ЧАСТЬ 2-Я:
СИСТЕМНОЕ ОБОБЩЕНИЕ МАТЕМАТИКИ

ГЛАВА 8. СИСТЕМА КАК ОБОБЩЕНИЕ МНОЖЕСТВА. СИСТЕМНОЕ ОБОБЩЕНИЕ МАТЕМАТИКИ И ЗАДАЧИ, ВОЗНИКАЮЩИЕ ПРИ ЭТОМ

В науке принято два основных принципа определения понятий:

– через подведение определяемого понятия под более общее понятие и выделение из него определяемого понятия путем указания одного или нескольких его специфических признаков (например, млекопитающие – это животные, выкармливающие своих детенышей молоком);

– процедурное определение, которое определяет понятие путем указания пути к нему или способа его достижения (магнитный северный полюс – это точка, в которую попадешь, если все время двигаться на север, определяя направление движения с помощью магнитного компаса).

Как это ни парадоксально, но понятия системы и множества могут быть определены друг через друга, т.е. трудно сказать, какое из этих понятие является более общим.

Определение системы через множество.

Система есть множество элементов, взаимосвязанных друг с другом, что дает системе новые качества, которых не было у элементов. Эти новые системные свойства еще называются эмерджентными, т.к. не очень просто понять, откуда они берутся. Чем больше сила взаимодействия элементов, тем сильнее свойства системы отличаются от свойств множества и тем выше уровень системности и синергетический эффект. Получается, что система – это множество элементов, но не всякое множество, а только такое, в котором элементы взаимосвязаны (это и есть специфический признак, выделяющий системы в множестве), т.е. множество – это более общее понятие.

Определение множества через систему.

Но можно рассуждать и иначе, считая более общим понятием систему, т.е. мы ведь можем определить понятие множества через понятие системы. Множество – это система, в которой сила взаимодействия между элементами равна нулю (это и есть отличительный признак, выделяющий множества среди систем). Тогда более общим понятием является система, а множества – это просто системы с нулевым уровнем системности.

Вторая точка зрения объективно является предпочтительной, т.к. совершенно очевидно, что понятие множества является предельной абстракцией от понятия системы и реально в мире существуют только системы, а множеств в чистом виде не существует, как не существует математической точки. Точнее сказать, что множества, конечно, существуют, но всегда исключительно и только в составе систем как их базовый уровень иерархии, на котором они основаны.

Из этого вытекает очень важный вывод: все понятия и теории, основанные на понятии множества, допускают обобщение путем замены понятия множества на понятие системы и тщательного прослеживания всех последствий этой замены. При этом более общие теории будут удовлетворять принципу соответствия, обязательному для более общих теорий, т.е. в асимптотическом случае, когда сила взаимосвязи элементов систем будет стремиться к нулю, системы будут все меньше отличаться от множеств и системное обобщение теории перейдет к классическому варианту, основанному на понятии множества. В предельном случае, когда сила взаимосвязи точно равна нулю, системная теория будет давать точно такие же результаты, как основанная на понятии множества.

Этот вывод верен для всех теорий, но в данной работе для авторов наиболее интересным и важным является то, что очень многие, если не практически все понятия современной математики основаны на понятии множества, в частности на математической теории множеств. К таким понятиям относятся понятия:

– математической операции: преобразования одного или нескольких исходных множеств в одно или несколько результирующих;

– функциональной зависимости: отображение множества значений аргумента на множество значений функции для однозначной функции одного аргумента или отображение множеств значений аргументов на множества значений функций для многозначной функции многих аргументов;

– «количество информации»: функция от свойств множества.

В монографии [99] впервые сформулирована, а в работе [186] подробно обоснована программная идея системного обобщения математики, суть которой состоит в тотальной замене понятия "множество" на более общее понятие "система" и прослеживании всех последствий этого. При этом обеспечивается соблюдение принципа соответствия, обязательного для более общей теории, т.к. при понижении уровня системности система по своим свойствам становится все ближе к множеству и система с нулевым уровнем системности и есть множество. Приводится развернутый пример реализации этой программной идеи в области теории информации, в качестве которого выступает предложенная в 2002 году системная теория информации [97], являющаяся системным обобщением теории информации Найквиста – Больцмана – Хартли – Шеннона и семантической теории информации Харкевича. Основа этой теории состоит в обобщении комбинаторного понятия информации Хартли I = Log₂N на основе идеи о том, что количество информации определяется не мощностью множества N, а мощностью системы, под которой предлагается понимать суммарное количество подсистем различного уровня иерархии в системе, начиная с базовых элементов исходного множества и заканчивая системой в целом. При этом в 2002 году, когда было предложено системное обобщение формулы Хартли, число подсистем в системе, т.е. мощность системы N_s, предлагалось рассчитывать по формуле:

.

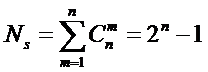Соответственно, системное обобщение формулы Хартли для количества информации в системе из n элементов предлагалось в виде:

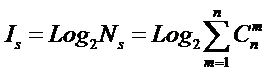
В работе [270] дано системное обобщение формулы Хартли для количества информации для квантовых систем, подчиняющиеся статистике как Ферми-Дирака, так и Бозе-Эйнштейна, и стало ясно, что предложенные в 2002 году в работе [97] вышеприведенные выражения имеют силу только для систем, подчиняющихся статистике Ферми-Дирака.

В работе [188] кратко описывается семантическая информационная модель системно-когнитивного анализа (СК-анализ), вводится универсальная информационная мера силы и направления влияния значений факторов (независимая от их природы и единиц измерения) на поведение объекта управления (основанная на лемме Неймана – Пирсона), а также неметрический интегральный критерий сходства между образами конкретных объектов и обобщенными образами классов, образами классов и образами значений факторов. Идентификация и прогнозирование рассматривается как разложение образа конкретного объекта в ряд по обобщенным образам классов (объектный анализ), что предлагается рассматривать как возможный вариант решения на практике 13-й проблемы Гильберта.

В статьях [189, 191] обоснована идея системного обобщения математики и сделан первый шаг по ее реализации: предложен вариант системной теории информации [97, 201]. В данной работе осуществлена попытка сделать второй шаг в этом же направлении: на концептуальном уровне рассматривается один из возможных подходов к системному обобщению математического понятия множества, а именно – подход, основанный на системной теории информации. Предполагается, что этот подход может стать основой для системного обобщения теории множеств и создания математической теории систем. Сформулированы задачи, возникающие на пути достижения этой цели (разработки системного обобщения математики) и предложены или намечены пути их решения:

Задача 1: найти способ представления системы как совокупности взаимосвязанных множеств.

Задача 2: сформулировать, чем отличаются друг от друга различные системы, состоящие из одних и тех же базисных элементов.

Задача 3: обосновать принципы геометрической интерпретации понятий: "элемент системы" и "система".

Задача 4: предложить способы аналитического описания (задания) подсистем как элементов системы.

Задача 5: описать системное семантическое пространство для отображения систем в форме эйдосов (эйдос-пространство).

Задача 6: описать принцип формирования эйдосов (включая зеркальные части).

Задача 7: показать, что базовая когнитивная концепция [97] формализуется многослойной системой эйдос-пространств (термин автора) различных размерностей.

Задача 8: показать, что системная теория информации позволяет непосредственно на основе эмпирических данных определять вид функций принадлежности, т.е. решать одну из основных задач теории нечетких множеств.

Задача 9: сформулировать перспективы: разработка операций с системами: объединение (сложение), пересечение (умножение), вычитание. Привести предварительные соображения по сложению систем.

Далее рассмотрим более подробно некоторые основные результаты перечисленных выше работ и некоторых других без дополнительных специальных ссылок на них, т.к. они уже даны.

8.1. Программная идея системного обобщения математики
и ее применение для создания системной теории информации

Фундаментом, находящимся в самом основании грандиозного здания современной математики, являются понятие множества и теория множеств. Теория множеств лежит в основе самого глубокого в настоящее время обоснования таких базовых математических понятий, как "число" и "функция". Определенное время этот фундамент казался незыблемым. Однако вскоре в работах выдающихся ученых XX века, прежде всего, Давида Гильберта, Бертрана Рассела и Курта Геделя, со всей очевидностью было обнажены фундаментальные логические и лингвистические проблемы, в частности, проявляющиеся в форме парадоксов теории множеств. Это, в свою очередь, привело к появлению ряда развернутых предложений по пересмотру самых глубоких оснований математики. В задачи данной работы не входит рассмотрение этой интереснейшей проблематики, а также истории возникновения и развития понятий числа и функции.

Однако очевиден тот факт, что Вселенная состоит из систем различных уровней иерархии.

Система представляет собой множество элементов, объединенных в целое за счет взаимодействия элементов друг с другом, т.е. за счет отношений между ними, и обеспечивает преимущества в достижении целей.

Преимущества в достижении целей обеспечиваются за счет системного эффекта.

Системный эффект состоит в том, что свойства системы не сводятся к сумме свойств ее элементов, т.е. система, как целое, обладает рядом новых, т.е. эмерджентных свойств, которых не было у ее элементов, взятых по отдельности [97].

Уровень системности тем выше, чем выше интенсивность взаимодействия элементов системы и сильнее отличаются свойства системы от свойств входящих в нее элементов, т.е. чем выше системный эффект, чем значительнее отличается система от множества [189].

Таким образом, система обеспечивает тем большие преимущества в достижении целей, чем выше ее уровень системности [189].

В частности, система с нулевым уровнем системности вообще ничем не отличается от множества образующих ее элементов, т.е. тождественна этому множеству и никаких преимуществ в достижении целей не обеспечивает. Этим самым достигается выполнение принципа соответствия между понятиями системы и множества, обязательного для более общей теории. Из соблюдения этого принципа для понятий множества и системы следует его соблюдение для математических понятий, в частности, понятий системной теории информации [253], основанных на теории множеств и их системных обобщений.

Поэтому проблема, решаемая в данной работе, состоит в явном несоответствии между системным характером объекта познания и несистемным характером современной математики, как средства познания. Он заключается в том, что, с одной стороны, мир, как объект познания, представляет собой совокупность систем различных уровней иерархии, а с другой – математика, как наиболее мощное средство познания и моделирования этого мира, основана не на теории систем, а на теории множеств.

Общеизвестна эффективность математики, которая тем более удивительна, если учесть, что она достигается уже фактически в нулевом приближении, т.е. при рассмотрении систем как множеств. Так, как может возрасти адекватность математики и ее мощь, как средства познания и универсального языка моделирования реальности, если удастся получить ее системное обобщение! Поэтому, на взгляд автора, актуальность разработки системного обобщения математики совершенно очевидна.

Предлагается следующая программная идея системного обобщения математики: обобщить все понятия математики, базирующиеся на теории множеств, путем тотальной замены понятия множества на понятие системы и тщательного отслеживания всех последствий этой замены.

Реализация данной программной идеи потребует, прежде всего, системное обобщение самой теории множеств и преобразование ее в "Математическую теорию систем", которая, согласно принципу соответствия, будет плавно переходить в современную классическую теорию множеств при уровне системности, стремящемся к нулю. При этом необходимо заметить, что существующая в настоящее время наука под названием "Теория систем" (а также: системный анализ, системный подход, информационная теория систем и т.п.) ни в коей мере не является обобщением математической теории множеств, и ее не следует путать с предлагаемой "Математической теорией систем". На наш взгляд, существуют некоторые возможности обобщения ряда понятий математики и без разработки математической теории систем. К таким понятиям относятся, прежде всего, "информация" и "функция".

Системному обобщению понятия информации и применениею этого понятия посвящены работы [93-279] и др. На основе предложенной системной теории информации (СТИ) были разработаны математическая модель и методика численных расчетов (структуры данных и алгоритмы), а также специальный программный инструментарий (система "Эйдос") автоматизированного системно-когнитивного анализа (АСК-анализ), который представляет собой системный анализ, автоматизированный путем его рассмотрения как метода познания и структурирования по базовым когнитивным операциям.

В АСК-анализе теоретически обоснована и реализована на практике в форме конкретной информационной методики и технологии процедура установления новой универсальной, сопоставимой в пространстве и времени, ранее не используемой количественной, т.е. выражаемой числами, меры соответствия между событиями или явлениями любого рода, получившей название "системная мера целесообразности информации", которая, по сути, является количественной мерой знаний [170]. Это является достаточным основанием для того, чтобы назвать эти числа "когнитивными" от английского слова "cognition" – "познание".

В настоящее время под функцией понимается соответствие друг другу нескольких множеств чисел. Поэтому виды функций можно классифицировать, по крайней мере, в зависимости от:

– природы этих чисел (натуральные, целые, дробные, действительные, комплексные и т.п.);

– количества и вида множеств чисел, связанных друг с другом в функции (функции одного, нескольких, многих, счетного или континуального количества аргументов, однозначные и многозначные функции, дискретные или континуальные функции);

– степени жесткости и меры силы связи между множествами чисел (детерминистские функции, функции, в которых в качестве меры связи используется вероятность, корреляция и другие меры);

– степени расплывчатости чисел в множествах и самой формы функции (четкие и нечеткие функции, использование различных видов шкал, в частности, интервальных оценок).

Так как функции, выявляемые модели предметной области методом АСК-анализа, связывают друг с другом множества когнитивных чисел, то предлагается называть их "когнитивными функциями" [280]. Учитывая перечисленные возможности классификации функций, когнитивные функции можно считать нечеткими интервальными недетерминистскими многозначными функциями многих аргументов, в которых в качестве меры силы связи между множествами значений аргумента и значений функции используется количество информации или знаний. Отметим, что детерминистские однозначные функции нескольких аргументов могут рассматриваться как частный случай когнитивных функций, к которому они сводятся при анализе жестко детерминированной предметной области, скажем макроскопических механических явлений, описываемых классической физикой.

Автором предлагается программная идея системного обобщения понятий математики, в частности теории информации, основанных на теории множеств, путем замены понятия множества на более содержательное понятие системы. Частично эта идея была реализована автором при разработке автоматизированного системно-когнитивного анализа (АСК-анализа), математическая модель которого основана на системном обобщении формул для количества информации Хартли и Харкевича. Реализация следующего шага – системное обобщение понятия функциональной зависимости рассматривается в работе [280], в ней же вводятся новые научные понятия и соответствующие термины "когнитивные функции" и "когнитивные числа". На численных примерах показано, что АСК-анализ обеспечивает выявление когнитивных функциональных зависимостей в многомерных зашумленных фрагментированных данных.

Вывод. Формулируется и обосновывается программная идея системного обобщения математики, суть которой состоит в тотальной замене понятия "множество" на более общее понятие "система" и прослеживание всех последствий этого. При этом обеспечивается соблюдение принципа соответствия, обязательного для более общей теории, т.к. система с нулевым уровнем системности есть множество. Приводится развернутый пример реализации этой программной идеи, в качестве которого выступает предложенная автором [97] системная теория информации, являющаяся системным обобщением теории информации Найквиста – Больцмана – Хартли – Шеннона и семантической теории информации Харкевича.

Необходимо отметить, что сходные идеи независимо развиваются В.Б. Вяткиным в ряде интересных работ[1], посвященных созданию синергетической теории информации (считаю это название очень удачным). Видимо, подобные идеи буквально "витают в воздухе".

8.2. Неформальная постановка и обсуждение задач,
возникающих при системном обобщении теории множеств

Данный раздел основан на работе [189]. Впервые программная идея системного обобщения математики и явной форме была сформулирована автором в 2005 году в работе [166], а системная теория информации (СТИ), явлюящяся ее реализацией в области теории информации, предложена в 2002 году [97], сами же идеи и математические модели развивались и ранее, фактически с 1979 года[2]. В работе поставлена цель – сделать второй шаг в том же направлении: на концептуальном уровне рассмотреть один из возможных подходов к системному обобщению математического понятия множества, а именно – подход, основанный на системной теории информации. Предполагается, что этот или подобный подход может способствовать созданию математической теории систем как системного обобщения теории множеств, что является весьма актуальным как для самой математики, так и для наук, использующих математику.

Для достижения данной цели осуществим ее декомпозицию в последовательность задач, являющихся этапами ее достижения:

Задача 1: найти способ представления системы как совокупности взаимосвязанных множеств.

Задача 2: сформулировать, чем отличаются друг от друга различные системы, состоящие из одних и тех же базисных элементов.

Задача 3: обосновать принципы геометрической интерпретации понятий: "элемент системы" и "система".

Задача 4: предложить способы аналитического описания (задания) подсистем как элементов системы.

Задача 5: описать системное семантическое пространство для отображения систем в форме эйдосов (эйдос-пространство).

Задача 6: описать принцип формирования эйдосов (включая зеркальные части).

Задача 7: показать, что базовая когнитивная концепция формализуется многослойной системой эйдос-пространство (термин автора) различных размерностей.

Задача 8: показать, что системная теория информации позволяет непосредственно на основе эмпирических данных определять вид функций принадлежности, т.е. решать одну из основных задач теории нечетких множеств.

Задача 9: сформулировать перспективы: разработка операций с системами: объединение (сложение), пересечение (умножение), вычитание. Привести предварительные соображения по сложению систем.

Кратко, на концептуальном уровне, т.е. на уровне идей, без разработки соответствующего математического формализма рассмотрим предлагаемый вариант решения этих задач.

Задача 1: найти способ представления системы как совокупности взаимосвязанных множеств.

Для того чтобы получить системное обобщение теории множеств, необходимо найти способ представления системы как совокупности взаимосвязанных множеств. Ожидается, что это позволит с минимальными доработками применить прекрасно разработанный аппарат теории множеств для описания систем.

Определение 1:

1. Система есть иерархическая структура подсистем.

2. В каждой системе существует нулевой наиболее фундаментальный уровень иерархии, представляющий собой классическое множество базисных элементов, не имеющих никаких свойств.

3. Каждая подсистема относится к определенному уровню иерархии системы, который определяется только количеством базисных элементов в данной подсистеме.

4. Элементами подсистем каждого уровня иерархии являются как подсистемы предыдущих более фундаментальных уровней иерархии, так и базисные элементы.

Таким образом, будем считать, что система отличается от множества базисных элементов, из которых она состоит, тем, что эти элементы образуют подсистемы различной структуры и сложности (рисунок 1).

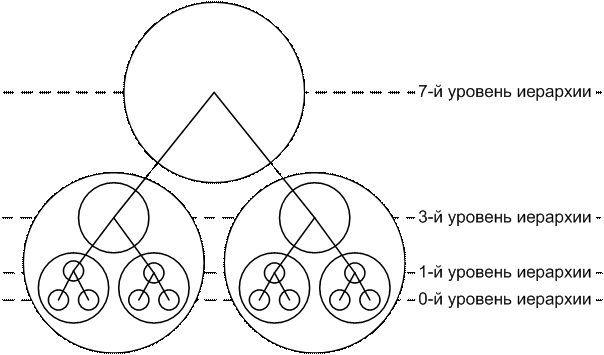
Рисунок 1 – Элементы-подсистемы различных уровней иерархии

В простейшем случае можно считать, что элементы системы (подсистемы) не имеют внутренней структуры, т.е. не включают в себя подсистемы, а являются подмножествами базисного множества, состоящими непосредственно из базисных элементов. Но вообще говоря это не так[3].

На рисунке 2 показаны как элементы-подмножества базисного уровня (23, 456 78910: отмечены зеленым цветом), так и элементы-подсистемы, включающие не только непосредственно элементы базисного уровня, но и их подмножества или подсистемы (123, 23456, 45678910: отмечены желтым цветом).

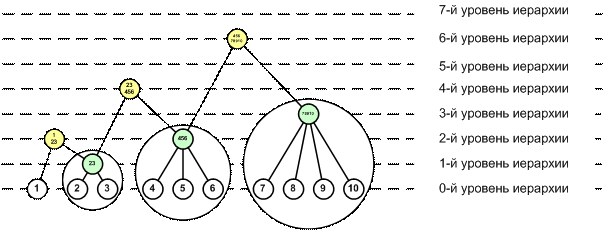
Рисунок 2 – Элементы-подмножества и элементы-подсистемы
различных уровней иерархии системы

Из рисунка 2 также видно, что различие между элементами-подмножествами и элементами-подсистемами возникает только для элементов, начиная со 2-го уровня иерархии, т.к. только для этих элементов возможен уровень сложности, достаточный для существования этого различия [170]. Например, видно, что элемент-подсистема 123 отличается от элемента-подмножества 456 наличием внутренней структуры, т.е. тем, что включает не только базисный элемент 1, но и подсистему 23, при этом и оба элемента: и 123, и 456 относятся ко 2-му уровню иерархии системы.

Таким образом, можно сделать вывод о том, что два элемента тождественны, если они состоят из одних и тех же базисных элементов и у них тождественна структура. Отметим, что поскольку у множеств нет структуры, то для тождества множеств достаточно тождества входящих в них элементов.

Для системы, состоящей из элементов-множеств, можно применять термин "аморфная система" (например: газ или жидкость), а из элементов-систем – "структурированная система" (например: кристалл). Аморфные и структурированные системы, состоящие из одних и тех же базисных элементов, можно считать различными фазовыми состояниями одной системы, отличающимися уровнем системности.

Задача 2: сформулировать, чем отличаются друг от друга различные системы, состоящие из одних и тех же базисных элементов.

Для того чтобы решить эту задачу, сформулируем несколько определений.

Определение 2: Полной или максимальной системой будем называть такую систему, в которой реализуются все формально возможные сочетания базисных элементов.

Таким образом, если в системе имеется n базисных элементов, то полная система включает подсистем, представляющих собой сочетания базисных элементов по m, где m={1, 2, 3, ..., n}. Подсистемы полной системы можно классифицировать различными способами, но одним из наиболее простых и естественных является классификация по их мощности (в смысле теории множеств), т.е. по количеству входящих в них базисных элементов.

Определение 3: Мощностью подсистемы будем называть количество входящих в нее базисных элементов.

Определение 4: k-й уровень иерархии системы состоит из всех ее подсистем мощности (k+1).

Из определений 3 и 4 следует, что:

0-й уровень иерархии системы состоит из подсистем, включающих 1 базисный элемент, это базисный уровень иерархии, на котором система не отличается от множества;

1-й уровень иерархии системы состоит из подсистем, включающих 2 базисных элемента;

2-й уровень иерархии системы состоит из подсистем, включающих 3 базисных элемента;

.......................

k-й уровень иерархии системы состоит из подсистем, включающих (k+1) базисных элемента.

Из этих определений следует также, что базисный уровень является 0-м (нулевым) уровнем иерархии системы и состоит из подсистем мощности 1. Это означает, что сами базисные элементы можно рассматривать как подсистемы, имеющие мощность, равную 1, т.е. в определенном смысле можно считать, что базисный элемент состоит из самого себя, в отличие от элементов других иерархических уровней системы, которые включают базисные элементы, но сами себя не включают. Необходимо отметить, что если бы элементы различных иерархических уровней системы включали не только базисные элементы, но и самих себя, то мощность подсистем различных уровней изменялась бы следующим образом:

– элементы 0-го уровня иерархии, т.е. базисные элементы: мощность 1;

– элементы 1-го уровня иерархии: мощность 3 (2 базисных элемента + 1, т.к. элемент включает сам себя);

– элементы 2-го уровня иерархии: мощность 4 (3 базисных элемента + 1, т.к. элемент включает сам себя);

.........................

– элементы k-го уровня иерархии: мощность (k+2) ((k+1) базисных элемента + 1, т.к. элемент включает сам себя), что, как мы считаем, неприемлемо, т.к. нарушает простую и очевидную логическую последовательность между 0-м и 1-м уровнями иерархии.

Определение 5: Реальной системой будем называть систему, в которой реализуются не все формально-возможные сочетания базисных элементов, а лишь некоторые из них.

В этом случае возникает естественный и закономерный вопрос: "По какой причине получается так, что в реальной системе реализуются не все, а лишь некоторые сочетания базисных элементов?" Для ответа на этот вопрос введем понятие "правила запрета".

Определение 6: Правилами запрета будем называть механизм или способ, с помощью которого обеспечивается формирование различной структуры систем, состоящих из одних и тех же базисных элементов.

Таким образом, правила запрета являются средством получения конкретных реальных систем из максимальной, включающей все возможные сочетания базисных элементов. Например, в квантовой механике существует Принцип запрета Паули для квнтовых систем, подчиняющихся квантовой статистике Ферми-Дирака.

Определение 7: n-тождественными системами (т.е. системами, тождественными на n-м уровне иерархии) будем называть системы, состоящие из одних и тех же элементов на n-м уровне иерархии. Два элемента-подсистемы тождественны, если они состоят из одних и тех же базисных элементов и у них тождественна структура, т.е. связи между базисными элементами.

В частности, 0-тождественными являются системы, состоящие из одних и тех же базисных элементов, независимо от того, отличаются ли они друг от друга связями между этими элементами, т.е. своей структурой.

Из определений 2 и 7 следует, что:

– реальные 0-тождественные системы являются подмножествами одной и той же полной системы;

– полная система является объединением всех возможных 0-тождественных реальных систем.

Отметим, что поскольку у множеств нет структуры, то для тождества множеств достаточно тождества входящих в них элементов.

Задача 3: обосновать принципы геометрической интерпретации понятий "элемент системы" и "система".

Основываясь на аналогии между базисными элементами и геометрическими точками (и первые и вторые не имеют никаких свойств, кроме свойства отличаться друг от друга), припишем базисным элементам смысл, аналогичный смыслу геометрической точки. Тогда элементы-подмножества различных иерархических уровней системы, отличающиеся друг от друга количеством базисных элементов, можно представить в виде систем из соответствующего количества точек. Однако как геометрически интерпретировать эти системы?

Для того чтобы ответить на этот вопрос, обратим внимание на то, что:

– пространство 0-й размерности есть одна точка 0-й размерности, т.е. классическая точка, известная в математике (в частности, в геометрии, дифференциальном и интегральном исчислении), а также в основанной на них физике;

– пространство 1-й размерности – это прямая линия, однозначно определяется системой из двух точек 0-й размерности;

– пространство 2-й размерности – это плоскость, однозначно определяется системой из трех точек 0-й размерности;

– пространство 3-й размерности – это пространство, однозначно определяется системой из четырех точек 0-й размерности;

......................

– пространство i-й размерности однозначно определяется системой из (i+1) точек 0-й размерности.

Однако различным количеством точек однозначно определяется не только положение пространства или гиперплоскости соответствующей размерности в многомерном пространстве, но и определенный тип геометрической фигуры:

– одна точка 0-й размерности задает точку;

– система из двух точек 0-й размерности задает отрезок прямой линии;

– система из трех точек 0-й размерности задает треугольник;

– система из четырех точек 0-й размерности задает тетраэдр (один из пяти 3-мерных многогранников Платона);

............................

– система из i точек 0-й размерности задает многомерную фигуру, называемую i-мерный симплекс.

В этой связи возникает один очень существенный вопрос: "Каким образом получается так, что геометрические фигуры, образованные из точек нулевой размерности, вдруг приобретают новое качество, а именно ненулевую размерность, которого ни в какой форме не было у базисных элементов, из которых они состоят?"

По мнению автора, ответ на это вопрос самым непосредственным образом связан с понятием системных или эмерджентных свойств, т.е. с тем, что система имеет качественно новые системные или эмерджентные свойства, которых не было у ее элементов (не сводящиеся к сумме свойств ее элементов). Кроме системного анализа, проблемами изучения системных свойств занимаются многие науки, в частности: химия, биология, физика, синергетика и математика, особенно теория фракталов.

Возникает известная "проблема кучи зерен", которую можно проиллюстрировать следующим образом: "Одно зерно – это явно не куча, два – тоже, и три, и четыре и пять – тоже, а вот 10 – это уже вроде как маленькая кучка, а вот "куча" – это, наверное, где-то от 1531 до 73568 зерен и более". В контексте данной работы и решаемой задачи "проблему кучи" можно переформулировать следующим образом: "Какой минимальный элемент пространства или геометрической фигуры некоторой размерности можно считать обладающим той же размерностью, что и само пространство или фигура?"

В химии аналогичный вопрос звучит примерно так: "Какой минимальный объем вещества обладает теми же химическими свойствами, что и макроколичество этого вещества". В химии ответ известен: это молекула данного вещества. Если молекулу любого вещества расщепить на элементы (атомы), перечисленные в таблице Д.И. Менделеева, из которых она состоит, то свойства этого вещества исчезнут, хотя элементы останутся. Однако что же при этом исчезает такое, что приводит к исчезновению свойств вещества? Ответ вполне очевиден: при расщеплении молекулы исчезают взаимосвязи между элементами (атомами), благодаря которым они и образовывали минимальную систему данного вещества, обладающую его химическим свойствами, т.е. его молекулу. Необходимо отметить, что приведенный пример имеет несколько упрощенный характер, т.к. элементы таблицы Д.И. Менделеева также образуют вещества, т.е. простейшей молекулой является сам элемент. С другой стороны, макрообъект не всегда состоит из молекул, он может быть, например, ионным кристаллом как NaCl (поваренная соль).

В информационной теории систем (ИТС), идеи которой мы пытаемся развивать в данной работе, предлагается считать, что минимальным элементом пространства или геометрической фигуры некоторой размерности, обладающим той же размерностью, что и само пространство или фигура, является точка этого пространства".

Получается, что пространства и геометрические фигуры различной размерности состоят из различных точек, т.е. точек также различной размерности. Поэтому геометрические фигуры можно рассматривать как системы, состоящие из точек различной размерности и имеющие различную структуру взаимосвязей между этими точками. Таким образом, геометрическим аналогом системы в рамках информационной теории систем является многомерная геометрическая фигура, состоящая из точек различной размерности и структуры, взаимосвязанных между собой в определенную структуру.

Отметим, что в рамках данной работы мы не рассматриваем вопросы топологической целостности (связности) элементов фигур и наличия у них некоторой сплошной гиперповерхности, ограничивающей некоторый гиперобъем. Вопрос, связанный с метрикой пространства, будет конкретизирован при рассмотрении следующих задач. Отметим, что вообще понятие "геометрическая фигура" связано с понятиями "топологическое пространство" и "геометрическое место точек", кроме того, фигура может быть определена операционально, например, в форме некоторой начальной фигуры и алгоритма ее преобразования для получения элементов фигуры, как это делается в теории фракталов.

Итак, системы можно представить как многомерные геометрические фигуры, состоящие из точек различной размерности и структуры, взаимосвязанных между собой в определенную структуру. При этом i-мерные точки, как системы, имеют эмерджентные свойства (i-гиперобъем), которых не было у точек меньших размерностей, из которых они состоят:

– 0-мерная точка не имеет никаких качеств (9-мера: S⁰);

– 1-мерная точка имеет длину (1-мера: S¹);

– 2-мерная точка имеет площадь (2-мера: S²);

– 3-мерная точка имеет объем (3-мера: S³);

...........................

– i-мерная точка имеет i-гиперобъем (i-мера: Sⁱ).

Смысл размерности пространства состоит в том, что она количественно показывает, на сколько быстро возрастает "содержимое" тела при увеличении его линейных размеров или при уменьшении линейных размеров объектов, "заполняющих" это тело.

Одним из наиболее распространенных и общепринятых способов определения размерности многомерной геометрической фигуры является применение известной формулы Хаусдорфа:

,

(1)

где

D – размерность многомерной геометрической фигуры;

S – обобщенный объем многомерной геометрической фигуры: S¹ – длина, S² – площадь, S³ – объем, ..., Sⁱ – i-гиперобъем;

L – линейный размер многомерной геометрической фигуры.

В соответствии с выражением (1), получаем:

– для линии (S^1):	,
– для плоскости (S^2):	,
– для объема (S^3):	.

Обращает на себя внимание следующая закономерность:

– при увеличении линейных размеров геометрической фигуры в 2 раза ее i-гиперобъем возрастает в 2ⁱ раз;

– при размерности пространства, равной i, минимальное количество i-мерных шаров, заполняющих i-мерный куб, равно N=2ⁱ (рисунок 3).

Эта закономерность формально точно совпадает с комбинаторной мерой Хартли для количества информации:

,

(2)

где

i – количество информации (в битах);

N – количество элементов в множестве.

В соответствии с представлением о кубической размерности фракталов (box dimension)[4], будем оценивать размерность "i" пространства по тому, как быстро возрастает количество i-мерных объектов, помещающихся в какое-либо i-мерное тело при увеличении его размеров или при уменьшении размеров объектов. Примем, в качестве множества "А" i-мерный куб (i-куб), а в качестве элементов множества – i-мерные шары (i-шар). Пусть N(r) – минимальное количество i-шаров радиуса r, заполняющих (покрывающих) "A" в i-мерной кубической укладке.

Если i-шары имеют очень большой диаметр, сопоставимый с длиной ребра i-куба, то ясно, что в i-кубе всегда, независимо от размерности пространства, будет помещаться только один i-шар. Поэтому диаметр i-шара нужно взять таким, чтобы в i-кубе поместилось несколько i-шаров. Например, достаточно взять начальный диаметр в два раза меньше длины ребра. Тогда при уменьшении диаметра i-шаров их будет помещаться в i-кубе все больше и больше, и мы все точнее сможем определить размерность пространства, которая, как ясно из вышесказанного, является пределом D:

,

(3)

при r, стремящемся к нулю. Этот предел, если он существует, и называется кубической размерностью пространства. Известно, что Хаусдорфова размерность не превосходит кубическую, а для самоподобных фракталов (определение фракталов, как самоподобных множеств, дано Дж. Хатчинсоном) они совпадают. Самоподобным называется множество, части которого образованы из целого множества путем таких его преобразований, как масштабирование, отражение, перенос и поворот.

Таким образом, размерность пространства можно рассматривать или интерпретировать как количество осей координат, которых необходимо и достаточно для однозначного определения положения объектов в этом пространстве.

Казалось бы, в этом утверждении нет ничего нового. Однако не будем спешить с выводами.

Дело в том, что каждое значение координат несет некоторое количество информации, необходимой для идентификации i-объекта, путем определения его положения в i-пространстве, причем это количество информации тем больше, чем выше размерность i-пространства.

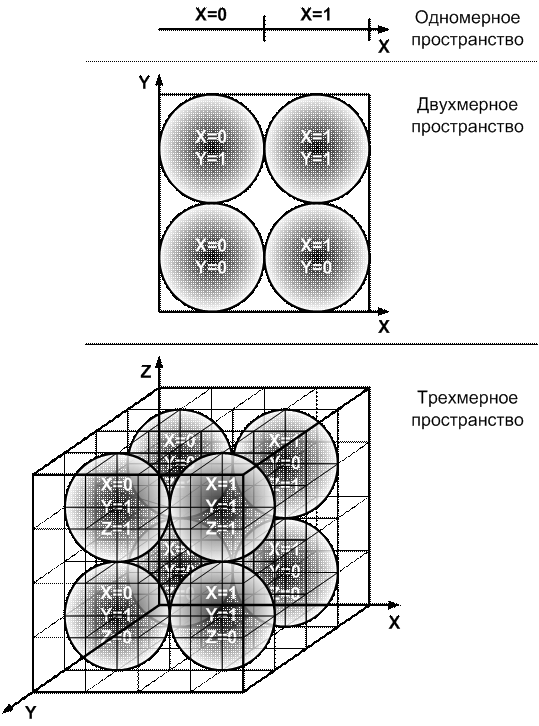
Рисунок 1 – Примеры плотной упаковки шаров в кубе, сторона

которого в два раза превышает диаметр шара, при различных

размерностях пространства и шаров (размерности: 1, 2 и 3)

Таким образом, координаты i-объекта в i-пространстве вполне обоснованно можно рассматривать как признаки этого объекта, с помощью которых он идентифицируется, т.е. отличается от остальных объектов. Причем эти признаки можно рассматривать как градации описательных шкал, в качестве которых выступают оси координат, а сами шкалы могут быть номинальные, порядковые (интервальные) или числовые (шкалы отношений). По эти признакам необходимо идентифицировать объект. Это уже формулировка задачи идентификации или распознавания, которую можно решать, в том числе с применением теории информации. Таким образом, появляется возможность исследования информационных свойств не только геометрического, но и физического пространства (если учесть, что общая теория относительности ОТО, т.е. теория гравитации Альберта Эйнштейна описывает гравитацию как искривление пространства).

Таким образом, мы видим важную аналогию между понятиями геометрии и теории информации, представленную в таблице.

Аналогия между геометрией и теорией информации

№	Геометрия		Теория информации
	S^i – i-гиперобъем	i – размерность пространства	N – количество элементов в множестве	i – количество информации (по Хартли)
1	2	1	2	1
2	4	2	4	2
3	8	3	8	3
4	16	4	16	4
5	32	5	32	5
6	64	6	64	6
7	128	7	128	7
8	256	8	256	8
...	...	...	...	...
i

Отметим также, что известна [21, 22] так называемая "фрактальная размерность" d₁ (4), которую часто называют информационной размерностью, т.к. она показывает, какое количество информации необходимо для определения местоположения точки в многомерном пространстве.

.

(4)

В выражении (4) обозначено:

– сторона гиперкубической ячейки i-пространства объемом: ;

– количество занятых ячеек, в которых содержится хотя бы одна точка;

– вероятность того, что некоторая точка содержится в i-й ячейке, при этом: ;

– количество точек в i-й ячейке.

Из данных таблицы, выражения (4) видно, что Хаусдорфа размерность пространства и информационная размерность соотносятся как комбинаторная мера Хартли для количества информации и статистическая мера информации Шеннона для неравновероятных событий.

Основываясь на этой существенной аналогии, можно сделать некоторые выводы и предположения, в том числе об информационных свойствах пространства и перемещающихся в них объектах:

1. Размерность пространства можно определить как его информационную емкость.

2. Поскольку информация связана с энтропией: численно равна ей, но имеет противоположный знак, то можно предположить, что чем выше размерность пространства, тем выше его антиэнтропийные свойства.

3. Энтропия связана с энергией:

– при сообщении энергии системе ее энтропия повышается, и уровень системности (организованности) уменьшается (вплоть до распада структуры системы), а при передаче энергии от системы (охлаждение) ее энтропия уменьшается, и уровень системности (организованности) возрастает;

– в замкнутых системах вектор потока энергии всегда направлен в сторону уменьшения ее плотности (закон возрастания энтропии);

– физические объекты представляют собой сложные системы, различные структурные уровни организации которых локализуются в пространствах различных размерностей: более глубокие (высокие) и фундаментальные (сущностные) структурные уровни локализуются в пространствах больших размерностей, а менее фундаментальные, внешние уровни (форма) – в пространствах меньших размерностей;

– объекты представляют собой каналы информационного и энергетического взаимодействия тех структурных уровней организации материи, на которых они локализованы (отличаются от окружающей среды), при этом при передаче информации осуществляется преобразование языковой формы ее представления;

– поток информации в объектах направлен из пространств высшей размерности в пространства низшей размерности, от сущности к форме, что придает антиэнтропийные свойства форме и позволяет ей сохранять устойчивость во внешней среде;

– одни объекты взаимодействуют с помощью других объектов (подобъектов), при этом подобъекты являются квантами поля, с помощью которого осуществляется взаимодействие объектов, а объекты – источниками этого поля (зарядами); заряды всегда локализуются в пространстве с меньшей размерностью, чем порождаемое ими поле, с помощью которого они взаимодействуют.

Любой объект, в т.ч. человек, является системой, которую можно представить себе в качестве i-точки некоторого i-пространства, причем не только абстрактного (фазового, семантического или иного), но и вполне "физического", в смысле реально "объективно" существующего.

Развитие любого объекта, в т. ч. человека, можно представить себе как движение в некотором пространстве, которое осуществляется путем чередования состояний двух типов: локализованного в пространстве, но с неопределенным направлением перемещения (бифуркационное состояние), и с определенным направлением перемещения, но с неопределенной локализацией (детерминистское состояние).

Для особого класса геометрических фигур-фракталов получаются не только целые, но и дробные значения размерности, причем обычно превосходящие размерность элементов, из которых строится фрактал. Это означает, что фрактал обладает качественно новыми эмерджентными, системными свойствами по сравнению со своими элементами, т.е. свойствами, которыми эти элементы не обладали, и, таким образом, является системой составляющих его элементов.

На этом даже может быть основано одно из определений фракталов: фракталом называется геометрическая фигура, размерность которой превосходит размерность геометрических объектов, из которых он состоит. На основании этого определения и вышесказанного мы можем высказать гипотезу о том, что все геометрические фигуры являются фракталами, а классические фигуры, для которых ранее считалось, что они не фракталы, также являются особым видом и частным случаем фракталов.

По аналогии с введенным автором понятием "антисистемы" [166], можно предложить и определение "антифрактала": это геометрическая фигура, размерность которой меньше размерности геометрических объектов, из которых он состоит.

Остается лишь добавить, что, по-видимому, классическая геометрия от Евклида до Римана изучает геометрические фигуры, размерность которых строго равна размерности геометрических объектов, из которых они состоят, т.е. фигуры, являющиеся не системами, а множествами. Однако множество является частным случаем системы [166]. Это означает, что в рамках классической геометрии все виды i-мерных точек "по умолчанию" ошибочно считались 0-точками, т.е. точками нулевой размерности, но обнаружить это возможно только в рамках более общей системной геометрии, являющейся системным обобщением классической геометрии. Это наводит на мысль о том, что, по-видимому, фрактальная геометрия является одним из первых разработанных разделов системной геометрии. В этой связи можно высказать геометрическую гипотезу о том, что геометрические фигуры классической геометрии являются фракталами с одним уровнем самоподобия, состоящими из системных точек, подобных фигуре в целом и той же размерности: "точка" – "фигура-в-целом" (по Дж. Хатчинсону). Это определение по смыслу совпадает с определением так называемой "истинной бесконечности" Г.В.Ф. Гегеля, согласно которому истинно бесконечной является система, подобная каждой своей части. Подобные системы, по Шеннону, обладают максимальной взаимной информацией и минимальной энтропией, к подобным системам относятся и фракталы (Дж. Хатчинсон), и живые организмы, состоящие из клеток, в каждой из которых находится полный геном, содержащий информацию о всем организме. Возможно, даже во Вселенной нет ни одного объекта, не являющегося истинно-бесконечным и не содержащего в своей сущности полной информации о всей Вселенной. Поэтому древние утверждали равенство или даже тождество "микро- и макрокосма".

Бенуа Мандельброт в своей основополагающей работе[5] пишет, что "размерность есть локальное свойство пространства", т.е. иначе говоря, она может изменяться от точки к точке, как квривзна. В связи с этим возникает физическая гипотеза о том, что, возможно, наше физическое пространство имеет размерность, не точно равную 3, а просто очень близкую к 3, причем эта размерность (и статистическое распределение i-мерных точек – систем разного типа) в принципе может изменяться с течением времени в разных областях пространства в зависимости от тех или иных физических условий, и совершенно не обязательно связанных только с гравитацией и гравитационной массой (вдруг, например, окажется, что размерность пространства изменяется во время ударов молний, землетрясений, ядерных взрывов, вблизи торнадо, а также в аномальных зонах). В этой связи возникает идея о разработке метода и прецизионной мобильной технологии измерения текущей фактической размерности пространства в различных его точках, и, если такая технология будет создана, то, возможно, также и о создании службы мониторинга и прогнозирования динамики размерности пространства. Соответсвенно можно ввести понятие «Поле размерности» и попытаться понять от чего зависит локальная размерность реального физического пространства. Мы уже не говорим о том, какие возможные перспективы открываются, если удастся теоретически найти и практически реализовать способы управления размерностью пространства.

Выше уже отмечалось, что смысл размерности пространства состоит в том, что она количественно показывает на сколько быстро возрастает "содержимое" тела при увеличении его линейных размеров или при уменьшении линейных размеров объектов, "заполняющих" тело. В рамках системной теории информации автором получены выражения для коэффициентов эмерджентности Хартли и Харкевича [1, 1–20], названные так автором в честь этих выдающихся ученых:

,

(5)

где

W – количество чистых (классических) состояний системы, т.е. количество базисных элементов;

j – коэффициент эмерджентности Хартли (уровень системной организации объекта, имеющего W чистых состояний).

Непосредственно из вида выражения для коэффициента эмерджентности Хартли (5) ясно, что он представляет собой относительное превышение количества информации в системе при учете системных эффектов (смешанных состояний, иерархической структуры ее подсистем и т.п.) над количеством информации без учета системности, т.е. этот коэффициент отражает уровень системности объекта.

Таким образом, коэффициент эмерджентности Хартли отражает уровень системности объекта и изменяется от 1 (системность минимальна, т.е. отсутствует) до W/Log₂W (системность максимальна). Очевидно, для каждого количества базисных элементов системы существует свой максимальный уровень системности, который никогда реально не достигается из-за действия правил запрета на реализацию в системе ряда подсистем различных уровней иерархии. Таким образом, коэффициент эмерджентности Хартли дает верхнюю оценку уровня системности i-точки из W базисных элементов.

Из сравнения коэффициент эмерджентности Хартли (5) с мерой Хаусдорфа (1) и кубической размерностью (3) видно, что коэффициент эмерджентности Хартли, отражающий "уровень системности", можно интерпретировать как своего рода размерность системы, т.е. скорость возрастания ее системных (эмерджентных) свойств при количественном увеличении мощности базисного множества системы.

Упрощенно можно считать, что:

– пространство 0-й размерности есть одна точка 0-й размерности, т.е. классическая точка, известная в математике (в частности в геометрии, дифференциальном и интегральном исчислении), а также в основанной на них физике;

– пространство 1-й размерности – это прямая линия, состоит из точек 1-й размерности, представляющих собой системы из 2-х точек 0-й размерности, т.е. отрезков, имеющих бесконечно малую длину (не нулевую);

– пространство 2-й размерности – это плоскость, состоит из точек 2-й размерности, представляющих собой системы из 3-х точек 0-й размерности, или точки 1-й размерности и точки 0-й размерности, т.е. треугольников, имеющих бесконечно малую площадь (не нулевую);

– пространство 3-й размерности – это пространство, состоит из точек 3-й размерности, представляющих собой системы из 4-х точек 0-й размерности, или точки 3-й размерности и точки 0-й размерности т.е. тетраэдров, имеющих бесконечно малый объем (не нулевой);

.....

– пространство i-й размерности состоит из точек i-й размерности, представляющих собой системы из (i+1)-х точек 0-й размерности, или точки i-й размерности и точки 0-й размерности, т.е. i-мерных симплексов, имеющих бесконечно малый i-гиперобъем (i-мера: Sⁱ) (не нулевую).

В заключение хотелось бы подчеркнуть, что все предложенные в данной работе мысли и положения высказываются исключительно в порядке обсуждения и ни в коей мере не претендуют на какую-либо полноту и завершенность.

Дальнейшее изложение основано на рабате [191], нумерация формул, рисунков и таблиц сохранены.

Задача 4: предложить способы аналитического описания (задания) подсистем, как элементов системы.

Для решения данной задачи необходимо найти способ представления в виде аналитической функции системы из (i+1) 0-мерных точек, произвольным образом расположенных в i-мерном пространстве. Предлагается представить эту систему точек в виде пространственных аппроксимирующих функций, вейвлетов и/или сплайнов в многомерном пространстве.

В геометрии существует один принципиальный вопрос, который, насколько известно, в явной форме не задавался: "Каким образом получается так, что из точек нулевой размерности, не обладающих никакими свойствами, образуются геометрические объекты, обладающие целым набором геометрических (и даже физических, как в теории гравитации А. Эйнштейна) свойств, таких как размерность, длина, площадь, объем, кривизна, кручение и т.д.?"

Предлагается следующий ответ на этот вопрос, основанный на программной идее системного обобщения математики: необходимо ввести понятие геометрической системы и признать, что новые свойства геометрических систем, отсутствующие у элементов, из которых они состоят, являются системными или эмерджентными свойствами, которые образуются за счет взаимосвязей между элементами этих систем. Фактически все исследуемые в геометрии объекты, называемые по-разному: "геометрическим местом точек", "многообразием" и т.д., в действительности являются геометрическими системами.

По мере усложнения кривых у них, соответственно, повышается уровень системности и появляются все новые и новые системные (эмерджентные) свойства: если прямая линия обладает только одним новым свойством: размерностью, которого не было у составляющих ее точек 0-вой размерности, то плоская кривая, т.е. кривая, полностью лежащая в плоскости, кроме того, обладает и кривизной, а пространственные кривые обладают еще и кручением.

Аналитически подобные кривые описываются и исследуются в дифференциальной геометрии и топологии с помощью векторного и тензорного анализа. Это описание может быть довольно сложным, поэтому в данной работе предлагается использовать параметрическое задание пространственных кривых через их проекции на координатные плоскости многомерного пространства. При обсуждении данной задачи для простоты будем предполагать, что это ортонормированное пространство с евклидовой метрикой. В общем случае если кривая однозначно задается системой из (i+1) 0-мерных точек, произвольным образом расположенных в i-мерном пространстве, для ее однозначного представления требуется i взаимно-ортогональных (координатных) плоскостей, на которые она проектируется. Сами же эти плоские проекции пространственной кривой можно аппроксимировать различными функциями, но мы предлагаем использовать для этого степенные полиномы различных степеней.

Для нас именно этот вариант аппроксимирующих функций наиболее удобен и интересен, т.к. известно, что полином i-й степени однозначно определяется (i+1) точками на плоскости и гарантировано проходит через них, т.е. не только однозначно определяется ими, но и сам однозначно определяет их.

В частности:

– полином 1-й степени однозначно определяется 2-мя точками 0-й размерности, гарантировано проходит через них и однозначно определяет аналитически точку пространства 1-й размерности, т.е. прямой линии;

– полином 2-й степени однозначно определяется 3-мя точками 0-й размерности, гарантировано проходит через них и однозначно определяет аналитически точку пространства 2-й размерности, т.е. плоскости;

– полином 3-й степени однозначно определяется 4-мя точками 0-й размерности, гарантировано проходит через них и однозначно определяет аналитически точку пространства 3-й размерности, т.е. трехмерного пространства;

.................................................................................................

– полином i-й степени однозначно определяется (i+1)-мя точками 0-й размерности, гарантировано проходит через них и однозначно определяет аналитически точку пространства i-й размерности.

Это и означает, что аппроксимация проекций пространственных кривых, задаваемых системой точек в многомерном пространстве степенными полиномами, является взаимно-однозначным (т.е. полностью адекватным) способом аналитического представления этой системы точек. Таким образом, системе из (i+1) 0-мерных точек в i-мерном пространстве аналитически соответствует система из i степенных полиномов i-й степени. Это утверждение и предлагается считать одним из вариантов решения задачи 4.

Приведем простой и наглядный пример, иллюстрирующий сформулированные выше положения. В качестве систем 0-мерных точек рассмотрим обобщенные образы классов, полученные путем обобщения конкретных образов железнодорожных составов, идущих на запад и на восток (рисунок 1). Этот пример приведен в учебном пособии [98, 101] в качестве лабораторной работы №1, описание этой работы находится в свободном общем доступе (http://lc.kubagro.ru/aidos/aidos06_lab/lab_01.htm), поэтому здесь подробно на нем останавливаться не будем.

	Используя технологию и методику применения автоматизированного системно-когнитивного анализа (АСК-анализ) [97], построим семантическую информационную модель (СИМ), позволяющую определить направление движения состава по его признакам. Формализация предметной области включает разработку классификационных и описательных шкал и градаций (таблица 1) и обучающей выборки (таблица 2).
Рисунок 1 – Примеры поездов, идущих на запад и на восток

Классификационные шкалы и градации:

1. Состав следует на восток.

2. Состав следует на запад.

Таблица 1 – ОПИСАТЕЛЬНЫЕ ШКАЛЫ И ГРАДАЦИИ

Наименование описательной шкалы	Градация описательной шкалы		Кол-во
	Наименование	Код
Количество вагонов в составе:	2	1	3
	3	2	4
	4	3	3
Форма вагона:	V-образная.	4	3
	Прямоугольная	5	10
	Ромбовидная	6	1
	U-образная.	7	4
	Эллипсоидная.	8	1
Длина вагона:	Короткий.	9	10
	Длинный	10	8
Количество осей вагона:	2	11	9
	3	12	4
Вид стенок вагона:	Одинарные	13	10
	Двойные	14	3
Вид крыши вагона:	Отсутствует	15	10
	Гофрированная	16	2
	Двухскатная	17	1
	Прямая (эллипсоидная)	18	6
Груз (количество и вид):	1 большой круг.	19	7
	2 маленьких круга	20	1
	3 маленьких круга	21	1
	1 квадрат	22	1
	3 квадрата.	23	1
	1 короткий прямоугольник.	24	3
	2 коротких прямоугольника	25	1
	1 длинный прямоугольник	26	3
	1 треугольник	27	7
	1 перевернутый треугольник.	28	1
	1 ромб.	29	2
	1 шестиугольник	30
	Груза нет	31	1

Таблица 2 – ОБУЧАЮЩАЯ ВЫБОРКА

№	Наименование состава	Коды класса	Коды признаков
1	Состав-1	1	3	5	5	5	5	9	9	10	10	11	11
			11	12	13	13	13	13	15	15	15	17	19
			29	27	23
2	Состав-2	1	2	5	4	7	9	9	9	2	2	2	13
			13	13	15	15	18	20	24	27
3	Состав-3	1	2	5	6	5	10	9	9	12	11	11	13
			13	13	18	18	15	28	27	19
4	Состав-4	1	3	5	8	5	4	9	9	9	9	13	13
			13	14	15	15	15	18	22	29	27	27	11
			11	11	11
5	Состав-5	1	2	5	5	5	9	9	10	11	11	12	13
			13	14	18	18	15	19	26	27
6	Состав-6	2	1	5	5	9	10	11	11	13	13	15	18
			27	21
7	Состав-7	2	2	5	5	7	10	9	9	11	11	11	13
			13	14	16	15	15	31	27	19
8	Состав-8	2	1	7	5	9	10	11	12	19	26	15	18
			13	13
9	Состав-9	2	3	4	4	5	5	9	9	9	10	11	11
			11	11	13	13	13	13	15	15	15	16	19
			24	26	19
10	Состав-10	2	1	5	7	9	10	11	11	13	13	15	15
			25	24

После ввода классификационных и описательных шкал и градаций, а также обучающей выборки в универсальную когнитивную аналитическую систему "Эйдос" (являющуюся программным инструментарием АСК-анализа), в результате синтеза СИМ была получена следующая матрица абсолютных частот (таблица 3).

Таблица 3 – МАТРИЦА АБСОЛЮТНЫХ ЧАСТОТ

Наименование описательной шкалы	Градация описательной шкалы		Наименования и коды классов (градаций классификационных шкал)		Кол-во
	Наименование	Код	Состав следует на восток	Состав следует на запад
Количество вагонов в составе:	2	1	0	3	3
	3	2	3	1	4
	4	3	2	1	3
Форма вагона:	V-образная.	4	2	1	3
	Прямоугольная	5	5	5	10
	Ромбовидная	6	1	0	1
	U-образная.	7	1	3	4
	Эллипсоидная.	8	1	0	1
Длина вагона:	Короткий.	9	5	5	10
	Длинный	10	3	5	8
Количество осей вагона:	2	11	4	5	9
	3	12	3	1	4
Вид стенок вагона:	Одинарные	13	5	5	10
	Двойные	14	2	1	3
Вид крыши вагона:	Отсутствует	15	5	5	10
	Гофрированная	16	0	2	2
	Двухскатная	17	1	0	1
	Прямая (эллипсоидная)	18	4	2	6
Груз (количество и вид):	1 большой круг.	19	3	4	7
	2 маленьких круга	20	1	0	1
	3 маленьких круга	21	0	1	1
	1 квадрат	22	1	0	1
	3 квадрата.	23	1	0	1
	1 короткий прямоугольник.	24	1	2	3
	2 коротких прямоугольника	25	0	1	1
	1 длинный прямоугольник	26	1	2	3
	1 треугольник	27	5	2	7
	1 перевернутый треугольник.	28	1	0	1
	1 ромб.	29	2	0	2
	1 шестиугольник	30	0	0	0
	Груза нет	31	0	1	1

Напомним, что мы предлагаем рассматривать описательные шкалы как оси координат в многомерном неортонормированном пространстве, а градации описательных шкал – как интервальные значения, т.е. координаты на этих осях (признаки). Для того чтобы построить в многомерном пространстве кривую, соответствующую некоторому заданному классу, в качестве значений по каждой координате будем рассматривать суммарное количество встреч данного признака у объектов этого класса.

Используя графическую систему SigmaPlot for Windows Version 10.0 фирмы Systat Software Inc., построим трехмерные образы исследуемых нами классов, выбрав три описательные шкалы, отмеченные светло-зеленым цветом, и предполагая, что пространство является ортонормированным. Последнее предположение в общем случае не выполняется (как и нашем примере), но этим обстоятельством на данном этапе мы вынуждены пренебречь, т.к. нам неизвестны системы, позволяющие строить по координатам точек в криволинейных или косоугольных координатах многомерные объекты и проектировать их в евклидово трехмерное или двумерное пространство.

Для построения графиков в системе SigmaPlot выполним подготовку исходных данных, выполнив следующие операции:

1. Выберем 3 описательные шкалы: форма вагона; вид крыши вагона и груз (количество и вид), в каждой из которых не менее 4-х градаций, что достаточно для получения наглядной кривой.

2. Система SigmaPlot предъявляет требование, чтобы по всем осям было равное количество координат, т.к. точка в многомерном пространстве задается координатами по всем осям. Однако в наших данных это требование не выполняется. Всего существует два варианта решить эту проблему: дополнить нулями недостающие координаты, ограничиться по всем осям тем количеством координат, которое в оси с минимальным их количеством. Мы выбираем второй вариант и оставляем по каждой из осей по 4 координаты, как в оси "Вид крыши вагона", в которой их минимальное количество.

3. Для большей наглядности перед построением графиков градации по каждой шкале рассортируем в порядке возрастания их значений для одного из классов (по каждой оси координат они могут быть оставлены в исходном порядке либо рассортированы в порядке возрастания или убывания).

В результате получим исходную таблицу данных для построения графиков в системе SigmaPlot (таблица 4) и сами графики (рисунок 2).

Таблица 4 – ДАННЫЕ ИЗ МАТРИЦЫ АБСОЛЮТНЫХ ЧАСТОТ
ДЛЯ ПОСТРОЕНИЯ ГРАФИКОВ В СИСТЕМЕ SIGMAPLOT

Ось	Наименование описательной шкалы	Градация описательной шкалы		Наименования и коды классов (градаций классификационных шкал)		Кол-во
		Наименование	Код	Состав следует на восток	Состав следует на запад
X	Форма вагона	U-образная.	7	1	3	4
		Эллипсоидная.	8	1	0	1
		V-образная.	4	2	1	3
		Прямоугольная	5	5	5	10
Y	Вид крыши вагона	Гофрированная	16	0	2	2
		Двухскатная	17	1	0	1
		Прямая (эллипсоидная)	18	4	2	6
		Отсутствует	15	5	5	10
Z	Груз (количество и вид)	1 перевернутый треугольник.	28	1	0	1
		1 ромб.	29	2	0	2
		1 большой круг.	19	3	4	7
		1 треугольник	27	5	2	7

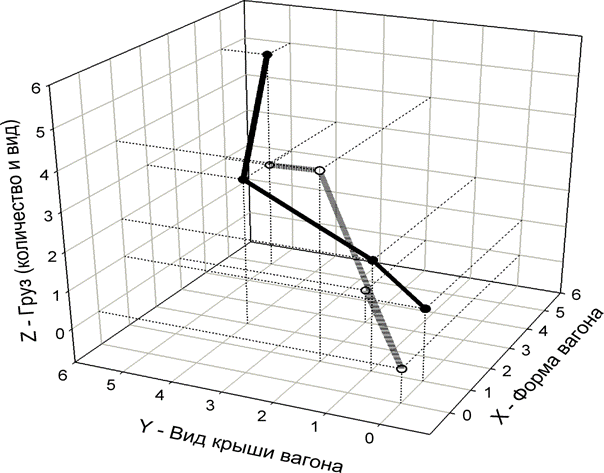
Рисунок 2 – Отображение фрагмента семантического пространства

с образами составов, следующих на восток (сплошная линия) и на запад (пунктир). Единица измерения по шкалам – количество встреч признака

Рассмотрим проекции этих пространственных кривых на координатные плоскости и аппроксимации этих проекций степенными полиномами. На основе данных таблицы 4 получим сочетания координат для точек проекций кривых, соответствующих поездам, следующим на восток и на запад, на координатные плоскости XY, XZ и YZ (таблица 5), а затем построим график проекции YZ и его аппроксимацию полиномом 3-й степени (рисунок 3).

Для примера выбрана именно данная проекция пространственной кривой класса "Поезда, следующие на восток", т.к. при выбранном способе сортировки координат по возрастанию значений она оказалась монотонно-возрастающей по обеим координатам, что является необходимым и достаточным условием для возможности аппроксимации кривой именно степенным полином.

Таблица 5 – СОЧЕТАНИЯ КООРДИНАТ ДЛЯ ТОЧЕК ПРОЕКЦИЙ КРИВЫХ НА КООРДИНАТНЫЕ ПЛОСКОСТИ XY, XZ И YZ

		Восток	Запад	Восток		Запад
X				XY		XY
Форма вагона	U-образная.	1	3	1	0	3	2
	Эллипсоидная.	1	0	1	1	0	0
	V-образная.	2	1	2	4	1	2
	Прямоугольная	5	5	5	5	5	5
Y				XZ		XZ
Вид крыши вагона	Гофрированная	0	2	1	1	3	0
	Двухскатная	1	0	1	2	0	0
	Прямая (эллипсоидная)	4	2	2	3	1	4
	Отсутствует	5	5	5	5	5	2
Z				YZ		YZ
Груз (количество и вид)	1 перевернутый треугольник.	1	0	0	1	2	0
	1 ромб.	2	0	1	2	0	0
	1 большой круг.	3	4	4	3	2	4
	1 треугольник	5	2	5	5	5	2

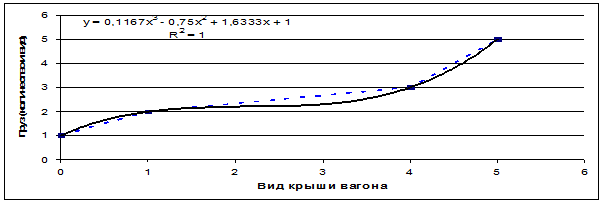
Рисунок 3 – Проекция пространственной кривой класса: "Поезда, следующие на восток" на координатную плоскость "YZ" (синий пунктир) и аппроксимация этой проекции полиномом 3-й степени (черная сплошная линия)

Задача 5: описать системное семантическое пространство для отображения систем в форме эйдосов (эйдос-пространство).

Прежде всего, отметим, что нас не устраивает в классическом семантическом пространстве, рассмотренном при обсуждении возможных подходов к решению предыдущей задачи.

Напомним, что в этом пространстве в качестве осей координат рассматривались описательные шкалы, в качестве координат на этих осях – градации описательных шкал (интервальные значения, признаки), а в качестве значений по каждой координате – суммарное количество встреч данного признака у объектов этого класса. При этом классическое семантическое пространство, вообще говоря (т.е. в общем случае), является многомерным неортонормированным пространством, т.к. углы между осями координат не являются прямыми, а единицы измерения по различным осям различны. Более того, это пространство может быть искривлено, скручено и т.п., не говоря уже о том, что его локальная фрактальная размерность может изменяться от точки к точке.

В качестве меры расстояния в этом пространстве обычно используют евклидову метрику (многомерный аналог теоремы Пифагора), как правило совершенно забывая при этом, что для корректного применения этой метрики необходимо, чтобы пространство было ортонормированным, и по всем осям использовалась бы одна и та же единица измерения, либо они все были безразмерными. Эти условия являются совершенно необходимыми и обязательными. Если для неортонормированного пространства существует обобщение теоремы Пифагора, и оно просто по неизвестным причинам не используется (правда более-менее простой аналитический вид это выражение имеет только для плоскости и трехмерного пространства), то вопрос о единицах измерения по осям просто игнорируется, т.е. не ставится и не осбуждается. Мы же напротив, обращаем на это внимание, как принципиальный вопрос [277], т.к. получается, что выбор единиц измерения сильно сказывается на результатах исследования, что некорректно.

Об этом вопросе упоминается в работе отечественных классиков системного анализа Ф.И. Перегудова и Ф.П. Тарасенко[6] (при рассмотрении многокритериального метода приятия решений и формировании интегрального критерия из частных критериев). Между тем, широко известно, что с размерностями в математических выражениях, в которые входят различные по смыслу величины, измеряемые в различных единицах измерения, нужно обращаться очень аккуратно. Даже на уроке физики в средней школе обязательно проверяют размерности получаемых в результате решения задач величин, и если они не соответствуют смыслу этих величин и принятым для них размерностям, то это является явным признаком ошибки в решении. Однако в статистических системах, системах анализа данных и системах искусственного интеллекта (кроме системы "Эйдос"), почему-то совершенно не задумываясь, спокойно совершают операции сложения, вычитания и другие более сложные математические операции с величинами, имеющими качественно различающийся смысл и, соответственно, измеряемыми в совершенно различных единицах измерения.

Удивительно, но такой подход на практике традиционен и в нем нет ничего необычного. Например, в известной статистической системе SPSS в разделе по изучению кластерного анализа приведены обучающие примеры, в которых между собой сравниваются различные модели автомобилей. При этом признаками для сравнения этих моделей являются: количество ведущих мостов, количество цилиндров, мощность двигателя, расход топлива и т.п. параметры, измеряемые количественно, естественно, в различных единицах измерения. Затем с использованием евклидовой меры сходства (корректность использования которой также еще нужно обосновать) вычисляется параметр сходства между этими моделями, строится матрица сходства, на основе которой и проводится кластерный анализ. Ясно, что это некорректно, т.к., например, 4 ведущих колеса или 4 цилиндра будут иметь одинаковый вес при определении сходства моделей, а мощность 80 л.с. будет иметь значение в 10 раз больше, чем расход топлива 8 литров на 100 километров. В исходной матрице данных в системе SPSS просто используются безразмерные количественные величины, т.е. числа, и даже не предусмотрено места для ввода единиц измерения. Но эти же величины в действительности не являются безразмерными, а лишь используются как безразмерные! Это примерно, как сложить 4 крокодила с 8 бегемотами и разделить затем на 6 секунд, за которые какой-то автомобиль разгоняется до 100 км/час, и получить в результате 2. Конечно, числа 4 и 5 формально сложатся и разделятся на 6, в результате получится 2, но чего именно 2, и какой смысл в выполнении подобных математических операций? Даже если величины измеряются в сходных по смыслу единицах измерения, то все равно перед выполнением с ними арифметических операций нужно привести их к одной общей единице измерения, например, если сложить 5 метров и 5 сантиметров, то будет не 10, а 5,05 метра или 505 сантиметров. Ясно, что и результаты измерения расстояний между объектами будет самым непосредственным образом зависеть от единиц измерения, с помощью которых, фактически, можно как угодно произвольно манипулировать этими расстояниями, чем многие с энтузиазмом и пользуются, что по сути превращает программу из инструмента исследования в программу для подбора нужных результатов.

Конечно, это совершенно не означает, что режим кластерного анализа системы SPSS невозможно использовать корректно. Для этого достаточно в матрицу исходных данных кластерного анализа ввести либо безразмерные (например, стандартизированные) величины, либо величины, приведенные к одной размерности, например, можно вычислить, как влияет тот или иной размерный параметр модели автомобиля на его цену, и вводить не сам этот параметр, а его влияние на цену автомобиля (например, в какой-либо валюте в индексированных ценах). Аналогично можно изучать влияние различных факторов на продолжительность жизни, вводя для исследования не сами значения этих факторов, а их влияние на эту продолжительность (например, в годах). При этом сами параметры или факторы могут измеряться в самых различных единицах измерения, например, количество сигарет, выкуренных за день, количество метров, пройденных пешком, количество минут, потраченных на утреннюю зарядку и т.п., но все это, в каких бы единицах измерения оно не измерялось, прибавляет или отнимает какие-то минуты нашей жизни. Проблема только в том, что это нужно понимать и делать самому, а система своими странными примерами правоцирует пользователей на некорректное применение.

Таким образом, мы считаем необходимым использовать для моделирования реальности не классическое семантическое пространство, а другое пространство (назовем его системным семантическим пространством или кратко эйдос-пространством), которое характеризуется следующими свойствами:

1. В качестве осей координат используются конструкты, т.е. понятия, имеющие смысловые полюса и спектр промежуточных смысловых значений с количественной или порядковой шкалой смыслового сходства и различия между ними. По всем осям координат используется одна и та же единица измерения.

2. Величины или значения координат выражаются количественными величинами, имеющими один и тот же смысл не только для одной оси, но и для всех осей координат, т.е. всего эйдос-пространства.

3. Значения координат несут информацию не только о положении точки в этом пространстве, но и о степени принадлежности этой точки к многомерному объекту, соответствующему обобщенному образу класса (будем называть этот образ "эйдос" (от греч. εἶδος – вид, образ) – идея, понятие, образ). Координаты образов классов в эйдос-пространстве – информативности, рассчитываемые согласно системной теории информации [97, 93-280]. Более того, эти значения координат являются величинами, учитывающими системный эффект взаимодействия всех классов в эйдос-пространстве со всеми градациями описательных шкал (поэтому для математической модели системы "Эйдос" и был предложен термин "нелокальная нейронная сеть" [138]), в отличие от классических нейронных сетей с обратным распространением ошибки. Предлагается считать координаты точек в эйдос-пространстве компонентами i-мерных когнитивных чисел [166], по аналогии с действительными числами (1-мерными), комплексными числами (2-мерными), кватернионами (3-мерными).

4. Интегральный критерий сходства образа конкретного объекта с классом, классов друг с другом, значений факторов друг с другом, т.е. метрика или "информационное расстояние" – свертка или скалярное произведение векторов классов или объекта и класса [1–20, 9, 10], величина, которую корректно использовать в случае неортонормированного пространства (в общем случае эйдос-пространство неортонормированно), так как: а) сами величины информативностей (см. п. 3) учитывают углы между описательными шкалами (если угол между двумя описательными шкалами равен 0, то информативности градаций этих шкал уменьшаются в два раза), б) свертка в координатной форме, по сути, является просто суммой информативностей тех признаков, которые есть у конкретного объекта, и математически никак не связана с предположением об ортонормированности или неортономированности эйдос-пространства.

5. Это эйдос-пространство является, вообще говоря, многомерным неортонормированным пространством с неевклидовой метрикой.

Мы осознаем мир, используя эйдос-пространство, а детально исследуем модели объектов внутреннего и внешнего мира, сформированные в этом пространстве, изучая их проекции на координатные плоскости, а чаще на оси координат, т.е. конструкты. Так, что мы действительно осознаем не сам мир, а лишь проекции его объектов, подобные теням на стенах пещеры Платона, причем в действительности эти тени даже не от самих объектов, а лишь от их моделей в нашем сознании (т.к. мы осознаем не непосредственно сами объекты "какие они есть на самом деле, т.е. сами по себе" (еще вопрос, возможно ли это хотя бы в принципе), а лишь отражения этих объектов в нашем сознании).

Продолжим изучение примера, который мы рассматривали при обсуждении предыдущей задачи. В таблице 6 приведено количество информации, рассчитанное согласно системной теории информации [97], которое содержится в градациях описательных шкал (признаках) о принадлежности конкретных объектов, обладающих этими признаками, к обобщенным классам: "Состав, следующий на восток", "Состав, следующий на запад".

Таблица 6 – МАТРИЦА ИНФОРМАТИВНОСТЕЙ (БИТ)

Наименование описательной шкалы	Градация описательной шкалы		Наименования и коды классов (градаций классификационных шкал)
	Наименование	Код	Состав следует на восток	Состав следует на запад
Количество вагонов в составе:	2	1	0,00000000	0,15333187
	3	2	0,07610294	-0,13573296
	4	3	0,05154327	-0,07574658
Форма вагона:	V-образная.	4	0,05154327	-0,07574658
	Прямоугольная	5	-0,00844310	0,00879946
	Ромбовидная	6	0,13608931	0,00000000
	U-образная.	7	-0,15297552	0,09334550
	Эллипсоидная.	8	0,13608931	0,00000000
Длина вагона:	Короткий.	9	-0,00844310	0,00879946
	Длинный	10	-0,06842948	0,05532850
Количество осей вагона:	2	11	-0,03300278	0,03076883
	3	12	0,07610294	-0,13573296
Вид стенок вагона:	Одинарные	13	-0,00844310	0,00879946
	Двойные	14	0,05154327	-0,07574658
Вид крыши вагона:	Отсутствует	15	-0,00844310	0,00879946
	Гофрированная	16	0,00000000	0,15333187
	Двухскатная	17	0,13608931	0,00000000
	Прямая (эллипсоидная)	18	0,05154327	-0,07574658
Груз (количество и вид):	1 большой круг.	19	-0,04058602	0,03664292
	2 маленьких круга	20	0,13608931	0,00000000
	3 маленьких круга	21	0,00000000	0,15333187
	1 квадрат	22	0,13608931	0,00000000
	3 квадрата.	23	0,13608931	0,00000000
	1 короткий прямоугольник.	24	-0,09298915	0,06878583
	2 коротких прямоугольника	25	0,00000000	0,15333187
	1 длинный прямоугольник	26	-0,09298915	0,06878583
	1 треугольник	27	0,06592940	-0,10788950
	1 перевернутый треугольник.	28	0,13608931	0,00000000
	1 ромб.	29	0,13608931	0,00000000
	1 шестиугольник	30	0,00000000	0,00000000
	Груза нет	31	0,00000000	0,15333187

Далее выберем из таблицы 6 только те информативности, которые соответствуют градациям описательных шкал, рассмотренных в предыдущей задаче (для обеспечения сопоставимости), и в результате получим таблицу 7 и ее графическое отображение на рисунке 4.

Таблица 7 – ДАННЫЕ ИЗ МАТРИЦЫ ИНФОРМАТИВНОСТЕЙ
ДЛЯ ПОСТРОЕНИЯ ГРАФИКОВ В СИСТЕМЕ SIGMAPLOT

Ось	Наименование описательной шкалы	Градация описательной шкалы		Наименования и коды классов (градаций классификационных шкал)
		Наименование	Код	Состав следует на восток	Состав следует на запад
X	Форма вагона	U-образная.	7	-0,15297552	0,09334550
		Прямоугольная	5	-0,00844310	0,00879946
		V-образная.	4	0,05154327	-0,07574658
		Эллипсоидная.	8	0,13608931	0,00000000
Y	Вид крыши вагона	Отсутствует	15	-0,00844310	0,00879946
		Гофрированная	16	0,00000000	0,15333187
		Прямая (эллипсоидная)	18	0,05154327	-0,07574658
		Двухскатная	17	0,13608931	0,00000000
Z	Груз (количество и вид)	1 большой круг.	19	-0,04058602	0,03664292
		1 треугольник	27	0,06592940	-0,10788950
		1 перевернутый треугольник.	28	0,13608931	0,00000000
		1 ромб.	29	0,13608931	0,00000000

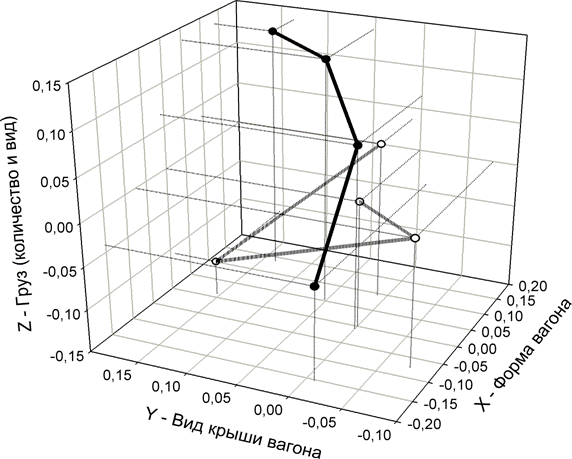
Рисунок 4 – Отображение фрагмента системного семантического
пространства (эйдос-пространства) с образами составов, следующих
на восток (сплошная линия) и на запад (пунктир). Единица измерения
по шкалам – биты

Рассмотрим проекции этих пространственных кривых на координатные плоскости и аппроксимации этих проекций степенными полиномами. На основе таблицы 7 получим сочетания координат для точек проекций кривых, соответствующих поездам, следующим на восток и на запад, на координатные плоскости XY, XZ и YZ (таблица 8), а затем построим график проекции XY и его аппроксимацию полиномом 3-й степени (рисунки 5 и 6). В таблице 8 области данных, отображенные на рисунках 5 и 6, обведены жирной рамкой.

Таблица 8 – СОЧЕТАНИЯ КООРДИНАТ ДЛЯ ПРОЕКЦИЙ КРИВЫХ ИЗ ЭЙДОС-ПРОСТРАНСТВА НА КООРДИНАТНЫЕ ПЛОСКОСТИ XY, XZ И YZ

		Восток	Запад	Восток		Запад
X				XY		XY
Форма вагона	U-образная.	-0,153	0,093	-0,153	-0,008	0,093	0,009
	Прямоугольная	-0,008	0,009	-0,008	0,000	0,009	0,153
	V-образная.	0,052	-0,076	0,052	0,052	-0,076	-0,076
	Эллипсоидная.	0,136	0,000	0,136	0,136	0,000	0,000
Y				XZ		XZ
Вид крыши вагона	Отсутствует	-0,008	0,009	-0,153	-0,041	0,093	0,037
	Гофрированная	0,000	0,153	-0,008	0,066	0,009	-0,108
	Прямая (эллипсоидная)	0,052	-0,076	0,052	0,136	-0,076	0,000
	Двухскатная	0,136	0,000	0,136	0,136	0,000	0,000
Z				YZ		YZ
Груз (количество и вид)	1 большой круг.	-0,041	0,037	-0,008	-0,041	0,009	0,037
	1 треугольник	0,066	-0,108	0,000	0,066	0,153	-0,108
	1 перевернутый треугольник.	0,136	0,000	0,052	0,136	-0,076	0,000
	1 ромб.	0,136	0,000	0,136	0,136	0,000	0,000

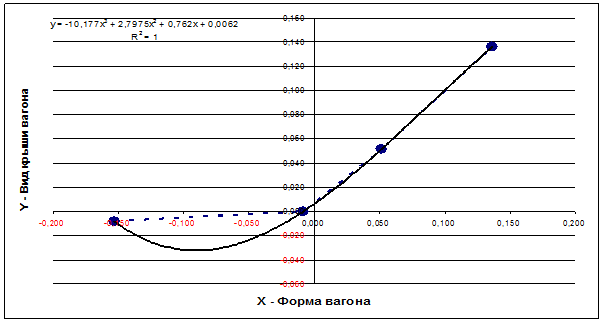
Рисунок 5 – Проекция эйдоса (класса): "Поезда, следующие на восток"

на координатную плоскость "XY" (синий пунктир) и аппроксимация этой

проекции полиномом 3-й степени (черная сплошная линия)

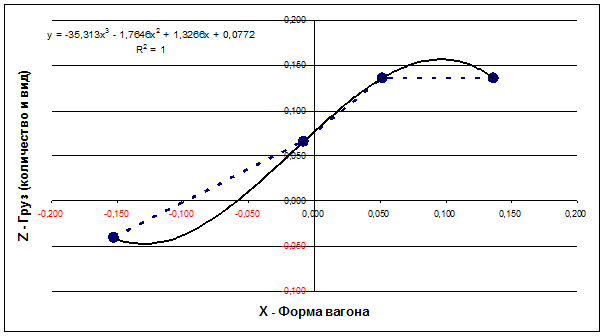
Рисунок 6 – Проекция эйдоса (класса): "Поезда, следующие на восток"

на координатную плоскость "XZ" (синий пунктир) и аппроксимация этой

проекции полиномом 3-й степени (черная сплошная линия)

Для примера выбраны именно проекции пространственной кривой (эйдоса) класса "Поезда, следующие на восток", т.к. при выбранном способе сортировки координат по возрастанию значений они оказались монотонно-возрастающими по обеим координатам, что является необходимым и достаточным условием для возможности аппроксимации кривой степенным полином. Отметим, что для аппроксимации всех проекций эйдосов на координатные плоскости с коэффциентом детерминации R²=1 (т.е. с нулевой погрешностью) оказалось достточно полиномов 3-й степени.

Задача 6: описать принцип формирования эйдосов (включая зеркальные части).

Автоматизированный системно-когнитивный анализ (АСК-анализ) [97] представляет собой метод, технологию и методику формирования эйдосов и включает следующие этапы:

1. Когнитивная структуризация, а затем и формализация предметной области.

2. Ввод данных мониторинга в базу прецедентов (обучающую выборку) за период, в течение которого имеется необходимая информация в электронной форме.

3. Синтез семантической информационной модели (СИМ).

4. Оптимизация СИМ.

5. Проверка адекватности СИМ (измерение внутренней и внешней, дифференциальной и интегральной валидности).

6. Анализ СИМ.

7. Решение задач идентификации состояний объекта управления, прогнозирования и поддержки принятия управленческих решений по управлению с применением СИМ.

На первых двух этапах АСК-анализа, детально рассмотренных в работах [9, 10], числовые величины сводятся к интервальным оценкам, как и информация об объектах нечисловой природы (фактах, событиях). Этот этап реализуется и в методах интервальной статистики.

На третьем этапе СК-анализа всем этим величинам (по единой методике, основанной на системном обобщении семантической теории информации А. Харкевича) сопоставляются количественные величины, с которыми в дальнейшем и производятся все операции моделирования.

Обобщенный образ класса (эйдос) представляет собой элемент определенного уровня иерархии системы, т.е. множество, в котором в качестве элементов-признаков выступают элементы предыдущего уровня иерархии системы.

Информационный портрет класса представляет собой список признаков этого класса, ранжированный в порядке убывания количества информации, содержащейся в этих признаках о принадлежности к данному классу. Этот информационный портрет может быть разделен на две части: позитивную: с положительными информативностями (эйдос), и негативную: с отрицательными информативностями (антиэйдос). Эйдос и антиэйдос представляют собой как бы зеркальные части информационного портрета.

Значения координат точки, входящей в эйдос, равны количеству информации в соответствующем признаке (градации описательной шкалы) о принадлежности конкретного обладающего этим признаком объекта к обобщенному образу класса (градации классификационной шкалы).

Если классические координаты точки в семантическом пространстве несут информацию только о положении точки в пространстве и все, то системные координаты точки в эйдос-пространстве, кроме этого, несут также и информацию о принадлежности объекта, в который входит данная точка, к эйдосу (обобщенному образу класса), т.е. к системе точек.

Подробнее задачу № 6 рассматривать в данной работе нецелесообразно, т.к. она неоднократно реализовалась в ряде приложений и исследований, проведенных по технологии АСК-анализа, о которых имеются многочисленные общедоступные публикации, в частности, размещенные по Internet-адресам:

– http://ej.kubagro.ru/a/viewaut.asp?id=11;

– http://lc.kubagro.ru/aidos/Eidos.htm.

Задача 7: показать, что базовая когнитивная концепция [97] формализуется многослойной системой эйдос-пространств.

Из базовой когнитивной концепции, предложенной в работе [97], следует иерархическая структура процесса познания (таблица 9).

Таблица 9 – ИЕРАРХИЧЕСКАЯ СТРУКТУРА ПРОЦЕССА ПОЗНАНИЯ

Уровень иерархии процесса познания	Элемент	Действие с элементами	Система
1	признаки	синтез	образы конкретных объектов
2	признаки, образы конкретных объектов	обобщение, многопараметрическая типизация	обобщенные образы классов
3	классы	нахождение наиболее сходных, обобщение	кластеры
4	кластеры	нахождение наиболее отличающихся	конструкты
5	конструкты	синтез	действующая парадигма предметной области

При этом на разных уровнях иерархии системы познания элементами являются: признаки, а системами – образы конкретных объектов, описанные системами признаков по 2, 3 и т.д., а на других элементами выступают уже конкретные образы, а системами – обобщенные образы классов, которые, в свою очередь, являются элементами систем-кластеров, а они – элементами систем-конструктов, система конструктов образует парадигму. В 1996 году в работе [94], а затем в работе [138] автором была предложена идея создания подобных многоуровневых моделей в АСК-анализе. В последующем в ряде работ автора с соавторами [102, 154, 99] и других были созданы и исследованы подобные многоуровневые модели, каждый из уровней которых формализуется эйдос-пространством определенной размерности.

Таким образом, можно сделать вывод о том, что базовая когнитивная концепция и реализующий ее АСК-анализ формализуются многослойной системой взаимосвязанных эйдос-пространств. Если на 2-м уровне иерархии оси координат представляют собой описательные шкалы, градациями которых являются признаки, а обобщенные образы классов (градации классификационных шкал) представляются пространственными кривыми в эйдос-пространстве, то на 3-м уровне иерархии градациями описательных шкал являются классы, а пространственные кривые – эйдосы отображают уже кластеры.

Задача 8: показать, что системная теория информации позволяет непосредственно на основе эмпирических данных определять вид функций принадлежности, т.е. решать одну из основных задач теории нечетких множеств.

В теории нечетких множеств, предложенной в 1965 году Лотфи А. Заде, понятие множества было обобщено, путем задания функции принадлежности элемента множеству, количественно задающей степень принадлежности элемента множеству (в классическом множестве элемент мог либо принадлежать, либо не принадлежать множеству). Было предложено несколько различных аналитических видов функций принадлежности и разработаны операции с нечеткими множествами, зависящие от вида этих априорно заданных функций.

Таким образом, в теории нечетких множеств математическое понятие множества было обогащено свойствами, и это несколько приблизило его к понятию "система" и позволило получить более общую теорию, чем классическая теория множеств.

Однако мы считаем, что теория нечетких множеств является лишь первым шагом и в этом направлении еще много работы. Например, ясно, что для реальных объектов, моделируемых множествами, фактический вид функции принадлежности может отличаться от ранее априорно определенных и затем аксиоматически постулированных и аналитически исследованных. Между тем именно фактический вид функции принадлежности характеризует специфику конкретного объекта исследования, и поэтому ее знание обуславливает адекватность моделирования этого объекта с помощью аппарата нечетких множеств. Поэтому возникает проблема определения вида функции принадлежности непосредственно на основе эмпирических данных и все значения и актуальность решения этой проблемы общим универсальным методом трудно переоценить. В настоящее время имеется ряд попыток найти подобный универсальный метод и разработать технологию и методику его применения на практике. В разделе 4.8 данной монографии приведен пример подхода, позволяющего решить эту проблему. Одной из таких попыток является интеграция теории нечетких множеств и нейронных сетей: так называемые нечеткие нейронные сети[7].

С применением системной теории информации (СТИ) также непосредственно на основе эмпирических данных определяется функция принадлежности элемента множеству, в частности:

– в информационном портрете определяется степень принадлежности признака классу;

– при идентификации объекта определяется степень его сходства с классами;

– при проведении кластерного анализа определяется степень сходства классов с кластерами.

На рисунке 7 в качестве примера приведена экранная форма системы "Эйдос", в которой показана степень принадлежности конкретных образов составов, описанных в обучающей выборке, к обобщенному образу класса: "Состав, следующий на запад". Таким образом, можно считать, что данный класс представляет собой нечеткое множество, включающее все составы, следующие на запад, но в разной степени. Состав-10 наиболее похож на обобщенный образ данного класса, т.е. является наиболее типичным для него, а состав-3 наименее типичным. Для составов 1, 2, 3, 4 и 5 степень принадлежности к классу "Состав, следующий на запад" отрицательна, т.е. они не относятся к этому классу в соответствии с созданной моделью.

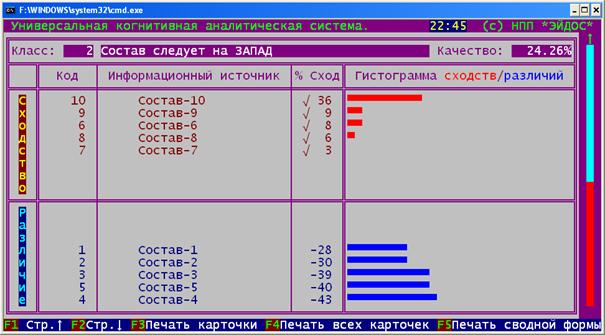
Рисунок 7 – Функция принадлежности конкретных образов
составов обучающей выборки к обобщенному образу класса:
"Состав, следующий на запад"

В таблице 10 приведен информационный портрет обобщенного образа класса: "Состав, следующий на запад", включая позитивную и негативную части, т.е. эйдос и антиэйдос.

Таблица 10 – ИНФОРМАЦИОННЫЙ ПОРТРЕТ КЛАССА РАСПОЗНАВАНИЯ:

Код: 2 Наименование: Состав следует на ЗАПАД

Позитивный и негативный портрет (эйдос и антиэйдос).

Фильтрации по кодам признаков нет.

Фильтрации по модулю информативности нет.

Код признака	Наименования описательных шкал и градаций	Информативность
		Бит	% от теоретически максимально возможной информативности	Сумма нарастающим итогом, %
1	КОЛИЧЕСТВО ВАГОНОВ В СОСТАВЕ:
1	2	0.153	15.33	15.3
6	ВИД КРЫШИ ВАГОНА:
16	Гофрированная	0.153	15.33	30.7
7	ГРУЗ (КОЛИЧЕСТВО И ВИД):
21	3 маленьких круга	0.153	15.33	46.0
7	ГРУЗ (КОЛИЧЕСТВО И ВИД):
25	2 коротких прямоугольника	0.153	15.33	61.3
7	ГРУЗ (КОЛИЧЕСТВО И ВИД):
31	Груза нет	0.153	15.33	76.7
2	ФОРМА ВАГОНА:
7	U-образная.	0.093	9.33	86.0
7	ГРУЗ (КОЛИЧЕСТВО И ВИД):
24	1 короткий прямоугольник.	0.069	6.88	92.9
7	ГРУЗ (КОЛИЧЕСТВО И ВИД):
26	1 длинный прямоугольник	0.069	6.88	99.7
3	ДЛИНА ВАГОНА:
10	Длинный	0.055	5.53	105.3
7	ГРУЗ (КОЛИЧЕСТВО И ВИД):
19	1 большой круг.	0.037	3.66	108.9
4	КОЛИЧЕСТВО ОСЕЙ ВАГОНА:
11	2	0.031	3.08	112.0
2	ФОРМА ВАГОНА:
5	Прямоугольная	0.009	0.88	112.9
3	ДЛИНА ВАГОНА:
9	Короткий.	0.009	0.88	113.8
5	ВИД СТЕНОК ВАГОНА:
13	Одинарные	0.009	0.88	114.7
6	ВИД КРЫШИ ВАГОНА:
15	Отсутствует	0.009	0.88	115.5
1	КОЛИЧЕСТВО ВАГОНОВ В СОСТАВЕ:
3	4	-0.076	-7.57	123.1
2	ФОРМА ВАГОНА:
4	V-образная.	-0.076	-7.57	130.7
5	ВИД СТЕНОК ВАГОНА:
14	Двойные	-0.076	-7.57	138.2
6	ВИД КРЫШИ ВАГОНА:
18	Прямая (эллипсоидная)	-0.076	-7.57	145.8
7	ГРУЗ (КОЛИЧЕСТВО И ВИД):
27	1 треугольник	-0.108	-10.79	156.6
1	КОЛИЧЕСТВО ВАГОНОВ В СОСТАВЕ:
2	3	-0.136	-13.57	170.2
4	КОЛИЧЕСТВО ОСЕЙ ВАГОНА:
12	3	-0.136	-13.57	183.7

Фоном светло-желтого цвета в информационном портрете выделены положительные информативности, а светло-зеленого – отрицательные, соответствующие эйдосу и антиэйдосу или эйдосу и его зеркальной части.

Информативность в битах – это количество информации, которое мы получаем о принадлежности некоторого объекта к данному классу, если узнаем, что он обладает этим признаком. Как показано в базовой когнитивной концепции [97], если мы анализируем только образы конкретных объектов и никак не обобщаем их, относя к каким-то классам и называя их обобщенными именами, то не можем определить, какие признаки этих объектов являются характерными для них, а какие случайными. Например, если маленький ребенок видит различные мячи впервые и не знает, что это все мячи, то такие признаки мячей, как круглый и пустой будут для него столь же важны, как цвет и рисунок на мяче. Однако при обобщении появляется возможность определить, какие признаки являются более характерными для того или иного обобщенного класса, какие менее, а какие – вообще случайными. Это и делается в АСК-анализе на основе системной теории информации: степень характерности признака для класса измеряется количеством информации, которое мы получаем из факта наблюдения этого признака о принадлежности к классу. Таким образом, характерные признаки в большей степени принадлежат классу, нехарактерные – менее, а случайные и принадлежащие другим классам, несходным с данным, вообще не принадлежат. Это и означает, что системная теория информации и АСК-анализ тесно связаны с теорией нечетких множеств и даже позволяют решать некоторые важные для этой теории задачи, такие, например, как определение вида функции принадлежности непосредственно на основе эмпирических данных и использование знания вида этой функции для решения задач идентификации, прогнозирования и поддержки принятия решений.

Процент от теоретически максимально возможной информативности – это процент, который составляет информативность в битах от теоретически максимально возможной информативности.

Теоретически-максимальная возможная информативность полностью определяется суммарным количеством градаций классификационных шкал, т.е. классов и равна количеству информации, которое мы получаем, когда достоверно узнаем, что некоторый объект принадлежит к определенному классу: это количество информации в битах равно двоичному логарифму от количества классов в семантической информационной модели (мера Хартли).

Суммарная информативность нарастающим итогом в процентах – это накопительная сумма от столбца: "Процент от теоретически максимально возможной информативности". Она показывает, насколько полно описан информационный потрет класса и есть ли в нем какая-либо избыточность описания. Если избыточность есть, т.е. суммарное количество информации в признаках, описывающих потрет, больше 100 %, то это означает, что существуют корреляции между признаками, т.е. пространство неортонормированное, если же описание неполное, то это означает, что для обеспечения полноты описания данного класса в модели необходимо увеличить размерность эйдос-пространства путем добавления в него новых, желательно, максимально независимых от уже имеющихся описательных шкал и градаций.

Во всех этих случаях определена, т.е. имеет смысл, не только положительная принадлежность, но и отрицательная. Например, отрицательная информативность признака несет информацию о непринадлежности конкретного объекта, обладающего этим признаком, к данному классу. Примеры определения конкретного вида функций принадлежности непосредственно на основе эмпирических данных и применения этих функций для идентификации и прогнозирования объектов в различных предметных областях можно обнаружить в работах автора по применению АСК-анализа: http://ej.kubagro.ru/a/viewaut.asp?id=11.

Правда, во всех этих случаях функция принадлежности в системе "Эйдос" (являющейся инструментарием АСК-анализа) задана таблично, но это не является особым ограничением, т.к. таблично-заданные функции всегда можно аппроксимировать наиболее подходящей в каком-то смысле аналитической зависимостью, например, степенными полиномами, полиномами Чебышева или Лагранжа, рядами функций различного вида, Фурье, степенными, показательными, рядами спецфункций или функций общего вида, как это принято в АСК-анализе.

Задача 9: сформулировать перспективы: разработка операций с системами: объединение (сложение), пересечение (умножение), вычитание. Привести предварительные соображения по сложению систем.

В качестве перспективы мы рассматриваем разработку математического формализма, обеспечивающего операции с системами: объединение (сложение), пересечение (умножение), вычитание.

В предварительном плане мы приведем здесь некоторые соображения по операции сложения систем. В отличие от сложения множеств, при сложении систем у системы-суммы появляются новые эмерджентные свойства, которых не было у систем-слагаемых. Именно эту особенность сложения систем отражает системная теория информации [97].

Элементы-подмножества системы отличаются не только количеством базисных элементов, но и тем, какие именно конкретно это базисные элементы, т.е. элементы, состоящие из одинакового количества базисных элементов, различаются, если различается, по крайней мере, один из этих базисных элементов.

Элементы-подсистемы, состоящие из одних и тех же базисных элементов (0-тождественные элементы), тождественны, если тождественна их структура, и отличаются друг от друга, если отличается их структура.

Приведем примеры.

Лингвистические системы, в том числе естественный язык (вербализация), являются одним из наиболее мощных, точных и удачных из всех выработанных человечеством средств моделирования реальности и отражения ее в сознании. Язык имеет многие системные свойства реальности, благодаря чему он и является достаточно адекватным для физического сознания средством ее отражения.

Поэтому в 1-м примере рассмотрим два предложения, естественно, состоящие из слов, написанных с помощью букв. Каждое предложение будем рассматривать как систему, состоящую на базисном уровне из букв, а на 1-м уровне иерархии – из слов. На 0-м уровне у них будет пересечение, состоящее из общих букв, а 1-м уровне – пересечение, состоящее из общих слов. Естественно, результаты пересечения систем на 1-м уровне будут различаться, если считать тождественными только те слова, которые полностью тождественны по всем буквам, или слова, являющиеся словоформами от одного слова. Рассмотрим два предложения (таблица 11).

Таблица 11 – ПЕРЕСЕЧЕНИЕ ЛИНГВИСТИЧЕСКИХ СИСТЕМ

НА 0-М И 1-М ИЕРАРХИЧЕСКИХ УРОВНЯХ ИХ СТРУКТУРЫ (ПРОЗА)

№	Система	0-й уровень иерархии (буквы)	1-й уровень иерархии (слова)
1	У лукоморья дуб зеленый	бдезйклмно р уыья	зеленый
2	Под дубом рос зеленый лук	бдезйклмнопрсуы	зеленый

Жирным шрифтом выделены буквы, общие в обоих предложениях. Видно, что 13 букв из 17, которые используются в этих предложениях, общие для обоих предложений, тогда как из 9 слов общее (тождественно) только одно. Таким образом, пересечение этих предложений как систем на базисном уровне составляет: 13/17´100=76,47 %, а на 1-м иерархическом уровне – 1/9´100=11,11 %.

Рассмотрим более сложный 2-й пример со стихами и былинами. При этом, так же как и в 1-м примере, будем считать каждое предложение системой, состоящей на базисном уровне из букв, а на 1-м уровне иерархии – из слов и рифм. Однако в отличие от 1-го примера, будем считать тождественными словоформы одного слова, кроме того, будем учитывать рифму, которую также отнесем к 1-му уровню иерархии.

Выделим одинаковым цветом тождественные слова и рифмы:

У лукоморья дуб зеленый,

Златая цепь на дубе том:

И днем, и ночью кот ученый

Все ходит по цепи кругом

(А.С. Пушкин "Руслан и Людмила")

Представим результаты анализа пересечений предложений в виде таблиц 12–15.

Таблица 12 – ПЕРЕСЕЧЕНИЕ ЛИНГВИСТИЧЕСКИХ СИСТЕМ

НА 0-М УРОВНЕ ИЕРАРХИИ В СИМВОЛАХ (СТИХИ)

KOD	PREDL	P01	P02	P03	P04
P01	У лукоморья дуб зелен-ый	-бдезйклмноруыь	-бдезлмноуья	-дейкмноуыь	-декмору
P02	Златая цепь на дубе т-ом	-бдезлмноуья	-абдезлмноптуць	-демнотуь	-демоптуц
P03	И днем, и ночью кот учен-ый	-дейкмноуыь	-демнотуь	,-деийкмнотучыь	-деикмоту
P04	Все ходит по цепи круг-ом	-декмору	-демоптуц	-деикмоту	-вгдеикмопрстух

Таблица 13 – ПЕРЕСЕЧЕНИЕ ЛИНГВИСТИЧЕСКИХ СИСТЕМ

НА 0-М УРОВНЕ ИЕРАРХИИ В ПРОЦЕНТАХ (СТИХИ)

KOD	PREDL	P01	P02	P03	P04
P01	У лукоморья дуб зелен-ый	100,000	70,588	75,000	56,250
P02	Златая цепь на дубе т-ом	70,588	100,000	62,500	62,500
P03	И днем, и ночью кот учен-ый	75,000	62,500	100,000	62,500
P04	Все ходит по цепи круг-ом	56,250	62,500	62,500	100,000

Таблица 14 – ПЕРЕСЕЧЕНИЕ ЛИНГВИСТИЧЕСКИХ СИСТЕМ

НА 1-М УРОВНЕ ИЕРАРХИИ В СЛОВОФОРМАХ (СТИХИ)

Код	PREDL	P01	P02	P03	P04
P01	У лукоморья дуб зелен-ый	дуб зелен лукоморья ый	дуб	ый
P02	Златая цепь на дубе т-ом	дуб	дубе златая на ом цепь		ом цепи
P03	И днем, и ночью кот учен-ый	ый		днем кот ночью учен ый
P04	Все ходит по цепи круг-ом		ом цепи		все круг ом по ходит цепи

Примечание: в таблицах 12–15 использован следующий технический прием: чтобы программа выделила рифмы, как структурные элементы 1-го уровня иерархии, они отделены знаком тире, используемым в качестве разделителя.

Таблица 15 – ПЕРЕСЕЧЕНИЕ ЛИНГВИСТИЧЕСКИХ СИСТЕМ

НА 1-М УРОВНЕ ИЕРАРХИИ В ПРОЦЕНТАХ (СТИХИ)

KOD	PREDL	P01	P02	P03	P04
P01	У лукоморья дуб зелен-ый	100,000	25,000	25,000	0,000
P02	Златая цепь на дубе т-ом	25,000	100,000	0,000	40,000
P03	И днем, и ночью кот учен-ый	25,000	0,000	100,000	0,000
P04	Все ходит по цепи круг-ом	0,000	40,000	0,000	100,000

Рассмотрим былинный текст:

У ласкова у князя у Владимира

Было пированице, почестен пир,

Для многих князей, для бояр,

Для русских могучих богатырей;

Красное солнышко к вечеру -

Почестный пир идет на веселие,

Все на пиру пьяны - веселы,

Все на пиру порасхвастались:

Богатый хвастает золотой казной,

Глупый хвастает молодой женой,

Умный хвастает старой матерью,

Сильный хвастает своей силою -

Силою, ухваткою богатырскою;

За тем за столом за дубовым

Сидит один богатырь -

Ничем-то он молодец не хвастает

(Русская былина "Сухман".

Владимиро-Суздальский период.

Cер. XII - конец XIII века)

Результаты анализа пересечений предложений из этого текста представлены в таблицах 16–19.

Тождественные или сходные слова, производные от одного слова (словоформы), рифмы и повторы, особенно широко использовавшиеся в русских былинах, повышают степень пересечения предложений текста на различных иерархических уровнях его организации и, тем самым, помогают организовать между ними смысловую связь, служат смысловыми маркерами, повышают количество связей в лингвистической системе, а значит повыщают ее уровень системности и легкость восприятия смысла, а также заряд нетождественности в тексте, т.е. его невербальную смысловую нагрузку. Таким образом, можно сделать вывод о том, что рифмы и повторы словоформ повышают уровень системности теста, вследствие чего стихи и былины можно считать более высокоорганизованной формой текста, чем проза.

Эти результаты получены с помощью программы, исходный текст которой приведен ниже, разработанной автором при подготовке данной работы специально с целью исследования пересечений лингвистических систем на 0-м и 1-м уровнях иерархии языка программирования (xBase++ или CLIPPER 5.01+TOOLS II):

********************************************************

*** ЛУЦЕНКО Е.В. 04/13/08 10:11am ***

*** Исследование пересечений лингвистических систем ***

*** на 0-м и 1-м уровнях иерархии (буквы, слова) ***

********************************************************

G_buf=SAVESCREEN(0,0,24,79)

FOR j=0 TO 24

@j,0 SAY REPLICATE("█",80) COLOR "n/n"

NEXT

***** Если БД исходных предложений нет, то создать ее и выйти

IF .NOT. FILE("LingvSys.dbf")

CLOSE ALL

CREATE Struc

APPEND BLANK

REPLACE Field_name WITH "Kod",;

Field_type WITH "C",;

Field_len WITH 5,;

Field_dec WITH 0

APPEND BLANK

REPLACE Field_name WITH "Predl",;

Field_type WITH "C",;

Field_len WITH 65,;

Field_dec WITH 0

APPEND BLANK

REPLACE Field_name WITH "ListChar",;

Field_type WITH "C",;

Field_len WITH 65,;

Field_dec WITH 0

APPEND BLANK

REPLACE Field_name WITH "ListWord",;

Field_type WITH "C",;

Field_len WITH 65,;

Field_dec WITH 0

CREATE LingvSys FROM Struc

Mess = "Необходимо ввести предложения в БД *LingvSys* и запустить программу !!!"

@20, 40-LEN(Mess)/2 SAY Mess COLOR "w+/n"

INKEY(0)

INKEY(0)

RESTSCREEN(0,0,24,79,G_buf)

QUIT

ENDIF

********************************************************************

***** 0-й УРОВЕНЬ ИЕРАРХИИ (БУКВЫ) *********************************

********************************************************************

***** Составить отсортированный список уникальных символов, входящих в предложения

***** Определить максимальную длину предложения и листа уникальных символов

CLOSE ALL

USE LingvSys EXCLUSIVE NEW // Открыть БД с предложениями

N_Predl = RECCOUNT() // Кол-во предложений в БД

Max_Pred = -999

Max_List = -999

DBGOTOP()

DO WHILE .NOT. EOF()

REPLACE ListChar WITH CHARSORT(CHARLIST(LOWER(Predl))) // Сформировать отсортированный список уникальных букв предложения

Max_Pred = MAX(Max_Pred, LEN(ALLTRIM(Predl)))

Max_List = MAX(Max_List, LEN(ALLTRIM(ListChar)))

DBSKIP(1)

ENDDO

***** Создать БД совпадения символов в предложениях

CLOSE ALL

CREATE Struc

APPEND BLANK

REPLACE Field_name WITH "Kod",;

Field_type WITH "C",;

Field_len WITH 5,;

Field_dec WITH 0

APPEND BLANK

REPLACE Field_name WITH "Predl",;

Field_type WITH "C",;

Field_len WITH Max_Pred,;

Field_dec WITH 0

FOR i = 1 TO N_Predl

APPEND BLANK

Fn = "P"+STRTRAN(STR(i,2)," ","0")

REPLACE Field_name WITH Fn,;

Field_type WITH "C",;

Field_len WITH Max_List,;

Field_dec WITH 0

NEXT

CREATE SovList0 FROM Struc

***** Создать БД % совпадения символов в предложениях

CLOSE ALL

CREATE Struc

APPEND BLANK

REPLACE Field_name WITH "Kod",;

Field_type WITH "C",;

Field_len WITH 5,;

Field_dec WITH 0

APPEND BLANK

REPLACE Field_name WITH "Predl",;

Field_type WITH "C",;

Field_len WITH Max_Pred,;

Field_dec WITH 0

FOR i = 1 TO N_Predl

APPEND BLANK

Fn = "P"+STRTRAN(STR(i,2)," ","0")

REPLACE Field_name WITH Fn,;

Field_type WITH "N",;

Field_len WITH 7,;

Field_dec WITH 3

NEXT

CREATE SovPerc0 FROM Struc

***** Заполнить БД совпадения символов в предложениях

***** и БД % совпадений пустыми записями

CLOSE ALL

USE SovPerc0 EXCLUSIVE NEW // Открыть БД совпадения предложений в %

USE SovList0 EXCLUSIVE NEW // Открыть БД совпадения символов в предложениях

USE LingvSys EXCLUSIVE NEW // Открыть БД с предложениями

FOR i = 1 TO N_Predl

SELECT LingvSys

DBGOTO(i)

M_Predl = Predl

SELECT SovList0

APPEND BLANK

Fn = "P"+STRTRAN(STR(i,2)," ","0")

REPLACE Kod WITH Fn

REPLACE Predl WITH M_Predl

SELECT SovPerc0

APPEND BLANK

REPLACE Kod WITH Fn

REPLACE Predl WITH M_Predl

NEXT

****** Построение БД пересечений предложений на уровне букв

SELECT LingvSys

FOR i=1 TO N_Predl // Цикл по предложениям

DBGOTO(i) // Переход на запись с 1-м предложением

Ar_List1 = ListChar // Присвоить переменной значение 1-го предложения

FOR j=1 TO N_Predl // Цикл по предложениям

DBGOTO(j) // Переход на запись со 2-м предложением

Ar_List2 = ListChar // Присвоить переменной значение 2-го предложения

M12 = CHARONE(CHARSORT(CHARONLY(Ar_List1,Ar_List2))) // Получить символы, общие для обоих предложений (убрав повторы) и отсортировать их

IF LEN(M12) > 0 // Если были общие символы

SELECT SovList0

DBGOTO(i);FIELDPUT(2+j, M12) // Записать пересечение

DBGOTO(j);FIELDPUT(2+i, M12)

SELECT Lingvsys // Сделать текущей БД исходных предложений

ENDIF

NEXT

NEXT

****** Расчет % сходства предложений на уровне букв: (% совпадающих букв

****** от суммарного количества уникальных букв обоих предложений)

SELECT SovList0

FOR i=1 TO N_Predl // Цикл по строкам предложениям

DBGOTO(i)

Ar_List1 = FIELDGET(2+i) // Присвоить переменной значение листа символов 1-го предложения

FOR j=i TO N_Predl // Цикл по столбцам предложениям

Ar_List2 = FIELDGET(2+j) // Присвоить переменной значение листа символов 2-го предложения

Ar_m12 := {} // Массив совпадающих символов обоих предложений

Ar_sum := {} // Массив всех уникальных символов обоих предложений

FOR k=1 TO LEN(Ar_List1)

L = SUBSTR(Ar_List1, k, 1) // k-й символ 1-го предложения

IF AT(L, Ar_List2) > 0

IF ASCAN(Ar_m12, L) = 0

AADD(Ar_m12, L)

ENDIF

ENDIF

IF ASCAN(Ar_sum, L) = 0

AADD(Ar_sum, L)

ENDIF

NEXT

FOR k=1 TO LEN(Ar_List2)

L = SUBSTR(Ar_List2, k, 1) // k-й символ 2-го предложения

IF ASCAN(Ar_sum, L) = 0

AADD(Ar_sum, L)

ENDIF

NEXT

IF LEN(Ar_sum) > 0

SELECT SovPerc0

DBGOTO(i);FIELDPUT(2+j, LEN(Ar_m12)/LEN(Ar_sum)*100)

DBGOTO(j);FIELDPUT(2+i, LEN(Ar_m12)/LEN(Ar_sum)*100)

SELECT SovList0

ENDIF

NEXT

NEXT

********************************************************************

***** 1-й УРОВЕНЬ ИЕРАРХИИ (СЛОВА) *********************************

********************************************************************

***** Составить отсортированный список уникальных слов, входящих в предложения

***** Определить максимальную длину предложения и листа уникальных слов

CLOSE ALL

USE LingvSys EXCLUSIVE NEW // Открыть БД с предложениями

N_Predl = RECCOUNT() // Кол-во предложений в БД

Max_Pred = -999

Max_List = -999

DBGOTOP()

DO WHILE .NOT. EOF()

*** Сформировать отсортированный список уникальных слов предложения

Ar_word := {}

M_Predl = Predl

FOR w=1 TO NUMTOKEN(M_Predl)

M_Word = ALLTRIM(LOWER(TOKEN(M_Predl, w)))

IF LEN(M_Word) > 1 // Исключение предлогов

IF ASCAN(Ar_word, M_Word) = 0 // Исключение повторов слов

AADD(Ar_word, M_Word) // Добавление слова в массив

ENDIF

ENDIF

NEXT

ASORT(Ar_word)

M_ListWord = ""

FOR w=1 TO LEN(Ar_word)

M_ListWord = M_ListWord + Ar_word[w] + " "

NEXT

REPLACE ListWord WITH ALLTRIM(M_ListWord)

Max_Pred = MAX(Max_Pred, LEN(ALLTRIM(M_Predl)))

Max_List = MAX(Max_List, LEN(ALLTRIM(M_ListWord)))

DBSKIP(1)

ENDDO

***** Создать БД совпадения слов в предложениях

CLOSE ALL

CREATE Struc

APPEND BLANK

REPLACE Field_name WITH "Kod",;

Field_type WITH "C",;

Field_len WITH 5,;

Field_dec WITH 0

APPEND BLANK

REPLACE Field_name WITH "Predl",;

Field_type WITH "C",;

Field_len WITH Max_Pred,;

Field_dec WITH 0

FOR i = 1 TO N_Predl

APPEND BLANK

Fn = "P"+STRTRAN(STR(i,2)," ","0")

REPLACE Field_name WITH Fn,;

Field_type WITH "C",;

Field_len WITH Max_List,;

Field_dec WITH 0

NEXT

CREATE SovList1 FROM Struc

***** Создать БД % совпадения слов в предложениях

CLOSE ALL

CREATE Struc

APPEND BLANK

REPLACE Field_name WITH "Kod",;

Field_type WITH "C",;

Field_len WITH 5,;

Field_dec WITH 0

APPEND BLANK

REPLACE Field_name WITH "Predl",;

Field_type WITH "C",;

Field_len WITH Max_Pred,;

Field_dec WITH 0

FOR i = 1 TO N_Predl

APPEND BLANK

Fn = "P"+STRTRAN(STR(i,2)," ","0")

REPLACE Field_name WITH Fn,;

Field_type WITH "N",;

Field_len WITH 7,;

Field_dec WITH 3

NEXT

CREATE SovPerc1 FROM Struc

ERASE("Struc.dbf")

***** Заполнить БД совпадения слов в предложениях

***** и БД % совпадений пустыми записями

CLOSE ALL

USE SovPerc1 EXCLUSIVE NEW // Открыть БД совпадения предложений в %

USE SovList1 EXCLUSIVE NEW // Открыть БД совпадения сслов в предложениях

USE LingvSys EXCLUSIVE NEW // Открыть БД с предложениями

FOR i = 1 TO N_Predl

SELECT LingvSys

DBGOTO(i)

M_Predl = Predl

SELECT SovList1

APPEND BLANK

Fn = "P"+STRTRAN(STR(i,2)," ","0")

REPLACE Kod WITH Fn

REPLACE Predl WITH M_Predl

SELECT SovPerc1

APPEND BLANK

REPLACE Kod WITH Fn

REPLACE Predl WITH M_Predl

NEXT

*** Построение БД пересечений предложений на уровне слов

FOR i=1 TO N_Predl // Цикл по предложениям

SELECT LingvSys

DBGOTO(i) // Переход на запись с 1-м предложением

******* Занести в массив значения слов 1-го предложения

Ar_List1 := {}

M_ListWord = LOWER(ListWord)

FOR w=1 TO NUMTOKEN(M_ListWord)

M_Word = ALLTRIM(TOKEN(M_ListWord, w))

IF ASCAN(Ar_List1, M_Word) = 0 // Исключение повторов слов

AADD(Ar_List1, M_Word) // Добваление слова в массив

ENDIF

NEXT

FOR j=1 TO N_Predl // Цикл по предложениям

DBGOTO(j) // Переход на запись со 2-м предложением

******* Занести в массив значения слов 2-го предложения

Ar_List2 := {}

M_ListWord = LOWER(ListWord)

FOR w=1 TO NUMTOKEN(M_ListWord)

M_Word = TOKEN(M_ListWord, w)

IF ASCAN(Ar_List2, M_Word) = 0 // Исключение повторов слов

AADD(Ar_List2, M_Word) // Добваление слова в массив

ENDIF

NEXT

*** Получить слова и словоформы, ОБЩИЕ для обоих предложений

*** (убрав повторы) и отсортировать их

*** Определить словоформы с использованием расстояния Левенштейна

Krs = 3 // Критерий сходства словоформ

Ar_m12 := {} // Массив общих словоформ

FOR w1=1 TO LEN(Ar_List1)

FOR w2=1 TO LEN(Ar_List2)

*** Сравнение сходства двух слов или словоформ

*** с использованием расстояния Левенштейна

IF STRDIFF(Ar_List1[w1], Ar_List2[w2]) <= Krs

Flag_ins = .F.

** Исключение тождественных повторов

IF ASCAN(Ar_m12, Ar_List1[w1]) = 0

Flag_ins = .T.

ENDIF

IF Flag_ins = .F.

*** Исключение повторов словоформ

*** т.е. сходных слов в массиве еще нет

LEN_Ar_m12 = LEN(Ar_m12)

n = 0

FOR k=1 TO LEN_Ar_m12

IF STRDIFF(Ar_m12[k], Ar_List1[w1]) > Krs

++n

ENDIF

NEXT

IF n = LEN_Ar_m12 // Все имеющиеся в массиве слова не похожи

Flag_ins = .T.

ENDIF

ENDIF

IF Flag_ins

AADD(Ar_m12, Ar_List1[w1]) // Добавление слова в массив

ENDIF

ENDIF

NEXT

NEXT

***** Сформировать переменную для записи в БД сходства слов

M_m12 = ""

FOR w=1 TO LEN(Ar_m12)

M_m12 = M_m12 + Ar_m12[w] + " "

NEXT

IF LEN(Ar_m12) > 0 // Если были общие слова

SELECT SovList1

DBGOTO(i);FIELDPUT(2+j, ALLTRIM(M_m12)) // Записать общие слова в БД совпадений

DBGOTO(j);FIELDPUT(2+i, ALLTRIM(M_m12)) // Записать общие слова в БД совпадений

SELECT Lingvsys // Сделать текущей БД исходных предложений

ENDIF

NEXT

NEXT

****** Расчет % сходства предложений на уровне слов: (% совпадающих слов

****** от суммарного количества уникальных слов обоих предложений)

SELECT SovList1

FOR i=1 TO N_Predl // Цикл по строкам предложениям

DBGOTO(i)

******** Занести в массив значения слов 1-го предложения

Ar_List1 := {}

M_ListWord = FIELDGET(2+i)

FOR w=1 TO NUMTOKEN(M_ListWord)

M_Word = TOKEN(M_ListWord, w)

AADD(Ar_List1, M_Word) // Добавление слова в массив

NEXT

FOR j=i TO N_Predl // Цикл по столбцам предложениям

******** Занести в массив значения слов 2-го предложения

Ar_List2 := {}

M_ListWord = FIELDGET(2+j)

FOR w=1 TO NUMTOKEN(M_ListWord)

M_Word = TOKEN(M_ListWord, w)

AADD(Ar_List2, M_Word) // Добавление слова в массив

NEXT

*** Получить слова, ОБЩИЕ для обоих предложений

*** (убрав повторы) и отсортировать их

*** Определить словоформы с использованием расстояния Левенштейна

Krs = 3 // Критерий сходства словоформ

Ar_m12 := {} // Массив совпадающих словоформ обоих предложений

FOR w1=1 TO LEN(Ar_List1)

FOR w2=1 TO LEN(Ar_List2)

*** Сравнение сходства двух слов или словоформ

*** с использованием расстояния Левенштейна

IF STRDIFF(Ar_List1[w1], Ar_List2[w2]) <= Krs

*** Исключение повторов словоформ, т.е. добавлять

*** только если сходных слов в массиве еще нет

LEN_Ar_m12 = LEN(Ar_m12)

n = 0

IF LEN_Ar_m12 > 0

FOR k=1 TO LEN_Ar_m12

IF STRDIFF(Ar_m12[k], Ar_List1[w1]) > Krs

++n

ENDIF

NEXT

ENDIF

IF n = LEN_Ar_m12 // Все имеющиеся в массиве слова не похожи

AADD(Ar_m12, Ar_List1[w1]) // Добавление слова в массив

ENDIF

ENDIF

NEXT

NEXT

****** Формирование массива уникальных слов

****** и словоформ, входящих в 1-е, 2-е или в оба предложения

Ar_sum := {} // Массив всех уникальных словоформ обоих предложений

FOR i1=1 TO LEN(Ar_List1)

AADD(Ar_sum, Ar_List1[i1]) // Добавление слова в массив

NEXT

FOR i1=1 TO LEN(Ar_sum)

FOR j1=1 TO LEN(Ar_List2)

*** Сравнение сходства двух слов или словоформ

*** с использованием расстояния Левенштейна

IF STRDIFF(Ar_sum[i1], Ar_List2[j1]) <= Krs

*** Исключение повторов словоформ, т.е. добавлять слово

*** только если сходных слов в массиве еще нет

LEN_Ar_sum = LEN(Ar_sum)

n = 0

IF LEN_Ar_sum > 0

FOR k=1 TO LEN_Ar_sum

IF STRDIFF(Ar_sum[k], Ar_List2[j1]) > Krs

++n

ENDIF

NEXT

ENDIF

IF n = LEN_Ar_sum // Все имеющиеся в массиве слова не похожи

AADD(Ar_sum, Ar_List2[j1]) // Добавление слова в массив

ENDIF

ENDIF

NEXT

NEXT

** Занесение информации в БД % сходства предложений на уровне слов

IF LEN(Ar_sum) > 0

SELECT SovPerc1

DBGOTO(i);FIELDPUT(2+j, LEN(Ar_m12)/LEN(Ar_sum)*100)

DBGOTO(j);FIELDPUT(2+i, LEN(Ar_m12)/LEN(Ar_sum)*100)

SELECT SovList1

ENDIF

NEXT

NEXT

Mess = "Исследование пересечений лингвистических систем успешно завершено !!!"

@20, 40-LEN(Mess)/2 SAY Mess COLOR "w+/n"

INKEY(0)

INKEY(0)

RESTSCREEN(0,0,24,79,G_buf)

QUIT

Более развитие подходы, основанные на АСК-анализе, в которых символы имеют различный вес для идентификации слов (в различной степени характерны для слов или принадлежат словам), а слова – различный вес для идентификации текстов (в различной степени характерны для текстов или принадлежат текстам), и эти веса вычисляются на основе примеров (и эти функции принадлежности вычисляются непосредственно на основе эмпирических данных), были апробированы автором при решении задач идентификации слов по входящим в них буквам [147] и атрибуции анонимных и псевдонимных текстов [150].

Итак, сделаем некоторые обобщения.

Две системы тождественны, если тождественны все их элементы на всех уровнях иерархии, а также тождества их структура, т.е. взмиосвязи между элементами. В теории множеств о структуре речи не было.

Если есть две системы, то в них могут входить различные 0-тождественные элементы-подсистемы. Это означает, что на 0-м уровне иерархии эти системы могут иметь пересечение в смысле теории множеств, а на последующих уровнях иерархии его может и не быть.

Определение 10: пересечением двух систем является система, состоящая из элементов, являющихся пересечением на каждом из имеющихся иерархических уровней этих систем.

Выводы

Ранее автором была обоснована программная идея системного обобщения математики и сделан первый шаг по ее реализации: предложен вариант системной теории информации (СТИ). В данной работе осуществлена попытка – сделать второй шаг в том же направлении: рассматривается один из возможных подходов к системному обобщению математического понятия множества, а именно – подход, основанный на системной теории информации. Предполагается, что этот подход может стать основой для системного обобщения теории множеств и создания математической теории систем.

По ходу обсуждения сформулированных задач и подходов к их решению было выяснено, что в современной науке уже созданы научные теории (более того, они общепризнанны), которые хорошо вписываются в предложенную программную идею системного обобщения математики как элементы мозаики в общую картину, контуры которой мы и пытались нащупать. В дальнейшем при реализации предложенной программной идеи системного обобщения математики эта мозаика будет дополняться новыми элементами и, в конце концов, мы увидим всю картину в целом.

Так что же это за теории?

Прежде всего, это общая теория относительности (ОТО) Альберта Эйнштейна, основанная на общей идее о том, что физические явления можно описывать свойствами пространства – времени, например, гравитацию можно рассматривать как искривление пространства. В последующем эта идея получила развитие в работах по геометродинамике Дж. Уиллера, однако, описать другие физические явления с помощью геометрии оказалось на данном этапе затруднительным, что, по мнению автора, обусловлено, в том числе, недостаточной развитостью самой геометрии, в частности бедностью набора свойств геометрических объектов. Будем надеяться, что разработка системного обобщения геометрии позволит кардинально преодолеть эту проблему и описать свойства физических (да и других) объектов и явлений как эмерджентные свойства геометрических систем, лежащих в их основе и этими свойствами не обладающих. Если эту идею довести до логического конца, то будет стерта непреодолимая граница между математикой и физикой, математикой и другими науками. С учетом того, что системная геометрия и системная теория информации оказываются тесно взаимосвязанными, можно высказать следующую гипотезу, которая кажется вполне обоснованной: любые процессы и явления внутреннего и внешнего мира независимо от их природы можно рассматривать как информационные процессы, в которых объекты информационно взаимодействуют друг с другом с помощью каналов связи с определенными характеристиками, и при этом, соответственно, выделяется или поглощается энергия, изменяется уровень организации, уровень системности взаимодействующих объектов, изменяется их структура и функции (свойства). Для целенаправленного изменения структуры и функций объектов и явлений любой природы, в т.ч. квантовых, можно использовать методы и средства теории автоматизированного управления, применяя при этом для воздействия на объекты с целью управления ими информационные, по своей природе, управляющие факторы (отметим, что эта идея в развитой форме была высказана и реализована еще в 1984 году[8]). Таким образом, теория информации, ее идеи и методы могут проникнуть во все области науки и практики, т.к. информация – это предельно общая категория, даже более общая, чем категории "бытие и небытие", "материя и сознание", так как что бы мы не говорили об этих или других категориях, мы, прежде всего, обмениваемся информацией об их содержании и строим их информационные модели.

Это и фрактальная геометрия Бенуа Мандельброта, в которой, пожалуй, впервые в геометрии со времен Евклида коренным образом изменено представление о геометрических объектах в бесконечно-малом, обобщено представление о размерности пространства, стали систематически рассматриваться эмерджентные свойства геометрических систем.

Это и теория нечетких множеств Лотфи Заде, в которой может быть еще не вполне осознанно и целенаправленно, но были обогащены свойства математических множеств, в результате чего, по сути, нечетким множествам были приписаны отдельные свойства систем.

Все это вселяет надежду, что программная идея системного обобщения математики является вполне оправданной и обоснованной, и у нее есть перспективы применения и развития, т.е. действительно может быть получено системное обобщение любого математического понятия, основанного на понятии множества, любой области математики, основанной на теории множеств, путем тотальной замены понятия "множество" на более общее понятие "система" и прослеживания всех последствий этого. То, что эта надежда не беспочвенна, подтверждается не только существованием уже перечисленных выше общепринятых теорий, но и появлением целого ряда новаторских работ, подобных работам [30, 31, 32], демонстрирующим качественно новый уровень понимания проблем, связанных с системами и информацией.

Замечание по вопросу о названии "Системного обобщения теории множеств", возможность которого мы обсуждали в данном разделе. Для этого обобщения были бы очень удачны термины: "Математическая теория систем" или "Информационная теория систем", однако эти термины уже есть в арсенале науки [24, 25], и при этом в них вкладывается иное смысловое содержание. Поэтому, видимо, придется либо несколько переосмыслить это содержание (что кажется более рациональным, т.к. в науке постоянно происходит процесс переосмысления ее содержания), либо научное направление, к которому относится данная работа, так и называть: "Системное обобщение теории множеств".

В заключение хотелось бы отметить, что авторы полностью осознают весьма спорный характер высказанных в данной работе мыслей и положений, но все же изложили их потому, что считают их интересными, поэтому все эти мысли и положения высказываются здесь исключительно в порядке научного обсуждения и ни в коей мере не претендуют на какую-либо полноту и завершенность.

ГЛАВА 9. РАЗВИТИЕ ИДЕИ СИСТЕМНОГО ОБОБЩЕНИЯ МАТЕМАТИКИ В ОБЛАСТИ ТЕОРИИ ИНФОРМАЦИИ: СИСТЕМНАЯ (ЭМЕРДЖЕНТНАЯ) ТЕОРИЯ ИНФОРМАЦИИ (СТИ)

Дальнейшее изложение основано на рабатах [97] и [280], нумерация формул, рисунков и таблиц сохранены теми же, что в работе [280].

Итак, классическая формула Хартли имеет вид:

( 1 )

Будем искать ее системное обобщение в виде:

( 2 )

где:

W – количество элементов в множестве.

j – коэффициент эмерджентности, названный автором в честь Хартли коэффициентом эмерджентности Хартли.

Примем, что системное обобщение формулы Хартли имеет вид:

( 3 )

^где:

^{– количество подсистем из m элементов;}

m – сложность подсистем;

M – максимальная сложность подсистем (максимальное число элементов подсистемы).

^{Так как , то при M=1 система переходит в множество и выражение (3) приобретает вид (1), т.е. для него выполняется принцип соответствия, являющийся обязательным для более общей теории.}

Учитывая, что при M=W:

( 4 )

в этом случае получаем:

( 5 )

Выражение (5) дает оценку максимального количества информации в элементе системы. Из выражения (5) видно, что при увеличении числа элементов W количество информации I быстро стремится к W (6) и уже при W>4 погрешность выражения (5) не превышает 1%:

( 6 )

Приравняв правые части выражений (2) и (3):

( 7 )

получим выражение для коэффициента эмерджентности Хартли:

( 8 )

Смысл этого коэффициента раскрыт в работе [97] и ряде других. Здесь отметим лишь, что при M®1, когда система асимптотически переходит в множество, имеем j®1 и (2) ® (1), как и должно быть согласно принципу соответствия.

С учетом (8) выражение (2) примет вид:

( 9 )

или при M=W и больших W, учитывая (4) и (5):

( 10 )

Выражение (9) и представляет собой искомое системное обобщение классической формулы Хартли, а выражение (10) – его достаточно хорошее приближение при большом количестве элементов в системе W.

Классическая формула А. Харкевича имеет вид:

( 11 )

где: – P_ij – условная вероятность перехода объекта в j-е состояние при условии действия на него i-го значения фактора;

– – безусловная вероятность перехода объекта в j-е состояние (вероятность самопроизвольного перехода или вероятность перехода, посчитанная по всей выборке, т.е. при действии любого значения фактора).

Придадим выражению (11) следующий эквивалентный вид (12), который и будем использовать ниже. Вопрос об эквивалентности выражений (11) и (12) рассмотрим позднее.

( 12 )

где: – индекс i обозначает признак (значение фактора): 1£ i £ M;

– индекс j обозначает состояние объекта или класс: 1£ j £ W;

– P_ij – условная вероятность наблюдения i-го значения фактора у объектов в j-го класса;

– – безусловная вероятность наблюдения i-го значения фактора по всей выборке.

Из (12) видно, что формула Харкевича для семантической меры информации по сути является логарифмом от формулы Байеса для апостериорной вероятности (отношение условной вероятности к безусловной).

Известно, что классическая формула Шеннона для количества информации для неравновероятных событий преобразуется в формулу Хартли при условии, что события равновероятны, т.е. удовлетворяет фундаментальному принципу соответствия. Поэтому теория информации Шеннона справедливо считается обобщением теории Хартли для неравновероятных событий. Однако, выражения (11) и (12) при подстановке в них реальных численных значений вероятностей P_ij, и не дает количества информации в битах, т.е. для этого выражения не выполняется принцип соответствия, обязательный для более общих теорий. Возможно, в этом состоит причина довольно сдержанного, а иногда и скептического отношения специалистов по теории информации Шеннона к семантической теории информации Харкевича.

Причину этого мы видим в том, что в выражениях (11) и (12) отсутствуют глобальные параметры конкретной модели W и M, т.е. в том, что А. Харкевич в своем выражении для количества информации не ввел зависимости от мощности пространства будущих состояний объекта W и количества значений факторов M, обуславливающих переход объекта в эти состояния.

Поставим задачу получить такое обобщение формулы Харкевича, которое бы удовлетворяло тому же самому принципу соответствия, что и формула Шеннона, т.е. преобразовывалось в формулу Хартли в предельном детерминистском равновероятном случае, когда каждому классу (состоянию объекта) соответствует один признак (значение фактора), и каждому признаку – один класс, и эти классы (а, значит и признаки), равновероятны, и при этом каждый фактор однозначно, т.е. детерминистским образом определяет переход объекта в определенное состояние, соответствующее классу.

В детерминском случае вероятность[9] P_ij наблюдения объекта j-го класса при обнаружении у него i-го признака:

.

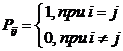Будем искать это обобщение (12) в виде:

( 13 )

Найдем такое выражение для коэффициента Y, названного нами в честь А. Харкевича "коэффициентом эмерджентности Харкевича", которое обеспечивает выполнение для выражения (13) принципа соответствия с классической формулой Хартли (1) и ее системным обобщением (2) и (3) в равновероятном детерминистском случае.

Для этого нам потребуется выразить вероятности P_ij, P_j и P_i через частоты наблюдения признаков по классам (см. табл. 1). В табл. 1 рамкой обведена область значений, переменные определены ранее.

Таблица 1 – МАТРИЦА АБСОЛЮТНЫХ ЧАСТОТ

		Классы					Сумма
		1	...	j	...	W
Значения факторов	1
	...
	i
	...
	M
Суммарное количество признаков

Алгоритм формирования матрицы абсолютных частот.

Объекты обучающей выборки описываются векторами (массивами) имеющихся у них признаков:

Первоначально в матрице абсолютных частот все значения равны нулю. Затем организуется цикл по объектам обучающей выборки. Если предъявленного объекта, относящегося к j-му классу, есть i-й признак, то:

Здесь можно провести очень интересную и важную аналогию между способом формирования матрицы абсолютных частот и работой многоканальной системы выделения полезного сигнала из шума. Представим себе, что все объекты, предъявляемые для формирования обобщенного образа некоторого класса, в действительности являются различными реализациями одного объекта – "Эйдоса" (в смысле Платона), по-разному зашумленного различными случайными обстоятельствами. И наша задача состоит в том, чтобы подавить этот шум и выделить из него то общее и существенное, что отличает объекты данного класса от объектов других классов. Учитывая, что шум чаще всего является "белым" и имеет свойство при суммировании с самим собой стремиться к нулю, а сигнал при этом, наоборот, возрастает пропорционально количеству слагаемых, то увеличение объема обучающей выборки приводит ко все лучшему отношению сигнал/шум в матрице абсолютных частот, т.е. к выделению полезной информации из шума. Примерно так мы начинаем постепенно понимать смысл фразы, которую мы сразу не расслышали по телефону и несколько раз переспрашивали. При этом в повторах шум не позволяет понять то одну, то другую часть фразы, но в конце концов за счет использования памяти и интеллектуальной обработки информации мы понимаем ее всю. Так и объекты, описанные признаками, можно рассматривать как зашумленные фразы, несущие нам информацию об обобщенных образах классов - "Эйдосах" [97, 206], к которым они относятся. И эту информацию мы выделяем из шума при синтезе модели.

Для выражения (11):

( 14 )

Для выражений (12) и (13):

( 15 )

Для выражений (11), (12) и (13):

( 16 )

В (16) использованы обозначения:

N_ij – суммарное количество наблюдений в исследуемой выборке факта: "действовало i-е значение фактора и объект перешел в j-е состояние";

– суммарное по всей выборке количество встреч различных факторов у объектов, перешедших в j-е состояние;

– суммарное количество встреч i-го фактора у всех объектов исследуемой выборки;

– суммарное количество встреч различных значений факторов у всех объектов исследуемой выборки.

Формирование матрицы условных и безусловных процентных распределений.

На основе анализа матрицы частот (табл. 1) классы можно сравнивать по наблюдаемым частотам признаков только в том случае, если количество объектов по всем классам одинаково, как и суммарное количество признаков по классам. Если же они отличаются, то корректно сравнивать классы можно только по условным и безусловным относительным частотам (оценкам вероятностей) наблюдений признаков, посчитанных на основе матрицы частот (табл. 1) в соответствии с выражениями (14) и (15), в результате чего получается матрица условных и безусловных процентных распределений (табл. 2).

При расчете матрицы оценок условных и безусловных вероятностей N_j из табл. 1 могут браться либо из предпоследней, либо из последней строки. В 1-м случае N_j представляет собой "Суммарное количество признаков у всех объектов, использованных для формирования обобщенного образа j-го класса", а во 2-м случае - это "Суммарное количество объектов обучающей выборки, использованных для формирования обобщенного образа j-го класса", соответственно получаем различные, хотя и очень сходные семантические информационные модели, которые мы называем СИМ-1 и СИМ-2. Оба этих вида моделей поддерживаются системой "Эйдос".

Таблица 2 – МАТРИЦА УСЛОВНЫХ И БЕЗУСЛОВНЫХ
ПРОЦЕНТНЫХ РАСПРЕДЕЛЕНИЙ

		Классы					Безусловная вероятность признака
		1	...	j	...	W
Значения факторов	1
	...
	i
	...
	M
Безусловная вероятность класса

Эквивалентность выражений (11) и (12) устанавливается, если подставить в них выражения относительных частот как оценок вероятностей P_ij, и через абсолютные частоты наблюдения признаков по классам из (14), (15) и (16). В обоих случаях из выражений (11) и (12) получается одно и то же выражение (17):

( 17 )

А из (13) - выражение (18), с которым мы и будем далее работать.

( 18 )

При взаимно-однозначном соответствии классов и признаков в равновероятном детерминистском случае имеем (таблица 3):

Таблица 3 – МАТРИЦА ЧАСТОТ В РАВНОВЕРОЯТНОМ ДЕТЕРМИНИСТСКОМ СЛУЧАЕ

		Классы					Сумма
		1	...	j	...	W
Значения факторов	1	1					1
	...		1				1
	i			1			1
	...				1		1
	M					1	1
Сумма		1	1	1	1	1

В этом случае к каждому классу относится один объект, имеющий единственный признак. Откуда получаем для всех i и j равенства (19):

( 19 )

Таким образом, обобщенная формула А. Харкевича (18) с учетом (19) в этом случае приобретает вид:

( 20 )

откуда:

( 21 )

или, учитывая выражение для коэффициента эмерджентности Хартли (8):

( 22 )

Подставив коэффициент эмерджентности А.Харкевича (21) в выражение (18), получим:

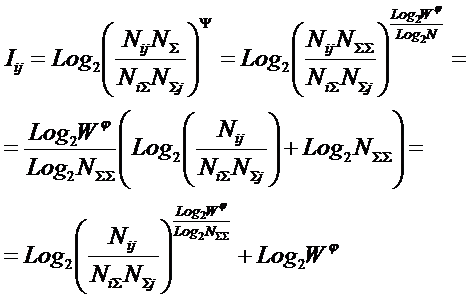
или окончательно:

( 23 )

Отметим, что 1-я задача получения системного обобщения формул Хартли и Харкевича и 2-я задача получения такого обобщения формулы Харкевича, которая удовлетворяет принципу соответствия с формулой Хартли – это две разные задачи. 1-я задача является более общей и при ее решении, которое приведено выше, автоматически решается и 2-я задача, которая является, таким образом, частным случаем 1-й.

Однако, представляет самостоятельный интерес и частный случай, в результате которого получается формула Харкевича, удовлетворяющая в равновероятном детерминистском случае принципу соответствия с классической формулой Хартли (1), а не с ее системным обобщением (2) и (3). Ясно, что эта формула получается из (23) при j=1.

( 24 )

Из выражений (21) и (22) видно, что в этом частном случае, т.е. когда система эквивалентна множеству (M=1), коэффициент эмерджентности А.Харкевича приобретает вид:

( 25 )

На практике для численных расчетов удобнее пользоваться не выражениями (23) или (24), а формулой (26), которая получается непосредственно из (18) после подстановки в него выражения (25):

( 26 )

Используя выражение (26) и данные таблицы 1 непосредственно прямым счетом получаем матрицу знаний (таблица 4):

Таблица 4 – МАТРИЦА ЗНАНИЙ (ИНФОРМАТИВНОСТЕЙ)

		Классы					Значимость фактора
		1	...	j	...	W
Значения факторов	1
	...
	i
	...
	M
Степень редукции класса

^{Здесь – это среднее количество знаний в i-м значении фактора:}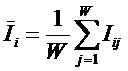

Когда количество информации Iij > 0 – i-й фактор способствует переходу объекта управления в j-е состояние, когда Iij < 0 – препятствует этому переходу, когда же Iij = 0 – никак не влияет на это. В векторе i-го фактора (строка матрицы информативностей) отображается, какое количество информации о переходе объекта управления в каждое из будущих состояний содержится в том факте, что данный фактор действует. В векторе j-го состояния класса (столбец матрицы информативностей) отображается, какое количество информации о переходе объекта управления в соответствующее состояние содержится в каждом из факторов.

Таким образом, матрица знаний (информативностей), приведенная в таблице 6, является обобщенной таблицей решений, в которой входы (факторы) и выходы (будущие состояния объекта управления) связаны друг с другом не с помощью классических (Аристотелевых) импликаций, принимающих только значения: "истина" и "ложь", а различными значениями истинности, выраженными в битах, и принимающими значения от положительного теоретически-максимально-возможного ("максимальная степень истинности"), до теоретически неограниченного отрицательного ("степень ложности"). Это позволяет автоматически формулировать прямые и опосредованные правдоподобные высказывания с расчетной степенью истинности.

Фактически предложенная модель позволяет осуществить синтез обобщенных таблиц решений для различных предметных областей непосредственно на основе эмпирических исходных данных и продуцировать прямые и обратные правдоподобные (нечеткие) логические рассуждения по неклассическим схемам с различными расчетными значениями истинности, являющимися обобщением классических импликаций.

Таким образом, данная модель позволяет рассчитать, какое количество информации содержится в любом факте о наступлении любого события в любой предметной области, причем для этого не требуется повторности этих фактов и событий. Если данные повторности осуществляются и при этом наблюдается некоторая вариабельность значений факторов, обуславливающих наступление тех или иных событий, то модель обеспечивает многопараметрическую типизацию, т.е. синтез обобщенных образов классов или категорий наступающих событий с количественной оценкой степени и знака влияния на их наступление различных значений факторов. Причем эти значения факторов могут быть как количественными, так и качественными и измеряться в любых единицах измерения, в любом случае в модели оценивается количество информации, которое в них содержится о наступлении событий, переходе объекта управления в определенные состояния или, просто, о его принадлежности к тем или иным классам. Другие способы метризации приведены в работе [277] (таблица 5):

Таблица 5 – ЧАСТНЫЕ КРИТЕРИИ ЗНАНИЙ, ИСПОЛЬЗУЕМЫЕ
В НАСТОЯЩЕЕ ВРЕМЯ В СК-АНАЛИЗЕ И СИСТЕМЕ «ЭЙДОС-Х++»

Наименование модели знаний и частный критерий	Выражение для частного критерия
	через относительные частоты	через абсолютные частоты
INF1, частный критерий: количество знаний по А.Харкевичу, 1-й вариант расчета относительных частот: – суммарное количество признаков по j-му классу. Относительная частота того, что если у объекта j-го класса обнаружен признак, то это i-й признак
INF2, частный критерий: количество знаний по А.Харкевичу, 2-й вариант расчета относительных частот: – суммарное количество объектов по j-му классу. Относительная частота того, что если предъявлен объект j-го класса, то у него будет обнаружен i-й признак.
INF3, частный критерий: Хи-квадрат: разности между фактическими и теоретически ожидаемыми абсолютными частотами	---
INF4, частный критерий: ROI - Return On Investment, 1-й вариант расчета относительных частот: – суммарное количество признаков по j-му классу[10]
INF5, частный критерий: ROI - Return On Investment, 2-й вариант расчета относительных частот: – суммарное количество объектов по j-му классу
INF6, частный критерий: разность условной и безусловной относительных частот, 1-й вариант расчета относительных частот: – суммарное количество признаков по j-му классу
INF7, частный критерий: разность условной и безусловной относительных частот, 2-й вариант расчета относительных частот: – суммарное количество объектов по j-му классу

Обозначения:

i – значение прошлого параметра;

j - значение будущего параметра;

N_ij – количество встреч j-го значения будущего параметра при i-м значении прошлого параметра;

M – суммарное число значений всех прошлых параметров;

W - суммарное число значений всех будущих параметров.

– количество встреч i-м значения прошлого параметра по всей выборке;

– количество встреч j-го значения будущего параметра по всей выборке;

– количество встреч j-го значения будущего параметра при i-м значении прошлого параметра по всей выборке.

I_ij – частный критерий знаний: количество знаний в факте наблюдения i-го значения прошлого параметра о том, что объект перейдет в состояние, соответствующее j-му значению будущего параметра;

Ψ – нормировочный коэффициент (Е.В.Луценко, 2002), преобразующий количество информации в формуле А.Харкевича в биты и обеспечивающий для нее соблюдение принципа соответствия с формулой Р.Хартли;

– безусловная относительная частота встречи i-го значения прошлого параметра в обучающей выборке;

P_ij – условная относительная частота встречи i-го значения прошлого параметра при j-м значении будущего параметра.

Все эти способы метризации с применением 7 частных критериев знаний (таблица 10) реализованы в системно-когнитивном анализе и интеллектуальной системе «Эйдос» и обеспечивают сопоставление градациям всех видов шкал числовых значений, имеющих смысл количества информации в градации о принадлежности объекта к классу. Поэтому является корректным применение интегральных критериев, включающих операции умножения и суммирования, для обработки числовых значений, соответствующих градациям шкал. Это позволяет единообразно и сопоставимо обрабатывать эмпирические данные, полученные с помощью любых типов шкал, применяя при этом все математические операции [277].

Частные критерии знаний, представленные в таблице 5, по сути, «являются формулами для преобразования абсолютных частот в количество информации и знания» (проф.В.И.Лойко, 2013). В будущем их предлагается дополнить критерием Г.Раша. Модель Г.Раша математически тесно связана с моделью логитов, предложенной в 1944 году Джозефом Берксоном (Joseph Berkson) и здесь мы ее не приводим, т.к. она подробно описана в литературе. Модель Г.Раша (с учетом ее модификаций) является чуть ли не единственной широко известной в настоящее время моделью метризации измерительных шкал.

Информационный портрет класса – это список значений факторов, ранжированных в порядке убывания силы их влияния на переход объекта управления в состояние, соответствующее данному классу. Информационный портрет класса отражает систему его детерминации. Генерация информационного портрета класса представляет собой решение обратной задачи прогнозирования, т.к. при прогнозировании по системе факторов определяется спектр наиболее вероятных будущих состояний объекта управления, в которые он может перейти под влиянием данной системы факторов, а в информационном портрете мы, наоборот, по заданному будущему состоянию объекта управления определяем систему факторов, детерминирующих это состояние, т.е. вызывающих переход объекта управления в это состояние. В начале информационного портрета класса идут факторы, оказывающие положительное влияние на переход объекта управления в заданное состояние, затем факторы, не оказывающие на это существенного влияния, и далее – факторы, препятствующие переходу объекта управления в это состояние (в порядке возрастания силы препятствования). Информационные портреты классов могут быть от отфильтрованы по диапазону факторов, т.е. мы можем отобразить влияние на переход объекта управления в данное состояние не всех отраженных в модели факторов, а только тех, коды которых попадают в определенный диапазон, например, относящиеся к определенным описательным шкалам.

Информационный (семантический) портрет фактора – это список классов, ранжированный в порядке убывания силы влияния данного фактора на переход объекта управления в состояния, соответствующие данным классам. Информационный портрет фактора называется также его семантическим портретом, т.к. в соответствии с концепцией смысла системно-когнитивного анализа, являющейся обобщением концепции смысла Шенка-Абельсона [149], смысл фактора состоит в том, какие будущие состояния объекта управления он детерминирует или обуславливает. Сначала в этом списке идут состояния объекта управления, на переход в которые данный фактор оказывает наибольшее влияние, затем состояния, на которые данный фактор не оказывает существенного влияния, и далее состояния – переходу в которые данный фактор препятствует. Информационные портреты факторов могут быть от отфильтрованы по диапазону классов, т.е. мы можем отобразить влияние данного фактора на переход объекта управления не во все возможные будущие состояния, а только в состояния, коды которых попадают в определенный диапазон, например, относящиеся к определенным классификационным шкалам.

Прямые и обратные, непосредственные и опосредованные правдоподобные логические рассуждения с расчетной степенью истинности в системной теории информации. Одним из первых ученых, поднявших и широко обсуждавшим в своих работах проблематику правдоподобных рассуждений, был известный венгерский, швейцарский и американский математик Дьердь Пойа[11], книги которого одному из авторов (тому, который потом стал профессором Е.В.Луценко) подарил еще в школе его учитель математики Михаил Ильич Перевалов (см. также раздел «Формализация логики правдоподобных рассуждений Д. Пойа», глава третья, параграф 7, с.158-163, исходящий из (репрезентативной) теории измерений).

В работе [97] предложена логическая форма представления правдоподобных логических рассуждений с расчетной степенью истинности, которая определяется в соответствии с системной теорией информацией непосредственно на основе эмпирических данных.

В качестве количественной меры влияния факторов, предложено использовать обобщенную формулу А.Харкевича, полученную на основе предложенной эмерджентной теории информации. При этом непосредственно из матрицы абсолютных частот рассчитывается база знаний (табл.1), которая и представляет собой основу содержательной информационной модели предметной области.

Весовые коэффициенты табл.1 непосредственно определяют, какое количество информации Iij система управления получает о наступлении события: "активный объект управления перейдет в j–е состояние", из сообщения: "на активный объект управления действует i–й фактор".

Принципиально важно, что эти весовые коэффициенты не определяются экспертами неформализуемым способом на основе интуиции и профессиональной компетенции (т.е., мягко говоря, «на глазок»), а рассчитываются непосредственно на основе эмпирических данных и удовлетворяют всем ранее обоснованным в работе [97] требованиям, т.е. являются сопоставимыми, содержательно интерпретируемыми, отражают понятия "достижение цели управления" и "мощность множества будущих состояний объекта управления" и т.д.

В [97] обосновано, что предложенная информационная мера обеспечивает сопоставимость индивидуальных количеств информации, содержащейся в факторах о классах, а также сопоставимость интегральных критериев, рассчитанных для одного объекта и разных классов, для разных объектов и разных классов.

Когда количество информации Iij>0 – i–й фактор способствует переходу объекта управления в j–е состояние, когда Iij<0 – препятствует этому переходу, когда же Iij=0 – никак не влияет на это. В векторе i–го фактора (строка матрицы информативностей) отображается, какое количество информации о переходе объекта управления в каждое из будущих состояний содержится в том факте, что данный фактор действует. В векторе j–го состояния класса (столбец матрицы информативностей) отображается, какое количество информации о переходе объекта управления в соответствующее состояние содержится в каждом из факторов.

Таким образом, матрица информативностей (табл.1) является обобщенной таблицей решений, в которой входы (факторы) и выходы (будущие состояния активного объекта управления (АОУ) связаны друг с другом не с помощью классических (Аристотелевских) импликаций, принимающих только значения: "Итина" и "Ложь", а различными значениями истинности, выраженными в битах и принимающими значения от положительного теоретически-максимально-возможного ("Максимальная степень истинности"), до теоретически неограниченного отрицательного ("Степень ложности").

Фактически предложенная модель позволяет осуществить синтез обобщенных таблиц решений для различных предметных областей непосредственно на основе эмпирических исходных данных и продуцировать на их основе прямые и обратные правдоподобные (нечеткие) логические рассуждения по неклассическим схемам с различными расчетными значениями истинности, являющимся обобщением классических импликаций (табл.5):

Таблица 5 – Прямые и обратные правдоподобные логические высказывания с расчетной в соответствии с системной теорией информации (СТИ) степенью истинности импликаций

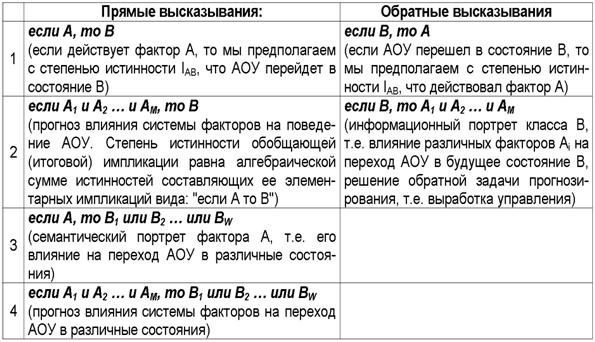
Приведем пример более сложного высказывания, которое может быть рассчитано непосредственно на основе матрицы информативностей – обобщенной таблицы решений (таблица 2):

Если A, со степенью истинности a(A,B), детерминирует B, и если С, со степенью истинности a(C,D), детерминирует D, и A совпадает по смыслу с C со степенью истинности a(A,C), то это вносит вклад в совпадение B с D, равный степени истинности a(B,D).

При этом в прямых рассуждениях как предпосылки рассматриваются факторы, а как заключение – будущие состояния АОУ, а в обратных – наоборот: как предпосылки – будущие состояния АОУ, а как заключение – факторы. Степень истинности i-й предпосылки – это просто количество информации Iij, содержащейся в ней о наступлении j-го будущего состояния АОУ. Если предпосылок несколько, то степень истинности наступления j-го состояния АОУ равна суммарному количеству информации, содержащемуся в них об этом. Количество информации в i-м факторе о наступлении j-го состояния АОУ, рассчитывается в соответствии с выражениями системной теории информации (СТИ).

Прямые правдоподобные логические рассуждения позволяют прогнозировать степень достоверности наступления события по действующим факторам, а обратные – по заданному состоянию восстановить степень необходимости и степень нежелательности каждого фактора для наступления этого состояния, т.е. принимать решение по выбору управляющих воздействий на АОУ, оптимальных для перевода его в заданное целевое состояние.

Приведем простой пример, когда безупречная классическая бинарная логика Аристотеля дает сбой. Рассмотрим высказывания:

А) если студент хорошо сдал экзамен по информационным системам, значит, он умеет хорошо программировать;

Б) если студент умеет хорошо программировать, то он может стать специалистом в области прикладной информатики.

Откуда средами логики предикатов получаем вывод:

В) если студент хорошо сдал экзамен по информационным системам, то он может стать специалистом в области прикладной информатики.

Если при рассмотрении каждого высказывания «А» и «Б» по отдельности у нас не возникает особых возражений, хотя мы сразу чувствуем здесь какой-то подвох, что это не совсем так или не всегда так и легко можем привести вполне реальные примеры, когда эти высказывания могут быть и ложными. то высказывание «В» уже само по себе выглядит очень сомнительным, т.е. проще говоря ложным, тогда как в логике предикатов оно является истинным. Интуитивно мы хорошо понимаем, почему так получается. Дело в том, что в этих высказываниях не отражен контент, т.е. та огромная слабо формализованная и вообще неформализованная информация об объекте моделирования, которой располагает человек, но не располагает логическая система. Например, в этих двух логических высказываниях не отражена информация, которой располагает каждый преподаватель и студент, о том, каким образом иногда сдаются экзамены, когда оценка вообще никак не зависит от знаний. Иначе говоря, чтобы эти высказывания были истинны необходимо, чтобы оценка определялась только знаниями. Но и этого мало. Предполагается, что факт получения хорошей оценки по дисциплине означает полное ее освоение, хотя все понимают, что для этого достаточно освоения только тех вопросов, которые были в билете и были заданы преподавателем.

При решении этой же задачи средами АСК-анализа мы формулируем эти высказывания в форме правдоподобных рассуждений:

А) если студент хорошо сдал экзамен по информационным системам, то в этом факте содержится I(A) информации о том, что он умеет хорошо программировать;

Б) если студент умеет хорошо программировать, то в этом факте содержится I(Б) информации о том он может стать специалистом в области прикладной информатики.

Откуда средами АСК-анализа получаем результирующее высказывание:

В) если студент хорошо сдал экзамен по информационным системам, то в этом факте содержится I(В) информации о том он может стать специалистом в области прикладной информатики.

Это высказывание не выглядит как истинное или ложное и может быть и истинным, и ложным, причем в различной степени, в зависимости от знака и модуля расчетной его степени истинности I(В). Для расчета этой величины нужны конкретные эмпирические данные, являющиеся репрезентативными для отражения определенной предметной области (генеральной совокупности), в которой этот вывод и будет иметь эти значения знака и величины степени истинности.

Необходимо отметить, что предложенная модель, основывающаяся на теории информации, обеспечивает автоматизированное формирования системы нечетких правил по содержимому входных данных, как и комбинация нечеткой логики Заде-Коско с нейронными сетями Кохонена. Принципиально важно, что качественное изменение модели путем добавления в нее новых классов не уменьшает достоверности распознавания уже сформированных классов. Кроме того, при сравнении распознаваемого объекта с каждым классом учитываются не только признаки, имеющиеся у объекта, но и отсутствующие у него, поэтому предложенной моделью правильно идентифицируются объекты, признаки которых образуют множества, одно из которых является подмножеством другого (как и в Неокогнитроне К.Фукушимы).

ГЛАВА 10. ИНФОРМАЦИОННЫЕ МЕРЫ
УРОВНЯ СИСТЕМНОСТИ – КОЭФФИЦИЕНТЫ ЭМЕРДЖЕНТНОСТИ, ВЫТЕКАЮЩИЕ ИЗ СИСТЕМНОЙ ТЕОРИИ ИНФОРМАЦИИ

Дальнейшее изложение основано на рабатах [98, 170, 270, 240, 241]. В работе [97] и работе [170] предлагаются теоретически обоснованные количественные меры, следующие из системной теории информации (СТИ), которые позволяют количественно оценивать влияние факторов на системы различной природы не по силе и направлению изменения состояния системы, а по степени возрастания или уменьшения ее эмерджентности (уровня системности) и степени детерминированности.

В работе [253] на простом численном примере рассматривается применение автоматизированного системно-когнитивного анализа (АСК-анализ) и его программного инструментария – интеллектуальной системы «Эйдос» для выявления и исследования детерминации эмерджентных макросвойств систем их составом и иерархической структурой, т.е. подсистемами различной сложности (уровней иерархии). Кратко обсуждаются некоторые методологические вопросы создания и применения формальных моделей в научном познании. Предложены системное обобщение принципа Уильяма Росса Эшби о необходимом разнообразии на основе системного обобщения теории множеств и системной теории информации, обобщенная формулировка принципа относительности Галилея-Эйнштейна, высказана гипотеза о его взаимосвязи с теоремой Эмми Нётер, а также предложена гипотеза «О зависимости силы и направления связей между базовыми элементами системы и ее эмерджентными свойствами в целом от уровня иерархии в системе»

В [270] предложены коэффициенты эмерджентности, применимые для систем, подчиняющихся классической или квантовой статистике. Дан алгоритм оценки уровня системности квантовых объектов. Рассмотрены квантовые системы, подчиняющиеся статистике Ферми-Дирака и Бозе-Эйнштейна, а также классические системы, подчиняющиеся статистике Максвелла-Больцмана. Установлено, что коэффициенты эмерджентности квантовых и классических систем отличаются между собой, как и коэффициенты квантовых систем ферми-частиц и бозе-частиц. Следовательно, коэффициент эмерджентности позволяет отличить классическую систему от квантовой системы, а квантовую систему ферми-частиц от квантовой системы бозе-частиц. Установлено также, что предложенные ранее в ряде работ, начиная с [97], различные варианты коэффициентов эмерджентности Хартли распространяются только на системы, подчиняющиеся статистике Ферми-Дирака.

Рассмотрим результаты этих работ подробнее.

10.1. Количественные меры возрастания эмерджентности в процессе эволюции систем (в рамках системной теории информации)

Дальнейшее изложение основано на рабате [170], нумерация формул, рисунков и таблиц сохранены.

Одного взгляда на Вселенную на всех ее структурных уровнях организации, начиная с микромира с его квантами, элементарными частицами и атомами и до макро- и мега масштабов, достаточно, чтобы убедиться, что Вселенная глубоко структурирована и состоит из глобально и нелокально взаимосвязанных систем различного масштаба, все свойства которых имеют эмерджентную природу, и во Вселенной ни на одном из уровней ее организации не наблюдается ничего похожего на унылую картину "Тепловой смерти". Сегодня уже совершенно очевидно, что закон возрастания энтропии (2-е начало термодинамики) является сильнейшей абстракцией и по сути во всей Вселенной нет ни одной системы, которая ему бы абсолютно точно и в полной мере соответствовала, т.к. не существует полностью изолированных от окружающей среды систем (адиабатически замкнутых систем, т.е. систем, энергетически не взаимодействующих со средой). Более того, если бы такие системы и существовали, то мы бы об этом никогда в принципе не узнали бы, т.к. не получили бы о них никакой информации, поэтому можно сказать еще и иначе: такие системы скорее относятся не к области бытия, а к области небытия.

Но для существования любой системы или подсистемы необходим системобразующий фактор и, естественно, возникает вопрос о том, что же является глобальным и нелокальным системообразующим фактором, общим для всех систем.

Это вопрос необычайной важности, так как именно этот фактор противодействует возрастанию энтропии на всех уровнях организации систем во Вселенной. Без действия этого фактора, т.е. если бы закон возрастания энтропии действительно был всеобщим законом природы, каковым его хотели некогда представить те самые французские академики, которые заодно запретили и существование метеоритов, то Вселенная была бы совершенно однородна (хаос или небытие, "Тепловая смерть") и об этом бы вообще некому и негде было бы рассуждать.

Из термодинамических представлений ясно, что этот глобальный нелокальный антиэнтропийный системообразующий фактор может быть отожествлен с некоторым источником энергии или информации, которые как известно взаимосвязаны в любой конкретной системе через ее энтропию. Каждая система во Вселенной (пока она существует) должна иметь прямой и непосредственный контакт с этим фактором и как только этот контакт прекращается – система распадается на подсистемы или элементы. Поэтому этот фактор должен быть не внешним, а внутренним по отношению к системам, а также обладать глобальностью и нелокальностью, возможно даже не только в пространстве, но и во времени (на эти мысли наталкивает анализ возможных механизмов принципа наименьшего действия, траекторной формулировки и опережающих потенциалов в КТП). Физической основой этого фактора может быть квантовое единство, которое существует с момента возникновения самого метрического пространства-времени еще с единого квантового состояния Вселенной-в-Целом до Большого Взрыва, с которого и начался процесс последовательной иерархической дифференциации. Сам физический механизм нелокального взаимодействия дифференцированной структуры системы с ее единой сущностью может быть аналогичным тому, который был предвосхищен А.Эйнштейном в известном парадоксе ЭПР.

Если этот фактор научиться сознательно использовать, то возможно будут решены энергетические и другие связанные с ними проблемы.

Таким образом на наш взгляд этот глобальный и нелокальный системообразующий фактор – это энергия и информация идущие к каждой системе из неизменной нелокальной сущности Вселенной, из того его состояния, которое оставаясь неизменным породило всю эту дифференцированную Вселенную, это состояние, которое есть лишенное частей единство в сущности каждой системы. Это не какое-либо место или время – это наиболее фундаментальный структурный уровень организации Вселенной – лишенная всех качеств основа всех качеств (предполагается, что все качества эмерджентны по своей природе). Возможно после Большого Взрыва Вселенная стала дифференцированной лишь по своей форме не изменяясь в своей единой и неделимой сущности, т.е. не переставая быть единой без частей ... и это непроявленное состояние есть ни что иное как неделимая сущность каждой системы и подсистемы во Вселенной ... причем она одна и та же у всех систем и внутри осознается как Сущность субъективности, а во вне – как сущность материи...

Похоже Никола Тесла был не просто гениальным ученым, инженером и изобретателем, а скорее Пророком технической эры, который понял с точки зрения физики что такое этот глобальный нелокальный системообразующий фактор и научился осознанно включать в его состав своих технических систем. До этого нечто подобное удавалось только музыкантам, художникам, скульпторам и архитекторам, а теперь похоже приближается время и программистов, прежде всего специалистов по системам искусственного интеллекта, виртуальной реальности и моделированию эволюции.

Итак, в самом общем виде существование систем во Вселенной можно объяснить тем, что существует некий гипотетический фактор, успешно противодействующий возрастанию энтропии на всех уровнях организации систем во Вселенной. Но что это за фактор и как влияют его свойства на характеристики систем? Попробуем конкретизировать ответы на эти вопросы.

Из общепринятого представления о том, что количество информации может быть измерено величиной уменьшения энтропии следует гипотеза о том, что этот антиэнтропийный системообразующий фактор представляет собой некий источник информации. Этот источник информации, обеспечивающий возникновение и существование системы, может локализоваться как внутри, так и вне ее, но реально осуществляется смешанный вариант.

В этом процессе формирования и развития системы под влиянием как внутренних, так и внешних информационных по своему существу факторов она претерпевает количественные и качественные изменения, т.е. проходит точки бифуркации и детерминистские участки траектории [97], в частности изменяются такие фундаментальные характеристики системы, как ее уровень системности и степень детерминированности.

Учитывая информационный характер антиэнтропийного системообразующего фактора предлагается применить теорию информации для количественной оценки этих фундаментальных характеристик систем.

Однако классическая теория информации не совсем подходит для этой цели, т.к. она основана на теории множеств, а не на теории систем. В работе [186] предлагается программная идея системного обобщения понятий математики, в частности понятий теории информации, основанных на теории множеств, путем замены понятия множества на более содержательное понятие системы. Частично эта идея была реализована в работе [97] при разработке автоматизированного системно-когнитивного анализа (АСК-анализа), математическая модель которого основана на системном обобщении формул для количества информации Хартли и Харкевича в рамках предложенной системной теории информации (СТИ).

Система представляет собой множество элементов, объединенных в целое за счет взаимодействия элементов друг с другом, т.е. за счет отношений между ними, и обеспечивает преимущества в достижении целей. Преимущества в достижении целей обеспечиваются за счет системного эффекта. Системный эффект состоит в том, что свойства системы не сводятся к сумме свойств ее элементов, т.е. система как целое обладает рядом новых, т.е. эмерджентных свойств, которых не было у ее элементов. Предполагается, что во Вселенной не существует элементов не являющихся системами. Таким образом все свойства любых систем в конечном счете являются эмерджентными. Уровень системности тем выше, чем выше интенсивность взаимодействия элементов системы друг с другом, чем сильнее отличаются свойства системы от свойств входящих в нее элементов, т.е. чем выше системный эффект, чем значительнее отличается система от множества.

Таким образом, система обеспечивает тем большие преимущества в достижении целей, чем выше ее уровень системности. В частности, система с нулевым уровнем системности вообще ничем не отличается от множества образующих ее элементов, т.е. тождественна этому множеству и никаких преимуществ в достижении целей не обеспечивает. Этим самым достигается выполнение принципа соответствия между понятиями системы и множества. Из соблюдения этого принципа для понятий множества и системы следует и его соблюдение для понятий системной теории информации, основанных на теории множеств и их системных обобщений.

На этой основе можно ввести и новое научное понятие: понятие "антисистемы", применение которого оправдано в случаях, когда централизация (монополизация, интеграция) не только не дает положительного эффекта, но даже сказывается отрицательно.

Антиподсистемой будем называть подсистему, включение которой в некоторую систему уменьшает ее уровень системности, т.е. это такое объедение некоторого множества элементов за счет их взаимодействия в целое, которое препятствует достижению целей системы в целом.

Фундаментом современной математики является теория множеств. Эта теория лежит и в основе самого глубокого на сегодняшний день обоснования таких базовых математических понятий, как "число" и "функция". Определенный период этот фундамент казался незыблемым. Однако вскоре работы целой плеяды выдающихся ученых XX века, прежде всего Давида Гильберта, Бертрана Рассела и Курта Гёделя, со всей очевидностью обнажили фундаментальные логические и лингвистические проблемы, в частности проявляющиеся в форме парадоксов теории множеств, что, в свою очередь, привело к появлению ряда развернутых предложений по пересмотру самых глубоких оснований математики.

В задачи данной работы не входит рассмотрение этой интереснейшей проблематики, а также истории возникновения и развития понятий числа и функции. Отметим лишь, что кроме рассмотренных в литературе вариантов существует возможность обобщения всех понятий математики, базирующихся на теории множеств, в частности теории информации, путем тотальной замены понятия множества на более общее понятие системы и тщательного отслеживания всех последствий этой замены. Это утверждение будем называть "программной идеей системного обобщения понятий математики".

Строго говоря, реализация данной программной идеи потребует прежде всего системного обобщения самой теории множеств и преобразования ее в математическую теорию систем, которая будет плавно переходить в современную теорию множеств при уровне системности, стремящемся к нулю. При этом необходимо заметить, что существующая в настоящее время наука под названием "Теория систем" ни в коей мере не является обобщением математической теории множеств, и ее не следует путать с математической теорией систем. Вместе с тем, на наш взгляд, существуют некоторые возможности обобщения ряда понятий математики и без разработки математической теории систем. К таким понятиям относятся прежде всего понятия "информация" и "функция".

Системному обобщению понятия информации посвящены работы автора [97] и др., поэтому здесь на этом вопросе мы останавливаться не будем. Отметим лишь, что на основе предложенной системной теории информации (СТИ) были разработаны математическая модель и методика численных расчетов (структуры данных и алгоритмы), а также специальный программный инструментарий (система "Эйдос") системно-когнитивного анализа (СК-анализ), который представляет собой системный анализ, автоматизированный путем его рассмотрения как метода познания и структурирования по базовым когнитивным операциям.

В СК-анализе теоретически обоснована и реализована на практике в форме конкретной информационной технологии процедура установления новой универсальной, сопоставимой в пространстве и времени, ранее не используемой количественной, т.е. выражаемой числами, меры соответствия между событиями или явлениями любого рода, получившей название "системная мера целесообразности информации", которая по существу является количественной мерой знаний [245]. Это является достаточным основанием для того, чтобы называть эту форму системного анализа системно-когнитивным анализом, от английского слова "cognition" – "познание".

В результате получены следующие выражения для системных обобщений формул для количества информации Хартли и Харкевича и плотности информации Шеннона,

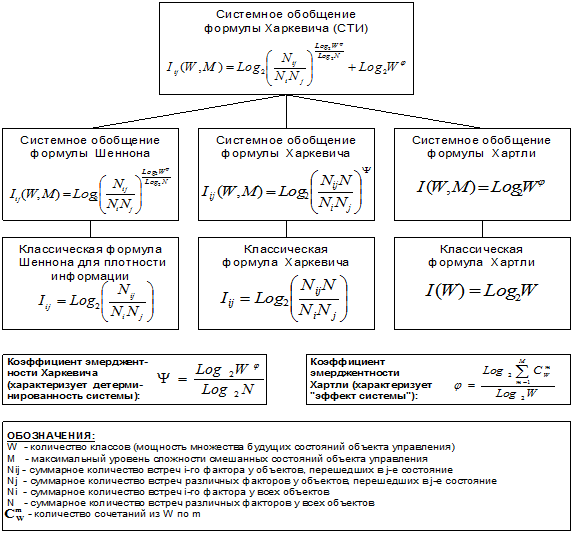
а также гипотезы о законе возрастания эмерджентности и аналитические выражения для коэффициентов Хартли и Харкевича, которые являются научно обоснованными в рамках системной теории информации (СТИ) количественными мерами уровня системности и степени детерминированности систем (рис. 1-2).

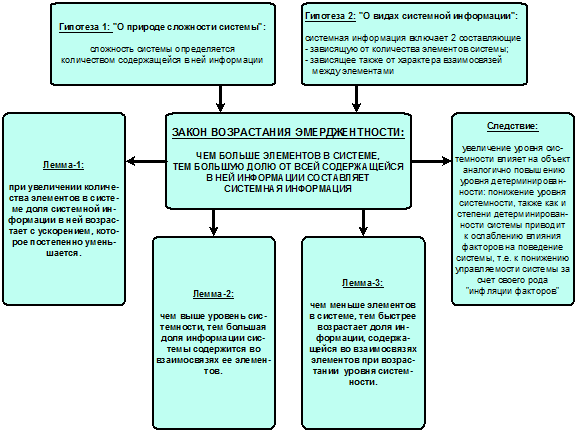
Рисунок 1. Гипотеза о законе возрастания эмерджентности

Рисунок 2. Интерпретация коэффициентов эмерджентности СТИ

Резюмируя рисунки 1 и 2, можно сказать, что в процессе эволюции систем есть по крайней мере два этапа:

– на 1-м этапе идет экстенсивный рост системы путем увеличения количества ее элементов; при этом объем информации в системе возрастает в основном за счет увеличения размера системы и количества элементов в ней;

– на 2-м этапе идет система развивается интенсивно за счет усложнения взаимосвязей между элементами и своей структуры; при этом объем информации в системе возрастает в основном за счет ее усложнения, т.е. повышения уровня системности или эмерджентности системы.

Так, например, управлять толпой из 729 человек значительно сложнее, чем воздушно-десантным полком той же численности. Процесс превращения 729 новобранцев в воздушно-десантный полк это и есть процесс повышения уровня системности и степени детерминированности системы. Этот процесс включает процесс последовательного иерархического структурирования (на отделения, взвода, роты, батальоны), а также процесс повышения степени детерминированности команд путем повышения дисциплины их исполнения путем соответствующих организующих воздействий. Эффективность этих организующих воздействий мы и предлагаем оценивать по изменению уровня системности и степени детерминированности с помощью коэффициентов эмерджентности, названных нами [97] в честь выдающихся ученых, внесших огромный вклад в создание теории информации Хартли и Харкевича.

Рассмотрим численный пример.

В работе [100] в разделе: "1.2.2.2.3. Конструирование системной численной меры на основе базовой", подразделе: "Системное обобщение формулы Хартли для количества информации", который размещен по адресу: http://lc.kubagro.ru/aidos/aidos06_lec/lec_04.htm приведено выражение для коэффициента эмерджентности Хартли (1):

(1)

где:

W – количество элементов в системе альтернативных будущих состояний АОУ (количество чистых состояний);

m – сложность подсистемы (количество элементов 1-го уровня иерархии в подсистеме);

M – максимальная сложность подсистем (количество элементов 1-го уровня иерархии в системе).

Непосредственно из вида выражения для коэффициента эмерджентности Хартли (1) ясно, что он представляет собой относительное превышение количества информации о системе при учете системных эффектов (смешанных состояний, иерархической структуры ее подсистем и т.п.) над количеством информации без учета системности, т.е. этот коэффициент отражает уровень системности объекта.

Необходимо отметить, что сходное выражение было предложено видным исследователем в области информационной теории систем А.А.Денисовым еще в 80-х годах[12], однако свое теоретическое обоснование это выражение получило лишь в рамках СТИ. Очень близкие идеи развиваются также в фундаментальных работах[13] (см., например, раздел: "2.6. Эволюционная динамика и эмерджентность" в работе Попова В.П.).

Первое слагаемое в выражении (1) дает количество информации по классической формуле Хартли, а остальные слагаемые – дополнительное количество информации, получаемое за счет системного эффекта, т.е. за счет наличия у системы иерархической структуры или смешанных состояний. По сути дела эта дополнительная информация является информацией об иерархической структуре системы, как состоящей из ряда подсистем различных уровней сложности.

Однако реально в любой системе осуществляются не все формально возможные сочетания элементов 1-го уровня иерархии, т.к. существуют различные правила запрета, различные для разных систем. Это означает, что возможно множество различных систем, состоящих из одинакового количества тождественных элементов, и отличающихся своей структурой, т.е. строением подсистем различных иерархических уровней. Эти различия систем как раз и возникают благодаря различию действующих для них этих правил запрета. По этой причине систему правил запрета предлагается назвать информационным проектом системы. Различные системы, состоящие из равного количества одинаковых элементов (например, дома, состоящие из 20000 кирпичей), отличаются друг от друга именно по причине различия своих информационных проектов.

Из статистики известно, что при M=W:

(2)

в этом случае для выражения (1) получаем:

(3)

Выражение (3) дает оценку максимального количества информации, которое может содержаться в элементе системы с учетом его вхождения в различные подсистемы ее структуры. Из этого выражения видно, что I быстро стремится к W при увеличении W:

(4)

В действительности уже при W>4 погрешность выражения (4) не превышает 1%, поэтому на практике в большинстве случаев при оценке величины теоретически максимально-возможного значения уровня системности не будет большой ошибкой вместо суммы числа сочетаний использовать просто W.

Таким образом, коэффициент эмерджентности Хартли отражает уровень системности объекта и изменяется от 1 (системность минимальна, т.е. отсутствует) до величины W/Log₂W (системность максимальна). Очевидно, для каждого количества элементов системы существует свой максимальный уровень системности, который никогда реально не достигается из-за действия правил запрета на реализацию в системе ряда подсистем различных уровней иерархии.

Будем считать, что полк является системой, имеющей иерархическую структуру (такие системы являются наиболее распространенными).

Если в толпе из 729 (или любого другого количества W) новобранцев (элементов 1-го уровня иерархии) нет ни одного командира, то ее уровень системности согласно выражения (1) равен 1:

(5)

Если в полку появляется командир полка, непосредственно (напрямую) дающий указания каждому из солдат (что вообще-то достаточно проблематично реализовать на практике), то появляется еще 729 дополнительных элементов 2-го уровня иерархии вида: "Командир полка + N-й солдат". В этом случае выражение (1) примет вид (6):

(6)

Но в реальном полку используется не двухуровневая, а многоуровневая иерархическая система управления, т.к. командир полка и любой другой командир из-за информационных, пространственных и временных ограничений реально может отдать конкретный детализированный приказ только очень ограниченному количеству нижестоящих командиров – системообразующих элементов следующего уровня иерархии. Рассмотрим структуру условного полка, приведенную на рисунке 3.

Рисунок 3. Иерархическая система управления полком (условно)

Проведем расчет уровня системности полка, иерархическая структура которого приведена на рисунке 3 с использованием формулы (1). При этом обращаем внимание на то обстоятельство, что приведенная иерархическая структура близка к фрактальной. По-видимому это не случайно, т.к. является одной из наиболее рациональных схем управления.

1-й уровень иерархии: 729 солдат. Уровень системности полка на 1-м уровне иерархии, как мы уже видели из формулы (5) равна 1.

2-й уровень иерархии: 81 отделение по 9 солдат в каждом. Добавление командиров отделений порождает в каждом из 81 отделений 9 элементов вида: "Командир i-го отделения + j-й солдат". Уровень системности полка на первых двух уровнях вычисляется по формуле (7):

(7)

Здесь необходимо отметить, что структурный элемент "отделение", как и подсистемы других уровней иерархии, рассматривается не как неделимые элементы, а именно как подсистемы, сами имеющие определенный уровень системности, определяемый их структурой. Возможны и другие подходы, рассматривающие подсистемы как элементы без учета их внутренней структуры, т.е. не учитывающие различное в общем случае содержание подсистем, но в данной работе они не рассматриваются. Вместе с тем приведенные выше аналитические выражения для коэффициентов эмерджентности имеют общий характер и применимы и в этом случае.

3-й уровень иерархии: 27 взводов по 3 отделения в каждом. Добавление командиров взводов порождает в каждом из 27 взводов по 3 элемента вида: "Командир i-го взвода + командир j-го отделения". Уровень системности полка на первых трех уровнях вычисляется по формуле (8):

(8)

4-й уровень иерархии: 9 рот по 3 взвода в каждой. Добавление командиров рот порождает в каждой из 9 рот по 3 элемента вида: "Командир i-й роты + командир j-го взвода".

(9)

5-й уровень иерархии: 3 батальона по 3 роты в каждом. Добавление командиров батальонов порождает в каждом из 3 батальонов по 3 элемента вида: "Командир i-го батальона + командир j-й роты".

(10)

6-й уровень иерархии: 1 командир полка. Добавление командира полка порождает 3 элемента вида: "Командир полка + командир j-го батальона".

(11)

В сводном виде эти данные приведены в таблице и на рисунке 4.

СВОДНЫЕ ДАННЫЕ О ВКЛАДЕ РАЗЛИЧНЫХ УРОВНЕЙ ИЕРАРХИИ СИСТЕМЫ УПРАВЛЕНИЯ В ОБЩИЙ УРОВЕНЬ СИСТЕМНОСТИ

	729 солдат	81 отде- ление	27 взво- дов	9 рот	3 бата- льона	1 полк		Уровень системности
	1-й ур.	2-й ур.	3-й ур.	4-й ур.	5-й ур.	6-й ур.	Всего:
Командир полка командует солдатами "на прямую"	729					729	1458	1,10515
1-й ур. толпа новобранцев)	729						729	1,00000
2-й ур.	729	81*9					1458	1,10515
3-й ур.	729	81*9	27*3				1539	1,11336
4-й ур.	729	81*9	27*3	9*3			1566	1,11600
5-й ур.	729	81*9	27*3	9*3	3*3		1575	1,11687
6-й ур.	729	81*9	27*3	9*3	3*3	1*3	1578	1,11715
Максимальный теоретически возможный уровень системности	729							76,65797

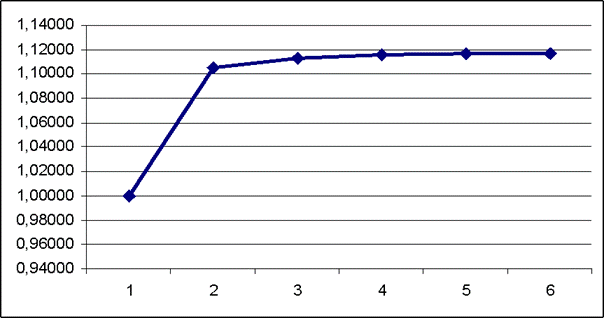
Рисунок 4. Зависимость эмерджентности системы от появления в ней
новых все более высоких иерархических уровней управления

Если проанализировать приведенную таблицу, рисунок 2, на котором показана динамика эмерджентности и выражения (6) – (11), то сразу бросается в глаза, что создание иерархической системы управления полком приводит к добавлению в систему значительно большего количества элементов, чем при реализации двухуровневого управления командиром полка напрямую каждым солдатом, если бы такое было возможно на практике. Соответственно это приводит к гораздо более значительному повышению уровня системности полка и более выраженному системному эффекту (эмерджентности), выражающемуся в том, что полк с иерархической структурой управления значительно более боеспособен и живуч, чем с одноуровневой. Видно, что добавление в систему новых все более высоких иерархических уровней управления приводит ко все меньшему увеличению системного эффекта (эмерджентности), т.е. в основном в этом смысле играет роль появление 1-го уровня иерархии (отделений, в нашем примере).

Кроме того из рассмотренных примеров можно сделать вывод о зависимости степени живучести системы в целом от степени ее иерархичности при нарушении системы управления: чем выше степень иерархичности системы управления, тем в меньшей степени ее нарушение изменяет уровень системности и тем более живуча система в целом в случае нарушения ее системы управления. Это можно объяснить наличием системообразующих факторов на различных уровнях организации системы (в нашем примере это командиры батальонов, рот, взводов и отделений). В частности при невозможности для командира полка выполнять свои функции по состоянию здоровья:

– в гипотетическом случае, когда он управлял каждым солдатом непосредственно полк бы сразу превратился из единого слаженного организма в дезорганизованную толпу, в которой каждый сражается сам за себя;

– в случае приведенной 6-уровневой иерархической системы управления полк исчез бы как единое целое, но продолжал бы достаточно эффективно сражаться в составе организованных отдельных батальонов, сохраняющих полную управляемость и боеспособность.

Но теоретически максимальный уровень системности нашего условного полка с 729 солдатами составляет: 729/Log₂729=76,65797. Можно предположить, что этот огромный уровень системности мог бы быть обеспечен, если бы весь полк состоял сплошь из одних джедаев, свободно непрерывно телепатически общающихся друг с другом и действующих как единое целое, т.е. практически как одно практически непобедимое существо (если даже с одним таким воином очень проблематично справиться, то можно себе представить какую силу представляет высокоорганизованная группа из 729 воинов без слов мгновенно и полностью понимающих друг друга независимо от того, где и в какой ситуации каждый из них находится).

Здесь необходимо отметить также известное положение из теории информации Шеннона состоящее в том, что энтропия системы тем меньше, чем больше взаимная информация в ее подсистемах друг о друге. В биологических системах до определенного иерархического уровня их организации (клетки) в каждой подсистеме вообще имеется полная информация о всей системе в целом (геном). Это обеспечивает слаженную работу различных подсистем организма и сводит к минимуму потребность в обмене информацией между ними.

Однако добавление новой подсистемы в состав организационной системы не всегда приводит к повышению ее уровня системности, как казалось бы можно было ожидать. Если продолжить пример с полком, то это соответствует случаю внедрения в полк вражеского разведчика или просто лишнего управленческого звена, которое не вносит в систему управления ничего нового и ценного, а лишь дублирует команды, и хорошо еще если делает это своевременно и без их искажения, а иногда и просто блокирует прохождение команд на исполнение. Именно о подобных случаях говорят: "Начальник уехал в служебную командировку и работа подразделения неожиданно стабилизировалась, наладилась, сотрудников перестало лихорадить". В организациях уровень системности может понижаться при неоправданном разбухании административного аппарата.

В технической системе при ее повреждении также уменьшается количество исправных функциональных элементов, а также узлов и подсистем, в результате чего уменьшается уровень системности и степень детерминированности, т.е. управляемости системы.

В этой связи предлагается специально различать управляющие воздействия, целью которых является перевод объекта управления в заранее заданное целевое состояние без изменения его уровня системности и степени детерминированности, т.е. использование объекта управления, и управляющие воздействия направленные на повышение самого уровня системности и степени детерминированности объекта управления, т.е. организующие управляющие воздействия, направленные на создание и развитие объекта управления.

Если в первом случае управляющие факторы можно оценивать по силе и направлению их влияния на объект управления, то во втором случае – по величине и направлению изменения уровня системности и степени детерминированности, которые можно количественно измерять с помощью предложенных выражений системной теории информации для коэффициентов эмерджентности Хартли и Харкевича, названных так в работе [97] в честь этих выдающихся ученых.

10.2. Исследование влияния подсистем различных уровней иерархии на эмерджентные свойства системы в целом с применением АСК-анализа и интеллектуальной системы "Эйдос" (микроструктура системы как фактор управления ее макросвойствами)

“Истинное знание – это знание причин”

Френсис Бэкон (1561–1626 гг.)

Дальнейшее изложение основано на рабате [253], нумерация формул, рисунков и таблиц сохранены.

Проблема, решаемая в научных исследованиях, состоит в выявлении силы и направления влияния состава и особенностей внутренней иерархической микроструктуры структуры систем на их внешне наблюдаемые на макроуровне свойства, т.е. по сути, в выявлении и исследовании вида причинно-следственных зависимостей между составом, внутренней структурой и эмерджентными свойствами систем.

Другой формой этой же проблемы является построение на основе эмпирических данных[14] формальной модели, количественно отражающей силу и направление влияния значений факторов на поведение моделируемого объекта, в частности на его переход в различные будущие состояния.

Такая формальная модель обеспечивает решение ряда как прямых, так и обратных задач.

Прямые задачи (задачи идентификации, распознавания и прогнозирования):

1. Прогнозирование свойств системы по ее составу и структуре.

2. Идентификация состояния системы по ее признакам.

3. Прогнозирование будущих состояний объекта управления по системе действующих на него значений факторов.

Задачи управления (обратные задачи прогнозирования):

4. Определение такого состава и такой структуры системы, которые обусловливают заранее заданные ее свойства.

5. Определение такой системы значений управляющих факторов, которая переводит объект управления в заранее заданное целевое состояние.

Идентификация и распознавание – это просто синонимы. При идентификации считается, что признаки объекта и его состояние, которое нужно определить по этим признакам, относятся к одному моменту времени[15]. Прогнозирование отличается от идентификации тем, что (признаки) значения факторов относятся к прошлому времени, а состояния объекта к будущему[16].

Задача управления (выработки управляющих воздействия) является обратной по отношению к задаче прогнозирования, так как при прогнозировании мы по значениям факторов, относящимся к прошлому, определяем будущее состояние объекта, а при управлении, наоборот, по заданному целевому (желательному) состоянию объекта управления определяем такую систему значений факторов, которая по определенным критериям[17] наиболее эффективно обусловливает (детерминирует) переход объекта в это целевое состояние.

Сформулированные задачи имеют очень общий характер, так как, по сути, являются вариациями одной математической задачи в различных областях науки и практики, например:

– в генетике: исследование и выявление силы и направления влияния признаков генома и окружающей среды на фенотип (смысловая интерпретация генома с применением технологий искусственного интеллекта: признаки генома и окружающей среды как факторы управления фенотипом);

– в психологии (управление персоналом): исследование зависимости личностных и профессиональных качеств человека от его реакции на осознаваемый и неосознаваемый стимульный материал (в частности на опросники); исследование влияния личностных и профессиональных качеств человека на успешность его работы на различных должностях; прогнозирование успешности деятельности конкретного человека на различных должностях на основе ранее выявленных его личностных и профессиональных качеств; разработка «Эйдос-реализации» психологических тестов на основе их опросников и шкал, включая среду применения, а также разработка интегральных тестов на основе стандартных тестов;

– в педагогике: исследование влияния педагогических технологий (в том числе: укомплектованности докторами и кандидатами наук, профессорами и доцентами, методов преподавания, технической оснащенности, учебно-методического обеспечения) на качество образования[18] вообще и уровень предметной обученности в частности, а также на успешность профессиональной деятельности по специальности после окончания обучения; оценка уровня преподавания в учебном заведении; прогнозирование учебных достижений учащихся по свойствам их личности и характеристикам образовательного и учебного процесса; выработка рекомендаций по совершенствованию образовательных технологий;

– в экономике: исследование влияния внутренней структуры предприятия на эффективность ее деятельности; исследование влияния технологических, экономических, социально-политических, природных и иных факторов на результаты экономической деятельности предприятий, отраслей и регионов; оценка и прогнозирование эффективности работы предприятий, выработка научно-обоснованных рекомендаций по совершенствованию деятельности; прогнозирование динамики и сценариев развития фондового рынка, поддержка принятия решений на фондовом рынке;

– в агрономии: исследование влияния агротехнологических факторов, биологических свойств сортов и факторов окружающей среды на количественные и качественные результаты выращивания сельскохозяйственных культур; прогнозирование результатов применения конкретных агротехнологий для выращивания конкретных культур в заданных условиях (почвы, предшественники, климат); разработка рекомендаций по системе агротехнологий, обеспечивающей заданный результат выращивания; определение степени соответствия условий зон и микрозон выращивания, требованиям, предъявляемым конкретными культурами и сортами;

– в кулинарии: исследование влияния рецептуры и технологии на вкусовые и потребительские свойства продуктов питания; разработка рекомендаций по рецептурам и технологиям, обеспечивающим получение продуктов питания с заданными вкусовыми и потребительскими свойствами;

– в металлургии: исследование влияния состава и технологии на свойства сплавов; разработка рекомендаций по составу и технологиям, обеспечивающим получение сплавов с заданными свойствами;

– в химии: исследование зависимости химических свойств химических элементов от структуры атомов; зависимость свойств химических соединений от элементного состава и структуры молекул; прогнозирование свойств новых элементов и химических соединений по их составу и структуре; разработка рекомендаций по составу и структуре новых соединений с заранее заданными свойствами;

– в физике: описание физических явлений и законов физики в различных областях физики на языке теории информации; применение теории управления для управления физическими процессами на различных уровнях организации материи;

– в технических науках: выявление зависимостей свойств новых материалов и технических систем от их состава, структуры и технологии создания; прогнозирование свойств новых материалов и технических систем и выработка рекомендаций по технологии их создания с заранее заданными свойствами;

– в теории управления: выявление и исследование силы и направления влияния значений факторов на свойства и поведение объекта управления; прогнозирование поведения объекта управления под воздействием заданной системы значений управляющих факторов; выработка такого управляющего воздействия, которое с наивысшей степенью детерминированности переведет объект управления в заданное целевое состояние;

– в медицине: исследование зависимости диагноза от клинической картины и симптоматики и зависимости плана лечения от диагноза; постановка диагноза и прогнозирование успешности лечения по симптоматике; выработка плана лечения по диагнозу;

– в биологии: исследование зависимости потребительских, технологических и адаптивных свойств сортов от их фенотипических (ботанических) признаков, физиологии и генотипа; выработка рекомендаций по получению новых сортов и культур;

– в ампелографии: создание семантической информационной модели, отражающей количество знаний, содержащихся в факте наблюдения каждого морфологического и биолого-хозяйственного признака у конкретного образца винограда о том, что этот образец относится к каждому из сортов, представленных в модели. Данную модель можно использовать для решения задач ампелографии, т.е. для идентификации образцов винограда или автоматизированного отнесения образца к сортам на основе его описания с определением количественной меры сходства образца с каждым сортом, а также для количественного определения степени сходства сортов друг с другом путем агломеративной и дивизивной древовидной кластеризации;

– в лингвистике: исследование взаимосвязи между символами и словами, между смыслом фразы и словами, из которых она состоит;

– в теории чисел: исследование взаимосвязи между свойствами цифр и чисел из них, между сложными числами и простыми числами, произведениями которых они являются, исследование других взаимосвязей между числами.

Эти примеры можно легко продолжить, но для целей данной работы и уже приведенных вполне достаточно. Остается добавить, что по многим из приведенных примеров автором проведены конкретные исследования и разработки интеллектуальных приложений[19], т.е. поставлены и решены перечисленные выше задачи идентификации, прогнозирования и поддержи принятия решений в различных предметных областях и сделано это на единой методологической и инструментально-технологической основе Автоматизированного системно-когнитивного анализа (АСК-анализ) и его программного инструментария – интеллектуальной системы «Эйдос».

Рассмотрим, как на теоретическом уровне, так и на простом численном примере, как решается поставленная проблема в АСК-анализе.

Система есть множество взаимосвязанных элементов, что обеспечивает возникновение новых, так называемых системных или эмерджентных свойств, которых не было у элементов системы до их объединения в систему, что обеспечивает системе преимущества в достижении целей. Таким образом, понятие системы основано на понятии множества, но выходит за его пределы, т.е. является его обобщением, т.к. включает также понятия взаимосвязей между элементами, за счет которых образуются подсистемы различных уровней иерархии, образующие структуру системы [97, 170, 189, 191, 196, 201, 240, 241, 245, 248]. На рисунках 1 и 2 представлены в условном виде все возможные подсистемы, образующиеся из 3-х и из 4-х базовых элементов, являющихся простыми числами, путем их перемножения в различных сочетаниях:

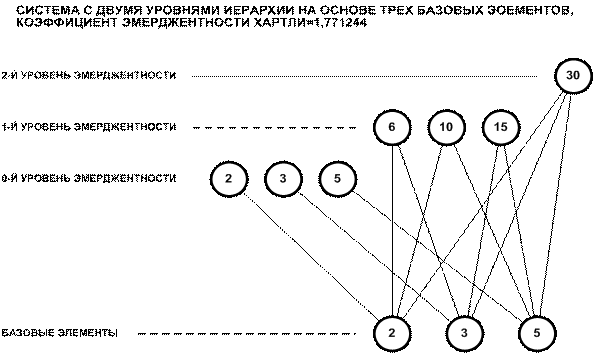
Рисунок 1. Пример системы сложных чисел,
основанных на 3 простых числах

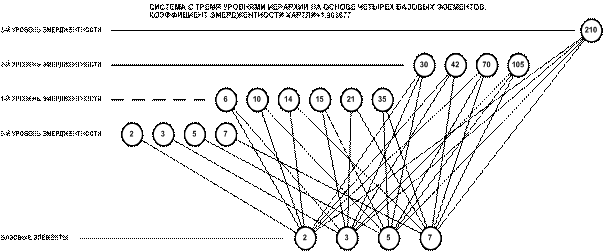
Рисунок 2. Пример системы сложных чисел,
основанных на 4 простых числах

Базовыми элементами будем называть элементы исходного множества, на основе которого образуется система. При этом подсистемы различных уровней иерархии некоторой системы, основанной на n базовых элементов, могут включать различное количество базовых элементов m, где m может изменяться от 1 до n. Конечно, реальные системы включают не все в принципе возможные подсистемы, а лишь некоторые из них, поэтому на одном и том же множество базовых элементов могут основываться большое количество различных систем, одинаковых по составу (базовым элементам), но отличающихся своими структурами (подсистемами). Уровень базовых элементов будем считать нулевым уровнем иерархии системы, подсистемы, состоящие из 2-х базовых элементов – 1-м уровнем иерархии, и т.д., т.е. подсистемы из m базовых элементов образуют k-й уровень иерархии, где k=m-1.

Отметим, что выбор в качестве примера системы, основанной на базовых элементах, являющихся простыми числами, с подсистемами, образующимися путем перемножения базовых элементов в различных сочетаниях, не накладывает каких-либо ограничений на применимость полученных на этом примере выводов в различных предметных областях, т.к. простые числа можно рассматривать как условные коды признаков систем или значений действующих на них факторов, а составные числа – кодами эмерджентных свойств этих систем, образующихся путем взаимодействия соответствующих базовых элементов, к тому же разложение сложных чисел на простые множители является единственным. Таким образом, приведенный в работе пример адекватно представляет в символической форме как все вышеперечисленные примеры решения прямых и обратных задач идентификации и прогнозирования в различных предметных областях, так и все не перечисленные аналогичные задачи.

Если выдвинуть весьма правдоподобную гипотезу, что свойства системы в целом обусловливаются ее составом и структурой, то можно считать, что между этими свойствами и подсистемами различных уровней иерархии существует взаимнооднозначное соответствие, т.е.:

– на нулевом уровне иерархии свойства системы соответствуют непосредственно самим элементам;

– на первом уровне иерархии свойства системы соответствуют подсистемам, образованных из пар базовых элементов в различных сочетаниях;

– на втором уровне иерархии свойства системы соответствуют подсистемам, образованных из троек базовых элементов в различных сочетаниях;

– на третьем уровне иерархии свойства системы соответствуют подсистемам, образованных из четверок базовых элементов в различных сочетаниях;

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

– на k-ом уровне иерархии свойства системы соответствуют подсистемам, образованных из m базовых элементов в различных сочетаниях, где k=m–1.

Таким образом, будем считать, что:

1. Система включает в свой состав не только базовые элементы, на которых она основана, но и различные подсистемы из тех же базовых элементов в различных сочетаниях и эти подсистемы образуют иерархическую структуру системы.

2. Базовые элементы системы будем считать ее подсистемами нулевого уровня иерархии.

3. Свойства системы в целом соответствуют ее подсистемам различных уровней иерархии, поэтому все уровни иерархии, за исключением нулевого, вполне обоснованно называть уровнями эмерджентности.

Ясно, что чем меньше базовых элементов в подсистемах, т.е. чем более простыми являются подсистемы, тем ближе свойства системы в целом к свойствам исходного множества базовых элементов, на которых основана данная система. На основании этого можно утверждать, что понятие системы является обобщением понятия множества. При этом выполнятся принцип соответствия[20] между этими понятиями, т.к. система плавно переходит в множество собственных базовых элементов при уменьшении сложности ее структуры, т.е. числа уровней иерархии и подсистем на этих уровнях до нуля.

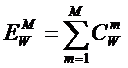Будем считать, что уровень системности (эмерджентность) системы тем выше, чем больше ее свойства отличаются от свойств множества базовых элементов, на которых она основана. Будем считать, что максимальное количество эмерджентных свойств системы в целом , состоящей из M базовых элементов, равно количеству ее подсистем различных уровней иерархии, т.е. различной сложности (1):

(1)

где:

W – количество подсистем в системе, т.е. количество состояний системы или количество ее эмерджентных свойств;

m – число базовых элементов в подсистеме (сложность подсистемы);

M – максимальное количество базовых элементов в подсистеме (максимальный уровень сложности подсистем) M <=W.

В работах [97, 170, 189, 191, 196, 201, 240, 241, 245, 248] предложены, обоснованы, развиты и исследованы абсолютные и относительные количественные меры уровня системности (эмерджентности) системы, в качестве которых автором в 2002 году предложены системное обобщение выражения Хартли для количества информации в системе (2), основанной на W базовых элементов и его отношение к классическому количеству информации по Хартли (3) в множестве тех же базовых элементов [97] (4):

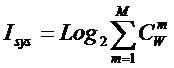(2)

(3)

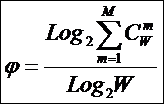(4)

Таким образом, этот коэффициент количественно отражает максимально возможную степень отличия системы от множества его базовых элементов. Поскольку выражение (4) основано на классическом выражении Хартли для количества информации (3) и его системном обобщении, предложенном автором (2), то в работе [97] для него было предложено название: «Коэффициент эмерджентности Хартли», однако, в работах ряда авторов эти и другие результаты преподносятся как собственные без ссылок на первоисточники[21], другие, напротив почему-то думают, что эта информационная мера уровня мера системности была предоложена самим Р.Хартли.

Из вышеизложенного ясно, что уровень системности (эмерджентности) системы или ее сложность определяется не только числом базовых элементов в ней, но и взаимосвязями между ними, т.е. структурой системы, и при уменьшении интенсивности и количества этих взаимосвязей система дезинтегрируется, т.е. структура системы упрощается, пока полностью не исчезнет и система не превратится в простое множество собственных базовых элементов. Значит уровень системности или эмерджентность системы тем выше, чем выше сила и сложность взаимосвязей между ее базовыми элементами. В работе [97] сформулирована и численно исследована гипотеза о законе возрастания эмерджентности (рисунок 3):

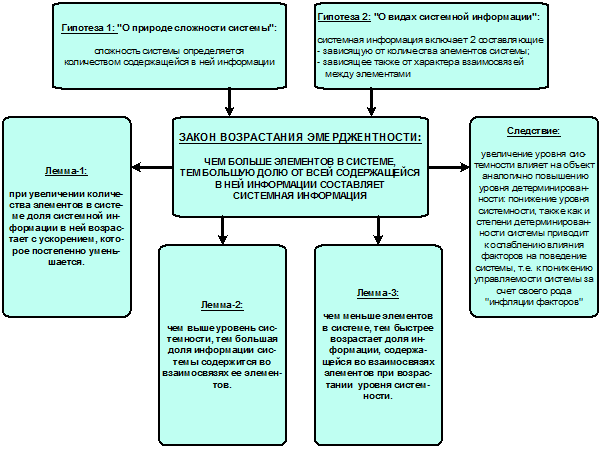
Рисунок 3. Гипотеза о законе возрастания эмерджентности [97]

Но как связан уровень системности с управляемостью системы? Интуитивно понятно, что чем сложнее система, тем сложнее ей управлять. Фундаментальный принцип, раскрывающий природу взаимосвязи между сложностью системы и проблематичностью управления ею предложен одним из основателей кибернетики Уильямом Россом Эшби и в современной науке носит его имя.

Уильям Росс Эшби, 1960 год.

Принцип Эшби: «Управление может быть обеспечено только в том случае, если разнообразие средств управляющего (в данном случае всей системы управления) по крайней мере не меньше, чем разнообразие управляемой им ситуации» [22]. Обычно принцип Эшби интерпретируется таким образом, что число факторов в модели должно быть не меньше числа состояний объекта управления.

Принцип Эшби не означает, что если модель объекта управления отражает не все действующие на него факторы[23], то управление им будет невозможно, а означает лишь, что в этом случае управление будет не полным, не детерминистским. При этом под фактором фактически понимается значение фактора и неявно предполагается, что каждое будущее состояние объекта управления детерминируется одним значением фактора и между значениями факторов и состояниями существует взаимнооднозначное соответствие, т.е. по сути, предполагается, что модель объекта управления является детерминистской, факторы не зависят друг от друга (ортонормированны) и не взаимодействуют друг с другом, т.е. по сути, образуют множество, а не систему факторов. Однако если рассматривать объект управления как систему в цикле управления (рисунок 4), то можно интерпретировать признаки как значения факторов, воздействующих на систему, а классы как эмерджентные свойства системы или ее будущие состояния, некоторые из которых являются целевыми, а некоторые нежелательными:

Рисунок 4. Объект управления как система в цикле управления

По мнению авторов это означает, что принцип Эшби может быть обобщен с учетом системных представлений следующим образом:

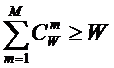«Для того чтобы управление было полным (детерминистским) модель объекта управления должна описывать силу и направление влияния на объект управления не меньшего суммарного количества различных сочетаний значений факторов, чем количество возможных будущих состояний объекта управления». Если записать это высказывание в форме математического выражения, то получим (5):

(5)

Из выражения (5), естественно при W<>0, следует эквивалентная форма 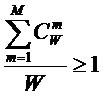(6):

(6)

Предлагается также следующая формулировка системного обобщения принципа Эшби: «Чем больше различных сочетаний значений факторов действует на объект управления, тем выше степень детерминированности управления им». Из сравнения выражений (6) и (4) можно сделать вывод о том, что из приведенной выше формулировки системного обобщения принципа Эшби вытекает следствие: «Степень детерминированности управления системой тем выше, чем выше ее эмерджентность (уровень системности), количественно измеряемая коэффициентом эмерджентности Хартли».

Если в классическом принципе Эшби объект управления рассматривается как многофакторный линейный черный ящик[24], т.е. черный ящик со многими входами и многими выходами не имеющий никакой внутренней структуры, то в системном обобщении принципа Эшби объект управления рассматривается как система однофакторных черных ящиков, каждый из которых имеет один вход и один выход, взаимодействующих между собой и образующих подсистемы, что приводит к нарушению линейности объекта управления. Таким образом, системное обобщение принципа Эшби основано на введении внутренней иерархической структуры черного ящика.

Объект управления называется линейным, если результат совместного действия на него совокупности факторов равен сумме результатов влияния на него каждого из этих факторов по отдельности [273]. Это означает, что в линейном объекте управления факторы не взаимодействуют между собой, не образуют подсистем детерминации, т.е. по сути, являются не системой, а множеством факторов. В нелинейных объектах управления факторы образуют систему с определенным уровнем системности, с новыми эмерджентными (системными) свойствами, не сводящимися к свойствам факторов, рассматриваемым по отдельности. Чем ниже эмерджентность (уровень системности) объекта управления, тем он как система ближе к множеству и к линейности.

В работе [97] для количественной оценки степени детерминированности системы предложен и численно исследован коэффициент эмерджентности, названный в честь А.А.Харкевича «Коэффициентом эмерджентности Харкевича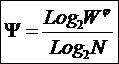» (7):

, (7)

где N – количество фактов, обобщенных в модели объекта управления. Фактом является одновременное наблюдение на опыте двух событий: «Объект управления перешел в j-е состояние» и «На объект управления действовало i-е значение фактора».

Александр Александрович Харкевич (21.1(3.2).1904 – 30.3.1965)

Александр Александрович Харкевич, директор Института проблем передачи информации АН СССР академик АН СССР, является выдающимся советским ученым, внесшим огромный вклад в создание семантической теории информации тем, что внес в теорию информации представление о цели (и тем самым об управлении) и фактически, как стало ясно уже в наше время [245, 248] предложившим количественную меру знаний.

Из вида выражения (7) для коэффициента эмерджентности Харкевича Y очевидно, что увеличение уровня системности φ влияет на семантическую информационную модель аналогично повышению уровня детерминированности системы: понижение уровня системности, также как и степени детерминированности системы приводит к ослаблению влияния факторов на поведение системы, т.е. к понижению управляемости системы за счет своего рода "инфляции факторов" [97]. Иначе говоря, если на объект управления действует ортонормированная система факторов, т.е. множество факторов, не связанных между собой, и к этой системе добавляется еще один фактор, тождественный по своему влиянию одному из уже имеющихся, то суммарное влияние этого нового фактора и тождественного останется тем же самым, т.е. распределится между ними поровну (рисунок 5).

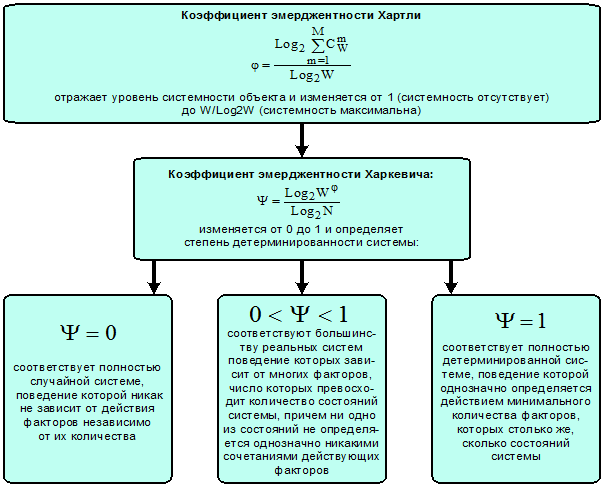
Рисунок 2. Интерпретация и взаимосвязь коэффициентов эмерджентности Хартли и Харкевича согласно [97]

Таким образом, коэффициенты эмерджентности Хартли и Харкевича можно обоснованно считать количественным выражением системного обобщения принципа Эшби.

Общим для всех сформулированных в начале работы задач, и обобщенных, и из разных предметных областей, является неизвестность характера или вида причинно-следственных зависимостей между составом, иерархической структурой и свойствами объектов, или между значениями действующих на объект значениями факторов и его поведением. Однако для решения задач идентификации (распознавания), прогнозирования и принятия решений необходимо знать вид этих зависимостей, следовательно, необходимо выявить и отразить их в формальной модели перед решением этих задач. При этом источником исходных данных для построения формальной модели могут быть только эмпирические данные, полученные из опыта путем наблюдения или в специально организованных экспериментах. Соответственно, возникает принципиальный вопрос, который можно сформулировать следующим образом: «Возможно ли на основе ряда примеров систем с известными внутренним составом и иерархической структурой с одной стороны, и внешне наблюдаемыми свойствами с другой стороны, выявить в количественной форме силу и направление причинно-следственных связей между ними?».

Автоматизированный системно-когнитивный анализ (АСК-анализ) и его программный инструментарий – интеллектуальная система «Эйдос» [97] позволяют утвердительно ответить на этот вопрос, т.к. предоставляют ряд новых возможностей для построения и верификации на основе эмпирических данных формальных моделей, отражающих силу и направление причинно-следственных связей между составом, структурой и свойствами объектов или между значениями действующих на объект значениями факторов и его поведением, а также для решения на основе этих моделей задач идентификации, прогнозирования и принятия решений.

Однако перед тем как непосредственно перейти к рассмотрению этих возможностей кратко обсудим некоторые методологические аспекты создания и применения формальных моделей в научном познании.

Основываясь на работе [245] будем считать, что:

– закономерности – это причинно-следственные зависимости, выявленные на исследуемой выборке и распространяемые лишь на саму эту выборку;

– эмпирический закон – это закономерности, выявленные на исследуемой выборке и распространяемые на некоторую более широкую предметную область, в которой действуют те же причины их существования, что и в исследуемой выборке и эта более широкая предметная область называется генеральной совокупностью, по отношению к которой исследуемая выборка репрезентативна.

Важно, что генеральная совокупность является более широкой, чем исследуемая выборка, причем не только в пространстве, но и во времени. Периоды времени, в течение которых закономерности в предметной области существенно не меняются, называются периодами эргодичности. Можно сказать, что эргодичность – это репрезентативность во времени. Границы между периодами эргодичности называются точками бифуркации. Будем считать, что генеральная совокупность эргодична по отношению к исследуемой выборке, а граница генеральной совокупности состоит из точек бифуркации.

Таким образом, если формальная модель адекватна, то по результатам ее применения невозможно определить в какой именно подобласти генеральной совокупности (области репрезентативности и эргодичности) она применяется. Важно отметить, что сформулированное положение никак не привязано к конкретной предметной области, исследуемой той или иной наукой.

В физике сходный, но более ограниченный смысл имеют принципы относительности Галилея и Эйнштейна: «Все физические процессы в инерциальных системах отсчёта[25] протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения[26]». При этом под «физическими процессами» в принципе относительности Галилея подразумеваются только механические явления, а Эйнштейна – кроме того, и электромагнитные, в частности оптические. Поэтому если мы находимся в замкнутой инерциальной системе отсчета, то по протеканию физических процессов невозможно определить, движется она или покоится, а также в каком месте пространства и в каком времени она движется иди покоится. Из принципа относительности Эйнштейна вытекают преобразования Лоренца, которые являются релятивистским обобщением преобразований Галилея и относительно которых инвариантны уравнения Максвелл, описывающие электромагнитные явления.

Это дает основания называть сформулированное положение «Обобщенным принципом относительности». Предлагается следующая формулировка обобщенного принципа относительности, относящегося не только к механическим и электромагнитным явлениям, но и вообще ко всем явлениям, в том числе еще не обнаруженным и даже к тем, которые в принципе никогда не будут обнаружены человечеством: «Законы природы открытые в одном месте и в определенное время действуют и в других местах и в другое время», поэтому по виду законов природы в замкнутой лаборатории невозможно определить в каком месте (пространства) и в каком времени эта лаборатория находится, т.е. по виду законов природы внутри лаборатории невозможно локализовать ее в пространстве-времени. По-видимому, из этого утверждения также могут быть выведены преобразования, являющиеся обобщением преобразований Лоренца для различных предметных областей, а не только для физики.

Обобщенный принцип относительности является методологической основой синтеза формальной модели объекта управления[27] на основе исследуемой выборки, и применения этой модели в течение периода эргодичности для решения задач идентификации, прогнозирования и принятия решений в некоторой генеральной совокупности, по отношению к которой исследуемая выборка репрезентативна.

На этом утверждении фактически основана вся современная наука, так как когда ученые открывают и исследуют в своих лабораториях новые явления природы и новые законы, то они при этом неявно предполагают, что открываемое ими новое знание будет использоваться не только лично ими, но в будущем пригодится и другим людям, причем и в других странах. Они также предполагают, что изучив законы природы в своих лабораториях они могут на их основе делать выводы об объектах и процессах, весьма удаленных в пространстве и времени, а также об объектах существенно других масштабов, чем изучаемые в лаборатории.

Пример-1. Исследуя излучение света нагретыми химическими элементами ученые могут по спектрам этого излучения определять химический состав веществ не только на Земле, но и химический состав далеких планет, Солнца и других звезд, в том числе в других галактиках. Правда наблюдается «красное смещение» спектральных линий, которое сегодня объясняется законом Хаббла[28] и расширением вселенной[29], хотя известно, что возможны и другие объяснения. Предлагается гипотеза о том, «красное смещение» может быть объяснено не только расширением вселенной, но и ускорением темпа времени в ней (или совместным действием этих факторов в разных сочетаниях степени их влияния на появление этого эффекта[30]). При этом фотоны, которые мы регистрируем на Земле, относятся к тем более отдаленному прошлому, чем дальше находится источник их излучения от Земли, и смещение их частоты в красную сторону отражает на сколько темп времени в источнике их излучения меньше, чем на Земле. В замкнутой системе отсчета нет возможности определить, изменился ли темп времени в ней, даже если он изменится в 1000 раз, но это возможно при взаимодействии нескольких систем отсчета с разным темпом времени в них. Например, когда человек спит, то в течение нескольких секунд может увидеть сон с событиями, которые занимают 2-3 часа и при этом ему не кажется, что эти события происходят в каком-то ускоренном темпе, но это только потому, что во время сна он не осознает событий в физической реальности и не имеет возможности сравнить темп их реализации.

Пример-2. Изучив законы гравитации на Земле и в Солнечной системе ученые могут применять их в масштабах нашей и других галактик, а также в масштабах метагалактики. Правда при этом обнаруживается фактическое несоблюдение этих законов даже уже в масштабах галактики и для объяснения этого предполагается существование «темной материи[31]» и «темной энергии», свойства которых и распределение в пространстве как раз таковы, что позволяют «объяснить» расхождение теории с фактом, хотя известно, что возможны и другие объяснения. Например, энергии гравитационного поля соответствует масса, которая в свою очередь создает гравитационное поле, т.е. гравитационное поле является нелинейным самосогласованным полем. Правда заметным это становится лишь при очень больших по напряженности или по объему гравитационных полях, т.е. как раз в очень больших масштабах, порядка размеров галактики и больше, или вблизи таких экзотических объектов, как черные дыры. Предлагается гипотеза, что никакой «темной материи и энергии» нет, но есть дополнительное гравитационное поле, которое объясняли их наличием, однако это дополнительное гравитационное поле создается самим гравитационным полем.

Ама́лия Э́мми Нётер[32] 23.03.1882 – 14.04.1935 (1935-04-14)

В соответствии с фундаментальной теоремой Эмми Нётер[33] из симметрий пространства-времени: однородности и изотропности пространства и однородностью времени, следуют, соответственно, законы сохранения импульса, момента количества движения и энергии[34]. Выполнение принципа относительности Галилея-Эйнштейна обусловлено тем, что законы физики не меняются при инерциальном смещении системы отсчета (в т.ч. в гравитационном поле), и одинаковы при смещении в разных направлениях, во времени, и при поворотах.

Получается, что есть основания сформулировать следующую гипотезу: «Принцип относительности выполняется по тем же причинам, по которым существуют законы сохранения и этими причинами являются симметрии пространства-времени».

В этой связи возникают два принципиальных вопроса:

Вопрос-1. В какой степени абстрактная модель полностью однородного и изотропного пространства-времени, рассматриваемая в теореме Нётер, соответствует свойствам реального пространства-времени, т.е. на сколько адекватно эта абстрактная модель отражает реальность?

Вопрос-2. Если реальные пространство не является полностью однородным и изотропным и реальное время не совсем однородно, то каким образом это отклонение их свойств от свойств абстрактного полностью однородного и изотропного пространства-времени сказывается на степени соблюдения законов сохранения импульса, момента импульса и энергии, а также на точности принципа относительности?

Естественно, 2-й вопрос становится актуальным в случае неполной адекватности абстрактной модели абсолютно однородного и изотропного пространства-времени, рассматриваемого в теореме Нётер.

Альберт Эйнштейн 14.03.1879 – 18.04.1955

В современной науке считается, что свойства реального (физического) пространства-времени определяются распределением масс, т.к. гравитация согласно модели общей теории относительности (ОТО)[35] Альберта Эйнштейна[36] представляет собой деформацию пространства-времени, т.е. нарушение его однородности и изотропности, вызванное распределением массы-энергии. Поэтому пространство-время может быть однородным и изотропным только в однородной и изотропной вселенной, в которой это условие выполняется для распределения массы-энергии как в микро, так и в мега масштабах[37].

Следовательно, ответ на 1-й вопрос, по сути, сводится к ответу на вопрос об однородности и изотропности распределения массы-энергии во вселенной.

На уровне микро масштабах об однородности и изотропности распределения масс не может быть и речи, т.к. всем хорошо известно, каким сложным образом движутся планеты вокруг Солнца и спутники планет вокруг них. Недавно в ряде работ с участием автора выяснилось[38], что это движение оказывает довольно заметное влияние на движение географического и магнитного полюсов Земли [243], на конфигурацию магнитного поля Земли, на частоту землетрясений на Земле, а также на поведение людей и их социальный статус.

Длительное время считалось, что вселенная однородна и изотропна в мега масштабах (космологический принцип[39]), однако в последнее время появились данные о том, что, по-видимому, и это тоже не так. В этой связи необходимо упомянуть работы по реликтовому излучению[40], великому аттрактору[41] и сенсационные исследования профессора Майкла Лонге[42] (США) с коллегами по ассиметрии распределения и ориентации спиральных галактик в метагалактике[43] (рисунок 6).

Анизотропия реликтового излучения. Источник изображения: http://upload.wikimedia.org/wikipedia/commons/2/28/WMAP_2008.png	Карта потоков галактик в метагалактике согласно http://www.atlasoftheuniverse.com/superc/cen.html Источник изображения: http://www.universe-review.ca/I03-02-attractor2.jpg	Анизотропия распределения спиральных галактик во Вселенной. Источник: http://www.modcos.com/news.php?id=115

Рисунок 6. Ассиметрия вселенной в масштабах метагалактики

Как мы видим из этих примеров реальная структура метагалактики весьма мало напоминает однородную и изотропную и может быть принята такую только в очень грубом приближении. Таким же грубым приближением к реальности являются и теории, основанные на этом предположении. Это и есть ответ на 1-й вопрос, который делает актуальным поиск ответа и на 2-й вопрос[44], который, по-видимому, будет найден в более общих и более точных физических теориях, чем современные.

Таким образом, есть основания полагать, что даже в физике принцип относительности имеет границы применимости, но на предметные области других наук он не распространяется [275] и поэтому в [253] и в данной работе предложен обобщенный принцип относительности: «Законы природы открытые в одном месте и в определенное время действуют и в других местах и в другое время», поэтому по виду законов природы в лаборатории невозможно определить в каком месте (пространства) и в каком времени эта лаборатория находится, т.е. по виду законов природы внутри лаборатории невозможно локализовать ее в пространстве-времени.

В частности, никакими экспериментами внутри полностью замкнутой виртуальной реальности (сном) невозможно определить, является эта реальность виртуальной (сном) или реальной. Но это можно установить, выйдя за пределы этой реальности, например, сняв амуницию виртуальной реальности или просто проснувшись. Поэтому внутри нашей реальности нет критериев, позволяющих обоснованно утверждать, что наша реальность не является виртуальной (сном). Из этого можно сделать очень важный вывод о том, что для того, чтобы давать истинные результаты способ определения степени истинности реальности сам должен быть истинным, т.е. он сам не должен относиться к той области реальности, которая с помощью него оценивается. Например, если мы хотим определить спим мы или нет, то сам способ, который мы используем для этого, не должен нам сниться, т.к. иначе он может дать результаты, которые тоже нам снятся, и, соответственно, могут быть какими угодно, в том числе и «подтверждающими», что мы не спим, и тем самым могут ввести нас в заблуждение [163, 164, 275][45]. Проще говоря нам может приснится, что мы бодрствуем и мы во сне сами можем придерживаться этого мнения, но от этого сон не станет бодрствованием. Из этого примера следует, по крайней мере, два вывода:

1. Принцип относительности описывает не саму реальность, а то, какой она осознается в замкнутой лаборатории, но как только мы связываем каналом передачи информации как минимум две до этого замкнутые лаборатории, то сразу очевидным, что этот принцип нарушается.

2. Наша «истинная» реальность имеет очень много общего с виртуальной реальностью, по крайней мере, внутри нее у нас нет способа и критериев это опровергнуть. Этот вывод усиливается и другими доводами, в частности наличием в нашем мире квантовых явлений[46] и релятивистских эффектов, а также различных аномальных явлений и их сходством с современными средствами трехмерной визуализации.

И не смотря на то, что на этом принципе, как было показано выше, по существу основана современная наука он, строго говоря, не верен, т.е. выполнятся лишь в первом весьма грубом приближении. Для всех наук, изучающих реальную область, кроме физики, это совершенно очевидно, и фактически современная наука (кроме физики) основана не только на этом принципе, но и на исследовании зависимости степени его несоблюдения от локализации лаборатории в пространстве-времени и масштабов изучаемых явлений, т.е. исследование региональных особенностей и их динамики[47]. Для обоснования этого положения достаточно привести несколько примеров из области социально-экономических, политологических и психологических исследований.

Пример-1: исследование региональных особенностей и их динамики в экономике, социологии, политологии.

Лауреат Нобелевской премии в области экономики, основатель математической экономики Василий Васильевич Леонтьев[48] разработал экономико-математические модели межотраслевого баланса. Однако эти модели с различной степенью адекватности описывали реальную экономику разных стран, а иногда вообще ее не описывали, например тех, в которых «экономика должна быть экономной». Можно было бы построить карту мира с наглядной визуализацией на ней степени адекватности этих моделей в динамике. Даже очень хорошие модели, заслужившие наивысшую оценку, имеют свои ограниченные в пространстве и времени области адекватности.

Социологи и политологи изучают общественное мнение по различными вопросам в разрезе по регионам и различным группам населения и также это делают в динамике.

Пример-2: «зарабатывание» на разнице в курсах ценных бумаг.

Приведем замечательную цитату из работы академика А.Б.Мигдала[49]: «… как неравномерность хода времени приводит к несохранению энергии. Допустим, что неравномерность хода времени проявилась в том, что начиная с некоторого момента стала периодически изменяться постоянная всемирного тяготения. Тогда легко построить машину, которая будет получать энергию из ничего, – "вечный двигатель". Для этого нужно поднимать грузы в период слабого тяготения и превращать приобретенную ими энергию в кинетическую, сбрасывая грузы в период увеличения тяготения[50]. Видите, неравномерность хода времени, то есть изменение относительного ритма разных процессов, приводит к нарушению закона сохранения энергии». Не правда ли, это весьма и весьма напоминает то, чем занимаются спекулянты на рынке ценных бумаг: покупают товар, когда цена на него падает до локального минимума и прогнозируется ее повышение, и продают, когда она достигает локального максимумам и ожидается ее понижение. Чем не нарушение закона сохранения энергии в экономике и не «экономический вечный двигатель»? Более того, спекулянты ведут себя так, как будто стараются нарушить закон сохранения энергии в максимально возможной степени [196], т.к. нет никакого экономического смысла в том, чтобы покупать и продавать ценные бумаги по одной и той цене и чем выше разница в цене приобретения и продажи, тем выше прибыль. Действия таможенников также приводят к нарушению закона сохранения энергии в экономике, по своему содержанию по сути ничем не отличаясь от действий «демонов Максвелла»[51], только на макроуровне. Аналогично и в пространстве товары перемещают из тех мест, где они дешевле (обычно там они и производятся), туда, где они дороже, т.е. логистические потоки информационные, финансовые, энергетические и материальные, направлены таким образом, чтобы в максимально возможной степени нарушать закон сохранения импульса в экономике [196]. Ясно, что нет никакого экономического смысла возить товары по путям, по которым их цена не меняется, а именно для этих областей экономического пространства выполняется закон сохранения импульса по данному виду товаров. Таким образом, вечный двигатель, невозможный в физике, вполне возможен в экономике из-за ярко-выраженного нарушения обобщенного принципа относительности, а также законов сохранения энергии и импульса в экономике. При этом финансовые и материальные потоки направлены в область максимального скорости изменения градиента или разности потенциалов что, по-видимому, связано с каким-то обобщением принципа наименьшего действия [196].

Пример-3: локализация и адаптация психологических тестов. В управлении персоналом часто используются психологические тесты. Как правило, их скачивают в Интернете или находят на пиратских компакт-дисках. При этом обычно не задаются вопросами о том, на сколько корректно применять эти тесты, например, в ООО «Сигнал» в России 2012 года, если они были разработаны в Стэндфордском университете США в 1970 году, т.е. ведут себя так, как будто предполагают, что для них соблюдается обобщенный принцип относительности[52]. Между тем даже в США они уже подвергались многократной адаптации, т.к. с течением времени закономерности в предметной области изменяются и там это прекрасно осознают и отслеживают в своих психологических измерительных инструментах эти изменения. Даже в США они локализуются для применения в других штатах, т.к. закономерности в предметной области изменяются в пространстве, и там это прекрасно осознают и отслеживают в своих психологических измерительных инструментах эти изменения. Между тем в России есть необходимые для этого технологии, но они не востребованы[53], т.к. по-видимому, легче и главное прибыльнее занимамться профанацией, чем реальными исследованиями и разработками.

Таким образом, свойства социально-экономического, политического и психологического пространства-времени разные в разных местах и весьма динамично изменяются с течением физического времени. Если бы для них существовал какой-то обобщенный вариант теоремы Нётер, то можно было бы сделать предположение о несоблюдении в этих предметных областях законов сохранения. Может быть даже, что это играет существенную роль в прогрессе человеческого общества, экспоненциальном росте объемов знаний в обществе, капиталов и технологического потенциала. Известно, что преобразование Лапласа[54] и особенно дискретное z-преобразование Лорана[55], описывают процесс затухания последствий от некоторой причины и в соответствующие интегралы и суммы входит экспоненциальный коэффициент затухания, т.к. если функция будут затухать медленнее, чем по экспоненте, то получается расходящийся интеграл (сумма), т.е. получается, что описываемая им причина будет иметь бесконечные последствия. Похоже, что общество как раз и является подобным бесконечным последствием, своего рода «эффектом бабочки»[56].

Но что делать, если обнаруживаются новые факты, которые неадекватно описываются или вообще не описываются существующей теорией или моделью? В этом случае эту теорию или модель необходимо развивать с учетом этих новых фактов (а не отрицать само существование этих «неудобных» фактов, что конечно проще), развивать так, чтобы эти новые факты тоже стали описываться теорией адекватно, так же как и все факты, известные до этого (принцип соответствия[57]). В терминологии, принятой АСК-анализе это означает следующее [245] (рисунок 7):

Рисунок 7. К пояснению смысла понятий:
«адаптация и пересинтез модели»

Новый факт («3» на рисунке 7) не описывается (не идентифицируется) адекватно существующей моделью, т.к. по-видимому, не относится к генеральной совокупности или периоду эргодичности, по отношению к которым репрезентативна обучающая выборка, на основе которой создана данная модель. В этом случае, для того чтобы восстановить адекватность модели, необходимо добавить данный факт к обучающей выборке (для чего обычно необходимо расширить классификационные и описательные шкалы градации) и произвести пересинтез модели. Это обеспечивает качественное изменение смысла признаков и образов классов, в результате чего предметная область адекватности модели, т.е. генеральная совокупность и период эргодичности расширяются.

Рассмотрим численный пример, демонстрирующий возможность выявления причинно-следственных связей между внутренней иерархической структурой системы и ее внешне наблюдаемыми на макроуровне системными или эмерджентными свойствами с применением технологий автоматизированного системно-когнитивного анализа и его программного инструментария – интеллектуальной системы «Эйдос». Рассмотрим также пример неадекватной идентификации объектов, не входящих в генеральную совокупность и пересинтез модели, позволяющий восстановить ее адекватность на более широкой генеральной совокупности (рисунок 7). Отметим, что автоматическое создание классификационных и описательных шкал и градаций для рассматриваемых ниже моделей при различных их параметрах обеспечивается стандартным режимом системы «Эйдос» _159, который полностью автоматизирует этап формализации предметной области АСК-анализа и включен в систему для учебных целей[58].

В качестве базовых элементов в полном соответствии с рисунком 2 будем рассматривать простые числа из диапазона от 2 до 7 включительно, а в качестве подсистем различных уровней иерархии – составные числа, образующиеся путем различных сочетаний базовых в качестве сомножителей по 1, 2, 3 и 4. Из этих базовых элементов путем их использования в качестве сомножителей во всех возможных различных сочетаниях по 1, 2, 3 и 4 образуются составные (сложные) числа, детерминирующие эмерджентные свойства числовых подсистем и системы в целом, в частности 0-го уровня эмерджентности, которому соответствуют свойства самих базовых элементов. Поэтому в качестве классов естественно рассматривать, как базовые элементы, так и составные числа (таблица 1).

Таблица 1 – СПРАВОЧНИК КЛАССОВ

KOD	NAME
1	2 = 2
2	3 = 3
3	5 = 5
4	7 = 7
5	6 = 2 * 3
6	10 = 2 * 5
7	14 = 2 * 7
8	15 = 3 * 5
9	21 = 3 * 7
10	35 = 5 * 7
11	30 = 2 * 3 * 5
12	42 = 2 * 3 * 7
13	70 = 2 * 5 * 7
14	105 = 3 * 5 * 7
15	210 = 2 * 3 * 5 * 7

Если в качестве признаков также как ив качестве классов рассматривать свойства подсистем, то задача становится тривиальной, т.к. при этом справочники признаков и классов полностью совпадают. В этом случае чтобы сформировать модель мы в качестве исходных данных для нее должны предварительно выявить и указать связи между базовыми элементами и подсистемами, которые на рисунке 8 изображены в виде линий, соединяющих базовые элементы с составными числами, образованными на их основе. Но больший научный и практический интерес представляет задача выявления силы и направления этих связей между базовыми элементами и эмерджентными свойствами системы в целом. Поэтому в качестве признаков будем рассматривать только базовые элементы (таблица 2):

Таблица 2 – СПРАВОЧНИК ПРИЗНАКОВ

KOD	NAME
1	2
2	3
3	5
4	7

В качестве объектов обучающей выборки рассматриваются числовые подсистемы различных уровней иерархии, приведенные на рисунке 8, закодированные с использованием таблиц 1 и 2 (таблица 3):

Таблица 3 – ОБУЧАЮЩАЯ ВЫБОРКА

KOD	NAME	Уровень эмерджент-ности	Коды классов															Коды признаков
			1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	1	2	3	4
1	Obj_1	Нулевой	1															1
2	Obj_2		2															2
3	Obj_3		3															3
4	Obj_4		4															4
5	Obj_5	Первый	1	2	5													1	2
6	Obj_6		1	3	6													1	3
7	Obj_7		1	4	7													1	4
8	Obj_8		2	3	8													2	3
9	Obj_9		2	4	9													2	4
10	Obj_10		3	4	10													3	4
11	Obj_11	Второй	1	2	3	5	6	8	11									1	2	3
12	Obj_12		1	2	4	5	7	9	12									1	2	4
13	Obj_13		1	3	4	6	7	10	13									1	3	4
14	Obj_14		2	3	4	8	9	10	14									2	3	4
15	Obj_15	Третий	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	1	2	3	4

На основе обучающей выборки посчитана матрица абсолютных частот (матрица сопряженности) (таблица 4), на основе которой с использованием четырех частных критериев знаний (таблица 5) получены четыре базы знаний, обеспечивающие различную среднюю достоверность с двумя интегральными критериями (таблица 6):

Таблица 4 – МАТРИЦА АБСОЛЮТНЫХ ЧАСТОТ
(МАТРИЦА СОПРЯЖЕННОСТИ)

Признаки		Классы (код, наименование, уровень эмерджентности)
Код	Наимен.	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
		2	3	5	7	2*3	2*5	2*7	3*5	3*7	5*7	2*3*5	2*3*7	2*5*7	3*5*7	2*3*5*7
		0-й уровень эмерджентности				1-й уровень эмерджентности						2-й уровень эмерджентности				3-й УЭ
1	2	8	4	4	4	4	4	4	2	2	2	2	2	2	1	1
2	3	4	8	4	4	4	2	2	4	4	2	2	2	1	2	1
3	5	4	4	8	4	2	4	2	4	2	4	2	1	2	2	1
4	7	4	4	4	8	2	2	4	2	4	4	1	2	2	2	1

Таблица 5 – РАЗЛИЧНЫЕ АНАЛИТИЧЕСКИЕ ФОРМЫ
ЧАСТНЫХ КРИТЕРИЕВ ЗНАНИЙ

Наименование модели знаний и частный критерий	Выражение для частного критерия
	через относительные частоты	через абсолютные частоты
СИМ-1, частный критерий: количество знаний по А.Харкевичу, 1-й вариант расчета вероятностей: Nj – суммарное количество признаков по j-му классу (предпоследняя строка таблицы 2)
СИМ-2, частный критерий: количество знаний по А.Харкевичу, 2-й вариант расчета вероятностей: Nj – суммарное количество объектов по j-му классу (последняя строка таблицы 2)
СИМ-3, частный критерий: разности между фактическими и теоретически ожидаемыми по критерию хи-квадрат абсолютными частотами	---
СИМ-4, частный критерий: ROI - Return On Investment
СИМ-5, частный критерий: разность условной и безусловной вероятностей

Смысл и поведение функций, приведенных в таблице 5, очень сходен, что очевидно из их математической формы. В работе [277] приведен более полный перечень функций, используемый в АСК-анализе и системе «Эйдос-Х++» для метризации шкал.

Таблица 6 – ДОСТОВЕРНОСТЬ МОДЕЛЕЙ С РАЗНЫМИ КОЛИЧЕСТВЕННЫМИ КРИТЕРИЯМИ ЗНАНИЙ И РАЗНЫМИ ИНТЕГРАЛЬНЫМИ КРИТЕРИЯМИ [10, 11]

Наименование модели	Вид интегрального критерия	Расчет проведен		Достоверность
		Дата	Идентификации	Идентификации	Идентификации	Средняя
СИМ-4	Корреляция	02-01-12	09:40:57	100,000	63,306	81,653
	Свертка	02-01-12	09:41:00	100,000	63,306	81,653
СИМ-3	Корреляция	02-01-12	09:41:04	100,000	63,306	81,653
	Свертка	02-01-12	09:41:06	100,000	63,306	81,653
СИМ-2	Корреляция	02-01-12	09:41:10	100,000	63,306	81,653
	Свертка	02-01-12	09:41:12	33,858	75,403	54,631
СИМ-1	Корреляция	02-01-12	09:41:17	100,000	63,306	81,653
	Свертка	02-01-12	09:41:20	100,000	77,823	88,911

Из таблицы 6 видно, что наилучшей достоверностью по двум видам ошибок обладает модель СИМ-1 с интегральным критерием: «сумма информации» (свертка), поэтому база знаний этой модели и приводится в таблице 7:

Таблица 7 – МАТРИЦА ЗНАНИЙ СИМ-1 (Биты × 1000)

Признаки		Классы (код, наименование, уровень эмерджентности)
Код	Наимен.	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
		2	3	5	7	2*3	2*5	2*7	3*5	3*7	5*7	2*3*5	2*3*7	2*5*7	3*5*7	2*3*5*7
		0-й уровень эмерджентности				1-й уровень эмерджентности						2-й уровень эмерджентности				3-й УЭ
1	2	352	-167	-167	-167	216	216	216	-304	-304	-304	100	100	100	-419	0
2	3	-167	352	-167	-167	216	-304	-304	216	216	-304	100	100	-419	100	0
3	5	-167	-167	352	-167	-304	216	-304	216	-304	216	100	-419	100	100	0
4	7	-167	-167	-167	352	-304	-304	216	-304	216	216	-419	100	100	100	0

База знаний, приведенная в таблице 7, является решением проблемы поставленной в разделе, т.к. отражает силу и направление влияния подсистем различных уровней иерархии на эмерджентные свойства системы в целом, причем в единой сопоставимой форме в единицах измерения информации и знаний: миллибитах. Знак чисел в таблице 7 показывает направление связи, а величина модуля – силу связи между признаками и классами.

При малой размерности модели таблица 7 может быть непосредственно обозримой и понятной для исследователя, поэтому в данной работе и приведена подобная модель. Однако при больших размерностях модели необходимы специальные режимы, позволяющие делать различные выборки из базы знаний и представлять информацию в удобной, понятной и наглядной форме. Для этой цели в системе «Эйдос» есть ряд режимов, позволяющих выводить информационные портреты классов и признаков, а также когнитивные функции (функции влияния) и другие текстовые и графические формы (которых более 110 различных видов).

Ниже кратко рассмотрим некоторые из них.

Нелокальные нейроны и интерпретируемые нейронные сети позволяют в наглядной графической форме отобразить систему детерминации будущих состояний [138].

Нелокальный нейрон представляет собой будущее состояние объекта управления с изображением наиболее сильно влияющих на него факторов с указанием силы и направления (способствует-препятствует) их влияния (рисунок 8):

Рисунок 8. Отображение базы знаний (таблица 7)
в форме нелокальных нейронов [138]

Нелокальная нейронная сеть представляет собой совокупность взаимосвязанных нейронов. В классических нейронных сетях связь между нейронами осуществляется по входным и выходным сигналам, а в нелокальных нейронных сетях – на основе общего информационного поля, реализуемого семантической информационной моделью. Система "Эйдос" обеспечивает построение любого подмножества многослойной нейронной сети с заданными или выбираемыми по заданным критериям рецепторами и нейронами, связанными друг с другом связями любого уровня опосредованности (рисунок 9):

Рисунок 9. Отображение базы знаний (таблица 7)
в форме Парето-подмножества нелокальной нейронной сети [138]

С использованием знаний о силе и направлении связей между составом и иерархической структурой системы, с одной стороны, и ее эмерджентными свойствами как целого, с другой стороны, приведенными в таблице 7 и рисунках 8, 9 можно изобразить иерархическую структур системы, приведенную на рисунке 2, с графическим указанием силы и направления связи между базовыми элементами системы и ее эмерджентными свойствами в форме толщины и цвета линий (рисунок 10):

Рисунок 10. Пример системы сложных чисел, основанных на 4
простых числах с указанием силы и направления связи между
базовыми элементами системы и ее эмерджентными свойствами
в форме толщины и цвета линий

На рисунке 10 толщина линии пропорциональна силе связи, черный цвет обозначает положительную связь, а красный – отрицательную. Из сравнения рисунков 9 и 10 можно сделать обоснованный вывод том, что АСК-анализ и его программный инструментарий – интеллектуальная система «Эйдос» обеспечивают выявление силы и направления связей между базовыми элементами системы и ее эмерджентными свойствами в целом на основе эмпирических данных и отображение внутренней иерархической структуры конкретной системы в наглядной графической форме нелокальной нейронной сети.

Анализ приведенного численного примера и нейронной сети на рисунке 10 дает нам основания сформулировать гипотезу «О зависимости силы и направления связей связи между базовыми элементами системы и ее эмерджентными свойствами в целом от уровня иерархии в системе»: чем выше уровень иерархии в системе, тем слабее положительные и сильнее отрицательные связи между базовыми элементами системы и ее эмерджентными свойствами в целом, т.к., возможно, это является конкретным проявлением соответствующей общей закономерности.

Информационный портрет класса – это список факторов, ранжированных в порядке убывания силы их влияния на переход объекта управления в состояние, соответствующее данному классу. Информационный портрет класса отражает систему его детерминации. Генерация информационного портрета класса представляет собой решение обратной задачи прогнозирования, т.к. при прогнозировании по системе факторов определяется спектр наиболее вероятных будущих состояний объекта управления, в которые он может перейти под влиянием данной системы факторов, а в информационном портрете мы наоборот, по заданному будущему состоянию объекта управления определяем систему факторов, детерминирующих это состояние, т.е. вызывающих переход объекта управления в это состояние. В начале информационного портрета класса идут факторы, оказывающие положительное влияние на переход объекта управления в заданное состояние, затем факторы, не оказывающие на это существенного влияния, и далее – факторы, препятствующие переходу объекта управления в это состояние (в порядке возрастания силы препятствования). Информационные портреты классов могут быть от отфильтрованы по диапазону факторов, т.е. мы можем отобразить влияние на переход объекта управления в данное состояние не всех отраженных в модели факторов, а только тех, коды которых попадают в определенный диапазон, например, относящиеся к определенным описательным шкалам. Пример информационного портрета класса приведен в таблице 8:

Таблица 8 – ИНФОРМАЦИОННЫЙ ПОРТРЕТ КЛАССА:
код: 11, наименование: 30=2*3*5

№	Признак		Количество информации
	Код	Наименование	В Битах	В % от теоретически максимально возможного
1	1	2	0,10004	2,56
2	2	3	0,10004	2,56
3	3	5	0,10004	2,56
4	4	7	-0,41925	-10,73

Таким образом, информационный портер класса содержит ту же информацию, что и нелокальный нейрон, но в форме таблицы.

Информационный (семантический) портрет фактора – это список классов, ранжированный в порядке убывания силы влияния данного фактора на переход объекта управления в состояния, соответствующие данным классам. Информационный портрет фактора называется также его семантическим портретом, т.к. в соответствии с концепцией смысла системно-когнитивного анализа, являющейся обобщением концепции смысла Шенка-Абельсона, смысл фактора состоит в том, какие будущие состояния объекта управления он детерминирует. Сначала в этом списке идут состояния объекта управления, на переход в которые данный фактор оказывает наибольшее влияние, затем состояния, на которые данный фактор не оказывает существенного влияния, и далее состояния – переходу в которые данный фактор препятствует. Информационные портреты факторов могут быть от отфильтрованы по диапазону классов, т.е. мы можем отобразить влияние данного фактора на переход объекта управления не во все возможные будущие состояния, а только в состояния, коды которых попадают в определенный диапазон, например, относящиеся к определенным классификационным шкалам. Пример информационного портрета признака (значения фактора) приведен в таблице 9:

Таблица 9– ИНФОРМАЦИОННЫЙ ПОРТРЕТ ПРИЗНАКА:
код: 11, наименование: 30=2*3*5

№	Класс		Количество информации
	Код	Наименование	В Битах	В % от теоретически максимально возможного
1	1	2 = 2	0,35211	9,01
2	5	6 = 2 * 3	0,21552	5,52
3	6	10 = 2 * 5	0,21552	5,52
4	7	14 = 2 * 7	0,21552	5,52
5	11	30 = 2 * 3 * 5	0,10004	2,56
6	12	42 = 2 * 3 * 7	0,10004	2,56
7	13	70 = 2 * 5 * 7	0,10004	2,56
8	15	210 = 2 * 3 * 5 * 7	0,00000	0,00
9	2	3 = 3	-0,16717	-4,28
10	3	5 = 5	-0,16717	-4,28
11	4	7 = 7	-0,16717	-4,28
12	8	15 = 3 * 5	-0,30376	-7,77
13	9	21 = 3 * 7	-0,30376	-7,77
14	10	35 = 5 * 7	-0,30376	-7,77
15	14	105 = 3 * 5 * 7	-0,41925	-10,73

Когнитивные функции (функции влияния) [12] представляет собой график зависимости вероятностей перехода объекта управления в будущие состояния под влиянием различных значений некоторого фактора. Если взять несколько информационных портретов факторов, соответствующих градациям одной описательной шкалы, отфильтровать их по диапазону градаций некоторой классификационной шкалы и взять из каждого информационного портрета по одному состоянию, на переход в которое объекта управления данная градация фактора оказывает наибольшее влияние, то мы и получим зависимость, отражающую вероятность перехода объекта управления в будущие состояния под влиянием различных значений некоторого фактора, т.е. функцию влияния. Функции влияния являются наиболее развитым средством изучения причинно-следственных зависимостей в моделируемой предметной области, предоставляемым системой "Эйдос". Необходимо отметить, что на вид функций влияния математической моделью СК-анализа не накладывается никаких ограничений, в частности, они могут быть и нелинейные. Пример нередуцированной когнитивной функции, генерируемой режимом _54 системы «Эйдос», приведен на рисунке 11:

Рисунок 11. Пример нередуцированной когнитивной функции

Классические когнитивные карты являются графической формой представления фрагментов СИМ, объединяющей достоинства таких форм, как нейроны и семантические сети факторов. Классическая когнитивная карта представляет собой нейрон, соответствующий некоторому состоянию объекта управления с рецепторами, каждый из которых соответствует фактору в определенной степени способствующему или препятствующему переходу объекта в это состояние. Рецепторы соединены связями как с нейроном, так и друг с другом. Связи рецепторов с нейроном отражают силу и направление влияния факторов, а связи рецепторов друг с другом, отображаемые в форме семантической сети факторов, – сходство и различие между рецепторами по характеру их влияния на объект управления. Таким образом, классическая когнитивная карта представляет собой нейрон с семантической сетью факторов, изображенные на одной диаграмме.

Обобщенные когнитивные карты позволяют объединить в одной графической форме семантические сети классов и факторов, объединенных нейронной сетью. Если объединить несколько классических когнитивных карт на одной диаграмме и изобразить на ней также связи между нейронами в форме семантической сети классов, то получим обобщенную (интегральную) когнитивную карту. Система "Эйдос" обеспечивает построение любого подмножества многоуровневой семантической информационной модели с заданными или выбираемыми по заданным критериям рецепторами и нейронами, связанными друг с другом связями любого уровня опосредованности в форме классических и обобщенных когнитивных карт. В частности, в системе полуавтоматически формируется задание на генерацию подмножеств обобщенной когнитивной карты. Пример интегральной когнитивной карты для построенной модели приведен на рисунке 12:

Рисунок 12. Пример интегральной когнитивной карты
для построенной модели

Матрица сходства классов по системе их детерминации представлена в таблице 10:

Таблица 10 – МАТРИЦА СХОДСТВА КЛАССОВ
ПО СИСТЕМЕ ИХ ДЕТЕРМИНАЦИИ

KOD	NAME	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	2 = 2	100	-33	-33	-33	58	58	58	-58	-58	-58	33	33	33	-100	0
2	3 = 3	-33	100	-33	-33	58	-58	-58	58	58	-58	33	33	-100	33	0
3	5 = 5	-33	-33	100	-33	-58	58	-58	58	-58	58	33	-100	33	33	0
4	7 = 7	-33	-33	-33	100	-58	-58	58	-58	58	58	-100	33	33	33	0
5	6 = 2 * 3	58	58	-58	-58	100	0	0	0	0	-100	58	58	-58	-58	0
6	10 = 2 * 5	58	-58	58	-58	0	100	0	0	-100	0	58	-58	58	-58	0
7	14 = 2 * 7	58	-58	-58	58	0	0	100	-100	0	0	-58	58	58	-58	0
8	15 = 3 * 5	-58	58	58	-58	0	0	-100	100	0	0	58	-58	-58	58	0
9	21 = 3 * 7	-58	58	-58	58	0	-100	0	0	100	0	-58	58	-58	58	0
10	35 = 5 * 7	-58	-58	58	58	-100	0	0	0	0	100	-58	-58	58	58	0
11	30 = 2 * 3 * 5	33	33	33	-100	58	58	-58	58	-58	-58	100	-33	-33	-33	0
12	42 = 2 * 3 * 7	33	33	-100	33	58	-58	58	-58	58	-58	-33	100	-33	-33	0
13	70 = 2 * 5 * 7	33	-100	33	33	-58	58	58	-58	-58	58	-33	-33	100	-33	0
14	105 = 3 * 5 * 7	-100	33	33	33	-58	-58	-58	58	58	58	-33	-33	-33	100	0
15	210 = 2 * 3 * 5 * 7	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

Любая подматрица матрицы сходства (таблица 10) (или любой заданный набор классов) может быть представлена в графическом виде в форме ориентированного графа – семантической сети (рисунок 13), которая в ряде работ называется также когнитивной диаграммой:

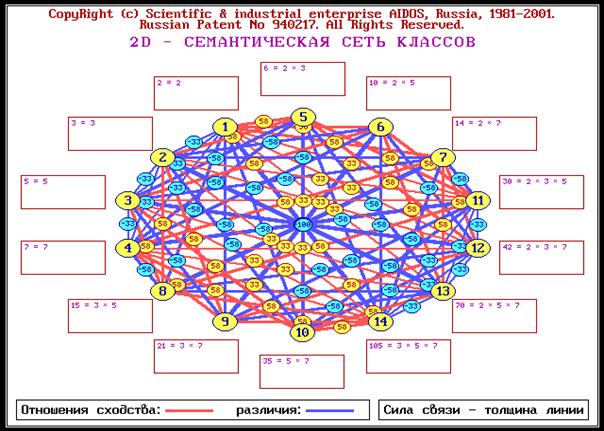
Рисунок 13. Матрицы сходства классов (таблица 10),
представленная в форме семантической сети классов

В таблице 11 представлен конструкт, представляющий собой систему противоположных кластеров со спектром промежуточных классов:

Таблица 11 – КОНСТРУКТ: «6-35»

№	Код	Наименование	Уровень сходства %
1	5	6 = 2 * 3	100,00
2	1	2 = 2	57,74
3	2	3 = 3	57,74
4	11	30 = 2 * 3 * 5	57,74
5	12	42 = 2 * 3 * 7	57,74
6	3	5 = 5	-57,74
7	4	7 = 7	-57,74
8	13	70 = 2 * 5 * 7	-57,74
9	14	105 = 3 * 5 * 7	-57,74
10	10	35 = 5 * 7	-100,00

На основе матрицы сходства (таблица 10) может быть проведена когнитивная кластеризация [248], результаты которой представлены на рисунках 13 и 14:

Рисунок 13. График пошагового изменения межкластерного
расстояния при когнитивной кластеризации в СИМ-1

Рисунок 14. Дендрограмма когнитивной кластеризации в СИМ-1

На рисунке 16 приведены результаты идентификации объекта распознаваемой выборки с классами, а на рисунке 17 – класса с объектами:

Рисунок 16. Результат идентификации объекта с классами
(экранная форма)

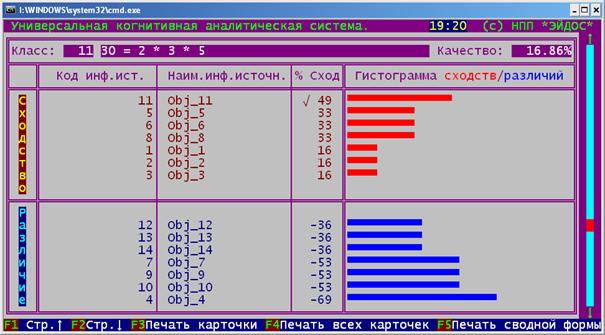
Рисунок 17. Результат идентификации классами с объектами
(экранная форма)

При добавлении еще одного базового элемента (например, простого числа: 11) без пересинтеза модели объекты, включающие этот базовый элемент, идентифицируются так же, как будто его нет. Например, результат идентификации объекта: 330 = 2 * 3 * 5 * 11 в этой модели будут такими же, как показано на рисунке 16, т.е. данный объект будет неверно идентифицироваться как 30 = 2 * 3 * 5. Это является признаком необходимости обобщения модели, т.е. создания модели, адекватно отражающей как все предыдущие, так и новые факты. Создание этой более общей модели обеспечивается выполнением следующих шагов:

– добавлением в справочник классов, соответствующих объектам, включающим данный элемент;

– добавлением данного базового элемента в справочник признаков;

– добавлением этого объекта и других объектов, включающих данный базовый элемент, в обучающую выборку;

– пересинтезом модели;

– проверкой ее на адекватность, в т.ч. на новых фактах.

Результат выполнения этих шагов представлен в таблицах 12-16:

Таблица 12 – СПРАВОЧНИК КЛАССОВ БОЛЕЕ ОБЩЕЙ МОДЕЛИ

KOD	NAME	KOD	NAME	KOD	NAME
1	2 = 2	11	21 = 3 * 7	21	154 = 2 * 7 * 11
2	3 = 3	12	33 = 3 * 11	22	105 = 3 * 5 * 7
3	5 = 5	13	35 = 5 * 7	23	165 = 3 * 5 * 11
4	7 = 7	14	55 = 5 * 11	24	231 = 3 * 7 * 11
5	11 = 11	15	77 = 7 * 11	25	385 = 5 * 7 * 11
6	6 = 2 * 3	16	30 = 2 * 3 * 5	26	210 = 2 * 3 * 5 * 7
7	10 = 2 * 5	17	42 = 2 * 3 * 7	27	330 = 2 * 3 * 5 * 11
8	14 = 2 * 7	18	66 = 2 * 3 * 11	28	462 = 2 * 3 * 7 * 11
9	22 = 2 * 11	19	70 = 2 * 5 * 7	29	770 = 2 * 5 * 7 * 11
10	15 = 3 * 5	20	110 = 2 * 5 * 11	30	1155 = 3 * 5 * 7 * 11

Таблица 13 – СПРАВОЧНИК ПРИЗНАКОВ БОЛЕЕ ОБЩЕЙ МОДЕЛИ

KOD	NAME
1	2
2	3
3	5
4	7
5	11

Таблица 14 – ОБУЧАЮЩАЯ ВЫБОРКА БОЛЕЕ ОБЩЕЙ МОДЕЛИ

KOD	NAME	Коды классов															Коды признаков
		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	1	2	3	4
1	Obj_1	1															1
2	Obj_2	2															2
3	Obj_3	3															3
4	Obj_4	4															4
5	Obj_5	5															5
6	Obj_6	1	2	6													1	2
7	Obj_7	1	3	7													1	3
8	Obj_8	1	4	8													1	4
9	Obj_9	1	5	9													1	5
10	Obj_10	2	3	10													2	3
11	Obj_11	2	4	11													2	4
12	Obj_12	2	5	12													2	5
13	Obj_13	3	4	13													3	4
14	Obj_14	3	5	14													3	5
15	Obj_15	4	5	15													4	5
16	Obj_16	1	2	3	6	7	10	16									1	2	3
17	Obj_17	1	2	4	6	8	11	17									1	2	4
18	Obj_18	1	2	5	6	9	12	18									1	2	5
19	Obj_19	1	3	4	7	8	13	19									1	3	4
20	Obj_20	1	3	5	7	9	14	20									1	3	5
21	Obj_21	1	4	5	8	9	15	21									1	4	5
22	Obj_22	2	3	4	10	11	13	22									2	3	4
23	Obj_23	2	3	5	10	12	14	23									2	3	5
24	Obj_24	2	4	5	11	12	15	24									2	4	5
25	Obj_25	3	4	5	13	14	15	25									3	4	5
26	Obj_26	1	2	3	4	6	7	8	10	11	13	16	17	19	22	26	1	2	3	4
27	Obj_27	1	2	3	5	6	7	9	10	12	14	16	18	20	23	27	1	2	3	5
28	Obj_28	1	2	4	5	6	8	9	11	12	15	17	18	21	24	28	1	2	4	5
29	Obj_29	1	3	4	5	7	8	9	13	14	15	19	20	21	25	29	1	3	4	5
30	Obj_30	2	3	4	5	10	11	12	13	14	15	22	23	24	25	30	2	3	4	5

Таблица 15 – ОЦЕНКА АДЕКВАТНОСТИ БОЛЕЕ ОБЩЕЙ МОДЕЛИ

Наименование модели	Вид интегрального критерия	Расчет проведен		Достоверность
		Дата	Идентификации	Идентификации	Идентификации	Средняя
СИМ-4	Корреляция	03-01-12	11:29:19	100,000	73,171	86,585
	Свертка	03-01-12	11:29:24	100,000	73,171	86,585
СИМ-3	Корреляция	03-01-12	11:29:32	100,000	73,171	86,585
	Свертка	03-01-12	11:29:37	100,000	73,171	86,585
СИМ-2	Корреляция	03-01-12	11:29:44	100,000	73,171	86,585
	Свертка	03-01-12	11:29:50	56,137	71,137	63,637
СИМ-1	Корреляция	03-01-12	11:29:59	100,000	73,171	86,585
	Свертка	03-01-12	11:30:04	70,179	87,400	78,789

Таблица 16 – РЕЗУЛЬТАТ ИДЕНТИФИКАЦИИ ОБЪЕКТА С КЛАССАМИ В БОЛЕЕ ОБЩЕЙ МОДЕЛИ (ВЫХОДНАЯ ФОРМА)

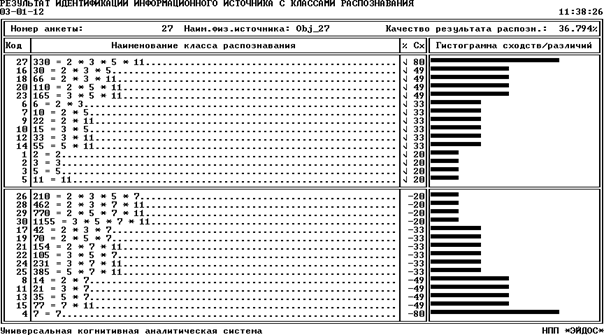
Из сравнения таблицы 16 с рисунком 16 видно, что полученная нами обобщенная модель удовлетворяет принципу соответствия с предыдущей моделью, т.к. дает вполне разумные результаты идентификации как объектов, верно идентифицируемых в старой модели, так и новых объектов, которые ранее идентифицировались неадекватно. Таким образом, подход, представленный на рисунке 7, дает ожидаемые положительные результаты.

Выводы. Таким образом, в разделе на простом, но универсальном численном примере рассмотрено применение автоматизированного системно-когнитивного анализа (АСК-анализ) и его программного инструментария – интеллектуальной системы «Эйдос» для выявления и исследования детерминации эмерджентных макросвойств систем их составом и иерархической структурой, т.е. подсистемами различной сложности (уровней иерархии). Тем самым продемонстрирована возможность решения этой проблемы в широком круге предметных областей с применением технологии и инструментария АСК-анализа.

Кратко обсуждаются некоторые методологические вопросы создания и применения формальных моделей в научном познании.

Предложены:

– системное обобщение принципа Уильяма Росса Эшби о необходимом разнообразии на основе системного обобщения теории множеств и системной теории информации;

– обобщенная формулировка принципа относительности Галилея-Эйнштейна, применимая не только в физике, но и в других науках, в частности в экономике, социологии и психологии;

– гипотеза о связи обобщенного принципа относительности с теоремой Эмми Нётер;

– гипотеза «О зависимости силы и направления связей между базовыми элементами системы и ее эмерджентными свойствами в целом от уровня иерархии в системе».

Системное обобщение принципа Эшби и следствие из него: «Чем больше различных сочетаний значений факторов действует на объект управления, тем выше степень детерминированности управления им», следовательно «Степень детерминированности управления системой тем выше, чем выше ее эмерджентность (уровень системности), количественно измеряемая коэффициентом эмерджентности Хартли». Коэффициенты эмерджентности Хартли и Харкевича можно обоснованно считать количественным выражением системного обобщения принципа Эшби.

Обобщенный принцип относительности Галилея-Эйнштейна: «Законы природы открытые в одном месте и в определенное время действуют и в других местах и в другое время», поэтому по виду законов природы в замкнутой лаборатории невозможно определить в каком месте (пространства) и в каком времени эта лаборатория находится, т.е. по виду законов природы внутри лаборатории невозможно локализовать ее в пространстве-времени. Из обобщенного принципа относительности вытекает важное следствие том, что способ определения степени истинности реальности сам должен быть истинным, чтобы давать истинные результаты, и сам не должен относится к той реальности, которая с помощью него оценивается. Обобщенный принцип относительности применим не только в физике, но и в других науках, в частности в экономике, социологии и психологии. Но в отличие от физики другие науки не только основаны на применении этого принципа, хотя и в явном виде не формулировали его, но и их исследования во многом состоят в изучении отклонений от этого принципа.

Гипотеза о связи обобщенного принципа относительности с теоремой Эмми Нётер: «Принцип относительности выполняется по тем же причинам, по которым существуют законы сохранения и этими причинами являются симметрии пространства-времени».

Гипотеза «О зависимости силы и направления связей между базовыми элементами системы и ее эмерджентными свойствами в целом от уровня иерархии в системе»: «Чем выше уровень иерархии в системе, тем слабее положительные и сильнее отрицательные связи между базовыми элементами системы и ее эмерджентными свойствами в целом».

Материалы работы могут быть использованы при проведении лекционных и лабораторных занятий по дисциплинам: «Интеллектуальные информационные системы» и «Концепции современного естествознания».для различных специальностей, а также для решения перечисленных в начале работы и других задач того же типа в различных предметных областях.

10.3. Коэффициент эмерджентности классических
и квантовых статистических систем

В данном разделе изложение полностью основано на рабате [270], нумерация формул, рисунков и таблиц сохранены.

В классической теории информации Хартли-Шеннона понятие информации определяется на основе теоретико-множественных и комбинаторных представлений на основе анализа поведения классического макрообъекта, который может переходить только в четко фиксированные альтернативные редуцированные состояния, например монета, может упасть либо на "орел", либо на "решку". Если эти варианты равновероятны, то при реализации одного из них по формуле Хартли мы получаем информацию в 1 бит, при реализации одного из W равновероятных состояний мы получаем информацию I=Log₂W бит, если неравновероятны, то для расчета среднего количества информации используется формула Шеннона [97].

Однако квантовые объекты могут быть одновременно в двух и более альтернативных для классических объектов состояниях [2]. Такие состояния будем называть смешанными.

Например, электрон может интерферировать, проходя одновременно через две щели[59] [2]. При этом наблюдаются эффекты, не сводящиеся к суперпозиции классических состояний, т.е. имеющие существенно квантовый, системный, эмерджентный, нелинейный характер.

Поэтому классическая теория информации Хартли-Шеннона может быть обобщена путем рассмотрения квантовых систем в качестве объектов, на основе анализа поведения которых формируется само основополагающее понятие информации. Обобщенную таким образом теорию информации предлагается называть системной или эмерджентной теорией информации.

Основным отличием эмерджентной теории информации от классической является учет свойства системности, как фундаментального и универсального свойства всех объектов, на уровне самого понятия информации. Достаточно рассмотреть квантовое обобщение теории Хартли, т.к. путь вывода теории Шеннона из теории Хартли хорошо известен [97].

В работе[60] Ричард Фейнман рассмотрел пример интерференции электрона на двух щелях при наблюдении этого процесса с помощью эффекта Комптона, т.е. путем рассеяния фотонов на электроне. В этом случае электрон всегда наблюдается в форме объекта с размером порядка длины волны света, и как выяснилось, его свойства самым существенным образом зависят от его наблюдаемого, а значит и фактического размера. Мы не будем детально приводить известную аргументацию Р. Фейнмана, но коснемся лишь моментов, играющих ключевую роль в квантовом (системном) обобщении понятия "информация".

Когда длина волны фотонов меньше расстояния между щелями, то видно, что электрон проходит через одну из щелей. В этом случае на экране за каждой щелью наблюдается классическое распределение плотности. Суммарная плотность N₁₂ является просто суммой распределений N₁ и N₂, полученных соответственно от щелей 1 и 2 – рис. 1. Следовательно, имеем в этом случае:

(1)

Когда длина волны фотонов порядка расстояния между щелями или больше, то видно, как он проходит через экран "накрывая" обе щели одновременно. В этом случае за ними наблюдается сложная интерференционная картина, нисколько не напоминающая сумму или суперпозицию классических распределений за 1-й и 2-й щелями, т.е. не являющуюся их суммой – рис. 2.

Рисунок 1. Классический объект, интерференции нет	Рисунок 2. Квантовый объект, интерференция есть

Введем следующие обозначения:

– волновая функция или амплитуда вероятности, квадрат модуля которой характеризует вероятность попадания электрона в точку x экрана через отверстие 1;

– волновая функция, квадрат модуля которой характеризует вероятность попадания электрона в точку x экрана через отверстие 2;

– суммарная амплитуда вероятности, квадрат модуля которой характеризует вероятность попадания электрона в точку x экрана через отверстия 1 и 2 одновременно.

Согласно законам квантовой механики, складываются волновые функции, а не вероятности, как в классическом случае, поэтому имеем:

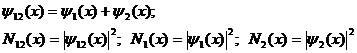(2)

Отсюда находим, что

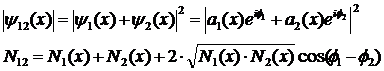(3)

Здесь – амплитуда и фаза волновой функции соответственно. Сравнивая выражения (1) и (3) видим, что квантовый эффект прохождения электрона через две щели одновременно приводит к появлению дополнительного слагаемого, описывающего интерференцию – рис. 2.

Это дополнительное слагаемое учитывает системный эффект состоящий в том, что состояния объекта, в классической теории считавшиеся альтернативными, т.е. одновременно не реализуемыми ни при каких условиях, в квантовой теории таковыми не являются и могут осуществляться одновременно, что приводит к возможности нахождения объекта в смешанных состояниях.

Если вероятность прохождения электрона через каждую из W щелей одинакова, то по классической теории Хартли в самом факте пролета электрона через одну из щелей содержится количество информации:

(4)

где W – количество щелей, или, в общем случае, классических состояний объекта.

В соответствии с концепцией эмерджентной теории информации, предлагается ввести в это выражение параметр, учитывающий квантовые системные эффекты нахождения объекта в смешанных состояниях. В результате количество состояний объекта возрастает и, следовательно, так же возрастает и количество информации, которое мы получаем, когда узнаем, что он перешел в одно из этих состояний:

(5)

где φ – степень эмерджентности системы (синоним: уровень системности объекта), в частности:

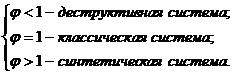
Для деструктивных систем свойства целого меньше свойств частей, для классических систем они совпадают, для синтетических систем свойства целого больше свойств частей и не сводятся к ним.

На первый взгляд можно было бы просто увеличить количество состояний системы W за счет учета смешанных состояний. Однако этот путь не удовлетворяет известному принципу соответствия, который в данном контексте требует, чтобы в предельном случае более общая теория переходила в уже известную, классическую теорию.

Здесь уместно привести теорему, впервые доказанную известным кибернетиком У. Эшби: у системы тем больше возможностей в выборе поведения, чем сильнее степень согласованности поведения ее частей.

Теорема Эшби описывает систему в точке бифуркации, причем, по сути, он при этом использует понятие "степень эмерджентности объекта", хотя в явном виде и не вводит его. Более того, он указывает на источник эмерджентности: – взаимодействие частей и связывает уровень системности или уровень системной организации со степенью взаимодействия этих частей.

В теории информации есть теорема, доказывающая, что энтропия системы в целом меньше суммы энтропии ее частей на величину взаимной информации частей друг о друге. Таким образом, можно утверждать, что способность системы к выбору прямо пропорциональная степени ее эмерджентности и самым непосредственным образом связана с ее способностью, противостоять действию закона возрастания энтропии.

Таким образом, и теоретико-информационное рассмотрение сложных активных самоорганизующихся систем, каким является человек и системы с участием человека, и рассмотрение квантовых систем, приводит к необходимости разработки эмерджентной теории информации, в которой используется обобщенное понятие информации, учитывающее эффект системности с помощью коэффициента эмерджентности.

Рассмотрим численный пример вычисления коэффициента эмерджентности для простого случая, когда все рассматриваемые места работы равновероятны. Пусть количество мест, куда может пойти работать выпускник после получения 1-й специальности будет равно: W₁=6, после получения 2-й специальности: W₂=10, а при одновременном получении обоих специальностей дополнительно появляется еще W=16 мест работы, откуда:

W₃= W₁+W₂+W =32

Тогда в 1-м случае, если мы узнаем, что выпускник устроился на определенное место работы, то мы получаем

I₁=Log₂W₁2,58 бит

информации, во 2-м случае, соответственно:

I₂=Log₂W₂3,32 бита

Но в 3-м случае мы получаем не

I₃=Log₂(W₁+W₂)=4 бита,

как можно было бы ожидать, если бы не было интерференции последствий, т.е. системного эффекта, а на 1 бит больше:

I₃=Log₂W₃=5 бит. (6)

Таким образом, при наблюдении за поведением объектов, при рассмотрении их как элементов некоторой системы, мы получаем больше информации, чем при рассмотрении их как автономных объектов, т.е. вне системы. Это можно объяснить тем, что дополнительная информация – это и есть информация о системе, о том, как она влияет на поведение своего элемента.

Указанные 16 дополнительных состояний (мест работы) выпускника в 3-м случае образовались за счет системного эффекта (эмерджентности) и являются "смешанными", образующимися за счет одновременного наличия у выпускника свойств, полученных при окончании и 1-й, и 2-й специальности, поэтому, учитывая выражения (4) и (5), получаем:

I₃=Log₂W₃= Log₂(W₁+W₂)^

Откуда:

Следовательно, одновременное окончание двух специальностей в рассмотренном случае дает системный эффект 1,25.

Таким образом, предлагаемый концептуальный подход к построению эмерджентной теории информации позволяет количественно учитывать системный эффект или эмерджентность непосредственно на уровне самого понятия "информация", что имеет большое значение для науки и практики применения теории информации и системного анализа для управления активными объектами.

Рассмотрим, что изложенный информационный подход может дать для оценки уровня системности квантовых объектов.

В 2002 году одним из авторов [97] было предложена идея, состоящая в том, что количество информации в системе больше количества информации во множестве образующих ее базовых элементов, т.к. подсистемы, состоящие из нескольких элементов, содержат информацию также как и базовые элементы [97]. Понятно, что базовые элементы также являются подсистемами, т.к. кроме систем в мире вообще ничего не существует, а подсистемы некоторого иерархического уровня системы, например, состоящие из m базовых элементов, могут рассматриваться как базовые элементы этого иерархического уровня [170, 196].

Если базовое множество содержит W элементов, то по Хартли количество информации, которое мы получаем, когда выбираем некоторый элемент, равно:

(7)

Если базовые элементы могут взаимодействовать друг с другом, то они могут образовывать подсистемы.

Здесь и возникают принципиальные вопросы о том:

– какие элементы могут образовывать подсистемы, а какие не могут;

– сколько подсистем различной сложности может быть образовано из W базовых элементов?

Ответы на эти вопросы зависят от того, какой квантовой статистике подчиняется образующаяся система.

Рассмотрим квантовую систему, состоящую из ряда подсистем, которые пронумеруем целым числом . Каждая подсистема характеризуется числом состояний и числом частиц , которые находятся в этих состояниях и обладают энергией . Определим число возможных способов распределения частиц по состояниям. В случае статистики Ферми в каждом состоянии может находиться не более чем одна частица, поэтому число способов равно[61]

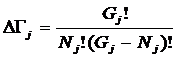(8)

В случае статистики Бозе в каждом состоянии может находиться любое число частиц, следовательно, число способов равно[62]

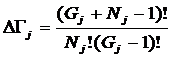(9)

Энтропия, общее число частиц и энергия системы равны по определению

(10)

Найдем числа , которые соответствуют экстремуму энтропии при условии постоянства общего числа частиц и энергии системы. Если число состояний и число частиц в каждой подсистеме достаточно велико, , то можно воспользоваться приближенной формулой для логарифма факториала . В этом случае выражение энтропии квантовых систем упрощается и принимает вид:

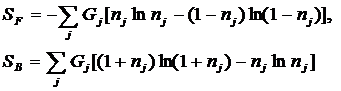(11)

Здесь первое выражение соответствует энтропии системы фермионов, а второе – системы бозонов.

Используя метод Лагранжа, составим функционал , где - некоторые постоянные. Экстремум энтропии достигается при условии

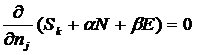
Отсюда находим два типа распределения

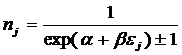(12)

Отметим, что знак плюс соответствует распределению Ферми, а знак минус – распределению Бозе.

Следовательно, в случае статистики Ферми на образование подсистем накладывается ограничение на число частиц, которые могут находиться в одном состоянии. С учетом этого ограничения все элементы базового множества могут образовывать подсистемы в любых сочетаниях, а их общее число определяется выражением (8), которое запишем в виде

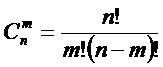(13)

Здесь n – число состояний системы; m – число частиц находящихся в этих состояниях.

Ясно, что при фиксированном числе состояний в системе могут быть подсистемы из 1, 2, 3, …, W элементов. При этом подсистемы из 1-го элемента это сами базовые элементы, а подсистема из W элементов – это вся система в целом (булеан) [7-8].

На всех иерархических уровнях системы от 1-го до W, суммарно будет содержаться общее число подсистем:

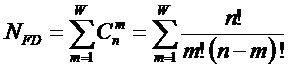(14)

В работе [97] предложено считать, что количество информации в системе можно рассчитывать по формуле Хартли (7), полагая, что элементами системы являются не только ее базовые элементы, но и состоящие из них подсистемы, количество которых в системе определяется выражением (14). Таким образом, количество информации в системе будет:

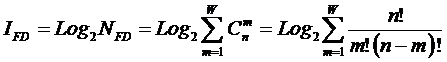(15)

Или окончательно:

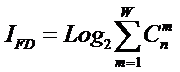(16)

Выражение (11) представляет собой системное обобщение формулы Хартли для количества информации в квантовой системе, подчиняющейся статистике Ферми-Дирака с заданным числом состояний и с переменным числом частиц.

В работе [97] предложено оценивать уровень системности или сложности системы отношением количества информации в системе (с учетом входящих в нее подсистем всех уровней иерархии) к количеству информации во множестве образующих ее базовых элементов:

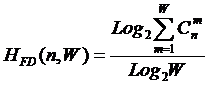(17)

Это выражение было названо в работе [97] коэффициентом эмерджентности Хартли, в честь этого выдающегося ученого, внесшего большой вклад в становление научной теории информации, а также потому, что в нем использовано классическое выражение Хартли для количества информации (7) и его системное обобщение (16).

На рис. 3 представлена зависимость коэффициента эмерджентности Хартли (17), представляющая собой поверхность. Отметим, что в области параметров , характерной для ядерных и атомных оболочек, коэффициент эмерджентности изменяется немонотонно с ростом W, что позволяет объяснить поведение энергии связи нуклонов в атомных ядрах[63].

Непосредственно из вида выражения для коэффициента эмерджентности Хартли (17) ясно, что он представляет собой относительное превышение количества информации в квантовой системе, подчиняющейся статистике Ферми-Дирака, при учете системных эффектов (смешанных состояний, иерархической структуры ее подсистем и т.п.) над количеством информации без учета системности.

Рис. 3. Поведение коэффициента эмерджентности Хартли в случае статистики Ферми-Дирака.

В работе [97] показано, что при n=W выражение (16) приобретает вид:

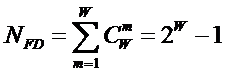(18)

Выражение (11) для количества информации в системе с учетом (18):

(19)

Выражение (19) дает оценку максимального количества информации, которое может содержаться в системе при условии вхождения всех элементов во все подсистемы различных уровней иерархической структуры, что на практике никогда не осуществляется (возможно, за исключением мира в целом).

Из выражения (19) видно, что I достаточно быстро стремится к W, поскольку

(20)

При W > 4 различие I и W в выражении (20) не превышает 1%. Таким образом, коэффициент эмерджентности Хартли (17) отражает уровень системности объекта, подчиняющегося статистике Ферми-Дирака. Этот коэффициент изменяется от 1 (системность минимальна, т.е. отсутствует) до W/Log₂W (системность максимальна).

Для каждого количества элементов системы существует свой максимальный уровень системности, который никогда реально не достигается из-за действия правил запрета на реализацию в системе ряда подсистем различных уровней иерархии. Например, не все сочетания букв русского алфавита образуют слова русского языка, и не все сочетания слов – предложения. В каждом состоянии может находиться только одна частица и т.п. По этой причине систему правил запрета в [97] предложено назвать информационным проектом системы. Различные системы, состоящие из равного количества одинаковых элементов, отличаются друг от друга именно по причине различия своих информационных проектов.

Одним из наиболее важных и известных в физике правил запрета, который действует на квантовые системы, подчиняющиеся статистике Ферми-Дирака, является принцип Паули. Это один из основополагающих принципов, влияющий на строение химических элементов, классифицированных в таблице Д. И. Менделеева[64] [201].

Таким образом, в работе [97] по сути, предложено системное обобщение формулы Хартли и коэффициент эмерджентности Хартли для случая квантовых систем, подчиняющихся статистике Ферми-Дирака. Однако статистике Ферми-Дирака подчиняются только квантовые системы с полуцелым спином, тогда как квантовые системы с целым спином описываются статистикой Бозе-Эйнштейна.

Для этой статистики число различных подсистем рассчитывается по формуле (9), которую запишем в форме

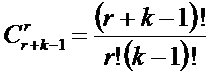(21)

Здесь k – число состояний, r – число частиц в системе. На всех иерархических уровнях квантовой системы, подчиняющейся статистике Бозе-Эйнштейна, от 1-го до W, суммарно будет содержаться общее число подсистем

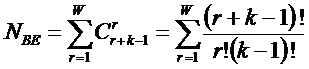(22)

Предположим, что количество информации в квантовой системе, подчиняющейся статистике Бозе-Эйнштейна, можно рассчитывать по формуле Хартли (7), полагая, что элементами системы являются не только ее базовые элементы, но и состоящие из них подсистемы, количество которых в системе определяется выражением (22). Таким образом, количество информации в такой квантовой системе, подчиняющейся статистике Бозе-Эйнштейна, будет:

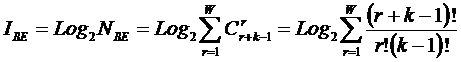(23)

Или окончательно:

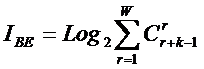(24)

Выражение (19) представляет собой системное обобщение формулы Хартли для количества информации в квантовой системе, подчиняющейся статистике Бозе-Эйнштейна.

Соответственно, выражение для коэффициента эмерджентности Хартли для случая квантовых систем, подчиняющихся статистике Бозе-Эйнштейна, будет иметь вид:

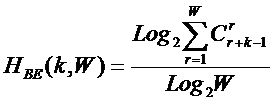(25)

На рис. 4 представлена зависимость коэффициента эмерджентности Хартли (25) в области параметров . Можно отметить существенное различие в поведении функции (25) и аналогичного коэффициента вычисленного для случая статистики Ферми-Дирака – см. рис. 3.

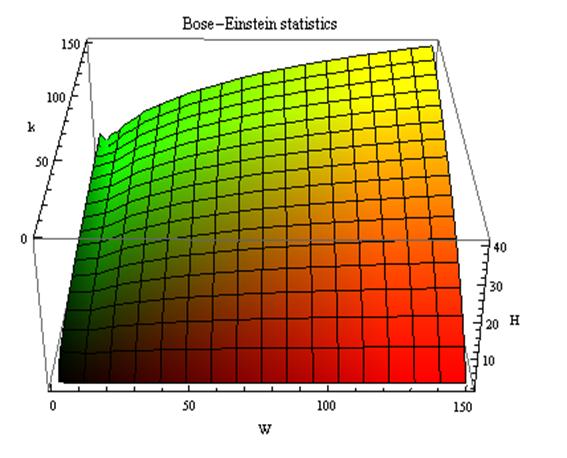
Рис. 4. Поведение коэффициента эмерджентности Хартли в случае статистики Бозе-Эйнштейна

Отметим, что обе квантовые статистики – и Ферми-Дирака, и Бозе-Эйнштейна, асимптотически приближаются к статистике Максвелла-Больцмана в пределе высоких температур и низких плотностей, что непосредственно следует из выражения (12). В случае статистики Максвелла-Больцмана число подсистем, которое можно образовать при заданном значении числа состояний определяется согласно[65] [5]

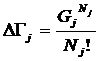(26)

Отсюда находим коэффициент эмерджентности классических систем в виде

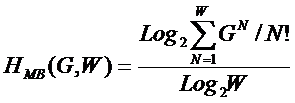(27)

Здесь N – число частиц, G – число состояний. На рис. 5 представлена зависимость (27) в области параметров . По характеру поведения коэффициент эмерджентности классических систем при малом числе состояний и частиц занимает промежуточное положение между аналогичными коэффициентами, вы численными для ферми- и бозе-систем – см. рис 3-4.

Рис. 5. Поведение коэффициента эмерджентности Хартли в случае статистики Максвелла-Больцмана

Наконец, рассмотрим поведение коэффициента эмерджентности всех трех систем для больших значений параметров числа состояний и частиц – рис. 6. Отметим, что максимальное число подсистем для данных, приведенных на рис. 6 составляет:

· статистика Ферми-Дирака - 3.50746621×10⁴⁵¹.

· статистика Бозе-Эйнштейна - 1.79196794×10⁹⁰¹.

· статистика Максвелла-Больцмана - 1.4015754×10⁶⁵¹.

При этом максимальное число состояний и частиц в каждом случае равно 1500. Общее число подсистем на всех уровнях иерархии, т.е. включающих по W=1, 2, 3, …, 10 элементов, для статистки Ферми-Дирака согласно выражения (14) для этого случая, т.е. при n=1500 уровней имеет вид:

{W, N_FD}

{1, 1500}

{2, 1125750}

{3, 562501250}

{4, 210657282125}

{5, 63071015719925}

{6, 15725776993138425}

{7, 3358594738459315425}

{8, 627221514672084598050}

{9, 104049830019224187006550}

{10, 15524360758047942656113900}

Все результаты, представленные на рис. 3-6, получены с использованием системы Wolfram Mathematica 9.0[66]. В этой системе максимальное число в вычислениях с плавающей точкой равно $MaxMachineNumber = 1.79769*10³⁰⁸. Максимальное же число, которое может быть представлено на компьютере, использованном в вычислениях приведенных выше данных, составляет $MaxNumber= 2.174188391646043*10^20686623745.

Рис. 6. Поведение коэффициента эмерджентности Хартли в случае классической и квантовой статистики. На правом нижнем рисунке поверхности коэффициента эмерджентности изображены для малого числа частиц и состояний

Из приведенных на рис. 6 данных следует, что с ростом числа состояний и числа частиц коэффициенты эмерджентности квантовых и классических систем отличаются между собой, как и коэффициенты квантовых систем ферми-частиц и бозе-частиц. Следовательно, коэффициент эмерджентности позволяет отличить классическую систему от квантовой системы, а квантовую систему ферми-частиц от квантовой системы бозе-частиц.

Полученные результаты могут оказаться полезными в молекулярной, атомной и ядерной физике, в физике высоких энергий в исследованиях структуры элементарных частиц, а также в математике, экономике, социологии, биологии и других науках, связанных с исследованием сложных систем [12-23].

Из рисунка 6 видно, что для коэффициента эмерджентности Хартли квантовых объектов, подчиняющихся статистике Ферми-Дирака (фермионов), существует максимум при примерно 650 частицах-элементах, а для бозонов и классических объектов подобного максимума не существует. В работе [196] обосновывается универсальный информационный вариационный принцип, согласно которому объекты выбирают путь изменения и развития [170], который приводит к наиболее быстрому возрастанию количеству содержащейся в них информации и их уровня системности. На основании этих двух положений можно сформулировать гипотезу, согласно которой уровень системности системы, которую можно создать из определенного количества частиц, будет выше для системы подчиняется статистике Бозе-Эйнштейна или классической Максвелла-Больцмана, и ниже – если статистике Ферми-Дирака, поэтому количество и размеры бозонов и классических объектов во вселенной должны превосходить количество и размеры фермионов.

10.4. Системное обобщение операций над множествами (на примере операции объединения булеанов) и обобщения локального коэффициента эмерджентности Хартли

В работе [240] рассматривается реализация математической операции объединения систем, являющаяся обобщением операции объединения множеств в рамках системного обобщения теории множеств. Эта операция сходна с операцией объединения булеанов классической теории множеств. Но в отличие от классической теории множеств в ее системном обобщении предлагается конкретный алгоритм объединения систем и обосновывается количественная мера системного (синергетического, эмерджентного) эффекта, возникающего за счет объединения систем. Для этой меры предложено название: «Обобщенный коэффициент эмерджентности Р. Хартли» из-за сходства его математической формы с локальным коэффициентом эмерджентности Хартли и отражающим степень отличия системы от множества её базовых элементов[67]. Приводится ссылка на авторскую программу, реализующую предложенный алгоритм и обеспечивающую численное моделирование объединения систем при различных ограничениях на сложность систем и при различной мощности порождающего множества, приводятся некоторые результаты численного моделирования.

В работе [241] предлагается общее математическое выражение для количественной оценки системного (синергетического) эффекта, возникающего при объединении булеанов (систем), являющихся обобщением множества в системном обобщении теории множеств и независящее от способа (алгоритма) образования подсистем в системе. Для этой количественной меры предложено название: «Обобщенный коэффициент эмерджентности Р.Хартли» из-за сходства его математической формы с локальным коэффициентом эмерджентности Хартли, отражающим степень отличия системы от множества его базовых элементов. Для локального коэффициента эмерджентности Хартли также предложено обобщение, независящее от способа (алгоритма) образования подсистем в системе. Приводятся численные оценки системного эффекта при объединении двух систем с применением авторской программы, на которую дается ссылка.

В работе [240] в общем виде сформулирована, обоснована и предложена программная идея системного обобщения математики, суть которой состоит в тотальной замене понятия "множество" на более общее понятие "система" и прослеживании всех математических последствий этого во всех разделах математики, основанных на теории множеств или использующих ее результаты. При этом обеспечивается соблюдение принципа соответствия, обязательного для более общей теории, т.к. чем ниже уровень системности, тем в меньшей степени система отличается от множества, а система с нулевым уровнем системности тождественно и есть множество. В работах [189, 191] приводится неформальная постановка и обсуждение задач, возникающих при системном обобщении теории множеств. В работе [97] обосновываются количественные меры уровня системности (эмерджентности, синергетического или системного эффекта[68] [170, 253, 270]). В работе [97] приводится развернутый пример реализации этой программной идеи системного обобщения математики, в качестве которого выступает предложенная автором системная теория информации.

10.4.1. Реализация операции объединения систем в системном
обобщении теории множеств (объединение булеанов)

Данный раздел основан на работах [240, 241] и посвящен разработке подхода к решению 9-й задачи, сформулированной в [189, 191]: «Разработать операции с системами: объединение (сложение), пересечение (умножение), вычитание. Привести предварительные соображения по реализации операции объединения систем».

В классической теории множеств, которую мы далее сокращенно будем называть «КТМ», операция объединения множеств реализуется следующим образом. «Объединение множеств (тж. сумма или соединение) [69] в теории множеств – множество, содержащее в себе все элементы исходных множеств. Объединение двух множеств A и B обычно обозначается , но иногда можно встретить запись в виде суммы A + B». Графически операция объединения двух множеств может быть представлена в форме диаграммы Эйлера-Венна, приведенной на рисунке 1.

Рисунок 1. Диаграмма Эйлера-Венна объединения двух множеств[70]

При объединении двух множеств с мощностями A и B образуется множество, включающее все элементы как 1-го, так и 2-го множеств с мощностью N_k, которая является просто суммой числа элементов 1-го и 2-го множеств:

(1)

(2)

В теории множеств выражения (1) и (2) считаются эквивалентными. Однако выражение (1) внешне выглядит так же, как арифметическое сложение двух количественных величин, которое совпадает по смыслу с объединением множеств только для непересекающихся множеств. Если же множества пересекаются, т.е. одно множество включают некоторые элементы, которые тождественны элементам другого множества, то при сложении эти элементы повторяются в сумме, а при объединении этих повторений в объединенном множестве нет (рисунок 2):

Рисунок 2. Диаграмма Эйлера-Венна пересечения двух множеств[71]

Особенно наглядно различие между арифметическим сложением и объединением видно, когда эти операции выполняются над тождественными множествами 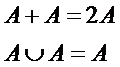(3):

(3)

Запись операции объединения множеств с использованием операции арифметического сложения их мощностей предполагает вычитание мощности пересечения множеств из арифметической суммы с целью исключения повторения тождественных элементов (4):

(4)

где: N_k – мощность объединенного множества.

Для непересекающихся множеств:

(5)

и в этом случае выражение (4) с учетом (5) приобретает вид (1) уже не только символически, но и фактически (арифметически).

По мнению автора это означает, что символика выражения (2) точнее или более удачно отражает смысл объединения множеств и его использование предпочтительнее.

В отличие от множеств, системы имеют иерархическое строение. Будем считать, что 1-м уровнем иерархии системы является множество базовых элементов, которое будем называть порождающим множеством.

В случае объединения двух систем, согласно системной теории множеств (СТМ), на втором и более высоких уровнях иерархии [189, 191] объединенной системы могут возникать новые составные элементы, которых до объединения не было ни в одной из исходных систем и состоящие из элементов обоих систем, что и приводит к системному эффекту S. В результате мощность объединения систем превосходит мощность объединения их порождающих множеств A и B на величину системного эффекта S, возникающего за счет объединения систем:

(6)

Кроме того, в каждой из систем могут возникать составные элементы из ее собственных базовых элементов. Это приводит к системному эффекту, в результате которого система отличается от множества, т.е. содержит больше элементов, чем в порождающем множестве. Этот вид системного эффекта аналитически выражается локальным коэффициентом эмерджентности Хартли (3), который был получен автором в 2001 году [97] и назван так в честь этого ученого, внесшего большой вклад с разработку научной теории информации[72]:

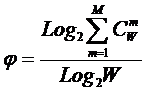(7)

где:

W – количество базовых элементов в системе;

m – сложность составного элемента системы, т.е. подсистемы (количество базовых элементов в составном элементе);

M – максимальная сложность подсистем (максимальное количество базовых элементов в составном элементе).

Фактически максимальная сложность подсистем M не может быть больше количества базовых элементов в системе W: , т.к. самым сложным элементом системы может быть элемент, состоящий из всех базовых элементов. Но формально это ограничение можно не соблюдать, т.к. при согласно выражения (7) будут получаться нулевые слагаемые под логарифмом в числителе, отражающие тот факт, что соответствующих составных элементов просто не существует. Поэтому за соблюдением этого условия можно особо не следить и математически объединять выражения, указывая один максимальный уровень сложности из всех возможных при различных количествах базовых элементов в разных системах, что пригодится нам в будущем.

Будем считать, что составные элементы в системах не могут образовываться за счет многократного использования одних и тех же базовых элементов в одном составном (повторений):

– это предполагается самим видом математического выражения (7) и понятием комбинаторики «число сочетаний из n по m»;

– в противном случае уровень сложности элементов и системы в целом, а также ее мощность, могли бы неограниченно возрастать, например, за счет наличия в системе элементов, представляющих собой сколь угодно высокую степень любого из базовых элементов.

Коэффициент эмерджентности Хартли исследован автором в ряде работ, в частности [97, 170]. Непосредственно из вида выражения для коэффициента эмерджентности Хартли (7) ясно, что он представляет собой относительное превышение количества информации в системе при учете системных эффектов (смешанных состояний, иерархической структуры ее подсистем и т.п.) над количеством информации без учета системности (только в базовом уровне или порождающем множестве), т.е. этот коэффициент отражает уровень системности объекта.

Получим аналитические выражения для количества элементов в объединенной системе и величины системного эффекта, образующегося не за счет объединения базовых элементов в отдельно-взятой системе (что отражается локальным коэффициентом эмерджентности Хартли), а за счет объединения систем, а затем проведем и количественные оценки с использованием этих выражений и численного моделирования.

Аксиома о максимальной мощности системы системной теории множеств (СТМ) и СТИ [97]: в системе, основанной на множестве из W неповторяющихся элементов, которые мы будем называть базовыми, может содержаться не более N_max элементов, включающих как все базовые элементы, так и составные элементы (подсистемы), образованные из всех возможных различных сочетаний базовых элементов по 2, 3, …, W элементов (без повторений):

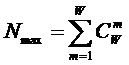(8)

Эта аксиома СТМ аналогична аксиоме булеана[73] классической теории множеств, в которой постулируется существование и единственность множества всех подмножеств некоторого множества из W элементов, т.е. булеана, а также доказывается[74], что мощность булеана равна 2^W.

В этой связи необходимо сделать два замечания.

Замечание 1: мощность системы, базирующейся на W элементах, всегда на 1 меньше мощности булеана, образованного на тех же элементах:

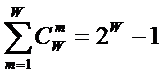(9)

Это связано с тем, что по определению булеан включает как элемент самого себя, а система не включает в качестве элемента саму себя, но включает элемент наивысшего уровня сложности (иерархии), состоящий из всех базовых элементов, т.е. в систему входит элемент: «Система-в-целом».

Замечание 2: в самой аксиоме булеана классической теории множеств не содержится алгоритма или способа нахождения всех элементов образуемого множества, но такой алгоритм предлагается в рамках СТМ и его идея основана на аксиоме о максимальной мощности системы: это алгоритм формирования всех возможных различных (без повторений) сочетаний базовых элементов системы. Подобные алгоритмы известны[75] и поэтому здесь не приводятся.

Однако, фактически количество элементов в системе всегда меньше максимального, т.к. действуют определенные правила запрета на образование некоторых составных элементов [97][76]. Среди таких правил запрета могут быть, например, ограничения на максимальное (или/и минимальное) количество базовых элементов в составных элементах (т.е. на их сложность), а также запрет на повторное включение базовых элементов в составные (когда один и тот же базовый элемент не может несколько раз входить в один и тот же составной элемент).

Если система образована на основе W базовых элементов, то в ней существует M уровней иерархии, на 1-м из которых находятся сами базовые элементы и этот уровень иерархии системы тождественно является порождающему множеству, на 2-м – составные элементы, образованные различными сочетаниями базовых элементов по 2, на 3-м – по 3, и на последнем – по M. Если количество уровней иерархии в системе M (будем называть его рангом системы) равно количеству ее базовых элементов W, то все базовые элементы входят в единственный элемент наивысшего уровня иерархии. В системе отсутствуют составные элементы, включающие больше базовых элементов, чем ранг системы.

Чтобы учесть в выражении (7) 1-е ограничение (на максимальную сложность составных элементов M) и получить выражение для количества элементов в системе ранга M, модифицируем его следующим образом:

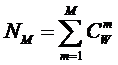(10)

В частности, если есть два множества, в 1-м из которых A элементов, а во 2-м – B, то согласно системной теории множеств (СТМ) на базе 1-го множества образуется система с числом элементов N_A:

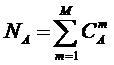, (11)

а на базе 2-го – с числом элементов N_B:

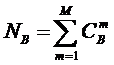, (12)

В случае объединения этих 2-х систем по правилам классической теории множеств (КТМ) (4), т.е. считая систему множеством всех ее элементов: и базовых, и составных, количество элементов в объединенной системе N_k равно просто сумме числа элементов 1-й и 2-й систем (11) и (12), как в случае множеств:

(13)

где:

N_A – множество всех элементов (базовых и составных) системы A;

N_B – множество всех элементов (базовых и составных) системы B.

Выражение (13) является системным аналогом теоретико-множественного выражения (4), но проще его записать аналогично (2):

(14)

Подставим в выражение (14) переменные N_A и N_B из (11) и (12):

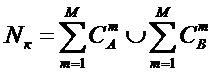(15)

В выражении (15) все элементы систем A и B (базовые и составные) по сути, рассматриваются как элементы множеств. Операторы суммирования вычисления количества сочетаний в выражении (15) понимаются не как арифметические операторы, а как символические порождающие операторы теории множеств, которые содержат обобщенное аналитическое описание алгоритма генерации элементов систем на базе порождающих множеств A и B.

Однако в системной теории множеств в случае объединения 2-х и более систем возникает системный (синергетический) эффект, состоящий в отклонении от аддитивности (6), т.е. в том, что сумма элементов в объединенной системе (16) превосходит[77] сумму элементов в исходных системах (15). Математически это можно выразить, добавив в выражение (15) еще одно слагаемое S, отражающее системный эффект:

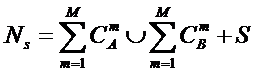(16)

Это слагаемое S равно числу тех составных элементов объединенной системы, которые могли возникнуть только в результате объединения этих 2-х систем, т.е. которые включают элементы как 1-й, так 2-й систем, и которых до объединения этих систем не было и не могло быть ни в одной из них.

Например, при объединении 2-х систем, содержащих на 1-м уровне иерархии простые числа, а на 2-м уровне составные числа, являющиеся произведениями различных пар простых сомножителей, образуется объединенная система, 1-й уровень которой является объединением 1-х уровней исходных систем, а 2-й образуется по тому же алгоритму, что и в них (рисунок 3):

Рисунок 3. Объединение 2-х систем из простых чисел на базовом уровне и сложных чисел, образованных из пар простых, на 2-м уровне[78]

Может возникнуть впечатление, что пример объединения символических числовых систем носит какой-то абстрактный и узко-специальный характер и не имеет отношения к реальным системам. Но это не так, что ясно уже из того, что элементы базового уровня реальных систем в самых разных предметных областях могут быть закодированы с помощью простых чисел, а их составные элементы, образованные из базовых – соответствующими составными числами, образованными этими простыми сомножителями, и между этими числовыми кодами и элементами реальных систем будет установлено взаимно-однозначное соответствие. Таким образом, рассматриваемую в данном примере символическую систему можно рассматривать как универсальную и адекватную модель реальных систем. Так если закодировать элементы таблицы Д.И.Менделеева простыми числами, то различным образованным из них химическим соединениям будут соответствовать сложные числа, образованные произведениями соответствующих простых сомножителей. Аналогично, если символам алфавита поставить в соответствие простые числа, то словам будут соответствовать числа, представляющие собой их произведения[79]. Если же взять логарифм от составного числа, то он будет равен сумме логарифмов его простых сомножителей (что соответствует переходу к логарифмической шкале и в некоторых случаях удобнее, т.к. размер чисел меньше и мультипликативность взаимно-однозначно заменяется аддитивностью).

В таблицах 1–4 приведены данные о том, какие составные числа произведениями каких простых являются в рассматриваемом примере:

Таблица 1 – СОСТАВ ЭЛЕМЕНТОВ 1-Й СИСТЕМЫ

Элемент	Уровень иерархии	Простые сомножители
		1-й	2-й
2	1	2
3	1	3
5	1	5
7	1	7
6	2	2	3
10	2	2	5
14	2	2	7
15	2	3	5
21	2	3	7
35	2	5	7

Таблица 2 – СОСТАВ ЭЛЕМЕНТОВ 2-Й СИСТЕМЫ

Элемент	Уровень иерархии	Простые сомножители
		1-й	2-й
11	1	11
13	1	13
17	1	17
19	1	19
143	2	11	13
187	2	11	17
209	2	11	19
221	2	13	17
247	2	13	19
323	2	17	19

Таблица 3 – СОСТАВ ЭЛЕМЕНТОВ ОБЪЕДИНЕННОЙ СИСТЕМЫ

Элемент	Уровень иерархии	Простые сомножители
		1-й	2-й
2	1	2
3	1	3
5	1	5
7	1	7
11	1	11
13	1	13
17	1	17
19	1	19
6	2	2	3
10	2	2	5
14	2	2	7
22	2	2	11
26	2	2	13
34	2	2	17
38	2	2	19
15	2	3	5
21	2	3	7
33	2	3	11
39	2	3	13
51	2	3	17
57	2	3	19
35	2	5	7
55	2	5	11
65	2	5	13
85	2	5	17
95	2	5	19
77	2	7	11
91	2	7	13
119	2	7	17
133	2	7	19
143	2	11	13
187	2	11	17
209	2	11	19
221	2	13	17
247	2	13	19
323	2	17	19

Таблица 4 – СОСТАВ ЭЛЕМЕНТОВ ПОДСИСТЕМЫ ОБЪЕДИНЕННОЙ СИСТЕМЫ, СОДЕРЖАЩЕЙ ЭЛЕМЕНТЫ, ОБРАЗОВАННЫЕ ЗА СЧЕТ СИСТЕМНОГО ЭФФЕКТА

Элемент	Уровень иерархии	Простые сомножители
		1-й	2-й
22	2	2	11
26	2	2	13
34	2	2	17
38	2	2	19
33	2	3	11
39	2	3	13
51	2	3	17
57	2	3	19
55	2	5	11
65	2	5	13
85	2	5	17
95	2	5	19
77	2	7	11
91	2	7	13
119	2	7	17
133	2	7	19

Числа, показанные на рисунке 3 черным цветом на 2-м уровне объединенной системы, есть на 2-м уровне либо 1-й системы, либо 2-й. Если бы системы объединялись как множества, то никаких других элементов на 2-м уровне объединенной системы и не было бы. Но при объединении систем в объединенной системе могут возникать элементы, образованные из сочетаний базовых элементов нескольких исходных систем одновременно, которых не было в исходных системах и которые могли образоваться только в объединенной системе. В нашем примере на рисунке 3 это числа, показанные более крупным шрифтом и красным цветом на 2-м уровне объединенной системы, образованные из различных пар простых чисел, одно из которых принадлежит 1-й системе, а 2-е – второй (см. таблицы 1–4).

Получим аналитическое выражение для этого числа элементов S. У нас уже есть одно выражение для мощности объединенной системы (16). Чтобы найти S, необходимо иметь еще одно независимое от выражения (16) выражение для N_s. Это выражение (17) совершенно аналогично выражениями (11) и (12), т.е. число всех элементов N_s в объеденной системе равно:

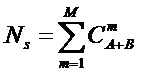(17)

или точнее:

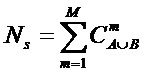(18)

Выражения (17) и (18) эквивалентны и являются системным обобщением соответственно выражений (1) и (2) классической теории множеств в рамках СТМ.

При уменьшении сложности системы M система все в меньшей степени отличается от множества своих базовых элементов и при M=1 система переходит в это множество (т.к. составных элементов в нем нет) и выражение (16) преобразуется в (4):

(19)

т.е. преобразуется в выражение (4). Это и означает выполнение принципа соответствия[80] между системным обобщением теории множеств (СТМ) и классической теорией множеств (КТМ), когда на основе базовых элементов множеств не создаются составные элементы, т.е. при уровне системности равном 1. Необходимо отметить, что выполнение принцип соответствия является обязательным для более общей теории, и системное обобщение теории множеств удовлетворяет этому принципу.

Если найти S из выражения (16) и подставить в него выражение N_S из выражения (18), то получим:

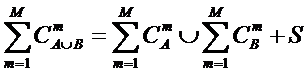(19)

откуда:

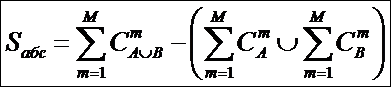(20)

Выражения (19) и (20) представляют собой искомые выражения для абсолютной величины системного эффекта, образующегося за счет объединения 2-х систем без повторяющихся элементов с правилом запрета в форме ограничения на максимальную сложность подсистем (составных элементов) или количество уровней иерархии в системе, равным M.

Обобщим выражения (19) и (20) на произвольное количество систем. Пусть дано не 2 системы, а семейство систем: . Как уже отмечалось выше в выражениях (20) и (21) в качестве значения M можно взять максимальный из уровней сложности всех систем:

⁽²²⁾

^{где: – уровень сложности системы . Тогда для случая многих систем выражения (20) и (21) обобщаются следующим образом:}

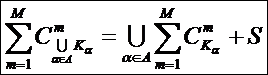(23)

В формуле (23) использованы символика и обозначения из статьи[81]. Непосредственно из (23) получаем выражение для величины системного эффекта S, получаемого при объединении систем семейства :

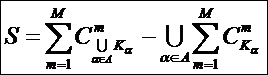(24)

Итак, абсолютная величина системного эффекта, образующегося за счет объединения систем, равна количеству составных элементов (подсистем), которые включают базовые элементы обоих систем и, следовательно, могут образоваться только после этого объединения.

Однако проблема интерпретации и оценки абсолютной величины системного эффекта (20) состоит в том, что по самому этому количеству сложно понять, большое оно, среднее или незначительное, т.к. его не с чем сравнивать, т.е. нет базы сравнения. В качестве естественной базы сравнения предлагается использовать суммарное количество элементов в исходных системах до объединения.

В результате получим выражение для относительной величины системного эффекта, образующегося за счет объединения 2-х систем с правилом запрета в форме ограничения на максимальную сложность подсистем (составных элементов), равным M:

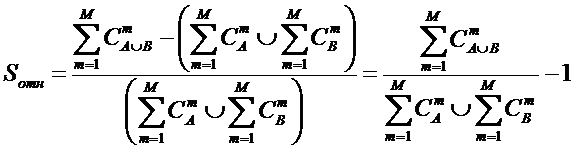
Или окончательно:

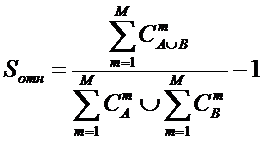(25)

Обратим внимание на то, что, как и в параметре ROI[82], вычитание 1 из отношения является одним из способов нормировки выражения, равного 1 к 0 при отсутствии системного эффекта, что более естественно и лучше приспособлено для его использования в качестве частного критерия в аддитивном интегральном критерии. Другим способом нормировки, дающим тот же результат (с точностью до единиц измерения), является взятие логарифма из этого отношения:

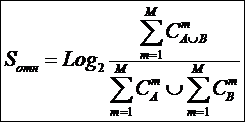(26)

Этот вариант более интересен чем (25) из-за прозрачной аналогии с формулой А.Харкевича для количественной меры семантической целесообразности информации, что позволяет привлечь для исследований в области СТМ богатейший идейный арсенал теории информации, ее применения для управления и управления знаниями.

Обобщение выражения (26) на произвольное количество систем семейства: :

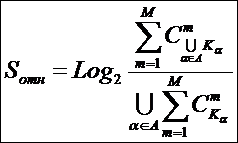⁽²⁷⁾

Рассмотрим связь системного обобщения теории множеств с теорией информации.

Понятие информации тесно связано с комбинаторными представлениями. По Р.Хартли[83] количество информации I, получаемое при идентификации элемента множества мощностью W при равновероятной встрече различных элементов, равно:

(28)

К.Шенноном на основе статистического подхода выражение Р.Хартли обобщено на случай неравновероятных событий[84]. А.Н.Колмогоров развил комбинаторный и алгоритмический подход к понятию сложности системы и на его основе разработал новое определение понятия информации и также получил формулу К.Шеннона[85], причем по некоторым данным даже значительно раньше самого К.Шеннона.

С современной точки зрения понятие информации теснейшим образом связано с понятием множества. Поэтому совершенно естественной выглядит мысль исследовать как меняется понятие информации при реализации программной идеи системного обобщения математики [186], т.е. в результате замены понятия множества более общим понятием системы. В работе [97] и ряде других [см.: 97-280] исследованы некоторые следствия реализации этой программы в теории информации. Продолжим эту работу с использованием результатов, полученных в данном разделе.

Если формулу (28) применить к системе, основанной на W базовых элементов с M уровней иерархии (10), то получим:

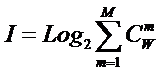(29)

Выражение (29) предложено автором в 2001 году и исследовано в работе [97]. Из применения выражения (29) для расчета количества информации, содержащегося в объединенной системе (18) и в исходных системах, рассматриваемых совместно как множества (15), следует выражение для количества информации, получаемого при идентификации элемента подсистемы, возникшей за счет системного эффекта при объединении двух подсистем:

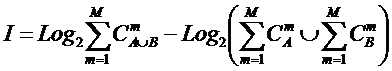(30)

Отметим, что из выражения (30) непосредственно вытекает (31)[86]:

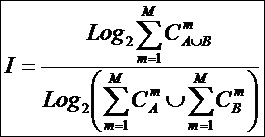(31)

Это и есть окончательное выражение для количества информации, получаемого при идентификации элемента подсистемы, возникшей за счет системного эффекта при объединении двух подсистем.

По своей математической форме выражение (31) очень напоминает коэффициент эмерджентности Хартли (7), отражающий уровень системности локальной системы, т.е. степень ее отличия от множества. Поэтому у нас есть все основания назвать выражение (31) обобщенным коэффициентом эмерджентности Хартли, который показывает степень отличия объединения систем от исходных систем за счет системного эффекта, возникающего за счет этого объединения.

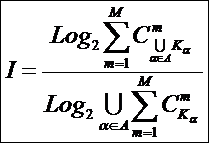Полученные выражения стандартно обобщаются на случай объединения многих систем. Например, выражение (31) для случая объединения систем семейства принимает вид (32):

⁽³²⁾

Все полученные выражения стандартно обобщаются также на непрерывный случай путем замены факториалов при расчете числа сочетаний на гамма-функции [1].

Рассмотрим примеры объединения систем, в т.ч. численные.

Наиболее яркие примеры системного эффекта, возникающего при объединении систем, можно наблюдать в процессе биологической эволюции. Логично предположить, что если системный эффект, возникающий за счет объединения двух систем (31), например, при оплодотворении, настолько велик, что сопоставим с уровнем системности локальной системы (7), аналогичной исходным, то за счет этого системного эффекта могут возникать новые локальные системы, подобные исходным 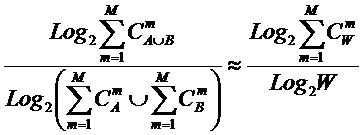(33):

(33)

На рисунке 4 приведен простой генетический алгоритм (ГА), являющийся моделью биологической эволюции [196]. Работа ГА представляет собой итерационный процесс, который продолжается до тех пор, пока поколения не перестанут существенно отличаться друг от друга, или не пройдет заданное количество поколений или заданное время. Для каждого поколения реализуются отбор, кроссовер (скрещивание), мутация и генерация следующего поколения. В этом алгоритме есть этапы, на которых проявляются системные эффекты, связанные с появлением следующего поколения в результате объединения особей предыдущего поколения. Рассмотрим этот алгоритм.

Рисунок 4. Простой генетический алгоритм

Шаг 1: генерируется начальная популяция, состоящая из N особей со случайными наборами признаков.

Шаг 2 (борьба за существование): вычисляется абсолютная приспособленность каждой особи популяции к условиям среды f(i) и суммарная приспособленность особей популяции, характеризующая приспособленность всей популяции. Затем при пропорциональном отборе для каждой особи вычисляется ее относительный вклад в суммарную приспособленность популяции P_s(i), т.е. отношение ее абсолютной приспособленности f(i) к суммарной приспособленности всех особей популяции 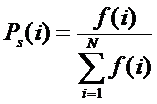(34):

(34)

В выражении (34) сразу обращает на себя внимание возможность сравнения абсолютной приспособленности i-й особи f(i) не с суммарной приспособленностью всех особей популяции, а со средней абсолютной приспособленностью особи популяции 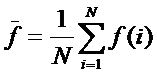(35):

(35)

Тогда получим 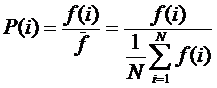(36):

(36)

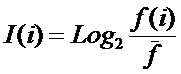Если взять логарифм по основанию 2 от выражения (36), т.е. перейти к логарифмической шкале (что соответствует закону Фехнера[87]), то получим количество информации, содержащееся в признаках особи о том, что она выживет и даст потомство (37):

(37)

Необходимо отметить, что эта формула совпадает с формулой для семантического количества информации А.Харкевича, если «целью» биологической эволюции считать индивидуальное выживание и продолжение рода (выживание вида). Это значит, что даже чисто формально приспособленность особи представляет собой количество информации, содержащееся в ее фенотипе о продолжении ее генотипа в последующих поколениях.

Поскольку количество потомства особи пропорционально ее приспособленности, то естественно считать, что если это количество информации:

– положительно, то данная особь выживает и дает потомство, численность которого пропорциональна этому количеству информации;

– равно нулю, то особь доживает до половозрелого возраста, но потомства не дает (его численность равна нулю);

– меньше нуля, то особь погибает до достижения половозрелого возраста.

Таким образом, можно сделать фундаментальный вывод, имеющий даже мировоззренческое звучание, о том, что естественный отбор представляет собой процесс генерации, накопления и передачи от прошлых поколений к будущим информации о выживании и продолжении рода в ряде поколений популяции, как системы.

Это накопление информации происходит на различных уровнях иерархии популяции, как системы, включающей:

– элементы системы: отдельные особи;

– взаимосвязи между элементами: отношения между особями в популяции, обеспечивающие передачу последующим поколениям максимального количества информации об их выживании и продолжении рода (путем скрещивания наиболее приспособленных особей и наследования рациональных приобретений);

– цель системы: сохранение и развитие популяции, реализуется через цели особей: индивидуальное выживание и продолжение рода.

Фенотип соответствует генотипу и представляет собой его внешнее проявление в признаках особи в условиях фактической среды. Особь взаимодействует с окружающей средой и другими особями в соответствии со своим фенотипом. В случае, если это взаимодействие удачно, то особь передает генетическую информацию, определяющую фенотип, последующим поколениям.

Шаг 3: начало цикла смены поколений.

Шаг 4: начало цикла формирования нового поколения.

Шаг 5 (отбор): осуществляется пропорциональный отбор особей, которые могут участвовать в продолжении рода. Отбираются только те особи популяции, у которых количество информации в фенотипе и генотипе о выживании и продолжении рода положительно, причем вероятность выбора пропорциональна этому количеству информации.

Шаг 6 (кроссовер): отобранные для продолжения рода на предыдущем шаге особи с заданной вероятностью P_c подвергаются скрещиванию или кроссоверу (рекомбинации). Если кроссовер происходит, то потомки получают по половине случайным образом определенных признаков от каждого из родителей.

Численность потомства пропорциональна суммарной приспособленности родителей, т.е. величине системного эффекта, возникающего за счет их объединения в систему 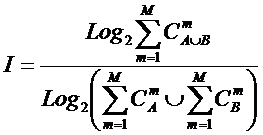(38).

(38)

В некоторых вариантах ГА потомки после своего появления заменяют собой родителей и переходят к мутации. Если кроссовер не происходит, то исходные особи – несостоявшиеся родители, переходят на стадию мутации.

Шаг 7 (мутация): выполняются операторы мутации. При этом признаки потомков с вероятностью P_m случайным образом изменяются на другие. Отметим, что использование механизма случайных мутаций роднит генетические алгоритмы с таким широко известным методом имитационного моделирования, как метод Монте-Карло.

Шаг 8 (борьба за существование): оценивается приспособленность потомков (по тому же алгоритму, что и на шаге 2).

Шаг 9: проверяется, все ли отобранные особи дали потомство.

Если нет, то происходит переход на шаг 5 и продолжается формирование нового поколения, иначе – переход на следующий шаг 10.

Шаг 10: происходит смена поколений:

– потомки помещаются в новое поколение;

– наиболее приспособленные особи из старого поколения переносятся в новое, причем для каждой из них это возможно не более заданного количества раз;

– полученная новая популяция замещает собой старую.

Шаг 11: проверяется выполнение условия останова генетического алгоритма. Выход из генетического алгоритма происходит либо тогда, когда новые поколения перестают существенно отличаться от предыдущих, т.е., как говорят, "алгоритм сходится", либо когда пройдено заданное количество поколений или заданное время работы алгоритма (чтобы не было "зацикливания" и динамического зависания в случае, когда решение не может быть найдено в заданное время ).

Если ГА сошелся, то это означает, что решение найдено, т.е. получено поколение, идеально приспособленное к условиям данной фиксированной среды обитания.

Иначе – переход на шаг 4 – начало формирования нового поколения.

В реальной биологической эволюции этим дело не ограничивается, т.к. любая популяция кроме освоения некоторой экологической ниши пытается также выйти за ее пределы освоить и другие ниши, как правило "смежные". Именно за счет этих процессов жизнь вышла из моря на сушу, проникла в воздушное пространство и поверхностный слой почвы, а сейчас осваивает космическое пространство.

Рассмотрим второй пример с объединением систем натуральных чисел, основанных на базовых элементах, являющихся простыми числами. Для этого автором разработана программа, которая обеспечивает:

1. Задание в диалоге двух диапазонов простых чисел, являющихся базовыми элементами 1-й и 2-й систем, а также задание диапазона изменения M (ограничения на сложность подсистем - составных чисел).

Для всех M:

2. Генерацию простых чисел без повторов в заданных диапазонах, являющихся соответственно базовыми элементами 1-й и 2-й системы.

3. Объединение множеств простых чисел, являющихся базовыми элементами 1-й и 2-й систем, и формирование множества базовых элементов объединенной системы (без повторов).

4. Генерацию на основе простых чисел, являющихся базовыми элементами 1-й и 2-й системы, составных натуральных чисел, являющихся произведениями 2, 3,..., M простых чисел и образующих вместе с базовыми простыми числами 1-ю и 2-ю системы.

5. Генерацию на основе простых чисел, являющихся базовыми элементами объединенной системы, составных натуральных чисел, являющихся произведениями 2, 3,..., M простых чисел и образующих вместе с базовыми простыми числами объединенную систему.

6. Поиск в объединенной системе составных чисел, которых нет ни в одной из исходных систем. Эти числа и составляют новую подсистему, образование которой и представляет собой системный эффект, возникающий при этом объединении, нарушающую аддитивность объединения систем и отличающую операцию объединения систем в системном обобщении теории множеств от объединения множеств в классической теории множеств.

7. Количественный расчет коэффициентов эмерджентности Хартли для 1-й, 2-й и объединенной локальных систем и обобщенного коэффициента эмерджентности Хартли, отражающего величину системного эффекта, возникающего при объединении этих двух числовых систем, образованных на простых числах заданных диапазонов. Печать поэлементного состава 1-й, 2-й и объединенной систем, а также подсистемы системного эффекта по уровням иерархии

8. Исследование зависимости системного эффекта от различных параметров объединяемых систем (количества базовых элементов, уровня сложности систем и других).

Экранная форма этой программы приведена на рисунке 5:

Рисунок 4. Экранная форма программы численного моделирования
объединения систем натуральных чисел, основанных на базовых элементах,
являющихся простыми числами

Исполнимый модуль, исходный текст (на языке программирования CLIPPER 5.01) и численный пример применения программы, моделирующий объединение 2-х систем с различными уровнями сложности приведены автором по адресу: http://www.twirpx.com/file/370725/.

Рассмотрим численные примеры объединения двух систем, смоделированные с помощью приведенной программы при различных параметрах.

При запуске программы с указанными ниже параметрами она формирует выходной файл с именем System.txt (считывается MS Word как DOS Text), приведенный ниже.

Объединение двух систем натуральных чисел, основанных

на базовых элементах, являющихся простыми числами,

при разных уровнях сложности систем.

(Системное обобщение теории множеств. Е.В.Луценко)

Диапазон базовых элементов 1-й системы: 2-10

Диапазон базовых элементов 2-й системы: 11-20

Диапазон уровней сложности: 1-7

УРОВЕНЬ СЛОЖНОСТИ=1

1-Я СИСТЕМА === Sys_1.dbf ============================

1-й уровень иерархии. Кол-во элементов=4

2 3 5 7

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=4, из них базовых: 4

Локальный коэффициент эмерджентности Хартли=1.0000000

======================================================

2-Я СИСТЕМА === Sys_2.dbf ============================

1-й уровень иерархии. Кол-во элементов=4

11 13 17 19

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=4, из них базовых: 4

Локальный коэффициент эмерджентности Хартли=1.0000000

======================================================

ОБЪЕДИНЕННАЯ СИСТЕМА === Sys_U.dbf ===================

1-й уровень иерархии. Кол-во элементов=8

2 3 5 7 11 13 17 19

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=8, из них базовых: 8

Локальный коэффициент эмерджентности Хартли=1.0000000

======================================================

СИСТЕМНЫЙ ЭФФЕКТ === Sys_s.dbf =======================

1-й уровень иерархии. Кол-во элементов=0

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=0, из них базовых: 0

======================================================

Обобщенный коэффициент эмерджентности Хартли=1.0000000

A=4. B=4. AUB=8. AUB-A-B=0

======================================================

Локальный коэффициент эмерджентности Хартли отражает

степень отличия системы от множества базовых элементов

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Обобщенный коэффициент эмерджентности Хартли отражает

величину системного эффекта, возникающего при объеди-

нении нескольких систем в одну

======================================================

УРОВЕНЬ СЛОЖНОСТИ=2

1-Я СИСТЕМА === Sys_1.dbf ============================

2-й уровень иерархии. Кол-во элементов=6

6 10 14 15 21 35

1-й уровень иерархии. Кол-во элементов=4

2 3 5 7

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=10, из них базовых: 4

Локальный коэффициент эмерджентности Хартли=1.6609640

======================================================

2-Я СИСТЕМА === Sys_2.dbf ============================

2-й уровень иерархии. Кол-во элементов=6

143 187 209 221 247 323

1-й уровень иерархии. Кол-во элементов=4

11 13 17 19

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=10, из них базовых: 4

Локальный коэффициент эмерджентности Хартли=1.6609640

======================================================

ОБЪЕДИНЕННАЯ СИСТЕМА === Sys_U.dbf ===================

2-й уровень иерархии. Кол-во элементов=28

6 10 14 15 21 22 26 33 34 35 38 39 51 55 57 65 77 85 91 95 119 133 143 187 209 221 247 323

1-й уровень иерархии. Кол-во элементов=8

2 3 5 7 11 13 17 19

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=36, из них базовых: 8

Локальный коэффициент эмерджентности Хартли=1.7233083

======================================================

СИСТЕМНЫЙ ЭФФЕКТ === Sys_s.dbf =======================

2-й уровень иерархии. Кол-во элементов=16

22 26 33 34 38 39 51 55 57 65 77 85 91 95 119 133

1-й уровень иерархии. Кол-во элементов=0

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=16, из них базовых: 0

======================================================

Обобщенный коэффициент эмерджентности Хартли=1.1962080

A=10. B=10. AUB=36. AUB-A-B=16

======================================================

Локальный коэффициент эмерджентности Хартли отражает

степень отличия системы от множества базовых элементов

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Обобщенный коэффициент эмерджентности Хартли отражает

величину системного эффекта, возникающего при объеди-

нении нескольких систем в одну

======================================================

УРОВЕНЬ СЛОЖНОСТИ=3

1-Я СИСТЕМА === Sys_1.dbf ============================

3-й уровень иерархии. Кол-во элементов=4

30 42 70 105

2-й уровень иерархии. Кол-во элементов=6

6 10 14 15 21 35

1-й уровень иерархии. Кол-во элементов=4

2 3 5 7

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=14, из них базовых: 4

Локальный коэффициент эмерджентности Хартли=1.9036775

======================================================

2-Я СИСТЕМА === Sys_2.dbf ============================

3-й уровень иерархии. Кол-во элементов=4

2431 2717 3553 4199

2-й уровень иерархии. Кол-во элементов=6

143 187 209 221 247 323

1-й уровень иерархии. Кол-во элементов=4

11 13 17 19

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=14, из них базовых: 4

Локальный коэффициент эмерджентности Хартли=1.9036775

======================================================

ОБЪЕДИНЕННАЯ СИСТЕМА === Sys_U.dbf ===================

3-й уровень иерархии. Кол-во элементов=56

30 42 66 70 78 102 105 110 114 130 154 165 170 182 190 195 231 238 255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627 646 663 665 715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261 2431 2717 3553 4199

2-й уровень иерархии. Кол-во элементов=28

6 10 14 15 21 22 26 33 34 35 38 39 51 55 57 65 77 85 91 95 119 133 143 187 209 221 247 323

1-й уровень иерархии. Кол-во элементов=8

2 3 5 7 11 13 17 19

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=92, из них базовых: 8

Локальный коэффициент эмерджентности Хартли=2.1745207

======================================================

СИСТЕМНЫЙ ЭФФЕКТ === Sys_s.dbf =======================

3-й уровень иерархии. Кол-во элементов=48

66 78 102 110 114 130 154 165 170 182 190 195 231 238 255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627 646 663 665 715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261

2-й уровень иерархии. Кол-во элементов=16

22 26 33 34 38 39 51 55 57 65 77 85 91 95 119 133

1-й уровень иерархии. Кол-во элементов=0

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=64, из них базовых: 0

======================================================

Обобщенный коэффициент эмерджентности Хартли=1.3569961

A=14. B=14. AUB=92. AUB-A-B=64

======================================================

Локальный коэффициент эмерджентности Хартли отражает

степень отличия системы от множества базовых элементов

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Обобщенный коэффициент эмерджентности Хартли отражает

величину системного эффекта, возникающего при объеди-

нении нескольких систем в одну

======================================================

УРОВЕНЬ СЛОЖНОСТИ=4

1-Я СИСТЕМА === Sys_1.dbf ============================

4-й уровень иерархии. Кол-во элементов=1

210

3-й уровень иерархии. Кол-во элементов=4

30 42 70 105

2-й уровень иерархии. Кол-во элементов=6

6 10 14 15 21 35

1-й уровень иерархии. Кол-во элементов=4

2 3 5 7

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=15, из них базовых: 4

Локальный коэффициент эмерджентности Хартли=1.9534453

======================================================

2-Я СИСТЕМА === Sys_2.dbf ============================

4-й уровень иерархии. Кол-во элементов=1

46189

3-й уровень иерархии. Кол-во элементов=4

2431 2717 3553 4199

2-й уровень иерархии. Кол-во элементов=6

143 187 209 221 247 323

1-й уровень иерархии. Кол-во элементов=4

11 13 17 19

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=15, из них базовых: 4

Локальный коэффициент эмерджентности Хартли=1.9534453

======================================================

ОБЪЕДИНЕННАЯ СИСТЕМА === Sys_U.dbf ===================

4-й уровень иерархии. Кол-во элементов=70

210 330 390 462 510 546 570 714 770 798 858 910 1122 1155 1190 1254 1326 1330 1365 1430 1482 1785 1870 1938 1995 2002 2090 2145 2210 2470 2618 2805 2926 3003 3094 3135 3230 3315 3458 3705 3927 4389 4522 4641 4845 4862 5005 5187 5434 6545 6783 7106 7293 7315 7735 8151 8398 8645 10659 11305 12155 12597 13585 17017 17765 19019 20995 24871 29393 46189

3-й уровень иерархии. Кол-во элементов=56

30 42 66 70 78 102 105 110 114 130 154 165 170 182 190 195 231 238 255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627 646 663 665 715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261 2431 2717 3553 4199

2-й уровень иерархии. Кол-во элементов=28

6 10 14 15 21 22 26 33 34 35 38 39 51 55 57 65 77 85 91 95 119 133 143 187 209 221 247 323

1-й уровень иерархии. Кол-во элементов=8

2 3 5 7 11 13 17 19

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=162, из них базовых: 8

Локальный коэффициент эмерджентности Хартли=2.4466167

======================================================

СИСТЕМНЫЙ ЭФФЕКТ === Sys_s.dbf =======================

4-й уровень иерархии. Кол-во элементов=68

330 390 462 510 546 570 714 770 798 858 910 1122 1155 1190 1254 1326 1330 1365 1430 1482 1785 1870 1938 1995 2002 2090 2145 2210 2470 2618 2805 2926 3003 3094 3135 3230 3315 3458 3705 3927 4389 4522 4641 4845 4862 5005 5187 5434 6545 6783 7106 7293 7315 7735 8151 8398 8645 10659 11305 12155 12597 13585 17017 17765 19019 20995 24871 29393

3-й уровень иерархии. Кол-во элементов=48

66 78 102 110 114 130 154 165 170 182 190 195 231 238 255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627 646 663 665 715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261

2-й уровень иерархии. Кол-во элементов=16

22 26 33 34 38 39 51 55 57 65 77 85 91 95 119 133

1-й уровень иерархии. Кол-во элементов=0

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=132, из них базовых: 0

======================================================

Обобщенный коэффициент эмерджентности Хартли=1.4958251

A=15. B=15. AUB=162. AUB-A-B=132

======================================================

Локальный коэффициент эмерджентности Хартли отражает

степень отличия системы от множества базовых элементов

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Обобщенный коэффициент эмерджентности Хартли отражает

величину системного эффекта, возникающего при объеди-

нении нескольких систем в одну

======================================================

УРОВЕНЬ СЛОЖНОСТИ=5

1-Я СИСТЕМА === Sys_1.dbf ============================

5-й уровень иерархии. Кол-во элементов=0

4-й уровень иерархии. Кол-во элементов=1

210

3-й уровень иерархии. Кол-во элементов=4

30 42 70 105

2-й уровень иерархии. Кол-во элементов=6

6 10 14 15 21 35

1-й уровень иерархии. Кол-во элементов=4

2 3 5 7

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=15, из них базовых: 4

Локальный коэффициент эмерджентности Хартли=1.9534453

======================================================

2-Я СИСТЕМА === Sys_2.dbf ============================

5-й уровень иерархии. Кол-во элементов=0

4-й уровень иерархии. Кол-во элементов=1

46189

3-й уровень иерархии. Кол-во элементов=4

2431 2717 3553 4199

2-й уровень иерархии. Кол-во элементов=6

143 187 209 221 247 323

1-й уровень иерархии. Кол-во элементов=4

11 13 17 19

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=15, из них базовых: 4

Локальный коэффициент эмерджентности Хартли=1.9534453

======================================================

ОБЪЕДИНЕННАЯ СИСТЕМА === Sys_U.dbf ===================

5-й уровень иерархии. Кол-во элементов=56

2310 2730 3570 3990 4290 5610 6006 6270 6630 7410 7854 8778 9282 9690 10010 10374 13090 13566 14586 14630 15015 15470 16302 17290 19635 21318 21945 22610 23205 24310 25194 25935 27170 33915 34034 35530 36465 38038 40755 41990 49742 51051 53295 57057 58786 62985 74613 85085 88179 92378 95095 124355 138567 146965 230945 323323

4-й уровень иерархии. Кол-во элементов=70

210 330 390 462 510 546 570 714 770 798 858 910 1122 1155 1190 1254 1326 1330 1365 1430 1482 1785 1870 1938 1995 2002 2090 2145 2210 2470 2618 2805 2926 3003 3094 3135 3230 3315 3458 3705 3927 4389 4522 4641 4845 4862 5005 5187 5434 6545 6783 7106 7293 7315 7735 8151 8398 8645 10659 11305 12155 12597 13585 17017 17765 19019 20995 24871 29393 46189

3-й уровень иерархии. Кол-во элементов=56

30 42 66 70 78 102 105 110 114 130 154 165 170 182 190 195 231 238 255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627 646 663 665 715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261 2431 2717 3553 4199

2-й уровень иерархии. Кол-во элементов=28

6 10 14 15 21 22 26 33 34 35 38 39 51 55 57 65 77 85 91 95 119 133 143 187 209 221 247 323

1-й уровень иерархии. Кол-во элементов=8

2 3 5 7 11 13 17 19

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=218, из них базовых: 8

Локальный коэффициент эмерджентности Хартли=2.5893948

======================================================

СИСТЕМНЫЙ ЭФФЕКТ === Sys_s.dbf =======================

5-й уровень иерархии. Кол-во элементов=56

2310 2730 3570 3990 4290 5610 6006 6270 6630 7410 7854 8778 9282 9690 10010 10374 13090 13566 14586 14630 15015 15470 16302 17290 19635 21318 21945 22610 23205 24310 25194 25935 27170 33915 34034 35530 36465 38038 40755 41990 49742 51051 53295 57057 58786 62985 74613 85085 88179 92378 95095 124355 138567 146965 230945 323323

4-й уровень иерархии. Кол-во элементов=68

330 390 462 510 546 570 714 770 798 858 910 1122 1155 1190 1254 1326 1330 1365 1430 1482 1785 1870 1938 1995 2002 2090 2145 2210 2470 2618 2805 2926 3003 3094 3135 3230 3315 3458 3705 3927 4389 4522 4641 4845 4862 5005 5187 5434 6545 6783 7106 7293 7315 7735 8151 8398 8645 10659 11305 12155 12597 13585 17017 17765 19019 20995 24871 29393

3-й уровень иерархии. Кол-во элементов=48

66 78 102 110 114 130 154 165 170 182 190 195 231 238 255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627 646 663 665 715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261

2-й уровень иерархии. Кол-во элементов=16

22 26 33 34 38 39 51 55 57 65 77 85 91 95 119 133

1-й уровень иерархии. Кол-во элементов=0

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=188, из них базовых: 0

======================================================

Обобщенный коэффициент эмерджентности Хартли=1.5831175

A=15. B=15. AUB=218. AUB-A-B=188

======================================================

Локальный коэффициент эмерджентности Хартли отражает

степень отличия системы от множества базовых элементов

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Обобщенный коэффициент эмерджентности Хартли отражает

величину системного эффекта, возникающего при объеди-

нении нескольких систем в одну

======================================================

УРОВЕНЬ СЛОЖНОСТИ=6

1-Я СИСТЕМА === Sys_1.dbf ============================

6-й уровень иерархии. Кол-во элементов=0

5-й уровень иерархии. Кол-во элементов=0

4-й уровень иерархии. Кол-во элементов=1

210

3-й уровень иерархии. Кол-во элементов=4

30 42 70 105

2-й уровень иерархии. Кол-во элементов=6

6 10 14 15 21 35

1-й уровень иерархии. Кол-во элементов=4

2 3 5 7

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=15, из них базовых: 4

Локальный коэффициент эмерджентности Хартли=1.9534453

======================================================

2-Я СИСТЕМА === Sys_2.dbf ============================

6-й уровень иерархии. Кол-во элементов=0

5-й уровень иерархии. Кол-во элементов=0

4-й уровень иерархии. Кол-во элементов=1

46189

3-й уровень иерархии. Кол-во элементов=4

2431 2717 3553 4199

2-й уровень иерархии. Кол-во элементов=6

143 187 209 221 247 323

1-й уровень иерархии. Кол-во элементов=4

11 13 17 19

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=15, из них базовых: 4

Локальный коэффициент эмерджентности Хартли=1.9534453

======================================================

ОБЪЕДИНЕННАЯ СИСТЕМА === Sys_U.dbf ===================

6-й уровень иерархии. Кол-во элементов=28

30030 39270 43890 46410 51870 67830 72930 81510 102102 106590 114114 125970 149226 170170 176358 190190 248710 255255 277134 285285 293930 373065 440895 461890 646646 692835 969969 1616615

5-й уровень иерархии. Кол-во элементов=56

2310 2730 3570 3990 4290 5610 6006 6270 6630 7410 7854 8778 9282 9690 10010 10374 13090 13566 14586 14630 15015 15470 16302 17290 19635 21318 21945 22610 23205 24310 25194 25935 27170 33915 34034 35530 36465 38038 40755 41990 49742 51051 53295 57057 58786 62985 74613 85085 88179 92378 95095 124355 138567 146965 230945 323323

4-й уровень иерархии. Кол-во элементов=70

210 330 390 462 510 546 570 714 770 798 858 910 1122 1155 1190 1254 1326 1330 1365 1430 1482 1785 1870 1938 1995 2002 2090 2145 2210 2470 2618 2805 2926 3003 3094 3135 3230 3315 3458 3705 3927 4389 4522 4641 4845 4862 5005 5187 5434 6545 6783 7106 7293 7315 7735 8151 8398 8645 10659 11305 12155 12597 13585 17017 17765 19019 20995 24871 29393 46189

3-й уровень иерархии. Кол-во элементов=56

30 42 66 70 78 102 105 110 114 130 154 165 170 182 190 195 231 238 255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627 646 663 665 715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261 2431 2717 3553 4199

2-й уровень иерархии. Кол-во элементов=28

6 10 14 15 21 22 26 33 34 35 38 39 51 55 57 65 77 85 91 95 119 133 143 187 209 221 247 323

1-й уровень иерархии. Кол-во элементов=8

2 3 5 7 11 13 17 19

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=246, из них базовых: 8

Локальный коэффициент эмерджентности Хартли=2.6475048

======================================================

СИСТЕМНЫЙ ЭФФЕКТ === Sys_s.dbf =======================

6-й уровень иерархии. Кол-во элементов=28

30030 39270 43890 46410 51870 67830 72930 81510 102102 106590 114114 125970 149226 170170 176358 190190 248710 255255 277134 285285 293930 373065 440895 461890 646646 692835 969969 1616615

5-й уровень иерархии. Кол-во элементов=56

2310 2730 3570 3990 4290 5610 6006 6270 6630 7410 7854 8778 9282 9690 10010 10374 13090 13566 14586 14630 15015 15470 16302 17290 19635 21318 21945 22610 23205 24310 25194 25935 27170 33915 34034 35530 36465 38038 40755 41990 49742 51051 53295 57057 58786 62985 74613 85085 88179 92378 95095 124355 138567 146965 230945 323323

4-й уровень иерархии. Кол-во элементов=68

330 390 462 510 546 570 714 770 798 858 910 1122 1155 1190 1254 1326 1330 1365 1430 1482 1785 1870 1938 1995 2002 2090 2145 2210 2470 2618 2805 2926 3003 3094 3135 3230 3315 3458 3705 3927 4389 4522 4641 4845 4862 5005 5187 5434 6545 6783 7106 7293 7315 7735 8151 8398 8645 10659 11305 12155 12597 13585 17017 17765 19019 20995 24871 29393

3-й уровень иерархии. Кол-во элементов=48

66 78 102 110 114 130 154 165 170 182 190 195 231 238 255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627 646 663 665 715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261

2-й уровень иерархии. Кол-во элементов=16

22 26 33 34 38 39 51 55 57 65 77 85 91 95 119 133

1-й уровень иерархии. Кол-во элементов=0

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=216, из них базовых: 0

======================================================

Обобщенный коэффициент эмерджентности Хартли=1.6186451

A=15. B=15. AUB=246. AUB-A-B=216

======================================================

Локальный коэффициент эмерджентности Хартли отражает

степень отличия системы от множества базовых элементов

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Обобщенный коэффициент эмерджентности Хартли отражает

величину системного эффекта, возникающего при объеди-

нении нескольких систем в одну

======================================================

УРОВЕНЬ СЛОЖНОСТИ=7

1-Я СИСТЕМА === Sys_1.dbf ============================

7-й уровень иерархии. Кол-во элементов=0

6-й уровень иерархии. Кол-во элементов=0

5-й уровень иерархии. Кол-во элементов=0

4-й уровень иерархии. Кол-во элементов=1

210

3-й уровень иерархии. Кол-во элементов=4

30 42 70 105

2-й уровень иерархии. Кол-во элементов=6

6 10 14 15 21 35

1-й уровень иерархии. Кол-во элементов=4

2 3 5 7

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=15, из них базовых: 4

Локальный коэффициент эмерджентности Хартли=1.9534453

======================================================

2-Я СИСТЕМА === Sys_2.dbf ============================

7-й уровень иерархии. Кол-во элементов=0

6-й уровень иерархии. Кол-во элементов=0

5-й уровень иерархии. Кол-во элементов=0

4-й уровень иерархии. Кол-во элементов=1

46189

3-й уровень иерархии. Кол-во элементов=4

2431 2717 3553 4199

2-й уровень иерархии. Кол-во элементов=6

143 187 209 221 247 323

1-й уровень иерархии. Кол-во элементов=4

11 13 17 19

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=15, из них базовых: 4

Локальный коэффициент эмерджентности Хартли=1.9534453

======================================================

ОБЪЕДИНЕННАЯ СИСТЕМА === Sys_U.dbf ===================

7-й уровень иерархии. Кол-во элементов=8

510510 570570 746130 881790 1385670 1939938 3233230 4849845

6-й уровень иерархии. Кол-во элементов=28

30030 39270 43890 46410 51870 67830 72930 81510 102102 106590 114114 125970 149226 170170 176358 190190 248710 255255 277134 285285 293930 373065 440895 461890 646646 692835 969969 1616615

5-й уровень иерархии. Кол-во элементов=56

2310 2730 3570 3990 4290 5610 6006 6270 6630 7410 7854 8778 9282 9690 10010 10374 13090 13566 14586 14630 15015 15470 16302 17290 19635 21318 21945 22610 23205 24310 25194 25935 27170 33915 34034 35530 36465 38038 40755 41990 49742 51051 53295 57057 58786 62985 74613 85085 88179 92378 95095 124355 138567 146965 230945 323323

4-й уровень иерархии. Кол-во элементов=70

210 330 390 462 510 546 570 714 770 798 858 910 1122 1155 1190 1254 1326 1330 1365 1430 1482 1785 1870 1938 1995 2002 2090 2145 2210 2470 2618 2805 2926 3003 3094 3135 3230 3315 3458 3705 3927 4389 4522 4641 4845 4862 5005 5187 5434 6545 6783 7106 7293 7315 7735 8151 8398 8645 10659 11305 12155 12597 13585 17017 17765 19019 20995 24871 29393 46189

3-й уровень иерархии. Кол-во элементов=56

30 42 66 70 78 102 105 110 114 130 154 165 170 182 190 195 231 238 255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627 646 663 665 715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261 2431 2717 3553 4199

2-й уровень иерархии. Кол-во элементов=28

6 10 14 15 21 22 26 33 34 35 38 39 51 55 57 65 77 85 91 95 119 133 143 187 209 221 247 323

1-й уровень иерархии. Кол-во элементов=8

2 3 5 7 11 13 17 19

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=254, из них базовых: 8

Локальный коэффициент эмерджентности Хартли=2.6628949

======================================================

СИСТЕМНЫЙ ЭФФЕКТ === Sys_s.dbf =======================

7-й уровень иерархии. Кол-во элементов=8

510510 570570 746130 881790 1385670 1939938 3233230 4849845

6-й уровень иерархии. Кол-во элементов=28

30030 39270 43890 46410 51870 67830 72930 81510 102102 106590 114114 125970 149226 170170 176358 190190 248710 255255 277134 285285 293930 373065 440895 461890 646646 692835 969969 1616615

5-й уровень иерархии. Кол-во элементов=56

2310 2730 3570 3990 4290 5610 6006 6270 6630 7410 7854 8778 9282 9690 10010 10374 13090 13566 14586 14630 15015 15470 16302 17290 19635 21318 21945 22610 23205 24310 25194 25935 27170 33915 34034 35530 36465 38038 40755 41990 49742 51051 53295 57057 58786 62985 74613 85085 88179 92378 95095 124355 138567 146965 230945 323323

4-й уровень иерархии. Кол-во элементов=68

330 390 462 510 546 570 714 770 798 858 910 1122 1155 1190 1254 1326 1330 1365 1430 1482 1785 1870 1938 1995 2002 2090 2145 2210 2470 2618 2805 2926 3003 3094 3135 3230 3315 3458 3705 3927 4389 4522 4641 4845 4862 5005 5187 5434 6545 6783 7106 7293 7315 7735 8151 8398 8645 10659 11305 12155 12597 13585 17017 17765 19019 20995 24871 29393

3-й уровень иерархии. Кол-во элементов=48

66 78 102 110 114 130 154 165 170 182 190 195 231 238 255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627 646 663 665 715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261

2-й уровень иерархии. Кол-во элементов=16

22 26 33 34 38 39 51 55 57 65 77 85 91 95 119 133

1-й уровень иерархии. Кол-во элементов=0

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Всего элементов=224, из них базовых: 0

======================================================

Обобщенный коэффициент эмерджентности Хартли=1.6280544

A=15. B=15. AUB=254. AUB-A-B=224

======================================================

Локальный коэффициент эмерджентности Хартли отражает

степень отличия системы от множества базовых элементов

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Обобщенный коэффициент эмерджентности Хартли отражает

величину системного эффекта, возникающего при объеди-

нении нескольких систем в одну

======================================================

Из приведенного примера видно, что при уровне сложности равном 1, объединение систем ничем не отличается от объединения множеств их базовых элементов, чем и обеспечивается выполнение принципа соответствия. При увеличении уровня сложности наблюдается все больший и больший системный эффект, количественно измеряемый обобщенным коэффициентом эмерджентности Хартли.

При этих же параметрах и уровне сложности 2 сформирован пример, приведенный на рисунке 3 и в таблицах 1–4. Данные таблицы сформированы на основе файлов (которые считываются в MS Excel): Sys#_1.dbf, Sys#_2.dbf, Sys#_U.dbf и Sys#_eff.dbf, где: # – уровень сложности.

В результате запуска этой программы с последовательно увеличивающимся параметром «уровень сложности» при одних и тех же диапазонах базовых элементов, указанных выше, получим результаты, сведенные в таблице 5 и на рисунке 6:

Таблица 5 – ЗАВИСИМОСТЬ ЛОКАЛЬНЫХ И ОБОБЩЕННОГО КОЭФФИЦИЕНТОВ ЭМЕРДЖЕНТНОСТИ ХАРТЛИ
ОТ СЛОЖНОСТИ ОБЪЕДИНЯЕМЫХ СИСТЕМ

Уровень сложности	Локальный коэффициент эмерджентности Хартли			Обобщенный коэффициент эмерджентности Хартли
	1-й системы	2-й системы	Объединенной системы
1	1,0000000	1,0000000	1,0000000	1,0000000
2	1,6609640	1,6609640	1,7233083	1,1962080
3	1,9036775	1,9036775	2,1745207	1,3569961
4	1,9534453	1,9534453	2,4466167	1,4958251
5	1,9534453	1,9534453	2,5893948	1,5831175
6	1,9534453	1,9534453	2,6475048	1,6186451
7	1,9534453	1,9534453	2,6628949	1,6280544

Рисунок 6. Зависимость локальных и обобщенного коэффициентов
эмерджентности Хартли от сложности объединяемых систем

На рисунке 6 использованы обозначения:

– LKEH_SYS1 – локальный коэффициент эмерджентности Хартли для систем Sys_1 и Sys_2;

– LKEH_SYSU – локальный коэффициент эмерджентности Хартли для объединенной системы (объединения систем Sys_1 и Sys_2), хорошо аппроксимируется кубическим степенным полиномом:

y = 0,009x³ - 0,1766x² + 1,1767x - 0,0055

R² = 0,9999;

– OKEH – обобщенный коэффициент эмерджентности Хартли.

Из таблицы 5 и рисунка 6 видно, что при повышении уровня сложности от 4 до 7 уровень системности 1-й и 2-й подсистем не увеличивается. Это связано с тем, что из-за небольшого количества базовых элементов в этих системах отсутствуют 5-й, 6-й и 7-й иерархические уровни, т.е. на них нет ни одного элемента. На других зависимостях также виден «эффект насыщения», проявляющийся в том, что с увеличением уровня сложности системный эффект увеличивается все медленнее и медленнее и выходит на некоторую асимптоту, определяемую количеством базовых элементов в исходных подсистемах.

Выводы. Итак, в разделе рассмотрена реализация операции объединения систем, являющаяся обобщением операции объединения множеств в рамках системного обобщения теории множеств. Эта операция сходна с операцией объединения булеанов классической теории множеств. Но в отличие от классической теории множеств в ее системном обобщении предлагается конкретный алгоритм объединения систем и обосновывается количественная мера системного (синергетического, эмерджентного) эффекта, возникающего за счет объединения систем. Для этой меры предложено название: «Обобщенный коэффициент эмерджентности Хартли» из-за сходства его математической формы с предложенным в 2001 году локальным коэффициентом эмерджентности Хартли, отражающим степень отличия системы от множества его базовых элементов. Приводится ссылка на авторскую программу, реализующую предложенный алгоритм и обеспечивающую численное моделирование объединения систем при различных ограничениях на сложность систем и при различной мощности порождающего множества, приводятся некоторые результаты численного моделирования.

Перспективы. В перспективе планируется более тщательно исследовать свойства объединения систем и разработать системные обобщения других операций над множествами[88].

10.4.2. Обобщенный коэффициент эмерджентности Хартли как количественная мера синергетического эффекта объединения булеанов в системном обобщении теории множеств

Данный раздел основан на работе [241]. В работе [240] предложено математическое выражение для обобщенного коэффициента эмерджентности Хартли[89], количественно отражающего величину системного эффекта, возникающего при объединении систем. Для двух систем, образованных на базовых элементах множеств A и B (240):

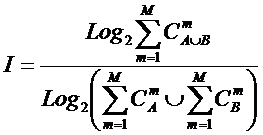(1)

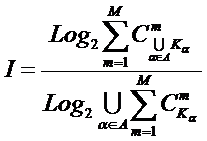Для объединения M систем семейства (2):

⁽²⁾

При получении этих выражений в работе [240] в соответствии с системной теорией информации (СТИ) [97] предполагается, что количество подсистем N_A в системе, образованной на некотором множестве базовых элементов A, равно сумме числа сочетаний этих элементов от 1 до M:

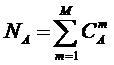(3)

Обобщим выражения (1) и (2) без использования этого предположения. Пусть – булеан (система), образованная на множестве базовых элементов A, а – система, образованная на множестве базовых элементов B. В объединение этих систем входят все подсистемы обоих этих подсистем, тогда как в систему , образованную на объединении базовых множеств , кроме того, входят подсистемы, включающие базовые элементы как 1-го, так и 2-го базовых множеств одновременно.

Поэтому система, образованная на объединении базовых множеств, имеет большую мощность, чем мощность объединения систем, образованных на исходных базовых множествах:

(4)

Вышесказанное практически полностью совпадает с классическим определением системного (синергетического, эмерджентного) эффекта: «Свойства системы превосходят сумму свойств ее частей и не сводятся к ним». При этом степень отличия свойств системы от свойств составляющих ее элементов (базового множества) обоснованно считать ее уровнем системности [240, 97, 186, 189, 191, 170, 196, 281].

Поэтому предлагается считать, что разность в мощности этих систем (системы, образованной на объединении базовых множеств, и системы, являющейся объединением систем, образованных на исходных базовых множествах) представляет собой системный эффект, возникший за счет их объединения:

(5)

Используем классическую формулу Р.Хартли для количества информации, получаемого при идентификации элемента множества, состоящего из N элементов:

(6)

для расчета количества информации, получаемого при идентификации одной из подсистем системы, образованной на объединении базовых множеств, и системы, являющейся объединением систем, образованных на исходных базовых множествах:

(7)

Откуда непосредственно[90] получаем выражение для обобщенного коэффициента эмерджентности Хартли, независящее от предположения о способе образования подсистем на основе элементов базовых множеств:

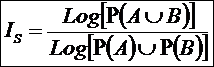(8)

Заметим, что основание логарифма в выражении (7) не является существенным, т.к. берется их отношение.

Обобщим выражение (7) на произвольное количество систем. Пусть дано не 2 системы, а семейство систем: . ^{Тогда для случая многих систем выражения (5) и (8) обобщаются следующим образом:}

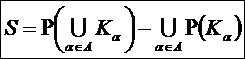(9)

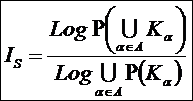(10)

Кроме того, в каждой из систем могут возникать составные элементы из ее собственных базовых элементов. Это приводит к системному эффекту, в результате которого система отличается от множества, т.е. содержит больше элементов, чем в порождающем множестве. Этот вид системного эффекта аналитически выражается локальным коэффициентом эмерджентности Хартли (11), который был получен автором в 2001 году [97] и назван так в честь этого ученого, внесшего большой вклад с разработку научной теории информации[91]:

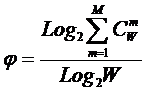(11)

где:

W – количество базовых элементов в системе;

m – сложность составного элемента системы, т.е. подсистемы (количество базовых элементов в составном элементе);

M – максимальная сложность подсистем (максимальное количество базовых элементов в составном элементе).

Обобщение локального коэффициента эмерджентности Хартли (11), независящее от способа образования подсистем, имеет вид 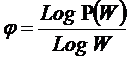(12):

(12)

Например, при объединении 2-х систем, содержащих на 1-м уровне иерархии простые числа, а на 2-м уровне составные числа, являющиеся произведениями различных пар простых сомножителей, образуется объединенная система, 1-й уровень которой является объединением 1-х уровней исходных систем, а 2-й образуется по тому же алгоритму, что и в них (рисунок 1):

Рисунок 1. Объединение 2-х систем из простых чисел на базовом уровне и сложных чисел, образованных из пар простых, на 2-м уровне[92]

В таблицах 1–4 приведены данные о том, какие составные числа произведениями каких простых являются в рассматриваемом примере:

Таблица 1 – СОСТАВ ЭЛЕМЕНТОВ 1-Й СИСТЕМЫ

Элемент	Уровень иерархии	Простые сомножители
		1-й	2-й
2	1	2
3	1	3
5	1	5
7	1	7
6	2	2	3
10	2	2	5
14	2	2	7
15	2	3	5
21	2	3	7
35	2	5	7

Таблица 2 – СОСТАВ ЭЛЕМЕНТОВ 2-Й СИСТЕМЫ

Элемент	Уровень иерархии	Простые сомножители
		1-й	2-й
11	1	11
13	1	13
17	1	17
19	1	19
143	2	11	13
187	2	11	17
209	2	11	19
221	2	13	17
247	2	13	19
323	2	17	19

Таблица 3 – СОСТАВ ЭЛЕМЕНТОВ ОБЪЕДИНЕННОЙ СИСТЕМЫ

Элемент	Уровень иерархии	Простые сомножители
		1-й	2-й
2	1	2
3	1	3
5	1	5
7	1	7
11	1	11
13	1	13
17	1	17
19	1	19
6	2	2	3
10	2	2	5
14	2	2	7
22	2	2	11
26	2	2	13
34	2	2	17
38	2	2	19
15	2	3	5
21	2	3	7
33	2	3	11
39	2	3	13
51	2	3	17
57	2	3	19
35	2	5	7
55	2	5	11
65	2	5	13
85	2	5	17
95	2	5	19
77	2	7	11
91	2	7	13
119	2	7	17
133	2	7	19
143	2	11	13
187	2	11	17
209	2	11	19
221	2	13	17
247	2	13	19
323	2	17	19

Таблица 4 – СОСТАВ ЭЛЕМЕНТОВ ПОДСИСТЕМЫ ОБЪЕДИНЕННОЙ СИСТЕМЫ, СОДЕРЖАЩЕЙ ЭЛЕМЕНТЫ, ОБРАЗОВАННЫЕ ЗА СЧЕТ СИСТЕМНОГО ЭФФЕКТА

Элемент	Уровень иерархии	Простые сомножители
		1-й	2-й
22	2	2	11
26	2	2	13
34	2	2	17
38	2	2	19
33	2	3	11
39	2	3	13
51	2	3	17
57	2	3	19
55	2	5	11
65	2	5	13
85	2	5	17
95	2	5	19
77	2	7	11
91	2	7	13
119	2	7	17
133	2	7	19

Числа, показанные на рисунке 3 черным цветом на 2-м уровне объединенной системы, есть на 2-м уровне либо 1-й системы, либо 2-й. Если бы системы объединялись как множества, то никаких других элементов на 2-м уровне объединенной системы и не было бы. Но при объединении систем в объединенной системе могут возникать элементы, образованные из сочетаний базовых элементов нескольких исходных систем одновременно, которых не было в исходных системах и которые могли образоваться только в объединенной системе. В нашем примере на рисунке 3 это числа, показанные более крупным шрифтом и красным цветом на 2-м уровне объединенной системы, образованные из различных пар простых чисел, одно из которых принадлежит 1-й системе, а 2-е – второй (см. таблицы 1–4).

Все полученные выражения стандартно обобщаются также на непрерывный случай путем замены факториалов при расчете числа сочетаний на гамма-функции [97].

В результате запуска этой программы с последовательно увеличивающимся параметром «уровень сложности» при одних и тех же диапазонах базовых элементов, указанных выше, получим результаты, сведенные в таблице 5 и на рисунке 2:

Таблица 5 – ЗАВИСИМОСТЬ ЛОКАЛЬНЫХ И ОБОБЩЕННОГО КОЭФФИЦИЕНТОВ ЭМЕРДЖЕНТНОСТИ ХАРТЛИ
ОТ СЛОЖНОСТИ ОБЪЕДИНЯЕМЫХ СИСТЕМ

Уровень сложности	Локальный коэффициент эмерджентности Хартли			Обобщенный коэффициент эмерджентности Хартли
	1-й системы	2-й системы	Объединенной системы
1	1,0000000	1,0000000	1,0000000	1,0000000
2	1,6609640	1,6609640	1,7233083	1,1962080
3	1,9036775	1,9036775	2,1745207	1,3569961
4	1,9534453	1,9534453	2,4466167	1,4958251
5	1,9534453	1,9534453	2,5893948	1,5831175
6	1,9534453	1,9534453	2,6475048	1,6186451
7	1,9534453	1,9534453	2,6628949	1,6280544
8	1,9534453	1,9534453	2,6647845	1,6292096
9	1,9534453	1,9534453	2,6647845	1,6292096

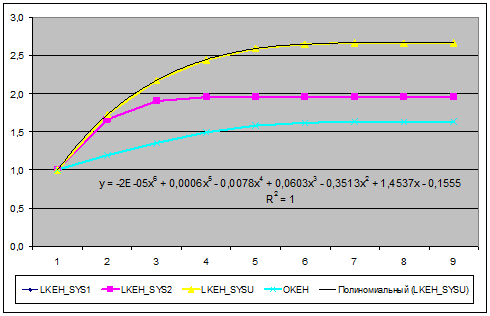
Рисунок 2. Зависимость локальных и обобщенного коэффициентов
эмерджентности Хартли от сложности объединяемых систем

На рисунке 2 использованы обозначения:

– LKEH_SYS1 – локальный коэффициент эмерджентности Хартли для систем Sys_1 и Sys_2;

– LKEH_SYSU – локальный коэффициент эмерджентности Хартли для объединенной системы (объединения систем Sys_1 и Sys_2), хорошо аппроксимируется кубическим степенным полиномом:

y = -2E-05x⁶ + 0,0006x⁵ - 0,0078x⁴ + 0,0603x³ - 0,3513x² + 1,4537x - 0,1555

R² = 1

– OKEH – обобщенный коэффициент эмерджентности Хартли.

Из таблицы 5 и рисунка 2 видно, что при повышении уровня сложности от 4 до 9 уровень системности 1-й и 2-й подсистем не увеличивается. Это связано с тем, что из-за небольшого количества базовых элементов этих системах отсутствуют иерархические уровни с 5-го по 9-й, т.е. на них нет ни одного элемента. На других зависимостях также виден «эффект насыщения», проявляющийся в том, что с увеличением уровня сложности системный эффект увеличивается все медленнее и медленнее и выходит на некоторую асимптоту, определяемую количеством базовых элементов в исходных подсистемах.

Выводы. В работе предлагается общее математическое выражение для количественной оценки системного (синергетического) эффекта, возникающего при объединении булеанов (систем), являющихся обобщением множества в системном обобщении теории множеств и независящее от способа (алгоритма) образования подсистем в системе. Для этой количественной меры предложено название: «Обобщенный коэффициент эмерджентности Р.Хартли» из-за сходства его математической формы с локальным коэффициентом эмерджентности Хартли, отражающим степень отличия системы от множества его базовых элементов. Для локального коэффициента эмерджентности Хартли также предложено обобщение, независящее от способа (алгоритма) образования подсистем в системе. Приводятся численные оценки системного эффекта при объединении двух систем с применением авторской программы, на которую дается ссылка.

Перспективы. В перспективе планируется более тщательно исследовать свойства объединения систем, конкретизировать полученные математические выражения для различных способов образования подсистем на основе элементов базовых множеств [257], разработать системные обобщения других операций над множествами[93].

ГЛАВА 11. КОГНИТИВНЫЕ ФУНКЦИИ КАК ОБОБЩЕНИЕ КЛАССИЧЕСКОГО ПОНЯТИЯ ФУНКЦИОНАЛЬНОЙ ЗАВИСИМОСТИ НА ОСНОВЕ ТЕОРИИ ИНФОРМАЦИИ
В АСК-АНАЛИЗЕ И СИСТЕМНОЙ НЕЧЕТКОЙ ИНТЕРВАЛЬНОЙ МАТЕМАТИКЕ

Данный раздел основан на статье [280].

11.1. Классическое понятие функции в математике

Кратко рассмотрим классическое понятие функциональной зависимости или функции в математике.

Под функциональной зависимостью (функцией) понимается закон или правило, по которому осуществляется отображение множества числовых значений аргумента (область определения) на множество числовых значений функции (область значений). В более общем определении область определения и область значений могут быть произвольными множествами, не обязательно числовыми.

В математике для классических функций обычно вводится большое количество различных ограничений, накладывающих соответствующие ограничения на возможности их практического применения, но позволяющих использовать и развивать математические конструкции, основанные на описанном выше понятии функции в математике. К этим ограничениям, прежде всего, относятся то, что множества значений аргумента и значений функции являются числовыми, чаще всего континуальными (интервал, луч прямая), и между ними существует взаимно-однозначное соответствие, т.е. функция является биективной. Обычно предполагается также, что эти множества или не обладают никакой структурой, или имеют алгебраическую структуру группы, кольца, поля или аналогичную.

Вместе с тем при определении и использовании функций необходимо различать математические, прагматические и компьютерные числа, учитывать, что множества могут быть нечеткими или случайными, элементами множеств могут быть не только числа, но и лингвистические переменные, а также результаты измерений в различных шкалах, в частности, в порядковых, кроме того множества могут образовывать системы. Всем этим обусловлены существенные ограничения, которые накладываются на возможности применения классического математического понятия функции для моделирования социально-экономических объектов. Как следствие, возникает необходимость разработки математического аппарата, снимающего эти ограничения. Кратко рассмотрим совокупность поставленных вопросов вопросы ниже.

11.2. Ограничения классического понятия функции
и формулировка проблемы

Математика – язык науки [1, с.18]. С появлением новых объектов обсуждения, изучения и практического применения этот язык развивается. «Между математикой и практикой всегда существует двусторонняя связь; математика предлагает практике понятия и методы исследования, которыми она уже располагает, а практика постоянно сообщает математике, что ей необходимо» [1, c.53].

В настоящей работе мы рассматриваем необходимость расширения математического понятия функциональной зависимости (функции) с целью учета присущих реальности нечеткости, интервальности, системности, а также основы соответствующего предлагаемого нами нового перспективного направления теоретической и вычислительной математики – системной нечеткой интервальной математики (СНИМ) [92]. Анализируя, следуя А.Н. Колмогорову [2], математику в ее историческом развитии, констатируем, что ее основой являются действительные числа и множества. Как подчеркнуто выше, функции обычно определяются с помощью множеств (области определения, области значений и подмножества декартова произведения этих областей, задающего отображение области определения на область значений. Число же является основным понятием математики с древнейших времен, и стержнем развития математики вплоть до XIX в. является развитие понятия числа. Еще один символ математики – фигуры и тела. И посвящена элементарная геометрия. Однако развитие этой области математики прекратилось в начале ХХ в. Сейчас элементарная геометрия – предмет изучения в средней школе, новые научные результаты в ней не появляются. Ее наследники - современные геометрические дисциплины, такие, как проективная геометрия, дифференциальная геометрия, общая топология, алгебраическая топология и др. – далеки от реального мира. Их чисто теоретические результаты практически не используются при решении прикладных задач.

Поэтому сосредоточимся на рассмотрении только двух понятий - числа и множества.

Констатируем необходимость расширения математического аппарата с целью учета присущих реальности нечеткости и интервальности. Такая необходимость отмечалась в ряде публикаций [25, 26, 27], но пока еще не стала общепризнанной. На описании неопределенностей с помощью вероятностных моделей не останавливаемся, поскольку такому подходу посвящено множество работ.

Подробное обоснование необходимости подобных подходов дано в 1-й части данной работы.

11.2.8. Система как обобщение множества. Системное обобщение
математики и задачи, возникающие при этом

В науке принято два основных принципа определения понятий:

– через подведение определяемого понятия под более общее понятие и выделение из него определяемого понятия путем указания одного или нескольких его специфических признаков (например, млекопитающие – это животные, выкармливающие своих детенышей молоком);

– процедурное определение, которое определяет понятие путем указания пути к нему или способа его достижения (магнитный северный полюс – это точка, в которую попадешь, если все время двигаться на север, определяя направление движения с помощью магнитного компаса).

Как это ни парадоксально, но понятия системы и множества могут быть определены друг через друга, т.е. трудно сказать, какое из этих понятие является более общим.

Определение системы через множество.

Система есть множество элементов, взаимосвязанных друг с другом, что дает системе новые качества, которых не было у элементов. Эти новые системные свойства еще называются эмерджентными (т.е. «возникающими»), т.к. не очень просто понять, откуда они берутся. Чем больше сила взаимодействия элементов, тем сильнее свойства системы отличаются от свойств множества и тем выше уровень системности и синергетический эффект. Получается, что система – это множество элементов, но не всякое множество, а только такое, в котором элементы взаимосвязаны (это и есть специфический признак, выделяющий системы среди множеств), т.е. множество – это более общее понятие.

Определение множества через систему.

Но можно рассуждать и иначе, считая более общим понятием систему, т.е. мы ведь можем определить понятие множества через понятие системы. Множество – это система, в которой сила взаимодействия между элементами равна нулю (это и есть отличительный признак, выделяющий множества среди систем). Тогда более общим понятием является система, а множества – это просто системы с нулевым уровнем системности.

Вторая точка зрения объективно является предпочтительной, т.к. совершенно очевидно, что понятие множества является предельной абстракцией от понятия системы и реально в мире существуют только системы, а множеств в чистом виде не существует, как не существует математической точки. Точнее сказать, что множества, конечно, существуют, но всегда исключительно и только в составе систем как их базовый уровень иерархии, на котором они основаны.

Из этого вытекает очень важный вывод: все понятия и теории, основанные на понятии множества, допускают обобщение путем замены понятия множества на понятие системы и тщательного прослеживания всех последствий этой замены. При этом более общие теории будут удовлетворять принципу соответствия, обязательному для всех более общих теорий, т.е. в асимптотическом случае, когда сила взаимосвязи элементов систем стремится к нулю, системы будут все меньше отличаться от множеств и системное обобщение теории перейдет к классическому варианту, основанному на понятии множества. В предельном случае, когда сила взаимосвязи точно равна нулю, системная теория будет давать точно такие же результаты, как основанная на понятии множества.

Этот вывод верен для всех теорий, но в данной работе для авторов наиболее интересным и важным является то, что очень многие, если не практически все понятия современной математики основаны на понятии множества, в частности на математической теории множеств. В частности, к таким понятиям относятся понятия:

– математической операции: преобразования одного или нескольких исходных множеств в одно или несколько результирующих;

– функциональной зависимости: отображение множества значений аргумента на множество значений функции для однозначной функции одного аргумента или отображение множеств значений аргументов на множества значений функций для многозначной функции многих аргументов;

– «количество информации»: функция от свойств множества.

В работе [186] впервые сформулирована и обоснована программная идея системного обобщения математики, суть которой состоит в тотальной замене понятия "множество" на более общее понятие "система" и прослеживании всех последствий этого. При этом обеспечивается соблюдение принципа соответствия, обязательного для более общей теории, т.к. при понижении уровня системности система по своим свойствам становится все ближе к множеству и система с нулевым уровнем системности и есть множество. Приводится развернутый пример реализации этой программной идеи в области теории информации, в качестве которого выступает предложенная в 2002 году системная теория информации [97], являющаяся системным обобщением теории информации Найквиста – Больцмана – Хартли – Шеннона и семантической теории информации Харкевича. Основа этой теории состоит в обобщении комбинаторного понятия информации Хартли I = Log₂N на основе идеи о том, что количество информации определяется не мощностью множества N, а мощностью системы, под которой предлагается понимать суммарное количество подсистем различного уровня иерархии в системе, начиная с базовых элементов исходного множества и заканчивая системой в целом. При этом в 2002 году, когда было предложено системное обобщение формулы Хартли, число подсистем в системе, т.е. мощность системы N_s, предлагалось рассчитывать по формуле:

.

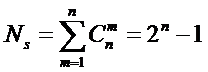Соответственно, системное обобщение формулы Хартли для количества информации в системе из n элементов предлагалось в виде:

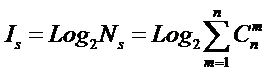
В работе [270] дано системное обобщение формулы Хартли для количества информации для квантовых систем, подчиняющиеся статистике как Ферми-Дирака, так и Бозе-Эйнштейна, и стало ясно, что предложенные в 2002 году в работе [97] вышеприведенные выражения имеют силу только для систем, подчиняющихся статистике Ферми-Дирака.

В работе [188] кратко описывается семантическая информационная модель системно-когнитивного анализа (СК-анализ), вводится универсальная информационная мера силы и направления влияния значений факторов (независимая от их природы и единиц измерения) на поведение объекта управления (основанная на лемме Неймана – Пирсона), а также неметрический интегральный критерий сходства между образами конкретных объектов и обобщенными образами классов, образами классов и образами значений факторов. Идентификация и прогнозирование рассматривается как разложение образа конкретного объекта в ряд по обобщенным образам классов (объектный анализ), что предлагается рассматривать как возможный вариант решения на практике 13-й проблемы Гильберта.

В статьях [189, 191] обоснована идея системного обобщения математики и сделан первый шаг по ее реализации: предложен вариант системной теории информации [97, 201]. В данной работе осуществлена попытка сделать второй шаг в этом же направлении: на концептуальном уровне рассматривается один из возможных подходов к системному обобщению математического понятия множества, а именно – подход, основанный на системной теории информации. Предполагается, что этот подход может стать основой для системного обобщения теории множеств и создания математической теории систем. Сформулированы задачи, возникающие на пути достижения этой цели (разработки системного обобщения математики) и предложены или намечены пути их решения:

Задача 1: найти способ представления системы как совокупности взаимосвязанных множеств.

Задача 2: сформулировать, чем отличаются друг от друга различные системы, состоящие из одних и тех же базисных элементов.

Задача 3: обосновать принципы геометрической интерпретации понятий: "элемент системы" и "система".

Задача 4: предложить способы аналитического описания (задания) подсистем как элементов системы.

Задача 5: описать системное семантическое пространство для отображения систем в форме эйдосов (эйдос-пространство).

Задача 6: описать принцип формирования эйдосов (включая зеркальные части).

Задача 7: показать, что базовая когнитивная концепция [97] формализуется многослойной системой эйдос-пространств (термин автора) различных размерностей.

Задача 8: показать, что системная теория информации позволяет непосредственно на основе эмпирических данных определять вид функций принадлежности, т.е. решать одну из основных задач теории нечетких множеств.

Задача 9: сформулировать перспективы: разработка операций с системами: объединение (сложение), пересечение (умножение), вычитание. Привести предварительные соображения по сложению систем.

11.2.9. Формулировка проблемы

Постоянно работая в области математического моделирования социально-экономических объектов и явлений и учитывая наличие всех вышеперечисленных ограничений, авторы пришли к выводу, что классическое математическое понятие функциональной зависимости недостаточно для адекватного отражения силы и величины причинно-следственной (или иной) связи между факторами, действующим на экономический (или иной) объект, и поведением этого объекта. Одно и тоже значение фактора влияет на переход экономического объекта в различные состояния, но в различной степени или даже с различным знаком, и переход объекта в каждое из состояний обусловлен действием большого количества различных факторов, вообще говоря, взаимодействующих между собой. Это значит, что одному значению аргумента соответствует не одно, а много различных значений функции, а каждому значению функции соответствует много различных значений аргумента, причем это соответствие может быть различным по величание и знаку. Очевидно, что простое представление о биективной функции не пригодно для формального математического моделирования подобных зависимостей. Обобщение классического понятия функции может осуществлено различными способами, – на основе теории нечеткости, интервальной математики, системного анализа.

11.3. Теоретическое решение проблемы в АСК-анализе

Очевидно, смысл процесса измерения в том, что в его результате мы получаем определенное количество информации о степени выраженности тех или иных свойств объекта измерения или о его состоянии. Информация может рассматриваться с двух точек зрения: с количественной и с качественной, т.е. содержательной, семантической. Парадокс заключается в том, что традиционно внимание обращается только на содержание информации, полуденной в процессе измерения, тогда как на количество этой информации обычно вообще не обращают никакого внимания. Между тем количество информации полученной в результате измерений также очень важно, т.к. непосредственно определяется точностью измерений.

По мнению авторов необходимо четко осознать, что когда мы спрашиваем чему равно значение некоторой функции при определенном значении ее аргумента, то, по сути, мы хотим получить некое количество информации об этом значении функции из значения ее аргумента, т.е. о том, какое количество информации об этом значении функции содержится в данном значении ее аргумента. Парадоксально, но мы никогда не спрашиваем, какое же конкретно количество информации мы получили при ответе на этот наш вопрос.

Ответом на этот вопрос являются когнитивные функции. Если мы отобразим в графической форме результаты измерения степени выраженности некоторого свойства объекта в зависимости от величины влияющего на нее фактора в виде функции с указанием не только самих значений функции, но и количества информации в ее аргументе о том, что функция будет иметь эти значения, то это и будет когнитивная функция.

С точки зрения теории управления когнитивная функция представляет собой зависимость вероятностей перехода объекта управления в будущие состояния, соответствующие классам, под влиянием различных значений некоторого фактора. Наглядные примеры когнитивных функций будут приведены ниже.

Когнитивная функции строится для подматриц матрицы информативностей (матрицы знаний) системы «Эйдос», образованных различными классификационными и описательными шкалами (одна из подматриц выделена жирной линией и фоном) (таблица 6):

Таблица 6 – К ПОЯСНЕНИЮ ПОНЯТИЯ:
«ПОДМАТРИЦЫ МАТРИЦЫ ЗНАНИЙ»

		1-я классификационная шкала			2-я классификационная шкала			3-я классификационная шкала
		1-я градация	2-я градация	3-я градация	1-я градация	2-я градация	3-я градация	1-я градация	2-я градация	3-я градация
1-я описательная шкала	1-я градация
	2-я градация
	3-я градация
2-я описательная шкала	1-я градация
	2-я градация
	3-я градация
3-я описательная шкала	1-я градация
	2-я градация
	3-я градация

Если взять несколько информационных портретов факторов, соответствующих градациям одной описательной шкалы, отфильтровать их по диапазону градаций некоторой классификационной шкалы и взять из каждого информационного портрета по одному состоянию, на переход в которое объекта управления данное значение фактора оказывает наибольшее влияние, то мы и получим когнитивную функциональную зависимость, отражающую вероятность перехода объекта управления в будущие состояния под влиянием различных значений некоторого фактора, т.е. полностью редуцированную когнитивную функцию.

Когнитивные функции являются наиболее развитым средством изучения причинно-следственных зависимостей в моделируемой предметной области, предоставляемым системой "Эйдос". Необходимо отметить, что на вид функций влияния математической моделью СК-анализа не накладывается никаких ограничений, в частности, они могут быть и нелинейные [273].

Введем определение когнитивной функции: когда функция используется для отображения причинно-следственной зависимости, т.е. информации (согласно концепции Шенка-Абельсона [235]), или знаний, если эта информация полезна для достижении целей, то будем называть такую функцию когнитивной функцией [166, 218, 226, 235, 239, 108, 243, 244, 254, 280], от англ. «cognition»[94].

Смысл когнитивной функциональной зависимости в том, что в значении аргумента содержится определенное количество информации о том, какое значение примет функция, т.е. когнитивная функция отражает знания о степени соответствия значений функции значениям аргумента.

Очень важно, что этот подход позволяет автоматически решить проблему сопоставимой обработки многих факторов, измеряемых в различных единицах измерения, т.к. в этом подходе рассматриваются не сами факторы, какой бы природы они не были и какими бы шкалами не формализовались, а количество информации, которое в них содержится о поведении моделируемого объекта [280].

Необходимо также отметить, что представление о полностью линейных объектах (системах) является абстракцией и реально все объекты являются принципиально нелинейными. Вместе с тем для большинства систем нелинейные эффекты можно считать эффектами второго и более высоких порядков и такие системы в первом приближении можно считать линейными. Возможны различные модели взаимодействия факторов, в частности, развиваемые в форме системного обобщения теории множеств [189, 191]. Этот подход в перспективе может стать одним из вариантов развития теории нелинейных систем.

Отметим, что математическая модель АСК-анализа (системная теория информации) органично учитывает принципиальную нелинейность всех объектов. Это проявляется в нелокальности нейронной сети системы «Эйдос» [138], приводящей к зависимости всех информативностей от любого изменения в исходных данных, а не как в методе обратного распространения ошибки[95]. В результате значения матрицы информативностей количественно отражают факторы не как множество, а как систему.

Объект может перейти в некоторое будущее состояние под действием различного количества факторов, но какая бы система факторов не обусловливала (детерминировала) этот переход, в ней не может содержаться информации больше, чем можно получить, точно узнав, что объект переходит в данное состояние. Это количество информации в АСК-анализе называется «Теоретически максимальное количество информации» и определяется только количеством классов (будущих состояний объекта), которые в детерминистском случае равновероятны, т.к. между классами и факторами выполняется взаимнооднозначное соответствие, когда каждое будущее состояние однозначно определяется единственным фактором. Формула А.Харкевича видоизменена в работе [97] таким образом, чтобы удовлетворять принципу соответствия с формулой Р.Хартли в детерминистском случае. Поэтому, чем меньше факторов, тем жестче ими детерминировано поведение объекта, и наоборот, чем больше этих факторов, тем меньше влияние каждого из них на поведение объекта. Например, если переход объекта в некоторое состояние однозначно определяется единственным фактором, то добавление в модель еще одного точно такого же фактора приводит к тому, что в сумме эти два фактора будут оказывать тоже самое влияние, которое делится между ними поровну.

Так в математической модели АСК-анализа учитывается взаимодействие факторов и отличие системы факторов от множества факторов [273], являющееся источником нелинейности моделируемого объекта.

Итак, в матрице информативнстей количественно отражены сила и направление влияния каждого значения фактора на переход объекта в каждое из состояний, а также учтено, что совокупность факторов является системой, а не множеством, т.е. учтены взаимодействие факторов и нелинейность моделируемого объекта. Результаты решения задач идентификации, прогнозирования, принятия решений и научного исследования моделируемой предметной области (в частности кластерно-конструктивного анализа), на основе матрицы информативностей инвариантны относительно формы частотного распределения объектов исследуемой выборки по классам, единиц измерения значений факторов и типа шкал, используемых для формализации факторов.

Это позволяет корректно использовать в АСК-анализе аддитивный интегральный критерий в форме суммы частных критериев не только для линейных, но и для нелинейных объектов.

Различие между матрицей информативностей и матрицей знаний. Если в модели отражены лишь причинно-следственные связи между факторами и будущими состояниями объекта, но не отражена степень желательности ли нежелательности этих будущих состояний, то мы имеем дело с матрицей информативностей. Если же некоторые из будущих событий классифицируются как желательные, т.е. целевые, а другие как нежелательные, то появляется возможность количественной оценки степени полезности информации о действии факторов для перевода объекта в эти состояния, т.е. для преобразования информации в знания.

Процесс преобразования информации в знания – это процесс оценки степени полезности информации для достижения желаемых будущих состояний, т.е. целей.

Таким образом, матрица знаний количественно отражает степень полезности (а также бесполезности и вредности) факторов для достижения целей: она содержит знания в количественной форме о величине и направлении влияния каждого значения фактора на перевод объекта в каждое из будущих состояний, как желаемое, так и нежелательное.

Факт – это единство экстенсионального и интенсинального описания события, обнаруженного эмпирическим путем, т.е. по сути, факт это определение события. Пример факта: «Кошка кормит котят молоком». Пример определения в науке: «Млекопитающее – это животное (более общее, интенсиональное понятие), вскармливающее своих детей молоком (экстенсиональный специфический признак)».

Закономерности – это причинно-следственные зависимости, выявленные на исследуемой выборке и распространяемые лишь на саму эту выборку.

Эмпирический закон – это причинно-следственные зависимости, выявленные на исследуемой выборке и распространяемые на некоторую предметную область, более широкую, чем исследуемая выборка, в которой действуют те же причины действия причинно-следственных зависимостей, что и в исследуемой выборке, на которой он обнаружены. Эта более широкая предметная область называется генеральной совокупностью, по отношению к которой исследуемая выборка репрезентативна. Эмпирический закон является феноменологическим, т.е. внешним описанием зависимости последствий от причин, который не раскрывает механизма или способа, которым реализуется эта зависимость.

Научный закон – это содержательная интерпретация механизма действия эмпирического закона, т.е. способа преобразования причин в следствия. Научный закон является содержательным объяснением и интерпретацией эмпирического закона. Это объяснение, когда оно разрабатывается, не сразу становится научным законом, а сначала имеет статус научной гипотезы и приобретает статус научного закона лишь после того, как на практике, т.е. эмпирически, подтверждаются предсказания существования новых, ранее неизвестных явлений, сделанные на основе научной гипотезы. Таким образом, научный закон – это научная гипотеза, адекватность и прогностическая сила которой подтверждены (верифицированы) эмпирически. Процесс преобразования научной гипотезы в научный закон – это процесс подтверждения на практике адекватности этой научной гипотезы.

Необходимо подчеркнуть, что существует принципиальная возможность создания многих различных моделей, одинаково адекватно отражающих одну и ту же предметную область. Иногда такие модели и действительно созданы. Тогда возникает вопрос о критериях выбора одной модели, в определенном смысле «наилучшей» из многих. Среди этих критериев следует отметить адекватность, удовлетворение принципу соответствия и широту адекватно отражаемой предметной области, а также ее простоту и красоту. Из многих моделей предпочтительная та, которая более адекватна, та, которая адекватно отражает более широкую предметную область и включает в себя на основе принципа соответствия другие известные модели, а также более простая и красивая модель. Однако часто бывает, что разработка многих моделей (научных теорий) весьма затруднительна и есть или известна всего лишь одна-единственная модель. Тогда эта модель автоматически становится наилучшей из всех известных.

Возникает соблазн неоправданно и необоснованно считать, что реальность устроена именно таким образом, какой она отражается в этой наилучшей по сформулированным выше критериям модели или научной теории, т.е. необоснованно придать онтологический статус абстрактной модели. В этом состоит широко распространенная малозаметная ошибка познания, называемая «Гипостазирование[96]». Однако эта ошибка влечет за собой целый шлейф весьма заметных последствий, важнейшим из которых является отрицание существования фактов, закономерностей и эмпирических законов, не вписывающихся в те или иные научные теории, даже если эти факты в буквальном смысле слова очевидны. Например, апологеты воздухоплавания отрицали возможность летательных аппаратов тяжелее воздуха, не смотря на птиц, которые садились и взлетали перед ними (или даже смотря на них, но не осознавая, что они видят). При этом они исходили из того, что принцип действия летальных аппаратов может быть основан только на законе Архимеда, как это следовало из единственной известной им научной теории полета. Однако существуют и другие принципы полета: в частности, баллистический, аэродинамический, ракетный, электромагнитный, на которых может быть основан принцип действия летательных аппаратов тяжелее воздуха, причем эти аппараты ни в коей мере не нарушают закон Архимеда и полностью ему подчиняются.

Признание существования факта не зависит от обнаружения закономерности. Признание существования закономерности не зависит от обнаружения соответствующего эмпирического закона. Признание существования эмпирических законов не зависит от наличия верифицированной содержательной интерпретации или научного закона, а если она есть, то от того, является ли она «правильной» или «неправильной» по тем или иным критериям или по чьему-то мнению. Таким образом, признание существования факта не зависит от наличия теории, которая его объясняет, и отсутствие такой теории не является основанием для отрицания существования или непризнания существования факта.

Когнитивные функции представляют собой новый перспективный инструмент отражения и наглядной визуализации закономерностей и эмпирических законов. Разработка содержательной научной интерпретации когнитивных функций представляет собой способ познания природы, общества и человека.

Когнитивные функции могут быть:

– прямые, отражающие зависимость классов от признаков, обобщающие информационные портреты признаков;

– обратные, отражающие зависимость признаков от классов, обобщающие информационные портреты классов;

– позитивные, показывающие чему способствуют система детерминации;

– негативные, отражающие чему препятствуют система детерминации;

– средневзвешенные, отражающие совокупное влияние всех значений факторов на поведение объекта;

– с различной степенью редукции или степенью детерминации, которая отражает в графической форме (в форме полосы) количество знаний в аргументе о значении функции и является аналогом и обобщением доверительного интервала.

Примеры когнитивных функций будут приведены ниже.

Прямая и обратная, а также позитивная и негативная когнитивные функции полностью совпадают (тождественны) друг с другом только для жестко (т.е. полностью) детерминированных систем. Это связано с тем, что матрица знаний, моделирующая полностью детерминированную систему, в которой между значениями аргумента и значениями функции существует взаимнооднозначное соответствие, представляет собой диагональную матрицу [273]. Можно обоснованно предположить, что степень совпадения прямой и обратной когнитивных функций пропорциональна степени детерминированности моделируемой системы. Если интерпретировать значения факторов, обусловливающих поведение системы, как ее экстениональное описание, относящееся к ее прошлому времени, а классы – как интенсиональное описание ее будущих состояний, то можно сказать, что степень детерминации поведения системы тем выше, чем более сходным являются влияние на нее прямой и обратной причинности, т.е. если влияние прошлого на будущее совпадет с влиянием будущего на прошлое. Чем сильнее влияние прошлого на будущее отличается от влияния будущего на прошлое, тем слабее детерминированность в поведении системы, тем ближе оно к случайному. При этом рассмотрение вопросов о физическом механизме прямой и обратной причинности, как и самом существовании обратной причинности, не входит в задачи данной работы.

Матрица информативности может быть использована для выявления и визуализации когнитивных функциональных зависимостей в фрагментированных и зашумленных данных большой размерности. Кратко поясним суть этого метода. Матрица информативностей рассчитывается на основе системной теории информации [97] непосредственно на основе эмпирических данных и представляет собой таблицу, в которой столбцы соответствуют обобщенным образам классов, т.е. будущим состояниям моделируемой системы, строки – значениям факторов, влияющих на эту систему, а на пересечениях строк и столбцов находится количество информации, которое содержится в факте действия значения фактора, соответствующего строке, на переход системы в состояние, соответствующее столбцу. Максимальное количество информации, которое может быть в значении фактора, определяется числом будущих состояний моделируемой системы. Модуль количества информации отражает силу влияния значения фактора, а знак – направление этого влияния, т.е. то, способствует он или препятствует наступлению данного состояния. Если последовательности классов и значений факторов образуют порядковые шкалы или шкалы отношений, т.е. соответственно, на них определены отношения «больше-меньше» или, кроме того, единица измерения, начало отсчета и арифметические операции, то матрица информативностей допускает наглядную графическую визуализацию, традиционного для функций типа, когда значения факторов рассматриваются в качестве значений аргумента, а классы, о наступлении которых в этих значениях факторов содержится максимальное количество информации – в качестве значений функции. Другие классы, менее обусловленные данным значением фактора, а также те, наступлению которых это значение препятствует в большей или меньшей степени, также могут отображаться соответствующими цветами, и это также может представлять интерес, т.к. позволяет задействовать мощные способности человека к анализу изображений. Когнитивные функции, представляемые в форме матрицы информативностей, соответствуют очень общему виду функциональной зависимости: многозначной функции многих аргументов, т.к. каждое значение фактора влияет на все состояния моделируемого объекта, и каждое его состояние обусловлено всеми значениями факторов. Простой пример визуализации матрицы информативностей, полученной на выборке, отражающей зависимость амплитуды затухающего гармонического колебания от времени, приведен на нижеследующем рисунке 1, в котором степень детерминации значения функции значением аргумента показана различными цветами: теплые цвета – высокая степень детерминации, холодные – низкая.

Рисунок 1. Количество информации в значении аргумента
о значении функции для нечеткой взаимнооднозначной когнитивной функции

11.3.2. Системное обобщение понятия функции и функциональной зависимости. Когнитивные функции. Матрицы знаний как нечеткое с расчетной степенью истинности отображение системы аргументов на систему значений функции

Выше кратко рассматривается программная идея системного обобщения понятий математики (в частности теории информации), основанных на теории множеств, путем тотальной замены понятия множества на более содержательное понятие системы и прослеживания всех последствий этого. Частично эта идея была реализована автором при разработке автоматизированного системно-когнитивного анализа (АСК-анализа) [97], математическая модель которого основана на системном обобщении формул для количества информации Хартли и Харкевича [97].

В работе [166] реализуется следующий шаг: предлагается системное обобщение понятия функциональной зависимости, и вводятся термины "когнитивные функции" и "когнитивные числа". На численных примерах показано, что АСК-анализ обеспечивает выявление когнитивных функциональных зависимостей в многомерных зашумленных фрагментированных данных.

В работе [140] намечены принципы применения многозначных функций многих аргументов для описания сложных систем и предложено матричное представление этих функций.

В работе [218] обсуждается возможность восстановления значений одномерных и двумерных функций как между значениями аргумента (интерполяция), так и за их пределами (экстраполяция) на основе использования априорной информации о взаимосвязи между признаками аргумента и значениями функции в опорных точках с применением системно-когнитивного анализа и его инструментария – системы «Эйдос». Приводятся численные примеры и визуализация результатов. Предлагается применение аппарата многомерных когнитивных функций для решения задач распознавания и прогнозирования на картографических базах данных.

В работе [226] на примере решения проблемы управления агропромышленным холдингом рассматривается технология когнитивных функций СК-анализа, обеспечивающая как выявление знаний из эмпирических данных, так и использование этих знаний для поддержки принятия решений по управлению холдингом в целом на основе управления характеристиками входящих в него предприятий.

В работе [235] рассматривается применение метода автоматизированного системно-когнитивного анализа и его программного инструментария – системы «Эйдос» для выявления причинно-следственных зависимостей из эмпирических данных. В качестве инструментария для формального представления причинно-следственных зависимостей предлагаются когнитивные функции.

Когнитивные функции представляют собой многозначные интервальные функции многих аргументов, в которых различные значения функции в различной степени соответствуют различным значениям аргументов, причем количественной мерой этого соответствия выступает знание, т.е. информация о причинно-следственных зависимостях в эмпирических данных, полезная для достижения целей.

В работе [239] на основе применения аппарата когнитивных функций впервые исследована зависимость параметров движения полюса Земли от положения небесных тел Солнечной системы. В последующем эти результаты развиты в монографии [108].

Наиболее полно метод визуализации когнитивных функций, как новый инструмент исследования эмпирических данных большой размерности, раскрыт в работе [243].

В работе [244] рассматривается новая версия системы искусственного интеллекта «Эйдос-астра» для решения прикладных задач с эмпирическими данными большой размерности. Приложение, написанное на языке JAVA, обеспечивает GUI (графический интерфейс пользователя) и позволяет подготовить и выполнить визуализацию матрицы знаний без ограничений, налагаемых реализацией предыдущих версий системы «Эйдос-астра». Отметим, что в системе Эйдос-Х++ все эти ограничения на размерность моделей также сняты в универсальной форме, не зависящей от предметной области.

В работе [254] рассмотрена глубокая взаимосвязь между теорией автоматизированного и автоматического управления и системно-когнитивным анализом и его программным инструментарием – системой «Эйдос» в их применении для интеллектуального управления сложными системами. Предлагается технология, позволяющая на практике реализовать интеллектуальное автоматизированное и даже автоматическое управление такими объектами управления, для которых ранее управление реализовалось лишь на слабоформализованном уровне, как правило, без применения математических моделей и компьютеров. К таким объектам управления относятся, например, технические системы, штатно качественно-изменяющиеся в процессе управления, биологические и экологические системы, социально-экономические и психологические системы. Намечены возможности получения когнитивных передаточных функций сложных многопараметрических нелинейных объектов управления на основе зашумленной фрагментированной эмпирической информации об их фактическом поведении под действием различных сочетаний значений факторов различной природы.

Приведем простейший пример (рисунок 2) когнитивной функции затухающего синусоидального колебания, восстановленной по табличным данным, включающим 360 значений функции, при разном числе интервальных значений аргумента и функции: 30 (верхний график) и 60 (нижний график):

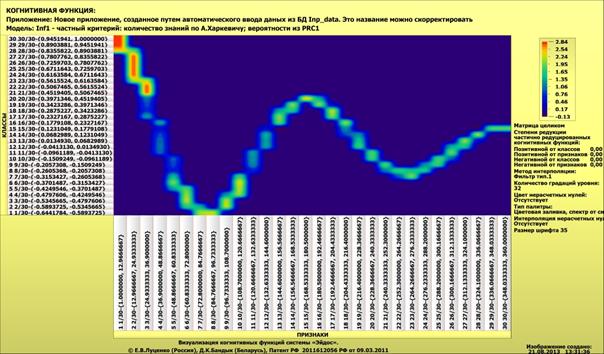
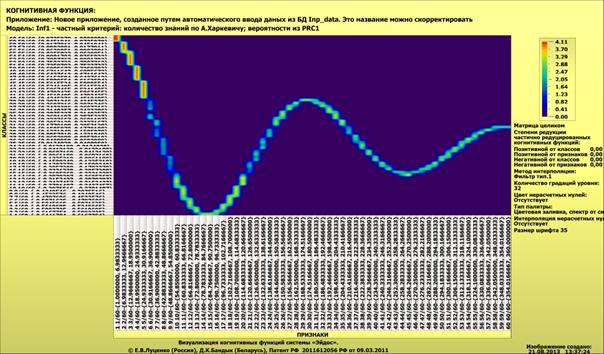
Рисунок 2. Когнитивная функция затухающего синусоидального
колебания, восстановленная по табличным данным, включающим 360
значений функции, при 30 (вверху) и 60 (внизу) интервальных
значениях аргумента и функции

Ясно, что если величина интервала будет стремиться к нулю, то интервальные функции, к которым относятся и когнитивные функции, будут асимптотически приближаться к абстрактным математическим функциям, которые можно считать интервальными функциями с нулевой величиной интервала. Соответственно при уменьшении величины интервала будет увеличиваться и суммарное количество информации, содержащееся в модели, т.е. в значениях аргумента о значениях когнитивной функции (эту зависимость планируется исследовать в новых работах). Поэтому интервальная математика может рассматриваться как более общая, чем точная математика с бесконечно малыми и для нее выполняется известный принцип соответствия, обязательный для более общих теорий.

В когнитивных функциях, представленных на рисунке 2, цветом отображено количество информации в интервальном значении аргумента об интервальном значении функции. Или выражаясь точнее, цветом отображено количество информации в интервальном значении аргумента о том, что (при этом значении аргумента) функция примет определенное интервальное значение. Или еще точнее, цветом отображено количество информации о том, что при значении аргумента, попадающем в данный интервал, функция примет определенное значение, попадающее в соответствующий интервал.

Из рисунка 2 мы видим, что об одних значениях функции в значениях аргумента содержится больше информации, а о других меньше. Это значит, что различные значения аргумента с разной степенью определенности обуславливают соответствующие значения функции. Иначе говоря, зная одни значения аргумента, мы весьма определенно можем сказать о соответствующем значении функции, а по другим значениям мы можем судить о значении функции лишь приблизительно, т.е. с гораздо большей погрешностью или неопределенностью.

Таким образом, когнитивная функция содержит информацию не только о соответствии значений функции значениям аргумента, как абстрактная математическая функция, но и о достоверности высказывания о том, что именно такое их соответствие имеет место в действительности, причем эта достоверность меняется от одних значений аргумента и функции к другим.

Получается, что в каждом значении аргумента содержится определенная информация о каждом значении функции. Эта информация может быть больше или меньше, она может быть положительная или отрицательная, т.е. в когнитивной функции каждому значению аргумента соответствуют все значения функции, но в различной степени. Из этого следует также, что каждое значение функции обуславливается различными значениями аргумента, но каждое из них обусловливает это значение в различной степени. Поэтому когнитивные функции являются многозначными функциями многих аргументов.

Это понятие напоминает доверительный интервал, но с той разницей, что доверительный интервал всегда растет со значением аргумента, а количество информации может и возрастать, и уменьшаться. Если осуществляется интерполяция или прогноз значения когнитивной функции, то при этом одновременно определяется и достоверность этой интерполяции или этого прогноза. На когнитивной функции, представленной на рисунке 3, эта достоверность представлена в форме полупрозрачной полосы, ширина которой обратно пропорциональна достоверности (как в доверительном интервале), т.е. чем точнее известно значение функции, тем уже полоса, и чем оно более неопределенно, тем она шире.

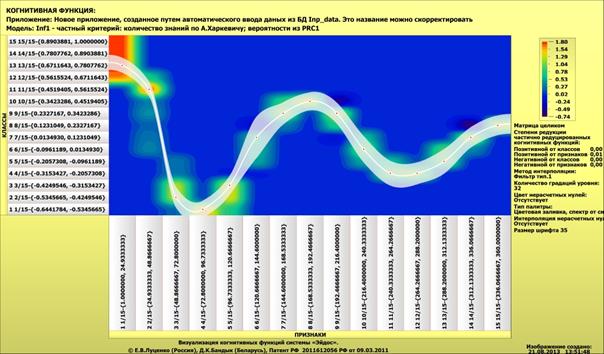
Рисунок 3. Когнитивная функция затухающего синусоидального
колебания, восстановленная по табличным данным, включающим 360
значений функции, при 15 интервальных значениях аргумента
и функции с указанием степени достоверности не только цветом,
но и в форме частично-редуцированной когнитивной функции,
аналогичной по смыслу доверительному интервалу

В теоретической математике нет меры причинно-следственной связи. Математика оперирует абстрактными понятиями, а понятие причинно-следственной связи является содержательным понятием, относящимся к конкретной изучаемой, в том числе и эмпирически, реальной предметной области. Математические понятия функциональной зависимости или корреляция не являются такой мерой. Правда, в статистике есть критерий хи-квадрат, который действительно является мерой причинно-следственной связи, но статистика специально разработана с целью изучения конкретных явлений и этим существенно отличается от абстрактной теоретической математики.

Мы рассматриваем числовые и лингвистические данные, как сырые данные, полученные непосредственно из опыта и еще не подвергнутые какой-либо обработке. Эти эмпирические данные могут быть преобразованы в информацию путем их анализа. Информация есть осмысленные данные. Смысл согласно концепции смысла Шешка-Абельсона, которой мы придерживаемся, представляет собой знание причинно-следственных зависимостей. Причинно-следственные зависимости возможны только между событиями, а не между данными. Поэтому анализ данных, в результате которого они преобразуются в информацию, включает два этапа:

– нахождение событий в данных;

– выявление причинно-следственных связей между событиями.

Знания представляют собой информацию, полезную для достижения цели. Если такой целью является решение задач прогнозирования, принятия решений и исследования моделируемой предметной области путем исследования ее модели (это корректно, если модель адекватна), то информационная модель является и когнитивной моделью, т.е. интеллектуальной моделью или моделью знаний.

Поэтому когнитивные функции являются наглядным графическим отображение наших знаний о причинно-следственных связях между интервальными или лингвистическими значениями аргумента и интервальными или лингвистическими значениями функции.

Когнитивные функции представляют собой графическое отображение сечений многомерного эйдос-пространства (базы знаний) системы «Эйдос-Х++» плоскостями, содержащими заданные описательные и классификационные шкалы с фактически имеющимися у них интервальными значениями (градациями).

11.3.3. Примеры известных функций, которые могут рассматриваться как аналоги когнитивных функций

11.3.3.1. Оцифрованные сигналы: аудио, графика, видео

В оцифрованных аудио, видео и других сигналах мы всегда знаем глубину кодирования, а значит и количество информации в значении аргументе о значении функции. В любых таблицах и базах данных числа всегда представлены с ограниченным числом знаков после запятой, а значит само множество таких чисел ограничено, и всегда можно посчитать, какие количество информации содержится в факте выборки как-то одного конкретного из этих чисел.

11.3.3.2. Таблично заданные функции, например таблицы Брадиса

Например, в известной таблице Брадиса[97] приводится 4 знака значения синуса после запятой. Это значит, что заданному углу соответствует одно из 9999 значений. По формуле Хартли получаем: I=Log₂N=Log₂9999~13.29 бит.

11.3.3.3. Доверительные интервалы как аналог количества информации в аргументе о значении функции и прогнозирование достоверности прогнозирования

В статистике принято не просто что-либо утверждать, а обязательно сопровождать каждое утверждение оценкой степени его достоверности. Например, для этой цели при решении задачи прогнозирования путем экстраполяции, т.е. оценки значения функции за пределами эмпирических значений аргумента, используется так называемый «доверительный интервал». Доверительный интервал представляет собой определенный диапазон значений функции, зависящий от значения аргумента, в который истинное значение функции попадает с определенной вероятностью (обычно 0,95). Наиболее известным свойством доверительного интервала при решении задачи прогнозирования является его монотонное увеличение по мере удаления от эмпирически известных значений аргумента и функции. Используя определение информации как количественной меры степени снятия неопределенности (энтропийная мера Больцмана) можно сказать, что чем больше величина доверительного интервала, тем меньше информации в значениях аргумента о значениях функции, т.е. тем выше неопределенность значений функции.

В теории и практике когнитивных функций оценкой достоверности прогноза о значении функции является количество информации в аргументе о том, что функция примет данное значение. Это количество информации может быть наглядно изображено цветом и толщиной частично-редуцированной когнитивной функции. Существенно, что это количество информации не обязательно уменьшается при удалении от области эмпирически известных значений, но может и уменьшаться и возрастать, в отличие от доверительного интервала [97]. Это означает, что АСК-анализ позволяет не только прогнозировать развитие процесса, но и позволяет прогнозировать достоверность этого прогнозирования. Это возможно также по разбросу точечных прогнозов [97].

11.3.3.4. Что представляют собой классические функции с точки зрения теории и практики когнитивных функций?

Рассмотрим с позиций теории информации, чем отличаются когнитивные функции от абстрактных математических функций. Формально по точному значению аргумента любой абстрактной математической функции возможно точно узнать ее точное значение. Но на практике это возможно лишь тогда, когда и значения аргумента, и значения функции являются целыми числами. Если же они являются иррациональными числами, то совершенно ясно, что точное их значение никогда не может быть ни вычислено на любом компьютере с ограниченной вычислительной мощностью, ни записано, ни на каких носителях с ограниченной информационной емкостью, ни передано ни по каким каналам связи с ограниченной пропускной способностью. Поэтому точное знание значения иррациональной функции означает доступ к бесконечному количеству информации. На практике же мы, конечно, всегда имеем дело с ограниченной точностью или знаем значения функции с некоторой погрешностью, т.е. оперируем конечным количеством информации в значениях аргумента о значениях функции. Но каким именно количеством информации? До разработки математического аппарата и программного инструментария когнитивных функций это вопрос как-то ребром не ставился и был в тени приоритетных направлений исследований. Ответом на это вопрос и является теория когнитивных функций, где каждому значению аргумента соответствует не только значение функции, но и количество информации в битах, содержащееся в этом значении аргумента о том, что ему соответствует данное значение функции.

Конкретные численные примеры когнитивных функций приведены в разделе 4.2.

Разработаны нередуцированные, частично и полностью редуцированные прямые и обратные когнитивные функции, а также программный инструментарий для их расчета (сама система Эйдос-Х++) и модуль визуализации когнитивных функций [133]. Однако в данной работе не целесообразно их рассматривать, т.к. этому посвящены многочисленные работы, ссылки на которые даны выше.

Таким образом, с точки зрения теории и практики когнитивных функций классические функции это предел, к которому стремятся полностью редуцированные когнитивные функции при неограниченном увеличении количества наблюдений, т.е. когнитивные функции, в значениях аргумента которых содержится бесконечное количество информации о значении функции (т.к. значение функции предполагается известным абсолютно точно). Ясно, что вообще говоря, на практике это невозможно в реальности классическим математическим функциям ничего не соответствует, т.е. они являются чистой абстракцией наподобие математической точки, бесконечно малой величины и т.п.

11.4. Практическое решение проблемы в программном
инструментарии АСК-анализа – интеллектуальной
системе «Эйдос»

11.4.1. Интеллектуальная система Эйдос-Х++ как инструментарий
АСК-анализа, реализующий идеи системного нечеткого интервального
обобщения математики

Система «Эйдос» за многие годы применения хорошо показала себя при проведении научных исследований в различных предметных областях и занятий по ряду научных дисциплин, связанных с искусственным интеллектом, представлениями знаний и управлению знаниями [234]. Однако в процессе эксплуатации системы были выявлены и некоторые недостатки, ограничивающие возможности и перспективы применения системы. Поэтому создана качественно новая версия системы (система Эйдос-Х++), в которой преодолены ограничения и недостатки предыдущей версии и реализованы новые важные идеи по ее развитию и применению в качестве программного инструментария системно-когнитивного анализа (СК-анализ) [260].

Авторы считают, что система Эйдос-Х++ является программным инструментарием, реализующим ряд идей системного нечеткого интервального обобщения математики.

11.4.2. Развернутый численный пример построения когнитивных функций на основе зашумленных данных в системе «Эйдос»

В системе «Эйдос» для учебных целей реализована возможность исследования зашумленных когнитивных функций. В качестве функции, на примере которой это осуществляется в настоящее время выбран затухающий свип-сигнал, т.е. гармонический сигнал с уменьшающейся амплитудой и изменяющийся частотой.

Рассмотрим последовательность действий при исследовании зашумленных когнитивных функций в системе «Эйдос» и их результаты этого исследования. Для генерации исходной выборки запустим диспетчер приложений, т.е. режим 1.3 (рисунок 4):

Рисунок 4. Запуск диспетчера приложений системы «Эйдос»
(режим 1.3)

Появляется окно данного режима (рисунок 5):

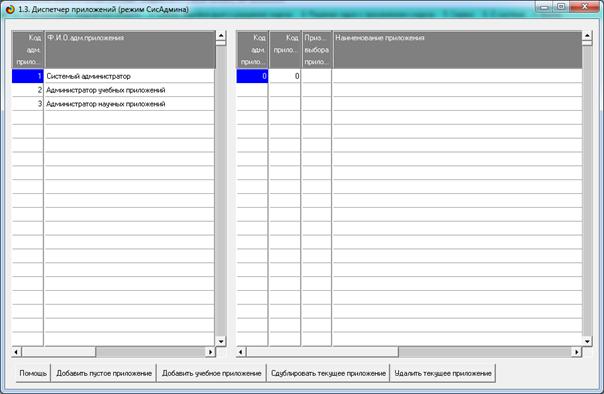
Рисунок 5. Окно диспетчера приложений системы «Эйдос» (режим 1.3)

По клику на кнопке «Добавить учебное приложение» появляется окно (рисунок 6):

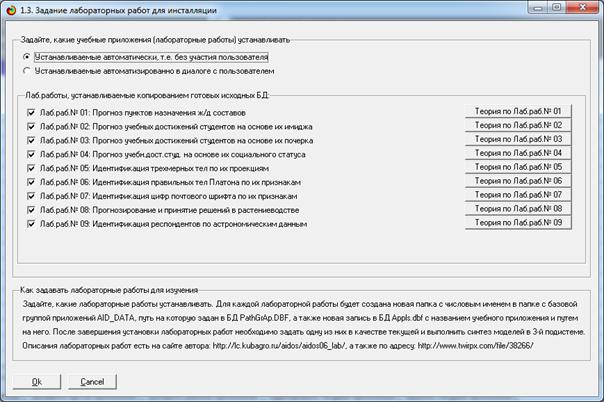
Рисунок 6. Первое окно режима выбора учебных приложений
для инсталляции

Выбираем опцию: «Устанавливаемые автоматизировано в диалоге с пользователем» и получаем (рисунок 7):

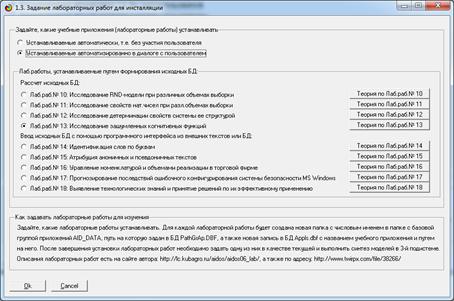
Рисунок 7. Второе окно режима выбора учебных приложений
для инсталляции

Выбираем учебное приложение №13 и нажимаем «ОК». Получаем окно, представленное на рисунке 8:

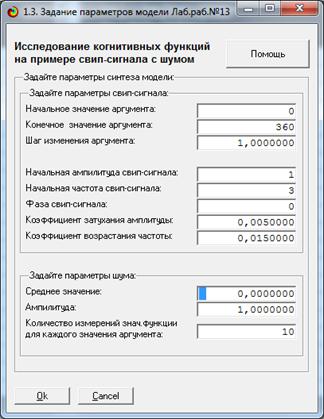
Рисунок 8. Окно задания параметров генерации зашумленного
свип-сигнала для исследования зашумленных когнитивных функций

Стадия процесса генерации обучающей выборки и прогноз времени исполнения отображается на окне, представленном на рисунке 9:

Рисунок 9. Окно отображения стадия процесса генерации обучающей выборки и прогноза времени исполнения

В результате выполнения данного режима генерируется обучающая выборка, состоящая из двух файлов: Inp_data.dbf с значениями функции для различных значений аргумента, причем для каждого значения аргумента просчитано 10 значений функций, и Inp_name.txt с наименованиями колонок файла Inp_data.dbf. Файл Inp_data.dbf представлен в таблице 7:

Таблица 7 – ИСХОДНЫЕ ДАННЫЕ ДЛЯ СИНТЕЗА МОДЕЛИ ИССЛЕДОВАНИЯ ЗАШУМЛЕННОЙ КОГНИТИВНОЙ ФУНКЦИИ (ФРАГМЕНТ)

Наименование объекта обучающей выборки	Значения функции			Значение шума		Значение аргумента
	Равномерно зашумленное (эмпирическое)	Нормально зашумленное (эмпирическое)	Истинное (теоретическое)	Равномерное распределение	Нормальное распределение
0	0,6507407	0,8494331	0,9986295	-0,3478888	-0,1491964	0,0000000
0	0,6423481	0,8423761	0,9986295	-0,3562814	-0,1562534	0,0000000
0	1,4927462	1,2906329	0,9986295	0,4941167	0,2920034	0,0000000
0	0,7181546	0,9006307	0,9986295	-0,2804749	-0,0979988	0,0000000
0	1,1079167	1,0137574	0,9986295	0,1092872	0,0151279	0,0000000
0	0,9321988	0,9930294	0,9986295	-0,0664308	-0,0056001	0,0000000
0	1,3841246	1,1805820	0,9986295	0,3854951	0,1819525	0,0000000
0	1,7984084	1,6942263	0,9986295	0,7997788	0,6955968	0,0000000
0	0,3177716	0,4729162	0,9986295	-0,6808579	-0,5257134	0,0000000
0	1,1989542	1,0491026	0,9986295	0,2003246	0,0504731	0,0000000
1	0,8676704	0,9706996	0,9894791	-0,1218087	-0,0187795	1,0000000
1	1,8432152	1,7656193	0,9894791	0,8537361	0,7761402	1,0000000
1	1,7012114	1,5580637	0,9894791	0,7117323	0,5685846	1,0000000
1	1,8043663	1,7074563	0,9894791	0,8148872	0,7179772	1,0000000
1	0,9903626	0,9894801	0,9894791	0,0008835	0,0000010	1,0000000
1	0,6544930	0,8508427	0,9894791	-0,3349860	-0,1386363	1,0000000
1	1,1558018	1,0243804	0,9894791	0,1663227	0,0349013	1,0000000
1	1,5639833	1,3760441	0,9894791	0,5745042	0,3865650	1,0000000
1	0,4903830	0,6919209	0,9894791	-0,4990961	-0,2975581	1,0000000
1	0,2341416	0,3587870	0,9894791	-0,7553375	-0,6306920	1,0000000
2	1,2346845	1,0601969	0,9776125	0,2570720	0,0825845	2,0000000
2	0,0278706	0,0550427	0,9776125	-0,9497419	-0,9225698	2,0000000
2	1,7419907	1,6213866	0,9776125	0,7643783	0,6437741	2,0000000
2	1,8483406	1,7794321	0,9776125	0,8707281	0,8018196	2,0000000
2	0,5440427	0,7496685	0,9776125	-0,4335697	-0,2279440	2,0000000
2	-0,0229405	-0,0232402	0,9776125	-1,0005530	-1,0008527	2,0000000
2	0,4398505	0,6355278	0,9776125	-0,5377619	-0,3420847	2,0000000
2	1,3910291	1,1857304	0,9776125	0,4134166	0,2081179	2,0000000
2	0,2706143	0,4156645	0,9776125	-0,7069982	-0,5619480	2,0000000
2	0,5239797	0,7291730	0,9776125	-0,4536328	-0,2484394	2,0000000
3	1,5783846	1,4013130	0,9630885	0,6152962	0,4382245	3,0000000
3	1,7041258	1,5732261	0,9630885	0,7410373	0,6101377	3,0000000
3	1,4467041	1,2435161	0,9630885	0,4836157	0,2804276	3,0000000
3	1,9246833	1,9038979	0,9630885	0,9615948	0,9408095	3,0000000
3	1,0482806	0,9722919	0,9630885	0,0851921	0,0092034	3,0000000
3	1,0711801	0,9778882	0,9630885	0,1080917	0,0147997	3,0000000
3	0,0678112	0,1239575	0,9630885	-0,8952772	-0,8391310	3,0000000
3	0,4612102	0,6624084	0,9630885	-0,5018783	-0,3006801	3,0000000
3	1,8572679	1,8005462	0,9630885	0,8941794	0,8374577	3,0000000
3	0,3946094	0,5839555	0,9630885	-0,5684791	-0,3791330	3,0000000

Эти данные аналогичны тем, которые мы получаем при многократных измерениях некоторой эмпирической величины. При этом все время получаются разные эмпирические значения, являющиеся суммой истинного значения и шума. Если шум обусловлен независимыми факторами, влияющими на результаты процессы измерения, то такой шум распределен нормально и называется аддитивным гауссовским шумом. В системе «Эйдос» генерируются последовательности значений функции и с гауссовским, и с равномерным шумом (рисунки 10 и 11):

Рисунок 10. Экранная форма с графическим представлением
исходных данных с гауссовским аддитивным шумом

Рисунок 11. Экранная форма с графическим представлением
исходных данных с равномерным аддитивным шумом

Если вид модели эмпирических данных, представленных в таблице 7 и на рисунках 10 и 11 чем-то не устраивает, то на этой стадии можно повторить процесс генерации исходных данных, т.к. никакого приложения еще не создано.

Чтобы теперь создать приложение необходимо запустить универсальный программный интерфейс импорта данных из внешних баз данных в систему «Эйдос», т.е. режим 2.3.2.2 при параметрах, созданных автоматически на предыдущем шаге (рисунок 12):

Рисунок 12. Запуск универсального программного интерфейса
импорта данных из внешних баз данных в систему «Эйдос»
(режим 2.3.2.2)

На рисунке 13 приведено первое окно режима 2.3.2.2:

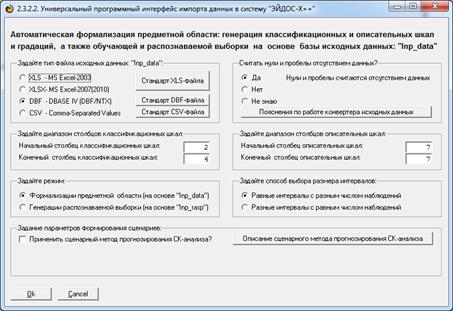
Рисунок 13. Первое окно универсального программного интерфейса импорта данных из внешних баз данных в систему «Эйдос»
(режим 2.3.2.2)

Обратим внимание на то, что в системе «Эйдос» реализованы режимы выбора либо равных интервальных значений в которых будет получаться разное число наблюдений, либо адаптивных интервалов разной величины, в которых будет получаться практически равное число наблюдений. Второй вариант соответствует рекомендациям, основанным на теореме Котельникова «Об отсчетах», т.к. размер интервала при этом подходе определяется распределением плотности наблюдений по шкале аргумента. При этом подходе, чем выше кривизна функции, тем чаще будут стоять отсчеты и тем меньше будут значения числовых интервалов, что обеспечивает максимальную точность модели при минимальном суммарном числе интервалов.

На экранной форме, представленной на рисунке 13, просто кликаем «ОК», т.к. все необходимые параметры импорта данных заданы по умолчанию на предыдущем этапе. Тогда появляется второе окно данного режима, представляющее собой калькулятор для выбора числа градаций числовых классификационных и описательных шкал (рисунок 14):

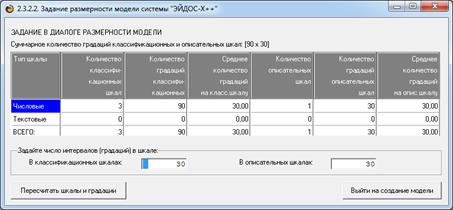
Рисунок 14. Второе окно универсального программного интерфейса импорта данных из внешних баз данных в систему «Эйдос»
(режим 2.3.2.2)

Здесь мы можем задать любое число градаций как в классификационных, так и в описательных числовых шкалах (в данном случае задано 30). Обратим внимание на то, что число градаций по классификационным и описательным шкалам задается раздельно и может не совпадать. В случае перезадания числа градаций необходимо выполнить пересчет шкал и градаций, кликнув на соответствующей кнопке в данной экранной форме. Если все устраивает необходимо выйти на создание модели. Экранная форма отображения стадии процесса и прогнозирования времени исполнения представлена на рисунке 15:

Рисунок 15. Третье окно универсального программного интерфейса импорта данных из внешних баз данных в систему «Эйдос»
(режим 2.3.2.2): отображение стадии процесса
и прогнозирования времени исполнения

В результате работы программного интерфейса создается новое приложение (рисунок 16), название которого может быть изменено вручную, что нами и было сделано.

Рисунок 16. Окно диспетчера приложений с информацией о том,
что новое приложение создано

Данное приложение автоматически определяется как текущее (рабочее). Универсальным программным интерфейсом созданы классификационные и описательные шкалы и градации в этом новом текущем приложении. Затем исходные данные закодированы с помощью классификационных и описательных шкал и градаций и тем самым преобразованы в обучающую выборку.

Таким образом, универсальный программный интерфейс автоматизирует выполнение этапа формализации предметной области АСК-анализа (рисунок 17). Дальнейшие процедуры преобразования, предусмотренные в АСК-анализе, осуществляются также в соответствии с диаграммой, приведенной на рисунке 17.

Кратко рассмотрим соотношение содержания понятий: «данные», «информация» и «знания» (рисунок 24). Данные – это информация, рассматриваемая безотносительно к ее смысловому содержанию, находящаяся на носителях или в каналах связи и представленная в определенной системе кодирования или на определенном языке (т.е. в формализованном виде). Информация – это осмысленные данные. Смысл, семантика, содержание (согласно концепции смысла Шенка-Абельсона [149]) – это знание причинно-следственных зависимостей. Знания – это информация, полезная для достижения целей, т.е. для управления, которая представляет собой технологию или «ноу-хау».

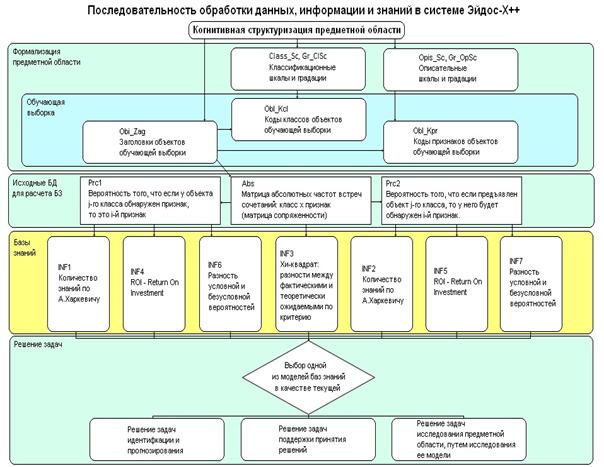
Рисунок 17. Последовательность преобразования исходных данных
в информацию, а ее в знания в системе «Эйдос-Х++»

Знания могут быть представлены в различных формах, характеризующихся различной степенью формализации:

– вообще неформализованные знания, т.е. знания в своей собственной форме, ноу-хау (мышление без вербализации есть медитация);

– знания, формализованные на естественном вербальном языке;

– знания, формализованные в виде различных методик, схем, алгоритмов, планов, таблиц и отношений между ними;

– знания в форме технологий, организационных производственных, социально-экономических и политических структур;

– знания, формализованные в виде математических моделей и методов представления знаний в автоматизированных интеллектуальных системах (логическая, фреймовая, сетевая, продукционная, нейросетевая, нечеткая и другие).

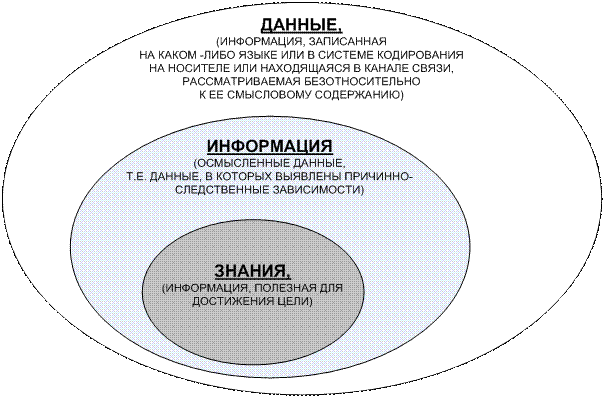
Рисунок 5. Соотношение содержания понятий:
«данные», «информация», «знания»

Таким образом, для решения задачи метризации шкал в АСК-анализе необходимо осознанно и целенаправленно последовательно повышать степень формализации исходных данных до уровня, который позволяет ввести исходные данные в интеллектуальную систему, а затем:

– преобразовать исходные данные в информацию;

– преобразовать информацию в знания;

– использовать знания для решения задач прогнозирования, принятия решений и исследования предметной области.

Для этого в АСК-анализе предусмотрены следующие этапы [17]:

1. Когнитивная структуризация предметной области, при которой определяется, что мы хотим прогнозировать и на основе чего (конструирование классификационных и описательных шкал).

2. Формализация предметной области:

– разработка градаций классификационных и описательных шкал (номинального, порядкового и числового типа);

– использование разработанных на предыдущих этапах классификационных и описательных шкал и градаций для формального описания (кодирования) исследуемой выборки.

3. Синтез и верификация (оценка степени адекватности) модели.

4. Если модель адекватна, то ее использование для решения задач идентификации, прогнозирования и принятия решений, а также для исследования моделируемой предметной области [97].

Для синтеза моделей в АСК-анализе в настоящее время используется 7 частных критериев знаний, а для верификации моделей и решения задачи идентификации и прогнозирования 2 интегральных критерия [97].

Итак, в результате работы универсального программного интерфейса получены классификационные и описательные шкалы и градации и обучающая выборка (рисунки 19, 20, 21):

Рисунок 19. Экранная форма с классификационными шкалами
и градациями

Рисунок 20. Экранная форма с описательной шкалой и градациями

Рисунок 21. Экранная форма с обучающей выборкой

Затем запускается режим синтеза всех частных моделей 3.4 (рисунок 22):

Рисунок 22. Запуск режима синтеза всех частных моделей 3.4

Затем необходимо выбрать все частные модели и кликнуть «ОК» (рисунок 23):

Рисунок 23. Первая экранная форма режима синтеза
всех частных моделей 3.4

В результате будут созданы статистические модели и модели знаний с частными критериями, приведенными в таблице 5. На рисунке 24 приведена результирующая экранная форма режима 3.4:

Рисунок 24. Результирующая экранная форма режима 3.4

В результате выполнения этих операций созданы базы знаний с различными частными критериями, представленными в таблице 5. Подматрицы этих баз знаний могут быть представлены в наглядной графической форме в виде когнитивных функций. Для получения этих когнитивных функций необходимо вызвать режим 4.5 (рисунок 25):

Рисунок 25. Запуск режима визуализации когнитивных функций

На рисунке 26 приведена первая экранная форма режима визуализации когнитивных функций:

Рисунок 26. Первая экранная форма режима визуализации
когнитивных функций:

Для запуска модуля визуализации когнитивных функций [40] кликаем по соответствующей кнопке и выходим на главное окно модуля визуализации (рисунок 27):

Рисунок 27. Главное окно модуля визуализации
когнитивных функций

Ниже, на рисунке 28 приведены когнитивные функции, полученные с помощью данного модуля визуализации подматриц баз знаний модели INF1 на основе частного критерия знаний А.Харкевича, а на рисунке 29 – на основе модели INF3 (хи-квадрат):

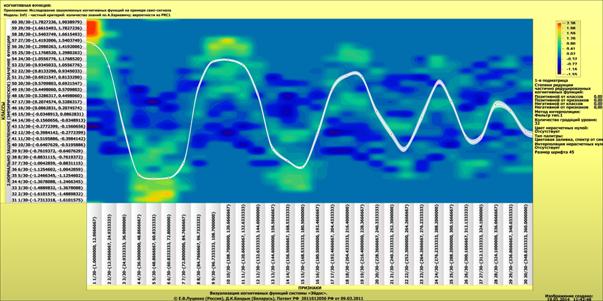
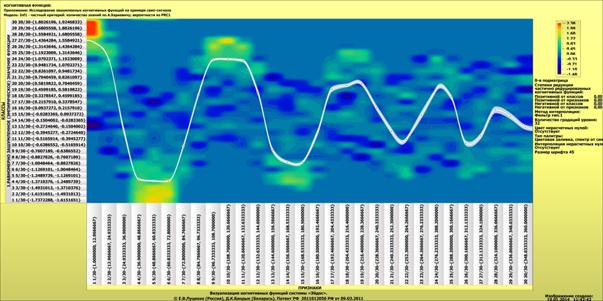
Рисунок 28. Когнитивные функции, полученные на основе частного критерия А.Харкевича

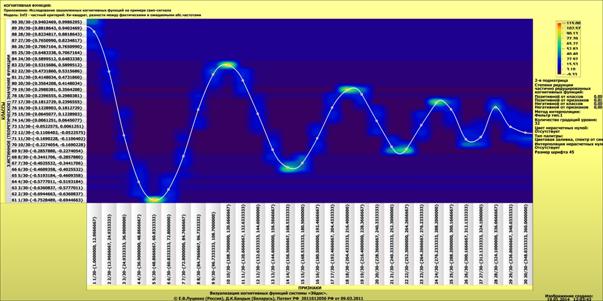
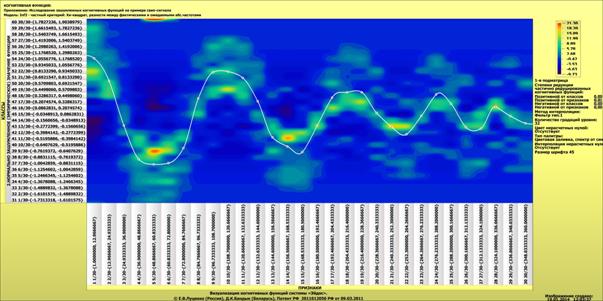
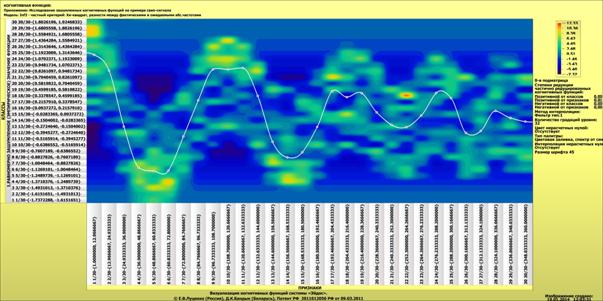
Рисунок 29. Когнитивные функции, полученные на основе частного критерия хи-квадрат

Из сравнения вида когнитивных функций, приведенных на рисунках 28 и 29 можно сделать выводы о том, что они вполне позволяют выявлять зависимости в зашумленных эмпирических данных.

11.5. Выводы

Кратко рассматриваются классическое понятие функциональной зависимости в математике, определяются ограничения применимости этого понятия для адекватного моделирования реальности и формулируется проблема, состоящая в поиске такого обобщения понятия функции, которое было бы более пригодно для адекватного отражения причинно-следственных связей в реальной области. Далее рассматривается теоретическое и практическое решения поставленной проблемы, состоящие в том, что

а) предлагается универсальный не зависящий от предметной области способ вычисления количества информации в значении аргумента о значении функции, т.е. когнитивные функции;

б) предлагается программный инструментарий: интеллектуальная система «Эйдос», позволяющая на практике осуществлять эти расчеты, т.е. строить когнитивные функции на основе фрагментированных зашумленных эмпирических данных большой размерности.

Предлагаются понятия нередуцированных, частично и полностью редуцированных прямых и обратных, позитивных и негативных когнитивных функций и метод формирования редуцированных когнитивных функций, являющийся обобщением известного взвешенного метода наименьших квадратов на основе учета в качсетве весов наблюдений количества информации в значениях аргумента о значениях функции.

Таким образом, предлагается теория (АСК-анализ), и реализующий ее программный инструментарий (система «Эйдос») для когнитивного функционального анализа. Эта технология была успешно применена при проведении ряда научных исследований [97-286] и может применяться как в научных исследованиях, так и при проведении лекционных и лабораторных занятий по дисциплинам: «Управление знаниями», «Интеллектуальные системы», «Представление знаний в интеллектуальных системах», «Функционально-стоимостной анализ при управлении персоналом» и других.

В качестве перспективы хотелось бы отметить возможность обобщения понятия когнитивных функций на многомерный случай с возможностью 3D-визуализации, а также визуализации в динамике. Эти идеи развивались в работаъ по системному обобщению математики.

ГЛАВА 12. ПОВЫШЕНИЕ СТЕПЕНИ ФОРМАЛИЗАЦИИ ВЗВЕШЕННОГО МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ ПУТЕМ ВЫБОРА В КАЧЕСТВЕ ВЕСОВ НАБЛЮДЕНИЙ КОЛИЧЕСТВА ИНФОРМАЦИИ В НИХ О ЗНАЧЕНИЯХ ФУНКЦИИ И АВТОМАТИЗАЦИИ ИХ РАСЧЕТА ПУТЕМ ПРИМЕНЕНИЯ АСК-АНАЛИЗА

Использование взвешенного метода наименьших квадратов (МНК) позволяет исследователю вручную регулировать вклад тех или иных данных в результаты построения моделей. Это необходимо в тех случаях, когда известно, что на зависимую переменную оказывали влияние какие-либо факторы кроме аргумента, заведомо не включенные в модель. В такой ситуации нужно попытаться исключить влияние неучтенных факторов заданием весов наблюдений. Обычно в статистических пакетах набор весов это числа от 0 до 100. По умолчанию все данные учитываются с единичными весами. Задание наблюдениям веса меньше 1 снижает их вклад в модель, а больше единицы увеличивает этот вклад. Ключевым моментом при применении взвешенного МНК является способ выбора и задания весов наблюдений. Считается[98], что разумным вариантом является выбор весов пропорционально ошибкам не взвешенной регрессии.

Подбор этих весов наблюдений вручную может являться сложной и практически неразрешимой задачей, как из-за сложной структуры данных (например, непостоянства дисперсии и среднего ошибок наблюдений), так и из-за возможной очень большой размерности данных. Таким образом, возникает задача автоматического определения весов наблюдений и разработка алгоритмов и программного инструментария, обеспечивающего автоматизацию определения и взвешивания весов наблюдений в МНК.

Предлагается новое, ранее не встречавшееся в специальной литературе, решение этой задачи и соответствующее обобщение метода наименьших квадратов (МНК), в котором точки (наблюдения) имеют вес, равный количеству информации в значении аргумента о значении функции. Ясно, что по сути, речь идет о применении когнитивных функций в взвешенном МНК.

Для этого предлагается два варианта.

11.1. Вариант 1-й: применение когнитивных функций в взвешенном МНК

Можно рассматривать точки когнитивных функций как «мультиточки», состоящие из определенного количества «элементарных точек», соответствующего их весу. При этом вес элементарной точки может быть принят равным единице младшего разряда.

В таблице 8 приведен фрагмент матрицы информативностей модели INF1 – мера А.Харкевича (см. таблицу 5, глава 9).

Таблица 5 – МАТРИЦА ИНФОРМАТИВНОСТИ МОДЕЛЬ
INF1 – МЕРА А.ХАРКЕИВЧА В БИТАХ (ФРАГМЕНТ)

Код	Наименование	Классы
		1	2	3	4	5	6
1	ЗНАЧЕНИЕ АРГУМЕНТА-1/30-{1.0000000, 12.9666667}	0,000	0,000	0,000	0,000	0,000	0,000
2	ЗНАЧЕНИЕ АРГУМЕНТА-2/30-{12.9666667, 24.9333333}	0,000	0,000	0,000	0,000	0,000	0,000
3	ЗНАЧЕНИЕ АРГУМЕНТА-3/30-{24.9333333, 36.9000000}	0,000	0,000	0,000	0,000	-0,562	0,533
4	ЗНАЧЕНИЕ АРГУМЕНТА-4/30-{36.9000000, 48.8666667}	1,408	1,408	1,199	1,165	0,892	0,708
5	ЗНАЧЕНИЕ АРГУМЕНТА-5/30-{48.8666667, 60.8333333}	1,893	1,610	1,683	0,754	0,563	0,849
6	ЗНАЧЕНИЕ АРГУМЕНТА-6/30-{60.8333333, 72.8000000}	1,408	1,765	1,527	1,366	0,691	0,142
7	ЗНАЧЕНИЕ АРГУМЕНТА-7/30-{72.8000000, 84.7666667}	0,000	0,000	0,074	0,114	0,407	0,626
8	ЗНАЧЕНИЕ АРГУМЕНТА-8/30-{84.7666667, 96.7333333}	0,000	0,000	0,000	0,000	0,000	0,000
9	ЗНАЧЕНИЕ АРГУМЕНТА-9/30-{96.7333333, 108.7000000}	0,000	0,000	0,000	0,000	0,000	0,000
10	ЗНАЧЕНИЕ АРГУМЕНТА-10/30-{108.7000000, 120.6666667}	0,000	0,000	0,000	0,000	0,000	0,000
11	ЗНАЧЕНИЕ АРГУМЕНТА-11/30-{120.6666667, 132.6333333}	0,000	0,000	0,000	0,000	0,000	0,000
12	ЗНАЧЕНИЕ АРГУМЕНТА-12/30-{132.6333333, 144.6000000}	0,000	0,000	0,000	0,000	0,000	0,000
13	ЗНАЧЕНИЕ АРГУМЕНТА-13/30-{144.6000000, 156.5666667}	0,000	0,000	0,000	0,397	0,563	-0,343
14	ЗНАЧЕНИЕ АРГУМЕНТА-14/30-{156.5666667, 168.5333333}	0,000	0,000	0,074	1,305	1,048	0,298
15	ЗНАЧЕНИЕ АРГУМЕНТА-15/30-{168.5333333, 180.5000000}	0,000	0,000	0,558	1,165	0,799	0,626
16	ЗНАЧЕНИЕ АРГУМЕНТА-16/30-{180.5000000, 192.4666667}	0,000	0,000	0,000	0,000	0,407	-0,343
17	ЗНАЧЕНИЕ АРГУМЕНТА-17/30-{192.4666667, 204.4333333}	0,000	0,000	0,000	0,000	0,000	0,000
18	ЗНАЧЕНИЕ АРГУМЕНТА-18/30-{204.4333333, 216.4000000}	0,000	0,000	0,000	0,000	0,000	0,000
19	ЗНАЧЕНИЕ АРГУМЕНТА-19/30-{216.4000000, 228.3666667}	0,000	0,000	0,000	0,000	0,000	0,000
20	ЗНАЧЕНИЕ АРГУМЕНТА-20/30-{228.3666667, 240.3333333}	0,000	0,000	0,000	0,000	0,000	-0,060
21	ЗНАЧЕНИЕ АРГУМЕНТА-21/30-{240.3333333, 252.3000000}	0,000	0,000	0,000	0,000	-0,077	0,298
22	ЗНАЧЕНИЕ АРГУМЕНТА-22/30-{252.3000000, 264.2666667}	0,000	0,000	0,000	0,000	0,691	0,626
23	ЗНАЧЕНИЕ АРГУМЕНТА-23/30-{264.2666667, 276.2333333}	0,000	0,000	0,000	0,000	-0,077	-0,827
24	ЗНАЧЕНИЕ АРГУМЕНТА-24/30-{276.2333333, 288.2000000}	0,000	0,000	0,000	0,000	0,000	0,000
25	ЗНАЧЕНИЕ АРГУМЕНТА-25/30-{288.2000000, 300.1666667}	0,000	0,000	0,000	0,000	0,000	0,000
26	ЗНАЧЕНИЕ АРГУМЕНТА-26/30-{300.1666667, 312.1333333}	0,000	0,000	0,000	0,000	0,563	0,425
27	ЗНАЧЕНИЕ АРГУМЕНТА-27/30-{312.1333333, 324.1000000}	0,000	0,000	0,000	0,000	-0,077	0,626
28	ЗНАЧЕНИЕ АРГУМЕНТА-28/30-{324.1000000, 336.0666667}	0,000	0,000	0,000	0,000	0,000	0,000
29	ЗНАЧЕНИЕ АРГУМЕНТА-29/30-{336.0666667, 348.0333333}	0,000	0,000	0,000	0,000	0,000	0,298
30	ЗНАЧЕНИЕ АРГУМЕНТА-30/30-{348.0333333, 360.0000000}	0,000	0,000	0,000	0,000	0,000	0,425

Чтобы применить предлагаемый подход, умножим в таблице 8 все значения на 1000 и оставим только целую часть, тогда получим таблицу 9.

Таблица 6 – МАТРИЦА ИНФОРМАТИВНОСТИ МОДЕЛЬ
INF1 – МЕРА А.ХАРКЕИВЧА В МИЛЛИБИТАХ (ФРАГМЕНТ)

Код	Наименование	Классы
		1	2	3	4	5	6	7
1	ЗНАЧЕНИЕ АРГУМЕНТА-1/30-{1.0000000, 12.9666667}
2	ЗНАЧЕНИЕ АРГУМЕНТА-2/30-{12.9666667, 24.9333333}
3	ЗНАЧЕНИЕ АРГУМЕНТА-3/30-{24.9333333, 36.9000000}					-562	533	105
4	ЗНАЧЕНИЕ АРГУМЕНТА-4/30-{36.9000000, 48.8666667}	1408	1408	1199	1165	892	708	717
5	ЗНАЧЕНИЕ АРГУМЕНТА-5/30-{48.8666667, 60.8333333}	1893	1610	1683	754	563	849	434
6	ЗНАЧЕНИЕ АРГУМЕНТА-6/30-{60.8333333, 72.8000000}	1408	1765	1527	1366	691	142	434
7	ЗНАЧЕНИЕ АРГУМЕНТА-7/30-{72.8000000, 84.7666667}			74	114	407	626	341
8	ЗНАЧЕНИЕ АРГУМЕНТА-8/30-{84.7666667, 96.7333333}							-535
9	ЗНАЧЕНИЕ АРГУМЕНТА-9/30-{96.7333333, 108.7000000}
10	ЗНАЧЕНИЕ АРГУМЕНТА-10/30-{108.7000000, 120.6666667}
11	ЗНАЧЕНИЕ АРГУМЕНТА-11/30-{120.6666667, 132.6333333}
12	ЗНАЧЕНИЕ АРГУМЕНТА-12/30-{132.6333333, 144.6000000}							-252
13	ЗНАЧЕНИЕ АРГУМЕНТА-13/30-{144.6000000, 156.5666667}				397	563	-343	773
14	ЗНАЧЕНИЕ АРГУМЕНТА-14/30-{156.5666667, 168.5333333}			74	1305	1048	298	516
15	ЗНАЧЕНИЕ АРГУМЕНТА-15/30-{168.5333333, 180.5000000}			558	1165	799	626	590
16	ЗНАЧЕНИЕ АРГУМЕНТА-16/30-{180.5000000, 192.4666667}					407	-343	341
17	ЗНАЧЕНИЕ АРГУМЕНТА-17/30-{192.4666667, 204.4333333}
18	ЗНАЧЕНИЕ АРГУМЕНТА-18/30-{204.4333333, 216.4000000}
19	ЗНАЧЕНИЕ АРГУМЕНТА-19/30-{216.4000000, 228.3666667}
20	ЗНАЧЕНИЕ АРГУМЕНТА-20/30-{228.3666667, 240.3333333}						-60	-252
21	ЗНАЧЕНИЕ АРГУМЕНТА-21/30-{240.3333333, 252.3000000}					-77	298	341
22	ЗНАЧЕНИЕ АРГУМЕНТА-22/30-{252.3000000, 264.2666667}					691	626	233
23	ЗНАЧЕНИЕ АРГУМЕНТА-23/30-{264.2666667, 276.2333333}					-77	-827	105
24	ЗНАЧЕНИЕ АРГУМЕНТА-24/30-{276.2333333, 288.2000000}
25	ЗНАЧЕНИЕ АРГУМЕНТА-25/30-{288.2000000, 300.1666667}							-1020
26	ЗНАЧЕНИЕ АРГУМЕНТА-26/30-{300.1666667, 312.1333333}					563	425	341
27	ЗНАЧЕНИЕ АРГУМЕНТА-27/30-{312.1333333, 324.1000000}					-77	626	233
28	ЗНАЧЕНИЕ АРГУМЕНТА-28/30-{324.1000000, 336.0666667}
29	ЗНАЧЕНИЕ АРГУМЕНТА-29/30-{336.0666667, 348.0333333}						298	-51
30	ЗНАЧЕНИЕ АРГУМЕНТА-30/30-{348.0333333, 360.0000000}						425	233

В таблице 9 рассматриваем отдельно только положительные числа или только отрицательные. Рассмотрим фрагмент таблицы 9, выделенный светло-желтым фоном:

– аргументу 14 соответствует 74 точки 3 класса, и 1305 точек 4-го класса;

– аргументу 15 соответствует 558 точек 3 класса, и 1165 точек 4-го класса.

После этого преобразования можно применять стандартный МНК.

11.2. Вариант 2-й: средневзвешенные значения функции в взвешенном МНК

Перед применением стандартного МНК для каждого значения аргумента предварительно рассчитывается средневзвешенное значение функции из всех ее значений с их весами.

Для двух точек выбор координаты средневзвешенной точки соответствует «правилу рычага», т.е. ее положение выбирается таким, чтобы рычаг, образованный двумя точками с координатами Y₁ и Y₂ и весами I₁ и I₂, находился в равновесии, если его опора будет в средневзвешенной точке с координатой Y:

Откуда находим Y. При двух точках, соответствующих одному значению аргумента, координата Y средневзвешенной точки, имеет вид:

.

Если же таких точек N, то предыдущее выражение принимает вид:

.

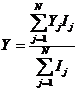В результате средневзвешенная точка находится тем ближе к некоторой точке, чем больше абсолютное и относительное количество информации в значении аргумента о том, что функция примет значение, соответствующее этой точке.

После этого преобразования можно применять стандартный МНК.

В модуле визуализации когнитивных функций [133] этот метод реализован программно для отображения частично и полностью редуцированных когнитивных функций. Математическому описанию этого метода планируются посвятить одну из будущих статей авторов.

Отметим, что кроме количества информации в значении аргумента о значении функции в качестве весов могут быть использованы и другие частные критерии из таблицы 5 главы 9.

ГЛАВА 13. МЕТОД КОГНИТИВНОЙ КЛАСТЕРИЗАЦИИ ИЛИ КЛАСТЕРИЗАЦИЯ НА ОСНОВЕ ЗНАНИЙ
(Кластеризация в системно-когнитивном анализе
и интеллектуальной системе «Эйдос»)

«Мышление – это обобщение, абстрагирование,

сравнение, и классификация»

Патанджали[99], II в. до н. э.

“Истинное знание – это знание причин”

Френсис Бэкон (1561–1626 гг.)

Кластерный анализ[100] (англ. Data clustering) – это задача разбиения заданной выборки объектов (ситуаций) на подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались. Кластерный анализ очень широко применяется как в науке, так и в различных направлениях практической деятельности. Значение кластерного анализа невозможно переоценить, оно широко известно[101] и нет необходимости его специально обосновывать.

Существует большое количество различных методов кластерного анализа, хорошо описанных в многочисленной специальной литературе[102] и прекрасных обзорных статьях[103]. Поэтому в данной работе мы не ставим перед собой задачу дать еще одно подобное описание, а обратим основное внимание на проблемы, существующие в кластерном анализе и вариант их решения, предлагаемый в автоматизированном системно-когнитивном анализе (АСК-анализ). Эти проблемы, в основном, хорошо известны специалистам, и поэтому наш краткий обзор будет практически полностью основан на уже упомянутых работах. Необходимо специально отметить, что специалисты небезуспешно работают над решением этих проблем, предлагая все новые и новые варианты, которые и являются различными вариантами кластерного анализа. Мы в данной работе также предложим еще один ранее не описанный в специальной литературе (т.е. новый, авторский) теоретически обоснованный и программно-реализованный вариант решения некоторых из этих проблем, а также проиллюстрируем его на простом численном примере.

Почему же разработано так много различных методов кластерного анализа, почему это было необходимо? Кажутся почти очевидными мысли о том, что различные методы кластерного анализа дают результаты различного качества, т.е. одни методы в определенном смысле «лучше», а другие «хуже», и это действительно так[104], и, следовательно, по-видимому, должен существовать только один-единственный метод кластеризации, всегда (т.е. на любых данных) дающий «правильные» результаты, тогда как все остальные методы являются «неправильными». Однако если задать аналогичный вопрос по поводу, например, автомобиля или одежды, то становится ясным, что нет просто наилучшего автомобиля, а есть лучшие по определенным критериям-требованиям или лучшие для определенных целей. При этом сами критерии также должны быть обоснованы и не просто могут быть различными, но и должны быть различными при различных целях, чтобы отражать цель и соответствовать ей. Так автомобиль, лучший для семейного отдыха не являются лучшим для гонок Формулы-1 или для представительских целей. Аналогично можно обоснованно утверждать, что одни методы кластерного анализа являются более подходящими для кластеризации данных определенной структуры, а другие – другой, т.е. не существует одного наилучшего во всех случаях универсального метода кластеризации, но существуют методы более универсальные и методы менее универсальные. Но все же многообразие разработанных методов кластерного анализа на наш взгляд указывает не только на это, но и на то, что их можно рассматривать как различные более или менее успешные варианты решения или попытки решения тех или иных проблем, существующих в области кластерного анализа.

Для структурирования дальнейшего изложения сформулируем требования к исходным данным в кластерном анализе и фундаментальные вопросы, которые решают разработчики различных методов кластерного анализа.

Считается[105], что кластерный анализ предъявляет следующие требования к исходным данным:

1. Показатели не должны коррелировать между собой.

2. Показатели должны быть безразмерными.

3. Распределение показателей должно быть близко к нормальному.

4. Показатели должны отвечать требованию «устойчивости», под которой понимается отсутствие влияния на их значения случайных факторов.

5. Выборка должна быть однородна, не содержать «выбросов».

Даже поверхностный анализ сформулированных требований к исходным данным сразу позволяет утверждать, что на практике они в полной мере никогда не выполняются, а приведение исходных данных к виду, удовлетворяющему этим требованиям, или очень сложно, т.е. представляет собой проблему, и не одну, или даже теоретически невозможно в полной мере. В любом случае пытаться это делать можно различными способами, хотя чаще всего на практике этого не делается вообще или потому, что необходимость этого плохо осознается исследователем, или чаще потому, что в его распоряжении нет соответствующих инструментов, реализующих необходимые методы[106]. Конечно, в последнем случае не приходится удивляться тому, что результаты кластерного анализа получаются мягко сказать «несколько странными», а если они соответствуют здравому смыслу и точке зрения экспертов, то можно сказать, что это получилось случайно или потому, что «просто повезло».

Остановимся подробнее на анализе перечисленных требований к исходным данным, а также проблем, возникающих при попытке их выполнения и решения.

Первое требование связано с использованием в большинстве методов кластеризации евклидова расстояния или различных его вариантов в качестве меры близости объектов и кластеров. Другими словами это требование означает, что описательные шкалы, рассматриваемые как оси семантического пространства, должны быть ортонормированны, т.к. в противном случае применение евклидова расстояния и большинства других метрик (таблица 1) (кроме расстояния Махалонобиса) теоретически необоснованно и некорректно.

Существуют и другие метрики, в частности: квадрат евклидова расстояния, расстояние городских кварталов (манхэттенское расстояние), расстояние Чебышева, степенное расстояние, процент несогласия, метрики Рао, Хемминга, Роджерса-Танимото, Жаккара, Гауэра, Воронина, Миркина, Брея-Кертиса, Канберровская и многие другие[107]. Когда корреляции между переменными равны нулю, расстояние Махаланобиса эквивалентно квадрату евклидового расстояния (там же). Это означает, что метрику Махаланобиса можно считать обобщением евклидовой метрики для неортонормированных пространств[108].

Таблица 1 – ОСНОВНЫЕ ТИПЫ МЕТРИК ПРИ КЛАСТЕР-АНАЛИЗЕ[109]

№	Наименование метрики	Тип признаков	Формула для оценки меры близости (метрики)
1	Эвклидово расстояние	Количественные
2	Мера сходства Хэмминга	Номинальные (качественные)	где число совпадающих признаков у образцов —  и
3	Мера сходства Роджерса–Танимото	Номинальные шкалы	где число совпадающих единичных признаков у образцов —  и ; , общее число —  единичных признаков у образцов и соответственно;
4	Манхэттенская метрика	Количественные
5	Расстояние Махаланобиса	Количественные	, где W ковариационная матрица выборки; — ;
6	Расстояние Журавлева	Смешанные	, где

Но на практике это требование никогда в полной мере не выполняется, а для его выполнения необходимо выполнить операцию ортонормирования семантического пространства, при которой из модели тем или иным методом[110] (реализованным в программной системе, в которой проводится кластерный анализ) исключаются все шкалы, коррелирующие между собой.

Таким образом, первое требование к исходным данным порождает две проблемы:

Проблема 1.1 выбора метрики, корректной для неортонормированных пространств.

Проблема 1.2 ортонормирования пространства.

Второе требование (безразмерности показателей) вытекает из того, что выбор единиц измерения по осям существенно влияет на результаты кластеризации. Казалось бы, одного этого должно быть достаточно для того, чтобы не делать этого, т.к. выбор единиц измерения, по сути, произволен (определяется исследователем), вследствие чего и результаты кластеризации, вместо того чтобы объективно отражать структуру данных и описываемой ими объективной реальности, также становятся произвольными и зависящими не только от самой исследуемой реальности, но и от произвола исследователя (причем неизвестно от чего больше: от реальности или исследователя). По сути, автоматизированная система кластеризации превращается в этих условиях из инструмента исследования структуры объективной реальности в автоматизированный инструмент рисования таких дендрограмм, какие больше нравятся пользователю. Непонятно также, какой содержательный смысл могут иметь, например корни квадратные из сумм квадратов разностей координат объектов, классов или кластеров, измеряемых в различных единицах измерения. Разве корректно складывать величины даже одного рода, измеряемые в различных единицах измерения, а тем более разного рода? Даже если сложить величины одного рода, но измеренные в разных единицах измерения, например расстояния от школы до подъезда дома 1.2 (километра), и от подъезда дома до квартиры 25 (метров), то получится 26,2 непонятно чего. Если же сложить разнородные по смыслу величины, т.е. величины различной природы, такие, например, как квадрат разности веса студентов с квадратом разности их роста, возраста, успеваемости и т.д., а потом еще извлечь из этой суммы квадратный корень, то получится просто бессмысленная величина, которая в традиционном кластерном анализе почему-то называется «Евклидово расстояние». В школе на уроке физики в 8-м классе за подобные действия сразу бы поставили «Неуд»[111]. Однако, как это ни удивительно, то, что «не прошло бы» на уроке физики в средней школе является вполне устоявшейся практикой в «статистике» и ее псевдонаучных применениях на уровне руководства системой образования.

В подтверждение тому, что подобная практика действительно существует, авторы не могут удержаться от искушения и не привести пространную цитату из работы[112]: «Заметим, что евклидово расстояние (и его квадрат) вычисляется по исходным, а не по стандартизованным данным. Это обычный способ его вычисления, который имеет определенные преимущества (например, расстояние между двумя объектами не изменяется при введении в анализ нового объекта, который может оказаться выбросом). Тем не менее, на расстояния могут сильно влиять различия между осями, по координатам которых вычисляются эти расстояния. К примеру, если одна из осей измерена в сантиметрах, а вы потом переведете ее в миллиметры (умножая значения на 10), то окончательное евклидово расстояние (или квадрат евклидова расстояния), вычисляемое по координатам, сильно изменится, и, как следствие, результаты кластерного анализа могут сильно отличаться от предыдущих.» (выделено нами, авт.)[113]. В той же работе просто констатируется факт этой ситуации, но ему не дается никакой оценки. Наша же оценка этой практике по перечисленным выше причинам сугубо отрицательная. Приведем еще цитату из той же работы: «Степенное расстояние. Иногда желают (!!!?)[114] прогрессивно увеличить или уменьшить вес, относящийся к размерности, для которой соответствующие объекты сильно отличаются. Это может быть достигнуто с использованием степенного расстояния. Степенное расстояние вычисляется по формуле:

расстояние(x,y) = (_i |x_i - y_i|^p)^1/r

где r и p - параметры, определяемые пользователем. Несколько примеров вычислений могут показать, как "работает" эта мера. Параметр p ответственен за постепенное взвешивание разностей по отдельным координатам, параметр r ответственен за прогрессивное взвешивание больших расстояний между объектами. Если оба параметра - r и p, равны двум, то это расстояние совпадает с расстоянием Евклида». Мы считаем, что еще какие-то комментарии здесь излишни, хотя сложно удержаться от того, чтобы не сказать, что подобный подход превращает науку из поиска истины в произвольную подтасовку данных и выводов.

Таким образом, второе требование к исходным данным порождает следующую проблему 2.1:

Проблема 2.1 сопоставимой обработки описаний объектов, описанных признаками различной природы, измеряемыми в различных единицах измерения (проблема размерностей).

Отметим также, что объекты чаще всего описаны не только признаками, измеряемыми в различных единицах измерения, но как количественными, так и качественными признаками, которые соответственно являются градациями как числовых шкал, так и номинальных (текстовых) шкал. Существует метрика для номинальных шкал: это «Процент несогласия»[115], однако для количественных шкал применяются другие метрики. Каким образом и с помощью какой комбинации классических метрик вычислять расстояния между объектами, описанными как количественными, так и качественными признаками, а также между кластерами, в которые они входят, вообще не понятно. Это порождает проблему 2.2.:

Проблема 2.2 формализации описаний объектов, имеющих как количественные, так и качественные признаки.

Третье требование (нормальности распределения показателей) вытекает из того, что статистическое обоснование корректности вышеперечисленных метрик существенным образом основано на этом предположении, т.е. эти метрики являются параметрическими. На практике это означает, что перед применением кластерного анализа с этими метриками необходимо доказать гипотезу о нормальности исходных данных либо применить процедуру их нормализации. И первое, и второе, весьма проблематично и на практике не делается, более того, даже вопрос об этом чаще всего не ставится. Процедура нормализации (или взвешивания, ремонта) исходных данных обычно предполагает удаление из исходной выборки тех данных, которые нарушают их нормальность. Ясно, что это непредсказуемым образом может повлиять на результаты кластеризации, которые, скорее всего, существенно изменяться и их уже нельзя будет признать результатами кластеризации исходных данных. Отметим, что на практике исходные данные, не подчиняющиеся нормальному распределению, встречаются достаточно часто, что и делает актуальными методы непараметрической статистики.

Таким образом, 3-е требование к исходным данным порождает проблемы 3.1., 3.2. и 3.3.:

Проблема 3.1 доказательства гипотезы о нормальности исходных данных.

Проблема 3.2 нормализации исходных данных.

Проблема 3.3 применения непараметрических методов кластеризации, корректно работающих с ненормализованными данными.

Что можно сказать о четвертом и пятом требованиях?[116] Эти требования взаимосвязаны, т.к. случайные факторы и порождают «выбросы». На практике, строго говоря, эти требования никогда не выполняются и вообще звучат несколько наивно, если учесть, что как случайные часто рассматриваются неизвестные факторы, а их влияние даже теоретически, т.е. в принципе, исключить невозможно. С другой стороны эти требования «удобны» тем, что неудачные, неадекватные или не интерпретируемые результаты кластеризации, полученные тем или иным методом кластерного анализа, всегда можно «списать» на эти неизвестные «случайные» факторы или скрытые параметры и порожденные ими выбросы. А поскольку ответственность за обеспечение отсутствия шума и выбросов в исходных данных возложена этими требованиями на самого исследователя, то получается, что если что-то получилось не так, то это связано уж не столько с методом кластеризации, сколько с каким-то недоработками самого исследователя. По этим причинам более логично и главное, более продуктивно было бы предъявить эти требования не к исходным данным и обеспечивающему их исследователю, а к самому методу кластерного анализа, который, по мнению авторов, должен корректно работать в случае наличия шума и выбросов в исходных данных и не перкладывать эту проблему «с больной головы на здоровую».

Таким образом, четвертое и пятое требования приводят к двум проблемам:

Проблема 4 разработки такого метода кластерного анализа, математическая модель и алгоритм и которого органично включали бы фильтр, подавляющий шум в исходных данных, в результате чего данный метод кластеризации корректно работал бы при наличии шума в исходных данных.

Проблема 5 разработки метода кластерного анализа, математическая модель и алгоритм и которого обеспечивали бы выявление «выбросов» (артефактов) в исходных данных и позволяли либо вообще не показывать их в дендрограммах, либо показывать, но так, чтобы было наглядно видно, что это артефакты.

Далее рассмотрим, как решаются (или не решаются) сформулированные выше проблемы в классических методах кластерного анализа. Для удобства дальнейшего изложения повторим формулировки этих проблем.

Проблема 1.1 выбора метрики, корректной для неортонормированных пространств.

Проблема 1.2 ортонормирования пространства.

Проблема 2.1 сопоставимой обработки описаний объектов, описанных признаками различной природы, измеряемыми в различных единицах измерения (проблема размерностей).

Проблема 2.2 формализации описаний объектов, имеющих как количественные, так и качественные признаки.

Проблема 3.1 доказательства гипотезы о нормальности исходных данных.

Проблема 3.2 нормализации исходных данных.

Проблема 3.3 применения непараметрических методов кластеризации, корректно работающих с ненормализованными данными.

Проблема 4 разработки такого метода кластерного анализа, математическая модель и алгоритм и которого органично включали бы фильтр, подавляющий шум в исходных данных, в результате чего данный метод кластеризации корректно работал бы при наличии шума в исходных данных.

Проблема 5 разработки метода кластерного анализа, математическая модель и алгоритм и которого обеспечивали бы выявление «выбросов» (артефактов) в исходных данных и позволяли либо вообще не показывать их в дендрограммах, либо показывать, но так, чтобы было наглядно видно, что это артефакты.

Сделать это удобнее всего, рассматривая какие ответы предлагают классические методы кластерного анализа на сформулированные в работе[117] вопросы:

– как вычислять координаты кластера из двух более объектов; 

– как вычислять расстояние до таких "полиобъектных" кластеров от "монокластеров" и между "полиобъектными" кластерами.

Дело в том, что эти вопросы имеют фундаментальное значение для кластерного анализа, т.к. разнообразные комбинации используемых метрик и методов вычисления координат и взаимных расстояний кластеров и порождают все многообразие методов кластерного анализа (см. туже работу). Мы бы несколько переформулировали эти вопросы, а также добавили бы еще один:

1. Каким методом вычислять координаты кластера, состоящего из одного и более объектов, т.е. каким образом объединять объекты в кластеры.

2. Каким методом сравнивать кластеры, т.е. как вычислять расстояния между кластерами, состоящими из различного количества объектов (одного и более).

3. Каким методом объединять кластеры, т.е. формировать обобщенные («многообъектные») кластеры.

Вопрос 1-й. Чаше всего ни в теории и математических моделях кластерного анализа, ни на практике между кластером, состоящим из одного объекта («моноообъектным» кластером) и самим объектом не делается никакого различия, т.е. считается, что это одно и тоже. «В агломеративно-иерархических методах (aggomerative hierarhical algorithms) … первоначально все объекты (наблюдения) рассматриваются как отдельные, самостоятельные кластеры состоящие всего лишь из одного элемента»[118]. В работе[119] также говорится, что древовидная «Диаграмма начинается с каждого объекта в классе (в левой части диаграммы)». Это решение сразу же порождает многие из вышеперечисленных проблем (1.1., 1.2., 2.1, 2.2), т.к. объекты могут быть описаны как количественными, так и качественными признаками различной природы, измеряемыми в различных единицах измерения, причем эти признаки взаимосвязаны (коррелируют) между собой.

Казалось бы, проблему размерностей (2.1) решает кластеризация не исходных переменных, а матриц сопряженности, содержащих абсолютные частоты наблюдения признаков по объектам или классам. Однако при таком подходе, например при сравнении моделей автомобилей, четыре и два цилиндра у этих моделей, а также четыре и два болта, которыми у них прикручен номер, будут давать одинаковый вклад в сходство-различие этих моделей, что едва ли разумно и приемлемо [8]. Тем ни менее матрица сопряженности анализируется в социологических и социометрических исследованиях, а в статистических системах, в разделах справки, посвященных кластерному анализу, приводятся примеры подобного рода.

Другое предложение по решению проблемы размерностей (2.1) основано на четком пожимании того, что изменение единиц измерения переменной меняет среднее ее значений и их разброс от этого среднего. Например, переход от сантиметров к миллиметрам увеличивает среднее и среднее отклонение от среднего в 10 раз. Речь идет о методе нормализации или стандартизации исходных данных, когда значения переменных заменяются их стандартизированными значения или z-вкладами [15]. Z-вклад показывает, сколько стандартных отклонений отделяет данное наблюдение от среднего значения:

,

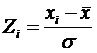^{где – значение данного наблюдения, – среднее, – стандартное отклонение.}

Однако этот метод имеет серьезный недостаток, описанный в вышеперечисленной литературе, а также работе[120]. Дело в том, что нормализация значений переменных приводит к тому, что независимо от значений их среднего и вариабельности до нормализации (т.е. значимости, измеряемой стандартным отклонением), после нормализации среднее становится равным нулю, а стандартное отклонение 1. Это значит, что нормализация выравнивает средние и отклонения по всем переменным, снижая, таким образом, вес значимых переменных, оказывающих большое влияние на объект, и завышая роль малозначимых переменных, оказывающих меньшее влияние и искажая, таким образом, картину. На взгляд авторов это не приемлемо. Другой важный недостаток, который в отличие от первого не отмечается в специальной литературе, состоит в том, что стандартизированные значения сложно как-то содержательно интерпретировать, т.е. устранение влияния единиц измерения достигается ценой потери смысла переменных, который как раз и содержался в единицах их измерения. В результате нормализации все переменные становятся как бы «на одно лицо». Это также недопустимо. Таким образом, можно обоснованно сделать вывод о том, нормализация и стандартизация исходных данных – это весьма радикальное решение проблемы 2.1 «в лоб и в корне», но решение неприемлемо дорогой ценой.

В классических методах кластерного анализа предлагается два основных варианта ответов на 1-й вопрос:

1. Вообще не формировать обобщенных классов или кластеров из объектов, а на всех этапах кластеризации рассматривать только сами первичные объекты.

2. Формировать обобщенные кластеры путем вычисления неких статистических характеристик кластера на основе характеристик входящих в него объектов.

О 1-м варианте ответа в работе[121] говорится: «Диаграмма начинается с каждого объекта в классе (в левой части диаграммы). Теперь представим себе, что постепенно (очень малыми шагами) вы "ослабляете" ваш критерий о том, какие объекты являются уникальными, а какие нет. Другими словами, вы понижаете порог, относящийся к решению об объединении двух или более объектов в один кластер. В результате, вы связываете вместе всё большее и большее число объектов и агрегируете (объединяете) все больше и больше кластеров, состоящих из все сильнее различающихся элементов». Этот подход, когда кластеры реально не формируются, т.к. им не соответствуют какие-либо конструкции математической модели, представляется авторам сомнительным, т.к., во-первых, как было показано выше, это порождает проблемы 1.1., 1.2., 2.1, 2.2, а во-вторых, никак не решает проблемы 3.1, 3.2, 3.3, 4 и 5. Между тем сам способ формирования кластеров из объектов, по мнению авторов, призван стать средством решения всех этих проблем.

2-й вариант ответа представляется более обоснованным, однако он сам в свою очередь порождает вопросы о степени корректности и научной обоснованности того или иного метода вычисления обобщенных характеристик кластера и главное о том, в какой степени этот метод позволяет решить сформулированные выше проблемы. Описание кластера на основе входящих в него объектов традиционно включает центр кластера, в качестве которого обычно используется среднее или центр тяжести от характеристик входящих в него объектов[122], а также какую-либо количественную оценку степени рассеяния объектов кластера от его центра (как правило, это дисперсия). Ответ на 2-й вопрос является продолжением ответа на 1-й вопрос.

Вопрос 2-й. В вышеупомянутых и других работах по кластерному анализу описывается большое количество различных мер и методов, которые можно применить как для измерения расстояний между кластерами, так и расстояний от объекта до кластеров. Например, в невзвешенном центроидном методе при определении расстояния от объекта до кластера, по сути, определяется расстояние до его центра[123]. В методе невзвешенного попарного среднего расстояние между двумя кластерами вычисляется как среднее расстояние между всеми парами объектов в них [там же]. При этом, как правило, не решаются перечисленные выше проблемы, т.к. не устраняются их причины: а именно средние вычисляются на основе мер расстояния, корректных только для ортонормированных пространств и при этом часто используются размерные или нормализованные формы представления признаков объектов, не формализуется описание объектов, обладающих как количественными, так и качественными признаками. Ответ на 3-й вопрос является продолжением ответа на 2-й вопрос.

Вопрос 3-й. При объединении кластеров характеристики вновь образованного обобщенного кластера обычно пересчитываются тем же методом, каким они рассчитывались для исходных кластеров. Это сохраняет нерешенными и все проблемы, которые были при определении характеристик исходных кластеров и расстояний между этими кластерами.

Далее рассмотрим вариант решения некоторых из сформулированных выше проблем кластерного анализа, предлагаемый в АСК-анализе и реализованный в интеллектуальной системе «Эйдос».

Обратимся к эпиграфам к данному разделу: «Мышление – это обобщение, абстрагирование, сравнение, и классификация» (Патанджали, II в. до н. э.), «Истинное знание – это знание причин» (Френсис Бэкон, 1561–1626 гг.). Итак, мышление, как процесс это [в том числе] классификация, результатом же мышления является знание, причем истинное знание есть знание причин. Истинное мышление есть мышление, дающее истинное знание. Соответственно ложное мышление – это мышление, приводящее к заблуждениям. Поэтому истинное мышление – это [в том числе] истинная (правильная, адекватная) классификация объектов по причинам их поведения, т.е. по системе их детерминации. Правильной классификацией будем считать ту, которая совпадает с классификацией экспертов, основанной на их высоком уровне компетенции, профессиональной интуиции и большом практическом опыте.

Если, как это принято в АСК-анализе [145], факторы формализовать в виде шкал различного типа (номинальных, порядковых и числовых), признаки рассматривать как значения факторов, т.е. их интервальные значения, более или менее жестко детерминирующих поведение объекта, а классы как будущие состояния, в которые объект переходит под влиянием различных значений этих факторов, то можно сказать, что признаки формализуют причины переходов объекта в состояния, соответствующие классам или кластерам. Если учесть, что классификация – это кластерный анализ, то можно сделать обоснованные выводы о том, что кластерный анализ это и есть мышление (но мышление не сводится только к кластерному анализу), а результаты кластерного анализа представляют собой знания. Степень истинности этих знаний, полученных в результате кластерного анализа, т.е. их адекватность или соответствие действительности, полностью определяются степенью истинности метода кластерного анализа, с помощью которого они получены. Поэтому столь важно решить сформулированные выше проблемы кластерного анализа.

В свою очередь классификация (в т.ч. кластерный анализ) как процесс основана на обобщении и сравнении. В монографии 2002 года [97] предлагается пирамида иерархической структуры процесса познания, входящая в базовую когнитивную концепцию (рисунок 1):

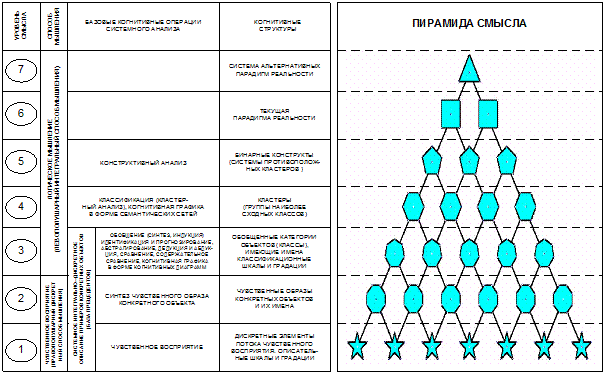
Рисунок 1 Обобщенная схема иерархической структуры процесса познания согласно базовой формализуемой когнитивной концепции[124]

В этой же монографии [97] предлагается математическая модель, основанная на семантической теории информации, обеспечивающая высокую степень формализацию данной когнитивной концепции, достаточную для разработки алгоритмов[125], структур данных и программной реализации в виде интеллектуальной программной системы. Такая система была создана автором и постоянно развивается, это система «Эйдос» [97, 100, 101].

Суть предлагаемых в АСК-анализе решений сформулированных выше проблем кластерного анализа состоит в следующем[126].

Основная идея решения проблем кластерного анализа, состоит в том, что для решения задачи кластеризации предлагается использовать математическое представление объектов не виде переменных со значениями, измеряемыми в различных единицах измерения и в шкалах разного типа, и не матрицу сопряженности с абсолютными частотами встреч признаков по классам или нормализованными Z-вкладами, а базы знаний, рассчитанные на основе матрицы сопряженности (матрицы абсолютных частот) с использованием различных аналитических выражений для частных критериев. При этом для всех значений всех переменных используется одна и та же размерность – это размерность количества информации (бит, байт и т.д.), что обеспечивает расчет на основе исходных данных силы и направления влияния на объект всех факторов и их значений и сопоставимую обработку значений переменных, изначальное (в исходных данных) представленных в разных единицах измерения и в шкалах разного типа (количественных – числовых, и качественных – текстовых).

1. Расстояния между объектом и кластером, а также между кластерами предлагается определять с использованием неметрических интегральных критериев, корректных для неортормированных пространств, одним и тем же методом: по суммарному количеству информации, которое содержится (соответственно) в системе признаков объекта о принадлежности к классу или кластеру, или которое содержится в обобщенных образах двух классов или кластеров об их принадлежности друг к другу.

2. Координаты кластера, возникающего как при включении в него одного единственного объекта, так и при объединении многих объектов в кластеры вычисляются тем же самым методом, что и координаты кластера, возникающего при объединении нескольких кластеров, а именно путем применения базовой когнитивной операции (БКОСА): «Обобщение», «Синтез», «Индукция» (БКОСА-3) АСК-анализа.

3. Объединять кластеры, т.е. формировать обобщенные («многообъектные») кластеры при объединении кластеров предлагается тем же самым методом, что и обобщенные образы классов при объединении конкретных образов объектов, т.е. путем применения базовой когнитивной операции (БКОСА): «Обобщение», «Синтез», «Индукция» (БКОСА-3) АСК-анализа.

Основная идея сводится к тому, чтобы кластеризовать не размерные переменные, абсолютные или относительные частоты или Z-вклады, а знания. Предложения 1-3 являются непосредственными ответами на сформулированные выше фундаментальные вопросы кластерного анализа.

Остановимся подробнее на математическом и алгоритмическом описании этих предложений и затем проиллюстрируем их на простом и наглядном численном примере.

Основная идея. Вспомним приведенный выше пример кластеризации моделей автомобилей, в котором четыре или два цилиндра в двигателе давали такой вклад в сходство-различие моделей, как четыре или два болта, которыми прикручивается регистрационный номер. Из этого примера ясно, что при сравнении объектов и кластеров основную роль должно играть не само количество разных деталей или элементов конструкции, а, например, их влияние на стоимость модели, выраженное в долларах или на степень ее пригодности (полезности) для поставленной цели, тоже выраженное в одних и тех же для всех переменных и их значений единицах измерения. В АСК-анализе предлагается более радикальное решение: измерять степень и направление влияния всех переменных и их значений на поведение объекта или принадлежность его к тому или иному классу или кластеру в одних и тех же универсальных единицах измерения, а именно единицах измерения количества информации. Ведь по сути, когда мы узнаем о том, что некий объект обладает определенным признаком, то мы получаем из этого факта некое количество информации о том, что принадлежит к определенной категории (классу, кластеру). А уж сами эти категории могут иметь совершенно различный смысл, в частности классифицировать текущие или будущие состояния объектов, или степень их полезности для достижения тех или иных целей. И что очень важно, при этом не играет абсолютно никакой роли в каких единицах измерения в какой шкале, количественной или качественной, изначально измерялся этот признак: килограммах, долларах, Омах, джоулях, или еще каких-то других.

Предложение 1-е. В этом смысле в АСК-анализе исчезает существенное различие между классом и кластером и эти термины можно использовать как синонимы. Классы в АСК-анализе могут быть различаться степенью обобщенности: чем больше объектов в классе и чем выше вариабельность этих объектов по их признакам, тем шире представляемая ими генеральная совокупность, по отношению к которой они представляют собой репрезентативную выборку, тем выше степень обобщения в объединяющем их классе. Классы включают один или насколько объектов. Наименьшей степенью обобщения обладают классы, включающие лишь один объект, но и они совершенно не тождественны объекту исходной выборки, т.к. в математической мидели АСК-анализа у них совершенно различные математические формы представления. Кластеры обычно являются классами более высокой степени обобщения, т.к. включают один или несколько классов.

Как реализуется базовая когнитивная операция АСК-анализа «Обобщение», «Синтез», «Индукция» (БКОСА-3) будет рассмотрено ниже при кратком изложении математической модели АСК-анализа.

Предложения 2-е и 3-е необходимо рассматривать в комплексе, т.к. их смысл в том, что объект при когнитивной кластеризации имеет другую математическую форму, чем объект в исходных данных, а именно такую же форму, как класс и как кластер, т.е. в АСК-анализе возможны классы и кластеры, включающие как один, так и много объектов. При этом для формирования класса состоящего из одного объекта, т.е. при добавлении в пустой кластер первого объекта, используется та же самая математическая процедура, что и при добавлении в него второго и вообще любого нового объекта (в АСК-анализе она называется БКОСА-3), и эта же самая процедура БКОСА-3 используется и при объединении классов или кластеров. При этом само объединение классов (кластеров) осуществляется путем создания «с нуля» нового класса (кластера) из всех объектов, входящих в объединяемые классы (кластеры), а затем удаления исходных классов (кластеров). Новый объединенный класс (кластер) создается «с нуля» тем же самым методом (БКОСА-3), каким впервые создается любой новый класс (кластер). Теперь рассмотрим, как же это реализовано математически и алгоритмически.

Рассмотрим предлагаемый алгоритм когнитивной кластеризации в графической и текстовой форме (рисунок 3):

Рисунок 3. Алгоритм когнитивной кластеризации
или кластеризации, основанной на знаниях

Дадим необходимые пояснения к приведенному алгоритму.

1. Если не соответствуют размерности баз данных (БД) классов, признаков и информативностей, то выдать сообщение о необходимости пересинтеза модели.

2. Создать БД абсолютных частот: ABS_KLAS, информативностей: INF_KLAS, сходства классов: MSK_KLAS, а также БД учета объединения классов IterObj1.dbf и занести в них начальную информацию по текущей модели.

Данный режим реализован в модуле _5126 системы «Эйдос» и обеспечивает работу с любой из четырех моделей или со всеми этими моделями по очереди, поддерживаемых системой и приведенных в таблице 3. При этом в базах данных этих моделей ничего не изменяется.

3. Цикл по моделям до тех пор, пока есть похожие классы.

4. Рассчитать матрицу сходства классов MSK_KLAS в текущей модели.

Эта матрица рассчитываемся на основе матрицы знаний модели, заданной при запуске режима (СИМ-1 – СИМ-7), путем расчета корреляции обобщенных образов классов (т.е. векторов или профилей классов).

5. Найти пару наиболее похожих классов в матрице сходства.

Здесь определяются два класса, у которых на предыдущем шаге было обнаружено наивысшее сходство. При этом при запуске режима задается параметр: «Исключать ли артефакты (выбросы)». Если задано исключать, то рассматриваются только положительные уровни сходства, если нет – то и отрицательные, т.е. в этом случае могут быть объединены и непохожие классы, но наименее непохожие из всех, если других нет. Считается, что непохожие кассы являются исключениями или «выбросами».

6. Объединить 2 класса с наибольшим уровнем сходства.

Данный пункт алгоритма требует наиболее детальных пояснений. Как же объединяются классы в методе когнитивной кластеризации? Сначала суммируются абсолютные частоты этих классов в таблице 2, причем сумма рассчитывается в столбце класса с меньшим кодом, а затем частоты класса с большим кодом обнуляются. После этого в базе знаний (таблица 4) с использованием частного критерия соответствующей модели (таблица 3) пересчитываются только изменившиеся столбцы и строки, т.е. пересчитывается столбец класса с меньшим кодом, а столбец класса с большим кодом обнуляется.

7. Отразить информацию об объединении классов в БД IterObj1.dbf.

8. Конец цикла итераций. Проверить критерий остановки и перейти на продолжение итераций (п.9) или на окончание работы (п.10).

9. Пересчитать в базе данных сходства классов (MSK_KLAS) только изменившиеся столбцы и строки. Конец цикла по моделям.

10. Нарисовать дерево объединения классов, псевдографическое: /TXT/AgKlastK.txt и графическое: /PCX/AGLKLAST/TrK-#-##.GIF.

Работа предлагаемой математической модели и реализующего ее алгоритма когнитивной кластеризации продемонстрированная на простом численном примере в работе [248], а в данной монографии некоторые выходные формы режима когнитивной кластеризации системы «Эйдос» приведены на рисунках 13 и 14 раздела 10.2.

ГЛАВА 14. ИНТЕЛЛЕКТУАЛЬНАЯ СИСТЕМА ЭЙДОС-Х++ КАК ИНСТРУМЕНТАРИЙ, РЕАЛИЗУЮЩИЙ ИДЕИ СИСТЕМНОГО НЕЧЕТКОГО ИНТЕРВАЛЬНОГО ОБОБЩЕНИЯ МАТЕМАТИКИ

Система «Эйдос» за многие годы применения хорошо показала себя при проведении научных исследований в различных предметных областях и занятий по ряду научных дисциплин, связанных с искусственным интеллектом, представлениями знаний и управлению знаниями [224]. Однако в процессе эксплуатации системы были выявлены и некоторые недостатки, ограничивающие возможности и перспективы применения системы. Поэтому создана качественно новая версия системы (система Эйдос-Х++), в которой преодолены ограничения и недостатки предыдущей версии и реализованы новые важные идеи по ее развитию и применению в качестве программного инструментария системно-когнитивного анализа (СК-анализ) [260].

Авторы считают, что система Эйдос-Х++ является программным инструментарием, реализующим ряд идей системного нечеткого интервального обобщения математики.

14.1. Система «Эйдос» – одна из старейших отечественных универсальных систем искусственного интеллекта, широко применяемых и развивающихся и в настоящее время

Системы искусственного интеллекта
помогают решать сложнейшие проблемы,
которые не возникали, пока этих систем не было

(IT-фольклор)

Универсальная когнитивная аналитическая система «Эйдос», по-видимому, является одной из первых реально работающих отечественных универсальных систем искусственного интеллекта, широко применяемых и развивающихся и в настоящее время. Математическая модель Универсальной когнитивной аналитической системы "Эйдос", а также методика численных расчетов (алгоритмы и структуры данных) и функциональная структура системы разработаны автором в 1979 году, когда он работал старшим инженером на вычислительном центре Краснодарского медицинского института^[127] и занимался разработкой математических моделей и алгоритмов медицинских диагностических систем. Впервые математическая модель системы «Эйдос» прошла экспериментальную апробацию в ходе численного эксперимента в 1981 году. С 1981 по 1992 система "Эйдос" неоднократно реализовалась автором в предметно-зависимых приложениях на платформе Wang (на компьютерах Wang-2200с) в среде персональной технологической системы «Вега» (1983 год)[128], во многом функционально аналогичной MS Excel (включая деловую графику), но опережавшей его лет на 10. Два акта внедрения ранней версии системы «Эйдос» (1987 год) приведен ниже.

Для IBM-совместимых персональных компьютеров система "Эйдос" была реализована в универсальной постановке (не зависящей от предметной области) в 1992 году и с тех она пор совершенствуется постоянно, вплоть до настоящего времени. В 1993 году впервые в более-менее полном виде была опубликована математическая модель системы «Эйдос» [284]. В 1994 году на систему  "Эйдос" и связанные с ней разработки получены 3 свидетельства РосПатента: №№ 940217, 940328 и 940334 [111, 112, 113], ставшие первыми в Краснодарском крае, а возможно и в России, патентами на системы искусственного интеллекта. Отметим, что именно в 1994 году в Российской Федерации впервые появилась возможность правовой защиты авторских прав на программы для ЭВМ. Позже были получены еще ряд свидетельств РосПатента [111-137]^[129].

Система «Эйдос» применялась для решения задач прогнозирования, поддержки принятия решений и научных исследований во многих предметных областях. Обзор применений системы «Эйдос» до 2002 года приведен в 7-й главе работы [97]^[130], где приведена и ссылка на акты внедрения. О применениях системы «Эйдос» с 2002 года по настоящее время можно судить по работам [93-286], а также публикациям в Научном журнале КубГАУ: http://ej.kubagro.ru/a/viewaut.asp?id=11 и материалам сайта автора: http://lc.kubagro.ru. Система "Эйдос" является высокоэффективным инструментом научных исследований в самых различных предметных областях, в которых требуется обобщение (многопараметрическая типизация), системная (многопараметрическая) идентификация, прогнозирование и принятие решений, сравнение, классификация, и была успешно применена в экономике, технических науках, педагогике, социологии, психологии, психофизиологии, биологии, медицине, агрономии, сельскохозяйственных науках (растениеводстве и плодоводстве), рекламных и маркетинговых исследованиях, геофизике, климатологии, мелиорации и других науках. Она была применена также при выполнении ряда кандидатских и докторских диссертационных работ по экономическим, техническим и психологическим наукам^[131]:

– 3 доктора экономических наук;

– 2 доктора технических наук;

– 4 кандидата психологических наук;

– 1 кандидат технических наук;

– 1 кандидат экономических наук;

– 1 кандидат медицинских наук.

С 1999 по 2002 год система «Эйдос» применялась в учебном процессе в Кубанском государственном технологическом университете (КубГТУ) при преподавании дисциплин: "Новые информационные технологии в учебном процессе", "Комплексные технологии в науке и образовании", «Основы теории и техники измерений». С 2002 года и по настоящее время система «Эйдос» применяется в Кубанском государственном аграрном университете (КубГАУ) и Кубанском государственном университете (КубГУ) при преподавании дисциплин: "Теория и техника измерений", "Методы принятия решений", "Основы теории информации", "Алгоритмы и структуры данных", "Вычислительные системы и сети", "Базы данных", "Новые информационные технологии в учебном процессе", "Комплексные технологии в науке и образовании", "Измерения в социально-экономических системах", "Информатика", "Интеллектуальные информационные системы", “Представление знаний в информационных системах”, "Основы теории управления (теория автоматического управления)", «Компьютерные технологии в строительной науке и образовании (магистратура)», «Современные технологии в образовании (магистратура)», «Управление знаниями (магистратура)», Введение в искусственный интеллект, Системно-когнитивный анализ, Информационные технологии управления бизнес-процессами / Корпоративные информационные системы (магистратура), Система искусственного интеллекта «Эйдос», Моделирование социально-экономических систем / Организационно-управленческие модели корпорации (магистратура), Введение в нейроматику и методы нейронных сетей (магистратура), Интеллектуальные и нейросетевые технологии в образовании (магистратура), Основы искусственного интеллекта, Эффективность АСУ (магистратура), Функционально-стоимостной анализ системы и технологии управления персоналом (магистратура), Компьютерная графика, Интеллектуальные технологии и представление знаний, Технологии и средства защиты информации (магистратура), Информационная среда обучения (магистратура).

Разработанный автором системно-когнитивный анализ (СК-анализ) и его программный инструментарий – Универсальная когнитивная аналитическая система "Эйдос", нашли свое отражение в Internet^[132].

14.1.1. Назначение и состав системы "Эйдос"

14.1.1.1. Цели и основные функции системы "Эйдос"

Универсальная когнитивная аналитическая система "Эйдос" (система «Эйдос») является отечественным лицензионным программным продуктом [111-137], созданным с использованием официально приобретенного лицензионного программного обеспечения. Система «Эйдос» включает базовую систему, ряд систем окружения и программные интерфейсы импорта данных из внешних баз данных различных стандартов.

По системе "Эйдос" и различным аспектам ее практического применения имеется более сотни публикаций автора с соавторами, в т.ч. 18 монографий и три учебных пособия с грифами УМО и министерства [93-110].

Система "Эйдос" является программным инструментарием, реализующим теоретическую концепцию, математическую модель и методику численных расчетов Системно-когнитивного анализа (СК-анализ) [97] и обеспечивает реализацию следующих основных функций:

1. Синтез и адаптация семантической информационной модели предметной области, включая активный объект управления и окружающую среду.

2. Идентификация и прогнозирование состояния активного объекта управления, а также разработка управляющих воздействий для его перевода в заданные целевые состояния.

3. Углубленный анализ семантической информационной модели предметной области.

Синтез содержательной информационной модели
предметной области

Синтез модели в СК-анализе осуществляется с применением подсистем: "Словари", "Обучение", "Оптимизация", "Распознавание" и "Анализ". Он включает следующие этапы:

1) формализация (когнитивная структуризация предметной области);

2) формирование исследуемой выборки и управление ею;

3) синтез или адаптация модели;

4) оптимизация модели;

5) измерение адекватности модели (внутренней и внешней, интегральной и дифференциальной валидности), ее скорости сходимости и семантической устойчивости.

Идентификация и прогнозирование состояния объекта управления, выработка управляющих воздействий

Данный вид работ осуществляется с помощью подсистем "Распознавание" и "Анализ". Эти подсистемы обеспечивают: ввод распознаваемой выборки; пакетное распознавание; вывод результатов распознавания и их оценку, в т.ч. с использованием данных по дифференциальной валидности модели.

Углубленный анализ содержательной информационной модели предметной области

Этот анализ выполняется в подсистеме "Типология", которая включает:

1. Информационный и семантический анализ классов и признаков.

2. Кластерно-конструктивный анализ классов распознавания и признаков, включая визуализацию результатов анализа в оригинальной графической форме когнитивной графики (семантические сети классов и признаков).

3. Когнитивный анализ классов и признаков (когнитивные диаграммы и диаграммы Вольфа Мерлина).

14.1.1.2. Обобщенная структура системы "Эйдос"

Система "Эйдос" включает семь подсистем, состоящих из режимов, подрежимов, функций и подфункций (включающих в свою очередь функциональное меню, пункты которого здесь не приводятся):

1. Формализация предметной области (ПО)

1.1. Классификационные шкалы и градации

1.2. Описательные шкалы (и градации)

1.3. Градации описательных шкал (признаки)

1.4. Иерархические уровни систем

1.4.1. Уровни классов

1.4.2. Уровни признаков

1.5. Программные интерфейсы для импорта данных

1.5.1. Импорт данных из TXT-фалов стандарта DOS-текст

1.5.2. Импорт данных из DBF-файлов стандарта проф. А.Н.Лебедева

1.5.3. Импорт из транспонированных DBF-файлов проф. А.Н.Лебедева

1.5.4. Генерация шкал и обучающей выборки RND-модели

1.5.5. Генерация шкал и обучающей выборки для исследования чисел

1.5.6. Транспонирование DBF-матриц исходных данных

1.5.7. Импорт данных из DBF-файлов стандарта Евгения Лебедева

1.5.8. Системно-когнитивный анализ стандартных графических шрифтов[133]

1.6. Почтовая служба по НСИ

1.6.1. Обмен по классам

1.6.2. Обмен по обобщенным признакам

1.6.3. Обмен по первичным признакам

1.7. Печать анкеты

2. Синтез СИМ

2.1. Ввод–корректировка обучающей выборки

2.2. Управление обучающей выборкой

2.2.1. Параметрическое задание объектов для обработки

2.2.2. Статистическая характеристика, ручной ремонт

2.2.3. Автоматический ремонт обучающей выборки

2.3. Синтез семантической информационной модели СИМ

2.3.1. Расчет матрицы абсолютных частот

2.3.2. Исключение артефактов (робастная процедура)

2.3.3. Расчет матрицы информативностей СИМ-1 и сделать ее текущей

2.3.4. Расчет условных процентных распределений СИМ-1 и СИМ-2

2.3.5. Автоматическое выполнение режимов 1–2–3–4

2.3.6. Зависимость достоверности СИМ от объема обучающей выборки, сходимость и устойчивость СИМ, поиск периодов эргодичности и точек бифуркации

2.3.7. Расчет матрицы информативностей СИМ-2 и сделать ее текущей

2.4. Почтовая служба по обучающей информации

2.5. Синтез СИМ и измерение ее адекватности

3. Оптимизация СИМ

3.1. Формирование ортонормированного базиса классов

3.2. Исключение признаков с низкой селективной силой

3.3. Удаление классов и признаков, по которым недостаточно данных

3.4. Разделение классов на типичную и нетипичную части

3.5. Генерация сочетанных признаков и перекодирование обучающей выборки

4. Распознавание

4.1. Ввод–корректировка распознаваемой выборки

4.2. Пакетное распознавание

4.3. Вывод результатов распознавания

4.3.1. Разрез: один объект – много классов

4.3.2. Разрез: один класс – много объектов

4.4. Почтовая служба по распознаваемой выборке

4.5. Построение когнитивных функций влияния

4.6. Докодирование сочетаний признаков в распознаваемой выборке

4.7. Назначения объектов на классы (задача о назначениях)[134]

4.7.1. Задание ограничений на ресурсы по классам

4.7.2. Ввод затрат на объекты

4.7.3. Назначение объектов на классы (LC-алгоритм)

4.7.4. Сравнение эффективности LC и RND алгоритмов

5. Типология

5.1. Типологический анализ классов распознавания

5.1.1. Информационные (ранговые) портреты (классов)

5.1.2. Кластерный и конструктивный анализ классов

5.1.2.1 Расчет матрицы сходства образов классов

5.1.2.2. Генерация кластеров и конструктов классов

5.1.2.3. Просмотр и печать кластеров и конструктов

5.1.2.4. Автоматическое выполнение режимов: 1,2,3

5.1.2.5. Вывод 2d семантических сетей классов

5.1.3. Когнитивные диаграммы классов

5.2. Типологический анализ первичных признаков

5.2.1. Информационные (ранговые) портреты признаков

5.2.2. Кластерный и конструктивный анализ признаков

5.2.2.1. Расчет матрицы сходства образов признаков

5.2.2.2. Генерация кластеров и конструктов признаков

5.2.2.3. Просмотр и печать кластеров и конструктов

5.2.2.4. Автоматическое выполнение режимов: 1,2,3

5.2.2.5. Вывод 2d семантических сетей признаков

5.2.3. Когнитивные диаграммы признаков

6. СК-анализ СИМ

6.1. Оценка достоверности заполнения объектов

6.2. Измерение адекватности семантической информационной модели

6.3. Измерение независимости классов и признаков

6.4. Просмотр профилей классов и признаков

6.5. Графическое отображение нелокальных нейронов

6.6. Отображение Паретто-подмножеств нейронной сети

6.7. Классические и интегральные когнитивные карты

6.8. Восстановление значений функций по признакам аргумента[135]

6.8.1. Восстановление значений и визуализация 1d-функций

6.8.2. Восстановление значений и визуализация 2d-функций

6.8.3. Преобразование 2d-матрицы в 1d-таблицу с признаками точек

6.8.4. Объединение многих БД: Inp_001.dbf и т.д., в Inp_data.dbf

6.8.5. Помощь по подсистеме (требования к исходным данным)

7. Сервис

7.1. Генерация (сброс) БД

7.1.1. Все базы данных

7.1.2. НСИ

7.1.2.1. Всех баз данных НСИ

7.1.2.2. БД классов

7.1.2.3. БД первичных признаков

7.1.2.4. БД обобщенных признаков

7.1.3. Обучающая выборка

7.1.4. Распознаваемая выборка

7.1.5. Базы данных статистики

7.2. Переиндексация всех баз данных

7.3. Печать БД абсолютных частот

7.4. Печать БД условных процентных распределений СИМ-1 и СИМ-2

7.5. Печать БД информативностей СИМ-1 и СИМ-2

7.6. Интеллектуальная дескрипторная информационно–поисковая система

7.7. Копирование основных баз данных СИМ

7.8. Сделать текущей матрицу информативностей СИМ-1

7.9. Сделать текущей матрицу информативностей СИМ-2

Структура и взаимодействие этих подсистем и режимов позволяют полностью реализовать все аспекты СК-анализа в удобной для пользователя форме. Обобщенной структуре соответствуют и структура управления и дерево диалога системы. Подробнее теоретическая концепция системы «Эйдос», ее подсистемы и режимы, реализуемые ей функции и операции, описаны в работах [93-286]. В данном разделе, в связи с ограниченностью объема монографии, приводится лишь краткая характеристика некоторых из них.

14.1.2. Пользовательский интерфейс, технология разработки и эксплуатации приложений управления знаниями в системе "ЭЙДОС"

Не смотря на то, что данный раздел посвящен интерфейсу системы "Эйдос", видеограммы и экранные формы в нем не приводятся в связи с ограничениями на объем и монографии, кроме того, они есть в работах [93-286]. В наименованиях разделов с описаниями подсистем и режимов системы "Эйдос" указаны коды реализуемых ими базовых когнитивных операций системного анализа (БКОСА) в соответствии с обобщенной схемой СК-анализа [97].

14.1.2.1. Начальный этап синтеза модели: когнитивная структуризация и формализация предметной области, подготовка исходных данных (подсистема "Словари") (БКОСА-1, БКОСА-2)

Подсистема "Словари" обеспечивает формализацию предметной области. Она реализует следующие режимы: классификационные шкалы и градации; описательные шкалы и градации; градации описательных шкал; иерархические уровни организации систем; автоматический ввод первичных признаков из текстовых файлов; ряд программных интерфейсов импорта данных из из внешних баз данных различных стандартов; почтовая служба по нормативно-справочной информации; печать анкеты.

Классификационные шкалы и градации (БКОСА-1.1)

Классификационные шкалы и градации предназначены для ввода справочника будущих состояний активного объекта управления – классов. Режим: "Классификационные шкалы и градации" обеспечивает ведение базы данных классификационных шкал и градаций классов: ввод; корректировку; удаление; распечатку (в текстовый файл); сортировку; поиск по базе данных.

Описательные шкалы и градации (БКОСА-1.2)

Описательные шкалы и градации предназначены для ввода справочников факторов, влияющих на поведение активного объекта управления – признаков. В этом режиме обеспечивается ввод, удаление, корректировка, копирование наименований описательных шкал и связанных с ними градаций. Характерной особенностью системы "Эйдос" является возможность использования неальтернативных градаций, которых может быть различное количество по различным шкалам (в широких пределах). Справочник позволяет работать непосредственно с градациями (с учетом связей со шкалами), видеть их общее количество, а также просматривать и распечатывать процентное распределение ответов респондентов по.

Уровни организации систем (уровни Вольфа Мерлина) являются независимым способом классификации классов и факторов, что позволяет легко создавать и анализировать различные их подмножества как сами по себе, так и в сопоставлении друг с другом. В.С.Мерлин предложил интегральную концепцию индивидуальности, в которой рассматривал взаимодействие и взаимообусловленность различных уровней свойств личности: от генетически предопределенных, до социально-обусловленных и отражающих сиюминутное состояние. В системе "Эйдос" предусмотрен аппарат, позволяющий классифицировать факторы таким образом, что становится возможным исследовать различные уровни их организации и взаимообусловленности. Уровни организации классов предназначены для классификации будущих состояний активного объекта управления, как целевых, так и нежелательных с точки зрения самого объекта управления и управляющей системы, а также различных вариантов сочетаний этих вариантов. Возможны и другие виды классификации.

Система "Эйдос" обеспечивает решение задач атрибуции анонимных и псевдонимных текстов (установления вероятного авторства), датировки текстов, определения их принадлежности к определенным традициям, школам или течениям мысли. При этом различные структуры, из которых состоят тексты, рассматриваются как их атрибуты. В системе "Эйдос" реализован специальный режим, обеспечивающий автоматическое выявление и ввод этих атрибутов текстов непосредственно из текстовых файлов.

Технология работы в системе "Эйдос" текущей версии не предусматривает одновременной работы многих пользователей с одними и теми же базами данных в режиме корректировки записей. Поэтому возможна эффективная организация распределенной работы по многомашинной технологии без использования ЛВС. Для обеспечения необходимой тождественности справочников на различных компьютерах служит режим "Почтовая служба по НСИ".

Классификационные шкалы и градации в экономических, социально-психологических и политологических исследованиях часто представляют собой опросники (анкеты). Для их распечатки в файл (в поддиректорию "TXT") служит режим: "Печать анкеты". В системе "Эйдос" все текстовые и графические входные и выходные формы автоматически сохраняются в виде файлов, удобных для использования в различных приложениях под Windows.

Ввод-корректировка обучающей информации (БКОСА-2.1)

Данная подсистема обеспечивает ввод и корректировку обучающей выборки, управление ею, синтез и адаптацию модели на основе данных обучающей выборки, экспорт и импорт данных с других компьютеров.

Для ввода-корректировки обучающей выборки служит соответствующий режим, имеющий двухоконный интерфейс, позволяющий ввести в обучающую выборку двухвекторные описания объектов. Левое окно служит для ввода классификационной характеристики объекта. В этом окне каждому объекту соответствует одна строка с прокруткой. В правом окне вводится описательная характеристика объекта на языке признаков. Каждому объекту соответствует окно с прокруткой. Переход между окнами осуществляется по нажатию клавиши "TAB". Количество объектов в обучающей выборке не ограничено. Имеется практический опыт проведения расчетов с объемами обучающей выборки до 70000 объектов, суммарным количеством градаций описательных шкал до 4000 и количеством классов до 3900. Реализована также возможность автоматического формирования объектов обучающей выборки путем кодирования текстовых файлов.

В системе реализован ряд программных интерфейсов, обеспечивающих автоматическое формирование классификационных и описательных шкал и градаций, а также обучающей выборки:

– импорт данных из файлов стандарта "Текст DOS";

– импорт данных из DBF-файлов, стандарта проф. А.Н.Лебедева;

– импорт данных из транспонированных DBF-файлов, стандарта профессора А.Н.Лебедева;

– генерация случайной модели;

– генерация учебной модели для исследования свойств натуральных чисел.

Управление составом обучающей информации (БКОСА-2.2)

Данный режим предназначен для управления обучающей выборкой путем параметрического задания подмножеств анкет для обработки, объединения классов, автоматического ремонта обучающей выборки ("ремонт или взвешивание данных"). Параметрическое выделение подмножества анкет для обработки может осуществляться логически и физически (рекомендуется 2-й вариант), это осуществляется путем сравнения с анкетой-маской. В ней задаются коды тех классов и признаков, которые обязательно должны присутствовать во всех анкетах обрабатываемого подмножества. Режим: "Статистическая характеристика обучающей выборки. Ручной ремонт" предназначен для выявления слабо представленных классов (по которым недостаточно данных) и объединения нескольких классов в один. При этом производится переформирование справочника классов и автоматическое перекодирование анкет обучающей выборки. В режиме "Автоматический ремонт обучающей выборки (ремонт или взвешивание данных)" реализуется БКОСА-2.2: задается частотное распределение объектов по категориям, характерное для генеральной совокупности (или другое), затем автоматически осуществляется формирование последовательных подмножеств анкет обучающей выборки (с увеличивающимся числом анкет), на каждом этапе максимально соответствующих заданному частотному распределению генеральной совокупности. При этом используется метод последовательных приближений по минимаксному критерию: максимизация корреляции и минимизация максимального отклонения. Система рекомендует оптимальное (по этим двум критериям) подмножество и позволяет исключить остальные анкеты из рассмотрения. При достижении минимакса можно говорить об обеспечении структурной репрезентативности [5].

14.1.2.2. Синтез модели: пакетное обучение системы распознавания (подсистема "Обучение") (БКОСА-3)

Данный режим обеспечивает: расчет матрицы абсолютных частот, поиск и исключение из дальнейшего анализа артефактов, расчет матрицы информативностей, расчет матрицы условных процентных распределений, пакетный режим автоматического выполнения вышеперечисленных 4-х режимов, а также исследовательский режим, обеспечивающий измерение скорости сходимости и семантической устойчивости сформированной содержательной информационной модели.

Расчет матрицы абсолютных частот (БКОСА-3.1.1)

В данном режиме осуществляется последовательное считывание всех анкет обучающей выборки и использование описаний объектов для формирования статистики встреч признаков в разрезе по классам. На экране в наглядной форме отображается стадия этого процесса, который может занимать значительное время при больших размерностях задачи и объеме обучающей выборки. Кроме того, на качественном уровне красным отображается заполнение матрицы абсолютных частот данными: классы соответствуют столбцам, а признаки – строкам. Поэтому значительная фрагментарность данных легко обнаруживается еще на этой стадии. Данный режим обеспечивает полную "развязку по данным" и независимость времени исполнения процессов синтеза модели и ее анализа от объема обучающей выборки. Кроме того, в данном режиме выявляются 4 типа формально-обнаружимых ошибок в исходных данных и по ним формируется файл отчета.

Исключение артефактов (робастная процедура) (БКОСА-3.1.2)

В данном режиме на основе исследования частотного распределения частот встреч признаков в матрице абсолютных частот, делаются выводы:

– об отсутствии статистики и невозможности обнаружения и исключения артефактов;

– о наличии статистики и возможности выявления артефактов (если частоты встреч признаков растут пропорционально объему обучающей выборки, то это нормально, артефактами считаются признаки, по которым эта закономерность нарушается).

На основе этих выводов рекомендуется частота, которая признается незначимой и характерной для артефактов и осуществляется переформирование баз данных с исключенными артефактами.

Расчет матриц информативностей (БКОСА-3.1.3, 3.2, 3.3)

В этом режиме непосредственно на основе матрицы абсолютных частот с применением системного обобщения формулы Харкевича, предложенного автором в рамках СТИ, рассчитывается матрица информативностей, определяются значимость признаков, степень сформированности обобщенных образов классов, а также обобщенный критерий сформированности модели Харкевича для всей матрицы информативностей в целом. На экране монитора наглядно отображается стадия выполнения процесса и структура заполнения матрицы информативностей значимыми данными (на качественном уровне). На основе матрицы абсолютных частот рассчитывается и матрица условных процентных распределений.

Автоматическое выполнение режимов 1-2-3-4. В данном пакетном режиме последовательно выполняются ранее перечисленные режимы обучения системы (кроме режима исключения артефактов).

Измерение сходимости и устойчивости модели

Для измерения сходимости и устойчивости модели СК-анализа задаются параметры, определяющие исследование скорости сходимости:

– порядок выборки анкет (физический, случайный, в порядке возрастания соответствия генеральной совокупности, в порядке убывания степени многообразия, вносимого анкетой в модель);

– количество и коды признаков, по которым исследуется сходимость модели;

– интервал сглаживания для расчета скользящей погрешности.

В данном режиме организован цикл по объектам обучающей выборки, в котором после учета каждой анкеты в матрице абсолютных частот перерассчитывается матрица информативностей и в отдельной базе данных запоминаются информативности для заданных признаков. Это позволяет измерять и графически отображать скорость сходимости и семантическую устойчивость модели. В работе [5] на примере прогнозирования фондового рынка, подробно рассматриваются вопросы сходимости и семантической устойчивости содержательной информационной модели.

Почтовая служба по обучающей информации обеспечивает экспорт и импорт баз данных обучающей выборки при решении задач в системе "Эйдос" по многомашинной технологии.

14.1.2.3. Оптимизация модели (подсистема "Оптимизация") (БКОСА-4)

В данной подсистеме реализовано несколько различных подходов к повышению адекватности модели: контролируемое существенное снижение размерности семантических пространств классов и атрибутов при несущественном уменьшении их объема без уменьшения адекватности модели; разделение классов на типичные и нетипичные части и друге, некоторые из которых кратко будут рассмотрены ниже.

Формирование ортонормированного базиса классов
(БКОСА-4.2)

Формирование ортонормированного базиса классов реализуется с применением одного из трех итерационных алгоритмов оптимизации, относящиеся к методу последовательных приближений:

1) исключение из модели заданного количества наименее сформированных классов;

2) исключение заданного процента количества классов от оставшихся (адаптивный шаг);

3) исключение классов, вносящих заданный процент степени сформированности от оставшегося суммарного (адаптивный шаг).

Критерий остановки процесса последовательных приближений – срабатывание хотя бы одного из заданных ограничений:

а) достигнуто заданное минимальное количество классов в модели;

б) достигнута заданная полнота описания признака.

Прокрутка окна вправо позволяет просмотреть дополнительные характеристики, позволяющие оценить степень сформированности образов классов и ортонормированность пространства классов.

Исключение признаков с низкой селективной силой
(БКОСА-4.1)

С этой целью реализовано три итерационных алгоритма оптимизации, относящиеся к методу последовательных приближений:

– путем исключения из модели заданного количества наименее значимых признаков;

– путем исключения заданного процента количества признаков от оставшихся (адаптивный шаг);

– путем исключения признаков, вносящих заданный процент значимости от оставшейся суммарной (адаптивный шаг).

Критерий остановки процесса исключения признаков с низкой селективной силой – срабатывание одного из заданных ограничений:

а) достигнуто заданное минимальное количество признаков в модели;

б) достигнуто заданное минимальное количество признаков на класс (полнота описания класса).

Удаление классов и признаков, по которым
недостаточно данных

В данном режиме реализована возможность удаления из модели всех классов и признаков, по которым или вообще нет данных, или их недостаточно в соответствии с заданным критерием. Этот режим сходен с режимом выявления и исключения артефактов.

Разделение классов на типичную и нетипичные части

Если объекты, относящиеся к классу, обладают незначительной вариабельностью по признакам, то обобщенный образ класса получается четким и хорошо идентифицируемым, если же эта вариабельность высока, то он получается аморфным, расплывчатым и класс плохо идентифицируемым, в результате чего во втором случае объекты, в действительности принадлежащие к данному классу иногда не относятся системой к нему, т.е. рассматриваются как нетипичные. В данном режиме (_34) реализован эффективный итерационный алгоритм, в котором на основе этих нетипичных объектов создаются новые классы с тем же названием, что и исходный и с указанием номера итерации, на которой они созданы. В результате классы с высокой внутренней вариабельностью входящих в них объектов разбиваются на подклассы с низкой внутренней вариабельностью и достоверность модели быстро возрастает.

14.1.2.4. Верификация модели (оценка ее адекватности) (БКОСА-5)

Данный режим исполняется после синтеза модели. Верификация модели осуществляется путем копирования обучающей выборки в распознаваемую, пакетного распознавания и последующего анализа в режиме "Измерение валидности системы распознавания" подсистемы "Анализ". Он показывает средневзвешенную погрешность идентификации (интегральная валидность) и погрешность идентификации в разрезе по классам. При этом объект считается отнесенным к классу, с которым у него наибольшее сходство. Необходимо отметить, что остальные классы, находящиеся по уровню сходства на второй и последующих позициях не учитываются. Это обусловлено тем, что их учет привел бы к завышению оценки валидности модели.

Классы, по которым дифференциальная валидность неприемлемо низка считаются не сформированными. Причинами этого может быть очень высокая вариабельность объектов, отнесенных к данным классам (тогда имеет смысл разделить их на несколько), а также недостаток достоверной классификационной и описательной информации по этим классам (некорректная работа экспертов).

14.1.2.5. Эксплуатация приложения в режиме адаптации и периодического синтеза модели (БКОСА-7, БКОСА-9, БКОСА-10)

Идентификация и прогнозирование (подсистема "Распознавание") (БКОСА-7)

Данная подсистема реализует режимы ввода и корректировки распознаваемой выборки; пакетного распознавания; вывода результатов и межмашинного обмена данными. Ввод-корректировка распознаваемых анкет осуществляется в двухоконном интерфейсе: в левом окне показаны заголовки идентифицируемых объектов, в которых отображаются их коды и условные наименования, а в правом окне – описания объектов на языке признаков. В левом окне каждому объекту соответствует строка, а в правом – окно с прокруткой. Переход между окнами происходит по нажатию клавиши "TAB". В данном режиме каждая анкета распознаваемой выборки последовательно идентифицируется с каждым классом. Вывод результатов распознавания (идентификации и прогнозирования) возможен в двух разрезах:

а) информация о сходстве каждого объекта со всеми классами;

б) информация о сходстве каждого класса со всеми объектами.

Система генерирует обобщающий отчет по итогам идентификации, в котором в каждой строке дана информация о классе, с которым распознаваемый объект имеет наивысший уровень сходства (в процентах). Качество результата идентификации – это эвристическая оценка качества, учитывающая максимальную величину сходства, различие между первым и вторым классами по уровню сходства и в (меньшей степени) общий вид распределения классов по уровням сходства с данным объектом. Каждой строке обобщающего отчета соответствует карточка результатов идентификации (прогнозирования), которая по сути дела представляет собой результат разложения вектора объекта в ряд по векторам классов. Эти карточки распечатываются в файл с полными наименованиями классов и содержат классы, с уровнем сходства выше заданного.

Почтовая служба по распознаваемым анкетам обеспечивает запись на дискету распознаваемой выборки и считывание распознаваемой выборки с дискеты с добавлением к имеющейся на текущем компьютере. Этот режим служит для объединения информации по идентифицируемым объектам, введенной на различных компьютерах.

Подсистема "Типология" обеспечивает типологический анализ классов и признаков.

Типологический анализ классов включает: информационные (ранговые) портреты; кластерно-конструктивный и когнитивный анализ классов.

Информационные портреты классов (БКОСА-9.1)

Информационный портрет класса представляет собой список признаков в порядке убывания количества информации о принадлежности к данному классу. Такой список представляет собой результат решения обратной задачи идентификации (прогнозирования). Фильтрация (F6) позволяет выделить из информационного портрета класса диапазон признаков (по кодам или уровням Мерлина) и, таким образом, исследовать влияние заданных признаков на переход активного объекта управления в состояние, соответствующее данному классу.

Кластерный и конструктивный анализ классов обеспечивает: расчет матрицы сходства классов; генерацию кластеров и конструктов; просмотр и печать кластеров и конструктов; пакетный режим, обеспечивающий автоматическое выполнение первых трех режимов при установках параметров "по умолчанию"; визуализацию результатов кластерно-конструктивного анализа в форме семантических сетей и когнитивных диаграмм.

Расчет матрицы сходства образов классов (БКОСА-10.1.1)

В данном режиме непосредственно на основе оптимизированной матрицы информативностей рассчитывается матрица сходства классов. На экране в наглядной форме отображается информация о текущей стадии выполнения этого процесса.

Генерация кластеров и конструктов классов (БКОСА-10.1.2)

В данном режиме пользователем задаются параметры для генерации кластеров и конструктов классов, позволяющие исключить из форм центральную часть конструктов (оставить только полюса), а также сформировать кластеры и конструкты для заданных (кодами или уровнями Мерлина) подматриц. В данном режиме обеспечивается отображение отчета по конструктам и вывод его в виде текстового файла. Реализован режим быстрого поиска заданного конструкта и быстрый выход на него по заданному классу.

Автоматическое выполнение режимов 1-2-3

В данном пакетном режиме автоматически выполняются вышеперечисленные 3 режима с параметрами "по умолчанию". Выполнение пакетного режима целесообразно в самом начале проведения типологического анализа для общей оценки его результатов. Более детальные результаты получаются при выполнении отдельных режимов с конкретными значениями параметров.

Вывод 2d-семантических сетей классов (БКОСА-10.1.3)

В данном режиме пользователем в диалоге с системой "Эйдос" задаются коды от 3 до 12 классов (ограничение связано с тем, что больше классов не помещается на мониторе при используемом разрешении), а затем на основе данных матрицы сходства классов отображается ориентированный граф, в вершинах которого находятся классы, а ребра соответствуют знаку (красный – "+", синий – "-") и величине (толщина линии) сходства/различия между ними. Посередине каждой линии уровень сходства/различия соответствующих классов отображается в числовой форме (в процентах). Такие графы в данной работе называются 2d-семантическими сетями классов (2d означает "двухмерные").

Когнитивные диаграммы классов (БКОСА-10.3.1, 10.3.2)

В системе "Эйдос" реализован двухоконный интерфейс ввода задания на формирование когнитивных диаграмм и пример такой диаграммы. Переход между окнами осуществляется по клавише "ТАВ", выбор класса для когнитивной диаграммы – по нажатию клавиши "Enter". В верхней левой части верхнего окна отображаются коды выбранных классов. Генерация и вывод когнитивной диаграммы для заданных классов выполняется по нажатию клавиши F5. Отображаемые диаграммы всегда записываются в виде графических файлов в соответствующие поддиректории. Имеются также пакетные режимы генерации диаграмм: генерацию когнитивных диаграмм для полюсов конструктов (F6), генерация всех возможных когнитивных диаграмм (F7), а также генерация диаграмм Вольфа Мерлина (F8). При задании всех этих режимов имеется возможность задания большого количества параметров, определяющих вид диаграмм и содержание отображаемой на них информации.

Типологический анализ атрибутов обеспечивает: формирование и отображение семантических портретов атрибутов (признаков), а также кластерно-конструктивный и когнитивный анализ атрибутов.

Семантические портреты атрибутов (БКОСА-9.2)

В данном режиме обеспечивается формирование семантического портрета заданного признака и его отображение в текстовой и графической формах. Окно для просмотра текстового отчета имеет прокрутку вправо, что позволяет отобразить количественные характеристики. Графическая диаграмма выводится по нажатию клавиши F5, и может быть непосредственно распечатана или записана в виде графического файла в соответствующую поддиректорию.

Кластерный и конструктивный анализ атрибутов обеспечивает: расчет матрицы сходства признаков; генерация кластеров и конструктов признаков: просмотр и печать результатов кластерно-конструктивного анализа; автоматическое выполнение перечисленных режимов; отображение результатов кластерно-конструктивного анализа в форме семантических сетей и когнитивных диаграмм.

Расчет матрицы сходства атрибутов (БКОСА-10.2.1)

Стадия выполнения расчета матрицы сходства признаков наглядно отображается на мониторе.

Генерация кластеров и конструктов атрибутов (БКОСА-10.2.2)

В данном режиме имеется возможность задания ряда параметров, детально определяющих обрабатываемые данные и форму вывода результатов анализа и отображаются результаты кластерно-конструктивного анализа. Имеются также многочисленные возможности манипулирования данными (различные варианты поиска, сортировки и фильтрации).

Автоматическое выполнение режимов 1-2-3. Автоматически реализуются три вышеперечисленные режима.

Вывод 2d-семантических сетей атрибутов (БКОСА-10.2.3)

Результаты кластерно-конструктивного анализа признаков отображаются для заданных признаков в наглядной графической форме семантических сетей.

Когнитивные диаграммы атрибутов (БКОСА-10.4.1, 10.4.2)

Это новый вид когнитивных диаграмм, не встречающийся в литературе. Частным случаем этих диаграмм являются инвертированные диаграммы Вольфа Мерлина (терм. авт.). При их генерации имеется возможность задания ряда параметров, определяющих обрабатываемые данные и форму отображения результатов.

В подсистеме "Анализ" реализованы режимы:

– оценки анкет по шкале лживости;

– измерения внутренней интегральной и дифференциальной валидности модели;

– измерения независимости классов и признаков (стандартный анализ c²);

– генерации большого количества разнообразных 2d & 3d графических форм на основе данных матриц абсолютных частот, условных процентных распределений и информативностей (2d & 3d означает: "двухмерные и трехмерные");

– генерации и графического отображения нелокальных нейронов, нейронных сетей, классических и интегральных когнитивных карт.

Оценка достоверности заполнения анкет

В данном режиме исследуются корреляции между ответами в каждой анкете, эти корреляции сравниваются с выявленными на основе всей обучающей выборки и все анкеты ранжируются в порядке уменьшения типичности обнаруженных в них корреляций. Считается, что если корреляции в анкете соответствуют "среднестатистическим", которые принимаются за "норму", то анкета отражает обнаруженные макрозакономерности, если же нет, то возникает подозрение в том, что она заполнена некорректно.

В режиме "Измерение независимости объектов и признаков" реализован стандартный анализ c², а также рассчитываются коэффициенты Пирсона, Чупрова и Крамера, популярные в экономических, социологических и политологических исследованиях. В системе задание на расчет матриц сопряженности вводится в специальный бланк, который служит также для отображения обобщающих результатов расчетов. На основе этого задания рассчитываются и записываются в форме текстовых файлов одномерные и двумерные матрицы сопряженности для заданных подматриц.

В отличие от матриц сопряженности, выводимых в известной системе SPSS, здесь они выводятся с текстовыми пояснениями на том языке, на котором сформированы классификационные и описательные шкалы, с констатацией того, обнаружена ли статистически-значимая связь на заданном уровне значимости. Необходимо также отметить, что в системе "Эйдос" не используются табулированные теоретические значения критерия c² для различных степеней свободы, а необходимые теоретические значения непосредственно рассчитываются системой, причем со значительно большей точностью, чем они приведены в таблицах (при этом численно берется обратный интеграл вероятностей).

Режим "Просмотр профилей классов и признаков". Система "Эйдос" текущей версии 12.5 позволяет генерировать и выводить более 54 различных видов 2d & 3d графических форм, каждая из которых выводится в форме, определяемой задаваемыми в диалоге параметрами.

Подсистема "Сервис". Реальная эксплуатация ни одной программной системы невозможна либо без тщательного сопровождения эксплуатации и без наличия в системе развитых средств обеспечения надежности эксплуатации. В системе "Эйдос" для этого служит подсистема "Сервис" в которой:

– автоматически ведется архивирование баз данных;

– создаются отсутствующие базы данных и индексные массивы;

– распечатываются в текстовые файлы служебные формы, являющиеся основой содержательной информационной модели (базы абсолютных частот, условных процентных распределений и информативностей).

В подсистему "Сервис" входит также интеллектуальная дескрипторная информационно-поисковая система, автоматически генерирующая нечеткие дескрипторы и имеющая интерфейс нечетких запросов на любом естественном языке, использующем кириллицу или латиницу (т.е. не только русском). Отчет по результатам запроса содержит информационные объекты базы данных системы, ранжированные в порядке уменьшения степени соответствия запросу.

14.1.3. Технические характеристики и обеспечение эксплуатации системы "ЭЙДОС" (версии 12.5)

14.1.3.1. Состав системы "Эйдос": базовая система, системы окружения и программные интерфейсы импорта данных

Система "Эйдос" (последней версии 12.5) включает базовую систему (система "Эйдос" в узком смысле слова), три системы окружения, а также ряд программных интерфейсов с внешними источниками данных:

– систему анализа и прогнозирования ситуация на фондовом рынке "Эйдос-фонд", разработанную совместно с Б.Х.Шульман [97, 111];

– систему комплексного психологического тестирования "Эйдос-Y", созданную совместно с С.Д.Некрасовым [97, 118];

– систему типизации и идентификации социального статуса респондентов по их астрономическим показателями на момент рождения "Эйдос-астра", разработанную совместно с А.П.Труневым и В.Н.Шашиным [104, 108, 122, 131, 173, 185, 187, 190, 204, 207, 208, 219, 222, 227, 228, 229, 234, 239, 242, 243, 244, 270, 276].

Системы окружения представляют собой развитие программные интерфейсы базовой системы "Эйдос" с внешними базами данных психологических тестов, биржевыми базами данных и базами данных социологической информации соответственно, а также выполняют ряд самостоятельных функций по предварительной обработке информации, визуализации результатов анализа и т.д. Кроме того, в саму базовую систему "Эйдос" включены программные интерфейсы, обеспечивающие формализацию предметной области и импорт данных из внешних источников данных различных стандартов (текстовых файлов и баз данных).

14.1.3.2. Отличия системы "Эйдос" от аналогов: экспертных и статистических систем

От экспертных систем система "Эйдос" отличается тем, что для ее обучения от экспертов требуется лишь само их решение о принадлежности того или иного объекта или его состояния к определенному классу, а не формулирование правил (продукций) или весовых коэффициентов, позволяющих прийти к такому решению (система генерирует их сама, т.е. автоматически). Дело в том, что часто эксперт не может или не хочет вербализовать, тем более формализовать свои способы принятия решений. Система "Эйдос" генерирует обобщенную таблицу решений непосредственно на основе эмпирических данных и их оценки экспертами.

От систем статистической обработки информации система "Эйдос" отличается, прежде всего, своими целями, которые состоят в следующем: формирование обобщенных образов исследуемых классов распознавания и признаков по данным обучающей выборки (т.е. обучение); исключение из системы признаков тех из них, которые оказались наименее ценными для решения задач системы; вывод информации по обобщенным образам классов распознавания и признаков в удобной для восприятия и анализа текстовой и графической форме (информационные или ранговые портреты); сравнение распознаваемых формальных описаний объектов с обобщенными образами классов распознавания (распознавание); сравнение обобщенных образов классов распознавания и признаков друг с другом (кластерно-конструктивный анализ); расчет частотных распределений классов распознавания и признаков, а также двумерных матриц сопряженности на основе критерия c² и коэффициентов Пирсона, Чупрова и Крамера; результаты кластерно-конструктивного и информационного анализа выводятся в форме семантических сетей и когнитивных диаграмм. Система "Эйдос" в универсальной форме автоматизирует базовые когнитивные операции системного анализа, т.е. является инструментарием СК-анализа. Таким образом, система "Эйдос" выполняет за исследователя-аналитика ту работу, которую при использовании систем статистической обработки ему приходится выполнять вручную, что чаще всего просто невозможно при реальных размерностях данных. Поэтому система "Эйдос" и называется универсальной когнитивной аналитической системой.

14.1.3.3. Некоторые количественные характеристики системы "Эйдос"

Система "Эйдос" обеспечивает генерацию и запись в виде файлов более 54 видов 2d & 3d графических форм и 50 видов текстовых форм.

При применении системы в самых различных предметных областях обеспечивается достоверность распознавания обучающей выборки: на уровне 90% (интегральная валидность), которая существенно повышается после Парето-оптимизации системы признаков (т.е. после исключения признаков с низкой селективной силой), удаления из модели артефактов, а также классов и признаков, по которым недостаточно данных, разделения классов на типичные и нетипичные части. Система "Эйдос" версии 12.5 обеспечивает синтез модели, включающей десятки тысяч классов и признаков при неограниченном объеме обучающей выборки, причем признаки могут быть не только качественные (да/нет), но и количественные, т.е. числовые. В некоторых режимах анализа модели имеются ограничения на ее размерность, которые на данном этапе преодолеваются путем снижения размерности модели. Реализована возможность разработки супертестов, в том числе интеграции стандартных тестов в свою среду, (при этом не играет роли известны ли методики интерпретации, т.е. "ключи" этих тестов). В системе имеется научная графика, обеспечивающая высокую степень наглядности, а также естественный словесный интерфейс при обучении Системы и запросах на распознавание.

Исходные тексты системы "Эйдос" и систем окружения "Эйдос-Y", "Эйдос-фонд" и «Эйдос-астра» в формате "Текст-DOS" имеют объем около 2.5 Мб; их распечатка 6-м шрифтом составляет около 800 страниц.

14.1.3.4. Обеспечение эксплуатации системы "Эйдос"

Универсальная когнитивная аналитическая система "Эйдос" представляет собой программную систему, и для ее эксплуатации, как и для эксплуатации любой программной системы, необходима определенная инфраструктура. Без инфраструктуры эксплуатации любая программная система остается лишь файлом, записанным на винчестере. В зависимости от масштабности решаемых задач управления и специфики предметной области данная структура может быть как довольно малочисленной, так и более развитой. Однако в любом случае ее основные функциональные и структурные характеристики остаются примерно одними и теми же. Кратко рассмотрим эту инфраструктуру на примере гипотетической организации, производящей определенные виды продукции.

Основная цель: обеспечивать информационную и аналитическую поддержку деятельности организации, направленную на производство запланированного объема продукции заданного качества, достижение высокой эффективности управления и устойчивого поступательного развития.

Данная основная цель предполагает выполнение информационных и аналитических работ с различными объектами деятельности, находящимися на различных структурных уровнях как самой организации, так и ее окружения: персональный уровень; уровень коллективов (подразделений); уровень организации в целом; окружающая среда (непосредственное, региональное, международное окружение). Для достижения основной цели для каждого класса объектов должны регулярно выполняться следующие работы: оценка (идентификация) текущего состояния с накоплением данных (мониторинг); прогнозирование развития (оперативное, тактическое и стратегическое); выработка рекомендаций по управлению. Необходимо особо подчеркнуть, что основная цель может быть достигнута только при условии соблюдения вполне определенной наукоемкой технологии, основы которой изложены в данном исследовании.

Задачи, решаемые для достижения цели работы:

1. Мониторинг: оценка и идентификация текущего (фактического, актуального) состояния объекта управления; накопление данных идентификации в базах данных в течение длительного времени.

2. Анализ: выявление причинно-следственных зависимостей путем анализа данных мониторинга.

3. Прогнозирование: оперативное, тактическое и стратегическое прогнозирование развития объекта управления и окружающей среды путем использования закономерностей, выявленных на этапе анализа данных мониторинга.

4. Управление: анализ взаимодействия объекта управления с окружающей средой и выработка рекомендаций по управлению.

Таким образом, по мнению автора, управление является высшей, существующей на данный момент формой обработки информации.

Для достижения основной цели и решения задач управления необходимо выполнять работы по следующим направлениям: регулярное получение исходной информации о состоянии объекта управления; обработка исходной информации на компьютерах; анализ обработанной информации, прогнозирование развития объекта управления, выработка рекомендаций по оказанию управляющих воздействий на объект управления; разработка и применение (или предоставление рекомендаций заказчикам) различных методов оказания управляющих воздействий на объект управления.

Для этого необходима определенная организационная структура: научно-методический отдел включает: научно-методический сектор; сектор разработки программного обеспечения; сектор внедрения и сопровождения программного обеспечения; сектор организационного и юридического обеспечения; отдел мониторинга: сектор исследования объекта управления; сектор по работе с независимыми экспертами; сектор по взаимодействию с поставляющими информацию организациями; сектор по анализу информации общего пользования; отдел обработки информации: сектор ввода исходной информации (операторы); сектор сетевых технологий и Internet; сектор внедрения, эксплуатации и сопровождения программных систем; сектор технического обслуживания компьютерной техники; сектор ведения архивов баз данных по проведенным исследованиям; аналитический отдел имеет структуру, обеспечивающую компетентный профессиональный анализ результатов обработки данных мониторинга по объектам, которые приняты для контроля и управления.

Для выполнения работ по этим направлениям необходимо определенное обеспечение деятельности: техническое, программное, информационное, организационное, юридическое и кадровое. Детально подобная структура и виды обеспечения ее деятельности описаны в работе [94].

14.1.4. АСК-анализ, как технология синтеза и эксплуатации рефлексивных АСУ активными объектами

Применение АСК-анализа обеспечивает выявление информационных зависимостей между факторами различной природы и будущими состояниями объекта управления, т.е. позволяет осуществить синтез содержательной информационной модели, а фактически – осуществить синтез АСУ. Применение АСК-анализа в составе АСУ обеспечивает ее эксплуатацию в режиме непрерывной адаптации модели (на детерминистских этапах), а когда это необходимо (т.е. после прохождения точек бифуркации) – и ее нового синтеза.

Ниже приведена технология системы "Эйдос" как инструментария АСК-анализа:

Шаг 1–й: формализация предметной области (БКОСА-1): разработка описательных и классификационных шкал и градаций, необходимых для формализованного описания предметной области. Описательные шкалы описывают факторы различной природы, влияющие на поведение активных объектов управления (АОУ), а классификационные – все его будущие состояния, в том числе целевые.

Шаг 2–й: формирование обучающей выборки (БКОСА-2): информация о состоянии среды и объекта управления, а также вариантах управляющих воздействий поступает на вход системы. Работа по преобразованию этой информации в формализованный вид (т.е. кодирование) осуществляется специалистами, обслуживающими систему с использованием описательных и классификационных шкал. Вся эта информация представляется в виде специальных кодированных бланков, используемых также для ввода информации в компьютер. В результате ее формируется так называемая "обучающая выборка".

Шаг 3–й: обучение (БКОСА-3): обучающая выборка обрабатывается обучающим алгоритмом, на основе чего им формируются решающие правила (обобщенные образы состояний АОУ, отражающие весь спектр будущих возможных состояний объекта управления) и определяется ценность факторов для решения задач подсистем идентификации, мониторинга, прогнозирования и выработки управляющих воздействий.

Шаг 4–й: оптимизация (БКОСА-4): факторы, не имеющие особой прогностической ценности, корректным способом удаляются из системы. Данный процесс осуществляется с помощью итерационных алгоритмов, при этом обеспечивается выполнение ряда ограничений, таких как результирующая размерность пространства факторов, его информационная избыточность и т.п.

Шаг 5–й: верификация модели (БКОСА-5): выполняется после каждой адаптации или пересинтеза модели. На этом шаге обучающая выборка копируется в распознаваемую и осуществляется ее автоматическая классификация (в режиме распознавания). Затем рассчитываются так называемые внутренняя дифференциальная и интегральная валидности, характеризующие качество решающих правил.

Шаг-6: принятие решения об эксплуатации модели или ее пересинтезе. Если результаты верификации модели удовлетворяют разработчиков рефлексивной АСУ активными объектами (РАСУ АО), то она переводится из пилотного (экспериментального) режима, при котором управляющие решения генерировались, но не исполнялись, в режим экспериментальной эксплуатации, а затем и опытно–производственной эксплуатации, когда они реально начинают использоваться для управления. Иначе, т.е. если же модель признана недостаточно адекватной, то необходимо осуществить ее пересинтез, начиная с шага 1. При этом используются следующие приемы: расширение набора факторов, т.к. значимые факторы могли не войти в модель; увеличение объема обучающей выборки, т.к. существенные примеры могли не войти в обучающую выборку; исключение артефактов, т.к. в модель могли вкрасться существенно искажающие ее не подтверждающиеся данные; пересмотр экспертных оценок и, если необходимость этого возникает систематически, то и переформирование экспертного совета, т.к. причиной этого могла быть некомпетентность экспертов; объединение некоторых классы, т.к. по ним недостаточно данных; разделение некоторых классов, т.к. по ним слишком высокая вариабельность объектов по признакам, и т.д.

Шаг 7-й: идентификация и прогнозирование состояния АОУ (БКОСА-7).

Шаг 8-й: оценка качества идентификации состояния АОУ. Если качество идентификации высокое, то состояние АОУ рассматривается как типовое, а значит, причинно-следственные взаимосвязи между факторами и будущими состояниями данного объекта управления считаются адекватно отраженными в модели и известными (т.е. если качество идентификации высокое, то считается, что объект относится к генеральной совокупности, по отношению к которой обучающая выборка репрезентативна). Поэтому в этом случае осуществляется переход на Шаг-9 (выработка управляющего воздействия и последующий анализ). Иначе – считается, что на вход системы идентификации попал объект, не относящийся к генеральной совокупности, адекватно представленной обучающей выборкой. Поэтому в этом случае информация о нем поступает на Шаг-13, начиная с которого запускается процедура пересинтеза модели, что приводит к расширению генеральной совокупности, представленной обучающей выборкой.

Шаг 9-й: выработка решения об управляющем воздействии (БКОСА-9) путем решения обратной задачи прогнозирования [97].

Шаг 10–й типологический анализ классов и факторов (БКОСА-10): кластерно-конструктивный и когнитивный анализ, семантические сети, когнитивные диаграммы состояний АОУ и факторов [97].

Шаг 11-й: многофакторное планирование и принятие решения о применении системы управляющих факторов (БКОСА-11).

Шаг 12-й: оценка адекватности принятого решения об управляющих воздействиях: если АОУ перешел в заданное целевое состояние, то осуществляется переход на вход адаптации содержательной информационной модели (Шаг-2): в подсистеме идентификации предусмотрен режим дополнения распознаваемой выборки к обучающей, чтобы в последующем, когда станут известны результаты управления, этой верифицированной (т.е. достоверной) оценочной информацией дополнить обучающую выборку и переформировать решающие правила (обучающая обратная связь). Иначе, т.е. если АОУ не перешел в заданное целевое состояние, переход на вход пересинтеза модели (Шаг-1), при этом могут быть изменены и описательные, и классификационные (оценочные) шкалы, что позволяет качественно расширить сферу адекватного функционирования РАСУ АО.

Шаг 13–й (неформализованный поиск нетипового решения об управляющем воздействии и подготовка данных для пересинтеза модели, как в случае, если решения оказалось удачным, так и в противном случае).

Таким образом, предложена технология применения системы "Эйдос" как инструментария применения АСК-анализа, основанного на системной теории информации, ориентированной на синтез рефлексивных АСУ АО. В процессе эксплуатации системы "Эйдос" успешно решаются все задачи АСК-анализа: формирование обобщенных образов состояний АОУ на основе обучающей выборки (обучение); идентификация состояний АОУ на основе его параметров (распознавание); определение влияния входных параметров на перевод АОУ в различные будущие состояния (обратная задача прогнозирования); прогнозирование поведения АОУ в условиях полного отсутствия управляющих воздействий; прогнозирование поведения АОУ при различных вариантах многофакторных управляющих воздействий.

Кроме того, выявленные в результате работы рефлексивной АСУ причинно-следственные зависимости между факторами различной природы и будущими состояниями объекта управления позволяют, при условии неизменности этих закономерностей в течение достаточно длительного времени, построить АСУ с постоянной моделью классического типа.

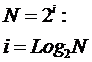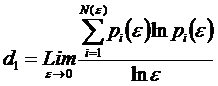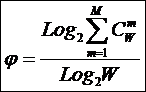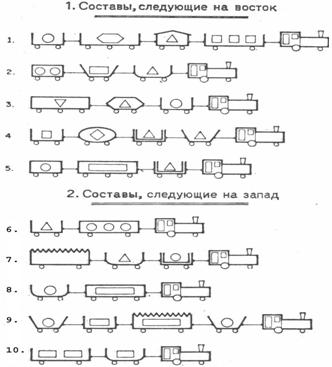
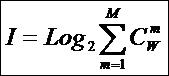
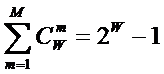
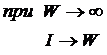
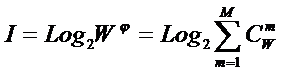
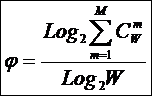
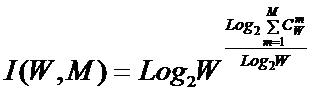
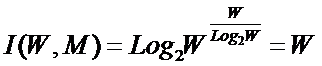
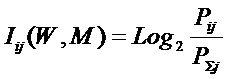
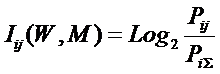
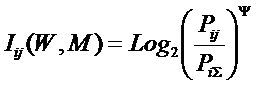
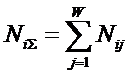
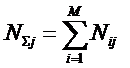
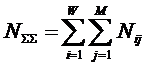
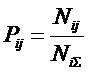
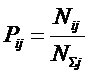
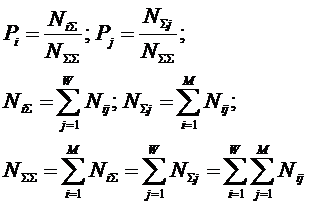
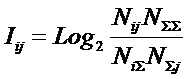
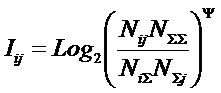
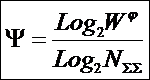
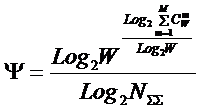
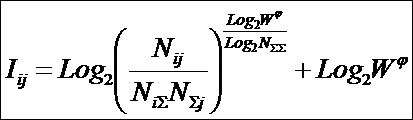
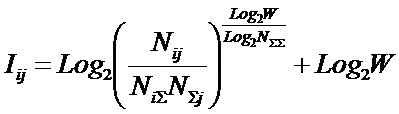
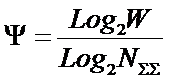
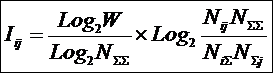
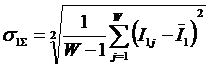
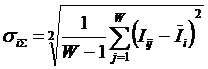
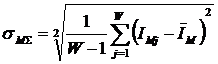
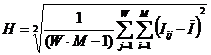
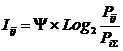
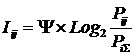
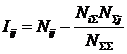
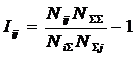
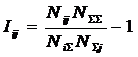
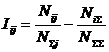
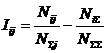
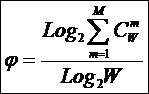
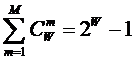
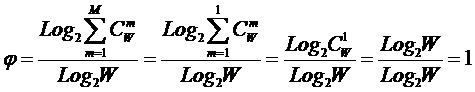
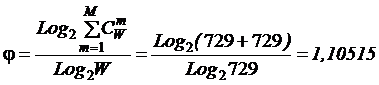
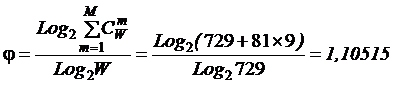
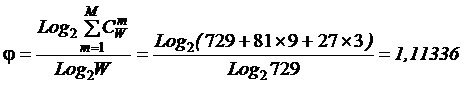
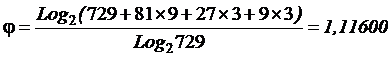
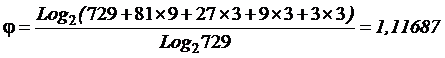
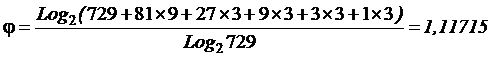
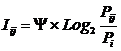
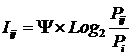
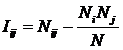
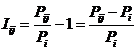
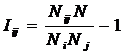
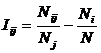
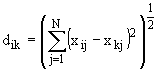
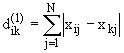
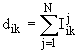14.1.5. Выводы

1. Создан программный и методический инструментарий СК-анализа – Универсальная когнитивная аналитическая система "Эйдос", рядом Свидетельств РосПатента РФ [111-137].

2. Система "Эйдос" на базе формализуемой когнитивной концепции успешно реализует предложенную семантическую информационную модель и алгоритмы базовых когнитивных операций системного анализа, и, таким образом, является специальным программным инструментарием для синтеза и экспулатации приложений управления знаниями. Система "Эйдос" является эффективным инструментарием СК-анализа. В функциях и структуре системы "Эйдос" нашли воплощение фундаментальные закономерности познания, связанные с функциональной асимметрией мозга и знаковых систем [94].

3. Технология синтеза и эксплуатации приложений системы "Эйдос", видеограммы ее пользовательского интерфейса и технические характеристики (текущая версия системы "Эйдос-12.5" позволяет обрабатывать десятки тысяч будущих состояний активных объектов управления и градаций факторов).

4. Технология разработки приложения управления знаниями в системе "Эйдос" включает: когнитивную структуризацию и формализацию предметной области (подсистема "Словари"); синтез модели (подсистема "Обучение"); оптимизацию модели (подсистема "Оптимизация"); верификацию модели (оценка степени адекватности, скорости сходимости и семантической устойчивости модели).

5. Технология эксплуатации приложения системы "Эйдос" в режиме адаптации и синтеза модели включает: идентификацию и прогнозирование (подсистема "Распознавание"); кластерно-конструктивный, семантический и когнитивный анализ (подсистема "Типология"); анализ достоверности, валидности, независимости (подсистема "Анализ"); средства и инструменты обеспечения надежности эксплуатации (подсистема "Сервис").

5. Система "Эйдос" является большой системой. Листинг ее исходных текстов (вместе с системами окружения "Эйдос-фонд", "Эйдос-Y" и «Эйдос-астра») 6-м шрифтом составляет около 800 страниц, в процессе работы система оперирует десятками баз данных (около 70).

6. Разработана инфраструктура применения системы "Эйдос", детализированы организационные, юридические, экономические, технические и другие аспекты информационной технологии применения данной системы для решения задач синтеза рефлексивных АСУ активными объектами и эксплуатации этих АСУ в режиме адаптации и периодического синтеза модели.

7. Разработана технология синтеза рефлексивных АСУ активными объектами и методики ее применения в конкретных предметных областях. Предложено рассматривать алгоритм СК-анализа, как алгоритм синтеза рефлексивных АСУ активными, а сам СК-анализ, как технологию синтеза рефлексивных АСУ активными объектами и их эксплуатации в режиме адаптации и периодического синтеза модели:

шаг 1–й: формализация предметной области (БКОСА-1);

шаг 2–й: формирование обучающей выборки (БКОСА-2);

шаг 3–й: обучение (БКОСА-3);

шаг 4–й: оптимизация (БКОСА-4);

шаг 5–й: верификация модели (БКОСА-5);

шаг 6-й: принятие решения об эксплуатации модели или ее пересинтезе;

шаг 7-й: идентификация и прогнозирование состояния АОУ (БКОСА-7);

шаг 8-й: оценка качества идентификации состояния АОУ;

шаг 9-й: выработка решения об управляющем воздействии (БКОСА-9);

шаг 10–й: типологический анализ классов и факторов (БКОСА-10);

шаг 11-й: многофакторное планирование и принятие решения о применении системы управляющих факторов (БКОСА-11);

шаг 12-й: оценка адекватности принятого решения об управляющих воздействиях;

шаг 13–й: (неформализованный поиск нетипового решения об управляющем воздействии и подготовка данных для пересинтеза модели, причем как в случае, если решение оказалось удачным, так и в противном случае).

Постановка и программная реализация системы «Эйдос» универсальна, т.е. не зависит от предметной области, потому она может быть эффективно применена в самых различных предметных областях.

14.1.6. Перспективы развития системы «Эйдос»

Основную перспективу развития Универсальной когнитивной аналитической системы «Эйдос» автор видит в разработке многоязычной (прежде всего русской и английской) Internet версии (система «Эйдос-net»), работающей в локальной сети Host-компьютера (на кластере), к которой был бы обеспечен доступ с любого компьютера, находящегося в Internet.

Основные отличия системы «Эйдос-net» от локальной версии состоят в наличии диспетчера приложений и нескольких уровней авторизации пользователей. Предполагается также пересмотреть структуру диалога системы, а также снять ограничения на размерности обрабатываемых моделей, имеющиеся в текущей версии. Подробнее перспективы развития СК-анализа и системы «Эйдос» описаны в 7-й главе работы [97][136].

Диспетчер приложений обеспечивает создание или выбор текущего приложения в пределах компетенции пользователя, определяемого уровнем авторизации. Предполагается несколько уровней авторизации:

Таблица – УРОВНИ АВТОРИЗАЦИИ И ПРАВА ПОЛЬЗОВАТЕЛЕЙ
СИСТЕМЫ «ЭЙДОС-NET»

№	Статус пользователя	Права пользователя	Источник полномочий
1	Администратор приложения	Создание и удаление своих приложений и в них пересинтез моделей; решение задач прогнозирования и поддержки принятия решений; исследование СИМ	Модератор: автор сайта – системы «Эйдос-net»
2	Специалист	Адаптация моделей, в которых он авторизован, решение в них задач прогнозирования и поддержки принятия решений	Модериратор: администратор приложения
3	Пользователь	Решение задач прогнозирования и поддержки принятия решений в приложениях, в которых он авторизован администратор приложения	Модериратор: администратор приложения
4	Ученик	Просмотр системы меню и публикаций по системе, возможность осваивать лабораторные работы	Немодерируемый доступ

В настоящее время автор работает над реализацией этого проекта.

Но необходимо отметить, что и сегодня имеется техническая возможность:

– одновременной интерактивной on-line демонстрации текущей «локальной» версии системы «Эйдос» на любом количестве компьютеров, подключенных к Internet;

– удаленной инсталляции системы «Эйдос» для дальнейшего использования на этих удаленных компьютерах;

– удаленного использования системы «Эйдос» на любых компьютерах, на которых она проинсталлирована.

Для обеспечения всех этих возможностей может быть использована, например, программа TeamViewer (http://www.teamviewer.com/). Эта программа, в отличие от RemoteAdmin (Radmin) и NetOP, обеспечивает доступ к удаленным компьютерам, в т.ч. и не имеющим внешних IP-адресов и находящимся за брандмауэром, прокси-сервером и другими экранами.

В режиме демонстрации на удаленных компьютерах отображается рабочий стол главного компьютера, с которого осуществляется демонстрация, и изображение с его монитора, но нет никакого другого доступа к этим удаленным компьютерам. При этом с главного компьютера есть возможность аудио- и видео-общения с аудиторией около удаленных компьютеров, т.е. можно комментировать презентацию, а также слышать вопросы слушателей и отвечать на них, т.е. автор может вести дистанционное преподавание с целью освоения системы «Эйдос», например, по лекционным и лабораторным курсам [98, 100, 101]. Удаленную инсталляцию системы «Эйдос» для дальнейшего использования на удаленных компьютерах осуществляет автор. Удаленное использование системы «Эйдос» на любых компьютерах, на которых она проинсталлирована, осуществляют те, кому автором предоставлено такое право.

14.2. Универсальная когнитивная аналитическая
система «Эйдос-Х++» – новое поколение
системы «Эйдос»

Данный раздел основан на работе [260]. Универсальная когнитивная аналитическая система "Эйдос" является отечественным лицензионным программным продуктом, который в разные годы реализовался на различных языках программирования на компьютерах различных платформ [224]. С 1992 года существует и версия системы «Эйдос» для IBM-совместимых персональных компьютеров. В качестве инструментальных средств программирования использовались следующие лицензионные средства, официально приобретенные Научно-производственным предприятием «Эйдос»[137]: CLIPPER 5.01 Rus, № CRX 202874; Tools-II Rus № 200932; BiGraph 3.01r1 № 247. Выбор этих средств в то время был совершенно оправданным и обоснованным, т.к. тогда эта система программирования несопоставимо превосходила все остальные, существовавшие в то время, по своим возможностям. В основе системы «Эйдос» использовались математические модели и алгоритмы, основанные на теории информации, впервые в полной форме описанные в 1993 году [284]. В 1994 году автором были получены первый в Краснодарском крае, а возможно и один из первых в России, патенты на систему искусственного интеллекта [111-113]. С тех пор данная версия системы непрерывно совершенствовалась на протяжении почти 20 лет вплоть до весны 2012 года, когда началась не посредственная разработка качественно новой версии. С применением этой системы было решено большое количество задач в различных предметных областях, чему существенно способствовало то, что система «Эйдос» изначально разрабатывалась в постановке, не зависящей от предметной области и могла применяться для решения задач, которые от человека требуют применения естественного интеллекта во всех предметных областях, в которых человек применяет свой естественный интеллект [93-286]. Поэтому в 2003 году ей было дано название: Универсальная когнитивная аналитическая система "Эйдос", подчеркивающее это важное обстоятельство [117]. По результатам проведенных с помощью системы исследований издано 18 научных монографий и учебных пособий с грифами УМО и министерства [93-110], сотни статей [93-286], в т.ч. в изданиях, входящих в Перечень ВАК РФ^[138], получено 27 патентов РФ, защищено 5 докторских и 7 кандидатских диссертаций по экономическим, техническим, психологическим и медицинским наукам^[139].

В состав системы «Эйдос» входит подсистема _152, содержащая ряд стандартных программных интерфейсов с внешними базами данных различных стандартов: текстовых, баз данных (БД) и графических, расширяющих сферу ее применения. Некоторые из подобных интерфейсов при своем развитии превратились в системы окружения: "Эйдос-фонд" [97, 111], "Эйдос-Ψ" [97, 118] и «Эйдос-астра» [104, 108, 122, 131, 234, 244] (рис. 1):

Рисунок 1. Базовая система «Эйдос» и системы окружения [260]

Таким образом, по мнению автора можно сделать обоснованный вывод о том, что система «Эйдос» является большой и довольно эффективной системой. Однако она обладала и рядом недостатков, среди которых в первую очередь необходимо отметить следующие:

1. Система была разработана за несколько лет до создания операционной системы MS Windows-95, и, естественно, не обладала стандартным для MS Windows так называемым GUI‑интерфейсом (сокр. от англ. Graphical user interface).

2. Она работала в основной памяти компьютера, имеющей размер 640 Кб, и не могла использовать внешнюю память (Extend Memory). Поэтому система «Эйдос» имела модульную оверлейную структуру и использовала диспетчер памяти (QEMM). Но со временем система на столько увеличилась, что и эта технология уже не обеспечивала ее развитие и пришлось разбить систему на десятки отдельно загружаемых модулей, связанных только по базам данных.

3. Система не могла работать в защищенном режиме и задействовать swapping-технологию MS Windows для использования внешней памяти в качестве оперативной. Внешняя память использовалась системой «Эйдос» только для кеширования обращения к внешней памяти и до, и после создания системы MS Windows.

4. В системе не было возможности интеграции с Windows и Internet-приложениями, например организации работы с базами данных, находящимися на Internet-сервере, хотя сам язык программирования, на котором она была написана, в принципе это позволял.

5. Размерности баз знаний были ограничены: 4000 классов на 4000 градаций факторов, размеры самих файлов баз знаний и баз данных системы также были ограничены 4 гигабайтами.

6. Система работала с интеллектуальным приложением, находящимся в текущей директории с исполнимыми модулями системы, т.е. в ней не было диспетчера приложений.

7. В системе не было подсистемы администрирования самой системы, а также пользователей и приложений.

8. Но самое главное, что система была 16-разрядным приложением и работала под Windows в режиме эмуляции MS DOS. Это было нормально во всех версиях системы MS Windows до 7. Под MS Windows 7 система «Эйдос» работала с использованием виртуальной машины, эмулирующей MS Windows XP.

Особо отметим, что отсутствие графики не являлось недостатком системы «Эйдос», т.к. в ней изначально использовалась мощная графическая библиотека (общая для CLIPPER, Pascal и C++) и было реализовано большое количество (более 60) различных графических форм, многие из которых не имеют аналогов в MS Windows и других системах и все это было в системе за несколько лет до создания MS Windows.

Наличие в системе перечисленных выше недостатков, а также некоторых других, более мелких, вызывало настоятельную потребность создания качественно новой версии системы «Эйдос», основывающейся на современной системе программирования, позволяющей решить все эти проблемы. Такая качественно-новая версия системы была задумана очень давно (около 10 лет назад) и о ней писалось в частности в работах [97, 224] и других, размещенных на сайте автора системы «Эйдос»: http://lc.kubagro.ru/. Однако по ряду причин создание новой версии затягивалось, хотя такие попытки неоднократно предпринимались автором на протяжении ряда лет и в разных системах программирования, в частности на Alaska xBase++, Delphi for PHP^[140] и на Java. Наконец к лету 2012 года благодаря помощи зав.кафедрой компьютерных технологий и систем Заслуженного деятеля науки РФ профессора В.И.Лойко и проректора по науке профессора Ю.П.Федулова (ФГБОУ ВПО «Кубанский государственный аграрный университет») удалось приобрести лицензионное программное обеспечение, являющееся современным развитием того, на котором была написана система «Эйдос»: Alaska Xbase++ (R) Version 1.90.355 SL1, TOOLS III, eXPress++ (C) Version 1.9 Build 255, Advantage Database Server (ADS) 10.0.

В настоящее время автором создана и запатентована [260, 135, 136, 137] качественно новая версия системы «Эйдос», получившая название: Универсальная когнитивная аналитическая система «Эйдос-Х++»^[141]. Конечно, в ней пока реализованы в основном базовые подсистемы и режимы, но она уже является полнофункциональной системой и непрерывно развивается. Первая публикация по системе Эйдос-Х++ вышла в 2012 году [282].

В новой версии системы сняты все вышеперечисленные, а также еще и следующие ограничения:

- на количество объектов обучающей и распознаваемой выборки (в базах данных заголовков и базах данных признаков);

- на размерность баз данных классов, признаков, на количество градаций описательных шкал в одной шкале;

- на количество классов, к которым относится объект обучающей и распознаваемой выборки;

- на размерность по признакам баз данных абсолютных частот, условных и безусловных процентных распределений и баз знаний;

- на размерность по классам баз данных абсолютных частот, условных и безусловных процентных распределений и баз знаний[142];

- вместо ранее используемых 4-х моделей знаний в новой версии используется 7, кроме того есть возможность использовать 3 статистические модели как модели знаний и сравнивать результаты их использования;

- новая версия системы «Эйдос» имеет стандартный GUI-интерфейс; режимы системного администратора, авторизацию и диспетчер приложений; возможность работы с группами приложений, как с одним приложением (как в системе Эйдос-астра);

- кроме локальной версии предусматривается возможность работы в локальной сети и через Internet;

- сняты проблемы с ограниченным использованием возможностей современных процессоров и операционных систем. Локальная версия системы «Эйдос-Х++» является 32-разрядным приложением и нормально работает во всех версиях MS Window, включая 7, но использует лишь одно ядро процессора и не более 2 Гб оперативной памяти. Однако с Advantage Database Server (ADS) эти ограничения снимаются, и она становится практически полноценным 64-разрядным приложением, работающим с базами данных размером до 16000 Гбайт^[143].

Универсальная когнитивная аналитическая система "Эйдос-Х++" является современным инструментарием системно-когнитивного анализа [97, 266], разработана в универсальной постановке, не зависящей от предметной области, и обеспечивает:

- формализацию предметной области;

- многопараметрическую типизацию, синтез, повышение качества и верификацию 3 статистических моделей и 7 моделей знаний предметной области;

- распознавание (системную идентификацию и прогнозирование);

- поддержку принятия решений и исследование модели, в т.ч.: дивизивную и агломеративную когнитивную кластеризацию, конструктивный и СК-анализ моделей: семантические и нейронные сети, когнитивные диаграммы, классические и интегральные когнитивные карты.

Есть в системе и ряд других новых возможностей. Переосмыслена иерархическая структура системы, учтен значительный опыт проведения научных исследований и преподавания ряда дисциплин с применением системы «Эйдос» и систем окружения[144]. Это нашло отражение в структуре системы и дереве диалога, приведенных в таблице 1:

ТАБЛИЦА 1 – СТРУКТУРА УНИВЕРСАЛЬНОЙ КОГНИТИВНОЙ АНАЛИТИЧЕСКОЙ СИСТЕМЫ "ЭЙДОС-Х++"
(БЕЗ КНОПОЧНЫХ МЕНЮ ЭКРАННЫХ ФОРМ)

Подсистема, режим, подрежим, функция	Комментарий
1. Администрирование	Подсистема администрирования
1.1. Авторизация	Авторизация сисадмина, администратора приложения или пользователя
1.2. Регистрация администратора приложения	Регистрация и удаление регистрации администраторов приложений и задание паролей пользователей. Этот режим доступен только системному администратору и администраторам приложений
1.3. Диспетчер приложений	Это подсистема администрирования приложений. Она предназначена для создания новых приложений, как пустых, так и на основе учебных примеров (лабораторных работ), имеющихся в системе, а также для выбора приложения для работы из уже имеющихся и удаления приложения. Выбор приложения для работы осуществляется путем отметки его любым символом. Удалять любые приложения разрешается только сисадмину, а Администратору приложений - только те, которые он сам создал
1.4. Выбор режима использования системы	Монопольный или многопользовательский (задается при инсталляции системы, но может быть изменен когда угодно сисадмином)
1.5. Задание путей на папки с группами приложений	Папки с различными группами приложениями могут быть на локальном компьютере, в локальной сети или в Internet. Пути на них задаются сисадмином при инсталляции системы и могут быть изменены им когда угодно. Один из этих путей, а именно первый из отмеченный специальных символов, считается текущим и используется при создании приложений в диспетчере приложений 1.3, а в последующем при запуске приложений на исполнение пути берутся уже из БД диспетчера приложений
1.6. Задание цветовой схемы главного меню	Задается по умолчанию если в папке с системой нет файла: ColorSch.arx при инсталляции системы, но может быть изменена когда угодно сисадмином
1.7. Задание размера главного окна в пикселях	Задается по умолчанию 1024 x 769 если в папке с системой нет файла: _MainWind.arx при инсталляции системы, но может быть изменена когда угодно сисадмином
1.8. Задание языка интерфейса на новые запуски	Задается по умолчанию если в папке с системой нет файла: _Language.arx при инсталляции системы, но может быть изменен когда угодно сисадмином
1.9. Прописывание путей по фактическому расположению системы	Доступно только сисадмину. Определяет фактическое месторасположение системы и приложений и прописывает пути на них в БД: PathGrAp.DBF и Appls.dbf, а также восстанавливает имена приложений в Appls.dbf на данные им при их создании
1.10. Удаление всех приложений и пользователей	Доступно только сисадмину. Определяет фактическое месторасположение системы и приложений и удаляет все директории приложений с поддиректориями и всеми файлами в них, а затем пересоздает и переиндексирует БД: PathGrAp.DBF, Appls.dbf и Users.dbf
2. Формализация предметной области	Разработка классификационных и описательных шкал и градаций и формирование обучающей выборки
2.1. Классификационные шкалы и градации	Ручной ввод-корректировка классификационных шкал и градаций'
2.2. Описательные шкалы и градации	Ручной ввод-корректировка описательных шкал и градаций'
2.3. Ввод обучающей выборки
2.3.1. Ручной ввод-корректировка обучающей выборки
2.3.2. Программные интерфейсы с внешними базами данных	Автоматизированная формализация предметной области
2.3.2.1. Импорт данных из TXT-фалов стандарта DOS-текст
2.3.2.2. Импорт данных из dbf-файлов стандарта проф.А.Н.Лебедева	Режим представляет собой универсальный программный интерфейс формализации предметной области и импорта данных в систему "Эйдос-Х++". Данный программный интерфейс обеспечивает автоматическое формирование классификационных и описательных шкал и градаций и обучающей выборки на основе DBF-файла с исходными данными описанного в Help режима стандарта
2.3.2.3. Импорт из транспонированных dbf-файлов проф.А.Н.Лебедева
2.3.2.4. Транспонирование dbf-матриц исходных данных
2.3.3. Управление обучающей выборкой
2.3.3.1. Параметрическое задание объектов для обработки
2.3.3.2. Статистическая характеристика, ручной ремонт
2.3.3.3. Автоматический ремонт обучающей выборки
2.3.4. Докодирование сочетаний признаков в обучающей выборке
3. Синтез, верификация и улучшение модели	Создание модели, повышение ее качества и оценка достоверности'
3.1. Формирование базы абсолютных частот	Загрузка по очереди описаний всех объектов обучающей выборки и расчет количества встреч различных сочетаний: Принадлежность объекта к j-му классу - наличие у него i-го признака'
3.2. Расчет процентных распределений	Расчет условных и безусловных процентных распределений'
3.3. Расчет заданных из 7 моделей знаний	Inf1~Prc1, Inf2~Prc2, Inf3-хи-квадрат, Inf4-roi~Prc1, Inf5-roi~Prc2, Inf6-Dp~Prc1, Inf7-Dp~Prc2'
3.4. Автоматическое выполнение режимов 1-2-3	По очереди исполняются режимы: 3.1., 3.2. и 3.3. для заданных стат.моделей и моделей знаний и затем заданная делается текущей'
3.5. Синтез и верификация заданных из 10 моделей	Оценивается достоверность (адекватность) заданных стат.моделей и моделей знаний. Для этого осуществляется синтез заданных моделей, обучающая выборка копируется в распознаваемую и в каждой заданной модели проводится распознавание с использованием двух интегральных критериев, подсчитывается количество верно идентифицированных и не идентифицированных, ошибочно идентифицированных и не идентифицированных объектов (ошибки 1-го и 2-го рода)
3.6. Синтез и верификация заданной группы моделей	Abs, Prc1, Prc2, Inf1~Prc1, Inf2~Prc2, Inf3-хи-квадрат, Inf4-roi~Prc1, Inf5-roi~Prc2, Inf6-Dp~Prc1, Inf7-Dp~Prc2
3.7. Повышение качества модели
3.7.1. Поиск и удаление артефактов (робастная процедура)
3.7.2. Формирование ортонормированного базиса классов
3.7.3. Исключение признаков с низкой селективной силой	Abs, Prc1, Prc2, Inf1~Prc1, Inf2~Prc2, Inf3-хи-квадрат, Inf4-roi~Prc1, Inf5-roi~Prc2, Inf6-Dp~Prc1, Inf7-Dp~Prc2
3.7.4. Удаление классов и признаков, по которым недостаточно данных
3.7.5. Разделение классов на типичную и нетипичную части
3.7.6. Генерация сочетанных признаков и докодирование обучающей выборки
3.7.7. Удаление малодостоверных данных в заданных или всех 10 моделях	Abs, Prc1, Prc2, Inf1~Prc1, Inf2~Prc2, Inf3-хи-квадрат, Inf4-roi~Prc1, Inf5-roi~Prc2, Inf6-Dp~Prc1, Inf7-Dp~Prc2
4. Решение задач с применением модели	Применение модели для решения задач идентификации (распознавания), прогнозирования и поддержки принятия решений (обратная задача прогнозирования), а также для исследования моделируемой предметной области путем исследования ее модели
4.1. Идентификация и прогнозирование
4.1.1. Ручной ввод-корректировка распознаваемой выборки
4.1.2. Пакетное распознавание в текущей модели	Распознаются по очереди все объекты распознаваемой выборки в стат.модели или базе знаний, заданной текущей в режиме 3.3 или 5.13.
4.1.3. Вывод результатов распознавания
4.1.3.1. Подробно наглядно: "Объект - классы"	Визуализация результатов распознавания в подробной наглядной форме в отношении: "Один объект - много классов" с двумя интегральными критериями сходства между конкретным образом распознаваемого объекта и обобщенными образами классов: "Семантический резонанс знаний" и "Сумма знаний"
4.1.3.2. Подробно наглядно: "Класс - объекты"	Визуализация результатов распознавания в подробной наглядной форме в отношении: "Один класс - много объектов" с двумя интегральными критериями сходства между конкретным образом распознаваемого объекта и обобщенными образами классов: "Семантический резонанс знаний" и "Сумма знаний"
4.1.3.3. Итоги наглядно: "Объект - класс"	Отображение итоговых результатов распознавания в наглядной форме: отображаются пары: "Объект-класс" у которых наибольшее сходство по двум интегральным критериям сходства: "Семантический резонанс знаний" и "Сумма знаний". Приводится информация о фактической принадлежности объекта к классу.
4.1.3.4. Итоги наглядно: "Класс - объект"	Отображение итоговых результатов распознавания в наглядной форме: отображаются пары: "Класс-объект" у которых наибольшее сходство по двум интегральным критериям сходства: "Семантический резонанс знаний" и "Сумма знаний". Приводится информация о фактической принадлежности объекта к классу.
4.1.3.5. Подробно сжато: "Объекты - классы"	В подробной сжатой (числовой) форме приводится информация об уровне сходства всех объектов со всеми классами по двум интегральным критериям сходства: "Семантический резонанс знаний" и "Сумма знаний", а также о фактической принадлежности объекта к классу.'
4.1.3.6. Обобщ.форма по достов.моделей при разных интегральных крит.	Отображаются обобщенные результаты измерения достоверности идентификации по всем моделям и интегральным критериям из БД: Dost_mod.DBF
4.1.3.7. Обобщ.стат.анализ результатов идент. по моделям и инт.крит.	Отображаются результаты обобщенного стат.анализа достоверности идентификации по всем моделям и интегральным критериям из БД: VerModALL.dbf
4.1.3.8. Стат.анализ результ. идент. по классам, моделям и инт.крит.	Отображаются результаты стат.анализа достоверности идентификации по всем классам, моделям и интегральным критериям из БД: VerModCls.dbf
4.1.3.9. Распределения уровн.сходства при разных моделях и инт.крит.	Отображаются частотные распределения уровней сходства верно и ошибочно идентифицированных и неидентифицированных объектов при разных моделях и интегральных критериях из БД: DostRasp.dbf
4.1.3.10.Достоверность идент. классов при разных моделях и инт.крит.' F4_1_3_10()}	Отображается достоверность идентификации объектов по классам при разных моделях (т.е. разных частных критериях) и при разных интегральных критериях из БД: Dost_cls.dbf
4.1.4. Пакетное распознавание в заданной группе моделей' Razrab()} Распознаются по очереди все объекты распознаваемой выборки в стат.модели или базе знаний, заданной текущей, в всех моделях заданной группы моделей'
4.1.5. Докодирование сочетаний признаков в распознаваемой выборке
4.1.6. Назначения объектов на классы (задача о назначениях)	Функционально-стоимостной анализ в управлении персоналом'
4.1.6.1. Задание ограничений на ресурсы по классам
4.1.6.2. Ввод затрат на объекты
4.1.6.3. Назначения объектов на классы (LC-алгоритм)
4.1.6.4. Сравнение эффективности LC и RND алгоритмов
4.1.7. Интерактивная идентификация - последовательный анализ Вальда
4.1.8. Мультираспознавание (пакетное распознавание во всех моделях)	При идентификации объекта распознаваемой выборки с каждым классом он сравнивается в той модели, в которой этот класс распознается наиболее достоверно, как в системе "Эйдос-астра"'
4.2. Типология классов и принятие решений'
4.2.1. Информационные портреты классов	Решение обратной задачи прогнозирования: выработка управляющих решений. Если при прогнозировании на основе значений факторов оценивается в какое будущее состояние перейдет объект управления, то при решении обратной задачи, наоборот, по заданному целевому будущему состоянию объекта управления определяется такая система значений факторов, которая в наибольшей степени обуславливает переход в это состояние'
4.2.2. Кластерный и конструктивный анализ классов
4.2.2.1. Расчет матрицы сходства образов классов
4.2.2.2. Генерация кластеров и конструктов классов
4.2.2.3. Просмотр и печать кластеров и конструктов
4.2.2.4. Автоматическое выполнение режимов: 1-2-3
4.2.2.5. Вывод 2d семантических сетей классов
4.2.2.6. Агломеративная древовидная кластеризация классов
4.2.3. Когнитивные диаграммы классов
4.3. Типологический анализ признаков
4.3.1. Информационные портреты признаков	Семантический (смысловой) портрет признака или значения фактора, т.е. количественная характеристика силы и направления его влияния на поведение объекта управления'
4.3.2. Кластерный и конструктивный анализ признаков
4.3.2.1. Расчет матрицы сходства образов признаков
4.3.2.2. Генерация кластеров и конструктов признаков
4.3.2.3. Просмотр и печать кластеров и конструктов
4.3.2.4. Автоматическое выполнение режимов: 1-2-3
4.3.2.5. Вывод 2d семантических сетей признаков
4.3.2.6. Агломеративная древовидная кластеризация признаков
4.3.3. Когнитивные диаграммы признаков
4.3.4. Восстановление значений функций по признакам аргумента
4.3.4.1. Восстановление значений и визуализация 1d-функций
4.3.4.2. Восстановление значений и визуализация 2d-функций
4.3.4.3. Преобразование 2d-матрицы в 1d-таблицу с признаками точек
4.3.4.4. Объединение многих БД: Inp_0001.dbf и т.д. в Inp_data.dbf
4.3.4.5. Помощь по подсистеме (требования к исходным данным)
4.4. Исследование предметной области путем исследования ее модели
4.4.1. Оценка достоверности обучающей выборки	Выявление объектов с нарушенными корреляциями между классами и признаками. Выявление очень сходных друг с другом объектов обучающей выборки'
4.4.2. Оценка достоверности распознаваемой выборки	Выявление очень сходных друг с другом объектов распознаваемой выборки'
4.4.3. Измерение адекватности 3 стат.моделей и 7 моделей знаний	Любой заданной или всех'
4.4.4. Измерение сходимости и устойчивости 10 моделей
4.4.5. Зависимость достоверности моделей от объема обучающей выборки
4.4.6. Измерение независимости классов и признаков (анализ хи-квадрат)
4.4.7. Графические профили классов и признаков
4.4.8. Графическое отображение нелокальных нейронов
4.4.9. Отображение Паретто-подмножеств нелокальной нейронной сети
4.4.10.Классические и интегральные когнитивные карты
4.5. Построение функций влияния (когнитивные функции)
5. Сервис	Конвертирование, печать и сохранение модели, пересоздание и переиндексация всех баз данных'
5.1. Конвертер приложения OLD => NEW	Преобразование модели из стандарта БД системы Эйдос-12.5 в стандарт Эйдос-X++. Для конвертирования старого приложения надо скопировать в папку: <OldAppls> файлы: Object.Dbf, Priz_Ob.Dbf, Priz_Per.Dbf, Priz_Per.Dbt, Obinfzag.Dbf, Obinfkpr.Dbf
5.1. Интерактивная конвертация классов OLD => NEW	Полуавтоматическое преобразование справочника классов из стандарта БД системы Эйдос-12.5 в стандарт Эйдос-X++ с использованием априорной информации от пользователя о наименованиях классификационных шкал и связях между классификационными шкалами и градациями классификационных шкал
5.3. Конвертер всех PCX (BMP) в GIF
5.4. Просмотрщик изображений
5.5. Просмотр основных БД всех моделей	Обеспечивает просмотр и экспорт в Excel основных баз данных всех статистических моделей: Abs, Prc1, Prc2 и моделей знаний: Inf1~Prc1, Inf2~Prc2, Inf3-хи-квадрат, Inf4-roi~Prc1, Inf5-roi~Prc2, Inf6-Dp~Prc1, Inf7-Dp~Prc2
5.6. Выбрать модель и сделать ее текущей	Данная функция позволяет выбрать среди ранее рассчитанных в 3-й подсистеме статистических баз Abs, Prc1, Prc2 и моделей знаний INF#, текущую модель для решения в 4-й подсистеме задач идентификации, прогнозирования, приятия решений и исследования предметной области путем исследования ее модели
5.7. Переиндексация всех баз данных	Заново создаются все необходимые для работы системы индексные массивы общесистемных баз данных (находящихся в папке с исполнимым модулем системы), а также баз данных текущего приложения, необходимые для работы с ним'
5.8. Сохранение основных баз данных модели
5.9. Восстановление модели из основных БД
5.10. Сброс всех БД текущего приложения	Доступно только сисадмину и администратору приложения
5.11. Интеллектуальная дескрипторная ИПС	Интеллектуальная дескрипторная информационно-поисковая система
5.12. Пояснения по частн.и инт.крит.и лаб.работам	Пояснения по смыслу частных и интегральных критериев и описания лабораторных работ'
6.1. Информация о системе, разработчике и средствах разработки
6.2. Ссылки на патенты, документацию и текущую системы	Internet-ссылки на патенты, монографии, учебные пособия, научные работы и самую новую на текущий момент версию системы "Эйдос-Х++, а также полный комплект документации на нее одним файлом
6.3. Карта системы (дерево диалога)
6.4. Порядок обработки данных, информации и знаний в системе	Последовательность обработки данных, информации и знаний в системе "Эйдос-Х++" с указанием имен баз данных'
6.5. Графическая заставка системы "Эйдос-12.5"
6.6. Roger Donnay[145], Professional Developer, Developer eXPress++	Roger Donnay, профессиональный разработчик программного обеспечения, разработчик высокоэффективной инструментальной системы программирования eXPress++, широко использованной при создании системы "Эйдос-Х++". Roger Donnay, Professional Developer, Developer eXPress++
6.7. Логотипы мультимоделей
6.8. Свидетельство РосПатента РФ на систему "Эйдос-Х++"
7. Выход	Закрыть все базы данных и корректно выйти из системы

Необходимо отметить, что все эти режимы, за исключением подсистемы администрирования и диспетчера приложений, были реализованы в предыдущей версии системы “Эйдос» и системах окружения. Кроме того, в системе «Эйдос-Х++» появляется все больше и больше режимов и функций, которых не было в предыдущей версии. Фрагмент дерева диалога системы «Эйдос-Х++» приведен на рисунке 2:

Рисунок 2. Фрагмент дерева диалога системы «Эйдос-Х++»

Приведенная структура меню не окончательная, т.к. система непрерывно развивается. Одним из наиболее существенных отличий системы Эйдос-Х++ от предыдущей версии системы «Эйдос» является то, что она обеспечивает одновременную работу с 3 статистическими моделями, которые есть и в статистических системах, а также с 7 моделями знаний[146], и позволяет во всех этих моделях решать задачи идентификации (прогнозирования), принятия решений и исследования предметной области с двумя интегральными критериями. При этом система Эйдос-Х++ оценивает эффективность применения различных частных и интегральных критериев для решения этих задач. Рассмотрим эти вопросы подробнее [283, 243, 245, 248, 254].

Управление – это достижение цели путем принятия и реализации решений об определенных действиях, способствующих достижению этой цели. Цели управления обычно заключаются в том, чтобы определенная система, которая называется объектом управления, находилась в определенном целевом (желаемом) состоянии или эволюционировала по определенному заранее известному или неизвестному сценарию. Действия, способствующие достижению цели, называются управляющими воздействиями. Решения об управляющих воздействиях принимаются управляющей системой. Управляющее воздействие вырабатывается управляющей системой на основе модели объекта управления и информации обратной связи о его состоянии и условиях окружающей среды.

Автоматизированные и автоматические системы управления отличаются друг от друга степенью формализации модели объекта управления и степенью автоматизации процесса выработки решения об управляющем воздействии:

– считается, что в системах автоматического управления (САУ) процесс выработки управляющего воздействия полностью автоматизирован, т.е. оно принимается управляющей системой автоматически, без участия человека;

– в автоматизированных системах управления (АСУ) решение об управляющем воздействии принимается управляющей системой с участием человека в процессе их взаимодействия.

Однако, по мнению автора, методологически неверно представлять себе дело таким образом, как будто САУ принимают решение полностью самостоятельно, без какого-либо участия человека. Гораздо правильнее было бы сказать, что в случае САУ решение принимаемся человеком, который сконструировал и создал эти САУ и «заложил» в них определенные математические модели и реализующие их алгоритмы принятия решений, которые в процессе работы САУ просто используются на практике. Разве это не является участием человека? Следовательно, точнее было бы говорить не об участии или неучастии человека в принятии управляющих решений, а об его участии в реальном времени в случае АСУ и отсроченном участии в случае САУ.

Естественно, далеко не для всех видов объектов управления удается построить их достаточно полную адекватную математическую модель, являющуюся основой для принятия управляющих решений. В более-менее полной мере это удается сделать лишь для достаточно простых, в основном чисто технических систем, и именно для них удается построить САУ. Для технологических же систем, а также других систем, включающих не только техническую компоненту, но людей в качестве элементов, это удается сделать лишь в неполной мере, т.е. степень формализации управления такими системами ниже, чем в САУ. В этом случае в процессе выработки решения об управляющем воздействии остаются вообще неформализованные или слабо формализованные этапы, которые пока не поддаются автоматизации, и, поэтому, решения об управляющем воздействии не удается принять на полностью формализованном уровне и тем самым полностью передать эту функцию системе управления. Этим и обусловлена необходимость включения человека непосредственно в цикл управления, что и приводит к созданию АСУ, в которых математические модели и алгоритмы используются не для принятия решений, а для создания человеку комфортных информационных условий, в которых он мог бы принимать решения на основе своего опыта и профессиональной компетенции. Поэтому и говорят, что АСУ не принимают решений, а лишь поддерживают принятие решений. Еще сложнее поддаются математическому моделированию и формализации биологические и экологические, а также социально-экономические и психологические системы, включающие отдельных людей и их коллективы, т.е. сложные системы. Поэтому сложные системы обычно являются слабо формализованными и на этой их особенности практически основано их определение. Конечно, управление такими системами тоже осуществляется, но уже практически без использования математических моделей и компьютерных технологий, т.е. преимущественно на слабо формализованном интуитивном уровне на основе опыта и профессиональной компетенции экспертов и лиц, принимающих решения (ЛПР). При этом в соответствии с принципом Эшби управляемость сложных систем является неполной.

Таким образом, виды управления различными объектами управления можно классифицировать по степени формализации процесса принятия решений об управляющих воздействиях и, соответственно, по степени участия человека в этом процессе:

– САУ: автоматическое принятие решения без непосредственного участия человека в реальном времени;

– АСУ: поддержка принятия решений, т.е. создание комфортных информационных условий для принятия решений человеком в реальном времени;

– менеджмент: управление на слабо формализованном уровне практически без применения математических моделей.

Перспектива развития методов управления сложными системами, по мнению автора, состоит в повышении степени формализации процессов принятия решений при выборе вариантов управляющих воздействий. Однако на пути реализации этой перспективы необходимо решить проблему разработки технологии, обеспечивающей создание формальной количественной модели сложного объекта управления на основе эмпирических данных о его поведении под действием различных факторов, модели, пригодной для решения задач прогнозирования и принятия решений.

В стационарных САУ и АСУ объект управления не изменяется качественно в процессе управления и, поэтому, его модель, созданная на этапе проектирования и создания системы управления не теряет адекватность и в процессе ее применения. Иначе обстоит дело в случае, когда объект управления изменяется качественно непосредственно в процессе управления, т.е. является динамичным. В этом случае модель объекта управления быстро теряет адекватность, как и управляющие воздействия, выработанные на ее основе. Реализация таких неадекватных управляющих воздействий приводит уже не к достижению цели управления, а к срыву управления. Поэтому проблема состоит не только в том, чтобы создать адекватную модель сложного объекта управления, но и в том, чтобы сохранить ее адекватность при существенном изменении этого объекта, т.е. при изменении характера взаимосвязей между воздействующими факторами и поведением объекта управления.

Это означает, что система управления сложными динамичными объектами должна быть интеллектуальной, т.к. именно системы этого класса позволяют проводить обучение, адаптацию или настройку модели объекта управления за счет накопления и анализа информации о поведении этого объекта при различных сочетаниях действующих на него факторов. Таким образом, решив первую проблему, т.е. разработав технологию создания модели сложного объекта управления, мы этим самым создаем основные предпосылки и для решения и второй проблемы, т.к. для этого достаточно применить эту технологию непосредственно в цикле управления.

Как показано в работе (1), непосредственно на основе матрицы сопряженности (абсолютных частот) или с использованием матрицы условных и безусловных процентных распределений с использованием количественных мер знаний можно получить 7 различных моделей знаний, приведенных в таблице 2:

ТАБЛИЦА 7 – РАЗЛИЧНЫЕ АНАЛИТИЧЕСКИЕ ФОРМЫ
ЧАСТНЫХ КРИТЕРИЕВ ЗНАНИЙ В СИСТЕМЕ «ЭЙДОС-Х++»

Наименование модели знаний и частный критерий	Выражение для частного критерия
	через относительные частоты	через абсолютные частоты
INF1, частный критерий: количество знаний по А.Харкевичу, 1-й вариант расчета вероятностей: Nj – суммарное количество признаков по j-му классу. Вероятность того, что если у объекта j-го класса обнаружен признак, то это i-й признак
INF2, частный критерий: количество знаний по А.Харкевичу, 2-й вариант расчета вероятностей: Nj – суммарное количество объектов по j-му классу. Вероятность того, что если предъявлен объект j-го класса, то у него будет обнаружен i-й признак.
INF3, частный критерий: Хи-квадрат: разности между фактическими и теоретически ожидаемыми абсолютными частотами	---
INF4, частный критерий: ROI - Return On Investment, 1-й вариант расчета вероятностей: Nj – суммарное количество признаков по j-му классу
INF5, частный критерий: ROI - Return On Investment, 2-й вариант расчета вероятностей: Nj – суммарное количество объектов по j-му классу
INF6, частный критерий: разность условной и безусловной вероятностей, 1-й вариант расчета вероятностей: Nj – суммарное количество признаков по j-му классу
INF7, частный критерий: разность условной и безусловной вероятностей, 2-й вариант расчета вероятностей: Nj – суммарное количество объектов по j-му классу

Система «ЭйдосХ++» обеспечивает синтез и верификацию всех этих моделей знаний. При этом верификация (оценка достоверности) модели может осуществляться как с использованием всей обучающей выборки в качестве распознаваемой, так и с использованием различных ее подмножеств на основе бутстрепного подхода. Диалог режима синтеза модели и ее верификации приведен на рисунке 3:

Рисунок 6. Диалог режима синтеза модели и ее верификации
в системе «ЭйдосХ++»

Количественные значения коэффициентов Iij таблицы 1 являются знаниями о том, что "объект перейдет в j-е состояние" если "на объект действует i-е значение фактора". Когда количество знаний Iij > 0 – i–й фактор способствует переходу объекта управления в j-е состояние, когда Iij < 0 – препятствует этому переходу, когда же Iij = 0 – никак не влияет на это. В векторе i-го фактора (строка матрицы знаний) отображается, какое количество знаний о переходе объекта управления в каждое из будущих состояний содержится в том факте, что данное значение фактора действует. В векторе j-го состояния класса (столбец матрицы знаний) отображается, какое количество знаний о переходе объекта управления в соответствующее состояние содержится в каждом из значений факторов, представленных в модели. Схема обработки данных и их преобразования в информацию и знания в системе Эйдос-Х++ представлена на рисунке 4:

Рисунок 7. Схема обработки данных и их преобразования в информацию
и знания в системе Эйдос-Х++

Все задачи идентификации, прогнозирования, приятия решений и исследования предметной области решаются в системе Эйдос-Х++ на основе моделей знаний, хотя для этого могут использоваться и статистические модели. Поэтому там, где возможности статистических систем заканчиваются, работа системы Эйдос-Х++ только начинается.

Таким образом, модель системы Эйдос-Х++ позволяет рассчитать какое количество знаний содержится в любом факте о наступлении любого события в любой предметной области, причем для этого не требуется повторности этих фактов. Если же эти повторности осуществляются и при этом наблюдается некоторая вариабельность значений факторов, обуславливающих наступление тех или иных событий, то модель обеспечивает многопараметрическую типизацию, т.е. синтез обобщенных образов классов или категорий наступающих событий с количественной оценкой силы и направления влияния на их наступление различных значений факторов. Причем эти факторы могут быть различной природы (физические, экономические, социальные, психологические, организационные и другие), как количественными, так и качественными и измеряться в различных единицах измерения и обрабатываться в одной модели знаний сопоставимо друг с другом за счет того, что для любых значений факторов в модели оценивается количество знаний, которое в них содержится о наступлении событий, переходе объекта управления в определенные состояния или просто о его принадлежности к тем или иным классам.

Рассмотрим поведение объекта управления при воздействии на него не одного, а целой системы значений факторов:

(1)

В теории принятия решений скалярная функция Ij векторного аргумента называется интегральным критерием. Основная проблема состоит в выборе такого аналитического вида функции интегрального критерия, который обеспечил бы эффективное решение задач, решаемых управляющей системой САУ и АСУ.

Учитывая, что частные критерии (таблица) имеют смысл количества знаний, а знания, как и информация, является аддитивной функцией, предлагается ввести интегральный критерий, как аддитивную функцию от частных критериев в виде:

(2)

В выражении (2) круглыми скобками обозначено скалярное произведение, т.е. свертка. В координатной форме это выражение имеет вид:

,

(3)

где:

– вектор j-го класса-состояния объекта управления;

– вектор состояния предметной области (объекта управления), включающий все виды факторов, характеризующих объект управления, возможные управляющие воздействия и окружающую среду (массив-локатор), т.е. Li=n, если i-й признак встречается у объекта n раз.

Таким образом, предложенный интегральный критерий представляет собой суммарное количество знаний, содержащихся в системе значений факторов различной природы (т.е. факторах, характеризующих объект управления, управляющее воздействие и окружающую среду) о переходе объекта управления в то или иное будущее состояние.

В многокритериальной постановке задача прогнозирования состояния объекта управления, при оказании на него заданного многофакторного управляющего воздействия Ij, сводится к максимизации интегрального критерия:

(4)

т.е. к выбору такого состояния объекта управления, для которого интегральный критерий максимален.

Результат прогнозирования поведения объекта управления, описанного данной системой факторов, представляет собой список его возможных будущих состояний, в котором они расположены в порядке убывания суммарного количества знаний о переходе объекта управления в каждое из них.

Задача принятия решения о выборе наиболее эффективного управляющего воздействия является обратной задачей по отношению к задаче максимизации интегрального критерия (идентификации и прогнозирования), т.е. вместо того, чтобы по набору факторов прогнозировать будущее состояние объекта, наоборот, по заданному (целевому) состоянию объекта определяется такой набор факторов, который с наибольшей эффективностью перевел бы объект управления в это состояние.

Предлагается обобщение фундаментальной леммы Неймана-Пирсона, основанное на косвенном учете корреляций между знаниями в векторе состояний при использовании средних по векторам. Соответственно, вместо простой суммы количеств информации предлагается использовать корреляцию между векторами состояния и объекта управления, которая количественно измеряет степень сходства этих векторов:

(5)

где:

– средняя информативность по вектору класса;

– среднее по вектору идентифицируемой ситуации (объекта).

– среднеквадратичное отклонение информативностей вектора класса;

– среднеквадратичное отклонение по вектору распознаваемого объекта.

Выражение (5) получается непосредственно из (3) после замены координат перемножаемых векторов их стандартизированными значениями. Необходимо отметить, что выражение для интегрального критерия сходства (5) по своей математической форме является корреляцией двух векторов, координатами которых являются частные критерии знаний (поэтому в системе «Эйдос-Х++» этот интегральный критерий называется «Смысловой или семантический резонанс знаний», а критерий (3) – «Сумма знаний»).

Таким образом, в системе «Эйдос-Х++» возможна оценка достоверности 7 моделей знаний, а также 3 статистических моделей, с использованием двух интегральных критериев сходства конкретного образа идентифицируемого объекта с обобщенным образом класса:

- «Резонанс знаний».

- «Сумма знаний».

При этом система генерирует несколько различных форм по достоверности моделей с этими интегральными критериями:

1. Обобщающая форма по достоверности моделей при разных интегральных критериях.

2. Обобщающий статистический анализ результатов идентификации по моделям

3. Достоверность идентификации классов в различных моделях

4. Распределение уровней сходства верно и ошибочно идентифицированных и не идентифицированных объектов в различных моделях.

5. Детальный статистический анализ результатов идентификации в различных моделях по классам

Объем работы не позволяет привести конкретные примеры этих форм, и здесь можно лишь отметить, что многочисленные численные эксперименты подтвердили возможность обоснованно выбрать на их основе наиболее достоверную модель в каждом конкретном случае. Это означает, что в системе «Эйдос-Х++» после синтеза модели мы имеем возможность не сразу применять ее для решения различных задач, а предварительно обосновано выбрать наиболее достоверную модель и уже затем использовать ее для решения конкретных задач.

Кроме того в системе «Эйдос-Х++» реализуется возможность идентификации объекта с каждым классом именно в той модели и с тем интегральным критерием, при которых была наиболее высокая достоверность идентификации. Этот алгоритм идентификации был впервые разработан и реализован совместно с А.П.Труневым в системе «Эйдос-астра» [104, 108] и продемонстрировал повышение вероятности верной идентификации и верной не идентификации около 20%. С приведенными монографиями можно ознакомиться на сайте автора системы «Эйдос» http://lc.kubagro.ru/ .

Выводы. Система «Эйдос» за многие годы применения хорошо показала себя при проведении научных исследований в различных предметных областях и занятий по ряду научных дисциплин, связанных с искусственным интеллектом, представлениями знаний и управлению знаниями. Однако в процессе эксплуатации системы были выявлены и некоторые недостатки, ограничивающие перспективы применения системы. Создана качественно новая версия системы (система Эйдос-Х++), в которой преодолены ограничения и недостатки предыдущей версии и реализованы новые важные идеи по ее развитию и применению в качестве программного инструментария системно-когнитивного анализа (СК-анализ) [97].

Автор системы «Эйдос-Х++» благодарен заведующему кафедрой компьютерных технологий и систем ФГБОУ ВПО «Кубанский государственный аграрный университет»Заслуженному деятелю науки РФ профессору В.И.Лойко, проректора по науке профессору Ю.П.Федулову за созданную возможность разработки системы «Эйлрс-Х++», а Roger Donnay, профессиональному разработчику программного обеспечения, разработчику высокоэффективной инструментальной системы программирования eXPress++, широко использованной при создании системы "Эйдос-Х++" (Roger Donnay, Professional Developer, Developer eXPress++, Boise, Idaho USA, http://donnay-software.com), Clifford Wiernik (CPA/CNE, Senior IT Analyst, www.aquafinance.com cwiernik@aquafinance.com Tel: 800-234-3663 x1126, Fax: 715-848-1411, Aqua Finance, Inc, One Corporate Dr, Ste 300, Wausau WI 54401, USA) и всем участникам форума http://bb.donnay-software.com:8080/phpBB3/, оказывающим автору действенную и бескорыстную помощь в разработке.

---

[1] См., например: http://www.vbvvbv.narod.ru/ http://ej.kubagro.ru/a/viewaut.asp?id=762 Отметим также, что эти работы польузются большой популярномстью у плагиаторов: http://trv-science.ru/2011/11/08/gruppovojj-plagiat-ot-studenta-do-ministra/

[2] См.: [189]

[3] http://quantmagic.narod.ru/volumes/VOL512008/p1215.pdf

[4] Акимов О.Е. Дискретная математика: логика, группы, графы, фракталы. [Электронный ресурс]. – Режим доступа: http://sceptic-ratio.narod.ru/ma/dm4-3.htm.

Мандельброт Бенуа. Фрактальная геометрия природы. – М.: Институт компьютерных исследований, 2002, – 656 с.

[5] Мандельброт Бенуа. Фрактальная геометрия природы. – М.: Институт компьютерных исследований, 2002, – 656 с.

[6] Перегудов, Ф.И. Введение в системный анализ: Учебное пособие / Ф.И. Перегудов, Ф.П. Тарасенко. – М.: Высшая школа, 1997. – 389 с.

[7] Николаев А.Б., Фоминых И.Б. Нейросетевые методы анализа и обработки данных: Учебное пособие. – М.: МАДИ (ГТУ), 2003. – 95 с. – Режим доступа: http://www.madi.ru/study/kafedra/asu/metod/neiroseti3.rar.

[8] Бутковский А.Г., Самойленко Ю.И. Управление квантово-механическими процессами. – М.: Наука, 1984. – 250 с.

[9] предел, к которому стремится частость при неограниченном увеличении числа наблюдений

[10] Применение предложено Л.О. Макаревич

[11] См., например: http://ru.wikipedia.org/wiki/Пойа,%20Дьёрдь

[12] Денисов А.А. Информационные основы управления. –Л.: Энергоатомиздат, 1983. –72 с.

Денисов А.А., Колесников Д.Н. Теория больших систем управления.–Л.: Энергоатомиздат, 1982.–287 с.

[13] Крайнюченко И. В., Попов В. П. Системное мировоззрение. Теория и анализ. Учебник для вузов. – Пятигорск.: ИНЭУ, 2005. – 218 с.

Попов В.П. Глобальный эволюционизм и синергетика ноосферы / В.П. Попов и И.В. Крайнюченко. - науч. изд.. - Ростов-на-Дону : ГНУ СКНЦ ВШ, 2003 . - 333 с.

[14] т.е. на основе описаний структуры, свойств и поведения объектов под влиянием различных воздействий, полученных из опыта

[15] Конечно, фактически и при идентификации признаки всегда относятся к прошлому, а идентифицируемые состояния к будущему, т.к. процесс получения информации о наличии признаков и сам процесс идентификации занимает определенное время.

[16] Может быть исследован вопрос влияния будущего на прошлое, а также влияния друг на друга одновременных событий, которые, по-видимому, причинно-следственно не связаны друг с другом.

[17] Например, с наибольшей силой или с наиболее дешево на единицу силы влияния.

[18] Образование – это обучение, воспитание и развитие. Обучение – это предметная обученность, т.е. знания, умения и навыки. Вопросы обучения в современной науке проработаны наиболее тщательно. Воспитание включает цели, ценности, мотивации и другие качеств личности. Какие именно из них формировать и каким способом – это изучено намного слабее, чем вопросы обучения. Что же такое развитие в настоящее время в науке вообще освещено слабо. Достаточно сказать, что в современной науке есть теория познания, но нет теории сознания.

[19] См., например: http://lc.kubagro.ru/aidos/index.htm http://ej.kubagro.ru/a/viewaut.asp?id=11

[20] См., например: http://ru.wikipedia.org/wiki/Принцип%20соответствия

[21] Об этом см., например: Вяткин В.В. Групповой плагиат: от студента до министра. // Троицкий вариант. № 91: 08.11.2011 – Электронный ресурс. – [Режим доступа]: http://trv-science.ru/2011/11/08/gruppovojj-plagiat-ot-studenta-do-ministra/

[22] http://ru.wikipedia.org/wiki/Эшби,%20Уильям

[23] Факторы, действующие на объект управления делятся на внутренние и внешние, а внешние в свою очередь на технологические факторы, т.е. факторы зависящие от управляющей системы, и факторы окружающей среды, независящие от нее.

[24] http://ru.wikipedia.org/wiki/Чёрный%20ящик

[25] http://ru.wikipedia.org/wiki/Инерциальная%20система%20отсчёта

[26] http://ru.wikipedia.org/wiki/Принцип%20относительности

[27] т.е. формальной модели, отражающей силу и направление причинно-следственного влияния значений факторов на поведение моделируемого объекта.

[28] http://ru.wikipedia.org/wiki/Закон%20Хаббла

[29] http://ru.wikipedia.org/wiki/Хаббл,%20Эдвин%20Пауэлл

[30] Расширение вселенной тоже должно приводить к ускорению темпа времени, т.к. должно сопровождаться уменьшением плотности массы и напряженности гравитационного поля.

[31] http://ru.wikipedia.org/wiki/Тёмная%20материя

[32] http://ru.wikipedia.org/wiki/Файл:Noether.jpg

[33] http://ru.wikipedia.org/wiki/Нётер,%20Эмми

[34] В современной физике законов сохранения гораздо больше и все они связаны с определенными симметриями пространства-времени, а также с динамическими симметриями, см., например: http://www.ugatu.ac.ru/ddo/KSE/01/0123/ks012300.htm

[35] См.:, например: http://ru.wikipedia.org/wiki/Общая%20теория%20относительности

[36] http://ru.wikipedia.org/wiki/Эйнштейн,%20Альберт

[37] Микро масштабом вселенной можно считать уровень звездных систем, например Солнечной системы, мега масштабами – структуру метагалактики.

[38] См.: http://ej.kubagro.ru/a/viewaut.asp?id=495

[39] См.: http://ru.wikipedia.org/wiki/Космологический_принцип

[40] Анизотропия реликтового излучения: http://ru.wikipedia.org/wiki/Реликтовое%20излучение

[41] http://ru.wikipedia.org/wiki/Великий%20аттрактор

[42] http://www.lsa.umich.edu/physics/directory/emeritus/ci.longomichael_ci.detail

[43] См.: http://www.modcos.com/news.php?id=115

[44] «О границах применения принципа относительности Галилея-Эйнштейна и законов сохранения»

[45] Луценко Е.В. Существование, несуществование и изменение как эмерджентные свойства систем // Квантовая Магия. – 2008. – Т. 5. – Вып. 1. – С. 1215–1239 [Электронный ресурс]. – Режим доступа: http://quantmagic.narod.ru/volumes/VOL512008/p1215.html

[46] В т.ч. действием принципа неопределенности Гейзенберга

[47] Такое исследование (зависимости степени несоблюдения принципа относительности и законов сохранения от локализации лаборатории в пространстве-времени) было бы интересно провести и в физике.

[48] http://ru.wikipedia.org/wiki/Леонтьев,%20Василий%20Васильевич

[49] Мигдал А. Б. Поиски истины. – М.: «Молодая гвардия», 1983. – 239 с., – Режим доступа: http://physiclib.ru/books/item/f00/s00/z0000024/index.shtml http://www.twirpx.com/file/438798/

[50] См.: http://physiclib.ru/books/item/f00/s00/z0000024/st014.shtml. Курсив мой, авт.

[51] См.: http://ru.wikipedia.org/wiki/Демон%20Максвелла и http://etherdynamic.ru/physics/82-yaponcam-udalos-sozdat-demon-maksvella.html

[52] Чаще те, кто это делает, не имеют об этом ни малейшего представления, т.е. занимается профанацией.

[53] http://lc.kubagro.ru/aidos/index.htm

[54] http://ru.wikipedia.org/wiki/Преобразование%20Лапласа

[55] http://ru.wikipedia.org/wiki/Z-преобразование

[56] http://ru.wikipedia.org/wiki/Эффект%20бабочки

[57] http://ru.wikipedia.org/wiki/Принцип%20соответствия

[58] Отметим, что модуль _159 системы «Эйдос» поддерживает формализацию предметной области и для этого случая, как и многих других, но в данной работе мы соответствующие модели рассматривать не будем. В системе Эйдос-Х++ есть значительно более мощный режим 2.3.2.2.

[59] Feynman, Richard P. The Character of Physical Law: The 1964 Messenger Lectures. MIT Press, 1967.

[60] Фейнман Р. Характер физических процессов. - М.: Мир, 1968. - 232с.

[61] L.D. Landau, E.M. Lifshitz. Statistical Physics. Vol. 5 (3rd ed.). Butterworth-Heinemann. 1980. Feynman, Richard P. Statistical Mechanics: A Set of Lectures. Reading, Mass: W. A. Benjamin, 1972.

[62] Там же

[63] Трунев А.П. Ядерные оболочки и периодический закон Д.И.Менделеева. Часть 2. // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета (Научный журнал КубГАУ) [Электронный ресурс]. – Краснодар: КубГАУ, 2012. – №07(81). С. 491 – 514. – Режим доступа: http://ej.kubagro.ru/2012/07/pdf/37.pdf

[64] Вяткин В.Б. Орбитальная система распределения электронов в атоме и структура периодической системы элементов / В.Б. Вяткин // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета (Научный журнал КубГАУ) [Электронный ресурс]. – Краснодар: КубГАУ, 2013. – №05(089). С. 1453 – 1485. – IDA [article ID]: 0891305100. – Режим доступа: http://ej.kubagro.ru/2013/05/pdf/100.pdf, 2,062 у.п.л.

Трунев А.П. Ядерные оболочки и периодический закон Д.И.Менделеева. Часть 2. // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета (Научный журнал КубГАУ) [Электронный ресурс]. – Краснодар: КубГАУ, 2012. – №07(81). С. 491 – 514. – Режим доступа: http://ej.kubagro.ru/2012/07/pdf/37.pdf

[65] L.D. Landau, E.M. Lifshitz. Statistical Physics. Vol. 5 (3rd ed.). Butterworth-Heinemann. 1980.

[66] Wolfram Mathematica 9.0/ http://www.wolfram.com/mathematica/

[67] Предложен автором в работе [97] в 2002 году. Напоминать об этом приходится по причинам, изложенным в статье: Вяткин В.Б. Групповой плагиат: от студента до министра. - Троицкий вариант — Наука - http://trv-science.ru - [Электронный ресурс]. Адрес доступа: http://trv-science.ru/2011/11/08/gruppovojj-plagiat-ot-studenta-do-ministra/ или: http://trv-science.ru/2011/11/08/gruppovojj-plagiat-ot-studenta-do-ministra/print/

[68] Системный эффект проявляется в отличии свойств системы от свойств ее элементов. Яркими примерами системного эффекта являются отличие свойств химических соединений от свойств химических элементов, их которых они состоят, дефект массы в физике, когда масса физической системы не совпадает с суммой масс ее частей. Системный эффект тем больше, чем сильнее взаимодействие элементов системы.

[69] http://ru.wikipedia.org/wiki/Объединение%20множеств

[70] http://ru.wikipedia.org/wiki/Диаграммы%20Эйлера-Венна

[71] http://ru.wikipedia.org/wiki/Пересечение%20множеств

[72] Приходится об этом напоминать, т.к. в ряде материалов, широко распространившихся в научной печати и в Internet, их авторы без ссылки на первичный источник информации о коэффициентах эмерджентности Хартли и Харкевича, т.е. работы автора, используют большие фрагменты из этих работ. Чтобы убедится в этом достаточно сделать запрос: «коэффициенты эмерджентности Хартли и Харкевича»

[73] http://ru.wikipedia.org/wiki/Аксиома%20булеана

[74] http://ru.wikipedia.org/wiki/Булеан

[75] См., например: Мамонтов Д.В., Волошин С.Б. Алгоритм формирования комбинаций при расчете перестановок, размещений и сочетаний. [Электронный ресурс]. – Режим доступа: http://www.voloshin-sb.ru/Portals/0/Download/Works/combinator.pdf

[76] Автор просит прощения за большое количество самоцитирований, которое обусловлено тем, что практически все работы автора образуют единую систему и основываются друг на друге, в частности посвящены развитию предложенного в 2000-2001 годах автоматизированного системно-когнитивного анализа [97], его математической модели – системной теории информации (СТИ), и реализующего их программного инструментария – универсальной когнитивной аналитической системы «Эйдос».

[77] Если же количество элементов в объединенной системе меньше числа элементов в исходных системах, то наблюдается эффект антисистемы [166].

[78] Пример разработан с помощью авторской программы, размещенной по адресу: http://www.twirpx.com/file/370725/ при параметрах «по умолчанию» и максимальным уровнем сложности

[79] Правда, для расчета количества подобных возможных сочетаний необходимо использовать формулы ^{числа сочетаний с повторениями}: . ^{С использованием этого выражения,} приводимые в работе формулы, могут быть обобщены на случай, когда повторения допустимы (формально чаще всего для этого достаточно поставить черточку на символом числа сочетаний). В словах играет роль порядок букв, но нет принципиальных проблем для обобщения полученных выражений и на этот случай.

[80] http://ru.wikipedia.org/wiki/Принцип%20соответствия

[81] http://ru.wikipedia.org/wiki/Объединение%20множеств

[82] См., например: http://ru.wikipedia.org/wiki/ROI, http://shuvalov.wmsite.ru/materialy-stati/analiz-raschety/roi

[83] Хартли Р.В.Л. Передача информации. // Теория информации и ее приложения. М.: Физматгиз, 1959 – с.5-35.

[84] Шеннон К. Работы по теории информации и кибернетике. – М.: Изд. иностр. лит., 1963 – 830с.

[85] Колмогоров А.Н. Теория информации и теория алгоритмов. – М.: Наука, 1987 – 304с.

[86]

[87] ru.wikipedia.org/wiki/Закон_Фехнера

[88] См.: http://ru.wikipedia.org/wiki/Операции%20над%20множествами

[89] Назван так автором в работе [1] в честь этого выдающегося ученого в связи со сходством математической формы данного коэффициента с локальным коэффициентом эмерджентности Хартли [2], отражающим уровень системности локальной системы.

[90]

[91] Приходится об этом напоминать, т.к. в ряде материалов, широко распространившихся в научной печати и в Internet, их авторы без ссылки на первичный источник информации о коэффициентах эмерджентности Хартли и Харкевича, т.е. работы автора, используют большие фрагменты из этих работ. Чтобы убедится в этом достаточно сделать запрос: «коэффициенты эмерджентности Хартли и Харкевича»

[92] Пример взят и работы (1) и разработан с помощью авторской программы, размещенной по адресу: http://www.twirpx.com/file/370725/ при параметрах «по умолчанию» и максимальным уровнем сложности

[93] См.: http://ru.wikipedia.org/wiki/Операции%20над%20множествами

[94] http://lingvo.yandex.ru/cognition/с%20английского/

[95] http://ru.wikipedia.org/wiki/Метод%20обратного%20распространения%20ошибки

[96] http://yandex.ru/yandsearch?text=гипостазирование

[97] См., например: http://www.vsetabl.ru/056.htm

[98] Замков О. О., Толстопятенко А. В., Черемных Ю. Н. Математические методы в экономике: Учебник /Московский государственный университет. - М.: ДИС, 1997. - 368 с. Носач В.В. Решение задач аппроксимации с помощью персональных компьютеров / М.: Микап, 1994. - 382 с.

[99] http://ru.wikipedia.org/wiki/Патанджали

[100] http://ru.wikipedia.org/wiki/Кластерный%20анализ

[101] http://yandex.ru/yandsearch?text=кластерный%20анализ

[102] Мандель И.Д. Кластерный анализ. - М.: Финансы и статистика. 1988. – 176с.

[103] Леонов В.П. Краткий обзор методов кластерного анализа. Сайт: http://www.biometrica.tomsk.ru/cluster_2.htm http://www.biometrica.tomsk.ru/cluster_3.htm

Леонов В.П. Литература и сайты по кластерному анализу. Сайт: http://www.biometrica.tomsk.ru/cluster_4.htm

Сайт Института Космических Исследований РАН: http://www.iki.rssi.ru/magbase/REFMAN/STATTEXT/modules/stcluan.html#general

Сайт Internet-сообщества закупщиков: http://zakup.vl.ru/132-metodi_klastern.html

[104] Баран О.И., Григорьев Ю.А., Жилина Н.М. Алгоритмы и критерии качества кластеризации // Общественное здоровье и здравоохранение: материалы XLV науч.-практ. конф. с международным участием «Гигиена, организация здравоохранения и профпатология» и семинара «Актуальные вопросы современной профпатологии», Новокузнецк, 17-18 ноября 2010 / под ред. В.В.Захаренкова. Кемерово: Примула, 2010. – С. 21-26.

[105] http://ru.wikipedia.org/wiki/Кластерный%20анализ

[106] Справедливости ради отметим, что подобных инструментов вообще мало и они практически недоступны исследователям

[107] Леонов В.П. Краткий обзор методов кластерного анализа. Сайт: http://www.biometrica.tomsk.ru/cluster_2.htm http://www.biometrica.tomsk.ru/cluster_3.htm

Леонов В.П. Литература и сайты по кластерному анализу. Сайт: http://www.biometrica.tomsk.ru/cluster_4.htm

Сайт Института Космических Исследований РАН: http://www.iki.rssi.ru/magbase/REFMAN/STATTEXT/modules/stcluan.html#general

[108] http://matlab.exponenta.ru/fuzzylogic/book1/12_1_3.php http://d3lpirt.narod.ru/dm/dm.htm

[109] Источник: проф. Зайченко Ю.П. http://www.masters.donntu.edu.ua/2005/kita/kapustina/library/cluster.htm

[110] Например, для ортонормирования семантического пространства может быть применен метод главных компонент: http://ru.wikipedia.org/wiki/Метод%20главных%20компонент

[111] Конечно, есть случаи, когда производят определенные математические операции над величинами различной природы, измеряемыми в различных единицах измерения, и это вполне корректно, правда это не операция сложения. Например, в физике так производятся вычисления по формулам. Но эти формулы теоретически обоснованы в соответствующих физических теориях. Если математические операции производятся так, что это не соответствует обоснованным формулам, то в результате получаются бессмысленные величины неизвестных науке размерностей. В этом случае говорят о проверке размерностей и нарушении размерностей. Такое впечатление, что в статистике подобные нарушения размерностей просто стали нормой.

[112] Сайт Института Космических Исследований РАН: http://www.iki.rssi.ru/magbase/REFMAN/STATTEXT/modules/stcluan.html#general

[113] Пространные цитаты здесь и далее для удобства читателей приведены мелким шрифтом.

[114] Пометка (!!!?) наша, авт.

[115] Сайт Института Космических Исследований РАН: http://www.iki.rssi.ru/magbase/REFMAN/STATTEXT/modules/stcluan.html#general

[116] 4. Показатели должны отвечать требованию «устойчивости», под которой понимается отсутствие влияния на их значения случайных факторов. 5. Выборка должна быть однородна, не содержать «выбросов».

[117] Леонов В.П. Краткий обзор методов кластерного анализа. Сайт: http://www.biometrica.tomsk.ru/cluster_2.htm http://www.biometrica.tomsk.ru/cluster_3.htm

[118] Леонов В.П. Краткий обзор методов кластерного анализа. Сайт: http://www.biometrica.tomsk.ru/cluster_2.htm http://www.biometrica.tomsk.ru/cluster_3.htm

[119] Сайт Института Космических Исследований РАН: http://www.iki.rssi.ru/magbase/REFMAN/STATTEXT/modules/stcluan.html#general

[120] Близоруков М. Г. Статистические методы анализа рынка: Учебно-метод. пособие / Близоруков М. Г. – Екатеринбург: Ин-т управления и предпринимательства Урал. гос. ун-та, 2008. – 75 с. – Режим доступа: http://elar.usu.ru/bitstream/1234.56789/1671/6/1334937_schoolbook.pdf

[121] Сайт Института Космических Исследований РАН: http://www.iki.rssi.ru/magbase/REFMAN/STATTEXT/modules/stcluan.html#general

[122] Леонов В.П. Краткий обзор методов кластерного анализа. Сайт: http://www.biometrica.tomsk.ru/cluster_2.htm http://www.biometrica.tomsk.ru/cluster_3.htm

[123] Сайт Института Космических Исследований РАН: http://www.iki.rssi.ru/magbase/REFMAN/STATTEXT/modules/stcluan.html#general

[124] http://lc.kubagro.ru/aidos/aidos02/2.3.htm

[125] http://lc.kubagro.ru/aidos/aidos02/4.2.htm http://lc.kubagro.ru/aidos/aidos02/4.3.htm

[126] Данные предложения приведены в том же порядке, что и переформулированные нами фундаментальные вопросы кластерного анализа согласно работе [248]

[127] http://lc.kubagro.ru/aidos/Auto0700.htm

[128] Луценко Е.В. Персональная система обработки информации "ВЕГА-М" для мини-ЭВМ "Искра-226". ИЛ о научно-техническом достижении №87-12. –Краснодар: КЦНТИ, 1987. Гос. рег. .№ 01.06.01.Н15.06.03.05.02. – 4с.

[129] http://lc.kubagro.ru/aidos/index.htm

[130] http://lc.kubagro.ru/aidos/aidos02/7.htm http://lc.kubagro.ru/aidos/aidos02/PR-4.htm

[131] http://lc.kubagro.ru/aidos/index.htm

^[132] http://yandex.ru/yandsearch?text=системно-когнитивный%20анализ&lr=10995

http://yandex.ru/yandsearch?text=универсальная%20когнитивная%20аналитическая%20система%20"эйдос"&lr=10995

[133] http://ej.kubagro.ru/2009/07/pdf/05.pdf

[134] http://ej.kubagro.ru/2009/07/pdf/04.pdf

[135] http://ej.kubagro.ru/2009/07/pdf/06.pdf

[136] http://lc.kubagro.ru/aidos/aidos02/7.htm

[137] Учредителем и директором которого был автор

[138] http://elibrary.ru/author_items.asp?authorid=123162, http://ej.kubagro.ru/a/viewaut.asp?id=11

[139] http://lc.kubagro.ru/aidos/index.htm

[140] http://www.delphiforphp.ru/ http://ru.wikipedia.org/wiki/Delphi_for_PHP

[141] “X++” в названии новой версии системы «Эйдос» – это дань используемому инструментальному программному обеспечению: Alaska Xbase++ (R) Version 1.90.355 SL1, TOOLS III, eXPress++ (C) Version 1.9 Build 255, Advantage Database Server (ADS) 10.0.

[142] В системе «Эйдос-Х++» проводился численный эксперимент по созданию моделей размерностью 10000 × 10000 классов и признаков, а используемые программные средства проверялись на размерности 100000 × 100000 классов и признаков. Во втором случае база знаний INF1 создавалась 34 минуты и имела размер 250 Гб.

[143] Имеется бесплатная локальная версия ADS: http://www.softscribe.ru

[144] В частности: Методы принятия решений, Интеллектуальные информационные системы, Представление знаний в информационных системах, Управление знаниями (магистратура), Основы искусственного интеллекта, Системно-когнитивный анализ, Информационные технологии управления бизнес-процессами / Корпоративные информационные системы (магистратура), Система искусственного интеллекта «Эйдос», Моделирование социально-экономических систем, Введение в нейроматику и методы нейронных сетей (магистратура), Интеллектуальные и нейросетевые технологии в образовании (магистратура), Функционально-стоимостной анализ системы и технологии управления персоналом (магистратура), Информационные системы в экономике, Математическое моделирование

[145] http://donnay-software.com/ http://donnay-software.com:8080/phpBB3/

[146] В предыдущей версии системы одновременно могла использоваться лишь одна модель знаний, а другие – если они выбраны в качестве текущей модели