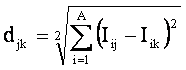2.3. ФОРМАЛИЗАЦИЯ БАЗОВЫХ КОГНИТИВНЫХ ОПЕРАЦИЙ СИСТЕМНОГО АНАЛИЗА
2.3.1. Исходные теоретические положения когнитивной концепции
В этой связи нами предложена формализуемая когнитивная концепция, не претендующая на вклад в когнитивную психологию, но удовлетворяющая требованиям, вытекающим из существа исследования.
Исходные положения этой когнитивной концепции:
1) процессы познания обеспечивают в целом адекватное отражение процессов природы и общества;
2) некоторые когнитивные (познавательные) операции возможно представить в виде математических и алгоритмических моделей (формализовать);
3) формализованные модели когнитивных операций допускают программную реализацию, т.е. передачу соответствующих функций, ранее выполнявшихся только человеком, интеллектуальным средствам труда. Это обеспечивает возможность выполнения данных функций вне ограничений, присущих человеку и высвобождает его ресурсы для выполнения более творческих функций.
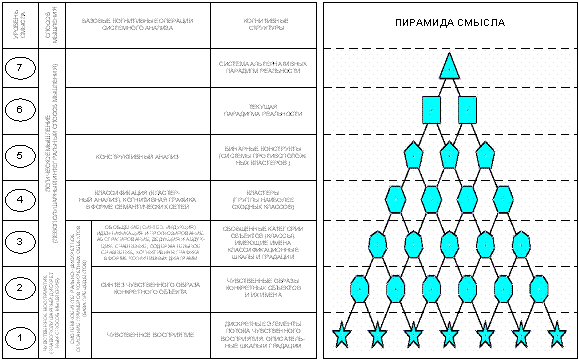
На базе выше сформулированных положений построена целостная система взглядов на процесс познания, т.е. когнитивная концепция (рисунок 2.14):
|
|
|
Рисунок 2. 14. Обобщенная схема предлагаемой |
Суть предложенной когнитивной концепции состоит в том, что процесс познания рассматривается как многоуровневая иерархическая система обработки информации, в которой каждый последующий уровень является результатом интеграции элементов предыдущего уровня. На 1-м уровне этой системы находятся дискретные элементы потока чувственного восприятия, которые на 2-м уровне интегрируются в чувственный образ конкретного объекта. Те, в свою очередь, на 3-м уровне интегрируются в обобщенные образы классов и факторов, образующие на 4-м уровне кластеры, а на 5-м конструкты. Система конструктов на 6-м уровне образуют текущую парадигму реальности (т.е. человек познает мир путем синтеза и применения конструктов). На 7-м же уровне обнаруживается, что текущая парадигма не единственно-возможная.
Ключевым для когнитивной концепции является понятие факта, под которым понимается соответствие дискретного и интегрального элементов познания (т.е. элементов разных уровней интеграции-иерархии), обнаруженное на опыте. Факт рассматривается как квант смысла, что является основой для его формализации. Таким образом, происхождение смысла связывается со своего рода "разностью потенциалов", существующей между смежными уровнями интеграции-иерархии обработки информации в процессах познания.
1. Процесс познания начинается с чувственного восприятия. Различные органы восприятия дают качественно-различную чувственную информацию в форме дискретного потока элементов восприятия. Эти элементы формализуются с помощью описательных шкал и градаций.
2. В процессе накопления опыта выявляются взаимосвязи между элементами чувственного восприятия: одни элементы часто наблюдаются с другими (имеет место их пространственно-временная корреляция), другие же вместе встречаются достаточно редко. Существование устойчивых связей между элементами восприятия говорит о том, что они отражают некую реальность, интегральную по отношению к этим элементам. Эту реальность будем называть объектами восприятия. Рассматриваемые в единстве с объектами элементы восприятия будем называть признаками объектов. Таким образом, органы восприятия дают чувственную информацию о признаках наблюдаемых объектов, процессов и явлений окружающего мира (объектов). Чувственный образ конкретного объекта представляет собой систему, возникающую как результат процесса синтеза признаков этого объекта. В условиях усложненного восприятия синтез чувственного образа объекта может быть существенно замедленным и даже не завершаться успехом в реальном времени.
3. Человек присваивает конкретным объектам названия (имена) и сравнивает объекты друг с другом. При сравнении выясняется, что одни объекты в различных степенях сходны по их признакам, а другие отличаются. Сходные объекты объединяются в обобщенные категории (классы), которым присваиваются имена, производные от имен входящих в категорию конкретных объектов. Классы формализуются с помощью классификационных шкал и градаций и обеспечивают интегральный способ описания действительности. Путем обобщения (синтеза, индукции) информации о признаках конкретных объектов, входящих в те или иные классы, формируются обобщенные образы классов. Накопление опыта и сравнение обобщенных образов классов друг с другом позволяет определить степень характерности признаков для классов, смысл признаков и ценность каждого признака для идентификации конкретных объектов с классами и сравнения классов, а также исключить наименее ценные признаки из дальнейшего анализа без существенного сокращения количества полезной информации о предметной области (абстрагирование). Абстрагирование позволяет существенно сократить затраты внутренних ресурсов системы на анализ информации. Идентификация представляет собой процесс узнавания, т.е. установление соответствия между чувственным описанием объекта, как совокупности дискретных признаков, и неделимым (целостным) именем класса, которое ассоциируется с местом и ролью воспринимаемого объекта в природе и обществе. Дискретное и целостное восприятие действительности поддерживаются как правило различными полушариями мозга: соответственно, правым и левым (доминантность полушарий). Таким образом именно системное взаимодействие интегрального (целостного) и дискретного способов восприятия обеспечивает возможность установление содержательного смысла событий. При выполнении когнитивной операции "содержательное сравнение" двух классов определяется вклад каждого признака в их сходство или различие.
4. После идентификации уникальных объектов с классами возможна их классификация и присвоение обобщающих имен группам похожих классов. Для обозначения группы похожих классов используем понятие "кластер". Но и сами кластеры в результате выполнения когнитивной операции "генерация конструктов" могут быть классифицированы по степени сходства друг с другом. Для обозначения системы двух противоположных кластеров, с "спектром" промежуточных кластеров между ними, будем использовать термин "бинарный конструкт", при этом сами противоположные кластеры будем называть "полюса бинарного конструкта". Бинарные конструкты классов и атрибутов, т.е. конструкты с двумя полюсами, наиболее типичны для человека и представляет собой когнитивные структуры, играющие огромную роль в процессах познания. Достаточно сказать, что познание можно рассматривать как процесс генерации, совершенствования и применения конструктов. Качество конструкта тем выше, чем сильнее отличаются его полюса, т.е. чем больше диапазон его смысла.
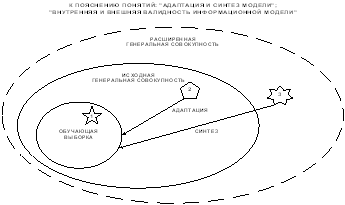
Результаты идентификации и прогнозирования, осуществленные с помощью модели, путем выполнения когнитивной операции "верификация" сопоставляются с опытом, после чего определяется целесообразность выполнения когнитивной операции "обучение". При этом может возникнуть три основных варианта, которые на рисунке 2.15 обозначены цифрами:
1. Объект, входит в обучающую выборку и достоверно идентифицируется (внутренняя валидность, в адаптации нет необходимости).
2. Объект, не входит в обучающую выборку, но входит в исходную генеральную совокупность, по отношению к которой эта выборка репрезентативна, и достоверно идентифицируется (внешняя валидность, добавление объекта к обучающей выборке и адаптация модели приводит к количественному уточнению смысла признаков и образов классов).
3. Объект не входит в исходную генеральную совокупность и идентифицируется недостоверно (внешняя валидность, добавление объекта к обучающей выборке и синтез модели приводит к качественному уточнению смысла признаков и образов классов, исходная генеральная совокупность расширяется).
|
|
|
Рисунок 2. 15. К пояснению смысла понятий: "Адаптация и синтез когнитивной модели предметной области", "Внутренняя и внешняя валидность информационной модели", |
2.3.2. Когнитивный конфигуратор и базовые когнитивные операции системного анализа
Познание предметной области с одной стороны безусловно является фундаментом, на котором строится все грандиозное здание системного анализа, а с другой стороны, процессы познания являются связующим звеном, органично объединяющим "блоки" принципов и методов системного анализа в стройное здание. Более того, процессы познания буквально пронизывают все методы и принципы системного анализа, входя в них как один из самых существенных элементов.
Однако, на этом основании неверным будет представлять, что когнитивные операции являются подмножеством понятия "системный анализ", скорее наоборот: системный анализ представляет собой один из теоретических методов познания, представимый в форме определенной последовательности когнитивных операций, тогда как другие последовательности этих операций позволяют образовать другие формы теоретического познания.
Поэтому разработка математических моделей, алгоритмов и программных систем, обеспечивающих автоматизацию применения когнитивной концепции в системном анализе, является актуальной научной и технической проблемой, заслуживающей внимания и усилий, как исследователей, так и разработчиков.
Сложность решения этой важнейшей проблемы состоит в ее ярко выраженном системном, комплексном, междисциплинарном характере, что определяет необходимость для ее решения активно и нетривиально использовать знания из таких областей науки, как когнитивная психология, системный анализ, математическое моделирование, теория информации, теория распознавания образов и принятия решений, а также применить на практике технологии программной реализации систем интеллектуального анализа данных и искусственного интеллекта.
Безусловно, в решении данной проблемы существует неограниченное поле деятельности для психологов, но в данной работе внимание акцентируется на научно-техническом аспекте, а именно на разработке соответствующих математических моделей, алгоритмов, программных систем, а также методологии, технологии и методики их применения для синтеза рефлексивных АСУ активными объектами.
В данной работе предлагается разрабатывается обоснованный вариант решения этой междисциплинарной проблемы. Вместе с тем этим самым не решается глобальная проблема автоматизации системного анализа, а лишь совершается один шаг в этом чрезвычайно перспективном направлении.
Конкретно путь достижения этой цели состоит в разработке:
1. Аналитической модели, позволяющей заложить основы для автоматизации когнитивных операций.
2. Алгоритмических моделей базовых когнитивных операций, обеспечивающих уровень конкретизации, позволяющий непосредственно приступить к их программной реализации.
Поэтому далее рассмотрим базовые когнитивные операции системного анализа и возможности их применения в рефлексивном управлении активными объектами.
2.3.3. Задачи формализации базовых когнитивных операций системного анализа
Выбор единой интерпретируемой численной меры для классов и атрибутов
При построении модели объекта управления одной из принципиальных проблем является выбор формализованного представления для индикаторов, критериев и факторов (далее: факторов). Эта проблема распадается на две подпроблемы:
1. Выбор и обоснование смысла выбранной
численной меры.
2. Выбор математической формы и способа
определения (процедуры, алгоритма) количественного выражения для значений,
отражающих степень взаимосвязи факторов
и будущих состояний АОУ.
Рассмотрим требования к численной мере,
определяемые существом подпроблем. Эти требования вытекают из необходимости
совершать с численными значениями факторов математические операции (сложение,
вычитание, умножение и деление), что в свою очередь необходимо для построения
полноценной математической модели.
Требование 1: из формулировки 1-й
подпроблемы следует, что все факторы должны быть приведены к некоторой общей и
универсальной для всех факторов единице измерения, имеющей какой-то
смысл, причем смысл, поддающийся единой сопоставимой в пространстве и времени
интерпретации.
Традиционно в специальной литературе [43, 167, 324]
рассматриваются следующие смысловые значения для факторов:
– стоимость (выигрыш-проигрыш или прибыль-убытки);
– полезность;
– риск;
– корреляционная или причинно-следственная
взаимосвязь.
Иногда предлагается использовать безразмерные меры
для факторов, однако, этот вариант не является удовлетворительным, т.к. не
позволяет придать смысл факторам и получить содержательную
интерпретацию выводов, полученных на основе математической модели.
Таким образом, возникает ключевая при выборе численной
меры проблема выбора смысла, т.е. по сути единиц измерения, для индикаторов,
критериев и факторов.
Требование 2: высокая степень
адекватности предметной области.
Требование 3: высокая скорость сходимости
при увеличении объема обучающей выборки.
Требование 4: высокая независимость от
артефактов.
Что касается конкретной математической формы и процедуры
определения числовых значений факторов в выбранных единицах измерения, то
обычно применяется метод взвешивания экспертных оценок, при котором эксперты
предлагают свои оценки, полученные как правило
неформализованным путем. При этом сами эксперты также обычно ранжированы по
степени их компетентности. Фактически при
таком подходе числовые значения факторов является не определяемой, искомой, а исходной
величиной. Иначе обстоит дело в факторном анализе, но в этом методе, опять
же на основе экспертных оценок важности факторов, требуется предварительно,
т.е. перед проведением исследования, принять решение о том, какие факторы
исследовать (из-за жестких ограничений на размерность задачи в факторном
анализе). Таким образом оба эти подхода реализуемы при
относительно небольших размерностях задачи, что с точки зрения достижения целей
настоящего исследования, является недостатком этих подходов.
Поэтому самостоятельной и одной из ключевых проблем
является обоснованный и удачный выбор математической формы для численной
меры индикаторов и факторов.
Эта математическая форма с одной стороны должна
удовлетворять предыдущим требованиям, прежде всего требованию 1, а также должна
быть процедурно вычислимой, измеримой.
Выбор неметрической меры сходства объектов в семантических пространствах
Существует большое количество мер сходства, из которых можно было бы упомянуть скалярное произведение, ковариацию, корреляцию, евклидово расстояние, расстояние Махалонобиса и др. [3, 4].
Проблема выбора меры
сходства состоит в том, что при выбранной численной мере для координат классов
и факторов она должна удовлетворять определенным критериям:
1. Обладать
высокой степенью адекватности предметной области, т.е. высокой валидностью, при
различных объемах выборки, как при очень малых, так и при средних и очень больших.
2. Иметь обоснованную,
четкую, ясную и интуитивно понятную интерпретацию.
3. Быть нетрудоемкой в
вычислительном отношении.
4. Обеспечивать корректное
вычисление меры сходства для пространств с неортонормированным базисом.
Из требования 4 сразу следует, что Евклидово
расстояние djk между j-м и k-м классами не подходит в качестве
метрики, т.к. оно предполагает ортонормированность пространства:
|
|
|
Известно, что для
неортнормированного базиса может быть использовано расстояние Махаланобиса.
Однако и одно не удовлетворяет сформулированным требованиям, т.к. дает не
расстояние между векторами, а расстояние от некоторого центра масс (центроида).
Поэтому в данном
исследовании предложено использовать в качестве меры сходства скалярное
произведение векторов, а также нормированное скалярное произведение, т.е. по
сути дела корреляцию. При этом координаты векторов должны представлять их
проекции на оси координат неортонормированного базиса.
Определение идентификационной и прогностической ценности атрибутов
Не все факторы имеют одинаковую ценность для решения задач идентификации, прогнозирования и управления. Традиционно считается, что факторы имеют одинаковую ценность только в тех случаях (обычно в психологии), когда определить их действительную ценность не представляется возможным по каким-либо причинам.
Для достижения целей, поставленных в данном данном исследовании, необходимо решить проблему определения
ценности факторов, т.е. разработать математическую модель и алгоритм, которые
допускают программную реализацию и обеспечивают на практике определение
идентификационной и прогностической ценности факторов.
Ортонормирование семантических пространств классов и атрибутов (Парето-оптимизация)
Если не все факторы имеют одинаковую ценность для решения задач идентификации, прогнозирования и управления, то возникает проблема исключения из системы факторов тех из них, которые не представляют особой ценности. Удаление малоценных факторов вполне оправданно и целесообразно, т.к. сбор и обработка информации по ним в среднем связана с такими же затратами времени, вычислительных и информационных ресурсов, как и при обработке ценных факторов. В этом состоит идея Парето-оптимизации. Однако это удаление должно осуществляться при вполне определенных граничных условиях, характеризующих результирующую систему:
– адекватность модели;
– количество признаков на класс;
– суммарное количество градаций признаков в описательных шкалах.
В противном случае удаление факторов может отрицательно сказываться на качестве решения задач.
Проблема состоит в том, что факторы вообще говоря коррелируют друг с другом и поэтому их ценность может изменяться при удалении любого из них, в том числе и наименее ценного. Поэтому просто взять и удалить наименее ценные факторы не представляется возможным и необходимо разработать корректный вычислительный алгоритм обеспечивающий решение этой проблемы при заданных граничных условиях.