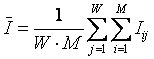1.2.2. ЛЕКЦИЯ-4.
Системная теория информации
и семантическая информационная модель

Учебные вопросы

1. Программа системного обобщения математики и предпосылки системной теории информации

2. Теоретические основы системной теории информации.

3. Семантическая информационная модель СК-анализа.

4. Некоторые свойства математической модели (сходимость, адекватность, устойчивость и др.).

5. Взаимосвязь математической модели СК-анализа с другими моделями.

1.2.2.1. Программа системного обобщения математики и предпосылки системной теории информации

Дадим определение понятия «система» классическим способом, т.е. путем его подведения под более общее понятие «множество» и выделение специфических признаков. Система представляет собой множество элементов, объединенных в целое за счет взаимодействия элементов друг с другом, т.е. за счет отношений между ними, и обеспечивающая преимущества в достижении целей. Преимущества в достижении целей обеспечиваются за счет системного эффекта. Системный эффект состоит в том, что свойства системы не сводятся к сумме свойств ее элементов, т.е. система как целое обладает рядом новых, т.е. эмерджентных свойств, которых не было у ее элементов. Уровень системности тем выше, чем выше интенсивность взаимодействия элементов системы друг с другом, чем сильнее отличаются свойства системы от свойств входящих в нее элементов, т.е. чем выше системный эффект, чем значительнее отличается система от множества. Элементы взаимодействуют (вступают в отношения) друг с другом с помощью имеющихся у них общих свойств, а также свойств, которые коррелируют между собой. Таким образом, система обеспечивает тем большие преимущества в достижении целей, чем выше ее уровень системности. В частности, система с нулевым уровнем системности вообще ничем не отличается от множества образующих ее элементов, т.е. тождественна этому множеству и никаких преимуществ в достижении целей не обеспечивает. Этим самым обеспечивается выполнение принципа соответствия между понятиями системы и множества. Из соблюдения это принципа для понятий множества и системы следует и его соблюдение для понятий, основанных на теории множеств и их системных обобщений.

На этой основе можно ввести и новое научное понятие: понятие «антисистемы», применение которого оправдано в случаях, когда централизация (монополизация, интеграция) не только не дает положительного эффекта, но даже сказывается отрицательно. Антисистемой называется система с отрицательным уровнем системности, т.е. это такое объедение некоторого множества элементов за счет их взаимодействия в целое, которое препятствует достижению целей.

Фундаментом, находящимся в самом основании современной математики, является теория множеств. Эта теория лежит и в основе самого глубокого на сегодняшний день обоснования таких базовых математических понятий, как «число» и «функция». Определенный период этот фундамент казался незыблемым. Однако вскоре работы целой плеяды выдающихся ученых XX века, прежде всего Давида Гильберта, Бертрана Рассела и Курта Гёделя, со всей очевидностью обнажили фундаментальные логические и лингвистические проблемы, в частности проявляющиеся в форме парадоксов теории множеств, что в свою очередь привело к появлению ряда развернутых предложений по пересмотру самых глубоких оснований математики [20].

В задачи данной статьи не входит рассмотрение этой интереснейшей проблематики, а также истории возникновения и развития понятий числа и функции. Отметим лишь, что кроме рассмотренных в литературе вариантов существует возможность обобщения всех понятий математики, базирующихся на теории множеств, в частности теории информации, путем тотальной замены понятия множества на понятие системы и тщательного отслеживания всех последствий этой замены. Это утверждение будем называть «программной идеей системного обобщения понятий математики».

Строго говоря, реализация данной программной идеи потребует прежде всего системного обобщения самой теории множеств и преобразование ее в математическую теорию систем, которая будет плавно переходить в современную теорию множеств при уровне системности стремящемся к нулю. При этом необходимо заметить, что существующая в настоящее время наука под названием «Теория систем» ни в коей мере не является обобщением математической теории множеств и ее не следует путать с математической теорией систем. Вместе с тем, на наш взгляд, существуют некоторые возможности обобщения ряда понятий математики и без разработки математической теории систем. К таким понятиям относятся прежде всего понятия «информация» и «функция».

Системному обобщению понятия информации посвящены работы автора [5, 6, 9, 10, 11] и другие, поэтому в данной статье на этом вопросе мы останавливаться не будем. Отметим лишь, что на основе предложенной системной теории информации (СТИ) были разработаны математическая модель и методика численных расчетов (структуры данных и алгоритмы), а также специальный программный инструментарий (система «Эйдос») автоматизированного системно-когнитивного анализа (АСК-анализ), который представляет собой системный анализ, автоматизированный путем его рассмотрения как метода познания и структурирования по базовым когнитивным операциям.

В АСК-анализе теоретически обоснована и реализована на практике в форме конкретной информационной технологии процедура установления новой универсальной, сопоставимой в пространстве и времени, ранее не используемой количественной, т.е. выражаемой числами, меры соответствия между событиями или явлениями любого рода, получившей название «системная мера целесообразности информации», которая по существу является количественной мерой знаний [10]. Это является достаточным основанием для того, чтобы назвать эти числа «когнитивными» от английского слова "cognition" – "познание".

В настоящее время функция понимается как соответствие друг другу нескольких множеств чисел. Поэтому виды функций можно классифицировать по крайней мере в зависимости от:

– природы этих чисел (натуральные, целые, дробные, действительные, комплексные и т.п.);

– количества и вида множеств чисел, связанных друг с другом в функции (функции одного, нескольких, многих, счетного или континуального количества аргументов, однозначные и многозначные функции, дискретные или континуальные функции) [10];

– степени жесткости и меры силы связи между множествами чисел (детерминистские функции, функции, в которых в качестве меры связи используется вероятность, корреляция и другие меры);

– степени расплывчатости чисел в множествах и самой формы функции (четкие и нечеткие функции, использование различных видов шкал, в частности интервальных оценок).

Так как функции, выявляемые модели предметной области методом АСК-анализа, связывают друг с другом множества когнитивных чисел, то предлагается называть их «когнитивными функциями». Учитывая перечисленные возможности классификации когнитивные функции, можно считать недетерминистскими многозначными функциями многих аргументов, в которых в качестве меры силы связи между множествами используется количественная мера знаний, т.е. системная мера целесообразности информации, основанными на интервальных оценках, номинальных и порядковых шкалах и шкалах отношений. Отметим, что детерминистские однозначные функции нескольких аргументов могут рассматриваться как частный случай когнитивных функций, к которому они сводятся при анализе жестко детерминированной предметной области, скажем явлений, описываемых классической физикой.

Итак, предлагается программная идея системного обобщения понятий математики, в частности теории информации, основанных на теории множеств, путем замены понятия множества на более содержательное понятие системы. Частично эта идея была реализована автором при разработке автоматизированного системно-когнитивного анализа (АСК-анализа), математическая модель которого основана на системном обобщении формул для количества информации Хартли и Харкевича. Реализация следующего шага: системного обобщения понятия функциональной зависимости рассматривается в работе [87], в ней же вводятся новые научные понятия и соответствующие термины: «когнитивные функции» и «когнитивные числа». На численных примерах показано, что АСК-анализ обеспечивает выявление когнитивных функциональных зависимостей в многомерных зашумленных фрагментированных данных.

1.2.2.2. Теоретические основы системной теории информации

1.2.2.2.1. Требования к математической модели и численной мере

Для практической реализации идеи решения проблемы необходимо сформулировать требования к математической модели и численной мере, вытекающие из когнитивной концепции и специфических свойств активного объекта управления в АПК (слабодетерминированность, многофакторность, активность).

Требования к математической модели предусматривают: содержательную интерпретируемость; эффективную вычислимость на основе непосредственно эмпирических данных (наличие эффективного численного метода); универсальность; адекватность; сходимость; семантическую устойчивость; сопоставимость результатов моделирования в пространстве и времени; непараметричность; формализацию базовых когнитивных операций системного анализа (прежде всего таких, как обобщение, абстрагирование, сравнение, классификация и др.); корректность работы на фрагментарных, неточных и зашумленных данных; возможность обработки данных очень больших размерностей (тысячи факторов и будущих состояний объекта управления); математическую и алгоритмическую ясность и простоту, эффективность программной реализации.

Требования к численной мере. Ключевым при построении математических моделей является выбор количественной меры, обеспечивающей учет степени причинно-следственной взаимосвязи исследуемых параметров. Эта мера должна удовлетворять следующим требованиям: 1) обеспечивать эффективную вычислимость на основе эмпирических данных, полученных непосредственно из опыта; 2) обладать универсальностью, т.е. независимостью от предметной области; 3) подчиняться единому для различных предметных областей принципу содержательной интерпретации; 4) количественно измеряться в единых единицах измерения а количественной шкале (шкала с естественным нулем, максимумом или минимумом); 5) учитывать понятия: "цели объекта управления", "цели управления"; "мощность множества будущих состояний объекта управления"; уровень системности объекта управления; степень детерминированности объекта управления; 6) обладать сопоставимостью в пространстве и во времени; 7) обеспечивать возможность введения метрики или неметрической функции принадлежности на базе выбранной количественной меры.

Для того, чтобы выбрать тип (класс) модели, удовлетворяющей сформулированным требованиям, необходимо решить на какой форме информации эта модель будет основана: абсолютной, относительной или аналитической.

1.2.2.2.2. Выбор базовой численной меры

Абсолютная, относительная и аналитическая информация.

Широко известны абсолютная и относительная формы информации. Абсолютная форма – это просто количество, частота. Относительная форма – это доли, проценты, относительные частоты и вероятности.

Менее знакомы специалисты с аналитической формой информации, примером которой является условные вероятности, стандартизированные статистические значения, эластичность и количество информации.

Очевидно, что и из относительной информации, взятой изолированно, вырванной из контекста, делать какие-либо обоснованные выводы не представляется возможным. Для того, чтобы о чем-то судить по процентам, нужен их сопоставительный анализ, т.е. анализ всего процентного распределения. Обычно для используется "база оценки", в качестве которой используется среднего по всей совокупности или "скользящее среднее" (нормативный подход: норма – среднее).

Аналитическая (сопоставительная) информация – это информация, содержащаяся в отношении вероятности (или процента) к некоторой базовой величине, например к средней вероятности по всей выборке. Аналитическими являются также стандартизированные величины в статистике и количество информации в теории информации.

Очевидно, именно аналитическая информация является наиболее кондиционной для употребления с той точки зрения, что позволяет непосредственно делать содержательные выводы об исследуемой предметной области (точнее будет сказать, что она сама и является выводом), тогда как для того, чтобы сделать аналогичные выводы на основе относительной, и особенно абсолютной информации требуется ее значительная предварительная обработка.

Выбор в качестве базовой численной меры количества информации

Как было показано в лекции 2, системный анализ представляет собой теоретический метод познания, т.е. информационный процесс, в котором поток информации направлен от познаваемого объекта к познающему субъекту. Процесс труда, напротив, представляет собой процесс, в котором поток информации направлен от субъекта к объекту. При этом информация передается по каналу связи, представляющему собой средства труда, и записывается в носитель информации (предмет труда), который в ходе этого процесса преобразуется в заранее заданную форму, т.е. в продукт труда. Таким образом, процесс труда по сути дела представляет собой информационный процесс, обратный по направлению потока информации процессу познания. Управление представляет собой процесс, на различных этапах которого выполняются функции, сходные с процессами труда (управляющее воздействие) и познания (обратная связь). По мнению автора, информационный подход к управлению является наиболее общим. Поэтому в качестве количественной меры взаимосвязи факторов и будущих состояний АОУ целесообразно использовать количество информации. Более подробное обоснование целесообразности выбора в качестве численной меры количества информации приведено в работе автора [81].

Однако, известно много различных информационных мер и, следовательно, возникает задача выбора одной из них, оптимальной по выбранным критериям. Различные выражения классической теории информации для количества информации: Хартли, Шеннона, Харкевича и др., учитывают различные аспекты информационного моделирования объектов (таблице 8):

Таблица 8 – СООТВЕТСТВИЕ ТРЕБОВАНИЯМ
ВЫРАЖЕНИЙ ДЛЯ КОЛИЧЕСТВА ИНФОРМАЦИИ

– формула Хартли учитывает количество классов (мощность множества состояний объекта управления) но никак не учитывает их признаков или факторов, переводящих объект в эти состояния, т.е. содержит интегральное описание объектов;

– формула Шеннона основывается на учете признаков, т.е. основывается на дискретном описании объектов;

– формула Харкевича учитывает понятие цели и также как формула Шеннона основана на статистике признаков, но не учитывает мощности множества будущих состояний объекта управления, включающего целевые и другие будущие состояния объекта управления и также как формула Шеннона основывается на дискретном описании объектов.

Как видно из таблицы 8, классическая формула Харкевича по учитываемым критериям имеет преимущества перед классическими формулами Хартли и Шеннона, т.к. учитывает как факторы, так и понятие цели, ключевое для системного анализа, теории и практики управления (в т.ч. АСУ). Поэтому именно выражение для семантической целесообразности информации Харкевича взято за основу при выводе обобщающего выражения, удовлетворяющего всем предъявляемым требованиям.

1.2.2.2.3. Конструирование системной численной меры на основе базовой

Системное обобщение формулы Хартли для количества информации

Классическая формула Хартли имеет вид:

(3. 1)

Будем искать ее системное обобщение в виде:

(3. 2)

где:

W – количество чистых (классических) состояний системы.

j – коэффициент эмерджентности Хартли (уровень системной организации объекта, имеющего W чистых состояний);

Учитывая, что возможны смешанные состояния, являющиеся нелинейной суперпозицией или одновременной реализацией чистых (классических) состояний "из W по m", всего возможно состояний системы, являющихся сочетаниями классических состояний. Таким образом, примем за аксиому, что системное обобщение формулы Хартли имеет вид [81]:

(3. 3)

где: W – количество элементов в системе альтернативных будущих состояний АОУ (количество чистых состояний); m – сложность смешанных состояний АОУ; M – максимальная сложность смешанных состояний АОУ.

Выражение (1) дает количество информации в активной системе, в которой чистые и смешанные состояния равновероятны. Смешанные состояния активных систем, возникающие под действием системы нелинейно-взаимодействующих факторов, считаются такими же измеримыми, как и чистые альтернативные состояния, возникающие под действием детерминистских факторов. Так как , то при M=1 выражение (3.3) приобретает вид (3.1), т.е. выполняется принцип соответствия, являющийся обязательным для более общей теории.

Рассмотрим подробнее смысл выражения (3.3), представив сумму в виде ряда слагаемых:

(3. 4)

Первое слагаемое в (3.4) дает количество информации по классической формуле Хартли, а остальные слагаемые – дополнительное количество информации, получаемое за счет системного эффекта, т.е. за счет наличия у системы иерархической структуры или смешанных состояний. По сути дела эта дополнительная информация является информацией об иерархической структуре системы, как состоящей из ряда подсистем различных уровней сложности.

Например, пусть система состоит из W пронумерованных элементов 1-го уровня иерархии. Тогда на 2-м уровне иерархии элементы соединены в подсистемы из 2 элементов 1-го уровня, на 3-м – из 3, и т.д. Если выборка любого элемента равновероятна, то из факта выбора n-го элемента по классической формуле Хартли мы получаем количество информации согласно (3.1). Если же при этом известно, что данный элемент входит в определенную подсистему 2-го уровня, то это дает дополнительное количество информации, за счет учета второго слагаемого, поэтому общее количество получаемой при этом информации будет определяться выражением (3.4) уже с двумя слагаемыми (M=2). Если элемент одновременно входит в M подсистем разных уровней, то количество информации, получаемое о системе и ее подсистемах при выборке этого элемента определяется выражением (3.4). Так, если мы вытаскиваем кирпич из неструктурированной кучи, состоящей из 32 кирпичей, то получаем 5 бит информации, если же из этих кирпичей сложен дом, то при аналогичном действии мы получаем дополнительное количество информации о том, из каких части дома (подсистем различного уровня иерархии) вытащен этот кирпич. Действия каменщика, укладывающего кирпич на место, предусмотренное проектом, значительно выше по целесообразности, чем у грузчика, складывающего кирпичи в кучу. Учитывая, что при M=W:

(3. 5)

в этом случае получаем:

(3. 6)

Выражение (3.5) дает оценку максимального количества информации, которое может содержаться в элементе системы с учетом его вхождения в различные подсистемы ее иерархической структуры.

Однако реально в любой системе осуществляются не все формально возможные сочетания элементов 1-го уровня иерархии, т.к. существуют различные правила запрета, различные для разных систем. Это означает, что возможно множество различных систем, состоящих из одинакового количества тождественных элементов, и отличающихся своей структурой, т.е. строением подсистем различных иерархических уровней. Эти различия систем как раз и возникают благодаря различию действующих для них этих правил запрета. По этой причине систему правил запрета предлагается назвать информационным проектом системы. Различные системы, состоящие из равного количества одинаковых элементов (например, дома, состоящие из 20000 кирпичей), отличаются друг от друга именно по причине различия своих информационных проектов.

Из выражения (3.5) очевидно, что I быстро стремится к W:

(3. 7)

В действительности уже при W>4 погрешность выражения (3.5) не превышает 1% (таблица 9):

Таблица 9 – ЗАВИСИМОСТЬ ПОГРЕШНОСТИ
ВЫРАЖЕНИЯ (3.5) ОТ КОЛИЧЕСТВА КЛАССОВ W

График зависимости погрешности выражения (3.5) от количества классов W приведен на рисунке 24.

Рисунок 24. Зависимость погрешности приближенного выражения системного обобщения формулы Хартли от количества классов W

Приравняв правые части выражений (3.2) и (3.3):

(3. 8)

получим выражение для коэффициента эмерджентности Хартли (терм. авт.):

(3. 9)

Непосредственно из вида выражения для коэффициента эмерджентности Хартли (3.9) ясно, что он представляет собой относительное превышение количества информации о системе при учете системных эффектов (смешанных состояний, иерархической структуры ее подсистем и т.п.) над количеством информации без учета системности, т.е. этот коэффициент отражает уровень системности объекта.

С учетом выражения (3.9) выражение (3.2) примет вид:

(3. 10)

или при M=W и больших W, учитывая (3.4 – 3.6):

(3. 11)

Выражение (3.10) и представляет собой искомое системное обобщение классической формулы Хартли, а выражение (3.11) – его достаточно хорошее приближение при большом количестве элементов или состояний системы (W).

Коэффициент эмерджентности Хартли представляет собой относительное превышение количества информации о системе при учете системных эффектов (смешанных состояний, иерархической структуры ее подсистем и т.п.) над количеством информации без учета системности, т.е. этот коэффициент является аналитическим выражением для уровня системности объекта. Таким образом, коэффициент эмерджентности Хартли отражает уровень системности объекта и изменяется от 1 (системность минимальна, т.е. отсутствует) до W/Log₂W (системность максимальна). Очевидно, для каждого количества элементов системы существует свой максимальный уровень системности, который никогда реально не достигается из-за действия правил запрета на реализацию в системе ряда подсистем различных уровней иерархии.

Например: из 32 букв русского алфавита может быть образовано не осмысленных 6-буквенных слов, а значительно меньше. Если мы услышим одно из этих в принципе возможных слов, то получим не 5´6=30 информации, содержащейся непосредственно в буквах (в одной букве содержится Log₂32=5 бит), а 30+19,79=49,79 бит, т.е. в 1.66 раз больше. Это и есть уровень системности иерархического уровня 6-буквенных слов русского языка. Уровень системности русского языка, как системы, состоящей из слов длиной от одной до 6 букв, согласно выражения (3.9) с учетом (3.5), равен примерно 6,4. Но при этом еще не была учтена информация, содержащаяся в последовательности слов, в последовательности предложений и т.д.

Итак, в предложении сдержится значительно больше информации, чем в буквах, с помощью которых оно написано, т.к. кроме букв информацию содержат слова, сочетания слов, последовательность предложений и т.д.. Буквы образуют 1-й иерархический уровень языка, слова – 2-й, предложения – 3-й, абзацы – 4-й, параграфы – 5-й, главы – 6-й, произведения – 7-й. Теория Шеннона концентрирует основное внимание на рассмотрении 1-го уровня, т.е. рассматривает тексты, прежде всего, как последовательность символов. Но именно иерархическая организация, не учитываемая в теории Шеннона и отраженная в системной теории информации, обеспечивает языку его удивительную мощь, как средства отражения и моделирования реальности.

Аналогично и в генах, этих своеобразных "символах генома", содержится значительно больше информации о фенотипе, чем предполагается в классической генетике Менделя, т.к. гены образуют ансамбли различных уровней иерархии в зависимости от влияния среды и технологий управления (явление адаптивности системы "генотип-среда", Драгавцев В.А., 1993). Если ген уподобить букве алфавита, а смысл фразы – фенотипическому признаку, то можно сказать, что возможно очень большое количество фраз с практически тождественным смысловым содержанием (тогда как в классической генетике считалось, что признак соответствует гену, хотя есть и такие). После расшифровки генома человека мы настолько же приблизились к его пониманию, как изучивший русскую или немецкую азбуку англичанин, не знающий этих языков, приблизился к чтению в оригинале и пониманию содержания "Войны и Мира" Льва Толстого или "Феноменологии Духа" Георга В.Ф.Гегеля.

На уровне слов верхняя оценка уровня системности русского языка с учетом (3.5) составляет огромную величину: 2616,48 (предполагается, что в русском языке 40000 слов и предложения могут иметь любую длину). Необходимо отметить, что правила запрета на порядок слов в русском языке значительно слабее, чем, например в английском, поэтому в русском языке возможно гораздо больше грамматически правильных и несущих различную информацию предложений из одних и тех же слов, чем в английском. Это значит, что уровень системности русского языка на уровне предложений, по-видимому, значительно превосходит уровень системности английского языка. При длине предложения до 2-х слов системность русского языка на уровне предложений согласно (3.9) составляет: 52330916.

Анализ выражения (3.9) показывает, что при М=1 оно преобразуется в (3.1), т.е. выполняется принцип соответствия. При М>1 количество информации в соответствии с системной теорией информации (СТИ) (3.9) будет превосходить количество информации, рассчитанное по классической теории информации (КТИ) (3.1). Непосредственно из выражения (3.2) получаем:

(3. 12)

Первое слагаемое в выражении (3.12) отражает количество информации, согласно КТИ, а второе – СТИ, т.е. доля системной информации.

Представляет несомненный интерес исследование закономерностей изменения доли системной информации в поведении элемента системы в зависимости от количества классов W и сложности смешанных состояний M.

В таблице 10 приведены результаты численных расчетов в соответствии с выражением (3.9). Сводные данные из таблицы 10 приведены в таблице 11, а в графическом виде они представлены на рисунке 25.

Таблица 10 – ЗАВИСИМОСТЬ I(W,M) ОТ КОЛИЧЕСТВА КЛАССОВ W И СЛОЖНОСТИ СМЕШАННЫХ СОСТОЯНИЙ М

Таблица 11 – ЗАВИСИМОСТЬ КОЛИЧЕСТВА ИНФОРМАЦИИ I(W,M) ОТ СЛОЖНОСТИ СМЕШАННЫХ СОСТОЯНИЙ M ДЛЯ РАЗЛИЧНОГО КОЛИЧЕСТВА КЛАССОВ W

Рисунок 25. Зависимость количества информации I(W,M)
от сложности смешанных состояний M
для разного количества классов W

Рост количества информации в СТИ по сравнению с КТИ обусловлен системным эффектом (эмерджентностью), который связан с учетом смешанных состояний, возникающих путем одновременной реализации (суперпозиции) нескольких чистых (классических) состояний под действием системы нелинейно-взаимодействующих недетерминистских факторов. Выражение (3.9) дает максимальную возможную оценку количества информации, т.к. могут существовать различные правила запрета на реализацию тех или иных смешанных состояний.

Фактически это означает, что в СТИ множество возможных состояний объекта рассматривается не как совокупность несвязанных друг с другом состояний, как в КТИ, а как система, уровень системности которой как раз и определяется коэффициентом эмерджентности Хартли j (3.9), являющегося монотонно возрастающей функцией сложности смешанных состояний M. Следовательно, дополнительная информация, которую мы получаем из поведения объекта в СТИ, по сути дела является информацией о системе всех возможных состояний объекта, элементом которой является объект в некотором данном состоянии.

Гипотеза о законе возрастания эмерджентности и следствия из него

Численные расчеты и аналитические выкладки в соответствии с СТИ показывают, что при возрастании количества элементов в системе доля системной информации в поведении ее элементов возрастает. Это обнаруженное нами новое фундаментальное свойство систем предлагается назвать законом возрастания эмерджентности.

Закон возрастания эмерджентности: "Чем больше элементов в системе, тем большую долю содержащейся в ней информации составляет информация, содержащаяся во взаимосвязях ее элементов".

На рисунках 26 и 27 приведены графики скорости и ускорения возрастания эмерджентности в зависимости от количества элементов W в системе.

Рисунок 26. Возрастание доли системной информации в поведении элемента системы при увеличении количества элементов W	Рисунок 27. Ускорение возрастания доли системной информации в поведении элемента системы от количества элементов W

Более детальный анализ предполагаемого закона возрастания эмерджентности с использованием конечных разностей первого и второго порядка (таблица 11) показывает, что при увеличении количества элементов в системе доля системной информации в ней возрастает с ускорением, которое постепенно уменьшается. Это утверждение будем называть леммой 1.

Продолжим анализ закона возрастания эмерджентности. Учитывая, что:

выражение (3.3) принимает вид:

(3. 13)

где: 1<=М<=W.

и учитывая, что Log₂1=0, выражение (3.13) приобретает вид:

(3. 14)

Где введены обозначения:

(3. 15)

С учетом (3.14) выражение (3.9) для коэффициента эмерджентности Хартли приобретает вид:

Заменяя в (3.13) факториал на Гамма-функцию, получаем обобщение выражения (3.3) на непрерывный случай:

Или окончательно:

(3. 16)

Для непрерывного случая обозначения (3.15) принимают вид:

(3. 17)

Учитывая выражения (3.9) и (3.16) получим выражение для коэффициента эмерджентности Хартли для непрерывного случая:

И окончательно для непрерывного случая:

(3. 18)

Анализируя выражения (3.14) и (3.16) видим, что количество информации, получаемое при выборке из системы некоторого ее элемента, состоит из двух слагаемых:

1) I(W), зависящего только от количества элементов в системе W (первое слагаемое);

2) I(W, M), зависящего как от количества элементов в системе W, так и от максимальной сложности, т.е. связности элементов подсистем M между собой (второе слагаемое).

Этот результат позволяет высказать гипотезы "О природе сложности системы" и "О видах системной информации":

– сложность системы определяется количеством содержащейся в ней информации;

– системная информация включает две составляющих: зависящее от количества элементов системы и зависящее также от характера взаимосвязей между элементами.

Изучим какой относительный вклад вносит каждое слагаемое в общее количество информации системы в зависимости от числа элементов в системе W и сложности подсистем M. Результаты численных расчетов показывают, что чем выше уровень системности, тем большая доля информации системы содержится во взаимосвязях ее элементов, и чем меньше элементов с системе, тем быстрее возрастает доля информации, содержащейся во взаимосвязях элементов при возрастании уровня системности. Эти утверждения будем рассматривать как леммы 2 и 3. Таким образом полная формулировка гипотезы о законе возрастания эмерджентности с гипотезой о видах информации в системе и тремя леммами приобретает вид:

Гипотеза о законе возрастания эмерджености:

"Чем больше элементов в системе, тем большую долю содержащейся в ней информации составляет информация, содержащаяся во взаимосвязях ее элементов" (рисунок 28).

Гипотеза 1: "О природе сложности системы": сложность системы определяется количеством содержащейся в ней информации.

Гипотеза 2: "О видах системной информации": системная информация включает две составляющие:

– зависящую от количества элементов системы;

– зависящую как от количества элементов системы, так и от сложности взаимосвязей между ними.

Лемма-1: при увеличении количества элементов в системе доля системной информации в ней возрастает с ускорением, которое постепенно уменьшается.

Лемма-2: чем выше уровень системности, тем большая доля информации системы содержится во взаимосвязях ее элементов.

Лемма-3: чем меньше элементов в системе, тем быстрее возрастает доля информации, содержащейся во взаимосвязях элементов при возрастании уровня системности.

Рисунок 28. Закон возрастания эмерджентности

Системное обобщение классической формулы Харкевича, как количественная мера знаний

Это обобщение представляет большой интерес, в связи с тем, что А.Харкевич впервые ввел в теорию информации понятие цели. Он считал, что количество информации, сообщенное объекту, можно измерять по изменению вероятности достижения цели этим объектом за счет использования им этой информации.

Рассмотрим таблицу 12, в которой столбцы соответствуют будущим состояниям АОУ (целевым и нежелательным), а строки факторам, характеризующим объект управления, управляющую систему и окружающую среду.

Таблица 12 – МАТРИЦА АБСОЛЮТНЫХ ЧАСТОТ

Классическая формула А.Харкевича имеет вид:

(3. 19)

где:

– W – количество классов (мощность множества будущих состояний объекта управления); M – максимальный уровень сложности смешанных состояний объекта управления;

– индекс i обозначает фактор: 1£ i £ M; индекс j обозначает класс: 1£ j £ W;

– P_ij – вероятность достижения объектом управления j-й цели при условии сообщения ему i-й информации;

– P_j – вероятность самопроизвольного достижения объектом управления j-й цели.

Из 3.19 видно, что формула Харкевича для семантической меры информации по сути является логарифмом от формулы Байеса (отношение условной вероятности к безусловной).

Ниже глобальные параметры модели W и M в выражениях для I опускаются, т.к. они являются константами для конкретной математической модели СК-анализа.

Однако: А.Харкевич в своем выражении для количества информации не ввел зависимости количества информации, от мощности пространства будущих состояний объекта управления, в т.ч. от количества его целевых состояний. Вместе с тем, один из возможных вариантов учета количества будущих состояний объекта управления обеспечивается классической и системной формулами Хартли (3.1) и (3.9); выражение (3.19) при подстановке в него реальных численных значений вероятностей P_ij и P_j не дает количества информации в битах; для выражения (3.19) не выполняется принцип соответствия, считающийся обязательным для обобщающих теорий. Возможно, в этом состоит одна из причин слабого взаимодействия между классической теорией информации Шеннона и семантической теорией информации.

Чтобы снять эти вопросы, приближенно выразим вероятности P_ij, P_i и P_j через частоты:

(3. 20)

В (3.20) использованы обозначения:

N_ij – суммарное количество наблюдений факта: "действовал i-й фактор и объект перешел в j-е состояние";

N_j – суммарное количество встреч различных факторов у объектов, перешедших в j-е состояние;

N_i – суммарное количество встреч i-го фактора у всех объектов;

N – суммарное количество встреч различных факторов у всех объектов.

Подставим в выражение (3.19) значения для P_ij и P_j из (3.20):

(3. 21)

Введем коэффициент эмерджентности Y в модифицированную формулу А.Харкевича:

(3. 22)

где: Y – коэффициент эмерджентности Харкевича (как будет показано выше, он определяет степень детерминированности объекта с уровнем системной организации j, имеющего W чистых состояний, на переходы в которые оказывают влияние M факторов, о чем в модели накоплено N фактов).

Известно, что классическая формула Шеннона для количества информации для неравновероятных событий преобразуется в формулу Хартли при условии, что события равновероятны, т.е. удовлетворяет фундаментальному принципу соответствия [81].

Естественно потребовать, чтобы и обобщенная формула Харкевича также удовлетворяла аналогичному принципу соответствия, т.е. преобразовывалась в формулу Хартли в предельном случае, когда каждому классу (состоянию объекта) соответствует один признак (фактор), и каждому признаку – один класс, и эти классы (а, значит и признаки), равновероятны. Иначе говоря факторов столько же, сколько и будущих состояний объекта управления, все факторы детерминистские, а состояния объекта управления – альтернативные, т.е. каждый фактор однозначно определяет переход объекта управления в определенное состояние.

В этом предельном случае отпадает необходимость двухвекторного описания объектов, при котором 1-й вектор (классификационный) содержит интегральное описание объекта, как принадлежащего к определенным классам, а 2-й вектор (описательный) – дискретное его описание, как имеющего определенные атрибуты. Соответственно, двухвекторная модель, предложенная в данной работе, преобразуется в "вырожденный" частный случай – стандартную статистическую модель. В этом случае количество информации, содержащейся в признаке о принадлежности объекта к классу является максимальным и равным количеству информации, вычисляемому по системной формуле Хартли (3.9).

Таким образом при взаимно-однозначном соответствии классов и признаков:

(3. 23)

формула А.Харкевича (3.13) приобретает вид:

(3. 24)

откуда:

(3. 25)

или, учитывая выражение для коэффициента эмерджентности Хартли (3.8):

(3. 26)

Смысл коэффициента эмерджентности Харкевича (3.25) проясняется, если учесть, что при количестве состояний системы W равном количеству фактов N о действии на эту систему различных факторов он равен 1. В этом случае факторы однозначно определяют состояния объекта управления, т.е. являются детерминистскими. Если же количество фактов N о действии на эту систему различных факторов превосходит количество ее состояний W, что является гораздо более типичным случаем, то этот коэффициент меньше 1. По-видимому, это означает, что в этом случае факторы как правило не однозначно (и не так жестко как детерминистские) определяют поведение объекта управления, т.е. являются статистическими.

Таким образом, коэффициент эмерджентности Харкевича Y изменяется от 0 до 1 и определяет степень детерминированности системы:

– Y=1 соответствует полностью детерминированной системе, поведение которой однозначно определяется действием минимального количества факторов, которых столько же, сколько состояний системы;

– Y=0 соответствует полностью случайной системе, поведение которой никак не зависит действия факторов независимо от их количества;

– 0<Y<1 соответствуют большинству реальных систем поведение которых зависит от многих факторов, число которых превосходит количество состояний системы, причем ни одно из состояний не определяется однозначно никакими сочетаниями действующих факторов (рисунок 29):

Рисунок 29. Интерпретация коэффициентов
эмерджентности СТИ

Из выражения (3.25) видно, что в частном случае, когда реализуются только чистые состояния объекта управления, т.е. M=1, коэффициент эмерджентности А.Харкевича приобретает вид:

(3. 27)

Подставив коэффициент эмерджентности А.Харкевича (3.25) в выражение (3.22), получим:

или окончательно:

(3. 28)

Из вида выражения (3.25) для Y очевидно, что увеличение уровня системности влияет на семантическую информационную модель (3.28) аналогично повышению уровня детерминированности системы: понижение уровня системности, также как и степени детерминированности системы приводит к ослаблению влияния факторов на поведение системы, т.е. к понижению управляемости системы за счет своего рода "инфляции факторов".

Например: управлять толпой из 1000 человек значительно сложнее, чем воздушно-десантным полком той же численности. Процесс превращения 1000 новобранцев в воздушно-десантный полк это и есть процесс повышения уровня системности и степени детерминированности системы. Этот процесс включает процесс иерархического структурирования (на отделения, взвода, роты, батальоны), а также процесс повышения степени детерминированности команд, путем повышения "степени беспрекословности" их исполнения. Оркестр, настраивающий инструменты, также весьма существенно отличается от оркестра, исполняющего произведение под управлением дирижера.

Необходимо отметить, что при повторном использовании той же самой обучающей выборки степень детерминированности модели уменьшается. Очевидно, с формальной математической точки зрения этого явления можно избежать, если перед расчетом информативностей признаков делить абсолютные частоты на количество объектов обучающей выборки.

С использованием выражения (3.28) непосредственно из матрицы абсолютных частот (таблица 12) рассчитывается матрица информативностей (таблица 13), содержащая связи между факторами и будущими состояниями АОУ и имеющая много различных интерпретаций и играющая основополагающую роль в данном исследовании.

Таблица 13 – МАТРИЦА ИНФОРМАТИВНОСТЕЙ

Из рассмотрения основополагающего выражения (3.28) видно, что:

1. При выполнении условий взаимно-однозначного соответствия классов и признаков (3.23) первое слагаемое в выражении (3.28) обращается в ноль и при всех реальных значениях входящих в него переменных оно отрицательно.

2. Выражение (3.28) является нелинейной суперпозицией двух выражений: системного общения формулы Хартли (второе слагаемое), и первого слагаемого, которое имеет вид формулы Шеннона для плотности информации и отличается от него тем, что выражение под логарифмом находится в степени, которая совпадает с коэффициентом эмерджентности Харкевича, а также способом взаимосвязи входящих в него абсолютных частот с вероятностями.

Это дает основание предположить, что первое слагаемое в выражении (3.28) является одной из форм системного обобщения выражения Шеннона для плотности информации:

(3. 29)

Поэтому вполне оправданным будет назвать степень в (3.29) коэффициентом эмерджентности Шеннона-Харкевича.

Генезис системной (эмерджентной) теории информации

Полученное системное обобщение формулы Харкевича (3.28) учитывает как взаимосвязь между признаками (факторами) и будущими, в т.ч. целевыми состояниями объекта управления, так и мощность множества будущих состояний объекта управления. Кроме того она объединяет возможности интегрального и дискретного описания объектов, учитывает уровень системности и степень детерминированности описываемой системы (таблица 14):

Таблица 14 – СООТВЕТСТВИЕ ТРЕБОВАНИЯМ ФОРМУЛ
"КТИ / СТИ"

При этом факторами являются управляющие факторы, т.е. управления со стороны системы управления, факторы окружающей среды, а также факторы, характеризующие текущее и прошлые состояния объекта управления. Все это делает полученное выражение (3.28) оптимальным по сформулированным критериям для целей построения содержательных информационных моделей активных объектов управления и для применения для синтеза адаптивных систем управления (см. диаграмму: "Генезис системного обобщения формулы Харкевича для количества информации", рисунок 30).

Рисунок 30. Генезис системной (эмерджентной) теории информации

Итак, различные выражения классической теории информации для количества информации: Хартли, Шеннона и Харкевича учитывают различные аспекты информационного моделирования объектов.

Полученное системное обобщение формулы А.Харкевича (3.28) учитывает как взаимосвязь между признаками (факторами) и будущими, в т.ч. целевыми состояниями объекта управления, так и мощность множества будущих состояний. Кроме того она объединяет возможности интегрального и дискретного описания объектов, учитывает уровень системности и степень детерминированности системы.

Различие между классическим понятием информации и его предложенным системным обобщением определяется различием между понятиями множества и системы, на основе которых они сформированы. Система при этом рассматривается как множество элементов, объединенных определенными видами взаимодействия ради достижения некоторой общей цели.

Все это делает полученное выражение (3.28) оптимальным по сформулированным критериям для целей построения содержательных информационных моделей активных объектов управления и для применения для синтеза рефлексивных АСУ активными объектами.

1.2.2.3. Семантическая информационная модель СК-анализа

Основная проблема, решаемая в аналитической модели: выбор способа вычисления весовых коэффициентов, отражающих степень и характер влияния факторов на переход активного объекта управления в различные состояния.

Основное отличие предлагаемого подхода от методов обобщения экспертных оценок состоит в том, что в предлагаемом подходе от экспертов требуется лишь само решение, а весовые коэффициенты автоматически подбираются в соответствии с моделью таким образом, что в сходных случаях будут приниматься решения, аналогичные предлагаемым экспертами. В традиционных подходах от экспертов требуют либо самих весовых коэффициентов, либо правил принятия решения (продукций).

1.2.2.3.1. Формализм динамики взаимодействующих семантических информационных пространств. Двухвекторное представление данных.

Не всегда и не все классы являются атрибутами, также не всегда и не все атрибуты являются классами по смыслу (в данной модели это может быть так в многослойной нейронной сети) Поэтому традиционное представление данных в форме одной матрицы с одинаковыми строками и столбцами представляется нецелесообразным и предлагается более общее – двухвекторное представление. В предлагаемой математической модели формальное описание объекта представляет собой совокупность его интенсионального и экстенсионального описаний.

Интенсиональное (дискретное) описание – это последовательность информативностей (но не кодов) тех и только тех признаков, которые реально фактически встретились у данного конкретного объекта.

Экстенсиональное (континуальное) описание состоит из информативностей (но не кодов) тех классов распознавания, для формирования образов которых по мнению экспертов целесообразно использовать интенсиональное описание данного конкретного объекта.

Именно взаимодействие и взаимная дополнительность этих двух взаимоисключающих видов описания объектов формирует то, что психологи, логики и философы называют "смысл".

Таким образом, формальное описание объекта в предлагаемой модели состоит из двух векторов. Первый вектор описывает к каким обобщенным категориям (классам распознавания) относится объект с точки зрения экспертов (вектор субъективной, смысловой, человеческой оценки). Второй же вектор содержит информацию о том, какими признаками обладает данный объект (вектор объективных характеристик). Необходимо особо подчеркнуть, что связь этих двух векторов друг с другом имеет вообще говоря не детерминистский, а вероятностный, статистический характер.

Если объект описан обоими векторами, то это описание можно использовать для формирования обобщенных образов классов распознавания, а также для проверки степени успешности выполнения этой задачи.

Если объект описан только вторым вектором – вектором признаков, то его можно использовать только для решения задачи распознавания (идентификации), которую можно рассматривать как задачу восстановления вектора классов данного объекта по его известному вектору признаков.

Предлагаемая модель удовлетворяет принципу соответствия, т.е. в ней одновекторный вариант описания предметной области получается как некоторое подмножество из возможных в ней вариантов, определяемое двумя ограничениями:

– справочник классов распознавания тождественно совпадает со справочником признаков;

– наличие какого-либо признака у объекта обучающей выборки однозначно (детерминистским образом) определяет принадлежность этого объекта к соответствующему классу распознавания (взаимно-однозначное соответствие классов и признаков).

Очевидно, эти ограничения приводят и к соответствующим ограничениям, накладываемым в свою очередь на варианты обработки информации и анализа данных в подобных системах.

Если говорить конкретнее, такая модель данных стирает различие между атрибутами и классами и не позволяет решать ряд задач, в которых эта абстракция является недопустимым упрощением. Эти задачи будут подробнее рассмотрены ниже.

Семантические пространства классов и атрибутов

Наглядно модель данных целесообразно представить себе в виде двух взаимосвязанных фазовых (т.е. абстрактных) пространств, в первом из которых осями координат служат шкалы атрибутов (пространство атрибутов), а во втором – шкалы классов (пространство классов).

В пространстве атрибутов векторами являются объекты обучающей выборки и обобщенные образы классов. Вектор класса представляет собой массив координат в фазовом пространстве, каждый элемент массива, т.е. координата, соответствует определенному атрибуту, а значение этой координаты – весовому коэффициенту, отражающему количество информации, содержащееся в факте наблюдения данного атрибута у объекта о принадлежности этого объекта к данному классу.

В пространстве классов векторами являются атрибуты. Вектор атрибута представляет собой массив координат в фазовом пространстве, каждый элемент массива, т.е. координата, соответствует определенному классу, а значение этой координаты – весовому коэффициенту, отражающему количество информации, содержащееся в факте наблюдения объекта данного класса о том, что у этого объекта будет определенный атрибут.

Таким образом, выбор смысла и математической формы значений весовых коэффициентов в виде количества информации вводит метрику в этих фазовых пространствах. Поэтому данные пространства являются нелинейными самосогласованными пространствами. Ясно, что линейная разделяющая функция в нелинейном пространстве является нелинейной функцией в линейном пространстве. Самосогласованность семантических пространств означает, что любое изменение одной координаты в общем случае связано с изменением всех остальных. Нелинейность и самосогласованность самым существенным образом отличает предложенные семантические информационные пространства классов и атрибутов от линейного семантического пространства, используемого в основном в психодиагностике [38], в котором осями являются признаки (шкалы), а значениями координат по осям являются непосредственно градации признаков.

Однако этого недостаточно. Чтобы над векторами в фазовых пространствах можно было корректно выполнять стандартные операции сложения, вычитания, скалярного и векторного умножения, выполнять преобразования системы координат, переход от одной системы координат к другой, и вообще применять аппарат линейной алгебры и аналитической геометрии, что представляет большой научный и практический интерес и является очень актуальным, необходимо корректно ввести в этих пространствах системы координат т.е. системы отсчета, удовлетворяющие определенным требованиям.

Требования к системам координат, свойства векторов классов и атрибутов, решение проблемы снижения размерности описания и ортонормирования

В качестве осей координат пространства атрибутов целесообразно выбрать вектора атрибутов, обладающие следующими свойствами:

1. Их должно быть минимальное количество, достаточное для полного описания предметной области.

2. Эти вектора должны пересекаться в одной точке.

3. Значения координат вектора должны измеряться в одной единице измерения, т.е. должны быть сопоставимы.

Для выполнения первого требования необходимо, чтобы математическая форма и смысл весовых коэффициентов были выбраны таким образом, чтобы модули векторов атрибутов в пространстве классов были пропорциональны их значимости для решения задач идентификации, прогнозирования и управления. Причем наиболее значимые вектора атрибутов не должны коррелировать друг с другом, т.е. должны быть ортонормированны. В этом случае при удалении векторов с минимальными модулями автоматически останутся наиболее значимые практически ортонормированные вектора, которые можно принять за базисные, т.е. в качестве осей системы координат.

Второе требование означает, что минимальное расстояние между этими векторами в пространстве классов должно быть равно нулю.

Третье требование предполагает соответствующий выбор математической формы для значений координат.

Эти идеальные требования практически никогда не будут соблюдаться на практике с абсолютной точностью. Однако этого и не требуется. Достаточно, чтобы реально выбранные в качестве базисных атрибуты отображались в пространстве классов векторами, для которых эти требования выполняются с точностью, достаточной для применения соответствующих математических моделей и математического аппарата на практике.

Аналогично обстоит дело и с минимизацией размерности пространства классов. В качестве базисных могут выбраны вектора классов, имеющие максимальную длину и взаимно (попарно) ортонормированные.

Очевидно, задача выбора базисных векторов имеет не единственное решение, т.е. может существовать несколько систем таких векторов, которые можно рассматривать как результат действия преобразований системы координат, состоящих из смещений и поворотов.

1.2.2.3.2. Применение классической теории информации К.Шеннона для расчета весовых коэффициентов и мер сходства

Формально, распознавание есть не что иное, как принятие решения о принадлежности распознаваемого объекта или его состояния к определенному классу (классам) [12, 125, 221]. Из этого следует внутренняя и органичная связь методов распознавания образов и принятия решений. Аналитический обзор позволяет сделать вывод, что наиболее глубокая основа этой связи состоит в том, что и распознавание образов, и принятие решений есть прежде всего снятие неопределенности. Распознавание снимает неопределенность в вопросе о том, к какому классу относится распознаваемый объект. Если до распознавания существовала неопределенность в вопросе о том, к какому классу относится распознаваемый объект или его состояние, то в результате распознавания эта неопределенность уменьшается, причем возможно и до нуля (когда объект идентифицируется однозначно). Принятие решения (выбор) также снимает неопределенность в вопросе о том, какое из возможных решений будет принято, если существовало несколько альтернативных вариантов решений и принимается одно из них.

Для строгого исследования процессов снятия неопределенности оптимальным является применение аппарата теории информации, которая как бы специально создана для этой цели. Из этого непосредственно следует возможность применения методов теории информации для решения задач распознавания и принятия решений в АСУ. Таким образом, теория информации может рассматриваться как единая основа методов распознавания образов и принятия решений.

Формальная постановка задачи

В рефлексивных АСУ активными объектами модели распознавания образов и принятия решений применимы в подсистемах идентификации состояния АОУ и выработки управляющего воздействия: идентификация состояния АОУ представляет собой принятие решения о принадлежности этого состояния к определенной классификационной категории (задача распознавания); выбор многофакторного управляющего воздействия из множества возможных вариантов представляет собой принятие решения (обратная задача распознавания).

Распознавание образов есть принятие решения о принадлежности объекта или его состояния к определенному классу. Если до распознавания существовала неопределенность в вопросе о том, к какому классу относится распознаваемый объект или его состояние, то в результате распознавания эта неопределенность уменьшается, в том числе может быть и до нуля (когда объект идентифицируется однозначно). Из данной постановки непосредственно следует возможность применения методов теории информации для решения задач распознавания образов и принятия решений в АСУ.

Информация как мера снятия неопределенности

Как было показано выше, теория информация применима в АСУ для решения задач идентификации состояния сложного объекта управления (задача распознавания) и принятия решения о выборе многофакторного управляющего воздействия (обратная задача распознавания).

Так в результате процесса познания уменьшается неопределенность в наших знаниях о состоянии объекта познания, а в результате процесса труда (по сути управления) – уменьшается неопределенность поведения продукта труда (или объекта управления). В любом случае количество переданной информации представляет собой количественную меру степени снятия неопределенности.

Процесс получения информации можно интерпретировать как изменение неопределенности в вопросе о том, от какого источника отправлено сообщение в результате приема сигнала по каналу связи. Подробно данная модель приведена в работе [81].

Количество информации в индивидуальных событиях и лемма Неймана–Пирсона

В классическом анализе Шеннона идет речь лишь о передаче символов по одному информационному каналу от одного источника к одному приемнику. Его интересует прежде всего передача самого сообщения.

В данном исследовании ставится другая задача: идентифицировать информационный источник по сообщению от него. Поэтому метод Шеннона был обобщен путем учета в математической модели возможности существования многих источников информации, о которых к приемнику по зашумленному каналу связи приходят не отдельные символы–признаки, а сообщения, состоящие из последовательностей символов (признаков) любой длины.

Следовательно, ставится задача идентификации информационного источника по сообщению от него, полученному приемником по зашумленному каналу. Метод, являющийся обобщением метода К.Шеннона, позволяет применить классическую теорию информации для построения моделей систем распознавания образов и принятия решений, ориентированных на применение для синтеза адаптивных АСУ сложными объектами.

Для решения поставленной задачи необходимо вычислять не средние информационные характеристики, как в теории Шеннона, а количество информации, содержащееся в конкретном i–м признаке (символе) о том, что он пришел от данного j–го источника информации. Это позволит определить и суммарное количество информации в сообщении о каждом информационном источнике, что дает интегральный критерий для идентификации или прогнозирования состояния АОУ.

Логично предположить, что среднее количество информации, содержащейся в системе признаков о системе классов

(3. 30)

является ничем иным, как усреднением (с учетом условной вероятности наблюдения) "индивидуальных количеств информации", которые содержатся в конкретных признаках о конкретных классах (источниках), т.е.:

(3. 31)

Это выражение определяет так называемую "плотность информации", т.е. количество информации, которое содержится в одном отдельно взятом факте наблюдения i–го символа (признака) на приемнике о том, что этот символ (признак) послан j–м источником.

Если в сообщении содержится M символов, то суммарное количество информации о принадлежности данного сообщения j–му информационному источнику (классу) составляет:

(3. 32)

Необходимо отметить, что применение сложения в выражении (3.43) является вполне корректным и оправданным, так как информация с самого начала вводилась как аддитивная величина, для которой операция сложения является корректной.

Преобразуем выражение (3.50) к виду, более удобному для практического применения (численных расчетов). Для этого выразим вероятности встреч признаков через частоты их наблюдения:

(3. 33)

Подставив (3.44) в (3.25), получим:

(3. 34)

Если ранжировать классы в порядке убывания суммарного количества информации о принадлежности к ним, содержащейся в данном сообщении (т.е. описании объекта), и выбирать первый из них, т.е. тот, о котором в сообщении содержится наибольшее количество информации, то мы получим обоснованную статистическую процедуру, основанную на классической теории информации, оптимальность которой доказывается в фундаментальной лемме Неймана–Пирсона [194].

Сравнивая выражения (3.34) и (3.28) видим, что в системное обобщенное формулы Харкевича входит слагаемое, сходное с выражением Шеннона для плотности информации. Различия состоят в том, что в выражении (3.28) это слагаемое возведено в степень, имеющую смысл коэффициента эмерджентности Харкевича. Необходимо отметить, что значения частот в этих формулах связаны с вероятностями несколько различным образом (выражения 3.20 и 3.33).

Если ранжировать классы в порядке убывания суммарного количества информации о принадлежности к ним, содержащейся в данном сообщении (т.е. описании объекта), и выбирать первый из них, т.е. тот, о котором в сообщении содержится наибольшее количество информации, то мы получим обоснованную статистическую процедуру, основанную на классической теории информации, оптимальность которой доказывается в фундаментальной лемме Неймана–Пирсона [194].

Таким образом, распознавание образов есть принятие решения о принадлежности объекта или его состояния к определенному классу. Если до распознавания существовала неопределенность в вопросе о том, к какому классу относится распознаваемый объект или его состояние, то в результате распознавания эта неопределенность уменьшается, в том числе может быть и до нуля. Понятие информации может быть определено следующим образом: "Информация есть количественная мера степени снятия неопределенности". Количество информации является мерой соответствия распознаваемого объекта (его состояния) обобщенному образу класса.

Количество информации имеет ряд вполне определенных свойств. Эти свойства позволяют ввести понятие "количество информации в индивидуальных событиях", которое является весьма перспективным для применения в системах распознавания образов и поддержки принятия решений.

1.2.2.3.3. Математическая модель метода распознавания образов и принятия решений, основанного на системной теории информации

Формальная постановка основной задачи рефлексивной АСУ активными объектами и ее декомпозиция

Рассмотрим некоторые основные понятия, необходимые для дальнейшего изложения. При этом будут использованы как литературные данные, так и результаты, полученные в предыдущих главах данной работы.

Принятие решения в АСУ – это выбор некоторого наиболее предпочтительного управляющего воздействия из исходного множества всех возможных управляющих воздействий, обеспечивающего наиболее эффективное достижение целей управления. В результате выбора неопределенность исходного множества уменьшается на величину информации, которая порождается самим актом выбора [81]. Следовательно, теория информации может быть применена как для идентификации состояний объекта управления, так и для принятия решений об управляющих воздействиях в АСУ.

Модель АСУ включает в себя: модель объекта управления, модель управляющей подсистемы, а также модель внешней среды. Управляющая подсистема реализует следующие функции: идентификация состояния объекта управления, выработка управляющего воздействия, реализация управляющего воздействия.

С позиций теории информации сложный объект управления (АОУ) может рассматриваться как шумящий (определенным образом) информационный канал, на вход которого подаются входные параметры , представляющие собой управляющие воздействия, а также факторы предыстории и среды, а на выходе фиксируются выходные параметры , связанные как с входными параметрами, так и с целевыми и иными состояниями объекта управления.

Одной из основных задач АСУ является задача принятия решения о наиболее эффективном управляющем воздействии. В терминах теории информации эта задача формулируется следующим образом: зная целевое состояние объекта управления, на основе его информационной модели определить такие входные параметры , которые с учетом предыстории и актуального состояния объекта управления, а также влияния среды с наибольшей эффективностью переведут его в целевое состояние, характеризующееся выходными параметрами .

С решением этой задачи тесно связана задача декодирования теории информации: "По полученному в условиях помех сообщению определить, какое сообщение было передано" [221]. Для решения данной задачи используются коды, корректирующие ошибки, а в более общем случае, - различные методы распознавания образов.

Учитывая вышесказанное, предлагается рассматривать принятие решения об управляющем воздействии в АСУ как решение обратной задачи декодирования, которая формулируется следующим образом: "Какое сообщение необходимо подать на вход зашумленного канала связи, чтобы на его выходе получить заранее заданное сообщение". Данная задача решается на основе математической модели канала связи.

Декомпозиция основной задачи в ряд частных подзадач

Построение аналитической модели АОУ затруднено из-за отсутствия или недостатка априорной информации об объекте управления, а также из-за ограниченности и сложности используемого математического аппарата. В связи с этим предлагается путь решения данной проблемы, состоящий в поэтапном решении следующих задач:

1–я задача: разработать абстрактную модель более общего класса (содержательную информационную);

2–я задача: обучить абстрактную информационную модель путем учета информации о реальном поведении АОУ, поступающей в процессе экспериментальной эксплуатации АСУ; на этом этапе адаптируется и конкретизируется абстрактная модель АОУ, т.е. в ней все более точно отражаются взаимосвязи между входными параметрами и состояниями АОУ;

3–я задача: на основе конкретной содержательной информационной модели разработать алгоритмы решения следующих задач АСУ:

3.1. Расчет влияния факторов на переход АОУ в различные возможные состояния (обучение, адаптация).

3.2. Прогнозирование поведения АОУ при конкретном управляющем воздействии и выработка многофакторного управляющего воздействия (основная задача АСУ).

3.3. Выявление факторов, вносящих основной вклад в детерминацию состояния АОУ; контролируемое удаление второстепенных факторов с низкой дифференцирующей способностью, т.е. снижение размерности модели при заданных ограничениях.

3.4. Сравнение влияния факторов. Сравнение состояний АОУ.

Сформулируем предлагаемую абстрактную модель АОУ, опишем способ ее конкретизации и приведем алгоритмы решения задач адаптивных АСУ АОУ на основе данной модели.

Решение задачи 1: "Синтез семантической информационной модели активного объекта управления"

Исходные данные для выявления взаимосвязей между факторами и состояниями объекта управления предлагается представить в виде корреляционной матрицы – матрицы абсолютных частот (таблица 15):

В этой матрице в качестве классов (столбцов) приняты будущие состояния объекта управления, как целевые, так и нежелательные, а в качестве атрибутов (строк) – факторы, которые разделены на три основных группы, математически обрабатываемые единообразно: факторы, характеризующие текущее и прошлые состояния объекта управления; управляющие факторы системы управления; факторы, характеризующие прошлые, текущее и прогнозируемые состояния окружающей среды. Отметим, что форма таблицы 15 является универсальной формой представления и обобщения фактов – эмпирических данных в единстве их дискретного и интегрального представления (причины – следствия, факторы – результирующие состояния, признаки – обобщенные образы классов, образное – логическое и т.п.).

Таблица 15 – МАТРИЦА АБСОЛЮТНЫХ ЧАСТОТ

Управляющие факторы объединяются в группы, внутри каждой из которых они альтернативны (несовместны), а между которыми - нет (совместны). В этом случае внутри каждой группы выбирают одно из доступных управляющих воздействий с максимальным влиянием. Варианты содержательной информационной модели без учета прошлых состояний объекта управления и с их учетом, аналогичны, соответственно, простым и составным цепям Маркова, автоматам без памяти и с памятью.

В качестве количественной меры влияния факторов, предложено использовать обобщенную формулу А.Харкевича (3.28), полученную на основе предложенной эмерджентной теории информации. При этом по формуле (3.28) непосредственно из матрицы абсолютных частот (таблица 15) рассчитывается матрица информативностей (таблица 16), которая и представляет собой основу содержательной информационной модели предметной области.

Весовые коэффициенты таблицы 3.28 непосредственно определяют, какое количество информации I_ij система управления получает о наступлении события: "активный объект управления перейдет в j–е состояние", из сообщения: "на активный объект управления действует i–й фактор".

Принципиально важно, что эти весовые коэффициенты не определяются экспертами неформализуемым способом, а рассчитываются непосредственно на основе эмпирических данных и удовлетворяют всем ранее сформулированным требованиям, т.е. являются сопоставимыми, содержательно интерпретируемыми, отражают понятия "достижение цели управления" и "мощность множества будущих состояний объекта управления" и т.д.

Таблица 16 – МАТРИЦА ИНФОРМАТИВНОСТЕЙ

В данной работе показано, что предложенная информационная мера обеспечивает сопоставимость индивидуальных количеств информации, содержащейся в факторах о классах, а также сопоставимость интегральных критериев, рассчитанных для одного объекта и разных классов, для разных объектов и разных классов.

Когда количество информации I_ij>0 – i–й фактор способствует переходу объекта управления в j–е состояние, когда I_ij<0 – препятствует этому переходу, когда же I_ij=0 – никак не влияет на это. В векторе i–го фактора (строка матрицы информативностей) отображается, какое количество информации о переходе объекта управления в каждое из будущих состояний содержится в том факте, что данный фактор действует. В векторе j–го состояния класса (столбец матрицы информативностей) отображается, какое количество информации о переходе объекта управления в соответствующее состояние содержится в каждом из факторов.

Таким образом, матрица информативностей (таблица 16) является обобщенной таблицей решений, в которой входы (факторы) и выходы (будущие состояния АОУ) связаны друг с другом не с помощью классических (Аристотелевских) импликаций, принимающих только значения: "Истина" и "Ложь", а различными значениями истинности, выраженными в битах и принимающими значения от положительного теоретически-максимально-возможного ("Максимальная степень истинности"), до теоретически неограниченного отрицательного ("Степень ложности").

Фактически предложенная модель позволяет осуществить синтез обобщенных таблиц решений для различных предметных областей непосредственно на основе эмпирических исходных данных и продуцировать на их основе прямые и обратные правдоподобные (нечеткие) логические рассуждения по неклассическим схемам с различными расчетными значениями истинности, являющимся обобщением классических импликаций (таблица 17).

Таблица 17 – ПРЯМЫЕ И ОБРАТНЫЕ ПРАВДОПОДОБНЫЕ ЛОГИЧЕСКИЕ ВЫСКАЗЫВАНИЯ С РАСЧЕТНОЙ (В СООТВЕТСТВИИ

С СТИ) СТЕПЕНЬЮ ИСТИННОСТИ ИМПЛИКАЦИЙ

Приведем пример более сложного высказывания, которое может быть рассчитано непосредственно на основе матрицы информативностей – обобщенной таблицы решений (таблица 16):

Если A, со степенью истинности a(A,B) детерминирует B, и если С, со степенью истинности a(C,D) детерминирует D, и A совпадает по смыслу с C со степенью истинности a(A,C), то это вносит вклад в совпадение B с D, равный степени истинности a(B,D).

При этом в прямых рассуждениях как предпосылки рассматриваются факторы, а как заключение – будущие состояния АОУ, а в обратных – наоборот: как предпосылки – будущие состояния АОУ, а как заключение – факторы. Степень истинности i-й предпосылки – это просто количество информации I_ij, содержащейся в ней о наступлении j-го будущего состояния АОУ. Если предпосылок несколько, то степень истинности наступления j-го состояния АОУ равна суммарному количеству информации, содержащемуся в них об этом. Количество информации в i-м факторе о наступлении j-го состояния АОУ, рассчитывается в соответствии с выражением (3.28) СТИ.

Прямые правдоподобные логические рассуждения позволяют прогнозировать степень достоверности наступления события по действующим факторам, а обратные – по заданному состоянию восстановить степень необходимости и степень нежелательности каждого фактора для наступления этого состояния, т.е. принимать решение по выбору управляющих воздействий на АОУ, оптимальных для перевода его в заданное целевое состояние.

Необходимо отметить, что предложенная модель, основывающаяся на теории информации, обеспечивает автоматизированное формирования системы нечетких правил по содержимому входных данных, как и комбинация нечеткой логики Заде-Коско с нейронными сетями Кохонена. Принципиально важно, что качественное изменение модели путем добавления в нее новых классов не уменьшает достоверности распознавания уже сформированных классов. Кроме того, при сравнении распознаваемого объекта с каждым классом учитываются не только признаки, имеющиеся у объекта, но и отсутствующие у него, поэтому предложенной моделью правильно идентифицируются объекты, признаки которых образуют множества, одно из которых является подмножеством другого (как и в Неокогнитроне К.Фукушимы) [243].

Данная модель позволяет прогнозировать поведение АОУ при воздействии на него не только одного, но и целой системы факторов:

(3. 35)

В теории принятия решений скалярная функция I_j векторного аргумента называется интегральным критерием. Основная проблема состоит в выборе такого аналитического вида функции интегрального критерия, который обеспечил бы эффективное решение сформулированной выше задачи АСУ.

Учитывая, что частные критерии (3.28) имеют смысл количества информации, а информация по определению является аддитивной функцией, предлагается ввести интегральный критерий, как аддитивную функцию от частных критериев в виде:

(3. 36)

В выражении (3.54) круглыми скобками обозначено скалярное произведение. В координатной форме это выражение имеет вид:

,

(3. 37)

где:

– вектор j–го состояния объекта управления;

– вектор состояния предметной области, включающий все виды факторов, характеризующих объект управления, возможные управляющие воздействия и окружающую среду (массив–локатор), т.е.:

В реализованной модели значения координат вектора состояния ПО принимались равными либо 1 (фактор действует), либо 0 (фактор не действует).

Таким образом, интегральный критерий представляет собой суммарное количество информации, содержащееся в системе факторов различной природы (т.е. факторах, характеризующих объект управления, управляющее воздействие и окружающую среду) о переходе активного объекта управления в будущее (в т.ч. целевое или нежелательное) состояние.

В многокритериальной постановке задача прогнозирования состояния объекта управления, при оказании на него заданного многофакторного управляющего воздействия I_j, сводится к максимизации интегрального критерия:

(3. 38)

т.е. к выбору такого состояния объекта управления, для которого интегральный критерий максимален.

Задача принятия решения о выборе наиболее эффективного управляющего воздействия является обратной задачей по отношению к задаче максимизации интегрального критерия (идентификации и прогнозирования), т.е. вместо того, чтобы по набору факторов прогнозировать будущее состояние АОУ, наоборот, по заданному (целевому) состоянию АОУ определяется такой набор факторов, который с наибольшей эффективностью перевел бы объект управления в это состояние.

Предлагается еще одно обобщение этой фундаментальной леммы, основанное на косвенном учете корреляций между информативностями в векторе состояний при использовании средних по векторам. Соответственно, вместо простой суммы количеств информации предлагается использовать корреляцию между векторами состояния и объекта управления, которая количественно измеряет степень сходства этих векторов:

(3. 39)

где:

– средняя информативность по вектору класса;

– среднее по вектору идентифицируемой ситуации (объекта).

– среднеквадратичное отклонение информативностей вектора класса;

– среднеквадратичное отклонение по вектору распознаваемого объекта.

Выражение (3.39) получается непосредственно из (3.37) после замены координат перемножаемых векторов их стандартизированными значениями:

Необходимо отметить, что выражение для интегрального критерия сходства (3.39) по своей математической форме является корреляцией двух векторов. Это означает, что если эти вектора являются суммой двух сигналов: полезного и белого шума, то при расчете интегрального критерия белый шум практически не будет играть никакой роли, т.е. его корреляция с самими собой равна нулю по определению. Это означает, что выбранный интегральный критерий сходства является высокоэффективным средством подавления белого шума и выделения полезной информации из шума, который неизбежно присутствует в эмпирических данных.

Результат прогнозирования поведения объекта управления, описанного данной системой факторов, представляет собой список его возможных будущих состояний, в котором они расположены в порядке убывания суммарного количества информации о переходе объекта управления в каждое из них.

Сравнения результатов идентификации и прогнозирования с опытными данными, с использованием выражений (3.37) и (3.39), показали, что при малых выборках они практически не отличаются, но при увеличении объема выборки до 400 и более (независимо от предметной области) выражение (3.39) дает погрешность идентификации (прогнозирования) на 5% – 7% меньше, чем (3.37). Поэтому в предлагаемой модели фактически используется не метрическая мера сходства (3.39).

В связи с тем, что в дальнейшем изложении широко применяются понятия теории АСУ, теории информации (связи), теории распознавания образов и методов принятия решений, приведем таблицу соответствия наиболее часто используемых нами терминов из этих научных направлений, имеющих сходный смысл (таблица 18):

Таблица 18 – СООТВЕТСТВИЕ ТЕРМИНОВ
РАЗЛИЧНЫХ НАУЧНЫХ НАПРАВЛЕНИЙ

Вывод системного обобщения формулы Харкевича (3.28) приведен в разделе 3.1 данной работы. Чрезвычайно важное для данного исследования выражение (3.28) заслуживает специального комментария. Прежде всего нельзя не обратить внимания на то, что оно по своей математической форме, т.е. формально, ничем не отличается от выражения для превышения сигнала над помехой для информационного канала [242]. Из этого, на первый взгляд, внешнего совпадения следует интересная интерпретация выражения (3.28). А именно: можно считать, что обнаружив некоторый i–й признак у объекта, предъявленного на распознавание, мы тем самым получаем сигнал, содержащий некоторое количество информации

о том, что этот объект принадлежит к j–му классу. По–видимому, это так и есть, однако чтобы оценить насколько много или мало этой информации нами получено, ее необходимо с чем–то сравнить, т.е. необходимо иметь точку отсчета или базу для сравнения. В качестве такой базы естественно принять среднее по всем признакам количество информации, которое мы получаем, обнаружив этот j–й класс:

Иначе говоря, если при предъявлении какого–либо объекта на распознавание у него обнаружен i–й признак, то для того, чтобы сделать из этого факта обоснованный вывод о принадлежности этого объекта к тому или иному классу, необходимо знать и учесть, насколько часто вообще (т.е. в среднем) обнаруживается этот признак при предъявлении объектов данного класса.

Фактически это среднее количество информации можно рассматривать как некоторый "информационный шум", который имеется в данном признаке и не несет никакой полезной информации о принадлежности объектов к тем или иным классам. Полезной же информацией является степень отличия от этого шума. Таким образом классическому выражению Харкевича (3.12) для семантической целесообразности информации может быть придан более привычный для теории связи вид:

который интерпретируется как вычитание шума из полезного сигнала. Эта операция является совершенно стандартной в системах шумоподавления.

Если полезный сигнал выше уровня шума, то его обнаружение несет информацию в пользу принадлежности объекта к данному классу, если нет – то, наоборот, в пользу не принадлежности.

Возвращаясь к выражению (3.12), необходимо отметить, что сам А.А.Харкевич рассматривал как вероятность достижения цели, при условии, что система получила информацию , а – как вероятность ее достижения при условии, что система этой информации не получала. Очевидно, что фактически соответствует вероятности случайного угадывания объектом управления правильного пути к цели, или, что тоже самое, вероятности самопроизвольного, т.е. без оказания управляющих воздействий, достижения АОУ целевого заданного состояния.

Необходимо отметить также, что каждый признак объекта управления как канала связи может быть охарактеризован динамическим диапазоном, равным разности максимально возможного (допустимого) уровня сигнала в канале и уровня помех в логарифмическом масштабе:

Максимальное количество информации, которое может содержаться в признаке, полностью определяется количеством классов распознавания W и равно количеству информации по Хартли: I=Log₂W.

Динамический диапазон признака является количественной мерой его полезности (ценности) для распознавания, но все же предпочтительней для этой цели является среднее количество полезной для классификации информации в признаке, т.е. исправленное выборочное среднеквадратичное отклонение информативностей:

(3. 40)

Очевидна близость этой меры к длине вектора признака в семантическом пространстве атрибутов:

(3. 41)

В сущности выражение (3.40) просто представляет собой нормированный вариант (3.41).

Решение задачи 2: "Адаптация модели объекта управления"

На основе обучающей выборки, содержащей информацию о том, какие факторы действовали, когда АОУ переходил в те или иные состояния, методом прямого счета формируется матрица абсолютных частот, имеющая вид, представленный в таблице 15. Необходимо отметить, что в случае АОУ в большинстве случаев нет возможности провести полный факторный эксперимент для заполнения матрицы абсолютных частот. В данной работе предполагается, что это и не обязательно, т.е. на практике достаточно воспользоваться естественной вариабельностью факторов и состояний АОУ, представленных в обучающей выборке. С увеличением объема обучающей выборки в ней со временем будут представлены все практически встречающиеся варианты сочетаний факторов и состояний АОУ.

В соответствии с выражением (3.28), непосредственно на основе матрицы абсолютных частот |||| (таблица 15) рассчитывается матрица информативностей факторов |||| (таблица 16).

Количество информации в i–м факторе о наступлении j–го состояния АОУ является статистической мерой их связи и количественной мерой влияния данного фактора на переход АОУ в данное состояние.

Решение задачи 3: "Разработка алгоритмов решения основных задач АСУ"

Как было показано в разделе 3.2, решение задачи 3 предполагает решение следующих подзадач.

Решение подзадачи 3.1: "Расчет влияния факторов на переход объекта управления в различные состояния (обучение, адаптация)"

При изменении объема обучающей выборки или изменении экспертных оценок прежде всего пересчитывается матрица абсолютных частот, а затем, на ее основании и в соответствии с выражением (3.28), - матрица информативностей. Таким образом, предложенная модель обеспечивает отображение динамических взаимосвязей, с одной стороны, между входными и выходными параметрами, а с другой, - между параметрами и состояниями объекта управления. Конкретно, это отображение осуществляется в форме так называемых векторов факторов и состояний.

В профиле (векторе) i–го фактора (строка матрицы информативностей) отображается, какое количество информации о переходе АОУ в каждое из возможных состояний содержится в том факте, что данный фактор действует.

В профиле (векторе) j–го состояния АОУ (столбец матрицы информативностей) отображается, какое количество информации о переходе АОУ в данное состояние содержится в каждом из факторов.

Решение подзадачи 3.2: "Прогнозирование поведения объекта управления при конкретном управляющем воздействии и выработка многофакторного управляющего воздействия (обратная задача прогнозирования)"

Прогнозирование состояния АОУ осуществляется следующим образом:

1. Собирается информация о действующих факторах, характеризующих состояние предметной области (активный объект управления описывается факторами, характеризующими его текущее и прошлые состояния; управляющая система характеризуется технологическими факторами, с помощью которых она оказывает управляющее воздействие на активный объект управления; окружающая среда характеризуется прошлыми, текущими и прогнозируемыми факторами, которые также оказывают воздействие на активный объект управления).

2. Для каждого возможного будущего состояния АОУ подсчитывается суммарное количество информации, содержащееся во всей системе факторов (согласно п.1), о наступлении этого состояния.

3. Все будущие состояния АОУ ранжируются в порядке убывания количества информации об их осуществлении.

Этот ранжированный список будущих состояний АОУ и представляет собой первичный результат прогнозирования.

Если задано некоторое определенное целевое состояние, то выбор управляющих воздействий для фактического применения производится из списка, в котором все возможные управляющие воздействия расположены в порядке убывания их влияния на перевод АОУ в данное целевое состояние. Такой список называется информационным портретом состояния АОУ [81].

Управляющие воздействия могут быть объединены в группы, внутри каждой из которых они альтернативны (несовместны), а между которыми - нет (совместны). В этом случае внутри каждой группы выбирают одно из фактически доступных управляющих воздействий с максимальным влиянием на достижение заданного целевого состояния АОУ.

Однако выбор многофакторного управляющего воздействия нельзя считать завершенным без прогнозирования результатов его применения. Описание АОУ в актуальном состоянии состоит из списка факторов окружающей среды, предыстории АОУ, описания его актуального (исходного) состояния, а также выбранных управляющих воздействий. Имея эту информацию по каждому из факторов в соответствии с выражением (3.39), нетрудно подсчитать, какое количество информации о переходе в каждое из состояний содержится суммарно во всей системе факторов. Данный метод соответствует фундаментальной лемме Неймана–Пирсона, содержащей доказательство оптимальности метода выбора той из двух статистических гипотез, о которой в системе факторов содержится больше информации. В то же время он является обобщением леммы Неймана–Пирсона, так как вместо информационной меры Шеннона используется системное обобщение семантической меры целесообразности информации Харкевича.

Предлагается еще одно обобщение этой фундаментальной леммы, основанное на косвенном учете корреляций между информативностями в профиле состояния при использовании среднего по профилю. Соответственно, вместо простой суммы количеств информации предлагается использовать ковариацию между векторами состояния и АОУ, которая количественно измеряет степень сходства формы этих векторов.

Результат прогнозирования поведения АОУ, описанного данной системой факторов, представляет собой список состояний, в котором они расположены в порядке убывания суммарного количества информации о переходе АОУ в каждое из них.

Решение подзадачи 3.3: "Выявление факторов, вносящих основной вклад в детерминацию состояния АОУ; снижение размерности модели при заданных ограничениях"

Естественно считать, что некоторый фактор является тем более ценным, чем больше среднее количество информации, содержащееся в этом факторе о поведении АОУ [81]. Но так как в предложенной модели количество информации может быть и отрицательным (если фактор уменьшает вероятность перехода АОУ в некоторое состояние), то простое среднее арифметическое информативностей может быть близко к нулю. При этом среднее будет равно нулю и в случае, когда все информативности равны нулю, и тогда, когда они будут велики по модулю, но с разными знаками. Следовательно, более адекватной оценкой полезности фактора является среднее модулей или, что наиболее точно, исправленное (несмещенное) среднеквадратичное отклонение информативностей по профилю признака.

Ценность фактора по сути дела определяется его полезностью для различения состояний АОУ, т.е. является его дифференцирующей способностью или селективностью.

Необходимо также отметить, что различные состояния АОУ обладают различной степенью обусловленности, т.е. в различной степени детерминированы факторами: некоторые слабо зависят от учтенных факторов, тогда как другие определяются ими практически однозначно. Количественно детерминируемость состояния АОУ предлагается оценивать стандартным отклонением информативностей вектора обобщенного образа данного состояния.

Предложено и реализовано несколько итерационных алгоритмов корректного удаления малозначимых факторов и слабодетерминированных состояний АОУ при заданных граничных условиях [81]. Решение задачи снижения размерности модели АОУ при заданных граничных условиях позволяет снизить эксплуатационные затраты и повысить эффективность РАСУ АО.

Решение подзадачи 3.4: "Сравнение влияния факторов. Сравнение состояний объекта управления"

Факторы могут сравниваться друг с другом по тому влиянию, которое они оказывают на поведение АОУ. Сами состояния могут сравниваться друг с другом по тем факторам, которые способствуют или препятствуют переходу АОУ в эти состояния. Это сравнение может содержать лишь результат, т.е. различные степени сходства/различия (в кластерном анализе), или содержать также причины этого сходства/различия (в когнитивных диаграммах).

Эти задачи играют важную роль в теории и практике РАСУ АО при необходимости замены одних управляющих воздействий другими, но аналогичными по эффекту, а также при изучении вопросов семантической устойчивости управления (различимости состояний АОУ по детерминирующим их факторам).

Этот анализ проводится над классами распознавания и над признаками. Он включает: информационный (ранговый) анализ; кластерный и конструктивный анализ, семантические сети; содержательное сравнение информационных портретов, когнитивные диаграммы.

Семантический информационный анализ

Предложенная математическая модель позволяет сформировать информационные портреты обобщенных эталонных образов классов распознавания и признаков.

Портреты классов распознавания представляют собой списки признаков в порядке убывания содержащегося в них количества информации о принадлежности к этим классам.

Информационный портрет класса распознавания показывает нам, каков информационный вклад каждого признака в общий объем информации, содержащейся в обобщенном образе этого класса.

В подходе к решению задач рефлексивных АСУ АО, основанном на применении методов распознавания образов, классам распознавания соответствуют, во–первых, исходные, а во–вторых, результирующие, в том числе целевые состояния объекта управления. Это значит, что в первом случае портреты классов используются для идентификации исходного состояния АОУ, потому что именно с ними сравнивается состояние объекта управления, а во втором – для выработки управляющего воздействия, так как его выбирают в форме суперпозиции неальтернативных факторов из информационного портрета целевого состояния, оказывающих наибольшее влияние на перевод АОУ в это состояние.

Портреты признаков представляют собой списки классов распознавания в порядке убывания количества информации о них, которое содержит данный признак. По своей сути информационный портрет признака раскрывает нам смысл данного признака, т.е. его семантическую нагрузку. В теории и практике рефлексивных АСУ АО информационный портрет фактора является развернутой количественной характеристикой, содержащей информацию о силе и характере его влияния на перевод АОУ в каждое из возможных результирующих состояний, в том числе в целевые. Информационные портреты классов и признаков допускают наглядную графическую интерпретацию в виде двухмерных (2d) и трехмерных (3d) диаграмм.

Кластерно-конструктивный анализ и семантические сети

Кластеры представляют собой такие группы классов распознавания (или признаков), внутри которых эти классы наиболее схожи друг с другом, а между которыми наиболее различны [81]. В данной работе, в качестве классов распознавания рассматриваются как исходные, так и результирующие, в том числе целевые состояния объекта управления, а в качестве признаков – факторы, влияющие на переход АОУ в результирующие состояния.

Исходные состояния АОУ, объединенные в кластер, характеризуются общими или сходными методами перевода в целевые состояния. Результирующие состояния АОУ, объединенные в кластер, являются слаборазличимыми по факторам, детерминирующим перевод АОУ в эти состояния. Это означает, что одно и то же управляющее воздействие при одних и тех же предпосылках (исходном состоянии и предыстории объекта управления и среды) могут привести к переводу АОУ в одно из результирующих состояний, относящихся к одному кластеру. Поэтому кластерный анализ результирующих состояний АОУ является инструментом, позволяющим изучать вопросы устойчивости управления сложными объектами.

При выборе управляющего воздействия как суперпозиции неальтернативных факторов часто возникает вопрос о замене одних управляющих факторов другими, имеющими сходное влияние на перевод АОУ из данного текущего состояния в заданное целевое состояние. Кластерный анализ факторов как раз и позволяет решить эту задачу: при невозможности применить некоторый управляющий фактор его можно заменить другим фактором из того же кластера.

При формировании кластеров используются матрицы сходства объектов и признаков, формируемые на основе матрицы информативностей.

В соответствии с предлагаемой математической моделью могут быть сформированы кластеры для заданного диапазона кодов классов распознавания (признаков) или заданных диапазонов уровней системной организации с различными критериями включения объекта (признака) в кластер.

Эти критерии могут быть сформированы автоматически либо заданы непосредственно. В последнем уровне кластеризации, в частности при задании одного уровня, в кластеры включаются не только похожие, но и все непохожие объекты (признаки), и, таким образом, формируются конструкты классов распознавания и признаков.

В данной работе под конструктом понимается система противоположных (наиболее сильно отличающихся) кластеров, которые называются "полюсами" конструкта, а также спектр промежуточных кластеров, к которым применима количественная шкала измерения степени их сходства или различия [81].

Понятия "кластер" и "конструкт" тесно взаимосвязаны:

– так как положительный и отрицательный полюса конструкта представляют собой кластеры, в наибольшей степени отличающиеся друг от друга, то конструкты могут быть получены как результат кластерного анализа кластеров;

– конструкт может рассматриваться как кластер с нечеткими границами, включающий в различной степени, причем не только в положительной, но и отрицательной, все классы (признаки).

В теории рефлексивных АСУ АО, конструктивный анализ позволяет решить такие задачи, как:

1. Определение в принципе совместимых и в принципе несовместимых целевых состояний АОУ. Совместимыми называются целевые состояния, для достижения которых необходимы сходные предпосылки и управляющие воздействия, а несовместимыми – для которых они должны быть диаметрально противоположными. Например, обычно сложно совмещаются такие целевые состояния, как очень высокое качество продукции и очень большое ее количество.

2. Определение факторов, имеющих не только сходное (это возможно и на уровне кластерного анализа), но и совершенно противоположное влияние на поведение сложного объекта управления.

Современный интеллект имеет дуальную структуру и, по сути дела, мыслит в системе кластеров и конструктов. Поэтому инструмент автоматизированного кластерно–конструктивного анализа может быть успешно применен для рефлексивного управления активными объектами.

Необходимо отметить, что формирование кластеров затруднено из-за проблемы комбинаторного взрыва, так как требует полного перебора и проверки "из n по m" сочетаний элементов (классов или признаков) в кластеры. Конструкты же формируются непосредственно из матрицы сходства прямой выборкой и сортировкой, что значительно проще в вычислительном отношении, так как конструктов значительно меньше, чем кластеров (всего n²). Поэтому учитывая, что при формировании конструктов автоматически формируются и их полюса, т.е. кластеры, в предложенной математической модели реализован не кластерный анализ, а сразу конструктивный (как более простой в вычислительном отношении и более ценный по получаемым результатам).

Диаграммы смыслового сходства–различия классов (признаков) соответствуют определению семантических сетей [81], т.е. представляют собой ориентированные графы, в которых признаки соединены линиями, соответствующими их смысловому сходству–различию.

Когнитивные диаграммы классов и признаков

В предложенной в настоящем исследовании математической модели в обобщенной постановке реализована возможность содержательного сравнения обобщенных образов классов распознавания и признаков, т.е. построения когнитивных диаграмм [81].

В информационных портретах классов распознавания мы видим, какое количество информации о принадлежности (или не принадлежности) к данному классу мы получаем, обнаружив у некоторого объекта признаки, содержащиеся в информационном портрете. В кластерно-конструктивном анализе мы получаем результаты сравнения классов распознавания друг с другом, т.е. мы видим, насколько они сходны и насколько отличаются. Но мы не видим, какими признаками они похожи и какими отличаются, и какой вклад каждый признак вносит в сходство или различие некоторых двух классов.

Эту информацию мы могли бы получить, если бы проанализировали и сравнили два информационных портрета. Эту работу и осуществляет режим содержательного сравнения классов распознавания.

Аналогично, в информационных портретах признаков мы видим, какое количество информации о принадлежности (или не принадлежности) к различным классам распознавания мы получаем, обнаружив у некоторого объекта данный признак. В кластерно-конструктивном анализе мы получаем результаты сравнения признаков друг с другом, т.е. мы видим, насколько они сходны и насколько отличаются. Но мы не видим, какими классами они похожи и какими отличаются, и какой вклад каждый класс вносит в смысловое сходство или различие некоторых двух признаков.

Эту информацию мы могли бы получить, если бы проанализировали и сравнили информационные портреты двух признаков. Эту работу и осуществляет режим содержательного (смыслового) сравнения признаков.

Содержательное (смысловое) сравнение классов

Обобщим математическую модель, предложенную и развиваемую в данной главе, на случай содержательного сравнения двух классов распознавания: J–го и L–го.

Признаки, которые есть по крайней мере в одном из классов, будем называть связями, так как благодаря тому, что они либо тождественны друг другу, либо между ними имеется определенное сходство или различие по смыслу, они вносят определенный вклад в отношения сходства/различия между классами.

Список выявленных связей сортируется в порядке убывания модуля силы связи, причем учитывается не более заданного количества связей.

Пусть, например:

у J–го класса обнаружен i–й признак,

у L–го класса обнаружен k–й признак.

Используем те же обозначения, что и в разделе 3.1.

На основе обучающей выборки системой рассчитывается матрица абсолютных частот встреч признаков по классам (таблица 15).

В разделе 3.1. получено выражение (3.28) для расчета количества информации в i–м признаке о принадлежности некоторого конкретного объекта к j–му классу (плотность информации), которое имеет вид:

(3.28)

Аналогично, формула для количества информации в k–м признаке о принадлежности к L–му классу имеет вид:

(3. 42)

Вклад некоторого признака i в сходство/различие двух классов j и l равен соответствующему слагаемому корреляции образов этих классов, т.е. просто произведению информативностей

(3. 43)

Классический коэффициент корреляции Пирсона, количественно определяющий степень сходства векторов двух классов: j и l, на основе учета вклада каждой связи, образованной i–м признаком, рассчитывается по формуле

(3. 44)

где:

	– средняя информативность признаков j–го класса;
	– средняя информативность признаков L–го класса;
	– среднеквадратичное отклонение информативностей признаков j–го класса;
	– среднеквадратичное отклонение информативностей признаков L–го класса.

Проанализируем, насколько классический коэффициент корреляции Пирсона (3.62) пригоден для решения важных задач:

– содержательного сравнения классов;

– изучения внутренней многоуровневой структуры класса.

Упростим анализ, считая, что средние информативности признаков по обоим классам близки к нулю, что при достаточно больших выборках (более 400 примеров в обучающей выборке) практически близко к истине.

Каждое слагаемое (3.43) суммы (3.44) отражает связь между классами, образованную одним i–м признаком. I–я связь существует в том и только в том случае, если i–й признак есть у обоих классов. Поэтому эти связи уместно называть одно–однозначными.

Этот подход можно назвать классическим для когнитивного анализа. Рассмотрим когнитивную диаграмму, приведенную на стр. 222 работы основной работы классика когнитивной психологии Р.Солсо (Когнитивная психология. /Пер. с англ. - М.: Тривола, 1996. - 600с.) (рисунок 31).

Рисунок 31. Когнитивная диаграмма из классической работы Роберта Солсо.

В приведенной когнитивной диаграмме наглядно в графической форме показано сравнение классов (обобщенных образов) "Малиновка" и "Птица" разных уровней общности по их атрибутам (признакам). Как видно из диаграммы, в ней:

1. Все атрибуты имеют одинаковый вес, т.е. не учитывается, что некоторые атрибуты более важны для идентификации класса, чем другие. Это соответствует предположению, что этот вес равен по модулю 1 для всех атрибутов.

2. Все признаки имеют одинаковый знак, т.е. они все характерны для классов и нет атрибутов нехарактерных. Это соответствует предположению, что вес всех признаков положительный, т.е. все признаки вносят вклад в сходство и нет признаков, вносящих вклад в различие.

3. Классы сравниваются только по тем атрибутам, которые есть одновременно у них обоих, т.е. признаки, имеющиеся у обоих классов вносят вклад в сходство классов, а признаки, которые есть только у одного из классов не вносят никакого вклада ни в сходство классов, ни в различие. Это соответствует предположению, что атрибуты ортонормированы, т.е. корреляция их друг с другом равна 0 (атрибуты семантически не связаны).

Каждое из этих трех допущений является довольно сильным и желательно их снять и, тем самым, обобщить принцип построения когнитивных диаграмм, приведенный в данном примере.

Но это означает, что данный подход не позволяет сравнивать классы, описанные различными, т.е. непересекающимися наборами признаков. Но даже если общие признаки и есть, то невозможность учета вклада остальных признаков является недостатком классического подхода, так как из содержательного анализа связей неконтролируемо исключается потенциально существенная информация. Таким образом, классический подход имеет ограниченную применимость при решении задачи №1. Для решения задачи №2 подход, основанный на формуле (3.44), вообще не применим, так как различные уровни системной организации классов образованы различными признаками и, следовательно, между уровнями не будет ни одной одно–однозначной связи.

Основываясь на этих соображениях, предлагается в общем случае учитывать вклад в сходство/различие двух классов, который вносят не только общие, но и остальные признаки. Логично предположить, что этот вклад (при прочих равных условиях) будет тем меньше, чем меньше корреляция между этими признаками.

Следовательно, для обобщения выражения для силы связи (3.43) необходимо умножить произведение информативностей признаков на коэффициент корреляции между ними, отражающий степень сходства или различия признаков по смыслу.

Таким образом, будем считать, что любые два признака (i,k) вносят определенный вклад в сходство/различие двух классов (j,l), определяемый сходством/различием признаков и количеством информации о принадлежности к этим классам, которое содержится в данных признаках:

(3. 45)

где: – классический коэффициент корреляции Пирсона, количественно определяющий степень сходства по смыслу двух признаков: i и k, на основе учета вклада каждой связи, образованной содержащейся в них информацией о принадлежности к j–му классу

(3. 46)

где

	– средняя информативность координат вектора i–го признака;
	– средняя информативность координат вектора k–го признака;
	– среднеквадратичное отклонение координат вектора i–го признака;
	– среднеквадратичное отклонение координат вектора k–го признака.

Коэффициент корреляции между признаками (3.46) рассчитывается на основе всей обучающей выборки, а не только объектов двух сравниваемых классов. Так как коэффициент корреляции между признаками (3.46) практически всегда не равен нулю, то каждый признак i образует связи со всеми признаками k, где k={1,...,A}, а каждый признак k в свою очередь связан со всеми остальными признаками. Это означает, что выражение (3.45) является обобщением (3.43) с учетом много-многозначных связей.

На основе этих представлений сформулируем выражение для обобщенного коэффициента корреляции Пирсона между двумя классами: j и l, учитывающего вклад в их сходство/различие не только одно–однозначных, но и много–многозначных связей, образуемых коррелирующими признаками. Когнитивные диаграммы с много–многозначными связями предлагается называть обобщенными когнитивными диаграммами.

(3. 47)

где K_ik определяется выражением (3.46).

Сравним классический (3.44) и обобщенный (3.47) коэффициенты корреляции Пирсона друг с другом. Очевидно, при i=k (3.47) преобразуется в (3.44), т.е. соблюдается принцип соответствия. Отметим, что модель позволяет задавать минимальный коэффициент корреляции (порог) между признаками, образующими учитываемые связи. При пороге 100% отображаются только одно–однозначные связи, учитываемые в классическом коэффициенте корреляции (3.44). Из выражений (3.47) и (3.44) видно, что

(3. 48)

так как в обобщенном коэффициенте корреляции учитываются связи между классами, образованные за счет учета корреляций между различными признаками. Ясно, что отношение

(3. 49)

отражает степень избыточности описания классов. В модели имеется возможность исключения из системы признаков наименее ценных из них для идентификации классов. При этом в первую очередь удаляются сильно коррелирующие друг с другом признаки. В результате степень избыточности системы признаков уменьшается, и она становится ближе к ортонормированной.

Рассмотрим вопрос о единицах измерения, в которых количественно выражаются связи между классами.

Сходство двух признаков выражается величиной от – 1 до +1.

Максимальная теоретически возможная информативность признака в Bit выражается формулой

(3. 50)

Таким образом, учитывая выражения (3.45) и (3.50) получаем, что максимальная теоретически возможная сила связи R_max равна

(3. 51)

В разработанном инструментарии СК-анализа, реализующем данную модель (описанном в лекции 6), реализован режим отображения когнитивной графики, где фактическая сила связи (3.45) в когнитивных диаграммах выражается в процентах от максимальной теоретически возможной силы связи (3.50). На графической диаграмме (рисунок 32) отображается 8 наиболее сильных по модулю связей, рассчитанных согласно формулы (3.47), причем знак связи изображается цветом (красный +, синий – ), а величина – толщиной линии.

Рисунок 32. Когнитивная диаграмма
конструкта классов "Качество-количество"

Имеется возможность выводить диаграммы только с положительными или только с отрицательными связями (для не цветных принтеров).

Частным случаем предложенных в данной работе обобщенных когнитивных диаграмм являются известные диаграммы В.С.Мерлина (Очерк интегрального исследования индивидуальности. - М., 1986. - 187с.). Эти диаграммы представляют обобщенные когнитивные диаграммы, формируемые в соответствии с предложенной моделью при следующих граничных условиях:

1. Класс сравнивается сам с собой.

2. Фильтрация левого и правого информационных портретов выбрана по уровням системной организации признаков (в данном случае – уровням Мерлина, терм. авт.).

3. Левый класс отображается с фильтрацией по одному уровню системной организации, а правый – по другому.

4. Диалог задания вида диаграмм предоставляет пользователю возможность задать следующие параметры:

– способ нормирования толщины линий, отображающих связи: нормирование по текущей диаграмме или по всем диаграммам;

– способ фильтрации признаков в информационных портретах диаграммы: по диапазону признаков или по диапазону уровней системной организации (уровням Мерлина);

– сами диапазоны признаков или уровней для левого и правого информационных портретов;

– максимальное количество связей, отображаемых на диаграмме;

– уровень сходства признаков, образующих одну связь, отображаемую на диаграмме: от 0 до 100%. При уровне сходства 100% в диаграммах отображаются только связи, образованные теми признаками, которые есть в обоих портретах одновременно, т.е. взаимно–однозначные связи. При уровне сходства менее 100% вообще говоря связи становятся много–многозначными, так как каждый признак корреляционно связан со всеми остальными;

– уровень сходства классов, отображаемых на диаграмме.

Таким образом, в предлагаемой математической модели в общем виде реализована возможность содержательного сравнения обобщенных образов состояний АОУ и факторов, т.е. построения когнитивных диаграмм [81], веса атрибутов определяются автоматически на основе исходных данных в соответствии с математической моделью и могут принимать различные по величине положительные и отрицательные значения. Кроме того на основе кластерного анализа атрибутов определяются корреляции между ними, которые учитываются при определении вклада атрибутов в сходство или различие классов. Поэтому отношения между атрибутами разных классов в когнитивной диаграмме не "один к одному", как в диаграмме на рисунке 31, а "многие ко многим" (рисунок 32).

В информационном портрете состояния АОУ показано, какое количество информации о принадлежности (не принадлежности) АОУ к данному состоянию, а также о переходе (не переходе) АОУ в данное состояние содержится в том факте, что на АОУ действуют факторы, содержащиеся в данном информационном портрете.

Кластерно-конструктивный анализ дает результат сравнения состояний АОУ друг с другом, т.е. показывает, насколько эти состояния сходны друг с другом и насколько отличаются друг от друга. Но он не показывает, какими факторами эти состояния АОУ похожи и какими отличаются, и какой вклад каждый фактор вносит в сходство или различие каждых двух состояний. Чтобы получить эту информацию, необходимо проанализировать два информационных портрета, что и делается при содержательном сравнении состояний АОУ .

Смысл и значение диаграмм Мерлина применительно к проблематике АСУ состоит в том, что они наглядно представляют внутреннюю структуру детерминации состояний АОУ, т.е. показывают, каким образом связаны друг с другом факторы и будущие состояния АОУ.

Таким образом:

– для моделирования процессов принятия решений в рефлексивных АСУ активными системами целесообразно применение многокритериального подхода с аддитивным интегральным критерием, в котором в качестве частных критериев используется семантическая мера целесообразности информации (Харкевич, 1960);

– предложенная математическая модель обеспечивает эффективное решение следующих задач, возникающих при синтезе адаптивных АСУ АОУ: разработка абстрактной информационной модели АОУ; адаптация и конкретизация абстрактной модели на основе апостериорной информации о реальном поведении АОУ; расчет влияния факторов на переход АОУ в различные возможные состояния; прогнозирование поведения АОУ при конкретном управляющем воздействии и выработка многофакторного управляющего воздействия (основная задача АСУ); выявление факторов, вносящих основной вклад в детерминацию состояния АОУ; контролируемое удаление второстепенных факторов с низкой дифференцирующей способностью, т.е. снижение размерности модели при заданных ограничениях; сравнение влияния факторов, сравнение целевых и других состояний АОУ.

Предложенная методология, основанная на теории информации, обеспечивает эффективное моделирование задач принятия решений в адаптивных АСУ сложными системами.

Содержательное (смысловое) сравнение признаков

Предложенная математическая модель позволяет осуществить содержательное сравнение информационных портретов двух признаков.

Выявляются классы, которые есть по крайней мере в одном из векторов. Такие классы называются связями, так как благодаря тому, что они либо тождественны друг другу, либо между ними имеется определенное сходство или различие, они вносят определенный вклад в отношения сходства/различия между признаками по смыслу.

Все связи между признаками сортируются в порядке убывания модуля, в соответствии с определенными ограничениями, связанными с тем, что нет необходимости учитывать очень слабые связи.

Для каждого класса известно, какое количество информации о принадлежности к нему содержит данный признак – это информативность. Здесь необходимо уточнить, что информативность признака – это не только количество информации в признаке о принадлежности к данному классу, но и количество информации в классе о том, что при нем наблюдается данный признак, т.е. это взаимная информация класса и признака.

Если бы классы были тождественны друг другу, т.е. это был бы один класс, то его вклад в сходство/различие двух признаков был бы просто равен соответствующему данному классу слагаемому корреляции этих признаков, т.е. просто произведению информативностей.

Но поскольку это в общем случае это могут быть различные классы, то, очевидно, необходимо умножить произведение информативностей на коэффициент корреляции между классами.

Таким образом, будем считать, что любые два класса (j,l) вносят определенный вклад в сходство/различие двух признаков (i,k), определяемый сходством/различием этих классов и количеством информации о принадлежности к ним, которое содержится в данных признаках

(3. 52)

Вывод формулы (3.52) обобщенного коэффициента корреляции Пирсона для двух признаков совершенно аналогичен выводу формулы (3.47), поэтому он здесь не приводится. Формулы для всех входящих в (3.52) величин приведены выше в предыдущем разделе.

Так же, как и в режиме содержательного сравнения классов, в данном режиме сила связи выражается в процентах от максимальной теоретически–возможной силы связи. На диаграммах отображается 16 наиболее значимых связей, рассчитанных согласно этой формуле, причем знак связи изображается цветом (красный +, синий –), а величина – толщиной линии. Имеется возможность вывода диаграмм только с положительными или только с отрицательными связями.

Математическая модель позволяет получить обобщенные инвертированные когнитивные диаграммы для любых двух заданных признаков, для пар наиболее похожих и непохожих признаков, для всех их возможных сочетаний, а также инвертированные диаграммы Мерлина.

Необходимо отметить, что понятия, соответствующие по смыслу терминам "обобщенная инвертированная когнитивная диаграмма" и "инвертированная диаграмма Мерлина" не упоминаются даже в фундаментальных руководствах по когнитивной психологии и впервые предложены автором в [125]. Эти диаграммы представляют собой частный случай обобщенных когнитивных диаграмм признаков, формируемых в соответствии с предложенной математической моделью при следующих ограничениях:

1. Признак сравнивается сам с собой.

2. Выбрана фильтрация левого и правого вектора по уровням системной организации классов (аналог уровней Мерлина для свойств).

3. Левый вектор отображается с фильтрацией по одному уровню системной организации классов, а правый – по другому.

Обоснование сопоставимости частных критериев I_ij

Применение этого метода корректно, если можно сравнивать суммарное количество информации о переходе АОУ в различные состояния, рассчитанное в соответствии с выражением (3.44), т.е. если они сопоставимы друг с другом.

Будем считать, что величины сопоставимы тогда и только тогда, когда одновременно выполняются следующие три условия:

1. Сопоставимы индивидуальные количества информации, содержащейся в признаках о принадлежности к классам.

2. Сопоставимы величины, рассчитанные для одного объекта и разных классов.

3. Сопоставимы величины, рассчитанные для разных объектов и разных классов.

Очевидно, для решения всех этих вопросов необходимо дать точное и полное определение самого термина "сопоставимость".

Считается, что величины сопоставимы, если существует некоторая количественная шкала для измерения этих величин.

Таким образом, в нашем случае сопоставимость обеспечивается, если на шкале определены направление и единица измерения, а также есть абсолютный минимум (ноль) или максимум.

Докажем теоремы о выполнении условий сопоставимости для упрощенной и полной информационных моделей объектов и классов распознавания. Для этого рассмотрим вышеперечисленные необходимые и достаточные условия сопоставимости для упрощенной и полной информационных моделей.

Теорема-1: Индивидуальные количества информации, содержащейся в признаках объекта о принадлежности к классам, сопоставимы между собой.

В упрощенной информационной модели класса и информационной модели объекта принято, что все признаки имеют одинаковый вес, который равен 1, если признак есть у класса, и 0, если его нет. Уже одним этим обеспечивается сопоставимость индивидуальных количеств информации в упрощенной модели.

В полной модели количество информации рассчитывается в соответствии с модифицированной формулой Харкевича (3.28). Таким образом, в полной информационной модели класса для каждого признака известно, какое количество информации о принадлежности к данному классу он содержит. Это количество информации может быть положительным, нулевым и отрицательным, но не может превосходить некоторой максимальной величины, определяемой количеством классов распознавания: I=Log₂W (мера Хартли), где W – количество классов распознавания. Следовательно, для полной информационной модели сопоставимость индивидуальных количеств информации также обеспечивается, так как для них применима шкала отношений.

Это означает, что индивидуальные количества информации можно суммировать и ввести интегральный критерий как аддитивную меру от индивидуальных количеств информации, что и требовалось доказать.

Теорема-2: Величины суммарной информации, рассчитанные для одного объекта и разных классов, сопоставимы друг с другом.

В упрощенной информационной модели вариант расстояния Хэмминга H^j, в котором учитываются только совпадения единиц (т.е. существующих признаков), для кодовых слов объекта и класса равно:

(3. 53)

где – кодовое слово (профиль, массив–локатор) j–го класса;

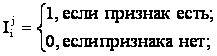
L_i – кодовое слово (профиль, массив–локатор) объекта.

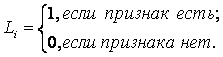
Пусть длина кодового слова (количество признаков) равна А. Длины кодовых слов объекта и классов одинаковы. Признаки могут принимать значения {0,1}. Тогда из этих условий и выражения (3.53) следует:

(3. 54)

Но выражение (3.54) является математическим определением шкалы отношений, что означает полную сопоставимость предложенной меры сходства для упрощенной информационной модели одного объекта и многих классов. Для обобщенной информационной модели этот вывод сохраняет силу, т.к. в этой модели информация в соответствии с выражением (3.28) измеряется в единицах измерения – битах, определенных на шкале измерения информации, и на этой шкале имеется 0 и теоретический максимум, определяемый в соответствии с выражением Хартли. В полной информационной модели мера сходства объекта с классом имеет вид, определяемый выражением (3.39).

Очевидно, величина нормирована:

(3. 55)

что и доказывает применимость шкалы отношений и полную сопоставимость меры сходства для полной информационной модели одного объекта и многих классов.

Это значит, что можно сравнивать меры сходства данного объекта с каждым из классов и ранжировать классы в порядке убывания сходства с данным объектом , что и требовалось доказать.

Теорема-3: Величины суммарной информации, рассчитанные для разных объектов и разных классов, а также классов и классов, признаков и признаков, взаимно-сопоставимы.

Очевидно, величина , рассчитанная по формуле (3.39) для различных объектов и классов нормирована:

(3. 56)

что и доказывает применимость шкалы отношений и полную сопоставимость мер сходства для полной информационной модели многих объектов и многих классов.

Это значит, что можно сравнивать меры сходства различных объектов с классами распознавания и делать выводы о том, что одни объекты распознаются лучше, а другие хуже на данном наборе классов и признаков, что и т.д.

Аналогичные рассуждения верны и для сравнения векторов классов друг с другом, а также векторов признаков друг с другом, что позволяет применить модели кластерно-конструктивного анализа и алгоритмы построения семантических сетей, что и требовалось доказать.

Теорема-4: Неметрический интегральный критерий сходства, основанный на модифицированной формуле А.Харкевича и обобщенной лемме Неймана-Пирсона, аддитивен.

Рассмотрим информационные модели распознаваемого объекта и классов распознавания, т.е. модели, основанные на теории кодирования – декодирования и расстоянии Хэмминга (кодовое расстояние) в качестве критерия сходства. Эта модель является упрощенной, но достаточно адекватной для решения вопроса об аддитивности меры сходства объектов и классов.

Информационная модель распознаваемого объекта представляет собой двоичное слово, каждый разряд которого соответствует определенному признаку. Если признак есть у распознаваемого объекта, то соответствующий разряд имеет значение 1, если нет – то 0. Двоичное слово с установленными в 1 разрядами, соответствующими признакам распознаваемого объекта, называется его кодовым словом.

Упрощенная информационная модель класса распознавания есть двоичное слово, каждый разряд которого соответствует определенному признаку. Соответствие между двоичными разрядами и признаками для классов то же самое, что и для распознаваемых объектов. Если признак есть у класса, то соответствующий разряд имеет значение 1, если нет – то 0. Двоичное слово с установленными в 1 разрядами, соответствующими признакам класса, называется его кодовым словом.

Такая модель класса является упрощенной, так как в ней принято, что все признаки имеют одинаковый вес равный 1, если он есть у класса, и 0, если его нет, тогда как в полной информационной модели класса для каждого признака известно, какое количество информации о принадлежности к данному классу он содержит. Это количество информации может быть положительным, нулевым и отрицательным, но не может превосходить некоторой максимальной величины, определяемой количеством классов распознавания: I=Log₂W (мера Хартли), где W – количество классов.

Таким образом, в упрощенной информационной модели различные классы распознавания отличаются друг от друга только наборами признаков, которые им соответствуют.

При использовании этих упрощенных моделей задача распознавания объекта сводится к задаче декодирования, т.е. кодовые слова объектов рассматриваются как искаженные зашумленным каналом связи кодовые слова классов. Распознавание состоит в том, что по кодовому слову объекта определяется наиболее близкое ему в определенном смысле кодовое слово класса. При этом естественной и наиболее простой мерой сходства между распознаваемым объектом и классом является расстояние Хэмминга между их кодовыми словами, т.е. количество разрядов, которыми они отличаются друг от друга.

Рассмотрим теперь вопрос об аддитивности количества информации как частного критерия в интегральном критерии.

Известно [194], что существует всего два варианта формирования интегрального критерия из частных критериев: аддитивный и мультипликативный, поэтому задача сводится к выбору одного из этих вариантов. Следует отметить, что аддитивный критерий может рассматриваться как логарифм мультипликативного, а т.к. логарифм является монотонно-возрастающей функцией, то в принципе разница между этими критериями для принятия решений не так уж и велика, что подтверждается и в их сравнительных численных исследованиях.

Рассмотрим эти варианты. Пусть кодовое слово объекта состоит из N разрядов. Тогда добавление еще одного разряда, отображающего имеющийся (1) или отсутствующий (0) признак, приведет к различным результатам в случаях, когда интегральный критерий есть аддитивная и мультипликативная функция индивидуальных количеств информации в признаках (таблица 19).

Таблица 19 – СРАВНЕНИЕ АДДИТИВНОГО И МУЛЬТИПЛИКАТИВНОГО ВАРИАНТОВ ИНТЕГРАЛЬНОГО КРИТЕРИЯ
Дополнительный признак	Аддитивная функция:	Мультипликативная функция:
Есть (1)
Нет (0)

Здесь предполагается, что: I=f(n), f(1)=1, f(0)=0.

Итак, если функция аддитивна – добавление еще одного разряда увеличит количество информации в кодовом слове на 1 бит, если соответствующий признак есть, и не изменит этого количества, если его нет; если же функция мультипликативна, – то это не изменит количества информации в кодовом слове, если соответствующий признак есть, и сделает его равным нулю, если его нет.

Очевидно, мультипликативный вариант интегрального критерия не соответствует классическим представлениям о природе информации, тогда как аддитивный вариант полностью им соответствует: требование аддитивности самой меры информации было впервые обосновано Хартли в 1928 году, подтверждено Шенноном в 1948 году, и в последующем развитии теории информации никогда не подвергалось сомнению. На аддитивности частных критериев, имеющих смысл количества информации, основана известная лемма Неймана-Пирсона [194, стр.152].

Пусть по выборке (т.е. совокупности факторов) {x=x_1,…, x_N} требуется отдать предпочтение одной из конкурирующих гипотез (H₁ или H₀), т.е. определить в какое будущее состояние перейдет объект управления, если известны распределения наблюдений при каждой из них (по данным обучающей выборки), т.е. р(х|H₀) и р(х|H₁). Как обработать предпочтительную гипотезу? Из теории информации известно, что никакая обработка не может увеличить количества информации, содержащегося в выборке {х}. Следовательно, выборке {х} нужно поставить в соответствие число, содержащее всю полезную информацию, т.е. обработать выборку без потерь. Возникает мысль о у том, чтобы вычислить индивидуальные количества информации в выборке {х} о каждой из гипотез и сравнить их:

Какой из гипотез отдать предпочтение, зависит теперь от величины Di и от того, какой порог сравнения мы назначим. Оптимальность данной статистической процедуры специально доказывается в математической статистике, – именно к этому сводится содержание фундаментальной Леммы Неймана-Пирсона, которая утверждает, что предпочтение следует отдавать той статистической гипотезе, о которой в выборке содержится больше информации.

Согласно описанной выше процедуре предполагается, что объект управления перейдет в то будущее состояние, о переходе в которое в системе факторов содержится большее суммарное количество информации.

Таким образом, аддитивность интегрального критерия, основанного на частных критериях, имеющих смысл количества информации, можно считать обоснованной, что и требовалось доказать.

Обобщение интегральной модели путем учета значений выходных параметров объекта управления

Выходные параметры– это свойства объекта управления, зависят от входных параметров (в том числе параметров, характеризующих среду) и связанны с его целевым состоянием сложным и неоднозначным способом:

Задача идентификации состояния АОУ по его выходным параметрам решается подсистемой идентификации управляющей подсистемы, работающей на принципах системы распознавания образов. При этом классами распознавания являются выходные состояния АОУ, а признаками – его выходные параметры.

Подсистема выработки управляющих воздействий, также основанная на алгоритмах распознавания образов, обеспечивает выбор управления , переводящего объект управления в целевое состояние .

При этом последовательно решаются следующие две обратные задачи распознавания:

во–первых, по заданному целевому состоянию определяются наиболее характерные для данного состояния выходные параметры объекта управления:

во–вторых, по определенному на предыдущем шаге набору выходных параметров определяются входные параметры , с наибольшей эффективностью переводящие объект управления в данное целевое состояние с этими выходными параметрами:

1. Таким образом, определенная ограниченность подхода Шеннона, рассмотренная в данной главе, преодолевается в семантической информационной математической модели СК-анализа, основанной на СТИ. В рамках СТИ установлено, что одной из наиболее перспективных конкретизаций апостериорного подхода, является подход, предложенный в 1960 году А.А.Харкевичем [242]. Для моделирования процессов принятия решений в рефлексивных АСУ активными объектами предложено применить многокритериальный подхода с аддитивным интегральным критерием, в котором в качестве частных критериев используется системная мера семантической целесообразности информации. При этом количество информации оценивается косвенно: по изменению степени целесообразности поведения системы, получившей эту информацию. В результате получения информации поведение системы улучшается (растет выигрыш), а в результате получения дезинформации – ухудшается (растет проигрыш). Известны и более развитые семантические меры информации [194], основанные на интересных и правдоподобных идеях, однако они наталкиваются на значительные математические трудности и сложности в программной реализации, поэтому их рассмотрение в данном исследовании признано нецелесообразным.

2. Предложенная математическая модель обеспечивает эффективное решение следующих задач, возникающих в рефлексивных АСУ АО:

– разработка абстрактной информационной модели АОУ;

– адаптация и конкретизация абстрактной модели на основе информации о реальном поведении АОУ;

– расчет влияния факторов на переход АОУ в различные возможные состояния;

– прогнозирование поведения АОУ при конкретном управляющем воздействии и выработка многофакторного управляющего воздействия (основная задача АСУ);

– выявление факторов, вносящих основной вклад в детерминацию состояния АОУ;

– корректное удаление второстепенных факторов с низкой дифференцирующей способностью, т.е. снижение размерности модели при заданных граничных условиях;

– сравнение влияния факторов, сравнение целевых и других состояний АОУ.

3. Показано, что предложенная методология, основанная на системном обобщении теории информации, обеспечивает эффективное моделирование задач принятия решений в РАСУ АОУ.

4. Доказана возможность сведения многокритериальной задачи принятия решений к однокритериальной, показана глубокая внутренняя взаимосвязь данной модели с математической моделью распознавания образов. На этой основе введено понятие "интегрального метода" распознавания и принятия решений и, после анализа и переосмысления основных понятий теории информации, предложена базовая математическая модель "интегрального метода", основанная на системной теории информации. Показано, что теория информации может рассматриваться как единая математическая и методологическая основа методов распознавания образов и теории принятия решений. При этом распознавание образов рассматривается как принятие решения о принадлежности объекта к определенному классу распознавания, прогнозирование – как распознавание будущих состояний, а принятие решения об управляющем воздействии на объект управления в АСУ как решение обратной задачи прогнозирования (распознавания).

5. Проведено исследование базовой математической модели на примере решения основной задачи АСУ – задачи принятия решения о наиболее эффективном управляющем воздействии. Осуществлена декомпозиция основной задачи в последовательность частных задач для каждой из которых найдено решение, показана взаимосвязь основной задачи АСУ с задачей декодирования теории информации.

1.2.2.4. Некоторые свойства математической модели (сходимость, адекватность, устойчивость и др.)

Под сходимостью семантической информационной модели в данной работе понимается:

а) зависимость информативностей факторов (в матрице информативностей) от объема обучающей выборки;

б) зависимость адекватности модели (интегральной и дифференциальной валидности) от объема обучающей выборки.

Для измерения сходимости в смыслах "а" и "б" в инструментарии СК-анализа – системе "Эйдос" реализован специальный исследовательский режим.

Под адекватностью модели понимается ее внутренняя и внешняя дифференциальная и интегральная валидность. Понятие валидности является уточнением понятия адекватности, для которого определены процедуры количественного измерения, т.е. валидность – это количественная адекватность. Это понятие количественно отражает способность модели давать правильные результаты идентификации, прогнозирования и способность вырабатывать правильные рекомендации по управлению. Под внутренней валидностью понимается валидность модели, измеренная после синтеза модели путем идентификации объектов обучающей выборки. Под внешней валидностью понимается валидность модели, измеренная после синтеза модели путем идентификации объектов, не входящих в обучающую выборку. Под дифференциальной валидностью модели понимается достоверность идентификации объектов в разрезе по классам. Под интегральной валидностью средневзвешенная дифференциальная валидность. Возможны все сочетания: внутренняя дифференциальная валидность, внешняя интегральная валидность и т.д. (таблица 20).

Таблица 20 – К ОПРЕДЕЛЕНИЮ ПОНЯТИЯ ВАЛИДНОСТИ
	Внутренняя валидность	Внешняя валидность
Дифференциальная валидность	Валидность модели, измеренная после синтеза модели путем идентификации объектов обучающей выборки в разрезе по классам	Валидность модели, измеренная после синтеза модели путем идентификации объектов, не входящих в обучающую выборку в разрезе по классам
Интегральная валидность	Средневзвешенная по всем классам достоверность идентификации объектов обучающей выборки	Средневзвешенная по всем классам достоверность идентификации объектов, не входящих в обучающую выборку

Под устойчивостью модели понимается ее способность давать незначительные различия в прогнозах и рекомендациях по управлению при незначительных различиях в исходных данных для решения этих задач.

1.2.2.4.1. Непараметричность модели. Робастные процедуры и фильтры для исключения артефактов

Предложенная семантическая информационная модель является непараметрической, т.к. не основана на предположениях о нормальности распределений исследуемой выборки. Под робастными понимаются процедуры, обеспечивающие устойчивую работу модели на исходных данных, зашумленных артефактами, т.е. данными, выпадающими из общих статистических закономерностей, которым подчиняется исследуемая выборка. Выявление артефактов возможно только при большой статистике, т.к. при малой статистике все частоты атрибутов малы и невозможно отличить артефакт от значимого атрибута. Критерий выявления артефактов основан на том, что при увеличении объема статистики частоты значимых атрибутов растут, как правило, пропорционально объему выборки, а частоты артефактов так и остаются чрезвычайно малыми, близкими к единице. В модели реализована такая процедура удаления наиболее вероятных артефактов, и она, как показывает опыт, существенно повышает качество (адекватность) модели.

1.2.2.4.2. Зависимость информативностей факторов от объема обучающей выборки

При учете в модели апостериорной информации, содержащейся в очередном объекте обучающей выборки, осуществляется перерасчет значений информативностей всех атрибутов. При этом изменяется количество информации, содержащейся в факте обнаружения у объекта данного атрибута о принадлежности объекта к определенному классу.

В этом процессе пересчета информативностей атрибута их значения "сходятся" к некоторому пределу в соответствии с двумя "сценариями":

1) процесс "последовательных приближений", напоминающего по своей форме "затухающие колебания" (рисунок 33);

2) относительно "плавное" возрастание или убывание с небольшими временными отклонениями от этой тенденции (рисунок 34).

Рисунок 33. Зависимость количества информации, содержащегося в атрибуте №1 о принадлежности объекта, обладающего этим атрибутом, к классу №4 от объема обучающей выборки

Рисунок 34. Зависимость количества информации, содержащегося в атрибуте №1 о принадлежности объекта, обладающего этим атрибутом, к классу №10 от объема обучающей выборки

Как показали численные эксперименты и специально проведенные исследования, других сценариев на практике не наблюдается.

В любом случае при накоплении достаточно большой статистики и сохранении закономерностей предметной области, отражаемых обучающей выборкой, модель стабилизируется в том смысле, что значения информативностей атрибутов перестают существенно изменяться.

Это дает основание утверждать, что при достижении этого состояния добавление новых примеров из обучающей выборки не вносит в модель ничего нового в модель и процесс обучения продолжать нецелесообразно. Это и является одним из критериев для принятия решения об остановке процесса обучения.

1.2.2.4.3. Зависимость адекватности семантической информационной модели от объема обучающей выборки (адекватность при малых и больших выборках)

При экспериментальном исследовании свойств предлагаемой математической модели было установлено следующее (рисунок 35).

Рисунок 35. Зависимость адекватности модели от объема обучающей выборки

1. При малых выборках адекватность модели (внутренняя интегральная и дифференциальная валидность) равна 100% (рисунок 35, диапазон "А"). Это можно объяснить тем, что при малых объемах выборки все выявленные закономерности имеют детерминистский характер.

2. При увеличении объема исследуемой выборки происходит понижение адекватности модели (переход: А®В) и стабилизация ее адекватности на некотором уровне около 95-98% (рисунок 35, диапазон "В").

3. Учет в модели объектов обучающей выборки, отражающих закономерности, качественно отличающиеся от ранее выявленных, приводит к понижению адекватности модели (переход: В®С) и ее стабилизации на уровне от 80 до 90% (рисунок 35, диапазон "С").

4. Внутри диапазона "В" вариабельность объектов обучающей выборки по закономерностям "атрибут®класс" меньше, чем в диапазоне "С", т.е. объекты обучающей выборки диапазона "В" более однородны, чем "С".

Выявленные в модели причинно-следственные закономерности имеют силу для определенного подмножества обучающей выборки, например, отражающих определенный период времени, который соответствует детерминистскому периоду развития предметной области. При качественном изменении закономерностей устаревшие данные могут даже на некоторое время (пока модель не сойдется к новым закономерностям) нарушать ее адекватность.

В многочисленных проведенных практических исследованных модель показала высокую скорость сходимости и высокую адекватность на малых выборках. На больших выборках (т.е. охватывающих несколько детерминистских и бифуркационных состояний предметной области) закономерности с коротким периодом "причина-следствие" переформировываются заново, а с длительным (охватывающим несколько детерминистских и бифуркационных состояний) – автоматически становятся незначимыми и не ухудшают адекватность модели, если процесс апериодический, или сохраняют силу, если они имеют фундаментальный характер.

Выявленные закономерности сходимости модели позволяют сформулировать следующий критерий остановки процесса обучения: если в модели ничего существенно не меняется при добавлении в обучающую выборку все новых и новых данных, то это означает, что модель адекватно отображает генеральную совокупность, к которой относятся эти данные, и продолжать процесс обучения нецелесообразно.

Здесь уместно рассмотреть ответ на следующий вопрос. Если для формирования образов классов распознавания предъявлено настолько малое количество обучающих объектов, что говорить об обобщении и статистике не приходится, то как это может повлиять на качество формирования модели и ее адекватность? При большой статистике, как показывает опыт, около 95% объектов, формирующих образ некоторого класса оказывается типичными для него, а остальные не типичными. Следовательно, если этот образ формируется на основе буквально одного - двух объектов, то вероятнее всего (т.е. с вероятностью около 95%) они являются типичными, и, следовательно, образ будет сформирован практически таким же, как и при большой статистике, т.е. правильным. При увеличении статистики в этом случае информативности признаков, составляющих образ практически не меняются). Но есть некоторая, сравнительно незначительная вероятность (около 5%), что попадется нетипичная анкета. Тогда при увеличении статистики образ быстро качественно изменится и "быстро сойдется" к адекватному, "нетипичная" анкета будет идентифицирована и ее данные либо будут удалены из модели, либо для нее специально будет создан свой класс.

При незначительной статистике относительный вклад каждого объекта в обобщенный образ некоторого класса, сформированный с его применением, будет достаточно велик. Поэтому в этом случае при распознавании модель уверенно относит объект к этому классу. При большой статистике модель также уверенно относит типичные объекты к классам, сформированным с их применением. Незначительное количество нетипичных объектов могут быть распознаны ошибочно, т.е. не отнесены моделью к тем классам, к которым их отнесли эксперты.

Наличие в системе очень сходных классов также может формально уменьшать валидность модели. Однако фактически эти очень сходные классы целесообразно объединить в один, т.к. по-видимому, их разделение объективно ничем не оправдано, т.е. не соответствует действительности. Для осуществления данной операции в математической модели целесообразно использовать режим: "Получение статистической характеристики обучающей выборки и объединение классов (ручной ремонт обучающей выборки)".

1.2.2.4.4. Семантическая устойчивость модели

Под семантической устойчивостью модели [81] нами понимается ее свойство давать малое различие в прогнозе при замене одних факторов, другими, мало отличающимися по смыслу (т.е. сходными по их влиянию на поведение АОУ). Проведенные автором исследования численные эксперименты в течение 1987 – 2005 годов показали, что разработанная математическая модель обладает очень высокой семантической устойчивостью.

1.2.2.4.5. Зависимость некоторых параметров модели от ее ортонормированности

Изучим зависимость уровня системности, степени детерминированности и адекватности модели от ее ортонормированности. В связи с тем, что соответствующий научно-исследовательский режим, позволяющий изучить эти зависимости методом численного эксперимента, на момент написания данной работы находится в стадии разработки, получим интересующие нас зависимости путем анализа выражений (3.9) и (3.25).

При этом будем различать ортонормированность модели по классам и ортонормированность по атрибутам.

Зависимость адекватности модели от ее ортонормированности

Модель изучалась методом численного эксперимента. При этом были получены следующие результаты.

На 1-м этапе ортонормирования адекватность модели (ее внутренняя дифференциальная и интегральная валидность) возрастает. Это можно объяснить тем, что, во-первых, уменьшается количество ошибок идентификации с близкими, т.е. коррелирующими классами, и, во-вторых, удаление из модели малоинформативных признаков по сути улучшает отношение "сигнал/шум" модели, т.е. качество идентификации.

На 2-м этапе ортонормирования адекватность модели стабилизируется и незначительно колеблется около максимума. Это объясняется тем, что атрибуты, удаляемые на этом этапе, не являются критическим для адекватности модели.

На 3-м этапе ортонормирования адекватность модели начинает уменьшаться, т.к. дальнейшее удаление атрибутов не позволяет адекватно описать предметную область.

При приближении процесса ортонормирования к 3-му этапу или его наступлении этот процесс должен быть остановлен.

Зависимость уровня системности модели от ее ортонормированности

Рассмотрим выражение (3.9):

(3.9)

При выполнении операции ортонормирования по классам из модели последовательно удаляются те из них, которые наиболее сильно корреляционно связаны друг с другом. В результате в модели остаются классы практически не коррелирующие, т.е. ортонормированные. Поэтому можно предположить, что в результате ортонормирования правила запрета на образование подсистем классов становятся более жесткими, и уровень системности модели уменьшается.

Зависимость степени детерминированности модели от ее ортонормированности

Рассмотрим выражение (3.25):

(3.25)

Так как каждый класс как правило описан более чем одним признаком, то при ортонормировании классов и удалении некоторых из них из модели суммарное количество признаков N будет уменьшаться быстрее, чем количество классов W, поэтому степень детерминированности будет возрастать.

При ортонормировании атрибутов числитель выражения (3.25) не изменяется, а знаменатель уменьшается, поэтому и в этом случае степень детерминированности возрастает.

Таким образом, ортонормирование модели приводит к увеличению степени ее детерминированности.

По этой причине предлагается считать "детерменированностью" и "системностью" модели не их значения в текущем состоянии модели, а тот предел, к которому стремятся эти величины при корректном ортонормировании модели при достижении ею точки максимума адекватности.

1.2.2.5. Взаимосвязь математической модели СК-анализа с другими моделями

1.2.2.5.1. Взаимосвязь системной меры целесообразности информации со статистикой c² и новая мера уровня системности предметной области

Статистика c² представляет собой сумму вероятностей совместного наблюдения признаков и объектов по всей корреляционной матрице или определенным ее подматрицам (т.е. сумму относительных отклонений частот совместного наблюдения признаков и объектов от среднего):

(3. 57)

где:

– N_ij – фактическое количество встреч i-го признака у объектов j-го класса;

– t – ожидаемое количество встреч i-го признака у объектов j-го класса.

(3. 58)

Отметим, что статистика c² математически связана с количеством информации в системе признаков о классе распознавания, в соответствии с системным обобщением формулы Харкевича для плотности информации (3.28)

(3. 59)

а именно из (3.58) и (3.59) получаем:

(3. 60)

Из (3.60) очевидно:

(3. 61)

Сравнивая выражения (3.57) и (3.61), видим, что числитель в выражении (3.57) под знаком суммы отличается от выражения (3.61) только тем, что в выражении (3.61) вместо значений N_ij и t взяты их логарифмы. Так как логарифм является монотонно возрастающей функцией аргумента, то введение логарифма не меняет общего характера поведения функции.

Фактически это означает, что:

(3. 62)

Если фактическая вероятность наблюдения i–го признака при предъявлении объекта j–го класса равна ожидаемой (средней), то наблюдение этого признака не несет никакой информации о принадлежности объекта к данному классу. Если же она выше средней – то это говорит в пользу того, что предъявлен объект данного класса, если же ниже – то другого.

Поэтому наличие статистической связи (информации) между признаками и классами распознавания, т.е. отличие вероятностей их совместных наблюдений от предсказываемого в соответствии со случайным нормальным распределением, приводит к увеличению фактической статистики c² по сравнению с теоретической величиной.

Из этого следует возможность использования в качестве количественной меры степени выраженности закономерностей в предметной области не матрицы абсолютных частот и меры c², а новой меры H, основанной на матрице информативностей и системном обобщении формулы Харкевича для количества информации:

(3. 63)

где:

– средняя информативность признаков по матрице информативностей.

Меру H в выражении (3.63) предлагается назвать обобщенным критерием сформированности модели Харкевича.

Значение данной меры показывает среднее отличие количества информации в факторах о будущих состояниях активного объекта управления от среднего количества информации в факторе (которое при больших выборках близко к 0). По своей математической форме эта мера сходна с мерами для значимости факторов и степени сформированности образов классов и коррелирует с объемом пространства классов и пространства атрибутов.

Описанная выше математическая модель обеспечивает инвариантность результатов ее синтеза относительно следующих параметров обучающей выборки: суммарное количество и порядок ввода анкет обучающей выборки; количество анкет обучающей выборки по каждому классу распознавания; суммарное количество признаков во всех анкетах обучающей выборки; суммарное количество признаков по эталонным описаниям различных классов распознавания; количество признаков и их порядок в отдельных анкетах обучающей выборки.

Это обеспечивает высокое качество решения задач системой распознавания на неполных и разнородных (в вышеперечисленных аспектах) данных как обучающей, так и распознаваемой выборки, т.е. при таких статистических характеристиках потоков этих данных, которые чаще всего и встречается на практике и которыми невозможно или очень сложно управлять.

1.2.2.5.2. Сравнение, идентификация и прогнозирование как разложение векторов объектов в ряд по векторам классов (объектный анализ)

В разделе 3.2.3 были введены неметрические интегральные критерии сходства объекта, описанного массивом-локатором L_i с обобщенными образами классов I_ij (выражения 3.35 – 3.37)

(3. 64)

В выражении (3.64) круглыми скобками обозначено скалярное произведение. В координатной форме это выражение имеет вид:

,

(3. 65)

где:

– вектор j–го состояния объекта управления;

– вектор состояния предметной области, включающий все виды факторов, характеризующих объект управления, возможные управляющие воздействия и окружающую среду (массив–локатор), т.е.:

Для непрерывного случая выражение (3.65) принимает вид:

(3. 66)

Таким образом, выражение (3.66) представляет собой вариант выражения (3.65) интегрального критерия сходства объекта и класса для непрерывного случая в координатной форме.

Интересно и очень важно отметить, что коэффициенты ряда Фурье по своей математической форме и смыслу сходны с ненормированными коэффициентами корреляции, т.е. по сути скалярными произведениями для непрерывных функций в координатной форме: выражение (3.66), между разлагаемой в ряд кривой f(x) и функциями Sin и Сos различных частот и амплитуд на отрезке [–L, L] [81]:

(3. 67)

где: n={1, 2, 3,…} – натуральное число.

Из сравнения выражений (3.66) и (3.67) следует вывод, что процесс идентификации и прогнозирования (распознавания), реализованный в предложенной математической модели, может рассматриваться как разложение вектора-локатора распознаваемого объекта в ряд по векторам информативностей классов распознавания (которые представляют собой произвольные функции, сформированные при синтезе модели на основе эмпирических данных).

Например, при результатах идентификации, представленных на рисунке 36.

Рисунок 36. Пример разложения профиля курсанта усл.№69
в ряд по обобщенным образам классов

Продолжая развивать аналогию с разложением в ряд, данный результат идентификации можно представить в векторной аналитической форме:

Или в координатной форме, более удобной для численных расчетов:

(3. 68)

где:

I(j) – интегральный критерий сходства массива-локатора, описывающего состояние объекта, и j-го класса, рассчитываемый согласно выражения (3.39):

(3.39)

I(i,j) – вектор обобщенного образа j-го класса, координаты которого рассчитываются в соответствии с системным обобщением формулы Харкевича (3.28):

(3.28)

Примечание: обозначения I(i,j) и I_ij, и т.п. эквивалентны. Смысл всех переменных, входящих в выражения (3.28) и (3.39) раскрыт в разделе 3.1.3 данной работы.

При дальнейшем развитии данной аналогии естественно возникают вопросы: о полноте, избыточности и ортонормированности системы векторов классов как функций, по которым будет вестись разложение вектора объекта; о сходимости, т.е. вообще возможности и корректности такого разложения.

В общем случае вектор объекта совершенно не обязательно должен разлагаться в ряд по векторам классов таким образом, что сумма ряда во всех точках точно совпадала со значениям исходной функции. Это означает, что система векторов классов может быть неполна по отношению к профилю распознаваемого объекта, и, тем более, всех возможных объектов.

Предлагается считать не разлагаемые в ряд, т.е. плохо распознаваемые объекты, суперпозицией хорошо распознаваемых объектов ("похожих" на те, которые использовались для формирования обобщенных образов классов), и объектов, которые и не должны распознаваться, так как объекты этого типа не встречались в обучающей выборке и не использовались для формирования обобщенных образов классов, а также не относятся к представляемой обучающей выборкой генеральной совокупности.

Нераспознаваемую компоненту можно рассматривать либо как шум, либо считать ее полезным сигналом, несущим ценную информацию о еще не исследованных объектах интересующей нас предметной области (в зависимости от целей и тезауруса исследователей). Первый вариант не приводит к осложнениям, так как примененный в математической модели алгоритм сравнения векторов объектов и классов, основанный на вычислении нормированной корреляции Пирсона (сумма произведений), является весьма устойчивым к наличию белого шума в идентифицируемом сигнале. Во втором варианте необходимо дообучить систему распознаванию объектов, несущих такую компоненту (в этой возможности и заключается адаптивность модели). Технически этот вопрос решается просто копированием описаний плохо распознавшихся объектов из распознаваемой выборки в обучающую, их идентификацией экспертами и дообучением системы. Кроме того, может быть целесообразным расширить справочник классов распознавания новыми классами, соответствующими этим объектам.

Но на практике гораздо чаще наблюдается противоположная ситуация (можно даже сказать, что она типична), когда система векторов избыточна, т.е. в системе классов распознавания есть очень похожие классы (между которыми имеет место высокая корреляция, наблюдаемая в режиме: "кластерно-конструктивный анализ"). Практически это означает, что в системе сформировано несколько практически одинаковых образов с разными наименованиями. Для исследователя это само по себе является очень ценной информацией. Однако, если исходить только из потребности разложения распознаваемого объекта в ряд по векторам классов (чтобы определить суперпозицией каких образов он является, т.е. "разложить его на компоненты"), то наличие сильно коррелирующих друг с другом векторов представляется неоправданным, так как просто увеличивает размерности данных, внося в них мало нового по существу. Поэтому возникает задача исключения избыточности системы классов распознавания, т.е. выбора из всей системы классов распознавания такого минимального их набора, в котором профили классов минимально коррелируют друг с другом, т.е. ортогональны в фазовом пространстве признаков. Это условие в теории рядов называется "ортонормируемостью" системы базовых функций, а в факторном анализе связано с идеей выделения "главных компонент".

В предлагаемой математической модели релизованы два варианта выхода из данной ситуации:

1) исключение неформирующихся, расплывчатых классов;

2) объединение почти идентичных по содержанию (дублирующих друг друга) классов.

Но выбрать нужный вариант и реализовать его, используя соответствующие режимы, пользователь технологии АСК-анализа должен сам. Вся необходимая и достаточная информация для принятия соответствующих решений предоставляется пользователю инструментария АСК-анализа.

Если считать, что функции образов составляют формально–логическую систему, к которой применима теорема Геделя, то можно сформулировать эту теорему для данного случая следующим образом: "Для любой системы базисных функций в принципе всегда может существовать по крайней мере одна такая функция, что она не может быть разложена в ряд по данной системе базисных функций, т.е. функция, которая является ортонормированной ко всей системе базисных функций в целом".

Очевидно, не взаимосвязанными друг с другом могут быть только четко оформленные, детерминистские образы, т.е. образы с высокой степенью редукции ("степень сформированности конструкта"). Поэтому в процессе выявления взаимно–ортогональных базисных образов в первую очередь будут выброшены аморфные "расплывчатые" образы, которые связаны практически со всеми остальными образами.

В некоторых случаях результат такого процесса представляет интерес и это делает оправданным его реализацию. Однако можно предположить, что и наличие расплывчатых образов в системе является оправданным, так как в этом случае система образов не будет формальной и подчиняющейся теореме Геделя, следовательно, система распознавания будет более полна в том смысле, что повысится вероятность идентификации любого объекта, предъявленного ей на распознавание. Конечно, уровень сходства с аморфным образом не может быть столь же высоким, как с четко оформленным, поэтому в этом случае может быть более уместно применить термин "ассоциация" или нечеткая, расплывчатая идентификация, чем "однозначная идентификация".

Итак, можно сделать следующий вывод: допустимость в математической модели СК-анализа не только четко оформленных (детерминистских) образов, но и образов аморфных, нечетких, расплывчатых является важным достоинством данной модели. Это обусловлено тем, что данная модель обеспечивает корректные результаты анализа, идентификации и прогнозирования даже в тех случаях, когда модели идентификации и информационно–поисковые системы детерминистского типа традиционных АСУ практически неработоспособны. В этих условиях данная модель СК-анализа работает как система ассоциативной (нечеткой) идентификации.

Таким образом, в предложенной семантической информационной модели при идентификации и прогнозировании по сути дела осуществляется разложение векторов идентифицируемых объектов по векторам классов распознавания, т.е. осуществляется "объектный анализ" (по аналогии с спектральным, гармоническим или Фурье–анализом), что позволяет рассматривать идентифицируемые объекты как суперпозицию обобщенных образов классов различного типа с различными амплитудами (3.68). При этом вектора обобщенных образов классов с математической точки зрения представляют собой произвольные функции, и не обязательно образуют полную и не избыточную (ортонормированную) систему функций.

Для любого объекта всегда существует такая система базисных функций, что вектор объекта может быть представлен в форме линейной суперпозиции (суммы) этих базисных функций с различными амплитудами. Это утверждение, по-видимому, является одним из следствий фундаментальной теоремы А.Н.Колмогорова, доказанной им в 1957 году (О представлении непрерывных функций нескольких переменных в виде суперпозиций непрерывных функций одного переменного и сложения // Докл. АН СССР, том 114, с. 953-956, 1957).

Теорема Колмогорова: Любая непрерывная функция от n переменных F(x₁, x₂, ..., x_n) может быть представлена в виде:

где g_j и h_ij – непрерывные функции, причем h_ij не зависят от функции F.

Эта теорема означает, что для реализации функций многих переменных достаточно операций суммирования и композиции функций одной переменной. Удивительно, что в этом представлении лишь функции g_j зависят от представляемой функции F, а функции h_ij универсальны. Необходимо отметить, что терема Колмогорова является обобщением теоремы В.И.Арнольда (1957), которая дает решение 13-й проблемы Гильберта.

К сожалению определение вида функций h_ij и g_j для данной функции F представляет собой математическую проблему, для которой пока не найдено общего строгого решения.

В данной работе предлагается рассматривать предлагаемую семантическую информационную модель как один из вариантов решения этой проблемы. В этом контексте функция F интерпретируется как образ идентифицируемого объекта, функция h_ij – как образ j-го класса, а функция g_j – как мера сходства образа объекта с образом класса.

1.2.2.5.3. Системно-когнитивный и факторный анализ. СК-анализ, как метод вариабельных контрольных групп

В науке широко известен "метод контрольных групп" (терм. авт.), позволяющий оценить влияние некоторого фактора на исследуемую группу по сравнению с контрольной, на которую он не влияет.

Обобщением метода контрольных групп является полный и дробный факторный анализ, при котором исследуется не одна контрольная группа, а столько, сколько факторов. При этом в каждой группе исследуется влияние одного фактора при остальных фиксированных. Таким образом факторный анализ можно было бы назвать "методом фиксированных контрольных групп". Факторный анализ требует проведения специально организованных экспериментов, что представляет собой проблему даже при нескольких факторах при большой длительности цикла управления (которая в АПК может составлять до десяти лет и более).

Например, для сбора исходных данных в факторном эксперименте при 3 факторах с 10 градациями каждый необходимо провести 10³=1000 экспериментов. На практике это редко осуществимо.

Поэтому перед проведением факторного эксперимента обычно выбирают небольшое количество наиболее значимых или интересных факторов для исследования. Вопрос о том, какие факторы исследовать, решается самим исследователем на основе неформальных методов.

СК-анализ является обобщением метода факторного анализа в том смысле, что контрольные группы отличаются не значениями одного фактора при остальных фиксированных, а в общем случае различными комбинациями значений действующих факторов. СК-анализ позволяет выявлять и корректно исследовать влияние тысяч факторов на объект управления на основе непосредственно эмпирических данных, причем неполных и неупорядоченных, как в факторном эксперименте. При этом определяется и значимость факторов, что позволяет обоснованно выбрать из них небольшое количество наиболее значимых для последующего более детального исследования методом факторного анализа. Необходимо отметить, что СК-анализ является непараметрическим методом, в отличие от факторного анализа.

1.2.2.5.4. Семантическая мера целесообразности информации и эластичность

Эластичность в непрерывном случае

Рассмотрим связь эластичности и семантической меры целесообразности информации, опираясь на результаты работ автора [81, 91, 115, 135]. Пусть численное значение некоторого параметра экономической системы описывается переменной y, зависящей от фактора x и эта зависимость описывается функцией y=f(x). Тогда степень и направление влияния фактора x на параметр y можно численно измерить производной (3.69), представляющей собой предел отношения абсолютных изменений величин y и x:

(3. 69)

Однако применение производной не очень удобно, т.к. она зависит от размерности величин y и x и, по этой причине, обладает недостаточной сопоставимостью в пространстве и времени. Кроме того, сама по себе скорость абсолютного изменения некоторого параметра объекта безотносительно к средней величине этого параметра, содержит недостаточно информации об этом объекте. Например, если на очередных выборах за некоторого кандидата отдано на 500 голосов больше, чем на предыдущих, то важно знать, а на сколько это процентов больше. Поэтому в экономике введено понятие эластичности E_x(y) функции y=f(x), которое определяется как предел отношения не абсолютных, а относительных изменений значений переменных y и x:

(3. 70)

Так как , и , то эластичность можно представить в виде логарифмической производной:

(3. 71)

Эластичность в дискретном случае

Для численных расчетов необходимо перейти к дискретному случаю, в частности для численного взятия производных используем метод конечных разностей. В конечных разностях выражение (3) принимает вид:

(3. 72)

Свойства эластичности

Рассмотрим некоторые свойства эластичности, которые, как мы заметили, удивительным образом полностью или частично совпадают со свойствами логарифма (таблица 21).

Таблица 21 – СВОЙСТВА ЭЛАСТИЧНОСТИ И ЛОГАРИФМА

№	ЭЛАСТИЧНОСТЬ	ЛОГАРИФМ	Примечание
1	Эластичность взаимно-обратной функции взаимно-обратна:	Логарифм взаимно-обратной функции равен той же функции с обратным знаком:	Совпадает по модулю (с точностью до знака)
2	Эластичность произведения двух функций одного аргумента равна сумме эластичностей функций:	Логарифм произведения двух функций одного аргумента равна сумме логарифмов функций:	Полностью совпадает
3	Эластичность частного двух функций одного аргумента равна разности эластичностей функций:	Логарифм частного двух функций одного аргумента равна разности логарифмов функций:	Полностью совпадает
4	Эластичность показательной функции пропорциональна показателю степени:	Логарифм показательной функции пропорционален показателю степени:	Полностью совпадает
5	Область значений эластичности: < E < .	Область значений логарифма: < ln < .	Полностью совпадает

Необходимо отметить, что ряд других свойств эластичности, таких как эластичность суммы функций, эластичность линейной функции и др., не совпадают со свойствами логарифма. Итак, учитывая свойства эластичности 2-5 (таблица 21) мы видим, что большинство свойств эластичности совпадают со свойствами логарифмической функции. Это позволяет высказать гипотезу, что свойства эластичности E_x(y) схожи со свойствами количества информации I, т.к. во все выражения для количества информации Хартли-Найквиста-Больцмана, Шеннона и Харкевича входит логарифмическая функция.

Какая же из этих мер информации в наибольшей степени соответствует понятию эластичности? Ключевым в решении этого вопроса является свойство 5 (таблица 21):

– область значений мер Хартли-Найквиста-Больцмана и Шеннона изменяется от 0 до ;

– область значений меры Харкевича, как и эластичности, изменяется от до , как и эластичности.

Однако классическая мера семантической целесообразности информации мера Харкевича не удовлетворяет принципу соответствия с мерой Хартли в детерминистском случае, поэтому автором данной работы в [81] предложена системная мера целесообразности информации (СМЦИ) – I_ij(W,M). В отличие от эластичности E_x(y), которая определена для однозначной функции одного аргумента, I_ij(W,M) определена для многозначной функции многих аргументов.

Таким образом, системная мера целесообразности информации, предложенная в настоящем исследовании, имеет математические свойства сходные со свойствами эластичности многозначной функции многих аргументов.

1.2.2.5.5. Связь семантической информационной модели с нейронными сетями

В 1943 году Дж. Маккалоки и У. Питт предложили формальную модель биологического нейрона как устройства, имеющего несколько входов (входные синапсы – дендриты), и один выход (выходной синапс – аксон). Дендриты получают информацию от источников информации (рецепторов) L_i, в качестве которых могут выступать и нейроны. Набор входных сигналов {L_i} характеризует объект или ситуацию, обрабатываемую нейроном. Каждому i-му входу j-го нейрона ставится в соответствие некоторый весовой коэффициент I_ij, характеризующий степень влияния сигнала с этого входа на аргумент передаточной (активационной) функции, определяющей сигнал Y_j на выходе нейрона. В нейроне происходит взвешенное суммирование входных сигналов, и далее это значение используется как аргумент активационной (передаточной) функции нейрона. На рисунке 37 данная модель приведена в обозначениях, принятых в настоящей работе.

Рисунок 37. Классическая модель нейрона Дж. Маккалоки и У. Питта (1943) в обозначениях системной теории информации

Метафора нейросетевого представления семантической информационной модели

В данной работе предлагается представление, согласно которому каждый нейрон отражает определенное будущее состояние активного объекта управления, а нейронная сеть в целом – систему будущих состояний, как желательных (целевых), так и нежелательных. Весовые коэффициенты на дендридах нейронов имеют смысл силы и направления влияния факторов на переход активного объекта управления в то или иное будущее состояние. Таким образом, предложенная в данной работе семантическая информационная модель в принципе допускает представление в терминах и понятиях нейронных сетей. Однако при более детальном рассмотрении выясняется, что семантическая информационная модель является более общей, чем нейросетевая и для полного их соответствия необходимо внести в нейросетевую модель ряд дополнений.

Соответствие основных терминов и понятий

Предлагается следующая система соответствий, позволяющая рассматривать термины и понятия из теории нейронных сетей и предложенной семантической информационной модели практически как синонимы. Нейрон – вектор обобщенного образа класса в матрице информативностей. Входные сигналы – факторы (признаки). Весовой коэффициент – системная мера целесообразности информации. Обучение сети – адаптация модели, т.е. перерасчет значений весовых коэффициентов дендридов для каждого нейрона (матрицы информативностей) и изменение вида активационной функции. Самоорганизация сети – синтез модели, т.е. изменение количества нейронов и дендридов, изменение количества нейронных слоев и структуры связей между факторами и классами, а затем адаптация (перерасчет матрицы информативностей). Таким образом, адаптация – это обучение сети на уровне изменения информационных весовых коэффициентов и активационной функции, а синтез – на уровне изменения размерности и структуры связей нейронов сети. 1-й (входной) слой нейронной сети – формирование обобщенных образов классов. Сети Хопфилда и Хэмминга – обучение с учителем, сопоставление описательной и классификационной информации, идентификация и прогнозирование. 2-й слой, сети Хебба и Кохонена – самообучение, анализ структуры данных без априорной классификационной информации, формирование кластеров классов и факторов. 3-й слой – формирование конструктов (в традиционных нейронных сетях не реализовано). Необходимо отметить, что любой слой нейронной сети является в предлагаемой модели не только обрабатывающим, но и выходным, т.е. с одной стороны дает результаты обработки информации, имеющие самостоятельное значение, а с другой – поставляет информацию для последующих слоев нейронной сети, т.е. более высоких уровней иерархии информационной системы (в полном соответствии с формализуемой когнитивной концепцией).

Недостатки нейронных сетей и пути их преодоления в семантической информационной модели

К основным недостаткам нейронных сетей можно отнести:

1. Сложность содержательной интерпретации смысла интенсивности входных сигналов и весовых коэффициентов ("проблема интерпретируемости весовых коэффициентов").

2. Сложность содержательной интерпретации и обоснования аддитивности аргумента и вида активационной (передаточной) функции нейрона ("проблема интерпретируемости передаточной функции").

3. "Комбинаторный взрыв", возникающий при определении структуры связей нейронов, подборе весовых коэффициентов и передаточных функций ("проблема размерности").

Проблемы интерпретируемости приводят к снижению ценности полученных результатов работы сети, а проблема размерности – к очень жестким ограничениям на количество выходных нейронов в сети, на количество рецепторов и на сложность структуры взаимосвязей нейронов с сети. Достаточно сказать, что количество выходных нейронов в реальных нейронных сетях, реализуемых на базе известных программных пакетов, обычно не превышает несколько сотен, а чаще всего составляет единицы и десятки.

Гипотеза о нелокальности нейрона и информационная нейросетевая парадигма

Модель нелокального нейрона: так как сигналы на дендридах различных нейронов вообще говоря коррелируют (или антикоррелируют) друг с другом, то, значения весовых коэффициентов, а значит и выходное значение на аксоне каждого конкретного нейрона вообще говоря не могут быть определены с использованием значений весовых коэффициентов на дендридах только данного конкретного нейрона, а должны учитывать интенсивности сигналов на всей системе дендридов нейронной сети в целом (рисунок 38).

Рисунок 38. Модель нелокального нейрона

в обозначениях системной теории информации

За счет учета корреляций входных сигналов (если они фактически присутствуют в структуре данных), т.е. наличия общего самосогласованного информационного поля исходных данных всей нейронной сети (информационное пространство), нелокальные нейроны ведут себя так, как будто связаны с другими нейронами, хотя могут быть и не связаны с ними синаптически по входу и выходу ни прямо, ни опосредованно. Самосогласованность семантического информационного пространства означает, что учет любого одного нового факта в информационной модели вообще говоря приводит к изменению всех весовых коэффициентов всех нейронов, а не только тех, на рецепторе которых обнаружен этот факт и тех, которые непосредственно или опосредованно синаптически с ним связаны.

В традиционной (т.е. локальной) модели нейрона весовые коэффициенты на его дендридах однозначно определяются заданным выходом на его аксоне и никак не зависят от параметров других нейронов, с которыми с нет прямой или опосредованной синаптической связи. Это связано с тем, что в общепринятой энергетической парадигме Хопфилда весовые коэффициенты дендридов имеют смысл интенсивностей входных воздействий. В методе "обратного распространения ошибки" процесс переобучения, т.е. интерактивного перерасчета весовых коэффициентов, начинается с нейрона, состояние которого оказалось ошибочным и захватывает только нейроны, ведущие от рецепторов к данному нейрону. Корреляции между локальными нейронами обусловлены сочетанием трех основных причин:

– наличием в исходных данных определенной структуры: корреляцией входных сигналов;

– синаптической связью локальных нейронов;

– избыточностью (дублированием) нейронной сети.

Решение проблемы интерпретируемости весовых коэффициентов (семантическая мера целесообразности информации и закон Фехнера)

В данной работе предлагается использовать такие весовые коэффициенты дендридов, чтобы активационная функция была линейной, т.е. по сути была равна своему аргументу: сумме. Этому условию удовлетворяют весовые коэффициенты, рассчитываемые с применением системного обобщения формулы Харкевича (3.28).

Очень важно, что данная мера, удовлетворяет известному эмпирическому закону Г.Фехнера (1860), согласно которому существует логарифмическая зависимость между интенсивностью фактора и величиной отклика на него биологической системы (в частности, величина ощущения прямо пропорциональна логарифму интенсивности раздражителя).

Предлагается информационный подход к нейронным сетям, по аналогии с энергетическим подходом Хопфилда (1980).

Суть этого подхода состоит в том, что интенсивности входных сигналов рассматриваются не сами по себе и не с точки зрения только их интенсивности, а как сообщения, несущие определенное количество информации или дезинформации о переходе нейрона и моделируемого им активного объекта управления в некоторое будущее состояние.

Под интенсивностью входного сигнала на определенном дендриде мы будем понимать абсолютную частоту (количество) встреч фактора (признака), соответствующего данному дендриду, при предъявлении нейронной сети объекта, соответствующего определенному нейрону. Таким образом матрица абсолютных частот рассматривается как способ накопления и первичного обобщения эмпирической информации об интенсивностях входных сигналов на дендридах в разрезе по нейронам.

Весовые коэффициенты, отражающие влияние каждого входного сигнала на отклик каждого нейрона, т.е. величину его возбуждения или торможения, представляют собой элементы матрицы информативностей, получающиеся из матрицы абсолютных частот методом прямого счета с использованием выражения для семантической меры целесообразности информации (3.28).

При этом предложенная мера семантической целесообразности информации, как перекликается с нейронными сетями Кохонена, в которых также принято стандартизировать (нормализовать) входные сигналы, что позволяет в определенной мере уйти от многообразия передаточных функций.

Наличие ясной и обоснованной интерпретации весовых коэффициентов, как количества информации, позволяет предложить в качестве математической модели для их расчета системную теорию информации (СТИ).

Семантическая информационная модель, как нелокальная нейронная сеть

Учитывая большое количество содержательных параллелей между семантической информационной моделью и нейронными сетями предлагается рассматривать данную модель как нейросетевую модель, основанную на системной теории информации. В данной модели предлагается вариант решения важных нейросетевых проблем интерпретируемости и ограничения размерности за счет введения меры целесообразности информации (системное обобщение формулы Харкевича), обеспечивающей прямой расчет интерпретируемых весовых коэффициентов на основе непосредственно эмпирических данных. Итак, в данной работе предлагается новый класс нейронных сетей, основанных на семантической информационной модели и информационном подходе. Для этих сетей предлагается полное наименование: "Нелокальные интерпретируемые нейронные сети прямого счета" и сокращенное наименование: "Нелокальные нейронные сети".

Нелокальная нейронная сеть является системой нелокальных нейронов, обладающей качественно новыми (системными, эмерджентными) свойствами, не сводящимися к сумме свойств нейронов. В такой сети поведение нейронов определяется как их собственными свойствами и поступающими на них входными сигналами, так и свойствами нейронной сети в целом, т.е. поведение нейронов в нелокальной нейронной сети согласовано друг с другом не только за счет их прямого и опосредованного синаптического взаимодействия (как в традиционных нейронных сетях), но за счет общего информационного поля весовых коэффициентов всех нейронов данной сети.

Гипотеза о физической природе нелокального взаимодействия нейронов в нелокальной нейронной сети

В данной работе предлагается математическая модель, численный метод и программный инструментарий нелокальных нейронных сетей (универсальная когнитивная аналитическая система "Эйдос"), успешно апробированные в ряде предметных областей. Данная система обеспечивает неограниченное количество слоев ННС при максимальном количестве весовых коэффициентов в слое до 16 миллионов и до 4000 выходных нейронов (в текущей версии 12.5 при решении ряда задач эти ограничения сняты). Но если рассматривать нелокальную нейронную сеть как модель реальных "биологических" нейронных сетей, то ясно, что формальной модели недостаточно и необходимо дополнить ее физической моделью о природе каналов нелокального взаимодействия нейронов в данной сети. По мнению автора данный механизм основан на парадоксе Эйнштейна-Подольского Розена (ЭПР) [10, 27, 264]. По мнению автора, физическая реализация нелокальных нейронов может быть осуществлена за счет соединения как минимум одного дендрита каждого нейрона с датчиком микротелекинетического воздействия, на который человек может оказывать влияние дистанционно. Некоторые из подобных датчиков описаны в работе [27] и более подробно на сайте автора http://lc.kubagro.ru. По мнению автора, квантовые компьютеры, основанные не на математических и программных моделях, а на физических нелокальных нейронах, могут оказаться во многих отношениях функционально эквивалентными физическому мозгу и организму.

Решение проблемы интерпретируемости передаточной функции

Вопрос об интерпретируемости передаточной функции нейрона включает два основных аспекта:

– об интерпретируемости аргумента передаточной функции;

– об интерпретируемости вида передаточной функции.

1. Возникает естественный вопрос о том, чем обосновано включение в состав модели нейрона Дж. Маккалоки и У. Питтом именно аддитивного элемента, суммирующего входные сигналы, а не скажем мультипликативного или в виде функции общего вида. По мнению автора такой выбор обоснован и имеет явную и убедительную интерпретацию именно в том случае, когда весовые коэффициенты имеют смысл количества информации, т.к. в этом случае данная мера представляет собой неметрический критерий сходства (3.37), основанный на лемме Неймана-Пирсона. Сумма весовых коэффициентов, соответствующих набору действующих факторов (входных сигналов) дает величину выходного сигнала на аксоне каждого нейрона.

2. Вид передаточной функции содержательно в теории нейронных сетей явно не обосновывается. Предлагается гипотеза, что на практике вид передаточной функции подбирается таким образом, чтобы соответствовать смыслу подобранных в данном конкретном случае весовых коэффициентов. Так как при применении в различных предметных областях смысл весовых коэффициентов в явном виде не контролируется и может отличаться, то выбор вида передаточной функции позволяет частично компенсировать эти различия.

Предлагаемый интерпретируемый вид весовых коэффициентов обеспечивает единую и стандартную интерпретацию аргумента и значения передаточной функции независимо от предметной области. Поэтому в нелокальной нейронной модели передаточная функция нейрона всегда линейна (аргумент равен функции). Следовательно в модели нелокального нейрона блок суммирования по сути дела объединен с блоком нелинейного преобразования (точнее, второй отсутствует, а его роль выполняет блок суммирования), в отличие от стандартных передаточных функций локальных нейронов: логистической, гиперболического тангенса, пороговой линейной, экспоненциально распределенной, полиномиальной и импульсно-кодовой.

Нелокальные нейроны как бы "резонируют" на ансамбли входных сигналов, причем этот резонанс может быть обоснованно назван семантическим (смысловым), т.к. весовые коэффициенты рассчитаны на основе предложенной семантической меры целесообразности информации. Таким образом, разложение вектора идентифицируемого объекта в ряд по векторам обобщенных образов классов осуществляется на основе семантического резонанса нейронов выходного слоя на ансамбль входных сигналов (признаков, факторов).

Решение проблемы размерности

Вместо итерационного подбора весовых коэффициентов путем полного перебора вариантов их значений при малых вариациях (методы обратного распространения ошибки и градиентного спуска к локальному экстремуму) предлагается прямой расчет этих коэффициентов на основе процедуры и выражений, обоснованных в предложенных системной теории информации и семантической информационной модели. Выигрыш во времени и используемых вычислительных ресурсах, получаемый за счет этого, быстро возрастает при увеличении размерности нейронной сети.

Моделирование причинно-следственных цепочек в нейронных сетях и семантической информационной модели

Факторы описывают причины, а классы – следствия. Но и следствия в свою очередь являются причинами более отдаленных последствий. Предлагаемая семантическая информационная модель позволяет рассматривать события, обнаружение которых осуществляется в режиме идентификации, как причины последующих событий, т.е. как факторы, их вызывающие. При этом факт наступления этих событий моделируется путем включения в модель факторов, соответствующих классам (событиям). В нейронных сетях этот процесс моделируется путем включения в сеть дополнительных нейронных слоев и создания обратных связей между слоями, обеспечивающих передачу в предыдущие слои результатов работы последующих слоев.

Моделирование иерархических структур обработки информации

Рассмотрим иерархическую структуру информации на примере использования психологического теста для оценки психологических качеств сотрудников и влияния этих качеств на эффективность работы фирмы. В нейронной сети иерархическим уровням обработки информации соответствуют слои, поэтому далее будем использовать термины "слой нейронной сети" и "иерархический уровень обработки информации" как синонимы. Рецепторы дают информацию по ответам сотрудника на опросник, нейроны 1-го слоя дают оценку психологических качеств и сигнал с их аксонов является входным для нейронов 2-го слоя, дающих оценку качества работы фирмы. В семантической информационной модели существует три варианта моделирования подобных иерархических структур обработки информации:

1. Заменить все слои одним слоем и выявлять зависимости непосредственно между исходными данными с первичных рецепторов и интересующими итоговыми оценками, например, ответами сотрудников на вопросы и результатами работы фирмы. Этот подход эффективен с прагматической точки зрения, но дает мало информации для теоретических обобщений.

2. Каждый слой моделируется отдельной семантической информационной моделью, включающей свои классификационные и описательные шкалы и градации, обучающую выборку, матрицы абсолютных частот и информативностей. Вся система иерархической обработки информации моделируется системой этих моделей, взаимосвязанных друг с другом по входу-выходу: результаты классификации объектов обучающей выборки 1-й моделью рассматриваются как свойства этих объектов во 2-й модели, в которой они используются для классификации 2-го уровня. Например, психологические качества сотрудников, установленные в результате психологического тестирования, рассматриваются как свойства сотрудников, влияющие на эффективность работы фирмы. Данный подход эффективен и с прагматической, и с теоретической точек зрения, но является громоздким в программной реализации.

3. Моделирование каждого слоя соответствующими подматрицами матриц абсолютных частот и информативностей (таблица 22).

Таблица 22 – ЛОГИЧЕСКАЯ МОДЕЛЬ СТРУКТУРЫ ДАННЫХ СЕМАНТИЧЕСКОЙ ИНФОРМАЦИОННОЙ МОДЕЛИ, СООТВЕТСТВУЮЩАЯ ТРЕХСЛОЙНОЙ НЕЛОКАЛЬНОЙ НЕЙРОННОЙ СЕТИ

Рецепторы – факторы, влияющие на поведение объекта управления	Нейроны - будущие состояния объекта управления			Дифференцирующая способность входного сигнала
	Нейроны 1-го слоя: психологические качества сотрудников	Нейроны 2-го слоя: успешность деятельности сотрудника	Нейроны 3-го слоя: успешность деятельности фирмы
Рецепторы 1-го слоя: ответы сотрудников на вопросы анкеты	Весовые коэффициенты 1-го слоя	– – –	– – –
Рецепторы 2-го слоя: психологические качества сотрудников	– – –	Весовые коэффициенты 2-го слоя	– – –
Рецепторы 3-го слоя: успешность деятельности сотрудника	– – –	– – –	Весовые коэффициенты 3-го слоя
Степень обученности нейрона				Степень обученности нейронной сети

Этот вариант обладает преимуществами первых двух и преодолевает их недостатки. В нем применяется следующий итерационный алгоритм послойного расчета, где n={1, 2, …, N}, N – количество слоев нейронной сети:

Шаг n: расчет весовых коэффициентов n-го слоя, идентификация объектов обучающей выборки в нейронах n-го слоя, если слой (n+1) существует, то занесение в обучающую выборку в качестве свойств объектов (n+1)-го слоя результатов их идентификации в нейронах n-го слоя.

Примечание: в таблице 22 представлена именно логическая структура данных, т.е. в реальных базах данных нет записей, содержащих информацию о влиянии рецепторов n-го слоя на нейроны слоев, номера которых не равны n.

Нейронные сети и СК-анализ

Известные в литературе нейронные сети, в отличие от предлагаемой семантической информационной модели и нелокальных нейронных сетей, не обеспечивают реализацию всех базовых когнитивных операций, входящих в когнитивный конфигуратор. В частности, традиционные нейронные сети решают лишь задачу идентификации (прогнозирования) и не обеспечивают решение обратной задачи (дедукции), необходимой для принятия решения о выборе многофакторного управляющего воздействия. Кроме того не решается вопрос об уменьшении размерности нейронной сети без ущерба для ее адекватности (абстрагирование).

Результаты численного моделирования и исследования свойств нейронных сетей этого класса при управлении в АПК и других предметных областях позволяют предположить, в качестве модели реальных когнитивных процессов они обладает более высокой адекватностью, чем нейронные сети других типов.

Графическое отображение нейронов и Паррето-подмножеств нелокальной нейронной сети

Ниже приводятся примеры графического отображения нелокального нейрона и Паретто-подмножества (нейронов с наиболее значимыми связями) нелокальной нейронной сети в системе "Эйдос" (рисунки 39 и 40).

Рисунок 39. Графическое отображение нелокального нейрона в системе "Эйдос"

Рисунок 40. Графическое отображение нелокальной нейронной сети в системе "Эйдос"

1.2.2.5.6. Математический метод СК-анализа в свете идей интервальной бутстрепной робастной статистики объектов нечисловой природы

Постановка проблемы

Современный этап развития информационных технологий характеризуется быстрым ростом производительности компьютеров облегчением доступа к ним. С этим связан возрастающий интерес к использованию компьютерных технологий для организации мониторинга различных объектов, анализа данных, прогнозирования и управления в различных предметных областях. И у исследователей, и у руководителей, имеются определенные ожидания и надежды на повышение эффективности применения компьютерных технологий.

Однако на пути реализации этих ожиданий имеются определенные сложности, связанные с относительным отставанием в развитии математических методов и реализующего их программного инструментария.

И анализ, и прогнозирование, и управление самым непосредственным образом основываются на математическом моделировании объектов. Математическое моделирование в свою очередь предполагают возможность выполнения всех арифметических операций (сложение, вычитание, умножение и деление) над отображениями объектов в моделях и над их элементами.

В практике интеллектуального анализа данных в экономике, социологии, психологии, педагогике и других предметных областях все чаще встречаются ситуации, когда необходимо в рамках единой математической модели совместно обрабатывать числовые и нечисловые данные.

В свою очередь числовые данные могут быть различной природы и, соответственно, измеряться в самых различных единицах измерения. Ясно, что арифметические операции можно выполнять только над числовыми данными, измеряемыми в одних единицах измерения.

Данные нечисловой природы, т.е. различные факты и события, характеризуются тем, что с ними вообще нельзя выполнять арифметические операции.

Соответственно, возникает потребность в математических методах и программном инструментарии, обеспечивающих совместную сопоставимую обработку разнородных числовых данных и данных нечисловой природы.

Традиционные пути решения проблемы

Традиционно при необходимости проведения подобных исследований реализуется один из двух вариантов, т.е. либо изучается подмножество однородных по своей природе данных, измеряемых в одних единицах измерения; либо перед исследованием данные приводятся к сопоставимому виду, например, широко используются процентные или другие относительные величины, реже – стандартизированные значения.

Ясно, что первый вариант является не решением проблемы, а лишь ее вынужденным обходом, обусловленным ограничениями реально имеющегося в распоряжении исследователей инструментария.

Второй вариант лишь частично решает проблему, т.к. хотя и снимает различие в единицах измерения, но не преодолевает принципиального различия между количественными и качественными (нечисловыми) величинами и не позволяет обрабатывать их совместно в рамках единой модели.

В последние годы развивается ряд новых методов статистики, полный обзор которых дан в работах А. И. Орлова [http://antorlov.chat.ru]. Прежде всего, это интервальная статистика, статистика объектов нечисловой природы, робастные, бутстрепные и непараметрические методы.

В частности методы интервальной статистики, позволяют сводить числовые величины к фактам попадания их значений в определенные интервалы, т.е. к событиям. При этом преодолевается проблема различия в размерности числовых величин. Это обеспечивает также обработку числовых величин, как событий совместно с информацией о других событиях, связанных с объектами нечисловой природы. Таким образом, интервальные методы сводят обработку числовых величин к методам обработки нечисловой информации и позволяет обрабатывать их единообразно по одной методике. И это является очень важным достижением.

Идея решения проблемы

Это, в общем-то, вполне очевидный и естественный ход. Однако достигается этот результат дорогой ценой, т.е. путем сведения числовых величин к нечисловым, т.е. путем сведения их к "низменному типу", что приводит к утрате ряда возможностей обработки. Это происходит потому, что для числовых величин существует гораздо больше методов и возможностей обработки, чем для нечисловых.

По нашему мнению более предпочтительным является противоположный подход, основанный на введении некоторой количественной меры, позволяющей единым и сопоставимым образом описывать как числовые данные различной природы, так и нечисловые величины с использованием всего арсенала возможностей, имеющегося при обработке числовых данных.

Аналогично, если у нас есть документы стандартов "Документ Word" и "Текст-DOS" и мы хотели бы обрабатывать их все в одном редакторе, то это можно сделать либо преобразовав все документы Word в "низменный стандарт" "Текст-DOS", либо наоборот, преобразовав "досовские" документы в формат Word.

В 1979 году автором разработана, а в 1981 году впервые применена математическая модель, обеспечивающая реализацию этой идеи. В последующем этот математический аппарат был развит в ряде работ, основной из которых является [81], был разработана соответствующая ему методика численных расчетов, включающая структуры данных и алгоритмы базовых когнитивных операций, а также создана программная система "Эйдос", реализующая математическую модель и методику численных расчетов [76-155, 185-192].

Предложенный метод получил название "Системно-когнитивный анализ" (СК-анализ) [81]. В СК-анализе нечисловым величинам тем же методом, что и числовым, приписываются сопоставимые в пространстве и времени, а также между собой, количественные значения, позволяющие обрабатывать их как числовые.

СК-анализ включает следующие этапы:

1. Когнитивная структуризация, а затем и формализация предметной области.

2. Ввод данных мониторинга в базу прецедентов за период, в течение которого имеется необходимая информация в электронной форме.

3. Синтез семантической информационной модели (СИМ).

4. Оптимизация СИМ.

5. Проверка адекватности СИМ (измерение внутренней и внешней, дифференциальной и интегральной валидности).

6. Анализ СИМ.

7. Решение задач идентификации состояний объекта управления, прогнозирование и поддержка принятия управленческих решений по управлению с применением СИМ.

На первых двух этапах СК-анализа, детально рассмотренных в работе [81], числовые величины сводятся к интервальным оценкам, как и информация об объектах нечисловой природы (фактах, событиях). Этот этап реализуется и в методах интервальной статистики.

На третьем этапе СК-анализа всем этим величинам по единой методике, основанной на системном обобщении семантической теории информации А.Харкевича, сопоставляются количественные величины, с которыми в дальнейшем и производятся все операции моделирования.

Математическая модель СК-анализа

Системное обобщение формулы Хартли

В выражении (3) приведено системное обобщение формулы Хартли для равновероятных состояний объекта управления.

	(1)		(4)
	(2)		(5)
	(3)	с очень малой и быстро уменьшающейся погрешностью	(6)

W – количество чистых (классических) состояний системы.

j – коэффициент эмерджентности Хартли (уровень системной организации объекта, имеющего W чистых состояний).

Гипотеза о Законе возрастания эмерджентности

Исследование математических выражений системной теории информации (7 – 12) позволило сформулировать гипотезу о существовании "Закона возрастания эмерджентности". Суть этой гипотезы в том, что в самих элементах системы содержится сравнительно небольшая доля всей содержащейся в ней информации, а основной ее объем составляет системная информация, содержащаяся в подсистемах различного уровня иерархии.

Различие между классическим и предложенным системным понятиями информации соответствует различию между понятиями МНОЖЕСТВА И СИСТЕМЫ, на основе которых они сформированы.

	(7)		(8)
	(9)		(10)
	(11)		(12)

Математическая формулировка:

Интерпретация

Системное обобщение формулы Харкевича

Ниже приведен вывод системного обобщения формулы Харкевича, а именно:

– классическая формула Харкевича через вероятности перехода системы в целевое состояние при условии сообщения ей определенной информации и самопроизвольно (13);

– выражение классической формулы Харкевича через частоты (14, 15);

– вывод коэффициента эмерджентности Харкевича на основе принципа соответствия с выражением Хартли в детерминистском случае (16 –19);

– вывод системного обобщения формулы Харкевича;

– окончательное выражение для системного обобщения формулы Харкевича (21).

Классическая формула Харкевича

(13)

P_ij – вероятность перехода объекта управления в j-е состояние в условиях действия i-го фактора;

P_j – вероятность самопроизвольного перехода объекта управления в j-е состояние, т.е. в условиях отсутствия действия i-го фактора или в среднем.

Известно, что корреляция не является мерой причинно-следственных связей. Если корреляция между действием некоторого фактора и переходом объекта управления в определенное состояние высока, то это еще не значит, что данный фактор является причиной этого перехода. Для того чтобы по корреляции можно было судить о наличии причинно-следственной связи необходимо сравнить исследуемую группу с контрольной группой, т.е. с группой, в которой данный фактор не действовал.

Также и высокая вероятность перехода объекта управления в определенное состояние в условиях действия некоторого фактора сама по себе не говорит о наличии причинно-следственной связи между ними, т.е. о том, что данный фактор обусловил переход объекта в это состояние. Это связано с тем, что вероятность перехода объекта в это состояние может быть вообще очень высокой независимо от действия фактора. Поэтому в качестве меры силы причинной обусловленности определенного состояния объекта действием некоторого фактора Харкевич предложил логарифм отношения вероятностей перехода в объекта в это состояние в условиях действия фактора и при его отсутствии или в среднем (13).

Таким образом семантическая мера информации Харкевича является мерой наличия причинно-следственных связей между факторами и состояниями объекта управления.

Выражение классической формулы Харкевича через частоты фактов

(14)

(15)

Вывод коэффициента эмерджентности Харкевича на основе принципа соответствия с выражением Хартли в детерминистском случае

Однако мера Харкевича (13) не удовлетворяет принципу соответствия мерой Хартли как мера Шеннона, т.е. не переходит в меру Хартли в детерминистском случае, т.е. когда каждому будущему состоянию объекта управления соответствует единственный уникальный фактор и между факторами и состояниями имеется взаимно однозначное соответствие (17).

(16)

(17)

Откуда:

(18)

(19)

Вывод системного обобщения формулы Харкевича

(20)

Окончательное выражение для системного обобщения формулы Харкевича

(21)

Связь системной теории информации (СТИ) с теорией Хартли-Найквиста-Больцмана и теорией Шеннона

Связь между выражениями для плотности информации в теориях Хартли, Шеннона и СТИ приведена на рисунке 41.

Рисунок 41. Связь между выражениями для плотности
информации в теориях Хартли, Шеннона и СТИ

Интерпретация коэффициентов эмерджентности СТИ

Интерпретация коэффициентов эмерджентности, предложенных в рамках системной теории информации, приведена на рисунке 42.

Рисунок 42. Интерпретация коэффициентов
эмерджентности СТИ

Коэффициент эмерджентности Хартли j (4) представляет собой относительное превышение количества информации о системе при учете системных эффектов (смешанных состояний, иерархической структуры ее подсистем и т.п.) над количеством информации без учета системности, т.е. этот коэффициент является аналитическим выражением для уровня системности объекта.

Коэффициент эмерджентности Харкевича Y, изменяется от 0 до 1 и определяет степень детерминированности системы.

Таким образом, в предложенном системном обобщении формулы Харкевича (21) впервые непосредственно в аналитическом выражении для самого понятия "Информация" отражены такие фундаментальные свойства систем, как "Уровень системности" и "Степень детерминированности" системы.

Матрица абсолютных частот

Основной формой первичного обобщения эмпирической информации в модели является матрица абсолютных частот (таблица 23). В этой матрице строки соответствуют факторам, столбцы – будущим целевым и нежелательным состояниям объекта управления, а на их пересечении приведено количество наблюдения фактов (по данным обучающей выборки), когда действовал некоторый i-й фактор и объект управления перешел в некоторое j-е состояние.

Таблица 23 – МАТРИЦА АБСОЛЮТНЫХ ЧАСТОТ

Матрица информативностей

Непосредственно на основе матрицы абсолютных частот с использованием системного обобщения формулы Харкевича (21) рассчитывается матрица информативностей (таблица 24).

Таблица 24 – МАТРИЦА ИНФОРМАТИВНОСТЕЙ

Матрица информативностей является универсальной формой представления смысла эмпирических данных в единстве их дискретного и интегрального представления (причины – последствия, факторы – результирующие состояния, признаки – обобщенные образы классов, образное – логическое, дискретное – интегральное).

Весовые коэффициенты матрицы информативностей непосредственно определяют, какое количество информации Iij система управления получает о наступлении события: "объект управления перейдет в j–е состояние", из сообщения: "на объект управления действует i–й фактор".

Когда количество информации Iij>0 – i–й фактор способствует переходу объекта управления в j–е состояние, когда Iij<0 – препятствует этому переходу, когда же Iij=0 – никак не влияет на это.

Таким образом, предлагаемая семантическая информационная модель позволяет непосредственно на основе эмпирических данных и независимо от предметной области рассчитать, какие количество информации содержится в любом событии о любом другом событии.

Этот вывод является ключевым для данной работы, т.к. конкретно показывает возможность числовой обработки в СК-анализе как числовой, так и нечисловой информации.

Матрица информативностей является также обобщенной (неклассической) таблицей решений, в которой входы (факторы) и выходы (будущие состояния объекта управления) связаны друг с другом не с помощью классических (Аристотелевских) импликаций, принимающих только значения: "Истина" и "Ложь", а различными значениями истинности, выраженными в битах и принимающими значения от положительного теоретически-максимально-возможного, до теоретически неограниченного отрицательного. Некоторые неклассические высказывания, генерируемые на основе матрицы информативности, приведены на плакате.

Неметрический интегральный критерий сходства, основанный на лемме Неймана-Пирсона

В выражениях (22 – 24) приведен неметрический интегральный критерий сходства, основанный на фундаментальной лемме Неймана-Пирсона, обеспечивающий идентификацию и прогнозирование в предложенных неортонормированных семантических пространствах с финитной метрикой, в которых в качестве координат векторов будущих состояний объекта управления и факторов выступает количество информации, рассчитанное в соответствии с системной теорией информации (21), а не Булевы координаты или частоты, как обычно.

(22)

(23)

Или в координатной форме:

(24)

(25)

– вектор j–го состояния объекта управления;

– вектор состояния предметной области, включающий все виды факторов, характеризующих объект управления, возможные управляющие воздействия и окружающую среду (массив–локатор), т.е.:

	(26)
	(27)

– средняя информативность по вектору класса;

– среднее по вектору идентифицируемой ситуации (объекта).

– среднеквадратичное отклонение информативностей вектора класса;

– среднеквадратичное отклонение по вектору распознаваемого объекта.

Необходимо особо отметить, что выражения идентичные (23-26) используются при определении понятия "белый шум": белым шумом называется сигнал, автокорреляция которого равна нулю. Это означает, что предложенный интегральный критерий сходства образа конкретного объекта, формализуемого в форме (массива-локатора, и обобщенного образа класса в форме массива информативностей обладает естественной защищенностью и устойчивостью от зашумленности белым шумом, т.е. подавляет его и выделяет полезный сигнал из шума. Это очень важно, т.к. на практике белый шум всегда присутствует в эмпирических данных из-за погрешностей в измерениях.

Связь системной меры целесообразности информации с критерием c²

В (28 – 33) показана связь системной меры целесообразности информации с известным критерием c², а также предложен новый критерий уровня системности предметной области, являющийся нормированным объемом семантического пространства (34, 35).

(28)

(29)

– N_ij – фактическое количество встреч i-го признака у объектов j-го класса;

– t – ожидаемое количество встреч i-го признака у объектов j-го класса.

	(30)				(31)
	(32)				(33)
			(34)		(35)

Предлагается более точный критерий уровня системности модели является объем неортонормированного семантического пространства, рассчитанный как объем многомерного параллелепипеда, ребрами которого являются оси семантического пространства. Однако для этой меры сложнее в общем виде записать аналитическое выражение и для ее вычисления могут быть использованы численные методы с использованием многомерного обобщения смешанного произведения векторов.

Абстрагирование (ортонормирование) существенно уменьшает размерность семантического пространства без существенного уменьшения его объема.

Оценка адекватности семантической информационной модели в СК-анализе и бутстрепные методы

Под адекватностью модели СК-анализа понимается ее внутренняя и внешняя дифференциальная и интегральная валидность. Понятие валидности является уточнением понятия адекватности, для которого определены процедуры количественного измерения, т.е. валидность – это количественная адекватность. Это понятие количественно отражает способность модели давать правильные результаты идентификации, прогнозирования и способность вырабатывать правильные рекомендации по управлению.

Под внутренней валидностью понимается валидность модели, измеренная после синтеза модели путем идентификации объектов обучающей выборки.

Под внешней валидностью понимается валидность модели, измеренная после синтеза модели путем идентификации объектов, не входящих в обучающую выборку.

Под дифференциальной валидностью модели понимается достоверность идентификации объектов в разрезе по классам.

Под интегральной валидностью средневзвешенная дифференциальная валидность.

Возможны все сочетания: внутренняя дифференциальная валидность, внешняя интегральная валидность и т.д.

Основная идея бутстрепа по Б.Эфрону [107] состоит в том, что методом Монте-Карло (статистических испытаний) многократно извлекаются выборки из эмпирического распределения. Эти выборки, естественно, являются вариантами исходной, напоминают ее.

Эта идея позволяет сконструировать алгоритм измерения адекватности модели, состоящий из двух этапов:

1. Синтез модели на одном случайном подмножестве обучающей выборки.

2. Измерение валидности модели на оставшемся подмножестве обучающей выборки, не использованном для синтеза модели.

Поскольку оба случайных подмножества имеют переменный состав по объектам обучающей выборки, то подобная процедура должна повторяться много раз, после чего могут быть рассчитаны статистические характеристики адекватности модели, например, такие как:

– средняя внешняя валидность;

– среднеквадратичное отклонение текущей внешней валидности от средней и другие.

Достоинство бутстрепного подхода к оценке адекватности модели состоит в том, что он позволяет измерить внешнюю валидность на уже имеющейся выборке и изучить статистические характеристики, характеризующие адекватность модели при изменении объема и состава выборки.

Непараметричность модели. Робастные процедуры и фильтры для исключения артефактов

Предложенная семантическая информационная модель является непараметрической, т.к. базируется на системной теории информации [81], которая никоим образом не основана на предположениях о нормальности распределений исследуемой выборки.

Под робастными понимаются процедуры, обеспечивающие устойчивую работу модели на исходных данных, зашумленных артефактами, т.е. данными, выпадающими из общих статистических закономерностей, которым подчиняется исследуемая выборка.

Критерий выявления артефактов, реализованный в СК-анализе, основан на том, что при увеличении объема статистики частоты значимых атрибутов растут, как правило, пропорционально объему выборки, а частоты артефактов так и остаются чрезвычайно малыми, близкими к единице. Таким образом, выявление артефактов возможно только при достаточно большой статистике, т.к. в противном случае недостаточно информации о поведении частот атрибутов с увеличением объема выборки.

В модели реализована такая процедура удаления наиболее вероятных артефактов, и она, как показывает опыт, существенно повышает качество (адекватность) модели.

Методика численных расчетов СК-анализа

Детальный список БКОСА и их алгоритмов

В таблице 25 приведен детальный список базовых когнитивных операций системного анализа, которым соответствует 24 алгоритма, которые здесь привести нет возможности из-за их объемности. Но они все приведены в полном виде в работе [81].

Таблица 25 – ДЕТАЛЬНЫЙ СПИСОК
БАЗОВЫХ КОГНИТИВНЫХ ОПЕРАЦИЙ СИСТЕМНОГО АНАЛИЗА (БКОСА)

№ алгоритма	Код БКОСА по схеме СК-анализа	№ БКОСА	Наименование БКОСА	Полное наименование базовых когнитивных операций системного анализа (БКОСА)
	1.1	1	Присвоение имен	Присвоение имен классам (интенсиональная, интегральная репрезентация)
	1.2			Присвоение имен атрибутам (экстенсиональная, дискретная репрезентация)
1	2.1.	2	Восприятие	Восприятие и запоминание исходной обучающей информации
2	2.2.			Репрезентация. Сопоставление индивидуального опыта с коллективным (общественным)
3	3.1.1.	3	Обобщение (синтез, индукция).	Накопление первичных данных
4	3.1.2.			Исключение артефактов
5	3.1.3.			Расчет истинности смысловых связей между предпосылками и результатами (обобщенных таблиц решений)
6	3.2.			Определение значимости шкал и градаций факторов, уровней Мерлина
7	3.3.			Определение значимости шкал и градаций классов, уровней Мерлина
8	4.1.	4	Абстраги- рование	Абстрагирование факторов (снижение размерности семантического пространства факторов)
9	4.2.			Абстрагирование классов (снижение размерности семантического пространства классов)
10	5.	5	Оценка адекватности	Оценка адекватности информационной модели предметной области
11	7.	6	Сравнение, идентификация и прогнозирование	Сравнение, идентификация и прогнозирование. Распознавание состояний конкретных объектов (объектный анализ)
12	9.1.	7	Анализ, дедукция и абдукция	Анализ, дедукция и абдукция классов (семантический анализ обобщенных образов классов, решение обратной задачи прогнозирования)
13	9.2.			Анализ, дедукция и абдукция факторов (семантический анализ факторов)
14	10.1.1.	8	Классификация и генерация конструктов	Классификация обобщенных образов классов
15	10.1.2.			Формирование бинарных конструктов классов
16	10.1.3.			Визуализация семантических сетей классов
17	10.2.1.			Классификация факторов
18	10.2.2.			Формирование бинарных конструктов факторов
19	10.2.3.			Визуализация семантических сетей факторов
20	10.3.1.	9	Содержательное сравнение	Содержательное сравнение классов
21	10.3.2.			Расчет и отображение многомногозначных когнитивных диаграмм, в т.ч. диаграмм Мерлина
22	10.4.1.			Содержательное сравнение факторов
23	10.4.2.			Расчет и отображение многомногозначных когнитивных диаграмм, в т.ч. инвертированных диаграмм Мерлина
24	11.	10	Планирование и управление	Многовариантное планирование и принятие решения о применении системы управляющих факторов

Иерархическая структура данных семантической информационной модели СК-анализа

На рисунке 43 приведена в обобщенном виде иерархическая структура баз данных семантической информационной модели системно-когнитивного анализа. На этой схеме базы данных обозначены прямоугольниками, а базовые когнитивные операции системного анализа, преобразующие одну базу в другую – стрелками с надписями. Имеются также базовые когнитивные операции, формирующие выходные графические формы. Из этой схемы видно, что одни базовые когнитивные операции готовят данные для других операций, относящихся к более высоким уровням иерархии системы процессов познания. Этим определяется возможная последовательность выполнения базовых когнитивных операций.

Рисунок 43. Иерархическая структура баз данных семантической информационной модели системно-когнитивного анализа

Специальный программный инструментарий СК-анализа – система "Эйдос"

На таблице 26 показана обобщенная схема когнитивной аналитической системы "Эйдос", которая реализует математическую модель и численный метод системно-когнитивного анализа и, таким образом, является его инструментарием.

В состав данной системы входит 7 подсистем.

Первые 3 подсистемы являются инструментальными, т.е. позволяют осуществлять синтез и адаптацию модели.

Остальные 4 подсистемы обеспечивают идентификацию, прогнозирование и кластерно-конструктивный анализ модели, в т.ч. верификацию модели и выработку управляющих воздействий.

Система "Эйдос" является довольно большой системой: распечатка ее исходных текстов 6-м шрифтом составляет около 800 листов, она генерирует 54 графических формы (двухмерные и трехмерные) и 50 текстовых форм. На данную систему и системы окружения получено 8 свидетельств РосПатента РФ.

Таблица 26 – ОБОБЩЕННАЯ СТРУКТУРА УНИВЕРСАЛЬНОЙ КОГНИТИВНОЙ АНАЛИТИЧЕСКОЙ СИСТЕМЫ "ЭЙДОС" (версии 12.5)

Подсистема	Режим	Функция	Операция
Группа-1: "Синтез и адаптация СИМ"
1. Словари	1. Классификационные шкалы и градации
	2. Описательные шкалы (и градации)
	3. Градации описательных шкал (признаки)
	4. Иерархические уровни систем	1. Уровни классов
		2. Уровни признаков
	5. Программные интерфейсы для импорта данных	1. Импорт данных из TXT-фалов стандарта DOS-текст
		2. Импорт данных из DBF-файлов стандарта проф. А.Н.Лебедева
		3. Импорт из транспонированных DBF-файлов проф. А.Н.Лебедева
		4. Генерация шкал и обучающей выборки RND-модели
		5. Генерация шкал и обучающей выборки для исследования чисел
		6. Транспонирование DBF-матриц исходных данных
	6. Почтовая служба по НСИ	1. Обмен по классам
		2. Обмен по обобщенным признакам
		3. Обмен по первичным признакам
	7. Печать анкеты
2. Обучение	1. Ввод–корректировка обучающей выборки
	2. Управление обучающей выборкой	1. Параметрическое задание объектов для обработки
		2. Статистическая характеристика, ручной ремонт
		3. Автоматический ремонт обучающей выборки
	3. Пакетное обучение системы распознавания	1. Накопление абсолютных частот
		2. Исключение артефактов (робастная процедура)
		3. Расчет информативностей признаков
		4. Расчет условных процентных распределений
		5. Автоматическое выполнение режимов 1–2–3–4
		6. Измерение сходимости и устойчивости модели	1. Сходимость и устойчивость СИМ
			2. Зависимость валидности модели от объема обучающей выборки
	4. Почтовая служба по обучающей информации
3. Оптимизация	1. Формирование ортонормированного базиса классов
	2. Исключение признаков с низкой селективной силой
	3. Удаление классов и признаков, по которым недостаточно данных
Группа-2: "СК-анализ СИМ"
4. Распознавание	1. Ввод–корректировка распознаваемой выборки
	2. Пакетное распознавание
	3. Вывод результатов распознавания	1. Разрез: один объект – много классов
		2. Разрез: один класс – много объектов
	4. Почтовая служба по распознаваемой выборке
5. Типология	1. Типологический анализ классов распознавания	1. Информационные (ранговые) портреты (классов)
		2. Кластерный и конструктивный анализ классов	1 Расчет матрицы сходства образов классов
			2. Генерация кластеров и конструктов классов
			3. Просмотр и печать кластеров и конструктов
			4. Автоматическое выполнение режимов: 1,2,3
			5. Вывод 2d семантических сетей классов
		3. Когнитивные диаграммы классов
	2. Типологический анализ первичных признаков	1. Информационные (ранговые) портреты признаков
		2. Кластерный и конструктивный анализ признаков	1. Расчет матрицы сходства образов признаков
			2. Генерация кластеров и конструктов признаков
			3. Просмотр и печать кластеров и конструктов
			4. Автоматическое выполнение режимов: 1,2,3
			5. Вывод 2d семантических сетей признаков
		3. Когнитивные диаграммы признаков
6. Анализ	1. Оценка достоверности заполнения объектов
	2. Измерение адекватности семантической информационной модели
	3. Измерение независимости классов и признаков
	4. Просмотр профилей классов и признаков
	5. Графическое отображение нелокальных нейронов
	6. Отображение Паретто-подмножеств нейронной сети
	7. Классические и интегральные когнитивные карты
Группа-3: "Администрирование"
7. Сервис	1. Генерация (сброс) БД	1. Все базы данных
		2. НСИ	1. Всех баз данных
			2. БД классов
			3. БД первичных признаков
			4. БД обобщенных признаков
		3. Обучающая выборка
		4. Распознаваемая выборка
		5. Базы данных статистики
	2. Переиндексация всех баз данных
	3. Печать БД абсолютных частот
	4. Печать БД условных процентных распределений
	5. Печать БД информативностей
	6. Интеллектуальная дескрипторная информационно–поисковая система
	7. Копирование основных баз данных информационной модели
8. О системе
9. Выход

Выводы

Интервальные оценки сводят анализ чисел к анализу фактов и позволяют обрабатывать количественные величины как нечисловые данные. Это ограничивает возможности обработки количественных величин методами обработки нечисловых данных. В математической модели СК-анализа, основанной на системной теории информации, наоборот, качественным, нечисловым данным, сопоставляются количественные величины. Это позволяет использовать все возможности количественных методов для исследования нечисловых данных.

Таким образом, в СК-анализе числовые и нечисловые данные обрабатываются единообразно на основе единой математической модели как числовые данные.

Рассматривается связь метода измерения адекватности модели в СК-анализе с бутстрепными методами.

Описывается робастная процедура выявления и устранения артефактов в СК-анализе.

Резюме

1. Сформулированы требования к математической модели и к численной мере. Затем на их основе обоснован выбор базовой численной меры. Для этого рассмотрены три вида информации: абсолютная, относительная и аналитическая информация. Предпочтение отдано аналитической форме информации, к которой принадлежат относительные вероятности, относительные проценты и количество информации. Вместо традиционных мер, основанных на понятии "стоимости" и "полезности" предложено использовать информационную меру. Рассмотрены различные аспекты применения теории информации для анализа процесса труда и средств труда как информационных систем. Показано, что принятие решения об управляющем воздействии есть обратный процесс по отношению к идентификации и прогнозированию, т.е. познанию. Установлена связь количества (синтаксиса) и качества (содержания, семантики) информации, записываемой в структуре предмета труда, с меновой и потребительной стоимостью. Сформулирована информационная теория стоимости, в которой информация рассматривается как сущность стоимости и как "первичный" и по сути единственный товар. Рассмотрены вопросы определения стоимости и амортизация интеллектуальных систем и баз знаний. Показано, что их стоимость как генераторов информации возрастает в процессе эксплуатации. С позиций теории информации раскрыт фундаментальный источник экономической эффективности АСУ и систем интеллектуальной обработки данных: понижение энтропии объекта управления как приемника сообщений в результате получения управляющей информации. Сделан вывод о целесообразности выбора в качестве базовой численной меры количества информации. Поставлена задача выбора или конструирования конкретной численной меры, основанной на понятии информации.

2. В классической теории информации Шеннона, созданной на основе обобщения результатов Больцмана, Найквиста и Хартли, само понятие информации определяется на основе теоретико-множественных и комбинаторных представлений путем анализа поведения классического макрообъекта, который может переходить только в четко фиксированные альтернативные редуцированные состояния. Однако, квантовые объекты и сложные активные рефлексивные системы могут оказываться одновременно в двух и более альтернативных для классических объектов состояниях. Такие состояния названы смешанными. Таким образом в реальности наблюдается картина последствий, не сводящаяся к простой сумме последствий альтернативных вариантов. Она больше напоминает квантовое физическое явление, которое называется интерференцией плотности вероятности. Это явление, безусловно имеющее системный характер, предлагается называть "интерференция последствий выбора".

3. Предлагается обобщение классической теория информации Хартли-Шеннона путем рассмотрения активных объектов в качестве объектов, на основе анализа которых формируется само основополагающее понятие информации. Обобщенную таким образом теорию информации предлагается называть системной или эмерджентной теорией информации (СТИ). Основным отличием эмерджентной теории информации от классической является учет свойства системности, как фундаментального и универсального свойства всех объектов, на уровне самого понятия информации, а не только в последующем изложении, как в классической теории.

4. Предложена системная модификация формулы Хартли для количества информации:

где:

W – количество чистых (классических) состояний системы;

– сочетания "по m" классических состояний.

Так как , то при M=1 выполняется принцип соответствия, являющийся обязательным для более общей теории. Данная формула дает верхнюю оценку возможного количества информации состоянии системы, т.к. возможны различные правила запрета и реальное количество возможных состояний системы будет меньшим, чем .

Предложено приближенное выражение для системной модификации формулы Хартли (при M=W):

При W>4 погрешность данного выражения не превышает 1%.

Дополнительная информация, которую мы получаем из поведения объекта в СТИ, по сути дела является информацией о множестве всех его возможных состояний, как системы, элементом которой является объект в некотором данном состоянии.

5. Численные расчеты и аналитические выкладки согласно СТИ показывают, что при возрастании количества элементов в системе доля системной информации в поведении ее элементов возрастает, причем возрастает ускоренно. Это установленное нами свойство систем названо "Законом возрастания эмерджентности".

6. Предложена системная модификация классической формулы А.Харкевича, являющееся нелинейной суперпозицией классических выражением для плотности информации Шеннона и количества информации Хартли.

где: j – коэффициент эмерджентности Хартли (уровень системной организации объекта, имеющего W чистых состояний):

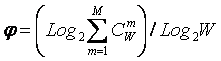
Установлено, что полученное выражение учитывает как взаимосвязь между признаками (факторами) и будущими, в т.ч. целевыми состояниями объекта управления, так и мощность множества будущих состояний. Эта мера отражает уровень системности и степень детерминированности объекта, объединяет возможности их интегрального и дискретного описания, что является основой формализации смысла, а также удовлетворяет принципу соответствия, т.е. преобразуется в формулу Хартли в предельном случае, когда каждому классу (состоянию объекта) соответствует один признак (фактор), и каждому признаку – один класс, и эти классы, а значит и признаки, равновероятны.

7. Все это делает семантическую меру целесообразности информации оптимальной по сформулированным критериям для целей построения семантической информационной модели активных объектов управления и для применения при синтезе рефлексивных АСУ активными системами.

8. В разработанной семантической информационной модели генерируется обобщенная таблица решений, в которой входы (факторы) и выходы будущие состояния активного объекта управления (АОУ) связаны друг с другом не с помощью классических (Аристотелевских) импликаций, принимающих только значения: "Истина" и "Ложь", а различными значениями истинности, выраженными в битах и принимающими значения от положительного теоретически-максимально-возможного ("Максимальная степень истинности"), до теоретически неограниченного отрицательного ("Степень ложности"). Синтез обобщенных таблиц решений для различных предметных областей осуществляется непосредственно на основе эмпирических исходных данных. На основе этих таблиц продуцируются прямые и обратные правдоподобные (нечеткие) логические рассуждения по неклассическим схемам с различными расчетными значениями истинности, являющимся обобщением классических импликаций. При этом в прямых рассуждениях как предпосылки рассматриваются факторы, а как заключения – будущие состояния АОУ, а в обратных – наоборот. Степень истинности i-й предпосылки – это количество информации I_ij, содержащейся в предпосылке о наступлении j-го будущего состояния активного объекта управления.

9. В качестве меры сходства объекта с классом, класса с классом и атрибута с атрибутом предложено использовать неметрический интегральный критерий, основанный на лемме Неймана-Пирсона, – суммарное количество информации. Если предпосылок несколько, то степень истинности наступления j-го состояния АОУ равна суммарному количеству информации, содержащемуся в них об этом:

Или в координатной форме:

_,

где: – вектор j–го состояния объекта управления, координаты которого в информационном семантическом пространстве рассчитываются согласно системного обобщения формулы Харкевича, приведенной в п.6; – булев вектор состояния предметной области, включающий все виды факторов, характеризующих объект управления, возможные управляющие воздействия и окружающую среду (массив–локатор). Обоснована замена значений координат этих векторов их стандартизированными значениями.

10. Предложенная семантическая информационная модель позволяет решать задачи идентификации и прогнозирования развития активных систем (разложение вектора объекта по векторам классов – "Объектный анализ"), а также вырабатывать эффективные управляющие воздействия путем решения обратной задачи прогнозирования и применения элементов нетрадиционной логики и правдоподобных (нечетких) рассуждений. В ней объединены преимущества содержательных и статистических моделей, созданы предпосылки для реализации СК-анализа.

11. Исследована взаимосвязь примененной в модели семантической меры Харкевича со статистикой c², и, на этой основе, предложена новая статистическая мера наличия причинно-следственных связей в предметной области H, основанная на модифицированной формуле Харкевича:

где:

– средняя информативность признаков по матрице информативностей.

Обоснована устойчивость модели при малых и больших выборках, дано обоснование сопоставимости частных критериев, разработана интерпретация распознавания как объектного анализа (разложение вектора объекта в ряд по векторам классов), предложены робастные процедуры, а также процедуры обеспечения структурной репрезентативности выборки.

12. Предлагается модель нелокального нейрона, являющаяся обобщением классической модели Дж. Маккалоки и У. Питта. Суть нелокальности данной модели состоит в том, что весовые коэффициенты каждого нейрона зависят не только от нейронов, прямо или косвенно соединенных с ним синаптически, но и от всех остальных нейронов сети, не затрагиваемых при обратном распространении ошибки от данного нейрона. Предлагается новый класс нейронных сетей: "Нелокальные интерпретируемые нейронные сети прямого счета" (нелокальные нейронные сети – ННС). Организация ННС обеспечивает один из вариантов решения традиционных для нейронных сетей проблем: содержательной интерпретации смысла интенсивности входных сигналов и весовых коэффициентов ("проблема интерпретируемости весовых коэффициентов"); содержательной интерпретации и обоснования аддитивности аргумента и вида активационной (передаточной) функции нейрона ("проблема интерпретируемости передаточной функции"); "Комбинаторного взрыва" при определении структуры связей нейронов, подборе весовых коэффициентов и передаточных функций ("проблема размерности"). Математическая модель ННС основана на предложенной автором системной теории информации и семантической информационной модели автоматизированного системно-когнитивного анализа (АСК-анализ), и в отличие от известных нейронных сетей, обеспечивают автоматизацию всех 10 базовых когнитивных операций, образующих "когнитивный конфигуратор". Предложены не только математическая модель, но также и соответствующий численный метод (включая алгоритмы и структуры данных), а также программный инструментарий нелокальных нейронных сетей (универсальная когнитивная аналитическая система "Эйдос" версии 12.5), успешно апробированные в ряде предметных областей. Данная система обеспечивает практически неограниченное количество слоев ННС, рецепторов, выходных нейронов и связывающих их весовых коэффициентов (десятки миллионов), а также автоматическую визуализацию и запись в виде графических файлов сформированных моделей нелокальных нейронов и Паретто-подмножеств нелокальной нейронной сети.

13. Введено в научный оборот новое понятие: коэффициент эмерджентности Хартли j, который представляет собой относительное превышение количества информации о системе при учете системных эффектов (смешанных состояний, иерархической структуры ее подсистем и т.п.) над количеством информации без учета системности, т.е. этот коэффициент отражает уровень системности объекта. Этот уровень системности объекта изменяется от 1 (системность минимальна, т.е. отсутствует) до W/Log₂W (системность максимальна). Для каждого количества элементов системы существует свой максимальный уровень системности, который никогда реально не достигается из-за действия правил запрета на реализацию в системе ряда подсистем различных уровней иерархии.

Введено в научный оборот новое понятие: коэффициент эмерджентности Харкевича Y, который изменяется от 0 до 1 и определяет степень детерминированности системы: Y=1 соответствует полностью детерминированной системе, поведение которой однозначно определяется действием минимальным количеством факторов, которых столько же, сколько состояний системы; Y=0 соответствует полностью случайной системе, поведение которой никак не зависит действия факторов независимо от их количества; 0<Y<1 соответствуют большинству реальных систем, поведение которых зависит от многих факторов, число которых превосходит количество состояний системы, причем ни одно из состояний не определяется однозначно никакими сочетаниями действующих факторов. Увеличение уровня системности влияет на семантическую информационную модель аналогично повышению уровня детерминированности. Понижение уровня системности, также как и степени детерминированности системы приводит к ослаблению влияния факторов на поведение системы, т.е. к своего рода "инфляции факторов".

Основной вывод:

В предложенном системном обобщении формулы Харкевича впервые непосредственно в аналитическом выражении для самого понятия "Информация" отражены такие фундаментальные свойства систем, как "Уровень системности" и "Степень детерминированности" системы, кроме того это выражение (как и формула Шеннона) удовлетворяет принципу соответствия с выражением Хартли в детерминистском случае, учитывает понятие цели и мощность множества будущих состояний объекта управления, объединяет возможности интегрального и дискретного описания объектов. По этим причинам полученное выражение является оптимальным и его целесообразно использовать в качестве основы для построения математической модели рефлексивных АСУ активными объектами.

Контрольные вопросы

1. Предпосылки и теоретические основы системной теории информации.

2. Требования к математической модели и численной мере СТИ. Выбор базовой численной меры СТИ.

3. Конструирование системной численной меры на основе базовой в СТИ.

4. Семантическая информационная модель СК-анализа.

5. Формализм динамики взаимодействующих семантических информационных пространств. Двухвекторное представление данных.

6. Применение классической теории информации Клода Шеннона для расчета весовых коэффициентов и мер сходства.

7. Математическая модель метода распознавания образов и принятия решений, основанного на системной теории информации.

8. Некоторые свойства математической модели СК-анализа (сходимость, адекватность, устойчивость и др.).

9. Непараметричность модели. Робастные процедуры и фильтры для исключения артефактов в математической модели СК-анализа.

10. Зависимость информативностей факторов от объема обучающей выборки.

11. Зависимость адекватности семантической информационной модели от объема обучающей выборки (адекватность при малых и больших выборках).

12. Семантическая устойчивость модели СК-анализа.

13. Зависимость параметров модели СК-анализа от ее ортонормированности.

14. Взаимосвязь математической модели СК-анализа с другими моделями.

15. Взаимосвязь системной меры целесообразности информации со статистикой Х² и новая мера уровня системности предметной области.

16. Сравнение, идентификация и прогнозирование как разложение векторов объектов в ряд по векторам классов (объектный анализ).

17. Системно-когнитивный и факторный анализ. СК-анализ, как метод вариабельных контрольных групп.

18. Семантическая мера целесообразности информации и эластичность.

19. Связь семантической информационной модели с нейронными сетями.

20. Математический метод СК-анализа в свете идей интервальной бутстрепной робастной статистики объектов нечисловой природы.

Рекомендуемая литература

1. Орлов А.И. "Высокие статистические технологии": http://antorlov.chat.ru.

2. Луценко Е.В. Автоматизированная система распознавания образов: математическая модель и опыт применения. //В сб.: "В.И. Вернадский и современность (к 130-летию со дня рождения)". - Краснодар: КНА, 1993. - С.37-42.

3. Луценко Е.В. Теоретические основы и технология адаптивного семантического анализа в поддержке принятия решений (на примере универсальной автоматизированной системы распознавания образов "ЭЙДОС-5.1"). – Краснодар: КЮИ МВД РФ, 1996. – 280с.

4. Луценко Е.В. Автоматизированный системно-когнитив-ный анализ в управлении активными объектами (системная теория информации и ее применение в исследовании экономических, социально-психологических, технологических и организационно-технических систем): Монография (научное издание). –Краснодар: КубГАУ. 2002. –605 с.

5. Пат. № 940217. РФ. Универсальная автоматизированная система распознавания образов "ЭЙДОС". /Е.В.Луценко (Россия); Заяв. № 940103. Опубл. 11.05.94. – 50с.

6. Пат. № 2003610986 РФ. Универсальная когнитивная аналитическая система "ЭЙДОС" / Е.В.Луценко (Россия); Заяв. № 2003610510 РФ. Опубл. от 22.04.2003. – 50с.

7. Эфрон Б. Нетрадиционные методы многомерного статистического анализа. - М.: Финансы и статистика, 1988. – 263 с.
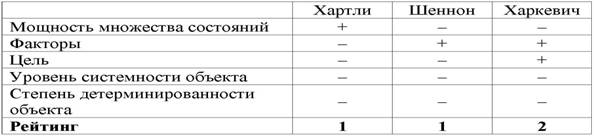
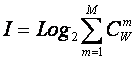
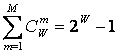
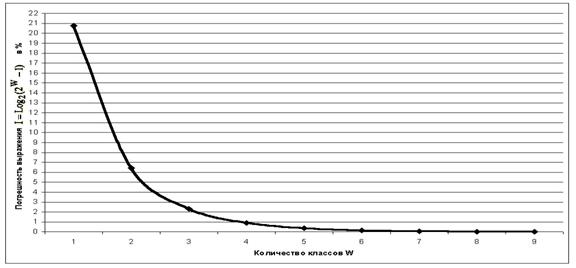
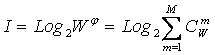
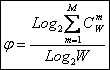
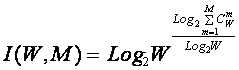
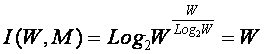
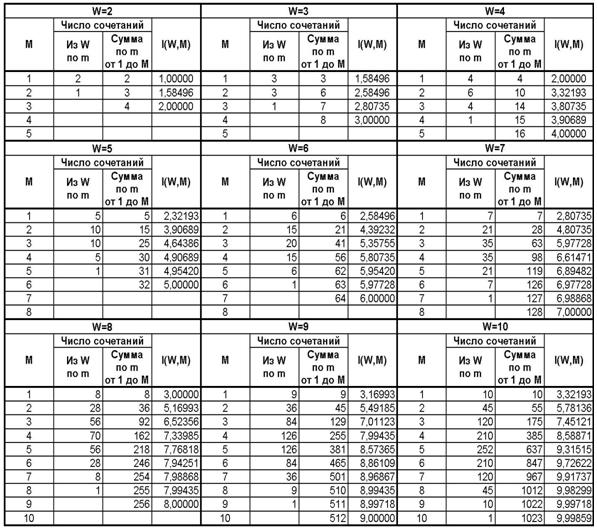
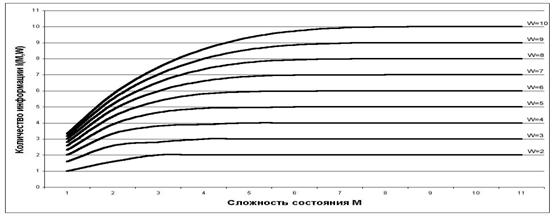
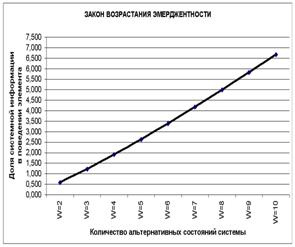
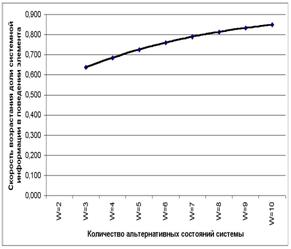
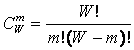
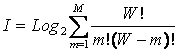
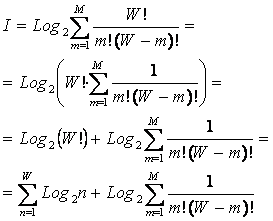
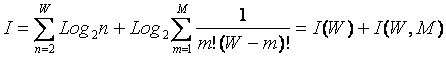
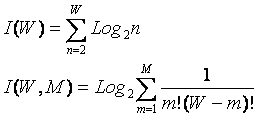
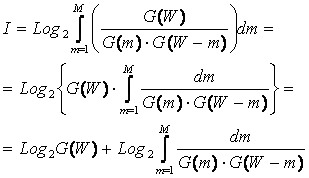
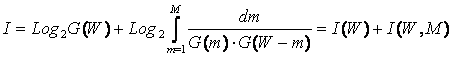
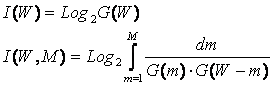
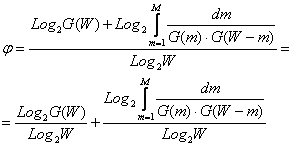
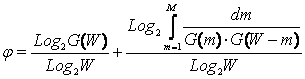
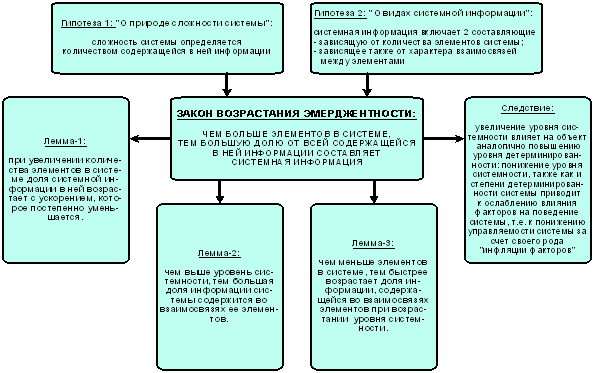
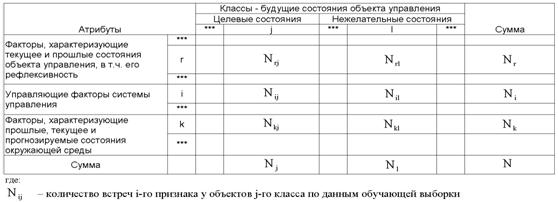
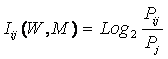
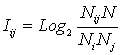
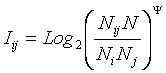
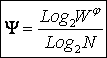
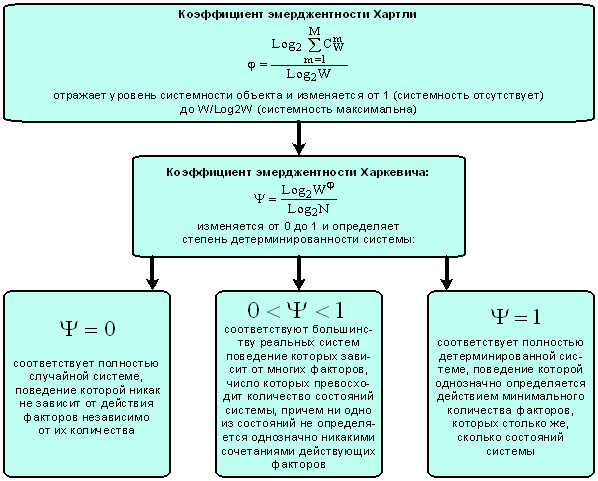
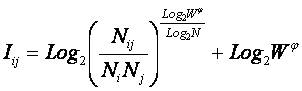
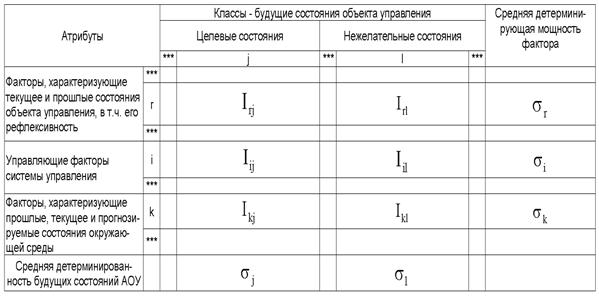
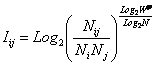
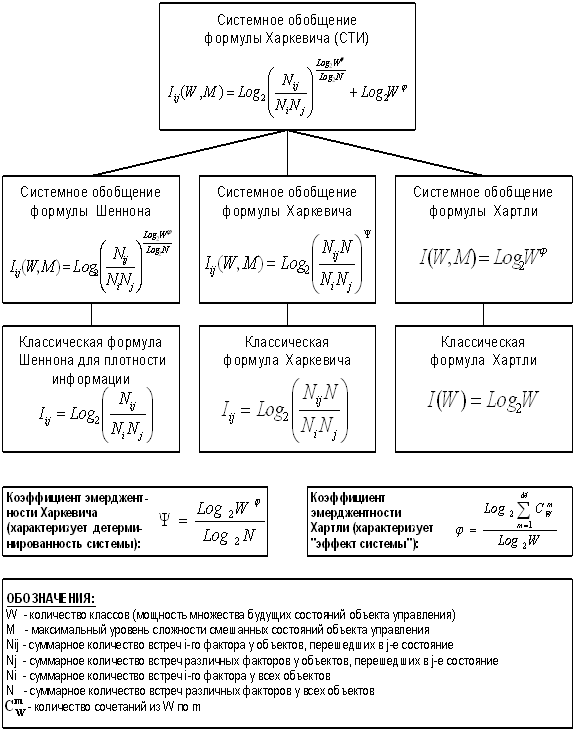
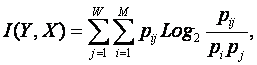
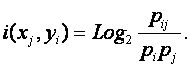
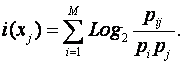
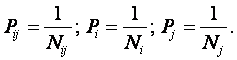
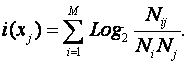
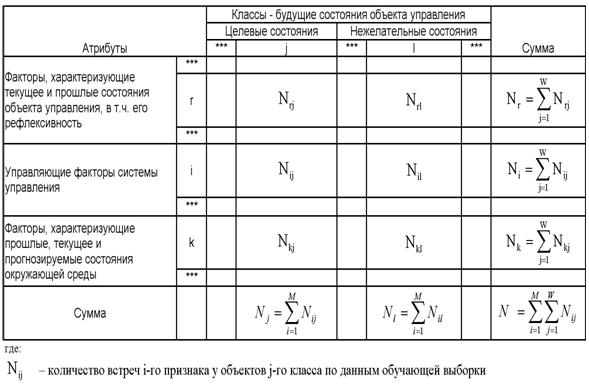
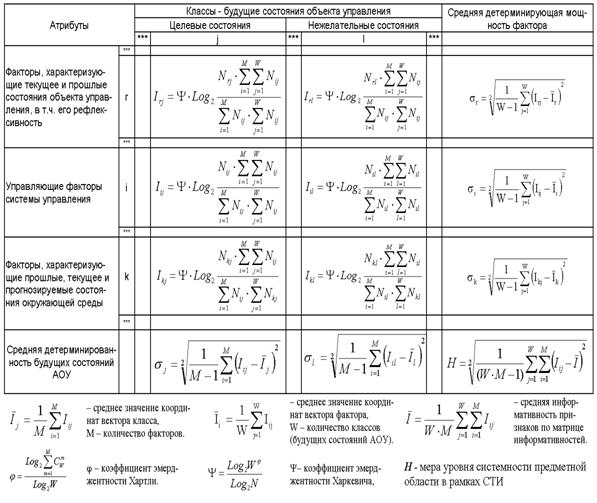
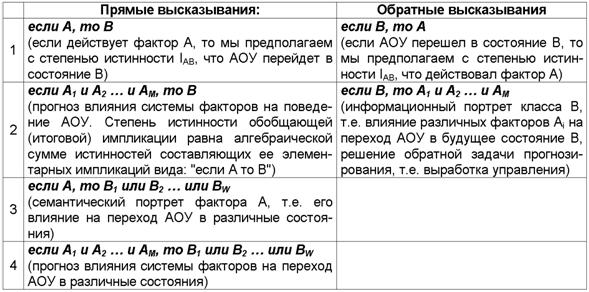
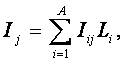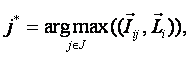
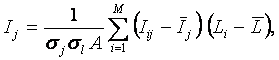
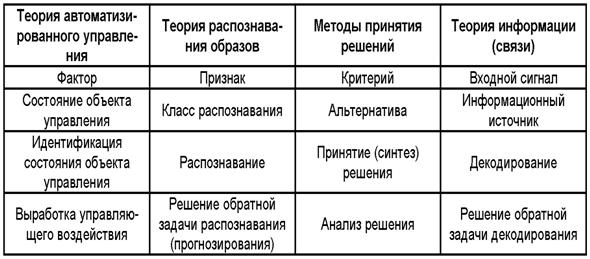
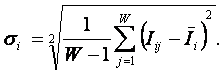
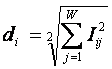
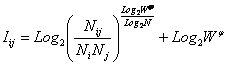
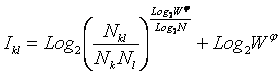
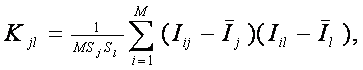
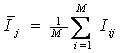
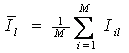
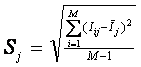
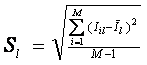
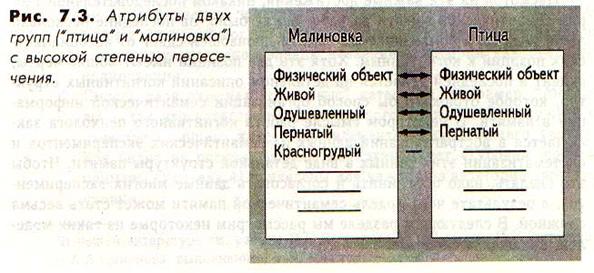
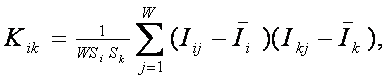
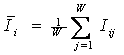
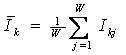
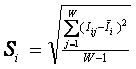
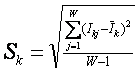
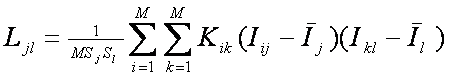
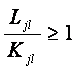
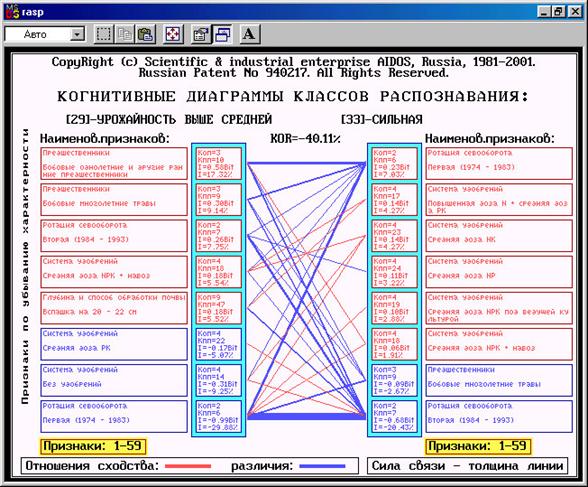
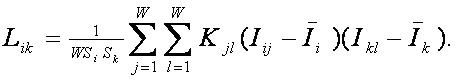
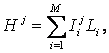
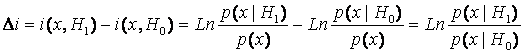
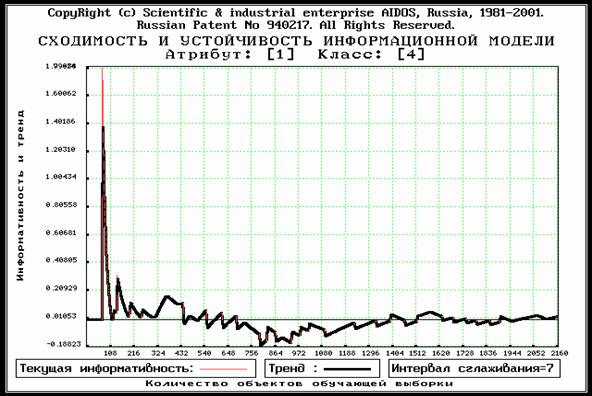
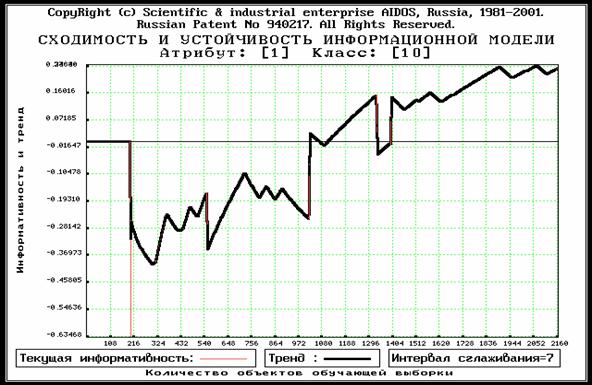
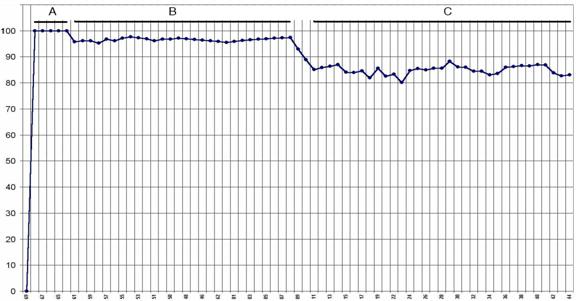
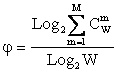
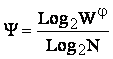
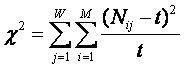
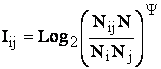
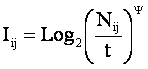
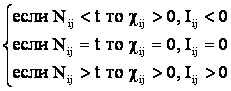
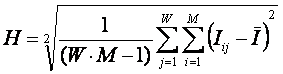
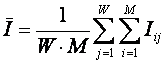
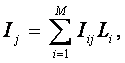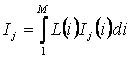
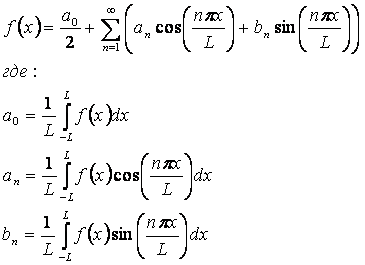
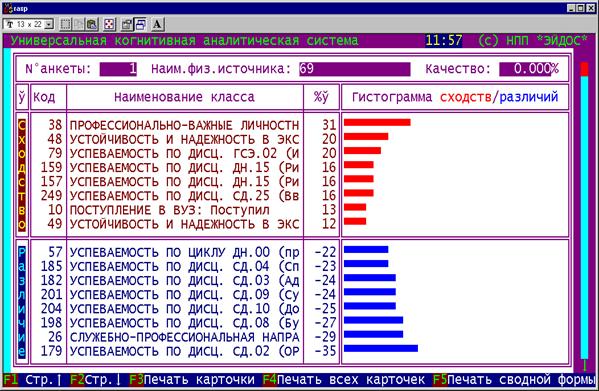
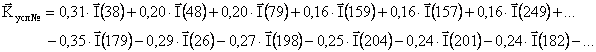
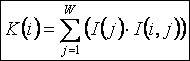
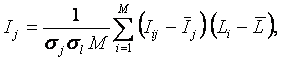
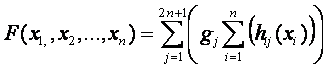
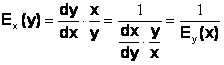
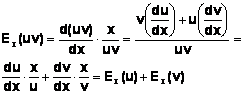
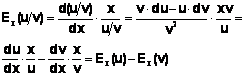
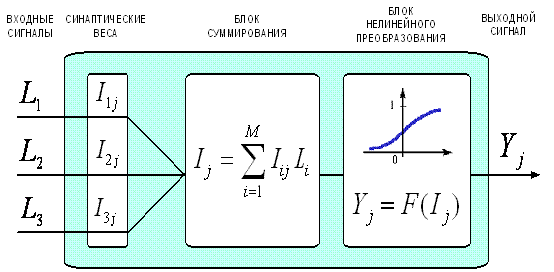
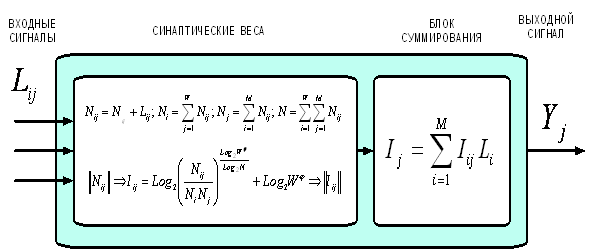
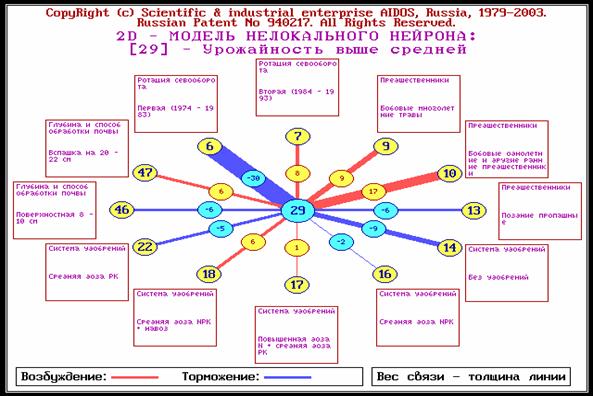
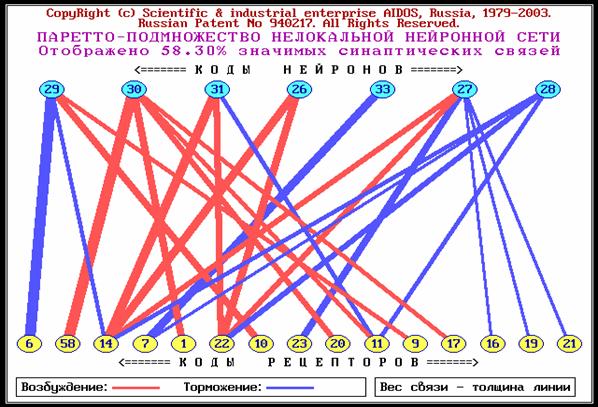
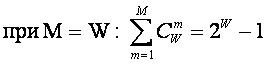
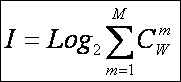
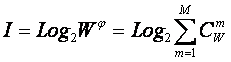
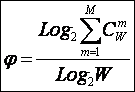
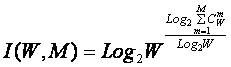
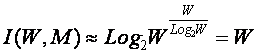
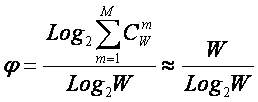
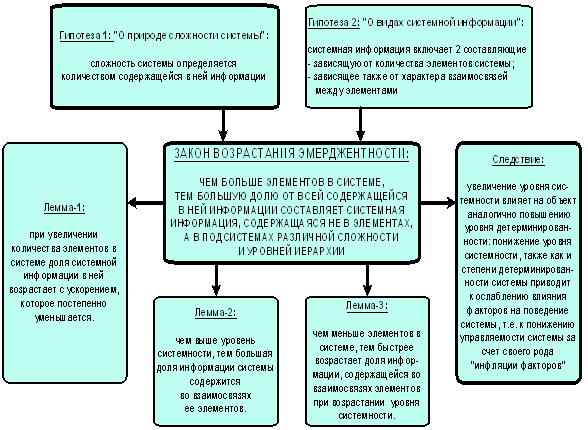
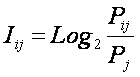
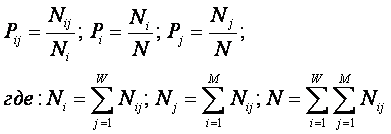
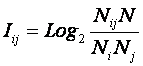
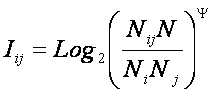
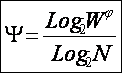
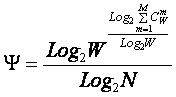
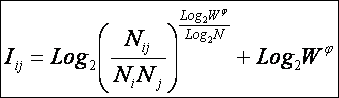
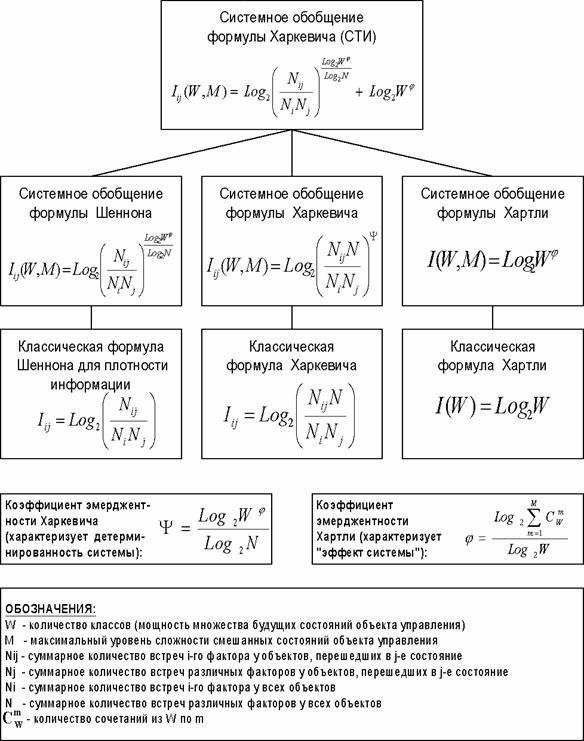
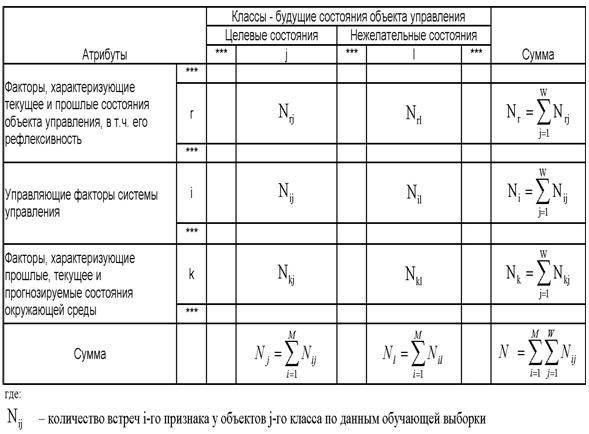
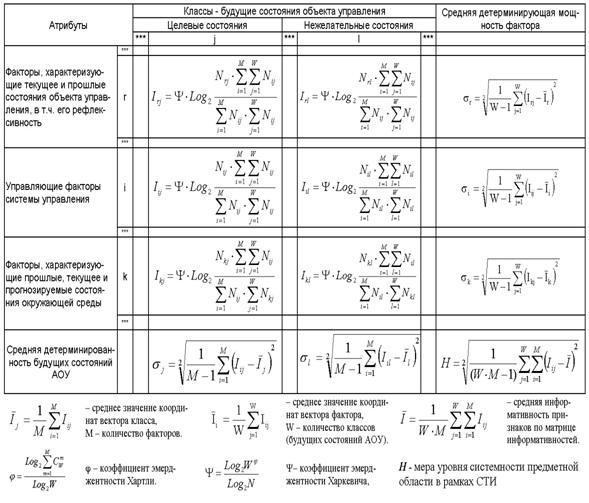
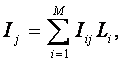
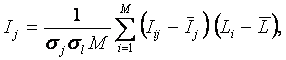
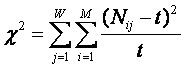
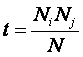
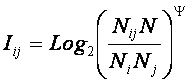
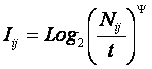
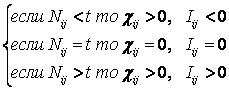
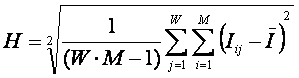
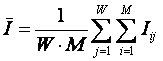
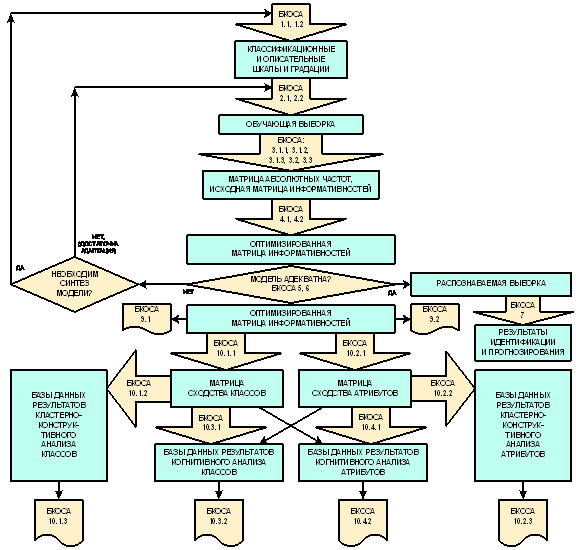
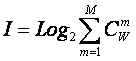
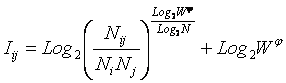
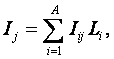