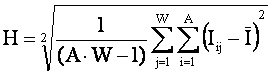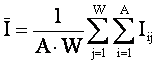Предлагается
теоретическое обоснование, методика
численных расчетов и программная реализация решения задач статистики, в
частности исследования статистических распределений, методами теории
информации. При этом непосредственно на основе эмпирических данных расчетным
путем определяется количество информации в наблюдениях, которое используется
для анализа статистических распределений. Предлагаемый способ расчета количества
информации не основан на предположениях о независимости наблюдений и их
нормальном распределении, т.е. является непараметрическим и обеспечивает
корректное моделирование нелинейных систем, а также позволяет сопоставимо
обрабатывать разнородные (измеряемые в шкалах различных типов) данные числовой
и нечисловой природы, измеряемые в различных единицах измерения. Таким образом,
АСК-анализ и система «Эйдос» представляют собой современную инновационную
(готовую к внедрению) технологию решения задач статистики методами теории
информации. Данный раздел может быть использован как описание
лабораторной работы по дисциплинам: интеллектуальные
системы; инженерия знаний и интеллектуальные системы; интеллектуальные
технологии и представление знаний; представление знаний в интеллектуальных
системах; основы интеллектуальных систем; введение в нейроматематику и методы
нейронных сетей; основы искусственного интеллекта; интеллектуальные технологии
в науке и образовании; управление знаниями; автоматизированный системно-когнитивный
анализ и интеллектуальная система «Эйдос»; которые автор ведет в настоящее
время, а также и в других дисциплинах, связанных с преобразованием данных в
информацию, а ее в знания и применением этих знаний для решения задач
идентификации, прогнозирования, принятия решений и исследования моделируемой
предметной области (а это практически все дисциплины во всех областях науки)
«... навыки мысли и аналитический аппарат
теории информации должны, по-видимому, привести к заметной перестройке здания математической
статистики»
А.Н.
Колмогоров [2,3,4]
В статистике существует проблема определения закона распределения наблюдений, а затем и
определения параметров этого распределения. Традиционно эта проблема решается путем проверки статистических гипотез, на основе
специально разработанных довольно многочисленных статистических
тестов и критериев с учетом ошибок первого и второго рода.
Эта теория детально разработана и общеизвестна. Однако
необходимо отметить, что по ряду причин на практике ей довольно редко
пользуются, а когда все же пользуются, то часто делают это некорректно. Довольно
многие просто пользуются теми или иными возможностями MS Excel или
статистических пакетов и при этом даже не задумываются, что применяемые ими
методы являются параметрическими,
т.е. существенным образом основаны
на предположении о выполнении для исследуемых наблюдений гипотезы о
нормальности распределения. Естественно они и не пытаются проверить, так ли
это. Детальный и исчерпывающий на сегодняшний день анализ причин некорректного
использования статистических технологий приведен в классической работе [1] и
здесь мы не будем на нем останавливаться. Отметим лишь, что этих причин так
много и они настолько разнообразны, что на наш взгляд ученый, собирающийся применить
статистику в своих исследованиях или при решении задач в своей области науки,
по-видимому, практически обречен на ее некорректное использование.
Общая идея решения сформулированной проблемы состоит в
предложении применить
непараметрические методы, в частности теорию
информации, для решения тех задач, которые традиционно решаются в параметрической
статистике.
Конечно, применение теории информации для решения
проблем и развития статистики не является абсолютно новой идеей. Как
указывает в своих работах [2, 3] профессор А.И.Орлов, сходные идеи развивал еще
в середине XX века С.Кульбак [4], а в эпиграф данного раздела вынесено программное
высказывание выдающегося российского математика А.Н. Колмогорова:
«... навыки мысли и аналитический аппарат теории информации должны,
по-видимому, привести к заметной перестройке
здания математической статистики», которое содержится в его предисловии к той
же книге С.Кульбака и также приведено в
работах [2, 3]. В наше время в этом направлении продуктивно работают Дуглас Хаббард
[5], а также известный российский математик, разработчик синергетической теории
информации В.Б.Вяткин [6-13].
В работе [1] в разделе «11.1. Проблема множественных проверок статистических гипотез»
профессор А.И.Орлов указывает, что регрессионный анализ является параметрическим
методом и при множественных проверках
статистических гипотез им пользоваться некорректно, т.к. однородные группы, полученные с помощью
какого-либо алгоритма классификации (кластеризации), подчиняются не нормальному
распределению, а усеченному нормальному.
Имеется определенный
положительный опыт решения поставленной проблемы путем применения теории
информации.
В статье [14] метод наименьших квадратов (МНК) широко
известен и пользуется заслуженной популярностью. Вместе с тем не прекращаются
попытки усовершенствования этого метода. Результатом одной из таких попыток
является взвешенный метод наименьших квадратов (ВМНК), суть которого в том,
чтобы придать наблюдениям вес обратно пропорциональный погрешностям их
аппроксимации. Этим самым, фактически, наблюдения игнорируются тем в большей
степени, чем сложнее их аппроксимировать. В результате такого подхода формально
погрешность аппроксимации снижается, но фактически это происходит путем
частичного отказа от рассмотрения «проблемных» наблюдений, вносящих большую
ошибку. Если эту идею, лежащую в основе ВМНК довести до крайности (и тем самым
до абсурда), то в пределе такой подход приведет к тому, что из всей
совокупности наблюдений останутся только те, которые практически точно ложатся
на тренд, полученный методом наименьших квадратов, а остальные просто будут
проигнорированы. Однако, по мнению автора, фактически это не решение проблемы,
а отказ от ее решения, хотя внешне и выглядит как решение. В работе
предлагается именно решение, основанное на теории информации: считать весом
наблюдения количество информации в аргументе о значении функции. Этот подход
был обоснован в рамках нового инновационного метода искусственного интеллекта:
метода автоматизированного системно-когнитивного анализа (АСК-анализа) и реализован
еще 30 лет назад в его программном инструментарии – интеллектуальной системе «Эйдос» в виде так называемых «когнитивных функций».
В данном разделе приводится алгоритм и программная реализация данного подхода,
проиллюстрированные на подробном численном примере.
В статье [15] кратко рассматриваются математическая
сущность предложенной автором модификации взвешенного
метода наименьших квадратов (ВМНК), в котором в качестве весов
наблюдений применяется количество информации в них. Предлагается два варианта
данной модификации ВМНК. В первом варианте взвешивание наблюдений производится
путем замены одного наблюдения с определенным количеством информации в нем
соответствующим количеством наблюдений
единичного веса, а затем к ним применяется стандартный метод
наименьших квадратов (МНК). Во втором варианте взвешивание наблюдений
производится для каждого значения аргумента путем замены всех наблюдений с
определенным количеством информации в них одним наблюдением единичного веса,
полученным как средневзвешенное от них, а затем к ним применяется стандартный
МНК. Подробно описана методика численных расчетов количества информации в
наблюдениях, основанная на теории автоматизированного системно-когнитивного
анализа (АСК-анализ) и реализованная в его программном инструментарии –
интеллектуальной системе «Эйдос». Приводится иллюстрация предлагаемого подхода
на простом численном примере.
Отметим также, что в статье [16] на небольшом численном примере рассматриваются новые
математическая модель, алгоритм и результаты агломеративной кластеризации,
основные отличия которых от ранее известных стоят в том, что: а) в них параметры
обобщенного образа кластера не вычисляются как средние от исходных объектов
(классов) или центры тяжести, а определяются с
помощью той же самой базовой когнитивной операции АСК-анализа, которая
применяется и для формирования обобщенных образов классов на основе примеров
объектов и которая действительно обеспечивает обобщение; б) в качестве критерия
сходства используется не евклидово расстояние или его варианты, а интегральный
критерий неметрической природы: «суммарное количество информации», применение
которого теоретически корректно и дает хорошие результаты в неортонормированных
пространствах, которые обычно и встречаются на практике; в) кластерный анализ
проводится не на основе исходных переменных или матрицы сопряженности,
зависящих от единиц измерения по осям, а в когнитивном пространстве, в котором
по всем осям (описательным шкалам) используется одна единица измерения:
количество информации, и поэтому результаты кластеризации не зависят от
исходных единиц измерения признаков объектов. Имеется и ряд других менее
существенных отличий. Все это позволяет получить результаты кластеризации,
понятные специалистам и поддающиеся содержательной интерпретации, хорошо
согласующиеся с оценками экспертов, их опытом и интуитивными ожиданиями, что
часто представляет собой проблему для классических методов кластеризации. Описанные
методы теоретически обоснованы в системно-когнитивном анализе (СК-анализ) и
реализованы в его программном инструментарии – интеллектуальной системе «Эйдос».
Таким образом, в работах автора [14, 15 и
16] по сути, намечается путь решения проблемы построения непараметрического
регрессионного анализа, основанного на теории информации, в том числе и для его
применения в относительно однородных группах, полученных путем когнитивной
кластеризации.
Задача № 1:
проверка статистических гипотез.
По сути, эта задача является частным вариантом задачи распознавания образов,
т.к. в ней по первичным и вторичным (расчетным) признакам наблюдений необходимо
определить вид статистического распределения и его параметры. А теория
информации хорошо позволяет решать подобные задачи распознавания, в том числе и
в условиях зашумленности исходных данных.
Задача № 2: исследование влияния уровня системности
действующих на объекты наблюдения факторов на степень отклонения статистического
распределения их характеристик от нормального. Данная задача тесно связана с системным обобщением
математики, в частности системной теорией информации, которые были предложены
автором в ряде работ [см., например: 17, 35, 36]. Решение этой задачи может заложить
основы системного обобщения статистики (системной статистики) в результате
применения идей системного обобщения математики в статистике. Эта задача тесно
связана с Центральными предельными теоремами
(ЦПТ) или законом больших чисел теории
вероятностей, утверждающих, что сумма достаточно большого количества слабо
зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из
слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет
статистическое распределение, стремящееся (сходящееся) к нормальному распределению.
С позиций системного обобщения математики независимые зависимые случайные
величины представляют собой множество случайных величин. Если же
между ними есть зависимости, то их уже нельзя (вернее можно, но это
некорректно) рассматривать как множество и более адекватным является
представление о них, как о системе
случайных величин [17]. Система имеет эмерджентные свойства, которых не было
у ее элементов и эти свойства тем ярче выражены, чем выше уровень системности.
Автором предложено несколько разных вариантов коэффициентов эмерджентности, которые
представляют собой количественные информационные меры уровня системности и
степени детерминированности систем.
Система факторов влияет на систему не так, так как их сумма, т.е. нелинейно. В
результате статистическое распределение системы случайных величин отклоняется
от нормального тем в большей степени, чем выше уровень системности и нелинейность.
Таким образом, вся параметрическая статистика описывает только линейные
системы, а для нелинейных систем она является неадекватной. Отметим, что к
нелинейным системам, имеющим высокий уровень системности и ярко выраженные
эмерджентные (синергетические) свойства, относятся все живые системы,
искусственные и естественные экосистемы, биоценозы, системы с участием людей
(социально-экономические, психологические, культурные, политические), вообще
все сложные и большие системы.
Задача № 3: нахождение
информативных подмножеств признаков в регрессионном анализе и в
автоматизированных системах управления. Данная задача сформулирована
профессором А.И.Орловым в работе [1] следующим образом: «…в большинстве важных
для практики случаев статистические свойства процедур анализа данных,
основанных на множественных проверках, остаются пока неизвестными. Примерами
являются процедуры нахождения информативных подмножеств признаков (коэффициенты
для таких и только таких признаков отличны от 0) в регрессионном анализе или выявления
отклонений параметров в автоматизированных системах управления». Решение этой
задачи давно (еще в 1979 году) предложено автором в теории АСК-анализа и
реализовано в его программном инструментарии – интеллектуальной системе «Эйдос»
и представляет собой базовую когнитивную операцию «Абстрагирование» [18]. Это
решение основано на использовании вариабельности количества информации в
значении аргумента (в признаке) о значении функции (классе) в качестве меры
информативности (ценности, дискриминантной, дифференцирующей способности)
данного значения аргумента (признака), т.е. его полезности для различения
классов.
Задача № 4: "стыковка"
статистических процедур. Данная задача также сформулирована профессором
А.И.Орловым в работе [1]: «Проблема
множественных проверок статистических гипотез – часть более общей проблемы
"стыковки" (сопряжения) статистических процедур. Дело в том, что
каждая процедура может применяться лишь при некоторых условиях, а в результате
применения предыдущих процедур эти условия могут нарушаться». Решению очень
сходной задачи посвящен АСК-анализ, в котором с единых позиций теории
информации рассматривается полная необходимая и достаточная система
(конфигуратор) базовых когнитивных операций [19, 20, 21]. По сути можно
сказать, что грандиозное здание статистики построено без единого плана, т.е. не
системно, и в результате отдельные его конструкции не всегда гармонично
сочетаются друг с другом и не образуют единого целого. Можно, конечно,
попытаться все это упорядочить и расписать на языке непосвященных, а также
снабдить их программным инструментарием, но эта задача в настоящее время,
похоже, никем не ставится. Автор предлагает другое, как это ни парадоксально,
но возможно более простое решение: не реформировать старое, а построить рядом
новое здание системной статистики и сделать это по единому проекту, единой теоретической
и методологической основе теории информации. По крайней мере, в совершенно
аналогичной ситуации с автоматизацией системного анализа второй вариант решения
оказался более эффективным, чем другие [19]. В частности оказалось
возможным создать и единую систему, основанную на этой единой теоретической и
металогической основе теории информации: интеллектуальную систему «Эйдос». Это
вселяет надежду на решение проблемы, о которой в работе [1] профессор А.И.Орлов
писал: «Математическая статистика
демонстрирует … виртуозную математическую технику для анализа частных случаев и
полную беспомощность при выдаче практических рекомендаций».
Задача № 5: конструирование системной информационной
меры взаимосвязи двух векторов, аналогичной коэффициенту корреляции. Это сделано в АСК-анализе и реализовано в системе
«Эйдос» и описано автором в монографии [37] еще в 1996 году в режиме «Содержательное сравнение двух классов».
Суть идеи состоит в том, что:
а) при расчете коэффициента корреляции учитываются не
сами значения аргумента, а количество информации о значениях функции, которое в
них содержится;
б) учитываются не только вклад в сходство-различие
значений аргумента с одинаковыми индексами, но и все их сочетания.
Разумеется, этим перечень задач статистики, которые на
взгляд автора могли бы быть решены с методами теории информации, в частности
АСК-анализа и системы «Эйдос», далеко не исчерпывается. Конечно, здесь
возникает естественный вопрос о том, какие вообще задачи статистики могут быть
решены с помощью теории информации. На это вопрос можно было бы ответить другим
вопросом: «А какие задачи статистики не могут быть решены с помощью теории
информации?» На наш взгляд любая
наука, а не только статистика, в процессе исследования и как его результат
получает определенную информацию об объекте исследования. Поэтому теория
информации в определенном смысле является метанаукой имеющей не меньшую
общность, чем философия, но в отличие от нее являющаяся естественной
высокоматематизированной наукой, имеющей свой программный инструментарий. Даже
мысленный эксперимент Альберта Эйнштейна с движущимся поездом и источниками
света на платформе, на основе которого в теории относительности формируется
представление об одновременности и времени, фактически является не более чем
описанием системы передачи информации в пространстве-времени с помощью световых
сигналов. Даже когда мы узнаем, чему равен предел функции или интеграл, то даже
если мы об этом и не знаем, то все равно на самом деле мы тоже получаем об этом
информацию, количество которой можно посчитать и выразить в битах. Поэтому
любая задача в любой области науки требует для своего решения практического
применения теории информации, которое чаще осуществляется всего неосознанно и
на качественном уровне. АСК-анализ и его программный инструментарий – система
«Эйдос», реализованная в универсальной постановке, не зависящей от предметной
области, позволяют осуществить это на осознанном уровне.
Задача № 6: исследование информационных моделей
статистических распределений. Решение
этой задачи включает кластерный и конструктивный анализ распределений, их
информационные портреты и многие другие исследования с использованием
возможностей АСК-анализа и системы «Эйдос» [21].
Далее в данном разделе кратко рассмотрим возможный
вариант применения теории информации для получения определенной информации о
статистическом распределении наблюдений. Это можно рассматривать как подготовку
к решению сформулированной выше задачи №1 и некоторых других
сформулированных задач.
Данная идея состоит в том, чтобы рассматривать статистические
распределения как когнитивные функции. Это открывает перспективы
использования теории информации для анализа функций, в т.ч. и статистических
распределений.
В АСК-анализе предложено новое понятие когнитивных функций, которое
рассмотрено и развито в ряде работ автора и соавторов [17, 22–34] и поэтому
здесь нет смысла подробно останавливаться на этом понятии. Отметим лишь суть. В
работе [17] кратко рассматриваются классическое понятие функциональной
зависимости в математике, определяются ограничения применимости этого понятия
для адекватного моделирования реальности и формулируется проблема, состоящая в
поиске такого обобщения понятия функции, которое было бы более пригодно для
адекватного отражения причинно-следственных связей в реальной области. Далее
рассматривается теоретическое и практическое решения поставленной проблемы,
состоящие в том, что:
а) предлагается универсальный не зависящий от
предметной области способ вычисления количества информации в значении аргумента
о значении функции, т.е. когнитивные функции;
б) предлагается программный инструментарий:
интеллектуальная система «Эйдос», позволяющая на практике осуществлять эти
расчеты, т.е. строить когнитивные функции на основе фрагментированных зашумленных
эмпирических данных большой размерности.
Предлагаются понятия нередуцированных, частично и
полностью редуцированных прямых и обратных, позитивных и негативных когнитивных
функций и метод формирования редуцированных когнитивных функций, являющийся
вариантом известного взвешенного метода наименьших квадратов, отличающимся от
стандартного ВМНК учетом в качестве весов
наблюдений количества информации в
значениях аргумента о значениях функции.
Идея применения теории информации для исследования
статистических распределений проста и базируется на двух вполне очевидных предпосылках.
Предпосылка № 1. Любое исследование, в т.ч. исследование статистических распределений,
представляет собой процесс получения информации об объекте исследования. Этот
процесс включает: источник информации, канал передачи информации и получатель
информации, т.е. представляет собой информационно-измерительную систему.
Поэтому применение теории информации для построения такой системы является
совершенно естественным и очевидным.
Предпосылка № 2. Понятия «Информация» и
«Статистического распределение» тесно взаимосвязаны. Широко известен
хрестоматийный пример определения количественной меры информации Хартли через
понятие равномерного распределения случайной величины: количество информации I=Log2N по Хартли равно
количеству информации, которое мы получаем, когда узнаем, что равномерно
распределенная случайная величина попала в некоторый определенный i-й интервал: один из N равных интервалов. На подобных
соображениях основан известный метод Монте-Карло. В работах [35, 36] предложено
развитие этих идей с использованием классической статистики Больцмана, также ее
квантовых обобщений статистик Ферми-Дирака и Бозе-Эйнтштейна. Оказалось, что
эти статистики математически тесно связаны с системным обобщением теории информации,
предложенным автором.
В данной
работе ставится задача дать ответ на несколько простых вопросов:
Вопрос 1-й. Какое количество информации о принадлежности случайной величины к
нескольким нормальным распределениям с разными параметрами мы получаем, когда
узнаем, что она попала в некоторый определенный i-й интервал: один из N
равных интервалов?
Вопрос 2-й. Какое суммарное количество информации о степени сходства эмпирического
распределения наблюдений с нормальными распределениями с различными параметрами
мы получаем, зная частоты попадания случайной величины в каждый из интервалов
при N равных интервалов?
Вопрос 3-й. Попадание случайной величины в какие интервалы при N равных интервалах является более
характерным и в какие менее характерным для нормальных распределений с
различными параметрами?
Для ответа на эти вопросы нам потребуется
универсальный не зависящий от предметной области способ вычисления количества
информации в наблюдениях, который мы рассмотрим ниже.
Ниже в наиболее упрощенном виде приводится методика
численных расчетов количества информации в наблюдениях, основанная на теории
автоматизированного системно-когнитивного анализа (АСК-анализ) и реализованная
в его программном инструментарии – интеллектуальной системе «Эйдос» [21].
Для удобства рассмотрения введем следующие
обозначения:
i – индекс значения аргумента;
j – индекс значения функции;
M – количество значений аргумента;
W – количество значений функции;
Nij
– количество встреч j-го значения функции при
i-м значении аргумента;
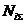 – суммарное количество наблюдений при i-м
значении аргумента по всей выборке;
– суммарное количество наблюдений при i-м
значении аргумента по всей выборке;
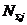 – суммарное количество наблюдений j-го значении функции по всей
выборке;
– суммарное количество наблюдений j-го значении функции по всей
выборке;
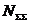 – суммарное количество наблюдений по всей
выборке;
– суммарное количество наблюдений по всей
выборке;
Iij
– количество информации в i-м значении аргумента о том, что функция имеет j-е значение, т.е. это количество
информации в наблюдении (i, j);
Ψ –
нормировочный коэффициент (Е.В.Луценко, 1979), преобразующий количество
информации в формуле А.Харкевича в биты и обеспечивающий для нее соблюдение
принципа соответствия с формулой Р.Хартли в равновероятном детерминистском
случае;
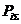 – безусловная относительная частота встречи i-го значения аргумента в обучающей
выборке;
– безусловная относительная частота встречи i-го значения аргумента в обучающей
выборке;
Pij – условная относительная частота встречи
j-го значения функции при i-м
значении аргумента.
Используя исходную выборку эмпирических наблюдений
посчитаем матрицу абсолютных частот (таблица 1):
Таблица 1 – МАТРИЦА АБСОЛЮТНЫХ ЧАСТОТ
|
|
Классы
|
Сумма
|
|
1
|
...
|
j
|
...
|
W
|
|
Значения
факторов
|
1
|
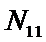
|
|
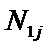
|
|
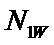
|
|
|
...
|
|
|
|
|
|
|
|
i
|
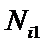
|
|
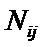
|
|
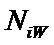
|
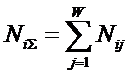
|
|
...
|
|
|
|
|
|
|
|
M
|
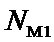
|
|
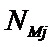
|
|
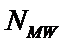
|
|
|
Суммарное
количество
признаков
|
|
|
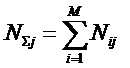
|
|
|
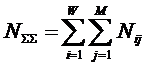
|
Алгоритм формирования матриц абсолютных частот и
условных и безусловных процентных распределений.
Объекты обучающей выборки описываются векторами
(массивами) 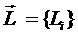 имеющихся у них
признаков:
имеющихся у них
признаков:
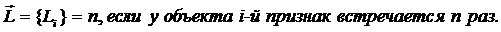
Первоначально в матрице абсолютных частот все значения
равны нулю. Затем организуется цикл по объектам обучающей выборки. Если у
предъявленного объекта, относящегося к j-му
классу, есть i-й признак, то:
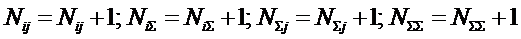 (1)
(1)
На основе анализа матрицы частот (табл. 1) классы
можно сравнивать по наблюдаемым частотам признаков только в том случае, если
количество объектов по всем классам одинаково, как и суммарное
количество признаков по классам. Если же они отличаются, то корректно
сравнивать классы можно только по условным и безусловным относительным частотам
(оценкам вероятностей) наблюдений признаков, посчитанных на основе матрицы
частот (табл. 1) в соответствии с выражениями (2), в результате чего
получается матрица условных и безусловных процентных распределений (табл. 2):
|
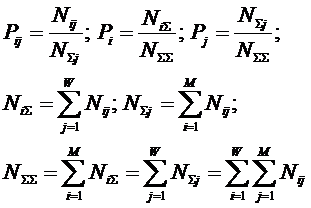
|
((2)
|
Таблица 2 – МАТРИЦА УСЛОВНЫХ И
БЕЗУСЛОВНЫХ
ПРОЦЕНТНЫХ РАСПРЕДЕЛЕНИЙ
|
|
Классы
|
Безусловная
вероятность
признака
|
|
1
|
...
|
j
|
...
|
W
|
|
Значения
факторов
|
1
|
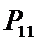
|
|
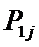
|
|
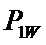
|
|
|
...
|
|
|
|
|
|
|
|
i
|
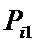
|
|
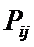
|
|
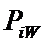
|
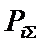
|
|
...
|
|
|
|
|
|
|
|
M
|
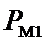
|
|
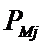
|
|
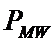
|
|
|
Безусловная
вероятность
класса
|
|
|
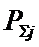
|
|
|
|
Далее произведем расчет количества информации в наблюдениях в соответствии
с выражением (3):
|
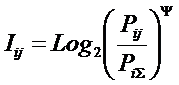
|
(3)
|
С
учетом (2) преобразуем (3) к виду (4):
|
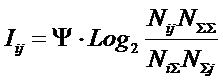
|
(4)
|
|

А.А.Харкевич
|
Здесь 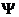 – упрощенная форма
коэффициента эмерджентности А.Харкевича (10), предложенный автором в 1979
году и названный так в честь известного советского ученого, внесшего большой
вклад в теорию информации, на работах которого основана излагаемая методика
численных расчетов количества информации в наблюдениях. – упрощенная форма
коэффициента эмерджентности А.Харкевича (10), предложенный автором в 1979
году и названный так в честь известного советского ученого, внесшего большой
вклад в теорию информации, на работах которого основана излагаемая методика
численных расчетов количества информации в наблюдениях.
|
|
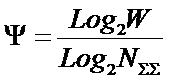
|
(5)
|
Используя выражения (3) и (5) на основе таблицы 2
рассчитывается матрицу информативностей
(таблица 3). Она также может быть получена :непосредственно из таблицы 1 с
использованием выражений (4) и (5):
Таблица 3 – МАТРИЦА ИНФОРМАТИВНОСТЕЙ
|
|
Классы
|
Значимость
фактора
|
|
1
|
...
|
j
|
...
|
W
|
|
Значения
факторов
|
1
|
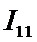
|
|
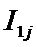
|
|
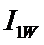
|
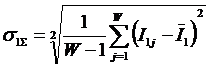
|
|
...
|
|
|
|
|
|
|
|
i
|
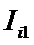
|
|
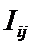
|
|
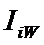
|
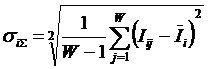
|
|
...
|
|
|
|
|
|
|
|
M
|
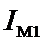
|
|
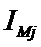
|
|
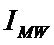
|
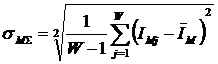
|
|
Степень
редукции
класса
|
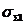
|
|
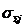
|
|
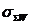
|
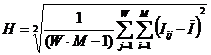
|
Здесь – 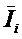 это среднее
количество информации в i-м значении
фактора:
это среднее
количество информации в i-м значении
фактора:
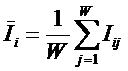
Когда количество информации Iij > 0 – i-й фактор
способствует переходу объекта управления в j-е состояние, когда Iij < 0 –
препятствует этому переходу, когда же Iij = 0 – никак не влияет на это. В
векторе i-го фактора (строка матрицы информативностей) отображается, какое
количество информации о переходе объекта управления в каждое из будущих
состояний содержится в том факте, что данный фактор действует. В векторе j-го
состояния класса (столбец матрицы информативностей) отображается, какое количество
информации о переходе объекта управления в соответствующее состояние содержится
в каждом из факторов.
Таким образом, данная модель позволяет рассчитать,
какое количество информации содержится в любом факте о наступлении любого события
в любой предметной области, причем для этого не требуется повторности этих
фактов и событий. Если данные повторности осуществляются и при этом наблюдается
некоторая вариабельность значений факторов, обуславливающих наступление тех или
иных событий, то модель обеспечивает многопараметрическую типизацию, т.е.
синтез обобщенных образов классов или категорий наступающих событий с количественной
оценкой степени и знака влияния на их наступление различных значений факторов.
Причем эти значения факторов могут быть как количественными, так и
качественными и измеряться в любых единицах измерения, в любом случае в модели
оценивается количество информации, которое в них содержится о наступлении
событий, переходе объекта управления в определенные состояния или, просто, о
его принадлежности к тем или иным классам. Другие способы метризации приведены
в работе [20].
Ниже на простом численном примере
мы кратко рассмотрим технологию, позволяющую на практике и в любой предметной
области посчитать, какое количество информации содержится в наблюдении. В связи
с ограничениями на объем статьи автор не имеет возможности полностью раскрыть все позиции на приведенных ниже
скриншотах и рисунках, т.е. фактически предполагается некоторое предварительное
знакомство читателя с системой «Эйдос». Если же такое знакомство недостаточно
полное, то автор отсылает автора к публикациям в списке литературы и к сайту: http://lc.kubagro.ru/.
Скачиваем и устанавливаем систему «Эйдос». Это наиболее полная на данный
момент незащищенная от несанкционированного копирования портативная (portable)
версия системы (не требующая инсталляции) с исходными текстами, находящаяся
в полном открытом бесплатном доступе (около 50 Мб). Обновление
имеет объем около 3 Мб.
ИНСТРУКЦИЯ
по скачиванию и установке системы «Эйдос» (объем около 50 Мб)
|
Система не требует инсталляции, не меняет никаких системных
файлов и содержимого папок операционной системы,
т.е. является портативной (portable)
программой. Но чтобы она работала необходимо аккуратно выполнить следующие
пункты.
1. Скачать самую новую на текущий момент версию системы «Эйдос-Х++»
по ссылкам:
http://lc.kubagro.ru/a.rar или: http://lc.kubagro.ru/Aidos-X.exe (ссылки для обновления системы даны в режиме
6.2).
2. Разархивировать этот архив в любую папку с правами на запись
с коротким латинским именем и путем доступа,
включающим только папки с такими же именами (лучше всего в корневой каталог
какого-нибудь диска).
3. Запустить систему. Файл запуска:  _AIDOS-X.exe * _AIDOS-X.exe *
4. Задать имя: 1 и пароль: 1 (потом их можно поменять в режиме
1.2).
5. Перед тем как запустить новый режим НЕОБХОДИМО ЗАВЕРШИТЬ предыдущий
(Help можно не закрывать). Окна закрываются в порядке, обратном порядку их
открытия.
|
|
* Разработана программа: « _START_AIDOS.exe»,
полностью снимающая с пользователя системы «Эйдос-Х++» заботу о проверке
наличия и скачивании обновлений. Эту программу надо просто скачать по ссылке: http://lc.kubagro.ru/Install_Aidos-X/_START_AIDOS.exe ,
поместить в папку с исполнимым модулем системы и всегда запускать систему с
помощью этого файла. _START_AIDOS.exe»,
полностью снимающая с пользователя системы «Эйдос-Х++» заботу о проверке
наличия и скачивании обновлений. Эту программу надо просто скачать по ссылке: http://lc.kubagro.ru/Install_Aidos-X/_START_AIDOS.exe ,
поместить в папку с исполнимым модулем системы и всегда запускать систему с
помощью этого файла.
При
запуске программы _START_AIDOS.EXE система Эйдос не должна быть запущена,
т.к. она содержится в файле обновлений и при его разархивировании возникнет
конфликт, если система будет запущена.
1. Программа  _START_AIDOS.exe определяет дату
системы Эйдос в текущей папке, и дату обновлений на FTP-сервере не скачивая
их, и, если система Эйдос в текущей папке устарела, скачивает обновления.
(Если в текущей папке нет исполнимого модуля системы Эйдос, то программа
пытается скачать полную инсталляцию системы, но не может этого сделать из-за
ограниченной функциональности демо-версии библиотеки Xb2NET.DLL). _START_AIDOS.exe определяет дату
системы Эйдос в текущей папке, и дату обновлений на FTP-сервере не скачивая
их, и, если система Эйдос в текущей папке устарела, скачивает обновления.
(Если в текущей папке нет исполнимого модуля системы Эйдос, то программа
пытается скачать полную инсталляцию системы, но не может этого сделать из-за
ограниченной функциональности демо-версии библиотеки Xb2NET.DLL).
2. После
этого появляется диалоговое окно с сообщением, что надо сначала
разархивировать систему, заменяя все файлы (опция: «Yes to All» или
«OwerWrite All»), и только после этого закрыть данное окно.
3. Потом программа  _START_AIDOS.exe запускает
обновления на разархивирование. После окончания разархивирования окно
архиватора с отображением стадии процесса исчезает. _START_AIDOS.exe запускает
обновления на разархивирование. После окончания разархивирования окно
архиватора с отображением стадии процесса исчезает.
4. После
закрытия диалогового окна с инструкцией (см. п.2), происходит запуск
обновленной версии системы Эйдос на исполнение.
Для работы программы  _START_AIDOS.exe необходима
библиотека: Xb2NET.DLL, которую можно скачать по ссылке: http://lc.kubagro.ru/Install_Aidos-X/Xb2NET.DLL .
Перед первым запуском этой программы данную библиотеку необходимо скачать и
поместить либо в папку с этой программой, а значит и исполнимым
модулем системы «Эйдос-Х++», либо в любую другую папку, на которую в
операционной системе прописаны пути поиска файлов, например в папку:
c:\Windows\System32\. Эта библиотека стоит около 500$ и у меня ее нет,
поэтому я даю только бесплатную демо-версию, которая выдает сообщение об
ограниченной функциональности, но для наших целей ее достаточно. _START_AIDOS.exe необходима
библиотека: Xb2NET.DLL, которую можно скачать по ссылке: http://lc.kubagro.ru/Install_Aidos-X/Xb2NET.DLL .
Перед первым запуском этой программы данную библиотеку необходимо скачать и
поместить либо в папку с этой программой, а значит и исполнимым
модулем системы «Эйдос-Х++», либо в любую другую папку, на которую в
операционной системе прописаны пути поиска файлов, например в папку:
c:\Windows\System32\. Эта библиотека стоит около 500$ и у меня ее нет,
поэтому я даю только бесплатную демо-версию, которая выдает сообщение об
ограниченной функциональности, но для наших целей ее достаточно.
|
|
Лицензия:
Автор отказывается от какой бы то ни было
ответственности за последствия применения или не применения Вами системы
«Эйдос».
Проще говоря, пользуйтесь если понравилось, а
если не понравилось – сотрите и забудьте, а лучше вообще не скачивайте.
|
В
диспетчере приложений системы «Эйдос» (режим 1.3) кликаем по кнопке «Добавить учебное
приложение» и выбираем лабораторную работу 2.05 «Исследование нормального
распределения» (рисунок 1):
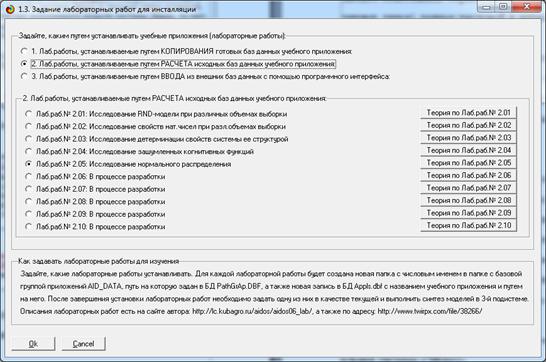
Рисунок 1 – Выбор режима инсталляции лабораторной
работы
На экранной форме (рисунок 2) задаем параметры
создаваемых распределений случайной величины:
Рисунок 2 – Экранная форма задания параметров
генерируемых распределений
Этапы генерации распределений приведены на рисунке 3:
Рисунок 3 – Экранная форма отображения стадии процесса
генерации
исследуемых распределений случайной величины
В результате созданы следующие распределения (рисунок
4), отличающиеся сочетаниями параметров
среднего и стандартного отклонения, заданными в режиме, экранная форма которого
приведена на рисунке 2:
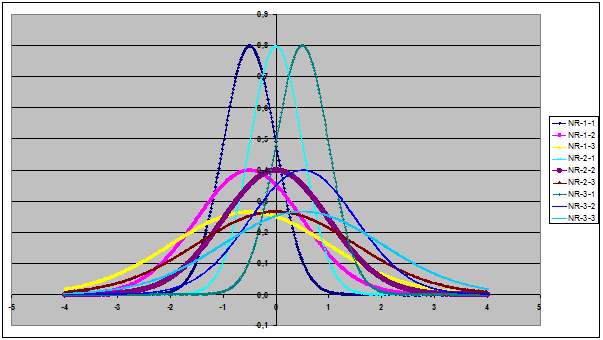
Рисунок 4. Исследуемые нормальные распределения,
полученные при
различных сочетаниях параметров среднего и стандартного отклонения
В таблице 1 приведены параметры созданных нормальных
распределений (на рисунке 4 и в таблице 1 выделено стандартное нормальное распределение
со средним значением 0 и стандартным отклонением 1):
Таблица 1 – Параметры созданных нормальных распределений
|
|
GAUSS
1-1
|
GAUSS
1-2
|
GAUSS
1-3
|
GAUSS
2-1
|
GAUSS
2-2
|
GAUSS
2-3
|
GAUSS
3-1
|
GAUSS
3-2
|
GAUSS
3-3
|
|
Среднее
|
-0,50
|
-0,50
|
-0,50
|
0,00
|
0,00
|
0,00
|
0,50
|
0,50
|
0,50
|
|
Ст.отклонение
|
0,50
|
1,00
|
1,50
|
0,50
|
1,00
|
1,50
|
0,50
|
1,00
|
1,50
|
На рисунке 5 приведена экранная форма задания
параметров генерации интервальных моделей, формируемые по умолчанию:
Рисунок 5 – Экранная форма задания параметров
генерации
интервальных моделей, формируемых по умолчанию
На рисунке 6 приведен внутренний калькулятор
параметров интервальных моделей:
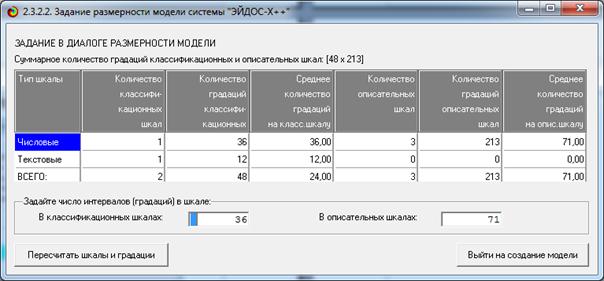
Рисунок 6 – Экранная форма внутреннего калькулятора
параметров интервальных моделей
На рисунке 7 приведена форма отображения стадии
процесса импорта исходных данных интервальных моделей:
Рисунок 7 – Экранная форма отображения стадии процесса
импорта исходных данных интервальных моделей
На рисунке 8 приведена экранная форма задания
параметров расчета статистических и информационных интервальных моделей, а на
рисунке 8 – стадии процесса их расчета:
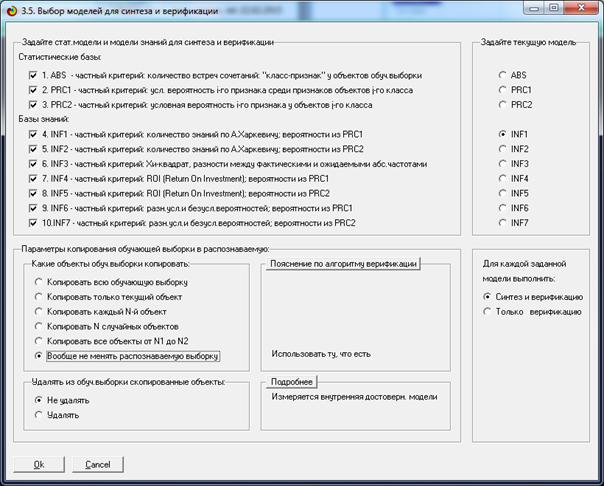
Рисунок 8 – Экранная форма задания параметров расчета
статистических и информационных интервальных моделей
Рисунок 9 – Экранная форма отображения стадии расчета
статистических и информационных интервальных моделей
Обращаем внимание на то, что в экранной форме на
рисунке 8 установлена опция: «Вообще не менять распознаваемую выборку». Это
сделано потому, что распознаваемая выборка сформирована ранее при генерации
нормальных распределений и отличается от обучающей выборки.
Полученные статистические распределения отображаются в
виде когнитивных функций (рисунок 10):
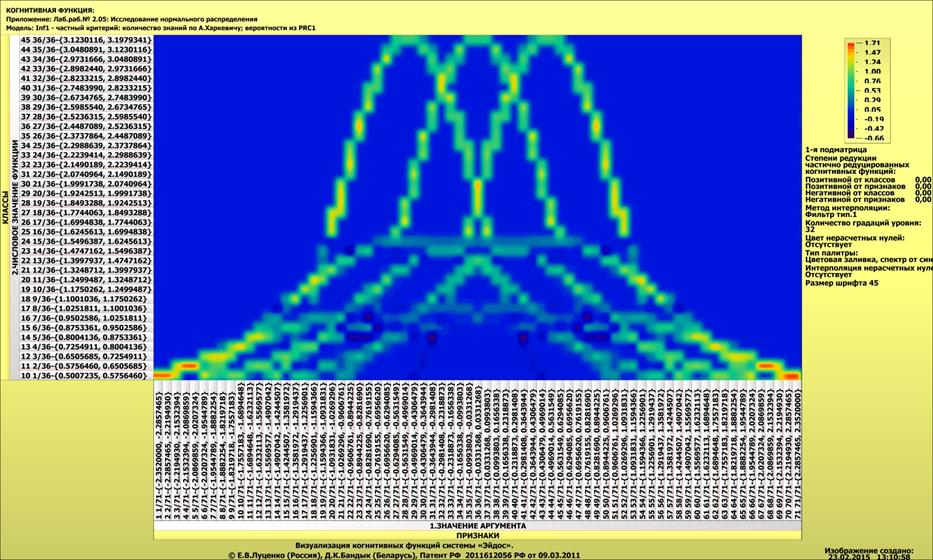
Рисунок 10 – Визуализация статистических распределений
в виде когнитивных функций
Из экранной формы, представленной на рисунке 11, мы видим,
что в различных интервальных значениях аргумента содержится различное количество
информации о значениях функции статистического распределения. Таким образом, мы
получили ответ на первый вопрос, ответ на который хотели получить в статье: «Вопрос
1-й. Какое количество информации о принадлежности случайной величины к
нескольким нормальным распределениям с разными параметрами мы получаем, когда
узнаем, что она попала в некоторый определенный i-й интервал: один из N равных
интервалов?»
Но система «Эйдос» позволяет получить ответ на этот
вопрос в самых разнообразных формах, которых очень много, например, в форме инвертированных
SWOT-диаграмм (предложены автором в работе [38]). Экранная форма
инвертированной SWOT-матрицы для одного из интервальных значений аргумента
приведена на рисунке 11, а соответствующая ей инвертированная SWOT-диаграмма –
на рисунке 12:
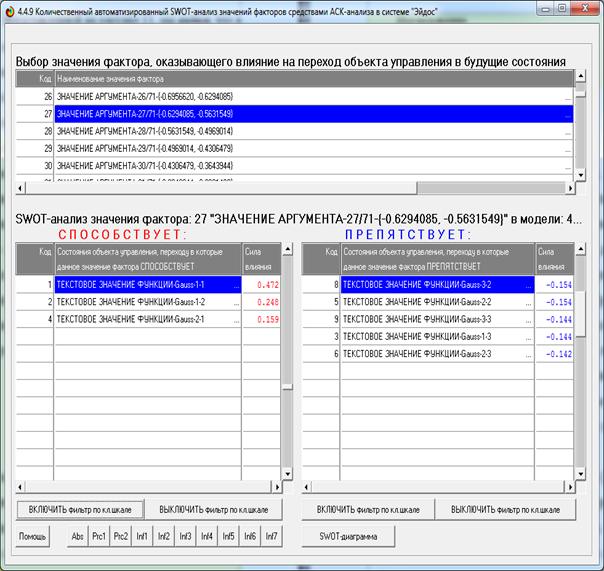
Рисунок 11 – Пример экранной формы инвертированной
SWOT-матрицы
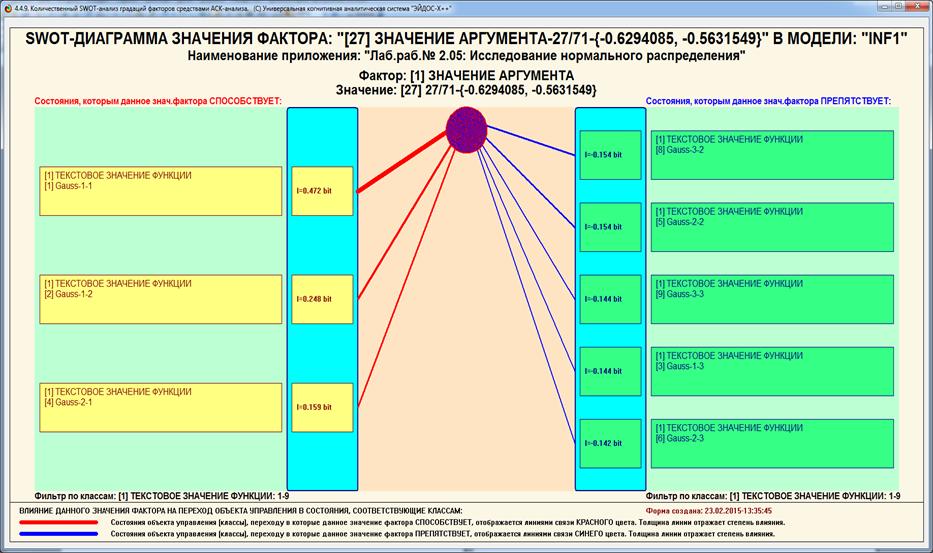
Рисунок 12 – Пример экранной формы инвертированной
SWOT-диаграммы
Рассмотрим теперь варианты различных по форме ответов
на второй вопрос: «Вопрос 2-й. Какое суммарное количество информации о степени сходства
эмпирического распределения наблюдений с нормальными распределениями с различными
параметрами мы получаем, зная частоты попадания случайной величины в каждый из
интервалов при N равных интервалов?», которые предоставляет система «Эйдос».
На рисунке 13 представлена экранная форма с
отображением фрагмента эмпирического распределения частот наблюдений №1, а на
рисунке 14, – результаты идентификации этого эмпирического распределения
по суммарному количеству информации, содержащемуся в нем.
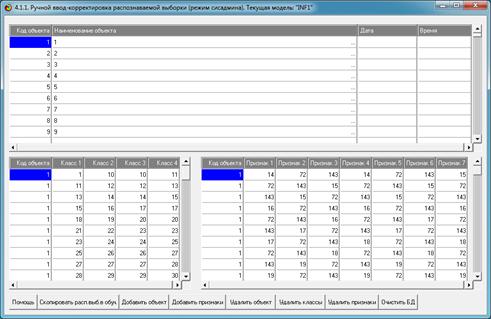
Рисунок 13 – Экранная форма с отображением
эмпирического
распределения частот наблюдений (фрагмент)
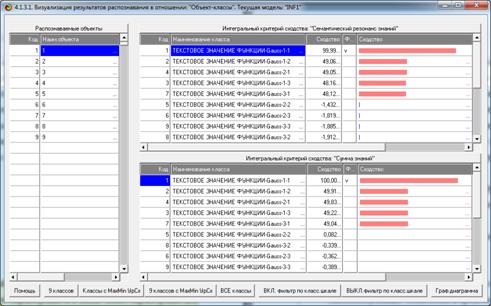
Рисунок 14 – Результаты определения вида и параметров
эмпирического
статистического распределения №1 по максимальному количеству
информации в нем о других распределениях, содержащихся в моделях
Мы видим, что в эмпирическом распределении №1 больше
всего информации содержится о его сходстве со стандартным нормальным распределением
Gauss-1-1, что и соответствует действительности.
Возникает вопрос: «А чем эта технология отличается от
расчета простой корреляции между эмпирическим и теоретическим
распределениями?». Есть несколько очень существенных отличий:
1. При расчете корреляции мы используем математический
аппарат параметрической статистики, что является корректным только в случае,
когда исследуемые данные подчиняются нормальному распределению. В данном же
случае использован математический аппарат, не основанный на этом предположении.
2. При расчете корреляции все координаты векторов
имеют одинаковый вес, равный 1, тогда как в данном случае вес наблюдений
различен, причем он может быть как положительным, так и отрицательным и равен
количеству информации в них [14, 15].
3. Расчет корреляции производится для одной группы,
тогда как количество информации рассчитывается на основе анализа модели,
отражающей условные и безусловные частотные распределения во всех группах и на
основе их сравнения. Таким образом, данный метод является обобщением метода
контрольных групп (на большое число групп), являющегося общепринятым в науке
для выявления влияния факторов.
Обратимся к ответу на «Вопрос 3-й. Попадание случайной
величины в какие интервалы при N равных интервалах является более характерным и
в какие менее характерным для нормальных распределений с различными параметрами?»
На качественном уровне ответ на этот вопрос дает
визуализация когнитивной функции на рисунке 10. На количественном – сама база
знаний, сформированная в системе, а также другие формы, полученные на ее основе.
В таблице 2 приведен фрагмент базы знаний с количеством информации в битах по
А.Харкевичу в интервальных значениях аргумента о том, что это значение
принадлежит статистическому распределению с определенными параметрами:
Таблица 2 – Количество информации в битах по
А.Харкевичу в интервальных значениях аргумента о том, что это значение
принадлежит нормальному распределению с определенными параметрами
|
Аргумент
|
G-1-1
|
G-1-2
|
G-1-3
|
G-2-1
|
G-2-2
|
G-2-3
|
G-3-1
|
G-3-2
|
G-3-3
|
|
1/71-{-2.3520000,
-2.2857465}
|
|
|
1,28688
|
|
|
|
|
|
|
|
2/71-{-2.2857465,
-2.2194930}
|
|
|
1,28688
|
|
|
|
|
|
|
|
3/71-{-2.2194930,
-2.1532394}
|
|
|
1,28688
|
|
|
|
|
|
|
|
4/71-{-2.1532394,
-2.0869859}
|
|
|
1,28688
|
|
|
|
|
|
|
|
5/71-{-2.0869859,
-2.0207324}
|
|
|
1,28688
|
|
|
|
|
|
|
|
6/71-{-2.0207324,
-1.9544789}
|
|
0,87429
|
0,88422
|
|
|
|
|
|
|
|
7/71-{-1.9544789,
-1.8882254}
|
|
0,87429
|
0,88422
|
|
|
|
|
|
|
|
8/71-{-1.8882254,
-1.8219718}
|
|
0,76838
|
0,77831
|
|
|
0,24853
|
|
|
|
|
9/71-{-1.8219718,
-1.7557183}
|
|
0,63875
|
0,64868
|
|
|
0,65119
|
|
|
|
|
10/71-{-1.7557183,
-1.6894648}
|
|
0,63875
|
0,64868
|
|
|
0,65119
|
|
|
|
|
11/71-{-1.6894648,
-1.6232113}
|
|
0,63875
|
0,64868
|
|
|
0,65119
|
|
|
|
|
12/71-{-1.6232113,
-1.5569577}
|
|
0,63875
|
0,64868
|
|
|
0,65119
|
|
|
|
|
13/71-{-1.5569577,
-1.4907042}
|
|
0,54920
|
0,55913
|
|
0,14654
|
0,56164
|
|
|
|
|
14/71-{-1.4907042,
-1.4244507}
|
-0,01163
|
0,40321
|
0,41314
|
|
0,40321
|
0,41565
|
|
|
|
|
15/71-{-1.4244507,
-1.3581972}
|
0,32982
|
0,34200
|
0,35193
|
|
0,34200
|
0,35444
|
|
|
|
|
16/71-{-1.3581972,
-1.2919437}
|
0,22391
|
0,23609
|
0,24602
|
|
0,23609
|
0,24853
|
|
|
0,24602
|
|
17/71-{-1.2919437,
-1.2256901}
|
0,22391
|
0,23609
|
0,24602
|
|
0,23609
|
0,24853
|
|
|
0,24602
|
|
18/71-{-1.2256901,
-1.1594366}
|
0,22391
|
0,23609
|
0,24602
|
|
0,23609
|
0,24853
|
|
|
0,24602
|
|
19/71-{-1.1594366,
-1.0931831}
|
0,32982
|
0,21237
|
0,22230
|
|
0,21237
|
0,22481
|
|
|
0,22230
|
|
20/71-{-1.0931831,
-1.0269296}
|
0,53702
|
0,14654
|
0,15647
|
|
0,14654
|
0,15898
|
|
|
0,15647
|
|
21/71-{-1.0269296,
-0.9606761}
|
0,45945
|
0,06897
|
0,07890
|
|
0,06897
|
0,08141
|
|
0,06897
|
0,07890
|
|
22/71-{-0.9606761,
-0.8944225}
|
0,39103
|
0,00055
|
0,01048
|
-0,01163
|
0,00055
|
0,01299
|
|
0,00055
|
0,01048
|
|
23/71-{-0.8944225,
-0.8281690}
|
0,45945
|
0,17488
|
-0,05073
|
-0,07284
|
-0,06066
|
-0,04822
|
|
-0,06066
|
-0,05073
|
|
24/71-{-0.8281690,
-0.7619155}
|
0,51000
|
0,28664
|
-0,10610
|
-0,12821
|
-0,11603
|
-0,10359
|
|
-0,11603
|
-0,10610
|
|
25/71-{-0.7619155,
-0.6956620}
|
0,51000
|
0,28664
|
-0,10610
|
-0,12821
|
-0,11603
|
-0,10359
|
|
-0,11603
|
-0,10610
|
|
26/71-{-0.6956620,
-0.6294085}
|
0,51000
|
0,28664
|
-0,10610
|
-0,12821
|
-0,11603
|
-0,10359
|
|
-0,11603
|
-0,10610
|
|
27/71-{-0.6294085,
-0.5631549}
|
0,47168
|
0,24832
|
-0,14441
|
0,15857
|
-0,15434
|
-0,14190
|
|
-0,15434
|
-0,14441
|
|
28/71-{-0.5631549,
-0.4969014}
|
0,45945
|
0,23609
|
-0,15664
|
0,22391
|
-0,16657
|
-0,15413
|
|
-0,16657
|
-0,15664
|
|
29/71-{-0.4969014,
-0.4306479}
|
0,44040
|
0,21704
|
-0,17569
|
0,20486
|
-0,18562
|
-0,17318
|
-0,73009
|
-0,18562
|
-0,17569
|
|
30/71-{-0.4306479,
-0.3643944}
|
0,41295
|
0,18959
|
-0,20314
|
0,17741
|
-0,21307
|
-0,20063
|
-0,22525
|
-0,21307
|
-0,20314
|
|
31/71-{-0.3643944,
-0.2981408}
|
0,33959
|
0,11622
|
-0,27651
|
0,28904
|
0,11622
|
-0,27400
|
-0,29862
|
-0,28644
|
-0,27651
|
|
32/71-{-0.2981408,
-0.2318873}
|
0,32982
|
0,10646
|
-0,28627
|
0,32982
|
0,10646
|
-0,28376
|
-0,30838
|
-0,29620
|
-0,28627
|
|
33/71-{-0.2318873,
-0.1656338}
|
0,32982
|
0,10646
|
-0,28627
|
0,32982
|
0,10646
|
-0,28376
|
-0,30838
|
-0,29620
|
-0,28627
|
|
34/71-{-0.1656338,
-0.0993803}
|
0,20278
|
-0,02058
|
-0,24619
|
0,36990
|
0,14654
|
-0,24368
|
-0,13867
|
-0,25612
|
-0,24619
|
|
35/71-{-0.0993803,
-0.0331268}
|
0,13436
|
-0,25612
|
-0,24619
|
0,36990
|
0,14654
|
-0,24368
|
0,13436
|
-0,25612
|
-0,24619
|
|
36/71-{-0.0331268,
0.0331268}
|
0,13436
|
-0,25612
|
-0,24619
|
0,36990
|
0,14654
|
-0,24368
|
0,13436
|
-0,25612
|
-0,24619
|
|
37/71-{0.0331268,
0.0993803}
|
0,13436
|
-0,25612
|
-0,24619
|
0,36990
|
0,14654
|
-0,24368
|
0,13436
|
-0,25612
|
-0,24619
|
|
38/71-{0.0993803,
0.1656338}
|
-0,13867
|
-0,25612
|
-0,24619
|
0,36990
|
0,14654
|
-0,24368
|
0,20278
|
-0,02058
|
-0,24619
|
|
39/71-{0.1656338,
0.2318873}
|
-0,30838
|
-0,29620
|
-0,28627
|
0,32982
|
0,10646
|
-0,28376
|
0,32982
|
0,10646
|
-0,28627
|
|
40/71-{0.2318873,
0.2981408}
|
-0,30838
|
-0,29620
|
-0,28627
|
0,32982
|
0,10646
|
-0,28376
|
0,32982
|
0,10646
|
-0,28627
|
|
41/71-{0.2981408,
0.3643944}
|
-0,29862
|
-0,28644
|
-0,27651
|
0,28904
|
0,11622
|
-0,27400
|
0,33959
|
0,11622
|
-0,27651
|
|
42/71-{0.3643944,
0.4306479}
|
-0,22525
|
-0,21307
|
-0,20314
|
0,17741
|
-0,21307
|
-0,20063
|
0,41295
|
0,18959
|
-0,20314
|
|
43/71-{0.4306479,
0.4969014}
|
-0,73009
|
-0,18562
|
-0,17569
|
0,20486
|
-0,18562
|
-0,17318
|
0,44040
|
0,21704
|
-0,17569
|
|
44/71-{0.4969014,
0.5631549}
|
|
-0,16657
|
-0,15664
|
0,22391
|
-0,16657
|
-0,15413
|
0,45945
|
0,23609
|
-0,15664
|
|
45/71-{0.5631549,
0.6294085}
|
|
-0,15434
|
-0,14441
|
0,15857
|
-0,15434
|
-0,14190
|
0,47168
|
0,24832
|
-0,14441
|
|
46/71-{0.6294085,
0.6956620}
|
|
-0,11603
|
-0,10610
|
-0,12821
|
-0,11603
|
-0,10359
|
0,51000
|
0,28664
|
-0,10610
|
|
47/71-{0.6956620,
0.7619155}
|
|
-0,11603
|
-0,10610
|
-0,12821
|
-0,11603
|
-0,10359
|
0,51000
|
0,28664
|
-0,10610
|
|
48/71-{0.7619155,
0.8281690}
|
|
-0,11603
|
-0,10610
|
-0,12821
|
-0,11603
|
-0,10359
|
0,51000
|
0,28664
|
-0,10610
|
|
49/71-{0.8281690,
0.8944225}
|
|
-0,06066
|
-0,05073
|
-0,07284
|
-0,06066
|
-0,04822
|
0,45945
|
0,17488
|
-0,05073
|
|
50/71-{0.8944225,
0.9606761}
|
|
0,00055
|
0,01048
|
-0,01163
|
0,00055
|
0,01299
|
0,39103
|
0,00055
|
0,01048
|
|
51/71-{0.9606761,
1.0269296}
|
|
0,06897
|
0,07890
|
|
0,06897
|
0,08141
|
0,45945
|
0,06897
|
0,07890
|
|
52/71-{1.0269296,
1.0931831}
|
|
|
0,15647
|
|
0,14654
|
0,15898
|
0,53702
|
0,14654
|
0,15647
|
|
53/71-{1.0931831,
1.1594366}
|
|
|
0,22230
|
|
0,21237
|
0,22481
|
0,32982
|
0,21237
|
0,22230
|
|
54/71-{1.1594366,
1.2256901}
|
|
|
0,24602
|
|
0,23609
|
0,24853
|
0,22391
|
0,23609
|
0,24602
|
|
55/71-{1.2256901,
1.2919437}
|
|
|
0,24602
|
|
0,23609
|
0,24853
|
0,22391
|
0,23609
|
0,24602
|
|
56/71-{1.2919437,
1.3581972}
|
|
|
0,24602
|
|
0,23609
|
0,24853
|
0,22391
|
0,23609
|
0,24602
|
|
57/71-{1.3581972,
1.4244507}
|
|
|
|
|
0,34200
|
0,35444
|
0,32982
|
0,34200
|
0,35193
|
|
58/71-{1.4244507,
1.4907042}
|
|
|
|
|
0,40321
|
0,41565
|
-0,01163
|
0,40321
|
0,41314
|
|
59/71-{1.4907042,
1.5569577}
|
|
|
|
|
0,14654
|
0,56164
|
|
0,54920
|
0,55913
|
|
60/71-{1.5569577,
1.6232113}
|
|
|
|
|
|
0,65119
|
|
0,63875
|
0,64868
|
|
61/71-{1.6232113,
1.6894648}
|
|
|
|
|
|
0,65119
|
|
0,63875
|
0,64868
|
|
62/71-{1.6894648,
1.7557183}
|
|
|
|
|
|
0,65119
|
|
0,63875
|
0,64868
|
|
63/71-{1.7557183,
1.8219718}
|
|
|
|
|
|
0,65119
|
|
0,63875
|
0,64868
|
|
64/71-{1.8219718,
1.8882254}
|
|
|
|
|
|
0,24853
|
|
0,76838
|
0,77831
|
|
65/71-{1.8882254,
1.9544789}
|
|
|
|
|
|
|
|
0,87429
|
0,88422
|
|
66/71-{1.9544789,
2.0207324}
|
|
|
|
|
|
|
|
0,87429
|
0,88422
|
|
67/71-{2.0207324,
2.0869859}
|
|
|
|
|
|
|
|
|
1,28688
|
|
68/71-{2.0869859,
2.1532394}
|
|
|
|
|
|
|
|
|
1,28688
|
|
69/71-{2.1532394,
2.2194930}
|
|
|
|
|
|
|
|
|
1,28688
|
|
70/71-{2.2194930,
2.2857465}
|
|
|
|
|
|
|
|
|
1,28688
|
|
71/71-{2.2857465,
2.3520000}
|
|
|
|
|
|
|
|
|
1,28688
|
Параметры, соответствующие распределениям, приведены в
таблице 1. Изображение несимметрично относительно аргумента из-за
использования небольшого количества интервальных значений аргумента.
Характеристика любого заданного распределения,
полученная на основе этой базы данных, приведена в SWOT-матрице (рисунок 15) и
соответствующей диаграмме (рисунок 16):
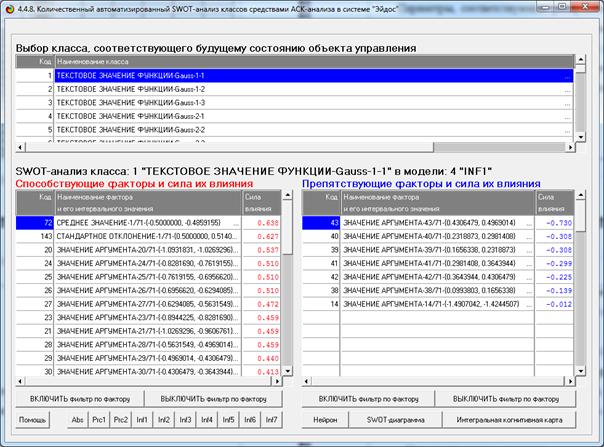
Рисунок 15 – Экранная форма с характеристикой
распределения
Gauss-1-1 в виде SWOT-матрицы
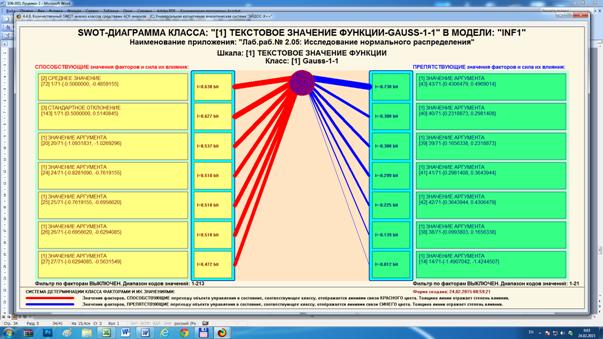
Рисунок 16 – Экранная форма с характеристикой
нормального распределения Gauss-1-1 в виде SWOT-диаграммы
Экранная форма задания на выполнение содержательного
сравнения двух заданных распределений приведена на рисунке 17, а результат сравнения
– в диаграмме на рисунке 18.
Отметим, что эти формы представляют собой результат
решения задачи № 5: одной из сформулированных в данном разделе
задач статистики, которую предположительно можно решить методами теории
информации.
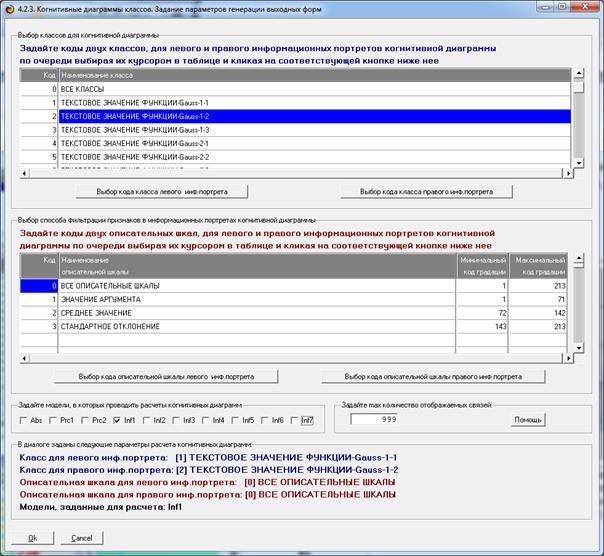
Рисунок 17 – Экранная форма задания на выполнение
содержательного сравнения двух заданных распределений

Рисунок 18 – Результат содержательного сравнения двух
распределений
На рисунке 19 приведена визуализация таблицы 2:
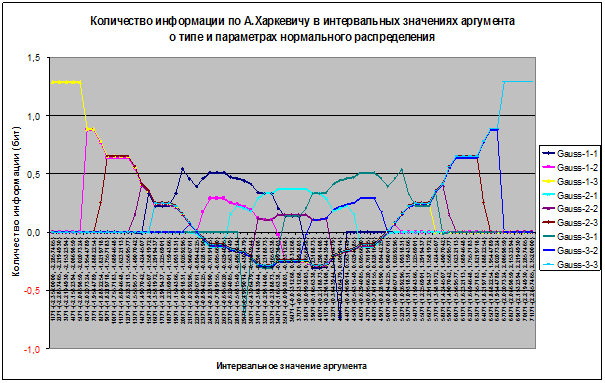
Рисунок 19 – Количество информации по А.Харкевичу в
интервальных значениях аргумента о том, что это значение принадлежит
нормальному распределению с определенными параметрами (визуализация таблицы 2)
Приведем две выходные форм, полученные в результате
решения Задачи № 6:
«исследование информационных моделей статистических распределений» (решение
этой задачи включает кластерный и конструктивный анализ распределений, их информационные
портреты и многие другие исследования с использованием возможностей АСК-анализа
и системы «Эйдос» [21]).
На рисунке 20 приведена экранная форма, а на рисунке
21 – соответствующая диаграмма, отражающие результаты кластерно-конструктивного
анализа смоделированных нормальных распределений:
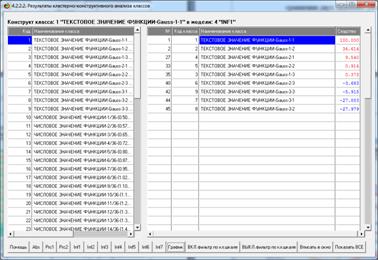
Рисунок 20 – Экранная форма с результатами
кластерно-конструктивного
анализа смоделированных нормальных распределений в модели
с количеством информации по А.Харкевичу (INF1)
(установлен фильтр по типу распределения)
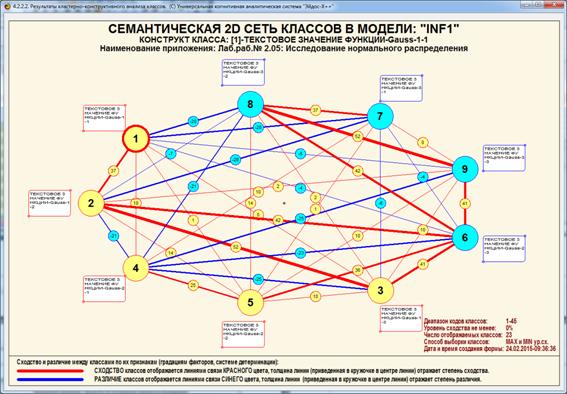
Рисунок 21 – Когнитивная диаграмма с результатами
кластерно-конструктивного анализа смоделированных нормальных распределений
в модели с количеством информации по А.Харкевичу (INF1)
(установлен фильтр по типу распределения)
Предлагается теоретическое
обоснование, методика численных расчетов
и программная реализация решения задач статистики, в частности исследования
статистических распределений, методами теории информации. При этом
непосредственно на основе эмпирических данных расчетным путем определяется
количество информации в наблюдениях, которое используется для анализа
статистических распределений. Предлагаемый способ расчета количества информации
не основан на предположениях о независимости наблюдений и их нормальном
распределении, т.е. является непараметрическим и обеспечивает корректное
моделирование нелинейных систем, а также позволяет сопоставимо обрабатывать
разнородные (измеряемые в шкалах различных типов) данные числовой и нечисловой
природы, измеряемые в различных единицах измерения.
Таким образом, АСК-анализ и
система «Эйдос» представляют собой современную инновационную (готовую к
внедрению) технологию решения задач статистики методами теории информации.
Данный раздел может быть использована как описание
лабораторной работы по дисциплинам:
– Интеллектуальные системы;
– Инженерия знаний и интеллектуальные системы;
– Интеллектуальные технологии и
представление знаний;
– Представление знаний в интеллектуальных
системах;
– Основы интеллектуальных систем;
– Введение в нейроматематику и методы
нейронных сетей;
– Основы искусственного интеллекта;
– Интеллектуальные технологии в науке и образовании;
– Управление знаниями;
– Автоматизированный системно-когнитивный
анализ и интеллектуальная система «Эйдос»;
которые автор ведет в настоящее время,
а также и в других дисциплинах, связанных с преобразованием данных в
информацию, а ее в знания и применением этих знаний для решения задач
идентификации, прогнозирования, принятия решений и исследования моделируемой
предметной области (а это практически все дисциплины во всех областях науки).
В данном разделе лишь намечены некоторые пути
применения теории информации для решения задач статистики. Для реального
решения сформулированных выше и других связанных с этим направлением задач
необходимы обширные научные исследования и разработки инструментальных средств,
что является делом будущего. Планируется описать уже решенные задачи, а также
решить некоторые из сформулированных выше задач, в частности использовать
статистические критерии в качестве вторичных признаков статистических
распределений и исследовать различные статистические распределения.
В данном разделе
кратко рассматриваются математическая сущность предложенной автором модификации взвешенного метода наименьших квадратов (ВМНК),
в котором в качестве весов наблюдений применяется количество информации
в них. Предлагается два варианта данной модификации ВМНК. В первом варианте
взвешивание наблюдений производится путем замены одного наблюдения с
определенным количеством информации в нем соответствующим количеством наблюдений единичного веса, а
затем к ним применяется стандартный метод наименьших
квадратов (МНК). Во втором варианте взвешивание наблюдений производится
для каждого значения аргумента путем замены всех наблюдений с определенным
количеством информации в них одним наблюдением единичного веса, полученным как
средневзвешенное от них, а затем к ним применяется стандартный МНК. Подробно
описана методика численных расчетов количества информации в наблюдениях,
основанная на теории автоматизированного системно-когнитивного анализа
(АСК-анализ) и реализованная в его программном инструментарии –
интеллектуальной системе «Эйдос». Приводится иллюстрация предлагаемого подхода
на простом численном примере. В будущем планируется дать более развернутое
математическое обоснование метода взвешенных наименьших квадратов, модифицированного
путем применения в качестве весов наблюдений количества информации в них, а
также исследовать его свойства
«... навыки
мысли и аналитический аппарат теории информации должны, по-видимому, привести к
заметной перестройке здания
математической статистики»
А.Н.
Колмогоров [1, 2, 19]
Данный раздел посвящен математическим аспектам нового
варианта взвешенного метода наименьших квадратов (ВМНК), модифицированного
путем применения в качестве весов наблюдений количества информации в них.
Данный подход предложен автором, в теоретическом плане основан на
автоматизированном системно-когнитивном анализе (АСК-анализ) и реализован в его
программном инструментарии – системе «Эйдос» [36].
В работе [36] подробно описаны проблемы стандартного
(классического) метода наименьших квадратов (МНК), состоящей в том, что в исходных данных обычно есть такие, которые
хуже, чем остальные вписываются в регрессионную модель, т.е. описываются ей с
большей погрешностью. По мнению автора, причина этого состоит не только в самих данных, но
и в способе их отражения в модели.
Иначе говоря, по-видимому, в принципе возможно построение разных моделей,
отражающих одни и те же эмпирические данные, причем количество этих моделей не
ограничено, и в одних моделях эта погрешность будет больше, а в других, более
удачных – меньше. Но фактически, т.е. на практике, часто выбор возможных
моделей ограничен одной. Поэтому актуальным является каждый новый
метод построения моделей, который может иметь некоторые преимущества перед уже
известными.
Традиционным решением этой проблемы является
взвешенный метод наименьших квадратов. В той же работе [36] обосновывается, что
подход, реализованный в ВМНК, на самом деле лишь создает видимость решения, а
фактически основан просто на игнорировании данных, причем тем в большей
степени, чем хуже они вписывающихся в регрессионную модель.
Рассмотрим еще
две проблемы, дополнительно к уже описанным в [36], которые обуславливают
актуальность предложенной модификации взвешенного метода наименьших квадратов.
Первая проблема ВМНК состоит в том, что
на практике ошибки наблюдений являются неизвестными, поэтому их обычно
принимают пропорциональными значениям переменных. «Суть взвешенного метода
наименьших квадратов состоит в том, что остаткам обобщённой модели регрессии
придаются определённые веса, которые равны обратным величинам соответствующих
дисперсий G2(εi).Однако
на практике значения дисперсий являются
величинами неизвестными, поэтому для вычисления наиболее подходящих весов
используется предположение о том, что они пропорциональны значениям факторных
переменных xt» (курсив мой, авт.).
Вторая проблема
ВМНК состоит в применении евклидовой меры
расстояния при определении ошибки наблюдений. Но эта мера адекватна только для ортонормированных пространств, которые
на практике вообще никогда не встречаются, как, кстати, и линейные системы. «Если
случайные ошибки модели регрессии подвержены гетероскедастичности (но являются
неавтокоррелированными), то для оценивания неизвестных коэффициентов модели
регрессии применяется взвешенный метод наименьших квадратов»1.
В качестве возможного решения поставленной проблемы в
работе [36] и предлагается модификация ВМНК, в которой:
– в качестве весов наблюдений используется количество
информации в них;
– в качестве меры расстояния применяется суммарное
количество информации (т.е. по сути свертка или скалярное произведение), т.е. информационное
расстояние, мера расстояния неметрической природы, вообще не предполагающая
ортонормированность пространства.
Кроме того очень важно, что АСК-анализе все факторы
рассматриваются с одной единственной точки зрения: сколько информации содержится в их значениях о переходе объекта, на
который они действуют, в определенные будущие состояния, и при этом сила и
направление влияния всех значений факторов на объект измеряется в одних общих
для всех факторов единицах измерения: единицах
количества информации [3]. Именно по
этой причине вполне корректно складывать силу и направление влияния всех
действующих на объект значений факторов, независимо от их природы, и определять
результат совместного влияния на
объект системы значений факторов. При
этом в общем случае объект является нелинейным
и факторы внутри него взаимодействуют друг с другом, т.е. для них не
выполняется принцип суперпозиции. Если же
разные факторы измеряются в различных единицах измерения, то результаты сравнения объектов будут зависеть от этих
единиц измерения, что совершенно недопустимо с теоретической точки
зрения [3].
Введем
определение когнитивной функции:
когда функция используется для отображения причинно-следственной зависимости,
т.е. информации (согласно концепции Шенка-Абельсона [34]), или знаний, если эта информация полезна для
достижении целей [35], то будем называть такую функцию когнитивной функцией, от англ. «cognition»
[3].
Смысл когнитивной функциональной зависимости в
том, что в значении аргумента содержится определенное количество информации
о том, какое значение примет функция, т.е. когнитивная функция отражает знания
о степени соответствия значений функции значениям аргумента [3].
Очень важно,
что этот подход позволяет автоматически решить проблему сопоставимой обработки
многих факторов, измеряемых в различных единицах измерения, т.к. в этом подходе рассматриваются не сами
факторы, какой бы природы они не были и какими бы шкалами не формализовались,
а количество информации, которое
в них содержится о поведении моделируемого объекта [3].
Необходимо также отметить, что представление о
полностью линейных объектах (системах) является абстракцией и реально все объекты являются принципиально
нелинейными. Вместе с тем для большинства систем нелинейные эффекты можно считать
эффектами второго и более высоких порядков и такие системы в первом приближении можно считать линейными. Возможны различные
модели взаимодействия факторов, в
частности, развиваемые в форме системного обобщения теории множеств. Этот
подход в перспективе может стать одним из вариантов развития теории нелинейных
систем [3].
Отметим, что математическая модель АСК-анализа
(системная теория информации) органично
учитывает принципиальную нелинейность всех объектов. Это проявляется в
нелокальности нейронной сети системы «Эйдос» [46], приводящей к зависимости всех
информативностей от любого изменения в исходных данных, а не как в методе обратного
распространения ошибки. В результате значения матрицы информативностей количественно
отражают факторы не как множество, а как систему.
В АСК-анализе ставится задача метризации шкал, т.е. преобразования к
наиболее формализованному виду, и предлагается 7 способов метризации всех типов
шкал, обеспечивающих совместную сопоставимую количественную обработку
разнородных факторов, измеряемых в различных единицах измерения за счет
преобразования всех шкал к одним универсальным единицам измерения в качестве
которых выбраны единицы измерения количества информации. Все эти способы метризации реализованы в
АСК-анализе и системе «Эйдос» [3]. В работах [4, 5, 6] кратко описаны суть и
история появления и развития метода АСК-анализа и его программного
инструментария – интеллектуальной системы «Эйдос», поэтому здесь мы их излагать
не будем. Отметим лишь, что эти методы созданы довольно давно и уже в 1987 году
были акты внедрения интеллектуальных приложений, в которых формировались
информационные портреты классов и и значений факторов [7].
Поэтому для
нас является вполне естественным предположить, что в качестве весов наблюдений целесообразно использовать количество
информации, которое содержится в этих наблюдениях о том, что интересующие
нас выходные параметры объекта моделирования примут те или иные значения или
сам объект моделирования перейдет в состояния, соответствующие тем или иным
классам или окажется принадлежащим к определенным обобщающим категориям
(группам). В этом и состоит основная идея
предлагаемого решения поставленной проблемы.
В АСК-анализе на основе системной теории информации [7, 17] развит математический аппарат,
обеспечивающий формальное описание поведения сложных нелинейных объектов
моделирования под воздействием систем управляющих факторов и окружающей среды,
а также созданы инструментальные средства, реализующие этот математический
аппарат.
В частности в АСК-анализе предложено понятие когнитивных функций, которое
рассмотрено и развито в ряде работ автора и соавторов [8, 9, 10, 11, 12, 13,
14, 15, 16, 17, 18] и поэтому здесь нет смысла подробно останавливаться на этом
понятии. Отметим лишь суть. В работе [16] кратко рассматриваются классическое
понятие функциональной зависимости в математике, определяются ограничения применимости
этого понятия для адекватного моделирования реальности и формулируется
проблема, состоящая в поиске такого обобщения понятия функции, которое было бы
более пригодно для адекватного отражения причинно-следственных связей в
реальной области. Далее рассматривается теоретическое и практическое решения
поставленной проблемы, состоящие в том, что:
а) предлагается универсальный не зависящий от
предметной области способ вычисления количества информации в значении аргумента
о значении функции, т.е. когнитивные функции;
б) предлагается программный инструментарий:
интеллектуальная система «Эйдос», позволяющая на практике осуществлять эти
расчеты, т.е. строить когнитивные функции на основе фрагментированных зашумленных
эмпирических данных большой размерности.
Предлагаются понятия нередуцированных, частично и
полностью редуцированных прямых и обратных, позитивных и негативных когнитивных
функций и метод формирования редуцированных когнитивных функций, являющийся
вариантом известного взвешенного метода наименьших квадратов, отличающимся от
стандартного ВМНК учетом в качестве весов наблюдений количества информации в значениях
аргумента о значениях функции.
Конечно, применение теории информации для решения
проблем и развития статистики не является абсолютно новой идеей. Как
указывает в своих работах [1, 2] профессор А.И.Орлов, сходные идеи развивал еще
в середине XX века С.Кульбак [19], а в эпиграф данного раздела вынесено программное
высказывание выдающегося российского математика А.Н. Колмогорова:
«... навыки мысли и аналитический аппарат теории информации должны,
по-видимому, привести к заметной перестройке
здания математической статистики», которые содержится в его предисловии к той
же книге С.Кульбака и также приведенное в
работах [1, 2]. В наше время в этом направлении продуктивно работают Дуглас Хаббард
[20], а также российский математик В.Б.Вяткин [21-28].
Кроме
того, иногда авторы, излагающие в частности взвешенный метод наименьших
квадратов, может быть не вполне осознанно используют слово «информация» не как
научный термин, а в обиходном разговорном смысле. Например, в работе, приведенной
на сайте: http://lib.alnam.ru/book_prs2.php?id=38,
автор пишет: «Чтобы учесть разницу в информации, которую
несет каждое наблюдение, для нахождения оценки необходимо минимизировать
взвешенную сумму
квадратов отклонений» (отмечено мной, авт.). Казалось бы, остается «лишь»
посчитать это количество информации и вариант взвешенного метода наименьших
квадратов, основанный на теории информации, готов, но, однако мы видим, что
ниже идет изложение стандартного ВМНК.
В работе [37]
автор пишет: «…по схеме скользящей
средней оценкой текущего уровня является взвешенное среднее всех предшествующих
уровней, причем веса при наблюдениях убывают по мере удаления от последнего
(текущего) уровня, т. е. информационная ценность наблюдений
тем больше, чем ближе они к концу периода наблюдений» (отмечено мной, авт.). Здесь мы тоже видим пример
применения слова «информация» и сочетания «информационная ценность наблюдений» в каком-то бытовом смысле, а не в качестве
научных терминов. Этот вывод можно сделать на основе подхода, примененного для
их расчета или оценки. Казалось бы, нужные слова произнесены и даже написаны и
опубликованы, и остается «только» а) прочитать их, б) понять,
что буквально сказано и в) сделать
это. Однако почему-то это никому не приходит в голову, т.е. никто не собирается
действительно взять да и посчитать это количество информации. Ведь ясно, что
эти подходы, описанные в приведенных выше статьях, не основаны на теории
информации. Примерно также на бытовом уровне все понимают, что когда мы
спрашиваем о том, какая температура на улице и нам отвечают, то этим самым
сообщают нам определенное количество информации. Но никому не приходит в голову
посчитать, какое именно количество информации нам сообщают в этом случае, как и
в других случаях.
Таким образом, даже если принять
в принципе изложенные выше идеи о применении количества информации в наблюдении
в качестве веса наблюдения во взвешенном методе наименьших квадратов, то все
равно остается очень существенный и принципиальный вопрос о том, каким
способом возможно реально посчитать это количество информации. Этот
вопрос разбивается на две части:
– с помощью какого
математического аппарата возможно посчитать количество информации в наблюдении?
– с помощью какого программного
инструментария, реализующего этот математический аппарат, возможно реально
посчитать количество информации в наблюдении?
Основная идея решения проблемы и
предложение автора состоит в том, что для этой цели вполне подходят
Автоматизированный системно-когнитивный анализ (АСК-анализ), его математическая
модель (системная теория информации), а также реализующий их программный
инструментарий АСК-анализа – система «Эйдос». АСК-анализ и система «Эйдос» представляют
собой современную интеллектуальную инновационную (полностью готовую к
внедрению) технологию взвешенного метода наименьших квадратов,
модифицированного путем применения в качестве весов наблюдений количества информации
в них.
У
интеллектуальных технологий есть одно слабое место: их никто не понимает, по
крайней мере, почти никто из тех, для кого они предназначены и кому они объективно
необходимы. А это значит, что для того, чтобы довести их до практики необходимо
придать им такую форму, в которой их и не надо понимать, а можно сразу применять.
Это пытается сделать автор в своих разработках, ведущихся в течение многих лет
[5], т.е. пытается создать универсальную инновационную (готовую к внедрению) интеллектуальную
технологию персонального уровня, т.е. не требующую от пользователя специальной
квалификации в области технологий искусственного интеллекта. Результатом этих
усилий и являются АСК-анализ
и система «Эйдос».
При принятии решений о применении для решения поставленной
проблемы этой интеллектуальной инновационной технологии естественно возникает
вопрос о степени точности восстановления в создаваемых с помощью нее моделях
исследуемых эмпирических зависимостей в АСК-анализе и системе «Эйдос».
Традиционно точность восстановления зависимости
оценивается дисперсиями и доверительным интервалами. В АСК-анализе смысловым
аналогом доверительного интервала, в определенной степени, конечно, является
количество информации в аргументе о значении функции. Поэтому необходимо
исследовать соотношение смыслового содержания этих понятий: доверительного
интервала и количества информации.
На математическом уровне это планируется сделать в
будущем, а в данном разделе отметим лишь, что чем больше доверительный
интервал, тем выше неопределенность наших знаний о значении функции,
соответствующем значению аргумента, а чем он меньше, тем эта определенность
выше. Но информация и определяется как количественная мера степени
снятия неопределенности. Учитывая это можно утверждать, что чем
больше доверительный интервал, тем меньше информации о значении функции,
соответствующем значению аргумента мы получаем, а чем он меньше, тем это
количество информации больше. Забегая вперед, отметим, что в частично-редуцированных
когнитивных функциях количество информации в значениях аргумента о значениях
функции наглядно изображено шириной полосы функции, что не только по смыслу, но
внешне очень сходно с доверительным интервалом. При этом отметим еще один
интересный момент, который состоит в том, что если традиционный доверительный
интервал при экстраполяции при удалении от эмпирических значений ко все далее
отстоящим от них в будущим все время увеличивается, то в степень редукции
когнитивной функции то увеличивается, то уменьшается. Это связано с тем, что АСК-анализ
и система «Эйдос» позволяют не только прогнозировать будущие события, но и
прогнозировать достоверность или риски этих прогнозов [7],
т.е. прогнозировать продолжительность периодов эргодичности и точки бифуркации
(качественного изменения закономерностей в моделируемой предметной области),
что наглядно и отображается в такой форме.
В частности при
этом при нулевом доверительном интервале формально
получается, что мы имеем бесконечное количество информации о значении функции,
но на практике это вообще невозможно
[17] и даже в теории возможно только для отдельных точек целых значений аргумента и функции. При бесконечном доверительном интервале
в значении аргумента функции содержится ноль информации о значении функции.
В переписке по содержанию статьи
профессор А.И.Орлов пишет: «Погрешность
средства измерения в ряде случаев меняется с изменением значения измеряемой величины.
Если закон изменения характеристик погрешностей
известен (например, внесен в паспорт средства измерения), то он дает обоснованные
веса. Из подобных соображений вытекает предложение Копаева изменить
минимизируемый функционал – вместо суммы квадратов абсолютных расхождений
минимизировать сумму квадратов относительных отклонений [40]» (курсив мой.
авт.).
Это очень глубокое замечание, из
которого вытекают интересные выводы, некоторые из которых мы кратко рассмотрим
ниже.
В статье [41] предлагается применить автоматизированный
системно-когнитивный анализ как для синтеза адаптивной интеллектуальной
измерительной системы, так и для ее использования не с целью измерения
параметров объектов, а для идентификации состояний измеряемых систем, т.е. для
так называемой системной идентификации. При этом задача измерения
рассматривается как предельно упрощенный вариант задачи идентификации или распознавания
образов, а задача синтеза измерительной системы – как предельно упрощенный
вариант синтеза системы распознавания образов. Программный инструментарий
автоматизированного системно-когнитивного анализа – интеллектуальную систему «Эйдос» предлагается применить как
универсальное средство для синтеза и эксплуатации адаптивных интеллектуальных измерительных систем в
различных предметных областях. Эта система позволяет вычислять количество информации,
содержащейся в результатах измерения, о том, что измеряемая величина примет то
или иное значение или объект системной идентификации находится в том или ином
состоянии. Применение данного подхода является корректным для измерения
состояния сложных многофакторных нелинейных динамических систем.
Упрощенно говоря, система «Эйдос» является
интеллектуальной измерительной системой и может рассматриваться в этом
качестве. При этом для нее «закон изменения характеристик погрешностей известен», так как в ней роль погрешностей
выполняет количество информации, а количество информации тесно связано с
понятиями неопределенности и погрешности. Общепринятым является представление
об информации, как количественной мере степени снятия неопределенности.
Погрешность также является мерой неопределенности наших знаний об истинном значении
измеряемой величины. Чем больше погрешность измерения, тем меньше информации мы
получаем в процессе измерения о значении измеряемой величины, чем меньше
погрешность – тем больше информации в наблюдении (измерении). Поэтому подход,
реализованный в предлагаемом варианте ВМНК, находится в согласии с предложением работы [40]. Подобные аргументы создают
теоретическое обоснование корректности использования количества информации в
наблюдениях в качестве их «обоснованных
весов» в предлагаемом варианте взвешенного метода наименьших квадратов.
В описании математического аппарата стандартного
метода наименьших квадратов (МНК) в данном разделе нет никакой необходимости,
т.к. этому посвящено большое количество общедоступных работ.
Поэтому в данном разделе мы рассмотрим только ключевые
моменты, позволяющие так преобразовать исходные данные о
наблюдениях, чтобы они учитывали количество информации в них, рассчитанное по методике численных расчетов
АСК-анализа, и чтобы к ним было возможно
применить стандартный МНК и при этом учитывалось количество информации в
наблюдениях.
В работе [9] предлагается два варианта данной
модификации взвешенного метода наименьших квадратов.
В первом варианте взвешивание наблюдений
производится путем замены одного наблюдения с определенным количеством
информации в нем соответствующим количеством наблюдений единичного веса, а
затем к ним применяется стандартный метод наименьших
квадратов (МНК). Фактически в этом
варианте решение задачи взвешивания наблюдений решается самим методом
наименьших квадратов. Алгоритм и программная реализация данного подхода
подробно описаны в статье [36].
В данной же работе, как и планировалось в [36], кратко
рассмотрим математические аспекты предлагаемого решения.
В стандартном методе наименьших квадратов
минимизируется сумма квадратов отклонений эмпирических значений
аппроксимируемой величины 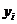 от расчетных значений
от расчетных значений 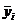 , вычисленных в соответствии с моделью (1):
, вычисленных в соответствии с моделью (1):
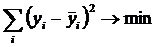 (1)
(1)
Во взвешенном методе наименьших квадратов
минимизируется сумма квадратов отклонений эмпирических значений
аппроксимируемой величины 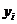 от расчетных значений
от расчетных значений 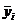 , вычисленных в соответствии с моделью, причем разным
наблюдениям приписывается разный вес
, вычисленных в соответствии с моделью, причем разным
наблюдениям приписывается разный вес 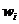 (2):
(2):
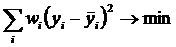 (2)
(2)
Ключевым моментом при применении
взвешенного МНК является способ выбора и задания весов наблюдений.
Традиционно считается, что разумным
вариантом является выбор весов пропорционально ошибкам не взвешенной регрессии
[38, 39]. Предполагается, что этим самым более надежным наблюдениям придается
больший вес, а сомнительным – меньший. Вроде выглядит разумно. Но проблема в
том, что к более надежными и или к сомнительными эмпирические наблюдения
относятся путем их сравнения с расчетными значениями, полученными с применением
создаваемой модели. Получается, что если модель хорошо описывает эмпирические
данные, то они считаются надежными, а если нет, то ненадежными. Как говорится
«если факты не соответствуют теории, то тем хуже для фактов». Автор не склонен
придерживаться подобной логики и поэтому видит возможность сделать из этого и
другой вывод: если модель хорошо
описывает эмпирические данные, то эта модель надежная, а если нет, то ненадежная,
и этот вывод выглядит гораздо более убедительным и разумным.
Подбор этих весов наблюдений вручную может
являться сложной и практически неразрешимой задачей, как из-за сложной
структуры данных (например, непостоянства дисперсии и среднего ошибок
наблюдений), так и из-за возможной очень большой размерности данных. Таким образом, возникает
задача автоматического определения весов наблюдений и
разработка алгоритмов и программного инструментария, обеспечивающего
автоматизацию определения и взвешивания весов наблюдений в МНК.
Предлагается новое, ранее не встречавшееся
в литературе, решение этой задачи и соответствующее обобщение метода наименьших
квадратов (МНК), в котором точки (наблюдения) имеют вес,
равный количеству информации в значении аргумента о значении функции. Ясно,
что по сути, речь идет о применении когнитивных функций [8-18] в
взвешенном МНК.
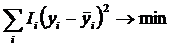 (3)
(3)
Здесь Ii
– количество информации в i-м наблюдении,
т.е. точнее говоря в i-м значении
аргумента 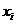 о том, что i-e функции примет значение
о том, что i-e функции примет значение 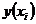 .
.
В выражениях (1), (2) и (3) не уточняется, могут ли
эмпирические значения функции 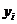 относиться к одному
значению аргумента и это не существенно для МНК. Но если точно известно, что
существует M значений аргумента и
одному значению аргумента
относиться к одному
значению аргумента и это не существенно для МНК. Но если точно известно, что
существует M значений аргумента и
одному значению аргумента 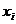 соответствует
соответствует 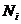 значений функции, то
для дальнейшего изложения нам удобнее записать выражения (1), (2) и (3) в
следующей форме, явно учитывающей это обстоятельство:
значений функции, то
для дальнейшего изложения нам удобнее записать выражения (1), (2) и (3) в
следующей форме, явно учитывающей это обстоятельство:
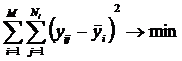 (1')
(1')
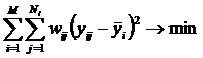 (2')
(2')
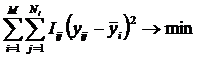 (3')
(3')
Отметим, что в случае, когда вес эмпирического
наблюдения 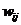 является целым числом, то выражение (2') эквивалентно
выражению:
является целым числом, то выражение (2') эквивалентно
выражению:
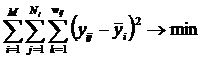 (2'')
(2'')
Этим мы и воспользовались в статье [36], когда
заменили одно наблюдение с весом 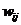 этим количеством
наблюдений с единичным весом.
этим количеством
наблюдений с единичным весом.
Во втором варианте взвешивание наблюдений
производится для каждого значения аргумента путем замены всех наблюдений с
определенным количеством информации в них одним наблюдением единичного веса,
полученным как средневзвешенное от них, а затем к ним применяется стандартный
МНК. В данном варианте ВМНК решение
задачи взвешивания наблюдений решается до
применения стандартного метода наименьших квадратов с помощью другого
инструментария, в качестве которого в частности может применяться и
интеллектуальная система «Эйдос».
Перед
применением стандартного МНК для каждого значения аргумента предварительно рассчитывается
средневзвешенное значение функции из всех ее значений с их весами.
Рассмотрим,
как по предлагаемой методике рассчитывается средневзвешенное значение функции с
учетом количества информации в аргументе о значении функции для одного значения аргумента.
Для двух точек выбор координаты средневзвешенной точки
y соответствует «правилу рычага»,
т.е. ее положение выбирается таким, чтобы рычаг, образованный двумя точками с координатами
y1 и y2 и весами I1
и I2, находился в
равновесии, если его опора будет в средневзвешенной точке с координатой 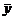 :
:
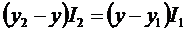 (4)
(4)
Откуда находим y.
При двух точках, соответствующих одному значению аргумента, координата y средневзвешенной точки, имеет вид:
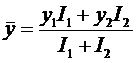 .
(5)
.
(5)
Если же для i-го
значения аргумента xi
таких точек 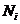 , то средневзвешенное значение функции
, то средневзвешенное значение функции 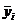 выражение (5) принимает вид (6):
выражение (5) принимает вид (6):
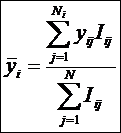 .
(6)
.
(6)
В результате средневзвешенная точка находится тем
ближе к некоторой точке, чем больше количество информации в значении аргумента
о том, что функция примет значение, соответствующее этой точке.
После этого преобразования можно применять стандартный
МНК.
В модуле визуализации когнитивных функций [11] этот
метод реализован программно по постановке автора разработчиком интеллектуальных
систем из Белоруссии Д.К.Бандык и обеспечивает отображение частично и полностью
редуцированных когнитивных функций.
Как говорилось выше,
ключевым моментом предлагаемой модификации ВМНК является способ определения
количества информации в наблюдениях. Поэтому далее в наиболее упрощенном виде
приводится методика численных расчетов количества информации в наблюдениях, основанная
на теории автоматизированного системно-когнитивного анализа (АСК-анализ) и
реализованная в его программном инструментарии – интеллектуальной системе «Эйдос»
[7, 17].
Для удобства
рассмотрения введем следующие обозначения:
i – индекс значения аргумента;
j – индекс значения функции;
M – количество значений аргумента;
W – количество значений функции;
Nij – количество встреч j-го
значения функции при i-м
значении аргумента;
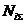 – суммарное количество наблюдений при i-м
значении аргумента по всей выборке;
– суммарное количество наблюдений при i-м
значении аргумента по всей выборке;
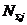 – суммарное количество наблюдений j-го значении функции по всей
выборке;
– суммарное количество наблюдений j-го значении функции по всей
выборке;
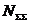 – суммарное количество наблюдений по всей
выборке;
– суммарное количество наблюдений по всей
выборке;
Iij – количество информации в
i-м значении аргумента о том,
что функция имеет j-е значение,
т.е. это количество информации в наблюдении (i, j);
Ψ – нормировочный коэффициент (Е.В.Луценко, 1979),
преобразующий количество информации в формуле А.Харкевича в биты и
обеспечивающий для нее соблюдение принципа соответствия с формулой Р.Хартли в
равновероятном детерминистском случае;
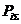 – безусловная относительная частота встречи i-го значения аргумента в обучающей
выборке;
– безусловная относительная частота встречи i-го значения аргумента в обучающей
выборке;
Pij – условная относительная частота встречи j-го значения функции при i-м значении аргумента.
Используя исходную
выборку эмпирических наблюдений посчитаем матрицу абсолютных частот (таблица
1):
Таблица 1 – МАТРИЦА АБСОЛЮТНЫХ ЧАСТОТ
|
|
Классы
|
Сумма
|
|
1
|
...
|
j
|
...
|
W
|
|
Значения
факторов
|
1
|
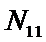
|
|
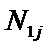
|
|
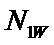
|
|
|
...
|
|
|
|
|
|
|
|
i
|
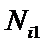
|
|
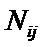
|
|
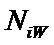
|
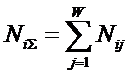
|
|
...
|
|
|
|
|
|
|
|
M
|
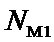
|
|
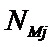
|
|
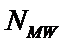
|
|
|
Суммарное
количество
признаков
|
|
|
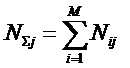
|
|
|
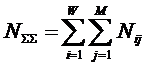
|
Алгоритм формирования матриц абсолютных частот и
условных и безусловных процентных распределений.
Объекты обучающей выборки описываются векторами
(массивами) 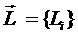 имеющихся у них
признаков:
имеющихся у них
признаков:
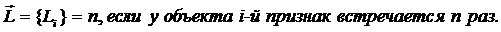
Первоначально в матрице абсолютных частот все значения
равны нулю. Затем организуется цикл по объектам обучающей выборки. Если у
предъявленного объекта, относящегося к j-му
классу, есть i-й признак, то:
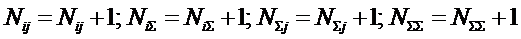 (7)
(7)
На основе анализа матрицы частот (табл. 1) классы
можно сравнивать по наблюдаемым частотам признаков только в том случае, если
количество объектов по всем классам одинаково, как и суммарное
количество признаков по классам. Если же они отличаются, то корректно
сравнивать классы можно только по условным и безусловным относительным частотам
(оценкам вероятностей) наблюдений признаков, посчитанных на основе матрицы
частот (табл. 1) в соответствии с выражениями (8), в результате чего
получается матрица условных и безусловных процентных распределений (табл. 2):
|
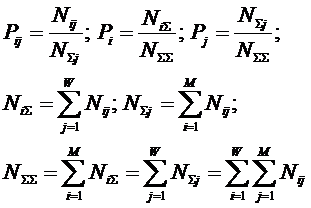
|
((8)
|
Таблица 2 – МАТРИЦА УСЛОВНЫХ И
БЕЗУСЛОВНЫХ
ПРОЦЕНТНЫХ РАСПРЕДЕЛЕНИЙ
|
|
Классы
|
Безусловная
вероятность
признака
|
|
1
|
...
|
j
|
...
|
W
|
|
Значения
факторов
|
1
|
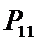
|
|
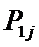
|
|
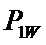
|
|
|
...
|
|
|
|
|
|
|
|
i
|
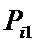
|
|
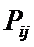
|
|
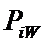
|
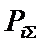
|
|
...
|
|
|
|
|
|
|
|
M
|
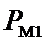
|
|
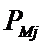
|
|
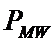
|
|
|
Безусловная
вероятность
класса
|
|
|
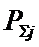
|
|
|
|
Далее произведем расчет количества информации в наблюдениях в
соответствии с выражением (9):
|
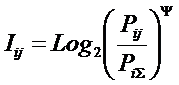
|
(9)
|
С
учетом (8) преобразуем (9) к виду (10):
|
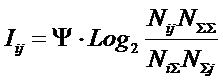
|
(10)
|
|

А.А.Харкевич
|
Здесь 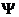 – упрощенная форма
коэффициента эмерджентности А.Харкевича (10), предложенный автором в 1979
году и названный так в честь известного советского ученого, внесшего большой
вклад в теорию информации, на работах которого основана излагаемая методика
численных расчетов количества информации в наблюдениях. – упрощенная форма
коэффициента эмерджентности А.Харкевича (10), предложенный автором в 1979
году и названный так в честь известного советского ученого, внесшего большой
вклад в теорию информации, на работах которого основана излагаемая методика
численных расчетов количества информации в наблюдениях.
|
|
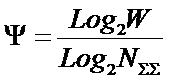
|
(11)
|
Используя выражения (9) и (11) на основе таблицы 2 рассчитывается
матрицу информативностей (таблица 3).
Она также может быть получена :непосредственно из таблицы 1 с использованием
выражений (10) и (11):
Таблица 3 – МАТРИЦА ИНФОРМАТИВНОСТЕЙ
|
|
Классы
|
Значимость
фактора
|
|
1
|
...
|
j
|
...
|
W
|
|
Значения
факторов
|
1
|
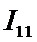
|
|
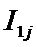
|
|
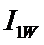
|
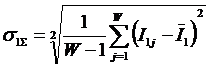
|
|
...
|
|
|
|
|
|
|
|
i
|
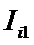
|
|
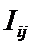
|
|
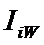
|
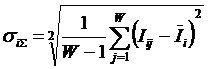
|
|
...
|
|
|
|
|
|
|
|
M
|
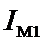
|
|
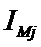
|
|
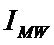
|
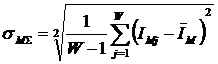
|
|
Степень
редукции
класса
|
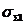
|
|
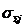
|
|
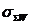
|
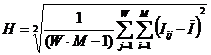
|
Здесь – 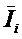 это среднее
количество информации в i-м значении
фактора:
это среднее
количество информации в i-м значении
фактора:
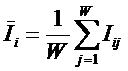
Когда количество информации Iij > 0 – i-й фактор
способствует переходу объекта управления в j-е состояние, когда Iij < 0 –
препятствует этому переходу, когда же Iij = 0 – никак не влияет на это. В
векторе i-го фактора (строка матрицы информативностей) отображается, какое
количество информации о переходе объекта управления в каждое из будущих
состояний содержится в том факте, что данный фактор действует. В векторе j-го
состояния класса (столбец матрицы информативностей) отображается, какое количество
информации о переходе объекта управления в соответствующее состояние содержится
в каждом из факторов.
Таким образом, данная модель позволяет рассчитать,
какое количество информации содержится в любом факте о наступлении любого события
в любой предметной области, причем для этого не требуется повторности этих
фактов и событий. Если данные повторности осуществляются и при этом наблюдается
некоторая вариабельность значений факторов, обуславливающих наступление тех или
иных событий, то модель обеспечивает многопараметрическую типизацию, т.е.
синтез обобщенных образов классов или категорий наступающих событий с
количественной оценкой степени и знака влияния на их наступление различных
значений факторов. Причем эти значения факторов могут быть как количественными,
так и качественными и измеряться в любых единицах измерения, в любом случае в
модели оценивается количество информации, которое в них содержится о
наступлении событий, переходе объекта управления в определенные состояния или,
просто, о его принадлежности к тем или иным классам. Другие способы метризации
приведены в работе [3].
Ниже на простом численном
примере мы кратко рассмотрим технологию, позволяющую на практике и в любой
предметной области посчитать, какое количество информации содержится в
наблюдении. В связи с ограничениями на объем статьи автор не имеет возможности полностью раскрыть все позиции на приведенных ниже
скриншотах и рисунках, т.е. фактически предполагается некоторое предварительное
знакомство читателя с системой «Эйдос». Если же такое знакомство недостаточно
полное, то автор отсылает автора к публикациям в списке литературы и к сайту: http://lc.kubagro.ru/.
Для иллюстрации предлагаемых подходов используем тот
же численный пример, что и в статье [36], но рассмотрим только второй вариант
предлагаемой модификации ВМНК, т.к. первый вариант был подробно рассмотрен в
[36].
Запустим режим 4.6 системы «Эйдос»,реализующий данный
метод, с параметрами, приведенными на рисунке 1:
Рисунок 1 – Экранная форма задания параметров режима
4.6 системы «Эйдос»
В результате выполнения режима создаются базы данных,
непосредственно считываемые MS Excel и содержащие данные для визуализации
когнитивных функций. Виды этих баз данных и способ формирования их имен
приведены в таблице 4.
Рассмотрим рисунок 22 из статьи [36] с результатами
применения первого варианта предлагаемого метода, приведенный ниже под номером 2:
Таблица 4 – Виды этих баз данных для визуализации когнитивных
функций и способ формирования их имен
|
Прямые
и обратные
|
Позитивные
и негативные
|
Вариант способа учета количества информации
в наблюдениях для одного значения аргумента
|
Имена баз данных
для MS Ecxel
|
|
Прямые:
Y=F[X]
|
Позитивные: количество информации I[X,Y] > 0
|
Учет только наблюдений для каждого значения аргумента
с MAX колич. информации
|
####-Y(X)-Pos-One_point-##-##.dbf
|
|
Замена всех наблюдений для каждого значения
аргумента одним средневзвешенным
|
####-Y(X)-Pos-All_points_Avr-##-##.dbf
|
|
Замена наблюдения с количеством информации Iij
наблюдениями с единичным весом
|
####-Y(X)-Pos-All_points_N1-##-##.dbf
|
|
Негативные: количество информации I[X,Y] < 0
|
Учет только наблюдений для каждого значения аргумента
с MAX колич. информации
|
####-Y(X)-Pos-One_point-##-##.dbf
|
|
Замена всех наблюдений для каждого значения
аргумента одним средневзвешенным
|
####-Y(X)-Pos-All_points_Avr-##-##.dbf
|
|
Замена наблюдения с количеством информации Iij
наблюдениями с единичным весом
|
####-Y(X)-Pos-All_points_N1-##-##.dbf
|
|
Обратные: X=F[Y]
|
Позитивные: количество информации I[X,Y] > 0
|
Учет только наблюдений для каждого значения аргумента
с MAX колич. информации
|
####-Y(X)-Pos-One_point-##-##.dbf
|
|
Замена всех наблюдений для каждого значения
аргумента одним средневзвешенным
|
####-Y(X)-Pos-All_points_Avr-##-##.dbf
|
|
Замена наблюдения с количеством информации Iij
наблюдениями с единичным весом
|
####-Y(X)-Pos-All_points_N1-##-##.dbf
|
|
Негативные: количество информации I[X,Y] < 0
|
Учет только наблюдений для каждого значения аргумента
с MAX колич. информации
|
####-Y(X)-Pos-One_point-##-##.dbf
|
|
Замена всех наблюдений для каждого значения
аргумента одним средневзвешенным
|
####-Y(X)-Pos-All_points_Avr-##-##.dbf
|
|
Замена наблюдения с количеством информации Iij
наблюдениями с единичным весом
|
####-Y(X)-Pos-All_points_N1-##-##.dbf
|
Примечание: В начале имени идет обозначение модели, в которой
получена когнитивная функция, а епосредственно перед расширением имен баз
данных через тире указываются коды описательной и классификационной шкал.
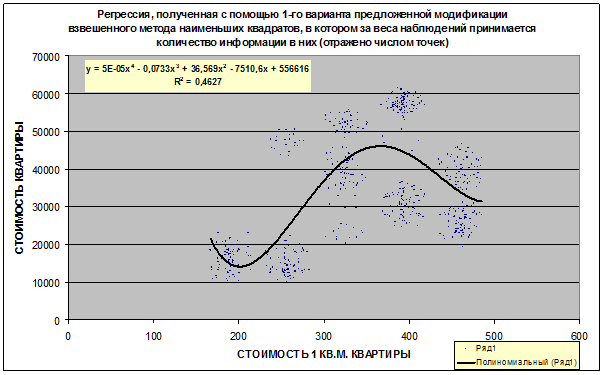
Рисунок 2 – Регрессия,
построенная на основе всех наблюдений с учетом
количества информации в них с использованием 1-го варианта
предлагаемой модификации ВМНК
В таблице 5 приводятся результаты взвешивания
наблюдений с учетом количества
информации в них с использованием 2-го варианта предлагаемой модификации ВМНК,
а на рисунке 3 показаны соответствующие регрессии, построенные по этим
данным:
Таблица 5 – Результаты взвешивания наблюдений с учетом количества информации в них с
использованием 2-го варианта предлагаемой модификации ВМНК
|
Наименование
аргумента
|
Наименование
значения функции
|
Значение
аргумента
|
Значение
функции
|
|
1/5-{154.2210000, 222.5048000}
|
2/10-{15617.4000000, 20523.4000000}
|
188,3629000
|
16260,8366534
|
|
2/5-{222.5048000, 290.7886000}
|
3/10-{20523.4000000, 25429.4000000}
|
256,6467000
|
23509,8510850
|
|
3/5-{290.7886000, 359.0724000}
|
7/10-{40147.4000000, 45053.4000000}
|
324,9305000
|
42225,3300638
|
|
4/5-{359.0724000, 427.3562000}
|
8/10-{45053.4000000, 49959.4000000}
|
393,2143000
|
45297,9398623
|
|
5/5-{427.3562000, 495.6400000}
|
5/10-{30335.4000000, 35241.4000000}
|
461,4981000
|
33211,6434714
|
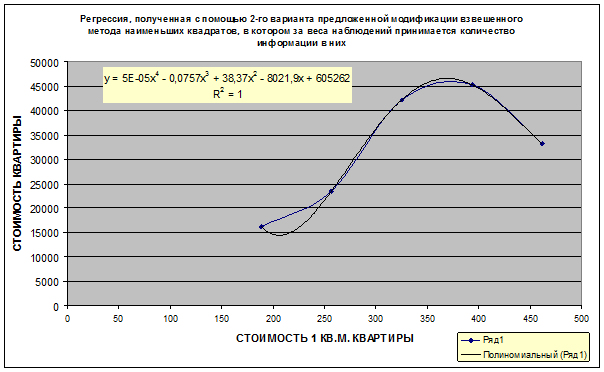
Рисунок 3 – Регрессия,
построенная на основе всех наблюдений с учетом количества информации в них с
использованием 2-го варианта предлагаемой модификации ВМНК
На рисунке 4 для удобства их сравнения совмещены
изображения с рисунков 2 и 3.
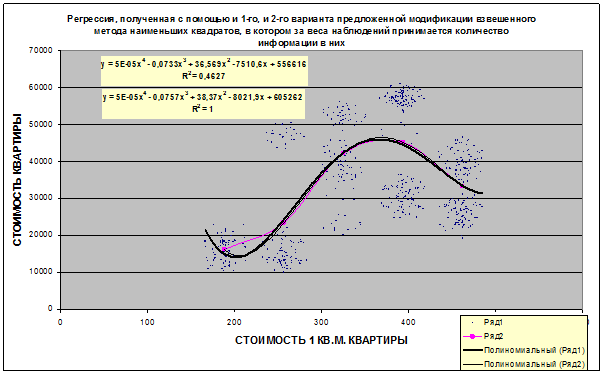
Рисунок 4 – Регрессии,
построенные на основе всех наблюдений с учетом количества информации в них с
использованием и 1-го, и 2-го вариантов предлагаемой модификации ВМНК
Из сравнения по рисункам 2, 3 и 4 и приведенным на них
уравнениям регрессий 1-го и 2-го вариантов взвешивания наблюдений с
использованием в качестве весов количества информации в наблюдениях мы можем
сделать вывод, что отличаются они весьма незначительно.
В данном разделе кратко рассмотрена математическая
сущность предложенной автором модификации взвешенного
метода наименьших квадратов (ВМНК), в котором в качестве весов
наблюдений применяется количество информации в них. Предлагается два варианта
данной модификации ВМНК. В первом варианте взвешивание наблюдений производится
путем замены одного наблюдения с определенным количеством информации в нем
соответствующим количеством наблюдений
единичного веса, а затем к ним применяется стандартный метод
наименьших квадратов (МНК). Во втором варианте взвешивание наблюдений
производится для каждого значения аргумента путем замены всех наблюдений с
определенным количеством информации в них одним наблюдением единичного веса,
полученным как средневзвешенное от них, а затем к ним применяется стандартный
МНК. Подробно описана методика численных расчетов количества информации в
наблюдениях, основанная на теории автоматизированного системно-когнитивного
анализа (АСК-анализ) и реализованная в его программном инструментарии –
интеллектуальной системе «Эйдос». Приводится иллюстрация предлагаемого подхода
на простом численном примере.
Главный вывод, который можно сделать по материалам статьи, состоит в том, что
предлагается обоснованное решение двух дополнительных проблем, сформулированных
в начале статьи, т.е. предлагается теоретическое обоснование, методика численных расчетов и программная
реализация модификации взвешенного метода наименьших квадратов, в котором в
качестве весов наблюдений применяется количество информации в них. Если в ВМНК
принимается гипотеза, что веса наблюдений тем больше (более надежны), чем
меньше ошибка, в качестве которой используется дисперсия, то в предлагаемой
модификации ВМНК непосредственно на основе эмпирических данных расчетным путем
определяется количество информации в наблюдениях, которое используется в качестве
весов наблюдений, вместо традиционной погрешности. Необходимо подчеркнуть, что
предлагаемый способ расчета количества информации не основан на предположениях
о независимости наблюдений и их нормальном распределении, т.е. является
непараметрическим и обеспечивает корректное моделирование нелинейных систем, а
также позволяет сопоставимо обрабатывать разнородные (измеряемые в шкалах
различных типов) данные числовой и нечисловой природы, измеряемые в различных
единицах измерения.
Таким образом, АСК-анализ и
система «Эйдос» представляют собой современную инновационную (готовую к
внедрению) технологию взвешенного метода наименьших квадратов,
модифицированного путем применения в качестве весов наблюдений количества
информации в них.
Данный раздел может быть использован как описание
лабораторной работы по дисциплинам:
– Интеллектуальные системы;
– Инженерия знаний и интеллектуальные системы;
– Интеллектуальные технологии и
представление знаний;
– Представление знаний в интеллектуальных
системах;
– Основы интеллектуальных систем;
– Введение в нейроматематику и методы
нейронных сетей;
– Основы искусственного интеллекта;
– Интеллектуальные технологии в науке и образовании;
– Управление знаниями;
– Автоматизированный системно-когнитивный
анализ и интеллектуальная система «Эйдос»;
которые автор ведет в настоящее время,
а также и в других дисциплинах, связанных с преобразованием данных в
информацию, а ее в знания и применением этих знаний для решения задач
идентификации, прогнозирования, принятия решений и исследования моделируемой
предметной области (а это практически все дисциплины во всех областях науки).
В данном разделе не ставилась задача исследовать
математические и прагматические свойства предлагаемой модификации ВМНК,
основанной на использовании в качестве весов наблюдений количества информации
в них. Это предполагается сделать в
будущих статьях, посвященных данному методу.
Профессор А.И.Орлов в переписке по поводу статьи
отмечает, что в будущем «…желательно
иметь вероятностно-статистическую теорию, в которой доказаны теоремы о
состоятельности оценок параметров зависимости, построены доверительные
интервалы для зависимости, как это сделано в классическом случае линейной зависимости
в моих книгах (см., например, п.5.1 в "Эконометрике" http://ibm.bmstu.ru/nil/biblio.html#books-13-econ ). К сожалению, вряд ли такую теорию
можно быстро построить».
Метод наименьших квадратов (МНК) широко
известен и пользуется заслуженной популярностью. Вместе с тем не прекращаются
попытки усовершенствования этого метода. Результатом одной из таких попыток
является взвешенный метод наименьших квадратов (ВМНК), суть которого в том,
чтобы придать наблюдениям вес обратно пропорциональный погрешностям их
аппроксимации. Этим самым, фактически, наблюдения игнорируются тем в большей
степени, чем сложнее их аппроксимировать. В результате такого подхода формально
погрешность аппроксимации снижается, но фактически это происходит путем
частичного отказа от рассмотрения «проблемных» наблюдений, вносящих большую
ошибку. Если эту идею, лежащую в основе ВМНК довести до крайности (и тем самым
до абсурда), то в пределе такой подход приведет к тому, что из всей
совокупности наблюдений останутся только те, которые практически точно ложатся
на тренд, полученный методом наименьших квадратов, а остальные просто будут
проигнорированы. Однако, по мнению автора, фактически это не решение проблемы,
а отказ от ее решения, хотя внешне и выглядит как решение. В работе
предлагается именно решение, основанное на теории информации: считать весом
наблюдения количество информации в аргументе о значении функции. Этот подход
был обоснован в рамках нового инновационного метода искусственного интеллекта:
метода автоматизированного системно-когнитивного анализа (АСК-анализа) и
реализован еще 30 лет назад в его программном инструментарии – интеллектуальной системе «Эйдос» в виде так называемых «когнитивных
функций». В данном разделе приводится алгоритм и программная реализация данного
подхода, проиллюстрированные на подробном численном примере. В будущем
планируется дать развернутое математическое обоснование метода взвешенных
наименьших квадратов, модифицированного путем применения теории информации для
расчета весовых коэффициентов наблюдений, а также исследовать его свойства
«... навыки мысли и аналитический аппарат
теории информации должны, по-видимому, привести к заметной перестройке здания математической
статистики»
А.Н.
Колмогоров [1, 2, 19]
|

René
Descartes
31.03.1596 – 11.02.1650
|
После ряда
основополагающих работ Рене Декарта стало понятно, что любой функции соответствует
график, а любому графику – функция. Построение графика по аналитически
заданной функции не представляет собой проблемы, т.к. известен способ, как
это сделать, т.е. это задача.
Решается эта задача
путем:
– расчета с
использованием аналитического выражения для функции таблицы ее значений
(таблица 1), соответствующих различным значениям аргумента;
– построения графика
параметрически заданной функции (1).Если функциональная зависимость y от x не
задана непосредственно y = f(x), а через промежуточную величину –
t, то формулы (1)
|
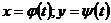 (1)
(1)
задают параметрическое представление
функции одной переменной.
Таблица 1 представляет
собой таблицу значений функции y и ее
аргумента x (1) для различных
значений параметра t.
Таблица 1 –
Параметрическое задание функции в виде таблицы
Однако решение обратной задачи, т.е. задачи
восстановления аналитической формы представления функции, т.е. формулы вида: 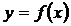 , по ее графику или таблично заданным значениям до сих пор
представляет собой проблему, не решенную в общем виде.
, по ее графику или таблично заданным значениям до сих пор
представляет собой проблему, не решенную в общем виде.
Решению этой проблемы
посвящен регрессионный анализ [32, 33], в котором широко применяется метод
наименьших квадратов (МНК), а также его взвешенный вариант. Однако этот метод
позволяет точно восстановить неизвестный истинный вид функции лишь в редких
частных случаях, а в общем виде решает лишь задачу поиска и подбора такого вида
функции из заранее определенного набора, которая в определенном смысле или по
определенным критериям наилучшим образом совпадает с этой неизвестной истинной
функцией.
Одним из общепринятых и
действительно наиболее убедительных критериев качества подбора функции,
аппроксимирующей эмпирические данные (типа таблицы 1), является минимизация
суммы квадратов отклонений эмпирических значений от этой аппроксимирующей их
функции.
Однако исследование этих
отклонений при аппроксимации различных эмпирических данных показало, что далеко
не всегда эти отклонения равномерно зависят от значения функции. Иначе говоря,
качество аппроксимации эмпирических данных ожжет изменяться для различных
значений аргумента, т.е. качество аппроксимации различно для различных фрагментов
функции и эмпирических данных.
Ясно, что качество
аппроксимирующей функции не может быть выше качества ее фрагмента, наиболее
плохо аппроксимирующего эти эмпирические данные. Вполне понятно и стремление
математиков-практиков повысить качество аппроксимации. Но что предлагают в этом
плане математики-теоретики?
Если эмпирических данных,
выпадающих из закономерности, отражаемой аппроксимирующей функцией, не очень
много, то их объявляют «артефактами» и это дает теоретические основания просто
игнорировать их путем удаления из
исследуемой выборки. Ясно, что после этой операции качество аппроксимации
заметно улучшается.
Но является ли это
решением проблемы? По мнению автора формально является, т.к. вроде как качество
модели возрастает, но конечно фактически это не решение, т.к. основано на
порочном принципе: «Если факты не вписываются в теорию (в нашем случае
аналитическую модель), то тем хуже для фактов». Фактически это «страусиный»
способ решения проблем, который состоит просто в том, чтобы не видеть их или
делать вид, что их не существует. При этом исследователь часто не отдает себе в
этом отчет и впадает в иллюзию (гипостазирование), что он моделирует саму
реальность и исследует ее путем исследования созданной им ее модели, тогда как
в действительности он исследует только ту часть реальности, которую смог
смоделировать при своих ограниченных возможностях моделирования. Профессор
А.И.Орлов пишет, что это равносильно тому, чтобы «искать под фонарем, а не там,
где потеряли» [1].
Конечно, разработка таких
более мощных методов моделирования ведется [2]. Но ознакомление с ними
математиков-практиков, и даже руководителей науки, далеко отстает от
фактической потребности применения этих методов [2].
Приведем простейший
пример, иллюстрирующий высказанные мысли. Если данные не вписываются в линейную
модель, то можно игнорировать или удалить из исследуемой те из них, которые
вносят основной вклад в суммарную ошибку, а можно использовать квадратичную
модель, которая точно описывает эти данные во всей их полноте (таблица 2, рисунки
1, 2 и 3):
Таблица 2 – Исходные данные для примера
|
Значение аргумента
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
Значение функции
|
1
|
4
|
9
|
16
|
25
|
36
|
49
|
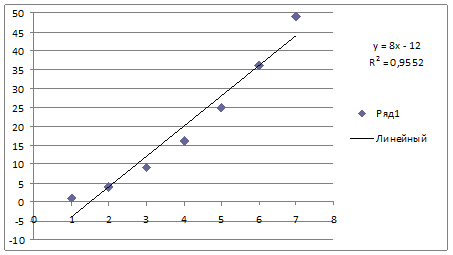
Рисунок 1 – Линейная модель не адекватно отражает
исходные данные
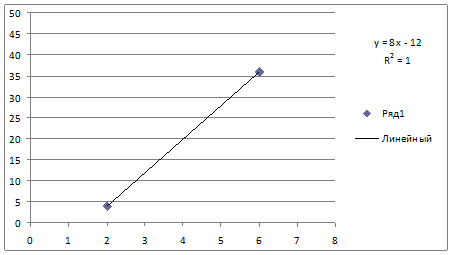
Рисунок 2 – Линейная модель адекватно отражает
исходные данные,
Из которых удалены все наблюдения, кроме 2-го и 6-го
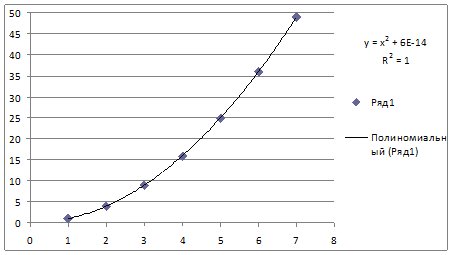
Рисунок 3 – Квадратичная модель адекватно отражает все
исходные данные
Но есть и более развитые идеи и методы улучшения
модели по формальным критериям качества: не вообще удалять неудобные данные, а
просто уменьшать их значение или вес и делать это тем в большей степени, чем
более эти данные неудобны, т.е. с чем
большей ошибкой они отражаются в модели. На этой идее основан взвешенный метод
наименьших квадратов (ВМНК), который является традиционным путем решения
поставленной проблемы. Фактически в этом методе
данные сначала преобразуются взвешиванием наблюдений (делением на величину,
пропорциональную предполагаемому стандартному отклонению случайных ошибок), а к
предварительно взвешенным данным уже применяется обычный стандартный метод наименьших
квадратов.
Профессор А.И.Орлов пишет о
том, что:
– на подавление выбросов нацелены робастные методы;
– вероятностно-статистическая модель порождения данных
– первична, а метод оценивания параметров качества модели – вторичен;
– точность восстановления зависимости традиционно
оценивается дисперсиями и доверительным интервалами;
– если в разные моменты времени проводится различное
количество наблюдений, вследствие чего их надежность, погрешности и другие характеристики,
вообще говоря, оказываются зависящими от времени, то взвешивание
данных действительно необходимо.
Тем ни менее к взвешенному методу наименьших квадратов
также может быть адресован ряд критических замечаний, которые мы кратко
рассмотрим ниже.
Все те возражения, которые были высказаны выше в
отношении процедуры удаления из исходных данных «артефактов» полностью сохранят
силу и для взвешенного метода наименьших квадратов.
Но здесь появляются и дополнительные возражения.
Прежде всего, возникают взаимосвязанные вопросы о цели
моделирования и цели повышения качества моделирования.
Если целью моделирования является наиболее полное и
адекватное отражение реальности в моделях, а так по наивности обычно все и думают,
то повышение качества моделирования должно осуществляться не путем выбора
наиболее легко и просто моделируемой предметной области, а путем
совершенствования математического аппарата и программного инструментария
моделирования.
Но если
исходить из этой логики, то в методе
взвешенных наименьших квадратов вес наблюдений должен быть принят не обратно
пропорциональным вносимым этими наблюдениями ошибкам аппроксимации простым МНК,
а наоборот пропорциональным этим
ошибкам. Проще говоря, чем сложнее некоторые данные отразить в модели, тем
более пристальное внимание должно быть им уделено, а не наоборот, как в ВМНК,
где фактически от таких данных просто отмахиваются игнорируя их и теоретически
обосновывая их якобы «несущественность».
Но в чем фактически
состоит причина, по которой эти данные вдруг стали считаться несущественными?
Да просто в том, что «они портят всю картину», такую стройную и удобную, т.е.
ухудшают формальное качество модели.
Поэтому если цель (точнее ее называть
самоцелью) моделирования состоит не в адекватном отражении реальности, а в повышении
формального качества модели, то от таких данных надо избавиться, но уже не
просто удалив их из исследуемой выборки как «артефакты», а более цивилизованным
способом, т.е. приписав им меньший вес, в т.ч. вес, равный нулю.
Более того, в статистических пакетах предоставлена возможность задавать
веса вручную, позволяет регулировать вклад тех или иных данных в результаты
построения моделей. Иначе говоря, предоставляется возможность вручную практически произвольно по своему
усмотрению влиять на модель путем подбора нужных весовых коэффициентов. Но
если так, то может быть проще использовать не статистические пакеты, а просто
взять и сразу написать в аналитическом отчете, что «компьютер посчитал так…» и
нарисовать в графическом редакторе нужные выходные формы. С аналогичными
подходами мы сталкиваемся и при проведении кластерного анализа [30].
В работах [1, 2] рассматриваются точки роста и перспективы статистических методов, и дается
положительная оценка методу автоматизированного системно-когнитивного анализа
(АСК-анализ) и его программному инструментарию – интеллектуальной системе
«Эйдос».
В АСК-анализе факторы формально описываются шкалами, а
значения факторов – градациями шкал [3]. Существует три основных группы
факторов: физические, социально-экономические и психологические (субъективные)
и в каждой из этих групп есть много различных видов факторов, т.е. есть много
различных физических факторов, много социально-экономических и много
психологических, но в АСК-анализе все факторы рассматриваются с
одной единственной точки зрения:
сколько информации содержится в их значениях о переходе объекта, на который они
действуют, в определенные будущие состояния, и при этом сила и направление
влияния всех значений факторов на объект измеряется в одних общих для всех
факторов единицах измерения: единицах
количества информации. Именно по этой
причине вполне корректно складывать силу и направление влияния всех
действующих на объект значений факторов, независимо от их природы, и определять
результат совместного влияния на
объект системы значений факторов. При
этом в общем случае объект является нелинейным
и факторы внутри него взаимодействуют друг с другом, т.е. для них не
выполняется принцип суперпозиции.
Если же
разные факторы измеряются в различных единицах измерения, то результаты
сравнения объектов будут зависеть от этих единиц измерения, что совершенно
недопустимо с теоретической точки зрения [3].
Введем
определение когнитивной функции:
когда функция используется для отображения причинно-следственной зависимости,
т.е. информации (согласно концепции Шенка-Абельсона [34]), или знаний, если эта информация полезна для
достижении целей [35], то будем называть такую функцию когнитивной функцией, от англ. «cognition»
[3].
Смысл когнитивной функциональной зависимости в
том, что в значении аргумента содержится определенное количество информации
о том, какое значение примет функция, т.е. когнитивная функция отражает знания
о степени соответствия значений функции значениям аргумента [3].
Очень важно,
что этот подход позволяет автоматически решить проблему сопоставимой обработки
многих факторов, измеряемых в различных единицах измерения, т.к. в этом подходе рассматриваются не сами
факторы, какой бы природы они не были и какими бы шкалами не формализовались,
а количество информации, которое
в них содержится о поведении моделируемого объекта [3].
Необходимо также отметить, что представление о
полностью линейных объектах (системах) является абстракцией и реально все объекты являются принципиально
нелинейными. Вместе с тем для большинства систем нелинейные эффекты можно считать
эффектами второго и более высоких порядков и такие системы в первом приближении можно считать линейными. Возможны различные
модели взаимодействия факторов, в
частности, развиваемые в форме системного обобщения теории множеств. Этот
подход в перспективе может стать одним из вариантов развития теории нелинейных
систем [3].
Отметим, что математическая модель АСК-анализа
(системная теория информации) органично
учитывает принципиальную нелинейность всех объектов. Это проявляется в
нелокальности нейронной сети системы «Эйдос» [46], приводящей к зависимости всех
информативностей от любого изменения в исходных данных, а не как в методе обратного
распространения ошибки. В результате значения матрицы информативностей количественно
отражают факторы не как множество, а как систему.
В АСК-анализе ставится задача метризации шкал, т.е. преобразования к
наиболее формализованному виду, и предлагается 7 способов метризации всех типов
шкал, обеспечивающих совместную сопоставимую количественную обработку
разнородных факторов, измеряемых в различных единицах измерения за счет
преобразования всех шкал к одним универсальным единицам измерения в качестве
которых выбраны единицы измерения количества информации. Все эти способы метризации реализованы в
АСК-анализе и системе «Эйдос» [3]. В работах [4, 5, 6] кратко описаны суть и
история появления и развития метода АСК-анализа и его программного инструментария
– интеллектуальной системы «Эйдос», поэтому здесь мы их излагать не будем. Отметим
лишь, что эти методы созданы довольно давно и уже в 1987 году были акты
внедрения интеллектуальных приложений, в которых формировались информационные
портреты классов и и значений факторов [7].
Поэтому для
нас является вполне естественным предположить, что в качестве весов наблюдений целесообразно использовать количество
информации, которое содержится в этих наблюдениях о том, что интересующие
нас выходные параметры объекта моделирования примут те или иные значения или
сам объект моделирования перейдет в состояния, соответствующие тем или иным
классам или окажется принадлежащим к определенным обобщающим категориям
(группам). В этом и состоит основная идея
предлагаемого решения поставленной проблемы.
В АСК-анализе на основе системной теории информации [7, 17] развит математический аппарат,
обеспечивающий формальное описание поведения сложных нелинейных объектов
моделирования под воздействием систем управляющих факторов и окружающей среды,
а также созданы инструментальные средства, реализующие этот математический
аппарат.
В частности в АСК-анализе предложено понятие когнитивных функций, которое
рассмотрено и развито в ряде работ автора и соавторов [8, 9, 10, 11, 12, 13, 14,
15, 16, 17, 18] и поэтому здесь нет смысла подробно останавливаться на этом
понятии. Отметим лишь суть. В работе [16] кратко рассматриваются классическое
понятие функциональной зависимости в математике, определяются ограничения
применимости этого понятия для адекватного моделирования реальности и
формулируется проблема, состоящая в поиске такого обобщения понятия функции,
которое было бы более пригодно для адекватного отражения причинно-следственных
связей в реальной области. Далее рассматривается теоретическое и практическое
решения поставленной проблемы, состоящие в том, что:
а) предлагается универсальный не зависящий от
предметной области способ вычисления количества информации в значении аргумента
о значении функции, т.е. когнитивные функции;
б) предлагается программный инструментарий:
интеллектуальная система «Эйдос», позволяющая на практике осуществлять эти
расчеты, т.е. строить когнитивные функции на основе фрагментированных зашумленных
эмпирических данных большой размерности.
Предлагаются понятия нередуцированных, частично и
полностью редуцированных прямых и обратных, позитивных и негативных когнитивных
функций и метод формирования редуцированных когнитивных функций, являющийся
вариантом известного взвешенного метода наименьших квадратов, отличающимся от
стандартного ВМНК учетом в качестве весов наблюдений количества информации в значениях
аргумента о значениях функции.
Конечно, применение теории информации для решения
проблем и развития статистики не является абсолютно новой идеей. Как
указывает в своих работах [1, 2] профессор А.И.Орлов, сходные идеи развивал еще
в середине XX века С.Кульбак [19], а в эпиграф данной статьи вынесено программное
высказывание выдающегося российского математика А.Н. Колмогорова:
«... навыки мысли и аналитический аппарат теории информации должны,
по-видимому, привести к заметной перестройке
здания математической статистики», которые содержится в его предисловии к той
же книге С.Кульбака и также приведенное в
работах [1, 2]. В наше время в этом направлении продуктивно работают Дуглас Хаббард
[20], а также российский математик В.Б.Вяткин [21-28].
Кроме
того, иногда авторы, излагающие в частности взвешенный метод наименьших
квадратов, может быть не вполне осознанно используют слово «информация» не как
научный термин, а в обиходном разговорном смысле. Например, в работе, приведенной
на сайте: http://lib.alnam.ru/book_prs2.php?id=38,
автор пишет: «Чтобы учесть разницу в информации, которую
несет каждое наблюдение, для нахождения оценки необходимо минимизировать
взвешенную сумму
квадратов отклонений» (отмечено мной, авт.). Казалось бы, остается «лишь»
посчитать это количество информации и вариант взвешенного метода наименьших
квадратов, основанный на теории информации, готов, но, однако мы видим, что
ниже идет изложение стандартного ВМНК.
Таким образом, даже если принять
в принципе изложенные выше идеи о применении количества информации в наблюдении
в качестве веса наблюдения во взвешенном методе наименьших квадратов, то все
равно остается очень существенный и принципиальный вопрос о том, каким
способом возможно реально посчитать это количество информации. Этот
вопрос разбивается на две части:
– с помощью какого
математического аппарата возможно посчитать количество информации в наблюдении?
– с помощью какого программного
инструментария, реализующего этот математический аппарат, возможно посчитать
количество информации в наблюдении?
Автоматизированный
системно-когнитивный анализ (АСК-анализ) и его математическая модель (системная
теория информации), а также реализующий их программный инструментарий
АСК-анализа – система «Эйдос» – это и есть ответы на этот вопрос. Таким
образом, АСК-анализ и система «Эйдос» представляют собой современную интеллектуальную
инновационную
(полностью готовую к внедрению) технологию взвешенного метода наименьших
квадратов, модифицированного путем применения в качестве весов наблюдений количества
информации в них.
При этом при принятии решений о применении для решения
поставленной проблемы этой интеллектуальной инновационной технологии
естественно возникает вопрос о степени точности восстановления в создаваемых с
помощью нее моделях исследуемых эмпирических зависимостей в АСК-анализе и
системе «Эйдос».
Традиционно точность восстановления зависимости
оценивается дисперсиями и доверительным интервалами. В АСК-анализе смысловым
аналогом доверительного интервала, в определенной степени, конечно, является
количество информации в аргументе о значении функции. Поэтому необходимо
исследовать соотношение смыслового содержания этих понятий: доверительного
интервала и количества информации.
На математическом уровне это планируется сделать в
будущем, а в данном разделе отметим лишь, что чем больше доверительный
интервал, тем выше неопределенность наших знаний о значении функции,
соответствующем значению аргумента, а чем он меньше, тем эта определенность
выше. Но информация и определяется как количественная мера степени
снятия неопределенности. Учитывая это можно утверждать, что чем
больше доверительный интервал, тем меньше информации о значении функции,
соответствующем значению аргумента мы получаем, а чем он меньше, тем это
количество информации больше. Забегая вперед, отметим, что в частично-редуцированных
когнитивных функциях, например изображенных на рисунке 15, количество
информации в значениях аргумента о значениях функции наглядно изображено
шириной полосы функции, что не только по смыслу, но внешне очень сходно с
доверительным интервалом. При этом отметим еще один интересный момент, который
состоит в том, что если традиционный доверительный интервал при экстраполяции
при удалении от эмпирических значений ко все далее отстоящим от них в будущим
все время увеличивается, то в степень редукции когнитивной функции то увеличивается,
то уменьшается. Это связано с тем, что АСК-анализ и система «Эйдос» позволяют не
только прогнозировать будущие события, но и прогнозировать достоверность или
риски этих прогнозов [7],
т.е. прогнозировать продолжительность периодов эргодичности и точки бифуркации
(качественного изменения закономерностей в моделируемой предметной области),
что наглядно и отображается в такой форме.
В частности при
этом при нулевом доверительном интервале формально
получается, что мы имеем бесконечное количество информации о значении функции,
но на практике это вообще невозможно
[17] и даже в теории возможно только для отдельных точек целых значений аргумента и функции. При бесконечном доверительном интервале
в значении аргумента функции содержится ноль информации о значении функции.
Ниже на простом численном
примере мы кратко рассмотрим технологию, позволяющую на практике и в любой
предметной области посчитать, какое количество информации содержится в
наблюдении. В связи с ограничениями на объем статьи автор не имеет возможности полностью раскрыть все позиции на приведенных ниже
скриншотах и рисунках, т.е. фактически предполагается некоторое предварительное
знакомство читателя с системой «Эйдос». Если же такое знакомство недостаточно
полное, то автор отсылает автора к публикациям в списке литературы и к сайту: http://lc.kubagro.ru/.
В АСК-анализе и системе «Эйдос» реализован аппарат
когнитивных функций, который может быть применен для иллюстрации варианта
взвешенного метода наименьших квадратов. На важность подобных наглядных
примеров также указывал А.Н. Колмогоров: «По-видимому, внедрение предлагаемых
методов в
практическую статистику будет облегчено, если тот же материал будет изложен
более доступно и проиллюстрирован на подробно разобранных содержательных
примерах» [1, 2, 19].
Для этой цели рассмотрим численный пример, основанный
на исходных данных, приведенных в работе (таблица 3) [29].
Необходимо отметить, что данные
в таблице 3 достаточно условные, поскольку не содержат
полного (адекватного) набора исходных данных, от которых зависит цена предложения квартиры
(которая, кстати, в них и не содержится). В частности в таблице 3 нет числа комнат, указаны не все
возможные типы домов, не учтена инфраструктура, как на сайте: http://1bezposrednikov.ru/krasnodar/kalkulyator_stoimosti/, не указано, входит ли площадь кухни в площадь
квартиры, т.е. что это за площадь: общая или жилая, и т.д. Вместе с тем для
целей данной статьи, т.е. для иллюстрации излагаемых в ней идей и методов, они
достаточны (после некоторых корректировок, о которых сказано ниже).
Таблица 3 –
Исходные данные для эконометрического моделирования
|
№ наблюдения
|
Стоимость 1 кв.м. квартиры (руб./м2)
|
Жилая площадь квартиры (м2)
|
Тип дома
|
Наличие балкона
|
Площадь кухни (м2)
|
Тип жилья
|
|
1
|
360,000
|
80
|
0
|
0
|
25
|
0
|
|
2
|
388,015
|
110
|
0
|
1
|
23
|
0
|
|
3
|
328,393
|
127
|
0
|
0
|
30
|
0
|
|
4
|
319,000
|
135
|
0
|
1
|
20
|
0
|
|
5
|
343,600
|
76
|
0
|
0
|
16
|
0
|
|
6
|
360,000
|
75
|
0
|
1
|
16
|
0
|
|
7
|
315,499
|
107
|
0
|
0
|
12
|
0
|
|
8
|
470,000
|
62
|
0
|
0
|
16
|
0
|
|
9
|
305,006
|
137
|
0
|
0
|
20
|
0
|
|
10
|
338,398
|
72
|
0
|
1
|
20
|
0
|
|
11
|
309,632
|
147
|
1
|
0
|
50
|
0
|
|
12
|
396,660
|
45
|
1
|
1
|
11,3
|
0
|
|
13
|
300,400
|
120
|
0
|
1
|
14
|
0
|
|
14
|
390,400
|
70
|
0
|
1
|
14
|
0
|
|
15
|
257,151
|
154
|
0
|
1
|
25
|
0
|
|
16
|
342,000
|
58
|
0
|
1
|
15
|
0
|
|
17
|
348,840
|
58
|
0
|
1
|
15,3
|
0
|
|
18
|
360,000
|
64
|
0
|
1
|
18
|
0
|
|
19
|
355,000
|
108
|
0
|
0
|
13
|
0
|
|
20
|
330,060
|
113
|
0
|
1
|
15
|
0
|
|
21
|
315,904
|
99
|
0
|
1
|
25
|
0
|
|
22
|
303,100
|
136
|
0
|
0
|
18
|
0
|
|
23
|
317,152
|
120
|
0
|
1
|
30
|
0
|
|
24
|
290,500
|
156
|
0
|
1
|
20
|
1
|
|
25
|
374,000
|
105
|
0
|
1
|
25
|
1
|
|
26
|
288,000
|
110
|
0
|
1
|
10,8
|
1
|
|
27
|
298,200
|
63
|
1
|
1
|
12
|
1
|
|
28
|
177,419
|
97
|
1
|
0
|
10
|
1
|
|
29
|
201,100
|
80
|
1
|
0
|
10
|
1
|
|
30
|
212,470
|
50
|
1
|
1
|
9
|
1
|
|
31
|
330,000
|
63
|
0
|
0
|
15
|
1
|
|
32
|
258,000
|
66
|
1
|
1
|
13
|
1
|
|
33
|
200,300
|
87
|
1
|
0
|
11
|
1
|
|
34
|
206,940
|
104
|
1
|
0
|
10
|
1
|
|
35
|
313,000
|
43
|
1
|
1
|
13
|
1
|
|
36
|
213,600
|
74
|
1
|
0
|
18
|
1
|
|
37
|
257,140
|
70
|
1
|
1
|
10
|
1
|
|
38
|
308,440
|
77
|
0
|
1
|
10,4
|
1
|
|
39
|
315,860
|
104
|
0
|
1
|
25
|
0
|
|
40
|
354,200
|
90
|
0
|
1
|
23
|
0
|
|
41
|
402,000
|
86
|
0
|
1
|
31
|
0
|
|
42
|
360,300
|
158
|
0
|
1
|
18
|
1
|
|
43
|
240,600
|
180
|
0
|
0
|
20
|
1
|
|
44
|
350,270
|
83
|
0
|
0
|
16
|
1
|
|
45
|
390,000
|
80
|
0
|
1
|
10
|
1
|
|
46
|
430,000
|
54
|
0
|
0
|
20
|
0
|
|
47
|
290,800
|
138
|
0
|
0
|
14
|
0
|
|
48
|
315,800
|
110
|
1
|
0
|
35
|
0
|
|
49
|
253,013
|
76
|
1
|
1
|
12
|
1
|
|
50
|
154,221
|
102
|
1
|
0
|
12,5
|
1
|
|
51
|
183,025
|
103
|
1
|
1
|
10,2
|
1
|
|
52
|
253,187
|
65
|
1
|
1
|
10
|
1
|
|
53
|
275,000
|
79
|
1
|
1
|
14
|
1
|
|
54
|
290,231
|
65
|
1
|
0
|
10
|
1
|
|
55
|
219,700
|
86
|
1
|
1
|
12
|
1
|
|
56
|
296,270
|
125
|
0
|
1
|
25
|
1
|
|
57
|
224,800
|
82
|
1
|
1
|
14
|
1
|
|
58
|
241,260
|
54
|
1
|
1
|
9,6
|
1
|
|
59
|
308,000
|
118
|
0
|
1
|
22,2
|
1
|
|
60
|
180,263
|
118
|
1
|
1
|
15
|
1
|
|
61
|
300,000
|
140
|
0
|
1
|
20
|
1
|
|
62
|
364,602
|
93
|
0
|
1
|
14
|
1
|
|
63
|
485,400
|
75
|
0
|
1
|
18
|
0
|
|
64
|
221,400
|
180
|
0
|
1
|
30
|
1
|
|
65
|
208,600
|
49
|
1
|
0
|
10
|
1
|
|
66
|
307,850
|
75
|
1
|
1
|
13
|
1
|
|
67
|
263,600
|
55
|
1
|
0
|
6,5
|
1
|
|
68
|
307,260
|
51
|
0
|
1
|
10
|
0
|
|
69
|
264,600
|
108
|
0
|
0
|
15
|
0
|
|
70
|
255,430
|
46
|
1
|
1
|
12
|
1
|
|
71
|
294,290
|
53
|
1
|
0
|
15
|
0
|
|
72
|
327,800
|
61
|
0
|
0
|
9
|
1
|
|
73
|
333,600
|
74
|
0
|
0
|
15
|
1
|
|
74
|
200,200
|
90
|
1
|
1
|
9
|
0
|
Факторы, от которых зависит
стоимость квартиры, делятся на 2 типа:
- Количественные:
– жилая площадь квартиры (без
площади кухни);
– площадь кухни.
- Качественные:
– тип дома: 0 – монолитный, 1
– панельный;
– наличие балкона: 0 – нет; 1
– есть;
– тип жилья: 0 – новостройка,
1 – вторичное жилье.
В таблице 3 произведена
замена числовых кодов качественных факторов на лингвистические переменные. Это
обеспечивает более высокую наглядность и читаемость выходных форм, а система
«Эйдос» обеспечивает такую возможность, поэтому эта замена и была произведена.
Кроме того добавлена расчетная колонка «Стоимость квартиры», равная
произведению стоимости
одного квадратного метра квартиры на ее общую площадь, а
общая площадь (в явном виде не указанная в таблице) равна сумме жилой площади квартиры и
площади кухни.
В результате этих операций
получена таблица 4, которая является исходной для ввода в систему «Эйдос» с
помощью одного и ее стандартных программных интерфейсов с внешними базами
данных (режим 2.3.2.2).
Таблица 4 – Исходные данные для разработки интеллектуального приложения,
иллюстрирующего модификацию
взвешенного метода наименьших квадратов путем применения в качестве весов наблюдений количества информации в
аргументе о значении функции
|
№ наблюдения
|
Стоимость квартиры (руб.)
|
Стоимость 1 кв.м. квартиры (руб./м2)
|
Жилая площадь квартиры (м2)
|
Тип дома
|
Наличие балкона
|
Площадь кухни (м2)
|
Тип жилья
|
|
1
|
30800,000
|
360,000
|
80
|
монолитный
|
нет
|
25,0
|
новостройка
|
|
2
|
45211,650
|
388,015
|
110
|
монолитный
|
есть
|
23,0
|
новостройка
|
|
3
|
45515,911
|
328,393
|
127
|
монолитный
|
нет
|
30,0
|
новостройка
|
|
4
|
45765,000
|
319,000
|
135
|
монолитный
|
есть
|
20,0
|
новостройка
|
|
5
|
27329,600
|
343,600
|
76
|
монолитный
|
нет
|
16,0
|
новостройка
|
|
6
|
28200,000
|
360,000
|
75
|
монолитный
|
есть
|
16,0
|
новостройка
|
|
7
|
35042,393
|
315,499
|
107
|
монолитный
|
нет
|
12,0
|
новостройка
|
|
8
|
30132,000
|
470,000
|
62
|
монолитный
|
нет
|
16,0
|
новостройка
|
|
9
|
44525,822
|
305,006
|
137
|
монолитный
|
нет
|
20,0
|
новостройка
|
|
10
|
25804,656
|
338,398
|
72
|
монолитный
|
есть
|
20,0
|
новостройка
|
|
11
|
52865,904
|
309,632
|
147
|
панельный
|
нет
|
50,0
|
новостройка
|
|
12
|
18358,200
|
396,660
|
45
|
панельный
|
есть
|
11,3
|
новостройка
|
|
13
|
37728,000
|
300,400
|
120
|
монолитный
|
есть
|
14,0
|
новостройка
|
|
14
|
28308,000
|
390,400
|
70
|
монолитный
|
есть
|
14,0
|
новостройка
|
|
15
|
43451,254
|
257,151
|
154
|
монолитный
|
есть
|
25,0
|
новостройка
|
|
16
|
20706,000
|
342,000
|
58
|
монолитный
|
есть
|
15,0
|
новостройка
|
|
17
|
21120,120
|
348,840
|
58
|
монолитный
|
есть
|
15,3
|
новостройка
|
|
18
|
24192,000
|
360,000
|
64
|
монолитный
|
есть
|
18,0
|
новостройка
|
|
19
|
39744,000
|
355,000
|
108
|
монолитный
|
нет
|
13,0
|
новостройка
|
|
20
|
38991,780
|
330,060
|
113
|
монолитный
|
есть
|
15,0
|
новостройка
|
|
21
|
33749,496
|
315,904
|
99
|
монолитный
|
есть
|
25,0
|
новостройка
|
|
22
|
43669,600
|
303,100
|
136
|
монолитный
|
нет
|
18,0
|
новостройка
|
|
23
|
41658,240
|
317,152
|
120
|
монолитный
|
есть
|
30,0
|
новостройка
|
|
24
|
48438,000
|
290,500
|
156
|
монолитный
|
есть
|
20,0
|
вторичное жилье
|
|
25
|
41895,000
|
374,000
|
105
|
монолитный
|
есть
|
25,0
|
вторичное жилье
|
|
26
|
32868,000
|
288,000
|
110
|
монолитный
|
есть
|
10,8
|
вторичное жилье
|
|
27
|
19542,600
|
298,200
|
63
|
панельный
|
есть
|
12,0
|
вторичное жилье
|
|
28
|
18179,643
|
177,419
|
97
|
панельный
|
нет
|
10,0
|
вторичное жилье
|
|
29
|
16888,000
|
201,100
|
80
|
панельный
|
нет
|
10,0
|
вторичное жилье
|
|
30
|
11073,500
|
212,470
|
50
|
панельный
|
есть
|
9,0
|
вторичное жилье
|
|
31
|
21735,000
|
330,000
|
63
|
монолитный
|
нет
|
15,0
|
вторичное жилье
|
|
32
|
17886,000
|
258,000
|
66
|
панельный
|
есть
|
13,0
|
вторичное жилье
|
|
33
|
18383,100
|
200,300
|
87
|
панельный
|
нет
|
11,0
|
вторичное жилье
|
|
34
|
22561,760
|
206,940
|
104
|
панельный
|
нет
|
10,0
|
вторичное жилье
|
|
35
|
14018,000
|
313,000
|
43
|
панельный
|
есть
|
13,0
|
вторичное жилье
|
|
36
|
17138,400
|
213,600
|
74
|
панельный
|
нет
|
18,0
|
вторичное жилье
|
|
37
|
18699,800
|
257,140
|
70
|
панельный
|
есть
|
10,0
|
вторичное жилье
|
|
38
|
24550,680
|
308,440
|
77
|
монолитный
|
есть
|
10,4
|
вторичное жилье
|
|
39
|
35449,440
|
315,860
|
104
|
монолитный
|
есть
|
25,0
|
новостройка
|
|
40
|
33948,000
|
354,200
|
90
|
монолитный
|
есть
|
23,0
|
новостройка
|
|
41
|
37238,000
|
402,000
|
86
|
монолитный
|
есть
|
31,0
|
новостройка
|
|
42
|
59771,400
|
360,300
|
158
|
монолитный
|
есть
|
18,0
|
вторичное жилье
|
|
43
|
46908,000
|
240,600
|
180
|
монолитный
|
нет
|
20,0
|
вторичное жилье
|
|
44
|
30400,410
|
350,270
|
83
|
монолитный
|
нет
|
16,0
|
вторичное жилье
|
|
45
|
32000,000
|
390,000
|
80
|
монолитный
|
есть
|
10,0
|
вторичное жилье
|
|
46
|
24300,000
|
430,000
|
54
|
монолитный
|
нет
|
20,0
|
новостройка
|
|
47
|
42062,400
|
290,800
|
138
|
монолитный
|
нет
|
14,0
|
новостройка
|
|
48
|
38588,000
|
315,800
|
110
|
панельный
|
нет
|
35,0
|
новостройка
|
|
49
|
20140,988
|
253,013
|
76
|
панельный
|
есть
|
12,0
|
вторичное жилье
|
|
50
|
17005,542
|
154,221
|
102
|
панельный
|
нет
|
12,5
|
вторичное жилье
|
|
51
|
19902,175
|
183,025
|
103
|
панельный
|
есть
|
10,2
|
вторичное жилье
|
|
52
|
17107,155
|
253,187
|
65
|
панельный
|
есть
|
10,0
|
вторичное жилье
|
|
53
|
22831,000
|
275,000
|
79
|
панельный
|
есть
|
14,0
|
вторичное жилье
|
|
54
|
19515,015
|
290,231
|
65
|
панельный
|
нет
|
10,0
|
вторичное жилье
|
|
55
|
19926,200
|
219,700
|
86
|
панельный
|
есть
|
12,0
|
вторичное жилье
|
|
56
|
40158,750
|
296,270
|
125
|
монолитный
|
есть
|
25,0
|
вторичное жилье
|
|
57
|
19581,600
|
224,800
|
82
|
панельный
|
есть
|
14,0
|
вторичное жилье
|
|
58
|
13546,440
|
241,260
|
54
|
панельный
|
есть
|
9,6
|
вторичное жилье
|
|
59
|
38963,600
|
308,000
|
118
|
монолитный
|
есть
|
22,2
|
вторичное жилье
|
|
60
|
23041,034
|
180,263
|
118
|
панельный
|
есть
|
15,0
|
вторичное жилье
|
|
61
|
44800,000
|
300,000
|
140
|
монолитный
|
есть
|
20,0
|
вторичное жилье
|
|
62
|
35209,986
|
364,602
|
93
|
монолитный
|
есть
|
14,0
|
вторичное жилье
|
|
63
|
37755,000
|
485,400
|
75
|
монолитный
|
есть
|
18,0
|
новостройка
|
|
64
|
45252,000
|
221,400
|
180
|
монолитный
|
есть
|
30,0
|
вторичное жилье
|
|
65
|
10711,400
|
208,600
|
49
|
панельный
|
нет
|
10,0
|
вторичное жилье
|
|
66
|
24063,750
|
307,850
|
75
|
панельный
|
есть
|
13,0
|
вторичное жилье
|
|
67
|
14855,500
|
263,600
|
55
|
панельный
|
нет
|
6,5
|
вторичное жилье
|
|
68
|
16180,260
|
307,260
|
51
|
монолитный
|
есть
|
10,0
|
новостройка
|
|
69
|
30196,800
|
264,600
|
108
|
монолитный
|
нет
|
15,0
|
новостройка
|
|
70
|
12301,780
|
255,430
|
46
|
панельный
|
есть
|
12,0
|
вторичное жилье
|
|
71
|
16392,370
|
294,290
|
53
|
панельный
|
нет
|
15,0
|
новостройка
|
|
72
|
20544,800
|
327,800
|
61
|
монолитный
|
нет
|
9,0
|
вторичное жилье
|
|
73
|
25796,400
|
333,600
|
74
|
монолитный
|
нет
|
15,0
|
вторичное жилье
|
|
74
|
18828,000
|
200,200
|
90
|
панельный
|
есть
|
9,0
|
новостройка
|
|
75
|
40999,920
|
495,640
|
78
|
монолитный
|
есть
|
30,0
|
новостройка
|
По условиям задачи,
рассматриваемой в данной работе в качестве численного примера применения
предлагаемого метода, на основе исходных данных, приведенных в таблице 4,
необходимо найти зависимости
стоимости квартиры от всех ее характеристик, приведенных в этих исходных данных.
Для решения этой задачи
прежде всего необходимо скачать и установить систему «Эйдос». Скачать систему «Эйдос-Х++»
(самую новую на текущий момент версию) или обновление системы до текущей версии,
можно на сайте: http://lc.kubagro.ru/
по адресу: http://lc.kubagro.ru/aidos/_Aidos-X.htm. По этой ссылке всегда находится наиболее
полная на данный момент незащищенная от несанкционированного копирования портативная
(portable) версия системы (не требующая инсталляции) с исходными текстами,
находящаяся в полном открытом бесплатном
доступе (около 50 Мб) (инструкция).
ИНСТРУКЦИЯ
по скачиванию и установке системы «Эйдос» (объем около 50 Мб)
|
Система не требует инсталляции, не меняет никаких системных
файлов и содержимого папок операционной системы, т.е. является портативной (portable) программой. Но чтобы она работала
необходимо аккуратно выполнить следующие пункты.
1. Скачать самую новую на текущий момент версию системы
«Эйдос-Х++» по ссылке:
http://lc.kubagro.ru/a.rar (ссылки для обновления системы даны
в режиме 6.2)
2. Разархивировать этот архив в любую папку с правами на запись
с коротким латинским именем и путем доступа, включающим только папки с такими же
именами (лучше всего в корневой каталог какого-нибудь диска).
3. Запустить систему. Файл запуска:  _AIDOS-X.exe * _AIDOS-X.exe *
4. Задать имя: 1 и пароль: 1 (потом их можно поменять в режиме
1.2).
5. Перед тем как запустить новый режим НЕОБХОДИМО ЗАВЕРШИТЬ предыдущий
(Help можно не закрывать). Окна закрываются в порядке, обратном порядку их
открытия.
|
|
* Разработана программа: « _START_AIDOS.exe»,
полностью снимающая с пользователя системы «Эйдос-Х++» заботу о проверке
наличия и скачивании обновлений. Эту программу надо просто скачать по ссылке: http://lc.kubagro.ru/Install_Aidos-X/_START_AIDOS.exe , поместить в папку с исполнимым
модулем системы и всегда запускать систему с помощью этого файла. _START_AIDOS.exe»,
полностью снимающая с пользователя системы «Эйдос-Х++» заботу о проверке
наличия и скачивании обновлений. Эту программу надо просто скачать по ссылке: http://lc.kubagro.ru/Install_Aidos-X/_START_AIDOS.exe , поместить в папку с исполнимым
модулем системы и всегда запускать систему с помощью этого файла.
При
запуске программы _START_AIDOS.EXE система Эйдос не должна быть запущена,
т.к. она содержится в файле обновлений и при его разархивировании возникнет
конфликт, если система будет запущена.
1.
Программа  _START_AIDOS.exe
определяет дату системы Эйдос в текущей папке, и дату обновлений на
FTP-сервере не скачивая их, и, если система Эйдос в текущей папке устарела,
скачивает обновления. (Если в текущей папке нет исполнимого модуля системы
Эйдос, то программа пытается скачать полную инсталляцию системы, но не может
этого сделать из-за ограниченной функциональности демо-версии библиотеки
Xb2NET.DLL). _START_AIDOS.exe
определяет дату системы Эйдос в текущей папке, и дату обновлений на
FTP-сервере не скачивая их, и, если система Эйдос в текущей папке устарела,
скачивает обновления. (Если в текущей папке нет исполнимого модуля системы
Эйдос, то программа пытается скачать полную инсталляцию системы, но не может
этого сделать из-за ограниченной функциональности демо-версии библиотеки
Xb2NET.DLL).
2. После
этого появляется диалоговое окно с сообщением, что надо сначала
разархивировать систему, заменяя все файлы (опция: «Yes to All» или
«OwerWrite All»), и только после этого закрыть данное окно.
3. Потом
программа  _START_AIDOS.exe
запускает обновления на разархивирование. После окончания разархивирования
окно архиватора с отображением стадии процесса исчезает. _START_AIDOS.exe
запускает обновления на разархивирование. После окончания разархивирования
окно архиватора с отображением стадии процесса исчезает.
4. После
закрытия диалогового окна с инструкцией (см. п.2), происходит запуск обновленной
версии системы Эйдос на исполнение.
Для
работы программы  _START_AIDOS.exe
необходима библиотека: Xb2NET.DLL, которую можно скачать по ссылке: http://lc.kubagro.ru/Install_Aidos-X/Xb2NET.DLL . Перед первым запуском этой
программы данную библиотеку необходимо скачать и поместить либо в папку с
этой программой, а значит и исполнимым
модулем системы «Эйдос-Х++», либо в любую другую папку, на которую в
операционной системе прописаны пути поиска файлов, например в папку:
c:\Windows\System32\. Эта библиотека стоит около 500$ и у меня ее нет,
поэтому я даю только бесплатную демо-версию, которая выдает сообщение об
ограниченной функциональности, но для наших целей ее достаточно. _START_AIDOS.exe
необходима библиотека: Xb2NET.DLL, которую можно скачать по ссылке: http://lc.kubagro.ru/Install_Aidos-X/Xb2NET.DLL . Перед первым запуском этой
программы данную библиотеку необходимо скачать и поместить либо в папку с
этой программой, а значит и исполнимым
модулем системы «Эйдос-Х++», либо в любую другую папку, на которую в
операционной системе прописаны пути поиска файлов, например в папку:
c:\Windows\System32\. Эта библиотека стоит около 500$ и у меня ее нет,
поэтому я даю только бесплатную демо-версию, которая выдает сообщение об
ограниченной функциональности, но для наших целей ее достаточно.
|
|
Лицензия:
Автор отказывается от какой бы то ни было
ответственности за последствия применения или не применения Вами системы
«Эйдос».
Проще говоря, пользуйтесь если понравилось, а
если не понравилось – сотрите и забудьте, а лучше вообще не скачивайте.
|
Необходимо отметить, что на папку с
системой у пользователя должны быть все права доступа, иначе система не сможет
корректировать свои базы данных и индексные массивы, что необходимо для ее
нормальной работы.
Затем записываем
таблицу 4 в виде Excel-файла с именем Inp_data.xls в папку:
c:\Aidos-X\AID_DATA\Inp_data\Inp_data.xls и запускаем систему (файл запуска:  _AIDOS-X.exe).
_AIDOS-X.exe).
При запуске системы появляется окно авторизации:
Рисунок 4 – Окно авторизации системы «Эйдос»
Вводим начальные имя 1 и пароль 1, которые в
последующем можно изменить в режиме 1.2.
Отметим, что система «Эйдос» является программным
инструментарием АСК-анализа и автоматизирует все его этапы, кроме первого:
1. Когнитивная структуризация предметной области
(неформализованный этап). На этом
этапе решается, что мы хотим прогнозировать и на основе чего.
2. Формализация предметной области. На этом этапе разрабатываются классификационные и
описательные шкалы и градации, а затем с их использованием исходные данные
кодируются и представляются в форме баз событий, между которыми могут быть
выявлены причинно-следственные связи.
3. Синтез и верификация моделей (оценка достоверности, адекватности). Повышение
качества модели. Выбор наиболее достоверной модели для решения в ней задач.
4. Решение задач идентификации и прогнозирования.
5. Решение задач принятия решений и управления.
6. Решение задач исследования моделируемой предметной
области путем исследования ее модели.
На рисунке 3 приведены автоматизированные в системе
«Эйдос» этапы АСК-анализа, которые обеспечивают последовательное повышение степени
формализации модели путем преобразования исходных данных в информацию, а далее
в знания:
Для выполнения 2-го этапа АСК-анализа запускаем
универсальный
программный интерфейс ввода данных из внешних баз данных (режим 2.3.2.2) (рисунок
6):
Рисунок 6 – Запуск универсального программного
интерфейса
ввода данных из внешних баз данных
Появляется следующая экранная форма (рисунок 7):

Рисунок 7 – Экранная форма задания параметров
универсального
программного интерфейса ввода данных из внешних баз данных
На рисунке 6 показаны нужные в данном случае значения
задаваемых параметров.
Help данного режима приведен на рисунке 8:
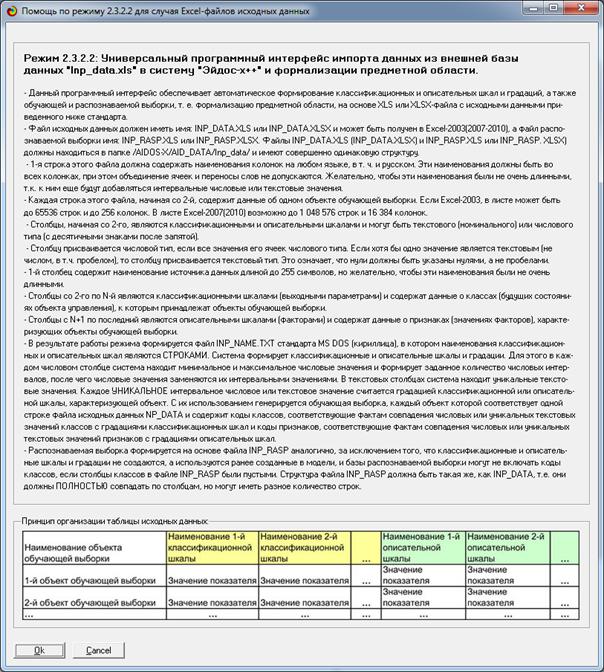
Рисунок 8 – Экранная форма Help универсального
программного
интерфейса ввода данных из внешних баз данных
Таблица 4 соответствует требованиям системы «Эйдос» к
внешним базам данных, приведенным на рисунке 8.
Если кликнуть OK на экранной форме, приведенной на
рисунке 6, то начинается автоматический процесс формализации предметной области,
который начинается с конвертирования Excel-файла в dbf-файл. При этом на заднем
фоне может возникнуть окно, приведенное на рисунке 9:
Рисунок 9 – Окно на заднем фоне, возникающее при
пересчете
Excel-файла в процессе его преобразования в dbf-файл
Чтобы увидеть это окно надо кликнуть по иконке системы
«Эйдос» на панели задач при всех свернутых окнах других приложений или их отсутствии.
На этом окне можно выбрать любой вариант, кроме отмены.
Сразу же после этого система находит классификационные
и описательные шкалы и градации, определяет тип данных в шкалах и отображает окно,
приведенное на рисунке 10:
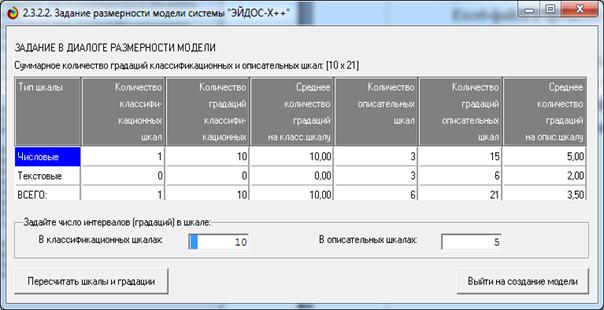
Рисунок 10 – Внутреннего калькулятора универсального
программного
интерфейса импорта данных из внешних баз данных
Если в таблице исходных данных есть числовые шкалы, то
появляется возможность задать количество интервальных числовых значений
(интервалов в числовых шкалах) в них отдельно для классификационных и
описательных шкал. Принцип определения разумного количества интервалов такой.
Если их задать очень много, то в некоторых интервалах вообще не будет данных
или будет очень мало (меньше 5), что нежелательно. Если задать интервалов очень
мало, то они будут очень большого размера и точность модели будет не высока.
Таким образом, можно сделать такой вывод, что чем больше объем выборки, тем
меньшего размера мы можем позволить себе задавать интервалы. Но не нужно этим
особенно увлекаться, т.е. если есть возможность сделать очень маленькие
интервалы, но нам не нужна такая точность, то лучше делать интервалы такого
размера, чтобы они обеспечили необходимую точность, но не меньшего размера. В
режиме 2.3.2.2 есть возможность задавать либо равные интервалы с разным числом
наблюдений, либо разные интервалы с примерно одинаковым числом измерений. Это
может иметь смысл, если в исходных данных в числовых шкалах представлен широкий
спектр частот, и мы не хотим терять высокочастотные гармоники, которые могут
оказаться не оцифрованными при равных интервалах. Это позволяет автоматически
ставить точки тем чаще, чем выше кривизна кривых, построенных на шкалах. Все
эти рассуждения напоминает какие-то следствия теоремы Котельникова об отсчетах.
В данной экранной форме задаем количество интервалов в
классификационных и описательных шкалах. Если оно изменяется, то необходимо
кликнуть по кнопке «Пересчитать шкалы и градации», а затем, когда будет выбран
окончательный вариант, выйти на создание модели.
Сразу же начинается процесс импорта данных в систему
«Эйдос», этапы и прогноз времени исполнения которого отображаются на экранной
форме (рисунок 11):
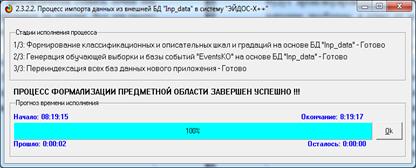
Рисунок 11 – Внутреннего калькулятора универсального
программного
интерфейса импорта данных из внешних баз данных
Затем в режиме 3.5 системы «Эйдос»с параметрами по
умолчанию (рисунок 12) выполняется 3-й этап АСК-анализа, т.е. синтез и верификация
модели:
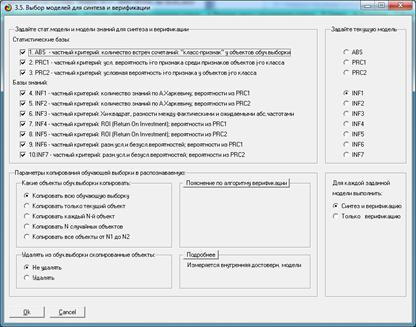
Рисунок 12 – Экранная форма задания параметров режима
синтеза и верификации модели системы «Эйдос»
Этапы выполнения данного режима и прогноз времени
исполнения отображаются на экранной форме (рисунок 13):
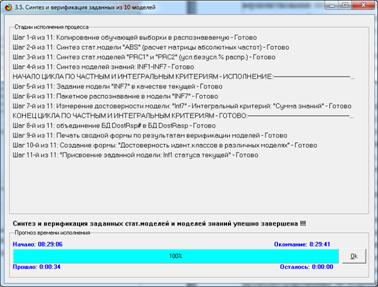
Рисунок 13 – Экранная форма с отображением этапов
прогнозом времени
исполнения режима синтеза и верификации модели системы «Эйдос»
Перейдем теперь в режим 4.5 «Визуализация когнитивных
функций» (рисунок 14):
Рисунок 14 – Начальная экранная форма режима
визуализации
когнитивных функций системы «Эйдос»
На рисунке 15 приведены визуализации когнитивной
функции (КФ) зависимости стоимости квартиры от стоимости одного квадратного
метра ее площади при разных способах определения и визуализации частично
редуцированных когнитивных функций.
Программная реализация данного режима визуализации
когнитивных функций разработан по постановке автора разработчиком
интеллектуальных, графических и музыкальных систем из Белоруссии Дмитрием
Константиновичем Бандык [30].
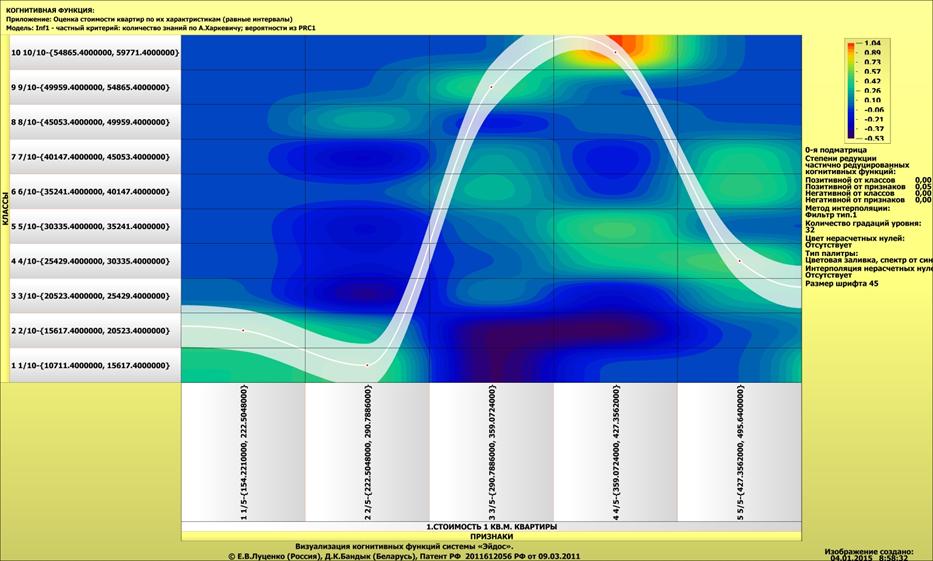
Рисунок 15-а – Визуализации когнитивной функции
зависимости стоимости квартиры от стоимости 1 кв.метра: частично-редуцированная
КФ проведена по значениям функции, о которых в аргументе содержится
максимальное количество информации
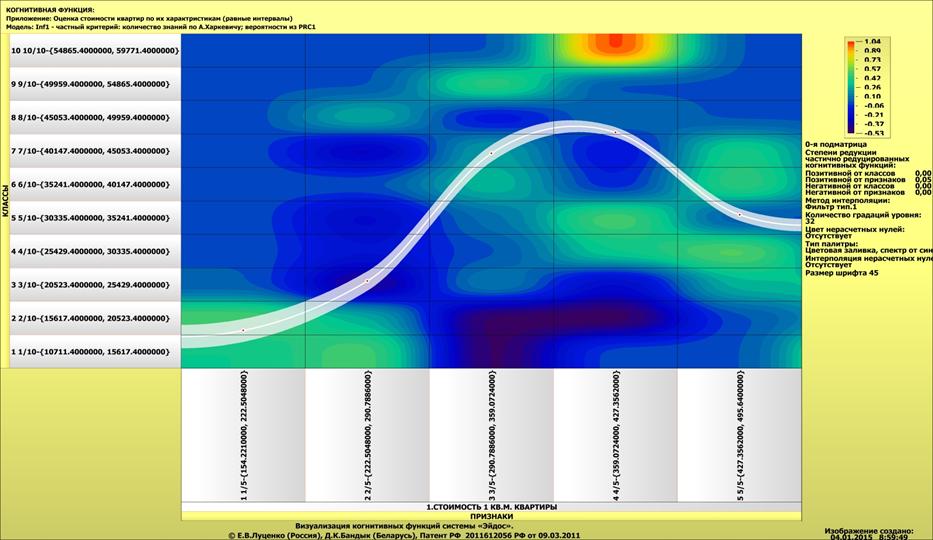
Рисунок
15-б – Визуализации когнитивной функции зависимости стоимости квартиры от
стоимости 1 кв.метра: частично-редуцированная КФ проведена по точкам,
полученным путем применения предложенной модификации
взвешенного метода наименьших квадратов, в котором в качестве весов
наблюдений используется количество информации в аргументе о значении функции.
При этом применены настройки параметров отображения
когнитивных функций, приведенные, приведенные на рисунке 16:
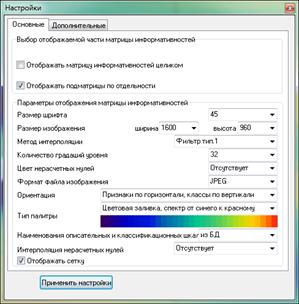
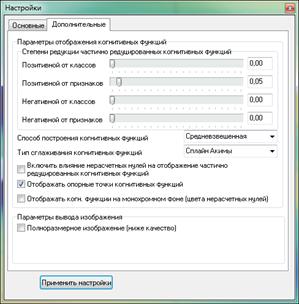
Рисунок 16 – Настройки параметров отображения
когнитивных функций
в режиме 4.5 системы «Эйдос»
Из рисунка 15 мы видим,
что у дешевых квартир минимальная стоимость 1 кв.метра, а максимальной она
вопреки ожиданиям является у просто дорогих квартир, а не у самых дорогих.
По соям координат
приведены интервальные числовые значения:
– по оси X: стоимости 1
квадратного метра жилья;
– по оси Y: стоимости
квартиры.
Графики оцененной
зависимости, полученные с помощью предложенной модификации взвешенного метода
наименьших квадратов, основанного на применении в качестве весов наблюдений
количества информации в аргументе о значении функции, будут приведены ниже.
Естественно возникает
вопрос о степени точности восстановления исследуемых эмпирических зависимостей
в моделях, созданных с применением АСК-анализе и системе «Эйдос».
Традиционно точность восстановления
зависимости оценивается дисперсиями и доверительным интервалами. В АСК-анализе смысловым
аналогом доверительного интервала, в определенной степени, конечно, является
количество информации в аргументе о значении функции. Поэтому необходимо
исследовать соотношение смыслового содержания этих понятий: доверительного
интервала и количества информации.
На математическом уровне
это планируется сделать в будущем, а в данном разделе отметим лишь, что чем
больше доверительный интервал, тем выше неопределенность наших знаний о
значении функции, соответствующем значению аргумента, а чем он меньше, тем эта
определенность выше. Но информация и определяется как количественная
мера степени снятия неопределенности. Учитывая это можно утверждать, что чем
больше доверительный интервал, тем меньше информации о значении функции,
соответствующем значению аргумента мы получаем, а чем он меньше, тем это
количество информации больше. Забегая вперед, отметим, что в частично-редуцированных
когнитивных функциях, например изображенных на рисунке 15, количество
информации в значениях аргумента о значениях функции наглядно изображено
шириной полосы функции, что не только по смыслу, но внешне очень сходно с
доверительным интервалом. При этом отметим еще один интересный момент, который
состоит в том, что если традиционный доверительный интервал при экстраполяции
при удалении от эмпирических значений ко все далее отстоящим от них в будущим
все время увеличивается, то в степень редукции когнитивной функции то увеличивается,
то уменьшается. Это связано с тем, что АСК-анализ и система «Эйдос» позволяют не
только прогнозировать будущие события, но и прогнозировать достоверность или
риски этих прогнозов [7],
т.е. прогнозировать продолжительность периодов эргодичности и точки бифуркации (качественного
изменения закономерностей в моделируемой предметной области), что наглядно и
отображается в такой форме.
В частности при этом при нулевом доверительном
интервале формально получается, что
мы имеем бесконечное количество информации о значении функции, но на практике это вообще невозможно [17]
и даже в теории возможно только для отдельных точек целых значений аргумента и функции. При бесконечном доверительном интервале
в значении аргумента функции содержится ноль информации о значении функции.
Когнитивные функции,
приведенные на рисунке 15, получены на основе модели знаний, основанной на мере
А.Харкевича, в которой учтены все переменные, т.е. факторы или описательные
шкалы модели и отражено их взаимное влияние друг на друга и выходные параметры.
Это влияние отражено в результатах кластерно-конструктивного анализа, отображенных
в форме семантических сетей на рисунках 17 и 18:
Итак, из рисунка 17 мы
видим, что классификационные шкалы, являющиеся осями в когнитивном пространстве
классов, зависят друг от друга, т.е. неоротнормированны. Из рисунка 18 мы
видим, что описательные шкалы (факторы), являющиеся осями в когнитивном
пространстве факторов, также зависят друг от друга, т.е. неоротнормированны.
Таким образом,
когнитивное (фазовое) пространство модели знаний системы «эйдос» является
неортонормированным, а модель, следовательно, является нелинейной. Поэтому
очень важно, что в АСК-анализе и системе «Эйдос» используется неметрический
интегральный критерий, не основанный на предположении об ортонормированности
пространства [7].
Рассмотрим теперь применение предложенной модификации взвешенного метода наименьших квадратов, в
котором в качестве весов наблюдений используется количество информации в
аргументе о значении функции. Для этой цели разработан режим 4.6 «Подготовка
баз данных для визуализации когнитивных функций в MS Excel».
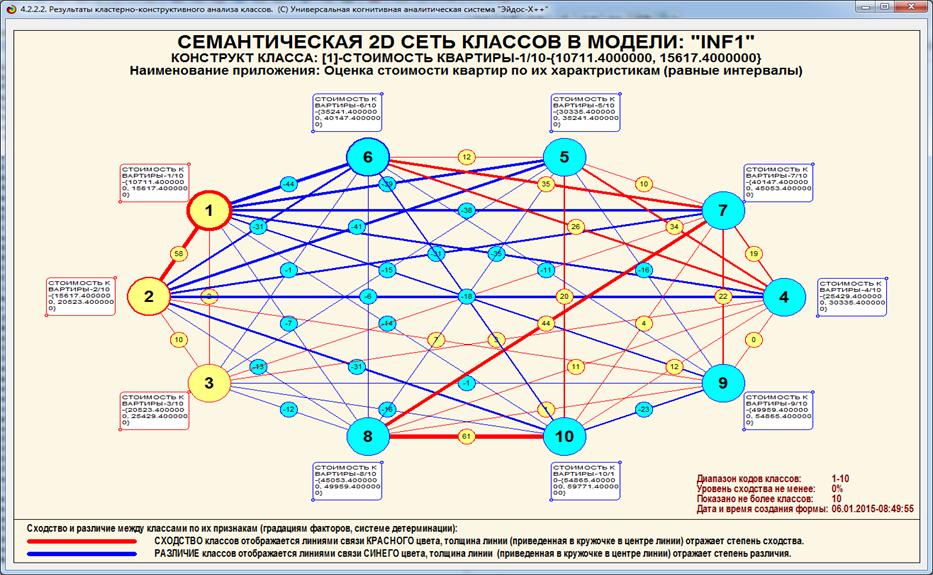
Рисунок 17 – Результаты кластерно-конструктивного
анализа классов, т.е. их сходство и различие по системе детерминации
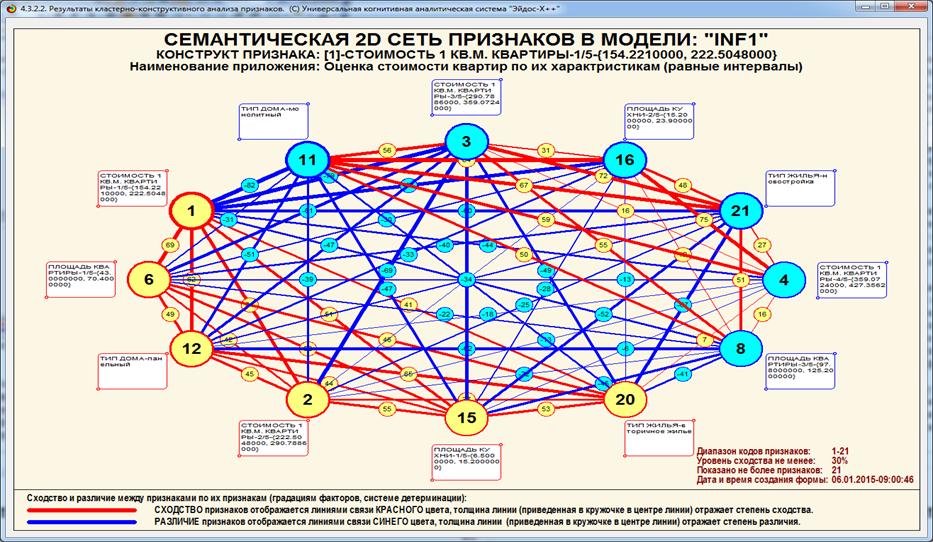
Рисунок 18. Результаты кластерно-конструктивного
анализа значений факторов, т.е. их сходство и различие по классам,
принадлежность и не принадлежность к которым они обуславливают
При разработке этого
режима использованы следующие идеи.
1. MS Excel (особенно
версии начиная с 2007) обладает очень удобными средствами регрессионного
анализа, использующими стандартный
метод наименьших квадратов, которые целесообразно использовать.
2. Однако, поскольку
MS Excel в регрессионном анализе использует лишь стандартный метод наименьших квадратов, в котором все наблюдения
имеют одинаковый (единичный) вес, то предлагается отражать вес наблюдения
количеством точек.
3. Поскольку вес
наблюдения в предлагаемой нами модификации взвешенного метода наименьших
квадратов равен количеству информации в аргументе о значении функции, то для
того, чтобы посчитать это количество точек для каждого наблюдения необходимо
приписать точке определенное количество информации.
4. Это можно сделать
расчетным путем для каждого наблюдения зная количество информации в данном
наблюдении и количество точек в наблюдении с максимальным количеством
информации. Количество информации в данном наблюдении определяется при синтезе
и верификации моделей в системе «Эйдос», а количество точек в наблюдении с максимальным
количеством информации необходимо задать в диалоге.
5. Если для каждого
наблюдения все точки, количество которых отражает количество информации в
данном наблюдении, отображать с их точными координатами, то они все попадают в
одну точке на изображении. Чтобы было видно, сколько этих точек в данном
наблюдении предлагается задавать небольшое случайное рассеяние этих точек
вокруг точки с точными значениями координат. Величину этого рассеяния можно
задавать в диалоге в процентах от диапазона значений описательной и классификационной
шкалы отображаемой подматрицы.
6. Стандартный режим
регрессионного анализа MS Excel будет строит регрессии с учетом всех точек
каждого наблюдения, сгенерированных в количестве, пропорциональном количеству
информации в этом наблюдении. Поэтому полученная регрессия будет соответствовать
предлагаемой модификации взвешенного метода наименьших квадратов.
При запуске режима 4.6
«Подготовка баз данных для визуализации когнитивных функций в MS Excel»
отображается окно настройки параметров (рисунок 19):
Выполняется этот режим
довольно быстро (несколько секунд), т.к. его алгоритм сводится к выборкам
данных из ранее посчитанных статистических баз и баз знаний, представленных в
системе «Эйдос» в нечеткой декларативной форме. Если бы в системе «Эйдос»
использовалась четкая процедурная модель представления знаний, при котором
генерация знаний производилась бы с различными степенями нечеткости непосредственно
перед их использованием, то данный режим работал бы на много порядков медленнее
и был бы непригоден для реального практического применения.
По окончании работы
режима выводится экранная форма, представленная на рисунке 20:
На рисунке 21 приведен скриншот, на котором показано
содержимое папки: ..\AID_DATA\A#######\System\Cogn_fun\
с базами данных для визуализации когнитивных функций и регрессий, созданных в
режиме 4.6 в соответствии с параметрами, приведенными на рисунке 19.
Из всех созданных баз данных рассмотрим только те,
которые позволяют отобразить те же подматрицы баз знаний (сочетания
классификационных и описательных шкал), что и на рисунке 15, это базы данных с
именами:
–
Inf1-Y(X)-Pos-One_point-1-1.dbf;
–
Inf1-Y(X)-Pos-All_points-1-1.dbf.
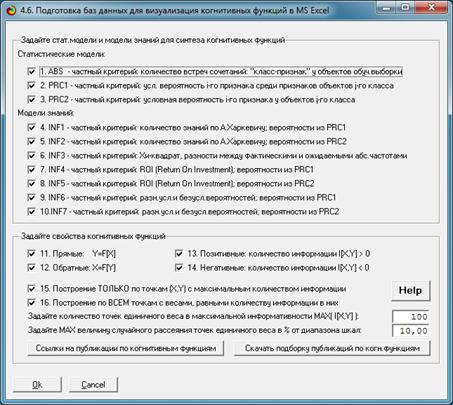
Рисунок 19. Настройки параметров создаваемых баз
данных
для визуализации когнитивных функций в режиме 4.6 системы «Эйдос»
Рисунок 20. Экранная форма, отображаемая по окончании
выполнения
режима 4.6 системы «Эйдос»
В результате работы режима 4.6 формируются базы данных
для визуализации редуцированных когнитивных функций, имена которых формируются
способом, который поясняет таблица 5.
Таблица 5 – Виды и имена баз данных для визуализации
когнитивных функций, формируемые в режиме 4.6
|
Прямые
и
обратные
|
Позитивные
и негативные
|
Построенные по точкам с максимальным количеством
информации или по ВСЕМ точкам с весами, равными количеству информации в них
|
Имена баз данных
для визуализации КФ в MS Ecxel
|
|
Прямые:
Y=F[X]
|
Позитивные: количество информации I[X,Y] > 0
|
Построение ТОЛЬКО по точкам
(X,Y) с максимальным количеством информации
|
КФ-1: ####-Y(X)-Pos-One_point-##-##.dbf
|
|
Построение по ВСЕМ точкам с
весами, равными количеству информации в них
|
КФ-2: ####-Y(X)-Pos-All_points-##-##.dbf
|
|
Негативные: количество информации I[X,Y] < 0
|
Построение ТОЛЬКО по точкам
(X,Y) с максимальным количеством информации
|
КФ-3: ####-Y(X)-Neg-One_point-##-##.dbf
|
|
Построение по ВСЕМ точкам с
весами, равными количеству информации в них
|
КФ-4: ####-Y(X)-Neg-All_points-##-##.dbf
|
|
Обратные: X=F[Y]
|
Позитивные: количество информации I[X,Y] > 0
|
Построение ТОЛЬКО по точкам
(X,Y) с максимальным количеством информации
|
КФ-5: ####-X(Y)-Pos-One_point-##-##.dbf
|
|
Построение по ВСЕМ точкам с
весами, равными количеству информации в них
|
КФ-6: ####-X(Y)-Pos-All_points-##-##.dbf
|
|
Негативные: количество информации I[X,Y] < 0
|
Построение ТОЛЬКО по точкам
(X,Y) с максимальным количеством информации
|
КФ-7: ####-X(Y)-Neg-One_point-##-##.dbf
|
|
Построение по ВСЕМ точкам с
весами, равными количеству информации в них
|
КФ-8: ####-X(Y)-Neg-All_points-##-##.dbf
|
Эти базы данных формируются
для всех моделей (в начале имен БД наименования моделей): {Abs, Prc1, Prc2, Inf1, Inf2, Inf3, Inf4, Inf5, Inf6, Inf7} и для
всех сочетаний классификационных и описательных шкал (в конце имен БД коды
шкал) и записываются в папку: ..\AID_DATA\A#######\System\Cogn_fun\.
Рисунок 21 – Скриншот, на котором показано содержимое
папки: ..\AID_DATA\A#######\System\Cogn_fun\ с базами данных для
визуализации когнитивных функций и регрессий, созданных в режиме 4.6 в
соответствии с параметрами, приведенными на рисунке 19
В таблице 6 приведена база данных Inf1-Y(X)-Pos-One_point-1-1.dbf,
а в таблице 7 – фрагмент базы данных Inf1-Y(X)-Pos-All_points-1-1.dbf.
Таблица 6 – База данных
«Inf1-Y(X)-Pos-One_point-1-1.dbf»
для визуализации когнитивных функций по точкам
с максимальным количеством информации в наблюдениях
|
Наименование
градации
описательной
шкалы
|
Наименование
градации
классификационной
шкалы
|
Градация
опис.шкалы
|
Градация
класс.шкалы
|
|
1/5-{154.2210000,
222.5048000}
|
2/10-{15617.4000000,
20523.4000000}
|
188,3629000
|
18070,4000000
|
|
2/5-{222.5048000,
290.7886000}
|
1/10-{10711.4000000,
15617.4000000}
|
256,6467000
|
13164,4000000
|
|
3/5-{290.7886000,
359.0724000}
|
9/10-{49959.4000000,
54865.4000000}
|
324,9305000
|
52412,4000000
|
|
4/5-{359.0724000,
427.3562000}
|
10/10-{54865.4000000,
59771.4000000}
|
393,2143000
|
57318,4000000
|
|
5/5-{427.3562000,
495.6400000}
|
4/10-{25429.4000000,
30335.4000000}
|
461,4981000
|
27882,4000000
|
Таблица 7 – База данных
«Inf1-Y(X)-Pos-All_points-1-1.dbf» для визуализации когнитивных функций по всем
наблюдениям с весами, равными количеству информации в наблюдениях (пример,
когда макс. количество информации отражено 10 точками)
|
Наименование
градации
описательной
шкалы
|
Наименование
градации
классификационной
шкалы
|
Градация
опис.шкалы
|
Градация
класс.шкалы
|
№
точки
|
Кол-во
Информации
(бит)
|
|
1/5-{154.2210000,
222.5048000}
|
1/10-{10711.4000000,
15617.4000000}
|
181,3450917
|
13836,3479983
|
1
|
0,3555752
|
|
1/5-{154.2210000,
222.5048000}
|
1/10-{10711.4000000,
15617.4000000}
|
184,1479638
|
11120,4317504
|
2
|
0,3555752
|
|
1/5-{154.2210000,
222.5048000}
|
1/10-{10711.4000000,
15617.4000000}
|
214,2460175
|
13164,3999991
|
3
|
0,3555752
|
|
1/5-{154.2210000,
222.5048000}
|
2/10-{15617.4000000,
20523.4000000}
|
194,2899689
|
19021,1910145
|
1
|
0,5120035
|
|
1/5-{154.2210000,
222.5048000}
|
2/10-{15617.4000000,
20523.4000000}
|
177,4300036
|
18394,0312272
|
2
|
0,5120035
|
|
1/5-{154.2210000,
222.5048000}
|
2/10-{15617.4000000,
20523.4000000}
|
186,5090552
|
17059,1910253
|
3
|
0,5120035
|
|
1/5-{154.2210000,
222.5048000}
|
2/10-{15617.4000000,
20523.4000000}
|
190,7028171
|
16524,8359564
|
4
|
0,5120035
|
|
1/5-{154.2210000,
222.5048000}
|
2/10-{15617.4000000,
20523.4000000}
|
215,2246262
|
18070,3999972
|
5
|
0,5120035
|
|
2/5-{222.5048000,
290.7886000}
|
1/10-{10711.4000000,
15617.4000000}
|
263,1092915
|
15879,1332606
|
1
|
0,4982368
|
|
2/5-{222.5048000,
290.7886000}
|
1/10-{10711.4000000,
15617.4000000}
|
239,6950459
|
15189,3525096
|
2
|
0,4982368
|
|
2/5-{222.5048000,
290.7886000}
|
1/10-{10711.4000000,
15617.4000000}
|
238,4616221
|
12770,1180014
|
3
|
0,4982368
|
|
2/5-{222.5048000,
290.7886000}
|
1/10-{10711.4000000,
15617.4000000}
|
261,9259384
|
11842,9811896
|
4
|
0,4982368
|
|
2/5-{222.5048000,
290.7886000}
|
1/10-{10711.4000000,
15617.4000000}
|
266,1218665
|
13164,3999952
|
5
|
0,4982368
|
|
2/5-{222.5048000,
290.7886000}
|
2/10-{15617.4000000,
20523.4000000}
|
249,5484524
|
19604,3972972
|
1
|
0,2777635
|
|
2/5-{222.5048000,
290.7886000}
|
2/10-{15617.4000000,
20523.4000000}
|
248,3602013
|
15067,0561877
|
2
|
0,2777635
|
|
2/5-{222.5048000,
290.7886000}
|
2/10-{15617.4000000,
20523.4000000}
|
282,0905272
|
18070,3999955
|
3
|
0,2777635
|
|
2/5-{222.5048000,
290.7886000}
|
8/10-{45053.4000000,
49959.4000000}
|
244,8125363
|
50085,6627054
|
1
|
0,2777635
|
|
2/5-{222.5048000,
290.7886000}
|
8/10-{45053.4000000,
49959.4000000}
|
246,2892018
|
45281,3162081
|
2
|
0,2777635
|
|
2/5-{222.5048000,
290.7886000}
|
8/10-{45053.4000000,
49959.4000000}
|
267,2780252
|
47506,3999981
|
3
|
0,2777635
|
|
3/5-{290.7886000,
359.0724000}
|
3/10-{20523.4000000,
25429.4000000}
|
330,3995391
|
22976,3999957
|
1
|
0,1335549
|
|
3/5-{290.7886000,
359.0724000}
|
5/10-{30335.4000000,
35241.4000000}
|
336,2903636
|
32788,3999976
|
1
|
0,0862421
|
|
3/5-{290.7886000,
359.0724000}
|
6/10-{35241.4000000,
40147.4000000}
|
311,5579867
|
38177,8804718
|
1
|
0,3067154
|
|
3/5-{290.7886000,
359.0724000}
|
6/10-{35241.4000000,
40147.4000000}
|
322,0267662
|
34029,3776279
|
2
|
0,3067154
|
|
3/5-{290.7886000,
359.0724000}
|
6/10-{35241.4000000,
40147.4000000}
|
345,0736688
|
37694,3999979
|
3
|
0,3067154
|
|
3/5-{290.7886000,
359.0724000}
|
7/10-{40147.4000000,
45053.4000000}
|
303,6228369
|
42600,4000020
|
1
|
0,2426704
|
|
3/5-{290.7886000,
359.0724000}
|
7/10-{40147.4000000,
45053.4000000}
|
351,0653550
|
42600,3999999
|
2
|
0,2426704
|
|
3/5-{290.7886000,
359.0724000}
|
9/10-{49959.4000000,
54865.4000000}
|
324,9305000
|
55754,6396374
|
1
|
0,4631437
|
|
3/5-{290.7886000,
359.0724000}
|
9/10-{49959.4000000,
54865.4000000}
|
318,2936322
|
52412,4000015
|
2
|
0,4631437
|
|
3/5-{290.7886000,
359.0724000}
|
9/10-{49959.4000000,
54865.4000000}
|
324,9305000
|
48191,0420545
|
3
|
0,4631437
|
|
3/5-{290.7886000,
359.0724000}
|
9/10-{49959.4000000,
54865.4000000}
|
333,6471197
|
52412,3999997
|
4
|
0,4631437
|
|
4/5-{359.0724000,
427.3562000}
|
4/10-{25429.4000000,
30335.4000000}
|
387,1796851
|
31381,3608947
|
1
|
0,3625915
|
|
4/5-{359.0724000,
427.3562000}
|
4/10-{25429.4000000,
30335.4000000}
|
385,3991840
|
27427,9773700
|
2
|
0,3625915
|
|
4/5-{359.0724000,
427.3562000}
|
4/10-{25429.4000000,
30335.4000000}
|
408,7770130
|
27882,3999987
|
3
|
0,3625915
|
|
4/5-{359.0724000,
427.3562000}
|
5/10-{30335.4000000,
35241.4000000}
|
397,3995679
|
33782,5078177
|
1
|
0,5104565
|
|
4/5-{359.0724000,
427.3562000}
|
5/10-{30335.4000000,
35241.4000000}
|
382,6745617
|
33842,3004182
|
2
|
0,5104565
|
|
4/5-{359.0724000,
427.3562000}
|
5/10-{30335.4000000,
35241.4000000}
|
373,9232543
|
31680,3234310
|
3
|
0,5104565
|
|
4/5-{359.0724000,
427.3562000}
|
5/10-{30335.4000000,
35241.4000000}
|
396,2378521
|
31184,3967189
|
4
|
0,5104565
|
|
4/5-{359.0724000,
427.3562000}
|
5/10-{30335.4000000,
35241.4000000}
|
394,3929650
|
32788,3999992
|
5
|
0,5104565
|
|
4/5-{359.0724000,
427.3562000}
|
8/10-{45053.4000000,
49959.4000000}
|
407,4816485
|
47506,3999964
|
1
|
0,0695099
|
|
4/5-{359.0724000,
427.3562000}
|
10/10-{54865.4000000,
59771.4000000}
|
395,3594729
|
58358,6771743
|
1
|
1,0437864
|
|
4/5-{359.0724000,
427.3562000}
|
10/10-{54865.4000000,
59771.4000000}
|
399,7423185
|
58346,4692167
|
2
|
1,0437864
|
|
4/5-{359.0724000,
427.3562000}
|
10/10-{54865.4000000,
59771.4000000}
|
390,3208291
|
58284,1852927
|
3
|
1,0437864
|
|
4/5-{359.0724000,
427.3562000}
|
10/10-{54865.4000000,
59771.4000000}
|
386,6324428
|
58108,7857112
|
4
|
1,0437864
|
|
4/5-{359.0724000,
427.3562000}
|
10/10-{54865.4000000,
59771.4000000}
|
368,9816470
|
57318,4000001
|
5
|
1,0437864
|
|
4/5-{359.0724000,
427.3562000}
|
10/10-{54865.4000000,
59771.4000000}
|
378,8259286
|
56283,9047843
|
6
|
1,0437864
|
|
4/5-{359.0724000,
427.3562000}
|
10/10-{54865.4000000,
59771.4000000}
|
387,5061798
|
54242,0098802
|
7
|
1,0437864
|
|
4/5-{359.0724000,
427.3562000}
|
10/10-{54865.4000000,
59771.4000000}
|
401,1296802
|
56338,7738351
|
8
|
1,0437864
|
|
4/5-{359.0724000,
427.3562000}
|
10/10-{54865.4000000,
59771.4000000}
|
411,7426326
|
54808,1590574
|
9
|
1,0437864
|
|
4/5-{359.0724000,
427.3562000}
|
10/10-{54865.4000000,
59771.4000000}
|
414,4819519
|
57318,3999978
|
10
|
1,0437864
|
|
5/5-{427.3562000,
495.6400000}
|
3/10-{20523.4000000,
25429.4000000}
|
452,2921759
|
26071,3518690
|
1
|
0,2899832
|
|
5/5-{427.3562000,
495.6400000}
|
3/10-{20523.4000000,
25429.4000000}
|
459,3299898
|
21906,1611866
|
2
|
0,2899832
|
|
5/5-{427.3562000,
495.6400000}
|
3/10-{20523.4000000,
25429.4000000}
|
465,1941402
|
22976,3999955
|
3
|
0,2899832
|
|
5/5-{427.3562000,
495.6400000}
|
4/10-{25429.4000000,
30335.4000000}
|
467,8300951
|
28755,7846561
|
1
|
0,5357519
|
|
5/5-{427.3562000,
495.6400000}
|
4/10-{25429.4000000,
30335.4000000}
|
458,4054364
|
28646,9649134
|
2
|
0,5357519
|
|
5/5-{427.3562000,
495.6400000}
|
4/10-{25429.4000000,
30335.4000000}
|
443,7581067
|
27314,1840382
|
3
|
0,5357519
|
|
5/5-{427.3562000,
495.6400000}
|
4/10-{25429.4000000,
30335.4000000}
|
466,2508313
|
24877,3928943
|
4
|
0,5357519
|
|
5/5-{427.3562000,
495.6400000}
|
4/10-{25429.4000000,
30335.4000000}
|
466,8937851
|
27882,3999948
|
5
|
0,5357519
|
|
5/5-{427.3562000,
495.6400000}
|
6/10-{35241.4000000,
40147.4000000}
|
461,4981000
|
39595,7426313
|
1
|
0,4631437
|
|
5/5-{427.3562000,
495.6400000}
|
6/10-{35241.4000000,
40147.4000000}
|
440,8689611
|
37694,4000022
|
2
|
0,4631437
|
|
5/5-{427.3562000,
495.6400000}
|
6/10-{35241.4000000,
40147.4000000}
|
461,4981000
|
33375,7515244
|
3
|
0,4631437
|
|
5/5-{427.3562000,
495.6400000}
|
6/10-{35241.4000000,
40147.4000000}
|
472,2978060
|
37694,3999977
|
4
|
0,4631437
|
|
5/5-{427.3562000,
495.6400000}
|
7/10-{40147.4000000,
45053.4000000}
|
461,4981000
|
44621,2671468
|
1
|
0,3990987
|
|
5/5-{427.3562000,
495.6400000}
|
7/10-{40147.4000000,
45053.4000000}
|
455,0021052
|
42600,4000026
|
2
|
0,3990987
|
|
5/5-{427.3562000,
495.6400000}
|
7/10-{40147.4000000,
45053.4000000}
|
461,4981000
|
39932,4565020
|
3
|
0,3990987
|
|
5/5-{427.3562000,
495.6400000}
|
7/10-{40147.4000000,
45053.4000000}
|
468,1049593
|
42600,3999976
|
4
|
0,3990987
|
Стандартными средствами MS Excel на основе таблиц 6 и
7 построены регрессии, изображенные на рисунке 22.
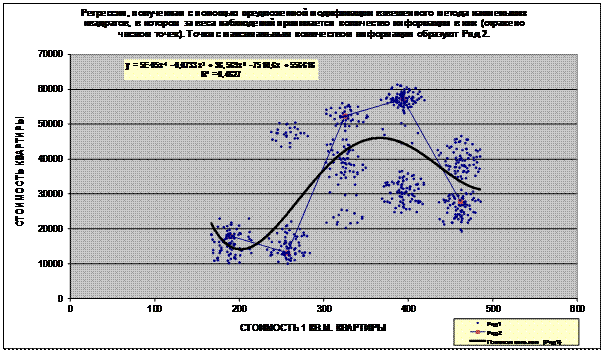
Рисунок 22 – Регрессия,
построенная на основе всех наблюдений с учетом
количества информации в них (в ряду 2 показаны также наблюдения
с максимальным количеством информации)
На рисунке 22 число точек, на которых строится
регрессия, значительно превосходит число параметров, т.к. каждая точка модели,
соответствующая наблюдению, представляется в форме ряда точек, количество
которых соответствует количеству информации в этом наблюдении.
Сравнивая когнитивные функции зависимости стоимости
квартиры от стоимости 1 кв.метра, приведенные на рисунке 15, с аппроксимацией
на рисунке 22 мы видим, что они совпадают. Это и не удивительно, т.е. так и
должно быть, т.к. они построены на основе одной и той же модели знаний.
Но здесь важно не только это, но и то, что режим
4.6 позволяет привлечь для построения и исследования когнитивных функций в виде регрессий весь
хорошо разработанный аппарат регрессионного анализа, в том числе и аппарат
оценки качества регрессий с помощью дисперсий и доверительных интервалов.
Программная
реализация режима подготовки баз
данных для визуализации когнитивных функций в MS Excel (режим 4.6) системы «Эйдос»
и исходный текст всей системы «Эйдос» приведена по ссылке: ftp://lc.kubagro.ru/Downloads.exe.
Для того, чтобы в исходном тексте системы «Эйдос», т.е. в файле _AIDOS-X.doc,
найти исходный текст программы описанного в данном разделе режима необходимо найти
в этом файле контекст: «N F4_6()».
Ниже приведен алгоритм
режима подготовки баз данных для визуализации когнитивных функций в MS
Excel, приведен ниже. Но с целью экономии места сделано это не в традиционной
форме блок-схемы, а в более компактной форме списка шагов.
Шаг-0. Вход режима
подготовки баз данных для визуализации когнитивных функций в MS Excel.
Шаг-1.
Определение массивов и переменных, используемых в режиме.
Шаг-2. Выйти
из режима, если нет авторизации в системе.
Шаг-3. Если не
запущен режим, работающий с БД, то
перейти в папку выбранного приложения
Шаг-4. Создать
папку для баз данных визуализации когнитивных функций "Cogn_fun" в
папке текущего приложения, если ее не было.
Шаг-5. Проверить созданы ли
в папке текущего приложения базы данных статистических моделей и моделей
знаний: {Abs.dbf, Prc1.dbf, Prc2.dbf, Inf1.dbf, Inf2.dbf, Inf3.dbf, Inf4.dbf,
Inf5.dbf, Inf6.dbf, Inf7.dbf}. Если их нет, то выдать сообщение о том, что для
того, чтобы создать их необходимо выполнить режим 3.4 или 3.5 и выйти из режима,
а иначе продолжить.
Шаг-6. Проверить,
существует ли файл с заданием на создание баз данных для визуализации
когнитивных функций. Если он существует, загрузить его и присвоить значения из
него массиву параметров диалога. Если же не существует – то присвоить значения
по умолчанию массиву параметров и записать его в виде файла.
Шаг-7. Организовать
экранную форум для задания параметров создания баз данных для визуализации
когнитивных функций с параметрами из массива с параметрами.
Шаг-8. Проверить, задана ли
хотя бы одна стат.модель или модель знаний для создания БД для визуализации КФ.
Если нет – выдать сообщение и выйти, иначе продолжить.
Шаг-9. Записать файл с
информацией о параметрах создания БД для визуализации КФ.
Шаг-10. Удалить все
dbf-файлов из папки: "Cogn_fun».
Шаг-11. Открыть базы данных
классификационных и описательных шкал и градаций.
Шаг-12. Определить
максимальную длину наименования градации описательной шкалы.
Шаг-13. Определить
максимальную длину наименования градации классификационной шкалы.
Шаг-14. Занести в БД
описательных и классификационных шкал информацию о начальной и конечной градации
каждой шкалы
Шаг-15. Открыть все базы
данных статистических моделей и моделей знаний: {Abs.dbf, Prc1.dbf, Prc2.dbf,
Inf1.dbf, Inf2.dbf, Inf3.dbf, Inf4.dbf, Inf5.dbf, Inf6.dbf, Inf7.dbf}.
Шаг-16. Определение число
операций, необходимых для создания БД для визуализации КФ. Это необходимо для
отображения стадии исполнения режима.
Шаг-17. Организовать
отображение стадии исполнения режима.
Шаг-18. Начало цикла по моделям: {Abs.dbf,
Prc1.dbf, Prc2.dbf, Inf1.dbf, Inf2.dbf, Inf3.dbf, Inf4.dbf, Inf5.dbf, Inf6.dbf,
Inf7.dbf}.
Шаг-19. Создавать КФ по
данной модели? Если да, то на следующий шаг, а иначе – на конец цикла по моделям.
Шаг-20. Создавать КФ-1: прямые, позитивные,
построенные ТОЛЬКО по точкам с максимальным количеством информации? Если да, то
на следующий шаг, иначе на проверку создания других видов КФ (Шаг-39).
Шаг-21. Начало цикла по
подматрицам текущей модели.
Шаг-22. Начало цикла по
классификационным шкалам.
Шаг-23. Определить диапазон
градаций текущей классификационной шкалы.
Шаг-24. Начало цикла по
описательным шкалам.
Шаг-25. Создать БД для
визуализации КФ с нужным именем и открыть ее.
Шаг-26. Определить диапазон
градаций текущей описательной шкалы.
Шаг-27. Начало цикла по
градациям описательной шкалы текущей модели.
Шаг-28. Для каждой градации
описательной шкалы найти градацию классификационной шкалы с Max информативностью
и занести их в БД КФ.
Шаг-29. Если градация
найдена, то на следующий шаг, а иначе на проверку, создавать ли следующий вид
когнитивных функций (Шаг-35).
Шаг-30. Извлечь
наименование градации описательной шкалы
Шаг-31. Если описательная
шкала числовая, то посчитать среднее значение числового интервала градации, а
иначе значением градации считать ее код.
Шаг-32. Если
классификационная шкала числовая, то посчитать среднее значение числового
интервала градации, а иначе значением градации считать ее код.
Шаг-33. Записать в БД
визуализации КФ новую запись с именами градаций описательной и классификационной
шкал и значениями этих градаций.
Шаг-34. Конец проверки на
наличие градации (Шаг-29).
Шаг-35. Конец цикла по по
градациям описательной шкалы текущей модели (Шаг-27).
Шаг-36. Закрыть БД
визуализации КФ.
Шаг-37. Конец цикла по
описательным шкалам (Шаг-24).
Шаг-38. Конец цикла по
классификационным шкалам (Шаг-22).
Шаг-39. Конец проверки на
создание 1-го вида когнитивных функций (Шаг-20).
Шаг-40. Создавать КФ-2: прямые, позитивные,
построение по ВСЕМ точкам с весами, равными количеству информации в них? Если
да, то на следующий шаг, иначе на проверку создания других видов КФ (Шаг-60).
Шаг-41. Начало цикла по
классификационным шкалам текущей модели.
Шаг-42. Определить диапазон
градаций текущей классификационной шкалы.
Шаг-43. Начало цикла по
описательным шкалам.
Шаг-44. Создать БД для
визуализации КФ с нужным именем и открыть ее.
Шаг-45. Определить диапазон
градаций текущей описательной шкалы.
Шаг 46. Найти максимальную
и минимальную информативность в подматрице БД INF# и использовать ее для
расчета весового коэффициента и определения количества точек с единичным весом
в единице информации для Iij > 0. Заодно определить диапазоны изменения
значений градаций классификационных и описательных шкал и градаций для
подматрицы функции.
Для каждой градации описательной шкалы найти все градации
классификационной шкалы и для каждой из них занести в БД визуализации КФ
количество точек единичного веса, соответствующее количеству информации в
значении аргумента о значении функции.
Шаг-47. Начало цикла по
градациям описательной шкалы текущей модели.
Шаг-48. Начало цикла по
градациям классификационной шкалы текущей модели.
Шаг-49. Извлечь из БД
текущей модели количество информации в текущей градации описательной шкалы о
текущей градации классификационной шкалы.
Шаг-50. Если это количество
информации положительное, то перейти на следующий шаг, а иначе – на проверку
следующего элемента матрицы текущей модели (Шаг-56).
Шаг-51. Определить диапазон
градаций текущей описательной шкалы.
Шаг-52. Определить диапазон
градаций текущей классификационной шкалы.
Шаг-53. Посчитать
количество точек, соответствующее количеству информации в градации.
Шаг-54. Посчитать угол в
градусах между соседними точками рассеяния.
Шаг-55. Занести в БД
визуализации КФ количество точек единичного веса, соответствующее количеству
информации в значении аргумента о значении функции (для каждой точки создать
запись в БД).
Шаг-56. Конец проверки на
положительность количества информации в элементе матрицы модели (Шаг-50).
Шаг-57. Конец цикла по градациям
классификационной шкалы текущей модели (Шаг-48).
Шаг-58. Конец цикла по
градациям описательной шкалы текущей модели (Шаг-47).
Шаг-59. Закрыть БД
визуализации КФ.
Шаг-60. Конец цикла по
описательным шкалам (Шаг-43).
Шаг-61. Конец цикла по
классификационным шкалам (Шаг-41).
Шаг-62. Конец проверки на
создание 2-го вида когнитивных функций (Шаг-40).
* * * *
Остальные 6 видов
когнитивных функций, классифицированные в таблице 5, рассчитываются аналогично
КФ-1 и КФ-2 с небольшими изменениями в алгоритмах их расчета по сравнению с
приведенными выше.
Шаг-63. Конец проверки на
расчет БД для данной модели.
Шаг-64. Конец цикла по
моделям.
Шаг-65. Закрытие структуры
отображения стадии исполнения.
Шаг-66. Закрытие всех баз
данных.
Шаг-67. Отображение окна с
информацией об окончании работы режима.
Шаг-68. Выход из режима
подготовки БД для визуализации КФ.
Конец алгоритма режима 4.6 системы «Эйдос».
Метод наименьших квадратов (МНК) широко известен и
пользуется заслуженной популярностью. Вместе с тем не прекращаются попытки
усовершенствования этого метода. Результатом одной из таких попыток является
взвешенный метод наименьших квадратов (ВМНК), суть которого в том, чтобы
придать наблюдениям вес обратно пропорциональный погрешностям их аппроксимации.
Этим самым фактически наблюдения игнорируются тем в большей степени, чем
сложнее их аппроксимировать. В результате такого подхода формально погрешность
аппроксимации снижается, но фактически это происходит путем частичного отказа
от рассмотрения «проблемных» наблюдений, вносящих большую ошибку. Если эту
идею, лежащую в основе ВМНК довести до крайности (и тем самым до абсурда), то в
пределе такой подход приведет к тому, что из всей совокупности наблюдений
останутся только те, которые практически точно ложатся на тренд, полученный
методом наименьших квадратов, а остальные просто будут проигнорированы. Однако,
по мнению автора, фактически это не решение проблемы, а отказ от ее решения,
хотя внешне и выглядит как решение. В работе предлагается именно решение,
основанное на теории информации: считать весом наблюдения количество информации
в аргументе о значении функции. Этот подход был обоснован в рамках нового
инновационного метода искусственного интеллекта: метода автоматизированного
системно-когнитивного анализа (АСК-анализа) и реализован еще 30 лет назад в его
программном инструментарии –
интеллектуальной системе «Эйдос» в виде
так называемых «когнитивных функций». В данном разделе приводится алгоритм и
программная реализация данного подхода, проиллюстрированные на подробном численном
примере.
Таким образом,
автоматизированный системно-когнитивный анализ (АСК-анализ) и его
математическая модель (системная теория информации), а также реализующий их
программный инструментарий АСК-анализа – система «Эйдос» – это и есть ответы на
этот вопрос. Таким образом, АСК-анализ и система «Эйдос» представляют собой
современную инновационную (готовую к внедрению) технологию взвешенного метода
наименьших квадратов, модифицированного путем применения в качестве весов наблюдений
количества информации в них.
Данный раздел может быть использован как описание
лабораторной работы по дисциплинам:
– Интеллектуальные системы;
– Инженерия знаний и интеллектуальные системы;
– Интеллектуальные технологии и
представление знаний;
– Представление знаний в интеллектуальных
системах;
– Основы интеллектуальных систем;
– Введение в нейроматематику и методы
нейронных сетей;
– Основы искусственного интеллекта;
– Интеллектуальные технологии в науке и образовании;
– Управление знаниями;
– Автоматизированный системно-когнитивный
анализ и интеллектуальная система «Эйдос»;
которые автор ведет в настоящее время,
а также и в других дисциплинах, связанных с преобразованием данных в
информацию, а ее в знания и применением этих знаний для решения задач идентификации,
прогнозирования, принятия решений и исследования моделируемой предметной
области (а это практически все дисциплины во всех областях науки).
В данном разделе не ставилась задача описать
математический метод АСК-анализа, обеспечивающий расчет количества информации в
наблюдениях, т.к. этому посвящено много монографий и статей автора, размещенных
в полном открытом бесплатном доступе:
– http://lc.kubagro.ru/;
– http://lc.kubagro.ru/aidos/index.htm;
– http://ej.kubagro.ru/a/viewaut.asp?id=11;
– http://www.twirpx.com/user/858406/;
– http://elibrary.ru/author_items.asp?authorid=123162.
В будущем планируется дать развернутое математическое
обоснование метода взвешенных наименьших квадратов, модифицированного путем
применения в качестве весов наблюдений количества информации в них и применения
теории информации для расчета этих весовых коэффициентов наблюдений, а также
исследовать свойства данной модификации метода взвешенных наименьших квадратов.
Интуитивно все понимают, что шум, это
сигнал, в котором нет информации или в котором на практике не удается выявить
информацию. Точнее, понятно, что некая последовательность элементов (ряд) тем в
большей степени является шумом, чем меньше информации содержится в значениях одних
элементов о значениях других. Тем более странно, что никто не предложил не
только способа, но даже идеи измерения количества информации в одних фрагментах
сигнала о других его фрагментах и его использования в качестве критерия оценки
степени близости данного сигнала к шуму. Авторами предложен асимптотический информационный
критерий качества шума, а также метод, технология и методика его применения на
практике. В качестве метода применения асимптотического информационного
критерия качества шума на практике предлагается автоматизированный
системно-когнитивный анализ (АСК-анализ), в качестве технологии – программный
инструментарий АСК-анализа: универсальная когнитивная аналитическая система
«Эйдос», в качестве методики – методика создания приложений в данной системе, а
также их использования для решения задач идентификации, прогнозирования,
принятия решений и исследования предметной области путем исследования ее
модели. Приводится наглядный численный пример, иллюстрирующий излагаемые идеи и
подтверждающий работоспособность предлагаемого асимптотического информационного
критерия качества шума, а также метода, технологии и методики его применения на
практике
«В начале было Слово»
Евангелие от
Иоанна
«…законы природы являются лишь высказываниями
о пространственно-временных совпадениях…»
Альберт
Эйнштейн
Данный раздел является продолжением серии работ
авторов, посвященных системной нечеткой интервальной математике [1, 2, 3] и
применению теории информации для решения задач математической статистики [4, 5,
6], в частности анализа текстов и рядов объектов числовой и нечисловой природы
(слов, чисел, символов, цифр).
Шум есть везде или выражаясь более точным языком
математики «почти везде». Любой сигнал, получаемый нами, может рассматриваться
как сумма истинного сигнала и шума. Понятие шума является одним из
основополагающих понятий в теории связи, в которой решается важнейшая задача
подавления шума и повышения отношения сигнал/шум [7, 8, 9]. Но смысл понятия
«Шум» гораздо шире, что будет видно из последующего обсуждения. Поэтому очень
важно уметь исследовать шум, выявлять его, идентифицировать тип шума, оценивать
качество шума, подавлять (отфильтровывать) шум, генерировать шум с
заранее заданными характеристиками и качеством и т.д.
В теоретическом исследовании и практических решениях
всех этих вопросов, связанных с шумом, большую роль играют физические и численные
эксперименты с шумом. В численных экспериментах в качестве источников шума
используются различные генераторы псевдослучайных последовательностей,
основанные на различных алгоритмах. На использовании этих генераторов основано
целое научное направление: «Метод статистических испытаний или статистического
моделирования Монте-Карло»
[10].
Понятно, что результаты статистического моделирования
напрямую зависят от качества используемых генераторов шума. Вопросам исследования
шума посвящено огромное количество научных работ. Надо отметить, что
используются разные терминологические системы. При рассмотрении пары сигнал/шум
говорят о выделении (или оценке) сигнала. Если есть зависимость от времени, то
обсуждают временные ряды (когда время лискретно) и случайные процессы (когда
время непрерывно). Решают задачи выделения тренда [49], оценки периода [50] и
др.
Однако, количественное измерение качества шума
остается недостаточно исследованной проблемой,
которую необходимо решать и теоретически, и практически. Данная статья
посвящена поиску подходов к решению этой проблемы с применением методов,
основных на теории информации.
В 60-х годах XX века А.Н.Колмогоров
связывал случайность с алгоритмизацией. Он считал, что последовательность чисел
является случайной, если ее нельзя задать с помощью алгоритма, заметно более
короткого по сравнению с длиной самой последовательности
[44 - 48]. Очевидно, все генераторы случайных
чисел задаются сравнительно короткими алгоритмами, а потому по А.Н.Колмогорову
получить с их помощью действительно случайную последовательность невозможно. По
этой причине будем использовать термин «псевдослучайный» и для самих
генераторов, и для получаемых с их помощью последовательностей.
Теоретически возможность создания
эффективных алгоритмов генерации псевдослучайных чисел обычно обосновывается с
помощью теорем теории чисел. Но с появлением в распоряжении исследователей
мощных компьютеров возрастает роль и численных экспериментов в исследованиях
шума.
В 1985 г. известным журналом
«Заводская лаборатория. Диагностика материалов»
была развернута научная дискуссия по поводу статистических свойств генерации
псевдослучайных последовательностей. Все началось с того, что И.Г.Журбенко (МГУ
им. М.В. Ломоносова) обнаружил, что в рядах, полученных с помощью распространенного
в те годы генератора псевдослучайных последовательностей, три последовательных значения довольно точно связаны линейной зависимостью. Такие аномалии для конкретных
датчиков обнаруживают и сейчас
Но что значит «Связаны»?
Интуитивно все понимают, что шум, это сигнал, в
котором нет информации или в котором на практике не удается выявить информацию.
Точнее, понятно, что некая последовательность элементов (ряд) тем в большей
степени является шумом, чем меньше информации содержится в значениях одних
элементов о значениях других. Тем более странно, что никто не предложил не
только способа, но даже лежащей на поверхности идеи измерения количества
информации в одних фрагментах сигнала о других его фрагментах и использования этого
количества информации в качестве критерия оценки степени близости данного
сигнала к шуму. При этом сходные подходы к приятию решений хорошо известны [7,
8, 9].
Авторы предлагают асимптотический информационный критерий
качества шума, представляющий собой вариабельность количества информации
в значениях одних элементов последовательности (ряда) о значениях других его
элементов.
Отметим, что в
работе [17] еще в 2002 году на стр. 290
одним из авторов было предложено использовать аналогичный критерий в качестве
количественной меры степени выраженности закономерностей в предметной области.
написано: «Из этого следует возможность использования
в качестве количественной меры
степени выраженности закономерностей в предметной области использовать не матрицу абсолютных
частот и меру X2, а
новую меру, основанную на матрице информативностей и системном обобщении формулы Харкевича для количества информации:
|
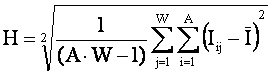
|
(3. 81)
|
где:
|
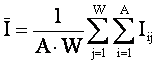
|
– средняя информативность признаков по
матрице информативностей.
|
Значение данной
меры показывает среднее отличие количества информации в факторах о будущих
состояниях активного объекта управления от среднего количества информации в
факторе (которое при больших выборках близко к 0). По своей математической
форме эта мера сходна с мерами для значимости факторов и степени сформированности образов
классов и коррелирует с
объемом пространства классов и пространства атрибутов». В данной же статье
предлагается количественную меру степени
выраженности закономерностей в предметной области использовать в качестве
критерия близости этой предметной области к шуму.
Данный критерий является асимптотическим, т.к. результаты измерения с помощью этого
критерия, по-видимому, должны сходится к истинному значению при увеличении
количества исследуемых элементов последовательности. Математические
формулировки этого утверждения о состоятельности критерия будут обсуждаться в
дальнейшем.
Количество информации может вычисляться для различных
элементов последовательности: например в значении каждого элемента о значении
последующего элемента, в паре элементов о паре последующих, в тройке значений
последовательных элементов о значении последующего и т.п., и т.д.
Количество информации может рассчитываться с помощью
различных количественных мер измерения информации: Найквиста, Хартли,
Больцмана, Шеннона, Харкевича, алгоритмических подходов к измерению информации
и др.
Вариабельность может рассчитываться с помощью
различных мер вариабельности: среднего модуля отклонения от среднего,
среднеквадратичного отклонения и др.
Поэтому существует много различных вариантов
применения предложенного критерия.
Как мы видели выше, понятие «Шум» тесно связано с
понятием «Информация», точнее с отсутствием информации в сигнале или
невозможностью ее извлечения из сигнала. Но как связано содержание понятий:
«Данные», «Информация», «Знания»? В рассмотрении этого вопроса будем
основываться на статье [11][33].
Данные –
это информация, записанная на каком-либо носителе или находящаяся в каналах
связи и представленная на каком-то языке или в системе кодирования и рассматриваемая
безотносительно к ее смысловому содержанию.
Исходные данные об объекте управления обычно представлены
в форме баз данных, чаще всего временных рядов, т.е. данных, привязанных ко
времени. В соответствии с методологией и технологией автоматизированного
системно-когнитивного анализа (АСК-анализ) [12, 17], для управления и принятия
решений использовать непосредственно исходные данные не представляется
возможным. Точнее сделать это можно, но результат управления при таком подходе
оказывается мало чем отличающимся от случайного. Для реального же решения
задачи управления необходимо предварительно преобразовать данные в информацию,
а ее в знания о том, какие воздействия на объект управления к каким его
изменениям обычно, как показывает опыт, приводят.
Информация
есть осмысленные данные.
Смысл данных, в соответствии с концепцией смысла
Шенка-Абельсона [13], состоит в том, что известны причинно-следственные
зависимости между событиями, которые описываются этими данными. Таким образом,
данные преобразуются в информацию в результате операции, которая называется
«Анализ данных» (этот термин используется и в иных смыслах, например, как
синоним термина "прикладная статистика" [41, 42]), которая состоит из
двух этапов:
1. Выявление событий в данных (разработка
классификационных и описательных шкал [15, 41] и градаций и преобразование с их
использованием исходных данных в обучающую выборку, т.е. в базу событий –
эвентологическую базу). По сути, этот этап является нормализацией базы исходных данных.
2. Выявление причинно-следственных зависимостей между
событиями.
В случае систем управления событиями в данных являются
совпадения определенных значений входных факторов и выходных параметров объекта
управления, т.е. по сути, случаи перехода объекта управления в определенные
будущие состояния под действием определенных сочетаний значений управляющих
факторов. Качественные значения входных факторов и выходных параметров
естественно формализовать в форме лингвистических переменных. Если же входные
факторы и выходные параметры являются числовыми, то их значения измеряются с
некоторой погрешностью и фактически представляют собой интервальные числовые
значения, которые также могут быть представлены или формализованы в форме
лингвистических переменных (типа: «малые», «средние», «большие» значения показателей)
[1].
Какие же математические меры могут быть использованы
для количественного измерения силы и направления причинно-следственных зависимостей?
Наиболее очевидным ответом на этот вопрос, который
обычно первым всем приходит на ум, является: «Корреляция». Однако, в статистике
это хорошо известно, что это совершенно не так (пассивный эксперимент дает
возможности выявить связи, но не причины). Для преобразования исходных данных в
информацию необходимо не только выявить события в этих данных, но и найти
причинно-следственные связи между этими событиями. В АСК-анализе предлагается 7
количественных мер причинно-следственных связей, основной из которых является
семантическая мера целесообразности информации по А.Харкевичу [15, 17].
Знания – это
информация, полезная для достижения целей.
Значит, для преобразования информации в знания необходимо:
1. Поставить цель (классифицировать будущие состояния
моделируемого объекта на целевые и нежелательные).
2. Оценить полезность информации для достижения этой
цели (знак и силу влияния).
Второй пункт, по сути, выполнен при преобразовании
данных в информацию. Поэтому остается выполнить только первый пункт, т.к.
классифицировать будущие состояния объекта управления как желательные (целевые)
и нежелательные. Отметим, что это делается, в частности, при SWOT и PEST
анализе [16].
Знания могут быть представлены в различных формах,
характеризующихся различной степенью формализации:
– вообще
неформализованные знания, т.е. знания в своей собственной форме, ноу-хау
(мышление без вербализации есть медитация);
– знания, формализованные в естественном вербальном
языке;
– знания, формализованные в виде различных методик,
схем, алгоритмов, планов, таблиц и отношений между ними (базы данных);
– знания в форме технологий, организационных,
производственных, социально-экономических и политических структур;
– знания, формализованные в виде математических
моделей и методов представления знаний в автоматизированных интеллектуальных
системах (логическая, фреймовая, сетевая, продукционная, нейросетевая, нечеткая
и другие).
Таким образом, для решения сформулированной проблемы
необходимо осознанно и целенаправленно последовательно повышать степень
формализации исходных данных до уровня, который позволяет ввести исходные
данные в интеллектуальную систему, а затем:
– преобразовать исходные данные в информацию;
– преобразовать информацию в знания;
– использовать знания для решения задач управления,
принятия решений и исследования предметной области.
Таким образом, понятие «Шум» по своему содержанию
наиболее близко к понятию «Данные». Для того, чтобы выяснить являются ли данные
просто шумом или содержат информацию, нужно выявить в них причинно-следственные
зависимости.
Процедуры преобразования данных в информацию, а ее в
знания, реализованные в системе «Эйдос», приведены на рисунке 2:
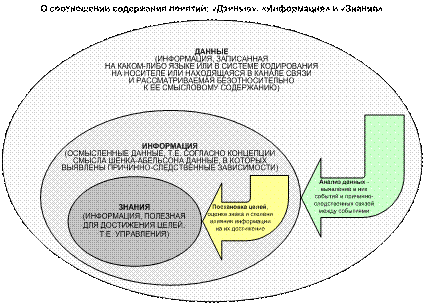
Рисунок 2 –Процедуры преобразования данных в
информацию, а ее в знания
Отметим в этой связи известное высказывание Альберта
Эйнштейна, приведенное в качестве эпиграфа к статье: «…законы природы являются
лишь высказываниями о пространственно-временных совпадениях…» [43]. Учитывая
вышесказанное, можно сказать, что законы природы отражают реально существующие
причинно-следственные зависимости, т.е. содержат информацию о них. Отметим
также, что расчет этого количества информации основывается на матрице
абсолютных частот, т.е. на предварительном определении абсолютного количества
этих совпадений (фактов), о которых говорит Альберт Эйнштейн. Фактом в
АСК-анализе является совпадение действия на моделируемый объект определенного
значения фактора и перехода этого объекта в определенное состояние.
Шум можно определить, как сигнал, в котором нет
закономерностей. Но как доказать что их нет? Возможно ли даже в
принципе доказать, что чего-то нет? Здесь необходимо вспомнить о критерии
Поппера и принципе Эшби [14]. По мнению авторов, это невозможно даже в
принципе. На практике возможно доказать лишь, что с помощью имеющихся в нашем
распоряжении методов обнаружения закономерностей их выявить не удалось. Это
позволяет провести различие между абстрактным теоретическим понятием шума и
понятием «практически шума». Реально мы всегда исследуем лишь практически шум.
В определение шума входит не только характеристика самого сигнала (отсутствие
закономерностей), но и характеристика нас самих, точнее наших возможностей
обнаружения закономерностей в этом сигнале. А они, во-первых, ограничены,
во-вторых, изменяются от места к месту (доступ к вычислительным ресурсам и
средствам обнаружения закономерностей), в третьих, изменяются со временем (вычислительные
технологии быстро эволюционируют). Поэтому то, что еще вчера считалось где-то
шумом, сегодня где-то уже им не будет признаваться.
Если в
результате применения процедур выявления причинно-следственных закономерностей
в данных, например, реализованных в системе «Эйдос», не удается выявить эти
закономерности, т.е. не удается преобразовать эти данные в информацию, то можно
говорить о том, что эти данные являются «практически шумом», т.е. на данном
этапе развития для нас неотличимы от
шума. Вопрос о том, являются ли «на самом деле» эти данные шумом, имеет скорее
философско-методологический характер [14].
Все свойства
систем имеют эмерджентную природу [1, 37]. Не является исключением и свойство
текстов иметь смысл. Любое сообщение на естественном языке является системой
символов некоторого алфавита, образующих иерархическую систему с многими
уровнями иерархии (например: слова, предложения, абзацы, параграфы, главы,
книги), и между элементами всех этих уровней существует множество горизонтальных
и вертикальных взаимосвязей, в результате чего у этой системы появляется новое
эмерджентное свойство, отсутствовавшее у элементов: смысл. Смысл – это эмерджентное свойство
символических систем. Уровень системной организации, количественно
измеряемый предложенным автором [1, 2, 27]
коэффициентом эмерджентности Хартли, своего рода «плотность смысла на символ» у
стихов выше, чем у прозы, а у песен, еще выше, чем у стихов.
С этой точки
зрения шум представляет собой
бессмысленное сообщение. Но как на практике сообщение может стать
бессмысленным? Это оказывается возможным, если нарушить или разрушить его
внутреннюю иерархическую структуру и взаимосвязи элементов в этой структуре.
Нечто подобное происходит с древними текстами, подвергшимся разрушительному
действию факторов окружающей среды в течение длительного времени. В качестве
других примеров можно привести костры из книг, а также действие уничтожителя
бумаги. Когда люди не хотят, чтобы содержимое записки стало кому-либо
известным, они просто разрывают ее на мелкие кусочки и кидают их в разные урны.
Если
в данных выявлены закономерности, то их можно использовать для сжатия данных,
т.е. создания архива. При этом если в архиве обнаружены закономерности, то его
можно еще сжать, но уже в меньшей степени. Чем лучше степень сжатия в архиве
(чем лучше архиватор), тем меньше в нем можно обнаружить закономерностей, т.е. тем больше он становится похожим
на шум, а наилучший архив вообще не отличим от шума. Идеальный архив
вообще невозможно сжать, как и шум, в котором вообще нет закономерностей. При
архивировании плотность записи информации на символ увеличивается.
Так может
быть шум, – это не бессмысленный сигнал, т.е. сигнал, в котором нет информации,
а наоборот, сигнал, с наивысшей в принципе возможной плотностью записью
информации?
Это
значит, что архиваторы можно считать генераторами шума.
По-видимому,
можно доказать теорему: при итерационном
применении архиватора к архиву этот архив сходится к шуму.
В
этом подходе, в отличие от подхода А.Н. Колмогорова [44 - 48], шум создается не
просто программой, но программой, использующей внешние данные, причем данные,
даже возможно, содержащие закономерности. Необходимо отметить, что эти исходные
данные могут быть весьма велики по объему, что делает шум более качественным,
несмотря на то, что алгоритм работы программы может быть очень коротким. В этом
важное отличие нашего подхода от подхода А.Н. Колмогорова.
Во
многих языках программирования (например, на Паскале) для улучшения
псевдослучайного сигнала перед запуском функции, возвращающей случайное число,
можно задать некоторое числовое значение, изменяющее ее работу. Ясно, что желательно,
чтобы и само это значение тоже не было постоянным, т.к. иначе работа генератора
псевдослучайных чисел будет изменяться одинаково. Поэтому часто в качестве
такого значения часто используется как-либо функция от текущего значения компьютерного
таймера.
Чтение, можно
рассматривать как извлечение информации из книги, т.е. дешифрованием
записанного в книге сигнала. Познание представляет собой извлечение информации
из объекта познания. Если провести аналогию между объектом познания и книгой,
то можно считать, что познание представляет собой чтение объекта познания,
пользуясь термином К. Маркса, его распредмечивание. С этой точки зрения вся
природа представляет собой зашифрованное послание, а познание представляет
собой ничто иное как чтение книги природы. Научный метод с этой точки зрения
представляет собой проверенный и доказавший свою высокую эффективность ключ
дешифрования книги природы, даже может быть своего рода отмычку, позволяющую
вскрыть «тайну за семью печатями». Конечно, при такой точке зрения возникает
закономерный вопрос об авторстве книги природы. Здесь ничего не приходит на ум,
кроме первых слов Евангелия от Иоанна, приведенных в качестве эпиграфа к
статье: «В начале было Слово» и далее по тексту. Слово, или выражаясь
современным языком – информация, преобразует первозданный Хаос во Вселенную,
полную чудес, информация способна структурировать бессмысленный набор символов
в гениальное высокоорганизованное литературное произведение [39].
Но человек не
только может читать книгу природы, он может и вносить в нее некоторые не очень
большие правки и дополнения. Труд представляет собой процессе записи
информации, содержащейся в субъективном образе будущего продукта труда, в
предмет труда [40], выражаясь термином К. Маркса: опредмечивание. С этой точки
зрения можно рассматривать труд и его результат – антропоморфное общество, как
внесение поправок и дополнений в книгу природы.
Шум – это
текст на неизвестном языке. Чтобы его расшифровать – надо перевести его на
известный язык.
В принципе не
взламываемый шифр – это шифр, в котором каждый символ встречается лишь один раз
и нет никаких «пространственно-временных совпадений», хотя бы в принципе
позволяющих выявить смысл. Примером такого шифра является замена каждого
символа исходного сообщения на номер этого символа в некотором очень большом
тексте (можно псевдослучайном), при этом каждый символ из большого текста
используется лишь один раз или не используется ни разу.
Таким образом,
системы
шифрования можно рассматривать как генераторы шума, и чем сложнее взломать
шифр, тем ближе зашифрованный сигнал к идеальному шуму.
Так может
быть шум, – это не бессмысленный сигнал, т.е. сигнал, в котором нет информации,
а наоборот, сигнал, с очень важной информацией, зашифрованный очень стойким
шифром?
По-видимому,
можно доказать теорему: при итерационном
применении шифрования (одного метода или различных методов в определенном
порядке) к уже зашифрованному сигналу результат шифрования сходится к шуму.
Для получения математических утверждений нужно тем или иным способом дать
строгие определения понятиях "шум" и "шифрование".
По-видимому, в момент большого взрыва (если принять
эту распространенную космогоническую модель, предложенную иезуитом Жоржем Леметром в 1927 г.) мир был
менее структурирован, чем сейчас, и имел более низкий, чем сейчас, уровень системности
[1].
Индусы в своих учениях говорили, что
дифференцированная вселенная периодически возникает и опять и переходит в не
проявленное состояние (день и ночь Брамы). Это очень напоминает архивирование
(или шифрование) и разархивирование (дешифрование) и опять архивирование и т.д.
Дух дифференцирует материю, затем материя одухотворяется (круг Сансары). Из хаоса, утверждали древние
греки, Вселенная родилась, и в Хаос же возвратится. Этому же учил Пифагор, об этом же
глубокомысленно и красноречиво молчит Дао. Вселенная периодически становится
более доступной для познания, как если бы Изида под нашим пристальным взором
иногда немного приоткрывала свое покрывало, скрывающее ее прекрасное (как
говорят) лицо. Можно утверждать, что сходные космогонические концепции
пронизывают все древние мировоззренческие системы и, похоже, в современной
науке получают еще одну интерпретацию, которая в чем-то глубже, а в чем-то
более поверхностна, чем древние.
Системный
анализ представляет собой современный метод научного познания, общепризнанный
метод решения проблем. Однако возможности практического применения системного
анализа ограничиваются отсутствием развернутого программного инструментария,
обеспечивающего его автоматизацию. Существуют программные системы,
автоматизирующие отдельные этапы или функции системного анализа в конкретных
предметных областях. Автоматизированный системно-когнитивный анализ
(АСК-анализ) представляет собой системный анализ, структурированный по базовым
когнитивным операциям (БКО), благодаря чему удалось разработать для него математическую
модель, методику численных расчетов (структуры данных и алгоритмы их обработки),
а также реализующую их программную систему – систему Эйдос [17, 18]. Система
Эйдос разработана в постановке, не зависящей от предметной области, и имеет ряд
программных интерфейсов с внешними данными различных типов. АСК-анализ может
быть применен как инструмент, многократно усиливающий возможности естественного
интеллекта во всех областях, где используется естественный интеллект.
АСК-анализ был успешно применен для решения задач идентификации, прогнозирования,
принятия решений и исследования моделируемого объекта путем исследования его
модели во многих предметных областях, в частности в экономике, технике, социологии,
педагогике, психологии, медицине, экологии, ампелографии (см. [14, 17, 31] и
др.).
7.3.4.1.1.
Истоки
Известно, что
системный анализ является одним из общепризнанных в науке методов решения
проблем и многими учеными рассматривается вообще как метод научного познания.
Однако как заметил еще в 1984 году проф. И. П. Стабин [19], на практике
применение системного анализа наталкивается на проблему. Суть этой проблемы в
том, что обычно системный анализ успешно применяется в сравнительно простых случаях,
в которых в принципе можно обойтись и без него, тогда как в действительно
сложных ситуациях, когда он действительно чрезвычайно востребован и у него нет
альтернатив, сделать это удается гораздо реже. Проф. И. П. Стабин предложил и
путь решения этой проблемы, который он видел в автоматизации системного анализа
[19].
Путь от идеи
до создания программной системы включает ряд этапов:
– выбрать теоретический
математический метод;
– разработать
методику численных расчетов, включающую структуры данных в оперативной памяти и
внешних баз данных (даталогическую и инфологическую модели) и алгоритмы
обработки этих данных;
– разработать
программную систему, реализующую эти математические методы и методики численных
расчетов.
Предпосылки решения проблемы
Перегудов Ф.
И. и Тарасенко Ф. П. в своих основополагающих работах 1989 и 1997 годов [20,
21] подробно рассмотрели математические методы, которые в принципе могли бы
быть применены для автоматизации отдельных этапов системного анализа. Однако
даже самые лучшие математические методы не могут быть применены на практике без
реализующих их программных систем, а путь от математического метода к
программной системе долог и сложен. Для этого необходимо разработать численные
методы или методики численных расчетов (алгоритмы и структуры данных), реализующие
математический метод, а затем разработать программную реализацию системы,
основанной на этом численном методе.
В числе
первых попыток реальной автоматизации системного анализа следует отметить
докторскую диссертацию проф. Симанкова В. С. (2001) [22]. Эта попытка была
основана на высокой детализации этапов системного анализа и подборе уже существующих
программных систем, автоматизирующих эти этапы. Идея была в том, что чем выше
детализация системного анализа, чем мельче этапы, тем проще их автоматизировать.
Эта попытка была реализована, однако, лишь для специального случая исследования
в области возобновляемой энергетики, т.к. объединяемые системы оказались различных
разработчиков, созданные с помощью различного инструментария и не имеющие
программных интерфейсов друг с другом, т.е. не образующие единой автоматизированной
системы. Эта попытка, безусловно, явилась большим шагом по пути, предложенному
проф. И. П. Стабиным, но и ее нельзя признать обеспечившей достижение поставленной
цели, сформулированной Стабиным И.П. (т.е. создание автоматизированного
системного анализа), т.к. она не привела к созданию единой универсальной программной
системы, автоматизирующий системный анализ, которую можно было бы применять в
различных предметных областях. Парадоксалаьно, но эта попытка автоматизации
системного анализа была несистемна.
Необходимо
отметить работы Дж. Клира по системологии и автоматизации решения системных
задач [23], которые внесли большой вклад в автоматизацию системного анализа
путем создания и применения универсального решателя системных задач (УРСЗ),
реализованного в рамках оригинальной экспертной системы. Обсуждение проблем
развития системного анализа продолжается (см., например, [51]).
АСК-анализ, как решение проблемы
Автоматизированный
системно-когнитивный анализ разработан профессором Е. В. Луценко и предложен в
2002 году [12, 17, 18]. Основная идея, позволившая сделать это, состоит в
рассмотрении системного анализа как метода познания (отсюда и «когнитивный» от
«cognitio» – знание, познание, лат.).
Это позволило структурировать системный анализ не по этапам, как пытались
сделать ранее, а по базовым когнитивным операциям системного анализа (БКОСА),
т.е. таким операциям, к комбинациям которых сводятся остальные. Эти операции
образуют минимальную систему, достаточную для описания системного анализа, как
метода познания, т.е. когнитивный конфигуратор (Лефевр В.А., 1962) [24] и их
оказалось не очень много, всего 10:
1) присвоение
имен;
2) восприятие
(описание конкретных объектов в форме отнологий, т.е. их признаками и
принадлежностью к обобщающим категориям - классам);
3) обобщение
(синтез, индукция);
4)
абстрагирование;
5) оценка
адекватности модели;
6) сравнение,
идентификация и прогнозирование;
7) дедукция и
абдукция;
8)
классификация и генерация конструктов;
9)
содержательное сравнение;
10)
планирование и поддержка принятия управленческих решений.
Каждая из
этих операций оказалась достаточно элементарна для формализации и программной
реализации.
Компоненты
АСК-анализа [12, 17, 18]:
–
формализуемая когнитивная концепция и следующий из нее когнитивный конфигуратор;
–
теоретические основы, методология, технология и методика АСК-анализа;
–
математическая модель АСК-анализа, основанная на системном обобщении теории
информации;
– методика
численных расчетов, в универсальной форме реализующая математическую модель
АСК-анализа, включающая иерархическую структуру данных и 24 детальных алгоритма
10 БКОСА;
– специальное
инструментальное программное обеспечение, реализующее математическую модель и
численный метод АСК-анализа – Универсальная когнитивная аналитическая система
"Эйдос".
Этапы
АСК-анализа:
1)
когнитивная структуризация предметной области;
2)
формализация предметной области (конструирование классификационных и
описательных шкал и градаций и подготовка обучающей выборки);
3) синтез
системы моделей предметной области (в настоящее время система Эйдос
поддерживает 3 статистические модели и 7 моделей знаний);
4)
верификация (оценка достоверности) системы моделей предметной области;
5) повышение
качества системы моделей;
6) решение
задач идентификации, прогнозирования и поддержки принятия решений;
7)
исследование моделируемого объекта путем исследования его моделей: кластерно-конструктивный
анализ классов и факторов; содержательное сравнение классов и факторов;
изучение системы детерминации состояний моделируемого объекта, нелокальные
нейроны и интерпретируемые нейронные сети прямого счета; построение
классических когнитивных моделей (когнитивных карт); построение интегральных когнитивных
моделей (интегральных когнитивных карт).
В АСК-анализе
все факторы рассматриваются с одной единственной точки зрения: сколько
информации содержится в их значениях о переходе объекта, на который они
действуют, в определенное состояние, и при этом сила и направление влияния всех
значений факторов на объект измеряется в одних общих для всех факторов единицах
измерения: единицах количества информации. Это напоминает подход Дугласа Хаббарда
[25], но, в отличие от него, имеет универсальный программный инструментарий,
разработанный в постановке, не зависящей от предметной области и находящийся в
полном открытом бесплатном доступе (даже с исходными текстами) на сайте автора:
http://lc.kubagro.ru/aidos/_Aidos-X.htm. Поэтому
АСК-анализ обеспечивает корректную сопоставимую обработку числовых и нечисловых
данных, представленных в разных типах измерительных шкал и разных единицах
измерения. Метод АСК-анализа является устойчивым непараметрическим методом,
обеспечивающим создание моделей больших размерностей при неполных и зашумленных
исходных данных о сложном нелинейном динамичном объекте управления. Этот метод
является чуть ли не единственным, обеспечивающим многопараметрическую типизацию
и системную идентификацию методов, инструментарий которого (интеллектуальная
система Эйдос) находится в полном открытом бесплатном доступе.
В развитии
различных теоретических и практических аспектов АСК-анализа приняли участие
многие ученые: Луценко Е.В., Лойко В.И.,
Трунев А.П. (Канада), Орлов А.И., Коржаков
В.Е., Барановская Т.П., Ермоленко В.В., Наприев И.Л., Некрасов С.Д., Лаптев В.Н.,
Третьяк В.Г., Щукин Т.Н., Симанков В.С., Ткачев А.Н., Сафронова Т.И., Макаревич
О.А., Макаревич Л.О., Сергеева Е.В. (Фомина Е.В.), Бандык Д.К., Артемов А.А.,
Крохмаль В.В., Рябцев В.Г. и другие.
Метод
системно-когнитивного анализа и его программный инструментарий интеллектуальная
система "Эйдос" были успешно применены при проведении научных
исследований, по результатам которых защищено довольно много докторских и кандидатских
диссертаций в различных направлениях науки: 3 доктора экономических наук (+1 в
стадии подтверждения в ВАК РФ, +1 в стадии подготовки к защите), 2 доктора
технических наук, 4 кандидата психологических наук, 1 кандидат технических
наук, 1 кандидат экономических наук, 1 кандидат медицинских наук:
АСК-анализ
был успешно применены при выполнении десятков грантов РФФИ и РГНФ различной
направленности за длительный период с 2002 года по настоящее время (2016 год).
По
проблематике АСК-анализа издана 21 монография, получено 28 патентов на системы
искусственного интеллекта, их подсистемы, режимы и приложения, опубликовано 196
статей в изданиях, входящих в Перечень ВАК РФ (по данным РИНЦ). В одном только
Научном журнале КубГАУ (входит в Перечень ВАК РФ с 26-го марта 2010 года)
автором АСК-анализа Луценко Е.В. опубликовано 175 статей по различным теоретическим
и практическим аспектам АСК-анализа, общим объёмом 297,246 у.п.л., в среднем
1,699 у.п.л. на одну статью.
По этим
публикациям, грантам и диссертационным работам видно, что АСК-анализ уже был
успешно применен в следующих предметных областях и научных направлениях:
экономика (региональная, отраслевая, предприятий, прогнозирование фондовых
рынков), социология, эконометрика, биометрия, педагогика (создание педагогических
измерительных инструментов и их применение), психология (личности,
экстремальных ситуаций, профессиональных и учебных достижений, разработка и
применение профессиограмм), сельское хозяйство (прогнозирование результатов применения
агротехнологий, принятие решений по выбору рациональных агротехнологий и микрозон
выращивания), экология, ампелография, геофизика (глобальное и локальное
прогнозирование землетрясений, параметров магнитного поля Земли, движения
полюсов Земли), климатология (прогнозирование Эль-Ниньо и Ла-Нинья), возобновляемая
энергетика, мелиорация и управление мелиоративными системами, и ряд других областей.
АСК-анализ
вызывает большой интерес во всем мире. Сайт автора АСК-анализа посетило около
500 тыс. посетителей с уникальными IP-адресами со всего мира. Еще около
500 тыс. посетителей (в расчете на фамилию автора) открывали статьи по
АСК-анализу в Научном журнале КубГАУ.
Все это
позволяет говорить о том, что АСК-анализ представляет собой современную
инновационную технологию искусственного интеллекта и постепенно превращается в
новое междисциплинарное научное направление.
В этом
качестве и для этой цели предлагается применить математическую
модель и методику численных расчетов (алгоритмы и структуры данных)
АСК-анализа, которая подробно описана в ряде работ [1, 2, 14, 17] и других.
Суть этой математической модели состоит в том, что сначала рассчитывается
матрица абсолютных частот, отражающая «пространственно-временные совпадения»,
т.е. факты, содержащиеся в исходных данных, а затем на основе на основе нее
рассчитываются матрицы условных и безусловных процентных распределений
(относительные частоты), матрица информативностей и другие модели знаний [15].
Методика
численных расчетов включает структуры внешних баз данных и данных в оперативной
памяти, а также алгоритмы их обработки, реализующие математическую модель [17].
Основными алгоритмами являются алгоритмы, реализующие базовые когнитивные
операции системного анализа (БКОСА).
Система
«Эйдос» является программным инструментарием АСК-анализа и
подробно описана в ряде работ [18], поэтому
здесь приведем лишь графическую схему преобразования данных в информацию, а ее
в знания и решения задач идентификации, прогнозирования, принятия решений и
исследования моделируемого объекта путем исследования его модели в системе
«Эйдос» (рисунок 2):
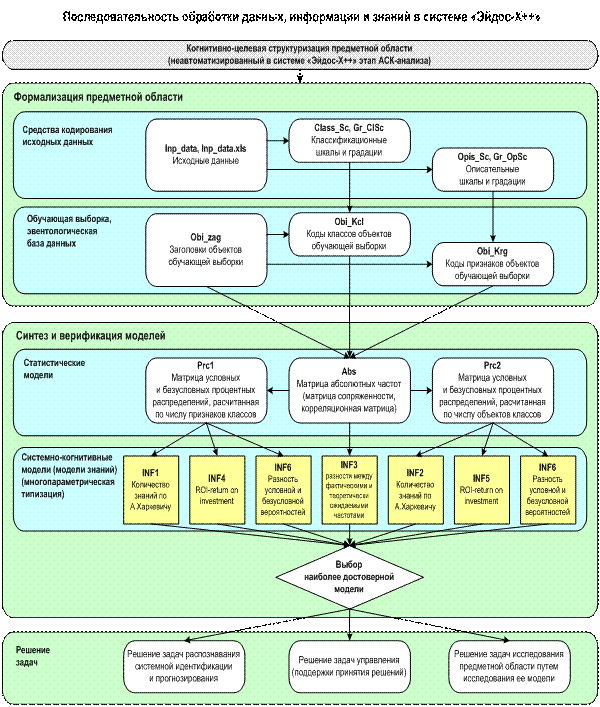
Рисунок 2 –
Схема преобразования данных в информацию, а ее в знания и решения задач
идентификации, прогнозирования, принятия решений и исследования моделируемого
объекта путем исследования его модели в системе «Эйдос»
При работе над данной статьей авторами разработана
специальная программа, скриншоты окна которой при выборе различных пунктов
приведены на рисунке 3:
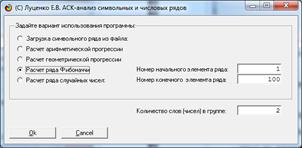
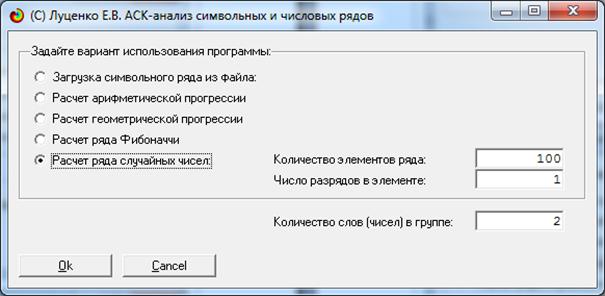
Рисунок 3 – Скриншоты окна программы подготовки
исходных данных
Эта программа предназначена для подготовки исходных
данных для системы «Эйдос» и обеспечивает
– ввод из внешнего DOS-TXT-файла числовой или
символьной последовательности с заданными параметрами (в качестве элементов
последовательности можно рассматривать числа-слова или цифра-символы, можно
переводить или не переводить символы в верхний регистр) и преобразования ее в
форму базы данных, непосредственно воспринимаемой одним из программных
интерфейсов системы «Эйдос» с внешними базами данных (стандарт этой базы данных
описан на рисунке 4);
– генерации известных неслучайных последовательностей:
арифметической и геометрической прогрессий и ряда Фибоначчи с заданными параметрами;
– генерации псевдослучайных последовательностей с
использованием стандартного генератора использованного языка программирования
(xBase++).
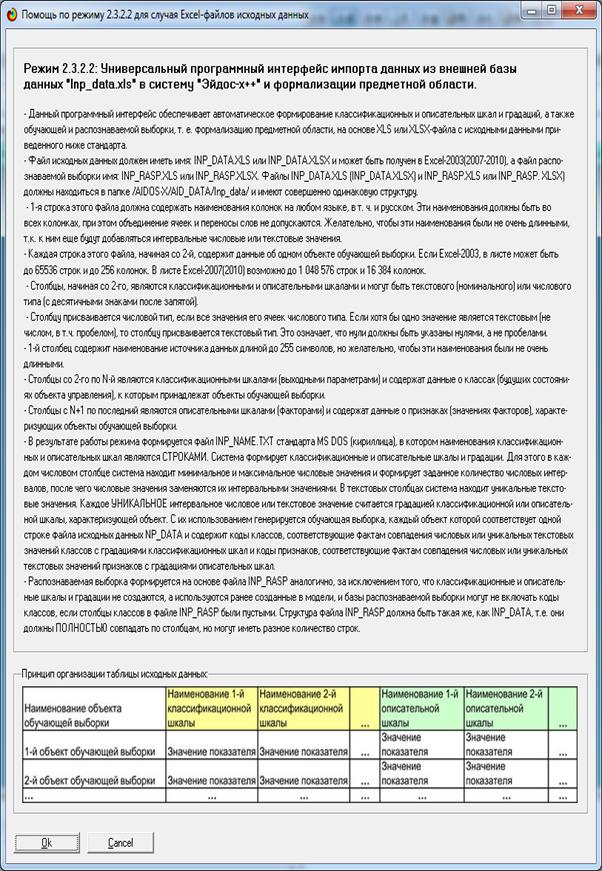
Рисунок 4 – Описание стандарта базы данных,
непосредственно воспринимаемой одним из программных интерфейсов системы «Эйдос»
с внешними базами данных
Исходный текст этой программы приведен ниже:
********************************************************************************
FUNCTION Main()
LOCAL
GetList[0], GetOptions, nColor, oMessageBox, oMenuWords, oDlg
DC_IconDefault(1000)
SET DECIMALS
TO 15
SET DATE
GERMAN
SET ESCAPE On
SET COLLATION
TO SYSTEM // Руссификация
*SET
COLLATION TO ASCII // Руссификация
PUBLIC aSay[30], Mess97, Mess98, Mess99 // Массив сообщений отображаемых
стадий исполнения (до 30 на экране)
PUBLIC Time_progress, Wsego, oProgress, lOk
PUBLIC nEvery := 100 // Количество
корректировок прогресс-бар
***********************************************************************************************************************
g = 0
s = 0
mRegim = 1
@g ,
0 DCGROUP oGroup1 CAPTION 'Задайте вариант использования программы:' SIZE 78.0,
7.5
@++s, 2 DCRADIO mRegim VALUE 1 PROMPT
'Загрузка символьного ряда из файла:' PARENT oGroup1
@++s, 2 DCRADIO mRegim VALUE 2 PROMPT
'Расчет арифметической прогрессии'
PARENT oGroup1
@++s, 2 DCRADIO mRegim VALUE 3 PROMPT
'Расчет геометрической прогрессии'
PARENT oGroup1
@++s, 2 DCRADIO mRegim VALUE 4 PROMPT 'Расчет ряда Фибоначчи' PARENT oGroup1
@++s, 2
DCRADIO mRegim VALUE 5 PROMPT 'Расчет ряда случайных чисел:' PARENT oGroup1
P1 = 45
P2 = 60
// Загрузка символьного ряда из файла
s = 1
cFile =
'Inp_data.txt'
nElement = 1
mUpper = .T.
@0.7,43
DCGROUP oGroup2 CAPTION '' SIZE 33, 5.5
HIDE {||.NOT.mRegim=1} PARENT oGroup1
@ 1+0.1, 4.5 DCSAY "Имя файла:"
EDITPROTECT {||.NOT.mRegim=1} HIDE {||.NOT.mRegim=1} PARENT oGroup2
@ 1,15
DCSAY "" GET cFile PICTURE "XXXXXXXXXXXX" EDITPROTECT {||.NOT.mRegim=1}
HIDE {||.NOT.mRegim=1} PARENT oGroup2
@ 2, 2 DCRADIO nElement VALUE 1 PROMPT 'Элементы-слова (числа)' EDITPROTECT {||.NOT.mRegim=1}
HIDE {||.NOT.mRegim=1} PARENT oGroup2
@ 3, 2 DCRADIO nElement VALUE 2 PROMPT 'Элементы-символы (цифры)' EDITPROTECT {||.NOT.mRegim=1} HIDE {||.NOT.mRegim=1} PARENT oGroup2
@ 4, 2 DCCHECKBOX mUpper PROMPT 'Перевести в заглавные' EDITPROTECT {||.NOT.mRegim=1} HIDE
{||.NOT.mRegim=1} PARENT oGroup2
P1 = 35
P2 = 61
// Расчет арифметической прогрессии
s = 2
N1 = 1
N2 = N1+99
D = 1
@
s+0.2, P1 DCSAY "Номер начального элемента ряда:" EDITPROTECT {||.NOT.mRegim=2} HIDE
{||.NOT.mRegim=2} PARENT oGroup1
@ s , P2 DCSAY "" GET N1 PICTURE
"##########" EDITPROTECT
{||.NOT.mRegim=2} HIDE {||.NOT.mRegim=2} PARENT oGroup1
@++s+0.2, P1
DCSAY "Номер конечного элемента ряда:" EDITPROTECT {||.NOT.mRegim=2} HIDE
{||.NOT.mRegim=2} PARENT oGroup1
@ s ,
P2 DCSAY "" GET N2 PICTURE "##########" EDITPROTECT {||.NOT.mRegim=2} HIDE
{||.NOT.mRegim=2} PARENT oGroup1
@++s+0.2, P1
DCSAY "Шаг прогрессии:" EDITPROTECT
{||.NOT.mRegim=2} HIDE {||.NOT.mRegim=2} PARENT oGroup1
@ s ,
P2 DCSAY "" GET D PICTURE
"##########" EDITPROTECT
{||.NOT.mRegim=2} HIDE {||.NOT.mRegim=2} PARENT oGroup1
// Расчет геометрической прогрессии
s = 3
N1 = 1
N2 = N1+99
Q =
1.1
@
s+0.2, P1 DCSAY "Номер начального элемента ряда:" EDITPROTECT {||.NOT.mRegim=3} HIDE
{||.NOT.mRegim=3} PARENT oGroup1
@ s , P2 DCSAY "" GET N1 PICTURE
"##########" EDITPROTECT
{||.NOT.mRegim=3} HIDE {||.NOT.mRegim=3} PARENT oGroup1
@++s+0.2, P1
DCSAY "Номер конечного элемента ряда:" EDITPROTECT
{||.NOT.mRegim=3} HIDE {||.NOT.mRegim=3} PARENT oGroup1
@ s ,
P2 DCSAY "" GET N2 PICTURE "##########" EDITPROTECT {||.NOT.mRegim=3} HIDE
{||.NOT.mRegim=3} PARENT oGroup1
@++s+0.2, P1
DCSAY "Знаменатель прогрессии:" EDITPROTECT {||.NOT.mRegim=3} HIDE
{||.NOT.mRegim=3} PARENT oGroup1
@ s ,
P2 DCSAY "" GET Q PICTURE
"###.######" EDITPROTECT
{||.NOT.mRegim=3} HIDE {||.NOT.mRegim=3} PARENT oGroup1
// Расчет ряда Фибоначчи
s
= 4
N1 =
1
N2 = N1+99
@
s+0.2, P1 DCSAY "Номер начального элемента ряда:" EDITPROTECT {||.NOT.mRegim=4} HIDE
{||.NOT.mRegim=4} PARENT oGroup1
@ s , P2 DCSAY "" GET N1 PICTURE
"##########" EDITPROTECT
{||.NOT.mRegim=4} HIDE {||.NOT.mRegim=4} PARENT oGroup1
@++s+0.2, P1
DCSAY "Номер конечного элемента ряда:" EDITPROTECT {||.NOT.mRegim=4} HIDE
{||.NOT.mRegim=4} PARENT oGroup1
@ s ,
P2 DCSAY "" GET N2 PICTURE "##########" EDITPROTECT {||.NOT.mRegim=4} HIDE
{||.NOT.mRegim=4} PARENT oGroup1
// Расчет ряда случайных чисел с равномерным рапределением
s
= 5
R1 =
100
R2 =
1
@
s+0.2, P1 DCSAY "Количество элементов ряда:" EDITPROTECT {||.NOT.mRegim=5} HIDE
{||.NOT.mRegim=5} PARENT oGroup1
@ s , P2 DCSAY "" GET R1 PICTURE
"##########" EDITPROTECT
{||.NOT.mRegim=5} HIDE {||.NOT.mRegim=5} PARENT oGroup1
@++s+0.2, P1
DCSAY "Число разрядов в элементе:" EDITPROTECT {||.NOT.mRegim=5} HIDE
{||.NOT.mRegim=5} PARENT oGroup1
@ s ,
P2 DCSAY "" GET R2 PICTURE "##########" EDITPROTECT {||.NOT.mRegim=5} HIDE
{||.NOT.mRegim=5} PARENT oGroup1
P1 = 35
P2 = 61
s
= 8.0
mGroup = 2
@
s+0.2,P1 DCSAY "Количество слов (чисел) в группе:"
@ s ,P2 DCSAY "" GET mGroup PICTURE
"##########"
DCGETOPTIONS
TABSTOP
DCREAD GUI ;
TO lExit ;
FIT ;
OPTIONS
GetOptions ;
ADDBUTTONS;
MODAL ;
TITLE '(C) Луценко Е.В. АСК-анализ символьных и числовых рядов'
********************************************************************
IF lExit
**
Button Ok
ELSE
QUIT
ENDIF
********************************************************************
***********************************************************************************************************************
***********************************************************************************************************************
T_Mess1 = "Начало: "+TIME() // Начало
Sec_1 =
(DOY(DATE())-1)*86400+SECONDS()
IF mRegim =
5 // Расчет ряда случайных чисел (с
равномерным рапределением)
N1 = 1
N2 = R1
ENDIF
nMax = N2 - N1 + 1
Mess =
'АСК-анализ рядов. Генерация ряда'
@ 4,5 DCPROGRESS oProgress SIZE 70,1.1 MAXCOUNT nMax
COLOR GRA_CLR_CYAN PERCENT EVERY 100
DCREAD GUI TITLE Mess PARENT @oDialog FIT EXIT
oDialog:show()
nTime = 0
DC_GetProgress(oProgress,0,nMax)
********
Формирование текстовой переменной с символами ******************
mInpData :=
"" // Текстовая
переменная для загрузки текстового файла
DO CASE
CASE mRegim = 1 // Загрузка символьного ряда из файла:
IF .NOT. FILE(cFile)
Mess
= 'В текущей папке нет файла: "#"'
Mess
= STRTRAN(Mess, "#", cFile)
LB_Warning(Mess)
CLOSE
ALL
RETURN
NIL
ELSE
mInpData = CharOne(' ',FILESTR(cFile)) // Загрузка cFile
IF
mUpper
// Перевести в заглавные
mInpData = UPPER(mInpData)
ENDIF
IF
nElement = 2 //
Элементы - символы (цифры)
mInpData2 = ""
FOR j=1 TO LEN(mInpData)
mInpData2 = mInpData2 + SUBSTR(mInpData,j,1) + " "
NEXT
mInpData = CharOne(' ', mInpData2) // Удалить подряд идущие пробелы
ENDIF
mOptions = 'Загрузка символьного
ряда из файла: "#". Количество слов (чисел) в группе: @"'
mOptions = STRTRAN(mOptions, "#", cFile)
mOptions = STRTRAN(mOptions, "@", ALLTRIM(STR(mGroup)))
ENDIF
CASE mRegim = 2 // Расчет арифметической прогрессии
FOR n = N1 TO N2
Xn =
ROUND(N1+D*(n-1), 0)
mInpData = mInpData + ALLTRIM(STR(Xn)) + " " // Текстовая переменная для
загрузки текстового файла
DC_GetProgress(oProgress, ++nTime, nMax)
NEXT
mOptions = 'Расчет элементов
арифметической прогрессии от: "#" до "@" с шагом
"D".'
mOptions = STRTRAN(mOptions, "#",
ALLTRIM(STR(N1)))
mOptions
= STRTRAN(mOptions, "@", ALLTRIM(STR(N2)))
mOptions
= STRTRAN(mOptions, "D", ALLTRIM(STR(D)))
CASE mRegim = 3 //
Расчет геометрической прогрессии
FOR n = N1 TO N2
Xn = ROUND(N1*Q^(n-1), 0)
mInpData = mInpData + ALLTRIM(STR(Xn)) + " " // Текстовая переменная для
загрузки текстового файла
DC_GetProgress(oProgress, ++nTime, nMax)
NEXT
mOptions = 'Расчет элементов
геометрической прогрессии от: "#" до "@" со знаменталем
"Q".'
mOptions = STRTRAN(mOptions, "#",
ALLTRIM(STR(N1)))
mOptions
= STRTRAN(mOptions, "@", ALLTRIM(STR(N2)))
mOptions
= STRTRAN(mOptions, "Q", ALLTRIM(STR(Q)))
CASE mRegim =
4 // Расчет ряда Фибоначчи
FOR n =
N1 TO N2
SQRT5 = SQRT(5)
Xn =
1/SQRT5*((1+SQRT5)/2)^n-1/SQRT5*((1-SQRT5)/2)^n
Xn =
ROUND(Xn, 0)
mInpData = mInpData + ALLTRIM(STR(Xn)) + " " // Текстовая переменная для загрузки текстового файла
DC_GetProgress(oProgress, ++nTime, nMax)
NEXT
mOptions = 'Расчет элементов ряда
Фибоначчи от: "#" до "@".'
mOptions = STRTRAN(mOptions, "#", ALLTRIM(STR(N1)))
mOptions
= STRTRAN(mOptions, "@", ALLTRIM(STR(N2)))
CASE mRegim = 5 //
Расчет ряда случайных чисел (с равномерным рапределением)
N1 = 1
N2 = R1
FOR j =
N1 TO N2
Xn = SUBSTR(ALLTRIM(STR(RANDOM())),1,R2) // Генерация
5-разрядного псевдослучайного числа, преобразование го в текстовую форму и получение
старшего разряда
mInpData = mInpData + ALLTRIM(Xn) +
" " //
Текстовая переменная для загрузки текстового файла
DC_GetProgress(oProgress, ++nTime, nMax)
NEXT
mOptions = 'Расчет # элементов ряда
$-разрядных случайных чисел (с равномерным рапределением).'
mOptions = STRTRAN(mOptions, "#",
ALLTRIM(STR(R1)))
mOptions
= STRTRAN(mOptions, "$", ALLTRIM(STR(R2)))
ENDCASE
STRFILE(mOptions, 'Options.txt')
STRFILE(mInpData, 'Inp_data.txt')
*MsgBox('STOP')
DC_GetProgress(oProgress,nMax,nMax)
oDialog:Destroy()
********
Формирование БД Inp_data.dbf на основе текстовой переменной ****
***** Создание БД Inp_data.dbf
CLOSE ALL
CrLf = CHR(13)+CHR(10) // Конец строки (записи)
mInpName := "" // TXT-переменная с наименованиями
полей
aStructure := { { "ObjName",
"C", 250, 0 }, ;
{ "Futur" ,
"C", 250, 0 }, ;
{ "Retro" ,
"C", 250, 0 } }
DbCreate( "Inp_data.dbf", aStructure )
mInpName = mInpName + "Futur" + CrLf +
"Retro" + CrLf
STRFILE(mInpName, "Inp_name.txt")
CLOSE ALL
USE Inp_data EXCLUSIVE NEW
IF NUMTOKEN(mInpData," ") >= mGroup + 1
nMax =
NUMTOKEN(mInpData," ") - mGroup - 1
Mess = 'АСК-анализ рядов. Формирование БД
"Inp_data.dbf"'
@ 4,5 DCPROGRESS oProgress2 SIZE 70,1.1 MAXCOUNT nMax
COLOR GRA_CLR_CYAN PERCENT EVERY 100
DCREAD GUI
TITLE Mess PARENT @oDialog2 FIT EXIT
oDialog2:show()
nTime = 0
DC_GetProgress(oProgress,0,nMax)
*** Начало цикла по словам *******
FOR t=1 TO NUMTOKEN(mInpData," ")
- mGroup - 1 // Цикл
по текущей дате
mWordR = ""
FOR j=1
TO mGroup // Прошлая группа
mWordR = mWordR + TOKEN(mInpData," ",t+j-1) + " "
NEXT
mWordF =
""
FOR j=1
TO mGroup //
Следующая группа
mWordF = mWordF + TOKEN(mInpData," ",t+mGroup+j-1) + "
"
NEXT
APPEND
BLANK
FIELDPUT(1, ALLTRIM(STR(t)))
FIELDPUT(2, mWordF)
FIELDPUT(3, mWordR)
DC_GetProgress(oProgress2, ++nTime, nMax)
NEXT
*
MsgBox('STOP')
DC_GetProgress(oProgress2,nMax,nMax)
oDialog2:Destroy()
ENDIF
CLOSE ALL
***** Прошло секунд с начала процесса
Sec_2 =
(DOY(DATE())-1)*86400+SECONDS() - Sec_1
Sec_2 = (DOY(DATE())-1)*86400+SECONDS() - Sec_1
ch2 =
INT(Sec_2/3600)
&& Часы
mm2 =
INT(Sec_2/60)-ch2*60
&& Минуты
cc2 =
Sec_2-ch2*3600-mm2*60
&& Секунды
Mess = 'Процесс создания БД "Inp_data.dbf" и "Inp_name.txt" завершился успешно! Время исполнения # секунд!'
Mess =
STRTRAN(Mess,"#",STRTRAN(STR(cc2,2)," ","0"))
LB_Warning(Mess, '(C) Луценко Е.В. АСК-анализ символьных и
числовых рядов')
RETURN NIL
***********************************************************************************************************************
FUNCTION LB_Warning( message, ctitle )
LOCAL aMsg :=
{}
DEFAULT cTitle
TO ''
IF
valtype(message) # 'A'
aadd(aMsg,message)
ELSE
aMsg :=
message
ENDIF
IF
LEN(ALLTRIM(cTitle)) > 0
DC_MsgBox( ,,aMsg,cTitle)
ELSE
DC_MsgBox( ,,aMsg,'Универсальная
когнитивная аналитическая система "Эйдос-Х++"')
ENDIF
RETURN NIL
*
Примечание: красным цветом выделена строка, в которой задается тип генератора
псевдослучайных чисел
Это сделано с целью
облегчить программистам ее реализацию на других языках программирования, если у
них возникнет такое желание.
В исследовании, описанном
ниже в данной статье, авторами исследовались числовые псевдослучайные
последовательности из одноразрядных чисел с различной длиной
последовательности, используемой в качестве обучающей выборки: 10, 20, 100,
1000, 2000, 3000, 5000, 7000, 10000, 20000, 30000 чисел. Эти последовательности
программа записывает в виде DOS-TXT-файла:
c:\Aidos-X\AID_DATA\Inp_data\100\Inp_data.txt в папку, из которой система
«Эйдос» берет внешние исходные данные.
При создании моделей была
исследована зависимость последующей группы из двух одноразрядных
псевдослучайных чисел на предыдущей. Вероятности верной идентификации и
неидентификации пар псевдослучайных чисел и значения асимптотического
информационного критерия качества шума в различных моделях, созданных на основе
10, 20, 100, 1000, 2000, 3000, 5000, 7000, 10000, 20000, 30000 чисел приведены
в таблице 1 на рисунках 5 и 6:
Таблица 1 – Вероятности
верной идентификации и неидентификации
в моделях, созданных на основе различных объемов выборки
|
Объем выборки
|
Вероятность
верной
идентификации
%
|
Вероятность
верной
неидентификации
%
|
Асимптотический информационный
критерий качества шума
|
|
% от теоретически максимально возможного
|
бит
|
|
10
|
100,00000
|
100,00000
|
15,656
|
0,99255
|
|
20
|
100,00000
|
91,28151
|
13,004
|
0,82445
|
|
100
|
100,00000
|
93,82898
|
11,343
|
0,71914
|
|
1000
|
99,29789
|
62,53239
|
8,049
|
0,51030
|
|
2000
|
82,82424
|
62,24528
|
7,409
|
0,46971
|
|
3000
|
79,31265
|
58,13248
|
7,113
|
0,45098
|
|
5000
|
73,86432
|
56,75676
|
6,663
|
0,42243
|
|
7000
|
72,67400
|
54,79248
|
6,119
|
0,38793
|
|
10000
|
68,23047
|
54,70407
|
5,994
|
0,38001
|
|
20000
|
63,56453
|
52,35414
|
5,232
|
0,33168
|
|
30000
|
60,07601
|
53,29280
|
5,130
|
0,32525
|
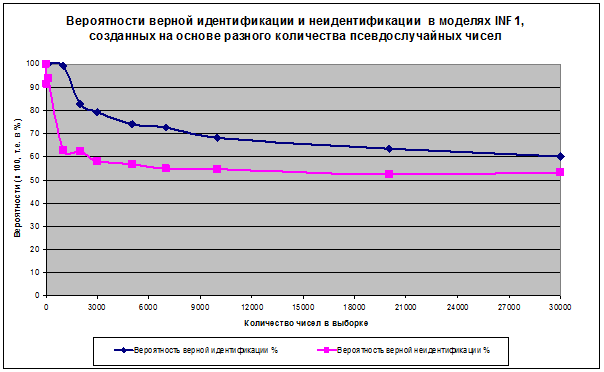
Рисунок 5 – Вероятности
верной идентификации и неидентификации
в моделях INF1 [15], созданных на основе разного количества псевдослучайных
чисел
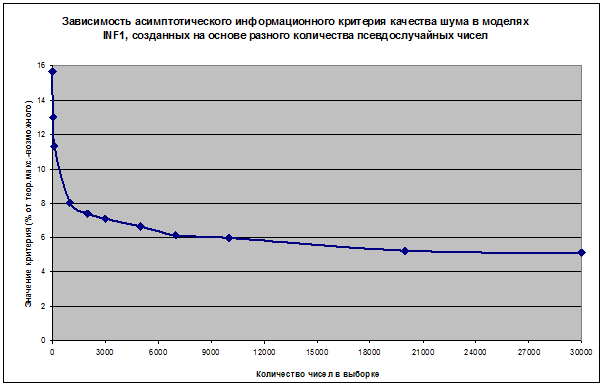
Рисунок 6 –
Зависимость асимптотического информационного критерия качества шума
в моделях INF1 [15], созданных на основе разного количества псевдослучайных чисел
Из таблицы 1
и рисунков 5 и 6 мы видим, что:
– модели,
созданные на основе сравнительно небольшого количества псевдослучайных чисел
(до 1000), имеют очень высокую достоверность идентификации пары последующих
чисел по паре предшествующих, близкую к 100%;
– при
увеличении объема выборки от 1000 до 10000 чисел достоверность сначала быстро,
а затем все медленнее и медленнее снижается, т.е. асимптотически сходится к
некоторому значению (пределу);
– при объемах
выборки от 10000 до 30000 чисел достоверность модели стабилизируется и
практически не меняется, асимптотически приближаясь к некоторому предельному
значению.
На основе
этих результатов можно сделать следующие выводы:
1. Системе
«Эйдос» успешно удается выявить закономерности взаимосвязи между предыдущей и
последующей парой псевдослучайных чисел. Это означает, что качество шума, генерируемого
стандартным генератором псевдослучайных чисел языка программирования xBbase++
(RANDOM()), можно считать довольно низким.
2. Когда
чисел менее 1000, то выявление закономерностей взаимосвязи между предыдущей и
последующей парой псевдослучайных чисел
для системы «Эйдос» является тривиальной (элементарной) задачей.
3. Но и для
моделей, созданных на основе значительно большего количества псевдослучайных
чисел: 10000, 20000 и 30000, тоже совершенно очевидно, что полученные
результаты были бы невозможны, если бы последовательность чисел была действительно
случайной, т.е. шум был качественным.
На основании
того факта, что при объемах выборки от 10000 до 30000 чисел достоверность
модели практически не меняется, асимптотически приближаясь к некоторому
предельному значению, можно сделать вывод о том, предложенный асимптотический
информационный критерий качества шума действительно работает.
То есть можно считать, что значение этого критерия для выборки 10000 уже
достаточно хорошо отражает качество шума и при дальнейшем увеличении объема
выборки меняется несущественно.
Отметим, что
для чистого шума количественное значение этого критерия должно быть равно 0 и
чем ближе критерий к этому значению при таких объемах выборки, при увеличении
которых этот критерий уже существенно не меняется, тем ближе к чистому шуму
сигнал, на основе которого создана модель.
Из вышесказанного следуют такие формулировки
асимптотического информационного критерия близости сигнала к шуму:
– сигнал
тем ближе к шуму, чем быстрее при неограниченном увеличении числа отсчетов
стремится к нулю количество информации в значениях одних его элементов о
значениях других элементов;
– для шума количество информации в
одних его элементах о значениях других асимптотически стремится к нулю при
неограниченном увеличении количества элементов.
Полученные
закономерности можно считать примерами действия закона больших чисел (в его
содержательной интерпретации; математические формулировки еще предстоит
получить).
В созданной
модели INF1 отражено, какое количество информации содержится в предшествующей
паре псевдослучайных чисел о последующей. Это количество информации может быть
положительным (если говорит о том, что произойдет),
и отрицательным (если говорит о том, чего не произойдет), также больше или
меньше по модулю (чем больше модуль – тем сильнее влияние).
Вся эта
информация отражена в SWOT-матрице и SWOT-диаграмме,
которые являются стандартными выходными формами системы “Эйдос” (рисунки 7, 8)
[16].
На
инвертированных SWOT-матрицах и SWOT-диаграммах (предложены автором в работе
[16]), мы видим, какие последующие пары псевдослучайных чисел обуславливает
предыдущая пара 1_1 (рисунки 9 и 10):
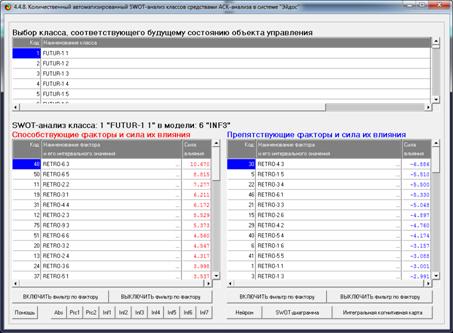
Рисунок 7 –
Пример SWOT-матрицы, показывающей зависимости между предыдущими парами чисел и
последующей парой 1_1 в модели INF1 [15], созданной основе 30000 псевдослучайных
чисел

Рисунок 8 –
Пример SWOT-диаграммы, показывающей зависимости между предыдущими парами чисел
и последующей парой 1_1 в модели INF1 [15], созданной основе 30000 псевдослучайных
чисел
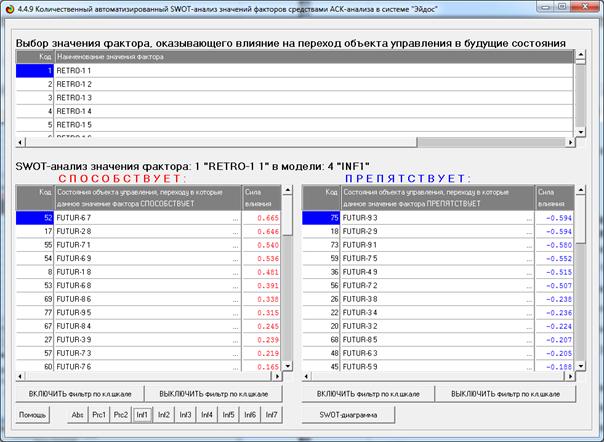
Рисунок 9 –
Пример SWOT-матрицы, показывающей зависимости между предыдущей парой чисел 1_1
и последующими в модели INF1 [15], созданной основе 30000 псевдослучайных чисел

Рисунок 10 –
Пример SWOT-диаграммы, показывающей зависимости между предыдущей парой чисел
1_1 и последующими в модели INF1 [15], созданной основе 30000 псевдослучайных
чисел
Из рисунков
7, 8 и 9, 10 хорошо видно, что система детерминации будущих пар псевдослучайных
чисел, выявленная системой «Эйдос», весьма мало напоминает случайную. При
использовании других датчиков псевдослучайных чисел картина может быть иной, но
это предмет дальнейших исследований.
Когнитивные функции – это наглядное графическое отображение
матриц различных моделей, создаваемых сисемой «Эйдос» и перечисленных на рисунке
(2) [1, 3].
Когнитивные
функции являются обобщением понятия функции, которое более пригодно для
адекватного отражения причинно-следственных зависимостей в реальной области, т.к. они отражают
количество информации содержится в значении аргумента о значении функции.
Определены
понятия нередуцированных, частично и полностью редуцированных прямых и
обратных, позитивных и негативных когнитивных функций и метод формирования
редуцированных когнитивных функций, являющийся обобщением известного
взвешенного метода наименьших квадратов на основе учета в качестве весов
наблюдений количества информации в значениях аргумента о значениях функции [1,
3].
Человек обладает естественной высокоразвитой
способностью обнаруживать в изображениях закономерности, и в некоторых случаях
эта способность на много превосходит аналогичные возможности программного
обеспечения и компьютеров. Поэтому когнитивные функции могут быть очень полезны
для решения задач, решаемых в данной статье.
В качестве примера рассмотрим две когнитивные функции:
матрицы абсолютных частот ABS и матрицы информативностей INF1 для модели
созданной на основе 30000 псевдослучайных чисел (рисунки 11 и 12):
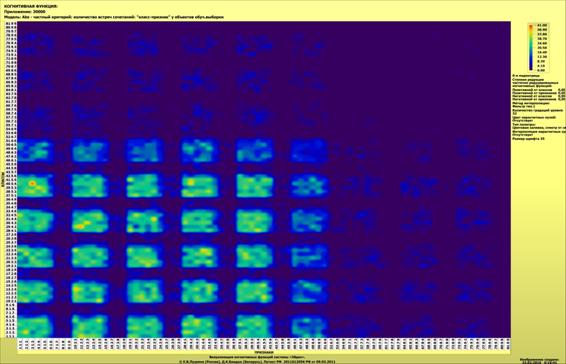
Рисунок 11 – Когнитивная функция матрицы абсолютных
частот ABS для модели,
созданной на основе 30000 псевдослучайных чисел
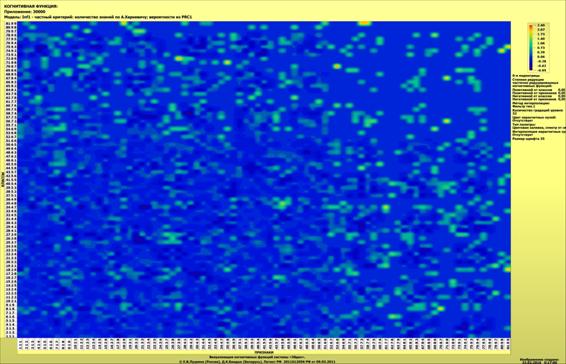
Рисунок 12 – Когнитивная функция матрицы
информативностей INF1 для модели,
созданной на основе 30000 псевдослучайных чисел
Из рисунков 11 и 12 также очень хорошо видно, что
система детерминации будущих пар псевдослучайных чисел, выявленная системой
«Эйдос», весьма мало напоминает случайную. Особенно на основании рисунка 11
можно сделать вывод о том, что определенные диапазоны пар предыдущих псевдослучайных
чисел гораздо чаще встречаются с определенными диапазонами пар последующих
чисел, чем с другими.
Предложен асимптотический информационный критерий
качества шума, а также метод, технология и методика его применения на практике.
В качестве метода применения асимптотического информационного критерия качества
шума на практике предлагается автоматизированный системно-когнитивный анализ
(АСК-анализ), в качестве технологии – программный инструментарий АСК-анализа:
универсальная когнитивная аналитическая система «Эйдос», в качестве методики –
методика создания приложений в данной системе, а также их использования для
решения задач идентификации, прогнозирования, принятия решений и исследования
предметной области путем исследования ее модели. Приводится наглядный численный
пример, иллюстрирующий излагаемые идеи и подтверждающий работоспособность
предлагаемого асимптотического информационного критерия качества шума, а также
метода, технологии и методики его применения на практике.
Применению на практике предложенного асимптотического
информационного критерия качестве шума на практике может способствовать и то,
что система «Эйдос» размещена в полном открытом бесплатном доступе на сайте
автора по адресу: http://lc.kubagro.ru/aidos/_Aidos-X.htm.
В частности, применить эту технологию могут и участники научной дискуссии по
методу Монте-Карло, проводимой журналом «Заводская лаборатория. Диагностика
материалов».
В лабораторных работах, встроенных в систему систему
«Эйдос-Х++», уже есть работа вычислительного типа 2.01: «Исследование
случайной семантической информационной модели при различных объемах выборки»
[38] (рисунок 13):
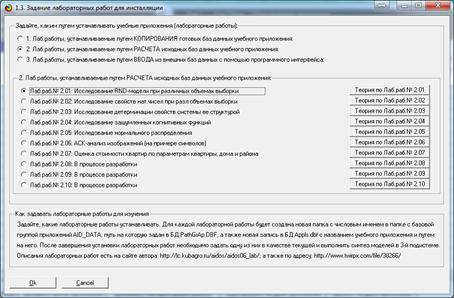
Рисунок 13. Экранная форма системы «Эйдос-Х++»,
обеспечивающая установку
лабораторной работы по исследованию псевдослучайных моделей
На основе материалов данной статьи может быть
реализована еще одна лабораторная работа (2.08) по дисциплинам, связанным с
интеллектуальными технологиями, представлением знаний и системами искусственного
интеллекта, а также в других областях [38].
В работах, приведенных в списке литературы [26-40],
приведены примеры применения сходных подходов к анализу текстов,
последовательности миллиона десятичных знаков числа 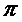 и др.
и др.
В качестве перспективы продолжения намеченного в данном
разделе направления исследований авторы планируют:
– усовершенствовать описанную выше программу генерации
исходных данных, которое обеспечит использование для генерации псевдослучайной
последовательности различные алгоритмы;
– усовершенствовать описанную выше программу генерации
исходных данных, которое обеспечит графическую визуализацию зависимости
последующих значений элементов ряда от предыдущих;
– интегрировать описанную выше программу генерации
исходных данных в состав системы «Эйдос» как один из видов программного
интерфейса с внешними данными и лабораторную работу вычислительного типа (2.01,
см. рисунок 13);
– провести численные исследования и сравнения качества
шума, получаемого с помощью различных алгоритмов, а также с помощью различных
архиваторов и методов шифрования;
– разработать в системе «Эйдос» выходную форму со
значениями предложенного в данном разделе асимптотического информационного критерия
качества шума для всех создаваемых в системе моделей;
– применить предельные теоремы теории вероятностей и
математической статистики для изучения асимптотических свойств предложенного
информационного критерия качества шума.
![]() – суммарное количество наблюдений при i-м
значении аргумента по всей выборке;
– суммарное количество наблюдений при i-м
значении аргумента по всей выборке;![]() – суммарное количество наблюдений j-го значении функции по всей
выборке;
– суммарное количество наблюдений j-го значении функции по всей
выборке;![]() – суммарное количество наблюдений по всей
выборке;
– суммарное количество наблюдений по всей
выборке;![]() – безусловная относительная частота встречи i-го значения аргумента в обучающей
выборке;
– безусловная относительная частота встречи i-го значения аргумента в обучающей
выборке;![]() имеющихся у них
признаков:
имеющихся у них
признаков:![]()
![]() (1)
(1)![]() это среднее
количество информации в i-м значении
фактора:
это среднее
количество информации в i-м значении
фактора: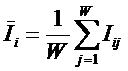









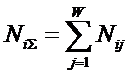
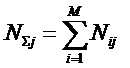
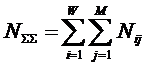
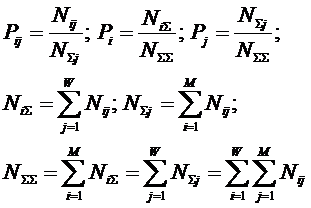
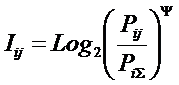
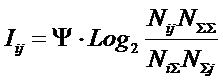

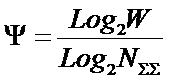
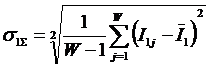
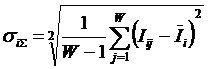
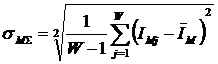
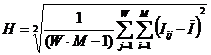












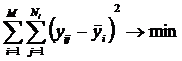
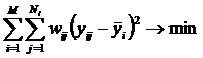
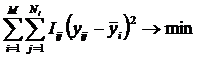
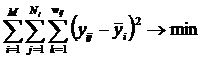
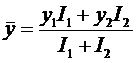 .
.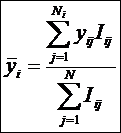 .
.