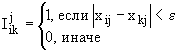ГЛАВА 13. МЕТОД КОГНИТИВНОЙ
КЛАСТЕРИЗАЦИИ ИЛИ
КЛАСТЕРИЗАЦИЯ НА ОСНОВЕ ЗНАНИЙ
(Кластеризация в системно-когнитивном анализе
и интеллектуальной системе «Эйдос»)
«Мышление – это обобщение,
абстрагирование,
сравнение, и классификация»
Патанджали[1],
II в. до н. э.
“Истинное знание – это знание причин”
Френсис Бэкон (1561–1626 гг.)
Кластерный
анализ[2]
(англ. Data clustering) – это задача разбиения заданной
выборки объектов (ситуаций) на подмножества, называемые кластерами,
так, чтобы каждый кластер состоял из схожих объектов, а объекты
разных кластеров существенно отличались. Кластерный анализ очень широко применяется
как в науке, так и в различных направлениях практической деятельности. Значение
кластерного анализа невозможно переоценить, оно широко известно[3]
и нет необходимости его специально обосновывать.
Существует большое количество различных методов кластерного анализа, хорошо
описанных в многочисленной специальной литературе[4]
и прекрасных обзорных статьях[5].
Поэтому в данной работе мы не ставим перед собой задачу дать еще одно подобное
описание, а обратим основное внимание на проблемы,
существующие в кластерном анализе и вариант их решения, предлагаемый в
автоматизированном системно-когнитивном анализе (АСК-анализ). Эти проблемы, в основном, хорошо известны
специалистам, и поэтому наш краткий обзор будет практически полностью основан
на уже упомянутых работах. Необходимо специально отметить, что специалисты
небезуспешно работают над решением этих проблем, предлагая все новые и новые
варианты, которые и являются различными вариантами кластерного анализа. Мы в
данной работе также предложим еще один ранее не описанный в специальной
литературе (т.е. новый, авторский) теоретически обоснованный и
программно-реализованный вариант решения некоторых из этих проблем, а также
проиллюстрируем его на простом численном примере.
Почему же разработано так много
различных методов кластерного анализа, почему это было необходимо? Кажутся
почти очевидными мысли о том, что различные методы кластерного анализа дают
результаты различного качества, т.е.
одни методы в определенном смысле
«лучше», а другие «хуже», и это действительно так[6],
и, следовательно, по-видимому, должен
существовать только один-единственный метод кластеризации, всегда (т.е. на любых данных) дающий «правильные» результаты, тогда
как все остальные методы являются «неправильными». Однако если задать аналогичный
вопрос по поводу, например, автомобиля или одежды, то становится ясным, что нет
просто наилучшего автомобиля, а есть лучшие по определенным
критериям-требованиям или лучшие для определенных целей. При этом сами критерии также должны быть обоснованы и не
просто могут быть различными, но и должны быть различными при различных целях,
чтобы отражать цель и соответствовать ей. Так автомобиль, лучший для семейного
отдыха не являются лучшим для гонок Формулы-1 или для представительских целей.
Аналогично можно обоснованно утверждать, что одни методы кластерного анализа
являются более подходящими для кластеризации данных определенной структуры, а
другие – другой, т.е. не существует одного наилучшего во всех случаях универсального метода кластеризации, но существуют
методы более универсальные и методы менее универсальные. Но все же многообразие
разработанных методов кластерного анализа на наш взгляд указывает не только на
это, но и на то, что их можно
рассматривать как различные более или
менее успешные варианты решения или попытки решения тех или иных проблем,
существующих в области кластерного анализа.
Для структурирования
дальнейшего изложения сформулируем требования к исходным данным в кластерном
анализе и фундаментальные вопросы, которые решают разработчики различных
методов кластерного анализа.
Считается[7],
что кластерный анализ предъявляет следующие требования
к исходным данным:
1. Показатели не должны
коррелировать между собой.
2. Показатели должны быть
безразмерными.
3. Распределение показателей
должно быть близко к нормальному.
4. Показатели должны отвечать
требованию «устойчивости», под которой понимается отсутствие влияния на их
значения случайных факторов.
5. Выборка должна быть
однородна, не содержать «выбросов».
Даже поверхностный анализ
сформулированных требований к исходным данным сразу позволяет утверждать, что на практике они в полной мере никогда не
выполняются, а приведение исходных данных к виду, удовлетворяющему этим
требованиям, или очень сложно, т.е. представляет собой проблему, и не одну, или даже
теоретически невозможно в полной мере. В любом случае пытаться это делать
можно различными способами, хотя чаще всего на практике этого не делается
вообще или потому, что необходимость этого плохо осознается исследователем,
или чаще потому, что в его распоряжении нет соответствующих инструментов,
реализующих необходимые методы[8].
Конечно, в последнем случае не приходится удивляться тому, что результаты
кластерного анализа получаются мягко сказать «несколько странными», а если они
соответствуют здравому смыслу и точке зрения экспертов, то можно сказать, что
это получилось случайно или потому, что «просто повезло».
Остановимся подробнее на
анализе перечисленных требований к исходным данным, а также проблем,
возникающих при попытке их выполнения и решения.
Первое
требование связано с использованием в большинстве методов
кластеризации евклидова расстояния
или различных его вариантов в качестве меры близости объектов и кластеров.
Другими словами это требование означает, что описательные шкалы, рассматриваемые
как оси семантического пространства, должны быть ортонормированны, т.к. в
противном случае применение евклидова расстояния и большинства других метрик
(таблица 1) (кроме расстояния Махалонобиса) теоретически необоснованно и некорректно.
Существуют и другие метрики, в
частности: квадрат евклидова расстояния, расстояние городских кварталов
(манхэттенское расстояние), расстояние
Чебышева, степенное расстояние, процент несогласия, метрики Рао,
Хемминга, Роджерса-Танимото, Жаккара, Гауэра, Воронина, Миркина, Брея-Кертиса,
Канберровская и многие другие[9]. Когда корреляции между переменными равны нулю, расстояние Махаланобиса
эквивалентно квадрату евклидового расстояния (там же). Это означает, что
метрику Махаланобиса можно считать обобщением евклидовой метрики для неортонормированных
пространств[10].
Таблица 1 – ОСНОВНЫЕ ТИПЫ МЕТРИК ПРИ КЛАСТЕР-АНАЛИЗЕ[11]
|
№ |
Наименование |
Тип признаков |
Формула для оценки меры близости (метрики) |
|
1 |
Эвклидово
расстояние |
Количественные |
|
|
2 |
Мера
сходства Хэмминга |
Номинальные
(качественные) |
|
|
3 |
Мера
сходства Роджерса–Танимото |
Номинальные шкалы |
|
|
4 |
Манхэттенская
метрика |
Количественные |
|
|
5 |
Расстояние
Махаланобиса |
Количественные |
|
|
6 |
Расстояние
Журавлева |
Смешанные |
|
Но на практике это требование никогда в полной мере не выполняется, а
для его выполнения необходимо выполнить операцию ортонормирования
семантического пространства, при которой из модели тем или иным методом[12]
(реализованным в программной системе, в которой проводится кластерный анализ) исключаются все шкалы, коррелирующие
между собой.
Таким образом, первое требование к исходным
данным порождает две проблемы:
Проблема
1.1 выбора метрики, корректной для неортонормированных
пространств.
Проблема
1.2 ортонормирования пространства.
Второе
требование
(безразмерности показателей) вытекает из того, что выбор единиц измерения по осям существенно влияет на результаты
кластеризации. Казалось бы, одного этого должно быть достаточно для того,
чтобы не делать этого, т.к. выбор единиц измерения, по сути, произволен
(определяется исследователем), вследствие чего и результаты кластеризации,
вместо того чтобы объективно отражать структуру данных и описываемой ими
объективной реальности, также становятся произвольными и зависящими не только
от самой исследуемой реальности, но и от произвола исследователя (причем
неизвестно от чего больше: от реальности или исследователя). По сути, автоматизированная система кластеризации
превращается в этих условиях из инструмента исследования структуры объективной
реальности в автоматизированный инструмент рисования таких дендрограмм, какие
больше нравятся пользователю. Непонятно также, какой содержательный смысл
могут иметь, например корни квадратные из сумм квадратов разностей координат
объектов, классов или кластеров, измеряемых
в различных единицах измерения. Разве
корректно складывать величины даже одного рода, измеряемые в различных
единицах измерения, а тем более разного рода? Даже если сложить
величины одного рода, но измеренные в разных единицах измерения, например расстояния от школы до подъезда дома 1.2
(километра), и от подъезда дома до квартиры 25 (метров), то получится 26,2 непонятно чего. Если же сложить разнородные
по смыслу величины, т.е. величины
различной природы, такие, например, как квадрат разности веса студентов с
квадратом разности их роста, возраста, успеваемости и т.д., а потом еще извлечь
из этой суммы квадратный корень, то получится просто бессмысленная величина, которая в традиционном кластерном анализе
почему-то называется «Евклидово расстояние». В школе на уроке физики в 8-м
классе за подобные действия сразу бы поставили «Неуд»[13].
Однако, как это ни удивительно, то, что «не прошло бы» на уроке физики в
средней школе является вполне устоявшейся практикой в «статистике» и ее псевдонаучных
применениях на уровне руководства системой образования.
В
подтверждение тому, что подобная практика действительно существует, авторы не
могут удержаться от искушения и не привести пространную цитату из работы[14]:
«Заметим, что евклидово расстояние (и
его квадрат) вычисляется по исходным, а не по стандартизованным данным. Это обычный способ его вычисления,
который имеет определенные преимущества (например, расстояние между двумя
объектами не изменяется при введении в анализ нового объекта, который может
оказаться выбросом). Тем не менее, на
расстояния могут сильно влиять различия между осями, по координатам которых
вычисляются эти расстояния. К примеру, если одна из осей измерена в
сантиметрах, а вы потом переведете ее в миллиметры (умножая значения на 10), то
окончательное евклидово расстояние (или квадрат евклидова расстояния),
вычисляемое по координатам, сильно изменится, и, как следствие, результаты
кластерного анализа могут сильно отличаться от предыдущих.» (выделено нами,
авт.)[15].
В той же работе просто констатируется факт этой ситуации, но ему не дается
никакой оценки. Наша же оценка этой практике по перечисленным
выше причинам сугубо отрицательная. Приведем еще
цитату из той же работы: «Степенное расстояние. Иногда желают (!!!?)[16]
прогрессивно увеличить или уменьшить вес, относящийся к размерности, для
которой соответствующие объекты сильно отличаются. Это может быть достигнуто с
использованием степенного расстояния. Степенное расстояние вычисляется
по формуле:
расстояние(x,y)
= (![]() i |xi
- yi|p)1/r
i |xi
- yi|p)1/r
где r
и p - параметры, определяемые
пользователем. Несколько примеров вычислений могут показать, как
"работает" эта мера. Параметр p
ответственен за постепенное взвешивание разностей по отдельным координатам,
параметр r ответственен за прогрессивное
взвешивание больших расстояний между объектами. Если оба параметра - r и p,
равны двум, то это расстояние совпадает с расстоянием Евклида». Мы считаем, что
еще какие-то комментарии здесь излишни, хотя сложно удержаться от того, чтобы
не сказать, что подобный подход превращает науку из поиска истины в произвольную подтасовку
данных и выводов.
Таким образом, второе требование к
исходным данным порождает следующую проблему 2.1:
Проблема
2.1 сопоставимой обработки
описаний объектов, описанных признаками различной природы, измеряемыми в различных
единицах измерения (проблема размерностей).
Отметим также, что объекты чаще
всего описаны не только признаками, измеряемыми в различных единицах измерения,
но как количественными, так и качественными признаками, которые соответственно
являются градациями как числовых шкал, так и номинальных (текстовых) шкал.
Существует метрика для номинальных шкал: это «Процент несогласия»[17], однако для количественных
шкал применяются другие метрики. Каким образом и с помощью какой комбинации
классических метрик вычислять расстояния между объектами, описанными как
количественными, так и качественными признаками, а также между кластерами, в
которые они входят, вообще не понятно. Это порождает проблему 2.2.:
Проблема
2.2 формализации описаний
объектов, имеющих как количественные, так и качественные признаки.
Третье
требование (нормальности распределения показателей)
вытекает из того, что статистическое обоснование корректности вышеперечисленных
метрик существенным образом основано на
этом предположении, т.е. эти метрики являются параметрическими. На практике это
означает, что перед применением кластерного анализа с этими метриками
необходимо доказать гипотезу о нормальности исходных данных либо применить процедуру
их нормализации. И первое, и второе, весьма проблематично и на практике не делается, более того, даже вопрос об
этом чаще всего не ставится. Процедура нормализации (или взвешивания,
ремонта) исходных данных обычно
предполагает удаление из исходной выборки тех данных, которые нарушают их нормальность.
Ясно, что это непредсказуемым образом может повлиять на результаты
кластеризации, которые, скорее всего, существенно изменяться и их уже нельзя
будет признать результатами кластеризации исходных данных. Отметим, что на практике
исходные данные, не подчиняющиеся нормальному распределению, встречаются
достаточно часто, что и делает актуальными методы непараметрической статистики.
Таким образом, 3-е требование к
исходным данным порождает проблемы 3.1., 3.2. и 3.3.:
Проблема
3.1 доказательства гипотезы
о нормальности исходных данных.
Проблема
3.2 нормализации исходных данных.
Проблема
3.3 применения
непараметрических методов кластеризации, корректно работающих с
ненормализованными данными.
Что можно сказать о четвертом и пятом
требованиях?[18] Эти
требования взаимосвязаны, т.к. случайные факторы и порождают «выбросы». На
практике, строго говоря, эти требования никогда не выполняются и вообще звучат несколько наивно, если учесть, что как
случайные часто рассматриваются неизвестные факторы, а их влияние даже
теоретически, т.е. в принципе, исключить невозможно. С другой стороны эти
требования «удобны» тем, что неудачные, неадекватные или не интерпретируемые
результаты кластеризации, полученные тем или иным методом кластерного анализа,
всегда можно «списать» на эти неизвестные «случайные» факторы или скрытые параметры
и порожденные ими выбросы. А поскольку
ответственность за обеспечение отсутствия шума и выбросов в исходных данных
возложена этими требованиями на самого исследователя, то получается, что если
что-то получилось не так, то это связано уж не столько с методом кластеризации,
сколько с каким-то недоработками самого исследователя. По этим причинам
более логично и главное, более продуктивно
было бы предъявить эти требования не к исходным данным и обеспечивающему их
исследователю, а к самому методу кластерного анализа, который, по мнению авторов, должен
корректно работать в случае наличия шума
и выбросов в исходных данных и не перкладывать эту проблему «с больной
головы на здоровую».
Таким образом, четвертое и пятое требования
приводят к двум проблемам:
Проблема
4 разработки такого метода кластерного
анализа, математическая модель и алгоритм и которого органично включали бы
фильтр, подавляющий шум в исходных данных, в результате чего данный метод
кластеризации корректно работал бы при наличии шума в исходных данных.
Проблема
5
разработки метода кластерного анализа, математическая модель и алгоритм
и которого обеспечивали бы выявление «выбросов» (артефактов) в исходных
данных и позволяли либо вообще не показывать их в дендрограммах, либо показывать,
но так, чтобы было наглядно видно, что это артефакты.
Далее
рассмотрим, как решаются (или не решаются) сформулированные выше проблемы в
классических методах кластерного анализа. Для удобства дальнейшего изложения повторим
формулировки этих проблем.
Проблема
1.1 выбора метрики, корректной для неортонормированных
пространств.
Проблема
1.2 ортонормирования пространства.
Проблема
2.1 сопоставимой обработки описаний объектов,
описанных признаками различной природы, измеряемыми в различных единицах
измерения (проблема размерностей).
Проблема
2.2 формализации описаний объектов, имеющих
как количественные, так и качественные признаки.
Проблема
3.1 доказательства гипотезы о нормальности
исходных данных.
Проблема
3.2
нормализации исходных данных.
Проблема
3.3 применения непараметрических методов кластеризации,
корректно работающих с ненормализованными данными.
Проблема
4 разработки такого метода кластерного
анализа, математическая модель и алгоритм и которого органично включали бы
фильтр, подавляющий шум в исходных данных, в результате чего данный метод
кластеризации корректно работал бы при наличии шума в исходных данных.
Проблема
5
разработки метода кластерного анализа, математическая модель и алгоритм
и которого обеспечивали бы выявление «выбросов» (артефактов) в исходных
данных и позволяли либо вообще не показывать их в дендрограммах, либо показывать,
но так, чтобы было наглядно видно, что это артефакты.
Сделать это удобнее
всего, рассматривая какие ответы предлагают классические методы кластерного
анализа на сформулированные в работе[19]
вопросы:
–
как вычислять координаты кластера из двух более объектов;
–
как вычислять расстояние до таких "полиобъектных" кластеров от
"монокластеров" и между "полиобъектными" кластерами.
Дело в том, что эти вопросы имеют
фундаментальное значение для кластерного анализа, т.к. разнообразные комбинации
используемых метрик и методов вычисления координат и взаимных расстояний
кластеров и порождают все многообразие методов кластерного анализа (см. туже
работу). Мы бы несколько переформулировали эти вопросы, а также добавили бы еще
один:
1. Каким методом вычислять координаты кластера, состоящего из одного и более объектов, т.е.
каким образом объединять объекты в кластеры.
2. Каким методом сравнивать кластеры, т.е. как вычислять расстояния между кластерами, состоящими из различного количества
объектов (одного и более).
3. Каким методом объединять кластеры, т.е.
формировать обобщенные («многообъектные»)
кластеры.
Вопрос
1-й. Чаше всего ни в теории и
математических моделях кластерного анализа, ни на практике между кластером, состоящим
из одного объекта («моноообъектным» кластером) и самим объектом не делается никакого различия, т.е. считается, что
это одно и тоже. «В агломеративно-иерархических методах (aggomerative
hierarhical algorithms) … первоначально все объекты (наблюдения)
рассматриваются как отдельные, самостоятельные кластеры состоящие всего лишь из
одного элемента»[20]. В
работе[21]
также говорится, что древовидная «Диаграмма начинается с каждого объекта в
классе (в левой части диаграммы)». Это решение сразу же порождает многие из вышеперечисленных проблем (1.1., 1.2., 2.1,
2.2), т.к. объекты могут быть описаны как количественными, так и качественными
признаками различной природы, измеряемыми в различных единицах измерения, причем
эти признаки взаимосвязаны
(коррелируют) между собой.
Казалось бы,
проблему размерностей (2.1) решает кластеризация не исходных переменных, а
матриц сопряженности, содержащих абсолютные
частоты наблюдения признаков по объектам или классам. Однако при таком
подходе, например при сравнении моделей автомобилей, четыре и два цилиндра у этих моделей, а также четыре и два болта, которыми у них прикручен номер, будут давать
одинаковый вклад в сходство-различие этих моделей, что едва ли разумно и
приемлемо [8]. Тем ни менее матрица сопряженности анализируется в
социологических и социометрических исследованиях, а в статистических системах,
в разделах справки, посвященных кластерному анализу, приводятся примеры
подобного рода.
Другое предложение по решению проблемы
размерностей (2.1) основано на четком пожимании того, что изменение единиц
измерения переменной меняет среднее ее значений и их разброс от этого среднего.
Например, переход от сантиметров к миллиметрам увеличивает среднее и среднее
отклонение от среднего в 10 раз. Речь идет о методе нормализации или
стандартизации исходных данных, когда значения переменных заменяются их стандартизированными
значения или z-вкладами [15]. Z-вклад показывает, сколько стандартных
отклонений отделяет данное наблюдение от среднего значения:
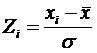 ,
,
где ![]() – значение
данного наблюдения,
– значение
данного наблюдения, ![]() – среднее,
– среднее, ![]() – стандартное
отклонение.
– стандартное
отклонение.
Однако этот метод имеет серьезный недостаток,
описанный в вышеперечисленной литературе, а также работе[22].
Дело в том, что нормализация значений переменных приводит к тому, что независимо
от значений их среднего и вариабельности до нормализации (т.е. значимости,
измеряемой стандартным отклонением), после нормализации среднее становится
равным нулю, а стандартное отклонение 1. Это значит, что нормализация выравнивает
средние и отклонения по всем переменным, снижая, таким образом, вес значимых
переменных, оказывающих большое влияние на объект, и завышая роль малозначимых
переменных, оказывающих меньшее влияние и искажая, таким образом, картину.
На взгляд авторов это не приемлемо. Другой важный недостаток, который в отличие
от первого не отмечается в специальной литературе, состоит в том, что стандартизированные значения сложно как-то
содержательно интерпретировать, т.е. устранение влияния единиц измерения
достигается ценой потери смысла переменных, который как раз и содержался в
единицах их измерения. В результате нормализации все переменные
становятся как бы «на одно лицо». Это также недопустимо. Таким образом, можно
обоснованно сделать вывод о том, нормализация и стандартизация исходных
данных – это весьма радикальное
решение проблемы 2.1 «в лоб и в корне», но решение неприемлемо дорогой ценой.
В классических методах кластерного анализа
предлагается два основных варианта ответов
на 1-й вопрос:
1. Вообще не формировать обобщенных классов или
кластеров из объектов, а на всех этапах кластеризации рассматривать только сами
первичные объекты.
2. Формировать обобщенные кластеры путем
вычисления неких статистических характеристик кластера на основе характеристик
входящих в него объектов.
О 1-м варианте ответа в работе[23]
говорится: «Диаграмма начинается с каждого объекта в классе (в левой части
диаграммы). Теперь представим себе, что постепенно (очень малыми шагами) вы
"ослабляете" ваш критерий о том, какие объекты являются уникальными,
а какие нет. Другими словами, вы понижаете порог, относящийся к решению об
объединении двух или более объектов в один кластер. В результате, вы связываете
вместе всё большее и большее число объектов и агрегируете (объединяете)
все больше и больше кластеров, состоящих из все сильнее различающихся
элементов». Этот подход, когда кластеры реально не формируются, т.к. им не
соответствуют какие-либо конструкции математической модели, представляется авторам
сомнительным, т.к., во-первых, как было показано выше, это порождает проблемы
1.1., 1.2., 2.1, 2.2, а во-вторых, никак
не решает проблемы 3.1, 3.2, 3.3, 4 и 5. Между
тем сам способ формирования кластеров из объектов, по мнению авторов, призван
стать средством решения всех этих проблем.
2-й вариант ответа представляется более
обоснованным, однако он сам в свою очередь порождает вопросы о степени корректности
и научной обоснованности того или иного метода вычисления обобщенных
характеристик кластера и главное о том, в
какой степени этот метод позволяет решить сформулированные выше проблемы.
Описание кластера на основе входящих в него объектов традиционно включает центр кластера, в качестве которого обычно
используется среднее или центр тяжести от характеристик входящих
в него объектов[24], а
также какую-либо количественную оценку степени рассеяния объектов кластера от
его центра (как правило, это дисперсия). Ответ на 2-й вопрос является
продолжением ответа на 1-й вопрос.
Вопрос
2-й. В вышеупомянутых и других работах по кластерному
анализу описывается большое количество различных мер и методов, которые можно
применить как для измерения расстояний между кластерами, так и расстояний от
объекта до кластеров. Например, в невзвешенном центроидном методе при определении расстояния от объекта
до кластера, по сути, определяется расстояние до его центра[25].
В методе невзвешенного попарного среднего расстояние между двумя
кластерами вычисляется как среднее расстояние между всеми парами объектов в них
[там же]. При этом, как правило, не решаются перечисленные выше проблемы, т.к. не устраняются их причины: а именно
средние вычисляются на основе мер расстояния, корректных только для
ортонормированных пространств и при этом часто используются размерные или
нормализованные формы представления признаков объектов, не формализуется
описание объектов, обладающих как количественными, так и качественными
признаками. Ответ на 3-й вопрос является продолжением ответа на 2-й вопрос.
Вопрос
3-й.
При объединении кластеров характеристики вновь образованного обобщенного
кластера обычно пересчитываются тем же методом, каким они рассчитывались для
исходных кластеров. Это сохраняет нерешенными и все проблемы, которые были при
определении характеристик исходных кластеров и расстояний между этими
кластерами.
Далее
рассмотрим вариант решения некоторых из сформулированных выше проблем
кластерного анализа, предлагаемый в АСК-анализе и реализованный в интеллектуальной
системе «Эйдос».
Обратимся к эпиграфам к данному разделу:
«Мышление – это обобщение, абстрагирование, сравнение, и классификация»
(Патанджали, II в. до н. э.), «Истинное знание – это знание причин»
(Френсис Бэкон, 1561–1626 гг.). Итак, мышление, как процесс это [в том числе]
классификация, результатом же мышления является знание, причем истинное знание
есть знание причин. Истинное мышление есть мышление, дающее истинное знание.
Соответственно ложное мышление – это мышление, приводящее к заблуждениям.
Поэтому истинное мышление – это [в том числе]
истинная (правильная, адекватная) классификация объектов по причинам их
поведения, т.е. по системе их детерминации. Правильной классификацией будем
считать ту, которая совпадает с классификацией экспертов, основанной на их
высоком уровне компетенции, профессиональной интуиции и большом практическом
опыте.
Если, как это принято в АСК-анализе [145],
факторы формализовать в виде шкал различного типа (номинальных, порядковых и
числовых), признаки рассматривать как значения факторов, т.е. их интервальные
значения, более или менее жестко детерминирующих поведение объекта, а классы
как будущие состояния, в которые объект переходит под влиянием различных
значений этих факторов, то можно сказать, что признаки формализуют причины переходов объекта в состояния,
соответствующие классам или кластерам. Если учесть, что классификация – это
кластерный анализ, то можно сделать обоснованные выводы о том, что кластерный
анализ это и есть мышление (но мышление не сводится только к кластерному
анализу), а результаты кластерного анализа представляют собой знания. Степень истинности этих знаний,
полученных в результате кластерного анализа, т.е. их адекватность или
соответствие действительности, полностью
определяются степенью истинности метода кластерного анализа, с помощью которого
они получены. Поэтому столь важно решить сформулированные выше проблемы кластерного
анализа.
В свою очередь классификация (в т.ч. кластерный анализ) как процесс основана на обобщении
и сравнении. В монографии 2002 года [97] предлагается пирамида
иерархической структуры процесса познания, входящая в базовую когнитивную концепцию
(рисунок 1):
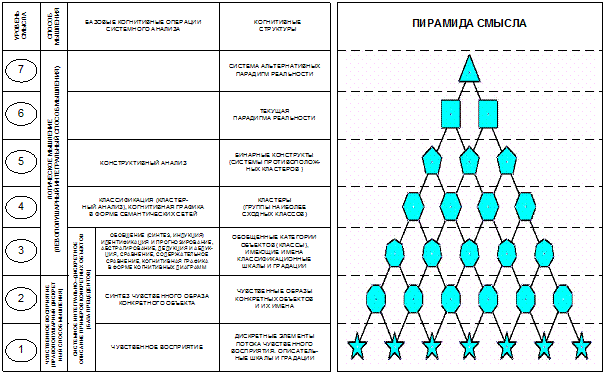
Рисунок 1 Обобщенная схема
иерархической структуры процесса познания согласно
базовой формализуемой когнитивной концепции[26]
В этой же монографии [97]
предлагается математическая модель, основанная на семантической теории
информации, обеспечивающая высокую степень формализацию данной когнитивной
концепции, достаточную для разработки алгоритмов[27],
структур данных и программной реализации в виде интеллектуальной программной
системы. Такая система была создана автором и постоянно развивается, это
система «Эйдос» [97, 100, 101].
Суть предлагаемых в АСК-анализе решений сформулированных
выше проблем кластерного анализа состоит в следующем[28].
Основная идея решения проблем
кластерного анализа, состоит в том, что для решения задачи кластеризации
предлагается использовать математическое представление объектов не виде
переменных со значениями, измеряемыми в различных единицах измерения и в шкалах
разного типа, и не матрицу сопряженности с абсолютными частотами встреч признаков
по классам или нормализованными Z-вкладами, а базы знаний, рассчитанные на основе матрицы сопряженности (матрицы
абсолютных частот) с использованием различных аналитических выражений для частных
критериев. При этом для всех значений всех переменных используется одна и та же размерность – это размерность количества информации (бит, байт и т.д.), что обеспечивает расчет на
основе исходных данных силы и направления влияния на объект всех факторов и их
значений и сопоставимую обработку значений переменных, изначальное (в исходных
данных) представленных в разных единицах измерения и в шкалах разного типа
(количественных – числовых, и качественных – текстовых).
1. Расстояния между объектом и
кластером, а также между кластерами предлагается определять с использованием
неметрических интегральных критериев, корректных для неортормированных
пространств, одним и тем же методом: по суммарному количеству информации,
которое содержится (соответственно) в системе признаков объекта о
принадлежности к классу или кластеру, или которое содержится в обобщенных
образах двух классов или кластеров об их принадлежности друг к другу.
2. Координаты кластера, возникающего как при включении в него одного единственного объекта, так и при объединении многих объектов в кластеры вычисляются тем
же самым методом, что и координаты кластера, возникающего при объединении нескольких
кластеров, а именно путем применения базовой когнитивной операции (БКОСА):
«Обобщение», «Синтез», «Индукция» (БКОСА-3) АСК-анализа.
3. Объединять кластеры, т.е. формировать обобщенные («многообъектные») кластеры при объединении кластеров
предлагается тем же самым методом,
что и обобщенные образы классов при объединении конкретных образов объектов,
т.е. путем применения базовой когнитивной операции (БКОСА): «Обобщение»,
«Синтез», «Индукция» (БКОСА-3) АСК-анализа.
Основная идея сводится к тому,
чтобы кластеризовать не размерные переменные, абсолютные или относительные
частоты или Z-вклады, а знания. Предложения 1-3 являются
непосредственными ответами на сформулированные выше фундаментальные вопросы
кластерного анализа.
Остановимся
подробнее на математическом и алгоритмическом описании этих предложений и затем
проиллюстрируем их на простом и наглядном численном примере.
Основная
идея.
Вспомним приведенный выше пример кластеризации моделей автомобилей, в котором
четыре или два цилиндра в двигателе давали такой вклад в сходство-различие моделей,
как четыре или два болта, которыми прикручивается регистрационный номер. Из
этого примера ясно, что при сравнении объектов и кластеров основную роль должно
играть не само количество разных
деталей или элементов конструкции, а, например, их влияние на стоимость модели, выраженное в долларах или на
степень ее пригодности (полезности) для
поставленной цели, тоже выраженное в
одних и тех же для всех переменных и их значений единицах измерения. В АСК-анализе предлагается более радикальное
решение: измерять степень и направление влияния всех переменных и их значений
на поведение объекта или принадлежность его к тому или иному классу или кластеру
в одних и тех же универсальных
единицах измерения, а именно единицах измерения количества информации. Ведь по
сути, когда мы узнаем о том, что некий объект обладает определенным признаком,
то мы получаем из этого факта некое количество информации о том, что
принадлежит к определенной категории (классу, кластеру). А уж сами эти категории могут иметь совершенно
различный смысл, в частности классифицировать текущие или будущие состояния
объектов, или степень их полезности для достижения тех или иных целей. И что
очень важно, при этом не играет абсолютно никакой роли в каких единицах
измерения в какой шкале, количественной или качественной, изначально измерялся
этот признак: килограммах, долларах, Омах, джоулях, или еще каких-то других.
Предложение
1-е. В этом смысле в АСК-анализе исчезает существенное различие
между классом и кластером и эти термины можно использовать как синонимы. Классы в АСК-анализе могут
быть различаться степенью обобщенности: чем больше объектов в классе и чем выше
вариабельность этих объектов по их признакам, тем шире представляемая ими
генеральная совокупность, по отношению к которой они представляют собой репрезентативную
выборку, тем выше степень обобщения в объединяющем их классе. Классы включают
один или насколько объектов. Наименьшей степенью обобщения обладают классы,
включающие лишь один объект, но и они совершенно не тождественны объекту
исходной выборки, т.к. в математической мидели АСК-анализа у них совершенно
различные математические формы представления. Кластеры обычно являются классами
более высокой степени обобщения, т.к. включают один или несколько классов.
Как реализуется базовая
когнитивная операция АСК-анализа «Обобщение», «Синтез», «Индукция» (БКОСА-3)
будет рассмотрено ниже при кратком изложении математической модели АСК-анализа.
Предложения
2-е и 3-е
необходимо рассматривать в комплексе, т.к. их смысл в том, что объект при
когнитивной кластеризации имеет другую математическую форму, чем объект в исходных
данных, а именно такую же форму, как класс и как кластер, т.е. в АСК-анализе
возможны классы и кластеры, включающие как один, так и много объектов. При этом
для формирования класса состоящего из одного объекта, т.е. при добавлении в
пустой кластер первого объекта, используется та же самая математическая
процедура, что и при добавлении в него второго и вообще любого нового объекта
(в АСК-анализе она называется БКОСА-3), и эта же самая процедура БКОСА-3
используется и при объединении классов или кластеров. При этом само объединение классов (кластеров)
осуществляется путем создания «с нуля» нового класса (кластера) из всех
объектов, входящих в объединяемые классы (кластеры), а затем удаления исходных
классов (кластеров). Новый объединенный класс (кластер) создается «с нуля» тем
же самым методом (БКОСА-3), каким
впервые создается любой новый класс (кластер). Теперь рассмотрим, как же
это реализовано математически и алгоритмически.
Рассмотрим
предлагаемый алгоритм когнитивной кластеризации
в графической и текстовой форме (рисунок 3):

Рисунок 3. Алгоритм когнитивной кластеризации
или кластеризации, основанной на знаниях
Дадим необходимые пояснения к
приведенному алгоритму.
1.
Если не соответствуют размерности баз данных (БД) классов, признаков и информативностей,
то выдать сообщение о необходимости пересинтеза модели.
2.
Создать БД абсолютных частот: ABS_KLAS, информативностей: INF_KLAS, сходства
классов: MSK_KLAS, а также БД учета объединения классов IterObj1.dbf и занести
в них начальную информацию по текущей модели.
Данный режим реализован в
модуле _5126 системы «Эйдос» и обеспечивает работу с любой из четырех моделей
или со всеми этими моделями по очереди, поддерживаемых системой и приведенных в
таблице 3. При этом в базах данных этих моделей ничего не изменяется.
3.
Цикл по моделям до тех пор, пока есть похожие классы.
4.
Рассчитать матрицу сходства классов MSK_KLAS в текущей модели.
Эта матрица рассчитываемся на
основе матрицы знаний модели, заданной при запуске режима (СИМ-1 – СИМ-7),
путем расчета корреляции обобщенных
образов классов (т.е. векторов или профилей классов).
5.
Найти пару наиболее похожих классов в матрице сходства.
Здесь определяются два класса,
у которых на предыдущем шаге было обнаружено наивысшее сходство. При этом при запуске
режима задается параметр: «Исключать ли артефакты (выбросы)». Если задано
исключать, то рассматриваются только положительные уровни сходства, если нет –
то и отрицательные, т.е. в этом случае могут быть объединены и непохожие классы, но наименее непохожие
из всех, если других нет. Считается, что непохожие кассы являются исключениями
или «выбросами».
6.
Объединить 2 класса с наибольшим уровнем сходства.
Данный пункт алгоритма требует
наиболее детальных пояснений. Как же объединяются классы в методе когнитивной
кластеризации? Сначала суммируются
абсолютные частоты этих классов в таблице 2, причем сумма рассчитывается в
столбце класса с меньшим кодом, а затем частоты класса с большим кодом
обнуляются. После этого в базе знаний (таблица 4) с использованием
частного критерия соответствующей модели (таблица 3) пересчитываются только изменившиеся столбцы и строки,
т.е. пересчитывается столбец класса с меньшим кодом, а столбец класса с большим
кодом обнуляется.
7.
Отразить информацию об объединении классов в БД IterObj1.dbf.
8.
Конец цикла итераций. Проверить критерий остановки и перейти на продолжение
итераций (п.9) или на окончание работы (п.10).
9.
Пересчитать в базе данных сходства классов (MSK_KLAS) только изменившиеся столбцы и строки. Конец
цикла по моделям.
10.
Нарисовать дерево объединения классов, псевдографическое: /TXT/AgKlastK.txt и графическое:
/PCX/AGLKLAST/TrK-#-##.GIF.
Работа предлагаемой
математической модели и реализующего ее алгоритма когнитивной кластеризации
продемонстрированная на простом численном примере в работе [248], а в данной
монографии некоторые выходные формы режима когнитивной кластеризации системы
«Эйдос» приведены на рисунках 13 и 14 раздела 10.2.
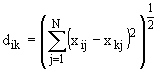
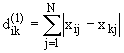
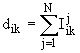 ,
,