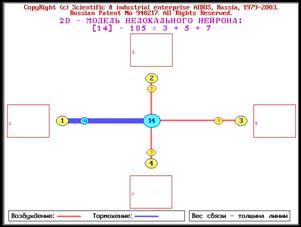
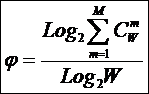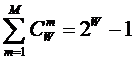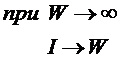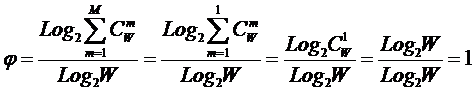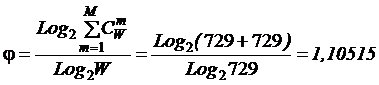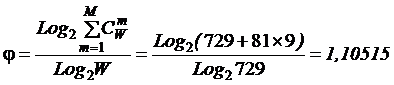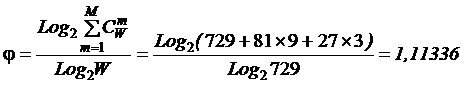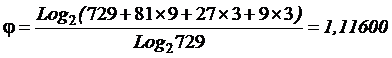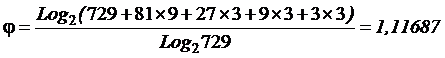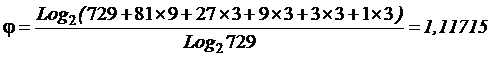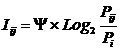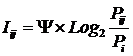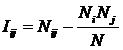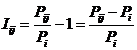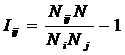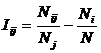ГЛАВА 10. ИНФОРМАЦИОННЫЕ МЕРЫ
УРОВНЯ СИСТЕМНОСТИ – КОЭФФИЦИЕНТЫ
ЭМЕРДЖЕНТНОСТИ, ВЫТЕКАЮЩИЕ ИЗ СИСТЕМНОЙ ТЕОРИИ ИНФОРМАЦИИ
Дальнейшее изложение основано на рабатах [98,
170, 270, 240, 241]. В работе [97] и работе [170] предлагаются теоретически
обоснованные количественные меры, следующие из системной теории информации
(СТИ), которые позволяют количественно оценивать влияние факторов на системы
различной природы не по силе и направлению изменения состояния системы, а по
степени возрастания или уменьшения ее эмерджентности (уровня системности) и
степени детерминированности.
В работе [253] на простом численном примере
рассматривается применение автоматизированного системно-когнитивного анализа
(АСК-анализ) и его программного инструментария – интеллектуальной системы
«Эйдос» для выявления и исследования детерминации эмерджентных макросвойств
систем их составом и иерархической структурой, т.е. подсистемами различной
сложности (уровней иерархии). Кратко обсуждаются некоторые методологические
вопросы создания и применения формальных моделей в научном познании. Предложены
системное обобщение принципа Уильяма Росса Эшби о
необходимом разнообразии на основе системного обобщения теории множеств и
системной теории информации, обобщенная формулировка принципа относительности
Галилея-Эйнштейна, высказана гипотеза о его взаимосвязи с теоремой Эмми Нётер, а также предложена гипотеза «О зависимости силы и
направления связей между базовыми элементами системы и ее эмерджентными
свойствами в целом от уровня иерархии в системе»
В [270] предложены коэффициенты
эмерджентности, применимые для систем, подчиняющихся классической или квантовой
статистике. Дан алгоритм оценки уровня системности квантовых объектов.
Рассмотрены квантовые системы, подчиняющиеся статистике Ферми-Дирака и
Бозе-Эйнштейна, а также классические системы, подчиняющиеся статистике
Максвелла-Больцмана. Установлено, что коэффициенты эмерджентности квантовых и
классических систем отличаются между собой, как и коэффициенты квантовых систем
ферми-частиц и бозе-частиц. Следовательно,
коэффициент эмерджентности позволяет отличить классическую систему от квантовой
системы, а квантовую систему ферми-частиц от квантовой системы бозе-частиц.
Установлено также, что предложенные ранее в ряде работ, начиная с [97], различные
варианты коэффициентов эмерджентности Хартли распространяются только на
системы, подчиняющиеся статистике Ферми-Дирака.
Рассмотрим результаты этих работ подробнее.
10.1. Количественные меры возрастания эмерджентности в процессе эволюции систем (в рамках системной теории информации)
Дальнейшее изложение основано на рабате [170],
нумерация формул, рисунков и таблиц сохранены.
Одного взгляда на Вселенную на
всех ее структурных уровнях организации, начиная с микромира с его квантами,
элементарными частицами и атомами и до макро- и мега масштабов, достаточно,
чтобы убедиться, что Вселенная глубоко структурирована и состоит из глобально и
нелокально взаимосвязанных систем различного масштаба, все свойства которых
имеют эмерджентную природу, и во Вселенной ни на одном из уровней ее
организации не наблюдается ничего похожего на унылую картину "Тепловой
смерти". Сегодня уже совершенно очевидно, что закон возрастания энтропии
(2-е начало термодинамики) является сильнейшей абстракцией и по сути во всей
Вселенной нет ни одной системы, которая ему бы абсолютно точно и в полной мере
соответствовала, т.к. не существует полностью изолированных от окружающей среды
систем (адиабатически замкнутых систем, т.е. систем, энергетически не
взаимодействующих со средой). Более того, если бы такие системы и существовали,
то мы бы об этом никогда в принципе не узнали бы, т.к. не получили бы о них
никакой информации, поэтому можно сказать еще и иначе: такие системы скорее
относятся не к области бытия, а к области небытия.
Но для существования любой системы или подсистемы необходим
системобразующий фактор и, естественно, возникает вопрос о
том, что же является глобальным и нелокальным системообразующим фактором, общим
для всех систем.
Это вопрос необычайной важности,
так как именно этот фактор противодействует возрастанию энтропии на всех
уровнях организации систем во Вселенной. Без действия этого фактора, т.е. если
бы закон возрастания энтропии действительно был всеобщим законом природы,
каковым его хотели некогда представить те самые французские академики, которые
заодно запретили и существование метеоритов, то Вселенная была бы совершенно
однородна (хаос или небытие, "Тепловая смерть") и об этом бы вообще
некому и негде было бы рассуждать.
Из термодинамических
представлений ясно, что этот глобальный нелокальный антиэнтропийный
системообразующий фактор может быть отожествлен с некоторым источником энергии
или информации, которые как известно взаимосвязаны в любой конкретной системе
через ее энтропию. Каждая система во Вселенной (пока она существует) должна
иметь прямой и непосредственный контакт с этим фактором и как только этот
контакт прекращается – система распадается на подсистемы или элементы. Поэтому
этот фактор должен быть не внешним, а внутренним
по отношению к системам, а также обладать глобальностью
и нелокальностью, возможно даже не
только в пространстве, но и во времени (на эти мысли наталкивает анализ
возможных механизмов принципа наименьшего действия, траекторной формулировки и
опережающих потенциалов в КТП). Физической основой этого фактора может быть
квантовое единство, которое существует с момента возникновения самого метрического
пространства-времени еще с единого квантового состояния Вселенной-в-Целом до
Большого Взрыва, с которого и начался процесс последовательной иерархической
дифференциации. Сам физический механизм нелокального взаимодействия
дифференцированной структуры системы с ее единой сущностью может быть аналогичным
тому, который был предвосхищен А.Эйнштейном в известном парадоксе ЭПР.
Если этот фактор научиться
сознательно использовать, то возможно будут решены энергетические и другие
связанные с ними проблемы.
Таким образом на наш взгляд этот
глобальный и нелокальный системообразующий фактор – это энергия и информация
идущие к каждой системе из неизменной нелокальной сущности Вселенной, из того
его состояния, которое оставаясь неизменным породило всю эту дифференцированную
Вселенную, это состояние, которое есть лишенное частей единство в сущности
каждой системы. Это не какое-либо место или время – это наиболее фундаментальный
структурный уровень организации Вселенной – лишенная всех качеств основа всех
качеств (предполагается, что все качества эмерджентны по своей природе).
Возможно после Большого Взрыва Вселенная стала дифференцированной лишь по своей
форме не изменяясь в своей единой и неделимой сущности, т.е. не переставая быть
единой без частей ... и это непроявленное состояние есть ни что иное как неделимая
сущность каждой системы и подсистемы во Вселенной ... причем она одна и та же у
всех систем и внутри осознается как Сущность субъективности, а во вне – как
сущность материи...
Похоже Никола Тесла был не просто
гениальным ученым, инженером и изобретателем, а скорее Пророком технической
эры, который понял с точки зрения физики что такое этот глобальный нелокальный
системообразующий фактор и научился осознанно включать в его состав своих
технических систем. До этого нечто подобное удавалось только музыкантам, художникам,
скульпторам и архитекторам, а теперь похоже приближается время и программистов,
прежде всего специалистов по системам искусственного интеллекта, виртуальной
реальности и моделированию эволюции.
Итак, в самом общем виде существование систем во Вселенной
можно объяснить тем, что существует некий гипотетический фактор, успешно
противодействующий возрастанию энтропии на всех уровнях организации систем во
Вселенной. Но что это за фактор и как влияют его свойства на характеристики систем?
Попробуем конкретизировать ответы на эти вопросы.
Из общепринятого представления о том, что количество информации
может быть измерено величиной уменьшения энтропии следует гипотеза о том, что этот антиэнтропийный системообразующий
фактор представляет собой некий источник информации. Этот источник
информации, обеспечивающий возникновение и существование системы, может
локализоваться как внутри, так и вне ее, но реально осуществляется смешанный вариант.
В этом процессе формирования и развития системы под
влиянием как внутренних, так и внешних информационных по своему существу
факторов она претерпевает количественные и качественные изменения, т.е.
проходит точки бифуркации и детерминистские участки траектории [97], в частности изменяются такие фундаментальные
характеристики системы, как ее уровень системности и степень
детерминированности.
Учитывая информационный характер антиэнтропийного
системообразующего фактора предлагается применить теорию информации для
количественной оценки этих фундаментальных характеристик систем.
Однако классическая теория информации не совсем подходит
для этой цели, т.к. она основана на теории множеств, а не на теории систем. В работе
[186] предлагается программная идея системного обобщения понятий математики, в
частности понятий теории информации, основанных на теории множеств, путем замены
понятия множества на более содержательное понятие системы. Частично эта идея
была реализована в работе [97] при разработке автоматизированного
системно-когнитивного анализа (АСК-анализа), математическая модель которого
основана на системном обобщении формул для количества информации Хартли и
Харкевича в рамках предложенной системной теории информации (СТИ).
Система представляет собой множество
элементов, объединенных в целое за счет взаимодействия элементов
друг с другом, т.е. за счет отношений между ними, и обеспечивает преимущества
в достижении целей. Преимущества в достижении целей обеспечиваются за
счет системного эффекта. Системный эффект состоит в том, что свойства
системы не сводятся к сумме свойств ее элементов, т.е. система как целое
обладает рядом новых, т.е. эмерджентных свойств, которых не было у ее
элементов. Предполагается, что во Вселенной не существует элементов не
являющихся системами. Таким образом все свойства любых систем в конечном счете
являются эмерджентными. Уровень системности тем выше, чем выше интенсивность
взаимодействия элементов системы друг с другом, чем сильнее отличаются свойства
системы от свойств входящих в нее элементов, т.е. чем выше системный эффект, чем значительнее отличается система от
множества.
Таким образом, система обеспечивает тем большие преимущества
в достижении целей, чем выше ее уровень системности. В частности, система с нулевым уровнем системности вообще
ничем не отличается от множества образующих ее элементов, т.е. тождественна
этому множеству и никаких преимуществ в достижении целей не обеспечивает. Этим самым достигается выполнение принципа
соответствия между понятиями системы и множества. Из соблюдения этого
принципа для понятий множества и системы следует и его соблюдение для понятий
системной теории информации, основанных на теории множеств и их системных
обобщений.
На этой основе можно ввести и новое научное понятие: понятие
"антисистемы", применение которого оправдано в случаях, когда
централизация (монополизация, интеграция) не только не дает положительного
эффекта, но даже сказывается отрицательно.
Антиподсистемой
будем называть подсистему, включение которой в некоторую систему уменьшает ее
уровень системности, т.е. это такое объедение некоторого множества элементов за
счет их взаимодействия в целое, которое препятствует достижению целей
системы в целом.
Фундаментом современной математики является теория
множеств. Эта теория лежит и в основе самого глубокого на сегодняшний день
обоснования таких базовых математических понятий, как "число" и
"функция". Определенный период этот фундамент казался незыблемым.
Однако вскоре работы целой плеяды выдающихся ученых XX века, прежде всего
Давида Гильберта, Бертрана Рассела и Курта Гёделя, со всей очевидностью обнажили
фундаментальные логические и лингвистические проблемы, в частности
проявляющиеся в форме парадоксов теории множеств, что, в свою очередь, привело
к появлению ряда развернутых предложений по пересмотру самых глубоких оснований
математики.
В задачи данной работы не входит рассмотрение этой интереснейшей
проблематики, а также истории возникновения и развития понятий числа и функции.
Отметим лишь, что кроме рассмотренных в литературе вариантов существует
возможность обобщения всех понятий математики, базирующихся на теории множеств,
в частности теории информации, путем тотальной замены понятия множества на
более общее понятие системы и тщательного отслеживания всех последствий этой
замены. Это утверждение будем называть "программной идеей
системного обобщения понятий математики".
Строго говоря, реализация данной программной идеи потребует
прежде всего системного обобщения самой теории множеств и преобразования ее в математическую
теорию систем, которая будет плавно переходить в современную теорию
множеств при уровне системности, стремящемся к нулю. При этом необходимо
заметить, что существующая в настоящее время наука под названием "Теория
систем" ни в коей мере не является обобщением математической теории множеств,
и ее не следует путать с математической теорией систем. Вместе с тем, на наш
взгляд, существуют некоторые возможности обобщения ряда понятий математики и
без разработки математической теории систем. К таким понятиям относятся прежде
всего понятия "информация" и "функция".
Системному обобщению понятия информации посвящены
работы автора [97] и др., поэтому здесь на этом
вопросе мы останавливаться не будем. Отметим лишь, что на основе предложенной
системной теории информации (СТИ) были разработаны математическая модель и
методика численных расчетов (структуры данных и алгоритмы), а также специальный
программный инструментарий (система "Эйдос") системно-когнитивного анализа
(СК-анализ), который представляет собой системный анализ, автоматизированный
путем его рассмотрения как метода познания и структурирования по базовым
когнитивным операциям.
В СК-анализе теоретически обоснована и реализована на
практике в форме конкретной информационной технологии процедура установления
новой универсальной, сопоставимой в пространстве и времени, ранее не
используемой количественной, т.е. выражаемой числами, меры соответствия
между событиями или явлениями любого рода, получившей название "системная
мера целесообразности информации", которая по существу является количественной мерой знаний
[245]. Это является достаточным основанием для того, чтобы называть эту форму
системного анализа системно-когнитивным анализом, от английского слова "cognition"
– "познание".
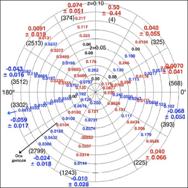
В результате получены следующие выражения для системных
обобщений формул для количества информации Хартли и Харкевича и плотности
информации Шеннона,
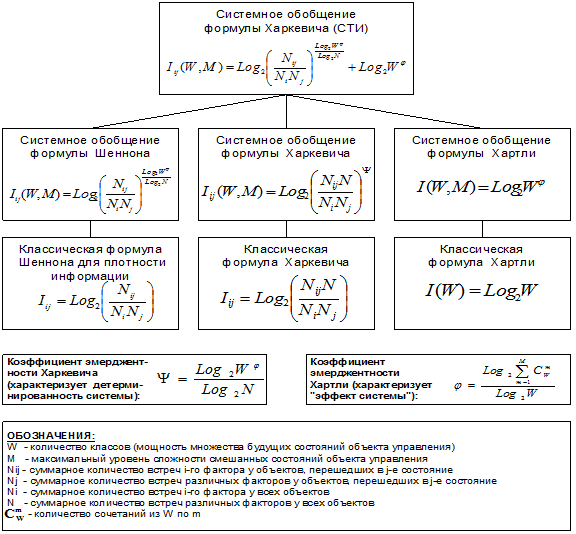
а также гипотезы о законе возрастания эмерджентности и
аналитические выражения для коэффициентов Хартли и Харкевича, которые являются
научно обоснованными в рамках системной теории информации (СТИ) количественными
мерами уровня системности и степени детерминированности систем (рис. 1-2).
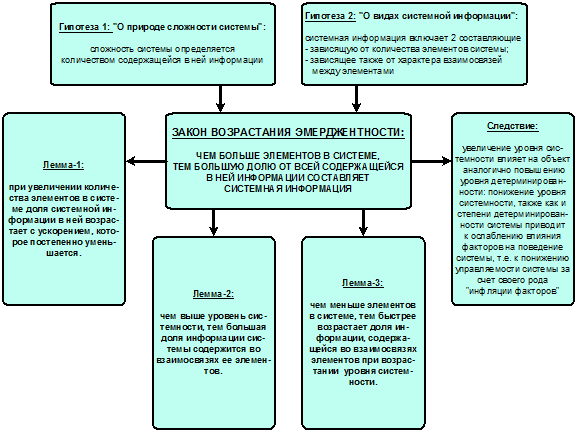
Рисунок 1. Гипотеза о
законе возрастания эмерджентности
Рисунок 2. Интерпретация коэффициентов эмерджентности
СТИ
Резюмируя рисунки 1
и 2, можно сказать, что в процессе эволюции систем есть по крайней мере два
этапа:
– на 1-м этапе идет
экстенсивный рост системы путем увеличения
количества ее элементов; при этом объем информации в системе возрастает в
основном за счет увеличения размера системы и количества элементов в ней;
– на
2-м этапе идет система развивается интенсивно за счет усложнения
взаимосвязей между элементами и своей структуры; при этом объем информации в
системе возрастает в основном за счет ее усложнения, т.е. повышения уровня
системности или эмерджентности системы.
Так, например,
управлять толпой из 729 человек значительно сложнее, чем воздушно-десантным
полком той же численности. Процесс превращения
729 новобранцев в воздушно-десантный полк это и есть процесс повышения уровня
системности и степени детерминированности системы. Этот процесс включает
процесс последовательного иерархического структурирования (на отделения,
взвода, роты, батальоны), а также процесс повышения степени детерминированности
команд путем повышения дисциплины их исполнения путем соответствующих организующих
воздействий. Эффективность этих организующих воздействий мы и предлагаем оценивать
по изменению уровня системности и степени детерминированности с помощью
коэффициентов эмерджентности, названных нами [97] в честь выдающихся ученых,
внесших огромный вклад в создание теории информации Хартли и Харкевича.
Рассмотрим
численный пример.
В работе [100] в разделе: "1.2.2.2.3. Конструирование системной
численной меры на
основе базовой",
подразделе: "Системное обобщение формулы Хартли для количества информации",
который размещен по адресу: http://lc.kubagro.ru/aidos/aidos06_lec/lec_04.htm приведено выражение для коэффициента эмерджентности Хартли
(1):
|
|
(1) |
где:
W – количество
элементов в системе альтернативных будущих состояний АОУ (количество чистых
состояний);
m – сложность
подсистемы (количество элементов 1-го уровня иерархии в подсистеме);
M – максимальная
сложность подсистем (количество элементов 1-го уровня иерархии в системе).
Непосредственно из вида выражения для коэффициента
эмерджентности Хартли (1) ясно, что он представляет собой относительное
превышение количества информации о системе при учете системных эффектов
(смешанных состояний, иерархической структуры ее подсистем и т.п.) над
количеством информации без учета системности, т.е. этот коэффициент отражает уровень системности объекта.
Необходимо
отметить, что сходное выражение было предложено видным исследователем в области
информационной теории систем А.А.Денисовым еще в 80-х годах[1],
однако свое теоретическое обоснование это выражение получило лишь в рамках СТИ.
Очень близкие идеи развиваются также в фундаментальных работах[2]
(см., например, раздел: "2.6. Эволюционная динамика и эмерджентность" в работе Попова В.П.).
Первое слагаемое в
выражении (1) дает количество информации по классической формуле Хартли, а
остальные слагаемые – дополнительное
количество информации, получаемое за счет системного эффекта, т.е. за счет
наличия у системы иерархической структуры или смешанных состояний. По сути дела эта дополнительная информация
является информацией об иерархической структуре системы, как состоящей из ряда
подсистем различных уровней сложности.
Однако реально в любой системе осуществляются не все
формально возможные сочетания элементов 1-го уровня иерархии, т.к. существуют
различные правила запрета,
различные для разных систем. Это означает, что возможно множество различных
систем, состоящих из одинакового количества тождественных элементов, и
отличающихся своей структурой, т.е. строением подсистем различных иерархических
уровней. Эти различия систем как раз и возникают благодаря различию действующих
для них этих правил запрета. По этой причине
систему правил запрета предлагается назвать информационным проектом системы. Различные системы, состоящие
из равного количества одинаковых элементов (например, дома, состоящие из 20000
кирпичей), отличаются друг от друга именно по причине различия своих
информационных проектов.
Из статистики известно, что при M=W:
|
|
(2) |
в этом случае для
выражения (1) получаем:
|
|
(3) |
Выражение (3) дает оценку
максимального количества информации, которое может содержаться в элементе
системы с учетом его вхождения в различные подсистемы ее структуры. Из этого
выражения видно, что I быстро
стремится к W при увеличении W:
|
|
(4) |
В действительности уже при W>4 погрешность выражения (4)
не превышает 1%, поэтому на практике в большинстве случаев при оценке величины
теоретически максимально-возможного значения уровня системности не будет
большой ошибкой вместо суммы числа сочетаний использовать просто W.
Таким образом, коэффициент эмерджентности Хартли отражает уровень
системности объекта и изменяется от 1 (системность минимальна, т.е.
отсутствует) до величины W/Log2W (системность максимальна). Очевидно, для каждого количества элементов
системы существует свой максимальный уровень системности, который
никогда реально не достигается из-за действия правил запрета на
реализацию в системе ряда подсистем различных уровней иерархии.
Будем считать, что полк является системой, имеющей иерархическую
структуру (такие системы являются наиболее распространенными).
Если в толпе из 729 (или любого другого количества W) новобранцев
(элементов 1-го уровня иерархии) нет ни одного командира, то ее уровень
системности согласно выражения (1) равен 1:
|
|
(5) |
Если в полку появляется командир полка, непосредственно (напрямую)
дающий указания каждому из солдат (что вообще-то достаточно проблематично
реализовать на практике), то появляется еще 729 дополнительных элементов 2-го уровня иерархии вида: "Командир
полка + N-й солдат". В этом случае выражение (1) примет вид (6):
|
|
(6) |
Но в реальном полку используется не двухуровневая, а многоуровневая
иерархическая система управления, т.к. командир полка и любой другой командир
из-за информационных, пространственных и временных ограничений реально может
отдать конкретный детализированный приказ только очень ограниченному количеству
нижестоящих командиров – системообразующих элементов следующего уровня
иерархии. Рассмотрим структуру условного полка, приведенную на рисунке 3.
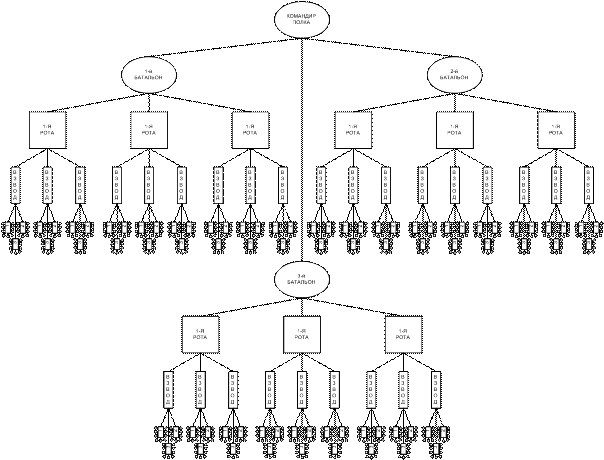
Рисунок 3. Иерархическая система
управления полком (условно)
Проведем расчет
уровня системности полка, иерархическая структура которого приведена на рисунке
3 с использованием формулы (1). При этом обращаем внимание на то обстоятельство,
что приведенная иерархическая структура близка к фрактальной. По-видимому это
не случайно, т.к. является одной из наиболее рациональных схем управления.
1-й уровень
иерархии: 729 солдат. Уровень
системности полка на 1-м уровне иерархии, как мы уже видели из формулы (5)
равна 1.
2-й уровень
иерархии: 81 отделение по 9 солдат в
каждом. Добавление командиров отделений порождает в каждом из 81 отделений 9
элементов вида: "Командир i-го отделения +
j-й солдат". Уровень системности полка на первых
двух уровнях вычисляется по формуле (7):
|
|
(7) |
Здесь необходимо
отметить, что структурный элемент "отделение", как и подсистемы
других уровней иерархии, рассматривается не как неделимые элементы, а именно
как подсистемы, сами имеющие определенный уровень системности, определяемый их
структурой. Возможны и другие подходы, рассматривающие подсистемы как элементы
без учета их внутренней структуры, т.е. не учитывающие различное в общем случае
содержание подсистем, но в данной работе они не рассматриваются. Вместе с тем
приведенные выше аналитические выражения для коэффициентов эмерджентности имеют
общий характер и применимы и в этом случае.
3-й уровень
иерархии: 27 взводов по 3 отделения в
каждом. Добавление командиров взводов порождает в каждом из 27 взводов по 3
элемента вида: "Командир i-го взвода +
командир j-го отделения". Уровень
системности полка на первых трех уровнях вычисляется по формуле (8):
|
|
(8) |
4-й уровень
иерархии: 9 рот по 3 взвода в каждой.
Добавление командиров рот порождает в каждой из 9 рот по 3 элемента вида:
"Командир i-й роты + командир j-го взвода".
|
|
(9) |
5-й уровень
иерархии: 3 батальона по 3 роты в
каждом. Добавление командиров батальонов порождает в каждом из 3 батальонов по
3 элемента вида: "Командир i-го батальона +
командир j-й роты".
|
|
(10) |
6-й уровень
иерархии: 1 командир полка.
Добавление командира полка порождает 3 элемента вида: "Командир полка +
командир j-го батальона".
|
|
(11) |
В сводном виде эти
данные приведены в таблице и на рисунке 4.
СВОДНЫЕ ДАННЫЕ О
ВКЛАДЕ РАЗЛИЧНЫХ УРОВНЕЙ ИЕРАРХИИ СИСТЕМЫ УПРАВЛЕНИЯ В ОБЩИЙ УРОВЕНЬ
СИСТЕМНОСТИ
|
|
729 солдат |
81 отде- ление |
27 взво- дов |
9 рот |
3 бата- льона |
1 полк |
|
Уровень системности |
|
|
1-й ур. |
2-й ур. |
3-й ур. |
4-й ур. |
5-й ур. |
6-й ур. |
Всего: |
|||
|
Командир полка командует солдатами "на прямую" |
729 |
|
|
|
|
729 |
1458 |
1,10515 |
|
|
1-й ур. толпа новобранцев) |
729 |
|
|
|
|
|
729 |
1,00000 |
|
|
2-й ур. |
729 |
81*9 |
|
|
|
|
1458 |
1,10515 |
|
|
3-й ур. |
729 |
81*9 |
27*3 |
|
|
|
1539 |
1,11336 |
|
|
4-й ур. |
729 |
81*9 |
27*3 |
9*3 |
|
|
1566 |
1,11600 |
|
|
5-й ур. |
729 |
81*9 |
27*3 |
9*3 |
3*3 |
|
1575 |
1,11687 |
|
|
6-й ур. |
729 |
81*9 |
27*3 |
9*3 |
3*3 |
1*3 |
1578 |
|
|
|
Максимальный теоретически возможный уровень системности |
729 |
|
|
|
|
|
|
76,65797 |
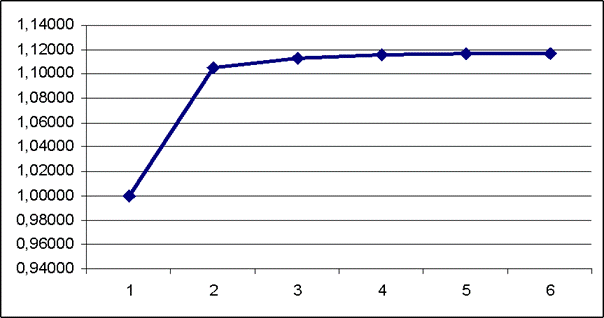
Рисунок 4. Зависимость эмерджентности
системы от появления в ней
новых все более высоких иерархических уровней управления
Если
проанализировать приведенную таблицу, рисунок 2, на котором показана динамика эмерджентности и выражения
(6) – (11), то сразу бросается в глаза, что создание иерархической системы
управления полком приводит к добавлению в систему значительно большего
количества элементов, чем при реализации двухуровневого управления командиром
полка напрямую каждым солдатом, если бы такое было возможно на практике. Соответственно
это приводит к гораздо более значительному повышению уровня системности полка и
более выраженному системному эффекту (эмерджентности), выражающемуся в том, что
полк с иерархической структурой управления значительно более боеспособен и
живуч, чем с одноуровневой. Видно, что добавление в систему новых все более
высоких иерархических уровней управления приводит ко все меньшему увеличению
системного эффекта (эмерджентности), т.е. в основном в этом смысле играет роль
появление 1-го уровня иерархии (отделений, в нашем примере).
Кроме того из
рассмотренных примеров можно сделать вывод о зависимости степени живучести
системы в целом от степени ее иерархичности при нарушении системы управления: чем выше степень иерархичности системы
управления, тем в меньшей степени ее нарушение изменяет уровень системности и
тем более живуча система в целом в случае нарушения ее системы управления.
Это можно объяснить наличием системообразующих факторов на различных уровнях
организации системы (в нашем примере это командиры батальонов, рот, взводов и
отделений). В частности при невозможности для командира полка выполнять свои
функции по состоянию здоровья:
– в гипотетическом
случае, когда он управлял каждым солдатом непосредственно полк бы сразу
превратился из единого слаженного организма в дезорганизованную толпу, в
которой каждый сражается сам за себя;
– в случае приведенной
6-уровневой иерархической системы управления полк исчез бы как единое целое, но
продолжал бы достаточно эффективно сражаться в составе организованных отдельных
батальонов, сохраняющих полную управляемость и боеспособность.
Но теоретически
максимальный уровень системности нашего условного полка с 729 солдатами
составляет: 729/Log2729=76,65797.
Можно предположить, что этот огромный
уровень системности мог бы быть обеспечен, если бы весь полк состоял сплошь
из одних джедаев, свободно непрерывно телепатически общающихся друг с другом и
действующих как единое целое, т.е. практически как одно практически непобедимое
существо (если даже с одним таким воином очень проблематично справиться, то
можно себе представить какую силу представляет высокоорганизованная группа из
729 воинов без слов мгновенно и полностью понимающих друг друга независимо от
того, где и в какой ситуации каждый из них находится).
Здесь необходимо
отметить также известное положение из теории информации Шеннона состоящее в
том, что энтропия системы тем меньше, чем
больше взаимная информация в ее подсистемах друг о друге. В биологических
системах до определенного иерархического уровня их организации (клетки) в каждой
подсистеме вообще имеется полная информация о всей системе в целом (геном). Это
обеспечивает слаженную работу различных подсистем организма и сводит к минимуму
потребность в обмене информацией между ними.
Однако добавление
новой подсистемы в состав организационной системы не всегда приводит к
повышению ее уровня системности, как казалось бы можно было ожидать. Если продолжить
пример с полком, то это соответствует случаю внедрения в полк вражеского
разведчика или просто лишнего управленческого звена, которое не вносит в
систему управления ничего нового и ценного, а лишь дублирует команды, и хорошо
еще если делает это своевременно и без их искажения, а иногда и просто блокирует
прохождение команд на исполнение. Именно о подобных случаях говорят:
"Начальник уехал в служебную командировку и работа подразделения
неожиданно стабилизировалась, наладилась, сотрудников перестало
лихорадить". В организациях уровень системности может понижаться при
неоправданном разбухании административного аппарата.
В технической
системе при ее повреждении также уменьшается количество исправных функциональных
элементов, а также узлов и подсистем, в результате чего уменьшается уровень системности
и степень детерминированности, т.е. управляемости системы.
В этой связи
предлагается специально различать управляющие воздействия, целью которых
является перевод объекта управления в заранее заданное целевое состояние без
изменения его уровня системности и степени детерминированности, т.е. использование
объекта управления, и управляющие
воздействия направленные на повышение самого уровня системности и степени
детерминированности объекта управления, т.е. организующие управляющие воздействия, направленные на создание и
развитие объекта управления.
Если в первом случае управляющие факторы можно оценивать
по силе и направлению их влияния на объект управления, то во втором случае – по
величине и направлению изменения уровня системности и степени
детерминированности, которые можно количественно измерять с помощью
предложенных выражений системной теории информации для коэффициентов эмерджентности
Хартли и Харкевича, названных так в работе [97] в честь этих выдающихся ученых.
10.2. Исследование влияния подсистем
различных уровней иерархии на эмерджентные свойства системы в целом с
применением АСК-анализа и интеллектуальной системы "Эйдос"
(микроструктура системы как фактор управления ее макросвойствами)
“Истинное знание – это знание
причин”
Френсис
Бэкон (1561–1626 гг.)
Дальнейшее изложение основано на рабате [253],
нумерация формул, рисунков и таблиц сохранены.
Проблема,
решаемая в научных исследованиях, состоит в выявлении силы и направления
влияния состава и особенностей внутренней иерархической микроструктуры
структуры систем на их внешне наблюдаемые на макроуровне свойства, т.е. по сути,
в выявлении и исследовании вида причинно-следственных зависимостей между
составом, внутренней структурой и эмерджентными свойствами систем.
Другой формой этой же проблемы является построение на основе эмпирических данных[3]
формальной модели, количественно
отражающей силу и направление влияния значений факторов
на поведение моделируемого объекта, в частности на его переход в различные
будущие состояния.
Такая формальная модель обеспечивает решение
ряда как прямых, так и обратных задач.
Прямые задачи (задачи идентификации, распознавания и прогнозирования):
1. Прогнозирование свойств системы по ее
составу и структуре.
2. Идентификация состояния системы по ее
признакам.
3. Прогнозирование будущих состояний объекта
управления по системе действующих на него значений факторов.
Задачи управления (обратные задачи прогнозирования):
4. Определение такого состава и такой
структуры системы, которые обусловливают заранее заданные ее свойства.
5. Определение такой системы значений
управляющих факторов, которая переводит объект управления в заранее заданное
целевое состояние.
Идентификация и распознавание – это просто
синонимы. При идентификации считается, что признаки объекта и его состояние,
которое нужно определить по этим признакам, относятся к одному моменту времени[4]. Прогнозирование
отличается от идентификации тем, что (признаки) значения факторов относятся к
прошлому времени, а состояния объекта к будущему[5].
Задача управления (выработки управляющих
воздействия) является обратной
по отношению к задаче прогнозирования, так как при прогнозировании мы по
значениям факторов, относящимся к прошлому, определяем будущее состояние
объекта, а при управлении, наоборот, по заданному целевому (желательному)
состоянию объекта управления определяем такую систему значений факторов,
которая по определенным критериям[6] наиболее эффективно
обусловливает (детерминирует) переход объекта в это целевое состояние.
Сформулированные задачи имеют очень общий
характер, так как, по сути, являются вариациями одной математической задачи в
различных областях науки и практики, например:
– в
генетике: исследование и выявление силы и направления влияния признаков
генома и окружающей среды на фенотип (смысловая интерпретация генома с
применением технологий искусственного интеллекта: признаки генома и окружающей
среды как факторы управления фенотипом);
– в
психологии (управление персоналом): исследование зависимости личностных
и профессиональных качеств человека от его реакции на осознаваемый и
неосознаваемый стимульный материал (в частности на опросники); исследование
влияния личностных и профессиональных качеств человека на успешность его работы
на различных должностях; прогнозирование успешности деятельности конкретного
человека на различных должностях на основе ранее выявленных его личностных и
профессиональных качеств; разработка «Эйдос-реализации» психологических
тестов на основе их опросников и шкал, включая среду применения, а также
разработка интегральных тестов на основе стандартных тестов;
– в
педагогике: исследование влияния педагогических технологий (в том
числе: укомплектованности докторами и кандидатами наук, профессорами и доцентами,
методов преподавания, технической оснащенности, учебно-методического
обеспечения) на качество образования[7] вообще и уровень
предметной обученности в частности, а также на успешность профессиональной
деятельности по специальности после окончания обучения; оценка уровня
преподавания в учебном заведении; прогнозирование учебных достижений учащихся
по свойствам их личности и характеристикам образовательного и учебного
процесса; выработка рекомендаций по совершенствованию образовательных технологий;
– в
экономике: исследование влияния внутренней структуры предприятия на
эффективность ее деятельности; исследование влияния технологических,
экономических, социально-политических, природных и иных факторов на результаты
экономической деятельности предприятий, отраслей и регионов; оценка и
прогнозирование эффективности работы предприятий, выработка научно-обоснованных
рекомендаций по совершенствованию деятельности; прогнозирование динамики и
сценариев развития фондового рынка, поддержка принятия решений на фондовом
рынке;
– в
агрономии: исследование влияния агротехнологических факторов,
биологических свойств сортов и факторов окружающей среды на количественные и
качественные результаты выращивания сельскохозяйственных культур; прогнозирование результатов применения
конкретных агротехнологий для выращивания конкретных культур в заданных
условиях (почвы, предшественники, климат); разработка рекомендаций по системе
агротехнологий, обеспечивающей заданный результат выращивания; определение
степени соответствия условий зон и микрозон выращивания, требованиям,
предъявляемым конкретными культурами и сортами;
– в
кулинарии: исследование влияния рецептуры и технологии на вкусовые и
потребительские свойства продуктов питания; разработка рекомендаций по
рецептурам и технологиям, обеспечивающим получение продуктов питания с
заданными вкусовыми и потребительскими свойствами;
– в
металлургии: исследование влияния состава и технологии на свойства
сплавов; разработка рекомендаций по составу и технологиям, обеспечивающим
получение сплавов с заданными свойствами;
– в
химии: исследование зависимости химических свойств химических элементов
от структуры атомов; зависимость свойств химических соединений от элементного
состава и структуры молекул; прогнозирование свойств новых элементов и химических
соединений по их составу и структуре; разработка рекомендаций по составу и
структуре новых соединений с заранее заданными свойствами;
– в
физике: описание физических явлений и законов физики в различных
областях физики на языке теории информации; применение теории управления для
управления физическими процессами на различных уровнях организации материи;
– в
технических науках: выявление зависимостей свойств новых материалов и
технических систем от их состава, структуры и технологии создания; прогнозирование
свойств новых материалов и технических систем и выработка рекомендаций по
технологии их создания с заранее заданными свойствами;
– в
теории управления: выявление и исследование силы и направления влияния
значений факторов на свойства и поведение объекта управления; прогнозирование поведения объекта управления
под воздействием заданной системы значений управляющих факторов; выработка
такого управляющего воздействия, которое
с наивысшей степенью детерминированности переведет объект управления в заданное
целевое состояние;
– в
медицине: исследование зависимости диагноза от клинической картины и
симптоматики и зависимости плана лечения от диагноза; постановка диагноза и
прогнозирование успешности лечения по симптоматике; выработка плана лечения по
диагнозу;
– в
биологии: исследование зависимости потребительских, технологических и
адаптивных свойств сортов от их фенотипических (ботанических) признаков,
физиологии и генотипа; выработка рекомендаций по получению новых сортов и
культур;
–
в ампелографии: создание семантической информационной модели,
отражающей количество знаний, содержащихся в факте наблюдения каждого морфологического
и биолого-хозяйственного признака у конкретного образца винограда о том, что
этот образец относится к каждому из сортов, представленных в модели. Данную
модель можно использовать для решения задач ампелографии, т.е. для
идентификации образцов винограда или автоматизированного отнесения образца к
сортам на основе его описания с определением количественной меры сходства
образца с каждым сортом, а также для количественного определения степени
сходства сортов друг с другом путем агломеративной и дивизивной древовидной
кластеризации;
– в лингвистике: исследование
взаимосвязи между символами и словами, между смыслом фразы и словами, из
которых она состоит;
– в
теории чисел: исследование взаимосвязи между свойствами цифр и
чисел из них, между сложными числами и простыми числами, произведениями которых
они являются, исследование других взаимосвязей между числами.
Эти примеры можно легко продолжить, но для
целей данной работы и уже приведенных вполне достаточно. Остается добавить, что
по многим из приведенных примеров автором проведены конкретные исследования и разработки интеллектуальных приложений[8], т.е. поставлены и решены
перечисленные выше задачи идентификации, прогнозирования и поддержи принятия
решений в различных предметных областях и сделано это на единой
методологической и инструментально-технологической основе Автоматизированного
системно-когнитивного анализа (АСК-анализ) и его программного инструментария –
интеллектуальной системы «Эйдос».
Рассмотрим, как на теоретическом уровне, так
и на простом численном примере, как решается поставленная проблема в
АСК-анализе.
Система есть множество взаимосвязанных элементов,
что обеспечивает возникновение новых,
так называемых системных или эмерджентных свойств, которых не было у элементов
системы до их объединения в систему, что обеспечивает системе преимущества в
достижении целей. Таким образом, понятие системы основано на понятии множества,
но выходит за его пределы, т.е. является его обобщением, т.к. включает также понятия взаимосвязей между элементами, за счет которых образуются подсистемы
различных уровней иерархии, образующие структуру
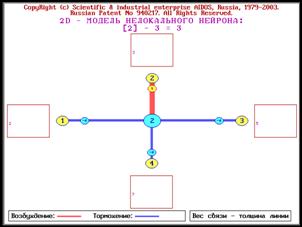
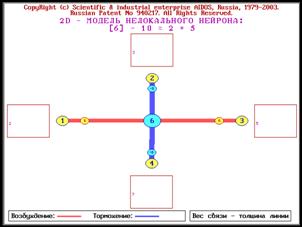
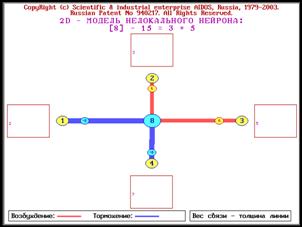
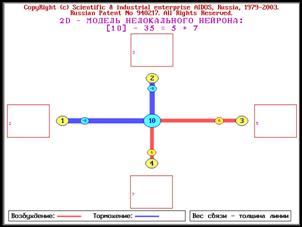
системы [97, 170, 189, 191, 196, 201, 240, 241, 245, 248]. На рисунках 1 и 2 представлены
в условном виде все возможные
подсистемы, образующиеся из 3-х и из 4-х базовых элементов, являющихся простыми
числами, путем их перемножения в различных сочетаниях:
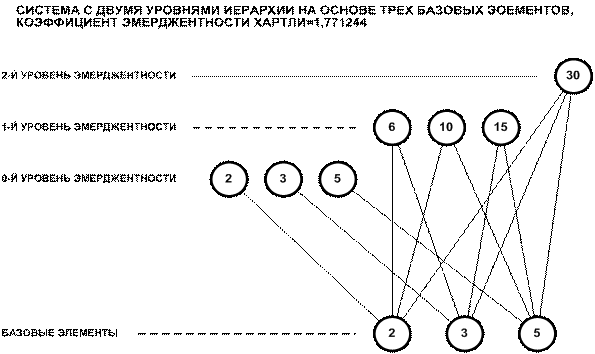
Рисунок 1. Пример системы сложных чисел,
основанных на 3 простых числах
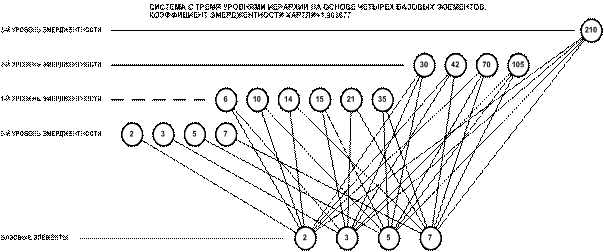
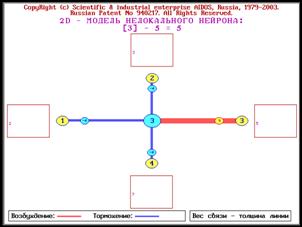
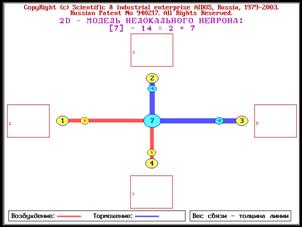
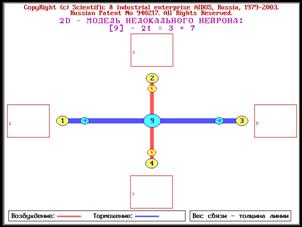
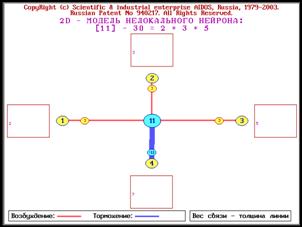
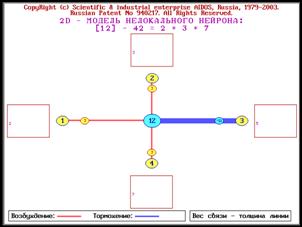
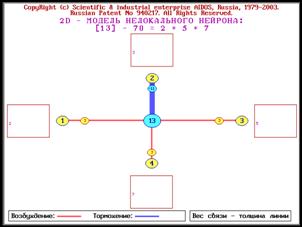
Рисунок 2. Пример системы сложных чисел,
основанных на 4 простых числах
Базовыми элементами будем называть элементы
исходного множества, на основе которого образуется система. При этом подсистемы
различных уровней иерархии некоторой
системы, основанной на n базовых элементов, могут
включать различное количество базовых элементов m, где m может изменяться от 1
до n. Конечно, реальные системы включают не все в принципе возможные подсистемы, а лишь некоторые из них, поэтому
на одном и том же множество базовых элементов могут основываться большое
количество различных систем, одинаковых по составу (базовым элементам), но
отличающихся своими структурами (подсистемами). Уровень базовых элементов будем
считать нулевым уровнем иерархии системы, подсистемы, состоящие из 2-х базовых
элементов – 1-м уровнем иерархии, и т.д., т.е. подсистемы из m базовых
элементов образуют k-й уровень иерархии, где k=m-1.
Отметим, что выбор в качестве примера
системы, основанной на базовых элементах, являющихся простыми числами, с
подсистемами, образующимися путем перемножения базовых элементов в различных
сочетаниях, не накладывает каких-либо ограничений на применимость полученных на
этом примере выводов в различных предметных областях, т.к. простые числа можно
рассматривать как условные коды
признаков систем или значений действующих на них факторов, а составные числа –
кодами эмерджентных свойств этих систем, образующихся путем взаимодействия
соответствующих базовых элементов, к тому же разложение сложных чисел на
простые множители является единственным.
Таким образом, приведенный в работе пример адекватно представляет в
символической форме как все вышеперечисленные примеры решения прямых и обратных
задач идентификации и прогнозирования в различных предметных областях, так и
все не перечисленные аналогичные задачи.
Если выдвинуть весьма правдоподобную
гипотезу, что свойства системы в целом
обусловливаются ее составом и структурой, то можно считать, что между этими
свойствами и подсистемами различных уровней иерархии существует взаимнооднозначное
соответствие, т.е.:
– на нулевом уровне иерархии свойства системы
соответствуют непосредственно самим элементам;
– на первом уровне иерархии свойства системы
соответствуют подсистемам, образованных из пар базовых элементов в различных
сочетаниях;
– на втором уровне иерархии свойства системы
соответствуют подсистемам, образованных из троек базовых элементов в различных
сочетаниях;
– на третьем уровне иерархии свойства системы
соответствуют подсистемам, образованных из четверок базовых элементов в
различных сочетаниях;
- - - - - - - - - - - - - - - - - - - - - - -
- - - - - - - - - - - - - - - - - - - - -
– на k-ом уровне иерархии свойства системы
соответствуют подсистемам, образованных из m базовых элементов в различных сочетаниях,
где k=m–1.
Таким образом, будем считать, что:
1. Система включает в свой состав не только базовые элементы, на
которых она основана, но и различные подсистемы из тех же базовых элементов в
различных сочетаниях и эти подсистемы образуют иерархическую структуру системы.
2. Базовые элементы системы будем считать ее подсистемами нулевого уровня иерархии.
3. Свойства системы в целом соответствуют ее
подсистемам различных уровней иерархии, поэтому все уровни иерархии, за
исключением нулевого, вполне обоснованно называть уровнями эмерджентности.
Ясно, что чем меньше базовых элементов в
подсистемах, т.е. чем более простыми
являются подсистемы, тем ближе свойства системы в целом к свойствам исходного
множества базовых элементов, на которых основана данная система. На основании
этого можно утверждать, что понятие
системы является обобщением понятия множества. При этом выполнятся принцип соответствия[9]
между этими понятиями, т.к. система плавно переходит в множество собственных
базовых элементов при уменьшении сложности ее структуры, т.е. числа уровней
иерархии и подсистем на этих уровнях до нуля.
Будем считать, что уровень системности (эмерджентность) системы тем выше, чем
больше ее свойства отличаются от свойств множества базовых элементов, на
которых она основана. Будем считать, что максимальное количество эмерджентных
свойств системы в целом 
, состоящей из M базовых элементов, равно количеству ее подсистем различных
уровней иерархии, т.е. различной сложности (1):
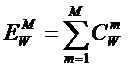(1)
где:
W – количество подсистем в системе, т.е. количество состояний
системы или количество ее эмерджентных свойств;
m – число базовых элементов в подсистеме (сложность
подсистемы);
M – максимальное количество базовых элементов в подсистеме
(максимальный уровень сложности подсистем) M
<=W.
В работах [97, 170, 189, 191, 196, 201, 240, 241, 245, 248] предложены,
обоснованы, развиты и исследованы абсолютные и относительные количественные меры уровня системности
(эмерджентности) системы, в качестве которых автором в 2002 году
предложены системное обобщение выражения Хартли для количества информации в системе (2), основанной на W базовых элементов и его отношение к
классическому количеству информации по Хартли (3) в множестве тех же базовых элементов [97] (4):
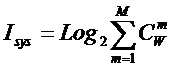(2)
(3)
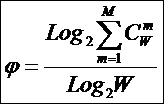(4)
Таким образом, этот коэффициент количественно
отражает максимально возможную степень отличия системы от множества его базовых
элементов. Поскольку выражение (4) основано на классическом выражении Хартли
для количества информации (3) и его системном обобщении, предложенном автором
(2), то в работе [97] для него было предложено
название: «Коэффициент эмерджентности Хартли», однако, в работах ряда авторов
эти и другие результаты преподносятся как собственные без ссылок на
первоисточники[10],
другие, напротив почему-то думают, что эта информационная мера уровня мера
системности была предоложена самим Р.Хартли.
Из вышеизложенного ясно, что уровень системности
(эмерджентности) системы или ее сложность
определяется не только числом базовых элементов в ней, но и взаимосвязями между ними, т.е. структурой системы, и при уменьшении интенсивности и количества
этих взаимосвязей система дезинтегрируется, т.е. структура системы
упрощается, пока полностью не исчезнет и система не превратится в простое
множество собственных базовых элементов. Значит уровень системности или
эмерджентность системы тем выше, чем выше сила и сложность взаимосвязей между
ее базовыми элементами. В работе [97] сформулирована и численно исследована гипотеза о
законе возрастания эмерджентности (рисунок 3):
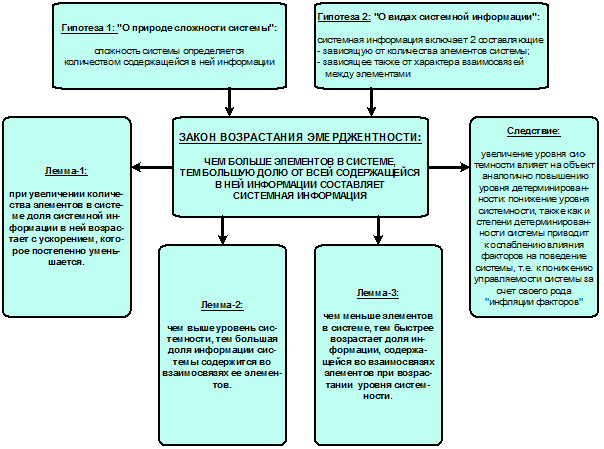
Рисунок 3. Гипотеза о
законе возрастания эмерджентности [97]
Но как связан уровень системности с
управляемостью системы? Интуитивно понятно, что чем сложнее система, тем сложнее
ей управлять. Фундаментальный принцип, раскрывающий природу взаимосвязи между сложностью системы и проблематичностью
управления ею предложен одним из основателей кибернетики Уильямом Россом Эшби и
в современной науке носит его имя.
|
1960 год. |
Принцип Эшби: «Управление может быть
обеспечено только в том случае, если разнообразие
средств управляющего (в данном случае всей системы управления) по крайней
мере не меньше, чем разнообразие
управляемой им ситуации» [11].
Обычно принцип Эшби интерпретируется таким
образом, что число факторов в модели должно быть не меньше числа состояний объекта
управления. |
Принцип Эшби не означает, что если модель объекта управления
отражает не все действующие на него факторы[12],
то управление им будет невозможно, а означает лишь, что в этом случае
управление будет не полным, не детерминистским. При этом под фактором
фактически понимается значение фактора и неявно предполагается, что каждое
будущее состояние объекта управления детерминируется одним значением фактора и
между значениями факторов и состояниями существует взаимнооднозначное соответствие,
т.е. по сути, предполагается, что модель
объекта управления является детерминистской, факторы не зависят друг от друга
(ортонормированны) и не взаимодействуют друг с другом, т.е. по сути, образуют
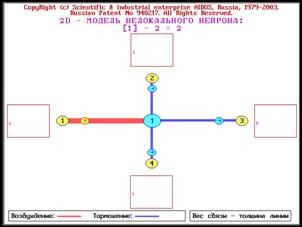
множество, а не систему факторов. Однако если
рассматривать объект управления как систему в цикле управления (рисунок 4),
то можно интерпретировать признаки как
значения факторов, воздействующих на систему, а классы как эмерджентные свойства системы или ее будущие состояния,
некоторые из которых являются целевыми, а некоторые нежелательными:
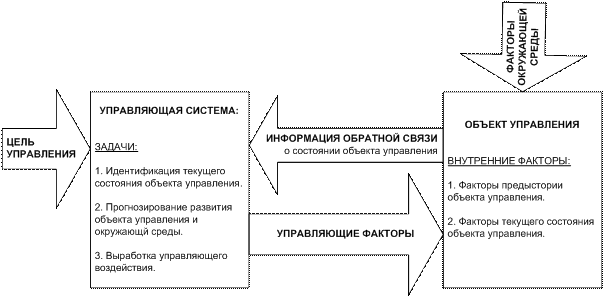
Рисунок 4. Объект управления как система в цикле управления
По мнению авторов это означает, что принцип Эшби
может быть обобщен с учетом системных представлений следующим образом:
«Для того
чтобы управление было полным (детерминистским) модель объекта управления должна
описывать силу и направление влияния на объект управления не меньшего суммарного
количества различных сочетаний значений факторов, чем количество возможных
будущих состояний объекта управления». Если записать это высказывание в форме
математического выражения, то получим
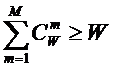(5):
(5)
Из выражения (5), естественно при W<>0,
следует эквивалентная форма 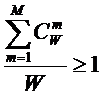(6):
(6)
Предлагается также следующая формулировка системного обобщения принципа Эшби:
«Чем больше различных сочетаний значений
факторов действует на объект управления, тем выше степень детерминированности
управления им». Из сравнения выражений (6) и (4) можно сделать вывод о том,
что из приведенной выше формулировки системного обобщения принципа Эшби
вытекает следствие: «Степень детерминированности управления
системой тем выше, чем выше ее эмерджентность (уровень системности),
количественно измеряемая коэффициентом эмерджентности Хартли».
Если в классическом принципе Эшби объект
управления рассматривается как многофакторный
линейный черный ящик[13],
т.е. черный ящик со многими входами и многими выходами не имеющий никакой
внутренней структуры, то в системном обобщении принципа Эшби объект управления
рассматривается как система однофакторных черных ящиков, каждый из которых имеет один вход и один выход, взаимодействующих между собой и образующих
подсистемы, что приводит к нарушению линейности объекта управления. Таким образом,
системное обобщение принципа Эшби основано на введении внутренней иерархической
структуры черного ящика.
Объект управления называется линейным, если результат совместного действия на него совокупности факторов равен
сумме результатов влияния на него каждого
из этих факторов по отдельности [273]. Это означает, что в линейном объекте управления факторы не взаимодействуют между собой,
не образуют подсистем детерминации, т.е. по сути, являются не системой, а множеством факторов. В нелинейных
объектах управления факторы образуют систему с определенным уровнем
системности, с новыми эмерджентными (системными) свойствами, не сводящимися к
свойствам факторов, рассматриваемым по отдельности. Чем ниже эмерджентность
(уровень системности) объекта управления, тем он как система ближе к множеству
и к линейности.
В работе [97] для количественной оценки степени
детерминированности системы предложен и численно исследован коэффициент
эмерджентности, названный в честь
А.А.Харкевича «Коэффициентом эмерджентности Харкевича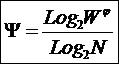» (7):
,
(7)
где N – количество фактов,
обобщенных в модели объекта управления. Фактом
является одновременное наблюдение на опыте двух событий: «Объект управления
перешел в j-е состояние» и «На объект
управления действовало i-е значение
фактора».
|
Александр Александрович (21.1(3.2).1904 – 30.3.1965) |
Александр Александрович Харкевич, директор
Института проблем передачи информации АН СССР академик АН СССР, является выдающимся
советским ученым, внесшим огромный вклад в создание семантической теории
информации тем, что внес в теорию информации представление о цели (и тем самым об управлении) и фактически, как стало ясно уже в наше время [245, 248] предложившим количественную меру знаний. |
Из вида выражения (7) для коэффициента эмерджентности
Харкевича Y очевидно, что увеличение уровня системности φ влияет
на семантическую информационную модель аналогично повышению уровня детерминированности
системы: понижение уровня системности, также как и степени детерминированности
системы приводит к ослаблению влияния факторов на поведение системы, т.е. к понижению
управляемости системы за счет своего рода "инфляции факторов"
[97]. Иначе говоря, если на объект управления действует ортонормированная система факторов, т.е. множество факторов, не
связанных между собой, и к этой системе добавляется еще один фактор, тождественный по своему влиянию одному
из уже имеющихся, то суммарное влияние этого нового фактора и тождественного
останется тем же самым, т.е. распределится между ними поровну (рисунок 5).
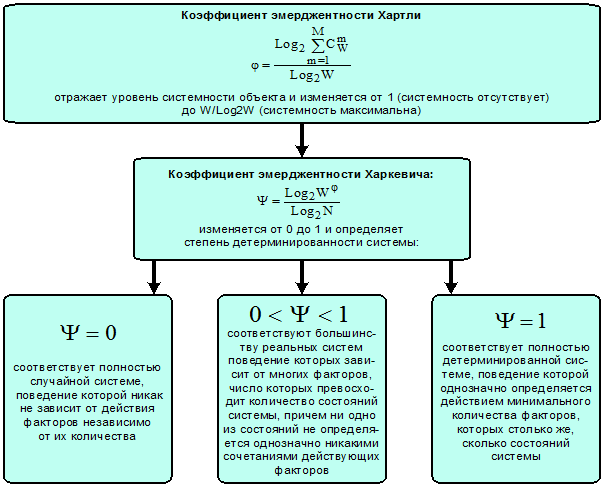
Рисунок 2. Интерпретация и взаимосвязь коэффициентов эмерджентности Хартли и Харкевича согласно [97]
Таким образом, коэффициенты эмерджентности
Хартли и Харкевича можно обоснованно считать количественным выражением
системного обобщения принципа Эшби.
Общим для всех сформулированных в начале работы задач,
и обобщенных, и из разных предметных областей, является неизвестность характера или вида причинно-следственных зависимостей
между составом, иерархической структурой и свойствами объектов, или между
значениями действующих на объект значениями факторов и его поведением. Однако
для решения задач идентификации (распознавания), прогнозирования и принятия
решений необходимо знать вид этих
зависимостей, следовательно, необходимо
выявить и отразить их в формальной модели перед решением этих задач. При
этом источником исходных данных для построения формальной модели могут быть только эмпирические данные, полученные
из опыта путем наблюдения или в специально организованных экспериментах.
Соответственно, возникает принципиальный вопрос, который можно сформулировать
следующим образом: «Возможно ли на основе
ряда примеров систем с известными внутренним составом и иерархической
структурой с одной стороны, и внешне наблюдаемыми свойствами с другой стороны,
выявить в количественной форме силу и направление причинно-следственных связей
между ними?».
Автоматизированный системно-когнитивный анализ
(АСК-анализ) и его программный инструментарий – интеллектуальная система
«Эйдос» [97] позволяют утвердительно ответить на этот вопрос, т.к.
предоставляют ряд новых возможностей для построения и верификации на основе
эмпирических данных формальных моделей, отражающих силу и направление
причинно-следственных связей между составом, структурой и свойствами объектов
или между значениями действующих на объект значениями факторов и его
поведением, а также для решения на основе этих моделей задач идентификации,
прогнозирования и принятия решений.
Однако перед тем как непосредственно перейти к
рассмотрению этих возможностей кратко обсудим некоторые методологические
аспекты создания и применения формальных моделей в научном познании.
Основываясь на работе [245] будем считать, что:
– закономерности – это
причинно-следственные зависимости, выявленные на исследуемой выборке и
распространяемые лишь на саму эту выборку;
– эмпирический закон – это
закономерности, выявленные на исследуемой выборке и распространяемые на
некоторую более широкую предметную область, в которой действуют те же причины их существования, что и в
исследуемой выборке и эта более широкая предметная область называется генеральной совокупностью, по отношению
к которой исследуемая выборка репрезентативна.
Важно, что генеральная совокупность является более широкой, чем исследуемая выборка,
причем не только в пространстве, но и во времени. Периоды времени, в
течение которых закономерности в предметной области существенно не меняются,
называются периодами эргодичности.
Можно сказать, что эргодичность – это
репрезентативность во времени. Границы между периодами эргодичности
называются точками бифуркации. Будем считать, что генеральная совокупность эргодична по отношению к исследуемой выборке,
а граница генеральной совокупности состоит из точек бифуркации.
Таким образом, если формальная модель адекватна, то по
результатам ее применения невозможно определить в какой именно подобласти
генеральной совокупности (области репрезентативности и эргодичности) она
применяется. Важно отметить, что сформулированное положение никак не привязано к конкретной предметной
области, исследуемой той или иной наукой.
В физике
сходный, но более ограниченный смысл
имеют принципы относительности Галилея и Эйнштейна:
«Все физические процессы в инерциальных
системах отсчёта[14]
протекают одинаково, независимо от того, неподвижна ли система или она
находится в состоянии равномерного и прямолинейного движения[15]».
При этом под «физическими процессами» в принципе относительности Галилея
подразумеваются только механические явления, а
Эйнштейна – кроме того, и электромагнитные, в частности оптические. Поэтому
если мы находимся в замкнутой инерциальной системе отсчета, то по протеканию
физических процессов невозможно определить, движется она или покоится, а также
в каком месте пространства и в каком времени она движется иди покоится. Из
принципа относительности Эйнштейна вытекают преобразования Лоренца, которые
являются релятивистским обобщением преобразований Галилея и относительно которых
инвариантны уравнения Максвелл, описывающие электромагнитные явления.
Это дает основания называть сформулированное положение
«Обобщенным принципом относительности». Предлагается следующая формулировка обобщенного принципа относительности,
относящегося не только к механическим и электромагнитным явлениям, но и вообще
ко всем явлениям, в том числе еще не обнаруженным и даже к тем, которые в
принципе никогда не будут обнаружены человечеством: «Законы природы открытые в
одном месте и в определенное время действуют и в других местах и в другое
время», поэтому по виду законов природы в
замкнутой лаборатории невозможно определить
в каком месте (пространства) и в каком времени эта лаборатория находится, т.е. по
виду законов природы внутри лаборатории невозможно локализовать ее в
пространстве-времени. По-видимому, из этого утверждения также могут быть
выведены преобразования, являющиеся обобщением преобразований Лоренца для различных
предметных областей, а не только для физики.
Обобщенный
принцип относительности является методологической основой синтеза формальной модели объекта управления[16] на основе исследуемой
выборки, и применения этой модели в
течение периода эргодичности для решения задач идентификации, прогнозирования и
принятия решений в некоторой генеральной совокупности, по отношению к которой
исследуемая выборка репрезентативна.
На этом утверждении фактически основана вся современная наука, так как когда ученые открывают и исследуют в своих лабораториях новые
явления природы и новые законы, то они при этом неявно предполагают, что
открываемое ими новое знание будет использоваться не только лично ими, но в будущем пригодится и другим людям,
причем и в других странах. Они также
предполагают, что изучив законы природы в своих лабораториях они могут на их
основе делать выводы об объектах и процессах, весьма удаленных в пространстве и
времени, а также об объектах существенно других масштабов, чем изучаемые в лаборатории.
Пример-1. Исследуя излучение света
нагретыми химическими элементами ученые могут по спектрам этого излучения
определять химический состав веществ не только на Земле, но и химический состав
далеких планет, Солнца и других звезд, в том числе в других галактиках. Правда
наблюдается «красное смещение» спектральных линий, которое сегодня объясняется
законом Хаббла[17]
и расширением вселенной[18], хотя известно, что возможны
и другие объяснения. Предлагается
гипотеза о том, «красное смещение» может быть объяснено не только
расширением вселенной, но и ускорением
темпа времени в ней (или совместным действием этих факторов в разных
сочетаниях степени их влияния на появление этого эффекта[19]). При этом фотоны,
которые мы регистрируем на Земле, относятся к тем более отдаленному прошлому,
чем дальше находится источник их излучения от Земли, и смещение их частоты в
красную сторону отражает на сколько темп времени в источнике их излучения меньше,
чем на Земле. В замкнутой системе отсчета нет возможности определить, изменился
ли темп времени в ней, даже если он изменится в 1000 раз, но это возможно при
взаимодействии нескольких систем отсчета с разным темпом времени в них.
Например, когда человек спит, то в течение нескольких секунд может увидеть сон
с событиями, которые занимают 2-3 часа и при этом ему не кажется, что эти
события происходят в каком-то ускоренном темпе, но это только потому, что во
время сна он не осознает событий в физической реальности и не имеет возможности
сравнить темп их реализации.
Пример-2. Изучив законы гравитации на
Земле и в Солнечной системе ученые могут применять их в масштабах нашей и
других галактик, а также в масштабах метагалактики. Правда при этом
обнаруживается фактическое
несоблюдение этих законов даже уже в масштабах галактики и для объяснения этого
предполагается существование «темной материи[20]» и «темной энергии»,
свойства которых и распределение в пространстве как раз таковы, что позволяют
«объяснить» расхождение теории с фактом, хотя известно, что возможны и другие
объяснения. Например, энергии гравитационного поля соответствует масса, которая
в свою очередь создает гравитационное поле, т.е. гравитационное поле является
нелинейным самосогласованным полем. Правда заметным это становится лишь при
очень больших по напряженности или по объему гравитационных полях, т.е. как раз
в очень больших масштабах, порядка размеров галактики и больше, или вблизи таких
экзотических объектов, как черные дыры. Предлагается
гипотеза, что никакой «темной материи и энергии» нет, но есть дополнительное гравитационное поле,
которое объясняли их наличием, однако это дополнительное гравитационное поле
создается самим гравитационным полем.
|
Ама́лия Э́мми
Нётер[21] 23.03.1882 – 14.04.1935 |
В соответствии с фундаментальной теоремой
Эмми Нётер[22]
из симметрий пространства-времени: однородности и изотропности пространства и
однородностью времени, следуют, соответственно, законы сохранения импульса,
момента количества движения и энергии[23]. Выполнение принципа
относительности Галилея-Эйнштейна обусловлено тем, что законы физики не меняются
при инерциальном смещении системы отсчета (в т.ч. в гравитационном поле), и
одинаковы при смещении в разных направлениях, во времени, и при поворотах. |
Получается, что есть основания сформулировать следующую
гипотезу: «Принцип относительности
выполняется по тем же причинам, по которым существуют законы сохранения и этими
причинами являются симметрии пространства-времени».
В этой связи возникают два принципиальных вопроса:
Вопрос-1. В какой степени абстрактная
модель полностью однородного и изотропного пространства-времени, рассматриваемая
в теореме Нётер, соответствует свойствам реального пространства-времени, т.е.
на сколько адекватно эта абстрактная модель отражает реальность?
Вопрос-2. Если реальные пространство не
является полностью однородным и изотропным и реальное время не совсем однородно,
то каким образом это отклонение их свойств от свойств абстрактного полностью
однородного и изотропного пространства-времени сказывается на степени
соблюдения законов сохранения импульса, момента импульса и энергии, а также на
точности принципа относительности?
Естественно, 2-й вопрос становится актуальным в
случае неполной адекватности абстрактной модели абсолютно однородного и
изотропного пространства-времени, рассматриваемого в теореме Нётер.
|
Альберт 14.03.1879 – 18.04.1955 |
В
современной науке считается, что свойства реального (физического) пространства-времени
определяются распределением масс, т.к. гравитация согласно модели общей теории относительности
(ОТО)[24]
Альберта Эйнштейна[25]
представляет собой деформацию пространства-времени, т.е. нарушение его однородности и изотропности, вызванное
распределением массы-энергии. Поэтому пространство-время может быть однородным
и изотропным только в однородной и изотропной вселенной, в которой это условие
выполняется для распределения массы-энергии как в микро, так и в мега масштабах[26]. |
Следовательно, ответ на 1-й вопрос, по сути,
сводится к ответу на вопрос об однородности и изотропности распределения
массы-энергии во вселенной.
На уровне микро масштабах об однородности и изотропности
распределения масс не может быть и речи, т.к. всем хорошо известно, каким
сложным образом движутся планеты вокруг Солнца и спутники планет вокруг них.
Недавно в ряде работ с участием автора выяснилось[27], что это движение оказывает довольно заметное влияние на движение
географического и магнитного полюсов Земли [243], на конфигурацию магнитного поля
Земли, на частоту землетрясений на Земле, а также на поведение людей и их
социальный статус.
Длительное время считалось, что вселенная однородна
и изотропна в мега масштабах (космологический
принцип[28]),
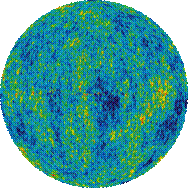
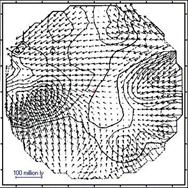
однако в последнее время появились данные о том, что, по-видимому, и это тоже не так. В этой связи необходимо упомянуть
работы по реликтовому излучению[29], великому аттрактору[30] и сенсационные
исследования профессора Майкла Лонге[31] (США) с коллегами по
ассиметрии распределения и ориентации спиральных галактик в метагалактике[32] (рисунок 6).
|
|
|
|
|
Анизотропия реликтового излучения. Источник изображения: http://upload.wikimedia.org/wikipedia/commons/2/28/WMAP_2008.png |
Карта потоков галактик в метагалактике
согласно http://www.atlasoftheuniverse.com/superc/cen.html Источник изображения: http://www.universe-review.ca/I03-02-attractor2.jpg |
Анизотропия распределения
спиральных галактик во Вселенной. Источник: http://www.modcos.com/news.php?id=115 |
Рисунок 6. Ассиметрия
вселенной в масштабах метагалактики
Как мы видим из этих примеров реальная структура метагалактики весьма мало напоминает однородную и изотропную и
может быть принята такую только в очень грубом приближении. Таким же грубым
приближением к реальности являются и теории, основанные на этом предположении.
Это и есть ответ на 1-й вопрос, который делает актуальным поиск ответа и на 2-й
вопрос[33], который, по-видимому,
будет найден в более общих и более точных физических теориях, чем современные.
Таким образом, есть основания полагать, что даже в
физике принцип относительности имеет границы применимости, но
на предметные области других наук он не распространяется [275] и поэтому в [253] и в данной
работе предложен обобщенный принцип относительности: «Законы природы открытые в одном месте и в определенное время действуют
и в других местах и в другое время», поэтому
по виду законов природы в лаборатории невозможно определить в
каком месте (пространства) и в каком времени эта лаборатория находится, т.е.
по виду законов природы внутри лаборатории невозможно локализовать ее в
пространстве-времени.
В частности, никакими экспериментами внутри полностью замкнутой виртуальной
реальности (сном) невозможно определить, является эта реальность виртуальной
(сном) или реальной. Но это можно установить, выйдя за пределы этой реальности, например, сняв амуницию
виртуальной реальности или просто проснувшись. Поэтому внутри нашей реальности нет критериев, позволяющих обоснованно
утверждать, что наша реальность не является виртуальной (сном). Из этого можно
сделать очень важный вывод о том, что для
того, чтобы давать истинные результаты способ
определения степени истинности реальности сам должен быть истинным, т.е. он сам
не должен относиться к той области реальности, которая с помощью него оценивается.
Например, если мы хотим определить спим мы или нет, то сам способ, который мы
используем для этого, не должен нам сниться, т.к. иначе он может дать
результаты, которые тоже нам снятся, и, соответственно, могут быть какими
угодно, в том числе и «подтверждающими», что мы не спим, и тем самым могут
ввести нас в заблуждение [163, 164, 275][34]. Проще говоря нам может
приснится, что мы бодрствуем и мы во сне сами можем придерживаться этого
мнения, но от этого сон не станет бодрствованием. Из этого примера следует, по
крайней мере, два вывода:
1. Принцип относительности описывает не саму реальность,
а то, какой она осознается в замкнутой лаборатории, но как только мы связываем
каналом передачи информации как минимум две до этого замкнутые лаборатории, то
сразу очевидным, что этот принцип нарушается.
2. Наша «истинная» реальность имеет очень много
общего с виртуальной реальностью, по крайней мере, внутри нее у нас нет способа
и критериев это опровергнуть. Этот вывод усиливается и другими доводами, в
частности наличием в нашем мире квантовых явлений[35] и релятивистских
эффектов, а также различных аномальных явлений и их сходством с современными
средствами трехмерной визуализации.
И не смотря на то, что на этом принципе, как было
показано выше, по существу основана современная наука он, строго говоря, не верен, т.е. выполнятся лишь в первом весьма
грубом приближении. Для всех наук, изучающих реальную область, кроме физики,
это совершенно очевидно, и фактически современная наука (кроме физики) основана не только на этом принципе, но и на
исследовании зависимости степени его несоблюдения от локализации лаборатории в
пространстве-времени и масштабов изучаемых явлений, т.е. исследование региональных особенностей и
их динамики[36]. Для обоснования этого положения достаточно привести несколько примеров
из области социально-экономических, политологических и психологических исследований.
Пример-1: исследование региональных особенностей и их динамики
в экономике, социологии, политологии.
Лауреат Нобелевской премии в области экономики,
основатель математической экономики Василий Васильевич Леонтьев[37] разработал
экономико-математические модели межотраслевого баланса. Однако эти модели с
различной степенью адекватности описывали реальную экономику разных стран, а иногда вообще ее не описывали, например тех, в
которых «экономика должна быть экономной». Можно было бы построить карту мира с
наглядной визуализацией на ней степени адекватности этих моделей в динамике.
Даже очень хорошие модели, заслужившие наивысшую оценку, имеют свои
ограниченные в пространстве и времени области адекватности.
Социологи и политологи изучают общественное мнение
по различными вопросам в разрезе по регионам и различным группам населения и
также это делают в динамике.
Пример-2: «зарабатывание» на разнице в
курсах ценных бумаг.
Приведем замечательную цитату из работы академика
А.Б.Мигдала[38]: «…
как неравномерность хода времени приводит к несохранению энергии. Допустим, что
неравномерность хода времени проявилась в том, что начиная с некоторого момента
стала периодически изменяться постоянная всемирного тяготения. Тогда легко
построить машину, которая будет получать энергию из ничего, – "вечный
двигатель". Для этого нужно поднимать
грузы в период слабого тяготения и превращать приобретенную ими энергию в
кинетическую, сбрасывая грузы в период увеличения тяготения[39].
Видите, неравномерность хода времени, то есть изменение относительного ритма
разных процессов, приводит к нарушению закона сохранения энергии». Не правда
ли, это весьма и весьма напоминает то, чем занимаются спекулянты на рынке
ценных бумаг: покупают товар, когда цена
на него падает до локального минимума и прогнозируется ее повышение, и продают,
когда она достигает локального максимумам и ожидается ее понижение. Чем не
нарушение закона сохранения энергии в экономике и не «экономический вечный двигатель»?
Более того, спекулянты ведут себя так,
как будто стараются нарушить закон сохранения энергии в максимально возможной
степени [196], т.к.
нет никакого экономического смысла в том, чтобы покупать и продавать ценные
бумаги по одной и той цене и чем выше разница
в цене приобретения и продажи, тем выше прибыль. Действия таможенников также
приводят к нарушению закона сохранения энергии в экономике, по своему содержанию
по сути ничем не отличаясь от действий «демонов
Максвелла»[40],
только на макроуровне. Аналогично и в пространстве
товары перемещают из тех мест, где они дешевле (обычно там они и производятся),
туда, где они дороже, т.е. логистические
потоки информационные, финансовые, энергетические и материальные, направлены
таким образом, чтобы в максимально возможной степени нарушать закон
сохранения импульса в экономике [196]. Ясно,
что нет никакого экономического смысла возить товары по путям, по которым их цена
не меняется, а именно для этих областей экономического пространства выполняется
закон сохранения импульса по данному виду товаров. Таким образом, вечный
двигатель, невозможный в физике, вполне возможен в экономике из-за
ярко-выраженного нарушения обобщенного принципа относительности, а также
законов сохранения энергии и импульса в экономике. При этом
финансовые и материальные потоки направлены в область максимального скорости
изменения градиента или разности потенциалов что, по-видимому, связано с каким-то
обобщением принципа наименьшего действия [196].
Пример-3: локализация и адаптация
психологических тестов. В управлении персоналом часто используются психологические
тесты. Как правило, их скачивают в Интернете или находят на пиратских
компакт-дисках. При этом обычно не задаются вопросами о том, на сколько
корректно применять эти тесты, например, в ООО «Сигнал» в России 2012 года,
если они были разработаны в Стэндфордском университете США в 1970 году, т.е.
ведут себя так, как будто предполагают,
что для них соблюдается обобщенный принцип относительности[41].
Между тем даже в США они уже подвергались многократной
адаптации, т.к. с течением времени закономерности в предметной области изменяются и там
это прекрасно осознают и отслеживают в своих психологических измерительных
инструментах эти изменения. Даже в США они локализуются для применения в других штатах, т.к. закономерности в предметной области
изменяются в пространстве, и там это прекрасно осознают и отслеживают в
своих психологических измерительных инструментах эти изменения. Между тем в
России есть необходимые для этого технологии, но они не востребованы[42], т.к. по-видимому, легче
и главное прибыльнее занимамться профанацией, чем реальными исследованиями и
разработками.
Таким образом, свойства
социально-экономического, политического и психологического пространства-времени
разные в разных местах и весьма динамично изменяются с течением физического
времени. Если бы для них существовал какой-то обобщенный вариант теоремы
Нётер, то можно было бы сделать предположение о несоблюдении в этих предметных
областях законов сохранения. Может быть даже, что это играет существенную роль
в прогрессе человеческого общества, экспоненциальном росте объемов знаний в
обществе, капиталов и технологического потенциала. Известно, что преобразование
Лапласа[43] и особенно дискретное
z-преобразование Лорана[44], описывают процесс
затухания последствий от некоторой причины и в соответствующие интегралы и
суммы входит экспоненциальный коэффициент затухания, т.к. если функция будут
затухать медленнее, чем по экспоненте, то получается расходящийся интеграл (сумма), т.е. получается, что описываемая им
причина будет иметь бесконечные
последствия. Похоже, что общество как раз и является подобным бесконечным
последствием, своего рода «эффектом бабочки»[45].
Но что делать, если обнаруживаются новые факты,
которые неадекватно описываются или вообще не описываются существующей теорией
или моделью? В этом случае эту теорию или модель необходимо развивать с учетом
этих новых фактов (а не отрицать само существование этих «неудобных» фактов,
что конечно проще), развивать так, чтобы эти новые факты тоже стали описываться
теорией адекватно, так же как и все факты, известные до этого (принцип соответствия[46]). В терминологии, принятой
АСК-анализе это означает следующее [245] (рисунок 7):
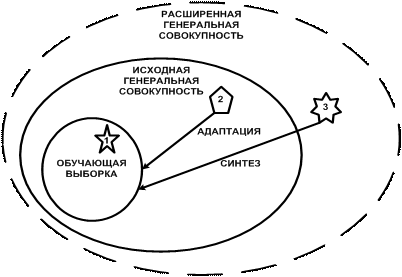
Рисунок 7. К пояснению
смысла понятий:
«адаптация и пересинтез модели»
Новый факт («3» на рисунке 7) не
описывается (не идентифицируется) адекватно существующей моделью, т.к.
по-видимому, не относится к генеральной совокупности или периоду эргодичности,
по отношению к которым репрезентативна обучающая выборка, на основе которой
создана данная модель. В этом случае, для того
чтобы восстановить адекватность модели, необходимо добавить данный факт к
обучающей выборке (для чего обычно необходимо расширить классификационные и описательные
шкалы градации) и произвести пересинтез модели. Это обеспечивает качественное изменение смысла признаков
и образов классов, в результате чего предметная область адекватности модели,
т.е. генеральная совокупность и период эргодичности расширяются.
Рассмотрим численный пример, демонстрирующий возможность
выявления причинно-следственных связей между внутренней иерархической
структурой системы и ее внешне наблюдаемыми на макроуровне системными или эмерджентными
свойствами с применением технологий автоматизированного системно-когнитивного
анализа и его программного инструментария – интеллектуальной системы «Эйдос».
Рассмотрим также пример неадекватной идентификации объектов, не входящих в
генеральную совокупность и пересинтез модели, позволяющий восстановить ее
адекватность на более широкой генеральной совокупности (рисунок 7). Отметим,
что автоматическое создание классификационных и описательных шкал и градаций
для рассматриваемых ниже моделей при различных их параметрах обеспечивается
стандартным режимом системы «Эйдос» _159, который полностью автоматизирует этап формализации предметной области
АСК-анализа и включен в систему для учебных целей[47].
В качестве базовых
элементов в полном соответствии с рисунком 2 будем рассматривать простые числа из диапазона от 2 до 7
включительно, а в качестве подсистем различных уровней иерархии – составные
числа, образующиеся путем различных сочетаний базовых в качестве сомножителей
по 1, 2, 3 и 4. Из этих базовых элементов путем их использования в качестве
сомножителей во всех возможных различных сочетаниях по 1, 2, 3 и 4 образуются
составные (сложные) числа, детерминирующие эмерджентные свойства числовых
подсистем и системы в целом, в частности 0-го уровня эмерджентности, которому
соответствуют свойства самих базовых элементов. Поэтому в качестве классов
естественно рассматривать, как базовые элементы, так и составные числа (таблица
1).
Таблица 1 – СПРАВОЧНИК
КЛАССОВ
|
KOD |
NAME |
|
1 |
2 = 2 |
|
2 |
3 = 3 |
|
3 |
5 = 5 |
|
4 |
7 = 7 |
|
5 |
6 = 2 * 3 |
|
6 |
10 = 2 * 5 |
|
7 |
14 = 2 * 7 |
|
8 |
15 = 3 * 5 |
|
9 |
21 = 3 * 7 |
|
10 |
35 = 5 * 7 |
|
11 |
30 = 2 * 3 * 5 |
|
12 |
42 = 2 * 3 * 7 |
|
13 |
70 = 2 * 5 * 7 |
|
14 |
105 = 3 * 5 * 7 |
|
15 |
210 = 2 * 3 * 5 * 7 |
Если в качестве признаков также как ив качестве
классов рассматривать свойства подсистем, то задача становится тривиальной,
т.к. при этом справочники признаков и классов полностью совпадают. В этом случае
чтобы сформировать модель мы в качестве исходных данных для нее должны предварительно выявить и указать
связи между базовыми элементами и подсистемами, которые на рисунке 8 изображены
в виде линий, соединяющих базовые элементы с составными числами, образованными
на их основе. Но больший научный и практический интерес представляет задача выявления силы и направления этих связей
между базовыми элементами и эмерджентными свойствами системы в целом. Поэтому в
качестве признаков будем рассматривать только базовые элементы (таблица 2):
Таблица 2 – СПРАВОЧНИК ПРИЗНАКОВ
|
KOD |
NAME |
|
1 |
2 |
|
2 |
3 |
|
3 |
5 |
|
4 |
7 |
В качестве объектов обучающей выборки рассматриваются
числовые подсистемы различных уровней иерархии, приведенные на рисунке 8,
закодированные с использованием таблиц 1 и 2 (таблица 3):
Таблица 3 – ОБУЧАЮЩАЯ ВЫБОРКА
|
NAME |
Уровень эмерджент-ности |
Коды классов |
Коды признаков |
||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
1 |
2 |
3 |
4 |
|||
|
1 |
Obj_1 |
Нулевой |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
Obj_2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
Obj_3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
4 |
Obj_4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
5 |
Obj_5 |
Первый |
1 |
2 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
6 |
Obj_6 |
1 |
3 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
|
|
|
7 |
Obj_7 |
1 |
4 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
|
|
|
|
8 |
Obj_8 |
2 |
3 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
|
9 |
Obj_9 |
2 |
4 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
|
|
|
10 |
Obj_10 |
3 |
4 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
4 |
|
|
|
|
11 |
Obj_11 |
Второй |
1 |
2 |
3 |
5 |
6 |
8 |
11 |
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
12 |
Obj_12 |
1 |
2 |
4 |
5 |
7 |
9 |
12 |
|
|
|
|
|
|
|
|
1 |
2 |
4 |
|
|
|
13 |
Obj_13 |
1 |
3 |
4 |
6 |
7 |
10 |
13 |
|
|
|
|
|
|
|
|
1 |
3 |
4 |
|
|
|
14 |
Obj_14 |
2 |
3 |
4 |
8 |
9 |
10 |
14 |
|
|
|
|
|
|
|
|
2 |
3 |
4 |
|
|
|
15 |
Obj_15 |
Третий |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
1 |
2 |
3 |
4 |
На основе обучающей выборки посчитана матрица
абсолютных частот (матрица сопряженности) (таблица 4), на основе которой с
использованием четырех частных критериев знаний (таблица 5) получены
четыре базы знаний, обеспечивающие различную среднюю достоверность с двумя
интегральными критериями (таблица 6):
Таблица 4 – МАТРИЦА
АБСОЛЮТНЫХ ЧАСТОТ
(МАТРИЦА СОПРЯЖЕННОСТИ)
|
Признаки |
Классы
(код, наименование, уровень эмерджентности) |
|||||||||||||||
|
Код |
Наимен. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
2 |
3 |
5 |
7 |
2*3 |
2*5 |
2*7 |
3*5 |
3*7 |
5*7 |
2*3*5 |
2*3*7 |
2*5*7 |
3*5*7 |
2*3*5*7 |
||
|
0-й
уровень эмерджентности |
1-й
уровень эмерджентности |
2-й
уровень эмерджентности |
3-й УЭ |
|||||||||||||
|
1 |
2 |
8 |
4 |
4 |
4 |
4 |
4 |
4 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
|
2 |
3 |
4 |
8 |
4 |
4 |
4 |
2 |
2 |
4 |
4 |
2 |
2 |
2 |
1 |
2 |
1 |
|
3 |
5 |
4 |
4 |
8 |
4 |
2 |
4 |
2 |
4 |
2 |
4 |
2 |
1 |
2 |
2 |
1 |
|
4 |
7 |
4 |
4 |
4 |
8 |
2 |
2 |
4 |
2 |
4 |
4 |
1 |
2 |
2 |
2 |
1 |
Таблица 5 – РАЗЛИЧНЫЕ
АНАЛИТИЧЕСКИЕ ФОРМЫ
ЧАСТНЫХ КРИТЕРИЕВ ЗНАНИЙ
|
Наименование модели знаний |
Выражение для частного критерия |
|
|
через |
через |
|
|
СИМ-1, частный
критерий: количество знаний по А.Харкевичу, 1-й вариант расчета вероятностей: Nj – суммарное количество признаков
по j-му классу (предпоследняя
строка таблицы 2) |
|
|
|
СИМ-2, частный
критерий: количество знаний по А.Харкевичу, 2-й вариант расчета вероятностей:
Nj – суммарное количество объектов
по j-му классу (последняя строка
таблицы 2) |
|
|
|
СИМ-3, частный критерий:
разности между фактическими и теоретически ожидаемыми по критерию хи-квадрат
абсолютными частотами |
--- |
|
|
СИМ-4,
частный критерий: ROI -
Return On Investment |
|
|
|
СИМ-5, частный
критерий: разность условной и безусловной вероятностей |
|
|
Смысл и поведение функций, приведенных в таблице
5, очень сходен, что очевидно из их математической формы. В работе [277]
приведен более полный перечень функций, используемый в АСК-анализе и системе
«Эйдос-Х++» для метризации шкал.
Таблица 6 –
ДОСТОВЕРНОСТЬ МОДЕЛЕЙ С РАЗНЫМИ КОЛИЧЕСТВЕННЫМИ КРИТЕРИЯМИ ЗНАНИЙ И РАЗНЫМИ
ИНТЕГРАЛЬНЫМИ КРИТЕРИЯМИ [10, 11]
|
Наименование |
Вид |
Расчет
проведен |
Достоверность |
|||
|
Дата |
Идентификации |
Идентификации |
Идентификации |
Средняя |
||
|
СИМ-4 |
Корреляция |
02-01-12 |
09:40:57 |
100,000 |
63,306 |
81,653 |
|
Свертка |
02-01-12 |
09:41:00 |
100,000 |
63,306 |
81,653 |
|
|
СИМ-3 |
Корреляция |
02-01-12 |
09:41:04 |
100,000 |
63,306 |
81,653 |
|
Свертка |
02-01-12 |
09:41:06 |
100,000 |
63,306 |
81,653 |
|
|
СИМ-2 |
Корреляция |
02-01-12 |
09:41:10 |
100,000 |
63,306 |
81,653 |
|
Свертка |
02-01-12 |
09:41:12 |
33,858 |
75,403 |
54,631 |
|
|
СИМ-1 |
Корреляция |
02-01-12 |
09:41:17 |
100,000 |
63,306 |
81,653 |
|
Свертка |
02-01-12 |
09:41:20 |
100,000 |
77,823 |
88,911 |
|
Из таблицы 6 видно, что наилучшей
достоверностью по двум видам ошибок обладает модель СИМ-1 с интегральным
критерием: «сумма информации» (свертка), поэтому база знаний этой модели и
приводится в таблице 7:
Таблица 7 – МАТРИЦА
ЗНАНИЙ СИМ-1 (Биты × 1000)
|
Признаки |
Классы
(код, наименование, уровень эмерджентности) |
|||||||||||||||
|
Код |
Наимен. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
2 |
3 |
5 |
7 |
2*3 |
2*5 |
2*7 |
3*5 |
3*7 |
5*7 |
2*3*5 |
2*3*7 |
2*5*7 |
3*5*7 |
2*3*5*7 |
||
|
0-й
уровень эмерджентности |
1-й
уровень эмерджентности |
2-й
уровень эмерджентности |
3-й УЭ |
|||||||||||||
|
1 |
2 |
352 |
-167 |
-167 |
-167 |
216 |
216 |
216 |
-304 |
-304 |
-304 |
100 |
100 |
100 |
-419 |
0 |
|
2 |
3 |
-167 |
352 |
-167 |
-167 |
216 |
-304 |
-304 |
216 |
216 |
-304 |
100 |
100 |
-419 |
100 |
0 |
|
3 |
5 |
-167 |
-167 |
352 |
-167 |
-304 |
216 |
-304 |
216 |
-304 |
216 |
100 |
-419 |
100 |
100 |
0 |
|
4 |
7 |
-167 |
-167 |
-167 |
352 |
-304 |
-304 |
216 |
-304 |
216 |
216 |
-419 |
100 |
100 |
100 |
0 |
База знаний,
приведенная в таблице 7, является решением проблемы поставленной в разделе,
т.к. отражает силу и направление влияния подсистем различных уровней иерархии на эмерджентные
свойства системы в целом, причем в единой сопоставимой форме в единицах
измерения информации и знаний: миллибитах. Знак
чисел в таблице 7 показывает направление
связи, а величина модуля – силу связи между признаками и классами.
При малой
размерности модели таблица 7 может быть непосредственно обозримой и понятной
для исследователя, поэтому в данной работе и приведена подобная модель. Однако
при больших размерностях модели необходимы специальные режимы, позволяющие
делать различные выборки из базы знаний и представлять информацию в удобной,
понятной и наглядной форме. Для этой цели в системе «Эйдос» есть ряд режимов,
позволяющих выводить информационные портреты классов и признаков, а также
когнитивные функции (функции влияния) и другие текстовые и графические формы
(которых более 110 различных видов).
Ниже кратко
рассмотрим некоторые из них.
Нелокальные нейроны
и интерпретируемые нейронные сети позволяют в наглядной графической форме
отобразить систему детерминации будущих состояний [138].
Нелокальный нейрон представляет собой будущее состояние объекта управления
с изображением наиболее сильно влияющих на него факторов с указанием силы и
направления (способствует-препятствует) их влияния (рисунок 8):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 8. Отображение базы знаний (таблица 7)
в форме нелокальных нейронов [138]
Нелокальная нейронная сеть представляет собой совокупность взаимосвязанных
нейронов. В классических нейронных сетях связь между нейронами осуществляется
по входным и выходным сигналам, а в нелокальных нейронных сетях – на основе
общего информационного поля, реализуемого семантической информационной моделью.
Система "Эйдос" обеспечивает построение любого подмножества
многослойной нейронной сети с заданными или выбираемыми по заданным критериям
рецепторами и нейронами, связанными друг с другом связями любого уровня
опосредованности (рисунок 9):
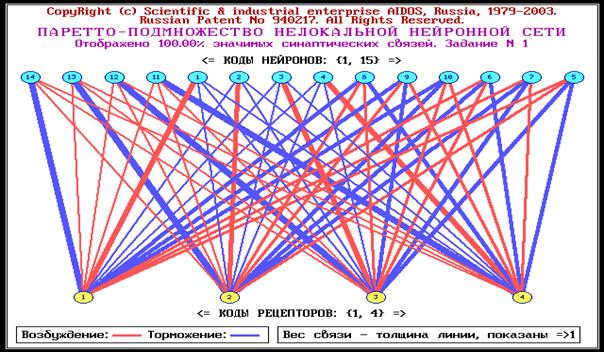
Рисунок 9. Отображение базы знаний (таблица 7)
в форме Парето-подмножества нелокальной нейронной сети [138]
С
использованием знаний о силе и
направлении связей между составом и иерархической структурой системы, с одной
стороны, и ее эмерджентными свойствами как целого, с другой стороны,
приведенными в таблице 7 и рисунках 8, 9 можно изобразить иерархическую
структур системы, приведенную на рисунке 2, с графическим указанием силы и
направления связи между базовыми элементами системы и ее эмерджентными
свойствами в форме толщины и цвета линий (рисунок 10):
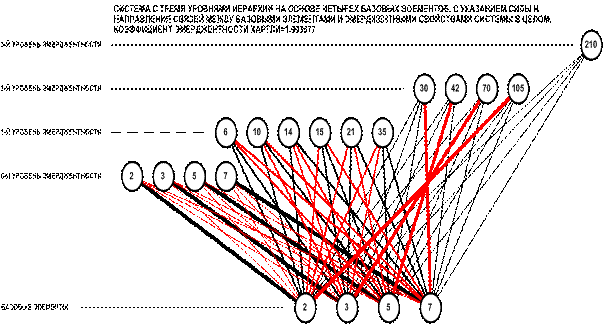
Рисунок 10. Пример системы сложных чисел, основанных
на 4
простых числах с указанием силы и направления связи между
базовыми элементами системы и ее эмерджентными свойствами
в форме толщины и цвета линий
На рисунке 10
толщина линии пропорциональна силе связи, черный цвет обозначает положительную
связь, а красный – отрицательную. Из сравнения рисунков 9 и 10 можно сделать
обоснованный вывод том, что АСК-анализ и
его программный инструментарий – интеллектуальная система «Эйдос» обеспечивают
выявление силы и направления связей между базовыми элементами системы и ее
эмерджентными свойствами в целом на основе эмпирических данных и отображение
внутренней иерархической структуры конкретной системы в наглядной графической
форме нелокальной нейронной сети.
Анализ приведенного численного примера и нейронной сети на рисунке
10 дает нам основания сформулировать гипотезу
«О зависимости силы и направления
связей связи между базовыми элементами системы и ее эмерджентными свойствами в
целом от уровня иерархии в системе»: чем выше уровень иерархии в
системе, тем слабее положительные и сильнее отрицательные связи между базовыми
элементами системы и ее эмерджентными свойствами в целом, т.к.,
возможно, это является конкретным проявлением соответствующей общей закономерности.
Информационный
портрет класса –
это список факторов, ранжированных в порядке убывания силы их влияния на
переход объекта управления в состояние, соответствующее данному классу.
Информационный портрет класса отражает систему его детерминации. Генерация
информационного портрета класса представляет собой решение обратной задачи
прогнозирования, т.к. при прогнозировании по системе факторов определяется
спектр наиболее вероятных будущих состояний объекта управления, в которые он
может перейти под влиянием данной системы факторов, а в информационном портрете
мы наоборот, по заданному будущему состоянию объекта управления определяем
систему факторов, детерминирующих это состояние, т.е. вызывающих переход
объекта управления в это состояние. В начале информационного портрета класса
идут факторы, оказывающие положительное влияние на переход объекта управления в
заданное состояние, затем факторы, не оказывающие на это существенного влияния,
и далее – факторы, препятствующие переходу объекта управления в это состояние
(в порядке возрастания силы препятствования). Информационные портреты классов
могут быть от отфильтрованы по
диапазону факторов, т.е. мы можем отобразить влияние на переход объекта
управления в данное состояние не всех отраженных в модели факторов, а только
тех, коды которых попадают в определенный диапазон, например, относящиеся к
определенным описательным шкалам. Пример информационного портрета класса приведен
в таблице 8:
Таблица 8 – ИНФОРМАЦИОННЫЙ ПОРТРЕТ КЛАССА:
код: 11, наименование: 30=2*3*5
|
№ |
Признак |
Количество
информации |
||
|
Код |
Наименование |
В Битах |
В % |
|
|
1 |
1 |
2 |
0,10004 |
2,56 |
|
2 |
2 |
3 |
0,10004 |
2,56 |
|
3 |
3 |
5 |
0,10004 |
2,56 |
|
4 |
4 |
7 |
-0,41925 |
-10,73 |
Таким образом, информационный портер класса содержит ту же
информацию, что и нелокальный нейрон, но в форме таблицы.
Информационный
(семантический) портрет фактора – это список классов, ранжированный в порядке убывания силы
влияния данного фактора на переход объекта управления в состояния,
соответствующие данным классам. Информационный портрет фактора называется также
его семантическим портретом, т.к. в
соответствии с концепцией смысла системно-когнитивного анализа, являющейся обобщением
концепции смысла Шенка-Абельсона, смысл
фактора состоит в том, какие будущие состояния объекта управления он
детерминирует. Сначала в этом списке идут состояния объекта управления, на
переход в которые данный фактор оказывает наибольшее влияние, затем состояния,
на которые данный фактор не оказывает существенного влияния, и далее состояния
– переходу в которые данный фактор препятствует. Информационные портреты
факторов могут быть от отфильтрованы
по диапазону классов, т.е. мы можем отобразить влияние данного фактора на
переход объекта управления не во все возможные будущие состояния, а только в
состояния, коды которых попадают в определенный диапазон, например, относящиеся
к определенным классификационным шкалам. Пример информационного портрета признака
(значения фактора) приведен в таблице 9:
Таблица 9– ИНФОРМАЦИОННЫЙ ПОРТРЕТ ПРИЗНАКА:
код: 11, наименование: 30=2*3*5
|
№ |
Класс |
Количество информации |
||
|
Код |
Наименование |
В Битах |
В % |
|
|
1 |
1 |
2 = 2 |
0,35211 |
9,01 |
|
2 |
5 |
6 = 2 * 3 |
0,21552 |
5,52 |
|
3 |
6 |
10 = 2 * 5 |
0,21552 |
5,52 |
|
4 |
7 |
14 = 2 * 7 |
0,21552 |
5,52 |
|
5 |
11 |
30 = 2 * 3 * 5 |
0,10004 |
2,56 |
|
6 |
12 |
42 = 2 * 3 * 7 |
0,10004 |
2,56 |
|
7 |
13 |
70 = 2 * 5 * 7 |
0,10004 |
2,56 |
|
8 |
15 |
210 = 2 * 3 * 5 * 7 |
0,00000 |
0,00 |
|
9 |
2 |
3 = 3 |
-0,16717 |
-4,28 |
|
10 |
3 |
5 = 5 |
-0,16717 |
-4,28 |
|
11 |
4 |
7 = 7 |
-0,16717 |
-4,28 |
|
12 |
8 |
15 = 3 * 5 |
-0,30376 |
-7,77 |
|
13 |
9 |
21 = 3 * 7 |
-0,30376 |
-7,77 |
|
14 |
10 |
35 = 5 * 7 |
-0,30376 |
-7,77 |
|
15 |
14 |
105 = 3 * 5 * 7 |
-0,41925 |
-10,73 |
Когнитивные
функции (функции влияния) [12] представляет собой график зависимости
вероятностей перехода объекта управления в будущие состояния под влиянием
различных значений некоторого фактора. Если взять несколько информационных
портретов факторов, соответствующих градациям одной описательной шкалы,
отфильтровать их по диапазону градаций некоторой классификационной шкалы и
взять из каждого информационного портрета по одному состоянию, на переход в
которое объекта управления данная градация фактора оказывает наибольшее
влияние, то мы и получим зависимость, отражающую вероятность перехода объекта
управления в будущие состояния под влиянием различных значений некоторого
фактора, т.е. функцию влияния. Функции влияния являются наиболее развитым средством
изучения причинно-следственных зависимостей в моделируемой предметной области,
предоставляемым системой "Эйдос". Необходимо отметить, что на вид
функций влияния математической моделью СК-анализа не накладывается никаких ограничений,
в частности, они могут быть и нелинейные.
Пример нередуцированной когнитивной функции, генерируемой режимом _54 системы
«Эйдос», приведен на рисунке 11:
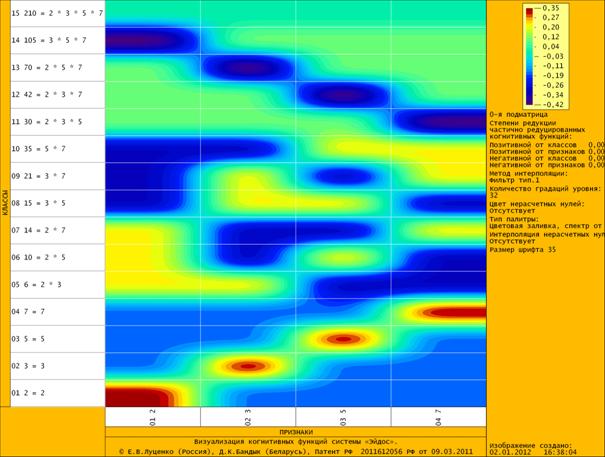
Рисунок 11. Пример нередуцированной когнитивной
функции
Классические когнитивные карты являются графической формой представления фрагментов
СИМ, объединяющей достоинства таких форм, как нейроны и семантические сети
факторов. Классическая когнитивная карта представляет собой нейрон, соответствующий
некоторому состоянию объекта управления с рецепторами, каждый из которых
соответствует фактору в определенной степени способствующему или
препятствующему переходу объекта в это состояние. Рецепторы соединены связями
как с нейроном, так и друг с другом. Связи рецепторов с нейроном отражают силу
и направление влияния факторов, а связи рецепторов друг с другом, отображаемые
в форме семантической сети факторов, – сходство и различие между рецепторами по
характеру их влияния на объект управления. Таким образом, классическая
когнитивная карта представляет собой нейрон с семантической сетью факторов,
изображенные на одной диаграмме.
Обобщенные когнитивные карты позволяют объединить в одной графической форме
семантические сети классов и факторов, объединенных нейронной сетью. Если
объединить несколько классических когнитивных карт на одной диаграмме и изобразить
на ней также связи между нейронами в форме семантической сети классов, то
получим обобщенную (интегральную) когнитивную карту. Система "Эйдос"
обеспечивает построение любого подмножества многоуровневой семантической
информационной модели с заданными или выбираемыми по заданным критериям
рецепторами и нейронами, связанными друг с другом связями любого уровня
опосредованности в форме классических и обобщенных когнитивных карт. В
частности, в системе полуавтоматически формируется задание на генерацию
подмножеств обобщенной когнитивной карты. Пример интегральной когнитивной карты
для построенной модели приведен на рисунке 12:
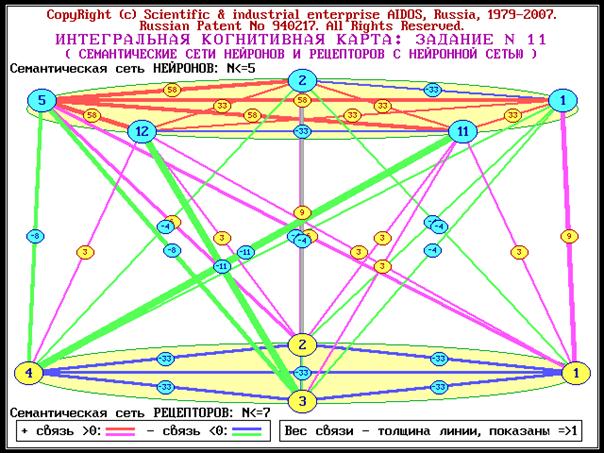
Рисунок 12. Пример интегральной когнитивной карты
для построенной модели
Матрица сходства классов по системе их
детерминации представлена в таблице 10:
Таблица 10 – МАТРИЦА СХОДСТВА КЛАССОВ
ПО СИСТЕМЕ ИХ ДЕТЕРМИНАЦИИ
|
KOD |
NAME |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
1 |
2 = 2 |
100 |
-33 |
-33 |
-33 |
58 |
58 |
58 |
-58 |
-58 |
-58 |
33 |
33 |
33 |
-100 |
0 |
|
2 |
3 = 3 |
-33 |
100 |
-33 |
-33 |
58 |
-58 |
-58 |
58 |
58 |
-58 |
33 |
33 |
-100 |
33 |
0 |
|
3 |
5 = 5 |
-33 |
-33 |
100 |
-33 |
-58 |
58 |
-58 |
58 |
-58 |
58 |
33 |
-100 |
33 |
33 |
0 |
|
4 |
7 = 7 |
-33 |
-33 |
-33 |
100 |
-58 |
-58 |
58 |
-58 |
58 |
58 |
-100 |
33 |
33 |
33 |
0 |
|
5 |
6 = 2 * 3 |
58 |
58 |
-58 |
-58 |
100 |
0 |
0 |
0 |
0 |
-100 |
58 |
58 |
-58 |
-58 |
0 |
|
6 |
10 = 2 * 5 |
58 |
-58 |
58 |
-58 |
0 |
100 |
0 |
0 |
-100 |
0 |
58 |
-58 |
58 |
-58 |
0 |
|
7 |
14 = 2 * 7 |
58 |
-58 |
-58 |
58 |
0 |
0 |
100 |
-100 |
0 |
0 |
-58 |
58 |
58 |
-58 |
0 |
|
8 |
15 = 3 * 5 |
-58 |
58 |
58 |
-58 |
0 |
0 |
-100 |
100 |
0 |
0 |
58 |
-58 |
-58 |
58 |
0 |
|
9 |
21 = 3 * 7 |
-58 |
58 |
-58 |
58 |
0 |
-100 |
0 |
0 |
100 |
0 |
-58 |
58 |
-58 |
58 |
0 |
|
10 |
35 = 5 * 7 |
-58 |
-58 |
58 |
58 |
-100 |
0 |
0 |
0 |
0 |
100 |
-58 |
-58 |
58 |
58 |
0 |
|
11 |
30 = 2 * 3 * 5 |
33 |
33 |
33 |
-100 |
58 |
58 |
-58 |
58 |
-58 |
-58 |
100 |
-33 |
-33 |
-33 |
0 |
|
12 |
42 = 2 * 3 * 7 |
33 |
33 |
-100 |
33 |
58 |
-58 |
58 |
-58 |
58 |
-58 |
-33 |
100 |
-33 |
-33 |
0 |
|
13 |
70 = 2 * 5 * 7 |
33 |
-100 |
33 |
33 |
-58 |
58 |
58 |
-58 |
-58 |
58 |
-33 |
-33 |
100 |
-33 |
0 |
|
14 |
105 = 3 * 5 * 7 |
-100 |
33 |
33 |
33 |
-58 |
-58 |
-58 |
58 |
58 |
58 |
-33 |
-33 |
-33 |
100 |
0 |
|
15 |
210 = 2 * 3 * 5 * 7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Любая подматрица матрицы сходства (таблица 10)
(или любой заданный набор классов) может быть представлена в графическом виде в
форме ориентированного графа – семантической сети (рисунок 13), которая в ряде
работ называется также когнитивной диаграммой:
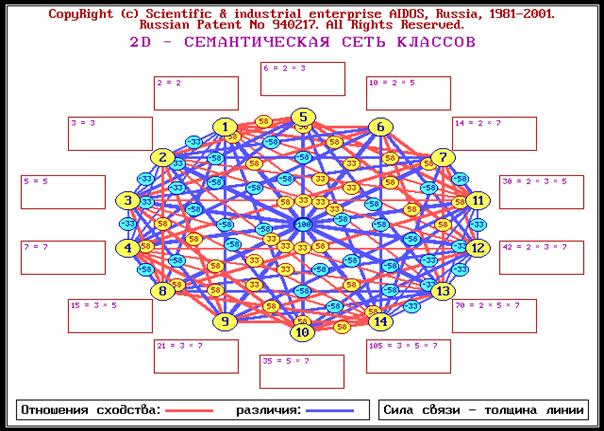
Рисунок 13. Матрицы сходства классов (таблица 10),
представленная в форме семантической сети классов
В таблице 11 представлен конструкт,
представляющий собой систему противоположных кластеров со спектром промежуточных
классов:
Таблица 11 – КОНСТРУКТ: «6-35»
|
№ |
Код |
Наименование |
Уровень |
|
1 |
5 |
6 = 2 * 3 |
100,00 |
|
2 |
1 |
2 = 2 |
57,74 |
|
3 |
2 |
3 = 3 |
57,74 |
|
4 |
11 |
30 = 2 * 3 * 5 |
57,74 |
|
5 |
12 |
42 = 2 * 3 * 7 |
57,74 |
|
6 |
3 |
5 = 5 |
-57,74 |
|
7 |
4 |
7 = 7 |
-57,74 |
|
8 |
13 |
70 = 2 * 5 * 7 |
-57,74 |
|
9 |
14 |
105 = 3 * 5 * 7 |
-57,74 |
|
10 |
10 |
35 = 5 * 7 |
-100,00 |
На основе матрицы сходства (таблица 10) может
быть проведена когнитивная кластеризация [248], результаты которой представлены
на рисунках 13 и 14:
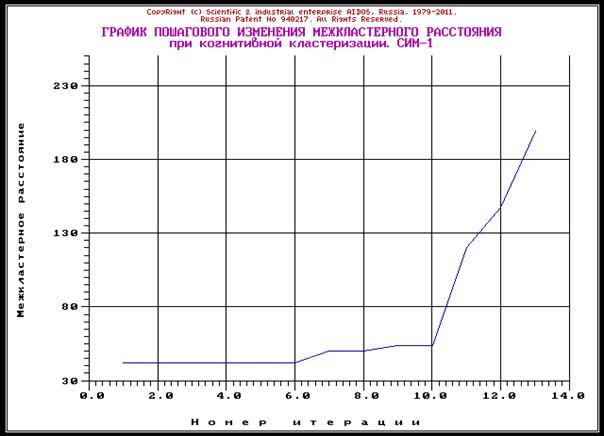
Рисунок 13. График пошагового изменения межкластерного
расстояния при когнитивной кластеризации в СИМ-1
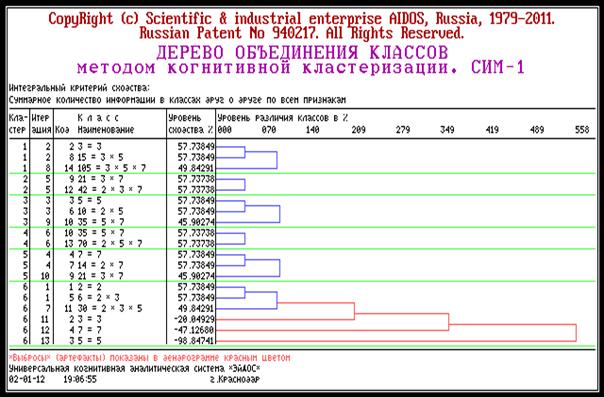
Рисунок 14. Дендрограмма когнитивной кластеризации в
СИМ-1
На рисунке 16 приведены результаты идентификации
объекта распознаваемой выборки с классами, а на рисунке 17 – класса с
объектами:
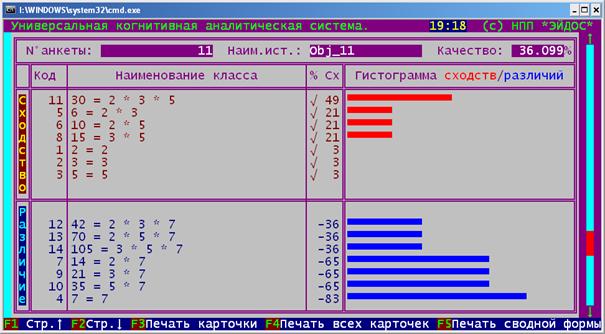
Рисунок 16. Результат идентификации объекта с классами
(экранная форма)
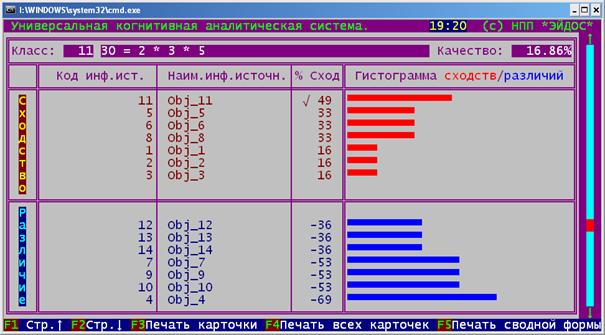
Рисунок 17. Результат идентификации классами с
объектами
(экранная форма)
При добавлении еще одного базового элемента
(например, простого числа: 11) без пересинтеза модели объекты, включающие этот
базовый элемент, идентифицируются так же, как будто его нет. Например,
результат идентификации объекта: 330 = 2 * 3 * 5 * 11 в этой модели будут
такими же, как показано на рисунке 16, т.е. данный объект будет неверно
идентифицироваться как 30 = 2 * 3 * 5. Это является признаком необходимости
обобщения модели, т.е. создания модели, адекватно отражающей как все
предыдущие, так и новые факты. Создание этой более общей модели обеспечивается
выполнением следующих шагов:
– добавлением в справочник классов,
соответствующих объектам, включающим данный элемент;
– добавлением данного базового элемента в
справочник признаков;
– добавлением этого объекта и других объектов,
включающих данный базовый элемент, в обучающую выборку;
– пересинтезом модели;
– проверкой ее на адекватность, в т.ч. на новых
фактах.
Результат выполнения этих шагов представлен в
таблицах 12-16:
Таблица 12 – СПРАВОЧНИК КЛАССОВ БОЛЕЕ ОБЩЕЙ МОДЕЛИ
|
KOD |
NAME |
KOD |
NAME |
KOD |
NAME |
|
1 |
2 = 2 |
11 |
21 = 3 * 7 |
21 |
154 = 2 * 7 * 11 |
|
2 |
3 = 3 |
12 |
33 = 3 * 11 |
22 |
105 = 3 * 5 * 7 |
|
3 |
5 = 5 |
13 |
35 = 5 * 7 |
23 |
165 = 3 * 5 * 11 |
|
4 |
7 = 7 |
14 |
55 = 5 * 11 |
24 |
231 = 3 * 7 * 11 |
|
5 |
11 = 11 |
15 |
77 = 7 * 11 |
25 |
385 = 5 * 7 * 11 |
|
6 |
6 = 2 * 3 |
16 |
30 = 2 * 3 * 5 |
26 |
210 = 2 * 3 * 5 * 7 |
|
7 |
10 = 2 * 5 |
17 |
42 = 2 * 3 * 7 |
27 |
330 = 2 * 3 * 5 * 11 |
|
8 |
14 = 2 * 7 |
18 |
66 = 2 * 3 * 11 |
28 |
462 = 2 * 3 * 7 * 11 |
|
9 |
22 = 2 * 11 |
19 |
70 = 2 * 5 * 7 |
29 |
770 = 2 * 5 * 7 * 11 |
|
10 |
15 = 3 * 5 |
20 |
110 = 2 * 5 * 11 |
30 |
1155 = 3 * 5 * 7 * 11 |
Таблица 13 – СПРАВОЧНИК ПРИЗНАКОВ БОЛЕЕ ОБЩЕЙ МОДЕЛИ
|
KOD |
NAME |
|
1 |
2 |
|
2 |
3 |
|
3 |
5 |
|
4 |
7 |
|
5 |
11 |
Таблица 14 – ОБУЧАЮЩАЯ ВЫБОРКА БОЛЕЕ ОБЩЕЙ МОДЕЛИ
|
KOD |
NAME |
Коды классов |
Коды признаков |
|||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
1 |
2 |
3 |
4 |
||
|
1 |
Obj_1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
Obj_2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
Obj_3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
4 |
Obj_4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
5 |
Obj_5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
6 |
Obj_6 |
1 |
2 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
7 |
Obj_7 |
1 |
3 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
|
|
8 |
Obj_8 |
1 |
4 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
|
|
|
9 |
Obj_9 |
1 |
5 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
5 |
|
|
|
10 |
Obj_10 |
2 |
3 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
11 |
Obj_11 |
2 |
4 |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
|
|
12 |
Obj_12 |
2 |
5 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
5 |
|
|
|
13 |
Obj_13 |
3 |
4 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
4 |
|
|
|
14 |
Obj_14 |
3 |
5 |
14 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
5 |
|
|
|
15 |
Obj_15 |
4 |
5 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
5 |
|
|
|
16 |
Obj_16 |
1 |
2 |
3 |
6 |
7 |
10 |
16 |
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
17 |
Obj_17 |
1 |
2 |
4 |
6 |
8 |
11 |
17 |
|
|
|
|
|
|
|
|
1 |
2 |
4 |
|
|
18 |
Obj_18 |
1 |
2 |
5 |
6 |
9 |
12 |
18 |
|
|
|
|
|
|
|
|
1 |
2 |
5 |
|
|
19 |
Obj_19 |
1 |
3 |
4 |
7 |
8 |
13 |
19 |
|
|
|
|
|
|
|
|
1 |
3 |
4 |
|
|
20 |
Obj_20 |
1 |
3 |
5 |
7 |
9 |
14 |
20 |
|
|
|
|
|
|
|
|
1 |
3 |
5 |
|
|
21 |
Obj_21 |
1 |
4 |
5 |
8 |
9 |
15 |
21 |
|
|
|
|
|
|
|
|
1 |
4 |
5 |
|
|
22 |
Obj_22 |
2 |
3 |
4 |
10 |
11 |
13 |
22 |
|
|
|
|
|
|
|
|
2 |
3 |
4 |
|
|
23 |
Obj_23 |
2 |
3 |
5 |
10 |
12 |
14 |
23 |
|
|
|
|
|
|
|
|
2 |
3 |
5 |
|
|
24 |
Obj_24 |
2 |
4 |
5 |
11 |
12 |
15 |
24 |
|
|
|
|
|
|
|
|
2 |
4 |
5 |
|
|
25 |
Obj_25 |
3 |
4 |
5 |
13 |
14 |
15 |
25 |
|
|
|
|
|
|
|
|
3 |
4 |
5 |
|
|
26 |
Obj_26 |
1 |
2 |
3 |
4 |
6 |
7 |
8 |
10 |
11 |
13 |
16 |
17 |
19 |
22 |
26 |
1 |
2 |
3 |
4 |
|
27 |
Obj_27 |
1 |
2 |
3 |
5 |
6 |
7 |
9 |
10 |
12 |
14 |
16 |
18 |
20 |
23 |
27 |
1 |
2 |
3 |
5 |
|
28 |
Obj_28 |
1 |
2 |
4 |
5 |
6 |
8 |
9 |
11 |
12 |
15 |
17 |
18 |
21 |
24 |
28 |
1 |
2 |
4 |
5 |
|
29 |
Obj_29 |
1 |
3 |
4 |
5 |
7 |
8 |
9 |
13 |
14 |
15 |
19 |
20 |
21 |
25 |
29 |
1 |
3 |
4 |
5 |
|
30 |
Obj_30 |
2 |
3 |
4 |
5 |
10 |
11 |
12 |
13 |
14 |
15 |
22 |
23 |
24 |
25 |
30 |
2 |
3 |
4 |
5 |
Таблица 15 – ОЦЕНКА АДЕКВАТНОСТИ БОЛЕЕ ОБЩЕЙ МОДЕЛИ
|
Наименование |
Вид |
Расчет проведен |
Достоверность |
|||
|
Дата |
Идентификации |
Идентификации |
Идентификации |
Средняя |
||
|
СИМ-4 |
Корреляция |
03-01-12 |
11:29:19 |
100,000 |
73,171 |
86,585 |
|
Свертка |
03-01-12 |
11:29:24 |
100,000 |
73,171 |
86,585 |
|
|
СИМ-3 |
Корреляция |
03-01-12 |
11:29:32 |
100,000 |
73,171 |
86,585 |
|
Свертка |
03-01-12 |
11:29:37 |
100,000 |
73,171 |
86,585 |
|
|
СИМ-2 |
Корреляция |
03-01-12 |
11:29:44 |
100,000 |
73,171 |
86,585 |
|
Свертка |
03-01-12 |
11:29:50 |
56,137 |
71,137 |
63,637 |
|
|
СИМ-1 |
Корреляция |
03-01-12 |
11:29:59 |
100,000 |
73,171 |
86,585 |
|
Свертка |
03-01-12 |
11:30:04 |
70,179 |
87,400 |
78,789 |
|
Таблица 16 – РЕЗУЛЬТАТ ИДЕНТИФИКАЦИИ ОБЪЕКТА С
КЛАССАМИ В БОЛЕЕ ОБЩЕЙ МОДЕЛИ (ВЫХОДНАЯ ФОРМА)
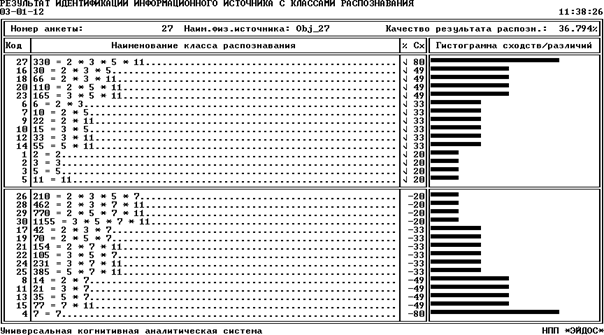
Из сравнения таблицы 16 с рисунком 16 видно, что
полученная нами обобщенная модель удовлетворяет принципу соответствия с
предыдущей моделью, т.к. дает вполне разумные результаты идентификации как
объектов, верно идентифицируемых в старой модели, так и новых объектов, которые
ранее идентифицировались неадекватно. Таким образом, подход, представленный на
рисунке 7, дает ожидаемые положительные результаты.
Выводы. Таким образом, в разделе
на простом, но универсальном численном примере рассмотрено применение автоматизированного
системно-когнитивного анализа (АСК-анализ) и его программного инструментария –
интеллектуальной системы «Эйдос» для выявления
и исследования детерминации эмерджентных макросвойств систем их составом и иерархической
структурой, т.е. подсистемами различной сложности (уровней иерархии). Тем
самым продемонстрирована возможность решения этой проблемы в широком круге
предметных областей с применением технологии и инструментария АСК-анализа.
Кратко обсуждаются некоторые методологические
вопросы создания и применения формальных моделей в научном познании.
Предложены:
– системное обобщение
принципа Уильяма Росса Эшби о необходимом разнообразии на основе системного
обобщения теории множеств и системной теории информации;
– обобщенная формулировка принципа
относительности Галилея-Эйнштейна, применимая не только в физике, но и в других
науках, в частности в экономике, социологии и психологии;
– гипотеза о связи обобщенного
принципа относительности с теоремой Эмми Нётер;
– гипотеза «О
зависимости силы и направления связей между базовыми элементами системы и ее
эмерджентными свойствами в целом от уровня иерархии в системе».
Системное
обобщение принципа Эшби и следствие из него: «Чем больше различных
сочетаний значений факторов действует на объект управления, тем выше степень
детерминированности управления им», следовательно «Степень детерминированности
управления системой тем выше, чем выше ее эмерджентность (уровень системности),
количественно измеряемая коэффициентом эмерджентности Хартли». Коэффициенты эмерджентности Хартли и Харкевича можно
обоснованно считать количественным выражением системного обобщения принципа
Эшби.
Обобщенный принцип относительности Галилея-Эйнштейна: «Законы природы открытые в одном
месте и в определенное время действуют и в других местах и в другое время»,
поэтому по виду законов природы в замкнутой лаборатории невозможно определить в
каком месте (пространства) и в каком времени эта лаборатория находится, т.е. по
виду законов природы внутри лаборатории невозможно локализовать ее в
пространстве-времени. Из обобщенного принципа относительности вытекает важное
следствие том, что способ определения
степени истинности реальности сам должен быть истинным, чтобы давать истинные
результаты, и сам не должен относится к той реальности, которая с помощью него
оценивается. Обобщенный принцип относительности
применим не только в физике, но и в других науках, в частности в экономике,
социологии и психологии. Но в отличие от физики другие науки не только основаны
на применении этого принципа, хотя и в явном виде не формулировали его, но и их
исследования во многом состоят в изучении отклонений от этого принципа.
Гипотеза о связи обобщенного принципа относительности с теоремой
Эмми Нётер: «Принцип относительности выполняется по тем же причинам, по
которым существуют законы сохранения и этими причинами являются симметрии
пространства-времени».
Гипотеза «О зависимости силы и направления связей между
базовыми элементами системы и ее эмерджентными свойствами в целом от уровня
иерархии в системе»: «Чем выше уровень иерархии в системе, тем слабее
положительные и сильнее отрицательные связи между базовыми элементами системы и
ее эмерджентными свойствами в целом».
Материалы работы могут быть использованы при
проведении лекционных и лабораторных занятий по дисциплинам: «Интеллектуальные
информационные системы» и «Концепции современного естествознания».для различных
специальностей, а также для решения перечисленных в начале работы и других
задач того же типа в различных предметных областях.
10.3. Коэффициент
эмерджентности классических
и квантовых статистических систем
В данном разделе изложение полностью основано на
рабате [270], нумерация формул, рисунков и таблиц сохранены.
В классической теории
информации Хартли-Шеннона понятие информации определяется на основе
теоретико-множественных и комбинаторных представлений на основе анализа
поведения классического макрообъекта, который может переходить только в
четко фиксированные альтернативные редуцированные состояния, например монета,
может упасть либо на "орел", либо на "решку". Если эти
варианты равновероятны, то при реализации одного из них по формуле Хартли мы
получаем информацию в 1 бит, при реализации одного из W равновероятных
состояний мы получаем информацию I=Log2W бит, если неравновероятны,
то для расчета среднего количества информации используется формула Шеннона [97].
Однако квантовые объекты могут
быть одновременно в двух и более альтернативных для классических
объектов состояниях [2]. Такие состояния будем называть смешанными.
Например, электрон может интерферировать, проходя
одновременно через две щели[48]
[2]. При этом наблюдаются эффекты, не сводящиеся к суперпозиции классических
состояний, т.е. имеющие существенно квантовый, системный, эмерджентный,
нелинейный характер.
Поэтому классическая теория
информации Хартли-Шеннона может быть обобщена путем рассмотрения квантовых
систем в качестве объектов, на основе анализа поведения которых формируется
само основополагающее понятие информации. Обобщенную таким образом теорию информации
предлагается называть системной или эмерджентной теорией информации.
Основным отличием эмерджентной
теории информации от классической является учет свойства системности, как
фундаментального и универсального свойства всех объектов, на уровне самого
понятия информации. Достаточно рассмотреть квантовое обобщение теории Хартли,
т.к. путь вывода теории Шеннона из теории Хартли хорошо известен [97].
В работе[49]
Ричард Фейнман рассмотрел пример интерференции электрона на двух щелях при
наблюдении этого процесса с помощью эффекта Комптона, т.е. путем рассеяния
фотонов на электроне. В этом случае электрон всегда наблюдается в форме объекта
с размером порядка длины волны света, и как выяснилось, его свойства самым
существенным образом зависят от его наблюдаемого, а значит и фактического
размера. Мы не будем детально приводить известную аргументацию Р. Фейнмана, но
коснемся лишь моментов, играющих ключевую роль в квантовом (системном)
обобщении понятия "информация".
Когда длина волны фотонов
меньше расстояния между щелями, то видно, что электрон проходит через одну из
щелей. В этом случае на экране за каждой щелью наблюдается классическое
распределение плотности. Суммарная плотность
N12 является просто суммой распределений N1 и N2, полученных соответственно от
щелей 1 и 2 – рис. 1. Следовательно, имеем в этом случае:
(1)
Когда длина волны фотонов
порядка расстояния между щелями или больше, то видно, как он проходит через
экран "накрывая" обе щели одновременно. В этом случае за ними
наблюдается сложная интерференционная картина, нисколько не напоминающая сумму
или суперпозицию классических распределений за 1-й и 2-й щелями, т.е. не
являющуюся их суммой – рис. 2.
|
|
|
|
Рисунок 1. Классический объект, |
Рисунок 2. Квантовый объект, |
Введем следующие обозначения:
– волновая функция или амплитуда вероятности, квадрат модуля
которой характеризует вероятность попадания электрона в точку x экрана через
отверстие 1;
– волновая функция, квадрат модуля которой характеризует
вероятность попадания электрона в точку x экрана через отверстие 2;
– суммарная амплитуда вероятности, квадрат модуля которой
характеризует вероятность попадания электрона в точку x экрана через отверстия
1 и 2 одновременно.
Согласно законам
квантовой механики, складываются волновые функции, а не вероятности, как в
классическом случае, поэтому имеем:
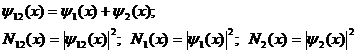(2)
Отсюда находим, что
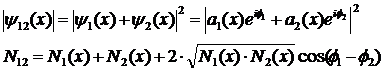(3)
Здесь 
– амплитуда и фаза
волновой функции соответственно. Сравнивая выражения (1) и (3) видим, что
квантовый эффект прохождения электрона через две щели одновременно приводит к
появлению дополнительного слагаемого, описывающего интерференцию – рис. 2.
Это дополнительное слагаемое
учитывает системный эффект состоящий в том, что состояния объекта, в
классической теории считавшиеся альтернативными, т.е. одновременно не реализуемыми
ни при каких условиях, в квантовой теории таковыми не являются и могут
осуществляться одновременно, что приводит к возможности нахождения объекта в
смешанных состояниях.
Если вероятность прохождения
электрона через каждую из W щелей одинакова, то по классической теории Хартли в
самом факте пролета электрона через одну из щелей содержится количество
информации:
(4)
где W – количество щелей, или, в общем
случае, классических состояний объекта.
В соответствии с концепцией
эмерджентной теории информации, предлагается ввести в это выражение параметр,
учитывающий квантовые системные эффекты нахождения объекта в смешанных
состояниях. В результате количество состояний объекта возрастает и,
следовательно, так же возрастает и количество информации, которое мы получаем,
когда узнаем, что он перешел в одно из этих состояний:
(5)
где φ – степень
эмерджентности системы (синоним: уровень системности объекта), в частности:
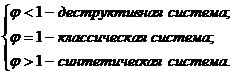
Для деструктивных систем свойства
целого меньше свойств частей, для классических систем они совпадают, для
синтетических систем свойства целого больше свойств частей и не сводятся к ним.
На первый взгляд можно было бы
просто увеличить количество состояний системы W за счет учета смешанных
состояний. Однако этот путь не удовлетворяет известному принципу соответствия,
который в данном контексте требует, чтобы в предельном случае более общая
теория переходила в уже известную, классическую теорию.
Здесь уместно привести теорему,
впервые доказанную известным кибернетиком У. Эшби: у системы тем больше возможностей
в выборе поведения, чем сильнее степень согласованности поведения ее частей.
Теорема Эшби описывает систему
в точке бифуркации, причем, по сути, он при этом использует понятие
"степень эмерджентности объекта", хотя в явном виде и не вводит его.
Более того, он указывает на источник эмерджентности: – взаимодействие частей и
связывает уровень системности или уровень системной организации со степенью
взаимодействия этих частей.
В теории информации есть
теорема, доказывающая, что энтропия системы в целом меньше суммы энтропии ее
частей на величину взаимной информации частей друг о друге. Таким образом,
можно утверждать, что способность системы к выбору прямо пропорциональная
степени ее эмерджентности и самым непосредственным образом связана с ее
способностью, противостоять действию закона возрастания энтропии.
Таким образом, и
теоретико-информационное рассмотрение сложных активных самоорганизующихся
систем, каким является человек и системы с участием человека, и рассмотрение
квантовых систем, приводит к необходимости разработки эмерджентной теории
информации, в которой используется обобщенное понятие информации, учитывающее
эффект системности с помощью коэффициента эмерджентности.
Рассмотрим численный пример
вычисления коэффициента эмерджентности для простого случая, когда все
рассматриваемые места работы равновероятны. Пусть количество мест, куда может
пойти работать выпускник после получения 1-й специальности будет равно: W1=6,
после получения 2-й специальности: W2=10, а при одновременном получении обоих специальностей дополнительно появляется еще W=16 мест работы, откуда:
W3=
W1+W2+W =32
Тогда в 1-м случае, если мы
узнаем, что выпускник устроился на определенное место работы, то мы получаем
I1=Log2W12,58
бит
информации, во 2-м случае, соответственно:
I2=Log2W23,32
бита
Но в 3-м случае мы получаем не
I3=Log2(W1+W2)=4
бита,
как можно было бы ожидать, если бы не было
интерференции последствий, т.е. системного эффекта, а на 1 бит больше:
I3=Log2W3=5
бит.
(6)
Таким образом, при наблюдении за поведением
объектов, при рассмотрении их как элементов некоторой системы, мы получаем
больше информации, чем при рассмотрении их как автономных объектов, т.е. вне системы.
Это можно объяснить тем, что дополнительная информация – это и есть информация
о системе, о том, как она влияет на поведение своего элемента.
Указанные 16 дополнительных
состояний (мест работы) выпускника в 3-м случае образовались за счет системного
эффекта (эмерджентности) и являются "смешанными", образующимися за
счет одновременного наличия у
выпускника свойств, полученных при окончании и 1-й, и 2-й специальности,
поэтому, учитывая выражения (4) и (5), получаем:
I3=Log2W3= Log2(W1+W2)
Откуда:
Следовательно, одновременное
окончание двух специальностей в рассмотренном случае дает системный эффект
1,25.
Таким образом, предлагаемый
концептуальный подход к построению эмерджентной теории информации позволяет количественно
учитывать системный эффект или эмерджентность непосредственно на уровне самого
понятия "информация", что имеет большое значение для науки и практики
применения теории информации и системного анализа для управления активными
объектами.
Рассмотрим, что изложенный
информационный подход может дать для оценки уровня системности квантовых
объектов.
В 2002 году одним из авторов [97] было
предложена идея, состоящая в том, что количество
информации в системе больше количества информации во множестве образующих ее
базовых элементов, т.к. подсистемы, состоящие из нескольких элементов, содержат
информацию также как и базовые элементы [97]. Понятно, что базовые элементы
также являются подсистемами, т.к. кроме систем в мире вообще ничего не
существует, а подсистемы некоторого иерархического уровня системы, например,
состоящие из m базовых элементов, могут рассматриваться как базовые элементы
этого иерархического уровня [170, 196].
Если базовое множество содержит W элементов, то
по Хартли количество информации, которое мы получаем, когда выбираем некоторый
элемент, равно:
(7)
Если базовые элементы могут взаимодействовать
друг с другом, то они могут образовывать подсистемы.
Здесь и возникают принципиальные вопросы о том:
– какие элементы могут образовывать подсистемы,
а какие не могут;
– сколько подсистем различной сложности может
быть образовано из W базовых элементов?
Ответы на эти вопросы зависят от того, какой
квантовой статистике подчиняется образующаяся система.
Рассмотрим квантовую систему, состоящую из ряда
подсистем, которые пронумеруем целым числом 
. Каждая подсистема характеризуется числом состояний 
и числом частиц 
, которые находятся в этих состояниях и обладают энергией 
. Определим число возможных способов распределения частиц по состояниям. В случае статистики Ферми в каждом состоянии
может находиться не более чем одна частица, поэтому число способов равно[50]
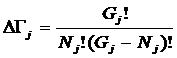(8)
В случае статистики Бозе в каждом состоянии
может находиться любое число частиц, следовательно, число способов равно[51]
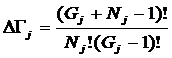(9)
Энтропия, общее число частиц и энергия системы
равны по определению
(10)
Найдем числа 
, которые соответствуют экстремуму энтропии при условии постоянства общего числа частиц и энергии
системы. Если число состояний и число
частиц в каждой подсистеме достаточно велико, 
, то можно воспользоваться приближенной формулой для
логарифма факториала 
. В этом случае выражение энтропии квантовых систем
упрощается и принимает вид:
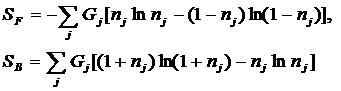(11)
Здесь первое выражение соответствует энтропии
системы фермионов, а второе – системы бозонов.
Используя метод Лагранжа, составим функционал 
, где 
- некоторые
постоянные. Экстремум энтропии достигается при условии
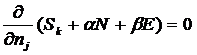
Отсюда находим два типа распределения
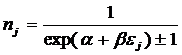(12)
Отметим, что знак плюс соответствует
распределению Ферми, а знак минус – распределению Бозе.
Следовательно, в случае статистики Ферми на
образование подсистем накладывается ограничение на число частиц, которые могут
находиться в одном состоянии. С учетом этого ограничения все элементы базового
множества могут образовывать подсистемы в любых сочетаниях, а их общее число
определяется выражением (8), которое запишем в виде
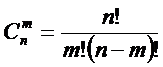(13)
Здесь n – число состояний системы; m – число
частиц находящихся в этих состояниях.
Ясно, что при фиксированном числе состояний в
системе могут быть подсистемы из 1, 2, 3, …, W элементов. При этом подсистемы
из 1-го элемента это сами базовые элементы, а подсистема из W элементов – это
вся система в целом (булеан) [7-8].
На всех иерархических уровнях системы от 1-го до
W, суммарно будет содержаться общее
число подсистем:
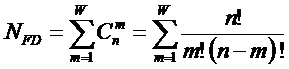(14)
В работе [97]
предложено считать, что количество информации в системе можно рассчитывать по
формуле Хартли (7), полагая, что элементами системы являются не только ее
базовые элементы, но и состоящие из них подсистемы, количество которых в
системе определяется выражением (14). Таким образом, количество информации в системе будет:
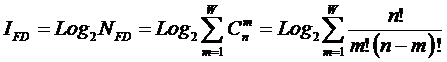(15)
Или окончательно:
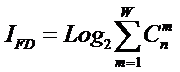(16)
Выражение
(11) представляет собой системное обобщение формулы Хартли для количества
информации в квантовой системе, подчиняющейся статистике Ферми-Дирака с
заданным числом состояний и с переменным числом частиц.
В работе [97] предложено оценивать уровень
системности или сложности системы отношением количества информации в системе (с
учетом входящих в нее подсистем всех уровней иерархии) к количеству информации
во множестве образующих ее базовых элементов:
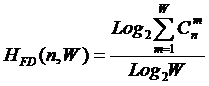(17)
Это выражение было названо в работе [97] коэффициентом эмерджентности Хартли, в
честь этого выдающегося ученого, внесшего большой вклад в становление научной
теории информации, а также потому, что в нем использовано классическое выражение
Хартли для количества информации (7) и его системное обобщение (16).
На рис. 3 представлена зависимость коэффициента
эмерджентности Хартли (17), представляющая собой поверхность. Отметим, что в
области параметров 
, характерной для ядерных и атомных оболочек, коэффициент
эмерджентности изменяется немонотонно с ростом W, что позволяет
объяснить поведение энергии связи нуклонов в атомных ядрах[52].
Непосредственно из
вида выражения для коэффициента эмерджентности Хартли (17) ясно, что он
представляет собой относительное превышение количества информации в квантовой
системе, подчиняющейся статистике Ферми-Дирака, при учете системных эффектов
(смешанных состояний, иерархической структуры ее подсистем и т.п.) над
количеством информации без учета системности.
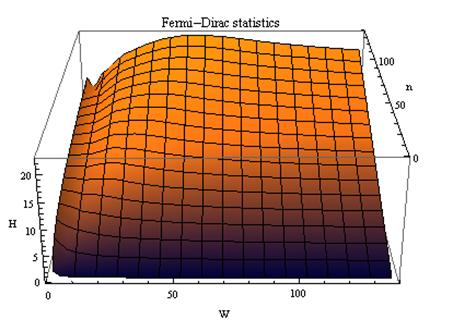
Рис. 3. Поведение коэффициента эмерджентности Хартли в
случае статистики Ферми-Дирака.
В работе [97]
показано, что при n=W выражение (16) приобретает вид:
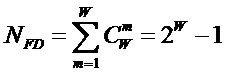(18)
Выражение
(11) для количества информации в системе с учетом (18):
(19)
Выражение
(19) дает оценку максимального количества
информации, которое может содержаться в системе при условии вхождения
всех элементов во все подсистемы различных уровней иерархической структуры, что
на практике никогда не осуществляется (возможно, за исключением мира в целом).
Из
выражения (19) видно, что I достаточно быстро стремится к W, поскольку
(20)
При
W > 4 различие I и W в выражении (20) не превышает 1%. Таким образом,
коэффициент эмерджентности Хартли (17) отражает уровень системности объекта,
подчиняющегося статистике Ферми-Дирака. Этот коэффициент изменяется от 1
(системность минимальна, т.е. отсутствует) до W/Log2W (системность
максимальна).
Для
каждого количества элементов системы существует свой максимальный уровень
системности, который никогда реально не достигается из-за действия правил запрета на реализацию в системе
ряда подсистем различных уровней иерархии. Например, не все сочетания букв
русского алфавита образуют слова русского языка, и не все сочетания слов –
предложения. В каждом состоянии может находиться только одна частица и т.п. По этой причине систему правил запрета в [97] предложено назвать информационным
проектом системы. Различные системы, состоящие из равного количества одинаковых
элементов, отличаются друг от друга именно по причине различия своих
информационных проектов.
Одним
из наиболее важных и известных в физике правил запрета, который действует на
квантовые системы, подчиняющиеся статистике Ферми-Дирака, является принцип Паули. Это один из
основополагающих принципов, влияющий на строение химических элементов, классифицированных
в таблице Д. И. Менделеева[53]
[201].
Таким образом, в работе [97] по сути, предложено
системное обобщение формулы Хартли и коэффициент эмерджентности Хартли для
случая квантовых систем, подчиняющихся статистике Ферми-Дирака. Однако
статистике Ферми-Дирака подчиняются только квантовые системы с полуцелым
спином, тогда как квантовые системы с целым спином описываются статистикой
Бозе-Эйнштейна.
Для этой статистики число различных подсистем
рассчитывается по формуле (9), которую запишем в форме
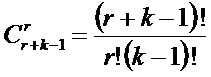(21)
Здесь k – число состояний, r –
число частиц в системе. На всех иерархических уровнях квантовой системы,
подчиняющейся статистике Бозе-Эйнштейна, от 1-го до W, суммарно будет содержаться
общее число подсистем
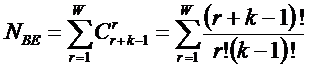(22)
Предположим, что количество информации в
квантовой системе, подчиняющейся статистике Бозе-Эйнштейна, можно рассчитывать
по формуле Хартли (7), полагая, что элементами системы являются не только ее
базовые элементы, но и состоящие из них подсистемы, количество которых в
системе определяется выражением (22). Таким образом, количество информации в
такой квантовой системе, подчиняющейся статистике Бозе-Эйнштейна, будет:
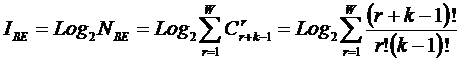(23)
Или окончательно:
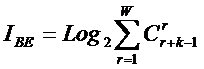(24)
Выражение
(19) представляет собой системное обобщение формулы Хартли для количества
информации в квантовой системе, подчиняющейся статистике Бозе-Эйнштейна.
Соответственно, выражение для коэффициента
эмерджентности Хартли для случая квантовых систем, подчиняющихся статистике
Бозе-Эйнштейна, будет иметь вид:
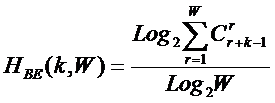(25)
На рис. 4 представлена зависимость коэффициента
эмерджентности Хартли (25) в области
параметров 
. Можно отметить существенное различие в поведении функции
(25) и аналогичного коэффициента вычисленного для случая статистики
Ферми-Дирака – см. рис. 3.
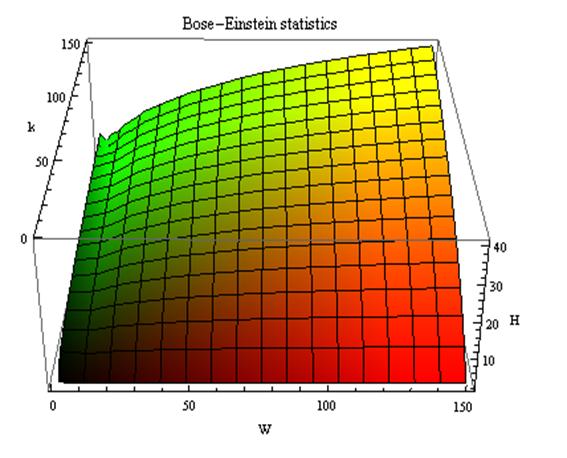
Рис. 4. Поведение коэффициента эмерджентности Хартли в
случае статистики Бозе-Эйнштейна
Отметим, что обе квантовые статистики – и
Ферми-Дирака, и Бозе-Эйнштейна, асимптотически приближаются к статистике
Максвелла-Больцмана в пределе высоких температур и низких плотностей, что непосредственно
следует из выражения (12). В случае
статистики Максвелла-Больцмана число подсистем, которое можно образовать при
заданном значении числа состояний определяется согласно[54]
[5]
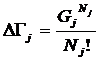(26)
Отсюда находим коэффициент эмерджентности
классических систем в виде
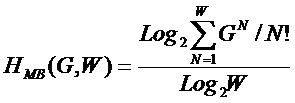(27)
Здесь N – число частиц, G –
число состояний. На рис. 5 представлена зависимость (27) в области параметров 
. По характеру поведения коэффициент эмерджентности классических
систем при малом числе состояний и частиц занимает промежуточное положение
между аналогичными коэффициентами, вы численными для ферми- и бозе-систем – см.
рис 3-4.
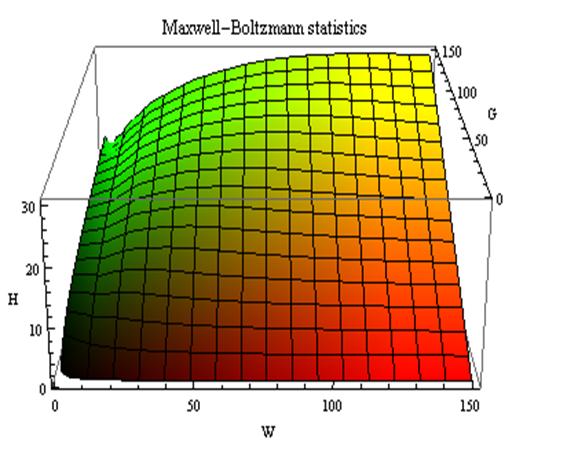
Рис. 5. Поведение коэффициента эмерджентности Хартли в
случае статистики Максвелла-Больцмана
Наконец, рассмотрим поведение
коэффициента эмерджентности всех трех систем для больших значений параметров
числа состояний и частиц – рис. 6. Отметим, что максимальное число подсистем
для данных, приведенных на рис. 6 составляет:
·
статистика Ферми-Дирака - 3.50746621×10451.
·
статистика Бозе-Эйнштейна - 1.79196794×10901.
·
статистика Максвелла-Больцмана -
1.4015754×10651.
При этом максимальное число
состояний и частиц в каждом случае равно 1500. Общее число подсистем на всех
уровнях иерархии, т.е. включающих по W=1, 2,
3, …, 10 элементов, для статистки Ферми-Дирака согласно выражения (14) для
этого случая, т.е. при n=1500
уровней имеет вид:
{W, NFD}
{1, 1500}
{2, 1125750}
{3, 562501250}
{4, 210657282125}
{5, 63071015719925}
{6, 15725776993138425}
{7, 3358594738459315425}
{8, 627221514672084598050}
{9, 104049830019224187006550}
{10, 15524360758047942656113900}
Все результаты, представленные
на рис. 3-6, получены с использованием системы
Wolfram Mathematica 9.0[55].
В этой системе максимальное число в вычислениях с плавающей точкой равно
$MaxMachineNumber = 1.79769*10308. Максимальное же число, которое
может быть представлено на компьютере, использованном в вычислениях приведенных
выше данных, составляет $MaxNumber= 2.174188391646043*1020686623745.
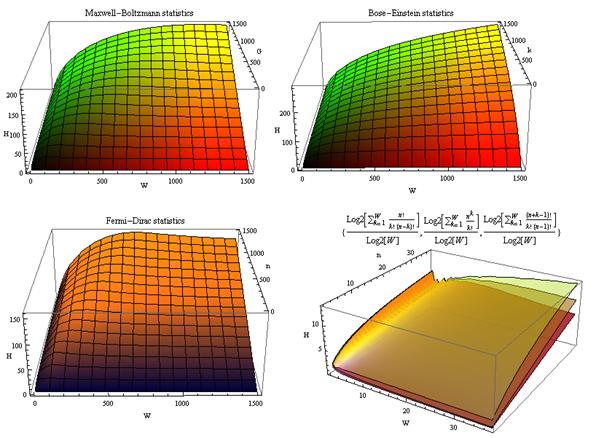
Рис. 6. Поведение коэффициента эмерджентности Хартли в
случае классической и квантовой статистики. На правом нижнем рисунке
поверхности коэффициента эмерджентности изображены для малого числа частиц и
состояний
Из приведенных на рис. 6 данных следует, что с
ростом числа состояний и числа частиц коэффициенты эмерджентности квантовых и
классических систем отличаются между собой, как и коэффициенты квантовых систем
ферми-частиц и бозе-частиц. Следовательно,
коэффициент эмерджентности позволяет отличить классическую систему от квантовой
системы, а квантовую систему ферми-частиц от квантовой системы бозе-частиц.
Полученные результаты могут оказаться полезными
в молекулярной, атомной и ядерной физике, в физике высоких энергий в
исследованиях структуры элементарных частиц, а также в математике, экономике,
социологии, биологии и других науках, связанных с исследованием сложных систем
[12-23].
Из рисунка 6 видно, что для коэффициента
эмерджентности Хартли квантовых объектов, подчиняющихся статистике Ферми-Дирака
(фермионов), существует максимум при примерно 650 частицах-элементах, а для
бозонов и классических объектов подобного максимума не существует. В работе
[196] обосновывается универсальный информационный вариационный принцип, согласно
которому объекты выбирают путь изменения и развития [170], который приводит к
наиболее быстрому возрастанию количеству содержащейся в них информации и их
уровня системности. На основании этих двух положений можно сформулировать гипотезу,
согласно которой уровень системности системы, которую можно создать из
определенного количества частиц, будет выше для системы подчиняется статистике
Бозе-Эйнштейна или классической Максвелла-Больцмана, и ниже – если статистике
Ферми-Дирака, поэтому количество и размеры бозонов и классических
объектов во вселенной должны превосходить количество и размеры фермионов.
10.4. Системное обобщение операций над множествами (на примере операции объединения булеанов) и обобщения локального коэффициента эмерджентности Хартли
В работе [240] рассматривается реализация
математической операции объединения систем, являющаяся обобщением операции объединения
множеств в рамках системного обобщения теории множеств. Эта операция сходна с
операцией объединения булеанов классической теории множеств. Но в отличие от
классической теории множеств в ее системном обобщении предлагается конкретный
алгоритм объединения систем и обосновывается количественная мера системного
(синергетического, эмерджентного) эффекта, возникающего за счет объединения
систем. Для этой меры предложено название: «Обобщенный коэффициент
эмерджентности Р. Хартли» из-за сходства его математической формы с локальным
коэффициентом эмерджентности Хартли и отражающим степень отличия системы от
множества её базовых элементов[56].
Приводится ссылка на авторскую программу, реализующую предложенный алгоритм и
обеспечивающую численное моделирование объединения систем при различных
ограничениях на сложность систем и при различной мощности порождающего
множества, приводятся некоторые результаты численного моделирования.
В работе [241] предлагается общее математическое
выражение для количественной оценки системного (синергетического) эффекта,
возникающего при объединении булеанов (систем), являющихся обобщением множества
в системном обобщении теории множеств и независящее от способа (алгоритма)
образования подсистем в системе. Для этой количественной меры предложено
название: «Обобщенный коэффициент эмерджентности Р.Хартли» из-за сходства его
математической формы с локальным коэффициентом эмерджентности Хартли,
отражающим степень отличия системы от множества его базовых элементов. Для
локального коэффициента эмерджентности Хартли также предложено обобщение,
независящее от способа (алгоритма) образования подсистем в системе. Приводятся
численные оценки системного эффекта при объединении двух систем с применением
авторской программы, на которую дается ссылка.
В работе [240] в
общем виде сформулирована, обоснована и предложена программная идея системного
обобщения математики, суть которой состоит в тотальной замене понятия
"множество" на более общее понятие "система" и
прослеживании всех математических последствий этого во всех разделах
математики, основанных на теории множеств или использующих ее результаты. При
этом обеспечивается соблюдение принципа соответствия, обязательного для более
общей теории, т.к. чем ниже уровень системности, тем в меньшей степени система
отличается от множества, а система с нулевым уровнем системности тождественно и
есть множество. В работах [189, 191] приводится неформальная постановка и
обсуждение задач, возникающих при системном обобщении теории множеств. В работе
[97] обосновываются количественные меры уровня системности (эмерджентности,
синергетического или системного эффекта[57]
[170, 253, 270]). В работе [97] приводится развернутый пример реализации этой
программной идеи системного обобщения математики, в качестве которого выступает
предложенная автором системная теория информации.
10.4.1.
Реализация операции объединения систем в системном
обобщении теории множеств (объединение булеанов)
Данный раздел основан на работах [240, 241] и посвящен
разработке подхода к решению 9-й задачи, сформулированной в [189, 191]:
«Разработать операции с системами: объединение (сложение), пересечение
(умножение), вычитание. Привести предварительные соображения по реализации
операции объединения систем».
В классической теории множеств, которую мы далее
сокращенно будем называть «КТМ», операция объединения множеств реализуется
следующим образом. «Объединение
множеств (тж. сумма или соединение) [58]
в теории множеств – множество, содержащее в себе все элементы исходных
множеств. Объединение двух множеств A и B обычно обозначается 
,
но иногда можно встретить запись в виде суммы A + B».
Графически операция объединения двух множеств может быть представлена в форме
диаграммы Эйлера-Венна, приведенной на рисунке 1.
Рисунок 1. Диаграмма Эйлера-Венна объединения двух множеств[59]
При объединении двух множеств с мощностями A и B
образуется множество, включающее все элементы как 1-го, так и 2-го множеств с
мощностью Nk, которая является
просто суммой числа элементов 1-го и
2-го множеств:
(1)
(2)
В теории множеств выражения (1) и (2) считаются эквивалентными.
Однако выражение (1) внешне выглядит так же, как арифметическое
сложение двух количественных величин, которое совпадает по смыслу с объединением
множеств только для непересекающихся множеств. Если же множества пересекаются,
т.е. одно множество включают некоторые элементы, которые тождественны элементам
другого множества, то при сложении эти элементы повторяются в сумме, а при
объединении этих повторений в объединенном множестве нет (рисунок 2):
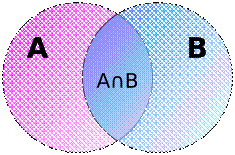
Рисунок 2. Диаграмма Эйлера-Венна пересечения двух множеств[60]
Особенно наглядно различие между арифметическим
сложением и объединением видно, когда эти операции выполняются над тождественными
множествами 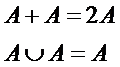(3):
(3)
Запись операции объединения множеств с
использованием операции арифметического сложения их мощностей предполагает
вычитание мощности пересечения множеств из арифметической суммы с целью
исключения повторения тождественных элементов (4):
(4)
где:
Nk – мощность
объединенного множества.
Для непересекающихся множеств:
(5)
и
в этом случае выражение (4) с учетом (5) приобретает вид (1) уже не только
символически, но и фактически (арифметически).
По мнению автора это означает, что символика
выражения (2) точнее или более удачно отражает смысл объединения множеств и его
использование предпочтительнее.
В отличие от множеств, системы имеют
иерархическое строение. Будем считать, что 1-м уровнем иерархии системы является
множество базовых элементов, которое
будем называть порождающим множеством.
В случае
объединения двух систем, согласно системной теории множеств (СТМ), на втором и более высоких уровнях иерархии [189, 191] объединенной системы могут возникать новые составные элементы, которых до объединения не было ни в одной из
исходных систем и состоящие из элементов обоих систем, что и приводит к системному эффекту S. В результате мощность объединения систем превосходит
мощность объединения их порождающих множеств A и B на величину системного
эффекта S, возникающего за счет объединения систем:
(6)
Кроме того, в каждой из систем могут возникать
составные элементы из ее собственных
базовых элементов. Это приводит к системному эффекту, в результате которого
система отличается от множества, т.е. содержит больше элементов, чем в порождающем
множестве. Этот вид системного эффекта аналитически выражается локальным
коэффициентом эмерджентности Хартли (3), который был получен автором в 2001 году [97]
и назван так в честь этого ученого, внесшего большой вклад с разработку научной
теории информации[61]:
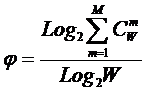(7)
где:
W –
количество базовых элементов в системе;
m –
сложность составного элемента системы, т.е. подсистемы (количество базовых
элементов в составном элементе);
M –
максимальная сложность подсистем (максимальное количество базовых элементов в
составном элементе).
Фактически
максимальная сложность подсистем M не
может быть больше количества базовых элементов в системе W: 
, т.к. самым сложным элементом системы может быть элемент, состоящий
из всех базовых элементов. Но формально это ограничение можно не соблюдать,
т.к. при 
согласно выражения (7) будут получаться нулевые слагаемые под логарифмом в числителе, отражающие тот факт,
что соответствующих составных элементов просто не существует. Поэтому за соблюдением
этого условия можно особо не следить и математически объединять выражения,
указывая один максимальный уровень
сложности из всех возможных при различных количествах базовых элементов в
разных системах, что пригодится нам в будущем.
Будем считать, что составные
элементы в системах не могут образовываться за счет многократного использования
одних и тех же базовых элементов в одном составном (повторений):
– это
предполагается самим видом математического выражения (7) и понятием
комбинаторики «число сочетаний из n
по m»;
– в противном
случае уровень сложности элементов и системы в целом, а также ее мощность,
могли бы неограниченно возрастать,
например, за счет наличия в системе элементов, представляющих собой сколь
угодно высокую степень любого из базовых элементов.
Коэффициент эмерджентности Хартли исследован
автором в ряде работ, в частности [97, 170].
Непосредственно из вида выражения для коэффициента эмерджентности Хартли (7)
ясно, что он представляет собой относительное превышение количества информации в
системе при учете системных эффектов (смешанных состояний, иерархической
структуры ее подсистем и т.п.) над количеством информации без учета системности
(только в базовом уровне или порождающем множестве), т.е. этот коэффициент отражает уровень системности объекта.
Получим аналитические выражения для количества
элементов в объединенной системе и величины системного эффекта, образующегося
не за счет объединения базовых элементов в отдельно-взятой системе (что
отражается локальным коэффициентом эмерджентности Хартли), а за счет
объединения систем, а затем проведем и количественные оценки с использованием
этих выражений и численного моделирования.
Аксиома о максимальной мощности системы системной теории
множеств (СТМ) и СТИ [97]: в системе, основанной
на множестве из W неповторяющихся
элементов, которые мы будем называть базовыми,
может содержаться не более Nmax
элементов, включающих как все базовые элементы, так и составные элементы (подсистемы), образованные из всех возможных
различных сочетаний базовых элементов по 2, 3, …, W элементов (без повторений):
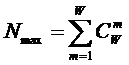(8)
Эта аксиома СТМ аналогична аксиоме булеана[62]
классической теории множеств, в которой постулируется существование и
единственность множества всех подмножеств некоторого множества из W элементов, т.е. булеана, а также
доказывается[63], что
мощность булеана равна 2W.
В этой связи необходимо сделать два замечания.
Замечание
1:
мощность системы, базирующейся на W
элементах, всегда на 1 меньше мощности булеана, образованного на тех же
элементах:
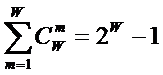(9)
Это связано с тем, что по определению булеан
включает как элемент самого себя, а система не включает в качестве элемента
саму себя, но включает элемент наивысшего уровня сложности (иерархии),
состоящий из всех базовых элементов, т.е. в систему входит элемент:
«Система-в-целом».
Замечание
2:
в самой аксиоме булеана классической теории множеств не содержится алгоритма или способа нахождения всех
элементов образуемого множества, но такой алгоритм предлагается в рамках СТМ и
его идея
основана на аксиоме о максимальной мощности системы: это алгоритм
формирования всех возможных различных
(без повторений) сочетаний базовых элементов системы. Подобные алгоритмы
известны[64] и
поэтому здесь не приводятся.
Однако, фактически количество элементов в
системе всегда меньше максимального, т.к. действуют определенные правила запрета на образование некоторых
составных элементов [97][65].
Среди таких правил запрета могут быть, например, ограничения на максимальное
(или/и минимальное) количество базовых элементов в составных элементах (т.е. на
их сложность), а также запрет на повторное
включение базовых элементов в составные (когда один и тот же базовый элемент не
может несколько раз входить в один и тот же составной элемент).
Если система образована на основе W базовых элементов, то в ней существует
M уровней иерархии, на 1-м из которых
находятся сами базовые элементы и этот уровень иерархии системы тождественно
является порождающему множеству, на 2-м – составные элементы, образованные
различными сочетаниями базовых элементов по 2, на 3-м – по 3, и на последнем –
по M.
Если количество уровней иерархии в системе M (будем называть его рангом системы) равно количеству ее базовых элементов
W, то все базовые элементы входят в единственный элемент наивысшего уровня
иерархии. В системе отсутствуют составные элементы, включающие больше
базовых элементов, чем ранг системы.
Чтобы учесть в выражении (7) 1-е ограничение (на
максимальную сложность составных элементов M)
и получить выражение для количества элементов в системе ранга M, модифицируем его следующим образом:
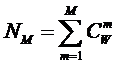(10)
В частности, если есть два множества, в 1-м из
которых A элементов, а во 2-м – B, то согласно системной теории множеств (СТМ) на базе 1-го множества
образуется система с числом элементов NA:
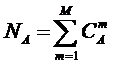, (11)
а
на базе 2-го – с числом элементов NB:
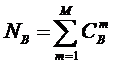, (12)
В случае объединения этих 2-х систем по правилам классической теории множеств (КТМ) (4), т.е. считая
систему множеством всех ее элементов: и базовых, и составных, количество
элементов в объединенной системе Nk
равно просто сумме числа элементов
1-й и 2-й систем (11) и (12), как в случае множеств:
(13)
где:
NA – множество всех
элементов (базовых и составных) системы A;
NB – множество всех
элементов (базовых и составных) системы B.
Выражение (13) является системным аналогом
теоретико-множественного выражения (4), но проще его записать аналогично (2):
(14)
Подставим в выражение (14) переменные NA и NB из (11) и (12):
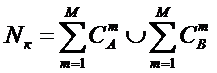(15)
В выражении (15) все элементы систем A и B
(базовые и составные) по сути, рассматриваются как элементы множеств. Операторы
суммирования вычисления количества сочетаний в выражении (15) понимаются не как
арифметические операторы, а как символические порождающие операторы теории
множеств, которые содержат обобщенное аналитическое описание алгоритма генерации
элементов систем на базе порождающих множеств A и B.
Однако в системной теории множеств в случае
объединения 2-х и более систем возникает системный (синергетический) эффект,
состоящий в отклонении от аддитивности (6), т.е. в том, что сумма элементов в
объединенной системе (16) превосходит[66]
сумму элементов в исходных системах (15). Математически это можно выразить,
добавив в выражение (15) еще одно слагаемое S,
отражающее системный эффект:
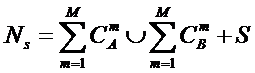(16)
Это слагаемое S равно числу тех составных
элементов объединенной системы, которые могли возникнуть только в результате объединения этих 2-х систем, т.е. которые
включают элементы как 1-й, так 2-й систем, и которых до объединения этих систем
не было и не могло быть ни в одной из них.
Например, при объединении 2-х систем, содержащих на 1-м
уровне иерархии простые числа, а на
2-м уровне составные числа,
являющиеся произведениями различных пар простых сомножителей, образуется
объединенная система, 1-й уровень которой является объединением 1-х уровней
исходных систем, а 2-й образуется по тому же алгоритму, что и в них (рисунок
3):
Рисунок 3. Объединение 2-х систем из простых чисел на базовом
уровне и сложных чисел, образованных из пар простых, на 2-м уровне[67]
Может возникнуть впечатление, что пример
объединения символических числовых систем носит какой-то абстрактный и
узко-специальный характер и не имеет отношения к реальным системам. Но это не
так, что ясно уже из того, что элементы базового уровня реальных систем в самых
разных предметных областях могут быть закодированы
с помощью простых чисел, а их составные элементы, образованные из базовых –
соответствующими составными числами, образованными этими простыми сомножителями,
и между этими числовыми кодами и элементами реальных систем будет установлено
взаимно-однозначное соответствие. Таким образом, рассматриваемую в данном
примере символическую систему можно рассматривать как универсальную и
адекватную модель реальных систем. Так если закодировать элементы таблицы
Д.И.Менделеева простыми числами, то различным образованным из них химическим
соединениям будут соответствовать сложные числа, образованные произведениями соответствующих простых
сомножителей. Аналогично, если символам алфавита поставить в соответствие
простые числа, то словам будут соответствовать числа, представляющие собой их
произведения[68]. Если
же взять логарифм от составного числа, то он будет равен сумме логарифмов его простых сомножителей (что соответствует
переходу к логарифмической шкале и в некоторых случаях удобнее, т.к. размер
чисел меньше и мультипликативность
взаимно-однозначно заменяется аддитивностью).
В таблицах 1–4 приведены данные о том, какие
составные числа произведениями каких простых являются в рассматриваемом
примере:
Таблица 1 – СОСТАВ
ЭЛЕМЕНТОВ 1-Й СИСТЕМЫ
|
Элемент |
Уровень иерархии |
Простые сомножители |
|
|
1-й |
2-й |
||
|
2 |
1 |
2 |
|
|
3 |
1 |
3 |
|
|
5 |
1 |
5 |
|
|
7 |
1 |
7 |
|
|
6 |
2 |
2 |
3 |
|
10 |
2 |
2 |
5 |
|
14 |
2 |
2 |
7 |
|
15 |
2 |
3 |
5 |
|
21 |
2 |
3 |
7 |
|
35 |
2 |
5 |
7 |
Таблица 2 – СОСТАВ
ЭЛЕМЕНТОВ 2-Й СИСТЕМЫ
|
Уровень иерархии |
Простые сомножители |
||
|
1-й |
2-й |
||
|
11 |
1 |
11 |
|
|
13 |
1 |
13 |
|
|
17 |
1 |
17 |
|
|
19 |
1 |
19 |
|
|
143 |
2 |
11 |
13 |
|
187 |
2 |
11 |
17 |
|
209 |
2 |
11 |
19 |
|
221 |
2 |
13 |
17 |
|
247 |
2 |
13 |
19 |
|
323 |
2 |
17 |
19 |
Таблица 3 – СОСТАВ
ЭЛЕМЕНТОВ ОБЪЕДИНЕННОЙ СИСТЕМЫ
|
Элемент |
Уровень иерархии |
Простые сомножители |
|
|
1-й |
2-й |
||
|
2 |
1 |
2 |
|
|
3 |
1 |
3 |
|
|
5 |
1 |
5 |
|
|
7 |
1 |
7 |
|
|
11 |
1 |
11 |
|
|
13 |
1 |
13 |
|
|
17 |
1 |
17 |
|
|
19 |
1 |
19 |
|
|
6 |
2 |
2 |
3 |
|
10 |
2 |
2 |
5 |
|
14 |
2 |
2 |
7 |
|
22 |
2 |
2 |
11 |
|
26 |
2 |
2 |
13 |
|
34 |
2 |
2 |
17 |
|
38 |
2 |
2 |
19 |
|
15 |
2 |
3 |
5 |
|
21 |
2 |
3 |
7 |
|
33 |
2 |
3 |
11 |
|
39 |
2 |
3 |
13 |
|
51 |
2 |
3 |
17 |
|
57 |
2 |
3 |
19 |
|
35 |
2 |
5 |
7 |
|
55 |
2 |
5 |
11 |
|
65 |
2 |
5 |
13 |
|
85 |
2 |
5 |
17 |
|
95 |
2 |
5 |
19 |
|
77 |
2 |
7 |
11 |
|
91 |
2 |
7 |
13 |
|
119 |
2 |
7 |
17 |
|
133 |
2 |
7 |
19 |
|
143 |
2 |
11 |
13 |
|
187 |
2 |
11 |
17 |
|
209 |
2 |
11 |
19 |
|
221 |
2 |
13 |
17 |
|
247 |
2 |
13 |
19 |
|
323 |
2 |
17 |
19 |
Таблица 4 – СОСТАВ
ЭЛЕМЕНТОВ ПОДСИСТЕМЫ ОБЪЕДИНЕННОЙ СИСТЕМЫ, СОДЕРЖАЩЕЙ ЭЛЕМЕНТЫ, ОБРАЗОВАННЫЕ ЗА
СЧЕТ СИСТЕМНОГО ЭФФЕКТА
|
Элемент |
Уровень иерархии |
Простые сомножители |
|
|
1-й |
2-й |
||
|
22 |
2 |
2 |
11 |
|
26 |
2 |
2 |
13 |
|
34 |
2 |
2 |
17 |
|
38 |
2 |
2 |
19 |
|
33 |
2 |
3 |
11 |
|
39 |
2 |
3 |
13 |
|
51 |
2 |
3 |
17 |
|
57 |
2 |
3 |
19 |
|
55 |
2 |
5 |
11 |
|
65 |
2 |
5 |
13 |
|
85 |
2 |
5 |
17 |
|
95 |
2 |
5 |
19 |
|
77 |
2 |
7 |
11 |
|
91 |
2 |
7 |
13 |
|
119 |
2 |
7 |
17 |
|
133 |
2 |
7 |
19 |
Числа, показанные на рисунке 3 черным цветом на
2-м уровне объединенной системы, есть на 2-м уровне либо 1-й системы, либо 2-й.
Если бы системы объединялись как множества, то никаких других элементов на 2-м
уровне объединенной системы и не было бы. Но при объединении систем в
объединенной системе могут возникать элементы, образованные из сочетаний
базовых элементов нескольких исходных систем одновременно, которых не было в
исходных системах и которые могли образоваться только в объединенной системе. В
нашем примере на рисунке 3 это числа, показанные более крупным шрифтом и красным
цветом на 2-м уровне объединенной системы, образованные из различных пар
простых чисел, одно из которых принадлежит 1-й системе, а 2-е – второй (см.
таблицы 1–4).
Получим аналитическое выражение для этого числа
элементов S. У нас уже есть одно
выражение для мощности объединенной системы (16). Чтобы найти S, необходимо иметь еще одно независимое от выражения (16) выражение для Ns. Это выражение (17)
совершенно аналогично выражениями (11) и (12), т.е. число всех элементов Ns в объеденной системе
равно:
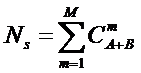(17)
или
точнее:
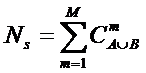(18)
Выражения (17) и (18) эквивалентны и являются
системным обобщением соответственно выражений (1) и (2) классической теории множеств
в рамках СТМ.
При уменьшении сложности системы M система все в меньшей степени
отличается от множества своих базовых элементов и при M=1 система переходит в это множество (т.к. составных элементов в
нем нет) и выражение (16) преобразуется в (4):
(19)
т.е.
преобразуется в выражение (4). Это и означает выполнение принципа соответствия[69]
между системным обобщением теории множеств (СТМ) и классической теорией
множеств (КТМ), когда на основе базовых элементов множеств не создаются составные
элементы, т.е. при уровне системности равном 1. Необходимо отметить, что выполнение принцип соответствия является обязательным
для более общей теории, и системное обобщение теории множеств удовлетворяет
этому принципу.
Если найти S
из выражения (16) и подставить в него выражение NS из выражения (18), то получим:
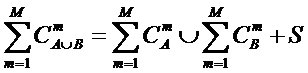(19)
откуда:
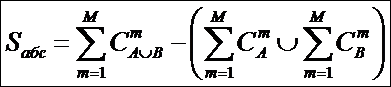(20)
Выражения (19) и (20) представляют собой искомые
выражения для абсолютной величины
системного эффекта, образующегося за счет объединения 2-х систем без
повторяющихся элементов с правилом запрета в форме ограничения на максимальную
сложность подсистем (составных элементов) или количество уровней иерархии в
системе, равным M.
Обобщим
выражения (19) и (20) на произвольное количество систем. Пусть дано не 2 системы,
а семейство систем: 
. Как уже отмечалось выше в выражениях (20) и (21) в качестве
значения M можно взять максимальный
из уровней сложности всех систем:
(22)
где: 
– уровень сложности системы 
. Тогда для случая многих систем выражения (20) и (21) обобщаются
следующим образом:
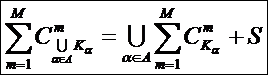(23)
В формуле (23) использованы символика и
обозначения из статьи[70].
Непосредственно из (23) получаем выражение для величины системного эффекта S, получаемого при объединении систем
семейства :
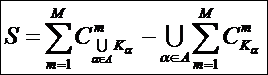(24)
Итак, абсолютная величина системного
эффекта, образующегося за счет объединения систем, равна количеству составных элементов
(подсистем), которые включают базовые элементы обоих систем и, следовательно,
могут образоваться только после этого объединения.
Однако проблема интерпретации и оценки абсолютной величины системного эффекта
(20) состоит в том, что по самому этому количеству сложно понять, большое оно,
среднее или незначительное, т.к. его не с
чем сравнивать, т.е. нет базы сравнения. В качестве естественной базы сравнения предлагается использовать
суммарное количество элементов в исходных системах до объединения.
В результате получим выражение для относительной
величины системного эффекта, образующегося за счет объединения 2-х систем с
правилом запрета в форме ограничения на максимальную сложность подсистем
(составных элементов), равным M:
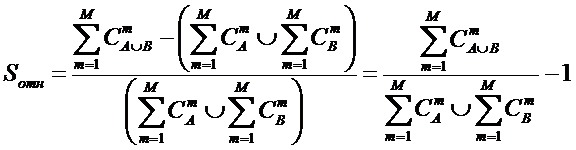
Или окончательно:
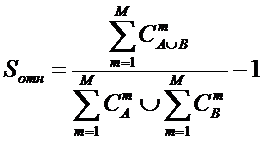(25)
Обратим внимание на то, что,
как и в параметре ROI[71],
вычитание 1 из отношения является одним из способов нормировки выражения, равного 1 к 0 при отсутствии системного эффекта, что более естественно и лучше
приспособлено для его использования в качестве частного критерия в аддитивном интегральном критерии. Другим
способом нормировки, дающим тот же результат (с точностью до единиц измерения),
является взятие логарифма из этого отношения:
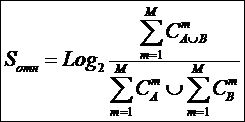(26)
Этот вариант более интересен
чем (25) из-за прозрачной аналогии с формулой А.Харкевича для количественной
меры семантической целесообразности информации, что позволяет привлечь для
исследований в области СТМ богатейший идейный арсенал теории информации, ее
применения для управления и управления знаниями.
Обобщение выражения (26) на
произвольное количество систем семейства: :
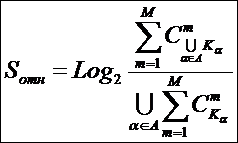(27)
Рассмотрим
связь системного обобщения теории множеств с теорией информации.
Понятие информации тесно
связано с комбинаторными представлениями. По Р.Хартли[72]
количество информации I, получаемое
при идентификации элемента множества мощностью W при равновероятной встрече различных элементов, равно:
(28)
К.Шенноном на основе
статистического подхода выражение Р.Хартли обобщено на случай неравновероятных
событий[73].
А.Н.Колмогоров развил комбинаторный и алгоритмический подход к понятию сложности
системы и на его основе разработал новое определение понятия информации и также
получил формулу К.Шеннона[74],
причем по некоторым данным даже значительно раньше самого К.Шеннона.
С современной точки зрения
понятие информации теснейшим образом связано с понятием множества. Поэтому
совершенно естественной выглядит мысль исследовать как меняется понятие
информации при реализации программной идеи системного
обобщения математики [186], т.е. в результате замены понятия множества
более общим понятием системы. В работе [97] и ряде других [см.: 97-280] исследованы некоторые следствия реализации
этой программы в теории информации. Продолжим эту работу с использованием результатов,
полученных в данном разделе.
Если формулу (28) применить к
системе, основанной на W базовых
элементов с M уровней иерархии (10),
то получим:
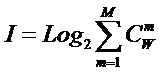(29)
Выражение (29) предложено
автором в 2001 году и исследовано в работе [97]. Из применения выражения (29) для расчета
количества информации, содержащегося в объединенной системе (18) и в исходных
системах, рассматриваемых совместно как множества (15), следует выражение для количества информации, получаемого при
идентификации элемента подсистемы, возникшей за счет системного эффекта при объединении
двух подсистем:
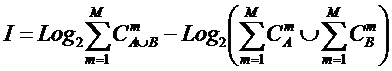(30)
Отметим, что из выражения (30) непосредственно вытекает (31)[75]:
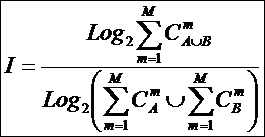(31)
Это и есть окончательное
выражение для количества информации,
получаемого при идентификации элемента подсистемы, возникшей за счет системного
эффекта при объединении двух подсистем.
По своей математической форме
выражение (31) очень напоминает коэффициент эмерджентности Хартли (7),
отражающий уровень системности локальной системы, т.е. степень ее отличия от
множества. Поэтому у нас есть все основания назвать выражение (31) обобщенным коэффициентом эмерджентности Хартли,
который показывает степень отличия объединения систем от исходных систем за
счет системного эффекта, возникающего за счет этого объединения.
Полученные выражения стандартно
обобщаются на случай объединения многих систем. Например, выражение (31) для случая
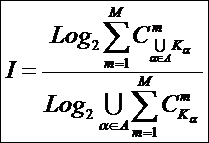объединения систем семейства принимает вид (32):
(32)
Все полученные выражения
стандартно обобщаются также на непрерывный случай путем замены факториалов при
расчете числа сочетаний на гамма-функции [1].
Рассмотрим
примеры объединения систем, в т.ч. численные.
Наиболее яркие примеры
системного эффекта, возникающего при объединении систем, можно наблюдать в
процессе биологической эволюции. Логично предположить, что если системный
эффект, возникающий за счет объединения двух систем (31), например, при
оплодотворении, настолько велик, что сопоставим с уровнем системности локальной
системы (7), аналогичной исходным, то за счет этого системного эффекта могут
возникать новые локальные системы, подобные исходным 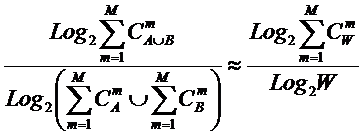(33):
(33)
На рисунке 4 приведен простой
генетический алгоритм (ГА), являющийся моделью биологической эволюции [196]. Работа
ГА представляет собой итерационный процесс, который продолжается до тех пор,
пока поколения не перестанут существенно отличаться друг от друга, или не
пройдет заданное количество поколений или заданное время. Для каждого поколения
реализуются отбор, кроссовер (скрещивание), мутация и генерация следующего
поколения. В этом алгоритме есть этапы, на которых проявляются системные
эффекты, связанные с появлением следующего поколения в результате объединения
особей предыдущего поколения. Рассмотрим этот алгоритм.
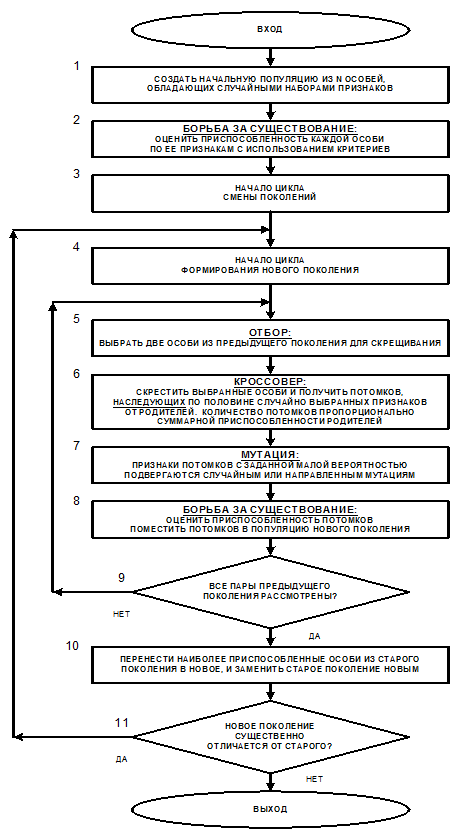
Рисунок 4. Простой генетический алгоритм
Шаг 1: генерируется начальная популяция, состоящая из N
особей со случайными наборами признаков.
Шаг 2
(борьба за существование):
вычисляется абсолютная приспособленность
каждой особи популяции к условиям среды f(i)
и суммарная приспособленность особей популяции, характеризующая
приспособленность всей популяции. Затем при пропорциональном
отборе для каждой особи вычисляется ее относительный
вклад в суммарную приспособленность популяции Ps(i), т.е. отношение ее абсолютной приспособленности f(i) к суммарной приспособленности всех
особей популяции 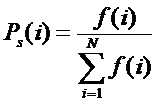(34):
(34)
В выражении (34)
сразу обращает на себя внимание возможность сравнения абсолютной
приспособленности i-й особи f(i) не с суммарной приспособленностью всех особей популяции, а со средней абсолютной приспособленностью
особи популяции 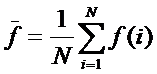(35):
(35)
Тогда получим 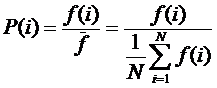(36):
(36)
Если взять логарифм
по основанию 2 от выражения (36), т.е. перейти к логарифмической шкале (что
соответствует закону Фехнера[76]),
то получим количество информации,
содержащееся в признаках особи о том, что она выживет и даст потомство
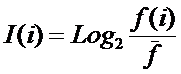(37):
(37)
Необходимо
отметить, что эта формула совпадает с формулой для семантического
количества информации А.Харкевича, если «целью» биологической эволюции считать индивидуальное выживание и продолжение
рода (выживание вида). Это значит, что даже чисто формально приспособленность особи представляет
собой количество информации, содержащееся в ее фенотипе о продолжении ее
генотипа в последующих поколениях.
Поскольку
количество потомства особи пропорционально ее приспособленности, то естественно
считать, что если это количество информации:
– положительно, то данная особь выживает и
дает потомство, численность которого пропорциональна этому количеству информации;
– равно нулю, то особь доживает до
половозрелого возраста, но потомства не дает (его численность равна нулю);
– меньше нуля, то особь погибает до
достижения половозрелого возраста.
Таким образом,
можно сделать фундаментальный вывод, имеющий даже мировоззренческое звучание, о
том, что естественный отбор представляет собой процесс генерации, накопления и
передачи от прошлых поколений к будущим информации о выживании и продолжении
рода в ряде поколений популяции, как системы.
Это накопление
информации происходит на различных уровнях иерархии популяции, как системы,
включающей:
– элементы
системы: отдельные особи;
– взаимосвязи
между элементами: отношения между особями в популяции, обеспечивающие
передачу последующим поколениям максимального количества информации об их
выживании и продолжении рода (путем скрещивания наиболее приспособленных особей
и наследования рациональных приобретений);
– цель системы:
сохранение и развитие популяции, реализуется через цели особей: индивидуальное
выживание и продолжение рода.
Фенотип
соответствует генотипу и представляет собой его внешнее проявление в признаках
особи в условиях фактической среды. Особь взаимодействует с окружающей средой и
другими особями в соответствии со своим фенотипом. В случае, если это
взаимодействие удачно, то особь передает генетическую информацию, определяющую
фенотип, последующим поколениям.
Шаг 3: начало цикла смены поколений.
Шаг 4: начало цикла формирования нового поколения.
Шаг 5
(отбор): осуществляется пропорциональный отбор особей, которые могут участвовать в продолжении рода. Отбираются
только те особи популяции, у которых количество информации в фенотипе и
генотипе о выживании и продолжении рода положительно, причем вероятность выбора
пропорциональна этому количеству информации.
Шаг 6
(кроссовер): отобранные для
продолжения рода на предыдущем шаге особи с заданной вероятностью Pc подвергаются скрещиванию
или кроссоверу
(рекомбинации).
Если кроссовер происходит, то потомки получают по половине случайным
образом определенных признаков от каждого из родителей.
Численность потомства пропорциональна суммарной приспособленности
родителей, т.е. величине системного эффекта, возникающего за счет их
объединения в систему 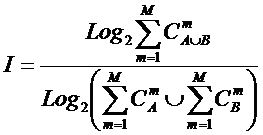(38).
(38)
В некоторых
вариантах ГА потомки после своего появления заменяют собой родителей и
переходят к мутации. Если кроссовер не происходит, то исходные особи –
несостоявшиеся родители, переходят на стадию мутации.
Шаг 7
(мутация): выполняются
операторы мутации. При этом признаки потомков с вероятностью Pm случайным образом
изменяются на другие. Отметим, что использование механизма случайных мутаций
роднит генетические алгоритмы с таким широко известным методом имитационного
моделирования, как метод Монте-Карло.
Шаг 8
(борьба за существование):
оценивается приспособленность потомков (по тому же алгоритму, что и на шаге 2).
Шаг 9: проверяется, все ли отобранные особи дали потомство.
Если нет, то
происходит переход на шаг 5 и продолжается формирование нового поколения, иначе
– переход на следующий шаг 10.
Шаг 10: происходит смена поколений:
– потомки
помещаются в новое поколение;
– наиболее
приспособленные особи из старого поколения переносятся в новое, причем для
каждой из них это возможно не более заданного количества раз;
– полученная новая
популяция замещает собой старую.
Шаг 11: проверяется выполнение условия останова генетического
алгоритма. Выход из генетического алгоритма происходит либо тогда, когда новые
поколения перестают существенно отличаться от предыдущих, т.е., как говорят,
"алгоритм сходится", либо когда пройдено заданное количество
поколений или заданное время работы алгоритма (чтобы не было
"зацикливания" и динамического зависания в случае, когда решение не
может быть найдено в заданное время ).
Если ГА сошелся, то это означает, что решение найдено, т.е. получено поколение, идеально приспособленное к
условиям данной фиксированной среды обитания.
Иначе – переход на
шаг 4 – начало формирования нового поколения.
В реальной биологической эволюции этим дело не ограничивается,
т.к. любая популяция кроме освоения некоторой экологической ниши пытается также
выйти за ее пределы освоить и другие ниши, как правило "смежные". Именно за счет этих процессов жизнь вышла из моря на
сушу, проникла в воздушное пространство и поверхностный слой почвы, а сейчас
осваивает космическое пространство.
Рассмотрим
второй пример с объединением систем натуральных чисел, основанных на базовых
элементах, являющихся простыми числами. Для этого автором разработана программа, которая
обеспечивает:
1. Задание в диалоге двух диапазонов простых
чисел, являющихся базовыми элементами 1-й и 2-й систем, а также задание диапазона
изменения M (ограничения на сложность подсистем - составных чисел).
Для всех M:
2. Генерацию простых чисел без повторов в
заданных диапазонах, являющихся соответственно базовыми элементами 1-й и 2-й
системы.
3. Объединение множеств простых чисел,
являющихся базовыми элементами 1-й и 2-й систем, и формирование множества
базовых элементов объединенной системы (без повторов).
4. Генерацию на основе простых чисел, являющихся
базовыми элементами 1-й и 2-й системы, составных натуральных чисел, являющихся
произведениями 2, 3,..., M простых
чисел и образующих вместе с базовыми простыми числами 1-ю и 2-ю системы.
5. Генерацию на основе простых чисел, являющихся
базовыми элементами объединенной системы, составных натуральных чисел,
являющихся произведениями 2, 3,..., M
простых чисел и образующих вместе с базовыми простыми числами объединенную
систему.
6. Поиск в объединенной системе составных чисел,
которых нет ни в одной из исходных систем. Эти числа и составляют новую
подсистему, образование которой и представляет собой системный эффект,
возникающий при этом объединении, нарушающую аддитивность объединения систем и
отличающую операцию объединения систем в системном обобщении теории множеств от
объединения множеств в классической теории множеств.
7. Количественный расчет коэффициентов
эмерджентности Хартли для 1-й, 2-й и объединенной локальных систем и обобщенного
коэффициента эмерджентности Хартли, отражающего величину системного эффекта,
возникающего при объединении этих двух числовых систем, образованных на простых
числах заданных диапазонов. Печать поэлементного состава 1-й, 2-й и
объединенной систем, а также подсистемы системного эффекта по уровням иерархии
8. Исследование зависимости системного эффекта
от различных параметров объединяемых систем (количества базовых элементов,
уровня сложности систем и других).
Экранная форма этой программы приведена на
рисунке 5:
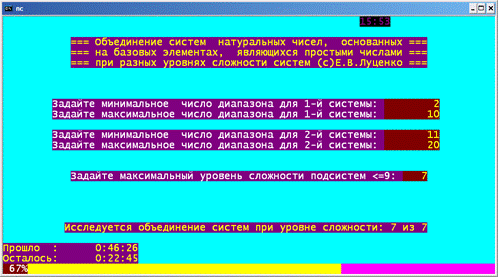
Рисунок 4. Экранная
форма программы численного моделирования
объединения систем натуральных чисел, основанных на базовых элементах,
являющихся простыми числами
Исполнимый модуль, исходный текст (на языке
программирования CLIPPER 5.01) и численный пример применения программы,
моделирующий объединение 2-х систем с различными уровнями сложности приведены
автором по адресу: http://www.twirpx.com/file/370725/.
Рассмотрим численные примеры объединения двух
систем, смоделированные с помощью приведенной программы при различных
параметрах.
При запуске программы с указанными ниже
параметрами она формирует выходной файл с именем System.txt (считывается MS
Word как DOS Text), приведенный ниже.
Объединение двух систем натуральных чисел, основанных
на базовых элементах, являющихся простыми числами,
при разных уровнях сложности систем.
(Системное обобщение теории множеств. Е.В.Луценко)
Диапазон базовых элементов 1-й системы: 2-10
Диапазон базовых элементов 2-й системы: 11-20
Диапазон уровней сложности: 1-7
УРОВЕНЬ СЛОЖНОСТИ=1
1-Я СИСТЕМА === Sys_1.dbf ============================
1-й уровень иерархии. Кол-во элементов=4
2 3 5 7
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=4, из них базовых: 4
Локальный коэффициент эмерджентности Хартли=1.0000000
======================================================
2-Я СИСТЕМА === Sys_2.dbf ============================
1-й уровень иерархии. Кол-во элементов=4
11 13 17 19
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=4, из них базовых: 4
Локальный коэффициент эмерджентности Хартли=1.0000000
======================================================
ОБЪЕДИНЕННАЯ СИСТЕМА === Sys_U.dbf ===================
1-й уровень иерархии. Кол-во элементов=8
2 3 5 7 11 13 17 19
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=8, из них базовых: 8
Локальный коэффициент эмерджентности Хартли=1.0000000
======================================================
СИСТЕМНЫЙ ЭФФЕКТ === Sys_s.dbf =======================
1-й уровень иерархии. Кол-во элементов=0
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=0, из них базовых: 0
======================================================
Обобщенный коэффициент эмерджентности Хартли=1.0000000
A=4. B=4. AUB=8. AUB-A-B=0
======================================================
Локальный коэффициент эмерджентности Хартли отражает
степень отличия системы от множества базовых элементов
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Обобщенный коэффициент эмерджентности Хартли отражает
величину системного эффекта, возникающего при объеди-
нении нескольких систем в одну
======================================================
УРОВЕНЬ СЛОЖНОСТИ=2
1-Я СИСТЕМА === Sys_1.dbf ============================
2-й уровень иерархии. Кол-во элементов=6
6 10 14 15 21 35
1-й уровень иерархии. Кол-во элементов=4
2 3 5 7
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=10, из них базовых: 4
Локальный коэффициент эмерджентности Хартли=1.6609640
======================================================
2-Я СИСТЕМА === Sys_2.dbf ============================
2-й уровень иерархии. Кол-во элементов=6
143 187 209 221 247 323
1-й уровень иерархии. Кол-во элементов=4
11 13 17 19
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=10, из них базовых: 4
Локальный коэффициент эмерджентности Хартли=1.6609640
======================================================
ОБЪЕДИНЕННАЯ СИСТЕМА === Sys_U.dbf ===================
2-й уровень иерархии. Кол-во элементов=28
6 10 14 15 21 22 26 33 34 35 38 39 51 55 57 65 77 85 91
95 119 133 143 187 209 221 247 323
1-й уровень иерархии. Кол-во элементов=8
2 3 5 7 11 13 17 19
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=36, из них базовых: 8
Локальный коэффициент эмерджентности Хартли=1.7233083
======================================================
СИСТЕМНЫЙ ЭФФЕКТ === Sys_s.dbf =======================
2-й уровень иерархии. Кол-во элементов=16
22 26 33 34 38 39 51 55 57 65 77 85 91 95 119 133
1-й уровень иерархии. Кол-во элементов=0
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=16, из них базовых: 0
======================================================
Обобщенный коэффициент эмерджентности Хартли=1.1962080
A=10. B=10. AUB=36. AUB-A-B=16
======================================================
Локальный коэффициент эмерджентности Хартли
отражает
степень отличия системы от множества базовых элементов
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Обобщенный коэффициент эмерджентности Хартли отражает
величину системного эффекта, возникающего при объеди-
нении нескольких систем в одну
======================================================
УРОВЕНЬ СЛОЖНОСТИ=3
1-Я СИСТЕМА === Sys_1.dbf ============================
3-й уровень иерархии. Кол-во элементов=4
30 42 70 105
2-й уровень иерархии. Кол-во элементов=6
6 10 14 15 21 35
1-й уровень иерархии. Кол-во элементов=4
2 3 5 7
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=14, из них базовых: 4
Локальный коэффициент эмерджентности Хартли=1.9036775
======================================================
2-Я СИСТЕМА === Sys_2.dbf ============================
3-й уровень иерархии. Кол-во элементов=4
2431 2717 3553 4199
2-й уровень иерархии. Кол-во элементов=6
143 187 209 221 247 323
1-й уровень иерархии. Кол-во элементов=4
11 13 17 19
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=14, из них базовых: 4
Локальный коэффициент эмерджентности Хартли=1.9036775
======================================================
ОБЪЕДИНЕННАЯ СИСТЕМА === Sys_U.dbf ===================
3-й уровень иерархии. Кол-во элементов=56
30 42 66 70 78 102 105 110 114 130 154 165 170 182 190
195 231 238 255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627
646 663 665 715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261
2431 2717 3553 4199
2-й уровень иерархии. Кол-во элементов=28
6 10 14 15 21 22 26 33 34 35 38 39 51 55 57 65 77 85 91
95 119 133 143 187 209 221 247 323
1-й уровень иерархии. Кол-во элементов=8
2 3 5 7 11 13 17 19
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=92, из них базовых: 8
Локальный коэффициент эмерджентности Хартли=2.1745207
======================================================
СИСТЕМНЫЙ ЭФФЕКТ === Sys_s.dbf =======================
3-й уровень иерархии. Кол-во элементов=48
66 78 102 110 114 130 154 165 170 182 190 195 231 238
255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627 646 663 665
715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261
2-й уровень иерархии. Кол-во элементов=16
22 26 33 34 38 39 51 55 57 65 77 85 91 95 119 133
1-й уровень иерархии. Кол-во элементов=0
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=64, из них базовых: 0
======================================================
Обобщенный коэффициент эмерджентности Хартли=1.3569961
A=14. B=14. AUB=92. AUB-A-B=64
======================================================
Локальный коэффициент эмерджентности Хартли
отражает
степень отличия системы от множества базовых элементов
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Обобщенный коэффициент эмерджентности Хартли отражает
величину системного эффекта, возникающего при объеди-
нении нескольких систем в одну
======================================================
УРОВЕНЬ СЛОЖНОСТИ=4
1-Я СИСТЕМА === Sys_1.dbf ============================
4-й уровень иерархии. Кол-во элементов=1
210
3-й уровень иерархии. Кол-во элементов=4
30 42 70 105
2-й уровень иерархии. Кол-во элементов=6
6 10 14 15 21 35
1-й уровень иерархии. Кол-во элементов=4
2 3 5 7
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=15, из них базовых: 4
Локальный коэффициент эмерджентности Хартли=1.9534453
======================================================
2-Я СИСТЕМА === Sys_2.dbf ============================
4-й уровень иерархии. Кол-во элементов=1
46189
3-й уровень иерархии. Кол-во элементов=4
2431 2717 3553 4199
2-й уровень иерархии. Кол-во элементов=6
143 187 209 221 247 323
1-й уровень иерархии. Кол-во элементов=4
11 13 17 19
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=15, из них базовых: 4
Локальный коэффициент эмерджентности Хартли=1.9534453
======================================================
ОБЪЕДИНЕННАЯ СИСТЕМА === Sys_U.dbf ===================
4-й уровень иерархии. Кол-во элементов=70
210 330 390 462 510 546 570 714 770 798 858 910 1122
1155 1190 1254 1326 1330 1365 1430 1482 1785 1870 1938 1995 2002 2090 2145 2210
2470 2618 2805 2926 3003 3094 3135 3230 3315 3458 3705 3927 4389 4522 4641 4845
4862 5005 5187 5434 6545 6783 7106 7293 7315 7735 8151 8398 8645 10659 11305
12155 12597 13585 17017 17765 19019 20995 24871 29393 46189
3-й уровень иерархии. Кол-во элементов=56
30 42 66 70 78 102 105 110 114 130 154 165 170 182 190
195 231 238 255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627
646 663 665 715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261
2431 2717 3553 4199
2-й уровень иерархии. Кол-во элементов=28
6 10 14 15 21 22 26 33 34 35 38 39 51 55 57 65 77 85 91
95 119 133 143 187 209 221 247 323
1-й уровень иерархии. Кол-во элементов=8
2 3 5 7 11 13 17 19
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=162, из них базовых: 8
Локальный коэффициент эмерджентности Хартли=2.4466167
======================================================
СИСТЕМНЫЙ ЭФФЕКТ === Sys_s.dbf =======================
4-й уровень иерархии. Кол-во элементов=68
330 390 462 510 546 570 714 770 798 858 910 1122 1155
1190 1254 1326 1330 1365 1430 1482 1785 1870 1938 1995 2002 2090 2145 2210 2470
2618 2805 2926 3003 3094 3135 3230 3315 3458 3705 3927 4389 4522 4641 4845 4862
5005 5187 5434 6545 6783 7106 7293 7315 7735 8151 8398 8645 10659 11305 12155
12597 13585 17017 17765 19019 20995 24871 29393
3-й уровень иерархии. Кол-во элементов=48
66 78 102 110 114 130 154 165 170 182 190 195 231 238
255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627 646 663 665
715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261
2-й уровень иерархии. Кол-во элементов=16
22 26 33 34 38 39 51 55 57 65 77 85 91 95 119 133
1-й уровень иерархии. Кол-во элементов=0
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=132, из них базовых: 0
======================================================
Обобщенный коэффициент эмерджентности Хартли=1.4958251
A=15. B=15. AUB=162. AUB-A-B=132
======================================================
Локальный коэффициент эмерджентности Хартли
отражает
степень отличия системы от множества базовых элементов
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Обобщенный коэффициент эмерджентности Хартли отражает
величину системного эффекта, возникающего при объеди-
нении нескольких систем в одну
======================================================
УРОВЕНЬ СЛОЖНОСТИ=5
1-Я СИСТЕМА === Sys_1.dbf ============================
5-й уровень иерархии. Кол-во элементов=0
4-й уровень иерархии. Кол-во элементов=1
210
3-й уровень иерархии. Кол-во элементов=4
30 42 70 105
2-й уровень иерархии. Кол-во элементов=6
6 10 14 15 21 35
1-й уровень иерархии. Кол-во элементов=4
2 3 5 7
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=15, из них базовых: 4
Локальный коэффициент эмерджентности Хартли=1.9534453
======================================================
2-Я СИСТЕМА === Sys_2.dbf ============================
5-й уровень иерархии. Кол-во элементов=0
4-й уровень иерархии. Кол-во элементов=1
46189
3-й уровень иерархии. Кол-во элементов=4
2431 2717 3553 4199
2-й уровень иерархии. Кол-во элементов=6
143 187 209 221 247 323
1-й уровень иерархии. Кол-во элементов=4
11 13 17 19
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=15, из них базовых: 4
Локальный коэффициент эмерджентности Хартли=1.9534453
======================================================
ОБЪЕДИНЕННАЯ СИСТЕМА === Sys_U.dbf ===================
5-й уровень иерархии. Кол-во элементов=56
2310 2730 3570 3990 4290 5610 6006 6270 6630 7410 7854
8778 9282 9690 10010 10374 13090 13566 14586 14630 15015 15470 16302 17290
19635 21318 21945 22610 23205 24310 25194 25935 27170 33915 34034 35530 36465
38038 40755 41990 49742 51051 53295 57057 58786 62985 74613 85085 88179 92378
95095 124355 138567 146965 230945 323323
4-й уровень иерархии. Кол-во элементов=70
210 330 390 462 510 546 570 714 770 798 858 910 1122
1155 1190 1254 1326 1330 1365 1430 1482 1785 1870 1938 1995 2002 2090 2145 2210
2470 2618 2805 2926 3003 3094 3135 3230 3315 3458 3705 3927 4389 4522 4641 4845
4862 5005 5187 5434 6545 6783 7106 7293 7315 7735 8151 8398 8645 10659 11305
12155 12597 13585 17017 17765 19019 20995 24871 29393 46189
3-й уровень иерархии. Кол-во элементов=56
30 42 66 70 78 102 105 110 114 130 154 165 170 182 190
195 231 238 255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627
646 663 665 715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261
2431 2717 3553 4199
2-й уровень иерархии. Кол-во элементов=28
6 10 14 15 21 22 26 33 34 35 38 39 51 55 57 65 77 85 91
95 119 133 143 187 209 221 247 323
1-й уровень иерархии. Кол-во элементов=8
2 3 5 7 11 13 17 19
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=218, из них базовых: 8
Локальный коэффициент эмерджентности Хартли=2.5893948
======================================================
СИСТЕМНЫЙ ЭФФЕКТ === Sys_s.dbf =======================
5-й уровень иерархии. Кол-во элементов=56
2310 2730 3570 3990 4290 5610 6006 6270 6630 7410 7854
8778 9282 9690 10010 10374 13090 13566 14586 14630 15015 15470 16302 17290
19635 21318 21945 22610 23205 24310 25194 25935 27170 33915 34034 35530 36465
38038 40755 41990 49742 51051 53295 57057 58786 62985 74613 85085 88179 92378
95095 124355 138567 146965 230945 323323
4-й уровень иерархии. Кол-во элементов=68
330 390 462 510 546 570 714 770 798 858 910 1122 1155
1190 1254 1326 1330 1365 1430 1482 1785 1870 1938 1995 2002 2090 2145 2210 2470
2618 2805 2926 3003 3094 3135 3230 3315 3458 3705 3927 4389 4522 4641 4845 4862
5005 5187 5434 6545 6783 7106 7293 7315 7735 8151 8398 8645 10659 11305 12155
12597 13585 17017 17765 19019 20995 24871 29393
3-й уровень иерархии. Кол-во элементов=48
66 78 102 110 114 130 154 165 170 182 190 195 231 238
255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627 646 663 665
715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261
2-й уровень иерархии. Кол-во элементов=16
22 26 33 34 38 39 51 55 57 65 77 85 91 95 119 133
1-й уровень иерархии. Кол-во элементов=0
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=188, из них базовых: 0
======================================================
Обобщенный коэффициент эмерджентности Хартли=1.5831175
A=15. B=15. AUB=218. AUB-A-B=188
======================================================
Локальный коэффициент эмерджентности Хартли
отражает
степень отличия системы от множества базовых элементов
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Обобщенный коэффициент эмерджентности Хартли отражает
величину системного эффекта, возникающего при объеди-
нении нескольких систем в одну
======================================================
УРОВЕНЬ СЛОЖНОСТИ=6
1-Я СИСТЕМА === Sys_1.dbf ============================
6-й уровень иерархии. Кол-во элементов=0
5-й уровень иерархии. Кол-во элементов=0
4-й уровень иерархии. Кол-во элементов=1
210
3-й уровень иерархии. Кол-во элементов=4
30 42 70 105
2-й уровень иерархии. Кол-во элементов=6
6 10 14 15 21 35
1-й уровень иерархии. Кол-во элементов=4
2 3 5 7
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=15, из них базовых: 4
Локальный коэффициент эмерджентности Хартли=1.9534453
======================================================
2-Я СИСТЕМА === Sys_2.dbf ============================
6-й уровень иерархии. Кол-во элементов=0
5-й уровень иерархии. Кол-во элементов=0
4-й уровень иерархии. Кол-во элементов=1
46189
3-й уровень иерархии. Кол-во элементов=4
2431 2717 3553 4199
2-й уровень иерархии. Кол-во элементов=6
143 187 209 221 247 323
1-й уровень иерархии. Кол-во элементов=4
11 13 17 19
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=15, из них базовых: 4
Локальный коэффициент эмерджентности Хартли=1.9534453
======================================================
ОБЪЕДИНЕННАЯ СИСТЕМА === Sys_U.dbf ===================
6-й уровень иерархии. Кол-во элементов=28
30030 39270 43890 46410 51870 67830 72930 81510 102102
106590 114114 125970 149226 170170 176358 190190 248710 255255 277134 285285
293930 373065 440895 461890 646646 692835 969969 1616615
5-й уровень иерархии. Кол-во элементов=56
2310 2730 3570 3990 4290 5610 6006 6270 6630 7410 7854
8778 9282 9690 10010 10374 13090 13566 14586 14630 15015 15470 16302 17290
19635 21318 21945 22610 23205 24310 25194 25935 27170 33915 34034 35530 36465
38038 40755 41990 49742 51051 53295 57057 58786 62985 74613 85085 88179 92378
95095 124355 138567 146965 230945 323323
4-й уровень иерархии. Кол-во элементов=70
210 330 390 462 510 546 570 714 770 798 858 910 1122
1155 1190 1254 1326 1330 1365 1430 1482 1785 1870 1938 1995 2002 2090 2145 2210
2470 2618 2805 2926 3003 3094 3135 3230 3315 3458 3705 3927 4389 4522 4641 4845
4862 5005 5187 5434 6545 6783 7106 7293 7315 7735 8151 8398 8645 10659 11305
12155 12597 13585 17017 17765 19019 20995 24871 29393 46189
3-й уровень иерархии. Кол-во элементов=56
30 42 66 70 78 102 105 110 114 130 154 165 170 182 190
195 231 238 255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627
646 663 665 715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261
2431 2717 3553 4199
2-й уровень иерархии. Кол-во элементов=28
6 10 14 15 21 22 26 33 34 35 38 39 51 55 57 65 77 85 91
95 119 133 143 187 209 221 247 323
1-й уровень иерархии. Кол-во элементов=8
2 3 5 7 11 13 17 19
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=246, из них базовых: 8
Локальный коэффициент эмерджентности Хартли=2.6475048
======================================================
СИСТЕМНЫЙ ЭФФЕКТ === Sys_s.dbf =======================
6-й уровень иерархии. Кол-во элементов=28
30030 39270 43890 46410 51870 67830 72930 81510 102102
106590 114114 125970 149226 170170 176358 190190 248710 255255 277134 285285
293930 373065 440895 461890 646646 692835 969969 1616615
5-й уровень иерархии. Кол-во элементов=56
2310 2730 3570 3990 4290 5610 6006 6270 6630 7410 7854
8778 9282 9690 10010 10374 13090 13566 14586 14630 15015 15470 16302 17290
19635 21318 21945 22610 23205 24310 25194 25935 27170 33915 34034 35530 36465
38038 40755 41990 49742 51051 53295 57057 58786 62985 74613 85085 88179 92378
95095 124355 138567 146965 230945 323323
4-й уровень иерархии. Кол-во элементов=68
330 390 462 510 546 570 714 770 798 858 910 1122 1155
1190 1254 1326 1330 1365 1430 1482 1785 1870 1938 1995 2002 2090 2145 2210 2470
2618 2805 2926 3003 3094 3135 3230 3315 3458 3705 3927 4389 4522 4641 4845 4862
5005 5187 5434 6545 6783 7106 7293 7315 7735 8151 8398 8645 10659 11305 12155
12597 13585 17017 17765 19019 20995 24871 29393
3-й уровень иерархии. Кол-во элементов=48
66 78 102 110 114 130 154 165 170 182 190 195 231 238
255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627 646 663 665
715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261
2-й уровень иерархии. Кол-во элементов=16
22 26 33 34 38 39 51 55 57 65 77 85 91 95 119 133
1-й уровень иерархии. Кол-во элементов=0
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=216, из них базовых: 0
======================================================
Обобщенный коэффициент эмерджентности Хартли=1.6186451
A=15. B=15. AUB=246. AUB-A-B=216
======================================================
Локальный коэффициент эмерджентности Хартли
отражает
степень отличия системы от множества базовых элементов
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Обобщенный коэффициент эмерджентности Хартли отражает
величину системного эффекта, возникающего при объеди-
нении нескольких систем в одну
======================================================
УРОВЕНЬ СЛОЖНОСТИ=7
1-Я СИСТЕМА === Sys_1.dbf ============================
7-й уровень иерархии. Кол-во элементов=0
6-й уровень иерархии. Кол-во элементов=0
5-й уровень иерархии. Кол-во элементов=0
4-й уровень иерархии. Кол-во элементов=1
210
3-й уровень иерархии. Кол-во элементов=4
30 42 70 105
2-й уровень иерархии. Кол-во элементов=6
6 10 14 15 21 35
1-й уровень иерархии. Кол-во элементов=4
2 3 5 7
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=15, из них базовых: 4
Локальный коэффициент эмерджентности Хартли=1.9534453
======================================================
2-Я СИСТЕМА === Sys_2.dbf ============================
7-й уровень иерархии. Кол-во элементов=0
6-й уровень иерархии. Кол-во элементов=0
5-й уровень иерархии. Кол-во элементов=0
4-й уровень иерархии. Кол-во элементов=1
46189
3-й уровень иерархии. Кол-во элементов=4
2431 2717 3553 4199
2-й уровень иерархии. Кол-во элементов=6
143 187 209 221 247 323
1-й уровень иерархии. Кол-во элементов=4
11 13 17 19
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=15, из них базовых: 4
Локальный коэффициент эмерджентности Хартли=1.9534453
======================================================
ОБЪЕДИНЕННАЯ СИСТЕМА === Sys_U.dbf ===================
7-й уровень иерархии. Кол-во элементов=8
510510 570570 746130 881790 1385670 1939938 3233230
4849845
6-й уровень иерархии. Кол-во элементов=28
30030 39270 43890 46410 51870 67830 72930 81510 102102
106590 114114 125970 149226 170170 176358 190190 248710 255255 277134 285285
293930 373065 440895 461890 646646 692835 969969 1616615
5-й уровень иерархии. Кол-во элементов=56
2310 2730 3570 3990 4290 5610 6006 6270 6630 7410 7854
8778 9282 9690 10010 10374 13090 13566 14586 14630 15015 15470 16302 17290
19635 21318 21945 22610 23205 24310 25194 25935 27170 33915 34034 35530 36465
38038 40755 41990 49742 51051 53295 57057 58786 62985 74613 85085 88179 92378
95095 124355 138567 146965 230945 323323
4-й уровень иерархии. Кол-во элементов=70
210 330 390 462 510 546 570 714 770 798 858 910 1122
1155 1190 1254 1326 1330 1365 1430 1482 1785 1870 1938 1995 2002 2090 2145 2210
2470 2618 2805 2926 3003 3094 3135 3230 3315 3458 3705 3927 4389 4522 4641 4845
4862 5005 5187 5434 6545 6783 7106 7293 7315 7735 8151 8398 8645 10659 11305
12155 12597 13585 17017 17765 19019 20995 24871 29393 46189
3-й уровень иерархии. Кол-во элементов=56
30 42 66 70 78 102 105 110 114 130 154 165 170 182 190
195 231 238 255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627
646 663 665 715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261
2431 2717 3553 4199
2-й уровень иерархии. Кол-во элементов=28
6 10 14 15 21 22 26 33 34 35 38 39 51 55 57 65 77 85 91
95 119 133 143 187 209 221 247 323
1-й уровень иерархии. Кол-во элементов=8
2 3 5 7 11 13 17 19
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=254, из них базовых: 8
Локальный коэффициент эмерджентности Хартли=2.6628949
======================================================
СИСТЕМНЫЙ ЭФФЕКТ === Sys_s.dbf =======================
7-й уровень иерархии. Кол-во элементов=8
510510 570570 746130 881790 1385670 1939938 3233230
4849845
6-й уровень иерархии. Кол-во элементов=28
30030 39270 43890 46410 51870 67830 72930 81510 102102
106590 114114 125970 149226 170170 176358 190190 248710 255255 277134 285285
293930 373065 440895 461890 646646 692835 969969 1616615
5-й уровень иерархии. Кол-во элементов=56
2310 2730 3570 3990 4290 5610 6006 6270 6630 7410 7854
8778 9282 9690 10010 10374 13090 13566 14586 14630 15015 15470 16302 17290
19635 21318 21945 22610 23205 24310 25194 25935 27170 33915 34034 35530 36465
38038 40755 41990 49742 51051 53295 57057 58786 62985 74613 85085 88179 92378
95095 124355 138567 146965 230945 323323
4-й уровень иерархии. Кол-во элементов=68
330 390 462 510 546 570 714 770 798 858 910 1122 1155
1190 1254 1326 1330 1365 1430 1482 1785 1870 1938 1995 2002 2090 2145 2210 2470
2618 2805 2926 3003 3094 3135 3230 3315 3458 3705 3927 4389 4522 4641 4845 4862
5005 5187 5434 6545 6783 7106 7293 7315 7735 8151 8398 8645 10659 11305 12155
12597 13585 17017 17765 19019 20995 24871 29393
3-й уровень иерархии. Кол-во элементов=48
66 78 102 110 114 130 154 165 170 182 190 195 231 238
255 266 273 285 286 357 374 385 399 418 429 442 455 494 561 595 627 646 663 665
715 741 935 969 1001 1045 1105 1235 1309 1463 1547 1615 1729 2261
2-й уровень иерархии. Кол-во элементов=16
22 26 33 34 38 39 51 55 57 65 77 85 91 95 119 133
1-й уровень иерархии. Кол-во элементов=0
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Всего элементов=224, из них базовых: 0
======================================================
Обобщенный коэффициент эмерджентности Хартли=1.6280544
A=15. B=15. AUB=254. AUB-A-B=224
======================================================
Локальный коэффициент эмерджентности Хартли
отражает
степень отличия системы от множества базовых элементов
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Обобщенный коэффициент эмерджентности Хартли отражает
величину системного эффекта, возникающего при объеди-
нении нескольких систем в одну
======================================================
Из приведенного примера видно, что при уровне
сложности равном 1, объединение систем ничем не отличается от объединения
множеств их базовых элементов, чем и обеспечивается выполнение принципа
соответствия. При увеличении уровня сложности наблюдается все больший и больший
системный эффект, количественно измеряемый обобщенным коэффициентом эмерджентности
Хартли.
При этих же параметрах и уровне сложности 2
сформирован пример, приведенный на рисунке 3 и в таблицах 1–4. Данные
таблицы сформированы на основе файлов (которые считываются в MS Excel):
Sys#_1.dbf, Sys#_2.dbf, Sys#_U.dbf и Sys#_eff.dbf, где: # – уровень сложности.
В результате запуска этой программы с
последовательно увеличивающимся параметром «уровень сложности» при одних и тех
же диапазонах базовых элементов, указанных выше, получим результаты, сведенные
в таблице 5 и на рисунке 6:
Таблица 5 – ЗАВИСИМОСТЬ
ЛОКАЛЬНЫХ И ОБОБЩЕННОГО КОЭФФИЦИЕНТОВ ЭМЕРДЖЕНТНОСТИ ХАРТЛИ
ОТ СЛОЖНОСТИ ОБЪЕДИНЯЕМЫХ СИСТЕМ
|
Уровень сложности |
Локальный коэффициент эмерджентности Хартли |
Обобщенный коэффициент эмерджентности Хартли |
||
|
1-й системы |
2-й системы |
Объединенной системы |
||
|
1,0000000 |
1,0000000 |
1,0000000 |
1,0000000 |
|
|
2 |
1,6609640 |
1,6609640 |
1,7233083 |
1,1962080 |
|
3 |
1,9036775 |
1,9036775 |
2,1745207 |
1,3569961 |
|
4 |
1,9534453 |
1,9534453 |
2,4466167 |
1,4958251 |
|
5 |
1,9534453 |
1,9534453 |
2,5893948 |
1,5831175 |
|
6 |
1,9534453 |
1,9534453 |
2,6475048 |
1,6186451 |
|
7 |
1,9534453 |
1,9534453 |
2,6628949 |
1,6280544 |
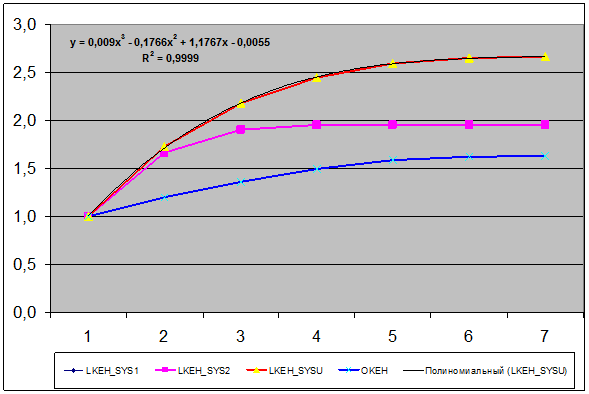
Рисунок 6. Зависимость
локальных и обобщенного коэффициентов
эмерджентности Хартли от сложности объединяемых систем
На рисунке 6 использованы обозначения:
– LKEH_SYS1 – локальный коэффициент
эмерджентности Хартли для систем Sys_1 и Sys_2;
– LKEH_SYSU – локальный коэффициент
эмерджентности Хартли для объединенной системы (объединения систем Sys_1 и
Sys_2), хорошо аппроксимируется кубическим степенным полиномом:
y = 0,009x3 - 0,1766x2 + 1,1767x - 0,0055
R2 = 0,9999;
– OKEH – обобщенный коэффициент эмерджентности
Хартли.
Из таблицы 5 и рисунка 6 видно, что при
повышении уровня сложности от 4 до 7 уровень системности 1-й и 2-й подсистем не
увеличивается. Это связано с тем, что из-за небольшого количества базовых
элементов в этих системах отсутствуют
5-й, 6-й и 7-й иерархические уровни, т.е. на них нет ни одного элемента. На
других зависимостях также виден «эффект насыщения», проявляющийся в том, что с
увеличением уровня сложности системный эффект увеличивается все медленнее и
медленнее и выходит на некоторую асимптоту, определяемую количеством базовых
элементов в исходных подсистемах.
Выводы. Итак, в разделе рассмотрена реализация
операции объединения систем, являющаяся обобщением операции объединения
множеств в рамках системного обобщения теории множеств. Эта операция сходна с
операцией объединения булеанов классической теории множеств. Но в отличие от
классической теории множеств в ее системном обобщении предлагается конкретный алгоритм объединения систем и
обосновывается количественная мера системного (синергетического, эмерджентного)
эффекта, возникающего за счет объединения систем. Для этой меры предложено
название: «Обобщенный коэффициент эмерджентности
Хартли» из-за сходства его математической формы с предложенным в 2001 году
локальным коэффициентом эмерджентности Хартли, отражающим степень отличия
системы от множества его базовых элементов. Приводится ссылка на авторскую
программу, реализующую предложенный алгоритм и обеспечивающую численное
моделирование объединения систем при различных ограничениях на сложность систем
и при различной мощности порождающего множества, приводятся некоторые результаты
численного моделирования.
Перспективы. В перспективе планируется более тщательно
исследовать свойства объединения систем и разработать системные обобщения
других операций над множествами[77].
10.4.2. Обобщенный коэффициент эмерджентности Хартли как количественная мера
синергетического эффекта объединения булеанов в системном обобщении теории множеств
Данный раздел
основан на работе [241]. В работе [240] предложено
математическое выражение для обобщенного коэффициента эмерджентности Хартли[78],
количественно отражающего величину системного эффекта, возникающего при объединении
систем. Для двух систем, образованных на базовых элементах множеств A и B
(240):
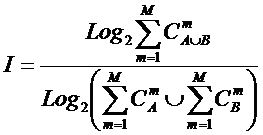(1)
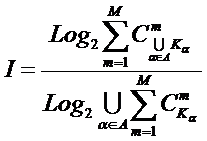Для объединения M систем семейства (2):
(2)
При получении этих выражений в работе [240] в
соответствии с системной теорией информации (СТИ) [97] предполагается, что
количество подсистем NA в
системе, образованной на некотором множестве базовых элементов A, равно сумме числа сочетаний этих
элементов от 1 до M:
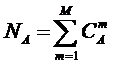(3)
Обобщим выражения (1) и (2) без использования
этого предположения. Пусть 
– булеан (система),
образованная на множестве базовых элементов A,
а 
– система, образованная
на множестве базовых элементов B. В
объединение этих систем 
входят все подсистемы
обоих этих подсистем, тогда как в систему 
, образованную на объединении базовых множеств 
, кроме того,
входят подсистемы, включающие базовые элементы как 1-го, так и 2-го базовых
множеств одновременно.
Поэтому система, образованная на объединении
базовых множеств, имеет большую мощность, чем мощность объединения систем,
образованных на исходных базовых множествах:
(4)
Вышесказанное практически полностью совпадает с
классическим определением системного (синергетического, эмерджентного) эффекта:
«Свойства системы превосходят сумму свойств ее частей и не сводятся к ним». При
этом степень отличия свойств системы от свойств составляющих ее элементов
(базового множества) обоснованно считать ее уровнем системности [240, 97, 186,
189, 191, 170, 196, 281].
Поэтому предлагается
считать, что разность в мощности этих систем (системы, образованной на
объединении базовых множеств, и системы, являющейся объединением систем, образованных
на исходных базовых множествах) представляет собой системный эффект, возникший
за счет их объединения:
(5)
Используем классическую формулу Р.Хартли для
количества информации, получаемого при идентификации элемента множества, состоящего
из N элементов:
(6)
для
расчета количества информации,
получаемого при идентификации одной из подсистем системы, образованной на объединении
базовых множеств, и системы, являющейся объединением систем, образованных на
исходных базовых множествах:
(7)
Откуда непосредственно[79]
получаем выражение для обобщенного коэффициента эмерджентности Хартли,
независящее от предположения о способе образования подсистем на основе элементов
базовых множеств:
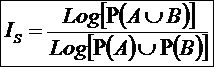(8)
Заметим, что основание логарифма в выражении (7)
не является существенным, т.к. берется их отношение.
Обобщим выражение (7) на произвольное количество
систем. Пусть дано не 2 системы, а
семейство систем: . Тогда для случая многих систем выражения (5) и (8)
обобщаются следующим образом:
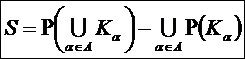(9)
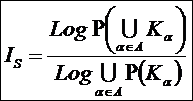(10)
Кроме того, в каждой из систем могут возникать
составные элементы из ее собственных
базовых элементов. Это приводит к системному эффекту, в результате которого
система отличается от множества, т.е. содержит больше элементов, чем в порождающем
множестве. Этот вид системного эффекта аналитически выражается локальным
коэффициентом эмерджентности Хартли (11), который был получен автором в 2001 году [97] и назван так в
честь этого ученого, внесшего большой вклад с разработку научной теории
информации[80]:
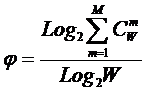(11)
где:
W –
количество базовых элементов в системе;
m –
сложность составного элемента системы, т.е. подсистемы (количество базовых
элементов в составном элементе);
M – максимальная
сложность подсистем (максимальное количество базовых элементов в составном
элементе).
Обобщение
локального коэффициента эмерджентности Хартли (11), независящее от способа
образования подсистем, имеет вид 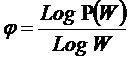(12):
(12)
Например, при объединении 2-х систем, содержащих на 1-м
уровне иерархии простые числа, а на
2-м уровне составные числа,
являющиеся произведениями различных пар простых сомножителей, образуется
объединенная система, 1-й уровень которой является объединением 1-х уровней
исходных систем, а 2-й образуется по тому же алгоритму, что и в них (рисунок
1):
Рисунок 1. Объединение 2-х систем из простых чисел на
базовом уровне и сложных чисел, образованных из пар простых, на 2-м уровне[81]
В таблицах 1–4 приведены данные о том, какие
составные числа произведениями каких простых являются в рассматриваемом
примере:
Таблица 1 – СОСТАВ ЭЛЕМЕНТОВ 1-Й СИСТЕМЫ
|
Элемент |
Уровень иерархии |
Простые сомножители |
|
|
1-й |
2-й |
||
|
2 |
1 |
2 |
|
|
3 |
1 |
3 |
|
|
5 |
1 |
5 |
|
|
7 |
1 |
7 |
|
|
6 |
2 |
2 |
3 |
|
10 |
2 |
2 |
5 |
|
14 |
2 |
2 |
7 |
|
15 |
2 |
3 |
5 |
|
21 |
2 |
3 |
7 |
|
35 |
2 |
5 |
7 |
Таблица 2 – СОСТАВ ЭЛЕМЕНТОВ 2-Й СИСТЕМЫ
|
Элемент |
Уровень иерархии |
Простые сомножители |
|
|
1-й |
2-й |
||
|
11 |
1 |
11 |
|
|
13 |
1 |
13 |
|
|
17 |
1 |
17 |
|
|
19 |
1 |
19 |
|
|
143 |
2 |
11 |
13 |
|
187 |
2 |
11 |
17 |
|
209 |
2 |
11 |
19 |
|
221 |
2 |
13 |
17 |
|
247 |
2 |
13 |
19 |
|
323 |
2 |
17 |
19 |
Таблица 3 – СОСТАВ ЭЛЕМЕНТОВ ОБЪЕДИНЕННОЙ СИСТЕМЫ
|
Элемент |
Уровень иерархии |
Простые сомножители |
|
|
1-й |
2-й |
||
|
2 |
1 |
2 |
|
|
3 |
1 |
3 |
|
|
5 |
1 |
5 |
|
|
7 |
1 |
7 |
|
|
11 |
1 |
11 |
|
|
13 |
1 |
13 |
|
|
17 |
1 |
17 |
|
|
19 |
1 |
19 |
|
|
6 |
2 |
2 |
3 |
|
10 |
2 |
2 |
5 |
|
14 |
2 |
2 |
7 |
|
22 |
2 |
2 |
11 |
|
26 |
2 |
2 |
13 |
|
34 |
2 |
2 |
17 |
|
38 |
2 |
2 |
19 |
|
15 |
2 |
3 |
5 |
|
21 |
2 |
3 |
7 |
|
33 |
2 |
3 |
11 |
|
39 |
2 |
3 |
13 |
|
51 |
2 |
3 |
17 |
|
57 |
2 |
3 |
19 |
|
35 |
2 |
5 |
7 |
|
55 |
2 |
5 |
11 |
|
65 |
2 |
5 |
13 |
|
85 |
2 |
5 |
17 |
|
95 |
2 |
5 |
19 |
|
77 |
2 |
7 |
11 |
|
91 |
2 |
7 |
13 |
|
119 |
2 |
7 |
17 |
|
133 |
2 |
7 |
19 |
|
143 |
2 |
11 |
13 |
|
187 |
2 |
11 |
17 |
|
209 |
2 |
11 |
19 |
|
221 |
2 |
13 |
17 |
|
247 |
2 |
13 |
19 |
|
323 |
2 |
17 |
19 |
Таблица 4 – СОСТАВ ЭЛЕМЕНТОВ ПОДСИСТЕМЫ ОБЪЕДИНЕННОЙ
СИСТЕМЫ, СОДЕРЖАЩЕЙ ЭЛЕМЕНТЫ, ОБРАЗОВАННЫЕ ЗА СЧЕТ СИСТЕМНОГО ЭФФЕКТА
|
Элемент |
Уровень иерархии |
Простые сомножители |
|
|
1-й |
2-й |
||
|
22 |
2 |
2 |
11 |
|
26 |
2 |
2 |
13 |
|
34 |
2 |
2 |
17 |
|
38 |
2 |
2 |
19 |
|
33 |
2 |
3 |
11 |
|
39 |
2 |
3 |
13 |
|
51 |
2 |
3 |
17 |
|
57 |
2 |
3 |
19 |
|
55 |
2 |
5 |
11 |
|
65 |
2 |
5 |
13 |
|
85 |
2 |
5 |
17 |
|
95 |
2 |
5 |
19 |
|
77 |
2 |
7 |
11 |
|
91 |
2 |
7 |
13 |
|
119 |
2 |
7 |
17 |
|
133 |
2 |
7 |
19 |
Числа, показанные на рисунке 3 черным цветом на
2-м уровне объединенной системы, есть на 2-м уровне либо 1-й системы, либо 2-й.
Если бы системы объединялись как множества, то никаких других элементов на 2-м
уровне объединенной системы и не было бы. Но при объединении систем в
объединенной системе могут возникать элементы, образованные из сочетаний
базовых элементов нескольких исходных систем одновременно, которых не было в
исходных системах и которые могли образоваться только в объединенной системе. В
нашем примере на рисунке 3 это числа, показанные более крупным шрифтом и красным
цветом на 2-м уровне объединенной системы, образованные из различных пар
простых чисел, одно из которых принадлежит 1-й системе, а 2-е – второй (см.
таблицы 1–4).
Все полученные выражения стандартно обобщаются
также на непрерывный случай путем замены факториалов при расчете числа
сочетаний на гамма-функции [97].
В результате запуска этой программы с
последовательно увеличивающимся параметром «уровень сложности» при одних и тех
же диапазонах базовых элементов, указанных выше, получим результаты, сведенные
в таблице 5 и на рисунке 2:
Таблица 5 – ЗАВИСИМОСТЬ ЛОКАЛЬНЫХ И ОБОБЩЕННОГО
КОЭФФИЦИЕНТОВ ЭМЕРДЖЕНТНОСТИ ХАРТЛИ
ОТ СЛОЖНОСТИ ОБЪЕДИНЯЕМЫХ СИСТЕМ
|
Уровень сложности |
Локальный коэффициент эмерджентности Хартли |
Обобщенный коэффициент эмерджентности Хартли |
||
|
1-й системы |
2-й системы |
Объединенной системы |
||
|
1 |
1,0000000 |
1,0000000 |
1,0000000 |
1,0000000 |
|
2 |
1,6609640 |
1,6609640 |
1,7233083 |
1,1962080 |
|
3 |
1,9036775 |
1,9036775 |
2,1745207 |
1,3569961 |
|
4 |
1,9534453 |
1,9534453 |
2,4466167 |
1,4958251 |
|
5 |
1,9534453 |
1,9534453 |
2,5893948 |
1,5831175 |
|
6 |
1,9534453 |
1,9534453 |
2,6475048 |
1,6186451 |
|
7 |
1,9534453 |
1,9534453 |
2,6628949 |
1,6280544 |
|
8 |
1,9534453 |
1,9534453 |
2,6647845 |
1,6292096 |
|
9 |
1,9534453 |
1,9534453 |
2,6647845 |
1,6292096 |
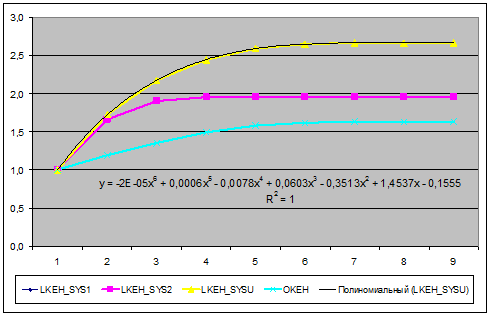
Рисунок 2. Зависимость локальных и обобщенного
коэффициентов
эмерджентности Хартли от сложности объединяемых систем
На рисунке 2 использованы обозначения:
– LKEH_SYS1 – локальный коэффициент
эмерджентности Хартли для систем Sys_1 и Sys_2;
– LKEH_SYSU – локальный коэффициент
эмерджентности Хартли для объединенной системы (объединения систем Sys_1 и
Sys_2), хорошо аппроксимируется кубическим степенным полиномом:
y = -2E-05x6
+ 0,0006x5 - 0,0078x4 + 0,0603x3 - 0,3513x2
+ 1,4537x - 0,1555
R2 = 1
– OKEH – обобщенный коэффициент эмерджентности
Хартли.
Из таблицы 5 и рисунка 2 видно, что при
повышении уровня сложности от 4 до 9 уровень системности 1-й и 2-й подсистем не
увеличивается. Это связано с тем, что из-за небольшого количества базовых
элементов этих системах отсутствуют
иерархические уровни с 5-го по 9-й, т.е. на них нет ни одного элемента. На
других зависимостях также виден «эффект насыщения», проявляющийся в том, что с
увеличением уровня сложности системный эффект увеличивается все медленнее и
медленнее и выходит на некоторую асимптоту, определяемую количеством базовых
элементов в исходных подсистемах.
Выводы. В работе предлагается
общее математическое выражение для количественной оценки системного (синергетического)
эффекта, возникающего при объединении булеанов (систем), являющихся обобщением
множества в системном обобщении теории множеств и независящее от способа
(алгоритма) образования подсистем в системе. Для этой количественной меры
предложено название: «Обобщенный коэффициент эмерджентности Р.Хартли» из-за
сходства его математической формы с локальным коэффициентом эмерджентности
Хартли, отражающим степень отличия системы от множества его базовых элементов.
Для локального коэффициента эмерджентности Хартли также предложено обобщение,
независящее от способа (алгоритма) образования подсистем в системе. Приводятся
численные оценки системного эффекта при объединении двух систем с применением
авторской программы, на которую дается ссылка.
Перспективы.
В
перспективе планируется более тщательно исследовать свойства объединения
систем, конкретизировать полученные математические выражения для различных
способов образования подсистем на основе элементов базовых множеств [257],
разработать системные обобщения других операций над множествами[82].
. С использованием этого выражения,
приводимые в работе формулы, могут быть обобщены на случай, когда повторения
допустимы (формально чаще всего для этого достаточно поставить черточку на
символом числа сочетаний). В словах играет роль порядок букв, но нет принципиальных проблем для обобщения
полученных выражений и на этот случай.
