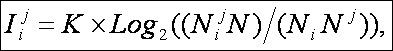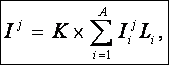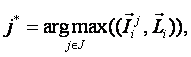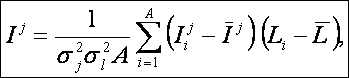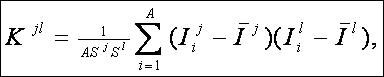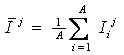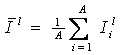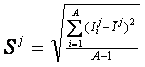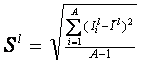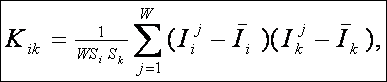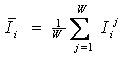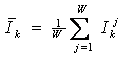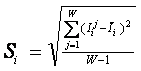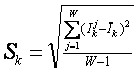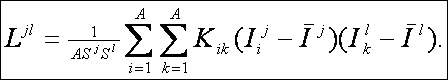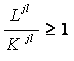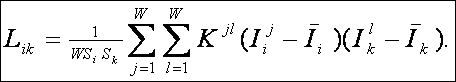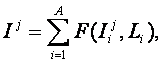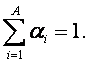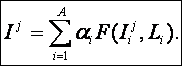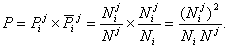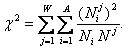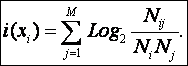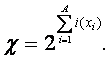ГЛАВА 5. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ИНТЕГРАЛЬНОГО
МЕТОДА РАСПОЗНАВАНИЯ ОБРАЗОВ
И ПРИНЯТИЯ РЕШЕНИЙ, ОСНОВАННОГО НА
МНОГОКРИТЕРИАЛЬНОМ ПОДХОДЕ
И ТЕОРИИ ИНФОРМАЦИИ
5.1. ФОРМАЛЬНАЯ ПОСТАНОВКА ОСНОВНОЙ ЗАДАЧИ
АСУ И ЕЕ ДЕКОМПОЗИЦИЯ
5.1.1. ОБЩИЕ ПОНЯТИЯ
Рассмотрим некоторые
основные понятия, необходимые для дальнейшего изложения. При этом будут
использованы как литературные данные, так и результаты, полученные в предыдущих
главах данной работы.
Принятие решения в АСУ – это выбор некоторого наиболее предпочтительного управляющего воздействия из исходного множества всех возможных управляющих воздействий, обеспечивающего наиболее эффективное достижение целей управления. В результате выбора неопределенность исходного множества уменьшается на величину информации, которая порождается самим актом выбора [273].
Следовательно, теория информации может быть применена как для идентификации состояний объекта управления, так и для принятия решений об управляющих воздействиях в АСУ.
Модель АСУ включает в себя: модель объекта управления, модель управляющей подсистемы, а также модель внешней среды. Управляющая подсистема реализует следующие функции: идентификация состояния объекта управления, выработка управляющего воздействия, реализация управляющего воздействия.
С
позиций теории информации сложный объект управления (СОУ) может рассматриваться
как шумящий (определенным образом) информационный канал, на вход которого
подаются входные параметры 
, представляющие собой управляющие воздействия, а также
факторы предыстории и среды, а на выходе фиксируются выходные параметры 
, связанные как с входными параметрами, так и с целевыми и
иными состояниями объекта управления.
5.1.2. ФОРМАЛЬНАЯ ПОСТАНОВКА ОСНОВНОЙ ЗАДАЧИ АСУ
Одной
из основных задач АСУ является задача принятия решения о наиболее эффективном
управляющем воздействии. В терминах теории информации эта задача формулируется
следующим образом: зная целевое состояние
объекта управления, на основе его информационной модели определить такие
входные параметры , которые с учетом предыстории и актуального состояния
объекта управления, а также влияния среды с наибольшей эффективностью переведут
его в целевое состояние, характеризующееся выходными параметрами .
С решением этой задачи тесно связана задача декодирования теории информации: по полученному в условиях помех сообщению определить, какое сообщение было передано [351]. Для решения данной задачи используются коды, корректирующие ошибки, а в более общем случае, - различные методы распознавания образов.
Учитывая вышесказанное, предлагается рассматривать принятие решения об управляющем воздействии в АСУ как решение обратной задачи декодирования: что надо передать, чтобы получить заранее заданное сообщение. Данная задача решается на основе математической модели канала связи.
5.1.3. ДЕКОМПОЗИЦИЯ ОСНОВНОЙ ЗАДАЧИ
В РЯД ЧАСТНЫХ ПОДЗАДАЧ
Построение аналитической модели СОУ затруднено из-за отсутствия или недостатка априорной информации об объекте управления [273, 333], а также из-за ограниченности и сложности используемого математического аппарата. В связи с этим предлагается путь решения данной проблемы, состоящий в поэтапном решении следующих задач:
1–я задача: отказавшись от попыток построения конкретной содержательной аналитической модели СОУ, разработать абстрактную модель более общего класса (матричную информационную);
2–я задача: обучить абстрактную информационную модель путем учета информации о реальном поведении СОУ, поступающей в процессе экспериментальной эксплуатации АСУ; на этом этапе адаптируется и конкретизируется абстрактная модель СОУ, т.е. в ней все более точно отражаются взаимосвязи между входными параметрами и состояниями СОУ;
3–я задача: на основе конкретной содержательной информационной модели разработать алгоритмы решения следующих задач АСУ:
3.1. Расчет влияния факторов на переход СОУ в различные возможные состояния (обучение, адаптация).
3.2. Прогнозирование поведения СОУ при конкретном управляющем воздействии и выработка многофакторного управляющего воздействия (основная задача АСУ).
3.3. Выявление факторов, вносящих основной вклад в детерминацию состояния СОУ; контролируемое удаление второстепенных факторов с низкой дифференцирующей способностью, т.е. снижение размерности модели при заданных ограничениях.
3.4. Сравнение влияния факторов. Сравнение состояний СОУ.
Сформулируем предлагаемую абстрактную модель СОУ, опишем способ ее конкретизации и приведем алгоритмы решения задач адаптивных АСУ СОУ на основе данной модели.
5.2. РЕШЕНИЕ ЗАДАЧИ 1: "РАЗРАБОТКА АБСТРАКТНОЙ
МОДЕЛИ ОБЪЕКТА УПРАВЛЕНИЯ"
Модель должна обеспечивать отражение взаимосвязей между входными и выходными параметрами СОУ и окружающей среды (факторами), с одной стороны, и будущими состояниями СОУ, – с другой. Как было показано выше, построить содержательную аналитическую модель СОУ не представляется возможным из–за дефицита априорной информации. Остается вариант использования феноменологической аналитической модели, например регрессионного типа, однако и для ее построения необходима исходная информация, которая, как это следует непосредственно из определения СОУ, может быть только апостериорной. Общепринятой стандартной формой представления исходной информации для анализа является матричная.
Поэтому предлагается представить информационную модель СОУ адаптивной АСУ в форме двумерной матрицы, столбцы которой соответствуют возможным будущим, конечным состояниям СОУ (в том числе – целевым), а строки – входным параметрам, т.е. факторам (табл. 5.1).
Таблица 5. 1
МАТРИЧНАЯ ИНФОРМАЦИОННАЯ МОДЕЛЬ
СЛОЖНОГО ОБЪЕКТА УПРАВЛЕНИЯ АДАПТИВНОЙ АСУ
|
Факторы |
Состояния СОУ |
Дифференцирующая |
||
|
... |
J |
... |
||
|
... |
|
|
|
|
|
i |
|
|
|
|
|
... |
|
|
|
|
|
Детерминированность |
|
|
|
|
Элементами
матрицы являются частные критерии 
, отражающие влияние i–го фактора на перевод СОУ в j–е
состояние.
В связи с тем, что в дальнейшем изложении широко применяются понятия теории АСУ, теории информации (связи) и теории распознавания образов, приведем таблицу соответствия наиболее часто используемых нами терминов из этих научных направлений (табл. 5.2).
Таблица 5. 2
СООТВЕТСТВИЕ ТЕРМИНОВ РАЗЛИЧНЫХ НАУЧНЫХ НАПРАВЛЕНИЙ
|
Теория |
Теория |
Теория информации |
|
Фактор |
Признак |
Входной
сигнал |
|
Состояние
объекта |
Класс
распознавания |
Информационный |
|
Идентификация |
Распознавание |
Декодирование |
|
Выработка |
Решение
обратной |
Решение
обратной |
В предыдущем изложении это соответствие было раскрыто содержательно.
Выбор
конкретного вида частных критериев является одним из ключевых моментов в построении
информационной модели СОУ. В качестве предлагается
применить семантическую меру целесообразности информации, введенную в 1960 году
А.А.Харкевичем [373] на основе апостериорного
подхода. Сущность этого подхода состоит в том, что количество информации
оценивается по изменению степени целесообразности
поведения системы в результате сообщения ей данной информации [351]. Но именно
это и происходит в АСУ: управляющая подсистема оказывает на СОУ управляющее
воздействие с целью перевода его в целевое состояние. Управляющее воздействие в
АСУ является прежде всего информационным воздействием, т.е. некоторым сообщением.
Понятие "целесообразность поведения" тесно связано с понятием "целевое состояние". Целевым состоянием называется конечное состояние системы, в которое она должна перейти в результате оказания управляющего воздействия [222]. Поведение системы считается "целесообразным", если приближает ее к переходу в целевое состояние, и "нецелесообразным" – в противном случае. Таким образом, управляющее воздействие может изменять целесообразность поведения системы, если изменяет вероятность ее перехода в целевое состояние. Множество целевых состояний является подмножеством конечных состояний объекта управления.
В наших обозначениях мера Харкевича имеет вид:
|
|
(5. 1) |
Целесообразность
выбора именно данной меры обусловлена самим смыслом величин 
и 
, обозначающих соответственно вероятность перехода СОУ
в j–е конечное состояние под
воздействием i–го фактора и
вероятность случайного (спонтанного, самопроизвольного) перехода СОУ в то же состояние.
То
же самое количество информации согласно Харкевичу может быть выражено и в другой
(эквивалентной) форме:
|
|
(5. 2) |
где
и 
обозначают вероятность обнаружения i–го фактора при переходе СОУ в j–е
состояние и вероятность обнаружения этого же фактора при переходе СОУ в любое
конечное состояние.
Выражения
(1) и (2)непосредственно определяют, какое количество информации 
АСУ получает о
наступлении события: {СОУ перейдет в j–е
состояние}, из сообщения: {на СОУ действует i–й
фактор}. Когда количество информации >0 – i–й фактор
способствует переходу СОУ в j–е
состояние, когда <0 – препятствует этому переходу, когда же =0 – никак не влияет на это.
Чрезвычайно важное для данного исследования выражение (1) заслуживает специального комментария. Прежде всего нельзя не обратить внимания на то, что оно по своей математической форме, т.е. формально, ничем не отличается от выражения для превышения сигнала над помехой для информационного канала [408]. Из этого, на первый взгляд, внешнего совпадения следует интересная интерпретация выражения (2). А именно: можно считать, что обнаружив некоторый i–й признак у объекта, предъявленного на распознавание, мы тем самым получаем сигнал, содержащий некоторое количество информации
о том, что этот объект принадлежит к j–му классу. По–видимому, это так и есть, однако чтобы оценить насколько много или мало этой информации нами получено, ее необходимо с чем–то сравнить, т.е. необходимо иметь точку отсчета или базу для сравнения. В качестве такой базы естественно принять среднее по всем классам распознавания количество информации, которое мы получаем, обнаруживая этот i–й признак:
Иначе говоря, если при предъявлении какого–либо объекта на распознавание у него обнаружен i–й признак, то для того, чтобы сделать из этого факта обоснованный вывод о принадлежности этого объекта к тому или иному классу, необходимо знать и учесть, насколько часто вообще (т.е. в среднем) обнаруживается этот признак при предъявлении объектов различных классов.
Фактически – это среднее количество информации можно рассматривать как некоторый "информационный шум", который имеется в данном признаке и не несет никакой полезной информации о принадлежности объектов к тем или иным классам.
Выражению (2) может быть придан более обычный для теории связи вид
который интерпретируется как вычитание шума из полезного сигнала. Эта операция является совершенно стандартной в системах шумоподавления.
Если полезный сигнал выше уровня шума, то
его обнаружение несет информацию в пользу принадлежности объекта к данному
классу, если нет – то, наоборот, в пользу не принадлежности.
Возвращаясь к выражению (1), необходимо
отметить, что сам А.А.Харкевич рассматривал 
как вероятность достижения цели, при условии, что
система получила информацию 
, а 
– как вероятность ее достижения при условии, что
система этой информации не получала. Очевидно, что фактически 
соответствует вероятности случайного угадывания
системой правильного пути к цели.
Необходимо отметить также, что каждый признак объекта управления как канала связи может быть охаректиризован динамическим диапазоном, равным разности максимально возможного (допустимого) уровня сигнала в канале и уровня помех в логарифмическом масштабе:
Максимальное количество информации, которое может содержаться в признаке, полностью определяется количеством классов распознавания W и равно количеству информации по Хартли: I=Log2W. Динамический диапазон признака является количественной мерой его полезности (ценности) для распознавания, но все же предпочтительней для этой цели, по мнению авторов, является применение среднего количества полезной для классификации информации в признаке, т.е. исправленное выборочное среднеквадратичное отклонение информативностей:
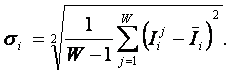
5.3. РЕШЕНИЕ ЗАДАЧИ 2: "АДАПТАЦИЯ И КОНКРЕТИЗАЦИЯ
АБСТРАКТНОЙ МОДЕЛИ ОБЪЕКТА УПРАВЛЕНИЯ"
На основе обучающей выборки, содержащей информацию о том, какие факторы действовали, когда СОУ переходил в те или иные состояния, методом прямого счета формируется матрица абсолютных частот, имеющая следующий вид (табл. 5.3).
Таблица 5. 3
МАТРИЦА АБСОЛЮТНЫХ ЧАСТОТ
|
Факторы |
Сумма |
|||
|
... |
j |
... |
||
|
... |
|
|
|
|
|
i |
|
|
|
|
|
... |
|
|
|
|
|
Сумма |
|
|
|
|
здесь
– количество
переходов СОУ в j–е состояние при
действующем i–м факторе по данным
обучающей выборки.
Необходимо отметить, что в случае СОУ в большинстве случаев нет возможности провести полный факторный эксперимент для заполнения матрицы абсолютных частот. Основываясь на результатах работы [153], авторы выдвигают гипотезу, что это и не обязательно (хотя и по большому счету желательно), т.е. на практике достаточно воспользоваться естественной вариабельностью факторов и состояний СОУ, представленных в обучающей выборке. С увеличением объема обучающей выборки в ней со временем будут представлены все практически встречающиеся варианты и из этих данных со временем может быть набрана выборка и для факторного эксперимента.
Подставив
в (1) 
и , рассчитанные из данной корреляционной матрицы по
очевидным формулам: 
, 
, или в (2) 
и , рассчитанные из той же матрицы по формулам: 
, 
, получим одно и то же выражение:
|
|
(5. 3) |
Окончательное выражение для расчета количества информации в i–м факторе о переходе СОУ в j–е состояние имеет вид:
|
|
(5. 4) |
где
– нормировочный коэффициент, переводящий
количество информации в двоичные единицы измерения информации – биты с учетом
количества возможных состояний СОУ: W, а также суммарного количества
зарегистрированных случаев действия различных факторов: N [15].
В
соответствии с выражением (4), непосредственно на основе матрицы абсолютных
частот ||
|| (табл. 5.3) рассчитывается матрица информативностей
факторов |||| (табл. 5.1).
Количество информации в i–м факторе о
наступлении j–го состояния СОУ является статистической мерой их связи и количественной
мерой влияния данного фактора на переход СОУ в данное состояние.
5.4. РЕШЕНИЕ ЗАДАЧИ 3: "РАЗРАБОТКА АЛГОРИТМОВ
РЕШЕНИЯ ОСНОВНЫХ ЗАДАЧ АСУ"
Как было показано в разделе 5.1, решение задачи 3 предполагает решение следующих подзадач.
5.4.1. РЕШЕНИЕ ПОДЗАДАЧИ 3.1: "РАСЧЕТ ВЛИЯНИЯ
ФАКТОРОВ НА ПЕРЕХОД ОБЪЕКТА УПРАВЛЕНИЯ
В РАЗЛИЧНЫЕ ВОЗМОЖНЫЕ СОСТОЯНИЯ
(ОБУЧЕНИЕ, АДАПТАЦИЯ)"
При
изменении объема обучающей выборки или изменении экспертных оценок прежде всего
пересчитывается матрица абсолютных частот, а затем, на ее основании и в
соответствии с выражением (28), -
матрица информативностей. Таким образом, предложенная
модель обеспечивает отображение динамических взаимосвязей, с одной стороны,
между входными и выходными параметрами, а с другой, - между параметрами и состояниями объекта управления.
Конкретно, это отображение осуществляется в форме так называемых профилей факторов
и состояний.
В профиле i–го фактора (строка матрицы информативностей) отображается, какое количество информации о переходе СОУ в каждое из возможных состояний содержится в том факте, что данный фактор действует.
В профиле j–го состояния СОУ (столбец матрицы информативностей) отображается, какое количество информации о переходе СОУ в данное состояние содержится в каждом из факторов.
5.4.2. РЕШЕНИЕ ПОДЗАДАЧИ 3.2: "ПРОГНОЗИРОВАНИЕ
ПОВЕДЕНИЯ ОБЪЕКТА УПРАВЛЕНИЯ ПРИ КОНКРЕТНОМ
УПРАВЛЯЮЩЕМ ВОЗДЕЙСТВИИ И ВЫРАБОТКА
МНОГОФАКТОРНОГО УПРАВЛЯЮЩЕГО ВОЗДЕЙСТВИЯ"
Данная модель позволяет прогнозировать поведение СОУ при воздействии на него не только одного, но и целой системы факторов:
|
|
(5. 5) |
В
теории принятия решений [451] скалярная функция 
векторного аргумента называется
интегральным критерием. Основная проблема состоит в выборе такого
аналитического вида интегрального критерия, который обеспечил бы эффективное
решение задачи АСУ.
Учитывая, что частные критерии (1) имеют смысл количества информации, а информация по определению является аддитивной функцией [332, 451], авторы предлагают ввести интегральный критерий, как аддитивную функцию от частных критериев:
|
|
(5. 6) |
В выражении (6) круглыми скобками обозначено скалярное произведение. Перепишем это выражение в координатной форме:
|
|
(5. 7) |
где
– профиль j–го состояния СОУ;
– профиль
текущего состояния СОУ (массив–локатор), т.е.:
фактор есть; фактора нет.
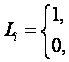
Таким образом, интегральным критерием является суммарное количество информации, содержащейся в факторах различной природы (т.е. факторах, характеризующих состояние среды, объекта управления, управляющее воздействие, прогнозную информацию) о переходе СОУ в целевое состояние.
В
многокритериальной постановке задача прогнозирования состояния СОУ, при
оказании на него заданного многофакторного управляющего воздействия , сводится к
максимизации интегрального критерия:
|
|
(5. 8) |
т.е. к выбору такого
состояния СОУ, для которого интегральный критерий максимален.
Задача принятия решения о выборе наиболее эффективного управляющего воздействия является обратной задачей по отношению к задаче максимизации интегрального критерия, т.е. вместо того, чтобы по набору факторов прогнозировать состояние СОУ, необходимо, наоборот, по заданному (целевому) состоянию СОУ определить такой набор факторов, который с наибольшей эффективностью перевел бы объект управления в это состояние.
Как
было показано при решении задачи 3.1, профиль
состояния показывает, какое количество информации о переходе СОУ в данное состояние
содержится в каждом из факторов.
Факторы могут быть разделены на две основные группы, в зависимости от того, могут ли они использоваться для управления или просто должны учитываться, но не могут быть изменены:
1) на управляющие воздействия (технологии);
2) факторы окружающей среды, а также факторы, характеризующие предысторию и актуальное состояние СОУ.
В предлагаемой методологии влияние предшествующих состояний СОУ можно учесть двумя способами:
- введя более подробную классификацию актуальных состояний, некоторые из которых, по–видимому тождественные, как раз и будут отличаться только своей предысторией;
- расширив список факторов, потенциально влияющих на поведение СОУ, факторами, связанными с его предшествующими состояниями.
Это различие соответствует различию между простыми и составными
цепями Маркова, автоматами без памяти и с памятью.
Если
задано некоторое определенное целевое состояние, то выбор управляющих
воздействий для фактического применения производится из списка, в котором все
возможные управляющие воздействия расположены в порядке убывания их влияния на
перевод СОУ в данное целевое состояние. Такой список называется информационным
портретом состояния СОУ [15].
Управляющие
воздействия могут быть объединены в группы, внутри каждой из которых они
альтернативны (несовместны), а между которыми - нет
(совместны). В этом случае внутри каждой группы выбирают одно из доступных
управляющих воздействий с максимальным влиянием.
Однако выбор многофакторного управляющего воздействия нельзя считать завершенным без прогнозирования результатов его применения. Описание СОУ в актуальном состоянии состоит из списка факторов окружающей среды, предыстории СОУ, описания его актуального (исходного) состояния, а также выбранных управляющих воздействий. Имея эту информацию по каждому из факторов в соответствии с выражением (7), нетрудно подсчитать, какое количество информации о переходе в каждое из состояний содержится суммарно во всей системе факторов.
Данный
метод соответствует фундаментальной лемме Неймана–Пирсона, содержащей
доказательство оптимальности метода выбора той из двух статистических гипотез,
о которой в системе факторов содержится больше информации. В то же время он
является обобщением леммы Неймана–Пирсона, так как, по предложению авторов,
вместо информационной меры Шеннона используется обобщенная мера семантической
информации Харкевича [15, 29, 30, 332, 408, 433, 451].
Предлагается еще одно обобщение этой фундаментальной леммы, основанное на косвенном учете корреляций между информативностями в профиле состояния при использовании среднего по профилю. Соответственно, вместо простой суммы количеств информации предлагается использовать ковариацию между профилями состояния и СОУ, которая количественно измеряет степень сходства формы этих профилей:
|
|
(5. 9) |
где
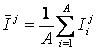– средняя информативность по профилю класса;
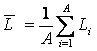– среднее по профилю распознаваемого объекта.
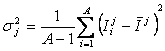– среднеквадратичное
отклонение информативностей профиля класса;
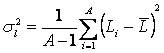– среднеквадратичное
отклонение по профилю распознаваемого объекта.
Выражение (9) получается непосредственно из (7) после замены координат перемножаемых векторов их стандартизированными значениями:
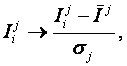
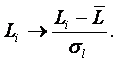
Результат прогнозирования поведения СОУ,
описанного данной системой факторов, представляет собой список состояний, в
котором они расположены в порядке убывания суммарного количества информации о
переходе СОУ в каждое из них.
Результаты сравнения качества результатов распознавания, полученных в соответствии с выражениями (7) и (9), показали, что при малых выборках они практически не отличаются, но при увеличении объема выборки до 400 и более выражение (9) дает на 5% – 7% более качественные результаты, чем (7). Поэтому базовым будем считать выражение (9).
Обоснование
сопоставимости частных критериев Iij
Применение
этого метода корректно, если можно сравнивать суммарное количество информации о
переходе СОУ в различные состояния, рассчитанное в соответствии с выражением
(9), т.е. если они сопоставимы друг с другом.
Будем считать, что величины сопоставимы тогда и только тогда, когда одновременно выполняются следующие три условия:
1. Сопоставимы индивидуальные количества информации, содержащейся в признаках о принадлежности к классам.
2. Сопоставимы величины, рассчитанные для одного объекта и разных классов.
3. Сопоставимы величины, рассчитанные для разных объектов и разных классов.
Очевидно, для решения
всех этих вопросов необходимо дать точное и полное определение самого термина
"сопоставимость".
Считается, что величины
сопоставимы, если существует некоторая количественная шкала для измерения этих
величин (табл. 5.4).
Таблица 5. 4
ХАРАКТЕРИСТИКА И ПРИМЕРЫ ИЗМЕРИТЕЛЬНЫХ ШКАЛ
|
Тип
шкалы |
Характеристики |
Примеры |
Сопоставимость |
|
Номинальная |
Объекты классифицированы, классам присвоены
словесные наименования или условные номера – коды. То, что номер одного
класса больше или меньше другого, еще ничего не говорит о свойствах объектов,
относящихся к этим классам, за исключением того, что они различаются |
Национальность, цвет глаз, пол, клинические диагнозы,
автомобильные номера |
Не |
|
Порядковая |
Объекты классифицированы, а классы обозначены
номерами (закодированы). Значения чисел, присваиваемых классам, качественно
отражают степень выраженности определенных свойств предметов, принадлежащих
этим классам, т.е. большим значениям кодов классов соответствует и большая степень
выраженности измеряемого свойства, на основании чего классы можно ранжировать |
Ранжирование по чертам личности, военные и гражданские
ранги, должности и звания. |
Частично |
|
Интервальная |
Существует единица измерения, с помощью которой
классы можно не только упорядочить, но и приписать им числа таким образом,
чтобы равные разности чисел, присвоенных классам, отражали равные различия в
количествах измеряемых свойств. Нулевая точка интервальной шкалы произвольна
(условна) и не указывает на отсутствие свойства |
Календарное время, шкалы температур по Фаренгейту и
Цельсию |
Обеспечивается |
|
Отношений |
Числа, присвоенные классам, обладают всеми
свойствами интервальной шкалы, но, помимо этого, на шкале существует
абсолютный нуль или абсолютный максимум, соответствующий полному отсутствию измеряемого
свойства или максимально возможному его присутствию. Отношения чисел, присвоенных
классам или объектам при измерении, отражают количественные отношения
измеряемого свойства |
Рост, вес, время, цена, температура по Кельвину
(есть абсолютный нуль), количество информации (есть абсолютный максимум) |
Полностью |
Таким образом, в нашем случае сопоставимость обеспечивается, если на шкале определены направление и единица измерения, а также есть абсолютный минимум (ноль) или максимум.
Проверим, выполняются ли эти условия для упрощенной и полной информационных моделей объектов и классов распознавания.
Рассмотрим вышеперечисленные необходимые и достаточные условия сопоставимости для упрощенной и полной информационных моделей.
Сопоставимость индивидуальных количеств информации,
содержащейся в признаках о принадлежности к
классам
В упрощенной информационной модели класса и информационной модели объекта принято, что все признаки имеют одинаковый вес, который равен 1, если признак есть у класса, и 0, если его нет.
Уже одним этим обеспечивается сопоставимость индивидуальных количеств информации в упрощенной модели.
В полной модели количество информации рассчитывается по видоизмененной авторами формуле Харкевича (36).
Таким образом, в полной информационной модели класса для каждого признака известно, какое количество информации о принадлежности к данному классу он содержит. Это количество информации может быть положительным, нулевым и отрицательным, но не может превосходить некоторой максимальной величины, определяемой количеством классов распознавания: I=Log2W (мера Хартли), где W – количество классов распознавания.
Следовательно, для полной информационной модели сопоставимость индивидуальных количеств информации также обеспечивается, так как для них применима шкала отношений.
Это означает, что индивидуальные количества информации можно суммировать и ввести интегральный критерий как аддитивную меру от индивидуальных количеств информации.
Сопоставимость величин суммарной информации,
рассчитанных для одного объекта и разных
классов
В упрощенной информационной модели вариант расстояния Хэмминга, в котором учитываются только совпадения 1 (т.е. существующих признаков), для кодовых слов объекта и класса равно:
|
|
(5. 10) |
где – кодовое слово (профиль, массив–локатор) j–го класса;
Li – кодовое слово (профиль, массив–локатор) объекта.
Пусть длина кодового слова (количество признаков) равна А. Длины кодовых слов объекта и классов одинаковы. Признаки могут принимать значения {0,1}. Тогда из этих условий и выражения (40) следует:
|
|
(5. 11) |
Но это и есть определение шкалы отношений, что
означает полную сопоставимость меры сходства для упрощенной информационной
модели одного объекта и многих классов.
В полной информационной модели мера сходства объекта с классом имеет вид, определяемый выражением (39).
Очевидно,
величина 
нормирована:
|
|
(5. 12) |
что и доказывает применимость шкалы отношений и полную сопоставимость меры сходства для полной информационной модели одного объекта и многих классов.
Это значит, что можно сравнивать меры сходства данного объекта с каждым из классов и ранжировать классы в порядке убывания сходства с данным объектом.
Сопоставимость величин суммарной информации,
рассчитанных для разных объектов и разных
классов
Очевидно,
величина , рассчитанная по формуле (39) для различных объектов и
классов нормирована:
|
|
(5. 13) |
что и доказывает применимость шкалы отношений и полную сопоставимость мер сходства для полной информационной модели многих объектов и многих классов.
Это значит, что можно сравнивать меры сходства различных объектов с классами распознавания и делать выводы о том, что одни объекты распознаются лучше, а другие хуже на данном наборе классов и признаков.
Обоснование
аддитивности интегрального критерия
Рассмотрим информационные модели распознаваемого объекта и классов распознавания, т.е. модели, основанные на теории кодирования – декодирования. Эта модель является упрощенной, но достаточно адекватной для решения вопроса об аддитивности меры сходства объектов и классов.
Информационная модель распознаваемого объекта представляет собой двоичное слово, каждый разряд которого соответствует определенному признаку. Если признак есть у распознаваемого объекта, то соответствующий разряд имеет значение 1, если нет – то 0. Двоичное слово с установленными в 1 разрядами, соответствующими признакам распознаваемого объекта, называется его кодовым словом.
Упрощенная информационная модель класса распознавания есть двоичное слово, каждый разряд которого соответствует определенному признаку. Соответствие между двоичными разрядами и признаками для классов то же самое, что и для распознаваемых объектов. Если признак есть у класса, то соответствующий разряд имеет значение 1, если нет – то 0. Двоичное слово с установленными в 1 разрядами, соответствующими признакам класса, называется его кодовым словом.
Такая модель класса является упрощенной, так как в ней принято, что все признаки имеют одинаковый вес равный 1, если он есть у класса, и 0, если его нет, тогда как в полной информационной модели класса для каждого признака известно, какое количество информации о принадлежности к данному классу он содержит. Это количество информации может быть положительным, нулевым и отрицательным, но не может превосходить некоторой максимальной величины, определяемой количеством классов распознавания: I=Log2N (мера Хартли), где N – количество классов.
Таким образом, в упрощенной информационной модели различные классы распознавания отличаются друг от друга только наборами признаков, которые им соответствуют.
При использовании этих упрощенных моделей задача распознавания объекта сводится к задаче декодирования, т.е. кодовые слова объектов рассматриваются как искаженные зашумленным каналом связи кодовые слова классов. Распознавание состоит в том, что по кодовому слову объекта определяется наиболее близкое ему в определенном смысле кодовое слово класса. При этом естественной и наиболее простой мерой сходства между распознаваемым объектом и классом является расстояние Хэмминга между их кодовыми словами, т.е. количество разрядов, которыми они отличаются друг от друга.
Рассмотрим теперь вопрос об аддитивности количества информации как частного критерия в интегральном критерии.
Известно [332], что существует всего два варианта формирования интегрального критерия из частных критериев: аддитивный и мультипликативный, поэтому задача сводится к выбору одного из этих вариантов.
Рассмотрим эти варианты. Пусть кодовое слово объекта состоит из N разрядов. Тогда добавление еще одного разряда, отображающего имеющийся (1) или отсутствующий (0) признак, приведет к различным результатам в случаях, когда интегральный критерий есть аддитивная и мультипликативная функция индивидуальных количеств информации в признаках (табл. 5.5).
Таблица 5. 5
СРАВНЕНИЕ
АДДИТИВНОГО И МУЛЬТИПЛИКАТИВНОГО
ВАРИАНТОВ СУПЕРКРИТЕРИЯ
|
Дополнительный |
Аддитивная
|
Мультипликативная
|
|
Есть (1) |
|
|
|
Нет (0) |
|
|
Здесь предполагается, что: I=f(n), f(1)=1, f(0)=0.
Итак, если функция аддитивна – добавление еще одного разряда увеличит количество информации в кодовом слове на 1 бит, если соответствующий признак есть, и не изменит этого количества, если его нет; если же функция мультипликативна, – то это не изменит количества информации в кодовом слове, если соответствующий признак есть, и сделает его равным нулю, если его нет.
Очевидно, мультипликативный вариант интегрального критерия не соответствует классическим представлениям о природе информации, тогда как аддитивный вариант полностью им соответствует: требование аддитивности самой меры информации было впервые обосновано Хартли в 1928 году, подтверждено Шенноном в 1948 году, и в последующем развитии теории информации никогда не подвергалось сомнению.
5.4.3. РЕШЕНИЕ ПОДЗАДАЧИ 3.3: "ВЫЯВЛЕНИЕ ФАКТОРОВ,
ВНОСЯЩИХ ОСНОВНОЙ ВКЛАД В ДЕТЕРМИНАЦИЮ
СОСТОЯНИЯ СОУ; СНИЖЕНИЕ РАЗМЕРНОСТИ МОДЕЛИ
ПРИ ЗАДАННЫХ ОГРАНИЧЕНИЯХ"
Естественно считать, что некоторый фактор является тем более ценным, чем больше среднее количество информации, содержащееся в этом факторе о поведении СОУ [15]. Но так как в предложенной модели количество информации может быть и отрицательным (если фактор уменьшает вероятность перехода СОУ в некоторое состояние), то простое среднее арифметическое информативностей может быть близко к нулю. При этом среднее будет равно нулю и в случае, когда все информативности равны нулю, и тогда, когда они будут велики по модулю, но с разными знаками. Следовательно, более адекватной оценкой полезности фактора, по мнению авторов, является среднее модулей или, что наиболее точно, исправленное (несмещенное) среднеквадратичное отклонение информативностей по профилю признака.
Ценность фактора по сути дела определяется его полезностью для различения состояний СОУ, т.е. является его дифференцирующей способностью или селективностью.
Необходимо также отметить, что различные состояния СОУ обладают различной степенью обусловленности, т.е. в различной степени детерминированы факторами: некоторые слабо зависят от учтенных факторов, тогда как другие определяются ими практически однозначно. Количественно детерминируемость состояния СОУ авторами предложено оценивать стандартным отклонением информативностей профиля обобщенного образа данного состояния.
Предложено и реализовано несколько итерационных алгоритмов корректного удаления малозначимых факторов и слабодетерминированных состояний СОУ при заданных граничных условиях [15, 196]. Решение задачи снижения размерности модели СОУ при заданных граничных условиях позволяет снизить эксплуатационные затраты и повысить эффективность адаптивной АСУ СС.
5.4.4. РЕШЕНИЕ ПОДЗАДАЧИ 3.4: "СРАВНЕНИЕ ВЛИЯНИЯ
ФАКТОРОВ. СРАВНЕНИЕ СОСТОЯНИЙ ОБЪЕКТА
УПРАВЛЕНИЯ"
Факторы могут сравниваться друг с другом по тому влиянию, которое они оказывают на поведение СОУ. Сами состояния могут сравниваться друг с другом по тем факторам, которые способствуют или препятствуют переходу СОУ в эти состояния. Это сравнение может содержать лишь результат, т.е. различные степени сходства/различия (в кластерном анализе), или содержать также причины этого сходства/различия (в когнитивных диаграммах).
Эти
задачи играют важную роль в теории и практике адаптивных АСУ СС при
необходимости замены одних управляющих воздействий другими, но аналогичными по
эффекту, а также при изучении вопросов устойчивости управления (различимости
состояний СОУ по детерминирующим их факторам).
Этот анализ проводится над классами распознавания и над признаками. Он включает:
- информационный (ранговый) анализ;
- кластерный и конструктивный анализ, семантические сети;
- содержательное сравнение информационных портретов, когнитивные диаграммы.
Предложенная математическая модель позволяет сформировать информационные портреты обобщенных эталонных образов классов распознавания и признаков.
Портреты классов распознавания представляют собой списки признаков в порядке убывания содержащегося в них количества информации о принадлежности к этим классам.
Информационный портрет класса распознавания показывает нам, каков информационный вклад каждого признака в общий объем информации, содержащейся в обобщенном образе этого класса.
В подходе к решению задач адаптивных АСУ СС, основанном на применении методов распознавания образов, развиваемом авторами в данной работе, классам распознавания соответствуют, во–первых, исходные, а во–вторых, результирующие, в том числе целевые состояния объекта управления. Это значит, что в первом случае портреты классов используются для идентификации исходного состояния СОУ, потому что именно с ними сравнивается состояние объекта управления, а во втором – для выработки управляющего воздействия, так как его выбирают в форме суперпозиции неальтернативных факторов из информационного портрета целевого состояния, оказывающих наибольшее влияние на перевод СОУ в это состояние.
Портреты признаков представляют собой списки классов распознавания в порядке убывания количества информации о них, которое содержит данный признак. По своей сути информационный портрет признака раскрывает нам смысл данного признака, т.е. его семантическую нагрузку. В теории и практике адаптивных АСУ СС информационный портрет фактора является развернутой количественной характеристикой, содержащей информацию о силе его влияния на перевод СОУ в каждое из возможных результирующих состояний, в том числе в целевые.
Информационные портреты классов и признаков допускают наглядную графическую интерпретацию в виде 2d и 3d диаграмм.
Кластерно–конструктивный анализ и
семантические сети
Кластеры представляют собой такие группы классов распознавания (или признаков), внутри которых эти классы наиболее схожи друг с другом, а между которыми наиболее различны [70, 177, 218].
В теории адаптивных АСУ СС, развиваемой в предлагаемой работе, классами распознавания являются как исходные, так и результирующие, в том числе целевые состояния объекта управления, а признаками – факторы, влияющие на переход СОУ в результирующие состояния.
Исходные состояния СОУ, объединенные в кластер, характеризуются общими или сходными методами перевода в целевые состояния.
Результирующие состояния СОУ, объединенные в кластер, являются слаборазличимыми по факторам, детерминирующим перевод СОУ в эти состояния. Это означает, что одно и то же управляющее воздействие при одних и тех же предпосылках (исходном состоянии и предыстории объекта управления и среды) могут привести к переводу СОУ в одно из результирующих состояний, относящихся к одному кластеру. Поэтому кластерный анализ результирующих состояний СОУ является инструментом, позволяющим изучать вопросы устойчивости управления сложными объектами.
При выборе управляющего воздействия как суперпозиции неальтернативных факторов часто возникает вопрос о замене одних управляющих факторов другими, имеющими сходное влияние на перевод СОУ из данного текущего состояния в заданное целевое состояние. Кластерный анализ факторов как раз и позволяет решить эту задачу: при невозможности применить некоторый управляющий фактор его можно заменить другим фактором из того же кластера.
При формировании кластеров используются матрицы сходства объектов и признаков, формируемые на основе матрицы информативностей.
В соответствии с предлагаемой математической моделью могут быть сформированы кластеры для заданного диапазона кодов классов распознавания (признаков) или заданных диапазонов уровней системной организации с различными критериями включения объекта (признака) в кластер.
Эти критерии могут быть сформированы автоматически либо заданы непосредственно. В последнем уровне кластеризации, в частности при задании одного уровня, в кластеры включаются не только похожие, но и все непохожие объекты (признаки), и, таким образом, формируются конструкты классов распознавания и признаков.
В
предлагаемой работе под конструктом авторы понимают систему противоположных (наиболее
сильно отличающихся) кластеров, которые называются "полюсами"
конструкта, а также спектр промежуточных кластеров, к которым применима количественная
шкала измерения степени их сходства или различия.
Понятия "кластер" и "конструкт" тесно взаимосвязаны:
- так как положительный и отрицательный полюса конструкта представляют собой кластеры, в наибольшей степени отличающиеся друг от друга, то конструкты могут быть получены как результат кластерного анализа кластеров;
- конструкт может рассматриваться как кластер с нечеткими границами, включающий в различной степени, причем не только в положительной, но и отрицательной, все классы (признаки).
В теории адаптивных АСУ СС, развиваемой авторами в данной работе, конструктивный анализ позволяет решить такие задачи, как:
1. Определение в принципе совместимых и в принципе несовместимых целевых состояний СОУ. Совместимыми называются целевые состояния, для достижения которых необходимы сходные предпосылки и управляющие воздействия, а несовместимыми – для которых они должны быть диаметрально противоположными. Например, обычно сложно совмещаются такие целевые состояния, как очень высокое качество продукции и очень большое ее количество.
2. Определение факторов, имеющих не только сходное (это возможно и на уровне кластерного анализа), но и совершенно противоположное влияние на поведение сложного объекта управления.
Современный интеллект имеет дуальную структуру и, по сути дела, мыслит в системе кластеров и конструктов [177, 196, 341, 367]. Поэтому инструмент автоматизированного кластерно–конструктивного анализа может быть успешно применен для интеллектуального управления сложными системами.
Необходимо отметить, что формирование
кластеров затруднено из-за проблемы комбинаторного взрыва, так как требует
полного перебора и проверки "из n по m", т.е. 
сочетаний элементов
(классов или признаков) в кластеры. Конструкты же формируются непосредственно
из матрицы сходства прямой выборкой и сортировкой, что значительно проще в
вычислительном отношении, так как конструктов значительно меньше, чем кластеров
(всего n2). Поэтому учитывая, что при формировании конструктов само
собой автоматически формируются и их полюса, т.е. кластеры, авторы реализовали
в предложенной математической модели не кластерный анализ, а сразу
конструктивный (как более простой в вычислительном отношении и более ценный по
получаемым результатам) [196, 326, 327].
Диаграммы смыслового сходства–различия классов (признаков) соответствуют определению семантических сетей [263], т.е. представляют собой ориентированные графы, в которых признаки соединены линиями, соответствующими их смысловому сходству–различию.
Когнитивные диаграммы
классов и признаков
В предложенной в настоящем исследовании математической модели в обобщенной постановке реализована возможность содержательного сравнения обобщенных образов классов распознавания и признаков, т.е. построения когнитивных диаграмм [196, 326, 327].
В информационных портретах классов распознавания мы видим, какое количество информации о принадлежности (или не принадлежности) к данному классу мы получаем, обнаружив у некоторого объекта признаки, содержащиеся в информационном портрете. В кластерно–конструктивном анализе мы получаем результаты сравнения классов распознавания друг с другом, т.е. мы видим, насколько они сходны и насколько отличаются.
Но мы не видим, какими признаками они
похожи и какими отличаются, и какой вклад каждый признак вносит в сходство
или различие некоторых двух классов.
Эту информацию мы могли бы получить, если бы проанализировали и сравнили два информационных портрета. Эту работу и осуществляет режим содержательного сравнения классов распознавания.
Аналогично, в информационных портретах признаков мы видим, какое количество информации о принадлежности (или не принадлежности) к различным классам распознавания мы получаем, обнаружив у некоторого объекта данный признак. В кластерно–конструктивном анализе мы получаем результаты сравнения признаков друг с другом, т.е. мы видим, насколько они сходны и насколько отличаются.
Но мы не видим, какими классами они
похожи и какими отличаются, и какой вклад каждый класс вносит в
смысловое сходство или различие некоторых двух признаков.
Эту информацию мы могли бы получить, если бы проанализировали и сравнили информационные портреты двух признаков. Эту работу и осуществляет режим содержательного (смыслового) сравнения признаков.
Содержательное (смысловое) сравнение классов
Обобщим математическую модель, предложенную и развиваемую в данной главе, на случай содержательного сравнения двух классов распознавания: J–го и L–го.
Признаки, которые есть по крайней мере в одном из классов, будем называть связями, так как благодаря тому, что они либо тождественны друг другу, либо между ними имеется определенное сходство или различие по смыслу, они вносят определенный вклад в отношения сходства/различия между классами.
Список выявленных связей сортируется в порядке убывания модуля силы связи, причем учитывается не более заданного количества связей.
Пусть, например:
- у J–го класса обнаружен i–й признак,
- у L–го класса обнаружен k–й признак.
Используем те же обозначения, что и в разделе 5.2.
На основе обучающей выборки системой рассчитывается матрица абсолютных частот встреч признаков по классам (табл. 5.6).
Таблица 5. 6
МАТРИЦА АБСОЛЮТНЫХ ЧАСТОТ
|
|
К л а с с ы |
|
||||
|
Признаки |
... |
j |
... |
l |
... |
Сумма |
|
... |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
Сумма |
|
|
|
|
|
|
В разделе 5.3 получено выражение (4) для расчета количества информации в i–м признаке о принадлежности некоторого конкретного объекта к j–му классу (плотность информации), которое имеет вид
|
|
(5. 14) |
Аналогично, формула для количества информации в k–м признаке о принадлежности к L–му классу имеет вид
|
|
(5. 15) |
Вклад некоторого признака i в сходство/различие двух классов j и l равен соответствующему слагаемому корреляции образов этих классов, т.е. просто произведению информативностей
|
|
(5. 16) |
Классический коэффициент корреляции Пирсона, количественно определяющий степень сходства профилей двух классов: j и l, на основе учета вклада каждой связи, образованной i–м признаком, рассчитывается по формуле
|
|
(5. 17) |
где
|
|
– средняя информативность признаков j–го класса; |
|
|
– средняя информативность признаков L–го класса; |
|
|
– среднеквадратичное отклонение информативностей признаков j–го класса; |
|
|
– среднеквадратичное отклонение информативностей признаков L–го класса. |
Проанализируем, насколько классический коэффициент корреляции Пирсона (17) пригоден для решения важных задач:
- содержательного сравнения классов;
- изучения внутренней многоуровневой структуры класса.
Упростим анализ, считая, что средние информативности признаков по обоим классам близки к нулю, что при достаточно больших выборках (более 400 примеров в обучающей выборке) практически близко к истине.
Каждое слагаемое (16) суммы (17) отражает связь между классами, образованную одним i–м признаком. I–я связь существует в том и только в том случае, если i–й признак есть у обоих классов. Поэтому эти связи уместно называть одно–однозначными. Но это означает, что данный подход не позволяет сравнивать классы, описанные различными, т.е. непересекающимися наборами признаков. Но даже если общие признаки и есть, то невозможность учета вклада остальных признаков, по мнению авторов, является недостатком классического подхода [9, 15], так как из содержательного анализа связей неконтролируемо исключается потенциально существенная информация. Таким образом, классический подход имеет ограниченную применимость при решении задачи №1. Для решения задачи №2 подход, основанный на формуле (17), вообще не применим, так как различные уровни системной организации классов образованы различными признаками и, следовательно, между уровнями не будет ни одной одно–однозначной связи.
Основываясь
на этих соображениях, авторы предлагают в общем случае учитывать вклад в
сходство/различие двух классов, который вносят не только общие, но и остальные
признаки. Логично предположить, что этот вклад (при прочих равных условиях)
будет тем меньше, чем меньше корреляция между этими признаками. Следовательно,
для обобщения выражения для силы связи (16) необходимо умножить произведение
информативностей признаков на коэффициент корреляции между ними, отражающий
степень сходства или различия признаков по смыслу.
Таким образом, будем считать, что любые два
признака (i,k) вносят определенный вклад в сходство/различие двух классов
(j,l), определяемый сходством/различием признаков и количеством информации о
принадлежности к этим классам, которое содержится в данных признаках:
|
|
(5. 18) |
где
– классический
коэффициент корреляции Пирсона, количественно определяющий степень сходства по
смыслу двух признаков: i и k, на основе учета вклада каждой связи, образованной
содержащейся в них информацией о принадлежности к j–му классу
|
|
(5. 19) |
где
|
|
– средняя информативность профиля i–го признака; |
|
|
– средняя информативность профиля k–го признака; |
|
|
– среднеквадратичное отклонение информативностей профиля i–го признака; |
|
|
–
среднеквадратичное отклонение информативностей профиля k–го признака. |
Коэффициент
корреляции между признаками (19) рассчитывается на основе всей обучающей
выборки, а не только объектов двух сравниваемых классов.
Так как коэффициент корреляции между признаками (19) практически всегда не равен нулю, то каждый признак i образует связи со всеми признаками k, где k={1,...,A}, а каждый признак k в свою очередь связан со всеми остальными признаками. Это означает, что выражение (18) является обобщением (16) на случай много–многозначных связей.
На основе этих представлений сформулируем выражение для обобщенного коэффициента корреляции Пирсона (термин авторов) между двумя классами: j и l, учитывающего вклад в их сходство/различие не только одно–однозначных, но и много–многозначных связей, образуемых коррелирующими признаками. Когнитивные диаграммы с много–многозначными связями предлагается называть обобщенными когнитивными диаграммами.
|
|
(5. 20) |
Сравним классический (17) и обобщенный (20) коэффициенты корреляции Пирсона друг с другом.
Очевидно, при i=k (20) преобразуется в (17), т.е. соблюдается принцип соответствия. Отметим, что модель позволяет задавать минимальный коэффициент корреляции (порог) между признаками, образующими учитываемые связи. При пороге 100% отображаются только одно–однозначные связи, учитываемые в классическом коэффициенте корреляции (17).
Из выражений (17) и (20) видно, что
|
|
(5. 21) |
так как в обобщенном коэффициенте корреляции учитываются связи между классами, образованные за счет учета корреляций между различными признаками. Ясно, что отношение
|
|
(5. 22) |
отражает степень избыточности описания классов. В модели имеется возможность исключения из системы признаков наименее ценных из них для идентификации классов. При этом в первую очередь удаляются сильно коррелирующие друг с другом признаки. В результате степень избыточности системы признаков уменьшается, и она становится ближе к ортонормированной [15].
Рассмотрим вопрос о единицах измерения, в которых количественно выражаются связи между классами.
Сходство
двух признаков выражается величиной
от — 1 до +1.
Максимальная теоретически возможная информативность признака в Bit выражается формулой
|
|
(5. 23) |
где Nobj – количество классов.
Таким образом, максимальная теоретически возможная сила связи Rmax равна
|
|
(5. 24) |
Сила связи в диаграммах выражается в процентах от максимальной теоретически возможной силы связи.
На
графической диаграмме отображается 8 наиболее сильных по модулю связей, рассчитанных
согласно формуле (20), причем знак связи изображается цветом (красный +, синий
— ), а величина – толщиной линии. Имеется возможность выводить диаграммы только
с положительными или только с отрицательными связями (для не цветных
принтеров).
Диаграммы Мерлина [190, 220] представляют собой частный случай обобщенных когнитивных диаграмм (т.е. с много–многозначными связями), т.е. диаграммы Мерлина – это когнитивные диаграммы, формируемые в соответствии с предложенной моделью при следующих граничных условиях:
1. Класс сравнивается сам с собой.
2. Фильтрация левого и правого информационных портретов выбрана по уровням системной организации признаков (в данном случае – уровням Мерлина).
3. Левый класс отображается с фильтрацией по одному уровню системной организации, а правый – по другому.
Диалог
задания вида диаграмм предоставляет пользователю возможность задать следующие
параметры:
- способ нормирования толщины линий, отображающих связи: нормирование по текущей диаграмме или по всем диаграммам;
- способ фильтрации признаков в информационных портретах диаграммы: по диапазону признаков или по диапазону уровней системной организации (уровням Мерлина);
- сами диапазоны признаков или уровней для левого и правого информационных портретов;
- максимальное количество связей, отображаемых на диаграмме;
- уровень сходства признаков, образующих одну связь, отображаемую на диаграмме: от 0 до 100%. При уровне сходства 100% в диаграммах отображаются только связи, образованные теми признаками, которые есть в обоих портретах одновременно, т.е. взаимно–однозначные связи. При уровне сходства менее 100% вообще говоря связи становятся много–многозначными, так как каждый признак корреляционно связан со всеми остальными;
- уровень сходства классов, отображаемых на диаграмме.
В предлагаемой математической модели в общем виде реализована возможность содержательного сравнения обобщенных образов состояний СОУ и факторов, т.е. построения когнитивных диаграмм [190, 196, 341].
В информационном портрете состояния СОУ показано, какое количество информации о принадлежности (не принадлежности) СОУ к данному состоянию, а также о переходе (не переходе) СОУ в данное состояние содержится в том факте, что на СОУ действуют факторы, содержащиеся в данном информационном портрете.
Кластерно–конструктивный анализ дает результат сравнения состояний СОУ друг с другом, т.е. показывает, насколько эти состояния сходны друг с другом и насколько отличаются друг от друга. Но он не показывает, какими факторами эти состояния СОУ похожи и какими отличаются, и какой вклад каждый фактор вносит в сходство или различие каждых двух состояний. Чтобы получить эту информацию, необходимо проанализировать два информационных портрета, что и делается при содержательном сравнении состояний СОУ .
Смысл
и значение диаграмм Мерлина применительно к проблематике АСУ состоит в том, что
они наглядно представляют внутреннюю структуру детерминации состояний СОУ,
т.е. показывают, каким образом связаны друг с другом предпосылки
(факторы среды, прошлые состояния СОУ, исходное состояние СОУ) и управляющие
воздействия, по тому влиянию, которое они оказывают на переход СОУ в заданное
состояние.
Таким
образом:
- для моделирования процессов принятия решений в адаптивных АСУ сложными системами целесообразно применение многокритериального подхода с аддитивным интегральным критерием, в котором в качестве частных критериев используется семантическая мера целесообразности информации (Харкевич, 1960);
- предложенная математическая модель обеспечивает эффективное решение следующих задач, возникающих при синтезе адаптивных АСУ СОУ: разработка абстрактной информационной модели СОУ; адаптация и конкретизация абстрактной модели на основе апостериорной информации о реальном поведении СОУ; расчет влияния факторов на переход СОУ в различные возможные состояния; прогнозирование поведения СОУ при конкретном управляющем воздействии и выработка многофакторного управляющего воздействия (основная задача АСУ); выявление факторов, вносящих основной вклад в детерминацию состояния СОУ; контролируемое удаление второстепенных факторов с низкой дифференцирующей способностью, т.е. снижение размерности модели при заданных ограничениях; сравнение влияния факторов, сравнение целевых и других состояний СОУ.
Предложенная методология, основанная на теории информации, обеспечивает эффективное моделирование задач принятия решений в адаптивных АСУ сложными системами.
Содержательное (смысловое) сравнение
признаков
Предложенная математическая модель позволяет осуществить содержательное сравнение информационных портретов двух признаков.
Выявляются классы, которые есть по крайней мере в одном из профилей. Такие классы называются связями, так как благодаря тому, что они либо тождественны друг другу, либо между ними имеется определенное сходство или различие, они вносят определенный вклад в отношения сходства/различия между признаками по смыслу.
Все связи между признаками сортируются в порядке убывания модуля, в соответствии с определенными ограничениями, связанными с тем, что нет необходимости учитывать очень слабые связи.
Для каждого класса известно, какое количество информации о принадлежности к нему содержит данный признак – это информативность. Здесь необходимо уточнить, что информативность признака – это не только количество информации в признаке о принадлежности к данному классу, но и количество информации в классе о том, что при нем наблюдается данный признак, т.е. это взаимная информация класса и признака.
Если бы классы были тождественны друг другу, т.е. это был бы один класс, то его вклад в сходство/различие двух признаков был бы просто равен соответствующему данному классу слагаемому корреляции этих признаков, т.е. просто произведению информативностей.
Но поскольку это в общем случае это могут быть различные классы, то, очевидно, необходимо умножить произведение информативностей на коэффициент корреляции между классами.
Таким образом, будем считать, что любые два класса (j,l) вносят определенный вклад в сходство/различие двух признаков (i,k), определяемый сходством/различием этих классов и количеством информации о принадлежности к ним, которое содержится в данных признаках
|
|
(5. 25) |
Вывод формулы (25) обобщенного коэффициента корреляции Пирсона для двух признаков совершенно аналогичен выводу формулы (20), поэтому он здесь не приводится. Формулы для всех входящих в (25) величин приведены выше в предыдущем разделе.
Так
же, как и в режиме содержательного сравнения классов, в данном режиме сила
связи выражается в процентах от максимальной теоретически–возможной силы связи.
На диаграмме (см. рис. 8.6 и 8.7) отображается 16 наиболее значимых связей,
рассчитанных согласно этой формуле, причем знак связи изображается цветом
(красный +, синий –), а величина – толщиной линии. Имеется возможность вывода
диаграмм только с положительными или только с отрицательными связями.
Математическая модель позволяет получить обобщенные инвертированные когнитивные диаграммы для любых двух заданных признаков, для пар наиболее похожих и непохожих признаков, для всех их возможных сочетаний, а также инвертированные диаграммы Мерлина.
Необходимо отметить, что понятия "обобщенная инвертированная когнитивная диаграмма" и "инвертированная диаграмма Мерлина" не упоминаются даже в фундаментальных руководствах по когнитивной психологии [394] и впервые предложены авторами в данной работе.
Эти диаграммы представляют собой частный случай обобщенных когнитивных диаграмм признаков, формируемых в соответствии с предложенной математической моделью при следующих ограничениях:
1. Признак сравнивается сам с собой.
2.
Выбрана фильтрация левого и правого профиля по уровням
системной организации классов (аналог уровней Мерлина для свойств).
3. Левый профиль отображается с фильтрацией по одному уровню системной организации классов, а правый – по другому.
5.5. ОБОБЩЕНИЕ ИНТЕГРАЛЬНОЙ МОДЕЛИ ПУТЕМ УЧЕТА
ЗНАЧЕНИЙ ВЫХОДНЫХ ПАРАМЕТРОВ ОБЪЕКТА
УПРАВЛЕНИЯ
Как
было показано в главе 2 данной работы (см. рис. 2.2), выходные параметры
– это свойства объекта управления, зависящие от входных
параметров (в том числе параметров, характеризующих среду) и связанные с его
целевым состоянием сложным и неоднозначным способом:
Задача идентификации состояния СОУ по его выходным параметрам решается подсистемой идентификации управляющей подсистемы, работающей на принципах системы распознавания образов. При этом классами распознавания являются выходные состояния СОУ, а признаками – его выходные параметры.
Подсистема
выработки управляющих воздействий, также основанная на алгоритмах распознавания
образов, обеспечивает выбор управления 
, переводящего объект управления в целевое состояние 
.
При этом
последовательно решаются следующие две обратные задачи распознавания:
во–первых,
по заданному целевому состоянию определяются наиболее
характерные для данного состояния выходные параметры объекта управления:
во–вторых,
по определенному на предыдущем шаге набору выходных параметров определяются входные параметры , с наибольшей эффективностью переводящие объект
управления в данное целевое состояние с этими выходными параметрами:
Системы
распознавания и принятия решений, применяемые в подсистемах идентификации и выработки
управляющих воздействий адаптивной АСУ СС, основаны на информационной мере
(9), которую в компактном виде можно записать в форме
|
|
(5. 26) |
где
|
|
(5. 27) |
Выражение (27) представляет собой слагаемое меры сходства выходного состояния объекта управления, обладающего i–м параметром с обобщенным образом j–го выходного состояния. Эта мера отражает информационное отношение, основанное на статистических закономерностях. Однако кроме информационного подхода оценки влияния параметров существуют и другие.
Например, метод экспертных оценок позволяет ранжировать параметры по их важности, исходя не из формальных статистических закономерностей, а учитывая их содержательное значение (смысл) и реальное значение, которое они играют в определении сущности тех или иных состояний СОУ. Это свойство авторами предложено назвать "значением параметра" и обозначить через ai.
Суммарное
значение всех параметров в целях обеспечения сопоставимости значений параметров
предлагается нормировать к 1:
|
|
(5. 28) |
Учитывая
нормировку значений параметров (28) в выражении (26), получаем итоговое
обобщенное выражение для меры сходства объекта управления в выходном состоянии,
обладающем выходными параметрами: 
с обобщенным
образом j–го результирующего
состояния:
|
|
(5. 29) |
Необходимо
отметить, что при 
выражение (29)
сводится к частному случаю (9). Соответственно, обобщаются и все выражения, в
которые входят 
.
Таким образом, в результате данного обобщения эксперт получает возможность влиять на принятие управляющих решений адаптивной АСУ СС не только на этапе обучения системы, но и в последующем без изменения обучающей выборки, а также при ее малом объеме или даже отсутствии. Это сближает предложенный подход с экспертными системами, существенно повышает адаптивные возможности системы, качественно расширяет возможности ее применения.
5.6. СВЯЗЬ МЕРЫ "IIJ" ШЕННОНА СО СТАТИСТИКОЙ "c2"
Предыдущий анализ позволяет сделать некоторые интересные сопоставления. Вероятность того, что предъявленный объект является j–м объектом, если у него обнаружен i–й признак:
Вероятность совместного появления двух независимых событий равна произведению их индивидуальных вероятностей. Таким образом, если рассматривать обнаружение данного j–го объекта и данного i–го признака как независимые события, то вероятность P их случайного совместного наблюдения при предъявлении j–го объекта
|
|
(5. 30) |
Очевидно, если фактическая вероятность
наблюдения i–го признака при предъявлении j–го объекта равна теоретической,
вычисленной по вышеприведенной формуле, то наблюдение данного признака никак
не связано с наблюдением данного объекта, т.е. не несет никакой информации о данном объекте.
Статистика c2 представляет собой просто сумму вероятностей совместного наблюдения признаков и объектов по всей корреляционной матрице или определенным ее подматрицам
|
|
(5. 31) |
Нельзя не обратить внимание на то, что статистика c2 простым образом связана с количеством информации в системе признаков о классе распознавания в соответствии с вариантом формулы Шеннона (4.27)
|
|
|
Сопоставляя выражения (5.31) и (4.27), получаем
|
|
(5. 32) |
Если
сравнить выражение (5.32) с формулой Хартли для количества информации (см.
табл. 4.1), то, очевидно, можно сделать вывод о том, что статистика c
может быть проинтерпретирована как мощность множества всех возможных вариантов
сочетаний признаков с классами распознавания при равномерном их распределении
(или нормальном, при достаточно больших выборках в соответствии с фундаментальным
свойством энтропии).
Поэтому наличие статистической связи (информации) между признаками и классами распознавания, т.е. отличие вероятностей их совместных наблюдений от предсказываемого в соответствии со случайным нормальным распределением, приводит к увеличению фактической статистики по сравнению с теоретической величиной.
5.7. РАСПОЗНАВАНИЕ КАК ОБЪЕКТНЫЙ АНАЛИЗ
(РАЗЛОЖЕНИЕ В РЯД ПО ПРОФИЛЯМ ОБРАЗОВ)
Интересно и очень важно отметить, что коэффициенты ряда Фурье по своей математической форме и смыслу представляют собой не что иное, как коэффициенты корреляции между разлагаемой в ряд кривой и функциями SIN и СOS соответствующих частот и амплитуд [78].
С этой точки зрения процесс распознавания, реализованный в предложенной математической модели, может рассматриваться как
разложение профиля распознаваемого объекта в ряд по профилям классов распознавания.
При развитии данной аналогии естественным образом возникают следующие вопросы:
- о полноте и избыточности системы профилей классов как функций, по которым будет вестись разложение профиля объекта;
- о сходимости, т.е. вообще возможности и корректности такого разложения.
В
общем случае профиль объекта совершенно не обязательно должен разлагаться в ряд
по профилям классов таким образом, что сумма ряда во всех точках будет в
точности равна значениям исходной функции. Это означает, что система профилей
классов не обязательно будет полна по отношению к профилю распознаваемого
объекта, и, тем более, всех возможных объектов. Авторами предлагается считать не разлагаемые в ряд, т.е. плохо распознаваемые объекты суперпозицией хорошо распознаваемых объектов ("похожих" на те, которые
использовались для формирования образов), и объектов, которые и не должны
распознаваться, так как объекты этого типа не встречались в обучающей выборке и не
использовались для формирования обобщенных образов классов.
Нераспознаваемую компоненту можно рассматривать либо как шум, либо считать ее полезным сигналом, несущим ценную информацию о еще не исследованных объектах интересующей нас предметной области (в зависимости от целей и тезауруса исследователей).
Первый вариант не приводит к осложнениям, так как примененный в математической модели алгоритм сравнения профилей объектов и классов, основанный на вычислении нормированной корреляции Пирсона (сумма произведений), является весьма устойчивым к наличию белого шума в идентифицируемом сигнале.
Во втором варианте необходимо дообучить систему распознаванию объектов, несущих такую компоненту (в этой возможности и заключается адаптивность модели). Технически этот вопрос решается просто копированием описаний плохо распознавшихся объектов из распознаваемой выборки в обучающую, их идентификацией экспертами и дообучением системы. Кроме того, может быть целесообразным расширить справочник классов распознавания новыми классами, соответствующими этим объектам.
Но на практике гораздо чаще наблюдается противоположная ситуация (можно даже сказать, что она типична), когда система профилей избыточна, т.е. в системе классов распознавания есть очень похожие классы (между которыми имеет место высокая корреляция, наблюдаемая в режиме: "кластерно–конструктивный анализ"). Практически это означает, что в системе сформировано несколько практически одинаковых образов с разными наименованиями. Для исследователя это само по себе является очень ценной информацией. Однако, если исходить только из потребности разложения распознаваемого объекта в ряд по профилям классов (чтобы определить суперпозицией каких образов он является, т.е. "разложить его на компоненты"), то наличие сильно коррелирующих друг с другом профилей представляется неоправданным, так как просто увеличивает размерности данных, внося в них мало нового по существу. Поэтому возникает задача исключения избыточности системы классов распознавания, т.е. выбора из всей системы классов распознавания такого минимального их набора, в котором профили классов минимально коррелируют друг с другом, т.е. ортогональны в фазовом пространстве признаков. Это условие в теории рядов называется "ортонормируемостью" системы базовых функций, а в факторном анализе связано с идеей выделения "главных компонент".
В предлагаемой математической модели есть два варианта выхода из данной ситуации:
- исключение неформирующихся, расплывчатых или дублирующих классов;
- объединение почти идентичных по содержанию классов.
Но выбрать вариант и реализовать его, используя соответствующие режимы, пользователь должен сам. Вся необходимая и достаточная информация для принятия соответствующих решений предоставляется пользователю системы.
По мнению авторов, если считать, что функции образов при соблюдении условия ортонормированности образуют формально–логическую систему, к которой применима теорема Геделя, то можно сформулировать эту теорему для данного случая следующим образом: "Для любой ортонормированной системы базисных функций всегда существует по крайней мере одна такая функция, что она не может быть разложена в ряд по данной системе базисных функций, т.е. всегда существует функция, которая является ортонормированной ко всей системе базисных функций в целом".
Если система базисных функций не является ортонормированной, то не существует ни одной функции, которая являлась бы ортонормированной ко всей этой системе базисных функций в целом. Следовательно, любая функция может быть разложена в ряд по неортонормированной системе функций.
Очевидно, не взаимосвязанными друг с другом могут быть только четко оформленные, детерминистские образы, т.е. образы с высокой степенью редукции ("степень сформированности конструкта"). Поэтому в процессе выявления взаимно–ортогональных базисных образов в первую очередь будут выброшены аморфные "расплывчатые" образы, которые связаны практически со всеми остальными образами.
В некоторых случаях результат такого процесса представляет интерес и это делает оправданным его реализацию. Однако можно предположить, что и наличие расплывчатых образов в системе является оправданным, так как в этом случае система образов не будет формальной и подчиняющейся теореме Геделя, следовательно, система распознавания будет более полна в том смысле, что повысится вероятность идентификации любого объекта, предъявленного ей на распознавание. Конечно, уровень сходства с аморфным образом не может быть столь же высоким, как с четко оформленным, поэтому в этом случае может быть более уместно применить термин "ассоциация", чем "однозначная идентификация".
Итак,
можно сделать следующий вывод: возможность наличия в системе образов не только
четко оформленных (детерминистских), но и аморфных, расплывчатых образов
является важным достоинством перспективной системы распознавания, так как обеспечивает
ей возможность устойчивой работы даже в тех случаях, в которых системы распознавания
(идентификации) и информационно–поисковые системы детерминистского типа
практически неработоспособны. В этих условиях перспективная система работает
как система ассоциативной идентификации.
Таким образом, перспективная система
распознавания образов по сути дела осуществляет разложение профилей распознаваемых объектов по профилям классов распознавания, т.е. осуществляет "объектный анализ" (по аналогии с
гармоническим или Фурье–анализом), что
позволяет рассматривать распознаваемые объекты как суперпозицию обобщенных образов классов
различного типа с различными амплитудами.
5.8. ЦЕННОСТЬ ПРИЗНАКА ДЛЯ РЕШЕНИЯ ЗАДАЧ
РАСПОЗНАВАНИЯ И ПРИНЯТИЯ РЕШЕНИЙ
В
работах [62, 160, 173, 180, 190, 194, 332, 417, 432, 451] описаны
многочисленные методы определения ценности признаков для решения задач
распознавания образов и принятия решений.
Естественно считать, что некоторый признак является тем более ценным для решения задач распознавания и принятия решений, чем больше математическое ожидание количества информации о принадлежности или непринадлежности обладающего этим признаком объекта к каждому из обрабатываемых классов распознавания
Поскольку в предложенной модели информация может быть и отрицательной (это информация о непринадлежности), то вместо математического ожидания целесообразно применить среднее модулей или исправленное (несмещенное) средне–квадратичное отклонение информативностей по профилю признака, что и предлагается авторами:
|
|
5.9. ВЫВОДЫ
1. Показано, что определенная ограниченность подхода Шеннона, рассмотренная в четвертой главе данной работы, преодолевается в апостериорном подходе. Обосновано, что одной из наиболее перспективных конкретизаций апостериорного подхода, является подход, предложенный в 1960 году А.А.Харкевичем [61, 408, 433]. Для моделирования процессов принятия решений в адаптивных АСУ сложными системами предложено применить многокритериальный подхода с аддитивным интегральным критерием, в котором в качестве частных критериев используется семантическая мера целесообразности информации. При апостериорном подходе количество информации оценивается косвенно: по изменению степени целесообразности поведения системы, получившей эту информацию. В результате получения информации поведение системы улучшается (растет выигрыш), а в результате получения дезинформации – ухудшается (растет проигрыш). Известны и более развитые обобщения, основанные на интересных и правдоподобных идеях, однако они наталкиваются на значительные математические трудности и намного более сложны в программной реализации, поэтому их рассмотрение в данном исследовании признано нецелесообразным [332, 451].
2. Предложенная математическая модель обеспечивает эффективное решение следующих задач, возникающих в адаптивных АСУ СС:
- разработка абстрактной информационной модели СОУ;
- адаптация и конкретизация абстрактной модели на основе информации о реальном поведении СОУ;
- расчет влияния факторов на переход СОУ в различные возможные состояния;
- прогнозирование поведения СОУ при конкретном управляющем воздействии и выработка многофакторного управляющего воздействия (основная задача АСУ);
- выявление факторов, вносящих основной вклад в детерминацию состояния СОУ; контролируемое удаление второстепенных факторов с низкой дифференцирующей способностью, т.е. снижение размерности модели при заданных граничных условиях;
- сравнение влияния факторов, сравнение целевых и других состояний СОУ.
3. Таким образом, предложенная методология, основанная на теории информации, обеспечивает эффективное моделирование задач принятия решений в адаптивных АСУ сложными системами.
4. На примере метода сведения многокритериальной задачи принятия решений к однокритериальной показана глубокая внутренняя взаимосвязь данной модели с математической моделью распознавания образов. На этой основе авторами введено понятие "интегрального метода" распознавания и принятия решений и, после изложения основных понятий теории информации, предложена базовая математическая модель "интегрального метода", основанная на теории информации. Показано, что теория информации может рассматриваться как единая основа методов РО и ПР, распознавание образов как принятие решения о принадлежности объекта к классу распознавания, прогнозирование как распознавание будущих состояний, принятие решения об управляющем воздействии на объект управления в АСУ как решение обратной задачи распознавания.
5. Проведено исследование базовой математической модели на примере решения основной задачи АСУ: задача принятия решения о наиболее эффективном управляющем воздействии. Осуществлена декомпозиция основной задачи в последовательность частных задач для каждой из которых найдено решение, показана взаимосвязь основной задачи АСУ с задачей декодирования теории информации, исследована взаимосвязь примененной в модели семантической меры Харкевича со статистикой Х2, обоснована устойчивость модели при малых выборках, дано обоснование сопоставимости частных критериев, разработана интерпретация распознавания как объектного анализа (разложение в ряд по профилям образов), предложены робастные процедуры, а также процедуры приведения структуры выборки к репрезентативной.