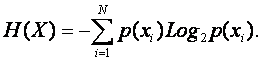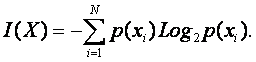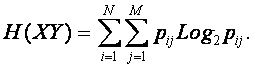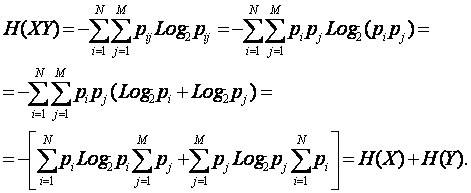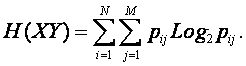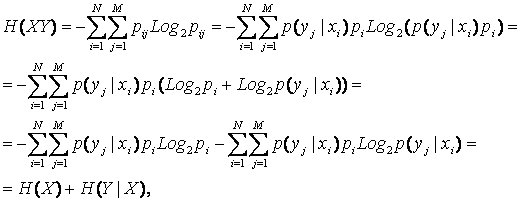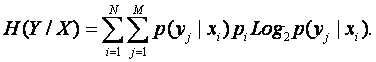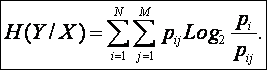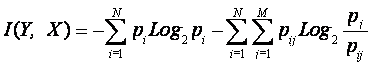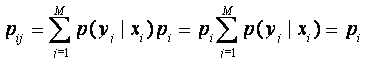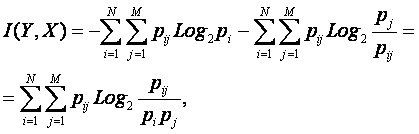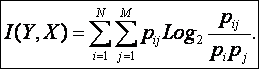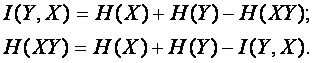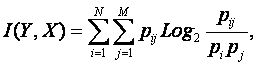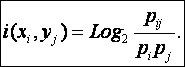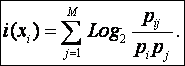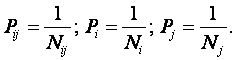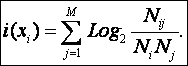ГЛАВА 4. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
РАСПОЗНАВАНИЯ ОБРАЗОВ
И
ПРИНЯТИЯ РЕШЕНИЙ В АСУ
НА ОСНОВЕ ТЕОРИИ ИНФОРМАЦИИ
Формально, распознавание есть не что иное, как принятие решения о принадлежности распознаваемого объекта или его состояния к определенному классу (классам) [295].
Из этого следует внутренняя и органичная связь методов распознавания образов и принятия решений. По мнению авторов, аналитический обзор позволяет сделать вывод, что наиболее глубокая основа этой связи состоит в том, что и распознавание образов, и принятие решений есть прежде всего снятие неопределенности.
Распознавание снимает неопределенность в вопросе о том, к какому классу относится распознаваемый объект. Если до распознавания существовала неопределенность в вопросе о том, к какому классу относится распознаваемый объект или его состояние, то в результате распознавания эта неопределенность уменьшается, причем возможно и до нуля (когда объект идентифицируется однозначно).
Принятие решения (выбор) также
снимает неопределенность в вопросе о том, какое из возможных решений будет
принято, если существовало
несколько альтернативных вариантов решений и принимается одно из них.
Для строгого исследования процессов снятия неопределенности оптимальным является применение аппарата теории информации, которая как бы специально создана для этой цели.
Из этого непосредственно следует возможность применения методов теории информации для решения задач распознавания и принятия решений в АСУ.
Таким образом, теория информации может рассматриваться как единая основа методов распознавания образов и принятия решений.
4.1. ФОРМАЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ
В адаптивных АСУ СОУ модели распознавания образов и принятия решений применимы в подсистемах идентификации состояния СОУ и выработки управляющего воздействия:
- идентификация состояния СОУ представляет собой принятие решения о принадлежности этого состояния к определенной классификационной категории (задача распознавания);
- выбор многофакторного управляющего воздействия из множества возможных вариантов представляет собой принятие решения (обратная задача распознавания).
Распознавание образов есть принятие решения о принадлежности объекта или его состояния к определенному классу. Если до распознавания существовала неопределенность в вопросе о том, к какому классу относится распознаваемый объект или его состояние, то в результате распознавания эта неопределенность уменьшается, в том числе может быть и до нуля (когда объект идентифицируется однозначно).
Из данной постановки непосредственно следует возможность применения методов теории информации для решения задач распознавания образов и принятия решений в АСУ. Однако возникает задача выбора конкретного математического метода, наиболее адекватного целям исследования.
В этой связи рассмотрим основные положения теории информации и такие ее ключевые понятия, как "энтропия" и "количество информации".
4.2. ТЕОРИЯ ИНФОРМАЦИИ И ЕЕ КЛЮЧЕВЫЕ ПОНЯТИЯ
Термин "информация" произошел от латинского слова informatio, которое означает разъяснение, осведомление [351]. Данное понятие является одним из ключевых понятий кибернетики и понимается как совокупность каких-либо сведений или данных.
В то же время это понятие относится к фундаментальным, исходным понятиям предельного уровня общности, и, как многие подобные понятия, не имеет общепринятого строго научного определения.
Современная наука о свойствах информации и закономерностях информационных процессов называется теорией информации. Содержание понятия "информация" можно раскрыть на примере двух исторически первых подходов к измерению количества информации: подходов Хартли и Шеннона. Первый из них основан на теории множеств и комбинаторике, а второй – на теории вероятностей.
В основе всей теории информации лежит открытие, сделанное Р. Хартли в 1928 году, и состоящее в том, что информация допускает количественную оценку [374]. Завершенный и полный вид этой теории придал в 1948 году К. Шеннон [390]. Большой вклад в дальнейшее развитие и обобщение теории информации внесли отечественные ученые А.Н. Колмогоров, А.А. Харкевич, Р.Л. Стратанович [373]. Недавно германские исследователи советских архивов сообщили о том, что теория, известная сегодня как теория Шеннона, была создана А.Н.Колмогоровым еще в 1938 году, но была засекречена, так как использовалась в военных разработках.
4.2.1. ПОДХОД Р. ХАРТЛИ
Подход Р. Хартли основан на весьма фундаментальных теоретико–множественных, по существу комбинаторных основаниях, а также нескольких интуитивно ясных и вполне очевидных предположениях.
Рассмотрим эти предположения. Будем считать, что если существует множество элементов и осуществляется выбор одного из них, то этим самым сообщается или генерируется определенное количество информации. Эта информация состоит в том, что если до выбора не было известно, какой элемент будет выбран, то после выбора это становится известным.
Найдем вид функции, связывающей количество информации, получаемой при выборе некоторого элемента из множества, с количеством элементов в этом множестве, т.е. с его мощностью.
Если множество элементов, из которых осуществляется выбор, состоит из одного–единственного элемента, то ясно, что его выбор предопределен, т.е. никакой неопределенности выбора нет. Таким образом, если мы узнаем, что выбран этот единственный элемент, то, очевидно, при этом мы не получаем никакой новой информации, т.е. получаем нулевое количество информации.
Если множество состоит из двух элементов, то неопределенность выбора минимальна. В этом случае минимально и количество информации, которое мы получаем, узнав, что совершен выбор одного из элементов.
Чем больше элементов в множестве, тем больше неопределенность выбора, тем больше информации мы получаем, узнав о том, какой выбран элемент.
Из этих очевидных соображений следует первое требование: информация есть монотонная функция от мощности исходного множества.
Рассмотрим множество, состоящее из чисел в двоичной системе счисления длиной I двоичных разрядов. При этом каждый из разрядов может принимать значения только 0 и 1 (табл. 4.1).
Таблица 4. 1
К ВЫВОДУ ФОРМУЛЫ КОЛИЧЕСТВА
ИНФОРМАЦИИ ПО Р.ХАРТЛИ
|
Кол-во двоичных разрядов (i) |
Кол-во состояний, которое можно пронумеровать i-разрядными двоичными
числами (N) |
Основание системы счисления |
||
|
10 |
16 |
2 |
||
|
1 |
2 |
0 1 |
0 1 |
0 1 |
|
2 |
4 |
0 1 2 3 |
0 1 2 3 |
00 01 10 11 |
|
3 |
8 |
0 1 2 3 4 5 6 7 |
0 1 2 3 4 5 6 7 |
000 001 010 011 100 101 110 111 |
|
4 |
16 |
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
0 1 2 3 4 5 6 7 8 9 A B C D E F |
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 |
|
*** |
*** |
|
|
|
|
i |
2i |
|
|
|
Очевидно, количество этих чисел (элементов) в множестве равно:
N = 2i.
Рассмотрим процесс выбора чисел из рассмотренного множества. До выбора вероятность выбрать любое число одинакова. Существует объективная неопределенность в вопросе о том, какое число будет выбрано. Эта неопределенность тем больше, чем больше N – количество чисел в множестве, а чисел тем больше – чем больше разрядность i этих чисел.
Примем, что выбор одного числа дает нам следующее количество информации:
i =
Log2(N).
Таким
образом, количество информации, содержащейся в двоичном числе, равно количеству
двоичных разрядов в этом числе.
Это выражение и представляет собой формулу Хартли для количества информации. Отметим, что оно полностью совпадает с выражением для энтропии (по Эшби), которая рассматривалась им как количественная мера степени неопределенности состояния системы.
При увеличении длины числа в два раза количество информации в нем также должно возрасти в два раза, несмотря на то, что количество чисел в множестве возрастает при этом по показательному закону (в квадрате, если числа двоичные), т.е. если
N2=(N1)2,
то
I2 = 2 * I1,
F(N1*N1)=
F(N1) + F(N1).
Это невозможно, если количество информации выражается линейной функцией от количества элементов в множестве. Но известна функция, обладающая именно таким свойством: это Log:
Log2(N2) =
Log2(N1)2= 2 * Log2(N1).
Это второе требование называется требованием аддитивности.
Таким образом, логарифмическая мера информации, предложенная Хартли, одновременно удовлетворяет условиям монотонности и аддитивности. Сам Хартли пришел к своей мере на основе эвристических соображений, подобных только что изложенным, но в настоящее время строго доказано, что логарифмическая мера для количества информации однозначно следует из этих двух постулированных им условий [391].
Минимальное количество информации получается при выборе одного из двух равновероятных вариантов. Это количество информации принято за единицу измерения и называется "бит".
4.2.2. ПОДХОД К.ШЕННОНА
Клод Шеннон основывается на теоретико–вероятностном подходе. Это связано с тем, что исторически шенноновская теория информации выросла из потребностей теории связи, имеющей дело со статистическими характеристиками передаваемых сообщений и каналов связи.
Пусть существует некоторое конечное множество событий (состояний системы): X={x1, x2, …, xN}, которые могут наступать с вероятностями: p(xi), соответственно, причем множество вероятностей удовлетворяет естественному условию нормировки:
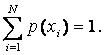
Исходное множество событий характеризуется некоторой неопределенностью, т.е. энтропией Хартли, зависящей, как мы видели выше, только от мощности множества. Но Шеннон обобщает это понятие, учитывая, что различные события в общем случае не равновероятны. Например, неопределенность системы событий: {монета упала "орлом", монета упала "решкой"}, значительно выше, чем неопределенность событий: {монета упала "орлом", монета упала "ребром"}, так как в первом случае варианты равновероятны, а во втором случае вероятности вариантов сильно отличаются:
|
|
(4. 1) |
Если измерять количество информации изменением степени неопределенности, то шенноновское количество информации численно совпадает с энтропией исходного множества:
|
|
(4. 2) |
4.2.3. СВЯЗЬ ФОРМУЛ К. ШЕННОНА И Р. ХАРТЛИ
Следуя
[391], приведем вывод
выражения Шеннона (4.2) непосредственно из выражения Хартли для количества
информации: I=Log2(N).
Пусть события исходного множества мощности N равновероятны:
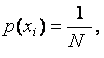
тогда учитывая, что

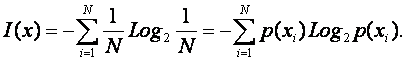
Остается предположить, что это выражение верно и для случая, когда события неравновероятны [391]. В этом предположении и состоит обобщение Клода Шеннона, составившее целую эпоху в развитии современной теории информации.
4.2.4. СРАВНЕНИЕ ПОДХОДОВ Р.ХАРТЛИ И К.ШЕННОНА
Чрезвычайно важным и принципиальным является то обстоятельство, что для построения меры Хартли используется лишь понятие "многообразие", которое накладывает на элементы исходного множества лишь одно условие (ограничение): должна существовать возможность отличать эти элементы один от другого.
В теории Шеннона существенным образом используется статистика, причем предполагается, что случайные события (состояния системы) распределены по нормальному закону.
Таким образом, различие между подходами Хартли и Шеннона к построению теории информации соответствует различию между непараметрическими и параметрическими методами в статистике.
Если говорить более конкретно, то очевидно, что мера Шеннона асимптотически переходит в меру Хартли при условии, что вероятности всех событий (состояний) равны.
В статистике доказано [273, 391] фундаментальное свойство энтропии случайного процесса, состоящее в том, что при условии нормальности распределения и достаточно больших выборках все множество событий можно разделить на две основные группы:
- высоковероятные события (считающиеся заслуживающими изучения);
- маловероятные события (считаются не заслуживающими особого внимания).
Причем высоковероятные события с высокой
точностью равновероятны. При
увеличении размерности выборки доля "заслуживающих внимания" событий
неограниченно уменьшается и мера Шеннона асимптотически переходит в меру
Хартли. Поэтому можно считать, что при больших нормально распределенных
выборках мера Хартли является оправданным упрощением меры Шеннона.
4.3. ИНФОРМАЦИЯ КАК МЕРА СНЯТИЯ НЕОПРЕДЕЛЕННОСТИ
Как было показано выше, теория информация применима в АСУ для решения задач идентификации состояния сложного объекта управления (задача распознавания) и принятия решения о выборе многофакторного управляющего воздействия (обратная задача распознавания). В данном разделе приведем математический аппарат из теории информации, позволяющий решить эти задачи на основе построения и применения информационной модели СОУ.
Процесс получения информации можно интерпретировать как изменение неопределенности в вопросе о том, от какого источника отправлено сообщение в результате приема сигнала по каналу связи.
Формально эту модель можно представить следующим образом. Пусть есть два взаимосвязанных множества:
1. Множество из N информационных источников {xi}, априорные вероятности предъявления которых равны p(xi).
2. Множество из M признаков {yj}, которые встречаются с априорными вероятностями p(yj) и условными вероятностями: p(xi|yj).
Априорная вероятность наблюдения признака – это средняя вероятность его наблюдения при предъявлении информационных источников (объектов) из исходного множества, а условная вероятность – вероятность его наблюдения при предъявлении определенного из них.
До получения информации ситуация характеризуется неопределенностью того, от какого источника она будет направлена, т.е. априорной энтропией:
|
|
(4. 3) |
Допустим, что множества информационных источников и сообщений о них никак не связаны (представляют собой независимые события), т.е. связаны совершенно случайным образом. Это означает, что события из этих двух множеств независимы друг от друга.
Пусть,
например, pij – есть
вероятность наступления события (xi,yj),
т.е. вероятность того, что если в сообщении был признак yj, то это сообщение от источника xi:
|
pij=pipj. |
(4. 4) |
Тогда в соответствии с фундаментальным определением Шеннона, энтропия множества XY, являющегося объединением множеств источников и сообщений, будет иметь вид:
|
|
(4. 5) |
Подставив в эту формулу выражение для вероятности (4), получим:
|
|
(4.
6) |
Здесь использовано классическое определение энтропии (1) и учтено условие нормировки вероятностей:
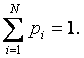
Таким образом, для независимых источников и сообщений получаем:
|
H(XY)=H(X)+H(Y). |
(4.
7) |
Обобщим это выражение на тот случай , когда содержание сообщений связано с тем, от какого они информационного источника.
Будем считать, что энтропия объединения множеств информационных источников и сообщений XY по прежнему определяется выражением Шеннона:
|
|
(4. 8) |
Однако вероятность совместного наступления зависимых событий:
- "активен i–й информационный источник";
- "в сообщении наблюдается j–й признак"
будет равна
|
|
(4. 9) |
где![]() – условная вероятность наблюдения признака yj в информационном сообщении
от источника xi. Тогда,
аналогично для энтропии объединенного множества получим выражение:
– условная вероятность наблюдения признака yj в информационном сообщении
от источника xi. Тогда,
аналогично для энтропии объединенного множества получим выражение:
|
|
(4. 10) |
|
H(XY)=H(X)+H(Y|X). |
(4. 11) |
В этом
выражении учтено условие нормировки: 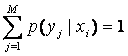 , а также приведенное выше выражение для энтропии H(X). Второе слагаемое обозначим: H(Y|X) и назовем условной энтропией
множества признаков из сообщений от информационных источников:
, а также приведенное выше выражение для энтропии H(X). Второе слагаемое обозначим: H(Y|X) и назовем условной энтропией
множества признаков из сообщений от информационных источников:
|
|
(4. 12) |
Учитывая (9), окончательно получаем:
|
|
(4. 13) |
Условной
энтропией H(Y|X) измеряется степень
неопределенности множества Y после
снятия неопределенности множества X.
Так как, очевидно, (xi,yj)=(yj,xi),
то аналогично, условной энтропией H(X/Y) измеряется степень неопределенности множества X после снятия
неопределенности множества Y:
|
H(XY)=H(X)+H(Y|X)=H(Y)+H(X|Y)=H(YX). |
(4. 14) |
Фактически,
условная энтропия H(X/Y) показывает нам, насколько много информации для
идентификации информационных источников мы в среднем получаем из
сообщений от них.
4.4. ИНФОРМАЦИЯ КАК МЕРА СООТВЕТСТВИЯ ОБЪЕКТОВ
ОБОБЩЕННЫМ ОБРАЗАМ КЛАССОВ
Количество информации является мерой соответствия распознаваемого объекта (его состояния) обобщенному образу класса, определенное на основе информации о признаках этого объекта.
Количество информации есть количественная мера степени снятия неопределенности: информация, содержащаяся в множестве Y относительно множества X есть уменьшение степени неопределенности множества X, возникающее в результате снятия неопределенности множества Y.
В нашем случае
первое множество – это множество признаков наблюдаемого объекта, а второе –
множество классов. До наблюдения объекта с системой признаков Y неопределенность наших знаний о принадлежности
этого объекта к классу была H(X)
(априорная энтропия), после наблюдения системы признаков Y эта неопределенность уменьшилась и стала равна H(X|Y) (апостериорная энтропия). Количество информации о том, что наблюдаемый
объект с системой признаков Y относится к классу X, равно уменьшению
неопределенности наших знаний об этом, которое произошло в результате
обнаружения у объекта признаков, т.е. равно разности априорной и апостериорной
энтропии этого класса:
|
|
(4. 15) |
Если после обнаружения системы признаков неопределенность знаний о
принадлежности объекта к классу стала равна нулю H(X|Y)=0, т.е. это стало
известно точно, то количество информации просто равно априорной энтропии. Если
же это стало известно лучше, но еще не до конца, то количество информации будет
меньше, чем априорная энтропия как раз на величину оставшейся, т.е. еще не
снятой неопределенности. Поэтому энтропия
– это недостающая информация (Больцман).
Перепишем выражение (15) в явной форме, подставив в него выражения для априорной и апостериорной энтропии из (3) и (13):
|
|
(4. 16) |
Учитывая, что
|
|
(4. 17) |
получаем выражение для среднего количества информации, которое содержится в сообщениях об источниках информации
|
|
(4. 18) |
или окончательно:
|
|
(4. 19) |
Находим выражение, связывающее информацию и взаимную энтропию, основываясь на (15):
|
|
(4. 20) |
Учитывая в выражении (20) условие симметричности (14), получаем:
|
I(X,Y)=I(Y,X), |
(4. 21) |
т.е. количество информации в
признаках об объектах (сообщениях об источниках информации) то же самое, что и
в объектах о признаках или в источниках информации о сообщениях, так как это одна и та же информация. По
этой причине эту информацию иногда называют взаимной,
так как она отражает определенное отношение двух множеств и не существует сама
по себе независимо от них или только когда есть лишь одно из них.
Подставляя H(X|Y) из (14) в выражение (20) получаем:
|
|
(4. 22) |
Таким образом, энтропия системы, состоящей
из объединения двух подсистем, меньше суммы индивидуальных энтропий этих
подсистем на величину взаимной информации, содержащейся в каждой из подсистем
относительно другой подсистемы.
АСУ как раз и выступает информационным системообразующим фактором, объединяющим подсистемы в единую систему, имеющую меньшую суммарную энтропию, чем ее части.
Это очень похоже на своеобразный
информационный аналог известного в физике "дефекта масс". Так
называется физический эффект, состоящий в том, что масса системы меньше сумм
масс ее частей на величину массы, соответствующей (по формуле E=mc2) энергии их взаимодействия [71, 392]. Подобные аналогии могут быть продолжены значительно
дальше [196]. Из этого следует, что информация это
и есть то интегрирующее начало, которое делает систему системой, объединяя
ее части в целое, т.е. по сути дела информация есть то, без чего система
разрушается на части.
4.5. КОЛИЧЕСТВО ИНФОРМАЦИИ В ИНДИВИДУАЛЬНЫХ
СОБЫТИЯХ И ЛЕММА НЕЙМАНА–ПИРСОНА
Следуя традиции, заложенной Шенноном, до сих пор анализировалось среднее количество информации, приходящееся на любую пару состояний (xi,yj) объекта X и сообщения Y. Эта характеристика естественна при рассмотрении особенностей стационарно функционирующих информационных систем, когда играют роль лишь их среднестатистические характеристики.
В классическом анализе Шеннона идет речь лишь о передаче символов по одному информационному каналу от одного источника к одному приемнику. Его интересует прежде всего передача самого сообщения.
В данном исследовании ставится другая задача: идентифицировать информационный источник по сообщению от него. Поэтому метод Шеннона был обобщен путем учета в математической модели возможности существования многих источников информации, о которых к приемнику по зашумленному каналу связи приходят не отдельные символы–признаки, а сообщения, состоящие из последовательностей символов (признаков) любой длины.
Следовательно, ставится задача идентификации информационного источника по сообщению от него, полученному приемником по зашумленному каналу. Метод, являющийся обобщением метода К.Шеннона, позволяет применить классическую теорию информации для построения моделей систем распознавания образов и принятия решений, ориентированных на применение для синтеза адаптивных АСУ сложными объектами.
Для решения поставленной задачи необходимо вычислять не средние
информационные характеристики, а количество информации, содержащееся в
конкретном j–м признаке (символе) о том, что он пришел от данного i–го
источника информации. Это позволит определить и суммарное количество информации
в сообщении о каждом информационном источнике, что дает интегральный критерий
для идентификации СОУ.
Логично предположить, что среднее количество информации, содержащейся в системе признаков о системе классов
|
|
(4. 23) |
является ничем иным, как усреднением (с учетом условной вероятности наблюдения) "индивидуальных количеств информации", которые содержатся в конкретных признаках о конкретных классах (источниках), т.е.:
|
|
(4. 24) |
Это выражение определяет так называемую
"плотность информации", т.е. количество информации, которое
содержится в одном отдельно взятом факте наблюдения j–го символа (признака) на
приемнике о том, что этот символ (признак) послан i–м источником.
Если в сообщении содержится M символов, то
суммарное количество информации о принадлежности данного сообщения i–му
информационному источнику (классу) составляет:
|
|
(4. 25) |
Необходимо отметить, что применение сложения в выражении (25) является вполне корректным и оправданным, так как информация с самого начала вводилась как аддитивная величина, для которой операция сложения является корректной.
Преобразуем выражение (25) к виду, более удобному для практического применения. Для этого, используя результаты работы [391], выразим вероятности встреч признаков через частоты их наблюдения:
|
|
(4. 26) |
Подставив (26) в (25), получим:
|
|
(4. 27) |
Если ранжировать классы в порядке убывания суммарного количества информации о принадлежности к ним, содержащейся в данном сообщении (т.е. описании объекта), и выбирать первый из них, т.е. тот, о котором в сообщении содержится наибольшее количество информации, то мы получим обоснованную статистическую процедуру, основанную на классической теории информации, оптимальность которой доказывается в фундаментальной лемме Неймана–Пирсона [273].
4.6. ЧИСЛЕННЫЙ ПРИМЕР АДАПТИВНОЙ АСУ СС,
ОСНОВАННОЙ НА МЕРЕ ШЕННОНА И ЛЕММЕ
НЕЙМАНА-ПИРСОНА
Рассмотрим упрощенный численный пример использования данного подхода для идентификации состояния сложной технической системы и выработки управляющего воздействия.
При этом в
качестве технической системы рассмотрим ФВЭУ,
т.е. продолжим конкретизацию 1-го технического примера из главы 1 данной
работы.
Различные имеющие практические значение режимы
энергораспределения ФВЭУ приведены в табл. 4.2 в соответствии с работой [316]:
Таблица 4. 2
РЕЖИМЫ ЭНЕРГОРАСПРЕДЕЛЕНИЯ
|
№ п/п |
Наименование градации |
|
1 |
Режим– 1: все группы потребителей
откл. Заряд накопителя |
|
2 |
Режим– 2: 2–4 группы потребителей
откл. Заряд накопителя |
|
3 |
Режим– 3: 3–4 группы потребителей
откл. Заряд накопителя |
|
4 |
Режим– 4: 4 группа потребителей откл. Заряд
накопителя |
|
5 |
Режим– 5: 3 группа потребителей откл. Заряд
накопителя |
|
6 |
Режим– 6: все группы потребителей
ПОДКЛ. Заряд накопителя |
|
7 |
Режим– 7: 2–4 группы потребителей
откл. Разряд накопителя |
|
8 |
Режим– 8: 3–4 группы потребителей
откл. Разряд накопителя |
|
9 |
Режим– 9: 4 группа потребителей откл. Разряд накопителя |
|
10 |
Режим–10: 3 группа потребителей откл. Разряд накопителя |
|
11 |
Режим–11: все группы потребителей
ПОДКЛ. Разряд накопителя |
В целях повышения наглядности опишем ФВЭУ минимальным количеством факторов (табл. 4.3):
Таблица 4. 3
ФАКТОРЫ
|
Кодирование |
Наименования шкал градаций |
||
|
Из[316] |
Новое |
||
|
Шкала 1: "Текущий баланс
энергосистемы" |
|||
|
X |
1 |
1 |
> 0 для 1–й, 2–й, 3–й, 4–й групп
нагрузок |
|
2 |
2 |
> 0 только для 1–й, 2–й, 3–й групп
нагрузок |
|
|
3 |
3 |
> 0 только для 1–й, 2–й групп
нагрузок |
|
|
4 |
4 |
> 0 только для 1–й группы нагрузок |
|
|
5 |
5 |
< 0 для 1–й группы нагрузок |
|
|
Шкала 2: "Состояние заряженности
аккумуляторной батареи" |
|||
|
Y |
1 |
6 |
Накопитель полностью заряжен 95%
<= Q <= 100% |
|
2 |
7 |
Накопитель хорошо заряжен 75% <= Q < 95% |
|
|
3 |
8 |
Накопитель слабо заряжен 30% <= Q < 75% |
|
|
4 |
9 |
Накопитель полностью разряжен 0%
<= Q <= 30% |
|
|
Шкала 3: "Прогноз поступления
возобновляемой энергии" |
|||
|
Z |
1 |
10 |
Прогнозируемый интегральный баланс
положителен |
|
2 |
11 |
Прогнозируемый интегральный баланс
отрицателен |
|
Задача выбора режима энергораспределения на основе значений факторов представляет собой сложную задачу, не имеющую однозначного решения. Поэтому были использованы экспертные оценки целесообразности выбора тех или иных режимов энергораспределения в зависимости от действующих факторов, обобщенные в табл. 4.4:
Таблица 4. 4
ОБУЧАЮЩАЯ ВЫБОРКА
|
№ п/п |
Факторы |
Режимы |
№ п/п |
Факторы |
Режимы |
||||||||||||||||||
|
X |
Y |
Z |
X |
Y |
Z |
||||||||||||||||||
|
1 |
1 |
6 |
10 |
11 |
|
|
|
|
|
|
|
21 |
1 |
6 |
11 |
6 |
|
|
|
|
|
|
|
|
2 |
1 |
7 |
10 |
10 |
11 |
|
|
|
|
|
|
22 |
1 |
7 |
11 |
5 |
6 |
|
|
|
|
|
|
|
3 |
1 |
8 |
10 |
9 |
10 |
11 |
|
|
|
|
|
23 |
1 |
8 |
11 |
4 |
5 |
6 |
|
|
|
|
|
|
4 |
1 |
9 |
10 |
8 |
9 |
10 |
11 |
|
|
|
|
24 |
1 |
9 |
11 |
3 |
4 |
5 |
6 |
|
|
|
|
|
5 |
2 |
6 |
10 |
10 |
11 |
|
|
|
|
|
|
25 |
2 |
6 |
11 |
5 |
6 |
|
|
|
|
|
|
|
6 |
2 |
7 |
10 |
9 |
10 |
11 |
|
|
|
|
|
26 |
2 |
7 |
11 |
4 |
5 |
6 |
|
|
|
|
|
|
7 |
2 |
8 |
10 |
8 |
9 |
10 |
11 |
|
|
|
|
27 |
2 |
8 |
11 |
3 |
4 |
5 |
6 |
|
|
|
|
|
8 |
2 |
9 |
10 |
7 |
8 |
9 |
10 |
11 |
|
|
|
28 |
2 |
9 |
11 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
9 |
3 |
6 |
10 |
9 |
10 |
11 |
|
|
|
|
|
29 |
3 |
6 |
11 |
4 |
5 |
6 |
|
|
|
|
|
|
10 |
3 |
7 |
10 |
8 |
9 |
10 |
11 |
|
|
|
|
30 |
3 |
7 |
11 |
3 |
4 |
5 |
6 |
|
|
|
|
|
11 |
3 |
8 |
10 |
7 |
8 |
9 |
10 |
11 |
|
|
|
31 |
3 |
8 |
11 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
12 |
3 |
9 |
10 |
1 |
7 |
8 |
9 |
10 |
11 |
|
|
32 |
3 |
9 |
11 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
13 |
4 |
6 |
10 |
8 |
9 |
10 |
11 |
|
|
|
|
33 |
4 |
6 |
11 |
3 |
4 |
5 |
6 |
|
|
|
|
|
14 |
4 |
7 |
10 |
7 |
8 |
9 |
10 |
11 |
|
|
|
34 |
4 |
7 |
11 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
15 |
4 |
8 |
10 |
1 |
7 |
8 |
9 |
10 |
11 |
|
|
35 |
4 |
8 |
11 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
16 |
4 |
9 |
10 |
1 |
1 |
7 |
8 |
9 |
|
|
|
36 |
4 |
9 |
11 |
1 |
1 |
2 |
3 |
4 |
|
|
|
|
17 |
5 |
6 |
10 |
7 |
8 |
9 |
10 |
11 |
|
|
|
37 |
5 |
6 |
11 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
18 |
5 |
7 |
10 |
1 |
7 |
8 |
9 |
10 |
11 |
|
|
38 |
5 |
7 |
11 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
19 |
5 |
8 |
10 |
1 |
1 |
7 |
8 |
9 |
10 |
11 |
|
39 |
5 |
8 |
11 |
1 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
20 |
5 |
9 |
10 |
1 |
1 |
1 |
7 |
8 |
9 |
10 |
11 |
40 |
5 |
9 |
11 |
1 |
1 |
1 |
2 |
3 |
4 |
5 |
6 |
На основе данных обучающей выборки получена матрица абсолютных частот (табл. 4.5), в которой отражено, сколько раз каждый фактор встретился при выборе каждого режима энергораспределения.
Таблица 4. 5
МАТРИЦА АБСОЛЮТНЫХ ЧАСТОТ
|
|
Режимы энергораспределения ФВЭУ |
|||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
||
|
Факторы |
1 |
0 |
0 |
0 |
2 |
3 |
4 |
0 |
0 |
2 |
3 |
5 |
|
2 |
0 |
0 |
2 |
3 |
4 |
4 |
0 |
2 |
3 |
4 |
4 |
|
|
3 |
2 |
2 |
3 |
4 |
4 |
4 |
2 |
3 |
4 |
4 |
4 |
|
|
4 |
6 |
3 |
4 |
4 |
4 |
4 |
3 |
4 |
4 |
3 |
3 |
|
|
5 |
12 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
|
|
6 |
0 |
0 |
2 |
3 |
4 |
5 |
0 |
2 |
3 |
4 |
5 |
|
|
7 |
2 |
2 |
3 |
4 |
5 |
5 |
2 |
3 |
4 |
5 |
5 |
|
|
8 |
6 |
3 |
4 |
5 |
5 |
5 |
3 |
4 |
5 |
5 |
5 |
|
|
9 |
12 |
4 |
5 |
5 |
5 |
5 |
4 |
5 |
5 |
4 |
5 |
|
|
10 |
10 |
0 |
0 |
0 |
0 |
0 |
10 |
14 |
17 |
18 |
20 |
|
|
11 |
10 |
10 |
14 |
17 |
19 |
20 |
0 |
0 |
0 |
0 |
0 |
|
Из матрицы абсолютных частот с применением выражения 4.26 рассчитана матрица информативностей (табл.4.6).
Таблица 4. 6
МАТРИЦА ИНФОРМАТИВНОСТЕЙ
|
|
Режимы энергораспределения ФВЭУ |
|||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
||
|
Факторы |
1 |
--- |
--- |
--- |
8,92 |
8,50 |
8,15 |
--- |
--- |
8,92 |
8,42 |
7,83 |
|
2 |
--- |
--- |
9,06 |
8,79 |
8,53 |
8,61 |
--- |
9,06 |
8,79 |
8,46 |
8,61 |
|
|
3 |
10,08 |
8,98 |
8,94 |
8,84 |
9,00 |
9,08 |
8,98 |
8,94 |
8,84 |
8,92 |
9,08 |
|
|
4 |
8,71 |
8,61 |
8,75 |
9,06 |
9,23 |
9,30 |
8,61 |
8,75 |
9,06 |
9,56 |
9,71 |
|
|
5 |
8,02 |
8,51 |
9,06 |
9,37 |
9,53 |
9,61 |
8,51 |
9,06 |
9,37 |
9,46 |
9,61 |
|
|
6 |
--- |
--- |
9,16 |
8,89 |
8,64 |
8,39 |
--- |
9,16 |
8,89 |
8,56 |
8,39 |
|
|
7 |
10,23 |
9,13 |
9,09 |
8,99 |
8,83 |
8,91 |
9,13 |
9,09 |
8,99 |
8,75 |
8,91 |
|
|
8 |
8,97 |
8,87 |
9,00 |
8,99 |
9,15 |
9,23 |
8,87 |
9,00 |
8,99 |
9,08 |
9,23 |
|
|
9 |
8,20 |
8,69 |
8,92 |
9,23 |
9,39 |
9,47 |
8,69 |
8,92 |
9,23 |
9,64 |
9,47 |
|
|
10 |
9,06 |
--- |
--- |
--- |
--- |
--- |
7,96 |
8,03 |
8,06 |
8,06 |
8,06 |
|
|
11 |
9,08 |
7,98 |
8,04 |
8,08 |
8,08 |
8,08 |
--- |
--- |
--- |
--- |
--- |
|
Данная матрица информативностей и представляет собой конкретную информационную модель ФВЭУ, на основе которой САУ может принимать решения о выборе наиболее целесообразного режима энергораспределения на основе данных о действующих факторах.
Если из табл. 4.6 выбрать строки, соответствующие действующей системе факторов (например: X=1, Y=1, Z=1), просуммировать количество информации в данной системе факторов для каждого режима энергораспределения ФВЭУ и проранжировать режимы в порядке убывания количества информации о них, то получим табл. 4.7.
Таблица 4. 7
РАСЧЕТ КОЛИЧЕСТВА ИНФОРМАЦИИ О РЕЖИМАХ ФВЭУ,
СОДЕРЖАЩЕЙСЯ В СИСТЕМЕ ФАКТОРОВ (X=1, Y=1, Z=1)
|
|
Режимы энергораспределения ФВЭУ |
|||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
||
|
X |
1 |
|
|
|
8,92 |
8,50 |
8,15 |
|
|
8,92 |
8,42 |
7,83 |
|
Y |
6 |
|
|
9,16 |
8,89 |
8,64 |
8,39 |
|
9,16 |
8,89 |
8,56 |
8,39 |
|
Z |
10 |
9,06 |
|
|
|
|
|
7,96 |
8,03 |
8,06 |
8,06 |
8,06 |
|
Сумма |
9,06 |
0,00 |
9,16 |
17,82 |
17,14 |
16,55 |
7,96 |
17,19 |
25,88 |
25,04 |
24,29 |
|
|
Ранг |
9 |
11 |
8 |
4 |
6 |
7 |
10 |
5 |
1 |
2 |
3 |
|
Если из табл. 4.7 выбрать режимы энергораспределения в порядке убывания их ранга, соответствующего количеству информации, то получим табл. 4.8.
Таблица 4. 8
ВЫБОР РЕЖИМА ФВЭУ (ПРИ X=1,
Y=1, Z=1)
Ранг |
Кол-во информации |
Код |
Наименование
режима |
|
1 |
25,88 |
9 |
Режим– 9: 4
гр.потр. откл. Разряд АБ |
|
2 |
25,04 |
10 |
Режим–10: 3
гр.потр. откл. Разряд АБ |
|
3 |
24,29 |
11 |
Режим–11: все гр.потр.ПОДКЛ. Разряд АБ |
|
4 |
17,82 |
4 |
Режим– 4: 4
гр.потр. откл. Заряд АБ |
|
5 |
17,19 |
8 |
Режим– 8: 3–4 гр.потр. откл. Разряд АБ |
|
6 |
17,14 |
5 |
Режим– 5: 3
гр.потр. откл. Заряд АБ |
|
7 |
16,55 |
6 |
Режим– 6: все гр.потр.ПОДКЛ. Заряд АБ |
|
8 |
9,16 |
3 |
Режим– 3: 3–4 гр.потр. откл. Заряд АБ |
|
9 |
9,06 |
1 |
Режим– 1: все гр.потр. откл. Заряд АБ |
|
10 |
7,96 |
7 |
Режим– 7: 2–4 гр.потр. откл. Разряд АБ |
|
11 |
0,00 |
2 |
Режим– 2: 2–4 гр.потр. откл. Заряд АБ |
Предложенная методология позволяет выбрать рациональный режим энергораспределения ФВЭУ: для реализации выбирается тот режим, о котором в системе факторов {X, Y, Z} содержится максимальное количество информации (или один из таких режимов, если они очень близки по этому параметру).
4.7. ВЫВОДЫ
1. Распознавание образов есть принятие решения о принадлежности объекта или его состояния к определенному классу. Если до распознавания существовала неопределенность в вопросе о том, к какому классу относится распознаваемый объект или его состояние, то в результате распознавания эта неопределенность уменьшается, в том числе может быть и до нуля. Понятие информации может быть определено следующим образом: "Информация есть количественная мера степени снятия неопределенности". Количество информации является мерой соответствия распознаваемого объекта (его состояния) обобщенному образу класса.
2. Количество информации имеет ряд вполне определенных свойств. Эти свойства позволяют ввести понятие "количество информации в индивидуальных событиях", которое является весьма перспективным для применения в системах распознавания образов и поддержки принятия решений.
3. Рассмотрены фундаментальные основания теории информации и подходы Хартли и Шеннона, а также различные варианты их обобщения. Показано, что подход Шеннона в принципе непосредственно применим для построения систем распознавания образов и принятия решений, ориентированных на использование для синтеза адаптивных АСУ СС. Соответствующая математическая модель относится к классу многокритериальных моделей принятия решений.
4. Однако подход Шеннона имеет два принципиальных ограничения, снижающих степень его адекватности для достижения цели исследования:
- во-первых, он не позволяет количественно описать понятие "дезинформации";
- во-вторых, является параметрическим, т.е. базируется на предположении о гауссовском (нормальном) характере СОУ.
Актуальной является
задача поиска или разработки подхода, преодолевающего эти недостатки.
5. Приведен численный пример использования информационной меры Шеннона для решения задачи идентификации состояния ФВЭУ и выбора оптимального режима энергораспределения.