По
литературным данным [50] во многих ранее разработанных и современных АСУ (которые
мы будем называть «традиционными») в подсистемах идентификации состояния
объекта управления и выработки управляющих воздействий используются
детерминистские математические модели «прямого счета», которые однозначно и
достаточно просто определяют что делать с объектом управления, если у него
наблюдаются определенные внешние параметры.
При
этом не ставится, а значит и не решается вопрос о том, как связаны эти параметры с теми или иными состояниями объекта управления. Эта
позиция соответствует точке зрения, состоящей в том, что «по умолчанию»
принимается их взаимно-однозначная связь. Поэтому термины: «параметры объекта
управления» и «состояния объекта управления» рассматриваются как синонимы, а
понятие «состояние объекта управления» в явном виде вообще не вводится. Однако
очевидно, что в общем случае связь между наблюдаемыми параметрами объекта
управления и его состоянием имеет динамичный и вероятностный характер.
Таким образом,
традиционные АСУ по сути дела являются системами параметрического управления,
т.е. системами, которые управляют не состояниями объекта управления, а
лишь его наблюдаемыми параметрами. Решение
об управляющем воздействии принимается в таких системах как бы «вслепую», т.е.
без формирования целостного образа объекта управления и окружающей среды в их
текущем состоянии, а также без прогнозировании развития среды и реакции объекта
управления на те или иные управляющие воздействия на него, действующие
одновременно с прогнозируемым влиянием среды.
С позиций подхода,
развиваемого в данной работе, термин «принятие решений» едва ли вообще в полной
мере применим к традиционным АСУ. Дело в том, что, по мнению авторов, «принятие
решений», как минимум, предполагает целостное видение объекта в окружающей
среде, причем не только в их актуальном состоянии, но и в динамике и во взаимодействии как друг с
другом, так и с системой управления, предполагает рассмотрение различных
альтернативных вариантов развития всей этой системы, а также сужение
многообразия (редукцию) этих альтернатив на основе определенных целевых
критериев. Ничего этого, очевидно, нет в традиционных АСУ, или есть, но в очень
упрощенном виде.
Конечно,
традиционный подход является адекватным и его применение вполне корректно и
оправдано в тех случаях, когда объект управления действительно является
стабильной и жестко детерминированной системой, а влиянием окружающей среды на
него можно пренебречь.
Однако
в других случаях этот подход малоэффективен.
Если
объект управления динамичен, то модели, лежащие в основе алгоритмов управления
им, быстро становятся неадекватными, так как изменяются отношения между
входными и выходными параметрами, а также сам набор существенных параметров. По
сути дела это означает, что традиционные АСУ способны управлять состоянием объекта
управления лишь вблизи точки равновесия путем слабых управляющих воздействий на
него, т.е. методом малых возмущений. Вдали же от состояния равновесия с
традиционной точки зрения поведение объекта управления выглядит непредсказуемым
и неуправляемым.
С
другой стороны если нет однозначной связи между входными и выходными параметрами
объекта управления (т.е. между входными параметрами и состоянием объекта),
иначе говоря эта связь имеет выраженный вероятностный характер, то
детерминистские модели, в которых предполагается, что результатом измерения
некоторого параметра является просто число, изначально неприменимы. Кроме того,
вид этой связи просто может быть неизвестным, и тогда необходимо исходить из
самого общего предположения: что она вероятностная.
Автоматизированная
система управления, построенная на традиционных принципах, может работать
только на основе параметров, закономерности связей которых уже известны, изучены
и отражены в математической модели, авторы же ставят задачу разработку таких
подходов к проектированию АСУ, которые позволят создать системы, способные
выявлять и набор наиболее значимых параметров, и определять характер связей
между ними и состояниями объекта управления.
В
этом случае необходимо применять более развитые и адекватные реальной ситуации
методы измерений:
1.
классификация или распознавание образов (обучение на основе обучающей выборки,
адаптивность алгоритмов распознавания, адаптивность наборов классов и
исследуемых параметров, выделение наиболее существенных параметров и снижение
размерности описания при сохранении заданной избыточности, и т.д.);
2. статистические
измерения, когда результатом измерения некоторого параметра является не
отдельное число, а вероятностное распределение: изменение статистической переменной
означает не изменение ее значения самого по себе, а изменение характеристик
вероятностного распределения ее значений.
В
итоге АСУ, основанные на традиционном детерминистском подходе, практически не работают
с многопараметрическими
слабодетерминированными объектами управления, такими, например, как макро-
и микросоциально-экономические системы в условиях динамичной экономики
«переходного периода», иерархические элитные и этнические группы, социум и электорат,
физиология и психика человека, природные и искусственные экосистемы, и многие
другие.
Весьма
знаменательно, что в середине 80-х годов школа И.Пригожина развивает подход,
согласно которому в развитии любой системы (в том числе и человека) чередуются
периоды, в течение которых система ведет себя то как «в основном
детерминированная», то как «в основном случайная». Естественно, реальная
система управления должна устойчиво управлять объектом управления не только на
«детерминистских» участках его истории, но и в точках, когда его дальнейшее
поведение становится в высокой степени неопределенным. Уже одно это означает,
что необходимо разрабатывать подходы к управлению системами, в поведении
которых есть большой элемент случайности (или того, что в настоящее время
описывается как случайность).
Поэтому с позиций,
развиваемых в данной работе, традиционные АСУ не представляют лишь частный интерес.
По мнению авторов, в
состав перспективных АСУ, управляющих многопараметрическими
слабодетерминированными системами [9], в качестве существенных функциональных
звеньев войдут подсистемы идентификации и прогнозирования состояний среды и
объекта управления, основанные на методах искусственного интеллекта (прежде
всего распознавания образов), методов поддержки принятия решений и теории
информации.
Идентификация – это процесс восстановления целостного образа
объекта по его разрозненным фрагментам (признакам) и сравнения образа объекта с
набором образов, уже имеющихся в системе идентификации. По мнению авторов,
детерминистская связь является частным случаем статистической, т.е это
статистическая связь с вероятностью равной 1. Поэтому, вообще говоря, признаки
связаны с образом статистически. Задача идентификации состояния объекта
представляет собой задачу распознавания образов.
В данной главе дан краткий обзор методов распознавания,
проанализированы перспективные направления развития методов распознавания
образов, раскрыта роль адаптивного семантического
анализа в процессах восприятия и познания, ориентации в среде и эффективного
управления. Сделаны выводы по основным направлениям данного исследования.
В данном разделе сформулированы принципы классификации
методов распознавания и кратко
освещена их суть. Кроме того эти методы проанализированы на предмет их
соответствия целям и задачам настоящего исследования. Отметим, что данный
раздел практически полностью основан на работе [50] и по сути является лишь
кратким изложением материалов, содержащихся в ней и на что большее не
претендует.
Распознаванием образов
называются задачи построения и применения формальных операций над числовыми или
символьными отображениями
объектов реального или идеального мира, результаты решения которых отражают
отношения эквивалентности между этими объектами. Отношения эквивалентности
выражают принадлежность оцениваемых объектов к каким-либо классам,
рассматриваемым как самостоятельные семантические единицы.
При построении алгоритмов распознавания классы
эквивалентности могут задаваться исследователем, который пользуется
собственными содержательными представлениями или использует внешнюю
дополнительную информацию о сходстве и различии объектов в контексте решаемой
задачи. Тогда говорят о “распознавании с учителем”
[145]. В противном случае, т.е. когда автоматизированная система решает задачу
классификации без привлечения внешней обучающей информации,
говорят об автоматической классификации или “распознавании без учителя”.
Большинство алгоритмов распознавания образов требует привлечения весьма значительных
вычислительных мощностей, которые могут быть обеспечены только высокопроизводительной
компьютерной техникой.
Различные авторы (Барабаш Ю.Л. [15],
Васильев В.И. [26], Горелик А.Л.,
Скрипкин В.А. [37], Дуда
Р., Харт П. [45],
Кузин Л.Т. [60],
Перегудов Ф.И., Тарасенко Ф.П. [99],
Темников Ф.Е. [121], Ту Дж., Гонсалес Р. [145],
Уинстон П. [126], Фу К. [130], Цыпкин Я.З. [133] и
др.) дают различную типологию методов распознавания образов. Одни
авторы различают параметрические, непараметрические и
эвристические методы, другие - выделяют группы методов, исходя из исторически
сложившихся школ и направлений в данной области. Например, в работе [46], в которой
дан прекрасный обзор методов распознавания, используется следующая типология
методов распознавания образов:
методы, основанные на принципе
разделения;
статистические методы;
методы, построенные на основе
“потенциальных функций”;
методы вычисления оценок (голосования);
методы, основанные на исчислении
высказываний, в частности на аппарате алгебры логики.
Подобная типология методов распознавания с той или
иной степенью детализации встречается во многих работах по распознаванию. В то же
время известные типологии не учитывают одну очень существенную характеристику,
которая отражает специфику способа
представления знаний о предметной области с помощью какого-либо формального
алгоритма распознавания образов. Д.А.Поспелов (1990)
выделяет два основных способа представления знаний [46]:
1. Интенсиональное представление
- в виде схемы связей между атрибутами (признаками).
2. Экстенсиональное представление
- с помощью конкретных фактов (объекты, примеры).
Интенсиональное представление
фиксируют закономерности и связи, которыми объясняется структура данных. Применительно
к диагностическим задачам такая фиксация заключается в определении операций над
атрибутами (признаками) объектов, приводящих к требуемому диагностическому
результату. Интенсиональные представления
реализуются посредством операций над значениями атрибутов и не предполагают
произведения операций над конкретными информационными фактами (объектами).
В свою очередь, экстенсиональные представления
знаний связаны с описанием и фиксацией конкретных объектов из предметной
области и реализуются в операциях, элементами которых служат объекты как
целостные системы.
Можно провести
аналогию между интенсиональными и экстенсиональными представлениями знаний и
механизмами, лежащими в основе деятельности левого и правого полушарий
головного мозга человека. Если для правого полушария характерна целостная прототипная репрезентация окружающего мира,
то левое полушарие оперирует закономерностями, отражающими связи атрибутов этого
мира [52, с.28-29].
Описанные выше два фундаментальных способа представления
знаний позволяют предложить следующую классификацию методов распознавания образов:
Интенсиональные методы
распознавания образов -
методы, основанные на операциях с признаками.
Экстенсиональные методы
распознавания образов -
методы, основанные на операциях с объектами.
Необходимо особо
подчеркнуть, что с по мнению авторов существование именно этих двух и только
двух групп методов распознавания (оперирующих с признаками, и
оперирующих с объектами) глубоко закономерно и отражает фундаментальные
характеристики взаимодействия Реальности и Сознания. С этой точки зрения ни
один из этих методов, взятый отдельно от другого, не позволяет сформировать
адекватное отражение Реальности. Стало быть между этими методами существует
отношение дополнительности в смысле Н.Бора [19] и перспективные системы
распознавания должны обеспечивать реализацию обоих этих методов, а не только
какого-либо одного из них.
В приводимой ниже классификации основное внимание уделено
формальным методам распознавания образов и
поэтому опущено рассмотрение эвристического подхода к распознаванию, получившего
полное и адекватное развитие в экспертных системах. По поводу этого подхода
ограничимся лишь несколькими замечаниями.
Эвристический подход основывается на
трудно формализуемых знаниях и интуиции исследователя. В этом подходе
исследователь сам определяет, какую информацию и каким образом нужно
использовать для достижения требуемого эффекта распознавания.
Отличительной особенностью интенсиональных методов
является то, что в качестве элементов операций при построении и применении
алгоритмов распознавания образов они
используют различные характеристики признаков и их связей. Такими элементами
могут быть отдельные значения или интервалы значений признаков, средние
величины и дисперсии, матрицы связи признаков и т. п., над которыми производятся
действия, выражаемые в аналитической или конструктивной форме. При этом объекты
в данных методах не рассматриваются как целостные информационные единицы, а
выступают в роли индикаторов для оценки взаимодействия и поведения своих
атрибутов.
Группа интенсиональных методов
распознавания образов
обширна, и ее деление на подклассы носит в определенной мере условный характер.
Эти методы распознавания образов
заимствованы из классической теории статистических решений, в которой объекты
исследования рассматриваются как реализации многомерной случайной величины,
распределенной в пространстве признаков по какому-либо закону [37]. Они
базируются на байесовской схеме
принятия решений, апеллирующей к априорным вероятностям принадлежности объектов
к тому или иному распознаваемому классу и условным плотностям распределения
значений вектора признаков. Данные методы сводятся к определению отношения
правдоподобия в различных областях многомерного пространства признаков.
Группа методов, основанных на оценке плотностей
распределения значений признаков имеет прямое отношение к методам
дискриминантного анализа.
Байесовский подход к принятию
решений и относится к наиболее разработанным в современной статистике так
называемым параметрическим методам, для которых считается известным
аналитическое выражение закона распределения (в данном случае нормальный закон)
и требуется оценить лишь небольшое количество параметров (векторы средних
значений и ковариационные матрицы).
К этой группе относится и метод вычисления отношения
правдоподобия для независимых признаков. Этот метод, за исключением
предположения о независимости признаков (которое в действительности практически
никогда не выполняется), не предполагает знания функционального вида закона
распределения. Поэтому его можно отнести к непараметрическим [46].
Другие непараметрические методы,
применяемые тогда, когда вид кривой плотности распределения неизвестен и нельзя
сделать вообще никаких предположений о ее характере, занимают особое положение.
К ним относятся известные метод многомерных гистограмм, метод
“k-ближайших соседей, метод евклидова расстояния,
метод потенциальных функций и др., обобщением которых является метод,
получивший название “оценки Парзена” [46]. Эти
методы формально оперируют объектами как целостными структурами, но в
зависимости от типа задачи распознавания могут
выступать и в интенсиональной и в
экстенсиональной ипостасях.
Непараметрические методы анализируют относительные
количества объектов, попадающих в заданные многомерные объемы, и используют
различные функции расстояния между объектами обучающей выборки и
распознаваемыми объектами [46]. Для количественных признаков, когда их число
много меньше объема выборки, операции с объектами играют промежуточную роль в
оценке локальных плотностей распределения условных вероятностей и объекты не
несут смысловой нагрузки самостоятельных информационных единиц. В то же время,
когда количество признаков соизмеримо или больше числа исследуемых объектов, а
признаки носят качественный или дихотомический характер, то ни о каких
локальных оценках плотностей распределения вероятностей не может идти речи. В
этом случае объекты в указанных непараметрических методах
рассматриваются как самостоятельные информационные единицы (целостные
эмпирические факты) и данные методы приобретают смысл оценок сходства и
различия изучаемых объектов.
Таким образом, одни и те же технологические операции
непараметрических методов в зависимости
от условий задачи имеют смысл либо локальных оценок плотностей распределения
вероятностей значений признаков, либо оценок сходства и различия объектов.
В контексте интенсионального представления
знаний здесь рассматривается первая сторона непараметрических методов, как
оценок плотностей распределения вероятностей. Многие авторы отмечают, что на
практике непараметрические методы типа
оценок Парзена работают
хорошо [46]. Основными трудностями применения указанных методов считаются
необходимость запоминания всей обучающей выборки для
вычисления оценок локальных плотностей распределения вероятностей и высокая
чувствительность к непредставительности обучающей
выборки.
В данной группе методов считается известным общий вид
решающей функции и задан функционал ее качества.
На основании этого функционала по обучающей последовательности ищется наилучшее
приближение решающей функции [124]. Самыми распространенными являются
представления решающих функций в виде линейных и обобщенных нелинейных полиномов. Функционал
качества решающего правила обычно связывают с ошибкой классификации.
Основным достоинством методов, основанных на предположениях
о классе решающих функций, является ясность математической постановки задачи
распознавания, как задачи
поиска экстремума [124].
Решение этой задачи нередко достигается с помощью каких-либо градиентных алгоритмов.
Многообразие методов этой группы объясняется широким спектром используемых
функционалов качества
решающего правила и алгоритмов поиска экстремума. Обобщением рассматриваемых
алгоритмов, к которым относятся, в частности, алгоритм Ньютона, алгоритмы
перцептронного типа и др.,
является метод стохастической аппроксимации. В отличие от
параметрических методов распознавания успешность применения данной группы методов
не так сильно зависит от рассогласования теоретических
представлений о законах распределения объектов в пространстве признаков с
эмпирической реальностью. Все операции подчинены одной главной цели -
нахождению экстремума функционала качества
решающего правила. В то же время результаты параметрических и рассматриваемых
методов могут быть похожими. Как показано выше, параметрические методы для
случая нормальных распределений объектов в различных классах с равными
ковариационными матрицами
приводят к линейным решающим функциям. Отметим также, что алгоритмы отбора информативных
признаков в линейных диагностических моделях, можно интерпретировать как
частные варианты градиентных алгоритмов поиска экстремума.
Возможности градиентных алгоритмов
поиска экстремума, особенно в
группе линейных решающих правил, достаточно хорошо изучены. Сходимость этих
алгоритмов доказана только для случая, когда распознаваемые классы объектов
отображаются в пространстве признаков компактными геометрическими структурами.
Однако стремление добиться достаточного качества решающего правила нередко
может быть удовлетворено с помощью алгоритмов, не имеющих строгого
математического доказательства сходимости решения к
глобальному экстремуму [46].
К таким алгоритмам относится большая группа процедур
эвристического программирования, представляющих направление эволюционного
моделирования. Эволюционное моделирование является бионическим методом,
заимствованным у природы. Оно основано на использовании известных механизмов
эволюции с целью замены процесса содержательного моделирования сложного объекта
феноменологическим моделированием его эволюции.
Известным представителем эволюционного моделирования в
распознавании образов является
метод группового учета аргументов (МГУА) [46]. В
основу МГУА положен принцип самоорганизации, и алгоритмы
МГУА воспроизводят схему массовой селекции. В алгоритмах МГУА особым образом
синтезируются и отбираются
члены обобщенного полинома, который
часто называют полиномом
Колмогорова-Габора. Этот синтез и отбор производится с нарастающим усложнением,
и заранее нельзя предугадать, какой окончательный вид будет иметь обобщенный полином. Сначала
обычно рассматривают простые попарные комбинации
исходных признаков, из которых составляются уравнения решающих функций, как
правило, не выше второго порядка. Каждое уравнение анализируется как
самостоятельная решающая функция, и по обучающей выборке тем
или иным способом находятся значения параметров составленных уравнений. Затем
из полученного набора решающих функций отбирается часть в некотором смысле
лучших. Проверка качества отдельных решающих функций осуществляется на
контрольной (проверочной) выборке, что иногда называют принципом внешнего
дополнения. Отобранные частные решающие функции рассматриваются далее как
промежуточные переменные, служащие исходными аргументами для аналогичного
синтеза новых решающих функций и т. д. Процесс такого иерархического синтеза
продолжается до тех пор, пока не будет достигнут экстремум критерия
качества решающей функции, что на практике проявляется в ухудшении этого
качества при попытках дальнейшего увеличения порядка членов полинома
относительно исходных признаков.
Принцип самоорганизации, положенный в
основу МГУА, называют
эвристической самоорганизацией, так как весь
процесс основывается на введении внешних дополнений, выбираемых эвристически.
Результат решения может существенно зависеть от этих эвристик. От того, как
разделены объекты на обучающую и проверочную
выборки, как определяется критерий качества распознавания, какое
количество переменных пропускается в следующий
ряд селекции и т. д., зависит результирующая диагностическая
модель.
Указанные особенности алгоритмов МГУА свойственны и
другим подходам к эволюционному моделированию. Но отметим здесь еще одну
сторону рассматриваемых методов. Это - их содержательная сущность. С помощью
методов, основанных на предположениях о классе решающих функций (эволюционных и
градиентных), можно
строить диагностические модели высокой сложности и получать практически
приемлемые результаты. В то же время достижению практических целей в данном
случае не сопутствует извлечение новых знаний о природе распознаваемых
объектов. Возможность извлечения этих знаний, в частности знаний о механизмах
взаимодействия атрибутов (признаков), здесь принципиально ограничена заданной
структурой такого взаимодействия, зафиксированной в выбранной форме решающих
функций. Поэтому максимально, что можно сказать после построения той или иной
диагностической модели - это перечислить комбинации признаков и сами признаки,
вошедшие в результирующую модель. Но
смысл комбинаций, отражающих природу и структуру распределений исследуемых
объектов, в рамках данного подхода часто остается нераскрытым.
Логические методы распознавания образов
базируются на аппарате алгебры логики и позволяют оперировать информацией,
заключенной не только в отдельных признаках, но и в сочетаниях значений
признаков. В этих методах значения какого-либо признака рассматриваются как
элементарные события [46].
В самом общем виде логические методы можно охарактеризовать
как разновидность поиска по обучающей выборке
логических закономерностей и формирование некоторой системы логических решающих
правил (например, в виде конъюнкций элементарных событий), каждое из
которых имеет собственный вес. Группа логических методов разнообразна и
включает методы различной сложности и глубины анализа. Для дихотомических
(булевых) признаков
популярными являются так называемые древообразные
классификаторы, метод тупиковых тестов, алгоритм
“Кора” и другие. Более сложные методы основываются на формализации индуктивных
методов Д.С.Милля. Формализация
осуществляется путем построения квазиаксиоматической теории и
базируется на многосортной многозначной
логике с кванторами по кортежам
переменной длины [46].
Алгоритм “Кора”, как и другие логические методы
распознавания образов,
является достаточно трудоемким, поскольку при отборе конъюнкций необходим
полный перебор. Поэтому при применении логических методов предъявляются высокие
требования к эффективной организации вычислительного процесса, и эти методы
хорошо работают при сравнительно небольших размерностях пространства
признаков и только на мощных компьютерах.
Лингвистические методы распознавания образов
основаны на использовании специальных грамматик порождающих языки, с помощью
которых может описываться совокупность свойств распознаваемых объектов [130].
Для различных классов объектов выделяются непроизводные (атомарные)
элементы (подобразы, признаки) и
возможные отношения между ними. Грамматикой называют правила построения объектов
из этих непроизводных элементов
[130]. Таким образом, каждый объект
представляется совокупностью непроизводных элементов, “соединенных” между собой
теми или иными способами или, другими словами, “предложением” некоторого
“языка”. Авторы хотели бы особо подчеркнуть очень значительную на их взгляд
мировоззренческую ценность этой мысли. Путем синтаксического анализа
(грамматического разбора) “предложения” устанавливается его синтаксическая
“правильность” или, что эквивалентно, - может ли некоторая фиксированная
грамматика (описывающая класс) породить имеющееся описание объекта.
Грамматический разбор производится так называемым “синтаксическим
анализатором”, который представляет полное синтаксическое описание объекта в
виде дерева грамматического разбора, если объект является синтаксически
правильным (принадлежит классу, описываемому данной грамматикой). В противном
случае, объект либо отклоняется, либо подвергается анализу с помощью других
грамматик, описывающих другие классы объектов. Известны бесконтекстные, автоматные и
другие типы грамматик. Однако задача восстановления (определения) грамматик по
некоторому множеству высказываний (предложений - описаний объектов), порождающих
данный язык, является трудно формализуемой. В литературе приводится описание
эвристических правил автоматического восстановления грамматик для
конструирования и применения лингвистических алгоритмов распознавания образов.
В методах данной группы, в отличие от интенсионального направления,
каждому изучаемому объекту в большей или меньшей мере придается самостоятельное
диагностическое значение. По своей сути эти методы
близки к клиническому подходу, который рассматривает людей не как
проранжированную по тому или
иному показателю цепочку объектов, а как целостные системы, каждая из
которых индивидуальна и имеет особенную диагностическую ценность [46]. Такое бережное отношение к объектам
исследования не позволяет исключать или утрачивать информацию о каждом
отдельном объекте, что происходит при применении методов интенсионального
направления, использующих объекты только для обнаружения и фиксации
закономерностей поведения их атрибутов.
Основными операциями в распознавании образов с
помощью обсуждаемых методов являются
операции определения сходства и различия объектов. Объекты в указанной группе методов играют роль диагностических
прецедентов. При этом в зависимости от условий конкретной задачи роль
отдельного прецедента может меняться в самых широких пределах от главной до
весьма косвенного участия в процессе распознавания. В свою
очередь, условия задачи могут требовать для успешного решения участия
различного количества диагностических прецедентов от одного в каждом распознаваемом
классе до полного объема выборки, а также разных способов вычисления мер
сходства и различия объектов. Этими требованиями объясняется дальнейшее
разделение экстенсиональных методов на подклассы.
Это наиболее простой экстенсиональный метод
распознавания. Он
применяется, например, тогда, когда распознаваемые классы отображаются в
пространстве признаков компактными геометрическими группировками. В таком
случае обычно в качестве точки - прототипа выбирается центр геометрической
группировки класса (или ближайший к центру объект).
Для классификации неизвестного объекта находится ближайший к
нему прототип, и объект относится к тому же классу, что и этот прототип. Очевидно, никаких обобщенных образов
классов в данном методе не формируется.
В качестве меры близости могут применяться различные типы расстояний.
Часто для дихотомических признаков используется расстояние Хэмминга, которое в
данном случае равно квадрату евклидова расстояния. При этом решающее правило
классификации объектов эквивалентно линейной решающей функции.
Указанный факт
следует особо отметить. Он наглядно демонстрирует связь прототипной и признаковой репрезентации информации о
структуре данных. Пользуясь приведенным представлением, можно, например, любую
традиционную измерительную шкалу, являющуюся линейной
функцией от значений дихотомических признаков, рассматривать как гипотетический
диагностический прототип. В свою очередь, если анализ пространственной
структуры распознаваемых классов позволяет сделать вывод об их геометрической
компактности, то каждый из этих классов достаточно заменить одним прототипом
который, фактически эквивалентен линейной диагностической модели.
На практике, конечно, ситуация часто бывает отличной от
описанного идеализированного примера. Перед исследователем, намеревающимся
применить метод распознавания, основанный
на сравнении с прототипами диагностических классов, встают непростые проблемы.
Это, в первую очередь, выбор меры близости (метрики), от которого может существенно
измениться пространственная конфигурация распределения объектов. И, во-вторых,
самостоятельной проблемой является анализ многомерных структур
экспериментальных данных. Обе эти проблемы
особенно остро встают перед исследователем в условиях высокой размерности пространства признаков, характерной
для реальных задач.
Метод k-ближайших соседей для решения задач дискриминантного анализа был
впервые предложен еще в 1952 году. Он заключается в следующем.
При классификации неизвестного объекта находится заданное
число (k) геометрически ближайших к нему в пространстве признаков других
объектов (ближайших соседей) с уже известной принадлежностью к распознаваемым
классам. Решение об отнесении неизвестного объекта к тому или иному
диагностическому классу принимается путем анализа информации об этой известной
принадлежности его ближайших соседей, например, с помощью простого подсчета голосов.
Первоначально метод k-ближайших соседей рассматривался как
непараметрический метод
оценивания отношения
правдоподобия. Для этого метода получены теоретические оценки его эффективности
в сравнении с оптимальным байесовским
классификатором. Доказано, что асимптотические вероятности
ошибки для метода k-ближайших соседей превышают ошибки правила Байеса не более чем в два раза.
Как отмечалось выше, в реальных задачах часто
приходится оперировать объектами, которые описываются большим количеством
качественных (дихотомических) признаков. При этом размерность пространства
признаков соизмерима или превышает объем исследуемой выборки. В таких условиях
удобно интерпретировать каждый объект обучающей выборки, как
отдельный линейный классификатор. Тогда тот или иной диагностический класс
представляется не одним прототипом, а набором линейных классификаторов. Совокупное
взаимодействие линейных классификаторов дает в итоге кусочно-линейную
поверхность, разделяющую в пространстве признаков распознаваемые классы. Вид
разделяющей поверхности, состоящей из кусков гиперплоскостей, может быть
разнообразным и зависит от взаимного расположения классифицируемых совокупностей.
Также можно использовать другую интерпретацию механизмов
классификации по правилу k-ближайших соседей. В ее основе лежит представление о
существовании некоторых латентных переменных, абстрактных или связанных
каким-либо преобразованием с исходным пространством признаков. Если в
пространстве латентных переменных попарные расстояния
между объектами такие же, как и в пространстве исходных признаков, и количество
этих переменных значительно меньше числа объектов, то интерпретация метода
k-ближайших соседей может рассматриваться под углом зрения сравнения
непараметрических оценок
плотностей распределения условных вероятностей. Приведенное здесь представление
о латентных переменных близко по своей сути к представлению об истинной
размерности и другим
представлениям, используемым в различных методах снижения размерности.
При использовании метода k-ближайших соседей для
распознавания образов
исследователю приходится решать сложную проблему выбора метрики для определения
близости диагностируемых объектов. Эта проблема в условиях высокой размерности пространства
признаков чрезвычайно обостряется вследствие достаточной трудоемкости данного
метода, которая становится значимой даже для высокопроизводительных
компьютеров. Поэтому здесь так же, как и в методе сравнения с прототипом,
необходимо решать творческую задачу анализа многомерной структуры
экспериментальных данных для минимизации числа объектов,
представляющих диагностические классы.
По мнению авторов
необходимость уменьшения числа объектов в обучающей выборке (диагностических
прецедентов)является недостатком данного метода, т.к. уменьшает
представительность обучающей выборки.
Принцип действия алгоритмов вычисления оценок (АВО) состоит в
вычислении приоритете (оценок сходства), характеризующих “близость” распознаваемого
и эталонных объектов по системе ансамблей признаков, представляющей собой
систему подмножеств заданного
множества признаков.
В отличие от всех ранее рассмотренных методов алгоритмы
вычисления оценок принципиально по-новому оперируют описаниями объектов. Для
этих алгоритмов объекты существуют одновременно в самых разных подпространствах пространства
признаков. Класс АВО доводит идею
использования признаков до логического конца: поскольку не
всегда известно, какие сочетания признаков наиболее информативны, то в АВО
степень сходства объектов вычисляется при
сопоставлении всех возможных или определенных сочетаний признаков, входящих в
описания объектов [46].
Используемые сочетания признаков (подпространства) авторы
называют опорными множествами или множествами частичных описаний объектов.
Вводится понятие обобщенной близости между распознаваемым объектом и объектами
обучающей выборки (с
известной классификацией), которые называют эталонными объектами. Эта близость
представляется комбинацией близостей
распознаваемого объекта с эталонными объектами, вычисленных на множествах
частичных описаний. Таким образом, АВО является
расширением метода k-ближайших соседей, в котором близость объектов
рассматривается только в одном заданном пространстве признаков.
Еще одним расширением АВО является то,
что в данных алгоритмах задача определения сходства и различия объектов
формулируется как параметрическая
и выделен этап настройки АВО по обучающей выборке, на
котором подбираются оптимальные значения введенных параметров. Критерием
качества служит ошибка распознавания, а параметризуется буквально
все:
правила вычисления близости объектов по
отдельным признакам,
правила вычисления близости объектов в
подпространствах признаков,
степень важности того или иного
эталонного объекта как диагностического прецедента,
значимость вклада каждого опорного
множества признаков в итоговую оценку сходства распознаваемого объекта с
каким-либо диагностическим классом.
Параметры АВО задаются в
виде значений порогов и (или) как веса указанных составляющих.
Теоретические возможности АВО превышают
или, по крайней мере, не ниже возможностей любого другого алгоритма
распознавания образов, так
как с помощью АВО могут быть реализованы все мыслимые операции с исследуемыми
объектами. Но, как это обычно бывает, расширение потенциальных возможностей
наталкивается на большие трудности их практического воплощения, особенно на
этапе построения (настройки) алгоритмов данного типа. Отдельные трудности
отмечались ранее при обсуждении метода k-ближайших соседей, который можно было
интерпретировать как усеченный вариант АВО. Его тоже можно рассматривать в
параметрическом виде и свести задачу к поиску взвешенной метрики выбранного
типа. В то же время уже здесь для высокоразмерных задач
возникают сложные теоретические вопросы и проблемы, связанные с организацией эффективного
вычислительном процесса. Для АВО, если попытаться использовать потенциальные
возможности данных алгоритмов в полном объеме, указанные трудности возрастают
многократно.
Отмеченные проблемы объясняют то, что на практике применение
АВО для решения высокоразмерных задач
сопровождается введением каких-либо эвристических ограничений и допущений. В
частности, известен пример использования АВО в психодиагностике, в котором апробирована
разновидность АВО, фактически эквивалентная методу k-ближайших соседей.
Заканчивая обзор методов распознавания образов,
остановимся еще на одном подходе. Это так называемые коллективы решающих
правил.
Так как различные алгоритмы распознавания проявляют
себя по-разному на одной и той же выборке объектов, то закономерно встает вопрос
о синтетическом решающем правиле, адаптивно использующем
сильные стороны этих алгоритмов. В синтетическом решающем правиле применяется
двухуровневая схема
распознавания. На первом уровне работают частные алгоритмы распознавания,
результаты которых объединяются на втором уровне в блоке синтеза. Наиболее
распространенные способы такого объединения основаны на выделении областей
компетентности того или иного частного алгоритма. Простейший способ нахождения
областей компетентности заключается в априорном разбиении пространства
признаков исходя из профессиональных соображений конкретной науки (например,
расслоение выборки по некоторому признаку). Тогда для каждой из выделенных
областей строится собственный распознающий алгоритм. Другой способ базируется
на применении формального анализа для определения локальных областей
пространства признаков как окрестностей распознаваемых объектов, для которых
доказана успешность работы какого-либо частного алгоритма распознавания.
Самый общий подход к
построению блока синтеза рассматривает результирующие показатели частных алгоритмов
как исходные признаки для построения нового обобщенного решающего правила.
В этом случае могут использоваться все перечисленные выше методы
интенсионального и
экстенсионального направлений в
распознавании образов. Эффективными
для решения задачи создания коллектива решающих правил являются логические
алгоритмы типа “Кора” и алгоритмы вычисления оценок (АВО), положенные
в основу так называемого алгебраического подхода, обеспечивающего исследование
и конструктивное описание алгоритмов распознавания, в рамки
которого укладываются все существующие типы алгоритмов [46].
Приведенные характеристики различных методов распознавания образов были
бы неполными без обсуждения вопроса о критериях
качества алгоритмов и о способах оценки этих критериев. Показателями
качества обычно являются либо собственно ошибка классификации, либо связанные с
ней некоторые функции потерь. При этом различают условную вероятность ошибочной
классификации, ожидаемую ошибку
алгоритма классификации на выборке заданного объема и асимптотическую ожидаемую
ошибку классификации. Функции потерь также разделяют на функцию средних потерь,
функцию ожидаемых потерь и
эмпирическую функцию средних потерь.
Для оценки
выбранного показателя качества того или иного алгоритма распознавания образов применяется три основных
экспериментальных способа.
Выборка
используется одновременно как обучающая и контрольная;
Выборка
разбивается на две части - обучающую и контрольную;
Из
всей выборки случайным образом извлекается один объект, а по оставшимся
синтезируется решающее правило и производится
распознавание извлеченного объекта. Процедура повторяется заданное число раз
(например, до полного перебора).
Первый способ дает завышенную
оценку качества распознавания по сравнению
с той же оценкой качества по независимым от обучения данным. Второй способ
является самым простым и убедительным. Им широко пользуются, если
экспериментальных данных достаточно. В то же время третий способ, называемый
также методом скользящего экзамена является наиболее предпочтительным, так как
дает меньшую дисперсию оценки вероятности ошибки. Однако этот метод является и
самым трудоемким, так как требует многократного построения правила распознавания.
Применительно к рассмотренным методам распознавания образов эта
трудоемкость наиболее существенна для многих методов интенсионального направления,
для которых необходимо на каждом шаге скользящего экзамена производить
коррекцию используемых характеристик признаков и их связей (например, средних
значений и ковариаций). Но для
экстенсиональных методов,
оперирующих объектами, достаточно просто не включать контрольный объект
в исследуемое правило распознавания. Поэтому данные методы (k-ближайших
соседей, АВО) как бы
приспособлены для реализации метода скользящего экзамена, который позволяет
избегать расточительного обращения с экспериментальным материалом и
одновременно получать наиболее эффективные оценки качества распознающих
алгоритмов.
Сравнение описанных выше методов распознавания образов
приводит к следующим выводам. Для решения реальных задач из
группы методов интенсионального направления
практическую ценность представляют параметрические методы и методы, основанные
на предложениях о виде решающих функций. Параметрические методы составляют
основу традиционной методологии конструирования показателей. Применение этих
методов в реальных задачах связано с
наложением сильных ограничений на структуру данных, которые приводят к линейным
диагностическим моделям с очень приблизительными оценками их параметров. При
использовании методов, основанных на предположениях о виде решающих функций,
исследователь также вынужден обращаться к линейным моделям. Это обусловлено
высокой размерностью пространства
признаков, характерной для реальных задач, которая при повышении степени полиноминальной решающей
функции дает огромный рост числа ее членов при проблематичном сопутствующем
повышении качества распознавания. Таким образом, спроецировав область
потенциального применения интенсиональных методов
распознавания на реальную проблематику,
получим картину, соответствующую хорошо отработанной традиционной методологии линейных
диагностических моделей.
Как отмечалось ранее, свойства линейных диагностических
моделей, в которых диагностический показатель представлен взвешенной суммой
исходных признаков, хорошо изучены. Результаты этих моделей (при
соответствующем нормировании) интерпретируются как расстояния
от исследуемых объектов до некоторой гиперплоскости в
пространстве признаков или, что эквивалентно, как проекции объектов на
некоторую прямую линию в данном пространстве. Поэтому линейные модели адекватны
только простым геометрическим конфигурациям областей пространства признаков, в
которые отображаются объекты разных диагностических классов. При более сложных
распределениях эти модели принципиально не могут отражать многие особенности
структуры экспериментальных данных. В то же время такие особенности способны
нести ценную диагностическую информацию.
Вместе с тем, появление в
какой-либо реальной задаче простых многомерных структур (в частности,
многомерных нормальных распределений) следует скорее расценивать как исключение,
чем как правило. Часто диагностические классы формируются на основании сложносоставных
внешних критериев, что автоматически влечет за собой геометрическую неоднородность
данных классов в пространстве признаков. Это особенно касается “жизненных”,
наиболее часто практически встречающихся критериев. В таких условиях применение
линейных моделей фиксирует только самые “грубые” закономерности
экспериментальной информации.
Применение экстенсиональных методов не
связано каким-либо предположениями о структуре экспериментальной информации
кроме того, что внутри распознаваемых классов должны существовать одна или
несколько групп чем-то похожих объектов, а объекты разных классов должны чем-то
отличаться друг от друга. Очевидно при любой конечной размерности обучающей выборки (а
другой она быть и не может) это требование выполняется всегда просто по той
причине, что существуют случайные различия между объектами. В качестве мер
сходства применяются различные меры близости (расстояния) объектов в
пространстве признаков. Поэтому эффективное использование экстенсиональных
методов распознавания образов зависит
от того, насколько удачно определены указанные меры близости, а также от того,
какие объекты обучающей выборки (объекты с известной классификацией) выполняют
роль диагностических прецедентов. Успешное решение данных задач дает результат,
приближающийся к теоретически достижимым пределам эффективности распознавания.
Достоинствам экстенсиональных методов
распознавания образов
противопоставлена, в первую очередь, высокая техническая сложность их
практического воплощения. Для высокоразмерных пространств
признаков внешне простая задача нахождения пар ближайших точек превращается в
серьезную проблему. Также многие авторы отмечают в качестве проблемы необходимость
запоминания достаточно большого количества объектов, представляющих распознаваемые
классы.
По мнению авторов,
само по себе это не является проблемой, однако воспринимается как проблема
(например, в методе k-ближайших соседей) по той причине, что при распознавании каждого объекта происходит полный
перебор всех объектов обучающей выборки.
В предложенной
авторами модели системы распознавания “ЭЙДОС” проблема полного перебора
объектов обучающей выборки снимается, так как он осуществляется лишь один
раз при формировании обобщенных образов классов распознавания. При самом же
распознавании осуществляется сравнение идентифицируемого объекта лишь с
обобщенными образами классов распознавания, количество которых фиксировано и
совершенно не зависит от размерности обучающей выборки. С другой
стороны этот подход позволяет увеличивать размерность обучающей выборки до тех пор,
пока не будет достигнуто требуемое высокое качество обобщенных образов,
совершенно при этом не опасаясь, что это может привести к неприемлемому
увеличению времени распознавания (т.к. время распознавания в данной модели
вообще не зависит от размерности обучающей выборки).
Теоретические проблемы применения экстенсиональных методов
распознавания связаны с
проблемами поиска информативных групп признаков, нахождения оптимальных метрик
для измерения сходства и различия объектов и анализа структуры
экспериментальной информации. В то же время успешное решение перечисленных
проблем позволяет не только конструировать эффективные распознающие алгоритмы,
но и осуществлять переход от экстенсионального знания
эмпирических фактов к интенсиональному знанию о
закономерностях их структуры.
Переход от экстенсионального знания к
интенсиональному происходит на
той стадии, когда формальный алгоритм распознавания уже
сконструирован и продемонстрировал свою эффективность. Тогда производится
изучение механизмов, за счет которых достигается полученная эффективность.
Такое изучение, связанное с анализом геометрической структуры данных, может,
например, привести к выводу, что достаточно заменить объекты, представляющие
тот или иной диагностический класс, одним типичным представителем (прототипом).
Это эквивалентно, как отмечалось выше, заданию традиционной линейной
диагностической шкалы. Также возможно, что каждый диагностический класс
достаточно заменить несколькими объектами, осмысленными как типичные
представители некоторых подклассов, что эквивалентно построению веера линейных
шкал. Возможны и другие варианты, которые будут рассмотрены ниже.
Таким образом обзор методов распознавания показывает,
что в настоящее время теоретически разработан целый ряд различных методов
распознавания образов. В литературе приводится развернутая их классификация.
Однако для большинства этих методов их программная реализация отсутствует, и
это глубоко закономерно, можно даже сказать “предопределено” характеристиками
самих методов распознавания. Об этом можно судить потому, что такие системы
мало упоминаются в специальной литературе, других общедоступных источниках
информации.
Следовательно остается недостаточно разработанным вопрос о
практической применимости тех или иных теоретических методов распознавания
для решения практических задач при реальных (т.е. довольно значительных)
размерностях
данных и на реальных современных компьютерах.
Вышеупомянутое обстоятельство может быть понято, если
напомнить, что сложность математической модели экспоненциально увеличивает
трудоемкость программной реализации системы и в такой же степени уменьшает
шансы на то, что эта система будет практически работать. Это означает, что
реально на рынке можно реализовать только такие программные системы, в основе
которых лежат достаточно простые и “прозрачные” математические модели. Поэтому
разработчик, заинтересованный в тиражировании своего программного продукта,
подходит к вопросу о выборе математической модели не с чисто научной точки зрения, а как прагматик, с учетом возможностей программной реализации. Он
считает, что модель должна быть как можно проще, а значит реализоваться с
меньшими затратами и более качественно, а также должна обязательно работать
(быть практически эффективной).
В этой связи особенно актуальной представляется задача
реализации в системах распознавания механизма обобщения
описаний объектов, относящихся к одному классу, т.е. механизм формирования компактных обобщенных образов.
Очевидно, что такой механизм обобщения позволит “сжать” любую по размерности обучающую выборку к
заранее известной по размерности базе обобщенных образов.
Забегая вперед отметим, что эта задача решена в
Универсальной автоматизированной системе распознавания образов
“ЭЙДОС”. Это
позволило поставить и решить в Системе “ЭЙДОС” ряд задач, которые даже не могут
быть сформулированы в таких методах распознавания, как метод сравнения с
прототипом, метод k-ближайших соседей и АВО. Это задачи:
определения информационного вклада признаков в информационный портрет
обобщенного образа, кластерно-конструктивный
анализ обобщенных образов, определение семантической нагрузки признака,
семантический кластерно-конструктивный анализ признаков, содержательное сравнение
обобщенных образов классов друг с другом и признаков друг с другом, и др.
Метод, который позволил достичь решения этих задач, также
отличает Систему “ЭЙДОС” от других
систем, как компиляторы отличаются от интерпретаторов, т.к. в благодаря
формированию обобщенных образов в Системе “ЭЙДОС” удалось достичь независимости
времени распознавания
от объемов обучающей
выборки. Известно, что именно существование этой зависимости
приводит к практически неприемлемым затратам машинного времени на распознавание в таких
методах, как метод k-ближайших соседей и АВО при таких
размерностях обучающей выборки,
когда можно говорить о статистике.
В заключение краткого обзора методов распознавания представим суть
вышеизложенного в сводной таблице, а также в форме в виде диаграмы:
1.
классификация методов распознавания;
2.
области применения методов распознавания;
3.
классификация ограничений методов распознавания.
Анализ перспективных направлений развития методов
распознавания показывает,
что для успешного достижения цели исследования необходимо решить (или обойти)
следующие проблемы:
комбинаторного взрыва;
достижения независимости времени
распознавания от
размерности обучающей выборки;
корректного снижения размерности пространства
признаков без существенной потери содержащейся в них значимой информации;
достижения высокой валидности результатов
анализа.
Первая и вторая проблемы имеют
сходное происхождение и возникают при попытке прямого перебора вариантов
кластеризации и во многих
методах распознавания.
Третья - при выявлении наиболее
существенного и отбрасывании относительно
несущественного в созданных Системой образах. Аналогичную проблему решает
художник, когда переносит на двумерный холст
изображение трехмерного пейзажа, причем так, чтобы при этом сохранилась
максимальная узнаваемость этого
пейзажа. Практически работающее программное средство, реализующее данную
функцию, должно корректно понижать размерность пространства
описания от нескольких тысяч, до сотен или даже десятков признаков. На практике
снижение размерности пространства
признаков сводится к двум задачам: во-первых определение ценности признаков для
решения задачи распознавания, и,
во-вторых, отбрасывание незначимых признаков.
Сделать это корректно не так просто в связи с тем, что все признаки, вообще
говоря, взаимосвязаны и ценность
одних признаков может меняться весьма значительно при отбрасывании других, даже
несущественных признаков.
Четвертая - при разработке
такой математической модели и программной реализации Системы, которые бы
обеспечивали наиболее высокий уровень соответствия существа выполняемых
Системой операций, моделирующих процессы восприятия и познания (а также их результатов)
интуитивному пониманию пользователем и экспертом подобных процессов в психике
человека. Из опыта математического эксперимента известно, что результаты
кластерного анализа и
даже идентификации к сожалению слишком часто не соответствуют
представлениям человека-эксперта о данной предметной области, хотя и
соответствуют логике математической модели. Это означает, что такие модели
обладают низкой внешней валидностью, т.е. не отражают
существо тех процессов обработки информации, с помощью которых нормальный компетентный
человек и в нормальном состоянии сознания реализует аналогичные когнитивные функции.
Следовательно, перспективная математическая модель и ее программная реализация
должны обеспечивать интуитивно понятную содержательную
интерпретацию при применении в тех предметных областях, в которых у
человека-эксперта имеется развитая и адекватная реальности система ориентации.
По мнению авторов, именно применение такого рода моделей можно считать
корректным, т.к. в противном случае трудно сказать, как можно применить результаты
их работы. Данный подход позволяет обоснованно надеяться на то, что и в новых малоизученных
областях такая модель даст корректные результаты и удовлетворит потребности
познающего человека в той или иной предметной области.
Уместно отметить, что многие перспективные разработки систем
распознавания ориентируются
на еще не созданные перспективные вычислительные системы или на очень мощные, а
значит редкие, дорогие и недоступные для массового пользователя компьютеры. Это обстоятельство переводит подобные
разработки в категорию фундаментальных научных исследований, которые в
настоящее время в реальных условиях мало кем могут быть реально использованы.
1. Рассматривая место и роль адаптивного распознавания и
содержательного информационного (семантического) анализа в процессах восприятия
окружающей среды (с точки зрения постановки цели и задач исследования) авторы
считает, что создание адаптивной модели распознавания
является ключевым моментом в теоретическом решении исследуемой проблемы. Под адаптацией понимается гибкая перестройка
механизма принятия решений, поддерживаемого Системой, за счет коррекции
смысла (семантической нагрузки) признаков и информационного содержания
образов, направленная на обеспечение их максимального соответствия
фактическим изменениям предметной области. Такая “подстройка”
интеллектуальной компьютерной системы к предметной области, призвана
обеспечивать непрерывную адекватность разработанных и применяемых на ее базе
приложений потребностям пользователей, работающих в динамичных предметных
областях.
Дело в том, что продукты, созданные с помощью традиционных
статических моделей, в связи с высокой динамичностью предметной области быстро
морально устаревают, т.е. со временем
работают все хуже и хуже, их адекватность падает. При их применении у
пользователя , образно говоря, “почва непрерывно уходит ног”, т.к. качество работы таких приложений постоянно
ухудшается, постепенно они перестают
давать корректные и сопоставимые даже друг с другом результаты и в конце
концов снимаются с эксплуатации. Адаптивные же модели
порождают приложения, практическая и научная ценность (и стоимость) которых
непрерывно возрастают, т.к. они являются “генераторами информации”. Собственно
говоря, ради этого они и создаются. Более того, адаптивные модели
позволяют изучать динамику смысла признаков и информационного содержания
образов, т.е. динамику самой предметной области.
Все отмеченные проблемы при прагматической оценке делают
очень широкий класс математических моделей распознавания практически
неинтересными (что не исключает их фундаментальную научную ценность), т.к. они
дают либо интуитивно-непонятные, т.е. неинтерпретируемые результаты,
либо приемлемые результаты, но требующие таких объемов вычислений, которые
непосильны для обычных персональных компьютеров.
2. Таким образом целесообразно сформулировать следующие
задачи исследования:
проанализировать состояние и развитие
современной теории и практики распознавания образов;
оценить место и роль адаптивного распознавания и семантического
информационного анализа в процессе восприятия и познания окружающей среды;
разработать теоретические основы и
технологию применения адаптивных
автоматизированных систем распознавания образов;
создать универсальную
автоматизированной систему адаптивного семантического
анализа, а также методологию ее применения;
разработать комплекс методик применения
этой системы для решения широкого спектра реальных задач.
3. Результатом решения указанных задач должно быть решение
проблемы, исследуемой в данной работе.
4. Различные перспективные модели предлагают свои варианты
решения некоторых из этих проблем, причем эти варианты в различной степени
подходят (или, точнее, не подходят) для программной реализации. Очевидно,
задача разработки адаптивной модели
семантического распознавания и анализа,
имеющей высокий уровень адекватности содержательной информационной
интерпретации и реализуемой в виде реальной программной системы, работающей на
обычном для России персональном
компьютере, - это задача значительной научной и практической сложности,
а также трудоемкости (достаточно сказать, что исходные тексты программ системы
“ЭЙДОС-6.2” составляет около 2Mb,
т.е. примерно 2500 листов А4, а беглый
показ режимов системы с краткими комментариями занимает не менее полутора
часов).
Авторский вариант комплексного
решения вышеперечисленных проблем отчасти практически реализован в
универсальной автоматизированной системе распознавания образов
“ЭЙДОС-6.2”, в технологии и опыте ее
применения, на основе которых выработано представление об определенной
оптимальной инфраструктуре применения данной системы (степень развития этой
инфраструктуры может быть очень различна: от одного человека до солидной организации,
в зависимости от решаемых задач). Система “ЭЙДОС-6.2” обеспечивает поддержку
адаптивных алгоритмов
распознавания и содержательный (семантический) анализ, т.е. позволяет измерять
смысловую нагрузку признаков, изучать смысловые взаимосвязи между различными
признаками, а также между смыслом признаков и категориями изучаемых объектов.
Система “ЭЙДОС-6.2” обеспечивает поддержку
когнитивных функций, характерных как для
левого, так и для правого полушария, рассмотренных в перспективной когнитивной концепции (см. п.12 и п.13
таблицы функций полушарий, раздел 1.3.1). Структура Системы “ЭЙДОС-6.2” отражает асимметричное
распределение этих функций по полушариям мозга.
Левополушарные функции: Объекты рассматриваются как
системы признаков (свойств). Формируемые системой обобщенные образы объектов выводятся в текстовом и
графическом виде (информационные портреты классов распознавания) и представляют собой описания
объектов на языке признаков (свойств) с указанием информационного вклада
каждого признака в суммарное количество информации, содержащейся в данном
образе. Сами признаки рассматриваются как “метки”, “указатели” на определенные
объекты. В текстовом и графическом виде выводится информация о том, в какой
степени каждый признак “указывает” на обобщенные образы объектов
(информационные портреты признаков). Обеспечивается синтез объектов по их
свойствам и признакам, распознавание и идентификация объектов.
Правополушарные функции: Объекты рассматривается как
нечто целостностное. Изучается сходство и различие
объектов (кластерно-конструктивный анализ классов
распознавания). Признаки (свойства)
рассматривается как нечто самостоятельное. Изучается сходство и различие между
признаками по их смыслу (кластерно-конструктивный анализ признаков). Результаты
конструктивного анализа признаков могут быть использованы для построения
семантических сетей признаков, т.е. ориентированных графов, в вершинах которых
находятся признаки, а ребра представляют собой семантические связи между признаками
(каждая семантическая связь характеризуется величиной и
знаком, т.е. является вектором).
В зависимости от
преобладающего типа мышления (формально-логического или образного) пользователи
отдают предпочтение соответствующим способам анализа данных, реализованным в Системе
“ЭЙДОС-6.2”, которые лично для них
более удобны, понятны и естественны.
Определение: принятие решения есть действие над множеством
альтернатив, в результате которого исходное множество альтернатив сужается. Это
действие называется «выбор».
Выбор является
действием, придающим всей деятельности целенаправленность. Именно через акты
выбора реализуется подчиненность всей деятельности определенной цели или совокупности
взаимосвязанных целей.
Таким образом, для
того, чтобы стал возможен акт выбора, необходимо следующее:
порождение или обнаружение множества альтернатив, на
котором предстоит совершить выбор;
определение целей, ради достижения которых
осуществляется выбор;
разработка и применение способа сравнения альтернатив
между собой, т.е. определение рейтинга предпочтения для каждой альтернативы,
согласно определенным критериям, позволяющим косвенно оценивать, насколько
каждая альтернатива соответствует цели.
Современные работы в
области поддержки принятия решений выявили характерную ситуацию, которая
состоит в том, что полная формализация нахождения наилучшего (в определенном
смысле) решения возможна только для хорошо изученных, относительно простых задач,
тогда как на практике чаще встречаются слабо структурированные задачи для
которых полностью формализованных алгоритмов не разработано (если не считать
полного перебора и метода проб и ошибок). Вместе с тем, опытные, компетентные и
способные специалисты, часто делают выбор, который оказывается достаточно
хорошим. Поэтому современная тенденция практики принятия решений в естественных
ситуациях состоит в сочетании способности человека решать неформализованные
задачи с возможностями формальных методов и компьютерного моделирования:
диалоговые системы поддержки принятия решений, экспертные системы, адаптивные
человеко-машинные автоматизированные системы управления, нейронные сети и
когнитивные системы.
Процесс получения
информации можно рассматривать как уменьшение неопределенности в результате
приема сигнала, а количество информации, как меру степени снятия неопределенности.
Но
в результате выбора некоторого подмножества альтернатив из множества, т.е. в результате принятия решения, происходит тоже самое
(уменьшение неопределенности). Это значит, что каждый выбор, каждое решение
порождает определенное количество информации, а значит может быть описано в
терминах теории информации.
Множественность
задач принятия решений связана с тем, что каждая компонента ситуации, в которой
осуществляется принятие решений может реализовываться в качественно различных
вариантах.
Вот
только некоторые из этих вариантов:
Множество
альтернатив с одной стороны может быть конечным, счетным или континуальным, а с
другой – закрытым (т.е. известным полностью), или открытым (включающим неизвестные
элементы).
Оценка
альтернатив может осуществляться по одному или нескольким критериям, которые, в
свою очередь, могут иметь количественный или качественный характер.
Режим
выбора может быть однократным (разовым), или многократным, повторяющимся, включающим
обратную связь по результатам выбора, т.е. допускающим обучение алгоритмов
принятия решений с учетом последствий предыдущих выборов.
Последствия
выбора каждой альтернативы могут быть точно известны заранее (выбор в условиях
определенности), иметь вероятностный характер, когда известны вероятности возможных
исходов после сделанного выбора (выбор в условиях риска), или иметь
неоднозначный исход с неизвестными вероятностями (выбор в условиях неопределенности).
Ответственность
за выбор может отсутствовать, быть индивидуальной или групповой.
Степень
согласованности целей при групповом выборе может варьироваться от полного
совпадения интересов сторон (кооперативный выбор), до их противоположности
(выбор в конфликтной ситуации). Возможны также промежуточные варианты:
компромисс, коалиция, нарастающий или затухающий конфликт.
Различные
сочетания перечисленных вариантов и приводят к многочисленным задачам принятия
решений, которые изучены в различной степени.
Приведем
иерархическую классификацию различных задач принятия решений, согласно [113].
--- РИСУНОК (СХЕМА) ---
Об
одном и том же явлении можно говорить на различных языках различной степени
общности адекватности. К настоящему времени сложилось три основных языка
описания выбора.
Самым
простым и наиболее развитым и наиболее популярным является критериальный язык.
Название этого языка связано с
основным предположением, состоящим в том, что каждую отдельно взятую
альтернативу можно оценить некоторым конкретным (одним) числом, после чего
сравнение альтернатив сводится к сравнению соответствующих им чисел.
Пусть, например, {X} – множество альтернатив, а x – некоторая определенная альтернатива,
принадлежащая этому множеству: x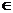 X. Тогда считается, что для всех x может быть задана функция: q(x),
которая называется критерием (критерием качества, целевой функцией, функцией
предпочтения, функцией полезности и т.п.), обладающая тем свойством, что если
альтернатива x1 предпочтительнее
x2: (обозначается: x1 > x2),
X. Тогда считается, что для всех x может быть задана функция: q(x),
которая называется критерием (критерием качества, целевой функцией, функцией
предпочтения, функцией полезности и т.п.), обладающая тем свойством, что если
альтернатива x1 предпочтительнее
x2: (обозначается: x1 > x2),
то:
q(x1)
> q(x2).
При этом выбор сводится к
отысканию альтернативы с наибольшим значением критериальной функции.
Однако, на практике использование лишь одного критерия
для сравнения степени предпочтительности альтернатив оказывается неоправданным
упрощением, т.к. более подробное рассмотрение альтернатив приводит к
необходимости оценивать их не по одному, а по многим критериям, которые могут
иметь различную природу и качественно отличаться друг от друга.
Например, при выборе наиболее
приемлемого для пассажиров и эксплуатирующей организации типа самолета на
определенных видах трасс сравнение идет одновременно по многим группам
критериев: техническим, технологическим, экономическим, социальным, эргономическим
и др.
Многокритериальные задачи не
имеют однозначного общего решения. Поэтому предлагается много способов придать
многокритериальной задаче частный вид, допускающий единственное общее решение.
Естественно, что для разных способов эти решения являются в общем случае
различными. Поэтому едва ли не главное в решении многокритериальной задачи –
обоснование данного вида ее постановки.
Используются различные варианты
упрощения многокритериальной задачи выбора. Перечислим некоторые из них.
1. Условная максимизация (находится не глобальный
экстремум суперкритерия, а локальный экстремум основного критерия).
2. Поиск альтернативы с заданными
свойствами.
3. Нахождение множества Парето.
4. Сведение многокритериальной задачи к
однокритериальной, путем ввода суперкритерия.
Рассмотрим подробнее формальную постановку метода
сведения многокритериальной задачи к однокритериальной.
Введем суперкритерий q0(x), как скалярную функцию
векторного аргумента:
q0(x)=
q0((q1(x), q2(x),…, qn(x)).
Суперкритерий позволяет
упорядочить альтернативы по величине q0,
выделив тем самым наилучшую (в смысле этого критерия). Вид функции q0 определяется тем, как конкретно мы
представляем себе вклад каждого критерия в суперкритерий. Обычно используют
аддитивные и мультипликативные функции:
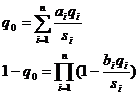
Коэффициенты si
обеспечивают:
1. безразмерность или единую
размерность числа aiqi/si
(различные частные критерии могут иметь разную размерность, и тогда над ними
нельзя производить арифметических операций и свести их в суперкритерий);
2. нормировку, т.е. обеспечение условия: biqi/si<1.
Коэффициенты ai и bi
отражают относительный вклад частных критериев qi в суперкритерий.
Итак, в многокритериальной
постановке задача принятия решения о выборе одной из альтернатив сводится к
максимизации суперкритерия:
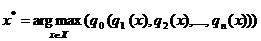
Основная проблема в
многокритериальной постановке задачи принятия решений состоит в том, что
необходимо найти такой аналитический вид коэффициентов ai и bi,
который бы обеспечил следующие свойства модели:
1. высокую степень адекватности
предметной области и точке зрения экспертов;
2. минимальные вычислительные
трудности максимизации суперкритерия, т.е. его расчета для разных альтернатив;
3. устойчивость результатов
максимизации суперкритерия от малых возмущений исходных данных.
Устойчивость решения означает, что малое изменение
исходных данных должно приводить к малому изменению величины суперкритерия, и,
соответственно, к малому изменению принимаемого решения. То есть практически на
тех же исходных данных должно приниматься или тоже самое, или очень близкое
решение.
Язык бинарных отношений является
обобщением многокритериального языка и основан на учете того факта, что когда
мы даем оценку некоторой альтернативе, то эта оценка всегда является
относительной, т.е. явно или чаще неявно в качестве базы или системы отсчета
для сравнения используются другие альтернативы из исследуемого множества или из
генеральной совокупности. Мышление человека основано на поиске и анализе
противоположностей (конструктов), поэтому, нам всегда проще выбрать один из
двух противоположных вариантов, чем один вариант из большого и никак
неупорядоченного их множества.
Таким образом, основные
предположения этого языка сводятся к следующему:
1.
отдельная альтернатива не оценивается, т.е. критериальная функция не вводится;
2.
для каждой пары альтернатив некоторым образом можно установить, что одна из них
предпочтительнее другой, либо они равноценны или несравнимы;
3.
отношение предпочтения в любой паре альтернатив не зависит от остальных
альтернатив, предъявленных к выбору.
Существуют различные способы
задания бинарных отношений: непосредственный, матричный, с использованием
графов предпочтений, метод сечений и др.
Отношения между альтернативами
одной пары выражают через понятия эквивалентности, порядка и доминирования.
Язык функций выбора основан на
теории множеств и позволяет оперировать с отображениями множеств на свои
подмножества, соответствующие различным вариантам выбора, без необходимости
перечисления элементов. Этот язык является весьма общим и потенциально
позволяет описывать любой выбор. Однако, математический аппарат обобщенных
функций выбора в настоящее время еще только разрабатывается и проверяется в
основном на задачах, которые уже решены с помощью критериального или бинарного
подходов.
Пусть имеется группа лиц, имеющих
право принимать участие в коллективном принятии решений. Предположим, что эта
группа рассматривает некоторый набор альтернатив, и каждый член группы
осуществляет свой выбор. Ставится задача о выработке решения, которое определенным
образом согласует индивидуальные выборы и в каком-то смысле выражает «общее
мнение» группы, т.е. принимается за групповой выбор.
Естественно, различным принципам
согласования индивидуальных решений будут соответствовать различные групповые
решения.
Правила согласования
индивидуальных решений при групповом выборе называются правилами голосования.
Наиболее распространенным является «правило большинства», при котором за
групповое решение принимается альтернатива, получившая наибольшее число голосов.
Необходимо понимать, что такое
решение отражает лишь распространенность различных точек зрения в группе, а не
действительно оптимальный вариант, за который вообще никто может и не
проголосовать. «Истина не определяется путем голосования».
Кроме того, существуют так
называемые «парадоксы голосования», наиболее известный из которых парадокс
Эрроу.
Эти парадоксы могут привести, и
иногда действительно приводят, к очень неприятным особенностям процедуры
голосования: например бывают случаи, когда группа вообще не может принять
единственного решения (нет кворума или каждый голосует за свой уникальный вариант,
и т.д.), а иногда (при многоступенчатом голосовании) меньшинство может навязать
свою волю большинству.
Выбор в условиях определенности – это
частный случай выбора в условиях неопределенности (когда неопределенность
близка к нулю).
Но неопределенность чего
конкретно имеется в виду?
В современной теории выбора
считается, что в задачах принятия решений существует три основных вида неопределенности:
1. информационная
(статистическая) неопределенность исходных данных для принятия решений;
2. неопределенность последствий
принятия решений (выбора);
3. расплывчатость в описании
компонент процесса принятия решений.
Рассмотрим их по порядку.
Данные, полученные о предметной
области, не могут рассматриваться как абсолютно точные. Кроме того, очевидно,
эти данные нас интересуют не сами по себе, а лишь в качестве сигналов, которые,
возможно, несут определенную информацию о том, что нас в действительности
интересует. То есть, реалистичнее считать, что мы имеем дело с данными, не
только зашумленными и неточными, но еще и косвенными, а возможно и не полными.
Кроме того эти данные касаются не всей исследуемой (генеральной) совокупности,
а лишь определенного ее подмножества, о котором мы смогли фактически собрать
данные, однако при этом мы хотим сделать выводы о всей совокупности, причем
хотим еще и знать достоверность этих выводов.
В этих условиях используется
теория статистических решений.
В этой теории существует два
основных источника неопределенности. Во-первых, неизвестно, какому
распределению подчиняются исходные данные. Во-вторых, неизвестно, какое
распределение имеет то множество (генеральная совокупность), о котором мы хотим
сделать выводы по его подмножеству, образующему исходные данные.
Статистические процедуры это и
есть процедуры принятия решений, снимающих оба эти виды неопределенности.
Необходимо отметить, что
существует ряд причин, которые приводят к некорректному применению статистических
методов:
1. статистические выводы, как и
любые другие, всегда имеют некоторую определенную надежность или достоверность.
Но, в отличие от многих других случаев, достоверность статистических выводов
известна и определяется в ходе статистического исследования;
2. качество решения, полученного
в результате применения статистической процедуры зависит, от качества исходных
данных;
3. не следует подвергать
статистической обработке данные, не имеющие статистической природы;
4. необходимо использовать
статистические процедуры, соответствующие уровню априорной информации об исследуемой
совокупности (например, не следует применять методы дисперсионного анализа к
негауссовым данным). Если распределение исходных данных неизвестно, то надо
либо его установить, либо использовать несколько различных методов и сравнить
результаты. Если они сильно отличаются – это говорит о неприменимости некоторых
из использованных процедур.
Когда последствия выбора той или
иной альтернативы однозначно определяются самой альтернативой, тогда можно не
различать альтернативу и ее последствия, считая само собой разумеющимся, что
выбирая альтернативу мы в действительности выбираем ее последствия.
Однако, в реальной практике
нередко приходится иметь дело с более сложной ситуацией, когда выбор той или
иной альтернативы неоднозначно определяет последствия сделанного выбора.
В случае дискретного набора
альтернатив и исходов их выбора, при условии, что сам набор возможных исходов
общий для всех альтернатив, можно считать, что различные альтернативы
отличаются друг от друга распределением вероятностей исходов. Эти распределения
вероятностей вообще говоря могут зависеть от результатов выбора альтернатив и
реально наступивших в результате этого исходов. В простейшем случае исходы
равновероятны. Сами исходы обычно имеют смысл выигрышей или потерь и выражаются
количественно.
Если исходы равны для всех
альтернатив, то выбирать нечего. Если же они различны, то можно сравнивать
альтернативы, вводя для них те или иные количественные оценки. Разнообразие
задач теории игр связано с различным выбором числовых характеристик потерь и
выигрышей в результате выбора альтернатив, различными степенями конфликтности
между сторонами, выбирающими альтернативы и т.д.
Любая задача выбора является
задачей целевого сужения множества альтернатив. Как формальное описание
альтернатив (сам их перечень, перечень их признаков или параметров), так и
описание правил их сравнения (критериев, отношений) всегда даются в терминах
той или иной измерительной шкалы (даже тогда, когда тот, кто это делает, не
знает об этом).
Известно, все шкалы размыты, но в
разной степени. Под термином «размытие» понимается свойство шкал, состоящее в
том, что всегда можно предъявить такие две альтернативы, которые различимы,
т.е. различны в одной шкале и неразличимы, т.е. тождественны в другой – более
размытой. Чем меньше градаций в некоторой шкале, тем более она размыта.
Таким образом, мы можем четко
видеть альтернативы, и одновременно нечетко их классифицировать, т.е. иметь
неопределенность в вопросе о том, к каким классам они относятся. Например, мы
можем совершенно четко видеть на улице негра и совершенно не представлять себе,
из какой страны он к нам приехал.
Уже в первой работе по принятию
решений в расплывчатой ситуации Беллман и Заде выдвинули идею, состоящую в том,
что и цели, и ограничения должны представляться как размытые (нечеткие)
множества на множестве альтернатив.
Во всех рассмотренных выше
задачах выбора и методах принятия решений проблема состояла в том, чтобы в
исходном множестве найти наилучшие в заданных условиях, т.е. оптимальные
в определенном смысле альтернативы.
Идея оптимальности является
центральной идеей кибернетики и прочно вошла в практику проектирования и эксплуатации
технических систем. Вместе с тем эта идея требует осторожного к себе отношения,
когда мы пытаемся перенести ее в область управления сложными, большими и слабо
детерминированными системами, такими, например, как социально-экономические
системы.
Для этого заключения имеются
достаточно веские основания. Рассмотрим некоторые из них.
1. Оптимальное решение нередко
оказывается неустойчивым: т.е. незначительные изменения в условиях задачи,
исходных данных или ограничениях могут привести к выбору существенно
отличающихся альтернатив.
2. Оптимизационные модели разработаны лишь для узких
классов достаточно простых задач, которые не всегда адекватно и системно
отражают реальные объекты управления. Чаще всего оптимизационные методы
позволяют оптимизировать лишь достаточно простые и хорошо формально описанные
подсистемы некоторых больших и сложных систем, т.е. позволяют осуществить лишь
локальную оптимизацию. Однако, если каждая подсистема некоторой большой системы
будет работать оптимально, то это еще совершенно не означает, что оптимально будет
работать и система в целом. То есть оптимизация подсистемы совсем не
обязательно приводит к такому ее поведению, которое от нее требуется при
оптимизации системы в целом. Более того, иногда локальная оптимизация может
привести к негативным последствиям для системы в целом.
3. Часто максимизация критерия
оптимизации согласно некоторой математической модели считается целью
оптимизации, однако в действительностью целью является оптимизация объекта
управления. Критерии оптимизации и математические модели всегда связаны с целью
лишь косвенно, т.е. более или менее адекватно, но всегда приближенно.
Итак, идею оптимальности,
чрезвычайно плодотворную для систем, поддающихся адекватной математической
формализации, нельзя перенести на сложные системы. Конечно, математические
модели, которые удается иногда предложить для таких систем, можно оптимизировать.
Однако всегда следует учитывать сильную упрощенность этих моделей, а также то,
что степень их адекватности фактически неизвестна. Поэтому не известно, какое
чисто практическое значение имеет эта оптимизация. Высокая практичность
оптимизации в технических системах не должна порождать иллюзий, что она будет
настолько же эффективна при оптимизации сложных систем. Содержательное
математическое моделирование сложных систем является весьма затруднительным,
приблизительным и неточным. Чем сложнее система, тем осторожнее следует
относится к идее ее оптимизации.
Поэтому, при разработке методов
управления сложными, большими слабо детерминированными системами, авторы
считают основным не оптимальность выбранного подхода с формальной
математической точки зрения, а его адекватность поставленной цели и самому характеру
объекта управления.
При исследовании сложных систем
часто возникают проблемы, которые по различным причинам не могут быть строго
поставлены и решены с применением разработанного в настоящее время
математического аппарата. В этих случаях прибегают к услугам экспертов (системных
аналитиков), чей опыт и интуиция помогают уменьшить сложность проблемы.
Однако, необходимо учитывать, что
эксперты сами представляют собой сверхсложные системы, и их деятельность сама
зависит от многих внешних и внутренних условий. Поэтому в методиках организации
экспертных оценок большое внимание уделяется созданию благоприятных внешних и
психологических условий для работы экспертов.
На работу эксперта оказывают влияние следующие
факторы:
- знание того, что привлекаются и другие
эксперты;
- наличие информационного контакта между
экспертами;
- межличностные отношения экспертов (если
между ними есть информационный контакт);
- личная заинтересованность эксперта в
результатах оценки;
- личностные качества экспертов (самолюбие,
конформизм, воля и др.)
Взаимодействие между экспертами
может как стимулировать, так и подавлять их деятельность. Поэтому в разных
случаях используют различные методы экспертизы, отличающиеся характером
взаимодействия экспертов друг с другом: анонимные и открытые опросы и анкетирования,
совещания, дискуссии, деловые игры, мозговой штурм и т.д.
Существуют различные методы
математической обработки мнений экспертов. Экспертам предлагают оценить
различные альтернативы либо одним, либо системой показателей. Кроме того им
предлагают оценить степень важности каждого показателя (его «вес» или «вклад»).
Самим экспертам также приписывается уровень компетентности, соответствующий его
вкладу в результирующее мнение группы.
Развитой методикой работы с
экспертами является метод «Дельфи». Основная идея этого метода состоит в том,
что критика и аргументация благотворно влияет на эксперта, если при этом не
задевается его самолюбие и обеспечиваются условия, исключающие персональную
конфронтацию.
Необходимо особо подчеркнуть, что
существует принципиальное различие в характере использования экспертных методов
в экспертных системах и в поддержке принятия решений. Если в первом случае от
экспертов требуется формализация способов принятия решений, то во втором, лишь
само решение, как таковое.
Поскольку эксперты привлекаются
для реализации именно тех функций, которые в настоящее время или вообще не
обеспечиваются автоматизированными системами, или выполняются ими хуже, чем
человеком, то перспективным направлением развития автоматизированных систем
является максимальная автоматизация этих функций.
Человек
всегда использовал помощников при принятии решений: это были и просто поставщики
информации об объекте управления, и консультанты (советники), предлагающие варианты
решений и анализирующие их последствия. Человек, принимающий решения, всегда
принимал их в определенном информационном окружении: для военачальника это
штаб, для ректор - ученый совет, для министра - коллегия.
В
наше время информационная инфраструктура принятия решений немыслима без автоматизированных
систем итерактивной оценки решений и особенно систем поддержки решений (DDS –
Decision Support Systems), т.е. автоматизированных систем, которые специально
предназначены для подготовки информации, необходимой человеку для принятия
решения. Разработка систем поддержки решений ведется, в частности, в рамках
интернационального проекта, осуществляемого под эгидой Международного института
прикладного системного анализа в Лаксенбурге (Австрия).
Выбор
в реальных ситуациях требует выполнения ряда операций, одни из которых более
эффективно выполняет человек, а другие - машина. Эффективное объединение их
достоинств при одновременной компенсации недостатков и воплощается в автоматизированных
системах поддержки принятия решений.
Человек
лучше чем машина принимает решения в условиях неопределенности, но и ему для
принятия верного решения необходима адекватная (полная и достоверная)
информация, характеризующая предметную область. Однако известно, что человек
плохо справляется с большими объемами «сырой» необработанной информации.
Поэтому роль машины в поддержке принятия решений может заключаться в том, чтобы
осуществить предварительную подготовку информации об объекте управления и неконтролируемых
факторах (среде), помочь просмотреть последствия принятия тех или иных решений,
а также в том, чтобы представить всю эту информацию в наглядном и удобном для
принятия решений виде.
Таким
образом, автоматизированные системы поддержки принятия решений компенсируют
слабые стороны человека, освобождая его от рутинной предварительной обработки
информации, и обеспечивают ему комфортную информационную среду, в которой он
может лучше проявить свои сильные стороны. Эти системы ориентированы не на автоматизацию
функций лица, принимающего решения (и, как следствие, отчуждение от него этих
функций, а значит и ответственности за принятые решения, что часто вообще
является неприемлемым), а на предоставлении ему помощи в поиске хорошего решения.
1.2.8. УПРАВЛЕНИЕ
ЭЛИТНЫМИ ГРУППАМИ
В
качестве типичного примера управления состоянием сложного слабо детерминированного
объекта, рассмотрим управление элитной группой.
Прагматическая
цель исследования: создать автоматизированную систему,
применимую в реально действующих автоматизированных системах управления в
качестве подсистемы поддержки принятия решений, как на этапе идентификации
состояний среды и объекта управления, так и на этапе прогнозирования их
развития и выработки управляющих воздействий.
Актуальность
данной прагматической цели обусловлена противоречием, возникшим в практике
применения АСУ, предназначенных для управления большими
социально-экономическими системами в динамичных и противоречивых условиях
экономики «переходного периода». Это противоречие состоит в том, что с одной
стороны потребность в подобных системах осознана уже практически всеми
руководителями аналитических служб всех трех ветвей власти, т.е. «социальный
заказ» на них есть, с другой же стороны соответствующих предложений еще очень
мало (на самом деле их практически их нет).
Одной
из причин такого положения является нерешенность научных проблем разработки
соответствующих математических и алгоритмических моделей, а также
технологическая сложность и высокая трудоемкость создания подобных
автоматизированных систем.
Научная
цель исследования: разработать математическую модель,
обеспечивающую адекватное компьютерное моделирование когнитивных (т.е.
познавательных) процессов человека, изучающего некоторую предметную область,
осознающего множество возможных альтернатив ее развития и осуществляющего
выбор, приводящий к сужению круга этих альтернатив, а также принимающего
решения по выбору управляющего воздействия, повышающего вероятность реализации
желаемых вариантов.
Актуальность данной
научной цели обусловлена противоречием, возникшим в науке: с одной стороны
наука располагает мощным математическим аппаратом, который имеет самое
непосредственное отношение к достижению сформулированной выше цели, с другой
стороны этот аппарат как правило имеет неизвестную адекватность, т.к. на его
основе не создано практически работающих автоматизированных систем, которые
позволили ли бы на практике проверить эффективность реализованных в них научных
подходов. Наиболее разработанный многокритериальный подход к принятию решений
не может быть непосредственно применен для достижения сформулированной выше
цели, т.к. нуждается в конкретизации (прежде всего необходимо получить вид
весовых коэффициентов матрицы: альтернативы / критерии). Зарубежные АСУ
основаны на содержательных математических моделях, адекватных тем условиям, для
которых они созданы и в которых используются, т.е. для условий развитой
стабильной рыночной экономики. В наших же совершенно иных по всем пунктам
условиях они обладает низкой адекватностью и практически неприменимы.
Основная
задача исследования: разработка и реализация метода
поддержки принятия решений, обеспечивающего идентификацию состояний и выработку
управляющих воздействий в АСУ сложными слабо детерминированными объектами
управления.
Частные
задачи исследования:
Обоснование
аналитического вида функции суперкритерия.
Вывод
аналитического выражения для весовых коэффициентов, отражающих относительный
вклад частных критериев в суперкритерий.
Решение
проблемы приведения частных критериев к общей единице измерения или к безразмерному
виду.
Разработка математической модели, содержащей формальные
модели следующих когнитивных операций:
-
восприятие: интенсиональное (дискретное) представление чувственного
образа конкретного объекта в форме совокупности признаков;
- присвоение формальных (знаковых) имен:
экстенсиональное (континуальное) представление чувственного образа конкретного
объекта в форме принадлежности к некоторым градациям определенных смысловых
шкал;
-
обобщение (синтез, индукция): формирование обобщенных образов различных
категорий объектов на основе одновременного использования экстенсиональных и
интенсиональных описаний конкретных объектов, которые используются в качестве
примеров;
- анализ обобщенных образов (дедукция): выявление
общего и особенного для каждого обобщенного образа;
- анализ признаков: выявление общего и особенного в
смысловом содержании каждого признака;
- абстрагирование: определение для каждого признака
его вклада в различие друг от друга обобщенных образов; контролируемое и
корректное удаление незначимых признаков с сохранением всей существенной информации;
-
классификация обобщенных образов: определение сходств и различий
обобщенных образов друг с другом; объединение сходных образов в кластеры;
формирование биполярных систем наиболее непохожих кластеров, т.е. конструктов
образов;
- классификация признаков: определение сходств и
различий признаков по их смыслу; объединение сходных по смыслу признаков в кластеры;
формирование биполярных систем наиболее непохожих кластеров, т.е. конструктов
признаков;
- содержательное сравнение обобщенных образов:
определение признаков, по которым заданные два образа несопоставимы, которыми
они сходны и которыми они отличаются друг от друга;
- содержательное сравнение признаков: определение
элементов смысла, по которым заданные два признака несопоставимы, которыми они
сходны и которыми они отличаются друг от друга;
- распознавание (идентификация) конкретных объектов:
сравнение чувственного образа конкретного объекта со всеми обобщенными образами.
Математическая модель должна разрабатываться с учетом
необходимости эксплуатировать основанную на ней программную систему с
практически значимыми приложениями больших размерностей на реальных компьютерах
при разумных затратах машинного времени. Для этого необходимо теоретически
найти, а затем воплотить в программной реализации решения в частности следующих
научных и технических проблем:
- проблема комбинаторного взрыва, которая возникает при
попытке классификации обобщенных образов и признаков путем объединения их в
кластеры в различных количествах и в различных сочетаниях в кластерах;
- проблема выбора адекватной меры смысла признака;
- проблема разработки адекватной семантической модели
признака;
- проблема разработки адекватной модели обобщенного образа
класса;
- проблема обеспечения работоспособности модели на
нерепрезентативных выборках и при отсутствии достаточной статистики;
- проблема обеспечения
структурной репрезентативности выборки (ремонт выборки и взвешивание данных);
- проблема обеспечения независимости времени распознавания
(идентификации) от объема обучающей выборки;
- проблема обеспечения адаптивности обобщенных образов за
счет учета информации обратной связи о правильности или ошибочности
идентификации конкретных объектов.
Решение
основной задачи исследования, а также многочисленных частные задачи, возможно
при условии применения адекватной методологии, т.е. прежде всего
научно-методического аппарата (метода), а также методики исследования.
Строго
говоря, принятие решения о выборе того или иного метода исследования является
сложно формализуемым процессом. К этому выбору вполне применимы все основные
закономерности, описанные выше в аналитическом обзоре. Вместе с тем, можно
привести ряд аргументов в пользу выбора методологии, который был сделан
авторами данного исследования.
В
качестве метода формального описания способа принятия решений, в данной
работе принят многокритериальный язык.
Этот
выбор обусловлен тем, что многокритериальный язык является интуитивно ясным и в
настоящее время наиболее полно разработанным, а также (по этим причинам)
наиболее популярным.
Различные
варианты многокритериального подхода отличаются друг от друга выбором функции
предпочтения, видом суперкритерия, способом обеспечения сопоставимости частных
критериев (проблема размерности), а также видом весовых коэффициентов,
отражающих вклад частных критериев в суперкритерий.
Методика
расчета весовых коэффициентов, предлагаемая авторами, основана на результатах
статистической теории информации, а именно на семантической мере информации
А.А.Харкевича [114, с.56]. С точки зрения этого подхода, выбор представляет
собой процесс и результат снятия неопределенности, т.е. сужение множества
альтернатив, тогда как количество информации выступает как мера степени снятия
неопределенности. Попутно это обеспечивает решение проблемы согласования
размерностей частных критериев, т.к. весовые коэффициенты всех частных
критериев просто измеряются в одной и той же единице измерения - в битах.
Данная
методология позволяет построить формальную математическую модель базовых
когнитивных операций, а также решить другие задачи и проблемы, сформулированные
выше.
Как
показывает опыт исследований и разработок в области принятия решений, в процессах
выбора в той или иной форме всегда используется ряд критериев оценки
предпочтения альтернатив. Этот процесс имеет ряд этапов, которые присутствуют
практически во всех методах принятия решений. На первом этапе формируется сам
набор альтернатив и критериев, затем альтернативы описываются на языке
критериев, и лишь затем они анализируются и сравниваются.
Поэтому
авторы считают, что многокритериальный подход является наиболее общим. В то же
время именно благодаря общности этого подхода в нем остается достаточно свободы
и неопределенности в вопросах выбора конкретных наиболее значимых критериев,
определения их относительного веса, учета их взаимосвязей и .т.п.
По
общему мнению необходимость решения этих и других конкретных вопросов и является
основной причиной сложности применения многокритериального подхода. Сам по себе
этот подход не снимает проблем неопределенности, а лишь меняет форму их
проявления, т.е. внешне снимая ее он в действительности как бы загоняет ее
вглубь: неопределенность в выборе альтернатив «загоняется» в неопределенность
выбора вида частных критериев и их весовых коэффициентов, наиболее адекватных
данной конкретной задаче. Для снятия неопределенности и на этих уровнях
авторами предложено применение статистической теории информации, прежде всего
семантической меры информации.
![]() X. Тогда считается, что для всех x может быть задана функция: q(x),
которая называется критерием (критерием качества, целевой функцией, функцией
предпочтения, функцией полезности и т.п.), обладающая тем свойством, что если
альтернатива x1 предпочтительнее
x2: (обозначается: x1 > x2),
X. Тогда считается, что для всех x может быть задана функция: q(x),
которая называется критерием (критерием качества, целевой функцией, функцией
предпочтения, функцией полезности и т.п.), обладающая тем свойством, что если
альтернатива x1 предпочтительнее
x2: (обозначается: x1 > x2),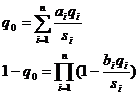
![]()