ГЛАВА 4. КОЛИЧЕСТВЕННАЯ ОЦЕНКА СТЕПЕНИ
МАНИПУЛИРОВАНИЯ ИНДЕКСОМ ХИРША
И ЕГО МОДИФИКАЦИЯ, УСТОЙЧИВАЯ
К МАНИПУЛИРОВАНИЮ
В СССР ВАК с 1975 и до самого распада СССР подчинялась не Министерству
образования и науки, а непосредственно Совету министров СССР. Однако с тех пор
существует устойчивая тенденция постепенного снижения статуса ВАК. Сегодня ВАК
уже не просто входит в Минобрнауки, а является всего лишь одним из
подразделений одной из его структур: Рособрнадзора. Снижение статуса ВАК
неизбежно приводит к снижению как статуса, так и адекватности присваиваемых им
ученых степеней и научных званий. Этот процесс обесценивания традиционных
ученых степеней и званий, присваиваемых ВАК, дошел до того, что несколько лет
назад отменили надбавки к заработной плате за них. Теперь вместо них каждым вузом
и НИИ разрабатывается свои локальные, т.е. несопоставимые друг с другом
наукометрические методики оценки результатов научной и педагогической
деятельности. При всем разнообразии этих методик, общим для всех них является
несоразмерно большая роль, которая отводится в них индексу Хирша. Значение
индекса Хирша начинает играть важную роль при защитах, при рассмотрении
конкурсных дел на замещение должностей, а также при определении величины
ежемесячного материального поощрения за результаты научной и педагогической
деятельности. Сам по себе, этот индекс теоретически вполне обоснован. Однако, в
связи с практикой его применения в наших условиях, в коллективном сознании
научного сообщества возникла своеобразная мания, которую авторы называют
«Хиршамания». Эта мания характеризуется повышенным нездоровым интересом к
самому значению индекса Хирша, а также к некорректному манипулированию его
значением, т.е. к искусственному неадекватному преувеличению этого значения, а
также рядом негативных последствий этого интереса. В данной работе делается
попытка сконструировать количественную меру для оценки степени некорректного
манипулирования значением индекса Хирша, а также предлагается
научно-обоснованная модификация индекса Хирша, нечувствительная (устойчивая) к
манипулированию им. Приводится методика всех численных расчетов, которая
достаточно проста, чтобы ее мог применить любой автор
Введение
Высшая аттестационная комиссия (ВАК) – это своего рода
отдел технического контроля (ОТК), оценивающий «качество продукции» не только
Министерства образования и науки, но и всех других министерств и ведомств, в
которых есть свои вузы и НИИ. В качестве продукции вузов и НИИ выступают не
только их разработки, но и сами ученые. ВАК, как и ОТК, обеспечивает обратную
связь, информируя управляющую систему о результатах ее работы. Из теории
управления известно, что если информация обратной связи неадекватна, то и
управляющие решения, принимаемые на ее основе, также будут неадекватными. Понятно,
что оценивающая структура не должна находится в подчинении у той структуры,
качество работы которой она оценивает. В противном случае нетрудно догадаться,
как она будет оценивать. В СССР ВАК с 1975 и до самого распада СССР
подчинялась не Министерству образования и науки, а непосредственно Совету
министров СССР, что соответствует этой логике. Однако с тех пор существует устойчивая тенденция постепенного
снижения статуса ВАК. Сегодня ВАК уже не просто входит в Минобрнауки, а
является всего лишь одним из подразделений одной из его структур:
Рособрнадзора. Снижение статуса ВАК неизбежно приводит к снижению как статуса, так и
адекватности присваиваемых им ученых степеней и научных званий. Этот
процесс обесценивания традиционных ученых степеней и званий, присваиваемых ВАК,
дошел до того, что несколько лет назад отменили надбавки к заработной плате за
них. Теперь вместо традиционных ученых степеней и званий, присваиваемых ВАК
практически каждым вузом и НИИ
разрабатывается свои локальные, т.е.
несопоставимые друг с другом наукометрические методики оценки результатов
научной и педагогической деятельности. При всем разнообразии этих методик
общим для всех них является несоразмерно большая роль, которая отводится в них
индексу Хирша. Значение индекса Хирша начинает играть важную роль при защитах,
при рассмотрении конкурсных дел на замещение должностей, а также при
определении величины ежемесячного материального поощрения за результаты научной
и педагогической деятельности. Сам по себе этот индекс теоретически вполне обоснован. Однако в связи с практикой применения индекса Хирша в
наших условиях в сознании научного сообщества возникла своеобразная мания, которую
авторы называют «Хиршамания» [1]. Эта мания характеризуется повышенным нездоровым
интересом к самому значению индекса Хирша, а также к некорректному манипулированию его
значением, т.е. к искусственному неадекватному преувеличению этого
значения, а также рядом негативных последствий этого интереса.
Возникают естественные вопросы:
1. Возможно ли как-то количественно оценить степень
манипулирования индексом Хирша, т.е. то, в какой степени его значение
«целенаправленно организовано»?
2. Возможно ли получить гипотетическое значение
индекса Хирша каким оно было бы в случае отсутствия манипулирования им?
В данной работе делается попытка найти конкретные
ответы на эти вопросы путем:
– конструирования количественной меры для оценки
степени некорректного манипулирования значением индекса Хирша;
– разработки научно-обоснованной модификации индекса
Хирша, нечувствительной (устойчивая) к попыткам манипулированию им.
Кроме собственно самих идей предлагается также
методика всех численных расчетов, достаточно простая, чтобы ее мог применить
каждый автор.
4.1. Что такое индекс Хирша
Если ранжировать все публикации ученого в порядке
убывания числа их цитирований («ранжированный список публикаций»),
то индекс Хирша h – это просто номер публикации в этом списке, процитированной
h раз. За этой публикацией идут публикации, процитированные менее h раз, а до
нее – более h раз.
Таким образом, индекс Хирша является абсциссой точки
пересечения графика числа цитирований для ранжированного списка публикаций с
биссектрисой первого квадранта (рис. 1).
Пусть f(h) - число цитирований публикации ранга h
(т.е. публикации с номером h в ранжированном списке публикаций). Тогда для
индекса Хирша h0 справедливы неравенства
f(h) > h при h < h0 и
f(h) < h при h > h0.
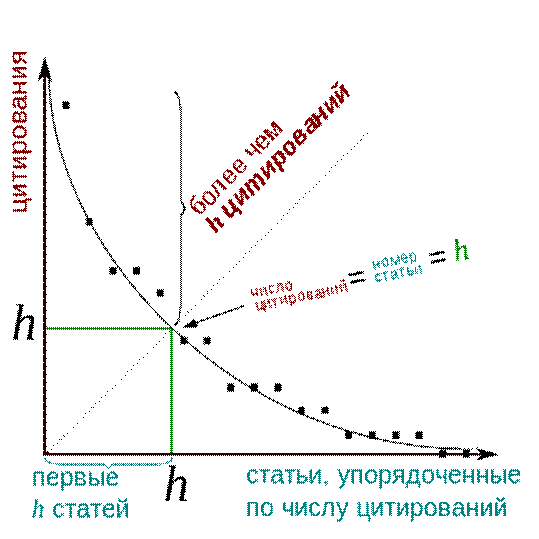
Рисунок 1. Распространенное в Internet пояснение к
понятию:
«индекс Хирша»[1]
4.2. Манипулирование индексом Хирша
при малом числе публикаций
4.2.1. Способ сформировать максимальное значение
индекса Хирша при малом числе публикаций
Из приведенного выше нехитрого алгоритма вычисления
значения индекса Хирша вполне понятно, как получить максимальное значение индекса
Хирша h при минимальном числе публикаций h+1. Для этого достаточно опубликовать
h+1 статей, в каждой из которых сослаться на все остальные [2].
4.2.2. Первый интегральный критерий
манипулирования индексом Хирша
Наверное приведенный выше
простой и доступный способ сформировать любое заданное значение индекса Хирша
первым приходит всем авторам на ум. И это дает нам в руки первый наиболее
простой критерий манипулирования индексом Хирша: «Чем более пологим является линейный тренд числа цитирований,
построенный по ранжированному списку публикаций, тем более вероятно, что был
применен описанный выше способ максимизации индекса Хирша при малом числе
публикаций».
Максимальный теоретически
возможный угол наклона линейного тренда, достижимый лишь асимптотически, равен
90°, а минимальный, естественно, равен нулю: 0°. Количественно этот 1-й частный
критерий по сути должен быть какой-то простой функцией от коэффициента наклона
линейного тренда ранжированного списка. Естественным было
нормировать 1-й частный критерий манипулирования индексом Хирша таким образом,
чтобы при наклоне тренда 90° он имел минимальное значение равное 0 (нет
манипулирования), а при наклоне 0° имел максимальное значение, равное 1 (полное
манипулирование).
Уравнение линейного тренда
выгладит следующим образом:
![]()
С учетом всех этих
соображений предлагается следующее выражение для 1-го частного критерия
манипулирования индексом Хирша K1
при малом числе публикаций:
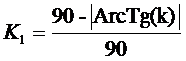 ,
,
где:
k – коэффициент при x в
линейном тренде ранжированного списка публикаций;
ArcTg(k) – арктангенс
коэффициента наклона – угол наклона линейного тренда ранжированного по числу
цитирований списка публикаций (в градусах).
Понятно, что чем более
пологим является линейный тренд графика числа цитирований, тем ближе
коэффициент b в линейном тренде к значению индекса Хирша h:
![]()
Предлагается следующее
выражение для 2-го частного критерия манипулирования индексом Хирша K2 при малом числе
публикаций:
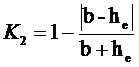 ,
,
где:
b – свободный член в
линейном тренде графика числа цитирований;
he – эмпирическое
значение индекса Хирша, т.е. полученное непосредственно из ранжированного
списка публикаций и построенного по нему графика числа цитирований.
Естественным было
нормировать 2-й частный критерий манипулирования индексом Хирша таким образом,
чтобы при эмпирическом индексе Хирша he=0 он был равен нулю (нет
манипулирования), при свободном члене b равном
эмпирическому индексу Хирша he он был равен 1 (полное
манипулирование), и при увеличении разницы между ними стремился к нулю (уменьшение
степени манипулирования) (таблица 1 и рисунок 2):
Таблица 1 – Зависимость 2-го
частного критерия манипулирования индексом Хирша от эмпирического значения
индекса Хирша
при постоянном свободном члене b=7
|
B |
H |
2-й частный критерий |
B |
H |
2-й частный критерий |
B |
H |
2-й частный критерий |
|
7 |
0 |
0,000000 |
7 |
13 |
0,700000 |
7 |
26 |
0,424242 |
|
7 |
1 |
0,250000 |
7 |
14 |
0,666667 |
7 |
27 |
0,411765 |
|
7 |
2 |
0,444444 |
7 |
15 |
0,636364 |
7 |
28 |
0,400000 |
|
7 |
3 |
0,600000 |
7 |
16 |
0,608696 |
7 |
29 |
0,388889 |
|
7 |
4 |
0,727273 |
7 |
17 |
0,583333 |
7 |
30 |
0,378378 |
|
7 |
5 |
0,833333 |
7 |
18 |
0,560000 |
7 |
31 |
0,368421 |
|
7 |
6 |
0,923077 |
7 |
19 |
0,538462 |
7 |
32 |
0,358974 |
|
7 |
7 |
1,000000 |
7 |
20 |
0,518519 |
7 |
33 |
0,350000 |
|
7 |
8 |
0,933333 |
7 |
21 |
0,500000 |
7 |
34 |
0,341463 |
|
7 |
9 |
0,875000 |
7 |
22 |
0,482759 |
7 |
35 |
0,333333 |
|
7 |
10 |
0,823529 |
7 |
23 |
0,466667 |
7 |
36 |
0,325581 |
|
7 |
11 |
0,777778 |
7 |
24 |
0,451613 |
7 |
37 |
0,318182 |
|
7 |
12 |
0,736842 |
7 |
25 |
0,437500 |
7 |
38 |
0,311111 |
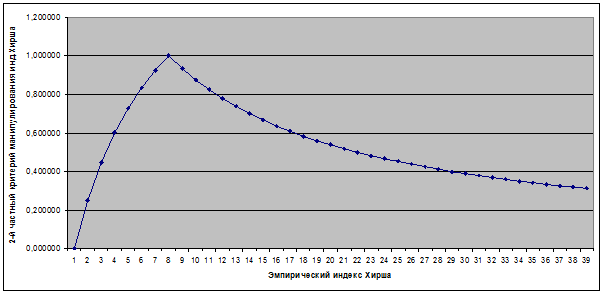
Рисунок 2. Зависимость 2-го
частного критерия манипулирования
индексом Хирша от эмпирического значения индекса Хирша
при постоянном свободном члене b=7
Если считать, что оба эти
частные критерия K1 и K2 имеют равный вес 0.5, то
можно предложить следующее выражение для 1-го интегрального критерия
манипулирования индексом Хирша при малом числе публикаций:
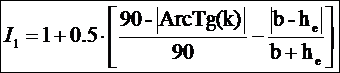 .
.
Все обозначения,
использованные в данном выражении, описаны выше.
Данный 1-й интегральный
критерий принимает значение равное 0 при отсутствии манипулирования и равное 1
при максимальном, т.е. полном манипулировании. Ниже приведена его вербальная
формулировка:
«Чем ближе к нулю коэффициент наклона
линейного тренда числа цитирований, построенного по ранжированному списку публикаций
и чем ближе свободный член в линейном тренде к эмпирическому значению индекса
Хирша, тем более вероятно, что был применен описанный выше способ максимизации
индекса Хирша при малом числе публикаций».
Конечно, понятно, что часть
цитирований могут естественными, не организованными автором, и они вместе тоже
могут формировать достаточно пологий тренд, т.е. понятно, что максимальное
значение индекса манипулирования еще не означает самого факта манипулирования,
а лишь является его признаком. Аналогично и заимствования сами по себе не означают
плагиата, т.к. могут быть снабжены ссылками на источники, а могут быть и
заимствованиями из работ самого автора, которые уже по главам порезаны на
рефераты и разошлись по всему интернету.
4.2.3. Примеры применения первого интегрального
критерия манипулирования индексом Хирша
на основе баз данных РИНЦ
Для того, чтобы применить
этот интегральный критерий к публикациям какого-либо автора выполняем следующие
действия:
1. Открываем сайт РИНЦ: http://elibrary.ru/.
2. В меню слева выбираем «Авторский указатель», задаем сортировку по
числу цитирований по убыванию без фильтра по региону. В результате получаем (на
момент написания работы) (рисунок 3):
Рисунок 3. Экранная форма
РИНЦ: «Авторский указатель»,
сортировка по числу цитирований по убыванию
без фильтра по региону
3. Выбираем автора, по
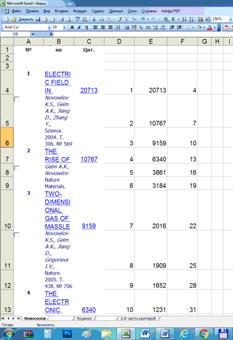
которому собираемся анализировать индекс Хирша (Новоселов К.С.), кликаем по
числу его работ (левее гистограммки: ![]() ),
выделяем блоком вместе с заголовком
таблицы первые его 100 публикаций (или все, если их меньше 100),
копируем его в буфер обмена и вставляем
в MS Excel (используем копировать: Ctrl+C, и вставить: Crtl+V или эти
пункты в меню, выскакивающему по клику на правой кнопке мыши).
),
выделяем блоком вместе с заголовком
таблицы первые его 100 публикаций (или все, если их меньше 100),
копируем его в буфер обмена и вставляем
в MS Excel (используем копировать: Ctrl+C, и вставить: Crtl+V или эти
пункты в меню, выскакивающему по клику на правой кнопке мыши).
4. Выделяем блоком весь лист
отменяем объединение ячеек.
5. Переносим колонку D
с числом цитирований в колонку C (если они не в колонке C).
6. Начиная с колонки D
вставляем следующие значения и формулы для построения графика цитирований и
расчета трендов (рисунок 4):
|
|
|
Рисунок 4. Значения и
формулы для построения графика
цитирований и расчета трендов
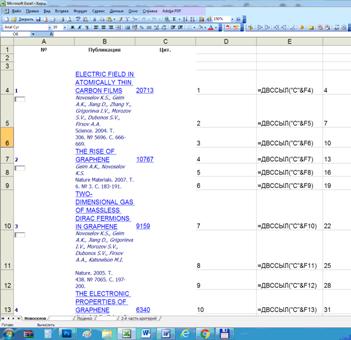
В колонке D просто
подряд пронумерованы строки c 1 до 100. В колонке F в подряд идущих
строках проставлены номера строк, в которых в колонке C приведено число
цитирований: 4, 7, 10, 13 и т.д. с шагом 3. В колонке E приведены
формулы ссылок на ячейки с числом цитирований из колонки C. Все это
сделано для того, чтобы значения числа цитирований для различных публикаций шли
в подряд идущих строках, а не в каждой третьей строке, начиная с 4-й, как это
сделано в РИНЦ. Отметим, что и в РИНЦ шаг 3 между строками с числом цитирований
может нарушаться, хотя это происходит и редко. Например, у автора: Новоселов
К.С. в 64-й публикации (193-я строка в списке РИНЦ) дано не совсем стандартное
описание. Поэтому для 65-й публикации вместо 196 строки указана 201-я, в
которой фактически находится число цитирований 65-й публикации. Далее и до 10-й
публикации они опять идут с стандартным шагом 3. Чтобы не пропустить подобные ситуации рекомендуется проверять
значения числа цитирований не только в первых, но и в последних строках списка.
7. Строим график по числу
цитирований. Для этого выделяем блоком ячейки в колонке E, в которых
есть число цитирований (удобнее это делать снизу вверх), и строим график
(рисунок 5):
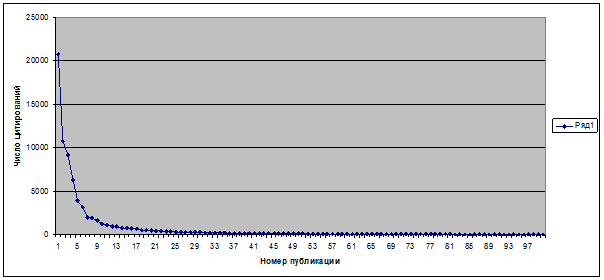
Рисунок 5. График числа цитирований, простроенный по
списку
публикаций Новоселова К.С., ранжированному по числу цитирований в порядке
убывания
8. Строим линейный тренд
графика числа цитирований с выводом формулы тренда и критерия качества
аппроксимации – коэффициента детерминации R2 (рисунок 6):
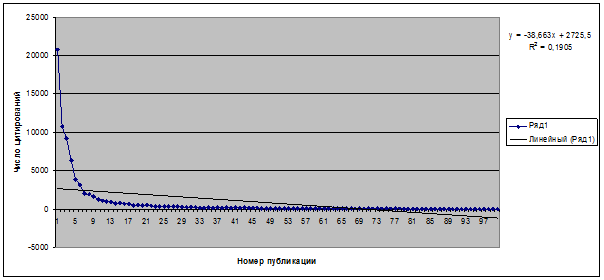
Рисунок 6. График числа цитирований публикаций
Новоселова К.С. с линейным трендом
9. Для расчета частных
критериев и интегрального критерия в MS Excel используем формулы, приведенные
на рисунке 7:
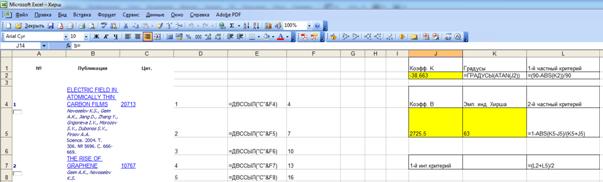
Рисунок 7. Формулы для
расчета частных критериев и 1-го
интегрального критерия манипулирования индексом Хирша
при малом числе публикаций
Значения коэффициентов k и b
из уравнения линейной регрессии, приведенного на рисунке 6, вручную вносим в ячейки J2 и J5
соответственно (выделены на рисунке 7 желтым цветом). В результате получим значения
частных критериев и интегрального критерия манипулирования индексом Хирша для
данного автора (рисунок 8), рассчитанные по приведенным выше формулам.
Из рисунка 8 видно, что все
эти значения очень близки к нулю, что означает полное отсутствие манипулирования в данном случае.
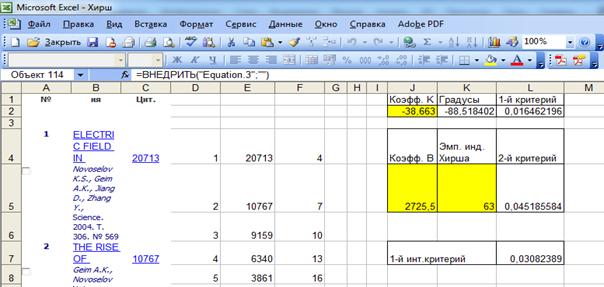
Рисунок 8. Значения частных
критериев и 1-го интегрального критерия манипулирования индексом Хирша для
автора:
Новоселов К.С.
Рассмотрим применение
предлагаемого интегрального критерия на примере 2-го автора, рейтинг,
Ф.И.О. и место работы которого мы не указываем из этических соображений.
На рисунке 9 приведен график числа цитирований с линейным трендом этого 2-го
автора, а в таблице 2 результаты расчета частных критериев и интегрального
критерия :
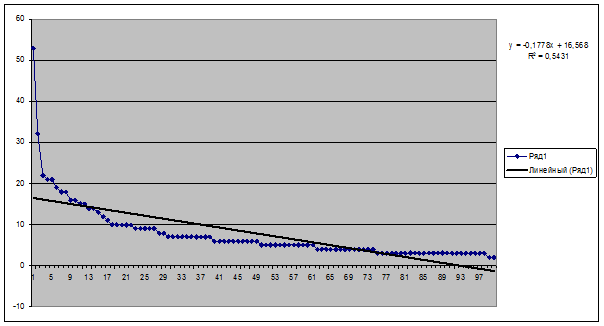
Рисунок 9. График числа цитирований публикаций 2-го
автора
с линейным трендом
Таблица 2 – Результаты расчетов частных критериев и 1-го
интегрального критерия манипулирования индексом Хирша при малом числе
публикаций для 2-го автора
|
Коэфф. K |
Градусы |
1-й частный критерий |
|
-0,1778 |
-10,081832 |
0,887979642 |
|
|
|
|
|
Коэфф. B |
Эмп. инд. Хирша |
2-й частный критерий |
|
16,568 |
14 |
0,915990578 |
|
|
|
|
|
1-й инт.критерий |
|
0,90198511 |
Из таблицы 2 видно, что доля
манипулирования индексом Хирша в данном случае значительно выше, т.к. значение
1-го интегрального критерия близко к 0,9.
Из приведенных графиков и
таблиц мы видим, что для лидера рейтинга РИНЦ по числу цитирований предлагаемый
1-й критерий манипулирования индексом Хирша дает значительно меньшую величину,
чем у 2-го автора. Видно, что этот результат получается за счет того, что у лидера различие между числом цитирований
наиболее и наименее цитируемых работ первой сотни работ. значительно больше, чем у обычного автора.
4.3. Манипулирование индексом Хирша
при большом числе публикаций
4.3.1. Способ увеличить значение индекса Хирша
при большом числе публикаций
Если у автора большое число
публикаций, то очевидно, использовать способ формирования максимального
значения индекса Хирша, который использовался при малом числе публикаций, т.е.
ссылаться во всех публикациях на все, не
представляется возможным по ряду причин. Понятно, что работа, у которой в
списке литературы приведено десятки источников и в основном автора самой этой работы,
будет выглядеть несколько странно[2].
Во многих журналах просто есть ограничение и на суммарное число источников в
списке литературы и на число источников автора публикации. Но цитирование всех
публикаций данного автора в каждой его публикации не только невозможно технически[3],
но и не имеет особого смысла, т.к.
увеличение числа цитирований статей, находящихся в ранжированном списке далеко
от значения индекса Хирша, не окажет влияния на его значение ни в ближайшее
время, ни в перспективе (за исключением может быть каких-то научных
«бестселлеров», которые сразу становятся очень цитируемыми и сохраняют
популярность длительное время).
Поэтому многие авторы, у которых большое количество
публикаций, приходят к тому, чтобы увеличивать
число ссылок не на все публикации, а только на те, которые оказывают самое непосредственное
влияние на значение индекса Хирша, т.е. на публикации в окрестности
индекса Хирша в ранжированном списке публикаций. В результате вблизи
значения индекса Хирша, причем как текущего, так и перспективного с точки
зрения этих авторов, формируется характерная «ступенька» или «полочка», которую
предлагается называть: «горб Хирша», показанная на рисунке 10 красным
цветом. К росту этого «горба Хирша» приводит и привязка ссылок к публикациям,
которую осуществляют администраторы системы Science Index, которые привязывают не все
публикации подряд, а в первую очередь те, которые в наибольшей степени влияют
на значение индекса Хирша. Так совместными усилиями авторов и администраторов
этот горб и выращивается.
В результате такого
манипулирования индекс Хирша приобретает вместо значения h некоторое большее
значение h2. При этом площадь под кривой числа цитирований, соответствующая
суммарному числу цитирований автора, увеличивается совершенно незначительно, а
значение индекса Хирша за счет этого возрастает довольно заметно, т.е. затраты
на это повышение оказываются весьма эффективными.
Вот как выглядит подобная
«полочка» на реальном графике числа цитирований, построенном по данным РИНЦ[4]
3-го автора (рисунок 11):
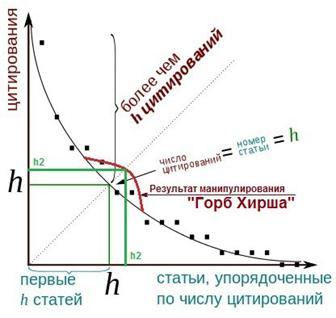
Рисунок 10. Результат манипулирования индексом Хирша
при большом числе публикаций: характерная «полочка» в окрестности индекса Хирша («горб Хирша») в ранжированном списке
публикаций (теория)
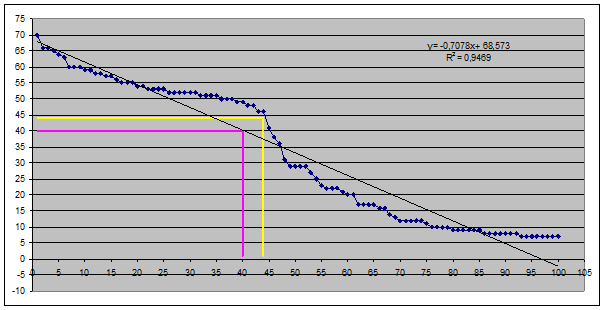
Рисунок 11. Результат манипулирования индексом Хирша
при большом числе публикаций: характерная «полочка» в окрестности
индекса Хирша («горб Хирша») в ранжированном списке публикаций
3-го автора (факт)
4.3.2. Научно-обоснованная модификация индекса
Хирша, нечувствительная (устойчивая)
к попыткам манипулированию им
Идея второго критерия
манипулирования индексом Хирша, применяемого при большом числе публикаций,
основана на том, что при цитирования статей в окрестностях текущего значения
индекса Хирша площадь под кривой числа цитирований, соответствующая суммарному
числу цитирований автора, увеличивается очень незначительно. А это в свою очередь
означает, что, по-видимому, если
аппроксимировать эту кривую с использованием метода наименьших квадратов (МНК),
то эта аппроксимация окажется малочувствительной или устойчивой к появлению
в результате манипулирования этой небольшой «полочки».
Это позволяет сформулировать
гипотезу о том, что значение
индекса Хирша, определенное не по классическому алгоритму, а посчитанное на
основе аппроксимации кривой числа цитирований, окажется менее чувствительным и
более устойчивым к попыткам манипулирования, чем классический индекс Хирша.
Но откуда взять эту
аппроксимацию кривой числа цитирований и как определить значение индекса Хирша
на ее основе? В общем виде все это довольно просто. Непосредственно из самого
определения классического индекса Хирша следует, что если аппроксимации кривой
числа цитирований выражается в виде уравнения:
![]()
то теоретическим значением индекса Хирша h будет
корень уравнения:
![]() .
.
Такого рода уравнения обычно
легко решаются численно итерационным методом, реализованным в частности, в MS
Excel.
Сам вид функции f() предлагается определять с
использованием аппарата аппроксимации трендов функциями различных видов в MS
Excel.
В принципе можно было бы каждый раз выбирать для аппроксимации тот
вид монотонной[5]
функции, который обеспечивает наивысший коэффициент детерминации R2,
т.е. наиболее хорошее приближение (наилучший тренд). В данном случае для аппроксимации графика числа
цитирований ранжированного списка публикаций уместно использовать лишь
монотонно возрастающие или убывающие функции: линейную, логарифмическую,
степенную, экспоненциальную, но не полиномиальную, т.к. она может иметь точки
перегиба и даже нарушения монотонности и является чувствительной к особенностям
графика, обусловленными манипулированием индексом Хирша.
Но можно выбрать какой-то
один вид функции, который чаще других обеспечивает наилучшее приближение. В
результате многочисленных численных экспериментов по аппроксимации кривых числа
цитирований различных авторов, проведенных по данным РИНЦ, было выявлено, что
наилучшее приближение с коэффициентом детерминации около 0,9 и выше, как
правило обеспечивается трендом в виде степенной функции:
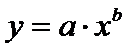 .
.
Поэтому предлагается
находить теоретическое значение индекса Хирша h путем решения уравнения:
![]() .
.
При этом само уравнение
тренда предлагается формировать в MS Excel непосредственно на основе данных
РИНЦ, как описано выше в разделе 2.3 при формировании линейной регрессии
(примеры приведены ниже).
Решение этого уравнения
легко находится аналитически:
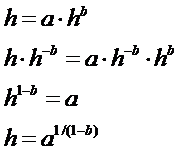
![]() .
.
4.3.3. Второй интегральный критерий
манипулирования индексом Хирша
И это дает нам в руки второй
более сложный второй критерий манипулирования индексом Хирша:
«Чем
больше отличаются друг от друга эмпирический индекс Хирша, определенный по
классическому алгоритму, и теоретический индекс Хирша, найденный путем решения
наилучшего уравнения тренда, тем больше вероятность того, что классический
индекс Хирша получен в результате манипулирования (хотя возможны и другие
варианты: шум и несовершенство алгоритма)».
Аналитически 2-й
интегральный критерий манипулирования индексом Хирша, т.е. относительное
превышение эмпирического значения индекса Хирша над теоретическим, может быть
выражен по-разному. Авторы предлагают измерять это превышение в долях от
теоретического значения, как более близкого к истинному:
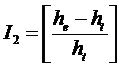
где:
he – классическое эмпирическое значение индекса Хирша;
ht – теоретическое значение индекса Хирша.
4.3.4. Примеры определения теоретических значений
индекса Хирша путем решения уравнений
трендов
Как и в разделе 2.3 примеры
рассмотрим на примере тех же авторов:
– Новоселов Константин
Сергеевич, имеющий 1-й рейтинг по числу цитирований по данным РИНЦ[6];
– 2-й и 3-й авторы, рейтинг
и Ф.И.О. и место работы которых мы не указываем из этических соображений.
Новоселов Константин Сергеевич.
На графике числа цитирований,
приведенном на рисунке 5, построим тренд в виде степенной функции (рисунок 12):
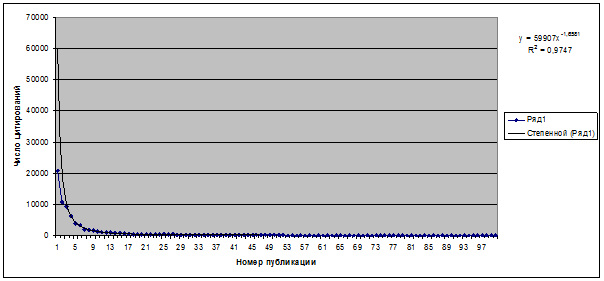
Рисунок 12. График числа цитирований публикаций
Новоселова К.С. и тренд в виде степенной функции
Мы видим, что уравнение
тренда имеет вид:
![]()
С очень хорошим качеством
аппроксимации: R2 = 0,9747.
Для нахождения
теоретического значения индекса Хирша необходимо решить уравнение тренда:
![]()
Для решения этого уравнения
воспользуемся on-line сервисом Вольфрам-математики по адресу: http://www.wolframalpha.com/. Введя решаемое
уравнение (заменив в нем запятые на точки, добавив знаки операций и скобки) в
окно сервиса, представленное на рисунке 13, получим: h=62.7, что после
округления с точностью до целых совпадает с эмпирическим значением h=63:
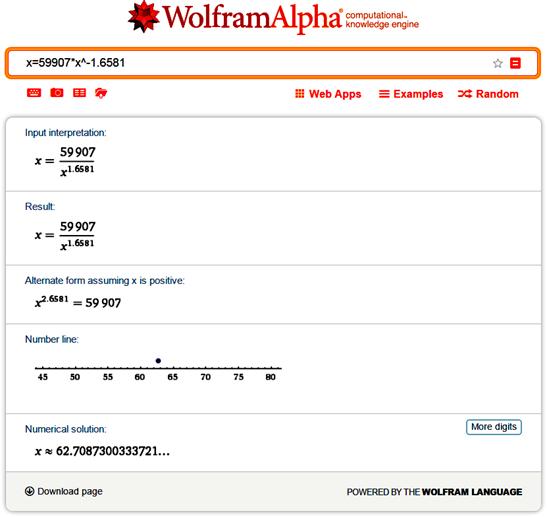
Рисунок 13. Выходной экран
on-line сервиса Вольфрам-математики
с решением уравнения тренда графика числа
цитирований
публикаций Новоселова К.С.
Найденное
on-line решение точно совпадает с полученным аналитически:
![]()
При решении в MS Excel по
этой формуле со значениями коэффициентов: a=59907; b=-1,6581 получаем ![]() или h=62.7087300333721,
что совпадает по всем знакам после запятой с решением, полученным on-line с
помощью Вольфрам-математики.
или h=62.7087300333721,
что совпадает по всем знакам после запятой с решением, полученным on-line с
помощью Вольфрам-математики.
В разделе 3.3. мы видели,
что 2-й интегральный критерий манипулирования индексом Хирша рассчитывается по
формуле:
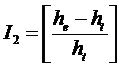
где:
he – классическое эмпирическое значение индекса Хирша;
ht – теоретическое значение индекса Хирша.
Для Новоселова К.С. это дает
значение, весьма близкое к нулю (десятые доли процента):
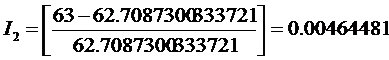 .
.
Фрагменты Excel-файла, в
которых проводятся расчеты по приведенным выше формулам, приведены на рисунках
14 (результаты расчетов) и 15 (формулы):
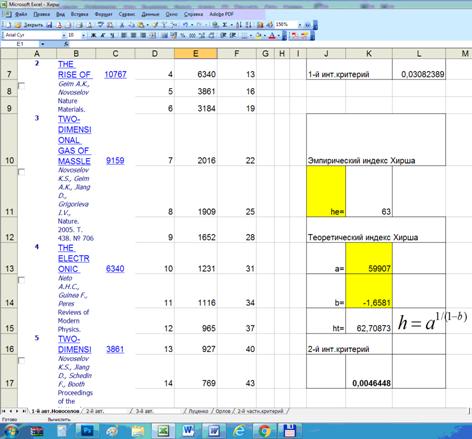
Рисунок 14. Фрагмент
Excel-файла с расчетами,
представленными в таблице 3 (результаты расчетов)
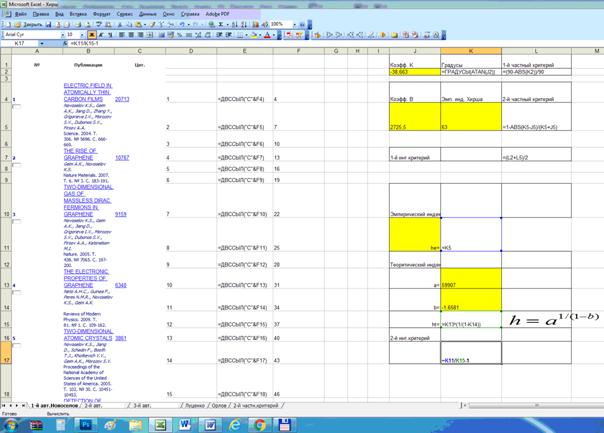
Рисунок 15. Фрагмент
Excel-файла с расчетами,
представленными в таблице 3 (расчетные формулы)
Для 2-го автора график
числа цитирований публикаций и тренд в виде степенной функции представлены на
рисунке 16:
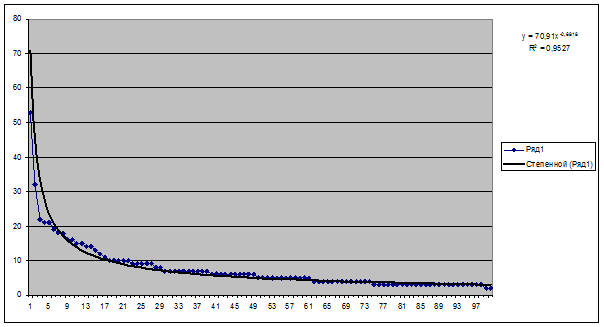
Рисунок 16. График числа цитирований публикаций 2-го
автора
и тренд в виде степенной функции
Таблица 3 – Эмпирический и
теоретический индексы Хирша и 2-й инт. критерий манипулирования индексом Хирша
для 2-го автора
|
Эмпирический индекс Хирша |
|
|
he= |
14 |
|
Теоретический индекс Хирша |
|
|
a= |
70,91 |
|
b= |
-0,6818 |
|
ht= |
12,6017994 |
|
2-й инт.критерий |
|
|
|
0,11095245 |
Для 2-го автора 2-й
интегральный критерий имеет значение порядка 10%.
Для 3-го автора
график числа цитирований публикаций и тренд в виде степенной функции
представлены на рисунке 17:

Рисунок 17. График числа цитирований публикаций 3-го
автора
(вырастившего внушительный «горб Хирша»)
и тренд в виде линейной функции
Для 3-го автора использован
линейный тренд, т.к. он дает приближение с более высоким коэффициентом
детерминации, чем степенная функция. Для 3-го автора эмпирическое значение
индекса Хирша равно 44, а теоретическое 40, что дает значение 2-го
интегрального критерия манипулирования индексом Хирша: I2=(44-40)/40=0.1.
Это значит, что в данном случае манипулирование привело к увеличению индекса
Хирша примерно на 10%.
Интересно, что у некоторых
авторов теоретическое значение индекса Хирша получается не меньше, а больше
эмпирического, т.е. эмпирическое значение «недооценено».
4.4. Согласованность 1-го и 2-го
интегральных
критериев манипулирования индексом Хирша
Рассмотрим сводную таблицу
4, в которой приведем все просчитанные в данной работе частные и интегральные
критерии по всем авторам:
Таблица 4 – Частные и
интегральные критерии по всем авторам
|
Автор |
1-й частный критерий |
2-й частный критерий |
1-й интегральный критерий |
Эмпирический индекс Хирша |
Теоретический индекс Хирша |
2-й интегральный критерий |
|
Новоселов К.С. |
0,01646 |
0,04518 |
0,03082 |
63 |
62,70873 |
0,00464 |
|
2-й автор |
0,88797 |
0,91599 |
0,90198 |
14 |
12,60179 |
0,11095 |
|
3-й автор |
0,60787 |
0,78171 |
0,69479 |
44 |
40 |
0,10000 |
Мы видим, что и частные
критерии, и оба интегральных критерия
манипулирования индексом Хирша дают согласованные, совпадающие по смыслу
результаты, т.е. когда мы не видим манипулирования по 1-му частному критерию,
то не видим его и по 2-му, т.е. эмпирический индекс Хирша практически совпадает
с теоретическим. Возможно это объясняется тем, что авторы, не занимавшиеся
манипулированием индексом Хирша, когда у них было мало публикаций, не начинают
занимаются этим и когда публикаций у них становится большое количество. Это
повышает степень обоснованности и достоверности этих критериев.
4.5. Выводы
Итак, на основе вышеизложенного можно считать, что:
1) существует некое неизвестное «истинное значение
индекса Хирша»;
2) есть «эмпирическое (классическое) значение индекса
Хирша», которое является истинным значением, измененным в результате совместного
действия факторов манипулирования (рассматривались в данной работе) а также
естественного шума и несовершенства алгоритма Хирша (в данной работе эти
факторы только упоминаются);
3) есть «теоретическое значение индекса Хирша», – это
решение уравнения наилучшего тренда графика числа цитирований ранжированного
списка публикаций.
«Теоретическое значение индекса Хирша»
– это новое научное понятие из области наукометрии, которое авторы предлагают
ввести в научный оборот и практику наукометрии по следующим причинам:
– теоретическое значение индекса Хирша является
устойчивым к манипулированию и другим факторам, искажающим истинное значение индекса
Хирша и может обоснованно считаться значительно более близким к истинному
значению индекса Хирша, чем классическое эмпирическое значение;
– технология получения теоретического значения индекса
Хирша (путем решение уравнения наилучшего тренда графика числа цитирований
ранжированного списка публикаций) проста и доступна авторам и организациям.
В работе предлагаются два убедительных количественных
частных критерия манипулирования индексом Хирша при малом числе статей и основанный
на них аддитивный интегральный критерий, основанные на линейном тренде графика
числа цитирований ранжированного списка публикаций.
Степень различия между эмпирическим и теоретическим значениями
индекса Хирша можно считать устойчивым интегральным критерием манипулирования индексом Хирша при любом числе публикаций.
Предлагается:
1. Применить результаты данной работы при расчетах в
РИНЦ и строить рейтинги авторов, журналов и организаций (подразделений) не
только на основе эмпирического классического индекса Хирша, но и на основе
теоретического индекса Хирша, а также по критериям манипулирования.
2. Не придавать излишне и
неоправданно большого значения классическому эмпирическому значению индекса
Хирша при оценках и принятии решений.