ГЛАВА 3. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ПРИКЛАДНОЙ СТАТИСТИКИ

3.1. Структура прикладной статистики

Прикладная статистика - наука о том, как обрабатывать статистические данные. Как самостоятельная научно-практическая область она развивается весьма быстро. В ее состав входят многочисленные широко и глубоко развитые научные направления. Те, кто применяет прикладную статистику и другие статистические методы, обычно ориентированы на конкретные области исследования, т.е. не являются специалистами по прикладной статистике. Поэтому представляется полезным провести критический анализ современного состояния прикладной статистики и обсудить тенденции развития статистических методов.

3.1.1. Что дает прикладная статистика народному хозяйству?

Такой вопрос часто задают специалисты различных областей науки, отраслей народного хозяйства, не владеющие методами прикладной статистики. В ответ нами была написана статья [1], в которой приводились многочисленные примеры успешного использования методов прикладной математической статистики. при решении практических задач. Перечень примеров можно продолжать практически безгранично. Например, можно сослаться на обобщающую монографию В. Г. Горского [2], на диссертацию А. Н. Гуды [3]. По данным Института информации Гарфилда (США) каждая из основополагающих книг В. В. Налимова [4, 5] цитировалась не менее 1000 раз (см. также монографию [6, с.270, 274, 373]). Практически в любом номере журнала "Заводская лаборатория. Диагностика материалов" есть работы, в которых те или иные методы прикладной статистики применяются для решения прикладных задач. Не раз публиковались в этом журнале и обобщающие статьи по вопросам применения прикладной статистики [7–10].

Итак, бесспорно совершенно, что методы прикладной статистики успешно применяются в различных отраслях народного хозяйства, практически во всех областях науки. Согласно докладу [11, с.157-158], в 1988 г. затраты в СССР на статистический анализ данных оценивались в 2 миллиарда рублей ежегодно.

Большая практическая значимость прикладной статистики оправдывает целесообразность проведения работ по развитию ее методологии, в которых эта область научной и прикладной деятельности рассматривалась бы как целое, "с высоты птичьего полета". Чтобы иметь возможность обсуждения тенденций развития прикладной статистики и других статистических методов, кратко рассмотрим их историю.

3.1.2. Об истории прикладной статистики

Типовые примеры раннего этапа применения статистических методов описаны в Ветхом Завете (см., например, Книгу Чисел - четвертую книгу Моисееву). С математической точки зрения они сводились к подсчетам числа попаданий значений наблюдаемых признаков в определенные градации. В дальнейшем результаты стали представлять в виде таблиц и диаграмм, как это и сейчас делает Федеральная служба государственной статистики (Росстат). Надо признать, что по сравнению с Ветхим Заветом есть прогресс - в Библии не было таблиц. Однако в работах Росстата нет продвижения по сравнению с работами российских статистиков конца девятнадцатого - начала двадцатого века (типовой монографией тех времен можно считать книгу [12], которая в настоящее время ещё легко доступна).

Сразу после возникновения теории вероятностей (Паскаль, Ферма, XXVII век) вероятностные модели стали использоваться при обработке статистических данных. Например, изучалась частота рождения мальчиков и девочек, было установлено отличие вероятности рождения мальчика от 0.5, анализировались причины того, что в парижских приютах эта вероятность не та, что в самом Париже, и т.д. Имеется достаточно много публикаций по истории теории вероятностей, однако в некоторых из них имеются неточные утверждения, что заставило академика Украинской АН Б. В. Гнеденко включить в шестое издание своего знаменитого курса [13] главу по истории математики случайного, выпущенную затем отдельным изданием [14].

Как установил Ф. Клейн, анализируя записные книжки великого немецкого математика и физика К. Гаусса, тот в 1794 г. разработал метод наименьших квадратов, один из наиболее популярных ныне статистических методов, и применил его при расчете орбиты астероида Церера - для борьбы с ошибками астрономических наблюдений [15]. Математические публикации К. Гаусса по методу наименьших квадратов появились лишь через 12 лет, когда близкие вопросы стали обсуждаться в литературе. В Х1Х веке заметный вклад в развитие практической статистики внес в развитие практической статистики внес бельгиец Ламбер Адольф Жак Кетле, на основе анализа большого числа реальных данных показавший устойчивость относительных статистических показателей, таких, как доля самоубийств среди всех смертей [16]. Важно отметить, что основные идеи статистического приемочного контроля и сертификации продукции глубоко анализировались российским академиком М. В. Остроградским и применялись в российской армии ещё в середине Х1Х в. [17, 18]. Статистические методы управления качеством, сертификации и классификации продукции сейчас весьма актуальны как с теоретической, так и с прикладной точек зрения [19, 20].

Современный этап развития прикладной статистики можно отсчитывать с 1900 г., когда англичанин К. Пирсон основал журнал "Biometrika". Мы полагаем, что именно 1900 г. следует считать началом развития прикладной математической статистики как самостоятельной науки, хотя вначале она выступала под другими именами (биометрика, актуарные исследования (т.е. исследования в области страхового дела) и др.). Первая треть ХХ в. прошла под знаком параметрической статистики. Изучались методы, основанные на анализе данных из параметрических семейств распределений, описываемых кривыми семейства Пирсона. Наиболее популярным было нормальное (гауссово) распределение. Для проверки гипотез использовались критерии Пирсона, Стьюдента, Фишера. Были предложены метод максимального правдоподобия, дисперсионный анализ, сформулированы основные идеи планирования эксперимента.

Разработанную в первой трети ХХ в. теорию будем называть параметрической статистикой, поскольку ее основной объект изучения - это выборки из распределений, описываемых одним или небольшим числом параметров. Наиболее общим является семейство кривых Пирсона, задаваемых четырьмя параметрами. Как правило, нельзя указать каких-либо веских причин, по которым конкретное распределение результатов наблюдений должно входить в то или иное параметрическое семейство. Исключения хорошо известны: если вероятностная модель предусматривает суммирование независимых случайных величин, то сумму естественно описывать нормальным распределением; если же в модели рассматривается произведение таких величин, то итог, видимо, приближается логарифмически нормальным распределением, и т.д. Однако в подавляющем большинстве реальных ситуаций подобных моделей нет, и приближение реального распределения с помощью кривых из семейства Пирсона или его подсемейств - чисто формальная операция. Именно из таких соображений критиковал параметрическую статистику академик С. Н. Бернштейн в 1927 г. в своем докладе на Всероссийском съезде математиков [21]. Однако эта теория, к сожалению, до сих пор остается основой преподавания статистических методов и продолжает использоваться основной массой прикладников, остающихся далекими от новых веяний в статистике. Почему так происходит? Чтобы попытаться ответить на этот вопрос, обратимся к наукометрии.

3.1.3. Наукометрия прикладной статистики

Проведенный в 1980-е годы (в ходе работ по созданию Всесоюзной статистической ассоциации [22]) анализ прикладной статистики как области научно-практической деятельности показал, в частности, что актуальными для специалистов в настоящее время являются не менее чем 100 тысяч публикаций (подробнее см. статьи [8, 23, 24]). Реально же каждый из нас знаком с существенно меньшим количеством книг и статей. Так, в наиболее обширном на русском языке сочинении по прикладной статистике - известном трехтомнике Кендалла и Стьюарта [25–27] - приведено около 2 тысяч литературных ссылок. При всей очевидности соображений о многократном дублировании в публикациях ценных идей приходится признать, что каждый специалист по прикладной статистике владеет лишь небольшой частью накопленных в этой области знаний (это утверждение в полной мере относится и к специалистам в других областях). Не удивительно, что приходится постоянно сталкиваться с игнорированием или повторением ранее полученных результатов, с уходом в тупиковые (с точки зрения практики) направления исследований, с беспомощностью при обращении к реальным данным, и т.д. Все это - одно из проявлений адапционного механизма торможения развития науки, о котором еще около 50 лет назад писали В. В. Налимов и другие науковеды (см., например, [28]).

Традиционный предрассудок состоит в том, что каждый новый результат, полученный исследователем - это кирпич в непрерывно растущее здание науки, который непременно будет проанализирован и использован научным сообществом. Реальная ситуация - совсем иная. Основа профессиональных знаний исследователя и инженера закладывается в период обучения. Затем они пополняются в том узком направлении, в котором работает специалист. Следующий этап - их тиражирование новому поколению. В результате вузовские учебники отстоят от современного развития на десятки лет. Так, учебники по математической статистике, по нашей экспертной оценке, в основном соответствуют 40–60-м годам ХХ в. А потому тем же годам соответствует большинство вновь публикуемых исследований и тем более - прикладных работ. Одновременно приходится признать, что результаты, которые не вошли в учебники, независимо от их ценности почти все забываются.

Активно продолжается развитие тупиковых направлений. Психологически это понятно. Приведем пример из опыта одного из авторов настоящей монографии. В свое время по заказу Госстандарта А. И. Орлов разработал методы оценки параметров гамма-распределения [29]. Поэтому ему близки и интересны работы по оцениванию параметров по выборкам из распределений, принадлежащих тем или иным параметрическим семействам, понятия функции максимального правдоподобия, эффективности оценок, использование неравенства Рао - Крамера и т.д. К сожалению, известно, что это - тупиковая ветвь, поскольку реальные данные не подчиняются каким-либо параметрическим семействам, надо применять иные статистические методы, о которых речь пойдет ниже. Понятно, что специалистам по параметрической статистике, потратившим многие годы на совершенствование в своей области, психологически трудно согласиться с этим утверждением. В том числе и одному из авторов настоящей монографии.

3.1.4. Точки роста

Отечественная литература по прикладной статистике столь же необозрима, как и мировая. Только в разделе "Математические методы исследования" журнала "Заводская лаборатория. Диагностика материалов" с 1960-х годов опубликовано более 1000 статей. Не будем даже пытаться перечислять коллективы исследователей или основные монографии в этой области (впрочем, см. статью [24]). Отметим только одно издание. По нашему мнению, наилучшей отечественной книгой по прикладной статистике является сборник статистических таблиц Л. Н. Большева и Н. В. Смирнова [30] с подробными комментариями, играющими роль учебника и справочника по классическим вопросам прикладной статистики.

С целью управления развитием статистической науки кратко рассмотрим "точки роста" прикладной статистики [31], т.е. те ее направления, которые представляются перспективными, но пока отодвинуты на задний план традиционными постановками. Двадцать пять лет назад при описании современного этапа развития статистических методов нами были выделены [32] пять актуальных направлений, в которых развивается современная прикладная статистика, т.е. пять "точек роста": непараметрика, робастность, бутстреп, статистика интервальных данных, нечисловая статистика. Обсудим их.

Непараметрическая статистика. В первой трети ХХ в., одновременно с параметрической статистикой, в работах Спирмена и Кендалла появились первые непараметрические методы, основанные на коэффициентах ранговой корреляции, носящих ныне имена этих статистиков. Но непараметрика, не делающая нереалистических предположений о том, что функции распределения результатов наблюдений принадлежат тем или иным параметрическим семействам распределений, стала заметной частью статистики лишь со второй трети ХХ века. В 30-е годы появились работы А. Н. Колмогорова и Н. В. Смирнова, предложивших и изучивших статистические критерии, носящие в настоящее время их имена (история этих работ подробно описана в статьях [33, 34]). Эти критерии основаны на использовании так называемого эмпирического процесса - разности между эмпирической и теоретической функциями распределения, умноженной на квадратный корень из объема выборки. В работе А. Н. Колмогорова 1933 г. изучено предельное распределение супремума модуля эмпирического процесса, называемого сейчас статистикой критерия Колмогорова. Затем Н. В. Смирнов исследовал супремум и инфимум эмпирического процесса, а также интеграл (по теоретической функции распределения) квадрата эмпирического процесса. Следует отметить, что встречающееся иногда в литературе [35] словосочетание "критерий Колмогорова - Смирнова", как подробно обосновано в [33, 34], некорректно, поскольку эти два статистика никогда не печатались вместе и не изучали один и тот же критерий. Корректно словосочетание "критерий типа Колмогорова - Смирнова", применяемое для обозначения критериев, основанных на использовании супремума функций от одного или нескольких эмпирических процессов или процессов более сложной природы.

После второй мировой войны развитие непараметрической статистики пошло быстрыми темпами [36, 37]. Большую роль сыграли работы американца Вилкоксона и его школы. К настоящему времени с помощью непараметрических методов можно решать практически тот же круг статистических задач, что и с помощью параметрических [35]. Все большую роль играют непараметрические оценки плотности, непараметрические методы регрессии и распознавания образов (дискриминантного анализа). В нашей стране непараметрические методы получили достаточно большую известность после выхода в 1965 г. первого издания упомянутого выше сборника статистических таблиц Л. Н. Большева и Н. В. Смирнова [30], содержащего подробные таблицы для основных непараметрических критериев. Тем не менее параметрические методы всё еще популярнее непараметрических, особенно среди тех прикладников, кто слабо знаком со статистическими методами. Неоднократно публиковались (см. сводки в [4, 38]) экспериментальные данные, свидетельствующие о том, что распределения реально наблюдаемых случайных величин, в частности, ошибок измерения, в подавляющем большинстве случаев отличны от нормальных (гауссовских). Тем не менее теоретики продолжают строить и изучать статистические модели, основанные на гауссовости, а практики - применять подобные методы и модели. Другими словами, как сказано в пословице, "ищут под фонарем, а не там, где потеряли".

Устойчивость статистических процедур (робастность). Если в параметрических постановках на данных накладываются слишком жесткие требования - их функции распределения должны принадлежать определенному параметрическому семейству, то в непараметрических, наоборот, излишне слабые - требуется лишь, чтобы функции распределения были непрерывны. При этом игнорируется априорная информация о том, каков "примерный вид" распределения. Априори можно ожидать, что учет этого "примерного вида" улучшит показатели качества статистических процедур. Развитием этой идеи является теория устойчивости (робастности) статистических процедур, в которой предполагается, что распределение исходных данных мало отличается от некоторого параметрического семейства. С 60-х годов эту теорию разрабатывали П. Хубер [39], Ф. Хампель [40] и многие другие. Из монографий на русском языке, трактующих о робастности и устойчивости статистических процедур, самой ранней и наиболее общей была книга [41], следующей - монография [42]. Современное состояние отражено в [43, 44]. Частными случаями реализации идеи робастности (устойчивости) статистических процедур являются рассматриваемые ниже статистика интервальных данных и нечисловая статистика.

Имеется большое разнообразие моделей робастности в зависимости от того, какие именно отклонения от заданного параметрического семейства допускаются. Сначала наиболее популярной [39, 40] была модель выбросов, в которой исходная выборка "засоряется" малым числом "выбросов", имеющих принципиально иное распределение. Однако эта модель представляется "тупиковой", поскольку в большинстве случаев большие выбросы либо невозможны из-за ограниченности шкалы прибора, либо от них можно избавиться, применяя статистики, построенные по центральной части вариационного ряда. Кроме того, в подобных моделях обычно считается известной частота засорения, что в сочетании со сказанным выше делает их малопригодными для практического использования. Более перспективной представляется модель, в которой расстояние между распределением каждого элемента выборки и базовым распределением не превосходит заданной малой величины.

Бутстреп (размножение выборок). Третье из упомянутых выше направлений - бутстреп - связано с интенсивным использованием возможностей вычислительной техники, т.е. с применением современных информационно-коммуникационных технологий. Основная идея состоит в том, чтобы теоретическое исследование дополнить или даже заменить вычислительным экспериментом [45, 46]. Вместо описания выборки распределением из параметрического семейства строим большое число "похожих" выборок, т.е. "размножаем" выборку. Затем вместо оценивания характеристик и параметров и проверки гипотез на основе свойств теоретического распределения решаем эти задачи вычислительным методом, рассчитывая интересующие нас статистики по каждой из "похожих" выборок и анализируя полученные при этом распределения. Например, вместо того, чтобы теоретическим путем находить распределение статистики, доверительные интервалы и другие характеристики, моделируют много выборок, похожих на исходную, рассчитывают соответствующие значения интересующей исследователя статистики и изучают их эмпирическое распределение. Квантили этого распределения задают доверительные интервалы, и т.д.

Термин "бутстреп" мгновенно получил известность после статьи Б. Эфрона 1979 г. [47] по этой тематике. Новый подход сразу же стал обсуждаться в массе публикаций, в том числе и научно-популярных [48]. В журнале "Заводская лаборатория. Диагностика материалов" была помещена подборка статей по бутстрепу [49], выпущен сборник статей Б.Эфрона [50]. Основная идея бутстрепа по Б. Эфрону состоит в том, что методом Монте-Карло (статистических испытаний) многократно извлекаются выборки из эмпирического распределения. Эти выборки, естественно, являются вариантами исходной, напоминают ее.

Сама по себе идея "размножения выборок" была известна гораздо раньше. Статья Б.Эфрона [47] называется так: "Бутстреп-методы: новый взгляд на метод складного ножа". Упомянутый "метод складного ножа" (jackknife) предложен М. Кенуем еще в 1949 г., за 30 лет до статьи Б. Эфрона. "Размножение выборок" при этом осуществляется путем исключения одного наблюдения. При этом для выборки объема n получаем n "похожих" на нее выборок объема (n - 1) каждая. Если же исключать по 2 наблюдения, то число "похожих" выборок возрастает до n (n - 1) / 2 объема (n - 2) каждая, и т.д.

Преимущества и недостатки бутстрепа как статистического метода обсуждаются в [51]. Там же и в [23] приводится информация о ряде аналогичных методов. Необходимо подчеркнуть, что бутстреп по Эфрону [47 - 50] - лишь один из вариантов методов "размножения выборки" (resampling), и, на наш взгляд, не самый удачный. Метод "складного ножа" представляется более полезным. На его основе можно сформулировать следующую простую практическую рекомендацию.

Вы по выборке делаете какие-либо статистические выводы и хотите узнать также, насколько эти выводы устойчивы. Если у Вас есть другие (контрольные) выборки, описывающие то же явление, то Вы можете применить к ним ту же статистическую процедуру и сравнить результаты. А если таких выборок нет? Тогда Вы можете построить их искусственно. Берете исходную выборку и исключаете один элемент. Получаете похожую выборку. Затем возвращаете этот элемент и исключаете другой. Получаете вторую похожую выборку. Поступив так со всеми элементами исходной выборки, получаете столько выборок, похожих на исходную, каков ее объем. Остается обработать их тем же способом, что и исходную, и изучить устойчивость получаемых выводов - разброс оценок параметров, частоты принятия или отклонения гипотез и т.д.

Можно изменять не выборку, а сами данные. Поскольку всегда имеются погрешности измерения, то реальные данные - это не числа, а интервалы (результат измерения плюс-минус погрешность). Нужна статистическая теория анализа таких данных.

Статистика интервальных данных. Перспективное и быстро развивающееся направление последних десятилетий - математическая статистика интервальных данных. Речь идет о развитии методов математической статистики в ситуации, когда статистические данные - не числа, а интервалы, в частности, порожденные наложением ошибок измерения на значения случайных величин. Полученные результаты отражены, в частности, в дискуссии [52] и в докладах международной конференции ИНТЕРВАЛ-92 [53]. Статистика интервальных данных идейно связана с интервальной математикой, в которой в роли чисел выступают интервалы (см., например, [54]). Это направление математики является дальнейшим развитием известных правил приближенных вычислений, посвященных выражению погрешностей суммы, разности, произведения, частного через погрешности тех чисел, над которыми осуществляются перечисленные операции. Как видно из докладов конференции ИНТЕРВАЛ-92 [53], уже к 1992 г. удалось решить, в частности, ряд задач теории интервальных дифференциальных уравнений, в которых коэффициенты, начальные условия и решения описываются с помощью интервалов.

Одна из ведущих научная школа в области статистики интервальных данных - это школа проф. А. П. Вощинина (1937–2008), активно работающая с конца 70-х годов. Полученные результаты отражены в ряде монографий (см., в частности, [55–57]), статей [52, 58, 59], докладов [53], диссертаций. В частности, изучены проблемы регрессионного анализа, планирования эксперимента, сравнения альтернатив и принятия решений в условиях интервальной неопределенности.

Рассмотрим другое - наше - направление в статистике интервальных данных, которое также представляется перспективным. В нем развиваются асимптотические методы статистического анализа интервальных данных при больших объемах выборок и малых погрешностях измерений. В отличие от классической математической статистики, сначала устремляется к бесконечности объем выборки и только потом - уменьшаются до нуля погрешности. В частности, с помощью такой асимптотики были сформулированы правила выбора метода оценивания параметров гамма-распределения в ГОСТ 11.011-83 [29]. Основные идеи статистики интервальных данных были разработаны нами при подготовке этого стандарта в начале 80-х, однако в научной печати появились лишь в начале 90-х [60, 61]. Общая схема исследования включает расчет нотны (максимально возможного отклонения статистики, вызванного интервальностью исходных данных) и рационального объема выборки (превышение которого не дает существенного повышения точности оценивания). Она применена к оцениванию математического ожидания, дисперсии, коэффициента вариации, параметров гамма-распределения и характеристик аддитивных статистик, при проверке гипотез о параметрах нормального распределения, в т.ч. с помощью критерия Стьюдента, а также гипотезы однородности с помощью критерия Смирнова. Разработаны подходы к рассмотрению интервальных данных в основных постановках регрессионного, дискриминантного и кластерного анализов. В частности, изучено влияние погрешностей измерений и наблюдений на свойства алгоритмов регрессионного анализа, разработаны способы расчета нотн и рациональных объемов выборок, введены и исследованы новые понятия многомерных и асимптотических нотн, доказаны соответствующие предельные теоремы. Начата разработка интервального дискриминантного анализа, в частности, рассмотрено влияние интервальности данных на введенный нами показатель качества классификации. Изучено асимптотическое поведение оценок метода моментов и оценок максимального правдоподобия (а также более общих - оценок минимального контраста), проведено асимптотическое сравнение этих методов в случае интервальных данных. Найдены общие условия, при которых, в отличие от классической математической статистики, метод моментов дает более точные оценки, чем метод максимального правдоподобия. Основные результаты разработанной нами статистики интервальных данных приведены как развернутые главы в книгах [62–65].

В области асимптотической математической статистики интервальных данных российская наука имеет мировой приоритет. Развертывание работ по рассматриваемой тематике позволит закрепить этот приоритет, получить теоретические результаты, основополагающие в новой области математической статистики и необходимые для обоснованного статистического анализа почти всех типов данных. Со временем во все виды статистического программного обеспечения должны быть включены алгоритмы интервальной статистики, "параллельные" обычно используемым алгоритмам прикладной математической статистики. Это позволит в явном виде учесть наличие погрешностей у результатов наблюдений, сблизить позиции метрологов и статистиков.

Статистика объектов нечисловой природы как часть прикладной статистики. Согласно классификации статистических методов, принятой в [9, 62], прикладная статистика делится на следующие четыре области: статистика (числовых) случайных величин, многомерный статистический анализ, статистика временных рядов и случайных процессов, статистика объектов нечисловой природы. Первые три из этих областей являются классическими. Остановимся на четвертой, только еще входящей в массовое сознание специалистов. Ее именуют также статистикой нечисловых данных или нечисловой статистикой [64].

Исходный объект в математической статистике - это выборка. В вероятностной теории статистики выборка - это совокупность независимых одинаково распределенных случайных элементов. Какова природа этих элементов? В классической математической статистике (той, что обычно преподают студентам) элементы выборки - это числа. В многомерном статистическом анализе - вектора. А в нечисловой статистике элементы выборки - это объекты нечисловой природы, которые нельзя складывать и умножать на числа. Другими словами, объекты нечисловой природы лежат в пространствах, не имеющих векторной структуры.

Примерами объектов нечисловой природы являются: значения качественных признаков, т.е. результаты кодировки объектов с помощью заданного перечня категорий (градаций); упорядочения (ранжировки) экспертами образцов продукции (при оценке её технического уровня и конкурентоспособности)) или заявок на проведение научных работ (при проведении конкурсов на выделение грантов); классификации, т.е. разбиения объектов на группы сходных между собой (кластеры); толерантности, т.е. бинарные отношения, описывающие сходство объектов между собой, например, сходства тематики научных работ, оцениваемого экспертами с целью рационального формирования экспертных советов внутри определенной области науки; результаты парных сравнений или контроля качества продукции по альтернативному признаку ("годен" - "брак"), т.е. последовательности из 0 и 1; множества (обычные или нечеткие), например, зоны, пораженные коррозией, или перечни возможных причин аварии, составленные экспертами независимо друг от друга; графы; слова, предложения, тексты; вектора, координаты которых - совокупность значений разнотипных признаков, например, результат составления статистического отчета о научно-технической деятельности (форма №1-наука) или заполненная компьютеризированная история болезни, в которой часть признаков носит качественный характер, а часть - количественный; ответы на вопросы экспертной, маркетинговой или социологической анкеты, часть из которых носит количественный характер (возможно, интервальный), часть сводится к выбору одной из нескольких подсказок, а часть представляет собой тексты; и т.д. Интервальные данные тоже можно рассматривать как пример объектов нечисловой природы, а именно, как частный случай нечетких множеств.

С начала 70-х годов под влиянием запросов прикладных исследований в технических, медицинских и социально-экономических науках в России активно развивается нечисловая статистика. В создании этой сравнительно новой области прикладной математической статистики приоритет принадлежит российским ученым. Большую роль сыграл основанный в 1973 г. научный семинар "Экспертные оценки и анализ данных". В 60-е годы советское научное сообщество стало интересоваться методами экспертных оценок (об их истории и современном состоянии см. [66, 67]). Началось знакомство с конкретными математизированными теориями, связанными с этими методами. Речь идет о репрезентативной теории измерений, ставшей известной в нашей стране по статье П. Суппеса и Дж. Зинеса [68] и книге И. Пфанцагля [69], о теории нечеткости Л. А. Заде [70], теории парных сравнений, описанной Г. Дэвидом [71]. К этому кругу идей примыкают теория случайных множеств (см., например, книгу Ж. Матерона [72]) и методы многомерного шкалирования (описаны А. Ю. Терехиной [73] и В. Т. Перекрестом [74]). Но наибольшее влияние оказали идеи Дж. Кемени, который аксиоматически ввел расстояние между ранжировками (теперь оно именуется в литературе расстоянием Кемени) и предложил использовать в качестве средней величины решение оптимизационной задачи (теперь - медиана Кемени). Его небольшая книга [75], написанная в соавторстве с Дж. Снеллом, породила большой поток исследований.

В течение 70-х годов на основе запросов теории экспертных оценок (а также социологии, экономики, техники и медицины) развивались конкретные направления нечисловой статистики. Были установлены связи между конкретными видами таких объектов, разработаны для них вероятностные модели [41, 64, 76].

Следующий этап - выделение нечисловой статистики в качестве самостоятельного направления в прикладной статистике, ядром которого являются методы статистического анализа данных произвольной природы. Программа развития этого нового научного направления впервые была сформулирована в 1979 г. в статье [77]. Реализация этой программы была осуществлена в 80-е годы. Для работ этого периода характерна сосредоточенность на внутренних проблемах нечисловой статистики. Ссылки на конкретные монографии, сборники, статьи и иные публикации нескольких десятков авторов приведены в обзорах [78–80]. Отметим лишь сборник [81], специально посвященный нечисловой статистике, и диссертацию [82], относящуюся к непараметрической теории парных сравнений (теории люсианов).

К 90-м годам статистика объектов нечисловой природы с теоретической точки зрения была достаточно хорошо развита, основные идеи, подходы и методы были разработаны и изучены математически, в частности, доказано достаточно много теорем. Однако она оставалась недостаточно апробированной на практике. Это было связано как с ее сравнительной молодостью, так и с общеизвестными особенностями организации науки в 80-е годы, когда отсутствовали достаточные стимулы для тому, чтобы теоретики занялись широким внедрением своих результатов. И в 90-е годы наступило время от математико-статистических исследований перейти к применению полученных результатов на практике.

Следует отметить, что в нечисловой статистике, как и в других областях прикладной математической статистики и прикладной математики вообще, одна и та же математическая схема может с успехом применяться и в технических исследованиях, и в медицине, и в социологии, и для анализа экспертных оценок, а потому ее лучше всего формулировать и изучать в наиболее общем виде, для объектов произвольной природы.

3.1.5. Основные идеи нечисловой статистики

В чем её принципиальная новизна? Для классической математической статистики характерна операция сложения. При расчете выборочных характеристик распределения (выборочное среднее арифметическое, выборочная дисперсия и др.), в регрессионном анализе и других областях этой научной дисциплины постоянно используются суммы. Математический аппарат - законы больших чисел, Центральная предельная теорема и другие теоремы - нацелены на изучение сумм. В нечисловой же статистике нельзя использовать операцию сложения, поскольку элементы выборки лежат в пространствах, где нет операции сложения. Методы обработки нечисловых данных основаны на принципиально ином математическом аппарате - на применении различных расстояний в пространствах объектов нечисловой природы.

Кратко рассмотрим несколько идей, развиваемых в статистике объектов нечисловой природы для данных, лежащих в пространствах произвольного вида. Решаются классические задачи описания данных, оценивания, проверки гипотез - но для неклассических данных, а потому неклассическими методами.

Первой обсудим проблему определения средних величин. В рамках репрезентативной теории измерений удается указать вид средних величин, соответствующих тем или иным шкалам измерения [41]. В классической математической статистике средние величины вводят с помощью операций сложения (выборочное среднее арифметическое, математическое ожидание) или упорядочения (выборочная и теоретическая медианы). В пространствах произвольной природы средние значения нельзя определить с помощью операций сложения или упорядочения. Теоретические и эмпирические средние приходится вводить как решения экстремальных задач. Для теоретического среднего это - задача минимизации математического ожидания (в классическом смысле) расстояния от случайного элемента со значениями в рассматриваемом пространстве до фиксированной точки этого пространства (минимизируется указанная функция от этой точки). Для эмпирического среднего математическое ожидание берется по эмпирическому распределению, т.е. берется сумма расстояний от некоторой точки до элементов выборки и затем минимизируется по этой точке. При этом как эмпирическое, так и теоретическое средние как решения экстремальных задач могут быть не единственным элементом пространства, а состоять из множества таких элементов, которое может оказаться и пустым. Тем не менее удалось сформулировать и доказать законы больших чисел для средних величин, определенных указанным образом, т.е. установить сходимость эмпирических средних к теоретическим [64].

Оказалось, что методы доказательства законов больших чисел допускают существенно более широкую область применения, чем та, для которой они были разработаны. А именно, удалось изучить асимптотику решений экстремальных статистических задач, к которым, как известно, сводится большинство постановок прикладной статистики. В частности, кроме законов больших чисел установлена и состоятельность оценок минимального контраста, в том числе оценок максимального правдоподобия и робастных оценок. К настоящему времени подобные оценки изучены также и в статистике интервальных данных.

В статистике в пространствах произвольной природы большую роль играют непараметрические оценки плотности, используемые, в частности, в различных алгоритмах регрессионного, дискриминантного, кластерного анализов. В нечисловой статистике предложен и изучен ряд типов непараметрических оценок плотности в пространствах произвольной природы, в частности, доказана их состоятельность, изучена скорость сходимости и установлен примечательный факт совпадения наилучшей скорости сходимости в произвольном случае с той, которая имеет быть в классической теории для числовых случайных величин.

Дискриминантный, кластерный, регрессионный анализы в пространствах произвольной природы основаны либо на параметрической теории - и тогда применяется подход, связанный с асимптотикой решения экстремальных статистических задач - либо на непараметрической теории - и тогда используются алгоритмы на основе непараметрических оценок плотности.

Для проверки гипотез могут быть использованы статистики интегрального типа, в частности, типа омега-квадрат. Любопытно, что предельная теория таких статистик, построенная первоначально в классической постановке [83], приобрела естественный (завершенный, изящный) вид именно для пространств произвольного вида [84], поскольку при этом удалось провести рассуждения, опираясь на базовые математические соотношения, а не на те частные (с общей точки зрения), что были связаны с конечномерным пространством.

Представляют интерес результаты, связанные с конкретными областями статистики объектов нечисловой природы, в частности, со статистикой нечетких множеств [85], со случайными множествами [41] (следует отметить, что теория нечетких множеств в определенном смысле сводится к теории случайных множеств [41, 86]), с непараметрической теорией парных сравнений [82], с аксиоматическим введением метрик в конкретных пространствах объектов нечисловой природы [81, 87].

Для анализа нечисловых, в частности, экспертных данных весьма важны методы классификации. С другой стороны, наиболее естественно ставить и решать задачи классификации, основанные на использовании расстояний или показателей различия, в рамках статистики объектов нечисловой природы. Это касается как распознавания образов с учителем (другими словами, дискриминантного анализа), так и распознавания образов без учителя (т.е. кластерного анализа). Современное состояние дискриминантного и кластерного анализа с точки зрения нечисловой статистики отражено работах в [88–90].

Статистические методы анализа нечисловых данных особенно хорошо приспособлены для применения в экономике, социологии и экспертных оценках, поскольку в этих областях от 50% до 90% данных являются нечисловыми [91].

3.1.6. Итоги анализа структуры прикладной статистики

Выше рассмотрены пять "точек роста" прикладной статистики. Разумеется, они не исчерпывают все многообразие фронта научных исследований в этой области. В частности, решены отнюдь не все проблемы, поставленные в конце 70-х годов в т.н. "цахкадзорской тетради" [92]. Кроме того, мы почти не затрагивали разнообразные применения статистических методов в конкретных прикладных областях. Много интересных проблем есть в планировании экспериментов, особенно кинетических, при анализе проблем надежности, в статистических методах управления качеством продукции, в вопросах экологии и безопасности и др.

В течение последних более чем 60 лет в России наблюдается огромный разрыв между государственной статистикой и научным сообществом специалистов по статистическим методам (подробнее об этом см. [24]). В учебнике по истории статистики [16], подготовленном ориентированными на обслуживание государственной статистики лицами, даже не упоминаются имена членов-корреспондентов АН СССР Н.В. Смирнова и Л.Н. Большева! Поэтому нет ничего удивительного в том, что тенденции развития современной прикладной математической статистики столь же мало обсуждаются отечественными авторами, как и ее история.

3.2. Теоретические инструменты статистических методов

Набор широко применяемых исследователями теоретических инструментов прикладной математической статистики и статистических методов в целом достаточно ограничен. В настоящем разделе собраны основные математические инструменты (теоремы, методы), постоянно используемые при обосновании новых результатов в области статистических методов. Эти инструменты отнюдь не всегда легко найти в литературе по теории вероятностей и математической статистике. Например, такие рассматриваемые далее теоремы и методы, как многомерная центральная предельная теорема, теоремы о наследовании сходимости и метод линеаризации, даже не включены в энциклопедию «Вероятность и математическая статистика» [1] – наиболее полный, по мнению составителей энциклопедии, свод знаний по заявленной тематике. Последний факт наглядно демонстрирует разрыв между математической дисциплиной «теория вероятностей и математическая статистика» и потребностями прикладной статистики и других статистических методов.

3.2.1. Законы больших чисел

Законы больших чисел позволяют описать поведение сумм случайных величин. Примером является следующий результат, доказанный русским математиком П. Л. Чебышёвым (1821–1894) в 1867 г. Пусть сначала вероятностное пространство состоит из конечного числа элементов.

Теорема Чебышёва. Пусть случайные величины Х₁, Х₂,…, Х_k попарно независимы и существует число С такое, что D(X_i) < C при всех i = 1, 2, …, k. Тогда для любого положительного ε выполнено неравенство

(1)

Частным случаем теоремы Чебышева является теорема Бернулли – первый в истории вариант закона больших чисел. Известный математики Якоб Бернулли (1654–1705), живший в городе Базель в Швейцарии, в самом конце XVII века доказал это утверждение в рамках математической модели (опубликовано доказательство было лишь после его смерти, в 1713 году). Современная формулировка теоремы Бернулли такова.

Теорема Бернулли. Пусть m – число наступлений события А в k независимых (попарно) испытаниях, и р есть вероятность наступления события А в каждом из испытаний. Тогда при любом справедливо неравенство

(2)

Ясно, что при росте k выражения в правых частях формул (1) и (2) стремятся к 0. Таким образом, среднее арифметическое попарно независимых случайных величин сближается со средним арифметическим их математических ожиданий.

Выше шла речь лишь о пространствах элементарных событий из конечного числа элементов. Однако приведенные теоремы верны и в общем случае, для произвольных пространств элементарных событий. Однако в список условий закона больших чисел необходимо добавить требование существования дисперсий. Легко видеть, что если существуют дисперсии, то существуют и математические ожидания. Закон больших чисел в форме Чебышёва приобретает следующий вид.

Теорема Чебышёва [2, с.147]. Если Х₁, Х₂,…, Х_k,… - последовательность попарно независимых случайных величин, имеющих конечные дисперсии, ограниченные одной и той же постоянной,

D(X₁)<C, D(X₂)<C,… D(Х_i)<C,…

то, каково бы ни было постоянное ε > 0,

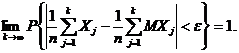(3)

С точки зрения прикладных статистических исследований ограниченность дисперсий вполне естественна. Она вытекает, например, из ограниченности диапазона изменения практически всех величин, используемых при реальных расчетах.

В 1923 г. А. Я. Хинчин показал, что если случайные величины не только независимы, но и одинаково распределены, то существование у них математического ожидания является необходимым и достаточным условием для применимости закона больших чисел [2, с.150]. Найдены и более экзотические варианты закона больших чисел. Например, такой.

Теорема [2, с.150–151]. Для того чтобы для последовательности Х₁, Х₂,…, Х_k,…(как угодно зависимых) случайных величин при любом положительном ε выполнялось соотношение (3), необходимо и достаточно, чтобы при n → ∞

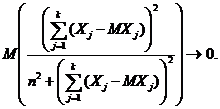
Законы больших чисел для случайных величин служат основой для аналогичных утверждений для случайных элементов в пространствах более сложной природы, в частности, в пространствах произвольной природы [3, 4]. Однако здесь мы ограничимся классическими формулировками, служащими основой для современных статистических методов.

Смысл классических законов больших чисел состоит в том, что выборочное среднее арифметическое независимых одинаково распределенных случайных величин приближается (сходится) к математическому ожиданию этих величин. Другими словами, выборочные средние сходятся к теоретическому среднему.

Это утверждение справедливо и для других видов средних. Например, выборочная медиана сходится к теоретической медиане. Это утверждение – тоже закон больших чисел, но не классический.

Существенным продвижением в теории вероятностей во второй половине ХХ в. явилось введение средних величин в пространствах произвольной природы и получение для них законов больших чисел, т.е. утверждений, состоящих в том, что эмпирические (т.е. выборочные) средние сходятся к теоретическим средним [3, 4].

3.2.2. Центральные предельные теоремы

Простейший вариант Центральной предельной теоремы (ЦПТ) теории вероятностей таков.

Центральная предельная теорема (для одинаково распределенных слагаемых). Пусть Х₁, Х₂,…, X_n, …– независимые одинаково распределенные случайные величины с математическими ожиданиями M(X_i) = m и дисперсиями D(X_i) = , i = 1, 2,…, n,… Тогда для любого действительного числа х существует предел

где Ф(х) – функция стандартного нормального распределения.

Эту теорему иногда называют теоремой Линдеберга – Леви [5, с.122].

В ряде прикладных задач не выполнено условие одинаковой распределенности. В таких случаях центральная предельная теорема обычно остается справедливой, однако на последовательность случайных величин приходится накладывать те или иные условия. Суть этих условий состоит в том, что ни одно слагаемое не должно быть доминирующим, вклад каждого слагаемого в среднее арифметическое должен быть пренебрежимо мал по сравнению с итоговой суммой. Наиболее часто используется теорема Ляпунова.

Теорема Ляпунова - Центральная предельная теорема (для разнораспределенных слагаемых). Пусть Х₁, Х₂,…, X_n, …– независимые случайные величины с математическими ожиданиями M(X_i) = m_i и дисперсиями D(X_i) = , i = 1, 2,…, n,… Пусть при некотором δ > 0 у всех рассматриваемых случайных величин существуют центральные моменты порядка 2+δ и безгранично убывает «дробь Ляпунова»:

где

Тогда для любого действительного числа х существует предел

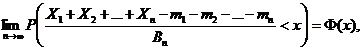(4)

где Ф(х) – функция стандартного нормального распределения.

В случае одинаково распределенных случайных слагаемых

и теорема Ляпунова переходит в теорему Линдеберга – Леви.

История получения центральных предельных теорем для числовых случайных величин растянулась на два века – от первых работ Муавра в 30-х гг. XVIII в. для необходимых и достаточных условий, полученных Линдебергом и Феллером в 30-х гг. XX в.

Теорема Линдеберга - Феллера. Пусть Х₁, Х₂,…, X_n, …– независимые случайные величины с математическими ожиданиями M(X_i) = m_i и дисперсиями D(X_i) = , i = 1, 2,…, n,… Предельное соотношение (4), т.е. Центральная предельная теорема, выполнено тогда и только тогда, когда при любом τ > 0

где F_k(x) обозначает функцию распределения случайной величины X_k.

Доказательства перечисленных в настоящем разделе центральных предельных теорем для случайных величин можно найти в классическом курсе теории вероятностей [2].

Для обоснования многих статистических методов большое значение имеет многомерная центральная предельная теорема. В ней речь идет не о сумме случайных величин, а о сумме случайных векторов.

Необходимое и достаточное условие многомерной сходимости [5, с.124]. Пусть F_n обозначает совместную функцию распределения k-мерного случайного вектора , n = 1, 2, …, и F_λn – функция распределения линейной комбинации . Необходимое и достаточное условие для сходимости F_n к некоторой k-мерной функции распределения F состоит в том, что F_λn имеет предел для любого вектора λ.

Приведенная теорема ценна тем, что с ее помощью сходимость распределений случайных векторов сводится к сходимости распределений линейных комбинаций их координат, т.е. к сходимости обычных (числовых) случайных величин, рассмотренных ранее. Однако она не дает возможности непосредственно указать предельное распределение. Это можно сделать с помощью следующей теоремы.

Теорема о многомерной сходимости [5]. Пусть F_n и F_λn – те же, что в предыдущей теореме. Пусть F - совместная функция распределения k-мерного случайного вектора . Если функция распределения F_λn сходится при росте объема выборки к функции распределения F_λ для любого вектора λ, где F_λ – функция распределения линейной комбинации , то F_n сходится к F.

Здесь сходимость F_n к F означает, что для любого k-мерного вектора такого, что функция распределения F непрерывна в , числовая последовательность F_n сходится при росте n к числу F. Другими словами, сходимость функций распределения понимается точно так же, как при обсуждении предельных теорем для случайных величин выше. Приведем многомерный аналог этих теорем.

Многомерная центральная предельная теорема [5]. Рассмотрим независимые одинаково распределенные k-мерные случайные вектора

где штрих обозначает операцию транспонирования вектора. Предположим, что случайные вектора U_n имеют моменты первого и второго порядка, т.е.

М(U_n) = μ, D(U_n) = Σ,

где μ – вектор математических ожиданий координат случайного вектора, Σ – его ковариационная матрица. Введем последовательность средних арифметических случайных векторов:

Тогда случайный вектор имеет асимптотическое k-мерное нормальное распределение , т.е. он асимптотически распределен так же, как k-мерная нормальная величина с нулевым математическим ожиданием, ковариационной Σ и плотностью

Здесь |Σ| - определитель матрицы Σ. Другими словами, распределение случайного вектора сходится к k-мерному нормальному распределению с нулевым математическим ожиданием и ковариационной матрицей Σ.

Напомним, что многомерным нормальным распределением с математическим ожиданием μ и ковариационной матрицей Σ называется распределение, имеющее плотность

Многомерная центральная предельная теорема показывает, что распределения сумм независимых одинаково распределенных случайных векторов при большом числе слагаемых хорошо приближаются с помощью нормальных распределений, имеющих такие же первые два момента (вектор математических ожиданий координат случайного вектора и его корреляционную матрицу), как и исходные вектора. От одинаковой распределенности можно отказаться, но это потребует некоторого усложнения символики. В целом из теоремы о многомерной сходимости вытекает, что многомерный случай ничем принципиально не отличается от одномерного.

Пример. Пусть X₁, … X_n ,…– независимые одинаково распределенные случайные величины. Рассмотрим k-мерные независимые одинаково распределенные случайные вектора

Их математическое ожидание – вектор теоретических начальных моментов, а ковариационная матрица составлена из соответствующих центральных моментов. Тогда - вектор выборочных центральных моментов. Многомерная центральная предельная теорема утверждает, что имеет асимптотически нормальное распределение. Как вытекает из теорем о наследовании сходимости и о линеаризации (см. ниже), из распределения можно вывести распределения различных функций от выборочных начальных моментов. А поскольку центральные моменты выражаются через начальные моменты, то аналогичное утверждение верно и для них.

3.2.3. Теоремы о наследовании сходимости

Суть проблемы наследования сходимости. Пусть распределения случайных величин X_n при n → ∞ стремятся к распределению случайной величины Х. При каких функциях f можно утверждать, что распределения случайных величин f(X_n) сходятся к распределению f(X), т.е. наследуется сходимость?

Хорошо известно, что для непрерывных функций f сходимость наследуется [5]. Однако в статистических методах используются различные обобщения этого утверждения. Необходимость обобщений связана с тремя обстоятельствами.

1) Статистические данные могут моделироваться не только случайными величинами, но и случайными векторами, случайными множествами, случайными элементами произвольной природы (т.е. функциями на вероятностном пространстве со значениями в произвольном множестве) [6, 7].

2) Переход к пределу должен рассматриваться не только для случая безграничного возрастания объема выборки, но и в более общих случаях. Например, если в постановке статистической задачи участвуют несколько выборок объемов n(1), n(2), … , n(k), то вполне обычным является предположение о безграничном росте всех этих объемов (что можно описать и как min{n(1), n(2), … , n(k)} → ∞).

3) Функция f не обязательно является непрерывной. Она может иметь разрывы. Кроме того, она может зависеть от параметров, по которым происходит переход к пределу. Например, может зависеть от объемов выборок. Например, в [8, гл.5] понадобилось рассмотреть функцию f = f(n(1), n(2), … , n(k)).

Расстояние Прохорова и сходимость по направленному множеству. Введем необходимые для дальнейшего изложения понятия.

Расстояние (метрика) Прохорова. Пусть С – некоторое пространство, А – его подмножество, d – метрика в С. Назовем ε-окрестностью множества А в метрике d следующее множество:

S(A,ε) = {x С: d(A,x) < ε}.

Таким образом, ε-окрестность множества А – это совокупность всех точек пространства С, отстоящих от А не более чем на положительное число ε. При этом расстояние от точки х до множества А – это точная нижняя грань расстояний от х до точек множества А, т.е.

d(A,x) = inf{d(x,y): yA}.

Пусть P₁ и P₂ – две вероятностные меры на С (т.е. распределения двух случайных элементов со значениями в С). Пусть D₁₂ – множество чисел ε > 0 таких, что

P₁(A) < P₂(S(A,ε)+ε

для любого замкнутого подмножества А пространства С. Пусть D₂₁ – множество чисел ε > 0 таких, что

P₂(A) < P₁(S(A,ε)+ε

для любого замкнутого подмножества А пространства С. Расстояние Прохорова L(P₁,P₂) между вероятностными мерами (его можно рассматривать и как расстояние между случайными элементами с распределениями P₁ и P₂ соответственно) вводится формулой

L(P₁,P₂) = max (inf D₁₂, inf D₂₁).

С помощью метрики Прохорова формализуется понятие сходимости распределений случайных элементов в произвольном пространстве.

Расстояние L(P₁,P₂) введено академиком АН СССР РАН Юрием Васильевичем Прохоровым (1929–2013) в середине ХХ в. [9] и широко используется в современной теории вероятностей.

Сходимость по направленному множеству [10, с.95-96]. Бинарное отношение > (упорядочение), заданное на множестве В, называется направлением на нем, если В не пусто и

(а) если m, n и p – такие элементы множества В, что m > n и n > p, то m > p;

(б) m > m для любого m из B;

(в) если m и n принадлежат B, то найдется элемент p из B такой, что p > m и p > n.

Направленное множество – это пара (В, >), где > - направление на множестве В. Направленностью (или «последовательностью по направленному множеству») называется пара (f, >), где f – функция, > - направление на ее области определения. Пусть f: B → Y, где Y – топологическое пространство. Направленность (f, >) сходится в топологическом пространстве Y к точке y₀, если для любой окрестности U точки y₀ найдется p из B такое, что f(q)U при любом q > p. В таком случае говорят также о сходимости по направленному множеству.

Пусть В = {(n(1), n(2), … , n(k))} – совокупность векторов, каждый из которых составлен из объемов k выборок. Пусть

(n(1), n(2), … , n(k)) > (n₁(1), n₁(2), … , n₁(k))

тогда и только тогда, когда n(i) > n₁(i) при всех i = 1, 2, …, k. Тогда (В, >) – направленное множество, сходимость по которому эквивалентна сходимости при min{n(1), n(2), … , n(k)} → ∞.

Чтобы охватить различные частные случаи, целесообразно предельные теоремы формулировать в терминах сходимости по направленному множеству. Будем писать B = {α}. Пусть запись α→∞ обозначает переход к пределу по направленному множеству.

Формулировка проблемы наследования сходимости. Пусть случайные элементы X_α со значениями в пространстве С сходятся при α→∞ к случайному элементу Х, где через α→∞ обозначен переход к пределу по направленному множеству. Сходимость случайных элементов означает, что L(X_α, X) → 0 при α→∞, где L – метрика Прохорова в пространстве С.

Пусть f_α: C → Y – некоторые функции. Какие условия надо на них наложить, чтобы из L(X_α, X) → 0 вытекало, что L₁(f_α(X_α), f_α(X)) → 0 при α→∞, где L₁ – метрика Прохорова в пространстве Y? Другими словами, какие условия на функции f_α: C → Y гарантируют наследование сходимости?

В работах [11, 12] найдены необходимые и достаточные условия на функции f_α: C → Y, гарантирующие наследование сходимости. Описанию этих условий посвящена оставшаяся часть подраздела.

Приведем для полноты изложения строгие формулировки математических предположений.

Математические предположения. Пусть С и У – полные сепарабельные метрические пространства [10]. Пусть выполнены обычные предположения измеримости: Х_α и Х – случайные элементы С, f_α(Х_α) и f_α(Х) – случайные элементы в У, рассматриваемые ниже подмножества пространств С и У лежат в соответствующих σ–алгебрах измеримых подмножеств, и т.д.

Понадобятся некоторые определения. Разбиение Т_n = {C_1n, C_2n, … , C_nn} пространства С – это такой набор подмножеств C_j, j = 1, 2, … , n, этого пространства, что пересечение любых двух из них пусто, а объединение совпадает с С. Диаметром diam(A) подмножества А множества С называется точная верхняя грань расстояний между элементами А, т.е.

diam(A) = sup {d(x,y), xA, yA},

где d(x,y) – метрика в пространстве С. Обозначим ∂А границу множества А, т.е. совокупность точек х таких, что любая их окрестность U(x) имеет непустое пересечение как с А, так и с C\А. Колебанием δ(f, B) функции f на множестве B называется δ(f, B) = sup {|f(x) – f(y)|, xB, yB}.

Достаточное условие для наследования сходимости. Пусть L(X_α,X) → 0 при α → ∞. Пусть существует последовательность Т_n разбиений пространства С такая, что Р(Х∂А) = 0 для любого А из Т_n и, основное условие, для любого ε > 0

(5)

при n →∞ и α→∞, где сумма берется по всем тем А из Т_n, для которых колебание функции f_α на А больше ε, т.е. δ(f_α, А) > ε. Тогда L₁(f_α(X_α), f_α(X)) → 0 при α→∞.

Необходимое условие для наследования сходимости. Пусть У – конечномерное линейное пространство, У = R^k. Пусть случайные элементы f_α(X) асимптотически ограничены по вероятности при α→∞, т.е. для любого ε > 0 существуют число S(ε) и элемент направленного множества α(ε) такие, что Р(||f_α(X)||> S(ε))<ε при α > α(ε), где ||f_α(X)|| - норма (длина) вектора f_α(X). Пусть существует последовательность Т_n разбиений пространства С такая, что

,

т.е. последовательность Т_n является безгранично измельчающейся. Самое существенное – пусть условие (5) не выполнено для последовательности Т_n. Тогда существует последовательность случайных элементов X_α такая, что L(X_α,X) → 0 при α → ∞, но L₁(f_α(X_α), f_α(X)) не сходится к 0 при α → ∞.

Несколько огрубляя, можно сказать, что условие (5) является необходимым и достаточным для наследования сходимости.

Пример 1. Пусть С и У – конечномерные линейные пространства, функции f_α не зависят от α, т.е. f_α ≡ f, причем функция f ограничена. Тогда условие (5) эквивалентно требованию интегрируемости по Риману - Стилтьесу функции f по мере G(A) = P(XA). В частности, условие (5) выполнено для непрерывной функции f.

В конечномерных пространствах С вместо сходимости L(X_α,X) → 0 при α → ∞ можно говорить о слабой сходимости функций распределения случайных векторов X_α к функции распределения случайного вектора X. Речь идет о «сходимости по распределению», т.е. о сходимости во всех точках непрерывности функции распределения случайного вектора X. В этом случае разбиения могут состоять из многомерных параллелепипедов [12, гл.2].

Пример 2. Полученные выше результаты дают обоснование для рассуждений типа следующего (ср., например, утверждения в [8, гл.5] выше). Пусть по двум независимым выборкам объемов m и n соответственно построены статистики X_m и Y_n. Пусть известно, что распределения этих статистик сходятся при безграничном росте объемов выборок к стандартным нормальным распределениям с математическим ожиданием 0 и дисперсией 1. Пусть a(m, n) и b(m, n) – некоторые коэффициенты. Тогда согласно результатам примера 1 распределение случайной величины Z(m, n) = a(m, n)X_m + b(m, n)Y_n сближается с распределением нормально распределенной случайной величины с математическим ожиданием 0 и дисперсией a²(m, n) + b²(m, n). Если же a²(m, n) + b²(m, n) = 1, например,

,

то распределение Z(m, n) сходится при безграничном росте объемов выборок к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1.

3.2.4. Метод линеаризации

При разработке статистических методов часто возникает следующая задача (см., например, [5, с.338]). Имеется последовательность k-мерных случайных векторов X_n = (X_1n, X_2n, … , X_kn), n = 1, 2, … , такая, что X_n → a = (a₁, a₂, … , a_k) при n → ∞, и последовательность функций f_n: R^k → R¹. Требуется найти распределение случайной величины f_n(X_n).

Основная идея – рассмотреть главный линейный член функции f_n в окрестности точки а. Из математического анализа известно, что

,

где остаточный член является бесконечно малой величиной более высокого порядка малости, чем линейный член. Таким образом, произвольная функция может быть заменена на линейную функцию от координат случайного вектора. Эта замена проводится с точностью до бесконечно малых более высокого порядка. Конечно, должны быть выполнены некоторые математические условия регулярности. Например, функции f_n должны быть дважды непрерывно дифференцируемы в окрестности точки а.

Если вектор X_n является асимптотически нормальным с математическим ожиданием а и ковариационной матрицей ∑/n, где ∑ = ||σ_ij||, причем σ_ij = nM(X_i – a_i)(X_j – a_j), то линейная функция от его координат также асимптотически нормальна. Следовательно, при очевидных условиях регулярности f_n(X_n) – асимптотически нормальная случайная величина с математическим ожиданием f_n(а) и дисперсией

.

Для практического использования асимптотической нормальности f_n(X_n) остается заменить неизвестные моменты а и ∑ на их оценки. Например, если X_n – это среднее арифметическое независимых одинаково распределенных случайных векторов, то а можно заменить на X_n, а ∑ - на выборочную ковариационную матрицу.

Пример. Пусть Y₁, Y₂, … , Y_n – независимые одинаково распределенные случайные величины с математическим ожиданием а и дисперсией σ². В качестве X_n (при k = 1) рассмотрим выборочное среднее арифметическое

.

Как известно, в силу закона больших чисел → а = М(У). Следовательно, для получения распределений функций от выборочного среднего арифметического можно использовать метод линеаризации. В качестве примера рассмотрим f_n(y) = f(y) = y². Тогда

.

Из этого соотношения следует, что с точностью до бесконечно малых более высокого порядка

.

Поскольку в соответствии с Центральной Предельной Теоремой выборочное среднее арифметическое является асимптотически нормальной случайной величиной с математическим ожиданием а и дисперсией σ²/n, то квадрат этой статистики является асимптотически нормальной случайной величиной с математическим ожиданием а² и дисперсией 4а²σ²/n. Для практического использования может оказаться полезной замена параметров (асимптотического нормального распределения) на их оценки, а именно, математического ожидания – на , а дисперсии – на , где s² – выборочная дисперсия.

Большое внимание (целая глава!) уделено методу линеаризации в классическом учебнике Е. С. Вентцель [13].

3.2.5. Принцип инвариантности

Пусть Y₁, Y₂, … , Y_n – независимые одинаково распределенные случайные величины с непрерывной функцией распределения F(x). Многие используемые в статистических методах функции от результатов наблюдений выражаются через эмпирическую функцию распределения F_n(x). К ним относятся, в частности, статистики Колмогорова, Смирнова, омега-квадрат [14]. Отметим, что и другие статистики выражаются через эмпирическую функцию распределения, например:

.

Полезным является преобразование Н.В.Смирнова t = F(x). Тогда независимые случайные величины Z_j = F(Y_j), j = 1, 2, … , n, имеют равномерное распределение на отрезке [0; 1]. Рассмотрим построенную по ним эмпирическую функцию распределения F_n(t), 0 < t < 1. Эмпирическим процессом называется случайный процесс

.

Рассмотрим критерии проверки согласия функции распределения выборки с фиксированной функцией распределения F(x). Статистика критерия Колмогорова записывается в виде

статистика критерия Смирнова – это

а статистика критерия омега-квадрат (Крамера - Мизеса - Смирнова) имеет вид

.

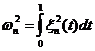Случайный процесс ξ_n(t) имеет нулевое математическое ожидание и ковариационную функцию Мξ_n(s)ξ_n(t) = min (s,t) – st. Рассмотрим гауссовский случайный процесс ξ(t) с такими же математическим ожиданием и ковариационной функцией. Он называется броуновским мостом. (Напомним, что гауссовским процесс именуется потому, что вектор (ξ(t₁), ξ(t₂), … , ξ(t_k)) имеет многомерное нормальное распределение при любых наборах моментов времени t₁, t₂, … , t_k.)

Пусть f – функционал, определенный на множестве возможных траекторий случайных процессов. Принцип инвариантности [1] состоит в том, что последовательность распределений случайных величин f(ξ_n) сходится при n → ∞ к распределению случайной величины f(ξ). Сходимость по распределению обозначим символом =>. Тогда принцип инвариантности кратко записывается так: f(ξ_n) => f(ξ). В частности, согласно принципу инвариантности статистика Колмогорова и статистика омега-квадрат сходятся по распределению к распределениям соответствующих функционалов от случайного процесса ξ:

=> , => .

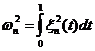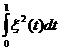Таким образом, от проблем прикладной статистики сделан переход к теории случайных процессов. Методами этой теории найдены распределения случайных величин

, .

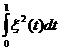Принцип инвариантности – инструмент получения предельных распределений функций от результатов наблюдений, используемых в прикладной статистике.

Обоснование принципу инвариантности может быть дано на основе теории сходимости вероятностных мер в функциональных пространствах [9, 15]. Более простой подход, позволяющий к тому же получать необходимые и достаточные условия в предельной теории статистик интегрального типа (принцип инвариантности к ним нельзя применить), рассмотрен в [16].

Почему «принцип инвариантности» так назван? Обратим внимание, что предельные распределения рассматриваемых статистик не зависят от их функции распределения F(x). Другими словами, предельное распределение инвариантно относительно выбора F(x).

В более широком смысле термин «принцип инвариантности» применяют тогда, когда предельное распределение не зависит от тех или иных характеристик исходных распределений [1]. В этом смысле наиболее известный «принцип инвариантности» - это Центральная предельная теорема, поскольку предельное стандартное нормальное распределение – одно и то же для всех возможных распределений независимых одинаково распределенных слагаемых (лишь бы слагаемые имели конечные математическое ожидание и дисперсию).

3.3. Распределения реальных статистических данных
не являются нормальными

В учебных курсах по теории вероятностей и математической статистике рассматривают различные параметрические семейства распределений числовых случайных величин. А именно, изучают семейства нормальных распределений, логарифмически нормальных, экспоненциальных, гамма-распределений, распределений Вейбулла - Гнеденко и др. Все они зависят от одного, двух или трех параметров. Поэтому для полного описания распределения достаточно знать или оценить одно, два или три числа. Очень удобно. Поэтому широко развита параметрическая теория математической статистики, в которой предполагается, что распределения результатов наблюдений принадлежат тем или иным параметрическим семействам. Эта традиция идет от Карла Пирсона, который в начале ХХ в. предложил использовать четырехпараметрическое семейство распределений [1]. Перечисленные выше семейства распределений - это подмножества четырехпараметрического семейства Пирсона.

К сожалению, параметрические семейства существуют лишь в головах авторов учебников по теории вероятностей и математической статистике. В реальной жизни их нет. Поэтому современная прикладная статистика [2 - 4] и эконометрика [5] используют в основном непараметрические методы [6, 7], в которых распределения результатов наблюдений могут иметь произвольный вид.

Сначала на примере нормального распределения достаточно подробно обсудим невозможность практического использования параметрических семейств для описания распределений конкретных статистических данных. Затем разберем параметрические методы отбраковки резко выделяющихся наблюдений и продемонстрируем невозможность практического использования ряда методов параметрической статистики, покажем ошибочность выводов, к которым они приводят.

3.3.1. Часто ли распределение результатов наблюдений является нормальным?

В эконометрических и экономико-математических моделях, применяемых, в частности, при изучении и оптимизации процессов маркетинга и менеджмента, управления предприятием и регионом, точности и стабильности технологических процессов, в задачах надежности, обеспечения безопасности, в том числе экологической, функционирования технических устройств и объектов, разработки организационных схем часто применяют понятия и результаты теории вероятностей и математической статистики. При этом зачастую используют те или иные параметрические семейства распределений вероятностей. Как уже отмечалось, наиболее популярно нормальное распределение. Используют также логарифмически нормальное распределение, экспоненциальное распределение, гамма-распределение, распределение Вейбулла-Гнеденко и т.д.

Очевидно, всегда необходимо проверять соответствие моделей реальности. Возникают два вопроса. Отличаются ли реальные распределения от используемых в модели? Насколько это отличие влияет на выводы?

Ниже на примере нормального распределения и основанных на нем методов отбраковки резко отличающихся наблюдений (выбросов) показано, что реальные распределения практически всегда отличаются от включенных в классические параметрические семейства, а имеющиеся отклонения от заданных семейств делают неверными выводы, в рассматриваемом случае, об отбраковке, основанные на использовании этих семейств.

Есть ли основания априори предполагать нормальность результатов измерений?

Иногда утверждают, что в случае, когда погрешность измерения (или иная случайная величина) определяется в результате совокупного действия многих малых факторов, то в силу Центральной Предельной Теоремы (ЦПТ) теории вероятностей эта величина хорошо приближается (по распределению) нормальной случайной величиной. Это утверждение, вообще говоря, неверно.

Точнее, такое утверждение справедливо, если малые факторы действуют аддитивно и независимо друг от друга. Если же они действуют мультипликативно (и независимо друг от друга), то в силу той же ЦПТ аппроксимировать распределение рассматриваемой величины надо логарифмически нормальным распределением. В прикладных задачах обосновать аддитивность, а не мультипликативность действия малых факторов обычно не удается.

Если же зависимость имеет общий характер, не приводится к аддитивному или мультипликативному виду, а также нет оснований принимать модели, дающие экспоненциальное, Вейбулла - Гнеденко, гамма или иные распределения, то о распределении итоговой случайной величины практически ничего не известно, кроме внутриматематических свойств типа регулярности.

При обработке конкретных данных иногда считают, что погрешности измерений имеют нормальное распределение. На предположении нормальности построены классические модели регрессионного, дисперсионного, факторного анализов, метрологические модели, которые еще продолжают встречаться как в отечественной ноpмативно-технической документации, так и в международных стандартах. На то же предположение опираются модели расчетов максимально достигаемых уровней тех или иных характеристик, применяемые при проектировании систем обеспечения безопасности функционирования экономических структур, технических устройств и объектов. Однако теоретических оснований для такого предположения нет. Необходимо экспериментально изучать распределения погрешностей.

3.3.2. Результаты экспериментов метрологов

Что же показывают результаты экспериментов? В классической монографии В. В. Налимова 1960 г. [8], посвященной применению математической статистики при анализе вещества, рассматриваемой проблеме посвящен специальный раздел "Отклонения от нормального распределения в аналитической работе" (гл. IV, параграф 4, с.122-134). Разбирается распространенное утверждение (со ссылкой на ЦПТ), что "истинное" распределение погрешностей - нормальное, а отклонения от нормальности - результат смешивания (разных генеральных совокупностей, например, серий измерений, проведенных в различных условиях). Вместе с тем приведены следующие экспериментальные данные: "В работе Клэнси [9] было изучено 250 распределений для различных аналитических методов, включающих в общей сложности 50 000 отдельных определений, и показано, что с практической точки зрения только в 10 - 15% случаев имеет место нормальное распределение" [8, с.122 - 123].

Развернутые исследования распределений погрешностей измерений проведены проф. П. В. Новицким (Ленинград) и его научной школой. Сводка, данная в монографии [10], позволяет утверждать, что в большинстве случаев распределение погрешностей измерений отличается от нормального. Так, в Машинно-электротехническом институте (г. Варна в Болгарии) было исследовано распределение погрешностей градуировки шкал аналоговых электроизмерительных приборов. Изучались приборы, изготовленные в Чехословакии, СССР и Болгарии. Согласно [10], закон распределения погрешностей оказался одним и тем же. Он имеет плотность

Были проанализированы данные о параметрах 219 фактических распределениях погрешностей, исследованных разными авторами, при измерении как электрических, так и не электрических величин самыми разнообразными (электрическими) приборами. В результате этого исследования оказалось, что 111 распределений, т.е. примерно 50%, принадлежат классу распределений с плотностью

где - параметр степени; b - параметр сдвига; - параметр масштаба; - гамма-функция от аргумента ;

(см. [10, с. 56]); 63 распределения, т.е. 30%, имеют плотности с плоской вершиной и пологими длинными спадами и не могут быть описаны как нормальные или, например, экспоненциальные. Оставшиеся 45 распределений оказались двухмодальными.

В другой книге известного метролога проф. П. В. Hовицкого [11] приведены результаты исследования законов распределения различного рода погрешностей измерения. Он изучил распределения погрешностей электромеханических приборов на кернах, электронных приборов для измерения температур и усилий, цифровых приборов с ручным уpавновешиванием. Объем выборок экспериментальных данных для каждого экземпляра составлял 100–400 отсчетов. Оказалось, что 46 из 47 распределений значимо отличались от нормального. Исследована форма распределения погрешностей у 25 экземпляров цифровых вольтметров Щ-1411 в 10 точках диапазона. Результаты аналогичны. Дальнейшие сведения содержатся в монографии [10].

В лаборатории прикладной математики Тартуского государственного университета проанализировано 2500 выборок из архива реальных статистических данных [12]. В 92% гипотезу нормальности пришлось отвергнуть.

Приведенные описания экспериментальных данных показывают, что погрешности измерений в большинстве случаев имеют распределения, отличные от нормальных. Это означает, в частности, что большинство применений критерия Стьюдента, классического регрессионного анализа и других статистических методов, основанных на нормальной теории, строго говоря, не является обоснованным, поскольку неверна лежащая в их основе аксиома нормальности распределений соответствующих случайных величин.

Очевидно, для оправдания или обоснованного изменения существующей практики анализа статистических данных требуется изучить свойства процедур анализа данных при "незаконном" применении. Изучение процедур отбраковки показало, что они крайне неустойчивы к отклонениям от нормальности, а потому применять их для обработки реальных данных нецелесообразно (см. ниже); поэтому нельзя утверждать, что произвольно взятая процедура устойчива к отклонениям от нормальности.

Иногда предлагают перед применением, например, критерия Стьюдента однородности двух выборок проверять нормальность. Хотя для этого имеется много критериев, но проверка нормальности - более сложная и трудоемкая статистическая процедура, чем проверка однородности (как с помощью статистик типа Стьюдента, так и с помощью непараметрических критериев). Для достаточно надежного установления нормальности требуется весьма большое число наблюдений. Так, чтобы гарантировать, что функция распределения результатов наблюдений отличается от некоторой нормальной не более, чем на 0,01 (при любом значении аргумента), требуется порядка 2500 наблюдений [3]. В большинстве экономических, технических, медико-биологических и других прикладных исследований число наблюдений существенно меньше. Особенно это справедливо для данных, используемых при изучении проблем, связанных с обеспечением безопасности функционирования экономических структур и технических объектов.

3.3.3. Скорость сходимости в Центральной предельной теореме

Иногда пытаются использовать ЦПТ для приближения распределения погрешности к нормальному, включая в технологическую схему измерительного прибора специальные сумматоры. Оценим полезность этой меры.

Пусть Z₁ , Z₂ ,…, Z_k - независимые одинаково распределенные случайные величины с функцией распределения H = H(x) такие, что Рассмотрим

Показателем обеспечиваемой сумматором близости к нормальности является

Тогда

Правое неравенство в последнем соотношении вытекает из оценок константы в неравенстве Берри - Эссеена, полученном в книге [13, с.172], а левое - из примера в монографии [14, с.140-141]. Для нормального закона =1,6, для равномерного = 1,3, для двухточечного =1 (это - нижняя граница для ). Следовательно, для обеспечения расстояния (в метрике Колмогорова) до нормального распределения не более 0,01 для "неудачных" распределений необходимо не менее k₀ слагаемых, где

В обычно используемых сумматорах слагаемых значительно меньше. Сужая класс возможных распределений H, можно получить, как показано в монографии [15], более быструю сходимость, но теория здесь еще не смыкается с практикой. Кроме того, не ясно, обеспечивает ли близость распределения к нормальному (в определенной метрике) также и близость распределения статистики, построенной по случайным величинам с этим распределением, к распределению статистики, соответствующей нормальным результатам наблюдений. Видимо, для каждой конкретной статистики необходимы специальные теоретические исследования, Именно к такому выводу приходит автор монографии [15]. В задачах отбраковки выбросов ответ: "Не обеспечивает" (см. ниже).

Отметим, что результат любого реального измерения записывается с помощью конечного числа десятичных знаков, обычно небольшого (2-5), так что любые реальные данные целесообразно моделировать лишь с помощью дискретных случайных величин, принимающих конечное число значений. Нормальное распределение - лишь аппроксимация реального распределения. Так, например, данные конкретного исследования, приведенные в работе [16], принимают значения от 1,0 до 2,2, т.е. всего 13 возможных значений. Из принципа Дирихле следует, что в какой-то точке построенная по данным работы [16] функция распределения отличается от ближайшей функции нормального распределения не менее чем на 1/26, т.е. на 0,04. Кроме того, очевидно, что для нормального распределения случайной величины вероятность попасть в дискретное множество десятичных чисел с заданным числом знаков после запятой равна 0.

Из сказанного выше следует, что результаты измерений и вообще статистические данные имеют свойства, приводящие к тому, что моделировать их следует случайными величинами с распределениями, более или менее отличными от нормальных. В большинстве случаев распределения существенно отличаются от нормальных, в других нормальные распределения могут, видимо, рассматриваться как некоторая аппроксимация, но никогда нет полного совпадения. Отсюда вытекает как необходимость изучения свойств классических статистических процедур в неклассических вероятностных моделях (подобно тому, как это сделано в [17] для критерия Стьюдента), так и необходимость разработки устойчивых (учитывающих наличие отклонений от нормальности) и непараметрических, в том числе свободных от распределения процедур, их широкого внедрения в практику статистической обработки данных.

Опущенные здесь рассмотрения для других параметрических семейств приводят к аналогичным выводам. Итог можно сформулировать так. Распределения реальных данных практически никогда не входят в какое-либо конкретное параметрическое семейство. Реальные распределения всегда отличаются от тех, что включены в параметрические семейства. Отличия могут быть большие или маленькие, но они всегда есть. Попробуем понять, насколько важны эти различия для проведения статистического анализа данных.

3.3.4. Неустойчивость параметрических методов отбраковки
резко выделяющихся результатов наблюдений

При обработке реальных статистических данных, полученных в процессе наблюдений, измерений, расчетов, иногда один или несколько результатов наблюдений резко выделяются, т.е. далеко отстоят от основной массы данных. Такие резко выделяющиеся результаты наблюдений часто считают содержащими грубые погрешности, соответственно называют промахами или выбросами. В рассматриваемых случаях возникает естественная мысль о том, что подобные наблюдения не относятся к изучаемой совокупности, поскольку содержат грубую погрешность, а получены в результате ошибки, промаха. В метрологии об этом явлении говорят так: "Грубые погрешности и промахи возникают из-за ошибок или неправильных действий оператора (его психофизиологического состояния, неверного отсчета, ошибок в записях или вычислениях, неправильного включения приборов и т.п.), а также при кратковременных резких изменений проведения измерений (вибрации, поступления холодного воздуха, толчка прибора оператором и т.п.). Если грубые погрешности и промахи обнаруживают в процессе измерений, то результаты, содержащие их, отбрасывают. Однако чаще всего их выявляют только при окончательной обработке результатов измерений с помощью специальных критериев оценки грубых погрешностей" [18, с.46-47].

Есть два подхода к обработке данных, которые могут быть искажены грубыми погрешностями и промахами:

1) отбраковка резко выделяющихся результатов наблюдений, т.е. обнаружение наблюдений, искаженных грубыми погрешностями и промахами, и исключение их из дальнейшей статистической обработки;

2) применение устойчивых (робастных) методов обработки данных, на результаты работы которых мало влияет наличие небольшого числа грубо искаженных наблюдений (см. [19 - 22] и др.).

В настоящем подразделе обсуждаются методы отбраковки.

Наиболее изучена ситуация, когда результаты наблюдений - числа x₁, x₂,…, x_n, резко выделяется один результат наблюдения, для определенности, максимальный x_max .

Простейшая вероятностно-статистическая модель такова [23]. При нулевой гипотезе H₀ результаты наблюдения x₁, x₂,…, x_n рассматриваются как реализация независимых одинаково распределенных случайных величин числа X₁, X₂,…, X_n с функцией распределения F(x). При альтернативной гипотезе H₁ случайные величины X₁, X₂,…, X_n также независимы, X₁, X₂,…, X_n-1 имеют распределение F(x), а X_n - распределение G(x), оно "существенно сдвинуто вправо" относительно F(x), например, G(x)=F(x - A), где A достаточно велико. Если альтернативная гипотеза справедлива, то при вероятность равенства

стремится к 1, поэтому естественно применять решающее правило следующего вида:

если x_max.> d, то принять H₁,

если x_max.< d, то принять H₀, (1)

где d - параметр решающего правила, значение которого следует определять из вероятностно-статистических соображений.

При справедливости нулевой гипотезы

Статистический критерий проверки гипотезы H₀ , основанный на решающем правиле вида (1), имеет уровень значимости , если

т.е.

(2)

Из соотношения (2) определяют граничное значение d = d(, n) в решающем правиле (1).

При больших n и малых

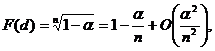(3)

поэтому в качестве хорошего приближения к d(, n) рассматривают (1-/n) - квантиль распределения F(x).

Пусть правило отбраковки задано в соответствии с выражениями (1) и (2) с некоторой функцией распределения F, однако выборка берется из функции распределения G, мало отличающейся от F в смысле расстояния Колмогорова

(4)

С помощью соотношения (3) получаем, что величина = G(d) для d из уравнения (2) находится между и . Уровень значимости критерия, построенного для F, при применении к наблюдениям из G есть 1- и может принимать любые значения в отрезке [1-; 1-]. В частности, при = 0,01, =0,05, n = 5 возможные значения уровня значимости заполняют отрезок [0; 0,1], т.е. уровень значимости может быть в 2 раза выше номинального, а если n возрастает до 30, то максимальный уровень значимости есть 0,297, т.е. почти в 6 раз выше номинального. При дальнейшем росте n верхняя граница для уровня значимости, как нетрудно видеть, приближается к 1.

Рассмотрим и другой вопрос - насколько правило отбраковки с уровнем значимости для G может отличаться от такового для F при справедливости неравенства (4). С использованием соотношения (3) заключаем, что из

(5)

следует, что где и выписаны выше. Решение уравнения (5) может принимать любое значение в отрезке []. В частности, при = 0,05 и n = 5 для стандартного нормального распределения F имеем d(, n) = 2,319, при = 0,01 решение уравнения (5) может принимать любое значение в отрезке [2,054; + ], при = 0,005 - любое значение в отрезке [2,170; 2,576].

При использовании любого другого расстояния между функциями распределения выводы о неустойчивости правил отбраковки также справедливы. Отметим, что проведенные рассмотрения выполнены в рамках "общей схемы устойчивости" (см. об устойчивости статистических процедур [19 - 22] и др.).

Рассмотренные примеры показывают, что при конкретном значении = 0,01 в неравенстве (4) весьма неустойчивы как уровни значимости при фиксированном правиле отбраковки, так и параметр d правила отбраковки при фиксированном уровне значимости. Обсудим, насколько реалистично определение функции распределения с точностью

Есть два подхода к определению функции распределения результатов наблюдений: эвристический подбор с последующей проверкой с помощью критериев согласия и вывод из некоторой вероятностной модели.

Пусть с помощью критерия согласия Колмогорова проверяется гипотеза о том, что выборка взята из распределения F. Пусть функции распределения F и G удовлетворяют соотношению (4). Пусть на самом деле выборка взята из распределения G, а не F. При каких не удастся различить F и G? Для определенности, при каких гипотеза согласия с F будет приниматься не менее чем в 50% случаев?

Критерий согласия Колмогорова основан на статистике

(6)

где расстояние между функциями распределения определено выше в формуле (4); H - та функция распределения, согласие с которой проверяется, а F_n - эмпирическая функция распределения (т.е. F_n(х) равно доле наблюдений, меньших х, в выборке объема n). Как показал А.Н. Колмогоров в 1933 г., функция распределения случайной величины при росте объема выборки n сходится к некоторой функции распределения К(х), которую ныне называют функцией Колмогорова [3, 23]. При этом К(1,36) = 0,95 и К(0,83) = 0,50.

Поскольку выборка взята из распределения G, то с вероятностью 0,50

(7)

(при больших n). Тогда для рассматриваемой выборки с учетом неравенства (4) и неравенства треугольника для расстояния Колмогорова и симметричности этого расстояния имеем

Если

т.е.

(8)

то, согласно формуле (6), гипотеза согласия принимается по крайней мере с той же вероятностью, с которой выполнено неравенств (7), т.е. с вероятностью не менее 0,50. Для = 0,01 это условие выполняется при n < 2809. Таким образом, для определения функции распределения с точностью с помощью критерия согласия Колмогорова необходимо несколько тысяч наблюдений, что для большинства прикладных задач нереально.

При втором из названных выше подходов к определению функции распределения ее конкретный вид выводится из некоторой системы аксиом, в частности, из некоторой модели порождения соответствующей случайной величины. Например, из модели суммирования вытекает нормальное распределение, а из мультипликативной модели перемножения - логарифмически нормальное распределение. Как правило, при выводе используется предельный переход. Так, из Центральной Предельной Теоремы теории вероятностей вытекает, что сумма независимых случайных величин может быть приближена нормальным распределением. Однако более детальный анализ, в частности, с помощью неравенства Берри - Эссеена (см. выше) показывает, что для гарантированного достижения точности необходимо более полутора тысяч слагаемых. Такого количества слагаемых реально, конечно, указать почти никогда нельзя. Это означает, что при решении практических задач теория дает возможность лишь сформулировать гипотезу о виде функции распределения, а проверять ее надо с помощью анализа реальной выборки объема, как показано выше, не менее нескольких тысяч. Таким образом, в большинстве реальных ситуаций определить функцию распределения с точностью невозможно.

Итак, показано, что правила отбраковки, основанные на использовании конкретной функции распределения, являются крайне неустойчивыми к отклонениям от нее распределения элементов выборки, а гарантировать отсутствие подобных отклонений невозможно. Поэтому отбраковка по классическим правилам математической статистики не является научно обоснованной, особенно при больших объемах выборок. Указанные правила целесообразно применять лишь для выявления "подозрительных" наблюдений, вопрос об отбраковке которых должен решаться из соображений соответствующей предметной области, а не из формально-математических соображений [24].

Выше для простоты изложения рассмотрен лишь случай полностью известного распределения F, для которого изучено правило отбраковки, заданное формулами (1) и (2). Аналогичные выводы о крайней неустойчивости правил отбраковки справедливы, если "истинное распределение" принадлежит какому-либо параметрическому семейству, например, нормальному, Вейбулла - Гнеденко, гамма.

Параметрическим методам отбраковки, основанным на моделях тех или иных параметрических семейств распределений, посвящены тысячи книг и статей. Приходится признать, что они имеют в основном внутриматематический интерес. При обработке реальных данных следует применять устойчивые методы (см. [19 - 22] и др.), в частности, непараметрические [25, 26].

3.4. Выборочные исследования

Термин «выборочные исследования» применяют, когда невозможно изучить все единицы представляющей интерес совокупности. Приходится знакомиться с частью совокупности - с выборкой, а затем с помощью вероятностно – статистических методов и моделей переносить выводы с выборки на всю совокупность. Выборочные исследования – способ получения статистических данных и важный раздел эконометрики и прикладной статистики [5]. Методы выборочных исследований используются при решении различных задач экономики и управления (менеджмента), в маркетинге и социологии.

3.4.1. Организация выборочных исследований

В качестве примера рассмотрим выборочные исследования предпочтений потребителей, которые часто проводят специалисты по маркетингу (изучению рынка).

Оценивание функции спроса. Функция спроса часто встречается в учебниках по экономической теории, но при этом обычно не рассказывается, как она получена. Между тем оценить ее по эмпирическим данным не так уж трудно. Например, можно выяснять ожидаемый спрос с помощью следующего простого приема - спрашиваем потенциальных потребителей: «Какую максимальную цену Вы заплатили бы за такой-то товар?» Пусть для определенности выборка состояла из 20 опрошенных. Они назвали следующие максимально допустимые для них цены:

40, 25, 30, 50, 35, 20, 50, 32, 15, 40,

20, 40, 45, 30, 50, 25, 35, 20, 35, 40.

Сначала названные опрошенными величины упорядочим в порядке возрастания. Результаты представлены в табл.1. В первом столбце - номера различных численных значений (в порядке возрастания), названных потребителями. Во втором столбце приведены сами значения цены, названные ими. В третьем столбце указано, сколько раз названо то или иное значение.

Таблица 1. – Эмпирическая оценка функции спроса и ее использование

№ п/п (i)	Цена	Повторы	Спрос	Прибыль	Прибыль	Прибыль
1	15	1	20	100	0	-
2	20	3	19	190	95	-
3	25	2	16	240	160	0
4	30	2	14	280	210	70
5	32	1	12	264	204	84
6	35	3	11	275	220	110
7	40	4	8	240	200	120
8	45	1	4	140	120	80
9	50	3	3	120	105	75

Таким образом, 20 потребителей назвали 9 конкретных значений цены (максимально допустимых, или приемлемых для них значений), каждое из значений, как видно из третьего столбца, названо от 1 до 4 раз. Теперь легко построить выборочную функцию спроса в зависимости от цены. Она будет представлена в четвертом столбце, который заполним снизу вверх. Спрос как функция от цены р обозначен D(p) (от demand (англ.) – спрос). Если мы будем предлагать товар по цене свыше 50 руб., то его не купит никто из опрошенных. При цене 50 руб. появляются 3 покупателя. Записываем 3 в четвертый столбец в девятую строку. А если цену понизить до 45? Тогда товар купят четверо – тот единственный, для кого максимально возможная цена - 45, и те трое, кто был согласен на более высокую цену – 50 руб. Таким образом, легко заполнить столбец 4, действуя по правилу: значение в клетке четвертого столбца равно сумме значений в находящейся слева клетке третьего столбца и в лежащей снизу клетке четвертого столбца. Например, за 30 руб. купят товар 14 человек, а за 20 руб. - 19.

Зависимость спроса от цены - это зависимость четвертого столбца от второго. Табл.1 дает нам девять точек такой зависимости. Зависимость можно представить на рисунке, в координатах «спрос – цена». Если абсцисса - это спрос, а ордината - цена, то девять точек на кривой спроса, перечисленные в порядке возрастания абсциссы, имеют вид:

(3; 50), (4; 45), (8; 40), (11; 35), (12; 32),

(14; 30), (16; 25), (19; 20), (20; 15).

Эти девять точек можно использовать для построения кривой спроса каким-либо графическим (сделайте чертеж!) или расчетным способом, например, методом наименьших квадратов. Кривая спроса, как и следует ожидать согласно учебникам экономической теории, убывает, имея направления от левого верхнего угла чертежа к правому. Однако заметны отклонения от гладкого вида функции, связанные, в частности, с естественным пристрастием потребителей к круглым числам. Заметьте, все опрошенные, кроме одного, назвали числа, кратные 5 руб.

Расчет оптимальной цены. Данные табл.1 могут быть использованы для выбора цены продавцом-монополистом. Или организацией, действующей на рынке монополистической конкуренции. Пусть расходы на изготовление или оптовую покупку единицы товара равны 10 руб. По какой цене ее продавать на том рынке, функцию спроса для которого мы только что нашли? Для ответа на этот вопрос вычислим суммарную прибыль, т.е. произведение прибыли на одной единице товара (p - 10) на число проданных (точнее, запрошенных) экземпляров D(p). Результаты приведены в пятом столбце табл.1. Видно, что максимальная прибыль, равная 280 руб., достигается при цене 30 руб. за единицу товара. При этом из 20 потенциальных покупателей окажутся в состоянии заплатить за книгу 14, т.е. 70% .

Если же удельные издержки производства, приходящиеся на одну единицу товара (или оптовая цена), повысятся до 15 руб., то данные столбца 6 табл.1 показывают, что максимальная прибыль, равная 220 руб. (она, разумеется, меньше, чем в предыдущем случае), достигается при более высокой цене - 35 руб. Эта цена доступна 11 потенциальным покупателям, т.е. 55% от всех возможных покупателей. При дальнейшем повышении издержек, скажем, до 25 руб., как вытекает из данных столбца 7 табл.1, максимальная прибыль, равная 120 руб., достигается при цене 40 руб. за единицу товара, что доступно 8 лицам, т.е. 40% покупателей. Отметьте, что при повышении оптовой цены на 10 руб. оказалось выгодным увеличить розничную лишь на 5, поскольку более резкое повышение привело бы к такому сокращению спроса, которое перекрыло бы эффект от повышения удельной прибыли (т.е. прибыли, приходящейся на одну проданную единицу товара).

Замечание. При более строгом подходе к использованию терминов надо вместо «прибыли» говорить о «маржинальной прибыли», а вместо «удельных издержек» – о «переменных издержках» (на одну единицу продукции), поскольку постоянные издержки не учитываем. Кроме того, спрос целесообразно выражать не в числе потребителей, а в процентах от общего числа потенциальных потребителей. Мы не сочли необходимым придерживаться подобных уточнений, поскольку цель настоящей главы – в демонстрации возможности использования в маркетинговых исследований подходов, основанных на организационно-экономическом моделировании.

Представляет интерес анализ оптимального объема выпуска при различных значениях удельных издержек (табл.2).

В табл.2 звездочками указаны максимальные значения прибыли при том или ином значении издержек, не включенном в табл.1. Для легкости обозрения результаты об оптимальных объемах выпуска и соответствующих ценах из табл.1 и табл.2 приведены в табл.3.

Как видно из табл.3, с ростом издержек оптимальный выпуск падает, а цена растет. При этом изменение издержек на 5 единиц может вызывать, а может и не вызывать повышения цены. В этом проявляется микроструктура функции спроса – небольшое повышение цены может привести к тому, что значительные группы покупателей откажутся от покупок, и прибыль упадет.

Таблица 2. – Прибыль при различных значениях издержек

№ (i)	Цена	Спрос	Прибыль	Прибыль	Прибыль	Прибыль	Прибыль
1	15	20	200	-	-	-	-
2	20	19	285	0	-	-	-
3	25	16	320	80	-	-	-
4	30	14	350 *	140	0	-	-
5	32	12	324	144	24	-	-
6	35	11	330	165 *	55	0	-
7	40	8	280	160	80 *	40	0
8	45	4	160	100	60	40	20
9	50	3	135	90	60	45 *	30 *

Таблица 3. – Зависимость оптимального выпуска и цены от издержек

Издержки	5	10	15	20	25	30	35	40
Оптимальный выпуск	14	14	11	11	8	8	3	3
Цена	30	30	35	35	40	40	50	50

Этот эффект напоминает известное в экономической теории разделение налогового бремени между производителем и потребителем. Неверно говорить, что производитель перекладывает издержки или, конкретно, налоги, на потребителя, повышая цену на их величину, поскольку при этом сокращается спрос (и выпуск), а потому и прибыль производителя.

Дальнейшее ясно - если оптовая цена будет повышаться, то и дающая максимальную прибыль розничная цена также будет повышаться, и все меньшая доля покупателей сможет приобрести товар. Крайняя точка - оптовая цена, равная 45 руб. Тогда только трое (15%) купят товар за 50 руб., а прибыль продавца составит только 15 руб. Наглядно видно, что повышение издержек производства приводит к ориентации производителя на наиболее богатые слои населения. Но и повышение цен (до оптимального для монополиста-производителя уровня) не приводит к повышению прибыли, напротив, она снижается, и при этом большинство потенциальных потребителей не в состоянии купить товар.

Отметим, что рыночные структуры не в состоянии обеспечить всех желающих – это просто не выгодно. Так, из 20 опрошенных лишь 14, т.е. 70%, могут рассчитывать на покупку, даже при минимальных издержках и ценах. Если общество желает чем-либо обеспечить всех граждан, оно должно раздавать это благо бесплатно, как это делается, например, с учебниками в школах.

Описанный здесь метод оценивания спроса был разработан в Институте высоких статистических технологий и эконометрики (Москва) в 1993 г.

Для изучения предпочтений потребителей часто используют более изощренные методы. Рассмотрим некоторые из них.

Маркетинговые опросы потребителей. Потенциального покупателя интересует не только цена, но и качество товара, красота упаковки (например, для подарочных наборов конфет) и многое другое. Хочешь узнать, чего желает потребитель - спроси его. Эта простая мысль объясняет популярность маркетинговых опросов.

Бесспорно, что основная цель производственной и торговой деятельности - удовлетворение потребностей людей. Как получить представление об этих потребностях? Очевидно, необходимо опросить потребителей. В американском учебнике по рекламному делу [6] подробно рассматриваются различные методы опроса потребителей и обработки результатов с помощью методов эконометрики. Расскажем о результатах опроса потребителей растворимого кофе. Исследование проведено Институтом высоких статистических технологий и эконометрики по заказу АОЗТ «Д-2» в апреле 1994 г. в Москве.

Сбор данных. Один из важнейших разделов прикладной статистики – сбор данных. Обсудим постановку задачи в случае опроса потребителей растворимого кофе. Заказчика интересуют предпочтения как продавцов кофе (розничных и мелкооптовых), так и непосредственно потребителей. В результате совместного обсуждения было признано целесообразным использовать для опроса и тех, и других одну и ту же анкету из 14 основных и 4 социально-демографических вопросов с добавлением двух вопросов специально для продавцов. Анкета была разработана совместно представителями заказчика и исполнителя и утверждена заказчиком. В табл.4 приведен несколько сокращенный вариант этой анкеты.

Таблица 4 – Анкета для потребителей растворимого кофе (в сокращении)

____________________________________________________

Дорогой потребитель растворимого кофе,

Институт высоких статистических технологий и эконометрики просит Вас ответить на несколько простых вопросов о том, какой кофе Вы любите. Ваши ответы позволят составить объективное представление о вкусах российских любителей кофе и будут способствовать повышению качества этого товара на российском рынке.

1. Часто ли Вы пьете растворимый кофе: иногда, каждый день 1 чашку, 2-3 чашки, больше, чем 3 чашки.

(Здесь и далее подчеркните нужное.)

2. Что Вы цените в кофе: вкус, аромат, крепость, цвет, отсутствие вредных для здоровья веществ, что-либо еще (сообщите нам, что именно) ____________________________.

3. Как часто покупаете кофе: по мере надобности или по возможности?

4. Какую марку растворимого кофе Вы обычно покупаете? ______

5. Какой объем упаковки Вы предпочитаете: в пакетиках, маленькая банка, средняя банка, большая банка, обязательно стеклянная банка, все равно.

6. Где покупаете растворимый кофе: в ларьках, в продуктовых магазинах, в специализированных отделах и магазинах, все равно, где купить, где-либо еще (опишите, пожалуйста) ______________.

7. Были ли случаи, когда купленный Вами кофе оказывался низкого качества? Да, нет.

8. Согласны ли Вы, что за высокое и гарантированное качество продукта можно и заплатить несколько дороже? Да, нет.

9. На сколько дороже Вы готовы платить за экологически безопасный кофе? _______________________________________

10. Считаете ли Вы нужным, чтобы вредные для здоровья вещества, в частности, ионы тяжелых металлов, не проникали из материала упаковки в растворимый кофе? Да, нет.

Мы планируем сравнить потребительские предпочтения различных категорий жителей нашей страны. Поэтому просим ответить еще на несколько вопросов.

11. Пол: женский, мужской.

12. Возраст: до 20, 20-30, 30-50, более 50.

13. Род занятий: учащийся, работающий, пенсионер, инженер, врач, преподаватель, служащий, менеджер, предприниматель, научный работник, рабочий, др. (пожалуйста, расшифруйте).

14. Вся Ваша семья любит растворимый кофе или же Вы - единственный любитель этого восхитительного напитка современного человека? Вся семья, я один (одна).

Спасибо за Ваше содействие работе по повышению качества продуктов на российском рынке!

Выбор метода опроса. Широко применяются процедуры опроса, когда респонденты (так социологи и маркетологи называют тех, от кого получают информацию, т.е. опрашиваемых) самостоятельно заполняют анкеты (розданные им или полученные по почте), а также личные и телефонные интервью. Из этих процедур нами было выбрано личное интервью по следующим причинам.

Возврат почтовых анкет сравнительно невелик (в данном случае можно было ожидать не более 5-10%), оттянут по времени и искажает структуру совокупности потребителей (наиболее динамичные люди вряд ли найдут время для ответа на подобную анкету).

Самостоятельное заполнение анкеты, как показали специально проведенные эксперименты, не позволяет получить полные ответы на поставленные вопросы. Респондент утомляется или отвлекается, отказывается отвечать на часть вопросов, иногда не понимает их или отвечает не по существу. Некоторые категории респондентов, например, продавцы в киосках, отказываются заполнять анкеты, но готовы устно ответить на вопросы.

Телефонный опрос искажает совокупность потребителей, поскольку наиболее активных индивидуумов трудно застать дома и уговорить ответить на вопросы анкеты. Репрезентативность нарушается также и потому, что на один номер телефона может приходиться различное количество продавцов и потребителей растворимого кофе, а некоторые из них не имеют телефонов вообще. Анкета достаточно длинна, и разговор по домашнему и тем более служебному телефону респондента может быть прекращен досрочно по его инициативе. Иногородних продавцов и потребителей растворимого кофе, приехавших в Москву, по телефону опросить практически невозможно.

Метод личного интервью лишен перечисленных недостатков. Соответствующим образом подготовленный интервьюер, получив согласие на интервью, удерживает внимание собеседника на анкете, добивается получения ответов на все её вопросы, контролируя при этом соответствие ответов реальной позиции респондента. Ясно, что успех интервьюирования зависит от личных качеств и подготовки интервьюера. Однако расходы на получение одной анкеты при использовании этого метода больше, чем для других рассмотренных методов.

Формулировки вопросов. В маркетинговых и социологических опросах используют три типа вопросов - закрытые, открытые и полузакрытые, они же полуоткрытые. При ответе на закрытые вопросы респондент может выбирать лишь из сформулированных составителями анкеты вариантов ответа. В качестве ответа на открытые вопросы респондента просят изложить свое мнение в свободной форме. Полузакрытые, они же полуоткрытые вопросы занимают промежуточное положение - кроме перечисленных в анкете вариантов, респондент может добавить свои соображения.

В социологических публикациях, посвященных выборочным исследованиям, продолжается дискуссия по поводу «мягких» и «жестких» форм сбора данных. Т.е. фактически о том, какого типа вопросы более целесообразно использовать - открытые или закрытые (см., например, статью известного социолога В. А. Ядова [7]).

Преимущество открытых вопросов состоит в том, что респондент может свободно высказать свое мнение так, как сочтет нужным. Их недостаток - в сложности сопоставления мнений различных респондентов. Для такого сопоставления и получения сводных характеристик организаторы опроса вынуждены сами шифровать ответы на открытые вопросы, применяя разработанную ими схему шифровки.

Преимущество закрытых вопросов в том и состоит, что такую шифровку проводит сам респондент. Однако при этом организаторы опроса уподобляются древнегреческому мифическому персонажу Прокрусту. Как известно, Прокруст приглашал путников заночевать у него. Укладывал их на кровать. Если путник был маленького роста, он вытягивал его ноги так, чтобы они и голова доставали до концов кровати. Если же путник оказывался высоким и ноги его торчали - он обрубал их так, чтобы достигнуть стандарта: «рост» путника должен равняться длине кровати. Так и организаторы опроса, применяя закрытые вопросы, заставляют респондента «вытягивать» или «обрубать» свое мнение, чтобы выразить его с помощью приведенных в формулировке вопроса возможных ответов.

Ясно, что для обработки данных по группам и сравнения групп между собой нужны формализованные данные, и фактически речь может идти лишь о том, кто - респондент или маркетолог (социолог, психолог и др.) - будет шифровать ответы. В проекте «Потребители растворимого кофе» практически для всех вопросов варианты ответов можно перечислить заранее, т.е. можно широко использовать закрытые вопросы. В отличие от опросов с вопросами типа: «Одобряете ли Вы идущие в России реформы?», в которых естественно просить респондента расшифровать, что он понимает под «реформами» (открытый вопрос). Поэтому в используемой в описываемом проекте анкете использовались в основном закрытые и полузакрытые вопросы. Как показали результаты обработки, этот подход оказался правильным - лишь в небольшом числе анкет оказались вписаны свои варианты ответов. Вместе с тем демонстрировалось уважение к мнению респондента, не выдвигалось требование обязательного выбора из заданного множества ответов - респондент мог добавить свое, но редко пользовался этой возможностью (не более чем в 5% случаев).

В последнем вопросе анкеты респонденту предлагалось стать постоянным участником опросов о качестве товаров народного потребления. Ряд респондентов откликнулся на это предложение, в результате стало возможным развертывание постоянной сети «экспертов по качеству», подобной аналогичным в США и других странах.

3.4.2. Модели случайных выборок

Статистические методы выборочных исследований основаны на вероятностных моделях, описывающих получение ответов опрашиваемых на вопросы анкет. В случае ответов типа «да» - «нет» наиболее распространенными являются две вероятностные модели—биномиальная и гипергеометрическая.

В биномиальной модели предполагается, что ответы n опрашиваемых можно рассматривать как совокупность n независимых одинаково распределенных случайных величин Х₁, Х₂,....,Х_n , где Х_i = 1, если i‑ый респондент сказал «да», и Х_i = 0, если его ответ - «нет». Тогда число Х ответов «да» в выборке равно

Х= Х₁+ Х₂+...+ Х_n . (1)

Из формулы (1) и Центральной предельной теоремы теории вероятностей (см. раздел 3.2 выше) вытекает, что при увеличении объема выборки n распределение Х сближается с нормальным распределением. Известно, что распределение Х имеет вид

Р(Х= k) = C_n^k p^k (1—p)^n-k , (2)

где C_n^k - число сочетаний из n элементов по k, а p - доля ответов «да» в генеральной совокупности, т.е. p = Р(Х_i = 1). Формула (2) задает биномиальное распределение, часто используемое при вероятностном моделировании реальных явлений и процессов.

Гипергеометрическое распределение соответствует иной схеме - случайному отбору респондентов в выборку. Пусть среди N лиц, составляющих генеральную совокупность, имеется D лиц, чье мнение - «да». Случайность отбора респондентов в выборку означает, что каждое лицо имеет одинаковые шансы быть отобранным. Мало того, ни одна пара потенциальных респондентов не должна иметь при отборе в выборку преимущества перед любой другой парой. То же самое — для троек, четверок и т.д. Это условие выполнено тогда и только тогда, когда каждое из сочетаний по n лиц из N имеет одинаковые шансы быть отобранным в качестве выборки. Вероятность того, что будет отобрано заранее заданное сочетание, равна, очевидно, 1/.

Пусть Y —число сказавших «да» лиц в случайной выборке, организованной таким образом. Известно, что тогда P(Y = k) – гипергеометрическое распределение, т.е.

. (3)

Отбор случайной выборки согласно описанным правилам организуют при проведении различных лотерей. Например, отбирают 6 номеров из 49. Тогда генеральная совокупность состоит из 49 единиц (номеров), а выборка - из 6. В этом случае отбирают номера, а не респондентов, но вероятностная модель - та же. Удобно говорить, что генеральная совокупность и выборка состоят из единиц. В одном случае единицы - это люди (лица, потенциальные респонденты), в другом - номера. В статистических метода управления качеством рассматриваются единицы продукции - детали или изделия.

Замечательный математический факт состоит в том, что биномиальная модель (2) и гипергеометрическая модель (3) весьма близки (с практической точки зрения совпадают), когда объем генеральной совокупности (партии) по крайней мере в 10 раз превышает объем выборки. Другими словами, можно принять, что

Р(Х = k) = P(Y = k), (4)

если объем выборки мал по сравнению с объемом партии. При этом в качестве p в левой части формулы (4) берут D/N.

Близость результатов, получаемых с помощью биномиальной и гипергеометрической моделей, весьма важна не только с практической, но и с методологической точки зрения. Дело в том, что эти модели исходят из принципиально различных методологических предпосылок. В биномиальной модели случайность присуща каждому респонденту. Он с какой-то вероятностью отвечает «да», а с какой-то - «нет» (сумма этих вероятностей, очевидно, равна 1). В то же время в гипергеометрической модели ответ респондента полностью определен, а случайность проявляется лишь в отборе, вносится социологом или маркетологом при составлении выборки.

В науках о человеке противоречие между рассматриваемыми моделями выборки четко выражено. В среде специалистов, изучающих человека (маркетологов, социологов, психологов, политологов и др.) давно идет дискуссия о роли случайности в поведении человека. А именно, о том, есть ли случайность в поведении отдельно взятого человека или же случайность проявляется лишь в отборе выборки из генеральной совокупности.

Биномиальная модель предполагает, что поведение человека, в частности, выбор им определенного варианта при ответе на вопрос, определяется с участием случайных причин. Например, человек может случайно сказать «да», случайно — «нет». Некоторые философы отрицают случайность, присущую поведению человека согласно биномиальной модели. Они верят в причинность и считают поведение конкретного человека практически полностью детерминированным (его взглядами, психофизиологическими особенностями, прежним опытом и др.). Поэтому они принимают гипергеометрическую модель и считают, что случайность отличия ответов в выборке от ответов во всей генеральной совокупности определяется всецело случайностью, вносимой при отборе единиц наблюдения в выборку.

Сформулированные выше математические результаты (соотношение (4)) показывают, что позиция в этой давней дискуссии практически не влияет на алгоритмы обработки данных. Следовательно, во многих случаях нет необходимости принимать чью-либо сторону в этом споре, поскольку обе модели дают близкие численные результаты.

Отличия проявляются лишь при обсуждении вопроса о том, какую выборку считать представительной. В терминах контроля качества продукции - является ли таковой выборка, составленная из 20 изделий, лежащих сверху в первом вскрытом ящике? В биномиальной модели вполне допустим ответ «да», в гипергеометрической - только «нет».

Биномиальная модель легче для теоретического изучения, поэтому будем её рассматривать в дальнейшем. Однако при реальном опросе лучше формировать выборку, исходя из гипергеометрической модели. Это делают, выбирая респондентов из списка избирателей (для включения в выборку) с помощью датчиков псевдослучайных чисел на ЭВМ или с помощью таблиц псевдослучайных чисел. Алгоритмы формирования выборки встраивают во все современные программные продукты, предназначенные для поддержки проведения маркетинговых или социологических опросов, организации статистического контроля качества и др.

Обоснование объема выборки и проведение опроса. Вернемся к анализу результатов опроса потребителей растворимого кофе, о котором шла речь в предыдущем разделе. Как уже говорилось, модели выборочных исследований часто опираются на предположение о том, что реальную выборку можно описывать как «случайную выборку из конечной совокупности». Типа той, когда из списков избирателей с помощью датчика случайных чисел отбирается необходимое число номеров для формирования жюри присяжных заседателей. В рассматриваемом исследовании нельзя обеспечить формирование подобной выборки - не существует реестра потребителей растворимого кофе. Однако в этом и нет необходимости. Поскольку гипергеометрическое распределение хорошо приближается биномиальным, если объем выборки по крайней мере в 10 раз меньше объема всей совокупности (в рассматриваемом случае это так), то правомерно использование биномиальной модели, согласно которой мнение респондента (ответы на все вопросы анкеты) рассматривается как случайный вектор, а все такие вектора независимы между собой. Другими словами, можно использовать модель простой случайной выборки.

3.4.3. Доверительное оценивание доли

Зачем проводятся выборочные исследования? Чтобы получить необходимую информацию о генеральной совокупности. Для этого необходимо перенести выводы с выборки на генеральную совокупность. Как и с какой точностью можно это сделать?

Рассмотрим эту проблему для простейшего случая одного вопроса с двумя возможными ответами - «да» и «нет».

Напомним, что биномиальная модель выборки как раз и применяется для описания ответов на закрытые вопросы, имеющие две подсказки, например, «да» и «нет». Конечно, пары подсказок могут быть иными. Например, «согласен» и «не согласен». Или при опросе потребителей кондитерских товаров первая подсказка может иметь такой вид: «Больше люблю «Марс», чем «Сникерс»«. А вторая тогда такова: «Больше люблю «Сникерс», чем «Марс»«.

Пусть объем выборки равен n. Тогда ответы опрашиваемых можно представить как X₁ , X₂ ,…,X_n , где X_i = 1, если i-й респондент выбрал первую подсказку, и X_i = 0, если i-й респондент выбрал вторую подсказку, i=1,2,…,n. В вероятностной модели предполагается, что случайные величины X₁ , X₂ ,…,X_n независимы и одинаково распределены. Поскольку эти случайные величины принимают два значения, то ситуация описывается одним параметром р - долей выбирающих первую подсказку во всей генеральной совокупности. Тогда

Р(X_i = 1) = р, Р(X_i = 0)= 1 - р, i=1,2,…,n.

Пусть m = X₁ + X₂ +…+X_n . Оценкой вероятности р является частота р*=m/n. При этом математическое ожидание М(р*) и дисперсия D(p*) имеют вид

М(р*) = р, D(p*)= p(1-p)/n.

По Закону Больших Чисел (ЗБЧ) теории вероятностей (в данном случае - по теореме Бернулли) частота р* сходится (т.е. безгранично приближается) к вероятности р при росте объема выборки (см. разд. 3.2 выше). Это означает, что оценивание проводится тем точнее, чем больше объем выборки. Точность оценивания можно указать. Займемся этим.

По теореме Муавра-Лапласа теории вероятностей

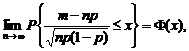
где - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1,

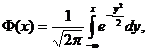
где = 3,1415925…-отношение длины окружности к ее диаметру, e = 2,718281828… - основание натуральных логарифмов. График плотности стандартного нормального распределения

был очень точно изображен на германской денежной банкноте в 10 немецких марок (до введения евро). Банкнота была посвящена великому немецкому математику Карлу Гауссу (1777–1855), среди основных работ которого есть относящиеся к нормальному распределению. Эта подробность демонстрирует, что в Германии (и тем более в англосаксонских странах) гораздо шире распространено знакомство с основами теории вероятностей и математической статистики, чем в нашей стране.

В настоящее время нет необходимости вычислять функцию стандартного нормального распределения и ее плотность по приведенным выше формулам, поскольку давно составлены подробные таблицы (см., например, [1]), а распространенные программные продукты содержат алгоритмы нахождения этих функций.

С помощью теоремы Муавра-Лапласа могут быть построены доверительные интервалы для неизвестной статистику вероятности. Сначала заметим, что из этой теоремы непосредственно следует, что

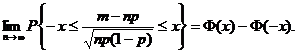
Поскольку функция стандартного нормального распределения симметрична относительно 0, т.е. то справедливо полезное равенство

Зададим характеристику надежности переноса выводов с выборки на генеральную совокупность - доверительную вероятность , близкую к 1. Пусть функция удовлетворяет условию

т.е.

Из последнего предельного соотношения следует, что

К сожалению, это соотношение нельзя непосредственно использовать для доверительного оценивания, поскольку верхняя и нижняя границы зависят от неизвестной вероятности. Однако с помощью метода наследования сходимости (см. раздел 3.2 выше или [3, п.2.4]) можно доказать, что

Следовательно, нижняя доверительная граница имеет вид

в то время как верхняя доверительная граница такова:

Наиболее распространенным (в прикладных исследованиях) значением доверительной вероятности является Иногда употребляют термин «95% доверительный интервал». Тогда

Пример 1. Пусть n = 500, m = 200. Тогда p* = 0,40. Найдем доверительный интервал для

Таким образом, хотя в достаточно большой выборке 40% респондентов говорят «да», можно утверждать лишь, что во всей генеральной совокупности таких от 35,7% до 44,3% - крайние значения отличаются на 8,6%.

Замечание. С достаточной для практики точностью можно заменить 1,96 на 2.

Величина

называется ошибкой выборки. Обычно, как в примере 1, используют значение доверительной вероятности и множитель

Удобные для использования в практической работе специалиста по выборочным исследованиям, маркетолога и социолога таблицы точности оценивания разработаны во ВЦИОМ (Всероссийском центре по изучению общественного мнения). Приведем здесь несколько модифицированный вариант одной из них (табл.5).

Таблица 5. – Допустимая величина ошибки выборки (в процентах)

Объем группы n	1000	750	600	400	200	100
Доля р*
Около 10% или 90%	2	3	3	4	5	7
Около 20% или 80%	3	4	4	5	7	9
Около 30% или 70%	4	4	4	6	9	10
Около 40% или 60%	4	4	5	6	8	11
Около 50%	4	4	5	6	8	11

В условиях рассмотренного выше примера надо взять вторую снизу строку. Объема выборки 500 нет в таблице, но есть объемы 400 и 600, которым соответствуют ошибки в 6% и 5% соответственно. Следовательно, в условиях примера целесообразно оценить ошибку как ((5+6)/2)% = 5,5%. Эта величина несколько больше, чем рассчитанная выше (4,3%). С чем связано это различие? Дело в том, что таблица ВЦИОМ связана не с доверительной вероятностью а с доверительной вероятностью которой соответствует множитель Расчет ошибки по приведенным выше формулам дает 5,65%, что практически совпадает со значением, найденным по табл.5.

Необходимый объем выборки. В биномиальной модели выборки оценивание характеристик происходит тем точнее, чем объем выборки больше. Часто спрашивают: «Какой объем выборки нужен?» Разработан ряд методов определения необходимого объема выборки. Они основаны на разных подходах. Либо на задании необходимой точности оценивания параметров. Либо на явной формулировке альтернативных гипотез, между которыми необходимо сделать выбор. Либо на учете погрешностей измерений (методы статистики интервальных данных). Ни один из этих подходов нельзя применить в рассматриваемом случае.

Минимальный из обычно используемых объемов выборки n в маркетинговых или социологических исследованиях - 100, максимальный - до 5000 (обычно в исследованиях, охватывающих ряд регионов страны, т.е. фактически разбивающихся на ряд отдельных исследований - как в ряде исследований ВЦИОМ). По данным Института социологии Российской академии наук [2], среднее число анкет в социологическом исследовании не превышает 700. Поскольку стоимость исследования растет, по крайней мере, как линейная функция объема выборки, а точность повышается как квадратный корень из этого объема, то верхняя граница объема выборки определяется обычно из экономических соображений. Объемы пилотных исследований (т.е. проводящихся впервые, предварительно или как первые в сериях подобных) обычно ниже, чем объемы исследований по обкатанной программе.

Нижняя граница определяется тем, что в минимальной по численности анализируемой подгруппе должно быть несколько десятков человек (не менее 30), поскольку по ответам попавших в эту подгруппу необходимо сделать обоснованные заключения, например, о предпочтениях соответствующей подгруппы в совокупности всех потребителей растворимого кофе. Учитывая деление опрашиваемых на продавцов и покупателей, на мужчин и женщин, на четыре градации по возрасту и восемь - по роду занятий, наличие 5 - 6 подсказок во многих вопросах, приходим к выводу о том, что в рассматриваемом проекте объем выборки должен быть не менее 400 - 500. Вместе с тем существенное превышение этого объема было признано нецелесообразным, поскольку исследование являлось пилотным.

Поэтому в проекте «Потребители растворимого кофе» объем выборки был выбран равным 500. Анализ полученных результатов позволяет утверждать, что в соответствии с целями исследования выборку следует считать репрезентативной.

3.4.4. Два прикладных выборочных исследования

Продолжим обсуждение выборочного исследования потребителей растворимого кофе.

Организация опроса. Интервьюерами работали молодые люди – студенты первого курса экономико-математического факультета Московского государственного института электроники и математики (технического университета) и лицея № 1140, проходившие обучение по экономике, всего 40 человек, имеющих специальную подготовку по изучению рынка и проведению маркетинговых опросов потребителей и продавцов (в объеме 8 часов). Опрос продавцов проводился на рынках г. Москвы, действующих в Лужниках, у Киевского вокзала и в других местах. Опрос покупателей проводился на рынках, в магазинах, на улицах около киосков и ларьков, а также в домашней и служебной обстановке.

Большое внимание уделялось качеству заполнения анкет. Интервьюеры были разбиты на шесть бригад, бригадиры персонально отвечали за качество заполнения анкет. Второй уровень контроля осуществляла специально созданная «группа организации опроса», третий происходил при вводе информации в базу данных. Каждая анкета заверена подписями интервьюера и бригадира, на ней указано место и время интервьюирования. Поэтому необходимо признать высокую достоверность собранных анкет.

Обработка данных. В соответствии с целью исследования основной метод первичной обработки данных - построение частотных таблиц для ответов на отдельные вопросы. Кроме того, проводилось сравнение различных групп потребителей и продавцов, выделенных по социально-демографическим данным, с помощью критериев проверки однородности выборок (см. ниже). При более углубленном анализе применялись различные методы статистики объектов нечисловой природы (более 90% маркетинговых и социологических данных имеют нечисловую природу [4]). Использовались средства графического представления данных.

Итоги опроса. Итак, по заданию одной из торговых фирм были изучены предпочтения покупателей и мелкооптовых продавцов растворимого кофе. Совместно с представителями заказчика был составлен опросный лист (анкета типа социологической) из 16 основных вопросов и 4 дополнительных, посвященных социально-демографической информации. Опрос проводился в форме интервью с 500 покупателями и продавцами кофе. Места опроса - рынки, лотки, киоски, продуктовые и специализированные магазины. Другими словами, были охвачены все виды мест продаж кофе. Интервью проводили более 40 специально подготовленных (примерно по 8-часовой программе) студентов и лицеистов, разбитых на 7 бригад. После тщательной проверки бригадирами и группой обработки информация была введена в специально созданную базу данных. Затем проводилась разнообразная статистическая обработка, строились таблицы и диаграммы, проверялись статистические гипотезы и т.д. Заключительный этап - осмысление и интерпретация данных, подготовка итогового отчета и предложений для заказчиков.

Технология организации и проведения маркетинговых опросов лишь незначительно отличается от технологии социологических опросов, многократно описанной в литературе. Так, мы предпочли использовать полуоткрытые вопросы, в которых для опрашиваемого дан перечень подсказок, а при желании он может высказать свое мнение в свободной форме. Не уложившихся в подсказки оказалось около 5 % , их мнения были внесены в базу данных и анализировались дополнительно. Для повышения надежности опроса о наиболее важных с точки зрения маркетинга моментах спрашивалось в нескольких вопросах. Были вопросы - ловушки, с помощью которых контролировалась «осмысленность» заполнения анкеты. Например, в вопросе: «Что Вы цените в кофе: вкус, аромат, крепость, наличие пенки...» ловушкой является включение «крепости» - ясно, что крепость зависит не от кофе самого по себе, а от его количества в чашке. В ловушку никто из 500 не попался - никто не отметил «крепость». Этот факт свидетельствует о надежности выводов проведенного опроса. Мы считали нецелесообразным задавать вопрос об уровне доходов (поскольку в большинстве случаев отвечают «средний», что невозможно связать с определенной величиной). Вместо такого вопроса мы спрашивали: «Как часто Вы покупаете кофе: по мере надобности или по возможности?». Поскольку кофе не является дефицитным товаром, первый ответ свидетельствовал о наличии достаточных денежных средств, второй - об их ограниченности (потребитель не всегда имел возможность позволить себе купить банку растворимого кофе).

Стоимость подобных исследований - 5–10 долларов США на одного обследованного. При этом трудоемкость (и стоимость) начальной стадии - подготовки анкеты и интервьюеров, пробный опрос и др. - 30% от стоимости исследования. Стоимость непосредственно опроса - тоже 30%, ввод информации в компьютер и проведение расчетов, построение таблиц и графиков - 20%, интерпретация результатов, подготовка итогового отчета и предложений для заказчиков - 20%. Таким образом, стоимость собственно опроса в два с лишним раза меньше стоимости остальных стадий исследования. И в выполнении работы участвуют различные специалисты. На первой стадии – в основном нужны высококвалифицированные аналитики. На второй – многочисленные интервьюеры, в роли которых могут выступать студенты и школьники, прошедшие конкретный курс обучения в 8–10 часов. На третьей – работа с компьютером (надо уметь строить и обсчитывать электронные таблицы или базы данных, использовать статистические пакеты, составлять и печатать таблицы и диаграммы и т.п.). На четвертой – опять в основном нужны высококвалифицированные аналитики.

Приведем некоторые из полученных результатов.

а) В отличие от западных потребителей, отечественные не отдавали предпочтения стеклянным банкам по сравнению с жестяными. Поскольку жестяные банки дешевле стеклянных, то можно было порекомендовать (в 1994 г., когда проходил опрос) с целью снижения расходов закупку кофе в жестяных банках.

б) Отечественные потребители готовы платить на 10–20% больше за экологически безопасный кофе более высокого качества, имеющий сертификат Минздрава и символ экологической безопасности на упаковке.

в) Средний объем потребления растворимого кофе одной семьей - 850 г в месяц.

г) Потребители растворимого кофе могут быть разделены на классы (в другой терминологии - кластеры). Есть «продвинутые» потребители, обращающие большое внимание на качество и экологическую безопасность, марку и страну производства, терпимо относящиеся к изменению цены. Эти «тонкие ценители» - в основном женщины от 30 до 50 лет, служащие, менеджеры, научные работники, преподаватели, врачи (т.е. лица с высшим образованием), пьющие кофе как дома, так и на работе, причем «кофейный ритуал» зачастую входит в процедуру деловых переговоров или совещаний. Противоположный по потребительскому поведению класс состоит из мужчин двух крайних возрастных групп - школьников и пенсионеров. Для них важна только цена, что очевидным образом объясняется недостатком денег.

Результаты были использованы заказчиком в рекламной кампании. В частности, в ней в соответствии с итогами опроса обращалось внимание на сертификат Минздрава и на экологическую безопасность упаковки.

Оценивание функции спроса и моделирование рынка. Выпускник программы «Топ-менеджер» Академии народного хозяйства при Правительстве Российской Федерации А. А. Пивень в 2003 г. оценил функцию спроса на продукцию своего предприятия. Расчет и установление оптимальной цены на изделие с точки зрения максимизации прибыли был произведен по описанному выше методу. В табл.6 приведена функция ожидаемого спроса в зависимости от цены. Как подсчитал А.А. Пивень, уровень издержек на производство 1 изделия составляет 42824,7 руб. (1350 у.е.). Для удобства все расчеты будем производить в условных единицах.

Таблица 6. – Функция ожидаемого спроса в зависимости от цены

№ п/п	Цена, у.е.	Объем продаж в год, шт.	Издержки на объем производства	Выручка, у.е.	Прибыль, у.е.
1	1 400	1 600	2 160 000	2 240 000	80 000
2	1 500	1 500	2 025 000	2 250 000	225 000
3	1 600	1 200	1 620 000	1 920 000	300 000
4	1 700	1 000	1 350 000	1 700 000	350 000
5	1 800	720	972 000	1 246 000	324 000
6	1 900	500	675 000	950 000	275 000
7	2 000	320	432 000	640 000	208 000
8	2 100	170	229 500	357 000	127 500
9	2 200	110	148 500	242 000	93 500

Как видно из приведенных расчетов, оптимальная цена на подъемник должна находиться в диапазоне 1600–1700 у.е.

На основе многомерной регрессионной зависимости методом наименьших квадратов была построена математическая модель рынка. Она довольно точно отражает реальное положение дел. При исходной цене 1650 у.е. продажи ориентировочно должны составить 1010 шт. На рис.1 приведена кривая спроса.

Эти расчеты были сделаны при допущении, что издержки не меняются в течение длительного промежутка времени. Однако, в реальных условиях постоянный рост стоимости энергоресурсов и непрекращающаяся инфляция издержек (рост затрат на сырье, материалы, комплектующие изделия, рабочую силу) приводит к увеличению издержек. Поэтому А. А. Пивень проанализировал оптимальный объем выпуска при их различных значениях. Данные его расчетов приведены в табл.7. Поскольку инфляция в нашей стране заметно искажает стоимостные характеристики, используем для их описания условные единицы (у.е.).

Рисунок 1 – Кривая спроса на изделие.

Для удобства восприятия рассмотренные результаты относительно оптимальных объемов производства при соответствующих ценах приведены в табл.8.

Таблица 7. – Прибыль в зависимости от цены и издержек

№ п/п	Цена, у.е.	Объем продаж, шт.	Прибыль (тыс. у.е.) при издержках на единицу продукции, у.е.
			1350	1400	1450	1500	1550	1600	1650	1700
1	1 400	1600	80	0	-	-	-	-	-	-
2	1 500	1500	225	150	75	0	-	-	-	-
3	1 600	1200	300	240	180	120	60	0	-	-
4	1 700	1000	350	300	250	200	150	100	50	0
5	1 800	720	324	288	252	216	180	144	108	72
6	1 900	500	275	250	225	200	175	150	125	100
7	2 000	320	208	192	176	160	144	128	112	96
8	2 100	170	127,5	119	110,5	102	93,5	85	76,5	68
9	2 200	110	93,5	88	82,5	77	71,5	66	60,5	55

Таблица 8. – Оптимальные выпуск и цена в зависимости от издержек

Издержки	1350	1400	1450	1500	1550	1600	1650	1700
Оптимальный выпуск	1000	1000	720	720	720	500	500	500
Цена	1700	1700	1800	1800	1800	1900	1900	1900

Как видно из табл.8, увеличение издержек ведет к снижению оптимального выпуска при росте цены. Хотя изменение издержек на 50 у.е. может не сразу привести к изменению цены. Необоснованная цена может “переключить” большую группу потребителей на другое, аналогичное изделие, имеющее сходный по уровню набор технических характеристик, но более низкую рыночную цену.

По данным функции спроса (табл.7) проведем расчет эластичности спроса по цене. Под ценовой эластичностью спроса понимается степень реагирования рыночного спроса на изменение цен. В классическом понимании эластичность спроса по цене показывает, насколько изменится объем спроса при изменении цены на 1%. Спрос квалифицируется как эластичный, если понижение цены вызывает такой рост оборота, при котором увеличение объема продаж с лихвой компенсирует более низкие цены. Если же понижение цены, приводя к некоторому увеличению объема продаж, тем не менее, не ведет к увеличению оборота или даже уменьшает его, то такой спрос называется неэластичным. Коэффициент ценовой эластичности спроса определяется по формуле:

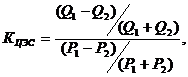
где Q₁, Q₂ – значения объема продаж; P₁, P₂ – значения цены изделия.

В рассматриваемом случае K_ЦЭС будет различен на протяжении всей функции спроса (рис.1). Однако, произведем расчет на той части кривой (в том диапазоне), где присутствует расчетная цена подъемника, а именно: Q₁=1200 шт.; Q₂=720 шт.; P₁=1600 у.е.; P₂=1800у.е. В этом случае

Коэффициент K_ЦЭС имеет отрицательный знак и абсолютную величину, значительно превышающую 1. Это говорит о сильной обратной зависимости объемов продаж от цены. Спрос на подъемник весьма эластичен. Валовая выручка увеличивается при снижении цены и уменьшается при ее повышении. Компании необходимо быть готовой к тому, что покупатели очень чутко реагируют на всякое повышение цены на изделие значительным снижением объемов закупок. Как отмечает А. А. Пивень, снижение эластичности спроса на изделие возможно только при общем росте благосостояния населения страны и в частности, значительного роста доходной части бюджетов промышленных предприятий.

3.4.5. Проверка однородности двух биномиальных выборок

Проверка однородности – одна из базовых проблем, решаемых статистическими методами. Она часто обсуждается в литературе, а методы проверки однородности применяются при решении многих практических задач. Например, как сравнить две группы - мужчин и женщин, молодых и пожилых, и т.п.? В маркетинге это важно для сегментации рынка. Если две группы не отличаются по ответам, значит, их можно объединить в один сегмент и проводить по отношению к ним одну и ту же маркетинговую политику, в частности, осуществлять одни и те же рекламные воздействия. Если же две группы различаются, то и относиться к ним надо по-разному. Это - представители двух разных сегментов рынка, требующих разного подхода при борьбе за их завоевание.

Обсуждаемая далее постановка задачи в статистических терминах такова. Рассматривается вопрос с двумя возможными ответами, например, «да» и «нет». В первой группе из n₁ опрошенных m₁ человек сказали «да», а во второй группе из n₂ опрошенных m₂ сказали «да». В вероятностной модели предполагается, что m₁ и m₂ - биномиальные случайные величины B(n₁, p₁) и B(n₂, p₂) соответственно. Запись B(n, p) означает, что случайная величина m имеет биномиальное распределение с параметрами n - объем выборки и p - вероятность определенного ответа (скажем, ответа «да»). Такая случайная величина может быть представлена в виде суммы m = X₁ + X₂ +…+X_n , где случайные величины X₁, X₂,…, X_n независимы, одинаково распределены, принимают два значения 1 и 0, причем Р(X_i = 1) = р, Р(X_i = 0)= 1 - р, i=1,2,…,n.

Однородность двух групп означает, что соответствующие им вероятности равны, неоднородность - что эти вероятности отличаются. В терминах прикладной математической статистики задача ставится так: необходимо проверить гипотезу однородности

H₀: p₁ = p₂

при альтернативной гипотезе о наличии эффекта

H₁: p₁ p₂

(Иногда представляют интерес односторонние альтернативные гипотезы и .)

Оценкой вероятности р₁ является частота р₁*=m₁/n₁, а оценкой вероятности р₂ является частота р₂*=m₂/n₂ . Даже при совпадении вероятностей р₁ и р₂ частоты, как правило, различаются. Как говорят, «по чисто случайным причинам». Рассмотрим случайную величину р₁* - р₂*. Тогда

M(р₁* - р₂*) = р₁ - р₂, D(р₁* - р₂*) = р₁ (1 - р₁)/n₁ + р₂(1-р₂)/n₂.

Из теоремы Муавра - Лапласа и теоремы о наследовании сходимости (см. разд. 3.2) следует, что

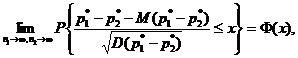
где - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. Для практического применения этого соотношения следует заменить неизвестную статистику дисперсию разности частот на оценку этой дисперсии:

D*(р₁* - р₂*) = р*₁ (1 - р*₁)/n₁ + р*₂ (1-р*₂)/n₂.

(Могут использоваться и другие оценки рассматриваемой дисперсии, например, при справедливости нулевой гипотезы - по объединенной выборке.) С помощью указанной выше математической техники можно показать, что при такой замене предельное распределение не меняется:

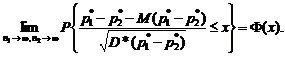
При справедливости гипотезы однородности (т.е. при отсутствии эффекта) имеем M(р₁* - р₂*) = 0. Поэтому правило принятия решения при проверке однородности двух выборок выглядит так:

1. Вычислить статистику

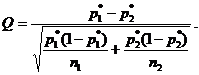
2. Сравнить значение модуля статистика |Q| с граничным значением K. Если |Q|<K, то принять гипотезу однородности H₀ . Если же |Q|>K, то заявить об отсутствии однородности и принять альтернативную гипотезу H₁.

Граничное значение К определяется выбором уровня значимости статистического критерия проверки однородности. Из приведенных выше предельных соотношений следует, что при справедливости гипотезы однородности H₀ для уровня значимости имеем (при

Следовательно, граничное значение в зависимости от уровня значимости целесообразно выбирать из условия

Здесь - функция, обратная к функции стандартного нормального распределения. В социально-экономических исследованиях наиболее распространен 5% уровень значимости, т.е. Для него К = 1,96.

Пример 2. Пусть в первой группе из 500 опрошенных мужчин ответили «да» 200, а во второй группе из 700 опрошенных женщин сказали «да» 350. Есть ли разница по доле отвечающих «да» между генеральными совокупностями, представленными этими двумя группами?

Для установления взаимопонимания с маркетологом уберем из формулировки примера относящийся к теории статистики термин «генеральная совокупность». Получим следующую постановку.

Пусть из 500 опрошенных мужчин ответили «да, я люблю пепси-колу» 200, а из 700 опрошенных женщин 350 сказали «да, я люблю пепси-колу». Есть ли разница между мужчинами и женщинами по доле отвечающих «да» на вопрос о любви к пепси-коле?

В рассматриваемом примере нужные для расчетов величины таковы: Вычислим статистику

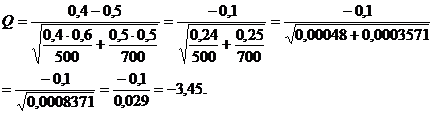
Поскольку |Q| = 3,45 > 1,96, то необходимо отклонить нулевую гипотезу и принять альтернативную. Таким образом, мужчины и женщины отличаются по рассматриваемому признаку - любви к пепси-коле.

Необходимо отметить, что результат проверки гипотезы однородности зависит не только от частот, но и от объемов выборок. Предположим, что частоты (доли) зафиксированы, а объемы выборок растут. Тогда числитель статистики Q не меняется, а знаменатель уменьшается, значит, вся дробь возрастает. Поскольку знаменатель стремится к 0, то дробь возрастает до бесконечности и рано или поздно превзойдет любую границу. Есть только одно исключение - когда в числителе стоит 0. Следовательно, при строгом подходе к формулировкам вывод статистика должен выглядеть так: «различие обнаружено» или «различие не обнаружено». Во втором случае различие, возможно, было бы обнаружено при увеличении объемов выборок.

Как и для доверительного оценивания вероятности, во ВЦИОМ разработаны две полезные таблицы, позволяющие оценить вызванные чисто случайными причинами допустимые расхождения между частотами в группах. Эти таблицы рассчитаны при выполнении нулевой гипотезы однородности и соответствуют ситуациям, когда частоты близки к 50% (табл.9) или к 20% (табл.10). Если наблюдаемые частоты - от 30% до 70%, то рекомендуется пользоваться первой из этих таблиц, если от 10% до 30% или от 70% до 90% - то второй. Если наблюдаемые частоты меньше 10% или больше 90%, то теорема Муавра-Лапласа и основанные на ней асимптотические формулы дают не очень хорошие приближения, целесообразно применять иные, более продвинутые математические средства, в частности, приближения с помощью распределения Пуассона.

В условиях разобранного выше примера табл.9 дает допустимое расхождение 7%. Действительно, объем первой группы 500 отсутствует в таблице, но строки, соответствующие объемам 400 и 600, совпадают для первых двух столбцов слева. Эти столбцы соответствуют объемам второй группы 750 и 600, между которыми расположен объем 700, данный в примере. Он ближе к 750, поэтому берем величину расхождения, стоящую на пересечении первого столбца и второй (и третьей) строк, т.е. 7%. Поскольку реальное расхождение (10%) больше, чем 7%, то делаем вывод о наличии значимого различия между группами. Естественно, этот вывод совпадает с полученным ранее расчетным путем.

Таблица 9. – Допустимые расхождения (в %) между частотами

в двух группах, когда наблюдаются частоты от 30% до 70%

Объемы групп	750	600	400	200	100
750	6	7	7	10	12
600	7	8	8	11	13
400	7	8	10	11	14
200	10	11	11	13	16
100	12	13	14	16	18

Таблица 10. – Допустимые расхождения (в %) между частотами в двух группах,
когда наблюдаются частоты от 10% до30% или от 70% до 90%

Объемы групп	750	600	400	200	100
750	5	5	6	8	10
600	5	6	7	8	10
400	6	7	8	9	11
200	8	8	9	10	12
100	10	10	11	12	14

Как и в случае табл.5, значения в таблицах 9 и 10 несколько больше, чем рассчитанные по приведенным выше формулам. Дело в том, что таблицы ВЦИОМ связаны не с уровнем значимости а с уровнем значимости которому соответствует граничное значение 2,58.

Допустимое расхождение между частотами нетрудно получить расчетным путем. Для этого достаточно воспользоваться формулой для статистики Q и определить, при каком максимальном расхождении частот все еще делается вывод о том, что верна гипотеза однородности. Следовательно, допустимое расхождение находится из уравнения

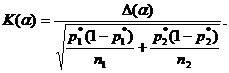
Таким образом,

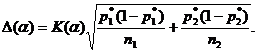
Для данных примера 2 = 1,96 0,029 = 0,057, или 5,7%, для уровня значимости 0,05.

Для других уровней значимости надо использовать другие коэффициенты Так, K(0,01) = 2,58 для уровня значимости 1% и K(0,10) = 1,64 для уровня значимости 10%. Для данных примера = 2,58 0,029 = 0,7482 0,075, или 7,5%, для уровня значимости 0,01. Если округлить до ближайшего целого числа процентов, то получим 7%, как при использовании таблицы 9 выше.

Анализ таблиц 9 и 10 показывает, что для обнаружения эффекта (констатации различия генеральных совокупностей) частоты должны отличаться не менее чем на 6%. А при некоторых объемах выборок - более чем на 10%, например, при объемах выборок 100 и 100 - на 19%. Если же частоты отличаются на 5% или менее, можно сразу сказать, что статистический анализ приведет к выводу о том, что различие не обнаружено (для выборок объемов не более 750).

В связи со сказанным возникает вопрос: каково типовое отличие частот в двух выборках из одной и той же совокупности? Разность частот в этом случае имеет нулевое математическое ожидание и дисперсию

Величина р(1 - р) достигает максимума при р = 1/2, и этот максимум равен 1/4. Если р = 1/2, а объемы двух выборок совпадают и равны 500, то дисперсия разности частот равна

Следовательно, среднее квадратическое отклонение равно 0,032, или 3,2%. Поскольку для стандартной нормальной случайной величины в 50% случаев ее значение не превосходит по модулю 0,67 (а в 50% случаев - больше 0,67), то типовой разброс равен 0,67, а в рассматриваемом случае - 2,1%.

Приведенные соображения дают возможность построить метод контроля правильности (корректности) проведения повторных опросов. Если частоты излишне устойчивы, значения при повторных опросах слишком близки - это подозрительно! Возможно, нарушены правила проведения опросов, выборки не являются случайными, ответы фальсифицированы, и т.д.

3.5. Проверка однородности

В конце предыдущего раздела шла речь о проверке однородности двух биномиальных выборок. В настоящем разделе продолжим обсуждать проблему однородности - рассмотрим систему эконометрических моделей и методов, предназначенных для проверки однородности двух независимых выборок. Подобные системы разработаны в прикладной статистике [21] для решения многих иных задач статистического анализа данных, однако объем настоящей монографии не позволяет провести подробный разбор всех таких задач и систем. Настоящий раздел следует рассматривать как пример разработки системы эконометрических моделей и методов, предназначенной для решения определенной задачи.

3.5.1. Система моделей проверки однородности двух независимых выборок

В прикладных исследованиях часто возникает необходимость выяснить, различаются ли генеральные совокупности, из которых взяты две независимые выборки. Например, надо выяснить, зависят ли от способа упаковки потребительские качества подшипников, измеренные через год после хранения. Или: влияет ли система оплаты на производительность труда.

В математико-статистических терминах постановка задачи такова: имеются две выборки x₁, x₂,...,x_m и y₁, y₂,...,y_n, требуется проверить их однородность. Напомним, что выборка моделируется как совокупность независимых одинаково распределенных случайных величин. Термин «однородность» уточняется ниже.

Противоположным понятием является «различие» (или «наличие эффекта»). Можно переформулировать задачу: требуется проверить, есть ли различие между выборками. Если различия нет, то для дальнейшего изучения две рассматриваемые выборки часто объединяют в одну.

Например, в маркетинге важно выделить сегменты потребительского рынка. Если установлена однородность двух выборок мнений потребителей, то возможно объединение сегментов, из которых эти выборки взяты, в один. В дальнейшем это позволит осуществлять по отношению к ним одинаковую маркетинговую политику (проводить одни и те же рекламные мероприятия и т.п.). Если же установлено различие, то поведение потребителей в двух сегментах различно, объединять эти сегменты нельзя, и могут понадобиться различные маркетинговые стратегии, своя для каждого из этих сегментов.

Вероятностная модель порождения данных. Для обоснованного выбора и применения организационно-экономических (эконометрических, статистических) методов необходимо прежде всего построить и обосновать вероятностную модель порождения данных. При проверке однородности двух выборок общепринята модель, в которой x₁, x₂, ..., x_m рассматриваются как результаты m независимых наблюдений некоторой случайной величины Х с функцией распределения F(x), неизвестной статистику, а y₁, y₂, ..., y_n - как результаты п независимых наблюдений, вообще говоря, другой случайной величины Y с функцией распределения G(x), также неизвестной статистику. Предполагается также, что наблюдения в одной выборке не зависят от наблюдений в другой, поэтому выборки и называют независимыми.

Возможность применения модели в конкретной реальной ситуации требует обоснования. Независимость и одинаковая распределенность результатов наблюдений, входящих в выборку, могут быть установлены или исходя из методики проведения конкретных наблюдений, или путем проверки статистических гипотез независимости и одинаковой распределенности с помощью соответствующих критериев проверки статистических гипотез [2].

Если проведено (т+п) измерений объемов продаж в (т+п) торговых точках, то описанную выше модель, как правило, можно применять. Если же, например, x_i и y_i - объемы продаж одного и того же товара до и после определенного рекламного воздействия, то рассматриваемую модель применять нельзя, поскольку очевидно, что эти объемы продаж определяются не только и не столько рекламным воздействием, сколько особенностями конкретной торговой точки (ее расположением, продолжительностью работы, репутацией и т.д.). В последнем случае используют модель связанных выборок. В ней обычно строят новую выборку z_i = x_i - y_i и используют статистические методы анализа одной выборки, а не двух. Методы проверки однородности для связанных выборок рассматриваются в [21].

При дальнейшем изложении принимаем описанную выше вероятностную модель двух выборок.

Классификация моделей по типам данных. В предыдущем разделе рассматривались результаты измерений по альтернативным признакам. Каждое из чисел x_i и y_i принимало одно из двух значений, для определенности, 0 или 1. Если респондент дает ответ «да» на вопрос анкеты, то x_i = 1, если его ответ – «нет», то x_i = 0. Такие признаки называют также дихотомическими или бинарными. Распределение элементов первой выборки x₁, x₂, ..., x_m описывается одним числом P(x_i = 1) = p₁. Распределение элементов второй выборки y₁, y₂, ..., y_n также описывается одним числом P(y_i = 1) = p₂. Проверка однородности двух независимых выборок состоит в проверке статистической гипотезы H₀: p₁ = p₂ при альтернативной гипотезе о наличии эффекта H₁: p₁ p₂. Метод проверки гипотезы H₀ разобран в конце предыдущего раздела. Есть и другие методы проверки этой гипотезы, основанные на использовании иных статистик [16].

Обобщением альтернативного признака является такой, значением которого является элемент некоторого конечного множества. Например, респондент выбирает не из двух ответов («да» или «нет»), а из трех («да», «нет», «может быть»). Пусть множество значений состоит из k элементов (их часто называют градациями признака). Занумеруем их натуральными числами j = 1, 2, …, k. Для простоты записи будем считать, что элемент выборки – это номер значения (градации), которое принимает признак. Тогда распределение случайного элементов двух выборок со значениями в одном и том же конечном множестве описывается вероятностями

P(x_i = j) = p_j(1), P(y_i = j) = p_j(2), j = 1, 2, …, k.

Таким образом, в отличие от альтернативного признака каждое распределение задается не одном числом, а k числами, неотрицательными и в сумме составляющими 1, так что «свободных параметров» всего (k – 1).

Подобные k-значные признаки обычно возникают при измерениях по качественным шкалам (наименований и порядковой). Однако иногда они возникают в результате группировки значений количественных (числовых) признаков. Будем называть их «признаки с конечным числом градаций». Проверка однородности для таких признаков – это проверка сложной гипотезы

.

Альтернативную гипотезу наиболее общего вида можно записать так:

.

Третий тип рассматриваемых здесь данных – количественные признаки, значения которых – действительные числа, а функции распределения непрерывны.

Уточнения понятия однородности для количественных данных. Понятие «однородность», т. е. «отсутствие различия», может быть формализовано в терминах вероятностной модели различными способами.

Наивысшая степень однородности (абсолютная однородность) достигается, если обе выборки взяты из одной и той же генеральной совокупности, т. е. справедлива нулевая гипотеза

H₀ : F(x)=G(x) при всех х.

Отсутствие абсолютной однородности означает, что верна альтернативная гипотеза, согласно которой

H₁ : F(x₀)¹G(x₀)

хотя бы при одном значении аргумента x₀. Если гипотеза H₀ принята, то выборки можно объединить в одну, если нет - то нельзя.

В некоторых случаях целесообразно проверять не совпадение функций распределения, а лишь совпадение некоторых характеристик случайных величин Х и Y - математических ожиданий, медиан, дисперсий, коэффициентов вариации и др. (однородность тех или иных характеристик). Например, однородность математических ожиданий означает, что справедлива гипотеза

H'₀ : M(X)=M(Y),

где M(Х) и M(Y) - математические ожидания случайных величин Х и Y, результаты наблюдений над которыми составляют первую и вторую выборки соответственно. Доказательство различия между выборками в рассматриваемом случае - это доказательство справедливости альтернативной гипотезы

H'₁ : M(X) ¹ M(Y).

Если гипотеза H₀ верна, то и гипотеза H'₀ верна, но из справедливости H'₀ , вообще говоря, не следует справедливость H₀. Математические ожидания могут совпадать для различающихся между собой функций распределения. В частности, если в результате обработки выборочных данных принята гипотеза H'₀, то отсюда не следует, что две выборки можно объединить в одну. Однако в ряде ситуаций целесообразна проверка именно гипотезы H'_{0 .} Например, пусть функция спроса на определенный товар или услугу оценивается путем опроса потребителей (первая выборка) или с помощью данных о продажах (вторая выборка). Тогда маркетологу важно проверить гипотезу об отсутствии систематических расхождений результатов этих двух методов, т.е. гипотезу о равенстве математических ожиданий. Другой пример – из производственного менеджмента. Пусть изучается эффективность управления бригадами рабочих на предприятии с помощью двух организационных схем, результаты наблюдения - объем производства продукции или услуг на одного члена бригады (производительность), а показатель эффективности организационной схемы - средний (по предприятию) объем производства на одного рабочего. Тогда для сравнения эффективности препаратов достаточно проверить гипотезу H'₀ .

Иногда нужно проверить однородность дисперсий. Например, различаются ли два способа измерения по величине случайной ошибки – т.е. по дисперсии случайных погрешностей.

Рассмотрим проверку однородности для признаков с конечным числом градаций, а затем – для количественных признаков.

3.5.2. Проверка согласия и однородности для признаков
с конечным числом градаций

Проведем в качестве примера обработку данных, относящихся к известной всем читателям тематике. Дональд А. Уиндзор подсчитал, сколько ученых родилось под каждым из знаков Зодиака (см. журнал «Химия и жизнь», 1976, №4, с.112–113). Им были взяты две научные специальности – таксономия (т.е. теория классификация биологических организмов) и молекулярная биология. Результаты приведены в табл.1.

Видно, что под знаком Овна родилось гораздо больше молекулярных биологов, чем под любым другим – почти в 1,5 раза больше, чем приходится в среднем на один знак Зодиака. Таксономисты чаще рождались под знаком Рака, а реже всего – под знаком Скорпиона. Для этой специальности среднее число рождений больше числа рождений под знаком Скорпиона почти в 1,6 раза, а отношение максимального числа в столбце таксономистов к минимальному равно 38/18 2,1 (!).

Разве все эти факты не доказывают, что специальность ученого и знак Зодиака, под которым он родился, связаны между собой, что молекулярные биологи, скажем, не случайно чаще всего рождаются под знаком Овна?

Таблица 1 – Специальности ученых и знаки Зодиака их дней рождений

Номер (i)	Знак Зодиака	Количество таксонометристов (mi(1))	Количество молекулярных биологов (m2i(2))
1	Овен	28	58
2	Телец	30	32
3	Близнецы	31	39
4	Рак	38	41
5	Лев	32	32
6	Дева	31	42
7	Весы	25	41
8	Скорпион	18	41
9	Стрелец	27	40
10	Козерог	25	33
11	Водолей	26	35
12	Рыба	31	36
Всего (ni)		342	470
В среднем на знак Зодиака (ni/12)		28,5	39,17

Нет, не доказывают. Почему превышение над средним уровнем в 1,5 раза считать большим, а, к примеру, в 1,1 раза – малым? Может быть, и то, и другое вызывается число случайными причинами?

Как теория организационно-экономического моделирования рекомендует поступать? Прежде всего необходимо сформулировать гипотезу, которую будем проверять. Или несколько гипотез. А для этого построим вероятностно-статистическую модель, в терминах которой сформулируем гипотезу. Модель нужна, чтобы дальнейшие расчеты опирались на теорию математической статистики.

Принимаем, что для каждой из двух генеральных совокупностей ученых (таксономистов и молекулярных биологов) существуют 12 вероятностей событий, состоящих в рождении ученого под определенным знаком Зодиака. Обозначим p₁(1) вероятность того, что таксономист родился под знаком Овна, p₂(1) – что он родился под знаком Тельца, и так далее до p₁₂(1) – вероятности рождения под знаком Рыбы (знаки Зодиака перенумерованы в табл.2.1). Кроме того, считаем, что n₁ = 342 изученных Дональдом А. Уиндзором таксономиста выбраны из всей совокупности ученых этой специальности таким способом, который никак не связан с днями и месяцами их рождений – ведь иначе мы не можем распространить выводы, полученные по выборке, на всю совокупность. Короче, рассматриваемая выборка является представительной.

Итак, вероятностно-статистическая модель такова. Считаем, что в столбце таксономистов табл.1 записаны результаты n₁ = 342 опытов, проведенных независимо друг от друга, в каждом из которых осуществляется одно из 12 событий – с вероятностью p₁(1) качественный признак принимает значение 1 (интерпретируется как «родился под знаком Овна), с вероятностью p₂(1) признак принимает значение 2 (т.е. «родился под знаком Тельца»), и так далее до значения 12 («родился под знаком Рыбы»), которое этот признак принимает с вероятностью p₁₂(1). Модель для описания результатов n₂ = 470 опытов, приведенных в столбце молекулярных биологов, отличается только другими обозначениями вероятностей, а именно, p₁(2), p₂(2), …, p₁₂(2) для рождений под знаками Овна, Тельца, …, Рыбы соответственно.

Самая простая гипотеза, которая приходит в голову, такова: шансы родиться под каждым знаком Зодиака одинаковы. Поскольку всего знаков 12, то имеется 1 шанс из 12 родиться под знаком Овна, 1 шанс из 12 – под знаком Тельца, и т.д. Значит, все вероятности равны между собой и потому равны 1/12. Речь идет о нулевых гипотезах

,

.

При взгляде на табл.1 возникает, скажем, гипотеза, что для таксономистов p₄(1) больше p₈(1) (вероятность родиться под знаком Рака больше, чем вероятность родиться под знаком Скорпиона). Если эта гипотеза справедлива, то знаки Зодиака не являются равноправными, и реальный мир устроен более сложно, чем в случае равных вероятностей. По принципу экономии мышления (известен также как «бритва Оккама»[1]) необходимо сначала проверить, не соответствуют ли всё-таки данные табл.1 гипотезе равноправности шансов, и только в случае обнаружения противоречия переходить к более сложным гипотезам.

Итак, мы пришли к следующим задачам проверки статистических гипотез: не противоречат ли данные табл.1 гипотезам H₀(1) и H₀(2)?

Критерий (хи-квадрат) для проверки согласия с фиксированным распределением. В математической статистике со времен великого английского статистика Карла Пирсона (1857–1936) рассматривают задачу проверки согласия эмпирического распределения с теоретическим. А именно, пусть в результате опыта осуществляется один и только один из k исходов. Пусть эти исходы занумерованы натуральными числами от 1 до k, и p₁, p₂, …, p_k – вероятности этих исходов. Пусть проведены n опытов, в результате которых m₁ раз осуществился первый исход, m₂ раз - второй, …, m_k раз – k-ый исход. По этим статистическим данным требуется проверить статистическую гипотезу о том, что вероятности исходов опыта совпадают с заданными:

.

Альтернативная гипотеза, которую обычно рассматривают, состоит в том, что нарушается хотя бы одно из этих равенств. Ее можно записать так:

.

Для проверки этой гипотезы согласия эмпирического распределения с теоретическим естественно исходить из того, что при ее справедливости случайная величина m_j имеет биномиальное распределение с вероятностью p_j0 и числом опытов n, а потому ее математическое ожидание равно np_j0. Следовательно, отклонение эмпирического распределения от теоретического описывается величинами m_j - np_j0. С некоторой естественной точки зрения [13] наилучший способ проверки согласия основан на введенной Карлом Пирсоном статистике критерия хи-квадрат, рассчитываемой по формуле

.

При росте объема выборки n распределение только что введенной статистики критерия хи-квадрат стремится к известному в теории вероятностей распределению хи-квадрат с (k - 1) степенью свободы, т.е. к распределению суммы (k - 1) независимых случайных величин, каждая из которых – квадрат стандартной нормальной случайной величины (с математическим ожиданием 0 и дисперсией 1). Исходя из этого математического утверждения, для проверки гипотезы согласия по уровню значимости находят квантиль порядка (1 - ) распределения хи-квадрат с (k - 1) степенью свободы (с помощью распространенных таблиц, имеющихся, в частности, в сборнике [2], или с помощью различных программных продуктов). Правило принятия решений при проверке гипотезы согласия таково: если рассчитанное по эмпирическим данным значение статистики хи-квадрат таково, что

,

то гипотезу согласия принимают на заданном уровне значимости (и констатируют, что эмпирические данные не противоречат гипотезе ); если же

,

то гипотезу согласия отклоняют (и принимают альтернативную гипотезу).

Замечание 1. Чтобы можно было опираться на предельное соотношение, требуется, чтобы величины np_j0 не были малыми. Для этого достаточно, чтобы np_j0 > 5 при всех j = 1, 2, …, k.

Замечание 2. В математической статистике еще несколько критериев проверки гипотез называются «критериями хи-квадрат», например, критерий для проверки однородности распределений значений конечнозначных признаков (см. ниже), критерий для проверки независимости признаков на основе таблицы сопряженности. Причина проста – распределения статистик этих критериев сходятся к распределению хи-квадрат.

Замечание 3. Если соответствующее опыту распределение мало отличается от теоретического, то при сравнительно небольшом объеме выборки скорее всего будет принята гипотеза согласия. При увеличении же объема выборки может быть обнаружено отличие распределения от теоретического. Поэтому в случае точнее формулировать вывод так: эмпирические данные не позволяют отклонить гипотезу согласия, в то время как в случае констатируем, что отклонение обнаружено.

Замечание 4. Если значение статистики мало, то данные, возможно, фальсифицированы. Это утверждение основано на то, что при справедливости гипотезы согласия распределение статистики близко к хи-квадрат распределению, а потому осуществление маловероятных событий – слишком большого или слишком малого значения статистики - практически невозможно.

Вернемся к данным табл.1. Соответственно числу знаков Зодиака k = 12. Проверяем гипотезу равновероятности, т.е. частный случай гипотезы согласия с p_j0 = 1/12, j = 1, 2, …, 12. Из последней строки табл.1 следует, что приведенное в замечании 1 условие выполнено.

Проведя расчеты по приведенной выше формуле, получаем, что для таксономистов = 9,36, а для молекулярных биологов = 13,85. По таблицам [2] (и любым другим) для числа степеней свободы k – 1 = 12 – 1 = 11 квантиль распределения хи-квадрат порядка 0,9 есть 17,3, а квантиль порядка 0,95 равен 19,7. Это значит, что гипотеза согласия принимается (точнее, не отклоняется) при уровнях значимости ) 0,1, а также 0,05 и всех иных, используемых на практике. По тем же таблицам

,

так что значения статистики попадают в среднюю часть распределения – они не слишком велики и не слишком малы.

Итак, данные табл.1 идеально согласуются с равномерным распределением моментов рождения по знакам Зодиака как для таксонометристов, так и для молекулярных биологов. Отклонения от равномерности, отмеченные в начале подраздела, объясняются чисто случайными причинами.

Критерий (хи-квадрат) проверки однородности распределений признаков с конечным числом градаций. Может быть, хотя гипотезу равноправности знаков Зодиака нельзя отвергнуть ни для одной группы ученых, но зато эти группы сильно различаются между собой, отклоняясь о среднего, как сказать, в разные стороны? Речь идет, очевидно, о проверке однородности распределений двух признаков с конечным числом градаций. Опишем соответствующую вероятностно-статистическую модель.

Пусть в результате опыта осуществляется один и только один из k исходов. Пусть эти исходы занумерованы натуральными числами от 1 до k. Пусть p₁(1), p₂(1), …, p_k(1) – вероятности этих исходов для одной генеральной совокупности, а p₁(2), p₂(2), …, p_k(2) – вероятности этих же исходов для другой генеральной совокупности. Другими словами, рассмотрим два признака (две случайные величины) X и Y, возможные значения которых – рассматриваемые k исходов. Распределения этих признаков таковы:

.

Пусть для признака X проведены n(1) независимых опытов, в результате которых m₁(1) раз осуществился первый исход, m₂(1) раз - второй, …, m_k(1) раз – k-ый исход. Другими словами, проведено n(1) независимых испытаний, в результате которых получено n(1) независимых значений случайной величины X, причем эта случайная величина m₁(1) раз приняла значение 1, m₂(1) раз – значение 2, …, m_k(1) раз – значение k. Аналогичным образом получены статистические данные для случайной величины Y – проведено n(2) независимых испытаний, в которых эта случайная величина m₁(2) раз приняла значение 1, m₂(2) раз – значение 2, …, m_k(2) раз – значение k. Причем испытания для X проведены независимо от испытаний для Y.

По этим статистическим данным, т.е. по двум независимым выборкам значений двух конечнозначных случайных величин, требуется проверить статистическую гипотезу о том, что распределения этих случайных величин совпадают. Другими словами, проверить гипотезу однородности распределений, т.е. сложную гипотезу

.

В качестве альтернативной обычно рассматривают гипотезу о том, что хотя бы одно из этих k равенств не выполнено. Эту гипотезу наиболее общего вида можно записать так:

.

Статистика критерия хи-квадрат имеет вид [22, с.275]:

.

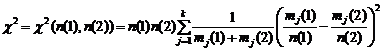Известно, что при росте объемов выборок n(1) и n(2) распределение статистики стремится к распределению хи-квадрат с (k - 1) степенями свободы. Поэтому при больших n(1) и n(2) правило принятия решений при проверке гипотезы однородности таково: если рассчитанное по эмпирическим данным значение статистики хи-квадрат таково, что

,

то гипотезу однородности принимают на заданном уровне значимости; если же

,

то гипотезу однородности отклоняют (и принимают альтернативную гипотезу). Здесь, как и ранее, - это квантиль порядка (1 - ) распределения хи-квадрат с (k-1) степенью свободы.

Замечание. Более точно, в случае можно констатировать, что обнаружено различие распределений (как говорят, доказано наличие эффекта (на данном уровне значимости), в том время как в случае можно сказать лишь, что эффект не обнаружен (нет оснований отвергнуть предположение о совпадении распределений).

Расчет по данным табл.1 дает, что

.

Таким образом, на любом из практически используемых уровней значимости констатируем однородность распределений. Наблюдаемое значение статистики (т.е. 14,22) попадает в среднюю часть распределения – при справедливости нулевой гипотезы значение статистики в 78% случаев меньше наблюдаемого и в 22% случаев больше наблюдаемого. Итак, не обнаружено никакой связи между специальностью ученого и знаком Зодиака, под которым он рожден.

3.5.3. Проверка однородности характеристик для количественных признаков

Перейдем к следующему элементу системы моделей, описанной в начале настоящего раздела – к моделям, нацеленным на проверку равенства характеристик двух распределений, из которых взяты две независимые выборки. Исходим из общепринятой базовой модели, в которой элементы первой выборки x₁, x₂, ..., x_m рассматриваются как результаты m независимых наблюдений некоторой числовой случайной величины Х с функцией распределения F(x), неизвестной статистику, а элементы второй выборки y₁, y₂, ..., y_n - как результаты п независимых наблюдений, вообще говоря, другой случайной величины Y с функцией распределения G(x), также неизвестной статистику. Предполагается также, что наблюдения в одной выборке не зависят от наблюдений в другой, поэтому выборки и называют независимыми.

Замечание. Обратите внимание, что объемы выборок обозначены здесь не так, как в предыдущем разделе. Это сделано специально, а именно, для того, чтобы у читателя не создавался ложный стереотип, мешающий воспринимать многообразие литературных источников с соответствующим многообразием обозначений.

Традиционный метод проверки однородности (критерий Стьюдента). Для дальнейшего критического разбора опишем традиционный статистический метод проверки однородности. Он широко использовался в течение всего ХХ в. Хотя к настоящему времени этот метод устарел (см. ниже), но продолжает встречаться в учебной литературе, и потому и применяться для анализа конкретных данных.

При использовании традиционного метода проверки однородности вычисляют выборочные средние арифметические в каждой выборке

,

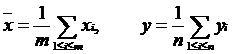затем выборочные дисперсии

,

и статистику Стьюдента t, на основе которой принимают решение,

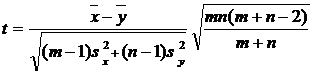. (1)

По заданному уровню значимости a и числу степеней свободы (m+n ^_ 2) из таблиц распределения Стьюдента (см., например, [2]) находят критическое значение t_кр. Если |t|>t_кр, то гипотезу однородности (отсутствия различия) отклоняют, если же |t|<t_кр, то принимают. (При односторонних альтернативных гипотезах вместо условия |t|>t_кр проверяют, что t>t_кр; эту постановку рассматривать не будем, так как в ней нет принципиальных отличий от обсуждаемой здесь.)

В литературе зачастую описывается только приведенный выше алгоритм. Этого недостаточно для квалифицированного анализа статистических данных. Рассмотрим условия применимости традиционного метода проверки однородности, основанного на использовании статистики t Стьюдента, а также обсудим современные методы проверки однородности двух выборок.

Классические условия применимости критерия Стьюдента. Согласно математико-статистической теории должны быть выполнены два классических условия применимости критерия Стьюдента, основанного на использовании статистики t, заданной формулой (1):

а) результаты наблюдений имеют нормальные распределения:

F(x)=N(x; m₁, s₁²), G(x)=N(x; m₂, s₂²)

с математическими ожиданиями m₁ и m₂ и дисперсиями s₁² и s₂² в первой и во второй выборках соответственно;

б) дисперсии результатов наблюдений в первой и второй выборках совпадают:

D(X)=s₁²=D(Y)=s₂².

Если условия а) и б) выполнены, то нормальные распределения F(x) и G(x) отличаются только математическими ожиданиями, а поэтому обе гипотезы H₀ и H'₀ (см. подраздел 3.5.1) сводятся к гипотезе

H"₀ : m₁ = m₂,

а обе альтернативные гипотезы H₁ и H'₁ сводятся к гипотезе

H"₁ : m₁ ¹ m₂ .

Если условия а) и б) выполнены, то статистика t при справедливости H"₀ имеет распределение Стьюдента с (т + п – 2) степенями свободы. Только в этом случае описанный выше традиционный метод обоснован безупречно. Если хотя бы одно из условий а) и б) не выполнено, то нет никаких оснований считать, что статистика t имеет распределение Стьюдента, поэтому применение традиционного метода, строго говоря, не обосновано. Обсудим возможность проверки этих условий и последствия их нарушений.

Имеют ли результаты наблюдений нормальное распределение? Как подробно показано в литературе (см. раздел 3.3 выше, а также, например, [21, гл.5.1], [20, гл.4.1]), априори нет оснований предполагать нормальность распределения результатов экономических, технико-экономических, технических, медицинских и иных наблюдений. Следовательно, нормальность надо проверять. Разработано много статистических критериев для проверки нормальности распределения результатов наблюдений [2]. Однако проверка нормальности - более сложная и трудоемкая статистическая процедура, чем проверка однородности (как с помощью статистики t Стьюдента, так и с использованием непараметрических критериев, рассматриваемых ниже).

Для достаточно надежного установления нормальности требуется весьма большое число наблюдений. В указанных выше литературных источниках показано, что для того, чтобы гарантировать, что функция распределения результатов наблюдений отличается от некоторой нормальной не более чем на 0,01 (при любом значении аргумента), требуется порядка 2500 наблюдений. В большинстве технических, экономических, медицинских и иных исследований число наблюдений существенно меньше.

Как отмечалось в литературе, есть и еще одна общая причина отклонений от нормальности: любой результат наблюдения записывается конечным (обычно 2–5) количеством цифр, а с математической точки зрения вероятность такого события равна 0. Точнее, для случайной величины с непрерывной плотностью распределения вероятность попадания в счетное множество рациональных чисел равна 0. Следовательно, при статистической обработке данных в организационно-экономических исследованиях распределение результатов наблюдений практически всегда более или менее отличается от нормального распределения.

Последствия нарушения условия нормальности. Если условие а) не выполнено, то распределение статистики t не является распределением Стьюдента. Однако можно показать, используя Центральную предельную теорему теории вероятностей и теоремы о наследовании сходимости [21, гл.4], что при справедливости H'₀ и условия б) распределение статистики t при росте объемов выборок приближается к стандартному нормальному распределению Ф(х) = N(x; 0, 1). К этому же распределению приближается распределение Стьюдента при возрастании числа степеней свободы. Другими словами, несмотря на нарушение условия нормальности традиционный метод (критерий Стьюдента) можно использовать (при определенных условиях!) для проверки гипотезы H'₀ при больших объемах выборок. При этом вместо таблиц распределения Стьюдента достаточно пользоваться таблицами стандартного нормального распределения Ф(х).

Сформулированное в предыдущем абзаце утверждение справедливо для любых функций распределения F(x) и G(x) таких, что M(X) = M(Y), D(X) = D(Y) и выполнены некоторые внутриматематические условия, обычно считающиеся справедливыми в реальных задачах. Если же M(X) ¹ M(Y), то нетрудно вычислить, что при больших объемах выборок

P(t<x)»Ф(x-a_mn), (2)

где

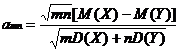. (3)

Формулы (2) - (3) позволяют приближенно вычислять мощность t-критерия (точность возрастает при увеличении объемов выборок т и п).

О проверке условия равенства дисперсий. Иногда условие б) вытекает из методики получения результатов наблюдений, например, когда с помощью одного и того же прибора или методики m раз измеряют характеристику первого объекта и п раз - второго, а параметры распределения погрешностей измерения при этом не меняются. Однако ясно, что в постановках большинства исследовательских и практических задач нет основании априори предполагать равенство дисперсий.

Целесообразно ли проверять равенство дисперсий статистическими методами, например, как это иногда предлагают, с помощью F-критерия Фишера? Этот критерий основан на нормальности распределений результатов наблюдений. А от нормальности неизбежны отклонения (см. выше). Причем хорошо известно, что в отличие от t-критерия распределение F-критерия Фишера сильно меняется при малых отклонениях от нормальности [3]. Кроме того, F-критерий отвергает гипотезу D(X) = D(Y) лишь при большом различии выборочных дисперсий. Так, для данных [2] о двух группах результатов химических анализов отношение выборочных дисперсий равно 1,95, т.е. существенно отличается от 1. Тем не менее, гипотеза о равенстве теоретических дисперсий принимается при применении F-критерия на 1%-м уровне значимости. Следовательно, при проверке однородности применение F-критерия для предварительной проверки равенства дисперсий с целью обоснования возможности использования критерия Стьюдента нецелесообразно.

Итак, в большинстве технических, экономических, медицинских и иных задач условие б) нельзя считать выполненным, а проверять его перед проверкой однородности нецелесообразно.

Последствия нарушения условия равенства дисперсий. Если объемы выборок т и п велики, то можно показать, что распределение статистики t описывается с помощью только математических ожиданий M(Х) и M(Y), дисперсий D(X), D(Y) и отношения объемов выборок, а именно:

P(t<x)»Ф(b_mnx-a_mn), (4)

где a_mn определено формулой (3),

. (5)

Если b_mn ¹ 1, то распределение статистики t отличается от распределения, заданного формулой (2), полученной в предположении равенства дисперсий. Когда b_mn=1? В двух случаях – при m = n и при D(X) = D(Y). Таким образом, при больших и равных объемах выборок требовать выполнения условия б) нет необходимости. Кроме того, ясно, что если объемы выборок мало различаются, то b_mn близко к 1. Так, для данных [2] о двух группах результатов химических анализов имеем b*_mn= 0,987, где b*_mn - оценка b_mn , полученная заменой в формуле (5) теоретических дисперсий на их выборочные оценки.

Область применимости традиционного метода проверки однородности с помощью критерия Стьюдента. Подведем итоги рассмотрения t-критерия. Он позволяет проверять гипотезу H'₀ о равенстве математических ожиданий, но не гипотезу H₀ о том, что обе выборки взяты из одной и той же генеральной совокупности. Классические условия применимости критерия Стьюдента в подавляющем большинстве технических, экономических, медицинских и иных задач не выполнены. Тем не менее, при больших и примерно равных объемах выборок его можно применять. При конечных объемах выборок традиционный метод носит неустранимо приближенный характер.

Критерий Крамера-Уэлча равенства математических ожиданий. Вместо критерия Стьюдента целесообразно для проверки H'₀ использовать критерий Крамера-Уэлча [12, с.492], основанный на статистике

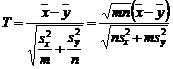. (6)

Критерий Крамера-Уэлча имеет прозрачный смысл – разность выборочных средних арифметических для двух выборок делится на естественную оценку среднего квадратического отклонения этой разности. Естественность указанной оценки состоит в том, что неизвестные статистику дисперсии заменены их выборочными оценками. Из многомерной центральной предельной теоремы и из теорем о наследовании сходимости [21, гл.4] вытекает, что при росте объемов выборок распределение статистики Т Крамера-Уэлча сходится к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1. Итак, при справедливости H'₀ и больших объемах выборок распределение статистики Т приближается с помощью стандартного нормального распределения Ф(х), из таблиц которого и следует брать критические значения.

При т = п, как следует из формул (1) и (6), t = T. При т ¹ п этого равенства нет. В частности, при в формуле (1) стоит множитель (m - 1), в формуле (6) - множитель п.

Если M(X) ¹ M(Y), то при больших объемах выборок

P(T<X)»Ф(x-c_mn), (7)

где

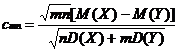. (8)

При т = п или D(X) = D(Y), согласно формулам (3) и (8), a_mn = c_mn , в остальных случаях равенства нет.

Из асимптотической нормальности статистики Т, формул (7) и (8) следует, что правило принятия решения для критерия Крамера-Уэлча выглядит так:

- если |T| < , то гипотеза однородности (равенства) математических ожиданий принимается на уровне значимости

- если же |T| > , то гипотеза однородности (равенства) математических ожиданий отклоняется на уровне значимости .

В прикладной статистике наиболее часто применяется уровень значимости Тогда значение модуля статистики Т Крамера-Уэлча надо сравнивать с граничным значением = 1,96.

Из сказанного выше следует, что применение критерия Крамера-Уэлча при анализе организационно-экономических данных более обосновано, чем применение критерия Стьюдента. Дополнительное преимущество критерия Крамера-Уэлча по сравнению с критерием Стьюдента - не требуется равенства дисперсий D(X) = D(Y). Распределение статистики Т не является распределением Стьюдента, однако и распределение статистики t, как показано выше, не является таковым в реальных ситуациях.

Распределение статистики Т при объемах выборок т = п = 6, 8, 10, 12 и различных функциях распределений выборок F(x) и G(x) изучено нами совместно с Ю.Э. Камнем и Я.Э. Камнем методом статистических испытаний (Монте-Карло). Рассмотрены различные варианты функций распределения F(x) и G(x). Результаты (частично опубликованы в статье [8]) показывают, что даже при таких небольших объемах выборок точность аппроксимации предельным стандартным нормальным распределением вполне удовлетворительна. Поэтому представляется целесообразным во всех тех случаях, когда в соответствии с устаревшими литературными источниками рекомендуют применять критерий Стьюдента, заменить его на критерий Крамера-Уэлча. Конечно, такая замена потребует переделки ряда нормативно-технических и методических документов, исправления учебников и учебных пособий для вузов.

Пример 1. Пусть объем первой выборки Для второй выборки Вычислим величину статистики Крамера-Уэлча

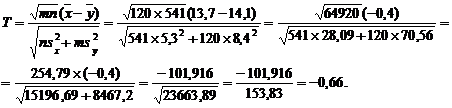
Поскольку полученное значение по абсолютной величине меньше 1,96, то гипотеза однородности математических ожиданий принимается на уровне значимости 0,05.

Непараметрические методы проверки однородности. В большинстве управленческих, технических, экономических, медицинских и иных задач представляет интерес не проверка равенства математических ожиданий или иных характеристик распределения, а обнаружение различия генеральных совокупностей, из которых извлечены выборки, т.е. проверка гипотезы H₀. Методы проверки гипотезы H₀ позволяют обнаружить не только изменение математического ожидания, но и любые иные изменения функции распределения результатов наблюдений при переходе от одной выборки к другой (увеличение разброса, появление асимметрии и т. д.). Как установлено выше, методы, основанные на использовании статистик t Стьюдента и Т Крамера-Уэлча, не позволяют проверять гипотезу H₀. Априорное предположение о принадлежности функций распределения F(x) и G(x) к какому-либо определенному параметрическому семейству (например, семействам нормальных, логарифмически нормальных, распределений Вейбулла - Гнеденко, гамма-распределений и др.), как также показано выше, обычно нельзя достаточно надежно обосновать. Поэтому для проверки H₀ следует использовать методы, пригодные при любом виде F(x) и G(x), т.е. непараметрические методы. (Напомним, что термин «непараметрический метод» означает, что при использовании этого метода нет необходимости предполагать, что функции распределения результатов наблюдений принадлежат какому-либо определенному параметрическому семейству.)

Для проверки гипотезы H₀ разработано много непараметрических методов - критерии Смирнова, типа омега-квадрат (Лемана - Розенблатта), Вилкоксона (Манна-Уитни), Ван-дер-Вардена, Сэвиджа, хи-квадрат и др. [5, 21, 24]. Распределения статистик всех этих критериев при справедливости H₀ не зависят от конкретного вида совпадающих функций распределения F(x) º G(x). Следовательно, таблицами точных и предельных (при больших объемах выборок) распределений статистик этих критериев и их процентных точек [21, 24] можно пользоваться при любых непрерывных функциях распределения результатов наблюдений.

Какой из непараметрических критериев применять? Как известно [3], для выбора одного из нескольких критериев необходимо сравнить их мощности, определяемые видом альтернативных гипотез. Сравнению мощностей критериев посвящена обширная литература.

Хорошо изучены свойства критериев при альтернативной гипотезе сдвига

H_1c : G(x) = F(x-d), d ¹ 0.

Критерии Вилкоксона, Ван-дер-Вардена и ряд других ориентированы для применения именно в этой ситуации. Если m раз измеряют характеристику одного объекта и п раз - другого, а функция распределения погрешностей измерения произвольна, но не меняется при переходе от объекта к объекту (это более жесткое требование, чем условие равенства дисперсий), то рассмотрение гипотезы H_1c оправдано. Однако в большинстве организационно-экономических, технических, медицинских и иных исследований нет оснований считать, что функции распределения, соответствующие выборкам, различаются только сдвигом.

3.5.4. Двухвыборочный критерий Вилкоксона

Рассмотрим подробнее часто используемый непараметрический критерий Вилкоксона. В частности, покажем (и это - основной теоретический результат настоящего подраздела), что двухвыборочный критерий Вилкоксона (в литературе его называют также критерием Манна-Уитни) предназначен для проверки гипотезы

H₀: P(X < Y) = 1/2,

где X - случайная величина, распределенная как элементы первой выборки, а Y - случайная величина, распределенная как элементы второй выборки. Это – непараметрическая гипотеза. Но из нее не следует, что функции распределения двух выборок совпадают. Обратное, конечно, верно: если X и Y одинаково распределены, то P(X < Y) = ½.

В описанной выше вероятностной модели двух независимых выборок без ограничения общности можно считать, что объем первой из них не превосходит объема второй, m < n, в противном случае выборки можно поменять местами. Обычно предполагается, что функции F(x) и G(x) непрерывны и строго возрастают. Из непрерывности этих функций следует, что с вероятностью 1 все m + n результатов наблюдений различны. При рассмотрении реальных статистических данных иногда наблюдаются совпадения результатов наблюдений, но сам факт их наличия - свидетельство нарушений предпосылок только что описанной базовой математической модели.

Расчет значения статистики критерия Вилкоксона и правило принятия решений. Статистика S двухвыборочного критерия Вилкоксона определяется следующим образом. Все элементы объединенной выборки X₁, X₂, ..., X_m, Y₁, Y₂, ..., Y_n упорядочиваются в порядке возрастания. Элементы первой выборки X₁, X₂, ..., X_m занимают в общем вариационном ряду места с номерами R₁, R₂, ..., R_m, другими словами, имеют ранги R₁, R₂, ..., R_m (напомним, что ранг – это номер в упорядоченном ряду). Тогда статистика Вилкоксона - это сумма рангов элементов первой выборки

S = R₁ + R₂ + ...+ R_m.

Статистика U Манна-Уитни определяется как число пар (X_i, Y_j) таких, что X_i < Y_j, среди всех mn пар, в которых первый элемент - из первой выборки, а второй - из второй. Как известно [5, с.160],

U = mn + m(m+1)/2 – S.

_{Поскольку} S и U линейно связаны, то обычно говорят не о двух критериях - Вилкоксона и Манна-Уитни, а об одном - критерии Вилкоксона (Манна-Уитни).

Критерий Вилкоксона - один из самых известных инструментов непараметрической статистики (наряду с критериями на основе статистик типа Колмогорова-Смирнова, омега-квадрат и коэффициентами ранговой корреляции). Свойствам этого критерия и таблицам его критических значений уделяется место во многих монографиях по математической и прикладной статистике (см., например, [2, 5, 21, 24]).

Однако в литературе имеются и неточные утверждения относительно возможностей критерия Вилкоксона. Так, отдельные авторы полагают, что с его помощью можно обнаружить любое различие между функциями распределения F(x) и G(x). По мнению других, этот критерий нацелен на проверку равенства медиан распределений, соответствующих выборкам. И то, и другое неверно. Это будет ясно из дальнейшего изложения.

Введем некоторые обозначения. Пусть F^-1(t) - функция, обратная к функции распределения F(x). Она определена на отрезке [0; 1]. Положим L(t) = G(F^-1(t)). Поскольку F(x) непрерывна и строго возрастает, то F^-1(t) и L(t) обладают теми же свойствами. Важную роль в дальнейшем изложении будет играть величина a = P(X < Y). Как нетрудно показать,

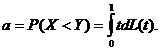
Введем также параметры

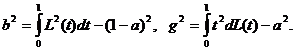
Тогда математические ожидания и дисперсии статистик Вилкоксона и Манна-Уитни согласно [5, с.160] выражаются через введенные величины:

М(U) = mna , М(S) = mn + m(m+1)/2 - М(U) = mn(1 - a) + m(m+1)/2,

D(S) = D(U) = mn [(n - 1) b² + (m - 1) g² + a(1 -a)]. (9)

Когда объемы обеих выборок безгранично растут, распределения статистик Вилкоксона и Манна-Уитни являются асимптотически нормальными (см., например, [5, гл. 5 и 6]) с параметрами, задаваемыми формулами (9).

Если выборки полностью однородны, т.е. их функции распределения совпадают, другими словами, справедлива гипотеза

H₀: F(x) = G(x) при всех x, (10)

то L(t) = t для t из отрезка [0, 1], L(t)= 0 для всех отрицательных t и L(t)= 1 для t > 1, соответственно a= 1/2. Подставляя в формулы (9), получаем, что

М(S) = m(m+n+1)/2, D(S) = mn(m+n+1)/12. (11).

Следовательно, распределение нормированной и центрированной статистики Вилкоксона

T = (S - m(m+n+1)/2) (mn(m+n+1)/12)^-1/2 (12)

при росте объемов выборок приближается к стандартному нормальному распределению (с математическим ожиданием 0 и дисперсией 1).

Из асимптотической нормальности статистики Т следует, что при больших объемах выборок правило принятия решения для критерия Вилкоксона выглядит так:

- если |T| < , то гипотеза (2.10) однородности (тождества) функций распределений принимается на уровне значимости

- если же |T| > , то гипотеза (2.10) однородности (тождества) функций распределений отклоняется на уровне значимости .

В прикладной статистике наиболее часто применяется уровень значимости Тогда значение модуля статистики Т Вилкоксона надо сравнивать с граничным значением=1,96.

Пример 1. Пусть даны две выборки. Первая содержит m = 12 элементов 17; 22; 3; 5; 15; 2; 0; 7; 13; 97; 66; 14. Вторая содержит n = 14 элементов 47; 30; 2; 15; 1; 21; 25; 7; 44; 29; 33; 11; 6; 15. Проведем проверку однородности функций распределения двух выборок с помощью критерия Вилкоксона.

Первым шагом является построение общего вариационного ряда для элементов двух выборок (табл.2). Общий вариационный ряд – в средней строке. Ниже для каждого его элемента указано, из какой выборки он взят. Построение верхней строки «Ранги» описано далее.

Хотя с точки зрения теории математической статистики вероятность совпадения двух элементов выборок равна 0, в реальных выборках статистических данных совпадения встречаются. Так, в рассматриваемых выборках, как видно из табл.2, два раза повторяется величина 2, два раза - величина 7 и три раза - величина 15. В таких случаях говорят о наличии «связанных рангов», а соответствующим совпадающим величинам приписывают среднее арифметическое тех рангов, которые они занимают (т.е среднее арифметическое номеров тех мест, которые они занимают в общем вариационном ряду). Так, величины 2 (из первой выборки) и 2 (из второй выборки) занимают в объединенном вариационном ряду места 3 и 4, поэтому им приписывается ранг (3+4)/2=3,5. Величины 7 и 7 занимают в объединенном вариационном ряду места 8 и 9, поэтому им приписывается ранг (8+9)/2=8,5. Величины 15, 15 и 15 занимают в объединенном вариационном ряду места 13, 14 и 15, поэтому им приписывается ранг (13+14+15)/3=14.

Таблица 2. – Общий вариационный ряд для элементов двух выборок

Ранги	1	2	3,5	3,5	5	6	7	8,5	8,5	10	11	12	14
Элементы выборок	0	1	2	2	3	5	6	7	7	11	13	14	15
Номера выборок	1	2	1	2	1	1	2	1	2	2	1	1	1
Ранги	14	14	16	17	18	19	20	21	22	23	24	25	26
Элементы выборок	15	15	17	21	22	25	29	30	33	44	47	66	97
Номера выборок	2	2	1	2	1	2	2	2	2	2	2	1	1

Таким образом, после построения объединенного вариационного ряда выделяют группы «связанных рангов» и проводят описанные выше расчеты. В итоге получают строку «Ранги».

Следующий шаг - подсчет значения статистики Вилкоксона, т.е. суммы рангов элементов первой выборки

S = R₁ + R₂ + ...+ R_{m =} 1+3,5+5+6+8,5+11+12+14+16+18+25+26=146.

Подсчитаем также сумму рангов элементов второй выборки

S₁ = 2+3,5+7+8,5+10+14+14+17+19+20+21+22+23+24= 205.

Величина S₁ может быть использована для контроля вычислений. Дело в том, что суммы рангов элементов первой выборки S и второй выборки S₁ вместе составляют сумму рангов объединенной выборки, т.е. сумму всех натуральных чисел от 1 до m+n. Следовательно,

S+ S₁ = (m+n)(m+n+1)/2= (12+14)(12+14+1)/2= 351.

В соответствии с ранее проведенными расчетами S+S₁ = 146 + 205 = 351. Необходимое условие правильности расчетов выполнено. Ясно, что справедливость этого условия не гарантирует правильности расчетов.

Перейдем к расчету статистики Т. Согласно формуле (11)

М(S) = 12(12+14+1)/ 2 = 162, D(S) = 12^.14(12+14+1)/ 12= 378 .

Следовательно,

T = (S – 162) (378)^-1/2 = (146–162) / 19,44 = - 0,82.

Поскольку |T |< 1,96, то гипотеза однородности принимается на уровне значимости 0,05.

Что будет, если поменять выборки местами, вторую назвать первой? Тогда вместо S надо рассматривать S₁ . Имеем

М(S₁) = 14(12+14+1)/2 = 189, D(S) = D(S₁) = 378,

T₁ = (S₁ – 189) (378)^-1/2 = (205–189) / 19,44 = 0,82.

Таким образом, значения статистики критерия отличаются только знаком (можно показать, что это утверждение верно всегда). Поскольку в правиле принятия решения используется только абсолютная величина статистики, то принимаемое решение не зависит от того, какую выборку считаем первой, а какую второй. Для уменьшения объема таблиц критических значений принято считать первой выборку меньшего объема.

Мощность критерия Вилкоксона. Продолжим обсуждение критерия Вилкоксона. Правила принятия решений и таблицы критических значений для критерия Вилкоксона строятся в предположении справедливости гипотезы полной однородности, описываемой формулой (10). А что будет, если эта гипотеза неверна? Другими словами, какова мощность критерия Вилкоксона?

Пусть объемы выборок достаточно велики, так что можно пользоваться асимптотической нормальностью статистики Вилкоксона. Тогда в соответствии с формулами (9) статистика T будет асимптотически нормальна с параметрами

М(T) = (12mn)^1/2 (1/2 - a) (m+n+1)^-1/2 ,

D(T) = 12 [(n - 1) b² + (m - 1) g² + a(1 - a)] (m+n+1)^-1. (13)

Из формул (13) видно большое значение гипотезы

H₀₁: a = P(X < Y) = 1/2. (14)

Если эта гипотеза неверна, то, поскольку m < n, справедлива оценка

|M(T)| > (12 m n (2n+1)^-1)^1/2 |1/2 - a|,

а потому |M(T)| безгранично растет при росте объемов выборок. В то же время, поскольку

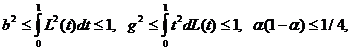
то

D(T) < 12 [(n - 1) + (m - 1) + 1/4] (m+n+1)^-1 < 12. (15)

Следовательно, вероятность отклонения гипотезы H₀₁, когда она неверна, т.е. мощность критерия Вилкоксона как критерия проверки гипотезы (14), стремится к 1 при возрастании объемов выборок, т.е. критерий Вилкоксона является состоятельным для этой гипотезы при альтернативе

АH₀₁ : a = P(X < Y) 1/2. (16) .

Если же гипотеза (14) верна, то статистика T асимптотически нормальна с математическим ожиданием 0 и дисперсией, определяемой формулой

D(T) = 12[(n - 1)b² + (m - 1)g² + 1/4](m+n+1)^-1. (17)

Гипотеза (14) является сложной, дисперсия (17), как показывают приводимые ниже примеры, в зависимости от значений b² и g² может быть как больше 1, так и меньше 1, но согласно неравенству (15) никогда не превосходит 12.

Критерий Вилкоксона не позволяет проверять абсолютную однородность. Приведем пример двух функций распределения F(x) и G(x) таких, что гипотеза (14) выполнена, а гипотеза (10) - нет. Поскольку

a = P(X < Y) = , 1 - a = P(Y < X) = (18)

и a = 1/2 в случае справедливости гипотезы (10), то для выполнения условия (14) необходимо и достаточно, чтобы

, (19) ,

а потому естественно в качестве F(x) рассмотреть функцию равномерного распределения на интервале (-1; 1). Тогда формула (19) переходит в условие

Это условие выполняется, если функция (G(x) – (x + 1)/2) является нечетной.

Пример 2. Пусть функции распределения F(x) и G(x) сосредоточены на интервале (-1; 1), на котором

F(x) = (x + 1)/2, G(x) = (x + 1 + 1/ sinx)/2.

Тогда

x=F^-1(t)=2t-1, L(t)=G(F^-1(t))=(2t+1/sin(2t-1))/2=t+1/2sin(2t-1).

Условие (19) выполнено, поскольку функция (G(x) - (x + 1)/2) является нечетной. Следовательно, a = 1/2. Начнем с вычисления

g² = 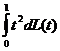- 1/4 =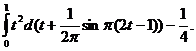

Поскольку

то

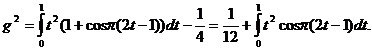
С помощью замены переменных t = (x +1) / 2 получаем, что

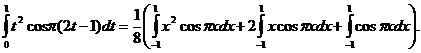
В правой части последнего равенства стоят табличные интегралы (см., например, справочник [23, с.71]). Проведя соответствующие вычисления, получаем, что в правой части стоит 1/8×(-4/²)= -1/(2²). Следовательно,

g² = 1/12 - 1/(2²) = 0,032672733...

Перейдем к вычислению b². Поскольку

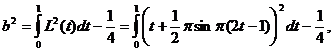
то

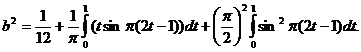
С помощью замены переменных t = (x+1)/2 переходим к табличным интегралам (см., например, справочник [23, с.65]):

Проведя необходимые вычисления, получим, что

Следовательно, для рассматриваемых функций распределения нормированная и центрированная статистика Вилкоксона (см. формулу (12)) асимптотически нормальна с математическим ожиданием 0 и дисперсией (см. формулу (17))

D(T) = (0,544 n + 0,392 m + 2,064) (m+n+1)^-1.

Как легко видеть, дисперсия всегда меньше 1. Это значит, что в рассматриваемом случае гипотеза полной однородности (10) при проверке с помощью критерия Вилкоксона будет приниматься чаще, чем если она на самом деле верна.

Сказанное означает, что критерий Вилкоксона нельзя считать критерием для проверки гипотезы (10) при альтернативе общего вида. Он не всегда позволяет проверить однородность - не при всех альтернативах. Точно так же критерии типа хи-квадрат нельзя считать критериями проверки гипотез согласия и однородности в случае непрерывных распределений - они позволяют обнаружить не все различия, поскольку некоторые из них «скрадывает» группировка.

Критерий Вилкоксона не позволяет проверять равенство медиан. Обсудим теперь, действительно ли критерий Вилкоксона нацелен на проверку равенства медиан распределений, соответствующих выборкам.

Пример 3. Построим семейство пар функций распределения F(x) и G(x) таких, что их медианы различны, но для F(x) и G(x) выполнена гипотеза (14). Пусть распределения сосредоточены на интервале (0; 1), и на нем G(x) = x , а F(x) имеет кусочно-линейный график с вершинами в точках (0; 0), (, 1/2), (, 3/4), (1; 1). Следовательно,

F(x) = 0 при x < 0;

F(x) = x/(2) на [0; );

F(x) = 1/2 + (x - )/(4 - 4) на [; );

F(x) = 3/4 + (x - )/(4 - 4) на [; 1];

F(x) = 1 при x > 1.

Очевидно, что медиана F(x) равна , а медиана G(x) равна 1/2 .

Согласно соотношению (17) для выполнения гипотезы (14) достаточно определить как функцию , т.е. = (), из условия

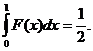
Вычисления дают

= () = 3(1 - )/2.

Учитывая, что лежит между и 1, не совпадая ни с тем, ни с другим, получаем ограничения на , а именно, 1/3 < < 3/5 . Итак, построено искомое семейство пар функций распределения.

Пример 4. Пусть, как и в примере 3, распределения сосредоточены на интервале (0; 1), и на нем F(x)=x. А G(x) - функция распределения, сосредоточенного в двух точках - и 1. Т.е. G(x) = 0 при x, не превосходящем ; G(x) = h на (; 1]; G(x) = 1 при x > 1. С такой функцией G(x) легко проводить расчеты. Однако она не удовлетворяет принятым выше условиям непрерывности и строгого возрастания. Вместе с тем легко видеть, что она является предельной (сходимость в каждой точке отрезка [0; 1]) для последовательности функций распределения, удовлетворяющих этим условиям. А распределение статистики Вилкоксона для пары функций распределения примера 4 является предельным для последовательности соответствующих распределений статистики Вилкоксона, полученных в рассматриваемых условиях непрерывности и строгого возрастания.

Условие P(X < Y) = 1/2 выполнено, если h = (1 - )^-1/2 (при из отрезка [0; 1/2]). Поскольку h > 1/2 при положительном , то очевидно, что медиана G(x) равна , в то время как медиана F(x) равна 1/2 . Значит, при = 1/2 медианы совпадают, при всех иных положительных - различны. При = 0 медианой G(x) является любая точка из отрезка [0; 1].

Легко подсчитать, что в условиях примера 4 параметры предельного распределения имеют вид

b² = (1- )^-1/4 , g² = (1- 2)/4.

Следовательно, распределение нормированной и центрированной статистики Вилкоксона будет асимптотически нормальным с математическим ожиданием 0 и дисперсией

D(T) = 3 [(n-1) (1- )^-1 + (m-1) (1-2) + 1] (m+n+1)^-1.

Проанализируем величину D(T) в зависимости от параметра и объемов выборок m и n. При достаточно больших m и n

D(T) = 3w(1 - )^-1 + 3(1 - w)(1 - 2)

с точностью до величин порядка (m+n)^-1, где w= n/(m+n). Значит, D(T) - линейная функция от w, а потому достигает экстремальных значений на границах интервала изменения w, т.е. при w = 0 и w = 1. Легко видеть, что при (1-)^-1 <1-2 минимум равен 3(1-)^-1 (при w = 1), а максимум равен 3(1 - 2) (при w = 0). В случае (1-)^-1 >1-2 максимум равен 3(1-)^-1 (при w = 1), а минимум равен 3(1 - 2) (при w = 0). Если же (1-)^-1 =1-2 (это равенство справедливо при =₀ = 1 - 2^-1/2 = 0,293), то D(T)=3(2^1/2-1)=1,2426... при всех w из отрезка [0; 1].

Первый из описанных выше случаев имеет быть при < ₀. При этом минимум D(T) возрастает от 0 (при =0, w=1 - предельный случай) до 3(2^1/2 - 1) (при =₀, w - любом), а максимум уменьшается от 3 (при =0, w=0 - предельный случай) до 3 (2^1/2 - 1) (при =₀, w - любом). Второй случай относится к из интервала (₀; 1/2]. При этом минимум убывает от приведенного выше значения для =₀ до 0 (при =1/2, w=0 - предельный случай) , а максимум возрастает от того же значения при =₀ до 3 (при =1/2 , w=0).

Таким образом, D(T) может принимать все значения из интервала (0; 3) в зависимости от значений и w. Если D(T) < 1, то при применении критерия Вилкоксона к выборкам с рассматриваемыми функциями распределения гипотеза однородности (10) будет приниматься чаще (при соответствующих значениях и w - с вероятностью, сколь угодно близкой к 1), чем если бы она самом деле была верна. Если 1<D(T)<3, то гипотеза (10) также принимается достаточно часто. Так, если уровень значимости критерия Вилкоксона равен 0,05, то (асимптотическая) критическая область этого критерия, как показано выше, имеет вид {T: |T| > 1,96}. Если - самый плохой случай - D(T)= 3, то гипотеза (10) принимается с вероятностью 0,7422.

Гипотеза сдвига. При проверке гипотезы однородности мы рассмотрели различные виды нулевых и альтернативных гипотез - гипотезу (10) и ее отрицание в качестве альтернативы, гипотезу (14) и ее отрицание, гипотезы о равенстве или различии медиан. В теоретических работах по математической статистике часто рассматривают гипотезу сдвига, в которой альтернативой гипотезе (10) является гипотеза

H₁: F(x) = G(x + r) (20)

при всех x и некотором сдвиге r, отличным от 0. Если верна альтернативная гипотеза H₁, то вероятность P(X < Y) отлична от 1/2, а потому при альтернативе (20) критерий Вилкоксона является состоятельным.

В некоторых прикладных постановках гипотеза (20) представляется естественной. Например, если одним и тем же прибором проводятся две серии измерений двух значений некоторой величины (физической, химической и т.п.). При этом функция распределения G(x) описывает погрешности измерения одного значения, а G(x+r) - другого. Вопреки распространенному заблуждению, хорошо известно, что распределение погрешностей измерений, как правило, не является нормальным (см. об этом раздел 3.3, а также [21, гл.5.1], [20, гл.4.1]). Однако при анализе подавляющего большинства конкретных статистических данных, как правило, нет никаких оснований считать, что отсутствие однородности всегда выражается столь однозначным образом, как следует из формулы (20). Поэтому для проверки однородности необходимо использовать статистические критерии, состоятельные против любого отклонения от гипотезы однородности (10), а не только против альтернативы сдвига.

Почему же математики так любят гипотезу сдвига (20)? Да потому, что она дает возможность доказывать глубокие математические результаты, например, об асимптотической оптимальности критериев. К сожалению, с точки зрения организационно-экономического моделирования это напоминает поиск ключей под фонарем, где светло, а не в кустах, где они потеряны.

Отметим еще одно обстоятельство. Часто говорят (в соответствии с классическим подходом математической статистики), что нельзя проверять нулевые гипотезы без рассмотрения альтернативных. Однако при анализе данных, полученных в ходе организационно-экономических, технических, медицинских или иных исследований, зачастую полностью ясна формулировка той гипотезы, которую желательно проверить (например, гипотезы абсолютной (иногда говорят, полной) однородности - см. формулу (10)), в то время как формулировка альтернативной гипотезы не очевидна. То ли это гипотеза о неверности равенства (10) хотя бы для одного значения x, то ли это альтернатива (16), то ли - альтернатива сдвига (20), и т. д. В таких случаях целесообразно «обернуть» постановку задачи - исходя из статистического критерия найти альтернативы, относительно которых он состоятелен. Именно это и проделано в настоящем подразделе для критерия Вилкоксона.

Подведем итоги рассмотрения критерия Вилкоксона.

1. Критерий Вилкоксона (Манна-Уитни) является одним из самых распространенных непараметрических ранговых критериев, используемых для проверки однородности двух выборок. Его значение не меняется при любом монотонном преобразовании шкалы измерения (т.е. он пригоден для статистического анализа данных, измеренных в порядковой шкале).

2. Распределение статистики критерия Вилкоксона определяется функциями распределения F(x) и G(x) и объемами m и n двух выборок. При больших объемах выборок распределение статистики Вилкоксона является асимптотически нормальным с параметрами, выписанными выше (см. формулы (9), (11) и (13)).

3. При альтернативной гипотезе, когда функции распределения выборок F(x) и G(x) не совпадают, распределение статистики Вилкоксона зависит от величины вероятности a = P(X < Y). Если a отличается от 1/2, то мощность критерия Вилкоксона стремится к 1, и он отличает нулевую гипотезу F G от альтернативной. Если же a = 1/2, то это не всегда имеет место. В примере 2 приведены две различные функции распределения выборок F(x) и G(x) такие, что гипотеза однородности F G при проверке с помощью критерия Вилкоксона будет приниматься чаще, чем если бы она на самом деле была верна.

4. Следовательно, в случае общей альтернативы критерий Вилкоксона не является состоятельным, т.е. не всегда позволяет обнаружить различие функций распределения. Однако это не лишает его практической ценности, точно так же, как несостоятельность критериев типа хи-квадрат при проверке согласия, независимости или однородности не мешает отклонять нулевую гипотезу во многих практически важных случаях. Однако принятие нулевой гипотезы с помощью критерия Вилкоксона может означать не совпадение F и G, а всего лишь выполнение равенства a = 1/2.

5. Иногда утверждают, что с помощью критерия Вилкоксона можно проверять равенство медиан функций распределения F и G. Это не так. В примерах 3 и 4 указаны функции распределения F и G с a = 1/2, но с различными медианами. Во многих случаях это различие нельзя обнаружить с помощью критерия Вилкоксона, как это показано при численном анализе асимптотической дисперсии в примере 4.

6. Указанные выше недостатки критерия Вилкоксона исчезают для специального вида альтернативы - т.н. «альтернативы сдвига» H₁: F(x) = G(x + r). В этом частном случае при справедливости альтернативной гипотезы мощность стремится к 1, различие медиан также всегда обнаруживается. Однако альтернатива сдвига не всегда естественна. Ее целесообразно принять, если одним и тем же прибором проводятся две серии измерений двух значений некоторой величины (физической, химической и т.п.). При этом функция распределения G(x) описывает результаты измерений (с погрешностями) одного значения, а F(x) = G(x+r) - другого. Другими словами, меняется лишь измеряемое значение, а собственно распределение погрешностей - одно и то же, присущее используемому средству измерения (и обычно описанное в его техническом паспорте). Однако в большинстве прикладных статистических исследований нет никаких оснований считать, что при альтернативе функция распределения второй выборки лишь сдвигается, но не меняется каким-либо иным образом.

7. При всех своих недостатках критерий Вилкоксона прост в применении и часто позволяет обнаруживать различие групп (поскольку оно часто сводится к отличию a = P(X < Y) от 1/2 ). Приведенные здесь критические замечания не следует понимать как призыв к полному отказу от использования критерия Вилкоксона. Однако для проверки гипотезы однородности в случае альтернативы общего вида можно порекомендовать состоятельные критерии, в частности, рассматриваемые в следующем разделе критерии Смирнова и типа омега-квадрат (Лемана-Розенблатта).

8. В литературе по прикладным статистическим методам соседствуют два стиля изложения. Один из них исходит из формулировок нулевой и альтернативных гипотез (или описания набора гипотез, из которого надо выбрать наиболее адекватную), для проверки которых строятся те или иные критерии. При другом стиле изложения упор делается на алгоритмическое описание критериев для проверки тех или иных гипотез, а об альтернативах даже не упоминается.

Например, в литературе по математической статистике часто говорится, что для проверки нормальности используются критерии асимметрии и эксцесса (они описаны, например, в лучшем справочнике 1960–1980-х годов [2, табл. 4.7]). Однако эти критерии позволяют проверять некоторые соотношения между моментами распределения, но отнюдь не являются состоятельными критериями нормальности (не все отклонения от нормальности обнаруживают). Впрочем, для прикладной статистики эти критерии большого практического значения не имеют, поскольку заранее известно, что распределения конкретных технических, экономических, медицинских и иных статистических данных скорее всего отличны от нормальных.

Так что недостатки критерия Вилкоксона не является исключением, мощность ряда иных популярных в математической статистике критериев заслуживает тщательного изучения, при этом заранее можно сказать, что зачастую они не позволяют проверять те гипотезы, с которыми традиционно связаны. При применении подобных критериев к анализу реальных данных необходимо тщательно взвешивать их достоинства и недостатки.

В организационно-экономических исследованиях начинать следует с построения вероятностно-статистической модели, формулировки в ее терминах проверяемых гипотез. Лишь на основе подобной модели можно изучить свойства тех или иных методов и алгоритмов обработки данных. За статистическим критерием всегда стоит вероятностно-статистическая модель порождения данных, определяющая его свойства.

3.5.5. Состоятельные критерии проверки однородности независимых выборок

В соответствии с методологией организационно-экономического моделирования естественно потребовать, чтобы рекомендуемый для массового использования в управленческих, экономических, технических, медицинских и иных исследованиях критерий однородности был состоятельным. Напомним: это значит, что для любых отличных друг от друга функций распределения F(x) и G(x) (другими словами, при справедливости альтернативной гипотезы H₁) вероятность отклонения гипотезы H₀ должна стремиться к 1 при увеличении объемов выборок т и п. Из перечисленных выше (в конце раздела 3.5.3) критериев однородности состоятельными являются только критерии Смирнова и типа омега-квадрат.

Проведенное в Институте высоких статистических технологий и эконометрики исследование мощности (методом статистических испытаний) первых четырех из перечисленных выше критериев (при различных вариантах функций распределения F(x) и G(x)) подтвердило преимущество критериев Смирнова и омега-квадрат и при малых объемах выборок 6–12. Рассмотрим эти критерии подробнее.

Критерий Смирнова однородности двух независимых выборок. Он был предложен членом-корреспондентом АН СССР Н. В. Смирновым в 1939 г. (см. справочник [2]). Единственное ограничение - функции распределения F(x) и G(x) должны быть непрерывными. Напомним, что согласно Л. Н. Большеву и Н. В. Смирнову [2] значение эмпирической функции распределения в точке х равно доле результатов наблюдений в выборке, меньших х. Критерий Смирнова основан на использовании эмпирических функций распределения F_m(x) и G_n(x), построенных по первой и второй выборкам соответственно. Значение статистики Смирнова

сравнивают с соответствующим критическим значением (см., например, [2]) и по результатам сравнения принимают или отклоняют гипотезу Н₀ о совпадении (однородности) функций распределения. Практически значение статистики D_m,п рекомендуется согласно монографии [2] вычислять по формулам

, (21)

, (22)

, (23)

где x'₁<x'₂<…<x'_m - элементы первой выборки x₁, x₂, … , x_m, переставленные в порядке возрастания, а y'₁ < y'₂ < … < y'_n - элементы второй выборки y₁, y₂, … , y_n , также переставленные в порядке возрастания. Поскольку функции распределения F(x) и G(x) предполагаются непрерывными, то вероятность совпадения каких-либо выборочных значений равна 0.

Пример 1. Рассчитаем значение статистики двухвыборочного критерия Смирнова для тех же выборок, для которых в предыдущем разделе было рассчитано значение статистики критерия Вилкоксона. Первая из них содержит m = 12 элементов. Переставим их в порядке возрастания 0 < 2 < 3 < 17 < 5 < 7 < 13 < 14 < 15 < 22 < 66 < 97. Вторая содержит n = 14 элементов. Также переставим их в порядке возрастания 1 < 2 < 6 < 7 < 11 < 15 = 15 < 21 < 25 < 29 < 30 < 33 < 44 < 47. Точнее, в порядке неубывания, поскольку два элемента совпадают. С точки зрения теории вероятность совпадения двух элементов равна 0, но из-за неизбежных округлений эта вероятность положительна. Поскольку совпадений мало (как внутри одной выборки, так и для элементов разных выборок), то использование теории, основанной на нулевой вероятности совпадения элементов выборок, является допустимым.

Расчет значений статистик представлен в табл.3 () и табл.4 ().

Беря максимум по столбцу (6) табл.3, получаем, что . Таков же максимум и по столбцу (9), как и должно быть в соответствии с приведенным выше равенством. Максимум по столбцу (6) табл.4 равен 0,262, в то время как максимум по столбцу (9) той же таблицы есть 0,312. Это различие вызвано тем, что некоторые выборочные значения совпадают, а потому равенство (22), справедливое при отсутствии совпадений, не выполняется. В таких случаях рекомендуют брать максимальное из полученных двумя способами значений, т.е. следует положить . По формуле (23) двухвыборочная статистика Смирнова .

Таблица 3. – Расчет значения статистики

№ п/п	Элементы выборок x	Номера выборок	Fm(x)	r/n	r/n – Fm(x)	Gn(x)		Gn(x)- (s-1)/m
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
1	0	1	0			0	0	0
2	1	2	0,083	0,071	-0,012	0
3	2	1	0,083			0,071	0,083	-0,012
4	2	2	0,083	0,143	0,06	0,071
5	3	1	0,167			0,143	0,167	-0,024
6	5	1	0,25			0,143	0,25	-0,107
7	6	2	0,333	0,214	-0,119	0,143
8	7	1	0,333			0,214	0,333	-0,119
9	7	2	0,333	0,286	-0,047	0,214
10	11	2	0,417	0,357	-0,06	0,286
11	13	1	0,417			0,357	0,417	-0,06
12	14	1	0,5			0,357	0,5
13	15	1	0,583			0,357	0,583	-0,226
14	15	2	0,583	0,429	-0,154	0,357
15	15	2	0,583	0,5	-0,083	0,357
16	17	1	0,667			0,5	0,667	-0,167
17	21	2	0,75	0,571	-0,179	0,5
18	22	1	0,75			0,571	0,75	-0,179
19	25	2	0,833	0,643	-0,19	0,571
20	29	2	0,833	0,714	-0,119	0,643
21	30	2	0,833	0,786	-0,047	0,714
22	33	2	0,833	0,857	0,024	0,786
23	44	2	0,833	0,929	0,096	0,857
24	47	2	0,833	1,0	0,167	0,929
25	66	1	0,833			1,0	0,883	0,167
26	97	1	0,917			1,0	0,883	0,167

В табл.6.5а справочника [2] приведены критические значения для двухвыборочной статистики Смирнова, соответствующие обычно используемым уровням значимости (см. табл.5). Поскольку полученное по статистическим данным значение меньше критического значения для уровня значимости = 0,1, а потому и для всех остальных рассматриваемых уровней значимости, то нет оснований отклонять гипотезу однородности. Как и при использовании критерия Вилкоксона, эффект не обнаружен, нулевую гипотезу абсолютной однородности принимаем.

Разработаны алгоритмы и программы для ЭВМ, позволяющие рассчитывать точные распределения, процентные точки и достигаемый уровень значимости для двухвыборочной статистики Смирнова , рассчитаны подробные таблицы (см., например, методику [14], содержащую описание алгоритмов, тексты программ и подробные таблицы).

Таблица 4. – Расчет значения статистики

№ п/п	Элементы выборок x	Номера выборок	Fm(x)	(r-1)/n	Fm(x) – (r-1)/n	Gn(x)	s/m	s/m – Gn(x)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
1	0	1	0			0	0,083	0,083
2	1	2	0,083	0	0,083	0
3	2	1	0,083			0,071	0,167	0,096
4	2	2	0,083	0,071	0,012	0,071
5	3	1	0,167			0,143	0,25	0,107
6	5	1	0,25			0,143	0,333	0,19
7	6	2	0,333	0,143	0,19	0,143
8	7	1	0,333			0,214	0,417	0,203
9	7	2	0,333	0,214	0,119	0,214
10	11	2	0,417	0,286	0,131	0,286
11	13	1	0,417			0,357	0,5	0,143
12	14	1	0,5			0,357	0,583
13	15	1	0,583			0,357	0,667	0,31
14	15	2	0,583	0,357	0,226	0,357
15	15	2	0,583	0,429	0,154	0,357
16	17	1	0,667			0,5	0,75	0,25
17	21	2	0,75	0,5	0,25	0,5
18	22	1	0,75			0,571	0,883	0,312
19	25	2	0,833	0,571	0,262	0,571
20	29	2	0,833	0,643	0,19	0,643
21	30	2	0,833	0,714	0,119	0,714
22	33	2	0,833	0,786	0,047	0,786
23	44	2	0,833	0,857	-0,024	0,857
24	47	2	0,833	0,929	-0,096	0,929
25	66	1	0,833			1,0	0,917	-0,083
26	97	1	0,917			1,0	0,917	-0,083

Таблица 5. – Критические значения и истинные уровни значимости
для двухвыборочной статистики Смирнова (m = 12, n = 14)

Номинальный уровень значимости	10%	5%	2%	1%
Критическое значение (дробь)	39/84	43/84	47/84	52/84
Критическое значение (десятичное число)	0,464	0,512	0,559	0,619
Истинный уровень значимости	8,7	4,4	2,0	0,8

Однако у критерия Смирнова есть и недостатки. Его распределение сосредоточено в сравнительно небольшом числе точек. Ясно, что принимаемые этой статистикой значения пропорциональны величине 1/L, где L – наименьшее общее кратное объемов выборок m и n. Поэтому функция распределения растет большими скачками. Для рассматриваемого примера L – наименьшее общее кратное 12 и 14, т.е. 84. Следовательно, принимаемые статистикой Смирнова входят в арифметическую прогрессию с шагом 1/84 = 0,012. Именно поэтому критические значения в сборнике [2] приведены в виде дроби с знаменателем L = 84.

Кроме того, не удается выдержать заданный уровень значимости. Реальный (другими словами, истинный) уровень значимости может значительно, даже в несколько раз отличаться от номинального (подробному обсуждению неклассического феномена существенного отличия реального уровня значимости от номинального посвящена работа [8] и раздел 3.5.6 ниже).

При больших объемах выборок можно воспользоваться доказанной Н. В. Смирновым в 1939 г. теоремой: в случае совпадения непрерывных функций распределения элементов двух независимых выборок

,

где K(y) – функция распределения Колмогорова, заданная формулой

.

Поскольку согласно [2] квантиль порядка 0,9 функции распределения Колмогорова равна 1,224, то критическое значение двухвыборочной статистики Смирнова , соответствующее уровню значимости 10%, при больших объемах выборок имеет вид

.

При m=12, n=14 эта формула дает 0,4815, в то время как точное значение равно 0,464 (см. табл.5 выше). Видим, что приближение удовлетворительное, т.е. рассматриваемые объемы выборок (более 10 элементов) можно считать большими. Для построения правил принятия решений на основе значений двухвыборочной статистики Смирнова, соответствующих другим уровням значимости, можно воспользоваться небольшой табл.6 квантилей функции распределения Колмогорова, взятой из справочника [2].

Таблица 6. – Квантили функции распределения Колмогорова

Величина a	0,8	0,9	0,95	0,98	0,99
Квантиль порядка a	1,07275	1,22385	1,35810	1,51743	1,62762

Критерий типа омега-квадрат (Лемана-Розенблатта). Статистика критерия типа омега-квадрат для проверки однородности двух независимых выборок имеет вид:

A = F_m(x) – G_n(x))² dH_m+n(x) ,

где H_m+n(x) – эмпирическая функция распределения, построенная по объединенной выборке. Легко видеть, что

H_m+n(x) = F_m(x) + G_n(x).

Статистика A типа омега-квадрат была предложена Э. Леманом в 1951 г., изучена М. Розенблаттом в 1952 г., а затем и другими исследователями. Она зависит лишь от рангов элементов двух выборок в объединенной выборке. Пусть - первая выборка, - соответствующий вариационный ряд, - вторая выборка, - вариационный ряд, соответствующий второй выборке. Поскольку функции распределения независимых выборок непрерывны, то с вероятностью 1 все выборочные значения различны, совпадения отсутствуют. Статистика А представляется в виде (см., например, [2]):

где r_i - ранг x'_i и s_j - ранг y'_j в общем вариационном ряду, построенном по объединенной выборке.

Правила принятия решений при проверке однородности двух выборок на основе статистик Смирнова и типа омега-квадрат, т.е. таблицы критических значений в зависимости от уровней значимости и объемов значимости приведены, например, в таблицах [2]. При достаточно больших объемах выборок правило принятия решения формулируется просто: если наблюдаемое значение статистики меньше соответствующего квантиля предельного распределения, гипотеза однородности принимается, в противном случае отклоняется.

Расчет значения статистики А типа омега-квадрат (статистики Лемана-Розенблатта) по тем же данным, по которым были найдены значения статистик критериев Вилкоксона и Смирнова, представлен в табл.7. Суммируя значения в столбце (6), получаем, что

.

Аналогично получаем с помощью столбца (9), что

.

Следовательно,

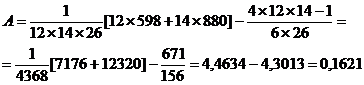
Таблица 7 – Расчет значения статистики А Лемана-Розенблатта

№ п/п	Элементы выборок x	Номера выборок	i	ri - i	(ri - i)^2	j	sj-j	(sj-j)^2
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
1	0	1	1	0	0
2	1	2				1	1	1
3	2	1	2	1	1
4	2	2				2	2	4
5	3	1	3	2	4
6	5	1	4	2	4
7	6	2				3	4	16
8	7	1	5	3	9
9	7	2				4	5	25
10	11	2				5	5	25
11	13	1	6	5	25
12	14	1	7	5	25
13	15	1	8	5	25
14	15	2				6	8	64
15	15	2				7	8	64
16	17	1	9	7	49
17	21	2				8	9	81
18	22	1	10	8	64
19	25	2				9	10	100
20	29	2				10	100	100
21	30	2				11	10	100
22	33	2				12	10	100
23	44	2				13	10	100
24	47	2				14	10	100
25	66	1	11	14	196
26	97	1	12	14	196

Известно [21], что

(в обозначениях [2]), где a₁(x) – предельная функция распределения классической статистики омега-квадрат (Крамера - Мизеса - Смирнова), используемой для проверки согласия эмпирического распределения с заданным теоретическим.

Квантили функции распределения a₁(x) приведены в табл.8. Известно [2, 21], что в случае статистики Лемана-Розенблатта предельным распределением можно пользоваться и для выборок умеренного объема (5 и 7, 6 и 7, 7 и 7,8 и 8 и т.д.). Поскольку наблюдаемое значение А = 0,1621 меньше любого критического значения в табл.8, то гипотезу однородности двух рассматриваемых выборок следует принять.

Таблица 8. – Квантили предельной функции распределения статистики
омега-квадрат (Крамера - Мизеса - Смирнова)

Величина a	0,8	0,9	0,95	0,98	0,99
Квантиль порядка a	0,245	0,347	0,461	0,620	0,743

Рекомендации по выбору критерия однородности. Для критерия типа омега-квадрат (Лемана-Розенблатта) нет выраженного эффекта различия между номинальными и реальными уровнями значимости. Поэтому мы рекомендуем для проверки однородности функций распределения (гипотеза H₀) применять статистику А типа омега-квадрат. Если методическое, табличное или программное обеспечение для статистики Лемана - Розенблатта отсутствует, рекомендуем использовать критерий Смирнова. Для проверки однородности математических ожиданий (гипотеза H'₀) целесообразно применять критерий Крамера-Уэлча. По нашему мнению, статистики Стьюдента, Вилкоксона и др. допустимо использовать лишь в отдельных частных случаях, рассмотренных выше.

Кратко сформулируем некоторые соображения о внедрении современных методов прикладной статистики в практику технических, экономических, медицинских и иных исследований. Даже из проведенного выше разбора лишь одной из типичных статистических задач организационно-экономического моделирования - задачи проверки однородности двух независимых выборок - можно сделать вывод о целесообразности широкого развертывания работ по критическому анализу сложившейся практики статистической обработки данных и по внедрению накопленного арсенала современных методов прикладной статистики. По нашему мнению, широкого внедрения заслуживают, в частности, методы многомерного статистического анализа, планирования эксперимента, статистики объектов нечисловой природы. Очевидно, рассматриваемые работы должны быть плановыми, организационно оформленными, проводиться мощными самостоятельными организациями и подразделениями. Целесообразно создание службы статистических консультаций в системе научно-исследовательских учреждений и вузов технического, экономического, медицинского профиля, а также в рамках корпораций и промышленных предприятий. Этот инновационный проект подробно разработан в специальной литературе [18, 19].

3.5.6. Реальные и номинальные уровни значимости в задачах
проверки статистических гипотез

Во многих монографиях, справочниках и таблицах (например, [1, 6, 7]) при проверке статистических гипотез критические значения статистик указаны для априорно фиксированных (номинальных в терминологии [8]) уровней значимости . В качестве таковых обычно используются значения из тройки чисел 0,01, 0,05, 0,1, к которым иногда добавляют еще несколько: 0,001, 0,005, 0,02 и др.

Однако ясно, что для дискретных статистик (т.е. статистик с дискретными функциями распределения), к которым, в частности, относятся все непараметрические статистические критерии [2, 24], реальные уровни значимости могут и не совпадать с номинальными. Под понимается максимально возможный уровень значимости дискретной статистики, не превосходящий заданный номинальный (т.е при переходе к следующему по величине возможному значению дискретной статистики соответствующий уровень значимости оказывается больше заданного номинального). Поэтому в лучших таблицах [2, 24] для ограниченных объемов выборок (2 - 100) табулируются точные распределения дискретных статистик. Для каждой конкретной статистики реальный уровень значимости - функция от объемов выборок n = (n₁, …, n_t), т.е. = (n). (Здесь t – число выборок, по которым рассчитывается значение статистики; рассматриваем в основном случай двух выборок, т.е. t = 2.)

В одних таблицах приведены [2, 24], в других - нет [1, 6, 7]. Возникает естественный вопрос: с чем это связано? Либо в работах [1, 6, 7] нарушена культура табулирования, либо реальные и номинальные уровни значимости практически совпадают для всех n. Продемонстрируем, что по крайней мере для некоторых статистик выполнено первое из этих двух утверждений.

В качестве примера рассмотрим критерий серий (Вольфовица) проверки однородности двух независимых выборок. Статистика этого критерия V – это число серий, т.е. частей общего вариационного ряда двух выборок, каждая из которых состоит из элементов одной выборки. При справедливости нулевой гипотезы о тождестве функций распределения, соответствующих двум независимым выборкам объемов n₁ и n₂, известно точное распределение [2, табл.6.7]

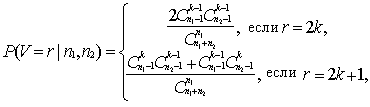
где r = 2, 3, …, 2n₁ при n₁ = n₂ и r = 2, 3, …, 2n₁ + 1 при n₁ < n₂ (без ограничения общности можно принять, что объем первой выборки не превосходит объема второй выборки, т.е. n₁ < n₂).

Несложный расчет для номинального уровня значимости = 0,05 показывается, что

при n₁ = n₂ = 6 реальный уровень значимости = 0,0260;

при n₁ = n₂ = 8 реальный уровень значимости = 0,0178;

при n₁ = n₂ = 10 реальный уровень значимости = 0,0370;

при n₁ = n₂ = 12 реальный уровень значимости = 0,0190.

Таким образом, для рассматриваемых объемов выборок реальный уровень значимости в 2–3 раза меньше, чем номинальный. Это, очевидно, необходимо учитывать при интерпретации результатов анализа реальных статистических данных.

Соотношение реальных (истинных) и номинальных уровней значимости было изучено нами [8] на примере непараметрических критериев проверки однородности двух независимых выборок. В табл.9, построенной в [8] по данным [2, 4, 24], для ряда непараметрических критериев проверки однородности двух независимых выборок приведены реальные уровни значимости (n) для номинального уровня значимости = 0,05 и объемов выборок n₁ = n₂ = 6, 8, 10, 12. Проанализированы пять критериев.

1. Двухвыборочный критерий Вилкоксона, являющийся линейной функцией от критерия Манна-Уитни и подробно рассмотренный выше в разд. 3.5.4. Напомним, что статистика Вилкоксона S - это сумма рангов элементов первой выборки

в общем вариационном ряду, построенном по объединенной выборке, включающей в себя все элементы обеих выборок (без ограничения общности можно принять, что объем первой выборки не превосходит объема второй выборки, т.е. n₁ < n₂).

2. Критерий Ван-дер-Вардена [2, 4], представляющий собой дальнейшее развитие (модификацию) критерия Вилкоксона и предназначенный для анализа выборок, распределение которых близко к нормальному. Статистика Х критерия Ван-дер-Вардена имеет вид

,

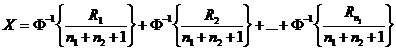где есть квантиль порядка p стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1, т.е. - обратная функция к .

3. Двухвыборочный двухсторонний критерий Смирнова однородности двух независимых выборок, рассмотренный в разд. 3.5.5. Он основан на использовании разности эмпирических функций распределения и построенных по первой и второй выборкам соответственно. Термин «двухсторонний» означает, что берется супремум модуля этой разности. Статистика двухвыборочного двухстороннего критерия Смирнова

в случае равенства объемов выборок n₁ = n₂ принимает значения, кратные 1/n₁, поскольку только такие значения принимают эмпирические функции распределения и , а потому рассматриваемая статистика имеет (n₁+1) возможных значений.

4. Критерий знаков Z используют в случае равенства объемов выборок n₁ = n₂. Статистика этого критерия равна числу положительных разностей X_k - Y_k элементов двух выборок с одинаковыми номерами. При справедливости нулевой гипотезы статистика Z имеет биномиальное распределение B(1/2; n₁), а потому имеет (n₁+1) возможных значений.

5. Критерий серий (Вольфовица) V, о котором шла речь выше в начале настоящего подраздела. Число его возможных значений не превосходит 2n₁.

Таблица 9. – Реальные уровни значимости (n) для = 0,05

Наименование и обозначение критерия	Объемы выборок n1 = n2				Примечания и ссылки
	6	8	10	12
Вилкоксона S	0,0320	0,0400	0,0480	0,0420	[24, с.280-281], [4, с.418 ]
Ван-дер-Вардена X	0,0498	0,0498	0,0500	0,0500	Рассчитано по мето- дике [4, с.249-250]
Смирнова D	0,0044	0,0372	0,0246	0,0158	[2, с.412], [24, с.406-427]
Знаков Z	0,0312	0,0078	0,0214	0,0386	[24, с.273-274]
Вольфовица (серий) V	0,0260	0,0178	0,0370	0,0190	Рассчитано по мето- дике [2, с.91-92]

Анализ содержания табл.9 подтверждает предположение о существенности отличия реальных уровней значимости (n) от номинальных уровней значимости .

Предположим теперь, что, несмотря на установленные отличия, мы используем при проверке гипотезы однородности таблицы [1, 6, 7], в которых указаны , а не . Это приводит к снижению мощности критерия по сравнению с соответствующим рандомизированным критерием, обеспечивающим равенство и .

Разъяснение. Поясним, что такое рандомизированный критерий. Пусть Y – статистика некоторого статистического критерия, принимающая дискретные значения, числа a и b, где a < b - два соседних значения этой статистики, такие, что P(Y > b) < и P(Y > a) > (вероятности взяты в предположении справедливости нулевой гипотезы). Если критическое значение критерия равно b, т.е. нулевая гипотеза принимается при Y < b, то = P(Y > b) < . Если же критическое значение равно следующему возможному (при движении в сторону уменьшения) значению a, т.е. нулевая гипотеза принимается при Y < a, то = P(Y > a) > . Рандомизированный критерий получим, если при Y = b в некоторой доле p случаев будем принимать нулевую гипотезу, а в остальных случаях – альтернативную. Поскольку

P(Y = b) = P(Y > a) - P(Y > b),

то (реальный) уровень значимости рандомизированного критерия равен

(1 – p) P(Y = b) + P(Y > b) = (1 – p) P(Y > a) + p P(Y > b).

Ясно, что при соответствующем выборе параметра рандомизации p уровень значимости рандомизированного критерия совпадет с заданным номинальным уровнем .

Для малых объемов выборок (2–20 элементов) понижение мощности из-за того, что , может быть существенным. Для иллюстрации этого в табл.10 приведены результаты моделирования наиболее употребительных (согласно [2]) критериев проверки однородности двух независимых выборок.

Таблица 10. – Мощности статистических критериев при = 0,05

Номер эксперимента	Объем выборок n1 = n2	Параметры				Мощность M статистического критерия
		m1	m2			S	V	X	D	t
1	6	0	1	1	1	0,318	0,006	0,298	0,238	0,396
2	8	0	1	1	1	0,452	0,104	0,426	0,068	0,484
3	10	0	1	1	1	0,520	0,180	0,534	0,116	0,598
4	12	0	1	1	1	0,632	0,076	0,618	0,462	0,682
5	6	0	2	1	1	0,828	0,308	0,808	0,716	0,904
6	8	0	2	1	1	0,958	0,510	0,954	0,458	0,976
7	10	0	2	1	1	0,984	0,704	0,990	0,632	0,988
8	12	0	2	1	1	0,996	0,568	0,996	0,978	0,998

Моделируются выборки одинакового объема из нормальных законов распределения с математическими ожиданиями m₁ и m₂ и дисперсиями и . Номинальный уровень значимости, определяющий конкретные критические значения для критериев, принят равным = 0,05. Мощность критерия определяется моделированием N = 5000 пар выборок. При использовании N = 5000 моделируемых пар выборок среднее квадратическое отклонение оценок мощности (при M > 0,95 имеем ).

Изучены критерии Вилкоксона S, Вольфовица V, Ван-дер-Вардена X, Смирнова D. Критерий Стьюдента t (см. например, [2]), как равномерно наиболее мощный в классе нормальных законов распределения, приведен для сравнительной оценки мощности рассматриваемых непараметрических критериев. (Моделирование и расчеты, приведенные в настоящем подразделе, выполнены Ю.Э. Камнем и Я.Э. Камнем [8].)

Замечание. Приведенные в табл.10 значения мощностей критериев интересны нам с точки зрения обсуждения их зависимости от различия реальных и номинальных уровней значимости. При этом необходимо подчеркнуть, что эти значения зависят от предположений, принятых при моделировании. Так, критерии Вилкоксона и Ван-дер-Вардена «настроены» на использование в случае распределений, близких к нормальному семейству. При проверке гипотезы о совпадении функций распределения двух независимых выборок из логистического распределения с альтернативой сдвига критерий Вилкоксона является асимптотически оптимальным. А в случае выборок из нормального распределения аналогичным свойством обладает критерий Ван-дер-Вардена, причем известно, что семейства нормальных и логистических распределений весьма близки – расстояние Колмогорова между ними не превышает 0,01 (см. по вопросам асимптотической оптимальности непараметрических критериев [10, 11, 15]). Поэтому нет ничего удивительного в том, что мощности критериев Вилкоксона и Ван-дер-Вардена близки к оптимуму в случае нормального распределения – к мощности критерия Стьюдента. При этом мощности критериев Смирнова и особенно критерия Вольфовица заметно меньше. Однако для выборок из других распределений (например, распределений Вейбулла-Гнеденко или гамма-распределений) ситуация иная – критерий Смирнова, как показывает компьютерное моделирование, оказывается более мощным, чем критерии Вилкоксона и Ван-дер-Вардена. Более того, критерий Смирнова – состоятельный, т.е. позволяет отклонить любую конкретную альтернативу (при соответствующих объемах выборок), а критерии Вилкоксона и Ван-дер-Вардена не являются состоятельными, некоторых альтернатив они «не чувствуют» (см. подраздел 3.5.4). Поэтому вполне обоснованной является рекомендация о широком использовании состоятельных критериев Смирнова и типа омега-квадрат (Лемана-Розенблатта), данная в подразделе 3.5.5. Что же касается критерия серий (Вольфовица), то из-за его отрицательных свойств (выраженной дискретности, низкой мощности) он в настоящее время выходит из употребления при анализе реальных данных, несмотря на прозрачность определения.

Рассмотрения настоящего раздела позволяют сделать следующие выводы [8].

1. При создании методик и таблиц, а также программных продуктов необходимо соблюдать определенную культуру табулирования. В качестве положительных примеров можно указать работы [2, 24].

2. При малых объемах выборок использовать номинальные уровни значимости вместо реальных уровней значимости для дискретных статистик недопустимо.

3. При конечных объемах выборок выбор того или иного критерия с дискретной статистикой должен сопровождаться исследованием влияния варьирования уровня значимости на качественную интерпретацию результатов проверки гипотез. В частности, выбор одного из двух конкурирующих непараметрических критериев K₁ и K₂ прежде всего должен зависеть от априорного выбора исследователем реального уровня значимости или , соответствующего первому критерию K₁ или второму K₂, в качестве номинального уровня значимости .

Последний вывод демонстрирует сложность сравнения критериев с дискретными статистиками между собой, поскольку точки скачков распределений их статистик не совпадают. Следовательно, в отличие от критериев с непрерывными статистиками нельзя выбрать единый фиксированный уровень значимости и сравнить свойства критериев при этом уровне значимости.

В заключение отметим, что для любого критерия проверки статистических гипотез реальный уровень значимости приближается к номинальному при безграничном возрастании объемов выборок, т.е. при . Поэтому для прикладных исследований значительный интерес представляет определение верхней оценки скорости сходимости (n) к . Соответствующие теоретические результаты для критериев проверки однородности двух независимых или связанных выборок можно получить, основываясь на оценках скорости сходимости в принципе инвариантности [21, гл.4]. Некоторые оценки приведены в [17, гл.2]. Скорость сходимости также может быть оценена методом статистических испытаний (Монте-Карло). Пример подобного исследования подробно рассмотрен в [9] в ходе обсуждения проблем вероятностно-статистического моделирования помех, создаваемых электровозами.

В настоящем разделе затронута лишь небольшая часть непараметрических методов анализа числовых статистических данных. В частности, обратим внимание на непараметрические оценки плотности, которые используются для описания данных, проверки однородности, в задачах восстановления зависимостей и других областях эконометрики. Непараметрические оценки плотности рассмотрены в [21, раздел 5.6].

3.6. Восстановление зависимости методом наименьших квадратов
на основе непараметрической модели с периодической составляющей

Метод наименьших квадратов восстановления зависимости – один из наиболее распространенных статистических методов анализа данных. В настоящем разделе рассмотрена непараметрическая постановка: восстанавливаемая зависимость – сумма линейной функции и периодической составляющей произвольного вида (с известным периодом), распределение случайных погрешностей (остатков, невязок) произвольно.

3.6.1. Задача восстановления линейной зависимости

Начнем с простейшего случая – задачи восстановления линейной зависимости. Пусть t – независимая переменная, а x – зависимая. Рассмотрим задачу восстановления зависимости x = x(t) на основе набора n пар чисел (t_k , x_k), k = 1,2,…,n, где t_k –– значения независимой переменной, а x_k – соответствующие им значения зависимой переменной.

Восстанавливать зависимость можно на основе различных моделей. Обычно применяют модели временных рядов, включающие три составляющие: трендовую (T), периодическую (S) и случайную (E). Рассматривают, как в [1] и аналогичных изданиях, аддитивную модель T + S + E и мультипликативную модель TSE.

Простейшая аддитивная модель имеет вид

x_k = a (t_k - )+ d + e_k = a (t_k - ) + d+ f(t_k) + E_k, k = 1,2,…,n. (1)

Здесь трендовая составляющая – линейная функция a (t_k - ) + d (такая запись тренда предпочтительнее для облегчения выкладок); периодическая составляющая f(t) обычно описывает сезонность, т.е период известен (в зависимости от моделируемой ситуации он равен году, неделе, суткам и т.п.); случайная составляющая представлена слагаемыми E_k, которые являются реализациями независимых одинаково распределенных случайных величин с нулевым математическим ожиданием и дисперсией , неизвестной статистику. В рассматриваемой модели e_k = f(t_k) + E_k, = 1,2,…,n, т.е. отклонения от линейного тренда e_k не являются одинаково распределенными. Однако их распределения отличаются лишь сдвигами (на значения детерминированной периодической составляющей).

Соответствующая модели (1) мультипликативная модель имеет вид

. (2)

В модели (2) сомножители имеют описанный выше смысл. При логарифмировании модель (2) переходит в аналог модели (1), следовательно, достаточно рассматривать модель (1).

Иногда принимают предположение о нормальности распределения погрешностей. Однако давно известно, что распределения реальных данных, как правило, отличаются от нормальных [2]. Поэтому далее рассматриваем непараметрическую модель, не предполагающую, что распределение погрешностей входит в то или иное параметрическое семейство. Отказ от задания распределения погрешностей в параметрическом виде – одно из оснований для того, чтобы именовать рассматриваемые модель и метод непараметрическими. Второе основание – отказ от выбора периодической составляющей из какого-либо параметрического семейства функций.

Практическая значимость модели (1) очевидна. Однако расчетные методы, описанные в [1] и аналогичных изданиях, являются эвристическими. Цель настоящей статьи - построить непараметрическую вероятностно-статистическую теорию прогноза временного ряда на базе линейного тренда с учетом аддитивной периодической составляющей.

Метод наименьших квадратов был разработан К. Гауссом в 1794 г. [2]. Согласно нему этому методу для расчета наилучшей функции, приближающей линейным образом зависимость x от t в модели (1), следует рассмотреть функцию двух переменных

.

Оценки метода наименьших квадратов (кратко: оценки МНК) - это такие значения a* и d*, при которых функция f(a,d) достигает минимума по всем значениям аргументов. Как известно (см., например, [2]), оценки МНК имеют вид

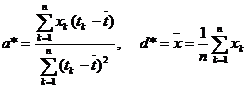. (3)

Следуя эвристическому подходу [1], изучим асимптотическое поведение оценок МНК a* и d*, заданных формулами (3), установим их асимптотическую нормальность в предположениях модели (19), а затем состоятельно оценим периодическую составляющую f(t) и построим интервальный прогноз для x(t).

3.6.2. Асимптотические распределения оценок параметров

Из формулы (3) следует, что

. (4)

Согласно Центральной предельной теореме (для выполнения ее условий необходимо предположить, например, что погрешности e_k , k = 1, 2, …, n, финитны или имеют конечный третий абсолютный момент; однако заострять внимание на этих внутриматематических «условиях регулярности» здесь нет необходимости) оценка d* имеет асимптотически нормальное распределение с математическим ожиданием и дисперсией , ее оценка приводится ниже. Из формул (3) и (4) вытекает, что

,

.

Последнее слагаемое во втором соотношении при суммировании по k обращается в 0, поэтому

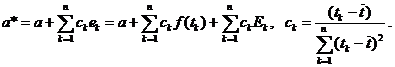(5)

Формулы (5) показывают, что оценка a* является асимптотически нормальной с математическим ожиданием и дисперсией

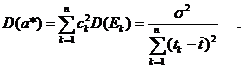
Отметим, что многомерная нормальность имеет быть, когда каждое слагаемое в формуле (5) мало сравнительно со всей суммой, т.е.

. (6)

Условие (6) выполнено, например, если t_k образуют (полную, т.е. без пропусков) арифметическую прогрессию, число членов которой безгранично растет.

Итак, дисперсии оценок МНК параметров a* и d* линейного тренда – те же, что и при отсутствии сезонных искажений (см., например, [2]). А вот их математические ожидания зависят от периодической составляющей. Однако в случае

(7)

оценки a* и d* являются несмещенными.

Условия (7) являются необходимыми и достаточными для несмещенности и состоятельности оценок МНК коэффициентов линейной зависимости. Проверка условий (7) рассмотрена в конце статьи.

Несмещенность (в предположениях (7) и асимптотическая нормальность оценок метода наименьших квадратов позволяют легко указывать для них асимптотические доверительные границы и проверять статистические гипотезы, например, о равенстве определенным значениям, прежде всего 0.

3.6.3. Асимптотическое распределение трендовой составляющей

Из формул (4) и (5) следует, что при справедливости соотношений (7)

т.е. оценка y*(t) = a* (t_k - )+ d* трендовой составляющей y(t) = a (t - )+ d рассматриваемой зависимости является несмещенной. Поэтому

При этом, поскольку погрешности E_k независимы в совокупности и M(E_k) = 0, то

Таким образом,

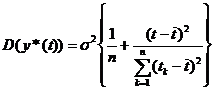. (8)

Итак, оценка y*(t) является несмещенной и асимптотически нормальной. Для ее практического использования (построения доверительных интервалов, проверки статистических гипотез) необходимо состоятельно уметь оценивать остаточную дисперсию .

В частности, не представляет труда выписывание нижней и верхней границ для трендовой составляющей прогностической функции:

где полуширина доверительного интервала имеет вид

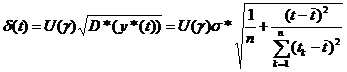. (9)

Здесь - доверительная вероятность, - квантиль нормального распределения порядка , т.е. , где - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. При = 0,95 (наиболее применяемое значение) имеем = 1,96. В формуле (9) - состоятельная оценка дисперсии y*(t). В соответствии с (8) она является произведением состоятельной оценки среднего квадратического отклонения случайных погрешностей E_k на известную исследователю детерминированную функцию от t.

3.6.4. Математическое ожидание остаточной суммы квадратов

В точках t_k , k = 1, 2, …, n, имеются исходные значения зависимой переменной x_k и восстановленные значения y*(t_k). Рассмотрим остаточную сумму квадратов

При отсутствии периодической составляющей используют [2] состоятельные оценки среднего квадратического отклонения случайных погрешностей, построенные на основе остаточной суммы квадратов или . Однако при наличии периодической составляющей так делать нельзя. Приходится использовать «обходный путь».

В соответствии с формулами (4) и (5) при справедливости условий (7)

.

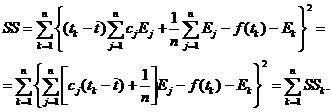Найдем математическое ожидание каждого из слагаемых:

.

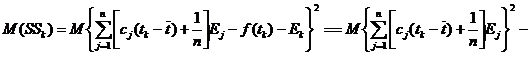
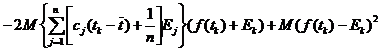Поскольку E_k независимы, одинаково распределены и имеют нулевое математическое ожидание, то

.

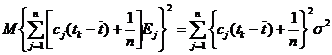Далее,

.

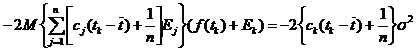Наконец,

.

На основе трех последних равенств можно показать, что при выполнении условия асимптотической нормальности (6)

.

Следовательно,

. (10)

В правой части (10) первое слагаемое соответствует вкладу случайной составляющей, второе – вкладу периодической составляющей.

В некоторых случаях второе слагаемое в правой части (10) может быть известно из предыдущего опыта или же оценено экспертами, однако в большинстве ситуаций целесообразно исходить из оценки периодической составляющей.

3.6.5. Оценивание периодической составляющей

В литературе рассматривают как параметрические, так и непараметрические подходы. Популярный метод исходит из того, что достаточно гладкую функцию можно разложить в ряд Фурье и получить хорошее приближение с помощью небольшого числа гармоник. В простейшем случае – одна гармоника. Так, динамику индекса инфляции можно попытаться изучать с помощью модели

x_k = a (t_k - ) + d+ f(t_k) + E_k = a (t_k - ) + d+ g + E_k, k = 1,2,…,n

(время t измеряется в годах). Тогда неизвестные параметры a, b, g оцениваются методом наименьших квадратов.

Однако обычно нет оснований предполагать, что периодическая составляющая входит в то или иное параметрическое семейство функций. Приходится строить непараметрические оценки. Опишем одну из возможных постановок.

Пусть в согласии с предположениями (7) рассматривается целое число периодов, т.е. n = mq, где n – объем наблюдений, m – количество периодов, q – число наблюдений в одном периоде. Предполагается, что первые q моментов наблюдения при сдвиге на длину периода дают следующие q моментов времени, при сдвиге на две длины периода дают третий набор из q моментов наблюдения, и т.д. Тогда в соответствии с определением периодической составляющей справедливы равенства

. (11)

Если наблюдения проводятся ежемесячно в течение m лет, то число наблюдений в одном периоде q = 12, общий объем наблюдений n = 12m, далее s – номер месяца в году, s = 1, 2, …, 12. Пусть g_s - общее значение в (11). Для оценки периодической составляющей требуется оценить g₁, g₂, …, g_q.

Естественный подход состоит в том. чтобы усреднить m значений x_k – y*(t_k), соответствующих моментам времени, отстоящим друг от друга на целое число периодов. Другими словами, усреднить «очищенные» от трендовой составляющей исходные данные, соответствующие одноименным месяцам различных лет. Речь идет об оценках

. (12)

Оценка периодической составляющей распространяется на весь интервал наблюдений очевидным образом:

. (13)

Сложив восстановленные значения трендовой и периодической оставляющей, получим оценку зависимости, «очищенную» от случайной составляющей

. (14)

Здесь оценки a* и d* находят по формулам (3), а оценки f*(t) – по формулам (12) – (13).

С помощью формулы (14) можно строить точечный прогноз, используя ее вне интервала наблюдений. Для этого достаточно распространить сезонную составляющую f*(t) вплоть до рассматриваемого момента времени по правилу (13) и суммировать ее с прогнозом трендовой составляющей y*(t). Интерполяция и экстраполяция на моменты времени t, не входящие в исходное множество {t_k, k = 1, 2, …, n} и множества, полученные из него сдвигами на целое число периодов, может быть осуществлена путем линейной интерполяции ближайших значений или иным методом сглаживания.

Обсудим свойства оценок (12) – (14).

При безграничном росте объема данных и справедливости условий (6) и (7) оценки a* и d* параметров трендовой составляющей являются состоятельными и несмещенными, а потому, как можно показать, в рассматриваемых в настоящей статье условиях суммы (12) оценивают периодическую составляющую состоятельно (при ) и несмещенно. Как следствие,

(15)

по вероятности при . В соответствии с (10) последнее соотношение дает возможность оценить , а затем построить интервальный прогноз для трендовой составляющей согласно (9).

Отметим, что в рассматриваемой ситуации, как правило, n растет, увеличиваясь на величины, кратные q – числу наблюдений в одном периоде. Как следствие, уменьшаемое в (15) – константа, зависимости от n нет. Эти особенности связаны с тем, что выполнение условий (7) предполагает рассмотрение целого числа периодов.

Рассмотрим оценки (12) подробнее. Как вытекает из (4.1.19), (11) и (12),

.

С учетом (4), (5) и (7) получаем, что

.

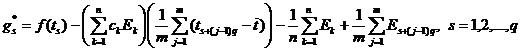Таким образом,

(16)

где , если , и при всех остальных значениях индекса суммирования k, здесь .

Соотношение (16) означает, что рассматриваемые оценки есть суммы независимых случайных величин, а потому с помощью Центральной предельной теоремы можно построить доверительные интервалы для рассматриваемых значений периодической составляющей (в предположении справедливости условий (6)).

3.6.6. Интервальный прогноз

Точечный прогноз строят по формуле (11) на основе x*(t) - оценки зависимости, «очищенной» от случайной составляющей, но включающей трендовый и периодический компоненты. Если выполнены условия (7), то

Mx*(t) = x(t) = a (t - ) + d + f(t),

т.е. оценка x*(t) является несмещенной.

При справедливости условий (7) с учетом (4), (5) и (16) получаем, что для момента времени t, входящего в исходное множество {t_k, k = 1, 2, …, n} или в множества, полученные из него сдвигами на целое число периодов,

. (17)

В (17) при определении значений коэффициентов h_ks в качестве s следует взять номер наименьшего из исходных моментов времени {t_k, k = 1, 2, …, n}, отстоящих от рассматриваемого момента t на целое число периодов. С помощью (16) заключаем, что

,

где , если , и при всех остальных значениях индекса суммирования k, здесь r_s – то же, что и в формуле (16).

В правой части формулы (17) стоит сумма независимых случайных величин, поэтому оценка x*(t) является асимптотически нормальной (при справедливости условий (6)) с математическим ожиданием x(t) и дисперсией

. (18)

Следовательно, нижняя и верхняя доверительные границы для прогностической функции (с учетом как трендовой, так и периодической составляющих) имеют вид:

,

где

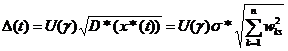. (19)

Здесь - доверительная вероятность, - квантиль нормального распределения порядка . В формуле (19) - состоятельная оценка дисперсии точечного прогноза x*(t). В соответствии с (18) она является произведением состоятельной оценки среднего квадратического отклонения случайных погрешностей E_k на известную статистику детерминированную функцию от t. Величину рассчитывают согласно (10) и (15).

3.6.7. Пример применения непараметрического метода наименьших квадратов
в модели с периодической составляющей

Обработаем фактические данные ОАО «Магнитогорский металлургический комбинат» о закупочных ценах на лом черных металлов [3]. Как показано в [3], может быть использована модель (1) линейного тренда с периодической составляющей. Для облегчения расчетов оставим из каждого квартала данные только по одному месяцу. Введем условные моменты времени, а именно, будем измерять время в кварталах, начиная с первого квартала 2003 г. Исходные данные для демонстрации примера применения непараметрического метода наименьших квадратов в модели с периодической составляющей - пары чисел (t_k , x_k), k = 1, 2, …, 12, - представлены в табл.1 в столбцах (3) и (4) соответственно.

По формулам (3) найдем оценки параметров a* и d*, что позволяет построить оценку трендовой составляющей

y*(t) = a*(t - ) + d* =212,26 (t – 6,5) + 3967,17 = 212,26 t + 2587,48.

Численные значения трендовой составляющей приведены в столбце (5) табл.1.

Рассчитав отклонения исходных значений закупочных цен от оценок трендовой составляющей (столбец (6) табл.1), возведя их в квадрат и сложив, получаем остаточную сумму квадратов SS = 4 539 214 и SS/n = SS/12 = 378 267,843.

Таблица 1 – Построение модели прогнозирования цен на лом марки 3А

№ п/п	Периоды времени	Условные моменты времени	Закупоч-ные цены, руб./т	Оценка тренда	Отклонения от оценки тренда	Восста-новлен-ные зна-чения	Кажу-щиеся невязки
k				y*()	-y*()
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
1	янв.03	1	2 750	2 800	- 50	2 424	326
2	апр.03	2	3 800	3 012	788	3 545	255
3	июл.03	3	2 900	3 224	- 324	2 655	245
4	окт.03	4	3 100	3 437	- 337	3 848	- 748
5	янв.04	5	2 761	3 649	- 888	3 273	- 512
6	апр.04	6	4 602	3 861	741	4394	208
7	июл.04	7	3 540	4 073	- 533	3504	36
8	окт.04	8	5 268	4 286	982	4 697	571
9	янв.05	9	4 307	4 498	- 191	4 122	185
10	апр.05	10	4 779	4 710	69	5 243	- 464
11	июл.05	11	4 071	4 922	- 851	4 353	- 280
12	окт.05	12	5 723	5 135	588	5546	177

Сгруппировав отклонения исходных значений закупочных цен от оценок трендовой составляющей по месяцам (табл.2), наглядно убеждаемся в наличии периодической составляющей. Взяв среднее арифметическое отклонений от тренда за конкретный месяц, рассчитываем оценку периодической составляющей (в соответствии с формулой (12)). Результаты приведены в табл.2.

Рассчитав по формуле (13) оценки периодической составляющей на весь интервал времени и сложив их с оценками трендовой составляющей, получаем в соответствии с формулой (14) оценку зависимости, «очищенную» от случайной составляющей, т.е. восстановленные значения (столбец (7) табл.1). Кажущиеся невязки, т.е. отклонения исходных значений закупочных цен от восстановленных значений, приведены в столбце (8) табл.1. Сравнивая столбцы (6) и (8), убеждаемся в целесообразности введения в модель периодической составляющей. В 9 случаях из 12 абсолютные величины отклонений уменьшились, в остальных трех, хотя и возросли, но линь до среднего уровня среди остальных.

Таблица 2 – Оценивание периодической составляющей

Номер квартала s	Месяц	Отклонения от тренда			Оценка периодической составляющей
		В 2003 г.	В 2004 г.	В 2005 г.
1	Январь	-50	- 888	-191	- 376
2	Апрель	788	741	69	533
3	Июль	- 324	- 533	- 851	- 569
4	Октябрь	- 337	982	588	411

Возведя в квадрат оценки периодической составляющей (табл.2), сложив эти квадраты, умножив на число лет и поделив на n, получаем, что = 229 537. В соответствии с формулой (10) оценкой дисперсии случайной составляющей является

= 378 267,83 - 229 537 = 148 731,

а оценкой среднего квадратического отклонения

.

В соответствии с формулами (4) и (5) оценим дисперсии оценок параметров:

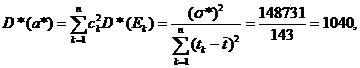
Средние квадратические отклонения a* и d* оцениваются как 32,25 и 111,33 соответственно, а доверительные интервалы для доверительной вероятности 0,95 таковы: .

Первое из условий (7) выполнено в силу построения оценок периодической составляющей по целому числу периодов. Действительно, согласно данным табл.2 сумма оценок периодической составляющей для 12 точек наблюдений равна (-3), незначительное отклонение от 0 вызвано ошибками округления.

В соответствии с формулой (5) смещение оценки a* оценивается как

.

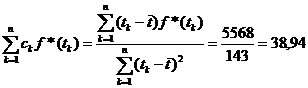Таким образом, смещение имеет тот же порядок, что и среднее квадратичное отклонение оценки а*, и заведомо меньше, чем полуширина доверительного интервала. Дальнейшее сравнение может быть проведено на основе оценки дисперсии смещения – случайной величины

.

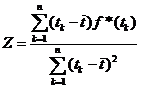Алгоритм вычисления дисперсии Z аналогичен таковым для периодической составляющей и интервального прогноза (см. (16) и (18) соответственно), но более сложен, поэтому не включен в статью. Таким образом, можно считать, что предположения (7) модели (1) выполнены для данных табл.1.

Перейдем к оценке дисперсий значений периодической составляющей. Как следует из равенства (16),

,

где , если , и при иных значениях индекса суммирования k, здесь .

Начнем со значения s = 1 (периодическая составляющая для января). Тогда . Понадобятся значения

.

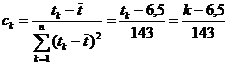Расчет удобно проводить с помощью таблицы (табл.3).

Таблица 3 – Расчет дисперсии периодической составляющей

k			-1/n	+1/m
(1)	(2)	(3)	(4)	(5)	(6)	(7)
1	- 5,5	0,0577	- 0,0833	0,3333	0,3077	0,09468
2	- 4,5	0,0472	- 0,0833	-	- 0,0361	0,00130
3	- 3,5	0,0367	- 0,0833	-	- 0,0466	0,00217
4	- 2,5	0,0262	- 0,0833	-	- 0,0571	0,00326
5	- 1,5	0,0157	- 0,0833	0,3333	0,2657	0,07060
6	- 0,5	0,0052	- 0,0833	-	- 0,0781	0,00610
7	0,5	- 0,0052	- 0,0833	-	- 0,0885	0,00783
8	1,5	- 0,0157	- 0,0833	-	- 0,0990	0,00980
9	2,5	- 0,0262	- 0,0833	0,3333	0,2238	0,05009
10	3,5	- 0,0367	-0,0833	-	0,1200	0,01440
11	4,5	- 0,0472	-0,0833	-	0,1305	0,01703
12	5,5	- 0,0577	-0,0833	-	0,1410	0,01988

В табл. 3 столбец (3) получен из столбца (2) умножением на , каждый элемент столбца (6) равен сумма элементов столбцов (3), (4) и (5), стоящих в той же строке, а в столбце (7) стоят квадраты соседних элементов из столбца (6). Цель построения табл.3 – расчет суммы элементов столбца (7). Эта сумма равна 0,28275. Следовательно,

.

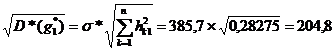Доверительный интервал для значения периодической составляющей в январе (- 376 – 1,96204,8; -376 + 1,96204,8) захватывает 0 (при доверительной вероятности 0,95), отличие значения периодической составляющей от 0 не значимо (на уровне значимости 0,05).

Аналогичный расчет для значения s = 2 (периодическая составляющая для апреля) дает

.

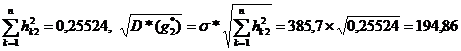Доверительный интервал для значения периодической составляющей в апреле (533 – 1,96194,86; 533 + 1,96194,86) = (533 – 381,93; 533 + 381,93) не захватывает 0 (при доверительной вероятности 0,95), отличие значения периодической составляющей от 0 значимо (на уровне значимости 0,05).

Приступим к завершающему этапу анализа данных табл.1 – построению интервального прогноза. Необходимо рассчитать величины , если , и при всех остальных значениях индекса суммирования k, где r_s – то же, что и в формуле (16), поскольку точечный прогноз x*(t) является несмещенным, асимптотически нормальным, а его дисперсия оценивается согласно (18) так:

.

Начнем с прогноза на январь 2006 г. (по данным за 2003 - 2005 гг.). Тогда t = 13, s = 1, , , если , и при всех остальных значениях индекса суммирования. При этом . Расчет удобно проводить с помощью таблицы (табл.4).

Сумма значений, стоящих в последнем столбце табл.4, равна 0,61299. Согласно формуле (19)

.

Согласно (14) точечный прогноз прогностической функции таков:

.

Нижняя и верхняя доверительные границы для прогностической функции (с учетом как трендовой, так и периодической составляющих) имеют вид:

.

Реальное значение согласно [3] равно 4336. Оно практически совпадает с нижней доверительной границей прогностической функции .

Таблица 4 – Расчет дисперсии прогностической функции

k		1/m
1	- 0,3077	0,3333	0,0256	0,00066
2	- 0,2517	-	- 0,2517	0,06336
3	- 0,1958	-	- 0,1958	0,03834
4	- 0,1399	-	- 0,1399	0,01957
5	- 0,0839	0,3333	0,2494	0,06220
6	- 0,0280	-	- 0,0280	0,00078
7	0,0280	-	0,0280	0,00078
8	0,0839	-	0,0839	0,00700
9	0,1399	0,3333	0,4732	0,22392
10	0,1958	-	0,1958	0,03834
11	0,2517	-	0,2517	0,06336
12	0,3077	-	0,3077	0,09468

Аналогичные расчеты для апреля 2006 г. (t = 14, s = 2, ) дают . Точечный прогноз равен x*(14) = 6092, а нижняя и верхняя доверительные границы таковы: . Реальное значение [3] – 5430. Оно практически совпадает с нижней доверительной границей прогностической функции .

3.6.8. Интервальный прогноз индивидуальных значений

Формула (19) позволяет строить интервальный прогноз для прогностической функции, т.е. для математического ожидания временного ряда. Наблюдаемое значение отличается от него на величину невязки. Распределение невязки можно оценить по значениям кажущихся невязок (см. столбец (8) в табл.1). Напомним, что это распределение не является нормальным, не описывается элементом какого-либо параметрического семейства. Интервальный прогноз индивидуального значения построить, скорректировав интервальный прогноз для прогностической функции с помощью выборочных квантилей кажущихся невязок.

Для рассмотренного выше примера вариационный ряд n = 12 кажущихся невязок таков: -748, - 512, - 464, - 280, 36, 177, 185, 208, 245, 255, 326, 571. Нижний дециль оценим как второй член вариационного ряда (-512), верхний – как предпоследний (одиннадцатый) член вариационного ряда 326. Для расчета нижней доверительной границы индивидуального значения надо взять нижнюю доверительную границу прогностической функции и отнять 512. Для расчета верхней доверительной границы индивидуального значения надо взять верхнюю доверительную границу прогностической функции и прибавить 326.

Итак, для данных табл.1 индивидуальные значения лежат «глубоко внутри» доверительных интервалов. Прогнозы полностью оправдались.

3.6.9. О проверке условий (7)

Рассмотрим три вопроса. Верны ли условия (7) в моделях, соответствующих реальным ситуациям? Как проверять справедливость условий по результатам наблюдений? Каковы свойства оценок, если эти условия оказываются невыполненными?

В условиях (7) важную роль играет система точек наблюдения t_k, k = 1, 2, …, n. Более тщательно рассмотрим ранее принятую модель с целым числом периодов, для которой справедливо соотношение (11). При этом объем наблюдений n = mq, где m – количество периодов, q – число наблюдений в одном периоде. Предполагается, что первые q моментов наблюдения при сдвиге на длину периода дают следующие q моментов времени, при сдвиге на две длины периода дают третий набор из q моментов наблюдения, и т.д. Для значений периодической составляющей выше построены точечные оценки и доверительные интервалы (в предположении, что количество периодов m безгранично растет), в чем и состоит оценивание периодической составляющей. (Для гладкой функции f(t) при безграничном росте числа наблюдений q в одном периоде можно получить сходимость оценок периодической составляющей не только в q точках, но и на всем периоде. При этом от оценок в q точках придется перейти к оценкам на всем периоде, например, кусочно-линейным, соединив соседние точки графика отрезками прямых.)

Описанная модель справедлива, когда, например, в течение некоторого числа лет имеются поквартальные или помесячные данные бухгалтерского учета. При изучения посещений сайта или торгового заведения – почасовые данные за целое число недель. Если в ряду наблюдений есть пропуски (временной ряд не является полным) – предпосылки модели не выполняются. Если система точек наблюдения не образует арифметическую прогрессию,

В рассматриваемой модели естественно принять, что

, (20)

суммарное отклонение значений восстанавливаемой функции от линейного тренда за один период является нулевым. Тогда первое из условий (7) выполнено:

.

В реальных ситуациях система точек наблюдения может включать в себя, кроме целого числа периодов, еще несколько начальных точек следующего периода. Можно априори принять первое условие (7), для этого изменив – при необходимости – величину свободного члена d в модели тренда (та же логика рассуждений, что и при принятии условий M(e_k) = 0 – в модели без периодической составляющей – и M(E_k) = 0 в общем случае). Однако возникает противоречие между первым условием (7) и условием (20). Условие первое условие (7) автоматически обеспечивается методом наименьших квадратов, а условие (20) соответствует логике моделирования. Однако поскольку рассматриваем асимптотическую теорию при безграничном росте числа периодов, указанное различие исчезает при . Таким образом, первое из условий (7) вытекает из свойств рассматриваемой модели и потому вообще не требует проверки по экспериментальным данным, в отличие от второго условия (7), которое выполнено не всегда.

Добавим к модели с целым числом периодов два предположения - симметричности множества {t_k, k = 1, 2, …, n} относительно и четности периодической составляющей f(t) относительно той же точки. Эти предположения выполнены, если, например, график f(t) симметричен относительно середины года. Тогда второе условие (7) выполнено. Ясно, что обычно нет оснований априори считать, что реальные данные описываются такой моделью.

3.6.10. Проверка второго условия (7) по экспериментальным данным

Естественно использовать статистику

,

где - ранее построенная оценка периодической составляющей f(t). Оценка является несмещенной, а потому

.

При справедливости (6) распределение Y является асимптотически нормальным (при безграничном росте количества периодов m). Для проверки второго условия (7), т.е. для проверки нулевой гипотезы H₀: M(Y) = 0 при альтернативной гипотезе о неравенстве математического ожидания 0 достаточно оценить дисперсию Y.

В соответствии с (11) формулу (16) можно записать для любого j = 1, 2, … , n, если под k = k(j) понимать k(j) = j – aq при максимально возможном a, при котором k(j) остается положительным, т.е. k(j) – это остаток от деления j на q, если этот остаток ненулевой, и k(j) = q при нулевом остатке. Таким образом,

, (21)

где h_ik – те же, что и в формуле (16). В соответствии с определением Y из (21) следует, что

. (22)

Изменим порядок суммирования во втором слагаемом в (22):

.

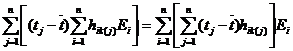Следовательно, поскольку E_i – независимые одинаково распределенные случайные величины с математическим ожиданием 0 и дисперсией , то

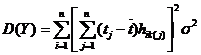. (23)

Величину оцениваем по формулам (10) и (15), величины описаны после формулы (16). Подставив оценку в (23), получаем оценку D*(Y) дисперсии Y.

В соответствии с асимптотической нормальностью Y правило принятия решений при проверке гипотезы H₀: M(Y) = 0 таково: если

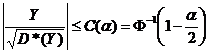, (24),

где - критическое значение, соответствующее уровню значимости , то нулевая гипотеза принимается (второе условие (7) выполнено), если же неравенство (24) не выполнено, то принимается альтернативная гипотеза (второе условие (7) не выполнено).

3.6.11. Асимптотическая несмещенность оценки параметра а

Приведем пример, когда второе условие (7) не выполнено. Измерять время будем в месяцах. Пусть данные берутся на середину квартала. Тогда последовательность моментов времени такова: 2, 5, 8, 11, 14, 17, 20, 23, … Задан период – год. Периодическая составляющая задается четырьмя числами: g₁ = - 1, g₂ = -2, g₃ = -3, g₄ = 6. Для таких данных выполнено равенство (20), т.е. . Следовательно, выполнено первое условие (7). Используя это условие, можно упростить второе условие (7):

.

Для простоты расчетов ограничимся двумя годами. Тогда

.

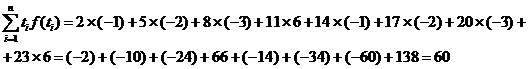Второе условие (7) не выполнено. Оно не будет выполнено и для любого иного числа лет. Действительно, если х – начало года (для первого года х = 0, для второго х = 12, и т.д.), то вклад этого года в рассматриваемую сумму будет равен

.

Причина нарушения второго условия (7) ясна – периодическая составляющая не симметрична в течение года. Такое поведение периодической составляющей естественно для сельскохозяйственных предприятий. Противоположную ситуацию демонстрирует периодическая составляющая для временного ряда цен на лом черных металлов (по данным Магнитогорского металлургического комбината), проанализированного выше.

Смещение оценки параметра а равно

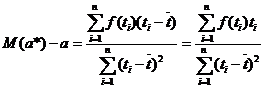. (25)

В рассматриваемом примере числитель за m лет равен 30m. А знаменатель, очевидно, имеет порядок m³. Смещение имеет порядок m^-2, т.е. быстро убывает с ростом числа периодов. Оценка а* параметра а является асимптотически несмещенной.

Нетрудно показать, что для модели с целым числом периодов всегда имеет асимптотическая несмещенность оценки а* параметра а. Если второе условие (7) выполнено – эта оценка является несмещенной, если не выполнено – смещенной, но смещение стремится к 0 при росте числа периодов. Таким образом, выполнение второго условия (7) не является необходимым для применения рассматриваемых методов. Тем не менее проверка второго условия (7) по экспериментальным данным является полезным для решения о том, можно ли пользоваться асимптотической несмещенностью оценки при имеющемся объеме данных.

3.6.12. Обсуждение полученных в разделе результатов

Подведем итоги. По сравнению с эвристическими алгоритмами, разобранными в [1] и других литературных источниках, разработанная в настоящем разделе теория позволила:

1) дать общее обоснование этим алгоритмам в рамках асимптотических методов математической статистики и указать условия их применимости (формула (6));

2) выявить принципиально важные условия (7), необходимые и достаточные для несмещенности и состоятельности рассматриваемых оценок;

3) построить доверительные интервалы для зависимости (прогностической функции), трендовой и периодической составляющих, индивидуальных значений временного ряда.

Обсуждение отдельных сторон рассматриваемой проблемы проведено в работах [2, 4, 5].

В рамках математической статистики удается провести анализ не всех распространенных эвристических алгоритмов. Так, довольно часто рекомендуют вначале провести сглаживание («выравнивание») временного ряда, например, методом скользящих средних [1, с.137]. При этом периодическая (сезонная) составляющая меняется (также сглаживается), а погрешности (отклонения от суммы трендовой и периодической составляющих) становятся зависимыми случайными величинами, что делает невозможным применение описанных в настоящем разделе методов.

Теория устойчивости [6] отвергает идею поиска оптимального метода, поскольку зачастую оказывается, что для любого выбранного для рассмотрения метода анализа данных можно подобрать такое понимание оптимальности, что именно этот метод является оптимальным. Например, метод наименьших квадратов в определенном смысле оптимален, если погрешности имеют нормальное распределение, в то время как метод наименьших модулей оптимален, если погрешности имеют распределение Лапласа. В задаче проверки однородности двух независимых выборок установлено [7], что для любого из обычно используемых критериев однородности существует такое распределение на множестве альтернативных гипотез, что рассматриваемый критерий является оптимальным (в том смысле, который определен в [7]).

Работа выполнена в рамках новой парадигмы прикладной (математической) статистики [8, 9]. Изучена непараметрическую модель, не предполагающая, что распределение погрешностей (ошибок, невязок) входит в то или иное параметрическое семейство. Второе основание для того, чтобы именовать рассматриваемые модель и метод непараметрическими – оценивание периодической составляющей произвольного вида, т.е. отказ от выбора периодической составляющей из какого-либо параметрического семейства функций.

Полученные в статье [10] научные результаты, касающиеся средних величин и законов больших чисел в пространствах произвольной природы, могут быть применены для анализа данных в различных научных и прикладных областях. В отличие от них результаты настоящей работы нацелены прежде всего на анализ динамических рядов экономических показателей (временных рядов), необходимость которого часто возникает при организационно-экономическом моделировании с целью решения задач управления хозяйственными единицами [11]. Именно потребности экономики и управления ставят во главу угла модели с одной независимой переменной – временем. Длина периода задается существом рассматриваемой прикладной задачи (для оценки длины периода по статистическим данным нужен другой математический аппарат, разработанный в [12]). Рассмотренные в настоящем разделе постановки можно относить к эконометрике [2], т.е. статистическим методам в экономике. Полученные результаты могут быть применены для прогнозирования и построения экономико-математических моделей, в частности, в рамках неформальной информационной экономики будущего [13].

---

[1] «Бритва (лезвие) О́ккама» — методологический принцип, получивший название по имени английского монаха-францисканца, философа-номиналиста Вильяма Оккама (Ockham, Ockam, Occam; ок. 1285–1349). В упрощенном виде он гласит: «Не следует множить сущее без необходимости» (либо «Не следует привлекать новые сущности без самой крайней на то необходимости»). Этот принцип формирует базис методологического редукционизма. Его называют также принципом бережливости, или законом экономии.