ЧАСТЬ 1-Я.
ВЫСОКИЕ СТАТИСТИЧЕСКИЕ ТЕХНОЛОГИИ
В КОНТРОЛЛИНГЕ

ГЛАВА 1. ВВЕДЕНИЕ. ЧТО ТАКОЕ КОНТРОЛЛИНГ. КОНТРОЛЛИНГ МЕТОДОВ

В обстановке замедления экономического роста нашей страны, а также современных внешнеполитических и внешнеэкономических реалий очевидна актуальность необходимости совершенствования систем и процедур управления промышленными предприятиями и организациями в других отраслях народного хозяйства. Обеспечить технологическую и политическую независимость наша страна может лишь путем перехода на инновационный путь развития. Перспективное направление управленческих инноваций связано с широким использованием контроллинга.

Система контроллинга – это система информационно-аналитической поддержки процесса принятия управленческих решений в организации [1]. Приведем недавнюю формулировку исполнительного директора «Объединения контроллеров» проф., д.э.н. С.Г. Фалько: “Сегодня контроллинг в практике управления российских предприятий понимается как «система информационно-аналитической и методической поддержки по достижению поставленных целей»” [2]. Контроллер разрабатывает правила принятия решений, руководитель принимает решения, опираясь на эти правила.

Инновации в сфере управления в промышленности и других отраслях народного хозяйства основаны, в частности, на использовании новых адекватных организационно-экономических методов. Контроллинг в этой области – это разработка процедур управления соответствием используемых и вновь создаваемых (внедряемых) организационно-экономических методов поставленным задачам. В деятельности управленческих структур выделяем интересующую нас сторону – используемые ими организационно-экономические методы. Такие методы рассматриваем с точки зрения их влияния на эффективность (в широком смысле) процессов управления промышленными предприятиями и организациями других отраслей народного хозяйства. Если речь идет о новых методах (для данного предприятия), то их разработка и внедрение – организационная инновация, соответственно контроллинг организационно-экономических методов можно рассматривать как часть контроллинга инноваций [3].

В статье [4] обосновано выделение в контроллинге новой области – контроллинг организационно-экономических методов. Обсудим содержание этой области, опираясь на предлагаемую нами базовую организационно-экономическую модель промышленного предприятия, в рамках которой описаны основные проблемы разработки современных организационно-экономических методов. В качестве примеров рассмотрим применение статистических методов на различных этапах жизненного цикла продукции, оценки и управления внутренних рисков на промышленном предприятии и учета инфляции при анализе хозяйственной деятельности организации.

1.1. Определения терминов и взаимосвязь понятий

Практика показывает, что основная доля бесплодных дискуссий связана с различным пониманием терминов спорящими сторонами. Например, специально проведенный опрос показал, что границы дохода, определяющие понятие «богатый», различаются на 2 порядка [5]. Поэтому приведем принятые нами определения.

Исходным пунктом обсуждения экономических проблем являются потребности физических или юридических лиц. Для их удовлетворения необходимо решить те или иные задачи. Основа нашего рассмотрения – практическая задача. Она может состоять в том, чтобы достичь определенной цели.

Согласно энциклопедическим источникам метод – систематизированная совокупность шагов, которые необходимо предпринять, чтобы выполнить определенную задачу или достичь определенной цели. Сужение этого понятия на область экономики и управления вслед за сложившейся практикой словоупотребления мы называем организационно-экономическим методом. Другими словами, организационно-экономический метод – это метод в рамках научно-практической специальности «экономика и управление в народном хозяйстве». (Более естественно было бы употреблять термин «экономико-управленческий метод», но массы специалистов говорят и пишут иначе.) Систематизированная совокупность шагов обычно оформляется в виде нормативно-методического документа (методических указаний, инструкции и т.п.) или алгоритма, включенного в корпоративную информационную систему (программный продукт).

Метод всегда основан на том или ином представлении о свойствах окружающего мира. Другими словами, в рассматриваемой области метод разрабатывают на основе той или иной организационно-экономической модели (хотя для формального применения метода знание модели не всегда необходимо).

Термин моде́ль (фр. Modèle) происходит от латинского слова modulus – мера, образец. В общем случае, модель - это объект, в достаточной степени повторяющий свойства моделируемого объекта (прототипа)), существенные для целей конкретного моделирования, и опускающий несущественные свойства, в которых он может отличаться от прототипа. Модель – любой образ, аналог (мысленный или условный: изображение, описание, схема, чертеж, график, карта и т. п.) какого-либо объекта, процесса или явления («оригинала» данной модели).

Как пишет философ, модель - создаваемый с целью получения и (или) хранения информации специфический объект (в форме мысленного образа, описания знаковыми средствами либо материальной системы), отражающий свойства, характеристики и связи объекта-оригинала произвольной природы, существенные для задачи, решаемой субъектом [6]. Модель может быть словесной, графической (чертежи, диаграммы, блок-схемы), математической (формулы, алгоритмы) и т.п. Соответственно организационно-экономическая модель - это модель в рамках научно-практической специальности «экономика и управление в народном хозяйстве».

В организационно-экономической модели выражены знания и представления о конкретном процессе управления, предназначенные для выработки метода решения той или иной задачи в рамках экономики и управления в народном хозяйстве. Зачастую такая модель формулируется в математических терминах. Однако нельзя относить ее к математике, поскольку цели ее разработки, изучения и применения лежат вне математики. Математика – это лишь инструмент, язык, на котором выражаются интересующие исследователя свойства.

Итак, промежуточным звеном на пути от практической задачи к методу ее решения является модель ситуации. Поэтому вполне естественно, что широко используется составной термин «организационно-экономические модели и методы» (или «… методы и модели»). С точки зрения контроллинга возникает ряд вопросов:

Соответствует ли модель реальности?

Соответствует ли метод модели?

Какой метод является наилучшим в рамках данной модели?

Какой модели соответствует используемый метод?

Позволяет ли определенный метод решить поставленную задачу? И т.д.

После того, как определенный метод разработан, необходимо выяснить его условия применимости. Дело в том, что практически полезный метод может быть разработан на основе неадекватной модели. Установить его применимость может как анализ практического опыта применения, так и рассмотрение в рамках другой модели, адекватной реальности.

Соотношение основных понятий в области организационно-экономического моделирования представлено на рисунке 1:

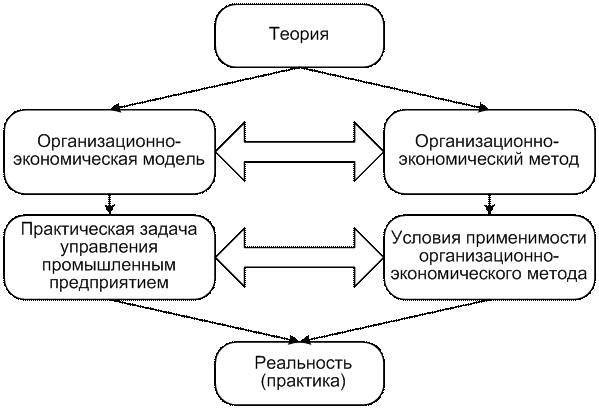
Рисунок 1. Соотношение основных понятий в области организационно-экономического моделирования.

Отметим, что два нижних прямоугольника относятся к реальному миру и должны обсуждаться в терминах практики, в то время как два верхних – к миру идей, теоретических представлений. В предисловии к своей книге 1979 г. [7] один из авторов привел следующую цитату, которую уместно повторить здесь: «Познание есть отражение человеком природы. Но это не простое, не непосредственно, не цельное отражение, а процесс ряда абстракций, формирования, образования понятий, законов etc, (мышление, наука = «логическая идея») и охватывают условно, приблизительно универсальную закономерность вечно движущейся и развивающейся природы» [8]. Применительно к нашей тематике надо сузить «природу» до практики управления промышленными предприятиями.

1.2. Базовая организационно-экономическая модель промышленного предприятия

Для успешного использования организационно-экономических методов с целью совершенствования (повышения эффективности) процессов управления промышленными предприятиями, казалось бы, необходимо рассмотреть промышленное предприятие как систему, выделить составляющие систему элементы и связи между ними. Т.е. исходить из организационной структуры предприятия. На практике используют различные управленческие структуры (см., например, [9, гл.1]). Однако отсутствуют типовые структуры. В одни и те же термины вкладывают разное содержание. Например, на одном предприятии главный инженер руководит всей технической стороной деятельности завода, в том числе всеми цехами. На другом цехами занимается начальник производства, а главный инженер отвечает лишь за вспомогательные службы. В одном случае лаборатория (например, центральная заводская лаборатория на крупном металлургическом предприятии численностью в 2 тыс. сотрудников) делится на отделы, а отделы – на отделения. В другом, наоборот, лаборатории объединяются в отделы, а отделы – в отделения. Вполне естественно, что управленческие структуры носят на себе отпечатки создавших их менеджеров и событий истории предприятия.

Поэтому исходим не из элементов организационной структуры, а из реализуемых на предприятии процессов управления, видов деятельности, в том числе процессов реализации тех или иных функций. Процессы управления с учетом трудоемкости их осуществления группируются по элементам организационной структуры, которая может иметь матричный вид. Другими словами, процессы управления первичны, организационная структура вторична.

Выявим базовую организационно-экономическую модель промышленного предприятия, на основе которой рассмотрим конкретные модели процессов управления предприятиями и их объединениями и организационно-экономические методы, предназначенные для повышения эффективности процессов управления промышленными предприятиями.

Для рациональной работы предприятия необходима организация основного процесса производства, средств производства, труда, инструментального производства, ремонтного хозяйства, технической подготовки производства, транспортного, энергетического и складского хозяйства, службы программно-математического и компьютерно-информационного обеспечения [10, с.6]. На машиностроительных предприятиях целесообразно выделить три существенно отличных вида процессов - производственные процессы, инновационные процессы и процессы функционального обслуживания производственных и инновационных процессов. При этом производственные процессы разделяют на основные (технологические), вспомогательные и обслуживающие. В инновационных процессах выделяют процессы исследования и изобретательства и процессы подготовки производства. К процессам функционального обслуживания относят материально-техническое снабжение, сбыт, планирование, учет, нормирование, финансовое обеспечение, подготовку кадров и др. [11, с.9-10].

Около 100 лет назад в качестве основных функций менеджмента А. Файоль выделял прогнозирование и планирование, проектирование организационных структур, руководство командой (распорядительство), координацию, контроль [12, 13]. Тогда основное внимание уделялось научной организации производства. Позже в связи с ускоряющимися темпами научно-технического прогресса возникла необходимость управления инновационным развитием и инвестициями. Возросшее внимание к предпочтениям потребителей выразилось в развитии маркетинговых исследований. Логистико-ориентированное проектирование бизнеса предполагает разработку организационно-экономических методов и моделей управления материальными ресурсами предприятия. Требованием времени является сертификация предприятий на соответствие стандартам ИСО 9000 по менеджменту качества и ИСО 14000 по экологическому менеджменту. Бурно развиваются системы информационно-аналитической и методической поддержки менеджмента – службы контроллинга [14]. В последние годы в промышленно развитых странах всё большее внимание уделяется управлению рисками, появляются соответствующие национальные стандарты. Можно ожидать, что в недалеком будущем среди топ-менеджеров в массовом порядке появятся директора по рискам, возглавляющие соответствующие интегрированные службы.

Все сказанное выше определяет спектр процессов управления на промышленном предприятии. Такие виды деятельности, как:

- прогнозирование,

- планирование,

- управление рисками,

пронизывают практически все управленческие процессы. Перспективна разработка организационно-экономических методов и моделей в таких функциональных областях управленческой деятельности промышленного предприятия, как:

- контроллинг;

- управление инновациями;

- управление инвестициями;

- менеджмент качества;

- экологический менеджмент;

- маркетинговые исследования;

- управление материальными ресурсами, и др.

Организационно-экономические методы и модели, относящиеся к перечисленным процессам управления, обладают определенным единством, в частности, общим инструментарием. При этом некоторые весьма важные виды деятельности, такие, как управление персоналом или налоговый учет, обладают выраженной спецификой, которую необходимо учитывать при разработке соответствующих организационно-экономических методов и моделей.

1.3. Актуальность разработки теории и методологии организационно-экономического моделирования

Анализ опыта применения организационно-экономических методов при решении конкретных задач управления промышленными предприятиями показал, что накопленный в рассматриваемой научно-практической области потенциал используется хотя и широко, но явно недостаточно и часто неадекватно. Поясним на примерах.

Распространена словесная модель: управленческие решения следует принимать на основе экономических соображений. Предлагаем ее заменить на современную: необходим учет всего комплекса социальных, технологических, экологических, экономических, технологических факторов (СТЭЭП-факторов). Неумение или нежелание учитывать те или иные из этих факторов зачастую приводит к заметным экономическим потерям для конкретного предприятия.

Использование номинальных стоимостных характеристик, таких, как данные бухгалтерского учета, в условиях роста цен и, следовательно, падения покупательной способности денежных единиц может привести, например, к неадекватной оценке финансово-хозяйственного положения предприятия и необоснованным управленческим решениям.

Многие экономические величины не могут принимать произвольные числовые значения. Например, цена или объем выпуска неотрицательны. Следовательно, моделирование таких величин с помощью нормального распределения неадекватно их природе (нормально распределенные случайные величины принимают значения из определенного интервала всегда с положительной вероятностью). Между тем зачастую применяют методы анализа данных, в частности, временных рядов, с использованием распределений Стьюдента, Фишера, хи-квадрат, т.е. опирающиеся на модель нормального распределения. Как неадекватность модели порождения данных влияет на управленческие решения? Известно, что иногда влияние весьма велико (например, при отбраковке выбросов), иногда заметно, иногда мало. В первых двух случаях необходим переход на другие методы [5].

Оценки экспертов или мнения потребителей обычно следует считать измеренными в порядковой шкале. Это значит, что опрашиваемые могут сказать, какой из двух вариантов они предпочитают, но не могут ответить, во сколько раз один из них лучше другого или на сколько лучше. Методы обработки данных должны соответствовать шкалам измерения, и в рассматриваемом случае для получения итогового мнения экспертов надо находить медиану их ответов, а не среднее арифметическое.

Важна проблема выбора адекватных моделей. Например, установлено, что устойчивость хозяйственных решений во времени эквивалентна использованию моделей с дисконтированием. Следовательно, проводить анализ эффективности инвестиционных проектов на предприятии с использованием таких характеристик, как NPV, IRR и т.п., можно лишь в предположении отсутствия резких изменений, например, вследствие научно-технического прогресса. Если же изменения прогнозируются, то целесообразно применять экспертные технологии разработки управленческих решений с учетом всей совокупности СТЭЭП-факторов). Важна также проблема зависимости оптимального решения в той или иной модели от горизонта планирования. Предлагаем использовать асимптотически оптимальные планы.

Обобщая, можно констатировать, что многообразие используемых на практике организационно-экономических методов должно быть упорядочено, проанализировано и доработано в соответствии с современными требованиями. Объем необходимого развития многообразия методов оказывается неожиданно большим. Отметим необходимость анализа устойчивости социально-экономических моделей к отклонениям значений исходных данных и предпосылок моделей [7], значимость рекомендаций, вытекающих из такого анализа. Например, установлено [15], что несмотря на отклонения от предпосылок модели Вильсона управления материальными ресурсами предприятия и неточность определения параметров модели ее использования позволяет добиться сокращения издержек не менее чем на 51,5%.

Для решения ряда практических задач в выделенных выше видах деятельности и функциональных областях управления на промышленном предприятии необходимо разрабатывать новые организационно-экономические методы, например, для оценки функции ожидаемого спроса, организации технико-экономического взаимодействия поставщика и потребителя в условиях нецелесообразности выходного контроля, экологического мониторинга в соответствии с требованиями стандартов ИСО серии 14000, создания корпоративной сети экспертов и т.п.

Таким образом, работы в области теории и методологии организационно-экономического моделирования направлены на:

- систематизацию используемых в практической работе организационно-экономических методов;

- развитие многообразия методов с целью обеспечения их адекватности решаемым задачам;

- разработку новых моделей и методов, необходимых для обеспечения адекватного управления промышленными предприятиями в современных условиях.

Перейдем к примерам. Рассмотрим три сюжета – многообразие одного основных классов организационно-экономических методов – статистических – в соотнесении с этапами жизненного цикла, варианты постановок задач оценки, анализа и управления внутренними рисками на промышленном предприятии и необходимость учета динамики цен (инфляции) при анализе хозяйственной деятельности организации.

1.4. Применение конкретных организационно-экономических методов на различных этапах жизненного цикла продукции

Чтобы продемонстрировать специфику практического применения различных видов организационно-экономических методов, рассмотрим их применение на различных этапах жизненного цикла промышленной продукции (ЖЦПП). Выделим 11 этапов, перечисленных в табл.1.

Таблица 1 – Статистические методы
на различных этапах ЖЦПП

№	Этапы жизненного цикла продукции (согласно ИСО 9004)	Вид методов					Спец. модели
		а	б	в	г	д
1	Маркетинг, поиски и изучение рынка	+	-	-	+	-	+
2	Проектирование и/или разработка технических требований, разработка продукции (опытного образца)	+	-	-	+	+	+
3	Поиски поставщиков и оптовых покупателей, организация материально-технического снабжения	+	-	-	-	-	+
4	Подготовка и разработка производственных (технологических) процессов	+	+	+	+	+	+
5	Производство продукции	+	+	+	+	-	+
6	Контроль качества продукции, проведение испытаний и обследований	+	+	+	+	+	+
7	Упаковка и хранение продукции	+	+	+	+	+	+
8	Реализация (сбыт) и распределение (доставка) продукции	+	+	-	-	-	+
9	Монтаж и эксплуатация продукции у потребителей	+	+	+	+	+	+
10	Технические помощь и обслуживание	+	-	-	-	-	+
11	Утилизация после использования	+	+	+	+	-	+

На каждом из этих этапов успешно применяются статистические методы, основанные на вероятностных моделях (т.е. моделях, описанных в терминах теории вероятностей и математической статистики). Если же выделить конкретные виды статистических методов, то проявляется специфика – на одних этапах жизненного цикла одни методы, на других – другие. В соответствии с практикой работы Центра статистических методов и информатики по созданию и внедрению программных продуктов в рассматриваемой области [16, гл.13] рассмотрим 5 видов статистических методов:

а) прикладная статистика (статистические методы оценки точности и стабильности технологических процессов);

б) статистический приемочный контроль (партий продукции);

в) статистическое регулирование технологических процессов (обнаружение разладки, статистический контроль процессов);

г) планирование эксперимента (с целью построения модели технологического процесса и нахождения оптимальных значений контролируемых факторов);

д) надежность и испытания (оценка и контроль надежности по результатам испытаний и эксплуатации промышленной продукции).

В табл.1 знак «+» показывает, что методы соответствующего вида активно применяются на соответствующем этапе ЖЦПП, знак «-» означает противоположное. Последний столбец посвящен специально разработанным специалистами организационно-экономическим моделям и методам, непосредственно учитывающим особенности конкретного производства. Практический опыт показывает, что все клетки в этом столбце должны быть отмечены знаком «+».

Сводка, приведенная в табл.1, показывает, что организационно-экономические (в данном случае – статистические) методы широко применяются на всех этапах жизненного цикла продукции.

1.5. СТЭЭП-факторы и моделирование рисков
предприятия

Важность теоретико-методологического анализа выпукло проявляется при рассмотрении второго примера – внутренних рисков промышленного предприятия. К ним естественно отнести:

- риски, связанные с выпуском дефектной продукции;

- риски аварий;

- экологические риски;

- инновационные риски;

- социальные риски (риски конфликтов).

Для предприятия важны и внешние риски, прежде всего коммерческие (связанные с деятельностью поставщиков, потребителей, конкурентов, партнеров) и финансовые (порожденные событиями на уровне государства). Каждый из этих видов рисков обычно рассматривается отдельно, специалистами в соответствующей области. Однако для нужд управления предприятием в соответствии с концепцией необходимости учета всей совокупности СТЭЭП-факторов [17] перечисленные виды рисков необходимо рассматривать совместно.

Термин «риск» использован для описания явления в реальном мире, связанного с неопределенностью, возможностями различного развития ситуации. Можно сказать, что риск – это нежелательная возможность. Для описания неопределенностей чаще всего используют вероятностно-статистические методы (прежде всего методы статистики нечисловых данных, в том числе интервальной статистики и интервальной математики). Полезны методы теории нечеткости и методы теории конфликтов (теории игр). Математический инструментарий применяется в имитационных, эконометрических, экономико-математических моделях, реализованных обычно в виде программных продуктов.

Некоторые виды неопределенностей связаны с безразличными к организации силами - природными (погодные условия) или общественными (смена правительства). Если явление достаточно часто повторяется, то его естественно описывать в вероятностных терминах. Так, прогноз дефектности при массовом производстве вполне естественно вести в вероятностных терминах. Если же событие единично, то вероятностное описание вызывает внутренний протест, поскольку частотная интерпретация вероятности невозможна. Так, для описания неопределенности, связанной с исходами выборов Совета директоров, лучше использовать методы теории нечеткости и интервальной математики (интервал – удобный частный случай описания нечеткого множества). Наконец, если неопределенность связана с активными действиями соперников или партнеров, целесообразно применять методы анализа конфликтных ситуаций, т.е. методы теории игр, прежде всего антагонистических игр, но иногда полезны и более новые методы кооперативных игр, нацеленных на получение устойчивого компромисса.

При вероятностно-статистическом моделировании риска применяют различные характеристики риска – математическое ожидание потерь, их дисперсия, медиана, другие квантили. В [4, 15] разработаны непараметрические оценки характеристик риска.

Цель управления риском формулируют по-разному. Так, она может состоять в минимизации:

1) математического ожидания (ожидаемых потерь),

2) квантиля распределения (например, медианы);

3) дисперсии (с целью обеспечения предсказуемости),

4) линейной комбинации математического ожидания и среднего квадратического отклонения;

5) математического ожидания функции ущерба, и т.д.

Естественной является двухкритериальная постановка, например, минимизация, как среднего ущерба, так и дисперсии (чем меньше дисперсия, тем точнее прогнозирование). От двухкритериальной постановки необходимо тем или иным образом перейти к однокритериальной. Обычно один из критериев переводят в ограничение. При таком подходе страхование рисков – это способ уменьшения неопределенности будущего развития ситуации при заданном ограничении на рост расходов предприятия.

Подчеркнем, что понятные на интуитивном уровне понятия риска и неопределенности могут анализироваться с помощью различных моделей, использующих тот или иной математический аппарат, многообразные постановки целей управления в рамках одной и той же модели. Многообразие организационно-экономических моделей управления риском нецелесообразно искусственно сужать.

1.6. Необходимость учет инфляции при анализе
хозяйственной деятельности организации

Организационно-экономические методы и модели полезны при решении различных задач информационно-аналитической поддержки процессов принятия решений при управлении предприятиями. В качестве примера обсудим использование индексов инфляции при анализе хозяйственной деятельности [16, гл.7]. Основные понятия здесь - потребительская корзина, т.е. перечень товаров и услуг и фиксированные объемы их потребления, S(t) – ее стоимость как функция времени t, индекс инфляции I(t₁, t₂) = S(t₂)/S(t₁).

Таблица 2 – Анализ динамики прибыли предприятия, млн. руб.

Год	Прибыль, млн. руб.	Индекс инфляции	Накопленная инфляция	Прибыль в сопоставимых ценах (на начало 2001 г.)
(1)	(2)	(3)	(4)	(5)
2000	1,0			1,0
2001	1,1	1,186	1,186	1,1/1,186 = 0,927
2002	1,3	1,151	1,365	1,3/1,365 = 0,952
2003	1,4	1,12	1,529	1,4/1,529 = 0,912
2004	1,5	1,117	1,708	1,5/1,708 = 0,878
2005	1,7	1,109	1,894	1,7/1,894 = 0,896
2006	1,8	1,09	2,064	1,8/2,064 = 0,872
2007	2,0	1,119	2,310	2,0/2,310 = 0,866

В табл.2 в столбце (2) приведены значения (по годам) одного из естественных показателей хозяйственной деятельности предприятия – прибыли (для определенности – фактической прибыли, т.е. полученной как разность (сальдо) фактических доходов и издержек за период, ср. обсуждение в [18, с. 185-186]). Наблюдаем рост прибыли на 100% за 7 лет (дальнейшие годы кризиса не рассматриваем). Казалось бы, предприятие успешно развивается. Однако происходил рост цен. Официальные данные (Росстата) об инфляции приведены в столбце (3) – погодовые, и в столбце (4) – накопленные с начала века. В столбце (5) приведены пересчитанные значения прибыли - в сопоставимых ценах на начало 2001 г. Видим, что реальное значение прибыли не растет, а наоборот, имеет тенденцию к снижению и к концу периода упала на 13,4% (а не выросла на 100%, как в номинальных ценах). Ясно, что это меняет оценку хозяйственной деятельности предприятия – с выраженной положительной на умеренно-отрицательную

Разработаны методы оценки динамики цен по независимо собранной информации, результаты анализа реальных данных приведены в [15, 19, 20].

* * *

Многие вопросы, затронутые во введении, с тех или иных позиций и с различной степенью подробности рассматривались в публикациях в журнале «Контроллинг» [21-25].

Контроллинг имеет ряд аспектов. Выделяют стратегический контроллинг [26], сущность которого: «Делать правильное дело», и оперативный контроллинг [27], посвященный тому, как следовать правилу: «Делать дело правильно» ([1], с.20). В статье [28] нами впервые выдвинута и обоснована концепция «контроллинга методов», которая может быть применена в любой из ранее выделенных областей контроллинга – в стратегическом и оперативном контроллинге, в контроллинге некоммерческих организаций, вузов, малых и средних предприятий и т.д. Инновации в сфере управления основаны, в частности, на использовании новых адекватных организационно-экономических (а также математических и статистических) методов, в частности, таких, как системно-когнитивный анализ [29, 30] Контроллинг в этой области – это разработка процедур управления соответствием используемых и вновь создаваемых (внедряемых) организационно-экономических методов поставленным задачам. В деятельности управленческих структур выделяем интересующую нас сторону – используемые ими организационно-экономические методы. Такие методы рассматриваем с точки зрения их влияния на эффективность (в широком смысле) процессов управления предприятиями и организациями. Если речь идет о новых методах (для данной организации), то их разработка и внедрение – управленческая инновация, соответственно контроллинг организационно-экономических методов можно рассматривать как часть контроллинга инноваций [3].

Современные организационно-экономические методы в значительной мере опираются на перспективное направление теоретической и вычислительной математики - системную нечеткую интервальную математику [32, 33].

ГЛАВА 2. ОБЩИЙ ВЗГЛЯД НА МАТЕМАТИЧЕСКИЕ
И ИНСТРУМЕНТАЛЬНЫЕ МЕТОДЫ КОНТРОЛЛИНГА

2.1. Новая парадигма математических
методов экономики

Математические и инструментальные методы экономики – одна из специальностей научных работников, относящаяся к экономическим наукам. Она посвящена разработке интеллектуальных инструментов для решения задач теории и практики экономического анализа.

Конкретные модели и методы экономики предприятия и организации производства основаны, в частности, на научных результатах таких научных областей, как организационно-экономическое и экономико-математическое моделирование, эконометрика и статистика. Эти научные области относятся к математическим методам экономики. Они предоставляют интеллектуальные инструменты для решения различных задач стратегического планирования и развития предприятий, организации производства и управления хозяйствующими субъектами, конструкторской и технологической подготовки производства. В монографии [34] на с.395-424 выделено 195 групп задач управления промышленными предприятиями и для них указаны базовые группы экономико-математических методов и моделей.

Развитие математических методов экономики привело к формированию новой парадигмы в этой области, существенно отличающейся от послевоенной парадигмы, созданной в 1950-1970 гг. и используемой многими преподавателями и научными работниками и в настоящее время. Настоящая статья посвящена основным идеям новой парадигмы математических методов экономики.

2.1.1. Основные понятия

Целесообразно начать с определений используемых понятий.

Термин «парадигма» происходит от греческого «paradeigma» – пример, образец и означает совокупность явных и неявных (и часто не осознаваемых) предпосылок, определяющих научные исследования и признанных на определенном этапе развития науки [35].

Организационно-экономическое моделирование – научная, практическая и учебная дисциплина, посвященная разработке, изучению и применению математических и статистических методов и моделей в экономике и управлении народным хозяйством, прежде всего промышленными предприятиями и их объединениями [36].

Экономико-математическое моделирование – описание экономических процессов и явлений в виде экономико-математических моделей. При этом экономико-математическая модель – математическое описание экономического процесса или объекта, произведенное в целях их исследования и управления ими: математическая запись решаемой экономической задачи (поэтому часто термины «модель» и «задача» употребляются как синонимы). В самой общей форме модель – условный образ объекта исследования, сконструированный для упрощения этого исследования. При построении модели предполагается, что ее непосредственное изучение дает новые знания о моделируемом объекте [37].

Эконометрика – это наука, изучающая конкретные количественные и качественные взаимосвязи экономических объектов и процессов с помощью математических и статистических методов и моделей [38]. Обычно используют несколько более узкое определение: эконометрика – это статистические методы в экономике [39].

Статистика исходит прежде всего из опыта; недаром ее зачастую определяют как науку об общих способах обработки результатов эксперимента [40]. Прикладная статистика – это наука о том, как обрабатывать данные [5].

Очевидна близость, переплетение, зачастую совпадение всех научных, практических и учебных дисциплин, рассмотренных выше. К ним можно прибавить еще несколько: теорию принятия решений, системный анализ, кибернетику, исследование операций… Исходя из нашего профессионального опыта, попытки искусственно ввести границы между этими дисциплинами не являются плодотворными.

На Вторых Чарновских чтениях [41] работала секция «Организационно-экономическое и экономико-математическое моделирование, эконометрика и статистика». Это название было получено путем объединения названий учебных дисциплин «Организационно-экономическое моделирование», «Эконометрика», «Прикладная статистика», «Статистика», которые изучаются студентами Научно-учебного комплекса «Инженерный бизнес и менеджмент», а также названия Лаборатории экономико-математических методов в контроллинге Научно-образовательного центра «Контроллинг и управленческие инновации» Московского государственного технического университета им. Н.Э. Баумана. На заседании секции была проведена дискуссия по выбору наиболее адекватного названия научной области, к которой относились представленные работы. Приведенное выше название признано слишком длинным. Название «Организационно-математическое моделирование» отклонено как малоизвестное и сужающее рассматриваемую тематику. Одобрено название «Математическое моделирование в организации производства», а при проведении конференций по более широкой тематике – «Математическое моделирование экономики и управления». Заметная доля исследований в этой области относятся к научной специальности «Математические и инструментальные методы экономики», практически все используют те или иные математические методы экономики.

2.1.2. Разработка новой парадигмы

Организационно-экономическое и экономико-математическое моделирование, эконометрика и статистика предоставляют интеллектуальные инструменты для решения различных задач организации производства и управления предприятиями и организациями. Например, в учебнике по организации и планированию машиностроительного производства (производственному менеджменту) [11] более 20 раз используются эконометрические (если угодно, математические и статистические) методы и модели [23].

Рассматриваемые методы широко используются для решения различных задач теории и практики экономического анализа. В частности, проводится когнитивное моделирование [42] развития наукоемкой промышленности (на примере оборонно-промышленного комплекса), модельное обоснование инновационного развития наукоемкого сектора российской экономики [43]. Моделируют организационные изменения [44], применяют информационные технологии [45]. Все шире используются экспертные оценки [46], в том числе для построения обобщенных показателей (рейтингов) [47].

Во второй половине 1980-х гг. в нашей стране развернулось общественное движение по созданию профессионального объединения специалистов в области организационно-экономического и экономико-математического моделирования, эконометрики и статистики (кратко – статистиков). Аналоги такого объединения - британское Королевское статистическое общество (основано в 1834 г.) и Американская статистическая ассоциация (создана в 1839 г.). К сожалению, деятельность учрежденной в 1990 г. Всесоюзной статистической ассоциации (ВСА) [48] оказалась парализованной в результате развала СССР.

В ходе организации ВСА проанализировано состояние и перспективы развития рассматриваемой области научно-прикладных исследований и осознаны основы уже сложившейся к концу 1980-х гг. новой парадигмы организационно-экономического моделирования, эконометрики и статистики.

В течение следующих лет новая парадигма развивалась и к настоящему времени оформлена в виде серии монографий и учебников для вузов, состоящей более чем из 10 книг (см. ниже).

2.1.3. Сравнение старой и новой парадигм

Типовые исходные данные в новой парадигме – объекты нечисловой природы (элементы нелинейных пространств, которые нельзя складывать и умножать на число, например, множества, бинарные отношения), а в старой – числа, конечномерные векторы, функции. Ранее (в старой парадигме) для расчетов использовались разнообразные суммы, однако объекты нечисловой природы нельзя складывать, поэтому в новой парадигме применяется другой математический аппарат, основанный на расстояниях между объектами нечисловой природы и решении задач оптимизации.

Изменились постановки задач анализа данных и экономико-математического моделирования. Старая парадигма математической статистики исходит из идей начала ХХ в., когда К. Пирсон предложил четырехпараметрическое семейство распределений для описания распределений реальных данных. В это семейство как частные случаи входят, в частности, подсемейства нормальных, экспоненциальных, Вейбулла-Гнеденко, гамма-распределений. Сразу было ясно, что распределения реальных данных, как правило, не входят в семейство распределений Пирсона (об этом говорил, например, академик С.Н. Бернштейн в 1927 г. в докладе на Всероссийском съезде математиков [49]. Однако математическая теория параметрических семейств распределений (методы оценивания параметров и проверки гипотез) оказалась достаточно интересной, и именно на ней до сих пор основано преподавание во многих вузах. Итак, в старой парадигме основной подход к описанию данных - распределения из параметрических семейств, а оцениваемые величины – их параметры, в новой парадигме рассматривают произвольные распределения, а оценивают - характеристики и плотности распределений, зависимости, правила диагностики и др. Центральная часть теории – уже не статистика числовых случайных величин, а статистика в пространствах произвольной природы, т.е. нечисловая статистика (см. основную монографию [36] по этой тематике).

В старой парадигме источники постановок новых задач - традиции, сформировавшиеся к середине ХХ века, а в новой - современные потребности математического моделирования и анализа данных (XXI век), т.е. запросы практики. Конкретизируем это общее различие. В старой парадигме типовые результаты - предельные теоремы, в новой - рекомендации для конкретных значений параметров, в частности, объемов выборок. Изменилась роль информационных технологий – ранее они использовались в основном для расчета таблиц (в частности, информатика находилась вне математической статистики), теперь же они - инструменты получения выводов (имитационное моделирование, датчики псевдослучайных чисел, методы размножение выборок, в т.ч. бутстреп, и др.). Вид постановок задач приблизился к потребностям практики – при анализе данных от отдельных задач оценивания и проверки гипотез перешли к статистическим технологиям (технологическим процессам анализа данных). Выявилась важность проблемы «стыковки алгоритмов» - влияния выполнения предыдущих алгоритмов в технологической цепочке на условия применимости последующих алгоритмов. В старой парадигме эта проблема не рассматривалась, для новой – весьма важна.

Если в старой парадигме вопросы методологии моделирования практически не обсуждались, достаточными признавались схемы начала ХХ в., то в новой парадигме роль методологии (учения об организации деятельности) [50] является основополагающей. Резко повысилась роль моделирования – от отдельных систем аксиом произошел переход к системам моделей. Сама возможность применения вероятностного подхода теперь – не «наличие повторяющегося комплекса условий» (реликт физического определения вероятности, использовавшегося до аксиоматизации теории вероятностей А.Н. Колмогоровым в 1930-х гг.), а наличие обоснованной вероятностно-статистической модели. Если раньше данные считались полностью известными, то для новой парадигмы характерен учет свойств данных, в частности, интервальных и нечетких. Изменилось отношение к вопросам устойчивости выводов – в старой парадигме практически отсутствовал интерес к этой тематике, в новой разработана развитая теория устойчивости (робастности) выводов по отношению к допустимым отклонениям исходных данных и предпосылок моделей.

Результаты сравнения парадигм удобно представить в виде табл. 1. Сопоставление будет продолжено в дальнейших разделах настоящей монографии. В частности, будет выявлена роль современных высоких статистических технологий, заменяющих неупорядоченную массу отдельных методов оценивания и проверки гипотез. Будут достаточно подробно рассмотрены основные "точки роста" современной прикладной математической статистики.

Таблица 3 – Сравнение основных характеристик
старой и новой парадигм

№	Характеристика	Старая парадигма	Новая парадигма
1	Типовые исходные данные	Числа, конечномерные вектора, функции	Объекты нечисловой природы [36]
2	Основной подход к моделированию данных	Распределения из параметрических семейств	Произвольные функции распределения
3	Основной математический аппарат	Суммы и функции от сумм	Расстояния и алгоритмы оптимизации [36]
4	Источники постановок новых задач	Традиции, сформировавшиеся к середине ХХ века	Современные прикладные потребности анализа данных (XXI век)
5	Отношение к вопросам устойчивости выводов	Практически отсутствует интерес к устойчивости выводов	Развитая теория устойчивости (робастности) выводов [34]
6	Оцениваемые величины	Параметры распределений	Характеристики, функции и плотности распределений, зависимости, правила диагностики и др.
7	Возможность применения	Наличие повторяющегося комплекса условий	Наличие обоснованной вероятностно-статистической модели
8	Центральная часть теории	Статистика числовых случайных величин	Нечисловая статистика [36]
9	Роль информационных технологий	Только для расчета таблиц (информатика находится вне статистики)	Инструменты получения выводов (датчики псевдослучайных чисел, размножение выборок, в т.ч. бутстреп, и др.)
10	Точность данных	Данные полностью известны	Учет неопределенности данных, в частности, интервальности и нечеткости [33]
11	Типовые результаты	Предельные теоремы (при росте объемов выборок)	Рекомендации для конкретных объемов выборок
12	Вид постановок задач	Отдельные задачи оценивания параметров и проверки гипотез	Высокие статистические технологии (технологические процессы анализа данных) [51]
13	Стыковка алгоритмов	Не рассматривается	Весьма важна при разработке процессов анализа данных
14	Роль моделирования	Мала (отдельные системы аксиом)	Системы моделей – основа анализа данных
15	Анализ экспертных оценок	Отдельные алгоритмы	Прикладное «зеркало» общей теории [52]
16	Роль методологии	Практически отсутствует	Основополагающая [34, 53]

2.2. Учебная литература, подготовленная
в соответствии с новой парадигмой

В 1992 г. на базе секции статистических методов Всесоюзной статистической ассоциации была организована Российская ассоциация статистических методов, а в 1996 г. – Российская академия статистических методов. В соответствии с новой парадигмой проводились научные исследования, публиковались статьи, по этой тематике были организованы семинары и конференции. Однако размах работ сокращался по сравнению с концом 1980-х годов, как и число участвующих в них исследователей. Поэтому на рубеже тысячелетий нами было принято решение сосредоточить усилия на подготовке учебной литературы, соответствующей новой парадигме.

Первым был учебник по эконометрике [39], переизданный в 2003 г. и в 2004 г. Четвертое издание «Эконометрики» [16] существенно переработано. Оно соответствует первому семестру курса, в отличие от первых трех изданий, содержащих материалы для годового курса. В учебник [16] включены новые разделы, в частности, полностью обновлена глава про индекс инфляции, добавлено методическое обеспечение.

В фундаментальном курсе по прикладной статистике [5], выпущенном в 2006 г., в рамках новой парадигмы рассмотрены как нечисловая статистика, так и классические разделы прикладной статистики, посвященные методам обработки элементов линейных пространств - чисел, векторов и функций (временных рядов).

В том же 2006 г. в рамках новой парадигмы был выпущен курс теории принятия решений [54]. Его сокращенный (в 1,5 раза) вариант вышел годом раньше [55].

В соответствии с потребностями практики в России в 2005 г. введена новая учебная специальность 220701 «Менеджмент высоких технологий», относящаяся к тогда же введенному направлению подготовки 220700 «Организация и управление наукоемкими производствами», предназначенному для обеспечения инженерами-менеджерами высокотехнологичных предприятий. Большинство студентов научно-учебного комплекса «Инженерный бизнес и менеджмент» МГТУ им. Н.Э. Баумана обучаются по этой специальности. Общий взгляд на нее представлен в учебнике [56].

Государственным образовательным стандартом по специальности «Менеджмент высоких технологий» предусмотрено изучение дисциплины «Организационно-экономическое моделирование». Одноименный учебник выпущен в трех частях (томах). Первая из них [36] посвящена сердцевине новой парадигмы – нечисловой статистике. Ее прикладное «зеркало» - вторая часть [52], современный учебник по экспертным оценкам. В третьей части [57] наряду с основными постановками задач анализа данных (чисел, векторов, временных радов) и конкретными статистическими методами анализа данных классических видов (чисел, векторов, временных рядов) рассмотрены вероятностно-статистические модели в технических и экономических исследованиях, медицине, социологии, истории, демографии, а также метод когнитивных карт (статистические модели динамики).

В названиях еще двух учебников есть термин «организационно-экономическое моделирование». Это книги по менеджменту [58] и по теории принятия решений [59], в которых содержание соответствует новой парадигме, в частности, подходам организационно-экономического моделирования. Отметим, что, в учебнике [59] значительно большее внимание по сравнению с более ранним учебником [54] уделено теории и практике экспертных оценок, в то время как проблемы менеджмента, составлявшиеся основное содержание первой части учебника [54], выделены для обсуждения в отдельное издание [58].

К рассмотренному выше корпусу учебников примыкают справочник по минимально необходимым (для использования наших учебников) понятиям теории вероятностей и прикладной математической статистики [60] и книги по промышленной и экологической безопасности [61] и [62], в которых большое место занимает изложение научных результатов в соответствии с новой парадигмой, в частности, активно используются современные статистические и экспертные методы, математическое моделирование. Опубликовано еще несколько изданий (в частности, пособие [15] и монография [34]), но от их рассмотрения воздержимся, чтобы не загромождать изложение излишними подробностями.

Публикация учебной литературы на основе новой парадигмы шла непросто. Зачастую издание удавалось с третьего-четвертого раза. Неоценима поддержка Научно-учебного комплекса «Инженерный бизнес и менеджмент» и МГТУ им. Н.Э. Баумана в целом, Учебно-методического объединения вузов по университетскому политехническому образованию.

Все перечисленные монографии, учебники, учебные пособия имеются в Интернете в свободном доступе. Соответствующие ссылки приведены на персональной странице одного из авторов настоящей монографии на сайте МГТУ им. Н.Э. Баумана http://www.bmstu.ru/ps/~orlov/ и в аналогичной теме нашего форума http://forum.orlovs.pp.ru/viewtopic.php?f=1&t=1370, однако целесообразно иметь в виду, что из-за растянутого по времени процесса издания иногда различны названия книг в бумажном и электронном вариантах.

Информация о новой парадигме появилась в печати недавно – в 2012 г. (см. ссылки на соответствующие публикации в [63]). Мы не без оснований опасались, что обладающие административной властью и связями сторонники старой парадигмы, отстаивая свое спокойствие и положение, могут помешать нам довести работу до конца. В своей издательской тактике мы следовали примеру Гаусса, который воздерживался от публикации работ по неевклидовой геометрии, опасаясь «криков беотийцев» [64, с.91].

На основе сказанного выше полагаем, что к настоящему моменту рекомендация Учредительного съезда ВСА по созданию комплекта учебной литературы на основе новой парадигмы выполнена. Предстоит большая работа по внедрению новой парадигмы организационно-экономического моделирования, эконометрики и статистики в научные исследования и преподавание.

2.3. Высокие статистические технологии

Новая парадигма математических методов экономики реализуется с помощью соответствующих моделей и методов. В области статистического анализа данных - с помощью высоких статистических технологий.

При практическом использовании методов прикладной статистики применяются, как известно всем реально работающим со статистическими данными исследователям, не отдельные методы описания данных, оценивания, проверки гипотез, а развернутые цельные процедуры - так называемые «статистические технологии». Понятие «статистическая технология» в анализе данных аналогично понятию «технологический процесс» в теории и практике организации производства.

Вполне естественно, что одни статистические технологии лучше соответствуют потребностям исследователя (пользователя, статистика), другие хуже, одни – современные, а другие – устаревшие, свойства одних изучены, а других – нет.

В различных областях человеческой деятельности применяют высокие технологии, под которыми понимают технологии, наиболее новые и прогрессивные на текущий момент времени. В начале XXI в. нами был введен термин «высокие статистические технологии». Первоначально он появился в печати в 2002 г. в первом издании нашего учебнике «Эконометрика» [39], а в следующем году вышла программная статья [51] (поступила в редакцию 16 марта 2001 г., т.е. ранее, чем мы приступили к подготовке учебника [39]). Наш основной сайт http://orlovs.pp.ru/ с книгами и статьями в открытом доступе получил название «Высокие статистические технологии». Сайт был введен в эксплуатацию в октябре 2004 г., к настоящему времени его посетили более 1 млн. раз. Многие учебники и справочники, размещенные (2008) на сайте Лаборатории экономико-математических методов Московского государственного технического университета им. Н.Э. Баумана http://ibm.bmstu.ru/nil/biblio.html, имеют названия из двух частей. Первая часть – серийное название «Высокие статистические технологии», вторая – название конкретной монографии. (В выпущенных позже печатных изданиях серийное название другое – «Организационно-экономическое моделирование»; оно было изменено в соответствии с названием учебной дисциплины по специальности «Менеджмент высоких технологий».)

Таким образом, термин «высокие статистические технологии» стал широко использоваться. Представляется целесообразным обсудить его содержание, подвести первые итоги применения понятия, обозначенного этим термином, в научных исследованиях и преподавании.

2.3.1. Статистические технологии

Статистический анализ конкретных данных, как правило, включает в себя целый ряд процедур и алгоритмов, выполняемых последовательно, параллельно или по более сложной схеме. В частности, с точки зрения организатора (а также контроллера) прикладного статистического исследования можно выделить следующие этапы:

- планирование статистического исследования (включая разработку анкет, бланков наблюдения и учета и других форм сбора данных; их апробацию; подготовку сценариев интервью и анализа данных и т.п.);

- организация сбора необходимых статистических данных по оптимальной или рациональной программе (планирование выборки, создание организационной структуры и подбор команды статистиков, подготовка кадров, которые будут заниматься сбором данных, а также контролеров данных и т.п.);

- непосредственный сбор данных и их фиксация на тех или иных носителях (с контролем качества сбора и отбраковкой ошибочных данных по соображениям предметной области);

- первичное описание данных (расчет различных выборочных характеристик, функций распределения, непараметрических оценок плотности, построение гистограмм, корреляционных полей, различных таблиц и диаграмм и т.д.),

- оценивание тех или иных числовых или нечисловых характеристик и параметров распределений (например, непараметрическое интервальное оценивание коэффициента вариации или восстановление зависимости между откликом и факторами, т.е. оценивание функции),

- проверка статистических гипотез (иногда их цепочек - после проверки предыдущей гипотезы принимается решение о проверке той или иной последующей гипотезы; например, после проверки адекватности линейной регрессионной модели и отклонения этой гипотезы может проверяться адекватность квадратичной модели),

- более углубленное изучение, т.е. одновременное применение различных алгоритмов многомерного статистического анализа, алгоритмов диагностики и построения классификации, статистики нечисловых и интервальных данных, анализа временных рядов и др.;

- проверка устойчивости полученных оценок и выводов относительно допустимых отклонений исходных данных и предпосылок используемых вероятностно-статистических моделей, в частности, изучение свойств оценок методом размножения выборок и другими численными методами;

- применение полученных статистических результатов в прикладных целях, т.е. для формулировки выводов в терминах содержательной области (например, для диагностики конкретных материалов, построения прогнозов, выбора инвестиционного проекта из предложенных вариантов, нахождения оптимальных режима осуществления технологического процесса, подведения итогов испытаний образцов технических устройств и др.),

- составление итоговых отчетов, в частности, предназначенных для тех, кто не является специалистами в статистических методах анализа данных, в том числе для руководства - «лиц, принимающих решения», с учетом возможности и использования - при необходимости - в суде и в арбитражном суде.

Возможны и иные структуризации различных статистических технологий, предназначенных для решения конкретных прикладных задач. Важно подчеркнуть, что квалифицированное и результативное применение статистических методов - это отнюдь не проверка одной отдельно взятой статистической гипотезы или оценка характеристик или параметров одного заданного распределения из фиксированного семейства. Подобного рода операции - только отдельные кирпичики, из которых складывается статистическая технология.

Итак, процедура статистического анализа данных – это информационный технологический процесс, другими словами, та или иная информационная технология. Статистическая информация подвергается разнообразным операциям (последовательно, параллельно или по более сложным схемам). В настоящее время об автоматизации всего процесса статистического анализа данных говорить было бы несерьезно, поскольку имеется слишком много нерешенных проблем, вызывающих дискуссии среди исследователей-статистиков. Наличие разногласий – причина того, что так называемые «экспертные системы в области статистического анализа данных» пока не стали рабочим инструментом статистиков. И вряд ли станут в обозримом будущем, поскольку для создания научно обоснованных экспертных систем в этой области необходимо провести развернутые научные исследования.

2.3.2. Проблема «стыковки» алгоритмов

В современной научной и особенно учебной литературе статистические технологии рассматриваются явно недостаточно. В частности, обычно все внимание сосредотачивается на том или ином элементе технологической цепочки, а переход от одного элемента к другому остается в тени. Между тем проблема «стыковки» статистических алгоритмов, как известно, требует специального рассмотрения (см., например, [65, 66]), поскольку в результате использования предыдущего алгоритма зачастую нарушаются условия применимости последующего. В частности, результаты наблюдений могут перестать быть независимыми, может измениться их распределение и т.п.

Так, вполне резонной выглядит рекомендация: сначала разбейте данные на однородные группы, а потом в каждой из групп проводите статистическую обработку, например, регрессионный анализ. Однако эта рекомендация под кажущейся прозрачностью содержит подводные камни. Действительно, как поставить задачу в вероятностно-статистических терминах? Если, как обычно, примем, что исходные данные - это выборка, т.е. совокупность независимых одинаково распределенных случайных элементов, то классификация приведет к разбиению этих элементов на группы. В каждой группе элементы будут зависимы между собой, а их распределение будет зависеть от группы, куда они попали. Отметим, что в типовых ситуациях границы классов стабилизируются, а это значит, что асимптотически элементы кластеров становятся независимыми. Однако их распределение не может быть нормальным. Например, если исходное распределение было нормальным, то распределения в классах будет усеченным нормальным. Это означает, что необходимо пользоваться непараметрическими методами.

Разберем другой пример. При проверке статистических гипотез большое значение имеют такие хорошо известные характеристики статистических критериев, как уровень значимости и мощность. Методы их расчета и использования при проверке одной гипотезы обычно хорошо известны. Если же сначала проверяется одна гипотеза, а потом с учетом результатов ее проверки (конкретнее, если первая гипотеза принята) - вторая, то итоговую процедуру также можно рассматривать как проверку некоторой (более сложной) статистической гипотезы. Она имеет характеристики (уровень значимости и мощность), которые, как правило, нельзя простыми формулами выразить через характеристики двух составляющих гипотез, а потому они обычно неизвестны. Лишь в некоторых простых случаях характеристики итоговой процедуры можно рассчитать. В результате итоговую процедуру нельзя рассматривать как научно обоснованную, она относится к эвристическим алгоритмам. Конечно, после соответствующего изучения, например, методом Монте-Карло, она может войти в число научно обоснованных процедур прикладной статистики.

2.3.3. Термин «высокие статистические технологии»

Термин «высокие технологии» популярен в современной научно-технической литературе. Он используется для обозначения наиболее передовых технологий, опирающихся на последние достижения научно-технического прогресса. Есть такие технологии и среди технологий статистического анализа данных - как в любой интенсивно развивающейся научно-практической области.

Примеры высоких статистических технологий и входящих в них алгоритмов анализа данных, подробный анализ современного состояния и перспектив развития даны при обсуждении «точек роста» прикладной статистики и других статистических методов [67], подробнее обсуждаются в следующем разделе. В качестве «высоких статистических технологий» были выделены технологии непараметрического анализа данных; устойчивые (робастные) технологии; технологии, основанные на размножении выборок, на использовании достижений статистики нечисловых данных и статистики интервальных данных.

Обсудим пока не вполне привычный термин «высокие статистические технологии». Каждое из трех слов несет свою смысловую нагрузку.

«Высокие», как и в других областях, означает, что статистическая технология опирается на современные достижения статистической теории и практики, в частности, на достижения теории вероятностей и прикладной математической статистики. При этом «опирается на современные научные достижения» означает, во-первых, что математическая основа технологии получена сравнительно недавно в рамках соответствующей научной дисциплины, во-вторых, что алгоритмы расчетов разработаны и обоснованы в соответствии в нею (а не являются т.н. «эвристическими»). Со временем новые подходы и результаты могут заставить пересмотреть оценку применимости и возможностей технологии, привести к замене ее более современной. В противном случае «высокие статистические технологии» переходят в «классические статистические технологии», такие, как метод наименьших квадратов. Итак, высокие статистические технологии - плоды недавних серьезных научных исследований. Здесь два ключевых понятия - «молодость» технологии (во всяком случае, не старше 50 лет, а лучше - не старше 10 или 30 лет) и опора на «высокую науку».

Термин «статистические» привычен, но коротко разъяснить его нелегко. Проще сослаться на введение и все содержание учебника [57], на фундаментальную энциклопедию в этой области [68], на справочник [69] - высшее достижение отечественной статистической мысли ХХ в., и др. В частности, отметим, что статистические данные – это результаты измерений, наблюдений, испытаний, анализов, опытов, замеров, исследований. А «статистические технологии» - это технологии анализа статистических данных.

Наконец, редко используемый применительно к статистике термин «технологии». Статистический анализ данных, как правило, включает в себя целый ряд процедур и алгоритмов, выполняемых последовательно, параллельно или по более сложной схеме. Структура типовой статистической технологии описана выше. Обработка статистических данных - это информационный технологический процесс, который относится к приоритетному направлению развития "Информационно-коммуникационные технологии".

2.3.4. Всегда ли нужны «высокие статистические
технологии»?

«Высоким статистическим технологиям» противостоят, естественно, «низкие статистические технологии» (а между ними помещаем «классические статистические технологии»). «Низкие статистические технологии» - это те технологии, которые не соответствуют современному уровню науки и практики. Обычно они одновременно и устарели, и не вполне адекватны сути решаемых статистических задач.

Примеры таких технологий неоднократно критически рассматривались нами. Достаточно вспомнить критику использования критерия Стьюдента для проверки однородности при отсутствии нормальности и равенства дисперсий [70, 71]. Или применение критерия Вилконсона для проверки совпадения теоретических медиан или функций распределения двух выборок [72, 73]. Или использование классических процентных точек критериев Колмогорова и омега-квадрат в ситуациях, когда параметры оцениваются по выборке и эти оценки подставляются в «теоретическую» функцию распределения [74, 75]. На первый взгляд вызывает удивление устойчивость «низких статистических технологий», их постоянное возрождение во все новых статьях, монографиях, учебниках. Поэтому, как ни странно, наиболее «долгоживущими» оказываются не работы, посвященные новым научным результатам, а публикации, разоблачающие ошибки, типа статьи [74]. Прошло уже 30 лет с момента ее публикации, но она по-прежнему актуальна, поскольку ошибочное применение критериев Колмогорова и омега-квадрат по-прежнему распространено, в том числе в разнообразных учебниках (см. многочисленные примеры в теме http://forum.orlovs.pp.ru/viewtopic.php?f=1&t=548 ).

Целесообразно отметить по крайней мере четыре обстоятельства, которые определяют эту устойчивость ошибок.

Во-первых, прочно закрепившаяся традиция. Так, многие учебники по курсам типа «Общая теория статистики», если беспристрастно проанализировать их содержание, состоят в основном из введения в прикладную статистику (в понимании нашего учебника [5]). Иногда изложение идет в стиле «низких статистических технологий», т.е. на уровне 1950-х годов, а во многом и на уровне начала ХХ в., причем обычно с ошибками. К «низкой» прикладной статистике добавлена некоторая информация о деятельности органов Госкомстата РФ. Новое поколение специалистов, обучившись «низким» подходам, идеям, алгоритмам, их использует, а с течением времени и достижением должностей, ученых званий и степеней – пишет новые учебники со старыми ошибками.

Второе обстоятельство связано с большими трудностями при оценке экономической эффективности применения статистических методов вообще и при оценке вреда от применения ошибочных методов в частности. (А без такой оценки как докажешь некоторым зацикленным на своих ошибках оппонентам, что «высокие статистические технологии» лучше «низких»?) При оценке вреда от применения ошибочных методов приходится учитывать, что общий успех в конкретной инженерной или научной работе вполне мог быть достигнут вопреки применению ошибочных методов, за счет «запаса прочности» других составляющих общей работы. Например, преимущество одного технологического приема (станка, оснастки, организации работы) над другим можно продемонстрировать как с помощью критерия Крамера-Уэлча [70, 71] проверки равенства математических ожиданий (что правильно), так и с помощью двухвыборочного критерия Стьюдента (что, вообще говоря, неверно, т.к. обычно не выполняются условия применимости этого критерия - нет ни нормальности распределения, ни равенства дисперсий).

Третье существенное обстоятельство – трудности со знакомством с высокими статистическими технологиями. В нашей стране в силу ряда исторических обстоятельств развития статистических методов в течение последних десятилетий только журнал «Заводская лаборатория. Диагностика материалов» предоставлял такие возможности (в последние годы активно присоединился «Научный журнал КубГАУ»; надо добавить также периодический (раз в год – два) межвузовский сборник научных трудов «Статистические методы оценивания и проверки гипотез»). К сожалению, поток современных отечественных и переводных статистических книг, выпускавшихся ранее, в частности, издательствами «Наука», «Мир», «Финансы и статистика», практически превратился в узкий ручеек…

Возможно, более существенным является влияние естественной задержки во времени между созданием «новых статистических технологий» и написанием полноценной и объемной учебной и методической литературы. Она должна позволять знакомиться с новой методологией, новыми методами, теоремами, алгоритмами, методами расчетов и интерпретации их результатов, статистическими технологиями в целом не по кратким оригинальным статьям, а при обычном вузовском и последипломном обучении. О выпущенных в XXI в. монографической, учебной и методической литературе, которая посвящена высоким статистическим технологиям и соответствуют новой парадигме математических методов экономики, рассказано в предыдущем разделе 2.1.

И, наконец, четвертое - наиболее важное. Всегда ли нужны высокие статистические технологии? Приведем аналогию - нужна ли современная сельскохозяйственная техника для обработки приусадебного участка? Нужны ли трактора и комбайны? Может быть, достаточно старинных технологий, основанных на использовании лопаты и граблей? Вернемся к данным государственной статистики. Применяются статистические технологии первичной обработки (описания) данных, основанные на построении разнообразных таблиц, диаграмм, графиков. Эти технологии соответствуют научному уровню XIX в. (и лишь незначительно развивают технологии времен Моисея, описанные в книге "Числа" Ветхого Завета - см. [5]. Подобное представление данных и их первичный анализ удовлетворяет большинство потребителей статистической информации.

Итак, чтобы высокие статистические технологии успешно использовались, необходимы два условия:

- чтобы они были объективно нужны для решения практической задачи;

- чтобы потенциальный пользователь технологий субъективно понимал это.

Таким образом, весь арсенал реально используемых в настоящее время эконометрических и статистических технологий можно распределить по трем потокам:

- высокие статистические технологии;

- классические статистические технологии,

- низкие статистические технологии.

Под классическими статистическими технологиями, как уже отмечалось, понимаем технологии почтенного возраста, сохранившие свое значение для современной статистической практики. Таковы технологии на основе метода наименьших квадратов (включая методы точечного оценивания параметров прогностической функции, непараметрические методы доверительного оценивания параметров и прогностической функции в целом, проверок различных гипотез о них), статистик типа Колмогорова, Смирнова, омега-квадрат, непараметрических коэффициентов корреляции Спирмена и Кендалла (относить их только к методам анализа ранжировок - значит делать уступку «низким статистическим технологиям») и многих других статистических процедур.

2.3.5. Основная проблема в области
статистических технологий

В настоящее время она состоит в том, чтобы в конкретных эконометрических исследованиях использовались только технологии первых двух типов.

Каковы возможные пути решения этой проблемы? Бороться с конкретными невеждами - дело почти безнадежное. Конечно, необходима демонстрация квалифицированного применения высоких статистических технологий. В 1960-70-х годах этим активно занималась Лаборатория статистических методов акад. А.Н. Колмогорова в МГУ им. М.В. Ломоносова. В разделе «Математические методы исследования» журнала «Заводская лаборатория» за последние 50 лет опубликовано более 1000 статей, выполненных на уровне «высоких статистических технологий». В настоящее время действует Институт высоких статистических технологий и эконометрики МГТУ им. Н.Э. Баумана и целый ряд других научных коллективов, работающих на уровне «высоких статистических технологий».

Очевидно, самое основное - это обучение. Какие бы новые научные результаты ни были получены, если они остаются неизвестными студентам, то новое поколение исследователей и инженеров, экономистов и менеджеров, специалистов других областей будет вынуждено осваивать их поодиночке, в порядке самообразования, а то и переоткрывать заново. Т.е. зачастую новые научные результаты практически исчезают из оборота научной и практической информации, едва появившись. Как ни странно это может показаться, избыток научных публикаций превратился в тормоз развития науки. По нашим оценкам (опубликованы в наших отчетах о Первом Всемирном конгрессе Общества математической статистики и теории вероятностей им. Бернулли [76 – 79]), уже к середине 1980-х годов по статистическим технологиям опубликовано не менее миллиона статей и книг, в основном во второй половине ХХ в. Из них не менее 100 тысяч являются актуальными для современного специалиста. При этом реальное число публикаций, которые способен освоить исследователь за свою профессиональную жизнь, по нашей оценке, не превышает 2 - 3 тысяч (именно таково число литературных ссылок в наиболее развернутом издании на русском языке по статистических методам – трехтомнике [79 – 81]). Сейчас, через 30 лет, сделанные тогда оценки только усугубились.

Итак, каждый специалист в области прикладной статистики знаком не более чем с 2 - 3% актуальных для него литературных источников. Поскольку существенная часть публикаций заражена «низкими статистическими технологиями», то исследователь-самоучка, увы, имеет мало шансов выйти на уровень «высоких статистических технологий». С подтверждениями этого печального вывода постоянно приходится сталкиваться. Одновременно приходится констатировать, что масса полезных результатов погребена в изданиях прошлых десятилетий и имеет мало шансов пробиться в ряды используемых в настоящее время «высоких статистических технологий» без специально организованных усилий современных специалистов.

Итак, основное - обучение. Несколько огрубляя, можно сказать так: что попало в учебные курсы и соответствующие учебные издания - то сохраняется, что не попало - то пропадает.

2.3.6. Необходимость высоких статистических
технологий

У профанов может возникнуть естественный вопрос: зачем нужны высокие статистические технологии, разве недостаточно обычных статистических методов? Специалисты по прикладной статистике справедливо считают и доказывают своими теоретическими и прикладными работами, что совершенно недостаточно. Так, совершенно очевидно, что многие данные в информационных системах имеют нечисловой характер, например, являются словами или принимают значения из конечных множеств. Нечисловой характер имеют и упорядочения, которые дают эксперты или менеджеры, например, выбирая главную цель, следующую по важности и т.д. Значит, нужна статистика нечисловых данных. Мы ее построили [36, 82]. Далее, многие величины известны не абсолютно точно, а с некоторой погрешностью - от и до. Другими словами, исходные данные - не числа, а интервалы. Нужна статистика интервальных данных. Мы ее развиваем [32, 33, 83]. В широко известной монографии по контроллингу [84] на с.138 хорошо сказано: «Нечеткая логика - мощный элегантный инструмент современной науки, который на Западе (и на Востоке - в Японии, Китае - А.О.) можно встретить в десятках изделий - от бытовых видеокамер до систем управления вооружениями, - у нас до самого последнего времени был практически неизвестен». Напомним, первая монография российского автора по теории нечеткости [85] содержит основы высоких статистических технологий, связанные с анализом выборок нечетких множеств (см. также [33]). Ни статистики нечисловых данных, ни статистики интервальных данных, ни статистики нечетких данных не было и не могло быть в классической статистике. Все эти области статистического анализа данных относятся к высоким статистическим технологиям. Они разработаны за последние десятилетия. К сожалению, многие распространенные в настоящее время вузовские курсы по общей теории статистики и по математической статистике разбирают только научные результаты, полученные в первой половине ХХ века, а потому далеко отстают от современного уровня развития математических методов экономики и, в частности, от уровня современной прикладной математической статистики.

Важная и весьма перспективная часть прикладной статистики - применение высоких статистических технологий к анализу конкретных данных, что зачастую требует дополнительных теоретических исследований по доработке статистических технологий применительно к конкретной ситуации. Большое значение имеют конкретные статистические модели, например, модели экспертных оценок или эконометрики качества. И конечно, такие конкретные применения, как расчет и прогнозирование индекса инфляции. Сейчас уже многим экономистам и менеджерам ясно, что годовой бухгалтерский баланс предприятия может быть использован для оценки его финансово-хозяйственной деятельности только с привлечением данных об инфляции.

2.3.7. Институт высоких статистических технологий
и эконометрики

Опишем опыт внедрения «высоких статистических технологий». Организованный нами в 1989 г. Институт высоких статистических технологий и эконометрики (ИВСТЭ) в настоящее время действует на базе кафедры ИБМ-2 «Экономика и организация производства» Московского государственного технического университета им. Н.Э. Баумана. Институт на хоздоговорных и госбюджетных началах занимается развитием, изучением и внедрением эконометрики и «высоких статистических технологий», т.е. наиболее современных технологий анализа экономических, технических, социологических, медицинских данных, ориентированных на использование в условиях современного производства и экономики. Основной интерес представляют применения «высоких статистических технологий» для анализа конкретных экономических данных, т.е. в эконометрике. Наиболее перспективным представляется применение «высоких статистических технологий» для поддержки принятия управленческих решений, прежде всего в таком новом (для России) современном направлении экономической науки и практики, как контроллинг (см., например, [1 - 3, 18, 84, 86]).

Термин «высокие статистические технологии» активно используется на Интернет-ресурсах научной школы кафедры ИБМ-2 по эконометрике – на сайтах с книгами и статьями в открытом доступе http://orlovs.pp.ru/ (сайт «Высокие статистические технологии», за 10 лет работы - более 1 млн. посетителей) и http://ibm.bmstu.ru/nil/biblio.html (сайт Лаборатории экономико-математических методов в контроллинге), в том числе в названиях учебников, а также на общем для этих сайтов форуме http://forum.orlovs.pp.ru/. При публикации научных статей представителей научной школы в журнале «Заводская лаборатория. Диагностика материалов» в качестве места работы часто указан ИВСТЭ МГТУ им. Н.Э. Баумана. Поэтому целесообразно рассмотреть историю ИВСТЭ.

Вначале ИВСТЭ действовал как Центр статистических методов и информатики в 1989 г., затем - как Всесоюзный центр статистических методов и информатики (1989-1992), затем - снова как Центр статистических методов и информатики (1992-1993). В 1993 г. он был преобразован в Лабораторию эконометрических исследований Московского государственного института электроники и математики (технического университета), а с 1997 г. действует под своим нынешним именем - Институт высоких статистических технологий и эконометрики МГТУ им. Н.Э.Баумана.

У Института высоких статистических технологий и эконометрики есть и предыстория. В 1978-1985 гг. активно действовала комиссия «Статистика объектов нечисловой природы и экспертные оценки» Научного Совета АН СССР по комплексной проблеме «Кибернетика». Зримым результатом ее работы является сборник научных статей [87], в котором были подведены итоги выполненных к тому времени исследований по созданию новой области прикладной статистики – статистики объектов нечисловой природы (статистики нечисловых данных, нечисловой статистики).

ИВСТЭ был создан как инструмент реализации инновационного проекта в области эконометрики. Опишем соответствующий инновационный процесс.

Рабочая группа по упорядочению системы стандартов по прикладной статистике и другим статистическим методам. С начала 1970-х годов стали разрабатываться государственные стандарты по статистическим методам управления качеством продукции. В связи с обнаружением в них грубых ошибок (с т очки зрения эконометрики) в 1985 г. была организована «Рабочая группа по упорядочению системы стандартов по прикладной статистике и другим статистическим методам». В ее работе приняли участие 66 специалистов, в том числе 15 докторов и 36 кандидатов наук. В соответствии с рекомендациями Рабочей группы 24 из 31 государственного стандарта по статистическим методам были отменены в 1986-87 гг.

В 1988-89 гг. наиболее активная часть Рабочей группы (10 докторов и 15 кандидатов наук) составила «Аванпроект комплекса методических документов и пакетов программ по статистическим методам стандартизации и управления качеством» (около 1600 стр.)

Центр статистических методов и информатики. К сожалению, Госстандарт не пожелал финансировать реализацию заказанного им «Аванпроекта». Тогда решено было действовать самостоятельно. На собрании в Политехническом музее 20 февраля 1989 г. был организован (на общественных началах) Центр статистических методов и информатики (ЦСМИ; в настоящее время - Институт высоких статистических технологий и эконометрики).

Организационное оформление последовало в конце того же года. Всесоюзный центр статистических методов и информатики (ВЦСМИ) Центрального правления Всесоюзного экономического общества создан на базе ЦСМИ Постановлением Президиума Центрального Правления Всесоюзного экономического общества № 5-7 от 25 декабря 1989 г.

К середине 1990 г. в ЦСМИ - ВЦСМИ были разработаны 7 диалоговых систем по современным статистическим методам управления качеством, а именно, СПК и АТСТАТ-ПРП (по статистическому приемочному контролю), СТАТКОН и АВРОРА-РС (по контролю процессов и обнаружению разладки, прежде всего с помощью контрольных карт Шухарта и кумулятивных сумм), ЭКСПЛАН и ПАСЭК (по планированию экспериментов), НАДИС (по надежности и испытаниям). В работе участвовали 128 специалистов. В дальнейшем к ЦСМИ присоединялись новые группы научно-технических работников, уже к концу 1991 г. нас было более 300. Информация о программных продуктах и другой деятельности ЦСМИ постоянно помещалась в журналах «Заводская лаборатория» и «Надежность и контроль качества». Программные продукты, разработанные Центром статистических методов и информатики, использовались более чем в 100 организациях и предприятиях. Среди них - производственные объединения «Уралмаш», «АвтоВАЗ», «Пластик», ЦНИИ черной металлургии им. Бардина, НИИ стали, ВНИИ эластомерных материалов и изделий, НИИ прикладной химии, ЦНИИ химии и механики, НПО «Орион», НИЦентр по безопасности атомной энергетики, ВНИИ экономических проблем развития науки и техники, ВНИИ нефтепереработки, МИИТ, Казахский политехнический институт, Ульяновский политехнический институт, Донецкий государственный университет, Институт питания (Алма-Ата) и многие другие организации и предприятия.

Всесоюзная статистическая ассоциация. Параллельно с выполнением работ по договорам с организациями и предприятиями ЦСМИ вел работу по объединению статистиков. В апреле 1990 г. в Большом Актовом Зале Московского Энергетического института прошла Учредительная конференция Всесоюзной организации по статистическим методам и их применениям. Через полгода на Учредительном съезде Всесоюзной статистической ассоциации (ВСА) в октябре 1990 г. в Московском экономико-статистическом институте эта организация вошла в состав ВСА в качестве секции статистических методов. В соответствии со своим Уставом эта организация (ВСА) продолжает существовать, хотя и номинально.

В соответствии с реальной структурой статистики ВСА делится на 4 секции: 1) практической статистики, 2) статистических методов и их применений, 3) статистики надежности, 4) социально-экономической статистики. Названия секций, зафиксированные в документах ВСА, не вполне соответствуют действительности. Первая секция состоит из работников государственной статистики (ЦСУ - Госкомстата - Росстата), большинство членов второй и третьей занимаются прикладными научными исследованиями, в том числе в социально-экономической области и оборонно-промышленном комплексе, а четвертая состоит из преподавателей статистических дисциплин. В 1992 г. после развала СССР и фактического прекращения работы ВСА на основе секции статистических методов ВСА в 1992 г. была организована Российская ассоциация по статистическим методам (РАСМ), а затем – в 1996 г. - и Российская академия статистических методов, существующие и в настоящее время.

Бизнес-идея. Задачи ЦСМИ и ВСА (и РАСМ) были взаимосвязаны. Роль ЦСМИ - производить товары и услуги, а именно, разрабатывать новые статистические методы, а прежде всего - программные и методические продукты в области эконометрики. Общественные объединения специалистов в области эконометрики (ВСА и РАСМ) занимаются их распространением и внедрением. К сожалению, бурный всплеск активности (1989-1991 гг.) сменился к 1993 г. полным развалом, поскольку в условиях либерализации цен спрос предприятий организаций на высокотехнологичную наукоемкую продукцию ЦСМИ весьма сократился.

Создание новой парадигмы статистических методов. В мероприятиях секции статистических методов ВСА и РАСМ активно участвовали несколько сот исследователей. Основной тематикой работ многих из этих специалистов являются статистические методы в сертификации (управлении качеством).

В 1989-90 гг. была проведена большая работа по анализу положения дел в области теории и практики статистики в нашей стране. В ЦСМИ и РАСМ, объединивших большинство ведущих российских специалистов, коллективными усилиями разработан единый подход к проблемам применения статистических методов в сертификации и управлении качеством, т.е. новая парадигма статистических методов.

Был сформулирован «социальный заказ» - разработать серию учебников согласно новой парадигме. К настоящему времени выполнен (см. раздел 2.1 выше). Перечень выпущенных учебников и их Интернет-версий приведен, например, на персональной странице А.И. Орлова на сайте МГТУ им. Н.Э. Баумана http://www.bmstu.ru/ps/~orlov/ .

Научные исследования ИВСТЭ. В условиях либерализации цен и резкого сокращения спроса предприятий и организаций на высокотехнологичную наукоемкую продукцию Институт от организации широкого внедрения высоких статистических технологий перешел к выполнению конкретных заказов. Он разрабатывал эконометрические методы анализа нечисловых данных, а также процедуры расчета и прогнозирования индекса инфляции (для Министерства обороны РФ) и валового внутреннего продукта. ИВСТЭ развивал методологию построения и использования математических моделей процессов налогообложения (для Министерства налогов и сборов РФ), методологию оценки рисков реализации инновационных проектов высшей школы (для Министерства промышленности, науки и технологий РФ). Институт оценивал влияние различных факторов на формирование налогооблагаемой базы ряда налогов (для Минфина РФ), прорабатывал перспективы применения современных статистических и экспертных методов для анализа данных о научном потенциале (для Министерства промышленности, науки и технологий РФ). Важное направление связано с эколого-экономической тематикой - разработка методологического, программного и информационного обеспечения анализа рисков химико-технологических объектов (для Международного научно-технического центра), методов использования экспертных оценок в задачах экологического страхования (совместно с Институтом проблем рынка РАН). Институт проводил маркетинговые исследования (в частности, для Institute for Market Research GfK MR, Промрадтехбанка, фирм, торгующих растворимым кофе, программным обеспечением, оказывающих образовательные услуги). Интерес вызывали работы Института по прогнозированию социально-экономического развития России методом сценариев [88 - 91], по экономико-математическому моделированию развития малых предприятий [92, 93] и созданию современных систем информационной поддержки принятия решений для таких организаций [94, 95], и др.

С 2010 г. Институт занимался проблемами прогнозирования и предотвращения авиационных происшествий, обеспечения безопасности полетов (см., например, [96 – 101]), с 2013 г. – организационно-экономическим обеспечением управления проектами создания изделий ракетно-космической техники (см., например, [102 - 107]).

Институт ведет фундаментальные исследования в области высоких статистических технологий и эконометрики, в частности, в рамках МГТУ им. Н.Э. Баумана и Российского фонда фундаментальных исследований. Информация об Институте представлена на сайтах в Интернете (http://orlovs.pp.ru, прежний вариант - http://antorlov.nm.ru, зеркала http://antorlov.euro.ru, http://www.newtech.ru/~orlov ), которые в 2000 – 2003 гг. ежегодно посещали более 10000 пользователей, а в 2006 г. – уже более 100000. Его деятельности посвящены страницы http://forum.orlovs.pp.ru/viewtopic.php?f=5&t=1760, http://forum.orlovs.pp.ru/viewtopic.php?f=5&t=1360. С 2000 г. Институтом издается электронный еженедельник «Эконометрика» (более 1,5 тыс. подписчиков, более 700 выпусков). Архив выпусков еженедельника «Эконометрика» можно рассматривать как хрестоматию по различным разделам эконометрики, а также по высоким статистическим технологиям (см. http://subscribe.ru/catalog/science.humanity.econometrika).

2.3.7. Эконометрика при решении задач экономики,
организации производства и контроллинга

Вокруг Института высоких статистических технологий и эконометрики выросла отечественная научная школа в области эконометрики. Для ее формирования Институт и его работы послужили стержнем. На основе научных статей были написаны учебники, соответствующие новой парадигме математических методов экономики.

Уместно сказать несколько слов об эконометрике. Как мы уже отмечали, область научных и практических работ по развитию и применению статистических методов в экономике и управлении организациями и территориями называется эконометрикой [16]. Эконометрика – это прежде всего статистические методы в экономике. Прикладная статистика – наука о том, как обрабатывать данные. Данные – любой вид зарегистрированной информации. Отечественная научная школа в области эконометрики базируется на кафедре ИБМ-2 "Экономика и организация производства" МГТУ им. Н.Э. Баумана (первой кафедре по этой тематике в нашей стране, организованной в 1929 г.). Научная школа кафедры ИБМ-2 по эконометрике занимается сбором и анализом экономической и управленческой информации, в том числе экспертной, хранящейся в базах и банках данных, а потому относится к приоритетному направлению развития - информационно-коммуникационным технологиям. Уже говорилось о том, что в предыстории ИВСТЭ - работа в рамках Научного Совета АН СССР по комплексной проблеме «Кибернетика». Само выделение прикладной статистики как самостоятельной научной области состоялось под эгидой кибернетики и информатики.

Эконометрика - один из наиболее эффективных инструментов контроллинга. Вначале наша научная школа занималась вопросами применения организационно-экономического моделирования, эконометрики и статистики при решении задач контроллинга (http://orlovs.pp.ru/econ.php#e2). Затем развернулись работы в конкретных областях контроллинга – в контроллинге методов, контроллинге рисков, контроллинге научной деятельности, контроллинге качества.

При решении задач организации производства используются разнообразные эконометрические методы и модели. Проанализируем учебник [11], подготовленный кафедрой ИБМ-2. В нем более 20 раз используются эконометрические методы и модели. Так, методы восстановления зависимости (регрессионного анализа) используются при изучении динамики производственных затрат в период освоения производства [11, с.95-97]. В частности, для выявления закономерностей изменения трудоемкости изготовления единицы продукции, снижения себестоимости и других показателей с течением времени или с ростом объемов изготовления и др. При нормировании труда косвенные методы основаны на регрессионном анализе [11, с.308-309]. Интегральный критерий эффективности проекта, применяемый при планировании инновационных процессов, строится с помощью многомерного статистического анализа [11, с.101]. Постоянно возникает необходимость строить те или иные интегральные показатели (критерии), объединяющие значения частных (единичных или групповых) показателей. Упомянем суммарный показатель качества продукции или проекта [11, с.244], коэффициент качества инженерного труда [11, с.269].

В организации производства часто используются задачи оптимизации. Так, с целью рационального расположения на территории завода складских помещений, заготовительных цехов, участков, оборудования решают задачу минимизации суммарных грузопотоков. Для максимально возможного совмещения отдельных производственных процессов во времени, что может существенно сократить время от запуска в производство до выпуска готовой продукции, решают соответствующую оптимизационную задачу [11, с.121-122]. Методы сокращения производственного цикла, в том числе снижения затрат труда на основные технологические операции, сокращения затрат времени на транспортные, складские и контрольные операции, предполагают применение методов оптимизации, в том числе дискретной оптимизации [11, с.134-136].

Особенно заметна роль оптимизации в задачах планирования производственно-хозяйственной деятельности предприятия. Предполагается построение экономико-математической модели объекта планирования, включающей целевую функцию по принятому критерию оптимальности и систему ограничений [11, с.339]. Среди основных методов планирования указаны экономико-математические методы [11, с.342]. Подробно рассматривается математическая модель построения оптимального плана реализации продукции, сводящаяся к задаче линейного программирования [11, с.352-354]. При планировании рыночных цен на продукцию решается задача максимизации прибыли как функции цены [11, с.409]. Расчет оптимальных размеров партии деталей основан на минимизации суммарных затрат [11, с.428].

Отметим важную роль математической теория оптимального управления запасами как части логистики [11, с.223-236], в том числе для организации материально-технического снабжения и складирования [11, с.217], организации обеспечения основного производства технологической оснасткой [11, с.208]. Есть и устоявшиеся неточности - «экономичный объем заказа» [11, с.227] является оптимальным лишь при большом интервале планирования [59, разд.16.3].

В производственном менеджменте широко применяются разнообразные эконометрические методы. Например, хронометраж [11, с. 311-316] – это типовое статистическое исследование. Отметим использование медианы для вычисления нормы времени [11, с.312], что совпадает с рекомендациями эконометрики [16]. На основе теории выборочных исследований указывается количество наблюдений, позволяющее сделать обоснованные выводы о структуре затрат рабочего времени [11, с.315].

Большой раздел эконометрики – статистические методы управления качеством продукции. Согласно международному стандарту ИСО 9004 в системах качества должно быть предусмотрено использование статистических методов [11, с.253]. При рассмотрении видов контроля качества продукции выделяются «выборочный» и «статистический» контроль [11, с.268]. Описываются методы статистического приемочного контроля и статистического контроля процессов (другими словами, статистического регулирования технологических процессов) [11, с.271-274]. В качестве одного из четырех основных методов определения показателей качества продукции указан экспертный метод [11, с.275]. Экспертные методы предлагается использовать и при построении причинно-следственной диаграммы (диаграммы Исикавы) для ранжирования факторов по их значимости и выделении наиболее важных [11, с.276]. Из методов обработки статистических данных разобрана методика анализа качества продукции машиностроения с помощью диаграмм Парето [11, с.277].

В производственном менеджменте большую роль играют методы принятия решений [11, с.25-28], различные специализированные эконометрические модели, например, модель минимизации сроков выполнения заказов на основе использования сетевого графика со случайными сроками выполнения отдельных работ [11, с.110-112].

Таким образом, эконометрические методы постоянно используются менеджерами, в том числе контроллерами. При решении задач организации производства необходимо применять эконометрические методы в соответствии с новой парадигмой в этой области (см. раздел 2.1 выше).

Термин «эконометрика» пока еще не всем известен в России. А между тем в мировой науке эконометрика занимает достойное место. Напомним, что Нобелевские премии по экономике получили эконометрики Ян Тильберген, Рагнар Фриш, Лоуренс Клейн, Трюгве Хаавельмо, Джеймс Хекман и Дэниель Мак-Фадден. В 2003 г. к ним добавились Энгл Грейнджер и Кеннет Риглз. Выпускается ряд научных журналов, полностью посвященных эконометрике, в том числе: Journal of Econometrics (Швеция), Econometric Reviews (США), Econometrica (США), Sankhya (Indian Journal of Statistics. Ser.D. Quantitative Economics. Индия), Publications Econometriques (Франция). Применение эконометрики дает заметный экономический эффект. Например, в США - не менее 20 миллиардов долларов ежегодно только в области статистического контроля качества [16].

Однако в нашей стране по ряду причин прикладная статистика и эконометрика до начала 1980-х годов не были сформированы как самостоятельные направления научной и практической деятельности, в отличие, например, от Польши, не говоря уже об англосаксонских странах. В результате специалистов в области прикладной статистики и эконометрики у нас на порядок меньше, чем в США и Великобритании.

Поэтому весьма важно создание и развитие отечественной научной школы по эконометрике [104]. За развитие работ по эконометрике отвечает секция «Организационно-экономическое моделирование, эконометрика и статистика» кафедры ИБМ-2. Члены секции преподают и активно используют при решении практических задач дисциплины «Эконометрика», «Организационно-экономическое моделирование», «Прикладная статистика», «Статистика» (дневное обучение), «Статистика», «Методы принятия управленческих решений» (второе высшее образование на факультете ИБМ), «Количественные методы, статистика и информатика», «Эконометрика» (Бизнес-школа МГТУ им. Н.Э. Баумана).

Для описания работ членов секции в качестве базового будем использовать термин «эконометрика». Терминологические дискуссии не представляются плодотворными в данном разделе настоящей монографии.

Научная работа ведется в рамках Института высоких статистических технологий и эконометрики (ИВСТЭ) и Лаборатории экономико-математических методов в контроллинге Научно-учебного центра «Контроллинг и управленческие инновации» МГТУ им. Н.Э. Баумана. Научная школа по эконометрике представлена в редколлегиях научных журналов «Заводская лаборатория. Диагностика материалов», «Контроллинг», «Социология: методология, методы, математическое моделирование», периодического сборника научных трудов «Управление большими системами» (все четыре издания входят в «список ВАК» - Перечень российских рецензируемых научных журналов, в которых должны быть опубликованы основные научные результаты диссертаций на соискание ученых степеней доктора и кандидата наук), научного журнала «IDO science (Innovation, Development, Outsourcing)», редакционных советов журналов «BIOCOSMOLOGY – NEO-ARISTOTELISM», «Инженерный журнал: наука и инновации», «Инновации в менеджменте», в составе ряда диссертационных советов и Ученого совета Научно-учебного комплекса «Инженерный бизнес и менеджмент» МГТУ им. Н. Э. Баумана.

Партнерами научной школы по эконометрике в соответствии с заключенными договорами являются академические институты – Институт проблем управления, Центральный экономико-математический институт, а также Кубанский государственный аграрный университет, в «Научном журнале КубГАУ» в 2013-2015 гг. опубликовано более 50 наших работ.

Ведутся прикладные научно-исследовательские работы, в частности, с Группой авиакомпаний «Волга-Днепр» (разработка Автоматизированной системы прогнозирования и предотвращения авиационных происшествий АСППАП), с космическим научным центром ЦНИИМАШ.

Активно работает научный семинар Лаборатории экономико-математических методов в контроллинге. В 2007 -2014 гг. проведено около 120 заседаний, на которых заслушано и обсуждено несколько сотен докладов.

В рамках научной школы защищено 9 кандидатских диссертаций, в том числе 6 – по экономическим наукам, 2 – по техническим, 1 – по физико-математическим

2.3.8. О подготовке специалистов по высоким
статистическим технологиям

Приходится с сожалением констатировать, что в России плохо налажена подготовка специалистов по высоким статистическим технологиям. В курсах по теории вероятностей и математической статистике обычно даются лишь классические основы этих дисциплин, разработанные в первой половине ХХ в., а преподаватели-математики свою научную деятельность предпочитают посвящать доказательству теорем, имеющих лишь внутриматематическое значение, а не развитию высоких статистических технологий. В настоящее время появилась надежда на эконометрику. В России развертываются эконометрические исследования и преподавание эконометрики. Экономисты, менеджеры и инженеры, прежде всего специалисты по контроллингу, должны быть вооружены современными средствами информационной поддержки, в том числе высокими статистическими технологиями и эконометрикой. Очевидно, преподавание должно идти впереди практического применения. Ведь как применять то, чего не знаешь?

Приведем два примера - отрицательный и положительный, - показывающие связь преподавания с внедрением передовых технологий.

Один раз - в 1990 – 1992 гг. мы уже обожглись на недооценке необходимости предварительной подготовки тех, для кого предназначены современные программные продукты. Наш коллектив (Всесоюзный центр статистических методов и информатики Центрального Правления Всесоюзного экономического общества, в настоящее время – Институт высоких статистических технологий и эконометрики) разработал систему диалоговых программных систем обеспечения качества продукции. Их созданием руководили ведущие специалисты страны. Но распространение программных продуктов шло на 1 - 2 порядка медленнее, чем мы ожидали. Причина стала ясна не сразу. Как оказалось, работники предприятий просто не понимали возможностей разработанных систем, не знали, какие задачи можно решать с их помощью, какой экономический эффект они дадут. А не понимали и не знали потому, что в вузах никто их не учил статистическим методам управления качеством. Без такого систематического обучения нельзя обойтись - сложные концепции «на пальцах» за пять минут не объяснишь.

Есть и противоположный пример - положительный. В середине 1980-х годов в советской средней школе ввели новый предмет «Информатика». И сейчас молодое поколение превосходно владеет компьютерами, мгновенно осваивая быстро появляющиеся новинки, и этим заметно отличается от тех, кому за 50 – 60 лет.

Если бы удалось ввести в средней школе курс теории вероятностей и статистики, то ситуация с внедрением высоких статистических технологий могла бы быть резко улучшена. Такой курс есть в Японии и США, Швейцарии, Кении и Ботсване, почти во всех странах (и ЮНЕСКО проводит всемирные конференции по преподаванию статистики в средней школе – см. сборник докладов [109]). Надо, конечно, добиться того, чтобы этот курс был построен на высоких статистических технологиях, а не на низких. Другими словами, он должен отражать современные достижения, а не концепции пятидесятилетней или столетней давности.

2.4. Точки роста статистических методов

Устаревшая научная и учебная литература, выполненная в соответствии с парадигмой середины XX в., создает впечатление, что математические методы экономики застыли на уровне пятидесятилетней давности, ничего существенно нового с тех пор не появлялось. Это впечатление полностью противоречит реальности. Новая парадигма породила массу новых идей, подходов, моделей, методов во всех разделах математических методов экономики - в прикладной статистике и других статистических методах (т.е. в эконометрике), теории принятия решений, экспертных технологиях, организационно-экономическом моделировании, экономико-математических методах и моделях. (Перечисленные разделы в значительной степени перекрываются, и нет необходимости заниматься их искусственным разделением.) В настоящем разделе рассмотрим точки роста математических методов экономики на примере статистических методов. На основе новой парадигмы прикладной математической статистики, анализа данных и математических методов экономики выделим и рассмотрим пять актуальных направлений, в которых развивается современная прикладная статистика и другие статистические методы, т.е. пять «точек роста» – непараметрическая статистика, робастность, компьютерно-статистические методы, статистика интервальных данных, статистика нечисловых данных.

Отечественная литература по прикладной статистике и другим статистическим методам столь же необозрима, как и мировая. Только в разделе «Математические методы исследования» журнала «Заводская лаборатория» (с 1994 г.- "Заводская лаборатория. Диагностика материалов") с 1960-х годов опубликовано более 1000 статей.

Не будем даже пытаться перечислять здесь коллективы исследователей или основные монографии в этой области. История развития прикладной статистики и других статистических методов в нашей стране в основных чертах рассмотрена в работах [110 - 113].

Отметим только одно издание. По нашему мнению, наилучшей отечественной книгой ХХ века по прикладной статистике является сборник статистических таблиц Л.Н. Большева и Н.В. Смирнова [69] с подробными комментариями, играющими роль сжатого учебника и справочника.

В настоящем разделе на основе новой парадигмы прикладной математической статистики [63, 114], анализа данных [115] и математических методов экономики [116] (см. подробнее раздел 2.1) выделим и обсудим основные «точки роста» прикладной статистики и других статистических методов, те их направления, которые представляются наиболее перспективными в будущем, в следующие десятилетия XXI века, но пока в большинстве учебных, справочных и даже научных изданий отодвинуты на задний план традиционными постановками.

На основе опыта научной (теоретической и прикладной) и научно-организационной деятельности полагаем, что при описании современного этапа развития статистических методов целесообразно выделить пять актуальных направлений, в которых развивается современная прикладная статистика, т.е. пять «точек роста»: непараметрика (т.е. непараметрическая статистика), робастность (устойчивость), компьютерно-статистические технологии (метод Монте-Карло, имитационное моделирование, автоматизированный системно-когнитивный анализ, бутстреп и др.), статистика интервальных данных, статистика нечисловых данных (в несколько иной терминологии - статистика объектов нечисловой природы). Дадим здесь краткую характеристику каждому из пяти перечисленных актуальных направлений исследований.

2.4.1. Непараметрическая статистика

В первой трети ХХ в., одновременно с параметрической статистикой Пирсона, Стьюдента и Фишера [110], в работах Спирмена и Кендалла появились первые непараметрические методы, основанные на коэффициентах ранговой корреляции, носящих ныне имена этих статистиков. Но непараметрика, не делающая нереалистических предположений о том, что функции распределения результатов наблюдений принадлежат тем или иным параметрическим семействам распределений, стала заметной частью статистики лишь со второй трети ХХ века. В 30-е годы появились работы А.Н. Колмогорова и Н.В. Смирнова, предложивших и изучивших статистические критерии, носящие в настоящее время их имена [111, 113]. Эти критерии основаны на использовании так называемого эмпирического процесса. (Как известно, эмпирический процесс – это разность между эмпирической и теоретической функциями распределения, умноженная на квадратный корень из объема выборки.) В работе А.Н. Колмогорова 1933 г. изучено предельное распределение супремума модуля эмпирического процесса, называемого сейчас критерием Колмогорова. Затем Н.В. Смирнов исследовал супремум и инфимум эмпирического процесса, а также интеграл (по теоретической функции распределения) квадрата эмпирического процесса.

Следует отметить, что встречающееся иногда в литературе словосочетание «критерий Колмогорова – Смирнова» некорректно, поскольку эти два статистика никогда не печатались вместе и не изучали один и тот же критерий схожими методами. Корректно сочетание «критерий типа Колмогорова – Смирнова», применяемое для обозначения критериев, основанных на использовании супремума функций от эмпирического процесса [75, 117].

После второй мировой войны развитие непараметрической статистики пошло быстрыми темпами. Большую роль сыграли работы американского статистика Ф. Вилкоксона и его научной школы. К настоящему времени с помощью непараметрических методов можно решать практически тот же круг статистических задач, что и с помощью параметрических. Однако для обеспечения широкого внедрения непараметрических методов необходимо провести еще целый комплекс теоретических и пилотных (т.е. пробных) прикладных работ. Все большую роль играют непараметрические оценки плотности [118], непараметрические методы регрессии [119] и распознавания образов (дискриминантного анализа) [120]. В нашей стране непараметрические методы получили достаточно большую известность после выхода в 1965 г. первого издания упомянутого выше сборника статистических таблиц Л.Н. Большева и Н.В.Смирнова [69], содержащего подробные таблицы для основных непараметрических критериев.

Тем не менее параметрические методы всё еще популярнее непараметрических, особенно среди тех прикладников, кто слабо знаком со статистическими методами. Неоднократно публиковались экспериментальные данные, свидетельствующие о том, что распределения реально наблюдаемых случайных величин, в частности, ошибок измерения, в подавляющем большинстве случаев отличны от нормальных, т.е. гауссовских (см., например, [5, 121]). Тем не менее, математики-теоретики продолжают строить и изучать статистические модели, основанные на гауссовости, а практики – применять подобные методы и модели. Другими словами, «ищут под фонарем, а не там, где потеряли».

2.4.2. Устойчивость (робастность) статистических
процедур

Если в параметрических постановках на вероятностные модели статистических данных накладываются слишком жесткие требования – их функции распределения должны принадлежать определенному параметрическому семейству, то в непараметрических, наоборот, излишне слабые – обычно требуется лишь, чтобы функции распределения были непрерывны. При этом игнорируется априорная информация о том, каков «примерный вид» распределения. Априори можно ожидать, что учет этого «примерного вида» улучшит показатели качества статистических процедур. Развитием этой идеи является теория устойчивости (робастности) статистических процедур, в которой предполагается, что распределение исходных данных мало отличается от некоторого параметрического семейства. За рубежом эту теорию разрабатывали П. Хубер (другое написание фамилии - Хьюбер), Ф. Хампель и многие другие. Из монографий на русском языке, трактующих о робастности и устойчивости статистических процедур и математических моделей социально-экономических явлений и процессов, самой ранней и наиболее общей была книга [7], следующей - монография [122]. Частными, но весьма важными случаями реализации идеи робастности (устойчивости) статистических процедур являются статистика объектов нечисловой природы и статистика интервальных данных (см. ниже).

Имеется большое разнообразие моделей робастности в зависимости от того, какие именно отклонения от заданного параметрического семейства допускаются (подробнее см. [34, 123, 124]). Среди теоретиков наиболее популярной оказалась модель выбросов, в которой исходная выборка «засоряется» малым числом «выбросов», имеющих принципиально иное распределение. Однако эта модель представляется «тупиковой», поскольку в большинстве случаев большие выбросы либо невозможны из-за ограниченности шкалы прибора либо интервала изменения измеряемой величины, либо от них можно избавиться, применяя для расчетов только статистики, построенные по центральной части вариационного ряда. Кроме того, в подобных моделях обычно считается известной частота засорения (от которой зависят рекомендации по выбору методов), что в сочетании со сказанным выше делает их малопригодными для практического использования.

Более перспективным представляется, например, модель малых отклонений распределений, в которой расстояние между распределением каждого элемента выборки и базовым распределением не превосходит заданной малой величины, и модель статистики интервальных данных.

2.4.3. Компьютерно-статистические технологии

Если еще в 70-е годы ХХ в. основным содержанием математической статистики считались предельные теоремы (см., например, [125, с.7 - 8]), то в настоящее время большую роль играют различные компьютерно-статистические технологии, основанные на методе статистических испытаний (Монте-Карло), имитационном моделировании, автоматизированном системно-когнитивном анализе (АСК-анализе), бутстрепе и др. Компьютерно-статистические технологии будут рассмотрены ниже в отдельном разделе. Здесь скажем несколько слов об АСК-анализе и бутстрепе.

В предисловии к переводу на русский язык книги С. Кульбака «Теория информации и статистика» [126] А.Н. Колмогоров писал: «... навыки мысли и аналитический аппарат теории информации должны, по-видимому, привести к заметной перестройке здания математической статистики» [126, с. 5 - 6]. Однако этого не произошло, поскольку поток исследований, имеющих целью указанную перестройку, в СССР и мире по каким-то причинам не возник. Работы Е.В. Луценко по разработке и применению автоматизированного системно-когнитивного анализа (см., например [127 - 130]) можно рассматривать как развитие указанного А.Н. Колмогоровым направления прикладной математической статистики, не столько в чисто-математическом плане, сколько в прагматически-прикладном. Реализуется рекомендация А.Н. Колмогорова: «По-видимому, внедрение предлагаемых методов в практическую статистику будет облегчено, если тот же материал будет изложен более доступно и проиллюстрирован на подробно разобранных содержательных примерах». Отметим оригинальность подхода и результатов Е.В. Луценко (по сравнению с книгой C. Кульбака), так что речь выше идет об идейных связях, а не о развитии конкретных научных результатов. Математический метод автоматизированного системно-когнитивного анализа (АСК-анализ) реализован в его программном инструментарии – универсальной когнитивной аналитической системе Эйдос-Х++. АСК-анализ основан на системной теории информации, которая создана в рамках реализации программной идеи обобщения всех понятий математики, в частности теории информации, базирующихся на теории множеств, путем тотальной замены понятия множества на более общее понятие системы и тщательного отслеживания всех последствий этой замены (см., например, [32, 33]). Благодаря математическим основам АСК-анализа этот метод является непараметрическим и позволяет сопоставимо обрабатывать десятки и сотни тысяч градаций факторов и будущих состояний объекта управления (классов) при неполных (фрагментированных), зашумленных данных числовой и нечисловой природы, измеряемых в различных единицах измерения.

Другая из упомянутых выше технологий - бутстреп (размножение выборок) - связана с интенсивным использованием возможностей компьютеров. Основная идея состоит в том, чтобы теоретическое исследование заменить вычислительным экспериментом. Например, вместо описания выборки распределением из параметрического семейства строим большое число «похожих» выборок, т.е. «размножаем» выборку. Затем вместо оценивания характеристик (и параметров) и проверки гипотез на основе свойств теоретического распределения решаем эти задачи вычислительным методом, рассчитывая интересующие нас статистики по каждой из «похожих» выборок и анализируя полученные при этом распределения. Например, вместо того, чтобы теоретическим путем находить распределение статистики, доверительные интервалы и другие характеристики, моделируют большое число выборок, похожих на исходную, затем рассчитывают соответствующие значения интересующей исследователя статистики и изучают их эмпирическое распределение. Квантили этого распределения задают доверительные интервалы, и т.д.

Термин «бутстреп» мгновенно получил широкую известность после первой же статьи Б. Эфрона 1979 г. по этой тематике. Он сразу же стал обсуждаться в массе публикаций, в том числе и научно-популярных. В «Заводской лаборатории» №10 за 1987 г. была помещена подборка статей по бутстрепу. На русском языке выпущен сборник статей Б. Эфрона [131]. Основная идея бутстрепа по Б. Эфрону состоит в том, что методом Монте-Карло (статистических испытаний) многократно извлекаются выборки из эмпирического распределения. Эти выборки, естественно, являются вариантами исходной, напоминают ее.

Сама по себе идея «размножения выборок» была известна гораздо раньше. Одна из статей Б. Эфрона в сборнике [131] называется так: «Бутстреп-методы: новый взгляд на метод складного ножа». Упомянутый «метод складного ножа» (jackknife) предложен М. Кенуем еще в 1949 г., за 30 лет до появления статьи Б.Эфрона. «Размножение выборок» при этом осуществляется путем исключения одного наблюдения. Таким путем для выборки объема n получаем n «похожих» на нее выборок объема (n - 1) каждая. Если же исключать по 2 наблюдения, то число «похожих» выборок возрастает до n(n - 1)/2 объема (n - 2) каждая.

Преимущества и недостатки бутстрепа как статистического метода в сравнении с рядом аналогичных методов обсуждаются в [132]. Необходимо подчеркнуть, что бутстреп по Эфрону - лишь один из вариантов методов «размножения выборки» (resampling), и, на наш взгляд, не самый удачный. Метод «складного ножа» представляется более полезным. На его основе можно сформулировать следующую простую практическую рекомендацию.

Предположим, что Вы по выборке делаете какие-либо статистические выводы. Вы хотите узнать также, насколько эти выводы устойчивы. Если у Вас есть другие (контрольные) выборки, описывающие то же явление, то Вы можете применить к ним ту же статистическую процедуру и сравнить результаты. А если таких выборок нет? Тогда Вы можете их построить искусственно. Берете исходную выборку и исключаете один элемент. Получаете похожую выборку (она взята из того же распределения, только объем на единицу меньше). Затем возвращаете этот элемент выборки и исключаете другой. Получаете вторую похожую выборку. Поступая таким образом со всеми элементами исходной выборки, получаете столько выборок, похожих на исходную, каков ее объем. Остается обработать их тем же способом, что и исходную, и изучить устойчивость получаемых выводов - разброс оценок параметров, частоты принятия или отклонения гипотез и т.д.

Можно изменять не выборку, а сами данные. Поскольку всегда имеются погрешности измерения, то реальные данные - это не числа, а интервалы (результат измерения плюс-минус погрешность). Нужна статистическая теория анализа таких данных.

2.4.4. Статистика интервальных данных

Перспективное и быстро развивающееся направление последних десятилетий - статистика интервальных данных [83]. Речь идет о развитии методов прикладной математической статистики в ситуации, когда статистические данные - не числа, а интервалы, в частности, порожденные наложением ошибок измерения на значения случайных величин.

Статистика интервальных данных идейно связана с интервальной математикой, в которой в роли чисел выступают интервалы. Это направление математики является дальнейшим развитием известных правил приближенных вычислений, посвященных выражению погрешностей суммы, разности, произведения, частного через погрешности тех чисел, над которыми осуществляются перечисленные операции. К настоящему времени удалось решить, в частности, ряд задач теории интервальных дифференциальных уравнений, в которых коэффициенты, начальные условия и решения описываются с помощью интервалов.

Одна из ведущих научных школ в области статистики интервальных данных - это школа проф. А.П. Вощинина (1937 - 2008), активно работающая с конца 70-х годов. В частности, ее представителями изучены проблемы регрессионного анализа, планирования эксперимента, сравнения альтернатив и принятия решений в условиях интервальной неопределенности.

Рассмотрим другое направление в статистике интервальных данных, которое также представляется перспективным. В нем развиваются асимптотические методы статистического анализа интервальных данных при больших объемах выборок и малых погрешностях измерений. Мы называем это направление асимптотической математической статистикой интервальных данных. В отличие от классической математической статистики, сначала устремляется к бесконечности объем выборки и только потом - уменьшаются до нуля погрешности. В частности, с помощью такой асимптотики в начале 1980-х годов были сформулированы правила выбора метода оценивания параметров гамма-распределения в ГОСТ 11.011-83 [133].

В рамках рассматриваемого научного направления разработана общая схема исследования, включающая введение и расчет нотны (максимально возможного отклонения статистики, вызванного интервальностью исходных данных) и рационального объема выборки (превышение которого не дает существенного повышения точности оценивания). Она применена к оцениванию математического ожидания, дисперсии, коэффициента вариации, параметров гамма-распределения и характеристик аддитивных статистик, при проверке гипотез о параметрах нормального распределения, в том числе с помощью критерия Стьюдента, а также гипотезы однородности с помощью критерия Смирнова. Разработаны подходы к рассмотрению интервальных данных в основных постановках регрессионного, дискриминантного и кластерного анализов. В частности, изучено влияние погрешностей измерений и наблюдений на свойства алгоритмов регрессионного анализа, разработаны способы расчета нотн и рациональных объемов выборок, введены и исследованы новые понятия многомерных и асимптотических нотн, доказаны соответствующие предельные теоремы. Начата разработка интервального дискриминантного анализа, в частности, рассмотрено влияние интервальности данных на введенный в статье [134] показатель качества классификации. Изучено асимптотическое поведение оценок метода моментов и оценок максимального правдоподобия (а также более общих оценок минимального контраста), проведено асимптотическое сравнение этих методов в случае интервальных данных. Найдены общие условия, при которых, в отличие от классической математической статистики, метод моментов дает более точные оценки, чем метод максимального правдоподобия. Подробное изложение дано в соответствующих главах монографий [5, 33, 36, 54].

В области асимптотической статистики интервальных данных российская наука имеет мировой приоритет. Во все виды статистического программного обеспечения необходимо включать алгоритмы интервальной статистики, «параллельные» обычно используемым алгоритмам прикладной математической статистики. Это позволяет в явном виде учесть наличие погрешностей у результатов наблюдений.

2.4.5. Статистика объектов нечисловой природы
как центральная часть прикладной статистики

Напомним, что согласно общепринятой в настоящее время классификации статистических методов [5] прикладная статистика делится на следующие четыре области:

статистика (числовых) случайных величин;

многомерный статистический анализ;

статистика временных рядов и случайных процессов;

статистика объектов нечисловой природы.

Первые три из этих областей являются классическими. Они были хорошо известны еще в первой половине ХХ в. Остановимся на четвертой, сравнительно недавно вошедшей в массовое сознание специалистов. Ее именуют также статистикой нечисловых данных или попросту нечисловой статистикой. Анализ динамики развития прикладной статистики приводит к выводу, что в XXI в. она станет центральной областью прикладной статистики, поскольку содержит наиболее общие подходы и результаты.

Исходный объект в прикладной математической статистике - это выборка. В вероятностной теории статистики выборка - это совокупность независимых одинаково распределенных случайных элементов. Какова природа этих элементов? В классической математической статистике элементы выборки - это числа. В многомерном статистическом анализе - вектора. А в нечисловой статистике элементы выборки - это объекты нечисловой природы, которые нельзя складывать и умножать на числа. Другими словами, объекты нечисловой природы лежат в пространствах, не имеющих векторной структуры. Примерами объектов нечисловой природы являются:

значения качественных признаков, т.е. результаты кодировки объектов с помощью заданного перечня категорий (градаций);

упорядочения (ранжировки) образцов продукции (при оценке её технического уровня и конкурентоспособности)) или заявок на проведение научных работ (при проведении конкурсов на выделение грантов), описывающие мнения экспертов;

классификации, т.е. разбиения совокупности объектов на группы сходных между собой (кластеры);

толерантности, т.е. бинарные отношения, описывающие сходство объектов между собой, например, сходство тематики научных работ, которое оценивается экспертами с целью рационального формирования экспертных советов внутри определенной области науки;

результаты парных сравнений или контроля качества продукции по альтернативному признаку («годен» - «брак»), т.е. последовательности из 0 и 1;

множества (обычные или нечеткие), например, зоны, пораженные коррозией; топокарты, полученные при кинетокардиографии; перечни возможных причин аварии, составленные экспертами независимо друг от друга; нечеткие экспертные оценки качества газовых плит;

слова, предложения, тексты;

вектора, координаты которых - совокупность значений разнотипных признаков, например, результат составления статистического отчета о научно-технической деятельности (т.н. форма № 1-наука) или заполненная компьютеризированная история болезни, в которой часть признаков носит качественный характер, а часть - количественный;

ответы на вопросы экспертной, маркетинговой или социологической анкеты, часть из которых носит количественный характер (возможно, интервальный), часть сводится к выбору одной из нескольких подсказок, а часть представляет собой тексты;

графы, и т.д.

Интервальные данные также можно рассматривать как пример объектов нечисловой природы, а именно, как частный случай нечетких множеств.

С начала 1970-х годов под влиянием запросов прикладных исследований в социально-экономических, технических, медицинских науках в России активно развивается статистика объектов нечисловой природы, известная также как статистика нечисловых данных или нечисловая статистика. В создании этой сравнительно новой области эконометрики и прикладной математической статистики приоритет принадлежит российским ученым.

Большую роль сыграл основанный в 1973 г. научный семинар «Экспертные оценки и анализ данных». В 1960-е годы советское научное сообщество стало интересоваться методами экспертных оценок (об их истории и современном состоянии см. ниже и [52, 135]). Как следствие, началось знакомство с конкретными математизированными теориями, связанными с этими методами. Речь идет о репрезентативной теории измерений, ставшей известной в нашей стране по статье П. Суппеса и Дж. Зинеса в сборнике [136] и книге И. Пфанцагля [137], о теории нечеткости, современный этап которой начался с работ Л.А. Заде [138], теории парных сравнений, описанной в монографии Г. Дэвида [139]. К этому кругу идей примыкают теория случайных множеств (см., например, книгу Ж. Матерона [140]) и методы многомерного шкалирования (описаны, в частности, в монографиях А.Ю. Терехиной [141] и В.Т. Перекреста [142]). Но наибольшее влияние оказали идеи американского исследователя проф. Дж. Кемени, который аксиоматически ввел расстояние между ранжировками (теперь оно именуется в литературе расстоянием Кемени) и предложил использовать в качестве средней величины решение оптимизационной задачи (теперь - медиана Кемени). Его скромная по объему книга [143], написанная в соавторстве с Дж. Снеллом, породила большой поток исследований.

В течение 1970-х годов на основе запросов теории экспертных оценок (а также социологии, экономики, техники и медицины) развивались конкретные направления статистики объектов нечисловой природы. Были установлены связи между конкретными видами таких объектов, разработаны для них вероятностные модели. Научные итоги этого периода подведены в монографиях [7, 144, 145].

Следующий этап - выделение статистики объектов нечисловой природы в качестве самостоятельного направления в прикладной статистике, ядром которого являются методы статистического анализа данных произвольной природы. Программа развития этого нового научного направления впервые была сформулирована в статье [146]. Реализация этой программы была осуществлена в основном в 1980-е годы. Для работ этого периода характерна сосредоточенность на внутренних проблемах нечисловой статистики. Ссылки на конкретные монографии, сборники, статьи и иные публикации нескольких сотен авторов приведены в [36, 82]. Отметим лишь сборник научных статей [87], первый сборник, полностью посвященный нечисловой статистике.

К началу 1990-х годов статистика объектов нечисловой природы с теоретической точки зрения была достаточно хорошо развита, основные идеи, подходы и методы были разработаны и изучены математически, в частности, доказано достаточно много теорем. Однако она оставалась недостаточно апробированной на практике. И в 1990-е годы наступило время от теоретических математико-статистических исследований перейти к применению полученных результатов при решении конкретных задач в различных областях науки и практики. В конце ХХ в. и начале XXI в. началось преподавание статистики объектов нечисловой природы, в частности, в учебных курсах «Прикладная статистика», «Эконометрика», «Организационно-экономическое моделирование», «Принятие решений» и др.

Важно отметить, что в статистике нечисловых данных, как и в других областях прикладной статистики и прикладной математики вообще, одна и та же математическая схема может с успехом применяться при решении различных задач анализа конкретных данных. В технических исследованиях, и в менеджменте, и в экономике, и в геологии, и в медицине, и в социологии, и для анализа экспертных оценок, и во многих иных областях. А потому ее лучше всего формулировать и изучать в наиболее общем виде, для объектов произвольной природы.

2.4.6. Основные идеи статистики объектов
нечисловой природы

В чем принципиальная новизна нечисловой статистики? Для классической математической статистики характерна операция сложения. При расчете выборочных характеристик распределения (выборочное среднее арифметическое, выборочная дисперсия и др.), в регрессионном анализе и других областях этой научной дисциплины постоянно используются суммы. Математический аппарат - законы больших чисел, Центральная предельная теорема и другие теоремы - нацелены на изучение сумм. В нечисловой же статистике нельзя использовать операцию сложения, поскольку элементы выборки лежат в пространствах, где нет операции сложения. Методы обработки нечисловых данных основаны на принципиально ином математическом аппарате - на применении различных расстояний в пространствах объектов нечисловой природы.

Кратко рассмотрим несколько идей, развиваемых в статистике объектов нечисловой природы для данных, лежащих в пространствах произвольного вида. Решаются классические задачи описания данных, оценивания, проверки гипотез - но для неклассических данных, а потому неклассическими методами.

Первой обсудим проблему определения средних величин. В рамках репрезентативной теории измерений удается указать вид средних величин, соответствующих тем или иным шкалам измерения. В классической математической статистике эмпирические и теоретические средние величины вводят с помощью операций сложения (выборочное среднее арифметическое, математическое ожидание) или упорядочения (выборочная и теоретическая медианы). В пространствах произвольной природы средние значения нельзя определить с помощью операций сложения или упорядочения. Теоретические и эмпирические средние приходится вводить как решения экстремальных задач. Для теоретического среднего это - задача минимизации математического ожидания (в классическом смысле) расстояния от случайного элемента со значениями в рассматриваемом пространстве до фиксированной точки этого пространства (минимизируется указанная функция от этой точки). Для эмпирического среднего математическое ожидание берется по эмпирическому распределению, т.е. берется сумма расстояний от некоторой точки до элементов выборки и затем минимизируется по этой точке. При этом как эмпирическое, так и теоретическое средние как решения экстремальных задач могут быть не единственными элементами пространства, а описываться множествами таких элементов, которые могут оказаться и пустыми. Несмотря на возможность неоднозначности или пустоты решений экстремальных задач, удалось сформулировать и доказать законы больших чисел для средних величин, определенных указанным образом, т.е. установить сходимость эмпирических средних к теоретическим.

Как обычно, хорошая общая теория дает больше того, что от нее вначале ожидалось. Так, удалось установить, что методы доказательства законов больших чисел допускают существенно более широкую область применения, чем та, для которой они были разработаны. А именно, с помощью этих методов удалось изучить асимптотику решений экстремальных статистических задач, к которым, как известно, сводится большинство постановок прикладной статистики. В частности, кроме законов больших чисел установлена и состоятельность оценок минимального контраста, в том числе оценок максимального правдоподобия и робастных оценок. К настоящему времени подобные оценки изучены также и в интервальной статистике.

В статистике в пространствах произвольной природы большую роль играют непараметрические оценки плотности, используемые, в частности, в различных алгоритмах регрессионного, дискриминантного, кластерного анализов. В нечисловой статистике предложен и изучен ряд типов непараметрических оценок плотности в пространствах произвольной природы, в частности, доказана их состоятельность, изучена скорость сходимости и установлен примечательный факт совпадения наилучшей скорости сходимости в произвольном случае с той, которая имеет быть в классической математико-статистической теории для числовых случайных величин.

Дискриминантный, кластерный, регрессионный анализы в пространствах произвольной природы основаны либо на параметрической теории - и тогда применяется подход, связанный с асимптотикой решения экстремальных статистических задач - либо на непараметрической теории - и тогда используются алгоритмы на основе непараметрических оценок плотности.

Для проверки гипотез могут быть использованы статистики интегрального типа, в частности, типа омега-квадрат. Любопытно, что предельная теория таких статистик, построенная первоначально в классической постановке [147] для конечномерного пространства, приобрела естественный (завершенный, изящный) вид именно для пространств произвольного вида [148, 148], поскольку при этом удалось провести рассуждения, опираясь на базовые математические соотношения, а не на те частные (с общей точки зрения), что были связаны с конечномерным пространством.

Представляют практический интерес результаты, связанные с конкретными областями статистики нечисловых данных. В частности, со статистикой нечетких и случайных множеств (напомним, что теория нечетких множеств в определенном смысле сводится к теории случайных множеств), с непараметрической теорией парных сравнений, с аксиоматическим введением метрик в конкретных пространствах объектов нечисловой природы, и с рядом других конкретных постановок.

Для анализа нечисловых, в частности, экспертных данных весьма важны методы классификации. С другой стороны, наиболее естественно ставить и решать задачи классификации, основанные на использовании расстояний или показателей различия, в рамках статистики нечисловых данных. Это касается как распознавания образов с учителем (другими словами, дискриминантного анализа), так и распознавания образов без учителя (т.е. кластерного анализа).

Статистические методы анализа нечисловых данных особенно хорошо приспособлены для применения в экономике, социологии и экспертных оценках, поскольку в этих областях от 50% до 90% данных являются нечисловыми [36].

Итак, статистика нечисловых данных является центром прикладной статистики. А ее теоретическая основа – статистика в пространствах произвольной природы – является стержнем математической статистики.

2.4.7. Другие точки роста

Выше рассмотрены пять основных «точек роста» прикладной статистики и других статистических методов. Разумеется, они не исчерпывают все многообразие фронта научных исследований в рассматриваемых областях. Кроме того, мы почти не затронули разнообразные применения статистических методов в конкретных прикладных исследованиях и разработках. Много интересных проблем есть в планировании экспериментов, особенно кинетических (см., например, [150]), при анализе проблем надежности, в новых статистических методах управления качеством продукции [16, 39], при анализе рисков [151], в вопросах экологии и промышленной безопасности [62] и др.

Необходимо отметить, что в течение последних более чем 60 лет в России наблюдается огромный разрыв между государственной статистикой и научным сообществом специалистов по статистическим методам (подробнее об этом см. статью [152]). Так, в учебнике по истории статистики [153] даже не упоминаются имена членов-корреспондентов АН СССР Н.В.Смирнова и Л.Н. Большева! А ведь они – единственные представители именно математической статистики как таковой в Академии наук в ХХ в. (еще ряд членов отечественной Академии наук имели математическую статистику среди своих интересов, но Н.В. Смирнов и Л.Н. Большев занимались практически только ею).

ГЛАВА 3. КОНКРЕТНЫЕ ОБЛАСТИ МАТЕМАТИЧЕСКИХ И ИНСТРУМЕНТАЛЬНЫХ МЕТОДОВ КОНТРОЛЛИНГА

Бросив общий взгляд на математические и инструментальные методы контроллинга, рассмотрев "с птичьего полета" эту обширную область теоретических и прикладных исследований, вполне естественно проанализировать ранее выделенные крупные научные направления. Двигаясь "сверху вниз", мы получим возможность обсуждать конкретные алгоритмы расчетов, однако за подробностями часто будем отсылать к соответствующим публикациям. По нашей оценке, современный этап развития науки характеризуется тем, что конкретные методы достаточно хорошо описаны в традиционных бумажных изданиях и в Интернет-ресурсах. Недостаточно проработан следующий иерархический этап - анализ совокупностей методов, предназначенных для решения задач в рамках конкретных научных направлений. Необходимо развитие методологии [50] математических и инструментальных методов контроллинга, т.е. организации деятельности в этой области исследований. Именно развитию методологии посвящена настоящая часть монографии. Начнем с анализа выделенных в предыдущей части точек роста.

3.1. Современное состояние непараметрической
статистики

Непараметрическая статистика – одна из пяти точек роста прикладной математической статистики и математических методов экономики в целом (включая контроллинг). Специалистам хорошо известно большое число публикаций по конкретным вопросам непараметрической статистики - статей и книг, полностью или частично посвященных этой тематике. Однако приходится констатировать, что внутренняя структура научного направления "Непараметрическая статистика" остается до настоящего времени непроявленной. Цель настоящего раздела – на основе сложившегося в практике научной деятельности определения непараметрической статистики рассмотреть ее деление на области и систематизировать исследования по непараметрическим статистическим методам.

Непараметрическая статистика – одна из пяти точек роста прикладной математической статистики, выделенных в разделе 2.3 (см. также статьи [67, 154, 155]). Она занимает важное место среди математических методов исследования. Однако, несмотря на большое число публикаций по конкретным вопросам непараметрической статистики, внутренняя структура этого научного направления оставалась до сих пор непроявленной. На основе сложившегося в практике научной деятельности определения непараметрической статистики проведем ее деление на области и сделаем первоначальную попытку систематизировать публикации по непараметрическим статистическим методам.

Как известно, непараметрика, или - подробнее - непараметрическая статистика, позволяет делать статистические выводы, в частности, оценивать характеристики распределения и проверять статистические гипотезы, без, как правило, слабо обоснованных предположений о том, что функция распределения элементов выборки входит в то или иное параметрическое семейство. Например, широко распространена вера в то, что статистические данные часто подчиняются нормальному распределению. Как говорят (частично в шутку, частично всерьез - распространенная фраза из научного фольклора), математики думают, что это - экспериментальный факт, установленный в прикладных исследованиях, в то время как прикладники уверены, что математики доказали нормальность результатов наблюдений. Между тем анализ конкретных результатов наблюдений, в частности, погрешностей измерений, приводит всегда к одному и тому же выводу - в подавляющем большинстве случаев реальные распределения существенно отличаются от нормальных [121]. Некритическое использование гипотезы нормальности часто приводит к значительным ошибкам, например, при отбраковке резко выделяющихся результатов наблюдений (выбросов) [156], при статистическом контроле качества и в других случаях. Поэтому целесообразно использовать непараметрические методы, в которых на функции распределения результатов наблюдений наложены лишь весьма слабые требования. Обычно предполагается лишь их непрерывность. На основе обобщения многочисленных исследований можно констатировать, что к настоящему времени с помощью непараметрических методов можно решать практически тот же круг задач, что ранее решался параметрическими методами. Являются несостоятельными встречающиеся в литературе заявления о том, что непараметрические методы имеют меньшую мощность или требуют большего объема выборки, чем параметрические. При этом в непараметрике, как и в математической статистике в целом, шире - во всей обширной области математических методов исследования, остается ряд нерешенных задач, некоторые из которых сформулированы в статье [157].

3.1.1. Параметрические и непараметрические
гипотезы

Начнем обсуждение понятия «непараметрическая статистика» с постановок задач проверки статистических гипотез, следуя подходу, зафиксированному в справочнике [60]. Уточнение исходных понятий необходимо, поскольку в литературе распространены неполные или даже неверные формулировки.

Статистическая гипотеза – любое предположение, касающееся неизвестного распределения случайных величин (элементов). Приведем формулировки нескольких статистических гипотез:

1. Результаты наблюдений имеют нормальное распределение с нулевым математическим ожиданием.

2. Результаты наблюдений имеют функцию стандартного нормального распределения c нулевым математическим ожиданием и единичной дисперсией (обычно такое распределение обозначается N(0,1)).

3. Результаты наблюдений имеют нормальное распределение.

4. Результаты наблюдений в двух независимых выборках имеют одно и то же нормальное распределение.

5. Результаты наблюдений в двух независимых выборках имеют одно и то же распределение.

Различают нулевую и альтернативную гипотезы. Нулевая гипотеза – гипотеза, подлежащая проверке. Альтернативная гипотеза – каждая допустимая гипотеза, отличная от нулевой. Нулевую гипотезу обозначают Н₀, альтернативную – Н₁ (от Hypothesis – «гипотеза» (англ.)). Выбор тех или иных нулевых или альтернативных гипотез определяется стоящими перед менеджером, экономистом, инженером, исследователем прикладными задачами. Рассмотрим примеры.

Пример 1. Пусть нулевая гипотеза – гипотеза 2 из приведенного выше списка, а альтернативная – гипотеза 1. Сказанное означает, что реальная ситуация описывается вероятностной моделью, согласно которой результаты наблюдений рассматриваются как реализации независимых одинаково распределенных случайных величин с функцией распределения N(0,σ), где параметр σ (среднее квадратичное отклонение) неизвестен статистику. В рамках этой модели нулевую гипотезу записывают так:

Н₀: σ = 1,

а альтернативную так:

Н₁: σ ≠ 1.

Пример 2. Пусть нулевая гипотеза – по-прежнему гипотеза 2 из приведенного выше списка, а альтернативная – гипотеза 3 из того же списка. Тогда в вероятностной модели управленческой, экономической или производственной ситуации предполагается, что результаты наблюдений образуют выборку из нормального распределения N(m, σ) при некоторых значениях m и σ. Гипотезы записываются так:

Н₀: m = 0, σ = 1

(оба параметра принимают фиксированные значения);

Н₁: m ≠ 0 и/или σ ≠ 1

(т.е. либо m ≠ 0, либо σ ≠ 1, либо и m ≠ 0, и σ ≠ 1).

Пример 3. Пусть Н₀ – гипотеза 1 из приведенного выше списка, а Н₁ – гипотеза 3 из того же списка. Тогда вероятностная модель – та же, что в примере 2,

Н₀: m = 0, σ произвольно;

Н₁: m ≠ 0, σ произвольно.

Пример 4. Пусть Н₀ – гипотеза 2 из приведенного выше списка, а согласно Н₁ результаты наблюдений имеют функцию распределения F(x), не совпадающую с функцией стандартного нормального распределения Ф(х). Тогда

Н₀: F(х) = Ф(х) при всех х (записывается как тождество F(х) ≡ Ф(х));

Н₁: F(х₀) ≠ Ф(х₀) при некотором х₀ (т.е. неверно, что F(х) ≡ Ф(х)).

Примечание. Здесь символ "≡" - знак тождественного совпадения функций (т.е. совпадения при всех возможных значениях аргумента х).

Пример 5. Пусть Н₀ – гипотеза 3 из приведенного выше списка, а согласно Н₁ результаты наблюдений имеют функцию распределения F(x), не являющуюся нормальной. Тогда

при некоторых m, σ;

Н₁: для любых m, σ найдется х₀ = х₀(m, σ) такое, что

.

Пример 6. Пусть Н₀ – гипотеза 4 из приведенного выше списка, согласно вероятностной модели две выборки извлечены из совокупностей с функциями распределения F(x) и G(x), являющихся нормальными с параметрами m₁, σ₁ и m₂, σ₂ соответственно, а Н₁ – отрицание Н₀. Тогда

Н₀: m₁ = m₂, σ₁ = σ₂, причем m₁ и σ₁ произвольны;

Н₁: m₁ ≠ m₂ и/или σ₁ ≠ σ₂.

Пример 7. Пусть в условиях примера 6 дополнительно известно, что σ₁ = σ₂. Тогда

Н₀: m₁ = m₂, σ > 0, причем m₁ и σ произвольны;

Н₁: m₁ ≠ m₂, σ > 0.

Пример 8. Пусть Н₀ – гипотеза 5 из приведенного выше списка, согласно вероятностной модели две выборки извлечены из совокупностей с функциями распределения F(x) и G(x) соответственно, а Н₁ – отрицание Н₀. Тогда

Н₀: F(x) ≡ G(x), где F(x) – произвольная функция распределения;

Н₁: F(x) и G(x) - произвольные функции распределения, причем

F(x) ≠ G(x) при некоторых х.

Пример 9. Пусть в условиях примера 7 дополнительно предполагается, что функции распределения F(x) и G(x) отличаются только сдвигом, т.е. G(x) = F(x - а) при некотором а. Тогда

Н₀: F(x) ≡ G(x), где F(x) – произвольная функция распределения;

Н₁: G(x) = F(x - а), а ≠ 0, где F(x) – произвольная функция распределения.

Пример 10. Пусть в условиях примера 4 дополнительно известно, что согласно вероятностной модели ситуации F(x) - функция нормального распределения с единичной дисперсией, т.е. имеет вид N(m, 1). Тогда

Н₀: m = 0 (т.е. F(х) = Ф(х) при всех х, F(х) ≡ Ф(х));

Н₁: m ≠ 0 (т.е. неверно, что F(х) ≡ Ф(х)).

Пример 11. При статистическом регулировании технологических, экономических, управленческих или иных процессов [97, 158] рассматривают выборку, извлеченную из совокупности с нормальным распределением и известной дисперсией, и гипотезы

Н₀: m = m₀,

Н₁: m = m₁,

где значение параметра m = m₀ соответствует налаженному ходу процесса, а переход к m = m₁ свидетельствует о разладке.

Пример 12. При статистическом приемочном контроле [16, 159, 160] число дефектных единиц продукции в выборке подчиняется гипергеометрическому распределению, неизвестным параметром является p = D/N – уровень дефектности, где N – объем партии продукции, D – общее число дефектных единиц продукции в партии. Используемые в нормативно-технической и коммерческой документации (стандартах, договорах на поставку и др.) планы контроля часто нацелены на проверку гипотезы

Н₀: p < AQL

против альтернативной гипотезы

Н₁: p > LQ,

где AQL – приемочный уровень дефектности, LQ – браковочный уровень дефектности (очевидно, что AQL < LQ).

Пример 13. В качестве показателей стабильности технологического, экономического, управленческого или иного процесса используют ряд характеристик распределений контролируемых показателей, в частности, коэффициент вариации v = σ/M(X). Требуется проверить нулевую гипотезу

Н₀: v < v₀

при альтернативной гипотезе

Н₁: v > v₀,

где v₀ – некоторое заранее заданное граничное значение.

Пример 14. Пусть вероятностная модель двух выборок – та же, что в примере 8, математические ожидания результатов наблюдений в первой и второй выборках обозначим М(Х) и М(У) соответственно. В ряде ситуаций проверяют нулевую гипотезу

Н₀: М(Х) = М(У)

против альтернативной гипотезы

Н₁: М(Х) ≠ М(У).

Пример 15. В статье [161] отмечалось большое значение в математической статистике функций распределения, симметричных относительно 0. При проверке симметричности

Н₀: F(-x) = 1 – F(x) при всех x, в остальном F произвольна;

Н₁: F(–x₀) ≠ 1 – F(x₀) при некотором x₀, в остальном F произвольна.

В вероятностно-статистических методах принятия решений используются и многие другие постановки задач проверки статистических гипотез.

Конкретная задача проверки статистической гипотезы полностью описана, если заданы нулевая и альтернативная гипотезы. Выбор метода проверки статистической гипотезы, свойства и характеристики методов определяются как нулевой, так и альтернативной гипотезами. Для проверки одной и той же нулевой гипотезы при различных альтернативных гипотезах следует использовать, вообще говоря, различные методы. Так, в примерах 4 и 10 нулевая гипотеза одна и та же, а альтернативные – различны. Поэтому в условиях примера 4 следует применять методы проверки согласия с фиксированным распределением (например, критерии Колмогорова или омега-квадрат), а в условиях примера 10 - критерий Стьюдента. Если в условиях примера 4 использовать критерий Стьюдента, то он не будет решать поставленных задач (не сможет обнаружить все варианты альтернативных гипотез). Если в условиях примера 10 использовать критерий согласия Колмогорова, то он, напротив, будет решать поставленные задачи, хотя, возможно, и хуже, чем специально приспособленный для этого случая критерий Стьюдента.

При обработке реальных данных большое значение имеет правильный выбор гипотез Н₀ и Н₁. Принимаемые предположения, например, нормальность распределения, должны быть тщательно обоснованы, в частности, статистическими методами. Отметим, что в подавляющем большинстве конкретных прикладных постановок распределение результатов наблюдений отлично от нормального [121].

Часто возникает ситуация, когда вид нулевой гипотезы вытекает из постановки прикладной задачи, а вид альтернативной гипотезы не ясен. В таких случаях следует рассматривать альтернативную гипотезу наиболее общего вида и использовать методы, решающие поставленную задачу при всех возможных Н₁. В частности, при проверке гипотезы 2 (из приведенного выше списка) как нулевой следует в качестве альтернативной гипотезы использовать Н₁ из примера 4, а не из примера 10, если нет специальных обоснований нормальности распределения результатов наблюдений при альтернативной гипотезе.

Статистические гипотезы разделяют на два класса - параметрические и непараметрические. Дадим определения этим терминам. Предположение, которое касается неизвестного значения параметра распределения, входящего в некоторое параметрическое семейство распределений, называется параметрической гипотезой (отметим, что параметр может быть и многомерным). Предположение, при котором вид распределения неизвестен (т.е. не предполагается, что оно входит в некоторое априори заданное параметрическое семейство распределений), называется непараметрической гипотезой. Таким образом, если распределение F(x) результатов наблюдений в выборке согласно принятой вероятностной модели входит в некоторое параметрическое семейство {F(x;θ), θΘ}, т.е. F(x) = F(x;θ₀) при некотором θ₀Θ, то рассматриваемая гипотеза – параметрическая, в противном случае – непараметрическая.

Если и Н₀ и Н₁ – параметрические гипотезы, то задача проверки статистической гипотезы – параметрическая. Если хотя бы одна из гипотез Н₀ и Н₁ – непараметрическая, то задача проверки статистической гипотезы – непараметрическая. Другими словами, если вероятностная модель ситуации – параметрическая, т.е. полностью описывается в терминах того или иного параметрического семейства распределений вероятностей, то и задача проверки статистической гипотезы – параметрическая. Если же вероятностная модель ситуации – непараметрическая, т.е. ее нельзя полностью описать в терминах какого-либо параметрического семейства распределений вероятностей, то и задача проверки статистической гипотезы – непараметрическая. В примерах 1 - 3, 6, 7, 10 - 12 даны постановки параметрических задач проверки гипотез, а в примерах 4, 5, 8, 9, 13 - 15 – непараметрических. Непараметрические задачи проверки гипотез делятся на два класса: в одном из них речь идет о проверке утверждений, касающихся функций распределения (примеры 4, 5, 8, 9, 15), во втором – о проверке утверждений, касающихся характеристик распределений (примеры 13, 14).

Статистическая гипотеза называется простой, если она однозначно задает распределение результатов наблюдений, вошедших в выборку. В противном случае статистическая гипотеза называется сложной. Гипотеза 2 из приведенного выше списка, нулевые гипотезы в примерах 1, 2, 4, 10, нулевая и альтернативная гипотезы в примере 11 – простые, все остальные упомянутые выше гипотезы – сложные.

Однозначно определенный способ проверки статистических гипотез называется статистическим критерием. Статистический критерий строится с помощью статистики U(x₁, x₂, …, x_n) – функции от результатов наблюдений x₁, x₂, …, x_n. В пространстве значений статистики U выделяют критическую область Ψ, т.е. область со следующим свойством: если значения применяемой статистики принадлежат данной области, то отклоняют (иногда говорят - отвергают) нулевую гипотезу, в противном случае – не отвергают (т.е. принимают).

Статистику U, используемую при построении определенного статистического критерия, называют статистикой этого критерия. Например, в задаче проверки статистической гипотезы, приведенной в примере 4, применяют критерий Колмогорова, основанный на статистике

.

При этом D_n называют статистикой критерия Колмогорова.

Частным случаем статистики U является векторзначная функция результатов наблюдений U₀(x₁, x₂, …, x_n) = (x₁, x₂, …, x_n), значения которой – набор результатов наблюдений. Если x_i – числа, то U₀ – набор n чисел, т.е. точка n–мерного пространства. Ясно, что статистика критерия U является функцией от U₀, т.е. U = f(U₀). Поэтому можно считать, что Ψ – область в том же n–мерном пространстве, нулевая гипотеза отвергается, если (x₁, x₂, …, x_n)Ψ, и принимается в противном случае.

В вероятностно-статистических методах обработки данных и принятия решений статистические критерии, как правило, основаны на статистиках U, принимающих числовые значения, и критические области имеют вид

Ψ = {U(x₁, x₂, …, x_n) > C}, (1)

где С – некоторые числа.

Статистические критерии делятся на параметрические и непараметрические: параметрические критерии используются в параметрических задачах проверки статистических гипотез, а непараметрические – в непараметрических задачах.

При проверке статистической гипотезы возможны ошибки. Есть два рода ошибок. Ошибка первого рода заключается в том, что отвергают нулевую гипотезу, в то время как в действительности эта гипотеза верна. Ошибка второго рода состоит в том, что принимают нулевую гипотезу, в то время как в действительности эта гипотеза неверна.

Вероятность ошибки первого рода называется уровнем значимости и обозначается α. Таким образом, α = P{UΨ | H₀}, т.е. уровень значимости α – это вероятность события {UΨ}, вычисленная в предположении, что верна нулевая гипотеза Н₀.

Уровень значимости однозначно определен, если Н₀ – простая гипотеза. Если же Н₀ – сложная гипотеза, то уровень значимости, вообще говоря, зависит от функции распределения результатов наблюдений, удовлетворяющей Н₀. Статистику критерия U обычно строят так, чтобы вероятность события {UΨ} не зависела от того, какое именно распределение (из удовлетворяющих нулевой гипотезе Н₀) имеют результаты наблюдений. Для статистик критерия U общего вида под уровнем значимости понимают максимально возможную ошибку первого рода. Максимум (точнее, супремум) берется по всем возможным распределениям, удовлетворяющим нулевой гипотезе Н₀, т.е. α = sup P{UΨ | H₀}.

Если критическая область имеет вид, указанный в формуле (1), то

P{U > C | H₀} = α. (2)

Если С задано, то из последнего соотношения определяют α. Часто поступают по иному - задавая α (обычно α = 0,05, иногда α = 0,01 или α = 0,1, другие значения α используются гораздо реже), определяют С из уравнения (2), обозначая его С_α, и используют критическую область Ψ = {U > C_α} с заданным уровнем значимости α.

Вероятность ошибки второго рода есть P{UΨ | H₁}. Обычно используют не эту вероятность, а ее дополнение до 1, т.е. P{UΨ | H₁} = 1 – P{UΨ | H₁}. Эта величина носит название мощности критерия. Итак, мощность критерия – это вероятность того, что нулевая гипотеза будет отвергнута, когда альтернативная гипотеза верна.

Понятия уровня значимости и мощности критерия объединяются в понятии функции мощности критерия – функции, определяющей вероятность того, что нулевая гипотеза будет отвергнута. Функция мощности зависит от критической области Ψ и действительного распределения результатов наблюдений. В параметрической задаче проверки гипотез распределение результатов наблюдений задается параметром θ. В этом случае функция мощности обозначается М(Ψ, θ) и зависит от критической области Ψ и действительного значения исследуемого параметра θ. Если

Н₀: θ = θ₀,

Н₁: θ = θ₁,

то

М(Ψ, θ₀) = α,

М(Ψ, θ₁) = 1 – β,

где α – вероятность ошибки первого рода, β - вероятность ошибки второго рода. В статистическом приемочном контроле α – риск изготовителя, β – риск потребителя. При статистическом регулировании технологического процесса α – риск излишней наладки, β – риск незамеченной разладки.

Функция мощности М(Ψ, θ) в случае одномерного параметра θ обычно достигает минимума, равного α, при θ = θ₀, монотонно возрастает при удалении от θ₀ и приближается к 1 при |θ - θ₀| → ∞.

В ряде вероятностно-статистических методов принятия решений используется оперативная характеристика L(Ψ, θ) - вероятность принятия нулевой гипотезы в зависимости от критической области Ψ и действительного значения исследуемого параметра θ. Ясно, что

L(Ψ, θ) = 1 - М(Ψ, θ).

Основной характеристикой статистического критерия является функция мощности. Для многих задач проверки статистических гипотез разработан не один статистический критерий, а целый ряд. Чтобы выбрать из них определенный критерий для использования в конкретной практической ситуации, проводят сравнение критериев по различным показателям качества [16, приложение 3], прежде всего с помощью их функций мощности. В качестве примера рассмотрим лишь два показателя качества критерия проверки статистической гипотезы – состоятельность и несмещенность.

Пусть объем выборки n растет, а U_n и Ψ_n – статистики критерия и критические области соответственно. Критерий называется состоятельным, если

т.е. вероятность отвергнуть нулевую гипотезу стремится к 1, если верна альтернативная гипотеза.

Статистический критерий называется несмещенным, если для любого θ₀, удовлетворяющего Н₀, и любого θ₁ , удовлетворяющего Н₁, справедливо неравенство

P{UΨ | θ₀} < P{UΨ | θ₁},

т.е. при справедливости Н₀ вероятность отвергнуть Н₀ меньше, чем при справедливости Н₁.

При наличии нескольких статистических критериев в одной и той же задаче проверки статистических гипотез следует использовать состоятельные и несмещенные критерии. Предлагаемый из каких-либо соображений критерий, предназначенный для определенной задачи проверки статистических гипотез, подлежит проверке – является ли он состоятельным и несмещенным. Можно поставить вопрос иначе: для какой задачи проверки статистических гипотез предназначен определенный критерий, т.е. для какой задачи он является состоятельным?

3.1.2. Место непараметрической статистики
в истории прикладной статистики

Типовые примеры раннего этапа применения статистических методов описаны в Ветхом Завете (см., например, Книгу Чисел). Там, в частности, описана перепись военнообязанных – подсчет числа воинов в различных племенах. С математической точки зрения дело сводилось к подсчету числа попаданий значений наблюдаемых признаков в определенные градации [110].

В дальнейшем результаты обработки статистических данных стали представлять в виде таблиц и диаграмм, как это и сейчас делают органы государственной статистики. Надо признать, что по сравнению с Ветхим Заветом есть прогресс – в Библии не было таблиц и диаграмм. Однако нет продвижения по сравнению с работами российских статистиков конца XIX – начала XX вв.

Сразу после возникновения теории вероятностей (Паскаль, Ферма, XVII в.) вероятностные модели стали использоваться при обработке статистических данных. Например, изучалась частота рождения мальчиков и девочек, было установлено отличие вероятности рождения мальчика от вероятности рождения девочки (и от 0,5), анализировались причины того, что в парижских приютах эта вероятность не та, что в самом Париже, и т.д. Имеется достаточно много публикаций по истории теории вероятностей с описанием раннего этапа развития статистических методов исследований; к лучшим из них относится очерк [162].

В 1794 г. К. Гаусс разработал метод наименьших квадратов, один из наиболее популярных ныне статистических методов, и применил его при расчете орбиты малой планеты (астероида) Церера – для борьбы с ошибками астрономических наблюдений [64]. В ХIХ веке заметный вклад в развитие практической статистики внес бельгиец А. Кетле, показавший на основе анализа большого числа реальных данных устойчивость относительных статистических показателей, таких, как доля самоубийств среди всех смертей [153]. Интересно, что основные идеи статистического приемочного контроля и сертификации продукции обсуждались академиком Петербургской Академии наук М.В. Остроградским (1801–1862) и применялись в российской армии ещё в середине ХIХ в. [16]. Статистические методы управления качеством и сертификации продукции сейчас весьма актуальны [16].

Отсчет современного этапа развития статистических методов можно начать с 1900 г., когда англичанин К. Пирсон основал журнал «Biometrika». Первая треть ХХ в. прошла под знаком параметрической статистики. Изучались методы, основанные на анализе данных из параметрических семейств распределений, описываемых кривыми семейства Пирсона. Наиболее популярным было нормальное (гауссово) распределение. Использовались экспоненциальные и логарифмически нормальные распределения, распределения Вейбулла – Гнеденко, гамма-распределения, биномиальное и гипергеометрическое распределения, распределение Пуассона и др. Для проверки гипотез применялись критерии Пирсона, Стьюдента, Фишера. Были предложены метод максимального правдоподобия, дисперсионный анализ, сформулированы основные идеи планирования эксперимента.

Разработанную в первой трети ХХ в. теорию статистического анализа данных называют параметрической статистикой, поскольку ее основной объект изучения – это выборки из распределений, описываемых одним или небольшим числом параметров. Наиболее общим является семейство кривых Пирсона, задаваемых четырьмя параметрами. Как правило, нельзя указать каких-либо веских причин, по которым распределение результатов конкретных наблюдений должно входить в то или иное параметрическое семейство. Исключения хорошо известны: если вероятностная модель предусматривает суммирование независимых случайных величин, то сумму естественно описывать нормальным распределением; если же в модели рассматривается произведение таких величин, то итог, видимо, приближается логарифмически нормальным распределением, и т.д. Однако подобных моделей нет в подавляющем большинстве реальных ситуаций, и приближение реального распределения с помощью кривых из семейства Пирсона или его подсемейств – чисто формальная операция. Именно из таких соображений критиковал параметрическую статистику академик АН СССР С.Н. Бернштейн в 1927 г. в своем докладе на Всероссийском съезде математиков [49].

В первой трети ХХ в., одновременно с параметрической статистикой, в работах Спирмена и Кендалла появились первые непараметрические методы, основанные на коэффициентах ранговой корреляции, носящих ныне имена этих статистиков. Но непараметрика, не делающая нереалистических предположений о том, что функции распределения результатов наблюдений принадлежат тем или иным параметрическим семействам распределений, стала заметной частью статистики лишь со второй трети ХХ века. В 1930-е годы появились работы А.Н. Колмогорова и Н.В. Смирнова, предложивших и изучивших статистические критерии, носящие в настоящее время их имена. Эти критерии основаны на использовании так называемого эмпирического процесса. (Как известно, эмпирический процесс – это разность между эмпирической и теоретической функциями распределения, умноженная на квадратный корень из объема выборки.) В работе А.Н. Колмогорова 1933 г. изучено предельное распределение супремума модуля эмпирического процесса, называемого сейчас критерием Колмогорова. Затем Н.В. Смирнов исследовал супремум и инфимум эмпирического процесса, а также интеграл (по теоретической функции распределения) квадрата эмпирического процесса. Следует отметить, что встречающееся иногда в литературе словосочетание «критерий Колмогорова-Смирнова» некорректно, поскольку эти два статистика никогда не печатались вместе и не изучали один и тот же критерий схожими методами. Корректно сочетание «критерий типа Колмогорова-Смирнова», применяемое для обозначения критериев, основанных на использовании супремума функций от эмпирических процессов [75, 117].

После Второй мировой войны развитие непараметрической статистики пошло быстрыми темпами. Большую роль сыграли работы американского статистика Ф. Вилкоксона и его школы (см., в частности, [72, 73]). Итог таков: по мнению ведущих специалистов по математической статистике к настоящему времени с помощью непараметрических методов можно решать практически тот же круг статистических задач, что и с помощью параметрических. В нашей стране непараметрические методы получили достаточно большую известность после выхода в 1965 г. первого издания сборника статистических таблиц Л.Н. Большева и Н.В. Смирнова [69], содержащего подробные таблицы для основных непараметрических критериев. Современному подходу к изучению предельного распределения непараметрических статистик посвящена работа [149].

Наше представление об основных этапах развития прикладной математической статистики представлено в табл.1. Названия этапов даны по впервые разработанным подходам. Вновь появляющиеся этапы не вытесняют полностью статистические методы, разработанные на предыдущих. В настоящее время активно используются методы всех четырех этапов.

Таблица 4 – Основные этапы развития прикладной
математической статистики

№	Этапы	Характерные черты	Годы
1	Описатель-ная статистика	Тексты, таблицы, графики. Отдельные расчетные приемы (МНК)	До 1900
2	Параметри-ческая статистика	Модели параметрических семейств распределений – нормальных, гамма и др. Теория оценивания параметров и проверки гипотез	1900 - 1933
3	Непарамет-рическая статистика	Произвольные непрерывные распределения. Непараметрические методы оценивания и проверки гипотез	1933 - 1979
4	Нечисловая статистика	Выборка – из элементов произвольных пространств. Использование показателей различия и расстояний	С 1979

В табл. 4 исходим из деления прикладной математической статистики на четыре области (табл.2). Статистику нечисловых данных (статистику объектов нечисловой природы, нечисловую статистику), ставшую знаменем современного четвертого этапа развития статистических методов (после непараметрической статистики), не рассматриваем в настоящем разделе. Этой области прикладной математической статистики посвящен специальный раздел настоящей монографии, а также достаточно много публикаций, в том числе монографий [5, 36] и обзоров [82, 163].

Таблица 5 – Области прикладной математической статистики

№	Вид статистических данных	Область прикладной статистики
1	Числа	Статистика (случайных) величин
2	Конечномерные вектора	Многомерный статистический анализ
3	Функции	Статистика случайных процессов и временных рядов
4	Объекты нечисловой природы	Статистика нечисловых данных

3.1.3. Три основные области непараметрической
статистики

Исходя из практики статистического анализа данных, опишем структуру непараметрической статистики, выделив основные ее области. Их, по нашему мнению, три:

- область на стыке параметрических и непараметрических методов;

- ранговые статистические методы;

- непараметрические оценки функций, прежде всего плотности распределения, регрессионной зависимости, а также статистик, используемых в теории классификации.

3.1.3.1. Сопоставление параметрических
и непараметрических методов анализа данных

Рассмотрим эти области. Первая из них относится прежде всего к статистике (случайных) величин (см. табл. 2), поскольку обсуждаются различные семейства распределений случайных величин, в то время как для случайных векторов широко известно лишь одно параметрическое семейство - многомерных нормальных распределений.

Многие алгоритмы анализа данных рассматривают как в параметрической, так и в непараметрической статистике. Например, выборочное среднее арифметическое и выборочная дисперсия являются оценками максимального правдоподобия (т.е. в определенном смысле наилучшими) для математического ожидания и дисперсии соответственно, если результаты наблюдения - выборка из нормального распределения. В непараметрической постановке они являются состоятельными оценками математического ожидания и дисперсии. Однако не всегда наилучшими - для оценивания центра распределения в ряде ситуаций предпочтительнее медиана [164]. Непараметрические и параметрические оценки характеристик распределения сопоставлены в статье [165].

Метод моментов проверки согласия с параметрическим семейством распределений [166], например, с нормальным семейством с помощью критериев асимметрии и эксцесса, основан на асимптотической нормальности выборочных моментов для выборок из произвольных распределений. Разработано много критериев согласия [167]. Однако достаточно достоверно отличить нормальное распределение от распределения другого типа можно лишь по выборкам, объем которых - сотни [168] или даже тысячи [5]. Часто критерии согласия применяются с ошибками (см. примеры в [60, 74, 75]. Констатируем, что в наиболее распространенном случае, когда объем выборки - не более нескольких десятков результатов измерений (наблюдений, испытаний, анализов, опытов), невозможно обосновать выбор определенного распределения из того или иного параметрического семейства.

Что происходит, если не выполнены предпосылки, при которых разработаны параметрические методы? Например, для проверки однородности двух независимых выборок в случае нормальности распределений и равенства дисперсий рекомендуют двухвыборочный критерий Стьюдента. Если же предпосылки нарушены, то для проверки равенства математических ожиданий следует использовать критерий Крамера-Уэлча [71]. Крайняя неустойчивость параметрических методов отбраковки резко выделяющихся наблюдений делает невозможным их практическое применение [156]. В то же время доверительные границы для математического ожидания в непараметрическом случае отличаются от таковых в случае нормального распределения только использованием квантилей нормального распределения вместо квантилей распределения Стьюдента, т.е. при росте объемов выборки различие исчезает (ср. с выводами в статье [165]).

Довольно часто предполагают, что погрешности (отклонения, ошибки, невязки) в методе наименьших квадратов имеют нормальное распределение. Однако это предположение не является обязательным. Так, непараметрическому оцениванию точки пересечения регрессионных прямых посвящены работы [169, 170], непараметрический метод наименьших квадратов для восстановления линейной зависимости с периодической составляющей разработан в статьях [119, 171].

3.1.3.2. Ранговые статистические методы

В этих методах используют не сами результаты измерений, а их ранги, т.е. места в упорядоченных рядах. Примерами являются критерии Колмогорова, Смирнова, омега-квадрат, коэффициенты ранговой корреляции Спирмена и Кендалла [69, 75, 117]. Все ранговые статистики измерены в порядковой шкале [5, 36, 82, 163], т.е. их значения не меняются при любом строго возрастающем преобразовании шкалы измерения.

Разработка и изучение ранговых статистик продолжается. Так. в [72, 73] разобраны два мифа, связанные с критерием Вилкоксона (Манна - Уитни) - о том, что этот критерий является состоятельным для проверки тождественного совпадения двух функций распределения (т.н. абсолютной однородности) или хотя бы для проверки равенства их медиан. Несмотря на выявленные недостатки, этот непараметрический критерий полезен для построения карт контроля качества продукции [172]. Состоятельные критерии проверки абсолютной однородности независимых выборок описаны в [173]. Интересный (как теоретически, так и практически) факт существенного различия реальных и номинальных уровней значимости в задачах проверки статистических гипотез с помощью непараметрических критериев выявлен в статье [174].

3.1.3.3. Непараметрические оценки функций

Базовыми являются непараметрические оценки плотности распределения в пространствах произвольной природы [118, 175]. На их основе разработаны методы непараметрического оценивания регрессионных зависимостей, классификации (распознавания образов, дискриминантного и кластерного анализов) [120, 176]. Эти методы, входящие в статистику нечисловых данных [5, 36, 82, 163], имеют большое прикладное значение.

Непараметрический дискриминантный анализ (синонимы: непараметрические методы диагностики, непараметрические методы распознавания образов) используется в задачах управления качеством [177], диагностики электрорадиоизделий [178]. Цикл работ [179 - 182] посвящен непараметрическим методам классификации текстовых документов.

3.1.3.4. О развитии непараметрической статистики

Проведенный анализ показывает, что к настоящему времени с помощью непараметрических методов можно решать практически тот же круг задач, что ранее решался параметрическими методами. Все большую роль играют непараметрические оценки плотности, непараметрические методы регрессии и распознавания образов (дискриминантного анализа).

Непараметрические методы не используют априорных (и в большинстве практических ситуаций недоступных проверке) предположений о том, что распределения результатов измерений (наблюдений, испытаний, анализов, опытов) входят в то или иное параметрическое семейство, а потому являются более обоснованными, чем параметрические.

В непараметрике, как и в математической статистике в целом, остается ряд нерешенных задач. Для обеспечения широкого внедрения непараметрических методов необходимо провести еще целый комплекс теоретических и пилотных (т.е. пробных) прикладных работ.

Методология современных статистических методов предполагает, что при решении конкретной прикладной задачи необходимо прежде всего построить (выбрать, описать) вероятностно-статистическую модель. А уже в рамках модели разрабатывается (подбирается, используется) соответствующий ей метод, согласно которому создаются алгоритмы и проводятся расчеты, делаются выводы и принимаются управленческие решения. Часто полезны иерархические системы моделей. Такая система на примере проверки однородности двух независимых выборок построена в статье [71], в которой, в частности, продемонстрирована польза несостоятельных критериев проверки статистических гипотез [166].

Непараметрическая статистика является лучше соответствует потребностям практики, представляет собой более передовой и более мощный (результативный, продуктивный) подход, чем параметрическая. Поэтому она должна применяться более широко, чем сейчас, вытеснять параметрическую из несвойственных последней областей использования. Преподавание математической статистики также должно быть приведено в соответствие с современными требованиями, место непараметрической статистики должно быть основным при рассмотрении задач статистики случайных величин, многомерного статистического анализа, статистики случайных процессов и временных рядов. Примером адекватного соотношения различных подходов, по нашему мнению, является учебник [5], соответствующий современному уровню развития прикладной математической статистики.

3.2. Подход к изучению устойчивости выводов
в математических моделях экономики

Раздел 3.2 основан на применении общей схемы изучения устойчивости выводов, полученных с помощью математических методов и моделей, относительно допустимых отклонений исходных данных и предпосылок моделей. Рассмотрены конкретные постановки задач устойчивости: по отношению к изменению данных, их объема и распределений, к допустимым преобразованиям шкал измерения, к временным характеристикам (моменту начала реализации проекта, горизонту планирования). Уменьшение неопределенности может проводиться путем изменения вида данных, т.е. путем перехода к нечисловым данным. Обсуждаются модели конкретных процессов управления промышленными предприятиями на примерах устойчивости характеристик инвестиционных проектов к изменению коэффициентов дисконтирования и устойчивости к изменению коэффициентов модели и объемов партий продукции в моделях управления запасами.

Математические модели дают лишь приближенное представление о реальных явлениях и процессах. Исходные данные известны лишь с некоторой точностью, математические зависимости всегда несколько отличаются от реальных. Поэтому изучение устойчивости выводов относительно допустимых отклонений исходных данных и предпосылок модели – один из этапов построения математической модели (см. [50, с.288-303], [183] и др.). Представим разработанный нами подход к изучению устойчивости выводов в математических моделях, используя примеры в основном из области математического моделирования процессов управления промышленными предприятиями. Рассмотрим общую схему устойчивости, выделим классы устойчивых моделей, приведем решения ряда конкретных задач.

Процессы управления промышленными предприятиями реализуются в реальных ситуациях с достаточно высоким уровнем неопределенности [9, 184]. Велика роль нечисловой информации как на «входе», так и на «выходе» процесса принятия управленческого решения. Неопределенность и нечисловая природа управленческой информации должны быть отражены при анализе устойчивости экономико-математических методов и моделей.

3.2.1. Основные понятия и базовые положения
подхода к изучению устойчивости выводов
в математических моделях социально-экономических явлений и процессов

Применение экономико-математических методов и моделей при разработке инструментария повышения эффективности управления промышленными предприятиями обычно предполагает последовательное осуществление трех этапов исследования. Первый - от исходной практической проблемы до теоретической чисто математической задачи. Второй – внутриматематическое изучение и решение этой задачи. Третий – переход от математических выводов обратно к практической проблеме.

Целесообразно выделять четверки проблем:

ЗАДАЧА – МОДЕЛЬ - МЕТОД - УСЛОВИЯ ПРИМЕНИМОСТИ.

Обсудим каждую из только что выделенных составляющих.

Задача, как правило, порождена потребностями той или иной прикладной области. Разрабатывается одна из возможных математических формализаций реальной ситуации. Например, при изучении предпочтений потребителей возникает вопрос: различаются ли мнения двух групп потребителей. При математической формализации мнения потребителей в каждой группе обычно моделируются как независимые случайные выборки, т.е. как совокупности независимых одинаково распределенных случайных величин, а вопрос маркетологов переформулируется в рамках этой модели как вопрос о проверке той или иной статистической гипотезы однородности. Речь может идти об однородности характеристик, например, о проверке равенства математических ожиданий, или о полной (абсолютной однородности), т.е. о совпадении функций распределения, соответствующих двух совокупностям.

Модель может быть порождена также обобщением потребностей (задач) ряда прикладных областей. Приведенный выше пример иллюстрирует эту ситуацию: к необходимости проверки гипотезы однородности приходят и медики при сравнении двух групп пациентов, и инженеры при сопоставлении результатов обработки деталей двумя способами, и т.д. Таким образом, одна и та же математическая модель может применяться для решения самых разных по своей прикладной сущности задач. Важно подчеркнуть, что выделение перечня задач находится вне математики.

Метод, используемый в рамках определенной математической модели - это уже во многом, если не в основном, дело математиков. В вероятностно-статистических моделях речь идет, например, о методе оценивания, о методе проверки гипотезы, о методе доказательства той или иной теоремы, и т.д. В первых двух случаях алгоритмы разрабатываются и исследуются математиками, но используются прикладниками, в то время как метод доказательства касается лишь самих математиков.

Отнюдь не все модели и методы непосредственно связаны с математикой. В организационно-экономических исследованиях широко используются графические модели описания спроса и предложения, равновесных цен. Предпочтения потребителей могут быть выявлены различными методами – выборочным опросом потребителей, путем наблюдения за их поведением, с помощью различных экспертных процедур. Ясно, что для решения той или иной задачи в рамках одной и той же принятой исследователем модели может быть предложено много методов.

Наконец, рассмотрим последний элемент четверки - условия применимости. При использовании математической модели он - полностью внутриматематический. С точки зрения математика замена условия (кусочной) дифференцируемости некоторой функции на условие ее непрерывности может представляться существенным научным достижением, в то время как экономист или менеджер оценить это достижение не смогут. Для них, как и во времена Ньютона и Лейбница, непрерывные функции мало отличаются от (кусочно) дифференцируемых. Точнее, они одинаково хорошо (или одинаково плохо) могут быть использованы для описания и решения реальных проблем.

Взаимоотношения моделей и методов заслуживают обсуждения. В процессе познания не всегда метод следует за математической моделью. Метод может быть разработан на основе эвристических соображений, словесной модели. Свойства метода можно изучать лишь в рамках той или иной модели. В рамках одной математической модели метод может быть оптимальным, в рамках другой – несостоятельным. Проблема состоит в создании или выборе модели, адекватной изучаемому явлению или процессу.

С точки зрения практической деятельности модели и методы нужны не сами по себе, а как инструменты разработки управленческих решений, которые могут описываться как выводы, заключения, планы мероприятий. Рассмотрим цепочку:

ДАННЫЕ – МЕТОД (их обработки) – ВЫВОДЫ.

Как обосновать адекватность выводов? Один из критериев – устойчивость метода обработки данных. Устойчивость можно изучать лишь в рамках определенной модели.

Для обоснованного практического применения математических моделей процессов управления промышленными предприятиями и основанных на них экономико-математических методов должна быть изучена устойчивость получаемых с их помощью выводов по отношению к допустимым отклонениям исходных данных и предпосылок моделей. Возможные применения результатов подобного исследования:

- заказчик научно-исследовательской работы получает представление о точности предлагаемого решения;

- удается выбрать из многих моделей наиболее адекватную;

- по известной точности определения отдельных параметров модели удается указать необходимую точность нахождения остальных параметров;

- переход к случаю «общего положения» позволяет получать более сильные с математической точки зрения результаты.

Можно рекомендовать обрабатывать данные несколькими способами (методами). Выводы, общие для всех способов, скорее всего отражают реальность (являются объективными). Выводы, меняющиеся от метода к методу, субъективны, зависят от исследователя, выбравшего тот или иной метод анализа данных. Здесь речь идет об устойчивости выводов по отношению к выбору метода.

3.2.2. Общая схема устойчивости

Проблемы устойчивости обсуждались многими авторами и с разных точек зрения. Так, случай «общего положения» соответствует переходу к «мягкой модели» в терминологии В.И. Арнольда [185]. В настоящем разделе рассматривается только система научных результатов, к которым авторы настоящей монографии имеют отношение, следовательно, она не претендует на обзор различных постановок задач изучения устойчивости.

Необходим математический аппарат для описания проблем устойчивости выводов, получаемых на основе математических моделей социально-экономических явлений и процессов. Предлагаем использовать следующие базовые понятия, впервые введенные в монографии [7].

Определение 1. Общей схемой устойчивости называется кортеж {A, B, f, d, E}, где:

A – множество, интерпретируемое как пространство исходных данных;

B – множество, называемое пространством решений;

f – способ получения выводов, т.е. однозначное отображение ;

d – показатель устойчивости, т.е. неотрицательная функция, определенная на подмножествах У множества B и такая, что из вытекает ;

– совокупность допустимых отклонений, т.е. система подмножеств множества A такая, что каждому элементу множества исходных данных и каждому значению параметра из некоторого множества параметров соответствует подмножество ) множества исходных данных. Оно называется множеством допустимых отклонений в точке х при значении параметра, равном .

Способ получения выводов иногда будем для краткости называть моделью. Во многих конкретных постановках устойчивости выводы получают с помощью определенного метода, основанного на некоторой модели. С прикладной точки зрения модель первична, метод – вторичен, поскольку результаты его применения определяются свойствами модели. Это соображение оправдывает принятую нами в [7] терминологию общей схемы устойчивости.

Часто показатель устойчивости d(Y) определяется с помощью метрики, псевдометрики или показателя различия (меры близости) как диаметр множества У, т.е. Т.е. в пространстве решений с помощью показателя устойчивости вокруг образа исходных данных сформирована система окрестностей. В пространстве исходных данных подобная система – это Е, т.е. совокупность допустимых отклонений, - окрестность радиуса вокруг точки х.

Определение 2. Показателем устойчивости в точке х при значении параметра, равном , называется число

,

т.е. диаметр образа множества допустимых отклонений при отображении, рассматриваемом в качестве модели (способа получения выводов).

Определение 3. Абсолютным показателем устойчивости в точке х называется число

.

Рассмотрим два конкретных типа математических моделей. В теории измерений (см., например, [7]) окрестностью исходных данных являются все те вектора, что получаются из исходного путем преобразования координат с помощью допустимого преобразования шкалы, которое берется из соответствующей группы допустимых преобразований. В статистике интервальных данных [5, 83] под окрестностью исходных данных естественно понимать – при описании выборки – куб с ребрами и центром в исходном векторе. В обоих случаях максимальное сужение не означает сужение к точке.

Определение 4. Абсолютным показателем устойчивости на пространстве исходных данных А по мере называется число

.

Определение 5. Максимальным абсолютным показателем устойчивости называется

.

Определение 6. Модель f называется абсолютно –устойчивой, если , где – максимальный абсолютный показатель устойчивости.

Пример. Если показатель устойчивости формируется с помощью метрики , а совокупность допустимых отклонений E – это совокупность всех окрестностей всех точек пространства исходных данных A, то 0–устойчивость модели f эквивалентна непрерывности модели f на множестве A.

Типовая проблема в общей схеме устойчивости – проверка –устойчивости данной модели f относительно данной системы допустимых отклонений E.

Проблема А (проблема характеризации устойчивых моделей). Даны пространство исходных данных A, пространство решений B, показатель устойчивости d, совокупность допустимых отклонений E и неотрицательное число . Описать достаточно широкий класс – устойчивых моделей f. Или: найти все –устойчивые модели среди моделей, обладающих данными свойствами, т.е. входящих в данное множество моделей.

Проблема Б (проблема характеризации систем допустимых отклонений). Даны пространство исходных данных A, пространство решений B, показатель устойчивости d, модель f и неотрицательное число . Описать достаточно широкий класс систем допустимых отклонений E, относительно которых модель f является –устойчивой. Или: найти все такие системы допустимых отклонений E среди совокупностей допустимых отклонений, обладающих данными свойствами, т.е. входящих в данное множество совокупностей допустимых отклонений.

Пример. Определение устойчивости по Ляпунову решения нормальной автономной системы дифференциальных уравнений с начальными условиями выразим в терминах общей схемы устойчивости.

Здесь пространство исходных данных A – конечномерное евклидово пространство, множество допустимых отклонений - окрестность радиуса точки , пространство решений B – множество функций на луче с метрикой

.

Модель f – отображение, переводящее начальные условия х в решение системы дифференциальных уравнений с этими начальными условиями .

В терминах общей схемы устойчивости положение равновесия а называется устойчивым по Ляпунову, если .

Для формулировки определения асимптотической устойчивости по Ляпунову надо ввести в пространстве решений B псевдометрику

.

Положение равновесия а называется асимптотически устойчивым, если для некоторого , где показатель устойчивости рассчитан с использованием псевдометрики .

Таким образом, общая схема устойчивости является обобщением классических постановок задач устойчивости по Ляпунову в теории дифференциальных уравнений. Соотношение общей схемы устойчивости с подходами других авторов обсуждается в [184, гл.8], [7, гл.1] и др. Отметим только структурную устойчивость (грубость динамических систем), введенную А. А. Андроновым и Л. С. Понтрягиным в 1937 г., работы Д.А. Молодцова по устойчивости принципов оптимальности [186] и теории мягких множеств [187].

Непосредственно из общей схемы устойчивости вытекает ряд практически полезных рекомендаций [7, гл.1], в частности, принцип уравнивания погрешностей, согласно которому целесообразно уравнять вклад погрешностей различной природы в общую погрешность. Принцип уравнивания погрешностей позволяет установить:

- рациональный объем выборки в статистике интервальных данных (см., например, [5, 83]);

- число градаций в анкетах, предназначенных для опроса потребителей [7, 57];

- необходимую точность оценивания параметров (платы за доставку и платы за дефицит) в моделях управления запасами (см., например, [54, 57]).

Перечислим ряд конкретных постановок проблем устойчивости в математических методах и моделях, в частности, используемых службами контроллинга при информационно-аналитической поддержке процессов управления деятельностью промышленных предприятий и организаций других отраслей народного хозяйства.

3.2.3. Устойчивость по отношению
к неопределенностям исходных данных

Исходные данные могут быть известны лишь с некоторыми неопределенностями (погрешностями, ошибками, невязками), присущими результатам измерений (наблюдений, испытаний, анализов, опытов). Для учета влияния неопределенностей на свойства процедур анализа данных используют модель сгруппированных данных [188, 189], статистику интервальных ([5, гл.12], [36, гл.4], [83] и др.) и нечетких [85, 190] данных.

Развернутый анализ различных подходов к учету неопределенностей исходных данных проведен в работах по системной нечеткой интервальной математике [32, 33], поэтому в настоящей книге мы ограничимся приведенными выше замечаниями и литературными ссылками.

3.2.4. Устойчивость к изменению объема данных
(объема выборки)

Асимптотические методы математической статистики нацелены на получение выводов, не меняющихся при изменении объемов данных, лишь бы эти объемы были достаточно велики. Отметим, что выводы, устойчивые к изменению объема выборки, т.е. полученные в результате предельного перехода, зачастую являются более общими, чем те, которые можно получить при рассмотрении конкретного объема выборки. Так, согласно Центральной предельной теореме теории вероятностей распределение центрированного и нормированного среднего арифметического независимых одинаково распределенных случайных величин приближается к вполне определенному распределению (нормальному распределению с математическим ожиданием 0 и дисперсией 1), каким бы ни было распределение слагаемых (в предположении, что дисперсия этого распределения конечна и отлична от 0).

Как писали Б.В. Гнеденко и А.Н. Колмогоров, «познавательная ценность теории вероятностей раскрывается только предельными теоремами» [191]. В этом полемически заостренном утверждении подчеркивается принципиальная важность получения выводов, устойчивых к изменению объема выборки.

Многообразие работ по асимптотическим методам математической статистики необозримо, включает в себя сотни тысяч статей и книг на различных языках. Полученные нами решения ряда задач асимптотической статистики рассмотрены, в частности, в монографиях [5, 7]. Проблемы изучения устойчивости к изменению объема данных (объема выборки) рассмотрены также в следующем разделе настоящнй монографии, посвященном компьютерно-статистическим технологиям.

3.2.5. Устойчивость (робастность) к изменению
распределений данных

До сих пор в книгах и статьях, выполненных в рамках старой парадигмы математических методов экономики, часто рассматривают различные параметрические семейства распределений числовых случайных величин. А именно – изучают семейства нормальных распределений, логарифмически нормальных, экспоненциальных, гамма-распределений, распределений Вейбулла – Гнеденко и др. Все они зависят от одного, двух или трех параметров. Поэтому для полного описания распределения достаточно знать или оценить одно, два или три числа. Широко развита и представлена в литературе параметрическая теория математической статистики, в которой предполагается, что распределения результатов наблюдений принадлежат тем или иным параметрическим семействам.

К сожалению, параметрические семейства существуют лишь виртуально, в теории, а именно, в моделях, созданных исследователями. Анализ конкретных данных показывает, что погрешности наблюдений (измерений, испытаний, анализов, опытов) в большинстве случаев имеют распределения, отличные от нормальных и от распределений из других параметрических семейств. Так, в научной школе метролога проф. П. В. Новицкого проведены исследования законов распределения различного рода погрешностей измерения. Изучены распределения погрешностей электромеханических приборов на кернах, электронных приборов для измерения температур и усилий, цифровых приборов с ручным уравновешиванием. Объем выборок экспериментальных данных для каждого экземпляра составлял 100–400 отсчетов. Оказалось, что 46 из 47 распределений значимо отличались от нормального. Исследована форма распределения погрешностей у 25 экземпляров цифровых вольтметров Щ-1411 в 10 точках диапазона. Результаты аналогичны. Дальнейшие сведения содержатся в монографии [192].

В лаборатории прикладной математики Тартуского государственного университета проанализировано 2500 выборок из архива реальных статистических данных. В 92% случаев гипотезу нормальности пришлось отвергнуть [16].

Анализ, проведенный в [5, 16], показал, что распределения реальных данных почти всегда отличаются от тех, которые включены в параметрические семейства. Отличия могут быть большими или меньшими, но они всегда есть. Каково влияние этих отличий на свойства процедур анализа данных? Иногда оно исчезает при росте объемов данных, как для доверительного оценивания математического ожидания, иногда является заметным (как при оценивании высших моментов), иногда делает процедуру полностью необоснованной (как для отбраковки выбросов) [5]. Следовательно, надо либо использовать непараметрические процедуры (в которых на функции распределения наложены лишь внутриматематические условия регулярности, например, условие непрерывности), в частности, при решении задач прогнозирования [193], либо изучать устойчивость основанных на параметрических моделях процедур по отношению к отклонениям распределений результатов наблюдений от предпосылок модели. Как говорят, изучать робастность статистических процедур (от robust (англ.) – крепкий, грубый) с использованием моделей и методов, приведенных в [7, 122, 194 – 197] и др. Статистику интервальных данных ([5, гл.12], [83], [36, гл.4]) также можно отнести к робастной статистике.

3.2.6. Устойчивость по отношению к допустимым
преобразованиям шкал измерения

Борьба с неопределенностью может проводиться путем изменения вида данных, т.е. путем перехода к нечисловым данным, например, к более слабым шкалам измерения.

Таблица 6 – Основные шкалы измерения

Тип шкалы	Определение шкалы	Примеры	Группа допустимых преобразований
Шкалы качественных признаков
Наи-мено-ваний	Числа используют для различения объектов	Номера телефонов, паспортов, пол, ИНН, штрих-коды, УДК	Все взаимно-однозначные преобразования
По-рядко-вая	Числа используют для упорядочения объектов	Оценки экспертов, баллы ветров, отметки в школе, полезность, номера домов	Все строго возрастающие преобразования
Шкалы количественных признаков (описываются началом отсчета и единицей измерения)
Интервалов	Начало отсчета и единица измерения произвольны	Потенциальная энергия, положение точки, температура по шкалам Цельсия и Фаренгейта^[1]	Все линейные преобразования φ(x) = ax + b, a и b произвольны, а>0
Отношений	Начало отсчета задано, единица измерения произвольна	Масса, длина, мощность, напряжение, сопротивление, темпе-ратура по Кельвину, цены	Все подобные преобразования φ(x) = ax, а произвольно, а>0
Разностей	Начало произ-вольно, единица измерения задана	Время^[2]**	Все преобразования сдвига φ(x) = x + b, b произвольно
Абсолютная	Начало отсчета и единица измерения заданы	Число людей в данном помещении	Только тождественное преобразование φ(x) = x

Примером нечисловых данных являются результаты измерений в шкалах, отличных от абсолютной. Теория измерений [198] – один из разделов нечисловой статистики [36, 82, 163]. Типы основных шкал измерения, их определения, примеры величин, измеренных в этих шкалах, группы допустимых преобразований приведены в табл.1.

Основное требование к статистическим алгоритмам: выводы, сделанные на основе данных, измеренных в шкале определенного типа, не должны меняться при допустимом преобразовании шкалы измерения этих данных. В частности, выводы могут быть адекватны реальности только тогда, когда они не зависят от того, какую единицу измерения предпочтет исследователь.

Это требование позволяет, например, указать вид допустимой средней величины в зависимости от шкалы, в которой измерены данные (табл.2). Определим термины.

Общее понятие средней величины введено Огюстеном Луи Коши: средней величиной (средним по Коши) является любая функция f(X₁, X₂,...,X_n) такая, что при всех возможных значениях аргументов значение этой функции не меньше, чем минимальное из чисел X₁, X₂,...,X_n, и не больше, чем максимальное из этих чисел.

Для чисел X₁, X₂,...,X_n средним по Колмогорову является

G{(F(X₁) + F(X₂) +...+ F(X_n))/n},

где F - строго монотонная функция (т.е. строго возрастающая или строго убывающая), G - функция, обратная к F.

Конкретизацией основного требования к алгоритмам анализа данных является условие устойчивости результата сравнения средних (УУРСС): неравенства

f(Y₁, Y₂,...,Y_n) < f(Z₁, Z₂,...,Z_n).

f((Y₁), (Y₂),..., (Y_n)) < f((Z₁), (Z₂),..., (Z_n)),должны быть равносильны для любых чисел Y₁, Y₂,...,Y_n, Z₁, Z₂,...,Z_n и любого допустимого преобразования из группы допустимых преобразований , задающей шкалу.

На основе математической теории, развитой в [7, 198, 200], получен цикл теорем, кратко описанный в табл.2. Правила выбора алгоритмов анализа данных в зависимости от шкал, в которых эти данные измерены, заслуживают дальнейшего изучения.

Таблица 7 – Выбор средних в зависимости
от шкалы измерения

Тип шкалы	Вид средних	Средние, удовлетворяющие УУРСС
Порядковая	По Коши	Члены вариационного ряда. Медианы
Интервальная	По Колмогорову	Среднее арифметическое
Отношений	По Колмогорову	Степенные средние с F(X)=X^C, С0, и среднее геометрическое

3.2.7. Нечисловая статистика как часть теории
устойчивости

В многообразии моделей и методов анализа данных нами выделена и развита как самостоятельная область нечисловая статистика [36] (синонимы: статистика объектов нечисловой природы [7, 163], статистика нечисловых данных [5]). Примерами объектов нечисловой природы (напомним здесь, чтобы не обращаться к другим разделам настоящей монографии), являются значения качественных признаков, т.е. результаты кодировки объектов с помощью заданного перечня категорий (градаций); упорядочения (ранжировки) экспертами образцов продукции (при оценке её технического уровня и конкурентоспособности)) или заявок на проведение научных работ (при проведении конкурсов на выделение грантов); классификации (отношения эквивалентности), т.е. разбиения объектов на группы сходных между собой (кластеры); толерантности, т.е. бинарные отношения, описывающие сходство объектов между собой, например, сходство организационных структур промышленных предприятий; результаты парных сравнений или контроля качества продукции по альтернативному признаку («годен» - «брак»), т.е. последовательности из 0 и 1; множества (обычные или нечеткие), например, перечни рекомендуемых к осуществлению инновационных проектов, составленные экспертами независимо друг от друга; слова, предложения, тексты; вектора, координаты которых - совокупность значений разнотипных признаков, например, результат составления отчета о деятельности промышленного предприятия или анкета эксперта, в которой ответы на часть вопросов носят качественный характер, а на часть - количественный; ответы на вопросы экспертной, маркетинговой или социологической анкеты, часть из которых носит количественный характер (возможно, интервальный), часть сводится к выбору одной из нескольких подсказок, а часть представляет собой тексты; графы [201] и т.д. Интервальные данные также можно рассматривать как пример объектов нечисловой природы, а именно, как частный случай нечетких множеств. Отметим, что теория нечетких множеств тесно связана с теорией случайных множеств, а именно, нечеткие множества естественно рассматривать как «проекции» случайных множеств, за каждой системой нечетких множеств видеть систему случайных множеств [5, 7, 16, 36, 85, 190].

В чем принципиальная новизна нечисловой статистики? Для классической статистики характерна операция сложения. При расчете выборочных характеристик распределения (выборочное среднее арифметическое, выборочная дисперсия и др.), в регрессионном анализе и других областях этой научной дисциплины постоянно используются суммы. Математический аппарат - законы больших чисел, Центральная предельная теорема и другие теоремы - нацелены на изучение сумм. В нечисловой же статистике нельзя использовать операцию сложения, поскольку элементы выборки лежат в пространствах, где нет операции сложения. Методы обработки нечисловых данных основаны на принципиально ином математическом аппарате - на применении различных расстояний в пространствах объектов нечисловой природы.

Как показали многочисленные опыты, человек более правильно (и с меньшими затруднениями) отвечает на вопросы качественного, например, - сравнительного, характера, чем количественного. Так, ему легче сказать, какая из двух гирь тяжелее, чем указать их примерный вес в граммах [144]. Поэтому нечисловая статистика отражает потребности экспертных оценок [52, 135, 202] и технологий управления (менеджмента), в частности, контроллинга [21, 28].

3.2.8. Устойчивость по отношению к временным
характеристикам (моменту начала реализации
проекта, горизонту планирования)

Перейдем к применению математических методов исследования для модернизации управления предприятиями и организациями. Для решения задач управления используют экономико-математические методы и модели. В качестве первого примера рассмотрим математические задачи, решенные для обоснования стратегического планирования.

При разработке стратегии развития промышленного предприятия одна из основных проблем – целеполагание. Поскольку естественных целей обычно несколько, то при построении формализованных экономико-математических моделей приходим к задачам многокритериальной оптимизации. Поскольку одновременно по нескольким критериям оптимизировать невозможно (например, невозможно добиться максимальной прибыли при минимуме затрат), то для адекватного применения экономико-математических методов и моделей необходимо тем или иным образом перейти к однокритериальной постановке (либо, выделив множество оптимальных по Парето альтернатив, применить экспертные технологии выбора). При выборе вида единого критерия целесообразно использовать следующую полученную нами характеризацию моделей с дисконтированием.

Пусть динамику развития рассматриваемой экономической системы можно описать последовательностью , где переменные x_j, j = 1, 2, ..., m, лежат в некотором пространстве Х, возможно, достаточно сложной природы. Положение экономической системы в следующий момент не может быть произвольным, оно связано с положением в предыдущий момент. Проще всего принять, что существует некоторое множество К такое, что . Результат экономической деятельности за j-й период описывается величиной . Зависимость не только от начального и конечного положения, но и от номера периода объясняется тем, что через номер периода осуществляется связь с общей (внешней) экономической ситуацией. Желая максимизировать суммарные результаты экономической деятельности, приходим к постановке стандартной задачи динамического программирования:

. (1)

При обычных математических предположениях максимум достигается.

Часто применяются модели, приводящие к частному случаю задачи (1):

. (2)

Это - модели с дисконтированием (- дисконт-фактор). Естественно выяснить, какими «внутренними» свойствами выделяются задачи типа (2) из всех задач типа (1).

Представляет интерес изучение и сравнение между собой планов возможного экономического поведения на k шагов и . Естественно сравнение проводить с помощью описывающих результаты экономической деятельности функций, участвующих в задачах (1) и (2): план Х₁ лучше плана Х₂ при реализации с момента i, если

(3)

Будем писать Х₁R(i)Х₂, если выполнено неравенство (3), где R(i) - бинарное отношение на множестве планов, задающее упорядочение планов отношением «лучше при реализации с момента i».

Ясно, что упорядоченность планов на k шагов, определяемая с помощью бинарного отношения R(i), может зависеть от i, т.е. «хорошесть» плана зависит от того, с какого момента i он начинает осуществляться. С точки зрения реальной экономики это вполне понятно. Например, планы действий, вполне рациональные для периода стабильного развития, нецелесообразно применять в период гиперинфляции. И наоборот, операции, приемлемые в период гиперинфляции, не принесут эффекта в стабильной обстановке.

Однако, как легко видеть, в моделях с дисконтированием (2) все упорядочения R(i) совпадают, i = 1,2, …, m - k. Оказывается, верно и обратное: если упорядочения совпадают, то мы имеем дело с задачей (2) - с задачей с дисконтированием, причем достаточно совпадения только при k = 1,2. Сформулируем более подробно предположения об устойчивости упорядочения планов.

(I). Пусть . Верно одно из двух: либо для всех , либо для всех .

(II). Пусть . Верно одно из двух: либо для всех , либо для всех .

Нами установлено [7, 203], что из условий устойчивости упорядоченности планов (I) и (II) следует существование констант и , таких, что . Поскольку прибавление константы не меняет точки, в которой функция достигает максимума, то последнее соотношение означает, что условия устойчивости упорядоченности планов (I) и (II) характеризуют (другими словами, однозначно выделяют) модели с дисконтированием среди всех моделей динамического программирования. Другими словами, устойчивость хозяйственных решений во времени эквивалентна использованию моделей с дисконтированием; применяя модели с дисконтированием, предполагаем, что экономическая среда стабильна; если прогнозируем существенное изменение взаимоотношений хозяйствующих субъектов, то вынуждены отказаться от использования моделей типа (2).

Перейдем к проблеме горизонта планирования. Только задав интервал времени, можно на основе экономико-математических методов и моделей принять оптимальные решения и рассчитать ожидаемую прибыль. Проблема «горизонта планирования» состоит в том, что оптимальное поведение зависит от того, на какое время вперед планируют, а выбор этого горизонта зачастую не имеет рационального обоснования. Однако от него зависят принимаемые решения и соответствующие этим решениям экономические результаты. Например, при коротком периоде планирования целесообразны лишь инвестиции (капиталовложения) в оборотные фонды предприятия, и лишь при достаточно длительном периоде – в основные фонды. Однозначный выбор горизонта планирования обычно не может быть обоснован, это – нечисловая экономическая величина. Предлагаем справиться с противоречием путем использования асимптотически оптимальных планов.

Рассмотрим модель (2) с , т.е. модель без дисконтирования

При каждом m существует оптимальный план , при котором достигает максимума оптимизируемая функция. Поскольку выбор горизонта планирования, как правило, нельзя рационально обосновать, хотелось бы построить план действий, близкий к оптимальному плану при различных горизонтах планирования. Это значит, что целью является построение бесконечной последовательности такой, что ее начальный отрезок длины m, т.е. , дает примерно такое же значение оптимизируемого функционала, как и значение для оптимального плана . Бесконечную последовательность с указанным свойством назовем асимптотически оптимальным планом.

Выясним, можно ли использовать для построения асимптотически оптимального плана непосредственно оптимальный план. Зафиксируем k и рассмотрим последовательность , m = 1, 2, ... . Примеры показывают, что, во-первых, элементы в этой последовательности будут меняться; во-вторых, они могут не иметь пределов. Следовательно, оптимальные планы могут вести себя крайне нерегулярно, а потому в таких случаях их нельзя использовать для построения асимптотически оптимальных планов.

Нами установлено [7, 54, 204] существование асимптотически оптимальных планов: можно указать такие бесконечные последовательности , что

С помощью такого подхода решается проблема горизонта планирования - надо использовать асимптотически оптимальные планы, не зависящие от горизонта планирования. Оптимальная траектория движения состоит из трех участков - начального, конечного и основного, а основной участок - это движение по магистрали (аналогия с типовым движением автотранспорта).

3.2.9. Устойчивость в моделях конкретных
процессов управления промышленными
предприятиями

В качестве примера рассмотрим устойчивость к изменению коэффициентов модели и объемов партий в моделях управления запасами. Так, для классической модели Вильсона управления материальными ресурсами в результате строгой постановки задачи оптимизации в ее естественной общности выявлен ряд неклассических эффектов [54].

Пусть - интенсивность спроса, s – плата за хранение единицы товара в течение единицы времени, g – плата за доставку одной партии, T – интервал (горизонт) планирования. По известной «формуле квадратного корня»

Найдем неотрицательное целое число n такое, что

Наименьшее из f(Q₁) и f(Q₂) – минимальные средние издержки, а то из Q₁ и Q₂, на котором достигается минимум – оптимальный размер партии,

.

Таким образом, «формула квадратного корня», как правило, не дает оптимальный план, а только асимптотически оптимальный.

По статистическим данным можно оценить возможные отклонения интенсивности спроса , а затем найти рациональную точность определения платы за хранение s и рациональную точность определения платы за доставку g согласно принципу уравнивания погрешностей:

Стремиться к более точному определению параметров s и g нецелесообразно, как следствие, нет необходимости выбирать между конкурирующими методиками их расчета.

Изучение устойчивости позволило получить практически полезные выводы. Так, для кальцинированной соды на Реутовской химбазе Московской области вызванное отклонениями параметров модели максимальное относительное увеличение суммарных затрат не превосходило 26% (колебания по кварталам от 22,5% до 25,95%). Фактические издержки составляли от 260% до 349% от оптимального уровня. внедрение модели Вильсона в практику управления запасами на Реутовской химбазе дает возможность снизить издержки по доставке и хранению кальцинированной соды в 2,1 раза.

Разработана [54, 205] двухуровневая модель управления материальными ресурсами промышленного предприятия для случая нестационарного спроса, найдены оптимальные значения управляющих параметров, установлена их устойчивость относительно изменения горизонта (интервала) планирования. В этой модели размеры заявок X_j независимы и одинаково распределены, τ(Т) – число заявок за время Т. Оптимальные уровни (при ) таковы:

, ,

где h – издержки от дефицита единицы товара в течение единицы времени.

3.2.10. Устойчивость характеристик инвестиционных
проектов к изменению коэффициентов
дисконтирования с течением времени

Эта задача – частный случай постановок задач устойчивости в рамках статистики интервальных данных ([5, разд.12.7], [206]). Другой частный случай – применение линейного регрессионного анализа интервальных данных при анализе и прогнозировании затрат предприятия ([36, разд.4.4], [207]).

***

Подведем итоги раздела. Нами разработана общая схема устойчивости, позволяющая проводить разработку и развитие математических методов и моделей на основе единого методологического подхода к изучению устойчивости выводов по отношению к допустимым отклонениям исходных данных и предпосылок модели. Возможности общего подхода продемонстрированы на примере восьми конкретных постановок задач устойчивости. Рассмотрена устойчивость по отношению к изменению данных (как частный случай - устойчивость характеристик инвестиционных проектов к изменению коэффициентов дисконтирования с течением времени), к изменению объема данных (объема выборки), к изменению распределений данных. Поскольку борьба с неопределенностью может проводиться путем изменения вида данных, т.е. путем перехода к нечисловым данным, то рассмотрены основные идеи нечисловой статистики, в том числе теории измерений. Обсуждается устойчивость по отношению к временным характеристикам (моменту начала реализации проекта, горизонту планирования) и устойчивость в моделях конкретных процессов управления промышленными предприятиями (на примере устойчивости к изменению коэффициентов модели и объемов партий в моделях управления запасами).

Для обоснованного практического применения математических и моделей процессов управления должна быть изучена устойчивость получаемых с их помощью выводов по отношению к допустимым отклонениям исходных данных и предпосылок моделей. Это требование вытекает из нужд практики и находится вне математики, оно относится к методологии [50] и философии математики [208]. В настоящем разделе описаны подходы к решению этой проблемы и приведены примеры, демонстрирующие теоретическую значимость и практическую пользу получаемых при изучении устойчивости научных результатов. Очевидна связь многих результатов настоящего раздела с новой областью теоретической и вычислительной математики – системной нечеткой интервальной математикой [32, 33].

3.3. Информационно-коммуникационные технологии
- инструменты контроллинга

Проанализируем современное состояние основных компьютерно-статистических методов, обсудим достижения и имеющиеся проблемы, наметим перспективы дальнейшего движения, сформулируем научные проблемы, которые следует решить в будущем. Основное внимание уделим обсуждению методов статистических испытаний (Монте-Карло), датчиков псевдослучайных чисел, имитационного моделирования, методов размножения выборок (будем их кратко называть "бутстреп-методы"), места среди автоматизированного системно-когнитивного анализа (АСК-анализа), имея в виду, что подробное обсуждение АСК-анализа будет дано в дальнейших разделах настоящей монографии. Рассмотрим применение компьютерной статистики в контроллинге и свойства статистических пакетов как инструментов исследователя.

Одним из отличительных признаков новой парадигмы математической [63] и прикладной [114] статистики, анализа данных и других статистических методов [115], математических методов экономики [116] является широкое применение компьютерно-статистических методов. В старой парадигме они применялись при вычислении выборочных характеристик, а при разработке инструментов статистического анализа данных - только для расчета таблиц (т.е. информационные технологии фактически находились вне статистической теории). Согласно новой парадигме информационные технологии – эффективные инструменты получения выводов (имеются в виду датчики псевдослучайных чисел, размножение выборок, в т.ч. бутстреп, автоматизированный системно-когнитивный анализ и др.). Наряду с математическими методами получения научных результатов, прежде всего с предельными теоремами теории вероятностей и математической статистики [209], компьютерно-статистические технологии позволяют изучать скорость сходимости распределений статистик, применяемых при оценивании параметров и проверке гипотез в статистике случайных величин, многомерном статистическом анализе, анализе временных рядов и нечисловой статистике, решать другие теоретические и прикладные задачи. Поэтому для дальнейшего развития и широкого использования статистических методов необходимо проанализировать современное состояние основных компьютерно-статистических методов, выявить достижения и имеющиеся проблемы, наметить перспективы дальнейшего движения, сформулировать задачи, которые следует решить.

3.3.1. Методы статистических испытаний
(Монте-Карло)

Многие информационные технологии в области прикладной статистики опираются на использование методов статистических испытаний. Этот термин применяется для обозначения компьютерных технологий, в которых в модель реального явления или процесса искусственно вводится большое число случайных элементов. Обычно моделируется последовательность независимых одинаково распределенных случайных величин или же последовательность, построенная на ее основе, например, последовательность накапливающихся (кумулятивных) сумм.

Необходимость в методе статистических испытаний возникает потому, что чисто теоретические методы дают точное решение, как правило, лишь в исключительных случаях. Либо тогда, когда исходные случайные величины имеют вполне определенные функции распределения, например, нормальные, чего, как правило, не бывает. Либо когда объемы выборок очень велики (с практической точки зрения - бесконечны).

Не только в задачах обработки данных возникает необходимость в методе статистических испытаний. Она не менее актуальна и при экономико-математическом моделировании технических, социально-экономических, медицинских и иных процессов. Представим себе всем знакомый объект - торговый зал самообслуживания по продаже продовольственных товаров. Сколько нужно работников в зале, сколько касс? Необходимо просчитать загрузку в разное время суток, в разные сезоны года, с учетом замены товаров и смены сотрудников. Нетрудно увидеть, что теоретическому анализу, например, с помощью теории массового обслуживания, подобная система не поддается, поскольку не выполнены необходимые для применения теории предположения, а компьютерному - вполне.

Методы статистических испытаний стали развиваться после второй мировой войны с появлением компьютеров. Второе название - методы Монте-Карло - они получили по наиболее известному игорному дому, а точнее, по его рулетке, поскольку исходный материал для получения случайных чисел с произвольным распределением - это случайные натуральные числа.

В методах статистических испытаний можно выделить две составляющие. Базой являются датчики псевдослучайных чисел. Результатом работы таких датчиков являются последовательности чисел, которые обладают некоторыми свойствами последовательностей случайных величин (в смысле теории вероятностей). Надстройкой являются различные алгоритмы, использующие последовательности псевдослучайных чисел.

Что же это могут быть за алгоритмы? Приведем примеры. Пусть мы изучаем распределение некоторой статистики при заданном объеме выборки. Тогда естественно много раз (например, 100000 раз) смоделировать выборку заданного объема (т.е. набор независимых одинаково распределенных случайных величин) и рассчитать значение статистики. Затем по 100000 значениям статистики можно достаточно точно построить функцию распределения изучаемой статистики, оценить ее характеристики. Однако эта схема годится лишь для так называемой «свободной от распределения» статистики, распределение которой не зависит от распределения элементов выборки. Если же такая зависимость есть, то одной точкой моделирования не обойдешься, придется много раз моделировать выборку, беря различные распределения, меняя параметры. Чтобы общее время моделирования было приемлемым, возможно, придется сократить число моделирований в одной точке, зато увеличив общее число точек. Точность моделирования может быть оценена по общим правилам выборочных обследований.

Второй пример - частично описанное выше моделирование работы торгового зала самообслуживания по продаже продовольственных товаров. Здесь одна последовательность псевдослучайных чисел описывает интервалы между появлениями покупателей, вторая, третья и т.д. связаны с выбором ими первого, второго и т.д. товаров в зале (например, число - номер в перечне товаров). Короче, все действия покупателей, продавцов, работников предприятия разбиты на операции, каждая операция, в продолжительности или иной характеристике которой имеется случайность, моделируется с помощью соответствующей последовательности псевдослучайных чисел. Затем итоги работы сотрудников торговой организации и зала в целом выражаются через характеристики случайных величин. Формулируется критерий оптимальности, решается задача оптимизации и находятся оптимальные значения параметров. В частности, оптимальные планы статистического контроля строятся на основе вероятностно-статистических моделей [16].

3.3.2. Датчики псевдослучайных чисел

Теперь обсудим свойства датчиков псевдослучайных чисел. Здесь стоит слово «псевдослучайные», а не «случайные». Это весьма важно. Дело в том, что за последние 50 лет обсуждались в основном три принципиально разных варианта получения последовательностей чисел, которые в дальнейшем использовались в методах статистических испытаний.

Первый - таблица случайных чисел. К сожалению, объем любой таблицы конечен, и сколько-нибудь сложные расчеты с ее помощью невозможны. Через некоторое время приходится повторять уже использованные числа. Кроме того, обычно обнаруживались те или иные отклонения от случайности.

Второй - физические датчики случайных чисел, в которых в качестве случайного числа рассматривается результат измерения некоторой физической величины. Основной недостаток - нестабильность, непредсказуемые отклонения от заданного распределения (обычно - равномерного).

Третий - расчетный. В простейшем случае каждый следующий член последовательности рассчитывается по предыдущему. Например, так:

где z₀ - начальное значение (заданное целое положительное число), M - параметр алгоритма (заданное целое положительное число), P = 2^m, где m - число двоичных разрядов представления чисел, с которыми манипулирует компьютер. Знак здесь означает теоретико-числовую операцию сравнения, т.е. взятие дробной части от числа и отбрасывание целой части.

В настоящее время обычно применяется именно третий вариант. Совершенно ясно, что он не соответствует интуитивному представлению о случайности. Например, интуитивно очевидно, что по предыдущему элементу случайной последовательности с независимыми элементами нельзя предсказать значение следующего элемента. А приведенная выше формула как раз и дает способ такого предсказания. Расчетный путь получения последовательности псевдослучайных чисел противоречит не только интуиции, но и подходу к определению случайности на основе теории алгоритмов, развитому акад. А.Н. Колмогоровым и его учениками в 1960-х гг. [210]. Однако во многих прикладных задачах он работает, и это основное.

Методу статистических испытаний посвящена обширная литература (см., например, монографии [211 – 213]). Время от времени обнаруживаются недостатки у популярных датчиков псевдослучайных чисел. Так, например, в середине 1980-х гг. выяснилось, что для одного из наиболее известных датчиков три последовательных значения связаны линейной зависимостью

После этого в 1985 г. в журнале «Заводская лаборатория» началась дискуссия о качестве датчиков псевдослучайных чисел, которая продолжалась до 1993 г. и закончилась статьей проф. С.М. Ермакова [214] и нашим комментарием [215].

Итоги можно подвести так. Во многих случаях решаемая методом статистических испытаний задача сводится к оценке вероятности попадания в некоторую область в многомерном пространстве фиксированной размерности. Тогда из чисто математических соображений теории чисел следует, что с помощью датчиков псевдослучайных чисел поставленная задача решается корректно. Сводка соответствующих математических обоснований приведена, например, в работе С.М. Ермакова [214].

В других случаях приходится рассматривать вероятности попадания в области в пространствах переменной размерности. Типичным примером является ситуация, когда на каждом шагу проводится проверка соответствующей статистической гипотезы, и по ее результатам либо остаемся в данном пространстве, либо переходим в пространство большей размерности. Например, в регрессионном анализе при оценивании степени многочлена либо останавливаемся на данной степени, либо увеличиваем степень, переходя в параметрическое пространство большей размерности [216]. Так вот, вопрос об обоснованности применения метода статистических испытаний (а точнее, о свойствах датчиков псевдослучайных чисел) в случае пространств переменной размерности остается в настоящее время открытым. О важности этой проблемы вдохновенно говорил академик РАН Ю.В. Прохоров на Первом Всемирном Конгрессе Общества математической статистики и теории вероятностей им. Бернулли (Ташкент, 1986 г.), как было отмечено в подготовленных нами отчетах о Конгрессе [76 – 78].

3.3.3. Имитационное моделирование

Поскольку постоянно обсуждаем проблемы моделирования, приведем несколько общих формулировок.

«Модель в общем смысле (обобщенная модель) - это создаваемый с целью получения и (или) хранения информации специфический объект (в форме мысленного образа, описания знаковыми средствами либо материальной системы), отражающей свойства, характеристики и связи объекта-оригинала произвольной природы, существенные для задачи, решаемой субъектом» (это определение взято из монографии [6, с.44]).

Например, в менеджменте производственных систем используют:

- модели технологических процессов (контроль и управление по технико-экономическим критериям, АСУ ТП - автоматизированные системы управления технологическими процессами);

- модели управления качеством продукции (в частности, модели оценки и контроля надежности);

- модели массового обслуживания (теории очередей);

- модели управления запасами (в современной терминологии - модели логистики, т.е. теории и практики управления материальными, финансовыми и информационными потоками);

- имитационные и эконометрические модели деятельности предприятия (как единого целого) и управления им (АСУ предприятием) и др.

Согласно академику РАН Н.Н. Моисееву [217, с.213], имитационная система - это совокупность моделей, имитирующих протекание изучаемого процесса, объединенная со специальной системой вспомогательных программ и информационной базой, позволяющих достаточно просто и оперативно реализовать вариантные расчеты. Другими словами, имитационная система - это совокупность имитационных моделей. А имитационная модель предназначена для ответов на вопросы типа: «Что будет, если…» Что будет, если параметры примут те или иные значения? Что будет с ценой на продукцию, если спрос будет падать, а число конкурентов расти? Что будет, если государство резко усилит вмешательство в экономику? Что будет, если остановку общественного транспорта перенесут на 100 м дальше от входа в торговый зал, о котором шла речь выше, и поток покупателей резко упадет? Кроме компьютерных моделей, на вопросы подобного типа часто отвечают эксперты при использовании метода сценариев [52, 218, 219].

При имитационном моделировании часто используется метод статистических испытаний (Монте-Карло). Теорию и практику машинных имитационных экспериментов с моделями экономических систем еще более 40 лет назад подробно разобрал Т. Нейлор в обширной классической монографии [220]. Рассмотрим применение датчиков псевдослучайных чисел в рамках статистических технологий.

3.3.4. Методы размножения выборок
(бутстреп-методы)

Прикладная статистика бурно развивается последние десятилетия. Серьезным (хотя, разумеется, не единственным и не главным) стимулом является стремительно растущая производительность вычислительных средств. Поэтому понятен острый интерес к статистическим методам, интенсивно использующим компьютеры. Одним из таких методов является так называемый «бутстреп», предложенный в 1977 г. Б. Эфроном из Станфордского университета (США).

Сам термин «бутстреп» - это английское слово «bootstrap», записанное русскими буквами. Оно буквально означает что-то вроде: «вытягивание себя (из болота) за шнурки от ботинок». Термин специально придуман и заставляет вспомнить о подвигах барона Мюнхгаузена.

В истории прикладной статистики было несколько более или менее успешно осуществленных рекламных кампаний. В каждой из них «раскручивался» тот или иной метод, который, как правило, отвечал нескольким условиям:

- по мнению его пропагандистов, полностью решал актуальную научную задачу;

- был понятен (при постановке задачи, при ее решении и при интерпретации результатов) широким массам потенциальных пользователей;

- использовал современные возможности вычислительной техники.

Пропагандисты метода, как правило, избегали беспристрастного сравнения его возможностей с возможностями иных статистических методов. Если сравнения и проводились, то с заведомо слабым «противником».

В нашей стране в условиях отсутствия массового систематического образования в области прикладной статистики подобные рекламные кампании находили особо благоприятную почву, поскольку у большинства затронутых ими специалистов не было достаточных знаний в области методологии построения моделей прикладной статистики для того, чтобы составить самостоятельное квалифицированное мнение.

Речь идет о таких методах и постановках, как бутстреп, нейронные сети, генетические алгоритмы, метод группового учета аргументов, робастные оценки по Тьюки-Хуберу, асимптотика пропорционального роста числа параметров и объема данных и др. Бывали локальные всплески неоправданного энтузиазма. Например, московские социологи в 1980-х гг. весьма активно пропагандировали так называемый «детерминационный анализ» - простой эвристический метод анализа таблиц сопряженности. Хотя в Новосибирске в это время давно уже было разработано (под руководством Г.С. Лбова) продвинутое математическое и программное обеспечение анализа векторов разнотипных признаков, включающее в себя «детерминационный анализ» как весьма частный случай.

Однако даже на фоне всех остальных рекламных кампаний судьба бутстрепа исключительна. Во-первых, признанный его автор Б. Эфрон с самого начала признавался, что в математико-статистической теории он ничего принципиально нового не сделал. Его исходная статья (первая в сборнике [131]) называлась: «Бутстреп-методы: новый взгляд на методы складного ножа». Тем самым Б. Эфрон честно признавал первенство за М. Кенуем – автором методов «складного ножа». Во вторых, сразу появились статьи и дискуссии в научных изданиях, публикации рекламного характера, и даже в научно-популярных журналах. Бурные обсуждения на конференциях, спешный выпуск книг. В 1980-е гг. финансовая подоплека всей этой активности, связанная с добыванием грантов на научную деятельность, содержание учебных заведений и т.п., была мало понятна отечественным специалистам, для которых упомянутые реалии науки и образования в капиталистических странах были практически незнакомы.

В чем основная идея группы методов «размножения выборок», наиболее известным представителем которых является бутстреп?

Пусть дана выборка . В вероятностно-статистической теории предполагаем, что это - набор независимых одинаково распределенных случайных величин. Пусть эконометрика интересует некоторая статистика Как изучить ее свойства? Подобными проблемами мы занимались на протяжении всей профессиональной научной жизни и знаем, насколько это непросто. Идея, которую предложил в 1949 г. М. Кенуй (это и есть «метод складного ножа») состоит в том, чтобы из одной выборки сделать много, исключая из нее по одному наблюдению (и возвращая ранее исключенные). Перечислим выборки, которые получаются из исходной:

;

…

;

…

;

Всего n новых (размноженных) выборок объемом (n - 1) каждая. По каждой из них можно рассчитать значение интересующей эконометрика статистики (с уменьшенным на 1 объемом выборки):

…

…

Полученные значения статистики позволяют судить о ее распределении и о характеристиках распределения - о математическом ожидании, медиане, квантилях, разбросе и др. Значения статистики, построенные по размноженным подвыборкам, не являются независимыми. Однако, как показано, например, в [57, гл.6] на примере ряда статистик, возникающих в методе наименьших квадратов и в кластер-анализе (при обсуждении возможности объединения двух кластеров), при росте объема выборки влияние зависимости может ослабевать, а потому со значениями статистик типа можно обращаться как с независимыми случайными величинами.

Однако и без всякой вероятностно-статистической теории разброс величин дает наглядное представление о том, какую точность может дать рассматриваемая статистическая оценка.

Сам М. Кенуй и его последователи использовали размножение выборок в основном для построения оценок с уменьшенным смещением. А вот Б. Эфрон предложил новый способ размножения выборок, существенно использующий датчики псевдослучайных чисел. А именно, он предложил строить новые выборки, моделируя выборки из эмпирического распределения. Другими словами, Б. Эфрон предложил взять конечную совокупность из n элементов исходной выборки и с помощью датчика псевдослучайных чисел сформировать из нее любое число размноженных выборок. Процедура, хотя и нереальна без ЭВМ, проста с точки зрения программирования. По сравнению с описанной выше процедурой Кенуя появляются новые недостатки - неизбежные совпадения элементов размноженных выборок и зависимость от качества датчиков псевдослучайных чисел. Однако существует математическая теория, позволяющая (при некоторых предположениях и безграничном росте объема выборки) обосновать процедуры бутстрепа (см. сборник статей [131]).

Есть много способов развития идеи размножения выборок (см., например, статью [132]). Можно по исходной выборке построить эмпирическую функцию распределения, а затем каким-либо образом от кусочно-постоянной функции перейти к непрерывной функции распределения, например, соединив точки отрезками прямых. Другой вариант - перейти к непрерывному распределению, построив непараметрическую оценку плотности [118]. После этого рекомендуется брать размноженные выборки из этого непрерывного распределения (являющегося состоятельной оценкой исходного), непрерывность защитит от совпадений элементов в этих выборках.

Другой вариант построения размноженных выборок - более прямой. Исходные данные не могут быть определены совершенно точно и однозначно. Поэтому предлагается к исходным данным добавлять малые независимые одинаково распределенные погрешности. При таком подходе соединяем вместе идеи устойчивости и бутстрепа. При внимательном анализе многие идеи прикладной статистики тесно друг с другом связаны (см. статью [132]).

В каких случаях целесообразно применять бутстреп, а в каких - другие методы прикладной статистики? В период рекламной кампании встречались, в том числе в научно-популярных журналах, утверждения о том, что и для оценивания математического ожидания полезен бутстреп. Как показано в статье [132], это совершенно не так. При росте числа испытаний методом Монте-Карло бутстреп-оценка приближается к классической оценке - среднему арифметическому результатов наблюдений. Другими словами, бутстреп-оценка отличается от классической оценки только шумом псевдослучайных чисел.

Аналогичной является ситуация и в ряде других случаев. Там, где эконометрическая теория хорошо развита, где найдены методы анализа данных, в том или иной смысле близкие к оптимальным, бутстрепу делать нечего. А вот в новых областях со сложными алгоритмами, свойства которых недостаточно ясны, он представляет собой ценный инструмент для изучения ситуации.

3.3.5. Автоматизированный системно-когнитивный
анализ

В предисловии к переводу на русский язык книги С. Кульбака «Теория информации и статистика» [126] А.Н. Колмогоров писал: «... навыки мысли и аналитический аппарат теории информации должны, по-видимому, привести к заметной перестройке здания математической статистики» (с. 5 – 6). Однако по неясным причинам этого не произошло. Несмотря на рекомендацию А.Н. Колмогорова, поток исследований, имеющих целью указанную перестройку математико-статистической теории и практики, в СССР и мире не возник. Работы Е.В. Луценко по разработке и применению автоматизированного системно-когнитивного анализа (см., например [127 - 130]) можно рассматривать как развитие указанного А.Н. Колмогоровым направления прикладной математической статистики, не только и не столько в чисто-математическом плане, сколько в прагматически-прикладном. Реализуется рекомендация А.Н. Колмогорова: «По-видимому, внедрение предлагаемых методов в практическую статистику будет облегчено, если тот же материал будет изложен более доступно и проиллюстрирован на подробно разобранных содержательных примерах». Отметим оригинальность подхода и результатов Е.В. Луценко (по сравнению с книгой C. Кульбака), так что речь выше идет об идейных связях, а не о конкретике. Математический метод автоматизированного системно-когнитивного анализа (АСК-анализ) реализован в его программном инструментарии – универсальной когнитивной аналитической системе Эйдос-Х++. АСК-анализ основан на системной теории информации, которая создана в рамках реализации программной идеи обобщения всех понятий математики, в частности теории информации, базирующихся на теории множеств, путем тотальной замены понятия множества на более общее понятие системы и тщательного отслеживания всех последствий этой замены (см., например, [32, 33]). Благодаря математическим основам АСК-анализа этот метод является непараметрическим и позволяет сопоставимо обрабатывать десятки и сотни тысяч градаций факторов и будущих состояний объекта управления (классов) при неполных (фрагментированных), зашумленных данных числовой и нечисловой природы, измеряемых в различных единицах измерения. За дальнейшей информацией – теоретическими разработками и многочисленными примерами успешного практического использования АСК-анализа отошлем к публикациям проф. Е.В. Луценко и его сотрудников, прежде всего в «Научном журнале КубГАУ».

3.3.6. Компьютерная статистика в контроллинге

В качестве примера применения компьютерной статистики рассмотрим конкретную прикладную область – контроллинг, т.е. современный подход к управлению организацией [1, 2, 4, 29, 30, 86, 221]. Контроллеру и сотрудничающему с ним статистику нужна разнообразная экономическая и управленческая информация, не менее нужны удобные инструменты ее анализа. Следовательно, информационная поддержка контроллинга необходима для успешной работы контроллера. Без современных компьютерных инструментов анализа и управления, основанных на продвинутых эконометрических и экономико-математических методах и моделях, невозможно эффективно принимать управленческие решения. Недаром специалисты по контроллингу большое внимание уделяют проблемам создания, развития и применения компьютерных систем поддержки принятия решений. Высокие статистические технологии и эконометрика - неотъемлемые части любой современной системы поддержки принятия экономических и управленческих решений.

Важная часть прикладной статистики - применение высоких статистических технологий к анализу конкретных экономических данных. Такие исследования зачастую требуют дополнительной теоретической работы по «доводке» статистических технологий применительно к конкретной ситуации. Большое значение для контроллинга имеют не только общие методы, но и конкретные эконометрические модели, например, вероятностно-статистические модели тех или иных процедур экспертных оценок или эконометрики качества, имитационные модели деятельности организации, прогнозирования в условиях риска. И конечно, такие конкретные применения, как расчет и прогнозирование индекса инфляции. Сейчас уже многим специалистам ясно, что годовой, квартальный или месячный бухгалтерский баланс предприятия может быть использован для оценки его финансово-хозяйственной деятельности только с привлечением данных об инфляции. Различные области экономической теории и практики в настоящее время еще далеко не согласованы. При оценке и сравнении инвестиционных проектов принято использовать такие характеристики, как чистая текущая стоимость, внутренняя норма доходности, основанные на введении в рассмотрение изменения стоимости денежной единицы во времени (это осуществляется с помощью дисконтирования). А вот при анализе финансово-хозяйственной деятельности организации на основе данных бухгалтерской отчетности изменение стоимости денежной единицы во времени по традиции не учитывают.

Специалисты по контроллингу должны быть вооружены современными средствами информационной поддержки, в том числе средствами на основе высоких статистических технологий и эконометрики. Очевидно, преподавание должно идти впереди практического применения. Ведь как применять то, чего не знаешь?

Статистические технологии применяют для анализа данных двух принципиально различных типов. Один из них - это результаты измерений (наблюдений, испытаний, анализов, опытов и др.) различных видов, например, результаты управленческого или бухгалтерского учета, данные Госкомстата и др. Короче, речь идет об объективной информации. Другой - это оценки экспертов, на основе своего опыта и интуиции делающих заключения относительно экономических явлений и процессов. Очевидно, это - субъективная информация. В стабильной экономической ситуации, позволяющей рассматривать длинные временные ряды тех или иных экономических величин, полученных в сопоставимых условиях, данные первого типа вполне адекватны. В быстро меняющихся условиях приходятся опираться на экспертные оценки. Такая новейшая часть прикладной статистики, как статистика нечисловых данных, была создана как ответ на запросы теории и практики экспертных оценок.

Для решения каких экономических задач могут быть полезны статистические методы? Практически для всех, использующих конкретную информацию о реальном мире. Только чисто абстрактные, отвлеченные от реальности исследования могут обойтись без нее. В частности, статистические методы необходима для прогнозирования, в том числе поведения потребителей, а потому и для планирования. Выборочные исследования, в том числе выборочный контроль, основаны на статистические методы. Но планирование и контроль - основа контроллинга. Поэтому статистические методы - важная составляющая инструментария контроллера, воплощенного в компьютерной системе поддержки принятия решений. Прежде всего оптимальных решений, которые предполагают опору на адекватные модели прикладной статистики. В производственном менеджменте это может означать, например, использование моделей экстремального планирования эксперимента (судя по накопленному опыту их практического использования, такие модели позволяют повысить выход полезного продукта на 30-300%).

Высокие статистические технологии предполагают адаптацию применяемых методов к меняющейся ситуации. Например, параметры прогностического индекса меняются вслед за изменением характеристик используемых для прогнозирования величин. Таков метод экспоненциального сглаживания. В соответствующем алгоритме расчетов значения временного ряда используются с весами. Веса уменьшаются по мере удаления в прошлое. Многие методы дискриминантного анализа основаны на применении обучающих выборок. Например, для построения рейтинга надежности банков можно с помощью экспертов составить две обучающие выборки - надежных и ненадежных банков. А затем с их помощью решать для вновь рассматриваемого банка, каков он - надежный или ненадежный, а также оценивать его надежность численно, т.е. вычислять значение рейтинга.

Автоматизированный системно-когнитивный анализ является перспективным инструментом контроллинга и менеджмента [29, 30, 86].

Один из способов построения адаптивных статистических моделей - нейронные сети (см., например, монографию [222]). При использовании нейронных сетей упор делается не на формулировку адаптивных алгоритмов анализа данных, а - в большинстве случаев - на построение виртуальной адаптивной структуры. Термин «виртуальная» означает, что «нейронная сеть» - это специализированная компьютерная программа, «нейроны» используются лишь при общении человека с компьютером. Методология нейронных сетей идет от начальных идей кибернетики 1940 - 50-х гг. В компьютере создается модель мозга человека (весьма примитивная с точки зрения физиолога). Основа модели - весьма простые базовые элементы, называемые нейронами. Они соединены между собой, так что нейронные сети можно сравнить с хорошо знакомыми экономистам и инженерам блок-схемами. Каждый нейрон находится в одном из заданного множества состояний. Он получает импульсы от соседей по сети, изменяет свое состояние и сам рассылает импульсы. В результате состояние множества нейтронов изменяется, что соответствует проведению статистических вычислений.

Нейроны обычно объединяются в слои (как правило, два-три). Среди них выделяются входной и выходной слои. Перед началом решения той или иной задачи производится настройка. Во-первых, устанавливаются связи между нейронами, соответствующие решаемой задаче. Во-вторых, проводится обучение, т.е. через нейронную сеть пропускаются обучающие выборки, для элементов которых требуемые результаты расчетов известны. Затем параметры сети модифицируются так, чтобы получить максимальное соответствие выходных значений заданным величинам.

С точки зрения точности расчетов (и оптимальности в том или ином статистическом смысле) нейронные сети не имеют преимуществ перед другими адаптивными системами прикладной статистики. Однако они более просты для восприятия, поэтому привлекательны для тех, кто плохо знаком с математико-статистической теорией.

Надо отметить, что в прикладной статистике используются и модели, промежуточные между нейронными сетями и «обычными» системами регрессионных уравнений (одновременных и с лагами). Они тоже используют блок-схемы, как, например, универсальный метод моделирования связей социально-экономических факторов ЖОК (этот метод подробно разработан в [5, 54, 57]).

Профессионалу в области контроллинга полезны многочисленные интеллектуальные инструменты анализа данных, относящиеся к высоким статистическим технологиям [51] и эконометрике [16]. В частности, заметное место в математико-компьютерном обеспечении принятия решений в контроллинге занимают методы теории нечеткости [190], входящие в системную нечеткую интервальную математику [32, 33].

3.3.7. Статистические пакеты – инструменты
исследователя

Рассмотрим проблемы разработки, внедрения и использования статистических пакетов (статистических программных продуктов) в России за последние 25 лет, дадим критический анализ популярных в настоящее время пакетов в сопоставлении с результатами современных научных исследований, наметим перспективы развития работ в области статистического программного обеспечения (ср. [223]).

Очевидно, что математические методы исследования, в том числе методы статистического анализа данных, требуют больших вычислений и зачастую невозможны без компьютеров. Продвинутое применение высоких статистических технологий (см., например, раздел 2.3 настоящей монографии и [51]) предполагает использование соответствующих программных продуктов. Статистические пакеты – постоянно используемые интеллектуальные инструменты исследователей, инженеров, управленцев, занимающихся анализом больших массивов данных.

В разделе «Математические методы исследования» журнала «Заводская лаборатория» (основном отечественном издании по статистическим методам) неоднократно рассматривались вопросы разработки и применения статистических пакетов. Так, более 20 статистических пакетов, разработанных Всесоюзным центром статистических метолов и информатики (директор – А.И. Орлов), в том числе пакеты СПК, АТСТАТ-ПРП, СТАТКОН, АВРОРА-РС, ЭКСПЛАН, ПАСЭК, НАДИС, проанализированы в [224, 225]. Перечисленные семь пакетов рассмотрены также в [226]. Сравнительному анализу четырех диалоговых систем по статистическому контролю посвящена статья [227], и т.д.

Однако наряду с очевидной пользой статистические пакеты могут приносить вред неискушенному пользователю. Например, в них зачастую пропагандируется применение двухвыборочного критерия Стьюдента (много раз этот критерий упомянут в статье [228], посвященной программному обеспечению статистического анализа данных), когда условия его применимости не проверены, а зачастую и не выполнены. Между тем хорошо известно, каковы последствия использования критерия Стьюдента вне сферы его применимости, а также и то, что применять его нет необходимости поскольку разработаны более адекватные критерии [71].

Другой пример. Малограмотность переводчиков в русифицированной версии MS Excel (по крайней мере в разделе «Анализ данных») шокирует специалиста по прикладной статистике: например, «объем выборки» именуется «счет». С сожалением приходится констатировать, что не соответствует современным требованиям и электронный учебник – обзор методов, реализованных в пакете STATISTICA6, о котором идет речь в статье [228].

К сожалению, анализ допущенных в документации к пакету недочетов занял бы не меньше места, чем сама документация. В [47] продемонстрировано, насколько трудоемким оказался критический анализ всего лишь нескольких десятков ГОСТов по статистическим методам управления качеством. Это замечание касается, конечно, не только пакетов. Из одной публикации в другую кочуют одни и те же ошибки. Для разоблачения каждой нужна развернутая публикация. Например, распространенная ошибка при использовании критериев Колмогорова и омега-квадрат разобрана в [74, 75], ошибочные утверждения о том, какие гипотезы можно проверять с помощью двухвыборочного критерия Вилкоксона, разоблачены в [72, 73].

Основное противоречие в области разработки статистических пакетов таково. Те, кто программирует, не являются специалистами по прикладной статистике, поскольку это не входит в их профессиональные обязанности. С другой стороны, специалисты по статистическим методам не берутся реализовывать их в пакетах, поскольку такая работа, весьма трудоемкая и ответственная, обычно не соответствует их профессиональным устремлениям. Судя по опыту Всесоюзного центра статистических методов и информатики, стоимость разработки (на профессиональном уровне) пакета среднего уровня сложности – порядка 70 тыс. руб. (в ценах 1990 г.), что соответствует порядка 10 млн. руб. в ценах 2014 г. (индекс инфляции за 25 лет равен примерно 150 при расчете по методике [16, гл.7]). Это означает, что разработкой, распространением и сопровождением статистических пакетов должны заниматься специализированные в этой области организации или подразделения.

В нашей стране активная работа по созданию развернутой системы отечественных статистических пакетов развернулась в 80-х годах [225, 226]. Как уже отмечалось, только Всесоюзным центром статистических метолов и информатики было разработано более 20 программных продуктов по прикладной статистике и другим статистическим методам. Эта работа проводилась в рамках более широкого проекта, нацеленного на объединение усилий специалистов по статистическим методам с целью повышения эффективности теоретических и прикладных исследований. Важным промежуточным итогом было создание в 1990 г. Всесоюзной организации по статистическим методам и их применениям и Всесоюзной статистической ассоциации [48, 229]. Планы тех лет отражены в статье [230]. Итогом виделось создание (развертывание, организационное оформление) новой отрасли прикладной науки по образцу метрологии.

Развал СССР, либерализация цен и гиперинфляция начала 90-х положили конец рассматриваемому проекту. Из плана работ реализована только подготовка современных учебников ([5, 16, 52, 54] и др. (см. также раздел 2.1 настоящей монографии), составленных на основе статей, опубликованных в «Заводской лаборатории» (учебники выложены в свободном доступе на сайте «Высокие статистические технологии» http://orlovs.pp.ru и на странице Лаборатории экономико-математических методов в контроллинге http://ibm.bmstu.ru/nil/biblio.html ). Предприятия и организации, лишившись оборотных средств из-за инфляции, перестали покупать статистические программные продукты, коллективы разработчиков распались, перестали поддерживать статистические пакеты в условиях быстрого обновления технических средств и базового программного обеспечения. В результате многообразие продуктов на отечественном рынке статистических пакетов резко сократилось, и монополистами оказались SPSS, STATISTICA, STATGRAPHICS (и немногие другие), о которых идет речь в статье О.С. Смирновой [228].

На опасность бездумного применения статистических пакетов В.В. Налимов обращал внимание более 40 лет назад [231]. Он имел в виду прежде всего склонность к проведению расчетов без знакомства с сутью применяемых методов. Необходимо обратить внимание также на научно-технический уровень самих пакетов и сопровождающей документации. Дополнительно к сказанному в начале этого подраздела приходится констатировать, что в популярных в настоящее время в России статистических пакетах нет примерно половины того, что разработано представителями отечественной вероятностно-статистической научной школы и включено в современные учебники [5, 16, 52, 54], подготовленные в соответствии с рекомендациями Всесоюзной статистической ассоциации и – позже - Российской ассоциации статистических методов. Сказанное легко проверить, сопоставив содержание указанных учебников и перечень методов, включенных в распространенные пакеты. Поэтому преподаватели МГТУ им. Н.Э. Баумана сознательно избегаем использования в учебном процессе пакетов SPSS, STATISTICA, STATGRAPHICS, чтобы не приучать студентов к статистике 60-70-х годов прошлого века. Однако, поскольку нет современных пакетов, приходится для практических расчетов использовать устаревшие программные продукты.

Тиражи пакетов и учебников сопоставимы. Пакет STATGRAPHICS имеет более 40 тыс. зарегистрированных пользователей, учебник «Прикладная статистика» [5] выпущен тиражом 3 тыс. экземпляров, электронную версию только с сайта «Высокие статистические технологии» скачали 45,7 тыс. пользователей (по состоянию на 04.02.2015). Поэтому состав пакетов и качество документации имеют большое значение. Они во многом определяют качество прикладных научных работ и обоснованность хозяйственных решений.

Отметим, что по сравнению с 1980-ми годами к настоящему времени наметился рост внимания к статистическим технологиям [51], а не только к их составляющим – конкретным методам обработки данных. В этом суть популярного ныне подхода Data Mining (на русском - «добыча данных», «интеллектуальный анализ данных»). Термин Data Mining введен эмигрантом из СССР Г. Пятецким-Шапиро в 1989 г. Задачи, решаемые Data Mining, – классификация, кластеризация, регрессия, ассоциация (поиск повторяющихся паттернов, например, поиск устойчивых связей) – это типичные задачи прикладной статистики. Новизна состоит в разработке технологий добычи полезных для практики выводов из данных путем решения ряда таких задач.

Еще более выражена отмеченная тенденция в технологии «Шесть сигм» [232]. Эта технология, первоначально позиционированная как «революционный метод управления качеством», основана на применении теории принятия решений [54] и прикладной статистики [5]. Мы ее рассматриваем как подход к совершенствованию бизнеса [25] и как новую систему внедрения математических методов исследования [233].

Итак, статистические пакеты – интеллектуальные инструменты, необходимые широким кругам научных работников, инженеров, менеджеров. Однако распространенные в настоящее время статистические программные продукты отстают от современного уровня научных исследований примерно на 30 лет. Весьма актуальна задача разработки статистических пакетов нового поколения, соответствующих современному научному уровню и одновременно обеспечивающих удобства пользователей, достигнутые в популярных ныне пакетах. Эта задача должна решаться одновременно с созданием систем обучения, сопровождения и внедрения пакетов нового поколения, в частности, в соответствии с технологиями типа «Шесть сигм».

3.4. Основы статистики интервальных данных

Как установлено в разделе 2.3, одной из точек роста статистических методов и математических методов экономики в целом является статистика интервальных данных. В настоящем разделе рассмотрим основные идеи асимптотической математической статистики интервальных данных, в которой элементы выборки – не числа, а интервалы.

Алгоритмы и выводы статистики интервальных данных принципиально отличаются от алгоритмов и выводов классической математической статистики. Приведем базовые результаты, связанные с основополагающими понятиями нотны и рационального объема выборки. Статистика интервальных данных является составной частью системной нечеткой интервальной математики [32, 33].

3.4.1. О развитии статистики интервальных данных

Перспективная и быстро развивающаяся область статистических исследований последних десятилетий – математическая статистика интервальных данных. Речь идет о развитии методов прикладной математической статистики в ситуации, когда статистические данные – не числа, а интервалы, в частности, порожденные наложением ошибок измерения на значения случайных величин. Полученные результаты были отражены, в частности, в выступлениях на проведенной в «Заводской лаборатории» дискуссии [234] и в докладах Международной конференции по интервальным и стохастическим методам в науке и технике ИНТЕРВАЛ-92 [235]. Приведем основные идеи весьма перспективного для вероятностно-статистических методов и моделей принятия решений асимптотического направления в статистике интервальных данных.

В настоящее время признается необходимым изучение устойчивости (робастности) оценок параметров к малым отклонениям исходных данных и предпосылок модели (см. раздел 3.2 настоящей монографии). Однако популярная среди теоретиков модель засорения (модель Тьюки-Хьюбера) во многих прикладных постановках представляется не вполне адекватной. Эта модель нацелена на изучение влияния больших «выбросов». Поскольку любые реальные измерения лежат в некотором фиксированном диапазоне, а именно, заданном в техническом паспорте средства измерения, то зачастую выбросы не могут быть слишком большими. Поэтому представляются полезными иные, более общие схемы устойчивости, впервые введенные в монографии [73], в которых, например, учитываются возможные отклонения распределений результатов наблюдений от предположений модели.

В одной из таких схем изучается влияние интервальности исходных данных на статистические выводы. Необходимость такого изучения стала очевидной следующим образом. В государственных стандартах СССР по прикладной статистике в обязательном порядке давалось справочное приложение «Примеры применения правил стандарта». При подготовке ГОСТ 11.011-83 [133] разработчикам стандарта были переданы для анализа реальные данные о наработке резцов до предельного состояния (в часах). Оказалось, что все эти данные представляли собой либо целые числа, либо полуцелые (т.е. после умножения на 2 становящиеся целыми). Ясно, что исходная длительность наработок искажена. Необходимо учесть в статистических процедурах наличие такого искажения исходных данных. Как это сделать?

Первое, что приходит в голову – модель группировки данных [236], согласно которой для истинного значения Х проводится замена на ближайшее число из множества {0,5n, n = 1, 2, 3, ...}. Однако эту модель целесообразно подвергнуть сомнению, а также рассмотреть иные модели. Так, возможно, что Х надо приводить к ближайшему сверху элементу указанного множества – если проверка качества поставленных на испытание резцов проводилась раз в полчаса. Другой вариант: если расстояния от Х до двух ближайших элементов множества {0,5n, n = 1, 2, 3, ...} примерно равны, то естественно ввести рандомизацию при выборе заменяющего числа, и т.д.

Целесообразно построить принципиально новую математико-статистическую модель, согласно которой результаты наблюдений – не числа, а интервалы. Например, если в таблице исходных данных приведено значение 53,5, то это значит, что реальное значение – какое-то число от 53,0 до 54,0, т.е. какое-то число в интервале [53,5 – 0,5; 53,5 + 0,5], где 0,5 – максимально возможная погрешность. Принимая эту модель, мы попадаем в новую научную область – статистику интервальных данных [237, 238]. Статистика интервальных данных идейно связана с интервальной математикой, в которой в роли чисел выступают интервалы (см., например, монографию [239]). Это направление математики является дальнейшим развитием хорошо известных правил приближенных вычислений, посвященных выражению погрешностей суммы, разности, произведения, частного через погрешности тех чисел, над которыми осуществляются перечисленные операции.

В интервальной математике сумма двух интервальных чисел [a, b] и [c, d] имеет вид [a, b] + [c, d] = [a + c, b + d], а разность определяется по формуле [a, b] – [c, d] = [a – d, b – c]. Для положительных a, b, c, d произведение определяется формулой [a, b] × [c, d] = [ac, bd], а частное имеет вид [a, b]/[c, d] = = [a/d, b/c]. Эти формулы получены при решении соответствующих оптимизационных задач. Пусть х лежит в отрезке [a, b], а у – в отрезке [c, d]. Каково минимальное и максимальное значение для х + у? Очевидно, a + c и b + d соответственно. Минимальные и максимальные значения для х – у, ху, х/у указывают нижние и верхние границы для интервальных чисел, задающих результаты арифметических операций. А от арифметических операций можно перейти ко всем остальным математическим алгоритмам. Так строится интервальная математика.

Как видно из сборника трудов Международной конференции [235], исследователям удалось решить ряд задач теории интервальных дифференциальных уравнений, в которых коэффициенты, начальные условия и решения описываются с помощью интервалов. По мнению некоторых специалистов, статистика интервальных данных является частью интервальной математики [239]. Впрочем, распространена и другая точка зрения, согласно которой такое включение нецелесообразно, поскольку статистика интервальных данных использует несколько иные подходы к алгоритмам анализа реальных данных, чем сложившиеся в интервальной математике (подробнее см. ниже).

В настоящем разделе рассматриваем асимптотические методы статистического анализа интервальных данных при больших объемах выборок и малых погрешностях измерений. В отличие от классической математической статистики, сначала устремляется к бесконечности объем выборки и только потом – уменьшаются до нуля погрешности (в классической математической статистике предельные переходы осуществляются в обратном порядке – сначала уменьшаются до нуля погрешности измерений, и только затем - устремляется к бесконечности объем выборки). В частности, еще в начале 1980-х годов с помощью такой асимптотики сформулированы правила выбора метода оценивания в ГОСТ 11.011-83 [133].

Нами разработана [240] общая схема исследования, включающая расчет нотны (максимально возможного отклонения статистики, вызванного интервальностью исходных данных) и рационального объема выборки (превышение которого не дает существенного повышения точности оценивания). Она применена к оцениванию математического ожидания и дисперсии [234], медианы и коэффициента вариации [241], параметров гамма-распределения [133, 242] и характеристик аддитивных статистик [240], при проверке гипотез о параметрах нормального распределения, в т.ч. с помощью критерия Стьюдента, а также гипотезы однородности с помощью критерия Смирнова [241]. Изучено асимптотическое поведение оценок метода моментов и оценок максимального правдоподобия (а также более общих – оценок минимального контраста), проведено асимптотическое сравнение этих методов в случае интервальных данных, найдены общие условия, при которых, в отличие от классической математической статистики, метод моментов дает более точные оценки, чем метод максимального правдоподобия [243].

Разработаны подходы к рассмотрению интервальных данных в основных постановках регрессионного, дискриминантного и кластерного анализов [244]. Изучено влияние погрешностей измерений и наблюдений на свойства алгоритмов регрессионного анализа, разработаны способы расчета нотн и рациональных объемов выборок, введены и исследованы новые понятия многомерных и асимптотических нотн, доказаны соответствующие предельные теоремы [244, 245]. Проведена первоначальная разработка интервального дискриминантного анализа, рассмотрено влияние интервальности данных на показатель качества классификации [244, 246]. Основные идеи и результаты рассматриваемого направления в статистике интервальных данных приведены в публикациях обзорного характера [237, 238].

Как показала Международная конференция ИНТЕРВАЛ-92, в области асимптотической математической статистики интервальных данных мы имеем мировой приоритет. По нашему мнению, со временем во все виды статистического программного обеспечения должны быть включены алгоритмы интервальной статистики, «параллельные» обычно используемым алгоритмам прикладной математической статистики. Это позволит в явном виде учесть наличие погрешностей у результатов наблюдений, сблизить позиции метрологов и статистиков.

Многие из утверждений статистики интервальных данных весьма отличаются от аналогов из классической математической статистики. В частности, не существует состоятельных оценок; средний квадрат ошибки оценки, как правило, асимптотически равен сумме дисперсии оценки, рассчитанной согласно классической теории, и некоторого положительного числа (равного квадрату т.н. нотны – максимально возможного отклонения значения статистики из-за погрешностей исходных данных) – в результате, метод моментов оказывается иногда точнее метода максимального правдоподобия [243]; нецелесообразно увеличивать объем выборки сверх некоторого предела (называемого рациональным объемом выборки) – вопреки классической теории, согласно которой чем больше объем выборки, тем точнее выводы.

В стандарт [133] включен раздел 5, посвященный выбору метода оценивания при неизвестных параметрах формы и масштаба и известном параметре сдвига и основанный на концепциях статистики интервальных данных. Теоретическое обоснование этого раздела стандарта опубликовано лишь через 5 лет в статье [242].

В 1982 г. при разработке стандарта [133] сформулированы основные идеи статистики интервальных данных. Однако из-за недостатка времени они не были полностью реализованы в ГОСТ 11.011-83, и этот стандарт написан в основном в классической манере. Развитие идей статистики интервальных данных продолжается уже в течение более чем 30 лет, и еще многое необходимо сделать! Большое значение статистики интервальных данных для современной прикладной статистики обосновано в [154, 247].

Вторая ведущая научная школа в области статистики интервальных данных – это школа проф. А.П. Вощинина (1937 - 2008), активно работающая с конца 70-х годов. Полученные результаты отражены в ряде монографий (см., прежде всего, [248, 249, 250]), статей [234, 251, 252], докладов, в частности, в трудах [235] Международной конференции ИНТЕРВАЛ-92, диссертациях [253, 254]. Изучены проблемы регрессионного анализа, планирования эксперимента, сравнения альтернатив и принятия решений в условиях интервальной неопределенности.

Рассматриваемое ниже наше научное направление отличается нацеленностью на асимптотические результаты, полученные при больших объемах выборок и малых погрешностях измерений, поэтому его полное название таково: асимптотическая математическая статистика интервальных данных.

3.4.2. Основные идеи статистики
интервальных данных

Сформулируем сначала основные идеи асимптотической математической статистики интервальных данных, а затем рассмотрим реализацию этих идей на простых примерах, отослав по поводу многочисленных конкретных результатов к имеющимся публикациям. Основные идеи достаточно просты, в то время как их проработка в конкретных ситуациях зачастую оказывается достаточно трудоемкой.

Пусть существо реального явления описывается выборкой x₁, x₂, ..., x_n. В вероятностной теории математической статистики, из которой мы исходим (см. справочник [60]), выборка – это набор независимых в совокупности одинаково распределенных случайных величин. Однако беспристрастный и тщательный анализ подавляющего большинства реальных задач показывает, что статистику известна отнюдь не выборка x₁, x₂, ..., x_n, а другие (искаженные) величины

y_j = x_j + e_j, j = 1, 2, ..., n,

где e₁, e₂, …, e_n – некоторые погрешности измерений, наблюдений, анализов, опытов, испытаний, исследований (например, инструментальные ошибки).

Одна из причин появления погрешностей – запись результатов наблюдений с конечным числом значащих цифр. Дело в том, что для случайных величин с непрерывными функциями распределения событие, состоящее в попадании хотя бы одного элемента выборки в множество рациональных чисел, согласно правилам теории вероятностей имеет вероятность 0, а такими событиями в теории вероятностей принято пренебрегать. Поэтому при рассуждениях о выборках из тех или иных непрерывных распределений из параметрических семейств - нормального, логарифмически нормального, экспоненциального, равномерного, гамма-распределений, распределения Вейбулла-Гнеденко и др. - приходится принимать, что эти распределения имеют элементы исходной выборки x₁, x₂, ..., x_n, в то время как статистической обработке доступны лишь искаженные значения y_j = x_j + e_j, записываемые конечным (и небольшим) числом значащих цифр, а потому входящие в множество рациональных чисел.

Введем обозначения

x = (x₁, x₂, ..., x_n), y = (y₁, y₂, ..., y_n), e = (e₁ + e₂ + … + e_n).

Пусть статистические выводы основываются на статистике f : Rⁿ ® R¹, используемой для оценивания параметров и характеристик распределения, проверки гипотез и решения иных статистических задач. Принципиально важная для статистики интервальных данных идея такова:

СТАТИСТИК ЗНАЕТ ТОЛЬКО f(y), НО НЕ f(x).

Очевидно, в статистических выводах необходимо отразить различие между f(y) и f(x). Одним из двух основных понятий статистики интервальных данных является понятие нотны.

Определение. Величину максимально возможного (по абсолютной величине) отклонения, вызванного погрешностями наблюдений e, известного статистику значения f(y) от истинного значения f(x), т.е.

N_f(x) = sup | f(y) – f(x) |,

где супремум берется по множеству возможных значений вектора погрешностей e (см. ниже), будем называть НОТНОЙ.

Если функция f имеет частные производные второго порядка, а ограничения на погрешности имеют вид

| e_i | £ D, i = 1, 2, …, n, (1)

причем D мало, то приращение функции f с точностью до бесконечно малых более высокого порядка описывается главным линейным членом, т.е.

Чтобы получить асимптотическое (при D ® 0) выражение для нотны, достаточно найти максимум и минимум линейной функции (главного линейного члена) на кубе, заданном неравенствами (1). Легко видеть, что максимум достигается, если положить

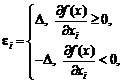
а минимум, отличающийся от максимума только знаком, достигается при = –e_i. Следовательно, нотна с точностью до бесконечно малых более высокого порядка имеет вид

Это выражение назовем асимптотической нотной.

Условие (1) означает, что исходные данные представляются статистику в виде интервалов [y_i – D; y_i + D], i = 1, 2, …, n (отсюда и название этого научного направления). Ограничения на погрешности могут задаваться разными способами – кроме абсолютных ошибок используются относительные или иные показатели различия между x и y.

Если задана не предельная абсолютная погрешность D, а предельная относительная погрешность d, т.е. ограничения на погрешности вошедших в выборку результатов измерений имеют вид

| e_i | £ d | x_i |, i = 1, 2, …, n,

то аналогичным образом получаем, что нотна с точностью до бесконечно малых более высокого порядка, т.е. асимптотическая нотна, имеет вид

При практическом использовании рассматриваемой концепции необходимо провести тотальную замену символов x на символы y. В каждом конкретном случае удается показать, что в силу малости погрешностей разность N_f(y) – N_f(x) является бесконечно малой более высокого порядка сравнительно с N_f(x) или N_f(y).

3.4.3. Основные результаты в вероятностной
модели

В классической вероятностной модели элементы исходной выборки x₁, x₂, ..., x_n рассматриваются как независимые одинаково распределенные случайные величины. Как правило, существует некоторая константа C > 0 такая, что в смысле сходимости по вероятности

(2)

Соотношение (2) доказывается отдельно для каждой конкретной задачи.

При использовании классических статистических методов в большинстве случаев используемая статистика f(x) является асимптотически нормальной. Это означает, что существуют константы а и s² такие, что

где F(x) – функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. При этом обычно оказывается, что

,

а потому в классической математической статистике средний квадрат ошибки статистической оценки равен

с точностью до членов более высокого порядка.

В статистике интервальных данных ситуация совсем иная – обычно можно доказать, что средний квадрат ошибки равен

(3)

Из соотношения (3) вытекает ряд важных следствий. Правая часть этого равенства, в отличие от правой части соответствующего классического равенства, не стремится к 0 при безграничном возрастании объема выборки. Она остается больше некоторого положительного числа, а именно, квадрата нотны. Следовательно, статистика f(x) не является состоятельной оценкой параметра a. Более того, состоятельных оценок вообще не существует.

Пусть доверительным интервалом для параметра a, соответствующим заданной доверительной вероятности g, в классической математической статистике является интервал (c_n(g); d_n(g)). В статистике интервальных данных аналогичный доверительный интервал является более широким. Он имеет вид (c_n(g) – N_f(y); d_n(g) + N_f(y)). Таким образом, его длина увеличивается на две нотны. Следовательно, при увеличении объема выборки длина доверительного интервала не может стать меньше, чем 2CD (см. формулу (2)).

В статистике интервальных данных методы оценивания параметров имеют другие свойства по сравнению с классической математической статистикой. Так, при больших объемах выборок метод моментов может быть заметно лучше, чем метод максимального правдоподобия (т.е. иметь меньший средний квадрат ошибки – см. формулу (3)), в то время как в классической математической статистике второй из названных методов всегда не хуже первого.

3.4.4. Рациональный объем выборки

Анализ формулы (3) показывает, что в отличие от классической математической статистики нецелесообразно безгранично увеличивать объем выборки, поскольку средний квадрат ошибки остается всегда большим квадрата нотны. Поэтому представляется полезным ввести понятие «рационального объема выборки» n_rat, при достижении которого продолжать наблюдения нецелесообразно.

Как установить «рациональный объем выборки»? Можно воспользоваться идеей применения «принципа уравнивания погрешностей», выдвинутой в монографии [7]. Речь идет о том, что вклад погрешностей различной природы в общую погрешность должен быть примерно одинаков. Этот принцип дает возможность выбирать необходимую точность оценивания тех или иных характеристик в тех случаях, когда это зависит от исследователя. В статистике интервальных данных в соответствии с «принципом уравнивания погрешностей» предлагается определять рациональный объем выборки n_rat из условия равенства двух величин – метрологической составляющей, связанной с нотной, и статистической составляющей – в среднем квадрате ошибки (3), т.е. из условия

Для практического использования выражения для рационального объема выборки неизвестные теоретические характеристики необходимо заменить их оценками. Это делается в каждой конкретной задаче по-своему.

Исследовательскую программу в области статистики интервальных данных можно «в двух словах» сформулировать так: для любого алгоритма анализа данных (алгоритма прикладной статистики) необходимо вычислить нотну и рациональный объем выборки. Или иные величины из того же понятийного ряда, возникающие в многомерном случае, при наличии нескольких выборок и при иных обобщениях описываемой здесь простейшей схемы. Затем проследить влияние погрешностей исходных данных на точность оценивания, доверительные интервалы, значения статистик критериев при проверке гипотез, уровни значимости и другие характеристики статистических выводов. Очевидно, классическая математическая статистика является (предельной) частью статистики интервальных данных, выделяемой условием D = 0.

Поясним теоретические концепции статистики интервальных данных на простых примерах оценивания математического ожидания и дисперсии.

3.4.5. Оценивание математического ожидания

Пусть необходимо оценить математическое ожидание случайной величины с помощью обычной оценки – среднего арифметического результатов наблюдений, т.е.

Тогда при справедливости ограничений (1) на абсолютные погрешности имеем N_f(x) = D. Таким образом, нотна полностью известна и не зависит от многомерной точки, в которой берется. Это утверждение вполне естественно: если каждый результат наблюдения известен с точностью до D, то и среднее арифметическое известно с той же точностью. Ведь возможна систематическая ошибка – если к каждому результату наблюдения добавить D, то и среднее арифметическое увеличится на D.

Поскольку

то в ранее введенных обозначениях

s² = D(x₁).

Следовательно, рациональный объем выборки равен

Для практического использования полученной формулы надо оценить дисперсию результатов наблюдений. Можно доказать, что, поскольку D мало, это можно сделать обычным способом, например, с помощью несмещенной выборочной оценки дисперсии

Здесь и далее рассуждения часто идут на двух уровнях. Первый – это уровень «истинных» случайных величин, обозначаемых в настоящем разделе «х», описывающих реальность, но неизвестных специалисту по анализу данных. Второй – уровень известных этому специалисту величин «у», отличающихся погрешностями от истинных. Погрешности малы, поэтому функции от х отличаются от функций от у на некоторые бесконечно малые величины. Эти соображения и позволяют использовать s²(y) как оценку D(x₁).

Итак, выборочной оценкой рационального объема выборки является

Уже на этом первом рассматриваемом примере видим, что рациональный объем выборки находится не где-то вдали, "в районе бесконечности", а непосредственно рядом с теми объемами, с которыми имеет дело любой практически работающий статистик. Например, если статистик знает, что

то n_rat = 36. А именно такова погрешность контрольных шаблонов во многих технологических процессах! Поэтому, занимаясь управлением качеством, необходимо обращать внимание на действующую на предприятии систему измерений.

По сравнению с классической математической статистикой доверительный интервал для математического ожидания (для заданной доверительной вероятности g) имеет другой вид, а именно:

(4)

где u(g) – квантиль порядка (1 + g)/2 стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.

По поводу формулы (4) была довольно жаркая дискуссия среди специалистов. Отмечалось, что она получена на основе Центральной предельной теоремы теории вероятностей и может быть использована при любом распределении результатов наблюдений (с конечной дисперсией). Если же имеется дополнительная информация, то, по мнению отдельных специалистов, формула (4) может быть уточнена. Например, если известно, что распределение x_i является нормальным, в качестве u(g) целесообразно использовать квантиль распределения Стьюдента. К этому надо добавить, что по небольшому числу наблюдений нельзя надежно установить нормальность, а при росте объема выборки квантили распределения Стьюдента приближаются к квантилям нормального распределения.

Вопрос о том, часто ли результаты наблюдений имеют нормальное распределение, подробно обсуждался среди специалистов. Выяснилось, что распределения встречающихся в практических задачах результатов измерений почти всегда отличны от нормальных [121]. А также и от распределений из иных параметрических семейств, описываемых в учебниках по теории вероятностей и математической статистике.

Применительно к оцениванию математического ожидания (но не к оцениванию других характеристик или параметров распределения) факт существования границы возможной точности, определяемой точностью исходных данных, неоднократно отмечался в литературе ([192, с. 230–234], [255, с. 121] и др.).

3.4.6. Оценивание дисперсии

Для статистики f(y) = s²(y), где s²(y) – выборочная дисперсия (несмещенная оценка теоретической дисперсии), при справедливости ограничений (1) на абсолютные погрешности имеем

Можно показать, что нотна N_f(y) сходится к константе

2DM | x₁ – M(x₁) |

по вероятности с точностью до o(D), когда n стремится к бесконечности. Это же предельное соотношение верно и для нотны N_f(х), вычисленной для исходных данных. Таким образом, в данном случае справедлива формула (2) с

C = 2M | x₁ – M(x₁) |.

Известно (см., например, [256]), что случайная величина

является асимптотически нормальной с математическим ожиданием 0 и дисперсией

Из сказанного вытекает: в статистике интервальных данных асимптотический доверительный интервал для дисперсии s² (соответствующий доверительной вероятности g) имеет вид

(s²(y) – A; s² + A),

где

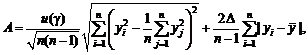
здесь u(g) обозначает тот же самый квантиль стандартного нормального распределения, что и выше в случае оценивания математического ожидания.

Рациональный объем выборки при оценивании дисперсии равен

а выборочную оценку рационального объема выборки n_sample–rat можно вычислить, заменяя теоретические моменты на соответствующие выборочные и используя доступные статистику результаты наблюдений, содержащие погрешности.

Что можно сказать о численной величине рационального объема выборки? Как и в случае оценивания математического ожидания, она отнюдь не выходит за пределы обычно используемых объемов выборок. Так, если принять, что распределение результатов наблюдений x_i является нормальным с математическим ожиданием 0 и дисперсией s², то в результате вычисления моментов случайных величин в предыдущей формуле получаем, что

где p – отношение длины окружности к диаметру, p = = 3,141592… Например, если D = s/6, то n_rat = 11. Это меньше, чем при оценивании математического ожидания в предыдущем примере.

3.4.7. Статистика интервальных данных
в прикладной статистике

Кратко рассмотрим положение статистики интервальных данных (СИД) среди других методов математического описания неопределенностей и анализа данных.

Нечеткость и СИД. С формальной точки зрения описание нечеткости интервалом – это частный случай описания ее нечетким множеством. В СИД функция принадлежности нечеткого множества имеет специфический вид – она равна 1 в некотором интервале и 0 вне его. Такая функция принадлежности описывается всего двумя параметрами (границами интервала). Эта простота описания делает математический аппарат СИД гораздо более прозрачным, чем аппарат теории нечеткости в общем случае (однако при этом надо иметь в виду, что, вопреки основополагающей идее Л.А. Заде, переход от "принадлежности к множеству" к "непринадлежности" является скачкообразным, а не непрерывным). Это, в свою очередь, позволяет исследователю продвинуться дальше, чем при использовании функций принадлежности произвольного вида.

Интервальная математика и СИД. Можно было бы сказать, что СИД – часть интервальной математики, что СИД так соотносится с прикладной математической статистикой, как интервальная математика – с математикой в целом. Однако исторически сложилось так, что интервальная математика занимается прежде всего вычислительным погрешностями. С точки зрения интервальной математики две известные формулы для выборочной дисперсии, а именно

,

имеют разные погрешности. А с точки зрения СИД эти две формулы задают одну и ту же функцию, и поэтому им соответствуют совпадающие нотны и рациональные объемы выборок. Интервальная математика прослеживает процесс вычислений, СИД этим не занимается. Необходимо отметить, что типовые постановки СИД могут быть перенесены в другие области математики, и, наоборот, вычислительные алгоритмы прикладной математической статистики и СИД заслуживают изучения в духе интервальной математики. Однако и то, и другое – скорее дело будущего, а не нынешнего уровня научных исследований в рассматриваемой области. Из уже сделанного отметим применение методов СИД при анализе такой основополагающей характеристики финансовых потоков инвестиционных проектов, как NPV – чистая текущая стоимость [16, гл.9].

Математическая статистика и СИД. Математическая статистика и СИД отличаются тем, в каком порядке делаются предельные переходы n ® ¥ и D ®0. При этом СИД переходит в математическую статистику при D = 0. Правда, тогда исчезают основные особенности СИД: нотна становится равной 0, а рациональный объем выборки – бесконечности. Рассмотренные выше методы СИД разработаны в предположении, что погрешности малы (но не исчезают), а объем выборки велик. СИД расширяет классическую математическую статистику тем, что в исходных статистических данных каждое число заменяет интервалом. С другой стороны, можно считать СИД новым этапом развития математической статистики.

Статистика объектов нечисловой природы и СИД. Статистика объектов нечисловой природы (СОНП) (см. [82] и следующий раздел настоящей монографии) расширяет область применения классической математической статистики путем включения в нее новых видов статистических данных. Естественно, при этом появляются новые виды алгоритмов анализа статистических данных и новый математический аппарат (в частности, происходит переход от методов суммирования к методам оптимизации). С точки зрения СОНП частному виду новых статистических данных – интервальным данным – соответствует СИД. Напомним, что одно из двух основных понятий СИД – нотна – определяется как решение оптимизационной задачи. Однако СИД, изучая классические методы прикладной статистики применительно к интервальным данным, по математическому аппарату ближе к классической математической статистике, чем другие части СОНП, например, статистика бинарных отношений.

Робастные методы статистики и СИД. Если понимать робастность согласно монографии [7] как теорию устойчивости статистических методов по отношению к допустимым отклонениям исходных данных и предпосылок модели, то в СИД рассматривается одна из естественных постановок робастности. Однако в массовом сознании специалистов термин «робастность» закрепился за моделью засорения выборки большими выбросами (модель Тьюки-Хубера), хотя эта модель не имеет большого практического значения [5]. К этой модели СИД не имеет отношения.

Теория устойчивости и СИД. Общей схеме устойчивости (см. [7, 123, 257] и раздел 3.2 настоящей монографии) математических моделей социально-экономических явлений и процессов по отношению к допустимым отклонениям исходных данных и предпосылок моделей СИД полностью соответствует. Она посвящена математико-статистическим моделям, используемым при анализе статистических данных, а допустимые отклонения – это интервалы, заданные ограничениями на погрешности. СИД можно рассматривать как пример теории, в которой учет устойчивости позволил сделать нетривиальные выводы. Отметим, что с точки зрения общей схемы устойчивости [7] устойчивость по Ляпунову в теории дифференциальных уравнений – весьма частный случай, в котором из-за его конкретности удалось весьма далеко продвинуться.

Минимаксные методы, типовые отклонения и СИД. Постановки СИД относятся к минимаксным. За основу берется максимально возможное отклонение. Это – «подход пессимиста», применяемый, например, в теории антагонистических игр. Использование минимаксного подхода позволяет подозревать СИД в завышении роли погрешностей измерения. Однако примеры изучения вероятностно-статистических моделей погрешностей, проведенные, в частности, при разработке методов оценивания параметров гамма-распределения [133, 242], показали, что это подозрение не подтверждается. Влияние погрешностей измерений по порядку такое же, только вместо максимально возможного отклонения (нотны) приходится рассматривать математическое ожидание соответствующего отклонения. Подчеркнем, что применение в СИД вероятностно-статистических моделей погрешностей не менее перспективно, чем минимаксных.

Подход научной школы А.П. Вощинина и СИД. Если в математической статистике неопределенность только статистическая, то в научной школе А.П. Вощинина – только интервальная. Можно сказать, что СИД лежит между классической прикладной математической статистикой и областью исследований научной школы А.П. Вощинина. Другое отличие состоит в том, что в этой школе разрабатывают новые методы анализа интервальных данных, а в СИД в настоящее время изучается устойчивость классических статистических методов по отношению к малым погрешностям. Подход СИД оправдывается распространенностью этих методов, однако в дальнейшем следует переходить к разработке новых методов, специально предназначенных для анализа интервальных данных.

Анализ чувствительности и СИД. При анализе чувствительности, как и в СИД, рассчитывают производные по используемым переменным, или непосредственно находят изменения при отклонении переменной на, например, ±10% от базового значения. Однако этот анализ делают по каждой переменной отдельно. В СИД все переменные рассматриваются совместно, и находится максимально возможное отклонение (нотна). При малых погрешностях удается на основе главного члена разложения функции в многомерный ряд Тейлора получить удобную формулу для нотны. Можно сказать, что СИД – это многомерный анализ чувствительности.

* * *

Асимптотической математической статистике интервальных данных посвящены обширные главы в монографиях [5, 33, 36, 54]. Продолжают интенсивно развиваться научные исследования как в научной школе А.П. Вощинина [258, 259], так и в СИД [83, 260, 261, 262].

По нашему мнению, во все виды статистического программного обеспечения должны быть включены алгоритмы интервальной статистики, «параллельные» обычно используемым в настоящее время алгоритмам прикладной математической статистики. Это позволит в явном виде учесть наличие погрешностей у результатов наблюдений (измерений, испытаний, анализов, опытов).

Статистика интервальных данных является составной частью системной нечеткой интервальной математики [32, 33, 263] – перспективного направления теоретической и вычислительной математики.

3.5. О развитии статистики нечисловых данных

Около тридцати пяти лет назад статистика нечисловых данных (синонимы - статистика объектов нечисловой природы, нечисловая статистика) была выделена как самостоятельная область математической статистики. Как показано в разделе 2.3.5, статистика нечисловых данных является центральной частью прикладной математической статистики. В настоящем разделе проанализируем разработку основных идей в этой области на фоне развития прикладной статистики в целом и в связи с формированием нового перспективного направления теоретической и прикладной математики - системной нечеткой интервальной математики [32, 33].

Термин "статистика объектов нечисловой природы" впервые появился в 1979 г. в монографии [7]. В том же году в статье [146] была развернута программа построения этой новой области статистических методов. В следующем году появилась коллективная обобщающая статья пяти авторов на эту тему [264]. Обсудим содержание, развитие и основные идеи статистики объектов нечисловой природы.

3.5.1. Послевоенное развитие отечественной
статистики

К 60-м годам ХХ в. в нашей стране (как и во всем мире) сформировалась научно-практическая дисциплина, которую называем классической математической статистикой. Статистики учились теории по книге Г. Крамера [265], написанной в военные годы и впервые изданной в нашей стране в 1948 г. Из прикладных руководств назовем учебник [266] и таблицы с комментариями [69].

Затем внимание многих специалистов сосредоточилось на изучении математических конструкций, используемых в статистике. Примером таких работ является монография [267]. В ней получены продвинутые математические результаты, но трудно (видимо - вообще невозможно) выделить рекомендации для статистика, анализирующего конкретные данные.

Как реакция на уход теоретиков-статистиков в математику выделилась новая научная дисциплина - прикладная статистика. В учебнике [5] в качестве рубежа, когда это стало очевидным, мы указали 1981 г. – дату выхода массовым тиражом (33 940 экз.) сборника [268], в названии которого использован термин «прикладная статистика». С этого времени линии развития математической статистики и прикладной статистики разошлись. Первая из этих дисциплин полностью ушла в математику, перестав интересоваться практическими делами. Вторая позиционировала себя в качестве науки об обработке данных – результатов наблюдений, измерений, испытаний, анализов, опытов [5].

Вполне естественно, что в прикладной статистике стали развиваться математические методы и модели. Необходимость их развития вытекает из потребностей конкретных прикладных исследований. Это математизированное ядро прикладной статистики хочется назвать теоретической статистикой. Тогда под собственно прикладной статистикой следует понимать обширную промежуточную область между теоретической статистикой и применением статистических методов в конкретных областях. В нее входят, в частности, вопросы формирования вероятностно-статистических моделей и выбора конкретных методов анализа данных (т.е. методология прикладной статистики и других статистических методов), проблемы разработки и применения информационных статистических технологий, организации сбора и анализа данных, т.е. разработки статистических технологий.

Таким образом, общая схема современной статистической науки выглядит следующим образом (от абстрактного к конкретному):

1. Математическая статистика – часть математики, изучающая статистические структуры. Сама по себе не дает рецептов анализа статистических данных, однако разрабатывает методы, полезные для использования в теоретической статистике. Можно вслед за Г. Крамером [265] в качестве названия этой области статистической науки использовать термин "Математические методы статистики".

2. Теоретическая статистика – наука, посвященная моделям и методам анализа конкретных статистических данных.

3. Прикладная статистика (в узком смысле) занимается статистическими технологиями сбора и обработки данных. Она включает в себя методологию статистических методов, вопросы организации выборочных исследований, разработки статистических технологий, создания и использования статистических программных продуктов.

4. Применение статистических методов в конкретных областях. Соответствующие области научно-прикладных исследований иногда имеют собственные названия (в экономике и менеджменте – эконометрика, в биологии – биометрика, в химии – хемометрия, в технических исследованиях – технометрика), а иногда специальных названий пока нет или они не устоялись (применения статистических методов в геологии, демографии, социологии, медицине, истории, и т.д.). Термин "социометрика" имеет более узкий смысл, чем можно было бы ожидать - под ним понимают не статистические методы в социологии, а всего лишь статистические методы изучения малых групп. Для обозначения математических и статистических метолов в истории иногда используют термин "клиометрика", но при этом не рассматривают основное достижение в этой области - новую статистическую хронологию [199]. И т.д., и т.п.

Часто позиции 2 и 3 вместе называют прикладной статистикой (как мы это сделали в учебнике [5], написанном в 2003 г. и изданном в 2006 г.). Иногда позицию 1 именуют теоретической статистикой (особенно в зарубежных изданиях). Эти терминологические расхождения связаны с тем, что описанное выше развитие рассматриваемой научно-прикладной области не сразу, не полностью и не всегда адекватно отражается в сознании специалистов. Так, до сих пор выпускают учебники, соответствующие уровню представлений середины ХХ века, т.е старой парадигме статистической науки (см. раздел 2.1 настоящей монографии).

Примечание. Здесь мы уточнили схему внутреннего деления статистической теории, предложенную в [152]. Естественный смысл приобрели термины «теоретическая статистика» и «прикладная статистика» (в узком смысле). Однако необходимо иметь в виду, что в сравнительно недавнем учебнике [5] прикладная статистика понимается в широком смысле, т.е. как объединение позиций 2 и 3.

К сожалению, в настоящее время невозможно отождествить теоретическую статистику с математической, поскольку последняя (как часть математики - научной специальности «теория вероятностей и математическая статистика») заметно оторвалась от задач практики. Однако начинают проявляться любопытные тенденции. Дело в том, что в нашей стране математическая статистика "вымирает". Исследователи в этой области с возрастом снижают активность, новые не появляются, число работ уменьшается, особенно диссертационных. В то же время прикладная статистика активно развивается. Можно предсказать, что в ближайшие десятилетия прикладная статистика полностью "поглотит" математическую, вместе с названием. Так завершится "раскол 1981 года". И снова будет единая "математическая статистика".

Как известно, издавна идут споры о том, существует ли прикладная математика. В частности, уиверждают, что вся математика является прикладной, а лишь математики делятся на тех, для кого теоремы важнее ("чистые"), и тех, для кого важнее приложения ("прикладные"). Аналогичные споры имели место и в статистической науке. Замечательный советский статистик член-корреспондент АН СССР Л.Н. Большев, один из авторов лучшего на русском языке сборника статистических таблиц [69], в конце 1970-х гг. в беседе с А.И. Орловым активно возражал против термина "прикладная статистика", поскольку, по его словам, "вся статистика является прикладной". При этом он отметил, что этот термин - реакция на развитие "аналитической статистики" (работы типа [267]), которая занимается внутриматематическими вопросами [268, с.7]. Прошло несколько десятилетий, и стало ясно, что Л.Н. Большев был прав - "вся статистика является прикладной", и имя ей - "математическая статистика", а внутриматематическая "аналитическая статистика" была модным увлечением математиков и ушла в прошлое.

Отметим, что математическая статистика, как и теоретическая с прикладной, заметно отличается от ведомственной науки органов официальной государственной статистики. ЦСУ, Госкомстат, Росстат применяли и применяют лишь проверенные временем приемы позапрошлого (девятнадцатого) века. Возможно, следовало бы от этого ведомства полностью отмежеваться и сменить название научной области, например, на «Анализ данных». В настоящее время компромиссным самоназванием нашей научно-практической дисциплины является термин «статистические методы».

Как уже говорилось, во второй половине 80-х годов развернулось общественное движение, имеющее целью создание профессионального объединения статистиков. Аналогами являются британское Королевское статистическое общество (основано в 1834 г.) и Американская статистическая ассоциация (создана в 1839 г.). К сожалению, деятельность учрежденной в 1990 г. Всесоюзной статистической ассоциации оказалась парализованной в результате развала СССР. Некоторую активность проявили созданные на базе ВСА Российская ассоциация статистических методов, Российская академия статистических методов, Белорусская статистическая ассоциация. Пришло время оживить их деятельность.

В ходе создания ВСА было проанализировано состояние и перспективы развития теоретической и прикладной статистики. В частности, выделены пять актуальных направлений, в которых развивается современная прикладная статистика, т.е. пять «точек роста» статистической науки: непараметрика, робастность, бутстреп, интервальная статистика, статистика объектов нечисловой природы. Первые четыре из этих направлений достаточно подробно рассмотрены выше в настоящей монографии в разделах 3.1 - 3.4 соответственно.

3.5.2. Краткая история статистики объектов
нечисловой природы

Перейдем к сути статистики объектов нечисловой природы (она же - статистика нечисловых данных, или нечисловая статистика). Типичный исходный объект в прикладной статистике - это выборка, т.е. совокупность независимых одинаково распределенных случайных элементов. Какова природа этих элементов? В классической математической статистике элементы выборки - это числа. В многомерном статистическом анализе - вектора. А в нечисловой статистике элементы выборки - это объекты нечисловой природы, которые нельзя складывать и умножать на числа. Другими словами, объекты нечисловой природы лежат в пространствах, не имеющих векторной структуры.

Примерами объектов нечисловой природы являются:

- значения качественных признаков, в том числе результаты кодировки объектов с помощью заданного перечня категорий (градаций);

- упорядочения (ранжировки) экспертами образцов продукции (при оценке её технического уровня, качества и конкурентоспособности)) или заявок на проведение научных работ (при проведении конкурсов на выделение грантов);

- классификации, т.е. разбиения объектов на группы сходных между собой (кластеры);

- толерантности, т.е. бинарные отношения, описывающие сходство объектов между собой, например, сходства тематики научных работ, оцениваемого экспертами с целью рационального формирования экспертных советов внутри определенной области науки;

- другие виды отношений на конечных множествах (унарных, бинарных, тернарных и др.);

- результаты парных сравнений или контроля качества продукции по альтернативному признаку («годен» - «брак»), т.е. последовательности из 0 и 1;

- множества (обычные или нечеткие), например, зоны, пораженные коррозией, или перечни возможных причин аварии, составленные экспертами независимо друг от друга;

- слова, предложения, тексты;

- вектора, координаты которых - совокупность значений разнотипных признаков, например, результат составления статистического отчета о научно-технической деятельности организации или анкета эксперта, в которой ответы на часть вопросов носят качественный характер, а на часть - количественный;

- ответы на вопросы экспертной, медицинской, маркетинговой или социологической анкеты, часть из которых носит количественный характер (возможно, интервальный), часть сводится к выбору одной из нескольких подсказок, а часть представляет собой тексты;

- графы;

- ориентированные графы;

- блок-схемы;

- кривые,

- фигуры;

- тела в пространстве;

- рисунки (образы, сцены);

- звуки (фонемы);

- алгоритмы;

- модели различных явлений и процессов;

- отношения в малой группе;

- предметы одежды;

- песни;

- цирковые номера;

- поэтические произведения;

- элементы метрического пространства;

- элементы произвольного пространства, и т.д.

Список можно продолжать сколь угодно долго, поскольку окружающие нас явления и процессы лишь в редких случаях можно адекватно описать с помощью чисел. (Хотя стоит напомнить, что любые символы кодируются в памяти компьютера с помощью последовательностей 0 и 1.)

Рассмотренные выше интервальные данные тоже можно рассматривать как пример объектов нечисловой природы, а именно, как частный случай нечетких множеств. Если характеристическая функция нечеткого множества равна 1 на некотором интервале и равна 0 вне этого интервала, то задание такого нечеткого множества эквивалентно заданию интервала. С методологической точки зрения важно, что теория нечетких множеств в определенном смысле сводится к теории случайных множеств. Цикл соответствующих теорем приведен в монографиях [7, 33], а также в учебниках [5, 16, 36, 54].

С 70-х годов в основном в ответ на запросы теории экспертных оценок (а также технических исследований, экономики, социологии и медицины) развивались различные направления статистики объектов нечисловой природы. Были установлены основные связи между конкретными видами таких объектов, разработаны для них базовые вероятностные модели. Сводка была дана в монографии [7], препринте [144].

Следующий этап (80-е годы) - выделение статистики объектов нечисловой природы в качестве самостоятельной дисциплины в рамках прикладной статистики (шире, математических методов исследования), ядром которого являются методы статистического анализа данных произвольной природы. Для работ этого периода характерна сосредоточенность на внутренних проблемах нечисловой статистики. Проводились всесоюзные конференции [269, 270], выпускались монографии [271 - 276], сборники трудов [277 - 279], защищались диссертации [280 - 286]. Наиболее представительным является сборник [87], подготовленный совместно комиссией «Статистика объектов нечисловой природы» Научного Совета АН СССР по комплексной проблеме «Кибернетика» и Институтом социологических исследований АН СССР.

К 90-м годам статистика объектов нечисловой природы с теоретической точки зрения была достаточно хорошо развита, основные идеи, подходы и методы были разработаны и изучены математически, в частности, доказано достаточно много теорем. Однако она оставалась недостаточно апробированной на практике. И в 90-е годы наступило время перейти от теоретико-статистических исследований к применению полученных результатов на практике и включить их в учебный процесс, что и было сделано (см., например, учебники [5, 16, 36, 54], написанные несколько позже, в первое десятилетие XXI в.). В 90-е годы опубликованы обзоры [287 - 289] по статистике объектов нечисловой природы и многочисленные конкретные исследования, к рассмотрению которых и переходим.

3.5.3. Основные идеи и направления статистики
объектов нечисловой природы

В чем принципиальная новизна нечисловой статистики? Для классической математической статистики характерна операция сложения. При расчете выборочных характеристик распределения (выборочное среднее арифметическое, выборочная дисперсия и др.), в регрессионном анализе и других областях этой научной дисциплины постоянно используются суммы. Математический аппарат - законы больших чисел, Центральная предельная теорема и другие теоремы - нацелены на изучение сумм. В нечисловой же статистике нельзя использовать операцию сложения, поскольку элементы выборки лежат в пространствах, где нет операции сложения. Методы обработки нечисловых данных основаны на принципиально ином математическом аппарате - на применении различных расстояний в пространствах объектов нечисловой природы.

Следует отметить, что в статистике объектов нечисловой природы одна и та же математическая схема может с успехом применяться во многих прикладных областях, для анализа данных различных типов, а потому ее целесообразно формулировать и изучать в наиболее общем виде, для объектов произвольной природы.

Кратко рассмотрим несколько идей, развиваемых в статистике объектов нечисловой природы для данных, лежащих в пространствах произвольного вида. Они нацелены на решение классических задач описания данных, оценивания, проверки гипотез - но для неклассических данных, а потому неклассическими методами.

Первой обсудим проблему определения средних величин. В рамках теории измерений удается указать вид средних величин, соответствующих тем или иным шкалам измерения. Теория измерений [7, 136, 137], в середине ХХ в. рассматривавшаяся как часть математического обеспечения психологии, к настоящему времени признана общенаучной дисциплиной. Современные достижения рассмотрены в статьях [198, 290 -292].

В классической математической статистике средние величины вводят с помощью операций сложения (выборочное среднее арифметическое, математическое ожидание) или упорядочения (выборочная и теоретическая медианы). В пространствах произвольной природы средние значения нельзя определить с помощью операций сложения или упорядочения. Теоретические и эмпирические средние приходится вводить как решения экстремальных задач. Теоретическое среднее определяется как решение задачи минимизации математического ожидания (в классическом смысле) расстояния от случайного элемента со значениями в рассматриваемом пространстве до фиксированной точки этого пространства (минимизируется указанная функция от этой точки). Для получения эмпирического среднего математическое ожидание берется по эмпирическому распределению, т.е. берется сумма расстояний от некоторой точки до элементов выборки и затем минимизируется по этой точке (примером является медиана Кемени [143]). При этом как эмпирическое, так и теоретическое средние как решения экстремальных задач могут быть не единственными элементами рассматриваемого пространства, а являться некоторыми множествами таких элементов, которые могут оказаться и пустыми. Тем не менее удалось сформулировать и доказать законы больших чисел для средних величин, определенных указанным образом, т.е. установить сходимость (в специально определенном смысле) эмпирических средних к теоретическим [5, 16, 293 - 295].

Оказалось, что методы доказательства законов больших чисел допускают существенно более широкую область применения, чем та, для которой они были разработаны. А именно, удалось изучить асимптотику решений экстремальных статистических задач, к которым, как известно, сводится большинство постановок прикладной статистики. В частности, кроме законов больших чисел установлена и состоятельность оценок минимального контраста, в том числе оценок максимального правдоподобия и робастных оценок. К настоящему времени подобные оценки изучены также и в интервальной статистике. Полученные результаты относительно асимптотики решений экстремальных статистических задач применяются в работах [296 - 300].

В статистике в пространствах произвольной природы большую роль играют непараметрические оценки плотности, используемые, в частности, в различных алгоритмах регрессионного, дискриминантного, кластерного анализов. В нечисловой статистике предложен и изучен ряд типов непараметрических оценок плотности в пространствах произвольной природы, в том числе в дискретных пространствах [175, 301 - 306]. В частности, доказана их состоятельность, изучена скорость сходимости и установлен (для ядерных оценок плотности) примечательный факт совпадения наилучшей скорости сходимости в произвольном пространстве с той, которая имеет быть в классической теории для числовых случайных величин [125].

Дискриминантный, кластерный, регрессионный анализы в пространствах произвольной природы основаны либо на параметрической теории - и тогда применяется подход, связанный с асимптотикой решения экстремальных статистических задач - либо на непараметрической теории - и тогда используются алгоритмы на основе непараметрических оценок плотности [36].

Для анализа нечисловых, в частности, экспертных данных весьма важны методы классификации [307 - 313]. Обзоры таких методов и наши научные результаты даны в работах [65, 120, 134, 176, 180, 314 - 320]. Интересно движение мысли в другом направлении в рамках новой парадигмы (см. разд. 2.1 настоящей монографии), согласно которой наиболее естественно ставить и решать задачи классификации, основанные на использовании расстояний или показателей различия, именно в рамках статистики объектов нечисловой природы (а не, скажем, многомерного статистического анализа). Это касается как распознавания образов с учителем (другими словами, дискриминантного анализа), так и распознавания образов без учителя (т.е. кластерного анализа). Аналогичным образом задачи многомерного шкалирования, т.е. визуализации данных [141, 142, 321], также естественно отнести к статистике объектов нечисловой природы.

Для проверки гипотез в пространствах нечисловой природы могут быть использованы статистики интегрального типа, в частности, типа омега-квадрат [71, 75, 161, 146, 173, 322]. Любопытно, что предельная теория таких статистик, построенная первоначально в классической постановке [323], приобрела естественный (завершенный, изящный) вид именно для пространств произвольного вида [149, 324], поскольку при этом удалось провести рассуждения, опираясь на базовые математические соотношения, а не на те частные (с общей точки зрения), что были связаны с конечномерным пространством.

Представляют практический интерес результаты, связанные с конкретными областями статистики объектов нечисловой природы, в частности, со статистикой нечетких множеств [85] и со статистикой случайных множеств (напомним, что теория нечетких множеств в определенном смысле сводится к теории случайных множеств), с непараметрической теорией парных сравнений и люсианов (бернуллиевских бинарных векторов), с аксиоматическим введением метрик в конкретных пространствах объектов нечисловой природы, а также с рядом других конкретных постановок. Отметим бурный рост интереса со стороны прикладников к математическому аппарату теории нечеткости [138, 325 - 328].

Результаты контроля штучной продукции по альтернативному (бинарному, дихотомическому) признаку представляют собой последовательности из 0 и 1 – объекты нечисловой природы, а потому теорию статистического контроля относят к нечисловой статистике [163, 287]. В рамках новой парадигмы статистических методов, шире, математических методов экономики постоянно публикуются работы по этой тематике, предназначенные для специалистов по статистическим методам управления качеством продукции [159, 160, 224, 329 - 332]. Для служб контроллинга особенно важны методы статистического контроля процессов, предназначенные для выявления отклонений методом контрольных карт [97, 158, 177, 333].

При статистическом анализе нечисловых данных возникает необходимость оценивать параметры модели. Вместо метода максимального правдоподобия целесообразно применять метод одношаговых оценок [334 - 337].

Интенсивно ведется разработка новых методов анализа конкретных видов нечисловых данных. Так, С.А. Смоляк рассматривает проблему восстановления функции многих переменных по ее точным или приближенным значениям в отдельных точках. Для функций числовых переменных – это обычная задача интерполяции, однако он решает задачу восстановления функции от номинальных или порядковых переменных и предлагает эвристические методы, основанные на формализации дискретного аналога понятия «гладкости» функции [338, 339]. А.Н. Горбач и Н.А. Цейтлин на основе практических потребностей (прежде всего, потребностей маркетинга) обосновывают необходимость построения статистической теории спонтанных последовательностей, вводят расстояния между ними [340] и разрабатывают методы анализа этого нового вида объектов нечисловой природы [341]. Бурно развивается раздел нечисловой статистики, посвященный организационным структурам [9, 56, 342 - 347].

Статистика объектов нечисловой природы порождена потребностями практики, прежде всего в области экспертных оценок. Вполне естественно, что названия сборников трудов неформального научного коллектива, развивающего нечисловую статистику, начинались со слов «Экспертные оценки» [348 - 351]. Различным вопросам теории и практики экспертных оценок посвящен ряд монографий, подготовленных членами нашего научного коллектива [52, 54, 55, 59, 145, 352 - 355]. Научные результаты последних лет постоянно публикуются в журналах «Заводская лаборатория» [356 - 365], «Автоматика и телемеханика» [202, 366 - 368], "Научном журнале КубГАУ" [135, 369, 370] и других [371, 372].

Экспертные методы, как и статистические, активно используются при прогнозировании. Тематике прогнозирования наш «незримый коллектив» уделяет значительное место [169, 170, 373 - 375]. Отметим цикл исследований по разработке научных основ создания автоматизированной системы прогнозирования и предотвращения авиационных происшествий [376 - 380].

Как показано в разд. 3.1, одна из основных областей непараметрической статистики – это ранговая статистика, т.е. основанная на рангах – номерах элементов выборок в вариационных рядах. Ранги измерены в порядковых шкалах, а значения ранговых статистик инвариантны относительно любых строго возрастающих преобразований - допустимых преобразований в таких шкалах. Это означает, что существенную часть непараметрической статистики [69, 380, 381] можно включить в нечисловую статистику. Тем более это касается статистики интервальных данных, изучающей методы анализа нечисловых данных конкретного вида – интервалов. Так, в учебнике [36] статистика интервальных данных включена в нечисловую статистику. Однако в настоящей монографии мы предпочли рассмотреть непараметрику, статистику интервальных данных и нечисловую статистику по отдельности. В частности, потому, что статистика в пространствах произвольной природы является центральной областью только для последнего из трех рассмотренных здесь направлений прикладной статистики.

Вопросы внедрения математических методов исследования всегда были в центре внимания нашего творческого сообщества, а потому и нашего раздела «Математические методы исследования» журнала «Заводская лаборатория» [224, 230, 382]. Подчеркивалось большое теоретическое и прикладное значение статистики объектов нечисловой природы [155], необходимость перехода от отдельных методов анализа данных к разработке высоких статистических технологий [51] и использования современных систем внедрения математических методов, таких как система «Шесть сигм» и ее аналоги [233]. Обсуждались проблемы программного обеспечения [223, 227, 228]. Однако приходится констатировать, что создание линейки современных программных продуктов по нечисловой статистике – пока дело будущего.

3.5.4. О некоторых нерешенных проблемах
нечисловой статистики

За каждым новым научным результатом открывается многообразие неизвестного. Рассмотрим несколько конкретных постановок.

В статистике в пространствах общей природы получены аналоги классического закона больших чисел. Но нет аналога центральной предельной теоремы. Какова скорость сходимости эмпирических средних к теоретическим? Как сравнить различные способы усреднения? В частности, что лучше применять для усреднения упорядочений – медиану Кемени или среднее по Кемени (среднее отличается от медианы тем, что в качестве показателя различия берется не расстояние Кемени, а его квадрат)? Какие конкретные представители различных классов непараметрических оценок плотности достойны рекомендации для использования в нацеленных на практическое применение алгоритмах и программных продуктах анализа нечисловых данных?

До сих пор не проведена полная классификация классических статистических методов с точки зрения теории измерений. Законченные результаты получены только для теории средних [5, 7, 16, 54, 200]. А именно, доказано, что для измерений в порядковой шкале в качестве средних можно использовать только порядковые статистики, например, медиану (при нечетном объеме выборки). Среднее арифметическое применять нельзя. Однако многочисленные эксперименты показывают, что упорядочения объектов по средним арифметическим рангов и по медианам рангов в подавляющем большинстве случаев совпадают или близки. Нужна теория, объясняющая этот экспериментальный факт. Ряд вопросов поставлен в статье [383].

Все более широкое распространение получает теория нечеткости. Давно установлено, что она в определенном смысле сводится к теории случайных множеств [33, 85]. Требуется на основе предложенного (или иного, если будет найден) метода сведения проанализировать различные теоретические и прикладные постановки теории нечеткости и рассмотреть их в рамках вероятностно-статистических методов и моделей. Представляет интерес оба направления движения - от нечетких множеств к случайным и, в обратном направлении, от случайных множеств к нечетким.

Перейдем к классическим областям статистики. Начнем с обсуждения влияния отклонений от традиционных предпосылок (ср. раздел 3.2 настоящей монографии). В вероятностной теории статистических методов выборка обычно моделируется как конечная последовательность независимых одинаково распределенных случайных величин или векторов. В парадигме середины ХХ в. часто предполагают, что эти величины (вектора) имеют нормальное распределение.

При внимательном взгляде совершенно ясна нереалистичность приведенных классических предпосылок. Независимость результатов измерений обычно принимается «из общих предположений», между тем во многих случаях очевидна их коррелированность. Одинаковая распределенность также вызывает сомнения из-за изменения во времени свойств измеряемых образцов, средств измерения и психофизического состояния специалистов, проводящих измерения (испытания, анализы, опыты). Даже обоснованность самого применения вероятностных моделей иногда вызывает сомнения, например, при моделировании уникальных измерений (согласно классическим воззрениям, теорию вероятностей обычно привлекают при изучении массовых явлений). И уж совсем редко распределения результатов измерений можно считать нормальными [5, 16].

Итак, методы классической математической статистики обычно используют вне сферы их обоснованной применимости. Какова влияние отклонений от традиционных предпосылок на статистические выводы? В настоящее время об этом имеются лишь отрывочные сведения. Приведем три примера.

Пример 1. Построение доверительного интервала для математического ожидания обычно проводят с использованием распределения Стьюдента (при справедливости гипотезы нормальности). Как следует их Центральной предельной теоремы (ЦПТ) теории вероятностей, в асимптотике (при большом объеме выборки) такие расчетные методы дают правильные результаты (из ЦПТ вытекает использование квантилей нормального распределения, а из классической теории - квантилей распределения Стьюдента, но при росте объема выборки квантили распределения Стьюдента стремятся к соответствующим квантилям нормального распределения). Подробнее об этом см. в статье [165].

Пример 2. Для проверки однородности двух независимых выборок (на самом деле, как показано в разд. 3.1.1 настоящей монографии, - для проверки равенства математических ожиданий) обычно рекомендуют использовать двухвыборочный критерий Стьюдента. Предпосылки его использования – это нормальность распределений, соответствующих выборкам, и равенство их дисперсий. Что будет при отклонении от нормальности распределений, из которых взяты выборки, от нормальности? Если объемы выборок равны или если дисперсии совпадают, то в асимптотике (когда объемы выборок безгранично возрастают) классический метод является корректным. Если же объемы выборок существенно отличаются или дисперсии различны, то критерий Стьюдента проверки гипотезы однородности применять нельзя, поскольку распределение двухвыборочной статистики Стьюдента будет существенно отличаться от классического. Поскольку проверка равенства дисперсий - более сложная задача, чем проверка равенства математических ожиданий, то для выборок разного объема использовать двухвыборочную статистику Стьюдента не следует, целесообразно применять критерий Крамера-Уэлча [5, 16, 71].

Пример 3. В задаче отбраковки (исключения) резко выделяющихся наблюдений (выбросов) расчетные методы, основанные на нормальности, являются крайне неустойчивыми по отношению к отклонениям от нормальности, что полностью лишает эти методы научной обоснованности [5, 16, 156].

Примеры 1 - 3 показывают весь спектр возможных свойств классических расчетных методов в случае отклонения от нормальности. Методы примера 1 оказываются вполне пригодными при таких отклонениях, примера 2 - пригодными в некоторых случаях, примера 3 - полностью непригодными.

Итак, имеется необходимость изучения свойств расчетных методов классической математической статистики, опирающихся на предположение нормальности, в ситуациях, когда это предположение не выполнено. Аппаратом для такого изучения наряду с методом Монте-Карло могут послужить предельные теоремы теории вероятностей, прежде всего Центральная Предельная Теорема, поскольку интересующие нас расчетные методы обычно используют разнообразные суммы. Пока подобное изучение не проведено, остается неясной научная ценность, например, применения основанного на предположении многомерной нормальности технологии факторного анализа к векторам из переменных, принимающих небольшое число градаций и к тому же измеренных в порядковой шкале. Очевиден выход за пределы предположений, в рамках которых разработана и обоснована технология факторного анализа. Неясно, какими свойствами обладают результаты расчетов вне области применимости этих расчетов.

Почему в современных условиях прежде всего необходимо изучение классических алгоритмов, а не построение новых, специально предназначенных для работы в условиях отклонения от классических предпосылок?

Во-первых, потому, что классические алгоритмы в настоящее время наиболее распространены (прежде всего из-за пороков сложившейся системы образования как прикладников, так и теоретиков). Например, для проверки однородности двух независимых выборок традиционно используют критерий Стьюдента, при этом условия его применимости не проверяют. Насколько обоснованными являются выводы? Как следует из примера 2, во многих случаях выводы нет оснований подвергать сомнению, хотя они получены с помощью некорректной процедуры.

Во-вторых, более новые подходы зачастую методологически уязвимы. Так, известная робастная модель засорения Тьюки-Хубера нацелена на борьбу с большими выбросами, которые зачастую физически невозможны из-за ограниченности интервала значений измеряемой характеристики, в котором работает конкретное средство измерения. Следовательно, модель Тьюки-Хубера-Хампеля [195, 196] имеет скорее теоретическое значение, чем практическое. Сказанное, конечно, не обозначает, что следует прекратить разработку, изучение и внедрение непараметрических и устойчивых методов, выделенных выше как «точки роста» современной прикладной статистики.

Нерешенным проблемам статистики посвящены статьи [157, 384]. Одна из важных проблем - использование асимптотических результатов при конечных объемах выборок. Конечно, естественно изучить свойства алгоритма с помощью метода Монте-Карло. Однако из какого конкретного распределения брать выборки при моделировании? От выбора распределения зависит результат. Кроме того, датчики псевдослучайных чисел лишь имитируют случайность. До сих пор неизвестно, каким датчиком целесообразно пользоваться в случае возможного безграничного роста размерности пространства (см. развернутое обсуждение затронутых проблем в разделе 3.3. настоящей монографии).

Другая проблема – обоснование выбора одного из многих критериев для проверки конкретной гипотезы. Например, для проверки однородности двух независимых выборок можно предложить критерии Стьюдента, Крамера-Уэлча, Лорда, хи-квадрат, Вилкоксона (Манна-Уитни), Ван-дер-Вардена, Сэвиджа, Н.В. Смирнова, типа омега-квадрат (Лемана-Розенблатта), Реньи, Г.В. Мартынова и др. [71, 174]. Какой выбрать?

Критерии однородности проанализированы в монографии [385]. Естественных подходов к сравнению критериев несколько - на основе асимптотической относительной эффективности по Бахадуру, Ходжесу-Леману, Питмену. И каждый критерий является оптимальным при соответствующей альтернативе или подходящем распределении на множестве альтернатив. При этом математические выкладки обычно используют альтернативу сдвига, сравнительно редко встречающуюся в практике анализа реальных статистических данных. Итог печален - блестящая математическая техника, продемонстрированная в [385], не позволяет дать рекомендации для выбора критерия проверки однородности при анализе реальных данных.

Проблемы разработки высоких статистических технологий поставлены в программной статье [51] (см. также сайт "Высокие статистические технологии" http://orlovs.pp.ru). Используемые при обработке реальных данных статистические технологии состоят из последовательности операций, каждая из которых, как правило, хорошо изучена, поскольку сводится к оцениванию (параметров, характеристик, распределений) или проверке той или иной гипотезы. Однако статистические свойства результатов обработки, полученных в результате последовательного применения таких операций, мало изучены. Необходима теория, позволяющая изучать свойства статистических технологий и так их конструировать, чтобы обеспечить высокое качество обработки данных.

В заключение отметим, что развернутое описание статистики нечисловых данных дано в монографиях [5, 7, 16, 36, 54]. При дальнейшем развитии исследований важно опираться на современную методологию [50]. Работы в области статистики объектов нечисловой природы активно продолжаются (см., например, [190, 295]). Эта область, как видно из проведенного выше анализа, имеет много общего с системной нечеткой интервальной математикой [32, 33, 263]. Статистика объектов нечисловой природы соответствует новой парадигме математической статистики, разобранной, например, в статье [63], более того, именно развитие этой научно-практической области стимулировало появление новой парадигмы математической статистики, прикладной статистики, математических методов экономики, шире - математических методов исследования (подробнее см. раздел 2.1 настоящей монографии, полностью посвященный новой парадигме математических методов экономики).

ГЛАВА 4. ЭКОНОМИКО-МАТЕМАТИЧЕСКАЯ
ПОДДЕРЖКА КОНТРОЛЛИНГА

4.1. Эконометрическая поддержка контроллинга

Эконометрика – один из наиболее эффективных инструментов контроллинга. Специалисты владеют этим инструментом. Поэтому они обычно рассказывают о полученных результатах, а не о приемах использования инструмента. В результате следующее поколение может и не познакомиться с основами, ограничившись повторением общих слов. Особенно актуальна эта проблема для современной России, в которой идет бурный процесс внедрения контроллинга.

В статье [21] рассмотрены общие проблемы применения эконометрических методов при решении задач контроллинга. Описанию конкретных методов посвящен, в частности, учебник "Эконометрика" [16]. В настоящем разделе рассмотрим конкретные задачи контроллинга, для решения которых необходимо использовать методы эконометрики.

4.1.1. Термин «эконометрика»

Однако вначале необходимо обсудить содержание термина «эконометрика». Согласно энциклопедическим источникам, эконометрика – это наука, изучающая конкретные количественные и качественные взаимосвязи экономических объектов и процессов с помощью математических и статистических методов и моделей [38]. Такие методы успешно используются в зарубежных и отечественных экономических и технико-экономических исследованиях, работах по управлению (менеджменту). Применение прикладной статистики и других эконометрических методов дает заметный экономический эффект. Например, в США - не менее 20 миллиардов долларов ежегодно только в области статистического контроля качества [16, 382]. В 1988 г. затраты на статистический анализ данных в нашей стране оценивались в 2 миллиарда рублей ежегодно [387]. Согласно расчетам сравнительной стоимости валют на основе потребительских паритетов, эту величину можно сопоставить с 2 миллиардами долларов США (по официальному курсу доллара на 1988 г. - 3 миллиарда долларов). Следовательно, объем отечественного "рынка статистических и эконометрических услуг" в 1988 г. был на порядок меньше, чем в США, что совпадает с оценками и по другим показателям, например, по числу специалистов.

В литературе встречается и более узкое понимание эконометрики. Так, в одном из наиболее распространенных в России вводных курсов западной экономической теории сказано: "Статистический анализ экономических данных называется эконометрикой, что буквально означает: наука об экономических измерениях" [386, с.25]. Согласно учебнику [16] эконометрические методы - это прежде всего методы статистического анализа конкретных экономических данных, естественно, с помощью компьютеров. В отличие от формулировок в энциклопедических источниках, здесь из эконометрики исключаются, например, оптимизационные задачи. Это оправдано, например, с точки зрения преподавания, поскольку в настоящее время методы статистического анализа и методы оптимизации рассматриваются в разных учебных курсах.

Однако при решении практических задач производственного менеджмента и контроллинга придерживаться такого разделения нет оснований. Поэтому в настоящей статье примем приведенное выше определение Большого Энциклопедического Словаря [38], согласно которому термин «эконометрика» фактически является синонимом термину «математические методы в экономике».

Точнее, в эконометрику согласно [38] не включают абстрактные экономико-математические методы и модели, не связанные с изучением конкретных явлений и процессов, например, теоремы о существовании точки равновесия. Однако подобные методы и модели, как правило, не используются при решении практических задач.

Итак, эконометрические методы - это прежде всего методы статистического анализа конкретных экономических данных, естественно, с помощью компьютеров. В нашей стране они пока сравнительно мало известны, хотя именно у нас наиболее мощная научная школа в области основы эконометрики – теории вероятностей.

В мировой науке эконометрика занимает достойное место. Как уже отмечалось в настоящей монографии, нобелевские премии по экономике получили эконометрики Ян Тильберген, Рагнар Фриш, Лоуренс Клейн, Трюгве Хаавельмо. В 2000 г. к ним добавились еще двое - Джеймс Хекман и Дэниель Мак-Фадден. Выпускается ряд научных журналов, полностью посвященных эконометрике, в том числе: Journal of Econometrics (Швеция), Econometric Reviews (США), Econometrica (США), Sankhya. Indian Journal of Statistics. Ser.D. Quantitative Economics (Индия), Publications Econometriques (Франция), электронный еженедельник "Эконометрика" (Россия).

Однако в нашей стране по ряду причин эконометрика не была сформирована как самостоятельное направление научной и практической деятельности, в отличие, например, от Польши, которая стараниями известного экономиста О. Ланге и его коллег покрыта сетью эконометрических "институтов" (в российской терминологии - кафедр вузов). Только примерно с 1997 г. в России развертываются эконометрические исследования (под собственным именем), начинается широкое преподавание этой дисциплины.

4.1.2. Эконометрика и контроллинг

Обсудим, что может дать эконометрика контроллеру, какие инструменты анализа данных она может предложить для решения типовых задач, стоящих перед контроллером.

Проблемы такого рода - а именно, что может дать эконометрика той или иной области, какие средства решения типовых задач она может предложить - возникают не впервые. Приходилось выступать и на весьма широкую тему: "Что дает прикладная статистика народному хозяйству?" [388]. В частности, ранее обсуждался набор эконометрических и экономико-математических инструментов, поддерживающих менеджмент и маркетинг малого бизнеса [389]. Средством поддержки проведения экспертных исследований, в частности, в задачах обеспечения химической безопасности биосферы и экологического страхования, служило автоматизированное рабочее место "Математика в экспертизе" (сокращенно АРМ МАТЭК) [390]. С целью эконометрической поддержки задач сертификации и обеспечения качества промышленной продукции нашим творческим коллективом была разработана обширная система программных продуктов по статистическому приемочному контролю, планированию эксперимента, контрольным картам, надежности и испытаниям, прикладной статистике и другим вопросам [224]. Обобщая, можно сказать, что любая достаточно важная и развитая прикладная сфера технико-экономической и управленческой деятельности требует создания адекватного эконометрического сопровождения. Это сопровождение дает рассматриваемой сфере деятельности инструменты (методы) анализа данных для решения стоящих перед нею задач.

Эконометрика - дисциплина методическая, посвящена методам, которые могут применяться в различных предметных областях. Напротив, контроллинг - предметная дисциплина, для решения задач своей предметной области привлекает те методы, которые оказываются полезными.

Прежде всего надо обсудить вопрос: полезны ли для решения задач контроллинга эконометрические методы?

Для ответа на этот вопрос проанализируем "Глоссарий по контроллингу", включенный в материалы симпозиума "Теория и практика контроллинга в России" (4-5 октября 2001 г., МГТУ им. Н.Э.Баумана). В нем, в частности, содержатся термины:

Абсолютные отклонения, Вербальные переменные, Индексы,

Интервальные данные, Исследование операций, Кривая опыта,

Кумулятивные отклонения, Метод сценариев,

Относительные отклонения, Принятие решений,

Размытые множества, Риски (угрозы), Ряды,

Системный анализ, Средние величины,

Управление по отклонениям, Фактические величины,

Шансы, Эконометрика, Эмпирико-индуктивные показатели.

Все эти многочисленные термины относятся к эконометрике и охватывают различные ее разделы - от классических (средние величины) до самых современных - статистики объектов нечисловой природы (включая вербальные и размытые переменные) и статистики интервальных данных.

Видимо, ответ на поставленный вопрос уже не вызывает сомнений у специалистов - эконометрические методы представляют собой важную часть научного инструментария контроллера, а их компьютерная реализация - важную часть информационной поддержки контроллинга. Обсуждать целесообразно содержание этого инструментария. Первоначальные соображения были высказаны в работе [392].

Классификация эконометрических инструментов может быть проведена по различным основаниям: по методам, по виду данных, по решаемым задачам и т.п. В частности, при классификации по методам целесообразно выделять следующие блоки:

1.1. Описание данных и их графическое представление.

1.2. Углубленный вероятностно-статистический анализ.

1.3. Поддержка экспертных исследований.

1.4. Методы сценариев и анализа рисков.

При классификации на основе вида данных эконометрические алгоритмы естественно делить по тому, каков вид данных "на входе":

2.1. Числа.

2.2. Конечномерные вектора.

2.3. Функции (временные ряды).

2.4. Объекты нечисловой природы, в том числе упорядочения (и другие бинарные отношения), вербальные (качественные) переменные, нечеткие (размытые, расплывчатые) переменные, интервальные данные, и др.

Наиболее интересна классификация по тем задачам контроллинга, для решения которых используются эконометрические методы. При таком подходе могут быть выделены блоки:

3.1. Поддержка прогнозирования и планирования.

3.2. Слежение за контролируемыми параметрами и обнаружение отклонений.

3.3. Поддержка принятия решений, и др.

От каких факторов зависит частота использования тех или иных эконометрических инструментов контроллинга? Как и при иных применениях эконометрики, основных групп факторов два - это решаемые задачи и квалификация специалистов.

Искусственная примитивизация перечня решаемых задач, естественно, приводит, к искусственному сокращению списка применяемых методов. Например, Госкомстат РФ так ограничил область своей деятельности, что для решения поставленных им перед собой задач вполне достаточно обычных статистических таблиц - инструментов XIX в. (Для подтверждения этой мысли достаточно обратиться к публикациям Госкомстата РФ.) Подчеркнем, что для решения этих задач ему не нужны разработки эконометриков, получивших за свои исследования нобелевские премии по экономике. Как не нужны и вообще все работы по эконометрике ХХ и XXI вв. Однако весь арсенал современной эконометрики может быть с успехом использован, если мы откажемся от искусственного ограничения перечня решаемых задач. В частности, если от описания существующего положения перейдем к прогнозированию на основе вероятностно-статистических моделей.

Как влияет квалификация специалистов? Она ограничивает круг решаемых задач и методов их решения. Зачастую то, что люди не знают - для них не существует. Однако конкурентная борьба требует поиска преимуществ по сравнению с другими фирмами. Знание эконометрических методов дает такие преимущества.

Здесь напрашивается вопрос со стороны практиков: "Что же такое эконометрика? Расскажите о ней." Достаточно подробное представление об эконометрике могут дать лишь монографии, содержащие описания основных подходов, идей, алгоритмов, Примером является учебное пособие [16]. В настоящем разделе эконометрика рассматривается "с птичьего полета". Такой подход дает возможность познакомиться с общей ситуацией, но не с конкретными алгоритмами анализа данных.

При практическом применении эконометрических методов в работе контроллера необходимо применять соответствующие программные системы. Могут быть полезны и общие статистические системы типа SPSS, Statgraphics, Statistica, ADDA, и более специализированные Statcon, SPC, NADIS, REST (по статистике интервальных данных), Matrixer и многие другие. Массовое внедрение программных продуктов, включающих современные эконометрические инструменты анализа конкретных экономических данных, можно рассматривать как один из эффективных способов ускорения научно-технического прогресса [225].

4.1.3. Высокие эконометрические технологии
и их возможности для решения задач
управления и контроллинга

Почему старые методы эконометрики не подходят для новых условий?

При взгляде на эконометрику со стороны часто возникает мысль о том, что за десятилетия развития этой научно-практической дисциплины все ее основные проблемы решены, остается только применять разработанные методы к тем конкретным экономическим данным, которые представляют интерес для исследователя. Эта мысль неверна в принципе, причем по двум основным причинам. Во-первых, прикладные исследования приводят к необходимости анализировать данные новой природы, например, являющиеся перечисленными выше видами объектов нечисловой природы (см. раздел 3.5 настоящей монографии). Во-вторых, выясняется необходимость более глубокого анализа классических методов. Быстрое развитие эконометрики как науки привело к появлению новой парадигмы математических методов экономики (см. раздел 2.1 настоящей монографии).

Хорошим примером для обсуждения являются методы проверки однородности двух выборок. Есть две совокупности, состоящие из чисел (результатов наблюдений, измерений, испытаний, анализов, опытов), и надо решить, различаются или совпадают. Для этого из каждой из них берут по выборке и применяют тот или иной эконометрический метод проверки однородности. Около 100 лет назад был предложен метод Стьюдента, широко рекомендуемый и применяемый и сейчас. Однако он имеет целый букет недостатков. Во-первых, распределения элементов выборок должны быть нормальными (гауссовыми). Как правило, это не так. Во вторых, он нацелен на проверку не однородности в целом (т.н. абсолютной однородности, т.е. совпадения функций распределения, соответствующих двум совокупностям), а только на проверку равенства математических ожиданий. Но, в-третьих, при этом обязательно предполагается, что дисперсии для элементов двух выборок совпадают. Самое интересное, что проверять равенство дисперсий, а тем более нормальность, гораздо труднее, чем равенство математических ожиданий. Поэтому критерий Стьюдента обычно применяют, не делая таких проверок. А тогда и выводы по критерию Стьюдента повисают в воздухе (подробности - в разделе 3.1 настоящей монографии).

Более продвинутые специалисты обращаются к другим критериям, например, к критерию Вилкоксона. Он является непараметрическим, т.е. не опирается на предположение нормальности. Но и он, как выяснилось, не лишен недостатков. С его помощью нельзя проверить абсолютную однородность (совпадение функций распределения, соответствующих двум совокупностям). Это можно сделать только с помощью т.н. состоятельных критериев, в частности, критериев Смирнова и типа омега-квадрат (Лемана-Розенблатта).

С практической точки зрения критерий Смирнова обладает необычным недостатком - его статистика принимает лишь небольшое число значений, ее распределение сосредоточено в небольшом числе точек, и не удается пользоваться традиционными уровнями значимости 0,05 и 0,01. Поэтому в настоящее время остается рекомендовать критерий типа омега-квадрат (Лемана-Розенблатта). Но - для него нет достаточно подробных таблиц, он не включен в популярные пакеты эконометрических программ.

Отметим фиаско математиков - специалистов по математической статистике. Они не в состоянии ответить на естественный вопрос: "Каким методом проверять однородность двух выборок?" Дело в том, что для каждого метода они могут указать определенную альтернативную гипотезу,при которой этот метод является наилучшим (в том смысле, который они рассматривают; этих смыслов несколько - оптимальность по Ходжесу-Леману, по Бахадуру и др.). Однако в практических задачах обычно совершенно непонятно, откуда брать "альтернативную гипотезу". Таким образом, в данной области математическая статистика выродилась в схоластику.

Проблему выбора наилучшего эконометрического метода проверки однородности двух выборок нельзя считать окончательно решенной. Нужны дальнейшие исследования.

Рассмотрим другой важный пример. Многие данные в информационных системах имеют нечисловой характер, например, являются словами или принимают значения из конечных множеств. Нечисловой характер имеют и упорядочения, которые дают эксперты или менеджеры, например, выбирая главную цель, следующую по важности и т.д. Значит, нужна статистика нечисловых данных. Далее, многие величины известны не абсолютно точно, а с некоторой погрешностью - от и до. Другими словами, исходные данные - не числа, а интервалы. Нужна статистика интервальных данных. В монографии [84, с.138] по контроллингу хорошо сказано: "Нечеткая логика - мощный элегантный инструмент современной науки, который на Западе (и на Востоке - в Японии, Китае - А.О.) можно встретить в десятках изделий - от бытовых видеокамер до систем управления вооружениями, - у нас до самого последнего времени был практически неизвестен". Напомним, первая монография российского автора по теории нечеткости была выпущена в 1980 г. [85], однако до широких масс специалистов эта теория доходит лишь постепенно. Ни статистики нечисловых данных, ни статистики интервальных данных, ни статистики нечетких данных нет и не могло быть в классической статистике. Все это - высокие эконометрические (статистические) технологии (см. раздел 2.2 настоящей монографии). Они разработаны за последние 10-30-50 лет.

Важная часть эконометрики - применение высоких эконометрических технологий к анализу конкретных экономических данных, что зачастую требует дополнительной теоретической работы по доработке технологий анализа данных применительно к конкретной ситуации. Большое значение имеют конкретные эконометрические модели, например, модели экспертных оценок или экономики качества. И конечно, такие конкретные применения, как расчет и прогнозирование индекса инфляции [16]. Сейчас уже многим ясно, что годовой бухгалтерский баланс предприятия может быть использован для оценки его финансово-хозяйственной деятельности только с привлечением данных об инфляции.

Весь арсенал используемых в настоящее время эконометрических и статистических технологий (методов) можно распределить по трем потокам:

– высокие эконометрические (статистические) технологии;

– классические эконометрические (статистические) технологии,

– низкие (неадекватные, устаревшие) эконометрические (статистические) технологии.

Основная современная проблема эконометрики состоит в обеспечении того, чтобы в конкретных эконометрических и статистических исследованиях использовались только технологии первых двух типов. При этом под классическими эконометрическими (статистическими) технологиями понимаем технологии почтенного возраста, сохранившие свое значение для современной статистической практики. Таковы метод наименьших квадратов, статистики Колмогорова, Смирнова, омега-квадрат, непараметрические коэффициенты корреляции Спирмена и Кендалла и многие другие эконометрические (статистические) процедуры.

Каковы возможные пути решения основной современной проблемы в области эконометрики? Как ускорить внедрение "высоких эконометрических (статистических) технологий"?

В нашей стране по ряду причин эконометрика не была сформирована как самостоятельное направление научной и практической деятельности, в отличие, например, от Польши, не говоря уже об англосаксонских странах. В результате специалистов - эконометриков у нас на порядок меньше, чем в США и Великобритании (Американская статистическая ассоциация включает более 20000 членов). Бороться с конкретными невеждами - дело почти безнадежное. Единственный путь - массовое обучение. Какие бы новые научные результаты ни были получены, если они остаются неизвестными студентам, то новое поколение исследователей и инженеров вынуждено осваивать их по одиночке, а то и переоткрывать. Несколько огрубляя, можно сказать: то, что попало в учебные курсы и соответствующие учебные пособия - то сохраняется, что не попало - то пропадает.

В России начинают развертываться эконометрические исследования и преподавание эконометрики. Среди технических вузов научно-учебный комплекс (факультет) "Инженерный бизнес и менеджмент" МГТУ им. Н.Э.Баумана имеет в настоящее время приоритет в преподавания эконометрики [108].

Мы полагаем, что экономисты, менеджеры и инженеры, прежде всего специалисты по контроллингу, должны быть вооружены современными средствами информационной поддержки, в том числе высокими статистическими технологиями и эконометрикой. Очевидно, преподавание должно идти впереди практического применения. Ведь как применять то, чего не знаешь?

Один раз - в 1990 - 1992 гг. - мы уже "обожглись" на недооценке необходимости предварительной подготовки тех, для кого предназначены современные компьютерные средства. Наш коллектив (Всесоюзный центр статистических методов и информатики Центрального правления Всесоюзного экономического общества) разработал систему диалоговых программных систем обеспечения качества продукции (см. о них в статьях [224, 225]). Их созданием руководили ведущие специалисты страны. Но распространение программных продуктов шло на 1 - 2 порядка медленнее, чем ожидалось (единицы и десятки, а не сотни и тысячи копий). Причина стала ясна не сразу. Как оказалось, работники предприятий просто не понимали возможностей разработанных систем, не знали, какие задачи можно решать с их помощью, какой экономический эффект они дадут. А не понимали и не знали потому, что в вузах никто их не учил статистическим методам управления качеством. Без такого систематического обучения нельзя обойтись - сложные концепции "на пальцах" за пять минут не объяснишь.

Есть и противоположный пример - положительный. В середине 1980-х годов в советской средней школе ввели новый предмет "Информатика". И сейчас молодое поколение превосходно владеет информационно-коммуникационными технологиями, компьютерами и прочими электронными устройствами, мгновенно осваивая быстро появляющиеся новинки, и этим заметно отличается от тех, кому за 50 - 60 лет. Если бы удалось ввести в средней школе курс теории вероятностей и математической статистики - а такой курс есть в Японии и США, Швейцарии, Кении и Ботсване, почти во всех странах (см. подготовленный ЮНЕСКО сборник докладов [109]) - то ситуация могла бы быть резко улучшена. Надо, конечно, добиться, чтобы такой курс был построен на высоких эконометрических (статистических) технологиях, а не на низких. Другими словами, он должен отражать современные достижения, а не концепции пятидесятилетней или столетней давности.

На основе опыта работы секции "Математические методы исследования" журнала "Заводская лаборатория. Диагностика материалов", более 50 лет публикующей работы по высоким эконометрическим (статистическим) методам, рассмотрим основные черты таких методов.

Основные направления работы секции - прикладная статистика и планирование эксперимента. В первом из них принимается, что экспериментатор не может выбирать точки (значения факторов), в которых проводятся измерения, во втором, напротив, выбор возможен, и основная задача - оптимальный подбор таких точек. Большое внимание уделяется вопросам оптимального управления технологическими процессами, в частности, статистическим методам управления качеством продукции. Рассматриваются также теория и практика экспертных оценок, применение нечетких множеств и др.

Публиковались статьи по статистике случайных величин, по многомерному статистическому анализу, в частности по алгоритмам выделения информативных подмножеств факторов в задачах регрессионного и дискриминантного анализа. ПРиведем пример. Как известно, во многих задачах требуется найти обратную матрицу, а определитель исходной матрицы может быть близок к 0. Для действий в подобных ситуациях разработан ряд методов. Другая проблема связана с тем, что классические методы хорошо работают, если число неизвестных параметров много меньше объема выборки. Между тем в реальных ситуациях часто число неизвестных параметров сравнимо с объемом выборки. Как быть? Новым методам, разработанным для этой неклассической ситуации, посвящен ряд публикаций.

В традициях отечественной вероятностно-статистической школы выдержана сводка основные терминов, определений и обозначений по теории вероятностей и прикладной статистике. Ее цель - обеспечить высокий научный уровень публикаций и помочь читателям овладеть современной научной терминологией по тематике секции. На основе этой сводки составлен справочник "Вероятность и прикладная статистика. Основные факты" [60].

Постоянно уделялось внимание теории измерений. Пропагандировалась концепция шкал измерения, а именно, шкал наименований, порядковой, интервалов, отношений, разностей, абсолютной. Установлено, какими алгоритмами анализа данных можно пользоваться в той или иной шкале, в частности, для усреднения результатов наблюдений. Так, для данных, измеренных в порядковой шкале, некорректно вычислять среднее арифметическое. В качестве средних для таких данных можно использовать порядковые статистики, в частности, медиану (см. также монографии [5, 7, 36, 54, 85]).

Рассматривались новые подходы и программное обеспечение в области эконометрических методов обеспечения качества. Предложен принципиально новый подход к выбору технико-экономической политики обеспечения качества [329]. Разработан метод проверки независимости результатов статистического контроля по двум альтернативным признакам [330]. Сопоставлены между собой различные диалоговые программные системы по статистическому приемочному контролю [227]. Проанализировано применение статистических методов на различных стадиях жизненного цикла продукции согласно международному стандарту ИСО 9004. Рассмотрены результаты анализа научной общественностью государственных стандартов по статистическим методам управления качеством продукции (см. статью [224]).

Эконометрические методы исследования часто опираются на использование современных информационных технологий. В частности, распределение статистики можно находить методами асимптотической математической статистики, а можно и путем статистического моделирования (метод Монте-Карло, он же - метод статистических испытаний). Вычислительная статистика широко представлена в публикациях секции.

4.1.4. Эконометрика в работах отечественных
контроллеров

В каждом номере журнала «Контроллинг» приведены многочисленные ссылки на эконометрические инструменты [23]. Так, С.Г. Фалько, К.А. Рассел и Л.Ф. Левин, анализируя знания, навыки и способности, необходимые контроллерам в США, выделяют оптимизацию процессов, а также компьютерные системы и операции [392]. Методы многокритериальной оптимизации позволяют согласовать цели предприятия за счет собственных и заемных источников финансирования [393]. Рассматривая место системы внутрифирменного контроллинга в функциональной структуре управления, Н.Г. Данилочкина выделяет блоки анализа, контроля, прогнозирования, оптимизации [394]. Во всех этих блоках велика доля эконометрических методов. Так, при выборочном контроле совокупности объектов необходимо применять методы статистического контроля, а при контроле процессов – методы обнаружения разладки. Прогнозирование базируется либо на объективных статистических данных, и тогда применяется метод наименьших квадратов и другие методы регрессионного анализа, либо на субъективных мнениях экспертов, и тогда используется теория экспертных оценок [16, 52].

Экспертные оценки широко используются при решении задач контроллинга. Для планирования продуктовой программы предприятия [395] и для оценки эффективности работы подразделения контроллинга [396] разработаны и подробно описаны конкретные методы сбора и анализа оценок экспертов.

Большое место в задачах управления, в том числе в контроллинге, занимают показатели эффективности. В монографии О.А. Дедова [397] рассмотрена система из 512 ключевых показателей экономической эффективности, имеющих широкое применение в странах с рыночной экономикой. Ясно, что из-за ограниченных возможностей человеческого мозга непосредственно использовать для управления значения 512 показателей нельзя. Приходится применять интегральные (обобщенные, итоговые) показатели, построенные на основе исходных показателей. Построению частных и интегральных показателей по уровням управления предприятием посвящена статья [398].

Эконометрика качества [16, гл.13] необходима В.В. Марущенко для организации поэтапного проведения реинжиниринга бизнес-процессов [399]. В работе [400] показано, что на всех этапах «петли качества», описывающей жизненный цикл продукции с точки зрения организатора производства, следует использовать эконометрические методы.

Отметим любопытное обстоятельство, связанное с соотношением объемов текстов, выделяемых для описания различных вопросов управления качеством. В одной из первых публикаций [401] Международной организации по стандартизации (ИСО) глава по управлению качеством почти полностью состояла из рассмотрения методов статистического приемочного контроля и других методов эконометрики качества. Другими словами, управление качеством практически приравнивалось к эконометрике качества. А вот в современном учебнике по качеству [402] содержится много материала по организации управления качеством, но статистический приемочный контроль не рассматривается (а контрольным картам уделено 5,5 стр.). Как могло появиться подобное сочинение, дезориентирующее читателей?

В стандартах ИСО серии 9000, посвященных менеджменту качества, статистические методы управления качеством указывались как необходимый элемент систем качества. При этом содержание этого элемента не раскрывалось. Почему? Да потому, что по этой тематике уже действовали многочисленные стандарты ИСО, а также региональные (например, стандарты CЭВ) и национальные стандарты [224]. Короче, статистические методы управления качеством были хорошо известны всем специалистам.

Затем к проблеме качества обратились новые лица (новые поколения). Они знали только стандарты ИСО серии 9000, но не знали всей предыстории. Вполне естественно, что они стали писать учебники, исходя из своих знаний. В результате следующее поколение, выучившись по учебникам типа [402], не сможет проанализировать имеющуюся нормативно-техническую документацию по управлению качеством, в том числе стандарты и договора на поставку (разделы «Правила приемки и методы контроля»), и тем более не смогут спроектировать оптимальную систему контроля. Историю деградации текстов по управлению качеством необходимо учесть при развитии работ по обучению и внедрению контроллинга.

Кроме эконометрических моделей управления качеством при решении задач контроллинга используются и другие вероятностно-статистические математические модели. Так, при информационном моделировании, имеющем целью реинжиниринг бизнес-процессов, В.В. Марущенко и А.В. Марущенко опирались на теорию массового обслуживания [403].

4.1.5. Эконометрика в производственном
менеджменте

Для получения более объемной картины использования эконометрических методов при управлении деятельностью организации обратимся к производственному менеджменту – основе контроллинга. Проанализируем базовый учебник "Организация и планирование машиностроительного производства (производственный менеджмент)" [404], подготовленный кафедрой «Экономика и организация производства» Московского государственного технического университета им. Н.Э. Баумана. В нем более 20 раз используются эконометрические методы и модели, что свидетельствует об эффективности такого инструмента менеджера, как эконометрика.

Приведем примеры. Методы восстановления зависимости (регрессионного анализа) используются при изучении динамики производственных затрат в период освоения производства [404, с.95-97]. В частности, для выявления закономерностей изменения трудоемкости изготовления единицы продукции, снижения себестоимости и других показателей с течением времени или с ростом объемов изготовления и др. При нормировании труда косвенные методы основаны на регрессионном анализе. Более того, разработанная НИИтруда формула для определения численности специалистов по функции «организация и оплата труда» также получена с его помощью [404, с.308-309]. Интегральный критерий эффективности проекта, применяемый при планировании инновационных процессов, строится с помощью многомерного статистического анализа [404, с.101].

Постоянно возникает необходимость строить те или иные интегральные показатели (критерии), объединяющие значения частных (единичных или групповых) показателей. Необходимо упомянуть суммарный показатель качества продукции или проекта [404, с.244], коэффициент качества инженерного труда [404, с.269].

В производственном менеджменте часто используются задачи оптимизации. Так, с целью рационального расположения на территории завода складских помещений, заготовительных цехов, участков, оборудования решают задачу минимизации суммарных грузопотоков. Для максимально возможного совмещения отдельных производственных процессов во времени, что может существенно сократить время от запуска в производство до выпуска готовой продукции, решают соответствующую оптимизационную задачу [404, с.121-122]. Методы сокращения производственного цикла, в том числе снижения затрат труда на основные технологические операции, сокращения затрат времени на транспортные, складские и контрольные операции, предполагают применение методов оптимизации, в том числе дискретной оптимизации [404, с.134-136].

Особенно заметна роль оптимизации в задачах планирования производственно-хозяйственной деятельности предприятия. В качестве одного из основных принципов планирования выдвигается принцип оптимальности. Предполагается построение экономико-математической модели объекта планирования, включающей целевую функцию по принятому критерию оптимальности и систему ограничений [404, с.339]. Среди основных методов планирования указаны экономико-математические методы [404, с.342]. Подробно рассматривается математическая модель построения оптимального плана реализации продукции, сводящаяся к задаче линейного программирования [404, с.352-354]. При планировании рыночных цен на продукцию решается задача максимизации прибыли как функции цены [404, с.409]. Расчет оптимальных размеров партии деталей основан на минимизации суммарных затрат [404, с.428].

В эконометрику входит и теория оптимального управления запасами. Эта теория используется для организации и управления материально-производственными запасами организации материально-технического снабжения и складирования [404, с.223-236], в том числе для организации материально-технического снабжения и складирования [404, с.217], организации обеспечения основного производства технологической оснасткой [404, с.208]. Отметим, что «экономичный объем заказа» [404, с.227] является оптимальным лишь при большом интервале планирования [7].

В производственном менеджменте широко применяются разнообразные эконометрические методы, относящиеся к «статистическому» крылу этой научно-практической дисциплины. Например, хронометраж [404, с.311-316] – это типовое статистическое исследование. Отметим использование медианы для вычисления нормы времени [404, с.312], что совпадает с рекомендациями эконометрики, основанными на теории измерений и теории устойчивости статистических процедур [7, 16]. На основе теории выборочных исследований указывается количество наблюдений, позволяющее сделать обоснованные выводы о структуре затрат рабочего времени [404, с.315].

Большой раздел эконометрики – статистические методы управления качеством продукции. Согласно международному стандарту ИСО 9004 в системах качества должно быть предусмотрено использование статистических методов [404, с.253]. При рассмотрении видов контроля качества продукции выделяются «выборочный» и «статистический» контроль [404, с.268]. Описываются методы статистического приемочного контроля и статистического контроля процессов (другими словами, статистического регулирования технологических процессов) [404, с.271-274]. В качестве одного из четырех основных методов определения показателей качества продукции указан экспертный метод [404, с.275]. Экспертные методы предлагается использовать и при построении причинно-следственной диаграммы (диаграммы Исикавы типа "рыбий скелет") для ранжирования факторов по их значимости и выделении наиболее важных [404, с.276]. Из методов обработки статистических данных разобрана методика анализа качества продукции машиностроения с помощью диаграмм Парето [404, с.277].

В производственном менеджменте большую роль играют методы принятия решений [404, с.25-28], различные специализированные эконометрические модели, например, модель минимизации сроков выполнения заказов на основе использования сетевого графика со случайными сроками выполнения отдельных работ [404, с.110-112].

Таким образом, эконометрические методы постоянно используются менеджерами, в том числе контроллерами. Вполне естественно, что ссылки на эти методы являются краткими. Предполагается, что читатели с ними знакомы. Да и странно было бы обсуждать вопросы эконометрики, например, в курсе организации и планирования производства или при рассказе о работе контроллеров в США.

Однако встанем на позицию специалиста, начинающего изучать и внедрять Контроллинг. Как ему овладеть таким эффективным инструментом контроллинга, как эконометрика? Кратких упоминаний в публикациях по контроллингу или по производственному менеджменту недостаточно. Необходимо обратиться к соответствующей литературе (см., например, [16]). Наблюдается и обратный процесс – в книгах по менеджменту все больше внимания уделяется инструментам менеджмента. Вполне естественно, что методы принятия решений, оптимизации, выборочного контроля и экспертных оценок подробно рассматриваются в учебном пособии по менеджменту в техносфере [61] в качестве отдельных глав.

Учитывая важность проблемы построения интегральных показателей, обсудим эту тему подробнее.

4.1.6. Анализ ситуации с помощью системы
показателей

В различных управленческих и экономических задачах используются показатели и системы показателей. Например, в теоретических обсуждениях популярен такой показатель, как рентабельность инвестиций (для достижения полной определенности ситуации надо фиксировать финансовый поток, дисконт-фактор и период рассмотрения). Широко известны развернутые системы показателей, предназначенных для оценки финансово-хозяйственной деятельности предприятий и организаций. Общее число показателей достигает многих десятков, сотен и даже тысяч. Особенно если используется иерархический подход к построению системы показателей (деревья показателей, в иной терминологии - единичные, групповые и обобщенные показатели и др.).

Как можно применять системы показателей для решения задач менеджмента, в частности, контроллинга? Обычно их используют для сравнения и выбора объектов (например, проектов, образцов продукции, предприятий) между собой. Требуется установить, какой объект лучше, какой хуже, упорядочить их между собой. Отсюда ясно, что сама по себе система показателей носят вспомогательный характер. Это – инструмент для решения задач сравнения и выбора.

Есть два основных подхода к упорядочению объектов на основе системы показателей. Первый из них основан на построении некоего обобщенного (интегрального) показателя. В простейшем случае строится линейная комбинация значений показателей, коэффициенты при этом оцениваются экспертно. Во втором подходе используют более изощренную технику многокритериальной оптимизации, в частности, оптимизации по Парето.

Оба подхода предполагают начальный этап – возможно большее сокращение числа показателей при минимально возможной потере содержащейся в них информации. После исключения дублирующих (функционально связанных) показателей целесообразно провести кластер-анализ [5, 16] оставшихся с целью выделения групп однородных показателей, а в них – показателей, которые будут представлять однородные группы. Связь между показателями естественно оценивать по статистическим данным с помощью, например, коэффициентов ранговой корреляции Кендалла или Спирмена. А кластер-анализ проводить методом k-средних, в качестве представителя группы брать легко вычисляемый (по реальным данным) показатель, расположенный вблизи центра группы. Число групп – до нескольких десятков.

Популярный подход на основе построения некоего обобщенного показателя, особенно когда строится линейная комбинация значений показателей, а коэффициенты при них оцениваются экспертно, плох тем, что, как правило, эксперты не в состоянии оценить коэффициенты достаточно точно. Разброс их значений недопустимо велик. Так, в свое время нам пришлось разбираться с ситуацией, в которой при оценке технологий уничтожения химического оружия разброс оценок американских экспертов составлял десятки процентов, что делало абсолютно бесполезной разработанную ими систему из 120 показателей. Причина описанного явления состоит в том, что человеку свойственно отвечать на вопросы качественного характера (типа: какой проект из представленных для анализа привлекательнее), чем на вопросы количественного характера (типа: во сколько раз привлекательнее, или - укажите коэффициенты при показателях). Гораздо точнее коэффициенты оцениваются с помощью экспертно-статистического метода, основанного на предварительном непосредственном сравнении (оценке) некоторого количества объектов с помощью высококвалифицированных экспертов.

Другой недостаток первого подхода (на основе построения некоего обобщенного показателя), когда строится линейная комбинация значений единичных показателей, а коэффициенты при них оцениваются экспертно, состоит в том, что для анализа данных, измеренных в порядковой шкале, нельзя использовать средние арифметические и вообще операцию сложения. Применять надо медианы. В крайнем случае – медианы и средние арифметические, а затем результаты согласовывать, как это предложено в [202] и описано в [16].

Во втором подходе используют многокритериальную оптимизацию, когда каждый параметр рассматривается как критерий. Первый шаг - оптимизация по Парето, т.е. отбрасывание вариантов, проигрывающих другим. Затем идет тщательный анализ оставшихся вариантов, сравнение их различными способами. Целесообразно применять выводы, полученные при использовании различных способов (устойчивые по отношению к способу обработки). При анализе системы показателей и сравнении объектов необходимо использовать различные экспертные методы.

Обсудим использование взвешенных агрегированных показателей в качестве интегральных показателей. Кроме взвешенной суммы значений единичных показателей, есть много иных способов. Опишем некоторые из них.

Пусть Х₁, Х₂,..., Х_К - частные (или групповые) числовые показатели. Пусть каждому из них приписан вес - А₁, А₂, ..., А_К соответственно, отражающий их относительную важность (оцененную экспертами или иным способом). Весовые коэффициенты неотрицательны и в сумме составляют 1.

Взвешенные агрегированные показатели можно определить следующим единообразным способом.

Введем (чисто формально) распределение вероятностей, приписывающее каждому значению Х_М, М = 1, 2, ..., К, вероятность А_М. Для этого распределения обычным образом определим такие характеристики, как математическое ожидание, медиана, начальные моменты, мода и т.д., которые и будем использовать в качестве взвешенных агрегированных показателей или при их расчете.

При этом математическое ожидание дает взвешенное среднее арифметическое, медиана - взвешенную медиану (в частном случае, когда одна из ступенек функции распределения приходится на высоту 0,5, целесообразно ввести понятия левой и правой медиан - т.е. левого и правого концов указанной ступеньки соответственно).

Начальный момент р-го порядка после извлечения корня р-ой степени дает взвешенное степенное. Аналогичным образом получаем обобщенное среднее по Колмогорову общего вида [5, 7, 16, 36, 54].

Мода указывает на значение наиболее важного показателя.

В соответствии с методологией устойчивости результатов обработки данных [7] при анализе конкретной ситуации целесообразно одновременно использовать несколько обобщенных показателей, например, взвешенную медиану и взвешенное среднее арифметическое (см. раздел 3.2 настоящей монографии). Хотя согласно теории измерений для усреднения показателей, измеренных в порядковой шкале, использование среднего арифметического некорректно, в отличие от применения медианы в качестве интегрального показателя, но расчет среднего арифметического имеет давние традиции [404]. Поэтому в эконометрике [16] разработана процедура построения итогового упорядочения объектов в два этапа. На первом этапе строятся два упорядочения - по средним арифметическим ответов экспертов и по медианам. На втором этапе рассчитывается упорядочение, согласующее эти два упорядочения.

4.1.7. Эконометрика при обучении контроллеров

Требования к профессиональной подготовке специалистов по контроллингу включают, в частности, требования к интеллектуальным инструментам, которыми должны владеть контроллеры. Одним из таких инструментов является эконометрика. Впервые в статье [21] была сделана попытка раскрыть содержание понятия «эконометрическая поддержка контроллинга». Из полученных в этой статье выводов мы исходим и сейчас.

В настоящее время эконометрика вызывает большой интерес у научных работников и преподавателей. Так, выпускаемое нами с июля 2000 г. еженедельное компьютерное издание «Эконометрика» имеет более 1500 подписчиков.

Организация обучения, в частности, составление учебных планов, программ, методических материалов и учебников, предполагает обсуждение объема и содержания соответствующей учебной дисциплины. В соответствии с цитированным выше определением Большого Энциклопедического Словаря к эконометрике следует относить математическое программирование, методы теории принятия решений, вообще все экономико-математические методы, кроме тех, которые используются для получения чисто теоретических качественных результатов, типа теорем о существовании магистрали в абстрактных моделях экономической динамики.

В наиболее распространенных представлениях об эконометрике внимание сосредотачивается на статистических методах и моделях. Именно так построено обучение в образовательных структурах научно-учебного комплекса (факультета) «Инженерный бизнес и менеджмент» МГТУ им. Н.Э.Баумана и соответствующий цикл учебников, начиная с [16] (см. раздел 2.1.4 настоящей монографии). При этом математическое программирование и ряд иных экономико-математических методов включаются не в курс эконометрики, а в иные дисциплины. Курсы теории вероятностей и математической статистики (как часть общего курса математики), статистики и эконометрики образуют естественную триаду.

Наконец, иногда эконометрику понимают предельно узко, как дисциплину, посвященную построению статистических моделей частного вида (систем линейных регрессионных и авторегрессионных моделей, типа приведенных в монографии Т. Нейлора [220]). На наш взгляд, эти модели являются излишне специальными для включения в систему образования специалистов по контроллингу и вообще в систему управленческого и экономического образования.

Содержание образования должно соответствовать современному научному уровню и давать знания, методы и навыки, полезные для практической работы. Назрела необходимость пересмотра содержания ряда учебных дисциплин и внесения изменений в учебные планы и соответствующие государственные образовательные стандарты. В частности, необходимо приветствовать введение дисциплины «Эконометрика» в ряд государственных образовательных стандартов по управленческим и экономическим дисциплинам. Однако содержание приведенных в них минимальных требований целесообразно привести в соответствие с новой парадигмой математических методов экономики (см. раздел 2.1 настоящей монографии) и реально читаемыми курсами эконометрики.

Курс «Теория вероятностей и математическая статистика» образует естественную основу эконометрики. Однако его необходимо привести в соответствие с современными требованиями, прежде всего с новой парадигмой математических методов экономики. В частности, необходимо рассматривать случайные элементы со значениями в произвольных пространствах, эмпирические и теоретические средние в таких пространствах, доказывать законы больших чисел в общих постановках. Необходимо исключить из программы курса «Теория вероятностей и математическая статистика» методы, опирающиеся на те предположения, которые не выполняются в конкретных экономических ситуациях. В частности, исключить одновыборочный и двухвыборочный критерии Стьюдента и заменить их на соответствующие непараметрические критерии (см. раздел 3.1 настоящей монографии).

Как преподавание контроллинга, так и преподавание эконометрики в настоящее время находятся в стадии становления. Нет опыта десятилетий. Необходимо отработать наиболее целесообразные формы преподавания. В частности, курс эконометрики может быть разбит на стадии. Первая стадия, как это и реализуется в настоящее время в МГТУ им. Н.Э. Баумана, должна следовать за курсами теории вероятностей и математической статистики (как части общего курса математики) и прикладной статистики [5], завершая фундаментальное образование по своему направлению. Ее место – третий или четвертый год дневного обучения бакалавров или специалистов. Однако в магистратуре или в конце обучения специалистов, на 10-м или 11-м семестре (включая бакалавриат), представляется полезным иметь эконометрический курс прикладной направленности, нацеленный на применение эконометрических методов в задачах прогнозирования, планирования, контроля, анализа внутренних и внешних рисков, принятия решений и др. Название курса может быть несколько иным, например, "Организационно-экономическое моделирование".

Актуальной является проблема разработки учебно-методической литературы, например, пособий по лабораторным работам по эконометрике, обмен опытом преподавания и научных исследований. Отметим, что подавляющее большинство эконометрических (т.е.статистических) методов могут быть успешно применены не только в контроллинге, менеджменте и экономике. Они могут быть использованы в технических, медицинских, геологических, социологических, психологических, исторических и иных социально-экономических исследованиях, практически в любой научной дисциплине и прикладной области. В частности, большой опыт накоплен за последние пятьдесят с лишним лет секцией «Математические методы исследования» научно-технического журнала «Заводская лаборатория. Диагностика материалов», основанной в начале 1960-х годов академиком АН УССР Б.В. Гнеденко и проф. В.В. Налимовым. В этой секции журнале опубликовано более тысячи статей по прикладной статистике и другим статистическим методам. На основе огромного накопленного опыта целесообразно приступить к широкому обучению основам современных статистических методов и эконометрики (на современном уровне, т.е. согласно новой парадигме прикладной статистики) студентов технических специальностей.

Поскольку контроллинг опирается на использование информационных систем управления предприятиями, то эконометрические программные продукты должны быть неотъемлемой составной частью таких систем [22].

Свободное владение такими инструментами контроллинга, как эконометрика, - признак профессионализма контроллера.

Однако из сказанного выше ясно, что эконометрика – дисциплина на стыке менеджмента и экономики, с одной стороны, прикладной математики и компьютерных наук, с другой стороны. Эконометрика рассматривается в паспорте научной специальности 08.00.13 "Математические и инструментальные методы экономики". Следовательно, специалист в области эконометрики должен владеть как организационно-экономическими, так и математическими знаниями, умениями, навыками, способностями. Нельзя требовать от каждого контроллера, чтобы он был специалистом в области эконометрики. Но внутри каждого достаточно крупного подразделения контроллинга целесообразно иметь такого специалиста.

Требования к профессиональной подготовке специалистов по контроллингу включают, в частности, знание инструментальной базы. Одним из инструментов контроллинга является эконометрика. В статье [21] впервые была сделана попытка раскрыть содержание понятия «эконометрическая поддержка контроллинга». Обширный перечень конкретных применений эконометрики при решении задач контроллинга был приведен в работах [23, 24]. Но на пути к получению адекватных знаний в этом направлении возникает ряд проблем.

Легко ли овладеть эконометрическими инструментами контроллинга? К сожалению, нелегко. То, что эконометрика – один из наиболее эффективных инструментов контроллинга, бесспорно. Специалисты владеют этим инструментом, поэтому они обычно рассказывают о полученных результатах, а не о приемах использования инструмента. В результате молодому поколению бывает сложно познакомиться с инструментальными основами. Начинающим специалистам крайне тяжело воспринимать ту или иную контроллинговую методику, если они не знают базовых подходов и методов, на основе которых она была сформирована. Зачастую они не постигают сущности методики, ограничиваясь повторением общих слов. Литературные источники также, к сожалению, не всегда дают исчерпывающую информацию по возникающим у начинающих специалистов вопросам.

Особенно актуальна эта проблема для современной России, в которой идет бурный процесс внедрения контроллинга. Большое значение имеет освоение зарубежного опыта. А эконометрические инструменты контроллинга в западных книгах не описываются, только упоминаются. Ведь они всем известны. На Западе. Но не у нас.

В качестве типичного примера проследим изменение во времени объемов текстов, выделяемых для описания различных вопросов управления качеством. В одной из первых публикаций [401] Международной организации по стандартизации (ИСО) глава по управлению качеством почти полностью состояла из рассмотрения методов статистического приемочного контроля и других методов эконометрики качества. Другими словами, управление качеством практически приравнивалось к эконометрике качества. А в недавно выпущенном отечественными авторами учебнике по качеству [402] содержится много материала по организации управления качеством, но статистический приемочный контроль вообще не рассматривается (а такому эффективному методу эконометрики качества, как контрольным картам, уделено лишь 5,5 стр.). Следовательно, по этому учебнику нельзя научиться использованию современных методов управления качеством.

Между тем в стандартах ИСО серии 9000, посвященных менеджменту качества, статистические методы управления качеством указываются как необходимый элемент систем качества, но содержание этого элемента не раскрывается. Почему? Скорее всего потому, что по этой тематике действуют многочисленные стандарты ИСО, а также региональные и национальные стандарты, посвященные конкретным методам (анализ отечественных стандартов по статистическим методам управления качеством дан в статье [224]). Таким образом, статистические методы управления качеством были хорошо известны всем специалистам.

Затем к проблеме качества обратилось новое поколение специалистов. Они работали уже только со стандартами ИСО серии 9000. Вполне естественно, что и учебники они писали, исходя из своих представлений об этой области. В этих учебниках об эконометрических инструментах управления качеством в лучшем случае только упоминается. В результате следующее поколение, выучившись по дефектным учебникам, не сможет профессионально проанализировать нормативно-техническую документацию по управлению качеством, в том числе стандарты и договора на поставку (разделы «Правила приемки и методы контроля») и, тем более, не сможет спроектировать оптимальную систему контроля. Наблюдаем деградацию теоретических и практических работ в области управления качеством. Причина деградации выглядит мелкой - необоснованное смещение акцентов в текстах учебников по управлению качеством. Ее необходимо учесть при развитии работ по обучению и внедрению контроллинга, чтобы не повторить печальную судьбу управления качеством.

Организация обучения, в частности, составление учебных планов, программ, методических материалов и учебников, предполагает обсуждение объема и содержания соответствующей учебной дисциплины.

Как уже говорилось, научно-учебный комплекс "Инженерный бизнес и менеджмент» МГТУ им. Н.Э.Баумана исходит из широко распространенного определения: "Статистический анализ экономических данных называется эконометрикой" [386, с.25]. Именно так построено обучение и соответствующий учебник [16]. При этом математическое программирование и ряд иных экономико-математических методов включаются не в курс эконометрики, а в другие дисциплины. Курсы теории вероятностей и математической статистики (как часть общего курса математики), прикладной статистики и эконометрики (именно в такой последовательности) образуют естественную триаду.

4.1.8. Содержание обучения эконометрике

Дадим описание эконометрических инструментов контроллинга, следуя программам курсов «Эконометрика-1» и «Эконометрика-2», которые кафедра ИБМ-2 "Экономика и организация производства" ведет на факультете «Инженерный бизнес и менеджмент» Московского государственного технического университета им. Н.Э. Баумана. Методическая база преподавания эконометрики развивается в соответствии с концепцией, впервые выдвинутой и обоснованной в докладе [405].

1. Выборочные исследования. Построение выборочной функции ожидаемого спроса и расчет оптимальной розничной цены при заданной оптовой цене (издержках). Пример маркетингового исследования потребителей растворимого кофе. Различные виды формулировок вопросов (открытый, закрытый, полузакрытый вопросы), их достоинства и недостатки. Биномиальная и гипергеометрическая модели выборки, их близость в случае большого объема генеральной совокупности по сравнению с выборкой. Асимптотическое распределение выборочной доли (в случае ответов типа "да" - "нет"). Интервальное оценивание доли и метод проверки гипотезы о равенстве долей.

2. Проверка однородности двух независимых выборок. Критерий Крамера-Уэлча для проверки равенства математических ожиданий. Некорректность использования двухвыборочного критерия Стьюдента. Расчет статистики двухвыборочного критерия Вилкоксона и правила принятия решения на основе ее асимптотической нормальности.

3. Метод наименьших квадратов для линейной прогностической функции. Подход к оцениванию параметров. Критерий правильности расчетов. Оценка остаточной дисперсии. Точечный и интервальный прогноз. Метод наименьших квадратов для модели, линейной по параметрам. Случай нескольких независимых переменных (регрессоров). Преобразования переменных. Оценивание коэффициентов многочлена. Оценка остаточной дисперсии как критерий качества эконометрической модели. Типовое поведение остаточной дисперсии при расширении множества регрессоров. Оценка степени полинома и описание асимптотического поведения этой оценки (геометрическим распределением со сдвигом).

4. Инфляция как рост цен. Разброс цен и возможная точность определения «рыночной цены». Потребительские корзины. Определение индекса инфляции. Теоремы умножения и сложения для него. Средний индекс (темп) инфляции. Инфляция в России. Динамика основных макроэкономических показателей России. Виды инфляции: спроса, издержек, административная. Применения индекса инфляции. Приведение к сопоставимым ценам. Прожиточный минимум. Вклады в банки и кредиты. Курс доллара в сопоставимых ценах. Инфляция и бухгалтерская отчетность. Инфляция и стоимость основных фондов предприятия.

5. Процедуры экспертного оценивания. Примеры. Использование в соревнованиях, при выборе, распределении финансирования. Военный Совет в Филях. Метод Дельфи. Мозговой штурм. Экологические экспертизы. Планирование и организация экспертного исследования. Рабочая группа и экспертная комиссия. Основные стадии проведения экспертного исследования. Экономические вопросы. Формирование целей экспертного исследования (сбор информации для ЛПР и/или подготовка проекта решения для ЛПР и др.). Роль диссидентов. Формирование состава экспертной комиссии: методы списков (реестров), "снежного кома", самооценки, взаимооценки. Проблема априорных предпочтений экспертов. Различные варианты организации экспертного исследования, различающиеся по числу туров (один, несколько, не фиксировано), порядку вовлечения экспертов (одновременно, последовательно), способу учета мнений (с весами, без весов), организации общения экспертов (без общения, заочное, очное с ограничениями ("мозговой штурм", Совет в Филях) или без ограничений). Нахождение итогового мнения экспертов: методы средних арифметических и медиан рангов. Построение согласующей ранжировки. Метод сценариев экспертного прогнозирования. Прогнозирование развития народного хозяйства России в условиях «открытой торговли».

6. Теория измерений. Определения, примеры, группы допустимых преобразований для шкал наименований, порядка, интервалов, отношений, разностей, абсолютной. Требование устойчивости статистических выводов относительно допустимых преобразований шкал. Средние по Коши и описание средних, результат сравнения которых устойчив в порядковой шкале. Средние по Колмогорову и описание средних, результат сравнения которых устойчив в шкалах интервалов и отношений. Применения к экспертному оцениванию.

7. Оптимизационный подход к определению средних величин. Примеры: математическое ожидание и среднее арифметическое, выборочная и теоретическая медианы, медиана Кемени. Нахождение медианы Кемени на основе матрицы попарных расстояний между элементами множества возможных ответов экспертов. Эмпирические и теоретические средние в пространствах произвольной природы. Законы больших чисел для нечисловых данных и их интерпретация в терминах теории экспертного опроса.

8. Статистический приемочный контроль - выборочный контроль, основанный на эконометрической теории. Его необходимость и эффективность. Планы контроля по альтернативному признаку. Одноступенчатый контроль. Оперативная характеристика. Риски поставщика и потребителя, приемочный и браковочный уровни дефектности. Расчеты для плана (n,0). Контроль с разбраковкой. Средний выходной уровень дефектности и его предел (ПСВУД). Расчет ПСВУД для плана (n,0). Выбор плана контроля на основе ПСВУД. Расчет приемочного и браковочного уровней дефектности для одноступенчатого плана с помощью теоремы Муавра-Лапласа. Выбор одноступенчатого плана контроля по заданным приемочным и браковочным уровням дефектности на основе асимптотических соотношений. Затраты, связанные с принятием решений при статистическом приемочном контроле. Ограниченные возможности использования экономических показателей при статистическом контроле.

9. Эконометрика качества. Арбитражная характеристика и принцип распределения приоритетов. Расчет планов контроля поставщика и потребителя на основе принципа распределения приоритетов. Геометрическая интерпретация результатов контроля и планов контроля при последовательной проверке единиц продукции. Усеченные планы контроля. Всегда ли нужен выходной контроль качества? Сравнение экономической эффективности сплошного контроля и увеличения объема партии; сплошного контроля и замены дефектных единиц продукции в системе гарантийного обслуживания. Статистические методы обеспечения качества (прикладная статистика, статистический приемочный контроль по альтернативному и количественному признаку, статистическое регулирование технологических процессов (контрольные карты Шухарта и кумулятивных сумм), планирование экспериментов, надежность и испытания).

10. Проблема обнаружения эффекта (проверки однородности в связанных выборках). Критерий знаков. Критерий проверки равенства 0 математического ожидания. Критерий типа омега-квадрат для проверки симметрии распределения.

11. Основы теории нечеткости. Описание неопределенностей с помощью теории нечетких множеств. Алгебра нечетких множеств. Понятие случайного множества. Распределения случайных множеств. Вероятность накрытия элемента случайным множеством. Сведение теории нечетких множеств к теории случайных множеств. Значение теории нечеткости при построении эконометрических моделей социально-экономических явлений и процессов.

12. Статистика интервальных данных. Погрешности измерения и интервальные данные. Операции над интервальными числами. Основная модель интервальной статистики. Понятие нотны - максимально возможного отклонения, вызванного интервальностью статистических данных. Расчет асимптотической нотны (для малой абсолютной погрешности). Основные результаты статистики интервальных данных. Рациональный объем выборки. Расчет асимптотической нотны, рационального объема выборки и доверительных интервалов при оценивании математического ожидания и дисперсии. Инвестиционные проекты и сравнение потоков платежей. Чистая текущая стоимость NPV – характеристика финансового потока. Необходимость изучения устойчивости выводов по отношению к отклонениям коэффициентов дисконтирования и величин платежей. Влияние интервальности дисконт-факторов на величину NPV. Формула для погрешности NPV.

13. Эконометрические методы классификации. Триада: построение классификаций - анализ классификаций - использование классификаций. Лемма Неймана-Пирсона и непараметрический дискриминантный анализ на основе непараметрических оценок плотности в пространствах произвольной природы. Линейный дискриминантный анализ (диагностика на два класса с помощью «индексов» - линейных функций от координат). Характеристики качества алгоритмов диагностики. Почему нельзя использовать такую характеристику, как «вероятность правильной классификации»? Асимптотическое распределение рекомендуемой корректной характеристики («прогностической силы»). Чем схожи и чем различаются задачи группировки и кластер-анализа. Агломеративные иерархические алгоритмы ближнего соседа, дальнего соседа и средней связи. Метод k-средних и проблема остановки алгоритма. Совместное (последовательное и параллельное) использование различных алгоритмов кластер-анализа. Двухкритериальная оптимизационная постановка кластер-анализа на основе внутрикластерного разброса и числа кластеров. Кластер-анализ признаков. Измерение расстояния между признаками с помощью линейного коэффициента корреляции Пирсона и непараметрического рангового коэффициента корреляции Спирмена. Понятие о методах многомерного шкалирования. Оптимизационные постановки и использование результатов.

14. Эконометрика риска. Понятие риска. Многообразие рисков. Характеристики рисков. Анализ, оценка и управление рисками. Аддитивно-мультипликативная модель оценки рисков.

Вслед за перечисленными базовыми разделами эконометрики могут быть изучены и применены дальнейшие эконометрические модели и методы, в частности, описанные в учебнике [16].

4.1.9. Внешняя среда эконометрики

Содержание образования должно соответствовать современному научному уровню и давать знания, методы и навыки, полезные для практической работы. Назрела необходимость пересмотра содержания ряда учебных дисциплин и внесения изменений в соответствующие государственные образовательные стандарты. В частности, необходимо обеспечить введение обязательного курса «Эконометрика» в ряд государственных образовательных стандартов по управленческим и экономическим дисциплинам. Содержание приведенных в стандартах минимальных требований целесообразно привести в соответствие с курсами эконометрики, реально читаемыми в соответствии с новой парадигмой математических методов экономики.

На основе современного подхода к преподаванию эконометрики следует сформулировать предложения по изменению преподавания смежных дисциплин. Так, курс «Теория вероятностей и математическая статистика» является основой для изучения эконометрики. Однако его необходимо привести в соответствие с современными требованиями. В частности, необходимо рассматривать такие понятия, как случайные элементы со значениями в произвольных пространствах, эмпирические и теоретические средние в таких пространствах, доказывать законы больших чисел в общих постановках. Одновременно с указанным расширением содержания курса целесообразно исключить из программы методы, опирающиеся на те предположения, которые не выполняются в конкретных экономических ситуациях. В частности, исключить одновыборочный и двухвыборочный критерии Стьюдента и заменить их соответствующими непараметрическими критериями.

Как уже отмечалось, и преподавание контроллинга, и преподавание эконометрики в настоящее время все еще находятся в стадии формирования. Нет опыта десятилетий, но нет и закостеневших традиций. Есть возможность и необходимость отработать наиболее эффективные формы преподавания. В частности, курс эконометрики может быть разбит на два этапа. Первый этап соответствует подготовке бакалавров. Он, как это и реализуется в настоящее время в МГТУ им. Н.Э. Баумана, следует за курсами теории вероятностей и математической статистики (как части общего курса математики) и прикладной статистики [5], завершая фундаментальное образование бакалавров по своему направлению. Его место – третий или четвертый год дневного обучения. Второй этап входит в подготовку магистров (или специалистов - на 10м или 11-м семестре). Представляется полезным предложить студентам эконометрический курс прикладной направленности, охватывающий применение эконометрических методов в задачах прогнозирования, планирования, контроля, анализа внутренних и внешних рисков, принятия решений и др. Аналогичные два этапа имеются в учебном плане второго образования на факультете "Инженерный бизнес и менеджмент", но с несколько измененными названиями дисциплин - соответственно "Статистика" и "Методы принятия управленческих решений". В Бизнес-школе МГТУ им. Н.Э. Баумана аналогичные дисциплины называются "Количественные методы, статистика и информатика" и "Эконометрика".

Актуальной является проблема разработки учебно-методической литературы, обмен опытом преподавания и научных исследований. Корпус базовых учебников подготовлен в соответствии с новой парадигмой математических методо в экономики (см. раздел 2.1.4 "Учебная литература, подготовленная в соответствии с новой парадигмой" настоящей монографии). Однако необходимы методические материалы следующего поколения - соответствующие конкретным используемым в преподавании учебным программам учебники, учебные пособия и конспекты лекций, практикумы по решению задач, методические указания по проведению лабораторных работ, наборы контрольных материалов для преподавателей и пособия по подготовке к экзаменам и зачетам для студентов, и т.д. Отметим, что подавляющее большинство эконометрических методов могут быть успешно применены не только в контроллинге, менеджменте и экономике. Они используются в технических, медицинских, геологических, социологических, исторических и иных социально-экономических исследованиях, практически в любой научной дисциплине и прикладной области. На основе новой парадигмы эконометрики (т.е. прежде всего прикладной статистики) и накопленного опыта прикладных исследований и преподавания целесообразно приступить к обучению основам современных статистических методов студентов технических специальностей в МГТУ им. Н.Э. Баумана и других вузах.

Поскольку службы контроллинга интенсивно используют информационные системы управления предприятиями, то эконометрические программные продукты должны быть неотъемлемой составной частью таких систем [22]. Очевидно, что включающие эконометрические и статистические методы распространенные программные продукты общего назначения должны соответствовать новой парадигме математических методов экономики. К сожалению, в настоящее время такого соответствия нет [223].

Свободное владение таким интеллектуальным инструментом решения проблем, как эконометрика, – признак профессионализма контроллера.

4.2. Проблемы внедрения математических
и инструментальных методов контроллинга

Как показывает практика, мало разработать перспективные современные научно обоснованные эффективные математические и инструментальные методы контроллинга. Чтобы эти методы использовались, необходимо, чтобы они были внедрены. Управление внедрением новшеств, т.е. инновационный менеджмент, вполне обоснованно является в настоящее время одним из наиболее обсуждаемых разделов экономики и организации производства, всей экономической науки в целом. Однако внедрение прикладной статистики и других статистических методов, более широко, математических и инструментальных методов контроллинга, имеет свою специфику. Мы столкнулись с ней в ходе развертывания деятельности Всесоюзного центра статистических методов и информатики Центрального правления Всесоюзного экономического общества и при создании Всесоюзной организации по статистическим методам (позже ставшей секцией Всесоюзной статистической ассоциации). Сделанные "по следам событий" выводы отражены в статьях [224, 230]. Уже в текущем столетии мы увидели в разработанной первоначально для в целях повышения качества продукции системе «Шесть сигм» новую систему внедрения математических методов контроллинга [25, 233]. В современных внешнеэкономических условиях вопросы модернизации систем управления предприятиями и народным хозяйством в целом, реиндустриализации, импортозамещения становятся все более актуальными. Соответственно растет значение проблем адекватного внедрения математических и инструментальных методов контроллинга. Обсудим их.

4.2.1. Болезни роста

Бурное развитие прикладной статистики и других математических методов контроллинга породило ряд проблем, которые, видимо, сопутствуют многим быстро развивающимся областям. Перечислим их.

1. Низкий научно-технический уровень многих работ (примеры даны в [74, 75, 85, 224]) объясняется тем, что статистическими методами занялись лица, не имеющие соответствующей подготовки, а актуальность этой тематики открыла им доступ на страницы научно-технических изданий. На современном этапе более важной задачей, чем дальнейший количественный рост числа лиц, занимающихся статистическими методами, является повышение качества работ в этой области, обеспечение их соответствия современному научно-техническому уровню, достигнутому в рамках научной специальности 01.01.05 "Теория вероятностей и математическая статистика". Уже на Четвертой международной Вильнюсской конференции по теории вероятностей и математической статистике (1985 г.) было 515 советских докладов, относящихся к этой специальности [407], поэтому дело не в том, что в нашей стране мало высококвалифицированных специалистов, а в том, что отсутствует система внедрения современных методов и вытеснения устаревших и неверных процедур анализа данных, а также система контроля за качеством работ в области статистических методов.

Ошибки при применении статистических методов встречаются в работах по различной тематике. Например, в учебниках по учебной дисциплине "общая теория статистики" [408, 409 и др.] постоянно повторяется одна и та же ошибка: для проверки гипотезы о принадлежности функции распределения выборки параметрическому семейству предлагается использовать критерий акад. А.Н. Колмогорова, при этом параметры теоретического распределения оцениваются по выборке, а процентные точки берутся для классического распределения критерия, полученного в предположении, что параметры точно известны. Дело в том, что в случае, когда параметры определяются по выборке, предельное распределение будет другим, процентные точки его примерно в 1,5 раза меньше, чем для классического распределения критерия А. Н. Колмогорова [74, 75].

В одной из лучших книг по применению статистических методов в медицине [410] допущена та же ошибка.

Как неоднократно отмечалось (см., например, [70, 85, 411, 412]), в большинстве медико-биологических исследований используются лишь самые элементарные статистические приемы: вычисление среднего арифметического и ошибки среднего, доли и ее ошибки, проверка однородности двух выборок с помощью критерия Стьюдента, вычисление коэффициента корреляции и проверка его значимости, к тому же иногда с ошибками (см. тщательный разбор причин ошибок в [413]). Подробный анализ ряда типичных ошибок при применении статистических методов дан в [414].

Ситуация практически во всех прикладных областях аналогична.

Применение статистических методов весьма широко. Практически во всех вузах и НИИ, на многих заводах имеются вычислительные центры, среди программ обычно имеются статистические. Большинство статей в технических, медицинских, социологических изданиях содержат упоминания о применении статистических методов. Конечно, эти методы обычно просты - расчет среднего, выборочной дисперсии, критерия Стьюдента, и часто применяются неквалифицированно - например, критерий Стьюдента используется для наблюдений, распределение которых явно отличается от нормального.

Обычно применяется одномерная статистика. Именно поэтому все 11 государственных стандартов по прикладной статистике относились к ней [415]. Многомерный статистический анализ, требующий расчетов на ЭВМ, применяется гораздо реже. Новые направления, такие, как статистика объектов нечисловой природы, используются пока в единичных случаях.

По нашей оценке, в России работают не менее 50 тысяч специалистов различных прикладных областей, постоянно использующих статистические методы в своей работе (в СССР к концу 1980-х годов имелось около 100 тысяч таких специалистов). Из-за отсутствия контрольной системы, низкой квалификации, огромного количества не всегда высококачественных публикаций по прикладной статистике деятельность этих специалистов зачастую нельзя считать научно обоснованной.

2. Отсутствие организационной структуры прикладной статистики как области прикладной (инженерной) деятельности связано с тем, что работы в этой области от пионерских попыток давно уже перешли к "массовому производству", однако факт указанного перехода недостаточно осознан как самими специалистами, так и организаторами науки и производства. В результате работы ведутся отдельными не связанными между собой подразделениями и специалистами, как следствие - дублирование и низкий научно-технический уровень разработок. Так, по данным, приведенным в монографии [416], в начале 1980-х годов в СССР эксплуатировалось более чем 400 компьютерных программ по регрессионному анализу, что, по крайней мере, на порядок превышает необходимое их количество, причем, что весьма важно, большая часть программ имела серьезные недостатки с точки зрения теории прикладной статистики. К настоящему времени ситуация не улучшилась, как показано в статье [223].

3. Для обеспечения широкого внедрения современных методов статистической обработки данных необходимо прежде всего установить основные требования к ним и те характеристики, которые необходимо учитывать при выборе метода для обработки конкретных данных и при описании метода в нормативно-технической и методической документации, а также в справочной, учебной, научной и технической литературе. Под нашим руководством был разработан соответствующий методический документ [417]. Однако широкое его обсуждение не было проведено. С сожалением приходится констатировать, что как сама идея необходимости установления требований к методам анализа данных, так и проект с формулировками таких требований остались вне внимания тех специалистов, которым они необходимы и были адресованы. В частном случае подобные требования приведены в "Методике сравнительного анализа родственных эконометрических моделей", помещенной в качестве Приложения 3 в учебнике "Эконометрика" [16]. Однако и она не дошла до адресата - специалистов, разрабатывающих новые методы анализа данных, поскольку учебники читают студенты и преподаватели, а не разработчики-исследователи.

Для обеспечения широкого внедрения статистических методов в практику работы инженеров, медиков, экономистов, биологов, социологов, геологов, химиков, представителей других специальностей необходима классификация этих методов, позволяющая прикладнику ориентироваться в море имеющихся методов. Удовлетворительной классификации подобного типа в настоящее время нет. Имеющиеся учебники, в том числе наши, можно рассматривать лишь как введение в предмет, специальные монографии посвящены отдельным направлениям, что связано обычно с субъективной оценкой значимости тех или иных направлений.

Очевидно, основная причина отсутствия приемлемой классификации статистических методов состоит в том, что объем знаний по прикладной статистике давно превысил индивидуальные возможности восприятия. Так, в наиболее полном издании по прикладной статистике на русском языке - трехтомнике Кендалла и Стьюарта [79 - 81] - приведено около 2000 ссылок, т.е. процитировано около 2% от имеющихся к настоящему времени актуальных работ (по экспертной оценке, данной в статьях [76 - 78]). Можно констатировать, что любой отдельный специалист знаком лишь с весьма малой частью (в лучшем случае единицы процентов) актуальных публикаций, относящихся к его специальности. Эту печальную ситуацию смягчает то, что одни и те же идеи обсуждаются во многих публикациях. Однако практика показывает, что знания о полученных научных результатах, как правило, распространяются недостаточно. В частности, создается впечатление, что если в настоящее время перепечатать достаточно обширный массив публикаций 1970-х годов по математической статистике, то подавляющим большинством читателей они будут восприняты как новые, отражающие только что полученные научные результаты.

Из сказанного вытекает, что необходим специальный методологический и гносеологический анализ массива публикаций по прикладной статистике, подобный проведенному в [418] для некоторых проблем классификации. Для проведения обоснованной классификации необходимо предварительное "освоение предметной области" [419]. Целям подобной "предклассификации" служит выделение основных характеристик статистических методов обработки данных. Этот подход относится к мерономии [420], в отличие от применяемой обычно таксономии с таксонами типа "регрессионный анализ", "дисперсионный анализ". Границу между указанными таксонами установить трудно, т.к. в обоих случаях, как известно, можно использовать одни и те же алгоритмы расчетов [421].

Кроме того, границы таксона "регрессионный анализ" по-разному понимаются специалистами. Так, обычно согласно устаревшей парадигме прикладной статистики считают, что независимые и зависимая переменные в регрессионном анализе - действительные числа [422]. В более современном направлении прикладной статистики (соответствующем новой парадигме математических методов экономики) - в статистике объектов нечисловой природы (впервые об этом сообщено в программной статье [423] – переменные могут иметь любую природу (подробнее об этих постановках - см. [314]). Если независимые переменные - порядковые или номинальные, принимающие конечное число градаций, а зависимая переменная - количественная, то с устаревшей точки зрения имеем дисперсионный анализ [422, с. 24], а с точки зрения статистики объектов нечисловой природы - частный случай регрессионного анализа [423, с. 82-84].

4. Изучение общих схем статистики объектов нечисловой природы позволяет единообразным образом получать результаты для наблюдений различной природы и тем самым способствует превращению прикладной статистики из хаотического набора методов в науку с выраженной внутренней структурой. При этом происходит разрушение ряда устарелых догм. Некоторые такие догмы рассмотрены в [314] на примерах регрессионного анализа и теории классификации.

5. Кроме перечня общих требований и характеристик, необходимы предназначенные для непосредственного применения методические документы по конкретным статистическим методам, выполненные на современном научном уровне. Чтобы вытеснить устаревшие и неверные методы, такие документы должны иметь ту или иную правовую основу.

Какие методы обработки данных целесообразно включать в нормативно-техническую документацию (НТД)?

Очевидно, те, которые применяются массово (иначе затраты на разработку НТД не окупятся), и те, что применяются в конфликтных ситуациях, возникающих, например, между поставщиками и потребителями промышленной продукции, в судебной медицине, при оценке ущерба от вредителей сельскохозяйственных культур [424] и т.д. Информация о разработанных стандартах по прикладной статистике дана в [415], о стандартах по статистическому контролю и статистическому регулированию технологических процессов - в [425] (большинство из них в настоящее время отменено, как содержащие грубые ошибки или устаревшие с развитием научно-технического прогресса).

4.2.2. Будущее прикладной статистики

Чтобы представить себе желательное будущее прикладной статистики (то будущее, к которому надо стремиться), сравним ее с метрологией - "наукой о единстве мира и точности измерений" [426, с. 5]. Это сравнение правомерно, поскольку с точки зрения современной теории измерений (см., например, [7, гл. 3]) результаты статистической обработки данных – это косвенные измерения, полученные расчетным путем по результатам прямых измерений - исходным данным.

Вопросами метрологии занимается в нашей стране целый ряд научно-исследовательских институтов - ВНИИМС, ВНИИМ, ВНИИФТРИ, ВНИИОФИ и др. Промышленные предприятия выпускают соответствующие средства измерения. Методики выполнения измерений стандартизованы, за состоянием средств измерения и правильностью их применения на предприятиях и в организациях всех отраслей народного хозяйства осуществляется метрологический надзор силами лабораторий государственного надзора территориальных органов Госстандарта [426].

А что в прикладной статистике? В метрологии три составляющие: наука об измерении, производство средств измерения, контроль за правильностью их использования - образуют стройную систему. В прикладной статистике подобной системы пока нет. Наилучшее положение в области науки - хотя в нашей стране нет ни одного научно-исследовательского института в этой области, приведенные выше данные о Вильнюсской конференции [407] свидетельствуют о наличии большого числа специалистов (порядка 1000), активно ведущих теоретические исследования. Аналогом средств измерения является нормативно-техническая, методическая и программная документация, а также сами программы и средства вычислительной техники. В настоящее время разработку ведут многие группы, малые по численности, в основном для нужд собственной организации (предприятия), без должной координации и обеспечения внедрения программных разработок, в результате чего наблюдается сочетание дублирования и низкого качества разработок. Что же касается контрольной системы, то она полностью отсутствует. Рецензии и отдельные критические разборы типа [74, 75] не имеют правовой силы.

Представляется своевременным рассмотреть вопрос о целесообразности реорганизации прикладной статистики, например, по образцу метрологии. С чего начать реорганизацию?

Обсудим положение специалиста прикладной области, желающего применить статистические методы в своей работе. Казалось бы, можно непосредственно воспользоваться научной или учебной литературой, пакетами программ. Однако, на этом пути встают два основных препятствия. Во-первых, научная литература имеет целью изложение новых научных результатов, а поэтому в подобной литературе и документации пакетов зачастую не удается найти подробной и законченной методики анализа статистических данных в определенной ситуации. Например, гамма-распределение широко обсуждается в научной литературе по крайней мере с 1921 г., когда Р. Фишер на его примере сравнивал эффективность различных методов оценивания параметров [80, с. 99], однако при разработке ГОСТ 11.011-83 [133] лишь примерно 50% его содержания нам удалось составить с помощью литературных источников, остальные 50% основаны на результатах исследований, проведенных при подготовке стандарта. Во-вторых, в литературе по статистическим методам встречается довольно большое число устаревших или попросту неверных утверждений (примеры даны в [74, 75, 85, 224]).

Из сказанного вытекает, что специалисту прикладной области необходимы методические материалы и хорошо документированные пакеты программ, содержащие полностью описанные алгоритмы обработки и интерпретации статистических данных и выполненные на современном научно-техническом уровне. Кроме того, необходимы правовые меры, позволяющие исключить из пользования ошибочные рекомендации.

Только научно-обоснованные нормативно-технические и методические документы позволят обеспечить современный научный уровень статистических методов, предназначенных для использования в производственных условиях, в прикладных НИИ и КБ.

Не менее важно использование современной добротной научно-технической документации при обработке данных, полученных в ходе научных исследований. Практика выработала определенное представление о способах обработки, признанных "стандартными" в соответствующих областях. Так, судя по медицинским журналам, в настоящее время в медицинских научных исследованиях "стандартной" является проверка однородности двух выборок (с целью обнаружения различия двух совокупностей) с помощью критерия Стьюдента.

Этот стихийно выработавшийся в середине ХХ в. "стандарт" не соответствует современным научным представлениям, согласно которым однородность целесообразно проверять с помощью непараметрических критериев - критерия Смирнова, Лемана - Розенблатта [173] или, при альтернативе сдвига, критерия Вилкоксона и др. [69 - 73, 427]. Регрессионный анализ прочно ассоциируется с "методом наименьших квадратов", хотя по современным воззрениям "метод наименьших модулей" [428] представляется более предпочтительным. Поразительно живучим является представление о широкой применимости нормального закона распределения, несмотря на отсутствие в большинстве прикладных областей подтверждений его применимости.

Современный подход состоит в использовании непараметрических [69, 427, 429, 430] и устойчивых (робастных) [7, 122, 194 - 197] методов. Задачи классификации многие связывают с построением иерархической системы типа биологической систематики живых организмов, хотя имеется масса иных подходов (см., например, [120]). Применимость вероятностно-статистических методов по традиции связывают с частотным подходом Мизеса, с наличием "статистической однородности", "статистического ансамбля", с возможностью проведения большого числа опытов, хотя уже более 50 лет теория вероятностей развивается как аксиоматическая математическая дисциплина, и мизесовский подход превратился в тормоз развития, хотя в начале ХХ в. он был прогрессивным [431].

Как уменьшить область влияния этих и других устаревших догм, ставших стандартами мышления? Один из создателей современной физики Макс Планк говорил: "Новая научная истина побеждает не потому, что ее противники убеждаются в ее правильности и прозревают, а лишь по той причине, что противники постепенно вымирают, а новое поколение усваивает эту истину буквально с молоком матери" (цитируем по [432]). Но у нас нет времени ждать "постепенного вымирания" сторонников устаревших догм.

Идея стандартизации математических методов имеет давнюю историю. Возможно, наиболее известной попыткой является многотомный трактат Н. Бурбаки "Элементы математики". Недаром один из разделов программной статьи Н.Бурбаки "Элементы математики" называется: "Стандартизация математических орудий" [433]. Изданные в нашей стране "Математическая энциклопедия" в пяти томах и энциклопедия "Вероятность и математическая статистика" [68] - отражение той же тенденции. По сравнению с трактатом Н. Бурбаки НТД по прикладной статистике и другим статистическим методам должны обладать тем преимуществом, что они должны содержать все необходимое для обработки конкретных реальных данных, в то время, как "Трактат" посвящен наиболее абстрактным разделам чистой математики, не имеющим отношения к проблемам реального мира.

Фактически в качестве "стандарта" иногда выступает многократно используемая программа расчетов на ЭВМ. В связи с лавинообразным ростом числа компьютеров, особенно персональных, особую актуальность приобретает задача обеспечения высокого качества пакетов прикладных статистических программ.

Итак, статистические методы опираются на развитую теорию и продемонстрировали свою полезность в отраслях народного хозяйства. Однако анализ положения дел в области применения статистических методов показывает явное неблагополучие, в результате которого накопленный в нашей стране научный потенциал используется далеко не в полной мере.

4.2.3. Применение статистических методов
как вид инженерной деятельности

Симптомом неблагополучия является анализ состава участников Вильнюсской конференции [407]. Из 515 докладов советских участников 201 приходится на 30 университетов, в том числе на МГУ - 50 и на Киевский университет - 42, и 57 - на 36 вузов, т.е. всего на учебные институты приходится половина докладов. Из оставшейся половины 123, т.е. около 25%, представлено сотрудниками 10 институтов математики и 75 - представителями 28 академических организаций. И только 59 докладов, т.е. 11%, приходится на сотрудников 54 организаций отраслей народного хозяйства. Эти данные показывают организационную разобщенность теоретической науки и ее применений - в области статистических методов.

Следовательно, необходимы специальные меры для усиления взаимосвязи между двумя типами специалистов в области статистических методов. Один тип - это математики, разрабатывающие и изучающие статистические методы; в настоящее время они сосредоточены в основном в вузах и академических институтах. Другой тип - это специалисты отраслей народного хозяйства, которые применяют статистические методы для решения задач своих отраслей. Грубо говоря, математики изготавливают инструмент, прикладники его применяют. Во втором случае применение статистических методов выступает как вид инженерной (управленческой, экономической, социологической, медицинской, исторической и т.п.) деятельности.

Статистические методы являются весьма эффективными как при управлении качеством продукции, так и при решении других производственных и научных задач во всех отраслях народного хозяйства. Они позволяют получать значительный экономический эффект, принимать научно-обоснованные решения. Эффективность применения этих методов в значительной степени повышается благодаря их унификации и стандартизации. При этом, с одной стороны, достигается упорядочение методов в зависимости от задач и условий применения, с другой - для широкого использования рекомендуются путем стандартизации хорошо обоснованные наукой и апробированные на практике методы. НТД на статистические методы должны излагаться и оформляться в доступной инженерам форме с удобными для пользования таблицами, программным обеспечением.

Наиболее эффективными формами внедрения в организациях и предприятиях народного хозяйства статистических методов является введение их в НТД (технические регламенты, национальные стандарты, технические условия и т.п.) на конкретные виды продукции в разделы "Приемка", "Методы контроля (испытаний, анализа, измерений)" или прямое их использование при разработке технологий контрольных операций, средств управления технологическими процессами и т.д.

В настоящее время статистические методы, особенно их современные модификации, активно применяются лишь на отдельных промышленных предприятиях и НИИ, хотя нормативно-техническая и методическая документация и пакеты программ (диалоговые системы), разработанные к настоящему времени, позволяют использовать их гораздо более широко. Причинами тому:

а) отсутствие в действующей нормативно-технической документации на конкретные виды продукции в разделах "Приемка" и "Методы контроля (испытаний, анализа, измерений)" для изготовителей и потребителей четких указаний о порядке обработки данных, вследствие чего в НТД допускаются противоречия, а иногда и неправильные толкования, которые по своему содержанию не соответствуют современному научно-техническому уровню;

б) слабое обоснование с правовой точки зрения разделов "Приемка" и "Методы контроля" многих действующих НТД на конкретные виды продукции, в которых применяются выборочные методы прикладной статистики, отсутствие в них четких указаний о взаимоотношениях поставщика и потребителя при оценке результатов обработки данных, при решении вопроса об экономической целесообразности тех или иных методов, гарантиях и т.д.;

в) отсутствие специальной подготовки инженерно-технических работников непосредственно на предприятиях и в НИИ, в т.ч. и знания пакетов программ и НТД по прикладной статистике и другим статистическим методам;

г) отсутствие на предприятиях заинтересованности во внедрении статистических методов.

4.2.4. Государственные стандарты по статистическим
методам в соотнесении с современной
математической статистикой

На 01.01.86 в СССР действовали 11 государственных стандартов системы "Прикладная статистика" (ГОСТ 11.001-73 - ГОСТ 11.011-83), 6 стандартов по статистическому регулированию технологических процессов. 8 стандартов по статистическому приемочному контролю, ряд методик и рекомендаций, 1 терминологический стандарт, 1 стандарт по организации внедрения статистических методов. Статистические методы использовались в ряде стандартов по вопросам надежности в технике, измерений, испытаний продукции, управления технологическими процессами, качеству продукции. Сопоставление включенных в стандарты статистических методов с современными научными результатами, представленными, в частности, в 1985 г. на Четвертой международной Вильнюсской конференции по теории вероятностей и математической статистике [407], приводит к неутешительным выводам.

Стандарты по прикладной статистике охватывали лишь небольшую часть методов прикладной статистики, доказавших свою полезность при решении прикладных задач в отраслях промышленности. Все они относились к одномерной статистике, не было ни одного стандарта по многомерному статистическому анализу, статистике случайных процессов и временных рядов, по большинству разделов статистики объектов нечисловой природы. Если возможны дискуссии о целесообразности разработки стандартов по таким бурно развивающимся областям статистики, как устойчивые статистические методы, математические методы классификации, ряд разделов статистики объектов нечисловой природы, то на 01.01.86 была несомненна целесообразность стандартизации устоявшихся и широко используемых методов непараметрической статистики, регрессионного анализа, дисперсионного анализа, планирования эксперимента и т.д. В частности, в одномерной статистике следовало стандартизировать непараметрические методы проверки статистической гипотезы однородности двух выборок.

Стандарты по статистическому регулированию технологических процессов основывались на научных результатах пятидесятых-шестидесятых годов. В них при регулировании по количественному признаку принято предположение нормальности контролируемого параметра, которое во многих реальных ситуациях является необоснованным. К рассматриваемому времени (к середине 1980-х годов) в нашей стране существенное развитие получили методы обнаружения разладки, получившие отражение, в частности, в работах А.Н. Ширяева (ныне академик РАН), Г.Ф. Филаретова, И.В. Никифорова, А.А. Новикова, Н. Клигенс и многих других. В свете этих работ рассматриваемые стандарты являются устаревшими. Кроме того, в стандартах по статистическому регулированию технологических процессов (по контрлльным картам Шухарта и кумулятивных сумм) были обнаружены принципиальные ошибки, делающие невозможным их применение.

Сказанное во многом справедливо и для стандартов по статистическому приемочному контролю. Наиболее известный из них - ГОСТ 18242-72 [434] - разработан по аналогии с американским военным стандартом MIL STD 105 D, подготовленного в годы второй мировой войны. При контроле по количественному признаку принято нереалистическое предположение нормальности. Современному научному уровню соответствует ГОСТ 24660-81 [435], подготовленный под руководством Ю.К. Беляева (МГУ) и Я.П. Лумельского (Пермский государственный университет). Важные результаты в области статистического приемочного контроля получены в работах И.Н. Володина, В.Ю. Королева, С.Х. Сираждинова, Н.Е. Боброва, Ю. Круописа и многих других.

Оценивая ситуацию в целом, необходимо констатировать, что комплекс государственных стандартов по статистическим методам во многом отставал от развития теоретических и прикладных работ по рассматриваемой тематике.

Более существенным недостатком обсуждаемого комплекса стандартов являлось наличие существенных ошибок в ряде документов. Так, в ГОСТ 11.006-74 имеются математические ошибки, частично разобранные в [74, 75]. Многочисленными ошибками выделяется терминологический стандарт [436], в котором даже определение такого основного понятия, как "случайная выборка", дано неверно. Имеется даже термин "выборочное среднее арифметическое в выборке". Резкая критика этого стандарта дана в [437]. Взамен безграмотного документа был подготовлен проект терминологического стандарта по теории вероятностей и математической статистике, но из-за противодействия виновников ошибок он не был утвержден. Позже на основе этого проекта была опубликована статья [438], терминологическое приложение в учебнике [16] и справочник "Вероятность и прикладная статистика: основные факты" [60].

При подготовке стандарта СЭВ и его введении в ГОСТ 18242-72 из текста документа "выпало" упоминание о возможности применения усеченных планов статистического приемочного контроля, т.е. планов, в которых разрешается прекратить контрольные операции, если ясен результат контроля (приемка или забракование партии продукции). Эта "забывчивость" приводит к тому, что стандарт [434] требует осуществления бессмысленных действий, влекущих ничем не оправданные затраты, на что справедливо указывают авторы статьи [439]. У этого стандарта есть и другие недостатки. Из сказанного ясно, что международные стандарты могут содержать грубые ошибки.

Крайне низким научно-техническим уровнем выделялся стандарт [440] по организации внедрения статистических методов. Он ориентировался на использование в основном устаревших методов, причем и это делалось с многочисленными ошибками. Особенно впечатляет, что стандарт предусматривал обучение всех категорий специалистов промышленного предприятия - рабочих и наладчиков, работников ОТК, ИТР, руководителей цехов и участков - по одной и той же программе в объеме 41 - 49 часов, причем в программу включены столь "необходимые" сведения, как информация о зарубежных стандартах по прикладной статистике, статистическим методам регулирования технологических процессов и статистическому приемочному контролю.

Каковы причины появления ошибок в государственных стандартах по статистическим методам ? Основной причиной, как установила Рабочая группа по упорядочению системы стандартов по прикладной статистике и другим статистическим методам, созданная в 1985 г., является низкая квалификация в области теории вероятностей и математической статистики специалистов, отвечающих за стандартизацию статистических методов в СССР, а также в советских частях Постоянной комиссии СЭВ по стандартизации и ИСО (Международной организации по стандартизации). Другой причиной являлось то, что разработка рассматриваемых стандартов велась в обход ведущих специалистов по теории вероятностей и математической статистике, стандарты не согласовывались с основными научными центрами по этой тематике.

Открывая Всесоюзную научно-техническую конференцию "Применение статистических методов в производстве и управлении" (Пермь, 31 мая - 2 июня 1984 г.), академик АН УССР Б. В. Гнеденко констатировал: "Большинство участников конференции даже не знают о существовании государственных стандартов по статистическим методам" [441]. Отрыв от масс специалистов промышленности имел место, несмотря на многотысячные тиражи указанных стандартов (6 - 20 тыс.экз.). За 15 лет развития комплекса стандартов по статистическим методам не были налажены регулярные контакты с отраслями, головным и базовым организациям не было вменено в обязанность руководство внедрением и использованием этих документов, не были установлены организации, ответственные за указанную работу в отраслях. Нельзя не согласиться со словами Б. В. Гнеденко при закрытии Пермской конференции: "Специалисты по статистике должны знать действующие государственные стандарты по статистическим методам и использовать их в своей работе" [441]. Этого не было, что снизило нанесенный стране ущерб от низкого качества стандартов.

4.2.5. О статусе документов по статистическим
методам стандартизации и управления
качеством продукции

Согласно технической политике органов стандартизации нашей страны (в настоящее время это Росстандарт, т.е. Федеральное агентство по техническому регулированию и метрологии) методические положения должны быть исключены из государственных стандартов. Стандарты не должны излишне регламентировать творческий труд работников предприятий и организаций. Недопустимо, чтобы стандарты становились тормозом на пути научно-технического прогресса.

Рабочая группа по упорядочению системы стандартов по прикладной статистике и другим статистическим методам действовала согласно указанной технической политике. Итоги подведены решениями Госстандарта СССР по отдельным документам и в решении НТС Госстандарта СССР "О стандартизации и применении статистических методов", утвержденном председателем Госстандарта СССР 27.07.87 г. Изложение этого решения опубликовано в [442].

Таким образом, дело не только в отдельных стандартах. Даже безупречные стандарты могут не учитывать конкретных ситуаций. Так, ГОСТ 11.002-73 [443], содержащий правила оценки анормальности результатов наблюдений, безупречен (в основном) с точки зрения математики, но его широкое использование может привести к грубым ошибкам, поскольку указанный стандарт опирается на предположение нормальности. Как правило, для реальных ситуаций характерно отсутствие нормальности, но практические работники об этом не задумываются. Бездумно применяя ГОСТ 11.002-73, они совершают действия, не имеющие научного обоснования. Стандарты могут стать тормозом на пути внедрения новых методов. В статье [382] отмечается, что прежние методы сами по себе являются заслоном на пути новых, если же старые методы еще и стандартами объявлены, то для их преодоления требуются огромные усилия. Так, ГОСТ 11.004-74 [444] по оценке параметров нормального распределения служит барьером на пути внедрения робастных методов оценивания математического ожидания и других параметров. Набор действующих государственных стандартов по статистическому контролю является тормозом на пути внедрения современных методов статистического контроля, например, принципа распределения приоритетов [445].

Так, в [446] продемонстрирована высокая экономическая эффективность применения на предприятиях металлургической промышленности отраслевого стандарта ОСТ 14-34-78 "Статистический контроль качества металлопродукции по корреляционной связи между параметрами", хотя методические указания Госстандарта СССР РД 50-605-86 запрещают применение подобного метода статистического контроля, поскольку он не включен в действующие стандарты по статистическом контролю.

Поэтому документы по статистическим методам должны иметь, как правило, рекомендательный, необязательный характер, быть методическими документами, а не нормативными. Лишь по отдельным вопросам, в частности, по организации статистического контроля, должны быть нормативные документы. Что же касается действовавших в конце 1980-х годов стандартов по статистическим методам, т.е. стандартов по статистическому контролю и терминологического стандарта, то они не могут быть нормативными документами, что было обосновано в статьях [445] и [437] соответственно. На основе государственных стандартов по статистическому контролю могут быть разработаны каталоги планов статистического контроля, носящие рекомендательный характер.

Перспективная форма документа - "методики измерений", разрабатываемые институтами Госстандарта СССР метрологического профиля. "Методика измерений" - это продукция соответствующего метрологического НИИ. Для конкретного предприятия или организации в отраслях народного хозяйства она становится обязательной после утверждения руководителем этого предприятия (организации). Это обеспечивает учет специфики предприятий и оперативное отслеживание научно-технического прогресса.

Ранее государственные стандарты выпускались на бумажном носителе. В связи с бурным развитием информационно-коммуникационных технологий встал вопрос о переходе на программные продукты. Традиционно подготовленный стандарт нельзя непосредственно использовать для создания таких продуктов. Так, обширные числовые таблицы традиционных стандартов нецелесообразно помещать в памяти ЭВМ, поскольку эффективнее применять специально разработанные алгоритмы, непосредственно рассчитывающие нужные величины по запросу пользователя.

В стандарте [447] и методике [448] были сделаны попытки включить программы в текст документов. Однако при этом выявились сложности, связанные с многообразием алгоритмических языков, типов компьютеров и соответствующих трансляторов, с необходимостью подготовки обширной программной документации, а также с дискуссиями программистов относительно того, какая программная реализация одного и того же алгоритма имеет преимущества в том или ином аспекте. Короче, создание программного обеспечения - самостоятельная область деятельности, следующая вслед за разработкой алгоритмического обеспечения.

Выяснилось также, что помещать весь текст документа только в память ЭВМ нецелесообразно, поскольку специалист должен иметь возможность работать с документом, не находясь за дисплеем компьютера.

Из сказанного вытекает, что на обозримое будущее можно предсказать симбиоз документов на традиционной бумажной основе и соответствующих им программных продуктов. При этом методические документы могут иметь более широкую сферу применения, не связанную с типом ЭВМ, имеющейся у пользователя, а пакеты программ могут различаться по используемым архитектуре, алгоритмическим языкам, системному обеспечению (от библиотек модулей до экспертных систем) и т.д.

Подведем итоги и обсудим направления дальнейшей деятельности в рассматриваемой области.

Научная и производственная работа на современном уровне невозможна без широкого и квалифицированного использования прикладной статистики и других статистических методов. В целях коренного улучшения использования накопленного научного потенциала в области теории вероятностей и математической статистики для повышения экономической мощи нашей страны необходим ряд организационных мер по развитию, внедрению и применению комплекса нормативно-технических и методических документов и пакетов программ по статистическим методам.

Для преодоления отрыва от науки и исключения возможности появления ошибок в НТД необходимо, чтобы разработкой стандартов рассматриваемого комплекса занимались специалисты в области теории вероятностей и математической статистики, а сами стандарты согласовывались с ведущими научными центрами по этой тематике.

Для преодоления отрыва от промышленности необходимо выделение системы головных и базовых организаций, ответственных за внедрение и использование статистических методов в отраслях (министерствах и ведомствах, корпорациях, холдингам), развертывание работ по ознакомлению специалистов с программными продуктами по современным статистическим методам, введение информации по этой тематике в учебные курсы в вузах и т.д.

Оценим массив накопленных научных результатов. Уже в 1980-х годах в реферативном журнале "Математика" в разделе "Математическая статистика" за год реферировалось около 2000 статей и книг. По нашей оценке, в настоящее время имеется не менее 100 тыс. актуальных публикаций по прикладной и математической статистике. Следовательно, можно ожидать, что конкретный специалист знаком лишь не более чем с 1% публикаций по прикладной статистике. Стихийность развития науки приводит к тому, что популярность того или иного результата или направления зачастую определяется вненаучными причинами. Коллективными усилиями надо разобраться в накопленном, рекомендовать лучшее для широкого внедрения, сформулировать нерешенные задачи, актуальные для приложений, скоординировать работу по переходу от теоретических результатов к НТД и программным продуктам, по проведению новых исследований. Квалифицированных специалистов по разработке методов прикладной статистики в нашей стране достаточно - несколько тысяч. Необходимо организовать их работу.

Итак, в настоящее время наблюдается большой разрыв между наукой о методах обработки данных (т.е. прикладной статистикой [5]) и практикой их использования. Из всего сказанного выше вытекает необходимость развертывания работ в следующих направлениях:

- адаптация накопленных в прикладной математической статистике результатов для нужд прикладных исследований, включая проведение чисто математического изучения тех или иных статистических процедур;

- разработка, унификация и стандартизация, распространение и внедрение методического и программного обеспечения статистических методов, используемых в прикладных исследованиях;

- помощь специалистам прикладных областей в организации и проведении исследований с использованием статистических методов, а также в обработке данных;

- контроль за правильностью применения статистических методов, а также качеством используемого методического и программного обеспечения.

Очевидно, эта работа должна быть плановой, организационно оформленной, ее должны проводить мощные самостоятельные подразделения. В частности, необходимо создать службу статистических консультаций (необходимость создания системы статистических консультаций обоснована В.В. Налимовым в [449, с. 200]).

Отметим, что по экспертным оценкам специалистов существенная часть статистической информации - от 50 до 90% - носит нечисловой характер [450]. Следовательно, для внедрения в прикладные разработки особый интерес представляет такой новый раздел математической статистики, как статистика объектов нечисловой природы (см. раздел 3.5 настоящей монографии).

4.2.6. «Шесть сигм» - новая система внедрения
перспективных математических
и инструментальных методов контроллинга

В XXI веке основное внимание исследователей и управленцев переносится с разработки отдельных математических и экономико-математических методов исследования на системы внедрения таких методов в практическую деятельность предприятий и организаций. Обсудим новую систему организации управления «Шесть сигм», основанную на интенсивном использовании современной компьютерной техники и информационных технологий [451 - 453]. По нашему мнению, она является не только новой технологией управления (менеджмента), но и системой внедрения математических и инструментальных методов в практику работы организации, предприятия, корпорации, региона. Мы рассматриваем ее как подход к совершенствованию бизнеса, как эффективный инструмент внедрения перспективных математических и инструментальных методов контроллинга.

Как улучшить качество продукции и организацию производства? Как увеличить эффективность управления предприятием? Как повысить качество научных исследований? Как оптимизировать деятельность центральной заводской лаборатории? Все эти проблемы - вечные. Их решали и сто лет назад, и пятьдесят, решают и сейчас. Но по-разному.

Последние десятилетия волна за волной накатывают на руководителей и специалистов все новые сочетания слов и стоящие за ними концепции: комплексные системы управления качеством продукции, АСУ, стандарты ИСО серии 9000, ИСУП, контроллинг... И в каждой волне есть что-то новое и что-то давно известное. Основное в очередной новации - иное направление взгляда на старые проблемы и методы.

И вот появилось еще одно новое модное поветрие - система «Шесть сигм». Что стоит за этими словами, наводящими на мысли о статистических методах (греческой буквой «сигма» традиционно обозначают показатель разброса статистических данных)?

Основные идеи системы «Шесть сигм». Как сказано в сравнительно недавно выпущенной книге [454], «Шесть сигм» - это более разумный способ управлять всей компанией или отдельным ее подразделением (например, литейным цехом или центральной заводской лабораторией). Фактически речь идет о развитии системы управления качеством и контроллинга на предприятии, в организации, фирме, компании. Концепция «Шесть сигм» ставит на первое место потребителя товаров и услуг и помогает, как утверждают ее разработчики, находить самые лучшие решения, опираясь на факты и данные. Она нацелена на три основные задачи:

- повысить удовлетворенность клиентов;

- сократить время цикла (производственного, операционного);

- уменьшить число дефектов.

Внедрение «Шести сигм» дает значительный экономический эффект. Исполнительный директор корпорации General Electric Джек Уэлч объявил в ежегодном докладе, что всего за три года система «Шесть сигм» сэкономила компании более 2 миллиардов долларов [454].

Совершенно справедливо систему «Шесть сигм» рассматривают как «революционный метод управления качеством». Согласно «Шести сигмам» следует стремиться к достижению самого малого (из возможных) разброса контролируемого параметра по сравнению с полем допуска. Точнее, желательно добиться, чтобы ширина поля допуска была по крайней мере в 6 раз больше типового разброса «плюс-минус сигма». Отсюда и название - «Шесть сигм». Соотношение поля допуска с полем разброса (в «сигмах») связывают с числом дефектов (на миллион возможностей) и с выходом годной продукции (в %). Так, 6 «сигм» согласно [454] соответствуют 3,4 дефектов на 1000000 возможностей, или выходу годной продукции 99,99966%.

А пока столь высокий уровень качества не достигнут, можно оценивать ситуацию в «сигмах». И промежуточная задача может формулироваться так: с уровня 2,5 «сигма» подняться до уровня 4 «сигма».

Инструменты системы «Шесть сигм». С помощью каких интеллектуальных инструментов достигается успех в системе «Шести сигм»? Перечислим их.

Это инструменты генерации идей и структурирования информации - экспертные оценки (различные варианты сбора информации и голосования, мозговой штурм и др.), диаграммы (сродства, древовидные, «рыбий скелет» - схема Исикава), блок-схемы.

Это инструменты сбора данных - разнообразные варианты выборочного метода, всевозможные методики измерений (наблюдений, анализов, опытов, испытаний). Сюда же относятся методы определения «голоса потребителя» (т.е. предпочтений потребителей), контрольные листки, а также инструменты систематизации данных - электронные таблицы и базы данных.

Третья группа - инструменты анализа процессов и данных - анализ течения процесса, добавленной ценности, различные графики и диаграммы. В том числе диаграмма Парето, график временного ряда (тренда), диаграмма разброса (корреляционное поле). Затем - многочисленные инструменты статистического анализа (описание данных, оценивание и проверка статистических гипотез, методы корреляции и регрессии, классификации, снижения размерности, планирования экспериментов, анализа временных рядов, статистики нечисловых и интервальных данных и др.).

Наконец, четвертая группа - инструменты реализации решений и управления процессами. Среди них - методы управления проектами (планирование, бюджетирование, составление графиков, оптимизация коммуникаций, управление коллективом, диаграммы Ганта и др.). А также анализ потенциальных проблем, изучение видов и последствий отказов, анализ заинтересованных сторон, диаграмма поля сил, документирование процесса, сбалансированная система показателей и «приборная» панель процесса.

Таким образом, инструментарий системы «Шести сигм» весьма широк. Эти интеллектуальные инструменты помогают принимать правильные решения, решать проблемы и управлять переменами. Среди них, как следует из проведенного выше перечисления, основное место занимают различные математические методы исследования, прежде всего статистические и экспертные инструменты. Однако нельзя считать, что система «Шести сигм» и инструменты «Шести сигм» - это одно и то же.

В чем новизна системы «Шесть сигм»? Как справедливо подчеркнуто в цитированной книге о системе «Шести сигм», возможно, вы говорите себе: «Мы уже давно делаем кое-что из этого». И уж, безусловно, вы читали почти обо всем из названных выше инструментов. Совершенно бесспорно, что многое в концепции «Шести сигм» не ново. Что действительно ново - так это соединение всех этих элементов системы и ее инструментов в согласованный процесс управления.

Действительно, различные виды инструментов повышения эффективности управления организацией, ее подразделениями, отдельными направлениями деятельности известны давно. Чтобы их успешно использовать, НУЖНА СИСТЕМА ВНЕДРЕНИЯ. Необходима тщательно разработанная методика создания и функционирования творческих коллективов, занимающихся анализом ситуации, подбором и внедрением современных инструментов управления. Такая методика и создана в системе «Шесть сигм». В этом и состоит суть нового шага в науке и практике управления предприятием и его подразделениями.

Шесть основных элементов системы «Шесть сигм». Выделяют [454] шесть основных элементов, составляющих квинтэссенцию системы «Шесть сигм». Это

- ориентация на потребителя;

- управление на основе данных и фактов;

- процессный подход (где действия, там и процессы);

- проактивное управление (т.е. основанное на прогнозировании);

а также два социально-психологических базисных положения:

- безграничное сотрудничество;

- стремление к совершенству без боязни поражений.

Конечно, каждый из этих элементов сам по себе хорошо известен в теории и практике управления (менеджмента). Дело в системе «Шесть сигм», в которую они объединены. В частности, в этой системе подробно расписаны роли различных участников команды - «черные пояса», «зеленые пояса», «мастера черных поясов», «чемпионы». В самих названиях ролей подчеркнута роль команды проекта по внедрению системы «Шесть сигм», соревнования между подразделениями и специалистами, энтузиазма в работе (аналогичного спортивному азарту), продвижения на основе освоенных знаний и полученных результатов (в спорте - переход от пояса к поясу). Весьма важна основополагающая роль членов высшего руководства компании, лично занимающихся развитием системы «Шесть сигм».

Анализ системы «Шесть сигм» показывает, что, несмотря не некоторое своеобразие терминов, связанное с корнями этой системы (лежащими в проблемах управления качеством), фактически «Шесть сигм» - это глубоко проработанная система внедрения современных подходов к управлению предприятием и его подразделениями, прежде всего контроллинга, на основе широкого и продвинутого использования математических методов исследования. Отметим большое место, которое занимают математические методы исследования, прежде всего статистические и экспертные методы, среди ее инструментов. Система «Шесть сигм» трудоемка, на внедрение нужны годы. Но и эффект велик.

Проблемы внедрения математических методов исследования. Полезно проанализировать изменение представлений о проблемах внедрения современных научных достижений в отечественную практику. В качестве примера для обсуждения рассмотрим теорию и методы планирования эксперимента, об истории которых в нашей стране рассказано в статье [455]. Как известно, локомотивом работ по планированию эксперимента в нашей стране являлся «незримый коллектив» под руководством В.В. Налимова, основные научные идеи этого коллектива и результаты их практического внедрения подробно описаны в научно-техническом журнале "Заводская лаборатория. Диагностика материалов".

Очевидно, совершенно необходимый первый этап - разработка самой научной теории до той стадии, когда предлагаемые рекомендации уже можно использовать на практике. Основной результат этого этапа - методические разработки и образцы внедрения. Для планирования эксперимента первый этап в основном завершился к началу 1970-х годов.

Термин «завершился» требует уточнения. Научные исследования, разумеется, продолжались после 1970 г. Они продолжаются сейчас, и будут продолжаться в дальнейшем, поскольку любая научная область может - при наличии энтузиастов - развиваться до бесконечности. Речь о другом - к началу 1970-х годов была создана методическая база для массового внедрения полученных к тому времени научных результатов.

Следующий этап - пропаганда возможностей методов планирования эксперимента, преподавание и подготовка кадров. В статье [455] рассказано о многочисленных акциях 1960-70-х годов в этом направлении. Казалось, что дальше всё пойдет самотеком. Но не получилось. Широкого потока внедренческих работ не последовало. Блестящие работы не стали образцами для подражания.

И не только для планирования эксперимента. Примерно так же развивалась ситуация с внедрением экономико-математических методов. Хотя были и некоторые незначительные отличия. Например, удалось организовать Центральный экономико-математический институт РАН, а вот академического института по планированию эксперимента (и по статистическим методам в целом) нет до сих пор. И Межфакультетская лаборатория статистических методов МГУ им. М.В. Ломоносова, которая занималась развитием теории и практическим внедрением методов планирования эксперимента, расформирована в середине 1970-х годов. Научный Совет АН СССР по комплексной проблеме "Кибернетика" после смерти его основателя А.И. Берга в 1979 г. перестал поддерживать работы по планированию эксперимента. Были и другие примеры того, что организационные успехи по тем или иным причинам не удавалось закрепить [455].

Стало ясно, что создания методов и их пропаганды недостаточно. Выявилась необходимость перехода к третьему этапу в развитии научно-практической дисциплины - этапу разработки организационных форм, обеспечивающих широкое внедрение. Наиболее ярким проявлением этого этапа было учреждение в 1990 г. Всесоюзной статистической ассоциации (ВСА), объединяющей - прежде всего в секции статистических методов - специалистов по математическим методам исследования [48]. В статье [230] тех лет, посвященной проблемам внедрения прикладной статистики и других статистических методов, была развернута программа создания сети научно-исследовательских и внедренческих институтов по этой тематике, аналогичной сети метрологических организаций. К сожалению, все эти глобальные планы организации внедрения рассматриваемых методов в государственном масштабе остались нереализованными из-за развала СССР и развертывания экономических «реформ» 1990-х годов, приведших к сокращению (в разы!) объемов научных исследований и численности работников в сфере науки и научного обслуживания.

Сейчас мы находимся на четвертом этапе. Надо разрабатывать и широко использовать новые организационные формы внедрения математических методов исследования на отдельных предприятиях. С похожими проблемами сталкиваются разработчики крупных информационных систем управления предприятиями (типа SAP R/3, Oracle, JD Edwards, Baan), занимающиеся их внедрением в конкретных организациях [22]. В частности, необходимо создание соответствующей службы под непосредственным началом одного из высших руководителей организации. Недаром внедрение контроллинга - современных методов управления предприятиями - обычно начинается именно с создания службы контроллинга и прорабатывания ее взаимодействия со всеми остальными структурами предприятия [84].

Система «Шесть сигм» ценна, прежде всего, своей организационной составляющей. Той, которой не уделяли внимания на ранних этапах истории внедрения современных математических методов исследования. Система «Шесть сигм» дает алгоритмы практической деятельности по организации внедрения. Чем она и интересна для отечественных специалистов.

4.3. Экспертные технологии - важная составная
часть инструментария контроллинга

Кроме вероятностно-статистических эконометрических методов, для контроллинга большое значение имеет такая важная область эконометрики, как экспертные оценки (обзор начального этапа развития этой научно-практической области проведен в статье [356], анализ современных проблем экспертных оценок дан в [99, 135, 365]). Нестабильность современной социально-экономической ситуации повысила интерес к применению экспертных оценок (и понизила практическое значение статистики временных рядов). Разнообразные процедуры экспертных оценок широко используются не только в контроллинге, но и в технико-экономическом анализе, в маркетинге, при оценке инвестиционных проектов и во многих иных областях. Повысился и интерес к теории экспертных оценок, в том числе в связи с преподаванием (новой парадигме математических методов экономики соответствует учебник [52]).

Среди взглядов на теорию экспертных оценок есть и экстремистские, согласно которым эту теорию надо еще создавать. Мы считаем, что теория экспертных оценок была в основном создана в течение 1970-1980 гг. В теории экспертных оценок выделяются вопросы организации экспертиз и математические модели поведения экспертов. Методы обработки экспертных данных всегда основаны на тех или иных моделях поведения экспертов. Так, при использовании многих методов предполагается, что ответы поведение экспертов можно моделировать как совокупность независимых одинаково распределенных случайных элементов. Эти элементы часто принадлежат тому или иному пространству объектов нечисловой природы, т.е. их нельзя складывать и умножать на число.

Статистика объектов нечисловой природы была разработана в ответ на запросы теории экспертных оценок и представляет собой математико-статистическую основу этой теории. Предварительные итоги были подведены в 1979-1981 гг. в обзорах [144, 264] и монографии [7], а также в ряде монографий и сборников тех времен. На наш взгляд, с выходом обзора пяти авторов [144] заканчивается начальный период развития экспертных оценок в нашей стране - от первоначальных публикаций до создания теории. Следующий этап, продолжающийся уже более 30 лет - развитие теории. Итоги по состоянию на 1995 г. подведены в широко цитируемом обзоре [356].

Третий этап, на котором созданная теория широко применяется, еще не наступил. Пока используются в основном наиболее простые (и примитивные) процедуры экспертных оценок, описанные еще в первоначальных публикациях 1960-х и начала 1970-х годов. Показателем перехода к третьему этапу будет массовое преподавание современной теории экспертных оценок.

Как отмечалось выше, статистика объектов нечисловой природы является одной из четырех основных областей современной эконометрики (и прикладной математической статистики), наряду с одномерной статистикой, многомерным статистическим анализом, статистикой временных рядов и случайных процессов [154]. Ее отличительной чертой является широкое использование операций оптимизации - нахождения решений оптимизационных задач (типа медианы Кемени), а не операций суммирования, как в остальных трех областях. Из конкретных видов объектов нечисловой природы обратим внимание на люсианы (конечные последовательности независимых испытаний Бернулли с, вообще говоря, различными вероятностями успеха). В частности, на их основе строится непараметрическая теория парных сравнений, для ответов экспертов проверяются гипотезы согласованности, однородности и независимости.

Теория экспертных оценок продолжает развиваться. Один из новых подходов к выделению общей части во мнениях экспертов, выраженных в виде кластеризованных ранжировок, а именно, метод согласования кластеризованных ранжировок, развит в статье [202]. Новым методам экспертного оценивания вероятностей редких событий посвящены работы [99, 100, 371, 378].

За последние 30 лет в теории экспертных оценок получено много полезных для практики результатов (в том числе подходов к сбору и анализу данных, методик проведения экспертных исследований, алгоритмов расчетов). Все ценное должно быть использовано для эконометрической поддержки контроллинга.

В настоящем разделе анализируется развитие теории и практики экспертных оценок в нашей стране в послевоенные годы. Рассмотрено многообразие экспертных технологий, приведены основные идеи и публикации, позволяющие выявить движущие силы развития в этой перспективной научно-практической области.

Экспертные оценки – один из эффективных инструментов разработки и принятия управленческих решений. Они широко используются в различных отраслях народного хозяйства. Однако специалистам, применяющим экспертные оценки, зачастую известны лишь отдельные методы и технологии из этой развитой научно-практической области. Поэтому целесообразно дать представление о многообразии работ по теории экспертных оценок, выполненных в нашей стране.

В настоящее время не существует научно обоснованной общепринятой классификации методов и технологий экспертных оценок и тем более - однозначных рекомендаций по их применению. По нашему мнению, наиболее продвинутые результаты в рассматриваемой области были получены в результате работы неформального научного коллектива вокруг комиссии «Экспертные оценки» Научного совета АН СССР по комплексной проблеме «Кибернетика», организованной в 70-х годах. Раздел подготовлен в рамках методологии, созданной этим научным коллективом.

4.3.1. Классические методы экспертных оценок

Экспертные оценки активно использовались с незапамятных времен. После Второй мировой войны в рамках мощного научного движения, на знаменах которого сверкали модные 60 лет назад термины «кибернетика», «исследование операций», «системный подход», выделилась самостоятельная научно-практическая дисциплина – экспертные оценки. Сложились методы сбора и анализа экспертных оценок, которые мы сейчас называем классическими. В 1960-е гг. они освоены в нашей стране, доработаны и успешно применены. И только потом, в 1970-е гг., начались активные самостоятельные научные исследования, была сформирована полностью оригинальная отечественная научная школа в области экспертных оценок. Нашей стране принадлежит мировой приоритет в целом ряде направлений, о некоторых из которых речь пойдет ниже.

Вполне естественно, что сначала в нашей стране появились публикации о классических методах экспертных оценок (см., например, [456 - 458]). Речь идет о простейших методах, не требующих развитого математического аппарата.

С одной стороны, такие публикации были полезны, позволив широким массам специалистов познакомиться с основными идеями экспертных оценок. До сих пор классические методы активно используются в практической работе и излагаются в учебной литературе.

С другой стороны, как обычно бывает во многих областях деятельности, первоначальные достаточно тривиальные соображения широко распространились, вошли в массовое сознание инженеров и управленцев (менеджеров) и стали тормозом на пути внедрения более новых продвинутых результатов в области экспертных оценок, описанных, например, в работах [217, 459 - 463].

Вспомним слова великого физика Макса Планка, создателя квантовой теории света: «Новая научная идея редко внедряется путем постепенного убеждения и обращения противников, редко бывает, что Савл становится Павлом. В действительности дело происходит так, что оппоненты постепенно вымирают, а растущее поколение с самого начала осваивается с новой идеей» [464, с.188-189].

Необычность рассматриваемой ситуации в области экспертных оценок состоит в том, что новые научные идеи появились всего через несколько лет после широкого распространения в нашей стране классических методов экспертных оценок. Но – головы возможных пользователей были уже оккупированы тривиальностями (а иногда и ошибками). В результате многие превосходные с научной точки зрения и высокоэффективные в приложениях результаты отечественных исследователей остаются малоизвестными, хотя получены еще в 70-е годы.

Центром исследований в научно-практической области "Экспертные технологии" является всесоюзный (ныне всероссийский) научно-исследовательский семинар «Экспертные оценки и анализ данных». Этот семинар был организован по предложению академика А.Н. Колмогорова на механико-математическом факультете МГУ Ю.Н. Тюриным, Б.Г. Литваком и П.Ф. Андруковичем. Он работает с 1973 г., сначала в МГУ им. М.В. Ломоносова, а затем в Институте проблем управления РАН. В разные годы им руководили д.ф.-м.н. Ю.Н. Тюрин, д-ра техн. наук Б.Г. Литвак, А.И. Орлов, А.А. Дорофеюк, Ф.Т. Алескеров, Д.А. Новиков, Ю.В. Сидельников. В работе семинара участвовали сотни исследователей.

4.3.2. Научные результаты мирового уровня

Участники неформального научного коллектива участников семинара обычно начинали с освоения современных зарубежных идей, переходя затем к самостоятельным исследованиям, приводящим, как правило, к новым научным результатам мирового значения. Рассмотрим несколько сюжетов, соответствующих этой общей схеме.

Так, освоив проблематику теории измерений, участники семинара перешли к изучению инвариантных алгоритмов. Основной полученный результат мирового уровня – характеризация средних величин шкалами измерения. Найдены необходимые и достаточные условия, выделяющие средние величины, результат сравнения которых инвариантен относительно допустимых преобразований в тех или иных шкалах. Цикл теорем о средних величинах – наиболее важное достижение в теории измерений, полученное в нашей стране.

В теории нечеткости также был получен принципиально важный результат мирового уровня – найден способ сведения теории нечетких множеств к теории случайных множеств. Это – основное отечественное достижение в теории нечеткости.

Большое влияние на развитие исследований в области экспертных оценок оказали работы американского математика Джона Кемени, прежде всего книга [143]. В ней был предложен подход к аксиоматическому введению расстояний между нечисловыми ответами экспертов (на примере упорядочений) и дан метод нахождения итогового мнения комиссии экспертов как решения оптимизационной задачи. Участники семинара по примеру Кемени построили аксиоматику для введения расстояний между различными объектами нечисловой природы. В обзоре [465] сведены вместе результаты более чем 150 исследований. В честь Дж. Кемени расстояния между элементами различных пространств бинарных отношений сейчас называют расстояниями Кемени, а введенные на их основе средние в этих пространствах – медианами Кемени.

Необходимо добавить, что и после 1985 г., когда была выпущена обзорная работа Г.В. Раушенбаха [465] по публикациям, базирующимся на подходе Кемени к аксиоматическому введению меры близости между нечисловыми ответами экспертов, появлялись новые результаты. Так, например, в работе Ю.В. Сидельникова [466] были введены пять аксиом и доказано, что эти аксиомы на множестве векторов предпочтения однозначно определяют меру близости. Аналогичный результат был получен и на множестве ранжирований. В работе [467] аксиоматически введена метрика подобия и изучена с помощью вероятностной модели.

Большое внимание уделялось различным вариантам парных и множественных сравнений. Если на Западе рассматривалась параметрическая теория (модели Льюса, Бредли-Терри, Терстоуна), то в нашей стране была построена не имеющая аналогов непараметрическая теория парных сравнений (люсианов), причем в асимптотике растущей размерности [369].

4.3.3. Итоги первого этапа работы семинара

В 70-е гг. было выпущено три сборника статей [348 - 350], содержащих научные труды участников семинара «Экспертные оценки и анализ данных». Эти сборники до сих пор являются актуальными, включенные в них работы содержат заметно более продвинутые научные результаты, чем публикации по «классическим методам экспертных оценок», поскольку последние опираются на идеи 40-60-х гг. Прошедшие десятилетия позволили более четко выявить теоретический смысл и прикладные возможности разработанных тогда подходов. Сборники статей [348 - 350] следует отнести к новой парадигме математических методов экономики (к периоду ее зарождения), а классические методы экспертных оценок [456 - 458] - к старой парадигме, не соответствующей современным требованиям.

Полученные результаты были обобщены в ряде монографий, написанных руководителями и участниками семинара [7, 85, 145, 468], и прежде всего в неоднократно изданном программном докладе пяти наиболее активных и продуктивных исследователей [144, 264]. К сожалению, этот принципиально важный доклад не был развернут в подробную монографию. «Доклад пяти» – веха в развитии отечественных исследований в области экспертных оценок. Закончился период становления самостоятельной научно-прикладной дисциплины. К концу 70-х гг. экспертные оценки получили и организационное оформление – в рамках комиссии «Экспертные оценки» Научного совета АН СССР по комплексной проблеме «Кибернетика».

4.3.4. Восьмидесятые годы

Научные исследования развивались вглубь и вширь. Регулярно выпускались сборники статей [351, 277 - 279], проводились всесоюзные конференции [269 - 270]. Разумеется, работы по экспертным оценкам публиковались не только в изданиях семинара, но и во многих иных. Укажем для примера на работы руководителей семинара А.А. Дорофеюка [469] и Ю.В. Сидельникова [354], на монографии по многомерному шкалированию экспертных и иных данных [141, 142]. Авторы «доклада пяти» защитили докторские (Б.Г. Литвак, А.И. Орлов, Ю.Н. Тюрин) и кандидатские (Г.А. Сатаров, Д.С. Шмерлинг) диссертации.

Были выполнены многочисленные прикладные работы. В частности, разработаны комплексы нормативно-методических документов по экспертным методам управления качеством продукции (ГОСТы, методические указания и др.) и по экспертизе научно-исследовательских работ в медицине и биологии (методические рекомендации по проведению экспертной оценки планируемых и законченных научных работ в области медицины и по подготовке и проведению конкурса проектов исследований и разработок в области физико-химической биологии и биотехнологии).

Исследования по экспертным оценкам шли в тесном контакте с работами в области прикладной статистики и других статистических методов (отраженными позже, уже в XXI в., в учебниках [5, 16]), многокритериальной оптимизации [470, 471], математических методов в социологии (как показано в обзоре [472]) и т.п. В литературе экспертные оценки иногда выступают под теми или иными «псевдонимами». Например, академик РАН Н.Н. Моисеев в своих выдающихся научных, учебных и научно-публицистических книгах [217, 462, 463, 474] использовал термин «неформальные процедуры».

4.3.5. Экспертные оценки и статистика
нечисловых данных

Основным отечественным достижением последней четверти ХХ в. в области статистических методов анализа данных является создание статистики нечисловых данных (в других терминах, нечисловой статистики, статистики объектов нечисловой природы). Ныне статистика нечисловых данных – одна из четырех основных областей прикладной статистики, наряду со статистикой числовых величин, многомерным статистическим анализом и статистикой временных рядов [5, 16, 36].

Для нас важно, что именно необходимость разработки адекватных методов анализа экспертных мнений стимулировала развитие статистики нечисловых данных. Не случайно основополагающая статья [146], излагающая программу построения новой области статистики, опубликована в одном из первых сборников трудов семинара. Эта статья интересна также переплетением, неразрывной связью основных идей статистики нечисловых данных и современной теорией экспертных оценок.

Кратко напомним суть статистики нечисловых данных. Начнем с того, что исходный объект в прикладной статистике - это выборка, т.е. совокупность независимых одинаково распределенных случайных элементов. Какова природа этих элементов? В классической математической статистике элементы выборки - это числа. В многомерном статистическом анализе - вектора. А в нечисловой статистике элементы выборки - это объекты нечисловой природы, которые нельзя складывать и умножать на числа. Объекты нечисловой природы лежат в пространствах, не имеющих векторной структуры.

Многочисленные примеры объектов нечисловой природы приведены в разделе 3.5 настоящей монографии. Наглядно видно, что подавляющее большинство объектов нечисловой природы могут быть получены в качестве ответов экспертов. К ним относятся, в частности:

- значения качественных признаков, т.е. результаты кодировки объектов экспертизы с помощью заданного перечня категорий (градаций);

- упорядочения (ранжировки) экспертами образцов продукции (при оценке её технического уровня и конкурентоспособности)) или заявок на проведение научных работ (при проведении конкурсов на выделение грантов);

- классификации, т.е. разбиения объектов экспертизы на группы сходных между собой (кластеры);

- толерантности, т.е. бинарные отношения, описывающие сходство объектов между собой, например, сходства тематики научных работ, оцениваемого экспертами с целью рационального формирования экспертных советов внутри определенной области науки;

- результаты проведенных экспертами парных сравнений или контроля качества продукции по альтернативному признаку («годен» - «брак»), т.е. последовательности из 0 и 1;

- множества (обычные или нечеткие), например, зоны, пораженные коррозией, или перечни возможных причин аварии, составленные экспертами независимо друг от друга;

- слова, предложения, составленные из них тексты, представленные экспертами по заданию организаторов экспертизы;

- векторы, координаты которых - совокупность значений разнотипных признаков, например, результат составления статистического отчета о научно-технической деятельности организации (т.н. форма № 1-наука) или анкета эксперта, в которой ответы на часть вопросов носят качественный характер, а на часть - количественный;

- ответы на вопросы экспертной, маркетинговой или социологической анкеты, часть из которых носит количественный характер (возможно, интервальный), часть сводится к выбору одной из нескольких подсказок, а часть представляет собой тексты; и т.д.

Интервальные оценки, полученные от экспертов, тоже можно рассматривать как пример объектов нечисловой природы, а именно, как частный случай нечетких множеств. А именно, если характеристическая функция нечеткого множества равна 1 на некотором интервале и равна 0 вне этого интервала, то задание нечеткого множества эквивалентно заданию интервала. Напомним, что теория нечетких множеств в определенном смысле сводится к теории случайных множеств [5, 7, 16].

С 70-х гг. в основном на основе запросов теории экспертных оценок (а также технических исследований, экономики, социологии и медицины) развивались конкретные направления статистики объектов нечисловой природы. Были установлены основные связи между конкретными видами таких объектов, разработаны для них базовые вероятностные модели. Итоги подведены в монографии [7], в предисловии к которой впервые появился термин «статистика объектов нечисловой природы», а в тексте постоянно рассматриваются вопросы сбора и анализа экспертных оценок.

Следующий этап (80-е гг.) - выделение статистики нечисловых данных в качестве самостоятельной дисциплины, ядром которой являются методы статистического анализа данных произвольной природы. Хотя для работ этого периода характерна сосредоточенность на внутренних проблемах нечисловой статистики, полученные результаты были нацелены на применение для статистического анализа субъективных данных - экспертных оценок. Основные результаты коллективного труда подведены в сборнике научных работ [87]. Характерно, что он был подготовлен совместно подкомиссией «Статистика объектов нечисловой природы» комиссии «Экспертные оценки» Научного совета АН СССР по комплексной проблеме «Кибернетика» и Институтом социологических исследований АН СССР. Видим, что статистика нечисловых данных на тот момент рассматьривалась как часть теории экспертных оценок.

К 90-м гг. статистика объектов нечисловой природы с теоретической точки зрения была достаточно хорошо развита, основные идеи, подходы и методы были разработаны и изучены математически, в частности, доказано достаточно много теорем. Однако она оставалась недостаточно апробированной на практике. И в 90-е гг. наступило время перейти от математико-статистических исследований к применению полученных результатов на практике. К этому периоду относится публикация большой серии статей в рамках раздела «Математические методы исследования» журнала «Заводская лаборатория» (основного места публикации в СССР и РФ работ по прикладной статистике), посвященных теории и практике нечисловой статистики.

В статистике объектов нечисловой природы одна и та же математическая схема может с успехом применяться во многих областях, а потому ее лучше всего формулировать и изучать в наиболее общем виде, для объектов произвольной природы.

Для классической математической статистики характерна операция сложения - при расчете выборочных характеристик распределения (выборочное среднее арифметическое, выборочная дисперсия и др.), в регрессионном анализе и других областях этой научной дисциплины постоянно используются суммы. Математический аппарат - законы больших чисел, Центральная предельная теорема и другие теоремы - нацелены на изучение сумм. В нечисловой же статистике нельзя использовать операцию сложения, поскольку элементы выборки лежат в пространствах, где нет операции сложения. Методы обработки нечисловых данных основаны на принципиально ином математическом аппарате - на применении различных расстояний (точнее, мер различия, близости, метрик и псевдометрик) в пространствах объектов нечисловой природы. (Псевдометрика отличается от метрики тем, что в системе из четырех аксиом метрики отбрасывается условие: если d(x, y) = 0, то x = y.)

Основные идеи статистики объектов нечисловой природы, принципиальная новизна нечисловой статистики раскрыты в разделе 3.5 настоящей монографии. Поэтому не будем рассматривать здесь принципиально новые идеи, развиваемые в статистике объектов нечисловой природы для данных, лежащих в пространствах произвольного вида. Цель - решение классических задач описания данных, оценивания, проверки гипотез - но для неклассических данных, а потому неклассическими методами.

4.3.6. Современный этап развития
экспертных оценок

С конца 80-х гг. число научных работников в нашей стране уменьшилось в разы. На порядок сократилось количество участников научных семинаров и конференций. Однако отечественная научная школа в области экспертных оценок успела достичь стадии зрелости и устояла. Этому способствовала и востребованность экспертных технологий во многих областях человеческой деятельности. Слово «эксперт» стало модным.

Зрелость научной области проявилась в том, что ведущие отечественные специалисты выпустили заметно большее число монографий, подводящих итоги исследования, чем в предыдущие десятилетия. Из них выделим книги [54, 55, 59, 342, 355, 475 - 481, 483, 485]. В рассматриваемом массиве публикаций экспертные оценки часто рассматривались вместе с проблемами принятия решений [54, 55, 59, 476, 477, 485]. Большое внимание уделялось проблеме выбора [478], в том числе в условиях многокритериальности [479]. Были проанализированы процедуры голосования в рамках комиссий экспертов [480].

Разделы, посвященные экспертным оценкам, на современном историческом этапе включают в учебники по различным дисциплинам, в частности, по теории принятия решений [54, 55, 59, 477], по эконометрике и прикладной статистике [5, 16]. Это свидетельствует о том, что теория и практика экспертных оценок вошла в «базовое ядро» знаний, которыми должны владеть инженеры, менеджеры, экономисты, специалисты в иных областях.

Поток новых идей, подходов, концепций, методологий, методов, конкретных постановок, моделей, теорем и алгоритмов в области экспертных оценок не только не иссякает, но год от году усиливается. Назовем некоторые из новшеств.

Теория организационных систем [342], прежде всего, теория активных систем [481], т.е. систем, элементы которых обладают собственными интересами и волей, позволяющей действовать независимо, нуждаются в развитии и применении современных методов экспертных оценок. Подходы теории активных систем особенно интересны для решения задач управления предприятиями и другими социально-экономическими структурами. Такой современный раздел менеджмента, как контроллинг [84, 482], немыслим без использования продвинутых методов экспертных оценок [21], реализованных на основе современных информационных технологий.

Принципиально важным является появление работ по экспертным технологиям [355, 483]. От разработки и изучения отдельных методов экспертных оценок осуществлен переход к разработке процедур, включающих все этапы технологического процесса сбора и анализа экспертной информации. Произошел качественный скачок – от отдельных инструментов интеллектуальной деятельности к целостным технологиям интеллектуальной деятельности. Аналогичный скачок осуществлен и в смежной области статистических методов – появились высокие статистические технологии [5, 16, 51, 391].

Из западных разработок наибольший интерес вызвал метод анализа иерархий Т. Саати [484]. К сожалению, он является некорректным [485 - 487]. К аргументам этих статей надо добавить, что метод Саати некорректен с точки зрения теории измерений, поскольку построен на неправомерной оцифровке (переходе к количественной шкале) данных, измеренных в порядковой шкале. От его недостатков удалось избавиться сотрудникам Института проблем управления им. В.А.Трапезникова. Они разработали метод векторной стратификации [488], согласно которому иерархическая структура показателей комплексного критерия формируется путем дихотомической конкретизации документированной формулировки цели.

Из недавно разработанных принципиально новых подходов укажем в качестве примера на метод согласования кластеризованных ранжировок [202]. «Турнирный» метод ранжирования вариантов впервые опубликован в 2005 г. [360], а в соседней статье дано его теоретическое обоснование [361]. Применению экспертных оценок для задач стратегического планирования посвящена работа [489]. Список легко продолжить. Мы ограничились здесь лишь наиболее заметными публикациями, в основном книжными.

Состояние и перспективы экспертных оценок неоднократно анализировались ведущими специалистами [356, 358, 367, 490]. Отмечалось, что перед исследователями – большое поле деятельности. Например, в [356] отмечалась актуальность разработки методов анализа интервальных экспертных оценок, в которых мнения экспертов выражены интервалами. Основой для разработки таких методов может послужить статистика интервальных данных, рассмотренная в [5, 54]. Однако теория интервальных экспертных оценок стоит лишь в начале своего пути, хотя ее перспективность очевидна.

Экспертным оценкам уделено большое внимание в основополагающей монографии по статистике нечисловых данных [36], в которой также приведен обширный список литературных источников по развитию экспертных оценок в нашей стране. Книги и статьи по рассматриваемой тематике имеются в открытом доступе на сайте «Высокие статистические технологии» [491], его форуме [492] и на сайте Лаборатории экономико-математических методов в контроллинге Научно-образовательного центра "Контроллинг и управленческие инновации" МГТУ им. Н.Э. Баумана [493].

4.3.7. О многообразии экспертных технологий

Итак, экспертные технологии – обширная совокупность интеллектуальных инструментов для решения научно-технических и социально-экономических задач, а также задач в других областях человеческой деятельности.

В чем основная причина все более широкого применения экспертных технологий? Для применения математических методов исследования, независимо от области их использования, нужны исходные данные. Есть два общих пути получения данных – объективные результаты измерений, наблюдений, испытаний, анализов, опытов и субъективные мнения высококвалифицированных специалистов (экспертов). Необходимость и целесообразность разработки и применения методов сбора и анализа экспертных оценок доказана практикой. Например, проведенное в начале 1960-х годов экспертное исследование позволило предсказать момент высадки человека на Луну с точностью до месяца [52].

Один из центров публикации научных работ по экспертным технологиям - раздел «Математические методы исследования» журнала «Заводская лаборатория. Диагностика материалов». В этом разделе опубликовано достаточно много статей, посвященных разработке новых методов экспертных оценок и обсуждению вопросов их практического применения [365]. В частности, развитие экспертных технологий в нашей стране с теоретической точки зрения проанализировано в обзоре [135, 494], а с прикладной – в работе [358] одного из ведущих отечественных исследователей в этой области Б.Г. Литвака (1940 - 2012).

По нашей экспертной оценке, отечественная научная школа в области теории и практики экспертных оценок создана неформальным исследовательским коллективом вокруг постоянно действующего научного семинара «Экспертные оценки и анализ данных», о котором уже упоминалось в начале настоящего раздела. Программная статья [264] наиболее активных руководителей и участников этого семинара Ю.Н. Тюрина, Б.Г. Литвака, А.И. Орлова, Г.А. Сатарова, Д.С. Шмерлинга во многом определила развитие теории и практики экспертных оценок в нашей стране на десятилетия вперед, вплоть до настоящего момента. К сожалению, выпущенный на основе этой статьи препринт [144] не был развернут в подробную монографию.

Экспертные технологии – не только проверенные временем инструменты решения конкретных прикладных задач. Это – быстро развивающаяся научная область. В частности, именно потребности теории и практики экспертных оценок стимулировали разработку новой парадигмы прикладной статистики [114]. Развитие современных технологий экспертных оценок шло в тесном взаимодействии с созданием центральной области современных статистических методов – статистики объектов нечисловой природы [163] (краткое название этой области прикладной математической статистики – нечисловая статистика [36]). Можно констатировать, что нечисловая статистика является теоретическим «зеркалом» современных экспертных технологий. Развитие информационно-коммуникационных технологий позволило разработать и внедрить новую область экспертных оценок – сетевую экспертизу [495]. Отметим, что модификация известного в теории экспертиз метода фокальных объектов дает новые возможности в научно-техническом творчестве [496].

Необходимость разработки новых математических методов исследования вызвана, в частности, тем, что эксперты дают оценки в различных шкалах измерения, прежде всего в порядковых шкалах, а также в вербальной форме. Поэтому значительная часть публикаций раздела «Математические методы исследования» журнала «Заводская лаборатория. Диагностика материалов» посвящена методам анализа нечисловых экспертных данных. Эти методы должны быть инвариантны относительно допустимых преобразований шкал измерения. Конкретная шкала выделяется группой допустимых преобразований. Например, для порядковой шкалы такой группой является совокупность всех строго возрастающих преобразований шкалы. Порядковую шкалу можно представить себе как резиновый стержень с нанесенными на него делениями, который можно произвольно растягивать и сжимать, но нельзя рвать. Порядковую шкалу иногда называют ранговой, поскольку инвариантные методы в этой шкале часто являются функциями от рангов результатов измерений. В обзоре [292] приведена сводка научных публикаций, относящихся к средним величинам, инвариантным относительно допустимых преобразований шкал измерения. Рядом помещена статья [198], в которой выделены основные результаты в рассматриваемой области. Ранее репрезентативная теория измерений была проанализирована с различных сторон в опубликованных рядом статьях [290, 291]. Уточнению (с помощью измеряемых данных) экспертных оценок, выставленных в ранговых шкалах, посвящена статья [497]. Предпочтительность использования медианы экспертных оценок (вместо среднего арифметического) обсуждается в работе [164].

Продолжается интенсивная разработка новых математических моделей получения, анализа и применения экспертных оценок. Так, в работе [322] проанализированы методы визуального представления тесноты связей. Квантификации (или, как говорят, оцифровке) предпочтений, выраженных в вербальной форме, посвящена статья [498]. Опыт практической работы по анализу дефектности отливок методом экспертных оценок разобран в публикации [358].

Экспертные оценки – важнейшая составная часть методов принятия решений, в частности, управления рисками и прогнозирования (см., например. обзор [499] по математическим методам оценки рисков). К теории принятия решений примыкают, в частности, работа [500] по определению весовых коэффициентов на основании экспертных оценок, исследование [501] по обоснованию вида рациональной экспертной оценки знаний учащихся, статья [360], посвященная математическим моделям квалиметрического анализа многофакторных объектов с бинарными факторами.

Вполне естественно, что именно авторами раздела «Математические методы исследования» журнала «Заводская лаборатория. Диагностика материалов» опубликованы основные отечественные монографии и учебники по теории и практике экспертных оценок [52, 355, 495, 496].

Современные методы экспертных оценок предоставляют собой эффективные интеллектуальные инструменты для решения прикладных задач во многих предметных областях, кроме того, сами являются источником дальнейших научных исследований. Экспертное оценивание является, зачастую, незаменимым инструментом, позволяющим разрабатывать обоснованные управленческие решения при отсутствии достаточного объема результатов наблюдений [52, 59, 494].

4.3.8. Экспертное оценивание вероятностей
редких событий

Экспертные технологии активно применяются, например, в Группе компаний «Волга-Днепр», осуществляющей нестандартные грузоперевозки на самых мощных в мире самолетах АН-124 «Руслан» и являющейся мировым монополистом в этой области. В ходе разработки автоматизированной системы прогнозирования и предотвращения авиационных происшествий (АСППАП) при организации и производстве воздушных перевозок экспертные опросы летного состава (всего около 20000 экспертных оценок) позволили получить исходные данные для деревьев событий и других математических моделей, предназначенных для оценки эффективности управленческих решений при создании систем обеспечения безопасности сложных технических систем [96, 98, 380]. При разработке АСППАП возникла необходимость применения экспертных технологий для оценивания вероятностей редких событий [379]. В частности, их необходимо использовать при моделировании на основе деревьев событий (многообразие моделей на основе деревьев событий рассмотрено в статье [98, 380]). Экспертами оценивались передаточные параметры для дерева событий при развитии авиационного события (происшествия) на основе логико-вероятностной модели [502] (представляющие из себя в первом приближении условные вероятности) в условиях почти полного отсутствия статистических данных. Отсутствие данных связано с несколькими причинами. Во-первых, для сбора части данных требовались большие человеческие и временные затраты, и к моменту проведения экспертного опроса они не были готовы. Во-вторых, часть данных для оценки условных вероятностей невозможно получить в принципе, поскольку промежуточные события из дерева событий [502], не приведшие к авиационному событию, часто никак и нигде не анализируются, не записываются и не сохраняются. Здесь можно привести простую аналогию: затруднительно статистически оценить, с какой вероятностью превышение скорости приведет к автомобильной аварии, поскольку большинство превышений скорости не приводят к авариям и остаются вне поля зрения исследователей.

Необходимо сопоставление двух подходов к получению важных для управления безопасностью полетов и предотвращения авиационных происшествий выводов (например, оценок вероятностей авиационных событий / происшествий) – на основе экспертных технологий и на основе анализа статистических данных. Дело в том, что рассматриваемые события зачастую встречаются в единичных случаях (менее 10 случаев за все время наблюдения), например, с частотой порядка 10^-5, поэтому доверительные границы для вероятностей весьма широки. Как следствие, нельзя априори утверждать, что анализ статистических данных дает более точные результаты, чем экспертные технологии. Предложенная нами экспертная технология оценки вероятностей редких событий позволила успешно решить задачи, стоявшие перед разработчиками системы АСППАП [378]. В терминах статьи [51] эту экспертную технологию следует отнести к высоким статистическим технологиям, которые можно применять для статистического анализа как результатов измерений (наблюдений, испытаний, анализов, опытов), так и ответов экспертов.

Подведем итоги раздела. В теории экспертных оценок применяются различные математические методы, прежде всего методы системной нечеткой интервальной математики [32, 33, 263]. При сборе и обработке мнений экспертов большое значение имеют метризация измерительных шкал различных типов и совместная сопоставимая количественная обработка разнородных факторов [128]. Потребности развития теории и практики экспертных оценок дали стимул к разработке статистики объектов нечисловой природы [82], а затем полученные в новой области математической статистики результаты позволили продвинуться в теории экспертных оценок, поднимающей научный уровень выполнения прикладных работ, как это подробно показано выше. Можно констатировать, что именно потребности развития теории и практики экспертных оценок привели к появлению новой парадигмы математической статистики [63].

---

[1] Если ⁰С - температура (в градусах) по шкале Цельсия, а ⁰F - температура по шкале Фаренгейта, то

[2] Согласно новой статистической хронологии (раздел нечисловой статистики), разработанной группой известного историка акад. РАН А.Т. Фоменко, Иисус Христос родился в 1152 г. [199].