ВВЕДЕНИЕ

Неизвестно, какая математика появилось раньше, вычислительная или теоретическая. Ясно, что вычислительная математика возникла тогда, когда возникла потребность в реальных практических вычислениях. Возможно, это было сделано на основе некоторых теоретических представлений, однако гораздо более правдоподобным является предположение, что сами эти теоретические представления возникли как обобщение опыта реальных вычислений.

Вычислители прошлого, не имевшие в своем распоряжении компьютеров, достигли больших высот в практических вычислениях. Однако именно с появлением компьютеров и информационных технологий началась новая современная эпоха бурного развития вычислительной математики, численных методов и дискретной математики (далее будем называть все эти направления вычислительной математикой).

На начальных этапах развития различных направлений современной вычислительной математики казалось очевидным, что все они развивались на грандиозном стволе теоретической математики подобно ветвям огромного дерева и питались его соками. Но недавно стало ясно, что в огромном количестве различных направлений вычислительной математики, которые в этой метафоре можно уподобить листьям, тоже возникает много новых перспективных идей, некоторые из которых вполне могут обогатить теоретическую математику и дать новый импульс ее развитию. Иначе говоря, сегодня наблюдается взаимопроникновение и взаимообогащение теоретической и вычислительной математики.

Кратко, не претендуя на полноту изложения, рассмотрим некоторые из подобных идей.

1. Числа и множества – основа современной математики

Математика – язык науки [1, с.18]. С появлением новых объектов обсуждения язык развивается. «Между математикой и практикой всегда существует двусторонняя связь; математика предлагает практике понятия и методы исследования, которыми она уже располагает, а практика постоянно сообщает математике, что ей необходимо» [1, c.53].

В настоящей работе мы рассматриваем необходимость расширения математического аппарата с целью учета присущих реальности нечеткости, интервальности, системности, а также основы соответствующего предлагаемого нами нового перспективного направления теоретической и вычислительной математики – системной нечеткой интервальной математики (СНИМ).

Анализируя, следуя А.Н. Колмогорову [2], математику в ее историческом развитии, констатируем, что ее основой являются действительные числа и множества. С прикладной точки зрения проанализируем эти понятия, обсудим необходимость обобщений и наметим пути таких обобщений.

Несколько слов о том, что известно всем специалистам, занимающимся разработкой и применением математических методов исследования.

Натуральные, рациональные, действительные числа используются в различных расчетах, основанных на математических моделях. Глубокое изучение натуральных числе было осуществлено уже в Древней Греции. В частности, была установлена бесконечность ряда натуральных чисел. Однако строгая теория действительных чисел была построена только во второй половине XIX в.

Тогда же была разработана теория множеств, оказавшаяся весьма удобной для определения понятий и построения математических моделей. Например, чтобы ввести функцию, задают два множества А и В – область определения и область значений соответственно, а функцию f описывают как отображение из А в В, т.е. как множество всех пар (x, f(x), где х – элемент множества А, а f(x) – соответствующий элемент множества В. Второй пример – чтобы сформулировать вероятностно-статистическую модель какого-либо реального явления, необходимо начать с пространства (множества) элементарных событий и случайных величин – функций, для которых это пространство является областью определения. Практика показывает, что игнорирование этих начальных определений приводит к недоразумениям и ошибкам.

Практически сразу же после появления теории множеств в ней были обнаружены противоречия (парадоксы). Один из них – парадокс Бертрана Рассела, открытый им в 1901 г. Дадим его краткое описание.

Пусть К— множество всех множеств, которые не содержат себя в качестве своего элемента. Содержит ли К само себя в качестве элемента? Если предположить, что содержит, то мы получаем противоречие с «не содержат себя в качестве своего элемента». Если предположить, что К не содержит себя, как элемент, то вновь возникает противоречие, ведь К — множество всех множеств, которые не содержат себя в качестве своего элемента, а значит, должно содержать все такие множества, включая и себя.

Конечно, парадокс Рассела можно сформулировать без употребления термина «множество». Пусть по определению брадобрей - это тот, кто бреет тех¸ кто сам не бреется. Должен ли брадобрей брить самого себя? Ответ «да» противоречит определению брадобрея. Ответ «нет» относит брадобрея к тем, кто сам не бреется, следовательно, он себя сам должен брить.

Противоречие в парадоксе Рассела возникает из-за использования в рассуждении внутренне противоречивого понятия «множества всех множеств» и представления о возможности неограниченного применения законов классической логики при работе с множествами [3, с.17-18]. Для преодоления этого парадокса было предложено несколько путей. Наиболее известный состоит в построении для теории множеств непротиворечивой аксиоматической теории, по отношению к которой являлись бы допустимыми все «действительно нужные» (в некотором смысле) способы оперирования с множествами.

Было предложено несколько возможных аксиоматических теорий, однако ни для одной из них до настоящего момента не найдено доказательства непротиворечивости. Более того, как показал К. Гёдель, доказав ряд теорем о неполноте, такого доказательства не может существовать (в строго определенном смысле). Отметим, что парадоксы ставят под сомнение не только теорию множеств и построенный на ее основе математический инструментарий, но и схемы логических рассуждений. Приходится констатировать, что здание современной математики и логики не имеет законченного обоснования, построено на песке.

Самое интересное состоит в том, что реально работающие математики, разрабатывающие теории и доказывающие теоремы, решающие прикладные задачи, обычно совсем не обеспокоены существованием парадокса Рассела и аналогичных ему. Они спокойно используют «наивную» теорию множеств, не обращая внимание на возможность парадоксов и не обращаясь к той или иной аксиоматической теории множеств. Заниматься такими теориями – удел специалистов по математической логике.

Однако само наличие парадокса Рассела и ему аналогичных показывает, что развитие математики не закончено. Требуется развитие новых концепций. О некоторых из них пойдет речь ниже в настоящей работе.

2. Математические, прагматические и компьютерные числа

Обсудим базовое для математики понятие числа. Будем считать, что читателю знакомы математические числа, о которых рассказывают в средней и высшей школе.

Констатируем, что реально используемые – назовем их прагматическими - числа зачастую не являются математическими. Так, результаты измерений обычно задаются небольшим количеством значащих цифр (от 1 до 5).

Например, записывать численность жителей страны с точностью до одного человека бессмысленно, поскольку указанная численность весьма быстро меняется. Так, для России начала текущего тысячелетия каждые пятнадцать секунд умирал человек, каждые двадцать секунд появлялся новорожденный, следовательно, каждую минуту численность населения уменьшалась на одного человека, а потому любое конкретное значение этой численности с точностью до одного человека могло соответствовать действительности в течение лишь одной минуты.

Экономические величины порядка миллиардов рублей бессмысленно записывать с точностью до копеек. Надо – с точностью до миллионов.

Расчеты обычно ведем, используя десятичную запись чисел. Напомним, что многие математические числа требуют для своей записи бесконечно много десятичных знаков. Например, длина диагонали квадрата со сторонами единичной длины не может быть выражена конечным числом десятичных знаков. Как и длина окружности единичного диаметра и основание натуральных логарифмов. И даже запись результата деления 1 на 3 состоит – в математике – из бесконечного числа десятичных знаков: 0,3333333... Десятичная запись - это декларативная форма представления числа, при которой число непосредственно готово для использования в вычислениях, а представление чисел в виде формул - это процедурная форма представления числа, подобная алгебраической, при которой перед использованием числа для вычислений необходимо предварительно еще вычислить его. Проблема в том, что это надо делать, но это не всегда возможно, даже в принципе (например в случае иррациональных чисел).

Итак, при решении реальных задач мы вынуждены пользоваться не математическими числами, а прагматическими. В результате тождества чистой математики не всегда выполняются при анализе данных, выраженных прагматическими числами.

Например, для выборочной дисперсии, рассчитанной по выборке x₁, x₂, …, x_n, с точки зрения чистой математики справедливо тождество, которое проверяется с помощью равносильных преобразований:

.

Однако расчеты по левой и правой частям этой формулы могут дать весьма различающиеся значения. Например, рассмотрим ситуацию, когда x_i = 10⁹ + y_i, i = 1, 2, …, n, где y_i – величины порядка 1 (для определенности, от (-3) до 3). Тогда в левой части формулы усредняются величины порядка 1 (числа от 0 до 9). А вот в правой из числа порядка 10¹⁸ вычитается число также порядка 10¹⁸, т.е. каждое из них имеет 18 знаков до запятой, и первые 17 из них должны совпасть. Ясно, что из-за погрешностей вычислений такое совпадение будет не всегда. Вычисления по правой части формулы для выборочной дисперсии могут число, заметно отличающееся от результата расчета по левой части. Например, может получиться отрицательное число. Приходилось видеть весьма недоумевающие лица прикладников, у которых дисперсия получилась отрицательной.

Кроме прагматических чисел, целесообразно выделить компьютерные. Они появляются из-за существования в любом компьютере «машинного нуля»: все числа, по абсолютной величине меньшие, чем «машинный нуль», компьютер воспринимает как 0. Как следствие существования «машинного нуля», некоторые результаты чистой математики неверны для расчетов на компьютерах. Например, с точки зрения чистой математики сумма

при росте числа слагаемых стремится к бесконечности (известно, что это сумма растет как lnn – натуральный логарифм числа слагаемых). При расчетах на компьютере при росте числа слагаемых наступит момент, когда очередное слагаемое станет меньше «машинного нуля», компьютер его воспримет как 0, сумма перестанет меняться, останется конечной. (Для конкретного случая можно разрабатывать специально для него приспособленные алгоритмы расчетов. Но это не меняет общего вывода об отличии компьютерных числе от математических.)

Принципиальное различие математических, прагматических и компьютерных чисел подробно обсуждает Е.М. Левич [4].

Приведем еще два парадокса, основанных на этом различии [5].

Как уже отмечалось, все реальные результаты наблюдений записываются рациональными числами (обычно десятичными числами с небольшим - от 2 до 5 - числом значащих цифр). Как известно, множество рациональных чисел счетно, а потому вероятность попадания значения непрерывной случайной величины в него равно 0. Следовательно, все рассуждения, связанные с моделированием непрерывными случайными величинами реальных результатов наблюдений - это рассуждения о том, что происходит внутри множества меры 0. Первый парадокс состоит в том, что множествами меры 0 в теории вероятностей принято пренебрегать. Другими словами, с точки зрения теории вероятностей всеми реальными данными можно пренебречь, поскольку они входят в одно фиксированное множество меры 0. Т.е. реальный мир не существует с точки зрения математика.

Глубже проанализируем ситуацию. Сколько всего чисел используется для записи реальных результатов наблюдений? Речь идет о типовых результатах наблюдений, измерений, испытаний, опытов, анализов в технических, естественнонаучных, экономических, социологических, медицинских и иных исследованиях. Если эти числа в десятичной записи имеют вид (a,bcde)10^k, где a принимает значения от 1 до 9, а стоящие после запятой b, c, d, e - от 0 до 9, в то время как показатель степени k меняется от (-100) до +100, то общее количество возможных чисел равно 9х10⁴х201=18 090 000, т.е. меньше 20 миллионов. А с учетом знака – 40 миллионов. Второй парадокс, усиливающий первый, состоит в том, что для описания реальных результатов наблюдений вполне достаточно 20 миллионов отдельных символов. Бесконечность натурального ряда и континуум числовой прямой - это математические абстракции, надстроенные над дискретной и состоящей из конечного числа элементов реальностью. (При изменении числа значащих цифр принципиальный вывод не меняется.) Таким образом, реальные данные лежат не только во множестве меры 0, но и в конечном множестве, причем число элементов в этом множестве вполне обозримо.

Из сказанного вытекает необходимость модернизации основ математики. Нужен математический аппарат, позволяющий оперировать с прагматическими и компьютерными числами.

3. От обычных множеств – к нечетким

В теории множеств переход от принадлежности элемента множеству к непринадлежности происходит скачком, что не всегда соответствует представлениям о свойствах реальных совокупностей. Следовательно, теорию множеств также необходимо модернизировать. Основное направление при этом – использование множеств с размытыми границами.

В 1965 г. в журнале «Информация и управление» появилась статья Лотфи А. Заде, профессора информатики Калифорнийского Университета в Беркли, специалиста по теории управления сложными системами. Она называлась необычно: «Fuzzy Sets». Второе слово этого названия переводится с английского языка привычным математическим термином «множества», а вот первое никогда до тех пор в математической и кибернетической литературе не использовалось. Согласно словарю, «fuzz» - пух, пушинка, «fuzzy» - пушистый. На русский язык термин «fuzzy» переводят по-разному: нечеткий, размытый, расплывчатый, реже – туманный, пушистый и т.п.

За прошедшие десятилетия «пушистой» тематике посвящены тысячи статей и книг. Появилось новое направление в вычислительной математике и математической кибернетике – теория нечеткости. Выходят международные научные журналы, проводятся конференции, в том числе и в нашей стране. Обсудим, почему необходимо учитывать нечеткость при описании мышления и восприятия человека.

Что такое «Куча»? Знаменитый софизм «Куча» обсуждали еще древнегреческие философы. Вот как можно его изложить: «Одно зерно не составляет кучу. Если к тому, что не оставляет кучи, добавить одно зерно, то куча не получится. Следовательно, никакое количество зерен не составляет кучу».

Рассуждение соответствует известному принципу математической индукции. База индукции – это утверждение: «Одно зерно не составляет кучу». Индуктивный переход: «Если к тому, что не оставляет кучи, добавить одно зерно, то куча не получится». И заключение: «Совокупность n зерен не составляет кучу при любом n». Другими словами: «Никакое количество зерен не составляет кучу».

Полученное утверждение явно нелепо: каждый согласится, что 100 миллионов зерен пшеницы – довольно большая куча (объемом около 6 кубометров). Как же возникает столь абсурдный вывод?

О чем говорит этот софизм? В нем обсуждаются два понятия – «несколько зерен» и «куча» - и показывается, что граница между ними в мышлении людей и в отражающем это мышление естественном языке (русском, английском, китайском, любом другом) нечетка, размыта.

В самом деле, разве можно указать такое число N, что совокупность из N зерен – уже куча, а из (N-1) зерна – еще нет? Можно ли допустить, например, что 325 647 зерен не образуют кучу, а 325 648 – образуют? Конечно, указание точной границы здесь бессмысленно. Ни один человек не сможет различить эти две совокупности зерен.

Представим теперь, что проводится специальная серия опытов: большому числу людей предлагают наборы из n зерен и спрашивают: «Это куча?» И пусть никто не уклоняется от ответа.

Что будет происходить? При малом n все единодушны: «Нет, это не куча, это всего лишь несколько зерен». При многих миллионах зерен все тоже будут едины в своем мнении: «Это куча». А при промежуточных значениях n мнения могут разделиться – одни выскажутся за «кучу», другие против.

Результаты описанного эксперимент допускает плодотворную интерпретацию: каждому числу зерен n можно сопоставить число p_n – долю опрошенных, которые считают n зерен кучей. С такой точки зрения понятие «куча» описывается не одним числом – границей между «несколькими зернами» и «кучей», а последовательностью p_n, n = 1, 2, …, члены которой равны нулю при малых n и единице – при больших.

Софизм «Куча» в начале ХХ в. обсуждал французский математик Эмиль Борель. Он предложил описывать понятие «куча» последовательностью p_n, n = 1, 2, …, и указал способ получения этой последовательности с помощью массового опроса. Исходил Э. Борель из глубокого анализа понятия физической непрерывности, выполненного великим математиком и физиком Анри Пуанкаре. В частности, Пуанкаре писал:

«… Непосредственные результаты опыта могут быть выражены следующими соотношениями:

А = В, В = С, A < C,

которые можно рассматривать как формулу физической непрерывности. Эта формула заключает в себе недопустимое разногласие с законом противоречия; необходимость избежать его и заставила нас изобрести идею математической непрерывности» [6, с.28].

Поясним мысль Пуанкаре. Пусть A(n) – гиря весом в n граммов. Пусть эксперт сравнивает две гири «вручную», т.е. не используя весов. Очевидно, эксперт не в состоянии уловить разницу в 1 грамм, поэтому естественно ожидать, что мнение эксперта будет выражено последовательностью равенств

А(1000) = А(1001), А(1001) = А(1002), …, А(1999) = А(2000).

Вместе с тем гири весом в 1 кг и в 2 кг эксперт сможет различить наверняка, так что по его мнению

А(1000) < A(2000).

Очевидно, два заключения одного и того же эксперта противоречат друг другу. В выводах эксперта нарушается транзитивность. Наблюдаем парадокс того же типа, что и софизм «Куча». Сказанное показывает, что процесс математического моделирования процессов измерений, в том числе получения экспертных мнений, нетривиален.

Понятие «куча» размыто не только для совокупности людей, но и для отдельно взятого человека. Представьте себе, что вам предъявляют один за другим наборы зерен, спрашивая: «Это куча?» Что вы будете отвечать? При малом числе зерен – «нет», при большом – «да», а при промежуточном станете колебаться. Если экспериментатор настойчив, он вытянет у вас ответ типа: «Это скорее куча, чем несколько зерен». А если он убедительно потребует от вас оценить числом степень вашей уверенности, то добьется чего-нибудь вроде: «Семьдесят пять шансов из ста за то, что это куча». В итоге ваше личное мнение будет выражено последовательностью p_n, n = 1, 2, …, того же типа, что и мнение большой совокупности экспертов.

Человек мыслит нечетко. Понятия, используемые людьми, отнюдь не всегда легко выразить числами. Например, что такое «оранжевый цвет»? Казалось бы, ответить на этот вопрос нетрудно – достаточно указать на шкале электромагнитных волн границы, между которыми лежит оранжевый цвет. В «Малой Советской Энциклопедии» (1930 г.) даже указаны конкретные числа: 589 микрометров – грань оранжевого и золотисто-желтого, 656 мкм – красного и оранжевого.

Но подумайте: неужели вы сможете ощутить разницу в цвете при переходе на 1 микрометр – от 655,5 мкм (оранжевый цвет) к 656,5 мкм (красный). Конечно, нет.

Размыты не только представления о цветах. Представьте себе, например, множество петухов. Представили? А теперь скажите: относится ли к нему леденцовый петушок на деревянной палочке? Задумались, не так ли? Вот и здесь расплывчатость…

Описанные ситуации типичны. Понятия естественного языка, с помощью которого мы общаемся друг с другом, как правило, размыты.

Нечеткость свойственна не только естественному языку, но и диалектам науки. Возьмем для примера физику. Зададимся вопросом: можно ли указать длину предмета (для определенности в метрах) с точностью до тридцатого знака после запятой? Вещество состоит из атомов, атомы из электронов, протонов и нейтронов. Можно ли указать абсолютно точно положение электрона? В квантовой механике получен принцип неопределенности: произведение неопределенности в определении импульса частицы на неопределенность в определении ее положения всегда больше вполне определенной величины – постоянной Планка. Импульс электрона в атоме не может достигать сколь угодно высоких значений (импульс – это произведение скорости на массу; скорость не превосходит скорости света, масса электрона известна). Таким образом, неопределенность импульса ограничена. Стало быть, неопределенность в положении электрона всегда больше некоторой величины – согласно расчетам, примерно 10^{-10 метра. Иными словами, неустранимая неточность подстерегает нас уже в десятом знаке после запятой, так что о тридцатом не может быть и речи. Отсюда вывод: длину любого тела следует задавать не одним определенным числом, а совокупностью чисел с размытыми границами, т.е. нечетким множеством.}

Бытует мнение, что непогрешимой четкостью отличается язык математики. Однако это не так. Например, мы уже не раз употребляли слово «множество». Повторим еще раз, это фундаментальное понятие лежит в основе современной математики. Существует математическая теория множеств. Как и во всякой математической теории, все ее положения базируются на системе аксиом. Эту систему можно строить по-разному. Выражаясь языком специалистов, теория множеств может быть аксиоматизирована различными способами. В получающихся при этом разновидностях теории множеств некоторые выводы оказываются прямо противоположными. Возьмем для примера так называемую континуум-гипотезу. При одних аксиоматизациях она верна, при других – верно ее отрицание.

Что же говорить о других менее точных науках? Одному из авторов настоящей работы в свое время пришлось столкнуться с таким любопытным фактом: по определению одной группы медиков «затяжное течение острой пневмонии» имеет место в шести случаях из ста, по мнению другой – в шестидесяти. Различие в 10 раз!

В подобных ситуациях возникает естественное желание навести четкость в понятиях и представлениях. Однако часто разные группы и даже отдельные лица понимают термины по-своему, например, как в только что приведенном примере с термином «затяжное течение острой пневмонии». Удастся ли договориться? Кроме того, в наведении четкости есть своя мера и своя опасная грань, за которой излишняя четкость становится вредной.

Например, при проведении некоторых социологических и экспертных исследований интересуются мнениями опрашиваемых, не учитывая, что эти мнения весьма нечетки или еще не сформировались. Вот вопросы одной, взятой наугад, анкеты: «Что прежде всего необходимо вам для счастья? Иметь интересную работу? Пользоваться уважением окружающих? Любить и быть любимым? Иметь много денег? Приносить пользу людям?» Сумеете ли вы с абсолютной уверенностью выбрать одну и только одну позицию из перечня? Ведь организаторы опроса настаивают на четкости. С расчетом на нее обычно и составляются анкеты. (Вспомним – ведь и мы, проводя мысленный опрос по поводу софизма «Куча», запрещали уклоняться от ответа на вопрос: «Это куча?» - и требовали отвечать либо «да», либо «нет».) И опрашивающие сами уже стараются сформулировать свое мнение поотчетливее. Однако эти мнения зачастую имеют довольно слабую связь с реальными представлениями людей, что порою приводит к существенным ошибкам в прогнозировании на основе подобных социологических или экспертных данных.

Разумно ли в таких ситуациях добиваться предельной четкости? Взвешивая этот вопрос, обратимся еще раз к математике. Как мы видели, даже в ней нет окончательной ясности с некоторыми важными понятиями. Между тем математики в массе своей применяют эти понятия весьма широко и обычно довольно успешно – эффективность математических методов в самых различных сферах знания и практической деятельности общеизвестна. Точно также естественный язык используется без особых затруднений, несмотря на свою нечеткость.

Итак, мы мыслим нечетко, и это нам не мешает. Более того, именно нечеткость мыслей и слов позволяет нам понимать друг друга, приходить к соглашению и действовать совместно. Только представьте, что было бы, если бы постоянно приходилось уточнять используемые в разговоре слова! Иногда приходится это делать – и тогда появляются огромные тексты договоров и инструкций. Стандартная инструкция к мобильному телефону занимает больше 200 страниц – кто же ее полностью прочитает, прежде чем сделает звонок…

Мы убедились, что, во-первых, мышлению человека органически присуща нечеткость, а во-вторых, эта нечеткость ничуть не зазорна: она естественна. Значит, при разработке математических моделей мышления и поведения человека надо учитывать эту нечеткость – игнорировать ее нельзя! Необходим соответствующий математический аппарат, моделирующий нечеткость восприятия, познания и принятия решений.

Но какие математические понятия следует при этом применять?

В основании современной математики лежит понятие множества. Чтобы задать то или иное конкретное множество предметов (объектов, элементов), надо относительно каждого предмета уметь ответить на вопрос: «Принадлежит данный предмет данному множеству или не принадлежит?» Но мы уже видели, что границы понятий, как правило, размыты, так что четкий ответ на подобный вопрос возможен далеко не всегда. Значит, для описания нечеткости надо взять за основу понятие множества, несколько отличающееся от привычного, более широкое, чем оно.

4. Теория нечетких множеств и «нечеткое удвоение» математики

Чтобы определить нечеткое множество, надо сначала задать совокупность всех тех элементов, для которых имеет смысл говорить о мере их принадлежности рассматриваемому нечеткому множеству. Эта совокупность называется универсальным множеством. Например, для «кучи» - это множество натуральных чисел, для описания цветов – отрезок шкалы электромагнитных волн, соответствующий видимому свету.

Пусть A - некоторое универсальное множество. Подмножество B множества A характеризуется своей характеристической функцией

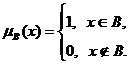(1)

Что такое нечеткое множество? Обычно говорят, что нечеткое подмножество C множества A характеризуется своей функцией принадлежности . Значение функции принадлежности в точке х показывает степень принадлежности этой точки нечеткому множеству. Нечеткое множество описывает неопределенность, соответствующую точке х – она одновременно и входит, и не входит в нечеткое множество С. За вхождение - шансов, за второе – (1- ) шансов.

Если функция принадлежности имеет вид (1) при некотором B, то C есть обычное (четкое) подмножество A. Таким образом, теория нечетких множество является не менее общей математической дисциплиной, чем обычная теория множеств, поскольку обычные множества – частный случай нечетких. Соответственно можно ожидать, что теория нечеткости как целое обобщает классическую математику. Однако позже мы увидим, что теория нечеткости в определенном смысле сводится к теории случайных множеств и тем самым является частью классической математики. Другими словами, по степени общности обычная математика и нечеткая математика эквивалентны. Однако для практического применения в теории принятия решений описание и анализ неопределенностей с помощью теории нечетких множеств весьма плодотворны.

Обычное подмножество можно было бы отождествить с его характеристической функцией. Этого математики не делают, поскольку для задания функции (в ныне принятом подходе) необходимо сначала задать множество. Нечеткое же подмножество с формальной точки зрения можно отождествить с его функцией принадлежности. Однако термин «нечеткое подмножество» предпочтительнее при построении математических моделей реальных явлений.

Теория нечеткости является обобщением интервальной математики (о ней подробнее ниже), в которой для описания реальных объектов вместо чисел используются интервалы. Действительно, функция принадлежности

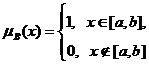(2)

задает интервальную неопределенность – про рассматриваемую величину известно лишь, что она лежит в заданном интервале [a,b]. Тем самым описание неопределенностей с помощью нечетких множеств является более общим, чем с помощью интервалов.

Начало современной теории нечеткости положено работой 1965 г. американского ученого азербайджанского происхождения Л.А. Заде. Основные определения, алгоритмы расчетов и выражающие их свойства теоремы приведены ниже. Рассуждения древнегреческих философов, математиков начала ХХ в. А. Пуанкаре и Э. Бореля обосновывают методологию теорию нечеткости, но как математическая дисциплина она началась с работы Заде. К настоящему времени по теории нечеткости опубликованы тысячи книг и статей, издается несколько международных журналов, выполнено достаточно много как теоретических, так и прикладных работ. В нашей стране концепция Заде активно обсуждалась еще в 60-е и 70-е гг. ХХ в. (см. обзор в [7]), однако первая книга российского автора по теории нечеткости – книга одного из авторов настоящей работы - вышла лишь в 1980 г. [8].

Л.А. Заде рассматривал теорию нечетких множеств как аппарат анализа и моделирования гуманистических систем, т.е. систем, в которых участвует человек. Его подход опирается на предпосылку о том, что элементами мышления человека являются не числа, а элементы некоторых нечетких множеств или классов объектов, для которых переход от «принадлежности» к «непринадлежности» не скачкообразен, а непрерывен. В настоящее время методы теории нечеткости используются почти во всех прикладных областях, в том числе при управлении предприятием, качеством продукции и технологическими процессами. Нет необходимости связывать теорию нечеткости только с гуманистическими системами.

Л.А. Заде использовал термин «fuzzy set» (нечеткое множество). На русский язык термин «fuzzy» переводили как нечеткий, размытый, расплывчатый, и даже как пушистый и туманный. Заде использовал термины «теория нечетких множеств» и «нечеткая логика». Мы предпочитаем говорить о теории нечеткости. Термин «нечеткая логика» не является синонимом к термину «теория нечеткости», поскольку логика – это наука о мышлении человека, а теория нечеткости применяется не только для моделирования мышления. Нечеткая логика – это часть теории нечеткости.

Аппарат теории нечеткости довольно громоздок. Не будем повторять здесь широко известные определения теоретико-множественных операций над нечеткими множествами. Отметим, что операции над множествами в теории нечеткости раздваиваются: объединению соответствуют объединение и сумма, пересечению – пересечение и произведение.

Некоторые равенства алгебры множеств сохраняются для нечетких множеств, другие же не сохраняются. Так, остаются справедливыми законы де Моргана. Дистрибутивный закон справедлив, если используются операции пересечения и объединения, и нарушается для операций произведения и суммы [7, 8].

Удвоение математики. Поскольку теория множеств – основа современной математики, понятие нечеткости позволяет «удвоить математику»: заменяя обычные множества нечеткими, мы можем каждому математическому объекту (понятию, термину) поставить в соответствие его нечеткий аналог. Рассматривают, например, нечеткие классификации, упорядочения, логики, теоремы, алгоритмы, правила принятия решений и т.д., и т.п. Чтобы это перечисление не выглядело для неискушенного читателя просто набором слов, разберем несколько примеров.

Первым в нашем списке упомянуты классификации. Под классификацией имеется в виду разбиение совокупности элементов на классы – группы сходных между собой элементов [9]. В четкой классификации каждый элемент относится к одному определенному классу. А в размытой – задается функция принадлежности элемента различным классам. Расплывчатая классификация обычно больше соответствует реальности, чем строгая.

Представьте себе – идет вам навстречу человек. Лишь в редких случаях вы с уверенностью скажете: «Это блондин». Чаще о цвете волос придется высказаться уклончиво: «Скорее шатен, чем брюнет». Так что, признайтесь, классификация встречных по цвету волос у вас нечеткая. Поэтому пушистые классификации надо изучать – этим и занимается соответствующая часть туманной математики.

Пример нечеткого упорядочения нетрудно найти в магазине, присмотревшись к поведению нерешительного покупателя. Надо приобрести часы, да вот какие? И «Слава» нравится, и «Ракета» современна. Другими словами, и «Слава» на сколько-то процентов привлекательна, и «Ракета» - тут и появляются функции принадлежности марок часов к множеству привлекательных. А ведь сравнивать можно по многим критериям – по внешнему виду, по цене, по надежности и т.д. Для каждого критерия – своя туманность, нужно эти расплывчатости сводить вместе, чтобы принять решение – покупать или не покупать… А для описания всего этого надо развивать математическую теорию нечетких упорядочений, принятия расплывчатых решений…

А что такое нечеткая логика? С позиций обычной логики утверждения бывают либо истинные, либо ложные. А в размытой логике – утверждения в какой-то степени истинны, а в какой-то – ложны. Присмотритесь к себе – очень многое, что вы говорите и думаете, имеет лишь относительную истинность. Например, вы сказали: «Вчера я хорошо поработал». Сразу возникают вопросы: «А разве нельзя было поработать еще лучше? Что значит – хорошо?» Согласитесь: ваши слова истинны не на сто процентов. И подобное можно сказать не только по части житейских высказываний, но и относительно утверждений науки.

Вот, скажем, как выглядит нечеткий аналог теоремы о том, что три медианы треугольника пересекаются в одной точке:

«Пусть АВ, ВС и СА – примерно прямые линии, которые образуют примерно треугольник с вершинами А, В и С. Пусть М₁, М₂, М₃ – примерно середины сторон ВС, СА и АВ соответственно. Тогда примерно прямые линии АМ₁, ВМ₂ и СМ₃ образуют примерно треугольник Т₁Т₂Т₃, который более или менее мал относительно треугольника АВС» [10, с.137-138].

Конечно, эта формулировка становится разумной только после того, как будет точно определен смысл слов «примерно» и «более или менее мал». Вот как, скажем, можно уточнить понятие «примерно отрезок АВ»: под ним будем понимать любую кривую, проходящую через точки А и В, такую, что расстояние (в обычном смысле) от любой точки кривой до отрезка АВ мало по отношению к длине АВ. Остается выяснить, что значит «мало». Ответ может даваться нечетким множеством со своей функцией принадлежности.

Нечеткие алгоритмы – тоже не экзотика. Многие инструкции в какой-то мере расплывчаты. Беря поваренную книгу, любая хозяйка знает: чтобы блюдо удалось, к печатным рецептам надо добавить свою интерпретацию, а также смекалку и удачу. Если же поручить роботу готовить суп, то придется нечеткие слова естественного языка определять с помощью функций принадлежности. Например, определить понятие «варить до готовности». Значит, нужна соответствующая математическая теория – теория нечетких алгоритмов.

Продолжать можно без конца. «Удвоение математики» - настоятельная необходимость. Однако «скоро сказка сказывается, да нескоро дело делается». Теория нечеткости молода. Всего лишь почти пятьдесят лет! Миг по сравнению с двадцатью пятью веками геометрии!

Польза нечеткости. Несмотря на свою молодость, нечеткая математика находит успешные приложения. Примеры описания неопределенностей с помощью нечетких множеств часто приводятся в литературе. Например, в [11] приведено описание понятия «богатый человек», разобрана разработка методики ценообразования на основе теории нечетких множеств.

Поскольку размытость свойственна самому восприятию и мышлению человека, теория нечеткости используется прежде всего в науках, изучающих эти стороны человеческой натуры: в психологии, в социологии, в исследовании операций… Зачастую в ходе социологических и экспертных опросов человеку легче сформулировать свое мнение расплывчато, а не предельно четко, и размытый ответ является к тому же более адекватным. Поэтому создаются методы сбора и анализа нечеткой информации.

Пример – система управления рыбным промыслом. Исходная информация – сообщения с судов и мнения экспертов. Они нечетки: в таком-то квадрате количество рыбы оценивается величиной между таким-то нижним и таким-то верхним пределами, суда стоит направить туда-то, и т.д. По этим данным согласно алгоритмам нечеткой математики производится оптимизация в расплывчатых условиях. И затем выдается четкий приказ: каким судам куда идти. (Результат его выполнения – количество выловленной рыбы – разумеется, нельзя предсказать точно: нечеткость исходной информации не устраняется четкостью приказа.)

Аппарат теории нечеткости оказался полезным в самых разных прикладных областях – в химической технологии и в медицине, при управлении движением автотранспорта и в экономической географии, в теории надежности и при контроле качества продукции.

Группа химиков во главе с академиком В.В. Кафаровым изучала процессы, протекающие в ванне стекловаренной печи при производстве листового стекла. Основное при этом – исследовать распределение поля температур в бассейне ванны. Можно это делать в классическом стиле, рассматривая дифференциальное уравнение в частных производных, которому удовлетворяет поле температур. Уравнение это можно решить хорошо известным среди специалистов методом Фурье. Но пушистые химики предлагают другой подход. В соответствии с ним приращение температуры при переходе от одной точки бассейна печи к другой является нечетким. Химики рассчитали поле температур размытым методом и сравнили свои результаты с числами, полученными по методу Фурье. Относительное расхождение не превышало 6%, что считается пренебрежимо малым в этой области. Но компьютерные расчеты заняли в 5-6 раз меньше машинного времени.

Парадокс теории нечеткости. В концепции размытости есть свой подход к познанию мира, к построению математических моделей реальных явлений. Хочется во всем увидеть нечеткость и смоделировать эту нечеткость подходящим расплывчатым объектов.

Мы уже рассмотрели много примеров, когда такой подход разумен и полезен. Возникает искушение провозгласить тезис: «Все в мире нечетко». Он выглядит особенно привлекательно в связи с большой вредностью излишней, обманчивой четкости. Но можно ли этот тезис провести последовательно?

Нечеткое множество задается функцией принадлежности. Обратим внимание на аргумент и на значение этой функции. Четкие это объекты или размытые? Тезис «все в мире нечетко» наталкивает на мысль, что они расплывчаты.

Действительно, вспомним примеры – скажем, софизм «Куча». Сначала поговорим про аргумент функции, т.е. про число зерен, относительно которых решается вопрос: «Куча это или не куча?» Число зерен в достаточно большой совокупности – разве может оно быть известно абсолютно точно? Как ни считай зерна – вручную, на вес, автоматически – всегда возможны ошибки (человек может ошибиться, автоматические весы измеряют с погрешностями (описаны в паспорте средства измерения), и даже – могут сломаться…). Или пройдемся по остальным примерам – всюду то же самое.

А теперь – о значении функции принадлежности. Оно уж тем более нечетко! Мнение человека – разве имеет смысл выражать его хотя бы с тремя значащими цифрами? В социологии общепринято, что человек в словесных оценках обычно не может различить больше трех, в лучшем случае – шести градаций (эти величины вытекают и из математической модели, разработанной в [12]). Отсюда можно вывести с помощью соответствующего расчета, что функция принадлежности, отражающее мнение одного человека, может быть определена лишь с точностью 0,17 – 0,33. Так что мнение отдельного лица следовало бы выразить не тонкой кривой – графиком функции, а довольно широкой полосой. Если же функция принадлежности строится как среднее (среднее арифметическое или медиана) индивидуальных мнений, то и тогда ее значения известны отнюдь не абсолютно точно из-за того, что опрашиваемая совокупность людей обычно не включает и малой доли тех, кого можно было опросить. И только если значения функции принадлежности определяются по аналитическим формулам, они известны абсолютно точно. Но тогда возникает законный вопрос: насколько обоснованы сами эти формулы? Обычно оказывается, что обоснование у них довольно слабое…

Каков итог? И аргумент, и значение функции принадлежности, как правило, необходимо считать нечеткими.

Что же из этого следует? Начнем опять с аргумента. Он сам является не строго определенной величиной, а некоторым нечетким множеством величин, значит, описывается некоторой функцией принадлежности – задается каким-то своим аргументом. А этот новый аргумент – он ведь тоже нечеток! Опять появляется функция принадлежности – с каким-то третьим аргументом. И так далее.

Остановимся ли мы когда-либо на этом пути? Если остановимся, то должны будем использовать четкие значения аргумента – а это противоречит тезису «все в мире нечетко». В соответствии с эти тезисом четкие значения фиктивны, им ничто в мире не соответствует. Если же не остановимся, то получим бесконечную последовательность нечетких моделей, в которой из каждого размытого множества, как из матрешки, вылезает новая расплывчатость. Возможны ли при этом обоснованные расчеты?

Далее, значение функции принадлежности также необходимо считать нечетким. Л.А. Заде разработал аппарат пушистых множеств с размытыми функциями принадлежности, благоразумно не вдаваясь при этом в рассуждения о том, на каком же шагу считать функции принадлежности четкой.

Итак, основной парадокс теории нечеткости состоит в том, что привлекательный тезис «все в мире нечетко» невозможно последовательно раскрыть в рамках математических моделей. Конечно, описанный парадокс не мешает успешно использовать расплывчатую математику в конкретных приложениях. Из него вытекает лишь необходимость указывать и обсуждать границы ее применимости.

5. О сведении теории нечетких множеств к теории случайных множеств

Нечеткость и случайность. С самого начала появления современной теории нечеткости в 1960-е годы началось обсуждение ее взаимоотношений с теорией вероятностей. Дело в том, что функция принадлежности нечеткого множества напоминает плотность распределения вероятностей. Отличие только в том, что сумма вероятностей по всем возможным значениям случайной величины (или интеграл, если множество возможных значений несчетно) всегда равна 1, а сумма S значений функции принадлежности (в непрерывном случае — интеграл от функции принадлежности) может быть любым неотрицательным числом. Возникает искушение пронормировать функцию принадлежности, т.е. разделить все ее значения на S (при S 0), чтобы свести ее к распределению вероятностей (или к плотности вероятности). Однако специалисты по нечеткости справедливо возражают против такого «примитивного» сведения, поскольку оно проводится отдельно для каждой размытости (нечеткого множества), и определения обычных операций над нечеткими множествами согласовать с ним нельзя. Последнее утверждение означает следующее. Пусть указанным образом преобразованы функции принадлежности нечетких множеств А и В. Как при этом преобразуются функции принадлежности АÇВ, АÈВ, А + В, АВ? Установить это невозможно в принципе. Последнее утверждение становится совершенно ясным после рассмотрения нескольких примеров пар нечетких множеств с одними и теми же суммами значений функций принадлежности, но различными результатами теоретико-множественных операций над ними. Причем и суммы значений соответствующих функций принадлежности для этих результатов теоретико-множественных операций, например, для пересечений множеств, также различны.

В работах по нечетким множествам время от времени утверждается, что теория нечеткости самостоятельный раздел прикладной математики и не имеет отношения к теории вероятностей. Некоторые авторы, обсуждавшие взаимоотношения теории нечеткости и теории вероятностей, подчеркивали различие между этими областями теоретических и прикладных исследований. Обычно сопоставляют аксиоматику и сравнивают области приложений.

Аргументы при втором типе сравнений не имеют доказательной силы, поскольку по поводу границ применимости даже такой давно выделившейся научной области, как вероятностно-статистические методы, имеются различные мнения. Более того, нет единства мнений об арифметике. Напомним, что итог рассуждений одного из наиболее известных французских математиков Анри Лебега по поводу границ применимости арифметики таков: «Арифметика применима тогда, когда она применима» (см. [7, 8]).

При сравнении различных аксиоматик теории нечеткости и теории вероятностей нетрудно увидеть, что списки аксиом различаются. Из этого, однако, отнюдь не следует, что между указанными теориями нельзя установить связь, типа известного сведения евклидовой геометрии на плоскости к арифметике (точнее к теории числовой системы R²). Эти две аксиоматики — евклидовой геометрии и арифметики — на первый взгляд весьма сильно различаются.

Можно понять желание энтузиастов теории нечеткости подчеркнуть принципиальную новизну своего научного аппарата. Однако не менее важно установить связи этого подхода с ранее известными.

Проекция случайного множества. Как оказалось, теория нечетких множеств тесно связана с теорией случайных множеств. Еще в 1975 г. доказано (см. [7, 8, 12]), что нечеткие множества естественно рассматривать как «проекции» случайных множеств. Рассмотрим этот метод сведения теории нечетких множеств к теории случайных множеств.

Определение 1. Пусть A = A(w) — случайное подмножество конечного множества Y. Нечеткое множество В, определенное на Y, называется проекцией А и обозначается Proj A, если

m_B(y) = P(y ÎA) (3)

при всех y Î Y.

Очевидно, каждому случайному множеству А можно поставить в соответствие с помощью формулы (3) нечеткое множество В = Proj A. Оказывается, верно и обратное.

Теорема 1. Для любого нечеткого подмножества В конечного множества Y существует случайное подмножество А множества Y такое, что В = Proj A.

Изучение связи между нечеткими и случайными множествами началось с введения случайных множеств с целью развития и обобщения аппарата нечетких множеств Л. Заде. Дело в том, что математический аппарат нечетких множеств не позволяет в должной мере учитывать различные варианты зависимости между понятиями (объектами), моделируемыми с его помощью, т.е. не является достаточно гибким. Так, для описания «общей части» двух нечетких множеств есть лишь две операции — произведение и пересечение. Если применяется первая из них, то фактически предполагается, что множества ведут себя как проекции независимых случайных множеств. Операция пересечения также накладывает вполне определенные ограничения на вид зависимости между множествами, причем в этом случае найдены даже необходимые и достаточные условия [7, 8, 12]. Желательно иметь более широкие возможности для моделирования зависимости между множествами (понятиями, объектами). Использование математического аппарата случайных множеств предоставляет такие возможности.

Цель сведения теории нечетких множеств к теории случайных множеств в том, чтобы за любой конструкцией из нечетких множеств увидеть конструкцию из случайных множеств, определяющую свойства первой, аналогично тому, как за плотностью распределения вероятностей мы видим случайную величину. Приведем один из результатов по сведению алгебры нечетких множеств к алгебре случайных множеств.

Теорема 2. Пусть B₁, B₂, B₃, …, B_t — некоторые нечеткие подмножества множества Y из конечного числа элементов. Рассмотрим результаты последовательного выполнения теоретико-множественных операций

B^m = ((…((B₁B₂)B₃)…)B_m–1) B_m, m = 1, 2, …, t,

где  — символ одной из следующих теоретико-множественных операций над нечеткими множествами: пересечение, произведение, объединение, сумма (на разных местах могут стоять разные символы). Тогда существуют случайные подмножества A₁, A₂, A₃, …, A_t того же множества Y такие, что

ProjA_i = B_i, i = 1, 2, …, t,

и, кроме того, результаты теоретико-множественных операций связаны аналогичными соотношениями

Proj{((…((A₁ Ä A₂) Ä A₃) Ä A_m–1) Ä A_m} = B^m, m = 1, 2, …, t,

где знак Ä означает, что на рассматриваемом месте стоит символ пересечения случайных множеств, если в определении B^m стоит символ пересечения или символ произведения нечетких множеств, и соответственно символ объединения случайных множеств, если в B^m стоит символ объединения или символ суммы нечетких множеств.

6. Интервальные числа как частный случай нечетких множеств

Интервальное число – это нечеткое множество с функцией принадлежности, заданной формулой (2). Проще говоря, интервальное число – это интервал [a, b]. Интервальные числа часто используются для описания результатов измерений, поскольку измерение всегда проводится с некоторой неопределенностью. Прогноз погоды, как и другие прогнозы, дается в виде интервала, например: «Температура завтра днем будет 15 – 17 градусов Цельсия».

Арифметические операции над интервальными числами [a, b] и [c, d] определяются следующим образом:

[a, b] + [c, d] = [a + c, b + d], [a, b] – [c, d] = [a – d+ c, b – c],

[a, b] [c, d] = [ac, bd], [a, b] / [c, d] = [a/d, b/c]

(формулы для умножения и деления приведены в случае положительных чисел a, b, c, d).

Определив арифметические операции, можем по аналогии с обычной математикой проводить различные расчеты, поскольку алгоритмы расчетов представляют собой последовательности арифметических действий.

7. Развитие интервальной математики. «Интервальное удвоение» математики

Первая монография по интервальной математике была опубликована Р.Е. Муром в 1966 г. (практически одновременно с первой статьей Л.А. Заде по нечетким множествам), а на русском языке – Ю.И. Шокиным в 1981 г. В дальнейшем интервальная математика активно развивалась, но не так быстро, как теория нечетких множеств. Исключением является статистика интервальных данных, в которой получено много интересных результатов (они приведены в одной из четырех глав монографии [7]), в то время как статистика нечетких данных до сих пор гораздо менее развита и представляет собой в основном результат применения общих подходов статистики объектов нечисловой природы, являющихся элементами пространств произвольного вида [7].

Любую математическую конструкцию, использующую числа, можно обобщить, заменив обычные числа на интервальные. Таким образом, применение интервальных чисел позволяет произвести «интервальное удвоение» математики. Открывается большое поле для теоретических исследований, имеющих непосредственный практический интерес. Вначале основные применения были связаны с автоматическим контролем ошибок округления при вычислениях на ЭВМ. Затем начали учитывать ошибки дискретизации численных методов и ошибки в начальных данных. Статистика интервальных данных исходит из модели, согласно которой элементы выборки известны лишь с точностью до «плюс-минус дельта», т.е. выборка состоит из интервалов фиксированной длины со случайными концами.

Констатируем необходимость расширения математического аппарата с целью учета присущих реальности нечеткости и интервальности. Такая необходимость отмечалась в ряде публикаций [35-37], но пока еще не стала общепризнанной. На описании неопределенностей с помощью вероятностных моделей не останавливаемся, поскольку такому подходу посвящено множество работ.

8. Система как обобщение множества. Системное обобщение математики и задачи, возникающие при этом

В науке принято два основных принципа определения понятий:

– через подведение определяемого понятия под более общее понятие и выделение из него определяемого понятия путем указания одного или нескольких его специфических признаков (например, млекопитающие – это животные, выкармливающие своих детенышей молоком);

– процедурное определение, которое определяет понятие путем указания пути к нему или способа его достижения (магнитный северный полюс – это точка, в которую попадешь, если все время двигаться на север, определяя направление движения с помощью магнитного компаса).

Как это ни парадоксально, но понятия системы и множества могут быть определены друг через друга, т.е. трудно сказать, какое из этих понятие является более общим.

Определение системы через множество.

Система есть множество элементов, взаимосвязанных друг с другом, что дает системе новые качества, которых не было у элементов. Эти новые системные свойства еще называются эмерджентными, т.к. не очень просто понять, откуда они берутся. Чем больше сила взаимодействия элементов, тем сильнее свойства системы отличаются от свойств множества и тем выше уровень системности и синергетический эффект. Получается, что система – это множество элементов, но не всякое множество, а только такое, в котором элементы взаимосвязаны (это и есть специфический признак, выделяющий системы в множестве), т.е. множество – это более общее понятие.

Определение множества через систему.

Но можно рассуждать и иначе, считая более общим понятием систему, т.е. мы ведь можем определить понятие множества через понятие системы. Множество – это система, в которой сила взаимодействия между элементами равна нулю (это и есть отличительный признак, выделяющий множества среди систем). Тогда более общим понятием является система, а множества – это просто системы с нулевым уровнем системности.

Вторая точка зрения объективно является предпочтительной, т.к. совершенно очевидно, что понятие множества является предельной абстракцией от понятия системы и реально в мире существуют только системы, а множеств в чистом виде не существует, как не существует математической точки. Точнее сказать, что множества, конечно, существуют, но всегда исключительно и только в составе систем как их базовый уровень иерархии, на котором они основаны.

Из этого вытекает очень важный вывод: все понятия и теории, основанные на понятии множества, допускают обобщение путем замены понятия множества на понятие системы и тщательного прослеживания всех последствий этой замены. При этом более общие теории будут удовлетворять принципу соответствия, обязательному для более общих теорий, т.е. в асимптотическом случае, когда сила взаимосвязи элементов систем будет стремиться к нулю, системы будут все меньше отличаться от множеств и системное обобщение теории перейдет к классическому варианту, основанному на понятии множества. В предельном случае, когда сила взаимосвязи точно равна нулю, системная теория будет давать точно такие же результаты, как основанная на понятии множества.

Этот вывод верен для всех теорий, но в данной работе для авторов наиболее интересным и важным является то, что очень многие, если не практически все понятия современной математики основаны на понятии множества, в частности на математической теории множеств. В частности, к таким понятиям относятся понятия:

– математической операции: преобразования одного или нескольких исходных множеств в одно или несколько результирующих;

– функциональной зависимости: отображение множества значений аргумента на множество значений функции для однозначной функции одного аргумента или отображение множеств значений аргументов на множества значений функций для многозначной функции многих аргументов;

– «количество информации»: функция от свойств множества.

В работе [186] впервые сформулирована и обоснована программная идея системного обобщения математики, суть которой состоит в тотальной замене понятия "множество" на более общее понятие "система" и прослеживании всех последствий этого. При этом обеспечивается соблюдение принципа соответствия, обязательного для более общей теории, т.к. при понижении уровня системности система по своим свойствам становится все ближе к множеству и система с нулевым уровнем системности и есть множество. Приводится развернутый пример реализации этой программной идеи в области теории информации, в качестве которого выступает предложенная в 2002 году системная теория информации [97], являющаяся системным обобщением теории информации Найквиста – Больцмана – Хартли – Шеннона и семантической теории информации Харкевича. Основа этой теории состоит в обобщении комбинаторного понятия информации Хартли I = Log₂N на основе идеи о том, что количество информации определяется не мощностью множества N, а мощностью системы, под которой предлагается понимать суммарное количество подсистем различного уровня иерархии в системе, начиная с базовых элементов исходного множества и заканчивая системой в целом. При этом в 2002 году, когда было предложено системное обобщение формулы Хартли, число подсистем в системе, т.е. мощность системы N_s, предлагалось рассчитывать по формуле:

.

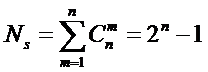Соответственно, системное обобщение формулы Хартли для количества информации в системе из n элементов предлагалось в виде:

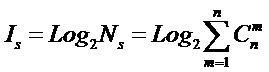
В работе [270] дано системное обобщение формулы Хартли для количества информации для квантовых систем, подчиняющиеся статистике как Ферми-Дирака, так и Бозе-Эйнштейна, и стало ясно, что предложенные в 2002 году в работе [97] вышеприведенные выражения имеют силу только для систем, подчиняющихся статистике Ферми-Дирака.

В работе [188] кратко описывается семантическая информационная модель системно-когнитивного анализа (СК-анализ), вводится универсальная информационная мера силы и направления влияния значений факторов (независимая от их природы и единиц измерения) на поведение объекта управления (основанная на лемме Неймана – Пирсона), а также неметрический интегральный критерий сходства между образами конкретных объектов и обобщенными образами классов, образами классов и образами значений факторов. Идентификация и прогнозирование рассматривается как разложение образа конкретного объекта в ряд по обобщенным образам классов (объектный анализ), что предлагается рассматривать как возможный вариант решения на практике 13-й проблемы Гильберта.

В статьях [189, 191] обоснована идея системного обобщения математики и сделан первый шаг по ее реализации: предложен вариант системной теории информации [97, 201]. В данной работе осуществлена попытка сделать второй шаг в этом же направлении: на концептуальном уровне рассматривается один из возможных подходов к системному обобщению математического понятия множества, а именно – подход, основанный на системной теории информации. Предполагается, что этот подход может стать основой для системного обобщения теории множеств и создания математической теории систем. Сформулированы задачи, возникающие на пути достижения этой цели (разработки системного обобщения математики) и предложены или намечены пути их решения:

Задача 1: найти способ представления системы как совокупности взаимосвязанных множеств.

Задача 2: сформулировать, чем отличаются друг от друга различные системы, состоящие из одних и тех же базисных элементов.

Задача 3: обосновать принципы геометрической интерпретации понятий: "элемент системы" и "система".

Задача 4: предложить способы аналитического описания (задания) подсистем как элементов системы.

Задача 5: описать системное семантическое пространство для отображения систем в форме эйдосов (эйдос-пространство).

Задача 6: описать принцип формирования эйдосов (включая зеркальные части).

Задача 7: показать, что базовая когнитивная концепция [97] формализуется многослойной системой эйдос-пространств (термин автора) различных размерностей.

Задача 8: показать, что системная теория информации позволяет непосредственно на основе эмпирических данных определять вид функций принадлежности, т.е. решать одну из основных задач теории нечетких множеств.

Задача 9: сформулировать перспективы: разработка операций с системами: объединение (сложение), пересечение (умножение), вычитание. Привести предварительные соображения по сложению систем.

В данной работе эти варианты решения не приводятся из-за ограниченности ее объема.

9. Системное обобщение операций над множествами (на примере операции объединения булеанов)

В работе [240] рассматривается реализация математической операции объединения систем, являющаяся обобщением операции объединения множеств в рамках системного обобщения теории множеств. Эта операция сходна с операцией объединения булеанов классической теории множеств. Но в отличие от классической теории множеств в ее системном обобщении предлагается конкретный алгоритм объединения систем и обосновывается количественная мера системного (синергетического, эмерджентного) эффекта, возникающего за счет объединения систем. Для этой меры предложено название: «Обобщенный коэффициент эмерджентности Р. Хартли» из-за сходства его математической формы с локальным коэффициентом эмерджентности Хартли и отражающим степень отличия системы от множества её базовых элементов[1]. Приводится ссылка на авторскую программу, реализующую предложенный алгоритм и обеспечивающую численное моделирование объединения систем при различных ограничениях на сложность систем и при различной мощности порождающего множества, приводятся некоторые результаты численного моделирования.

В работе [241] предлагается общее математическое выражение для количественной оценки системного (синергетического) эффекта, возникающего при объединении булеанов (систем), являющихся обобщением множества в системном обобщении теории множеств и независящее от способа (алгоритма) образования подсистем в системе. Для этой количественной меры предложено название: «Обобщенный коэффициент эмерджентности Р.Хартли» из-за сходства его математической формы с локальным коэффициентом эмерджентности Хартли, отражающим степень отличия системы от множества его базовых элементов. Для локального коэффициента эмерджентности Хартли также предложено обобщение, независящее от способа (алгоритма) образования подсистем в системе. Приводятся численные оценки системного эффекта при объединении двух систем с применением авторской программы, на которую дается ссылка.

10. Системное обобщение понятия функции и функциональной зависимости. Когнитивные функции. Матрицы знаний как нечеткое с расчетной степенью истинности отображение системы аргументов на систему значений функции

Выше кратко рассматривается программная идея системного обобщения понятий математики (в частности теории информации), основанных на теории множеств, путем тотальной замены понятия множества на более содержательное понятие системы и прослеживания всех последствий этого. Частично эта идея была реализована автором при разработке автоматизированного системно-когнитивного анализа (АСК-анализа) [266], математическая модель которого основана на системном обобщении формул для количества информации Хартли и Харкевича [97].

В работе [166] реализуется следующий шаг: предлагается системное обобщение понятия функциональной зависимости, и вводятся термины "когнитивные функции" и "когнитивные числа". На численных примерах показано, что АСК-анализ обеспечивает выявление когнитивных функциональных зависимостей в многомерных зашумленных фрагментированных данных.

В работе [140] намечены принципы применения многозначных функций многих аргументов для описания сложных систем и предложено матричное представление этих функций.

В работе [218] обсуждается возможность восстановления значений одномерных и двумерных функций как между значениями аргумента (интерполяция), так и за их пределами (экстраполяция) на основе использования априорной информации о взаимосвязи между признаками аргумента и значениями функции в опорных точках с применением системно-когнитивного анализа и его инструментария – системы «Эйдос». Приводятся численные примеры и визуализация результатов. Предлагается применение аппарата многомерных когнитивных функций для решения задач распознавания и прогнозирования на картографических базах данных.

В работе [226] на примере решения проблемы управления агропромышленным холдингом рассматривается технология когнитивных функций СК-анализа, обеспечивающая как выявление знаний из эмпирических данных, так и использование этих знаний для поддержки принятия решений по управлению холдингом в целом на основе управления характеристиками входящих в него предприятий.

В работе [235] рассматривается применение метода автоматизированного системно-когнитивного анализа и его программного инструментария – системы «Эйдос» для выявления причинно-следственных зависимостей из эмпирических данных. В качестве инструментария для формального представления причинно-следственных зависимостей предлагаются когнитивные функции.

Когнитивные функции представляют собой многозначные интервальные функции многих аргументов, в которых различные значения функции в различной степени соответствуют различным значениям аргументов, причем количественной мерой этого соответствия выступает знание, т.е. информация о причинно-следственных зависимостях в эмпирических данных, полезная для достижения целей.

В работе [239] на основе применения аппарата когнитивных функций впервые исследована зависимость параметров движения полюса Земли от положения небесных тел Солнечной системы. В последующем эти результаты развиты в монографии [108].

Наиболее полно метод визуализации когнитивных функций, как новый инструмент исследования эмпирических данных большой размерности, раскрыт в работе [243].

В работе [244] рассматривается новая версия системы искусственного интеллекта «Эйдос-астра» для решения прикладных задач с эмпирическими данными большой размерности. Приложение, написанное на языке JAVA, обеспечивает GUI (графический интерфейс пользователя) и позволяет подготовить и выполнить визуализацию матрицы знаний без ограничений, налагаемых реализацией предыдущих версий системы «Эйдос-астра». Отметим, что в системе Эйдос-Х++ все эти ограничения на размерность моделей также сняты в универсальной форме, не зависящей от предметной области.

В работе [254] рассмотрена глубокая взаимосвязь между теорией автоматизированного и автоматического управления и системно-когнитивным анализом и его программным инструментарием – системой «Эйдос» в их применении для интеллектуального управления сложными системами. Предлагается технология, позволяющая на практике реализовать интеллектуальное автоматизированное и даже автоматическое управление такими объектами управления, для которых ранее управление реализовалось лишь на слабоформализованном уровне, как правило, без применения математических моделей и компьютеров. К таким объектам управления относятся, например, технические системы, штатно качественно-изменяющиеся в процессе управления, биологические и экологические системы, социально-экономические и психологические системы. Намечены возможности получения когнитивных передаточных функций сложных многопараметрических нелинейных объектов управления на основе зашумленной фрагментированной эмпирической информации об их фактическом поведении под действием различных сочетаний значений факторов различной природы.

Ясно, что если величина интервала будет стремиться к нулю, то интервальные функции, к которым относятся и когнитивные функции, будут асимптотически приближаться к абстрактным математическим функциям, которые можно считать интервальными функциями с нулевой величиной интервала. Поэтому интервальная математика может рассматриваться как более общая, чем точная и для нее выполняется известный принцип соответствия[2], обязательный для более общих теорий.

В когнитивных функциях, представленных на рис. 1, цветом отображено количество информации в интервальном значении аргумента об интервальном значении функции. Или выражаясь точнее, цветом отображено количество информации в интервальном значении аргумента о том, что (при этом значении аргумента) функция примет определенное интервальное значение. Или еще точнее, цветом отображено количество информации о том, что при значении аргумента, попадающем в данный интервал, функция примет определенное значение, попадающее в соответствующий интервал.

Из рис. 1 мы видим, что об одних значениях функции в значениях аргумента содержится больше информации, а о других меньше. Это значит, что различные значения аргумента с разной степенью определенности обуславливают соответствующие значения функции. Иначе говоря, зная одни значения аргумента, мы весьма определенно можем сказать о соответствующем значении функции, а по другим значениям мы можем судить о значении функции лишь приблизительно, т.е. с гораздо большей погрешностью или неопределенностью.

Таким образом, когнитивная функция содержит информацию не только о соответствии значений функции значениям аргумента, как абстрактная математическая функция, но и о достоверности высказывания о том, что именно такое их соответствие имеет место в действительности, причем эта достоверность меняется от одних значений аргумента и функции к другим.

Получается, что в каждом значении аргумента содержится определенная информация о каждом значении функции. Эта информация может быть больше или меньше, она может быть положительная или отрицательная, т.е. в когнитивной функции каждому значению аргумента соответствуют все значения функции, но в различной степени. Из этого следует также, что каждое значение функции обуславливается различными значениями аргумента, но каждое из них обусловливает это значение в различной степени. Поэтому когнитивные функции являются многозначными функциями многих аргументов.

Это понятие напоминает доверительный интервал, но с той разницей, что доверительный интервал всегда растет со значением аргумента, а количество информации может и возрастать, и уменьшаться. Если осуществляется интерполяция или прогноз значения когнитивной функции, то при этом одновременно определяется и достоверность этой интерполяции или этого прогноза. На когнитивной функции эта достоверность представлена в форме полупрозрачной полосы, ширина которой обратно пропорциональна достоверности (как в доверительном интервале), т.е. чем точнее известно значение функции, тем уже полоса, и чем оно более неопределенно, тем она шире.

В теоретической математике нет меры причинно-следственной связи. Математика оперирует абстрактными понятиями, а понятие причинно-следственной связи является содержательным понятием, относящимся к конкретной изучаемой, в том числе и эмпирически, предметной области. Математические понятия функциональной зависимости или корреляция не являются такой мерой. Правда, в статистике есть критерий хи-квадрат, который действительно является мерой причинно-следственной связи, но статистика специально разработана с целью изучения конкретных явлений и этим существенно отличается от абстрактной теоретической математики.

Мы рассматриваем числовые и лингвистические данные, как сырые данные, полученные непосредственно из опыта и еще не подвергнутые какой-либо обработке. Эти эмпирические данные могут быть преобразованы в информацию путем их анализа. Информация есть осмысленные данные. Смысл согласно концепции смысла Шешка-Абельсона, которой мы придерживаемся, представляет собой знание причинно-следственных зависимостей. Причинно-следственные зависимости возможны только между событиями, а не между данными. Поэтому анализ данных, в результате которого они преобразуются в информацию, включает два этапа:

– нахождение событий в данных;

– выявление причинно-следственных связей между событиями.

Знания представляют собой информацию, полезную для достижения цели. Если такой целью является решение задач прогнозирования, принятия решений и исследования моделируемой предметной области путем исследования ее модели (это корректно, если модель адекватна), то информационная модель является и когнитивной моделью, т.е. интеллектуальной моделью или моделью знаний.

Поэтому когнитивные функции являются наглядным графическим отображение наших знаний о причинно-следственных связях между интервальными или лингвистическими значениями аргумента и интервальными или лингвистическими значениями функции.

Когнитивные функции представляют собой графическое отображение сечений многомерного эйдос-пространства (базы знаний) системы «Эйдос-Х++» плоскостями, содержащими заданные описательные и классификационные шкалы с фактически имеющимися у них интервальными значениями (градациями).

Рассмотрим с позиций теории информации, чем отличаются когнитивные функции от абстрактных математических функций. Формально по точному значению аргумента любой абстрактной математической функции возможно точно узнать ее точное значение. Но на практике это возможно лишь тогда, когда и значения аргумента, и значения функции являются целыми числами. Если же они являются иррациональными числами, то совершенно ясно, что точное их значение никогда не может быть ни вычислено на любом компьютере с ограниченной вычислительной мощностью, ни записано, ни на каких носителях с ограниченной информационной емкостью, ни передано ни по каким каналам связи с ограниченной пропускной способностью. Поэтому точное знание значения иррациональной функции означает доступ к бесконечному количеству информации. На практике же мы, конечно, всегда имеем дело с ограниченной точностью или знаем значения функции с некоторой погрешностью, т.е. оперируем конечным количеством информации в значениях аргумента о значениях функции. Но каким именно количеством информации? До разработки математического аппарата и программного инструментария когнитивных функций это вопрос как-то ребром не ставился и был в тени приоритетных направлений исследований. Ответом на это вопрос и является теория когнитивных функций, где каждому значению аргумента соответствует не только значение функции, но и количество информации в битах, содержащееся в этом значении аргумента о том, что ему соответствует данное значение функции. В оцифрованных аудио, видео и других сигналах мы всегда знаем глубину кодирования, а значит и количество информации в значении аргументе о значении функции. В любых таблицах и базах данных числа всегда представлены с ограниченным числом знаков после запятой, а значит само множество таких чисел ограничено, и всегда можно посчитать, какие количество информации содержится в факте выборки как-то одного конкретного из этих чисел. Например, в известной таблице Брадиса[3] приводится 4 знака значения синуса после запятой. Это значит, что определенному углу (от 0 до 90°) соответствует одно из 9999 значений. По формуле Хартли получаем: I=Log₂N=Log₂9999~13.29 бит.

Разработаны нередуцированные, частично и полностью редуцированные прямые и обратные когнитивные функции, а также программный инструментарий для их расчета (сама система Эйдос-Х++) и визуализации [40]. Однако в данной работе не целесообразно их рассматривать, т.к. этому посвящены работы [24, 27-30] и ряд других.

11. Модификация метода наименьших квадратов при аппроксимации когнитивных функций

Предлагается модификация метода наименьших квадратов для аппроксимации когнитивных функций, в котором точки имеют вес, равный количеству информации в значении аргумента о значении функции. Для упрощения можно рассматривать точки когнитивных функций как «мультиточки», состоящие из определенного количества «элементарных точек», соответствующего их весу. Другой вариант состоит в том, что перед применением стандартного МНК для каждого значения аргумента рассчитывается средневзвешенное значение функции из всех с их весами. В модуле визуализации когнитивных функций [40] этот метод реализован программно для отображения частично и полностью редуцированных когнитивных функций. Математическому описанию этого метода планируются посвятить одну из будущих статей авторов.

12. Развитие идеи системного обобщения математики в области теории информации. Системная (эмерджентная) теория информации (СТИ)

Простейшая комбинаторная количественная мера информации по Хартли рассчитывается как логарифм от числа элементов множества N:

.

В 2002 году у автора [97] возникла простая мысль о том, что если рассматривать как элементы множества не только его элементы по одному, как у Хартли, но и подсистемы, состоящие из 2, 3, …, N элементов, то формулу Хартли легко обобщить, придав ей вид, учитывающий наличие подсистем:

.

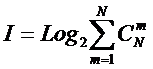Аналогично обобщаются и другие количественные меры информации, в частности Шеннона и Харкевича, и в результате получается вариант теории информации, органично приспособленный для учета как обычной (классической), так и системной информации.

13. Информационные меры уровня системности – коэффициенты эмерджентности

В работе [97] и работе [170] предлагаются теоретически обоснованные количественные меры, следующие из системной теории информации (СТИ), которые позволяют количественно оценивать влияние факторов на системы различной природы не по силе и направлению изменения состояния системы, а по степени возрастания или уменьшения ее эмерджентности (уровня системности) и степени детерминированности.

В работе [253] на простом численном примере рассматривается применение автоматизированного системно-когнитивного анализа (АСК-анализ) и его программного инструментария – интеллектуальной системы «Эйдос» для выявления и исследования детерминации эмерджентных макросвойств систем их составом и иерархической структурой, т.е. подсистемами различной сложности (уровней иерархии). Кратко обсуждаются некоторые методологические вопросы создания и применения формальных моделей в научном познании. Предложены системное обобщение принципа Уильяма Росса Эшби о необходимом разнообразии на основе системного обобщения теории множеств и системной теории информации, обобщенная формулировка принципа относительности Галилея-Эйнштейна, высказана гипотеза о его взаимосвязи с теоремой Эмми Нётер, а также предложена гипотеза «О зависимости силы и направления связей между базовыми элементами системы и ее эмерджентными свойствами в целом от уровня иерархии в системе»

В [270] предложены коэффициенты эмерджентности, применимые для систем, подчиняющихся классической или квантовой статистике. Дан алгоритм оценки уровня системности квантовых объектов. Рассмотрены квантовые системы, подчиняющиеся статистике Ферми-Дирака и Бозе-Эйнштейна, а также классические системы, подчиняющиеся статистике Максвелла-Больцмана. Установлено, что коэффициенты эмерджентности квантовых и классических систем отличаются между собой, как и коэффициенты квантовых систем ферми-частиц и бозе-частиц. Следовательно, коэффициент эмерджентности позволяет отличить классическую систему от квантовой системы, а квантовую систему ферми-частиц от квантовой системы бозе-частиц. Установлено также, что предложенные ранее в ряде работ, начиная с [97], различные варианты коэффициентов эмерджентности Хартли распространяются только на системы, подчиняющиеся статистике Ферми-Дирака.

14. Прямые и обратные, непосредственные и опосредованные правдоподобные логические рассуждения с расчетной степенью истинности

Одним из первых ученых, поднявших и широко обсуждавшим в своих работах проблематику правдоподобных рассуждений, был известный венгерский, швейцарский и американский математик Дьердь Пойа[4], книги которого одному из авторов (тому, который потом стал профессором Е.В.Луценко) подарил еще в школе его учитель математики Михаил Ильич Перевалов (см. также в книге: Д. Пойа «Формализация логики правдоподобных рассуждений», глава третья, параграф 7, с.158-163, исходящий из (репрезентативной) теории измерений).

В работе [97] предложена логическая форма представления правдоподобных логических рассуждений с расчетной степенью истинности, которая определяется в соответствии с системной теорией информацией непосредственно на основе эмпирических данных.

В качестве количественной меры влияния факторов, предложено использовать обобщенную формулу А.Харкевича, полученную на основе предложенной эмерджентной теории информации. При этом непосредственно из матрицы абсолютных частот рассчитывается база знаний (табл.1), которая и представляет собой основу содержательной информационной модели предметной области.

Весовые коэффициенты табл.1 непосредственно определяют, какое количество информации Iij система управления получает о наступлении события: "активный объект управления перейдет в j–е состояние", из сообщения: "на активный объект управления действует i–й фактор".

Принципиально важно, что эти весовые коэффициенты не определяются экспертами неформализуемым способом на основе интуиции и профессиональной компетенции (т.е., мягко говоря, «на глазок»), а рассчитываются непосредственно на основе эмпирических данных и удовлетворяют всем ранее обоснованным в работе [97] требованиям, т.е. являются сопоставимыми, содержательно интерпретируемыми, отражают понятия "достижение цели управления" и "мощность множества будущих состояний объекта управления" и т.д.

В [97] обосновано, что предложенная информационная мера обеспечивает сопоставимость индивидуальных количеств информации, содержащейся в факторах о классах, а также сопоставимость интегральных критериев, рассчитанных для одного объекта и разных классов, для разных объектов и разных классов.

Когда количество информации Iij>0 – i–й фактор способствует переходу объекта управления в j–е состояние, когда Iij<0 – препятствует этому переходу, когда же Iij=0 – никак не влияет на это. В векторе i–го фактора (строка матрицы информативностей) отображается, какое количество информации о переходе объекта управления в каждое из будущих состояний содержится в том факте, что данный фактор действует. В векторе j–го состояния класса (столбец матрицы информативностей) отображается, какое количество информации о переходе объекта управления в соответствующее состояние содержится в каждом из факторов.

Таким образом, матрица информативностей матрица информативностей является обобщенной таблицей решений, в которой входы (факторы) и выходы (будущие состояния активного объекта управления (АОУ) связаны друг с другом не с помощью классических (Аристотелевских) импликаций, принимающих только значения: "Итина" и "Ложь", а различными значениями истинности, выраженными в битах и принимающими значения от положительного теоретически-максимально-возможного ("Максимальная степень истинности"), до теоретически неограниченного отрицательного ("Степень ложности").

Фактически предложенная модель позволяет осуществить синтез обобщенных таблиц решений для различных предметных областей непосредственно на основе эмпирических исходных данных и продуцировать на их основе прямые и обратные правдоподобные (нечеткие) логические рассуждения по неклассическим схемам с различными расчетными значениями истинности, являющимся обобщением классических импликаций.

Более сложные правдоподобные опосредованные высказывания могут быть рассчитаны непосредственно на основе матрицы информативностей – обобщенной таблицы решений.

Если A, со степенью истинности a(A,B), детерминирует B, и если С, со степенью истинности a(C,D), детерминирует D, и A совпадает по смыслу с C со степенью истинности a(A,C), то это вносит вклад в совпадение B с D, равный степени истинности a(B,D).

При этом в прямых рассуждениях как предпосылки рассматриваются факторы, а как заключение – будущие состояния АОУ, а в обратных – наоборот: как предпосылки – будущие состояния АОУ, а как заключение – факторы. Степень истинности i-й предпосылки – это просто количество информации Iij, содержащейся в ней о наступлении j-го будущего состояния АОУ. Если предпосылок несколько, то степень истинности наступления j-го состояния АОУ равна суммарному количеству информации, содержащемуся в них об этом. Количество информации в i-м факторе о наступлении j-го состояния АОУ, рассчитывается в соответствии с выражениями системной теории информации (СТИ).

Прямые правдоподобные логические рассуждения позволяют прогнозировать степень достоверности наступления события по действующим факторам, а обратные – по заданному состоянию восстановить степень необходимости и степень нежелательности каждого фактора для наступления этого состояния, т.е. принимать решение по выбору управляющих воздействий на АОУ, оптимальных для перевода его в заданное целевое состояние.

Необходимо отметить, что предложенная модель, основывающаяся на теории информации, обеспечивает автоматизированное формирования системы нечетких правил по содержимому входных данных, как и комбинация нечеткой логики Заде-Коско с нейронными сетями Кохонена. Принципиально важно, что качественное изменение модели путем добавления в нее новых классов не уменьшает достоверности распознавания уже сформированных классов. Кроме того, при сравнении распознаваемого объекта с каждым классом учитываются не только признаки, имеющиеся у объекта, но и отсутствующие у него, поэтому предложенной моделью правильно идентифицируются объекты, признаки которых образуют множества, одно из которых является подмножеством другого (как и в Неокогнитроне К.Фукушимы).

15. Интеллектуальная система Эйдос-Х++ как инструментарий, реализующий идеи системного нечеткого интервального обобщения математики

Система «Эйдос» за многие годы применения хорошо показала себя при проведении научных исследований в различных предметных областях и занятий по ряду научных дисциплин, связанных с искусственным интеллектом, представлениями знаний и управлению знаниями [224]. Однако в процессе эксплуатации системы были выявлены и некоторые недостатки, ограничивающие возможности и перспективы применения системы. Поэтому создана качественно новая версия системы (система Эйдос-Х++), в которой преодолены ограничения и недостатки предыдущей версии и реализованы новые важные идеи по ее развитию и применению в качестве программного инструментария системно-когнитивного анализа (СК-анализ) [260].

Авторы считают, что система Эйдос-Х++ является программным инструментарием, реализующим ряд идей системного нечеткого интервального обобщения математики.

Таким образом, в монографии кратко рассмотрены перспективы и некоторые «точки роста» современной теоретической и вычислительной математики, в частности: числа и множества - основа современной математики; математические, прагматические и компьютерные числа; от обычных множеств - к нечетким; теория нечетких множеств и «нечеткое удвоение» математики; о сведении теории нечетких множеств к теории случайных множеств; интервальные числа как частный случай нечетких множеств; развитие интервальной математики (интервальное удвоение математики); система как обобщение множества; системное обобщение математики и задачи, возникающие при этом; системное обобщение операций над множествами (на примере операции объединения булеанов); системное обобщение понятия функции и функциональной зависимости; когнитивные функции; матрицы знаний как нечеткое с расчетной степенью истинности отображение системы аргументов на систему значений функции; модификация метода наименьших квадратов при аппроксимации когнитивных функций; развитие идеи системного обобщения математики в области теории информации - системная (эмерджентная) теория информации; информационные меры уровня системности - коэффициенты эмерджентности; прямые и обратные, непосредственные и опосредованные правдоподобные логические рассуждения с расчетной степенью истинности; интеллектуальная система Эйдос-Х++ как инструментарий, реализующий идеи системного нечеткого интервального обобщения математики.

Отметим, что нумерация формул, рисунков и таблиц везде по тексту, где это специально не оговорено, ведется внутри разделов. При необходимости ссылки на формулу, рисунок или таблицу в другом разделе в тексте будет об этом прямо упомянуто, например: «используя выражение (3) из раздела 4.2» и т.д.

Кроме того необходимо отметить, что данная монография представляет собой обобщающую работу, подводящую своеобразный итог по двум научным направлениям [92]:

- «Статистика объектов нечисловой природы» (предложено и разработано проф. А.А. Орловым)

- «Автоматизированный системно-когнитивный анализ (АСК-анализ)» (предложено и разработано проф. Е.В.Луценко).

Развитием этих научных направлений авторы занимаются и в настоящее время. Поэтому просим читателей правильно понять большое количество ссылок авторов на собственные работы.

Некоторые мысли, излагаемые в монографии, носят спорный и дискуссионный характер и высказаны в порядке научного обсуждения.

---

[1] Предложен в работе [97] в 2002 году. Напоминать об этом приходится по причинам, изложенным в статье: Вяткин В.Б. Групповой плагиат: от студента до министра. - Троицкий вариант — Наука - http://trv-science.ru - [Электронный ресурс]. Адрес доступа: http://trv-science.ru/2011/11/08/gruppovojj-plagiat-ot-studenta-do-ministra/ или: http://trv-science.ru/2011/11/08/gruppovojj-plagiat-ot-studenta-do-ministra/print/

[2] См., например: http://ru.wikipedia.org/wiki/Принцип%20соответствия

[3] См., например: http://www.vsetabl.ru/056.htm

[4] См., например: http://ru.wikipedia.org/wiki/Пойа,%20Дьёрдь