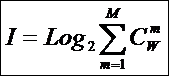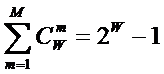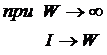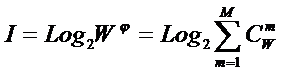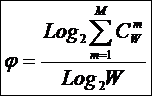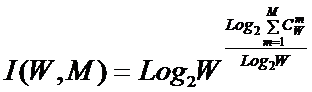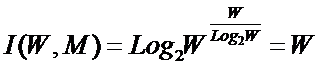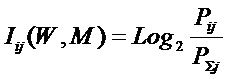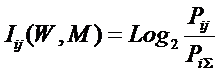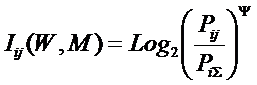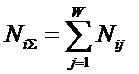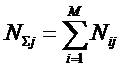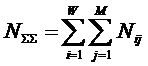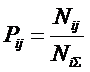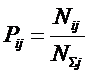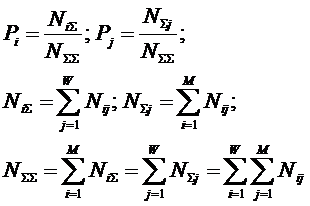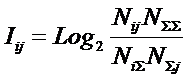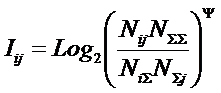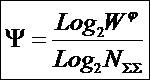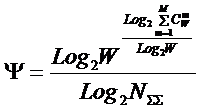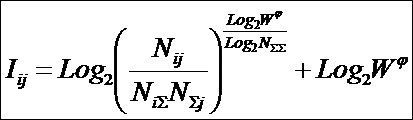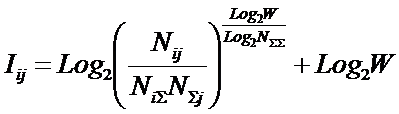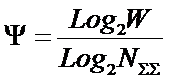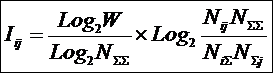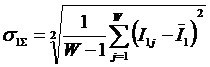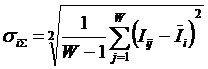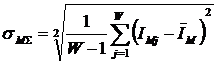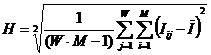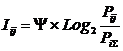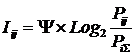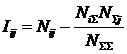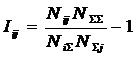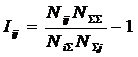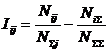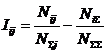ГЛАВА 9. РАЗВИТИЕ ИДЕИ СИСТЕМНОГО ОБОБЩЕНИЯ МАТЕМАТИКИ В ОБЛАСТИ ТЕОРИИ ИНФОРМАЦИИ: СИСТЕМНАЯ (ЭМЕРДЖЕНТНАЯ) ТЕОРИЯ ИНФОРМАЦИИ (СТИ)
Дальнейшее изложение основано на рабатах [97] и
[280], нумерация формул, рисунков и таблиц сохранены теми же, что в работе [280].
Итак, классическая формула Хартли имеет
вид:
|
|
( 1 ) |
Будем искать ее системное обобщение в
виде:
|
|
( 2 ) |
где:
W –
количество элементов в множестве.
j – коэффициент эмерджентности, названный автором в
честь Хартли коэффициентом эмерджентности Хартли.
Примем, что
системное обобщение формулы Хартли имеет вид:
|
|
( 3 ) |
где:
– количество подсистем из m элементов;
m –
сложность подсистем;
M – максимальная
сложность подсистем (максимальное число элементов подсистемы).
Так как 
, то при M=1
система переходит в множество и выражение (3) приобретает вид (1), т.е. для
него выполняется принцип соответствия,
являющийся обязательным для более общей теории.
Учитывая, что при M=W:
|
|
( 4 ) |
в этом случае получаем:
|
|
( 5 ) |
Выражение (5) дает оценку
максимального количества информации в элементе системы. Из выражения (5)
видно, что при увеличении числа элементов W
количество информации I быстро стремится
к W (6) и уже при W>4 погрешность выражения (5) не
превышает 1%:
|
|
( 6 ) |
Приравняв
правые части выражений (2) и (3):
|
|
( 7 ) |
получим
выражение для коэффициента эмерджентности Хартли:
|
|
( 8 ) |
Смысл этого коэффициента раскрыт в работе [97] и ряде других.
Здесь отметим лишь, что при M®1, когда система асимптотически
переходит в множество, имеем j®1 и
(2) ® (1), как и должно быть согласно
принципу соответствия.
С
учетом (8) выражение (2) примет вид:
|
|
( 9 ) |
или
при M=W и больших W, учитывая (4) и (5):
|
|
( 10 ) |
Выражение (9) и представляет собой искомое системное
обобщение классической формулы Хартли, а выражение (10) – его достаточно
хорошее приближение при большом количестве элементов в системе W.
Классическая формула А. Харкевича имеет вид:
|
|
( 11 ) |
где: – Pij – условная вероятность
перехода объекта в j-е состояние при условии действия на него i-го значения фактора;
– 
– безусловная вероятность перехода объекта
в j-е состояние (вероятность
самопроизвольного перехода или вероятность перехода, посчитанная по всей
выборке, т.е. при действии любого
значения фактора).
Придадим выражению
(11) следующий эквивалентный вид (12), который и будем использовать ниже.
Вопрос об эквивалентности выражений (11) и (12) рассмотрим позднее.
|
|
( 12 ) |
где: – индекс i обозначает признак (значение фактора): 1£ i £ M;
– индекс j обозначает состояние объекта или
класс: 1£ j £ W;
– Pij – условная вероятность
наблюдения i-го значения фактора у
объектов в j-го класса;
– 
– безусловная вероятность наблюдения i-го значения фактора по всей выборке.
Из (12) видно, что формула Харкевича для семантической меры
информации по сути является логарифмом от формулы Байеса для
апостериорной вероятности (отношение условной вероятности к безусловной).
Известно, что
классическая формула Шеннона для количества информации для неравновероятных
событий преобразуется в формулу Хартли при условии, что события равновероятны,
т.е. удовлетворяет фундаментальному принципу
соответствия. Поэтому теория информации Шеннона справедливо считается
обобщением теории Хартли для неравновероятных событий. Однако, выражения (11) и (12) при подстановке в них реальных
численных значений вероятностей Pij,
и не дает количества
информации в битах, т.е. для этого выражения не выполняется принцип соответствия, обязательный для
более общих теорий. Возможно, в этом состоит причина довольно сдержанного, а иногда
и скептического отношения специалистов по теории информации Шеннона к
семантической теории информации Харкевича.
Причину этого мы
видим в том, что в выражениях (11) и (12) отсутствуют глобальные параметры конкретной
модели W и M, т.е. в том, что А. Харкевич в своем выражении для количества
информации не ввел зависимости от
мощности пространства будущих состояний объекта W и количества значений
факторов M, обуславливающих переход объекта в эти состояния.
Поставим задачу
получить такое обобщение формулы Харкевича, которое бы удовлетворяло тому
же самому принципу соответствия,
что и формула Шеннона, т.е. преобразовывалось в формулу Хартли в предельном
детерминистском равновероятном случае, когда каждому классу (состоянию объекта)
соответствует один признак (значение фактора), и каждому признаку – один класс,
и эти классы (а, значит и признаки), равновероятны,
и при этом каждый фактор однозначно,
т.е. детерминистским образом
определяет переход объекта в определенное состояние, соответствующее классу.
В детерминском
случае вероятность[1] Pij
наблюдения объекта j-го класса при
обнаружении у него i-го признака:
.
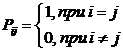Будем искать это
обобщение (12) в виде:
|
|
( 13 ) |
Найдем такое
выражение для коэффициента Y, названного нами в честь А. Харкевича "коэффициентом эмерджентности
Харкевича", которое обеспечивает выполнение для выражения (13) принципа
соответствия с классической формулой Хартли (1) и ее системным обобщением (2) и
(3) в равновероятном детерминистском
случае.
Для этого нам
потребуется выразить вероятности Pij,
Pj и Pi через частоты наблюдения признаков по классам (см.
табл. 1). В табл. 1 рамкой обведена область значений, переменные определены
ранее.
Таблица 1 – МАТРИЦА АБСОЛЮТНЫХ ЧАСТОТ
|
|
Классы |
Сумма |
|||||
|
1 |
... |
j |
... |
W |
|||
|
Значения факторов |
1 |
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
Суммарное количество признаков |
|
|
|
|
|
|
|
Алгоритм
формирования матрицы абсолютных частот.
Объекты обучающей
выборки описываются векторами (массивами)
имеющихся у них
признаков:
Первоначально в
матрице абсолютных частот все значения равны нулю. Затем организуется цикл по
объектам обучающей выборки. Если предъявленного объекта, относящегося к j-му классу, есть i-й признак, то:
Здесь можно провести
очень интересную и важную аналогию между способом формирования матрицы
абсолютных частот и работой многоканальной системы выделения полезного сигнала из шума. Представим себе, что
все объекты, предъявляемые для формирования обобщенного образа некоторого
класса, в действительности являются различными реализациями одного объекта –
"Эйдоса" (в смысле Платона), по-разному зашумленного различными
случайными обстоятельствами. И наша задача состоит в том, чтобы подавить этот
шум и выделить из него то общее и существенное, что отличает объекты данного
класса от объектов других классов. Учитывая, что шум чаще всего является
"белым" и имеет свойство при суммировании с самим собой стремиться к
нулю, а сигнал при этом, наоборот, возрастает пропорционально количеству
слагаемых, то увеличение объема обучающей выборки приводит ко все лучшему
отношению сигнал/шум в матрице абсолютных частот, т.е. к выделению полезной
информации из шума. Примерно так мы начинаем постепенно понимать смысл фразы, которую
мы сразу не расслышали по телефону и несколько раз переспрашивали. При этом в
повторах шум не позволяет понять то одну, то другую часть фразы, но в конце
концов за счет использования памяти и интеллектуальной обработки информации мы
понимаем ее всю. Так и объекты, описанные
признаками, можно рассматривать как зашумленные фразы, несущие нам информацию
об обобщенных образах классов - "Эйдосах" [97, 206], к которым они
относятся. И эту информацию мы выделяем из шума при синтезе модели.
Для выражения (11):
|
|
( 14 ) |
Для выражений (12)
и (13):
|
|
( 15 ) |
Для выражений (11),
(12) и (13):
|
|
( 16 ) |
В (16) использованы
обозначения:
Nij – суммарное количество наблюдений в
исследуемой выборке факта:
"действовало i-е значение
фактора и объект перешел в j-е состояние";
– суммарное по всей выборке количество
встреч различных факторов у объектов, перешедших в j-е состояние;
– суммарное количество встреч i-го фактора у всех объектов исследуемой
выборки;
– суммарное количество встреч различных
значений факторов у всех объектов исследуемой выборки.
Формирование матрицы условных и безусловных процентных
распределений.
На основе анализа матрицы частот (табл. 1) классы можно
сравнивать по наблюдаемым частотам признаков только в том случае, если
количество объектов по всем классам одинаково, как и суммарное
количество признаков по классам. Если же они отличаются, то корректно
сравнивать классы можно только по условным и безусловным относительным частотам
(оценкам вероятностей) наблюдений признаков, посчитанных на основе матрицы
частот (табл. 1) в соответствии с выражениями (14) и (15), в результате
чего получается матрица условных и безусловных процентных распределений (табл.
2).
При расчете матрицы оценок условных и безусловных вероятностей
Nj из табл. 1 могут
браться либо из предпоследней, либо из последней строки. В 1-м случае Nj представляет собой "Суммарное количество признаков у
всех объектов, использованных для формирования обобщенного образа j-го класса", а во 2-м случае - это
"Суммарное количество объектов обучающей выборки, использованных для
формирования обобщенного образа j-го
класса", соответственно получаем различные, хотя и очень сходные
семантические информационные модели, которые мы называем СИМ-1 и СИМ-2. Оба
этих вида моделей поддерживаются системой "Эйдос".
Таблица 2 – МАТРИЦА УСЛОВНЫХ И БЕЗУСЛОВНЫХ
ПРОЦЕНТНЫХ РАСПРЕДЕЛЕНИЙ
|
|
Классы |
Безусловная вероятность признака |
|||||
|
1 |
... |
j |
... |
W |
|||
|
Значения факторов |
1 |
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
Безусловная вероятность класса |
|
|
|
|
|
|
|
Эквивалентность выражений (11) и (12)
устанавливается,
если подставить в них выражения относительных частот как оценок вероятностей Pij, и через абсолютные
частоты наблюдения признаков по классам из (14), (15) и (16). В обоих случаях из выражений (11) и (12) получается
одно и то же выражение (17):
|
|
( 17 ) |
А из (13) - выражение
(18), с которым мы и будем далее работать.
|
|
( 18 ) |
При взаимно-однозначном соответствии классов и признаков в равновероятном детерминистском случае
имеем (таблица 3):
Таблица 3 – МАТРИЦА ЧАСТОТ В РАВНОВЕРОЯТНОМ ДЕТЕРМИНИСТСКОМ
СЛУЧАЕ
|
|
Классы |
Сумма |
|||||
|
1 |
... |
j |
... |
W |
|||
|
Значения факторов |
1 |
1 |
|
|
|
|
1 |
|
... |
|
1 |
|
|
|
1 |
|
|
i |
|
|
1 |
|
|
1 |
|
|
... |
|
|
|
1 |
|
1 |
|
|
M |
|
|
|
|
1 |
1 |
|
|
Сумма |
1 |
1 |
1 |
1 |
1 |
|
|
В этом случае к
каждому классу относится один объект, имеющий единственный признак. Откуда
получаем для всех i и j равенства (19):
|
|
( 19 ) |
Таким образом, обобщенная
формула А. Харкевича (18) с учетом (19) в этом случае приобретает вид:
|
|
( 20 ) |
откуда:
|
|
( 21 ) |
или, учитывая выражение для
коэффициента эмерджентности Хартли (8):
|
|
( 22 ) |
Подставив
коэффициент эмерджентности А.Харкевича (21) в выражение (18), получим:
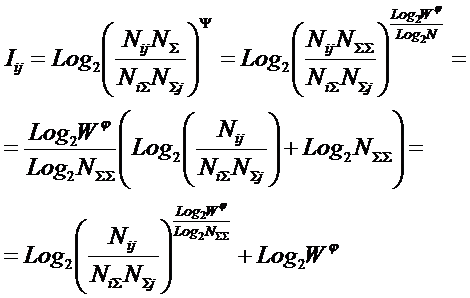
или окончательно:
|
|
( 23 ) |
Отметим, что 1-я
задача получения системного обобщения формул Хартли и Харкевича и 2-я задача
получения такого обобщения формулы Харкевича, которая удовлетворяет принципу
соответствия с формулой Хартли – это две разные задачи. 1-я задача является
более общей и при ее решении, которое приведено выше, автоматически решается и 2-я задача, которая является, таким
образом, частным случаем 1-й.
Однако, представляет
самостоятельный интерес и частный случай, в результате которого получается
формула Харкевича, удовлетворяющая в равновероятном
детерминистском случае принципу соответствия с классической формулой Хартли
(1), а не с ее системным обобщением (2) и (3). Ясно, что эта формула получается
из (23) при j=1.
|
|
( 24 ) |
Из выражений (21) и
(22) видно, что в этом частном случае, т.е. когда система эквивалентна
множеству (M=1), коэффициент эмерджентности А.Харкевича приобретает вид:
|
|
( 25 ) |
На практике
для численных расчетов удобнее
пользоваться не выражениями (23) или (24), а формулой (26), которая получается непосредственно из
(18) после подстановки в него выражения (25):
|
|
( 26 ) |
Используя выражение
(26) и данные таблицы 1 непосредственно прямым счетом получаем матрицу знаний (таблица 4):
Таблица 4 – МАТРИЦА ЗНАНИЙ (ИНФОРМАТИВНОСТЕЙ)
|
|
Классы |
Значимость фактора |
|||||
|
1 |
... |
j |
... |
W |
|||
|
Значения факторов |
1 |
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
Степень редукции класса |
|
|
|
|
|
|
|
Здесь – 
это среднее
количество знаний в i-м значении
фактора: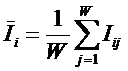 
Когда количество
информации Iij > 0 – i-й фактор способствует переходу объекта управления в
j-е состояние, когда Iij < 0 – препятствует этому переходу, когда же Iij = 0
– никак не влияет на это. В векторе i-го фактора (строка матрицы информативностей)
отображается, какое количество информации о переходе объекта управления в
каждое из будущих состояний содержится в том факте, что данный фактор
действует. В векторе j-го состояния класса (столбец матрицы информативностей)
отображается, какое количество информации о переходе объекта управления в
соответствующее состояние содержится в каждом из факторов.
Таким образом,
матрица знаний (информативностей), приведенная в таблице 6, является обобщенной
таблицей решений, в которой входы (факторы) и выходы (будущие состояния объекта
управления) связаны друг с другом не с помощью классических (Аристотелевых)
импликаций, принимающих только значения: "истина" и "ложь",
а различными значениями истинности, выраженными в битах, и принимающими
значения от положительного теоретически-максимально-возможного
("максимальная степень истинности"), до теоретически неограниченного
отрицательного ("степень ложности"). Это позволяет автоматически
формулировать прямые и опосредованные правдоподобные высказывания с расчетной
степенью истинности.
Фактически
предложенная модель позволяет осуществить синтез обобщенных таблиц решений для
различных предметных областей непосредственно на основе эмпирических исходных
данных и продуцировать прямые и обратные правдоподобные (нечеткие) логические
рассуждения по неклассическим схемам с различными расчетными значениями истинности,
являющимися обобщением классических импликаций.
Таким образом, данная
модель позволяет рассчитать, какое количество информации содержится в любом
факте о наступлении любого события в любой предметной области, причем для этого
не требуется повторности этих фактов и событий. Если данные повторности
осуществляются и при этом наблюдается некоторая вариабельность значений
факторов, обуславливающих наступление тех или иных событий, то модель
обеспечивает многопараметрическую типизацию, т.е. синтез обобщенных образов классов
или категорий наступающих событий с количественной оценкой степени и знака
влияния на их наступление различных значений факторов. Причем эти значения
факторов могут быть как количественными, так и качественными и измеряться в любых
единицах измерения, в любом случае в модели оценивается количество информации,
которое в них содержится о наступлении событий, переходе объекта управления в
определенные состояния или, просто, о его принадлежности к тем или иным классам.
Другие способы метризации приведены в работе [277] (таблица 5):
Таблица 5 – ЧАСТНЫЕ
КРИТЕРИИ ЗНАНИЙ, ИСПОЛЬЗУЕМЫЕ
В НАСТОЯЩЕЕ ВРЕМЯ В СК-АНАЛИЗЕ И СИСТЕМЕ «ЭЙДОС-Х++»
|
Наименование модели знаний |
Выражение для частного критерия |
|
|
через |
через |
|
|
INF1, частный критерий: количество знаний по
А.Харкевичу, 1-й вариант расчета относительных частот: |
|
|
|
INF2, частный критерий: количество знаний по
А.Харкевичу, 2-й вариант расчета относительных частот: |
|
|
|
INF3, частный критерий: Хи-квадрат: разности между
фактическими и теоретически ожидаемыми абсолютными частотами |
--- |
|
|
INF4, частный критерий: ROI - Return On Investment,
1-й вариант расчета относительных частот:
|
|
|
|
INF5, частный критерий: ROI - Return On
Investment, 2-й вариант расчета относительных частот: |
|
|
|
INF6, частный критерий: разность условной и безусловной
относительных частот, 1-й вариант расчета относительных частот: |
|
|
|
INF7, частный критерий: разность условной и безусловной
относительных частот, 2-й вариант расчета относительных частот: |
|
|
Обозначения:
i – значение прошлого
параметра;
j - значение будущего параметра;
Nij
– количество встреч j-го
значения будущего параметра при i-м
значении прошлого параметра;
M – суммарное число
значений всех прошлых параметров;
W - суммарное число
значений всех будущих параметров.
– количество встреч i-м значения прошлого
параметра по всей выборке;
– количество встреч j-го значения будущего
параметра по всей выборке;
– количество встреч j-го значения будущего
параметра при i-м значении
прошлого параметра по всей выборке.
Iij
– частный критерий знаний:
количество знаний в факте наблюдения
i-го значения прошлого параметра о том, что объект перейдет в состояние,
соответствующее j-му значению будущего
параметра;
Ψ –
нормировочный коэффициент (Е.В.Луценко, 2002), преобразующий количество
информации в формуле А.Харкевича в биты и обеспечивающий для нее соблюдение
принципа соответствия с формулой Р.Хартли;
– безусловная относительная частота встречи i-го значения прошлого параметра в обучающей
выборке;
Pij – условная
относительная частота встречи i-го
значения прошлого параметра при j-м значении
будущего параметра.
Все эти способы метризации с применением 7
частных критериев знаний (таблица 10) реализованы в системно-когнитивном
анализе и интеллектуальной системе «Эйдос» и обеспечивают сопоставление
градациям всех видов шкал числовых значений, имеющих смысл количества
информации в градации о принадлежности объекта к классу. Поэтому является
корректным применение интегральных критериев, включающих операции умножения и
суммирования, для обработки числовых значений, соответствующих градациям шкал.
Это позволяет единообразно и сопоставимо обрабатывать эмпирические данные,
полученные с помощью любых типов шкал, применяя при этом все математические операции [277].
Частные критерии знаний, представленные в
таблице 5, по сути, «являются формулами для преобразования абсолютных частот в
количество информации и знания» (проф.В.И.Лойко, 2013). В
будущем их предлагается дополнить критерием Г.Раша. Модель Г.Раша математически
тесно связана с моделью логитов, предложенной в 1944 году Джозефом Берксоном (Joseph
Berkson) и здесь мы ее не приводим, т.к. она подробно описана в литературе.
Модель Г.Раша (с учетом ее модификаций) является чуть ли не единственной
широко известной в настоящее время моделью метризации измерительных шкал.
Информационный портрет класса – это список значений факторов, ранжированных в
порядке убывания силы их влияния на переход объекта управления в состояние,
соответствующее данному классу. Информационный портрет класса отражает систему
его детерминации. Генерация информационного портрета класса представляет собой
решение обратной задачи прогнозирования, т.к. при прогнозировании по системе
факторов определяется спектр наиболее вероятных будущих состояний объекта
управления, в которые он может перейти под влиянием данной системы факторов, а
в информационном портрете мы, наоборот, по заданному будущему состоянию объекта
управления определяем систему факторов, детерминирующих это состояние, т.е.
вызывающих переход объекта управления в это состояние. В начале информационного
портрета класса идут факторы, оказывающие положительное влияние на переход
объекта управления в заданное состояние, затем факторы, не оказывающие на это существенного
влияния, и далее – факторы, препятствующие переходу объекта управления в это
состояние (в порядке возрастания силы препятствования). Информационные портреты
классов могут быть от отфильтрованы
по диапазону факторов, т.е. мы можем отобразить влияние на переход объекта
управления в данное состояние не всех отраженных в модели факторов, а только
тех, коды которых попадают в определенный диапазон, например, относящиеся к
определенным описательным шкалам.
Информационный (семантический) портрет фактора – это список классов, ранжированный в порядке
убывания силы влияния данного фактора на переход объекта управления в состояния,
соответствующие данным классам. Информационный портрет фактора называется также
его семантическим портретом, т.к. в
соответствии с концепцией смысла системно-когнитивного анализа, являющейся
обобщением концепции смысла Шенка-Абельсона [149], смысл фактора состоит в том, какие будущие состояния объекта управления
он детерминирует или обуславливает. Сначала в этом списке идут состояния
объекта управления, на переход в которые данный фактор оказывает наибольшее
влияние, затем состояния, на которые данный фактор не оказывает существенного
влияния, и далее состояния – переходу в которые данный фактор препятствует.
Информационные портреты факторов могут быть от отфильтрованы по диапазону классов, т.е. мы можем отобразить
влияние данного фактора на переход объекта управления не во все возможные
будущие состояния, а только в состояния, коды которых попадают в определенный
диапазон, например, относящиеся к определенным классификационным шкалам.
Прямые и
обратные, непосредственные и опосредованные правдоподобные логические
рассуждения с расчетной степенью истинности в системной теории информации. Одним из первых ученых,
поднявших и широко обсуждавшим в своих работах проблематику правдоподобных рассуждений,
был известный венгерский, швейцарский и американский математик Дьердь Пойа[3],
книги которого одному из авторов (тому, который потом стал профессором
Е.В.Луценко) подарил еще в школе его учитель математики Михаил Ильич Перевалов
(см. также раздел «Формализация логики правдоподобных рассуждений Д. Пойа»,
глава третья, параграф 7, с.158-163, исходящий из (репрезентативной) теории измерений).
В работе [97] предложена логическая форма
представления правдоподобных логических рассуждений с расчетной степенью
истинности, которая определяется в соответствии с системной теорией информацией
непосредственно на основе эмпирических данных.
В качестве количественной меры влияния факторов,
предложено использовать обобщенную формулу А.Харкевича, полученную на основе
предложенной эмерджентной теории информации. При этом непосредственно из
матрицы абсолютных частот рассчитывается база знаний (табл.1), которая и
представляет собой основу содержательной информационной модели предметной области.
Весовые коэффициенты табл.1 непосредственно
определяют, какое количество информации Iij
система управления получает о наступлении события: "активный объект
управления перейдет в j–е
состояние", из сообщения: "на активный объект управления действует i–й фактор".
Принципиально важно, что эти весовые
коэффициенты не определяются экспертами неформализуемым способом на основе
интуиции и профессиональной компетенции (т.е., мягко говоря, «на глазок»), а
рассчитываются непосредственно на основе эмпирических данных и удовлетворяют
всем ранее обоснованным в работе [97] требованиям, т.е. являются сопоставимыми,
содержательно интерпретируемыми, отражают понятия "достижение цели
управления" и "мощность множества будущих состояний объекта управления"
и т.д.
В [97] обосновано, что предложенная информационная
мера обеспечивает сопоставимость индивидуальных количеств информации,
содержащейся в факторах о классах, а также сопоставимость интегральных
критериев, рассчитанных для одного объекта и разных классов, для разных объектов
и разных классов.
Когда количество информации Iij>0 – i–й фактор
способствует переходу объекта управления в j–е
состояние, когда Iij<0 –
препятствует этому переходу, когда же Iij=0
– никак не влияет на это. В векторе i–го
фактора (строка матрицы информативностей) отображается, какое количество
информации о переходе объекта управления в каждое из будущих состояний
содержится в том факте, что данный фактор действует. В векторе j–го состояния класса (столбец матрицы
информативностей) отображается, какое количество информации о переходе объекта
управления в соответствующее состояние содержится в каждом из факторов.
Таким образом, матрица
информативностей (табл.1) является обобщенной таблицей решений, в которой входы
(факторы) и выходы (будущие состояния активного объекта управления (АОУ)
связаны друг с другом не с помощью классических (Аристотелевских) импликаций,
принимающих только значения: "Итина" и "Ложь", а различными
значениями истинности, выраженными в битах и принимающими значения от
положительного теоретически-максимально-возможного ("Максимальная степень
истинности"), до теоретически неограниченного отрицательного
("Степень ложности").
Фактически предложенная модель
позволяет осуществить синтез обобщенных таблиц решений для различных предметных
областей непосредственно на основе эмпирических исходных данных и продуцировать
на их основе прямые и обратные правдоподобные (нечеткие) логические рассуждения
по неклассическим схемам с различными расчетными значениями истинности,
являющимся обобщением классических импликаций (табл.5):
Таблица 5 – Прямые и обратные
правдоподобные логические высказывания с расчетной в соответствии с системной
теорией информации (СТИ) степенью истинности импликаций
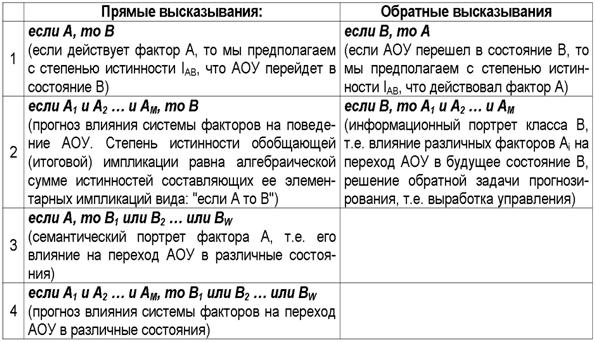
Приведем пример более сложного
высказывания, которое может быть рассчитано непосредственно на основе матрицы информативностей
– обобщенной таблицы решений (таблица 2):
Если A, со степенью истинности a(A,B), детерминирует B, и если С, со степенью
истинности a(C,D), детерминирует D,
и A совпадает по смыслу с C со степенью истинности a(A,C), то это вносит вклад в совпадение B с D,
равный степени истинности a(B,D).
При этом в прямых рассуждениях
как предпосылки рассматриваются факторы, а как заключение – будущие состояния
АОУ, а в обратных – наоборот: как предпосылки – будущие состояния АОУ, а как
заключение – факторы. Степень истинности i-й
предпосылки – это просто количество информации Iij, содержащейся в ней о наступлении j-го будущего состояния АОУ. Если предпосылок несколько, то степень
истинности наступления j-го состояния
АОУ равна суммарному количеству информации, содержащемуся в них об этом.
Количество информации в i-м факторе о
наступлении j-го состояния АОУ,
рассчитывается в соответствии с выражениями системной теории информации (СТИ).
Прямые правдоподобные
логические рассуждения позволяют прогнозировать степень достоверности
наступления события по действующим факторам, а обратные – по заданному состоянию
восстановить степень необходимости и степень нежелательности каждого фактора
для наступления этого состояния, т.е. принимать решение по выбору управляющих
воздействий на АОУ, оптимальных для перевода его в заданное целевое состояние.
Приведем простой пример, когда
безупречная классическая бинарная логика Аристотеля дает сбой. Рассмотрим
высказывания:
А) если студент хорошо сдал
экзамен по информационным системам, значит, он умеет хорошо программировать;
Б) если студент умеет хорошо
программировать, то он может стать специалистом в области прикладной
информатики.
Откуда средами логики
предикатов получаем вывод:
В) если студент хорошо сдал
экзамен по информационным системам, то он может стать специалистом в области
прикладной информатики.
Если при рассмотрении каждого
высказывания «А» и «Б» по отдельности у нас не возникает особых возражений,
хотя мы сразу чувствуем здесь какой-то подвох, что это не совсем так или не
всегда так и легко можем привести вполне реальные примеры, когда эти
высказывания могут быть и ложными. то высказывание «В» уже само по себе
выглядит очень сомнительным, т.е. проще говоря ложным, тогда как в логике предикатов оно является истинным.
Интуитивно мы хорошо понимаем, почему так получается. Дело в том, что в этих
высказываниях не отражен контент, т.е. та огромная слабо
формализованная и вообще неформализованная информация об объекте моделирования,
которой располагает человек, но не располагает логическая система. Например, в
этих двух логических высказываниях не отражена информация, которой располагает
каждый преподаватель и студент, о том, каким образом иногда сдаются экзамены,
когда оценка вообще никак не зависит от знаний. Иначе говоря, чтобы эти
высказывания были истинны необходимо, чтобы оценка определялась только
знаниями. Но и этого мало. Предполагается, что факт получения хорошей оценки по
дисциплине означает полное ее
освоение, хотя все понимают, что для этого достаточно освоения только тех
вопросов, которые были в билете и были заданы преподавателем.
При решении этой же задачи
средами АСК-анализа мы формулируем эти высказывания в форме правдоподобных рассуждений:
А) если студент хорошо сдал
экзамен по информационным системам, то в этом факте содержится I(A) информации
о том, что он умеет хорошо программировать;
Б) если студент умеет хорошо
программировать, то в этом факте содержится I(Б) информации о том он может
стать специалистом в области прикладной информатики.
Откуда средами АСК-анализа
получаем результирующее высказывание:
В) если студент хорошо сдал
экзамен по информационным системам, то в этом факте содержится I(В) информации
о том он может стать специалистом в области прикладной информатики.
Это высказывание не выглядит
как истинное или ложное и может быть и истинным, и ложным, причем в различной
степени, в зависимости от знака и модуля расчетной его степени истинности I(В).
Для расчета этой величины нужны
конкретные эмпирические данные,
являющиеся репрезентативными для отражения определенной предметной области
(генеральной совокупности), в которой этот вывод и будет иметь эти значения
знака и величины степени истинности.
Необходимо отметить, что
предложенная модель, основывающаяся на теории информации, обеспечивает
автоматизированное формирования системы нечетких правил по содержимому входных
данных, как и комбинация нечеткой логики Заде-Коско с нейронными сетями
Кохонена. Принципиально важно, что качественное изменение модели путем
добавления в нее новых классов не уменьшает достоверности распознавания уже
сформированных классов. Кроме того, при сравнении распознаваемого объекта с
каждым классом учитываются не только признаки, имеющиеся у объекта, но и
отсутствующие у него, поэтому предложенной моделью правильно идентифицируются
объекты, признаки которых образуют множества, одно из которых является
подмножеством другого (как и в Неокогнитроне К.Фукушимы).