ГЛАВА 7. СТАТИСТИКА ИНТЕРВАЛЬНЫХ ДАННЫХ

В статистике интервальных данных элементы выборки — не числа, а интервалы. Это приводит к алгоритмам и выводам, принципиально отличающимся от классических. Настоящая работа посвящена основным идеям и подходам асимптотической статистики интервальных данных. Приведены результаты, связанные с основополагающими в рассматриваемой области прикладной математической статистики понятиями нотны и рационального объема выборки.

7.1. Развитие статистики интервальных данных

Перспективная и быстро развивающаяся область статистических исследований последних десятилетий — математическая статистика интервальных данных. Речь идет о развитии методов прикладной математической статистики в ситуации, когда статистические данные — не числа, а интервалы, в частности, порожденные наложением ошибок измерения на значения случайных величин. Полученные результаты отражены в выступлениях на проведенной в журнале «Заводская лаборатория» дискуссии [28] и в докладах Международной конференции ИНТЕРВАЛ-92 [29]. Приведем основные идеи весьма перспективного для вероятностно-статистических и интервальных методов и моделей принятия решений асимптотического направления в статистике интервальных данных, в котором синтезируются идеи интервальной математики и математической статистики.

В настоящее время признается необходимым изучение устойчивости (робастности) оценок параметров к малым отклонениям исходных данных и предпосылок модели. Однако популярная среди теоретиков модель засорения (Тьюки-Хьюбера) представляется не вполне адекватной. Эта модель нацелена на изучение влияния больших «выбросов». Поскольку любые реальные измерения лежат в некотором фиксированном диапазоне, а именно, заданном в техническом паспорте средства измерения, то зачастую выбросы не могут быть слишком большими. Поэтому представляются полезными иные, более общие схемы устойчивости, введенные в монографии [13], в которых, например, учитываются отклонения распределений результатов наблюдений от предположений модели.

В одной из таких схем изучается влияние интервальности исходных данных на статистические выводы. Необходимость такого изучения стала очевидной следующим образом. В государственных стандартах СССР по прикладной статистике в обязательном порядке давалось справочное приложение «Примеры применения правил стандарта». При подготовке ГОСТ 11.011-83 [30] разработчикам стандарта были переданы для анализа реальные данные о наработке резцов до предельного состояния (в часах). Оказалось, что все эти данные представляли собой либо целые числа, либо полуцелые (т.е. после умножения на 2 становящиеся целыми). Ясно, что исходная длительность наработок искажена. Необходимо учесть в статистических процедурах наличие такого искажения исходных данных. Как это сделать?

Первое, что приходит в голову — модель группировки данных, согласно которой для истинного значения Х проводится замена на ближайшее число из множества {0,5n, n = 1, 2, 3, ...}. Однако эту модель целесообразно подвергнуть сомнению, а также рассмотреть иные модели. Так, возможно, что Х надо приводить к ближайшему сверху элементу указанного множества — если проверка качества поставленных на испытание резцов проводилась раз в полчаса. Другой вариант: если расстояния от Х до двух ближайших элементов множества {0,5n, n = 1, 2, 3, ...} примерно равны, то естественно ввести рандомизацию при выборе заменяющего числа, и т.д.

Целесообразно построить новую математико-статистическую модель, согласно которой результаты наблюдений — не числа, а интервалы. Например, если в таблице приведено значение 53,5, то это значит, что реальное значение — какое-то число от 53,0 до 54,0, т.е. какое-то число в интервале [53,5 – 0,5; 53,5 + 0,5], где 0,5 — максимально возможная погрешность. Принимая эту модель, мы попадаем в новую научную область — статистику интервальных данных [31, 32]. Статистика интервальных данных идейно связана с интервальной математикой, в которой в роли чисел выступают интервалы (см., например, монографию [24]). Это направление математики является дальнейшим развитием всем известных правил приближенных вычислений, посвященных выражению погрешностей суммы, разности, произведения, частного через погрешности тех чисел, над которыми осуществляются перечисленные операции.

Как видно из сборника трудов Международной конференции [29], исследователям удалось решить ряд задач теории интервальных дифференциальных уравнений, в которых коэффициенты, начальные условия и решения описываются с помощью интервалов. По мнению ряда специалистов, статистика интервальных данных является частью интервальной математики [24]. Впрочем, распространена и другая точка зрения, согласно которой такое включение нецелесообразно, поскольку статистика интервальных данных использует несколько иные подходы к алгоритмам анализа реальных данных, чем сложившиеся в интервальной математике (подробнее см. ниже).

В настоящей главе развиваем асимптотические методы статистического анализа интервальных данных при больших объемах выборок и малых погрешностях измерений. В отличие от классической математической статистики, сначала устремляется к бесконечности объем выборки и только потом — уменьшаются до нуля погрешности (в классической математической статистике предельные переходы осуществляются в обратном порядке – сначала уменьшаются до нуля погрешности измерений, и только затем - устремляется к бесконечности объем выборки). В частности, еще в начале 1980-х годов с помощью такой асимптотики сформулированы правила выбора метода оценивания в ГОСТ 11.011-83 [30].

Нами разработана [33] общая схема исследования, включающая расчет нотны (максимально возможного отклонения статистики, вызванного интервальностью исходных данных) и рационального объема выборки (превышение которого не дает существенного повышения точности оценивания). Она применена к оцениванию математического ожидания и дисперсии [28], медианы и коэффициента вариации [34], параметров гамма-распределения [30, 35] и характеристик аддитивных статистик [33], при проверке гипотез о параметрах нормального распределения, в т.ч. с помощью критерия Стьюдента, а также гипотезы однородности с помощью критерия Смирнова [34]. Изучено асимптотическое поведение оценок метода моментов и оценок максимального правдоподобия (а также более общих — оценок минимального контраста), проведено асимптотическое сравнение этих методов в случае интервальных данных, найдены общие условия, при которых, в отличие от классической математической статистики, метод моментов дает более точные оценки, чем метод максимального правдоподобия [36].

Разработаны подходы к рассмотрению интервальных данных в основных постановках регрессионного, дискриминантного и кластерного анализов [37]. Изучено влияние погрешностей измерений и наблюдений на свойства алгоритмов регрессионного анализа, разработаны способы расчета нотн и рациональных объемов выборок, введены и исследованы новые понятия многомерных и асимптотических нотн, доказаны соответствующие предельные теоремы [37, 38]. Проведена первоначальная разработка интервального дискриминантного анализа, рассмотрено влияние интервальности данных на показатель качества классификации [37, 39]. Основные идеи и результаты рассматриваемого направления в статистике интервальных данных приведены в публикациях обзорного характера [31, 32].

Как показала Международная конференция ИНТЕРВАЛ-92, в области асимптотической математической статистики интервальных данных мы имеем мировой приоритет. По нашему мнению, со временем во все виды статистического программного обеспечения должны быть включены алгоритмы интервальной статистики, «параллельные» обычно используемым алгоритмам прикладной математической статистики. Это позволит в явном виде учесть наличие погрешностей у результатов наблюдений, сблизить позиции метрологов и статистиков.

Многие из утверждений статистики интервальных данных весьма отличаются от аналогов из классической математической статистики. В частности, не существует состоятельных оценок; средний квадрат ошибки оценки, как правило, асимптотически равен сумме дисперсии оценки, рассчитанной согласно классической теории, и некоторого положительного числа (равного квадрату т.н. нотны — максимально возможного отклонения значения статистики из-за погрешностей исходных данных) — в результате, метод моментов оказывается иногда точнее метода максимального правдоподобия [36]; нецелесообразно увеличивать объем выборки сверх некоторого предела (называемого рациональным объемом выборки) — вопреки классической теории, согласно которой чем больше объем выборки, тем точнее выводы.

В стандарт [30] включен раздел 5, посвященный выбору
метода оценивания при неизвестных параметрах формы и масштаба и известном параметре сдвига и основанный на концепциях статистики интервальных данных. Теоретическое обоснование этого раздела стандарта опубликовано лишь через 5 лет в работе [35].

В 1982 г. при разработке стандарта [30] сформулированы основные идеи статистики интервальных данных. Однако из-за недостатка времени они не были полностью реализованы в ГОСТ 11.011-83, и этот стандарт написан в основном в классической манере. Развитие идей статистики интервальных данных продолжается уже более 30 лет, и еще многое необходимо сделать! Большое значение статистики интервальных данных для современной прикладной статистики обосновано в [40, 41].

Вторая (наряду с научной школой проф. А.И. Орлова) ведущая научная школа в области статистики интервальных данных — это школа проф. А.П. Вощинина (1937 - 2008), активно работающая с конца 70-х годов. Полученные результаты отражены в ряде монографий (см., прежде всего, [42, 43, 44]), статей [28, 45, 46, 47, 48], докладов, в частности, в трудах [29] Международной конференции ИНТЕРВАЛ-92, диссертациях [49, 50]. Изучены проблемы регрессионного анализа, планирования эксперимента, сравнения альтернатив и принятия решений в условиях интервальной неопределенности.

Рассматриваемое ниже наше научное направление отличается нацеленностью на асимптотические результаты, полученные при больших объемах выборок и малых погрешностях измерений, поэтому его полное название таково: асимптотическая математическая статистика интервальных данных.

7.2. Основные идеи и результаты
статистики интервальных данных

Сформулируем сначала основные идеи асимптотической математической статистики интервальных данных, а затем рассмотрим реализацию этих идей на перечисленных выше примерах. Основные идеи достаточно просты, в то время как их проработка в конкретных ситуациях зачастую оказывается достаточно трудоемкой.

Пусть существо реального явления описывается выборкой x₁, x₂, ..., x_n. В вероятностной теории математической статистики, из которой мы исходим (см. справочник [51]), выборка — это набор независимых в совокупности одинаково распределенных случайных величин. Однако беспристрастный и тщательный анализ подавляющего большинства реальных задач показывает, что статистику известна отнюдь не выборка x₁, x₂, ..., x_n, а величины

y_j = x_j + e_j, j = 1, 2, ..., n,

где e₁, e₂, …, e_n — некоторые погрешности измерений, наблюдений, анализов, опытов, исследований (например, инструментальные ошибки).

Одна из причин появления погрешностей — запись результатов наблюдений с конечным числом значащих цифр. Дело в том, что для случайных величин с непрерывными функциями распределения событие, состоящее в попадании хотя бы одного элемента выборки в множество рациональных чисел, согласно правилам теории вероятностей имеет вероятность 0, а такими событиями в теории вероятностей принято пренебрегать. Поэтому при рассуждениях о выборках из нормального, логарифмически нормального, экспоненциального, равномерного, гамма-распределений, распределения Вейбулла-Гнеденко и др. приходится принимать, что эти распределения имеют элементы исходной выборки x₁, x₂, ..., x_n, в то время как статистической обработке доступны лишь искаженные значения y_j = x_j + e_j.

Введем обозначения

x = (x₁, x₂, ..., x_n), y = (y₁, y₂, ..., y_n), e = (e₁ + e₂ + … + e_n).

Пусть статистические выводы основываются на статистике f : Rⁿ ® R¹, используемой для оценивания параметров и характеристик распределения, проверки гипотез и решения иных статистических задач. Принципиально важная для статистики интервальных данных идея такова: СТАТИСТИК ЗНАЕТ ТОЛЬКО f(y), НО НЕ f(x).

Очевидно, в статистических выводах необходимо отразить различие между f(y) и f(x). Одним из двух основных понятий статистики интервальных данных является понятие нотны.

Определение. Величину максимально возможного (по абсолютной величине) отклонения, вызванного погрешностями наблюдений e, известного статистику значения f(y) от истинного значения f(x), т.е.

N_f(x) = sup | f(y) – f(x) |,

где супремум берется по множеству возможных значений вектора погрешностей e (см. ниже), будем называть НОТНОЙ.

Если функция f имеет частные производные второго порядка, а ограничения на погрешности имеют вид[1]

| e_i | £ D, i = 1, 2, …, n, (1)

причем D мало, то приращение функции f с точностью до бесконечно малых более высокого порядка описывается главным линейным членом, т.е.

Чтобы получить асимптотическое (при D ® 0) выражение для нотны, достаточно найти максимум и минимум линейной функции (главного линейного члена) на кубе, заданном неравенствами (1). Легко видеть, что максимум достигается, если положить

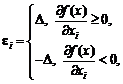
а минимум, отличающийся от максимума только знаком, достигается при = –e_i. Следовательно, нотна с точностью до бесконечно малых более высокого порядка имеет вид

Это выражение назовем асимптотической нотной.

Условие (1) означает, что исходные данные представляются статистику в виде интервалов [y_i – D; y_i + D], i = 1, 2, …, n (отсюда и название этого научного направления). Ограничения на погрешности могут задаваться разными способами — кроме абсолютных ошибок используются относительные или иные показатели различия между x и y.

Если задана не предельная абсолютная погрешность D, а предельная относительная погрешность d, т.е. ограничения на погрешности вошедших в выборку результатов измерений имеют вид

| e_i | £ d | x_i |, i = 1, 2, …, n,

то аналогичным образом получаем, что нотна с точностью до бесконечно малых более высокого порядка, т.е. асимптотическая нотна, имеет вид

При практическом использовании рассматриваемой концепции необходимо провести тотальную замену символов x на символы y. В каждом конкретном случае удается показать, что в силу малости погрешностей разность N_f(y) – N_f(x) является бесконечно малой более высокого порядка сравнительно с N_f(x) или N_f(y).

Основные результаты в вероятностной модели. В классической вероятностной модели элементы исходной выборки x₁, x₂, ..., x_n рассматриваются как независимые одинаково распределенные случайные величины. Как правило, существует некоторая константа C > 0 такая, что в смысле сходимости по вероятности

(2)

Соотношение (2) доказывается отдельно для каждой конкретной задачи.

При использовании классических статистических методов в большинстве случаев используемая статистика f(x) является асимптотически нормальной. Это означает, что существуют константы а и s² такие, что

где F(x) — функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. При этом обычно оказывается, что

и

а потому в классической математической статистике средний квадрат ошибки статистической оценки равен

с точностью до членов более высокого порядка.

В статистике интервальных данных ситуация совсем иная — обычно можно доказать, что средний квадрат ошибки равен

(3)

Из соотношения (3) вытекает ряд важных следствий. Правая часть этого равенства, в отличие от правой части соответствующего классического равенства, не стремится к 0 при безграничном возрастании объема выборки. Она остается больше некоторого положительного числа, а именно, квадрата нотны. Следовательно, статистика f(x) не является состоятельной оценкой параметра a. Более того, состоятельных оценок вообще не существует.

Пусть доверительным интервалом для параметра a, соответствующим заданной доверительной вероятности g, в классической математической статистике является интервал (c_n(g); d_n(g)). В статистике интервальных данных аналогичный доверительный интервал является более широким. Он имеет вид (c_n(g) – N_f(y); d_n(g) + N_f(y)). Таким образом, его длина увеличивается на две нотны. Следовательно, при увеличении объема выборки длина доверительного интервала не может стать меньше, чем 2CD (см. формулу (2)).

В статистике интервальных данных методы оценивания параметров имеют другие свойства по сравнению с классической математической статистикой. Так, при больших объемах выборок метод моментов может быть заметно лучше, чем метод максимального правдоподобия (т.е. иметь меньший средний квадрат ошибки — см. формулу (3)), в то время как в классической математической статистике второй из названных методов всегда не хуже первого.

Рациональный объем выборки. Анализ формулы (3) показывает, что в отличие от классической математической статистики нецелесообразно безгранично увеличивать объем выборки, поскольку средний квадрат ошибки остается всегда большим квадрата нотны. Поэтому представляется полезным ввести понятие «рационального объема выборки» n_rat, при достижении которого продолжать наблюдения нецелесообразно.

Как установить «рациональный объем выборки»? Можно воспользоваться идеей «принципа уравнивания погрешностей», выдвинутой в монографии [13]. Речь идет о том, что вклад погрешностей различной природы в общую погрешность должен быть примерно одинаков. Этот принцип дает возможность выбирать необходимую точность оценивания тех или иных характеристик в тех случаях, когда это зависит от исследователя. В статистике интервальных данных в соответствии с «принципом уравнивания погрешностей» предлагается определять рациональный объем выборки n_rat из условия равенства двух величин — метрологической составляющей, связанной с нотной, и статистической составляющей — в среднем квадрате ошибки (3), т.е. из условия

Для практического использования выражения для рационального объема выборки неизвестные теоретические характеристики необходимо заменить их оценками. Это делается в каждой конкретной задаче по-своему.

Исследовательскую программу в области статистики интервальных данных можно «в двух словах» сформулировать так: для любого алгоритма анализа данных (алгоритма прикладной статистики) необходимо вычислить нотну и рациональный объем выборки. Или иные величины из того же понятийного ряда, возникающие в многомерном случае, при наличии нескольких выборок и при иных обобщениях описываемой здесь простейшей схемы. Затем проследить влияние погрешностей исходных данных на точность оценивания, доверительные интервалы, значения статистик критериев при проверке гипотез, уровни значимости и другие характеристики статистических выводов. Очевидно, классическая математическая статистика является частью статистики интервальных данных, выделяемой условием D = 0.

Поясним теоретические концепции статистики интервальных данных на простых примерах.

7.3. Оценивание математического ожидания и дисперсии

Пусть необходимо оценить математическое ожидание случайной величины с помощью обычной оценки — среднего арифметического результатов наблюдений, т.е.

Тогда при справедливости ограничений (1) на абсолютные погрешности имеем N_f(x) = D. Таким образом, нотна полностью известна и не зависит от многомерной точки, в которой берется. Вполне естественно: если каждый результат наблюдения известен с точностью до D, то и среднее арифметическое известно с той же точностью. Ведь возможна систематическая ошибка — если к каждому результату наблюдения добавить D, то и среднее арифметическое увеличится на D.

Поскольку

то в ранее введенных обозначениях

s² = D(x₁).

Следовательно, рациональный объем выборки равен

Для практического использования полученной формулы надо оценить дисперсию результатов наблюдений. Можно доказать, что, поскольку D мало, это можно сделать обычным способом, например, с помощью несмещенной выборочной оценки дисперсии

Здесь и далее рассуждения часто идут на двух уровнях. Первый — это уровень «истинных» случайных величин, обозначаемых «х», описывающих реальность, но неизвестных специалисту по анализу данных. Второй — уровень известных этому специалисту величин «у», отличающихся погрешностями от истинных. Погрешности малы, поэтому функции от х отличаются от функций от у на некоторые бесконечно малые величины. Эти соображения и позволяют использовать s²(y) как оценку D(x₁).

Итак, выборочной оценкой рационального объема выборки является

Уже на этом первом рассматриваемом примере видим, что рациональный объем выборки находится не где-то вдали, а непосредственно рядом с теми объемами, с которыми имеет дело любой практически работающий статистик. Например, если статистик знает, что

то n_rat = 36. А именно такова погрешность контрольных шаблонов во многих технологических процессах! Поэтому, занимаясь управлением качеством, необходимо обращать внимание на действующую на предприятии систему измерений.

По сравнению с классической математической статистикой доверительный интервал для математического ожидания (для заданной доверительной вероятности g) имеет другой вид:

(4)

где u(g) — квантиль порядка (1 + g)/2 стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.

По поводу формулы (4) была довольно жаркая дискуссия среди специалистов. Отмечалось, что она получена на основе Центральной предельной теоремы теории вероятностей и может быть использована при любом распределении результатов наблюдений (с конечной дисперсией). Если же имеется дополнительная информация, то, по мнению отдельных специалистов, формула (4) может быть уточнена. Например, если известно, что распределение x_i является нормальным, в качестве u(g) целесообразно использовать квантиль распределения Стьюдента. К этому надо добавить, что по небольшому числу наблюдений нельзя надежно установить нормальность, а при росте объема выборки квантили распределения Стьюдента приближаются к квантилям нормального распределения.

Вопрос о том, часто ли результаты наблюдений имеют нормальное распределение, подробно обсуждался среди специалистов. Выяснилось, что распределения встречающихся в практических задачах результатов измерений почти всегда отличны от нормальных [52]. А также и от распределений из иных параметрических семейств, описываемых в учебниках.

Применительно к оцениванию математического ожидания (но не к оцениванию других характеристик или параметров распределения) факт существования границы возможной точности, определяемой точностью исходных данных, неоднократно отмечался в литературе ([53, с. 230–234], [54, с. 121] и др.).

Оценивание дисперсии. Для статистики f(y) = s²(y), где s²(y) — выборочная дисперсия (несмещенная оценка теоретической дисперсии), при справедливости ограничений (1) на абсолютные погрешности имеем

Можно показать, что нотна N_f(y) сходится к

2DM | x₁ – M(x₁) |

по вероятности с точностью до o(D), когда n стремится к бесконечности. Это же предельное соотношение верно и для нотны N_f(х), вычисленной для исходных данных. Таким образом, в данном случае справедлива формула (2) с

C = 2M | x₁ – M(x₁) |.

Известно [55], что случайная величина

является асимптотически нормальной с математическим ожиданием 0 и дисперсией

Из сказанного вытекает: в статистике интервальных данных асимптотический доверительный интервал для дисперсии s² (соответствующий доверительной вероятности g) имеет вид

(s²(y) – A; s² + A),

где

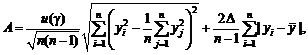
здесь u(g) обозначает тот же самый квантиль стандартного нормального распределения, что и выше в случае оценивания математического ожидания.

Рациональный объем выборки при оценивании дисперсии равен

а выборочную оценку рационального объема выборки n_sample–rat можно вычислить, заменяя теоретические моменты на соответствующие выборочные и используя доступные статистику результаты наблюдений, содержащие погрешности.

Что можно сказать о численной величине рационального объема выборки? Как и в случае оценивания математического ожидания, она отнюдь не выходит за пределы обычно используемых объемов выборок. Так, если распределение результатов наблюдений x_i является нормальным с математическим ожиданием 0 и дисперсией s², то в результате вычисления моментов случайных величин в предыдущей формуле получаем, что

где p — отношение длины окружности к диаметру, p = = 3,141592… Например, если D = s/6, то n_rat = 11. Это меньше, чем при оценивании математического ожидания в предыдущем примере.

7.4. Интервальные данные в задачах оценивания

Поясним теоретические концепции статистики интервальных данных на нескольких простых примерах.

Пример 1. Аддитивные статистики. Пусть g : R¹ ® R¹ — некоторая непрерывная функция. Аддитивные статистики имеют вид

Тогда

по вероятности при n ® ¥, если математические ожидания в правых частях двух последних соотношений существуют. Применяя рассмотренные выше общие соображения, получаем, что при малых фиксированных D и d и достаточно больших n значения f(y) могут принимать любые величины из разрешенных (например, записываемых заданным числом значащих цифр) в замкнутом интервале

(5)

при ограничениях (1) на абсолютные ошибки и в замкнутом интервале

(6)

при ограничениях на относительные погрешности результатов наблюдений. Обратим внимание, что длины этих интервалов независимы от объема выборки, в частности, не стремятся к 0 при его росте.

К каким последствиям это отсутствие стремления к 0 приводит в задачах статистического оценивания? Поскольку для статистик аддитивного типа

(7)

по вероятности при n ® ¥, если математическое ожидание в правой части формулы (7) существует, то аддитивную статистику f(x) естественно рассматривать как непараметрическую оценку этого математического ожидания. Термин «непараметрическая» означает, что не делается предположений о принадлежности функции распределения выборки к тому или иному параметрическому семейству распределения. Распределение статистики f(x) зависит от распределения результатов наблюдений. Однако для любого распределения результатов наблюдений с конечной дисперсией статистика f(x) является состоятельной и асимптотически нормальной оценкой для математического ожидания, указанного в правой части формулы (7).

Как известно, в рамках классической математической статистики в предположении существования ненулевой дисперсии Dg(x₁) в силу асимптотической нормальности аддитивной статистики f(x) асимптотический доверительный интервал, соответствующий доверительной вероятности g, имеет вид

где s(g(x)) — выборочное среднее квадратическое отклонение, построенное по g(x₁), g(x₂),…, g(x_n), а — квантиль стандартного нормального распределения порядка

В рассматриваемой модели порождения интервальных данных вместо f(x) необходимо использовать f(y), а вместо g(x_i) — соответственно, g(y_i), i = 1, 2, …, n. При этом доверительный интервал необходимо расширить с учетом формул (5) и (6).

В соответствии с проведенными рассуждениями для аддитивных статистик асимптотическая нотна имеет вид

при ограничениях (1) на абсолютную погрешность и

при ограничениях на относительную погрешность. В первом случае нотна является обобщением понятия предельной абсолютной систематической ошибки, во втором — предельной относительной систематической ошибки. Отметим, что, как и в примерах 1 и 2, асимптотическая нотна не зависит от точки, в которой вычисляется. Таким образом, она является константой для конкретного метода статистического анализа данных.

Поскольку n велико, а D и d малы, можно пренебречь отличием выборочного среднего квадратического отклонения s(g(y)), вычисленного по выборке преобразованных значений g(y₁), g(y₂), …, g(y_n), от выборочного среднего квадратического отклонения s(g(x)), построенного по выборке g(x₁), g(x₂), …, g(x_n). Разность этих двух величин является бесконечно малой, они приближаются к одной и той же положительной константе.

В статистике интервальных данных выборочный доверительный интервал для Mg(x₁) имеет вид

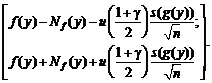
В асимптотике его длина такова:

(8)

где s² — дисперсия g(x₁), в то время как в классической теории математической статистики имеется только второе слагаемое. Соотношение (8) — аналог суммарной ошибки у метрологов [53]. Поскольку первое слагаемое положительно, то оценивание Mg(x₁) с помощью f(y) не является состоятельным.

Для аддитивных статистик при больших n максимум (по возможным погрешностям) среднего квадрата отклонения оценки имеет вид

(9)

с точностью до членов более высокого порядка. Исходя из принципа уравнивания погрешностей в общей схеме устойчивости [13], нецелесообразно второе слагаемое в (9) делать меньше первого за счет увеличения объема выборки n. Рациональный объем выборки, т.е. тот объем, при котором равны погрешности оценивания (или проверки гипотез), вызванные погрешностями исходных данных, и статистические погрешности, рассчитанные по обычным правилам математической статистики (при e_i º 0), для аддитивных статистик согласно (9) имеет вид

(10)

В качестве примера рассмотрим экспоненциально распределенные результаты наблюдений x_iс M(x₁) = D(x₁) = 1. Оцениваем математическое ожидание с помощью выборочного среднего арифметического при ограничениях на относительную погрешность. Тогда согласно формуле (10)

В частности, если относительная погрешность измерений d = 10%, то рациональный объем выборки равен 100. Формуле (10) соответствует также рассмотренный выше пример 1.

Пример 2. Оценивание медианы распределения с помощью выборочной медианы. Хотя нельзя выделить главный линейный член из-за недифференцируемости функции f(x), выражающей выборочную медиану через элементы выборки, непосредственно из определения нотны следует, что при ограничениях на абсолютные погрешности

а при ограничениях на относительные погрешности

с точностью до бесконечно малых более высокого порядка, где x_med — теоретическая медиана. Доверительный интервал для медианы имеет вид

где [a₁(x); a₂(x)] — доверительный интервал для медианы, вычисленный по классическим правилам непараметрической статистики [56]. Для нахождения рационального объема выборки можно использовать асимптотическую дисперсию выборочной медианы. Она, как известно (см., например, [57, с. 178]), равна

где p(x_med) — плотность распределения результатов измерений в точке x_med. Следовательно, рациональный объем выборки имеет вид

при ограничениях на абсолютные и относительные погрешности результатов измерений соответственно. Для практического использования этих формул следует оценить плотность распределения результатов измерений в одной точке — теоретической медиане. Это можно сделать с помощью тех или иных непараметрических оценок плотности [56].

Если результаты наблюдений имеют стандартное нормальное распределение с математическим ожиданием 0 и дисперсией 1, то

В этом случае рациональный объем выборки в p/2 раз больше, чем для оценивания математического ожидания (см. выше). Однако для других распределений рассматриваемое соотношение объемов может быть иным, в частности, меньше 1. Как вытекает из работы А.Н. Колмогорова 1931 г. [58], рассматриваемое соотношение объемов может принимать любое значение между 0 и 3.

Пример 3. Оценивание коэффициента вариации. Рассмотрим выборочный коэффициент вариации

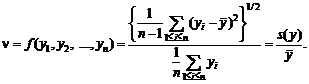
Как нетрудно подсчитать,

В случае ограничений на относительную погрешность

На основе этого предельного соотношения и формулы для асимптотической дисперсии выборочного коэффициента вариации, приведенной в [56], могут быть найдены по описанной выше схеме доверительные границы для теоретического коэффициента вариации и рациональный объем выборки.

Замечание. Формулы для рационального объема выборки получены на основе асимптотической теории, а применяются для получения конечных объемов — 36 и 100 в рассмотренных ранее примерах. Как всегда при использовании асимптотических результатов математической статистики, необходимы дополнительные исследования для изучения точности асимптотических формул при конечных объемах выборок.

Перейдем от отдельных примеров к более общей ситуации. Рассмотрим классическую в прикладной математической статистике параметрическую задачу оценивания. Исходные данные — выборка x₁, x₂, …, x_n, состоящая из n действительных чисел. В вероятностной модели простой случайной выборки ее элементы x₁, x₂, …, x_n считаются набором реализаций n независимых одинаково распределенных случайных величин. Будем считать, что эти величины имеют плотность f(x). В параметрической статистической теории предполагается, что плотность f(x) известна с точностью до конечномерного параметра, т.е., f(x) = f(x, q₀) при некотором q₀ Î Q Í R^k. Это, конечно, весьма сильное предположение, которое требует обоснования и проверки; однако в настоящее время параметрическая теория оценивания широко используется в различных прикладных областях.

Все результаты наблюдений определяются с некоторой точностью, в частности, записываются с помощью конечного числа значащих цифр (обычно 2–5). Следовательно, все реальные распределения результатов наблюдений дискретны. Обычно считают, что эти дискретные распределения достаточно хорошо приближаются непрерывными. Уточняя это утверждение, приходим к уже рассматривавшейся модели, согласно которой статистику доступны лишь величины

y_j = x_j + e_j, j = 1, 2, …, n,

где x_i — «истинные» значения, e₁, e₂, …, e_n — погрешности наблюдений (включая погрешности дискретизации). В вероятностной модели принимаем, что n пар

(x₁, e₁), (x₂, e₂), …, (x_n, e_n)

образуют простую случайную выборку из некоторого двумерного распределения, причем x₁, x₂, ..., x_n — выборка из распределения с плотностью f(x) = f(x, q₀). Необходимо учитывать, что x_i и e_i — реализации зависимых случайных величин (если считать их независимыми, то распределение y_i будет непрерывным, а не дискретным). Поскольку систематическую ошибку, как правило, нельзя полностью исключить [53, с. 141], то необходимо рассматривать случай Me_i ¹ 0. Нет оснований априори принимать и нормальность распределения погрешностей (согласно сводкам экспериментальных данных о разнообразии форм распределения погрешностей измерений, приведенным в [53, с. 148] и [56, с. 71–77], в подавляющем большинстве случаев гипотеза о нормальном распределении погрешностей оказалась неприемлемой для средств измерений различных типов). Таким образом, все три распространенных представления о свойствах погрешностей не адекватны реальности. Влияние погрешностей наблюдений на свойства статистических моделей необходимо изучать на основе иных моделей, а именно, моделей интервальной статистики.

Пусть e — характеристика величины погрешности, например, средняя квадратическая ошибка В классической математической статистике e считается пренебрежимо малой (e ® 0) при фиксированном объеме выборки n. Общие результаты доказываются в асимптотике n ® ¥. Таким образом, в классической математической статистике сначала делается предельный переход e ® 0, а затем предельный переход n ® ¥. В статистике интервальных данных принимаем, что объем выборки достаточно велик (n ® ¥), но всем измерениям соответствует одна и та же характеристика погрешности e ¹ 0. Полезные для анализа реальных данных предельные теоремы получаем при e ® 0. В статистике интервальных данных сначала делается предельный переход n ® ¥, а затем предельный переход e ® 0. Итак, в обеих теориях используются одни и те же два предельных перехода: n ® ¥ и e ® 0, но в разном порядке. Утверждения обеих теорий принципиально различны.

В дальнейшем изложение идет на примере оценивания параметров гамма-распределения, хотя аналогичные результаты можно получить и для других параметрических семейств, а также для задач проверки гипотез (см. ниже) и т.д. Наша цель — продемонстрировать основные черты подхода статистики интервальных данных. Его разработка была стимулирована подготовкой ГОСТ 11.011-83 [30].

Отметим, что постановки статистики объектов нечисловой природы соответствуют подходу, принятому в общей теории устойчивости [13, 56]. В соответствии с этим подходом выборке x = (x₁, x₂, ..., x_n) ставится в соответствие множество допустимых отклонений G(x), т.е. множество возможных значений вектора результатов наблюдений y = (y₁, y₂, ..., y_n). Если известно, что абсолютная погрешность результатов измерений не превосходит D, то множество допустимых отклонений имеет вид

G(x, D) = {y :| y_i – x_i | £ D, i = 1, 2, …, n}.

Если известно, что относительная погрешность не превосходит d, то множество допустимых отклонений имеет вид

Теория устойчивости позволяет учесть «наихудшие» отклонения, т.е. приводит к выводам типа минимаксных, в то время как конкретные модели погрешностей позволяют делать заключения о поведении статистик «в среднем».

Оценки параметров гамма-распределения. Как известно, случайная величина Х имеет гамма-распределение, если ее плотность такова [30]:

где a — параметр формы, b — параметр масштаба, G(a) — гамма-функция. Отметим, что есть и иные способы параметризации семейства гамма-распределений [59].

Поскольку M(X) = ab, D(X) = ab², то оценки метода имеют вид

где — выборочное среднее арифметическое, а s² — выборочная дисперсия. Можно показать, что при больших n

(11)

с точностью до бесконечно малых более высокого порядка.

Оценка максимального правдоподобия a^* имеет вид [30]:

(12)

где — функция, обратная к функции

При больших n с точностью до бесконечно малых более высокого порядка

Как и для оценок метода моментов, оценка максимального правдоподобия b^* параметра масштаба имеет вид

b^* = /a^*.

При больших n с точностью до бесконечно малых более высокого порядка

Используя свойства гамма-функции, можно показать [30], что при больших а

с точностью до бесконечно малых более высокого порядка. Сравнивая с формулами (11), убеждаемся в том, что средние квадраты ошибок для оценок метода моментов больше соответствующих средних квадратов ошибок для оценок максимального правдоподобия. Таким образом, с точки зрения классической математической статистики оценки максимального правдоподобия имеют преимущество по сравнению с оценками метода моментов.

Необходимость учета погрешностей измерений. Положим

Из свойств функции следует [30, с. 14], что при малых v

a^*~ 1/(2n). (13)

В силу состоятельности оценки максимального правдоподобия a^* из формулы (13) следует, что n ® 0 по вероятности при a ® ¥.

Согласно модели статистики интервальных данных результатами наблюдений являются не x_i, а y_i, вместо v по реальным данным рассчитывают

Имеем

(14)

В силу Закона больших чисел при достаточно малой погрешности e, обеспечивающей возможность приближения
ln(1 + a) ~ a для слагаемых в формуле (14), или, что эквивалентно, при достаточно малых предельной абсолютной погрешности D в формуле (1) или достаточно малой предельной относительной погрешности d имеем при n ® ¥

по вероятности (в предположении, что все погрешности одинаково распределены). Таким образом, наличие погрешностей вносит сдвиг, вообще говоря, не исчезающий при росте объема выборки. Следовательно, если c ¹ 0, то оценка максимального правдоподобия не является состоятельной. Имеем

где величина a^*(y) определена по формуле (12) с заменой x_i на y_i, i = 1, 2, …, n. Из формулы (13) следует [30], что

a^*(y) – a » –2(a^*)²c, (15)

т.е. влияние погрешностей измерений увеличивается по мере роста а.

Из формул для v и w следует, что с точностью до бесконечно малых более высокого порядка

(16)

С целью нахождения асимптотического распределения w выделим, используя формулу (16) и формулу для v, главные члены в соответствующих слагаемых

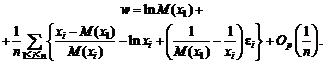(17)

Таким образом, величина w представлена в виде суммы независимых одинаково распределенных случайных величин (с точностью до зависящего от случая остаточного члена порядка 1/n). В каждом слагаемом выделяются две части — одна, соответствующая v, и вторая, в которую входят e_i. На основе представления (17) можно показать, что при n ® ¥, e ® 0 распределения случайных величин v и w асимптотически нормальны, причем

M(w) » M(v) + c, D(w) » D(v).

Из асимптотического совпадения дисперсий v и w, вида параметров асимптотического распределения (при a ® ¥) оценки максимального правдоподобия a^* и формулы (15) вытекает одно из основных соотношений статистики интервальных данных

(18)

Соотношение (18) уточняет утверждение о несостоятельности a^*. Из него следует также, что не имеет смысла безгранично увеличивать объем выборки n с целью повышения точности оценивания параметра а, поскольку при этом уменьшается только второе слагаемое в (18), а первое остается постоянным.

В соответствии с общим подходом статистики интервальных данных в стандарте [30] предлагается определять рациональный объем выборки n_rat из условия «уравнивания погрешностей» (это условие было впервые предложено в монографии [13]) различных видов в формуле (18), т.е. из условия

Упрощая это уравнение в предположении a ® ¥, получаем, что

Согласно сказанному выше, целесообразно использовать лишь выборки с объемами n £ n_rat. Превышение рационального объема выборки n_rat не дает существенного повышения точности оценивания.

Применение методов теории устойчивости. Найдем асимптотическую нотну. Как следует из вида главного линейного члена в формуле (17), решение оптимизационной задачи

w – v ® max, |e_i| £ D,

соответствующей ограничениям на абсолютные погрешности, имеет вид

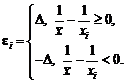
Однако при этом пары (x_i, e_i) не образуют простую случайную выборку, т.к. в выражения для e_i входит . Однако при n ® ¥ можно заменить на М(х₁). Тогда получаем, что

w – v » AD

при a > 1, где

Таким образом, с точностью до бесконечно малых более высокого порядка нотна имеет вид

N_a*(y) = 2(a^*)²c, c = AD.

Применим полученные результаты к построению доверительных интервалов. В постановке классической математической статистики (т.е. при e = 0) доверительный интервал для параметра формы а, соответствующий доверительной вероятности g, имеет вид [30]

где — квантиль порядка стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1,

В постановке статистики интервальных данных (т.е. при e ¹ 0) следует рассматривать доверительный интервал

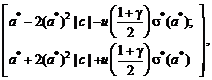
где

в вероятностной постановке (пары (x_i, e_i) образуют простую случайную выборку) и c = AD в оптимизационной постановке. Как в вероятностной, так и в оптимизационной постановках длина доверительного интервала не стремится к 0 при n ® ¥.

Если ограничения наложены на предельную относительную погрешность, задана величина d, то значение с можно найти с помощью следующих правил приближенных вычислений [60, с. 142].

(I). Относительная погрешность суммы заключена между наибольшей и наименьшей из относительных погрешностей слагаемых.

(II). Относительная погрешность произведения и частного равна сумме относительных погрешностей сомножителей или, соответственно, делимого и делителя.

Можно показать, что в рамках статистики интервальных данных с ограничениями на относительную погрешность правила (I) и (II) являются строгими утверждениями при d ® 0.

Обозначим относительную погрешность некоторой величины t через ОП(t), абсолютную погрешность — через АП(t).

Из правила (I) следует, что ОП() = d, а из правила (II) — что

Поскольку рассмотрения ведутся при a ® ¥, то в силу неравенства Чебышева

(19)

по вероятности при a ® ¥, поскольку и числитель, и знаменатель в (19) с близкой к 1 вероятностью лежат в промежутке где константа d может быть определена с помощью упомянутого неравенства Чебышева.

Поскольку при справедливости (19) с точностью до бесконечно малых более высокого порядка

то с помощью трех последних соотношений имеем

(20)

Применим еще одно правило приближенных вычислений [60, с. 142].

(III). Предельная абсолютная погрешность суммы равна сумме предельных абсолютных погрешностей слагаемых.

Из (20) и правила (III) следует, что

АП(v) = 2d.

Из этого соотношения и (15) вытекает [30, с. 44, ф-ла (18)], что

АП(a^*) = 4a²d,

откуда в соответствии с ранее полученной формулой для рационального объема выборки с заменой c = 2d получаем, что

В частности, при a = 5,00; d = 0,01 получаем n_rat = 50, т.е. в ситуации, в которой были получены данные о наработке резцов до предельного состояния (см. табл. 1, составленную согласно [30, с. 29]), проводить более 50 наблюдений нерационально.

Таблица 1

Наработка резцов до предельного состояния, ч

№ п/п	Наработка, ч	№ п/п	Наработка, ч	№ п/п	Наработка, ч
1	9	18	47,5	35	63
2	17,5	19	48	36	64,5
3	21	20	50	37	65
4	26,5	21	51	38	67,5
5	27,5	22	53,5	39	68,5
6	31	23	55	40	70
7	32,5	24	56	41	72,5
8	34	25	56	42	77,5
9	36	26	56,5	43	81
10	36,5	27	57,5	44	82,5
11	39	28	58	45	90
12	40	29	59	46	96
13	41	30	59	47	101,5
14	42,5	31	60	48	117,5
15	43	32	61	49	127,5
16	45	33	61,5	50	130
17	46	34	62

В соответствии с ранее проведенными рассмотрениями асимптотический доверительный интервал для a, соответствующий доверительной вероятности g = 0,95, имеет вид

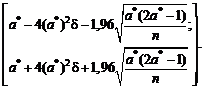
В частности, при a^* = 5,00, d = 0,01, n = 50 имеем асимптотический доверительный интервал [2,12; 7,86] вместо [3,14; 6,86] при d = 0.

При больших а в силу соображений, приведенных при выводе формулы (19), можно связать между собой относительную и абсолютную погрешности результатов наблюдений x_i:

(21)

Следовательно, при больших а имеем

Таким образом, проведенные рассуждения дали возможность вычислить асимптотику интеграла, задающего величину А.

Сравнение методов оценивания. Изучим влияние погрешностей измерений (с ограничениями на абсолютную погрешность) на оценку метода моментов. Имеем

Погрешность s² зависит от способа вычисления s². Если используется формула

(22)

то необходимо использовать соотношения

АП(x_i – ) = 2D, АП[(x_i – )²] » 2|x_i – | D.

По сравнению с анализом влияния погрешностей на оценку a^* здесь возникает новый момент — необходимость учета погрешностей в случайной составляющей отклонения оценки от оцениваемого параметра, в то время как при рассмотрении оценки максимального правдоподобия погрешности давали лишь смещение. Примем в соответствии с неравенством Чебышева

(23)

тогда

Замечание.( Если вычислять s² по формуле

(24)

то аналогичные вычисления дают, что

АП(s²) » 4abD,

т.е. погрешность при больших а существенно больше. Хотя правые части формул (22) и (24) тождественно равны, но погрешности вычислений по этим формулам весьма отличаются. Связано это с тем, что в формуле (24) последняя операция — нахождение разности двух больших чисел, примерно равных по величине (для выборки из гамма-распределения при большом значении параметра формы).)

Из полученных результатов следует, что

При выводе этой формулы использована линеаризация влияния погрешностей (выделение главного линейного члена). Используя связь (21) между абсолютной и относительной погрешностями, можно записать

Эта формула отличается от приведенной в [30, с. 44, формула (19)]

поскольку в [30] вместо (23) использовалась оценка

Используя соотношение (23), мы характеризуем влияние погрешностей «в среднем».

Доверительный интервал, соответствующий доверительной вероятности 0,95, имеет вид

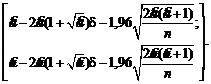
Если = 5,00; d = 0,01; n = 50, то получаем доверительный интервал [2,54; 7,46] вместо [2,86; 7,14] при d = 0. Хотя при d = 0 доверительный интервал для a при использовании оценки метода моментов шире, чем при использовании оценки максимального правдоподобия а^*, при d = 0,01 результат сравнения длин интервалов противоположен.

Необходимо выбрать способ сравнения двух методов оценивания параметра а, поскольку в длины доверительных интервалов входят две составляющие — зависящая от доверительной вероятности и не зависящая от нее. Выберем d = 0,68, т.е. . Тогда оценке максимального правдоподобия а^* соответствует полудлина доверительного интервала

(25)

а оценке метода моментов соответствует полудлина доверительного интервала

(26)

Ясно, что больших а или больших n справедливо неравенство n(a^*) > n(), т.е. метод моментов лучше метода максимального правдоподобия, вопреки классическим результатам Р. Фишера при d = 0 [61, с. 99].

Из (25) и (26) элементарными преобразованиями получаем следующее правило принятия решений. Если

то n(a^*) ³ n() и следует использовать ; а если то n(a^*) < n() и надо применять а^*. Для выбора метода оценивания при обработке реальных данных целесообразно использовать B() (см. раздел 5 в ГОСТ 11.011-83 [30, с. 10–11]).

Пример анализа реальных данных опубликован в [30].

На основе рассмотрения проблем оценивания параметров гамма-распределения можно сделать некоторые общие выводы. Если в классической теории математической статистики:

а) существуют состоятельные оценки a_n параметра а,

б) для повышения точности оценивания объем выборки целесообразно безгранично увеличивать;

в) оценки максимального правдоподобия лучше оценок метода моментов,

то в статистике интервальных данных, учитывающей погрешности измерений, соответственно:

а) не существует состоятельных оценок: для любой оценки a_n существует константа с такая, что

б) не имеет смысла рассматривать объемы выборок, большие «рационального объема выборки» n_rat;

в) оценки метода моментов в обширной области параметров (a, n, d) лучше оценок максимального правдоподобия, в частности, при a ® ¥ и при n ®¥.

Ясно, что приведенные выше результаты справедливы не только для рассмотренной задачи оценивания параметров гамма-распределения, но и для многих других постановок прикладной математической статистики.

Метрологические, методические, статистические и вычислительные погрешности. Целесообразно выделить ряд видов погрешностей статистических данных. Погрешности, вызванные неточностью измерения исходных данных, называем метрологическими. Их максимальное значение можно оценить с помощью нотны. Впрочем, выше на примере оценивания параметров гамма-распределения показано, что переход от максимального отклонения к реально имеющемуся в вероятностно-статистической модели не меняет выводы (с точностью до умножения предельных значений погрешностей D или d на константы). Как правило, метрологические погрешности не убывают с ростом объема выборки.

Методические погрешности вызваны неадекватностью вероятностно-статистической модели, отклонением реальности от ее предпосылок. Неадекватность обычно не исчезает при росте объема выборки. Методические погрешности целесообразно изучать с помощью «общей схемы устойчивости» [13, 56], обобщающей популярную в теории робастных статистических процедур модель засорения большими выбросами. В настоящей главе методические погрешности не рассматриваются.

Статистическая погрешность — это та погрешность, которая традиционно рассматривается в математической статистике. Ее характеристики — дисперсия оценки, дополнение до 1 мощности критерия при фиксированной альтернативе и т.д. Как правило, статистическая погрешность стремится к 0 при росте объема выборки.

Вычислительная погрешность определяется алгоритмами расчета, в частности, правилами округления. На уровне чистой математики справедливо тождество правых частей формул (22) и (24), задающих выборочную дисперсию s², а на уровне вычислительной математики формула (22) дает при определенных условиях существенно больше верных значащих цифр, чем вторая [62, с. 51–52].

Выше на примере задачи оценивания параметров гамма-распределения рассмотрено совместное действие метрологических и вычислительных погрешностей, причем погрешности вычислений оценивались по классическим правилам для ручного счета [60]. Оказалось, что при таком подходе оценки метода моментов имеют преимущество перед оценками максимального правдоподобия в обширной области изменения параметров. Однако, если учитывать только метрологические погрешности, как это делалось выше в примерах 1–3, то с помощью аналогичных выкладок можно показать, что оценки этих двух типов имеют (при достаточно больших n) одинаковую погрешность.

Вычислительную погрешность здесь подробно не рассматриваем. Ряд интересных результатов о ее роли в статистике получили Н.Н. Ляшенко и М.С. Никулин [63].

Проведем сравнение методов оценивания параметров в более общей постановке.

В теории оценивания параметров классической математической статистики установлено, что метод максимального правдоподобия, как правило, лучше (в смысле асимптотической дисперсии и асимптотического среднего квадрата ошибки), чем метод моментов. Однако в интервальной статистике это, вообще говоря, не так, что продемонстрировано выше на примере оценивания параметров гамма-распределения. Сравним эти два метода оценивания в случае интервальных данных в общей постановке. Поскольку метод максимального правдоподобия — частный случай метода минимального контраста, начнем с разбора этого несколько более общего метода.

Оценки минимального контраста. Пусть Х — пространство, в котором лежат независимые одинаково распределенные случайные элементы x₁, x₂, …, x_n, … Будем оценивать элемент пространства параметров Q с помощью функции контраста f : X ´ Q ® R¹. Оценкой минимального контраста называется

Если множество q_n состоит из более чем одного элемента, то оценкой минимального контраста называют также любой элемент q_n.

Оценками минимального контраста являются многие робастные статистики [13, 64]. Эти оценки широко используются в статистике объектов нечисловой природы [3, 56], поскольку при X = Q переходят в эмпирические средние, а если X = Q — пространство бинарных отношений — в медиану Кемени.

Пусть в Х имеется мера m (заданная на той же s-алгебре, что участвует в определении случайных элементов x_i), и p(x; q) — плотность распределения x_i по мере m. Если

f(x; q) = –ln p(x; q),

то оценка минимального контраста переходит в оценку максимального правдоподобия.

Асимптотическое поведение оценок минимального контраста в случае пространств Х и Q общего вида хорошо изучено [65], в частности, известны условия состоятельности оценок. Здесь ограничимся случаем X = R¹, но при этом введя погрешности измерений e_i. Примем также, что Q = (q_min, q_max) Í R¹.

В рассматриваемой математической модели предполагается, что статистику известны лишь искаженные значения y_i = x_i + e_i, i = 1, 2, …, n. Поэтому вместо q_n он вычисляет

Будем изучать величину – q_n в предположении, что погрешности измерений e_i малы. Цель этого изучения — продемонстрировать идеи статистики интервальных данных при достаточно простых предположениях. Поэтому естественно следовать условиям и ходу рассуждений, которые обычно принимаются при изучении оценок максимального правдоподобия [66, п. 33.3].

Пусть q₀ — истинное значение параметра, функция f(x; q) трижды дифференцируема по q, причем

при всех x, q. Тогда

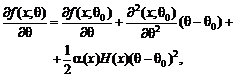(27)

где |a(x)| < 1.

Используя обозначения векторов x = (x₁, x₂, ..., x_n), y =
= (y₁, y₂, ..., y_n), введем суммы

Аналогичным образом введем функции B₀(y), B₁(y), R(y), в которых вместо x_i стоят y_i, i = 1, 2, …, n.

Поскольку в соответствии с теоремой Ферма оценка минимального контраста q_т удовлетворяет уравнению

(28)

то, подставляя в (27) x_i вместо x и суммируя по i = 1, 2, …, n, получаем, что

(29)

откуда

(30)

Решения уравнения (28) будем также называть оценками минимального контраста. Хотя уравнение (28) — лишь необходимое условие минимума, такое словоупотребление не будет вызывать трудностей.

Теорема 1[2]. Пусть для любого x выполнено соотношение (27). Пусть для случайной величины х₁ с распределением, соответствующим значению параметра q = q₀, существуют математические ожидания

(31)

Тогда существуют оценки минимального контраста q_n такие, что q_n ® q₀ при n ® ¥ (в смысле сходимости по вероятности).

Доказательство. Возьмем e > 0 и d > 0. В силу Закона больших чисел (теорема Хинчина) существует n(e, d) такое, что для любого n > n(e, d) справедливы неравенства

P{|B₀| ³ d²} < e/3, P{|B₁| < |A|/2} < e/3, P{R(x) > 2M} < e/3.

Тогда с вероятностью не менее 1 – e одновременно выполняются соотношения

|B₀| £ d², |B₁| ³ |A|/2, R(x) £ 2M. (32)

При q Î [q₀ – d; q₀ + d] рассмотрим многочлен второй степени

(см. формулу (29)). С вероятностью не менее 1 – e выполнены соотношения

Если 0 < 2(M + 1)d < |A|, то знак y(q) в точках q₁ = q₀ – d и q₂ = q₀ + d определяется знаком линейного члена B₁(q_i – q₀), i = 1, 2, следовательно, знаки y(q₁) и y(q₂) различны, а потому существует q_n Î [q₀ – d; q₀ + d] такое, что y(q_n) = 0, что и требовалось доказать.

Теорема 2. Пусть выполнены условия теоремы 1 и, кроме того, для случайной величины х₁, распределение которой соответствует значению параметра q = q₀, существует математическое ожидание

Тогда оценка минимального контраста имеет асимптотически нормальное распределение:

(33)

для любого х, где Ф(x) — функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.

Доказательство. Из Центральной предельной теоремы вытекает, что числитель в правой части формулы (30) асимптотически нормален с математическим ожиданием 0 и дисперсией s². Первое слагаемое в знаменателе формулы (30) в силу условий (31) и Закона больших чисел сходится по вероятности к A ¹ 0, а второе слагаемое по тем же основаниям и с учетом теоремы 1 — к 0. Итак, знаменатель сходится по вероятности к A ¹ 0. Доказательство теоремы 2 завершает ссылка на теорему о наследовании сходимости [8, Приложение 1].

Нотна оценки минимального контраста. Аналогично (30) нетрудно получить, что

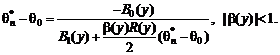(34)

Следовательно, есть разность правых частей формул (30) и (34). Найдем максимально возможное значение (т.е. нотну) величины при ограничениях (1) на абсолютные погрешности результатов измерений.

Покажем, что при D ® 0 для некоторого C > 0 нотна имеет вид

(35)

Поскольку то из (33) и (35) следует, что

(36)

Можно сказать, что наличие погрешностей e_i приводит к появлению систематической ошибки (смещения) у оценки метода максимального правдоподобия, и нотна является максимально возможным значением этой систематической ошибки.

В правой части (36) первое слагаемое — квадрат асимптотической нотны, второе соответствует статистической ошибке. Приравнивая их, получаем рациональный объем выборки

Остается доказать соотношение (35) и вычислить С. Укажем сначала условия, при которых (по вероятности) при n ® ¥ одновременно с D ® 0.

Теорема 3. Пусть существуют константа D₀ и функции g₁(x), g₂(x), g₃(x) такие, что при 0 £ D £ D₀ и –1 £ g £ 1 выполнены неравенства (ср. формулу (27))

(37)

при всех x. Пусть для случайной величины х₁, распределение которой соответствует q = q₀, существуют m₁ = Mg₁(x₁), m₂ = Mg₂(x₁) и m₃ = Mg₃(x₁). Пусть выполнены условия теоремы 1. Тогда (по вероятности) при D ® 0, n ® ¥.

Доказательство. Проведем по схеме доказательства теоремы 1. Из неравенств (37) вытекает, что

(38)

.

Возьмем e > 0 и d > 0. В силу Закона больших чисел (теорема Хинчина) существует n(e, d) такое, что для любого n >
> n(e, d) справедливы неравенства

Тогда с вероятностью не менее 1 – e одновременно выполняются соотношения

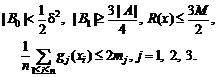
В силу (38) при этом

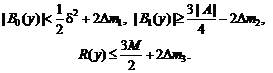
Пусть

Тогда с вероятностью не менее 1 – e одновременно выполняются соотношения (ср. (32))

Завершается доказательство дословным повторением такового в теореме 1, с единственным отличием — заменой в обозначениях x на y.

Теорема 4. Пусть выполнены условия теоремы 3 и, кроме того, существуют математические ожидания (при q = q₀)

(39)

Тогда выполнено соотношение (35) с

(40)

Доказательство. Воспользуемся следующим элементарным соотношением. Пусть a и b — бесконечно малые по сравнению с Z и B соответственно. Тогда с точностью до бесконечно малых более высокого порядка

Чтобы применить это соотношение к анализу – q_n в соответствии с (30), (34) и теоремой 2, положим

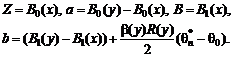
В силу условий теоремы 4 при малых e_i с точностью до членов более высокого порядка

.

При D ® 0 эти величины бесконечно малы, а потому с учетом сходимости B₁(x) к А и теоремы 3

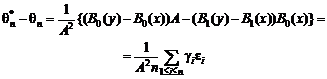
с точностью до бесконечно малых более высокого порядка, где

Ясно, что задача оптимизации

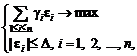(41)

имеет решение

при этом максимальное значение линейной формы есть . Поэтому

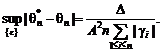(42)

С целью упрощения правой части (42) воспользуемся тем, что

(43)

где |a| £ 1. Поскольку при n ® ¥

по вероятности, то второе слагаемое в (43) сходится к 0, а первое в силу закона больших чисел с учетом (39) сходится к СА², где С определено в (40). Теорема 4 доказана.

Оценки метода моментов. Пусть g : R^k ® R¹, h_j : R¹ ® R¹, j = 1, 2, …, k, — некоторые функции. Рассмотрим аналоги выборочных моментов

Оценки метода моментов имеют вид

(x) = g(m₁, m₂, …, m_k)

(функции g и h_j должны удовлетворять некоторым дополнительным условиям [55, с. 80], которые здесь не приводим). Очевидно, что

(44)

с точностью до бесконечно малых более высокого порядка, а потому с той же точностью

(45)

Теорема 5. Пусть при q = q₀ существуют математические ожидания

функция g дважды непрерывно дифференцируема в некоторой окрестности точки (M₁, M₂, …, M_k). Пусть существует функция t : R¹ ® R¹ такая, что

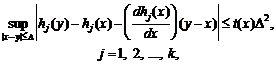(46)

причем Mt(x₁) существует. Тогда

с точностью до бесконечно малых более высокого порядка, причем

Доказательство теоремы 5 сводится к обоснованию проведенных ранее рассуждений, позволивших получить формулу (45). В условиях теоремы 5 собраны предположения, достаточные для такого обоснования. Так, условие (46) дает возможность обосновать соотношения (44); существование обеспечивает существование С₁, и т.д. Завершает доказательство ссылка на решение задачи оптимизации (41) и применение Закона больших чисел.

Полученные в теоремах 4 и 5 нотны оценок минимального контраста и метода моментов, асимптотические дисперсии этих оценок (см. теорему 2 и [67] соответственно) позволяют находить рациональные объемы выборок, строить доверительные интервалы с учетом погрешностей измерений, а также сравнивать оценки по среднему квадрату ошибки (36). Подобное сравнение проведено для оценок максимального правдоподобия и метода моментов параметров гамма-распределения. Установлено, что классический вывод о преимуществе оценок максимального правдоподобия [61, с. 99–100] неверен в случае D > 0.

7.5. Интервальные данные в задачах проверки гипотез

С позиций статистики интервальных данных целесообразно изучить все практически используемые процедуры прикладной математической статистики, установить соответствующие нотны и рациональные объемы выборок. Это позволит устранить разрыв между математическими схемами прикладной статистики и реальностью влияния погрешностей наблюдений на свойства статистических процедур. Статистика интервальных данных — часть теории устойчивых статистических процедур, развитой в монографии [13]. Часть, более адекватная реальной статистической практике, чем некоторые другие постановки, например, с засорением нормального распределения большими выбросами.

Рассмотрим подходы статистики интервальных данных в задачах проверки статистических гипотез. Пусть принятие решения основано на сравнении рассчитанного по выборке значения статистики критерия f = f(y₁, y₂, …, y_n) с граничным значением С: если f > C, то гипотеза отвергается, если же f £ C, то принимается. С учетом погрешностей измерений выборочное значение статистики критерия может принимать любое значение в интервале [f(y) – N_f(y); f(y) + N_f(y)]. Это означает, что «истинное» значение порога, соответствующее реально используемому критерию, находится между C – N_f(y) и C + N_f(y), а потому уровень значимости описанного правила (критерия) лежит между 1 – P(C + N_f(y)) и 1 – P(C – N_f(y)), где P(Z) = P(f < Z).

Пример 1[3]. Пусть x₁, x₂, …, x_n — выборка из нормального распределения с математическим ожиданием а и единичной дисперсией. Необходимо проверить гипотезу H₀: a = 0 при альтернативе H₁ : a ¹ 0.

Как известно из любого учебного курса математической статистики, следует использовать статистику f = и порог C = F(1 – a/2), где a — уровень значимости, Ф(×) — функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. В частности, С = 1,96 при a = 0,05.

При ограничениях (1) на абсолютную погрешность N_f(y) = D. Например, если D = 0,1, а n = 100, то N_f(y) = 1,0. Это означает, что истинное значение порога лежит между 0,96 и 2,96, а истинный уровень значимости — между 0,003 и 0,34. Можно сделать и другой вывод: нулевую гипотезу H₀ допустимо отклонить на уровне значимости 0,05 лишь тогда, когда
f > 2,96.

Если же n = 400 при D = 0,1, то N_f(y) = 2,0 и C – N_f(y) =
= –0,04, в то время как C + N_f(y) = 3,96. Таким образом, даже в случае x = 0 гипотеза H₀ может быть отвергнута только из-за погрешностей измерений результатов наблюдений.

Вернемся к общему случаю проверки гипотез. С учетом погрешностей измерений граничное значение C_a в статистике интервальных данных целесообразно заменить на C_a + N_f(y). Такая замена дает гарантию, что вероятность отклонения нулевой гипотезы H₀, когда она верна, не более a. При проверке гипотез аналогом статистической погрешности, рассмотренной выше в задачах оценивания, является C_α. Суммарная погрешность имеет вид C_a + N_f(y). Исходя из принципа уравнивания погрешностей [13], целесообразно определять рациональный объем выборки из условия

C_α = N_f(y).

Если f = |f₁|, где f₁ при справедливости H₀ имеет асимптотически нормальное распределение с математическим ожиданием 0 и дисперсией s² / n, то

(47)

при больших n, где u(1 – a/2) — квантиль порядка 1 – a/2 стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. Из (47) вытекает, что в рассматриваемом случае

В условиях примера 1 f₁ = и

Пример 2. Рассмотрим статистику одновыборочного критерия Стьюдента

где n — выборочный коэффициент вариации. Тогда с точностью до бесконечно малых более высокого порядка нотна для t имеет вид

где N_n(y) — рассмотренная ранее нотна для выборочного коэффициента вариации. Поскольку распределение статистики Стьюдента t сходится к стандартному нормальному, то небольшое изменение предыдущих рассуждений дает

Пример 3. Рассмотрим двухвыборочный критерий Смирнова, предназначенный для проверки однородности (совпадения) функций распределения двух независимых выборок [68]. Статистика этого критерия имеет вид

где F_m(x) — эмпирическая функция распределения, построенная по первой выборке объема m, извлеченной из генеральной совокупности с функцией распределения F(x), а G_n(x) — эмпирическая функция распределения, построенная по второй выборке объема n, извлеченной из генеральной совокупности с функцией распределения G(x). Нулевая гипотеза имеет вид H₀ : F(x) º G(x), альтернативная состоит в ее отрицании: H₁ : F(x) ¹ G(x) при некотором x. Значение статистики сравнивают с порогом D(a, m, n). зависящим от уровня значимости a и объемов выборок m и n. Если значение статистики не превосходит порога, то принимают нулевую гипотезу, если больше порога — альтернативную. Пороговые значения D(a, m, n) берут из таблиц [69]. Описанный критерий иногда неправильно называют критерием Колмогорова-Смирнова. История вопроса описана в [70].

При ограничениях (1) на абсолютные погрешности и справедливости нулевой гипотезы H₀ : F(x) º G(x) нотна имеет вид (при больших объемах выборок)

Если F(x) = G(x) = x при 0 £ x £ 1, то N_D = 2D. С помощью условия C_a = N_f(y) при уровне значимости a = 0,05 и достаточно больших объемах выборок (т.е. используя асимптотическое выражение для порога согласно [68, 69]) получаем, что выборки имеет смысл увеличивать, если

Правая часть этой формулы при D = 0,1 равна 46. Если m = n, то последнее неравенство переходит в n £ 92.

Теоретические результаты в области статистических методов входят в практику через алгоритмы расчетов, воплощенные в программные средства (пакеты программ, диалоговые системы). Ввод данных в современной статистической программной системе должен содержать запросы о погрешностях результатов измерений. На основе ответов на эти запросы вычисляются нотны рассматриваемых статистик, а затем — доверительные интервалы при оценивании, разброс уровней значимости при проверке гипотез, рациональные объемы выборок. Необходимо использовать систему алгоритмов и программ статистики интервальных данных, «параллельную» подобным системам для классической математической статистики.

7.6. Линейный регрессионный анализ интервальных данных

Перейдем к многомерному статистическому анализу. Сначала с позиций асимптотической математической статистики интервальных данных рассмотрим оценки метода наименьших квадратов (МНК).

Статистическое исследование зависимостей — одна из наиболее важных задач, которые возникают в различных областях науки и техники. Под словами «исследование зависимостей» имеется в виду выявление и описание существующей связи между исследуемыми переменными на основании результатов статистических наблюдений. К методам исследования зависимостей относятся: регрессионный анализ, многомерное шкалирование, идентификация параметров динамических объектов, факторный анализ, дисперсионный анализ, корреляционный анализ и др. Однако многие реальные ситуации характеризуются наличием данных интервального типа, причем известны допустимые границы погрешностей (например, из технических паспортов средств измерения).

Если какая-либо группа объектов характеризуется переменными Х₁, Х₂, ..., Х_m и проведен эксперимент, состоящий из n опытов, где в каждом опыте эти переменные измеряются один раз, то экспериментатор получает набор чисел: Х_1j, Х_2j, ..., Х_mj (j = 1, …, n).

Однако процесс измерения, какой бы физической природы он ни был, обычно не дает однозначный результат. Реально результатом измерения какой-либо величины Х являются два числа: Х_H — нижняя граница и Х_B — верхняя граница. Причем Х_ИСТ Î [Х_H, Х_B], где Х_ИСТ — истинное значение измеряемой величины. Результат измерения можно записать как X: [Х_H, Х_B]. Интервальное число X может быть представлено другим способом, а именно, X: [Х_m, D_x], где Х_H = Х_m — D_x, Х_H = Х_m + D_x. Здесь Х_m — центр интервала (как правило, не совпадающий с Х_ИСТ), а D_x — максимально возможная погрешность измерения.

Метод наименьших квадратов для интервальных данных. Пусть математическая модель задана следующим образом:

у = Q(x, b) + e,

где х = (х₁, х₂, ..., х_m) — вектор влияющих переменных (факторов), поддающихся измерению; b = (b₁, b₂, ..., b_r) — вектор оцениваемых параметров модели; у — отклик модели (скаляр); Q(x, b) — скалярная функция векторов х и b; наконец, e — случайная ошибка (невязка, погрешность).

Пусть проведено n опытов, причем в каждом опыте измерены (один раз) значения отклика (у) и вектора факторов (х). Результаты измерений могут быть представлены в следующем виде:

Х = {х_ij; i = 1, …, n; j = 1, …, m}, Y = (y₁, y₂, …, y_n ), Е = (e₁, e₂, …, e_n),

где Х — матрица значений измеренного вектора (х) в n опытах; Y — вектор значений измеренного отклика в n опытах; Е — вектор случайных ошибок. Тогда выполняется матричное соотношение:

Y = Q(X, b) + Е,

где Q(X, b) = (Q(x₁, b), Q(x₂, b), ..., Q(x_n, b))^T, причем x₁, x₂, ..., x_n — m-мерные вектора, которые составляют матрицу Х = (x₁, x₂, ..., x_n)^T.

Введем меру близости d(Y, Q) между векторами Y и Q. В МНК в качестве d(Y, Q) берется квадратичная форма взвешенных квадратов невязок e_i = y_i – Q(x_i, b), т.е.

d(Y, Q) = [Y – Q(X, b)]^T W[Y – Q(X, b)],

где W = {w_ij, i, j = 1, …, n} — матрица весов, не зависящая от b. Тогда в качестве оценки b можно выбрать такое b^*, при котором мера близости d(Y, Q) принимает минимальное значение, т.е.

b^* = {b : d(Y, Q) ®

В общем случае решение этой экстремальной задачи может быть не единственным. Поэтому в дальнейшем будем иметь в виду одно из этих решений. Оно может быть выражено в виде некоторой вектор-функции b^* = f(X, Y), где f(X, Y) = (f₁(X, Y), f₂(X, Y), ..., f_r(Х, У))^T, причем действительнозначные функции f_i(X, Y) непрерывны и дифференцируемы по (X, Y) Î Z, где Z — область определения функции f(X, Y). Эти свойства функции f(X, Y) дают возможность использовать подходы статистики интервальных данных.

Преимущество метода наименьших квадратов заключается в сравнительной простоте и универсальности вычислительных процедур. Однако не всегда оценка МНК является состоятельной (при функции Q(X, b), не являющейся линейной по векторному параметру b), что ограничивает его применение на практике.

Важным частным случаем является линейный МНК, когда Q(x, b) есть линейная функция от b:

у = b_ox_o + b₁x₁ + ... + b_mx_m + e = bх^T + e,

где, возможно, x_o = 1, а b_o — свободный член линейной комбинации. Как известно, в этом случае МНК-оценка имеет вид:

b^* = (X^TWX)^–1X^TWY.

Если матрица X^TWX не вырождена, то эта оценка является единственной. Если матрица весов W единичная, то

b^* = (X^TX)^–1X^TY.

Пусть выполняются следующие предположения относительно распределения ошибок e_i :

– ошибки e_i имеют нулевые математические ожидания М{e_i} = 0;

– результаты наблюдений имеют одинаковую дисперсию D{e_i} = σ²;

– ошибки наблюдений некоррелированы, т.е. cov{e_i, e_j} = 0.

Тогда, как известно, оценки МНК являются наилучшими линейными оценками, т.е. состоятельными и несмещенными оценками, которые представляют собой линейные функции результатов наблюдений и обладают минимальными дисперсиями среди множества всех линейных несмещенных оценок. Далее именно этот наиболее практически важный частный случай рассмотрим более подробно.

Как и в других постановках асимптотической математической статистики интервальных данных, при использовании МНК измеренные величины отличаются от истинных значений из-за наличия погрешностей измерения. Запишем истинные данные в следующей форме:

где R — индекс, указывающий на то, что значение истинное. Истинные и измеренные данные связаны следующим образом:

X = X_R + DX, Y = Y_R + DY,

где

Предположим, что погрешности измерения отвечают граничным условиям

(48)

аналогичным ограничениям (1).

Пусть множество W возможных значений (X_R, Y_R) входит в Z — область определения функции f(X, Y). Рассмотрим b^*R — оценку МНК, рассчитанную по истинным значениям факторов и отклика, и b^* — оценку МНК, найденную по искаженным погрешностями данным. Тогда

Ввести понятие нотны придется несколько иначе, чем это было сделано выше, поскольку оценивается не одномерный параметр, а вектор. Положим:

Будем называть n(1) нижней нотной, а n(2) верхней нотной. Предположим, что при безграничном возрастании числа измерений n, т.е. при n → ∞, вектора n(1), n(2) стремятся к постоянным значениям N(1), N(2) соответственно. Тогда N(1) будем называть нижней асимптотической нотной, а N(2) — верхней асимптотической нотной.

Рассмотрим доверительное множество B_a=B_a(n, b^*R) для вектора параметров b, т.е. замкнутое связное множество точек в r-мерном евклидовом пространстве такое, что P(b Î B_a) = a, где a — доверительная вероятность, соответствующая B_a (a ≈ 1). Другими словами, B_a(n, b^*R) есть область рассеивания (аналог эллипсоида рассеивания) случайного вектора b^*R с доверительной вероятностью a и числом опытов n.

Из определения верхней и нижней нотн следует, что всегда b^*R Î [b^* – n(1); b^* + n(2)] (т.е. по каждой координате выполнено соответствующее неравенство). В соответствии с определением нижней асимптотической нотны и верхней асимптотической нотны можно считать, что b^*R Î [b^* – N(1); b^* + N(2)] при достаточно большом числе наблюдений n. Этот многомерный интервал описывает r-мерный гиперпараллелепипед P.

Каким-либо образом разобьем P на L гиперпараллелепипедов. Пусть b_k — внутренняя точка k-го гиперпараллелепипеда. Учитывая свойства доверительного множества и устремляя L к бесконечности, можно утверждать, что P(b Î C) ³ a, где

Таким образом, множество C характеризует неопределенность при оценивании вектора параметров b. Его можно назвать доверительным множеством в статистике интервальных данных.

Введем некоторую меру М(X), характеризующую «величину» множества X Í R^r. По определению меры она удовлетворяет условию: если и то M(X) =
= M(Z) + M(Y). Примерами такой меры являются площадь для r = 2 и объем для r = 3. Тогда:

М(C) = М(P) + М(F), (49)

где F = C\P. Здесь М(F) характеризует меру статистической неопределенности, в большинстве случаев она убывает при увеличении числа опытов n. В то же время М(P) характеризует меру интервальной (метрологической) неопределенности, и, как правило, М(P) стремится к некоторой постоянной величине при увеличении числа опытов n. Пусть теперь требуется найти то число опытов, при котором статистическая неопределенность составляет d-ю часть общей неопределенности, т.е.

М(F) = dМ(C), (50)

где d < 1. Тогда, подставив соотношение (50) в равенство (49) и решив уравнение относительно n, получим искомое число опытов. В асимптотической математической статистике интервальных данных оно называется «рациональным объемом выборки». При этом d есть «степень малости» статистической неопределенности М(P) относительно всей неопределенности. Она выбирается из практических соображений. При использовании «принципа уравнивания погрешностей» согласно [13] имеем d = 1/2.

Метод наименьших квадратов для линейной модели. Рассмотрим наиболее важный для практики частный случай МНК, когда модель описывается линейным уравнением (см. выше).

Для простоты описания преобразований пронормируем переменные х_ij, у_i следующим образом:

где

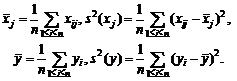
Тогда

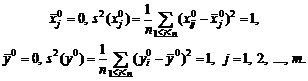
В дальнейшем изложении будем считать, что рассматриваемые переменные пронормированы описанным образом, и верхние индексы ⁰ опустим. Для облегчения демонстрации основных идей примем достаточно естественные предположения.

1. Для рассматриваемых переменных существуют следующие пределы:

2. Количество опытов n таково, что можно пользоваться асимптотическими результатами, полученными при n ® ¥.

3. Погрешности измерения удовлетворяют одному из следующих типов ограничений.

Тип 1. Абсолютные погрешности измерения ограничены согласно (48).

Тип 2. Относительные погрешности измерения ограничены:

Тип 3. Ограничения наложены на сумму погрешностей:

(Поскольку все переменные пронормированы, т.е. представляют собой относительные величины, то различие в размерностях исходных переменных не влияет на возможность сложения погрешностей.)

Перейдем к вычислению нотны оценки МНК. Справедливо равенство:

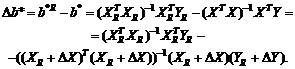
Воспользуемся следующей теоремой из теории матриц [71].

Теорема. Если функция f(l) разлагается в степенной ряд в круге сходимости |l – l₀| < r, т.е.

то это разложение сохраняет силу, если скалярный аргумент заменить любой матрицей А, характеристические числа которой l_k, k = 1, …, n, лежат внутри круга сходимости.

Из этой теоремы вытекает, что

если

Легко убедиться, что:

где

Это вытекает из последовательности равенств:

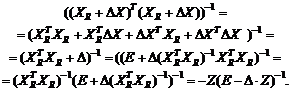
Применим приведенную выше теорему из теории матриц, полагая А = DZ и принимая, что собственные числа этой матрицы удовлетворяют неравенству |l_k| < 1. Тогда получим:

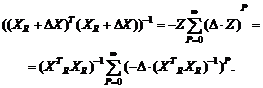
Подставив последнее соотношение в заключение упомянутой теоремы, получим:

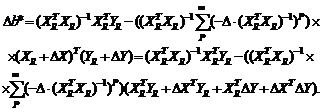
Для дальнейшего анализа понадобится вспомогательное утверждение. Исходя из предположений 1–3, докажем, что:

Доказательство. Справедливо равенство

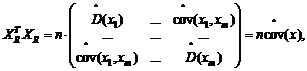
где — состоятельные и несмещенные оценки дисперсий и коэффициентов ковариации, т.е.

тогда

где

Другими словами, каждый элемент матрицы, обозначенной как о(1/n), есть бесконечно малая величина порядка 1/n. Для рассматриваемого случая cov(x) = E, поэтому

Предположим, что n достаточно велико и можно считать, что собственные числа матрицы О(1/n) меньше единицы по модулю, тогда

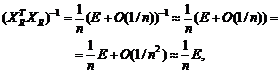
что и требовалось доказать.

Подставим доказанное асимптотическое соотношение в формулу для приращения b^*, получим

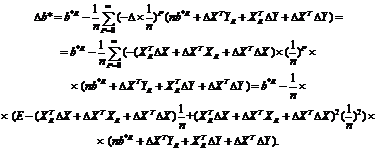
Выразим Db^* относительно приращений DХ, DY до 2-ro порядка

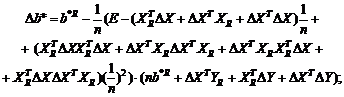
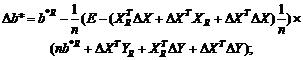
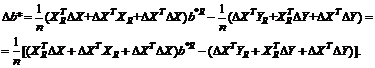
Перейдем от матричной к скалярной форме, опуская индекс (R):

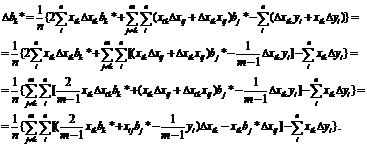
Будем искать max(|Db_k*|) по Dx_ij и Dy_i (i = 1, …, п; j = 1, …, m). Для этого рассмотрим все три ранее введенных типа ограничений на ошибки измерения.

Тип 1 (абсолютные погрешности измерения ограничены). Тогда:

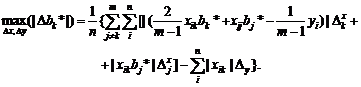
Тип 2 (относительные погрешности измерения ограничены). Аналогично получим:

Тип З (ограничения наложены на сумму погрешностей). Предположим, что достигает максимального значения при таких значениях погрешностей Dx_ij и Dy_i, которые мы обозначим как:

Тогда:

Ввиду линейности последнего выражения и выполнения ограничения типа 3:

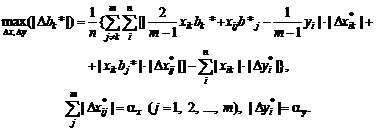
Для простоты записей выкладок сделаем следующие замены:

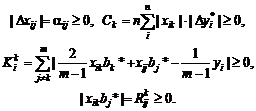
Теперь для достижения поставленной цели можно сформулировать следующую задачу, которая разделяется на m типовых задач оптимизации:

где

при ограничениях

Перепишем минимизируемые функции в следующем виде:

Очевидно, что f_i^k > 0.

Легко видеть, что

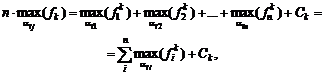
где

Следовательно, необходимо решить nm задач

при ограничениях «типа равенства»:

где

причем

Сформулирована типовая задача поиска экстремума функции. Она легко решается. Поскольку

то максимальное отклонение МНК-оценки k-ого параметра равно

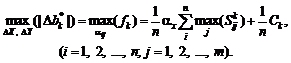
Кроме рассмотренных выше трех видов ограничений на погрешности могут представлять интерес и другие, но для демонстрации типовых результатов ограничимся только этими тремя видами.

Оценивание линейной регрессионной связи. В качестве примера рассмотрим оценивание линейной регрессионной связи случайных величин у и х₁, х₂, ..., х_m с нулевыми математическими ожиданиями. Пусть эта связь описывается соотношением:

где b₁, b₂, ..., b_m — постоянные, а случайная величина е некоррелирована с х₁, х₂, ..., х_m. Допустим, необходимо оценить неизвестные параметры b₁, b₂, ..., b_m по серии независимых испытаний:

Здесь при каждом i = 1, 2, …, n имеем новую независимую реализацию рассматриваемых случайных величин. В этой частной схеме оценки наименьших квадратов , …, параметров b₁, b₂, ..., b_m являются, как известно, состоятельными [72].

Пусть величины х₁, х₂, ..., х_m в дополнение к попарной независимости имеют единичные дисперсии. Тогда из Закона больших чисел [72] следует существование следующих пределов (см. предположение 1 выше):

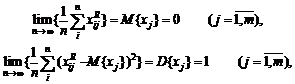
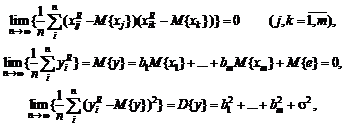
где s — среднее квадратическое отклонение случайной величины е.

Пусть измерения производятся с погрешностями, удовлетворяющими ограничениям типа 1, тогда максимальное приращение величины как показано выше, равно:

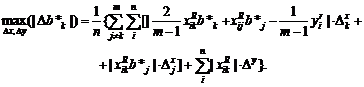
Перейдем к предельному случаю и выпишем выражение для нотны:

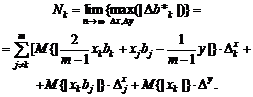
В качестве примера рассмотрим случай m = 2. Тогда

Приведенное выше выражение для максимального приращения метрологической погрешности не может быть использовано в случае m = 1. Для m = 1 выведем выражение для нотны, исходя из соотношения:

Подставив m = 1, получим:

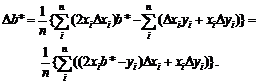
Следовательно, нотна выглядит так:

N_f = M{|2xb^* – y|}D^x + M{|x|}D^y.

Для нахождения рационального объема выборки необходимо сделать следующее.

Этап 1. Выразить зависимость размеров и меры области рассеивания B_a(n, b) от числа опытов n (см. выше).

Этап 2. Ввести меру неопределенности и записать соотношение между статистической и интервальной неопределенностями.

Этап 3. По результатам этапов 1 и 2 получить выражение для рационального объема выборки.

Для выполнения этапа 1 определим область рассеивания следующим образом. Пусть доверительным множеством B_a(n, b) является m-мерный куб со сторонами длиною 2k, для которого

P(b Î B_a(n, b^*R)) = a.

Исследуем случайный вектор b^* и

Как известно, если элементы матрицы А = {а_ij} —случайные, т.е. А — случайная матрица, то ее математическим ожиданием является матрица, составленная из математических ожиданий ее элементов, т.е. М{А} = {М{а_ij}}.

Утверждение 1. Пусть А = {а_ij} и В = {b_ij} — случайные матрицы порядка (m х n) и (n х r) соответственно, причем любая пара их элементов (а_ij, b_kl) состоит из независимых случайных величин. Тогда математическое ожидание произведения матриц равно произведению математических ожиданий сомножителей, т.е. M{AB} = M{A} M{B}.

Доказательство. На основании определения математического ожидания матрицы заключаем, что

но так как случайные величины а_ik, b_kj независимы, то

что и требовалось доказать.

Утверждение 2. Пусть А = {а_ij} и В = {b_ij} — случайные матрицы порядка (m ´ n) и (n ´ r) соответственно. Тогда математическое ожидание суммы матриц равно сумме математических ожиданий слагаемых, т.е. М{А + В} = М{А} + М{В}.

Доказательство. На основании определения математического ожидания матрицы заключаем, что

M{А + В} = {М{а_ij + b_ij}} = {М{а_ij} + М{b_ij}} = M{A} + M{B},

что и требовалось доказать.

Найдем математическое ожидание и ковариационную матрицу вектора b^* с помощью утверждений 1, 2 и выражения для b^*R, приведенного выше. Имеем

Но так как M{e} = 0, то M{b^*R} = b. Это означает, что оценка МНК является несмещенной.

Найдем ковариационную матрицу:

Можно доказать, что

Но M{e×e^T} = D{e} = s²E, поэтому

Как выяснено ранее, для достаточно большого количества опытов n выполняется приближенное равенство

(51)

тогда при больших n

Осталось определить вид распределения вектора b^*R. Из выражения для b^*R, приведенного выше, и асимптотического соотношения (51) следует, что

Можно показать, что вектор b^*R имеет асимптотически нормальное распределение, т.е.

Тогда совместная функция плотности распределения вероятностей случайных величин , , …, будет иметь в асимптотике вид:

(52)

где

Тогда справедливы соотношения

Подставим в формулу (52), получим

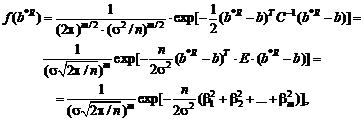
где

Вычислим асимптотическую вероятность попадания описывающего реальность вектора параметров b в m-мерный куб с длиной стороны, равной 2k, и с центром b^*R.

Сделаем замену

Тогда

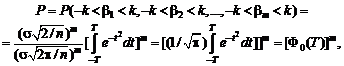
где Т = (n/2)^1/2(k/s), а F₀(Т) — интеграл Лапласа,

где — функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. Из последнего соотношения получаем

Т = (P^1/m),

где Ф^–1(Р) — обратная функция Лапласа. Отсюда следует, что

k = s (2/n)^1/2 Ф₀^–1 (Р^1/m). (53)

Напомним, что доверительная область B_a(n, b) — это
m-мерный куб, длина стороны которого равна К, т.е.

P(b Î B_a(n, b)) = P (–K < b₁ < K, –K < b₂ < K, …, –K < b_m < K) = a.

Подставляя P = a в формулу (53), получим

К = k = s (2/n)^1/2Ф₀^–1(a ^1/m). (54)

Соотношение (54) выражает зависимость размеров доверительной области (т.е. длины ребра куба К) от числа опытов n, среднего квадратического отклонения s ошибки е и доверительной вероятности a. Это соотношение понадобится для определения рационального объема выборки.

Переходим к этапу 2. Необходимо ввести меру разброса (неопределенности) и установить соотношение между статистической и интервальной (метрологической) неопределенностями с соответствии с ранее сформулированным общим подходом.

Пусть A — некоторое измеримое множество точек в m-мерном евклидовом пространстве, характеризующее неопределенность задания вектора а Î A. Тогда необходимо ввести некую меру М(А), измеряющую степень неопределенности. Такой мерой может служить m-мерный объем V(A) множества А (т.е. его мера Лебега или Жордана), М(А) = V(A).

Пусть P — m-мерный параллелепипед, характеризующий интервальную неопределенность. Длины его сторон равны значениям нотн 2N₁, 2N₂, …, 2N_m, а центр а (точка пересечений диагоналей параллелепипеда) находится в точке b^*R. Пусть C — измеримое множество точек, характеризующее общую неопределенность. В рассматриваемом случае это m-мерный параллелепипед, длины сторон которого равны 2(N₁ + K), 2(N₂ + K), …, 2(N_m + K), а центр находится в точке b^*R. Тогда

M(P) = V(P) = 2^mN₁N₂…N_m, (55)

M(C) = V(C) = 2^m (N₁ + K)(N₂ + K)…(N_m + K). (56)

Справедливо соотношение (49), согласно которому М(C) = М(P) + М(F), где множество F = C\P характеризует статистическую неопределенность.

На этапе 3 получаем по результатам этапов 1 и 2 выражение для рационального объема выборки. Найдем то число опытов, при котором статистическая неопределенность составит d 100% от общей неопределенности, т.е. согласно правилу (50)

M(F) = М(C) – М(P) = dM(C) (57)

где 0 < d < 1. Подставив (55) и (56) в (57), получим

Следовательно,

Преобразуем эту формулу:

откуда

Если статистическая погрешность мала относительно метрологической, т.е. величины K/Ni малы, то

При m = 1 эта формула является точной. Из нее следует, что для дальнейших расчетов можно использовать соотношение

Отсюда нетрудно найти К:

(58)

Подставив в формулу (58) зависимость K = K(n), полученную в формуле (54), находим приближенное (асимптотическое) выражение для рационального объема выборки:

При m = 1 эта формула также справедлива, более того, является точной.

Переход от произведения к сумме является обоснованным при достаточно малом d, т.е. при достаточно малой статистической неопределенности по сравнению с метрологической.
В общем случае можно находить К и затем рациональный объем выборки тем или иным численным методом.

Пример 1. Представляет интерес определение n_рац для случая, когда m = 2, поскольку простейшая линейная регрессия с m = 2 широко применяется. В этом случае базовое соотношение имеет вид

(1 + К/N₁)(1 + К/N₂) = 1/(1 – d).

Решая это уравнение относительно К, получаем

К = 0,5{ –(N₁ + N₂) + [(N₁ + N₂)² + 4N₁N₂ (d/(1 –d)]^1/2}.

Далее, подставив в формулу (54), получим уравнение для рационального объема выборки в случае m = 2:

s(2/n)^1/2Ф^–1(a^1/2) = 0,5{–(N₁ + N₂) + [(N₁ + N₂)²+4N₁N₂(d/(1 – d)]^1/2}.

Следовательно,

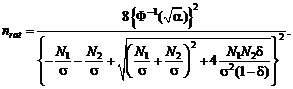
При использовании «принципа уравнивания погрешностей» согласно [3] d = 1/2. При доверительной вероятности имеем и согласно [42] Для этих численных значений

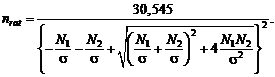
Если то Если же то Если первое из этих чисел превышает обычно используемые объемы выборок, то второе находится в «рабочей зоне» регрессионного анализа.

Парная регрессия. Наиболее простой и одновременно наиболее широко применяемый частный случай парной регрессии рассмотрим подробнее. Модель имеет вид

Здесь x_i — значения фактора (независимой переменной), y_i — значения отклика (зависимой переменной), e_i — статистические погрешности, a, b — неизвестные параметры, оцениваемые методом наименьших квадратов. Она переходит в модель (используем альтернативную запись линейной модели)

если положить

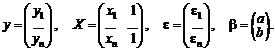
Естественно принять, что погрешности факторов описываются матрицей

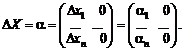
В рассматриваемой модели интервального метода наименьших квадратов

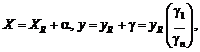
где X, y — наблюдаемые (т.е. известные статистику) значения фактора и отклика; X_R, y_{R —} истинные значения переменных;
a, g — погрешности измерений переменных. Пусть b^* — оценка метода наименьших квадратов, вычисленная по наблюдаемым значениям переменных; — аналогичная оценка, найденная по истинным значениям. В соответствии с ранее проведенными рассуждениями

(59)

с точностью до бесконечно малых более высокого порядка по |a| и |g|. В формуле (59) использовано обозначение Вычислим правую часть в (59), выделим главный линейный член и найдем нотну.

Легко видеть, что

(60)

где суммирование проводится от 1 до n. Для упрощения обозначений в дальнейшем до конца настоящего пункта не будем указывать эти пределы суммирования. Из (60) вытекает, что

(61)

Легко подсчитать, что

(62)

Положим

Тогда знаменатель в (61) равен Из (61) и (62) следует, что

(63)

Здесь и далее опустим индекс i, по которому проводится суммирование. Это не может привести к недоразумению, поскольку всюду суммирование проводится по индексу i в интервале от 1 до n. Из (61) и (63) следует, что

(64)

где

Наконец, вычисляем основной множитель в (59)

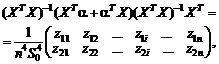(65)

где

Перейдем к вычислению второго члена с в (59). Имеем

(67)

где

Складывая правые части (65) и (67) и умножая на у, получим окончательный вид члена с a в (59):

(68)

где

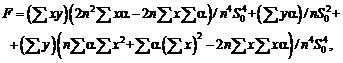(69)

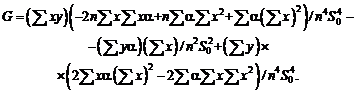
Для вычисления нотны выделим главный линейный член. Сначала найдем частные производные. Имеем

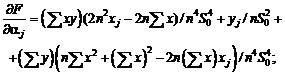(70)

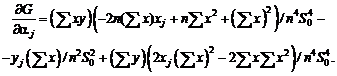
Если ограничения имеют вид

то максимально возможное отклонение оценки а^* параметра а из-за погрешностей a_j таково:

где производные заданы формулой (70).

Пример 2. Пусть вектор (х, y) имеет двумерное нормальное распределение с нулевыми математическими ожиданиями, единичными дисперсиями и коэффициентом корреляции r. Тогда

(71)

При этом

следовательно, максимально возможному изменению параметра b^* соответствует сдвиг всех x_i в одну сторону, т.е. наличие систематической ошибки при определении х-ов. В то же время согласно (71) значения в асимптотике выбираются по правилу

Таким образом, максимальному изменению а^* соответствуют не те a_j, что максимальному изменению b^*. В этом состоит новое по сравнению с одномерным случаем. В зависимости от вида ограничений на возможные отклонения, в частности, от вида метрики в пространстве параметров, будут «согласовываться» отклонения по отдельным параметрам. Ситуация аналогична той, что возникает в классической математической статистике в связи с оптимальным оцениванием параметров. Если параметр одномерен, то ситуация с оцениванием достаточно прозрачна — есть понятие эффективных оценок, показателем качества оценки является средний квадрат ошибки, а при ее несмещенности — дисперсия. В случае нескольких параметров возникает необходимость соизмерить точность оценивания по разным параметрам. Есть много критериев оптимальности (см., например, [73]), но нет признанных правил выбора среди них.

Вернемся к формуле (59). Интересно, что отклонения вектора параметров, вызванные отклонениями значений факторов a и отклика g, входят в (59) аддитивно. Хотя

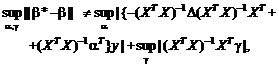
но для отдельных компонент (не векторов!) имеет место равенство.

В случае парной регрессии

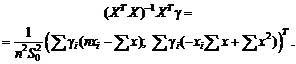(72)

Из формул (68), (69) и (72) следует, что

где F и G определены в (69), а

Итак, продемонстрирована возможность применения основных подходов статистики интервальных данных в регрессионном анализе.

Пример использования интервального регрессионного анализа. Методы статистики интервальных данных наряду с классическими методами оказываются полезными не только в традиционных статистических задачах, но и во многих других областях, в частности, в экономике и управлении промышленными предприятиями [56, 74]. Пример использования статистики интервальных данных в инвестиционном менеджменте подробно описан в [56] (см. также соответствующий раздел ниже). Перспективы применения статистики интервальных данных в контроллинге рассмотрены в [75]. Компьютерный анализ данных и использование статистических методов в информационных системах управления предприятием при решении задач контроллинга рассмотрены в [76]. Рассмотрим практический пример применения интервального регрессионного анализа при анализе и прогнозировании затрат предприятия [77].^[4]

Выпуск продукции y зависит от величины суммарных переменных затрат х. Условные исходные данные для предприятия «Омега» приведены в табл. 1. Необходимо построить уравнение регрессии и найти нотну. В данном случае n = 12, k = 2. Зависимость ищется в виде y = ax + b.

Таблица 1

Исходные данные для предприятия «Омега», тыс. руб.

№ п/п	х	y	№ п/п	х	y
1	15,1	89,0	7	44,3	145,9
2	16,8	110,8	8	46,0	151,8
3	25,0	104,4	9	46,8	153,7
4	30,7	116,1	10	53,4	161,8
5	33,2	127,8	11	56,5	175,8
6	44,2	143,3	12	65,4	193,4

Пусть как для х, так и для y максимально возможная погрешность l = 10. Можно доказать [37], что указанное значение l допустимо считать малым, поскольку под «малостью» следует понимать малость относительно типовых значений х и y. Построим уравнение регрессии согласно методу наименьших квадратов:

Оценим максимально возможное изменение (приращение) вектора (a^*, b^*) оценок параметров линейной зависимости методом наименьших квадратов при изменении исходных данных, когда a и g малы (см. формулу (59) выше). Для этого найдем нотны — максимально возможные изменения координат этого вектора в предположении и

N_a*(x, y) = 0,87; N_b*(x, y) = 32,98.

Найдем доверительные интервалы для параметров a и b согласно [56, п. 5.1] при доверительной вероятности 0,95. Для параметра a (т.е. для переменных затрат на единицу выпуска) нижняя доверительная граница а верхняя — Доверительный интервал для параметра a с учетом нотны равен [1,595 – 0,87; 2,233 + 0,87] или [0,73; 3,1]. Ширина «классического» доверительного интервала d₁ = a_B(0,95) – a_H(0,95) равна 0,63, что несколько меньше, чем нотна 0,87.

Для параметра b (т.е. для постоянных затрат) нижняя доверительная граница а верхняя — b_B(0,95) = 68,13. Ширина «классического» доверительного интервала для параметра b^* равна 9,63, т.е. почти в 3 раза меньше, чем нотна 32,98. Доверительный интервал для параметра b с учетом нотны равен [58,51 – 32,98; 68,13 + 32,98] или [25,53; 101,12].

Итак, восстановленная зависимость с учетом метрологических и статистических погрешностей имеет вид

Исходя из погрешностей коэффициентов линейной зависимости, можно указать нижнюю и верхнюю доверительные границы для функции

Более точно доверительные границы для значения функции в определенной точке можно указать, если найти нотну и статистическую погрешность не для коэффициентов, а непосредственно для значения функции [56, п. 5.1].

Полученные результаты дают возможность оценивать точность прогнозирования с помощью восстановленной зависимости, рассчитывая нижние и верхние границы для значения зависимой переменной. Например, при х = 100 нижняя и верхняя границы интервала равны

y_н (100) = (1,914 — 1,187)100 + 63,32 – 37,79 = 98,23;

y_в (100) = (1,914 + 1,187)100 + 63,32 + 37,79 = 411,21.

Некоторые замечания. На основе использования вероятностных моделей регрессионного анализа [56, гл. 5.1] удается построить доверительные границы для восстановленной зависимости. Однако при практическом применении вероятностных моделей не всегда легко обосновать предположения, наложенные на вектор невязок e (независимость и одинаковую распределенность его координат). Кроме того, при моделировании экономических явлений и процессов обычно нет оснований использовать нормально распределенные случайные величины [56, гл. 4.1], следовательно, нельзя применять методы регрессионного анализа, основанные на нормальном распределении погрешностей. При этом объем данных обычно таков, что применение асимптотических формул непараметрического регрессионного анализа [56, гл. 5] не вполне оправдано. Поэтому описанный выше подход интервального регрессионного анализа представляется не менее оправданным, чем подход на основе вероятностных моделей. В этом мы согласны с А.П. Вощининым [46]. Представляется необходимым использование интервального регрессионного анализа в различных областях научных и прикладных исследований, прежде всего, в технических, экономических, управленческих разработках.

7.7. Интервальный дискриминантный анализ

Перейдем к задачам классификации в статистике интервальных данных. Как известно [78], важная их часть — задачи дискриминации (диагностики, распознавания образов с учителем). В этих задачах заданы классы (полностью или частично, с помощью обучающих выборок), и необходимо принять решение — к какому из этих классов отнести вновь поступающий объект.

В линейном дискриминантном анализе правило принятия решений основано на линейной функции f(x) от распознаваемого вектора Рассмотрим для простоты случай двух классов. Правило принятия решений определяется константой С — при f(x) > C распознаваемый объект относится к первому классу, при f(x) £ C — ко второму.

В первоначальной вероятностной модели Р. Фишера предполагается, что классы заданы обучающими выборками объемов N₁ и N₂, соответственно, из многомерных нормальных распределений с разными математическими ожиданиями, но одинаковыми ковариационными матрицами. В соответствии с леммой Неймана-Пирсона, дающей правило принятия решений при проверке статистических гипотез, дискриминантная функция является линейной. Для ее практического использования теоретические характеристики распределения необходимо заменить на выборочные. Тогда дискриминантная функция приобретает следующий вид

Здесь — выборочное среднее арифметическое по первой выборке а — выборочное среднее арифметическое по второй выборке В роли S может выступать любая состоятельная оценка общей для выборок ковариационной матрицы. Обычно используют следующую оценку, естественным образом сконструированную на основе выборочных ковариационных матриц:

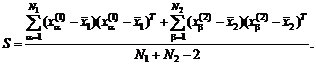
В соответствии с подходом статистики интервальных данных считаем, что специалисту по анализу данных известны лишь значения с погрешностями

Таким образом, вместо f(x) статистик делает выводы на основе искаженной линейной дискриминантной функции f₁(x), в которой коэффициенты рассчитаны не по исходным данным а по искаженным погрешностями значениям

Это модель с искаженными параметрами дискриминантной функции. Следующая модель — такая, в которой распознаваемый вектор x также известен с ошибкой. Далее, константа С может появляться в модели различными способами. Она может задаваться априори абсолютно точно. Может задаваться с какой-то ошибкой, не связанной с ошибками, вызванными конечностью обучающих выборок. Может рассчитываться по обучающим выборкам, например, с целью уравнять ошибки классификации, т.е. провести плоскость дискриминации через середину отрезка, соединяющего центры классов. Итак, целый спектр моделей ошибок.

На какие статистические процедуры влияют ошибки в исходных данных? Здесь тоже много постановок. Можно изучать влияние погрешностей измерений на значения дискриминантной функции f, например, в той точке, куда попадает вновь поступающий объект х. Очевидно, случайная величина f(x) имеет некоторое распределение, определяемое распределениями обучающих выборок. Выше описана модель Р. Фишера с нормально распределенными совокупностями. Однако реальные данные, как правило, не подчиняются нормальному распределению [56]. Тем не менее линейный статистический анализ имеет смысл и для распределений, не являющихся нормальными (при этом вместо свойств многомерного нормального распределения приходится опираться на многомерную центральную предельную теорему и теорему о наследовании сходимости [13]). В частности, приравняв метрологическую ошибку, вызванную погрешностями исходных данных, и статистическую ошибку, получим условие, определяющее рациональность объемов выборок. Здесь два объема выборок, а не один, как в большинстве рассмотренных постановок статистики интервальных данных. С подобным мы сталкивались ранее при рассмотрении двухвыборочного критерия Смирнова.

Естественно изучать влияние погрешностей исходных данных не при конкретном х, а для правила принятия решений в целом. Может представлять интерес изучение характеристик этого правила по всем х или по какому-либо отрезку. Более интересно рассмотреть показатель качества классификации, связанный с пересчетом на модель линейного дискриминантного анализа [56, 79].

Математический аппарат изучения перечисленных моделей развит выше в предыдущих разделах настоящей главы. Некоторые результаты приведены в [39]. Из-за большого объема выкладок ограничимся приведенными здесь замечаниями.

7.8. Интервальный кластер-анализ

Кластер-анализ, как известно [78], имеет целью разбиение совокупности объектов на группы сходных между собой. Многие методы кластер-анализа основаны на использовании расстояний между объектами. (Степень близости между объектами может измеряться также с помощью мер близости и показателей различия, для которых неравенство треугольника выполнено не всегда.) Рассмотрим влияние погрешностей измерения на расстояния между объектами и на результаты работы алгоритмов кластер-анализа.

С ростом размерности р евклидова пространства диагональ единичного куба растет как А какова погрешность определения евклидова расстояния? Пусть двум рассматриваемым объектам соответствуют и — вектора размерности р. Они известны с погрешностями и , т.е. статистику доступны лишь вектора Легко видеть, что

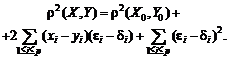(73)

Пусть ограничения на абсолютные погрешности имеют вид

Такая запись ограничений предполагает, что все переменные имеют примерно одинаковый разброс. Трудно ожидать этого, если переменные имеют различные размерности. Однако рассматриваемые ограничения на погрешности естественны, если переменные предварительно стандартизованы, т.е. центрированы и пронормированы (т.е. из каждого значения вычтено среднее арифметическое, а разность поделена на выборочное среднее квадратическое отклонение).

Пусть Тогда последнее слагаемое в (73) не превосходит поэтому им можно пренебречь. Тогда из (73) следует, что нотна евклидова расстояния имеет вид

с точностью до бесконечно малых более высокого порядка. Если случайные величины имеют одинаковые математические ожидания и для них справедлив закон больших чисел (эти предположения естественны, если переменные перед применением кластер-анализа стандартизованы), то существует константа С такая, что

с точностью до бесконечно малых более высокого порядка при малых D, больших р и pD² ® 0.

Из рассмотрений настоящего пункта вытекает, что

(74)

при некотором q таком, что |q| < 1.

Какое минимальное расстояние является различимым? По аналогии с определением рационального объема выборки при проверке гипотез предлагается уравнять слагаемые в (74), т.е. определять минимально различимое расстояние r_min из условия

. (75)

Естественно принять, что расстояния, меньшие r_min, не отличаются от 0, т.е. точки, лежащие на расстоянии r £ r_min, не различаются между собой.

Каков порядок величины С? Если x_i и y_i независимы и имеют стандартное нормальное распределение с математическим ожиданием 0 и дисперсией 1, то, как легко подсчитать, и соответственно С = 4,51. Следовательно, в этой модели

Формула (75) показывает, что хотя с ростом размерности пространства р растет диаметр (длина диагонали) единичного куба — естественной области расположения значений переменных, с той же скоростью растет и естественное квантование расстояния с помощью порога неразличимости r_min, т.е. увеличение размерности (вовлечение новых переменных), вообще говоря, не улучшает возможности кластер-анализа.

Можно сделать выводы и для конкретных алгоритмов. В дендрограммах (например, результатах работы иерархических агломеративных алгоритмах ближнего соседа, дальнего соседа, средней связи) можно порекомендовать склеивать (т.е. объединять) уровни, отличающиеся менее чем на r_min. Если все уровни склеятся, то можно сделать вывод, что у данных нет кластерной структуры, они однородны. В алгоритмах типа «Форель» центр тяжести текущего кластера определяется с точностью ±D по каждой координате, а порог для включения точки в кластер (радиус шара R) из-за погрешностей исходных данных может измениться согласно (74) на

Поэтому кроме расчетов с R рекомендуется провести также расчеты с радиусами R₁ и R₂, где

,

и сравнить полученные разбиения. Быть адекватными реальности могут только выводы, общие для всех трех расчетов. Эти рекомендации развивают общую идею [3] о целесообразности проведения расчетов при различных значениях параметров алгоритмов с целью выделения выводов, инвариантных по отношению к выбору конкретного алгоритма.

7.9. Интервальные данные в инвестиционном менеджменте

Методы статистики интервальных данных оказываются полезными не только в традиционных технических и эконометрических задачах, но и во многих других областях, например, в инвестиционном менеджменте.

Основная идея формулируется так. Все знают, что любое инженерное измерение проводится с некоторой погрешностью. Эту погрешность обычно приводят в документации и учитывают при принятии решений. Ясно, что и любое экономическое измерение также проводится с погрешностью. А вот какова она? Необходимо уметь ее оценивать, поскольку ошибки при принятии экономических решений обходятся дорого.

Например, как принимать решение о выгодности или невыгодности инвестиционного проекта? Как сравнивать инвестиционные проекты между собой? Как известно, для решения этих задач используют такие экономические характеристики, как NPV (Net Present Value) — чистая текущая стоимость (этот термин переводится с английского также как чистый дисконтированный доход, чистое приведенное значение и др.), внутренняя норма доходности, срок окупаемости, показатели рентабельности и др.

С экономической точки зрения инвестиционные проекты описываются финансовыми потоками, т.е. функциями от времени, значениями которых являются платежи (и тогда значения этих функций отрицательны) и поступления (значения функций положительны). Сравнение инвестиционных проектов — это сравнение функций от времени с учетом внешней среды, проявляющейся в виде дисконт-функции (как результата воздействия социальных, технологических, экологических, экономических и политических факторов), и представлений законодателя или инвестора — обычно ограничений на финансовые потоки платежей и на горизонт планирования. Основная проблема при сравнении инвестиционных проектов такова: что лучше — меньше, но сейчас, или больше, но потом? Как правило, чем больше вкладываем сейчас, тем больше получаем в более или менее отдаленном будущем. Вопрос в том, достаточны ли будущие поступления, чтобы покрыть нынешние платежи и дать приемлемую для инвестора прибыль?

В настоящее время широко используются различные теоретические подходы к сравнению инвестиционных проектов и облегчающие расчеты компьютерные системы, в частности, ТЭО-ИНВЕСТ, Project Expert, COMFAR, PROPSIN, Альт-Инвест. Однако ряд важных моментов в них не учтен.

Введем основные понятия.

Дисконт-функция как функция от времени показывает, сколько стоит для фирмы 1 руб. в заданный момент времени, если его привести к начальному моменту. Если дисконт-функция — константа для разных отраслей, товаров и проектов, то эта константа называется дисконт-фактором, или просто дисконтом. Дисконт-функция определяется совместным действием различных факторов, в частности, реальной процентной ставки и индекса инфляции. Реальная процентная ставка описывает «нормальный» рост экономики (т.е. без инфляции). В стабильной ситуации доходность от вложения средств в различные отрасли, в частности, в банковские депозиты, примерно одинакова. Сейчас она, по оценке ряда экспертов, около 12%. Итак, нынешний 1 руб. превращается в 1,12 руб. через год, а потому 1 руб. через год соответствует 1/1,12 = 0,89 руб. сейчас — это и есть максимум дисконта.

Обозначим дисконт буквой С. Если q — банковский процент (плата за депозит), т.е. вложив в начале года в банк 1 руб., в конце года получим (1 + q) руб., то дисконт определяется по формуле С = 1/(1 + q). При таком подходе полагают, что банковские проценты одинаковы во всех банках. Более правильно было бы считать q, а потому и С, нечисловыми величинами, а именно, интервалами [q₁; q₂] и [С₁; С₂]. Следовательно, экономические выводы должны быть исследованы на устойчивость (применяют и термин «чувствительность») по отношению к возможным отклонениям.

Как функцию времени t дисконт-функцию обозначим C(t). При постоянстве дисконт-фактора имеем C(t) = С^t. Если q = 0,12, С = 0,89, то 1 руб. за 2 года превращается в 1,12² = 1,2544, через 3 — в 1,4049. Итак, 1 руб., получаемый через 2 года, соответствует 1/1,2544 = 0,7972 руб., т.е. 79,72 коп. сейчас, а 1 руб., обещанный через 3 года, соответствует 0,71 руб. сейчас. Другими словами, С(2) = 0,80, а С(3) = 0,71. Если дисконт-фактор зависит от времени, в первый год равен С₁, во второй — С₂, в третий — С₃, ..., в t-ый год — С_t, то C(t)= С₁, С₂, С₃, ..., С_t.

Рассмотрим характеристики потоков платежей. Срок окупаемости — тот срок, за который доходы покроют расходы. Обычно предполагается, что после этого проект приносит только прибыль. Это верно не всегда. Простейший вариант, для которого не возникает никаких парадоксов, состоит в том, что все инвестиции (капиталовложения) делаются сразу, в начале, а затем инвестор получает только доход. Сложности возникают, если проект состоит из нескольких очередей, вложения распределены во времени.

Примитивный способ расчета срока окупаемости состоит в делении объема вложений А на ожидаемый ежегодный доход В. Тогда срок окупаемости равен А/В. Этот способ некорректен. Если дисконт-фактор равен С, то максимально возможный суммарный доход равен

ВС + ВС² + ВС³ + ВС⁴ + ВС⁵ + ... = ВС (1 + С + С² + С³ + С⁴ + ...) = ВС/(1 – С).

Если А/В меньше С/(1 – С), то можно рассчитать срок окупаемости проекта, но он будет больше, чем А/В. Если же А/В больше или равно С/(1 – С), то проект не окупится никогда. Поскольку максимум С равен 0,89, то проект не окупится никогда, если А/В не меньше 8,09.

Пусть вложения равны 1 млн. руб., ежегодная прибыль составляет 500 тыс., т.е. А/В = 2, дисконт-фактор С = 0.8. При примитивном подходе (при С = 1) срок окупаемости равен 2 годам. А на самом деле? За k лет будет возвращено

ВС (1 + С + С² + С³ + С⁴ + ... + C^k) = ВС(1 – С^k+1) / (1 – С).

Срок окупаемости k получаем из уравнения 1=0,5´0,8(1 – 0,8^{k + 1})/(1 – 0,8), откуда k = 2,11. Он оказался равным 2,11 лет, т.е. увеличился примерно на 6 недель. Это немного. Однако если В = 0,2, то имеем уравнение 1 = 0,2´0,8(1 – 0,8^{k + 1}) / (1 – 0,8). У этого уравнения нет корней, поскольку А/В = 5 > С/(1 – С) = 0.8/(1 – 0,8) = 4. Проект не окупится никогда. Прибыль можно ожидать лишь при А/В < 4. Рассмотрим промежуточный случай, В = 0,33, с «примитивным» сроком окупаемости 3 года. Тогда имеем уравнение 1 = 0,33 ´ 0,8 (1 – 0,8^{k + 1})/ (1 – 0,8), откуда k = 5,40.

Рассмотрим финансовый поток a(0), a(1), a(2), a(3), ..., a(t), ... . (для простоты примем, что платежи или поступления происходят раз в год). Выше рассмотрен поток с одним платежом a(0) = (–А) и дальнейшими поступлениями a(1) = a(2) = a(3) = ... = a(t) = .... = В. Чистая текущая стоимость (Net Present Value, сокращенно NPV) рассчитывается для финансового потока путем приведения затрат и поступлений к начальному моменту времени:

NPV = a(0) + a(1)С(1) + a(2)С(2) + a(3)С(3) + ... + a(t)С(t) + ...,

где С(t) — дисконт-функция. В простейшем случае, когда дисконт-фактор не меняется год от года и имеет вид С = = 1/(1 + q), формула для NPV конкретизируется:

NPV = NPV(q) = a(0) + a(1)/(1 + q) + a(2)/(1 + q)² +
+ a(3)/(1 + q)³ + ... +a(t)/(1 + q)^t + ...

Пусть, например, a(0) = –10, a(1) = 3, a(2) = 4, a(3) = 5. Пусть q = 0,12, тогда

NPV(0,12) = –10 + 3 ´ 0,89 + 4 ´ 0.80 + 5 ´ 0,71 =
= –10 + 2,67 + 3,20 + 3,55 = –0,58.

Итак, проект невыгоден для вложения капитала, поскольку NPV(0,12) отрицательна. При отсутствии дисконтирования (при С = 1, q = 0) вывод иной:

NPV(0) = –10 + 3 + 4 + 5 = 2,

проект выгоден.

Срок окупаемости и сам вывод о прибыльности проекта зависят от неизвестного дисконт-фактора С или даже от неизвестной дисконт-функции — ибо какие у нас основания считать будущую дисконт-функцию постоянной? Экономическая история России последних лет показывает, что банки часто меняют проценты платы за депозит. Часто предлагают использовать норму дисконта, равную приемлемой для инвестора норме дохода на капитал. Это значит, что экономисты явным образом обращаются к инвестору как к эксперту, который должен назвать им некоторое число исходя из своего опыта и интуиции (т.е. экономисты перекладывают свою работу на инвестора). Кроме того, при этом игнорируется изменение указанной нормы во времени,

Приведем пример исследования NPV на устойчивость (чувствительность) к малым отклонениям значений дисконт-функции. Для этого надо найти максимально возможное отклонение NPV при допустимых отклонениях значений дисконт-функции (или, если угодно, значений банковских процентов). В качестве примера рассмотрим

NPV = NPV (a(0), a(1), С(1), a(2), С(2), a(3), С(3)) = a(0) + a(1)С(1) + a(2)С(2) + a(3)С(3).

Предположим, что изучается устойчивость (чувствительность) для ранее рассмотренных значений

a(0) = (–10), a(1) = 3, a(2) = 4, a(3) = 5, С(1) = 0,89, С(2) = 0,80, С(3) = 0,71.

Пусть максимально возможные отклонения С(1), С(2), С(3) равны ±0,05. Тогда максимум значений NPV равен

NPVmax = (–10) + 3 ´ 0,94 + 4 ´ 0.85 + 5 ´ 0,76 = (–10) + 2,82 + 3,40 + 3,80 = 0,02,

в то время как минимум значений NPV есть

NPVmin = (–10) + 3 ´ 0,84 + 4 ´ 0.75 + 5 ´ 0,66 = (–10) + 2,52 + 3,00 + 3,30 = –1,18.

Для NPV получаем интервал от (–1,18) до (+0,02). В нем есть и положительные, и отрицательные значения. Следовательно, нет однозначного заключения — проект убыточен или выгоден. Для принятия решения не обойтись без экспертов.

Для иных характеристик, например, внутренней нормы доходности, выводы аналогичны. Дополнительные проблемы вносит неопределенность горизонта планирования, а также будущая инфляция. Если считать, что финансовый поток должен учитывать инфляцию, то это означает, что до принятия решений об инвестициях необходимо на годы вперед спрогнозировать рост цен, а это до сих пор еще не удавалось ни одной государственной или частной исследовательской структуре. Если же рост цен не учитывать, то отдаленные во времени доходы могут «растаять» в огне инфляции. На практике риски учитывают, увеличивая q на десяток-другой процентов.

7.10. Статистика интервальных данных
в прикладной статистике

Кратко рассмотрим положение статистики интервальных данных (СИД) среди других методов описания неопределенностей и анализа данных [80]. Проще говоря, положение СИД в прикладной статистике [81].

Нечеткость и СИД. С формальной точки зрения описание нечеткости интервалом — это частный случай описания ее нечетким множеством. В СИД функция принадлежности нечеткого множества имеет специфический вид — она равна 1 в некотором интервале и 0 вне его. Такая функция принадлежности описывается всего двумя параметрами (границами интервала). Эта простота описания делает математический аппарат СИД гораздо более прозрачным, чем аппарат теории нечеткости в общем случае. Это, в свою очередь, позволяет исследователю продвинуться дальше, чем при использовании функций принадлежности произвольного вида.

Интервальная математика и СИД. Можно было бы сказать, что СИД — часть интервальной математики, что СИД так соотносится с прикладной математической статистикой, как интервальная математика — с математикой в целом. Однако исторически сложилось так, что интервальная математика занимается прежде всего вычислительным погрешностями. С точки зрения интервальной математики две известные формулы для выборочной дисперсии, а именно

,

имеют разные погрешности. А с точки зрения СИД эти две формулы задают одну и ту же функцию, и поэтому им соответствуют совпадающие нотны и рациональные объемы выборок. Интервальная математика прослеживает процесс вычислений, СИД этим не занимается. Необходимо отметить, что типовые постановки СИД могут быть перенесены в другие области математики, и, наоборот, вычислительные алгоритмы прикладной математической статистики и СИД заслуживают изучения. Однако и то, и другое — скорее дело будущего. Из уже сделанного отметим применение методов СИД при анализе такой характеристики финансовых потоков, как NPV — чистая текущая стоимость [56, гл.9].

Математическая статистика и СИД. Математическая статистика и СИД отличаются тем, в каком порядке делаются предельные переходы n ® ¥ и D ®0. При этом СИД переходит в математическую статистику при D = 0. Правда, тогда исчезают основные особенности СИД: нотна становится равной 0, а рациональный объем выборки — бесконечности. Рассмотренные выше методы СИД разработаны в предположении, что погрешности малы (но не исчезают), а объем выборки велик. СИД расширяет классическую математическую статистику тем, что в исходных статистических данных каждое число заменяет интервалом. С другой стороны, можно считать СИД новым этапом развития математической статистики, соответствующим ее новой парадигме [83, 84, 85].

Статистика объектов нечисловой природы и СИД. Статистика объектов нечисловой природы (СОНП) [85] (другие названия – статистика нечисловых данных, нечисловая статистика [8]) - расширяет область применения классической математической статистики путем включения в нее новых видов статистических данных. Естественно, при этом появляются новые виды алгоритмов анализа статистических данных и новый математический аппарат (в частности, происходит переход от методов суммирования к методам оптимизации). С точки зрения СОНП частному виду новых статистических данных — интервальным данным — соответствует СИД. Напомним, что одно из двух основных понятий СИД — нотна — определяется как решение оптимизационной задачи. Однако СИД, изучая классические методы прикладной статистики применительно к интервальным данным, по математическому аппарату ближе к классической математической статистике, чем другие части СОНП, например, статистика бинарных отношений.

Робастные методы статистики и СИД. Если понимать робастность согласно [13] как теорию устойчивости статистических методов по отношению к допустимым отклонениям исходных данных и предпосылок модели, то в СИД рассматривается одна из естественных постановок робастности. Однако в массовом сознании специалистов термин «робастность» закрепился за моделью засорения выборки большими выбросами (модель Тьюки-Хубера), хотя эта модель не имеет большого практического значения [81]. К этой модели СИД не имеет отношения.

Теория устойчивости и СИД. Общей схеме устойчивости [13, 86, 87] математических моделей социально-экономических явлений и процессов по отношению к допустимым отклонениям исходных данных и предпосылок моделей СИД полностью соответствует. Она посвящена математико-статистическим моделям, используемым при анализе статистических данных, а допустимые отклонения — это интервалы, заданные ограничениями на погрешности. СИД можно рассматривать как пример теории, в которой учет устойчивости позволил сделать нетривиальные выводы. Отметим, что с точки зрения общей схемы устойчивости [13] устойчивость по Ляпунову в теории дифференциальных уравнений — весьма частный случай общей теории устойчивости, в котором из-за его конкретности удалось весьма далеко продвинуться.

Минимаксные методы, типовые отклонения и СИД. Постановки СИД относятся к минимаксным. За основу берется максимально возможное отклонение. Это — «подход пессимиста», применяемый, например, в теории антагонистических игр. Использование минимаксного подхода позволяет подозревать СИД в завышении роли погрешностей измерения. Однако примеры изучения вероятностно-статистических моделей погрешностей, проведенные, в частности, при разработке методов оценивания параметров гамма-распределения [30, 35], показали, что это подозрение не подтверждается. Влияние погрешностей измерений по порядку такое же, только вместо максимально возможного отклонения (нотны) приходится рассматривать математическое ожидание соответствующего отклонения. Подчеркнем, что применение в СИД вероятностно-статистических моделей погрешностей не менее перспективно, чем минимаксных.

Подход научной школы А.П. Вощинина и СИД. Если в математической статистике неопределенность только статистическая, то в научной школе А.П. Вощинина — только интервальная. Можно сказать, что СИД лежит между классической прикладной математической статистикой и областью исследований научной школы А.П. Вощинина. Другое отличие состоит в том, что в этой школе разрабатывают новые методы анализа интервальных данных, а в СИД в настоящее время изучается устойчивость классических статистических методов по отношению к малым погрешностям. Подход СИД оправдывается распространенностью этих методов, однако в дальнейшем следует переходить к разработке новых методов, специально предназначенных для анализа интервальных данных.

Анализ чувствительности и СИД. При анализе чувствительности, как и в СИД, рассчитывают производные по используемым переменным, или непосредственно находят изменения при отклонении переменной на ±10% от базового значения. Однако этот анализ делают по каждой переменной отдельно. В СИД все переменные рассматриваются совместно, и находится максимально возможное отклонение (нотна). При малых погрешностях удается на основе главного члена разложения функции в многомерный ряд Тейлора получить удобную формулу для нотны. Можно сказать, что СИД — это многомерный анализ чувствительности.

Заключительные замечания. Асимптотической математической статистике интервальных данных посвящены главы в учебниках [81, 88, 89]. Развиваются научные исследования как в научной школе А.П. Вощинина [47, 48], так и в СИД [59, 77, 90].

По нашему мнению, во все виды статистического программного обеспечения должны быть включены алгоритмы интервальной статистики, «параллельные» обычно используемым в настоящее время алгоритмам прикладной математической статистики. Это позволит в явном виде учесть наличие погрешностей у результатов наблюдений (измерений, испытаний, анализов, опытов).

Статистика интервальных данных является составной частью системной нечеткой интервальной математики [91, 92] – перспективного направления теоретической и вычислительной математики.

---

[1] Нумерация формул здесь начинается заново.

[2] Нумерация теорем \начинается заново.

[3] Нумерация примеров в каждом разделе начинается заново.

[4] Пример рассмотрен и расчеты проведены Е.А. Гуськовой.