ГЛАВА 5. О СВЕДЕНИИ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ К ТЕОРИИ СЛУЧАЙНЫХ МНОЖЕСТВ

5.1. Нечеткость и случайность

С самого начала появления современной теории нечеткости в 1960-е годы началось обсуждение ее взаимоотношений с теорией вероятностей. Дело в том, что функция принадлежности нечеткого множества напоминает плотность распределения вероятностей. Отличие только в том, что сумма вероятностей по всем возможным значениям случайной величины (или интеграл, если множество возможных значений несчетно) всегда равна 1, а сумма S значений функции принадлежности (в непрерывном случае — интеграл от функции принадлежности) может быть любым неотрицательным числом. Возникает искушение пронормировать функцию принадлежности, т.е. разделить все ее значения на S (при S 0), чтобы свести ее к распределению вероятностей (или к плотности вероятности). Однако специалисты по нечеткости справедливо возражают против такого «примитивного» сведения, поскольку оно проводится отдельно для каждой размытости (нечеткого множества), и определения обычных операций над нечеткими множествами согласовать с ним нельзя. Последнее утверждение означает следующее. Пусть указанным образом преобразованы функции принадлежности нечетких множеств А и В. Как при этом преобразуются функции принадлежности АÇВ, АÈВ, А + В, АВ? Установить это невозможно в принципе. Последнее утверждение становится совершенно ясным после рассмотрения нескольких примеров пар нечетких множеств с одними и теми же суммами значений функций принадлежности, но различными результатами теоретико-множественных операций над ними. Причем и суммы значений соответствующих функций принадлежности для этих результатов теоретико-множественных операций, например, для пересечений множеств, также различны.

В работах по нечетким множествам время от времени утверждается, что теория нечеткости самостоятельный раздел прикладной математики и не имеет отношения к теории вероятностей ((см., например, обзор литературы в монографиях [9, 13]). Некоторые авторы, обсуждавшие взаимоотношения теории нечеткости и теории вероятностей, подчеркивали различие между этими областями теоретических и прикладных исследований. Обычно сопоставляют аксиоматику и сравнивают области приложений.

Аргументы при втором типе сравнений не имеют доказательной силы, поскольку по поводу границ применимости даже такой давно выделившейся научной области, как вероятностно-статистические методы, имеются различные мнения. Более того, нет единства мнений об арифметике. Итог рассуждений одного из наиболее известных французских математиков Анри Лебега по поводу границ применимости арифметики таков: «Арифметика применима тогда, когда она применима» (см. его монографию [17, с.21-22]).

При сравнении различных аксиоматик теории нечеткости и теории вероятностей нетрудно увидеть, что списки аксиом различаются. Из этого, однако, отнюдь не следует, что между указанными теориями нельзя установить связь, типа известного сведения евклидовой геометрии на плоскости к арифметике (точнее к теории числовой системы R² - см., например, монографию [18]). Эти две аксиоматики — евклидовой геометрии и арифметики — на первый взгляд весьма сильно различаются.

Можно понять желание энтузиастов теории нечеткости подчеркнуть принципиальную новизну своего научного аппарата. Однако не менее важно установить связи этого подхода с ранее известными.

Как оказалось, теория нечетких множеств тесно связана с теорией случайных множеств.

5.2. Случайные множества

Что такое случайное множество? Начнем с понятия случайной величины. Это величина, зависящая от случая, т.е. функция от элементарного исхода (события). Скажем, результат наблюдения, зависящий от случайных привходящих факторов. А случайное множество – это множество, зависящее от случая. Другими словами, функция, область определения которой – пространство элементарных событий, а область значений – совокупность множеств, например, совокупность всех подмножеств некоторого конкретного множества.

Случайные множества используются во многих прикладных задачах [13]. В монографиях [14, 15] случайные множества использовались для моделирования распространения лесных пожаров. Пусть пожар начался с загорания в определенной точке. В следующий момент времени загорятся некоторые из соседних точек. А некоторые не загорятся. Через час огнем будет охвачено некоторое множество. Форма пожара будет описываться случайным множеством, зависящим от времени.

От чего зависит форма пожара? Конечно, от того, как «устроен» лес – какие в нем породы деревьев, сколько сухостоя, есть ли естественные преграды для огня (ручьи, овраги), а также от метеорологических условий – куда дует ветер, сколько осадков выпало за последнее время, какова температура воздуха… Все эти условия неизвестны в точности наблюдателю на самолете. Поэтому для него вполне естественно моделировать распространение пожара с помощью теории вероятностей. Эти модели, разработанные на основе теории случайных множеств, находят применение в лесном хозяйстве [14, 15].

Теория нечетких множеств сводится к теории случайных множеств с помощью понятия «проекция случайного множества». С каждым случайным множеством можно связать некоторую функцию – вероятность того, что элемент принадлежит множеству. Эта функция обладает всеми свойствами функции принадлежности нечеткого множества. Соответствующее нечеткое множество и называют проекцией исходного случайного множества. Оказывается, верно и обратное – для любого размытого множества можно подобрать случайное множество так, что вероятность принадлежности элемента случайному множеству всюду совпадает с функцией принадлежности заданного размытого множества. Подобное соответствие можно установить так, что результаты операций над множествами тоже будут соответствовать друг другу.

Есть все основания полагать, что связь между размытостью и вероятностью позволит применить в теории нечеткости методы и результаты, накопленные в теории случайных множеств. И наоборот, даст возможность перенести понятия и постановки задач из первой теории во вторую, что послужит прогрессу в обеих.

Почему же специалисты по нечетким множествам порою «открещиваются» от теории вероятностей? Одна из причин – устаревшее на три четверти века представление о математике случая, согласно которой она рассматривается как «наука о массовых явлениях»: вероятность мыслится как предел частоты, а случайное событие – как то, которое может произойти, а может не произойти. Всё это – отголоски далекого прошлого, когда теория вероятностей недостаточно отделялась от ее приложений. Ныне она опирается на четкую систему аксиом, обычно – на аксиоматику А.Н. Колмогорова. В 1933 г. им опубликована основополагающая монография [16], заложившая научные основы современной теории вероятностей. Теоремы в ней доказываются точно так же, как и в любом другом разделе математики, без всяких ссылок на свойства реального мира. Ее выводы могут применяться при анализе весьма различных реальных явлений – как массовых, так и таких, где нет и речи о массовости и частоте. Именно таковы многие расплывчатости, «нечастотную» природу которых специалисты по нечетким множествам зачастую рассматривают как причину несводимости к понятиям теории вероятностей.

Разберем подробнее связи между теорией нечеткости и теорией случайных множеств.

5.3. Нечеткие множества как проекции случайных множеств.

Рассмотрим метод сведения теории нечетких множеств к теории случайных множеств.

Определение 2. Пусть - случайное подмножество конечного множества У. Нечеткое множество В, определенное на У, называется проекцией А и обозначается Proj A, если

(8)

при всех

Очевидно, каждому случайному множеству А можно поставить в соответствие с помощью формулы (8) нечеткое множество В = Proj A. Оказывается, верно и обратное.

Теорема 3. Для любого нечеткого подмножества В конечного множества У существует случайное подмножество А множества У такое, что В = Proj A.

Доказательство. Достаточно задать распределение случайного множества А. Пусть У₁ - носитель В (см. определение 1 выше). Без ограничения общности можно считать, что при некотором m и элементы У₁ занумерованы в таком порядке, что

Введем множества

Положим

Для всех остальных подмножеств Х множества У положим Р(А=Х)=0. Поскольку элемент y_t входит во множества Y(1), Y(2),…, Y(t) и не входит во множества Y(t+1),…, Y(m), то из приведенных выше формул следует, что Если то, очевидно, Теорема 3 доказана.

Распределение случайного множества с независимыми элементами, как следует из [8], полностью определяется его проекцией. Для конечного случайного множества общего вида это не так. Для уточнения сказанного понадобится следующая теорема.

Теорема 4. Для случайного подмножества А множества У из конечного числа элементов наборы чисел

и

выражаются один через другой.

Доказательство. Второй набор выражается через первый следующим образом:

Элементы первого набора выразить через второй можно с помощью формулы включений и исключений из формальной логики, в соответствии с которой

В этой формуле в первой сумме у пробегает все элементы множества Y\X, во второй сумме переменные суммирования у₁ и у₂ не совпадают и также пробегают это множество, и т.д. Ссылка на формулу включений и исключений завершает доказательство теоремы 4.

В соответствии с теоремой 4 случайное множество А можно характеризовать не только распределением, но и набором чисел В этом наборе а других связей типа равенств нет. В этот набор входят числа следовательно, фиксация проекции случайного множества эквивалентна фиксации k = Card(Y) параметров из (2^k-1) параметров, задающих распределение случайного множества А в общем случае. (Здесь символом Card(Y) обозначено число элементов множества Y.)

Будет полезна следующая теорема.

Теорема 5. Если Proj A = B, то Proj

Для доказательства достаточно воспользоваться тождеством из теории случайных множеств формулой для вероятности накрытия , определением отрицания нечеткого множества и тем, что сумма всех P(A=X) равна 1. Под формулой для вероятности накрытия имеется в виду следующее утверждение: чтобы найти вероятность накрытия фиксированного элемента q случайным подмножеством S конечного множества Q, достаточно вычислить

где суммирование идет по всем подмножествам A множества Q, содержащим q.

5.4. Пересечения и произведения нечетких
и случайных множеств

Выясним, как операции над случайными множествами соотносятся с операциями над их проекциями. В силу законов де Моргана (теорема 1) и теоремы 5 достаточно рассмотреть операцию пересечения случайных множеств.

Теорема 6. Если случайные подмножества А₁ и А₂ конечного множества У независимы, то нечеткое множество является произведением нечетких множеств Proj A₁ и Proj A₂.

Доказательство. Надо показать, что для любого

(9)

По формуле для вероятности накрытия точки случайным множеством (см. выше)

(10)

Легко проверить, что распределение пересечения случайных множеств можно выразить через их совместное распределение следующим образом:

(11)

Из соотношений (10) и (11) следует, что вероятность накрытия для пересечения случайных множеств можно представить в виде двойной суммы

(12)

Заметим теперь, что правую часть формулы (12) можно переписать следующим образом:

(13)

Действительно, формула (12) отличается от формулы (13) лишь тем, что в ней сгруппированы члены, в которых пересечение переменных суммирования принимает постоянное значение. Воспользовавшись определением независимости случайных множеств и правилом перемножения сумм, получаем, что из (12) и (13) вытекает равенство

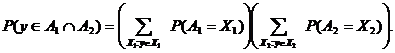
Для завершения доказательства теоремы 6 достаточно еще раз сослаться на формулу для вероятности накрытия точки случайным множеством.

Определение 3. Носителем случайного множества С называется совокупность всех тех элементов для которых

Теорема 7. Равенство

Proj = (ProjProj A₂)

верно тогда и только тогда, когда пересечение носителей случайных множеств и пусто.

Доказательство. Необходимо выяснить условия, при которых

(14)

Положим

Тогда равенство (14) сводится к условию

(15)

Ясно, что соотношение (15) выполнено тогда и только тогда, когда р₂р₃=0 при всех т.е. не существует ни одного элемента такого, что одновременно и , а это эквивалентно пустоте пересечения носителей случайных множеств и . Теорема 7 доказана.

5.5. Сведение последовательности операций над нечеткими
множествами к последовательности операций
над случайными множествами

Выше получены некоторые связи между нечеткими и случайными множествами. Изучение этих связей [9, 13] началось с введения случайных множеств с целью развития и обобщения аппарата нечетких множеств Л.А. Заде. Дело в том, что математический аппарат нечетких множеств не позволяет в должной мере учитывать различные варианты зависимости между понятиями (объектами), моделируемыми с его помощью, не является достаточно гибким. Так, для описания «общей части» двух нечетких множеств есть лишь две операции - произведение и пересечение. Если применяется первая из них, то фактически предполагается, что множества ведут себя как проекции независимых случайных множеств (см. выше теорему 6). Операция пересечения также накладывает вполне определенные ограничения на вид зависимости между множествами (см. выше теорему 7), причем в этом случае найдены даже необходимые и достаточные условия. Желательно иметь более широкие возможности для моделирования зависимости между множествами (понятиями, объектами). Использование математического аппарата случайных множеств предоставляет такие возможности.

Цель сведения теории нечетких множеств к теории случайных множеств - за любой конструкцией из нечетких множеств увидеть конструкцию из случайных множеств, определяющую свойства первой, аналогично тому, как за плотностью распределения вероятностей мы видим случайную величину. Приведем результаты по сведению алгебры нечетких множеств к алгебре случайных множеств.

Определение 4. Вероятностное пространство {Ω, G, P} назовем делимым, если для любого измеримого множества ХG и любого положительного числа , меньшего Р(Х), можно указать измеримое множество такое, что

Пример. Пусть - единичный куб конечномерного линейного пространства, G есть сигма-алгебра борелевских множеств, а P - мера Лебега. Тогда {Ω, G, P} - делимое вероятностное пространство.

Таким образом, делимое вероятностное пространство - это не экзотика. Обычный куб является примером такого пространства.

Доказательство сформулированного в примере утверждения проводится стандартными математическими приемами. Они основаны на том, что измеримое множество можно сколь угодно точно приблизить открытыми множествами, последние представляются в виде суммы не более чем счетного числа открытых шаров, а для шаров делимость проверяется непосредственно (от шара Х тело объема отделяется соответствующей плоскостью).

Теорема 8. Пусть даны случайное множество А на делимом вероятностном пространстве {Ω, G, P} со значениями во множестве всех подмножеств множества Y из конечного числа элементов, и нечеткое множество D на Y. Тогда существуют случайные множества С₁, С₂, С₃, С₄ на том же вероятностном пространстве такие, что

Proj Proj Proj

Proj Proj

где B = Proj A.

Доказательство. В силу справедливости законов де Моргана для нечетких (см. теорему 1 выше) и для случайных множеств, а также теоремы 5 выше (об отрицаниях) достаточно доказать существование случайных множеств С₁ и С₂.

Рассмотрим распределение вероятностей во множестве всех подмножеств множества Y, соответствующее случайному множеству С такому, что Proj C = D (оно существует в силу теоремы 3). Построим случайное множество С₂ с указанным распределением, независимое от А. Тогда по теореме 6.

Перейдем к построению случайного множества С₁. По теореме 7 необходимо и достаточно определить случайное множество так, чтобы ProjC₁ = D и пересечение носителей случайных множеств и было пусто, т.е.

для и

для .

Построим , исходя из заданного случайного множества Пусть Исключим элемент у₁ из для стольких элементарных событий , чтобы для полученного случайного множества было справедливо равенство

(именно здесь используется делимость вероятностного пространства, на котором задано случайное множество ). Для , очевидно,

Аналогичным образом последовательно исключаем у из для всех и добавляем у в для всех , меняя на каждом шагу только для так, чтобы

(ясно, что при рассмотрении случайное множество не меняется). Перебрав все элементы Y, получим случайное множество , для которого выполнено требуемое. Теорема 8 доказана.

Основной результат о сведении теории нечетких множеств к теории случайных множеств дается следующей теоремой.

Теорема 9. Пусть - некоторые нечеткие подмножества множества Y из конечного числа элементов. Рассмотрим результаты последовательного выполнения теоретико-множественных операций

где - символ одной из следующих теоретико-множественных операций над нечеткими множествами: пересечение, произведение, объединение, сумма (на разных местах могут стоять разные символы). Тогда существуют случайные подмножества того же множества Y такие, что

Proj

и, кроме того, результаты теоретико-множественных операций связаны аналогичными соотношениями

Proj

где знак означает, что на рассматриваемом месте стоит символ пересечения случайных множеств, если в определении B^m стоит символ пересечения или символ произведения нечетких множеств, и соответственно символ объединения случайных множеств, если в B^m стоит символ объединения или символ суммы нечетких множеств.

Комментарий. Поясним содержание теоремы. Например, если

то

Как совместить справедливость дистрибутивного закона для случайных множеств (вытекающего из его справедливости для обычных множеств) с теоремой 2 выше, в которой показано, что для нечетких множеств, вообще говоря, ? Дело в том, что хотя в соответствии с теоремой 9 для любых трех нечетких множеств В₁, В₂ и В₃ можно указать три случайных множества А₁, А₂ и А₃ такие, что

Proj Proj Proj,

где

но при этом, вообще говоря,

Proj

и, кроме случаев, указанных в теореме 2,

Proj

Доказательство теоремы 9 проводится по индукции. При t = 1 распределение случайного множества строится с помощью теоремы 3. Затем конструируется само случайное множество А₁, определенное на делимом вероятностном пространстве (нетрудно проверить, что на делимом вероятностном пространстве можно построить случайное подмножество конечного множества с любым заданным распределением именно в силу делимости пространства). Далее случайные множества А₂, А₃, …, A_t строим по индукции с помощью теоремы Теорема 9 доказана.

Замечание. Проведенное доказательство теоремы 9 проходит и в случае, когда при определении B^m используются отрицания, точнее, кроме B^m ранее введенного вида используются также последовательности результатов теоретико-множественных операций, очередной шаг в которых имеет вид

А именно, сначала при помощи законов де Моргана (теорема 1 выше) проводится преобразование, в результате которого в последовательности B^m остаются только отрицания отдельных подмножеств из совокупности , а затем с помощью теоремы 5 вообще удается избавиться от отрицаний и вернуться к условиям теоремы 9.

Итак, в настоящей главе описаны связи между такими объектами нечисловой природы, как нечеткие и случайные множества, установленные в нашей стране в первой половине 70-х годов, начиная с работы [19]. Через несколько лет, а именно, в начале 80-х годов, близкие подходы стали развиваться и за рубежом. Одна из работ [20] носит примечательное название «Нечеткие множества как классы эквивалентности случайных множеств».

В эконометрике и прикладной статистике разработан ряд методов статистического анализа нечетких данных, в том числе методы классификации, регрессии, проверки гипотез о совпадении функций принадлежности по опытным данным и т.д., при этом оказались полезными общие подходы статистики объектов нечисловой природы [8]. Методологические и прикладные вопросы теории нечеткости широко обсуждаются в литературе. Приведем пример.

5.6. Нечеткий экспертный выбор в контроллинге инноваций

Обсудим одно применение экспертных технологий, разработанных на основе теории нечеткости.

В настоящее время активно разрабатывается подход к управлению инновационными проектами, основанный на методологии контроллинга. Одной из главных причин возникновения и внедрения концепции контроллинга для разработки инноваций на промышленных предприятиях стала необходимость в системной интеграции различных аспектов управления инновационными проектами. Контроллинг обеспечивает методическую и инструментальную базу для поддержки основных функций менеджмента: планирования, учета, контроля и анализа, а также оценки ситуаций для принятия управленческих решений [21].

Этапы контроллинга инноваций. Согласно [22], контроллинг инноваций включает в себя:

- оценку реализуемости проекта;

- информационную поддержку планирования разработки инновационного проекта;

- информационную поддержку контроля над осуществлением инновационного проекта;

- информационную поддержку функции анализа.

На первом этапе контроллеру проекта необходимо ответить на вопрос: достигнет ли предприятие поставленных перед ним целей, если приступит к реализации проекта. Цели проекта - как и цели самого предприятия, должны иметь ясный смысл, результаты, полученные при достижении цели, должны быть измеримы, а заданные ограничения (по времени, рамкам бюджета, выделенным ресурсам и качеству получаемых результатов) выполнимы. Если при реализации проекта общефирменные цели не достигаются, то подразделение контроллинга вырабатывает предложения об альтернативных вариантах реализации проекта, способных удовлетворить поставленные цели.

На этом этапе возникает задача выбора варианта реализации проекта, позволяющего достичь общефирменные цели.

Для решения этой задачи можно воспользоваться эконометрическими методами. Эконометрика - это наука, изучающая конкретные количественные и качественные взаимосвязи экономических объектов и процессов с помощью математических и статистических методов и моделей, поэтому именно в эконометрике следует искать методы для решения поставленной задачи.

Каждый предложенный вариант реализации проекта имеет свои преимущества и недостатки. Он может характеризоваться как количественными экономическими показателями, такими, как затраты, поступления и др., техническими показателями, описывающими характеристики качества разрабатываемого продукта, так и качественными показателями, выраженными в виде терминов, например, крошечный, маленький, средний.

Целесообразно выделить эталонный вариант реализации проекта и его характеристики. Характеристики подбираются таким образом, чтобы проект был оптимальным с точки зрения предъявляемых к нему требований. Чтобы сравнить варианты реализации проекта с эталонным вариантом и выбрать из них лучший, можно применить эконометрические методы, основанные на алгоритмах анализа качественных и количественных данных. Такие методы подробнее рассматриваются ниже.

На втором этапе осуществляется разработка планово-организационных мероприятий. Подразделение контроллинга разрабатывает методики и инструменты планирования, наилучшим образом подходящие в данных условиях и обеспечивающие наиболее точные результаты. Подготовленный план проверяется на реализуемость, затем решаются вопросы, связанные с координацией участников проекта, с организацией информационного потока, с организацией работ и назначением ответственных.

На третьем этапе устанавливается время проведения контрольных мероприятий, связанное с выполнением определенных блоков работ. Выбираются подконтрольные показатели, характеризующие финансовое и организационное состояние проекта. Устанавливаются допустимые отклонения выбранных показателей, превышение которых может привести к негативным последствиям. Проводится учет показателей, фиксация отклонений. Выявляются причины и виновники отклонений.

На заключительном четвертом этапе подразделение контроллинга оценивает влияние выявленных отклонений на дальнейшие шаги реализации проекта. Выясняет, как выявленные отклонения повлияли на основные управляемые параметры проекта.

По окончанию цикла контроллер проекта подготавливает отчет с предложением вариантов решения возникших проблем и изменением плановых величин на следующий период.

Эконометрические методы сравнения и выбора. На первом этапе контроллинга инноваций необходимо решить задачу выбора варианта реализации проекта. Выбор между вариантами очевиден, если один из вариантов лучше другого по всем рассматриваемым показателям. В реальных ситуациях выбора варианты обычно несравнимы - первый лучше по одним показателям, второй - по другим. Для сравнения вариантов целесообразно прибегать к экспертным технологиям [12].

Одна группа экспертных технологий нацелена на выявление объективного упорядочения вариантов в результате усреднения мнений экспертов. Используют различные способы расчета на основе средних рангов (прежде всего средних арифметических и медиан). Для моделирования результатов парных сравнений применяют теорию люсианов. Для экспертных оценок находят медиану Кемени, и т.д.

Другая группа экспертных технологий нацелена на получение коэффициентов весомости (важности, значимости) отдельных показателей. Итоговая оценка варианта реализации проекта получается в результате суммирования произведений значений показателей на соответствующие коэффициенты весомости. Иногда эти коэффициенты оцениваются экспертами на основе иерархической системы показателей. Более обоснованным является экспертно-статистический метод, согласно которому на основе обучающей выборки восстанавливается зависимость между показателями варианта реализации инновационного проекта и его итоговой оценкой.

Использование теории нечеткости. Для сравнения вариантов реализации инновационного проекта и выбора из них лучшего можно использовать подход, основанный на описании качественных характеристик нечеткими множествами. Опишем его [22].

Пусть S = {S_i, i = 1, 2, …, n} – множество, состоящее из n вариантов реализации инновационного проекта. Для каждого варианта S_i определено m характеристик Q_ij, j = 1, 2, …, m. В зависимости от конкретных условий набор характеристик может меняться.

Необходимо выделить эталонный вариант реализации проекта S_o и его характеристики Q_0j. Характеристики подбираются таким образом, чтобы проект был оптимальным с точки зрения предъявляемых к нему требований.

Требуется проранжировать имеющиеся варианты S реализации инновационного проекта по заданным m характеристикам на соответствие эталону.

Для каждой характеристики Q_ij, согласно рассматриваемой методике, строится нечеткое множество . Для этого сначала определяются возможные значения переменной x_j, удовлетворяющие характеристике Q_ij. Предполагается, что они составляют отрезок X_ij. Определяется середина q_ij и полуширина (радиус) отрезка X_ij: Таким образом,

.

Для описания критерия Q_ij могут применяться различные функции принадлежности. В соответствии с [22] используем функцию принадлежности следующего вида:

.

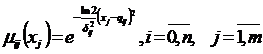Исходя из построения множества X_ij, в точке q_ij функция имеет максимум, в пределах множества X_ij функция принадлежности принимает значения больше 0,5, а вне X_ij – меньше:

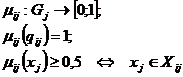
В результате получаем нечеткие множества

,

описывающие критерии Q_ij.

Чтобы определить, в какой мере характеристика варианта s_i близка характеристике эталонного варианта s_o, вычисляют степень равенства v_ij соответствующих нечетких множеств:

.

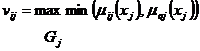Значение максимина достигается в точке пересечения функций принадлежности:

,

где

.

Произведя взвешенное голосование, получают интегральную оценку v_i соответствия совокупности характеристик варианта реализации проекта s_i совокупности характеристик эталонного варианта s₀:

,

где

.

Здесь является весом j-го критерия и показывает уровень его важности.

При обсуждении различных подходов к выбору наилучшего варианта реализации инновационного проекта иногда противопоставляют вероятностно-статистические модели и методы теории нечеткости. С обоснованной выше методологической точки зрения весьма важно, что такое противопоставление лишено оснований.