ГЛАВА 4. ТЕОРИЯ НЕЧЕТКИХ МНОЖЕСТВ
И «НЕЧЕТКОЕ УДВОЕНИЕ» МАТЕМАТИКИ

 

Чтобы определить нечеткое множество, надо сначала задать совокупность всех тех элементов, для которых имеет смысл говорить о мере их принадлежности рассматриваемому нечеткому множеству. Эта совокупность называется универсальным множеством. Например, для «кучи» - это множество натуральных чисел, для описания цветов – отрезок шкалы электромагнитных волн, соответствующий видимому свету.

 

4.1. Функции принадлежности

 

Пусть A - некоторое универсальное множество. Подмножество B множества A характеризуется своей характеристической функцией

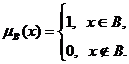                                               (1)

Что такое нечеткое множество? Обычно говорят, что нечеткое подмножество C множества A характеризуется своей функцией принадлежности . Значение функции принадлежности в точке х показывает степень принадлежности этой точки нечеткому множеству. Нечеткое множество описывает неопределенность, соответствующую точке х – она одновременно и входит, и не входит в нечеткое множество С. За вхождение -  шансов, за второе – (1- ) шансов.

Если функция принадлежности  имеет вид (1) при некотором B, то C есть обычное (четкое) подмножество A. Таким образом, теория нечетких множество является не менее общей математической дисциплиной, чем обычная теория множеств, поскольку обычные множества – частный случай нечетких. Соответственно можно ожидать, что теория нечеткости как целое обобщает классическую математику. Однако позже мы увидим, что теория нечеткости в определенном смысле сводится к теории случайных множеств и тем самым является частью классической математики. Другими словами, по степени общности обычная математика и нечеткая математика эквивалентны. Однако для практического применения в теории принятия решений описание и анализ неопределенностей с помощью теории нечетких множеств весьма плодотворны.

Обычное подмножество можно было бы отождествить с его характеристической функцией. Этого математики не делают, поскольку для задания функции (в ныне принятом подходе) необходимо сначала задать множество. Нечеткое же подмножество с формальной точки зрения можно отождествить с его функцией принадлежности. Однако термин «нечеткое подмножество» предпочтительнее при построении математических моделей реальных явлений.

Теория нечеткости является обобщением интервальной математики (о ней подробнее ниже), в которой для описания реальных объектов вместо чисел используются интервалы. Действительно, функция принадлежности

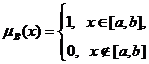                                            (2)

задает интервальную неопределенность – про рассматриваемую величину известно лишь, что она лежит в заданном интервале [a,b]. Тем самым описание неопределенностей с помощью нечетких множеств является более общим, чем с помощью интервалов.

 

4.2. Современная теория нечетких множеств

 

Начало современной теории нечеткости положено работой 1965 г. американского ученого азербайджанского происхождения Л.А. Заде. Основные определения, алгоритмы расчетов и выражающие их свойства теоремы приведены ниже. Рассуждения древнегреческих философов, французов Пуанкаре и Бореля начала ХХ в. обосновывают методологию теорию нечеткости, но как математическая дисциплина она началась с работы Заде.

За десятилетия, прошедшие с появления работы Л.А. Заде [6], «пушистой» тематике посвящены тысячи статей и книг. Выполнено достаточно много как теоретических, так и прикладных работ. Появилось новое направление в прикладной математике – теория нечеткости. Выходят международные научные журналы, проводятся конференции. В нашей стране концепция Заде активно обсуждалась еще в 60-е и 70-е гг. (см. обзор в [8]), однако первая книга российского автора по теории нечеткости вышла лишь в 1980 г. [9].

Л.А. Заде рассматривал теорию нечетких множеств как аппарат анализа и моделирования гуманистических систем, т.е. систем, в которых участвует человек. Его подход опирается на предпосылку о том, что элементами мышления человека являются не числа, а элементы некоторых нечетких множеств или классов объектов, для которых переход от «принадлежности» к «непринадлежности» не скачкообразен, а непрерывен. В настоящее время методы теории нечеткости используются почти во всех прикладных областях, в том числе при управлении предприятием, качеством продукции и технологическими процессами. Нет необходимости связывать теорию нечеткости только с гуманистическими системами.

Л.А. Заде использовал термины «теория нечетких множеств» и «нечеткая логика». Мы предпочитаем говорить о теории нечеткости. Термин «нечеткая логика» не является синонимом к термину «теория нечеткости», поскольку логика – это наука о мышлении человека, а теория нечеткости применяется не только для моделирования мышления. Нечеткая логика – это часть теории нечеткости.  

Аппарат теории нечеткости довольно громоздок. В качестве примера дадим определения теоретико-множественных операций над нечеткими множествами. Пусть C и D – два нечетких подмножества универсального множества A с функциями принадлежности и соответственно. Пересечением , произведением CD, объединением , отрицанием , суммой C+D называются нечеткие подмножества A с функциями принадлежности

соответственно.

Для демонстрации специфики нечетких множеств рассмотрим некоторые их свойства. 

В дальнейшем считаем, что все рассматриваемые нечеткие множества являются подмножествами одного и того же множества Y.

 

4.3. Законы де Моргана для нечетких множеств

 

Как известно, законами де Моргана называются следующие тождества алгебры множеств

       (2)

  Теорема 1. Для нечетких множеств справедливы тождества

       (3)

             (4)

Доказательство теоремы 1 состоит в непосредственной проверке (как это сделано ниже при доказательстве теоремы 2) справедливости соотношений (3) и (4) путем вычисления значений функций принадлежности участвующих в этих соотношениях нечетких множеств на основе определений, данных выше.

Тождества (3) и (4) назовем законами де Моргана для нечетких множеств. В отличие от классического случая соотношений (2), они состоят из четырех тождеств, одна пара которых относится к операциям объединения и пересечения, а вторая - к операциям произведения и суммы. Как и соотношение (2) в алгебре множеств, законы де Моргана в алгебре нечетких множеств позволяют преобразовывать выражения и формулы, в состав которых входят операции отрицания.

 

4.4. Дистрибутивный закон для нечетких множеств

 

Некоторые свойства операций над множествами не выполнены для нечетких множеств. Так,  за исключением случая, когда А - «четкое» множество (т.е. функция принадлежности принимает только значения 0 и 1).

Верен ли дистрибутивный закон для нечетких множеств? В литературе иногда расплывчато утверждается, что «не всегда». Внесем полную ясность.

Теорема 2. Для любых нечетких множеств А, В и С

       (5)

В то же время равенство

            (6)

справедливо тогда и только тогда, когда при всех  

Доказательство. Фиксируем произвольный элемент . Для сокращения записи обозначим  Для доказательства тождества (5) необходимо показать, что

         (7)

Рассмотрим различные упорядочения трех чисел a, b, c. Пусть сначала  Тогда левая часть соотношения (7) есть  а правая  т.е. равенство (7) справедливо.

Пусть  Тогда в соотношении (7) слева стоит  а справа  т.е. соотношение (7) опять является равенством.

Если  то в соотношении (7) слева стоит  а справа  т.е. обе части снова совпадают.

Три остальные упорядочения чисел a, b, c разбирать нет необходимости, поскольку в соотношение (6) числа b и c входят симметрично. Тождество (5) доказано.

Второе утверждение теоремы 2 вытекает из того, что в соответствии с определениями операций над нечеткими множествами 

и

Эти два выражения совпадают тогда и только тогда, когда, когда  что и требовалось доказать.

Определение 1. Носителем нечеткого множества А называется совокупность всех точек , для которых  

Следствие теоремы 2. Если носители нечетких множеств В и С совпадают с У, то равенство (6) имеет место тогда и только тогда, когда А - «четкое» (т.е. обычное, классическое, не нечеткое) множество.

Доказательство. По условию  при всех . Тогда из теоремы 2 следует, что  т.е.  или , что и означает, что А - четкое множество.

4.5. Нечеткое удвоение математики

 

Поскольку теория множеств – основа современной математики, понятие нечеткости позволяет «удвоить математику»: заменяя обычные множества нечеткими, мы можем каждому математическому объекту (понятию, термину) поставить в соответствие его нечеткий аналог. Рассматривают, например, нечеткие классификации, упорядочения, логики, теоремы, алгоритмы, правила принятия решений и т.д., и т.п. Чтобы это перечисление не выглядело для неискушенного читателя просто набором слов, разберем несколько примеров.

Первым в нашем списке упомянуты классификации. Под классификацией имеется в виду разбиение совокупности элементов на классы – группы сходных между собой элементов [10]. В четкой классификации каждый элемент относится к одному определенному классу. А в размытой – задается функция принадлежности элемента различным классам. Расплывчатая классификация обычно больше соответствует реальности, чем строгая.

Представьте себе – идет вам навстречу человек. Лишь в редких случаях вы с уверенностью скажете: «Это блондин». Чаще о цвете волос придется высказаться уклончиво: «Скорее шатен, чем брюнет». Так что, признайтесь, классификация встречных по цвету волос у вас нечеткая. Поэтому пушистые классификации надо изучать – этим и занимается соответствующая часть туманной математики.

Пример нечеткого упорядочения нетрудно найти в магазине, присмотревшись к поведению нерешительного покупателя. Надо приобрести часы, да вот какие? И «Слава» нравится, и «Ракета» современна. Другими словами, и «Слава» на сколько-то процентов привлекательна, и «Ракета» - тут и появляются функции принадлежности марок часов к множеству привлекательных. А ведь сравнивать можно по многим критериям – по внешнему виду, по цене, по надежности и т.д. Для каждого критерия – своя туманность, нужно эти расплывчатости сводить вместе, чтобы принять решение – покупать или не покупать… А для описания всего этого надо развивать математическую теорию нечетких упорядочений, принятия расплывчатых решений…

А что такое нечеткая логика? С позиций обычной логики утверждения бывают либо истинные, либо ложные. А в размытой логике – утверждения в какой-то степени истинны, а в какой-то – ложны. Присмотритесь к себе – очень многое, что вы говорите и думаете, имеет лишь относительную истинность. Например, вы сказали: «Вчера я хорошо поработал». Сразу возникают вопросы: «А разве нельзя было поработать еще лучше? Что значит – хорошо?» Согласитесь: ваши слова истинны не на сто процентов. И подобное можно сказать не только по части житейских высказываний, но и относительно утверждений науки.

Вот, скажем, как выглядит нечеткий аналог теоремы о том, что три медианы треугольника пересекаются в одной точке:

«Пусть АВ, ВС и СА – примерно прямые линии, которые образуют примерно треугольник с вершинами А, В и С. Пусть М1, М2, М3 – примерно середины сторон ВС, СА и АВ соответственно. Тогда примерно прямые линии АМ1, ВМ2 и СМ3 образуют примерно треугольник Т1Т2Т3, который более или менее мал относительно треугольника АВС» [11, с.137-138].

Конечно, эта формулировка становится разумной только после того, как будет точно определен смысл слов «примерно» и «более или менее мал». Вот как, скажем, можно уточнить понятие «примерно отрезок АВ»: под ним будем понимать любую кривую, проходящую через точки А и В, такую, что расстояние (в обычном смысле) от любой точки кривой до отрезка АВ мало по отношению к длине АВ. Остается выяснить, что значит «мало». Ответ может даваться нечетким множеством со своей функцией принадлежности.

Нечеткие алгоритмы – тоже не экзотика. Многие инструкции в какой-то мере расплывчаты. Беря поваренную книгу, любая хозяйка знает: чтобы блюдо удалось, к печатным рецептам надо добавить свою интерпретацию, а также смекалку и удачу. Если же поручить роботу готовить суп, то придется нечеткие слова естественного языка определять с помощью функций принадлежности. Например, определить понятие «варить до готовности». Значит, нужна соответствующая математическая теория – теория нечетких алгоритмов.

Продолжать можно без конца. «Удвоение математики» - настоятельная необходимость. Однако «скоро сказка сказывается, да нескоро дело делается». Теория нечеткости молода. Всего лишь почти пятьдесят лет! Миг по сравнению с двадцатью пятью веками геометрии!

 

4.6. Польза нечеткости

 

Несмотря на свою молодость, нечеткая математика находит успешные приложения. Примеры описания неопределенностей с помощью нечетких множеств часто приводятся в литературе. Например, в [12] приведено описание понятия «богатый человек», разобрана разработка методики ценообразования на основе теории нечетких множеств.

Поскольку размытость свойственна самому восприятию и мышлению человека, теория нечеткости используется прежде всего в науках, изучающих эти стороны человеческой натуры: в психологии, в социологии, в исследовании операций… Зачастую в ходе социологических и экспертных опросов человеку легче сформулировать свое мнение расплывчато, а не предельно четко, и размытый ответ является к тому же более адекватным. Поэтому создаются методы сбора и анализа нечеткой информации.

Пример – система управления рыбным промыслом. Исходная информация – сообщения с судов и мнения экспертов. Они нечетки: в таком-то квадрате количество рыбы оценивается величиной между таким-то нижним и таким-то верхним пределами, суда стоит направить туда-то, и т.д. По этим данным согласно алгоритмам нечеткой математики производится оптимизация в расплывчатых условиях. И затем выдается четкий приказ: каким судам куда идти. (Результат его выполнения – количество выловленной рыбы – разумеется, нельзя предсказать точно: нечеткость исходной информации не устраняется четкостью приказа.)

Аппарат теории нечеткости оказался полезным в самых разных прикладных областях – в химической технологии и в медицине, при управлении движением автотранспорта и в экономической географии, в теории надежности и при контроле качества продукции.

Группа химиков во главе с академиком В.В. Кафаровым изучала процессы, протекающие в ванне стекловаренной печи при производстве листового стекла. Основное при этом – исследовать распределение поля температур в бассейне ванны. Можно это делать в классическом стиле, рассматривая дифференциальное уравнение в частных производных, которому удовлетворяет поле температур. Уравнение это можно решить хорошо известным среди специалистов методом Фурье. Но пушистые химики предлагают другой подход. В соответствии с ним приращение температуры при переходе от одной точки бассейна печи к другой является нечетким. Химики рассчитали поле температур размытым методом и сравнили свои результаты с числами, полученными по методу Фурье. Относительное расхождение не превышало 6%, что считается пренебрежимо малым в этой области. Но компьютерные расчеты заняли в 5-6 раз меньше машинного времени. В этом и состояла польза применения методлов теории нечеткости.

 

4.7. Парадокс теории нечеткости

 

В концепции размытости есть свой подход к познанию мира, к построению математических моделей реальных явлений. Хочется во всем увидеть нечеткость и смоделировать эту нечеткость подходящим расплывчатым объектов.

Мы уже рассмотрели много примеров, когда такой подход разумен и полезен. Возникает искушение провозгласить тезис: «Все в мире нечетко». Он выглядит особенно привлекательно в связи с большой вредностью излишней, обманчивой четкости. Но можно ли этот тезис провести последовательно?

Нечеткое множество задается функцией принадлежности. Обратим внимание на аргумент и на значение этой функции. Четкие это объекты или размытые? Тезис «все в мире нечетко» наталкивает на мысль, что они расплывчаты.

Действительно, вспомним примеры – скажем, софизм «Куча». Сначала поговорим про аргумент функции, т.е. про число зерен, относительно которых решается вопрос: «Куча это или не куча?» Число зерен в достаточно большой совокупности – разве может оно быть известно абсолютно точно? Как ни считай зерна – вручную, на вес, автоматически – всегда возможны ошибки (человек может ошибиться, автоматические весы измеряют с погрешностями (описаны в паспорте средства измерения), и даже – могут сломаться…). Или пройдемся по остальным примерам – всюду то же самое.

А теперь – о значении функции принадлежности. Оно уж тем более нечетко! Мнение человека – разве имеет смысл выражать его хотя бы с тремя значащими цифрами? В социологии общепринято, что человек в словесных оценках обычно не может различить больше трех, в лучшем случае – шести градаций (эти величины вытекают и из математической модели, разработанной в [13]). Отсюда можно вывести с помощью соответствующего расчета, что функция принадлежности, отражающее мнение одного человека, может быть определена лишь с точностью 0,17 – 0,33. Так что мнение отдельного лица следовало бы выразить не тонкой кривой – графиком функции, а довольно широкой полосой. Если же функция принадлежности строится как среднее (среднее арифметическое или медиана) индивидуальных мнений, то и тогда ее значения известны отнюдь не абсолютно точно из-за того, что опрашиваемая совокупность людей обычно не включает и малой доли тех, кого можно было опросить. И только если значения функции принадлежности определяются по аналитическим формулам, они известны абсолютно точно. Но тогда возникает законный вопрос: насколько обоснованы сами эти формулы? Обычно оказывается, что обоснование у них довольно слабое…

Каков итог? И аргумент, и значение функции принадлежности, как правило, необходимо считать нечеткими.

Что же из этого следует? Начнем опять с аргумента. Он сам является не строго определенной величиной, а некоторым нечетким множеством величин, значит, описывается некоторой функцией принадлежности – задается каким-то своим аргументом. А этот новый аргумент – он ведь тоже нечеток! Опять появляется функция принадлежности – с каким-то третьим аргументом. И так далее.

Остановимся ли мы когда-либо на этом пути? Если остановимся, то должны будем использовать четкие значения аргумента – а это противоречит тезису «все в мире нечетко». В соответствии с эти тезисом четкие значения фиктивны, им ничто в мире не соответствует. Если же не остановимся, то получим бесконечную последовательность нечетких моделей, в которой из каждого размытого множества, как из матрешки, вылезает новая расплывчатость. Возможны ли при этом обоснованные расчеты?

Далее, значение функции принадлежности также необходимо считать нечетким. Л.А. Заде разработал аппарат пушистых множеств с размытыми функциями принадлежности, благоразумно не вдаваясь при этом в рассуждения о том, на каком же шагу считать функции принадлежности четкой.

Итак, основной парадокс теории нечеткости состоит в том, что привлекательный тезис «все в мире нечетко» невозможно последовательно раскрыть в рамках математических моделей. Конечно, описанный парадокс не мешает успешно использовать расплывчатую математику в конкретных приложениях. Из него вытекает лишь необходимость указывать и обсуждать границы ее применимости. 

 

4.8. Примеры описания неопределенностей
с помощью нечетких множеств

 

Один пример подробно обсуждался выше – понятие «Куча». Второй пример – понятие «богатый». Оно часто используется при обсуждении социально-экономических проблем, в том числе и в связи с подготовкой и принятием решений. Однако очевидно, что разные лица вкладывают в это понятие различное содержание. Сотрудники Института высоких статистических технологий и эконометрики МГТУ им. Н.Э. Баумана провели (в 1996 г.) социологическое исследование представления различных слоёв населения о понятии «богатый человек».

         Мини-анкета опроса выглядела так:

         1. При каком месячном доходе (в млн. руб. на одного человека) Вы считали бы себя богатым человеком?

         2. Оценив свой сегодняшний доход, к какой из категорий Вы себя относите:

         а) богатые;                                    

         б) достаток выше среднего;               

         в) достаток ниже среднего;

         г) бедные;

         д) за чертой бедности?

(В дальнейшем вместо полного наименования категорий будем оперировать буквами, например «в» - категория, «б» -  категория и т.д.)

         3. Ваша профессия, специальность.

         Всего опрошено 74 человека, из них 40 - научные работники и преподаватели, 34 человека - не занятых в сфере науки и образования, в том числе 5 рабочих и 5 пенсионеров. Из всех опрошенных только один (!) считает себя богатым. Несколько типичных ответов научных работников и преподавателей приведено в табл. 1, а аналогичные сведения для работников коммерческой сферы – в табл. 2.

Таблица 1

Типичные ответы научных работников и преподавателей

Ответы на вопрос 3

Ответы на вопрос 1, млн. руб./чел.

Ответы на вопрос 2

Пол

Кандидат наук

1

д

ж

Преподаватель

1

в

ж

Доцент

1

б

ж

Учитель

10

в

м

Старший научный сотрудник

10

д

м

Инженер-физик

24

д

ж

Программист

25

г

м

Научный работник

45

г

м

 

Таблица 2

Типичные ответы работников коммерческой сферы.

Ответы на вопрос 3

Ответы
на вопрос 1

Ответы
на вопрос 2

Пол

Вице-президент банка

100

а

ж

Зам. директора банка

50

б

ж

Начальник. кредитного отдела

50

б

м

Начальник отдела ценных бумаг

10

б

м

Главный бухгалтер

20

д

ж

Бухгалтер

15

в

ж

Менеджер банка

11

б

м

Начальник отдела проектирования

10

в

ж

         Разброс ответов на первый вопрос – от 1 до 100 млн. руб. в месяц на человека. Результаты опроса показывают, что критерий богатства у финансовых работников в целом несколько выше, чем у научных (см. гистограммы на рис. 1 и рис. 2 ниже).

         Опрос показал, что выявить какое-нибудь конкретное значение суммы, которая необходима «для полного счастья», пусть даже с небольшим разбросом, нельзя, что вполне естественно. Как видно из таблиц 1 и 2, денежный эквивалент богатства колеблется от 1 до 100 миллионов рублей в месяц. Подтвердилось мнение, что работники сферы образования в подавляющем большинстве причисляют свой достаток к категории «в» и ниже (81% опрошенных), в том числе к категории «д» отнесли свой достаток 57%.

         Со служащими коммерческих структур и бюджетных организаций иная картина: «г» - категория 1 человек (4%), «д» - категория 4 человека (17%), «б» - категория - 46% и 1 человек «а» - категория.

         Пенсионеры, что не вызывает удивления, отнесли свой доход к категории «д» (4 человека), и лишь один человек указал «г» - категорию. Рабочие же ответили так: 4 человека - «в», и один человек - «б».

         Для представления общей картины в табл. 3 приведены данные об ответах работников других профессий.

Таблица 3

Типичные ответы работников различных профессий.

Ответы на вопрос 3

Ответы

на вопрос 1

Ответы

на вопрос 2

Пол

Работник торговли

1

б

ж

Дворник

2

в

ж

Водитель

10

в

м

Военнослужащий

10

в

м

Владелец бензоколонки

20

б

ж

Пенсионер

6

д

ж

Начальник фабрики

20

б

м

Хирург

5

в

м

Домохозяйка

10

в

ж

Слесарь-механик

25

в

м

Юрист

10

б

м

Оператор ЭВМ

20

д

м

Работник собеса

3

д

ж

Архитектор

25

б

ж

         Прослеживается интересное явление: чем выше планка богатства для человека, тем к более низкой категории относительно этой планки он себя относит.

         Для сводки данных естественно использовать гистограммы. Для этого необходимо сгруппировать ответы. Использовались 7 классов (интервалов):

         1 – до 5 миллионов рублей в месяц на человека (включительно);

         2 – от 5 до 10 миллионов;

         3- от 10 до 15 миллионов;

         4 – от 15 до 20 миллионов;

         5 – от 20 до 25 миллионов;

         6 – от 25 до 30 миллионов;

         7 – более 30 миллионов.

(Во всех интервалах левая граница исключена, а правая, наоборот – включена.)

         Сводная информация представлена на рис. 1 (для научных работников и преподавателей) и рис. 2 (для всех остальных, т.е. для лиц, не занятых в сфере науки и образования - служащих иных бюджетных организаций, коммерческих структур, рабочих, пенсионеров).

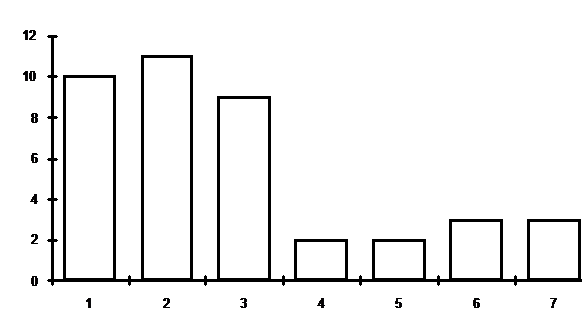
         Рис. 1. Гистограмма ответов на вопрос 1 для научных работников и преподавателей (40 человек)

 

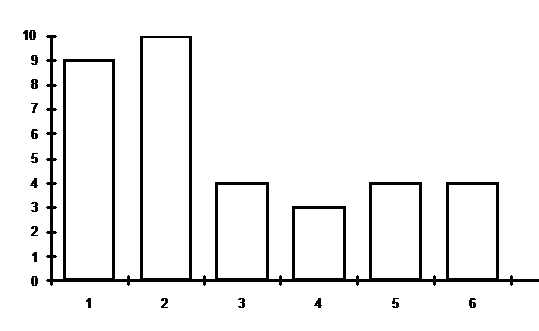
         Рис. 2. Гистограмма ответов на вопрос 1 для лиц, не занятых в сфере науки и образования (34 человека)

        

         Для двух выделенных групп, а также для некоторых подгрупп второй группы рассчитаны сводные средние характеристики – выборочные средние арифметические, медианы, моды. При этом медиана группы - количество млн. руб., названное центральным по порядковому номеру опрашиваемым в возрастающем ряду ответов на вопрос 1, а мода группы - интервал, на котором столбик гистограммы  - самый высокий, т.е. в него «попало» максимальное количество опрашиваемых. Результаты приведены в табл. 4.

Таблица 4

Сводные средние характеристики ответов на вопрос 1

для различных групп (в млн. руб. в мес. на чел.).

Группа опрошенных

Среднее

арифметическое

медиана

мода

Научные работники и преподаватели

11,66

7,25

(5; 10)

Лиц, не занятых в сфере науки и образования

14,4

10

(5; 10)

Служащие коммерческих структур и бюджетных организаций

17,91

10

(5; 10)

Рабочие

15

13

-

Пенсионеры

10,3

10

-

         Построим нечеткое множество, описывающее понятие «богатый человек» в соответствии с представлениями опрошенных. Для этого составим табл. 5 на основе рис. 1 и рис. 2 с учетом размаха ответов на первый вопрос.

 

Таблица 5

Характеристики ответов, попавших в интервалы

№

Номер интервала

0

1

2

3

4

1

Интервал, млн. руб. в месяц 

(0;1)

[1;5]

(5;10]

(10;15]

(15;20]

2

Число ответов в интервале

0

19

21

13

5

3

Доля ответов в интервале

0

0,257

0,284

0,176

0,068

4

Накопленное число ответов

0

19

40

53

58

5

Накопленная доля ответов

0

0,257

0,541

0,716

0,784

 

Продолжение таблицы 5

№

Номер интервала

5

6

7

8

1

Интервал, млн. руб. в месяц

(20;25]

(25;30]

(30;100)

[100;+∞)

2

Число ответов в интервале

6

7

2

1

3

Доля ответов в интервале

0,081

0,095

0,027

0,013

4

Накопленное число ответов

64

71

73

74

5

Накопленная доля ответов

0,865

0,960

0,987

1,000

 

         Пятая строка табл. 5 задает функцию принадлежности нечеткого множества, выражающего понятие «богатый человек» в терминах его ежемесячного дохода. Это нечеткое множество является подмножеством множества из 9 интервалов, заданных в строке 2 табл. 5. Или множества из 9 условных номеров {0, 1, 2, …, 8}. Эмпирическая функция распределения, построенная по выборке из ответов 74 опрошенных на первый вопрос мини-анкеты, описывает понятие «богатый человек» как нечеткое подмножество положительной полуоси.

         О разработке методики ценообразования на основе теории нечетких множеств. Для оценки значений показателей, не имеющих количественной оценки, можно использовать методы нечетких множеств. Например, П.В. Битюков применял нечеткие множества при моделировании задач ценообразования на электронные обучающие курсы, используемые при дистанционном обучении (см. [12, гл.8]). Им проведено исследование значений фактора «Уровень качества курса» с использованием нечетких множеств. В ходе практического использования предложенной П.В. Битюковым методики ценообразования значения ряда других факторов могут также определяться с использованием теории нечетких множеств. Например, ее можно использовать для определения прогноза рейтинга специальности в вузе с помощью экспертов, а также значений других факторов, относящихся к группе «Особенности курса». Опишем подход П.В. Битюкова как пример практического использования теории нечетких множеств.

         Значение оценки, присваиваемой каждому интервалу для фактора «Уровень качества курса», определяется на универсальной шкале [0,1], где необходимо разместить значения лингвистической переменной «Уровень качества курса»: НИЗКИЙ, СРЕДНИЙ, ВЫСОКИЙ. Степень принадлежности некоторого значения вычисляется как отношение числа ответов, в которых оно встречалось в определенном интервале шкалы, к максимальному (для этого значения) числу ответов по всем интервалам. 

         В ходе работы над диссертацией проведен опрос экспертов о степени влияния уровня качества электронных курсов на их потребительную ценность. Каждому эксперту в процессе опроса предлагалось оценить с позиции потребителя ценность того или иного класса курсов в зависимости от уровня качества. Эксперты давали свою оценку для каждого класса курсов по 10-ти балльной шкале (где 1 - min, 10 - max). Для перехода к универсальной шкале [0,1], все значения 10-ти балльной шкалы оценки ценности были разделены на максимальную оценку 10.

         Используя свойства функции принадлежности, необходимо предварительно обработать данные с тем, чтобы уменьшить искажения, вносимые опросом. Естественными свойствами функций принадлежности являются наличие одного максимума и гладкие, затухающие до нуля фронты. Для обработки статистических данных можно воспользоваться так называемой матрицей подсказок. Предварительно удаляются явно ошибочные элементы. Критерием удаления служит наличие нескольких нулей в строке вокруг этого элемента.

         Элементы матрицы подсказок вычисляются по формуле:

,

где  - элемент таблицы с результатами анкетирования, сгруппированными по интервалам.

         Матрица подсказок представляет собой строку, в которой выбирается максимальный элемент: , и далее все ее элементы преобразуются по формуле:

.

 Для столбцов, где , применяется линейная аппроксимация:

.

         Результаты расчетов сводятся в таблицу, на основании которой строятся функции принадлежности. Для этого находятся максимальные элементы по строкам:

.

Функция принадлежности вычисляется по формуле:

.

         Результаты расчетов приведены в табл. 6.

 

Таблица 6

Значения функции принадлежности лингвистической переменной

μi

Интервал на универсальной шкале

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

μ1

0

0,2

1

1

0,89

0,67

0

0

0

0

μ2

0

0

0

0

0

0,33

1

1

0

0

μ3

0

0

0

0

0

0

0

0

1

1

 

         На рис. 3 сплошными линиями показаны функции принадлежности значений лингвистической переменной «Уровень качества курса» после обработки таблицы, содержащей результаты опроса. Как видно из графика, функции принадлежности удовлетворяют описанным выше свойствам. Для сравнения пунктирной линией, выделенной крестиками, показана функция принадлежности лингвистической переменной для значения НИЗКИЙ* без обработки данных.

 

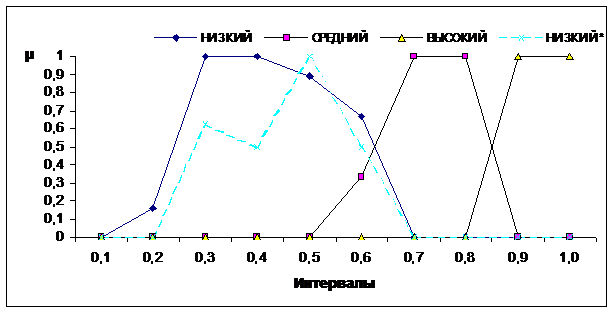         Рис. 3. График функций принадлежности значений лингвистической переменной «Уровень качества курса».

 

         Сбор и описание нечетких данных. Разработано большое количество процедур описания нечеткости. Так, согласно Э. Борелю понятие «Куча» описывается с помощью функции распределения – при каждом конкретном х значение функции принадлежности – это доля людей, считающих совокупность из х зерен кучей. Результат подобного опроса может дать и кривую иного вида, например, по поводу понятия «молодой» (слева будут отделены «дети», а справа – «люди зрелого и пожилого возраста»). Нечеткая толерантность может оцениваться с помощью случайных толерантностей (см. [12, разд. 7.2]).

         Целесообразно попытаться выделить наиболее практически полезные простые формы функций принадлежности. Видимо, наиболее простой является «ступенька» - внутри некоторого интервала функция принадлежности равна 1, а вне этого интервала равна 0. Это – простейший способ «размывания» числа путем замены его интервалом. Нечеткое множество описывается двумя числами – концами интервала. Оценки этих чисел можно получить с помощью экспертов. Статистическая теория подобных нечетких множеств, т.е. статистика интервальных данных, рассмотрена ниже. Связь с практикой очевидна – при прогнозировании погоды температура обычно описывается интервалами.

         Тремя числами a < b < c описывается функция принадлежности типа треугольника. При этом левее числа а и правее числа с функция принадлежности равна 0. В точке b функция принадлежности принимает значение 1. На отрезке [a; b] функция принадлежности линейно растет от 0 до 1, а на отрезке [b;c] – линейно убывает от 1 до 0. Оценки трех чисел a < b < c получают при опросе экспертов.

         Следующий по сложности вид функции принадлежности – типа трапеции – описывается четырьмя числами a < b < c < d. Левее a и правее d функция принадлежности равна 0. На отрезке [a; b] она линейно возрастает от 0 до 1, на отрезке [b; c] во всех точках равна 1, а на отрезке [c; d] линейно убывает от 1 до 0. Для оценивания четверки чисел a < b < c < d используют экспертов.

         Ряд результатов статистики нечетких данных приведен в первой монографии российского автора по нечетким множествам [9] и во многих дальнейших публикациях, в том числе в [8, 12, 88].

         Вторая часть настоящей книги посвящена системному обобщению математики. В частности, глава 11 посвящена когнитивным функциям – обобщению классического понятия функциональной зависимости на основе теории информации. Когнитивную функцию можно рассматривать как вариант нечеткой функциональной зависимости, для которой значение функции принадлежности, соответствующей конкретному значению зависимой переменной, определяется с помощью количества информации об этом значении в значении аргумента. Очень важно, что это количество информации рассчитывается на основе теоретически обоснованной модели непосредственно на основе эмпирических данных. Ценность такого подхода определяется тем, что специалисты по математическому моделированию, разрабатывая модели на основе теории нечетких множеств, зачастую не рассматривают вопрос о том, откуда брать функции принадлежности, другими словами, начинают рассмотрение с различных весьма произвольных гипотез о том, что эти функции имеют тот или иной вид. Здесь же, в теории когнитивных функций (см. главу 11), предлагается простой и понятный способ, как обоснованно рассчитывать функции принадлежности.

 

4.9. О статистике нечетких множеств

 

Обсудим некоторые вопросы статистического анализа нечетких данных. Нечеткие множества – частный вид объектов нечисловой природы. Поэтому при обработке выборки, элементами которой являются нечеткие множества, могут быть использованы различные методы анализа статистических данных произвольной природы - расчет средних, непараметрических оценок плотности, построение диагностических правил и т.д. [81].

         Среднее значение нечеткого множества. Однако иногда используются методы, учитывающие специфику нечетких множеств. Например, пусть универсальным множеством для рассматриваемого нечеткого множества является конечная совокупность действительных чисел {x1, x2, ..., xn}. Тогда под средним значением нечеткого множества иногда понимают число. А именно, среднее значение нечеткого множества определяют по формуле:

,

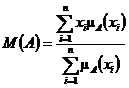где  - функция принадлежности нечеткого множества A. Если знаменатель равен 1, то эта формула определяет математическое ожидание случайной величины, для которой вероятность попасть в точку xi равна . Такое определение наиболее естественно, когда нечеткое множество A интерпретируется как нечеткое число.

         Очевидно, наряду с М(А) может оказаться полезным использование эмпирических средних, определяемых (согласно статистике в пространствах произвольной природы как части нечисловой статистики [8]) путем решения соответствующих оптимизационных задач. Для конкретных расчетов необходимо ввести то или иное расстояние между нечеткими множествами.

         Расстояния в пространствах нечетких множеств. Как известно, многие методы статистики нечисловых данных базируются на использовании расстояний (или показателей различия) в соответствующих пространствах нечисловой природы. Расстояние между нечеткими подмножествами А и В множества Х = {x1, x2, …, xk} можно определить как

где - функция принадлежности нечеткого множества A, а - функция принадлежности нечеткого множества B. Может использоваться и другое расстояние:

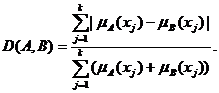
(Примем это расстояние равным 0, если функции принадлежности тождественно равны 0.)

         В соответствии с аксиоматическим подходом к выбору расстояний (метрик) в пространствах нечисловой природы разработан обширный набор систем аксиом, из которых выводится тот или иной вид расстояний (метрик) в конкретных пространствах, в том числе в пространствах нечетких множеств (см. [8, 81]). При использовании вероятностных моделей расстояние между случайными нечеткими множествами (т.е. между случайными элементами со значениями в пространстве нечетких множеств) само является случайной величиной, имеющей в ряде постановок асимптотически нормальное распределение.

         Проверка гипотез о нечетких множествах. Пусть ответ эксперта – нечеткое множество. Естественно считать, что его ответ, как показание любого средства измерения, содержит погрешности. Если есть несколько экспертов, то в качестве единой оценки (группового мнения) естественно взять эмпирическое среднее их ответов. Но возникает естественный вопрос: действительно ли все эксперты измеряют одно и то же? Может быть, глядя на реальный объект, они оценивают его с разных сторон? Например, на научную статью можно смотреть как с теоретической точки зрения, как и с прикладной, и соответствующие оценки будут, скорее всего, различны (если они совпадают, то работа либо никуда не годится, либо является выдающейся).

         Итак, возник вопрос: как проверить согласованность мнений экспертов? Надо сначала определить понятие согласованности. Пусть А – нечеткий ответ эксперта. Будем считать, что соответствующая функция принадлежности есть сумма двух слагаемых:

,

где N(A) – «истинное» нечеткое множество, а ξA(u) – «погрешность» эксперта как прибора. Естественно рассмотреть две постановки.

         Мнения экспертов А(1), А(2), …, А(m) будем считать согласованными, если

N(А(1)) = N(А(2)) = …, N(А(m)).

         Рассмотрим две группы экспертов. В первой у всех «истинное» мнение N(A), а во второй у всех - N(В). Две группы будем считать согласованными по мнениям, если

N(A) = N(В).

         Согласованность определена. Как же ее проверить? Если экспертов достаточно много, то эти гипотезы можно проверять отдельно для каждого элемента множества – общего носителя нечетких ответов. Проверка последней гипотезы переходит в проверку однородности двух независимых выборок [81]. Здесь ограничимся приведенными выше постановками основных гипотез.

         Восстановление зависимости между нечеткими переменными. Рассмотрим две нечеткие переменные А и В. Пусть каждый из n испытуемых выдает в ответ на вопрос два нечетких множества Ai и Bi, i = 1, 2, …, n. Необходимо восстановить зависимость В от А, другими словами, наилучшим образом приблизить В с помощью А.

         Для иллюстрации основной идеи ограничимся парной линейной регрессией нечетких множеств. Нечеткое множество С назовем линейной функцией от нечеткого множества А, если для любого х из носителя А функции принадлежности множеств А и С таковы, что µС(х) = µА(у) при х = αу + β. Другими словами,

µС(х) = µА((х - β)/α)

для любого х из носителя А. В таком случае естественно писать

С = αА +β.

         Однако нечеткие переменные, как и привычные для статистиков числовые переменные, обычно несколько отклоняются от линейной связи. Наилучшее линейное приближение нечеткой переменной В с помощью линейной функции от нечеткой переменной А естественно искать, решая задачу минимизации по α, β расстояния от В до С. Пусть

ρ(В, α0А + β0) = min ρ(B, αA + β),

где ρ – некоторое расстояние между нечеткими множествами, а минимизация проводится по всем возможным значениям α и β. Тогда наилучшей линейной аппроксимацией В является α0А + β0. Если рассматриваемый минимум равен 0, то имеет место точная линейная зависимость.

         Для восстановления зависимости по выборочным парам нечетких переменных естественно воспользоваться подходом, развитым в статистике в пространствах произвольной природы для параметрической регрессии (аппроксимации). В соответствии с методами статистики нечисловых данных [8] в качестве наилучших оценок параметров линейной зависимости следует рассматривать

.

Тогда наилучшим линейным приближением В является С* = α*А + β*.

         Вероятностно-статистическая теория регрессионного анализа нечетких переменных строится как частный случай аналогичной теории для переменных произвольной природы [8, 81]. В частности, при обычных предположениях оценки α*, β* являются состоятельными, т.е. α* → α0 и β* → β0 при n → ∞.

         Кластер-анализ нечетких переменных. Строить группы сходных между собой нечетких переменных (кластеры) можно многими способами. Опишем два семейства алгоритмов.

         Пусть на пространстве, в котором лежат результаты наблюдений, т.е. на пространстве нечетких множеств, заданы две меры близости ρ и τ (например, это могут быть введенные выше расстояния d и D). Берется один из результатов наблюдений (нечеткое множество) и вокруг него описывается шар радиуса R, определяемый мерой близости ρ. (Напомним, что шаром с центром в х относительно ρ называется множество всех элементов у рассматриваемого пространства таких, что ρ(х, у) < R.) Берутся результаты наблюдений (элементы выборки), попавшие в этот шар, и находится их эмпирическое среднее относительно второй меры близости τ. Оно берется за новый центр, вокруг которого снова описывается шар радиуса R относительно ρ, и процедура повторяется. (Чтобы алгоритм был полностью определен, необходимо сформулировать правило выбора элемента эмпирического среднего в качестве нового центра, если эмпирическое среднее состоит более чем из одного элемента.) 

         Когда центр шара зафиксируется (перестанет меняться), попавшие в этот шар элементы объявляются первым кластером и исключаются из дальнейшего рассмотрения. Алгоритм применяется к совокупности оставшихся результатов наблюдений, выделяет из нее второй кластер и т.д.

         Всегда ли центр шара остановится? При реальных расчетах в течение многих лет так было всегда. Соответствующая теория построена лишь в 1978 г. (см. [8, 81]). Доказано, что описанный выше процесс всегда остановится через конечное число шагов. Причем число шагов до остановки оценивается через максимально возможное число результатов наблюдений в шаре радиуса R относительно ρ.

         Обширное семейство образуют алгоритмы кластер-анализа типа «Дендрограмма», известные также под названием «агломеративные иерархические алгоритмы средней связи». На первом шаге алгоритма из этого семейства каждый результат наблюдения рассматривается как отдельный кластер. Далее на каждом шагу происходит объединение двух самых близких кластеров. Название «Дендрограмма» объясняется тем, что результат работы алгоритма обычно представляется в виде дерева. Каждая его ветвь соответствует кластеру, появляющемуся на каком-либо шагу работы алгоритма. Слияние ветвей соответствует объединению кластеров, а ствол – заключительному шагу, когда все наблюдения оказываются объединенными в один кластер.

         Для работы алгоритмов кластер-анализа типа «Дендрограмма» необходимо определить расстояние между кластерами. Естественно использовать ассоциативные средние, которыми, как известно, являются средние по Колмогорову всевозможных попарных расстояний между элементами двух рассматриваемых кластеров. Итак, расстояние между кластерами K и L, состоящими из n1 и n2 элементов соответственно, определяется по формуле:

,

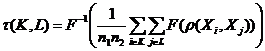где ρ – некоторое расстояние между нечеткими множествами;

F – строго монотонная функция (строго возрастающая или строго убывающая).

         Соображения теории измерений позволяют ограничить круг возможных алгоритмов типа «Дендрограмма». Естественно принять, что единица измерения расстояния выбрана произвольно. Тогда измерения проводятся в шкале отношений, и согласно результатам теории измерений [8] из всех средних по Колмогорову годятся только степенные средние, т.е.

F(z) = zλ при λ ≠ 0 или F(z) = ln(z).

         Чтобы получить разбиение на кластеры, надо «разрезать» дерево на определенной высоте, т.е. объединять кластеры лишь до тех пор, пока расстояние между ними меньше заранее выбранной константы. При альтернативном подходе заранее фиксируется число кластеров. Рассматривают и двухкритериальную постановку, когда минимизируют сумму (или максимум) внутрикластерных разбросов и число кластеров. Для решения задачи двухкритериальной минимизации либо один из критериев заменяют ограничением, либо два критерия «свертывают» в один, либо применяют иные подходы (последовательная оптимизация, построение поверхности Парето и др.).

         При классификации нечетких множеств полезны все подходы теории классификации [10], основанные только на использовании расстояний.