ГЛАВА 12. ПОВЫШЕНИЕ СТЕПЕНИ ФОРМАЛИЗАЦИИ ВЗВЕШЕННОГО МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ ПУТЕМ ВЫБОРА В КАЧЕСТВЕ ВЕСОВ НАБЛЮДЕНИЙ КОЛИЧЕСТВА ИНФОРМАЦИИ В НИХ О ЗНАЧЕНИЯХ ФУНКЦИИ И АВТОМАТИЗАЦИИ ИХ РАСЧЕТА ПУТЕМ ПРИМЕНЕНИЯ АСК-АНАЛИЗА
Использование взвешенного
метода наименьших квадратов (МНК) позволяет исследователю вручную регулировать
вклад тех или иных данных в результаты построения моделей. Это необходимо в тех
случаях, когда известно, что на зависимую переменную оказывали влияние
какие-либо факторы кроме аргумента, заведомо не включенные в модель. В такой
ситуации нужно попытаться исключить влияние неучтенных факторов заданием весов
наблюдений. Обычно в статистических пакетах набор весов это числа от 0 до 100.
По умолчанию все данные учитываются с единичными весами. Задание наблюдениям
веса меньше 1 снижает их вклад в модель, а больше единицы увеличивает этот
вклад. Ключевым моментом при применении
взвешенного МНК является способ выбора и задания весов наблюдений. Считается[1],
что разумным вариантом является выбор весов пропорционально ошибкам не
взвешенной регрессии.
Подбор этих весов наблюдений
вручную может являться сложной и практически неразрешимой задачей, как из-за
сложной структуры данных (например, непостоянства дисперсии и среднего ошибок
наблюдений), так и из-за возможной очень большой размерности данных. Таким
образом, возникает задача автоматического определения весов наблюдений и разработка алгоритмов и программного
инструментария, обеспечивающего автоматизацию определения и взвешивания весов наблюдений
в МНК.
Предлагается новое, ранее не
встречавшееся в специальной литературе, решение этой задачи и соответствующее
обобщение метода наименьших квадратов (МНК), в котором точки (наблюдения) имеют вес, равный количеству информации в значении
аргумента о значении функции. Ясно, что по сути, речь идет о применении
когнитивных функций в взвешенном МНК.
Для этого предлагается два варианта.
11.1. Вариант 1-й: применение когнитивных
функций в взвешенном МНК
Можно
рассматривать точки когнитивных функций как «мультиточки», состоящие из
определенного количества «элементарных точек», соответствующего их весу. При
этом вес элементарной точки может быть принят равным единице младшего разряда.
В таблице 8 приведен фрагмент матрицы
информативностей модели INF1 – мера А.Харкевича (см. таблицу 5, глава 9).
Таблица 5 – МАТРИЦА ИНФОРМАТИВНОСТИ МОДЕЛЬ
INF1 – МЕРА А.ХАРКЕИВЧА В БИТАХ
(ФРАГМЕНТ)
|
Код |
Наименование |
Классы |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
||
|
1 |
ЗНАЧЕНИЕ
АРГУМЕНТА-1/30-{1.0000000, 12.9666667} |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
|
2 |
ЗНАЧЕНИЕ
АРГУМЕНТА-2/30-{12.9666667, 24.9333333} |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
|
3 |
ЗНАЧЕНИЕ
АРГУМЕНТА-3/30-{24.9333333, 36.9000000} |
0,000 |
0,000 |
0,000 |
0,000 |
-0,562 |
0,533 |
|
4 |
ЗНАЧЕНИЕ
АРГУМЕНТА-4/30-{36.9000000, 48.8666667} |
1,408 |
1,408 |
1,199 |
1,165 |
0,892 |
0,708 |
|
5 |
ЗНАЧЕНИЕ
АРГУМЕНТА-5/30-{48.8666667, 60.8333333} |
1,893 |
1,610 |
1,683 |
0,754 |
0,563 |
0,849 |
|
6 |
ЗНАЧЕНИЕ
АРГУМЕНТА-6/30-{60.8333333, 72.8000000} |
1,408 |
1,765 |
1,527 |
1,366 |
0,691 |
0,142 |
|
7 |
ЗНАЧЕНИЕ
АРГУМЕНТА-7/30-{72.8000000, 84.7666667} |
0,000 |
0,000 |
0,074 |
0,114 |
0,407 |
0,626 |
|
8 |
ЗНАЧЕНИЕ
АРГУМЕНТА-8/30-{84.7666667, 96.7333333} |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
|
9 |
ЗНАЧЕНИЕ
АРГУМЕНТА-9/30-{96.7333333, 108.7000000} |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
|
10 |
ЗНАЧЕНИЕ
АРГУМЕНТА-10/30-{108.7000000, 120.6666667} |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
|
11 |
ЗНАЧЕНИЕ
АРГУМЕНТА-11/30-{120.6666667, 132.6333333} |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
|
12 |
ЗНАЧЕНИЕ
АРГУМЕНТА-12/30-{132.6333333, 144.6000000} |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
|
13 |
ЗНАЧЕНИЕ
АРГУМЕНТА-13/30-{144.6000000, 156.5666667} |
0,000 |
0,000 |
0,000 |
0,397 |
0,563 |
-0,343 |
|
14 |
ЗНАЧЕНИЕ
АРГУМЕНТА-14/30-{156.5666667, 168.5333333} |
0,000 |
0,000 |
0,074 |
1,305 |
1,048 |
0,298 |
|
15 |
ЗНАЧЕНИЕ
АРГУМЕНТА-15/30-{168.5333333, 180.5000000} |
0,000 |
0,000 |
0,558 |
1,165 |
0,799 |
0,626 |
|
16 |
ЗНАЧЕНИЕ
АРГУМЕНТА-16/30-{180.5000000, 192.4666667} |
0,000 |
0,000 |
0,000 |
0,000 |
0,407 |
-0,343 |
|
17 |
ЗНАЧЕНИЕ
АРГУМЕНТА-17/30-{192.4666667, 204.4333333} |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
|
18 |
ЗНАЧЕНИЕ
АРГУМЕНТА-18/30-{204.4333333, 216.4000000} |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
|
19 |
ЗНАЧЕНИЕ
АРГУМЕНТА-19/30-{216.4000000, 228.3666667} |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
|
20 |
ЗНАЧЕНИЕ
АРГУМЕНТА-20/30-{228.3666667, 240.3333333} |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
-0,060 |
|
21 |
ЗНАЧЕНИЕ
АРГУМЕНТА-21/30-{240.3333333, 252.3000000} |
0,000 |
0,000 |
0,000 |
0,000 |
-0,077 |
0,298 |
|
22 |
ЗНАЧЕНИЕ
АРГУМЕНТА-22/30-{252.3000000, 264.2666667} |
0,000 |
0,000 |
0,000 |
0,000 |
0,691 |
0,626 |
|
23 |
ЗНАЧЕНИЕ
АРГУМЕНТА-23/30-{264.2666667, 276.2333333} |
0,000 |
0,000 |
0,000 |
0,000 |
-0,077 |
-0,827 |
|
24 |
ЗНАЧЕНИЕ
АРГУМЕНТА-24/30-{276.2333333, 288.2000000} |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
|
25 |
ЗНАЧЕНИЕ
АРГУМЕНТА-25/30-{288.2000000, 300.1666667} |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
|
26 |
ЗНАЧЕНИЕ
АРГУМЕНТА-26/30-{300.1666667, 312.1333333} |
0,000 |
0,000 |
0,000 |
0,000 |
0,563 |
0,425 |
|
27 |
ЗНАЧЕНИЕ
АРГУМЕНТА-27/30-{312.1333333, 324.1000000} |
0,000 |
0,000 |
0,000 |
0,000 |
-0,077 |
0,626 |
|
28 |
ЗНАЧЕНИЕ
АРГУМЕНТА-28/30-{324.1000000, 336.0666667} |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
|
29 |
ЗНАЧЕНИЕ
АРГУМЕНТА-29/30-{336.0666667, 348.0333333} |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,298 |
|
30 |
ЗНАЧЕНИЕ
АРГУМЕНТА-30/30-{348.0333333, 360.0000000} |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,425 |
Чтобы применить предлагаемый
подход, умножим в таблице 8 все значения на 1000 и оставим только целую часть,
тогда получим таблицу 9.
Таблица 6 – МАТРИЦА ИНФОРМАТИВНОСТИ МОДЕЛЬ
INF1 – МЕРА А.ХАРКЕИВЧА В МИЛЛИБИТАХ
(ФРАГМЕНТ)
|
Код |
Наименование |
Классы |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||
|
1 |
ЗНАЧЕНИЕ
АРГУМЕНТА-1/30-{1.0000000, 12.9666667} |
|
|
|
|
|
|
|
|
2 |
ЗНАЧЕНИЕ
АРГУМЕНТА-2/30-{12.9666667, 24.9333333} |
|
|
|
|
|
|
|
|
3 |
ЗНАЧЕНИЕ
АРГУМЕНТА-3/30-{24.9333333, 36.9000000} |
|
|
|
|
-562 |
533 |
105 |
|
4 |
ЗНАЧЕНИЕ
АРГУМЕНТА-4/30-{36.9000000, 48.8666667} |
1408 |
1408 |
1199 |
1165 |
892 |
708 |
717 |
|
5 |
ЗНАЧЕНИЕ
АРГУМЕНТА-5/30-{48.8666667, 60.8333333} |
1893 |
1610 |
1683 |
754 |
563 |
849 |
434 |
|
6 |
ЗНАЧЕНИЕ
АРГУМЕНТА-6/30-{60.8333333, 72.8000000} |
1408 |
1765 |
1527 |
1366 |
691 |
142 |
434 |
|
7 |
ЗНАЧЕНИЕ
АРГУМЕНТА-7/30-{72.8000000, 84.7666667} |
|
|
74 |
114 |
407 |
626 |
341 |
|
8 |
ЗНАЧЕНИЕ
АРГУМЕНТА-8/30-{84.7666667, 96.7333333} |
|
|
|
|
|
|
-535 |
|
9 |
ЗНАЧЕНИЕ
АРГУМЕНТА-9/30-{96.7333333, 108.7000000} |
|
|
|
|
|
|
|
|
10 |
ЗНАЧЕНИЕ
АРГУМЕНТА-10/30-{108.7000000, 120.6666667} |
|
|
|
|
|
|
|
|
11 |
ЗНАЧЕНИЕ
АРГУМЕНТА-11/30-{120.6666667, 132.6333333} |
|
|
|
|
|
|
|
|
12 |
ЗНАЧЕНИЕ
АРГУМЕНТА-12/30-{132.6333333, 144.6000000} |
|
|
|
|
|
|
-252 |
|
13 |
ЗНАЧЕНИЕ
АРГУМЕНТА-13/30-{144.6000000, 156.5666667} |
|
|
|
397 |
563 |
-343 |
773 |
|
14 |
ЗНАЧЕНИЕ
АРГУМЕНТА-14/30-{156.5666667, 168.5333333} |
|
|
74 |
1305 |
1048 |
298 |
516 |
|
15 |
ЗНАЧЕНИЕ
АРГУМЕНТА-15/30-{168.5333333, 180.5000000} |
|
|
558 |
1165 |
799 |
626 |
590 |
|
16 |
ЗНАЧЕНИЕ
АРГУМЕНТА-16/30-{180.5000000, 192.4666667} |
|
|
|
|
407 |
-343 |
341 |
|
17 |
ЗНАЧЕНИЕ
АРГУМЕНТА-17/30-{192.4666667, 204.4333333} |
|
|
|
|
|
|
|
|
18 |
ЗНАЧЕНИЕ
АРГУМЕНТА-18/30-{204.4333333, 216.4000000} |
|
|
|
|
|
|
|
|
19 |
ЗНАЧЕНИЕ
АРГУМЕНТА-19/30-{216.4000000, 228.3666667} |
|
|
|
|
|
|
|
|
20 |
ЗНАЧЕНИЕ
АРГУМЕНТА-20/30-{228.3666667, 240.3333333} |
|
|
|
|
|
-60 |
-252 |
|
21 |
ЗНАЧЕНИЕ
АРГУМЕНТА-21/30-{240.3333333, 252.3000000} |
|
|
|
|
-77 |
298 |
341 |
|
22 |
ЗНАЧЕНИЕ
АРГУМЕНТА-22/30-{252.3000000, 264.2666667} |
|
|
|
|
691 |
626 |
233 |
|
23 |
ЗНАЧЕНИЕ
АРГУМЕНТА-23/30-{264.2666667, 276.2333333} |
|
|
|
|
-77 |
-827 |
105 |
|
24 |
ЗНАЧЕНИЕ
АРГУМЕНТА-24/30-{276.2333333, 288.2000000} |
|
|
|
|
|
|
|
|
25 |
ЗНАЧЕНИЕ
АРГУМЕНТА-25/30-{288.2000000, 300.1666667} |
|
|
|
|
|
|
-1020 |
|
26 |
ЗНАЧЕНИЕ
АРГУМЕНТА-26/30-{300.1666667, 312.1333333} |
|
|
|
|
563 |
425 |
341 |
|
27 |
ЗНАЧЕНИЕ
АРГУМЕНТА-27/30-{312.1333333, 324.1000000} |
|
|
|
|
-77 |
626 |
233 |
|
28 |
ЗНАЧЕНИЕ
АРГУМЕНТА-28/30-{324.1000000, 336.0666667} |
|
|
|
|
|
|
|
|
29 |
ЗНАЧЕНИЕ
АРГУМЕНТА-29/30-{336.0666667, 348.0333333} |
|
|
|
|
|
298 |
-51 |
|
30 |
ЗНАЧЕНИЕ
АРГУМЕНТА-30/30-{348.0333333, 360.0000000} |
|
|
|
|
|
425 |
233 |
В таблице 9 рассматриваем отдельно только положительные числа или
только отрицательные. Рассмотрим фрагмент таблицы 9, выделенный светло-желтым
фоном:
– аргументу 14
соответствует 74 точки 3 класса, и 1305 точек 4-го класса;
– аргументу 15 соответствует
558 точек 3 класса, и 1165 точек 4-го класса.
После
этого преобразования можно применять стандартный МНК.
11.2. Вариант 2-й: средневзвешенные значения
функции в взвешенном МНК
Перед
применением стандартного МНК для каждого значения аргумента предварительно
рассчитывается средневзвешенное значение функции из всех ее значений с их
весами.
Для двух точек выбор координаты средневзвешенной
точки соответствует «правилу рычага», т.е. ее положение выбирается таким, чтобы
рычаг, образованный двумя точками с координатами Y1 и Y2
и весами I1 и I2, находился в равновесии,
если его опора будет в средневзвешенной точке с координатой Y:
![]()
Откуда находим Y. При двух точках,
соответствующих одному значению аргумента, координата Y средневзвешенной точки,
имеет вид:
![]() .
.
Если же таких точек N, то предыдущее выражение
принимает вид:
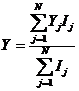 .
.
В результате средневзвешенная точка находится
тем ближе к некоторой точке, чем больше абсолютное и относительное количество
информации в значении аргумента о том, что функция примет значение, соответствующее
этой точке.
После
этого преобразования можно применять стандартный МНК.
В модуле визуализации когнитивных функций [133]
этот метод реализован программно для отображения частично и полностью
редуцированных когнитивных функций. Математическому описанию этого метода
планируются посвятить одну из будущих статей авторов.
Отметим, что кроме количества информации в
значении аргумента о значении функции в качестве весов могут быть использованы
и другие частные критерии из таблицы 5 главы 9.