ГЛАВА 11. КОГНИТИВНЫЕ ФУНКЦИИ КАК ОБОБЩЕНИЕ
КЛАССИЧЕСКОГО ПОНЯТИЯ ФУНКЦИОНАЛЬНОЙ ЗАВИСИМОСТИ НА ОСНОВЕ ТЕОРИИ ИНФОРМАЦИИ
В АСК-АНАЛИЗЕ И СИСТЕМНОЙ НЕЧЕТКОЙ ИНТЕРВАЛЬНОЙ
МАТЕМАТИКЕ
Данный раздел основан на
статье [280].
11.1. Классическое понятие функции в
математике
Кратко рассмотрим классическое понятие
функциональной зависимости или функции в математике.
Под функциональной зависимостью (функцией)
понимается закон или правило, по которому осуществляется отображение множества
числовых значений аргумента (область определения) на множество числовых
значений функции (область значений). В более общем определении область
определения и область значений могут быть произвольными множествами, не
обязательно числовыми.
В математике для классических функций обычно
вводится большое количество различных ограничений, накладывающих
соответствующие ограничения на возможности их практического применения, но позволяющих использовать и развивать
математические конструкции, основанные на описанном выше понятии функции в
математике. К этим ограничениям, прежде всего, относятся то, что множества
значений аргумента и значений функции являются числовыми, чаще всего
континуальными (интервал, луч прямая), и между ними существует
взаимно-однозначное соответствие, т.е. функция является биективной. Обычно предполагается также, что эти множества или
не обладают никакой структурой, или имеют алгебраическую структуру группы,
кольца, поля или аналогичную.
Вместе с тем при
определении и использовании функций необходимо различать математические,
прагматические и компьютерные числа, учитывать, что множества могут быть
нечеткими или случайными, элементами множеств могут быть не только числа, но и
лингвистические переменные, а также результаты измерений в различных шкалах, в
частности, в порядковых, кроме того множества могут образовывать системы. Всем
этим обусловлены существенные ограничения, которые накладываются на возможности
применения классического математического понятия функции для моделирования
социально-экономических объектов. Как следствие, возникает необходимость
разработки математического аппарата, снимающего эти ограничения. Кратко рассмотрим
совокупность поставленных вопросов вопросы ниже.
11.2. Ограничения классического понятия
функции
и
формулировка проблемы
Математика – язык науки [1,
с.18]. С
появлением новых объектов обсуждения, изучения и практического применения этот
язык развивается. «Между математикой и практикой всегда существует двусторонняя
связь; математика предлагает практике понятия и методы исследования, которыми
она уже располагает, а практика постоянно сообщает математике, что ей необходимо»
[1, c.53].
В настоящей работе мы рассматриваем
необходимость расширения математического понятия функциональной зависимости
(функции) с целью учета присущих реальности нечеткости, интервальности,
системности, а также основы соответствующего предлагаемого нами нового
перспективного направления теоретической и вычислительной математики –
системной нечеткой интервальной математики (СНИМ) [92]. Анализируя, следуя А.Н. Колмогорову
[2], математику в ее историческом развитии, констатируем, что ее основой
являются действительные числа и множества.
Как подчеркнуто выше, функции обычно определяются с помощью множеств
(области определения, области значений и подмножества декартова произведения
этих областей, задающего отображение области определения на область значений.
Число же является основным понятием математики с древнейших времен, и стержнем
развития математики вплоть до XIX в. является развитие понятия числа. Еще один
символ математики – фигуры и тела. И посвящена элементарная геометрия. Однако
развитие этой области математики прекратилось в начале ХХ в. Сейчас
элементарная геометрия – предмет изучения в средней школе, новые научные
результаты в ней не появляются. Ее наследники - современные геометрические
дисциплины, такие, как проективная геометрия, дифференциальная геометрия, общая
топология, алгебраическая топология и др. – далеки от реального мира. Их чисто
теоретические результаты практически не используются при решении прикладных задач.
Поэтому сосредоточимся на рассмотрении только
двух понятий - числа и множества.
Констатируем необходимость расширения
математического аппарата с целью учета присущих реальности нечеткости и интервальности.
Такая необходимость отмечалась в ряде публикаций [25, 26, 27],
но пока еще не стала общепризнанной. На описании неопределенностей с помощью
вероятностных моделей не останавливаемся, поскольку такому подходу посвящено
множество работ.
Подробное обоснование необходимости подобных
подходов дано в 1-й части данной работы.
11.2.8. Система как обобщение множества. Системное обобщение
математики и задачи,
возникающие при этом
В науке принято два основных принципа
определения понятий:
– через подведение определяемого понятия под более общее понятие и выделение из него
определяемого понятия путем указания одного или нескольких его специфических признаков (например,
млекопитающие – это животные, выкармливающие своих детенышей молоком);
– процедурное определение, которое определяет
понятие путем указания пути к нему
или способа его достижения (магнитный северный полюс – это точка, в которую
попадешь, если все время двигаться на север, определяя направление движения с помощью
магнитного компаса).
Как это ни парадоксально, но понятия системы и
множества могут быть определены друг через друга, т.е. трудно сказать, какое из
этих понятие является более общим.
Определение системы через множество.
Система
есть множество элементов, взаимосвязанных друг с другом, что дает системе новые
качества, которых не было у элементов. Эти новые системные свойства еще называются
эмерджентными (т.е. «возникающими»), т.к. не очень просто понять, откуда они
берутся. Чем больше сила взаимодействия элементов, тем сильнее свойства системы
отличаются от свойств множества и тем выше уровень системности и
синергетический эффект. Получается, что система – это множество элементов, но
не всякое множество, а только такое, в котором элементы взаимосвязаны (это и
есть специфический признак, выделяющий системы среди множеств), т.е. множество
– это более общее понятие.
Определение множества через систему.
Но можно рассуждать и иначе, считая более общим
понятием систему, т.е. мы ведь можем определить понятие множества через понятие
системы. Множество – это система, в
которой сила взаимодействия между элементами равна нулю (это и есть отличительный
признак, выделяющий множества среди систем). Тогда более общим понятием
является система, а множества – это просто системы с нулевым уровнем системности.
Вторая точка зрения объективно является
предпочтительной, т.к. совершенно очевидно, что понятие множества является предельной абстракцией от понятия системы и
реально в мире существуют только системы, а множеств в чистом виде не существует,
как не существует математической точки. Точнее сказать, что множества,
конечно, существуют, но всегда исключительно и только в составе систем как их базовый уровень иерархии, на котором
они основаны.
Из этого вытекает очень важный вывод: все понятия и теории, основанные
на понятии множества, допускают обобщение путем замены понятия множества на
понятие системы и тщательного прослеживания всех последствий этой замены.
При этом более общие теории будут удовлетворять принципу соответствия,
обязательному для всех более общих теорий, т.е. в асимптотическом случае, когда сила взаимосвязи элементов систем
стремится к нулю, системы будут все меньше отличаться от множеств и системное
обобщение теории перейдет к классическому варианту, основанному на понятии
множества. В предельном случае, когда
сила взаимосвязи точно равна нулю,
системная теория будет давать точно
такие же результаты, как основанная на понятии множества.
Этот вывод верен для всех теорий, но в данной работе
для авторов наиболее интересным и важным является то, что очень многие, если не
практически все понятия современной математики
основаны на понятии множества, в частности на математической теории множеств. В
частности, к таким понятиям относятся понятия:
– математической операции: преобразования одного
или нескольких исходных множеств в одно или несколько результирующих;
– функциональной зависимости: отображение
множества значений аргумента на множество значений функции для однозначной
функции одного аргумента или отображение множеств значений аргументов на
множества значений функций для многозначной функции многих аргументов;
– «количество информации»: функция от свойств
множества.
В работе [186]
впервые сформулирована и обоснована программная идея системного обобщения
математики, суть которой состоит в тотальной замене понятия
"множество" на более общее понятие "система" и
прослеживании всех последствий этого. При этом обеспечивается соблюдение
принципа соответствия, обязательного для более общей теории, т.к. при понижении
уровня системности система по своим свойствам становится все ближе к множеству
и система с нулевым уровнем системности и есть множество. Приводится
развернутый пример реализации этой программной идеи в области теории
информации, в качестве которого выступает предложенная в 2002 году системная
теория информации [97], являющаяся системным обобщением теории
информации Найквиста – Больцмана – Хартли – Шеннона и семантической теории
информации Харкевича. Основа этой теории состоит в обобщении комбинаторного
понятия информации Хартли I = Log2N
на основе идеи о том, что количество информации определяется не мощностью
множества N, а мощностью системы, под
которой предлагается понимать суммарное
количество подсистем различного уровня иерархии в системе, начиная с базовых
элементов исходного множества и заканчивая системой в целом. При этом в 2002
году, когда было предложено системное обобщение формулы Хартли, число подсистем
в системе, т.е. мощность системы Ns,
предлагалось рассчитывать по формуле:
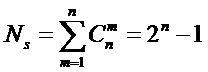 .
.
Соответственно,
системное обобщение формулы Хартли для количества информации в системе из n элементов предлагалось в виде:
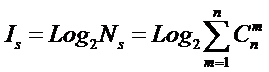
В работе [270]
дано системное обобщение формулы Хартли для
количества информации для квантовых систем, подчиняющиеся статистике как
Ферми-Дирака, так и Бозе-Эйнштейна, и стало ясно, что предложенные в 2002 году
в работе [97] вышеприведенные
выражения имеют силу только для систем, подчиняющихся статистике Ферми-Дирака.
В работе [188] кратко описывается семантическая информационная
модель системно-когнитивного анализа (СК-анализ), вводится универсальная
информационная мера силы и направления влияния значений факторов (независимая
от их природы и единиц измерения) на поведение объекта управления (основанная
на лемме Неймана – Пирсона), а также неметрический интегральный критерий
сходства между образами конкретных объектов и обобщенными образами классов,
образами классов и образами значений факторов. Идентификация и прогнозирование
рассматривается как разложение образа
конкретного объекта в ряд по обобщенным образам классов (объектный анализ), что
предлагается рассматривать как возможный вариант решения на практике 13-й проблемы Гильберта.
В статьях [189, 191]
обоснована идея системного обобщения математики и сделан первый шаг по ее
реализации: предложен вариант системной теории информации [97, 201].
В данной работе осуществлена попытка сделать второй шаг в этом же направлении:
на концептуальном уровне рассматривается один из возможных подходов к
системному обобщению математического понятия множества, а именно – подход,
основанный на системной теории информации. Предполагается, что этот подход
может стать основой для системного обобщения теории множеств и создания
математической теории систем. Сформулированы задачи, возникающие на пути
достижения этой цели (разработки системного обобщения математики) и предложены
или намечены пути их решения:
Задача 1: найти способ представления системы как совокупности
взаимосвязанных множеств.
Задача 2: сформулировать, чем отличаются друг от друга различные
системы, состоящие из одних и тех же базисных элементов.
Задача 3: обосновать принципы геометрической интерпретации
понятий: "элемент системы" и "система".
Задача 4: предложить способы аналитического описания (задания)
подсистем как элементов системы.
Задача 5: описать системное семантическое пространство
для отображения систем в форме эйдосов (эйдос-пространство).
Задача 6: описать принцип формирования эйдосов (включая
зеркальные части).
Задача 7: показать, что базовая когнитивная концепция [97]
формализуется многослойной системой эйдос-пространств (термин автора)
различных размерностей.
Задача 8: показать, что системная теория информации позволяет
непосредственно на основе эмпирических данных определять вид функций принадлежности,
т.е. решать одну из основных задач теории нечетких множеств.
Задача 9: сформулировать перспективы: разработка операций
с системами: объединение (сложение), пересечение (умножение), вычитание.
Привести предварительные соображения по сложению систем.
11.2.9. Формулировка
проблемы
Постоянно работая в области математического
моделирования социально-экономических объектов и явлений и учитывая наличие
всех вышеперечисленных ограничений, авторы пришли к выводу, что классическое
математическое понятие функциональной зависимости недостаточно для адекватного
отражения силы и величины причинно-следственной (или иной) связи между
факторами, действующим на экономический (или иной) объект, и поведением этого
объекта. Одно и тоже значение фактора влияет на переход экономического объекта
в различные состояния, но в различной степени или даже с различным знаком, и переход
объекта в каждое из состояний обусловлен действием большого количества
различных факторов, вообще говоря, взаимодействующих между собой. Это значит,
что одному значению аргумента соответствует не одно, а много различных значений
функции, а каждому значению функции соответствует много различных значений
аргумента, причем это соответствие может быть различным по величание и знаку.
Очевидно, что простое представление о биективной функции не пригодно для формального
математического моделирования подобных зависимостей. Обобщение классического
понятия функции может осуществлено различными способами, – на основе теории
нечеткости, интервальной математики, системного анализа.
11.3. Теоретическое решение проблемы в
АСК-анализе
Очевидно, смысл процесса
измерения в том, что в его результате мы получаем определенное количество информации
о степени выраженности тех или иных свойств объекта измерения или о его состоянии.
Информация может рассматриваться с двух точек зрения: с количественной и с
качественной, т.е. содержательной, семантической. Парадокс заключается в том,
что традиционно внимание обращается только на содержание информации, полуденной в процессе измерения, тогда как
на количество этой информации обычно
вообще не обращают никакого внимания. Между тем количество информации
полученной в результате измерений также очень важно, т.к. непосредственно
определяется точностью измерений.
По мнению авторов необходимо
четко осознать, что когда мы спрашиваем чему равно значение некоторой функции
при определенном значении ее аргумента, то, по сути, мы хотим получить некое количество информации об этом
значении функции из значения ее аргумента, т.е. о том, какое количество информации об этом значении функции содержится в
данном значении ее аргумента. Парадоксально, но мы никогда не спрашиваем,
какое же конкретно количество информации
мы получили при ответе на этот наш вопрос.
Ответом на этот вопрос
являются когнитивные функции. Если мы отобразим в графической форме результаты
измерения степени выраженности некоторого свойства объекта в зависимости от
величины влияющего на нее фактора в виде функции с указанием не только самих
значений функции, но и количества информации в ее аргументе о том, что функция
будет иметь эти значения, то это и будет когнитивная функция.
С точки
зрения теории управления когнитивная функция представляет собой зависимость вероятностей перехода объекта
управления в будущие состояния, соответствующие классам, под влиянием различных
значений некоторого фактора. Наглядные примеры когнитивных функций будут приведены
ниже.
Когнитивная функции строится для подматриц матрицы
информативностей (матрицы знаний) системы «Эйдос», образованных различными классификационными
и описательными шкалами (одна из подматриц выделена жирной линией и фоном)
(таблица 6):
Таблица 6 – К ПОЯСНЕНИЮ ПОНЯТИЯ:
«ПОДМАТРИЦЫ МАТРИЦЫ ЗНАНИЙ»
|
|
1-я |
2-я |
3-я |
|||||||
|
1-я градация |
2-я градация |
3-я градация |
1-я градация |
2-я градация |
3-я градация |
1-я градация |
2-я градация |
3-я градация |
||
|
1-я |
1-я градация |
|
|
|
|
|
|
|
|
|
|
2-я градация |
|
|
|
|
|
|
|
|
|
|
|
3-я градация |
|
|
|
|
|
|
|
|
|
|
|
2-я |
1-я градация |
|
|
|
|
|
|
|
|
|
|
2-я градация |
|
|
|
|
|
|
|
|
|
|
|
3-я градация |
|
|
|
|
|
|
|
|
|
|
|
3-я |
1-я градация |
|
|
|
|
|
|
|
|
|
|
2-я градация |
|
|
|
|
|
|
|
|
|
|
|
3-я градация |
|
|
|
|
|
|
|
|
|
|
Если взять несколько информационных портретов факторов,
соответствующих градациям одной описательной шкалы, отфильтровать их по
диапазону градаций некоторой классификационной шкалы и взять из каждого
информационного портрета по одному
состоянию, на переход в которое объекта управления данное значение фактора
оказывает наибольшее влияние, то мы и получим когнитивную функциональную
зависимость, отражающую вероятность перехода объекта управления в будущие состояния
под влиянием различных значений некоторого фактора, т.е. полностью
редуцированную когнитивную функцию.
Когнитивные функции являются наиболее развитым средством
изучения причинно-следственных зависимостей в моделируемой предметной области,
предоставляемым системой "Эйдос". Необходимо отметить, что на вид
функций влияния математической моделью СК-анализа не накладывается никаких ограничений,
в частности, они могут быть и нелинейные
[273].
Введем определение когнитивной функции: когда функция используется для отображения
причинно-следственной зависимости, т.е. информации (согласно концепции
Шенка-Абельсона [235]), или знаний, если эта информация полезна для
достижении целей, то будем называть такую функцию когнитивной функцией [166, 218, 226, 235, 239, 108, 243, 244, 254, 280], от англ. «cognition»[1].
Смысл когнитивной
функциональной зависимости в том, что в значении аргумента содержится
определенное количество информации о том, какое значение примет функция,
т.е. когнитивная функция отражает знания о степени соответствия значений
функции значениям аргумента.
Очень важно, что этот подход позволяет автоматически решить
проблему сопоставимой обработки многих факторов, измеряемых в различных
единицах измерения, т.к. в этом подходе
рассматриваются не сами факторы, какой бы природы они не были и какими бы
шкалами не формализовались, а количество
информации, которое в них содержится о поведении моделируемого объекта
[280].
Необходимо также
отметить, что представление о полностью линейных объектах (системах) является абстракцией и реально все объекты
являются принципиально нелинейными. Вместе с тем для большинства систем
нелинейные эффекты можно считать эффектами второго и более высоких порядков и
такие системы в первом приближении
можно считать линейными. Возможны различные модели взаимодействия факторов, в частности, развиваемые в форме
системного обобщения теории множеств [189, 191]. Этот подход в
перспективе может стать одним из вариантов развития теории нелинейных систем.
Отметим, что
математическая модель АСК-анализа (системная теория информации) органично учитывает принципиальную
нелинейность всех объектов. Это проявляется в нелокальности нейронной сети
системы «Эйдос» [138], приводящей к зависимости всех информативностей от любого
изменения в исходных данных, а не как в методе обратного распространения ошибки[2]. В результате значения матрицы информативностей количественно
отражают факторы не как множество, а как систему.
Объект может перейти в
некоторое будущее состояние под действием различного количества факторов, но
какая бы система факторов не обусловливала (детерминировала) этот переход, в
ней не может содержаться информации больше, чем можно получить, точно узнав,
что объект переходит в данное состояние. Это количество информации в
АСК-анализе называется «Теоретически максимальное количество информации» и
определяется только количеством классов (будущих состояний объекта), которые в
детерминистском случае равновероятны, т.к. между классами и факторами
выполняется взаимнооднозначное соответствие, когда каждое будущее состояние
однозначно определяется единственным фактором. Формула А.Харкевича видоизменена
в работе [97] таким образом, чтобы
удовлетворять принципу соответствия с формулой Р.Хартли в детерминистском
случае. Поэтому, чем меньше факторов, тем жестче ими детерминировано поведение
объекта, и наоборот, чем больше этих факторов, тем меньше влияние каждого из
них на поведение объекта. Например, если переход объекта в некоторое состояние
однозначно определяется единственным фактором, то добавление в модель еще
одного точно такого же фактора
приводит к тому, что в сумме эти два фактора будут оказывать тоже самое
влияние, которое делится между ними поровну.
Так в математической
модели АСК-анализа учитывается взаимодействие
факторов и отличие системы факторов
от множества факторов [273], являющееся источником нелинейности моделируемого объекта.
Итак, в матрице информативнстей количественно отражены
сила и направление влияния каждого значения фактора на переход объекта в каждое
из состояний, а также учтено, что совокупность факторов является системой, а не
множеством, т.е. учтены взаимодействие факторов и нелинейность моделируемого
объекта. Результаты решения задач идентификации, прогнозирования, принятия
решений и научного исследования моделируемой предметной области (в частности
кластерно-конструктивного анализа), на основе матрицы информативностей инвариантны относительно формы
частотного распределения объектов исследуемой выборки по классам, единиц измерения
значений факторов и типа шкал, используемых для формализации факторов.
Это позволяет корректно
использовать в АСК-анализе аддитивный интегральный критерий в форме суммы частных критериев не только для линейных,
но и для нелинейных объектов.
Различие между матрицей информативностей и матрицей знаний. Если в модели отражены лишь причинно-следственные связи
между факторами и будущими состояниями объекта, но не отражена степень
желательности ли нежелательности этих будущих состояний, то мы имеем дело с
матрицей информативностей. Если же некоторые из будущих событий
классифицируются как желательные, т.е. целевые, а другие как нежелательные, то
появляется возможность количественной оценки степени полезности информации о действии факторов для перевода объекта в
эти состояния, т.е. для преобразования информации в знания.
Процесс преобразования
информации в знания – это процесс оценки степени полезности информации для
достижения желаемых будущих состояний, т.е. целей.
Таким образом, матрица
знаний количественно отражает степень полезности (а также бесполезности и
вредности) факторов для достижения целей: она содержит знания в количественной
форме о величине и направлении
влияния каждого значения фактора на перевод объекта в каждое из будущих
состояний, как желаемое, так и нежелательное.
Факт – это единство экстенсионального и интенсинального описания
события, обнаруженного эмпирическим
путем, т.е. по сути, факт это определение
события. Пример факта: «Кошка кормит котят молоком». Пример определения в
науке: «Млекопитающее – это животное (более общее, интенсиональное понятие),
вскармливающее своих детей молоком (экстенсиональный специфический признак)».
Закономерности – это причинно-следственные зависимости, выявленные на
исследуемой выборке и распространяемые лишь на саму эту выборку.
Эмпирический закон – это причинно-следственные зависимости, выявленные на
исследуемой выборке и распространяемые на некоторую предметную область, более
широкую, чем исследуемая выборка, в которой действуют те же причины действия причинно-следственных зависимостей, что и в
исследуемой выборке, на которой он обнаружены. Эта более широкая предметная
область называется генеральной совокупностью, по отношению к которой
исследуемая выборка репрезентативна. Эмпирический закон является
феноменологическим, т.е. внешним описанием зависимости последствий от причин,
который не раскрывает механизма или способа, которым реализуется эта зависимость.
Научный закон – это содержательная интерпретация механизма действия
эмпирического закона, т.е. способа
преобразования причин в следствия. Научный закон является содержательным объяснением и интерпретацией
эмпирического закона. Это объяснение, когда оно разрабатывается, не сразу
становится научным законом, а сначала имеет статус научной гипотезы и приобретает
статус научного закона лишь после того, как на
практике, т.е. эмпирически, подтверждаются предсказания существования
новых, ранее неизвестных явлений, сделанные на основе научной гипотезы. Таким
образом, научный закон – это научная гипотеза, адекватность и прогностическая
сила которой подтверждены (верифицированы) эмпирически. Процесс преобразования
научной гипотезы в научный закон – это процесс подтверждения на практике
адекватности этой научной гипотезы.
Необходимо подчеркнуть,
что существует принципиальная возможность создания многих различных моделей, одинаково адекватно отражающих одну и ту
же предметную область. Иногда такие модели и действительно созданы. Тогда
возникает вопрос о критериях выбора
одной модели, в определенном смысле «наилучшей» из многих. Среди этих критериев
следует отметить адекватность, удовлетворение принципу соответствия и широту
адекватно отражаемой предметной области, а также ее простоту и красоту. Из
многих моделей предпочтительная та, которая более адекватна, та, которая
адекватно отражает более широкую предметную область и включает в себя на основе
принципа соответствия другие известные модели, а также более простая и красивая
модель. Однако часто бывает, что разработка многих моделей (научных теорий)
весьма затруднительна и есть или известна всего лишь одна-единственная модель.
Тогда эта модель автоматически становится наилучшей из всех известных.
Возникает соблазн
неоправданно и необоснованно считать, что реальность устроена именно таким
образом, какой она отражается в этой наилучшей по сформулированным выше
критериям модели или научной теории, т.е. необоснованно
придать онтологический статус абстрактной модели. В этом состоит широко
распространенная малозаметная ошибка познания, называемая «Гипостазирование[3]». Однако эта ошибка влечет за собой целый шлейф весьма
заметных последствий, важнейшим из которых является отрицание существования
фактов, закономерностей и эмпирических законов, не вписывающихся в те или иные
научные теории, даже если эти факты в буквальном смысле слова очевидны. Например, апологеты
воздухоплавания отрицали возможность летательных аппаратов тяжелее воздуха, не
смотря на птиц, которые садились и взлетали перед ними (или даже смотря на них,
но не осознавая, что они видят). При этом они исходили из того, что принцип
действия летальных аппаратов может быть основан только на законе Архимеда, как
это следовало из единственной известной им научной теории полета. Однако
существуют и другие принципы полета: в частности, баллистический, аэродинамический,
ракетный, электромагнитный, на которых может быть основан принцип действия
летательных аппаратов тяжелее воздуха, причем эти аппараты ни в коей мере не
нарушают закон Архимеда и полностью ему подчиняются.
Признание существования
факта не зависит от обнаружения закономерности. Признание существования
закономерности не зависит от обнаружения соответствующего эмпирического закона.
Признание существования эмпирических законов не зависит от наличия
верифицированной содержательной интерпретации или научного закона, а если она
есть, то от того, является ли она «правильной» или «неправильной» по тем или
иным критериям или по чьему-то мнению. Таким образом, признание существования факта не зависит от наличия теории, которая его
объясняет, и отсутствие такой теории не является основанием для отрицания
существования или непризнания существования факта.
Когнитивные функции
представляют собой новый перспективный инструмент отражения и наглядной
визуализации закономерностей и эмпирических законов. Разработка содержательной научной интерпретации когнитивных
функций представляет собой способ познания природы, общества и человека.
Когнитивные функции
могут быть:
– прямые,
отражающие зависимость классов от признаков, обобщающие информационные портреты
признаков;
– обратные,
отражающие зависимость признаков от классов, обобщающие информационные портреты
классов;
– позитивные,
показывающие чему способствуют система детерминации;
– негативные,
отражающие чему препятствуют система детерминации;
– средневзвешенные,
отражающие совокупное влияние всех значений факторов на поведение объекта;
– с различной степенью
редукции или степенью детерминации, которая отражает в графической форме (в
форме полосы) количество знаний в аргументе о значении функции и является
аналогом и обобщением доверительного интервала.
Примеры когнитивных
функций будут приведены ниже.
Прямая и
обратная, а также позитивная и негативная
когнитивные функции полностью
совпадают (тождественны) друг с другом
только для жестко (т.е. полностью) детерминированных систем. Это связано с
тем, что матрица знаний, моделирующая полностью детерминированную систему, в
которой между значениями аргумента и значениями функции существует взаимнооднозначное
соответствие, представляет собой диагональную матрицу [273]. Можно обоснованно предположить, что степень совпадения прямой и обратной
когнитивных функций пропорциональна степени детерминированности моделируемой
системы. Если интерпретировать
значения факторов, обусловливающих поведение системы, как ее экстениональное
описание, относящееся к ее прошлому времени, а классы – как интенсиональное
описание ее будущих состояний, то можно сказать, что степень детерминации
поведения системы тем выше, чем более сходным являются влияние на нее прямой и
обратной причинности, т.е. если влияние прошлого на будущее совпадет с влиянием
будущего на прошлое. Чем сильнее влияние прошлого на будущее отличается от
влияния будущего на прошлое, тем слабее детерминированность в поведении
системы, тем ближе оно к случайному. При этом рассмотрение вопросов о
физическом механизме прямой и обратной причинности, как и самом существовании
обратной причинности, не входит в задачи данной работы.
Матрица
информативности может быть использована для выявления и визуализации когнитивных функциональных зависимостей
в фрагментированных и зашумленных данных большой размерности. Кратко поясним
суть этого метода. Матрица информативностей рассчитывается на основе системной
теории информации [97]
непосредственно на основе эмпирических данных и представляет собой таблицу, в
которой столбцы соответствуют обобщенным
образам классов, т.е. будущим состояниям моделируемой системы, строки –
значениям факторов, влияющих на эту систему, а на пересечениях строк и столбцов
находится количество информации, которое содержится в факте действия значения
фактора, соответствующего строке, на переход системы в состояние,
соответствующее столбцу. Максимальное количество информации, которое может быть
в значении фактора, определяется числом будущих состояний моделируемой системы.
Модуль количества информации отражает силу влияния значения фактора, а знак –
направление этого влияния, т.е. то, способствует он или препятствует
наступлению данного состояния. Если последовательности классов и значений
факторов образуют порядковые шкалы или шкалы отношений, т.е. соответственно, на
них определены отношения «больше-меньше» или, кроме того, единица измерения,
начало отсчета и арифметические операции, то матрица информативностей допускает
наглядную графическую визуализацию, традиционного
для функций типа, когда значения факторов рассматриваются в качестве значений
аргумента, а классы, о наступлении которых в этих значениях факторов содержится
максимальное количество информации –
в качестве значений функции. Другие классы, менее обусловленные данным
значением фактора, а также те, наступлению которых это значение препятствует в
большей или меньшей степени, также могут отображаться соответствующими цветами,
и это также может представлять интерес, т.к. позволяет задействовать мощные способности
человека к анализу изображений. Когнитивные функции, представляемые в форме
матрицы информативностей, соответствуют очень общему виду функциональной
зависимости: многозначной функции многих
аргументов, т.к. каждое значение фактора влияет на все состояния
моделируемого объекта, и каждое его состояние обусловлено всеми значениями
факторов. Простой пример визуализации матрицы информативностей, полученной на
выборке, отражающей зависимость амплитуды затухающего гармонического колебания
от времени, приведен на нижеследующем рисунке 1, в
котором степень детерминации значения функции значением аргумента показана
различными цветами: теплые цвета – высокая степень детерминации, холодные – низкая.
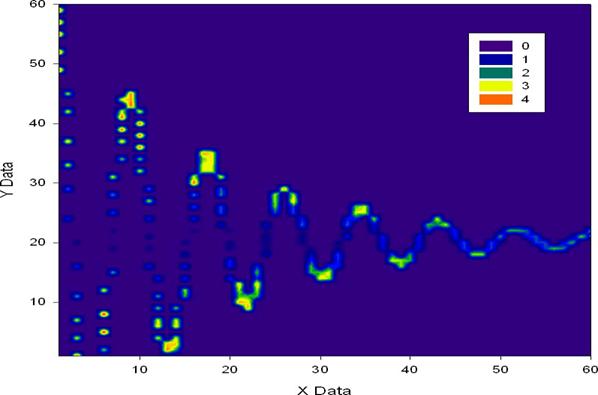
Рисунок 1.
Количество информации в значении аргумента
о значении функции для нечеткой взаимнооднозначной когнитивной
функции
11.3.2. Системное обобщение понятия функции и
функциональной зависимости. Когнитивные функции. Матрицы знаний как нечеткое с
расчетной степенью истинности отображение системы аргументов на систему значений
функции
Выше кратко
рассматривается программная идея системного обобщения понятий математики (в
частности теории информации), основанных на теории множеств, путем тотальной
замены понятия множества на более содержательное понятие системы и
прослеживания всех последствий этого. Частично эта идея была реализована
автором при разработке автоматизированного системно-когнитивного анализа
(АСК-анализа) [97], математическая модель которого основана на системном
обобщении формул для количества информации Хартли и Харкевича [97].
В работе [166] реализуется следующий шаг: предлагается системное
обобщение понятия функциональной зависимости, и вводятся термины
"когнитивные функции" и "когнитивные числа". На численных
примерах показано, что АСК-анализ обеспечивает выявление когнитивных
функциональных зависимостей в многомерных зашумленных фрагментированных данных.
В работе [140] намечены принципы применения многозначных функций многих
аргументов для описания сложных систем и предложено матричное представление
этих функций.
В работе [218] обсуждается возможность восстановления значений одномерных
и двумерных функций как между значениями аргумента (интерполяция), так и за их
пределами (экстраполяция) на основе использования априорной информации о взаимосвязи
между признаками аргумента и
значениями функции в опорных точках с применением системно-когнитивного анализа
и его инструментария – системы «Эйдос». Приводятся численные примеры и
визуализация результатов. Предлагается применение аппарата многомерных
когнитивных функций для решения задач распознавания и прогнозирования на
картографических базах данных.
В работе [226] на примере решения проблемы управления агропромышленным
холдингом рассматривается технология когнитивных функций СК-анализа, обеспечивающая
как выявление знаний из эмпирических данных, так и использование этих знаний
для поддержки принятия решений по управлению холдингом в целом на основе
управления характеристиками входящих в него предприятий.
В работе [235] рассматривается применение метода автоматизированного
системно-когнитивного анализа и его программного инструментария – системы
«Эйдос» для выявления причинно-следственных зависимостей из эмпирических
данных. В качестве инструментария для формального представления
причинно-следственных зависимостей предлагаются когнитивные функции.
Когнитивные
функции представляют
собой многозначные интервальные функции многих аргументов, в которых различные
значения функции в различной степени соответствуют различным значениям
аргументов, причем количественной мерой этого соответствия выступает знание,
т.е. информация о причинно-следственных зависимостях в эмпирических данных,
полезная для достижения целей.
В работе [239] на основе применения
аппарата когнитивных функций впервые исследована зависимость параметров движения
полюса Земли от положения небесных тел Солнечной системы. В последующем эти
результаты развиты в монографии [108].
Наиболее полно метод
визуализации когнитивных функций, как новый инструмент исследования
эмпирических данных большой размерности, раскрыт в работе [243].
В работе [244]
рассматривается новая версия системы искусственного интеллекта «Эйдос-астра» для решения прикладных задач с
эмпирическими данными большой размерности. Приложение, написанное на языке
JAVA, обеспечивает GUI (графический интерфейс пользователя) и позволяет
подготовить и выполнить визуализацию матрицы знаний без ограничений, налагаемых
реализацией предыдущих версий системы «Эйдос-астра». Отметим, что в системе
Эйдос-Х++ все эти ограничения на размерность моделей также сняты в
универсальной форме, не зависящей от предметной области.
В работе [254] рассмотрена глубокая взаимосвязь между теорией
автоматизированного и автоматического управления и системно-когнитивным
анализом и его программным инструментарием – системой «Эйдос» в их применении
для интеллектуального управления сложными системами. Предлагается технология,
позволяющая на практике реализовать интеллектуальное автоматизированное и даже
автоматическое управление такими объектами управления, для которых ранее
управление реализовалось лишь на слабоформализованном уровне, как правило, без
применения математических моделей и компьютеров. К таким объектам управления
относятся, например, технические системы, штатно качественно-изменяющиеся в
процессе управления, биологические и экологические системы,
социально-экономические и психологические системы. Намечены возможности
получения когнитивных передаточных функций сложных многопараметрических
нелинейных объектов управления на основе зашумленной фрагментированной
эмпирической информации об их фактическом поведении под действием различных
сочетаний значений факторов различной природы.
Приведем простейший
пример (рисунок 2) когнитивной функции затухающего синусоидального колебания,
восстановленной по табличным данным, включающим 360 значений функции, при
разном числе интервальных значений
аргумента и функции: 30 (верхний график) и 60 (нижний график):
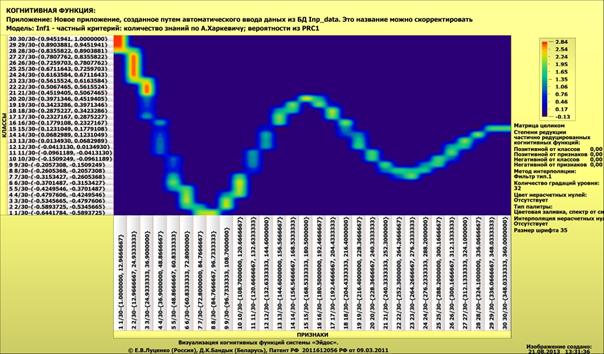
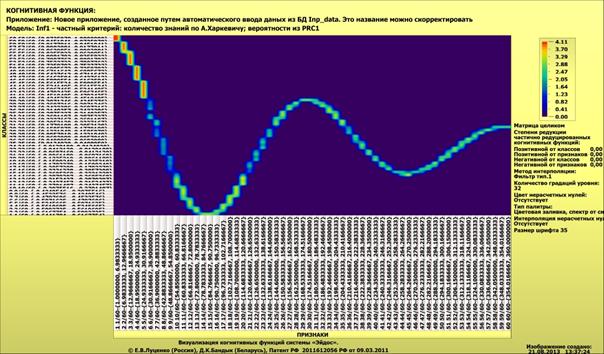
Рисунок 2.
Когнитивная функция затухающего синусоидального
колебания, восстановленная по табличным данным, включающим 360
значений функции, при 30 (вверху) и 60
(внизу) интервальных
значениях аргумента и функции
Ясно,
что если величина интервала будет стремиться к нулю, то интервальные функции, к
которым относятся и когнитивные функции, будут асимптотически приближаться к
абстрактным математическим функциям, которые можно считать интервальными
функциями с нулевой величиной интервала. Соответственно при уменьшении величины
интервала будет увеличиваться и суммарное количество информации,
содержащееся в модели, т.е. в значениях аргумента о значениях когнитивной
функции (эту зависимость планируется исследовать в новых работах). Поэтому
интервальная математика может рассматриваться как более общая, чем точная
математика с бесконечно малыми и для нее выполняется известный принцип соответствия, обязательный для
более общих теорий.
В
когнитивных функциях, представленных на рисунке 2, цветом отображено количество
информации в интервальном значении аргумента об интервальном значении
функции. Или выражаясь точнее, цветом отображено количество информации в интервальном
значении аргумента о том, что (при этом значении аргумента) функция примет
определенное интервальное значение. Или еще точнее, цветом отображено количество
информации о том, что при значении аргумента, попадающем в данный
интервал, функция примет определенное значение, попадающее в соответствующий интервал.
Из
рисунка 2 мы видим, что об одних значениях функции в значениях аргумента
содержится больше информации, а о других меньше. Это значит, что различные значения
аргумента с разной степенью определенности обуславливают соответствующие
значения функции. Иначе говоря, зная одни значения аргумента, мы весьма
определенно можем сказать о соответствующем значении функции, а по другим
значениям мы можем судить о значении
функции лишь приблизительно, т.е. с гораздо большей погрешностью или
неопределенностью.
Таким
образом, когнитивная функция содержит
информацию не только о соответствии значений функции значениям аргумента, как
абстрактная математическая функция, но и о достоверности высказывания о том,
что именно такое их соответствие имеет место в действительности, причем эта
достоверность меняется от одних значений аргумента и функции к другим.
Получается,
что в каждом значении аргумента содержится определенная информация о каждом
значении функции. Эта информация может быть больше или меньше, она может быть положительная
или отрицательная, т.е. в когнитивной
функции каждому значению аргумента
соответствуют все значения функции, но в различной степени. Из этого следует
также, что каждое значение функции
обуславливается различными значениями аргумента, но каждое из них обусловливает
это значение в различной степени. Поэтому когнитивные функции являются многозначными
функциями многих аргументов.
Это
понятие напоминает доверительный интервал, но с той разницей, что доверительный
интервал всегда растет со значением аргумента, а количество информации может и
возрастать, и уменьшаться. Если
осуществляется интерполяция или прогноз значения когнитивной функции, то при
этом одновременно определяется и достоверность этой интерполяции или этого
прогноза. На когнитивной функции, представленной на рисунке 3, эта достоверность представлена в форме
полупрозрачной полосы, ширина которой обратно пропорциональна достоверности
(как в доверительном интервале), т.е. чем точнее известно значение функции, тем
уже полоса, и чем оно более неопределенно, тем она шире.
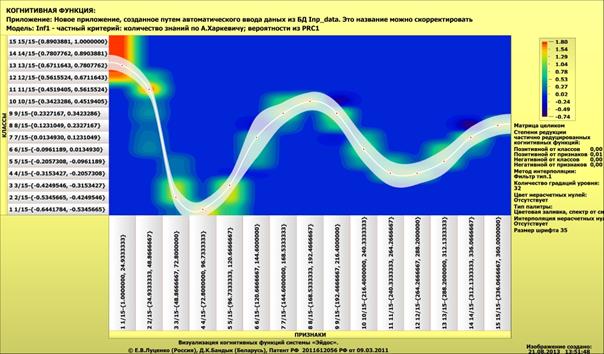
Рисунок 3.
Когнитивная функция затухающего синусоидального
колебания, восстановленная по табличным данным, включающим 360
значений функции, при 15 интервальных значениях аргумента
и функции с указанием степени достоверности не только цветом,
но и в форме частично-редуцированной когнитивной функции,
аналогичной по смыслу доверительному интервалу
В теоретической математике нет меры причинно-следственной
связи. Математика оперирует
абстрактными понятиями, а понятие
причинно-следственной связи является содержательным
понятием, относящимся к конкретной изучаемой, в том числе и эмпирически, реальной предметной области. Математические понятия
функциональной зависимости или корреляция не являются такой мерой. Правда, в статистике есть критерий хи-квадрат,
который действительно является мерой причинно-следственной связи, но статистика
специально разработана с целью изучения конкретных явлений и этим существенно
отличается от абстрактной теоретической математики.
Мы рассматриваем
числовые и лингвистические данные, как сырые данные, полученные непосредственно
из опыта и еще не подвергнутые какой-либо обработке. Эти эмпирические данные могут
быть преобразованы в информацию путем их анализа. Информация есть осмысленные
данные. Смысл согласно концепции смысла Шешка-Абельсона, которой мы
придерживаемся, представляет собой знание причинно-следственных зависимостей.
Причинно-следственные зависимости возможны только между событиями, а не между
данными. Поэтому анализ данных, в результате
которого они преобразуются в информацию, включает два этапа:
– нахождение событий в
данных;
– выявление
причинно-следственных связей между событиями.
Знания представляют
собой информацию, полезную для достижения цели. Если такой целью является
решение задач прогнозирования, принятия решений и исследования моделируемой
предметной области путем исследования ее модели (это корректно, если модель
адекватна), то информационная модель является и когнитивной моделью, т.е.
интеллектуальной моделью или моделью знаний.
Поэтому когнитивные функции являются наглядным графическим
отображение наших знаний о причинно-следственных связях между
интервальными или лингвистическими значениями аргумента и интервальными или
лингвистическими значениями функции.
Когнитивные функции
представляют собой графическое отображение сечений многомерного
эйдос-пространства (базы знаний) системы «Эйдос-Х++» плоскостями, содержащими
заданные описательные и классификационные шкалы с фактически имеющимися у них
интервальными значениями (градациями).
11.3.3. Примеры известных функций,
которые могут рассматриваться как аналоги когнитивных функций
11.3.3.1. Оцифрованные сигналы:
аудио, графика, видео
В оцифрованных аудио,
видео и других сигналах мы всегда знаем глубину кодирования, а значит и
количество информации в значении аргументе о значении функции. В любых таблицах
и базах данных числа всегда представлены с ограниченным числом знаков после
запятой, а значит само множество таких чисел ограничено, и всегда можно
посчитать, какие количество информации содержится в факте выборки как-то одного
конкретного из этих чисел.
11.3.3.2. Таблично заданные
функции, например таблицы Брадиса
Например, в известной
таблице Брадиса[4] приводится 4 знака значения синуса после запятой. Это
значит, что заданному углу соответствует одно из 9999 значений. По формуле
Хартли получаем: I=Log2N=Log29999~13.29
бит.
11.3.3.3. Доверительные интервалы
как аналог количества информации в аргументе о значении функции и
прогнозирование достоверности прогнозирования
В статистике принято не просто что-либо утверждать, а обязательно сопровождать
каждое утверждение оценкой степени его достоверности. Например, для этой цели
при решении задачи прогнозирования путем экстраполяции, т.е. оценки значения
функции за пределами эмпирических значений аргумента, используется так
называемый «доверительный интервал». Доверительный интервал представляет собой
определенный диапазон значений функции, зависящий от значения аргумента, в
который истинное значение функции попадает с определенной вероятностью (обычно
0,95). Наиболее известным свойством доверительного интервала при решении задачи
прогнозирования является его монотонное увеличение по мере удаления от
эмпирически известных значений аргумента и функции. Используя определение
информации как количественной меры степени снятия неопределенности (энтропийная
мера Больцмана) можно сказать, что чем больше величина доверительного
интервала, тем меньше информации в значениях аргумента о значениях функции,
т.е. тем выше неопределенность значений функции.
В теории и практике когнитивных функций оценкой достоверности прогноза о
значении функции является количество информации в аргументе о том, что функция
примет данное значение. Это количество информации может быть наглядно изображено
цветом и толщиной частично-редуцированной когнитивной функции. Существенно, что
это количество информации не обязательно уменьшается при удалении от области
эмпирически известных значений, но может и уменьшаться и возрастать, в отличие
от доверительного интервала [97]. Это означает, что
АСК-анализ позволяет не только прогнозировать развитие процесса, но и позволяет
прогнозировать достоверность этого прогнозирования. Это возможно также по
разбросу точечных прогнозов [97].
11.3.3.4. Что представляют собой
классические функции с точки зрения теории и практики когнитивных функций?
Рассмотрим с позиций
теории информации, чем отличаются когнитивные функции от абстрактных математических функций. Формально по точному значению
аргумента любой абстрактной
математической функции возможно точно узнать ее точное значение. Но на практике
это возможно лишь тогда, когда и значения аргумента, и значения функции
являются целыми числами. Если же они являются иррациональными числами, то
совершенно ясно, что точное их значение никогда не может быть ни вычислено на
любом компьютере с ограниченной вычислительной мощностью, ни записано, ни на
каких носителях с ограниченной информационной емкостью, ни передано ни по каким
каналам связи с ограниченной пропускной способностью. Поэтому точное знание
значения иррациональной функции означает доступ к бесконечному количеству
информации. На практике же мы, конечно, всегда имеем дело с ограниченной
точностью или знаем значения функции с некоторой погрешностью, т.е. оперируем
конечным количеством информации в значениях аргумента о значениях функции. Но
каким именно количеством информации? До разработки математического аппарата и
программного инструментария когнитивных функций это вопрос как-то ребром не
ставился и был в тени приоритетных направлений исследований. Ответом на это
вопрос и является теория когнитивных функций, где каждому значению аргумента
соответствует не только значение функции, но и количество информации в битах,
содержащееся в этом значении аргумента о том, что ему соответствует данное
значение функции.
Конкретные численные
примеры когнитивных функций приведены в разделе 4.2.
Разработаны
нередуцированные, частично и полностью редуцированные прямые и обратные
когнитивные функции, а также программный инструментарий для их расчета (сама
система Эйдос-Х++) и модуль визуализации когнитивных функций [133]. Однако в
данной работе не целесообразно их рассматривать, т.к. этому посвящены многочисленные
работы, ссылки на которые даны выше.
Таким
образом, с точки зрения теории и практики когнитивных функций классические функции это предел, к которому стремятся полностью
редуцированные когнитивные функции при неограниченном увеличении количества
наблюдений, т.е. когнитивные функции, в значениях аргумента которых содержится бесконечное количество
информации о значении функции (т.к. значение функции предполагается известным абсолютно точно). Ясно, что
вообще говоря, на практике это невозможно в реальности классическим математическим
функциям ничего не соответствует, т.е. они являются чистой абстракцией
наподобие математической точки, бесконечно малой величины и т.п.
11.4. Практическое решение проблемы в
программном
инструментарии АСК-анализа – интеллектуальной
системе «Эйдос»
11.4.1. Интеллектуальная система Эйдос-Х++ как инструментарий
АСК-анализа, реализующий идеи системного нечеткого интервального
обобщения математики
Система «Эйдос»
за многие годы применения хорошо показала себя при проведении научных исследований
в различных предметных областях и занятий по ряду научных дисциплин, связанных
с искусственным интеллектом, представлениями знаний и управлению знаниями [234].
Однако в процессе эксплуатации системы были выявлены и некоторые недостатки,
ограничивающие возможности и перспективы применения системы. Поэтому создана
качественно новая версия системы (система Эйдос-Х++), в которой преодолены
ограничения и недостатки предыдущей версии и реализованы новые важные идеи по
ее развитию и применению в качестве программного
инструментария системно-когнитивного анализа (СК-анализ) [260].
Авторы считают, что система Эйдос-Х++ является
программным инструментарием,
реализующим ряд идей системного нечеткого интервального обобщения математики.
11.4.2.
Развернутый численный пример построения когнитивных функций на основе
зашумленных данных в системе «Эйдос»
В системе «Эйдос» для
учебных целей реализована возможность исследования зашумленных когнитивных
функций. В качестве функции, на примере которой это осуществляется в настоящее
время выбран затухающий свип-сигнал, т.е. гармонический сигнал с уменьшающейся
амплитудой и изменяющийся частотой.
Рассмотрим
последовательность действий при исследовании зашумленных когнитивных функций в
системе «Эйдос» и их результаты этого исследования. Для генерации исходной
выборки запустим диспетчер приложений, т.е. режим 1.3 (рисунок 4):
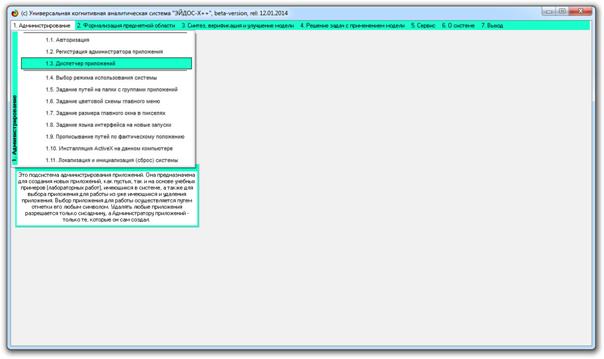
Рисунок 4. Запуск диспетчера приложений системы «Эйдос»
(режим 1.3)
Появляется окно данного
режима (рисунок 5):
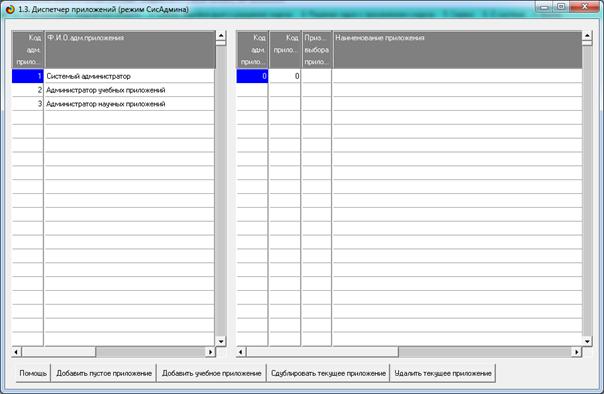
Рисунок 5. Окно диспетчера приложений системы «Эйдос» (режим 1.3)
По клику на кнопке «Добавить
учебное приложение» появляется окно (рисунок 6):
Рисунок 6. Первое окно режима выбора учебных
приложений
для инсталляции
Выбираем опцию:
«Устанавливаемые автоматизировано в диалоге с пользователем» и получаем
(рисунок 7):
Рисунок 7. Второе окно режима выбора учебных
приложений
для инсталляции
Выбираем учебное приложение
№13 и нажимаем «ОК». Получаем окно, представленное на рисунке 8:
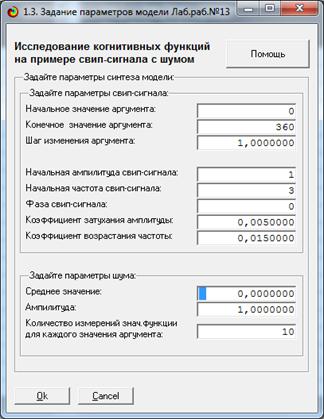
Рисунок 8. Окно задания параметров генерации
зашумленного
свип-сигнала для исследования зашумленных когнитивных функций
Стадия процесса генерации
обучающей выборки и прогноз времени исполнения отображается на окне,
представленном на рисунке 9:
Рисунок 9. Окно отображения стадия процесса генерации
обучающей выборки и прогноза времени исполнения
В результате выполнения
данного режима генерируется обучающая выборка, состоящая из двух файлов:
Inp_data.dbf с значениями функции для различных значений аргумента, причем для
каждого значения аргумента просчитано 10 значений функций, и Inp_name.txt с наименованиями колонок файла Inp_data.dbf.
Файл Inp_data.dbf представлен в таблице 7:
Таблица 7 – ИСХОДНЫЕ ДАННЫЕ ДЛЯ СИНТЕЗА МОДЕЛИ
ИССЛЕДОВАНИЯ ЗАШУМЛЕННОЙ КОГНИТИВНОЙ ФУНКЦИИ (ФРАГМЕНТ)
|
Наименование |
Значения функции |
Значение шума |
Значение |
|||
|
Равномерно |
Нормально |
Истинное |
Равномерное |
Нормальное |
||
|
0 |
0,6507407 |
0,8494331 |
0,9986295 |
-0,3478888 |
-0,1491964 |
0,0000000 |
|
0 |
0,6423481 |
0,8423761 |
0,9986295 |
-0,3562814 |
-0,1562534 |
0,0000000 |
|
0 |
1,4927462 |
1,2906329 |
0,9986295 |
0,4941167 |
0,2920034 |
0,0000000 |
|
0 |
0,7181546 |
0,9006307 |
0,9986295 |
-0,2804749 |
-0,0979988 |
0,0000000 |
|
0 |
1,1079167 |
1,0137574 |
0,9986295 |
0,1092872 |
0,0151279 |
0,0000000 |
|
0 |
0,9321988 |
0,9930294 |
0,9986295 |
-0,0664308 |
-0,0056001 |
0,0000000 |
|
0 |
1,3841246 |
1,1805820 |
0,9986295 |
0,3854951 |
0,1819525 |
0,0000000 |
|
0 |
1,7984084 |
1,6942263 |
0,9986295 |
0,7997788 |
0,6955968 |
0,0000000 |
|
0 |
0,3177716 |
0,4729162 |
0,9986295 |
-0,6808579 |
-0,5257134 |
0,0000000 |
|
0 |
1,1989542 |
1,0491026 |
0,9986295 |
0,2003246 |
0,0504731 |
0,0000000 |
|
1 |
0,8676704 |
0,9706996 |
0,9894791 |
-0,1218087 |
-0,0187795 |
1,0000000 |
|
1 |
1,8432152 |
1,7656193 |
0,9894791 |
0,8537361 |
0,7761402 |
1,0000000 |
|
1 |
1,7012114 |
1,5580637 |
0,9894791 |
0,7117323 |
0,5685846 |
1,0000000 |
|
1 |
1,8043663 |
1,7074563 |
0,9894791 |
0,8148872 |
0,7179772 |
1,0000000 |
|
1 |
0,9903626 |
0,9894801 |
0,9894791 |
0,0008835 |
0,0000010 |
1,0000000 |
|
1 |
0,6544930 |
0,8508427 |
0,9894791 |
-0,3349860 |
-0,1386363 |
1,0000000 |
|
1 |
1,1558018 |
1,0243804 |
0,9894791 |
0,1663227 |
0,0349013 |
1,0000000 |
|
1 |
1,5639833 |
1,3760441 |
0,9894791 |
0,5745042 |
0,3865650 |
1,0000000 |
|
1 |
0,4903830 |
0,6919209 |
0,9894791 |
-0,4990961 |
-0,2975581 |
1,0000000 |
|
1 |
0,2341416 |
0,3587870 |
0,9894791 |
-0,7553375 |
-0,6306920 |
1,0000000 |
|
2 |
1,2346845 |
1,0601969 |
0,9776125 |
0,2570720 |
0,0825845 |
2,0000000 |
|
2 |
0,0278706 |
0,0550427 |
0,9776125 |
-0,9497419 |
-0,9225698 |
2,0000000 |
|
2 |
1,7419907 |
1,6213866 |
0,9776125 |
0,7643783 |
0,6437741 |
2,0000000 |
|
2 |
1,8483406 |
1,7794321 |
0,9776125 |
0,8707281 |
0,8018196 |
2,0000000 |
|
2 |
0,5440427 |
0,7496685 |
0,9776125 |
-0,4335697 |
-0,2279440 |
2,0000000 |
|
2 |
-0,0229405 |
-0,0232402 |
0,9776125 |
-1,0005530 |
-1,0008527 |
2,0000000 |
|
2 |
0,4398505 |
0,6355278 |
0,9776125 |
-0,5377619 |
-0,3420847 |
2,0000000 |
|
2 |
1,3910291 |
1,1857304 |
0,9776125 |
0,4134166 |
0,2081179 |
2,0000000 |
|
2 |
0,2706143 |
0,4156645 |
0,9776125 |
-0,7069982 |
-0,5619480 |
2,0000000 |
|
2 |
0,5239797 |
0,7291730 |
0,9776125 |
-0,4536328 |
-0,2484394 |
2,0000000 |
|
3 |
1,5783846 |
1,4013130 |
0,9630885 |
0,6152962 |
0,4382245 |
3,0000000 |
|
3 |
1,7041258 |
1,5732261 |
0,9630885 |
0,7410373 |
0,6101377 |
3,0000000 |
|
3 |
1,4467041 |
1,2435161 |
0,9630885 |
0,4836157 |
0,2804276 |
3,0000000 |
|
3 |
1,9246833 |
1,9038979 |
0,9630885 |
0,9615948 |
0,9408095 |
3,0000000 |
|
3 |
1,0482806 |
0,9722919 |
0,9630885 |
0,0851921 |
0,0092034 |
3,0000000 |
|
3 |
1,0711801 |
0,9778882 |
0,9630885 |
0,1080917 |
0,0147997 |
3,0000000 |
|
3 |
0,0678112 |
0,1239575 |
0,9630885 |
-0,8952772 |
-0,8391310 |
3,0000000 |
|
3 |
0,4612102 |
0,6624084 |
0,9630885 |
-0,5018783 |
-0,3006801 |
3,0000000 |
|
3 |
1,8572679 |
1,8005462 |
0,9630885 |
0,8941794 |
0,8374577 |
3,0000000 |
|
3 |
0,3946094 |
0,5839555 |
0,9630885 |
-0,5684791 |
-0,3791330 |
3,0000000 |
Эти данные аналогичны тем,
которые мы получаем при многократных измерениях некоторой эмпирической
величины. При этом все время получаются разные эмпирические значения,
являющиеся суммой истинного значения и шума. Если шум обусловлен независимыми
факторами, влияющими на результаты процессы измерения, то такой шум распределен
нормально и называется аддитивным гауссовским шумом. В системе «Эйдос»
генерируются последовательности значений функции и с гауссовским, и с
равномерным шумом (рисунки 10 и 11):
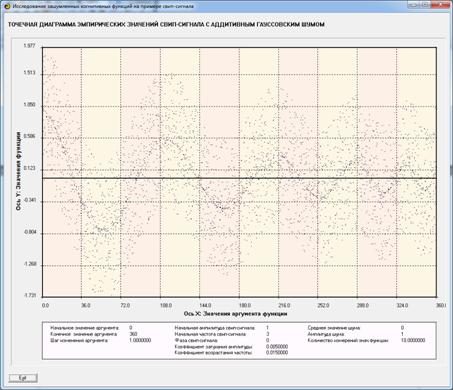
Рисунок 10. Экранная форма с графическим
представлением
исходных данных с гауссовским аддитивным шумом
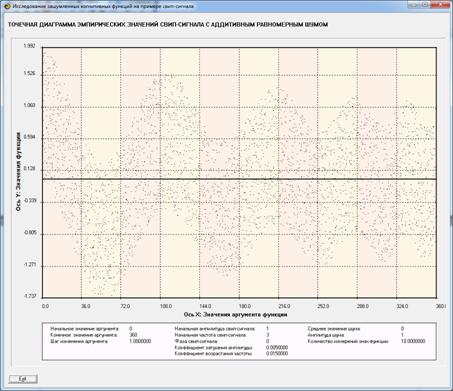
Рисунок 11. Экранная форма с графическим
представлением
исходных данных с равномерным аддитивным шумом
Если вид модели эмпирических данных, представленных в таблице 7 и на рисунках
10 и 11 чем-то не устраивает, то на этой стадии можно повторить процесс генерации
исходных данных, т.к. никакого приложения еще не создано.
Чтобы теперь создать приложение необходимо запустить универсальный
программный интерфейс импорта данных из внешних баз данных в систему «Эйдос»,
т.е. режим 2.3.2.2 при параметрах, созданных автоматически на предыдущем шаге
(рисунок 12):
Рисунок 12. Запуск универсального программного интерфейса
импорта данных из внешних баз данных в систему «Эйдос»
(режим 2.3.2.2)
На рисунке 13 приведено
первое окно режима 2.3.2.2:
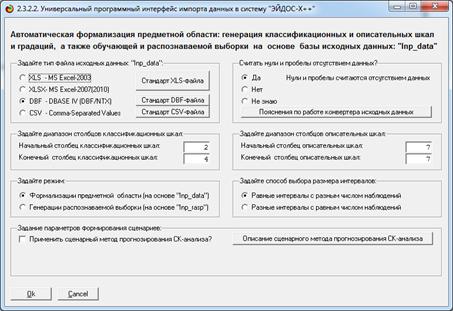
Рисунок 13. Первое окно универсального программного интерфейса
импорта данных из внешних баз данных в систему «Эйдос»
(режим 2.3.2.2)
Обратим внимание на то, что
в системе «Эйдос» реализованы режимы выбора либо равных интервальных значений в
которых будет получаться разное число наблюдений, либо адаптивных интервалов
разной величины, в которых будет получаться практически равное число
наблюдений. Второй вариант соответствует рекомендациям, основанным на теореме
Котельникова «Об отсчетах», т.к. размер интервала при этом подходе определяется
распределением плотности наблюдений по шкале аргумента. При этом подходе, чем
выше кривизна функции, тем чаще будут стоять отсчеты и тем меньше будут
значения числовых интервалов, что обеспечивает максимальную точность модели при
минимальном суммарном числе интервалов.
На экранной форме,
представленной на рисунке 13, просто кликаем «ОК», т.к. все необходимые
параметры импорта данных заданы по умолчанию на предыдущем этапе. Тогда
появляется второе окно данного режима, представляющее собой калькулятор для
выбора числа градаций числовых классификационных и описательных шкал (рисунок
14):
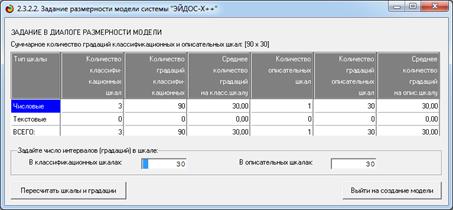
Рисунок 14. Второе окно универсального программного интерфейса
импорта данных из внешних баз данных в систему «Эйдос»
(режим 2.3.2.2)
Здесь мы можем задать любое
число градаций как в классификационных, так и в описательных числовых шкалах (в
данном случае задано 30). Обратим внимание на то, что число градаций по
классификационным и описательным шкалам задается раздельно и может не
совпадать. В случае перезадания числа градаций необходимо выполнить пересчет
шкал и градаций, кликнув на соответствующей кнопке в данной экранной форме.
Если все устраивает необходимо выйти на создание модели. Экранная форма
отображения стадии процесса и прогнозирования времени исполнения представлена
на рисунке 15:
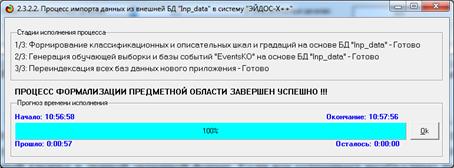
Рисунок 15. Третье окно универсального программного интерфейса
импорта данных из внешних баз данных в систему «Эйдос»
(режим 2.3.2.2): отображение стадии процесса
и прогнозирования времени исполнения
В результате работы программного интерфейса создается новое приложение
(рисунок 16), название которого может быть изменено вручную, что нами и
было сделано.
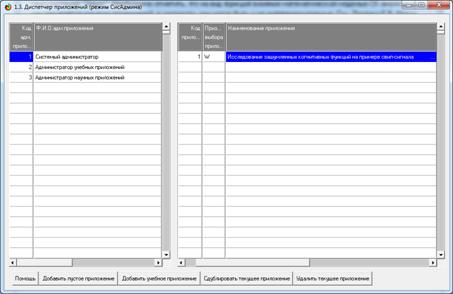
Рисунок 16. Окно диспетчера
приложений с информацией о том,
что новое приложение создано
Данное приложение автоматически определяется как текущее (рабочее).
Универсальным программным интерфейсом созданы классификационные и описательные
шкалы и градации в этом новом текущем приложении. Затем исходные данные закодированы
с помощью классификационных и описательных шкал и градаций и тем самым
преобразованы в обучающую выборку.
Таким образом, универсальный программный интерфейс автоматизирует
выполнение этапа формализации предметной области АСК-анализа (рисунок 17).
Дальнейшие процедуры преобразования, предусмотренные в АСК-анализе, осуществляются также в соответствии с
диаграммой, приведенной на рисунке 17.
Кратко рассмотрим соотношение
содержания понятий: «данные», «информация» и «знания» (рисунок 24). Данные
– это информация, рассматриваемая безотносительно к ее смысловому содержанию,
находящаяся на носителях или в каналах связи и представленная в определенной
системе кодирования или на определенном языке (т.е. в формализованном виде). Информация
– это осмысленные данные. Смысл,
семантика, содержание (согласно концепции смысла Шенка-Абельсона [149]) – это
знание причинно-следственных зависимостей. Знания – это информация, полезная
для достижения целей, т.е. для управления, которая представляет собой
технологию или «ноу-хау».
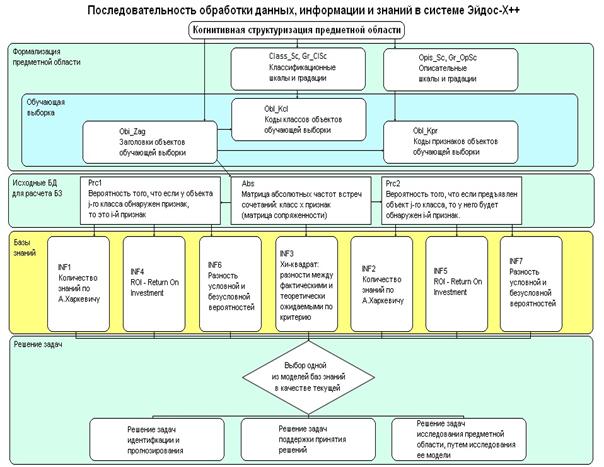
Рисунок
17. Последовательность преобразования исходных данных
в информацию, а ее в
знания в системе «Эйдос-Х++»
Знания могут быть представлены
в различных формах, характеризующихся различной степенью формализации:
– вообще неформализованные знания, т.е. знания
в своей собственной форме, ноу-хау (мышление без вербализации есть медитация);
– знания, формализованные на
естественном вербальном языке;
– знания, формализованные в
виде различных методик, схем, алгоритмов, планов, таблиц и отношений между
ними;
– знания в форме технологий,
организационных производственных, социально-экономических и политических
структур;
– знания, формализованные в
виде математических моделей и методов представления знаний в автоматизированных
интеллектуальных системах (логическая, фреймовая, сетевая, продукционная,
нейросетевая, нечеткая и другие).
Рисунок 1. Соотношение содержания понятий:
«данные», «информация»,
«знания»
Таким образом, для решения
задачи метризации шкал в АСК-анализе необходимо осознанно и целенаправленно последовательно
повышать степень формализации исходных данных до уровня, который
позволяет ввести исходные данные в интеллектуальную систему, а затем:
– преобразовать исходные данные
в информацию;
– преобразовать информацию в
знания;
– использовать знания для
решения задач прогнозирования, принятия решений и исследования предметной
области.
Для этого в АСК-анализе
предусмотрены следующие этапы [17]:
1. Когнитивная структуризация
предметной области, при которой определяется, что мы хотим прогнозировать и на
основе чего (конструирование классификационных и описательных шкал).
2. Формализация предметной
области:
– разработка градаций
классификационных и описательных шкал (номинального, порядкового и числового
типа);
– использование разработанных
на предыдущих этапах классификационных и описательных шкал и градаций для формального
описания (кодирования) исследуемой выборки.
3. Синтез и верификация (оценка
степени адекватности) модели.
4. Если модель адекватна, то ее использование для решения задач
идентификации, прогнозирования и принятия решений, а также для исследования
моделируемой предметной области [97].
Для синтеза моделей в
АСК-анализе в настоящее время используется 7 частных критериев знаний, а для
верификации моделей и решения задачи идентификации и прогнозирования 2 интегральных
критерия [97].
Итак, в результате работы
универсального программного интерфейса получены классификационные и
описательные шкалы и градации и обучающая выборка (рисунки 19, 20, 21):
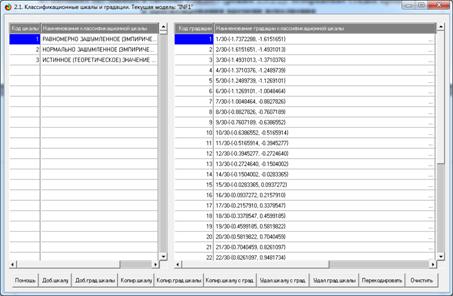
Рисунок 19. Экранная форма с классификационными
шкалами
и градациями
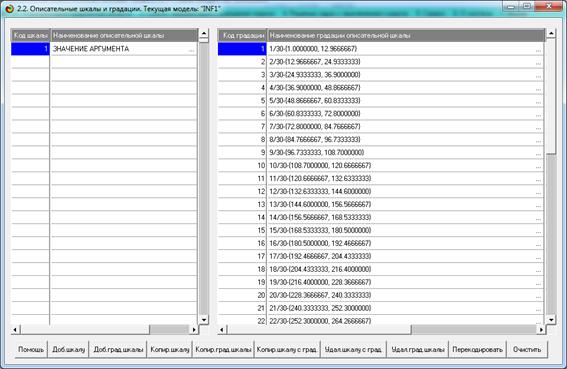
Рисунок 20. Экранная форма с описательной шкалой и
градациями
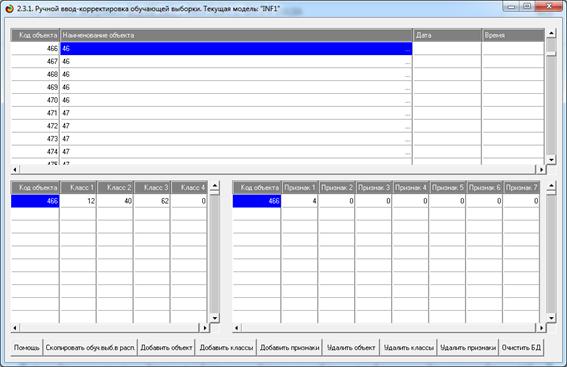
Рисунок 21. Экранная форма с обучающей выборкой
Затем запускается режим
синтеза всех частных моделей 3.4 (рисунок 22):
Рисунок 22. Запуск режима синтеза всех частных моделей 3.4
Затем
необходимо выбрать все частные модели и кликнуть «ОК» (рисунок 23):
Рисунок 23. Первая экранная форма режима синтеза
всех частных моделей 3.4
В результате будут созданы
статистические модели и модели знаний с частными критериями, приведенными в
таблице 5. На рисунке 24 приведена результирующая экранная форма режима 3.4:
Рисунок 24. Результирующая экранная форма режима 3.4
В результате выполнения этих
операций созданы базы знаний с различными частными критериями, представленными
в таблице 5. Подматрицы этих баз знаний могут быть представлены в наглядной
графической форме в виде когнитивных функций. Для получения этих когнитивных
функций необходимо вызвать режим 4.5 (рисунок 25):

Рисунок 25. Запуск режима визуализации когнитивных
функций
На рисунке 26 приведена
первая экранная форма режима визуализации
когнитивных функций:
Рисунок 26. Первая экранная форма режима визуализации
когнитивных функций:
Для запуска модуля
визуализации когнитивных функций [40] кликаем по соответствующей кнопке и
выходим на главное окно модуля визуализации (рисунок 27):
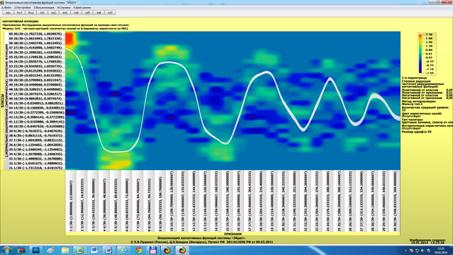
Рисунок 27. Главное окно модуля
визуализации
когнитивных функций
Ниже,
на рисунке 28 приведены когнитивные функции, полученные с помощью данного модуля
визуализации подматриц баз знаний модели INF1 на основе частного критерия
знаний А.Харкевича, а на рисунке 29 – на основе модели INF3 (хи-квадрат):
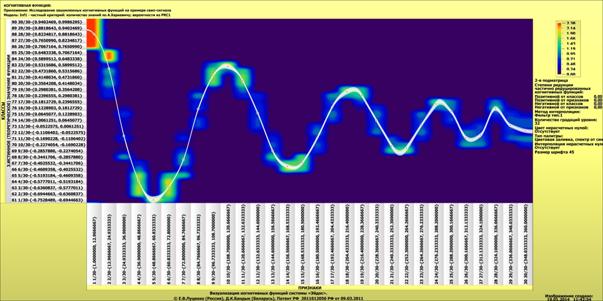
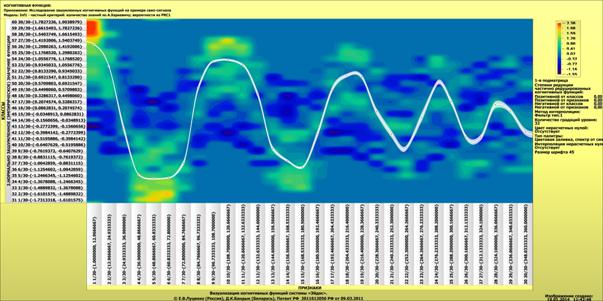
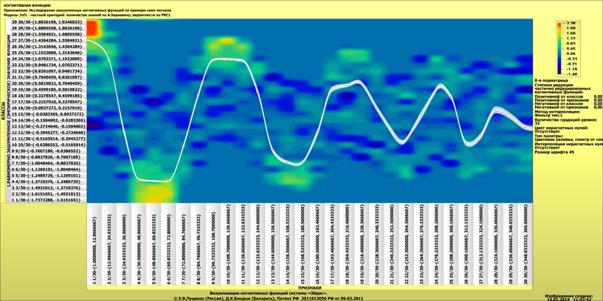
Рисунок 28.
Когнитивные функции, полученные на основе частного критерия А.Харкевича
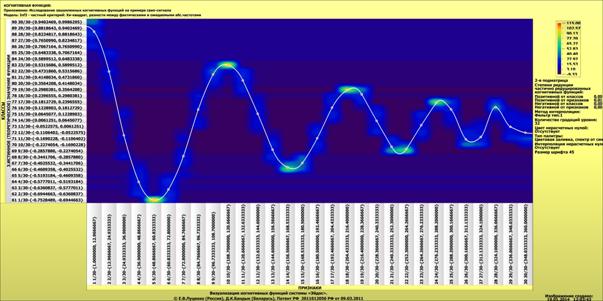
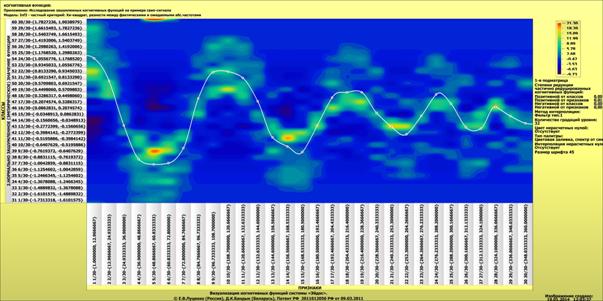
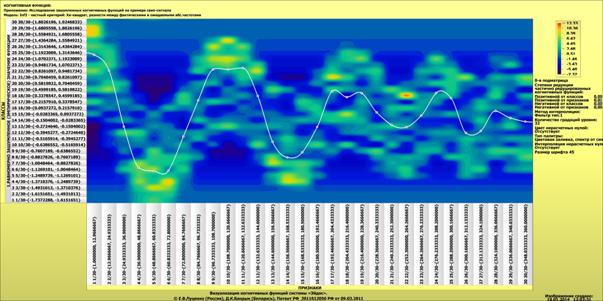
Рисунок 29.
Когнитивные функции, полученные на основе частного критерия хи-квадрат
Из
сравнения вида когнитивных функций, приведенных на рисунках 28 и 29 можно
сделать выводы о том, что они вполне позволяют выявлять зависимости в зашумленных
эмпирических данных.
11.5.
Выводы
Кратко рассматриваются
классическое понятие функциональной зависимости в математике, определяются
ограничения применимости этого понятия для адекватного моделирования реальности
и формулируется проблема, состоящая в поиске такого обобщения понятия функции,
которое было бы более пригодно для адекватного отражения причинно-следственных
связей в реальной области. Далее рассматривается теоретическое и практическое
решения поставленной проблемы, состоящие в том, что
а) предлагается универсальный
не зависящий от предметной области способ вычисления количества информации в
значении аргумента о значении функции, т.е. когнитивные функции;
б) предлагается программный
инструментарий: интеллектуальная система «Эйдос», позволяющая на практике
осуществлять эти расчеты, т.е. строить когнитивные функции на основе фрагментированных
зашумленных эмпирических данных большой размерности.
Предлагаются понятия
нередуцированных, частично и полностью редуцированных прямых и обратных, позитивных
и негативных когнитивных функций и метод формирования редуцированных
когнитивных функций, являющийся обобщением известного взвешенного метода
наименьших квадратов на основе учета в качсетве весов наблюдений количества
информации в значениях аргумента о значениях функции.
Таким образом, предлагается
теория (АСК-анализ), и реализующий ее программный инструментарий (система
«Эйдос») для когнитивного функционального анализа. Эта технология была успешно
применена при проведении ряда научных исследований [97-286] и может применяться как в
научных исследованиях, так и при проведении лекционных и лабораторных занятий
по дисциплинам: «Управление знаниями», «Интеллектуальные системы»,
«Представление знаний в интеллектуальных системах», «Функционально-стоимостной
анализ при управлении персоналом» и других.
В качестве перспективы хотелось
бы отметить возможность обобщения понятия когнитивных функций на многомерный случай
с возможностью 3D-визуализации, а также визуализации в динамике. Эти идеи
развивались в работаъ по системному обобщению математики.