ГЛАВА 2. СИСТЕМНО-КОГНИТИВНЫЙ АНАЛИЗ
И СИСТЕМНАЯ ТЕОРИЯ ИНФОРМАЦИИ
– ТЕОРЕТИЧЕСКИЕ ОСНОВЫ СИСТЕМЫ «ЭЙДОС»

2.1. Перспективная когнитивная концепция

Перспективная когнитивная концепция была предложена автором в работе [4] в 1996 году.

Выявление сходств и различий между обобщенными образами различных видами объектов Реальности позволяет выявить среди них образы двух основных “крайних” или “полярных” типов, - это образы, которые с некоторой степенью условности можно назвать “жесткие” (“детерминистские”) и “аморфные” (“статистические”).

Жесткие (детерминистские) образы - это четко оформленные образы, практически совершенно не связанные (не имеющие сходства или антисходства - различия) с другими образами, описанные в основном детерминистскими признаками с очень высокой информативностью. Детерминистские признаки являются таковыми, т.к. практически не встречаются у остальных образов. Поэтому обнаружение таких признаков у некоторого объекта позволяет без труда и практически однозначно отнести данный объект к соответствующему обобщенному образу (классу).

Аморфные (статистические, вероятностные) образы - это расплывчатые, слабо сформированные образы, которые сильно связаны с другими такими же аморфными образами, т.е. имеют с ними высокий уровень сходства или антисходства (различия). Аморфные образы описываются статистическими признаками, которые встречаются и у них, и у других образов с различными вероятностями: у одних чаще, чем в среднем по всем образам, а у других реже, чем в среднем, но также встречаются. Поэтому, естественно, статистические признаки имеют значительно меньшую информативность, чем детерминистские.

Реально формируемые в процессе познания обобщенные образы различных видов объектов реальности, их состояний и различных явлений всегда находятся где-то между этими крайними полюсами, по своей степени “жесткости” или “аморфности”, как и их признаки, которые, соответственно, в различной степени близки к детерминистским - высокоинформативным или к практически бесполезным для идентификации “всегда встречающимся” признакам.

Исходя из этого может показаться, что в системе признаков, описывающих некоторую предметную область желательно иметь как можно больше детерминистских и как можно меньше статистических признаков. Если ставить перед собой только задачу идентификации (различения друг от друга, распознавания) объектов этой предметной области, то это верно. Однако существуют и другие важные задачи, например задача объективной классификации объектов, которая сводится к определению степени их сходства и различия, объединению наиболее сходных друг с другом объектов в кластеры, определение наиболее непохожих друг на друга кластеров и формирование конструктов.

Конструктом называется понятие, имеющее противоположные смысловые полюса и спектр промежуточных смысловых значений, расположенных по некоторой шкале [127]. Например, понятие “температура” имеет полюса “горячее” и “холодное” с промежуточными значениями “теплое” и “прохладное” и шкалой Цельсия для количественного измерения температуры. Другие примеры конструктов: “вес”, “размер”, “возраст”, “цвет”, “нота” и т.д. Часто бывает, что конструкт четко выражен своими полюсами и спектром, но не имеет своего конструктивного названия. Например: “Дух-материя”, “добро-зло”. Свойство человеческого интеллекта мыслить бинарными конструктами (т.е. конструктами с двумя полюсами) является одним из наиболее фундаментальных его свойств. Как правило, люди мыслят именно полюсами конструктов, а не промежуточными смысловыми оттенками.

Очевидно, без наличия общих, т.е. статистических признаков все объекты будут максимально непохожими друг на друга и вообще не будут иметь какого-либо сходства. Следовательно, задача классификации будет иметь очень неинтересное тривиальное решение: в каждом кластере будет по одному объекту, а конструкты вообще не образуются.

Итак:

– создание обобщенных образов без некоторой вариабельности признаков у входящих в эти образы объектов и наличия статистических признаков невозможно;

– только наличие статистических признаков позволяет решить задачу формирования кластеров и конструктов.

Роль жестких и аморфных образов в процессе познания реальности можно сравнить, соответственно, с ролью ствола и крупных ветвей, как опоры “древа познания жизни”, и мелких веточек и листьев - как его бесконечного многообразия, “которое вечно цветет и зеленеет”.

“Драма идей”, ареной которой является сам процесс становления и развития процесса познания, является предметом рассмотрения в нашей “когнитивной концепции”, т.к. имеет самое непосредственное отношение к проблемам принципиальной распознаваемости (идентифицируемости) и теме данной работы в целом. Рассмотрим “эту драму” подробнее.

Упрощенное (естественнонаучное, формально-логическое) мышление, сосредотачивающееся на наиболее фундаментальных (базовых) закономерностях познаваемой предметной области, стремится освободится от аморфных образов и свести все многообразие этой предметной области к минимальному количеству детерминистских, “жестких” образов. Этот процесс освобождения от аморфных образов по существу является процессом абстрагирования и может быть назван также процессом ВЫЯВЛЕНИЯ БАЗИСНЫХ ВЗАИМНО ОРТОНОРМИРОВАННЫХ ПОНЯТИЙ.

Значение этого процесса невозможно переоценить. Например известно, что осознание А.Лобачевским независимости (ортогональности) образа аксиомы о параллельности прямых от системы образов остальных аксиом геометрии привело к созданию неевклидовой геометрии. Дальнейшим развитием по пути “неевклидовости” явилась геометрия Римана, ставшая основой теории гравитации А.Эйнштейна.

Другим ярким примером такого естественно-научного формально-логического подхода является классическая механика, которая сводит невообразимо громадное многообразие по-видимому различных явлений к небольшому числу таких фундаментальных понятий, как трехмерное пространство (три координаты которого взаимно перпендикулярны, т.е. ортогональны), время, масса и энергия. Очень важно заметить, что в рамках классической механики возможно два по существу эквивалентных и взаимноодназначно получающихся одно из другого описания любого явления: пространственно-временное и импульсно-энергетическое. Это означает, что в действительности взаимно ортогональными являются с одной стороны, только понятия трех измерений пространства и времени, а с другой стороны, энергии и импульса. Это в дальнейшем развитии познания нашло отражение в создании четырехмерного формализма Г.Минковского и “геометродинамике” общей теории относительности А.Эйнштейна, в которой существует только четыре взаимно ортогональных измерения единого пространства-времени, а гравитационные силы и энергия сводятся к искривлениям пространства-времени.

Успехи данного направления развития познания породили своеобразную “ЭЙФОРИЮ ДЕТЕРМИНИЗМА И ДЕДУКЦИИ”, которой “отдали дань” Лейбниц и Конан-Дойль, но которую лучше всего (по мнению автора) выразил Пьер Лаплас в своем знаменитом высказывании: “Мы должны рассматривать существующее состояние Вселенной как следствие предыдущего состояния и как причину последующего. Ум, который в данный момент знал бы все силы, действующие в природе, и относительное положение всех составляющих ее сущностей, если бы он был еще столь обширным, чтобы ввести в расчет все эти данные, охватил бы единой формулой движения крупнейших тел Вселенной и легчайших атомов. Ничего не было бы для него недостоверным, и будущее, как и прошлое, стояло бы перед его глазами.”

В этом высказывании есть очень много “если”, т.е. предположений, которые должны быть истинными, чтобы все высказывание было истинным. Они заслуживают того, чтобы рассмотреть их по порядку:

Во-первых, Лаплас абсолютно убежден в жесткой и ничем не ограниченной детерминированности явлений самой природы.

Однако, квантовая теория открыла “многослойность” явлений и объектов Реальности, а также фазовые переходы объектов между этими слоями из нередуцированного состояния в редуцированное и обратно, которые имеют принципиально вероятностный характер. Таким образом, с точки зрения современной науки свойства Реальности таковы, что строгого логического алгоритма, описывающего наблюдаемые явления, не может существовать даже в принципе. В современной теории физического вакуума (из которой как частные случаи вытекают ОТО и КТП), вводится также понятие “кручения” пространства-времени и связанные с этим разновидность гравитационных полей, которая называется торсионными полями. С этими последними видами физических полей связываются надежды на физическое объяснение ряда психологических явлений.

Во-вторых, Лаплас представлял себе эту всеобъемлющую теорию как теорию такого же типа, какие ему были известны, т.е. наподобие классической механики И.Ньютона. В качестве языка, на котором должна быть изложена эта теория, предполагалось использовать язык математики, прежде всего дифференциальное и интегральное исчисление, язык дифференциальных уравнений.

Само по себе это предположение выглядит чрезвычайно странным и даже наивным, т.к. в развитии науки мы видим, что изменяется не только “содержание”, но и сами принципы построения научных теорий, эволюционируют сами “научные парадигмы”. Кроме того, это “очень сильное” предположение, что Вселенная-в-целом, а также все процессы и явления в ней протекающие, могут быть описана ограниченным (счетным, или даже “небольшим”) числом фундаментальных, т.е. независимых друг от друга (физических?) законов, из “суперпозиции” которых строятся все остальные закономерности Реальности.

В-третьих, Лаплас ВЕРИТ в принципиальную возможность создания, а может быть даже существование, такой ЛОГИЧЕСКОЙ ТЕОРИИ, которая абсолютно точно отражает процессы ВСЕЛЕННОЙ В ЦЕЛОМ, т.е. теории, которая представляет собой логически полную знаковую модель, абсолютно изоморфную Реальности.

Очевидно, что если бы такая теория даже и была бы возможна, то пользоваться ей мог бы только разум, либо имеющий доступ к бесконечным вычислительным ресурсам, либо сам обладающий ими. Допускать существование такой всеобъемлющей теории практически тоже самое, что допускать существование такого разума или компьютера с бесконечными возможностями. Естественно, в их существование можно только верить (или не верить), но доказательство их существования - это задача не для логики.

Но что можно сказать сегодня о Вселенной-в-целом, т.е. о предмете всеобъемлющей теории? По-видимому, только то, что она существует. Очевидно, также, что существуют ее части. Почти очевидным является и то, что Вселенная-в-целом состоит из своих частей. Эти части образуют системы, различного уровня иерархии. Но как отразить в теории Вселенную-в-целом? По-видимому, всеобъемлющая теория должна описывать как взаимодействуют части Вселенной-в-целом друг с другом и с самой Вселенной-в-целом.

Однако даже самый первый вопрос о логическом понимании существования частей Вселенной-в-целом наталкивается на непреодолимые логические трудности. В теории множеств существует парадокс “О множестве всех множеств”, которое может быть простейшей логической моделью Вселенной-в-целом. Если такое множество существует, то оно является одновременно и целым, которое включает все множества, а значит включает и самого себя, а также частью, которое входит в состав этого целого, т.е. является частью самого себя. Следовательно (с точки зрения логики), либо Вселенная-в-целом вообще не является множеством, включающем части, т.е. является “пустым” множеством, либо она не существует.

Читателю предоставляется решить, существование чего для него более достоверно установлено:

– существование частей (но тогда неизвестно частей чего, но уж точно не Вселенной-в-целом),

– либо существование целого, т.е. Вселенной-в-целом (но тогда неизвестно, что же мы все наблюдаем, как мир многообразия),

а также подумать, как совместить по крайней мере все это в рамках логически непротиворечивой и полной действительно всеобъемлющей теории. Эти проблемы имеют непосредственное отношению к семейству логических парадоксов, построенных по принципу парадокса Рассела (более того, само это высказывание также является парадоксом Рассела).

Примечание: автором предложена следующая система вложенных парадоксов Рассела. “Нет правил без исключений. Предыдущее высказывание является правилом. Следовательно и у него существует исключение. Этим исключением является само это правило”.

Современная наука не предлагает решения всех этих проблем, - она просто доказывает принципиальную некорректность самой постановки вопроса о логическом познании Вселенной-в-целом, т.к. эта задача, по-видимому, значительно более сложная, чем построение карты рельефа Солнца путем ползания по нему и ощупывания пальцами. Здесь, по мнению автора, естественным образом возникают следующие вопросы:

о совершенствовании самой логики, разработки многозначной (даже “бесконечно-значной”) и “нечеткой” логики;

о возможном выходе науки за пределы логической формы познания;

об использовании учеными исследователями других форм сознания, которые могут более адекватными для познания (и “освоения”) других “слоев” или форм Реальности.

Начиная с XIX века логика была математизирована, а математика логизирована. Понятие логического рассуждения и вывода приобрело математически четкий смысл. Появился шанс решить уже возникшие в науке логические проблемы (дать определение понятия “проблема”) на новом уровне. И вот в числе 23-х наиболее актуальных математических проблем, провозглашенных Гильбертом на 2-м Международном конгрессе математиков была сформулирована и следующая: “Математическое изложение аксиом физики”. Если бы это удалось сделать, то появилась бы надежда на принципиальную достижимость идеала Лапласа. Это был бы триумф логической формы познания, доказательство бесконечной ничем не ограниченной силы логики, перед которой не только практически, даже в принципе не может быть никаких преград.

Однако в 1931 году выдающийся логик и математик современности Курт Гедель доказал свою знаменитую первую теорему - “теорему о неполноте”, согласно которой утверждение о непротиворечивости формальной логической системы невозможно доказать в рамках самой этой системы, если эта логическая система непротиворечива. Если же формальная логическая система противоречива, то в ней можно доказать ЛЮБОЕ утверждение, в том числе и утверждение, что она непротиворечива.

Таким образом, попытка построения формально-логической системы, в которой было бы доказано, что она является логически полной и непротиворечивой, может привести к тому, что все грандиозное здание логики рухнет, как карточный домик, когда него вытаскивают “не ту карту”. Может показаться, что этого делать не следует, однако по мнению автора (и последователей Зен) как раз это и является “прямым и кратчайшим путем наверх”. Формальная система либо непротиворечива и неполна, либо противоречива и полна. Может быть поэтому не стоит особенно выискивать логические противоречия в Библии и других эзотерических текстах. Похоже что Истина не может быть выражена непротиворечивым способом, т.е. действительно, “гений - парадоксов друг”.

В последующем было доказано существование в любой формально-логической системе неограниченного количества таких корректно сформулированных на ее языке утверждений, которые в рамках данной системы нельзя ни доказать, ни опровергнуть. Включение любого из этих утверждений (вместе с определенным утверждением о ее истинности или ложности) в качестве аксиомы в систему аксиом данной формально-логической системы, “порождает” новую логически непротиворечивую формально-логическую систему.

Аналогично, системе распознавания всегда может быть предъявлен объект, который имеет практически нулевое сходство с образами всех сформированных в данной системе классов распознавания. Добавление данного объекта в качестве образца нового класса распознавания принципиально расширяет предметную область применимости данной системы распознавания.

Теорема Геделя доказана для всех формальных логических систем достаточно развитых, чтобы включать в себя формальную арифметику. Работа Геделя была первым строгим исследованием ВОЗМОЖНОСТЕЙ ДЕДУКТИВНОГО МЕТОДА ПОЗНАНИЯ ВООБЩЕ, и важнейшим и полностью обоснованным результатом этого исследования является вывод о том, процедуры дедуктивного и вычислительного характера обладают определенной внутренней ограниченностью, вследствие которой достаточно развитый процесс познания (начиная с математики) не может быть представлен в форме завершенной формальной системы, т.е. не может быть сведен к системе аксиом и правил вывода заключений из них. Проще говоря, ПРОЦЕСС ПОЗНАНИЯ НЕ СВОДИТСЯ ИСКЛЮЧИТЕЛЬНО К ФОРМАЛЬНО ЛОГИЧЕСКОМУ ПРОЦЕССУ. О том, какие еще способы познания, кроме формально-логического, необходимы для полноценного развития достаточно сложного процесса познания, об этом в теореме Геделя содержательной информации не содержится, т.е. “она об этом говорит в отрицательной форме”. Автор предполагает, что в данном случае в теореме Геделя, “речь идет” о таких формах познания как интуиция и вдохновение, которые играют исключительно большую, часто решающую роль в творчестве всех выдающихся и гениальных ученых, особенно на первых этапах создания ими своих новаторских концепций.

Возникает также вопрос о способности формально-логической системы адекватно отражать всю полноту Реальности не только в целом, но даже в каком-либо из ее аспектов. Одно из следствий теоремы Геделя состоит в том, что по-видимому, Реальность по своей природе несводима к формально-логической схеме и в принципе не может быть полно и адекватно отражена формально-логическим средствами, т.е. в принципе невозможно построить логически полную знаковую модель, абсолютно изоморфную Реальности.

Автор считает, что теорема К.Геделя является одним из наивысших в принципе возможных достижений интеллекта, и весьма удивительным и закономерным, преисполненным глубочайшего смысла является то обстоятельство, что именно в этом своем непревзойденном взлете интеллект отчетливо увидел границы своих собственных возможностей и возможностей интеллектуальной формы познания вообще.

По мнению автора, чтобы “компенсировать” принципиальную неполноту формально-логических систем необходима другая форма познания Реальности, основанная на совершенно иных принципах (если о ней вообще уместно говорить, что она основана на каких-то “принципах”).

Это гуманитарное, образное мышление, которое видит в богатстве ассоциаций и связей аморфных образов возможность для более тонкого изучения таких проблем, в которых применение “жестких” образов выглядит грубым, даже вульгарным, и совершенно неприемлемым. Сердце и интуиция с успехом ведут нас к таким высотам, где слова и логика бессильно замолкают.

Очевидно, оба эти способа мышления (формально-логический, т.е. вербальный, и образный, т.е. невербальный) функционально дополняют друг друга в смысле принципа дополнительности Н.Бора, т.е. полноценное познание Реальности невозможно с использованием только одного из этих способов познания.

Интересно и очень важно, что эти два способа познания поддерживаются у большинства людей различными полушариями головного мозга, т.е. существует функциональная (и даже морфологическая) асимметрия полушарий. Распределение функций по полушариям отличается у правшей и левшей, но это различие более сложное, чем просто противоположность. Нейрофизиология изучила функции полушарий используя данные о больных с поражением одного из полушарий, нарушением их взаимодействия. Но основной объем данных получен с использованием метода электрошокового торможения деятельности, который позволяет “выключить” заданное полушарие на определенное время как бы “усыпив” его, оставив при этом второе полушарие активно действующим, “бодрствующим”. При этом выявились интереснейшие и очень глубокие закономерности, основные из которых приведены ниже в таблице 2 «Функциональная асимметрия полушарий».

Грамотные китайцы, корейцы и японцы (но, конечно, не только они) пользуются одновременно иероглификой - понятийным словесным письмом, в котором каждое значение передается определенным иероглифом, и слоговой азбукой, записывающей звучание слов, но не их смысл. При поражении левого полушария у представителей этих народов страдает слоговое письмо (хиригана и катакана), но совершенно не страдает иероглифика.

Таблица 2 – Функциональная асимметрия полушарий

№	ЛЕВОЕ ПОЛУШАРИЕ	ПРАВОЕ ПОЛУШАРИЕ
1	Левое, мужское, ЯН	Правое, женское, ИНЬ
2	Звуковая оболочка, т.е. звучание слов	Содержание, т.е. смысл слов
3	Логическая структура речи	Интонация, “выражение” речи, смысл речи
4	Абстрактное	Конкретное
5	Знак	Значение
6	Синтаксис, грамматика	Семантика
7	Вербальное	Невербальное
8	Формальное, логическое	Наглядное, образное
9	Абстрактно-логическое “Истинное” и “ложное”, формальная “Истинность”	Конкретное “Истинное”, практическое соответствие действительности
10	Сознательное критическое мышление, все подвергающее сомнению (действие “цензора”)	Подсознание, некритическое восприятие информации “как данного”, внушение
11	Математическое (естественно-научное)	Гуманитарное
12	Объект рассматривается как состоящий из частей. Анализ, изучение состава, признаков и свойств объектов	Объект рассматривается как нечто целостностное. Изучение сходств и различий объектов
13	Свойства и признаки рассматриваются как “метки”, “указатели” на определенные объекты. Синтез объектов по их свойствам и признакам, распознавание и идентификация объектов	Признак (свойство) рассматривается как нечто самостоятельное от объекта (например: “улыбка Чеширского кота”). Изучение смысловых сходств и различий между признаками
14	Фонетическое (звуковое) письмо	Иероглифы
15	Текст, числа	Пиктограммы, графика
16	Музыкальные ритмы	Музыкальные мелодии
17	Звуки высокого тона (женская речь)	Звуки низкого тона (мужская речь)
18	Формальный анализ и планирование будущего	Эмоциональное переживание настоящего (“здесь и теперь”, вечное “сейчас”)
19	Грамматический порядок слов и знаков в тексте	Индивидуальные особенности почерка (аналог интонации)
	Звуковое чтение “по слогам”, смысл извлекается из слов только после их звукового воспроизведения, хотя бы в форме внутренней речи. Скорость извлечения смысла ограничена скоростью звукового воспроизведения (350-500 слов в минуту)	Семантическое чтение по словам - “скорочтение”, слова рассматриваются как иероглифы, непосредственно несущие смысл без необходимости их звукового воспроизведения даже в форме внутренней речи. Скорость чтения не ограничена скоростью внутренней речи и достигает до 20000 слов в минуту.
20	Глагольные предложения, формально-логическое отражение движения	Именные предложения, “телеграфный стиль” (Например: “Ночь. Улица. Фонарь. Аптека. Бессмысленный и тусклый свет.” А.Блок). Движения нет, есть вечное “здесь и сейчас”

Каждому целостному наглядному образу объекта в правом полушарии соответствует его представление в левом полушарии в виде последовательности дискретных символов (свойств - признаков). Процесс познания и понимания состоит в установлении связи (тождества) между этими двумя альтернативными формами отражения объекта. Глубинный структура языка образуется рядом наглядных чувственно-эмоциональных образов которые облекаются во внешнюю дискретную языковую оболочку, построенную по правилам логики и грамматики, которая образует внешнюю структуру языка. В естественном языке далеко не каждое грамматически правильное сочетание слов является осмысленным предложением. Свободная генерация левым полушарием при неработающем правом грамматически правильных но бессмысленных предложений называется “вербальным бредом”. И наоборот, свободная манифестация подсознания, например в сновидениях, представляет собой осмысленный ряд образов не выраженных в языковой форме. Символы подсознания имеют, по-видимому, иероглифический характер. Здесь уместно заметить, что психоанализ, по нашему мнению, представляет собой попытку выразить содержание подсознания в форме речи, и, таким образом, осознать его. С помощью языка человек освобождается от той власти, которую имеют над ним неосознаваемые явления внутреннего и внешнего мира. И наоборот, того, чья власть признается, избегают называть по имени.

По соотношению и относительной роли соответствующих форм познания действительности вполне можно говорить о “левополушарных” и “правополушарных” культурах (цивилизациях). Так Европейская - “Западная”, а также африканская культура являются ярко выраженными “левополушарными” культурами, а Азиатская - “Восточная”, прежде всего китайская, японская, а также Русская и Индийская культура являются “правополушарными”. Люди с доминантностью левого или правого полушария, т.е. истинные “правши” или “левши” соответственно, отличаются друг от друга доминирующим типом мышления (формально-логическое или образное), а также очевидными различиями в своей ориентацией в пространстве, а также очень интересными различиями в ориентации во времени. Последнее проявляется в особенностях музыки, которая нравится правшам или левшам (ритмичная - или мелодичная соответственно), а также в том, что правши к прошлому относятся чувственно-эмоционально (переживают о нем), а к будущему формально-логически (“строят планы”), тогда как левши - наоборот: живут будущим, а к прошлому относятся “по-философски”. Во второй половине ХХ века стала заметной тенденция к синтезу обоих этих видов культур. Известно также, что при переходе в высшие формы сознания функции правого и левого полушарий изменяются таким образом, что преодолевается ярко выраженная доминантность какого-либо одного из них.

Необходимо также отметить, что основное отличие напечатанного (на машинке, принтере или в типографии) текста и рукописного состоит в том, что рукописный текст содержит невербальную информацию, характеризующую самого писавшего, а не то, о чем он пишет. Информация о самом писавшем, содержащаяся в почерке, обычно рассматривается как помеха для восприятия смысла написанного (почерк может быть и “неразборчивый”), однако это верно только в том случае, если мы стремимся воспринять только этот чисто формальный смысл. Если же представляет интерес не только то что написано, но и кем написано, т.е. интересен сам автор, то рукопись имеет очевидное преимущество перед напечатанным текстом. Один лист подлинной рукописи Пушкина стоит значительно дороже, чем целый том его стихов, отпечатанный в типографии. Психографология (изучение автора по почерку) невозможна по шрифтам пишущих машинок или принтеров. Искусство каллиграфии сродни искусству писать иероглифы. Японские стихи, написанные поэтом иероглифами не могут быть напечатаны фонетической азбукой без потери очень существенной своей части, более того, сами иероглифы должны быть воспроизведены не в своем “типичном”, т.е. типографском начертании, а именно в начертании поэта, т.к. в этом содержится важный компонент его творчества и искусства.

Попытка адекватно и корректно отобразить движение логическими средствами по-видимому является исторически первой задачей при решении которой человечество впервые столкнулось с принципиальной ограниченностью самой логики (необходимо отметить, что в эзотерических учениях это было известно ВСЕГДА). Известные парадоксы (апории) Зенона, которые логически доказывают “невозможность движения вообще, а также невозможность движения с разными скоростями” в действительности доказывают лишь невозможность адекватно отразить сущность движения средствами, которые принадлежат самому миру движения, т.е. средствами субъективной относительной логики. Логика, собственными средствами осознала собственную принципиальную ограниченность в тереме Курта Геделя “О неполноте” - и это является наивысшим возможным достижением ограниченной относительной субъективной логики.

Существование этого достижения позволяет поставить задачу такого логического анализа апорий Зенона, который вскрыл бы в самой логике причины невозможности логического отражения движения. Эту же проблему можно сформулировать и в более общей и глубокой форме. Известно, что язык как таковой является не просто средством общения между людьми и людьми, но и между людьми и самой Реальностью. Поэтому с необходимостью язык является не только средством отображения Реальности, например в науке, но и сам является отображением Реальности. Очевидно, без этого он не мог бы выполнять и других своих функций. Поэтому, вообще говоря, все объекты и явления Реальности можно рассматривать как некоторые тексты на некотором языке. Вспомним самые первые слова Библии: “В Начале было Слово...”. Ясно, конечно, что это было не совсем такое слово, какие мы произносим много раз за день. То есть, в самой структуре языка отражены самые глубокие закономерности Реальности. Каждый язык отражает специфический исторический опыт познания Реальности того народа, который создал этот язык.

Фокусом логических проблем, связанных с адекватностью логического отражения движения, очевидно является логический статус глагола. Логическое мышление о движении локализовано в левом полушарии. Глагол образуется из столкновения двух результатов, двух образов - начального и конечного. Сцепление двух образов передает отношение между ними, т.е. соответствует по смыслу глаголу. Сами образы локализуются в правом полушарии и в языке отображаются существительными. Когда два существительных ставится рядом, то между ними может быть вставлен глагол, отображающий трансформацию первого существительного во второе. Например: “Зерно. Земля. Вода. Цветок.” приводит к: “Возьми зерно. Посади зерно в землю. Полей землю водой. Тогда из зерна вырастет цветок”. Однако глагол представляет собой лишь обозначение и констатацию факта процесса трансформации, но не вскрывает механизма этой трансформации. Очевидно, для отображения механизма движения необходимо представить глагол в форме цепочки существительных. Однако это требует осознания времени в форме, в которой мы сейчас осознаем пространство. Условия, при которых это возможно, требуют специального исследования и не являются общедоступными. Поэтому логика позволяет отобразить лишь результат движения, т.е. перемещение, но не позволяет ухватить сам механизм движения. Самая глубокая причина этой ситуации состоит в том, что сущность механизма движения и самого времени не принадлежит тому миру, в котором родилась и существует относительная субъективная логика.

До доказательства Куртом Геделем своей знаменитой теоремы “О неполноте” господствовало мнение, что парадоксы и антиномии указывают на незавершенность здания логики. Считалось, что в корректно работающем логическом аппарате парадоксов не должно быть. Гедель доказал, что формальная система либо непротиворечива и неполна, либо противоречива и полна. В то время как одни математики и логики как-то сразу смирились с принципиальной неполнотой развиваемых ими логических систем, другие начали исследования естественных и формальных языков с целью локализовать и выявить те языковые конструкции, которые и приводят к логическим парадоксам (являющимся конкретным проявлением неполноты). В этих исследованиях были выявлены так называемые “ЭГОцентрические слова” - которые имеют различный смысл, зависящий от того, кто их употребляет. В числе таких слов на первом месте без сомнения нужно назвать слово “Я” и его производные, затем все местоимения: “ОН”, “ОНА”, “ОНО”, “ОНИ”, слова “ЭТО”, “ЗДЕСЬ”, “СЕЙЧАС”, а также производные от этих слов и некоторые другие. В известном “парадоксе лжеца”: “Это утверждение, которое я здесь и сейчас делаю, ложно” эгоцентрические слова, выделенные жирным шрифтом, буквально взрывают смысл всего высказывания. В естественном языке парадокс вызывается СУБЪЕКТИВНОСТЬЮ языка, благодаря которой в самом высказывании содержаться отсылки к нему самому - в эгоцентрических словах. По мнению Бертрана Рассела, который и ввел термин “эгоцентрические слова”, “Целью как науки, так и обыденного здравого смысла является замещение изменчивой субъективности эгоцентрических слов нейтральными общественными терминами... в этом процессе нашего избавления от субъективности истолкование эгоцентрических слов представляет собой один из существенных шагов”. Исследования речи людей с “выключенным” с помощью электрошока правым полушарием показало, что в речи таких людей резко возрастает количество “эгоистических слов”, в частности личных местоимений первого лица. Этот признак сближает продукты субъективной логики с “вербальным бредом”. Из работ автора по измененным, в частности высшим формам сознания, следует, что процесс развития сознания можно рассматривать как процесс последовательного преодоления ЭГО. Само ЭГО имеет сложную структуру, модель которой также была предложена автором. Исходя из всего вышеизложенного автор предполагает, что в принципе возможна объективная логика, не содержащая никаких эгоцентрческих слов, но это логика не может быть логикой какого-либо существа, которое считает, что “Я есть ЭТО”, или “Я есть ТО”, таким образом неэгоцентрическая логика - это логика Вселенной-в-целом. Это не означает, что она недоступна никакому конечному существу, а означает лишь, что это существо должно иметь такую ФОРМУ СОЗНАНИЯ, при которой оно не отождествляет себя с какой-либо конечной материальной структурой, например структурой типа физического тела. Мышление такого существа может быть в принципе не отличается от самой Реальности (в индийском эзотеризме есть глубочайшая идея, что весь Мир - это сон Шивы). Роберт Г.Джан и Бренда Дж.Данн, наиболее выдающиеся исследователи микротелекинеза и других Ψ-явлений современными научными методами, высказывают глубокую мысль, что поскольку физическая реальность зависит от сознания (а именно это доказано ими с небывалой надежностью и убедительностью), то строго говоря не существует непреодолимого барьера между физической и психической реальностью. Из этого вытекают очень значительные мировоззренческие выводы, которые далеко выходят за границы данной монографии.

В этой связи представляет интерес глубокая аналогия между задачей Учителя (такого как И.А.Соколянский), который обучает слепо-глухо-немых и делает их полноценными членами нашего общества (видящих, слышащих и говорящих на физическом уровне Реальности), и задачей Гуру - который ведет нас - слепых, глухих и немых на высших уровнях Реальности к высшим формам сознания. Мы все действительно являемся слепыми, глухими и немыми с точки зрения человека, у которого раскрыты центры высшего сознания (чакры). Действительно можно с полным основанием ожидать, что преодолев физическое ЭГО и перейдя в ментальное сознание человек овладеет абсолютной объективной логикой, лишенной в своей структуре тех причин неполноты, которые имеются в относительной субъективной логике и которые с наивысшей убедительностью вскрыты в теореме Курта Геделя и последовавшими за ней исследованиях Бертрана Рассела и Х.Рейхенбаха.

Что же можно сегодня сказать об этой абсолютной логике? Некоторое представление о ней можно получить, если в предельно обостренной форме поставить человека перед логическими проблемами, принципиально неразрешимыми средствами субъективной логики. Если человек решает эти проблемы - он переходит в высшую форму сознания. Такие ситуации, из которых существует только один выход, а именно выход вверх, называются в Дзен-буддизме коанами. Внешне с формальной точки зрения коаны чаще всего являются неразрешимыми парадоксами. Таким образом парадокс если и не выражает саму истину, то во всяком случае прозрачно намекает на ее существование и в определенном смысле указывает на истину. Традиция выражать некоторые высшие знания в форме парадоксов или системы взаимно исключающих высказываний (антиномий), о которых утверждается что они оба верны, глубоко укоренилась в эзотерической традиции. Учитывая результаты Геделя очевидно, что такой подход до основания разрушает субъективную логическую машину, делая её полной, но и внутренне противоречивой. Абсолютная объективная логика выходит за пределы как непротиворечивой и неполной субъективной логики, так и ее абсолютного отрицания - полной и противоречивой субъективной логики.

Рассмотрим подробнее два момента в предложенной нами концепции, имеющие с нашей точки зрения особое значение: это адаптивность и семантический анализ.

2.2. Базовая когнитивная концепция и синтез когнитивного конфигуратора

2.2.1. Понятие когнитивного конфигуратора и необходимость естественнонаучной (формализуемой) когнитивной концепции

В данном разделе приводится когнитивная концепция, разработанная автором исследования в 1998 году, с учетом двух основных требований:

1. Адекватное отражение в когнитивной концепции реальных процессов, реализуемых человеком в процессах познания.

2. Высокая степень приспособленности когнитивной концепции для формализации в виде достаточно простых математических и алгоритмических моделей, допускающих прозрачную программную реализацию в автоматизированной системе.

Определение понятия конфигуратора

Понятие конфигуратора, по-видимому, впервые предложено В.А.Лефевром, хотя безусловно это понятие использовалось и раньше, но, во-первых, оно не получало самостоятельного названия, а, во-вторых, использовалось в частных случаях и не получало теоертического обобщения.

Под конфигуратором В.А.Лефевр понимал минимальный полный набор понятийных шкал или конструктов, достаточный для адекватного описания предметной области.

Примеры конфигураторов:

1. Декартова система координат является исторически первым геометрическим конфигуратором, позволяющим построить аналитическую геометрию реального 3-х мерного пространства. Позже были предложены сферические, цилиндрические и другие системы координат, также позволяющие решать эту задачу.

2. Фундаментальные понятия классической механики (координаты в пространстве-времени, скорость, ускорение, перемещение, вращение, масса, энергия, импульс, сила) образуют "классический механический конфигуратор", обеспечивающий адекватное описание макроскопических классических механических явлений. Обобщениями классического механического конфигуратора являются квантовый и релятивистский конфигураторы.

3. Профессиограммы, включающие качества личности с количественной оценкой их важности для успешности профессиональной деятельности по тем или иным направлениям. При этом качества, не играющие роль в профессиограмму не входят. Таким образом, профессиограмму можно определить как "профессиональный конфигуратор личности".

Понятие когнитивного конфигуратора

В исследованиях по когнитивной психологии изучается значительное количество различных операций, связанных с процессом познания. Однако, насколько известно из литературы, психологами не ставился вопрос о выделении из всего множества когнитивных операций такого минимального (базового) набора наиболее элементарных из них, из которых как составные могли бы строится другие операции. Ясно, что для выделения таких базовых когнитивных операций (БКО) необходимо построить их иерархическую систему, в фундаменте которой будут находится наиболее элементарные из них, на втором уровне – производные от них, и т.д. Таким образом, под когнитивным конфигуратором будем понимать минимальный полный набор базовых когнитивных операций, достаточный для представления различных процессов познания.

Когнитивные концепции и операции

Проведенный анализ когнитивных концепций показал, что они разрабатывались ведущими психологами (Пиаже, Солсо, Найсер) без учета требований, связанных с их дальнейшей формализацией и автоматизацией. Поэтому имеющиеся концепции когнитивной психологии слабо подходят для этой цели; в когнитивной психологии не ставилась и не решалась задача конструирования когнитивного конфигуратора и, соответственно, не сформулировано понятие базовой когнитивной операции.

2.2.2. Предлагаемая когнитивная концепция

Ставить цель автоматизировать процесс познания в целом в настоящее время не вполне реалистично, но вполне возможно автоматизировать отдельные операции, выполняемые человеком в процессе познания, т.е. когнитивные операции.

Оптимальной системой когнитивных операций (когнитивным конфигуратором) будем называть такую систему, которая одновременно удовлетворяет требованиям полноты и минимальной избыточности. Когнитивные операции, образующие оптимальную систему, будем называть базовыми когнитивными операциями.

Соответственно, возникает задача выявления и определения базовых когнитивных операций, сделать это предлагается на основе когнитивной концепции.

Средство труда (компьютер и программная система) для автоматизации когнитивных операций будем обозначать вслед за Фукушимой термином "Когнитрон" (хотя и будем вкладывать в этот термин другой смысл, чем в теории нейронных сетей).

Автоматизация оптимальной системы когнитивных операций обеспечивает новое перераспределение функций в процессах познания и труда между человеком и средством труда в пользу последнего. Такое перераспределение функций между человеком и средством труда вполне закономерно и очень перспективно с точки зрения предложенных автором еще в 1980 году "Информационно-функциональной теории развития техники" и "Закона повышения качества базиса" и знаменуют собой новый этап развития технологий.

В данном исследовании не ставится задача рассматривать концепции, принятые в философской теории познания (гносеологии) и в психологии процессов познания (когнитивной психологии). Отметим лишь следующее:

– весь процесс возникновения наук путем последовательного "отслаивания" их предмета от предмета интегральной сверх и преднауки философии в определенной последовательности по мере усложнения предмета исследования (физика, химия, биология, история) и применения естественнонаучного метода, говорит о том, что этот метод в перспективе должен быть применен к диалектике, логике и теории познания, а в конце концов – и к постановке и решению основного вопроса философии (автор, 1979, 1990, 1994).

– системный анализ, как неоднократно заявляли классики системного анализа [2], по сути дела представляет собой современное естественнонаучное воплощение диалектики. В этом контексте учение о развитии систем путем чередования детерминистских и бифуркационных состояний представляет собой ничто иное, как естественнонаучное трактовку закона диалектики "Перехода количественных изменений в качественные". Иначе говоря, детерминистские этапы – это этапы количественного, эволюционного изменения объекта управления, а бифуркационные – этапы его качественного, революционного преобразования.

Поэтому системный анализ рассматривается в данной работе как теоретический метод познания детерминистско-бифуркационной динамики систем. Таким образом, логически системный анализ можно считать результатом выполнения программы естественнонаучного развития диалектики, хотя исторически он и возник иначе. Саму когнитивную психологию также в определенной мере можно рассматривать как результат выполнения программы естественнонаучного развития гносеологии.

Автоматизировать процесс познания в целом безусловно значительно сложнее, чем отдельные операции процесса познания. Но для этого прежде всего необходимо выявить эти операции и найти место каждой из них в системе или последовательности процесса познания.

Сделать это предлагается в форме когнитивной концепции, которая должна удовлетворять следующим требованиям:

– адекватность, т.е. точное отражение сущности процессов познания, характерных для человека, в частности описание процессов вербализации, семантической адаптации и семантического синтеза (уточнения смысла слов и понятий и включения в словарь новых слов и понятий);

– высокая степень детализации и структурированности до уровня достаточно простых базовых когнитивных операций;

– возможность математического описания, формализации и автоматизации.

Однако приходится констатировать, что даже концепции когнитивной психологии, значительно более конкретные, чем гносеологические, разрабатывались без учета необходимости построения реализующих их математических и алгоритмических моделей и программных систем. Более того, в когнитивной психологии из всего многообразия различных исследуемых когнитивных операций не выделены базовые, к суперпозиции и различным вариантам сочетаний которых сводятся различные процессы познания.

Поэтому для достижения целей данного исследования концепции когнитивной психологии мало применимы. В связи с этим в данном исследовании предлагается когнитивная концепция, удовлетворяющая сформулированным выше требованиям. Эта концепция достаточно проста, иначе было бы невозможно ее формализовать, многие ее положения интуитивно очевидны или хорошо известны. Тем ни менее эта концепция должна быть вербализована, чтобы образовать систему, позволяющую продвинуться еще на шаг к решению поставленной в данной работе проблемы: выявить базовые когнитивные операции, их содержание и последовательность. Положения когнитивной концепции приведены в определенном порядке, соответствующем реальному ходу процесса познания "от конкретных эмпирических исходных данных к содержательным информационным моделям, а затем к их верификации, адаптации и, в случае необходимости, к пересинтезу".

Системный анализ представляет собой теоретический метод познания, т.е. сложный многоступенчатый, итерационный, иерархически организованный когнитивный процесс.

Исходные данные для системного анализа поставляются из нескольких независимых информационных источников, имеющих качественно различную природу, которые мы будем условно называть "органы чувств". Данные от органов чувств также имеют качественно различную природу, обусловленную конкретным видом информационного источника. Для обозначения этих исходных данных будем использовать термин "атрибут". В результате выполнения когнитивной операции "присвоение имен" атрибутам могут быть присвоены уникальные имена, т.е. они могут быть отнесены к некоторым градациям номинальных шкал. Получение информации о предметной области в атрибутивной форме осуществляется когнитивной операцией "восприятие".

Исходные данные содержат внутренние закономерности, объединяющие качественно разнородные исходные данные от различных информационных источников.

После восприятия предметной области может быть проведен ее первичный анализ путем выполнения когнитивной операции: "сопоставление опыта, воплощенного в модели, с общественным", т.е. с результатами восприятия той же предметной области другими. Это делается с целью исключения из дальнейшего анализа всех наиболее явных расхождений, как сомнительных.

Однако, закономерности в предметной области могут быть выявлены путем выполнения когнитивной операции "обобщение" только после накопления в результате мониторинга достаточно большого объема исходных данных в памяти.

Наличие этих закономерностей позволяют предположить, что:

– существуют некие интегративные структуры, не сводящиеся ни к одному из качественно-различных аспектов исходных данных и обладающие по отношению к ним системными, т.е. эмерджентными свойствами, которые не могут быть предметом прямого восприятия с помощью органов чувств, но могут являться предметом для других форм познания, например логической формы. Для обозначения этих структур будем использовать термин "объект";

– "объекты" считаются причинами существования взаимосвязей между атрибутами.

Объектам приписывается объективное существование, в том смысле, что любой объект обнаруживается несколькими независимыми друг от друга способами с помощью различных органов чувств (этот критерий объективного существования в физике называется "принцип наблюдаемости").

После обобщения возможны когнитивные операции: "определение значимости шкал и градаций атрибутов" и "определение степени сформированности шкал и градаций классов".

Путем выполнения когнитивной операции "присвоение имен" конкретным объектам могут быть присвоены уникальные имена, т.е. они могут быть отнесены к некоторым градациям номинальной шкалы, которые мы будем называть "классами". В данном случае класс представляет собой отображение объекта шкалу, т.е. это своего рода целостный образ объекта. После этого возможно выполнение когнитивной операции "идентификация" объектов, т.е. их "узнавание": при этом по атрибутам объекта определяется класс, к которому принадлежит объект. При этом все атрибуты, независимо от их качественно различной природы, рассматриваются с одной-единственной точки зрения: "Какое количество информации они несут о принадлежности данного объекта к каждому из классов".

Кроме того возможно выполнение когнитивной операции: "дедукция и абдукция, обратная задача идентификации и прогнозирования", имеющей очень важное значение для управления, т.е. вывод всех атрибутов в порядке убывания содержащегося в них количества информации о принадлежности к данному классу.

Аналогично, может быть выполнена когнитивная операция: "семантический анализ атрибута", представляющий собой список классов, в порядке убывания количества информации о принадлежности к ним, содержащейся в данном атрибуте.

Таким образом возможно два взаимно-дополнительных способа отображения объекта: в форме принадлежности к некоторому классу (целостное, интегральное, экстенсиональное); в форме системы атрибутов (дискретное, интенсиональное).

Дальнейшее изучение атрибутов позволяет ввести понятия "порядковая шкала" и "градация". Порядковая шкала представляет собой способ классификации атрибутов одного качества, обычно по степени выраженности (интенсивности). Градация – это конкретное положение или диапазон на шкале, которому ставится в соответствие конкретный атрибут, соответствующее определенной степени интенсивности. Каждому виду атрибутов, информация о которых получается с помощью определенного "органа чувств", ставится в соответствие одна шкала. Таким образом, если при анализе в номинальных шкалах, можно было в принципе ввести одну шкалу для всех атрибутов, то в порядковых шкалах каждому атрибуту будет соответствовать своя шкала.

После идентификации уникальных объектов с классами возможна их классификация и присвоение обобщающих имен группам похожих классов. Для обозначения группы похожих классов используем понятие "кластер". Формирование кластеров осуществляется с помощью когнитивной операции "классификация". Кластер представляет собой своего рода "объект, состоящий из объектов", т.е. объект 2-го порядка. Если объект выполняет интегративную функцию по отношению к атрибутам, то кластер – по отношению к объектам.

Необходимо подчеркнуть, что термин "класс" используется не только для обозначения образов уникальных объектов, но и для обозначения их кластеров, т.е. классу может соответствовать не уникальное, а обобщающее имя, в этом случае мы имеем дело с обобщенным классом. Да и кластеры могут быть не только кластерами уникальных объектов, но и обобщенных классов.

Если объективное существование уникальных объектов мало у кого вызывает сомнение, то вопрос об объективном существовании интегративных структур 2-го и более высоких порядков остается открытым. В некоторых философских системах подобным объектам приписывался даже более высокий статус существования, чем самим объектам, например обычные объекты рассматриваются лишь как "тени" "Эйдосов" (Платон). Известны и другие понятия для обозначения объектов высоких порядков, например "архетип" (Юм), "эгрегор" (Андреев) и др. Нельзя не отметить, что в современной физике (специальной и общей теории относительности) есть подобное понятие пространственно-временного интервала, который проявляется как движение объекта. По-видимому, статус существования структур реальности, отражаемых когнитивными структурами тем выше, чем выше интегративный уровень этих структур.

Являясь объектами 2-го порядка сами кластеры в результате выполнения когнитивной операции "генерация конструктов" могут быть классифицированы по степени сходства друг с другом. Для обозначения системы двух противоположных кластеров, с "спектром" промежуточных кластеров между ними, будем использовать термин "бинарный конструкт", при этом сами противоположные кластеры будем называть "полюса бинарного конструкта". Таким образом конструкт представляет собой объект 3-го порядка.

Словом "бинарный" определяется, что в данном случае полюсов у конструкта всего два, но этим самым подчеркивается, что в принципе их может быть 3, 4 и больше. Бинарный конструкт можно формально представить в виде порядковой шкалы или даже шкалы отношений, на которой градациям соответствуют кластеры, а значит и сами классы и соответствующие объекты. Конструкты с количеством полюсов больше 2 могут быть представлены графически в форме семантических сетей в которых полюса являются вершинами, а дуги имеют цвет и толщину, соответствующие степени сходства-различия этих вершин. Семантические сети можно считать также просто графической формой представления результатов кластерного анализа.

Аналогично кластерам и конструктам классов формируются кластеры и конструкты атрибутов. В кластеры объединяются атрибуты, имеющие наиболее сходный смысл. В качестве полюсов конструктов выступают кластеры атрибутов, противоположных по смыслу.

Бинарные конструкты классов и атрибутов представляет собой когнитивные структуры, играющие огромную роль в процессах познания. Не будет преувеличением сказать, что познание представляет собой процесс генерации, совершенствования и применения конструктов. Будем считать, что конструкт тем более совершенен и тем выше его качество, чем сильнее отличаются его полюса, т.е. чем больше диапазон его области значений.

В кластерном анализе определялась степень сходства или различия классов, а не то, чем конкретно сходны или отличаются. При выполнении когнитивной операции "содержательное сравнение" двух классов определяется вклад каждого атрибута в их сходство или различие. Результаты содержательного сравнения выводятся в наглядной графической форме когнитивных диаграмм, в которых изображаются информационные портреты классов с наиболее характерными и нехарактерными для них атрибутами и атрибуты разных классов соединяются линиями, цвет и толщина которых соответствуют величине и знаку вклада этих атрибутов в сходство или различие данных классов.

Результаты идентификации и прогнозирования, осуществленные с помощью модели, путем выполнения когнитивной операции "верификация" сопоставляются с опытом, после чего определяется выполнять ли когнитивную операцию "обучение", состоящую в том, что параметры модели могут изменяться количественно, и тогда мы имеем дело с адаптацией, или качественно, и тогда идет речь о переформировании модели.

2.2.3. Предлагаемый когнитивный конфигуратор

Таким образом из предложенной когнитивной концепции вытекает существование по крайней мере 10 базовых когнитивных операций к которым сводятся процедуры системного анализа (таблица 3):

Таблица 3 – Обобщенный список БКОСА
(когнитивный конфигуратор)

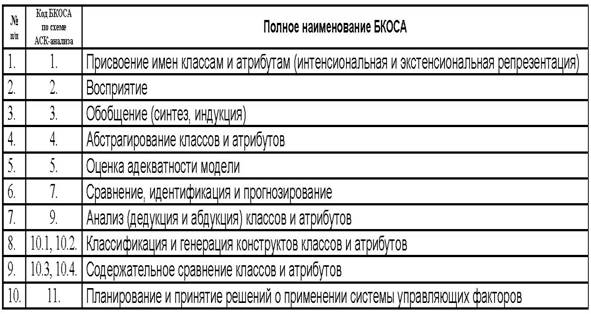
Необходимо отметить, что классификация операций системного анализа по В.М.Казиеву ближе всего к позиции, излагаемой в данной работе, т.к. этим автором названы 6 из 10 базовых когнитивных операций системного анализа: формализация; синтез (индукция); абстрагирование; анализ (дедукция); распознавание, и идентификация образов; классификация. Вместе с тем им не приводятся математическая модель, алгоритмы и инструментарий реализации этих операций и не ставится задача их разработки, кроме того некоторые из них приведены дважды под разными названиями, например: анализ и синтез это тоже самое, что дедукция и индукция.

По-видимому, впервые идея сведения мышления и процессов познания к когнитивным операциям была четко сформулирована в V веке до н.э.: "Сущность интеллекта проявляется в способностях обобщения, абстрагирования, сравнения и классификации" (цит.по пам., Патанжали, Йога-Сутра).

Эти операции представляют собой иерархическую систему: 1-е является элементарными, 2-е используют 1-е в качестве элементов в схеме обработки информации, и т.д. Поэтому на очередность (последовательность) выполнения этих операций существуют определенные ограничения: операции более высокого уровня иерархии (интегративности) не могут быть выполнены раньше операций предыдущих уровней иерархии.

2.3. Формализация базовых когнитивных операций системного анализа

2.3.1. Исходные теоретические положения когнитивной концепции

В этой связи нами предложена формализуемая когнитивная концепция, не претендующая на вклад в когнитивную психологию, но удовлетворяющая требованиям, вытекающим из существа исследования.

Исходные положения этой когнитивной концепции:

1) процессы познания обеспечивают в целом адекватное отражение процессов природы и общества;

2) некоторые когнитивные (познавательные) операции возможно представить в виде математических и алгоритмических моделей (формализовать);

3) формализованные модели когнитивных операций допускают программную реализацию, т.е. передачу соответствующих функций, ранее выполнявшихся только человеком, интеллектуальным средствам труда. Это обеспечивает возможность выполнения данных функций вне ограничений, присущих человеку и высвобождает его ресурсы для выполнения более творческих функций.

На базе выше сформулированных положений построена целостная система взглядов на процесс познания, т.е. когнитивная концепция (рисунок 9):

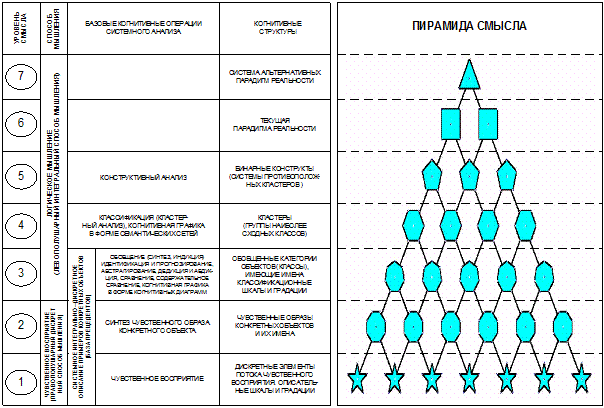
Рисунок 9. Обобщенная схема предлагаемой
когнитивной концепции

Суть предложенной когнитивной концепции состоит в том, что процесс познания рассматривается как многоуровневая иерархическая система обработки информации, в которой каждый последующий уровень является результатом интеграции элементов предыдущего уровня. На 1-м уровне этой системы находятся дискретные элементы потока чувственного восприятия, которые на 2-м уровне интегрируются в чувственный образ конкретного объекта. Те, в свою очередь, на 3-м уровне интегрируются в обобщенные образы классов и факторов, образующие на 4-м уровне кластеры, а на 5-м конструкты. Система конструктов на 6-м уровне образуют текущую парадигму реальности (т.е. человек познает мир путем синтеза и применения конструктов). На 7-м же уровне обнаруживается, что текущая парадигма не единственно-возможная.

Ключевым для когнитивной концепции является понятие факта, под которым понимается соответствие дискретного и интегрального элементов познания (т.е. элементов разных уровней интеграции-иерархии), обнаруженное на опыте. Факт рассматривается как квант смысла, что является основой для его формализации. Таким образом, происхождение смысла связывается со своего рода "разностью потенциалов", существующей между смежными уровнями интеграции-иерархии обработки информации в процессах познания.

1. Процесс познания начинается с чувственного восприятия. Различные органы восприятия дают качественно-различную чувственную информацию в форме дискретного потока элементов восприятия. Эти элементы формализуются с помощью описательных шкал и градаций.

2. В процессе накопления опыта выявляются взаимосвязи между элементами чувственного восприятия: одни элементы часто наблюдаются с другими (имеет место их пространственно-временная корреляция), другие же вместе встречаются достаточно редко. Существование устойчивых связей между элементами восприятия говорит о том, что они отражают некую реальность, интегральную по отношению к этим элементам. Эту реальность будем называть объектами восприятия. Рассматриваемые в единстве с объектами элементы восприятия будем называть признаками объектов. Таким образом, органы восприятия дают чувственную информацию о признаках наблюдаемых объектов, процессов и явлений окружающего мира (объектов). Чувственный образ конкретного объекта представляет собой систему, возникающую как результат процесса синтеза признаков этого объекта. В условиях усложненного восприятия синтез чувственного образа объекта может быть существенно замедленным и даже не завершаться успехом в реальном времени.

3. Человек присваивает конкретным объектам названия (имена) и сравнивает объекты друг с другом. При сравнении выясняется, что одни объекты в различных степенях сходны по их признакам, а другие отличаются. Сходные объекты объединяются в обобщенные категории (классы), которым присваиваются имена, производные от имен входящих в категорию конкретных объектов. Классы формализуются с помощью классификационных шкал и градаций и обеспечивают интегральный способ описания действительности. Путем обобщения (синтеза, индукции) информации о признаках конкретных объектов, входящих в те или иные классы, формируются обобщенные образы классов. Накопление опыта и сравнение обобщенных образов классов друг с другом позволяет определить степень характерности признаков для классов, смысл признаков и ценность каждого признака для идентификации конкретных объектов с классами и сравнения классов, а также исключить наименее ценные признаки из дальнейшего анализа без существенного сокращения количества полезной информации о предметной области (абстрагирование). Абстрагирование позволяет существенно сократить затраты внутренних ресурсов системы на анализ информации. Идентификация представляет собой процесс узнавания, т.е. установление соответствия между чувственным описанием объекта, как совокупности дискретных признаков, и неделимым (целостным) именем класса, которое ассоциируется с местом и ролью воспринимаемого объекта в природе и обществе. Дискретное и целостное восприятие действительности поддерживаются как правило различными полушариями мозга: соответственно, правым и левым (доминантность полушарий). Таким образом именно системное взаимодействие интегрального (целостного) и дискретного способов восприятия обеспечивает возможность установление содержательного смысла событий. При выполнении когнитивной операции "содержательное сравнение" двух классов определяется вклад каждого признака в их сходство или различие.

4. После идентификации уникальных объектов с классами возможна их классификация и присвоение обобщающих имен группам похожих классов. Для обозначения группы похожих классов используем понятие "кластер". Но и сами кластеры в результате выполнения когнитивной операции "генерация конструктов" могут быть классифицированы по степени сходства друг с другом. Для обозначения системы двух противоположных кластеров, с "спектром" промежуточных кластеров между ними, будем использовать термин "бинарный конструкт", при этом сами противоположные кластеры будем называть "полюса бинарного конструкта". Бинарные конструкты классов и атрибутов, т.е. конструкты с двумя полюсами, наиболее типичны для человека и представляет собой когнитивные структуры, играющие огромную роль в процессах познания. Достаточно сказать, что познание можно рассматривать как процесс генерации, совершенствования и применения конструктов. Качество конструкта тем выше, чем сильнее отличаются его полюса, т.е. чем больше диапазон его смысла.

Результаты идентификации и прогнозирования, осуществленные с помощью модели, путем выполнения когнитивной операции "верификация" сопоставляются с опытом, после чего определяется целесообразность выполнения когнитивной операции "обучение". При этом может возникнуть три основных варианта, которые на рисунке 10 обозначены цифрами:

1. Объект, входит в обучающую выборку и достоверно идентифицируется (внутренняя валидность, в адаптации нет необходимости).

2. Объект, не входит в обучающую выборку, но входит в исходную генеральную совокупность, по отношению к которой эта выборка репрезентативна, и достоверно идентифицируется (внешняя валидность, добавление объекта к обучающей выборке и адаптация модели приводит к количественному уточнению смысла признаков и образов классов).

3. Объект не входит в исходную генеральную совокупность и идентифицируется недостоверно (внешняя валидность, добавление объекта к обучающей выборке и синтез модели приводит к качественному уточнению смысла признаков и образов классов, исходная генеральная совокупность расширяется).

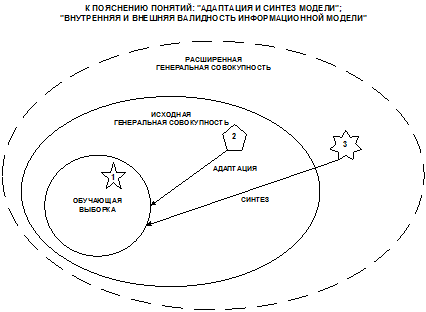
Рисунок 10. К пояснению смысла понятий: "Адаптация и синтез
когнитивной модели предметной области", "Внутренняя и внешняя валидность информационной модели",

2.3.2. Когнитивный конфигуратор и базовые когнитивные операции системного анализа

Познание предметной области с одной стороны безусловно является фундаментом, на котором строится все грандиозное здание системного анализа, а с другой стороны, процессы познания являются связующим звеном, органично объединяющим "блоки" принципов и методов системного анализа в стройное здание. Более того, процессы познания буквально пронизывают все методы и принципы системного анализа, входя в них как один из самых существенных элементов.

Однако, на этом основании неверным будет представлять, что когнитивные операции являются подмножеством понятия "системный анализ", скорее наоборот: системный анализ представляет собой один из теоретических методов познания, представимый в форме определенной последовательности когнитивных операций, тогда как другие последовательности этих операций позволяют образовать другие формы теоретического познания.

Поэтому разработка математических моделей, алгоритмов и программных систем, обеспечивающих автоматизацию применения когнитивной концепции в системном анализе, является актуальной научной и технической проблемой, заслуживающей внимания и усилий, как исследователей, так и разработчиков.

Сложность решения этой важнейшей проблемы состоит в ее ярко выраженном системном, комплексном, междисциплинарном характере, что определяет необходимость для ее решения активно и нетривиально использовать знания из таких областей науки, как когнитивная психология, системный анализ, математическое моделирование, теория информации, теория распознавания образов и принятия решений, а также применить на практике технологии программной реализации систем интеллектуального анализа данных и искусственного интеллекта.

Безусловно, в решении данной проблемы существует неограниченное поле деятельности для психологов, но в данной работе внимание акцентируется на научно-техническом аспекте, а именно на разработке соответствующих математических моделей, алгоритмов, программных систем, а также методологии, технологии и методики их применения для синтеза рефлексивных АСУ активными объектами.

В данной работе предлагается разрабатывается обоснованный вариант решения этой междисциплинарной проблемы. Вместе с тем этим самым не решается глобальная проблема автоматизации системного анализа, а лишь совершается один шаг в этом чрезвычайно перспективном направлении.

Конкретно путь достижения этой цели состоит в разработке:

1. Аналитической модели, позволяющей заложить основы для автоматизации когнитивных операций.

2. Алгоритмических моделей базовых когнитивных операций, обеспечивающих уровень конкретизации, позволяющий непосредственно приступить к их программной реализации.

Поэтому далее рассмотрим базовые когнитивные операции системного анализа и возможности их применения в рефлексивном управлении активными объектами.

2.3.3. Задачи формализации базовых когнитивных операций системного анализа

Выбор единой интерпретируемой численной меры для классов и атрибутов

При построении модели объекта управления одной из принципиальных проблем является выбор формализованного представления для индикаторов, критериев и факторов (далее: факторов). Эта проблема распадается на две подпроблемы:

1. Выбор и обоснование смысла выбранной численной меры.

2. Выбор математической формы и способа определения (процедуры, алгоритма) количественного выражения для значений, отражающих степень взаимосвязи факторов и будущих состояний АОУ.

Рассмотрим требования к численной мере, определяемые существом подпроблем. Эти требования вытекают из необходимости совершать с численными значениями факторов математические операции (сложение, вычитание, умножение и деление), что в свою очередь необходимо для построения полноценной математической модели.

Требование 1: из формулировки 1-й подпроблемы следует, что все факторы должны быть приведены к некоторой общей и универсальной для всех факторов единице измерения, имеющей какой-то смысл, причем смысл, поддающийся единой сопоставимой в пространстве и времени интерпретации.

Традиционно в специальной литературе рассматриваются следующие смысловые значения для факторов:

– стоимость (выигрыш-проигрыш или прибыль-убытки);

– полезность;

– риск;

– корреляционная или причинно-следственная взаимосвязь.

Иногда предлагается использовать безразмерные меры для факторов, однако, этот вариант не является удовлетворительным, т.к. не позволяет придать смысл факторам и получить содержательную интерпретацию выводов, полученных на основе математической модели.

Таким образом, возникает ключевая при выборе численной меры проблема выбора смысла, т.е. по сути единиц измерения, для индикаторов, критериев и факторов.

Требование 2: высокая степень адекватности предметной области.

Требование 3: высокая скорость сходимости при увеличении объема обучающей выборки.

Требование 4: высокая независимость от артефактов.

Что касается конкретной математической формы и процедуры определения числовых значений факторов в выбранных единицах измерения, то обычно применяется метод взвешивания экспертных оценок, при котором эксперты предлагают свои оценки, полученные, как правило, неформализованным путем. При этом сами эксперты также обычно ранжированы по степени их компетентности. Фактически при таком подходе числовые значения факторов является не определяемой, искомой, а исходной величиной. Иначе обстоит дело в факторном анализе, но в этом методе, опять же на основе экспертных оценок важности факторов, требуется предварительно, т.е. перед проведением исследования, принять решение о том, какие факторы исследовать (из-за жестких ограничений на размерность задачи в факторном анализе). Таким образом оба эти подхода реализуемы при относительно небольших размерностях задачи, что с точки зрения достижения целей настоящего исследования, является недостатком этих подходов.

Поэтому самостоятельной и одной из ключевых проблем является обоснованный и удачный выбор математической формы для численной меры индикаторов и факторов.

Эта математическая форма с одной стороны должна удовлетворять предыдущим требованиям, прежде всего требованию 1, а также должна быть процедурно вычислимой, измеримой.

Выбор неметрической меры сходства объектов в семантических пространствах

Существует большое количество мер сходства, из которых можно было бы упомянуть скалярное произведение, ковариацию, корреляцию, евклидово расстояние, расстояние Махалонобиса и другие.

Проблема выбора меры сходства состоит в том, что при выбранной численной мере для координат классов и факторов она должна удовлетворять определенным критериям:

1. Обладать высокой степенью адекватности предметной области, т.е. высокой валидностью, при различных объемах выборки, как при очень малых, так и при средних и очень больших.

2. Иметь обоснованную, четкую, ясную и интуитивно понятную интерпретацию.

3. Быть нетрудоемкой в вычислительном отношении.

4. Обеспечивать корректное вычисление меры сходства для пространств с неортонормированным базисом.

Из требования 4 сразу следует, что Евклидово расстояние d_jk между j-м и k-м классами не подходит в качестве метрики, т.к. оно предполагает ортонормированность пространства:

Известно, что для неортнормированного базиса может быть использовано расстояние Махаланобиса. Однако и одно не удовлетворяет сформулированным требованиям, т.к. дает не расстояние между векторами, а расстояние от некоторого центра масс (центроида).

Поэтому в данном исследовании предложено использовать в качестве меры сходства скалярное произведение векторов, а также нормированное скалярное произведение, т.е. по сути дела корреляцию. При этом координаты векторов должны представлять их проекции на оси координат неортонормированного базиса.

Определение идентификационной и прогностической ценности атрибутов

Не все факторы имеют одинаковую ценность для решения задач идентификации, прогнозирования и управления. Традиционно считается, что факторы имеют одинаковую ценность только в тех случаях (обычно в психологии), когда определить их действительную ценность не представляется возможным по каким-либо причинам.

Для достижения целей, поставленных в данном данном исследовании, необходимо решить проблему определения ценности факторов, т.е. разработать математическую модель и алгоритм, которые допускают программную реализацию и обеспечивают на практике определение идентификационной и прогностической ценности факторов.

Ортонормирование семантических пространств классов и атрибутов (Парето-оптимизация)

Если не все факторы имеют одинаковую ценность для решения задач идентификации, прогнозирования и управления, то возникает проблема исключения из системы факторов тех из них, которые не представляют особой ценности. Удаление малоценных факторов вполне оправданно и целесообразно, т.к. сбор и обработка информации по ним в среднем связана с такими же затратами времени, вычислительных и информационных ресурсов, как и при обработке ценных факторов. В этом состоит идея Парето-оптимизации. Однако это удаление должно осуществляться при вполне определенных граничных условиях, характеризующих результирующую систему:

– адекватность модели;

– количество признаков на класс;

– суммарное количество градаций признаков в описательных шкалах.

В противном случае удаление факторов может отрицательно сказываться на качестве решения задач.

Проблема состоит в том, что факторы вообще говоря коррелируют друг с другом и поэтому их ценность может изменяться при удалении любого из них, в том числе и наименее ценного. Поэтому просто взять и удалить наименее ценные факторы не представляется возможным и необходимо разработать корректный вычислительный алгоритм обеспечивающий решение этой проблемы при заданных граничных условиях.

2.3.4. Структурирование системного анализа до уровня базовых когнитивных операций

На рисунке 11 наглядно прослеживается сходство с когнитивным анализом.

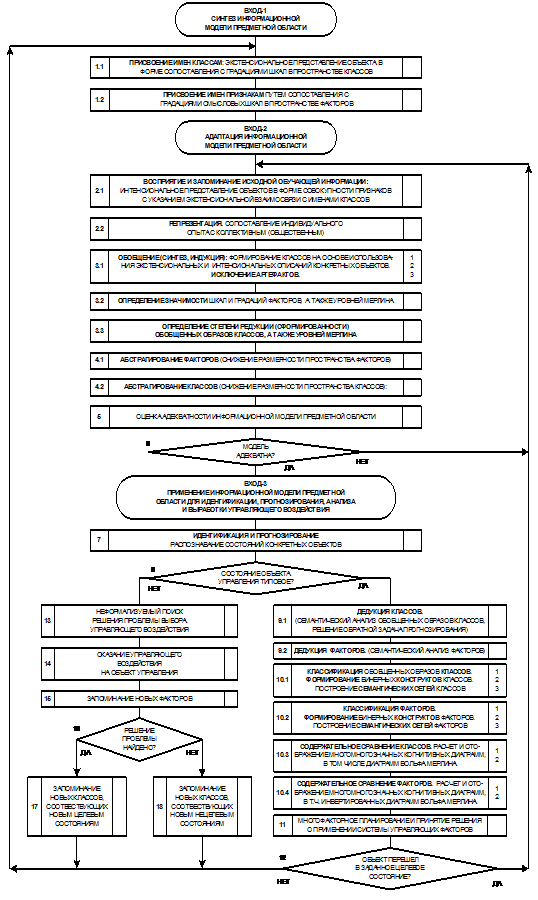
Рисунок 11. Обобщенная схема этапов АСК-анализа

Это естественно, т.к. системный анализ рассматриваться многими авторами, как одна из форм теоретического познания. Учитывая это и с целью создания условий для дальнейшей декомпозиции системного анализа до уровня, достаточного для разработки алгоритмов и программной реализации, предлагается структурировать системный анализ до уровня базовых когнитивных операций.

В порядке обсуждения предлагается рассматривать системный анализ, структурированный до уровня базовых когнитивных операций, как системно-когнитивный анализ (СК-анализ). Необходимо отметить, что впервые понятие "СК-анализ" предложено А.Е.Кибрик и Е.А.Богдановой в работе: "Русская лексема САМ: системно-когнитивный анализ" (Вопросы языкознания, 3, 1995). Однако этими авторами данное понятие было введено в другой предметной области, ими в это понятие не вкладывалось то содержание, которое вкладываем мы, но главное ими не ставилась и не решалась задача автоматизации СК-анализа.

В связи с тем, что СК-анализ структурируется нами до уровня БКОСА, его автоматизация становится решаемой на практике задачей, в отличие от автоматизация непосредственно системного анализа или детализированного системного анализа.

Отсюда органично вытекает 2-й этап решения проблемы – структурирование системного анализа до уровня базовых когнитивных (познавательных) операций.

Учитывая структуру когнитивного конфигуратора (таблица 4) конкретизируем обобщенную схему этапов системного анализа, ориентированного на интеграцию с когнитивными технологиями (рисунок 11), в результате чего получим обобщенную схему этапов АСК-анализа [7]. Предложенная схема представляет собой схему системного анализа, структурированного до уровня базовых когнитивных операций (АСК-анализа). Нумерация блоков на рисунке 11 соответствует этапам СА в таблице 5.

Схема, АСК-анализа, представленная на рисунке 11 определяет место каждой из базовых когнитивной операций в системном анализе.

2.3.5. Описание алгоритмов базовых когнитивных операций системного анализа

В данном разделе приведены 24 детальных алгоритма всех 10 базовых когнитивных операций системного анализа (таблицы 4 и 5), коды которых полностью соответствуют схеме АСК-анализа (рисунок 11).

Таблица 4 – Базовые когнитивные операции
системного анализа (БКОСА)

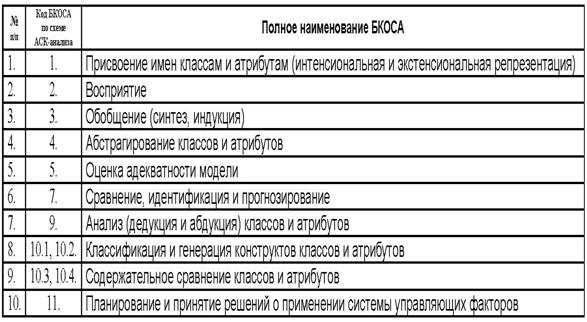
В таблице 5 приведена структура каждой базовой когнитивной операции и даны наименования программных модулей и функций Универсальной когнитивной аналитической системы "Эйдос", реализующих данные когнитивные операции.

Таблица 5 – Соответствие БКОСА программным модулям,
процедурам и функциям системы "Эйдос"

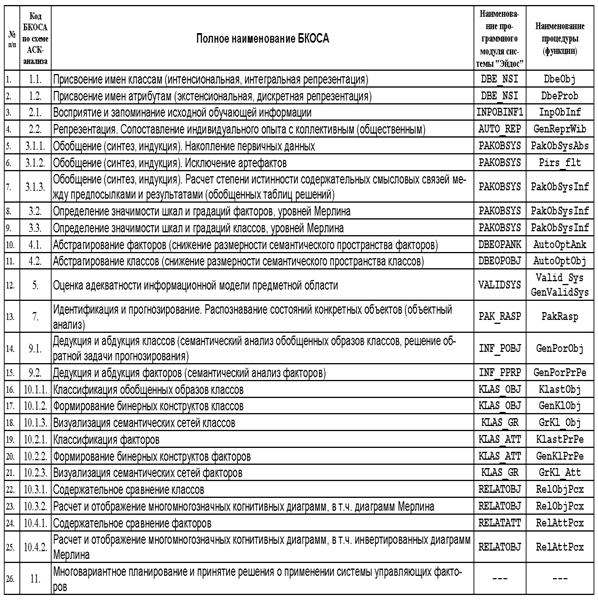
Детальные алгоритмы базовых когнитивных операций системного анализа приведены на рисунках 12-35 [7].

БКОСА-2.1. "Восприятие и запоминание исходной обучающей информации"

В базы данных вводятся двухвекторные (дискретно-интегральные) описания объектов, включающие как их описание на языке признаков, так и принадлежность к определенным классификационным категориям – классам.

БКОСА-2.2. "Репрезентация. Сопоставление индивидуального опыта с коллективным (общественным)"

В ряде случаев, особенно при проведении политологических исследований, необходимо, чтобы исследуемая выборка корректно представляла генеральную совокупность не только в смысле традиционно понимаемой репрезентативности, но и по распределению респондентов по категориям (т.е. структурно) соответствовала ей. Добиться этого путем подбора объектов для исследования затруднительно, т.к. каждый объект может относится одновременно ко многим классификационным категориям. Данный алгоритм обеспечивает выборку из исследуемого множества объектов последовательных подмножеств, наиболее близких по частотному распределению объектов по категориям к заданному распределению. Данная операция называется также "взвешивание или ремонт данных".

БКОСА-3.1.1. "Обобщение (синтез, индукция). Накопление первичных данных"

На основе анализа обучающей выборки обеспечивается накопление в базах данных первичных элементов смысла, т.е. фактов, состоящих в том, что определенный признак встретился у объекта определенного класса.

БКОСА-3.1.2. "Обобщение (синтез, индукция). Исключение артефактов"

При отсутствии статистики невозможно отличить закономерные факты от не вписывающихся в общую складывающуюся картину и искажающих ее, т.е. артефактов. При накоплении же достаточной статистики это возможно и данный алгоритм позволяет выявить и исключить из дальнейшего анализа артефакты. Необходимо отметить, что в результате действия данного алгоритма существенно повышается качество содержательной модели предметной области, в частности ее валидность.

БКОСА-3.1.3. "Обобщение (синтез, индукция). Расчет степени истинности содержательных смысловых связей между предпосылками и результатами (обобщенных таблиц решений)"

Непосредственно на основе матрицы абсолютных частот позволяет вычислить количество информации, содержащейся в факте наблюдения у некоторого объекта определенного признака о том, что данный объект принадлежит к определенной классификационной категории.

БКОСА-3.2. "Определение значимости шкал и градаций факторов, уровней Мерлина"

Рассчитывается среднее количество информации, которое система управления получает о поведении АОУ из фактов о действии тех или иных факторов и их значений. Кроме того, если факторы классифицированы независимым способом по уровням Мерлина, то определяется и значимость этих уровней.

БКОСА-3.3. "Определение значимости шкал и градаций классов, уровней Мерлина"

Рассчитывается среднее количество информации, которое система управления получает из одного признака, если известен класс. Если классы относятся к уровням Мерлина, то определяется и их значимость.

БКОСА-4.1. "Абстрагирование факторов (снижение размерности семантического пространства факторов)"

С помощью метода последовательных приближений (итерационный алгоритм) при заданных граничных условиях снижается размерность пространства атрибутов без существенного уменьшения его объема. Критерий остановки итерационного процесса – достижение одного из граничных условий.

БКОСА-4.2. "Абстрагирование классов (снижение размерности семантического пространства классов)"

С помощью метода последовательных приближений (итерационный алгоритм) при заданных граничных условиях снижается размерность пространства классов без существенного уменьшения его объема. Критерий остановки итерационного процесса – достижение одного из граничных условий.

БКОСА-5. "Оценка адекватности информационной модели предметной области"

Осуществляется идентификация объектов обучающей выборки (классификационный вектор которых уже известен) и затем рассчитывается средневзвешенная погрешность идентификации (интегральная валидность), а также погрешность идентификации с каждым классом (дифференциальная валидность). Если модель имеет приемлемый уровень адекватности, то принимается решение о возможности ее использования в адаптивном режиме на объектах, не входящих в обучающую выборку, но относящихся к генеральной совокупности, по отношению к которой эта выборка репрезентативна. Если же модель недостаточно адекватна, то продолжаются работы по синтезу адекватной модели путем увеличения количества классов и факторов, а также корректировки описаний объектов обучающей выборки и увеличения их количества.

БКОСА-7. "Сравнение, идентификация и прогнозирование. Распознавание состояний конкретных объектов (объектный анализ)"

Рассчитывается количество информации, содержащееся в описании идентифицируемого объекта о его принадлежности к каждому из классов. Все классы ранжируются в порядке убывания количества информации о принадлежности к ним в описании данного объекта. Таким образом, вектор объекта разлагается в ряд по векторам классов. Кроме того все объекты ранжируются в порядке убывания сходства с каждым классом. Таким образом, вектор класса разлагается в ряд по векторам объектов.

БКОСА-9.1. "Дедукция и абдукция классов (семантический анализ обобщенных образов классов, решение обратной задачи прогнозирования)"

Координаты вектора класса (т.е. факторы) ранжируются в порядке убывания их значений. Таким образом, в начале списка оказываются факторы, оказывающие наиболее сильное влияние на переход АОУ в состояние, соответствующее данному классу, а в конце списка – препятствующие этому. Это позволяет выбрать факторы для управляющего воздействия, целью которого является перевод АОУ в состояние, соответствующее данному классу. Механизм фильтрации позволяет "изолированно" рассматривать влияние различных групп факторов: например, факторов, характеризующих объект управления, управляющую систему или окружающую среду.

БКОСА-9.2. "Дедукция и абдукция факторов (семантический анализ факторов)"

Классы ранжируются в порядке убывания влияния данного фактора на переход АОУ в состояния, соответствующие этим классам. В начале списка оказываются состояния, на переход в которые данный фактор оказывает наибольшее влияние, а в конце – на переход в которые данный фактор препятствует. Этот список является развернутой характеристикой смысла фактора.

БКОСА-10.1.1. "Классификация обобщенных образов классов"

Сравниваются вектора классов и формируется диагональная матрица сходства классов, в которой по обоим осям расположены коды классов а в клетках находятся нормированные коэффициенты, численно отражающие степень сходства или различия векторов соответствующих классов.

БКОСА-10.1.2. "Формирование бинерных конструктов классов"

На основе матрицы сходства классов для каждого из них формируется ранжированный список остальных, в котором они расположены в порядке убывания сходства с данным классом. Такие списки представляют собой бинарные конструкты, а их полюса соответствуют кластерам.

БКОСА-10.1.3. "Визуализация семантических сетей классов"

На основе матрицы сходства классов визуализируются ориентированные графы, вершинам которых соответствуют классы, а ребрам – степени их сходства или различия. Знак связи обозначается цветом: красный цвет – сходство, синий – различие, толщина линии соответствует модулю (силе) связи. Необходимо отметить, что для подобных графов в литературе пока нет устоявшегося общепринятого названия: в данном исследовании, как и в предшествующих работах автора, они называются семантическими сетями, в литературе по когнитивному анализу их называют когнитивными картами, а в литературе по когнитивному анализу – когнитивными картами или схемами.

БКОСА-10.2.1. "Классификация факторов"

Сравниваются вектора факторов и формируется диагональная матрица сходства факторов, в которой по обоим осям расположены коды факторов а в клетках находятся нормированные коэффициенты, численно отражающие степень сходства или различия векторов соответствующих факторов.

БКОСА-10.2.2. "Формирование бинерных конструктов факторов"

На основе матрицы сходства факторов для каждого из них формируется ранжированный список остальных, в котором они расположены в порядке убывания сходства с данным фактором. Такие списки представляют собой бинарные конструкты, а их полюса соответствуют кластерам.

БКОСА-10.2.3. "Визуализация семантических сетей факторов"

На основе матрицы сходства факторов визуализируются ориентированные графы, вершинам которых соответствуют заданные факторы, а ребрам – степени их сходства или различия. Знак связи обозначается цветом: красный цвет – сходство, синий – различие, толщина линии соответствует модулю (силе) связи.

БКОСА-10.3.1. "Содержательное сравнение классов"

Каждая связь между классами в семантической сети, отражающая степень их сходства или различия, имеет определенную структуру, описанную в разделе 3.2.3 исследования. Эта структура включает ряд элементов, каждый из которых соответствует одному слагаемому обобщенной меры сходства векторов классов.

БКОСА-10.3.2. "Расчет и отображение многомногозначных когнитивных диаграмм, в т.ч. диаграмм Вольфа Мерлина"

Из всех составляющих связи между классами выбираются 8 наиболее сильных и отображаются в форме линий, цвет которых означает знак, а толщина – модуль силы связи. Классы изображаются в форме наиболее значимых фрагментов их информационных портретов. При этом учитываются корреляции между факторами.

БКОСА-10.4.1. "Содержательное сравнение факторов"

Каждая связь между факторами в семантической сети, отражающая степень их сходства или различия, имеет определенную структуру. Эта структура включает ряд элементов, каждый из которых соответствует одному слагаемому обобщенной меры сходства векторов факторов.

БКОСА-10.4.2. "Расчет и отображение многомногозначных когнитивных диаграмм, в т.ч. инвертированных диаграмм Мерлина"

Из всех составляющих связи между факторами выбираются 16 наиболее сильных и отображаются в форме линий, цвет которых означает знак, а толщина – модуль силы связи. Факторы отображаются в форме наиболее значимых фрагментов их семантических портретов. При этом учитываются корреляции между классами.

БКОСА-11. "Многовариантное планирование и принятие решения о применении системы управляющих факторов"

Выполняется в несколько этапов:

1) выполняется прогноз развития АОУ в условиях отсутствия управляющих воздействий, т.е. реализуется БКОСА-7 ("движение по инерции");

2) если в соответствии с прогнозом по п.1 АОУ достигает заданного целевого состояния (т.е. прогноз "удовлетворительный"), то планирование прекращается (переход на п.6); иначе – выполняется п.3;

3) путем решения обратной задачи прогнозирования (БКОСА-9.1) определяется набор факторов, оптимальный для перевода АОУ в заданное целевое состояние;

4) если все эти факторы есть возможность использовать для управления, то на этом планирование прекращается (переход п.6); иначе переход на п.5;

5) используя результаты кластерно-конструктивного анализа факторов (БКОСА 10.2.1, 10.2.2, 10.2.3) последовательно ищется замена для факторов, которые нет возможности использовать и после каждой замены выполняется прогнозирование (БКОСА-7); если результаты прогнозирования удовлетворительные – окончание планирования (переход на п.6); иначе принятие решения о невозможности выработки корректного управляющего воздействия;

6) окончание планирования.

2.3.6. Детальные алгоритмы БКОСА

Рисунок 12. Алгоритм БКОСА-2.1. "Восприятие и запоминание
исходной обучающей информации"

Рисунок 13. Алгоритм БКОСА-2.2. "Репрезентация.
Сопоставление индивидуального опыта с коллективным"

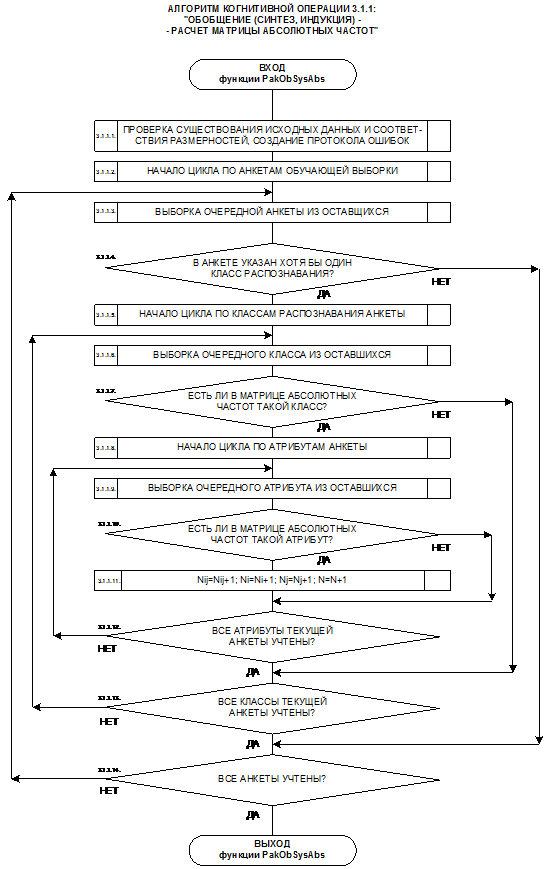
Рисунок 14. Алгоритм БКОСА-3.1.1. "Обобщение (синтез, индукция).
Накопление первичных данных"

Рисунок 15. Алгоритм БКОСА-3.1.2. "Обобщение (синтез, индукция). Исключение артефактов"

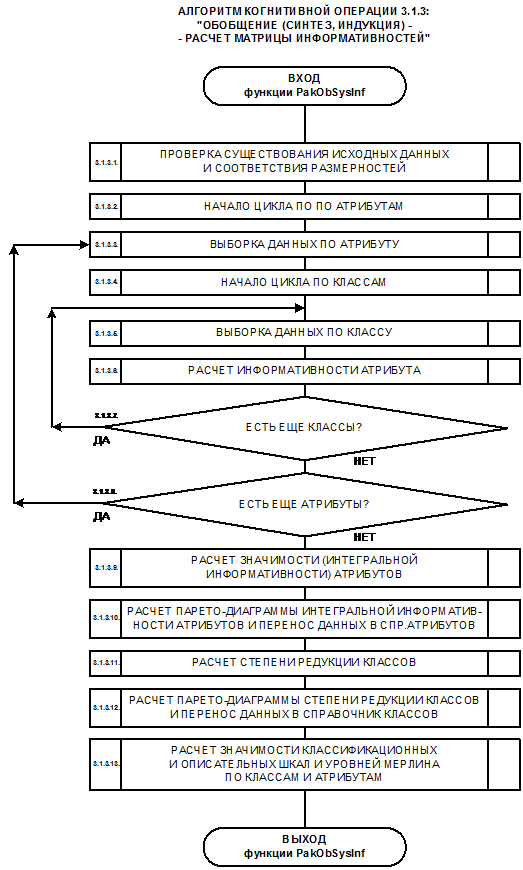
Рисунок 16. Алгоритм БКОСА-3.1.3. "Обобщение (синтез, индукция). Расчет степени истинности содержательных смысловых связей между предпосылками и результатами (обобщенных таблиц решений)"

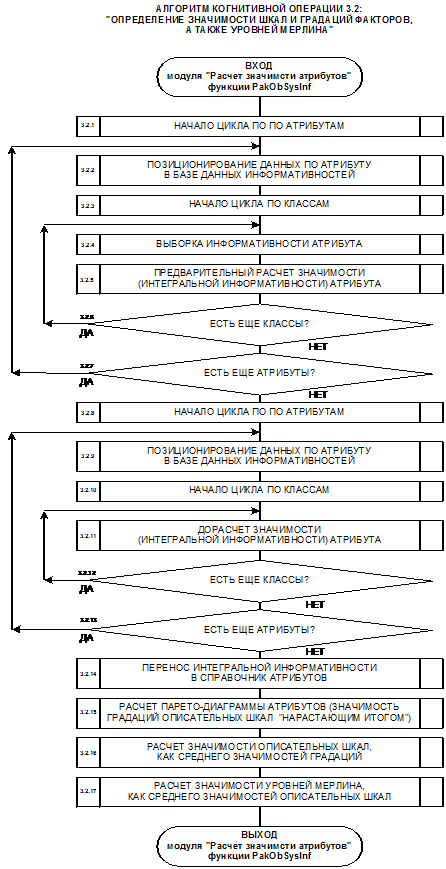
Рисунок 17. Алгоритм БКОСА-3.2. "Определение значимости шкал
и градаций факторов, уровней Мерлина"

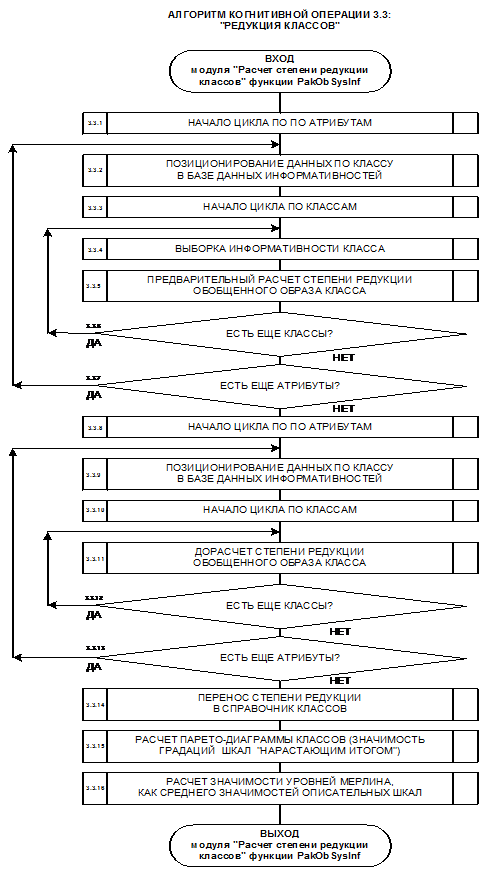
Рисунок 18. Алгоритм БКОСА-3.3. "Определение значимости шкал
и градаций классов, уровней Мерлина"

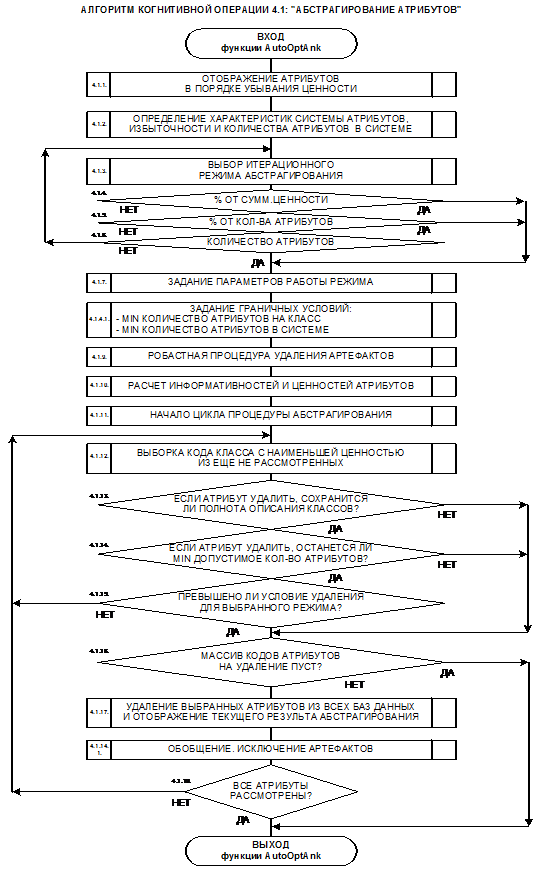
Рисунок 19. Алгоритм БКОСА-4.1. "Абстрагирование факторов
(снижение размерности семантического пространства факторов)"

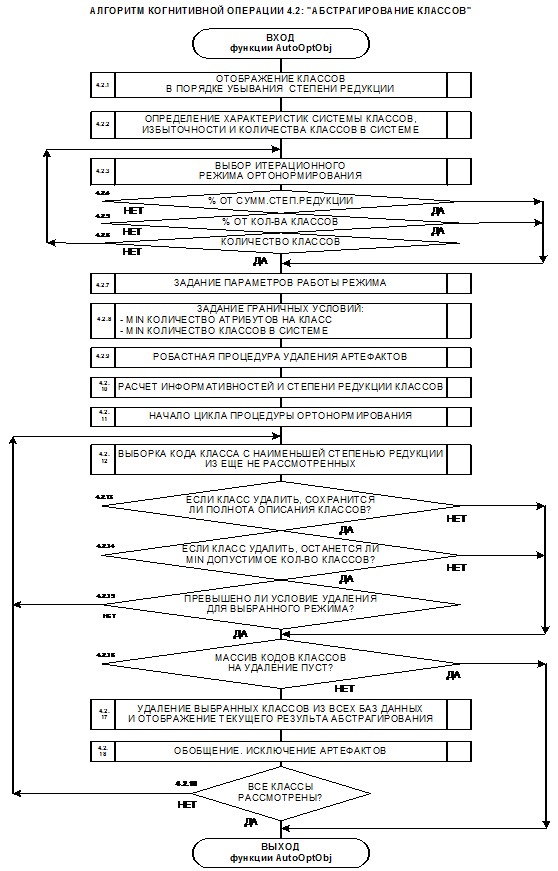
Рисунок 20. Алгоритм БКОСА-4.2. "Абстрагирование классов
(снижение размерности семантического пространства классов)"

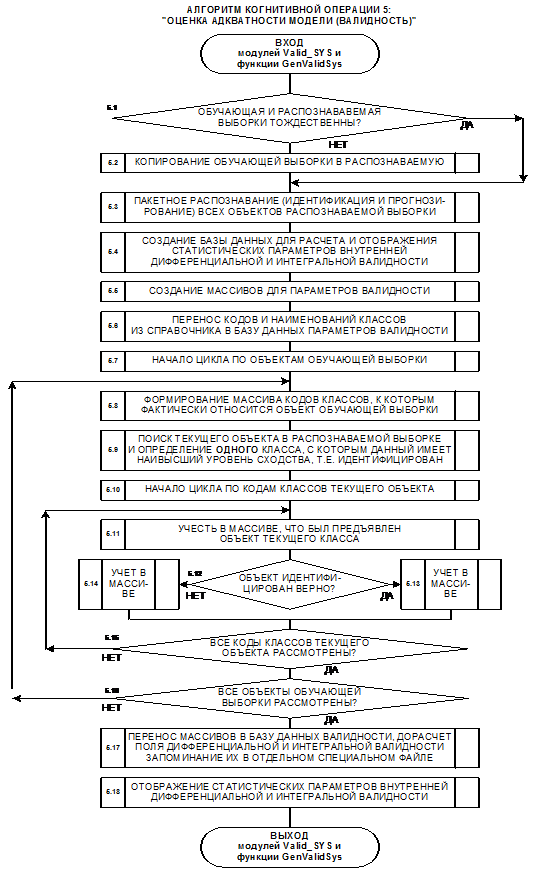
Рисунок 21. Алгоритм БКОСА-5. "Оценка адекватности семантической
информационной модели предметной области"

Рисунок 22. Алгоритм БКОСА-7. "Идентификация и прогнозирование.
Распознавание состояний конкретных объектов (объектный анализ)"

Рисунок 23. Алгоритм БКОСА-9.1. "Дедукция и абдукция классов
(семантический анализ обобщенных образов классов,
решение обратной задачи прогнозирования)"

Рисунок 24. Алгоритм БКОСА-9.2. "Дедукция и абдукция факторов
(семантический анализ факторов)"

Рисунок 25. Алгоритм БКОСА-10.1.1.
"Классификация обобщенных образов классов"

Рисунок 26. Алгоритм БКОСА-10.1.2. "Формирование бинерных
конструктов классов"

Рисунок 27. Алгоритм БКОСА-10.1.3. "Визуализация семантических
сетей классов" (когнитивная графика)

Рисунок 28. Алгоритм БКОСА10.2.1. "Классификация факторов"

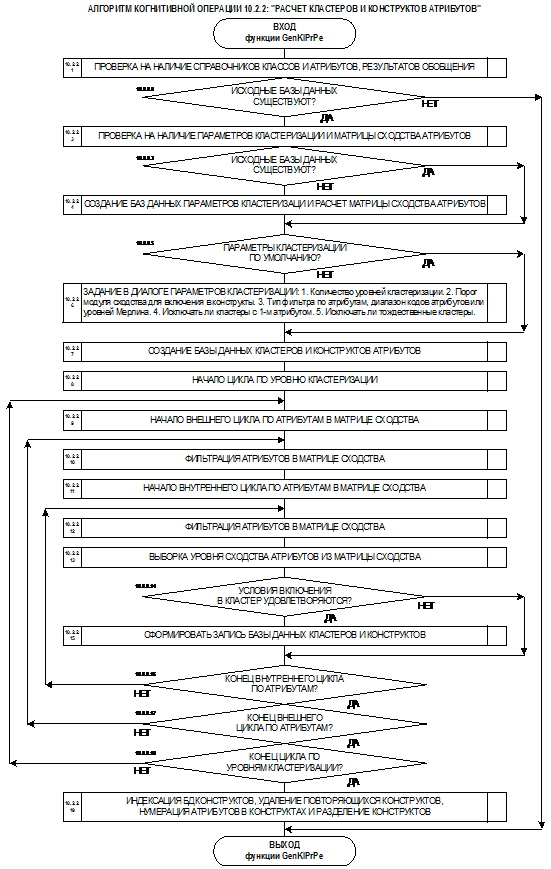
Рисунок 29. Алгоритм БКОСА-10.2.2. "Формирование бинерных
конструктов факторов"

Рисунок 30. Алгоритм БКОСА-10.2.3. "Визуализация семантических
сетей факторов" (когнитивная графика)

Рисунок 31. Алгоритм БКОСА-10.3.1. "Содержательное сравнение классов"

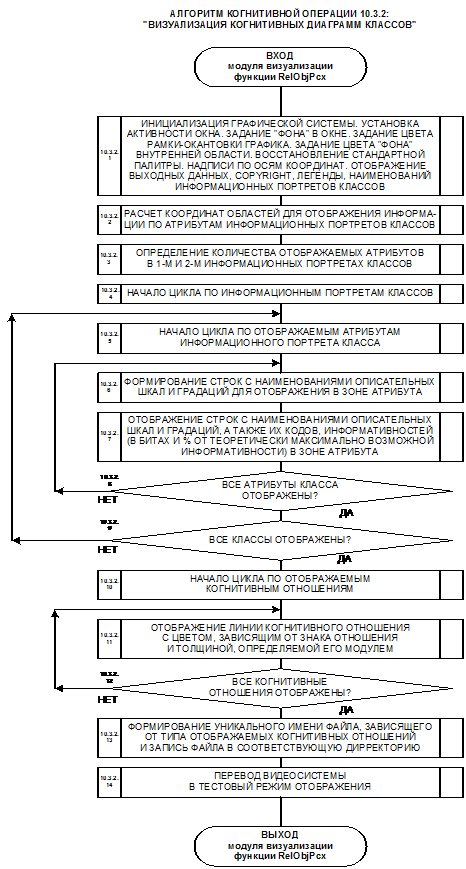
Рисунок 32. Алгоритм БКОСА-10.3.2. "Расчет и отображение
много-многозначных когнитивных диаграмм, в т.ч. диаграмм Мерлина"
(когнитивная графика)

Рисунок 33. Алгоритм БКОСА-10.4.1. "Содержательное сравнение факторов"

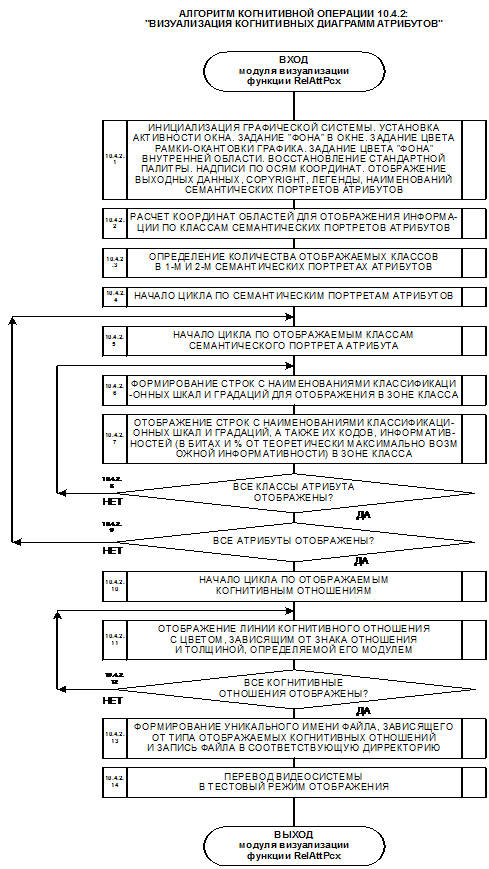
Рисунок 34. Алгоритм БКОСА-10.4.2. "Расчет и отображение много-многозначных когнитивных диаграмм, в т.ч. инвертированных
диаграмм Мерлина" (когнитивная графика)

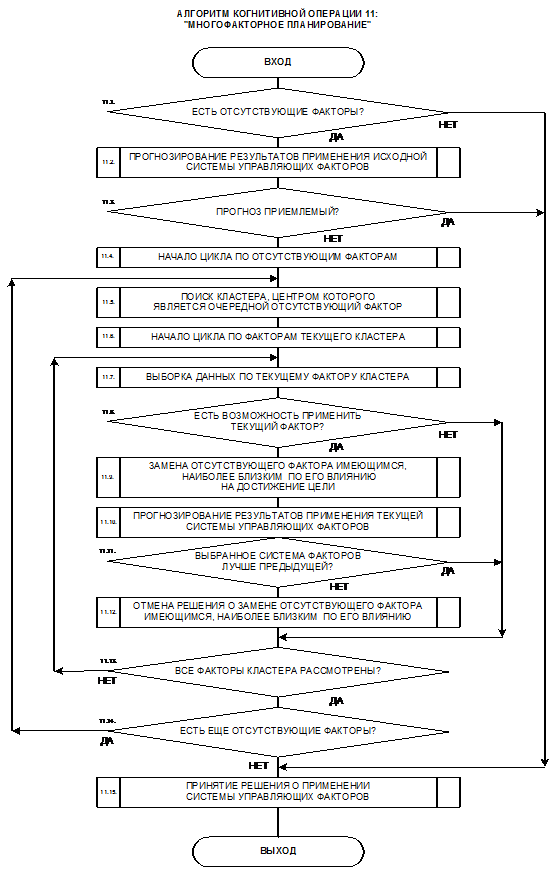
Рисунок 35. Алгоритм БКОСА-11. "Многовариантное планирование
и принятие решения о применении системы управляющих факторов"

Учитывая, что когнитивные диаграммы представляют собой детализацию семантических сетей, давая расшифровку структуры вершин и семантической сети и связей между ними, предлагается понятие "Семантическая когнитивная сеть", представляющая собой систему когнитивных диаграмм, объединенных в макроструктуру, соответствующую структуре семантической сети.

2.4. Системная теория информации – математическая модель системы «Эйдос»

В данном разделе на основе работы [7] кратко описана математическая сущность системной теории информации (СТИ), являющейся математической моделью системно-когнитивного анализа (СК-анализ) реализуемой в его программном инструментарии – универсальной когнитивной аналитической системе "Эйдос".

В работах [69, 71, 74] и других предложена и развита программная идея системного обобщения математики путем тотальной замены понятия множества на более общее и содержательное понятие системы и тщательное прослеживания всех последствий этого во всех понятиях математики, основанных на понятии множества. Частично эта идея была реализована при разработке автоматизированного системно-когнитивного анализа (АСК-анализа) [7], математическая модель которого основана на системном обобщении формул для количества информации Найквиста-Хартли и Харкевича, в результате чего удалось объединить семантическую теорию информации Харкевича с теорией информации Шеннона. Полученная в результате этого обобщенная теория названа системной теорией информации (СТИ). Системное обобщение понятия функциональной зависимости рассматривается в работах [48, 94, 106, 117б 121, 125, 126], в них же вводятся новые научные понятия и соответствующие термины: "когнитивные функции" и "когнитивные числа". Различные аспекты СТИ рассмотрены в работах [3-190]. Таким образом, существует много работ, в том числе монографий и учебных пособий, в которых изложена системная теория информации. Однако, как раз то, что этих работ много и они довольно объемны не вдохновляет потенциальных читателей.

Поэтому в данном разделе ставится цель описать математическую суть системной теории информации на столько кратко, на сколько это вообще возможно. Своеобразной "ценой" за это является то, что пришлось пожертвовать подробной смысловой интерпретацией полученных математических выражений, за которой мы отсылаем к уже упомянутым работам.

Итак, классическая формула Хартли имеет вид:

( 1 )

Будем искать ее системное обобщение в виде:

( 2 )

где:

W – количество элементов в множестве.

j – коэффициент эмерджентности, названный автором в честь Хартли коэффициентом эмерджентности Хартли.

Примем, что системное обобщение формулы Хартли имеет вид:

( 3 )

^где:

^{– количество подсистем и m элементов;}

m – сложность подсистем;

M – максимальная сложность подсистем.

^{Так как , то при M=1 система переходит в множество и выражение (3) приобретает вид (1), т.е. для него выполняется принцип соответствия, являющийся обязательным для более общей теории.}

Учитывая, что при M=W:

( 4 )

в этом случае получаем:

( 5 )

Выражение (5) дает приближенную оценку максимального количества информации в элементе системы. Из выражения (5) видно, что при увеличении числа элементов W количество информации I быстро стремится к W (6) и уже при W>4 погрешность выражения (5) не превышает 1%:

( 6 )

Приравняв правые части выражений (2) и (3):

( 7 )

получим выражение для коэффициента эмерджентности Хартли:

( 8 )

Смысл этого коэффициента раскрыт в работе [7] и ряде других. Здесь отметим лишь, что при M®1 когда система асимптотически переходит в множество j®1 и (2) ® (1), как и должно быть согласно принципу соответствия.

С учетом (8) выражение (2) примет вид:

( 9 )

или при M=W и больших W, учитывая (4 и 5):

( 10 )

Выражение (9) и представляет собой искомое системное обобщение классической формулы Хартли, а выражение (10) – его достаточно хорошее приближение при большом количестве элементов в системе W.

Классическая формула А.Харкевича имеет вид:

( 11 )

где: – P_ij – условная вероятность перехода объекта в j-е состояние при условии действия на него i-го значения фактора;

– P_j – безусловная вероятность перехода объекта в j-е состояние (вероятность самопроизвольного перехода или вероятность перехода, посчитанная по всей выборке, т.е. при действии любого значения фактора).

Придадим выражению (11) следующий эквивалентный вид, который и будем использовать ниже:

( 12 )

где: – индекс i обозначает признак (значение фактора): 1£ i £ M;

– индекс j обозначает состояние объекта или класс: 1£ j £ W;

– P_ij – условная вероятность наблюдения i-го значения фактора у объектов в j-го класса;

– P_i – безусловная вероятность наблюдения i-го значения фактора по всей выборке.

Из (12) видно, что формула Харкевича для семантической меры информации по сути является логарифмом от формулы Байеса для апостериорной вероятности (отношение условной вероятности к безусловной). Вопрос об эквивалентности выражений (11) и (12) рассмотрим позднее.

Известно, что классическая формула Шеннона для количества информации для неравновероятных событий преобразуется в формулу Хартли при условии, что события равновероятны, т.е. удовлетворяет фундаментальному принципу соответствия. Поэтому теория информации Шеннона справедливо считается обобщением теории Хартли для неравновероятных событий. Однако, выражения (11) и (12) при подстановке в них реальных численных значений вероятностей P_ij, P_j и P_i не дает количества информации в битах, т.е. для этого выражения не выполняется принцип соответствия, обязательный для более общих теорий. Возможно, в этом состоит причина довольно сдержанного, а иногда и скептического отношения специалистов по теории информации Шеннона к семантической теории информации Харкевича.

Причину этого мы видим в том, что в выражениях (11) и (12) отсутствуют глобальные параметры конкретной модели W и M, т.е. в том, что А.Харкевич в своем выражении для количества информации не ввел зависимости от мощности пространства будущих состояний объекта W и количества значений факторов M, обуславливающих переход объекта в эти состояния.

Поставим задачу получить такое обобщение формулы Харкевича, которое бы удовлетворяло тому же самому принципу соответствия, что и формула Шеннона, т.е. преобразовывалось в формулу Хартли в предельном детерминистском равновероятном случае, когда каждому классу (состоянию объекта) соответствует один признак (значение фактора), и каждому признаку – один класс, и эти классы (а, значит и признаки), равновероятны, и при этом каждый фактор однозначно, т.е. детерминистским образом определяет переход объекта в определенное состояние, соответствующее классу.

Будем искать это обобщение (12) в виде:

( 13 )

Найдем такое выражение для коэффициента Y, названого нами в честь А.Харкевича "коэффициентом эмерджентности Харкевича", которое обеспечивает выполнение для выражения (13) принципа соответствия с классической формулой Хартли (1) и ее системным обобщением (2 и 3) в равновероятном детерминистском случае.

Для этого нам потребуется выразить вероятности P_ij, P_j и P_i через частоты наблюдения признаков по классам (таблица 6). В таблице 6 рамкой обведена область значений, переменные определены ранее.

Таблица 6 – Матрица абсолютных частот

		Классы					Сумма
		1	...	j	...	W
Значения факторов	1
	...
	i
	...
	M
Суммарное количество признаков
Суммарное количество объектов обучающей выборки							N

Алгоритм формирования матрицы абсолютных частот.

Объекты обучающей выборки описываются векторами (массивами) имеющихся у них признаков:

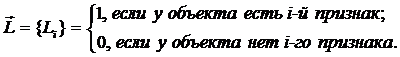
Первоначально в матрице абсолютных частот все значения равны нулю. Затем организуется цикл по объектам обучающей выборки. Если предъявленного объекта относящегося к j-му классу есть i-й признак, то:

Здесь можно провести очень интересную и важную аналогию между способом формирования матрицы абсолютных частот и работой многоканальной системы выделения полезного сигнала из шума. Представим себе, что все объекты, предъявляемые для формирования обобщенного образа некоторого класса в действительности являются различными реализациями одного объекта – "Эйдоса" (в смысле Платона), по-разному зашумленного различными случайными обстоятельствами. И наша задача состоит в том, чтобы подавить этот шум и выделить из него то общее и существенное, что отличает объекты данного класса от объектов других классов. Учитывая, что шум чаще всего является "белым" и имеет свойство при суммировании с самим собой стремиться к нулю, а сигнал при этом наоборот возрастает пропорционально количеству слагаемых, то увеличение объема обучающей выборки приводит ко все лучшему отношению сигнал/шум в матрице абсолютных частот, т.е. к выделению полезной информации из шума. Примерно так мы начинаем постепенно понимать смысл фразы, которую мы сразу не расслышали по телефону и несколько раз переспрашивали. При этом в повторах шум не позволяет понять то одну, то другую часть фразы, но в конце-концов за счет использования памяти и интеллектуальной обработки информации мы понимаем ее всю. Так и объекты, описанные признаками, можно рассматривать как зашумленные фразы, несущие нам информацию об обобщенных образах классов: "Эйдосах", к которым они относятся. И эту информацию мы выделяем из шума при синтезе модели.

Для выражения (11):

( 14 )

Для выражений (12) и (13):

( 15 )

Для выражений (11), (12) и (13):

( 16 )

В (16) использованы обозначения:

N_ij – суммарное количество наблюдений в исследуемой выборке факта: "действовало i-е значение фактора и объект перешел в j-е состояние";

N_j – суммарное количество встреч различных факторов у объектов, перешедших в j-е состояние;

N_i – суммарное количество встреч i-го фактора у всех объектов исследуемой выборки;

N – суммарное количество встреч различных факторов у всех объектов исследуемой выборки.

Формирование матрицы условных и безусловных вероятностей .

На основе анализа матрицы частот (таблица 6) классы можно сравнивать по наблюдаемым частотам признаков только в том случае, если количество объектов по всем классам одинаково, как и суммарное количество признаков по классам. Если же они отличаются, то корректно сравнивать классы можно только по условным и безусловным вероятностям наблюдения признаков, посчитанных на основе матрицы частот (таблица 6) в соответствии с выражениями (14) и (15), в результате чего получается матрица условных и безусловных процентных распределений (таблица 7).

При расчете матрицы условных и безусловных вероятностей N_j из таблицы 6 могут браться либо из предпоследней, либо из последней строки. В 1-м случае N_j представляет собой "Суммарное количество признаков у всех объектов, использованных для формирования обобщенного образа j-го класса", а во 2-м случае, это "Суммарное количество объектов обучающей выборки, использованных для формирования обобщенного образа j-го класса", соответственно получаем различные, хотя и очень сходные семантические информационные модели, которые мы называем СИМ-1 и СИМ-2. Оба этих вида моделей поддерживаются системой "Эйдос".

Таблица 7 – Матрица условных и безусловных вероятностей

		Классы					Безусловная вероятность признака
		1	...	j	...	W
Значения факторов	1
	...
	i
	...
	M
Безусловная вероятность класса

Эквивалентность выражений (11) и (12) устанавливается, если подставить в них выражения вероятности P_ij, P_j и P_i через частоты наблюдения признаков по классам из (14), (15) и (16). В обоих случаях из выражений (11) и (12) получается одно и тоже выражение (17):

( 17 )

А из (13) выражение (18), с которым мы и будем далее работать.

( 18 )

При взаимно-однозначном соответствии классов и признаков в равновероятном детерминистском случае имеем (таблица 8):

Таблица 8 – Матрица частот в равновероятном
детерминистском случае

		Классы					Сумма
		1	...	j	...	W
Значения факторов	1	1					1
	...		1				1
	i			1			1
	...				1		1
	M					1	1
Сумма		1	1	1	1	1	N

В этом случае к каждому классу относится один объект, имеющий единственный признак. Откуда получаем для всех i и j (19):

( 19 )

Таким образом, обобщенная формула А.Харкевича (18) с учетом (19) в этом случае приобретает вид:

( 20 )

откуда:

( 21 )

или, учитывая выражение для коэффициента эмерджентности Хартли (8):

( 22 )

Подставив коэффициент эмерджентности А.Харкевича (21) в выражение (18), получим:

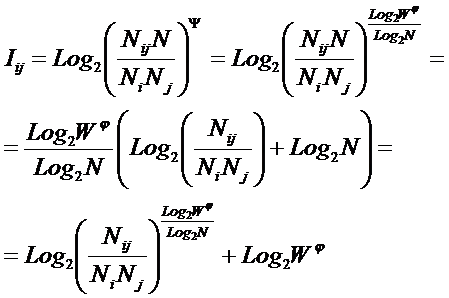
или окончательно:

( 23 )

Отметим, что 1-я задача получения системного обобщения формул Хартли и Харкевича и 2-я задача получения такого обобщения формулы Харкевича, которая удовлетворяет принципу соответствия с формулой Хартли – это две разные задачи. 1-я задача является более общей и при ее решении, которое приведено выше, автоматически решается и 2-я задача, которая является, таким образом, частным случаем 1-й.

Однако, представляет самостоятельный интерес и частный случай, в результате которого получается формула Харкевича удовлетворяющая в равновероятном детерминистском случае принципу соответствия с классической формулой Хартли (1), а не с ее системным обобщением (2) и (3). Ясно, что эта формула получается из (23) при j=1.

( 24 )

Из выражений (21) и (22) видно, что в этом частном случае, т.е. когда система эквивалентна множеству (M=1), коэффициент эмерджентности А.Харкевича приобретает вид:

( 25 )

На практике для численных расчетов на удобнее пользоваться не выражениями (23) или (24), а формулой (26), которая получается непосредственно из (18) после подстановки в него выражения (25):

( 26 )

В классическом анализе Шеннона идет речь лишь о передаче символов по одному информационному каналу от одного источника к одному приемнику. Его интересует прежде всего передача самого сообщения.

В данном разделе ставится другая задача: идентифицировать или распознать информационный источник по сообщению от него. Поэтому метод Шеннона был обобщен путем учета в математической модели возможности существования многих источников информации, о которых к приемнику по зашумленному каналу связи приходят не отдельные символы-признаки, а сообщения, состоящие из последовательностей символов (признаков) любой длины.

Следовательно, ставится задача идентификации информационного источника по сообщению от него, полученному приемником по зашумленному каналу. Метод, являющийся обобщением метода К.Шеннона, позволяет применить классическую теорию информации для построения моделей систем распознавания образов и принятия решений, ориентированных на применение для синтеза адаптивных АСУ сложными объектами.

Для решения поставленной задачи необходимо вычислять не средние информационные характеристики, как в теории Шеннона, а количество информации, содержащееся в конкретном i-м признаке (символе) о том, что он пришел от данного j-го источника информации. Это позволит определить и суммарное количество информации в сообщении о каждом информационном источнике, что дает интегральный критерий для идентификации или прогнозирования состояния объекта.

Логично предположить, что среднее количество информации, содержащейся в системе признаков о системе классов

( 27 )

является ничем иным, как усреднением (с учетом условной вероятности наблюдения) "индивидуальных количеств информации", которые содержатся в конкретных признаках о конкретных классах (источниках), т.е.:

( 28 )

Это выражение определяет так называемую "плотность информации", т.е. количество информации, которое содержится в одном отдельно взятом факте наблюдения i-го символа (признака) на приемнике о том, что этот символ (признак) послан j-м источником.

Если в сообщении содержится M символов, то суммарное количество информации о принадлежности данного сообщения j-му информационному источнику (классу) составляет:

( 29 )

Необходимо отметить, что применение сложения в выражении (29) является вполне корректным и оправданным, так как информация с самого начала вводилась как аддитивная величина, для которой операция сложения является корректной.

Преобразуем выражение (29) к виду, более удобному для применения на практике для численных расчетов. Для этого традиционным для теории информации Шеннона способом выразим вероятности встреч признаков через частоты их наблюдения:

( 30 )

Подставив (30) в (29), получим:

( 31 )

Минус в выражении (31) в дальнейшем можно опустить, т.к. он не несет существенной смысловой нагрузки.

Если ранжировать классы в порядке убывания суммарного количества информации о принадлежности к ним, содержащейся в данном сообщении (т.е. описании объекта), и выбирать первый из них, т.е. тот, о котором в сообщении содержится наибольшее количество информации, то мы получим обоснованную статистическую процедуру, основанную на классической теории информации, оптимальность которой доказывается в фундаментальной лемме Неймана-Пирсона [7].

Подставим значения вероятностей из (30) в (28) и получим выражением для плотности информации Шеннона, выраженное не через вероятности, а через частоты наблюдения символов, которые рассматриваются как признаки объектов, т.е. количество информации, содержащееся в отдельном i-м признаке о том, что другом конце канала связи находится j-й объект (32):

( 32 )

Сравнивая выражения (23) и (32) видим, что в системном обобщении формулы Харкевича 1-е слагаемое практически тождественно выражению Шеннона для плотности информации, а 2-е слагаемое представляющем собой плотность информации по Хартли.

Различия состоят в том, что в выражении (23) это слагаемое возведено в степень, имеющую смысл коэффициента эмерджентности Харкевича. Поэтому вполне оправданным называть это слагаемое не коэффициентом эмерджентности Харкевича, а коэффициентом эмерджентности Шеннона-Харкевича. Необходимо отметить также, что значения частот в этих формулах связаны с вероятностями несколько различным образом (выражения 14-16 и 30).

Из этого следует также, что полученное выражение (23) представляет собой нелинейную суперпозицию выражений для плотности информации Шеннона и Хартли, и, таким образом, является обобщающим выражением для плотности информации, которое при различных условиях асимптотически переходит в классические выражения Хартли и Харкевича, а от выражения Шеннона отличается лишь константой, т.е. 2-м слагаемым, характеризующим мощность множества состояний объекта в модели.

Это позволяет нам обоснованно высказать гипотезу о том, что системная теория информации (СТИ), базирующаяся на выражении (23) для плотности информации, является более общей, чем теории Хартли, Шеннона и Харкевича и асимптотически связана с ними через принцип соответствия (рисунок 36).

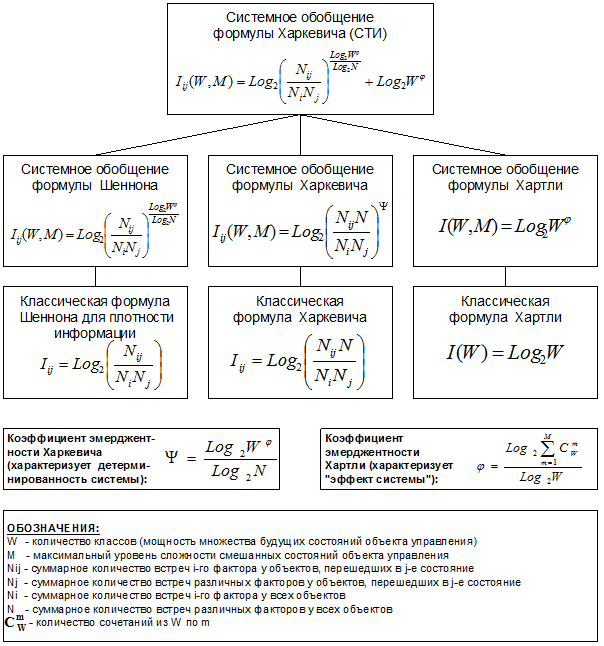
Рисунок 36. Генезис системной (эмерджентной)
теории информации [7]

Взаимосвязь системной меры целесообразности информации со статистикой c² и новая мера уровня системности предметной области

Статистика c² представляет собой сумму вероятностей совместного наблюдения признаков и объектов по всей корреляционной матрице или определенным ее подматрицам (т.е. сумму относительных отклонений частот совместного наблюдения признаков и объектов от среднего):

,

( 33 )

где

N_ij – фактическое количество встреч i-го признака у объектов j-го класса;

t – ожидаемое количество встреч i-го признака у объектов j-го класса (34).

.

( 34 )

Отметим, что статистика c² математически связана с количеством информации в системе признаков о классе распознавания в соответствии с системным обобщением формулы Харкевича для плотности информации (18):

,

( 35 )

а именно, из (34) и (35) получаем:

.

( 36 )

Из (36) очевидно:

.

( 37 )

Сравнивая выражения (33) и (37), видим, что числитель в выражении (33) под знаком суммы отличается от выражения (37) только тем, что в выражении (37) вместо значений N_ij и t взяты их логарифмы. Так как логарифм является монотонно возрастающей функцией аргумента, то введение логарифма не меняет общего характера поведения функции.

Фактически это означает, что:

.

( 38 )

Из изложенного следует интерпретация системной меры информации (35) с учетом статистики c² (33): если фактическая вероятность наблюдения i-го признака при предъявлении объекта j-го класса равна ожидаемой (средней), то наблюдение этого признака не несет никакой информации о принадлежности объекта к данному классу. Если она выше средней, то это свидетельствует в пользу того, что предъявлен объект данного класса, если ниже – то другого.

Поэтому наличие статистической связи (информации) между признаками и классами распознавания, т.е. отличие вероятностей их совместных наблюдений от предсказываемого в соответствии со случайным нормальным распределением, приводит к увеличению фактической статистики c² по сравнению с теоретической величиной.

Из этого следует возможность использования в качестве количественной меры степени выраженности закономерностей в предметной области не матрицы абсолютных частот и меры c², а новой меры H, основанной на матрице информативностей и системном обобщении формулы Харкевича для количества информации:

,

( 39 )

где

– средняя информативность признаков по матрице информативностей.

Меру H в выражении (39) предлагается назвать обобщенным критерием степени сформированности модели Харкевича.

Значение данной меры показывает среднее отличие количества информации в факторах о будущих состояниях активного объекта управления от среднего количества информации в факторе (которое при больших выборках близко к 0). По своей математической форме эта мера сходна с мерами для значимости (интегральной информативности) факторов и степени сформированности образов классов и коррелирует с объемом неортонормированного семантического информационного пространства классов и семантического информационного пространства атрибутов.

Вышеописанная математическая модель обеспечивает инвариантность результатов ее синтеза относительно следующих параметров обучающей выборки: суммарное количество и порядок ввода анкет обучающей выборки; количество анкет обучающей выборки по каждому классу распознавания; суммарное количество признаков во всех анкетах обучающей выборки; суммарное количество признаков по классам распознавания; количество признаков и их порядок в отдельных анкетах обучающей выборки. Это обеспечивает высокую степень качества решения задач распознавания на неполных и разнородных (в вышеперечисленных аспектах) данных как обучающей, так и распознаваемой выборки, т.е. при таких статистических характеристиках потоков этих данных, которые чаще всего и встречается на практике и которыми невозможно или очень сложно управлять.

Получение матрицы знаний (информативностей).

На основе анализа матрицы условных и безусловных вероятностей (таблица 7) наблюдений признаков по классам и всей выборке можно сравнивать признаки друг с другом по их роли для сравнения классов друг с другом и конкретных объектов с обобщенными классами. При этом существует 3 основных группы признаков:

Группа 1-я. Которые в одном классе встречаются, а в других нет. Это детерминистские признаки, обнаружение такого признака у объекта однозначно определяет его принадлежность к соответствующему классу.

Группа 2-я. Которые в одном классе встречаются чаще, чем в других. Это статистические признаки, обнаружение такого признака у объекта несет некоторую информацию о его принадлежности к соответствующему классу.

Группа 3-я. Которые в разных классах встречаются одной и той же вероятностью. Это признаки, обнаружение которых у объекта не несет никакой информации о его принадлежности к тем или иным классам.

Таким образом, мы видим, что если используя таблицу 7 анализировать условные вероятности (или процентные распределения) признаков по классам, то можно вынести правдоподобные суждения о принадлежности объектов, обладающих этими признакам к тем или иным классам.

Однако в таком методе сравнения есть по крайней мере два существенных недостатка:

1. Для того, чтобы отнести признак к одной из вышеперечисленных групп необходимо сравнивать вероятности его наблюдения по классам, т.е. каждый раз при таком сравнении выполнять соответствующую необходимую для этого работу.

2. При отнесении признака ко 2-й группе этого самого по себе еще недостаточно для его использования с целью идентификации объекта, а необходимо еще оценить количество информации, которое содержится в факте обнаружения у объекта этого признака о принадлежности этого объекта к каждому из классов, а для этого необходим соответствующий математический и численный метод.

Что касается 1-го недостатка, то о нем можно сказать, что для реальных задач большой размерности выполнение этого сравнения вручную практически невозможно, а значит тем более невозможно и использование результатов этого сравнения для решения задач идентификации, прогнозирования и поддержки принятия решений, а тем более для исследования предметной области путем исследования ее модели. Все это обусловлено тем, что результат сравнения вероятностей встречи признака по классам не представляется при ручной обработке в количественной форме некоторого одного числа: частного критерия, величина и знак которого отражали бы результат такого сравнения.

2-й недостаток преодолевается методом, который предложен А.Харкевичем в выражениях (11) и (12) и уточнен нами в системном обобщении этих выражений (18). В этом методе предложено сравнивать не условные вероятности наблюдения признаков по различным классам друг с другом, а условную вероятность наблюдения признака по классу с безусловной вероятностью его наблюдения по всей выборке.

Это предложение по своей сути полностью соответствует известному статистическому методу отклонений от средних и нормативному подходу, когда в качестве базы сравнения выбирается норма, т.е. среднее по всей группе. На основе этого подхода формируются и критерии сравнения, т.е. можно сказать, что критериальный подход изначально основан на нормативном.

Если такое сравнение провести по всем признакам и классам, то получится матрица, снимающая оба указанных недостатка: используя выражение (18) и данные таблицы 7 непосредственно прямым счетом получаем матрицу знаний (таблица 9):

Таблица 9 – Матрица знаний (информативностей)

		Классы					Значимость фактора
		1	...	j	...	W
Значения факторов	1
	...
	i
	...
	M
Степень редукции класса		s1		sj		sW

^{Здесь – это среднее количество знаний в i-м значении фактора:}

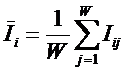
При расчете матрицы знаний N_j из таблицы 6 могут браться либо из предпоследней, либо из последней строки. В 1-м случае N_j представляет собой "Суммарное количество признаков у всех объектов, использованных для формирования обобщенного образа j-го класса", а во 2-м случае, это "Суммарное количество объектов обучающей выборки, использованных для формирования обобщенного образа j-го класса", соответственно получаем различные, хотя и очень сходные семантические информационные модели, которые мы называем СИМ-1 и СИМ-2. Оба этих вида моделей поддерживаются системой "Эйдос".

Количественные значения коэффициентов I_ij таблицы 9 являются знаниями о том, что "объект перейдет в j-е состояние" если "на объект действует i-е значение фактора".

Принципиально важно, что эти весовые коэффициенты не определяются экспертами на основе опыта интуитивным неформализуемым способом, а рассчитываются непосредственно на основе эмпирических данных на основе теоретически обоснованной модели, хорошо зарекомендовавшей себя на практике при решении широкого круга задач в различных предметных областях.

Когда количество информации I_ij>0 – i–й фактор способствует переходу объекта управления в j-е состояние, когда I_ij<0 – препятствует этому переходу, когда же I_ij=0 – никак не влияет на это. В векторе i-го фактора (строка матрицы информативностей) отображается, какое количество информации о переходе объекта управления в каждое из будущих состояний содержится в том факте, что данный фактор действует. В векторе j-го состояния класса (столбец матрицы информативностей) отображается, какое количество информации о переходе объекта управления в соответствующее состояние содержится в каждом из факторов.

Таким образом, матрица информативностей (таблица 9) является обобщенной таблицей решений, в которой входы (факторы) и выходы (будущие состояния объекта управления) связаны друг с другом не с помощью классических (Аристотелевских) импликаций, принимающих только значения: "Истина" и "Ложь", а различными значениями истинности, выраженными в битах и принимающими значения от положительного теоретически-максимально-возможного ("Максимальная степень истинности"), до теоретически неограниченного отрицательного ("Степень ложности").

Фактически предложенная модель позволяет осуществить синтез обобщенных таблиц решений для различных предметных областей непосредственно на основе эмпирических исходных данных и продуцировать на их основе прямые и обратные правдоподобные (нечеткие) логические рассуждения по неклассическим схемам с различными расчетными значениями истинности, являющимся обобщением классических импликаций.

Таким образом данная модель позволяет рассчитать какое количество информации содержится в любом факте о наступлении любого события в любой предметной области, причем для этого не требуется повторности этих фактов и событий. Если же эти повторности осуществляются и при этом наблюдается некоторая вариабельность значений факторов, обуславливающих наступление тех или иных событий, то модель обеспечивает многопараметрическую типизацию, т.е. синтез обобщенных образов классов или категорий наступающих событий с количественной оценкой степени и знака влияния на их наступление различных значений факторов. Причем эти значения факторов могут быть как количественными, так и качественными и измеряться в любых единицах измерения, в любом случае в модели оценивается количество информации которое в них содержится о наступлении событий, переходе объекта управления в определенные состояния или просто о его принадлежности к тем или иным классам.

Данная модель позволяет прогнозировать поведение объекта управления при воздействии на него не только одного, но и целой системы факторов:

( 40 )

В теории принятия решений скалярная функция I_j векторного аргумента называется интегральным критерием. Основная проблема состоит в выборе такого аналитического вида функции интегрального критерия, который обеспечил бы эффективное решение сформулированной выше задачи АСУ.

Учитывая, что частные критерии (18) имеют смысл количества информации, а информация по определению является аддитивной функцией, предлагается ввести интегральный критерий, как аддитивную функцию от частных критериев в виде:

( 41 )

В выражении (41) круглыми скобками обозначено скалярное произведение, т.е. свертка. В координатной форме это выражение имеет вид:

,

( 42 )

где: – вектор j-го класса-состояния объекта управления;

– вектор состояния предметной области, включающий все виды факторов, характеризующих объект управления, возможные управляющие воздействия и окружающую среду (массив-локатор), т.е.:

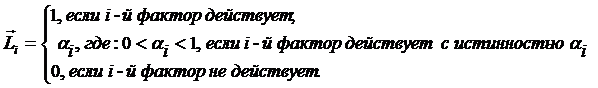В реализованной модели значения координат вектора состояния предметной области принимались равными либо 1 (фактор действует), либо 0 (фактор не действует).

Таким образом, интегральный критерий представляет собой суммарное количество информации, содержащееся в системе значений факторов различной природы (т.е. факторах, характеризующих объект управления, управляющее воздействие и окружающую среду) о переходе объекта управления в то или иное будущее состояние.

В многокритериальной постановке задача прогнозирования состояния объекта управления, при оказании на него заданного многофакторного управляющего воздействия I_j, сводится к максимизации интегрального критерия:

( 43 )

т.е. к выбору такого состояния объекта управления, для которого интегральный критерий максимален.

Задача принятия решения о выборе наиболее эффективного управляющего воздействия является обратной задачей по отношению к задаче максимизации интегрального критерия (идентификации и прогнозирования), т.е. вместо того, чтобы по набору факторов прогнозировать будущее состояние объекта, наоборот, по заданному (целевому) состоянию объекта определяется такой набор факторов, который с наибольшей эффективностью перевел бы объект управления в это состояние.

Предлагается еще одно обобщение фундаментальной леммы Неймана-Пирсона, основанное на косвенном учете корреляций между информативностями в векторе состояний при использовании средних по векторам. Соответственно, вместо простой суммы количеств информации предлагается использовать корреляцию между векторами состояния и объекта управления, которая количественно измеряет степень сходства этих векторов:

( 44 )

где:

– средняя информативность по вектору класса;

– среднее по вектору идентифицируемой ситуации (объекта).

– среднеквадратичное отклонение информативностей вектора класса;

– среднеквадратичное отклонение по вектору распознаваемого объекта.

Выражение (44) получается непосредственно из (42) после замены координат перемножаемых векторов их стандартизированными значениями:

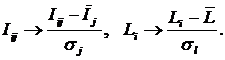
Необходимо отметить, что выражение для интегрального критерия сходства (42) по своей математической форме является корреляцией двух векторов. Это означает, что если эти вектора являются суммой двух сигналов: полезного и белого шума, то при расчете интегрального критерия белый шум практически не будет играть никакой роли, т.е. его корреляция с самими собой равна нулю по определению. Поэтому интегральный критерий сходства объекта со случным набором признаков с любыми образами классов, или реального объекта с образами классов, сформированными случайным образом, будет равен нулю. Это означает, что выбранный интегральный критерий сходства является высокоэффективным средством подавления белого шума и выделения полезной информации из шума, который неизбежно присутствует в эмпирических данных.

Важно также отметить неметрическую природу предложенного интегрального критерия сходства, благодаря чему его применение является корректным и при неортонормированном семантическом информационном пространстве, каким оно в подавляющем количестве случае и является, т.е. в общем случае.

Результат прогнозирования поведения объекта управления, описанного данной системой факторов, представляет собой список его возможных будущих состояний, в котором они расположены в порядке убывания суммарного количества информации о переходе объекта управления в каждое из них.

Сравнение, идентификация и прогнозирование как разложение векторов объектов в ряд по векторам классов (объектный анализ)

Выше были введены неметрические интегральные критерии сходства объекта, описанного массивом-локатором L_i с обобщенными образами классов I_ij (выражения 40-42).

Для непрерывного случая выражение (42) принимает вид:

.

( 45 )

Таким образом, выражение (45) представляет собой обобщение интегрального критерия сходства конкретного объекта и обобщенного класса (42) для непрерывного случая в координатной форме.

Отметим, что коэффициенты ряда Фурье (24) по своей математической форме и смыслу сходны с ненормированными коэффициентами корреляции, т.е. по сути скалярными произведениями для непрерывных функций в координатной форме: выражением (45) между разлагаемой в ряд кривой f(x) и функциями Sin и Сos различных частот и амплитуд [7].

,

( 46 )

где n={1, 2, 3,…} – натуральное число.

Из сравнения выражений (45) и (46) следует вывод о том, что процесс идентификации и прогнозирования (распознавания), реализованный в предложенной математической модели, может рассматриваться как разложение вектора-локатора распознаваемого объекта в ряд по векторам информативностей классов распознавания (которые представляют собой произвольные функции, сформированные при синтезе модели путем многопараметрической типизации на основе эмпирических данных).

Например, результаты идентификации представим на рисунке 37:

Рисунок 37. Пример разложения профиля курсанта усл.№69
в ряд по обобщенным образам классов

Продолжая развивать аналогию с разложением в ряд, данный результат идентификации можно представить в векторной аналитической форме:

или в координатной форме, более удобной для численных расчетов:

,

( 47 )

Предполагается, что . Таким образом массив-локатор, характеризующий распознаваемый объект, рассматривается как сумма произведений профилей классов на интегральный критерий сходства массива-локатора с этими профилями (т.е. взвешенная суперпозиция или разложение в ряд по профилям классов).

В выражении (47):

I(j) – интегральный критерий сходства массива-локатора, описывающего состояние объекта и j-го класса, рассчитываемый, согласно выражений (42) или (44):

( 48 )

I(i,j) – вектор обобщенного образа j-го класса, координаты которого рассчитываются в соответствии с системным обобщением формулы Харкевича (18):

.

( 49 )

Примечание: обозначения I(i,j) и I_ij, и т.п. эквивалентны. Смысл всех переменных, входящих в выражения (48) и (49) раскрыт выше.

При дальнейшем развитии данной аналогии естественно возникают вопросы: о полноте, избыточности и ортонормированности системы векторов классов как функций, по которым проводится разложение вектора объекта; о сходимости, т.е. вообще возможности и корректности такого разложения.

В общем случае вектор объекта совершенно не обязательно должен разлагаться в ряд по векторам классов таким образом, что сумма ряда во всех точках точно совпадала со значениями исходной функции. Это означает, что система векторов классов может быть неполна по отношению к профилю распознаваемого объекта, и, тем более, всех возможных объектов.

Предлагается считать не разлагаемые в ряд, т.е. плохо распознаваемые объекты, суперпозицией хорошо распознаваемых объектов ("похожих" на те, которые использовались для формирования обобщенных образов классов), и объектов, которые и не должны распознаваться, так как объекты этого типа не встречались в обучающей выборке и не использовались для формирования обобщенных образов классов, а также не относятся к представляемой обучающей выборкой генеральной совокупности.

Нераспознаваемую компоненту можно рассматривать либо как шум, либо считать ее полезным сигналом, несущим ценную информацию о неисследованных объектах интересующей нас предметной области (в зависимости от целей и тезауруса исследователей). Первый вариант не приводит к осложнениям, так как примененный в математической модели алгоритм сравнения векторов объектов и классов, основанный на вычислении нормированной корреляции Пирсона (сумма произведений), является весьма устойчивым к наличию белого шума в идентифицируемом сигнале. Во втором варианте необходимо дообучить систему распознаванию объектов, несущих такую компоненту (в этой возможности и заключается адаптивность модели). Технически этот вопрос решается просто копированием описаний плохо распознавшихся объектов из распознаваемой выборки в обучающую, их идентификацией экспертами и дообучением системы. Кроме того, может быть целесообразным расширить справочник классов распознавания новыми классами, соответствующими этим объектам, и осуществить пересинтез модели.

Однако на практике гораздо чаще наблюдается противоположная ситуация (можно даже сказать, что она типична), когда система векторов избыточна, т.е. в системе классов распознавания есть очень похожие классы (между которыми имеет место высокая корреляция, наблюдаемая в режиме: "кластерно-конструктивный анализ"). Практически это означает, что в системе сформировано несколько практически одинаковых образов с разными наименованиями. Для исследователя это само по себе является очень ценной информацией. Однако если исходить только из потребности разложения распознаваемого объекта в ряд по векторам классов (чтобы определить суперпозицией каких образов он является, т.е. "разложить его на компоненты"), то наличие сильно коррелирующих друг с другом векторов представляется неоправданным, так как просто увеличивает размерности данных, внося в них мало нового по существу. Поэтому возникает задача исключения избыточности системы классов распознавания, т.е. выбора из всей системы классов распознавания такого минимального их набора, в котором профили классов минимально коррелируют друг с другом, т.е. ортогональны в фазовом пространстве признаков. Это условие в теории рядов называется "ортонормируемостью" системы базовых функций, а в факторном анализе связано с идеей выделения "главных компонент".

В предлагаемой математической модели реализованы два варианта выхода из данной ситуации:

1) исключение неформирующихся, расплывчатых классов;

2) объединение почти идентичных по содержанию (дублирующих друг друга) классов.

Однако выбрать нужный вариант и реализовать его, используя соответствующие режимы, пользователь технологии АСК-анализа должен сам. Вся необходимая и достаточная информация для принятия соответствующих решений предоставляется пользователю инструментария АСК-анализа.

Если считать, что функции образов составляют формально-логическую систему, к которой применима теорема Геделя, то можно сформулировать эту теорему для данного случая следующим образом: "Для любой системы базисных функций в принципе всегда может существовать по крайней мере одна такая функция, что она не может быть разложена в ряд по данной системе базисных функций, т.е. функция, которая является ортонормированной ко всей системе базисных функций в целом". Поэтому для адекватного отражения подобных функций в модели необходимо повышение размерности семантического информационного пространства.

Очевидно, не взаимосвязанными друг с другом могут быть только четко оформленные, детерминистские образы, т.е. образы с высокой степенью редукции ("степень сформированности конструкта"). Поэтому в процессе выявления взаимно-ортогональных базисных образов, в первую очередь, будут выброшены аморфные "расплывчатые" образы, которые связаны практически со всеми остальными образами.

В некоторых случаях результат такого процесса представляет интерес, и это делает оправданным его реализацию. Однако можно предположить, что наличие расплывчатых образов в системе является оправданным, так как в этом случае система образов не будет формальной и подчиняющейся теореме Геделя. Следовательно, система распознавания будет более полна в том смысле, что увеличится вероятность идентификации любого объекта, предъявленного ей на распознавание. Конечно, уровень сходства с аморфным образом не может быть столь высоким, как с четко оформленным. Поэтому в этом случае более уместно применить термин "ассоциация" или нечеткая, расплывчатая идентификация, чем "однозначная идентификация".

Итак, можно сделать следующий вывод: допустимость в математической модели СК-анализа не только четко оформленных (детерминистских) образов, но и образов аморфных, нечетких, расплывчатых является важным достоинством данной модели. Это обусловлено тем, что данная модель обеспечивает корректные результаты анализа, идентификации и прогнозирования даже в тех случаях, когда модели идентификации и информационно-поисковые системы детерминистского типа традиционных АСУ практически неработоспособны. В этих условиях данная модель СК-анализа работает как система ассоциативной (нечеткой) идентификации.

Таким образом, в предложенной семантической информационной модели при идентификации и прогнозировании, по сути, осуществляется разложение векторов идентифицируемых объектов по векторам классов распознавания, т.е. осуществляется "объектный анализ" (по аналогии с спектральным, гармоническим или Фурье-анализом), что позволяет рассматривать идентифицируемые объекты как суперпозицию обобщенных образов классов различного типа с различными амплитудами (25). При этом вектора обобщенных образов классов, с математической точки зрения, представляют собой произвольные функции и не обязательно образуют полную и не избыточную (ортонормированную) систему функций.

Для любого объекта всегда существует такая система базисных функций, что вектор объекта может быть представлен в форме линейной суперпозиции (суммы) этих базисных функций с различными амплитудами. Это утверждение, по-видимому, является одним из следствий фундаментальной теоремы А.Н. Колмогорова, доказанной им в 1957 году (О представлении непрерывных функций нескольких переменных в виде суперпозиций непрерывных функций одного переменного и сложения // Докл. АН СССР, Т. 114, С. 953–956, 1957).

Теорема Колмогорова: Любая непрерывная функция от n переменных F(x₁, x₂, ..., x_n) может быть представлена в виде:

,

где g_j и h_ij – непрерывные функции, причем h_ij не зависят от функции F.

Эта теорема означает, что для реализации функций многих переменных достаточно операций суммирования и композиции функций одной переменной. Удивительно, что в этом представлении лишь функции g_j зависят от представляемой функции F, а функции h_ij универсальны. Необходимо отметить, что теорема Колмогорова является обобщением теоремы В.И. Арнольда (1957), которая дает решение 13-й проблемы Гильберта.

К сожалению, определение вида функций h_ij и g_j для данной функции F представляет собой математическую проблему, для которой пока не найдено общего строгого решения.

В данной работе предлагается рассматривать предлагаемую семантическую информационную модель как один из вариантов решения этой проблемы. В этом контексте функция F интерпретируется как образ идентифицируемого объекта, функция h_ij – образ j-го класса, а функция g_j – мера сходства образа объекта с образом класса.

Таким образом, в разделе кратко описана математическая сущность предложенной автором системной теории информации СТИ), являющейся математической моделью системно-когнитивного анализа (СК-анализ) и реализуемой в его программном инструментарии – универсальной аналитической системе "Эйдос" [3-190].
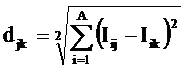
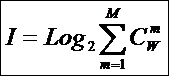
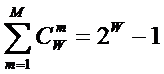
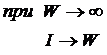
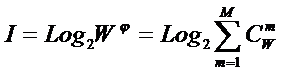
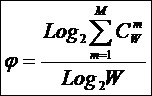
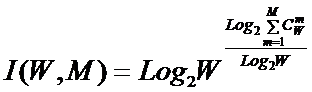
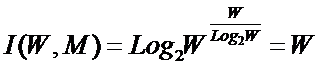
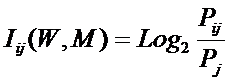
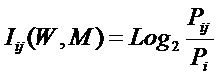
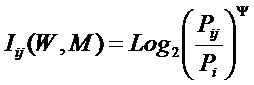
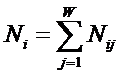
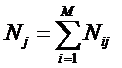
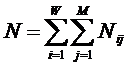
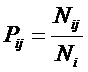
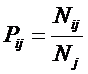
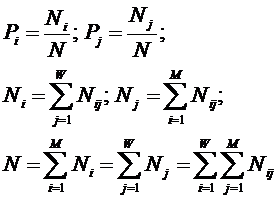
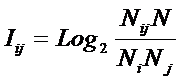
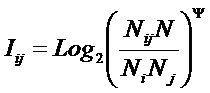
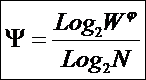
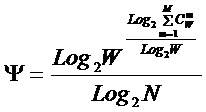
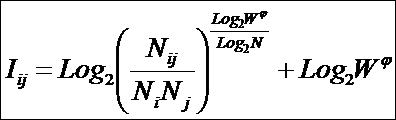
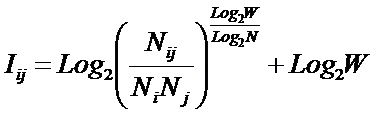
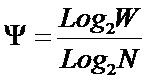
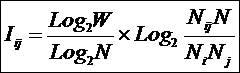
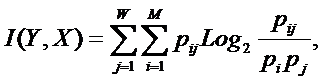
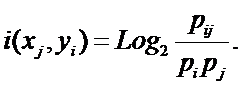
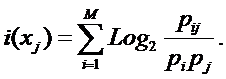
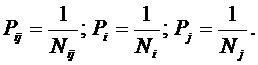
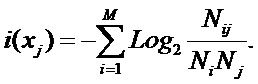
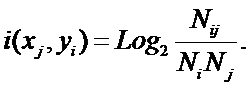
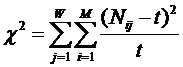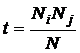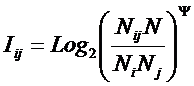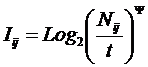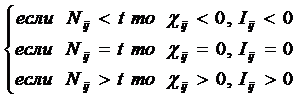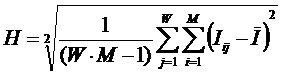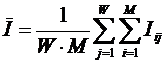
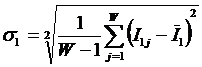
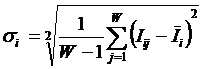
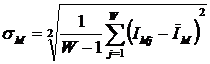
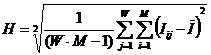
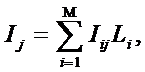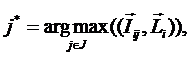
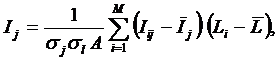
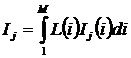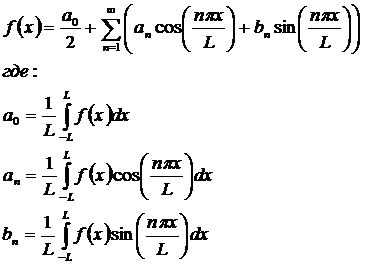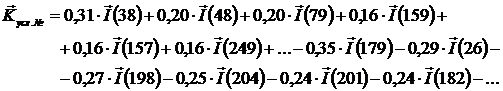
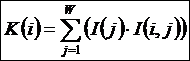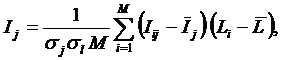
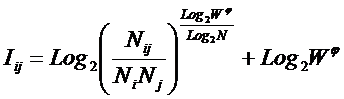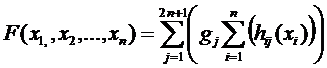