ГЛАВА 7. КОРРЕЛЯЦИЯ ФОНДОВОГО ИНДЕКСА
S & P 500 С АСТРОНОМИЧЕСКИМИ
И ГЕОФИЗИЧЕСКИМИ ПАРАМЕТРАМИ

7.1. Информационная модель

В предыдущей главе была развита модель прогнозирования землетрясений по астрономическим данным с учетом геофизических параметров смещения магнитного и географического полюса, основанная на семантических информационных моделях с использованием всемирной базы землетрясений /57/, данных по магнитному полю из всемирной базы /61/ и данных смещения географического полюса /60/. Была исследована совокупность 128320 событий землетрясений с магнитудой , произошедших на нашей планете в период с 9 февраля 1963 года по 31 декабря 2006 г (всего 16032 дня). На основе исследования семантических информационных моделей глобальной сейсмической активности было установлено, что индукция магнитного поля Земли и интегральные параметры сейсмической активности зависят от комбинаций астрономических параметров Урана и Нептуна, которые соответствуют дипольному излучению этих планет. Это дает основание предположить, что существует электромагнитный механизм, запускающий землетрясения.

В таком случае должна быть определенная взаимосвязь между параметрами глобальной сейсмической активности и развитием мировой экономики, на что неоднократно указывали различные авторы. Действительно, развитие промышленного производства на нашей планете в огромной степени зависит от потребляемых энергетических мощностей, включая электроэнергию и углеводороды – нефть и газ. Современные энергетические установки имеют достаточную мощность, чтобы вызвать заметные колебания магнитного поля Земли, что с учетом обнаруженной в работе /55/ взаимосвязи сейсмических событий с колебаниями магнитного поля, дает основания предположить наличие механизма антропогенного влияния на сейсмическую активность нашей планеты.

В данной главе исследованы семантические информационные модели, содержащие данные о сейсмических событиях /57/, астрономические параметры небесных тел, параметры магнитного поля Земли из всемирной базы /61/, параметры смещения географического полюса по данным /60/, а также биржевой индекс S & P 500 /63/. Установлено, что добавление в информационную модель /55/ данных по биржевому индексу S & P 500 позволяет увеличить достоверность прогноза землетрясений, что указывает на существование антропогенных механизмов влияние на сейсмическую активность.

Обнаружена сильная взаимосвязь биржевого индекса S & P 500 с данными по магнитной индукции, полученными на различных станциях. С учетом этих данных построена корреляционная модель зависимости логарифма объема продаж акций 500 крупнейших компаний США от дипольных моментов Урана и Нептуна. Полученные результаты находятся в согласии с данными работы /65/, в которой была построена общая корреляционная модель зависимости котировок валют на мировых валютных биржах от астрономических параметров.

Подробное описание информационной модели содержится в предыдущей главе. Для распознавания категорий используется автоматизированный системно-когнитивный анализ /3/ и система «Эйдос-астра» /7/. Рассмотрим задачу распознавания категорий по астрономическим, геофизическим и экономическим данным. Имеется множество событий A, которому ставится в соответствие множество категорий C_i. Событием можно считать регистрацию землетрясения сейсмологической станцией, а категорией – его магнитуду, лежащую в определенном интервале и глубину гипофокуса. В геофизике и экономике событием будем называть результат любого измерения геофизических или экономических параметров – магнитного поля, ориентации оси вращения, температуры, скорости, цены, объема продаж и т.п., путем многопараметрической типизации (обобщения) которых формируются обобщенные образы категорий (классы). Каждое такое событие характеризуется моментом времени и географическими координатами места его происхождения. По этим данным можно построить матрицу, содержащую координаты небесных тел – углы долготы, широты и расстояния, а также геофизические и экономические параметры – G_k. Будем считать, что заданы частотные распределения N_i – число событий, имеющих отношение к данной категории C_i.

Определим число случаев реализации событий данной категории, которое приходится на заданный интервал изменения астрономических, геофизических и экономических параметров, имеем в дискретном случае:

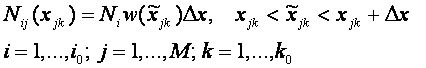(101)

Здесь w – плотность распределения событий вдоль нормированной координаты, i₀ – число распознаваемых категорий, М – число интервалов разбиения параметров (номер семантической модели), k₀ – общее число параметров, используемых в задаче. Нормированная переменная определяется через угловые и радиальную координаты, а также через амплитуды геофизических и экономических параметров следующим образом:

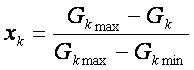
где - минимальное и максимальное значение параметра.

Определим матрицу информативности согласно

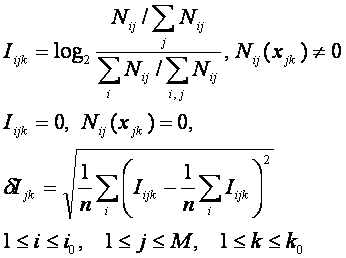(102)

Каждой категории можно сопоставить вектор информативности параметров размерности Мk₀, составленный из элементов матрицы информативности, путем последовательной записи столбцов, соответствующих нормированной координате, в один столбец, т.е.

(103)

С другой стороны, процесс идентификации, распознавания и прогнозирования может рассматриваться как разложение вектора распознаваемого объекта в ряд по векторам категорий (классов распознавания) /3/. Этот вектор, состоящий из единиц и нулей, можно определить по координатам небесных тел, соответствующих дате и месту происхождения события l в виде

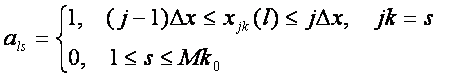(104)

Таким образом, если нормированная координата из данных по объекту исследуемой выборки попадает в заданный интервал, элементу вектора придается значение 1, а во всех остальных случаях – значение 0. Перечисление координат осуществляется последовательно, для каждого параметра G_k.

В случае, когда система векторов (103) является полной, можно любой вектор (104) представить в виде линейной комбинации векторов системы (103). Коэффициенты этого разложения будут соответствовать уровню сходства данного события с данной категорией. В случае неполной системы векторов (103) точная процедура заменяется распознаванием или разложением в ряд с некоторой погрешностью. При этом уровень сходства данных события с той или иной категорией можно определить по величине скалярного произведения вектора (104) на вектор (103), т.е. в координатной форме:

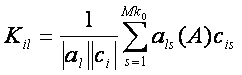(105)

Отметим, что возможны четыре исхода, при которых можно истинно или ложно отнести или не отнести данное событие к данной категории. Для учета этих исходов распознавание категорий в системе искусственного интеллекта «Эйдос-астра» осуществляется по параметру сходства, который определяется следующим образом /2, 4/:

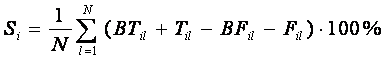(106)

S_i – достоверность идентификации «i-й» категории;

N – количество событий в распознаваемой выборке;

BT_il– уровень сходства «l-го» события с «i-й» категорией, к которой он был правильно отнесен системой;

T_il – уровень сходства «l-го» события с «i-й» категорией, к которой он был правильно не отнесен системой;

BF_il – уровень сходства «l-го» события с «i-й» категорией, к которой он был ошибочно отнесен системой;

F_il – уровень сходства «l-го» события с «i-й» категорией, к которой он был ошибочно не отнесен системой.

При таком определении параметр сходства изменяется в пределах от -100% до 100%, как обычный коэффициент корреляции в статистике. При этом ошибки 1-го и 2-го рода (ошибки ложной идентификации и ложной неидентификации) приводят к уменьшению параметра сходства. Очевидно, что параметр сходства должен удовлетворять критерию простой проверки

В монографии /2/ и других работах авторов было показано, что процедура распознавания по параметру сходства (106), реализованная в системе искусственного интеллекта «Эйдос-астра» /7/, является устойчивой как относительно объема выборки, так и относительно числа ячеек модели. Математическое обоснование этой процедуры дано в монографии /3/.

Исследуемая база данных сейсмических событий была сформирована на основе базы данных Международного сейсмологического центра (ISC) /57/, содержащей 20489816 записей регистрации различными сейсмостанциями событий землетрясений, произошедших на нашей планете в период с 1 января 1961 года по 31 декабря 2006 г.

В состав системы «Эйдос-астра» /7/ входят программные интерфейсы /80/, позволяющие объединять разрозненные данные /57/ в единую базу данных, выделять различные сегменты данных, производить необходимые вычисления со всеми исследованными базами исходных данных. С применением одного из программных интерфейсов из исходных данных /57/ было образовано несколько различных БД для исследования влияния астрономических параметров на магнитуду и глубину гипофокуса, на ежедневное число землетрясений, а также на средние параметры сейсмической активности. В настоящей работе исследована совокупность 128320 событий землетрясений с магнитудой , произошедших на нашей планете в период с 9 февраля 1963 года по 31 декабря 2006 г (всего 16032 дня).

В качестве астрономических параметров были использованы долгота (LON), широта (LAT) и расстояние – R, от Земли до десяти небесных тел – Солнца, Луны, Марса, Меркурия, Венеры, Юпитера, Сатурна, Урана, Нептуна и Плутона, и долгота Северного Узла Луны. Астрономические параметры вычислялись на каждый день в фиксированной точке с географическими координатами Гринвича в 12:00 GMT в топоцентрической системе координат. Отметим, что выбор этой точки не является существенным для решаемого класса задач.

Кроме того, в модели были использованы координаты географического полюса – X, Y /60/, данные по магнитной индукции /61/, полученные вблизи Северного магнитного полюса на станции Resolute Bay (IAGA Code: RES; lat: 74.69; long: 265.105) – параметры BxRES, ByRES, BzRES, и на станции Eskdalemuir (IAGA Code: ESK lat: 55.317 long: 356.8) – параметр BzESK, а также взвешенные данные по котировкам и объемам торгов акций 500 крупнейших компаний США – индекс S&P 500 /63/ - параметры ADJ_CLOSE и VOLUME соответственно. Отметим, что индекс S&P 500 называют барометром американской экономики, так как он довольно точно отражает ее состояние.

Из астрономических параметров, координат географического полюса, параметров индукции магнитного поля, индекса S&P 500 и категорий сейсмической активности была создана база данных, содержащая 16032 записи с обобщенной информацией о ежедневной сейсмической, геофизической и экономической активности различных сфер Земли: ноосферы, литосферы, магнитосферы.

Решение прямой задачи включает в себя нормирование входных параметров и приведение их к одному масштабу изменения в интервале (0;360), разбиение интервалов на М частей, вычисление матрицы абсолютных частот и информативности, в соответствии с формулами (101)-(102). Отметим, что в системе «Эйдос-астра» реализован режим автоматического синтеза системы из нескольких частных семантических информационных моделей, в которых число ячеек принимает любое заданное значение М=2,3,...,173.

Решение обратной задачи включает в себя распознавание категорий по заданным астрономическим параметрам, в соответствии с уравнениями (103)-(106). Частным случаем задачи распознавания является определение достоверности идентификации категорий по астрономическим данным в каждой модели.

7.2. Параметр сходства категорий магнитуды с учетом индекса S&P 500

В исходной БД /57/ сейсмические события характеризуются магнитудой mb, которой можно сопоставить категорию магнитуды – таблица 64. Поскольку события с одной и той же магнитудой могут повторяться в один день, каждому значению магнитуды сопоставляется несколько типов категорий, а именно:

A – событие с магнитудой mb повторяется один раз;

B – событие с магнитудой mb повторяется два раза;

C – событие с магнитудой mb повторяется три раза.

Кроме того, можно рассмотреть случай, когда, например, категория А усекается, путем отбрасывания некоторых событий. Таким образом, была образована категория _.

На рис. 171 и в таблице 64 представлен параметр сходства категории магнитуда в четырех информационных моделях:

· M12 [1], М170 [1] – модели, описанные в главе 6, содержат астрономические параметры, координаты географического полюса и параметр индукции магнитного поля;

· M12 S&P 500, М170 S&P 500 – модели настоящей работы, описанные выше.

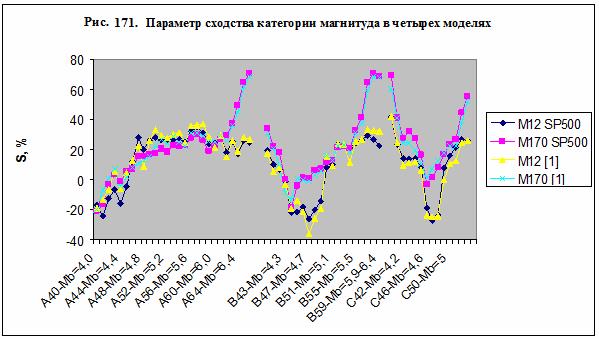
Таблица 64. Параметр сходства категории магнитуда
в четырех моделях

Категория	M12 S&P500	M170 S&P500	M12 [1]	M170 [1]	Число случаев
A40-Mb=4,0	-16,945	-20,748	-18,882	-20,037	938
A41-Mb=4,1	-24,193	-16,317	-13,237	-6,813	1065
A42-Mb=4,2	-12,319	-3,044	-6,400	0,637	1235
A43-Mb=4,3	-6,661	3,292	5,872	7,037	1525
A44-Mb=4,4	-15,917	-1,207	-5,835	-4,510	1850
A45-Mb=4,5	-4,519	5,295	4,907	1,890	2294
A46-Mb=4,6	12,174	7,017	12,681	8,161	2818
A47-Mb=4,7	28,028	15,356	22,570	10,887	3295
A48-Mb=4,8	20,131	15,732	8,539	12,764	3424
A49-Mb=4,9	26,515	16,998	26,116	15,614	3482
A50-Mb=5	27,758	17,432	33,384	22,451	3400
A51-Mb=5,1	26,620	20,625	29,249	26,773	3182
A52-Mb=5,2	26,989	18,567	27,784	23,767	2896
A53-Mb=5,3	26,259	22,927	30,490	29,035	2460
A54-Mb=5,4	27,093	22,667	31,482	24,969	2068
A55-Mb=5,5	24,984	22,859	24,281	22,462	1651
A56-Mb=5,6	32,286	28,096	35,661	31,337	1345
A57-Mb=5,7	34,827	30,524	36,326	31,225	1030
A58-Mb=5,8	31,242	26,476	37,398	28,725	801
A59-Mb=5,9	23,691	18,945	28,279	25,450	596
A60-Mb=6,0	24,478	22,556	21,362	25,074	442
A61-Mb=6,1	27,728	27,074	29,407	29,190	299
A62-Mb=6,2	18,074	29,295	15,215	25,934	212
A63-Mb=6,3	25,441	37,888	25,804	36,412	144
A64-Mb=6,4	16,929	49,667	19,235	45,038	90
A65-Mb=6,5	25,807	64,794	28,302	62,048	53
A66-Mb=6,6-7,0	24,905	70,761	26,985	68,781	47
B40-Mb=4,0	19,619	34,168	17,555	30,855	293
B41-Mb=4,1	10,304	21,757	5,406	21,036	434
B42-Mb=4,2	6,669	18,006	8,001	9,861	556
B43-Mb=4,3	-1,197	0,457	-3,087	-8,597	637
B44-Mb=4,4	-21,599	-18,440	-19,069	-13,509	761
B45-Mb=4,5	-21,251	-4,181	-13,723	0,992	817
B46-Mb=4,6	-18,429	1,067	-21,478	-0,022	981
B47-Mb=4,7	-26,095	0,677	-36,301	-1,349	1141
B48-Mb=4,8	-19,848	6,164	-25,838	3,183	1273
B49-Mb=4,9	-14,632	7,359	-19,474	5,508	1125
B50-Mb=5	8,344	11,713	15,540	16,131	979
B51-Mb=5,1	10,308	12,577	9,195	12,782	828
B52-Mb=5,2	23,691	21,405	23,793	22,561	633
B53-Mb=5,3	22,503	21,819	23,453	22,979	420
B54-Mb=5,4	21,174	20,747	11,687	18,494	283
B55-Mb=5,5	24,198	32,925	25,281	31,170	179
B56-Mb=5,6	26,286	41,501	27,069	37,841	116
B57-Mb=5,7	29,209	64,798	33,270	60,019	58
B58-Mb=5,8	26,724	70,712	32,825	68,742	45
B59-Mb=5,9-6,4	22,528	68,464	32,159	68,168	47
C40-Mb=4,0	41,728	69,040	41,965	60,331	66
C41-Mb=4,1	23,238	41,081	24,450	40,927	162
C42-Mb=4,2	14,072	27,344	9,682	24,192	232
C43-Mb=4,3	13,760	32,465	11,337	24,474	295
C44-Mb=4,4	14,017	27,572	12,233	19,482	325
C45-Mb=4,5	8,639	16,471	6,317	10,782	319
C46-Mb=4,6	-18,760	-3,110	-24,014	1,491	336
C47-Mb=4,7	-27,215	1,111	-24,764	6,989	365
C48-Mb=4,8	-23,937	8,221	-24,128	12,503	302
C49-Mb=4,9	7,525	17,136	-0,116	17,397	311
C50-Mb=5	16,286	23,353	10,743	22,289	233
C51-Mb=5,1	21,638	27,107	12,694	22,638	200
C52-Mb=5,2	26,769	44,347	24,367	38,506	110
C53-Mb=5,3-6,0	25,714	55,628	26,105	52,017	75
Среднее значение	11,859	22,541	12,297	22,052	944

Добавление в модель индекса биржевой активности позволяет заметно повысить параметр сходства при распознавании событий с большой магнитудой в модели М170, что свидетельствует о возможном влиянии экономики США и мировой экономики на параметры глобальной сейсмической активности. Другой возможной причиной этого может являться зависимость мировой экономики от некоторого неизвестного фактора, который влияет также на глобальную сейсмическую активность. Поэтому учет данных по мировой экономике при прогнозировании сейсмической активности эквивалентен косвенному учету этого фактора, что и приводит к повышению достоверности модели.

Для выяснения возможного механизма этого влияния рассмотрим корреляционные связи всех параметров задачи.

7.3. Корреляция индекса S&P 500 с астрономическими и геофи-зическими параметрами

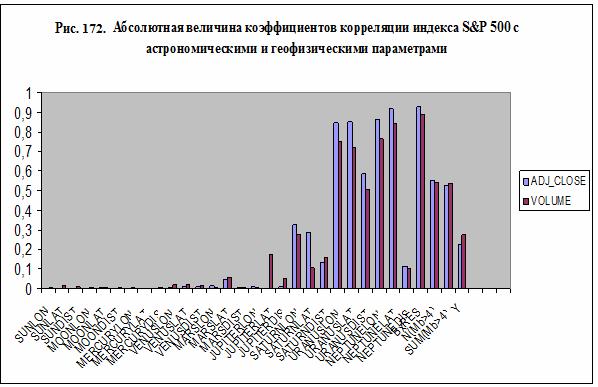
На рис. 102 и в таблице 65 представлены коэффициенты корреляции всех параметров задачи. Наибольшее значение коэффициента корреляции как самого индекса S&P 500, так и объема торгов – 0,927 и 0,891 соответственно, наблюдается с параметром BxRES – меридиональной составляющей магнитной индукции по измерениям на станции Resolute Bay (Канада). Примерно такую же величину имеет коэффициент корреляции индекса S&P 500 и объема торгов с параметром широты Нептуна – 0,92 и 0,84 соответственно. Отметим, что астрономические параметры Урана и Нептуна, а также параметры индукции магнитного поля Земли связаны с индексом S&P 500 и объемом торгов акциями 500 крупнейших компаний США заметно сильнее, чем другие параметры задачи. На втором месте по величине коэффициента корреляции c индексом S&P 500 и объемом торгов оказались параметры глобальной сейсмической активности – число и суммарная магнитуда землетрясений с магнитудой mb>4 – параметры N(Mb>4), SUM(Mb>4).

Таблица 65. Коэффициенты корреляции индекса S&P 500 с геофизическими параметрами полученные методом Pearson Product Moment Correlation по программе SigmaPlot: для Р<0,05 корреляционные связи являются достоверными. N – число точек по которым вычисляется корреляция.

	N(Mb>4)	BzESK	BxRES	ByRES	BzRES	X	Y	VOLUME	ADJ_CLOSE
SUM(Mb>4)	0,996	0,476	0,507	-0,46	-0,401	0,0617	0,142	0,537	0,522
P	0	0	0	0	0	7,32E-15	3,42E-72	0	0
N	15862	15839	15497	15397	15862	15862	15862	10924	10924
N(Mb>4)		0,494	0,532	-0,483	-0,424	0,0614	0,147	0,563	0,548
P		0	0	0	0	9,80E-15	1,68E-77	0	0
N		15839	15497	15397	15862	15862	15862	10924	10924
BzESK			0,954	-0,72	-0,539	0,137	0,343	0,776	0,842
P			0	0	0	4,11E-68	0	0	0
N			15644	15543	16009	16009	16009	11029	11029
BxRES				-0,866	-0,705	0,12	0,339	0,891	0,927
P				0	0	1,20E-51	0	0	0
N				15566	15667	15667	15667	10797	10797
ByRES					0,869	-0,0787	-0,246	-0,856	-0,861
P					0	8,24E-23	4,97E-213	0	0
N					15566	15566	15566	10724	10724
BzRES						-0,0667	-0,216	-0,693	-0,787
P						2,87E-17	1,19E-168	0	0
N						16032	16032	11048	11048
X							0,0476	0,0862	0,0938
P							1,63E-09	1,16E-19	4,92E-23
N							16032	11048	11048
Y								0,227	0,274
P								5,55E-129	4,39E-190
N								11048	11048
VOLUME									0,867
P									0
N									11048

В работе /55/ были построены корреляционные зависимости индукции магнитного поля Земли от дипольных моментов Урана и Нептуна, которые определяются в случае Урана следующим образом:

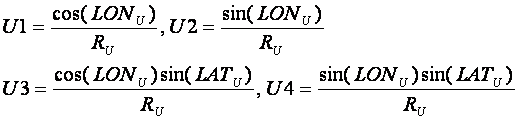
В случае Нептуна используются аналогичные выражения, но с заменой долготы, широты и расстояния на параметры, соответствующие этой планете, т.е.

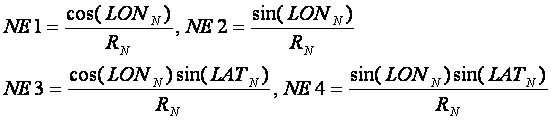
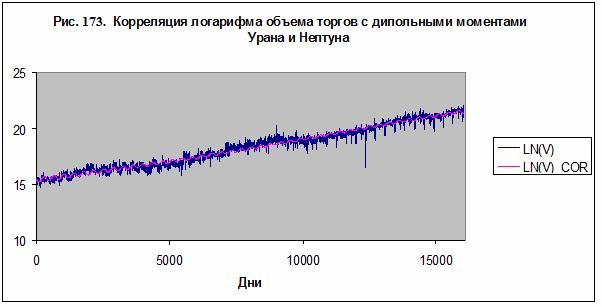
Путем применения многопараметрической регрессии была получена зависимость логарифма объема торгов от дипольных моментов Урана и Нептуна, имеющая высокую степень точности – рис. 173:

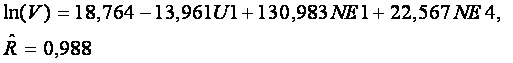
Таким образом, установлено, что индекс S&P 500 связан с индукцией магнитного поля Земли и с астрономическими параметрами Урана и Нептуна. Полученные результаты, по-видимому, означают, что существует взаимное влияние мировой экономики, тенденции которой частично отражает индекс S&P 500, и геофизических параметров, характеризующих индукцию магнитного поля Земли и сейсмическую активность. С другой стороны, и параметры мировой экономики и геофизические параметры зависят от астрономических параметров небесных тел Солнечной системы. Предположительно механизм влияния небесных тел на индекс S&P 500 можно понять через механизм связи индекса S&P 500 с индукцией магнитного поля Земли и параметрами сейсмической активности.

Для этой цели может быть использован аппарат выявления и визуализации когнитивных функциональных зависимостей, развитый в математической модели системно-когнитивного анализа (СК-анализ) и реализованный в его программном инструментарии – системах «Эйдос» и «Эйдос-астра». Этот аппарат основан на информационном подходе к пониманию функциональной зависимости, суть которого состоит в осознании того, что в каждом значении аргумента содержится определенное количество информации о том, что значение функции примет каждое из возможных значений.

В случае однозначных функций одного аргумента в каждом значении аргумента содержится максимальное количество информации о соответствии ему одного-единственного значения функции, а об остальных – ноль информации. В случае многозначных функций одного аргумента в каждом значении аргумента содержится определенное количество информации о реализации каждого возможного значения функции. В случае многозначных функций многих аргументов каждое значение функции определяется одновременно многими значениями аргументов, причем каждым – в различной степени, соответствующей количеству информации, содержащемуся в этих значениях аргумента о том, что функция примет данное значение. В СК-анализе реализован общий случай, т.е. выявление многозначных функций многих аргументов.

Аппарат когнитивных функций СК-анализа ассоциируется с рядом направлений математики:

– нечёткой логикой и теорией нечётких множеств, развитой Лотфи Зазе, но отличается от нее тем, что в СК-анализе аналог функции принадлежности, т.е. количество информации в значении аргумента о соответствии ему значения функции, имеет произвольный (не заданный заранее) вид и определяется непосредственно на основе эмпирических данных;

– классической статистикой с теорией доверительных интервалов, но отличается от нее тем, в статистике доверительный интервал при прогнозировании может только возрастать, тогда как аналог доверительного интервала в СК-анализе, т.е. количество информации в значении аргумента о соответствии ему значения функции, сам является предметом прогноза и может как возрастать (при прогнозировании точек бифуркации), так и уменьшаться (на периодах эргодичности);

– теоремой В.А.Котельникова об отсчетах, которая определяет точность представления функции с определенным спектром (полосой) при дискретных (или интервальных) значениях аргумента, т.к. в СК-анализе мы имеем дело именно с дискретными.

Отметим, что понятия математической точки (материальной точки) и бесконечно-малых величин, лежащих в основе математического понятия функции, являются сильнейшей абстракцией, т.к. реально на практике встречаются только интервальные значения аргумента и функции. Абсолютно точное значение функции содержит бесконечное количество информации и лишено физического смысла, в частности в принципе не может быть записано ни на одном материальном носителе или передано по реальному каналу связи за любое время. «Чистых математиков» это, кажется, не особенно беспокоит, по-видимому, потому, что математика сделала саму иерархию бесконечности предметом своего исследования и, возможно, является одной из немногих наук наряду с философией, способных исследовать бесконечность корректным образом. Однако это само по себе породило ряд новых уже чисто математических и логических проблем, в частности известных как парадоксы теории множеств и проблемы оснований математики. На сущность этих проблем проливает свет знаменитая теорема Геделя о неполноте.

С другой стороны физиков, экономистов и представителей других наук, использующих математику для моделирования объектов, процессов и явлений реальной области эта ситуация с бессмысленной бесконечностью не может устраивать и они в своих теориях пытаются разработать методы преодоления этих трудностей. Естественно, эти исследователи пытаются найти выход из этой непростой ситуации, когда модель дает бессмысленные результаты. Поучительным примером преодоления подобных трудностей, возникающих из-за неадекватности математического аппарата, является история расходимости в квантовой теории поля (КТП) в физике. Также в физике известно соотношение неопределенности Гейзенберга , а в теории измерений – его аналог: неравенство Крамера – Рао накладывающее принципиальное ограничение на максимальный объем информации Фишера , который можно «одновременно» получить (на самом деле за определенный промежуток времени) и о координате, и об импульсе физической системы с применением классических макроскопических измерительных приборов. Таким образом, можно считать, что уже установлена фундаментальная взаимосвязь между квантовой механикой (а значит и квантовой теорией поля, и теорией относительности) и теорией информации. Это дает основание надеяться на получение фундаментального соотношения между количеством информации, количеством энергии, массой, длиной волны и частотой волны де Бройля, скоростью света и постоянной Планка. Остается «лишь» получить из фундаментального соотношения квантовой теории поля для энергии:

(а)

выражение, по своей математической форме совпадающее с соотношением неопределенности Гейзенберга:

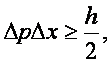(б)

где h – приведенная постоянная Планка:

n – частота волны де Бройля.

С этой целью учитывая, что , преобразуем выражение (а):

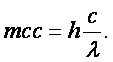
Откуда получим:

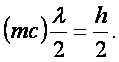(в)

В выражении (в) первый сомножитель имеет размерность импульса, второй – расстояния, а в правой части в обоих выражениях – одна и та же константа, таким образом, выражение (в) по своей математической форме полностью совпадает с соотношением неопределенности Гейзенберга (б).

Рассмотрим, какое суммарное количество информации можно получить о системе, одновременно измеряя ее координату и импульс. Если считать значения DV принадлежащими интервалу: 0 £ DV £ c, где с – скорость света, то количество N_p интервальных значений импульса будет равно:

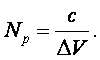
Считая эти значения импульса равновероятными и используя поэтому выражение Хартли получим количество информации, которое информационно-измерительная система получает при наблюдении у физической системы определенного интервального значения импульса DV:

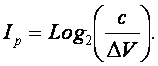
Если считать, что l/2 представляет собой диапазон изменения координаты x, т.е. 0 £ Dx £ l/2 , то количество интервальных значений координаты будет равно:

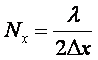
Считая эти значения координат равновероятными и используя поэтому выражение Хартли получим количество информации, которое информационно-измерительная система получает при наблюдении у физической системы определенного интервального значения координаты Dx:

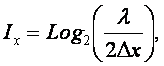
Таким образом, суммарное количество информации, полученное о физической системе при одновременном измерении интервальных значений ее импульса и координаты, будет:

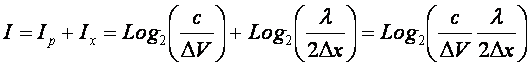
Или окончательно:

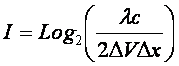(г)

Преобразуем выражение (б) учитывая, что неопределенность импульса обусловливается неопределенностью скорости: Dp=mDV:

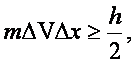
откуда:

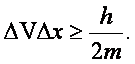(д)

Подставляя (д) в (г) получим:

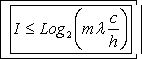(е)

Это и есть выражение для максимального количества информации, которое по мнению авторов в принципе возможно получить о физической системе с массой m и длиной волны де Бройля l с применением классической информационно-измерительной системы. Это выражение отражает глубинную взаимосвязь квантовой теории поля (т.е. и квантовой механики, и специальной теории относительности), с теорией информации.

Из выражения (е) получаем:

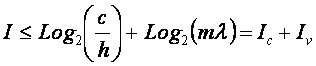
Из этого выражения видно, что количество информации в физическом объекте состоит из двух слагаемых, первое из которых постоянно и полностью определяется мировыми константами (и имеет огромную величину), а второе переменное и определяется массой объекта его длиной волны де Бройля.

Для выявления когнитивных функциональных зависимостей в фрагментированных и зашумленных данных большой размерности в СК-анализе используется матрица информативности (102). Этот подход может быть эффективно использован при решении задачи статьи. Кратко поясним суть этого метода. Матрица информативностей (102) рассчитывается на основе системной теории информации /3/ непосредственно на основе эмпирических данных и представляет собой таблицу, в которой столбцы соответствуют обобщенным образам классов, т.е. будущим состояниям моделируемой системы, строки – интервальным значениям факторов, влияющих на эту систему, а на пересечениях строк и столбцов находится количество информации, которое содержится в факте действия значения фактора, соответствующего строке, на переход системы в состояние, соответствующее столбцу. Максимальное количество информации, которое может быть в значении фактора, определяется количеством будущих состояний моделируемой системы. Модуль количества информации отражает силу влияния значения фактора, а знак – направление этого влияния, т.е. то, способствует он или препятствует наступлению данного состояния. Если последовательности классов и значений факторов образуют порядковые шкалы или шкалы отношений, т.е. соответственно, на них определены отношения «больше-меньше» или, кроме того, единица измерения, начало отсчета и арифметические операции, то матрица информативностей допускает наглядную графическую визуализацию, традиционного для функций типа, когда значения факторов рассматриваются в качестве значений аргумента, а классы, о наступлении которых в этих значениях факторов содержится максимальное количество информации – в качестве значений функции. Другие классы, менее обусловленные данным значением фактора, а также те, наступлению которых это значение препятствует в большей или меньшей степени, также могут отображаться соответствующими цветами, и это также может представлять интерес, т.к. позволяет задействовать мощные способности человека к анализу изображений. Когнитивные функции, представляемые в форме матрицы информативностей, соответствуют очень общему виду функциональной зависимости: многозначной функции многих аргументов, т.к. каждое значение фактора влияет на все состояния моделируемого объекта, и каждое его состояние обусловлено всеми значениями факторов. Подобные функции аналитически могут быть представлены использованием тензорного анализа и матричной алгебры. Визуализация этих зависимостей может осуществляться как средствами системы «Эйдос», так и с использованием других систем, например SigmaPlot, в которой количество информации в значениях аргумента о значениях функции представлено цветом и цветовым зонированием. Это гораздо нагляднее и удобнее, чем приписывать каждой точке свой доверительный интервал.

Учитывая роль наблюдателя в квантовой механике и систем отсчета в теории относительности можно говорить о том, что научные модели отражают не реальность, «какой она является на самом деле», а лишь реальность, какой она предстает пред нами при ее наблюдении (измерении) с помощью средств наблюдения определенного типа. Причин этого две: 1-я состоит в том, что любое конкретное средство наблюдения взаимодействуют не со всей реальностью, а лишь с вполне определенными ее подсистемами, 2-я причина в том, что средства наблюдения сами изменяют реальность, с которой они взаимодействуют. Задачей научного исследования часто является выявление функциональных зависимостей в эмпирических данных, т.е. по сути, получение информации об объекте исследования, а именно вычисление на основе эмпирических данных количества информации, содержащегося в интервальных значениях факторов о переходе объекта исследования (или управления) под их действием в различные возможные состояния. С этой точки зрения любая наука, получающая информацию об объекте исследования в процессе научного исследования, может рассматриваться как прикладной раздел теории информации. Поэтому аппарат выявления когнитивных функциональных зависимостей в многомерных зашумленных фрагментированных данных СК-анализа является универсальным и адекватным инструментом научных исследований.

Приведем широко известные примеры функциональных зависимостей, в которых их информационный характер наиболее ясен и очевиден, особенно для специалистов в области компьютерных технологий.

Пример 1-й. При оцифровке аналогового сигнала, например звукового сигнала с микрофона с помощью звуковой карты, получается временной ряд, накапливаемый в базе данных, в которой значения функции привязаны ко времени снятия отсчета (измерения). Значения функции в этом случае могут принимать только дискретные интервальные значения из определенного ограниченного набора, количество вариантов N в котором определяется разрядностью звуковой карты I по формуле: N=2^I. Так для 8-разрядной карты это 256 вариантов значения функции, а для 16-разрядной – 65536. Соответственно в каждом значении аргумента звукового сигнала в 1-м случае содержится 1 байт информации, а во 2-м случае – 2 байта.

Пример 2-й. Изображение на мониторе можно рассматривать как визуализацию функции, в которой сквозной номер пикселя (по сути, адрес в видеопамяти) содержит некоторое количество информации о его цвете. Значения функции в этом случае также могут принимать только дискретные интервальные значения из определенного ограниченного набора, количество вариантов N в котором определяется разрядностью видеокарты I по формуле: N=2^I. Так для 8-разрядной видеокарты (VGA) это 256 вариантов значения функции (цветов), а для 16-разрядной (SVGA) – 65536 цветов, реально сейчас используются видеокарты с 32 битами кодирования цвета (глубина кодирования цвета), обеспечивающие передачу 4294967296 цветов. Соответственно в каждом значении аргумента видеосигнала в 1-м случае содержится 1 байт информации, а во 2-м случае – 2 байта, а в 3-м – 4 байта.

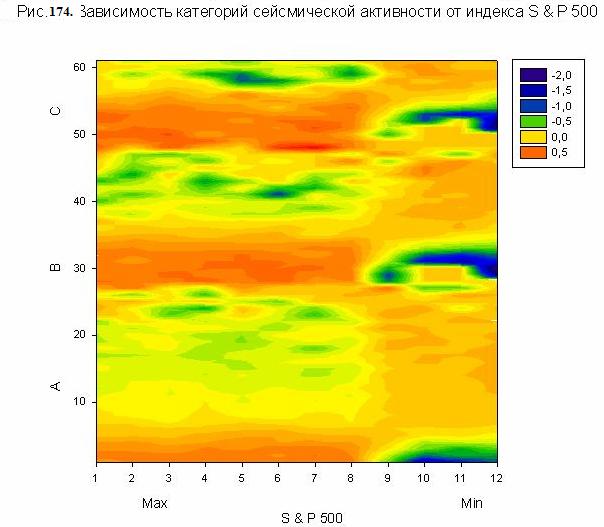
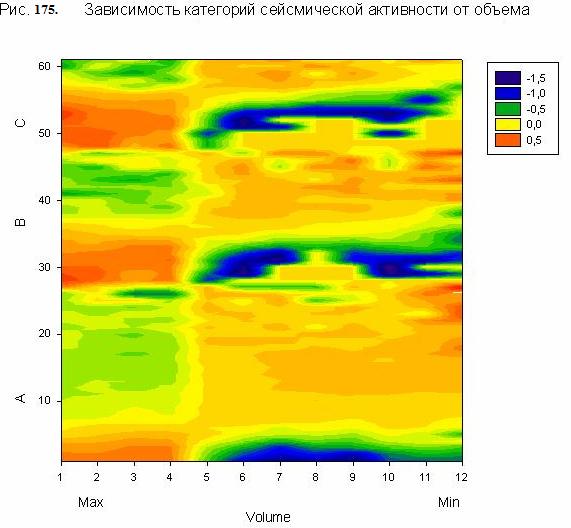
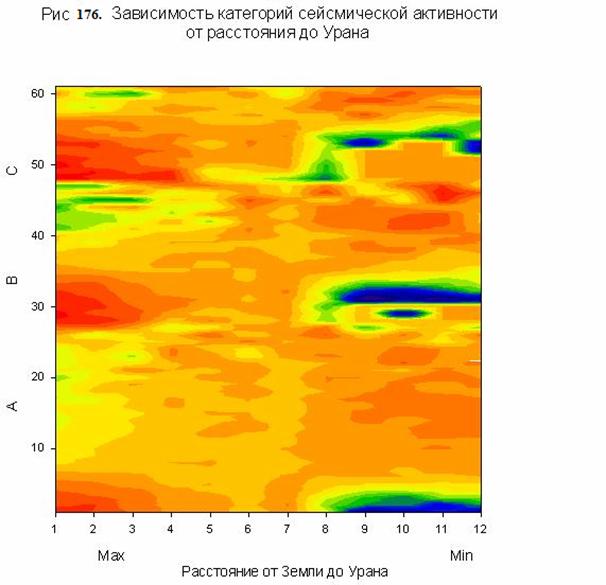
На рис. 174-176 представлены фрагменты матрицы информативности модели M12 S&P 500, позволяющие оценить степень влияния индекса S&P 500 и объема торгов, а также расстояния от Земли до Урана на категории A, B, C сейсмической активности из таблицы 64. Можно отметить, что данные на рис. 104-106 отражают общую закономерность, которая была обнаружена в работе /55/ и которая указывает на существование электромагнитного механизма, запускающего землетрясения.

В этой связи заметим, что влияние Нептуна и Урана на магнитное поле Земли обусловлено взаимной индукцией планет по механизму, описанному в работе /1/. Но современная промышленность включает в себя энергетические системы, системы связи и информационные системы, причем каждая из перечисленных систем базируется на сети, обладающей огромной индуктивностью. Поэтому предположительно можно говорить об индуктивном влиянии планет на электрические сети энергетики, связи и информационных систем по механизму взаимной индукции. Наконец, человеческий фактор, играющий основную роль в формировании экономических категорий, также базируется на биологических нейросетях, обладающих собственной индуктивностью.

Совокупная индуктивность всех перечисленных сетей, охватывающих целые материки, имеет огромную величину, поэтому колебания магнитного поля Земли вызывают немедленный отклик в промышленных сетях по законам Фарадея-Генри и Джоуля-Ленца. В свою очередь, колебания энергии в промышленных сетях может вызвать изменение в магнитном поле Земли по закону Ампера-Максвелла. Землетрясения же являются лишь одним из многих чувствительных природных индикаторов, реагирующих на изменения в электромагнитном поле Земли. Не менее чувствительным индикатором, реагирующим на колебания электромагнитного поля Земли, является биржа, основанная на информационных сетях и нейросетях агентов, участвующих в торгах.

Отметим, что согласно данным, приведенным в таблице 65 и на рис. 172, коэффициенты корреляции индекса S & P 500 с параметрами индукции магнитного поля Земли с астрономическими параметрами Урана и Нептуна имеют величину, близкую к величине коэффициента корреляции этого индекса с объемом торгов – 0,867. Но объем торгов является важнейшим экономическим показателем, на котором основываются сделки. Тем не менее, реакция на некий, казалось бы второстепенный фактор, обусловленный изменением магнитного поля Земли, является такой же по силе, как и реакция на изменение объема торгов. Здесь, видимо, имеет место масштабный эффект, который вынуждает реагировать совокупную гигантскую нейросеть всех биржевых агентов на изменения в магнитном поле по закону индукции, тогда как каждый агент принимает решение исходя их текущей обстановки. Следовательно, можно предположить, что существует электромагнитный механизм, влияющий на основные фондовые индексы.

Отметим, что возможно этот механизм имеет и другую природу. Но независимо от того, каков механизм обнаруженных взаимосвязей и какова их физическая или иная природа, знание самих этих зависимостей само по себе является новым знанием, которое может быть успешно использовано для прогнозирования и поддержки принятия решений.

Таким образом, на основе информационных моделей обнаружена корреляция фондового индекса S & P 500 с астрономическими и геофизическими параметрами, что указывает на взаимное влияния природных и экономических систем по механизму взаимной индукции. Этот факт может иметь большое значение для развития мировой экономики.

7.5. Воздействие глобальных и региональных природных факторов на фондовый индекс S&P 500 и курс EUR/USD

Корреляция S & P 500 с параметрами индукции магнитного поля Земли

Хорошо известно, что на курсы национальных валют влияют такие макроэкономические показатели, как валовой национальный продукт, объем промышленного производства, уровень занятости или безработицы, темп инфляции, а также уровень процентной ставки, торговый баланс страны, доверие к национальной валюте и некоторые другие /100/. Перечисленные факторы влияют на основной курс валюты, тогда как текущий курс зависит, главным образом, от ожиданий агентов, участвующих в торгах и текущими условиями на финансовых рынках /101/. С другой стороны, в работе /55/ была обнаружена высокая степень корреляции индекса S & P 500 с параметрами индукции магнитного поля Земли и с астрономическими параметрами Урана и Нептуна. В главе 5 были развиты модели прогнозирования курсов валют по астрономическим данным. Эти результаты указывают на зависимость курсов валют от неких природных факторов, не связанных на прямую с экономическими факторами. Возникает вопрос о механизме этого влияния. Ниже предложена модель влияния природных факторов на курсы валют и фондовые индексы.

Индекс S&P 500 представляет собой взвешенные данные по котировкам и объемам торгов акций 500 крупнейших компаний США /63/. Индекс S&P 500 называют барометром американской экономики, так как он довольно точно отражает ее состояние.

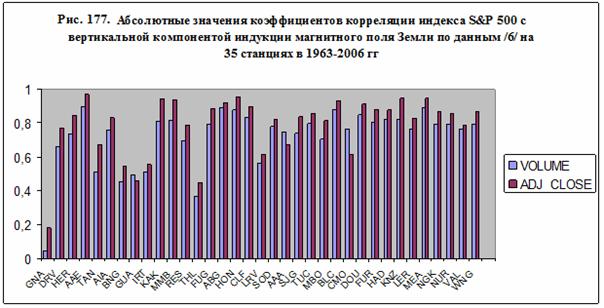
На рис. 177 приведены абсолютные значения параметров корреляции индекса S & P 500 с вертикальной компонентой индукции магнитного поля по данным /61/ на 35 станциях наблюдения в период с 1963 по 2006 гг. Отметим, что согласно данным, приведенным на рис. 177, коэффициенты корреляции индекса S & P 500 с параметрами индукции магнитного поля Земли имеют величину, близкую к величине коэффициента корреляции этого индекса с объемом торгов – 0,867. Но объем торгов является важнейшим экономическим показателем, на котором основываются сделки. Тем не менее, реакция на некий, казалось бы второстепенный фактор, обусловленный изменением магнитного поля Земли, является такой же по силе, как и реакция на изменение объема торгов.

Можно предположить, что имеет место масштабный эффект, который вынуждает реагировать совокупную гигантскую нейросеть всех биржевых агентов на изменения в магнитном поле по закону индукции, тогда как каждый агент принимает решение исходя их текущей обстановки. С другой стороны, современная промышленность включает в себя энергетические системы, системы связи и информационные системы, причем каждая из перечисленных систем базируется на сети, обладающей огромной индуктивностью. Поэтому предположительно можно говорить об индуктивном влиянии магнитного поля Земли на электрические сети энергетики, связи и информационных систем по механизму взаимной индукции. Человеческий фактор, играющий основную роль в формировании экономических категорий, базируется на биологических нейросетях, обладающих собственной индуктивностью. Совокупная индуктивность всех перечисленных сетей, охватывающих целые материки, имеет огромную величину, поэтому колебания магнитного поля Земли вызывают немедленный отклик в промышленных сетях по законам электродинамики. Следовательно, существует электромагнитный механизм, влияющий на основные фондовые индексы.

Действительно, определим индуктивность и емкость сети агентов, предполагая, что они связаны между собой коаксиальным кабелем, используя известные формулы электродинамики /102/:

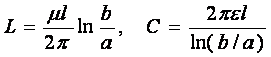(107)

Здесь использованы стандартные обозначения - диэлектрическая и магнитная проницаемость, a,b – внутренний и внешний диаметр кабеля, l – длина кабеля.

Основным параметром, влияющим на характеристики сети агентов является длина соединения, как это следует из выражений (102). Под агентами следует понимать не только прямых участников торгов, но и инвесторов и даже потребителей сети. Поэтому длина сети складывается из трех факторов – длины нейросети всех агентов, длины сети региона (страны) и длины сети отдельных кластеров (городов, населенных пунктов):

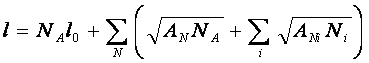(108)

Здесь N_A – общее число агентов в сети, l₀ – длина биологической нейросети отдельного агента, А_N – площадь региона (страны), А_Ni – площадь кластера (города, населенного пункта).

Характерная частота колебаний сети определяется согласно известной формуле /102/:

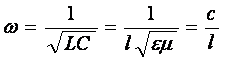(109)

Где с – скорость света. Отметим, что согласно выражению (3) собственная частота сети зависит только от ее длины. Отсюда можно определить длину индивидуальной нейросети, используя известную величину ее характерной частоты:

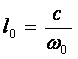(110)

Как известно, электрическая активность человеческого мозга характеризуется набором частот (ритмов ЭЭГ), среди которых выделяется альфа-ритм, бета-ритм, гамма-ритм, дельта-ритм, тета-ритм, каппа-ритм, мю-ритм, сигма-ритм и некоторые другие. В сети агентов должен доминировать один из этих ритмов, который предстоит определить. Используя выражения (107)-(110), находим характерный период экономической активности:

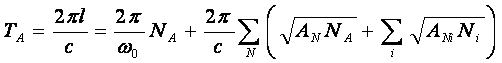(111)

Таким образом, длительность циклов экономической активности определяется, главным образом, числом действующих в сети агентов и характерной частотой ритма электрической активности их мозга.

Чтобы определить влияние индукции магнитного поля на период экономической активности, рассмотрим поток индукции магнитного поля через суммарную поверхность сети, длина которой определяется выражением (108), имеем

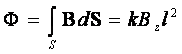(112)

Здесь k – численный коэффициент, зависящий от топологии сети. Рассмотрим выражение (112) в двух случаях, важных с точки зрения экономики.

1. Поток индукции сохраняется, тогда из выражения (112) следует, что

(113)

Следовательно, в этом случае между длиной сети и величиной вертикальной компоненты индукции магнитного поля наблюдается антикорреляция.

2. Изменение потока индукции связано с емкостью сети и величиной заряда по формуле, справедливой для параллельного соединения индуктивности и емкости:

(114)

Выражая емкость через длину сети из второго уравнения (107) и длину сети через поток индукции согласно (112), и подставляя результат в уравнение (114), получим

(115)

Интегрируя уравнение (115), находим

(116)

Полученное соотношение является обобщением выражения (113) на случай нестационарного потока индукции. Используя выражения (113) и (116), выразим квадрат длины сети в виде

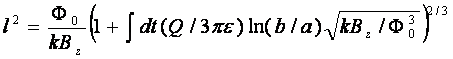(117)

Предположим, что площадь сети имеет положительную корреляцию с вертикальной компонентой индукции магнитного поля, . Используя это соотношение, находим из (117)

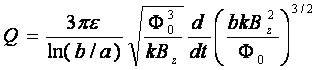(118)

Следовательно, в этом случае заряд в сети зависит только от изменения индукции магнитного поля.

Наше следующее предположение касается объема торгов акциями 500 крупнейших компаний США. Наиболее реалистичная связь, вытекающая непосредственно из выражения (108), имеет вид:

(119)

Следовательно, общий объем торгов определяется совокупной площадью региональных сетей. В зависимости от региона будет выполняться либо уравнение (113), либо уравнение (117), поэтому, в общем случае имеем:

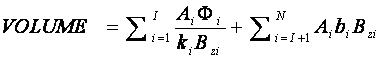(120)

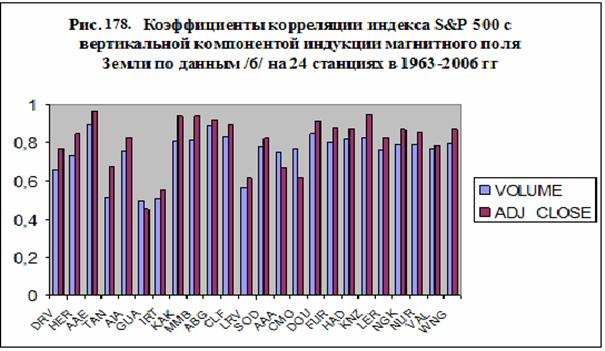
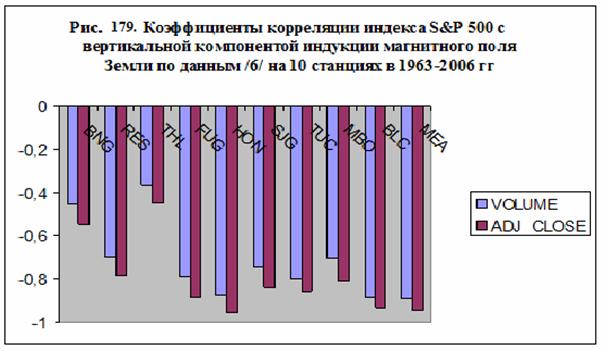
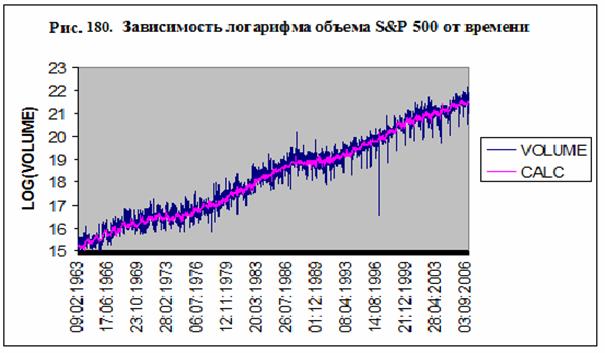
На рис. 178-179 показаны примеры корреляции и антикорреляции объема продаж с вертикальной компонентой индукции магнитного поля на различных станциях, координаты которых приведены в таблице 66. Используя уравнение (120) можно вычислить коэффициенты модели линейной регрессии. Наилучшее согласование данных с моделью (120) получается при сравнении логарифмов объема – рис. 180. При этом в модель можно внести еще некоторые существенные факторы, например, астрономические параметры долготы и расстояния до Урана и Нептуна, с которыми наблюдается корреляция S&P 500 /55/, а также удалить линейно зависимые величины, характеризующие магнитное поле Земли. В результате модель логарифма объема оказывается зависящей от 29 параметров, приведенных в таблице 67.

Таблица 66. Географические координаты магнитных обсерваторий

Station	Dumont d'Urville	Hermanus	Gnangara	Fuquene	Guam	Alibag	Honolulu	Kakioka
IAGA Code	DRV	HER	GNA	FUQ	GUA	ABG	HON	KAK
Lat	-66,667	-34,425	-31,8	5,47	13,59	18,638	21,32	36,232
Long	140,009	19,227	118	286,265	144,89	72,874	204	140,188
Station	Chambon-la-Foret	Fursten-feldbruck	Dourbes	Hartland	Niemegk	Patrony	Meanook	Lerwick
IAGA Code	CLF	FUR	DOU	HAD	NGK	IRT	MEA	LER
Lat	48,017	48,17	50,1	51	52,072	52,167	54,615	60,133
Long	2,269	11,3	4,8	355,519	12,675	104,47	246,655	358,817
Station	Baker Lake	Resolute Bay	Qaanaaq (Thule)	Sodankyla	Alma Ata	Addis Ababa	Antananarivo	San Juan
IAGA Code	BLC	RES	THL	SOD	AAA	AAE	TAN	SJG
Lat	64,333	74,69	77,483	67,367	43,25	9,03	-18,917	18,117
Long	263,969	265,105	290,833	26,633	76,917	38,765	47,552	293,85
Station	MBour	Faraday Islands	Apia	Bangui	Tucson	Byrd Station 2	Meanook	Cape Wellen (Uelen)
IAGA Code	MBO	AIA	API	BNG	TUC	BYR	MEA	CWE
Lat	14,384	-65,245	-13,807	4,333	32,17	66,163	54,615	66,163
Long	343,033	295,742	188,225	18,867	249,27	240,483	246,653	190,165
Station	Nurmijarvi	Valentia	Wingst	College	Kanozan	Niemegk	Memambetsu	Leirvogur
IAGA Code	NUR	VAL	WNG	CMO	KNZ	NGK	MMB	LRV
Lat	60,508	51,933	53,743	64,87	35,256	52,072	43,91	64,183
Long	24,655	349,75	9,073	212,14	139,956	12,675	144,189	338,5

Таблица 67. Модель линейной регрессии логарифма объема S&P 500, R²=0,992

Ln(VOLUME) = 222,878 - (0,00151 * BzGNA ) + (0,000544 * BzDRV) + (0,00139 * BzHER) + (0,000241 * BzAAE ) + (0,0000601 * BzTAN) - (0,000164 * BzAIA ) - (0,00131 * BzBNG) + (0,00235 * BzGUA) - (0,000540 * BzIRT ) - (0,000728 * BzKAK) + (0,000244 * BzRES) - (0,000212 * BzTHL) + (0,000371 * BzFUG) + (0,000498 * BzABG ) + (0,000328 * BzCLF) - (0,00000313 * BzLRV) - (0,000855 * BzSOD) + (0,000509 * BzAAA) - (0,0000115 * BzSJG) - (0,00110 * BzTUC) + (0,000392 * BzBLC) + (0,000133 * BzCMO) + (0,000315 * BzDOU) + (0,000219 * BzLER) - (0,00482 * BzVAL) + (0,0123 * URANUSLON) + (1,467 * URANUSLAT) - (0,0547 * URANUSDIST) + (0,0714 * NEPTUNEDIS)

Не смотря на высокую точность модели регрессии, приведенной в таблице 67, расчетная кривая не воспроизводит данные во всех деталях, как это видно из рис. 180. Реальный шум оказывается значительно больше, чем модельный. Тем не менее, сам факт воспроизведения с высокой степенью точности кривой логарифма объема S&P 500 на основе данных по магнитному полю Земли можно считать доказанным. Отклонение же расчетной величины от реальных данных не является удивительным, учитывая исключительную простоту модели (120), которая не содержит никаких других данных, кроме данных по магнитному полю и четырех астрономических параметров – см. таблицу 67. В работе /70/ и других было показано, что изменение магнитного поля Земли зависит от дипольных моментов небесных тел, в основном Урана и Нептуна. Поэтому использование астрономических параметров этих планет в модели (120) эквивалентно учету неких региональных составляющих магнитного поля, которые не содержатся в базе данных /61/.

Моделирование курса EUR/USD

В главе 5 были рассмотрены вопросы моделирования курсов валют усредненных за день, час и 15 минут. В качестве входных параметров информационной модели использовались астрономические параметры долготы и расстояния до десяти небесных тел. Были получены прогнозы курсов на день и неделю вперед, согласующиеся с реальными курсами. Возникает вопрос, чем определяются колебания мгновенного курса в пределах, например, одного часа – рис. 181.

Было установлено, что мгновенные колебания курсов валют, вообще говоря, не зависят от объема сделок, а курсы Ask и Bid тесно связаны между собой – рис. 182. В то же время объемы сделок Ask и Bid практически не связаны между собой – таблица 68. Это означает, что мгновенные колебания курса на протяжении часа определяются некими природными факторами. На это указывает и специфический природный ландшафт, представленный на рис. 181, образованный из данных 3688 сделок, осуществленных по продажам/покупкам валют.

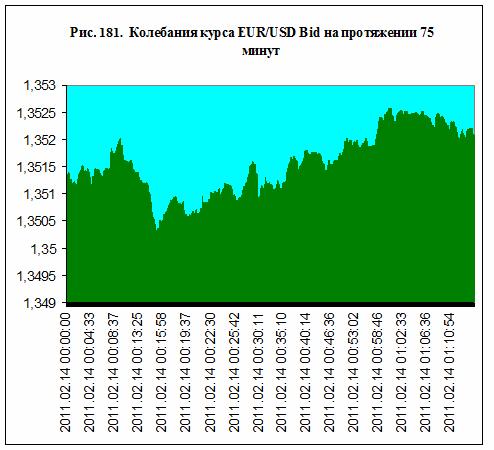
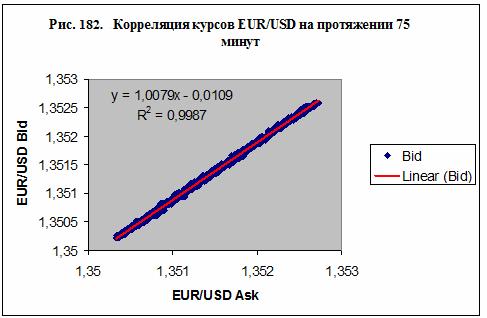
Таблица 68. Коэффициенты корреляции запрашиваемых и реализованных цен и объемов сделок EUR/USD на протяжении 20 часов при общем числе сделок - 65535

EUR/USD	Bid	AskVolume	BidVolume
Ask	1	-0,0152	-0,0246
P Value	0	9,49E-05	3,1E-10
Number of Samples	65535	65535	65535
Bid		-0,0158	-0,0251
P Value		4,96E-05	1,27E-10
N		65535	65535
AskVolume			-0,0602
P Value			1,15E-53
N			65535

Зависимость мгновенного курса валюты от природных факторов непосредственно следует из результатов, представленных в гл 5. Однако сами природные факторы в этом случае, видимо, являются региональными. Действительно, валютные торги можно рассматривать как процесс выравнивания потенциалов двух региональных сетей в соответствии с уравнением (114), причем национальная валюта изменяется как заряд на конденсаторе сети, следовательно

(121)

Наличие заряда в сети означает выполнение уравнения (118) при условии . Используя общее уравнение (112), находим

(122)

Таким образом, мгновенные колебания курса валюты определяется отношением региональных вариаций вертикальной компоненты индукции магнитного поля, т.е. зависят только от естественных факторов. Этот результат полностью согласуется с данными, приведенными на рис. 181.

Не смотря на видимую простоту модели, установление зависимости (122) является сложной задачей, поскольку исследуемые сети охватывают практически весь мир, как это следует из результатов моделирования индекса S&P 500 – см. таблицу 67. Можно лишь предполагать, что среди региональных составляющих магнитного потока должны доминировать регионы с максимальной плотностью агентов, типа Нью-Йорка, Парижа, Берлина, Лондона и т.п., поэтому колебания курса определяются конечным числом данных, подобно индексу S&P 500.

Упрощение модели достигается в том случае, когда сохраняется суммарный поток индукции в двух сетях, т.е.

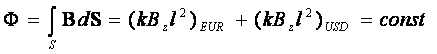(123)

Тогда из (122) и (123) следует, что

(124)

В соответствии с гипотезами (113) и (118) отсюда можно вывести уравнение типа (120), имеем

(124)

На рис. 183 представлены коэффициенты корреляции курса EUR/USD с вертикальной компонентой индукции магнитного поля Земли на 30 станциях по данным /61/ на протяжении 5 лет в 2000-2004 гг. Для сравнения на этом рисунке даны коэффициенты корреляции EUR/USD с объемом и ценой индекса S&P 500 и коэффициенты корреляции ADJ_CLOSE индекса S&P 500 с вертикальной компонентой индукции магнитного поля.

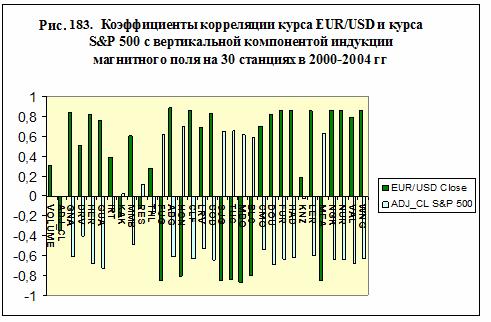
Отметим, что коэффициенты корреляции курса EUR/USD с вертикальной компонентой индукции магнитного поля Земли заметно превосходят по абсолютной величине аналогичные коэффициенты ADJ_CLOSE индекса S&P 500 в исследованный период.

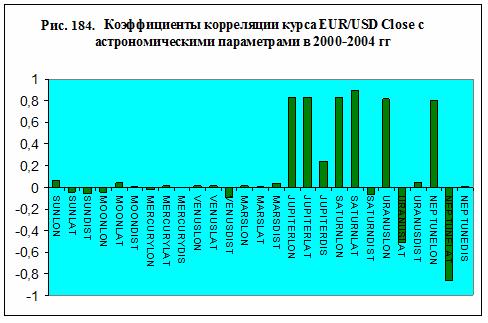
Как было установлено в главе 5, существует зависимость курсов валют от астрономических параметров долготы (LON), широты (LAT) и расстояния до небесных тел (DIST) – рис. 184. Поэтому модель (124) можно дополнить некоторой совокупностью астрономических параметров, для повышения ее точности. При этом вместо угловых параметров долготы и широты небесных тел используются функции, определение которых дано в главе 6.

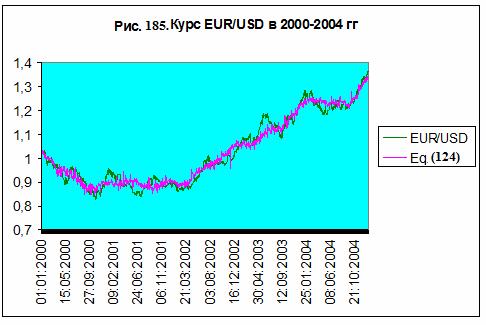
Дополненная модель (124) была использована для моделирования курса EUR/USD в 2000-2004 гг – см. рис. 185. Отклонение расчетной кривой от данных курса EUR/USD довольно велико, что, видимо, объясняется линейностью модели (124), на основе которой сделан расчет, а также влияние факторов рыночного регулирования, не учтенных в этой модели.

Модель регрессии, на основе которой сделан расчет, имеет вид:

EUR/USD Close = -15,665 - (0,708 * J1) - (1,564 * J2) - (0,592 * J3) - (5,908 * S1) - (5,677 * S2) - (11,511 * S3) + (75,956 * U1) - (62,555 * U2) - (28,685 * U3) - (131,688 * N1) - (0,250 * BzFUG) + (4,675 * BzABG) + (43,346 * BzHON) - (6,523 * BzCLF) + (13,926 * BzLRV) + (2,596 * BzSOD) - (0,00676 * BzMBO) - (1,430 * BzBLC) - (2,493 * BzCMO) - (39,368 * BzDOU)

Здесь J1,J2,J3 комплексы астрономических параметров Юпитера; S1,S2,S3 – комплексы Сатурна; U1,U2,U3 – комплексы Урана; N1 – комплекс Нептуна. В качестве параметров индукции магнитного поля используются соответствующие данные /61/, нормированные на их значения на 1 января 2000 г.

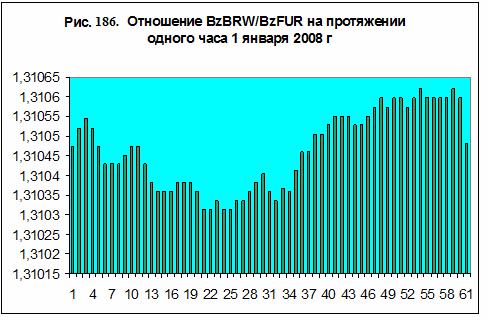
Возвращаясь к исходному вопросу о происхождении мгновенных вариаций курса EUR/USD, рассмотрим еще одно следствие обсуждаемой модели, связанное с длительностью заметных подъемов и спадов на кривой курса – рис. 181. Как следует из модели (124), в каждый момент времени курс складывается из вариаций магнитного поля, которые возникают на разных сторонах планеты – рис. 186. Колебания магнитного поля с характерным периодом около 500 секунд являются, видимо, следствием взаимодействия магнитосфер Солнца и Земли. Действительно, поделив среднее расстояние от Земли до Солнца на скорость света, находим период колебаний стоячих электромагнитных волн, связывающих два небесных тела – 499 сек. 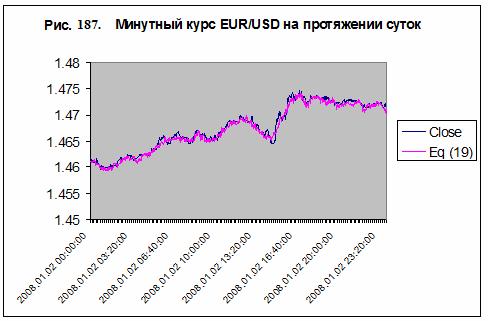Эти колебания хорошо прослеживаются на кривой мгновенного курса EUR/USD – рис. 181. Используя минутные данные по вертикальной компоненте индукции магнитного поля /61/, можно с большой степенью точности смоделировать минутный курс EUR/USD на протяжении суток – рис. 187.

Модель минутного курса EUR/USD на протяжении суток 2 января 2008 г в зависимости от нормированных параметров вертикальной компоненты индукции магнитного поля на 35 станциях по данным /61/ имеет вид (для обозначения локальных нормированных парметров Bz(t)/Bz(0)-1 использованы IAGA коды станций наблюдения):

EUR/USD Close = 1.461 + (0.0760 * AAE) - (4.244 * AIA) + (8.295 * AMS) + (6.017 * ASC) - (5.039 * ASP ) - (14.090 * BDV) - (14.034 * BFE) + (19.200 * BOU) - (3.327 * BSL) - (0.694 * CBB) + (8.148 * CLF) - (1.456 * CMO) + (0.000627 * CNB) - (0.155 * CTA) + (4.193 * DOB) - (11.125 * ESK) - (9.934 * FRD) - (3.828 * FRN) - (7.541 * FUR) + (2.257 * GCK) + (3.375 * GNA) + (1.569 * GUA) - (4.540 * GZH) + (7.200 * HAD) + (1.586 * HER) + (2.820 * HLP) - (0.0472 * HUA) - (21.128 * IRT) + (4.941 * IZN) - (4.465 * KDU) + (7.361 * KNY ) - (0.310 * KNZ ) - (0.577 * KOU ) + (7.193 * LER) + (2.012 * LRM)

Кроме локальных параметров на курсы валют влияют глобальные параметры, например, положения небесных тел относительно Земли. Физически влияние небесных тел сводится к гравитационному и электромагнитному взаимодействию, что приводит к изменениям в параметрах магнитного поля и полюса Земли. На основе этого в главе 5 был развит метод прогнозирования курсов валют по астрономическим данным на основе системы искусственного интеллекта «Эйдос-астра» /7/.

Метод прогнозирования курсов валют был осуществлен на основе данных FOREX о ежечасных и 15 минутных курсах валют на момент открытия (Open), высокий (High), низкий (Low) и на момент закрытия (Close), из которых формируются категории повышения (1)/снижения (0) курса. Для 15-минутного курса EUR/USD получено хорошее согласование расчетного курса с реальным курсом на протяжении недели.

Нами была создана информационная модель минутного курса EUR/USD с использованием данных по вертикальной компоненте индукции магнитного поля /61/. Изменение курса характеризуют 12 категорий повышения (2), снижения (0), постоянного (1) курса на момент открытия (Open) - A, высокий (High) - B, низкий (Low) -C и на момент закрытия (Close) – D. На рис. 188 представлена визуализация фрагментов матрицы информативностей категорий повышения/снижения курса EUR/USD в зависимости от нормированного параметра Bz(t)/Bz(0)-1 на станции GUA. Частотные характеристики категорий курса образуют своеобразный алфавит, расшифровка которого осуществляется на основе системы искусственного интеллекта /7/.

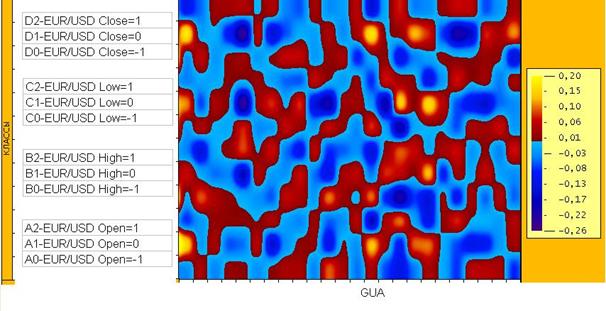
Рис. 188. Визуализация матрицы информативностей частоты 12 категорий курса EUR/USD в зависимости от нормированного параметра Bz(t)/Bz(0)-1 на станции GUA.

Таким образом, установлено, что курсы валют и биржевых индексов зависят от вертикальной компоненты индукции магнитного поля Земли и от астрономических параметров небесных тел. Предложены модели, описывающие курс S&P 500 в 1963-2006 гг и курс EUR/USD в 2000-2004 гг. Сочетание параметров магнитного поля и астрономических параметров небесных тел позволяет повысить точность расчетных моделей. Как уже отмечалось выше, магнитное поле Земли, в свою очередь, зависит от астрономических параметров /55/, поэтому включение астрономических параметров в модель (124) равносильно учету неких региональных составляющих индукции магнитного поля, не отраженных в базе данных /61/.

Полученные результаты означают, что стихийное рыночное регулирование курсов акций и валют равносильно возникновению зависимости курсов от природных региональных факторов, главным из которых является магнитное поле Земли. Сильная зависимость курсов валют и акций от вариаций магнитного поля Земли объясняется индукцией и емкостью совокупной сети, образовавшейся в результате экономической деятельности субъектов и корпораций.

Причина, в силу которой агенты принимают решения о возможном изменении курса в зависимости от местной величины индукции магнитного поля, заключается, видимо, в электрической активности мозга и в способности прогнозировать тенденции локального изменения индукции магнитного поля. Здесь будет уместна аналогия с биологической популяцией, которая само организуется под влиянием внешних факторов среды. Не вызывает сомнения, что современная популяция людей находится в сильной зависимости от электромагнитной энергии, широко используемой, как в быту, так и в промышленности. Так, например, мировое потребление энергии в 2008 году оценивается в 1,504*10¹³ Вт, причем основное потребление приходится на крупные города и промышленные центры. Очевидно, что изменение энергии такого масштаба способно вызвать заметный отклик в окружающей среде. Реакция же магнитного поля Земли, в свою очередь, вызывает заметный отклик в параметрах, характеризующих мировую экономику.

Влияние солнечных пятен и магнитных бурь на самочувствие людей, политику и экономику было обнаружено еще в 20-30-х годах прошлого столетия /93-95/, однако в настоящее время прогнозы магнитных бурь используются, главным образом, в медицинских целях /96/.

Самосогласованная система, включающая магнитное поле Земли и сеть, связывающую агентов, имеет собственную динамику, которая находит свое отражения в текущих курсах валют и биржевых индексов. Регулирование этой сложной системы, охватывающей материки, является сложной, практически невыполнимой задачей. В отсутствии же механизмов эффективного регулирования мировая экономика находится под влиянием глобальных и региональных природных факторов, которые, как было продемонстрировано в настоящей работе, вносят собственные ритмы в ее развитие.