ГЛАВА 6. ПРОГНОЗИРОВАНИЕ
ЗЕМЛЕТРЯСЕНИЙ
6.1. Прогнозирование землетрясений по астрономическим данным с
использованием системы искусственного интеллекта
В работе /11/ была сформулирована теорема
астросоциотипологии, которая устанавливает зависимость функции распределения
случайных событий, происходящих на Земле от кинематических и динамических
параметров нашей планеты при ее движении вокруг Солнца. Одним из следствий этой
теоремы является то, что любые непрерывные или дискретные распределения событий
по времени при их представлении в зависимости от координат небесных тел
содержат когерентные колебания, обусловленные движением небесных тел.
В работе /18/ высказана гипотеза о том, что эти
когерентные колебания могут быть использованы для распознавания событий любой
природы, например, социальных или экономических категорий, а также природных
явлений.
Ниже развита модель прогнозирования землетрясений по астрономическим
данным на основе системы искусственного интеллекта «Эйдос-астра» /7/. База
данных землетрясений была сформирована на основе оперативного сейсмологического
каталога ГС РАН /56/, содержащего 65541 запись событий землетрясений,
произошедших в различных регионах мира в период с 1 января 1993 года по 20
ноября 2008 г.
Моделирование событий осуществлялось по параметру сходства,
который является аналогом коэффициента
корреляции в статистике. Обнаружена
зависимость параметра сходства от магнитуды, глубины очага (гипофокуса) и числа
землетрясений, происходящих ежедневно на нашей планете, как в месячном, так и в
2-3 дневном прогнозе. В работе /52/
обсуждается гипотеза, что этот эффект обусловлен гравитацией небесных тел. Для
проверки гипотезы было исследовано влияние 12 гравитационных комплексов на всю
совокупность 65541 событий и выделены наиболее информативные астрономические
признаки землетрясений.
Задача о распознавании категорий событий в поле
центральных сил
Вообще говоря, каждому моменту времени можно сопоставить
множество категорий событий, происходящих в данном месте на нашей (или иной)
планете. События могут иметь детерминированную или случайную природу. По мнению
авторов целесообразно считать, что в общем случае система детерминации любого
события включает в различных соотношениях и детерминированную, и случайную
компоненты. Чтобы установить характер
(закономерность) последовательности событий и описать ее в виде функции,
можно сопоставить ее с другой последовательностью
или совокупностью последовательностей, которая рассматривается как аргумент
этой функции. При этом если эти последовательности являются детерминированными,
они могут играть роль времени, отличного от линейного времени Ньютона. Можно
сформулировать задачу распознавания категорий событий, используя
детерминированные последовательности. Частным случаем этой задачи является
распознавания категорий событий по астрономическим данным положений небесных
тел Солнечной системы в астросоциотипологии и распознавание категорий курсов
валют – см. главу 4-5 соответственно.
Рассмотрим задачу распознавания категорий по
астрономическим данным. Итак, имеется множество событий A, которому ставится в
соответствие множество категорий Ci. Событием можно считать
регистрацию землетрясения сейсмологической станцией, а категорией – его
магнитуду, лежащую в определенном интервале и глубину гипофокуса. Каждое
событие землетрясения характеризуется моментом времени и географическими координатами
места его происхождения. По этим данным можно построить матрицу, содержащую
координаты небесных тел, например углы долготы и расстояния. Будем считать, что заданы частотные
распределения Ni – число
событий, имеющих отношение к данной категории Ci.
Определим число случаев реализации данной категории,
которое приходится на заданный интервал изменения астрономических параметров,
имеем в дискретном случае:
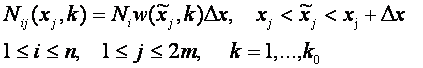
Здесь w –
плотность распределения событий вдоль нормированной координаты. Нормированная
переменная определяется через угловую и радиальную координаты следующим
образом:
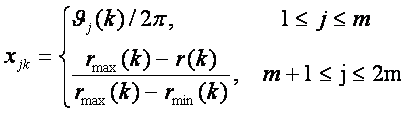
где ![]() - минимальное и максимальное удаление планеты
от центра масс системы, k0
– число небесных тел, используемых в задаче.
- минимальное и максимальное удаление планеты
от центра масс системы, k0
– число небесных тел, используемых в задаче.
Определим матрицу информативности согласно /3/
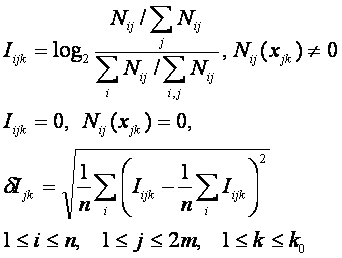
Каждой категории можно сопоставить вектор информативности
астрономических параметров размерности 2mk0,
составленный из элементов матрицы информативности, путем последовательной
записи столбцов, соответствующих нормированной координате, в один столбец, т.е.
![]() (68)
(68)
С другой стороны, процесс идентификации и
распознавания может рассматриваться как разложение вектора распознаваемого
объекта в ряд по векторам категорий (классов распознавания) /3/. Этот вектор,
состоящий из единиц и нулей, можно определить по координатам небесных тел, соответствующих
дате и месту происхождения события l
в виде
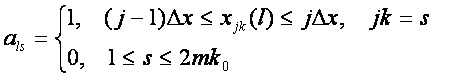 (69)
(69)
Таким образом, если нормированная координата небесного
тела из данных по объекту исследуемой выборки попадает в заданный интервал,
элементу вектора придается значение 1, а во всех остальных случаях – значение
0. Перечисление координат осуществляется последовательно, для каждого небесного
тела.
В случае, когда система векторов (68) является полной,
можно любой вектор (69) представить в виде линейной комбинации векторов системы
(68). Коэффициенты этого разложения будут соответствовать уровню сходства
данного события с данной категорией. В случае неполной системы векторов (68)
точная процедура заменяется распознаванием. При этом уровень сходства данных события
с той или иной категорией можно определить по величине скалярного произведения
вектора (68) на вектор (69), т.е.
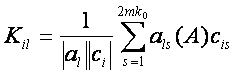 (70)
(70)
Отметим, что возможны четыре исхода, при которых можно
истинно или ложно отнести или не отнести данное событие к данной категории. Для
учета этих исходов распознавание категорий в системе искусственного интеллекта «Эйдос-астра»
/7/ осуществляется по параметру сходства, который определяется следующим
образом /2-6/:
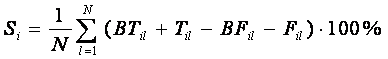 (71)
(71)
Si – достоверность идентификации «i-й»
категории;
N – количество событий в распознаваемой выборке;
BTil – уровень сходства «l-го» события с «i-й» категорией, к
которой он был правильно отнесен системой;
Til – уровень сходства «l-го» события с «i-й» категорией, к которой
он был правильно не отнесен системой;
BFil – уровень сходства «l-го» события с «i-й» категорией, к
которой он был ошибочно отнесен системой;
Fil – уровень сходства «l-го» события с «i-й» категорией, к которой
он был ошибочно не отнесен системой.
При таком определении параметр сходства изменяется в
пределах от -100% до 100%, как обычный коэффициент корреляции в статистике.
Очевидно, что параметр сходства должен удовлетворять критерию простой проверки
![]()
В работах /3-4/ и других было показано, что процедура
распознавания по параметру сходства (70), реализованная в системе
искусственного интеллекта «Эйдос-астра» /7/,
является устойчивой как относительно объема выборки, так и относительно
числа ячеек модели. Математическое обоснование этой процедуры дано в монографии
/3/. Причина, по которой оказывается возможным идентифицировать подмножества
(категории) событий различной даже случайной природы, используя астрономические
параметры, достаточно очевидна. Ведь фактически идентифицируются распределения,
которые образуются при модулировании исходных распределений астрономическими
параметрами. В некоторых случаях этого достаточно, чтобы осуществить
распознавание категорий. Эту задачу можно сравнить с разложением солнечного
света призмой. Свет представляет собой смесь случайных электромагнитных
колебаний, но после прохождения призмы свет разлагается в спектр категорий
цвета. При этом случайная природа самого света не меняется.
Исходные данные и технология моделирования
землетрясений
База данных землетрясений была сформирована на основе
оперативного сейсмологического каталога ГС РАН /56/, содержащего 65541 запись
событий землетрясений, произошедших в различных регионах мира в период с 1
января 1993 года по 20 ноября 2008 г.
Из исходной
базы было образовано несколько различных БД для исследования влияния
астрономических параметров на магнитуду и глубину гипофокуса, на ежедневное
число землетрясений и на их локализацию.
Категория «Магнитуда» была получена из исходной базы
данных путем умножения параметра MPSP на 10 и добавления символа А – см.
таблицу 41. Всего было образовано 47 категорий этого типа, которые
соответствуют изменению параметра MPSP от 3 до 7.5 с шагом 0.1 (46 категорий)
плюс одна категория А0, соответствующая тем случаям, когда по данным каталога
/56/ параметр MPSP=0. Отметим, что магнитуда MPSP рассчитывается по
максимальной скорости смещения в объемных волнах /56/.
ТАБЛИЦА. 41. Фрагмент базы данных категории «Магнитуда»
|
I |
NAME |
CATS1 |
SUNLON |
SUNDIST |
MOONLON |
MOONDIST |
|
1 |
01.01.1993
|
A54:A54:A56:A53: |
280.9686023746710 |
0.9832953224852 |
13.6193309143572 |
0.0026758287293 |
|
2 |
02.01.1993
|
A51:A49: |
281.9877769647200 |
0.9832827412929 |
25.8047627280948 |
0.0026514329751 |
|
3 |
03.01.1993
|
A60:A52:A46:A62:A53:A54: |
283.0068945266630 |
0.9832755597314 |
38.2524447909018 |
0.0026206202125 |
|
4 |
04.01.1993
|
A62:A53:A56:A60:A60: |
284.0259498778590 |
0.9832740284513 |
51.0313074310990 |
0.0025854001894 |
|
5 |
05.01.1993
|
A48: |
285.0449399774140 |
0.9832784151922 |
64.1942901475346 |
0.0025483733705 |
|
6 |
06.01.1993
|
A49:A58: |
286.0638619286330 |
0.9832889650152 |
77.7694840563520 |
0.0025125186647 |
|
7 |
07.01.1993
|
A61:A0:A57:A0: |
287.0827135891120 |
0.9833058932933 |
91.7514779908947 |
0.0024808734659 |
|
8 |
08.01.1993
|
A55:A55:A46: |
288.1014940625240 |
0.9833293611578 |
106.0953151556760 |
0.0024561346250 |
|
9 |
09.01.1993
|
A49:A56:A52:A47: |
289.1202049674210 |
0.9833594500691 |
120.7161775556960 |
0.0024402538842 |
|
10 |
10.01.1993
|
A66: |
290.1388517853630 |
0.9833961422425 |
135.4972701770000 |
0.0024341353125 |
Данные по глубине гипофокуса обрабатывались по формуле:
![]()
где глубина выражена в километрах. Всего было выделено
54 категории, соответствующие глубине гипофокуса от 0 до 812 км. В таблице 42
представлен фрагмент базы данных категорий глубины гипофокуса.
ТАБЛИЦА. 42. Фрагмент базы данных категории
«Глубина гипофокуса»
|
ID |
NAME |
CATS1 |
SUNLON |
SUNDIST |
MOONLON |
MOONDIST |
|
1 |
01.01.1993
|
B35:B35:B35:B53: |
280.9686023746710 |
0.9832953224852 |
13.6193309143572 |
0.0026758287293 |
|
2 |
02.01.1993
|
B35:B34: |
281.9877769647200 |
0.9832827412929 |
25.8047627280948 |
0.0026514329751 |
|
3 |
03.01.1993
|
B39:B11:B60:B41:B40:B40: |
283.0068945266630 |
0.9832755597314 |
38.2524447909018 |
0.0026206202125 |
|
4 |
04.01.1993
|
B42:B35:B43:B37:B35: |
284.0259498778590 |
0.9832740284513 |
51.0313074310990 |
0.0025854001894 |
|
5 |
05.01.1993
|
B36: |
285.0449399774140 |
0.9832784151922 |
64.1942901475346 |
0.0025483733705 |
|
6 |
06.01.1993
|
B35:B35: |
286.0638619286330 |
0.9832889650152 |
77.7694840563520 |
0.0025125186647 |
|
7 |
07.01.1993
|
B11:B23:B35:B35: |
287.0827135891120 |
0.9833058932933 |
91.7514779908947 |
0.0024808734659 |
|
8 |
08.01.1993
|
B11:B35:B63: |
288.1014940625240 |
0.9833293611578 |
106.0953151556760 |
0.0024561346250 |
|
9 |
09.01.1993
|
B35:B35:B35:B35: |
289.1202049674210 |
0.9833594500691 |
120.7161775556960 |
0.0024402538842 |
|
10 |
10.01.1993
|
B35: |
290.1388517853630 |
0.9833961422425 |
135.4972701770000 |
0.0024341353125 |
В качестве
астрономических параметров были использованы долгота и расстояние от Земли до
десяти небесных тел – Солнца, Луны, Марса, Меркурия, Венеры, Юпитера, Сатурна,
Урана, Нептуна и Плутона, и долгота Северного Узла Луны. Астрономические
параметры вычислялись на каждый день в фиксированной точке с географическими
координатами (36.61666667E; 55.08333333N) в 9:00 GMT в топоцентрической системе
координат. Отметим, что выбор этой точки не является существенным для решаемого
класса задач.
Для проверки различных
гипотез из астрономических параметров расстояний было образовано шесть
гравитационных комплексов G1-G6:
суммарный нормированный
гравитационный потенциал восьми небесных тел – Луны, Марса, Меркурия, Венеры,
Юпитера, Сатурна, Урана, Нептуна;
суммарный нормированный
гравитационный потенциал семи небесных тел – Луны, Марса, Меркурия, Венеры,
Сатурна, Урана, Нептуна;
суммарный нормированный
гравитационный потенциал шести небесных тел – Марса, Меркурия, Венеры, Сатурна,
Урана, Нептуна;
суммарный нормированный
гравитационный потенциал пяти небесных тел – Марса, Меркурия, Венеры, Урана,
Нептуна;
суммарный нормированный
гравитационный потенциал четырех небесных тел – Марса, Меркурия, Урана,
Нептуна;
суммарный нормированный
гравитационный потенциал девяти небесных тел – Солнца, Луны, Марса, Меркурия,
Венеры, Юпитера, Сатурна, Урана, Нептуна.
Таким образом, по
определению
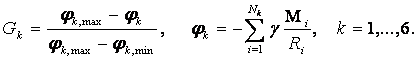 (72)
(72)
Здесь ![]() –
гравитационная постоянная и масса небесного тела соответственно. Из этих
комплексов были также образованы шесть других комплексов G7-G12,
представляющих собой суточное изменение (первую производную по времени) каждого
из комплексов G1-G6 соответственно.
–
гравитационная постоянная и масса небесного тела соответственно. Из этих
комплексов были также образованы шесть других комплексов G7-G12,
представляющих собой суточное изменение (первую производную по времени) каждого
из комплексов G1-G6 соответственно.
Решение прямой задачи
включает в себя нормирование входных параметров и приведение их к одному
масштабу изменения в интервале (0;360), разбиение интервалов на М частей,
вычисление матрицы абсолютных частот и информативности. Отметим, что в системе «Эйдос-астра»
реализован режим синтеза нескольких моделей, в которых число ячеек принимает
любое заданное значение М=2,3,...,173 /4/. Очевидно, что модель М12 наилучшим
образом подходит для осуществления месячного прогноза, а модель М120 может быть
использована для 3 дневного прогноза.
Решение обратной задачи
включает в себя распознавание (прогнозирование) категорий по заданным
астрономическим параметрам. Частным случаем задачи распознавания является определение
достоверности идентификации категорий по астрономическим данным в каждой
модели. Рассмотрим решение этой задачи в
случае исследуемой совокупности событий
землетрясений.
Достоверность идентификации категорий магнитуды
Путем обработки исходных
данных было получено распределение событий по величине магнитуды – рис. 106.
Заметим, что среди исследуемых событий преобладают легкие и умеренные
землетрясения, тогда как в природе преобладают слабые (около 49000 ежегодно) и
очень слабые землетрясения (около 9000 ежедневно). С другой стороны, умеренные
и сильные землетрясения, произошедшие в мире в исследуемый период, практически
все отражены в каталоге /56/. Поэтому
можно ожидать, что именно эти события будут распознаваться наиболее достоверно.
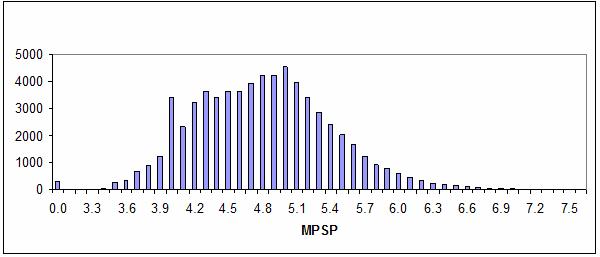
Рис. 106. Распределение
событий по величине магнитуды землетрясений.
Действительно, на рис. 107 представлены параметр
сходства в зависимости от магнитуды в пяти моделях – М12 (месячный прогноз),
М28 (двухнедельный прогноз), М90
(четырехдневный прогноз), М120 и М160 (2-х и 3-х дневной прогноз). Из этих данных
следует, что достоверность идентификации магнитуды по астрономическим
параметрам на 20-60% выше для умеренных и сильных землетрясений, чем для
легких.
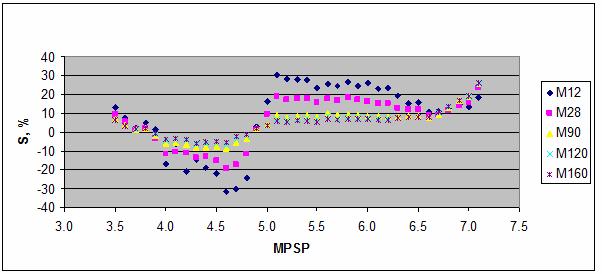
Рис. 107. Зависимость
параметра сходства от магнитуды
В месячном прогнозе достоверность идентификации магнитуды
умеренных и сильных землетрясений достигает 30%, тогда как в 2-4-дневном
прогнозе максимальное значение параметра сходства не превосходит 10%. Для
сравнения укажем, что в задачах распознавания социальных категорий по
астрономическим данным параметр сходства достигает 80% /3-4/. В задачах распознавания
экономических категорий по астрономическим данным достоверность 15-минутного
прогноза категорий повышения/понижения
курсов валют достигает 82% на протяжении
недели и 100% в часовом прогнозе – см. Главу 5.
Тем не менее, развитая модель позволяет осуществлять
прогноз умеренных и сильных землетрясений, как будет показано ниже. Разумеется,
что ценность такого прогноза возрастает, если кроме магнитуды указать еще и
координаты события, например, глубину залегания очага (гипофокуса)
землетрясения.
Достоверность идентификации глубины гипофокуса
Распределение событий по глубине залегания очагов землетрясений
содержит два пика, которые приходятся на глубину 10 и 33 км – рис. 108. Первый
пик, видимо, соответствует кровле «гранитного» слоя. Второй пик лежит ниже
поверхности «базальтового» слоя (границы Конрада).
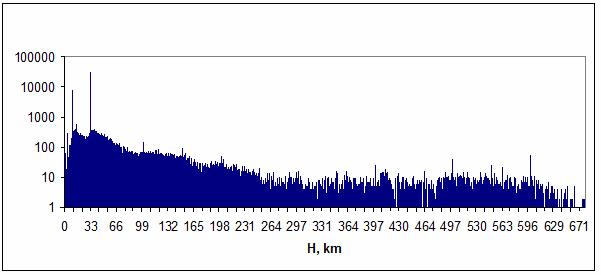
Рис. 108. Распределение
событий по глубине залегания очагов землетрясений
Параметр сходства категории глубины залегания очага землетрясения
(гипофокуса) имеет два максимума, которые приходятся на глубину 3 и 33 км
соответственно – рис. 109.
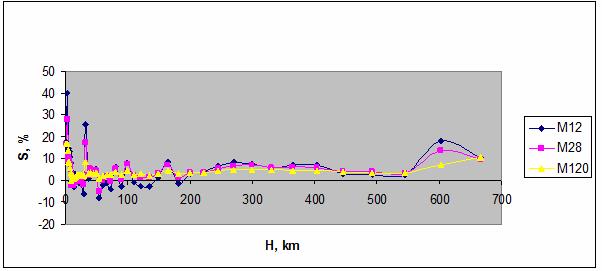
Рис. 109. Параметр сходства в
зависимости от глубины залегания очагов землетрясений в трех моделях.
Неглубокие (3-7 км, 33 км) и глубокие (600 км)
землетрясения распознаются лучше, чем средней глубины. Различие между плохо
распознаваемыми и хорошо распознаваемыми случаями достигает 47%, что
свидетельствует о заметном влиянии небесных тел на некоторые сейсмические процессы. Физический механизм этого влияния
пока неизвестен, однако, скачкообразное изменение параметра сходства с ростом
магнитуды – см. рис. 107, указывает на триггерный (пороговый) механизм, как при
подземных взрывах /81/. Иначе говоря, влияние небесных тел лишь запускает
сейсмический процесс, но не создает деформации, приводящие к разлому. Причем
максимальное влияние небесных тел проявляется в земной коре, а также в зонах
субдукции на глубине 600 км, вызывая умеренные и сильные землетрясения с МPSP
> 5.
Достоверность идентификации частоты событий
Диаграмма ежедневного числа событий представлена на
рис. 109, в результат распознавания частоты событий – на рис. 110. Среди событий хорошо распознаются дни с малым
числом умеренных и сильных землетрясений ( < 5) и с большим их числом ( >
20). Вместо ежедневного числа событий можно использовать их суммарную
магнитуду, поделенную на 5, т.е. параметр
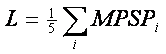 (73)
(73)
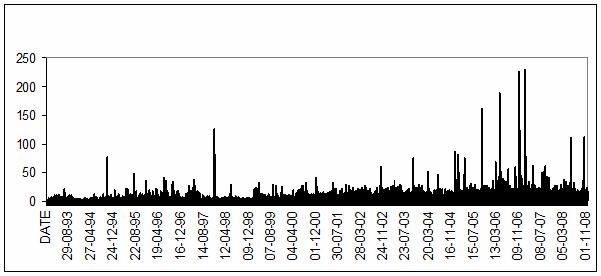
Рис. 109. Ежедневное число
событий
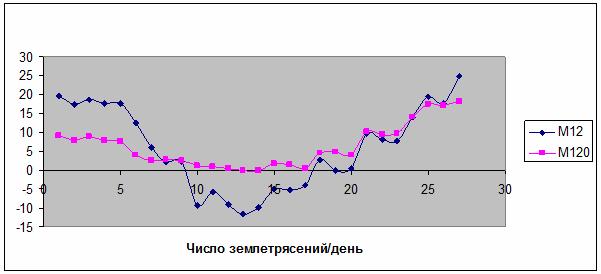
Рис. 110. Зависимость
параметра сходства от числа землетрясений в двух моделях
На рис. 111 представлена частота событий в зависимости
от параметра L, а на рис. 112 – результат распознавания этих событий. Кривые на
рис. 108 и 110 имеют сходно поведение, однако величина параметра сходства при
распознавании по параметру L в 3 раза больше, чем при распознавании частоты
событий. Следовательно, параметр L является более информативным, нежели частота
событий и может служить сейсмической характеристикой дня. Дни с низкой
сейсмичностью (L < 5) и с высокой сейсмичностью (L > 20) распознаются
достаточно достоверно, причем прогноз может быть дан как на месяц, так и на 3
дня вперед. Полученные результаты позволяют сделать вывод о зависимости некоторых
сейсмических процессов от положения небесных тел.
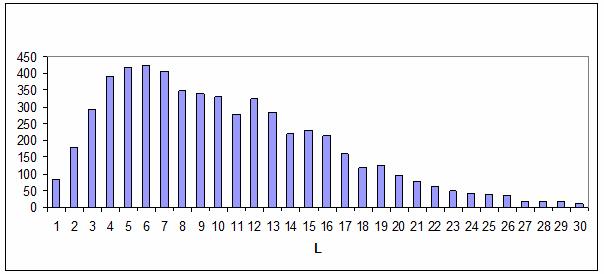
Рис. 111. Частота
распределения событий
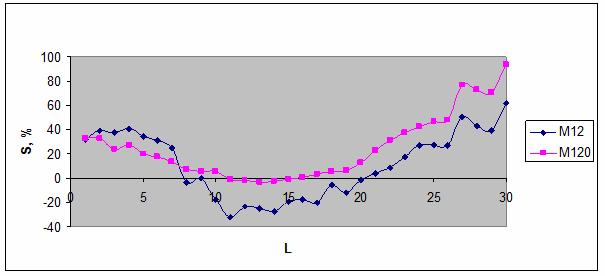
Рис. 112. Зависимость
параметра сходства от парметра L.
Проверка
гравитационных гипотез
Среди механизмов влияния небесных тел на процессы, происходящие
в недрах нашей планеты, в первую очередь необходимо исследовать гравитацию.
Технология моделирования на основе системы искусственного интеллекта «Эйдос-астра»
позволяет установить, какие астрономические признаки являются наиболее
информативными при распознавании тех или иных категорий, т.е. оказывают на них
наибольшее влияние. Это можно сделать как путем прямой оценки информативности,
так и путем оценки возбуждающих и тормозящих связей нейронов.
Заметим, что из
65541 записи событий в каталоге /56/ в 30016 случаях положение гипофокуса
определено на глубине 33 км. Параметр сходства на этой глубине имеет локальный
максимум – см. рис. 109. Сравним эти события, имеющие, видимо, отношение к
процессам в магме, с событиями, происходящими
на глубине 3 км (напряжения и трещины в земной коре) и на глубине
545-665 км (зоны субдукции). В таблице 43 приведены данные по информативности
астрономических признаков трех типов событий в модели М120. В фигурных скобках
указан диапазон изменения признака. Отметим, что все признаки нормированы и
приведены к одному интервалу изменения с долготой небесных тел – (0;360).
Каждый из признаков отражает влияние гравитации преимущественно одного
небесного тела, а именно:
G6, G12 – Солнца;
G1, G7 – Юпитера;
G2, G8 – Сатурна, Луны;
G3, G9 – Сатурна, Венеры;
G4, G10 – Венеры;
G5, G11 – Урана, Марса.
Таблица. 43. Информативность
(бит) астрономических признаков 12 гравитационных комплексов G1-G12
в трех различных зонах формирования землетрясений
|
Кора 3km |
Магма 33km |
Зоны субдукции 545-665 km |
|||
|
Астропризнак |
Бит |
Астропризнак |
Бит |
Астропризнак |
Бит |
|
G2 {342, 345} |
1.628714 |
G9 {333, 336} |
0.632511 |
G3 {345, 348} |
1.166759 |
|
G3 {351, 354} |
1.565744 |
G7 {3, 6} |
0.570593 |
G2 {348, 351} |
1.043125 |
|
G1 {357, 360} |
1.563297 |
G8 {345, 348} |
0.570593 |
G9 {330, 333} |
0.914688 |
|
G8 {39, 42} |
1.307307 |
G8 {351, 354} |
0.570593 |
G3 {351, 354} |
0.907268 |
|
G3 {354, 357} |
1.302067 |
G3 {348, 351} |
0.441355 |
G8 {27, 30} |
0.858413 |
|
G5 {18, 21} |
1.286695 |
G9 {339, 342} |
0.431437 |
G3 {348, 351} |
0.832646 |
|
G2 {348, 351} |
1.276722 |
G7 {345, 348} |
0.422928 |
G5 {12, 15} |
0.796496 |
|
G2 {351, 354} |
1.238849 |
G8 {357, 360} |
0.422928 |
G5 {24, 27} |
0.785046 |
|
G2 {354, 357} |
1.140866 |
G3 {342, 345} |
0.416945 |
G11 {12, 15} |
0.762961 |
|
G3 {12, 15} |
1.105452 |
G1 {9, 12} |
0.414573 |
G11 {36, 39} |
0.752301 |
|
G9 {45, 48} |
1.098683 |
G1 {18, 21} |
0.389067 |
G4 {3, 6} |
0.731689 |
|
G2 {345, 348} |
1.092011 |
G9 {345, 348} |
0.382582 |
G3 {15, 18} |
0.711954 |
|
G8 {21, 24} |
1.078948 |
G1 {12, 15} |
0.369877 |
G5 {9, 12} |
0.702393 |
|
G10 {342, 345} |
1.057963 |
G9 {357, 360} |
0.336634 |
G2 {351, 354} |
0.683843 |
|
G2 {27, 30} |
1.053878 |
G1 {0, 3} |
0.324544 |
G5 {87, 90} |
0.674839 |
|
G3 {357, 360} |
0.991198 |
G2 {114, 117} |
0.324544 |
G2 {123, 126} |
0.672615 |
|
G11 {306, 309} |
0.970354 |
G3 {357, 360} |
0.319902 |
G9 {6, 9} |
0.666007 |
|
G5 {42, 45} |
0.955314 |
G1 {357, 360} |
0.317164 |
G8 {327, 330} |
0.648831 |
|
G9 {42, 45} |
0.917441 |
G2 {345, 348} |
0.311103 |
G9 {36, 39} |
0.648831 |
|
G10 {12, 15} |
0.808547 |
G2 {354, 357} |
0.311103 |
G11 {351, 354} |
0.648831 |
|
G4 {66, 69} |
0.797887 |
G3 {351, 354} |
0.311103 |
G10 {342, 345} |
0.636354 |
|
G11 {309, 312} |
0.790914 |
G7 {12, 15} |
0.311103 |
G3 {102, 105} |
0.628219 |
|
G9 {48, 51} |
0.786323 |
G2 {351, 354} |
0.292553 |
G1 {39, 42} |
0.620224 |
|
G5 {255, 258} |
0.778557 |
G3 {339, 342} |
0.292553 |
G2 {39, 42} |
0.600820 |
|
G10 {102, 105} |
0.777275 |
G1 {15, 18} |
0.289532 |
G5 {15, 18} |
0.600820 |
|
G2 {15, 18} |
0.770603 |
G2 {342, 345} |
0.289532 |
G5 {0, 3} |
0.595779 |
|
G6 {87, 90} |
0.614583 |
G6 {285, 288} |
0.059968 |
G6 {261, 264} |
0.505014 |
|
G12 {234, 237} |
0.606144 |
G12 {249, 252} |
0.059032 |
G12 {207, 210} |
0.489212 |
Как следует из данных,
приведенных в таблице 43, во всех случаях преобладающее влияние на формирование
очагов оказывают Юпитер, Сатурн, Луна и Венера. В коре и в зонах субдукции велика
роль гравитационного потенциала, в магме главным фактором является производная
гравитационного потенциала по времени. Этот результат хорошо соотносится с
механикой процессов формирования очагов землетрясений. Действительно в коре и в
зонах субдукции главным фактором разрушения является напряженное состояние,
вызванное избыточным давлением. Но во внешнем
гравитационном поле давление изменяется пропорционально гравитационному
потенциалу. В магме же преобладают гидродинамические процессы, чувствительные к
изменению давления во времени. Таким процессом является, например, схлопывание
пузыря вблизи твердой поверхности.
Вообще говоря, астрономические признаки
(значения факторов) могут оказывать как возбуждение, так и торможение, т.е. как
способствовать наступлению события, так и препятствовать этому.
На рис. 113-115 представлены
модели нелокальных нейронов трех типов процессов, перечисленных в таблице 43.

Рис. 113. Модель нелокального
нейрона 300 событий землетрясений с глубиной гипофокуса 3 км.
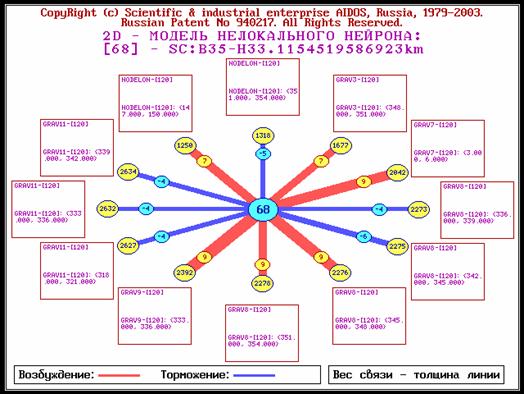
Рис. 114. Модель нелокального
нейрона 30016 событий землетрясений с глубиной гипофокуса 33 км.
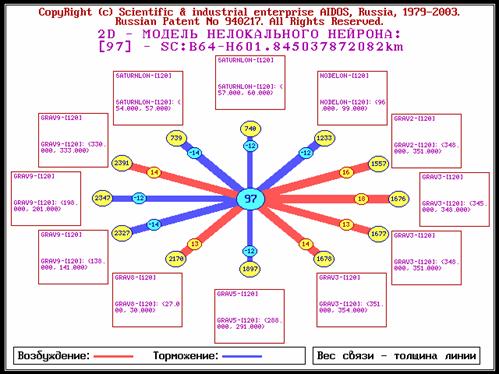
Рис. 115. Модель нелокального
нейрона 336 событий землетрясений с
глубиной гипофокуса 545-665 км.
Из данных, приведенных на рис. 113, 115 следует, что
комплексы G1, G2, G3 (GRAV1-GRAV3) оказывают
возбуждающее влияние на процессы в земной коре, а комплексы G2, G3 , G8
, G9 – в зонах субдукции. Процессы в магме возбуждают комплексы G3, G7, G8 ,
G9. Из этого можно предположить, что процессы в зонах субдукции
носят смешанный характер, т.е. включают, как тектонические процессы, так и
процессы в магме.
Полученные результаты носят предварительный, качественный характер. Для получения количественных
результатов сравним годичные изменения гравитационных потенциалов, входящих в
комплексы G1, G2, G3 , с величиной гидростатического давления на глубине 3 км –
рис. 116. Отметим, что второй и третий комплексы практически не отличаются
между собой в этом масштабе, а годичные изменения всех трех комплексов сравнимы
с величиной гидростатического давления. Разумеется, что это лишь потенциальная
энергия. Неизвестно, какая доля этой энергии способна аккумулироваться в форме
упругих напряжений, однако ясно, что если существует механизм поглощения и накопления
этой энергии в форме тектонических напряжений, тогда совокупное влияние
Юпитера, Луны и Сатурна способно вызвать сейсмические события не только глубине
3 км, но даже и на большей глубине.
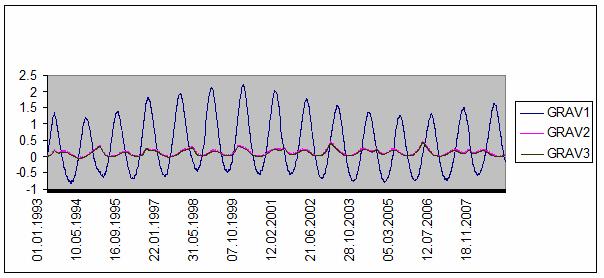
Рис. 116. Годичные изменения
гравитационных потенциалов, нормированных на величину гидростатического
давления на глубине 3 км.
В некоторых нестационарных процессах, например, в конвекции
важны не абсолютные значения параметров, а их изменения во времени (т.е. их
первые производные по времени). На рис. 117 представлены ежедневные абсолютные изменения трех гравитационных
комплексов G1, G2, G3 (обозначены GRAV7-GRAV9
соответственно). Отметим, что в этом масштабе комплексы G8 , G9
значительно различаются между собой, что обусловлено быстрым движением Луны
вокруг Земли по сравнению с относительно медленным движением Юпитера и
Сатурна.
В сплошной среде, такой, как магма, могут возникать разрывы, ведущие к образованию пузырьков /12/. Для
таких неоднородных включений изменение
гравитационного потенциала равносильно изменению внешнего давления. За сутки в
магме индуцированное изменение давление составляет в некоторые месяцы 15-20
атмосфер. Таким образом, гравитационное воздействие небесных тел может
значительно усиливаться за счет неоднородностей плотности среды, таких как
пузырьки и микротрещины.
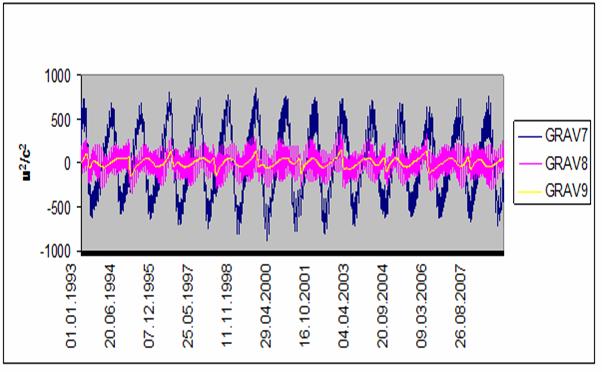
Рис. 117. Изменение гравитационных
комплексов 1993-2008 гг
Достоверность
прогноза землетрясений
В сейсмологии широко используются энергетические оценки
силы землетрясения, одной из которых является уравнение
Гуттенберга-Рихтера /82/:
![]()
где Es – сейсмическая энергия в джоулях, a
= 1.5, b = 11.8, MS – магнитуда поверхностных волн. Используя это уравнение
можно составить два энергетических критерия для оценки сейсмической активности
на каждый день:
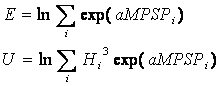 (73)
(73)
На рис. 118 представлен результат распознавания
событий по критериям (73). Параметр сходства при распознавании по
энергетическим критериям понизился в 2-3 раза по сравнению с результатом
распознавания по критерию магнитуды (72). Это связано с тем, что сейсмические
данные не отличаются большой точностью, поэтому их обработка по нелинейным
формулам типа (73) понижает достоверность распознавания.
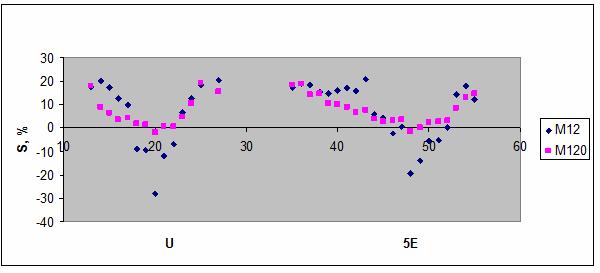
Рис. 118. Зависимость
параметра сходства от энергетических критериев.
Высокая степень неопределенности данных магнитуды является
ограничением достоверности распознавания событий по этому параметру – см. рис.
107. С другой стороны, сумма магнитуды
нескольких событий за день, как
оказалось, является более достоверным параметром, нежели магнитуда отдельного
события, поэтому повышается достоверность распознавания дней с высокими и
низкими значениями L – рис. 112. Предположительно это можно объяснить тем, что
при суммировании зашумленных сигналов возрастает отношение сигнал/шум, за счет
того, что при неограниченном увеличении выборки сумма шума стремится к нулю.
Заметим, что из 65541 записи событий в каталоге /56/ в
30016 случаях положение гипофокуса определено на глубине 33 км. Среди этих
событий, имеющих, видимо, отношение к процессам в магме, в 7376 случаях
регистрировались поверхностные волны. По этим данным можно определить
корреляционные зависимости магнитуды поверхностных и объемных волн в виде:
MS = 1.2288MPSP – 1.7109, R2 = 0.6317; H=33
km. (74)
MPSP = 0.5141MS + 2.8968, R2 = 0.6317; H=33
km.
Полученные зависимости (74) не согласованы друг с другом.
Можно согласовать второе уравнение (74) с первым, но при этом значительно
понижается достоверность аппроксимации:
MPSP = 0.8085MS + 1.3923, R2 = 0.4208; H=33
km. (75)
Таким образом, сравнительно низкая достоверность распознавания
событий землетрясений по величине магнитуды – см. рис. 107, обусловлена, в том
числе, рассеянием данных. Тем не
менее, полученные результаты позволяют сделать вывод о зависимости некоторых
сейсмических процессов от положения, скоростей и ускорений небесных тел.
6.2. Прогнозирование сейсмической активности и климата на основе
семантических информационных моделей
Технология
моделирования сейсмической активности
База данных землетрясений была сформирована на основе
оперативного сейсмологического каталога ГС РАН /56/, содержащего 65541 запись
событий землетрясений, произошедших в различных регионах мира в период с 1
января 1993 года по 20 ноября 2008 г.
Из исходной базы
было образовано несколько различных БД для исследования влияния астрономических
параметров на магнитуду и глубину гипофокуса, на ежедневное число землетрясений
и на их локализацию, а также на средние параметры сейсмической активности. Эти параметры можно определить следующим
образом.
Как известно, в сейсмологии широко используются энергетические
оценки силы землетрясения, одной из которых является уравнение
Гуттенберга-Рихтера /72/:
![]()
где Es – сейсмическая энергия в джоулях, a
= 1.5, b = 11.8, MS – магнитуда поверхностных волн. Используя это уравнение
можно составить два энергетических критерия для оценки сейсмической активности
на каждый день (эти определения отличаются от аналогичных формул (73),
введенных ввыше):
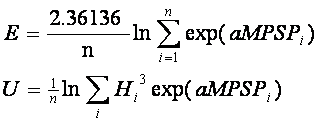 (76)
(76)
Здесь n, MPSP, H
– число ежедневных событий, магнитуда и глубина гипофокуса каждого события
соответственно. При таком определении параметры (76) изменяются в одной шкале.
Определим среднюю магнитуду ежедневных событий в виде
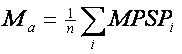 (77)
(77)
Отметим, что магнитуда MPSP рассчитывается по максимальной скорости смещения в объемных
волнах /56/. Из трех параметров (76)-(77)
было образовано 45 категорий сейсмической активности – таблица 44.
ТАБЛИЦА 44. Категории
сейсмической активности, абсолютная частота их встречаемости и максимальный
параметр сходства
|
KOD |
CATS |
ABS |
S_MAX, % |
|
1 |
A0-E=0 |
362 |
-9.605 |
|
2 |
A1-E=1 |
1928 |
-37.019 |
|
3 |
A2-E=2 |
1183 |
-20.912 |
|
4 |
A3-E=3 |
744 |
38.983 |
|
5 |
A4-E=4 |
453 |
49.805 |
|
6 |
A5-E=5 |
344 |
49.421 |
|
7 |
A6-E=6 |
141 |
46.146 |
|
8 |
A7-E=7 |
220 |
75.936 |
|
9 |
A8-E=8 |
31 |
38.345 |
|
10 |
A9-E=9 |
86 |
53.624 |
|
11 |
A10-E=10 |
137 |
50.854 |
|
12 |
A20-E=11-E=20 |
173 |
57.542 |
|
13 |
B0-U=0 |
389 |
-13.074 |
|
14 |
B1-U=1 |
1851 |
-32.437 |
|
15 |
B2-U=2 |
1246 |
-12.785 |
|
16 |
B3-U=3 |
739 |
28.199 |
|
17 |
B4-U=4 |
455 |
51.124 |
|
18 |
B5-U=5 |
275 |
50.278 |
|
19 |
B6-U=6 |
268 |
53.806 |
|
20 |
B7-U=7 |
110 |
62.876 |
|
21 |
B8-U=8 |
62 |
48.741 |
|
22 |
B9-U=9 |
142 |
50.915 |
|
23 |
B10-U=10 |
61 |
51.204 |
|
24 |
B20-U=11-U=20 |
204 |
52.375 |
|
25 |
C0-Ma=0 |
46 |
46.180 |
|
26 |
C41-Ma=1.6-Ma=4.1 |
104 |
38.956 |
|
27 |
C42-Ma=4.2 |
63 |
16.343 |
|
28 |
C43-Ma=4.3 |
165 |
-0.015 |
|
29 |
C44-Ma=4.4 |
367 |
-27.216 |
|
30 |
C45-Ma=4.5 |
546 |
-38.508 |
|
31 |
C46-Ma=4.6 |
724 |
-45.789 |
|
32 |
C47-Ma=4.7 |
753 |
-48.349 |
|
33 |
C48-Ma=4.8 |
636 |
-40.118 |
|
34 |
C49-Ma=4.9 |
526 |
-3.210 |
|
35 |
C50-Ma=5 |
422 |
18.823 |
|
36 |
C51-Ma=5.1 |
361 |
38.507 |
|
37 |
C52-Ma=5.2 |
293 |
44.078 |
|
38 |
C53-Ma=5.3 |
253 |
39.206 |
|
39 |
C54-Ma=5.4 |
197 |
43.987 |
|
40 |
C55-Ma=5.5 |
131 |
44.823 |
|
41 |
C56-Ma=5.6 |
87 |
48.499 |
|
42 |
C57-Ma=5.7 |
46 |
67.604 |
|
43 |
C58-Ma=5.8 |
42 |
72.045 |
|
44 |
C59-Ma=5.9 |
13 |
66.755 |
|
45 |
C60-Ma=6-Ma=6.9 |
27 |
70.916 |
|
|
Всего случаев |
17406 |
|
ТАБЛИЦА. 45. Фрагмент базы данных категорий
сейсмической активности
|
ID |
NAME |
CATS1 |
SUNLON |
SUNDIST |
MOONLON |
MOONDIST |
|
1 |
01.01.1993 |
A5:B5:C54: |
280.9686024 |
0.983295322 |
13.61933091 |
0.002675829 |
|
2 |
02.01.1993 |
A9:B9:C49: |
281.987777 |
0.983282741 |
25.80476273 |
0.002651433 |
|
3 |
03.01.1993 |
A4:B4:C54: |
283.0068945 |
0.98327556 |
38.25244479 |
0.00262062 |
|
4 |
04.01.1993 |
A4:B4:C58: |
284.0259499 |
0.983274028 |
51.03130743 |
0.0025854 |
|
5 |
05.01.1993 |
A20:B20:C47: |
285.04494 |
0.983278415 |
64.19429015 |
0.002548373 |
|
6 |
06.01.1993 |
A10:B9:C53: |
286.0638619 |
0.983288965 |
77.76948406 |
0.002512519 |
|
7 |
07.01.1993 |
A5:B4:C41: |
287.0827136 |
0.983305893 |
91.75147799 |
0.002480873 |
|
8 |
08.01.1993 |
A7:B8:C51: |
288.1014941 |
0.983329361 |
106.0953152 |
0.002456135 |
|
9 |
09.01.1993 |
A5:B4:C50: |
289.120205 |
0.98335945 |
120.7161776 |
0.002440254 |
|
10 |
10.01.1993 |
A20:B20:C60: |
290.1388518 |
0.983396142 |
135.4972702 |
0.002434135 |
В качестве астрономических параметров были использованы
долгота и расстояние от Земли до десяти небесных тел – Солнца, Луны, Марса,
Меркурия, Венеры, Юпитера, Сатурна, Урана, Нептуна и Плутона, и долгота
Северного Узла Луны. Астрономические параметры вычислялись на каждый день в
фиксированной точке с географическими координатами (36.61E; 55.08N) в 9:00 GMT
в топоцентрической системе координат. Отметим, что выбор этой точки не является
существенным для решаемого класса задач. Из астрономических параметров и категорий
сейсмической активности была создана база данных – таблица 45.
Для проверки различных гипотез из астрономических параметров
расстояний было образовано шесть гравитационных комплексов G1-G6:
суммарный нормированный гравитационный потенциал
восьми небесных тел - Луны, Марса,
Меркурия, Венеры, Юпитера, Сатурна, Урана, Нептуна;
суммарный нормированный гравитационный потенциал семи
небесных тел - Луны, Марса, Меркурия,
Венеры, Сатурна, Урана, Нептуна;
суммарный нормированный гравитационный потенциал шести
небесных тел - Марса, Меркурия, Венеры,
Сатурна, Урана, Нептуна;
суммарный нормированный гравитационный потенциал пяти
небесных тел - Марса, Меркурия, Венеры,
Урана, Нептуна;
суммарный нормированный гравитационный потенциал четырех
небесных тел - Марса, Меркурия, Урана,
Нептуна;
суммарный нормированный гравитационный потенциал девяти
небесных тел - Солнца, Луны, Марса, Меркурия, Венеры, Юпитера, Сатурна, Урана,
Нептуна.
Таким образом, по определению
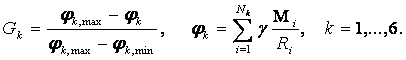 (78)
(78)
Здесь ![]() – гравитационная постоянная и
масса небесного тела соответственно. Отметим, что согласно (78) суммы jk являются
положительно определенными, т.е. взяты с иным знаком, нежели гравитационные
потенциалы небесных тел в классической теории. Из этих комплексов были также
образованы шесть других комплексов G7-G12, представляющих
собой суточное изменение каждого из комплексов
G1-G6 соответственно. Таким образом, параметры jk имеют размерность квадрата скорости, а комплексы Gk
являются безразмерными.
– гравитационная постоянная и
масса небесного тела соответственно. Отметим, что согласно (78) суммы jk являются
положительно определенными, т.е. взяты с иным знаком, нежели гравитационные
потенциалы небесных тел в классической теории. Из этих комплексов были также
образованы шесть других комплексов G7-G12, представляющих
собой суточное изменение каждого из комплексов
G1-G6 соответственно. Таким образом, параметры jk имеют размерность квадрата скорости, а комплексы Gk
являются безразмерными.
Решение прямой задачи включает в себя нормирование
входных параметров и приведение их к одному масштабу изменения в интервале
(0;360), разбиение интервалов на М частей, вычисление матрицы абсолютных частот
и информативности. Решение обратной задачи включает в себя распознавание категорий
по заданным астрономическим параметрам. Частным случаем задачи распознавания
является определение достоверности идентификации категорий по астрономическим
данным в каждой модели. Решение этой
задачи в случае исследуемой совокупности
событий землетрясений было рассмотрено выше. Здесь мы изучим вопрос повышения
достоверности идентификации в частной семантической информационной модели.
На рис. 119-120
представлен параметр сходства для 12 категорий параметров сейсмической
активности Е и U в 10 моделях М6-М13,
М24 и М12Opt. Последняя модель получена путем оптимизации модели М12 в соответствии с алгоритмом /5/.
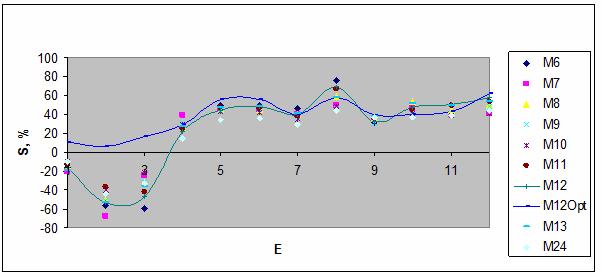
Рис. 119. Параметр сходства
для 12 категорий Е в 10 моделях.
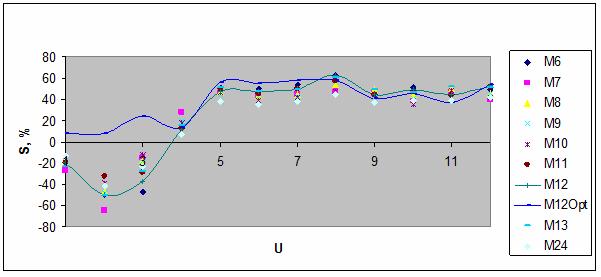
Рис. 120. Параметр сходства
для 12 категорий U в 10 моделях.
В результате разделения
классов на типичную и нетипичную части с образованием новых классов, удается
существенно повысить параметр сходства для плохо распознаваемых категорий в
модели M12Opt – см. рис. 119-120.
В главе 2 было показано,
что матрица информативности может быть использована для выявления и
визуализации когнитивных функциональных
зависимостей в фрагментированных и зашумленных данных большой размерности.
Кратко поясним суть этого метода. Матрица информативностей рассчитывается на
основе системной теории информации [3] непосредственно на основе эмпирических
данных и представляет собой таблицу, в которой столбцы соответствуют обобщенным образам классов, т.е. будущим
состояниям моделируемой системы, строки – значениям факторов, влияющих на эту
систему, а на пересечениях строк и столбцов находится количество информации,
которое содержится в факте действия значения фактора, соответствующего строке,
на переход системы в состояние, соответствующее столбцу. Максимальное
количество информации, которое может быть в значении фактора, определяется
числом будущих состояний моделируемой системы. Модуль количества информации
отражает силу влияния значения фактора, а знак – направление этого влияния,
т.е. то, способствует он или препятствует наступлению данного состояния. Если
последовательности классов и значений факторов образуют порядковые шкалы или
шкалы отношений, т.е. соответственно, на них определены отношения «больше-меньше»
или, кроме того, единица измерения, начало отсчета и арифметические операции,
то матрица информативностей допускает наглядную графическую визуализацию, традиционного для функций типа, когда
значения факторов рассматриваются в качестве значений аргумента, а классы, о
наступлении которых в этих значениях факторов содержится максимальное количество информации – в качестве значений функции.
Другие классы, менее обусловленные данным значением фактора, а также те,
наступлению которых это значение препятствует в большей или меньшей степени,
также могут отображаться соответствующими цветами, и это также может
представлять интерес, т.к. позволяет задействовать мощные способности человека
к анализу изображений. Когнитивные функции, представляемые в форме матрицы информативностей,
соответствуют очень общему виду функциональной зависимости: многозначной функции многих аргументов,
т.к. каждое значение фактора влияет на все состояния моделируемого объекта, и
каждое его состояние обусловлено всеми значениями факторов.
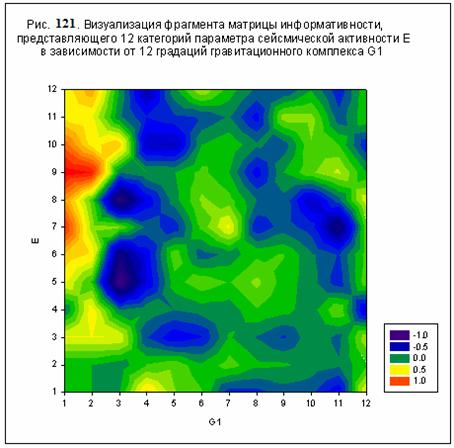
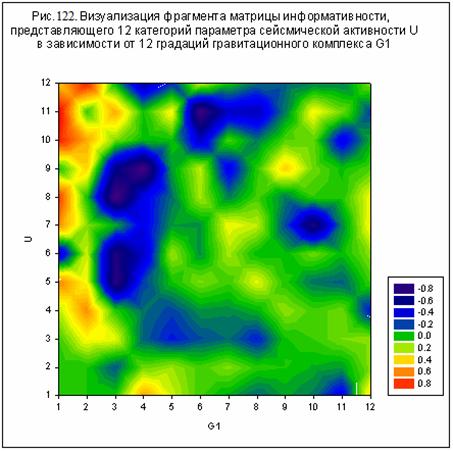
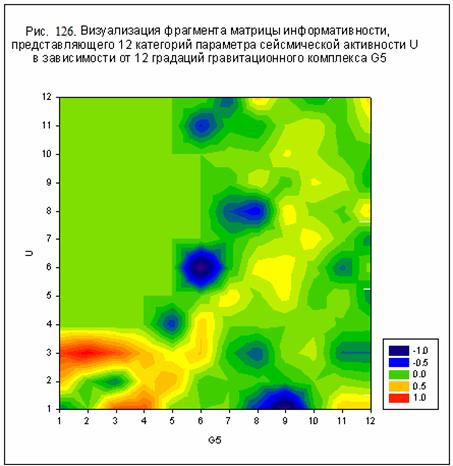
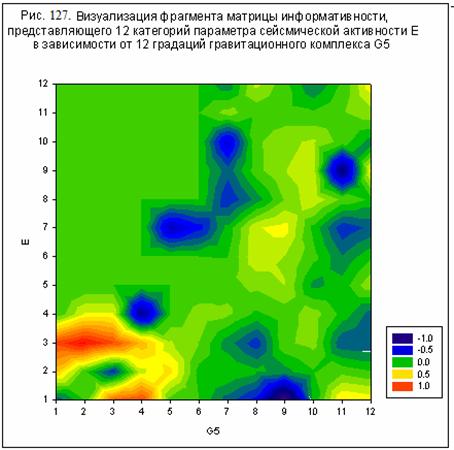
Матрица информативности
оптимизированной модели отличается высокой контрастностью при ее визуализации.
На рис. 121-126 даны некоторые примеры
визуализации фрагментов матрицы информативности, позволяющие оценить степень
влияния гравитационных комплексов G1-G12 на параметры
сейсмической активности (76)-(77).
Так, например, из данных,
представленных на рис. 121-122 следует, что влияние гравитационного комплекса
G1 на энергетические критерии E,U (7) является однотипным и сосредоточено в
области, где согласно (78), сумма j1 достигает максимального значения.
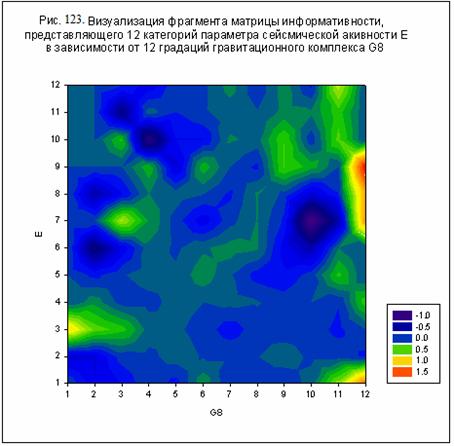
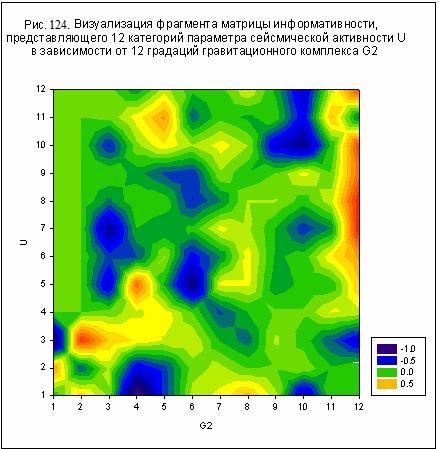
Влияние же гравитационных комплексов G8 и G2, напротив, сосредоточено в
области, где сумма j8 или j2 достигает минимального значения см.
рис. 123-124.
Отметим, что каждый из
гравитационных комплексов отражает влияние гравитации преимущественно одного
небесного тела, а именно:
G1 – Юпитера (рис.
121-122);
G8 - Луны (рис. 123);
G2 – Сатурна (рис. 124);
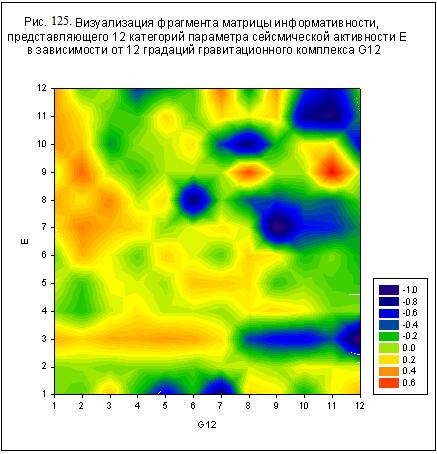
G12 – Солнца (рис. 125);
G5 – Урана (рис.
126-127).
По данным на рис. 121-127
невозможно установить, какой из гравитационных комплексов влияет сильнее на
интенсивность землетрясений. Однако, сравнивая данные на рис. 126-127 (влияние
гравитации Урана) с данными на рис. 121-122 (влияние гравитации Юпитера), можно
сделать вывод, что влияние Юпитера имеет отношение к событиям с большой
сейсмической энергией, тогда как влияние Урана связано с событиями с низкой
энергией. Влияние Луны и Сатурна (рис. 123-124 соответственно) охватывает
область событий со средней сейсмической энергией. Гравитационное влияние Солнца
(рис. 125) охватывает как область событий с малой сейсмической энергией, так и
область событий со средней и большой энергией, причем все области влияния четко
разделены. Эти результаты хорошо соотносятся с интенсивностью действующих
факторов, которая велика в случае Юпитера и Солнца, мала в случае Урана и имеет
среднее значение в случае Луны и Сатурна.
Далее рассмотрим один пример визуализации матрицы информативности для
хорошо изученного природного процесса (погоды), наблюдение за которым ведется на протяжении многих лет.
Технология моделирования
климата
Описанный метод распознавания категорий по астрономическим
данным можно применить для исследования любых природных процессов, например,
климата. Рассмотрим решение этой задачи для одного города (Оксфорда). В
качестве климатических категорий были выбраны усредненные за месяц данные по максимальной
температуре, осадкам и заморозкам, собранные в единую базу данных /62/ на
станции наблюдения за погодой в Оксфорде за период с января 1853 г по сентябрь
2009 г – всего 1881 запись.
Из данных /62/ было образовано 53 категории климатических
параметров, в том числе: 22 категории температуры (градус С), 14 категорий
осадков (мм) и 17 категорий заморозка (дней в месяц). Из этих категорий и из
астрономических параметров, вычисленных на середину каждого месяца, была
образована БД, на основе которой были синтезирована семантические информационные
модели.
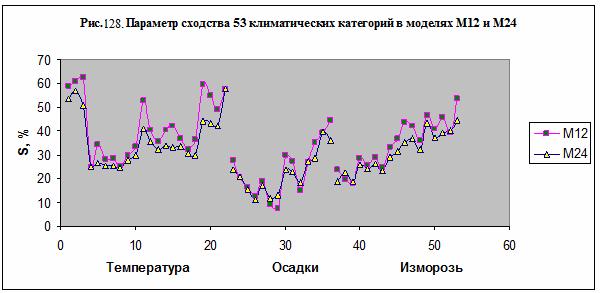
На рис. 128 представлен параметр сходства 53 климатических
категорий в моделях М12 и М24. Отметим, что параметр сходства является
положительным для всех категорий, а его значение довольно велико в
исследованных моделях. Это означает, что климатические параметры зависят от
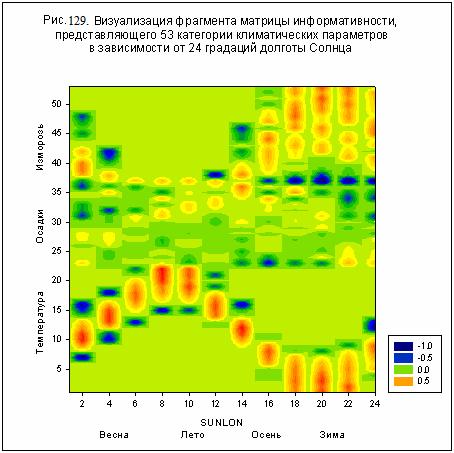
астрономических данных. Чтобы установить характер этой зависимости, рассмотрим
визуализацию фрагмента матрицы информативности модели М24 (для наглядности),
представляющего 53 климатические категории в зависимости от 24 градаций долготы
Солнца – рис. 129.
В нижней части рис. 129 хорошо просматривается сезонный ход
температуры воздуха в приземном слое атмосферы, что обусловлено, главным
образом, колебанием потока солнечной радиации, связанным с движением нашей
планеты вокруг Солнца (описывается долготой Солнца).
Заметим, что данные /62/ являются ежемесячными, что хорошо
отражено на рис. 129, содержащем 12 областей (окрашены в красный цвет),
соответствующих максимальной температуре воздуха. Данные по осадкам менее
информативны в сравнении с температурой, а данные по заморозкам (иней в
воздухе), хотя и являются информативными, неоднозначны, т.е. в разные годы
число дней заморозка в данный месяц изменяется в широких пределах.
Таким образом, метод визуализации матрицы информативности
позволяет установить наличие зависимости категорий от астрономических
параметров, хотя бы качественно. Например, по данным на рис. 129 видно, что
зимой заморозки более вероятны, нежели летом, а осадки в Оксфорде более
вероятны летом, нежели весной.
Модель сейсмической активности
Возвращаясь к данным на рис. 121-122, отметим, что параметры
сейсмической активности Е и U зависят от гравитационного комплекса G1, причем
эта зависимость в наибольшей степени проявляется при минимальном расстоянии от
Земли до Юпитера – рис. 130. Отметим,
что аналогичная зависимость от расстояния проявляется в случае Луны, тогда как
в случае Сатурна максимум влияния приходится на максимальное расстояние от
Земли до этой планеты – рис. 124, что соответствует соединению (по долготе)
Сатурна и Солнца.
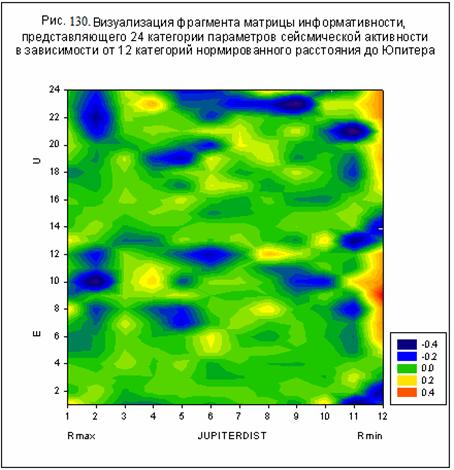
Данные на рисунке 130 свидетельствуют о наличии зависимости
параметров сейсмической активности от гравитационного комплекса G1. Прямая же фильтрация данных позволяет установить
характер этой зависимости – рис. 131.
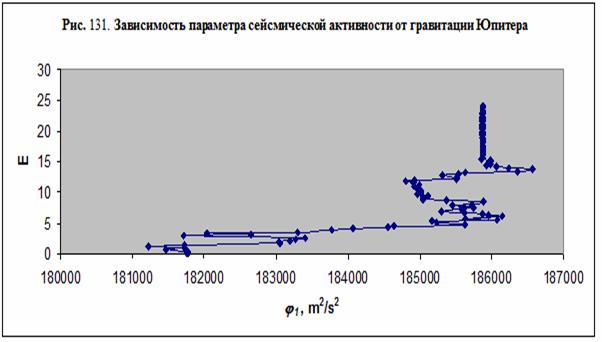
Полученная зависимость параметра сейсмической активности
от гравитационного комплекса Юпитера не является однозначной, но она
свидетельствует о накоплении данных с высокой энергией вблизи более высокого
значения j1,
а данных с низкой энергией вблизи более низкого значения гравитационного комплекса
Юпитера.
Аналогичная зависимость была получена и в случае гравитационного
комплекса Солнца. В этом случае разделение данных с высокой и низкой
сейсмической энергией является более заметным. Отбрасывая данные с высокой сейсмической
энергией из условия 0<E<13, и нормируя параметр j12 на
число секунд в сутках, находим линию тренда – рис. 132.
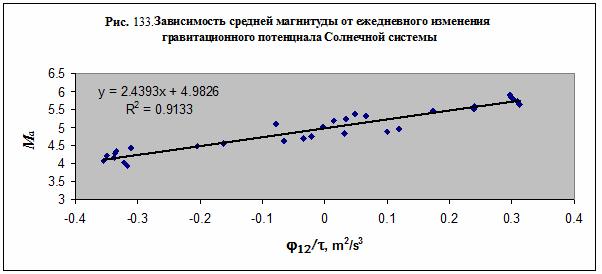
Однако наиболее четко происходит разделение событий по
средней за сутки магнитуде MPSP – рис. 133. В этом случае линия тренда определяется
с наибольшей достоверностью. Отметим, что данные на рис. 131-133 получены путем
обработки и сглаживания исходных данных /56/.
Приведем окончательные формулы зависимостей для параметров
сейсмической активности от параметра гравитации небесных тел:
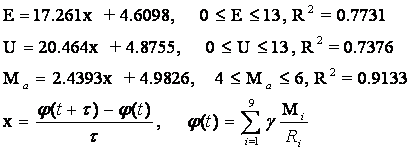 (79)
(79)
Здесь t=86400 – число секунд в сутках.
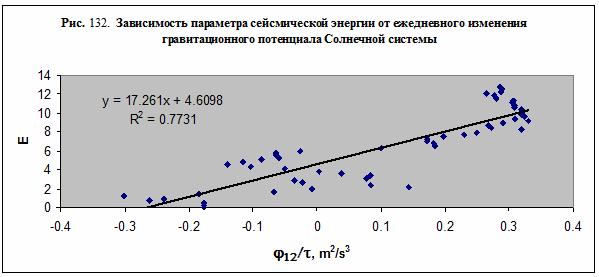
Полученные уравнения (79) свидетельствуют о наличии некого
механизма перехода гравитационной энергии Солнца и других небесных тел в сейсмическую
энергию.
Для установления природы этого эффекта заметим, что в
указанных в (79) пределах все параметры
связаны между собой линейной зависимостью, поэтому для определения сейсмической
энергии можно использовать любой из них. Потенцируя третье из уравнений (79) и,
используя уравнение Гуттенберга-Рихтера /82/, представим физический параметр
средней сейсмической энергии в виде:
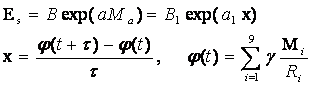 (80)
(80)
Здесь a, B – константы в уравнении
Гуттенберга-Рихтера, B1=Bexp(4.9826a), a1=2.4393a.
Используя уравнение связывающее магнитуду поверхностных
и объемных волн, находим a1
=10.3527. Отметим что формула (80) описывает диапазон изменения сейсмической
энергии, занимающий три порядка.
Уравнению (80)
можно придать наглядный вид, используя идею о процессе активации сейсмических
событий на молекулярном уровне, в котором скорость реакции имеет вид:
![]() (81)
(81)
Здесь m0 – масса молекулы, DjG –
изменение гравитационного потенциала, k=1.380662*10-23 Дж/К -
постоянная Больцмана, T – абсолютная температура. Следовательно, константа a1 в уравнении (80) связана с
молекулярными свойствами вещества, используя же величину этой константы, можно
оценить массу молекулы вещества, вовлеченной в реакцию активации, имеем:
![]()
Отметим, что эта величина вычислена при температуре
300К, а при более высокой температуре масса молекулы может быть больше.
Полученный результат свидетельствует, что механизм активации сейсмических
событий, видимо, действительно обусловлен молекулярными процессами, причем в
этот процесс вовлечены тяжелые молекулы типа группы оливина - Fe2SiO4, Mn2SiO4
и т.п..
В заключение укажем, что развитая модель сейсмической
активности позволяет прогнозировать средние за сутки параметры для всей Земли в
целом. Для нахождения же распределения сейсмических событий по долготе и широте
необходимо исследовать региональные базы данных. Решение этой задачи, которая
может иметь большое практическое значение, сопряжено с определенными
трудностями, главным образом, с недостатком данных, необходимых для
формирования семантической информационной модели. Исключение составляют лишь
сейсмически активные регионы, для которых можно сделать достаточно достоверный
прогноз.
6.3. Системно-когнитивный анализ и прогнозирование сейсмической
активности литосферы Земли, как глобальной активной геосистемы
Технология
моделирования глобальных геосистем
К глобальным активным геосистемам относятся ноосфера,
биосфера, атмосфера, гидросфера и литосфера. Поведение любого объекта
определяется действующими на него внутренними и внешними факторами. Внутренние
факторы отражают текущее состояние объекта и предысторию его развития. Внешние
факторы можно разделить на зависящие от нашей воли, которые можно рассматривать
как управляющие факторы, и независящие от нее, т.е. факторы (влияния)
окружающей среды. Для глобальных систем управляющие факторы, по сути,
отсутствуют или неизвестны, а факторами окружающей среды, очевидно, являются
космические факторы, т.к. именно космос представляет собой окружающую среду для
Земли и глобальных активных геосистем.
Активным называется объект, имеющий внутренний источник
самодвижения (энергии), систему моделирования себя и окружающей среды, включая
внешние управляющие системы, а также собственную систему поддержки принятия
решений, т.е. ведущий себя так, как будто он стремится к собственной определенной
цели. «Классическими» активными объектами являются системы с участием людей:
экономические, социально-психологические, технологические и
организационно-технические, а также биологические и экологические системы
(включая искусственные экосистемы). Однако и поведение объектов так называемой «неживой»
природы, подается блестящему теоретическому описанию на основе представления о
том, что они стремятся к некоторой «объективной цели». Это позволяет расширить
представление об активных объектах на все объекты и считать представление об
абсолютно пассивном объекте чистейшей абстракцией, которой в реальности ничего
не соответствует, если не считать Кантовской «вещи в себе». Дело в том, что абсолютно
пассивный объект не смог бы взаимодействовать ни с какими объектами.
Тем ни менее вполне оправдано говорить о степени активности
объектов и о существовании конструкта, спектра или иерархии объектов по степени
их активности: от объектов с очень высокой активностью до объектов с очень
низкой активностью. Активность объекта (системы) однозначно определяется его
уровнем системности, т.е. степенью отличия свойств системы от суммы свойств ее
элементов. С этой точки зрения спектр систем по их активности выглядит
следующим образом: механические, химические, биологические,
социально-экономические системы. Между тем уровень системности в свою очередь
обусловливается интенсивностью взаимосвязей между элементами системы и
сложностью ее внутренней организации, а значит и ее масштабами. Это значит, что
чем больше и сложнее система, состоящая из элементов определенной активности,
чем больше она включает элементов, тем сложнее могут быть взаимосвязи между
ними и тем выше общий уровень системности и активности системы в целом. С
другой стороны если системы состоят из одинакового количества элементов, но эти
элементы обладают разной сложностью, то и системы будут отличаться по своей
сложности. Это значит, что большие и сложные системы, состоящие из очень
большого количества относительно простых элементов, могут иметь такой же общий
уровень системности, как системы сравнительно небольшого размера, имеющие очень
сложную внутреннюю организацию и состоящие из очень сложных элементов.
Поэтому вполне оправданно ввести новое научное понятие
удельного уровня системности (или удельной системностью), под которым авторы
предлагают понимать уровень системности на единицу массы системы.
По удельной системности человек, по-видимому, имеет наивысший
уровень системности из известных систем, и, например, намного превосходит,
отдельно взятое дерево. Однако по общему уровню системности лесной массив, как
экосистема, может быть сопоставимым с человеком или даже превосходить его,
вплоть до проявления в системе реагирования элементов, которые мы бы могли
квалифицировать как проявления психики. Отдельный вирус не сопоставимо ниже
человека по уровню системности, однако, по последним данным эпидемия в целом
ведет себя по отношению к людям, изобретающим все новые средства борьбы с ней,
как армия, под руководством опытного полководца, осаждающая крепости-города.
Авторы предлагают гипотезу, согласно которой, не смотря на то, что удельная
системность литосферы на многие порядки ниже удельной системности биосферы, не
говоря уже о ноосфере (социально-экономических системах), однако, учитывая
огромную массу и масштабы литосферы можно предположить, что ее суммарный
уровень системности сопоставим с биосферой и даже с ноосферой.
Поведение простых объектов с низким уровнем
системности и активности практически полностью определяется внешними факторами.
Поведение же активных объектов практически полностью определяется внутренними
факторами, т.е. их внутренней организацией, текущим состоянием и предысторией.
Внешние факторы также оказывают влияние на поведение активного объекта, но не
непосредственно, а опосредованно его внутренней организацией. При этом
реагирование активной системы на внешние воздействия осуществляется таким
образом, что основную роль играет не мощность или суммарные затраты энергии
этих внешних воздействий (как в простых системах), а внутренняя организация
этих воздействий, точнее – их информационная составляющая. Конечно, активные
системы имеют иерархическое строение и обычно включают некую базовую структуру,
имеющую относительно низкий уровень системности. Например, автомобиль в
заглушенном состоянии можно рассматривать как систему с низким уровнем
системности, и, поэтому, для его транспортировки на стоянку в этом состоянии
необходим эвакуатор, однако если автомобиль завести, то практически без затрат
энергии на управляющие воздействия можно легко переместить его в ту же точку и
даже отбуксировать туда сам эвакуатор.
Развитие активных систем происходит путем чередования
периодов эргодичности и точек бифуркации. На периодах эргодичности законы
поведения объекта практически не изменяются и накапливаются количественные
изменения, которые, в конце концов, приводят к его скачкообразному
качественному изменению и переходу в новый период эргодичности. Для активных
систем точки бифуркации, по сути, представляют собой точки принятия решений,
определяющих эволюцию системы на следующем периоде эргодичности. При этом сами
моменты времени, в которые осуществляются переходы активной системы в точки
бифуркации могут определяться низко энергетическими, по существу
информационными внешними воздействиями, эффект влияния которых абсолютно не
сопоставим с их мощностью и общей затраченной энергией.
Ниже представлены результаты прогнозирования параметров
сейсмической активности по астрономическим данным на основе семантических
информационных моделей с использованием всемирной базы землетрясений /57/,
исследована совокупность 128320 событий землетрясений с магнитудой ![]() , произошедших на нашей
планете в период с 9 февраля 1963 года по 31 декабря 2006 г (всего 16032
дня).
, произошедших на нашей
планете в период с 9 февраля 1963 года по 31 декабря 2006 г (всего 16032
дня).
Исследуемая база данных сейсмических событий была
сформирована на основе базы данных Международного сейсмологического центра
(ISC) /57/, содержащей 20489816 записей
регистрации различными сейсмостанциями событий землетрясений, произошедших на
нашей планете в период с 1 января 1961 года по 31 декабря 2006 г.
Из исходной
базы было образовано несколько различных БД для исследования влияния
астрономических параметров на магнитуду и глубину гипофокуса, на ежедневное
число землетрясений, а также на средние параметры сейсмической активности. В
настоящей работе исследована совокупность 128320 событий землетрясений с
магнитудой ![]() , произошедших на нашей
планете в период с 9 февраля 1963 года по 31 декабря 2006 г (всего 16032 дня).
, произошедших на нашей
планете в период с 9 февраля 1963 года по 31 декабря 2006 г (всего 16032 дня).
В качестве астрономических параметров были использованы
долгота и расстояние от Земли до десяти небесных тел – Солнца, Луны, Марса,
Меркурия, Венеры, Юпитера, Сатурна, Урана, Нептуна и Плутона, и долгота
Северного Узла Луны. Астрономические параметры вычислялись на каждый день в
фиксированной точке с географическими координатами Гринвича в 12:00 GMT в
топоцентрической системе координат. Отметим, что выбор этой точки не является
существенным для решаемого класса задач. Из астрономических параметров и
категорий сейсмической активности была создана база данных, содержащая 16032
записи с обобщенной информацией о ежедневной
сейсмической активности Земли.
Решение прямой задачи включает в себя нормирование
входных параметров и приведение их к одному масштабу изменения в интервале
(0;360), разбиение интервалов на М частей, вычисление матрицы абсолютных частот
и информативности. Решение обратной задачи включает в себя распознавание категорий
по заданным астрономическим параметрам. Частным случаем задачи распознавания
является определение достоверности идентификации категорий по астрономическим
данным в каждой модели. Решение этой
задачи по данным /56/ было рассмотрено выше. Аналогичные результаты были
получены и в случае исследуемой совокупности 128320 сейсмических событий,
отобранных из базы данных /57/ по критерию mb>4. Отметим, что исследованные
БД, сформированные по данным /56/ и /57/ существенно различаются как по числу событий (65541 и 128320 соответственно), так и по
интервалу времени их реализации (5082 и 16032 дня соответственно).
Параметр
сходства категорий магнитуды
В исходной БД /57/ сейсмические события
характеризуются магнитудой mb, которой можно сопоставить категорию магнитуды –
таблица 46. Поскольку события с одной и той же магнитудой могут повторяться в
один день, каждому значению магнитуды сопоставляется несколько типов категорий,
а именно:
A – событие с магнитудой mb повторяется один раз;
B – событие с магнитудой mb повторяется два раза;
C – событие с
магнитудой mb повторяется три раза.
Кроме того, можно рассмотреть случай, когда,
например, категория А усекается, путем
отбрасывания некоторых событий. Таким образом, была образована категория ![]() .
.
Определим среднюю магнитуду ежедневных событий в виде:
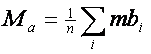 (82)
(82)
Здесь n – число ежедневных событий Отметим, что магнитуда
mb рассчитывается по максимальной
скорости смещения в короткопериодных объемных волнах по формулам /57/:
![]() (83)
(83)
где, А – амплитуда P-волн смещение грунта в мкм (рассчитывается
по максимальной амплитуде), T – периода в секундах, T <3с; Q (Δ, H)
– функция ослабления Гутенберг и Рихтер
(1956), Δ – эпицентральное расстояние в градусах, 21 ° ≤ Δ
≤ 100 °, H – глубина очага.
Таблица 46. Параметр сходства
категории магнитуда в трех моделях
|
Категория |
M12 |
M60 |
M160 |
Число случаев |
|
SC:A40-Mb=4,0 |
-18,645 |
-17,718 |
-14,543 |
1362 |
|
SC:A41-Mb=4,1 |
-22,916 |
-12,889 |
-7,703 |
1580 |
|
SC:A42-Mb=4,2 |
-17,617 |
-13,679 |
-5,874 |
1796 |
|
SC:A43-Mb=4,3 |
-8,763 |
0,169 |
5,257 |
2224 |
|
SC:A44-Mb=4,4 |
-28,171 |
-29,273 |
-6,789 |
2744 |
|
SC:A45-Mb=4,5 |
3,790 |
-14,328 |
-2,657 |
3358 |
|
SC:A46-Mb=4,6 |
20,900 |
2,565 |
5,996 |
4119 |
|
SC:A47-Mb=4,7 |
39,484 |
13,454 |
7,019 |
4768 |
|
SC:A48-Mb=4,8 |
28,408 |
13,262 |
10,024 |
4954 |
|
SC:A49-Mb=4,9 |
43,895 |
25,348 |
17,167 |
5008 |
|
SC:A50-Mb=5 |
46,332 |
32,051 |
23,112 |
4904 |
|
SC:A51-Mb=5,1 |
43,111 |
42,708 |
29,482 |
4582 |
|
SC:A52-Mb=5,2 |
40,011 |
34,899 |
26,342 |
4134 |
|
SC:A53-Mb=5,3 |
42,942 |
48,017 |
31,181 |
3563 |
|
SC:A54-Mb=5,4 |
50,842 |
44,806 |
29,391 |
3010 |
|
SC:A55-Mb=5,5 |
45,132 |
42,487 |
29,667 |
2367 |
|
SC:A56-Mb=5,6 |
49,463 |
51,507 |
33,892 |
1940 |
|
SC:A57-Mb=5,7 |
54,546 |
53,187 |
36,704 |
1460 |
|
SC:A58-Mb=5,8 |
46,835 |
43,283 |
31,282 |
1179 |
|
SC:A59-Mb=5,9 |
46,949 |
37,433 |
28,150 |
864 |
|
SC:A60-Mb=6,0 |
38,112 |
35,960 |
28,131 |
656 |
|
SC:A61-Mb=6,1 |
51,948 |
46,844 |
35,117 |
453 |
|
SC:A62-Mb=6,2 |
18,356 |
30,766 |
25,179 |
319 |
|
SC:A63-Mb=6,3 |
39,993 |
43,459 |
44,459 |
202 |
|
SC:A64-Mb=6,4 |
35,076 |
39,972 |
46,195 |
137 |
|
SC:A65-Mb=6,5 |
41,575 |
48,548 |
58,413 |
87 |
|
SC:A66-Mb=6,6-7,0 |
24,572 |
44,561 |
64,549 |
68 |
|
SC:B40-Mb=4,0 |
3,238 |
26,482 |
27,545 |
446 |
|
SC:B41-Mb=4,1 |
-16,761 |
-8,606 |
4,534 |
660 |
|
SC:B42-Mb=4,2 |
-2,641 |
-10,099 |
1,097 |
835 |
|
SC:B43-Mb=4,3 |
-24,940 |
-36,007 |
-20,915 |
955 |
|
SC:B44-Mb=4,4 |
-19,278 |
-18,572 |
-10,029 |
1099 |
|
SC:B45-Mb=4,5 |
-27,600 |
-16,025 |
-5,392 |
1223 |
|
SC:B46-Mb=4,6 |
-37,301 |
-26,465 |
-5,463 |
1455 |
|
SC:B47-Mb=4,7 |
-54,429 |
-28,247 |
-4,877 |
1612 |
|
SC:B48-Mb=4,8 |
-39,839 |
-25,311 |
-1,564 |
1817 |
|
SC:B49-Mb=4,9 |
-20,898 |
-18,403 |
0,840 |
1636 |
|
SC:B50-Mb=5 |
17,207 |
7,494 |
9,294 |
1428 |
|
SC:B51-Mb=5,1 |
12,708 |
14,084 |
13,464 |
1206 |
|
SC:B52-Mb=5,2 |
36,838 |
33,745 |
24,356 |
936 |
|
SC:B53-Mb=5,3 |
42,487 |
38,522 |
26,413 |
617 |
|
SC:B54-Mb=5,4 |
19,274 |
22,367 |
23,406 |
422 |
|
SC:B55-Mb=5,5 |
35,939 |
40,120 |
34,838 |
261 |
|
SC:B56-Mb=5,6 |
26,795 |
30,797 |
31,723 |
180 |
|
SC:B57-Mb=5,7 |
37,705 |
45,247 |
57,825 |
93 |
|
SC:B58-Mb=5,8 |
33,556 |
49,648 |
63,011 |
73 |
|
SC:B59-Mb=5,9-6,4 |
35,260 |
53,885 |
65,006 |
69 |
|
SC:C40-Mb=4,0 |
35,203 |
47,253 |
49,768 |
130 |
|
SC:C41-Mb=4,1 |
21,147 |
37,018 |
35,416 |
259 |
|
SC:C42-Mb=4,2 |
-7,800 |
11,979 |
17,220 |
362 |
|
SC:C43-Mb=4,3 |
-7,354 |
6,156 |
14,811 |
436 |
|
SC:C44-Mb=4,4 |
-3,149 |
-2,670 |
10,142 |
482 |
|
SC:C45-Mb=4,5 |
-10,944 |
-16,065 |
-1,734 |
468 |
|
SC:C46-Mb=4,6 |
-23,303 |
-5,223 |
6,164 |
515 |
|
SC:C47-Mb=4,7 |
-37,997 |
-10,425 |
3,659 |
501 |
|
SC:C48-Mb=4,8 |
-32,301 |
0,375 |
9,615 |
450 |
|
SC:C49-Mb=4,9 |
-15,689 |
8,794 |
11,992 |
447 |
|
SC:C50-Mb=5 |
0,790 |
16,317 |
20,876 |
356 |
|
SC:C51-Mb=5,1 |
-0,442 |
19,160 |
20,863 |
293 |
|
SC:C52-Mb=5,2 |
20,407 |
29,572 |
34,016 |
166 |
|
SC:C53-Mb=5,3-6,0 |
26,412 |
34,451 |
48,087 |
105 |
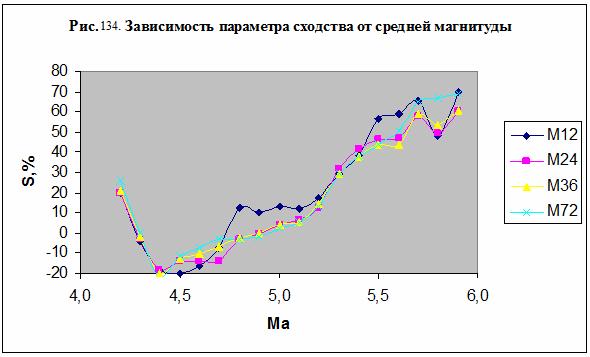
На рис. 134 и в таблице
47 представлен параметр сходства для
категорий параметра сейсмической активности Ma в 4 семантических информационных моделях
М12, М24, М36 и М72. Параметр средней магнитуды представляет особый интерес, поскольку,
как было установлено – см. (79), он с достоверностью R2=0.9133
связан с ежедневным изменением гравитационного потенциала Солнечной системы в
окрестностях Земли.
Отметим, что дни с
большим (Ма>4,8) или малым (Ma<4,2) значением
средней магнитуды распознаются лучше, нежели со средним значением (таблица 47 и
рисунок 134).
Таблица 47. Параметр сходства средней
магнитуды в 4-х моделях
|
Категории сейсмической активности |
Ma |
M12 |
M24 |
M36 |
M72 |
Число случаев |
|
1 |
<4 |
78,590 |
67,976 |
62,621 |
63,882 |
198 |
|
2 |
4,0-4,2 |
19,951 |
19,826 |
20,812 |
25,768 |
162 |
|
3 |
4,30 |
-4,403 |
-3,354 |
-2,001 |
-0,065 |
419 |
|
4 |
4,40 |
-18,255 |
-18,110 |
-19,947 |
-21,992 |
976 |
|
5 |
4,50 |
-20,077 |
-14,069 |
-12,985 |
-11,692 |
1313 |
|
6 |
4,60 |
-16,477 |
-14,057 |
-10,571 |
-7,356 |
1204 |
|
7 |
4,70 |
-7,601 |
-14,119 |
-6,729 |
-3,306 |
1180 |
|
8 |
4,80 |
12,552 |
-3,130 |
-2,762 |
-3,069 |
1713 |
|
9 |
4,90 |
9,900 |
-0,780 |
-0,102 |
-1,746 |
2317 |
|
10 |
5,00 |
12,920 |
4,356 |
4,321 |
2,246 |
2360 |
|
11 |
5,10 |
11,986 |
6,577 |
5,470 |
5,117 |
1831 |
|
12 |
5,20 |
17,283 |
12,770 |
14,051 |
12,924 |
1150 |
|
13 |
5,30 |
29,206 |
31,593 |
29,519 |
29,262 |
596 |
|
14 |
5,40 |
38,451 |
41,314 |
38,004 |
37,867 |
276 |
|
15 |
5,50 |
56,575 |
46,446 |
43,646 |
43,823 |
145 |
|
16 |
5,60 |
59,094 |
46,589 |
44,102 |
50,332 |
79 |
|
17 |
5,70 |
65,799 |
57,741 |
58,914 |
65,128 |
49 |
|
18 |
5,80 |
47,868 |
49,268 |
53,657 |
66,910 |
26 |
|
19 |
5,9-6,6 |
69,869 |
60,323 |
60,671 |
69,324 |
38 |
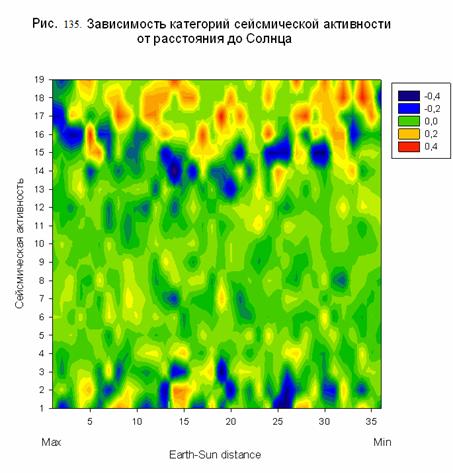
На рис. 135 представлен фрагмент матрицы информативности
модели М36, позволяющий оценить степень влияния расстояния о Земли до Солнца на
категории сейсмической активности из таблицы 46. Можно видеть, что категории
соответствующие высокой сейсмической активности более информативны, т.е.
обнаруживают связь с расстоянием до Солнца. Заметим, что изменение
гравитационного потенциала Солнечной системы на поверхности нашей планеты
связано, главным образом, с изменением расстояния от Земли до Солнца. Таким
образом, полученные результаты подтверждают установленную выше взаимосвязь
средней магнитуды и ежедневного изменения гравитационного потенциала Солнечной
системы в окрестностях Земли.
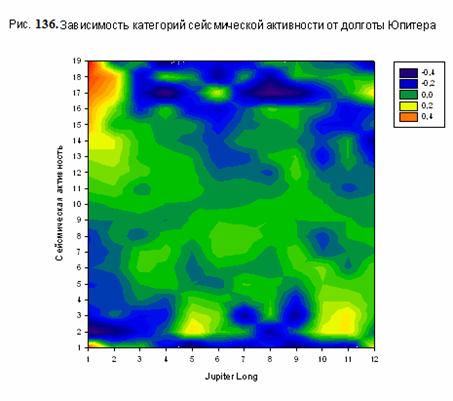
Еще один интересный результат, который был получен с
помощью визуализации фрагмента матрицы информативности, представлен на
рис. 136. Эти данные демонстрируют зависимость категорий сейсмической
активности от долготы Юпитера в модели М12 (отметим, что в других исследованных
моделях получается аналогичный результат). Каждой категории долготы на рис. 136
соответствует сектор 30о , причем первая категория соответствует
знаку Овна. Таким образом, Юпитер в знаке Овна, видимо, возбуждает сильные
землетрясения. Этот результат находится
в согласии с уравнениями (79), в
которых средняя сейсмическая энергия Е пропорциональна абсолютной величине гравитационного
потенциала Юпитера. Но в исследуемый период 1963-2006 годов точка перигелия
Юпитера приходится на 14-15 градус Овна. Следовательно, расстояние от Земли до
Юпитера минимально, а абсолютная величина гравитационного потенциала Юпитера
максимальна при нахождении Юпитера в знаке Овна.
На рис. 137 представлен параметр сходства для трех
типов категорий и для категории АА в семантических информационных моделях М12,
М60 и М160. Отметим, что в этих моделях наблюдается типичное поведение
параметра сходства от магнитуды, обнаруженное ранее на более коротких рядах.
Такое поведение указывает на существование нескольких
различных механизмов возбуждения (инициации) землетрясений, в одном из
которых определяющую роль играют небесные тела, составляющие космическое
окружение Земли.
На рис. 138 представлена диаграмма распределения среднего
(1) и максимального (2) значения параметра сходства различных
типов категорий в моделях М12 и М60. Наивысшее среднее значение параметра
сходства (28%) достигается в модели М12 (месячный прогноз) для категорий
магнитуды типа А. Наибольшее максимальное значение (66,8%) имеет категория типа
АА в модели М12. Это можно сравнить с наибольшим средним (7,87%) и максимальным
(30,9%) значением параметра сходства категории магнитуды типа А, полученным в
модели М12 на основе базы /56/.
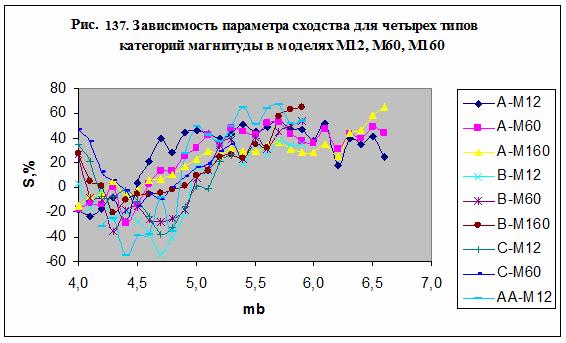
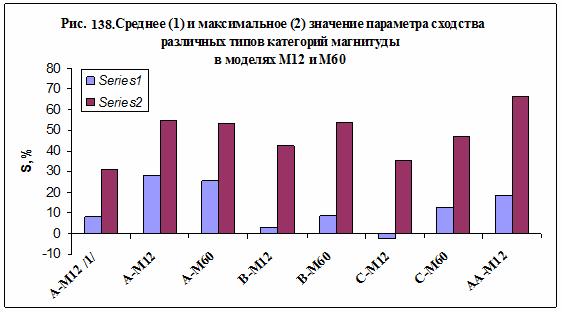
Таким образом, увеличение длины ряда с 5082 до 16032
дней и числа событий с 65541 до 128320 позволяет существенно поднять как
среднее так максимальное значение параметра сходства категории типа А
(магнитуда однократных событий). Это означает, что с увеличением количества событий
и длины временного ряда исследуемых сейсмический событий (землетрясений)
возрастает степень когерентности данных и достоверность прогнозирования событий
по астрономическим данным. Но такое поведение возможно только в том случае,
если воздействие небесных тел существенно влияет на формирование умеренных и
сильных землетрясений, т.к. повышение достоверности прогнозирования при
увеличении объема исследуемой выборки происходит за счет повышения отношения
сигнал/шум при улучшении условий работы системы подавления шума системы «Эйдос-астра».
Механизм
влияния небесных тел Солнечной системы на сейсмическую активность Земли
Для объяснения полученных результатов можно обратиться
к гипотезе приливного воздействия
небесных тел, широко обсуждаемой в литературе /83/.
Одним из первых теоретиков сейсмологии был Иммануил
Кант, который после знаменитого Лиссабонского землетрясения, произошедшего 1
ноября 1755 года, выдвинул теорию об определяющем
влиянии приливных сил Солнца и Луны в формировании землетрясений. Идея о
влиянии приливных сил на тектонические процессы и землетрясения развивалась
многими авторами, вплоть до создания самостоятельного научного направления астрогеологии,
которое получило развитие в связи с космическими исследованиями. Выше было
показано, что сейсмическая энергия Земли связана с изменением гравитационного
потенциала Солнечной системы, что полностью подтверждает идею Канта.
Для определения физического фактора, влияющего на подготовку
землетрясений, рассмотрим безразмерный комплекс, характеризующий отношение
вариаций гравитационной энергии элементарных частиц, атомов и молекул в
гравитационном поле Солнечной системы, к их тепловой энергии:
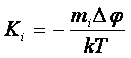 (84)
(84)
Здесь ![]() – масса частицы, изменение гравитационного
потенциала Солнечной системы в данной точке на поверхности Земли, постоянная
Больцмана и абсолютная температура соответственно.
– масса частицы, изменение гравитационного
потенциала Солнечной системы в данной точке на поверхности Земли, постоянная
Больцмана и абсолютная температура соответственно.
На рис. 139 показано сезонное изменение безразмерного
комплекса Ki для
электронов, протонов, атомов железа и молекул группы оливина (Fe2SiO4) при
температуре Т=1000К. Ранее было установлено /23-25/, что в случае электронов
малые вариации этого комплекса при комнатной температуре приводят к сезонным вариациям
индуктивности и сопротивления, а в случае нейтронов и протонов к сезонному
изменению скорости радиоактивного распада ядер изотопов /26-27/.
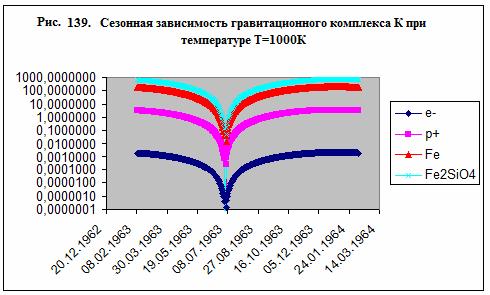
В случае атомов железа параметр Ki
изменяется в пределах от нуля до примерно 200. Столь большая амплитуда
колебаний должна иметь какой-то заметный физический эффект. Можно предположить,
что усталостное скачкообразное разрушение материала, инициирующее
землетрясение, обусловлено изменением некоторых физико-химических свойств
вещества, возникающих при периодическом изменении комплекса Ki , что индуцирует пропорциональное изменение давления
в некоторой ограниченной области пространства. Рассмотрим эту модель более
подробно.
Как известно,
во внешнем гравитационном поле химический потенциал изменяется на величину,
пропорциональную потенциальной энергии молекул, а условием равновесия является
постоянство химического потенциала, т.е.:
![]() (85)
(85)
Здесь P,T –
давление и температура тела, u –
потенциальная энергия молекулы, индексом 0 обозначен химический потенциал без
внешнего поля. Уравнение (85) применимо при достаточно медленном изменении
внешнего поля, чтобы поддерживалось состояние термодинамического равновесия.
Тогда изменение давления можно определить путем дифференцирования уравнения
(85) по времени при постоянной температуре:
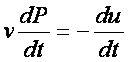
Где ![]() – удельный объем. Отсюда, используя определение потенциальной
энергии и выражение (84), находим
– удельный объем. Отсюда, используя определение потенциальной
энергии и выражение (84), находим
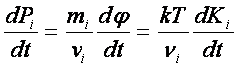 (86)
(86)
Таким образом, переменное гравитационное поле индуцирует
на границе двух сред скачок давления, пропорциональный разности плотностей и
величине изменения гравитационного потенциала.
Следовательно, эффект приливного воздействия небесных тел будет особенно
заметным в зонах, разделяющих различные тектонические образования, например при
наползании друг на друга разноплотных слоев земной коры, при переходе от плотности
земной коры к плотности магмы, в зонах субдукции и т.п., т.е. там, где по
современным представлениям концентрируются источники землетрясений.
Полученные ваше результаты могут служить основой для
развития модели подготовки землетрясений по механизму накопления повреждений в
земной коре под влиянием приливного воздействия небесных тел.
6.4. Семантические информационные модели глобальной сейсмической
активности при смещении географического и магнитного полюса
Механизмы формирования
сейсмических событий
В работах /52-53/ была развита модель прогнозирования
землетрясений по астрономическим данным, опирающаяся на теорию и модели
астросоциотипологии /2/. Эти модели обеспечивают многопараметрическую типизацию
(обобщение) конкретных землетрясений, описанных астрономическими данными, и
формирование обобщенных образов (классов) землетрясений, в которые они
объединяются по их магнитуде и глубине гипофокуса. Моделирование сейсмических событий
осуществлялось по параметру сходства между описаниями конкретных землетрясений
и обобщенными образами классов на основе системы искусственного интеллекта «Эйдос-астра»
/7/. База данных землетрясений была сформирована на основе оперативного
сейсмологического каталога ГС РАН /56/, содержащего 65541 запись событий
землетрясений, произошедших в различных регионах мира в период с 1 января 1993
года по 20 ноября 2008 г.
Была обнаружена зависимость параметра сходства от магнитуды,
глубины очага (гипофокуса) и числа землетрясений, происходящих ежедневно на
нашей планете, как в месячном, так и в 2-3 дневном прогнозе.
В работе /54/ представлены результаты прогнозирования
параметров сейсмической активности по астрономическим данным на основе
семантических информационных моделей с использованием всемирной базы
землетрясений /57/, была исследована совокупность 128320 событий землетрясений
с магнитудой ![]() , произошедших на нашей
планете в период с 9 февраля 1963 года по 31 декабря 2006 г (всего 16032 дня).
Полученные в работе /54/ результаты находятся в согласии с данными /52-53/, что
позволяет расширить область применения развитых в этих работах моделей. Как
было установлено, увеличение длины ряда с 5082 до 16032 дней и числа событий с
65541 до 128320 позволяет существенно поднять как среднее так максимальное
значение параметра сходства категории магнитуда.
, произошедших на нашей
планете в период с 9 февраля 1963 года по 31 декабря 2006 г (всего 16032 дня).
Полученные в работе /54/ результаты находятся в согласии с данными /52-53/, что
позволяет расширить область применения развитых в этих работах моделей. Как
было установлено, увеличение длины ряда с 5082 до 16032 дней и числа событий с
65541 до 128320 позволяет существенно поднять как среднее так максимальное
значение параметра сходства категории магнитуда.
Это означает, что с увеличением количества событий и
длины временного ряда исследуемых сейсмический событий (землетрясений)
возрастает степень когерентности данных и достоверность прогнозирования событий
по астрономическим данным. По мнению авторов это происходит за счет улучшения
условий для подавления шума при увеличении объема выборки и подтверждает, что
воздействие небесных тел является фактором, существенно влияющим на
формирование умеренных и сильных землетрясений.
Вместе с тем, по-видимому, среди факторов, влияющих на
глобальную сейсмическую активность Земли, следует учесть не только внешние для
нее космические факторы, такие как приливное воздействие, но и внутренние,
чисто Земные, такие, как смещение географического и магнитного полюсов. В
работе /55/ исследованы семантические информационные модели, содержащие данные
о сейсмических событиях /57/, астрономические параметры небесных тел, параметры
смещения географического полюса по данным /60/, а также параметры
магнитного поля Земли, полученные вблизи
магнитных полюсов, из всемирной базы /61/. Установлено, что добавление в
информационную модель данных по магнитному полю и смещению географических
полюсов позволяет увеличить достоверность прогноза землетрясений, что указывает
на существование глобальных общепланетарных механизмов формирования
сейсмических событий.
Модели сейсмической
активности
Исследуемая база данных сейсмических событий была
сформирована на основе базы данных Международного сейсмологического центра
(ISC) /57/, содержащей 20489816 записей
регистрации различными сейсмостанциями событий землетрясений, произошедших на
нашей планете в период с 1 января 1961 года по 31 декабря 2006 г.
В состав
системы «Эйдос-астра» /7/ входят программные интерфейсы, позволяющие объединять
разрозненные данные /57/ в единую базу данных, выделять различные сегменты
данных, производить необходимые вычисления
со всеми исследованными базами исходных данных. С применением данного
программного интерфейса из исходных данных /57/ было образовано несколько
различных БД для исследования влияния астрономических параметров на магнитуду и
глубину гипофокуса, на ежедневное число землетрясений, а также на средние
параметры сейсмической активности. Ниже исследована совокупность 128320 событий
землетрясений с магнитудой ![]() , произошедших на нашей
планете в период с 9 февраля 1963 года по 31 декабря 2006 г (всего 16032 дня).
, произошедших на нашей
планете в период с 9 февраля 1963 года по 31 декабря 2006 г (всего 16032 дня).
В качестве
астрономических параметров были использованы долгота и расстояние от Земли до
десяти небесных тел – Солнца, Луны, Марса, Меркурия, Венеры, Юпитера, Сатурна,
Урана, Нептуна и Плутона, и долгота Северного Узла Луны. Астрономические
параметры вычислялись на каждый день в фиксированной точке с географическими
координатами Гринвича в 12:00 GMT в топоцентрической системе координат.
Отметим, что выбор этой точки не является существенным для решаемого класса
задач.
Кроме того, в модели были
использованы координаты географического полюса – xEOP, yEOP /60/,
а также данные по вертикальной компоненте магнитной индукции - Bz,
полученные вблизи Северного магнитного полюса на станции Resolute Bay (IAGA
Code: RES; lat: 74.69; long: 265.105) /61/. Отметим, что параметр Bz
достаточно точно отражает не только ежедневную вариацию магнитного поля,
обусловленную, например, солнечной активностью, но и величину смещения
магнитного полюса, поскольку он получен путем измерения магнитного поля на
станции с фиксированными географическими координатами.
Из астрономических
параметров, координат географического полюса, параметра индукции магнитного
поля Bz и категорий сейсмической активности была создана база
данных, содержащая 16032 записи с обобщенной информацией о ежедневной сейсмической и геофизической активности Земли.
Решение прямой задачи
включает в себя нормирование входных параметров и приведение их к одному
масштабу изменения в интервале (0;360), разбиение интервалов на М частей,
вычисление матрицы абсолютных частот и информативности. Отметим, что в системе «Эйдос-астра»
реализован режим автоматического синтеза нескольких семантических
информационных моделей, в которых число ячеек принимает любое заданное значение
М=2,3,...,173.
Решение обратной задачи
включает в себя распознавание категорий по заданным астрономическим параметрам,
в соответствии с уравнениями (68-70). Частным случаем задачи распознавания
является определение достоверности идентификации категорий по астрономическим
данным в каждой модели. Решение этой
задачи по данным /56/ было рассмотрено в работах /52-53/, а по данным /57/ в
работах /54-55/.
Параметр сходства категорий
магнитуды
В исходной БД /57/ сейсмические события
характеризуются магнитудой mb, которой можно сопоставить категорию магнитуды –
таблица 48. Поскольку события с одной и той же магнитудой могут повторяться в
один день, каждому значению магнитуды сопоставляется несколько типов категорий,
а именно:
A – событие с магнитудой mb повторяется один раз;
B – событие с магнитудой mb повторяется два раза;
C – событие с
магнитудой mb повторяется три раза.
Кроме того, можно рассмотреть случай, когда,
например, категория А усекается, путем
отбрасывания некоторых событий. Таким образом, была образована категория ![]() .
.
На рис. 140 и в таблице 48 представлен параметр
сходства категории магнитуда в трех информационных моделях:
M160(G) – содержит только астрономические параметры;
M160(G,EOP) – астрономические параметры и координаты
географического полюса xEOP, yEOP;
M160(G,EOP,Bz) – астрономические параметры,
координаты географического полюса и параметр индукции магнитного поля.
Таблица
48. Параметр сходства категории магнитуда
в трех моделях
|
Категория |
M160(G) |
M160(G,EOP) |
M160(G,EOP,Bz) |
Число случаев |
|
A40-Mb=4,0 |
-18,593 |
-15,505 |
-19,975 |
1362 |
|
A41-Mb=4,1 |
-8,208 |
-5,448 |
-7,362 |
1580 |
|
A42-Mb=4,2 |
-1,797 |
0,993 |
0,934 |
1796 |
|
A43-Mb=4,3 |
4,889 |
8,250 |
7,752 |
2224 |
|
A44-Mb=4,4 |
-4,445 |
-1,930 |
-2,027 |
2744 |
|
A45-Mb=4,5 |
-0,364 |
0,716 |
-0,140 |
3358 |
|
A46-Mb=4,6 |
8,102 |
9,573 |
8,900 |
4119 |
|
A47-Mb=4,7 |
11,303 |
11,363 |
9,578 |
4768 |
|
A48-Mb=4,8 |
13,381 |
12,652 |
11,214 |
4954 |
|
A49-Mb=4,9 |
17,503 |
17,331 |
16,008 |
5008 |
|
A50-Mb=5 |
26,141 |
26,952 |
24,753 |
4904 |
|
A51-Mb=5,1 |
29,802 |
28,582 |
25,574 |
4582 |
|
A52-Mb=5,2 |
25,101 |
25,280 |
22,211 |
4134 |
|
A53-Mb=5,3 |
30,307 |
30,245 |
28,191 |
3563 |
|
A54-Mb=5,4 |
28,031 |
28,697 |
26,795 |
3010 |
|
A55-Mb=5,5 |
24,238 |
23,532 |
22,688 |
2367 |
|
A56-Mb=5,6 |
32,491 |
32,121 |
31,139 |
1940 |
|
A57-Mb=5,7 |
31,689 |
31,439 |
30,717 |
1460 |
|
A58-Mb=5,8 |
28,160 |
28,003 |
27,846 |
1179 |
|
A59-Mb=5,9 |
24,738 |
25,299 |
24,705 |
864 |
|
A60-Mb=6,0 |
23,495 |
23,873 |
22,988 |
656 |
|
A61-Mb=6,1 |
29,394 |
29,719 |
29,672 |
453 |
|
A62-Mb=6,2 |
23,934 |
24,791 |
24,343 |
319 |
|
A63-Mb=6,3 |
35,651 |
35,849 |
35,507 |
202 |
|
A64-Mb=6,4 |
42,810 |
42,797 |
44,097 |
137 |
|
A65-Mb=6,5 |
55,802 |
57,674 |
60,501 |
87 |
|
A66-Mb=6,6-7,0 |
63,169 |
65,357 |
67,766 |
68 |
|
B40-Mb=4,0 |
28,361 |
28,268 |
30,290 |
446 |
|
B41-Mb=4,1 |
18,857 |
19,805 |
20,165 |
660 |
|
B42-Mb=4,2 |
9,046 |
8,452 |
8,179 |
835 |
|
B43-Mb=4,3 |
-6,859 |
-6,084 |
-9,191 |
955 |
|
B44-Mb=4,4 |
-14,986 |
-12,157 |
-15,705 |
1099 |
|
B45-Mb=4,5 |
-1,494 |
1,128 |
0,257 |
1223 |
|
B46-Mb=4,6 |
-1,678 |
0,533 |
-0,159 |
1455 |
|
B47-Mb=4,7 |
-1,317 |
-1,172 |
-1,871 |
1612 |
|
B48-Mb=4,8 |
3,926 |
4,644 |
2,945 |
1817 |
|
B49-Mb=4,9 |
3,783 |
4,491 |
4,802 |
1636 |
|
B50-Mb=5 |
15,492 |
15,632 |
15,572 |
1428 |
|
B51-Mb=5,1 |
13,093 |
12,787 |
12,390 |
1206 |
|
B52-Mb=5,2 |
22,413 |
22,473 |
22,553 |
936 |
|
B53-Mb=5,3 |
24,482 |
23,816 |
22,955 |
617 |
|
B54-Mb=5,4 |
21,194 |
20,821 |
19,912 |
422 |
|
B55-Mb=5,5 |
30,487 |
30,712 |
30,184 |
261 |
|
B56-Mb=5,6 |
33,408 |
33,861 |
34,219 |
180 |
|
B57-Mb=5,7 |
56,994 |
57,037 |
59,599 |
93 |
|
B58-Mb=5,8 |
61,514 |
64,016 |
66,800 |
73 |
|
B59-Mb=5,9-6,4 |
62,605 |
64,548 |
66,552 |
69 |
|
C40-Mb=4,0 |
53,018 |
55,308 |
59,797 |
130 |
|
C41-Mb=4,1 |
35,327 |
36,118 |
39,149 |
259 |
|
C42-Mb=4,2 |
22,208 |
22,766 |
24,794 |
362 |
|
C43-Mb=4,3 |
21,621 |
22,491 |
23,921 |
436 |
|
C44-Mb=4,4 |
19,875 |
19,035 |
20,244 |
482 |
|
C45-Mb=4,5 |
11,685 |
11,468 |
10,396 |
468 |
|
C46-Mb=4,6 |
2,741 |
4,193 |
1,167 |
515 |
|
C47-Mb=4,7 |
5,517 |
8,352 |
7,265 |
501 |
|
C48-Mb=4,8 |
10,420 |
12,862 |
12,103 |
450 |
|
C49-Mb=4,9 |
15,730 |
16,235 |
16,365 |
447 |
|
C50-Mb=5 |
20,558 |
21,439 |
22,122 |
356 |
|
C51-Mb=5,1 |
22,202 |
23,067 |
23,448 |
293 |
|
C52-Mb=5,2 |
35,702 |
35,504 |
37,099 |
166 |
|
C53-Mb=5,3-6,0 |
48,043 |
50,344 |
52,712 |
105 |
|
Среднее значение |
20,995 |
21,820 |
21,564 |
1374 |
Из данных, приведенных на рис. 140 и в таблице 48
следует, что добавление геофизических параметров, связанных со смещением
географического и магнитного полюса и с ежедневной вариацией планетарного
магнитного поля приводит к росту как среднего, так и максимального параметр
сходства. Однако этот рост не столь велик, как можно было бы ожидать, если бы
механизм формирования землетрясений был автономным, зависящим только от местных
условий. Фактически на долю геофизических параметров приходится не более 5-6%,
причем их вклад увеличивается для сильных и многократно повторяющихся
сейсмических событий.
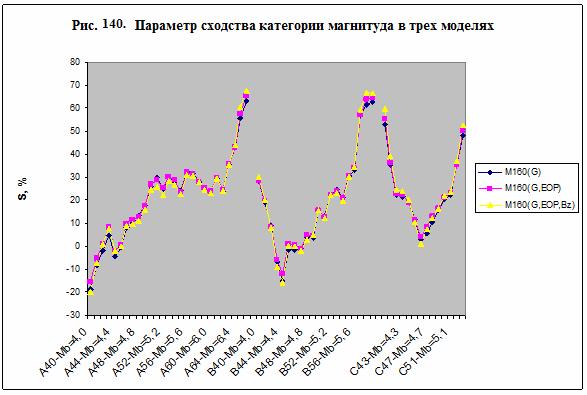
На рис. 141 представлены фрагменты матрицы информативности
модели M12(G,EOP), позволяющие оценить степень влияния параметров смещения
географического полюса на категории сейсмической активности из таблицы 48. Было
установлено, что параметры xEOP, yEOP влияют на категории
магнитуды несимметрично и что их влияние сильнее проявляется в случае многократных
событий.
Из сопоставления данных на рис. 141-142 хорошо видно,
что параметр yEOP влияет на
однократные события во всей области своего изменения, тогда как параметр xEOP
влияет жестко, возбуждая сильные землетрясения при отклонении в минимальное положение.
Отметим, что параметр xEOP соответствует движению земной оси вдоль
меридиана Гринвич, а параметр yEOP
описывает движение вдоль перпендикулярной к меридиану Гринвич оси - 90o
W. Механизм влияния смещения земной оси на сейсмические события в настоящее
время не установлен, хотя предпринимались неоднократные попытки определить
обратное влияние сейсмических событий на скорость вращения Земли.
На рис. 143 представлен фрагмент матрицы информативности
модели M12(G,EOP,Bz), на основе которого можно оценить степень
влияния параметра магнитной индукции на
категории A, B, C сейсмической активности из таблицы 1.
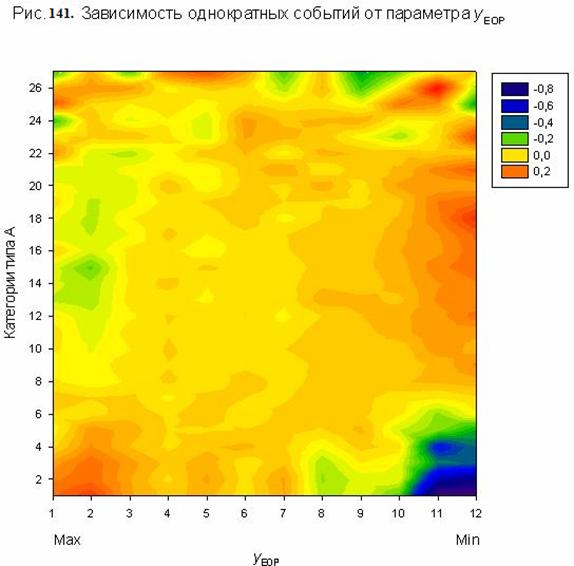
Из этих данных следует, что вариации напряженности магнитного
поля заметно влияют на события трех типов, увеличивая вероятность проявления
многократных событий с уменьшением вертикальной компоненты вектора магнитной
индукции. Механизм влияния магнитного поля
на сейсмические события в настоящее время неизвестен, хотя установлен обратный эффект влияния
сейсмического электромагнитного излучения на магнитосферу – это т.н. сейсмомагнитосферные связи /18/.
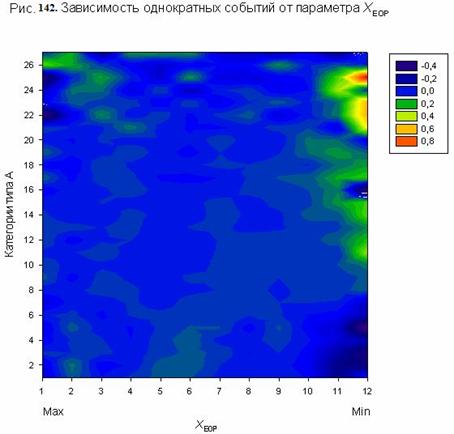
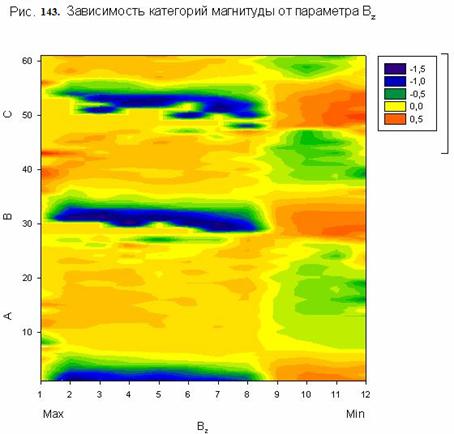
Корреляционные связи
гравитационных, сейсмических и геофизических параметров
Чтобы выяснить, являются ли геофизические механизмы
возбуждения землетрясений автономными, или они зависят в свою очередь от
параметров небесных тел, рассмотрим корреляционные связи всех параметров
задачи.
Определим суммарную и среднюю магнитуду, магнитуду
энергии и объема в виде:
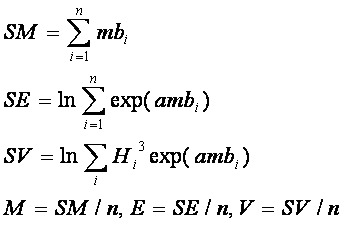 (87)
(87)
Здесь n –
число ежедневных событий, H – глубина
очага. Параметр энергии задан постоянным и равным a=1.5.
Отметим, что магнитуда mb рассчитывается по максимальной скорости смещения в
короткопериодных объемных волнах по
формулам /11/:
![]() (88)
(88)
где, А – амплитуда P-волн смещение грунта в мкм (рассчитывается
по максимальной амплитуде), T – периода в секундах, T <3с; Q (Δ, H)
– функция ослабления Гутенберг и Рихтер
(1956), Δ – эпицентральное расстояние в градусах, 21 ° ≤ Δ
≤ 100 °.
Определим параметр гравитационной энергии Солнечной
системы и его ежедневное изменение в виде
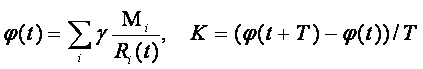 (89)
(89)
Здесь ![]() – гравитационная постоянная,
масса небесного тела и расстояние от него до Земли соответственно, Т – длительность
земных суток. Суммирование осуществляется по всем небесным телам, параметры
которых используются в модели.
– гравитационная постоянная,
масса небесного тела и расстояние от него до Земли соответственно, Т – длительность
земных суток. Суммирование осуществляется по всем небесным телам, параметры
которых используются в модели.
Рассмотрим
таблицу корреляционных связей между всеми параметрами задачи – таблица
49.
Таблица 49. Корреляционные
связи параметров задачи, полученные методом
Spearman Rank Order Correlation по программе SigmaPlot: для Р<0,05
корреляционные связи являются достоверными. N
– число точек по которым вычисляется корреляция.
|
|
Bz |
xEOP |
yEOP |
SM |
SE |
SU |
M |
E |
V |
n |
|
K |
-0,00898 |
-0,41 |
0,168 |
-0,0143 |
0,00101 |
-0,00131 |
0,0327 |
0,019 |
0,0192 |
-0,0181 |
|
P |
0,255 |
2E-07 |
2E-07 |
0,0711 |
0,899 |
0,869 |
3,78E-05 |
0,0167 |
0,0155 |
0,0226 |
|
N |
16031 |
16031 |
16031 |
15861 |
15861 |
15861 |
15861 |
15861 |
15861 |
15861 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Bz |
|
-0,067 |
-0,219 |
0,477 |
0,191 |
0,172 |
-0,444 |
-0,511 |
-0,49 |
0,494 |
|
P |
|
2E-07 |
2E-07 |
2E-07 |
2E-07 |
2E-07 |
2E-07 |
2E-07 |
2E-07 |
2E-07 |
|
N |
|
16031 |
16031 |
15861 |
15861 |
15861 |
15861 |
15861 |
15861 |
15861 |
|
|
|
|
|
|
|
|
|
|
|
|
|
xEOP |
|
|
0,04 |
-0,0699 |
-0,0429 |
-0,0314 |
0,0324 |
0,071 |
0,0681 |
-0,0692 |
|
P |
|
|
4E-07 |
2E-07 |
6,69E-08 |
7,68E-05 |
0,000044 |
2E-07 |
2E-07 |
2E-07 |
|
N |
|
|
16031 |
15861 |
15861 |
15861 |
15861 |
15861 |
15861 |
15861 |
|
|
|
|
|
|
|
|
|
|
|
|
|
yEOP |
|
|
|
-0,206 |
-0,105 |
-0,0768 |
0,145 |
0,214 |
0,211 |
-0,211 |
|
P |
|
|
|
2E-07 |
2E-07 |
2E-07 |
2E-07 |
2E-07 |
2E-07 |
2E-07 |
|
N |
|
|
|
15861 |
15861 |
15861 |
15861 |
15861 |
15861 |
15861 |
|
|
|
|
|
|
|
|
|
|
|
|
|
SM |
|
|
|
|
0,823 |
0,419 |
-0,321 |
-0,97 |
-0,977 |
0,992 |
|
P |
|
|
|
|
2E-07 |
2E-07 |
2E-07 |
2E-07 |
2E-07 |
2E-07 |
|
N |
|
|
|
|
15861 |
15861 |
15861 |
15861 |
15861 |
15861 |
|
|
|
|
|
|
|
|
|
|
|
|
|
SE |
|
|
|
|
|
0,351 |
0,11 |
-0,714 |
-0,759 |
0,775 |
|
P |
|
|
|
|
|
2E-07 |
2E-07 |
2E-07 |
2E-07 |
2E-07 |
|
N |
|
|
|
|
|
15861 |
15861 |
15861 |
15861 |
15861 |
|
|
|
|
|
|
|
|
|
|
|
|
|
SV |
|
|
|
|
|
|
-0,145 |
-0,404 |
-0,281 |
0,419 |
|
P |
|
|
|
|
|
|
2E-07 |
2E-07 |
2E-07 |
2E-07 |
|
N |
|
|
|
|
|
|
15861 |
15861 |
15861 |
15861 |
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
0,49 |
0,424 |
-0,422 |
|
|
P |
|
|
|
|
|
|
|
2E-07 |
2E-07 |
2E-07 |
|
N |
|
|
|
|
|
|
|
15861 |
15861 |
15861 |
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
0,976 |
-0,986 |
|
P |
|
|
|
|
|
|
|
|
2E-07 |
2E-07 |
|
N |
|
|
|
|
|
|
|
|
15861 |
15861 |
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
-0,985 |
|
P |
|
|
|
|
|
|
|
|
|
2E-07 |
|
N |
|
|
|
|
|
|
|
|
|
15861 |
Из анализа данных,
приведенных в таблице 49, следует, что существует положительная корреляционная
связь вариаций магнитного поля с числом землетрясений с коэффициентом 0,494, а
также положительная корреляционная связь этого параметра с суммарной магнитудой
с коэффициентом 0,477. Согласно полученным выше результатам по распознаванию
событий, эта связь является двухсторонней. Отметим, что связь возмущений магнитного
поля с происходящими землетрясениями, а также с движением Луны была установлена
еще в работах Булгакова Н.А. /84-85/.
Гипотеза о связи
землетрясений с подземными электрическими разрядами высказывалась неоднократно /86/, однако доказать
наличие этой связи на основании только представленных выше данных не
представляется возможным, тогда как обратное влияние землетрясений на
возмущения магнитного поля не только легко обнаруживается и является весьма
существенным, но и может быть использовано для прогнозирования землетрясений.
Тем не менее, можно предположить, что имеется некий механизм влияния возмущений
магнитного поля Земли на глобальную сейсмическую активность. Дадим обоснование
этой гипотезе.
Отметим сильную
несимметричную связь смещений географического полюса с ежедневным изменением
гравитационного потенциала. При этом вертикальная компонента магнитной индукции также связана со смещениями
географического полюса, однако связь Bz с параметром гравитационного
поля К довольно слабая. Поставим вопрос, связано ли магнитное поле Земли с положением
небесных тел?
Чтобы ответить на этот
вопрос были изучены все корреляционные связи вектора магнитной индукции с
астрономическими параметрами долготы, широты и расстояний до небесных тел –
таблица 50. Было обнаружено, что имеется сильная корреляционная связь с
определенными комбинациями астрономических параметров Урана и Нептуна, которые
соответствуют дипольному излучению этих планет. В настоящее время механизм
этого явления неизвестен. Однако интегральные параметры сейсмических событий
(87), в свою очередь, связаны с указанными комбинациями, поэтому рассмотрим
этот вопрос, не вникая в физику процесса.
Таблица 50. Корреляционные
связи* координат географического полюса по данным /60/ и магнитной индукции по измерениям на
трех станциях /61/ с координатами небесных тел: Alert (IAGA Code: ALE; lat: 82.5;
long: 297.65), Vostok (IAGA Code:
VOS lat:-78.45 long: 106.867), Resolute Bay (IAGA Code: RES; lat: 74.69;
long: 265.105)
|
|
BzALE |
BzVOS |
BzRES |
BxRES |
ByRES |
xEOP |
yEOP |
|
SUNLON |
0,0948 |
0,0347 |
0,0514 |
-0,014 |
-0,0145 |
-0,0769 |
-0,325 |
|
P |
1,95E-08 |
0,00486 |
7,16E-11 |
0,0762 |
0,067 |
1,75E-22 |
0 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
SUNLAT |
-0,117 |
-0,052 |
-0,0672 |
0,0129 |
0,0204 |
0,093 |
0,395 |
|
P |
4,12E-12 |
0,0000243 |
1,70E-17 |
0,101 |
0,0101 |
3,67E-32 |
0 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
SUNDIST |
-0,107 |
-0,0539 |
-0,0703 |
0,0159 |
0,0161 |
0,212 |
0,384 |
|
P |
1,96E-10 |
0,000012 |
4,99E-19 |
0,0441 |
0,0416 |
1,50E-161 |
0 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
MOONLON |
-0,0000556 |
-0,0153 |
0,00564 |
-0,00809 |
0,00477 |
-0,00174 |
-0,000344 |
|
P |
0,997 |
0,216 |
0,475 |
0,306 |
0,547 |
0,826 |
0,965 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
MOONLAT |
-0,0483 |
-0,000536 |
-0,00965 |
0,00478 |
-0,000313 |
0,00494 |
0,0196 |
|
P |
0,00427 |
0,965 |
0,222 |
0,545 |
0,968 |
0,532 |
0,0133 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
MOONDIST |
0,0093 |
-0,00316 |
0,0103 |
-0,00398 |
-0,00355 |
-0,00103 |
-0,00205 |
|
P |
0,582 |
0,798 |
0,194 |
0,614 |
0,654 |
0,897 |
0,795 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
MERCURYLON |
0,0663 |
0,0597 |
0,0598 |
-0,0161 |
-0,00634 |
-0,0176 |
-0,307 |
|
P |
0,0000857 |
0,00000124 |
3,68E-14 |
0,041 |
0,424 |
0,0258 |
0 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
MERCURYLAT |
0,0157 |
0,00974 |
0,0104 |
-0,00163 |
-0,00139 |
-0,0754 |
-0,049 |
|
P |
0,352 |
0,429 |
0,189 |
0,836 |
0,861 |
1,15E-21 |
5,53E-10 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
MERCURYDIS |
0,00316 |
0,00559 |
0,0153 |
-0,00404 |
-0,00592 |
0,00141 |
-0,11 |
|
P |
0,852 |
0,65 |
0,0528 |
0,609 |
0,455 |
0,859 |
3,29E-44 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
VENUSLON |
0,024 |
0,0529 |
0,0388 |
-0,00925 |
-0,0189 |
-0,0456 |
-0,282 |
|
P |
0,156 |
0,0000173 |
8,65E-07 |
0,242 |
0,0172 |
7,48E-09 |
5,28E-290 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
VENUSLAT |
-0,0199 |
0,0077 |
0,00504 |
0,00546 |
-0,00865 |
-0,152 |
-0,00226 |
|
P |
0,238 |
0,532 |
0,523 |
0,49 |
0,275 |
2,37E-83 |
0,775 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
VENUSDIST |
-0,0952 |
-0,0491 |
-0,0041 |
-0,0017 |
-0,0139 |
-0,016 |
-0,0283 |
|
P |
1,66E-08 |
0,0000662 |
0,604 |
0,829 |
0,0795 |
0,0423 |
0,000343 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
MARSLON |
0,116 |
-0,0833 |
-0,00527 |
-0,0000542 |
-0,0332 |
-0,00171 |
-0,135 |
|
P |
5,65E-12 |
1,26E-11 |
0,505 |
0,995 |
0,0000281 |
0,828 |
1,31E-65 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
MARSLAT |
-0,279 |
0,0978 |
0,0307 |
-0,0521 |
0,0315 |
-0,131 |
-0,0572 |
|
P |
1,29E-63 |
1,74E-15 |
0,000103 |
4,27E-11 |
0,00007 |
1,36E-62 |
4,24E-13 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
MARSDIST |
-0,0798 |
-0,0335 |
-0,00558 |
-0,00809 |
-0,00161 |
0,0227 |
-0,00678 |
|
P |
0,00000229 |
0,00661 |
0,48 |
0,306 |
0,839 |
0,00398 |
0,391 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
JUPITERLON |
0,829 |
0,192 |
0,0721 |
0,0485 |
0,052 |
0,0234 |
0,063 |
|
P |
0 |
7,03E-56 |
6,29E-20 |
8E-10 |
5,08E-11 |
0,00301 |
1,36E-15 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
JUPITERLAT |
0,712 |
0,246 |
-0,0696 |
0,138 |
-0,133 |
0,00718 |
0,0575 |
|
P |
0 |
2,02E-91 |
1,15E-18 |
1,59E-68 |
5,08E-64 |
0,364 |
3,22E-13 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
JUPITERDIS |
0,094 |
0,0968 |
-0,0345 |
0,0397 |
-0,0405 |
0,00919 |
0,0403 |
|
P |
2,54E-08 |
3,36E-15 |
0,0000128 |
0,00000051 |
3,09E-07 |
0,245 |
0,00000033 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
SATURNLON |
-0,741 |
-0,295 |
0,0225 |
-0,187 |
0,0444 |
-0,0105 |
-0,00187 |
|
P |
0 |
8,66E-133 |
0,0044 |
1,50E-126 |
2,06E-08 |
0,185 |
0,813 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
SATURNLAT |
-0,466 |
0,861 |
0,552 |
-0,073 |
0,23 |
0,0329 |
0,0571 |
|
P |
5,10E-188 |
0 |
0 |
2,05E-20 |
1,60E-189 |
0,0000315 |
4,61E-13 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
SATURNDIST |
-0,334 |
-0,113 |
0,00839 |
-0,0846 |
0,0357 |
-0,0632 |
0,0872 |
|
P |
9,49E-92 |
2,47E-20 |
0,288 |
6,90E-27 |
0,00000652 |
1,16E-15 |
1,86E-28 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
URANUSLON |
0,96 |
0,993 |
-0,59 |
0,956 |
-0,768 |
0,13 |
0,348 |
|
P |
0 |
0 |
0 |
0 |
0 |
3,87E-61 |
0 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
URANUSLAT |
-0,716 |
-0,939 |
0,66 |
-0,948 |
0,802 |
-0,15 |
-0,353 |
|
P |
0 |
0 |
0 |
0 |
0 |
7,48E-82 |
0 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
URANUSDIST |
0,0132 |
0,21 |
-0,44 |
0,633 |
-0,57 |
0,143 |
0,0724 |
|
P |
0,436 |
2,95E-66 |
0 |
0 |
0 |
4,20E-74 |
4,46E-20 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
NEPTUNELON |
0,944 |
0,99 |
-0,613 |
0,965 |
-0,786 |
0,118 |
0,353 |
|
P |
0 |
0 |
0 |
0 |
0 |
7,89E-51 |
0 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
NEPTUNELAT |
-0,763 |
-0,942 |
0,726 |
-0,989 |
0,875 |
-0,13 |
-0,319 |
|
P |
0 |
0 |
0 |
0 |
0 |
1,30E-61 |
0 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
NEPTUNEDIS |
0,105 |
0,00149 |
0,16 |
-0,141 |
0,0986 |
-0,0875 |
-0,399 |
|
P |
5,64E-10 |
0,904 |
1,51E-92 |
1,16E-71 |
1,08E-35 |
1,23E-28 |
0 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
PLUTOLON |
0,959 |
0,991 |
-0,623 |
0,965 |
-0,794 |
0,126 |
0,338 |
|
P |
0 |
0 |
0 |
0 |
0 |
1,25E-57 |
0 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
PLUTOLAT |
0,886 |
0,911 |
0,878 |
-0,835 |
0,926 |
-0,105 |
-0,18 |
|
P |
0 |
0 |
0 |
0 |
0 |
2,54E-40 |
1,24E-116 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
PLUTODIST |
-0,606 |
-0,795 |
-0,0444 |
-0,355 |
0,0706 |
0,0792 |
-0,347 |
|
P |
0 |
0 |
1,93E-08 |
0 |
4,40E-19 |
9,86E-24 |
0 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
NODELON |
0,658 |
0,299 |
0,214 |
-0,187 |
0,346 |
0,00778 |
-0,0177 |
|
P |
0 |
1,86E-136 |
5,87E-165 |
1,57E-126 |
0 |
0,324 |
0,025 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
NODEDIST |
0,0136 |
0,14 |
0,0435 |
0,0232 |
0,0221 |
0,0185 |
0,000237 |
|
P |
0,422 |
3,02E-30 |
3,69E-08 |
0,00325 |
0,00537 |
0,0192 |
0,976 |
|
N |
3500 |
6589 |
16032 |
16032 |
15931 |
16032 |
16032 |
* Корреляционные связи параметров получены
методом Pearson Product Moment
Correlation по программе SigmaPlot: для Р<0,05 корреляционные связи являются
достоверными. N – число точек по которым
вычисляются коэффициенты корреляции. LON – longitude, LAT – latitude, DIST –
distance.
Связь магнитного поля Земли с астрономическими параметрами
Урана
Из параметров долготы (LON), широты (LAT) и
расстояния до планеты (R) можно составить комбинации, которые соответствуют
дипольному излучению:
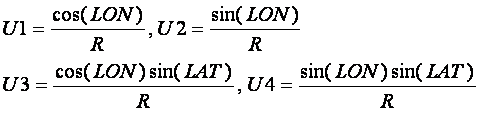 (89)
(89)
В таблице 51 приведены коэффициенты
корреляции магнитной индукции для трех станций наблюдения, расположенных вблизи
магнитных полюсов. Отметим, что R
измеряется в астрономических единицах (а.е.)
- 1 а.е.= 149 597 870,691 км.
Таблица 51. Корреляция
магнитной индукции с комбинациями астрономических параметров Урана для трех
станций: Alert (IAGA Code: ALE; lat:
82.5; long: 297.65), Vostok (IAGA Code: VOS lat:-78.45 long:
106.867), Resolute Bay (IAGA Code: RES;
lat: 74.69; long: 265.105) /16/.
|
|
U1 |
U2 |
U3 |
U4 |
|
BzALE |
-0,329 |
-0,96 |
0,314 |
-0,954 |
|
P |
4,53E-89 |
0 |
7,26E-81 |
0 |
|
N |
3500 |
3500 |
3500 |
3500 |
|
|
|
|
|
|
|
BzVOS |
0,819 |
-0,989 |
0,914 |
-0,863 |
|
P |
0 |
0 |
0 |
0 |
|
N |
6589 |
6589 |
6589 |
6589 |
|
|
|
|
|
|
|
BzRES |
-0,732 |
-0,179 |
0,322 |
-0,904 |
|
P |
0 |
5,83E-115 |
0 |
0 |
|
N |
16032 |
16032 |
16032 |
16032 |
|
|
|
|
|
|
|
BxRES |
0,966 |
-0,343 |
0,0567 |
0,653 |
|
P |
0 |
0 |
6,63E-13 |
0 |
|
N |
16032 |
16032 |
16032 |
16032 |
|
|
|
|
|
|
|
ByRES |
-0,853 |
-0,00252 |
0,172 |
-0,79 |
|
P |
0 |
0,75 |
1,80E-106 |
0 |
|
N |
15931 |
15931 |
15931 |
15931 |
Отметим, что коэффициенты корреляции магнитной индукции
с параметрами U1-U4 имеют высокие значения для всех перечисленных станций
наблюдения. Не задаваясь вопросом о природе этих связей, рассмотрим зависимость
индукции от параметров U1-U4, которую
можно установить методом многопараметрической регрессии – таблица 52.
Таблица 52. Зависимость
магнитной индукции (nT) от комбинаций астрономических параметров Урана для трех станций: Alert (IAGA Code: ALE; lat: 82.5;
long: 297.65), Vostok (IAGA Code:
VOS lat:-78.45 long: 106.867), Resolute Bay (IAGA Code: RES; lat: 74.69;
long: 265.105) /16/.
|
BzALE |
= 55550,543 -
(2665,273 * U1) - (21506,135 * U2) + (150151,509 * U3) + (979818,061 * U4) |
R = 0,963 |
|
BzVOS |
= -60493,835 -
(2611,044 * U1) - (27667,459 * U2) + (94108,464 * U3) + (545622,014 * U4) |
R = 0,992 |
|
BzRES |
= 58267,077 -
(2763,148 * U1) - (2831,565 * U2) + (133499,310 * U3) - (482593,967 * U4) |
R = 0,978 |
|
BxRES |
= 865,864 +
(15785,104 * U1) + (2203,794 * U2) - (238153,901 * U3) - (565326,409 * U4) |
R = 0,994 |
|
ByRES |
= -986,541 - (3679,303 * U1) - (2003,570 * U2) + (654,962
* U3) - (3139,044 * U4) |
R = 0,968 |
Как следует из приведенных в таблице 52 формул, данные
по магнитной индукции на трех станциях наблюдения с большой степенью точности
описываются комбинациями астрономических параметров Урана (89), которые
соответствуют дипольному излучению этой планеты.
Происхождение комбинаций Ui можно понять, рассматривая
электромагнитное излучение диполя, который вращается вокруг некоторой оси
(планеты), сохраняющей постоянное направление в пространстве. При этом надо
учесть, что отклонение орбиты Урана от плоскости эклиптики является
незначительным, поэтому параметр LAT<<1, т.е. в слагаемых, содержащих функцию
cos(LAT), можно положить cos(LAT)=1.
На рис. 144-146 представлены зависимости вертикальной
и горизонтальной составляющей магнитной индукции по данным /61/ вместе с корреляционными зависимостями, приведенными
в таблице 52. Можно отметить не только
хорошее совпадение данных с корреляционной зависимостью, но и различия, которые
заключаются в несовпадении колебаний магнитного поля и корреляционной зависимости.
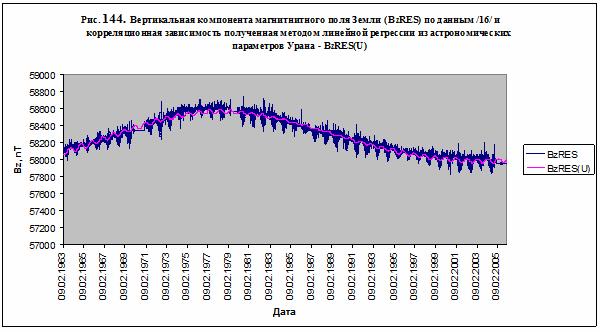
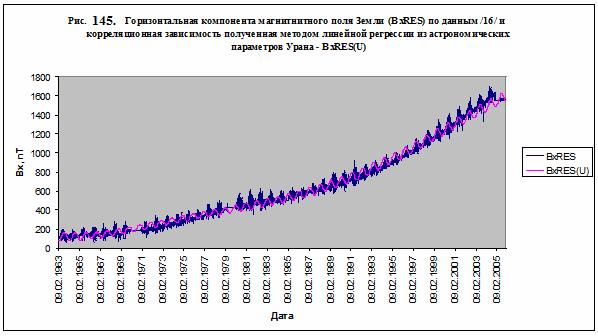
Можно предположить, что наряду с Ураном на колебания
магнитного поля оказывают влияние другие планеты-гиганты – Юпитер, Сатурн и
Нептун. Однако добавление в модель соответствующих комбинаций астрономических
параметров этих планет не улучшает существенно полученные зависимости, что свидетельствует
о наличии других источников возмущений магнитного поля Земли, например,
связанных с колебанием солнечной активности, с полярным сиянием и
землетрясениями.
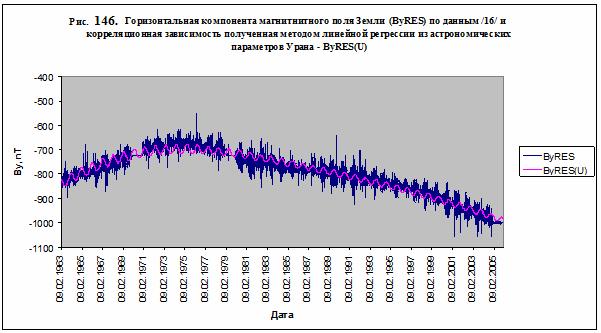
Связь параметров
сейсмической активности с астрономическими параметрами Урана и Нептуна
Определим комбинации астрономических параметров Нептуна,
которые соответствуют дипольному излучению этой планеты:
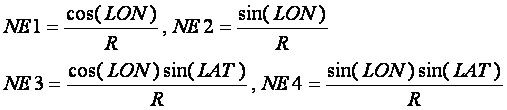 (90)
(90)
Учитывая, что имеется корреляционная связь магнитной индукции
с интегральными параметрами сейсмической активности (87), а магнитная индукция связана с
параметрами дипольного излучения (89) и (90), рассмотрим корреляционные связи
параметров (7), (10) и (11) – таблица 53.
Таблица
53. Корреляционные связи параметров задачи, полученные методом Pearson Product Moment Correlation по программе
SigmaPlot: для Р<0,05 корреляционные связи являются достоверными. N – число точек по которым вычисляется
корреляция.
|
|
SM |
SE |
SV |
M |
E |
V |
n |
|
U1 |
0,474 |
0,286 |
0,0138 |
0,00416 |
0,0108 |
-0,199 |
0,492 |
|
P |
0 |
8,37E-297 |
0,0821 |
0,6 |
0,175 |
8,51E-141 |
0 |
|
N |
15861 |
15861 |
15862 |
15862 |
15862 |
15862 |
15861 |
|
|
|
|
|
|
|
|
|
|
U2 |
-0,067 |
-0,176 |
0,00466 |
0,00222 |
0,00614 |
0,0871 |
-0,0548 |
|
P |
2,97E-17 |
1,90E-110 |
0,557 |
0,78 |
0,439 |
4,53E-28 |
5,16E-12 |
|
N |
15861 |
15861 |
15862 |
15862 |
15862 |
15862 |
15861 |
|
|
|
|
|
|
|
|
|
|
NE1 |
0,471 |
0,306 |
0,0141 |
0,00466 |
0,011 |
-0,207 |
0,488 |
|
P |
0 |
0 |
0,0751 |
0,557 |
0,168 |
3,06E-153 |
0 |
|
N |
15861 |
15861 |
15862 |
15862 |
15862 |
15862 |
15861 |
|
|
|
|
|
|
|
|
|
|
NE2 |
0,276 |
0,022 |
0,0188 |
0,00937 |
0,0183 |
-0,0505 |
0,303 |
|
P |
2,70E-274 |
0,00566 |
0,0176 |
0,238 |
0,0213 |
1,95E-10 |
0 |
|
N |
15861 |
15861 |
15862 |
15862 |
15862 |
15862 |
15861 |
|
|
|
|
|
|
|
|
|
|
U3 |
-0,0985 |
0,0665 |
-0,00765 |
0,000464 |
-0,00789 |
-0,00658 |
-0,122 |
|
P |
1,69E-35 |
5,29E-17 |
0,335 |
0,953 |
0,321 |
0,407 |
8,57E-54 |
|
N |
15861 |
15861 |
15862 |
15862 |
15862 |
15862 |
15861 |
|
|
|
|
|
|
|
|
|
|
U4 |
0,308 |
0,127 |
0,00377 |
-0,00259 |
0,00213 |
-0,106 |
0,32 |
|
P |
0 |
1,04E-57 |
0,635 |
0,744 |
0,788 |
7,59E-41 |
0 |
|
N |
15861 |
15861 |
15862 |
15862 |
15862 |
15862 |
15861 |
|
|
|
|
|
|
|
|
|
|
NE3 |
0,275 |
0,255 |
0,0027 |
-0,00041 |
0,000225 |
-0,154 |
0,276 |
|
P |
1,29E-272 |
7,80E-234 |
0,734 |
0,959 |
0,977 |
4,45E-85 |
2,37E-274 |
|
N |
15861 |
15861 |
15862 |
15862 |
15862 |
15862 |
15861 |
|
|
|
|
|
|
|
|
|
|
NE4 |
0,505 |
0,269 |
0,0173 |
0,00584 |
0,0143 |
-0,196 |
0,53 |
|
P |
0 |
6,75E-261 |
0,0294 |
0,462 |
0,0708 |
6,84E-137 |
0 |
|
N |
15861 |
15861 |
15862 |
15862 |
15862 |
15862 |
15861 |
Как следует из данных, приведенных в таблице 53, существует
довольно сильные корреляционные связи интегральных параметров сейсмической
активности - суммарной магнитуды (SM), суммарной магнитуды
энергии (SE) и ежедневного числа землетрясений с магнитудой mb>4, с
комбинациями астрономических параметров (89)-(90), которые соответствуют
дипольному излучению планет-гигантов – Урана и Нептуна. Отметим, что эти
корреляционные связи убедительно свидетельствуют, что влияние в данном случае
исходит от планет-гигантов – Урана и Нептуна, дипольное излучение которых
вызывает и колебания магнитного поля Земли, и изменение параметров сейсмической
активности.
Механизм этого влияния в настоящее время неизвестен,
но можно предположить, что между магнитным полем Земли и магнитными полями
Урана и Нептуна осуществляется обмен путем взаимной индукции. Детальный расчет
этого обмена выходит за рамки настоящей работы. Общая модель
явления взаимной индукции небесных тел представлена ниже.
Естественно возникает вопрос, какая же из планет –
Уран или Нептун, вносит больший вклад в колебания магнитного поля Земли? На
рис. 147-148 представлены фрагменты матрицы информативности модели M12(G,EOP,Bz),
на основе которых можно оценить влияние расстояния от Земли до Урана и Нептуна
соответственно на категории A, B, C сейсмической активности из таблицы 48. Сравнивая рис. 143 и 147, видим, что они как
бы являются зеркальным отражением друг друга, что указывает на зависимость
индукции магнитного поля Земли от параметров дипольного излучения Урана (90). С
другой стороны, данные на рис. 148 никак не соотносятся с данными на рис. 143,
что указывает на относительно малый (но заметный!) вклад дипольного излучения
Нептуна в колебания магнитного поля Земли вблизи полюсов.
Интересно, что в отношении интегральных параметров
сейсмической активности Уран и Нептун выступают вполне симметрично, как следует
из данных таблицы 53. Можно предположить, что магнитное взаимодействие Земли с
Ураном и Нептуном приводит не только к изменению магнитного поля, но и вызывает
механическое перемещение магнитного ядра планеты.
Действительно, в таблице 54 представлены коэффициенты
корреляции смещений географического полюса с параметрами дипольного излучения
(89)-(90), которые по величине превосходят соответствующие коэффициенты
корреляции с индукцией магнитного поля – см. Таблицу 50. Обнаруженные
корреляционные связи являются несимметричными: смещение географического полюса
вдоль меридиана 90oW сильнее связано с дипольным излучением Урана и
Нептуна, нежели смещение вдоль меридиана Гринвич (но смещение вдоль меридиана
Гринвич сильнее связано с изменением гравитационного потенциала – см. Таблицу
49).
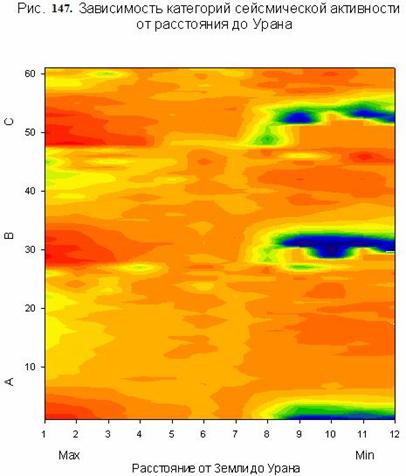
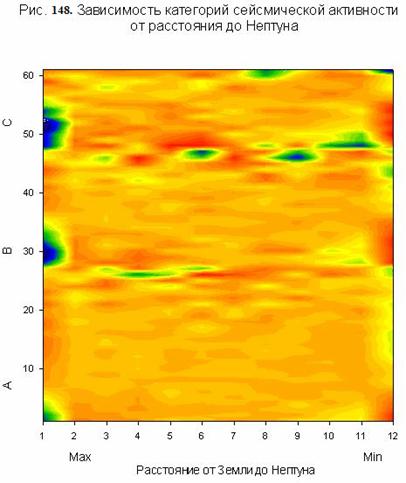
Таблица 54. Корреляционные
связи параметров смещения географического полюса с параметрами дипольного излучения
(10-11), полученные методом Pearson
Product Moment Correlation по программе SigmaPlot: для Р<0,05
корреляционные связи являются достоверными.
|
|
U1 |
U2 |
NE1 |
NE2 |
U3 |
U4 |
NE3 |
NE4 |
|
xEOP |
0,135 |
-0,111 |
0,124 |
-0,0299 |
0,103 |
0,0885 |
0,123 |
0,122 |
|
P |
1,91E-66 |
2,79E-45 |
4,89E-56 |
0,000152 |
3,42E-39 |
3,03E-29 |
3,15E-55 |
1,41E-54 |
|
N |
16032 |
16032 |
16032 |
16032 |
16032 |
16032 |
16032 |
16032 |
|
|
|
|
|
|
|
|
|
|
|
yEOP |
0,345 |
-0,231 |
0,351 |
-0,0709 |
0,139 |
0,238 |
0,314 |
0,28 |
|
P |
0 |
5,42E-193 |
0 |
2,61E-19 |
3,95E-70 |
1,32E-204 |
0 |
5,48E-286 |
|
N |
16032 |
16032 |
16032 |
16032 |
16032 |
16032 |
16032 |
16032 |
О взаимной индукции планет
Наиболее убедительным фактом внешнего влияния на магнитное
поле Земли является синхронное поведение вертикальной компоненты вектора
магнитной индукции на Северном и Южном полюсе. На рис. 149 представлена
зависимость вертикальной составляющей вектора магнитной индукции по данным
/61/, полученным на станции Восток (IAGA Code: VOS lat:-78.45 long: 106.867) в
Антарктиде, вместе с корреляционной зависимостью, приведенной в
таблице 52. Сравнивая данные на рис. 144 и 149, можно видеть, что вертикальная
компонента вектора магнитной индукции возрастает в 1963-1975 гг синхронно на
противоположных полюсах. Но такое возможно только если к вектору магнитной
индукции Земли добавляется внешний вектор с одинаковой ориентацией на
противоположных полюсах.
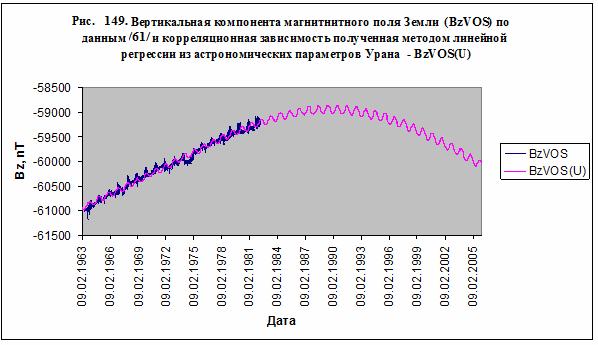
Изменение магнитной индукции в средних широтах и на
больших отрезках времени хорошо описывается комбинацией дипольных слагаемых
Нептуна и Урана (89)-(90). На рис. 11 представлены данные /61/ по вертикальной
компоненте вектора магнитной индукции, полученные на станции Eskdalemuir (IAGA
Code: ESK lat: 55.317 long: 356.8) в 1911-2008 гг вместе с корреляционной
зависимостью, полученной методом регрессии:
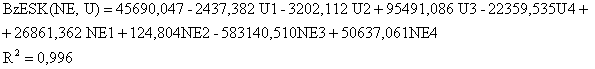

Хотя данные на рис.150
описываются с большой степенью точности комбинацией дипольных слагаемых
(89)-(90), степень корреляции можно еще повысить, включив в корреляционную зависимость
дипольные слагаемые Сатурна. Это справедливо и для данных, приведенных на рис. 144-146. Как можно объяснить столь
высокую степень корреляции данных по магнитному полю Земли с дипольным
излучением планет-гигантов?
Согласно классической
электродинамике магнитные поля планет образованы циркулирующими токами, контур
которых имеет конечную индуктивность. Кроме индуктивности, циркулирующие токи
планет могут обладать взаимной индуктивностью, что равносильно наличию у двух
контуров индуктивности общего магнитного потка. Чтобы обеспечить синхронность
поведения компоненты Bz на противоположных полюсах, надо
предположить, что контур индуцированного тока создает собственный магнитный
момент, который добавляется к магнитному моменту Земли. Дополнительный
магнитный момент изменяет не только величину собственного магнитного момента
Земли, но и его ориентацию в пространстве, что приводит к наблюдаемому смещению
магнитного и геомагнитного полюса — таблица 55.
Таблица 55. Координаты геомагнитного и магнитного полюса
по данным /61/.
|
Год |
North geomagnetic
pole |
South geomagnetic
pole |
North magnetic pole
|
South magnetic pole |
||||
|
|
Lat. |
Long.
|
Lat. |
Long.
|
Lat. |
Long.
|
Lat. |
Long. |
|
1900 |
78.6N |
68.8W |
78.6S |
111.2E |
70.5N |
96.2W |
71.7S |
148.3E |
|
1905 |
78.6N |
68.7W |
78.6S |
111.3E |
70.7N |
96.5W |
71.5S |
148.6E |
|
1910 |
78.6N |
68.7W |
78.6S |
111.3E |
70.8N |
96.7W |
71.2S |
148.7E |
|
1915 |
78.6N |
68.6W |
78.6S |
111.4E |
71.0N |
97.0W |
70.8S |
148.5E |
|
1920 |
78.6N |
68.4W |
78.6S |
111.6E |
71.3N |
97.4W |
70.4S |
148.2E |
|
1925 |
78.6N |
68.3W |
78.6S |
111.7E |
71.8N |
98.0W |
70.0S |
147.6E |
|
1930 |
78.5N |
68.3W |
78.5S |
111.7E |
72.3N |
98.7W |
69.5S |
147.0E |
|
1935 |
78.5N |
68.4W |
78.5S |
111.6E |
72.8N |
99.3W |
69.1S |
145.8E |
|
1940 |
78.5N |
68.5W |
78.5S |
111.5E |
73.3N |
99.9W |
68.6S |
144.6E |
|
1945 |
78.5N |
68.5W |
78.5S |
111.5E |
73.9N |
100.2W |
68.2S |
144.5E |
|
1950 |
78.5N |
68.8W |
78.5S |
111.2E |
74.6N |
100.8W |
67.9S |
143.6E |
|
1955 |
78.5N |
69.2W |
78.5S |
110.8E |
75.2N |
101.4W |
67.2S |
141.5E |
|
1960 |
78.5N |
69.5W |
78.5S |
110.5E |
75.3N |
101.0W |
66.7S |
140.2E |
|
1965 |
78.5N |
69.9W |
78.5S |
110.1E |
75.6N |
101.3W |
66.3S |
139.5E |
|
1970 |
78.6N |
70.2W |
78.6S |
109.8E |
75.9N |
101.0W |
66.0S |
139.4E |
|
1975 |
78.7N |
70.5W |
78.7S |
109.5E |
76.2N |
100.7W |
65.7S |
139.5E |
|
1980 |
78.8N |
70.8W |
78.8S |
109.2E |
76.9N |
101.7W |
65.4S |
139.3E |
|
1985 |
79.0N |
70.9W |
79.0S |
109.1E |
77.4N |
102.6W |
65.1S |
139.1E |
|
1990 |
79.1N |
71.1W |
79.1S |
108.9E |
78.1N |
103.7W |
64.9S |
138.9E |
|
1995 |
79.3N |
71.4W |
79.3S |
108.6E |
79.0N |
105.2W |
64.8S |
138.7E |
|
2000 |
79.5N |
71.6W |
79.5S |
108.4E |
81.0N |
109.7W |
64.7S |
138.4E |
|
2005 |
79.7N |
71.8W |
79.7S |
108.2E |
83.1N |
117.8W |
64.5S |
137.8E |
|
2006 |
79.8N |
71.9W |
79.8S |
108.1E |
83.8N |
122.0W |
64.5S |
137.7E |
|
2007 |
79.9N |
72.0W |
79.9S |
108.0E |
84.0N |
123.2W |
64.5S |
137.6E |
|
2008 |
79.9N |
72.0W |
79.9S |
108.0E |
84.2N |
124.9W |
64.5S |
137.6E |
|
2009 |
80.0N |
72.1W |
80.0S |
107.9E |
84.9N |
131.0W |
64.5S |
137.5E |
|
2010 |
80.0N |
72.2W |
80.0S |
107.8E |
85.0N |
132.6W |
64.4S |
137.3E |
|
2011 |
80.1N |
72.3W |
80.1S |
107.7E |
85.1N |
134.0W |
64.4S |
137.2E |
|
2012 |
80.1N |
72.4W |
80.1S |
107.6E |
85.9N |
147.0W |
64.4S |
137.1E |
|
2013 |
80.2N |
72.5W |
80.2S |
107.5E |
85.9N |
148.0W |
64.4S |
137.0E |
|
2014 |
80.2N |
72.5W |
80.2S |
107.5E |
85.9N |
149.0W |
64.3S |
136.8E |
|
2015 |
80.3N |
72.6W |
80.3S |
107.4E |
86.1N |
153.0W |
64.3S |
136.7E |
Как известно, взаимная индукция двух контуров индуктивности
определяется только расстоянием между ними и геометрией проводящих элементов,
поэтому в случае двух планет можно предположить, что изменение магнитного
момента Земли при взаимной индукции с небесными телами определяется как
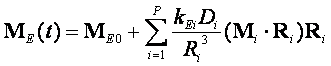 (91)
(91)
Здесь ![]() - безразмерный параметр взаимной индукции,
диаметр планеты и расстояние от Земли до небесного тела; ME0 – собственный магнитный
момент Земли; Mi – магнитный момент
небесного тела.
- безразмерный параметр взаимной индукции,
диаметр планеты и расстояние от Земли до небесного тела; ME0 – собственный магнитный
момент Земли; Mi – магнитный момент
небесного тела.
Выражение (91) согласуется с формулами (89)—(90), использованными
для получения корреляционных зависимостей, приведенных на рис. 144-146 и
149-150, а также в таблице 52. Заметим, что модель (91) легко обобщается с
учетом влияния Солнца. В последнем случае взаимная индукция определяется, в том
числе, геометрией солнечных пятен. Рассмотрим применение модели (91) к описанию
взаимной индукции Земли и Урана.
Как известно, Уран вращается вокруг оси, наклоненной
на 97,77° относительно орбитальной плоскости с периодом 17 ч
14 мин 24 с /87/. Его ось вращения ориентирована в сторону звезды Сабик
и проецируется на эклиптику на 257,311°, т.е. 17,311° знака Стрельца. Магнитное
поле Урана не является чисто дипольным: ось север-юг магнитного поля отклонена
на 59 градусов относительно оси вращения, а магнитный момент составляет приблизительно
MU =3,9 x 1017 T m3 , что почти в 50 раз
больше магнитного момента Земли /88/.
Земля вращается вокруг оси, наклоненной на 23,439291°
относительно нормали к орбитальной плоскости с периодом 0,99726968 дней. Ось
вращения Земли ориентирована в сторону Полярной звезды и проецируется на
эклиптику на 90°, т.е. на 0° знака Рака. Магнитное поле Земли похоже на поле
магнитного диполя, ось которого несколько отклоняется от оси вращения, причем в
последнее время наблюдается изменение как ориентации диполя, так и положения
магнитных и геомагнитных (теоретических) полюсов /61/ - таблица 55. Полный
магнитный момент Земли на 1995 год составлял около ME=7,812 х 1015
Т м3. Согласно /61/,
магнитный момент Земли снижается каждый год приблизительно на 4х1012
Т м3.
Взаимное движение планет по орбитам создает переменное
магнитное поле, что эквивалентно некоторому переменному току в контурах
индуктивности Земли и Урана. Топология магнитных силовых линий в системе
Земля-Уран имеет весьма сложный вид, поскольку Уран при движении по орбите поворачивается
к Земле то северным, то южным полюсом. Когда Уран находился в знаке Стрельца
(1981-1987 гг), вблизи точки проекции своей полярной оси, с Земли можно было
наблюдать только южный полюс Урана,
поэтому в эти периоды времени взаимная индукция максимальна и магнитный
момент Земли имеет максимальное значение. Когда Уран находился в знаках Девы
(1962-1968 гг) или Рыб (2003-2010 гг), с Земли можно наблюдать весь магнитный
момент Урана, поэтому взаимная индукция двух планет минимальна и магнитный
момент Земли принимает минимальное значение, что сказывается на величине
магнитного поля.
Если бы изменение магнитного момента Земли было целиком
обусловлено только влиянием Урана, тогда можно было бы ожидать увеличения
напряженности магнитного поля Земли в ближайшие 20 лет, поскольку Уран движется
в сторону знака Близнецов, где он будет находится 2025-2031 гг. В это время с Земли можно будет
наблюдать только северный полюс планеты. Поэтому взаимная индукция Земли и
Урана, согласно (91) будет максимальна. Однако влияние Нептуна несколько
изменяет этот прогноз, поскольку ось вращения Нептуна направлена в сторону
звезды BS7638 и проецируется приблизительно на 318,51° эклиптики - 18,51° знака
Водолея. Следовательно, в настоящее время взаимная индукция Земли и Нептуна
максимальна (а Урана и Земли — минимальна).
Наконец заметим, что модель (91) позволяет объяснить наблюдаемый
сдвиг магнитных полюсов (см. таблицу 55), не привлекая гипотезу об инверсии
магнитного поля Земли.
Таким образом, установлено, что добавление в информационную
модель глобальной сейсмической активности параметров магнитной индукции и
смещения географического полюса позволяет повысить достоверность распознавания
сейсмических событий.
Обнаружена взаимосвязь смещений географического полюса
Земли с изменением гравитационного потенциала Солнечной системы и с параметрами
дипольного излучения Урана и Нептуна.
Установлена высокая степень корреляции колебаний магнитного
поля Земли вблизи магнитных полюсов с дипольным излучением Урана, что позволило
создать достоверную модель изменения магнитного поля Земли на трех станциях -
Alert (IAGA Code: ALE; lat: 82.5; long: 297.65), Vostok (IAGA Code: VOS lat:-78.45 long:
106.867), Resolute Bay (IAGA Code: RES;
lat: 74.69; long: 265.105),
расположенных вблизи магнитных полюсов. В этой связи отметим, что стандартная
модель магнитного поля Земли IGRF 10 /61/ вообще не согласуется с
экспериментальными данными, представленными на рис. 144-146, что обусловлено
большим различием в настоящем (фактическом) положении магнитного полюса и его
теоретической модели – геомагнитного полюса.
Установлена высокая степень корреляции колебаний магнитного
поля Земли в средних широтах с дипольным излучением Урана и Нептуна, что
позволило создать достоверную модель изменения магнитного поля на станции Eskdalemuir (IAGA Code: ESK lat: 55.317
long: 356.8) в 1911-2008 гг. - рис. 150.
На основе исследования семантических информационных
моделей глобальной сейсмической активности установлено, что индукция магнитного
поля Земли и интегральные параметры сейсмической активности зависят от
комбинаций астрономических параметров Урана и Нептуна, которые соответствуют дипольному
излучению этих планет. Это дает основание предположить, что существует
электромагнитный механизм, запускающий землетрясения.
Отметим также, что использование в качестве инструмента систем искусственного
интеллекта открывает новые возможности научного исследования в астрономии и
геофизике, в том числе позволяет выявлять новые знания из общедоступных официальных
баз данных. При этом на конкретном содержательном уровне подтверждается, что
Земля является одним из элементов космической системы и некоторые процессы на
ней сложно понять, если рассматривать ее изолированно от космического
окружения, неоправданно абстрагируясь от ее взаимодействия с другими элементами
и с системой в целом.
6.5. Автоматизированный системно-когнитивный анализ влияния тел
солнечной системы на движение полюса
Земли и визуализация причинно-следственных зависимостей в виде
когнитивных функций
Технология моделирования
движения полюса Земли
В работах /70-71/ развита модель вынужденной нутации,
основанная на гипотезе о существовании гравитационного механизма обмена
механическим моментом в Солнечной системе. На основе данных /60/ и модели /71/
была сделана оценка момента сил, обусловленного гравитационным воздействием
небесных тел на нашу планету в период с 1963 по 2006 г, а также исследованы
механизмы взаимного влияния сейсмических событий, вариаций магнитного поля
Земли и движения полюса.
Ниже обсуждается технология моделирования и прогнозирования
движения полюса Земли на основе системы искусственного интеллекта «Эйдос-астра»
/7, 79-80/ с использованием семантических информационных моделей и АСК-анализа
/3/.
Исследуемая база данных категорий движения полюса Земли
была сформирована на основе данных IERS /60/,
в период с 1 января 1963 года по 31 декабря 2010 г. При создании моделей
в настоящей работе были использованы данные по координатам географического
полюса – X, Y /60/, данные по индукции магнитного поля Земли /61/, а
также данные по сейсмическим событиям /57/.
Из исходной базы было образовано несколько различных
БД для исследования влияния астрономических параметров на координаты и скорость
движения полюса. Для сравнения с данными моделирования сейсмических событий
была образована база, охватывающая 16032 дня наблюдений с 9 февраля 1963 г по
31 декабря 2006 г.
В качестве астрономических параметров были использованы
долгота, широта и расстояние от Земли до десяти небесных тел – Солнца, Луны,
Марса, Меркурия, Венеры, Юпитера, Сатурна, Урана, Нептуна и Плутона, и долгота
Северного Узла Луны. Астрономические параметры вычислялись на каждый день в
фиксированной точке с географическими координатами Гринвича в 12:00 GMT в
топоцентрической системе координат. Отметим, что выбор этой точки не является
существенным для решаемого класса задач. Из астрономических параметров и
категорий движения полюса Земли была создана база данных, содержащая 16032
записи с обобщенной информацией о динамике вращения нашей планеты.
В работах /70-71/ была построена модель линейной регрессии
с использованием 27 комбинаций астрономических параметров, характеризующих
влияние каждого небесного тела:
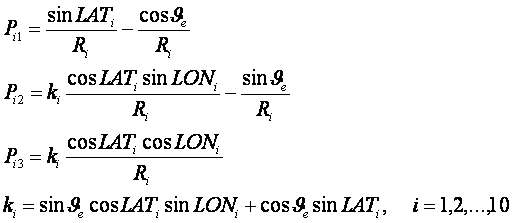 (92)
(92)
Здесь долгота (LON), широта (LAT) и расстояние (R) определяется
для каждого из 10 небесных тел, ![]() - угол наклона земной оси
относительно нормали к орбитальной плоскости. Структура комплексов (92)
вытекает из аналогии электромагнитных и гравитоэлектромагнитных (GEM) явлений
/70/. Отметим, что данные для расстояний от Земли до небесных тел вычисляются в
формулах (92) в астрономических единицах. Параметры (92) были использованы в
настоящей работе наряду с астрономическими параметрами.
- угол наклона земной оси
относительно нормали к орбитальной плоскости. Структура комплексов (92)
вытекает из аналогии электромагнитных и гравитоэлектромагнитных (GEM) явлений
/70/. Отметим, что данные для расстояний от Земли до небесных тел вычисляются в
формулах (92) в астрономических единицах. Параметры (92) были использованы в
настоящей работе наряду с астрономическими параметрами.
Решение прямой задачи включает в себя нормирование
входных параметров и приведение их к одному масштабу изменения в интервале
(0;360), разбиение интервалов на М частей, вычисление матрицы абсолютных частот
и информативности. Решение обратной задачи включает в себя распознавание категорий
по заданным астрономическим параметрам. Частным случаем задачи распознавания
является определение достоверности идентификации категорий по астрономическим
данным в каждой модели.
Параметр сходства категорий координат полюса
В таблице 56 и на рис. 151 приведены данные параметра
сходства 62 категорий X смещения полюса вдоль меридиана Гринвич и 60 категорий
Y смещения полюса вдоль меридиана 900W в двух моделях – М12, М160.
Отметим, что параметр сходства в модели М160 является положительным для всех
категорий. Наилучшим образом распознаются редко встречающиеся категории,
которые соответствуют максимальным и минимальным значениям координат полюса
Земли. Наихудшим же образом распознаются значения в окрестности нуля, но не
само нулевое значение.
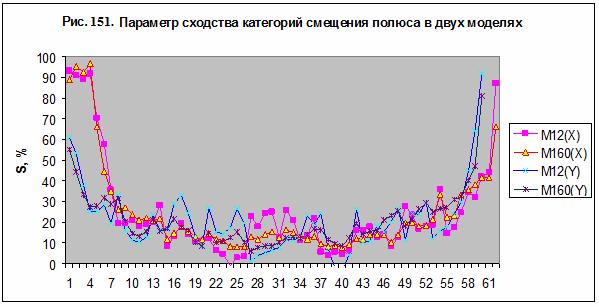
Таблица 56. Параметр сходства
категорий смещения полюса в двух семантических моделях М12, М160
|
Категория X смещения
полюса вдоль меридиана Гринвич |
ABS |
M12 |
M160 |
Категория Y смещения
полюса вдоль меридиана 900W |
ABS |
M12 |
M160 |
|
A1-X=-0,29609 |
11 |
93,107 |
88,988 |
B1-Y=-0,01292 |
30 |
61,036 |
55,179 |
|
A2-X=-0,28609 |
8 |
91,055 |
95,316 |
B2-Y=-0,00292 |
55 |
53,183 |
44,306 |
|
A3-X=-0,27609 |
8 |
89,336 |
92,669 |
B3-Y=0,00708 |
114 |
37,995 |
33,260 |
|
A4-X=-0,26609 |
7 |
91,621 |
96,861 |
B4-Y=0,01708 |
139 |
25,248 |
27,607 |
|
A5-X=-0,25609 |
17 |
70,335 |
65,907 |
B5-Y=0,02708 |
116 |
25,213 |
27,947 |
|
A6-X=-0,24609 |
70 |
57,702 |
44,554 |
B6-Y=0,03708 |
95 |
28,379 |
31,812 |
|
A7-X=-0,23609 |
99 |
35,539 |
35,023 |
B7-Y=0,04708 |
104 |
19,764 |
28,860 |
|
A8-X=-0,22609 |
140 |
19,810 |
25,902 |
B8-Y=0,05708 |
123 |
33,302 |
31,396 |
|
A9-X=-0,21609 |
125 |
19,597 |
27,046 |
B9-Y=0,06708 |
217 |
16,505 |
20,378 |
|
A10-X=-0,20609 |
194 |
21,118 |
23,567 |
B10-Y=0,07708 |
248 |
11,289 |
14,486 |
|
A11-X=-0,19609 |
199 |
18,063 |
21,047 |
B11-Y=0,08708 |
253 |
10,220 |
13,106 |
|
A12-X=-0,18609 |
188 |
18,909 |
21,982 |
B12-Y=0,09708 |
207 |
12,915 |
15,611 |
|
A13-X=-0,17609 |
173 |
19,857 |
21,195 |
B13-Y=0,10708 |
247 |
23,425 |
20,932 |
|
A14-X=-0,16609 |
238 |
28,145 |
21,646 |
B14-Y=0,11708 |
274 |
16,227 |
15,888 |
|
A15-X=-0,15609 |
378 |
8,537 |
11,882 |
B15-Y=0,12708 |
256 |
16,528 |
17,000 |
|
A16-X=-0,14609 |
269 |
13,379 |
14,533 |
B16-Y=0,13708 |
314 |
28,854 |
21,424 |
|
A17-X=-0,13609 |
272 |
19,133 |
17,768 |
B17-Y=0,14708 |
317 |
32,831 |
17,615 |
|
A18-X=-0,12609 |
269 |
14,176 |
15,673 |
B18-Y=0,15708 |
346 |
24,592 |
16,005 |
|
A19-X=-0,11609 |
340 |
10,618 |
12,692 |
B19-Y=0,16708 |
375 |
12,902 |
10,448 |
|
A20-X=-0,10609 |
354 |
10,659 |
11,908 |
B20-Y=0,17708 |
451 |
8,930 |
8,559 |
|
A21-X=-0,09609 |
271 |
12,111 |
14,500 |
B21-Y=0,18708 |
427 |
26,717 |
14,763 |
|
A22-X=-0,08609 |
299 |
6,271 |
11,823 |
B22-Y=0,19708 |
432 |
15,429 |
10,270 |
|
A23-X=-0,07609 |
302 |
4,794 |
11,088 |
B23-Y=0,20708 |
422 |
14,422 |
10,601 |
|
A24-X=-0,06609 |
342 |
-0,911 |
8,386 |
B24-Y=0,21708 |
341 |
17,412 |
12,475 |
|
A25-X=-0,05609 |
385 |
2,857 |
8,350 |
B25-Y=0,22708 |
372 |
26,525 |
15,371 |
|
A26-X=-0,04609 |
379 |
3,558 |
8,250 |
B26-Y=0,23708 |
478 |
19,320 |
10,211 |
|
A27-X=-0,03609 |
515 |
22,894 |
12,881 |
B27-Y=0,24708 |
417 |
1,393 |
6,239 |
|
A28-X=-0,02609 |
406 |
17,953 |
11,932 |
B28-Y=0,25708 |
374 |
3,806 |
7,833 |
|
A29-X=-0,01609 |
460 |
24,370 |
14,177 |
B29-Y=0,26708 |
340 |
5,304 |
8,526 |
|
A30-X=-0,00609 |
421 |
25,153 |
15,487 |
B30-Y=0,27708 |
332 |
6,288 |
8,569 |
|
A31-X=0,00391 |
441 |
12,979 |
12,421 |
B31-Y=0,28708 |
333 |
7,823 |
10,256 |
|
A32-X=0,01391 |
336 |
25,834 |
16,397 |
B32-Y=0,29708 |
338 |
11,746 |
12,531 |
|
A33-X=0,02391 |
347 |
21,116 |
14,917 |
B33-Y=0,30708 |
356 |
11,338 |
12,865 |
|
A34-X=0,03391 |
347 |
11,430 |
12,814 |
B34-Y=0,31708 |
400 |
12,730 |
12,000 |
|
A35-X=0,04391 |
369 |
13,517 |
11,956 |
B35-Y=0,32708 |
427 |
23,162 |
14,102 |
|
A36-X=0,05391 |
419 |
21,901 |
13,179 |
B36-Y=0,33708 |
369 |
18,989 |
16,950 |
|
A37-X=0,06391 |
469 |
5,804 |
9,755 |
B37-Y=0,34708 |
370 |
24,196 |
16,550 |
|
A38-X=0,07391 |
382 |
4,051 |
8,123 |
B38-Y=0,35708 |
341 |
6,711 |
11,836 |
|
A39-X=0,08391 |
414 |
5,878 |
8,821 |
B39-Y=0,36708 |
379 |
-1,910 |
9,542 |
|
A40-X=0,09391 |
402 |
4,779 |
7,705 |
B40-Y=0,37708 |
450 |
-3,692 |
8,444 |
|
A41-X=0,10391 |
410 |
6,197 |
9,395 |
B41-Y=0,38708 |
372 |
4,202 |
12,603 |
|
A42-X=0,11391 |
350 |
15,945 |
12,187 |
B42-Y=0,39708 |
351 |
26,035 |
19,635 |
|
A43-X=0,12391 |
371 |
15,923 |
11,843 |
B43-Y=0,40708 |
289 |
10,195 |
14,458 |
|
A44-X=0,13391 |
416 |
17,905 |
13,800 |
B44-Y=0,41708 |
301 |
10,906 |
15,810 |
|
A45-X=0,14391 |
267 |
12,607 |
13,914 |
B45-Y=0,42708 |
335 |
18,085 |
16,250 |
|
A46-X=0,15391 |
280 |
14,193 |
13,761 |
B46-Y=0,43708 |
207 |
15,311 |
21,195 |
|
A47-X=0,16391 |
284 |
8,112 |
10,425 |
B47-Y=0,44708 |
214 |
20,315 |
23,139 |
|
A48-X=0,17391 |
258 |
12,484 |
13,870 |
B48-Y=0,45708 |
241 |
26,258 |
25,316 |
|
A49-X=0,18391 |
257 |
28,020 |
19,737 |
B49-Y=0,46708 |
229 |
11,786 |
18,155 |
|
A50-X=0,19391 |
250 |
23,533 |
19,989 |
B50-Y=0,47708 |
282 |
24,120 |
21,504 |
|
A51-X=0,20391 |
300 |
16,840 |
18,145 |
B51-Y=0,48708 |
181 |
23,767 |
26,280 |
|
A52-X=0,21391 |
256 |
18,280 |
18,455 |
B52-Y=0,49708 |
131 |
29,472 |
29,443 |
|
A53-X=0,22391 |
294 |
18,553 |
21,527 |
B53-Y=0,50708 |
125 |
12,019 |
24,905 |
|
A54-X=0,23391 |
181 |
35,659 |
33,488 |
B54-Y=0,51708 |
115 |
15,706 |
26,731 |
|
A55-X=0,24391 |
170 |
14,493 |
22,535 |
B55-Y=0,52708 |
122 |
17,515 |
27,229 |
|
A56-X=0,25391 |
190 |
17,541 |
23,124 |
B56-Y=0,53708 |
132 |
23,829 |
31,025 |
|
A57-X=0,26391 |
79 |
24,478 |
33,086 |
B57-Y=0,54708 |
147 |
29,622 |
32,487 |
|
A58-X=0,27391 |
92 |
34,609 |
35,690 |
B58-Y=0,55708 |
103 |
45,056 |
40,347 |
|
A59-X=0,28391 |
78 |
32,166 |
38,276 |
B59-Y=0,56708 |
68 |
64,349 |
47,098 |
|
A60-X=0,29391 |
56 |
42,094 |
41,916 |
B60-Y=0,57708 |
14 |
91,879 |
81,030 |
|
A61-X=0,30391 |
72 |
43,858 |
41,414 |
|
|
|
|
|
A62-X=0,31391 |
23 |
87,191 |
66,197 |
|
|
|
|
Путем визуализации матрицы информативностей, можно
установить некоторые особенности влияния небесных тел на движение полюса.
На рис. 152 представлена зависимость
категорий координат полюса от долготы Солнца. Как следует из данных,
приведенных на рис. 152, координаты полюса в зависимости от долготы Солнца
образуют жгуты, которые формируются из отдельных годичных движений на
протяжении многих лет.
Параметр сходства категорий скорости движения полюса
В таблице 57 и на рис. 153 приведены данные параметра
сходства 62 категорий X1 угловой скорости движения полюса вдоль меридиана
Гринвич и 60 категорий Y1 угловой скорости движения полюса вдоль меридиана 900W
в двух моделях – М12, М160. Параметр сходства категорий угловой скорости
движения полюса в среднем несколько выше, чем аналогичный параметр категорий
координат. Особенно это заметно в модели М12. В этой связи отметим, что модель
регрессии для угловой скорости в зависимости от комплексов (92) является более
точной, нежели для координат – см. /71/.
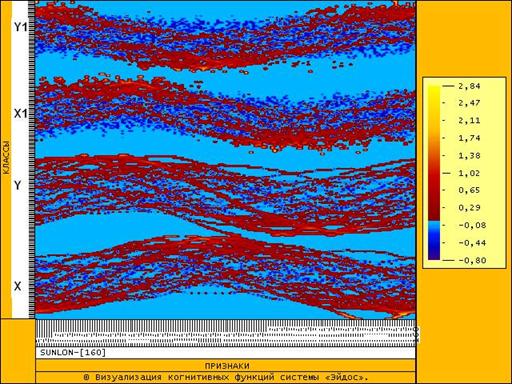
Рис. 152. Зависимость
категорий координат и угловой скорости полюса от долготы Солнца в модели М160
Это связано, видимо, с тем, что гравитомагнитное поле,
ответственное за обмен механическим моментом в Солнечной системе, также имеет
размерность угловой скорости. Поэтому отклик системы на внешнее
гравитомагнитное поле непосредственно сказывается на угловой скорости, т.е.
Земля откликается на гравитомагнитное поле подобно тому, как ведет себя,
например, парамагнетик во внешнем магнитном поле.
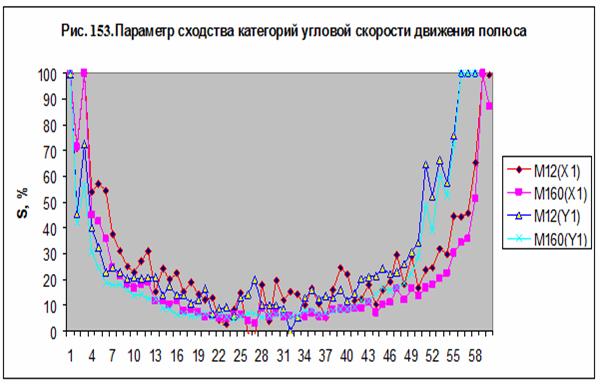
Таблица. 57. Параметр
сходства категорий угловой скорости движения полюса в двух семантических
моделях М12, М160
|
Категория X1 угловой
скорости движения полюса вдоль меридиана
Гринвич |
ABS |
M12 |
M160 |
Категория Y1 угловой
скорости движения полюса вдоль меридиана
900W |
ABS |
M12 |
M160 |
|
A1-X1=-0,006 |
1 |
99,725 |
99,675 |
B2-Y1=-0,00554 |
1 |
99,680 |
99,969 |
|
A2-X1=-0,0058 |
2 |
70,590 |
71,316 |
B4-Y1=-0,00514 |
6 |
45,287 |
42,220 |
|
A3-X1=-0,0056 |
1 |
99,859 |
99,934 |
B5-Y1=-0,00494 |
4 |
72,499 |
56,604 |
|
A4-X1=-0,0054 |
5 |
53,839 |
45,123 |
B6-Y1=-0,00474 |
20 |
40,100 |
30,589 |
|
A5-X1=-0,0052 |
7 |
57,302 |
42,458 |
B7-Y1=-0,00454 |
42 |
32,357 |
24,554 |
|
A6-X1=-0,005 |
11 |
54,621 |
35,796 |
B8-Y1=-0,00434 |
46 |
22,713 |
19,021 |
|
A7-X1=-0,0048 |
23 |
37,634 |
24,757 |
B9-Y1=-0,00414 |
93 |
24,723 |
17,790 |
|
A8-X1=-0,0046 |
32 |
30,911 |
21,562 |
B10-Y1=-0,00394 |
130 |
22,768 |
18,098 |
|
A9-X1=-0,0044 |
47 |
24,977 |
17,773 |
B11-Y1=-0,00374 |
137 |
20,453 |
16,030 |
|
A10-X1=-0,0042 |
67 |
22,690 |
16,653 |
B12-Y1=-0,00354 |
169 |
20,565 |
14,077 |
|
A11-X1=-0,004 |
136 |
26,969 |
18,290 |
B13-Y1=-0,00334 |
204 |
20,357 |
14,163 |
|
A12-X1=-0,0038 |
150 |
31,164 |
18,825 |
B14-Y1=-0,00314 |
258 |
20,864 |
12,509 |
|
A13-X1=-0,0036 |
202 |
15,518 |
11,747 |
B15-Y1=-0,00294 |
345 |
21,111 |
12,375 |
|
A14-X1=-0,0034 |
265 |
24,420 |
11,938 |
B16-Y1=-0,00274 |
315 |
13,998 |
8,848 |
|
A15-X1=-0,0032 |
309 |
19,899 |
10,474 |
B17-Y1=-0,00254 |
390 |
17,637 |
8,590 |
|
A16-X1=-0,003 |
354 |
22,633 |
11,884 |
B18-Y1=-0,00234 |
434 |
13,957 |
6,512 |
|
A17-X1=-0,0028 |
356 |
15,218 |
7,964 |
B19-Y1=-0,00214 |
433 |
14,048 |
6,865 |
|
A18-X1=-0,0026 |
383 |
18,923 |
8,511 |
B20-Y1=-0,00194 |
446 |
10,650 |
5,886 |
|
A19-X1=-0,0024 |
335 |
14,455 |
7,676 |
B21-Y1=-0,00174 |
440 |
12,032 |
6,055 |
|
A20-X1=-0,0022 |
434 |
12,164 |
5,481 |
B22-Y1=-0,00154 |
449 |
16,426 |
6,890 |
|
A21-X1=-0,002 |
445 |
12,807 |
6,249 |
B23-Y1=-0,00134 |
473 |
6,882 |
5,484 |
|
A22-X1=-0,0018 |
412 |
4,158 |
5,159 |
B24-Y1=-0,00114 |
500 |
8,409 |
6,347 |
|
A23-X1=-0,0016 |
398 |
2,533 |
4,913 |
B25-Y1=-0,00094 |
586 |
9,229 |
5,616 |
|
A24-X1=-0,0014 |
422 |
8,313 |
6,455 |
B26-Y1=-0,00074 |
542 |
5,963 |
4,506 |
|
A25-X1=-0,0012 |
449 |
14,589 |
6,295 |
B27-Y1=-0,00054 |
581 |
12,833 |
5,776 |
|
A26-X1=-0,001 |
403 |
-0,734 |
4,042 |
B28-Y1=-0,00034 |
515 |
14,283 |
6,859 |
|
A27-X1=-0,0008 |
510 |
-2,492 |
2,903 |
B29-Y1=-0,00014 |
587 |
19,942 |
6,792 |
|
A28-X1=-0,0006 |
595 |
17,817 |
8,823 |
B30-Y1=0,00006 |
521 |
10,034 |
5,417 |
|
A29-X1=-0,0004 |
515 |
3,814 |
5,450 |
B31-Y1=0,00026 |
614 |
9,894 |
6,085 |
|
A30-X1=-0,0002 |
574 |
19,726 |
7,302 |
B32-Y1=0,00046 |
612 |
10,022 |
6,436 |
|
A31-X1=0 |
656 |
12,227 |
5,598 |
B33-Y1=0,00066 |
575 |
8,582 |
6,329 |
|
A32-X1=0,0002 |
554 |
15,275 |
6,135 |
B34-Y1=0,00086 |
468 |
-0,114 |
5,879 |
|
A33-X1=0,0004 |
575 |
14,428 |
5,177 |
B35-Y1=0,00106 |
427 |
5,314 |
6,043 |
|
A34-X1=0,0006 |
546 |
10,138 |
5,655 |
B36-Y1=0,00126 |
403 |
12,713 |
7,883 |
|
A35-X1=0,0008 |
458 |
16,298 |
7,303 |
B37-Y1=0,00146 |
503 |
16,086 |
8,266 |
|
A36-X1=0,001 |
473 |
10,571 |
5,879 |
B38-Y1=0,00166 |
554 |
12,632 |
6,357 |
|
A37-X1=0,0012 |
503 |
5,448 |
5,546 |
B39-Y1=0,00186 |
456 |
13,519 |
7,070 |
|
A38-X1=0,0014 |
469 |
16,092 |
8,329 |
B40-Y1=0,00206 |
438 |
12,850 |
7,777 |
|
A39-X1=0,0016 |
485 |
24,756 |
8,437 |
B41-Y1=0,00226 |
427 |
16,062 |
8,730 |
|
A40-X1=0,0018 |
428 |
22,297 |
8,701 |
B42-Y1=0,00246 |
328 |
11,936 |
8,402 |
|
A41-X1=0,002 |
338 |
11,861 |
8,893 |
B43-Y1=0,00266 |
271 |
14,477 |
9,277 |
|
A42-X1=0,0022 |
343 |
12,497 |
9,012 |
B44-Y1=0,00286 |
306 |
20,212 |
11,669 |
|
A43-X1=0,0024 |
344 |
17,778 |
11,092 |
B45-Y1=0,00306 |
246 |
20,904 |
11,661 |
|
A44-X1=0,0026 |
353 |
10,304 |
7,121 |
B46-Y1=0,00326 |
197 |
21,319 |
14,674 |
|
A45-X1=0,0028 |
257 |
16,147 |
10,179 |
B47-Y1=0,00346 |
170 |
24,327 |
16,691 |
|
A46-X1=0,003 |
329 |
19,453 |
11,078 |
B48-Y1=0,00366 |
132 |
22,188 |
15,592 |
|
A47-X1=0,0032 |
239 |
29,729 |
16,390 |
B49-Y1=0,00386 |
99 |
22,965 |
17,315 |
|
A48-X1=0,0034 |
192 |
18,143 |
12,274 |
B50-Y1=0,00406 |
60 |
26,150 |
18,723 |
|
A49-X1=0,0036 |
175 |
28,827 |
16,365 |
B51-Y1=0,00426 |
37 |
30,890 |
22,624 |
|
A50-X1=0,0038 |
132 |
16,837 |
13,455 |
B52-Y1=0,00446 |
15 |
34,345 |
28,762 |
|
A51-X1=0,004 |
106 |
23,704 |
16,669 |
B53-Y1=0,00466 |
5 |
64,495 |
49,100 |
|
A52-X1=0,0042 |
83 |
24,797 |
17,781 |
B54-Y1=0,00486 |
8 |
52,283 |
39,026 |
|
A53-X1=0,0044 |
65 |
31,835 |
20,242 |
B55-Y1=0,00506 |
3 |
66,328 |
60,267 |
|
A54-X1=0,0046 |
41 |
30,067 |
22,400 |
B56-Y1=0,00526 |
4 |
57,425 |
52,381 |
|
A55-X1=0,0048 |
15 |
44,628 |
30,233 |
B59-Y1=0,00586 |
2 |
75,633 |
71,968 |
|
A56-X1=0,005 |
11 |
44,362 |
34,462 |
B62-Y1=0,00646 |
1 |
100,000 |
100,000 |
|
A57-X1=0,0052 |
9 |
45,857 |
35,776 |
B64-Y1=0,00686 |
1 |
99,899 |
99,973 |
|
A58-X1=0,0054 |
5 |
65,268 |
51,362 |
B65-Y1=0,00706 |
1 |
99,882 |
99,969 |
|
A59-X1=0,0056 |
1 |
99,527 |
99,883 |
|
|
|
|
|
A60-X1=0,0058 |
2 |
99,453 |
87,213 |
|
|
|
|
На рис. 152 представлена зависимость категорий угловой
скорости полюса Земли в зависимости от долготы Солнца в модели М160, полученная
путем визуализации матрицы информативностей. Отметим, что категории угловой
скорости не образуют достаточно четких нитевидных структур, подобных тем, что образуют категории координат.
Такое поведение угловой скорости полюса в зависимости
от долготы Солнца обусловлено наличием случайной составляющей, связанной с
движением атмосферы и океана относительно земной коры /89/. Случайная
составляющая угловой скорости меняется ежесуточно, поэтому угловое ускорение
полюса, вычисленное по данным /60/, также содержит случайную составляющую.
Увеличение же точности измерения координат полюса на три порядка в 1963-2006 гг
привело к росту на порядок величины амплитуды случайной составляющей в угловом
ускорении. Случайная компонента углового ускорения полюса Земли превосходит
регулярную составляющую, что делает прогноз движения полюса крайне сложной
задачей, которая не нашла еще окончательного решения /89/.
Следовательно, предполагаемая причинность событий в соответствии
с законом Ньютона, в котором зависимость координат от времени является точной,
заведомо не выполняется. В этом смысле любые оценки действующих сил и моментов,
входящих в закон Ньютона, являются произвольными, что хорошо видно при анализе
современной теории вращения Земли, в которой неизвестные силы заменяются
гипотетическими силами, обусловленными неизвестным движением в атмосфере,
Мировом океане и в мантии /89/. В таком случае с равным успехом можно моделировать
неизвестные силы, как обусловленные только влиянием небесных тел, что было
показано в цитированных работах /70-71/, в которых были развиты модели
регрессии для оценки момента сил, вызванного гравитомагнитным влияние небесных
тел.
Модель движения полюса Земли
Используя матрицу информативностей, можно оценить зависимости
угловой скорости движения полюса от координат – рис. 154-155. Из приведенных на
этих рисунках данных следует, что движение полюса Земли можно описать системой
уравнений /71/:
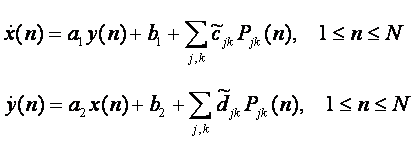 (93)
(93)
Рис. 154. Зависимость угловой
скорости движения полюса от координаты X (смещение вдоль меридиана Гринвич) в
модели М170
Как известно, на протяжении 100 лет наблюдается дрейф
полюса /90/. Для учета этого явления в правой части уравнений (93) введены
константы скорости. Параметры модели
(93) меняются в зависимости от исследуемого периода – см. таблицу 58. Период собственных колебаний системы (93)
определяется в виде
![]()
Согласно
полученным данным, период собственных колебаний системы изменяется
незначительно, в пределах 12 дней, тогда как скорость дрейфа меняет знак, что
указывает на неопределенность этого понятия во внешнем гравитомагнитном поле.
Таблица 58. Параметры модели
(93) в различные годы
|
Годы |
1990-2006 |
1963-2006 |
1963-1980 |
1980-1996 |
|
N |
6210 |
16031 |
6209 |
6054 |
|
a1 |
0,0144 |
0,0148 |
0,0145 |
0,0145 |
|
a2 |
-0,0144 |
-0,0145 |
-0,014 |
-0,0143 |
|
b1 |
0,0957 |
0,0122 |
-0,0238 |
0,0588 |
|
b2 |
0,0455 |
-0,0208 |
-0,0755 |
0,0162 |
|
Период колебаний, солнечных суток |
436,332313 |
428,9088521 |
440,9931559 |
436,3428345 |

Рис. 155. Зависимость угловой
скорости движения полюса от координаты Y (смещение вдоль меридиана 900W)
в модели М170
Стандартная модель движения полюса Земли может быть
выведена из уравнений Эйлера с переменным тензором инерции /90/. В качестве основы используется уравнение
изменения механического момента во вращающейся системе координат
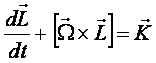 (94)
(94)
Здесь ![]() – векторы угловой скорости
вращения Земли, углового момент и углового момент сил соответственно. Угловой
момент связан с угловой скоростью и тензором инерции по формуле
– векторы угловой скорости
вращения Земли, углового момент и углового момент сил соответственно. Угловой
момент связан с угловой скоростью и тензором инерции по формуле
![]() (95)
(95)
Где ![]() – относительный угловой момент, обусловленный
перемещением текучих сред относительно центра масс
– относительный угловой момент, обусловленный
перемещением текучих сред относительно центра масс
![]() (96)
(96)
Проецируя уравнения (95) на главные оси инерции,
находим систему уравнений в форме Эйлера:
 (97)
(97)
Здесь ![]() – эффективный угловой момент сил с учетом вариаций
углового момента и тензора инерции. Полагая в первом и втором уравнениях
системы (97)
– эффективный угловой момент сил с учетом вариаций
углового момента и тензора инерции. Полагая в первом и втором уравнениях
системы (97) ![]() , получим линейную подсистему,
собственная частота которой определяется в виде
, получим линейную подсистему,
собственная частота которой определяется в виде
![]() (98)
(98)
Используя данные /60/, находим, что период колебаний,
соответствующий частоте (98), составляет 304,57 сидерических суток. В этом
случае система (97) описывает нутацию Эйлера, т.е. движение полюса
недеформируемой Земли. Реально же Земля имеет сложное строение, включающее
мантию и ядро. В случае вязкоупругой модели Земли частота собственных колебаний
системы (97) отличается от частоты нутации Эйлера. В этом случае в модель (97)
необходимо добавить вязкие слагаемые. Период колебаний, вычисленный по модели
(93) приведен в таблице 59.
Сравнивая данные, приведенные в таблицах 58-59,
находим, что периоды собственных колебаний систем (93) и (97) совпадают в
интервале 1963-2006 гг. Полученный в
результате период – 428,9 средних солнечных суток, близок по величине к периоду
428 дней, который впервые установил в 1891 г американский астроном Сет Карло
Чандлер.
Таблица 59. Период
собственных колебаний (средних солнечных суток) и параметр вязкости (1/средние
солнечные сутки) на различных интервалах времени
|
Интервал |
1963-1980 |
1963-1980 |
1963-2006 |
1963-2006 |
1990-2006 |
1990-2006 |
|
Координата |
X |
Y |
X |
Y |
X |
Y |
|
Период колебаний |
405,5779 |
455,8302 |
428,9089 |
428,9089 |
433,581 |
433,581 |
|
Параметр вязкости |
0,000373 |
-0,00295 |
-0,0003 |
-0,00023 |
0,000306 |
-0,00022 |
Как известно, колебания полюса Земли связаны, в том числе,
с синоптическими процессами в атмосфере, следовательно, используя прогноз для
вариаций угловой скорости вращения, можно предсказать синоптические процессы
/91/. В указанной работе была высказана гипотеза, что колебания полюса Земли
можно использовать для предсказания сейсмической и вулканической активности, а
также эпидемий и социально-экономических категорий.
Однако прогноз движения полюса Земли является сложной
задачей, которая не нашла еще окончательного решения. Благодаря систематическим
наблюдениям за положением внегалактических радиоисточников на основе сети
станций VLBI, была реализована
Международная небесная система координат ICRS, точность определения осей
которой составляет 10-5 угловой секунды (IERS, 2009). Столь высокая
степень точности определения параметров вращения нашей планеты стала доступна
лишь в последнее время, во многом, благодаря развитию модели /89/, которая содержит более 80000 параметров
(сводные таблицы 5.2a, 5.2b, 5.2c, 5.3a, 5.3b, 5.4 из раздела 5 с сайта ftp.maia.usno.navy.mil), отражающих, в том числе, приливное воздействие
небесных тел с учетом взаимного относительного движения атмосферы, океана и
коры.
Семантические информационные модели движения полюса
Для исследования влияния астрономических параметров небесных
тел на движение полюса Земли было сформировано несколько семантических
информационных моделей – М12, М80, М120, М142, М143, М144, М160, М170, в
которых использовались комбинации параметров в виде (92), а также сами астрономические
параметры. Всего было исследовано 18 семантических информационных моделей.
Было установлено, что параметр сходства слабо зависит
от числа разбиения N (номер модели), а также от используемых комбинаций
астрономических параметров. На рис. 156 представлен параметр сходства 236
категорий, объединяющих координаты и угловую скорость движения полюса, в двух
моделях – М80 и М160, в которых в качестве входных параметров использовалась
долгота и расстояние до небесных тел.
На рис. 157 представлен
параметр сходства категорий угловой скорости в пяти моделях, в которых в
качестве входных использовались параметры (7) в сочетании с широтой (LAT) и координатами
полюса (эти модели использовались для получения данных на рис. 4-5).

Как следует из данных, приведенных на рис.
156-157, параметр сходства слабо зависит как от числа разбиения, так и от
сочетаний параметров небесных тел при неизменном их числе (в текущей версии «Эйдос-астра»
используется 23 входных параметра, из которых образуются 23N признаков). На
рис. 158 представлена обобщенная зависимость параметра сходства от частоты
повторяемости категорий координат и угловой скорости движения полюса в моделях
М80 и М160, зависящих от долготы и расстояний до небесных тел. Параметр
сходства монотонно убывает с ростом абсолютного числа случаев повторяемости
категорий. Это означает, видимо, что увеличение длины рядов событий не ведет к
повышению параметра сходства в данной задаче.
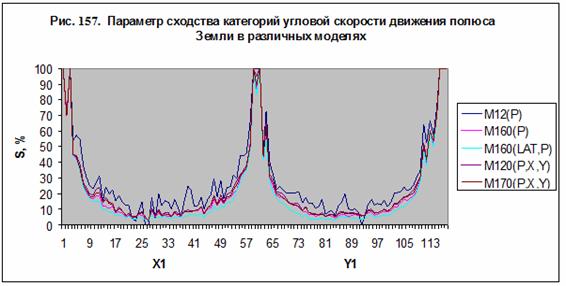
Другой целью исследования было обнаружение когерентных
структур в распределении параметров, подобных тем, что приведены на рис. 152,
154-155. На рис. 159 представлены зависимости категорий угловой скорости
движения полюса Земли от комплексов Pi1
для Солнца, Сатурна, Урана и Нептуна, с которыми угловая скорость имеет
наибольший коэффициент корреляции. Отметим, что эти комплексы дают наибольший
вклад в изменение углового момента нашей планеты – см. /71/. Из приведенных на рис. 159 данных
следует, что для указанных небесных тел исследуемые зависимости являются
однотипными. Это свидетельствует о существовании общего механизма влияния небесных
тел на движение полюса Земли, обусловленного гравитационным полем /70/.
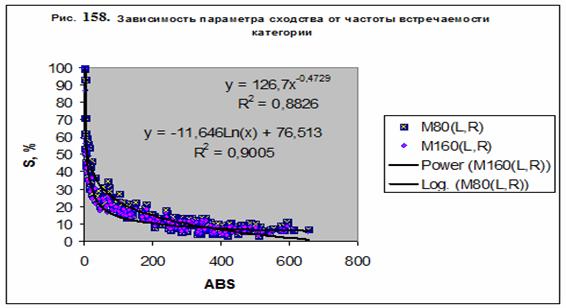
Результаты, приведенный в
работах /70-71,74/ свидетельствуют, что прогноз сейсмической активности,
вариаций магнитного поля и движения полюса Земли можно осуществлять на основе астрономических
параметров небесных и, в том числе, с использованием комплексов ![]() , отражающих
подобие гравитационного и электромагнитного взаимодействия в Солнечной системе.
Таким образом, гипотеза о всеобщей взаимосвязи процессов, протекающих на нашей
планете и охватывающих различные сферы – магнитосферу, атмосферу, земную кору,
ядро и т.п., находит свое подтверждение в перечисленных исследованиях /2,
64-65,70-71, / и других работах авторов.
Однако источником возмущений в этих сферах является не движение оси
вращения Земли само по себе, а движение небесных тел Солнечной системы
относительно нашей планеты и, видимо, движение самой Солнечной системы
относительно центра Галактики и скопления галактик в созвездии Девы.
, отражающих
подобие гравитационного и электромагнитного взаимодействия в Солнечной системе.
Таким образом, гипотеза о всеобщей взаимосвязи процессов, протекающих на нашей
планете и охватывающих различные сферы – магнитосферу, атмосферу, земную кору,
ядро и т.п., находит свое подтверждение в перечисленных исследованиях /2,
64-65,70-71, / и других работах авторов.
Однако источником возмущений в этих сферах является не движение оси
вращения Земли само по себе, а движение небесных тел Солнечной системы
относительно нашей планеты и, видимо, движение самой Солнечной системы
относительно центра Галактики и скопления галактик в созвездии Девы.
Ранее было установлено,
что существует взаимосвязь сейсмических событий, вариаций индукции магнитного
поля и параметров движения полюса Земли, что обусловлено влиянием небесных тел.
В таблицах 60-61 приведены коэффициенты корреляции параметров сейсмической
активности, вычисленных по данным /57/,
а также вертикальной компоненты индукции магнитного поля на восьми
станциях /61/ с комплексами ![]() . Из данных,
приведенных в таблицах 60-61 следует, что в случае Урана и Нептуна параметры
сейсмических событий и индукция магнитного поля Земли сильнее связаны с
комплексами
. Из данных,
приведенных в таблицах 60-61 следует, что в случае Урана и Нептуна параметры
сейсмических событий и индукция магнитного поля Земли сильнее связаны с
комплексами ![]() , нежели с комплексом
, нежели с комплексом ![]() . Угловая же
скорость движения полюса Земли, напротив, сильнее связана с комплексом
. Угловая же
скорость движения полюса Земли, напротив, сильнее связана с комплексом ![]() .
.

Рис. 159. Зависимость угловой
скорости движения полюса Земли от комплексов астрономических параметров ![]() Солнца, Сатурна, Урана и Нептуна в модели М170
Солнца, Сатурна, Урана и Нептуна в модели М170
Таблица 60. Коэффициенты
корреляции средних параметров сейсмической активности по данным /57/ с
комплексами ![]() Сатурна, Урана и Нептуна на протяжении 6009
дней: SUM, SUM_M, SUM_E, SUM_V – ежедневное число, суммарная магнитуда,
суммарная энергия и суммарный объем
землетрясений с магнитудой
Сатурна, Урана и Нептуна на протяжении 6009
дней: SUM, SUM_M, SUM_E, SUM_V – ежедневное число, суммарная магнитуда,
суммарная энергия и суммарный объем
землетрясений с магнитудой ![]() ; AVR_M, AVR_E, AVR_V –
средние значения магнитуды, энергии и объема.
; AVR_M, AVR_E, AVR_V –
средние значения магнитуды, энергии и объема.
|
|
SATURN1 |
SATURN2 |
SATURN3 |
URANUS1 |
URANUS2 |
URANUS3 |
NEPTUNE1 |
NEPTUNE2 |
NEPTUNE3 |
|
SUM |
-0,194 |
0,0703 |
0,0513 |
0,127 |
-0,419 |
-0,201 |
0,0279 |
-0,421 |
-0,401 |
|
SUM_M |
-0,184 |
0,0685 |
0,0358 |
0,115 |
-0,389 |
-0,179 |
0,0256 |
-0,391 |
-0,37 |
|
SUM_E |
-0,136 |
0,0817 |
-0,031 |
0,061 |
-0,268 |
-0,0813 |
0,00564 |
-0,272 |
-0,241 |
|
SUM_V |
-0,135 |
0,0474 |
0,106 |
0,0482 |
-0,277 |
-0,187 |
-0,026 |
-0,272 |
-0,283 |
|
AVR_M |
0,258 |
0,0241 |
-0,425 |
-0,211 |
0,632 |
0,569 |
-0,0157 |
0,615 |
0,697 |
|
AVR_E |
0,244 |
-0,008 |
-0,271 |
-0,14 |
0,518 |
0,416 |
0,00801 |
0,508 |
0,555 |
|
AVR_V |
0,231 |
-0,0128 |
-0,25 |
-0,135 |
0,492 |
0,386 |
0,0045 |
0,483 |
0,523 |
Таблица 61. Коэффициенты
корреляции вертикальной компоненты индукции магнитного поля Земли по данным
/61/ с комплексами ![]() Сатурна, Урана и Нептуна на протяжении 6009
дней.
Сатурна, Урана и Нептуна на протяжении 6009
дней.
|
Station |
SATURN1 |
SATURN2 |
SATURN3 |
URANUS1 |
URANUS2 |
URANUS3 |
NEPTUNE1 |
NEPTUNE2 |
NEPTUNE3 |
|
GNA |
-0,294 |
0,494 |
-0,103 |
0,187 |
-0,941 |
-0,119 |
-0,0156 |
-0,956 |
-0,806 |
|
GUA |
-0,438 |
0,233 |
0,43 |
0,272 |
-0,965 |
-0,649 |
0,00239 |
-0,946 |
-0,984 |
|
IRT |
-0,429 |
0,0404 |
0,538 |
0,282 |
-0,887 |
-0,781 |
0,0224 |
-0,86 |
-0,971 |
|
KAK |
-0,436 |
0,0292 |
0,55 |
0,28 |
-0,882 |
-0,793 |
0,0195 |
-0,855 |
-0,97 |
|
MMB |
-0,437 |
0,0749 |
0,503 |
0,281 |
-0,911 |
-0,754 |
0,0196 |
-0,887 |
-0,979 |
|
RES |
0,344 |
-0,109 |
-0,344 |
-0,124 |
0,879 |
0,612 |
0,141 |
0,871 |
0,911 |
|
THL |
0,136 |
0,21 |
-0,408 |
0,117 |
0,413 |
0,584 |
0,309 |
0,4 |
0,542 |
|
DRV |
-0,393 |
0,278 |
0,252 |
0,378 |
-0,932 |
-0,481 |
0,151 |
-0,927 |
-0,893 |
В случае Сатурна влияние всех трех комплексов ![]() на параметры сейсмических событий и магнитное
поле является однотипным, как следует из данных, приведенных в таблицах 60-61.
Возникает вопрос, подобно ли влияние Сатурна и вариаций магнитного поля Земли
на сейсмические события? Для ответа на этот вопрос была создана семантическая
информационная модель М170, в которой использовались астрономические параметры
небесных тел, вертикальная компонента индукции магнитного поля Земли на 12
станциях по данным /57/ и категории однократных (А), двукратных (В) и
трехкратных (С) сейсмических событий с магнитудой
на параметры сейсмических событий и магнитное
поле является однотипным, как следует из данных, приведенных в таблицах 60-61.
Возникает вопрос, подобно ли влияние Сатурна и вариаций магнитного поля Земли
на сейсмические события? Для ответа на этот вопрос была создана семантическая
информационная модель М170, в которой использовались астрономические параметры
небесных тел, вертикальная компонента индукции магнитного поля Земли на 12
станциях по данным /57/ и категории однократных (А), двукратных (В) и
трехкратных (С) сейсмических событий с магнитудой ![]() .
.
На рис. 160 представлены фрагменты матрицы информативностей указанной модели М170. Данные, приведенные на
рис. 160, демонстрирую подобие влияния долготы Сатурна и вариаций магнитного
поля Земли на частоту появления категорий сейсмических событий. Можно
предположить, что гравитационное и электромагнитное влияние Сатурна возбуждает
общий механизм, влияющий и на магнитное поле, и на сейсмические события, и на
движение полюса Земли. В этой связи отметим, что существует заметная корреляция
углового момента сил от Сатурна со средними параметрами сейсмических событий и
с вариациями индукции магнитного поля /70/, тогда как аналогичный коэффициент
корреляции углового момента сил от Урана и Нептуна с параметрами сейсмических событий
и вариациями индукции магнитного поля на порядок меньше по абсолютной величине
(см. таблицы 3-5 из работы /70/).
Таким образом, механизмы влияния Сатурна и Урана/Нептуна
на сейсмических событий, вариаций индукции магнитного поля и параметры движения
полюса Земли различаются. Это объясняется нарушением подобия электромагнитного
и гравитационного взаимодействия Земли с Ураном и Нептуном, что обусловлено
релятивистскими эффектами /70/.
Наконец,
заметим, что прогностические возможности исследованных в настоящей работе
семантических информационных моделей движения полюса Земли невелики, поэтому
они могут быть использованы в прогнозах только совместно с динамическими
моделями типа (93) и (97). Тем не менее, полученные на основе семантических
информационных моделей результаты представляют самостоятельный интерес при
решении проблемы взаимосвязи событий, явлений и процессов, обусловленных
влиянием небесных тел на землетрясения, магнитное поле и движение полюса Земли.
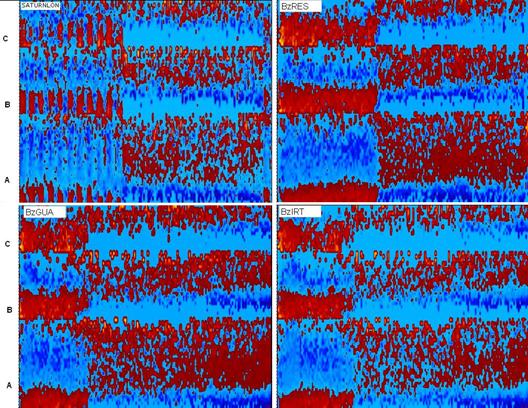
Рис. 160. Зависимость частоты категорий
однократных (А), двукратных (В) и трехкратных (С) сейсмических событий с
магнитудой ![]() от долготы Сатурна и вариаций вертикальной
компоненты индукции магнитного поля Земли на трех станциях в 1963-2006 гг по
данным /57/ в модели М170.
от долготы Сатурна и вариаций вертикальной
компоненты индукции магнитного поля Земли на трех станциях в 1963-2006 гг по
данным /57/ в модели М170.
Необходимо
отметить, что развитый в автоматизированном системно-когнитивном анализе
аппарат выявления и визуализации причинно-следственных зависимостей в форме
когнитивных функций позволяет очень наглядно буквально увидеть такие объективно
существующие явления и закономерности, о самом существовании которых еще
недавно в науке вообще не было известно и которые весьма проблематично
обнаружить другими методами. Это позволяет обоснованно говорить о том, что автоматизированный
системно-когнитивный анализ [3] и его программный инструментарий – система «Эйдос-астра»
[7] и базовая система «Эйдос» представляют собой новый инструмент исследования
в астрономии и геофизике, своего рода «математический телескоп», открывающий
качественно новые, ранее недоступные возможности исследования.
История науки наглядно демонстрирует, что появление новых
инструментов исследования, обеспечивающих новые возможности исследования, ранее
всегда приводило к возникновению новых направлений в науке. Так создание
микроскопа позволило открыть целый мир микроорганизмов и привело к возникновение
микробиологии, создание оптического телескопа позволило Галилео Галилею сразу
же открыть спутники Юпитера и привело к созданию оптической астрономии,
создание радиотелескопа привело к возникновению радиоастрономии, и.т.д. Авторы
считают, что применение систем искусственного интеллекта для анализа баз
данных, содержащих информацию об огромном количестве событий на Земле в
различных глобальных системах, позволяет выявить в этих данных влияние небесных
тел Солнечной системы на эти события и, позволяет
открыть существование новых, ранее неизвестных объективно существующих явлений
и закономерностей. По сути это означает, что применение технологий
искусственного интеллекта для исследования влияния небесных тел Солнечной
системы на глобальные геосистемы: ноосферу, биосферу, атмосферу, магнитосферу,
геосферу и другие, представляет собой новое перспективное направление исследований
в науке.
6.6. Семантические
информационные модели влияния солнечных пятен на сейсмическую
активность, движение полюса и магнитное поле Земли
Задача о распознавании
категорий событий солнечных пятен
Солнечные пятна, открытые китайскими астрономами еще
до нашей эры, являются одним из показателей солнечной активности. Согласно
существующим представлениям, солнечные пятна возникают в результате
взаимодействия плазмы с магнитным полем /92/. Ежедневное число пятен меняется
от 0 до >300, а их диаметр может превышать 80000 км. Температура пятен изменяется в пределах
3000-4500 К, что делает их заметными на фоне высокой температуры окружающей
среды (около 5780К). Эти образования
могут служить индикатором солнечной активности, так как связаны, с одной
стороны, с вариациями потока солнечной радиации и вспышками на Солнце, а с другой
– с изменением полярности солнечного магнитного диполя /92/. Оба фактора весьма
значимы для земного магнетизма, поскольку могут вызвать магнитные бури и
полярные сияния. Установлено, что солнечные пятна связаны с циклами солнечной
активности, влияющими на погоду, а
также, на здоровье и поведение людей, социальные и экономические процессы, и
технические системы /93-96/.
В силу важности этого влияния было разработано
несколько критериев для описания, как
самих солнечных пятен, так и магнитных бурь. В настоящее время эти критерии уже
используются в средствах массовой информации с целью предсказания космической погоды, наряду с
обычными прогнозами погоды.
В данном разделе на основе модифицированной системы
искусственного интеллекта «Эйдос-астра» /80/ с использованием данных /57,60-61,
72/ построена информационная модель влияния солнечных пятен на сейсмические
события с магнитудой ![]() , магнитное
поле и движение полюса Земли. Обсуждается модель взаимодействия магнитных полей
Солнца и Земли, в которой источником возмущений геомагнитного поля служит
дипольное излучение небесных тел, индуцированное солнечными пятнами.
, магнитное
поле и движение полюса Земли. Обсуждается модель взаимодействия магнитных полей
Солнца и Земли, в которой источником возмущений геомагнитного поля служит
дипольное излучение небесных тел, индуцированное солнечными пятнами.
Рассмотрим задачу распознавания категорий по астрономическим
данным. Имеется множество событий Е, которому ставится в соответствие множество
категорий Кi. Событиями можно считать, например, землетрясения,
происходящие на нашей планете ежедневно, а категориями – число одно- (А), двух-
(В) или трехкратных событий (С), магнитуда которых лежит в заданном интервале.
Каждое такое событие характеризуется моментом времени и географическими
координатами места его происхождения. По этим данным можно построить матрицу,
содержащую координаты небесных тел, например углы долготы, широты и
расстояния. Будем считать, что заданы
частотные распределения Ni
– число событий, имеющих отношение к данной категории Кi.
Определим число случаев реализации данной категории, которое
приходится на заданный интервал изменения астрономических параметров, имеем в
дискретном случае:
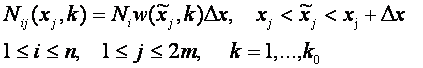
Здесь w –
плотность распределения событий вдоль нормированной координаты.
Определим матрицу информативностей согласно
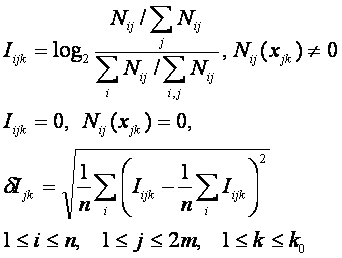
Каждой категории можно сопоставить вектор информативности
астрономических параметров размерности 2mk0,
составленный из элементов матрицы информативности, путем последовательной
записи столбцов, соответствующих нормированной координате, в один столбец, т.е.
![]()
С другой стороны, процесс идентификации, распознавания
и прогнозирования может рассматриваться как разложение вектора распознаваемого
объекта в ряд по векторам категорий (классов распознавания). Этот вектор,
состоящий из единиц и нулей, можно определить по координатам небесных тел,
соответствующих дате и месту происхождения события l в виде
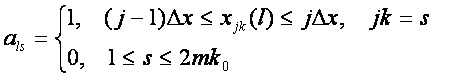
Таким образом, если нормированная координата небесного
тела из данных по объекту исследуемой выборки попадает в заданный интервал,
элементу вектора придается значение 1, а во всех остальных случаях – значение
0. Перечисление координат осуществляется последовательно, для каждого небесного
тела. В качестве астрономических параметров были использованы долгота, широта и
расстояние от Земли до десяти небесных тел – Солнца, Луны, Марса, Меркурия,
Венеры, Юпитера, Сатурна, Урана, Нептуна и Плутона, и долгота Северного Узла
Луны. Астрономические параметры вычислялись на каждый день в фиксированной
точке с географическими координатами Гринвича в 12:00 GMT в топоцентрической
системе координат. Отметим, что выбор этой точки не является существенным для
решаемого класса задач.
При создании моделей в настоящей работе были использованы
данные ежедневного числа солнечных пятен по наблюдениям американских астрономов
/72/ – параметр RADAILY, данные по индукции магнитного поля Земли /61/, данные
по сейсмическим событиям /57/, а также координаты географического полюса – X, Y
/60/. Данные по индукции магнитного поля были взяты со следующих 23
станций (приведены только IAGA коды): GNA, GUA, IRT, KAK, MMB, RES, THL, DRV,
HER, FUG, ABG, HON, CLF, LRV, SOD, AAE, AAA, TAN, SJG, AIA, TUC, BNG, MBO.
Без ограничения общности можно заменить координату любого
небесного тела иным исследуемым параметром, например, координатами и скоростью
движения полюса Земли, компонентами вектора индукции магнитного поля,
гравитационным потенциалом или числом пятен на Солнце, как в данной задаче.
В частности, в работах /70-71/ была построена модель линейной
регрессии с использованием комбинаций астрономических параметров,
характеризующих влияние каждого небесного тела. Структура приведенных ниже
комплексов вытекает из аналогии электромагнитных и гравитоэлектромагнитных
(GEM) явлений /71/ с учетом влияния солнечных пятен:
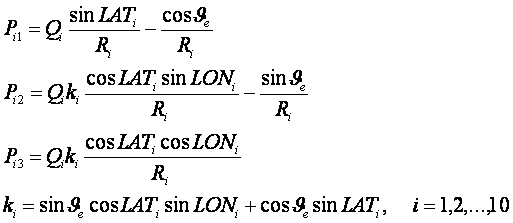 (99)
(99)
Здесь ![]() , Q0i – интегральный параметр,
описывающий предысторию влияния солнечных пятен на магнитосферу данного
небесного тела; долгота (LON), широта (LAT) и расстояние (R) определяется для
каждого из 10 небесных тел;
, Q0i – интегральный параметр,
описывающий предысторию влияния солнечных пятен на магнитосферу данного
небесного тела; долгота (LON), широта (LAT) и расстояние (R) определяется для
каждого из 10 небесных тел; ![]() - угол
наклона земной оси относительно нормали к орбитальной плоскости. Отметим, что
данные для расстояний от Земли до небесных тел вычисляются в формулах (99) в
астрономических единицах. Параметры (99) были использованы в настоящей работе
наряду с астрономическими параметрами.
- угол
наклона земной оси относительно нормали к орбитальной плоскости. Отметим, что
данные для расстояний от Земли до небесных тел вычисляются в формулах (99) в
астрономических единицах. Параметры (99) были использованы в настоящей работе
наряду с астрономическими параметрами.
Решение прямой задачи включает в себя нормирование
входных параметров и приведение их к одному масштабу изменения в интервале
(0;360), разбиение интервалов на М частей, вычисление матрицы абсолютных частот
и информативности. Решение обратной задачи включает в себя распознавание категорий
по заданным астрономическим параметрам. Частным случаем задачи распознавания
является определение достоверности идентификации категорий по астрономическим
данным в каждой модели.
Семантические
информационные модели влияния солнечных пятен, магнитного поля и долготы на
сейсмические события
Технология моделирования
сейсмических событий на основе системы «Эйдос-астра» подробна описана в
предыдущих пунктах. Исследуемая база данных сейсмических событий была
сформирована на основе базы данных Международного сейсмологического центра
(ISC) /57/, содержащей 20489816 записей
регистрации различными сейсмостанциями событий землетрясений, произошедших на
нашей планете в период с 1 января 1961 года по 31 декабря 2006 г. Была
исследована совокупность 128320 событий землетрясений с магнитудой ![]() , произошедших
на нашей планете в период с 9 февраля 1963 года по 31 декабря 2006 г (всего
16032 дня).
, произошедших
на нашей планете в период с 9 февраля 1963 года по 31 декабря 2006 г (всего
16032 дня).
В исходной БД /57/
сейсмические события характеризуются магнитудой mb, которой можно сопоставить
категорию магнитуды – таблица 62. Поскольку события с одной и той же магнитудой
могут повторяться в один день, каждому значению магнитуды из заданного
интервала сопоставляется несколько типов категорий, а именно:
A – событие с магнитудой
mb повторяется один раз;
B – событие с магнитудой
mb повторяется два раза;
C – событие с магнитудой mb повторяется три
раза.
Для целей настоящего
исследования было сформировано несколько информационных моделей, включая
следующие:
M160(L,R) – содержит
только астрономические параметры долготы и расстояния;
M160(RA,L,R) – содержит
параметр RADAILY и астрономические параметры долготы и расстояния;
M170(RA,L,Р) – содержит
параметр RADAILY, астрономические параметры долготы и 12 параметров (5),
вычисленных для Юпитера, Сатурна, Урана и Нептуна;
M170(В,L) – содержит
астрономические параметры долготы и параметры индукции магнитного поля на 13
станциях;
M120(В, Р) – содержит
параметры индукции магнитного поля на 13 станциях и 12 параметров (5),
вычисленных для Юпитера, Сатурна, Урана и Нептуна при Qi =1;
M160(L, Р68) – содержит
астрономические параметры долготы и 12 параметров (5), вычисленных для Юпитера,
Сатурна, Урана и Нептуна при Q0i
=68;
M160(L, Р68) – содержит
астрономические параметры долготы и 12 параметров (5), вычисленных для Юпитера,
Сатурна, Урана и Нептуна при Q0i
=365;
M160(L, ASP) – содержит
астрономические параметры долготы и взаимные аспекты Солнца, Юпитера, Сатурна,
Урана и Нептуна.
M170(RES,L,R) – содержит
астрономические параметры долготы и расстояния и параметр индукции магнитного
поля на станции RES;
M160(X,Y,L,R) – содержит
астрономические параметры долготы и расстояния, и координаты географического полюса;
M160(X,Y,RES,L,R) –
содержит астрономические параметры, координаты географического полюса и
параметр индукции магнитного поля на станции RES.
В таблице 62 представлен
параметр сходства категории магнитуда в четырех информационных моделях, а на
рис. 161 - аналогичный параметр сходства в семи перечисленных выше моделях. Из
данных, приведенных в таблице 161 и на рис. 62 следует, что добавление в
информационную модель параметра RADAILY – ежедневного числа солнечных пятен по
наблюдениям американских астрономов, приводит к понижению среднего и максимального
параметра сходства. Напротив, добавление параметра индукции магнитного поля
RES, связанного с ежедневной вариацией планетарного магнитного поля приводит к
росту как среднего, так и максимального параметр сходства. Следовательно, между
параметрами RES и RADAILY нет однозначной связи в смысле их влияния на
сейсмические события.
Таблица 62. Параметр сходства категории
магнитуда в четырех моделях
|
Категория |
Число случаев |
M160(L,R)) |
M160(RA,L,R) |
M170(RA,L,P)) |
M170(RES,L,R) |
|
A40-Mb=4,0 |
1362 |
-18,593 |
-12,149 |
-14,462 |
-20,037 |
|
A41-Mb=4,1 |
1580 |
-8,208 |
-6,109 |
-3,077 |
-6,813 |
|
A42-Mb=4,2 |
1796 |
-1,797 |
-0,407 |
2,698 |
0,637 |
|
A43-Mb=4,3 |
2224 |
4,889 |
5,069 |
8,640 |
7,037 |
|
A44-Mb=4,4 |
2744 |
-4,445 |
-3,647 |
-1,136 |
-4,510 |
|
A45-Mb=4,5 |
3358 |
-0,364 |
0,486 |
3,546 |
1,890 |
|
A46-Mb=4,6 |
4119 |
8,102 |
7,114 |
2,359 |
8,161 |
|
A47-Mb=4,7 |
4768 |
11,303 |
7,139 |
1,431 |
10,887 |
|
A48-Mb=4,8 |
4954 |
13,381 |
8,852 |
2,838 |
12,764 |
|
A49-Mb=4,9 |
5008 |
17,503 |
10,799 |
6,597 |
15,614 |
|
A50-Mb=5 |
4904 |
26,141 |
19,409 |
11,462 |
22,451 |
|
A51-Mb=5,1 |
4582 |
29,802 |
20,595 |
14,006 |
26,773 |
|
A52-Mb=5,2 |
4134 |
25,101 |
18,918 |
13,014 |
23,767 |
|
A53-Mb=5,3 |
3563 |
30,307 |
22,368 |
17,016 |
29,035 |
|
A54-Mb=5,4 |
3010 |
28,031 |
20,712 |
13,964 |
24,969 |
|
A55-Mb=5,5 |
2367 |
24,238 |
17,492 |
10,680 |
22,462 |
|
A56-Mb=5,6 |
1940 |
32,491 |
23,640 |
21,515 |
31,337 |
|
A57-Mb=5,7 |
1460 |
31,689 |
23,066 |
22,448 |
31,225 |
|
A58-Mb=5,8 |
1179 |
28,16 |
22,760 |
20,935 |
28,725 |
|
A59-Mb=5,9 |
864 |
24,738 |
19,841 |
18,139 |
25,450 |
|
A60-Mb=6,0 |
656 |
23,495 |
20,666 |
17,798 |
25,074 |
|
A61-Mb=6,1 |
453 |
29,394 |
25,123 |
22,496 |
29,190 |
|
A62-Mb=6,2 |
319 |
23,934 |
20,695 |
21,355 |
25,934 |
|
A63-Mb=6,3 |
202 |
35,651 |
28,722 |
28,901 |
36,412 |
|
A64-Mb=6,4 |
137 |
42,81 |
37,909 |
39,716 |
45,038 |
|
A65-Mb=6,5 |
87 |
55,802 |
47,917 |
51,895 |
62,048 |
|
A66-Mb=6,6-7,0 |
68 |
63,169 |
53,843 |
56,396 |
68,781 |
|
B40-Mb=4,0 |
446 |
28,361 |
18,736 |
23,423 |
30,855 |
|
B41-Mb=4,1 |
660 |
18,857 |
12,704 |
14,817 |
21,036 |
|
B42-Mb=4,2 |
835 |
9,046 |
6,722 |
6,265 |
9,861 |
|
B43-Mb=4,3 |
955 |
-6,859 |
-2,669 |
-8,075 |
-8,597 |
|
B44-Mb=4,4 |
1099 |
-14,986 |
-8,869 |
-10,093 |
-13,509 |
|
B45-Mb=4,5 |
1223 |
-1,494 |
-0,076 |
2,080 |
0,992 |
|
B46-Mb=4,6 |
1455 |
-1,678 |
-1,113 |
1,722 |
-0,022 |
|
B47-Mb=4,7 |
1612 |
-1,317 |
0,130 |
1,591 |
-1,349 |
|
B48-Mb=4,8 |
1817 |
3,926 |
4,190 |
5,574 |
3,183 |
|
B49-Mb=4,9 |
1636 |
3,783 |
3,855 |
2,818 |
5,508 |
|
B50-Mb=5 |
1428 |
15,492 |
11,992 |
11,574 |
16,131 |
|
B51-Mb=5,1 |
1206 |
13,093 |
10,956 |
9,329 |
12,782 |
|
B52-Mb=5,2 |
936 |
22,413 |
19,267 |
16,803 |
22,561 |
|
B53-Mb=5,3 |
617 |
24,482 |
20,240 |
17,872 |
22,979 |
|
B54-Mb=5,4 |
422 |
21,194 |
18,464 |
15,913 |
18,494 |
|
B55-Mb=5,5 |
261 |
30,487 |
23,114 |
26,050 |
31,170 |
|
B56-Mb=5,6 |
180 |
33,408 |
28,321 |
30,616 |
37,841 |
|
B57-Mb=5,7 |
93 |
56,994 |
47,736 |
52,339 |
60,019 |
|
B58-Mb=5,8 |
73 |
61,514 |
52,517 |
55,427 |
68,742 |
|
B59-Mb=5,9-6,4 |
69 |
62,605 |
54,655 |
59,161 |
68,168 |
|
C40-Mb=4,0 |
130 |
53,018 |
42,336 |
51,118 |
60,331 |
|
C41-Mb=4,1 |
259 |
35,327 |
27,456 |
34,395 |
40,927 |
|
C42-Mb=4,2 |
362 |
22,208 |
14,780 |
20,365 |
24,192 |
|
C43-Mb=4,3 |
436 |
21,621 |
15,521 |
18,421 |
24,474 |
|
C44-Mb=4,4 |
482 |
19,875 |
14,973 |
11,957 |
19,482 |
|
C45-Mb=4,5 |
468 |
11,685 |
9,127 |
8,575 |
10,782 |
|
C46-Mb=4,6 |
515 |
2,741 |
3,117 |
-0,391 |
1,491 |
|
C47-Mb=4,7 |
501 |
5,517 |
5,687 |
5,406 |
6,989 |
|
C48-Mb=4,8 |
450 |
10,42 |
9,536 |
8,836 |
12,503 |
|
C49-Mb=4,9 |
447 |
15,73 |
13,178 |
14,786 |
17,397 |
|
C50-Mb=5 |
356 |
20,558 |
16,937 |
15,841 |
22,289 |
|
C51-Mb=5,1 |
293 |
22,202 |
18,100 |
17,483 |
22,638 |
|
C52-Mb=5,2 |
166 |
35,702 |
30,512 |
31,979 |
38,506 |
|
C53-Mb=5,3-6,0 |
105 |
48,043 |
37,886 |
44,190 |
52,017 |
|
Среднее значение |
1374 |
20,995 |
17,063 |
16,874 |
22,052 |
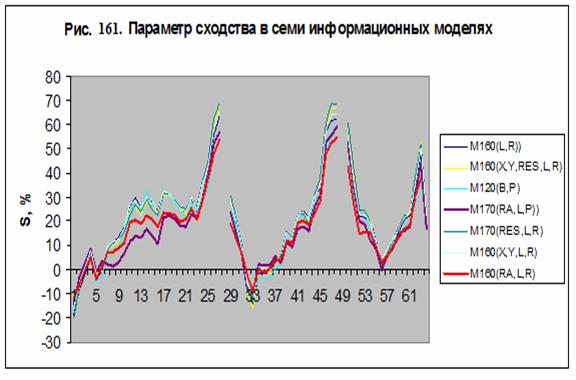
На рис. 162 представлены
фрагменты матрицы информативностей моделей M170(RA,L,Р) и M170(В,L).
Визуализация этих фрагментов осуществлялась на основе программы InfVisual v.
2.2 (авторы: Д. Бандык и Е.В. Луценко). Из представленных на рис. 162 данных
следует, что существует влияние солнечных пятен на сейсмические события, но это
влияние не подобно влиянию индукции магнитного поля.
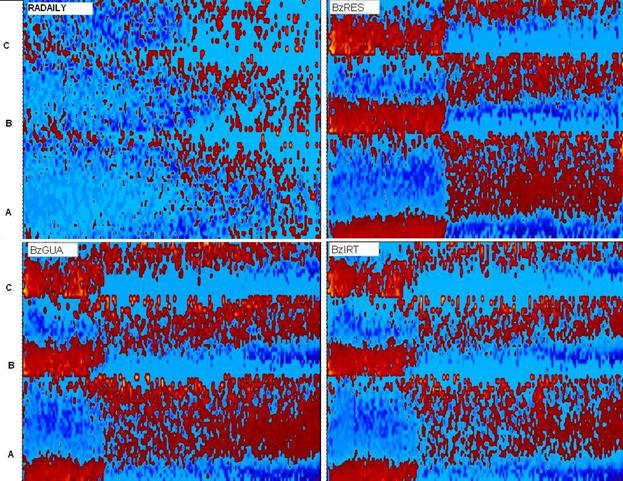
Рис. 162. Зависимость частоты
категорий однократных (А), двукратных (В) и трехкратных (С) сейсмических
событий с магнитудой ![]() от параметра RADAILY и вариаций вертикальной
компоненты индукции магнитного поля Земли на трех станциях в 1963-2006 гг по
данным /10/ в модели М170.
от параметра RADAILY и вариаций вертикальной
компоненты индукции магнитного поля Земли на трех станциях в 1963-2006 гг по
данным /10/ в модели М170.
На рис. 163. представлены
фрагменты матрицы информативностей моделей M160(L,Р365) и M160(L,R). Из
представленных на рис. 1633 данных следует, что существует влияние солнечных
пятен на сейсмические события через посредство комплексов Р3 Урана и
Нептуна, и что это влияние подобно влиянию индукции магнитного поля и долготы
Сатурна.
Можно предположить, что
основную роль во влиянии на сейсмические события играет возбуждение
магнитосферы небесных тел солнечным ветром. Однако, как было установлено, влияние
Юпитера, обладающего самой большой по объему магнитосферой среди планет, не
подобно влиянию Урана и Нептуна. На рис.
164. представлены фрагменты матрицы информативностей моделей M160(L,Р365) и
M160(L,R). Из представленных на рис. 164 данных следует, что существует влияние
солнечных пятен на сейсмические события через посредство комплекса Р3
Юпитера, но оно не подобно влиянию магнитного поля Земли, Уран, Нептуна и
Сатурна.
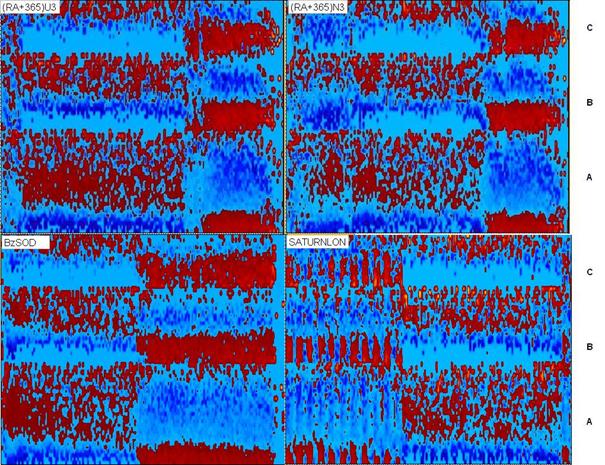
Рис. 163. Зависимость частоты
категорий однократных (А), двукратных (В) и трехкратных (С) сейсмических
событий с магнитудой ![]() от параметра P3 вычисленного для Урана и
Нептуна при Q0i =365,
долготы Сатурна и вариаций вертикальной компоненты индукции магнитного поля
Земли на станции SOD в 1963-2006 гг по данным /10/ в модели М160.
от параметра P3 вычисленного для Урана и
Нептуна при Q0i =365,
долготы Сатурна и вариаций вертикальной компоненты индукции магнитного поля
Земли на станции SOD в 1963-2006 гг по данным /10/ в модели М160.

Рис. 164. Зависимость частоты
категорий однократных (А), двукратных (В) и трехкратных (С) сейсмических
событий с магнитудой ![]() от параметра P3 вычисленного для
Юпитера при Q=1; Q0 =68 и Q0
=365, и долготы Юпитера.
от параметра P3 вычисленного для
Юпитера при Q=1; Q0 =68 и Q0
=365, и долготы Юпитера.
В рамках семантических информационных моделей можно
решить вопрос о влиянии взаимных аспектов небесных тел, которые определяются
как разность долготы двух небесных тел. Исследовалось влияние на сейсмические
события разности долготы Солнца и четырех небесных тел - Юпитера, Сатурна,
Урана и Нептуна. В результате установлено, что
заметного влияния аспектов Солнца с Юпитером, Сатурном, Ураном и Нептуном на сейсмические события
нет, хотя система «Эйдос-астра» позволяет отфильтровать несколько пиков для
каждого из аспектов – см. рис. 165.
Исследовалось влияния разности долготы четырех
небесных тел - Юпитера, Сатурна, Урана и Нептуна между собой. Наиболее значимы
оказались взаимные аспекты (в порядки значимости):
Уран/Нептун - влияние на общее число землетрясений, на
суммарную магнитуду, на среднюю энергию и на средний объем;
Сатурн/Нептун - влияние на общее число землетрясений,
на суммарную магнитуду, на среднюю магнитуду;
Сатурн/Уран - влияние на среднюю магнитуду;
Юпитер/Сатурн - влияние на общее число землетрясений и
на суммарную магнитуду.
У перечисленных аспектов ярко выраженное влияние, похожее
на влияние магнитного поля Земли – см. рис. 165 и 162.

Рис. 165. Зависимость частоты
категорий однократных (А), двукратных (В) и трехкратных (С) сейсмических
событий с магнитудой ![]() от взаимных аспектов Солнца, Юпитера, Сатурна,
Урана и Нептуна.
от взаимных аспектов Солнца, Юпитера, Сатурна,
Урана и Нептуна.
На данных для аспектов Юпитера на рис. 165 хорошо просматриваются
всплески, соответствующие некоторым аспектам Юпитер/Уран и Юпитер/Нептун.
Полосы, обнаруженные на данных для долготы Юпитера на рис. 164, видимо, соответствуют этим аспектам.
Влияние солнечных пятен на магнитное поле Земли
Как известно, число солнечных пятен связано с
изменением полярности солнечного магнитного диполя /92, 97/. Поэтому, можно
ожидать, что есть прямая связь между параметром RADAILY и вариациями индукции
магнитного поля Земли. На рис. 166. приведены коэффициенты корреляции параметра
RADAILY с вертикальной компонентой индукции магнитного поля на протяжении 16032
дней по измерениям на 23 станциях, перечисленных выше. Средний коэффициент
корреляции по всем станциям составляет около -0,00409, что, на первый взгляд,
свидетельствует об отсутствии связи между числом пятен на Солнце и вариациями
магнитного поля Земли. С другой стороны, наличие такой связи хорошо известно
/98-99/. Для объяснения этого парадокса была разработана специальная методика
вычисления геомагнитных индексов, которые изменяются подобно параметру RADAILY
или числу Вольфа. Такие индексы
составляются на основе часового, трехчасового,
суточного, месячного или годового изменения энергии магнитного поля. В
частности, в монографии /99/ были построены месячные и годичные средние комбинации
вариаций магнитного поля, которые имеют коэффициент корреляции с числом пятен
на Солнце 0,654 и 0,884 соответственно.
Начиная с 1 января 1964 года IAGA было рекомендовано
не использовать вертикальную компоненту индукции магнитного поля при вычислении
индексов геомагнитной активности, поскольку влияние местных аномалий может быть
весьма велико для вертикальной компоненты поля. Это представляется несколько
странным, так как в средних и высоких широтах вертикальная компонента поля
превосходит горизонтальную составляющую.
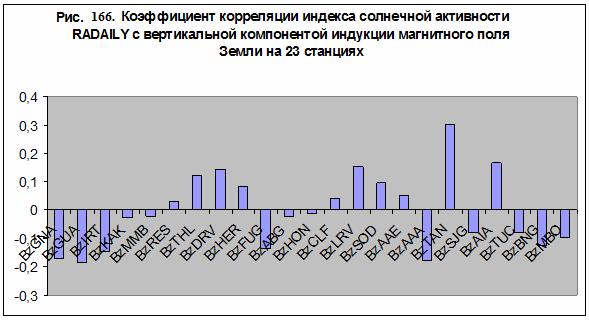
Можно предположить, что некоторые выборки их рядов
данных RADAILY будут иметь более высокий
коэффициент корреляции с вертикальной компонентой индукции магнитного поля,
нежели весь ряд. Таким образом были образованы новые ряды данных,
удовлетворяющие условию RADAILY>C, а также годичный ряд и ряд 74 дня –
таблица 62. Укороченные ряды действительно имеют более высокий коэффициент
корреляции на некоторых станциях, однако средний по всем 23 станциям коэффициент
корреляции имеет максимум 0,06 для годичного ряда, что значительно меньше
величины 0,884, полученной авторами /99/ для корреляции средне годичных величин
геомагнитного индекса и числа солнечных пятен.
Полученные
результаты означают, что влияние солнечных пятен на магнитное поле Земли
является опосредованным. Согласно /98-99/ в механизм этого влияния включены
такие сложные системы, как земная магнитосфера и ионосфера, а также солнечная
корона.
С другой стороны, в работах /50, 70/ и других было
показано, что на магнитное поле Земли существенное влияние оказывают небесные
тела Солнечной системы. Особая роль в этом влиянии принадлежит Урану и Нептуну.
Гипотеза опосредованного влияния солнечных пятен на земную магнитосферу находит
свое подтверждение в рамках модели /70/, в которой параметры (99) вычисляются с
учетом влияния числа солнечных пятен. Физический смысл выражений (99) довольно
очевиден: опосредованное влияние солнечных пятен включает медленный интегральный
процесс и быстрый процесс, который распространяется со скоростью света. При
этом предполагается, что солнечные пятна индуцируют дипольное излучение путем
воздействия на магнитосферу небесного тела.
Таблица 62. Изменение
коэффициента корреляции параметра RADAILY с вариацией вертикальной компоненты
индукции магнитного поля на шести станциях и среднее значение по 23 станциям
для различной выборки данных.
|
RADAILY |
BzGNA |
BzGUA |
BzIRT |
BzTHL |
BzDRV |
BzLRV |
AVERAGE23 |
|
N=16032 |
-0,172 |
-0,186 |
-0,145 |
0,121 |
0,143 |
0,152 |
-0,00408696 |
|
N(RA>9)=13890 |
-0,187 |
-0,209 |
-0,152 |
0,119 |
0,134 |
0,124 |
-0,01105652 |
|
N(RA>50)=8459 |
-0,238 |
-0,257 |
-0,189 |
0,133 |
0,0904 |
0,129 |
-0,02345044 |
|
N=5162(RA>90) |
-0,227 |
-0,248 |
-0,211 |
0,127 |
0,00867 |
0,0934 |
-0,03587739 |
|
N=3749(RA>110) |
-0,249 |
-0,242 |
-0,213 |
0,113 |
0,00505 |
0,096 |
-0,0374187 |
|
N=365 |
-0,0578 |
0,146 |
0,295 |
-0,126 |
-0,129 |
-0,212 |
0,06005909 |
|
N=74 |
-0,152 |
-0,00877 |
-0,146 |
0,172 |
0,521 |
0,227 |
-0,02464864 |
На рис. 167 представлены абсолютные значения коэффициентов
корреляции комплексов (99) в случае Урана и Нептуна с вертикальной компонентой индукции
магнитного поля Земли. Отметим, что в отличие от параметра RADAILY – см. рис.
166, комплексы (99) имеют высокий, вплоть до 0,98, коэффициент корреляции с
вертикальной компонентой индукции. Интегральный параметр, фигурирующий в
выражениях (99), принят постоянным и равным H0i
=365. Это значение не было оптимизировано для указанных небесных тел.
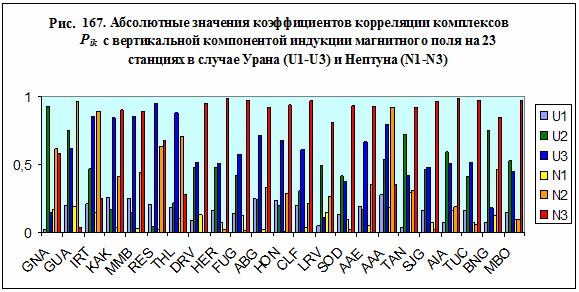
Влияние солнечных пятен на движение полюса Земли
Предложенную выше модель опосредованного влияния солнечных
пятен на магнитное поле Земли можно
обобщить на тот случай, когда изменение числа солнечных пятен сказывается непосредственно
на скорости движения полюса, вследствие чего в ускорении полюса возникает
случайная составляющая. Солнечный ветер вносит также вклад в угловой момент сил
за счет взаимодействия заряженных частиц с магнитным полем Земли. Оба эффекта
приводят к наблюдаемому сложному движению полюса. Для проверки этой гипотезы
были созданы семантические информационные модели.
Исследуемая база данных категорий движения полюса Земли
была сформирована на основе данных IERS /60/,
в период с 1 января 1963 года по 31 декабря 2010 г. Из исходной базы
было образовано несколько различных БД для исследования влияния астрономических
параметров на координаты и скорость движения полюса. Для сравнения с данными
моделирования была образована база, охватывающая 16032 дня наблюдений с 9
февраля 1963 г по 31 декабря 2006 г.
Визуализация матрицы информативностей – рис. 168, позволяет
установить, что влияние солнечных пятен на движение полюса Земли подобно их
влиянию на сейсмические события – см. рис. 162. Детальный механизм этого
влияния не известен. Можно предположить, что солнечные пятна влияют на климат
планеты, а синоптические процессы, в свою очередь, влияют на скорость движения
полюса. В этом случае существенную роль
играет приливное воздействие небесных тел.
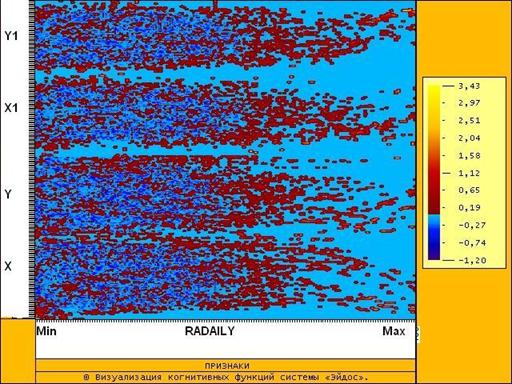
Рис. 168. Зависимость
координат и угловой скорости движения полюса Земли от параметра RADAILY
Для проверки этой гипотезы было образованы комплексы,
описывающие взаимодействие нашей планеты с гравитационным полем небесных тел в
виде
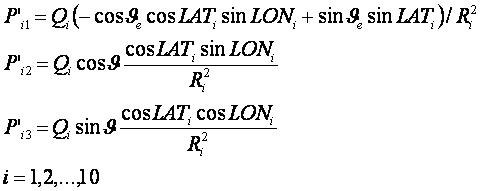 (100)
(100)
![]() , Q0i
– интегральный параметр.
, Q0i
– интегральный параметр.
На рис. 169 представлен фрагмент матрицы информативностей
модели М160, демонстрирующий линейную зависимость координат и угловой скорости
движения полюса Земли от комплексов (100) в случае Солнца, а также подобие
влияния Солнца и Юпитера на движение полюса, синхронизированное с влиянием
солнечных пятен. Механизм этой
синхронизации, видимо, обусловлен изменением параметров атмосферы и океана при
вариациях солнечной активности.
Как было установлено, комплексы (100), вычисленные для
Сатурна, Урана и Нептуна, имеют высокий, вплоть до 0,997, коэффициент
корреляции с вертикальной компонентой индукции магнитного поля – рис. 170, а
также средний по величине - с параметрами сейсмической активности – таблица
63.
Полученные результаты свидетельствуют в пользу
гипотезы приливного воздействия небесных тел, которое в информационной модели
описывается комплексами (100).
Таблица 63. Коэффициенты
корреляции средних параметров сейсмической активности с комплексами ![]() Сатурна, Урана и Нептуна на протяжении 16032
дней: SUM, SUM_M, SUM_E, SUM_V – ежедневное число, суммарная магнитуда,
суммарная энергия и суммарный объем
землетрясений с магнитудой
Сатурна, Урана и Нептуна на протяжении 16032
дней: SUM, SUM_M, SUM_E, SUM_V – ежедневное число, суммарная магнитуда,
суммарная энергия и суммарный объем
землетрясений с магнитудой ![]() ; AVR_M,
AVR_E, AVR_V – средние значения магнитуды, энергии и объема.
; AVR_M,
AVR_E, AVR_V – средние значения магнитуды, энергии и объема.
|
|
SAT1 |
SAT2 |
SAT3 |
URA1 |
URA2 |
URA3 |
NEP1 |
NEP2 |
NEP3 |
|
SUM |
-0,254 |
0,253 |
0,005 |
0,036 |
-0,041 |
-0,485 |
-0,293 |
0,274 |
-0,488 |
|
SUM_M |
-0,224 |
0,225 |
0,012 |
0,049 |
-0,054 |
-0,467 |
-0,267 |
0,248 |
-0,470 |
|
SUM_E |
-0,089 |
0,091 |
0,081 |
0,168 |
-0,170 |
-0,285 |
-0,025 |
0,013 |
-0,306 |
|
SUM_V |
-0,103 |
0,103 |
0,035 |
0,124 |
-0,126 |
-0,265 |
-0,051 |
0,039 |
-0,279 |
|
AVR_M |
0,323 |
-0,321 |
0,093 |
0,099 |
-0,097 |
0,217 |
0,240 |
-0,232 |
0,218 |
|
AVR_E |
0,196 |
-0,196 |
-0,015 |
-0,206 |
0,209 |
0,450 |
0,080 |
-0,061 |
0,473 |
|
AVR_V |
0,186 |
-0,187 |
-0,017 |
-0,201 |
0,204 |
0,435 |
0,077 |
-0,058 |
0,457 |

Рис. 169. Зависимость
координат и угловой скорости движения полюса Земли от параметров SUN2, SUN3,
вычисленных по уравнениям (9) при Q=1
и от параметров SUN1, JUPITER1, вычисленных
при Q0
=0.
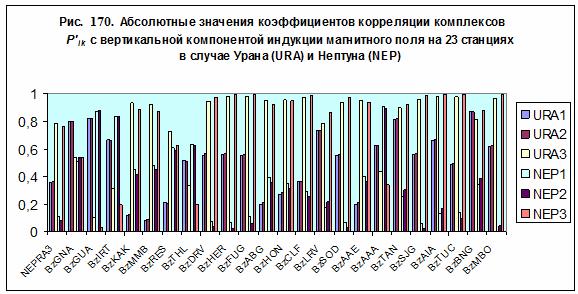
Наконец, заметим, что
развитый в автоматизированном системно-когнитивном анализе аппарат выявления и
визуализации причинно-следственных зависимостей в форме когнитивных функций
позволяет очень наглядно буквально увидеть такие объективно существующие
явления и закономерности, о самом существовании которых еще недавно в науке
вообще не было известно и которые весьма проблематично обнаружить другими
методами. Это позволяет обоснованно говорить о том, что автоматизированный
системно-когнитивный анализ /3/ и его программный инструментарий – система «Эйдос-астра»
/7/ и базовая система «Эйдос» представляют собой новый инструмент исследования
в астрономии и геофизике, своего рода «математический телескоп», открывающий качественно
новые, ранее недоступные возможности исследования.
Авторы считают, что
применение систем искусственного интеллекта для анализа баз данных, содержащих
информацию об огромном количестве событий на Земле в различных глобальных
системах, позволяет выявить в этих данных влияние небесных тел Солнечной
системы на эти события и, позволяет
открыть существование новых, ранее неизвестных объективно существующих явлений
и закономерностей. По сути это означает, что применение технологий
искусственного интеллекта для исследования влияния небесных тел Солнечной
системы на глобальные геосистемы: ноосферу, биосферу, атмосферу, магнитосферу,
геосферу и другие, представляет собой новое перспективное направление
исследований в науке.