ГЛАВА 4. О МЕХАНИЗМАХ ВЛИЯНИЯ НЕБЕСНЫХ ТЕЛ НА ХАРАКТЕР И СПОСОБНОСТИ ЛЮДЕЙ

4.1. Гравитационная гипотеза влияния небесных тел

Вопрос о влиянии планет Солнечной системы на психику людей исследовался многими авторами, главным образом, в эпоху античности и средневековья. Но лишь недавно был получен ответ на вопрос о механизмах такого влияния [20-23]. Эта фундаментальная проблема распадется на множество самостоятельных задач, которые можно сформулировать следующим образом:

1) существует ли зависимость физиологических функций организма и мозга от положения планет на небесном своде?

2) какое из фундаментальных взаимодействий, известных современной физике ответственно за передачу информации в мозг человека?

3) каков физиологический механизм восприятия сигналов, исходящих от планет?

4) как влияет на психику человека изменение физиологического состояния мозга при изменении положения планет?

5) каким образом положение планет на момент рождения запечатлевается навсегда в памяти человека?

Это далеко не полный перечень проблем, связанных с научным определением основных положений астросоциотипологии.

Идея о том, что мозг человека каким то образом воспринимает параметры состояния Солнечной системы, широко обсуждалась в литературе 19 века, куда она проникла, очевидно, из индийской философии.

Каким же образом возникает зависимость отделов мозга от тех или иных планет? Обратимся к строению мозга, который на клеточном уровне состоит из нейронов, являющихся проводниками электрических импульсов. Если проводимость нейронов зависит от гравитационного потенциала планет, тогда группы нейронов могут создавать в мозгу области, настроенные на те или иные планеты. В работе [25] были обнаружены сезонные колебания сопротивления и индуктивности при измерении по мостовой схеме в термостате. Теория этого явления дана в работах [24,26]. 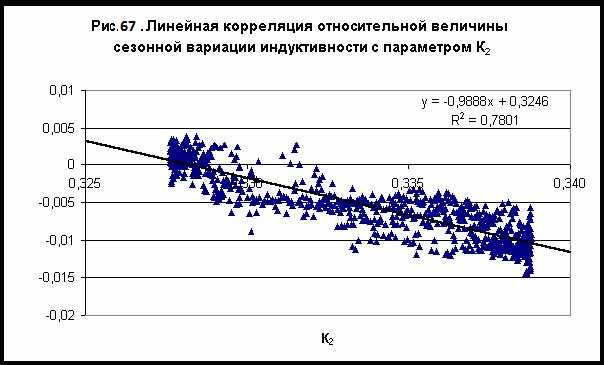Согласно [24], изменение электрического сопротивления можно объяснить колебаниями уровня энергии Ферми электронов проводимости, вызванными изменением суммарного гравитационного потенциала планет Солнечной системы на поверхности нашей планеты. Экспериментальные данные [25] по сезонным вариациям электрического сопротивления и индуктивности можно обобщить линейными зависимостями в виде [24]:

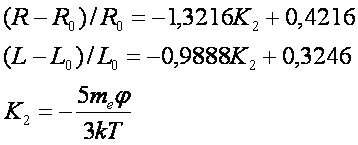
Здесь m_e – масса электрона, j - суммарный гравитационный потенциал небесных тел Солнечной системы, k=1,3806505^.10^-23 Дж/К- постоянная Больцмана, T – абсолютная температура, R₀=2,69 кОм; L₀=151,64 mH.

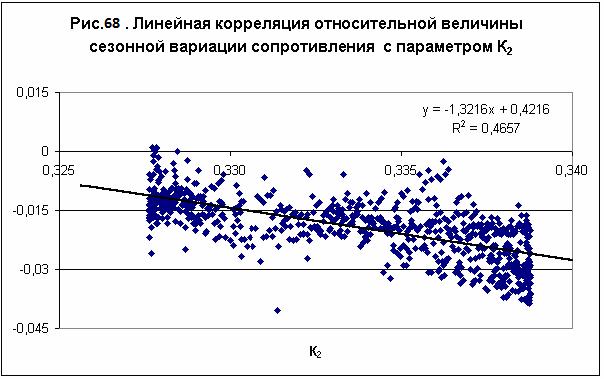
Таким образом, было установлено, что сопротивление и индуктивность электрической цепи, измеренные по мостовой схеме при постоянной температуре Т=293,15К, изменяются прямо пропорционально величине суммарного гравитационного потенциала – рис. 67-68.

Нейроны обладают электрическим сопротивлением и индуктивностью, поэтому могут изменять свои характеристики при изменении гравитационного потенциала. Неизвестно, существует ли дифференциация нейронов по их реакциям на сезонные и суточные колебания гравитационного потенциала. Но если такая дифференциация существует, она может приводить к появлению отделов мозга, зависящих от гравитационного потенциала тех или иных планет.

Эта модель позволяет объяснить влияние небесных тел на физиологию мозга и, соответственно, на психологию индивида. Вообще говоря, гравитационный потенциал может влиять не только на проводимость, но и на скорость биохимических реакций. Рассмотрим этот вопрос более подробно.

4.2. Гравитация и жизнь

Среди всех факторов планетного влияния на биохимические процессы на первое место следует поставить гравитацию. Действительно, каждая из планет Солнечной системы оказывает свое специфическое влияние на жизненные процессы. Но по суммарной энергии взаимодействия гравитация далеко превосходит все другие виды энергии, включая излучение Солнца, которое существует только благодаря силам гравитационного сжатия звезды. Планеты Солнечной системы, находясь в различных аспектах по отношению к Солнцу, оказывают циклическое влияние на объекты, расположенные на Земле. Одним из механизмов планетного влияния является периодическое изменение потенциалов гравитационных полей планет на поверхности Земли. Потенциал гравитационного поля в свою очередь влияет на параметры потоков энергии в неравновесных процессах, протекающих в пределах атмосферы, гидросферы, а также в центральной части планеты, где имеется твердое ядро, окруженное жидким слоем (так называемое приливное воздействие). Роль приливных сил и их влияние на геологические процессы и геомагнетизм в настоящее время мало изучены.

Известно, например, что приливное воздействие Луны способно вызывать подъем уровня воды на океаническом побережье на 10-15 метров дважды в сутки. Но никто точно не знает, как действует Луна на физико-химические процессы в атмосфере Земли особенно на такие, как испарение влаги или конденсация паров, которые чувствительны к малым вариациям действующих сил, а также на атмосферное электричество. Тем более трудно оценить воздействие Луны на процессы, протекающие в центральной части планеты, из-за сложности такого рода наблюдений.

Приливное воздействие дальних планет, таких как Юпитер и Сатурн, практически не изучено. Легко подсчитать, что за год гравитационный потенциал Юпитера, регистрируемый на поверхности Земли, изменяется в больших пределах, приблизительно от j=140000 м²/сек² до j=210000 м²/сек² . Но что означает изменение гравитационного потенциала Юпитера для жителя нашей планеты?

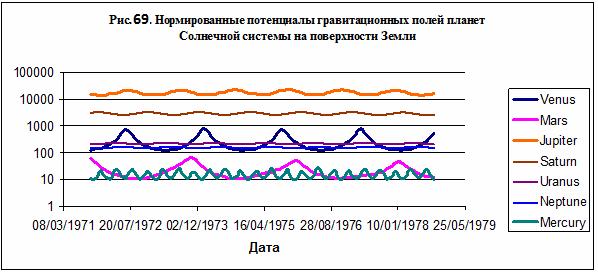
Можно представить образную картину приливного воздействия, если нормировать гравитационный потенциал планет на величину ускорения свободного падения g=9,7805 м/сек². Тогда гравитационные потенциалы планет будут измеряться в метрах, что равносильно восхождению на вершину горы соответствующей высоты, тогда приливное воздействие Юпитера эквивалентно перемещению с высоты 14,5 км на высоту 22 км над поверхностью Земли и обратно. Венера действует так, что это равносильно перемещению с высоты 100 метров на высоту около 800 метров. Влияние Сатурна равносильно периодическому перемещению с высоты 2,5 км на высоту 3,2 км. Можно сказать, что амплитуды изменения потенциала Венеры и потенциала Сатурна приблизительно равны. Марс действует слабее и его приливное воздействие распространяется от 10 метров до 60 метров. Потенциал Меркурия вполовину меньше, чем у Марса, и действует от 10 до 24 метров. Приблизительно такую же амплитуду изменения имеет потенциал Урана, хотя он находится в пределах от 188 до 208 метров – рис. 69.

Обращает внимание периодичность повторения пиковых значений потенциала. Так, за семь лет потенциалы Юпитера, Сатурна и Урана имеют приблизительно по 7 пиков, потенциал Марса – около 4 пиков, потенциал Венеры – около 5 пиков, а потенциал Меркурия – почти 22 пика. Можно также обратить внимание, что потенциалы Марса и Венеры изменяются быстрее вблизи максимальных значений и медленнее вблизи минимальных. В этом смысле их потенциалы похожи между собой.

Заметим, что энергия гравитационного взаимодействия двух планет является отрицательной величиной. Но отрицательная энергия снижает уровень энтропии в термодинамических процессах и понижает пороговые значения энергий в неравновесных термодинамических процессах, таких как химические и биохимические реакции синтеза. Учитывая, что стратегия выживания на нашей планете основана на простом воспроизведении клеток, что, в свою очередь, зависит от скорости синтеза белков, можно предположить, что влияние удаленных планет может проявляться уже на клеточном уровне.

Главное отличие гравитационного потенциала от электромагнитных полей заключается в том, что не существует способа, с помощью которого можно было бы экранировать гравитационное поле. Поэтому гравитационное поле пронизывает материю насквозь, действуя на каждый атом. В то же время поток солнечного электромагнитного излучения, несмотря на его видимую мощь, рассеивается в основном в поверхностном слое плотного вещества, например в подкожном слое человека, загорающего на пляже. Солнечное электромагнитное излучение не проникает вглубь живого организма, хотя растения приспособились использовать энергию этого излучения в процессе фотосинтеза.

Конечно, большое влияние на изменение гравитационного потенциала имеет Луна, которая максимально приближена и быстро вращается вокруг Земли. Солнце также вносит свой вклад в приливное воздействие.

Обращение небесной сферы вследствие суточного вращения планеты, годичное движение по орбите вокруг Солнца, интенсивность излучений и другие астрофизические параметры порождают циклическое воздействие планет и звездных систем на земные объекты. Ясно, что живые организмы, включая человека, вынуждены адаптироваться к изменяющимся условиям существования.

4.3. Фундаментальные законы распознавания социальных категорий по астрономическим данным на момент рождения

В работах [13-16] на основе системы искусственного интеллекта «Эйдос-астра» [7] было выполнено распознавание 37 представительных социальных категорий 20007 респондентов с общим числом случаев 86314. В качестве входных данных модели были использованы астрономические параметры долготы и расстояния до десяти небесных тел - Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна и Плутона, а также долготы углов 12 домов в системе Плацидуса. Из исходных астрономических параметров было образовано три базы данных, а именно:

1) долготы десяти небесных тел и 12 углов домов – банк LH исследованный в работе [4];

2) долготы и расстояния до десяти небесных тел – банк LR исследованный в работах [13-14];

3) расстояния до 10 небесных тел и долготы углов 12 домов – банк HR исследованный в работах [13-14].

Моделирование осуществлялось на сетках различного масштаба, полученных путем разбиения солярного зодиака на N=2, 3, …, 173 сектора. Были установлены фундаментальные закономерности распознавания категорий при изменении числа секторов разбиения [4], а также зависимость дисперсии информативности от расстояния до небесных тел [13] и от долготы угла первого, четвертого, седьмого и девятого дома [14].

В работе [22] выполнено подробное исследование фундаментальных зависимостей, полученных в работах [13-14]. Установлены основные закономерности поведения интегральной информативности в зависимости от расстояния до небесных тел. Найдены параметры подобия, позволяющие обобщить данные моделирования для всех исследованных моделей.

Постановка задачи и метод моделирования

Исходные параметры задачи представляют собой банк данных, содержащий 20007 записей биографий реальных личностей, отобранных из AstroDatabank [8]. Эти данные включают социальные и персональные категории, дату, время и место рождения, а также астрономические параметры, вычисленные на момент рождения. В настоящем исследовании была использована база данных, образованная из исходной путем комбинации входных параметров долготы и расстояние от Земли до центра масс 10 небесных тел - Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна и Плутона– банк LR исследованный в работах [13-14].

Среди социальных категорий были отобраны только представительные, число повторений которых в банке данных превышает 1000 – см. таблицу 25. Для того чтобы можно было сравнить влияние долготы и расстояния в одном масштабе, признаки расстояний нормировались по формуле:

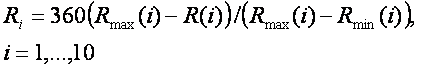
Здесь R_max(i), R_min(i) максимальное и минимальное расстояние до i-го небесного тела соответственно.

Моделирование осуществляется в два этапа на сетках различного масштаба – М6, М12, М20, М21, М22, М23, М24, М25, М26, М27, М28, М29,М32,М36,М72,М150, М170 (число ячеек совпадает с номером модели), с использованием системы искусственного интеллекта «Эйдос-астра» [7]. На первом этапе формируется обобщенный информационный портрет каждой социальной категории. Астрономические параметры на каждой сетке с числом ячеек М разбиваются на М признаков, соответствующих занимаемому интервалу с номером m=1, 2,…,M. Каждому астрономическому признаку (долготе или расстоянию из данного интервала) соответствует некоторое количество информации, по которому для каждой категории вычисляется информативность данного признака – см. таблицу 20. Интегральная информативность (ИИ) представляет собой среднеквадратичное отклонение информативности данного признака, вычисленное для 37 категорий, перечисленных в таблице 25.

Таблица 25. Список 37 социальных категорий

KOD	NAME	Частота
1	SC:М-	13640
2	SC:Ж-	5125
3	SC:A53-Sports	4567
4	SC:A1-Book Collection	4471
5	SC:A15-Famous	3373
6	SC:A42-Medical	2910
7	SC:A323-Sexuality	2675
8	SC:A5-Entertainment	2577
9	SC:A9-Relationship	2442
10	SC:A40-Occult Fields	2396
11	SC:B111-Sports:Basketball	2385
12	SC:B329-Sexuality:Sexual perversions	2360
13	SC:A55-Art	2232
14	SC:A19-Writers	2223
15	SC:A129-Death	2168
16	SC:A25-Personality	2083
17	SC:A68-Childhood	1996
18	SC:A31-Business	1813
19	SC:C330-Sexuality:Sexual perversions:Homosexual	1807
20	SC:B45-Famous:Greatest hits	1795
21	SC:A29-Parenting	1754
22	SC:B173-Sports:Football	1613
23	SC:B97-Occult Fields:Astrologer	1480
24	SC:B21-Relationship:Number of marriages	1417
25	SC:B2-Book Collection:Profiles Of Women	1389
26	SC:A92-Birth	1343
27	SC:B14-Entertainment:Actor/ Actress	1256
28	SC:?- (Неопределенный пол)	1242
29	SC:B49-Book Collection:American Book	1178
30	SC:B26-Personality:Body	1163
31	SC:B189-Medical:Illness	1159
32	SC:B6-Entertainment:Music	1086
33	SC:A99-Financial	1075
34	SC:B48-Famous:Top 5% of Profession	1073
35	SC:A38-Politics	1039
36	SC:A23-Psychological	1007
37	SC:A108-Education	1002
	Всего случаев	86314

По смыслу своего определения интегральная информативность является мерой отклика множества респондентов на воздействие небесных тел, проявляющегося через ряд категорий из таблицы 25. Чем выше значение интегральной информативности, тем больше расщепление информативности отдельных категорий, тем достовернее зависимость категорий от положения небесного тела или другого параметра – таблица 26 (колонка многоточия соответствует остальным 30 категориям из таблицы 25).

Таблица 26. Фрагмент матрицы информативности признаков расстояния до Солнца в модели М22. В последней колонке указана интегральная информативность. Единица измерения: Бит´100

SUNDIST	SC:М-	SC:Ж-	SC:A53	SC:A1	SC:A15	SC:A42	SC:A323	…	Sum	Average	II
{0.000, 16.364}.	-0,627	2,454	-0,464	-1,012	-3,270	-1,096	3,066	…	-6,476	-0,175	2,681
{16.364, 32.727}	0,726	0,742	1,576	-3,311	-2,001	2,392	1,817	…	-16,371	-0,442	3,835
{32.727, 49.091}	-0,766	-0,078	-2,474	2,122	1,751	-2,270	0,221	…	11,400	0,308	3,223
{49.091, 65.455}	-0,372	-3,833	-2,729	-0,206	-0,801	4,020	2,347	…	-0,578	-0,016	3,912
{65.455, 81.818}	-2,836	1,112	-3,832	0,861	2,722	0,891	2,313	…	18,696	0,505	3,547
{81.818, 98.182}	1,025	0,402	2,886	1,109	3,688	6,670	-0,226	…	-36,259	-0,980	4,609
{98.182, 114.545}	0,597	-0,199	1,540	-4,585	-1,787	0,842	-1,287	…	-3,715	-0,100	3,464
{114.545, 130.909}	-2,204	2,078	-2,555	1,994	-0,239	-4,824	-2,259	…	3,172	0,086	5,106
{130.909, 147.273}	0,284	2,317	2,341	-2,463	-1,490	2,258	3,211	…	-29,003	-0,784	4,871
{147.273, 163.636}	-0,230	-0,476	3,690	-0,335	-0,011	-1,693	-1,329	…	-17,193	-0,465	4,733
{163.636, 180.000}	-3,460	2,875	-2,326	3,871	4,879	-1,332	0,925	…	14,722	0,398	5,051
{180.000, 196.364}	1,179	-1,386	3,799	-1,130	-1,441	-6,504	-5,067	…	-19,620	-0,530	5,347
{196.364, 212.727}	-0,997	1,799	-2,713	0,231	1,484	-1,928	-0,199	…	-10,369	-0,280	5,267
{212.727, 229.091}	0,662	-1,290	1,172	1,439	4,062	3,669	-5,305	…	-10,934	-0,296	4,827
{229.091, 245.455}	2,807	-4,415	2,068	-1,110	-0,048	-0,523	4,959	…	-28,212	-0,762	5,015
{245.455, 261.818}	1,813	2,458	6,186	0,976	1,366	-4,853	-3,246	…	-51,358	-1,388	4,917
{261.818, 278.182}	0,460	-0,001	0,444	-0,573	-0,938	4,091	4,241	…	-28,972	-0,783	4,569
{278.182, 294.545}	0,478	-2,843	0,723	2,488	0,394	3,745	-2,089	…	-9,971	-0,269	4,315
{294.545, 310.909}	0,032	2,229	0,656	1,035	3,352	-0,748	-2,804	…	-9,397	-0,254	4,302
{310.909, 327.273}	-0,795	0,724	-2,996	1,851	1,044	-1,092	-1,414	…	10,403	0,281	3,322
{327.273, 343.636}	0,075	-3,458	-1,451	-1,242	1,265	-1,596	-0,120	…	8,486	0,229	3,632
{343.636, 360.000}	1,040	-1,733	-0,284	0,062	-2,084	-0,623	-2,899	…	-5,292	-0,143	2,152

На втором этапе осуществляется распознавание социальных категорий по параметру сходства, который определяется следующим образом:

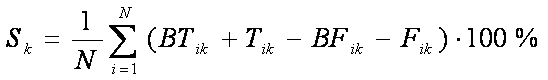
S_k – достоверность идентификации «k-й» категории;

N – количество респондентов в распознаваемой выборке;

BT_ik– уровень сходства «i-го» респондента с «k-й» категорией, к которой он был правильно отнесен системой;

T_ik – уровень сходства «i-го» респондента с «k-й» категорией, к которой он был правильно не отнесен системой;

BF_ik – уровень сходства «i-го» респондента с «k-й» категорией, к которой он был ошибочно отнесен системой;

F_ik – уровень сходства «i-го» респондента с «k-й» категорией, к которой он был ошибочно не отнесен системой.

При таком определении параметр сходства изменяется в пределах от -100% до 100%, как обычный коэффициент корреляции в статистике. В работе [6] было выполнено исследование зависимости параметра сходства от объема распознаваемой выборки для различных баз данных. Было установлено, что уже при N >150 происходит стабилизация параметра сходства различных категорий. В данной работе для всех 37 категорий был выбран объем N =100.

Заметим, что все исследованные модели имеют большую размерность, а общее количество фактов, учтенных во всех моделях более 30 миллионов.

Логарифмическая зависимость среднего параметра сходства от числа ячеек сетки

Для каждого масштаба сетки распознаются все 37 категорий, определяется их параметр сходства и средний параметр сходства для всех 37 категорий, что соответствует 86314 случаям. Такая представительная статистика позволяет выполнить параметрические исследования зависимости среднего параметра сходства от числа ячеек и определить эту зависимость с высокой достоверностью. На рис. 70 представлены обобщенные данные среднего параметра сходства в зависимости от числа ячеек для двух БД. Данные обобщаются зависимостью, которую можно представить в виде (сплошная линия ST на рис. 70):

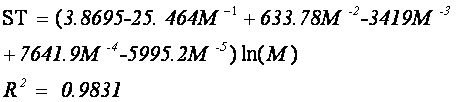
Данные работы [22] лежат в среднем несколько выше данных работы [4] - сплошная линия ST1 на рис. 70:

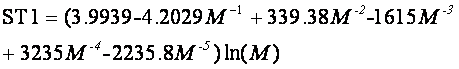
Такое поведение означает, что в среднем категории из таблицы 25 распознаются лучше по долготе небесных тел и расстоянию до них, чем по долготе небесных тел и углов домов. При больших значениях числа ячеек модели это различие является небольшим, поэтому им можно пренебречь.

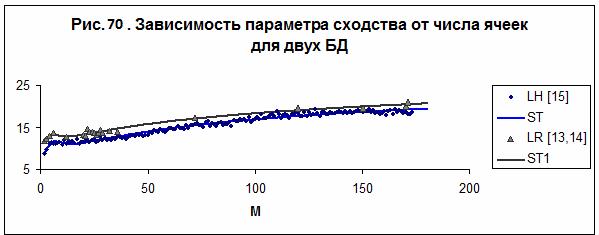
Асимптотически, при числе ячеек модели стремящемся к бесконечности, средний параметр сходства зависит от числа ячеек как логарифмическая функция. Подобная зависимость характерна для сеточной энтропии, которая пропорциональна логарифму числа элементов множества. Заметим, что логарифмическая зависимость среднего параметра сходства от числа ячеек модели для двух БД указывает на высокую степень соответствия полученных результатов распознавания, хотя в деталях для разных категорий эти результаты могут отличаться довольно сильно.

Зависимость интегральной информативности от расстояния до Солнца

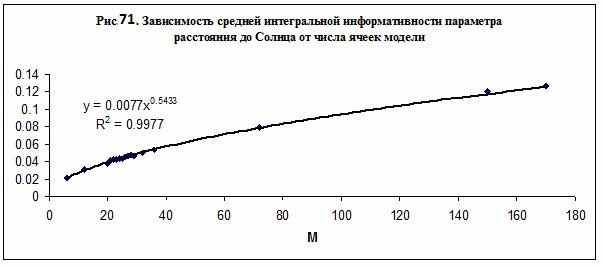
При моделировании влияния расстояния до Солнца на интегральную информативность было обнаружено, что средняя для данной модели величина интегральной информативности возрастает с ростом числа ячеек модели по степенному закону – рис. 71. Для сравнения данных, полученных в различных моделях, вместо ИИ использовалось нормированное значение этого параметра, полученное путем деления ИИ на его среднее значение для данной модели. Во всех изученных моделях поведение нормированного значения ИИ в зависимости от расстояния описывается параболой. Наиболее достоверно зависимость ИИ от расстояния выявляется в модели М22 – рис. 72. 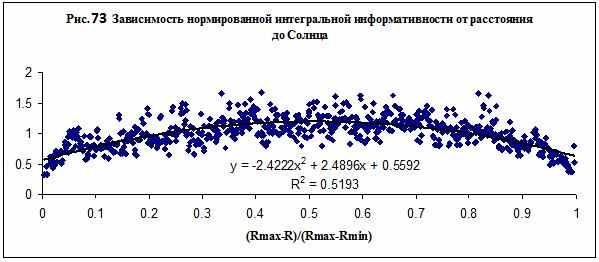Существенно, однако, что данные всех моделей обобщаются также параболической зависимостью – см. рис. 73, которая мало отличается от параболической зависимости на рис. 72. Иначе говоря, зависимость на рис. 73 является универсальной, что позволяет сформулировать закон взаимодействия группы субъектов с Солнцем, используя любую из них.

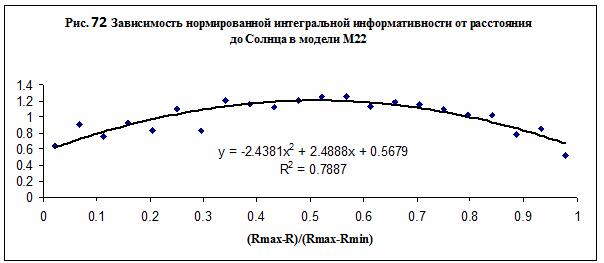
Зависимость нормированной интегральной информативности от расстояния до Солнца в общем случае можно представить в виде:

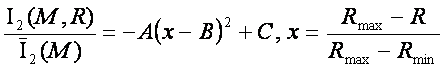(50)

Здесь численные коэффициенты, определенные по совокупности данных на рис. 73, равны:

A=2.4222, B=0.5139, C=0.8233.

Входящее в выражение (50) нормированное расстояние можно связать с гравитационным потенциалом Солнца, используя классическое выражение:

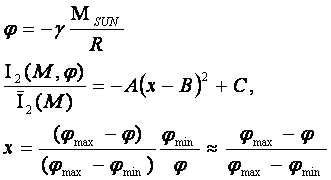(51)

Здесь - гравитационная постоянная и масса Солнца соответственно.

Полученное выражение (51), связывающее интегральную информативность с вариациями гравитационного потенциала Солнца, позволяет сформулировать модель взаимодействия группы субъектов с Солнцем. Отметим главные особенности этого взаимодействия:

амплитуда сигнала зависит только от относительной величины вариации гравитационного потенциала, но не от самой величины потенциала;

при увеличении или уменьшении амплитуды сигнала относительно некоторой величины В, величина ИИ, характеризующая реакцию на воздействие, всегда убывает, что свидетельствует о наличии отрицательной обратной связи.

Как известно в организме на принципе отрицательной обратной связи основаны механизмы нервной регуляции, поддерживающие параметры гомеостаза (терморегуляция, дыхание и т.п.).

Зависимость интегральной информативности от расстояния до Урана

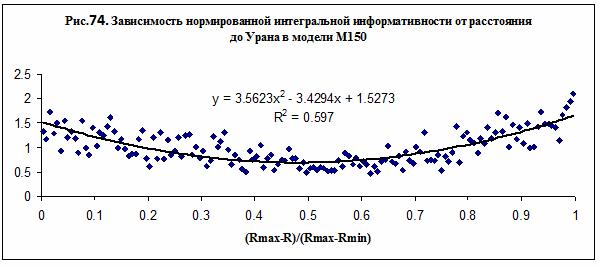
Как было установлено в работах [13-14], интегральная информативность зависит от расстояния до десяти небесных тел Солнечной системы - Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна и Плутона. Однако, наиболее точное соответствие выражениям (50-51) может быть получено по данным для планеты Уран – рис. 74. В этом случае зависимость интегральной информативности от расстояния до планеты описывается уравнением

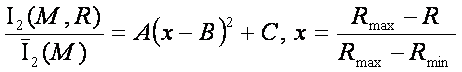(52)

Здесь параметры уравнения (52) вычисляются согласно данным, представленным на рис. 74:

A=3.5623, B= 0.4813, C= 1.2956

Используя выражение гравитационного потенциала, зависимость нормированной интегральной информативности от расстояния до Урана (52) можно представить в форме:

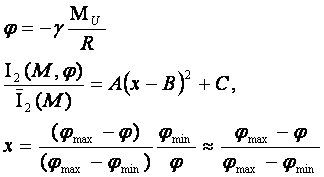(53)

Где - масса планеты Уран. Отметим, что зависимость нормированной интегральной информативности от расстояния до Урана имеет минимум в середине интервала – рис. 74, тогда как аналогичная зависимость в случае Солнца имеет максимум в середине интервала – см. рис. 73. Это отличие указывает на различную реакцию группы субъектов на воздействие Солнца и Урана, хотя сам механизм взаимодействия является общим в двух этих случаях, что непосредственно следует из сравнения выражений (51) и (53). Сформулируем закон взаимодействия субъектов с гравитационным полем Урана:

амплитуда сигнала зависит только от относительной величины вариации гравитационного потенциала, но не от самой величины потенциала;

при увеличении или уменьшении амплитуды сигнала относительно некоторой величины В, величина ИИ, характеризующая реакцию на воздействие, всегда возрастает, что свидетельствует о наличии положительной обратной связи.

Как известно, на принципе положительной обратной связи работает защитный механизм иммунной системы, обеспечивающий сохранность организма при проникновении инфекций. Таким образом, сравнивая воздействие Солнца и Урана, можно сделать следующие выводы:

воздействие гравитационного поля Солнца адаптируется организмом на уровне нейрорегуляторных функций типа терморегуляции и дыхания;

воздействие относительно слабого гравитационного поля Урана адаптируется организмом на уровне функций иммунной системы, воспринимающей это воздействие как инородный фактор, проникший в организм, вопреки установленным барьерам.

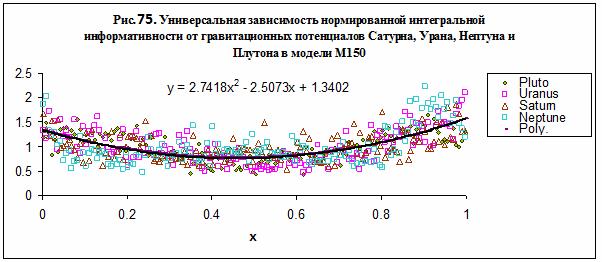
Универсальная зависимость нормированной интегральной информативности для далеких планет и модель взаимодействия

Для далеких планет – Сатурна, Урана, Нептуна и Плутона можно получить универсальную зависимость нормированной интегральной информативности от безразмерного параметра х – рис. 75. Используя данные на рис. 75, представим эту зависимость в виде:

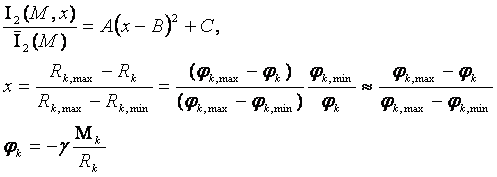(54)

где А=2.7418, В=0.4572, С=1.1311, k=1,2,3,4.

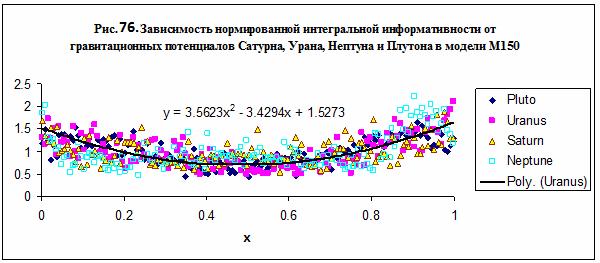
Заметим, что эта зависимость несколько отличается от таковой для Урана – рис. 74. поскольку для ее нахождения использованы данные для четырех планет, имеющие довольно широкий разброс. Поскольку это не меняет конечных выводов о характере влияния далеких планет, без ограничения общности полученных результатов можно было бы использовать для аппроксимации данных для четырех планет параболу, полученную для Урана – см. рис. 76. Такая замена слегка снижает точность аппроксимации, но не меняет самого характера поведения нормированной интегральной информативности в зависимости от амплитуды воздействия.

Полученные результаты позволяют сформулировать общую модель взаимодействия группы субъектов с удаленными небесными телами - Сатурном, Ураном, Нептуном и Плутоном:

амплитуда сигнала зависит только от относительной величины вариации гравитационного потенциала, но не от самой величины потенциала;

при увеличении или уменьшении амплитуды сигнала относительно некоторой величины В, величина ИИ, характеризующая реакцию на воздействие, всегда возрастает, что свидетельствует о наличии положительной обратной связи.

Как известно, в организме по механизму положительной обратной связи организована работа иммунной системы. Можно предположить, что слабые гравитационные поля удаленных планет Солнечной системы вызывают ответную реакцию организма такого же типа, как при проникновении возбудителей инфекционных заболеваний.

Зависимость интегральной информативности от расстояния до Луны, Марса, Меркурия, Юпитера и Венеры

Поведение интегральной информативности в зависимости от приведенного расстояния до Луны, Марса, Меркурия и Юпитера представлено на рис. 77. Для построения зависимости были выбраны данные моделирования семи моделей – М6, М12, М20, М21, М22, М23 и М24. Полученные результаты для каждого небесного тела могут быть аппроксимированы полиномом четвертого порядка, но наилучшая достоверность при аппроксимации данных достигается в случае Марс – см. рис. 77.

Используя выражение гравитационного потенциала, зависимость нормированной интегральной информативности от гравитационного поля Марса можно представить в форме:

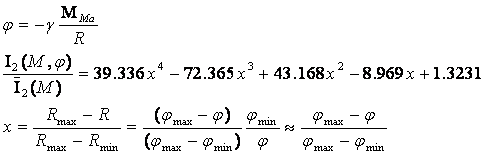(55)

Здесь - масса планеты Марс.

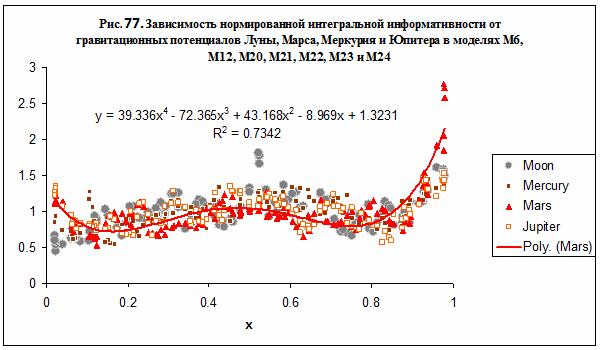
Универсальная зависимость нормированной интегральной информативности от безразмерного параметра х для четырех небесных тел – Луны, Марса, Меркурия и Юпитера (см. рис. 77), имеет вид:

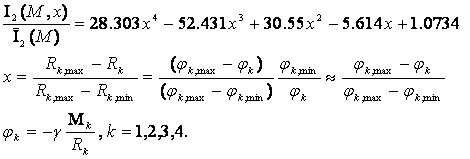(56)

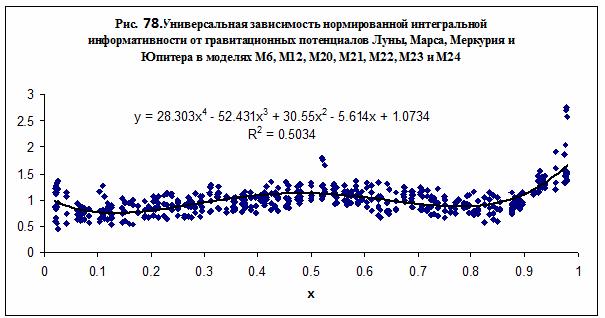
Анализируя зависимости на рис. 77-78, можно сделать вывод, что реакция группы субъектов на гравитационное воздействие Луны, Марса, Меркурия и Юпитера происходит по смешанному механизму положительной и отрицательной обратной связи. Можно предположить, что для поддержания гомеостазиса при малом отклонении от равновесного значения х=0.5, включается нейрорегуляторный механизм типа дыхания и терморегуляции, а при значительном отклонении включается механизм иммунной защиты.

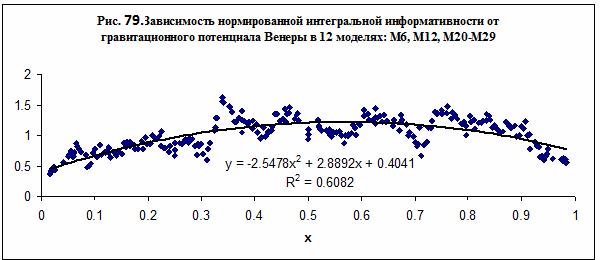
В случае Венеры зависимость нормированной интегральной информативности от гравитационного потенциала – рис. 79, вычисленная по данным моделирования в 12 моделях – М6, М12, М20-М29, имеет вид как в случае Солнца (см. рис. 73). Зависимость, представленная на рис. 79 с приемлемой точностью можно аппроксимировать параболой:

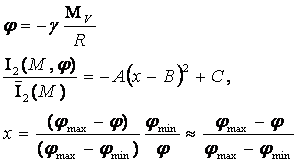(57)

Где - масса планеты Венера, А=2.5478, В=0.567, С= 0.7256.

Таким образом, в случае Венеры выполняются закономерности, отмеченные для Солнца, а именно:

амплитуда сигнала зависит только от относительной величины вариации гравитационного потенциала, но не от самой величины потенциала;

при увеличении или уменьшении амплитуды сигнала относительно некоторой величины В, величина ИИ, характеризующая реакцию на воздействие, всегда убывает, что свидетельствует о наличии отрицательной обратной связи.

Отметим, что в организме на принципе отрицательной обратной связи основаны механизмы нервной регуляции, поддерживающие параметры гомеостаза (терморегуляция, дыхание и т.п.). Следовательно, группа субъектов реагирует на воздействие гравитационного поля Венеры и Солнца по механизму отрицательной обратной связи, тогда как реакция на воздействие остальных небесных тел происходит преимущественно по механизму положительной обратной связи или по механизму обратной связи переменного типа. При этом Луна, Марс, Меркурий и Юпитер составляют одну группу планет, гравитационные поля которых возбуждают механизм обратной связи переменного типа. Сатурн, Уран, Нептун и Плутон составляют вторую группу планет, возбуждающих своими полями механизм положительной обратной связи.

Таким образом, была изучена реакция группы субъектов на воздействие Солнца, Луны и планет Солнечной системы – Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна и Плутона. В результате выполненных исследований установлено, что механизм взаимодействия может быть описан общей моделью, включающей нормированную интегральную информативность для описания реакции и амплитуду воздействия, зависящую от относительной величины гравитационного потенциала небесных тел.

Сформулируем общие законы взаимодействия субъектов с гравитационными полями небесных тел:

Амплитуда сигнала зависит только от относительной величины вариации гравитационного потенциала, но не от самой величины потенциала;

При увеличении или уменьшении амплитуды сигнала относительно некоторой величины В, величина ИИ, характеризующая реакцию на воздействие гравитационных полей Солнца и Венеры, всегда убывает, что свидетельствует о наличии отрицательной обратной связи.

При увеличении или уменьшении амплитуды сигнала относительно некоторой величины В, величина ИИ, характеризующая реакцию на воздействие гравитационных полей Сатурна, Урана, Нептуна и Плутона всегда возрастает, что свидетельствует о наличии положительной обратной связи.

При увеличении или уменьшении амплитуды сигнала относительно некоторой средней величины, реакция группы субъектов на воздействие гравитационных полей Луны, Марса, Меркурия и Юпитера осуществляется по механизму обратной связи переменного типа.

Полученные результаты можно интерпретировать следующим образом:

выбор тех или иных социальных категорий при воздействии небесных тел обусловлен адаптационными возможностями организма,

которые изменяются как на уровне нервной регуляции по механизму отрицательной обратной связи под воздействием Солнца или Венеры, а также при определенных условиях под воздействием Луны, Марса, Меркурия и Юпитера,

так и на уровне иммунной системы под воздействием слабых гравитационных полей Сатурна, Урана, Нептуна и Плутона, и при определенных условиях под воздействием Луны, Марса, Меркурия и Юпитера.

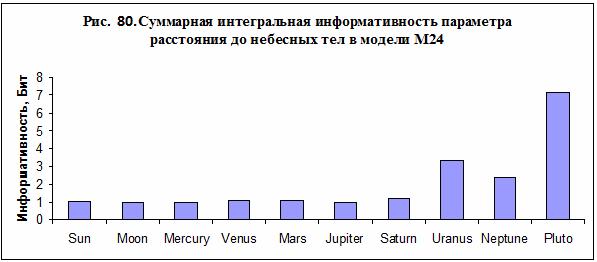
Обнаруженная зависимость интегральной информативности от расстояния до небесных тел свидетельствует о том, что взаимодействие субъектов с ближним космическим окружением носит, вообще говоря, субстанциональный характер. Что же лежит в основе этого взаимодействия? Сравним суммарную по всем ячейкам интегральную информативность параметра расстояния до небесных тел для заданной модели, например, М24 – рис. 80. Из данных, представленных на рис. 80, следует, что семь видимых глазом небесных тел – Солнце, Луна, Меркурий, Венера, Марс, Юпитер и Сатурн имеют примерно равное влияние на суммарную интегральную информативность, тогда как невидимые планеты – Уран, Нептун и Плутон влияют заметно сильнее, особенно Плутон.

Отсюда следует, что агентом влияния, скорее всего, является не электромагнитное поле, а некое другое, способное выравнивать влияние видимых небесных тел и усиливать влияние невидимых невооруженным глазом планет. Сформулируем энергетический критерий взаимодействия субъектов с небесными телами, используя известное из теории информации соотношение между информацией и энтропией:

Возводя это соотношение в квадрат, находим

Следовательно, интегральная информативность (среднеквадратичное отклонение количества информации) совпадает со среднеквадратичным отклонением для энтропии.

Заметим, что субъективное восприятие планет происходит не только и не столько на физическом уровне, сколько на уровне потоков информации. В свою очередь потоки информации формируются путем обработки сигналов. Чем слабее сигнал, приходящий со стороны небесного тела, тем больше затраты энергии на его обработку. При этом все сигналы, имеющие амплитуду выше пороговой, обрабатываются с одинаковыми затратами энергии. Поэтому семь видимых небесных тел, сигнал которых превышает пороговый, имеют примерно равную суммарную интегральную информативность. На обработку же сигналов невидимых небесных тела – Уран, Нептун и Плутон, требуется значительно больше энергии, поэтому им соответствует большая величина суммарной интегральной информативности.

В настоящее время не существует физической теории объясняющей это влияние. Можно лишь предположить в качестве рабочей гипотезы, что основным агентом влияния может быть гравитационный потенциал. Под воздействием гравитационного потенциала меняется статистика фермионов - электронов проводимости и нуклонов в атомных ядрах. Это, в свою очередь, приводит к изменению электрических и магнитных свойств материалов, а также фундаментальных констант радиоактивного распада [24-27].

Поскольку человеческий мозг состоит из системы нейронов, вырабатывающих электрические импульсы и связанных между собой проводниками электрических импульсов (дендритами и аксонами), можно предположить, что эта система может иметь отклик на изменение гравитационного потенциала (но не силы гравитации!). Поскольку в настоящей работе использованы данные рождения 20007 реальных субъектов, следует предположить, что субъект каким-то образом запоминает положение небесных тел на момент рождения. Физиология этого явления пока не изучена, известно, однако, что в состоянии гипноза люди способны воспроизвести некоторые обстоятельства, сопутствующие своему рождению.

Можно выдвинуть и альтернативную гипотезу об информационном поле, способном распространяться в космическом пространстве путем диффузии. Эта гипотеза позволяет объяснить зависимость интегральной информативности от скорости сближения и радиального ускорения. Но для обоснования этой гипотезы нет достаточных экспериментальных данных.

В настоящее время еще не изучен детальный механизм, описывающий указанные выше процессы, но сам факт их наличия подтверждается полученными результатами, которые могут иметь, по нашему мнению, фундаментальное значение для развития науки и техники.

Зависимость интегральной информативности от долготы углов домов

В работах [13-14] была обнаружена регулярная зависимость интегральной информативности от расстояния до небесных тел. Это означает, что влияние небесных тел на психологию группы индивидов имеет субстанциональный характер. Какая именно субстанция является агентом влияния остается пока под вопросом. Есть основания предполагать, что таковой субстанцией может являться гравитационный потенциал, под влиянием которого меняются статистические характеристики системы фермионов, что в свою очередь приводит к изменению электрических и магнитных свойств проводников, а также скорости радиоактивного распада [24-26].

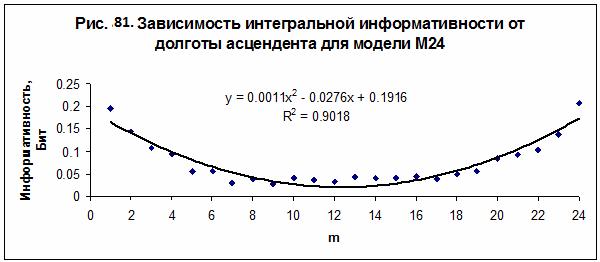
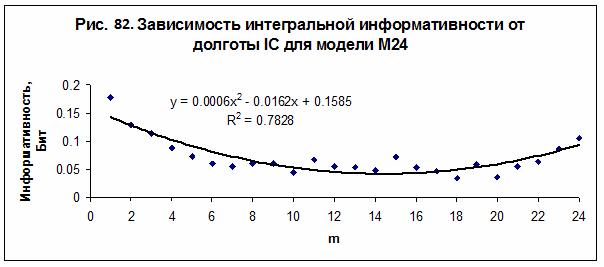
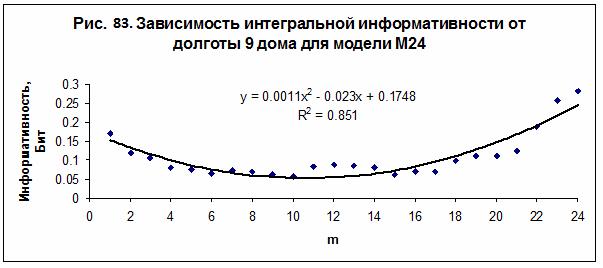
В работе [13] было выполнено исследование зависимости интегральной информативности от долготы углов домов. Обнаружена регулярная зависимость интегральной информативности от долготы угла первого дома (асцендента) – рис. 81, от долготы угла 4 дома (IC) – рис. 82, и от долготы угла 9 дома – рис. 83. Полученные зависимости являются однотипными во всех исследованных моделях - М24, М36, М72, М100 и М170. Наилучшая достоверность при интерполяции данных квадратичным полиномом наблюдается в модели М24.

Анализ полученных данных показывает, что существует асимметрия пространства вдоль оси знаков Овен - Весы. В настоящее время неизвестно, чем вызвана эта асимметрия. Возможно, что это обусловлено движением нашей Галактики в сторону гигантского скопления галактик в созвездии Девы со скоростью . Тогда точка осеннего равноденствия, которая в настоящее время проецируется в созвездие Девы рядом со скоплением галактик, будет выделена этим движением, как и противоположная ей точка весеннего равноденствия (обе точки находятся на оси Овен - Весы). Скопление галактик обладает колоссальным гравитационным потенциалом, который, видимо, на два порядка превосходит гравитационный потенциал Солнца на поверхности Земли. Неизвестно, однако, могут ли вариации этого потенциала, вызванные суточным вращением нашей планеты, создать заметное изменение в ритмах психической активности, или же влияние скопления проявляется на уровне восприятия информации.

Можно рассмотреть и другие причины, например, движение Солнца в направление созвездия Лебедя вокруг центра Галактики. Пока лишь можно утверждать, опираясь на полученные данные, что группа индивидов чувствует асимметрию пространства, что в свою очередь отражается на выборе социальных категорий. Кроме того, можно однозначно утверждать, что время суток в момент рождения, от которого зависит положение углов домов, влияет на выбор социальной специализации.

4.4. Роль гравитации в типичных ферментативных реакциях

В качестве прикладного примера реакции с участием белков (ферментов) рассмотрим уравнение МИХАЭЛИСА-МЕНТЕН [20]. Это простейшая ферментативная реакция, в которой участвует субстрат (S) и фермент (E), в результате появляется фермент-субстратный комплекс (ES), при распаде которого образуется продукт (P). Формула реакции имеет вид [38-39]:

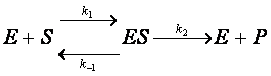
Здесь k₁, k_-1 - константы скоростей прямой и обратной реакций образования фермент-субстратного комплекса; k₂ - константа скорости образования продукта. При определенных предположениях находим уравнение изменения концентрации конечного продукта и субстрата

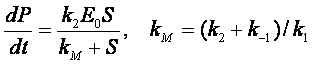(58)

Где Е₀ – начальная концентрация фермента, k_M - константа Михаэлиса. Поскольку фермент E участвует во всех стадиях реакции, имея при этом наибольшую массу, константы k_i во внешнем гравитационном поле определяются согласно уравнению:

(59)

Здесь m_E – масса молекулы фермента, k=1.372*10^-16 эрг/К - постоянная Больцмана, T – абсолютная температура (для процессов, происходящих в организме человека температуру можно считать постоянной и равной приблизительно 309.6К или 36.6С).

Заметим, что отношение скоростей реакций в знаменателе в правой части уравнения (58) – константа Михаэлиса, не меняется во внешнем поле. Чтобы не изменилась и эффективная константа скорости реакции, необходимо потребовать, чтобы выполнялось соотношение:

(60)

Следовательно, для автоматического регулирования выхода продукта при любых отклонениях гравитационного потенциала от некоторой начальной величины, потребуется дополнительное количество фермента:

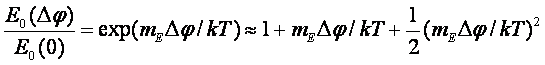(61)

Таким образом, для сохранения скорости производства продукта в простых ферментативных реакциях при изменении гравитационного потенциала необходимо изменять концентрацию фермента пропорционально отклонению гравитационного потенциала.

Сравним этот результат с типичной социальной реакцией большой группы респондентов (всего 20007) на воздействие гравитационных полей далеких небесных тел – Сатурна, Урана, Нептуна и Плутона – см. уравнение (53). Подобие выражений (61) и (53) указывает на общий механизм взаимодействия и на простой физиологически обусловленный характер социальной реакции, в ответ на воздействие гравитационных полей далеких небесных тел. Естественно, возникает вопрос, каким же образом осуществляется избирательность по отношению к влиянию полей конкретных планет? Ведь выражение (61) содержит в правой части суммарный потенциал, тогда как выражение (53) зависит от потенциала отдельного небесного тела. Кроме того, не определено время воздействия и нет явной связи со временем протекания реакции. Тем не менее, эта простая теория позволяет объяснить некоторые характерные особенности установления равновесной концентрации активных соединений в организме, таких как гормоны.

4.5. Роль гравитации в реакциях с участием гормонов

Рассмотрим уравнение (58) при условии, что изменение потенциала лимитировано временем реакции, т.е.

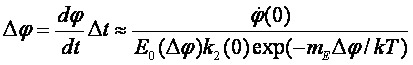
В этом случае вместо выражения (61) находим следующую зависимость концентрации гормона:

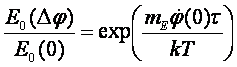(62)

Производную по времени от суммарного гравитационного потенциала можно представить в виде суммы производных потенциалов небесных тел:

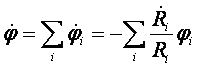(63)

Заметим, что основной вклад в скорость изменения потенциала вносит Солнце. Используя соответствующие Солнцу параметры, находим сезонную зависимость концентрации гормона вазопрессин, регулирующего величину осмотического давления жидкостей в организме – см. рис. 84. В качестве эффективного времени процесса использована длительность реакции одного типа с участием одной молекулы гормона – около 60 сек.

Аналогичная зависимость может быть получена для тиреоидных гормонов Т3 и Т4, осуществляющих перенос электронов в ферментных системах с молекулы донора на субстрат - рис. 84. В этом случае в качестве эффективного времени реакции выступает общее время участия одной молекулы гормона в реакции одного типа, что составляет 200 секунд. Для этих гормонов экспериментально установлена сезонная зависимость их концентрации в крови. Отметим основное действие этих гормонов [40-42]:

1) метаболическое, регуляция обменных процессов, увеличение синтеза белка, повышение распада жиров и углеводов, особенно в клетках нервной системы, регулируют энергетический обмен, обмен белков, жиров и углеводов, кальция во всех клетках организма, в том числе и нервной системе, регулируют уровень содержания сахара в крови;

2) контроль образования тепла, скорости поглощения кислорода клетками, поддержание нормального функционирования дыхательного центра, иммунитета;

3) наряду с гормонами коры надпочечников обеспечивают физиологическую адаптацию.

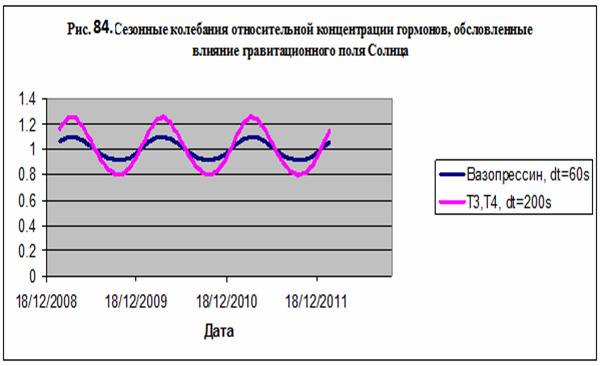
Таким образом, установлено, что концентрация двух типов гормонов, ответственных за регулирование давления и температуры тела, может испытывать сезонные колебания, связанные с воздействием гравитационных полей Солнца.

Отметим, что в сумме в правой части выражение (64) некоторые слагаемые могут обращаться в нуль. Так, например, производная гравитационного потенциала Солнца вносит основной вклад в сумму в правой части выражения (65), но в периоды летнего и зимнего солнцестояния вклад Солнца равен нулю, поскольку в это время производная от расстояния до Солнца обращается в нуль. В этом случае становится заметным влияние других небесных тел. Среди них наиболее существенное влияние (после Солнца) может оказывать Юпитер. Но даже его поля недостаточно, чтобы заметно повлиять на концентрацию гормонов с небольшой молекулярной массой. Не исключено, однако, что Юпитер может повлиять на концентрацию в крови тиреоглобулина (ТГ), обладающего большой молекулярной массой, при условии, что это соединение может принимать участие в длительных, порядка минуты ферментативных реакциях – рис. 85.

Таблица 27. Типичные соединения, концентрация которых зависит от сезонных колебаний гравитационного поля

Соединение	mЕ , дальтон	Е0(0) , нг/мл	Период полураспада, час
Тиреоглобулин (ТГ)	660000	18,57	78-96
Вазопрессин, пептидный гормон гипофиза	1084	0.002	0.20-0.25
Тиреоидные гормоны — трийодтиронин (ТЗ); Тироксин (Т4)	551; 777	46-105 (T4)	148 (Т4)

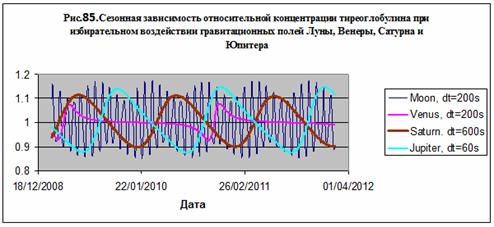
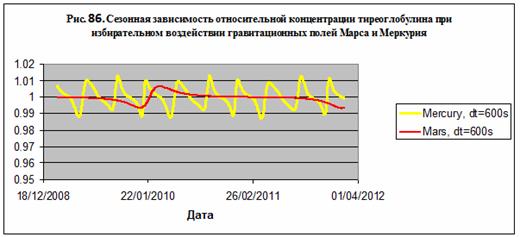
В некоторых случаях в нуль может обратиться производная суммы гравитационных потенциалов Солнца и Юпитера. Тогда заметным становится гравитационное воздействие Луны и Венеры, которые могут повлиять на концентрацию ТГ в крови в реакциях длительностью 200 сек – рис. 85. Наконец, в исключительных случаях, проявляют себя в ферментативных реакциях с участием тиреоглобулина, длительностью не менее 600 сек, гравитационные поля Сатурна, Марса и Меркурия – рис. 86. Отметим, что полученные результаты носят предварительный характер, поскольку не указаны конкретные реакции, в которых могли бы проявиться гравитационные поля небесных тел. Общее требование к таким реакциям с участием ферментов заключается в том, чтобы молекулярная масса фермента была достаточно большой, а время реакции исчислялось бы секундами и минутами. Кроме того, развитая теория относится к такому типу гормонов, концентрация которых имеют отчетливую сезонную и суточную зависимость. В этом случае теория предсказывает, что максимальная концентрация гормонов будет наблюдаться весной, а минимальная – осенью.

Вообще говоря, механизм установления равновесной концентрации тиреоидных гормонов Т3 и Т4 является довольно сложным, поскольку они производятся с участием тиреоглобулина под влияние гипоталамо-гипофизарной системы. Снижение концентрации тиреоидных гормонов приводит к повышению концентрации тиреотропного гормона (ТТГ) гипофиза, что в свою очередь приводит увеличению скорости синтеза тиреоглобулина и высвобождению Т3, Т4. Регуляция осуществляется по принципу отрицательной обратной связи, однако секреция ТТГ тормозится не только Т3 и Т4, но и соматостатином и дофамином, а стимулируется тиреотропин-рилизинг-гормоном гипоталамуса -тиреолиберином. Такая сложная цепочка не может быть описана одним уравнением, типа (58), но должна включать все стадии процесса регулирования, в том числе модель накопления сигнала в памяти.

Рассмотрим три модели накопления сигнала:

1) в случае, когда сигнал является очень слабым, что выполняется для Сатурна, Урана, Нептуна и Плутона, тогда его накопление идет непрерывно, в соответствии с выражением (61);

2) в том случае, когда сигнал является очень сильным, что выполняется для Солнца, тогда его накопление происходит за ограниченное время, в соответствии с выражением (62), после чего происходит сброс сигнала;

3) для сигналов средней интенсивности, приходящих от Луны, Меркурия, Марса и Юпитера в окрестности точек поворота выполняется модель 1, а в средней части зависимости ИИ от расстояния выполняется модель 2.

Эти модели позволяют описать все основные особенности зависимости ИИ от расстояния до различных небесных тел, полученные в работах [13-16, 21-23].

Таким образом, можно утверждать, что гравитационная чувствительность появляется в системах с памятью в ответ на изменение скоростей биохимических реакций с участием гормонов.

Влияние гравитационного потенциала Земли в состоянии динамической невесомости было впервые обнаружено при наблюдении за космонавтами во время длительных космических полетов [42]. Полученные выше результаты позволяют понять механизм этого влияния, связанный с изменением скоростей биохимических реакций во внешних гравитационных полях. Действительно, в этом случае сила, приложенная к телу космонавта, равна нулю, но гравитационный потенциал Земли не равен нулю. Поэтому гравитация продолжает действовать так, как будто космонавт находится на вершине горы эквивалентной высоты. При значительном удалении от Земли гравитационный потенциал падает по абсолютной величине. Обнаруженная в опытах статическая невесомость, вызывающая значительные физиологические изменения, наступает только на расстоянии более 37 тысяч километров от поверхности Земли [42].

Следует заметить, что потенциал гравитационного поля в нерелятивистском приближении описывается уравнением Лапласа. Но это уравнение не изменяется при переходе к неинерциальной системе координат, связанной с местом наблюдения на нашей планете или с кабиной космического корабля (в отличие от уравнения Ньютона, в котором появляются фиктивные силы инерции). Квантовая система молекул чувствует гравитационный потенциал, но не чувствует силы инерции, которые, вообще говоря, малы по сравнению с силами межмолекулярного взаимодействия. Таким образом, система молекул реагирует на изменение гравитационного потенциала, но не реагирует на систему сил, сумма которых равна нулю в лабораторной системе координат. Это и порождает эффекты, связанные с влиянием гравитационного потенциала [26].

Выражению (62) можно придать наглядный вид, выполнив осреднение для большой группы субъектов, тогда получим:

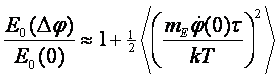(64)

Выражение (64) можно упростить с учетом того, что основной вклад в производную вносит изменение гравитационного потенциала Солнца. Производную гравитационного потенциала можно определить по формуле (63), используя простое выражение для изменения расстояния от Земли до Солнца:

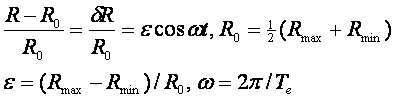(65)

Здесь R_max, R_min - максимальное и минимальное расстояние от Земли до Солнца, T_e – годичный период обращения Земли, время отсчитывается от точки максимального удаления (летнее солнцестояние в северном полушарии). С учетом этого выражения находим:

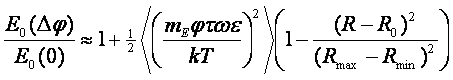(66)

Таким образом, в случае Солнца выражение (66) позволяет предсказать, что максимальное отклонение в концентрации будет наблюдаться весной и осенью в точках равноденствия, а минимальное – летом и зимой в точках солнцестояния. Сравним полученный результат с зависимостью нормированной интегральной информативности от расстояния до Солнца – см. уравнение (51). Подобие выражений (66) и (51) указывает на простой гормональный механизм отклика группы респондентов на воздействие гравитационного поля Солнца.

Предложенная выше теория позволяет сделать оценку влияния небесных тел на протекание ферментативных реакций с участием гормонов. Дальнейшее развитие теории может помочь в объяснении возникновения некоторых заболеваний, обусловленных нарушением гормонального баланса в организме.