ГЛАВА 3. ОСНОВНЫЕ МОДЕЛИ АСТРОСОЦИОТИПОЛОГИИ И РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

3.1. Социологические и астросоциотипологические базы данных

В социологии и экономике, в медицине и в статистике, во многих других отраслях знаний приходится иметь дело с огромными массивами специализированной информации в виде данных различной природы. Вплоть до середины 20-го века такого рода данные хранились обычно в виде справочников. Стоит ли говорить, сколь неудобным был такой способ хранения. Сразу же после создания первых компьютеров, данные начали переносить на магнитные носители в форме компьютерных баз данных (БД). В настоящее время для хранения и обработки этих данных используются специализированные компьютерные программы, среди которых наиболее известными являются Clipper, Excel, Quattro Pro и другие. В социологии для обработки данных широко применяется система SPSS. В настоящей работе для обработки и моделирования данных были использованы системы искусственного интеллекта «Эйдос» [36] и «Эйдос-астра» [7].

Компьютерные базы данных являются удобным инструментом для научных исследований. В настоящей работе были использованы первая и четвертая версии известной социологической и астросоциотипологической базы данных AstroDatabank [8]. Эти версии отличаются числом записей: в четвертой версии добавлено 5000 данных новых респондентов. Эта БД интересна тем, что в ней содержатся данные рождения и биографии известных людей и частных персон, относящихся к определенной категории. Всего в AstroDatabank 4.00 содержится 31012 записей, в том числе:

23217 данных респондентов с биографией;

6644 данных рождения респондентов относящихся к определенной категории;

1151 данных мировых событий.

Этим записям соответствует 113110 записей категорий, т.е. приблизительно 3,647 категорий на одного респондента (событие) – рис. 35.

 Все категории условно можно разделить на социальные, куда относятся и профессиональные категории, на психофизические и на события определенного типа. В нашем анализе было использовано минимум 4 категории [6], максимум 870 категорий – рис. 2.

 

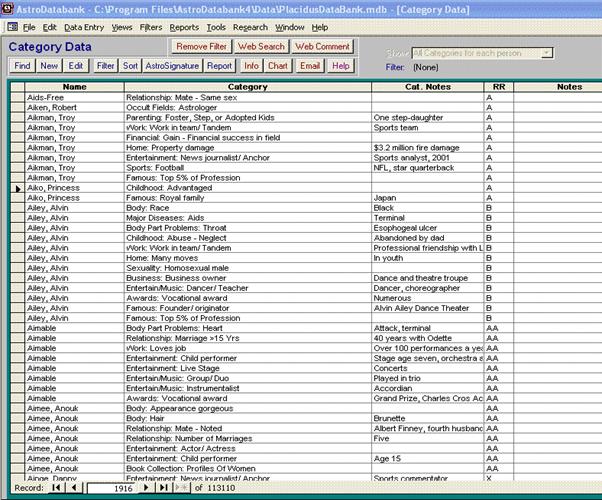
Рис. 35. Скриншот данных категорий AstroDatabank 4.00

 

Из исходных данных, содержащихся в AstroDatabank, было создано более десяти различных БД, для проверки тех или иных гипотез [1-2, 4-6]. Данные, импортированные непосредственно из AstroDatabank v. 4.00, были преобразованы в DBF4 формат, который воспринимается системами «Эйдос» [36] и «Эйдос-астра» [7]. Эти данные содержат как описание данных рождения и категорий, так и астрономические параметры долготы и склонения десяти небесных тел – Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна и Плутона, а также долготы Северного узла Луны, асцендента (ASC) и середины неба (МС), т.е. всего 23 астрономических параметра. Было использовано 9897 записей, соответствующих 5 категориям, объединенным в 4 класса – таблица 8, а. Среди этих записей 184 повторяются, поскольку они соответствуют 2, 3 или 4 категориям.

 

Таблица 8, а. Четыре класса, пять категорий и соответствующее число респондентов в случае Database0 и Database1

KOD_OBJ

NAME

ABS

1

Politics, Science

1876

2

Medical: Physician

347

3

Sports

6032

4

Psychological

1642

 

Из этих записей было создано две БД для проверки влияния склонения на качество распознавания:.

Database1 с 23 астрономическими параметрами для каждой записи, причем параметр склонения отображался на интервал (0; 360) с использованием формулы Declination1 = (Declination +30)*6;

Database0 с 11 астрономическими параметрами для каждой записи, соответствующими долготе десяти небесных тел – Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна и Плутона, а также долготе Северного узла (Луны).

Данные, импортированные из первой версии AstroDatabank, были конвертированы в формат баз данных JDataStore фирмы Borland, а затем сортированы с использованием SQL запросов и специальных функций на языке Java. В результате были получены астрономические и биографические данные для 20007 уникальных персон и 16360 записей событий, происходивших с ними. Для них всех с помощью библиотеки швейцарских эфемерид (www.astro.com) были вычислены координаты небесных тел (долгота и широта в градусах и расстояние в астрономических единицах). Для записей с точным временем вычислялась долгота углов домов в системе Плацидуса. С настоящем исследовании были использованы только параметры долготы следующих небесных тел: Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна и Плутона, а также Северного узла Луны. Вместе с параметрами долготы углов 12 домов это составляет 23 параметра, как и в случае Database0, Database1. Это позволяет представить все базы данных в одном формате и исследовать их на основе идентичных алгоритмов.

Из этих данных были образованы восемь БД для проверки различных гипотез:

Database A содержащая 20007 записей данных респондентов соответствующих 500 представительных категорий (каждая категория представлена не менее чем 26 записями);

Database B содержащая 15007 записей данных респондентов, соответствующих 500 представительным категориям (эта БД использовалась для тренировки нейросети);

Database C содержащая 5000 записей данных респондентов, соответствующих 500 представительным категориям (эта БД использовалась для определения эффективности распознавания);

Database D содержащая 20007 записей данных респондентов соответствующих 240 непредставительных категорий (каждая категория представлена числом записей более 2 и менее 25) – низкочастотный предел;

Database E D содержащая 20007 записей данных респондентов соответствующих 870 категориям (каждая категория представлена числом записей более 2) – наиболее полная база данных;

Database F содержащая 20007 записей данных респондентов соответствующих 37 категориям (каждая категория представлена числом записей более 1000) – высокочастотный предел;

Database F1 содержащая 20007 записей данных респондентов соответствующих 100 категориям (каждая категория представлена числом записей более 174);

Database G содержащая 20007 записей данных респондентов соответствующих 4 категориям, перечисленным в таблице 8,б. Заметим, что в этой базе данных 8150 записей не используется в моделировании, поскольку они не соответствуют какой-либо из 4 категорий.

 

Таблица 8, б. Четыре класса, четыре категории

и соответствующее число записей в базе данных G.

KOD_OBJ

NAME

ABS

1

Famous

3373

2

Medical

2910

3

Sports

4567

4

Psychological

1007

Следующим шагом является сортировка персон по категориям. В результате было получено XML дерево категорий исходной базы данных. Для этой цели была написана процедура, позволяющая безошибочно изменять категории, сортируя его. Далее база данных была полностью экспортирована в формат Excel, а из него – в формат DBF4, воспринимаемый интеллектуальной системой «Эйдос». 

 

3.2. Технология моделирования

Система «Эйдос» оперирует с кодами объектов, типа номеров в правых колонках в таблицах 2 а,б. Астрономические параметры также имеют собственные коды, именуемые шкалы или масштабы. Например в случае модели М3 (разбиение круга зодиака на три сектора), имеем 23 основных масштаба и 69=23х3 шкал, шесть из которых показаны ниже, в таблице 9.

Если обнаружено, что запись в обучающей базе данных содержит долготу Солнца, принадлежащую интервалу (0.000; 120.000), тогда частота соответствующего кода 1 возрастает на единицу. Таким образом, частота появления масштабов в обучающей базе данных может быть вычислена, что в свою очередь позволяет определить матрицу частот и информационную матрицу. Например, в случае модели М2 (разбиение круга зодиака на два сектора) и обучающей базы данных Database F фрагменты матрицы частот и информационной матрицы представлены в таблицах 10 и 11 соответственно. 

 

Таблица 9. Коды и шкалы модели М3 (указаны только шесть шкал, соответствующих долготе Солнца и Луны).

Code

Name of scale

1

SUNLON-[3]: {0.000, 120.000}

2

SUNLON-[3]: {120.000, 240.000}

3

SUNLON-[3]: {240.000, 360.000}

4

MOONLON-[3]: {0.000, 120.000}

5

MOONLON-[3]: {120.000, 240.000}

6

MOONLON-[3]: {240.000, 360.000}

 

Таблица 10. Фрагмент матрицы частот в случае модели М2
и обучающей базы данных Database F
(частоты даны в абсолютных величинах)

Code of

scale

Code of category

1

2

3

4

5

6

7

8

9

10

11

12

1

6744

2623

2281

2201

1671

1477

1378

1271

1222

1201

1230

1208

2

6896

2502

2286

2270

1702

1433

1297

1306

1220

1195

1155

1152

3

6786

2539

2325

2187

1689

1445

1330

1273

1207

1211

1218

1177

4

6854

2586

2242

2284

1684

1465

1345

1304

1235

1185

1167

1183

5

6261

2401

2070

2039

1561

1343

1307

1185

1125

1086

1134

1156

6

7379

2724

2497

2432

1812

1567

1368

1392

1317

1310

1251

1204

7

6907

2688

2332

2274

1735

1510

1422

1301

1263

1193

1232

1263

8

6733

2437

2235

2197

1638

1400

1253

1276

1179

1203

1153

1097

9

7137

2760

2443

2344

1754

1500

1454

1341

1269

1223

1330

1279

10

6503

2365

2124

2127

1619

1410

1221

1236

1173

1173

1055

1081

 

Заметим, что в действительности информация вычисляется в системе с высокой точностью с 8 десятичными знаками, но в таблице 11 показаны только два десятичных знака (числа умножены на 100). Положительная или отрицательная величина информации в ячейке ij в таблице 10 означает, что категория j имеет соответственно позитивную или негативную корреляцию с масштабом i.

 

Таблица 11. Фрагмент информационной матрицы в случае
модели М2 и обучающей базы данных Database F
(информация дана в единицах Bit*100)

Code of

scale

Code of category

1

2

3

4

5

6

7

8

9

10

11

12

1

3

-1

17

-2

-3

-0

-3

-3

-3

-3

22

-4

2

4

-3

17

-0

-3

-1

-5

-2

-3

-3

20

-5

3

3

-2

18

-2

-3

-1

-4

-3

-3

-3

22

-4

4

3

-2

16

-0

-3

-1

-4

-2

-2

-4

20

-5

5

3

-2

16

-2

-3

-1

-2

-3

-3

-4

22

-2

6

3

-3

17

-1

-3

-1

-6

-2

-2

-3

20

-6

7

3

-1

17

-1

-3

-1

-3

-3

-2

-4

21

-3

8

4

-3

17

-1

-3

-1

-5

-2

-3

-2

21

-6

9

3

-1

17

-1

-3

-2

-3

-3

-3

-4

23

-3

10

3

-3

16

-1

-3

-0

-5

-2

-2

-2

19

-6

 

При завершении обучения нейросети для каждой из моделей, запускается процесс распознавания, начинающийся с определения числа записей в распознаваемом образце. В случае баз данных Database0, Database1 или Database G, содержащих только четыре класса, разумное число записей может быть N=400 или 100 записей на класс. Тренированная компьютерная нейросеть реагирует на любые входные данные, похожие на те, что содержатся в обучающей базе данных. Следовательно, каждая запись из N может быть подвергнута анализу и четыре возможные реакции нейросети могут быть измерены:

¾             Запись с номером n из N принадлежит категории с номером m и это истина, при этом параметр сходства (корреляция) записи с номером n с категорией номер m равен BTnm;

¾             Запись с номером n из N не принадлежит категории с номером m и это истина, при этом параметр сходства (корреляция) записи с номером n с категорией номер m равен Tnm;

¾             Запись с номером n из N принадлежит категории с номером m и это ложь, при этом параметр сходства (корреляция) записи с номером n с категорией номер m равен BFnm;

¾             Запись с номером n из N не принадлежит категории с номером m и это ложь, при этом параметр сходства (корреляция) записи с номером n с категорией номер m равен Fnm.

Эффективная система искусственного интеллекта должна быть сконструирована таким образом, чтобы минимизировать ложные предсказания и увеличить процент верных предсказаний. Для наилучшего понимания результатов пакетного распознавания в работе [4] было предложено специальное эвристическое выражение параметра подобия в форме (10):

 

 

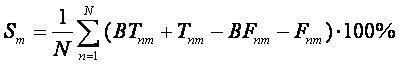
Согласно этому определению параметр подобия изменяется от -100% до 100%, как обычный коэффициент статистической корреляции. Заметим, что если, например Sm=0, то это означает, что категория с номером m распознается плохо, даже если BTnm =0.95 для каждой истиной записи (это может показаться очень хорошим результатом с точки зрения статистики). С другой стороны, если Sm=0.5, то это действительно хороший результат даже если при этом BTnm =0.5 для каждой истиной записи (это означает, что в пакете нет ложных записей и каждая истинная запись была опознана). Рассмотрим ряд экспериментов по распознаванию нескольких категорий.

Эксперимент 1.

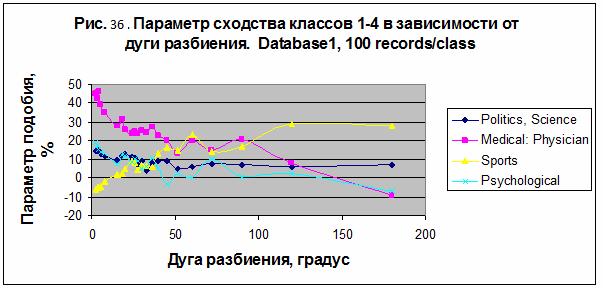
В первом эксперименте мультимодель из 22 моделей, включая M2, M3, M4, M5, M6, M7, M8, M9, M10, M11, M12, M13, M14, M15, M18, M20, M24, M48, M72, M90, M96, M150 (номер модели равен числу сектров разбиения) была создана и затем 22 модели были обучены с базой данных Database1, содержащей 9897 записей. В результате был создан информационный портрет каждого класса. Параметр сходства классов 1-4 из таблицы 8а в случае пакетного распознавания 100 записей на класс представлен на рис. 36 в зависимости от величины дуги разбиения круга зодиака. 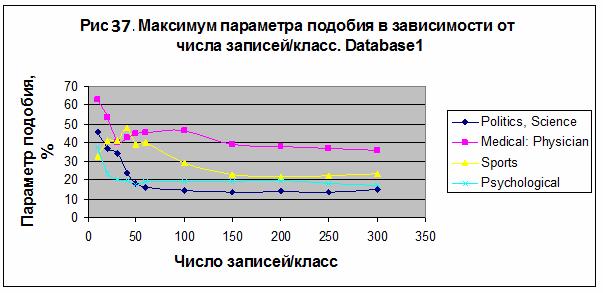Зависимость параметра сходства от параметра числа записей на класс представлена на рис. 37, где отображена величина максимума параметра сходства для каждого из разбиений круга зодиака.

В первом эксперименте наилучший результат получен для категории «Medical: Physician» – S= 45.908% в случае модели M90 для 100 записей/класс. Снижая число записей на класс можно увеличить параметр сходства категории «Medical: Physician» вплоть до 62.722% в случае модели M150 и для 10 записей/класс – см. рис. 37. Для категории «Sport» наилучший результат S= 47.526% получен в случае модели M4 для 40 записей/класс. Заметим, что это меньше, чем вероятность случайного угадывания для этой категории (60.9478%).

 

KOD_OBJ

NAME

ABS

1

Politics, Science

1876

 

2

Medical: Physician

347

3

Sports

6032

4

Psychological

1642

 

 

 

Интересно, что для категории «Medical: Physician» параметр сходства на порядок больше, чем вероятность случайного угадывания (3.5061%). Это свидетельствует, что распознавание в системе «Эйдос-астра» не связано с вероятностью случайного угадывания, на что было указано выше, в главе 2.

 

 

Эксперимент 2.

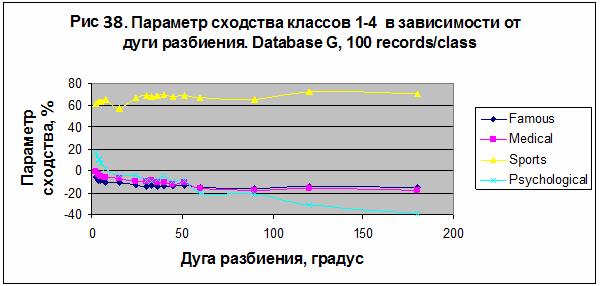
Во втором эксперименте были выполнены все этапы моделирования первого эксперимента, но с базой данных Database G, содержащей 20007 записей. Результаты моделирования представлены на рис. 38 и 39. В этом эксперименте наилучший результат был получен для категории «Sport», S= 72.273% в случае модели M3 для 100 записей на класс.

Class

NAME

ABS

1

Famous

3373

2

Medical

2910

3

Sports

4567

4

Psychological

1007

 

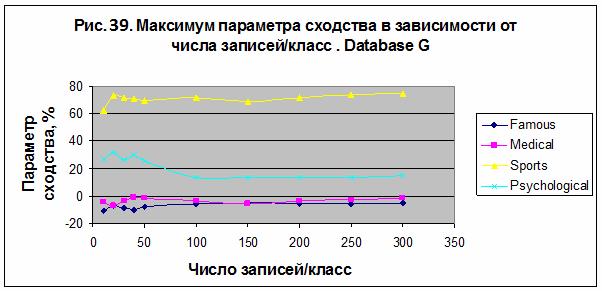
Сравнивая результаты, полученные в экспериментах 1 и 2, находим существенное отличие в поведении параметра сходства категории «Sport» в зависимости от числа секторов разбиения. В первом случае параметр сходства возрастает от -5,936% до 28,935% (рис. 36), а во втором случае колеблется в пределах от 56,716% до 72,273% (см. рис. 38). Это различие объясняется структурой входных параметров двух мульти-моделей, в первой из которых использованы долгота и склонение планет, а во второй только долгота планет и долгота углов 12 домов. Чтобы проверить эту гипотезу, был выполнен

Эксперимент 3.

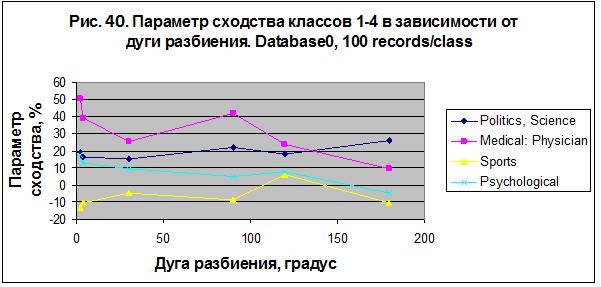
В этом эксперименте мульти-модель из 6 моделей, включая M2, M3, M4, M12, M90 и M150 была сгенерирована и обучена с базой данных Database0 (9897 записей). На рис. 40 представлен параметр сходства классов 1-4 из таблицы 8,а в зависимости от дуги разбиения в случае пакетного распознавания 100 записей на класс. Можно видеть существенное различие с данными экспериментов 1 и 2 для категории «Sport» (смотрите рис. 36 и 38 соответственно). Это особенно заметно для моделей, обученных с базами данных Database1 (рис.36) и Database0 (рис. 40), которые содержат идентичное число записей, но разное число масштабов (23 и 11 соответственно). Полученные результаты свидетельствует о том, что распознавание осуществляется именно по астрономическим параметрам, сокращение числа которых приводит к ухудшению качества распознавания в случае категории «Sport». Интересно отметить, что в этом эксперименте наилучший результат получен для категории «Medical: Physician» – S= 50.634% в случае модели M150, что сравнимо с аналогичными данными, полученными в первом эксперименте (рис. 36). Отсюда можно сделать вывод, что некоторые категории хорошо распознаются по положению планет в зодиаке, тогда как для других категорий требуется знать склонение и положение планет относительно линии горизонта.

Во всех трех экспериментах категория «Sport» распознается наилучшим образом в модели М3 (разбиение на три сектора), тогда как, например, категория «Psychological» наилучшим образом распознается в моделе М150. Отметим, что с ростом числа секторов разбиения параметр сходства трех категорий из четырех, представленных в таблице 8 а, заметно возрастает. Очевидно, что этот эффект можно использовать для повышения качества распознавания. Другой метод повышения качества – это дифференциация категорий на более однородные по составу подкатегории.

Class

NAME

ABS

1

Politics, Science

1876

2

Medical: Physician

347

3

Sports

6032

4

Psychological

1642

 

Для иллюстрации этого метода рассмотрим

Эксперимент 4.

В этом эксперименте мульти-модель составленная из 172 моделей, включая M2, M3, M4, …, M172 и M173 была создана и обучена с базой данных Database F (20007 записей). В этом эксперименте можно сравнить параметр сходства для категории «Sports» и двух подкатегорий – футбол и баскетбол, перечисленных в таблице 12. На рис. 41 представлен параметр сходства категории «Sports» и двух подкатегорий в зависимости от числа секторов разбиения. Наилучший результат распознавания S= 85.864 был получен для подкатегории «Sports: Football» в случае модели М3. Данные параметра сходства для первых пяти разбиений представлены в таблице 13.

 

Таблица 12. Категория «Sports» разбитая на три класса и соответствующее число записей в базе данных Database F.

Class

NAME

ABS

1

Sports

4567

2

Sports: Football

1613

3

Sports: Basketball

2385

 

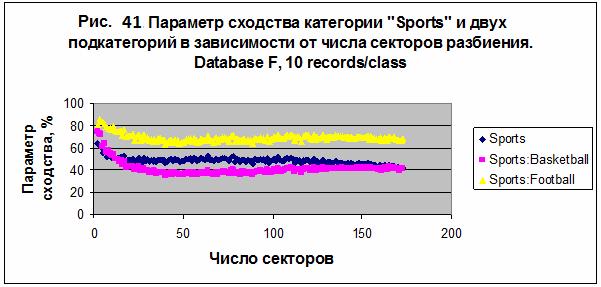
Таблица 13. Параметр сходства категории «Sports» и двух подкатегорий для пяти разбиений.

Число секторов

2

3

4

5

6

Sports

64,398

62,092

60,932

55,065

58,065

Sports:Basketball

74,773

72,722

71,733

61,489

64,101

Sports:Football

80,705

85,864

83,773

83,244

81,443

 

Отметим, что в этом эксперименте категория «Sports» достигает максимального значения при разбиении на 2 сектора. Метод разделения категории на подкатегории особенно эффективен в случае плохо распознаваемых категорий, типа категории «Psychological» на рис. 40. Для иллюстрации рассмотрим

Эксперимент 5.

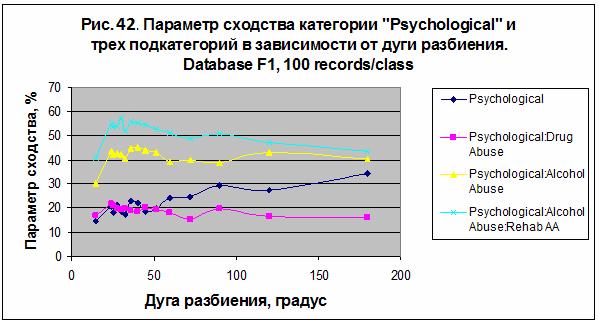
В этом эксперименте мультимодель из 15 моделей, включая M2,M3,M4,M5,M6,M7,M8,M9,M10,M11,M12,M13,M14,M15,M24 была создана и обучена с базой данных Database F1 (20007 записей). На рис. 42 представлены данные для параметра сходства категории «Psychological» и трех подкатегорий, перечисленных в таблице 14. Наилучший результат S= 57.244 был получен для подкатегории «Psychological: Alcohol Abuse: Rehab AA» в случае модели M12. Интересно отметить, что в этой модели категория «Psychological» распознается значительно лучше, чем в других, созданных в экспериментах 1-4.

Результаты распознавания можно также улучшить путем разбиения категории на типичную и нетипичную часть [5].

 

Таблица 14. Категория «Psychological» и три ее подкатегории.

Database F1

Class

NAME

ABS

1

SC:A23-Psychological

1007

2

SC:B112-Psychological:Drug Abuse

282

3

SC:B24-Psychological:Alcohol Abuse

481

4

SC:C457-Psychological:Alcohol Abuse:Rehab AA

267

 

 

 

Кроме того, для повышения достоверности можно использовать эвристический метод: если категория К распознается на нескольких разбиениях с параметром сходства не менее 20%, тогда на пяти разбиениях ее параметр сходства приближается к 100%. Рассмотрим этот вопрос более подробно.

 

3.3. Метод пакетного распознавания карт рождения в системе искусственного интеллекта

Алгоритмы сеточного моделирования, в которых сгущение сетки позволяет улучшить сходимость решения задачи, широко используются в современной науке. Мы применили этот метод для пакетного (совместного) распознавания респондентов из разных стран мира в системе искусственного интеллекта «Эйдос» [36]. Для этого осуществлялось нахождение решение задачи распознавания на 19 сетках различного масштаба, содержащих 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72 секторов соответственно (ряд делителей числа 360). В каждом случае вычислялся параметр сходства для 500 категорий, характеризующих профессиональные качества и обстоятельства жизни 20007 людей, чьи карты были отобраны для формирования первичной базы данных Database A. В качестве входных параметров модели использовались координаты долготы углов 12 домов (в системе Плацидуса), Лунных Узлов и 10 небесных тел – Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна, Плутона.

На рис. 43 представлены результаты пакетного распознавания в координатах параметр сходства (%) – логарифм (десятичный) величины дуги одного сектора разбиения. Можно видеть, что в каждом тестовом примере данные рассеяны вокруг среднего значения, максимум которого приходится на величину дуги в 120 градусов, что соответствует разбиению круга зодиака на три сектора. Для наглядности на рис. 44 представлена средняя величина параметра сходства в зависимости от числа секторов разбиения.

Как было установлено, средний параметр сходства монотонно снижается с увеличением числа секторов разбиения, когда их больше 3. Поэтому в дальнейшем анализе использовались 18 разбиений круга Зодиака вплоть до 60 секторов включительно. Для каждой карты рождения можно определить максимальную величину параметра сходства, что соответствует некоторой категории. Переходя на сетки другого масштаба моделирования, находим ряд 18 значений максимальной величины параметра сходства и ряд из 18 соответствующих категорий, номера которых лежат в интервале от 1 до 500. Если бы категории были случайными, то вероятность появления любой из них в этом ряду составляла бы 18/500=0,036. Вероятность двукратного появления составляет уже (18/500)2= 0,001296, трехкратного – (18/500)3=0,000046656, четырехкратного – (18/500)4= 0,000001679616 и т.д.

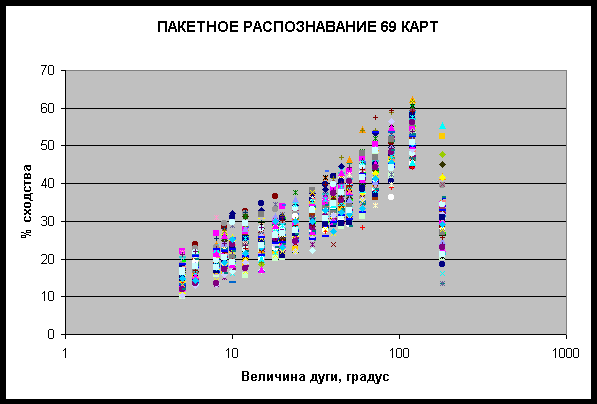
Рис. 43. Зависимость параметра сходства от величины дуги разбиения при пакетном распознавании 69 карт (логарифмическая шкала по горизонтальной оси).

 

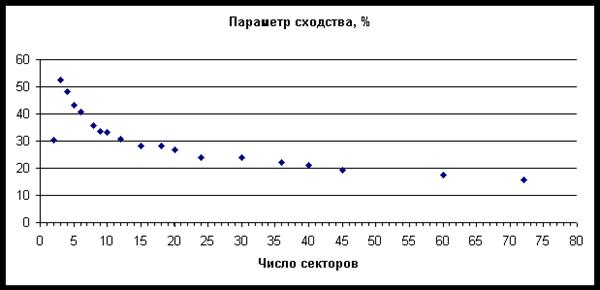
Рис. 44. Зависимость средней величины параметра сходства при распознавании 69 респондентов от числа секторов разбиения.

 

Если категория появилась 3 и более раз подряд, то ее можно формально рассматривать как закономерное проявление качества, присущего данному респонденту.

Во всех изученных картах было обнаружено трехкратное появление одной категории в 18 тестах, а в 47 картах из 69 одна категория проявилась 6 и более раз. На рис. 45 представлены данные распознавания карты типичного респондента в координатах число секторов – номер категории. Из этих данных можно видеть, что категория «487» повторяется 10 раз подряд, категория «127» – шесть раз, и две категории представлены по одному разу. Интересно отметить, что в этом примере повторяющиеся категории «487» и «127» дублируют друг друга по смыслу и означают «Развод родителей». Но одна из них является обстоятельством жизни, а другая событием. Объединяя их вместе, находим, что «Развод родителей» был опознан в данной карте в 16 случаях из 18 тестов на сетках разного масштаба. Это означает, что данная карта была опознана с высокой точностью.

Для нахождения всех категорий, присущих данному респонденту, поступим следующим образом. Зададим минимальный уровень сходства, например 20%. Ограничимся 10 сетками с числом секторов разбиения 3, 4, 5, 6, 9, 12, 15, 18, 20, 24 соответственно. Составим таблицу распознанных категорий на сетке каждого масштаба. Для карты №1 находим всего 373 распознанных категорий с уровнем сходства, не менее 20%, среди которых есть повторяющиеся. Отберем те из них, которые повторяются 4 и более раз. Составим таблицу 15, в которой указан номер категории, ее описание и частота повторения. Среди категорий есть такие, которые уже реализовались в жизни субъекта – это категории под номером 3, 5, 29, 65, 66, 159, 247, 269, 292, 423. Остальные категории имеют смысл прогноза для этого молодого человека. Например, для преуспевания в США ему можно рекомендовать профессии дизайнера, менеджера, полицейского или фотографа.

 

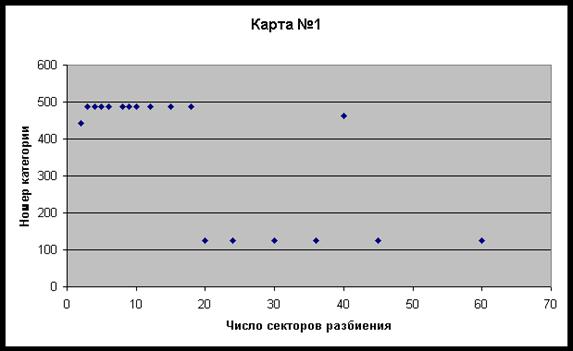
Рис 45. Данные идентификации карты №1
на сетках 18 масштабов.

 

Данный подход отличается тем, что при распознавании образов используются корреляционные связи, которые вычисляются на каждой сетке отдельно. Эти связи выявляются путем многокритериальной типизации респондентов обучающей выборки по исследуемым категориям. При этом на этапе синтеза модели рассчитывается количество информации, которое содержится в фактах попадания долгот углов в интервалы (рассматриваемые как критерии), о принадлежности респондента к тем или иным категориям, а на этапе идентификации эта информация используется для расчета степени сходства конкретных респондентов с обобщенными категориями.

 

Таблица 15. Список повторяющихся категорий
при распознавании карты №1

Категория

Описание категории

Частота
повторения

3

CATEGORIES: ###-Advantaged

8

5

CATEGORIES: ###-Affluent family

6

6

CATEGORIES: ###-Age 80

5

29

CATEGORIES: ###-Boxing

4

40

CATEGORIES: ###-Coach

4

65

CATEGORIES: ###-Family large

4

66

CATEGORIES: ###-Family noted

8

77

CATEGORIES: ###-Gracious

4

87

CATEGORIES: ###-Infant mortality

4

96

CATEGORIES: ###-Lottery

5

126

CATEGORIES: ###-Parent absent

10

127

CATEGORIES: ###-Parents divorced

8

137

CATEGORIES: ###-Production jobs

9

140

CATEGORIES: ###-Public relations

6

159

CATEGORIES: ###-Siblings

5

174

CATEGORIES: ###-Suicide Attempt

5

184

CATEGORIES: ###-Verbal abuse

4

188

CATEGORIES: ###-Winnings

5

195

CATEGORIES: A3-Criminal Victim

4

234

CATEGORIES: B2612-Missing person

4

247

CATEGORIES: B36-Noted kids

4

269

CATEGORIES: B803-Constitution strong

4

283

CATEGORIES: C10628-Photography

9

292

CATEGORIES: C12063-Unusual

7

349

CATEGORIES: C19244-Designer

9

356

CATEGORIES: C206-Surgery

5

367

CATEGORIES: C2354-Manager

7

407

CATEGORIES: C7589-Police

10

423

CATEGORIES: C9318-Physical

4

462

EVENT_LIFE: Family trauma

8

480

EVENT_LIFE: Medical procedure

5

482

EVENT_LIFE: Missing Person

5

487

EVENT_LIFE: Parents divorced

10

491

EVENT_LIFE: Retain professional help

4

494

EVENT_LIFE: Sex Victimization/Rape

4

 

Предложенный метод распознавания позволяет не только идентифицировать субъекта по ряду признаков и категорий, но и прогнозировать некоторые обстоятельства и события его жизни. Этот метод удается обобщить, путем добавления новых алгоритмов распознавания на множестве сеток различного масштаба.

 

3.4. Алгоритмы и законы типизации
и идентификации субъектов
по астрономическим данным
на момент рождения

 

Входные данные задачи представляют собой таблицу, содержащую 20007 записей (строк) независимых респондентов, каждый из которых характеризуется номером записи, именем, полом, датой и временем рождения, местом рождения, собственной биографией и набором категорий и событий жизни. В настоящем исследовании для повышения достоверности идентификации из списка категорий были отобраны только те из них, которые соотносятся с профессиями. 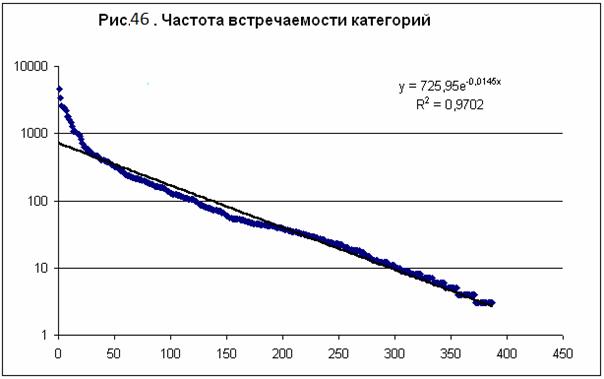Полученный список профессиональных категорий содержит только 387 наименований (см. Приложение 1 монографии [2]), которые представлены в исходной БД с разной частотой встречаемости – рис. 46. Частотное распределение с большой степенью точности описывается экспонентой (распределение Пуассона) – прямая сплошная линия на рис. 46. Суммируя все частоты, находим общее число исследуемых случаев N= 69742. Учитывая, что в исходной БД содержится только 20007 данных независимых респондентов, находим среднее число категорий, приходящихся на одну карту, n=N/20007=3,49. В качестве входных астрономических параметров модели использовались координаты долготы углов 12 домов (в системе Плацидуса), Лунных Узлов и 10 небесных тел – Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна, Плутона. Поскольку модель является дискретной, координаты долготы задавались на 12 сетках различного масштаба с числом секторов разбиения 3, 4, 5, 6, 9, 12, 15, 18, 20, 24, 36, 72 соответственно.

При исследовании частных моделей были установлены некоторые статистические закономерности распознавания, позволяющие повысить эффективность моделей. Во-первых, во всех частных моделях наблюдается обратная зависимость параметра сходства от частоты встречавшийся категории: чем выше частота, тем ниже параметр сходства. На рис. 47 представлены результаты распознавания категорий в модели с 72 секторами. В этом случае зависимость параметра сходства от частоты описывается степенной функцией с показателем степени b=-0,5355. Аналогичная зависимость наблюдается и для максимального по всем моделям параметра сходства – рис. 48 (на рисунках 15-16 по горизонтальной оси дана абсолютная частота, т.е. общее число случаев данной категории).

 

 

Во-вторых, параметр сходства зависит от числа секторов разбиения. Все категории можно разбить на три класса в зависимости от величины частоты повторяемости и поведения параметра сходства при изменении числа секторов разбиения. Первый класс составляют категории, для которых параметр сходства убывает с ростом числа секторов разбиения. Этот класс категорий характеризуется высокой частотой повторяемости при высоком уровне распознавания, что соответствует данным, лежащим выше линии корреляционной зависимости на рис. 46-47. Некоторые категории этого класса приведены в таблице 16 вместе с корреляционными зависимостями параметра сходства от числа секторов разбиения.

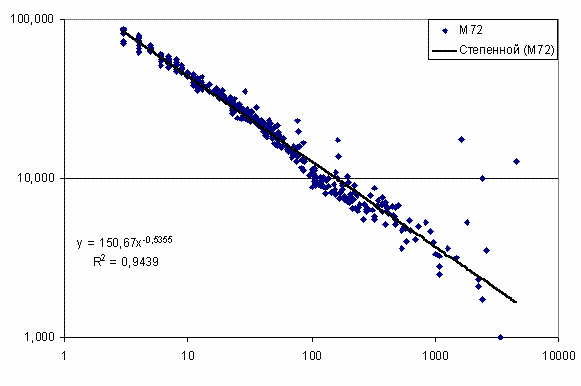
Рис. 47. Зависимость параметра сходства от частоты
встречаемости категории в модели М72

 

Второй класс составляют категории, для которых параметр сходства возрастает с ростом числа секторов разбиения. Этот класс категорий характеризуется низкой частотой повторяемости и относительно высоким параметром сходства, что соответствует данным, группирующимся вблизи линии корреляционной зависимости на рис. 47-48. Большая часть исследуемой в настоящей работе БД представлена категориями этого класса, поэтому средний параметр сходства возрастает с ростом числа секторов – рис. 49. Отметим, что в прикладных целях используется именно этот класс категорий, поэтому для повышения вероятности распознавания широко применяется анализ на множестве сеток, полученных при разбиении круга зодиака вплоть до градусов и минут. Третий класс составляют категории, для которых параметр сходства изменяется немонотонно с ростом числа секторов разбиения. Как правило, эти категории имеют среднюю частоту повторяемости и относительно небольшую величину параметра сходства. Общее их число невелико в исследуемой БД, поэтому они не оказывают существенного влияния на поведение среднего параметра распознавания.

 

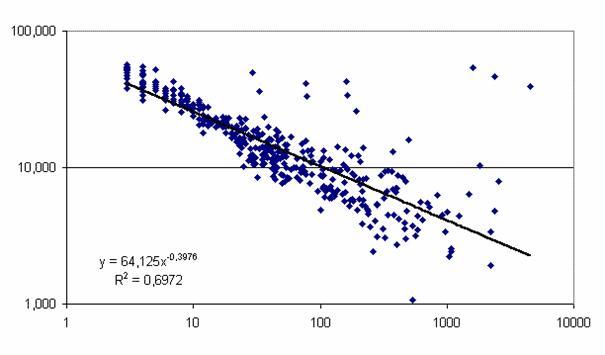
Рис. 48. Зависимость максимального параметра сходства от частоты повторяемости категории в 12 моделях

 

Таблица 16. Категории первого класса, их абсолютная частота повторяемости и корреляционная зависимость параметра сходства от числа секторов разбиения.

Категории

Частота

Корреляционная

зависимость

SC:A53-Sports

4567

y = 75,297x-0,3888

R2 = 0,9747

SC:B111-Sports:Basketball

2385

y = 109,23x-0,5494

R2 = 0,9909

SC:B173-Sports:Football

1613

y = 108,72x-0,3949

R2 = 0,9627

SC:B41-Occult Fields:UFO sighting

502

y = 24,008x-0,3275

R2 = 0,8406

SC:B404-Business:Sex Business

194

y = 45,03x-0,3428

R2 = 0,9783

SC:C78-Famous:Awards:Olympics

162

y = 67,868x-0,3678

R2 = 0,8959

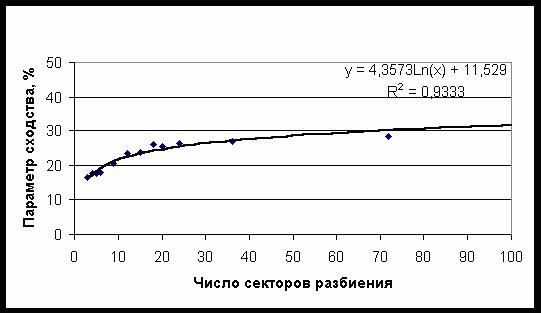
Рис. 49. Зависимость среднего параметра сходства от числа секторов разбиения

 

Насколько представительной является исследуемая БД и какое поколение в ней представлено? Только 2576 карт принадлежат людям, родившимся до 1901 года, остальные родились в 20 веке вплоть до 1998 года включительно. Распределение Солнца, Юпитера и Сатурна по знакам зодиака является достаточно однородным – рис. 50, однако распределение Урана указывает на преобладание карт поколения 1941-1948 (Уран в знаке Близнецов) и 1949-1956 (Уран в знаке Рака).

 

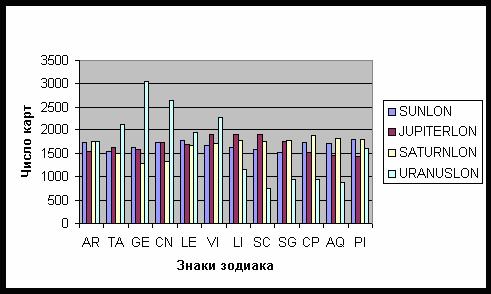
Рис. 50. Распределение планет по знакам зодиака

 

Для обработки результатов пакетного распознавания на множестве сеток выше был предложен алгоритм, который был дополнен еще четырьмя алгоритмами, для выбора наиболее эффективного из них. Таким образом, сравнивались пять алгоритмов, получивших общее название РЕЖИМЫ ГОЛОСОВАНИЯ МОДЕЛЕЙ:

1.               Для нахождения всех категорий, присущих данному респонденту, зададим минимальный уровень сходства, например 20%, составим таблицу распознанных категорий на сетке каждого масштаба с числом секторов разбиения 3, 4, 5, 6, 9, 12, 15, 18, 20, 24 соответственно и отберем те из них, которые повторяются 4 и более раз [2].

2.               Результаты распознавания в частных моделях просто УСРЕДНЯЮТСЯ, т.е. в итоговой карточке идентификации для каждого класса уровень сходства респондента с обобщенным классом является СРЕДНИМ его уровней сходства с этим классом всех частных карточек идентификации.

3.               В итоговую карточку идентификации респондента берется уровень сходства этого респондента с классом из той частной карточки идентификации, в которой он МАКСИМАЛЬНЫЙ (из всех частных карточек).

4.               Когда в итоговую карточку идентификации респондента берется уровень сходства этого респондента с каждым классом из частной карточки идентификации, полученной в той частной модели, которая по результатам измерения достоверности распознавания ДАННОГО КЛАССА показала МАКСИМАЛЬНУЮ достоверность из всех исследованных моделей.

5.               Результаты распознавания в частных моделях УСРЕДНЯЮТСЯ с учетом достоверности идентификации классов в различных частных моделях, например, берется СРЕДНЕЕ СУММЫ ПРОИЗВЕДЕНИЙ уровней сходства с данным классом на достоверность его идентификации в частных моделях.

Сравнение осуществлялось следующим образом. Согласно первому алгоритму выбирался список распознанных категорий, определялось их число, а затем по 4 другим моделям выбирался список с таким же числом категорий, распознанных наилучшим образом по данному алгоритму. В таблице 11 дан пример такого сопоставления. Путем сопоставления номеров категорий можно определить те из них, которые присутствуют во всех пяти моделях. В данном случае это 18 категорий, собранных в таблице 17.

 

Таблица 17. Категории, опознанные в пяти моделях и
упорядоченные по параметру сходства первой модели

№

Категория

Параметр сходства

165

SC:B781-Law:Police/Security.

10

387

SC:E793-Medical:Doctor:Alternative methods:Psychic healer:Hypnoth

10

36

SC:B1330-Sports:Martial Arts.

9

323

SC:C802-Work:Maintenance Field:Cleaning service.

9

357

SC:D258-Famous:Greatest hits:Art field:Photography field.

9

360

SC:D376-Business:Sports Business:Coach/ Manager/ Owner:Manager.

9

203

SC:C1257-Education:Teacher:Coach.

8

298

SC:C657-Art:Commercial artist:Pro.

8

35

SC:B1295-Law:Fire department.

7

193

SC:C1151-Education:Teacher:Medicine.

7

20

SC:B1040-Work:Self-employed.

6

68

SC:B256-Art:Photography.

6

191

SC:C1130-Education:Teacher:Nursing.

6

273

SC:C560-Education:Teacher:Astrology.

6

315

SC:C760-Art:Fine art artist:Secondary.

6

65

SC:B246-Financial:Winnings/ Lottery.

5

220

SC:C175-Business:Business/Marketing:Public relations.

5

386

SC:E748-Business:Sex Business:Porno Market:Films:Superstar/star.

5

 

Поскольку категории в таблице 17 распознаются по всем пяти алгоритмам, все пять алгоритмов можно считать эквивалентными в смысле определения множества категорий из таблицы 17. Различие же алгоритмов может проявиться в установлении приоритета категорий. Например, категория 165 (SC:B781-Law:Police/Security) распознается по первому алгоритму как наиболее достоверная, по второму алгоритму она оказывается на 4 месте, по третьему – на 7, по 4 – на 15, а по 5 – на 33. С другой стороны, категория 36 (SC:B1330-Sports:Martial Arts), которая распознается по пятому алгоритму с наибольшей достоверностью, также хорошо распознается и по первому алгоритму, но плохо распознается по третьему. Это означает, что каждый из алгоритмов имеет погрешность по отношению к другому, а наиболее эффективным может оказаться алгоритм, являющейся комбинацией указанных выше пяти алгоритмов. Такой комбинацией может быть описанный метод определения пересечения множества категорий, распознанных по каждому алгоритму.

 

3.5. Метод разделения категорий в задаче типизации и идентификации субъектов по астрономическим данным на момент рождения

В предыдущем пункте выполнено исследование моделей распознавания субъектов по астрономическим данным на момент рождения с целью определения наиболее эффективного алгоритма идентификации и типизации для профессиональной базы данных (БД) содержащей 387 категорий на 12 сетках различного масштаба. Было установлено, что категории можно разбить на три класса в зависимости от поведения параметра сходства от числа секторов. К первому классу были отнесены категории, для которых параметр сходства убывает с ростом числа секторов. Ко второму классу относятся категории, у которых параметр сходства возрастает с ростом числа секторов, а к третьему классу – категории, у которых параметр сходства ведет себя немонотонно. Логично предположить, что если отобрать категории первого класса в отдельную базу данных, то для их распознавания достаточно будет сетки, например, из четырех секторов. В данном разделе изучен вариант модели распознавания субъектов по астрономическим данным на момент рождения для профессиональной БД содержащей 184 категории первого и третьего класса на сетке из 4-х секторов. Мы покажем, что для этих категорий параметр сходства практически не зависит от частоты повторяемости категорий в исходной БД, содержащей 20007 данных независимых респондентов. Путем исключения категорий первого и третьего класса из профессионально БД содержащей 387 категорий, получена база данных категорий второго класса в составе 203 категорий.

Из списка категорий исследуемой БД отберем те из них, которые соотносятся с профессиями и для которых параметр сходства убывает с ростом числа секторов или изменяется немонотонно. Полученный список профессиональных категорий содержит только 184 наименования (см. Приложение 2 монографии [2]), которые представлены в исходной БД с разной частотой повторяемости – рис. 51. Частотное распределение с большой степенью точности описывается экспонентой (распределение Пуассона) – прямая сплошная линия на рис. 51. Суммируя все частоты, находим общее число исследуемых случаев N= 60011. Учитывая, что в исходной БД содержится 20007 данных независимых респондентов, находим среднее число категорий, приходящихся на одну карту, n=N/20007=2,9995.

 

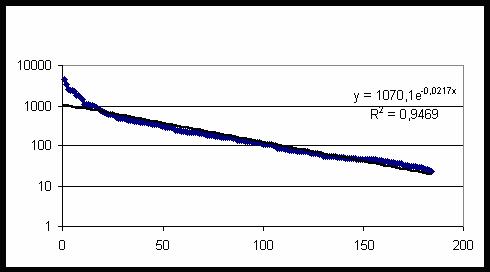
Рис. 51. Частота повторяемости 184 категорий первого класса

 

Распознавание отобранных 184 категорий осуществлялось на сетке из 4-х секторов, полученных путем деления круга зодиака на 4 части, начиная с нулевого градуса знака Овна. Как оказалось, для отобранных категорий параметр сходства практически не зависит от частоты повторяемости категории – рис. 52, тогда как в аналогичной задаче исследованной выше, параметр сходства убывает с ростом частоты – рис. 47. Можно сравнить параметры сходства идентичных категорий в этих двух задачах – рис. 53. Как следует из полученных данных, эти параметры связаны линейной зависимостью, причем параметр сходства при распознавании категорий в составе БД из 184 категорий приблизительно на 10% выше, чем в составе БД из 387 категорий (см. рис. 53).

 

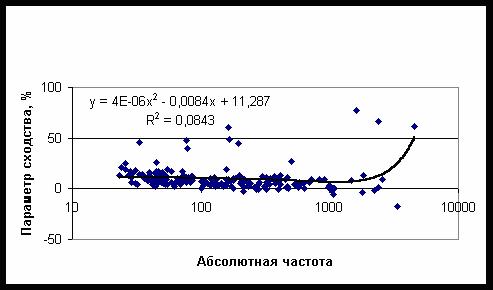
Рис. 52. Зависимость параметра сходства от частоты повторяемости 184 категорий первого класса

 

Отсюда следует, что обратная зависимость параметра сходства от частоты, возникает из-за наличия в исследованной БД 203 категорий второго класса. Эти категории отличаются малой частотой повторяемости, поэтому вероятность их случайного угадывания является крайне низкой. При распознавании категорий этого класса требуется большое число входных параметров, поэтому они хорошо распознаются на сетках с большим числом секторов (число входных параметров задачи пропорционально числу секторов).

Упорядочивая данные по параметру сходства, можно выделить наиболее хорошо распознаваемые категории первого класса – таблица 12. Среди 32 категорий, приведенных в этой таблице, 8 составляют спортивные категории, 6 – различный бизнес, 5 – оккультные, 3 – медицинские доктора, 3 – дизайнеры, фотографы и художники, 2 – писатели детективов и фантастики, 2 – игроки, 2 – строители и 1 – экипажи судов, поездов и автобусов.

 

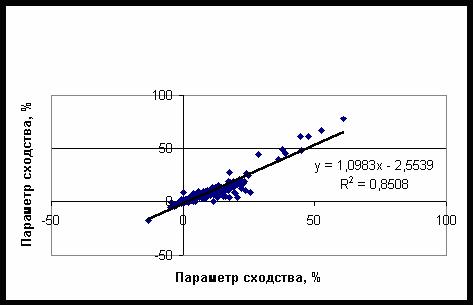
Рис. 53. Зависимость параметра сходства при распознавании 184 категорий первого класса от параметра сходства при распознавании 387 смешанных категорий

 

 

 

Таблица 18. Список наиболее хорошо распознаваемых
категорий первого класса

NAME

Абсолютная

частота

Параметр

сходства

SC:B173-Sports:Football

1613

77,51

SC:B111-Sports:Basketball

2385

66,58

SC:A53-Sports

4567

61,06

SC:B626-Occult Fields:Out of Body exper

162

60,57

SC:C405-Business:Sex Business:Prostitut

165

48,61

SC:C1198-Occult Fields:Psychic/ Medium/

77

47,68

SC:C1340-Medical:Doctor:Chiropractor

33

45,49

SC:B404-Business:Sex Business

194

44,53

SC:C170-Medical:Doctor:Psyhotherapist

79

39,61

SC:B41-Occult Fields:UFO sighting

502

27,02

SC:B236-Business:CPA/ Auditor/ Accounta

45

26,46

SC:B406-Art:Stage/ Set design

26

24,51

SC:B437-Sports:Skiing

24

20,81

SC:B238-Business:Clerical/ Secretarial

158

19,03

SC:C422-Occult Fields:Psychic/ Medium/

26

18,92

SC:B496-Sports:Boxing

55

18,70

SC:B272-Art:Cartoonist

31

18,33

SC:B246-Financial:Winnings/ Lottery

59

17,44

SC:B715-Sports:Field and Track

47

17,43

SC:B492-Sports:Skating

45

17,09

NAME

Абсолютная

частота

Параметр

сходства

SC:B256-Art:Photography

47

17,04

SC:B54-Sports:Baseball

72

16,96

SC:B217-Travel:Crew/ Ship, Train, Bus

28

16,69

SC:D988-Occult Fields:Astrologer:Pro:AF

50

16,54

SC:B374-Business:Sports Business

40

16,36

SC:C709-Medical:Doctor:Surgeon

30

16,32

SC:C303-Business:Business/Marketing:Sto

30

16,14

SC:C250-Work:Building Trades:Builder

44

15,16

SC:B259-Writers:Sci-Fi/ Fantasy/ Horror

47

14,76

SC:B511-Writers:Detective/ Mystery

33

14,60

SC:B315-Financial:Gambling

35

14,26

SC:C631-Work:Building Trades:Architect/

48

13,59

 

Плохо распознаваемые категории этого класса приведены в таблице 19. Из 32 категорий этого типа 12 составляют различные знаменитости (!), 6 – наука и образование, 5 – журналисты, писатели и издатели журналов, 2 – политики, 2 – юристы, 2 – музыканты-инструменталисты и по одной категории фермеров, оккультистов и финансистов. Интересно, что если знаменитостей сгруппировать в отдельные категории по характеру получаемой премии, то они попадают во второй класс и распознаются довольно хорошо. Рассмотрим этот вопрос более подробно.

 

Таблица 19. Плохо распознаваемые категории
первого класса

NAME

Абсолютная

частота

Параметр

сходства

SC:A108-Education

1002

3,024

SC:C149-Famous:Greatest hits: Occult field

118

2,834

SC:C603-Work:Food and Beverage:Farmer/

44

2,774

SC:C636-Famous:Awards:Hall of Fame

62

2,732

SC:B16-Famous:News figure

130

2,341

SC:B33-Writers:Columnist/ journalist

213

2,31

SC:A120-Science

466

1,999

SC:C125-Science:Biology:Medicine

311

1,98

SC:C110-Education:Teacher:High school t

150

1,967

SC:C296-Famous:Greatest hits:Astrology

173

1,915

SC:B171-Writers:Playwright/ script

233

1,828

SC:C260-Famous:Greatest hits:Writing fi

262

1,779

SC:B46-Famous:Awards

973

1,755

SC:A40-Occult Fields

2396

1,694

SC:C11-Entertainment:Music:Instrumental

461

1,12

SC:B105-Writers:Textbook/ Non-fiction

569

0,875

SC:B158-Politics:Public office

475

0,729

SC:C551-Famous:Greatest hits:Science fi

100

0,684

SC:B6-Entertainment:Music

1086

0,563

SC:B109-Education:Teacher

636

0,43

SC:A99-Financial

1075

0,017

SC:B505-Education:Public speaker

179

-0,067

SC:B152-Law:Attorney

280

-0,644

SC:A151-Law

400

-0,842

SC:B52-Famous:Historic figure

322

-0,923

SC:B106-Writers:Publisher/ Editor

271

-0,929

SC:A19-Writers

2222

-1,255

SC:A38-Politics

1039

-1,875

SC:B340-Famous:Royal family

214

-3,105

SC:B45-Famous:Greatest hits

1794

-4,091

SC:B48-Famous:Top 5% of Profession

1073

-5,363

SC:A15-Famous

3372

-16,945

 

Общие свойства категорий второго класса

Список категорий второго класса, упорядоченных по частоте повторяемости, приведен в Приложении 3 монографии [2] вместе с параметром сходства, полученным на сетке, содержащей 72 сектора. Частотное распределение категорий второго класса с большой степенью точности описывается степенной функцией – рис. 54.

Зависимость параметра сходства от частоты также описывается степенной функцией – рис. 55. Поскольку вероятность случайного угадывания пропорциональна частоте повторяемости, из этих данных следует, что для второго класса категорий параметр сходства обратно пропорционален вероятности случайного угадывания в степени a=0,5594.

 

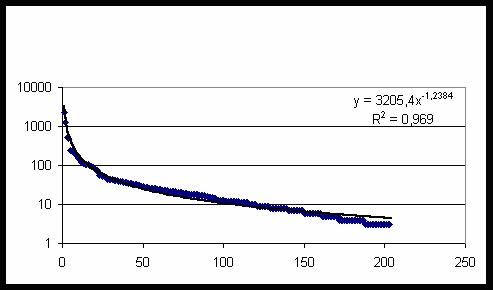
Рис. 54. Частота повторяемости категорий второго класса

 

 

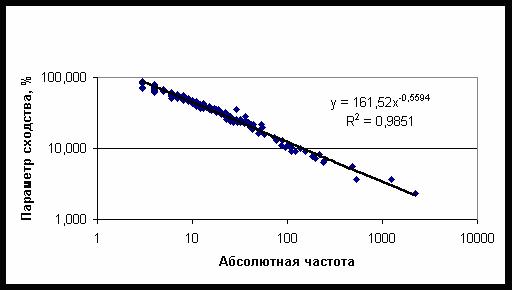
Рис. 55. Зависимость параметра сходства от частоты повторяемости категорий второго класса.

 

Рассмотрим категорию ЗНАМЕНИТЫЙ (Famous), разбитую на малые группы по характеру получаемой премии или социальному отличию – таблица 14. Из данных этой таблицы следует, что обладатели редких премий распознаются лучше, нежели обладатели известных, но широко распространенных премий. Становится понятной и закономерность, отраженная на рис. 55. Малочисленные группы в ряду многочисленных групп всегда более заметны, поэтому распознаются лучше. Например, эфиоп на улицах Москвы будет более заметен, нежели в ряду соплеменников на улицах Аддис-Абебы, поэтому его легко будет распознать. С другой стороны, блондин из Москвы, впервые попавший на улицы Аддис-Абебы, немедленно попадет в малочисленную категорию белых людей, поэтому будет легко узнаваем. В этом смысле распознавание в системе искусственного интеллекта «Эйдос»  существенно отличается от простой статистики, в которой главным критерием достоверности является отклонение от генеральной совокупности.

 

Таблица 20. Категория Famous (знаменитый) разбитая на малые группы по характеру премии

NAME

Абсолютная

частота

Параметр

сходства

SC:C1234-Famous:Awards:Peabody

3

85,512

SC:D258-Famous:Greatest hits:Art field:Photography field

12

36,07

SC:C1043-Famous:Awards:Honorary degrees

17

33,782

SC:D635-Famous:Greatest hits:Art field:Fashion field

23

25,813

SC:C587-Famous:Awards:Grammy

37

23,461

SC:B750-Famous:Socialite

37

23,413

SC:D150-Famous:Greatest hits:Occult field:Spiritual field

43

18,411

SC:C690-Famous:Awards:Pulitzer prize

52

18,231

SC:C362-Famous:Greatest hits:Business field

50

16,385

SC:C588-Famous:Awards:Emmy

76

12,811

SC:D307-Famous:Greatest hits:Social field:Political field

95

10,432

SC:C306-Famous:Greatest hits:Social field

110

10,186

SC:C344-Famous:Awards:Oscar

153

9,158

SC:D60-Famous:Greatest hits:Art field:Beauty

184

7,649

SC:D67-Famous:Greatest hits:Art field:Music field

237

6,256

SC:C59-Famous:Greatest hits:Art field

534

3,65

 

При объединении знаменитостей в одну категорию A15-Famous получается довольно многочисленная группа (3372 случая), которая не имеет никаких общих признаков, кроме того, что эти люди знамениты. Поэтому параметр сходства/различия у этой группы имеет значение -16,945, что указывает на неоднородность группы. При разбиении же группы на малые подгруппы с ярко выраженными профессиональными признаками, параметр сходства становится положительным, что указывает на возросшую однородность состава подгрупп. Аналогичный пример дает категория ОБРАЗОВАНИЕ – таблица 21. Малые группы преподавателей, объединенные по специальностям, распознаются на порядок лучше, чем общая категория A108-Education, содержащая 1002 случая. При этом подгруппы общей категории относятся ко второму классу, т.е. хорошо распознаются на сетке из 72 секторов, а общая категория относится к первому классу, т.е. лучше всего распознается на сетке из 4 секторов.

 

Таблица 21. Категория ОБРАЗОВАНИЕ
разбитая на малые подгруппы

NAME

Абсолютная

частота

Параметр

сходства

SC:D1256-Education:Teacher:Science:Computer science

3

87,215

SC:C1486-Education:Public speaker:Brilliant orator

3

86,079

SC:D1246-Education:Teacher:Science:Philosophy

3

85,142

SC:C1130-Education:Teacher:Nursing

3

85,135

SC:D1414-Education:Teacher:Science:Psychology

3

81,323

SC:C1434-Education:Teacher:Adult Education

4

77,007

SC:C1257-Education:Teacher:Coach

4

76,057

SC:C1262-Education:Teacher:Special Ed

4

73,722

SC:E508-Education:Public speaker:Lecturer:Astrology

lecturer:Speaker at AFA conventions

3

73,083

SC:D1105-Education:Teacher:Science:Physics

6

57,329

SC:D1180-Education:Teacher:Science:History

6

57,29

SC:B762-Education:Librarian

7

56,983

SC:D951-Education:Teacher:Art:Dance

6

56,144

SC:D755-Education:Teacher:Occult teacher:Religous

8

56,121

SC:D507-Education:Public speaker:

Lecturer:Astrology lecturer

6

54,198

SC:C229-Education:Engineer:Chemical

9

50,112

SC:C1151-Education:Teacher:Medicine

9

48,512

SC:C983-Education:Engineer:Civil

8

48,31

SC:C1219-Education:Teacher:Communications

10

46,212

SC:C783-Education:Teacher:

Physical education/Gymnastic/Sport

12

40,93

SC:D1010-Education:Public speaker:

Lecturer:International lecturer

12

38,247

SC:C619-Education:Teacher:Language/English

19

35,764

SC:C705-Education:Teacher:Occult teacher

18

35,053

SC:C1174-Education:Engineer:Electrical

19

33,407

SC:C159-Education:Teacher:Art

25

28,574

SC:C500-Education:Teacher:Music

25

27,795

SC:C637-Education:Engineer:Aerospace

24

26,285

SC:C803-Education:Engineer:Mechanical

30

23,321

SC:C684-Education:Teacher:School/College teacher

35

22,535

SC:C560-Education:Teacher:Astrology

35

22,291

SC:D451-Education:Teacher:

High school teacher:Professor

109

9,1

SC:C506-Education:Public speaker:Lecturer

122

9,088

 

Существуют категории, например, B173-Sports:Football, которые характеризуют заведомо однородные группы, объединенные по яркому профессиональному признаку. У этой группы самый высокий параметр сходства среди категорий первого класса, несмотря на ее многочисленность (1613 случаев). На втором месте по параметру сходства оказалась группа баскетболистов. Но если объединить футболистов и баскетболистов в одну большую группу СПОРТ, параметр сходства понижается, поскольку группа становится неоднородной – рис. 39. Такие многочисленные однородные по составу группы хорошо распознаются на сетке из четырех секторов. С другой стороны, малочисленные однородные группы хорошо распознаются на сетках с большим числом секторов (в данной случае распознавание осуществлялось на сетке, включающей 72 сектора). На первый взгляд кажется, что признаки малочисленных профессиональных групп не могут быть использованы для тестирования, поскольку не выполнены статистические критерии достоверности. На самом же деле критерий сходства отличается от стандартных критериев достоверности, типа критерия Стьюдента. Критерий сходства хорошо иллюстрирует следующий пример. Предположим, что у нас есть база данных, включающая 20007 фотографий известных людей. Мы хотим протестировать фотографии неизвестных людей, чтобы выяснить, на кого они более всего похожи внешне. У нас есть интеллектуальная система, которая позволяет отобрать из БД насколько десятков фотографий и расставить их по параметру сходства. При этом оказывается, что на одних фотографиях схожесть достигается за счет формы носа, на других за счет овала лица, на третьих за счет разреза глаз и т.д. Заменим теперь фотографии на карты рождения, включающие описание астрономических параметров, социальных и психологических категорий. Задача распознавания при этом не изменилась, но на выходе мы получим набор категорий, характеризующих тестируемого субъекта. Если при этом субъект оказался похож на малочисленную профессиональную категорию, то это нельзя назвать простым совпадением. Ведь совпадение с малочисленной группой маловероятно. Кроме того, путем прямых экспериментов доказано, что вероятность распознавания по астрономическим данным на момент рождения в много раз превосходит вероятность случайного угадывания [4]. Следовательно, полученные результаты так или иначе могут быть отнесены к числу характеристик субъекта, но при этом необходимо помнить, что сходство и подобие не означает тождество.

Заметим, что первые эксперименты по идентификации и типизации субъектов по астрономическим данным на момент рождения были выполнены на смешанной базе данных, содержащей 500 социальных (профессиональных) и личностных (в т.ч. психологических) категорий [1]. Для повышения уровня параметра сходства и достоверности идентификации была образована новая база данных, содержащая только 387 социальных (профессиональных) категорий. Полученные с ее помощью результаты отличаются высокой степенью достоверности идентификации. Рассмотренный метод позволяет повысить параметр сходства путем разделения категорий на классы, не увеличивая числа входных параметров задачи.

 

3.5. Типизации и идентификации субъектов
по астрономическим данным на момент
рождения на базе 500 психологических
и персональных категорий

 

В этом разделе изучен вариант модели распознавания субъектов по астрономическим данным на момент рождения для БД, содержащей 500 психологических и личностных категорий на 12 сетках различного масштаба с числом секторов разбиения 3, 4, 5, 6, 9, 12, 15, 18, 20, 24, 36, 72 соответственно. Методом разделения категорий установлены общие закономерности распознавания категорий первого и второго класса.

Исходные данные задачи представляют собой таблицу, содержащую 20007 записей (строк) независимых респондентов, каждый из которых характеризуется номером записи, именем, полом, датой и временем рождения, местом рождения, собственной биографией и набором категорий и событий жизни. На основе данных места и времени рождения вычислялись астрономические параметры. В качестве входных астрономических параметров модели использовались координаты долготы углов 12 домов (в системе Плацидуса), Лунных Узлов и 10 небесных тел – Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна, Плутона.

Из списка категорий были отобраны те из них, которые соотносятся с психологическими и личностными характеристиками. Полученный список категорий содержит 500 наименований. Частотное распределение категорий с хорошей степенью точности описывается степенной функцией – прямая сплошная линия на рис. 56.1 Суммируя все частоты, находим общее число исследуемых случаев N= 65143 и среднее число категорий, приходящихся на одну карту, n=N/20007=3,256.

Результаты распознавания для модели, содержащей 72 сектора, даны на рис. 56.2. Как и в случае социальных и профессиональных категорий, наблюдается обратная зависимость параметра сходства от частоты повторяемости категорий, которую можно аппроксимировать степенной функцией с показателем степени -0,4956. Используя полученные данные для моделей с 4 и 72 секторами, можно разделить все категории на два класса по признаку уменьшения или увеличения параметра сходства:

1) категория относится к первому классу, если Si(4)>Si(72);

2) категория относится ко второму классу, если Si(4)<Si(72),

где Si(4), Si(72) – значения параметра сходства категории i в модели с 4 и 72 секторами соответственно. Третий класс можно определить как промежуточный между первыми двумя путем задания условной границы скорости изменения параметра сходства, dS, при изменении числа секторов, в виде:

3) категория относится к третьему классу, если

-dS<(Si(72)-Si(4))/(72-4)<dS

 

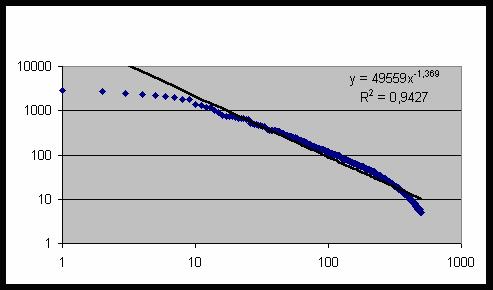
Рис. 56.1 Частота повторяемости 500 категорий

 

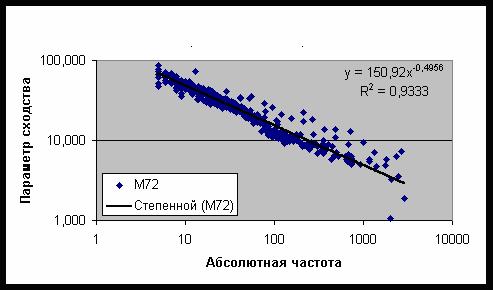
Рис. 56.2. Зависимость параметра сходства от частоты
повторяемости 500 категорий

 

При распознавании третий класс удобно будет отнести к одному из двух других классов, например, к первому (для его распознавания требуется меньше затрат машинного времени).

В результате разделения оказалось, что в первый класс попали только 84 категории, а во второй соответственно 416. Отметим, что в аналогичной задаче, рассмотренной в предыдущем пункте, при разделении на классы получилось 72 в первом классе и 315 – во втором. Но за счет отнесения категорий третьего класса к первому классу числа категорий изменились на 184 и 203 соответственно. В данном случае можно отнести 95 категорий второго класса к первому классу и, таким образом получить две БД в составе 179 категорий для смешанного класса и 321 – для второго.

Категории первого и третьего класса

Список категорий первого и третьего класса, упорядоченный по частоте повторяемости, приведен в Приложении 4 монографии [2] вместе с параметром сходства, полученным в модели с 4 секторами. Эти категории отличаются слабой зависимостью параметра сходства от частоты повторяемости – рис. 56.3.

 

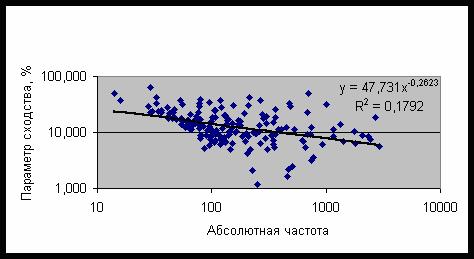
Рис. 56.3 Зависимость параметра сходства от частоты
повторяемости категорий первого класса

 

Само наличие этих категорий свидетельствует о влиянии времени года на новорожденного, что сказывается в его судьбе, как в плане социальной адаптации, так и в психологическом смысле. Отметим, что в человеческой практике большое значение придается положению Солнца, от которого зависят сезоны – весна, лето, осень и зима. Обнаруженный в данном исследовании феномен подчеркивает роль деления круга зодиака на четыре части по числу сезонов при распознавании категорий первого класса. Причем сезоны следует начинать от кардинальных точек эклиптики, совпадающих с началом знаков Овна, Рака, Весов и Козерога, для весны, лета, осени и зимы соответственно. Отметим, что, например, в Канаде принято именно такое деление года на сезоны.

Наиболее хорошо распознаваемые категории первого класса приведены в таблице 22.

 

Таблица 22. Список наиболее хорошо распознаваемых
категорий первого класса

Параметр

сходства

Категория

Абсолютная

частота

62,869

SC:C170-Medical:Doctor:Psyhotherapist

29

49,613

SC:A138-Religion

707

49,563

SC:B112-Psychological:Drug Abuse

14

42,988

SC:B395-Religion:12 step group

213

42,966

SC:C1340-Medical:Doctor:Chiropractor

33

38,512

SC:C1707-Medical:Doctor:Therapist

79

37,965

SC:B450-Mind:Extensive education

120

37,612

SC:B179-Birth:Test tube baby

53

37,446

SC:C457-Psychological:Alcohol Abuse:Rehab AA

267

36,693

SC:C1042-Medical:Cancer:Colon

16

34,862

SC:C1327-Birth:Infant mortality:SIDS

95

33,088

SC:B1557-Personality:Disasters

78

32,997

SC:C127-Medical:Accidents:Heart attack

33

32,969

SC:B240-Birth:Short labor <3 hrs

481

32,256

SC:C1239-Birth:Defects, Handicaps:Down's Syndrome

55

31,435

SC:A23-Psychological

1007

30,673

SC:B135-Death:Accidental

210

30,565

SC:B178-Birth:Cesarean

156

29,172

SC:B207-Medical:Cancer

490

28,843

SC:C155-Death:Long life >80 yrs:Age >100

78

28,816

SC:B703-Criminal Perpetrator:Terrorist

28

28,089

SC:B577-Sexuality:Celibacy/ Minimal

122

28,05

SC:B24-Psychological:Alcohol Abuse

41

27,926

SC:C1324-Birth:Twin, triplet, etc.:Triplets

41

26,276

SC:C208-Medical:Cancer:Breast

47

25,389

SC:C609-Sexuality:Sexual perversions:Lesbian

362

25,144

SC:B866-Birth:Stillborn

105

25,082

SC:C241-Death:Long life >80 yrs:Age 91-99

108

24,873

SC:D1125-Religion:Ecclesiastics/ western:Priest:monk/nun

36

24,217

SC:C644-Medical:Cancer:Lung

46

24,022

SC:C709-Medical:Doctor:Surgeon

30

23,845

SC:B1046-Sexuality:Voyeur

34

22,969

SC:B546-Psychological:Bi-Polar Disorder

29

 

Мы намеренно разместили в этой базе данных профессиональную категорию МЕДИЦИНСКИЙ ДОКТОР, чтобы показать корреляцию профессии и соответствующей группы заболеваний. Действительно, в таблице 22 находим профессию психотерапевт и психологические категории, соответствующие различным психическим отклонениям:

SC:C170-Medical:Doctor:Psyhotherapist

SC:A23-Psychological

SC:B101-Psychological:Eating Disorder

SC:B112-Psychological:Drug Abuse

SC:B24-Psychological:Alcohol Abuse

SC:B383-Psychological:Phobias

SC:B388-Psychological:Depression

SC:B546-Psychological:Bi-Polar Disorder

SC:C457-Psychological:Alcohol Abuse:Rehab AA

В этот список не попали категория SC:B524-Psychological:Schizophrenia, поскольку была отнесена ко второму классу, причем попала на условную границу между вторым и третьим классами. Две другие профессиональные категории – терапевт и хирург, оказываются в одном списке с набором раковых и сердечных заболеваний:

SC:C1707-Medical:Doctor:Therapist

SC:C709-Medical:Doctor:Surgeon

SC:B207-Medical:Cancer

SC:C1042-Medical:Cancer:Colon

SC:C208-Medical:Cancer:Breast

SC:C644-Medical:Cancer:Lung

SC:C127-Medical:Accidents:Heart attack.

Отметим, что категория SC:C1340-Medical:Doctor:Chiropractor также оказалась в этой таблице.

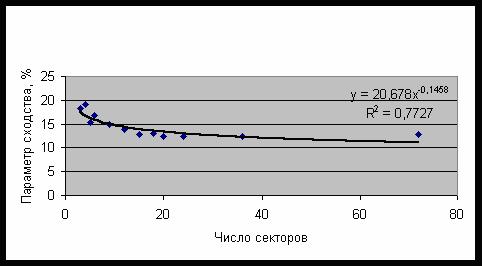
Рис. 56.4. Зависимость среднего параметра сходства от числа секторов разбиения для 84 категорий первого класса

 

 

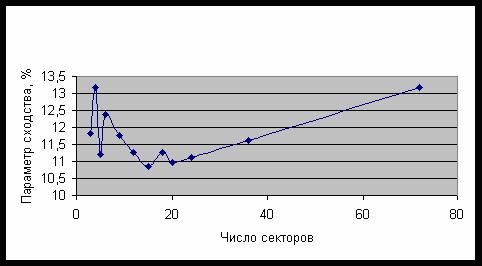
Рис. 56.5. Зависимость среднего параметра сходства от числа секторов разбиения для 89 категорий третьего класса

 

Перечисленные заболевания, скорее всего, носят сезонный характер и обусловлены климатическими изменениями, поэтому они хорошо распознаются при разбиении круга зодиака на четыре сектора, соответствующие сезонам.

На рис. 56.5 дана зависимость среднего параметра сходства от числа секторов разбиения для 84 категорий первого класса. Хорошо видно, что максимальный параметр сходства достигается при разбиении на 4 сектора. Возможно, что у этой функции имеется еще один максимум при числе секторов более 100. Этот максимум обусловлен примесью категорий третьего класса.

Категории второго класса

Список категорий второго класса, упорядоченных по величине параметра сходства, дан в Приложении 5 монографии [2]. Параметр сходства этих категорий убывает с ростом частоты повторяемости. С хорошей точностью эту зависимость можно аппроксимировать степенной функцией с показателем степени -0,5357. Аналогичная зависимость наблюдается и для всех 500 категорий исследуемой БД – рис. 47.

Среднее значение параметра сходства, вычисленное для 321 категории возрастает с ростом числа секторов разбиения. Если зависимость аппроксимировать степенной функцией и экстраполировать до значения параметра сходства 100%, то соответствующее число секторов окажется приблизительно равным 1557, а дуга одного сектора составит 832 угловых секунды, т.е. чуть меньше половины углового размера диска Луны или Солнца. Дальнейшие исследования покажут, действительно ли можно добиться 100% значения параметра сходства при увеличении числа секторов разбиения.

Действительно, среди категорий третьего класса можно выделить центральное ядро из 89 категорий с однотипным поведением – рис. 60. Приведенная на этом рисунке зависимость среднего параметра сходства от числа секторов разбиения имеет два максимума – при разбиении на 4 и 72 сектора соответственно. Это свойство позволяет отнести категории третьего класса к двум другим классам, поскольку они распознаются с одинаковым уровнем сходства для разбиения на 4 сектора, на котором достигается максимум распознавания категорий первого класса, и для разбиения на 72 сектора, на котором категории второго класса имеют максимум параметра сходства.

Максимальное значение параметра сходства у категорий второго класса реализуется при минимальном значении частоты повторяемости, которое в данном случае равно 5. Наилучшим образом распознается категория SC:B1112-Personality:Diplomatic, т.е. наличие у субъекта дипломатических способностей. Наихудшим образом на уровне 0% распознается категория SC:A129-Death – смерть без указания ее причины. Однако, если указать причину смерти, то уровень распознавания резко возрастает, например, категория SC:C1698-Death:Suicide:Subway – самоубийство в метро, распознается на уровне 40,8%; категория SC:C1395-Death:Suicide:Gassed – самоубийство путем отравления газом, на уровне 44,6%; а редкий случай ритуального самоубийства – категория SC:C622-Death:Suicide:Cult ritual, на уровне 52,6%. Иначе говоря, чем реже случай, тем лучше он распознается в рамках данной модели. Это можно объяснить тем, что в мало представленных категориях меньше вариабельность и поэтому задача идентификации с ними упрощается.

 

3.6. Исследование астросоциотипов
с применением семантических
информационных мультимоделей

 

В данной главе дан обзор работ [4-5], в которых приводятся основные научные результаты по семантической информационной мультимодели, обеспечивающей как выявление зависимостей между астропризнаками и принадлежностью респондентов к обобщенным социальным категориям, так и использование знания этих зависимостей для идентификации респондентов по этим категориям. Исследованная в [4] мультимодель включает 172 частные модели на 37 обобщенных категорий, причем каждая из категорий представлена не менее чем 1000 респондентов при общем объеме выборки 20007 респондентов.

Основным источником данных, подготовленной для системы «Эйдос», является AstroDatabank [8]. Использованная нами четвертая версия этого банка данных содержит 31012 записей, из которых 23217 составляют карты рождения известных личностей с описанием их биографии, 6643 карты рождения людей без имени, отнесенных к определенной категории и 1152 карты мунданных событий, типа землетрясения, авиационных катастроф и т.п. Общий объем банка данных составляет около 300 Мб. В нем содержатся астрономические параметры в 4 системах домов, поэтому в данной версии можно экспортировать в использованный нами DBF4 формат астрономические параметры, включая долготу и склонение планет, а также положение углов домов. Достоинством этого банка данных является то, что, все события жизни классифицированы, а все профессиональные и иные категории упорядочены. В результате сортировки исходных данных были получены астрономические и биографические данные для 20007 уникальных персон и 16360 записей событий, происходивших с ними. Для них всех были вычислены координаты небесных тел. Для записей с точным временем вычислялись куспиды домов в системе Плацидуса. В анализе были использованы эфемериды следующих небесных тел: Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна и Плутона.

Однако в процессе исследований выяснилось, что данная база данных обладает рядом недостатков, среди которых хотелось бы отметить крайне неравномерное распределение респондентов по категориям: из 11000 категорий, к которым относятся респонденты этой базы лишь 37 представлены 1000 респондентов и более. Поэтому выводы, полученные различным категориям, обладают разной степенью статистической достоверности: по хорошо представленным категориям можно говорить о надежно выявленных эмпирических законах, а по мало представленным – об исследовании неких зависимостей, которые нет возможности классифицировать как случайные или закономерные.

Дело в том, что чем меньше респондентов относится к категории, тем меньше вариабельность параметров респондентов, отнесенных к категории. В предельном случае, когда образ категории сформирован на примере одного респондента, вариабельность полностью отсутствует. В этом случае, по сути, задача распознавания вырождается (редуцируется) до задачи информационного поиска, т.е. становится тривиальной. Поэтому достоверность решения этой задачи максимальна и практически равна 100 %. Чем больше респондентов относится к некоторой категории, тем выше вариабельность параметров респондентов (астропризнаков) внутри категории, тем сложнее получить обобщенный образ этой категории и тем сложнее достоверно осуществить идентификацию конкретного респондента с этим образом. Однако именно это, т.е. определение уровня сходства конкретного респондента с обобщенным образом, сформированным на основе большого количества респондентов, относящихся к данной категории, и представляет и научный, и прагматический интерес.

Таким образом возникает проблема, состоящая в том, что для повышения статистической достоверности выводов необходимо увеличивать количество респондентов, относящихся к обобщенным категориям, однако это приводит к понижению достоверности идентификации респондентов с этими категориями из-за возрастания вариабельности внутри категорий.

Решение данной проблемы позволяет одновременно повысить и адекватность, и статистическую достоверность идентификации респондентов с астросоциотипами, что имеет высокую практическую значимость для служб, связанных с управлением персоналом. В этом и состоит актуальность решения данной проблемы.

Одним из эффективных методов повышения адекватности модели является сортировка исходных записей базы данных и удаление из нее нетипичных представителей данных категорий [5]. Рассмотрим этот метод более подробно на одном примере.

Объектом исследования являются модели, отражающие взаимосвязи между астропризнаками респондентов и принадлежностью этих респондентов к астросоциотипам, а предметом исследования – частные информационные семантические модели с 2, 3, 12 и 128 секторами.

Выбор именно этих частных моделей для исследования был обусловлен тем, что они представляют три группы частных моделей: с малым (2, 3), средним (12) и большим (128) количеством секторов, что позволяет оценить зависимость эффективности метода, применяемого для решения проблемы, от количества секторов в частной модели.

Целью исследования является повышение адекватности идентификации респондентов в частных моделях по хорошо статистически представленным астросоциотипам.

Данную цель предполагается достичь путем ее декомпозиции в следующую последовательность задач, являющихся этапами ее достижения:

1.                               Разработка дерева обобщенных категорий, к которым относятся респонденты, представленные в исходной базе данных.

2.                               Расчет распределения респондентов по категориям.

3.                               Удаление из списка категорий всех, к которым относится менее 1000 респондентов.

4.                               Синтез частных моделей для наиболее представленных социальных категорий с различным количеством секторов.

5.                               Выбор метода повышения адекватности и исследование частных моделей с малым (2, 3), средним (12) и большим (128) количеством секторов выбранным методом.

Решение задач 1-4 приведено в работе [4], а решение 5-й задачи в работе [5].

Обоснование требований к методу решения проблемы. Метод должен обеспечивать возможность работы с частными моделями, созданными в системе «Эйдос-астра» [7] и при этом повышать адекватность отдельной заданной модели, т.е. не использовать алгоритмы голосования (коллективы решающих правил), которые уже были исследованы в [4].

На сколько можно судить по литературным данным сформулированным требованиям в принципе удовлетворяют две системы: это SPSS и система «Эйдос» [36].

В системе SPSS можно методами кластерного анализа исследовать матрицу информативностей и построить дерево классов, отражающее их сходство и различие. Ясно, что сходство классов тем выше, чем больше респондентов относится одновременно к обоим этим классам, т.е. чем больше их пересечение по исходным данным, чем выше корреляция между ними. На основе этого можно попытаться сконструировать такую систему классов, которые бы имели минимальное пересечение по исходным данным, т.е. провести ортонормирование системы классов. При этом из системы классов будут удалены те из них, которые наиболее сильно коррелируют друг с другом. Это теоретически возможно, но практически осуществимо лишь для очень небольших обучающих выборок и небольших наборов классов, т.к. после изменения набора классов необходимо соответственно перекодировать обучающую выборку, и провести пересинтез модели. Для исследуемых нами баз данных с помощью системы SPSS это практически неосуществимо. Кроме того система SPSS вообще не обеспечивает многопараметрическую типизацию (обобщение, формирование обобщенных образов категорий) на основе описаний респондентов.

В системе «Эйдос» [36] реализованы режимы ортонормирования семантического пространства классов и семантического пространства атрибутов, а также режим разделения классов на типичную и нетипичную части, автоматизирующие все необходимые для этого функции, причем в процессе выполнения этих режимов создаются различные частные модели и при этом используется многопараметрическая типизация.

По этим причинам для решения сформулированной проблемы авторами принято решение применить метод разделения классов на типичную и нетипичную части, реализованный в системе «Эйдос». Необходимо отметить, что этот метод уже апробирован для решения подобных задач в других предметных областях и при этом продемонстрировал очень высокую эффективность, но для решения поставленной проблемы применяется впервые.

Описание метода. Данный метод представляет собой итерационный процесс синтеза частных моделей, отличающихся наборами классов (обобщенных категорий). Цикл итераций начинается с копирования исходной модели в директорию для первой итерации. В последующих итерациях частная модель копируется из директории с текущей итерацией в директорию с последующей итерацией. Выход из цикла итераций происходит при достижении заданной достоверности идентификации или 100% достоверности, заданного количества итераций или при стабилизации достоверности (ее неизменности в двух итерациях).

В каждой итерации проводится синтез модели и идентификация респондентов обучающей выборки с обобщенными категориями. Если респондент не отнесен системой к обобщенной категории, хотя в действительности по данным обучающей выборки относится к ней, то это означает, что он является нетипичным для этой категории, в которой, видимо, очень высока вариабельность параметров, и это означает, что надо разделить эту категорию на несколько таким образом, чтобы вариабельность параметров внутри каждой из них была минимальной и достаточной для наиболее достоверной идентификации респондентов. При этом формируется дерево разделения категорий, похожее на формирующееся при древовидной кластеризации, причем на каждой итерации каждая обобщенная категория разделяется не более, чем на две категории.

Описание методики (технологии) применения метода на практике. На практике для применения данного режима системы «Эйдос» (_35) были выполнены следующие работы:

¾              создана директория Razd_kl для исследования моделей методом разделения классов на типичную и нетипичную части;

¾              внутри этой директории созданы директории Razd_002, Razd_003, Razd_012, Razd_128 для исследования частных моделей с 2, 3, 12 и 128 секторами соответственно;

¾              в каждую из этих директорий скопированы папки с исходной частной моделью (из директории с мультимоделью, содержащей 172 ранее созданные частные модели) и папка с системой «Эйдос»;

¾              для каждой частной модели: все файлы из директории с исходной моделью скопированы в директорию с системой «Эйдос»;

¾              для каждой частной модели: система «Эйдос» запускается на исполнение и затем запускается режим _35: «Разделение классов на типичную и нетипичную части» (при этом задается 7 итераций);

¾              данный режим исполняется и формирует директории с именами вида: Razd_kl\razd_002\ITER_##, где ## – номер итерации;

¾              в поддиректории TXT каждой директории с итерацией содержится файл: Razd_kl\razd_002\ITER_02\TXT\NCD_TREE.TXT, содержащий в псевдографическом виде дерево классов для данной итерации;

¾              в базах данных DOSTITER.DBF содержится информация о достоверности идентификации по всей обучающей выборке, достигнутая в текущей итерации.

В таблице 23 приведены сводные данные по достоверности идентификации всех 20007 респондентов обучающей выборки в частных моделях, полученных из исходных частных моделей с 2, 3, 12 и 128 секторами на различных итерациях.

Таблица 23. Достоверность идентификации
20007 респондентов на различных итерациях

Номер

итерации

Количество секторов в частной модели

2

3

12

128

1

66,311

72,562

72,374

73,923

2

82,678

80,240

81,702

80,022

3

83,829

79,802

82,348

81,599

4

82,974

79,840

82,480

82,171

5

82,515

79,927

82,474

82,528

6

82,460

80,043

82,556

82,756

7

82,472

80,182

82,622

82,922

Из приведенных таблицы следует вывод о высокой эффективности применения выбранного метода разделения классов на типичную и нетипичную части, который обеспечил уже на 1-й итерации достоверность идентификации обучающей выборки, включающей 20007 респондентов, 65-75%, а уже на 2-й и 3-й итерациях эта достоверность достигает 82-83%. Видно также, что наибольший эффект дают уже первые три итерации, а последующие мало что меняют в эффективности частных моделей.

Главный научный вывод, который можно обоснованно сделать на основе проведенного исследования состоит в том, что метод разделения классов на типичную и нетипичную части позволяет получить семантические информационные модели с очень высокой достоверностью идентификации респондентов, достигающей 83% на огромной тестирующей выборке из 20007 респондентов.

Второй вывод состоит в том, что для получения модели с высокой достоверностью не играет особой роли количество секторов в исходной модели, т.е. эффективность метода практически не зависит от количества секторов в частных моделях.

В работе [5] приводится дерево категорий для частной модели с 2 секторами, полученное на 7-й итерации. Из этого дерева категорий можно сделать вывод о том, что одни категории обладают более высокой внутренней вариабельностью и разделяются в процессе итераций на большее количество классов, чем другие, которые идентифицируются с большей достоверностью. Ярким примером категории 2-го типа является SC:A53-Sports.

Примененный метод разделения классов на типичную и нетипичную части продемонстрировал свою высокую эффективность. Полученные в результате применения данного метода семантические информационные модели имеют достоверность идентификации достаточно высокую для того, чтобы применять эти модели на практике в консультирующих системах.

Необходимо отметить очень высокие затраты машинного времени и других вычислительных ресурсов на расчеты, связанные с получением новых более достоверных частных моделей. Этим и объясняется выбор для данного исследования всего 4-х частных моделей, а не всех 172-х, полученных ранее, а также то обстоятельство, что количество итераций было ограничено 7-ю. В вычислительных экспериментах на моделях меньшей размерности в других предметных областях и при большем количестве итераций этим же методом были получены модели со 100% достоверностью [37].

В работе [4] была изучена эффективность пяти алгоритмов голосования по сравнению со случайным угадыванием – таблица 17. Сравнивались алгоритмы распознавания в мультимоделях, когда за параметр сходства принимается:

А1. СУММАРНАЯ ЧАСТОТА ИДЕНТИФИКАЦИИ респондента с каждым классом, рассчитанная по всем частным моделям.

А2. СРЕДНЕЕ уровней сходства с этим классом из всех карточек идентификации частных моделей.

А3. Уровень сходства этого респондента с классом из той частной карточки идентификации, в которой он МАКСИМАЛЬНЫЙ.

А4. Уровень сходства из карточки идентификации той частной модели, которая показала МАКСИМАЛЬНУЮ достоверность распознавания ДАННОГО КЛАССА из всех моделей.

А5. СРЕДНЕЕ СУММЫ ПРОИЗВЕДЕНИЙ уровней сходства с данным классом на достоверность его идентификации в частных моделях.

Из анализа данных, приведенных в таблице 24, видно, что использование мультимодели и алгоритмов голосования дает результаты идентификации (по большинству категорий), существенно отличающиеся от случайного угадывания (в лучшую сторону). Из статистики известно, что если достоверность идентификации выше вероятности случайного угадывания в 2.5 раза, то вывод о том, что существует закономерность имеет достоверность 95%. Из этого можно сделать три важных вывода:

1) в обучающей выборке выявлены взаимосвязи между астрономическими признаками респондентов на момент рождения (астропризнаками) и обобщенными социальными категориями (астросоциотипами), показывающие, что эта выборка существенно отличается от случайной;

2) знание этих выявленных закономерностей позволяет относить респондентов к обобщенным социальным категориям с достоверностью, значительно превосходящей вероятность случайного угадывания;

3) достоверность предыдущих двух выводов, как статистических высказываний, составляет значительно более 95 %.

 

Таблица 24. Эффективность алгоритмов голосования
по сравнению со случайным угадыванием

Имя категории

А1

А2

А3

А4

А5

SC:М-

5,781

9,25

3,262

2,323

10,947

SC:A323-Sexuality

8,409

6,167

18,271

7,645

7,708

SC:B329-Sexual perversions

8,81

8,222

10,883

1,996

5,389

SC:C330- Homosexual m

10,277

15,418

6,159

9,136

9,679

SC:B189-Medical:Illness

11,936

6,379

8,968

10,242

3,85

SC:A53-Sports

12,333

36,996

6,371

4,068

7,113

SC:A42-Medical

12,758

9,25

5,139

12,432

3,997

SC:A5-Entertainment

13,704

11,212

4,791

12,589

12,432

SC:A9-Relationship

14,231

6,981

3,482

0,961

3,557

SC:A29-Parenting

16,088

4,302

4,567

3,61

0,903

SC:B21- Number of marriages

16,088

20,555

6,491

5,609

7,175

SC:A31-Business

16,088

18,501

10,242

8,712

3,263

SC:B26-Personality:Body

16,088

6,981

7,255

8,094

7,631

SC:A23-Psychological

17,618

9,487

21,763

20,483

3,652

SC:A25-Personality

19,474

16,088

9,992

3,7

5,668

SC:A19-Writers

21,763

11,212

3,706

6,662

11,419

SC:A129-Death

21,763

8,409

2,868

5,073

7,645

SC:A1-Book Collection

23,127

8,604

6,049

4,509

9,922

SC:B111-Sports:Basketball

23,127

24,667

10,883

9,024

8,804

SC:B14-Entertainment:Actor/ Actress

24,667

16,088

8,222

6,395

9,282

SC:A15-Famous

26,427

2,782

1,393

2,847

22,652

SC:A55-Art

28,458

8,409

8,409

10,999

4,441

SC:B49-Book Collection:Am. Book

28,458

7,551

9,024

7,604

7,604

SC:A38-Politics

30,836

7,872

11,551

3,807

6,662

SC:B173-Sports:Football

30,836

10,277

12,318

7,113

7,362

SC:A99-Financial

30,836

15,418

8,604

5,867

3,034

SC:B48-:Top 5% of Profession

33,636

9,737

14,799

6,483

11,674

SC:B6-Entertainment:Music

33,636

12,333

9,737

2,43

1,858

SC:A68-Childhood

36,996

11,936

13,683

2,337

6,605

SC:Ж-

36,996

16,818

6,727

5,011

4,365

SC:A108-Education

41,118

11,212

13,704

9,282

17,922

SC:B45-Famous:Greatest hits

46,253

17,618

3,362

10,781

9,626

SC:B2-Book Collection:Profiles Of W

46,253

6,852

4,556

7,362

6,578

SC:A92-Birth

52,854

10

6,066

13,703

3,584

SC:?-

52,854

23,127

20,555

20,555

18,271

SC:A40-Occult Fields

74,019

13,214

26,427

26,427

2,368

SC:B97-Occult Fields:Astrologer

92,507

28,458

9,25

12,182

2,575

Среднее значение

19,336

9,668

6,364

5,396

5,147

 

Итак, в мультимодели, основанной на солидной базе прецедентов (20007 респондентов) с огромной статистической представительностью категорий (не менее 1000 респондентов на категорию), получены результаты идентификации респондентов тестирующей выборки из 370 респондентов, подобранных таким образом, чтобы их было не менее 10 на категорию.

Полученные результаты идентификации подтверждают:

1. В созданной с помощью системы «Эйдос-астра» мультимодели выявлены зависимости между астропризнаками респондентов на момент их рождения и принадлежностью этих респондентов к обобщенным социальным категориям (типам).

2. Эти зависимости имеют такую силу, что их знание, по-видимому, может быть успешно использовано для идентификации респондентов по категориям.

3. Методы голосования моделей (коллективы решающих правил) позволяют повысить достоверность полученных результатов идентификации до 21 %, по сравнению с наихудшими частными моделями, поэтому это может представлять не только чисто научный, но, по-видимому, и практический интерес. Полученные результаты показывают, что достоверность идентификации с помощью мультимодели часто в 2,5 раза, а иногда – и в десятки раз превышает вероятность случайного угадывания, значит, их достоверность, как статистических высказываний, в этих случаях выше 95 %.

4. Выявлены категории, по которым уровень достоверности идентификации особенно высок или очень низкий. С учетом этого, предлагается при отнесении респондента системой к категориям второго типа не принимать эти результаты слишком серьезно.

5. Результаты экспериментального тестирования показали, что научные разработки, описанные выше, представляют не только научный, но и практический интерес, т.к. совпадение прогноза с фактом является довольно высоким и вполне очевидным как для консультанта, так и для его клиентов.

Рассмотрим, каким образом полученные результаты могут быть использованы в социологии.

 

3.7. Теория сходства в социологии – астросоциотипология

Профессиограммой будем называть перечень личностных качеств с указанием в количественной форме степени их необходимости для успешного выполнения определенного вида деятельности.

Сами эти личностные качества могут быть различной природы:

– конституционные или генетически предопределенные (в т.ч., пол, национальность, темперамент, генетические заболевания, определенные виды способностей);

– физические;

– физиологические;

– психологические;

– социально-приобретенные, т.е. зависящие от конкретной истории жизни человека, его биографии, образования, семейного и социального статуса, возраста, а также других обстоятельств.

Конституционные качества во многом предопределяют и физические, и физиологические, и психологические параметры личности, а значит во многом предопределяют и ее «Судьбу». Кроме того в соответствии с интегральной моделью индивидуальности Вольфа Мерлина считается, что конституционные качества личности составляют как бы фундамент или фон, на котором развиваются ее социально-приобретенные качества. При этом определенный фон является благоприятным для развития одних социально-приобретенных качеств, для развития других он является неблагоприятным, и наконец есть и такие качества, для развития которых он является нейтральным.

Таким образом можно считать, что социально-приобретенные личностные качества являются результатом совместного действия конституционных личностных качеств и окружающей среды. В частности, для растений справедливо высказывание: «Фенотип определяется взаимодействием генотипа и окружающей среды».

Есть замечательное латинское высказывание: «Желающего судьба ведет, а не желающего тащит». Это очень точно характеризует роль конституционных качеств человека в его жизни. Если человек развивается в направлении, в котором у него «карт-бланш», выданный самой судьбой, то успех ему обеспечен, если же он пытается спорить со своей судьбой, пытается действовать вопреки или без согласия с ней, то он либо ничего особого не добивается, либо вообще погибает не достигнув никакой самореализации. Поэтому совпадение жизни с астросоциотипологическим прогнозами выше у тех людей, которые следовали своему призванию, предназначению и реализовали себя. Обычно люди, реализовавшие себя, более счастливы, чем люди со сломанной судьбой.

Астросоциотипология основана на гипотезе, что конституционные качества личности включают не только предопределенные генотипом, но и ряд других качеств, не обусловленных генотипом: – это так называемые астросоциотипологические характеристики личности, связанные с местом и временем рождения.

В свою очередь астросоциотипологические характеристики личности также могут рассматриваться как иерархическая система, включающая:

– первичные астросоциотипологические признаки (определенная планета в определенном сегменте модели);

– вторичные астросоциотипологические признаки (сочетания планет по сегментам модели).

Астросоциотипологические признаки разных уровней иерархии также могут быть включены в систему конституционных и социально-обусловленных качеств личности при разработке профессиограмм.

Такие профессиограммы, которые включают не только конституционные и социально-обусловленные, но и астросоциотипологические качества личности различных уровней иерархии будем называть «астропрофессиограммами».

Однако даже разработка обычных профессиограмм представителями таких вроде бы уже общепризнанных научных направлений как психология или психофизиология также является очень сходным весьма слабо формализованным процессом, также самым существенным образом основанным на творческим, и во многом основан на жизненном опыте и интуиции ученого разработчика и исследователя.

В тоже время необходимо отметить, что в области формализации процесса разработки профессиограмм уже достигнуты определенные успехи. В последние годы создан целый ряд тестов, позволяющих оценивать респондентов на профессиональную пригодность в различных направлениях деятельности. Вместе с тем сама технология разработки подобных тестов является весьма наукоемкой, трудоемкой и дорогостоящей и этот процесс пока далек от стандартизации и малодоступен не только для потенциальных заказчиков на продукты подобных технологий, но и для самих ученых. Достаточно отметить, что в СССР существовало всего две научных школы, которые имели научный, информационный и технологический потенциал (включая ноу-хау), позволяющий решать подобные задачи: это Ленинградская и Киевская психологические научные школы. Сегодня Киевская школа оказалась за границей, а Ленинградская (Санкт-Петербургская) известна в основном по коммерческим работам фирмы «Иматон». А между тем психологические тесты сегодня используются все шире прежде всего в службах управления персоналом для решения весьма ответственных вопросов, влияющих на судьбы людей. Это как минимум означает, что эти тесты должны быть не только адаптированы и локализованы, но и применяться для тех целей, для решения которых они были предназначены разработчиками, и при удовлетворении всех этих условий – официально сертифицированы. Наша действительность в этом плане выглядит удручающе: на практике в службах персонала чаще всего применяются не лицензионные морально и физически устаревшие тестовые программы, взятые с компакт-дисков, причем эти программы никто и не думал адаптировать, локализовать и сертифицировать.

Разработчики современных технологий разработки профессиограмм должны поставить перед собой и решить по крайней мере следующие вопросы. Каким образом могут быть установлены личностные качества, какие для этого существуют инструментальные средства и процедуры? Как определить в количественной форме, какие личностные качества являются необходимыми для определенных видов деятельности, а какие вредны, а какие нейтральны? Как исключить из рассмотрения те личностные качества, которые не играют особой роли для определения успешности или не успешности определенных видов деятельности и тем исключить непроизводительные затраты труда и времени на сбор и обработку несущественной информации? Иначе говоря как разработать эффективные профессиограммы? Но если профессиограммы уже разработаны, то как их применять на практике? Какой инструментарий, а также какие технологии и методики его применения необходимы для разработки и применения профессиограмм?

Некоторые конституционные и социально-приобретенные личностные качества достаточно просто могут быть установлены непосредственно, другие же требуют для применения специальных средств методик и оцениваются косвенно на основе непосредственно-наблюдаемых и их выявление требует большого труда и использования специальных инструментов съема и обобщения информации.

Автоматизированный системно-когнитивный анализ (АСК-анализ) является успешно апробированной современной автоматизированной технологией, позволяющей решать эти проблемы. Методы, изложенные в предыдущих главах, позволяют определить набор социальных и психофизических категорий для каждого респондента, используя только его данные рождения.

Остаются нерешенным о причинах существования обнаруженных взаимосвязей между астропризнаками и социотипами и о конкретных механизмах осуществления этих взаимосвязей. По этому вопросу могут быть самые разные точки зрения. Однако, на взгляд авторов, интересной является идея о решающей роли времени. Если посчитать корреляцию между показаниями часов и различными видами активности людей, то будет обнаружено, что между ними существуют довольно сильные корреляционные зависимости. Мы ведь далеки от мысли считать, что показания часов детерминируют поведение людей. Все понимают, что и показания часов, и деятельность людей зависят от некоторого общего фактора, который влияет и на первое, и на второе, а именно – от времени. Именно ход или течение времени, а не показания часов детерминирует поведение людей (когда они просыпаются и ложатся спать, идут на работу и с работы, принимают пищу и т.д.). Наши обычные часы синхронизированы с суточным солнечным ритмом, т.к. он, совершенно очевидно, является основным ритмом, наиболее сильно влияющим на нашу деятельность. В данной модели влияние этот ритма моделируется путем разбиения суточного цикла на 12 частей, именуемых домами Плацидуса. Астрономические параметры на момент рождения также представляют собой показания определенных, а именно астрономических часов, циферблат которых размечен не в соответствии с суточным циклом, а на месяцы (цикл Луны), годы (циклы Солнца, Меркурия, Венеры, Марса), десятки (циклы Юпитера, Сатурна, Урана) или даже сотни лет (циклы Нептуна и Плутона). Наличие выявленных закономерностей между астропризнаками и социотипами говорит в пользу того, что на нашу жизнь оказывает влияние не только солнечное и лунное, но и планетарное время Солнечной системы. В следующей главе рассмотрены вопросы о механизмах этого влияния.

Теорема астросоциотипологии

В работах [11-12] была сформулирована теорема астросоциотипологии, которая устанавливает зависимость функции распределения случайных событий, происходящих на Земле от кинематических и динамических параметров нашей планеты при ее движении вокруг Солнца, а именно:

социальная реакция большой группы субъектов на воздействие любого небесного тела Солнечной системы может быть описана функцией среднеквадратичного отклонения нормированной частоты выбора, зависящей от радиальной скорости в системе Земля - небесное тело.

Некоторые следствия этой теоремы:

1) социальная реакция большой группы субъектов на воздействие любого небесного тела Солнечной системы, кроме Солнца может быть описана функцией среднеквадратичного отклонения нормированной частоты выбора, зависящей от углового аспекта небесного тела с Солнцем при наблюдении с Земли (от разности долготы небесного тела и долготы Солнца);

2) социальная реакция большой группы субъектов на воздействие Солнца может быть описана функцией среднеквадратичного отклонения нормированной частоты выбора, зависящей от долготы Солнца.

 Одним из следствий этой теоремы является то, что любые непрерывные во времени распределения событий при их представлении в зависимости от координат небесных тел содержат когерентные колебания, обусловленные движением небесных тел. В работе [12] высказана гипотеза о том, что когерентные колебания могут быть использованы для распознавания событий в астросоциотипологии. В работах [18-19] обсуждается проблема распознавания событий в поле центральных сил. Дано решение проблемы на основе системной теории информации. Развита модель прогнозирования курсов валют с использованием астрономических параметров.

При выводе теоремы астросоциотипологии предполагается [11-12], что на планете происходит ряд однородных событий, число которых в единицу времени описывается функцией W(t), нормированной на единицу за один период обращения планеты вокруг центрального светила, т.е.

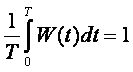                                                   (28)

Период обращения связан с угловой скоростью движения по орбите интегральным соотношением

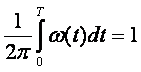
Для замкнутых траекторий эта теорема является следствием дифференциального уравнения, связывающего плотность функции распределения вдоль радиальной и угловой координаты в полярной системе координат 

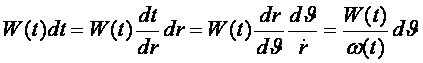                  (29)

 

Отметим связь кинематических параметров:

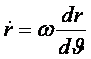                                                         (30)

Как известно, в поле центральных сил тело совершает финитное движение по эллипсу, уравнение которого в полярной системе координат можно представить в виде:

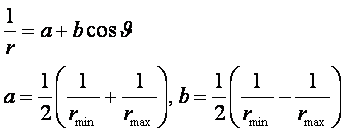                          (31)

Здесь  - минимальное и максимальное удаление планеты от центра масс системы.

В поле центральных сил выполняется закон сохранения момента импульса в форме

Отсюда и из уравнений (29-30) вытекают простые соотношения

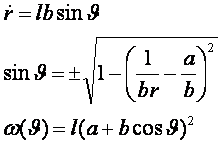                                   (32)

В случае равновероятных событий положим в уравнениях (29)  W(t)=1, и, используя (30), находим плотности распределения событий вдоль угловой и радиальной координаты

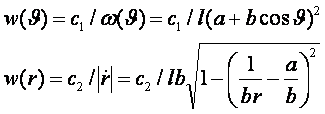                                (33)

Здесь с1, с2 – постоянные множители, которые можно найти из условия нормирования. Отметим, что полученные плотности (33) зависят от полярного угла (или долготы Солнца) и радиальной координаты, хотя исходное распределение не зависит от времени. Плотность функции распределения в зависимости от расстояния имеет особенности в точках остановки, где радиальная скорость обращается в нуль.

В дискретном случае, рассмотренном в работах по астросоциотипологии [1-2, 4-6] и других  вместо уравнения (28) используются нормированные частоты и их стандартные отклонения: 

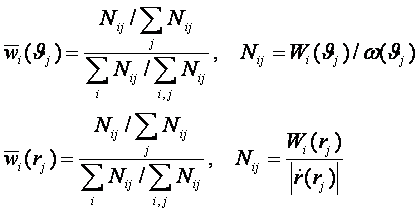
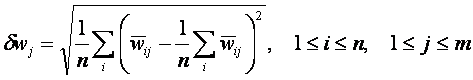         (34)

Теорема астросоциотипологии непосредственно следует из определений (35), которые не содержат никаких внешних параметров, кроме угловой и радиальной скорости.

Отметим, что при наблюдении с Земли за небесным телом, орбита которого близка к окружности, радиальная скорость в системе Земля – небесное тело связана с разностью долготы соотношением [11]:

                                       (35)

Здесь  – радиус, угловая скорость Земли, и долгота Солнца соответственно, - угловая скорость вращения небесного тела по орбите вокруг Солнца и его долгота соответственно.

Предположим, что известна функция распределения событий вдоль угловой координаты, , которую нормируем на единицу

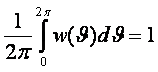                                               (36)

Функция плотности распределения вдоль радиальной координаты может быть получена из дифференциального соотношения:

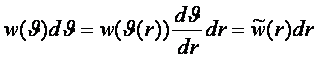                        (37)

Отметим, что функция плотности распределения отличается от функции с тильдой в правой части (37) на постоянный множитель, который определяется из условия нормировки. Вместо радиальной переменной удобно использовать нормированную переменную

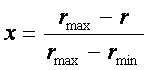
Тогда уравнение (29) приобретает вид

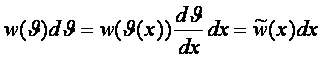                          (38)

Отсюда следует, что отношение плотностей вдоль угловой и нормированной координаты (с учетом нормировки и положительной определенности плотности) в случае Солнца равно

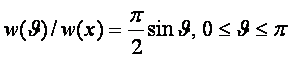                             (39)

В случае произвольного небесного тела, используя уравнение (35), находим:

                               (40)

Здесь С – постоянный множитель, который определяется из условия нормировки. 

Отметим, что уравнение (40) выполняется с точностью до величины эксцентриситета земной орбиты (или орбиты небесного тела). С той же точностью можно связать между собой функцию плотности распределения событий по времени  W(t) и функцию .  Действительно, используя уравнение (29), находим

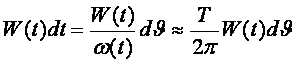
Таким образом, если использовать вместо истинной угловой скорости ее среднее значение, определяемое по периоду обращения планеты, тогда плотность распределения событий по углу связана с плотностью распределения событий по времени простым соотношением:

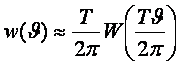                                      (41)

Далее заметим, что если функция W(t) является регулярной, то и функция  является регулярной в силу (41). Но тогда функция   может иметь особенности в точках, где , в силу уравнения (39) или в точках, где , в силу уравнения (40). Очевидно, что эти свойства относятся к непрерывным распределениям событий, тогда как в случае дискретных событий особенности заменяются конечными величинами – пиками событий [11-12].     

Можно показать, что в случае дискретных распределений уравнение (39) имеет дискретный аналог

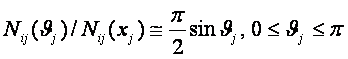                           (42)

Уравнение (42) выполняется тем точнее, чем больше общее число случаев и число ячеек модели, а также число случаев, приходящихся на одну ячейку.

На рис. 57 представлены данные отношения распределений  реализации выбора 20007 респондентов из 37 категорий для одной категории с общим числом случаев 13640 в зависимости от нормированного угла  в модели М120. Числа  определялись на основе комплекса программ «Эйдос-астра» [7] путем суммирования записей банка данных, относящихся к данной категории в данной ячейке. Сплошная линия на рис. 57 представляет правую часть уравнения (67). Наблюдается линейная корреляция данных с теоретической кривой с коэффициентом R2 = 0.6443.    

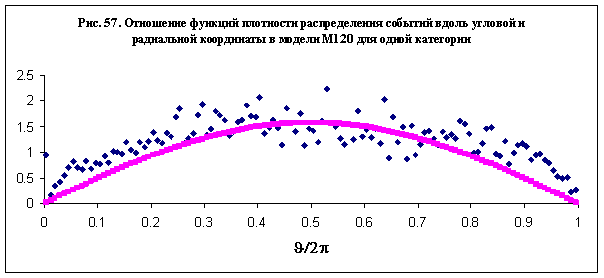
Менее представительные категории имеют большее рассеяние данных относительно теоретической кривой.  Поэтому по мере роста числа категорий рассеяние данных возрастает. Тем не менее, данные всех 37 исследованных категорий ложатся вокруг теоретической кривой. На рис. 58 представлены данные отношения распределений  реализации выбора 20007 респондентов из 37 категорий для десяти наиболее представительных категорий из таблицы 22 с общим числом случаев 44176 в зависимости от нормированного угла , в модели М120. Сравнивая данные на рис. 57 и 58 можно сделать вывод, что рассеяние данных относительно теоретической кривой (67) заметно растет с ростом числа категорий.  Это связано с тем, что при уменьшении общего числа случаев приходящихся на категорию, уменьшается и число случаев, приходящихся на одну ячейку модели. 

 

 

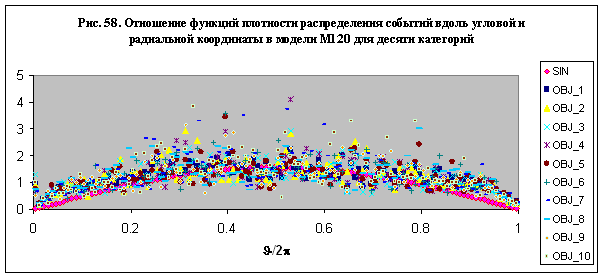
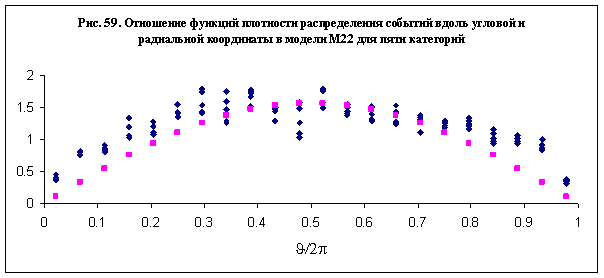
Уменьшая число ячеек модели, можно понизить рассеяние данных относительно теоретической кривой за счет увеличения числа случаев, приходящихся на одну ячейку. На рис. 59 представлены данные отношения распределений  реализации выбора 20007 респондентов из 37 категорий для пяти наиболее представительных категорий с общим числом случаев 31176 в зависимости от нормированного угла  в модели М22. Для совокупности этих данных наблюдается линейная корреляция с теоретической кривой (представлена квадратными символами на рис. 59) с коэффициентом R2 = 0.7928.

Таким образом, данные, представленные на рис. 57-59, свидетельствуют, что дискретный аналог уравнения (39) в форме (42) действительно существует. Докажем это утверждение, используя интегральную форму выражения числа событий в данной ячейке и теорему о средней точке, имеем: 

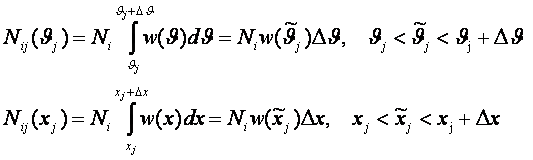
Здесь Ni – общее число случаев данного типа.  С учетом полученных выражений составим отношение

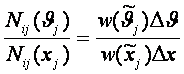
Далее заметим, что в дискретном случае при выборе равномерной сетки по угловой и радиальной координате, как в работах [13-16], отношение  . Без ограничения общности можно выбрать эту константу так, чтобы получить выражение (42).  Следовательно, уравнение (39) действительно выполняется в дискретном случае, причем невязка, необходимая для согласования правой и левой части уравнения (42), определяется выбором средней точки в соответствующих интервалах, т.е.

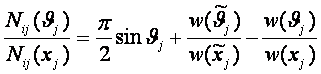                       (43)

Для дифференцируемой функции плотности распределения легко показать, что невязка в правой части уравнения (43) стремится к нулю при  условии, что . Однако, для дискретных распределений это выполняется лишь в том случае, если число случаев, приходящихся на одну ячейку, достаточно велико, что заведомо не выполняется в задачах с конечным числом событий. Для таких задач можно оптимизировать невязку, путем перебора числа ячеек сетки. В частности, для данных, приведенных на рис. 57-59, оптимальное число ячеек сетки М=22. 

Полученные выше результаты касаются свойств функции плотности распределения событий по угловой и радиальной координате Солнца относительно нашей планеты. К сожалению, для других небесных тел солнечной системы не удается получить простой дискретный аналог уравнения (40), поскольку в правую часть этого уравнения входит разность углов, а не один угол, как в уравнении (39). Кроме того,  даже если исходное распределение событий W(t) является случайным, распределения событий вдоль долготы и расстояния до небесных тел содержат когерентную составляющую, обусловленную периодическим движением нашей планеты.

На рис. 60 представлены данные отношения распределений по долготе и расстоянию до Венеры -  , реализации выбора 20007 респондентов из 37 категорий для десяти наиболее представительных категорий из таблицы 22 с общим числом случаев 44176 в зависимости от нормированного угла  в модели М120. В распределении данных отчетливо наблюдаются когерентные колебания, обусловленные периодическим движением Земли и Венеры.    

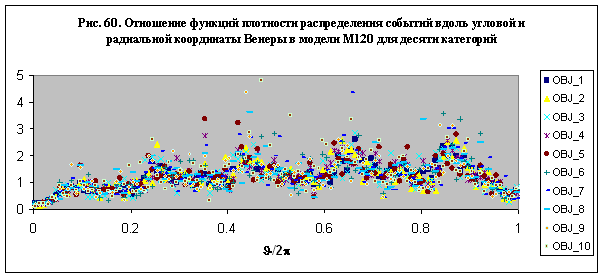
На рис. 61 представлены данные абсолютных распределений  реализации выбора 20007 респондентов из 37 категорий для пяти наиболее представительных категорий с общим числом случаев 31176 в зависимости от  долготы Венеры в модели М120. Из этих данных следует, что распределение событий по долготе Венеры содержит колебания, обусловленные изменением угловой скорости в системе Венера-Земля.

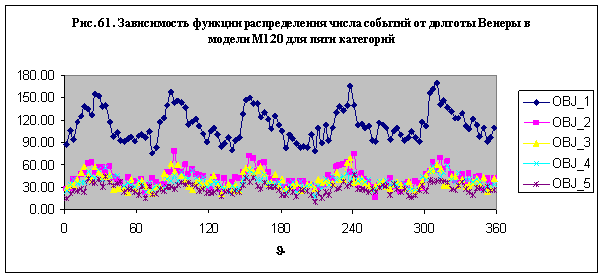
Действительно, как это следует из уравнения (29), плотность распределения событий вдоль угловой координаты изменяется обратно пропорционально угловой скорости, т.е.

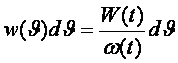                                        (44)

В случае Солнца это изменение невелико и дается первым уравнение (33). В случае других небесных тел относительное движение велико, что приводит к большому изменению относительной угловой скорости и к появлению колебаний в распределении числа событий, как это видно из данных на рис. 61.                

Заметим, что указанным свойством квазипериодичности, обусловленным изменением знака относительной угловой скорости, обладают и распределения относительно долготы других небесных тел. При этом, влияние каждого небесного тела на функцию распределения можно достаточно легко идентифицировать по внешнему виду кривой отношения функций плотности распределения вдоль угловой и радиальной координаты. На рис. 62-65 представлены данные отношения распределений по долготе и расстоянию -  , реализации выбора 20007 респондентов из 37 категорий для десяти наиболее представительных категорий из таблицы 1 работы /9/ с общим числом случаев 44176 в зависимости от нормированного угла  в модели М120 для Меркурия, Марса  Юпитера и Луны соответственно. Можно видеть, что данные на рис. 62-65 группируются сходным образом, но иначе, чем данные для Солнца (рис. 58) и Венеры (рис.60).

  

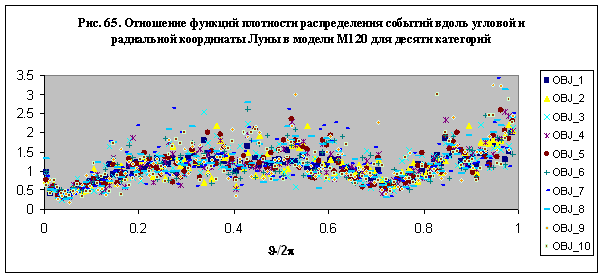
Данные для Юпитера на рис. 64 содержат 12 пиков, обусловленных взаимным когерентным движением Земли и Юпитера на протяжении 12-летнего цикла. Данные для Марса и Меркурия при внешнем сходстве рис. 62 и 63 имеют разное рассеяние относительно среднего значения.  Данные для Луны группируются аналогично данным для Меркурия и Марса, но со своими специфическими особенностями. Отметим, что все данные на рис. 58, 60, 62-65 изменяются пропорционально радиальной скорости в системе Земля – соответствующее небесное тело.    

Таким образом, в силу уравнения (29), данные распределений относительно координат любого небесного тела – расстояния и долготы, содержат когерентные составляющие, обусловленные периодическим движением небесного тела относительно Земли.  Зададимся вопросом, можно ли использовать когерентные возмущения функции плотности распределения данных, обусловленные движением небесных тел для распознавания самих данных по астрономическим параметрам, заданным в момент события W(t)? Ответ является положительным в задачах астросоциотипологии, связанных с распознаванием социальных категорий, причем можно утверждать, что чем больше использовано разнородных входных астрономических параметров, тем выше вероятность распознавания. Например, сочетание параметров долготы и расстояния должно приводить к повышению вероятности распознавания, что было обнаружено в работе [11]. С другой стороны, при замене независимых от долготы небесных тел углов домов на зависимые от долготы параметры склонения, вероятность распознавания должна снижаться, что было обнаружено в работе [6].

Теорема астросоциотипологии имеет еще одно интересное следствие, которое позволяет понять природу зависимости интегральной информативности от величины гравитационного потенциала.  Вычислим производную по времени от потенциала  гравитационного поля вдоль траектории движения, имеем с учетом первого уравнения (30):

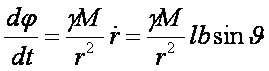
Учитывая, что расстояние от Земли до Солнца изменяется относительно слабо, можно сделать вывод, что скорость изменения потенциала гравитационного поля пропорциональна радиальной скорости перемещения нашей планеты. Учитывая эту связь, можно декларировать зависимость ИИ от производной потенциала гравитационного поля по времени, что и было сделано в работах [20-21].  

Наконец, заметим, что в работе [27] была обнаружена зависимость скорости радиоактивного распада ядер 32Si и 226Ra от расстояния от Земли до Солнца. Аналогичная зависимость была также установлена в работе [24] по данным [25] для сопротивления и индуктивности. В работе [26] была высказана гипотеза, что полученные в [25, 27] результаты можно объяснить зависимостью статистики фермионов от величины потенциала гравитационного поля Солнца. Учитывая полученные выше результаты, можно однозначно утверждать, что существует связь многолетних рядов наблюдений с радиальной скоростью движения нашей планеты или с производной потенциала гравитационного поля по времени.     

 

Проблема распознавания социальных категорий в поле центральных сил

Сформулируем задачу распознавания социальных категорий, рассматривая их как совокупность событий выбора самих категорий множеством респондентов. Тогда момент рождения респондентов можно отнести к началу события. Действительно, выбор социальной категории, например, профессии, не является одномоментным событием. Обычно ему предшествуют периоды воспитания и образования, практической подготовки. Однако для упрощения задачи удобно отнести это событие ко времени рождения респондентов, поскольку в этой задаче нет никакого другого выделенного момента времени, кроме рождения индивида.

Итак, имеется множество респондентов A, которому ставится в соответствие множество категорий Ci. Каждый респондент характеризуется моментом времени и местом рождения (географические координаты места рождения). По данным рождения можно построить матрицу, содержащую координаты небесных тел, например углы долготы и расстояния, а по биографическим данным респондентов можно определить частотные распределения Ni – число респондентов, имеющих отношение к данной категории Ci. В частности, для банка данных [8] соответствующие распределения приведены в работе [2]. Отметим, что один респондент может иметь отношение к нескольким категориям.

Определим число случаев реализации данной категории, которое приходится на заданный интервал изменения астрономических параметров, имеем в дискретном случае:

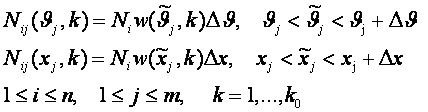                (45)

  Здесь k0 – число небесных тел, используемых в задаче,  нормированная переменная определена следующим образом:

     

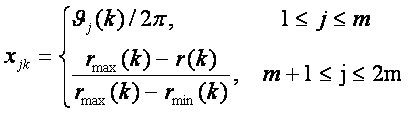
В системе искусственного интеллекта [7], используемой для решения задач астросоциотипологии, осуществляется фильтрация сигнала путем определения матрицы информативности в виде [3]

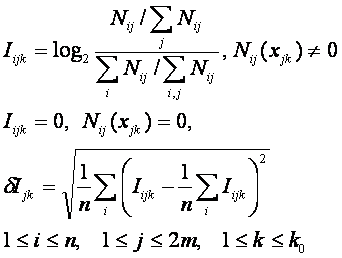                        (46)

Первая величина (46) называется информативность признака, а вторая величина является стандартным отклонением информативности или интегральная информативность (ИИ).

В случае непрерывных распределений событий определенная согласно (46) информативность явно не зависит от кинематических параметров небесных тел. Однако в дискретных задачах было обнаружено, что ИИ зависит от расстояния до небесных тел, что обусловлено невязкой, возникающей в формулах типа (43).

На рис. 66 представлены результаты расчетов интегральной информативности в зависимости от расстояния до Солнца в модели М22 выбора из 27-37 категорий (маркеры С27-С37 соответственно) для 20007 респондентов из банка данных [8]. Отметим, что зависимость типа представленной на рис. 66 наблюдается в широком диапазоне изменения числа интервалов разбиения от 6 до 172, числа категорий от 11 до 100 и общего числа случаев от 13479 до 123671 /8-9/. Таким образом, эту закономерность можно признать фундаментальным фактом.  По характеру распределения данных на рис. 66  можно сделать вывод, что ИИ изменяется пропорционально радиальной скорости, что непосредственно следует из основной теоремы астросоциотипологии [10-12].  

 

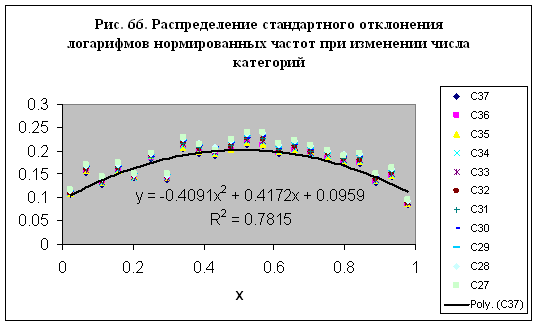
Следовательно, зависимость статистических параметров от кинематических параметров небесных тел сохраняется в матрице информативности, определенной согласно первому уравнению (46).  Определим размерность этой матрицы для примеров, приведенных на рис. 57-66. В модели М120 матрица информативности содержит 37х120х20=88800 элементов для 37 категорий и 20 параметров десяти небесных тел, разбитых на 120 ячеек. Соответственно в модели М22 матрица информативности содержит 37х22х20=16280 элементов.

Каждой категории можно сопоставить вектор информативности астрономических параметров размерности 2mk0, составленный из элементов матрицы информативности, путем последовательной записи столбцов, соответствующих нормированной координате, в один столбец, т.е.

                               (47)

С другой стороны, процесс идентификации и распознавания может рассматриваться как разложение вектора распознаваемого объекта в ряд по векторам категорий (классов распознавания) [3]. Этот вектор, состоящий из единиц и нулей, можно определить по координатам небесных тел, соответствующих дате и месту рождения респондента  l  в виде

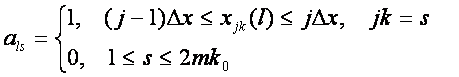    (48)

Таким образом, если нормированная координата небесного тела из данных респондента попадает в заданный интервал, элементу вектора придается значение 1, а во всех остальных случаях – значение 0. Перечисление координат осуществляется последовательно, для каждого небесного тела.    

В случае, когда система векторов (47) является полной, можно любой вектор (48) представить в виде линейной комбинации векторов системы (47). Коэффициенты этого разложения будут соответствовать уровню сходства данного респондента с данной категорией. В случае неполной системы векторов (47) точная процедура заменяется распознаванием. При этом уровень сходства данных респондента с той или иной категорией можно определить по величине скалярного произведения вектора (48) на вектор (47), т.е.

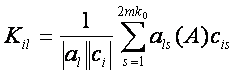                               (49)

Отметим, что возможны четыре исхода, при которых можно истинно или ложно отнести или не отнести данного респондента к данной категории. Для учета этих исходов распознавание социальных категорий в системе «Эйдос-астра» [7] осуществляется по параметру сходства, который определяется согласно (10).

На рис. 5  представлен параметр сходства четырех категорий при изменении объема выборки, взятый из работы [6]. Можно отметить, что уже при  N >150 происходит стабилизация параметра сходства различных категорий.  Очевидно, что параметр сходства должен удовлетворять критерию простой проверки

На рис. 2  представлена зависимость параметра сходства 870 категорий от частоты повторяемости в модели М72. В этом примере минимальная частота равна 3, а критерий простой проверки выполняется, согласно уравнению степенной зависимости, при Ni=1.7545, т.е. в интервале от 1 до 2. Следовательно, при малом объеме выборки сравнение данных в системе [7] осуществляется простым перебором, а при большом объеме выборки используются статистические методы.

При заданном объеме выборки и при фиксированном числе небесных тел, параметр сходства зависит от числа ячеек модели. Как было установлено [2], средний параметр сходства 37 категорий, данные для которых приведены на рис. 57-66, возрастает с числом ячеек модели по логарифмическому закону - см. рис. 32.

Эти результаты показывают, что процедура распознавания по параметру сходства (10), реализованная в системе «Эйдос-астра» [7],  является устойчивой как относительно объема выборки, так и относительно числа ячеек модели. Математическое обоснование этой процедуры дано в монографии [3], где также указана связь использованной меры (49) со статистикой c2.  

Естественно возникает вопрос, можно ли распознать произвольного респондента, не входящего в исходное множество А? Чтобы ответить на этот вопрос, разобьем исходное множество А на два подмножества – А1, А2. Сформируем матрицу информативности категорий, используя только подмножество А1. Выполним процедуру распознавания респондентов из подмножества А2. Теоретически определить процент угадывания при таком распознавании можно только при случайном выборе. Практический  же ответ на поставленный вопрос был получен в работе [4]. Так, например, из 5000 респондентов тестируемой выборки А2, чьи данные представлены на сайте [8], в системе «Эйдос-астра» [7] социальные категории были определены правильно у 68,75% респондентов. Обучение системы осуществлялось в этой задаче на базе данных 15007 респондентов. 

  Причина, по которой оказывается возможным идентифицировать подмножества (категории) событий различной даже случайной природы, используя астрономические параметры и матрицу информативности, достаточно очевидна. Ведь фактически идентифицируются распределения, которые образуются при модулировании исходных распределений астрономическими параметрами. В некоторых случаях этого достаточно, чтобы осуществить распознавание категорий.

Эту задачу можно сравнить с разложением солнечного света призмой. Свет представляет собой смесь случайных электромагнитных колебаний, но после прохождения призмы свет разлагается в спектр категорий цвета. При этом природа самого света не меняется.

Аналогично множество W(t) может представлять собой смесь случайных событий, но в процессе обработки системой  формируется матрица информативности астрономических параметров, которую можно использовать для распознавания категорий. При этом случайная природа множества W(t) не меняется.