ГЛАВА 8. МЕТОДИКА И ПОТОКОВЫЕ МОДЕЛИ УПРАВЛЕНИЯ ЭФФЕКТИВНОСТЬЮ ХЛЕБОПРОДУКТОВЫХ ПРОИЗВОДСТВЕННЫХ ОБЪЕДИНЕНИЙ

8.1. Комплекс методик и моделей
управления эффективностью

В процессе исследования был разработан комплекс методик и моделей повышения эффективности деятельности хлебопродуктовых производственных объединений АПК, который представлен на рис 8.1 [11, 67].

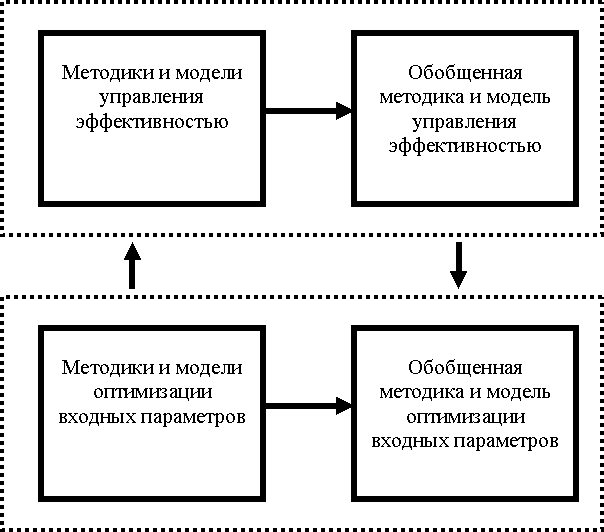
Рисунок 8. 1. Комплекс методик и моделей управления
эффективностью хлебопродуктовых производственных
объединений АПК

Первый подкомплекс включает в себя методики и модели управления эффективностью и разработанную на их основе обобщенную методику и модель управления эффективностью, второй подкомплекс включает в себя методики и модели оптимизации входных параметров и разработанную на их основе обобщенную методику и модель оптимизации входных параметров. Оба подкомплекса взаимосвязаны между собой и позволяют увеличить эффективность хлебопродуктовых систем АПК.

Полученные модели управления эффективностью содержат в качестве управляющих параметров такие величины как входной денежный поток d₁, входной материальный поток М₁ и количество циклов m, трактовка которых не является однозначной. Поэтому чтобы получить в этом вопросе определенность и попытаться оптимизировать их значения, с целью оптимизации эффективности был разработан подкомплекс моделей в основе которых лежит теория управления запасами. В итоге были получены модели для определения оптимального объема исходного материального потока M_1o, минимального объема исходного финансового потока и оптимальное число производственных циклов m, которые приведены на рисунке 4.2.

Полученная обобщенная модель для расчета входных параметров технологической цепи вместе с моделями эффективности, составляют математическую основу комплексной количественной методики оценки эффективности и определения входных параметров хлебопродуктового объединения с вертикальной (технологической) интеграцией.

На рисунке 8.2 показана информационная взаимосвязь и порядок расчетов выходных параметров в предложенном комплексе моделей, где

a – интенсивность спроса; S - организационные издержки; c - стоимость подлежащего переработке продукта; h - издержки содержания запасов; р - скорость поставки сырья; k - норма прибыли объединения; m - число циклов в исследуемый период, ρ - доля дополнительных расходов на организацию производственного процесса в одном; E₁ – расчетная эффективность; - оптимальный объем исходного материального потока; m₀ – оптимальное число циклов; - минимальный объем исходного финансового потока; Е – расчетная эффективность; d_2max – финансовый поток реализованных товаров, 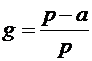- относительная скорость поставки.

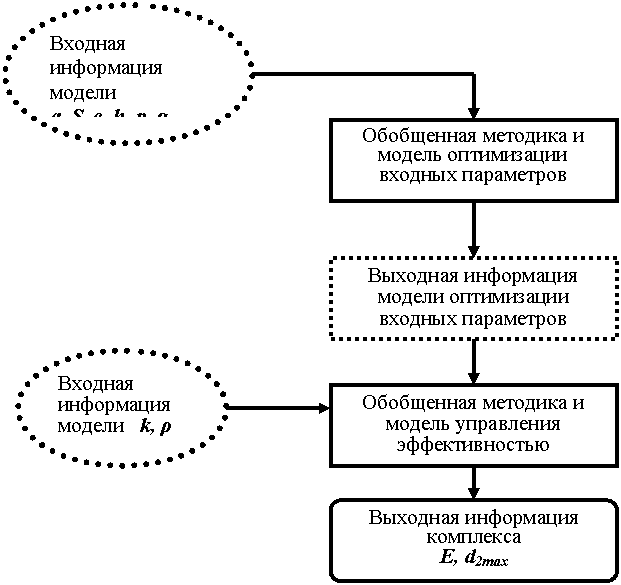
Рисунок 8. 2. Информационное взаимодействие
моделей комплекса

8.2. Эффективность трехступенной
структуры объединения

На рис. 8.3. представлена наиболее распространенная трехступенная структура системы хлебопродуктового производственного объединения с технологической (вертикальной) интеграцией предприятий, входящих в объединение. В этой структуре мукомольный завод не входит в объединение, но выступает в качестве сырьевой базы производства. Материальный поток движется по технологической цепи, образованной последовательностью предприятий, не затрагивая управляющую компанию (УК).

Отсутствие между ступенями технологической цепочки денежных потоков, способствует ритмичной работе отдельных производств и всей системы в целом. В системе действуют только два денежных потока: от УК к мукомольному заводу (поток d₁) и к УК от сегмента рынка, после реализации товара на рынке (поток d₂). Такая организация денежных потоков снимает их влияние на внутренний цикл производства, что очень важно в современных условиях.

Функционирование системы организовано следующим образом.

На основе анализа и синтеза информации о потребностях рынка, ценах, технологических и технических возможностях производства и других данных определяется объем денежных средств d₁, необходимый для закупки у хлебозавода достаточного для организации технологического цикла количества исходного материального ресурса (муки).

При этом учитывается, что прибавочная стоимость, полученная на каждом технологическом этапе, передается на следующий этап.

При исследовании структуры, изображенной на рис. 4.3, воспользуемся подходом, предложенным в работах. Будем считать, что норма прибыли принята одинаковой для всех предприятий, входящих в объединение, и равна k. Это возможно, если с точки зрения формы собственности, предприятия структуры образуют холдинг. Действительно, холдинговая организация дает больший синергический эффект и более чувствительна к управляющим воздействиям головной компании.

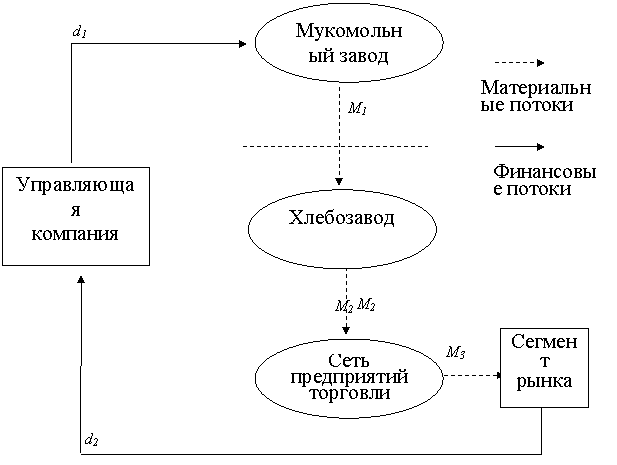
Рисунок 8. 3. Структура системы с технологической интеграцией, наиболее распространенной в хлебопродуктовой отрасли

На первом этапе объем закупленного ресурса М₁ (мука) эквивалентен денежным средствам d₁, т.е.

М₁~ d₁.

Соответственно материальный поток М₂ (хлебопекарные изделия) эквивалентен денежным средствам (1+k) d₁, то есть

М₂ ~ (1+k) d_{1 .}

Здесь k – норма прибыли объединения, а kd₁ – эквивалент прибавочной стоимости, созданной в технологическом звене (хлебозаводе).

Поток М₃ – это тот же поток хлебопекарных изделий М₂, поступающий на потребительский рынок через торговую сеть кооперации с торговой наценкой k.

После реализации на рынке товарного потока М₃ (хлебопекарных изделий), выручка B = d₂ составит

B = d₂ = (1+k)² d₁ .

В зависимости от вида технологии переработки и ее организации, в течение исследуемого периода (например, года) возможно несколько циклов производства (многократное прохождение технологической цепочки).

Число циклов может быть определено по количеству поставок исходного для производства сырья в течение года, поскольку каждая поставка сопровождается возникновением финансового потока d₁ для ее оплаты предприятию-производителю сырья.

Если обозначить число циклов в исследуемый период через m, то формула для выручки B принимает вид

B = m (1 + k)² d₁. (8.1)

Обозначим через ρ долю от d₁ дополнительных расходов на организацию производственного процесса в одном цикле (оплата труда, амортизация основных средств и т. п.). В этом случае общие расходы за период составят

P = d₁ + mρd₁ = d₁ (1 + mρ). (8.2)

Тогда чистый доход (прибыль)

D = B – P

Используя выражения для B и P и проведя преобразования, получим чистый доход, выраженный через исходный денежный поток, коэффициент прибыли (норму прибыли), число этапов (ступеней) технологической цепочки и количество циклов за исследуемый период:

D = d₁ [m (1 + k)² - (1 + mρ)] . (8.3)

Эффективность E₁ хлебопродуктового производственного объединения потребительской кооперации с технологической (вертикальной) интеграцией предприятий, определим как отношение выручки B к суммарным расходам Р:

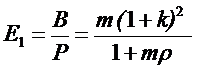. (8.4)

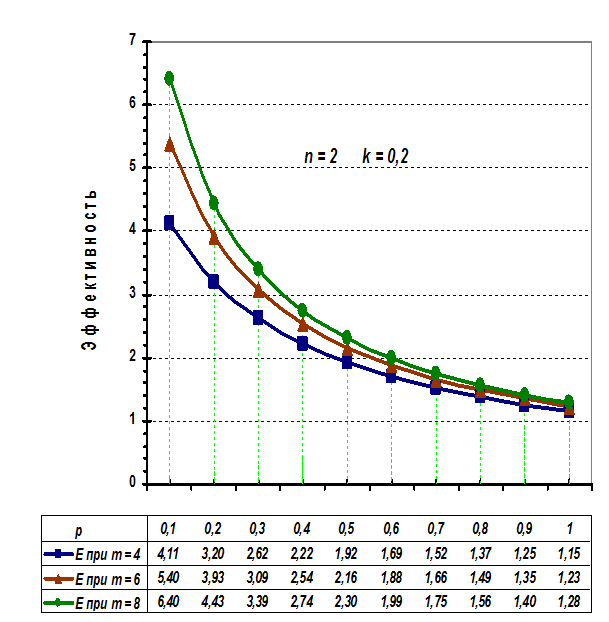
Рисунок 8. 4. График зависимости эффективности E₁ трехступенной структуры от доли расходов ρ при норме прибыли k = 0,2

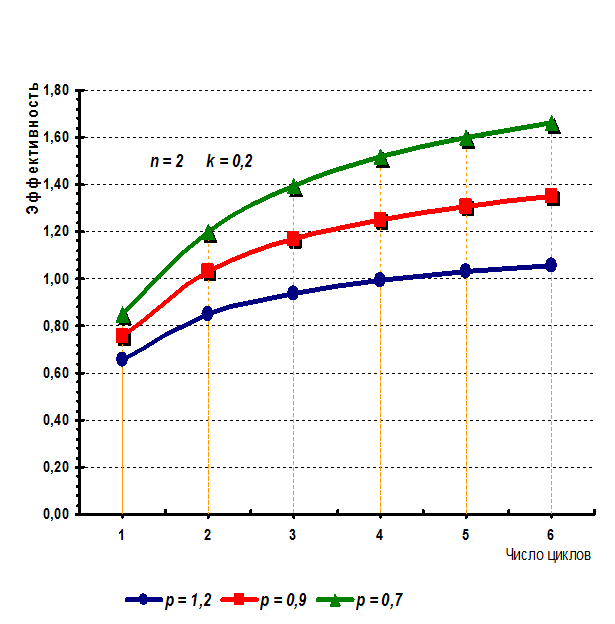
Рисунок 8. 5. График зависимости эффективности E₁ трехступенной структуры от числа циклов m при норме прибыли k = 0,2

Из (8.4) видно, что эффективность этой структуры нелинейно зависит от всех аргументов (факторов). Причем, нелинейности от числа циклов m и доли расходов ρ выражены сильнее, чем от нормы прибыли. Объяснить это можно тем, что, во-первых, удельный вес значений числа циклов выше, чем у нормы прибыли, а во-вторых, переменная доли расходов стоит в знаменателе выражения (8.4), что определяет гиперболический вид зависимости.

По полученным соотношениям, в том числе тем, которые приведены в последующих параграфах, были проведены численные эксперименты, подтвердившие сделанные выше выводы. На рисунках 8.4 – 8.6 приведены графики зависимости эффективности E₁ трехступенной структуры системы с технологической интеграцией, наиболее распространенной в хлебопродуктовой отрасли Краснодарского края. Они построены по результатам численных экспериментов (на этих рисунках n – число предприятий, входящих в состав объединения).

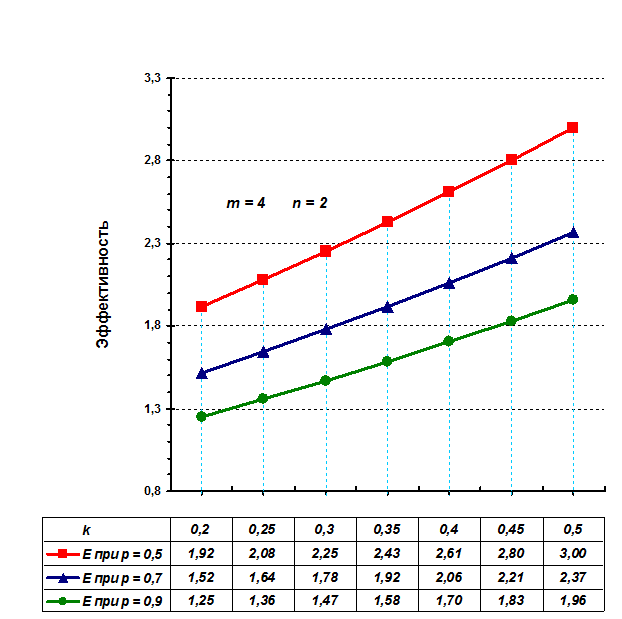
Рисунок 8. 6. График зависимости эффективности E₁ трехступенной структуры от нормы прибыли k при числе циклов m = 4

Очевидно, для рентабельной работы объединения необходимо, чтобы его эффективность была больше единицы, то есть E > 1. Заменив E₁ его выражением из (8.4), получим условие рентабельного функционирования объединения:

m (1 + k)² > (1 + mρ)

Разрешив (8.5) по отношению к ρ, получим условие-ограничение для максимально допустимого значения относительной доли расходов:

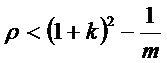(8.5)

Исходя из проведенного исследования движения материально-финансовых потоков хлебопродуктового производственного объединения потребительской кооперации с технологической (вертикальной) интеграцией, можно сделать вывод о том, что вторая степень в выражениях (8.1 – 8.4) определена количеством предприятий, вошедших в объединение.

Следовательно, для повышения эффективности хлебопродуктового производственного объединения необходимо наращивать количество звеньев технологической цепочки и стремиться к созданию структуры, образующей полный технологический набор производственных звеньев.

8.3. Эффективность четырехступенной
структуры объединения

Включение в состав хлебопродуктового производственного объединения мукомольного завода позволило бы повысить общую эффективность производства и реализации хлебопекарных изделий. В этом случае схема производственной структуры примет вид, изображенный на рис. 8.7.

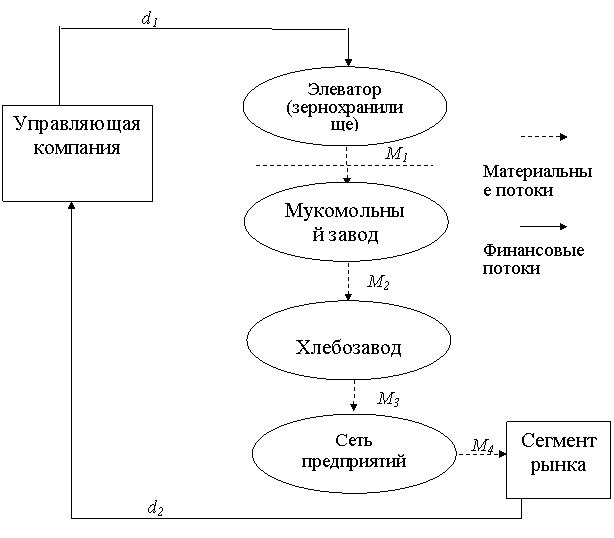
Рисунок 8. 7. Хлебопродуктовое производственное объединение
с мукомольным заводом

Соотношение для расчета эффективности E₂, расширенного за счет включения мукомольного завода в состав производственного объединения будет выглядеть так:

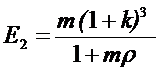. (8.6)

Поскольку в структуру объединения, изображенного на
рис. 8.7, входит три предприятия, то этим объясняется кубическая зависимость эффективности E₂ от внутренней нормы прибыли объединения k.

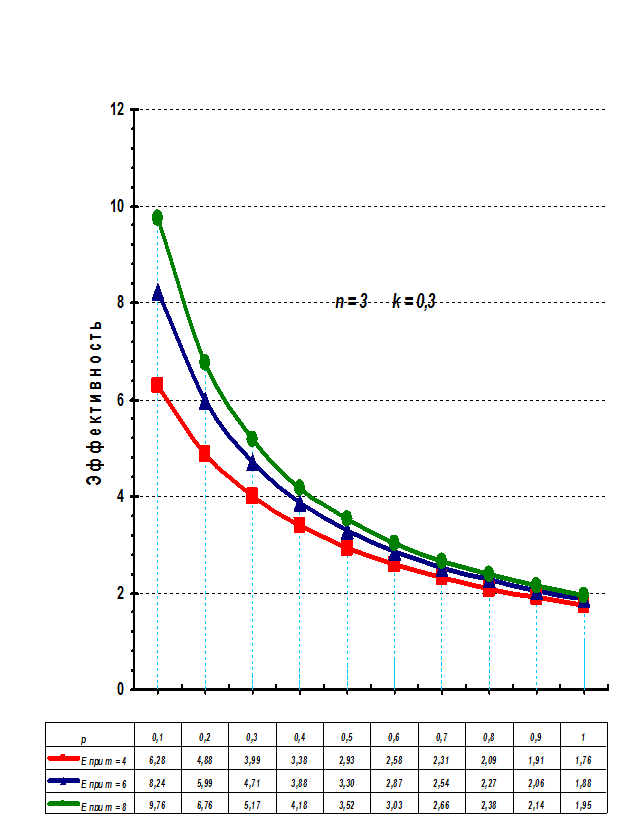
Рисунок 8. 8. График зависимости эффективности E₂ четырехступенной структуры от доли расходов ρ при норме прибыли k = 0,3

На рисунках 8.8 – 8.10. приведены графики зависимости эффективности E₂ четырехступенной структуры хлебопродуктовой системы с технологической интеграцией, аналогичные построенным для трехступенной структуры..

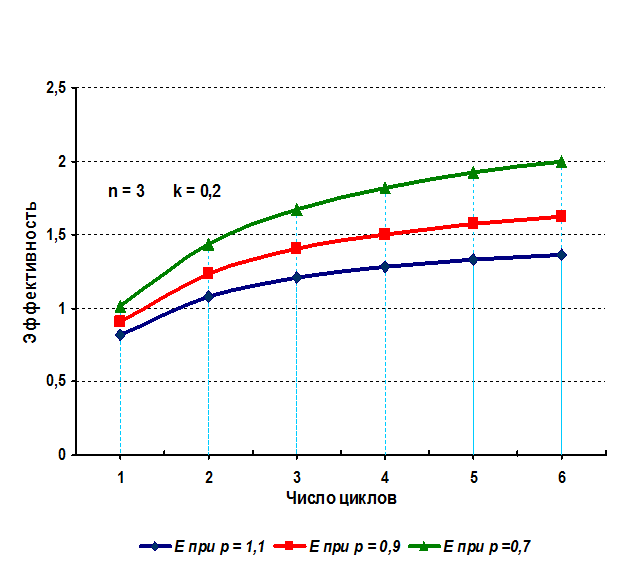
Рисунок 8. 9. График зависимости эффективности E₂ четырехступенной структуры от числа циклов m при норме прибыли k = 0,2

Если принять равными количество циклов m и доли расходов ρ в первой (рис. 8.3) и второй (рис. 8.4) структурах, то относительная эффективность Э₂₁ второй структуры по сравнению с первой запишется следующим образом:

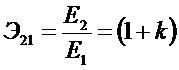. (8.7)

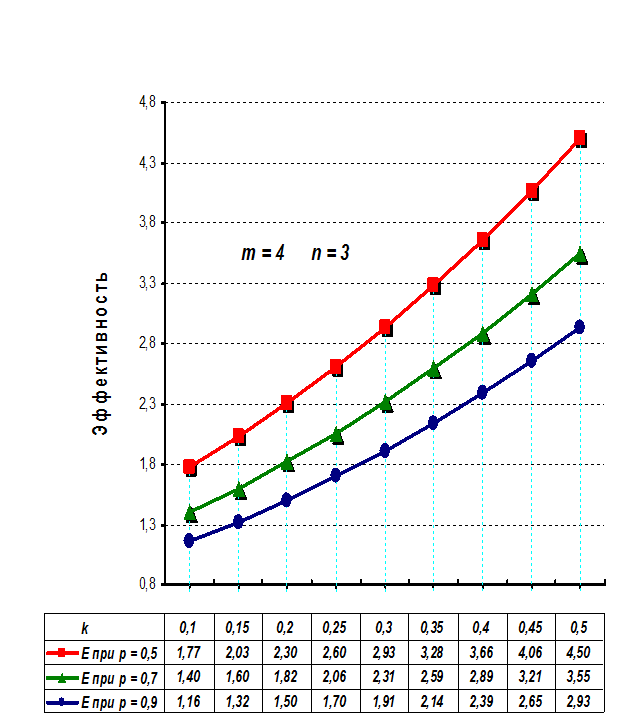
Рисунок 8. 10. График зависимости эффективности E₂ четырехступенной структуры от нормы прибыли k при числе циклов m = 4

Другими словами, добавление каждого нового звена в технологическую цепь объединения увеличивает общую эффективность производства в (1+k) раз.

8.4. Эффективность технологически
полной структуры

Полный технологический цикл производства хлебопекарных изделий можно обеспечить, если объединить агропредприятие зернового направления, элеватор, мукомольный завод, хлебозавод и сеть реализации.

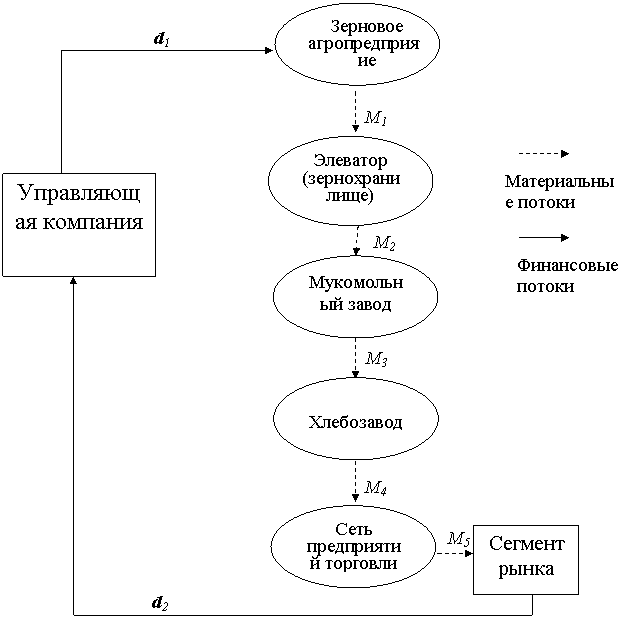
Рисунок 8. 11. Хлебопродуктовое производственное объединение с технологически полным циклом производства

Объединение может быть реализовано на различных принципах, но главным должно быть то, что создается технологически полная замкнутая цепь производства. При подобном объединении возникает структура интегрированной системы, изображенной на рис. 8.12.

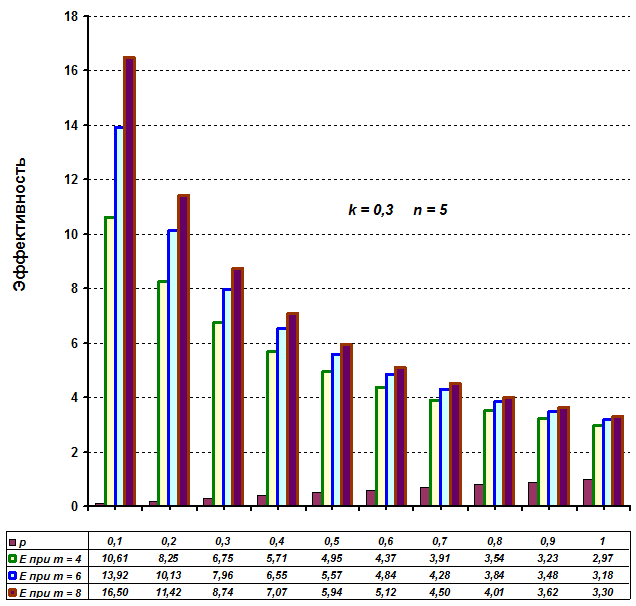
Рисунок 8. 12. График зависимости эффективности E₃ технологически полной структуры от доли расходов ρ (норма прибыли k = 0,3)

Соотношение для расчета эффективности E₃ производственного объединения с полным технологическим циклом с учетом (8.2), (8.3) и (8.4) можно записать так:

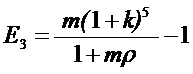. (8.8)

Здесь k – норма прибыли объединения;

m – количество циклов в год, начиная от потока зерна с элеватора.

На рисунках 8.12 – 8.14 приведены графики зависимости эффективности E₃ технологически полной структуры хлебопродуктовой, аналогичные построенным для четырехступенной структуры.

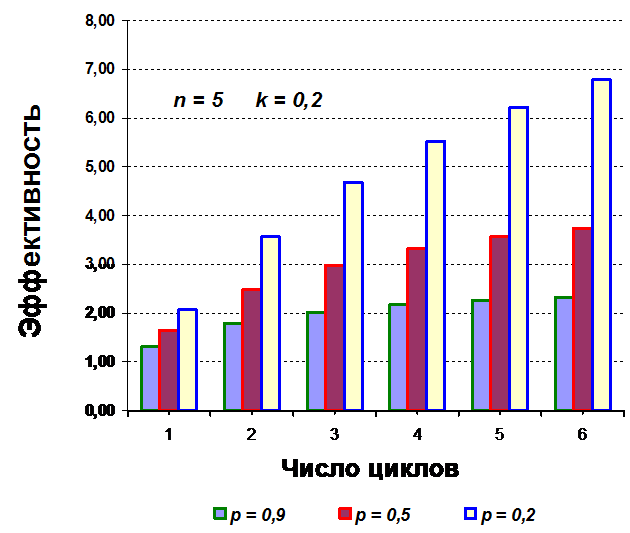
Рисунок 8. 13. График зависимости эффективности E₃ технологически полной структуры от числа циклов m (норма прибыли k = 0,2)

В общем случае, нормы прибыли могут быть различными во всех предприятиях объединения. Тогда формула (4.8) преобразуется к виду (8.9):

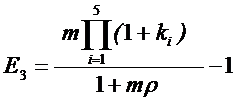, (8.9)

где i – номер предприятия в технологической цепочке;

m – количество циклов в год, начиная с элеватора.

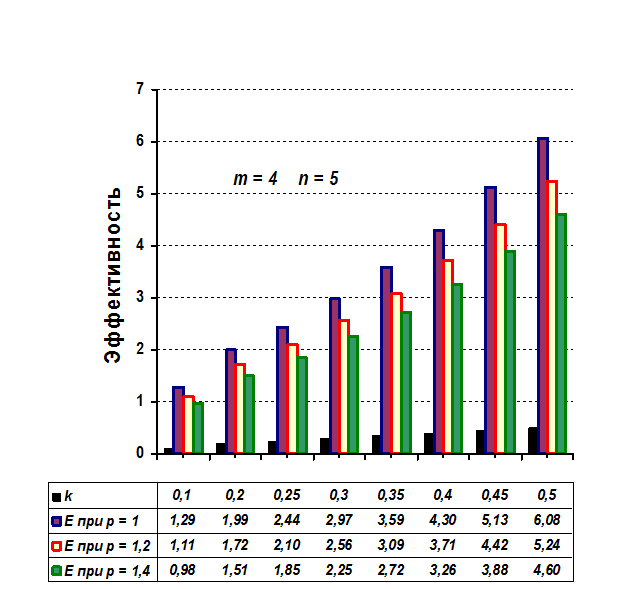
Рисунок 8. 14. График зависимости эффективности E₃ технологически полной структуры от нормы прибыли k (число циклов m = 4)

Как и для второй структуры сравним эффективность структуры с полным технологическим циклом производства (рис. 8.11.) с эффективностью ныне наиболее распространенной схемы производства и реализации хлебопекарных изделий в Краснодарском крае (рис. 8.3).

Приняв равными количество циклов m и доли расходов ρ в первой (рис. 8.3) и третьей (рис. 8.11) структурах, получим, путем деления (8.10) на (8.4), для относительной эффективности Э₃₁ третьей структуры по сравнению с первой следующее соотношение:

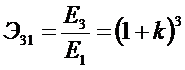. (8.10)

Из этой формулы следует то, что включение в хлебопродуктовое объединение всех производственных технологических звеньев (предприятий) позволяет получить существенно большую эффективность производства и реализации хлебопекарных изделий населению.

Возрастание экономической эффективности при увеличении числа производственных технологических звеньев вертикально интегрированной структуры объясняется возникновением синергического эффекта, который проявляется в передаче прибавочной стоимости, созданной в предыдущем технологическом звене, последующему звену, тем самым, увеличивая создаваемую им прибавочную стоимость. При определенных условиях общая прибавочная стоимость, созданная вертикально интегрированной производственной системой может превысить исходную стоимость (ее эквивалентом является финансовый поток d₁ на входе приведенных, на рисунках 8.3, 8.7 и 8.11 структур).

Одним из материальных воплощений социальной миссии государства является производство и продажа хлебобулочных изделий населению по разумным ценам и в достаточном количестве. С этой точки зрения из анализа полученных соотношений можно сделать вывод о том, что включение в объединение каждого дополнительного производственного технологического звена позволяет при тех же затратах и исходном финансовом потоке получать либо в (1 + k) раз больший объем выпекаемых хлебобулочных изделий, либо в среднем в (1 + k) раз уменьшить цены хлеб. Поэтому набольший социальный эффект достигается при создании в объединении полной технологической цепи предприятий по производству хлебопекарных изделий.

Предложенные модели и методики были апробированы в хлебопродуктовых объединениях потребительской кооперации Гулькевичского и Выселковского РПС.

8.5. Методика и модели оптимизации входных
параметров технологической цепи
хлебопродуктового объединения

Рассмотрим наиболее типичные вертикально интегрированные структуры хлебопродуктовых объединений (рисунки 8.3 и 8.5).

Годовой объем необходимого сырья для переработки, а значить и годовой объем финансовых средств для его закупки, может быть рассчитан, исходя из годового спроса на хлебопекарную продукцию сегмента рынка потребительской кооперации. Если сразу закупить (или произвести) годовой объем исходного продукта переработки (для структуры рис. 8.5 это зерно, а для структуры рис. 8.3 - мука), то за год будет реализован всего один цикл. В этом случае сразу возникает почти неразрешимая проблема (как финансовая, так и складская) хранения такого большого объема запасов. Если же производить закупки мелкими партиями (большое число циклов в году), проблемой становятся резко увеличившиеся затраты, связанные с частыми заказами (документация, транспортировка, погрузочно-разгрузочные работы и т.п.).

Таким образом, возникает задача оптимизации числа циклов m и связанных с ним объемов финансового d₁ и материального М₁ потоков.

Как указывалось в п. 8.3, число циклов может быть определено по количеству поставок исходного для производства сырья в течение года. Для закупки и организации поставки необходимо возникновение исходного финансового потока d₁, компенсирующего произведенные начальные издержки и, таким образом, запускающего производственный цикл вертикально интегрированной системы.

Для бесперебойного функционирования технологической цепи необходимо, чтобы на входе каждого ее звена в любой производственный момент времени находилось достаточное количество исходного для переработки сырья, или другими словами, запасов. Поскольку производственные запасы в течение технологического процесса расходуются, то их необходимо возобновлять. С этой целью вновь создается финансовый поток d₁, инициирующий возобновление уменьшившихся до минимального уровня производственных запасов, и так далее. Возникают типичные производственные циклы, причем их длительность и количество прямо связаны со скоростью расходования созданных в начале цикла запасов.

В связи с выше сказанным, воспользуемся для определения числа циклов m и объемов исходных финансового d₁ и материального M₁ потоков в вертикально интегрированной хлебопродуктовой производственной системе теорией управления запасами.

Необходимость запасов объяснятся случайными процессами, протекающими в производственных системах. Нельзя быть уверенным в том, что продукты для переработки поступят на склад технологического звена именно в тот момент времени, когда они понадобятся. Если на некоторой стадии процесса производства потребуется какой-то вид сырья, а этого сырья не окажется в запасе, т. е. образовался дефицит, то процесс производства может задержаться или вообще остановиться.

Очевидно, что таких ситуаций необходимо по возможности избегать: на складах технологических звеньев (предприятий) хлебопродуктового объединения всегда должно быть нужное количество данного вида сырья. Однако если запасы увеличить, соответственно возрастет плата за их хранение. Управления запасами состоит в том, чтобы выбрать компромиссное решение среди других или даже оптимальное при определенных условиях или ограничениях.

Независимо от того, какого рода систему управления запасами имеет производство, основные решения, которые может принять управляющий орган, состоят в следующем:

· какое количество товара должно находиться в запасе;

· в какое время производить пополнение запаса.

Предметом исследования является связь между количеством Q запаса, имеющегося на складе производственного звена технологической цепи, и временем t, для которого рассматривается этот запас. Таким образом, мы исследуем функцию Q = f (t), соответствующую величине запаса в момент времени t. Под Q будем понимать запасы только одного вида.

8.5.1. Модель для идеальных условий

Согласно классической модели Харриса, рассматривается непрерывное расходование запасов и мгновенное их поступление.

На рис. 8.15. показан пример графика изменения запасов для такой модели.

В течение длительности цикла T идет расходование запаса и в момент спада запасов до нуля происходит их восстановление до уровня q. Этот момент называют «точкой заказа», положение которой определяет длительность цикла.

Рисунок 8. 15. График изменения запасов в модели Харриса

В системах управления запасами основными вопросами являются состав и размеры издержек управления.

Рассматриваемые в модели величины, их обозначения, а также принятые относительно этих величин допущения, сведены в табл. 8.1.

Таблица 8. 1 – ПАРАМЕТРЫ СИСТЕМЫ УПРАВЛЕНИЯ ЗАПАСАМИ

Величина	Обозначение	Единицы измерения	Допущения
Интенсивность спроса	a	Единицы товара в год	Спрос постоянен и непрерывен
Организационные издержки	S	Рублей за одну партию	Организационные издержки постоянны
Стоимость подлежащего переработке продукта	c	Рублей за единицу товара	Цена единицы товара постоянна
Издержки содержания запасов	h	Рублей за единицу товара в год	Стоимость хранения постоянна
Размер партии поставки	q	Единицы товара в год	Постоянная величина.

Рассмотрим ситуации, в которых издержки, связанные с запасами, могут быть объяснены независимо друг от друга.

1. Организационные издержки – расходы, связанные с оформлением и доставкой подлежащего переработке продукта (товара), необходимые для каждого цикла складирования. Эти затраты связаны с подготовительно-заключительными операциями при поступлении сырья и подаче заявок.

2. Издержки содержания запасов – затраты, связанные с хранением и амортизацией в процессе хранения (товары могут портиться, устаревать, их количество может уменьшаться и т.п.).

3. Издержки, связанные с дефицитом – поставка не может быть выполнена, это допускается в моделях с дефицитом, что приводит к дополнительным издержкам, обусловленных отказом.

Уравнение издержек С, связанных с запасами, сделанными в течение года, может быть записано, в соответствии с табл. 8.1 следующим образом:

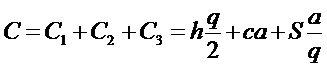, (8.11)

где С₁ = h - общие издержки содержания запасов;

С₂ = ca - стоимость товара;

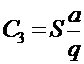- общие организационные издержки.

На рис. 8.16 показан приближенный график функции С = f(q), отвечающий формуле (8.11).

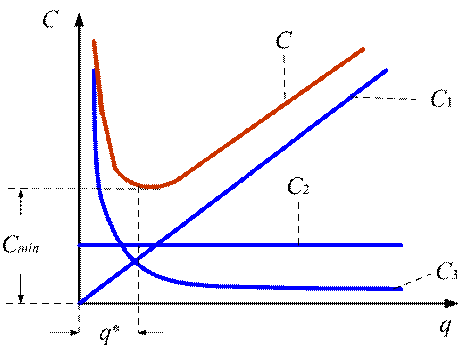
Рисунок 8. 16. График изменения издержек

Чтобы найти значение партии поставки, обращающее С в минимум, используем необходимое условие экстремума 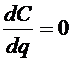. Это действительно точка минимума, так как .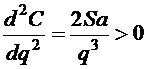

Следовательно, справедливо

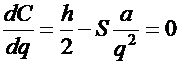(8.12)

Решая последнее уравнение относительно q, найдем оптимальный размер партии поставки q^*, а значит и оптимальный объем исходного материального потока M_1o:

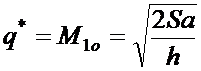(8.13)

Величина q^* называется оптимальным размером партии поставки товарного запаса. Уравнение (8.13) иногда называют формулой оптимального заказа.

Чтобы полностью удовлетворить годовой спрос a при размере поставки, равном q^*, необходимо сделать a/q^* поставок за год.

Таким образом, число циклов m технологической цепи в течение года можно определить как

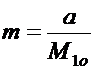, (8.14)

где a – годовая потребность в сырье для переработки;

М_1о – оптимальный объем исходного материального потока, вычисляемый по формуле (8.13).

Или, если подставить вместо объема исходного материального потока М_1о в формуле (8.14) его выражение из (8.13), получим оптимальное число циклов m_o:

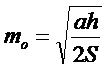(8.15)

Минимальный объем финансового потока d_1min, запускающего технологический цикл, определим по типу соотношения (8.11), в котором учтем, что рассматривается один цикл, а значит, и один оптимальный по объему материальный поток :

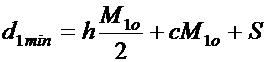(8.16)

Если подставить в (8.14) выражение из (8.13), получим соотношение для расчета минимального объема финансового потока d_1min, зависящее только от параметров поставок и хранения сырья:

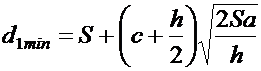(8.17)

8.5.2. Модель для производственных условий

В реальных производственных условиях, во-первых, не может быть мгновенных поставок партий исходного продукта переработки, а во-вторых, технологический процесс, как правило, является непрерывным, и в течение выполнения с определенной скоростью р поставки сырья происходит его потребление, тоже с определенной скоростью a. Причем, очевидно, что скорость поставки сырья должна превышать скорость его потребления
( р > a ).

Задача управления запасами в этих условиях может быть сформулирована практически так же, как и предыдущая задача, с тем отличием, что поставки партий сырья на склад производятся не мгновенно, а равномерно в течение определенного промежутка времени t_п, т.е. задана и скорость поставки р (рис. 8.17).

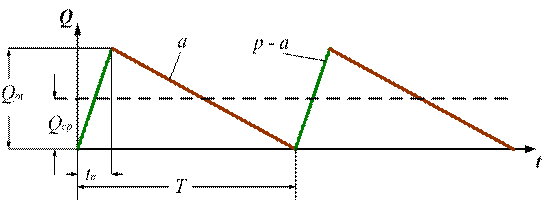
Рисунок 8. 17. График изменения запасов в производственных условиях

Допущения здесь те же, что и в задаче Харриса, кроме дополнительного, которое формулируется так:

при уменьшении запасов на складе до нуля начинаются поставки и продолжаются до тех пор, пока не будет поставлена одна партия. При этом отгрузка поставляемого сырья для осуществления технологического процесса не прекращается.

Суммарные издержки в заданной системе могут быть записаны в виде:

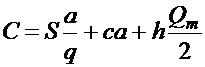, (8.18)

где Q_m – максимальный уровень запасов на складе.

Уровень запасов Q_m , для размещения которого должны быть подготовлены складские помещения, может быть определен как произведение длительности поставки сырья t_п и разности скоростей его поставки р и отгрузки d:

. (8.19)

Размер партии поставки определяется как произведение скорости поставки и ее длительности

.

Откуда

(8.20)

Подставив значение t_n из (8.20) в формулу (8.19), получим для Q_m :

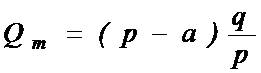(8.21)

А выражение для издержек после подстановки (8.21) приобретет вид:

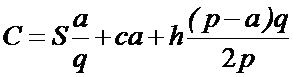(8.22)

Продифференцировав C по q и приравняв производную нулю, получим формулу для оптимальных размера партии поставки и объема исходного материального потока:

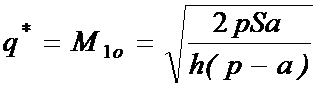(8.23)

Чтобы полностью удовлетворить годовой спрос при оптимальном объеме исходного материального потока необходимо осуществить число циклов, равное

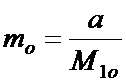, (8.24)

Или, если подставить вместо оптимального объема исходного материального потока в формуле (8.24) его выражение из (8.23), получим:

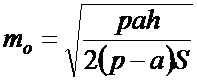(8.25)

Минимальный объем финансового потока d_1min, запускающего технологический цикл, определим по типу соотношения (8.22), в котором учтем, что рассматривается один цикл, а значит, и один оптимальный по объему материальный поток :

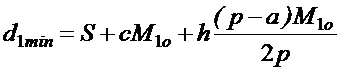(8.26)

Или, подставив в (8.26) соотношение для из (8.23), получим

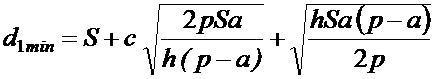. (8.27)

Оптимальные длительность поставки t_no и пиковый объем поставляемого сырья Q_mo будут определяться по формулам:

;

.

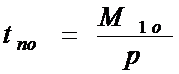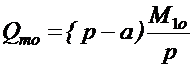Или:

;

.

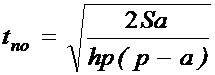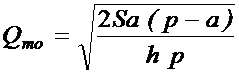8.5.3. Обобщенная модель определения
оптимальных входных параметров

Сравнительный анализ формул, полученных для числа циклов и исходных объемов финансового и материального потоков технологической цепи хлебопродуктового объединения, позволяет сделать вывод о том, что они отличаются лишь коэффициентом (назовем его относительной скоростью поставки и обозначим через g) в выражениях для размера партии поставки, равным 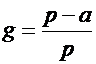. Исследование этого коэффициента показывает, что во-первых, для работоспособной технологической цепи он должен быть больше нуля (скорость поставки сырья должна быть больше скорости его отгрузки на переработку), во-вторых, его значение находиться в интервале от нуля до единицы и зависит от скорости поставки сырья: при p = a, g = 0; при p >> a, g = 1. Очевидно, что, если p >> a, то формулы второй группы, полученные для производственных условий, превращаются в формулы первой группы (идеальные условия). Таким образом, первая группа формул представляет собой частный случай второй группы при p >> a.

Используя выражение для коэффициента g, перепишем основные соотношения, представляющие обобщенную модель для расчета параметров технологической цепи хлебопродуктового объединения.

Оптимальный объем исходного материального потока:

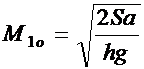. (8.28)

Оптимальное число циклов:

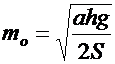. (8.29)

Минимальный объем исходного финансового потока:

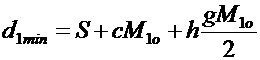, (8.30)

или

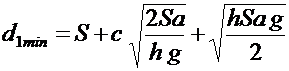. (8.31)

В хлебопродуктовой производственной структуре с полным технологическим набором предприятий (рис. 8.11) первые два звена характеризуются годичным циклом, обусловленным сезонностью производства в растениеводстве. Поэтому входные потоки d₁ и М₁ имеют годовые объемы, а оптимизация материальных потоков начинается только с потока М₂.

Полученная обобщенная модель для расчета входных параметров технологической цепи вместе с моделями эффективности, разработанными в п. 8.3, составляют математическую основу комплексной количественной методики оценки эффективности и определения входных параметров хлебопродуктового объединения с вертикальной (технологической) интеграцией.

Для апробации разработанных методик и моделей (оптимизации входных параметров) нами был проведен расчет для Гулькевического хлебопродуктового трехзвенного объединения (хлебокомбинат – торговая сеть). По данным этого объединения за 2003 год:

· Интенсивность спроса (муки в год) - 4225 т / год,

· Организационные издержки – 207,3 тыс. руб. / год

· Издержки содержания запасов – 28,7 тыс. руб. / год

· Размер партии поставки – 30 тонн

· Стоимость подлежащего переработке продукта (мука) - 13712,4 тыс. руб./ год.

Таким образом, затраты на управление запасами в объединении составили в 2003 году 236 тыс. рублей. Количество партий поставок (циклов) – 141. Средний уровень запасов в году – 15 тонн. Организационные издержки на одну партию поставки 1500 руб. Издержки на хранение 1 тонны муки в год – 1900 руб. Стоимость 1 тонны муки – 3245 руб.

Расчет по формуле 4.13 оптимального размера партии поставки q^*, что тоже самое оптимального исходного материального потока цикла составил 81 тонну. Учитывая интенсивность годового спроса предприятия по формуле 8.14 была получено, что оптимальное количество циклов m_o в течении года составляет 52. Подсчет затрат на управление запасами при оптимальных размерах исходного материального потока и числа циклов дал сумму в 154 тысячи рублей.

Таблица 8. 2 – СРАВНИТЕЛЬНЫЙ АНАЛИЗ РЕАЛЬНЫХ И ОПТИМАЛЬНЫХ ВХОДНЫХ ПАРАМЕТРОВ ПРЕДПРИЯТИЙ ХЛЕБОПЕКАРНОЙ ОТРАСЛИ КРАСНОДАРСКОГО КРАЙПОТРЕБСОЮЗА

№ п/п	Потребительские общества и союзы	Интенсивность спроса на муку, тонн	Количество муки на 1 цикл М1	Количество циклов m	Оптимальное количество муки на один цикл М01	Оптимальное количество циклов, m0	Изменение организационных издержек %
1	Абинский РПС	16875,6	116,3	145	468,7	36	32,0
2	Гулькевичский РПС	4077,4	26,8	152	78,4	52	35,0
3	Кореновское райпо	3635,7	24,2	150	62,6	58	28,0
4	Красноармейский РПС	5978,9	27,8	218	142,3	42	38,2
5	Крымское райпо	4278,5	28,1	152	99,5	43	32,7
6	Лабинское райпо	3567,3	24,6	145	63,7	56	30,4
7	Пашковский РПС	3876,6	28,9	134	71,7	54	24,4
8	Темрюкский РПС	8765,8	56,9	154	203,8	43	22,3
9	Тимашевский РПС	6239,0	42,7	146	102,3	61	24,7
10	Усть-Лабинский РПС	5765,4	39,76	145	108,8	53	34,6
11	Выселковское райпо	2104,5	28,8	73	56,9	37	26,7

Таким образом, выигрыш при оптимальных входных параметрах составляет 82 тысячи рублей в год, т.е. расходы на управление запасами уменьшаются на 35%.

Стоимость исходного материального потока за 1 цикли издержками управления запасами в цикле при оптимальных входных параметрах определили исходный финансовый поток d_1min (формула 8.16) который составил 266660 рублей.

По данным за 2003 год по 11 хлебопродуктовым объединениям потребкооперации были проведены расчеты, результаты которых приведены в табл.4.2., показавшие, что в случае применения оптимальных входных параметров расходы на организацию материального потока уменьшаются от 22,2 до 38,2%, а эффективность возрастает на величину от 20 до 50%.

8.6. Выводы по 8-й главе

Полученные в восьмой главе монографии научные результаты позволяют сделать следующие выводы.

1. Расширена трактовка понятия синергического эффекта, как эффекта умножения прибавочных стоимостей, создаваемых технологическими звеньями в вертикально интегрированных производственных системах.

2. Предложены модели и методика определения эффективности хлебопродуктовых производственных объединений, позволяющие проводить их сравнительную количественную оценку и рассчитывать параметры рентабельного функционирования.

3. Разработаны модели и методика определения числа производственных циклов хлебопродуктовых производственных объединений, дающие возможность так же определять периодичность поставок между технологическими звеньями и оптимальный размер партий поставок.

4. Разработана модель производственного цикла хлебопродуктового объединения, основанная на теории управления запасами, позволившая установить функциональную взаимозависимость между числом циклов и периодичностью и оптимальным размером партии производственных поставок в технологические звенья производственной системы.

5. Предложен комплекс взаимосвязанных моделей управления хлебопродуктовым производственным объединением.