ГЛАВА 2. АНАЛИЗ ЭФФЕКТИВНОСТИ
И УСТОЙЧИВОСТИ АПК НА ОСНОВЕ
ПОТОКОВЫХ МОДЕЛЕЙ СТОИМОСТИ

 

2.1. Структурная схема товарно-денежного
обращения

 

Основой и движущей силой любых экономических процессов является стоимость товарно-денежной массы и вложенного в них труда [9, 62, 83]. При этом стоимость многолика и бывает потребительной, меновой, рыночной, прибавочной и т.д. Однако сущностью всей экономической системы как целого бесспорно является полезность производимой этой системой продукции, характеризуемая степенью (вероятностью) р удовлетворения потребностей общества. А.А. Денисов предлагает исчислять сущность (полезность) системы следующим образом [23, 24, 27, 28]:

,                                            (2.1)

где в случае двоичных логарифмов полезность выражается в битах.

Применительно к экономике вместо сущности или полезности представляется более уместным термин "эффективность", которым в дальнейшем будем пользоваться.

Согласно (2.1) эффективность (или потенциал) Н0  экономики тем выше, чем выше степень р удовлетворения ею потребностей общества. Если эти потребности удовлетворяются полностью, т.е. р = 1 (что, конечно, никогда не бывает), то Н0 = ¥, т.е. эффективность экономики беспредельна. Если же потребности удовлетворяются наполовину, т.е.   

р = 0,5, то Н0=1 бит. Наконец, если потребности общества вообще никак не удовлетворяются, т.е. р = 0 (что также не реально), то Н0 = 0, т.е. экономика обладает нулевой эффективностью.

Сравнение экономических систем только по эффективности страдает однобокостью, поскольку сравнительно малоэффективная экономика, несмотря на свой невысокий потенциал Н0, может обеспечивать огромный оборот I товаров и услуг (как было в СССР). В то же время сравнительно эффективная экономика, несмотря на свой высокий потенциал, может обладать невысоким оборотом (как в Швеции). Поэтому исчерпывающей характеристикой, пригодной для сравнения любых экономических систем, является их экономическая мощь которая учитывает как качественные, так и объемные показатели системы:

N= Н0 I                                           (2.2)

Из (2.2), нетрудно понять, почему СССР по экономической мощи занимал второе после США место в мире. Ведь он, хотя и в меньшей степени по сравнению с другими развитыми странами, но удовлетворял потребности гораздо большего числа людей, т.е. имел намного больший оборот I товаров и услуг, несмотря на низкую их эффективность Н0.

Итак, эффективность экономики, в роли которой выступает полезность товаров и услуг, служит той движущей силой, которая побуждает экономическую систему функционировать. Ведь если товары и услуги не обладают полезностью, то никто не будет их ни производить, ни потреблять. Напротив, чем больше Н0, тем больше желание потребителей иметь соответствующие товары и тем больше желание предпринимателей их произвести. Значит, Н0 возбуждает экономические процессы, которые текут в последовательности: производство - обмен - потребление. Однако, производству препятствуют капиталовложения, частично "омертвляющие" эффективность на величину ΔН:

Н = Н0 - ΔН.                                          

Что касается обмена, то до изобретения денег он выступал на рынке в форме натурального обмена товаров, произведенных одними людьми, на товары, произведенные другими. Сейчас эта форма, чаще именуемая бартером, сохраняется как рудимент, параллельный товарно-денежному обмену. Последний же на современном рынке доминирует в форме обмена товаров, произведенных одними людьми, на деньги (продажа) с последующим обменом денег на товары, произведенные другими людьми (покупка).

Таким образом, схематично вся процедура товарно-денежного обращения выглядит так, как показано на рис. 2.1.

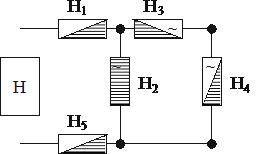
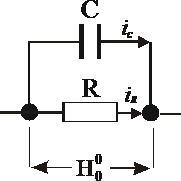
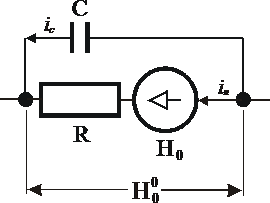
Рисунок 2. 1. Схема товарно-денежного обращения

 

На рис. 2.1 горизонтальной штриховкой выделены участки обращения товара, без цвета - участки обращения труда, а волнистым знаком - участки обращения денег. В блоке "производство" труд превращается в товар, придавая ему свою стоимость Н1. В блоке "бартер" затраты труда на обмен товаров придают им прибавочную стоимость Н2, которая на современном рынке распределяется между блоками "продажа" и "покупка", так что

 

                                        (2.3)

где Н3 оптовая наценка, Н4 - розничная наценка, так что цена товара составляет ΔН + Н1 + Н3 + Н5.

Наконец, в блоке "потребление" товар идет на воспроизводство труда (рабочей силы), сохраняя за собой потребительную стоимость Н5, которую обычно именуют "спросом". Таким образом, согласно схеме

 

,                                (2.4)

где Н = Н0 - ΔН.

Обратим внимание, что в отличие от материальных ценностей, которые создаются в процессе производства и исчезают в процессе потребления, проходя этот путь в направлении стрелок, деньги лишь символизируют стоимость и, циркулируя между блоками "продажа" и "покупка", являются нерасходуемым материалом. Поэтому они не стоимость, а информация о стоимости, и как всякая информация, будучи однажды созданы, используются многократно и безрасходно подобно законам Ома, Кулона или Ньютона. И пока информация о стоимости адекватна стоимости -деньги полноценны. Если же эта информация превосходит стоимость - деньги соответственно обесцениваются, а доверие к тем номиналам, что изображены на денежных купюрах, падает, как к не вполне истинной информации.

 

2.2. Экономическая интерпретация диалектического формализма

 

Независимо от того, отдаем мы себе в этом отчет или нет, во всех своих рассуждениях мы пользуемся диалектической логикой, формализм которой сводится к шести законам.

Первый из них - это закон об обратной зависимости между объемом C понятия и его содержанием Н:

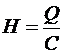,                                           (2.5)

где Q - суммарное свойство всех C объектов, охватываемых понятием Н.

Закон этот вполне очевиден, если принять, что понятие Н есть всего лишь среднее значение соответствующего свойства Q в расчете на один объект.

Сущностью Н всех экономических процессов является категория стоимости. При этом согласно (2.5) Q есть стоимость всех С объектов, Н - средняя стоимость каждого из них.

В производстве разного рода изделий Q1 - стоимость труда, а C1 -количество условных единиц трудозатрат в изделии. Таким образом, Н1 - стоимость единицы ΔН трудозатрат A1, a

 

C1 = A1/ΔA                                     (2.6)

 

 

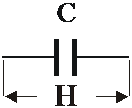
Рисунок 2. 2. Схематическое изображение объема понятия

 

Объем понятия C1, представляет трудоемкость изделия и схематически может быть изображен, как на рис. 2.2.

Q5 представляет собой потребительную стоимость изделия, а Н5 - потребительную стоимость его товарной единицы. Отметим, что пользоемкость С5 изделия не имеет никакого отношения к трудоемкости С1, ибо определяется не затратами труда, а исключительно потребительными свойствами, так что С5 - количество единиц потребления в изделии.

В потреблении, как и в производстве изделия, имеет место соотношение (2.5):

 

Q5 = C5Н5.                                                       

 

Это же соотношение относится и ко всем остальным процессам. В частности, к бартеру.

Вопреки мнению сторонников трудовой теории стоимости обмен товаров происходит отнюдь не только по капитало- и трудозатратам (по себестоимости), но и по полезности с точки зрения потребления (по потребительной стоимости). В самом деле, из двух равнотрудоемких продуктов всегда дороже тот, что полезнее. А из двух равно полезных продуктов дороже более трудоемкий. Это значит, что реально обмен товаров учитывает сумму их капиталоемкости, трудоемкости и полезности, причем прибавка, связанная с последней, и образует прибавочную стоимость Н2 по срав­нению с себестоимостью, так что реальный обмен товаров идет по ΔН + Н1 + Н2 , т.е. по меновой стоимости.

При этом ΔН + Н1 представляет фундамент себестоимости, а Н2 - прибыль, если производитель сам занимается обменом, не поручая его посредникам.

Второй закон диалектики - закон изменчивости ("Все течет, и все изменяется") - означает, что реализация каждой единицы трудозатрат или полезности не происходит мгновенно, а требует времени R. В результате все C единиц товара реализуются в течение RC, так что в единицу времени реализуется товарооборот

 

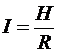                                             (2.7)

 

который представляет стоимость, производимую или потребляемую в единицу времени. При этом R по существу представляет сопротивление обороту, так и будем его именовать.

Но, поскольку речь в обоих законах идет об одной и той же стоимости H00 , то согласно (2.5) и (2.7) имеет место

 

                                  

 

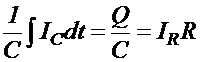
из чего для всех процессов на схеме рис. 3 следует обозначение, приведенное на рис. 2.3.

 

Рисунок 2. 3. Обозначение процесса

 

Параллельные цепочки на рис. 2.3 символизируют диалектические тезис и антитезис. Из верхней следует, что стоимостью обладает готовое изделие, а из нижней, что стоимостью обладает процесс трудовложения или потребления.

 

 

Рисунок 2. 4. Обозначение процесса в блоке эффективности

 

Особенность блока эффективности Н состоит в том, что его цепь включает полезность H0, как показано на рис. 6.

Закон единства противоположностей означает в данном случае, что тезис и антитезис обладают общей сущностью H00 (стоимостью) и потому на рис. 2.3 обе цепочки и соединены параллельно.

Эти противоположности, как подобает диалектике, взаимоп-роникают друг в друга через переходный член, описываемый законом отрицания отрицания. Взаимопроникновение тезиса и антитезиса выражается в том, что в переходном члене оба процесса налагаются друг на друга в форме общего оборота I = In+ Iτ. A это значит, что переходный член последователен с цепочкой на рис. 2.3, как показано на рис.2.5. Все это означает, что если процесс в нижней цепочке отрицает верхнюю цепочку, то переходный член отрицает нижнюю цепочку, тем самым отрицая отрицание верхней.

 

 

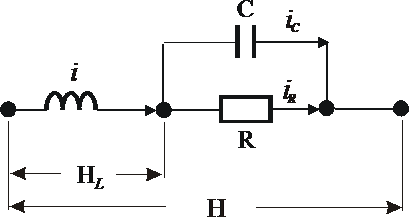
Рисунок 2. 5. Полное изображение экономического процесса

 

Практически это выражается в том, что переходный член препятствует любому изменению процессов в форме

 

                                              (2.8)

 

где НL - стоимость отрицания отрицания, т.е. стоимость преодоления стереотипов, догматизма, неповоротливости и иных форм инерции; L - ригидность процесса, т.е. квадрат времени изменения оборота на 1 ед/с.

Итак, R- время мобилизации единицы ресурсов; L - ригидность резервной системы, т.е. квадрат времени увеличения или уменьшения резервов на единицу, R2 - время реализации единицы трудозатрат, L1 - ригидность производства, т.е. квадрат времени освоения новой продукции, R2 - время обмена единицы товара по бартеру, L2 - ригидность бартера, т.е. квадрат времени становления бартера, R3 - время продажи единицы продукции, L3 - квадрат времени становления сбыта новой продукции, R4 - время покупки потребительной единицы товара, L4 - квадрат времени привыкания к приобретению нового, R5 - время потребления (службы) единицы товара, l5 - квадрат времени освоения использования нового товара.

В результате, для любого из экономических процессов с учетом (2.5), (2.7), (2.8) имеем

 

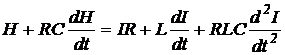                                     (2.9)

 

Исключение составляет лишь блок эффективности (полезности), уравнение которого хотя и аналогично (2.9), но содержит в правой части еще слагаемое Н0, что соответствует схеме на рис. 2.4.

Применительно к каждому блоку структурной схемы на рис. 2.1, это дифференциальное уравнение описывает динамическую взаимосвязь между соответствующим оборотом и его стоимостью.

Шестой по счету закон диалектики - перехода количественных изменений в качественные означает, что раньше или позже, но всегда в кризисных ситуациях, константы C, R и L процессов должны изменяться, что надо постоянно иметь в виду. В частности, эти параметры изменяются во время войн, революций, стихийных бедствий, экономических кризисов и других стрессовых ситуаций.

Согласно структурной схеме на рис. 2.1 макроэкономическое управление осуществляется исключительно путем изменения параметров C, R , L всех процессов. В установившемся режиме функционирования это изменение сопротивления R обороту в одном или нескольких звеньях системы, а в переходных режимах это изменение трудоемкости или пользоемкости C товаров и услуг, либо (и) изменение ригидности L соответствующих процессов и участвующих в них людей (руководителей, производителей, потребителей).

В производстве уменьшение R1 , достигается посредством технического прогресса как в смысле совершенствования, модернизации технологии, так и в смысле перехода на более совершенную и менее трудозатратную продукцию. Изменение трудоемкости C1 связано исключительно с изменением номенклатуры изделий, т.е. с переходом на более сложную и потому более трудоемкую продукцию, либо наоборот. Изменение ригидности L1, производства достигается, с одной стороны, внедрением гибких технологий, позволяющих сравнительно легко переходить от одних изделий к другим, увеличивать или уменьшать оборот I в зависимости от потребностей рынка, а, с другой стороны, изменением психологии руководителей и производителей продукции, повышением квалификации персонала в сторону универсализации, предрасположенности ко всякого рода новациям.

В сфере потребления сопротивление обороту R5 изменяется путем изменения долговечности предметов потребления, перехода от многоразового их использования к одноразовому и, наоборот. Пользоемкость H5 предметов потребления изменяется в зависимости от их качества, а ригидность L5 потребителей управляется посредством целенаправленной рекламы новых товаров и услуг.

Сопротивление R2  бартера является предметом соглашений между производителем и потребителем товаров и услуг в рыночной экономике, либо назначается директивно в чисто плановой экономике в интересах производителей или потребителей в зависимости от преобладания во власти тех или других политических сил. Но в любых обстоятельствах R2  изменяется от нуля в случае абсолютного преобладания интересов потребителей до R5 - R1 в случае абсолютного преобладания интересов производителей.

Те же обстоятельства определяют и соотношение трудоемкости и пользоемкости товаров, изменяя C2 от нуля в пользу потребителей до C2 = C1 C5/(C5 – C1) в пользу производителей товаров. Ригидность обмена проявляется в привычном соотношении интересов потребителя и производителя товаров.

Вышеизложенное справедливо и для товарно-денежного обмена с той лишь разницей, что последний распадается на два этапа: товар-деньги и деньги-товар, на каждом из которых действуют те же факторы, что и при бартере. Впрочем, при товарно-денежном обмене в баланс интересов потребителя и производителя товаров вмешиваются еще интересы работников бюджетной сферы и налогоплательщиков, что требует более детального рассмотрения.

Наконец, размеры резервов и накоплений регулируются емкостью C хранения блока эффективности, а его ригидность L регулируется в зависимости от принятой парадигмы расходов.

 

2.3. Экономическая цепь (потоковая модель
стоимости) АПК

 

Структура системы АПК, содержащая рыночную среду как поле взаимодействия товарно-денежных потоков, даже в упрощенном виде (рис. 2.7) сложна для анализа существующими экономико-математическими методами. Задача анализа состоит в том, чтобы определить математически точную взаимосвязь между элементами системы и их характеристиками. Из существующих подходов к анализу экономических систем представляется плодотворным подход А.А. Денисова, использующий для математического описания экономических логистических потоковых процессов аппарат формализации законов диалектической логики и методологические основы теории цепей. Ниже приведены схемы экономических цепей и потоковые модели стоимости системы АПК.

Каждая структурная составляющая  системы АПК может быть представлена в виде схемы рис. 2.1 . Учитывая, что в настоящее время в России практически отсутствует рынок автодорожных услуг, уберем из общей цепи АПК контур автодорог.  Тогда схема логистических процессов АПК будет иметь вид рис. 2.6.

 

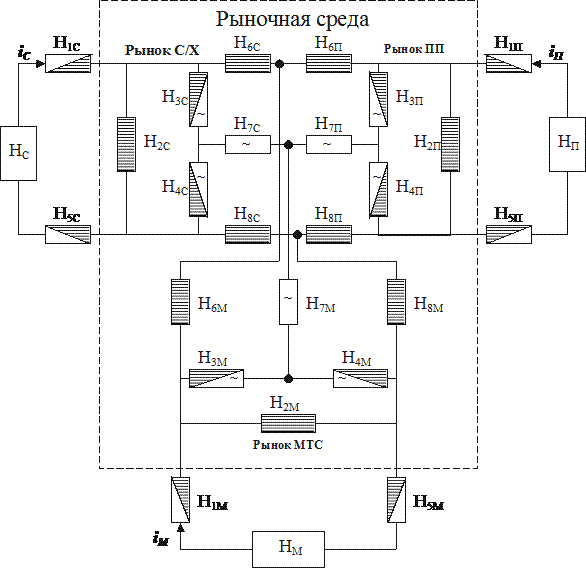
Рисунок 2. 6. Схема товарно-денежного обращения в системе АПК

 

На схеме рис. 2.6 введены следующие обозначения:

Hk=(Hok-ΔHk) - экономический потенциал (эффективность) блока системы;

 H1k  - процесс производства k–го блока системы (труд-товар);

H2k  - процесс бартерного обмена k –го блока (товар-товар);

H3k  - процесс продажи продукции k –го блока (товар-деньги);

H4k  - процесс покупки товаров k –го блока (деньги- товар);

H5k  - процесс потребления k –го блока (товар-труд);

H6k  - процесс перехода продукции с других рынков на k –й рынок;

H7k  - процесс перехода денег с других рынков на k –й рынок;

H8k  - процесс перехода продукции с k -го рынка на потребление в других блоках АПК;

k ЄL;

 L= c,  п, м,

 где с – сельское хозяйство, п– пищеперерабатывающая промышленность, м – материально-техническое снабжение;

ik  - оборот стоимостей в k –м блоке АПК.

В полной схеме цепи логистических процессов АПК, изображенной на рис. 2.6, процессы  H2k, H3k и H4k  образуют цепь процессов, протекающих на соответствующем (k -м) рынке. Все вместе они объединяются в цепь рыночной среды АПК. Как видно, получившаяся цепь имеет высокий порядок математической сложности. Учитывая, что каждый процесс имеет две независимые реактивные составляющие, а общее число процессов в изображенной цепи 27, система уравнений, описывающая экономическое равновесие цепи, будет содержать 27 компонентных дифференциальных уравнений второго порядка плюс топологические уравнения для узлов и контуров цепи.

Цепь можно упростить, если учесть следующее.

1.    Рыночная среда, состоящая из цепей рынков отдельных блоков АПК, является внутренним рынком России, поэтому препятствия движению товарно-денежных масс типа таможенных ограничений практически отсутствуют. Поэтому процессы H6k , H7k  и H8k могут быть исключены из схемы.

2.    На современном этапе развития рыночных отношений в России удельный вес бартера в процессах обмена мал, в основном обмену сопутствуют два процесса: «товар-деньги» и «деньги-товар». С учетом сказанного процессы H2k из схемы также можно удалить.

3.    Отдельные рынки блоков имеют специализированный характер, поэтому, например, попытки реализации продукции материально-технического снабжения на рынке пищевых продуктов будут обречены на неудачу и наоборот. Другими словами, специализированные рынки по процессу продаж разделены и, следовательно, перетекание товаров на продажу с одного рынка на другой отсутствует.

4.    В отличие от разделенных процессов продаж процессы покупок на отдельных специализированных рынках параллельно объединяются в общий процесс обмена типа «деньги-товар». Причем, этот объединенный процесс включает в себя не только денежно-товарные процессы специализированных рынков АПК, но и других рынков, внешних по отношению к рыночной среде системы АПК.

Проведя соответствующие упрощения на схеме рис. 2.6, получим цепь логистических процессов АПК в упрощенном виде (рис. 2.7).

 

 

 

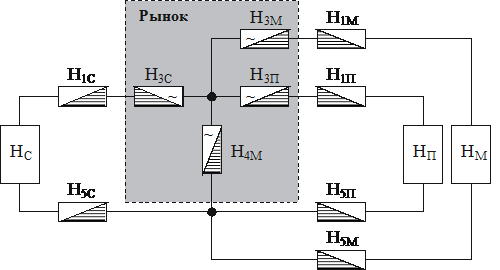
Рисунок 2. 7. Упрощенная схема товарно-денежного обращения в системе АПК

 

На схеме рис. 2.7 процесс H4 представляет собой общий процесс покупок, протекающий параллельно на всех специализированных рынках, на которых покупают производители АПК. Для того, чтобы проанализировать полученную цепь процессов, представим ее более полно, то есть раскроем для каждого процесса его компонентное содержание. Любой из изображенных на рис. 2.6 и 2.7 процессов может быть заменен   RLC-цепью первого или второго вида. Произведя замены, получим схему, приведенную на рис. 2.8.

 

Рисунок 2. 8. Упрощенная экономическая цепь АПК

 

Для полного математического описания такой цепи, то есть нахождения зависимостей, позволяющих определить значения оборота стоимостей и падения потенциала в каждой ветви цепи, даже, если RLC -цепь каждого процесса будет рассматриваться как одно комплексное сопротивление, потребуется составление 4 независимых топологических уравнений и 10 компонентных. Причем каждое компонентное уравнение – это дифференциальное уравнение второго порядка. Таким образом, дифференциальное уравнение, изображенной на рис. 2.8 экономической цепи, имеет высокий порядок сложности  и записывается в общем случае в виде:

 

,                         

 

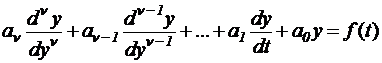где – y искомая реакция цепи (оборот стоимостей или падение потенциала в какой-либо ветви);

a0, a1, …, aν - коэффициенты, определяемые параметрами пассивных элементов.

Правая часть этого уравнения – линейная комбинация функций, описывающих внешнее воздействие x(t) на цепь, и их производных. При выключении всех источников экономического потенциала она становится равной нулю.

Дифференциальное уравнение такого порядка сложности является трудно обозримым, и хотя при современных машинных методах его решение не вызывает сомнений, анализ полученного решения является сложной задачей.

Очевидно, для экономики с установившимися экономическими процессами, анализ цепи значительно упрощается, поскольку дифференциальное уравнение цепи приобретает алгебраическую форму, а внешние воздействия не зависят от времени. Для переходной экономики, каковой является экономика России, установившийся процесс длится ограниченное время, после чего возникает либо скачкообразное внешнее возмущение, либо скачкообразное изменение параметра одного или нескольких элементов экономической цепи. Следствием подобных скачков является возникновение переходных процессов, после протекания которых экономическая система переходит в новое устойчивое состояние. Характер переходных процессов (апериодический или колебательный) оказывает существенное влияние на социально-экономическую жизнь страны. При колебательном переходном процессе социально-экономические условия жизни людей существенно ухудшаются, в обществе нарастает напряженность, В отличие от колебательного, апериодический переходной процесс позволяет достаточно плавно перевести экономику из одного состояния в другое, и если траектория переходов направлена на экономический рост, то социально-экономическая атмосфера на каждом переходе улучшается. Целенаправленное движение возможно только при условии управления системой, что проявляется в грамотном изменении параметров элементов и экономических потенциалов -  источников экономической цепи, моделирующей эту систему.

Сказанное выше относится и к подсистемам экономики страны, одной из которых является агропромышленный комплекс, включающий пищеперерабатывающее производство и его инфраструктуру.

Учитывая сказанное об особенностях переходной экономики, можно предложить следующую (двухэтапную) методику анализа экономической системы и системы АПК в частности по ее моделирующей экономической цепи.

 

1-й этап. Анализ установившегося режима цепи:

а) составление системы алгебраических уравнений экономического равновесия цепи;

б) разрешение системы относительно выбранной ветви; в) анализ полученного решения.

2-й этап. Анализ переходных процессов цепи:

а) анализ реакции экономической цепи на скачок источника экономического потенциала;

б) анализ реакции экономической цепи на скачок параметра элемента цепи.

При выполнении пунктов а) и б) второго этапа может быть использована одна из методик анализа переходных процессов в линейных инвариантных во времени цепях.

 

2.4. Анализ установившегося режима
экономики АПК

 

В установившемся режиме в экономической цепи действуют постоянные во времени обороты стоимостей и экономические потенциалы. В этом режиме реактивные составляющие процессов не оказывают влияния, и эквивалентная схема цепи может быть представлена на рис. 2.9.

На схеме рис. 2.9 числа в круглых скобках обозначают номера узлов (и ветвей). Топологический граф этой цепи является планарным, и его расширенное представление изображено на рис. 2.10а.

 

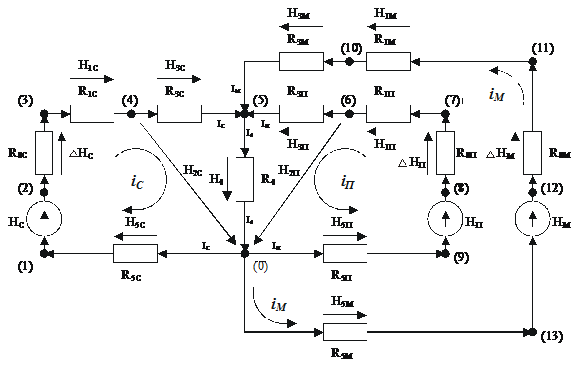
Рисунок 2. 9. Расширенное топологическое описание цепи оборота стоимостей системы АПК

 

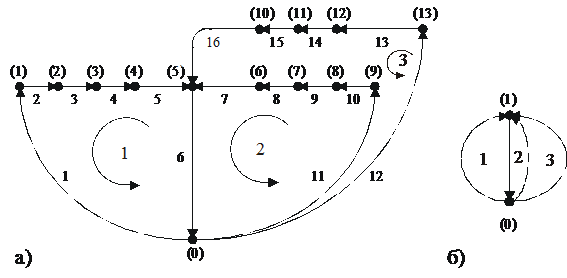
Рисунок 2. 10. Топологический граф цепи рис. 2.9

 

После преобразования, т.е. уменьшения количества ветвей и узлов, получим сокращенный топологический граф цепи, изображенный на рис. (2.10б) (тоже планарный), содержащий два узла, четыре ветви и три окна (ячейки). С помощью графов рис. 2.10 составим систему топологических уравнений цепи, содержащую три уравнения равновесия потенциалов и одно – равновесия оборотов стоимостей.

Приведенному на рис. 2.10а расширенному графу соответствует матрица В0 трех основных контуров, в которой номера строк соответствуют номерам основных контуров, а номера столбцов – номерам ветвей:

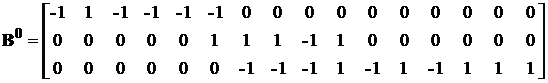(2.10)

Вектор стоимостей цепи в соответствии с графом (рис. 2.10а) имеет вид:

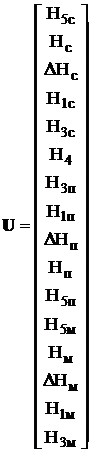                                               (2.11)

 

Тогда баланс потенциалов цепи запишем как

.                                                (2.12)

Или в виде системы уравнений:

 

-Н5с+Нс-ΔНс-Н1с-Н3с-Н4=0                                                        

Н4+Н3п+Н1п+ΔНп-Нп+Н5п=0                                                   

-Н3п-Н1п-ΔНп+Нп-Н5п+Н5м-Нм+ΔНм+Н1м+Н3м=0.               

 

После преобразования система независимых уравнений баланса стоимостей цепи (рис.2.9) примет вид:

 

ΔНс+Н1с+Н3с+Н4+Н5с=Нс                                      (2.13)

ΔНп+Н1п+Н3п+Н4+Н5п=Нп                                              (2.14)

Нп-(ΔНп+Н1п+Н3п)=Нм-(ΔНм+Н1м+Н3м)                       (2.15)

 

Топологическое уравнение равновесия оборотов будет иметь вид:

Ic+Iм+Iм=I4                                               (2.16)

К полученным четырем топологическим уравнениям (2.13) – (2.16) добавятся 13 компонентных уравнений:

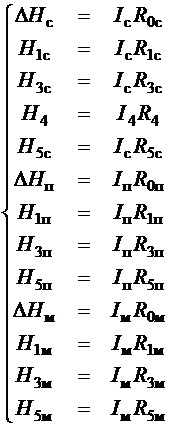                               (2.17)

Эти 17 независимых уравнений представляют собой систему уравнений равновесия цепи схемы рис. 2.9 и позволяют при заданных экономических потенциалах (эффективностях) источников и сопротивлениях процессов определить значения приведенных стоимостей Н всех процессов и их оборотов I.

Общей ветвью моделируемой цепи является ветвь R4 – общий рынок, на котором покупателями являются производители 3-х подсистем (сельского хозяйства, пищеперерабатывающей промышленности и материально-технического снабжения). Товарооборот I4, протекающий по этой ветви, определяется уравнением (2.16), а товарообороты в левой части этого уравнения определяются соотношениями:

 

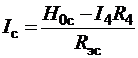   ;                                           (2.18)

 

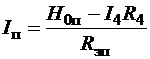   ;                                         (2.19)

 

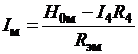.                                               (2.20)

 

В этих соотношениях

 

Rэс=R0с+R1с+R3с+R5с ,                                      (2.21)

 

Rэп=R0п+R1п+R3п+R5п ,                                    (2.22)

 

Rэм=R0м+R1м+R3м+R5м                                     (2.23)

 

Подставив обороты контуров подсистем в (2.16) и проведя преобразования, получим для рыночного оборота I4:

 

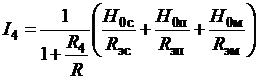,                       (2.24)

 

где 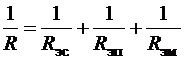     -  проводимость цепи по отношению к зажимам ветви R4.

При R4  <<  R товарооборот на общем рынке зависит только от суммы оборотов контуров подсистем АПК. В противном случае величина 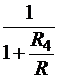   меньше единицы, и тем меньше, чем больше сопротивление рыночному обороту R4 по сравнению с R. В частности, при R4  = R оборот на общем рынке покупок составляет половину суммарного оборота контуров подсистем.

 

2.5. Сбалансированность экономики АПК

 

Выделим из общей цепи рис. 2.9 один из контуров, например, контур сельского хозяйства.

 

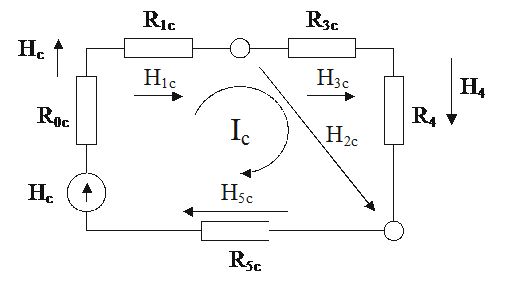
Рисунок 2. 11. Контур подсистемы сельского хозяйства

 

Сбалансированность подразумевает равенство производства и потребления (доходов и расходов), из чего следует, что в установившемся режиме для баланса экономики подсистемы рис. 2.11 должно быть:

 

ΔНс+Н1с+Н3с+Н4=Н5с=.                                      (2.25)

Если выделить в одном из контуров искомый процесс, например прибыль производителя товаров R3, а сопротивление остальной части контура обозначить Z, тогда схема контура упростится и примет вид, показанный на рис. 2.12.

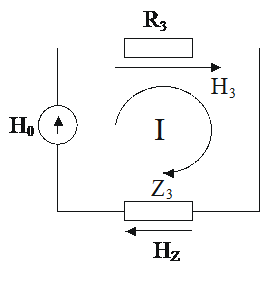
Рисунок 2. 12. Упрощенная схема контура одной из подсистем

 

Мощность прибыли производителя N3 составляет:

 

N3=H3I3=I2R3=,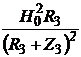                                

где Z3=R0+R1+R4+R5 (см. рис. 2.9).

Взяв производную по R и приравняв ее нулю, получим значение R3, соответствующее максимальной прибыли производителя в единицу времени:

R3 опт= Z3.                                       (2.26)

Любое отступление от этого соотношения приводит к уменьшению мгновенной прибыли.

Если выполнить условие (17), то прибыль производителя достигнет значения

,                                             

то она равна половине экономического потенциала подсистемы.

Очевидно, подобные соотношения получим и для других процессов. Иными словами, все процессы подсистемы будут стремиться достигнуть максимума потенциала Н, равного .

На рынке идет борьба за выгоду всех со всеми, поэтому соглашение достигается при взаимной выгоде производителя и продавца товара. Определим максимальную солидарную прибыль их обоих, исходя из максимума прибыли каждого из них. Требование максимальной прибыли производителя соответствует .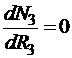

Откуда следует

,                                                   

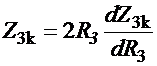где     Z3k=Z3+R3.

Аналогично для продавца 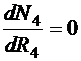 и, следовательно:

,                                                   

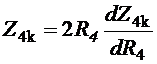где Z4k=Z4+R4.

Солидарная максимальная прибыль достигается при Z3k=Z4k, то есть при

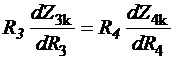 .                             (2.27)

Для контуров рис.2.9, ввиду последовательности соединения процессов, то есть всех сопротивлений, производные в выражении (2.27) равны единицам. Следовательно, условием максимизации солидарной прибыли для всех подсистем является:

 

R3=R4=Rp.                                       (2.28)

 

То есть у всех подсистем сопротивления продаж R3  должны быть равны общему сопротивлению покупок R4, что эквивалентно равенству оптовых и розничных наценок.

При выполнении условия (19) для всех контуров, в них достигаются оптимальные значения оборотов стоимостей, а с учетом условия сбалансированности (16) получим для оптимального оборота каждого контура Iопт.

 

Iопт=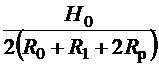                                   (2.29)

 

Учитывая, что R4  является общим для всех контуров, в выражении (2.29) третье слагаемое в скобках у всех контуров должно быть одинаковым. Поскольку этот же оборот Iопт идет через сопротивление потребления R5 и падение потенциала на нем тоже равно , получим:

R0 + R1  +2 Rp = R5.                                          

Откуда для получения оптимального оборота Iопт, максимизирующего солидарную прибыль производителя и продавца при одновременном соблюдении условия сбалансированности, полуразность сопротивления потреблению R5 и суммы внутреннего сопротивления производству R1 в каждой подсистеме АПК должна быть равна величине рыночных сопротивлений, то есть

 

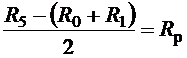.                                     (2.30)

 

2.6. Анализ переходных процессов
в экономической цепи АПК

 

Все экономические процессы, протекающие в моделирующей цепи, могут быть, как было показано в п.3.1, схематично изображены в виде рис. 2.13.

 

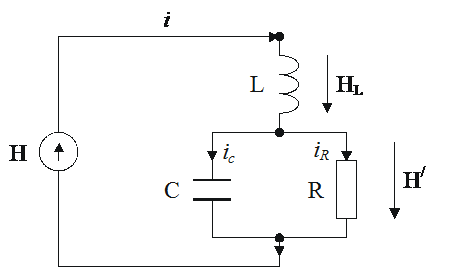
Рисунок 2. 13. Эквивалентная схема экономического процесса

 

Использую законы Кирхгофа для цепей, получим для баланса оборотов:

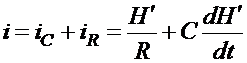 .                        (2.31)

Для баланса стоимостей:

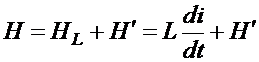  .                    (2.32)

Из (2.32) получим:

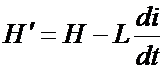 .                               (2.33)

Подставив выражение для  из (2.33) в (2.31) и проведя преобразования, получим дифференциальное уравнение экономического процесса в виде:

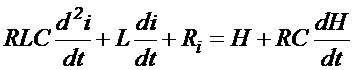,             (2.34)

где  i  - искомый оборот стоимостей;

R, L, C – параметры процесса.

Правая часть уравнения (2.34) описывает внешнее воздействие на процесс стоимости Н и ее производной.

Уравнениями, подобными (2.34), описываются все экономические процессы АПК, кроме блоков эффективности (полезности) каждой из подсистем. Уравнения этих блоков аналогичны, но в правой части содержат Н0.

Применительно к каждой ветви схемы рис. 2.8 эти дифференциальные уравнения описывают динамическую взаимосвязь между соответствующим оборотом и его стоимостью. Учитывая закон всеобщей взаимозависимости явлений, отраженный моделирующей цепью, для полного макроописания переходных процессов в макроэкономике АПК необходимо решение системы из 13 дифференциальных уравнений вида (2.34), связанных топологическими уравнениями. Цепь рис. 2.8 характеризуется достаточно высоким порядком сложности, и полный анализ ее устойчивости на переходных режимах экономики возможен лишь машинными методами.

Однако, можно сделать некоторые качественные суждения о реакции системы АПК на скачки внешнего воздействия по результатам анализа переходных процессов в отдельном блоке, имеющем лишь второй порядок сложности цепи.

 

Реакция цепи отдельного экономического процесса
на скачок стоимости

Пусть на цепь экономического процесса (рис. 2.13) действует источник стоимости, изменяющийся по закону

                                                    

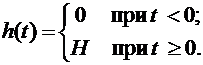
При подобном законе изменения h(t) независимые начальные условия цепи имеют нулевые значения, а уравнения цепи запишутся в виде:

 

i - iC - iR = 0                                                               

                                                       

.                                                      

 

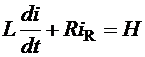
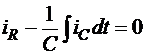Для свободной составляющей оборота iсв все правые части уравнений равны нулю, а характеристическое уравнение цепи

 

RLC p2 + Lp + R = 0                               (2.35)

имеет два корня:

                                             

где 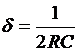 - коэффициент затухания цепи;

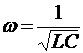  - резонансная частота цепи.

Как известно, при малой добротности контура (δ <ω0) характеристическое уравнение имеет два различных вещественных отрицательных корня, а выражение для свободной составляющей оборота после коммутации

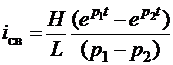.                                          (2.36)

В этом случае переходной процесс в цепи носит апериодический характер, причем вследствие того, что , экспонента затухает быстрее экспоненты , из-за чего наблюдается некоторый подъем оборота iсв с последующим спадом до нуля (рис. 2.14). 

 

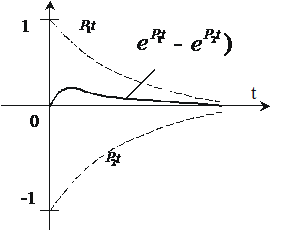
Рисунок 2. 14. Апериодический переходной процесс

 

При большой добротности контура (δ <ω0) характеристическое уравнение (2.35) имеет два комплексно-сопряженных корня

,                                                 

где  - частота свободных колебаний в цепи.

Тогда уравнение (27), может быть преобразовано к виду:

 

                   

 

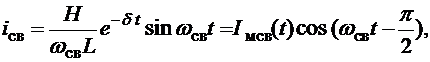
где   =

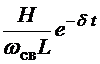
При δ =ω0 наступает критический (неустойчивый) режим цепи, определяющий границу между апериодическим и колебательным режимами.

Учитывая выражения для δ и ω0  через параметры элементов цепи, получим условия:

 

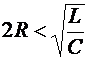 - для апериодического режима;                            (2.37)

 

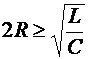  для неустойчивого (колебательного) режима.  (2.38)

 

Другими словами, экономический процесс в переходном режиме имеет апериодический характер, если удвоенное сопротивление обороту стоимости будет меньше корня квадратного из отношения регидности к емкости процесса.

Для получения временной характеристики полного оборота стоимости воспользуемся операторным методом анализа. Операторная эквивалентная схема экономического процесса приведена на рис. 2.15.

 

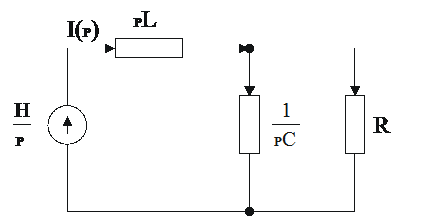
Рисунок 2. 15. Операторная эквивалентная схема экономического процесса

 

Для изображения оборота стоимости I(p) получим:

 

,          

 

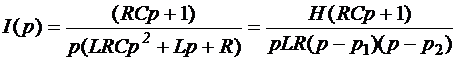где p1 и  p2 - корни характеристического уравнения, полученные ранее (2.35).

Преобразуем это выражение к виду, удобному для перехода к оригиналу:

 

                     

 

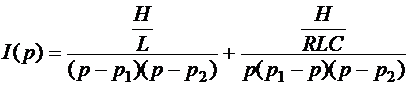
Оригиналом полученного изображения будет полный оборот в цепи экономического процесса:

 

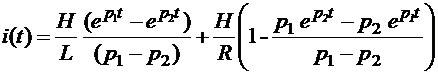.      (2.39)

 

Это выражение позволяет определить оборот стоимости в цепи экономического процесса в любой момент времени в диапазоне от t =0 до  t →∞.

Первое слагаемое в правой части уравнения (2.39) – это уже исследованная свободная составляющая переходного процесса, второе слагаемое – принужденная составляющая, усложняющая вид переходного процесса. Но поскольку корни характеристического уравнения (2.35) определяют и ход процесса во втором слагаемом, условие отсутствия колебаний остается прежним (2.37).

В проведенном анализе цепи величина H - это величина скачка, вызванная скачком эффективности (полезности) подсистемы Hк и определяемая коэффициентом передачи для соответствующей ветви. Но в процессе функционирования системы установившийся режим может быть нарушен из-за скачкообразного изменения одного или нескольких сопротивлений обороту. В этом случае переходной процесс в цепи отдельного экономического блока будет протекать аналогично рассмотренному, а величина скачка H может быть определена из анализа установившихся процессов до и после скачка.

Наиболее чувствительными к изменению экономической, финансовой и политической среды в цепи АПК является сопротивление обороту на общем рынке R4 . Поэтому предположим, что произошло скачкообразное изменение  на величину Δ R4. Так как сопротивление R4  является общим для всех контуров (см. рис. 2.9), то в каждом из них произойдет скачек товарооборота в большую или меньшую сторону в зависимости от знака скачка Δ R4.

,                                              

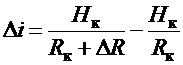где    Hк- эффективность соответствующего контура;

Rк=R0к+R1к+R3к+R 4+R5к - суммарное сопротивление оборота соответствующего контура до скачка.

Скачок же стоимости на R4 составит

 

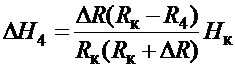,                                     (2.40)

 

где R4 - рыночное сопротивление  обороту до скачка.

Из выражения (31) с очевидностью следует, что завышение цен на общем рынке после окончания переходного процесса вовсе не соответствует ожидаемой прибыли у продавцов, так как ΔR  находится как в числителе, так и в знаменателе.

Чтобы определить ΔRопт, при котором скачок стоимости  ΔH4 достигает максимума, приравниваем производную (2.40) по ΔR нулю. Получим   ΔRопт= R4, т.е. для максимального скачка ΔH4 прибыли продавцов, необходимо увеличение R4  в два раза.

Однако, если продавцы решили увеличить в два раза сопротивление обороту (ΔRопт= R4), надеясь на двойную прибыль, то в связи с уменьшением товарооборота прирост прибыли составит только

 

.                                              

 

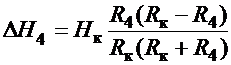Эта формула действительна только для скачка  ΔR= R4, и показывает, что реальное увеличение прибыли существенно ниже ожидаемого. Например, при  R4 =0,125 Rк, что соответствует более менее солидарному распределению прибыли при балансе экономики, получим прирост прибыли

ΔH4 ≈ Hк,                                                

а рыночный оборот при этом уменьшится на величину Δiк ≈ 0,11iк, где iк – оборот в контуре до скачка R4.

Увеличение же мощности прибыли продавцов произойдет на величину:

 

ΔN4= N4-- N4+= 0,79i22R4- i2R4=0,58N,                           

 

где    N4-- – мощность прибыли продавцов до скачка;

N4+ - мощность прибыли продавцов после скачка .

 

2.7. Выводы по 2-й главе

 

1.                Обосновано применение аппарата диалектической логики и теории цепей при анализе экономических процессов.

2.               Предложена методика макроэкономического моделирования эффективности и устойчивости системы АПК, использующая потоковые модели стоимости.

3.               Разработана эквивалентная экономическая цепь системы АПК и получены уравнения ее эффективности и устойчивости в установившемся режиме.

4.               Исследованы переходные режимы отдельного экономического процесса и показаны условия его устойчивости.

5.               Проведен анализ системы АПК для скачка сопротивления обороту стоимостей на общем рынке и получены соотношения, позволяющие прогнозировать уровни скачков цен и мощностей товарооборота.

6.               Проведенный макроэкономический анализ системы АПК показал, что при использовании потоковых моделей стоимости устанавливаются строгие соотношения между параметрами экономических процессов, и управление ими может осуществляться как изменением эффективностей соответствующих подсистем, так и изменением R, C, L.

7.               Однако, если эффективности соответствующих подсистем еще можно подсчитать с достаточной степенью точности, то параметры процессов, такие как сопротивления обороту, трудоемкости, емкости рынков, ригидности – расчету хотя и поддаются, но с большими погрешностями (из-за недостатка и некорректности информации, отсутствия методик ее сбора и подготовки, отсутствия методик расчета параметров), что сводит на нет высокую точность аналитических моделей. Таким образом, следующим шагом в исследованиях, использующих изложенный в этой главе подход, должны стать разработки методик и моделей расчета параметров потоковых процессов, протекающих в экономических системах.