ГЛАВА 6. О МЕХАНИЗМАХ ВЛИЯНИЯ НЕБЕСНЫХ ТЕЛ НА ХАРАКТЕР И СПОСОБНОСТИ ЛЮДЕЙ

6.1. Логика звезд и физиология мозга

Вопрос о влиянии планет Солнечной системы на психику людей исследовался многими авторами, но лишь недавно был получен ответ на вопрос о механизмах такого влияния /13-14/. Эта фундаментальная проблема распадется на множество самостоятельных задач, которые можно сформулировать следующим образом:

1) существует ли зависимость физиологических функций организма и мозга от положения планет на небесном своде?

2) какое из фундаментальных взаимодействий, известных современной физике ответственно за передачу информации в мозг человека?

3) каков физиологический механизм восприятия сигналов, исходящих от планет?

4) как влияет на психику человека изменение физиологического состояния мозга при изменении положения планет?

5) каким образом положение планет на момент рождения запечатлевается навсегда в памяти человека?

Это далеко не полный перечень проблем, связанных с научным определением основных положений астросоциотипологии.

Идея о том, что мозг человека каким то образом воспринимает параметры состояния Солнечной системы, широко обсуждалась в литературе 19 века, куда она проникла, очевидно, из индийской философии. Профессор Тони Найдер /28/ придал этой идее законченный вид. Он установил соответствие планет и отделов головного мозга, ответственных за физиологию.

В его схеме центральная часть мозга – таламус соответствует Солнцу. Гипоталамус, отвечающий за эмоции и физиологические реакции, связанные с ними, соответствует Луне. Субталамус, который осуществляет дифференциацию сигналов, поступающих от других отделов – это Меркурий мозга. Субстанция нигра, контролирующая воспроизводящие функции – это Венера. Амигдала, контролирующая эмоции страха и управляющая функциями движения соответствует Марсу. Глобус паллидус, отвечающий за управление высокого уровня, соответствует Юпитеру. Структура путамен, находящаяся на периферии центральной части мозга и выполняющая служебные функции соответствует Сатурну. Наконец, Caudate Nucleus – структура, имеющая голову и хвост, соответствует Лунным узлам.

Последнее обстоятельство является довольно любопытным. Можно понять, например, почему мозг, будучи материальным образованием, воспроизводит строение Солнечной системы. Ведь мозг предназначен главным образом для того, чтобы ориентироваться в пространстве и во времени. А светила и видимые планеты как нельзя лучше подходят на роль ориентиров. Таким образом, не было бы ничего удивительно, если бы мозг содержал целые отделы, моделирующие движение соответствующих им планет, как это предполагает Тони Найдер. Но Лунные узлы не видны на небе и не соответствуют ничему материальному. Почему же они имеют в качестве проекции большую по объему структуру Caudate Nucleus, охватывающую всю центральную часть мозга? Кроме того, известно, что Лунные узлы считаются наряду с планетами важными элементами, т.е. узлы предстают в одном ряду с материальными планетами, в то время как они вообще не существуют, но являются математической абстракцией.

Чтобы ответить на этот вопрос, обратимся к существующей тесной аналогии светил – Луны и Солнца. В годичном движении Солнца имеются четыре важные пункта, намечающие оси солярного Зодиака. Это моменты весеннего и осеннего равноденствия, задающие ось Овен – Весы, а также моменты летнего и зимнего солнцестояния, которому соответствует ось Рак – Козерог. В точке весеннего равноденствия Солнце переходит из южной полусферы в северную полусферу. Это является сигналом для многочисленных животных и растительных видов, насекомых и рыб о том, что настал самый важный момент, связанный с весенней линькой. Именно в это время заяц из белого становится серым, в стволах деревьев начинается ток жизненных соков, призванных пробудить спящие почки. Природа оживает после зимней спячки, готовится к летнему периоду.

Как известно, процессы линьки у животных связаны с возбуждением гормональной цепочки гипоталамус – гипофиз – надпочечники. Исходные сигналы зарождаются в ядрах гипоталамуса, где производится нейрогормон. Очевидно, что такой важный процесс как линька, происходит рефлекторно, в ответ на изменения в окружающей среде. В северном полушарии одним из важнейших видимых изменений в природе является переход Солнца из южной полусферы в северную полусферу. После этого день становится более продолжительным, чем ночь, что является сигналом для всего живого, что пора готовиться к линьке. Если обратиться к аналогии Луна-Солнце, тогда точка весеннего равноденствия будет соответствовать Голове Дракона или Северному узлу. При переходе через точку Северного узла, Луна оказывается в северной полусфере, что может также восприниматься как сигнал к очередной линьке. И хотя реально линька не происходит, но рефлекторная реакция ее вызывающая, уже запущена, вызывая выброс соответствующего нейрогормона. Кроме весенней линьки существует и осенняя линька, когда серый заяц становится белым. В этом случае основным сигналом является увеличение продолжительности ночи по сравнению с длительностью дня, т.е. переход Солнца через точку осеннего равноденствия. Очевидно, что точка осеннего равноденствия аналогична Южному узлу. Отметим, что кроме рефлекторных реакций процессы линьки могут быть вызваны и генетической памятью о предыдущих линьках, т.е. происходить спонтанно, при наступлении соответствующего периода. Заметим также, что гормональные реакции, связанные с сезонными изменениями, свойственны не только животным, но и человеку.

Тот факт, что процессы линьки запускаются именно из гипоталамуса, заставляет критически подойти к схеме Тони Найдера. Как было указано выше, именно гипоталамус является начальным звеном во всей цепочке гормональных изменений, приводящих к линьке. Но гормональные реакции в гипоталамусе возбуждаются в ответ на изменение положения Солнца, а не Луны. Следовательно, гипоталамус в большей степени соотносится с Солнцем, а не с Луной. Следует заметить, что схема с центральным Солнцем–таламусом, которую предложил профессор Тони Найдер, является моделью гелиоцентрической системы, в то время как реальный человек находится в топоцентрической или геоцентрической системе координат. В такой систем координат таламус соответствует скорее Земле и центру гороскопа, нежели Солнцу. В этой схеме существуют и другие несоответствия, как будет показано ниже. Тем не менее, можно считать большим достижением уже тот факт, что в монографии /28/ была указана принципиальная связь между планетами и отделами мозга, отвечающими за физиологию.

Чтобы понять связь планет и отделов мозга, рассмотрим два типичных заболевания:

1) Parkinson's Disease. Parkinson's disease involves degeneration of neurons of the substantia nigra, and is characterized by resting tremor, rigidity and bradykinesia. Болезнь Паркинсона, которая характеризуется дегенерацией нейронов в субстанции нигра и главным симптомом которой является дрожание членов.

2) Huntington's Disease. Huntington's disease is a genetic disorder characterized by degeneration of neurons in the striatum, particularly the caudate nucleus. Typically it manifests as involuntary choreiform movements and, in later stages of the disease, as dementia. Arrows point to the severely atrophied caudate nucleus. Болезнь Хантингтона, которая характеризуется атрофией Caudate Nucleus и главным симптомом которой является dementia (потеря рассудка, сумасшествие).

Согласно известным данным, болезнь Паркинсона следует приписать влиянию Луны. Но тогда субстанция нигра должна соответствовать Луне, а вовсе не Венере. Второе заболевание, связанное с сумасшествием зависит скорее от Сатурна, нежели от Лунных Узлов. Следовательно, структуру Caudate Nucleus следует приписать Сатурну. Далее заметим, что Солнце по нашим представлениям отвечает за гипоталамус, ведь гипоталамус управляет, в том числе, кровяным давлением, откуда становится очевидной его связь с Солнцем. Кроме этих несоответствий в схеме, которую предложил профессор Тони Найдер, есть и другие. Например, не ясно, почему из всех многочисленных функциональных отделов мозга Тони Найдер выбрал только 8, тогда как некоторые значительные отделы остались без планетарного управления. Известно также, что качества планет различаются в зависимости от знака, которым они управляют. Так, если Меркурий, как управитель знака Близнецов может быть соотнесен с отделом сабталамус, то Меркурий как управитель знака Девы больше соответствует путамену, выполняющему служебные функции.

Можно преложить следующую, далеко не полную схему соответствия отделов мозга и планет – рис. 28:

¾ Таламус – центр, эго, линия горизонта, асцендент (ASC)

¾ Гипоталамус – Солнце

¾ Сабталамус – Меркурий,

¾ Путамен, выполняющий служебные функции – Меркурий,

¾ Субстанция нигра – Луна

¾ Caudate Nucleus – Сатурн (левая и правая половины этой структуры)

¾ Амигдала, контролирующая эмоции страха и управляющая функциями движения – Марс.

¾ Глобус паллидус, отвечающий за управление высокого уровня – Юпитер.

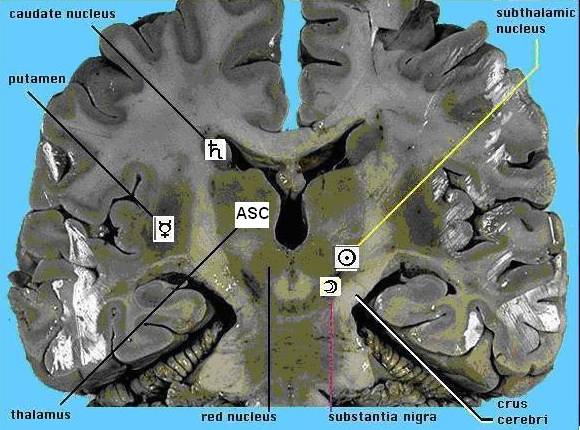
Рис. 28. Схема соответствия отделов мозга и планет

Эту схему предстоит дополнить еще, по крайней мере, тремя десятками связей, путем простого соответствия функций отделов мозга и функций планет.

Каким же образом возникает зависимость отделов мозга от тех или иных планет? Обратимся к строению мозга, который на клеточном уровне состоит из нейронов, являющихся проводниками электрических импульсов. Если проводимость нейронов зависит от гравитационного потенциала планет, тогда группы нейронов могут создавать в мозгу области, настроенные на те или иные планеты. В работе /30/ были обнаружены сезонные колебания сопротивления и индуктивности при измерении по мостовой схеме в термостате. Теория этого явления дана в работах /31-32/. Согласно /32/, изменение электрического сопротивления можно объяснить колебаниями уровня энергии Ферми электронов проводимости, вызванными изменением суммарного гравитационного потенциала планет Солнечной системы на поверхности нашей планеты. Экспериментальные данные /30/ по сезонным вариациям электрического сопротивления и индуктивности можно обобщить линейными зависимостями в виде /32/:

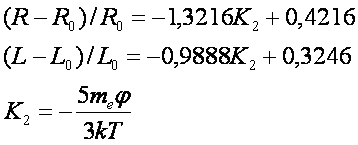
Здесь m_e – масса электрона, j - суммарный гравитационный потенциал небесных тел Солнечной системы, k=1,3806505^.10^-23 Дж/К- постоянная Больцмана, T – абсолютная температура, R₀=2,69 кОм; L₀=151,64 mH.

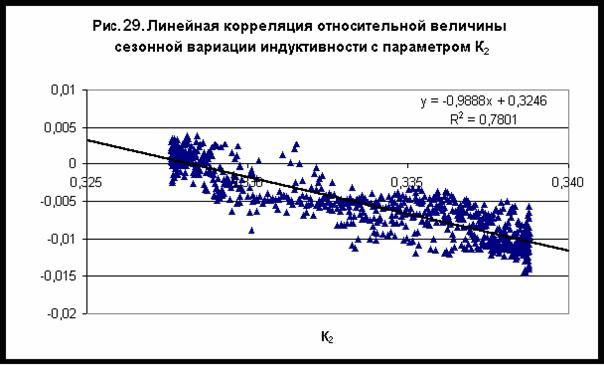
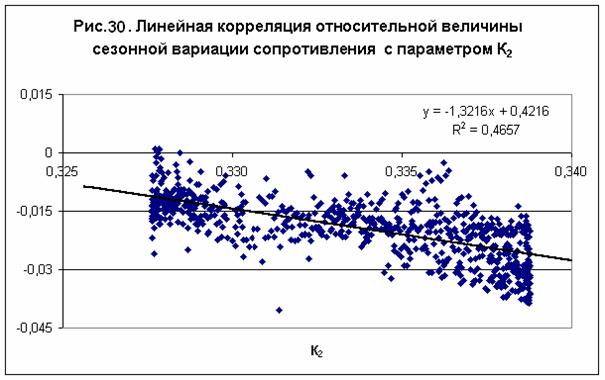
Таким образом, было установлено, что сопротивление и индуктивность электрической цепи, измеренные по мостовой схеме при постоянной температуре Т=293,15К, изменяются прямо пропорционально величине суммарного гравитационного потенциала – рис. 29-30.

Нейроны обладают электрическим сопротивлением и индуктивностью, поэтому могут изменять свои характеристики при изменении гравитационного потенциала. Неизвестно, существует ли дифференциация нейронов по их реакциям на сезонные и суточные колебания гравитационного потенциала. Но если такая дифференциация существует, она может приводить к появлению отделов мозга, зависящих от гравитационного потенциала тех или иных планет.

Эта модель позволяет объяснить влияние небесных тел на физиологию мозга и, соответственно, на психологию индивида. Вообще говоря, гравитационный потенциал может влиять не только на проводимость, но и на скорость биохимических реакций. Рассмотрим этот вопрос более подробно.

6.2. Гравитация и жизнь

Среди всех факторов планетного влияния на биохимические процессы на первое место следует поставить гравитацию. Действительно, каждая из планет Солнечной системы оказывает свое специфическое влияние на жизненные процессы. Но по суммарной энергии взаимодействия гравитация далеко превосходит все другие виды энергии, включая излучение Солнца, которое существует только благодаря силам гравитационного сжатия звезды. Планеты Солнечной системы, находясь в различных аспектах по отношению к Солнцу, оказывают циклическое влияние на объекты, расположенные на Земле. Одним из механизмов планетного влияния является периодическое изменение потенциалов гравитационных полей планет на поверхности земли. Потенциал гравитационного поля в свою очередь влияет на параметры потоков энергии в неравновесных процессах, протекающих в пределах атмосферы, гидросферы, а также в центральной части планеты, где имеется твердое ядро, окруженное жидким слоем (так называемое приливное воздействие). Роль приливных сил и их влияние на геологические процессы и геомагнетизм в настоящее время мало изучены.

Известно, например, что приливное воздействие Луны способно вызывать подъем уровня воды на океаническом побережье на 10-15 метров дважды в сутки. Но никто точно не знает, как действует Луна на физико-химические процессы в атмосфере Земли особенно на такие, как испарение влаги или конденсация паров, которые чувствительны к малым вариациям действующих сил, а также на атмосферное электричество. Тем более трудно оценить воздействие Луны на процессы, протекающие в центральной части планеты, из-за сложности такого рода наблюдений.

Приливное воздействие дальних планет, таких как Юпитер и Сатурн, практически не изучено. Легко подсчитать, что за год гравитационный потенциал Юпитера, регистрируемый на поверхности Земли, изменяется в больших пределах, приблизительно от j=140000 м²/сек² до j=210000 м²/сек². Но что означает изменение гравитационного потенциала Юпитера для жителя нашей планеты?

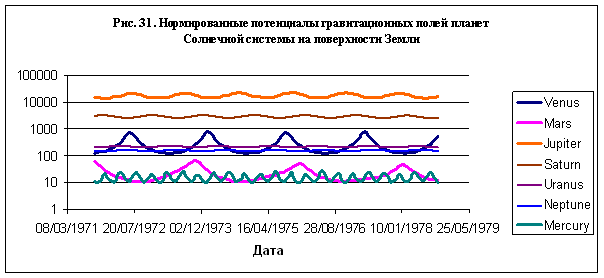
Можно представить образную картину приливного воздействия, если нормировать гравитационный потенциал планет на величину ускорения свободного падения g=9,7805 м/сек². Тогда гравитационные потенциалы планет будут измеряться в метрах, что равносильно восхождению на вершину горы соответствующей высоты, тогда приливное воздействие Юпитера эквивалентно перемещению с высоты 14,5 км на высоту 22 км над поверхностью Земли и обратно. Венера действует так, что это равносильно перемещению с высоты 100 метров на высоту около 800 метров. Влияние Сатурна равносильно периодическому перемещению с высоты 2,5 км на высоту 3,2 км. Можно сказать, что амплитуды изменения потенциала Венеры и потенциала Сатурна приблизительно равны. Марс действует слабее и его приливное воздействие распространяется от 10 метров до 60 метров. Потенциал Меркурия вполовину меньше, чем у Марса, и действует от 10 до 24 метров. Приблизительно такую же амплитуду изменения имеет потенциал Урана, хотя он находится в пределах от 188 до 208 метров – рис. 31.

Обращает внимание периодичность повторения пиковых значений потенциала. Так, за семь лет потенциалы Юпитера, Сатурна и Урана имеют приблизительно по 7 пиков, потенциал Марса – около 4 пиков, потенциал Венеры – около 5 пиков, а потенциал Меркурия – почти 22 пика. Можно также обратить внимание, что потенциалы Марса и Венеры изменяются быстрее вблизи максимальных значений и медленнее вблизи минимальных. В этом смысле их потенциалы похожи между собой.

Заметим, что энергия гравитационного взаимодействия двух планет является отрицательной величиной. Но отрицательная энергия снижает уровень энтропии в термодинамических процессах и понижает пороговые значения энергий в неравновесных термодинамических процессах, таких как химические и биохимические реакции синтеза. Учитывая, что стратегия выживания на нашей планете основана на простом воспроизведении клеток, что, в свою очередь, зависит от скорости синтеза белков, можно предположить, что влияние удаленных планет может проявляться уже на клеточном уровне.

Главное отличие гравитационного потенциала от электромагнитных полей заключается в том, что не существует способа, с помощью которого можно было бы экранировать гравитационное поле. Поэтому гравитационное поле пронизывает материю насквозь, действуя на каждый атом. В то же время поток солнечного электромагнитного излучения, несмотря на его видимую мощь, рассеивается в основном в поверхностном слое плотного вещества, например в подкожном слое человека, загорающего на пляже. Солнечное электромагнитное излучение не проникает вглубь живого организма, хотя растения приспособились использовать энергию этого излучения в процессе фотосинтеза.

Конечно, большое влияние на изменение гравитационного потенциала имеет Луна, которая максимально приближена и быстро вращается вокруг Земли. Солнце также вносит свой вклад в приливное воздействие.

Гравитация и деструкция белков

Обращение небесной сферы вследствие суточного вращения планеты, годичное движение по орбите вокруг Солнца, интенсивность излучений и другие астрофизические параметры порождают циклическое воздействие планет и звездных систем на земные объекты. Ясно, что живые организмы, включая человека, вынуждены адаптироваться к изменяющимся условиям существования. Рассмотрим влияние гравитации планет на деструкцию белков в человеческом организме. Уравнение распада белковых молекул будем описывать химической реакцией первого порядка

dN/dt=-N/t₀(11)

где t₀ – характерный период распада, для которого примем формулу Аррениуса:

1/t₀=Аexp(-E_a/kT) (12)

Здесь E_a – энергия активации, которая совпадает с температурой деструкции основных белковых молекул, что составляет около 333К. Температура тела постоянна и равна T=309.6К (36.6С). Постоянная Больцмана k=1.372^.10^-16 эрг/К. Константа А в формуле (12) является индивидуальной характеристикой белка.

Во внешнем гравитационном поле энергия активации изменяется на величину, пропорциональную массе молекулы и приложенному потенциалу:

E_a =E₀+nm_pU

Где n_–число нуклонов в молекуле, m_p =1.67^.10^{-24 г – средняя масса нуклона.}

Нормируем гравитационный потенциал на величину ускорения свободного падения, тогда его размерность совпадает с пространственным масштабом, т.е. положим

U=-gL

Подставляя эти выражения в исходное уравнение, имеем

dN/dt=-N Аexp[-(E₀-nm_pgL)/kT] (13)

Особенность уравнения (3) состоит в том, что его решение существенно зависит от начального момента времени. Рассмотрим для простоты воздействие отдельно взятой планеты, из тех, чьи потенциалы даны на рис 31. Представим себе, что реакция началась в момент времени, когда величина L максимальна. Тогда эту функцию можно представить в виде L=L(0)-L1(t), где L1(t) – неотрицательная функция. Подставляя это разложение в уравнение (13), находим

dN/dt=-N Аexp[-(E'₀+nm_pgL1)/kT] (13,а)

Но параметр E'₀ совпадает с E₀ поскольку температура деструкции не изменилась. Следовательно, в данном случае будет наблюдаться только замедление скорости распада со временем. Например, снижение скорости старения организма по отношению к некоторому среднему уровню. Соответственно увеличение продолжительности биологической жизни.

Второй типичный случай, когда начало реакции, совпадает с минимумом функции L. В этом случае L=L(0)+L1(t), где L1(t) – неотрицательная функция. Подставляя это разложение в уравнение (13), имеем

dN/dt=-N Аexp[-(E'₀-nm_pgL1)/kT] (13,б)

Здесь мы имеем случай ускорения скорости распада со временем. Соответственно старение организма протекает более интенсивно, а длительность жизни сокращается.

Постоянный параметр этой задачи, не зависящий от типа белка, имеет размерность обратной длины

m_pg/kT=3.86^.10^-9 см^-1 (14)

Другой важный параметр, имеющий размерность длины, связан с температурой деструкции

E₀ /m_pg=2.8^.10⁸ см (15)

Малая величина параметра (14) и большая величина параметра (15) являются главными причинами, почему гравитационные силы обычно не принимаются в расчет. Действительно, гравитационное воздействие удаленных планет становится существенным, если только

nL1=E₀ /m_pg (16)

Это выполняется быстрее в тот момент, когда L1(t) достигает максимума. Но эта величина различна, для различных планет, как видно из данных на рис. 31. Значит, каждая планета имеет свой масштаб влияния, в том смысле, что критическое число нуклонов, содержащихся в белке, обратным образом зависит от величины L1. Типичные значения n, вычисленные по формуле (16) приведены в таблице 18.

Гравитационные потенциалы Луны и Солнца оказывают существенное влияние втечение суток. Для этих источников число нуклонов в молекуле должно быть не мене 500. К таким органическим молекулам, играющим существенную роль в процессах жизнедеятельности, относятся нуклеиновые кислоты и аминокислоты. Юпитер существенно влияет на молекулы с числом нуклонов около 400. Но его период влияния составляет около года. Венера и Сатурн действуют на крупные молекулы с числом нуклонов около 5000. К таким белкам относятся основные ферменты, участвующие в синтезе ДНК. Марс активен в области более крупных образований с числом нуклонов не менее 60000. К таким молекулам относится, например, гемоглобин. Уран, Нептун и Меркурий действуют на очень большие молекулы с числом нуклонов не менее 150000. Это, к примеру, наследственная ДНК. Наконец, Плутон и Варуна, а также ряд крупных астероидов и звезды могут оказать влияние на устойчивость гигантских образований типа хромосом.

Таблица 18. Влияние небесных тел на биохимические
реакции молекул с различным числом нуклонов

Юпитер, Солнце, Луна

Венера, Сатурн

Марс

Меркурий, Уран, Нептун,

Ядро Галактики

Плутон, астероиды, звезды

n=4*10²

4*10³

6*10⁴

1.5*10⁵

10⁷

Аминокислоты

Нуклеиновые кислоты

Ферменты

Гемоглобин

Наследственная ДНК

Хромосомы,

Клеточные структуры

Можно только предполагать, какую длительную эволюцию должна совершить машина жизни, чтобы уверенно противостоять гравитации планет солнечной системы. Одним из очевидных механизмов снижения вероятности распада белков является обратная по отношению к деструкции реакция коагуляции продуктов распада. Например, обмен участками между компонентами двойной спирали ДНК позволяет снизить вероятность деструкции из-за воздействия гравитации планет.

Гравитация и синтез белков

Находясь в растворе, продукты распада вступают во взаимодействие, создавая условия для синтеза белка. Если предположить для упрощения задачи, что исходная молекула белка распадается на две равные части, тогда обратный к распаду процесс коагуляции описывается уравнением второго порядка:

dN/dt=X²Bexp[-(E₀-nm_pgL/2)/kT) (17)

где Х – концентрация продуктов распада, В – константа скорости реакции синтеза. Если масса системы сохраняется, то в каждый момент времени концентрации компонентов связаны уравнением

X/2 +Y=1 (18)

Выражая отсюда величину Х, подставляя ее в уравнение (17) и комбинируя его с уравнением (13), находим

dY/dt==-Y (19)

Аexp[-(E₀-nm_pgL)/kT]+(1-Y)²4Bexp[-(E₀-nm_pgL/2)/kT]

Здесь также будет уместно рассмотреть два случая. Если исходная система (19) сформировалась в момент времени, когда величина L максимальна, тогда эту функцию можно представить в виде L=L(0)-L1(t), а его решение в стационарном случае имеет вид

Y=1/[1+(A/4B)exp(-nm_pgL1/2kT)] (20)

При L1=0 реализуется нормальное равновесное состояние

Y₀=1/(1+A/4B)

При L1>0 равновесное состояние смещается в сторону повышения концентрации белков, поскольку всегда Y>Y₀.

Во втором случае, когда система сформировалась при минимальной величине L , эту функцию можно представить как L=L(0)+L1(t), а решение уравнения (19) в стационарном случае имеет вид

Y=1/[1+(A/4B)exp(nm_pgL1/2kT)] (20,а)

В этом случае равновесное состояние всегда смещается в сторону понижения концентрации белков.

Возможно, здесь мы имеем ключ к разгадке механизма иммунитета. Действительно, иммунитет определяется в основном содержанием в крови специфических белков. Если их концентрация падает, иммунитет снижается и, наоборот, при повышении концентрации белков иммунитет возрастает.

В таком случае иммунитет зависит в основном от положения Солнца, Луны и Юпитера на момент рождения. Например, Солнце в зените заведомо лучше, чем Солнце в надире, поскольку величина L максимальна при положении Солнца в зените. То же самое касается и Луны. Значит, Солнце и Луна в дневных домах улучшают здоровье. При этом Юпитер должен находиться в ночных домах, тогда он максимально приближен к Земле и дает максимальный вклад в величину L.

Здесь открываются большие возможности для объяснения влияния аспектов планет на иммунитет и здоровье.

Учитывая, что L1(t)=L(0)-L(t), представим выражение (20) в общем случае в виде

Y=1/[1+(A/4B)exp[nm_pg(L(t)-L(0))/2kT)] (20,б)

Этим выражением можно воспользоваться при оптимизации выбора времени рождения с целью повышения иммунитета.

Важным фактором является положение планет в Зодиаке. В пределах нашей Галактики наиболее мощный центр притяжения сосредоточен на границе знаков Стрельца и Козерога. Большинство астрономов считают, что там находится ядро нашей Галактики, хотя мы и не можем его видеть, так как оно скрыто звездными облаками. Согласно последним астрономическим данным Солнечная система находится на расстоянии приблизительно 30 тысяч световых лет от этого центра. Если вычислить гравитационный потенциал ядра Галактики исходя из этого расстояния и из величины галактического года, то можно прийти к выводу о том, что потенциал ядра галактики почти в 70 раз превосходит гравитационный потенциал Солнца, регистрируемый на поверхности Земли. Однако потенциал ядра Галактики заметно изменяется лишь втечение галактического года, т.е. за 225 миллионов лет. Ясно, что столь медленные изменения могут сказаться лишь в масштабе биологической эволюции.

Через этот центр проходит ось Рак-Козерог. Гравитационный потенциал Галактики, регистрируемый на поверхности земли, изменяется при движении по орбите вокруг Солнца. Годичные вариации гравитационного потенциала Галактики составляют около 10 метров, что сравнимо с влиянием Урана и Нептуна. В отличие от влияния планет, которые перемещаются по кругу Зодиака, влияние потенциала центра Галактики имеет четкий период, привязанный к годичному видимому движению Солнца. Таким образом, это влияние представляет собой как бы репер-сигнал, сообщающий долгоживущим организмам важную информацию, например, о процессии земной орбиты. Такого рода информация необходима популяциям живых существ, сохраняющих свое потомство на протяжении миллионов лет. Рассмотрим эти вопросы более подробно.

6.3. Фундаментальные законы распознавания социальных категорий по астрономическим данным на момент рождения

В работах /13-15/ на основе системы искусственного интеллекта «Эйдос-астра» /3/ было выполнено распознавание 37 представительных социальных категорий 20007 респондентов с общим числом случаев 86314. В качестве входных данных модели были использованы астрономические параметры долготы и расстояния до десяти небесных тел - Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна и Плутона, а также долготы углов 12 домов в системе Плацидуса. Из исходных астрономических параметров было образовано три базы данных, а именно:

1) долготы десяти небесных тел и 12 углов домов – банк LH исследованный в работе /15/;

2) долготы и расстояния до десяти небесных тел – банк LR исследованный в работах /13-14/;

3) расстояния до 10 небесных тел и долготы углов 12 домов – банк HR исследованный в работах /13-14/.

Моделирование осуществлялось на сетках различного масштаба, полученных путем разбиения солярного зодиака на N=2, 3, …, 173 сектора. Были установлены фундаментальные закономерности распознавания категорий при изменении числа секторов разбиения /15/, а также зависимость дисперсии информативности от расстояния до небесных тел /13/ и от долготы угла первого, четвертого, седьмого и девятого дома /14/.

В работе /29/ выполнено подробное исследование фундаментальных зависимостей, полученных в работах /13-14/. Установлены основные закономерности поведения интегральной информативности в зависимости от расстояния до небесных тел. Найдены параметры подобия, позволяющие обобщить данные моделирования для всех исследованных моделей.

Постановка задачи и метод моделирования

Исходные параметры задачи представляют собой банк данных, содержащий 20007 записей биографий реальных личностей, отобранных из AstroDatabank /5/. Эти данные включают социальные и персональные категории, дату, время и место рождения, а также астрономические параметры, вычисленные на момент рождения. В настоящем исследовании была использована база данных, образованная из исходной путем комбинации входных параметров долготы и расстояние от Земли до центра масс 10 небесных тел - Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна и Плутона– банк LR исследованный в работах /13-14/.

Среди социальных категорий были отобраны только представительные, число повторений которых в банке данных превышает 1000 – см. таблицу 19. Для того чтобы можно было сравнить влияние долготы и расстояния в одном масштабе, признаки расстояний нормировались по формуле:

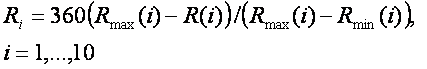
Здесь R_max(i), R_min(i) максимальное и минимальное расстояние до i-го небесного тела соответственно.

Моделирование осуществляется в два этапа на сетках различного масштаба – М6, М12, М20, М21, М22, М23, М24, М25, М26, М27, М28, М29,М32,М36,М72,М150, М170 (число ячеек совпадает с номером модели), с использованием системы искусственного интеллекта «Эйдос-астра» [3]. На первом этапе формируется обобщенный информационный портрет каждой социальной категории. Астрономические параметры на каждой сетке с числом ячеек М разбиваются на М признаков, соответствующих занимаемому интервалу с номером m=1, 2,…,M. Каждому астрономическому признаку (долготе или расстоянию из данного интервала) соответствует некоторое количество информации, по которому для каждой категории вычисляется информативность данного признака – см. таблицу 20. Интегральная информативность (ИИ) представляет собой среднеквадратичное отклонение информативности данного признака, вычисленное для 37 категорий, перечисленных в таблице 19.

Таблица 19. Список 37 социальных категорий

KOD	NAME	Частота
1	SC:М-	13640
2	SC:Ж-	5125
3	SC:A53-Sports	4567
4	SC:A1-Book Collection	4471
5	SC:A15-Famous	3373
6	SC:A42-Medical	2910
7	SC:A323-Sexuality	2675
8	SC:A5-Entertainment	2577
9	SC:A9-Relationship	2442
10	SC:A40-Occult Fields	2396
11	SC:B111-Sports:Basketball	2385
12	SC:B329-Sexuality:Sexual perversions	2360
13	SC:A55-Art	2232
14	SC:A19-Writers	2223
15	SC:A129-Death	2168
16	SC:A25-Personality	2083
17	SC:A68-Childhood	1996
18	SC:A31-Business	1813
19	SC:C330-Sexuality:Sexual perversions:Homosexual	1807
20	SC:B45-Famous:Greatest hits	1795
21	SC:A29-Parenting	1754
22	SC:B173-Sports:Football	1613
23	SC:B97-Occult Fields:Astrologer	1480
24	SC:B21-Relationship:Number of marriages	1417
25	SC:B2-Book Collection:Profiles Of Women	1389
26	SC:A92-Birth	1343
27	SC:B14-Entertainment:Actor/ Actress	1256
28	SC:?- (Неопределенный пол)	1242
29	SC:B49-Book Collection:American Book	1178
30	SC:B26-Personality:Body	1163
31	SC:B189-Medical:Illness	1159
32	SC:B6-Entertainment:Music	1086
33	SC:A99-Financial	1075
34	SC:B48-Famous:Top 5% of Profession	1073
35	SC:A38-Politics	1039
36	SC:A23-Psychological	1007
37	SC:A108-Education	1002
	Всего случаев	86314

По смыслу своего определения интегральная информативность является мерой отклика множества респондентов на воздействие небесных тел, проявляющегося через ряд категорий из таблицы 19. Чем выше значение интегральной информативности, тем больше расщепление информативности отдельных категорий, тем достовернее зависимость категорий от положения небесного тела или другого параметра – таблица 20 (колонка многоточий соответствует остальным 30 категориям из таблицы 19).

Таблица 20. Фрагмент матрицы информативности признаков расстояния до Солнца в модели М22. В последней колонке указана интегральная информативность. Единица измерения: Бит´100

SUNDIST	SC:М-	SC:Ж-	SC:A53	SC:A1	SC:A15	SC:A42	SC:A323	…	Sum	Average	II
{0.000, 16.364}.	-0,627	2,454	-0,464	-1,012	-3,270	-1,096	3,066	…	-6,476	-0,175	2,681
{16.364, 32.727}	0,726	0,742	1,576	-3,311	-2,001	2,392	1,817	…	-16,371	-0,442	3,835
{32.727, 49.091}	-0,766	-0,078	-2,474	2,122	1,751	-2,270	0,221	…	11,400	0,308	3,223
{49.091, 65.455}	-0,372	-3,833	-2,729	-0,206	-0,801	4,020	2,347	…	-0,578	-0,016	3,912
{65.455, 81.818}	-2,836	1,112	-3,832	0,861	2,722	0,891	2,313	…	18,696	0,505	3,547
{81.818, 98.182}	1,025	0,402	2,886	1,109	3,688	6,670	-0,226	…	-36,259	-0,980	4,609
{98.182, 114.545}	0,597	-0,199	1,540	-4,585	-1,787	0,842	-1,287	…	-3,715	-0,100	3,464
{114.545, 130.909}	-2,204	2,078	-2,555	1,994	-0,239	-4,824	-2,259	…	3,172	0,086	5,106
{130.909, 147.273}	0,284	2,317	2,341	-2,463	-1,490	2,258	3,211	…	-29,003	-0,784	4,871
{147.273, 163.636}	-0,230	-0,476	3,690	-0,335	-0,011	-1,693	-1,329	…	-17,193	-0,465	4,733
{163.636, 180.000}	-3,460	2,875	-2,326	3,871	4,879	-1,332	0,925	…	14,722	0,398	5,051
{180.000, 196.364}	1,179	-1,386	3,799	-1,130	-1,441	-6,504	-5,067	…	-19,620	-0,530	5,347
{196.364, 212.727}	-0,997	1,799	-2,713	0,231	1,484	-1,928	-0,199	…	-10,369	-0,280	5,267
{212.727, 229.091}	0,662	-1,290	1,172	1,439	4,062	3,669	-5,305	…	-10,934	-0,296	4,827
{229.091, 245.455}	2,807	-4,415	2,068	-1,110	-0,048	-0,523	4,959	…	-28,212	-0,762	5,015
{245.455, 261.818}	1,813	2,458	6,186	0,976	1,366	-4,853	-3,246	…	-51,358	-1,388	4,917
{261.818, 278.182}	0,460	-0,001	0,444	-0,573	-0,938	4,091	4,241	…	-28,972	-0,783	4,569
{278.182, 294.545}	0,478	-2,843	0,723	2,488	0,394	3,745	-2,089	…	-9,971	-0,269	4,315
{294.545, 310.909}	0,032	2,229	0,656	1,035	3,352	-0,748	-2,804	…	-9,397	-0,254	4,302
{310.909, 327.273}	-0,795	0,724	-2,996	1,851	1,044	-1,092	-1,414	…	10,403	0,281	3,322
{327.273, 343.636}	0,075	-3,458	-1,451	-1,242	1,265	-1,596	-0,120	…	8,486	0,229	3,632
{343.636, 360.000}	1,040	-1,733	-0,284	0,062	-2,084	-0,623	-2,899	…	-5,292	-0,143	2,152

На втором этапе осуществляется распознавание социальных категорий по параметру сходства, который определяется следующим образом:

S_k – достоверность идентификации «k-й» категории;

N – количество респондентов в распознаваемой выборке;

BT_ik– уровень сходства «i-го» респондента с «k-й» категорией, к которой он был правильно отнесен системой;

T_ik – уровень сходства «i-го» респондента с «k-й» категорией, к которой он был правильно не отнесен системой;

BF_ik – уровень сходства «i-го» респондента с «k-й» категорией, к которой он был ошибочно отнесен системой;

F_ik – уровень сходства «i-го» респондента с «k-й» категорией, к которой он был ошибочно не отнесен системой.

При таком определении параметр сходства изменяется в пределах от -100% до 100%, как обычный коэффициент корреляции в статистике. В работе [7] было выполнено исследование зависимости параметра сходства от объема распознаваемой выборки для различных баз данных. Было установлено, что уже при N >150 происходит стабилизация параметра сходства различных категорий. В данной работе для всех 37 категорий был выбран объем N =100.

Заметим, что все исследованные модели имеют большую размерность, а общее количество фактов, учтенных во всех моделях более 30 миллионов.

Логарифмическая зависимость среднего параметра сходства от числа ячеек сетки

Для каждого масштаба сетки распознаются все 37 категорий, определяется их параметр сходства и средний параметр сходства для всех 37 категорий, что соответствует 86314 случаям. Такая представительная статистика позволяет выполнить параметрические исследования зависимости среднего параметра сходства от числа ячеек и определить эту зависимость с высокой достоверностью. На рис. 1 представлены обобщенные данные среднего параметра сходства в зависимости от числа ячеек для двух БД. Данные /15/ обобщаются зависимостью, которую можно представить в виде (сплошная линия ST на рис. 32):

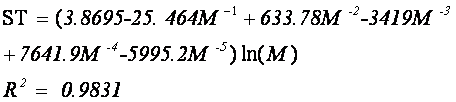
Данные работы /29/ лежат в среднем несколько выше данных работы /15/ - сплошная линия ST1 на рис. 32:

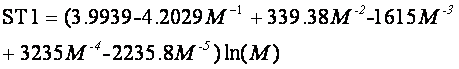
Такое поведение означает, что в среднем категории из таблицы 19 распознаются лучше по долготе небесных тел и расстоянию до них, чем по долготе небесных тел и углов домов. При больших значениях числа ячеек модели это различие является небольшим, поэтому им можно пренебречь.

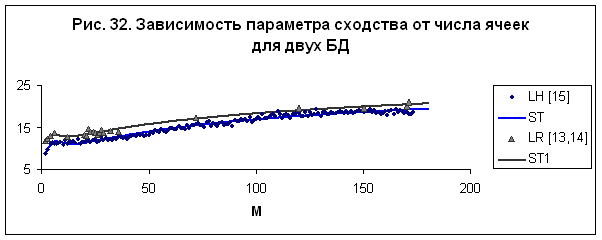
Асимптотически, при числе ячеек модели стремящемся к бесконечности, средний параметр сходства зависит от числа ячеек как логарифмическая функция. Подобная зависимость характерна для сеточной энтропии, которая пропорциональна логарифму числа элементов множества. Заметим, что логарифмическая зависимость среднего параметра сходства от числа ячеек модели для двух БД указывает на высокую степень соответствия полученных результатов распознавания, хотя в деталях для разных категорий эти результаты могут отличаться довольно сильно.

Зависимость интегральной информативности от расстояния до Солнца

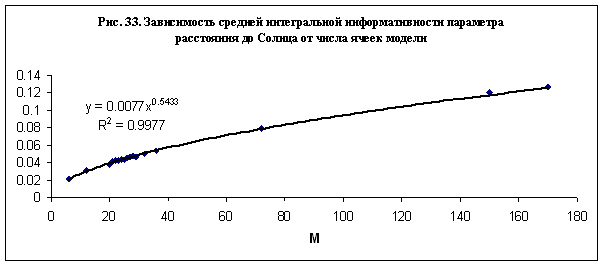
При моделировании влияния расстояния до Солнца на интегральную информативность было обнаружено, что средняя для данной модели величина интегральной информативности возрастает с ростом числа ячеек модели по степенному закону – рис. 2. Для сравнения данных, полученных в различных моделях, вместо ИИ использовалось нормированное значение этого параметра, полученное путем деления ИИ на его среднее значение для данной модели. 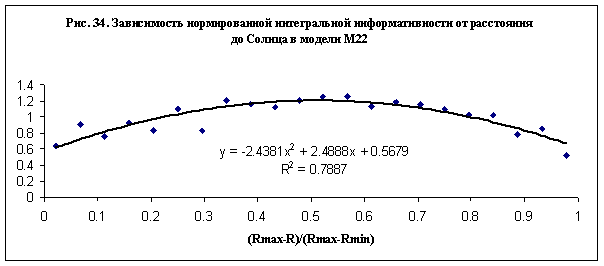Во всех изученных моделях поведение нормированного значения ИИ в зависимости от расстояния описывается параболой. Наиболее достоверно зависимость ИИ от расстояния выявляется в модели М22 – рис. 33. Существенно, однако, что данные всех моделей обобщаются также параболической зависимостью – см. рис. 34, которая мало отличается от параболической зависимости на рис. 33. Иначе говоря, зависимость на рис. 33-34 является универсальной, что позволяет сформулировать закон взаимодействия группы субъектов с Солнцем, используя любую из них.

Зависимость нормированной интегральной информативности от расстояния до Солнца в общем случае можно представить в виде:

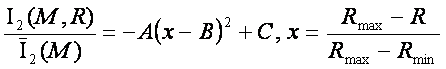(21)

Здесь численные коэффициенты, определенные по совокупности данных на рис. 35, равны:

A=2.4222, B=0.5139, C=0.8233.

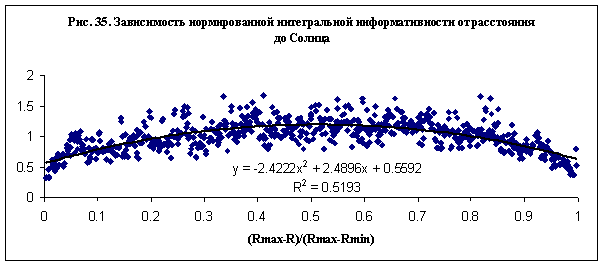
Входящее в выражение (21) нормированное расстояние можно связать с гравитационным потенциалом Солнца, используя классическое выражение:

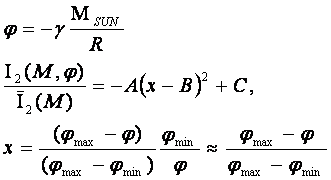(22)

Здесь - гравитационная постоянная и масса Солнца соответственно.

Полученное выражение (22), связывающее интегральную информативность с вариациями гравитационного потенциала Солнца, позволяет сформулировать модель взаимодействия группы субъектов с Солнцем. Отметим главные особенности этого взаимодействия:

1) амплитуда сигнала зависит только от относительной величины вариации гравитационного потенциала, но не от самой величины потенциала;

2) при увеличении или уменьшении амплитуды сигнала относительно некоторой величины В, величина ИИ, характеризующая реакцию на воздействие, всегда убывает, что свидетельствует о наличии отрицательной обратной связи.

Как известно в организме на принципе отрицательной обратной связи основаны механизмы нервной регуляции, поддерживающие параметры гомеостаза (терморегуляция, дыхание и т.п.).

Зависимость интегральной информативности от расстояния до Урана

Как было установлено в работах /13-14/, интегральная информативность зависит от расстояния до десяти небесных тел Солнечной системы - Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна и Плутона. Однако, наиболее точное соответствие выражениям (21-22) может быть получено по данным для планеты Уран – рис. 36. В этом случае зависимость интегральной информативности от расстояния до планеты описывается уравнением

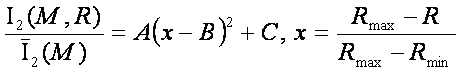(23)

Здесь параметры уравнения (23) вычисляются согласно данным, представленным на рис. 36:

A=3.5623, B= 0.4813, C= 1.2956

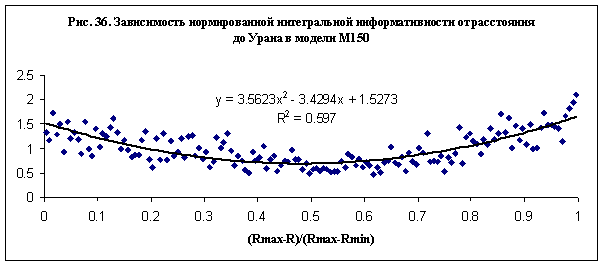
Используя выражение гравитационного потенциала, зависимость нормированной интегральной информативности от расстояния до Урана (23) можно представить в форме:

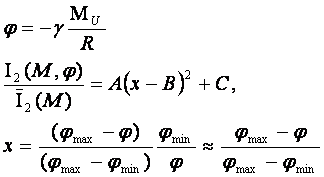(24)

Где - масса планеты Уран. Отметим, что зависимость нормированной интегральной информативности от расстояния до Урана имеет минимум в середине интервала – рис. 36, тогда как аналогичная зависимость в случае Солнца имеет максимум в середине интервала – см. рис. 35. Это отличие указывает на различную реакцию группы субъектов на воздействие Солнца и Урана, хотя сам механизм взаимодействия является общим в двух этих случаях, что непосредственно следует из сравнения выражений (22) и (24). Сформулируем закон взаимодействия субъектов с гравитационным полем Урана:

2) при увеличении или уменьшении амплитуды сигнала относительно некоторой величины В, величина ИИ, характеризующая реакцию на воздействие, всегда возрастает, что свидетельствует о наличии положительной обратной связи.

Как известно, на принципе положительной обратной связи работает защитный механизм иммунной системы, обеспечивающий сохранность организма при проникновении инфекций. Таким образом, сравнивая воздействие Солнца и Урана, можно сделать следующие выводы:

1) воздействие гравитационного поля Солнца адаптируется организмом на уровне нейрорегуляторных функций типа терморегуляции и дыхания;

2) воздействие относительно слабого гравитационного поля Урана адаптируется организмом на уровне функций иммунной системы, воспринимающей это воздействие как инородный фактор, проникший в организм, вопреки установленным барьерам.

Универсальная зависимость нормированной интегральной информативности для далеких планет и модель взаимодействия

Для далеких планет – Сатурна, Урана, Нептуна и Плутона можно получить универсальную зависимость нормированной интегральной информативности от безразмерного параметра х – рис. 37. Используя данные на рис. 37, представим эту зависимость в виде:

(25)

где А=2.7418, В=0.4572, С=1.1311, k=1,2,3,4.

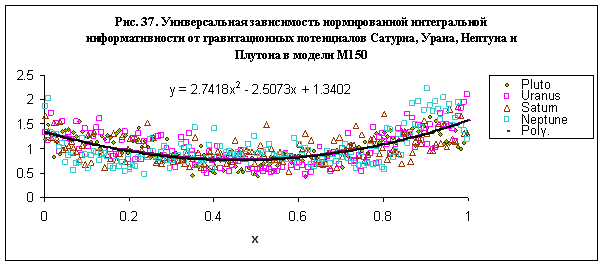
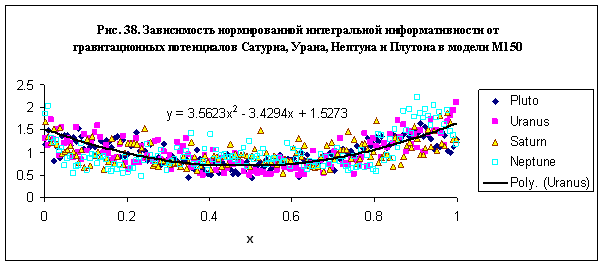
Заметим, что эта зависимость несколько отличается от таковой для Урана – рис. 37. поскольку для ее нахождения использованы данные для четырех планет, имеющие довольно широкий разброс. Поскольку это не меняет конечных выводов о характере влияния далеких планет, без ограничения общности полученных результатов можно было бы использовать для аппроксимации данных для четырех планет параболу, полученную для Урана – см. рис. 38. Такая замена слегка снижает точность аппроксимации, но не меняет самого характера поведения нормированной интегральной информативности в зависимости от амплитуды воздействия.

Полученные результаты позволяют сформулировать общую модель взаимодействия группы субъектов с удаленными небесными телами - Сатурном, Ураном, Нептуном и Плутоном:

Как известно, в организме по механизму положительной обратной связи организована работа иммунной системы. Можно предположить, что слабые гравитационные поля удаленных планет Солнечной системы вызывают ответную реакцию организма такого же типа, как при проникновении возбудителей инфекционных заболеваний.

Зависимость интегральной информативности от расстояния до Луны, Марса, Меркурия, Юпитера и Венеры

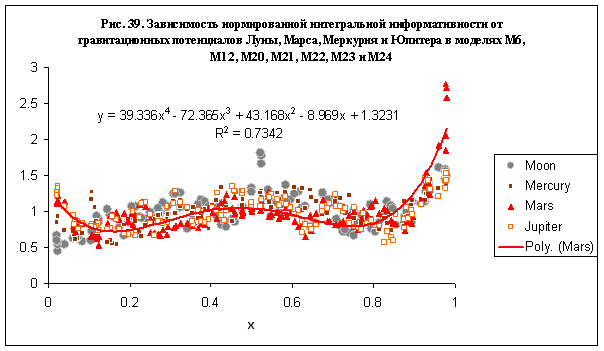
Поведение интегральной информативности в зависимости от приведенного расстояния до Луны, Марса, Меркурия и Юпитера представлено на рис. 39. Для построения зависимости были выбраны данные моделирования семи моделей – М6, М12, М20, М21, М22, М23 и М24. Полученные результаты для каждого небесного тела могут быть аппроксимированы полиномом четвертого порядка, но наилучшая достоверность при аппроксимации данных достигается в случае Марс – см. рис. 39.

Используя выражение гравитационного потенциала, зависимость нормированной интегральной информативности от гравитационного поля Марса можно представить в форме:

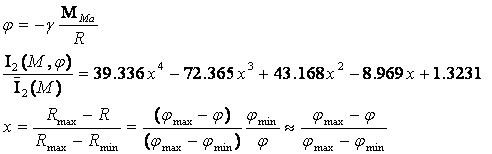(26)

Здесь - масса планеты Марс.

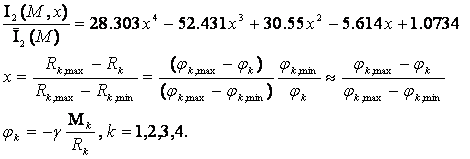
Универсальная зависимость нормированной интегральной информативности от безразмерного параметра х для четырех небесных тел – Луны, Марса, Меркурия и Юпитера (см. рис. 39), имеет вид:

(27)

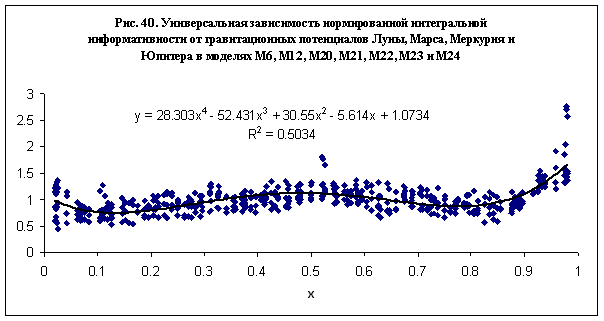
Анализируя зависимости на рис. 39-40, можно сделать вывод, что реакция группы субъектов на гравитационное воздействие Луны, Марса, Меркурия и Юпитера происходит по смешанному механизму положительной и отрицательной обратной связи. Можно предположить, что для поддержания гомеостазиса при малом отклонении от равновесного значения х=0.5, включается нейрорегуляторный механизм типа дыхания и терморегуляции, а при значительном отклонении включается механизм иммунной защиты.

В случае Венеры зависимость нормированной интегральной информативности от гравитационного потенциала – рис. 41, вычисленная по данным моделирования в 12 моделях – М6, М12, М20-М29, имеет вид как в случае Солнца (см. рис. 35). Зависимость, представленная на рис. 41 с приемлемой точностью можно аппроксимировать параболой:

(27)

Где - масса планеты Венера, А=2.5478, В=0.567, С= 0.7256.

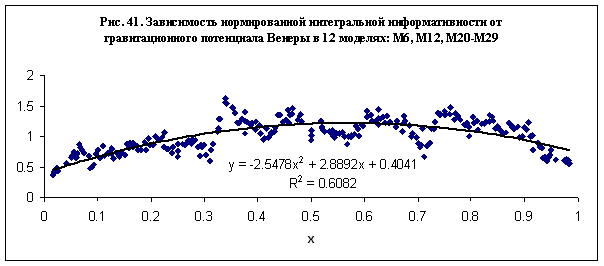Таким образом, в случае Венеры выполняются закономерности, отмеченные для Солнца, а именно:

1. амплитуда сигнала зависит только от относительной величины вариации гравитационного потенциала, но не от самой величины потенциала;

2. при увеличении или уменьшении амплитуды сигнала относительно некоторой величины В, величина ИИ, характеризующая реакцию на воздействие, всегда убывает, что свидетельствует о наличии отрицательной обратной связи.

Отметим, что в организме на принципе отрицательной обратной связи основаны механизмы нервной регуляции, поддерживающие параметры гомеостаза (терморегуляция, дыхание и т.п.). Следовательно, группа субъектов реагирует на воздействие гравитационного поля Венеры и Солнца по механизму отрицательной обратной связи, тогда как реакция на воздействие остальных небесных тел происходит преимущественно по механизму положительной обратной связи или по механизму обратной связи переменного типа. При этом Луна, Марс, Меркурий и Юпитер составляют одну группу планет, гравитационные поля которых возбуждают механизм обратной связи переменного типа. Сатурн, Уран, Нептун и Плутон составляют вторую группу планет, возбуждающих своими полями механизм положительной обратной связи.

Таким образом, была изучена реакция группы субъектов на воздействие Солнца, Луны и планет Солнечной системы – Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна и Плутона. В результате выполненных исследований установлено, что механизм взаимодействия может быть описан общей моделью, включающей нормированную интегральную информативность для описания реакции и амплитуду воздействия, зависящую от относительной величины гравитационного потенциала небесных тел.

Сформулируем общие законы взаимодействия субъектов с гравитационными полями небесных тел:

1. Амплитуда сигнала зависит только от относительной величины вариации гравитационного потенциала, но не от самой величины потенциала;

2. При увеличении или уменьшении амплитуды сигнала относительно некоторой величины В, величина ИИ, характеризующая реакцию на воздействие гравитационных полей Солнца и Венеры, всегда убывает, что свидетельствует о наличии отрицательной обратной связи.

3. При увеличении или уменьшении амплитуды сигнала относительно некоторой величины В, величина ИИ, характеризующая реакцию на воздействие гравитационных полей Сатурна, Урана, Нептуна и Плутона всегда возрастает, что свидетельствует о наличии положительной обратной связи.

4. При увеличении или уменьшении амплитуды сигнала относительно некоторой средней величины, реакция группы субъектов на воздействие гравитационных полей Луны, Марса, Меркурия и Юпитера осуществляется по механизму обратной связи переменного типа.

Полученные результаты можно интерпретировать следующим образом:

1) выбор тех или иных социальных категорий при воздействии небесных тел обусловлен адаптационными возможностями организма,

2) которые изменяются как на уровне нервной регуляции по механизму отрицательной обратной связи под воздействием Солнца или Венеры, а также при определенных условиях под воздействием Луны, Марса, Меркурия и Юпитера,

3) так и на уровне иммунной системы под воздействием слабых гравитационных полей Сатурна, Урана, Нептуна и Плутона, и при определенных условиях под воздействием Луны, Марса, Меркурия и Юпитера.

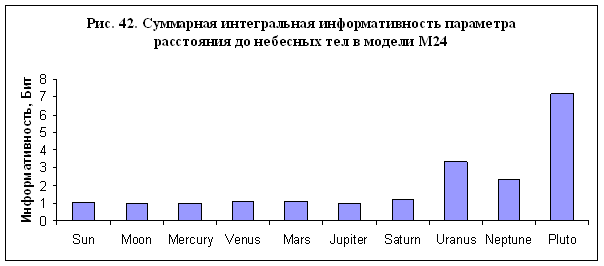
Обнаруженная зависимость интегральной информативности от расстояния до небесных тел свидетельствует о том, что взаимодействие субъектов с ближним космическим окружением носит, вообще говоря, субстанциональный характер. Что же лежит в основе этого взаимодействия? Сравним суммарную по всем ячейкам интегральную информативность параметра расстояния до небесных тел для заданной модели, например, М24 – рис. 42. Из данных, представленных на рис. 42, следует, что семь видимых глазом небесных тел – Солнце, Луна, Меркурий, Венера, Марс, Юпитер и Сатурн имеют примерно равное влияние на суммарную интегральную информативность, тогда как невидимые планеты – Уран, Нептун и Плутон влияют заметно сильнее, особенно Плутон.

Отсюда следует, что агентом влияния, скорее всего, является не электромагнитное поле, а некое другое, способное выравнивать влияние видимых небесных тел и усиливать влияние невидимых невооруженным глазом планет. Сформулируем энергетический критерий взаимодействия субъектов с небесными телами, используя известное из теории информации соотношение между информацией и энтропией:

Возводя это соотношение в квадрат, находим

Следовательно, интегральная информативность (среднеквадратичное отклонение количества информации) совпадает со среднеквадратичным отклонением для энтропии.

Заметим, что субъективное восприятие планет происходит не только и не столько на физическом уровне, сколько на уровне потоков информации. В свою очередь потоки информации формируются путем обработки сигналов. Чем слабее сигнал, приходящий со стороны небесного тела, тем больше затраты энергии на его обработку. При этом все сигналы, имеющие амплитуду выше пороговой, обрабатываются с одинаковыми затратами энергии. Поэтому семь видимых небесных тел, сигнал которых превышает пороговый, имеют примерно равную суммарную интегральную информативность. На обработку же сигналов невидимых небесных тела – Уран, Нептун и Плутон, требуется значительно больше энергии, поэтому им соответствует большая величина суммарной интегральной информативности.

В настоящее время не существует физической теории объясняющей это влияние. Можно лишь предположить в качестве рабочей гипотезы, что основным агентом влияния может быть гравитационный потенциал. Под воздействием гравитационного потенциала меняется статистика фермионов - электронов проводимости и нуклонов в атомных ядрах. Это, в свою очередь, приводит к изменению электрических и магнитных свойств материалов, а также фундаментальных констант радиоактивного распада /31-32, 39/.

Поскольку человеческий мозг состоит из системы нейронов, вырабатывающих электрические импульсы и связанных между собой проводниками электрических импульсов (дендритами и аксонами), можно предположить, что эта система может иметь отклик на изменение гравитационного потенциала (но не силы гравитации!). Поскольку в настоящей работе использованы данные рождения 20007 реальных субъектов, следует предположить, что субъект каким-то образом запоминает положение небесных тел на момент рождения. Физиология этого явления пока не изучена, известно, однако, что в состоянии гипноза люди способны воспроизвести некоторые обстоятельства, сопутствующие своему рождению.

Можно выдвинуть и альтернативную гипотезу об информационном поле, способном распространяться в космическом пространстве путем диффузии. Эта гипотеза позволяет объяснить зависимость интегральной информативности от скорости сближения и радиального ускорения. Но для обоснования этой гипотезы нет достаточных экспериментальных данных. Наконец, модификация уравнения гравитационного потенциала и сведение его к уравнению диффузии (или Шредингера), также позволяет воспользоваться теорией [12] для объяснения полученных выше результатов.

В настоящее время еще не изучен детальный механизм, описывающий указанные выше процессы, но сам факт их наличия подтверждается полученными результатами, которые могут иметь, по нашему мнению, фундаментальное значение для развития науки и техники.

Зависимость интегральной информативности от долготы углов домов

В работах /13-14/ была обнаружена регулярная зависимость интегральной информативности от расстояния до небесных тел. Это означает, что влияние небесных тел на психологию группы индивидов имеет субстанциональный характер. Какая именно субстанция является агентом влияния остается пока под вопросом. Есть основания предполагать, что таковой субстанцией может являться гравитационный потенциал, под влиянием которого меняются статистические характеристики системы фермионов, что в свою очередь приводит к изменению электрических и магнитных свойств проводников, а также скорости радиоактивного распада /30-32, 39/.

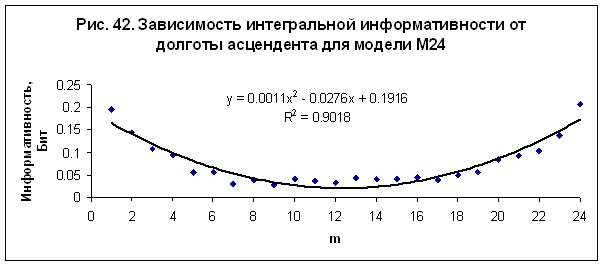
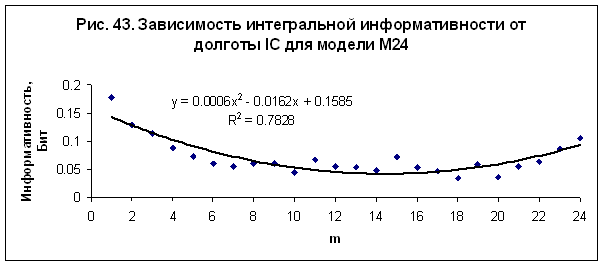
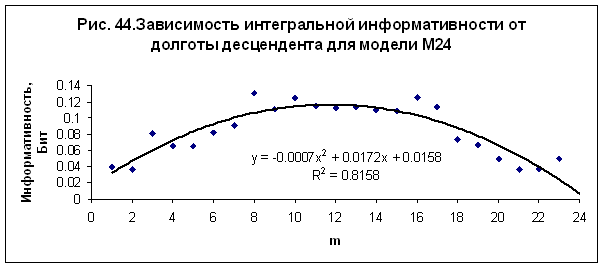
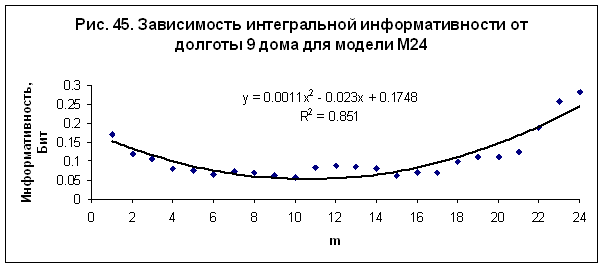
В работе /13/ было выполнено исследование зависимости интегральной информативности от долготы углов домов. Обнаружена регулярная зависимость интегральной информативности от долготы угла первого дома (асцендента) – рис. 42, от долготы угла 4 дома (IC) – рис. 43, от долготы угла 7 дома (десцендента) – рис. 44, и от долготы угла 9 дома – рис. 45. Полученные зависимости являются однотипными во всех исследованных моделях - М24, М36, М72, М100 и М170. Наилучшая достоверность при интерполяции данных квадратичным полиномом наблюдается в модели М24.

Анализ полученных данных показывает, что существует асимметрия пространства вдоль оси знаков Овен - Весы. В настоящее время неизвестно, чем вызвана эта асимметрия. Возможно, что это обусловлено движением нашей Галактики в сторону гигантского скопления галактик в созвездии Девы со скоростью . Тогда точка осеннего равноденствия, которая в настоящее время проецируется в созвездие Девы рядом со скоплением галактик, будет выделена этим движением, как и противоположная ей точка весеннего равноденствия (обе точки находятся на оси Овен - Весы). Скопление галактик обладает колоссальным гравитационным потенциалом, который, видимо, на два порядка превосходит гравитационный потенциал Солнца на поверхности земли. Неизвестно, однако, могут ли вариации этого потенциала, вызванные суточным вращением нашей планеты, создать заметное изменение в ритмах психической активности, или же влияние скопления проявляется на уровне восприятия информации.

Можно рассмотреть и другие причины, например, движение Солнца в направление созвездия Лебедя вокруг центра Галактики. Пока лишь можно утверждать, опираясь на полученные данные, что группа индивидов чувствует асимметрию пространства, что в свою очередь отражается на выборе социальных категорий. Кроме того, можно однозначно утверждать, что время суток в момент рождения, от которого зависит положение углов домов, влияет на выбор социальной специализации.

6.4. Информационная теория влияния
небесных тел на психологию индивида

Как следует из данных работы /35/, астероиды (в данном случае Хирон) могут вносить заметный вклад, сравнимый с вкладом планет и светил (этот эффект также был обнаружен при моделировании 20007 карт рождения на основе системы "Эйдос"). Мы не можем дать этому иного объяснения, чем просто предположить, что каждое небесное тело имеет определенный топологический "заряд", который не зависит от его массы и других физических параметров. Этот "заряд" распространяет свое влияние на "заряды" других небесных тел, взаимодействуя с их "зарядами" и создавая специфическое астральное поле.

Это поле, наряду с гравитационным, видимо, является источником влияния на психологию субъекта, что было обнаружено за долго до изобретения понятия полевого взаимодействия. Среди философов средневековья это поле получило название астральный флюид, а в трудах ученых 19 века оно вновь появилось уже как эфир – основа электромагнитных явлений. В дальнейшем с развитием физики элементарных частиц эфир был заменен вакуумом. Не исключено, однако, что астральный флюид имеет более фундаментальную природу, чем элементарные частицы, которые возникли как логические абстракции для объяснения результатов физических экспериментов.

Согласно Парацельсу, астральный флюид является разумной субстанцией в том смысле, что подчиняется воле разумного существа. Для философов средневековья было очевидно, что мир сотворенный Богом должен подчиняться воле разумного существа, а потому в его основе должна быть разумная субстанция. Современная наука, материалистическая в своей основе, заместила разумную субстанцию на ряд логических абстракций – элементарных частиц, наделив их заданными свойствами типа спина, заряда, массы и т.п.

Заметим, что элементарные частицы – электрон, протон и нейтрон, были открыты при исследовании атомов. В дальнейшем число элементарных частиц, открытых физиками, оказалось столь велико, что вызывает сомнение сам термин элементарная частица. Поэтому, для объяснения строения элементарных частиц были изобретены еще более элементарные частицы – кварки. Это ненаблюдаемые частицы, обладающие заданными свойствами. Пока для объяснения строения других элементарных частиц потребовалось шесть кварков, которые получили название Верхний, Нижний, Странный, Очарованный, Прелестный, Истинный. Это наводит на мысль, что кварки, подобно четырем буквам генетического алфавита, представляют собой информационные кванты, составляющие "язык" материи. Этот "язык" пытаются расшифровать физики путем постановки хитроумных экспериментов. Но тогда в основе мироздания действительно находится разумная субстанция, обладающая собственным языком, логикой и алгоритмами физических законов. Не удивительно поэтому, что физические законы часто имеют совершенную форму математических уравнений.

Конечно, разумная субстанция ближе мировоззрению современного человека, воспитанного в эпоху развития информационных технологий, нежели косная материя. Модель разумной субстанции можно построить по аналогии с мозгом, в котором есть две половины. Поэтому вселенную можно сразу разбить на мир и антимир, что согласуется с физикой элементарных частиц, в которой каждой частице соответствует античастица. Можно предположить, что такое разбиение существует в природе не случайно, а в силу необходимости, связанной с постоянным копированием информации. Если антимир представляет собой законченную, совершенную модель Вселенной, тогда мир является копией, находящейся в состоянии становления. Поэтому в нашем мире много несовершенных форм, неидеальных законов, ошибочных алгоритмов. По мере совершенствования нашего мира, он становится все более точной копией антимира. Когда соответствие становится полным, антимир разрушается, создавая основу для новой копии. Цикл повторяется неограниченное число раз, причем информация дублируется подобно тому, как это происходит при дублировании молекулы ДНК.

Для дублирования информации необходимо иметь базовые частицы, имеющие смысл алфавита, основу, на которую записывается сообщение, матрицу с которой считывается сообщение и алгоритм, обеспечивающий правильность записи. Такими частицами могут быть, например, протон и нейтрон, из которых состоят ядра атомов. Протон (1) и нейтрон (0) обеспечивают двоичное кодирование информации в атомных ядрах. Правильность записи обеспечивается силами взаимодействия, приводящими к распаду неустойчивых ядер. Каждый химический элемент является носителем определенного объема информации, который легко подсчитать. Так ядро атома водорода состоит из одного протона – это единица нашего мира. Ядро дейтерия включает один протон и один нейтрон поэтому его код 10, ядро трития состоит из протона и двух нейтронов – 100, ядро гелия из двух протонов и двух нейтронов – 1100 и т.д.

Любой объем вещества содержит атомы химических элементов, которые являются носителями информации, записанной в двоичных кодах. Это позволяет определить функцию плотности информации путем суммирования информации ядер отдельных атомов в виде:

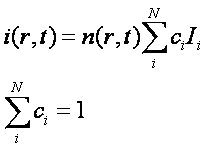(28)

Здесь n – число атомов в единице объема, c_i – концентрация i-го компонента смеси, I_i – информация, приходящаяся на один атом компонента смеси.

При таком определении функция плотности информации пропорциональна плотности вещества. Поэтому гравитационный потенциал и информация связаны между собой простым соотношением через массу планеты. Но существует ли взаимодействие, осуществляющее прямое распространение информации? Если бы первое выражение (28) было образовано из случайных компонентов, не имеющих какого-либо смысла, тогда для его передачи не требовалось бы никакого канала. Но если первое выражение (28) имеет определенный смысл, соответствующий гипотезе копирования информации, тогда об этом должно быть известно в других частях нашего мира. При этом скорость распространения информации не должна быть лимитирована, иначе процесс копирования никогда не завершится. Смыслом сообщения могут быть сведения об уникальном составе (формуле) вещества, способном обеспечить необходимую точность воспроизведения копируемой информации.

Как известно, таким свойством обладают решения уравнения диффузии. Т.о. можно предположить, что в свободном пространстве информация о составе вещества распространяется согласно уравнению:

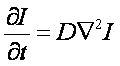(22)

Здесь D – коэффициент диффузии, который для информации этого типа можно выразить через постоянную Планка и массу протона по формуле .

В области, в которой плотность информации отлична от нуля, уравнение (22) необходимо доопределить с учетом распределенного источника в виде:

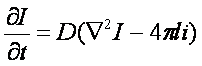(29)

где l – масштаб длины, который для протонов и нейтронов можно по порядку величины принять равным комптоновской длине волны и оценить по формуле .

В случае стационарной задачи имеем хорошо известное из теории потенциала решение затухающее на бесконечности как 1/r:

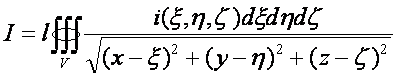(30)

Здесь интеграл берется по замкнутой области, в которой плотность информации отлична от нуля. На большом удалении от планеты решение (30) можно представить в виде ряда по степеням 1/r. Главный член разложения имеет вид:

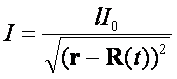(31)

^где 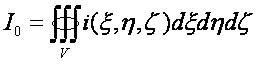^{, R(t) –
расстояние до центра планеты. Этому решению соответствует поток информации}

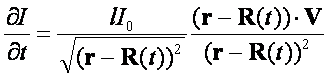(32)

Здесь V – скорость планеты.

С точки зрения уравнения (29) поток информации соответствует распределенному источнику, который в силу уравнения (24) порождает еще одно решение типа

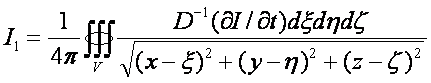(33)

В свою очередь это решение порождает поток информации, который зависит от ускорения планеты:

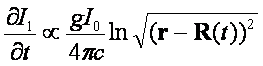(34)

где .

Выражение (28) интересно тем, что оно не зависит от параметров процесса диффузии, поэтому в исходных уравнениях нуклоны можно заменить на любые другие частицы. Дадим его другой вывод, опираясь на уравнение Шеннона (7).

Как известно, любой канал связи, по которому распространяется информация, характеризуется полосой частот , мощностью сигнала, мощностью шума и скоростью передачи информации. Согласно теории информации эти величины связаны уравнением Шеннона (7) :

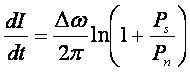
Отметим также, что поток информации однозначно связан с энтропией сообщения уравнением Бриллюэна: dH=-dI.

При наблюдении за планетой или звездой с поверхности земли мощность сигнала зависит от ориентации площадки dA, на которую падает излучение, от радиус-вектора планеты R_p и от суммарной интенсивности потока излучения с поверхности планеты i_p по формуле:

(35)

Мощность шума зависит от разрешающей способности прибора, с помощь которого ведется наблюдение. Предположим, что прибор сконструирован таким образом, что уровень шума зависит только от интенсивности потока энергии приходящего излучения и от угловых размеров прибора, т.е.

(36)

где, P₀ – мощность фонового излучения, а – численный коэффициент, L_b – база прибора. Параметр называется параллакс. Отметим, что в современной астрономии одним из методов определения расстояния до звезд и планет является измерение параллакса – изменения углового положения небесного объекта относительно статического фона при его наблюдении из разных точек пространства. Для определения расстояния до ближайших звезд используется годичный параллакс, возникающий при вращении Земли вокруг Солнца. Смещение звезды на одну угловую секунду соответствует расстоянию в один парсек, т.о. 1 парсек = 3,085678×10¹⁶ м. Для определения расстояний до планет Солнечной системы используется суточный параллакс. Параллакс используется также в геодезии, фотографии и в бинокулярном зрении.

Подставляя выражения (29-30) в исходное уравнение Шеннона, находим для прибора этого типа

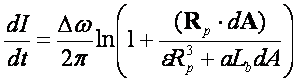(37)

Согласно уравнению (37) поток информации зависит только от радиуса вектора наблюдаемой планеты, поэтому такой прибор позволяет осуществлять интерференцию сигналов, приходящих от разных источников. Если при этом площадку dA ориентировать в направлении максимального сигнала, т.е. положить в уравнении (37)

тогда приходим к уравнению

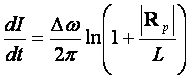(38)

Здесь обозначено .

Отметим, что модель (32) зависит от одного неизвестного параметра L, влияние которого исключается путем нормировки сигнала. Если интенсивность сигнала значительно превосходит интенсивность шума, тогда уравнение (32) несколько упрощается и принимает вид

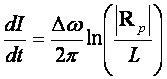₍₃₉₎

Наконец, полагая в уравнении (39) 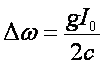, приходим к выражению (34).

Модель (39) получена в предположении, что канал информации связан с потоком электромагнитного излучения. Известно, что в астросоциотипологии учитывается влияние небесных тел находящихся как выше линии горизонта, так и ниже, когда видимый свет не доходит до наблюдателя. Кроме того, учитывается влияние невидимых глазом планет – Урана, Нептуна, Плутона и даже некоторых астероидов. Для объяснения этого влияния привлекаются различные поля, включая гравитационное поле /33/. В этом смысле модель (39) имеет более широкую область применения, поскольку не зависит от характера взаимодействия, осуществляющего перенос информации.

Применим уравнение (39) к системе, в которой галактики разбегаются со скоростью пропорциональной расстоянию до центра наблюдения по закону Хаббла:

(40)

где H – постоянная Хаббла, которая по данным разных авторов составляет от 55 до140 км/с на Мпс, или в среднем 3*10^-18с^-1 .

Интегрируя уравнение (39) с учетом (40), находим

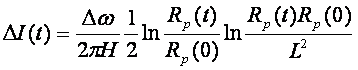(41)

Уравнение (41) позволяет оценить максимальный объем информации, который может быть получен путем наблюдения за удаленными звездами и галактиками. Теоретически при длительном наблюдении, сравнимом со временем жизни Солнечной системы, этот объем очень велик. Так, при наблюдении в видимой части спектра с характерной длиной волны 400-760 нм общий объем информации составит не менее 10³² Непер на один объект наблюдения. Отметим, что этот объем превосходит не только все запасы знаний, накопленных человечеством, но и весь объем наследственной информации, накопленной во всей биосфере Земли. Таким образом, удаленные звезды и галактики являются неисчерпаемым источником информации с точки зрения земных обитателей.

Очевидно, диффузия сама по себе не может обеспечить избирательность передачи информации в зависимости от смысла сообщения. Смысл сообщения необходимо определить как граничное условие для уравнения (29). Смыслом сообщения могут быть сведения о составе литосферы и атмосферы. Как известно, состав земной литосферы, гидросферы и атмосферы не меняется на протяжении миллионов лет, создавая основу для воспроизведения биологических видов. Это уникальные составы, которые могут быть использованы всюду во вселенной. Поэтому информация об этих составах распространяется по закону диффузии, механизм которой обеспечивается физическими свойствами вакуума.

Но тогда параметр I₀в правой части выражений (31-32, 34) является некоторой фундаментальной константой или "зарядом", характеризующим степень готовности небесного тела в процессе копирования информации. Поэтому каждая планета или астероид имеет свой цвет, запах, очарование и т.п. – смысловые характеристики, свойственные наблюдаемым системам. В свою очередь наблюдатель, находящийся на поверхности нашей планеты, фиксирует ускорение небесного тела в неинерциальной системе координат. Поэтому ускорение небесного тела складывается из его собственного ускорения относительно центра масс Солнечной системы, из ускорения Земли относительно Солнца и из ускорения, обусловленного суточным вращением нашей планеты. Поэтому в астросоциотипологии используется две системы координат одна из которых связана с линией горизонта (т.н. система домов для описания положения небесного тела относительно линии горизонта, изменяющегося втечение суток), а вторая связана с точкой весеннего равноденствия (т.н. знаки зодиака для описания положения небесного тела в плоскости эклиптики).

Рассмотрим еще вопрос о механизме влияния взаимных угловых аспектов на психологию индивида. Ответ на этот вопрос тесно связан с фундаментальной проблемой, которую можно сформулировать следующим образом, каков механизм астрсоциотипологического влияния планет вообще? Последний же вопрос может получить объяснение на основе физиологии мозга, в котором, очевидно, имеются процессы, протекающие синхронно с положением Солнца, Луны и планет Солнечной системы. Такая точка зрения позволяет объяснить влияние планет, как чисто информационный процесс, при котором мозг реагирует на сигналы о положении планет, каков бы не был физический механизм передачи этих сигналов. Тогда аспекты можно объяснить просто как результат интерференции сигналов, приходящих от разных источников. Представленные выше модели позволяют развить количественную теорию влияния аспектов планет.

Однако остается не решенным еще один вопрос, связанный с предсказанием будущего, а именно: каков механизм предвидения? В работах /37-38/ дана теория этого феномена, опирающаяся на модель пятимерной Вселенной /36/. Суть феномена заключается в том, что реальные события происходят на плоскости времени, а не в одном его измерении. Поэтому появляются пути передачи информации не только из прошлого в будущее, но и из будущего в прошлое без нарушения принципа причинности. Соотношение масштабов на плоскости времени в модели /38/ зависит от величины гравитационного потенциала, вариациии которого приводят к иллюзорному восприятию событий на субъективном уровне, как линейно упорядоченных во времени, хотя сами события лежат на окружности круга конечного радиуса в комплексной плоскости времени.

6.5. Роль гравитации в типичных ферментативных реакциях

В качестве прикладного примера реакции с участием белков (ферментов) рассмотрим уравнение МИХАЭЛИСА-МЕНТЕН /33/. Это простейшая ферментативная реакция, в которой участвует субстрат (S) и фермент (E), в результате появляется фермент-субстратный комплекс (ES), при распаде которого образуется продукт (P). Формула реакции имеет вид /41/:

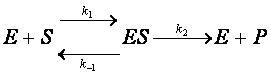
Здесь k₁, k_-1 - константы скоростей прямой и обратной реакций образования фермент-субстратного комплекса; k₂ - константа скорости образования продукта. При определенных предположениях находим уравнение изменения концентрации конечного продукта и субстрата

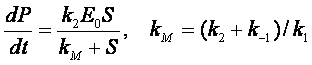(42)

Где Е₀ – начальная концентрация фермента, k_M - константа Михаэлиса. Поскольку фермент E участвует во всех стадиях реакции, имея при этом наибольшую массу, константы k_i во внешнем гравитационном поле определяются согласно уравнению (13):

(43)

Здесь m_E – масса молекулы фермента, k=1.372*10^-16 эрг/К - постоянная Больцмана, T – абсолютная температура (для процессов, происходящих в организме человека температуру можно считать постоянной и равной приблизительно 309.6К или 36.6С).

Заметим, что отношение скоростей реакций в знаменателе в правой части уравнения (42) – константа Михаэлиса, не меняется во внешнем поле. Чтобы не изменилась и эффективная константа скорости реакции, необходимо потребовать, чтобы выполнялось соотношение:

(44)

Следовательно, для автоматического регулирования выхода продукта при любых отклонениях гравитационного потенциала от некоторой начальной величины, потребуется дополнительное количество фермента:

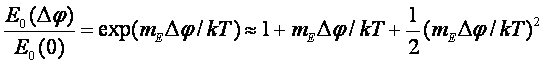(45)

Таким образом, для сохранения скорости производства продукта в простых ферментативных реакциях при изменении гравитационного потенциала необходимо изменять концентрацию фермента пропорционально отклонению гравитационного потенциала.

Сравним этот результат с типичной социальной реакцией большой группы респондентов (всего 20007) на воздействие гравитационных полей далеких небесных тел – Сатурна, Урана, Нептуна и Плутона – см. уравнение (25). Подобие выражений (45) и (25) указывает на общий механизм взаимодействия и на простой физиологически обусловленный характер социальной реакции, в ответ на воздействие гравитационных полей далеких небесных тел. Естественно, возникает вопрос, каким же образом осуществляется избирательность по отношению к влиянию полей конкретных планет? Ведь выражение (45) содержит в правой части суммарный потенциал, тогда как выражение (25) зависит от потенциала отдельного небесного тела. Кроме того, не определено время воздействия и нет явной связи со временем протекания реакции. Тем не менее, эта простая теория позволяет объяснить некоторые характерные особенности установления равновесной концентрации активных соединений в организме, таких как гормоны.

6.6. Роль гравитации в реакциях с участием гормонов

Рассмотрим уравнение (44) при условии, что изменение потенциала лимитировано временем реакции, т.е.

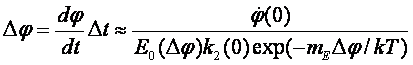
В этом случае вместо выражения (45) находим следующую зависимость концентрации гормона:

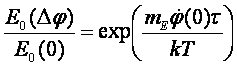(46)

Производную по времени от суммарного гравитационного потенциала можно представить в виде суммы производных потенциалов небесных тел:

(47)

Заметим, что основной вклад в скорость изменения потенциала вносит Солнце. Используя соответствующие Солнцу параметры, находим сезонную зависимость концентрации гормона вазопрессин, регулирующего величину осмотического давления жидкостей в организме – см. рис. 46. В качестве эффективного времени процесса использована длительность реакции одного типа с участием одной молекулы гормона – около 60 сек.

Аналогичная зависимость может быть получена для тиреоидных гормонов Т3 и Т4, осуществляющих перенос электронов в ферментных системах с молекулы донора на субстрат - рис. 46. В этом случае в качестве эффективного времени реакции выступает общее время участия одной молекулы гормона в реакции одного типа, что составляет 200 секунд. Для этих гормонов экспериментально установлена сезонная зависимость их концентрации в крови. Отметим основное действие этих гормонов /41-44/:

1) метаболическое, регуляция обменных процессов, увеличение синтеза белка, повышение распада жиров и углеводов, особенно в клетках нервной системы, регулируют энергетический обмен, обмен белков, жиров и углеводов, кальция во всех клетках организма, в том числе и нервной системе, регулируют уровень содержания сахара в крови;

2) контроль образования тепла, скорости поглощения кислорода клетками, поддержание нормального функционирования дыхательного центра, иммунитета;

3) наряду с гормонами коры надпочечников обеспечивают физиологическую адаптацию.

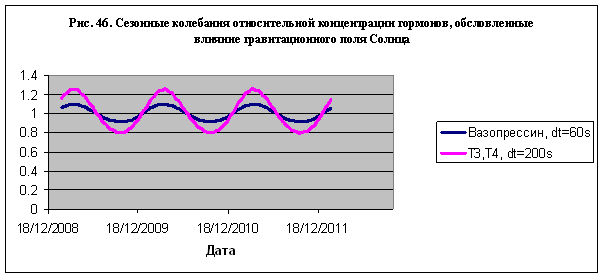
Таким образом, установлено, что концентрация двух типов гормонов, ответственных за регулирование давления и температуры тела, может испытывать сезонные колебания, связанные с воздействием гравитационных полей Солнца.

Отметим, что в сумме в правой части выражение (47) некоторые слагаемые могут обращаться в нуль. Так, например, производная гравитационного потенциала Солнца вносит основной вклад в сумму в правой части выражения (47), но в периоды летнего и зимнего солнцестояния вклад Солнца равен нулю, поскольку в это время производная от расстояния до Солнца обращается в нуль. В этом случае становится заметным влияние других небесных тел. Среди них наиболее существенное влияние (после Солнца) может оказывать Юпитер. Но даже его поля недостаточно, чтобы заметно повлиять на концентрацию гормонов с небольшой молекулярной массой. Не исключено, однако, что Юпитер может повлиять на концентрацию в крови тиреоглобулина (ТГ), обладающего большой молекулярной массой, при условии, что это соединение может принимать участие в длительных, порядка минуты ферментативных реакциях – рис. 47.

В некоторых случаях в нуль может обратиться производная суммы гравитационных потенциалов Солнца и Юпитера. Тогда заметным становится гравитационное воздействие Луны и Венеры, которые могут повлиять на концентрацию ТГ в крови в реакциях длительностью 200 сек – рис. 47. Наконец, в исключительных случаях, проявляют себя в ферментативных реакциях с участием тиреоглобулина, длительностью не менее 600 сек, гравитационные поля Сатурна, Марса и Меркурия – рис. 48.

Таблица 21. Типичные соединения, концентрация которых зависит от сезонных колебаний гравитационного поля

Соединение	m_Е , дальтон	Е₀(0), нг/мл	Период полураспада, час
Тиреоглобулин (ТГ)	660000	18,57	78-96
Вазопрессин, пептидный гормон гипофиза	1084	0.002	0.20-0.25
Тиреоидные гормоны — трийодтиронин (ТЗ); Тироксин (Т4)	551; 777	46-105 (T4)	148 (Т4)

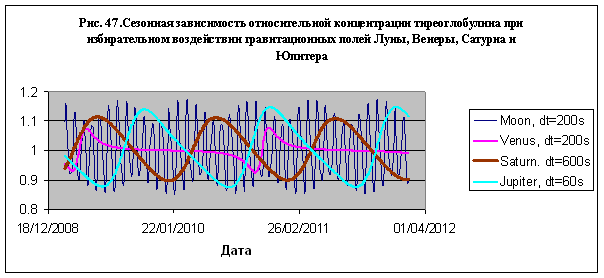
Отметим, что полученные результаты носят предварительный характер, поскольку не указаны конкретные реакции, в которых могли бы проявиться гравитационные поля небесных тел. Общее требование к таким реакциям с участием ферментов заключается в том, чтобы молекулярная масса фермента была достаточно большой, а время реакции исчислялось бы секундами и минутами. Кроме того, развитая теория относится к такому типу гормонов, концентрация которых имеют отчетливую сезонную и суточную зависимость. В этом случае теория предсказывает, что максимальная концентрация гормонов будет наблюдаться весной, а минимальная – осенью.

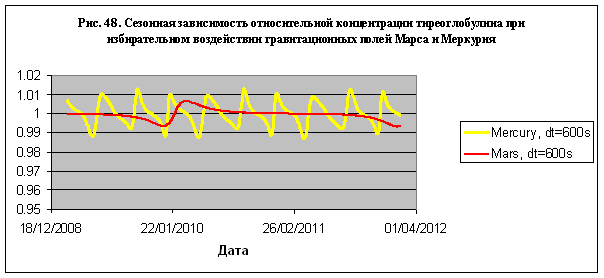
Вообще говоря, механизм установления равновесной концентрации тиреоидных гормонов Т3 и Т4 является довольно сложным, поскольку они производятся с участием тиреоглобулина под влияние гипоталамо-гипофизарной системы. Снижение концентрации тиреоидных гормонов приводит к повышению концентрации тиреотропного гормона (ТТГ) гипофиза, что в свою очередь приводит увеличению скорости синтеза тиреоглобулина и высвобождению Т3, Т4. Регуляция осуществляется по принципу отрицательной обратной связи, однако секреция ТТГ тормозится не только Т3 и Т4, но и соматостатином и дофамином, а стимулируется тиреотропин-рилизинг-гормоном гипоталамуса -тиреолиберином. Такая сложная цепочка не может быть описана одним уравнением, типа (42), но должна включать все стадии процесса регулирования, в том числе модель накопления сигнала в памяти.

Рассмотрим три модели накопления сигнала:

1) в случае, когда сигнал является очень слабым, что выполняется для Сатурна, Урана, Нептуна и Плутона, тогда его накопление идет непрерывно, в соответствии с выражением (45);

2) в том случае, когда сигнал является очень сильным, что выполняется для Солнца, тогда его накопление происходит за ограниченное время, в соответствии с выражением (46), после чего происходит сброс сигнала;

3) для сигналов средней интенсивности, приходящих от Луны, Меркурия, Марса и Юпитера в окрестности точек поворота выполняется модель 1, а в средней части зависимости ИИ от расстояния выполняется модель 2.

Эти модели позволяют описать все основные особенности зависимости ИИ от расстояния до различных небесных тел, полученные в работах /13-14, 29/.

Таким образом, можно утверждать, что гравитационная чувствительность появляется в системах с памятью в ответ на изменение скоростей биохимических реакций с участием гормонов.

Отметим, что полученные результаты носят предварительный характер, поскольку не указаны конкретные реакции, в которых могли бы проявиться гравитационные поля небесных тел. Общее требование к таким реакциям с участием ферментов заключается в том, чтобы молекулярная масса фермента была достаточно большой, а время реакции исчислялось бы секундами и минутами. Тем не менее, сам факт влияния гравитационных полей небесных тел на любой стадии процесса, удовлетворяющей сформулированным выше условиям, не вызывает сомнения.

Влияние гравитационного потенциала Земли в состоянии динамической невесомости было впервые обнаружено при наблюдении за космонавтами во время длительных космических полетов /44/. Полученные выше результаты позволяют понять механизм этого влияния, связанный с изменением скоростей биохимических реакций во внешних гравитационных полях. Действительно, в этом случае сила, приложенная к телу космонавта, равна нулю, но гравитационный потенциал Земли не равен нулю. Поэтому гравитация продолжает действовать так, как будто космонавт находится на вершине горы эквивалентной высоты. При значительном удалении от Земли гравитационный потенциал падает по абсолютной величине. Обнаруженная в опытах статическая невесомость, вызывающая значительные физиологические изменения, наступает только на расстоянии более 37 тысяч километров от поверхности земли /44/.

Следует заметить, что потенциал гравитационного поля в нерелятивистском приближении описывается уравнением Лапласа. Но это уравнение не изменяется при переходе к неинерциальной системе координат, связанной с местом наблюдения на нашей планете или с кабиной космического корабля (в отличие от уравнения Ньютона, в котором появляются фиктивные силы инерции). Квантовая система молекул чувствует гравитационный потенциал, но не чувствует силы инерции, которые, вообще говоря, малы по сравнению с силами межмолекулярного взаимодействия. Таким образом, система молекул реагирует на изменение гравитационного потенциала, но не реагирует на систему сил, сумма которых равна нулю в лабораторной системе координат. Это и порождает эффекты, связанные с влиянием гравитационного потенциала /39/.

Выражению (46) можно придать наглядный вид, выполнив осреднение для большой группы субъектов, тогда получим:

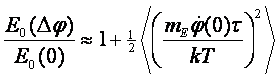(48)

Выражение (48) можно упростить с учетом того, что основной вклад в производную вносит изменение гравитационного потенциала Солнца. Производную гравитационного потенциала можно определить по формуле (47), используя простое выражение для изменения расстояния от земли до Солнца:

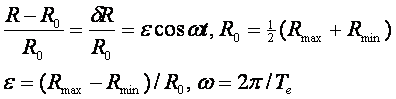(49)

Здесь R_max, R_min - максимальное и минимальное расстояние от земли до Солнца, T_e – годичный период обращения Земли, время отсчитывается от точки максимального удаления (летнее солнцестояние в северном полушарии). С учетом этого выражения находим:

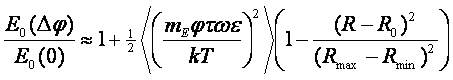(50)

Таким образом, в случае Солнца выражение (50) позволяет предсказать, что максимальное отклонение в концентрации будет наблюдаться весной и осенью в точках равноденствия, а минимальное – летом и зимой в точках солнцестояния. Сравним полученный результат с зависимостью нормированной интегральной информативности от расстояния до Солнца – см. уравнение (22). Подобие выражений (50) и (22) указывает на простой гормональный механизм отклика группы респондентов на воздействие гравитационного поля Солнца.

Предложенная выше теория позволяет сделать оценку влияния небесных тел на протекание ферментативных реакций с участием гормонов. Дальнейшее развитие теории может помочь в объяснении возникновения некоторых заболеваний, обусловленных нарушением гормонального баланса в организме.

6.7. Устойчивость зависимости интегральной информативности от расстояния до небесных тел

Исходные параметры задачи, рассмотренной выше в п. 6.3, представляют собой банк данных, содержащий 20007 записей биографий реальных личностей, отобранных из AstroDatabank /5/. Эти данные включают социальные и персональные категории, дату, время и место рождения, а также астрономические параметры, вычисленные на момент рождения. При решении задачи была использована база данных, образованная из исходной путем комбинации входных параметров долготы и расстояние от Земли до центра масс 10 небесных тел - Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна и Плутона– банк LR исследованный в работах /13-14/. Все основные результаты были получены для 37 категорий, представленных в таблице 19. Спрашивается, насколько эти результаты чувствительны к составу категорий?

Чтобы ответить на этот вопрос, среди социальных категорий были отобраны 100 наиболее представительных, число повторений которых в банке данных равно или превышает 375 – см. таблицу 22, с общим числом случаев - 123671. Первые 37 категорий таблицы 22 были изучены в работах /12-16/ и других.

Таблица 22. Список 100 социальных категорий

KOD	NAME	ABS
1	SC:М-	13640
2	SC:Ж-	5125
3	SC:A53-Sports	4567
4	SC:A1-Book Collection	4471
5	SC:A15-Famous	3373
6	SC:A42-Medical	2910
7	SC:A323-Sexuality	2675
8	SC:A5-Entertainment	2577
9	SC:A9-Relationship	2442
10	SC:A40-Occult Fields	2396
11	SC:B111-Sports:Basketball	2385
12	SC:B329-Sexuality:Sexual perversions	2360
13	SC:A55-Art	2232
14	SC:A19-Writers	2223
15	SC:A129-Death	2168
16	SC:A25-Personality	2083
17	SC:A68-Childhood	1996
18	SC:A31-Business	1813
19	SC:C330-Sexuality:Sexual perversions:Homosexual m	1807
20	SC:B45-Famous:Greatest hits	1795
21	SC:A29-Parenting	1754
22	SC:B173-Sports:Football	1613
23	SC:B97-Occult Fields:Astrologer	1480
24	SC:B21-Relationship:Number of marriages	1417
25	SC:B2-Book Collection:Profiles Of Women	1389
26	SC:A92-Birth	1343
27	SC:B14-Entertainment:Actor/ Actress	1256
28	SC:?-	1242
29	SC:B49-Book Collection:American Book	1178
30	SC:B26-Personality:Body	1163
31	SC:B189-Medical:Illness	1159
32	SC:B6-Entertainment:Music	1086
33	SC:A99-Financial	1075
34	SC:B48-Famous:Top 5% of Profession	1073
35	SC:A38-Politics	1039
36	SC:A23-Psychological	1007
37	SC:A108-Education	1002
38	SC:B46-Famous:Awards	974
39	EL:A17-Financial	932
40	SC:B72-Parenting:1-3 Kids	922
41	SC:B95-Art:Entertainers	913
42	EL:A49-Relationship	910
43	EL:A87-Personality	908
44	EL:A11-Social	902
45	SC:A70-Work	834
46	SC:A17-Criminal Perpetrator	780
47	EL:B10-Death:Death by Disease	763
48	SC:A65-Mind	742
49	SC:B69-Childhood:Family noted	737
50	SC:B64-Book Collection:Culture Collection	735
51	SC:B169-Medical:Doctor	724
52	SC:A138-Religion	707
53	SC:C164-Occult Fields:Astrologer:Pro	697
54	SC:B154-Death:Long life >80 yrs	681
55	SC:B130-Death:Illness/ Disease	680
56	EL:A45-Health	665
57	SC:C146-Relationship:Number of marriages:One	657
58	SC:B123-Book Collection:Occult/ Misc. Collection	650
59	SC:B126-Medical:Accidents	636
60	SC:B109-Education:Teacher	636
61	EL:B18-Financial:Prize	625
62	SC:B13-Relationship:Noted partner	625
63	SC:A85-Home	622
64	SC:A165-Military	619
65	SC:B61-Art:Musicians	589
66	EL:B38-Death:Others	586
67	SC:C7-Entertainment:Music:Vocalist	581
68	SC:B105-Writers:Textbook/ Non-fiction	569
69	SC:B134-Book Collection:Crime Collection	561
70	EL:B29-Social:Gain social status	560
71	EL:B20-Work:New Job	547
72	SC:B141-Politics:Politicians	537
73	SC:C59-Famous:Greatest hits:Art field	534
74	SC:B403-Death:Suicide	526
75	EL:A5-Crime	509
76	SC:A3-Criminal Victim	503
77	SC:B41-Occult Fields:UFO sighting	502
78	SC:B207-Medical:Cancer	490
79	SC:B24-Psychological:Alcohol Abuse	481
80	SC:D8-Entertainment:Music:Vocalist:Rock, Pop, etc	479
81	SC:B158-Politics:Public office	475
82	SC:B269-Entertainment:Stage	472
83	SC:B284-Childhood:Family trauma	471
84	SC:A120-Science	466
85	SC:C11-Entertainment:Music:Instrumentalist	461
86	SC:B89-Childhood:Siblings	458
87	SC:B210-Relationship:Term long >15 Yrs	449
88	SC:B50-Famous:Sports Figures	449
89	SC:B290-Childhood:Advantaged	435
90	SC:B86-Home:Expatriate	420
91	SC:B35-Writers:Fiction	417
92	SC:B117-Business:Entertain/Business	411
93	SC:B93-Birth:Twin, triplet, etc.	407
94	SC:B56-Art:Beauty	404
95	SC:A151-Law	400
96	SC:B166-Military:Military service	397
97	SC:A216-Travel	396
98	SC:B142-Parenting:>3 Kids	384
99	SC:B20-Writers:Autobiographer	380
100	SC:B293-Writers:Astrology	375
	Всего случаев:	123671

Из 100 категорий, перечисленных в таблице 1, были созданы 12 различных моделей, содержащих от 5 до 100 категорий с общим числом случаев от 5196 до 123671 соответственно. Описание моделей дано в таблице 23.

Для того чтобы можно было сравнить влияние долготы и расстояния в одном масштабе, признаки расстояний нормировались по формуле:

Здесь R_max(i), R_min(i) максимальное и минимальное расстояние до i-го небесного тела соответственно.

Моделирование осуществляется на сетке одного масштаба М22 с использованием системы искусственного интеллекта «Эйдос-астра». В результате моделирования формируется обобщенный информационный портрет каждой социальной категории. Астрономические параметры на сетке с числом ячеек М=22 разбиваются на М признаков, соответствующих занимаемому интервалу с номером m=1, 2,…,M. Каждому астрономическому признаку (долготе или расстоянию из данного интервала) соответствует некоторое количество информации, по которому для каждой категории вычисляется информативность данного признака. Интегральная информативность (ИИ) представляет собой среднеквадратичное отклонение информативности данного признака, вычисленное для отдельных категорий, перечисленных в таблице 22.

Таблица 23. Описание моделей

Модель Mod	Число категорий Cat	Число случаев N	Описание модели
C100	100	123671	Включает 100 категорий представленных в таблице 1
C64	64	45804	Включает 64 категории модели С100 с информативностью по признакам Солнца выше 0.1 бит.
С37	37	86314	Базовая модель /2, 4/ включающая 37 категорий с частотой встречаемости не менее 1000
С37D	37	86314	Модель С37 с двойной точностью
C37D7R	37	58833	Модель С37D в которой 7 категорий с наименьшим параметром сходства заменены на 7 следующих по частоте встречаемости из таблицы 1
C37D25R	37	31486	Модель С37D в которой 25 категорий с наименьшим параметром сходства заменены на 25 следующих по частоте встречаемости из таблицы 1
C34D	34	66307	Модель С37D в которой удалены 3 категории с наименьшим параметром сходства
C31	31	54627	Модель C37 в которой удалены 6 категорий с наименьшим параметром сходства
C30D	30	62113	Модель С37D в которой удалены 7 категорий с наименьшим параметром сходства
C22D	22	32316	Модель С37D в которой удалены 15 категорий с наименьшим параметром сходства
C11D	11	13479	Модель С37D в которой удалены 26 категорий с наименьшим параметром сходства
C5D	5	5196	Модель C11D в которой удалены 6 категорий с наибольшей частотой встречаемости

В процессе моделирования было установлено, что полученные результаты для ИИ в моделях С37 и C37D совпадают с точностью до 11 знака после запятой. Таким образом, можно без особой погрешности использовать одну из этих моделей. На рис. 2 представлены данные нормированной интегральной информативности для Солнца в 10 моделях, перечисленных в таблице 23. Зависимость нормированной интегральной информативности от расстояния до Солнца и Венеры в общем случае можно представить в виде:

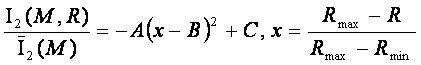(51)

Здесь численные коэффициенты определяются по совокупности данных для каждой модели. Наиболее достоверно зависимость ИИ от расстояния до Солнца выявляется в модели C34D. В этом случае имеем:

A=2.6592, B=0.5035, C=1.2211.

Достоверность аппроксимации данных квадратным полиномом для других моделей приведена в таблице 24. Наихудшая достоверность получается в модели C11D, содержащей наименьшее число категорий и описывающей наименьшее число случаев. Отметим, что в работах /13-14/ путем обработки данных для модели С37 на сетках нескольких масштабов были получены следующие значения коэффициентов формулы (1): A=2.4222, B=0.5139, C=0.8233. Таким образом, значения коэффициентов, полученных в наилучшей модели C34D, не слишком сильно отличаются от средних значений, полученных в модели С37.

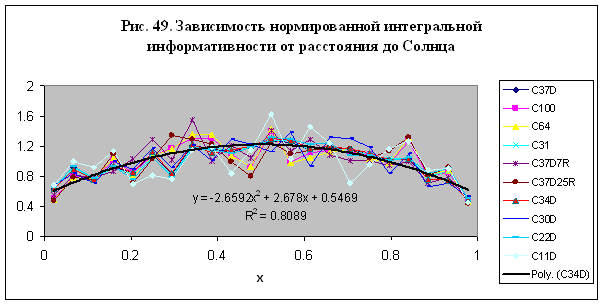
На рис. 2 представлена зависимость ИИ от расстояния до Плутона во всех исследованных моделях. Из приведенных на этом рисунке данных можно сделать вывод, что некоторые детали зависимости ИИ от расстояния до Плутона повторяются во всех моделях. Зависимость нормированной интегральной информативности от расстояния до Сатурна, Урана, Нептуна и Плутона в общем случае можно представить в виде:

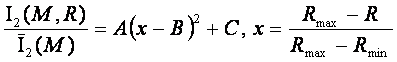(52)

Здесь численные коэффициенты определяются по совокупности данных для каждого небесного тела в каждой модели.

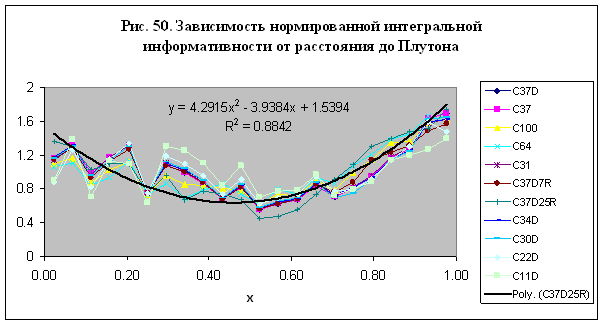
Таблица. 24. Достоверность аппроксимации ИИ от расстояния до небесных тел в различных моделях – R². Максимальные значения выделены жирным шрифтом.

Mod	C100	C64	C37D	C37D7R	C37D25R	C34D	C31	C30D	C22D	C11D
Cat	100	64	37	37	37	34	31	30	22	11
N	123671	45804	86314	58833	31486	66307	54627	62113	32316	13479
Sun	0.648	0.5774	0.7815	0.7228	0.5163	0.8089	0.778	0.6727	0.7058	0.2865
Venus	0.7506	0.757	0.515	0.5526	0.5905	0.4871	0.4855	0.5137	0.4223	0.3064
Saturn	0.6778	0.6919	0.577	0.4897	0.441	0.5432	0.5857	0.5317	0.8343	0.4965
Uranus	0.9043	0.8886	0.8466	0.8458	0.8581	0.8432	0.8467	0.8378	0.7662	0.8143
Neptune	0.7973	0.7249	0.7975	0.796	0.7538	0.8026	0.7976	0.8003	0.7662	0.7855
Pluto	0.8382	0.8739	0.7181	0.7299	0.8842	0.6978	0.6922	0.6667	0.4389	0.2003

Наибольшая достоверность при аппроксимации данных квадратичным полиномом достигается для Плутона в модели C37D25R - см. таблицу 5. Для этого случая находим:

A=4.2915, B=0.4587, C=0.615.

Отметим, что среднее значение этих коэффициентов, полученное по совокупности данных для Сатурна, Урана, Нептуна и Плутона в модели М150 составляет А=2.7418, В=0.4572, С=1.1311. Для удаленных небесных тел Солнечной системы – Урана и Нептуна наблюдается относительная устойчивость зависимости ИИ от расстояния при изменении числа категорий и общего числа случаев – см. таблицу 3. Это можно объяснить тем, что эти зависимости формируется под влиянием годичного движения Земли вокруг Солнца, что способствует накоплению сигнала. В случае Плутона это правило нарушается, хотя в деталях нормированные значения ИИ для этого небесного тела повторяются довольно точно – рис. 50. Для Венеры наилучшая аппроксимация зависимости ИИ от расстояния наблюдается в модели С64 – рис. 51, а наихудшая – в модели C11D, как и для Солнца.

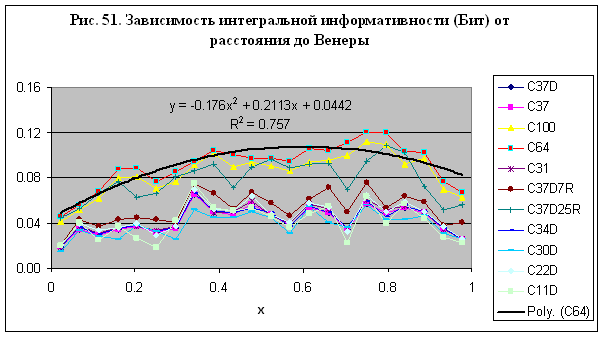
Отметим, что во всех рассмотренных случаях существует такая комбинация категорий, своя для каждого небесного тела, что зависимость ИИ от расстояния до соответствующего тела имеет наибольшую достоверность аппроксимации. Отсюда можно сделать вывод, что каждое небесное тело воспринимается независимо от других, причем характер восприятия можно установить путем анализа категорий соответствующей модели. Например, зависимость ИИ от расстояния до Урана и Нептуна одинаково хорошо распознается в любой модели при любой комбинации параметров, т.е. характер зависимости ИИ от расстояния до этих небесных тел практически не изменяется при изменении числа категорий – рис. 52-53. Следовательно, влияние этих небесных тел проявляется через все категории, затрагивает все стороны жизни субъектов. С другой стороны, Венера наилучшим образом распознается в моделях С100 и С64, содержащих большое число высокоспециализированных категорий, а влияние Сатурна наиболее заметно в модели C22D – рис. 54 .

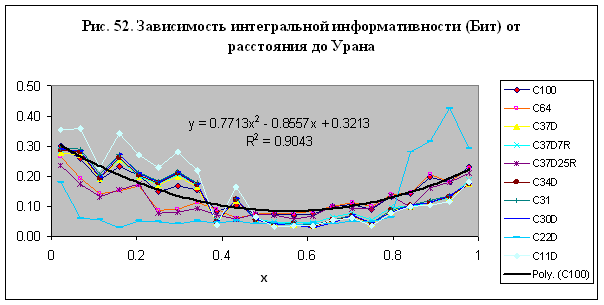
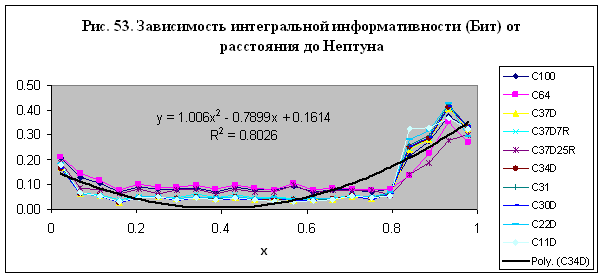
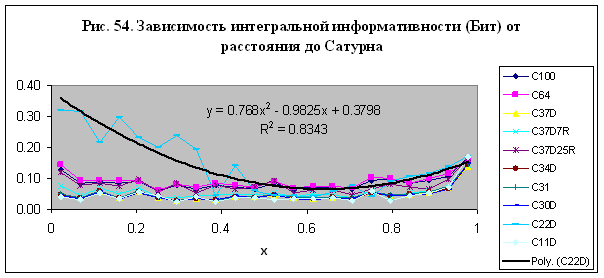
Отметим, что данные на рис. 51-54 представлены в абсолютных единицах (Бит) (тогда как на рис. 49-50 приведены нормированные значения ИИ), что позволяет сравнить масштаб изменения ИИ для трех планет – Венеры, Урана и Нептуна. Можно заметить, что хотя гравитационные потенциалы Венеры, Урана и Нептуна изменяются в одном масштабе – рис. 31, реакция на воздействие этих планет не является одинаковой.

Учитывая, что ИИ характеризует дисперсию информативности, вычисленную для данного множества категорий модели (аналог температуры), можно построить зависимость средней (по 22 ячейкам модели М22) интегральной информативности от общего числа случаев – рис. 55. Из этих данных следует, что при изменении общего числа случаев от 5196 до 123671 (т.е. более чем на порядок), среднее значение ИИ для всех небесных тел изменяется немонотонно. Реакция на воздействие видимых небесных тел – Солнца, Венеры и Сатурна, является избирательной, зависящей от состава категорий, тогда как реакция на воздействие далеких небесных тел – Урана, Нептуна и Плутона, является однотипной, охватывающей все категории – рис. 56. В этом случае можно обобщить данные для среднего значения ИИ, используя прараметр энтропии системы, который определяется согласно уравнению:

Соответствующие результаты представлены на рис. 56. Как следует из данных, приведенных на этом рисунке, данные по ИИ для Урана, Нептуна и Плутона описываются однотипной зависимостью, которая с хорошей точностью может быть интерполированна кубическим полиномом.

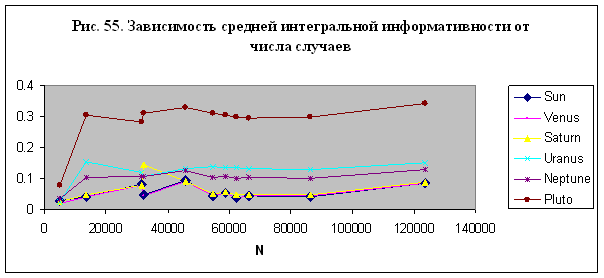
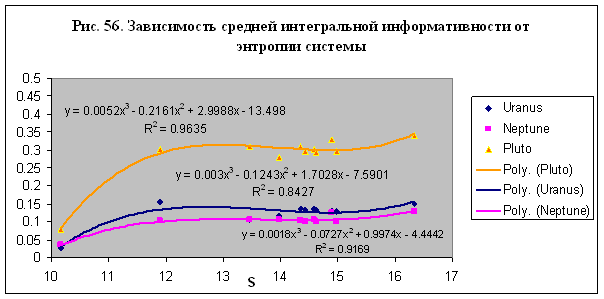
Отметим, что зависимости (51-52), установленные в работах /13-14/, наблюдаются во всех исследованных моделях, что хорошо видно при сравнении данных для нормированных значений ИИ, как на рис. 49-50. В случае Урана и Нептуна рассеяние данных не слишком велико даже для ненормированных значений ИИ – рис. 52-53. Для Венеры, как и для Солнца, характерно значительное рассеяние данных, полученных в разных моделях, поэтому эти данные необходимо сравнивать в приведенных координатах, как на рис. 49. В этом случае данные легко обобщаются на основе уравнения (51) простой параболической зависимостью /45/.

6.8. О зависимости курсов валют
от астрономических параметров
небесных тел Солнечной системы

Вообще говоря, тонкое влияние планет распространяется не только на процессы в живых организмах, но и на экономические процессы, что особенно сказывается на курсах валют. Разумеется, курсы валют формируются под влиянием игроков на рынке, психология которых зависит от положения планет. Ниже представлены результаты моделирования курсов валют из работы /35/.

Моделирование курсов валют является одной из популярных задач математической экономики. Существует несколько подходов к решению этой задачи. Наиболее содержательные результаты можно получить путем применения интеллектуальных систем на основе нейросетей. Принципиальным вопросом здесь является оценка степени влияния параметров отдельных планет на курсы валют. В работе /35/ была исследована задача о зависимости курсов валют двадцати стран (см. список валют в таблице 25) от астрономических параметров одиннадцати небесных тел Солнечной системы – Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Хирона, Сатурна, Урана, Нептуна и Плутона в период с 1 января 2000 года по 15 июня 2006 года. Для моделирования этой задачи была разработана нейросеть, позволяющая установить относительную значимость входных параметров. Среди входных параметров вводились астрономические параметры небесных тел, время в секундах, а также календарное время – год, месяц, день месяца и день недели. В качестве астрономических параметров использовались: синус и косинус долготы, широта и расстояние от Земли до центра небесного тела. База данных была подготовлена в виде одного массива, в котором наряду с данными валютных рядов были введены астрономические параметры.

Предсказательная сила такого рода модели сильно варьируется для разных стран – см. данные таблицы 25. Так, при прогнозе на день вперед модель позволяет правильно установить знак скорости изменения курса для 14 валют из 20. При этом уровень прогноза изменяется для валют разных стран от 37% (Новая Зеландия) до 76% (Китай) правильных предсказаний на 100 случаев прогноза. Иначе говоря, не все валютные ряды прогнозируются в равной степени хорошо или плохо. Можно выделить группу стран, для которых уровень прогноза курсов валют превосходит 2/3, но есть и такая группа стран, для которых уровень прогноза не выше 1/2. Это связано, видимо, с тем что, во-первых, система входных параметров модели не является полной, а во вторых, в реальном случае следует учитывать поведение игроков на рынке, оказывающих влияние на формирование цен. Тем не менее, эта модель позволяет установить относительную роль входных параметров, что представляет самостоятельный интерес.

На рис. 57 и в таблицах 26 А, Б представлена в процентах относительная роль входных параметров. Как было установлено, наиболее важным параметром для всей исследованной совокупности валют является календарный месяц. Относительный вклад этого параметра составляет около 14%. Очевидно, что календарный месяц наилучшим образом описывает сезонные колебания валют, которые являются самыми значительными в валютных рядах. Отметим, что деление года на месяцы соответствует разбиению зодиакального круга на знаки. Интересным и наиболее интригующим является то, что суммарный вклад параметров планет в 4 раза превосходит вклад календарного (циклического) времени и в 100 раз превосходит вклад линейного времени, которое обычно используется для моделирования не только физических процессов, но и в экономике. То, что линейное время оказалось, по уровню значимости ниже, чем астрономические параметры небесных тел, свидетельствует в пользу астросоциотипологии, как адекватной модели "случайных" экономических процессов. Более того, среди всех астрономических параметров суммарный вклад расстояния составляет только 22,68%, тогда как на долю угловых параметров и времени (входные параметры астросоциотипологических моделей) в сумме приходится 77,32% – см. таблицу 25.

Таблица 25. Уровень предсказания курсов валют 20 стран на день вперед. True (T) – правильные предсказания, False (F) – ложные предсказания.

Страна	True/False	ln(T/F)	T%	F%
UK	1,142857	0,133531	53%	47%
TAIWAN	1,454545	0,374693	59%	41%
SWITZERLAND	1,545455	0,435318	61%	39%
SINGAPORE	2	0,693147	67%	33%
AUSTRALIA	1	0	50%	50%
SWEDEN	1,071429	0,068993	52%	48%
NEW ZEALAND	0,578947	-0,54654	37%	63%
NORWAY	0,928571	-0,07411	48%	52%
MEXICO	0,928571	-0,07411	48%	52%
MALAYSIA	2,428571	0,887303	71%	29%
KOREA	1,9	0,641854	66%	34%
JAPAN	0,733333	-0,31015	42%	58%
INDIA	1,363636	0,310155	58%	42%
HONG KONG	0,833333	-0,18232	45%	55%
EURO	1,333333	0,287682	57%	43%
DENMARK	1,357143	0,305382	58%	42%
CHINA	3,2	1,163151	76%	24%
CANADA	1,307692	0,268264	57%	43%
BRAZIL	1,285714	0,251314	56%	44%
SOUTH_AFRICA	1,818182	0,597837	65%	35%

Среди всех планет наибольший вклад в валютные тренды вносит Юпитер (9,59%), затем идут Меркурий (9,05%), Луна (8,63%) и Венера (8,55%) – см. таблицу 26 А. Интересно, что вклад астероида Хирон (8,44%) превосходит вклад Сатурна (8,09%). Солнце (6,14%) вносит наименьший вклад среди семи видимых планет. Вклады невидимых глазу планет Урана (4,07%) и Нептуна (3,97%) в два раза меньше, чем, например, вклад Сатурна. Но при этом вклад сравнительно небольшой планеты Плутон (5,07%) превосходит вклад Урана или Нептуна, Марс вносит 7,84%. Но пара планет Марс и Плутон вносит уже 12,91%.

Таблица 26 А. Относительный вклад входных параметров модели для 11 небесных тел, %%

	Солнце	Луна	Меркурий	Венера	Марс	Юпитер	Сатурн	Уран	Нептун	Плутон	Хирон
Синус долготы	1,80	3,27	1,12	1,38	1,24	1,25	5,06	0,74	0,69	1,94	4,48
Косинус долготы	0,86	2,70	1,36	1,77	2,59	2,13	0,90	1,07	0,83	0,91	1,18
Широта	1,54	1,52	3,19	2,34	1,67	1,82	0,84	0,98	0,85	0,85	1,89
Расстояние	1,94	1,14	3,38	3,06	2,34	4,39	1,29	1,28	1,60	1,37	0,89
Итого:	6,14	8,63	9,05	8,55	7,84	9,59	8,09	4,07	3,97	5,07	8,44

Таблица 26 Б. Относительный вклад календарного
(циклического) времени и линейного времени

День месяца	2,69%
День недели	2,38%
Месяц	14,07%
Год, начиная с 2000 г.	0,60%
Линейное время	0,82%
Итого:	20,56%

Таблица 24. Сравнительная роль угловых параметров,
расстояния и времени.

Синус долготы	22,97%
Косинус долготы	16,30%
Широта	17,49%
Расстояние	22,68%
Циклическое и линейное время	20,56%

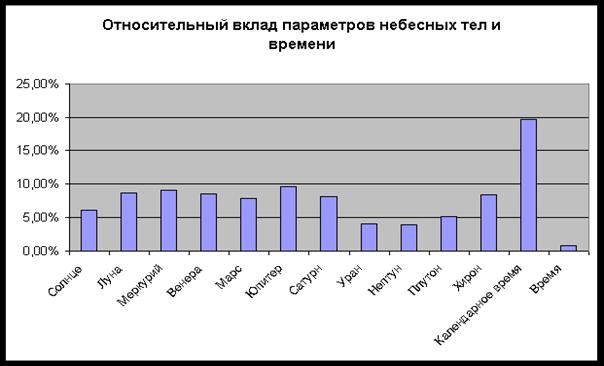
Рис. 58. Относительный вклад входных параметров 11 небесных тел, календарного (циклического) и линейного времени

Выполненное исследование позволяет по-новому взглянуть на астросоциотипологию, как на прогностическую модель. Во-первых, ясно, что астросоциотипология вполне может быть использована для описания процессов в экономике. Во-вторых, очевидно, что уровень прогноза сильно варьируется от случая к случаю и никогда не достигает 100%, Поэтому не следует требовать от этой модели слишком высокой точности прогноза в любом случае, но надо сосредоточить внимание на тех процессах, для которых уровень прогноза превосходит, например, 2/3.

6.2. Гравитация и жизнь

6.3. Фундаментальные законы распознавания социальных категорий по астрономическим данным на момент рождения

6.4. Информационная теория влияния небесных тел на психологию индивида

6.6. Роль гравитации в реакциях с участием гормонов

6.4. Информационная теория влияния
небесных тел на психологию индивида