ГЛАВА 3. ОСНОВНЫЕ МОДЕЛИ И РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

3.1. Социологические и астросоциотипологические базы данных

В социологии и экономике, в медицине и в статистике, во многих других отраслях знаний приходится иметь дело с огромными массивами специализированной информации в виде данных различной природы. Вплоть до середины 20-го века такого рода данные хранились обычно в виде справочников. Стоит ли говорить, сколь неудобным был такой способ хранения. Сразу же после создания первых компьютеров, данные начали переносить на магнитные носители в форме компьютерных баз данных (БД). В настоящее время для хранения и обработки этих данных используются специализированные компьютерные программы, среди которых наиболее известными являются Clipper, Excel, Quattro Pro и другие. В социологии для обработки данных широко применяется система SPSS. В настоящей работе для обработки и моделирования данных были использованы системы искусственного интеллекта "Эйдос" /2/ и "Эйдос-астра" /3/.

Компьютерные базы данных являются удобным инструментом для научных исследований. В настоящей работе были использованы первая и четвертая версии известной социологической и астросоциотипологической базы данных AstroDatabank /5/. Эти версии отличаются числом записей: в четвертой версии добавлено 5000 данных новых респондентов. Эта БД интересна тем, что в ней содержатся данные рождения и биографии известных людей и частных персон, относящихся к определенной категории. Всего в AstroDatabank 4.00 содержится 31012 записей, в том числе:

23217 данных респондентов с биографией;

6644 данных рождения респондентов относящихся к определенной категории;

1151 данных мировых событий.

Этим записям соответствует 113110 записей категорий, т.е. приблизительно 3,647 категорий на одного респондента (событие) – рис. 3.

 Все категории условно можно разделить на социальные, куда относятся и профессиональные категории, на психофизические и на события определенного типа. В нашем анализе было использовано минимум 4 категории /15/, максимум 870 категорий – рис. 2.

 

Рис. 3. Скриншот данных категорий AstroDatabank 4.00

 

Из исходных данных, содержащихся в AstroDatabank, было создано более десяти различных БД, для проверки тех или иных гипотез /6-17/. Данные, импортированные непосредственно из AstroDatabank v. 4.00, были преобразованы в DBF4 формат, который воспринимается системами "Эйдос" /2/ и "Эйдос-астра" /3/. Эти данные содержат как описание данных рождения и категорий, так и астрономические параметры долготы и склонения десяти небесных тел – Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна и Плутона, а также долготы Северного узла Луны, асцендента (ASC) и середины неба (МС), т.е. всего 23 астрономических параметра. Было использовано 9897 записей, соответствующих 5 категориям, объединенным в 4 класса – таблица 2, а. Среди этих записей 184 повторяются, поскольку они соответствуют 2, 3 или 4 категориям.

 

Таблица 2, а. Четыре класса, пять категорий и соответствующее число респондентов в случае Database0 и Database1

KOD_OBJ

NAME

ABS

1

Politics, Science

1876

2

Medical: Physician

347

3

Sports

6032

4

Psychological

1642

 

Из этих записей было создано две БД для проверки влияния склонения на качество распознавания:.

Database1 с 23 астрономическими параметрами для каждой записи, причем параметр склонения отображался на интервал (0; 360) с использованием формулы Declination1 = (Declination +30)*6;

Database0 с 11 астрономическими параметрами для каждой записи, соответствующими долготе десяти небесных тел – Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна и Плутона, а также долготе Северного узла (Луны).

Данные, импортированные из первой версии AstroDatabank, были конвертированы в формат баз данных JDataStore фирмы Borland, а затем сортированы с использованием SQL запросов и специальных функций на языке Java. В результате были получены астрономические и биографические данные для 20007 уникальных персон и 16360 записей событий, происходивших с ними. Для них всех с помощью библиотеки швейцарских эфемерид (www.astro.com) были вычислены координаты небесных тел (долгота и широта в градусах и расстояние в астрономических единицах). Для записей с точным временем вычислялась долгота углов домов в системе Плацидуса. С настоящем исследовании были использованы только параметры долготы следующих небесных тел: Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна и Плутона, а также Северного узла Луны. Вместе с параметрами долготы углов 12 домов это составляет 23 параметра, как и в случае Database0, Database1. Это позволяет представить все базы данных в одном формате и исследовать их на основе идентичных алгоритмов.

Из этих данных были образованы восемь БД для проверки различных гипотез:

Database A содержащая 20007 записей данных респондентов соответствующих 500 представительных категорий (каждая категория представлена не менее чем 26 записями);

Database B содержащая 15007 записей данных респондентов, соответствующих 500 представительным категориям (эта БД использовалась для тренировки нейросети);

Database C содержащая 5000 записей данных респондентов, соответствующих 500 представительным категориям (эта БД использовалась для определения эффективности распознавания);

Database D содержащая 20007 записей данных респондентов соответствующих 240 непредставительных категорий (каждая категория представлена числом записей более 2 и менее 25) – низкочастотный предел;

Database E D содержащая 20007 записей данных респондентов соответствующих 870 категориям (каждая категория представлена числом записей более 2) – наиболее полная база данных;

Database F содержащая 20007 записей данных респондентов соответствующих 37 категориям (каждая категория представлена числом записей более 1000) – высокочастотный предел;

Database F1 содержащая 20007 записей данных респондентов соответствующих 100 категориям (каждая категория представлена числом записей более 174);

Database G содержащая 20007 записей данных респондентов соответствующих 4 категориям, перечисленным в таблице 2,б. Заметим, что в этой базе данных 8150 записей не используется в моделировании, поскольку они не соответствуют какой-либо из 4 категорий.

 

 

Таблица 2, б. Четыре класса, четыре категории

и соответствующее число записей в базе данных G.

KOD_OBJ

NAME

ABS

1

Famous

3373

2

Medical

2910

3

Sports

4567

4

Psychological

1007

 

Следующим шагом является сортировка персон по категориям. В результате было получено XML дерево категорий исходной базы данных. Для этой цели была написана процедура, позволяющая безошибочно изменять категории, сортируя его. Далее база данных была полностью экспортирована в формат Excel, а из него – в формат DBF4, воспринимаемый интеллектуальной системой "Эйдос". 

 

3.2. Технология моделирования

Система "Эйдос" оперирует с кодами объектов, типа номеров в правых колонках в таблицах 2 а,б. Астрономические параметры также имеют собственные коды, именуемые шкалы или масштабы. Например в случае модели М3 (разбиение круга зодиака на три сектора), имеем 23 основных масштаба и 69=23х3 шкал, шесть из которых показаны ниже, в таблице 3:

 

Таблица 3. Коды и шкалы модели М3 (указаны только шесть шкал, соответствующих долготе Солнца и Луны).

Code

Name of scale

1

SUNLON-[3]: {0.000, 120.000}

2

SUNLON-[3]: {120.000, 240.000}

3

SUNLON-[3]: {240.000, 360.000}

4

MOONLON-[3]: {0.000, 120.000}

5

MOONLON-[3]: {120.000, 240.000}

6

MOONLON-[3]: {240.000, 360.000}

 

Если обнаружено, что запись в обучающей базе данных содержит долготу Солнца, принадлежащую интервалу (0.000; 120.000), тогда частота соответствующего кода 1 возрастает на единицу. Таким образом, частота появления масштабов в обучающей базе данных может быть вычислена, что в свою очередь позволяет определить матрицу частот и информационную матрицу. Например, в случае модели М2 (разбиение круга зодиака на два сектора) и обучающей базы данных Database F фрагменты матрицы частот и информационной матрицы представлены в таблицах 4 и 5 соответственно.

 

Таблица 4. Фрагмент матрицы частот в случае модели М2
и обучающей базы данных Database F
(частоты даны в абсолютных величинах)

Code of

scale

Code of category

1

2

3

4

5

6

7

8

9

10

11

12

1

6744

2623

2281

2201

1671

1477

1378

1271

1222

1201

1230

1208

2

6896

2502

2286

2270

1702

1433

1297

1306

1220

1195

1155

1152

3

6786

2539

2325

2187

1689

1445

1330

1273

1207

1211

1218

1177

4

6854

2586

2242

2284

1684

1465

1345

1304

1235

1185

1167

1183

5

6261

2401

2070

2039

1561

1343

1307

1185

1125

1086

1134

1156

6

7379

2724

2497

2432

1812

1567

1368

1392

1317

1310

1251

1204

7

6907

2688

2332

2274

1735

1510

1422

1301

1263

1193

1232

1263

8

6733

2437

2235

2197

1638

1400

1253

1276

1179

1203

1153

1097

9

7137

2760

2443

2344

1754

1500

1454

1341

1269

1223

1330

1279

10

6503

2365

2124

2127

1619

1410

1221

1236

1173

1173

1055

1081

 

Заметим, что в действительности информация вычисляется в системе с высокой точностью с 8 десятичными знаками, но в таблице 5 показаны только два десятичных знака (числа умножены на 100). Положительная или отрицательная величина информации в ячейке ij в таблице 5 означает, что категория j имеет соответственно позитивную или негативную корреляцию с масштабом i.

 

Таблица 5. Фрагмент информационной матрицы в случае
модели М2 и обучающей базы данных Database F
(информация дана в единицах Bit*100)

Code of

scale

Code of category

1

2

3

4

5

6

7

8

9

10

11

12

1

3

-1

17

-2

-3

-0

-3

-3

-3

-3

22

-4

2

4

-3

17

-0

-3

-1

-5

-2

-3

-3

20

-5

3

3

-2

18

-2

-3

-1

-4

-3

-3

-3

22

-4

4

3

-2

16

-0

-3

-1

-4

-2

-2

-4

20

-5

5

3

-2

16

-2

-3

-1

-2

-3

-3

-4

22

-2

6

3

-3

17

-1

-3

-1

-6

-2

-2

-3

20

-6

7

3

-1

17

-1

-3

-1

-3

-3

-2

-4

21

-3

8

4

-3

17

-1

-3

-1

-5

-2

-3

-2

21

-6

9

3

-1

17

-1

-3

-2

-3

-3

-3

-4

23

-3

10

3

-3

16

-1

-3

-0

-5

-2

-2

-2

19

-6

 

При завершении обучения нейросети для каждой из моделей, запускается процесс распознавания, начинающийся с определения числа записей в распознаваемом образце. В случае баз данных Database0, Database1 или Database G, содержащих только четыре класса, разумное число записей может быть N=400 или 100 записей на класс. Тренированная компьютерная нейросеть реагирует на любые входные данные, похожие на те, что содержатся в обучающей базе данных. Следовательно, каждая запись из N может быть подвергнута анализу и четыре возможные реакции нейросети могут быть измерены:

¾             Запись с номером n из N принадлежит категории с номером m и это истина, при этом параметр сходства (корреляция) записи с номером n с категорией номер m равен BTnm;

¾             Запись с номером n из N не принадлежит категории с номером m и это истина, при этом параметр сходства (корреляция) записи с номером n с категорией номер m равен Tnm;

¾             Запись с номером n из N принадлежит категории с номером m и это ложь, при этом параметр сходства (корреляция) записи с номером n с категорией номер m равен BFnm;

¾             Запись с номером n из N не принадлежит категории с номером m и это ложь, при этом параметр сходства (корреляция) записи с номером n с категорией номер m равен Fnm.

Эффективная система искусственного интеллекта должна быть сконструирована таким образом, чтобы минимизировать ложные предсказания и увеличить процент верных предсказаний. Для наилучшего понимания результатов пакетного распознавания в работе /15/ было предложено специальное эвристическое выражение параметра подобия в форме (10):

 

 

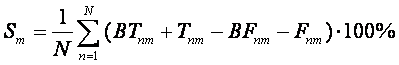
Согласно этому определению параметр подобия изменяется от -100% до 100%, как обычный коэффициент статистической корреляции. Заметим, что если, например Sm=0, то это означает, что категория с номером m распознается плохо, даже если BTnm =0.95 для каждой истиной записи (это может показаться очень хорошим результатом с точки зрения статистики). С другой стороны, если Sm=0.5, то это действительно хороший результат даже если при этом BTnm =0.5 для каждой истиной записи (это означает, что в пакете нет ложных записей и каждая истинная запись была опознана). Рассмотрим ряд экспериментов по распознаванию нескольких категорий.

Эксперимент 1.

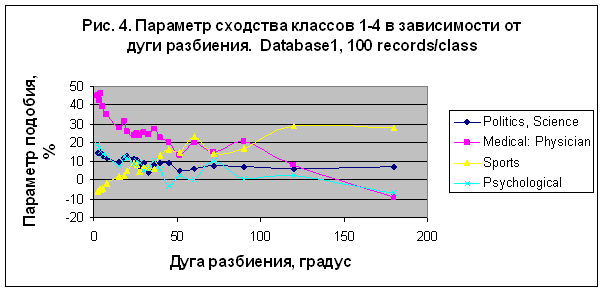
В первом эксперименте мультимодель из 22 моделей, включая M2, M3, M4, M5, M6, M7, M8, M9, M10, M11, M12, M13, M14, M15, M18, M20, M24, M48, M72, M90, M96, M150 (номер модели равен числу сектров разбиения) была создана и затем 22 модели были обучены с базой данных Database1, содержащей 9897 записей. В результате был создан информационный портрет каждого класса. Параметр сходства классов 1-4 из таблицы 2а в случае пакетного распознавания 100 записей на класс представлен на рис. 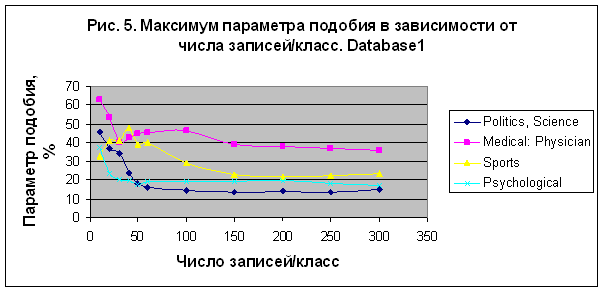4 в зависимости от величины дуги разбиения круга зодиака. Зависимость параметра сходства от параметра числа записей на класс представлена на рис. 5, где отображена величина максимума параметра сходства для каждого из разбиений круга зодиака.

В первом эксперименте наилучший результат получен для категории "Medical: Physician" – S= 45.908% в случае модели M90 для 100 записей/класс. Снижая число записей на класс можно увеличить параметр сходства категории "Medical: Physician" вплоть до 62.722% в случае модели M150 и для 10 записей/класс – см. рис. 5. Для категории "Sport" наилучший результат S= 47.526% получен в случае модели M4 для 40 записей/класс. Заметим, что это меньше, чем вероятность случайного угадывания для этой категории (60.9478%).

 

KOD_OBJ

NAME

ABS

1

Politics, Science

1876

2

Medical: Physician

347

3

Sports

6032

4

Psychological

1642

 

 

Интересно, что для категории "Medical: Physician" параметр сходства на порядок больше, чем вероятность случайного угадывания (3.5061%). Это свидетельствует, что распознавание в системе "Эйдос-астра" не связано с вероятностью случайного угадывания, на что было указано выше, в главе 2.

Эксперимент 2.

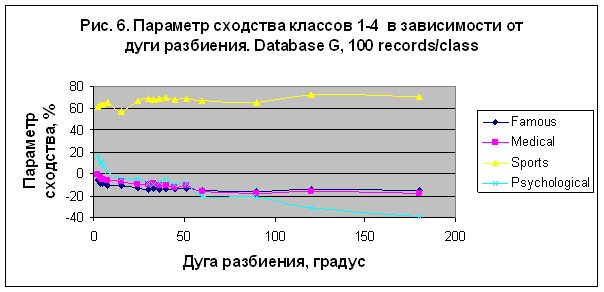
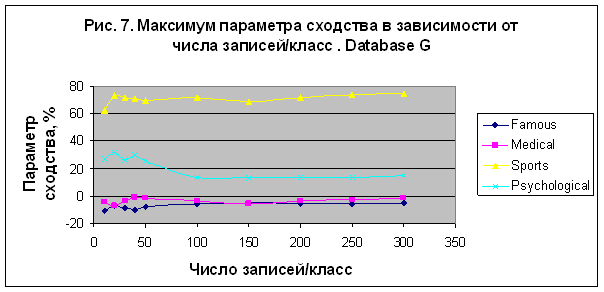
Во втором эксперименте были выполнены все этапы моделирования первого эксперимента, но с базой данных Database G, содержащей 20007 записей. Результаты моделирования представлены на рис. 6 и 7. В этом эксперименте наилучший результат был получен для категории "Sport", S= 72.273% в случае модели M3 для 100 записей на класс.

Class

NAME

ABS

1

Famous

3373

2

Medical

2910

3

Sports

4567

4

Psychological

1007

 

Сравнивая результаты, полученные в экспериментах 1 и 2, находим существенное отличие в поведении параметра сходства категории "Sport" в зависимости от числа секторов разбиения. В первом случае параметр сходства возрастает от -5,936% до 28,935% (рис. 4), а во втором случае колеблется в пределах от 56,716% до 72,273% (см. рис. 6). Это различие объясняется структурой входных параметров двух мульти-моделей, в первой из которых использованы долгота и склонение планет, а во второй только долгота планет и долгота углов 12 домов. Чтобы проверить эту гипотезу, был выполнен

Эксперимент 3.

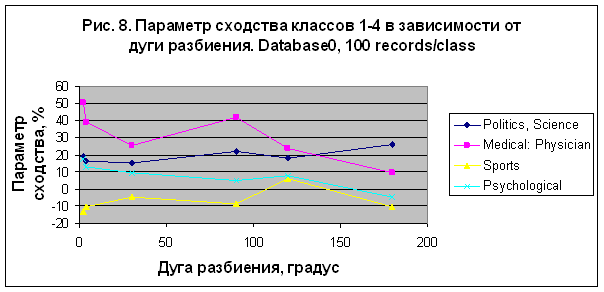
В этом эксперименте мульти-модель из 6 моделей, включая M2, M3, M4, M12, M90 и M150 была сгенерирована и обучена с базой данных Database0 (9897 записей). На рис. 8 представлен параметр сходства классов 1-4 из таблицы 2,а в зависимости от дуги разбиения в случае пакетного распознавания 100 записей на класс. Можно видеть существенное различие с данными экспериментов 1 и 2 для категории "Sport" (смотрите рис. 4 и 6 соответственно). Это особенно заметно для моделей, обученных с базами данных Database1 (рис.4) и Database0 (рис. 8), которые содержат идентичное число записей, но разное число масштабов (23 и 11 соответственно). Полученные результаты свидетельствует о том, что распознавание осуществляется именно по астрономическим параметрам, сокращение числа которых приводит к ухудшению качества распознавания в случае категории "Sport". Интересно отметить, что в этом эксперименте наилучший результат получен для категории "Medical: Physician" – S= 50.634% в случае модели M150, что сравнимо с аналогичными данными, полученными в первом эксперименте (рис. 4). Отсюда можно сделать вывод, что некоторые категории хорошо распознаются по положению планет в зодиаке, тогда как для других категорий требуется знать склонение и положение планет относительно линии горизонта.

Во всех трех экспериментах категория "Sport" распознается наилучшим образом в модели М3 (разбиение на три сектора), тогда как, например, категория "Psychological" наилучшим образом распознается в моделе М150. Отметим, что с ростом числа секторов разбиения параметр сходства трех категорий из четырех, представленных в таблице 2 а, заметно возрастает. Очевидно, что этот эффект можно использовать для повышения качества распознавания. Другой метод повышения качества – это дифференциация категорий на более однородные по составу подкатегории.

Class

NAME

ABS

1

Politics, Science

1876

2

Medical: Physician

347

3

Sports

6032

4

Psychological

1642

 

Для иллюстрации этого метода рассмотрим

Эксперимент 4.

В этом эксперименте мульти-модель составленная из 172 моделей, включая M2, M3, M4, …, M172 и M173 была создана и обучена с базой данных Database F (20007 записей). В этом эксперименте можно сравнить параметр сходства для категории "Sports" и двух подкатегорий – футбол и баскетбол, перечисленных в таблице 6. На рис. 9 представлен параметр сходства категории "Sports" и двух подкатегорий в зависимости от числа секторов разбиения. Наилучший результат распознавания S= 85.864 был получен для подкатегории "Sports: Football" в случае модели М3. Данные параметра сходства для первых пяти разбиений представлены в таблице 7.

 

Таблица 6. Категория "Sports" разбитая на три класса и соответствующее число записей в базе данных Database F.

Class

NAME

ABS

1

Sports

4567

2

Sports: Football

1613

3

Sports: Basketball

2385

 

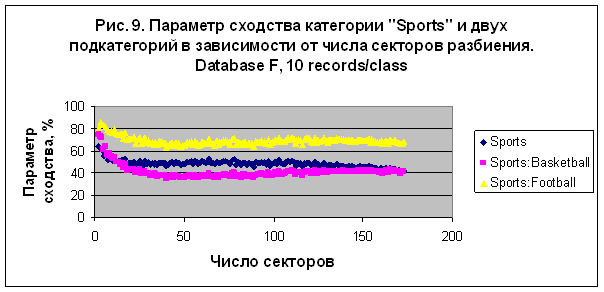
Таблица 7. Параметр сходства категории "Sports" и двух подкатегорий для пяти разбиений.

Число секторов

2

3

4

5

6

Sports

64,398

62,092

60,932

55,065

58,065

Sports:Basketball

74,773

72,722

71,733

61,489

64,101

Sports:Football

80,705

85,864

83,773

83,244

81,443

 

Отметим, что в этом эксперименте категория "Sports" достигает максимального значения при разбиении на 2 сектора. Метод разделения категории на подкатегории особенно эффективен в случае плохо распознаваемых категорий, типа категории "Psychological" на рис. 6. Для иллюстрации рассмотрим

Эксперимент 5.

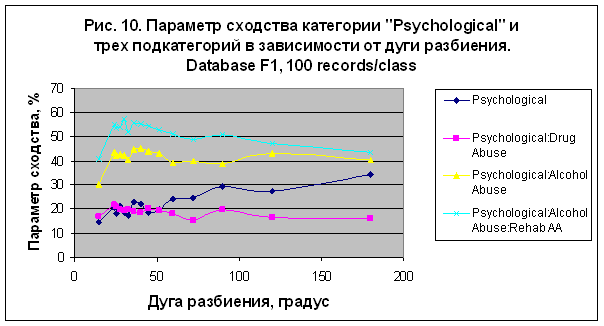
В этом эксперименте мультимодель из 15 моделей, включая M2,M3,M4,M5,M6,M7,M8,M9,M10,M11,M12,M13,M14,M15,M24 была создана и обучена с базой данных Database F1 (20007 записей). На рис. 10 представлены данные для параметра сходства категории "Psychological" и трех подкатегорий, перечисленных в таблице 8. Наилучший результат S= 57.244 был получен для подкатегории "Psychological: Alcohol Abuse: Rehab AA" в случае модели M12. Интересно отметить, что в этой моделе категория "Psychological" распознается значительно лучше, чем в других, созданных в экспериментах 1-4.

Результаты распознавания можно также улучшить путем разбиения категории на типичную и нетипичную часть /16/.

 

Таблица 8. Категория "Psychological" и три ее подкатегории.

Database F1

Class

NAME

ABS

1

SC:A23-Psychological

1007

2

SC:B112-Psychological:Drug Abuse

282

3

SC:B24-Psychological:Alcohol Abuse

481

4

SC:C457-Psychological:Alcohol Abuse:Rehab AA

267

 

 

 

Кроме того, для повышения достоверности можно использовать эвристический метод: если категория К распознается на нескольких разбиениях с параметром сходства не менее 20%, тогда на пяти разбиениях ее параметр сходства приближается к 100%. Рассмотрим этот вопрос более подробно.

3.3. Метод пакетного распознавания карт рождения в системе искусственного интеллекта

Алгоритмы сеточного моделирования, в которых сгущение сетки позволяет улучшить сходимость решения задачи, широко используются в современной науке. Мы применили этот метод для пакетного (совместного) распознавания респондентов из разных стран мира в системе искусственного интеллекта "Эйдос" /3/. Для этого осуществлялось нахождение решение задачи распознавания на 19 сетках различного масштаба, содержащих 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72 секторов соответственно (ряд делителей числа 360). В каждом случае вычислялся параметр сходства для 500 категорий, характеризующих профессиональные качества и обстоятельства жизни 20007 людей, чьи карты были отобраны для формирования первичной базы данных Database A. В качестве входных параметров модели использовались координаты долготы углов 12 домов (в системе Плацидуса), Лунных Узлов и 10 небесных тел – Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна, Плутона.

На рис. 11 представлены результаты пакетного распознавания в координатах параметр сходства (%) – логарифм (десятичный) величины дуги одного сектора разбиения. Можно видеть, что в каждом тестовом примере данные рассеяны вокруг среднего значения, максимум которого приходится на величину дуги в 120 градусов, что соответствует разбиению круга зодиака на три сектора. Для наглядности на рис. 12 представлена средняя величина параметра сходства в зависимости от числа секторов разбиения.

Как было установлено, средний параметр сходства монотонно снижается с увеличением числа секторов разбиения, когда их больше 3. Поэтому в дальнейшем анализе использовались 18 разбиений круга Зодиака вплоть до 60 секторов включительно. Для каждой карты рождения можно определить максимальную величину параметра сходства, что соответствует некоторой категории. Переходя на сетки другого масштаба моделирования, находим ряд 18 значений максимальной величины параметра сходства и ряд из 18 соответствующих категорий, номера которых лежат в интервале от 1 до 500. Если бы категории были случайными, то вероятность появления любой из них в этом ряду составляла бы 18/500=0,036. Вероятность двукратного появления составляет уже (18/500)2= 0,001296, трехкратного – (18/500)3=0,000046656, четырехкратного – (18/500)4= 0,000001679616 и т.д.

 

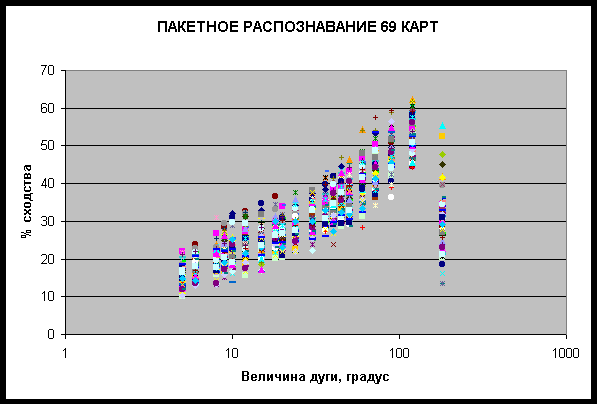
Рис. 11. Зависимость параметра сходства от величины дуги разбиения при пакетном распознавании 69 карт (логарифмическая шкала по горизонтальной оси).

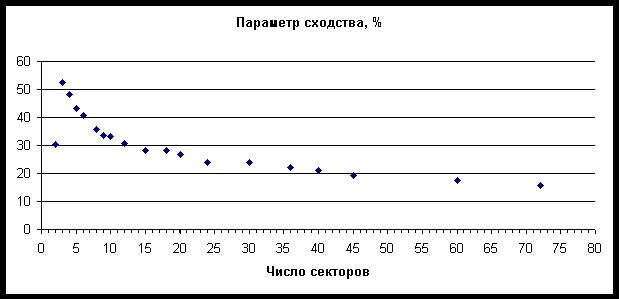
Рис. 12. Зависимость средней величины параметра сходства при распознавании 69 респондентов от числа секторов разбиения.

 

Если категория появилась 3 и более раз подряд, то ее можно формально рассматривать как закономерное проявление качества, присущего данному респонденту.

Во всех изученных картах было обнаружено трехкратное появление одной категории в 18 тестах, а в 47 картах из 69 одна категория проявилась 6 и более раз. На рис. 13 представлены данные распознавания карты типичного респондента в координатах число секторов – номер категории. Из этих данных можно видеть, что категория "487" повторяется 10 раз подряд, категория "127" – шесть раз, и две категории представлены по одному разу. Интересно отметить, что в этом примере повторяющиеся категории "487" и "127" дублируют друг друга по смыслу и означают "Развод родителей". Но одна из них является обстоятельством жизни, а другая событием. Объединяя их вместе, находим, что "Развод родителей" был опознан в данной карте в 16 случаях из 18 тестов на сетках разного масштаба. Это означает, что данная карта была опознана с высокой точностью.

Для нахождения всех категорий, присущих данному респонденту, поступим следующим образом. Зададим минимальный уровень сходства, например 20%. Ограничимся 10 сетками с числом секторов разбиения 3, 4, 5, 6, 9, 12, 15, 18, 20, 24 соответственно. Составим таблицу распознанных категорий на сетке каждого масштаба. Для карты №1 находим всего 373 распознанных категорий с уровнем сходства, не менее 20%, среди которых есть повторяющиеся. Отберем те из них, которые повторяются 4 и более раз. Составим таблицу 9, в которой указан номер категории, ее описание и частота повторения. Среди категорий есть такие, которые уже реализовались в жизни субъекта – это категории под номером 3, 5, 29, 65, 66, 159, 247, 269, 292, 423. Остальные категории имеют смысл прогноза для этого молодого человека. Например, для преуспевания в США ему можно рекомендовать профессии дизайнера, менеджера, полицейского или фотографа.

 

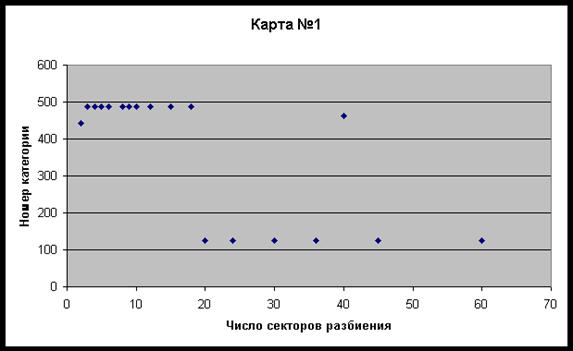
Рис 13. Данные идентификации карты №1
на сетках 18 масштабов.

 

Данный подход отличается тем, что при распознавании образов используются корреляционные связи, которые вычисляются на каждой сетке отдельно. Эти связи выявляются путем многокритериальной типизации респондентов обучающей выборки по исследуемым категориям. При этом на этапе синтеза модели рассчитывается количество информации, которое содержится в фактах попадания долгот углов в интервалы (рассматриваемые как критерии), о принадлежности респондента к тем или иным категориям, а на этапе идентификации эта информация используется для расчета степени сходства конкретных респондентов с обобщенными категориями.

 

Таблица 9. Список повторяющихся категорий
при распознавании карты №1

Категория

Описание категории

Частота
повторения

3

CATEGORIES: ###-Advantaged

8

5

CATEGORIES: ###-Affluent family

6

6

CATEGORIES: ###-Age 80

5

29

CATEGORIES: ###-Boxing

4

40

CATEGORIES: ###-Coach

4

65

CATEGORIES: ###-Family large

4

66

CATEGORIES: ###-Family noted

8

77

CATEGORIES: ###-Gracious

4

87

CATEGORIES: ###-Infant mortality

4

96

CATEGORIES: ###-Lottery

5

126

CATEGORIES: ###-Parent absent

10

127

CATEGORIES: ###-Parents divorced

8

137

CATEGORIES: ###-Production jobs

9

140

CATEGORIES: ###-Public relations

6

159

CATEGORIES: ###-Siblings

5

174

CATEGORIES: ###-Suicide Attempt

5

184

CATEGORIES: ###-Verbal abuse

4

188

CATEGORIES: ###-Winnings

5

195

CATEGORIES: A3-Criminal Victim

4

234

CATEGORIES: B2612-Missing person

4

247

CATEGORIES: B36-Noted kids

4

269

CATEGORIES: B803-Constitution strong

4

283

CATEGORIES: C10628-Photography

9

292

CATEGORIES: C12063-Unusual

7

349

CATEGORIES: C19244-Designer

9

356

CATEGORIES: C206-Surgery

5

367

CATEGORIES: C2354-Manager

7

407

CATEGORIES: C7589-Police

10

423

CATEGORIES: C9318-Physical

4

462

EVENT_LIFE: Family trauma

8

480

EVENT_LIFE: Medical procedure

5

482

EVENT_LIFE: Missing Person

5

487

EVENT_LIFE: Parents divorced

10

491

EVENT_LIFE: Retain professional help

4

494

EVENT_LIFE: Sex Victimization/Rape

4

Предложенный метод распознавания позволяет не только идентифицировать субъекта по ряду признаков и категорий, но и прогнозировать некоторые обстоятельства и события его жизни. Этот метод удается обобщить, путем добавления новых алгоритмов распознавания на множестве сеток различного масштаба.

 

3.4. Алгоритмы и законы типизации
и идентификации субъектов
по астрономическим данным
на момент рождения

Входные данные задачи представляют собой таблицу, содержащую 20007 записей (строк) независимых респондентов, каждый из которых характеризуется номером записи, именем, полом, датой и временем рождения, местом рождения, собственной биографией и набором категорий и событий жизни. 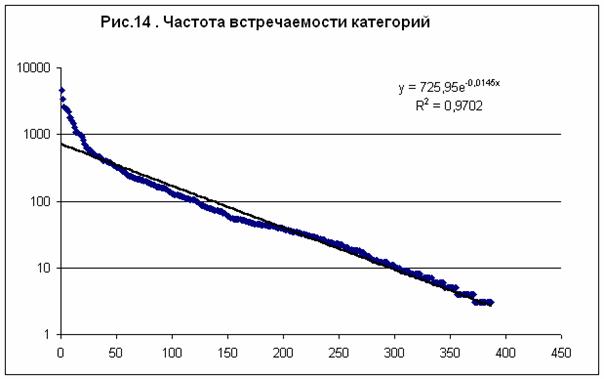В настоящем исследовании для повышения достоверности идентификации из списка категорий были отобраны только те из них, которые соотносятся с профессиями. Полученный список профессиональных категорий содержит только 387 наименований (см. Приложение 1), которые представлены в исходной БД с разной частотой встречаемости – рис. 14. Частотное распределение с большой степенью точности описывается экспонентой (распределение Пуассона) – прямая сплошная линия на рис. 14. Суммируя все частоты, находим общее число исследуемых случаев N= 69742. Учитывая, что в исходной БД содержится только 20007 данных независимых респондентов, находим среднее число категорий, приходящихся на одну карту, n=N/20007=3,49. В качестве входных астрономических параметров модели использовались координаты долготы углов 12 домов (в системе Плацидуса), Лунных Узлов и 10 небесных тел – Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна, Плутона. Поскольку модель является дискретной, координаты долготы задавались на 12 сетках различного масштаба с числом секторов разбиения 3, 4, 5, 6, 9, 12, 15, 18, 20, 24, 36, 72 соответственно.

 

При исследовании частных моделей были установлены некоторые статистические закономерности распознавания, позволяющие повысить эффективность моделей. Во-первых, во всех частных моделях наблюдается обратная зависимость параметра сходства от частоты встречаемости категории: чем выше частота, тем ниже параметр сходства. На рис. 15 представлены результаты распознавания категорий в модели с 72 секторами. В этом случае зависимость параметра сходства от частоты описывается степенной функцией с показателем степени b=-0,5355. Аналогичная зависимость наблюдается и для максимального по всем моделям параметра сходства – рис. 16 (на рисунках 15-16 по горизонтальной оси дана абсолютная частота, т.е. общее число случаев данной категории).

Во-вторых, параметр сходства зависит от числа секторов разбиения. Все категории можно разбить на три класса в зависимости от величины частоты встречаемости и поведения параметра сходства при изменении числа секторов разбиения. Первый класс составляют категории, для которых параметр сходства убывает с ростом числа секторов разбиения. Этот класс категорий характеризуется высокой частотой встречаемости при высоком уровне распознавания, что соответствует данным, лежащим выше линии корреляционной зависимости на рис. 15-16. Некоторые категории этого класса приведены в таблице 10 вместе с корреляционными зависимостями параметра сходства от числа секторов разбиения.

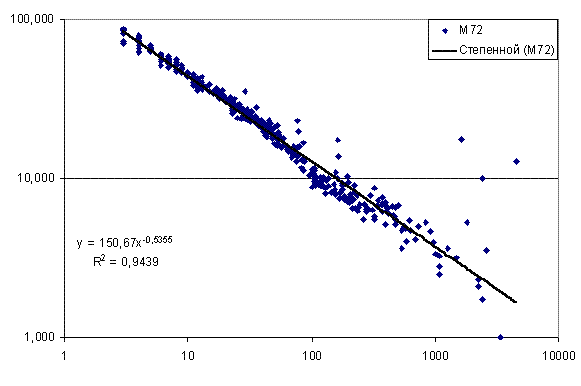
Рис. 15. Зависимость параметра сходства от частоты
встречаемости категории в модели М72

 

Второй класс составляют категории, для которых параметр сходства возрастает с ростом числа секторов разбиения. Этот класс категорий характеризуется низкой частотой встречаемости и относительно высоким параметром сходства, что соответствует данным, группирующимся вблизи линии корреляционной зависимости на рис. 15-16. Большая часть исследуемой в настоящей работе БД представлена категориями этого класса, поэтому средний параметр сходства возрастает с ростом числа секторов – рис. 17. Отметим, что в прикладных целях используется именно этот класс категорий, поэтому для повышения вероятности распознавания широко применяется анализ на множестве сеток, полученных при разбиении круга зодиака вплоть до градусов и минут. Третий класс составляют категории, для которых параметр сходства изменяется немонотонно с ростом числа секторов разбиения. Как правило, эти категории имеют среднюю частоту встречаемости и относительно небольшую величину параметра сходства. Общее их число невелико в исследуемой БД, поэтому они не оказывают существенного влияния на поведение среднего параметра распознавания.

 

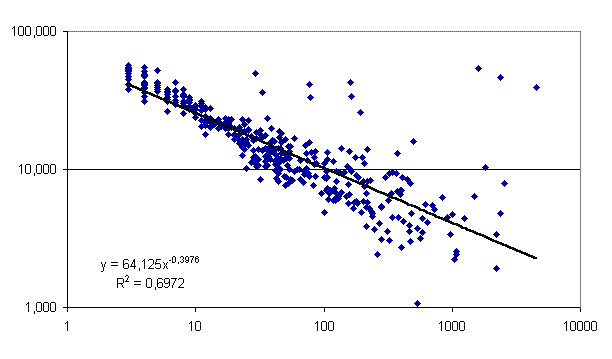
Рис. 16. Зависимость максимального параметра сходства от частоты встречаемости категории в 12 моделях

 

Таблица 10. Категории первого класса, их абсолютная частота встречаемости и корреляционная зависимость параметра сходства от числа секторов разбиения.

Категории

Частота

Корреляционная

зависимость

SC:A53-Sports

4567

y = 75,297x-0,3888

R2 = 0,9747

SC:B111-Sports:Basketball

2385

y = 109,23x-0,5494

R2 = 0,9909

SC:B173-Sports:Football

1613

y = 108,72x-0,3949

R2 = 0,9627

SC:B41-Occult Fields:UFO sighting

502

y = 24,008x-0,3275

R2 = 0,8406

SC:B404-Business:Sex Business

194

y = 45,03x-0,3428

R2 = 0,9783

SC:C78-Famous:Awards:Olympics

162

y = 67,868x-0,3678

R2 = 0,8959

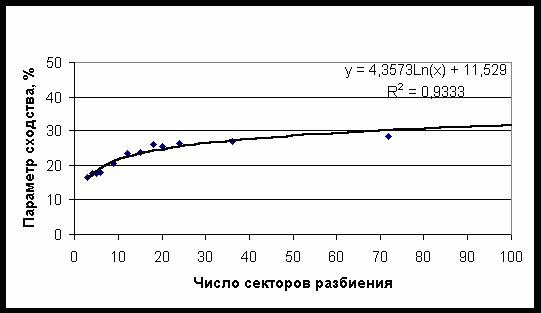
Рис. 17. Зависимость среднего параметра сходства от числа секторов разбиения

 

Насколько представительной является исследуемая БД и какое поколение в ней представлено? Только 2576 карт принадлежат людям, родившимся до 1901 года, остальные родились в 20 веке вплоть до 1998 года включительно. Распределение Солнца, Юпитера и Сатурна по знакам зодиака является достаточно однородным – рис. 18, однако распределение Урана указывает на преобладание карт поколения 1941-1948 (Уран в знаке Близнецов) и 1949-1956 (Уран в знаке Рака).

 

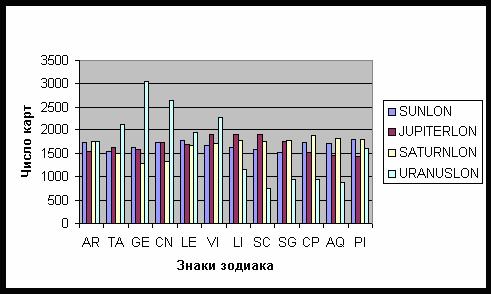
Рис. 18. Распределение планет по знакам зодиака

 

Для обработки результатов пакетного распознавания на множестве сеток выше был предложен алгоритм, который был дополнен еще четырьмя алгоритмами, для выбора наиболее эффективного из них. Таким образом, сравнивались пять алгоритмов, получивших общее название РЕЖИМЫ ГОЛОСОВАНИЯ МОДЕЛЕЙ:

1.               Для нахождения всех категорий, присущих данному респонденту, зададим минимальный уровень сходства, например 20%, составим таблицу распознанных категорий на сетке каждого масштаба с числом секторов разбиения 3, 4, 5, 6, 9, 12, 15, 18, 20, 24 соответственно и отберем те из них, которые повторяются 4 и более раз /3,4/.

2.               Результаты распознавания в частных моделях просто УСРЕДНЯЮТСЯ, т.е. в итоговой карточке идентификации для каждого класса уровень сходства респондента с обобщенным классом является СРЕДНИМ его уровней сходства с этим классом всех частных карточек идентификации.

3.               В итоговую карточку идентификации респондента берется уровень сходства этого респондента с классом из той частной карточки идентификации, в которой он МАКСИМАЛЬНЫЙ (из всех частных карточек).

4.               Когда в итоговую карточку идентификации респондента берется уровень сходства этого респондента с каждым классом из частной карточки идентификации, полученной в той частной модели, которая по результатам измерения достоверности распознавания ДАННОГО КЛАССА показала МАКСИМАЛЬНУЮ достоверность из всех исследованных моделей.

5.               Результаты распознавания в частных моделях УСРЕДНЯЮТСЯ с учетом достоверности идентификации классов в различных частных моделях, например, берется СРЕДНЕЕ СУММЫ ПРОИЗВЕДЕНИЙ уровней сходства с данным классом на достоверность его идентификации в частных моделях.

Сравнение осуществлялось следующим образом. Согласно первому алгоритму выбирался список распознанных категорий, определялось их число, а затем по 4 другим моделям выбирался список с таким же числом категорий, распознанных наилучшим образом по данному алгоритму. В таблице 11 дан пример такого сопоставления. Путем сопоставления номеров категорий можно определить те из них, которые присутствуют во всех пяти моделях. В данном случае это 18 категорий, собранных в таблице 11.

 

Таблица 11. Категории, опознанные в пяти моделях и
упорядоченные по параметру сходства первой модели

№

Категория

Параметр сходства

165

SC:B781-Law:Police/Security.

10

387

SC:E793-Medical:Doctor:Alternative methods:Psychic healer:Hypnoth

10

36

SC:B1330-Sports:Martial Arts.

9

323

SC:C802-Work:Maintenance Field:Cleaning service.

9

357

SC:D258-Famous:Greatest hits:Art field:Photography field.

9

360

SC:D376-Business:Sports Business:Coach/ Manager/ Owner:Manager.

9

203

SC:C1257-Education:Teacher:Coach.

8

298

SC:C657-Art:Commercial artist:Pro.

8

35

SC:B1295-Law:Fire department.

7

193

SC:C1151-Education:Teacher:Medicine.

7

20

SC:B1040-Work:Self-employed.

6

68

SC:B256-Art:Photography.

6

191

SC:C1130-Education:Teacher:Nursing.

6

273

SC:C560-Education:Teacher:Astrology.

6

315

SC:C760-Art:Fine art artist:Secondary.

6

65

SC:B246-Financial:Winnings/ Lottery.

5

220

SC:C175-Business:Business/Marketing:Public relations.

5

386

SC:E748-Business:Sex Business:Porno Market:Films:Superstar/star.

5

 

Поскольку категории в таблице 11 распознаются по всем пяти алгоритмам, все пять алгоритмов можно считать эквивалентными в смысле определения множества категорий из таблицы 11. Различие же алгоритмов может проявиться в установлении приоритетности категорий. Например, категория 165 (SC:B781-Law:Police/Security) распознается по первому алгоритму как наиболее достоверная, по второму алгоритму она оказывается на 4 месте, по третьему – на 7, по 4 – на 15, а по 5 – на 33. С другой стороны, категория 36 (SC:B1330-Sports:Martial Arts), которая распознается по пятому алгоритму с наибольшей достоверностью, также хорошо распознается и по первому алгоритму, но плохо распознается по третьему. Это означает, что каждый из алгоритмов имеет погрешность по отношению к другому, а наиболее эффективным может оказаться алгоритм, являющейся комбинацией указанных выше пяти алгоритмов. Такой комбинацией может быть описанный метод определения пересечения множества категорий, распознанных по каждому алгоритму.

3.5. Метод разделения категорий в задаче типизации и идентификации субъектов по астрономическим данным на момент рождения

В предыдущем пункте выполнено исследование моделей распознавания субъектов по астрономическим данным на момент рождения с целью определения наиболее эффективного алгоритма идентификации и типизации для профессиональной базы данных (БД) содержащей 387 категорий на 12 сетках различного масштаба. Было установлено, что категории можно разбить на три класса в зависимости от поведения параметра сходства от числа секторов. К первому классу были отнесены категории, для которых параметр сходства убывает с ростом числа секторов. Ко второму классу относятся категории, у которых параметр сходства возрастает с ростом числа секторов, а к третьему классу – категории, у которых параметр сходства ведет себя немонотонно. Логично предположить, что если отобрать категории первого класса в отдельную базу данных, то для их распознавания достаточно будет сетки, например, из четырех секторов. В данном разделе изучен вариант модели распознавания субъектов по астрономическим данным на момент рождения для профессиональной БД содержащей 184 категории первого и третьего класса на сетке из 4-х секторов. Мы покажем, что для этих категорий параметр сходства практически не зависит от частоты встречаемости категорий в исходной БД, содержащей 20007 данных независимых респондентов. Путем исключения категорий первого и третьего класса из профессионально БД содержащей 387 категорий, получена база данных категорий второго класса в составе 203 категорий.

Из списка категорий исследуемой БД отберем те из них, которые соотносятся с профессиями и для которых параметр сходства убывает с ростом числа секторов или изменяется немонотонно. Полученный список профессиональных категорий содержит только 184 наименования (см. Приложение 2), которые представлены в исходной БД с разной частотой встречаемости – рис. 19. Частотное распределение с большой степенью точности описывается экспонентой (распределение Пуассона) – прямая сплошная линия на рис. 19. Суммируя все частоты, находим общее число исследуемых случаев N= 60011. Учитывая, что в исходной БД содержится 20007 данных независимых респондентов, находим среднее число категорий, приходящихся на одну карту, n=N/20007=2,9995.

 

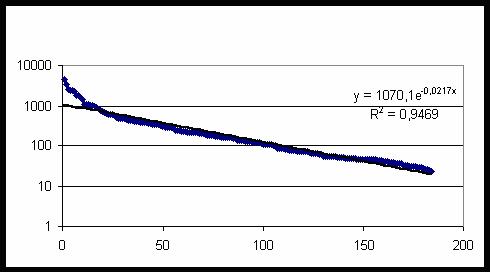
Рис. 19. Частота встречаемости 184 категорий первого класса

 

Распознавание отобранных 184 категорий осуществлялось на сетке из 4-х секторов, полученных путем деления круга зодиака на 4 части, начиная с нулевого градуса знака Овна. Как оказалось, для отобранных категорий параметр сходства практически не зависит от частоты встречаемости категории – рис. 20, тогда как в аналогичной задаче исследованной выше, параметр сходства убывает с ростом частоты – рис. 15. Можно сравнить параметры сходства идентичных категорий в этих двух задачах – рис. 21. Как следует из полученных данных, эти параметры связаны линейной зависимостью, причем параметр сходства при распознавании категорий в составе БД из 184 категорий приблизительно на 10% выше, чем в составе БД из 387 категорий (см. рис. 21).

 

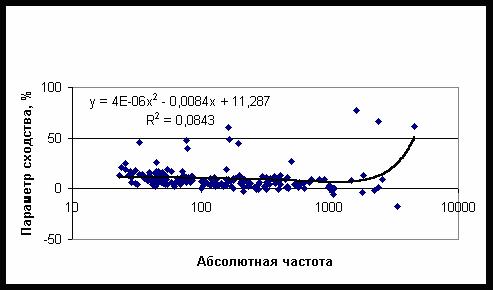
Рис. 20. Зависимость параметра сходства от частоты встречаемости 184 категорий первого класса

 

Отсюда следует, что обратная зависимость параметра сходства от частоты, возникает из-за наличия в исследованной БД 203 категорий второго класса. Эти категории отличаются малой частотой встречаемости, поэтому вероятность их случайного угадывания является крайне низкой. При распознавании категорий этого класса требуется большое число входных параметров, поэтому они хорошо распознаются на сетках с большим числом секторов (число входных параметров задачи пропорционально числу секторов).

Упорядочивая данные по параметру сходства, можно выделить наиболее хорошо распознаваемые категории первого класса – таблица 12. Среди 32 категорий, приведенных в этой таблице, 8 составляют спортивные категории, 6 – различные бизнесы, 5 – оккультные, 3 – медицинские доктора, 3 – дизайнеры, фотографы и художники, 2 – писатели детективов и фантастики, 2 – игроки, 2 – строители и 1 – экипажи судов, поездов и автобусов.

 

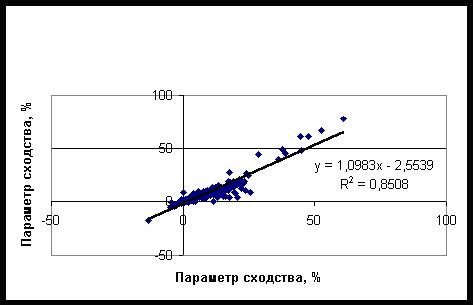
Рис. 21. зависимость параметра сходства при распознавании 184 категорий первого класса от параметра сходства при распознавании 387 смешанных категорий

 

 

 

Таблица 12. Список наиболее хорошо распознаваемых
категорий первого класса

NAME

Абсолютная

частота

Параметр

сходства

SC:B173-Sports:Football

1613

77,51

SC:B111-Sports:Basketball

2385

66,58

SC:A53-Sports

4567

61,06

SC:B626-Occult Fields:Out of Body exper

162

60,57

SC:C405-Business:Sex Business:Prostitut

165

48,61

SC:C1198-Occult Fields:Psychic/ Medium/

77

47,68

SC:C1340-Medical:Doctor:Chiropractor

33

45,49

SC:B404-Business:Sex Business

194

44,53

SC:C170-Medical:Doctor:Psyhotherapist

79

39,61

SC:B41-Occult Fields:UFO sighting

502

27,02

SC:B236-Business:CPA/ Auditor/ Accounta

45

26,46

SC:B406-Art:Stage/ Set design

26

24,51

SC:B437-Sports:Skiing

24

20,81

SC:B238-Business:Clerical/ Secretarial

158

19,03

SC:C422-Occult Fields:Psychic/ Medium/

26

18,92

SC:B496-Sports:Boxing

55

18,70

SC:B272-Art:Cartoonist

31

18,33

SC:B246-Financial:Winnings/ Lottery

59

17,44

SC:B715-Sports:Field and Track

47

17,43

SC:B492-Sports:Skating

45

17,09

NAME

Абсолютная

частота

Параметр

сходства

SC:B256-Art:Photography

47

17,04

SC:B54-Sports:Baseball

72

16,96

SC:B217-Travel:Crew/ Ship, Train, Bus

28

16,69

SC:D988-Occult Fields:Astrologer:Pro:AF

50

16,54

SC:B374-Business:Sports Business

40

16,36

SC:C709-Medical:Doctor:Surgeon

30

16,32

SC:C303-Business:Business/Marketing:Sto

30

16,14

SC:C250-Work:Building Trades:Builder

44

15,16

SC:B259-Writers:Sci-Fi/ Fantasy/ Horror

47

14,76

SC:B511-Writers:Detective/ Mystery

33

14,60

SC:B315-Financial:Gambling

35

14,26

SC:C631-Work:Building Trades:Architect/

48

13,59

 

Плохо распознаваемые категории этого класса приведены в таблице 13. Из 32 категорий этого типа 12 составляют различные знаменитости (!), 6 – наука и образование, 5 – журналисты, писатели и издатели журналов, 2 – политики, 2 – юристы, 2 – музыканты-инструменталисты и по одной категории фермеров, оккультистов и финансистов. Интересно, что если знаменитостей сгруппировать в отдельные категории по характеру получаемой премии, то они попадают во второй класс и распознаются довольно хорошо. Рассмотрим этот вопрос более подробно.

 

Таблица 13. Плохо распознаваемые категории
первого класса

NAME

Абсолютная

частота

Параметр

сходства

SC:A108-Education

1002

3,024

SC:C149-Famous:Greatest hits: Occult field

118

2,834

SC:C603-Work:Food and Beverage:Farmer/

44

2,774

SC:C636-Famous:Awards:Hall of Fame

62

2,732

SC:B16-Famous:News figure

130

2,341

SC:B33-Writers:Columnist/ journalist

213

2,31

SC:A120-Science

466

1,999

SC:C125-Science:Biology:Medicine

311

1,98

SC:C110-Education:Teacher:High school t

150

1,967

SC:C296-Famous:Greatest hits:Astrology

173

1,915

SC:B171-Writers:Playwright/ script

233

1,828

SC:C260-Famous:Greatest hits:Writing fi

262

1,779

SC:B46-Famous:Awards

973

1,755

SC:A40-Occult Fields

2396

1,694

SC:C11-Entertainment:Music:Instrumental

461

1,12

SC:B105-Writers:Textbook/ Non-fiction

569

0,875

SC:B158-Politics:Public office

475

0,729

SC:C551-Famous:Greatest hits:Science fi

100

0,684

SC:B6-Entertainment:Music

1086

0,563

SC:B109-Education:Teacher

636

0,43

SC:A99-Financial

1075

0,017

SC:B505-Education:Public speaker

179

-0,067

SC:B152-Law:Attorney

280

-0,644

SC:A151-Law

400

-0,842

SC:B52-Famous:Historic figure

322

-0,923

SC:B106-Writers:Publisher/ Editor

271

-0,929

SC:A19-Writers

2222

-1,255

SC:A38-Politics

1039

-1,875

SC:B340-Famous:Royal family

214

-3,105

SC:B45-Famous:Greatest hits

1794

-4,091

SC:B48-Famous:Top 5% of Profession

1073

-5,363

SC:A15-Famous

3372

-16,945

 

Общие свойства категорий второго класса

Список категорий второго класса, упорядоченных по частоте встречаемости, приведен в Приложении 3 вместе с параметром сходства, полученным на сетке, содержащей 72 сектора. Частотное распределение категорий второго класса с большой степенью точности описывается степенной функцией – рис. 22.

Зависимость параметра сходства от частоты также описывается степенной функцией – рис. 23. Поскольку вероятность случайного угадывания пропорциональна частоте встречаемости, из этих данных следует, что для второго класса категорий параметр сходства обратно пропорционален вероятности случайного угадывания в степени a=0,5594.

 

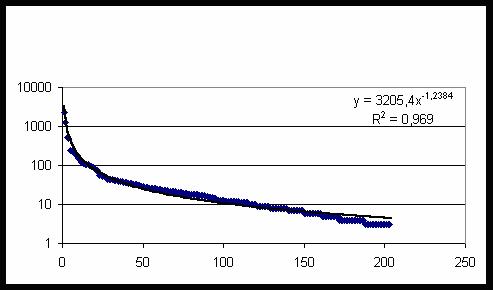
Рис. 22. Частота встречаемости категорий второго класса

 

 

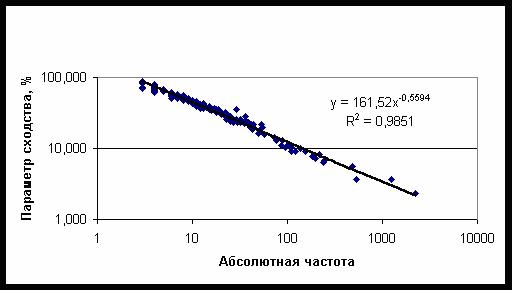
Рис. 23. Зависимость параметра сходства от частоты встречаемости категорий второго класса.

Рассмотрим категорию ЗНАМЕНИТЫЙ (Famous), разбитую на малые группы по характеру получаемой премии или социальному отличию – таблица 14. Из данных этой таблицы следует, что обладатели редких премий распознаются лучше, нежели обладатели известных, но широко распространенных премий. Становится понятной и закономерность, отраженная на рис. 23. Малочисленные группы в ряду многочисленных групп всегда более заметны, поэтому распознаются лучше. Например, эфиоп на улицах Москвы будет более заметен, нежели в ряду соплеменников на улицах Аддис-Абебы, поэтому его легко будет распознать. С другой стороны, блондин из Москвы, впервые попавший на улицы Аддис-Абебы, немедленно попадет в малочисленную категорию белых людей, поэтому будет легко узнаваем. В этом смысле распознавание в системе искусственного интеллекта "Эйдос" /3/ существенно отличается от простой статистики, в которой главным критерием достоверности является отклонение от генеральной совокупности.

 

Таблица 14. Категория Famous (знаменитый) разбитая на малые группы по характеру премии

NAME

Абсолютная

частота

Параметр

сходства

SC:C1234-Famous:Awards:Peabody

3

85,512

SC:D258-Famous:Greatest hits:Art field:Photography field

12

36,07

SC:C1043-Famous:Awards:Honorary degrees

17

33,782

SC:D635-Famous:Greatest hits:Art field:Fashion field

23

25,813

SC:C587-Famous:Awards:Grammy

37

23,461

SC:B750-Famous:Socialite

37

23,413

SC:D150-Famous:Greatest hits:Occult field:Spiritual field

43

18,411

SC:C690-Famous:Awards:Pulitzer prize

52

18,231

SC:C362-Famous:Greatest hits:Business field

50

16,385

SC:C588-Famous:Awards:Emmy

76

12,811

SC:D307-Famous:Greatest hits:Social field:Political field

95

10,432

SC:C306-Famous:Greatest hits:Social field

110

10,186

SC:C344-Famous:Awards:Oscar

153

9,158

SC:D60-Famous:Greatest hits:Art field:Beauty

184

7,649

SC:D67-Famous:Greatest hits:Art field:Music field

237

6,256

SC:C59-Famous:Greatest hits:Art field

534

3,65

При объединении знаменитостей в одну категорию A15-Famous получается довольно многочисленная группа (3372 случая), которая не имеет никаких общих признаков, кроме того, что эти люди знамениты. Поэтому параметр сходства/различия у этой группы имеет значение -16,945, что указывает на неоднородность группы. При разбиении же группы на малые подгруппы с ярко выраженными профессиональными признаками, параметр сходства становится положительным, что указывает на возросшую однородность состава подгрупп. Аналогичный пример дает категория ОБРАЗОВАНИЕ – таблица 15. Малые группы преподавателей, объединенные по специальностям, распознаются на порядок лучше, чем общая категория A108-Education, содержащая 1002 случая. При этом подгруппы общей категории относятся ко второму классу, т.е. хорошо распознаются на сетке из 72 секторов, а общая категория относится к первому классу, т.е. лучше всего распознается на сетке из 4 секторов.

 

Таблица 15. Категория ОБРАЗОВАНИЕ
разбитая на малые подгруппы

NAME

Абсолютная

частота

Параметр

сходства

SC:D1256-Education:Teacher:Science:Computer science

3

87,215

SC:C1486-Education:Public speaker:Brilliant orator

3

86,079

SC:D1246-Education:Teacher:Science:Philosophy

3

85,142

SC:C1130-Education:Teacher:Nursing

3

85,135

SC:D1414-Education:Teacher:Science:Psychology

3

81,323

SC:C1434-Education:Teacher:Adult Education

4

77,007

SC:C1257-Education:Teacher:Coach

4

76,057

SC:C1262-Education:Teacher:Special Ed

4

73,722

SC:E508-Education:Public speaker:Lecturer:Astrology

lecturer:Speaker at AFA conventions

3

73,083

SC:D1105-Education:Teacher:Science:Physics

6

57,329

SC:D1180-Education:Teacher:Science:History

6

57,29

SC:B762-Education:Librarian

7

56,983

SC:D951-Education:Teacher:Art:Dance

6

56,144

SC:D755-Education:Teacher:Occult teacher:Religous

8

56,121

SC:D507-Education:Public speaker:

Lecturer:Astrology lecturer

6

54,198

SC:C229-Education:Engineer:Chemical

9

50,112

SC:C1151-Education:Teacher:Medicine

9

48,512

SC:C983-Education:Engineer:Civil

8

48,31

SC:C1219-Education:Teacher:Communications

10

46,212

SC:C783-Education:Teacher:

Physical education/Gymnastic/Sport

12

40,93

SC:D1010-Education:Public speaker:

Lecturer:International lecturer

12

38,247

SC:C619-Education:Teacher:Language/English

19

35,764

SC:C705-Education:Teacher:Occult teacher

18

35,053

SC:C1174-Education:Engineer:Electrical

19

33,407

SC:C159-Education:Teacher:Art

25

28,574

SC:C500-Education:Teacher:Music

25

27,795

SC:C637-Education:Engineer:Aerospace

24

26,285

SC:C803-Education:Engineer:Mechanical

30

23,321

SC:C684-Education:Teacher:School/College teacher

35

22,535

SC:C560-Education:Teacher:Astrology

35

22,291

SC:D451-Education:Teacher:

High school teacher:Professor

109

9,1

SC:C506-Education:Public speaker:Lecturer

122

9,088

 

Существуют категории, например, B173-Sports:Football, которые характеризуют заведомо однородные группы, объединенные по яркому профессиональному признаку. У этой группы самый высокий параметр сходства среди категорий первого класса, несмотря на ее многочисленность (1613 случаев). На втором месте по параметру сходства оказалась группа баскетболистов. Но если объединить футболистов и баскетболистов в одну большую группу СПОРТ, параметр сходства понижается, поскольку группа становится неоднородной – рис. 9. Такие многочисленные однородные по составу группы хорошо распознаются на сетке из четырех секторов. С другой стороны, малочисленные однородные группы хорошо распознаются на сетках с большим числом секторов (в данной случае распознавание осуществлялось на сетке, включающей 72 сектора). На первый взгляд кажется, что признаки малочисленных профессиональных групп не могут быть использованы для тестирования, поскольку не выполнены статистические критерии достоверности. На самом же деле критерий сходства отличается от стандартных критериев достоверности, типа критерия Стьюдента. Критерий сходства хорошо иллюстрирует следующий пример. Предположим, что у нас есть база данных, включающая 20007 фотографий известных людей. Мы хотим протестировать фотографии неизвестных людей, чтобы выяснить, на кого они более всего похожи внешне. У нас есть интеллектуальная система, которая позволяет отобрать из БД насколько десятков фотографий и расставить их по параметру сходства. При этом оказывается, что на одних фотографиях схожесть достигается за счет формы носа, на других за счет овала лица, на третьих за счет разреза глаз и т.д. Заменим теперь фотографии на карты рождения, включающие описание астрономических параметров, социальных и психологических категорий. Задача распознавания при этом не изменилась, но на выходе мы получим набор категорий, характеризующих тестируемого субъекта. Если при этом субъект оказался похож на малочисленную профессиональную категорию, то это нельзя назвать простым совпадением. Ведь совпадение с малочисленной группой маловероятно. Кроме того, путем прямых экспериментов доказано, что вероятность распознавания по астрономическим данным на момент рождения в много раз превосходит вероятность случайного угадывания /15/. Следовательно, полученные результаты так или иначе могут быть отнесены к числу характеристик субъекта, но при этом необходимо помнить, что сходство и подобие не означает тождество.

Заметим, что первые эксперименты по идентификации и типизации субъектов по астрономическим данным на момент рождения были выполнены на смешенной базе данных, содержащей 500 социальных (профессиональных) и личностных (в т.ч. психологических) категорий /8, 10/. Для повышения уровня параметра сходства и достоверности идентификации была образована новая база данных, содержащая только 387 социальных (профессиональных) категорий /7/. Полученные с ее помощью результаты отличаются высокой степенью достоверности идентификации. Рассмотренный метод позволяет повысить параметр сходства путем разделения категорий на классы, не увеличивая числа входных параметров задачи.

 

3.5. Типизации и идентификации субъектов
по астрономическим данным на момент
рождения на базе 500 психологических
и персональных категорий

 

В этом разделе изучен вариант модели распознавания субъектов по астрономическим данным на момент рождения для БД, содержащей 500 психологических и личностных категорий на 12 сетках различного масштаба с числом секторов разбиения 3, 4, 5, 6, 9, 12, 15, 18, 20, 24, 36, 72 соответственно. Методом разделения категорий установлены общие закономерности распознавания категорий первого и второго класса.

Исходные данные задачи представляют собой таблицу, содержащую 20007 записей (строк) независимых респондентов, каждый из которых характеризуется номером записи, именем, полом, датой и временем рождения, местом рождения, собственной биографией и набором категорий и событий жизни. На основе данных места и времени рождения вычислялись астрономические параметры. В качестве входных астрономических параметров модели использовались координаты долготы углов 12 домов (в системе Плацидуса), Лунных Узлов и 10 небесных тел – Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна, Плутона.

Из списка категорий были отобраны те из них, которые соотносятся с психологическими и личностными характеристиками. Полученный список категорий содержит 500 наименований. Частотное распределение категорий с хорошей степенью точности описывается степенной функцией – прямая сплошная линия на рис. 24. Суммируя все частоты, находим общее число исследуемых случаев N= 65143 и среднее число категорий, приходящихся на одну карту, n=N/20007=3,256.

Результаты распознавания для модели, содержащей 72 сектора, даны на рис. 25. Как и в случае социальных и профессиональных категорий, наблюдается обратная зависимость параметра сходства от частоты встречаемости категорий, которую можно аппроксимировать степенной функцией с показателем степени -0,4956. Используя полученные данные для моделей с 4 и 72 секторами, можно разделить все категории на два класса по признаку уменьшения или увеличения параметра сходства:

1) категория относится к первому классу, если Si(4)>Si(72);

2) категория относится ко второму классу, если Si(4)<Si(72),

где Si(4), Si(72) – значения параметра сходства категории i в модели с 4 и 72 секторами соответственно. Третий класс можно определить как промежуточный между первыми двумя путем задания условной границы скорости изменения параметра сходства, dS, при изменении числа секторов, в виде:

3) категория относится к третьему классу, если

-dS<(Si(72)-Si(4))/(72-4)<dS

 

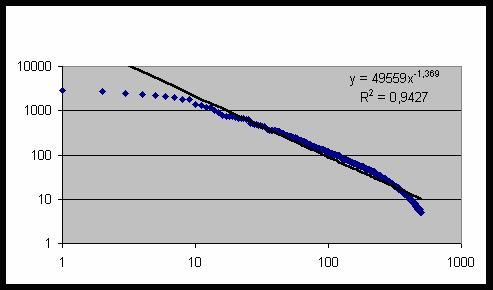
Рис. 24. Частота встречаемости 500 категорий

 

 

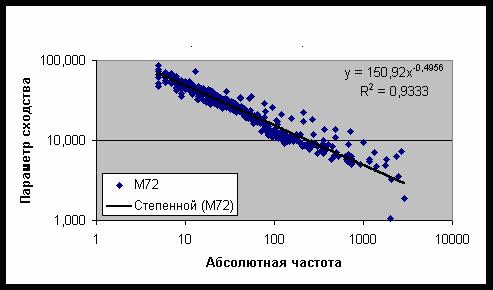
Рис. 25. Зависимость параметра сходства от частоты встречаемости 500 категорий

 

При распознавании третий класс удобно будет отнести к одному из двух других классов, например, к первому (для его распознавания требуется меньше затрат машинного времени).

В результате разделения оказалось, что в первый класс попали только 84 категории, а во второй соответственно 416. Отметим, что в аналогичной задаче, рассмотренной в предыдущем пункте, при разделении на классы получилось 72 в первом классе и 315 – во втором. Но за счет отнесения категорий третьего класса к первому классу числа категорий изменились на 184 и 203 соответственно. В данном случае можно отнести 95 категорий второго класса к первому классу и, таким образом получить две БД в составе 179 категорий для смешанного класса и 321 – для второго.

Категории первого и третьего класса

Список категорий первого и третьего класса, упорядоченный по частоте встречаемости, приведен в Приложении 4 вместе с параметром сходства, полученным в модели с 4 секторами. Эти категории отличаются слабой зависимостью параметра сходства от частоты встречаемости – рис. 26.

 

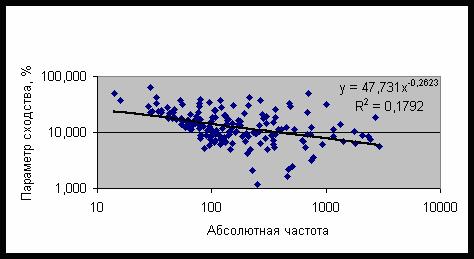
Рис. 26. Зависимость параметра сходства от частоты
встречаемости категорий первого класса

 

Само наличие этих категорий свидетельствует о влиянии времени года на новорожденного, что сказывается в его судьбе, как в плане социальной адаптации, так и в психологическом смысле. Отметим, что в человеческой практике большое значение придается положению Солнца, от которого зависят сезоны – весна, лето, осень и зима. Однако ни в одной системе нет явного выделения сезона, как самостоятельного сегмента круга зодиака. Обнаруженный в данном исследовании феномен подчеркивает роль деления круга зодиака на четыре части по числу сезонов при распознавании категорий первого класса. Причем сезоны следует начинать от кардинальных точек эклиптики, совпадающих с началом знаков Овна, Рака, Весов и Козерога, для весны, лета, осени и зимы соответственно. Отметим, что, например, в Канаде принято именно такое деление года на сезоны.

Наиболее хорошо распознаваемые категории первого класса приведены в таблице 16.

 

Таблица 16. Список наиболее хорошо распознаваемых
категорий первого класса

Параметр

сходства

Категория

Абсолютная

частота

62,869

SC:C170-Medical:Doctor:Psyhotherapist

29

49,613

SC:A138-Religion

707

49,563

SC:B112-Psychological:Drug Abuse

14

42,988

SC:B395-Religion:12 step group

213

42,966

SC:C1340-Medical:Doctor:Chiropractor

33

38,512

SC:C1707-Medical:Doctor:Therapist

79

37,965

SC:B450-Mind:Extensive education

120

37,612

SC:B179-Birth:Test tube baby

53

37,446

SC:C457-Psychological:Alcohol Abuse:Rehab AA

267

36,693

SC:C1042-Medical:Cancer:Colon

16

34,862

SC:C1327-Birth:Infant mortality:SIDS

95

33,088

SC:B1557-Personality:Disasters

78

32,997

SC:C127-Medical:Accidents:Heart attack

33

32,969

SC:B240-Birth:Short labor <3 hrs

481

32,256

SC:C1239-Birth:Defects, Handicaps:Down's Syndrome

55

31,435

SC:A23-Psychological

1007

30,673

SC:B135-Death:Accidental

210

30,565

SC:B178-Birth:Cesarean

156

29,172

SC:B207-Medical:Cancer

490

28,843

SC:C155-Death:Long life >80 yrs:Age >100

78

28,816

SC:B703-Criminal Perpetrator:Terrorist

28

28,089

SC:B577-Sexuality:Celibacy/ Minimal

122

28,05

SC:B24-Psychological:Alcohol Abuse

41

27,926

SC:C1324-Birth:Twin, triplet, etc.:Triplets

41

26,276

SC:C208-Medical:Cancer:Breast

47

25,389

SC:C609-Sexuality:Sexual perversions:Lesbian

362

25,144

SC:B866-Birth:Stillborn

105

25,082

SC:C241-Death:Long life >80 yrs:Age 91-99

108

24,873

SC:D1125-Religion:Ecclesiastics/ western:Priest:monk/nun

36

24,217

SC:C644-Medical:Cancer:Lung

46

24,022

SC:C709-Medical:Doctor:Surgeon

30

23,845

SC:B1046-Sexuality:Voyeur

34

22,969

SC:B546-Psychological:Bi-Polar Disorder

29

 

Мы намеренно разместили в этой базе данных профессиональную категорию МЕДИЦИНСКИЙ ДОКТОР, чтобы показать корреляцию профессии и соответствующей группы заболеваний. Действительно, в таблице 16 находим профессию психотерапевт и психологические категории, соответствующие различным психическим отклонениям:

SC:C170-Medical:Doctor:Psyhotherapist

SC:A23-Psychological

SC:B101-Psychological:Eating Disorder

SC:B112-Psychological:Drug Abuse

SC:B24-Psychological:Alcohol Abuse

SC:B383-Psychological:Phobias

SC:B388-Psychological:Depression

SC:B546-Psychological:Bi-Polar Disorder

SC:C457-Psychological:Alcohol Abuse:Rehab AA

В этот список не попали категория SC:B524-Psychological:Schizophrenia, поскольку была отнесена ко второму классу, причем попала на условную границу между вторым и третьим классами. Две другие профессиональные категории – терапевт и хирург, оказываются в одном списке с набором раковых и сердечных заболеваний:

SC:C1707-Medical:Doctor:Therapist

SC:C709-Medical:Doctor:Surgeon

SC:B207-Medical:Cancer

SC:C1042-Medical:Cancer:Colon

SC:C208-Medical:Cancer:Breast

SC:C644-Medical:Cancer:Lung

SC:C127-Medical:Accidents:Heart attack.

Отметим, что категория SC:C1340-Medical:Doctor:Chiropractor также оказалась в этой таблице.

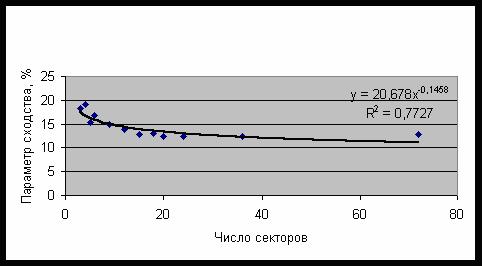
Рис. 27. Зависимость среднего параметра сходства от числа секторов разбиения для 84 категорий первого класса

 

 

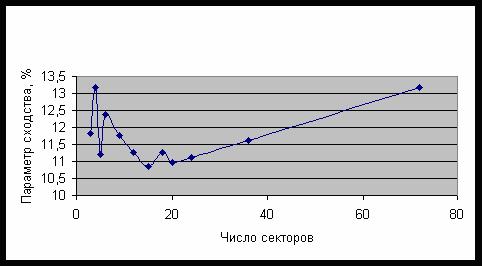
Рис. 28. Зависимость среднего параметра сходства от числа секторов разбиения для 89 категорий третьего класса

 

Перечисленные заболевания, скорее всего, носят сезонный характер и обусловлены климатическими изменениями, поэтому они хорошо распознаются при разбиении круга зодиака на четыре сектора, соответствующие сезонам.

На рис. 27 дана зависимость среднего параметра сходства от числа секторов разбиения для 84 категорий первого класса. Хорошо видно, что максимальный параметр сходства достигается при разбиении на 4 сектора. Возможно, что у этой функции имеется еще один максимум при числе секторов более 100. Этот максимум обусловлен примесью категорий третьего класса.

Категории второго класса

Список категорий второго класса, упорядоченных по величине параметра сходства, дан в Приложении 5. Параметр сходства этих категорий убывает с ростом частоты встречаемости – рис. 29. С хорошей точностью эту зависимость можно аппроксимировать степенной функцией с показателем степени -0,5357. Аналогичная зависимость наблюдается и для всех 500 категорий исследуемой БД – рис. 25.

Среднее значение параметра сходства, вычисленное для 321 категории возрастает с ростом числа секторов разбиения – рис. 30. Если зависимость аппроксимировать степенной функцией и экстраполировать до значения параметра сходства 100%, то соответствующее число секторов окажется приблизительно равным 1557, а дуга одного сектора составит 832 угловых секунды, т.е. чуть меньше половины углового размера диска Луны или Солнца. Дальнейшие исследования покажут, действительно ли можно добиться 100% значения параметра сходства при увеличении числа секторов разбиения.

Действительно, среди категорий третьего класса можно выделить центральное ядро из 89 категорий с однотипным поведением – рис. 28. Приведенная на этом рисунке зависимость среднего параметра сходства от числа секторов разбиения имеет два максимума – при разбиении на 4 и 72 сектора соответственно. Это свойство позволяет отнести категории третьего класса к двум другим классам, поскольку они распознаются с одинаковым уровнем сходства для разбиения на 4 сектора, на котором достигается максимум распознавания категорий первого класса, и для разбиения на 72 сектора, на котором категории второго класса имеют максимум параметра сходства.

 

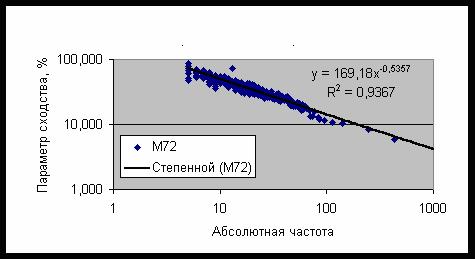
Рис. 29. Зависимость параметра сходства от частоты встречаемости категорий второго класса

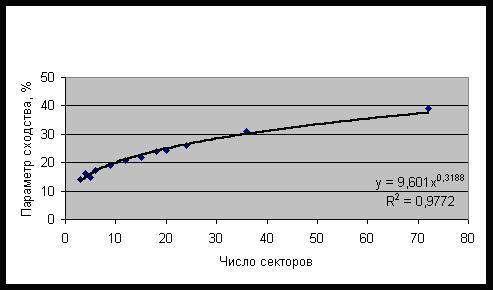
Рис. 30. Зависимость среднего параметра сходства от числа секторов разбиения для 321 категории второго класса

 

Максимальное значение параметра сходства у категорий второго класса реализуется при минимальном значении частоты встречаемости, которое в данном случае равно 5. Наилучшим образом распознается категория SC:B1112-Personality:Diplomatic, т.е. наличие у субъекта дипломатических способностей. Наихудшим образом на уровне 0% распознается категория SC:A129-Death – смерть без указания ее причины. Однако, если указать причину смерти, то уровень распознавания резко возрастает, например, категория SC:C1698-Death:Suicide:Subway – самоубийство в метро, распознается на уровне 40,8%; категория SC:C1395-Death:Suicide:Gassed – самоубийство путем отравления газом, на уровне 44,6%; а редкий случай ритуального самоубийства – категория SC:C622-Death:Suicide:Cult ritual, на уровне 52,6%. Иначе говоря, чем реже случай, тем лучше он распознается в рамках данной модели. Это можно объяснить тем, что в малопредставленных категориях меньше вариабельность и поэтому задача идентификации с ними упрощается.