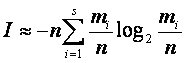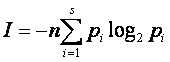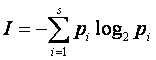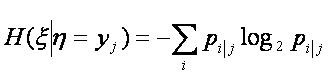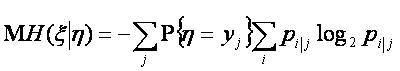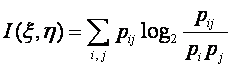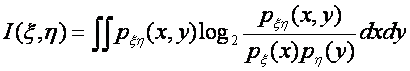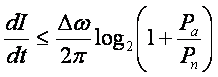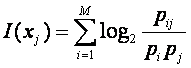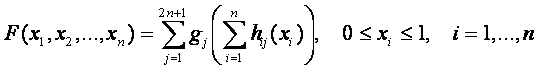ГЛАВА 1. ТЕОРИЯ ИНФОРМАЦИИ И
СИСТЕМА ИСКУССТВЕННОГО ИНТЕЛЛЕКТА "ЭЙДОС"
Жизнь людей немыслима
без источников информации в форме, телефона, радио, телевидения, книг, газет и журналов.
Люди постоянно пополняют запас своих знаний, обмениваются ими с другими людьми,
извлекают новые знания из собственного и коллективного опыта. Между тем, математическая
теория, описывающая процессы передачи информации по каналам связи возникла сравнительно
недавно, в конце сороковых годов 20 века, благодаря трудам Фишера, Хартли, Котельникова,
Шеннона, Колмогорова, Хинчина и других (см. гл. 3 в работе /20/).
H(x1,x2,…,xk)= H(x1)+ H(x2)+…+
H(xk).
Информацию в x1 относительно x2 можно определить по формуле
где n=m1+…+ms. Количество информации этого словаря
составляет
При ![]() справедлива асимптотическая формула
справедлива асимптотическая формула
В случае совместного распределения
вероятностей двух случайных объектов ![]()
при заданном значении ![]() находим условное распределение
находим условное распределение
Количество информации, которое
необходимо для указания точного значения ![]() равно, согласно (3)
равно, согласно (3)
Вычисляя среднее значение этого
выражения, находим
Величина информации относительно
![]() содержащаяся в задании
содержащаяся в задании ![]() определяется в виде
определяется в виде
Эту формулу можно записать в
симметричном виде:
Здесь ![]() – мощность сигнала и шума соответственно.
– мощность сигнала и шума соответственно.
В классической теории Шеннона /23/ исследуется
передача символов по одному информационному каналу от одного источника к одному
приемнику. В общем случае можно поставить другую задачу: идентифицировать информационный
источник по сообщению от него /18/.
Эта задача является своего рода обобщением метода идентификации
искусственного интеллекта, предложенного Аланом Тьюрингом и известной как
"тест Тьюринга" /25/. Тьюринг предлагал использовать этот тест для того,
чтобы эксперты-люди по сообщениям от системы искусственного интеллекта и
человека определили кто из них кто. А теперь возникает вопрос о том, может ли
искусственный интеллект по сообщениям, т.е. на основании информации, полученной
от объектов различной природы, в т.ч. людей, идентифицировать их, т.е. отнести
к тем или иным обобщенным категориям. Это задача известна как задача "распознавания
образов", к которой сводятся также задачи идентификации и прогнозирования.
Для решения этой задачи метод Шеннона был обобщен путем
учета в математической модели возможности существования многих источников
информации, от которых по одному зашумленному каналу связи приходят к приемнику
не отдельные символы, а сообщения, состоящие из последовательностей символов
(признаков) любой длины.
Задача идентификации информационного источника по сообщению
от него, полученному приемником по зашумленному каналу может быть решена методом,
являющимся обобщением метода К. Шеннона /23/. Это позволяет применить классическую
теорию информации для построения моделей систем распознавания образов и принятия
решений /18/.
Для решения поставленной задачи необходимо вычислять не
средние информационные характеристики, как в теории Шеннона, а количество информации,
содержащееся в конкретном i–м признаке
(символе) о том, что он пришел от данного j–го
источника информации. Это позволит определить суммарное количество информации в
сообщении о каждом информационном источнике, что дает интегральный критерий для
идентификации.
Логично предположить, что среднее количество информации,
содержащейся в системе признаков о системе классов (5) является усреднением порций
информации (слов или символов типа i),
приходящих от индивидуальных источников типа j:
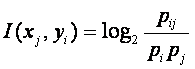 (8)
(8)
Если сообщение содержит М символов, то общее количество
информации, приходящей от источника типа j
определяется путем суммирования выражения (8):
где gj и hij
– непрерывные функции, причем hij
не зависят от функции F.
АСК-анализ представляет собой непараметрический метод искусственного
интеллекта, основанный не на статистике, а на системном обобщении теории информации,
системном анализе и когнитивном моделировании /1, 18-19/. Этот метод позволяет выделять
полезный сигнал о связи признаков с обобщенными категориями из шума путем обобщения
(многоканальной или многопараметрической типизации), осуществлять синтез информационным
моделей больших размерностей, а также использовать их для решения задач идентификации
(прогнозирования), поддержки принятия решений и просто исследования предметной области
путем исследования ее модели.
Метод и технология АСК-анализа включает:
– базовую когнитивную концепцию;
– математическую модель;
– методику численных расчетов;
– специальный программный инструментарий – универсальную
когнитивную аналитическую систему "Эйдос" /2/.
Базовая когнитивная концепция АСК-анализа рассматривает
процесс познания, как многоуровневую иерархическую систему обработки информации,
причем когнитивные структуры каждого уровня являются результатом интеграции структур
предыдущего уровня.
На 1-м уровне этой системы находятся дискретные элементы
потока чувственного восприятия, которые на 2-м уровне интегрируются в чувственный
образ конкретного объекта. Те, в свою очередь, на 3-м уровне интегрируются в обобщенные
образы классов и факторов, образующие на 4-м уровне кластеры, а на 5-м конструкты.
Система конструктов на 6-м уровне образуют текущую парадигму реальности (т.е. человек
познает мир путем синтеза и применения конструктов). На 7-м же уровне обнаруживается,
что текущая парадигма не единственно возможная, т.к. существуют другие формы сознания
и реальности, кроме известных до этого.
Ключевым для когнитивной концепции является понятие факта,
под которым понимается соответствие дискретного и интегрального элементов познания
(т.е. элементов разных уровней интеграции-иерархии), обнаруженное на опыте. Факт
рассматривается как квант смысла, что является основой для его формализации. Мысль
представляет собой действие над данными, извлекающее из них смысл. Таким образом,
происхождение смысла связывается со своего рода "разностью потенциалов",
существующей между смежными уровнями интеграции-иерархии обработки информации в
процессах познания. Между когнитивными структурами разных уровней иерархии существует
отношение "дискретное – интегральное". Именно это служит основой формализации
смысла. Из базовой когнитивной концепции следует когнитивный конфигуратор, представляющий
собой минимальную полную систему когнитивных операций, названных "базовые когнитивные
операции системного анализа".
Всего выявлено 10 таких операций, каждая из которых оказалась
достаточно элементарной для формализации и программной реализации:
1)
присвоение имен;
2)
восприятие;
3)
обобщение (синтез,
индукция);
4)
абстрагирование;
5)
оценка адекватности
модели;
6)
сравнение, идентификация
и прогнозирование;
7)
дедукция и абдукция;
8)
классификация и генерация
конструктов;
9)
содержательное сравнение;
10)
планирование и принятие
решений об управлении.
Математическая модель АСК-анализа основана на системной
теории информации, которая создана в рамках реализации программной идеи обобщения
всех понятий математики, в частности теории информации, базирующихся на теории множеств,
путем тотальной замены понятия множества на более общее понятие системы и тщательного
отслеживания всех последствий этой замены. Благодаря математической модели, положенной
в основу АСК-анализа, этот метод является непараметрическим и позволяет сопоставимо
обрабатывать тысячи градаций факторов (астропризнаков) и будущих состояний объекта
управления (категорий) при неполных (фрагментированных), зашумленных данных различной
природы, т.е. измеряемых в различных единицах измерения.
При этом на этапе синтеза модели осуществляется многокритериальная
типизация респондентов обучающей выборки по исследуемым категориям, т.е. рассчитывается
количество информации, которое содержится в фактах попадания долгот углов в интервалы
(рассматриваемые как критерии), о принадлежности респондента к тем или иным категориям,
а на этапе идентификации эта информация используется для расчета степени сходства
конкретных респондентов с обобщенными категориями.
Результат идентификации респондента, описанного данной
системой астропризнаков, представляет собой список обобщенных категорий (классов),
в котором они расположены в порядке убывания суммарного количества информации о
принадлежности респондента к каждому из них. Математическая модель позволяет сформировать
информационные портреты классов и астропризнаков, а также осуществить их кластерный
и конструктивный анализ.
Информационный портрет класса (обобщенной категории) показывает
какое количество информации содержит каждый астропризнак о принадлежности респондента
к данной категории.
Информационный (семантический) портрет астропризнака является
его развернутой смысловой количественной характеристикой, в которой содержится информация
о принадлежности респондента, обладающего данным признаком, ко всем обобщенным категориям.
Кластеры классов представляют собой группы категорий, сходных
по характерным для них астропризнакам.
Кластеры астропризнаков представляют собой группы признаков,
сходных по их смыслу, т.е. по тому, какую информацию о принадлежности респондентов,
обладающих этими признаками к обобщенным категориям они содержат.
Под конструктом понимается система противоположных (наиболее
сильно отличающихся) кластеров, которые называются "полюсами" конструкта,
а также спектр промежуточных кластеров, к которым применима количественная шкала
измерения степени их сходства или различия.
Конструкты могут быть получены как результат кластерного
анализа кластеров категорий или астропризнаков, при этом конструкт рассматривается
как кластер с нечеткими границами, включающий в различной степени, причем не только
в положи-
тельной, но и в отрицательной, все классы или астропризнаки.
Конструктивный анализ позволяет определить в принципе совместимые
и в принципе несовместимые по характерным для них астропризнакам классы или обобщенные
категории. Совместимыми называются классы, для которых характерны сходные системы
астропризнаков, а несовместимыми – для которых они диаметрально противоположны и
одновременно неосуществимы.
По результатам кластерно-конструктивного анализа строятся
диаграммы смыслового сходства-различия классов (признаков), соответствующие определению
семантических сетей и нечетких когнитивных схем, т.е. представляющие собой ориентированные
графы, в которых классы (признаки) соединены линиями, толщина которых соответствует
модулю, а цвет знаку их сходства-различия.
Предложенная математическая модель в обобщенной постановке
обеспечивает содержательное сравнение классов друг с другом и астропризнаков друг
с другом, т.е. построение когнитивных диаграмм. Например, информационные портреты
классов содержат информацию о характерности признаков для классов. Кластерно-конструктивный
анализ обеспечивает сравнение классов друг с другом, т.е. дает степень их сходства
и различия. Но он не дает информации о том, какими признаками эти классы похожи
и какими отличаются, и какой вклад каждый признак вносит в сходство или различие
некоторых двух классов. Информация об этом генерируется на основе анализа и сравнения
двух информационных портретов, что и осуществляется при содержательном сравнении
классов. Каждая пара признаков, принадлежащих сравниваемым классам, образует "смысловую
связь", вносящую определенный вклад в сходство/различие между этими классами
если эти признаки тождественны друг другу или между ними имеется определенное сходство/различие
по смыслу. Список связей сортируется в порядке убывания модуля силы связи, причем
учитывается не более заданного их количества (это связано с ограничениями при графическом
отображении). Графической визуализацией результатов содержательного сравнения классов
являются когнитивные диаграммы с многозначными связями. На когнитивной диаграмме
классов отображены их информационные портреты, в которых факторы расположены в порядке
убывания их характерности для этих классов, а линии, соединяющие астропризнаки,
имеют толщину и цвет, соответствующие модулю и знаку их вклада в сходстворазличие
классов. Когнитивная диаграмма классов дает детальную расшифровку структуры конкретной
линии связи семантической сети. Кроме того, предложены и реализованы в модели инвертированные
когнитивные диаграммы, детально раскрывающие сходство-различие двух астропризнаков
по их влиянию на принадлежность респондента к различным категориям, а также прямые
и инвертированные диаграммы В.С. Мерлина (1986), в которых показаны уровни и знаки
связей между астропризнаками различных уровней интегративности по их характерности
для различных категорий. Предложены и реализованы также классические и интегральные
когнитивные карты, представляющие собой диаграммы, объединяющие семантические сети
классов и признаков и нелокальные нейронные сети /25/.
Методика численных расчетов АСК-анализа включает структуры
данных, способы представления и формализации (кодирования) входных, промежуточных
и выходных данных, а также алгоритмы реализации базовых когнитивных операций системного
анализа.
Специальный программный инструментарий АСК-анализа – универсальная
когнитивная аналитическая система "Эйдос" (см. таблицу 1.1) обеспечивает:
– формализацию предметной области;
– подготовку обучающей выборки и управление ей, в т.ч.
взвешивание или "ремонт" данных;
– синтез семантической информационной модели предметной
области (обобщение или типизация);
– оптимизацию модели;
– проверку адекватности модели;
– идентификацию и прогнозирование;
– типологический анализ (включая решение обратной задачи
идентификации и прогнозирования, семантический информационный и кластерно-конструктивный
анализ классов и факторов);
– оригинальную графическую визуализацию результатов анализа
в форме когнитивной графики (простых и интегральных когнитивных карт, семантических
сетей и когнитивных диаграмм).
Общая структура системы "Эйдос" представлена
в таблице 1.
Таблица 1. Общая структура универсальной когнитивной аналитической
системы "Эйдос"
|
Подсистема |
Режим |
Функция |
Операция |
|
1. Формализация ПО |
1. Классификационные
шкалы и градации |
||
|
2. Описательные
шкалы (и градации) |
|||
|
3. Градации описательных
шкал (признаки) |
|||
|
4. Иерархические
уровни систем |
1. Уровни классов |
||
|
2. Уровни признаков |
|||
|
5. Программные
интерфейсы для импорта данных |
1. Импорт данных
из TXT-фалов стандарта DOS-текст |
||
|
2. Импорт данных
из DBF-файлов стандарта проф. А.Н.Лебедева |
|||
|
3. Импорт из
транспонированных DBF-файлов проф. А.Н.Лебедева |
|||
|
4. Генерация
шкал и обучающей выборки RND-модели |
|||
|
5. Генерация
шкал и обучающей выборки для исследования чисел |
|||
|
6. Транспонирование
DBF-матриц исходных данных |
|||
|
7. Импорт данных
из DBF-файлов стандарта Евгения Лебедева |
|||
|
6. Почтовая служба
по НСИ |
1. Обмен по классам |
||
|
2. Обмен по обобщенным
признакам |
|||
|
3. Обмен по первичным
признакам |
|||
|
7. Печать анкеты |
|||
|
2. Синтез СИМ |
1. Ввод–корректировка
обучающей выборки |
||
|
2. Управление
обучающей выборкой |
1. Параметрическое
задание объектов для обработки |
||
|
2. Статистическая
характеристика, ручной ремонт |
|||
|
3. Автоматический
ремонт обучающей выборки |
|||
|
3. Синтез семантической
информационной модели СИМ |
1. Расчет матрицы
абсолютных частот |
||
|
2. Исключение
артефактов (робастная процедура) |
|||
|
3. Расчет матрицы
информативностей СИМ-1 и сделать ее текущей |
|||
|
4. Расчет условных
процентных распределений СИМ-1 и СИМ-2 |
|||
|
5. Автоматическое
выполнение режимов 1–2–3–4 |
|||
|
6. Измерение
сходимости и устойчивости модели |
1. Сходимость
и устойчивость СИМ |
||
|
2. Зависимость
валидности модели от объема обучающей выборки |
|||
|
7. Расчет матрицы
информативностей СИМ-2 и сделать ее текущей |
|||
|
4. Почтовая служба
по обучающей информации |
|||
|
3. Оптимизация СИМ |
1. Формирование
ортонормированного базиса классов |
||
|
2. Исключение
признаков с низкой селективной силой |
|||
|
3. Удаление классов
и признаков, по которым недостаточно данных |
|||
|
4. Разделение
классов на типичную и нетипичную части |
|||
|
5. Генерация
сочетанных признаков и перекодирование обучающей выборки |
|||
|
4. Распознавание |
1. Ввод–корректировка
распознаваемой выборки |
||
|
2. Пакетное распознавание |
|||
|
3. Вывод результатов
распознавания |
1. Разрез: один
объект – много классов |
||
|
2. Разрез: один
класс – много объектов |
|||
|
4. Почтовая служба
по распознаваемой выборке |
|||
|
5. Построение
функций влияния |
|||
|
6. Докодирование
сочетаний признаков в распознаваемой выборке |
|||
|
5. Типология |
1. Типологический
анализ классов распознавания |
1. Информационные
(ранговые) портреты (классов) |
|
|
2. Кластерный
и конструктивный анализ классов |
1 Расчет матрицы
сходства образов классов |
||
|
2. Генерация
кластеров и конструктов классов |
|||
|
3. Просмотр и
печать кластеров и конструктов |
|||
|
4. Автоматическое
выполнение режимов: 1,2,3 |
|||
|
5. Вывод 2d семантических
сетей классов |
|||
|
3. Когнитивные
диаграммы классов |
|||
|
2. Типологический
анализ первичных признаков |
1. Информационные
(ранговые) портреты признаков |
||
|
2. Кластерный
и конструктивный анализ признаков |
1. Расчет матрицы
сходства образов признаков |
||
|
2. Генерация
кластеров и конструктов признаков |
|||
|
3. Просмотр и
печать кластеров и конструктов |
|||
|
4. Автоматическое
выполнение режимов: 1,2,3 |
|||
|
5. Вывод 2d семантических
сетей признаков |
|||
|
3. Когнитивные
диаграммы признаков |
|||
|
6. СК-анализ СИМ |
1. Оценка достоверности
заполнения объектов |
||
|
2. Измерение
адекватности семантической информационной модели |
|||
|
3. Измерение
независимости классов и признаков |
|||
|
4. Просмотр профилей
классов и признаков |
|||
|
5. Графическое
отображение нелокальных нейронов |
|||
|
6. Отображение
Паретто-подмножеств нейронной сети |
|||
|
7. Классические
и интегральные когнитивные карты |
|||
|
7. Сервис |
1. Генерация
(сброс) БД |
1. Все базы данных |
|
|
2. НСИ |
1. Всех баз данных
НСИ |
||
|
2. БД классов |
|||
|
3. БД первичных
признаков |
|||
|
4. БД обобщенных
признаков |
|||
|
3. Обучающая
выборка |
|||
|
4. Распознаваемая
выборка |
|||
|
5. Базы данных
статистики |
|||
|
2. Переиндексация
всех баз данных |
|||
|
3. Печать БД
абсолютных частот |
|||
|
4. Печать БД
условных процентных распределений СИМ-1 и СИМ-2 |
|||
|
5. Печать БД
информативностей СИМ-1 и СИМ-2 |
|||
|
6. Интеллектуальная
дескрипторная информационно–поисковая система |
|||
|
7. Копирование
основных баз данных СИМ |
|||
|
8. Сделать текущей
матрицу информативностей СИМ-1 |
|||
|
9. Сделать текущей
матрицу информативностей СИМ-1 |
|||
В монографии /19/ приведен перечень этапов системно-когнитивного
анализа, которые необходимо выполнить, чтобы осуществить синтез и исследование модели
объекта управления:
¾
Когнитивная
структуризация, а затем и формализация предметной области.
¾
Ввод
данных мониторинга в базу прецедентов (обучающую выборку).
¾
Синтез
семантической информационной модели (СИМ).
¾
Оптимизация
СИМ (в случае целесообразности).
¾
Проверка
адекватности СИМ (верификация модели, измерение внутренней и внешней, дифференциальной
и интегральной валидности).
¾
Решение задач идентификации состояний объекта управления,
прогнозирование и поддержка принятия управленческих решений по управлению с применением
СИМ.
¾
Системно-когнитивный
анализ СИМ.
Важной особенностью АСК-анализа является возможность единообразной
числовой обработки разнотипных числовых и нечисловых данных. Это обеспечивается
тем, что нечисловым величинам тем же методом, что и числовым, приписываются сопоставимые
в пространстве и времени, а также между собой, количественные значения, позволяющие
обрабатывать их как числовые:
¾
на
первых двух этапах АСК-анализа числовые величины сводятся к интервальным оценкам,
как и информация об объектах нечисловой природы (фактах, событиях) (этот этап реализуется
и в методах интервальной статистики);
¾
на
третьем этапе АСК-анализа всем этим величинам по единой методике, основанной на
системном обобщении семантической теории информации /1, 18/, сопоставляются количественные
величины (имеющие смысл количества информации в признаке о принадлежности объекта
к классу), с которыми в дальнейшем и производятся все операции моделирования (этот
этап является уникальным для АСК-анализа).
Хотя система искусственного интеллекта
"Эйдос" /2/ была создана специально для решения задач распознавания в
самом широком смысле, ее применение для исследования проблем астросоциотипологии
столкнулось с требованием автоматизации расчетов при изменении числа секторов разбиения
круга зодиака. Поэтому была разработана специализированная система искусственного
интеллекта "Эйдос-астра" /3/, позволяющая осуществлять пакетное распознавание
категорий респондентов на совокупности моделей с применением пяти алгоритмов "голосования"
/15/.