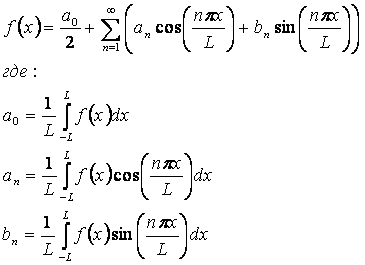
ГЛАВА 2.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ И ТЕХНОЛОГИЯ ПРИМЕНЕНИЯ АВТОМАТИЗИРОВАННОГО СИСТЕМНО-КОГНИТИВНОГО АНАЛИЗА

 

2.1. Теоретические предпосылки СК-анализа

Системно-когнитивный анализ представляет собой системный анализ, рассматриваемый как метод познания и структурированный по базовым когнитивным (познавательным) операциям (БКОСА) [5, 100].

Сам набор БКОСА следует из предложенной в [5] формализуемой когнитивной концепции, рассматривающей процесс познания, как многоуровневую иерархическую систему обработки информации в которой когнитивные структуры каждого уровня являются результатом интеграции структур предыдущего уровня.

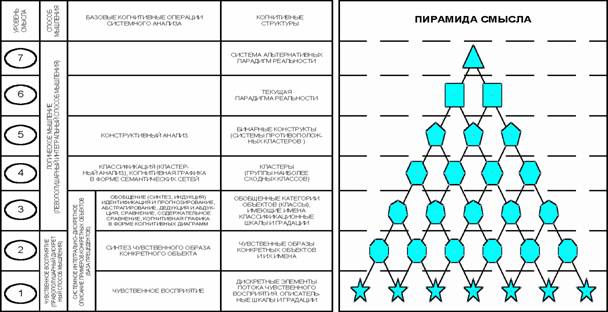
На 1-м уровне этой системы находятся дискретные элементы потока чувственного восприятия, которые на 2-м уровне интегрируются в чувственный образ конкретного объекта. Те, в свою очередь, на 3-м уровне интегрируются в обобщенные образы классов и факторов, образующие на 4-м уровне кластеры, а на 5-м конструкты. Система конструктов на 6-м уровне образуют текущую парадигму реальности (т.е. человек познает мир путем синтеза и применения конструктов). На 7-м же уровне обнаруживается, что текущая парадигма не единственно-возможная (рисунок 5).

Ключевым для когнитивной концепции является понятие факта, под которым понимается соответствие дискретного и интегрального элементов познания (т.е. элементов разных уровней интеграции-иерархии), обнаруженное на опыте. Факт рассматривается как квант смысла, что является основой для его формализации.

Таким образом, происхождение смысла связывается со своего рода "разностью потенциалов", существующей между смежными уровнями интеграции-иерархии обработки информации в процессах познания. В полном виде когнитивная концепция приведена в работах 1-5 основного списка литературы.

Рисунок 5. Обобщенная схема формализуемой когнитивной концепции
(иерархия базовых когнитивных операций)

 

Из данной концепции выводятся структура когнитивного конфигуратора, система базовых когнитивных операций и обобщенная схема автоматизированного системного анализа, структурированного до уровня базовых когнитивных операций (СК-анализ) (рисунок 6).

Между когнитивными структурами разных уровней иерархии существует отношение "дискретное – интегральное". Именно это служит основой формализации смысла.

Когнитивный конфигуратор, представляет собой минимальную полную систему когнитивных операций, названных "базовые когнитивные операции системного анализа" (БКОСА). Всего выявлено 10 таких операций, каждая из которых достаточно элементарна для формализации и программной реализации:

1) присвоение имен;

2) восприятие;

3) обобщение (синтез, индукция);

4) абстрагирование;

5) оценка адекватности модели;

6) сравнение, идентификация и прогнозирование;

7) дедукция и абдукция;

8) классификация и генерация конструктов;

9) содержательное сравнение;

10) планирование и принятие решений об управлении.

В работе [5] предложены математическая модель, методика счисленных расчетов, включающая структуры данных и алгоритмы реализации БКОСА, а также программный инструментарий СК-анализа – универсальная когнитивная аналитическая система "Эйдос".

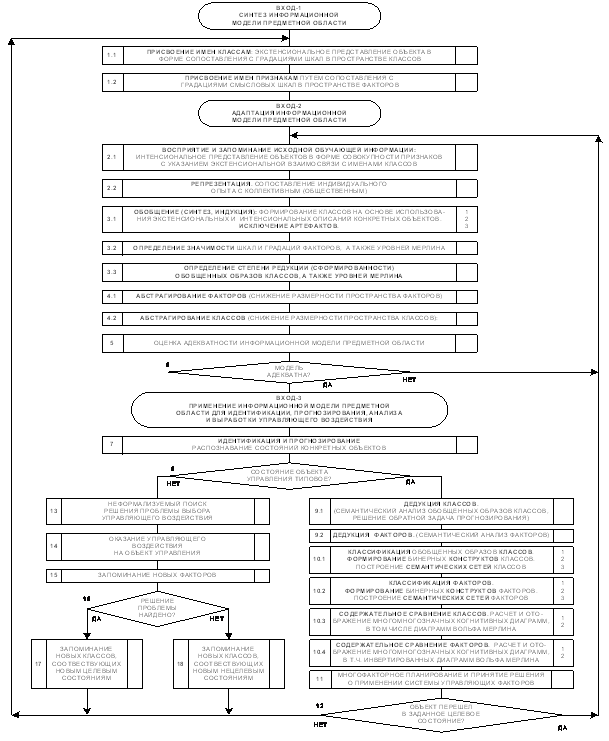
Рисунок 6. Обобщенная схема

системно-когнитивного анализа (СК-анализа)

2.2. Математическая модель АСК-анализа: системная теория информации (СТИ)

В работах [5, 66, 110, 112-114, 122-126, 132, 138, 154, 203-208, 215] предложена и развита программная идея системного обобщения математики путем тотальной замены понятия множества на более общее и содержательное понятие системы и тщательное прослеживания всех последствий этого во всех понятиях математики, основанных на понятии множества. Частично эта идея была реализована при разработке автоматизированного системно-когнитивного анализа (АСК-анализа) [5], математическая модель которого основана на системном обобщении формул для количества информации Найквиста-Хартли и Харкевича, в результате чего удалось объединить семантическую теорию информации Харкевича с теорией информации Шеннона. Полученная в результате этого обобщенная теория названа системной теорией информации (СТИ). Системное обобщение понятия функциональной зависимости рассматривается в работах [121, 122, 126, 154], в них же вводятся новые научные понятия и соответствующие термины: "когнитивные функции" и "когнитивные числа". Различные аспекты СТИ рассмотрены в работах [1-12]. Таким образом, существует много работ, в том числе монографий и учебных пособий, в которых изложена системная теория информации. Однако, как раз то, что этих работ много и они довольно объемны не вдохновляет потенциальных читателей.

Поэтому в данной работе ставится цель описать математическую суть системной теории информации на столько кратко, на сколько это вообще возможно, естественно без ущерба полноты и строгости изложения. Своеобразной "ценой" за это является то, что пришлось пожертвовать подробной смысловой интерпретацией полученных математических выражений, за которой мы отсылаем к уже упомянутым выше работам.

 

2.2.1. Системное обобщение формулы Хартли

Итак, классическая формула Хартли имеет вид:

( 1 )

Будем искать ее системное обобщение в виде:

( 2 )

где:

W – количество элементов в множестве.

j – коэффициент эмерджентности, названный автором в честь Хартли коэффициентом эмерджентности Хартли.

Примем, что системное обобщение формулы Хартли имеет вид:

( 3 )

где:

– количество подсистем и m элементов;

m – сложность подсистем;

M – максимальная сложность подсистем.

Так как , то при M=1 система переходит в множество и выражение (3) приобретает вид (1), т.е. для него выполняется принцип соответствия, являющийся обязательным для более общей теории.

Учитывая, что при M=W:

( 4 )

в этом случае получаем:

( 5 )

Выражение (5) дает приближенную оценку максимального количества информации в элементе системы. Из выражения (5) видно, что при увеличении числа элементов W количество информации I быстро стремится к W (6) и уже при W>4 погрешность выражения (5) не превышает 1%:

( 6 )

Приравняв правые части выражений (2) и (3):

( 7 )

получим выражение для коэффициента эмерджентности Хартли:

( 8 )

Смысл этого коэффициента раскрыт в работах [5, 168, 171, 172]. Здесь отметим лишь, что при M®1 когда система асимптотически переходит в множество j®1 и (2) ® (1), как и должно быть согласно принципу соответствия.

С учетом (8) выражение (2) примет вид:

( 9 )

или при M=W и больших W, учитывая (4 и 5):

( 10 )

Выражение (9) и представляет собой искомое системное обобщение классической формулы Хартли, а выражение (10) – его достаточно хорошее приближение при большом количестве элементов в системе W.

 

2.2.2. Системное обобщение формулы Харкевича

Классическая формула А.Харкевича имеет вид:

( 11 )

где: – Pij – условная вероятность перехода объекта в j-е состояние при условии действия на него i-го значения фактора;

– Pj – безусловная вероятность перехода объекта в j-е состояние (вероятность самопроизвольного перехода или вероятность перехода, посчитанная по всей выборке, т.е. при действии любого значения фактора).

Придадим выражению (11) следующий эквивалентный вид, который и будем использовать ниже:

( 12 )

где:

– индекс i обозначает признак (значение фактора): 1£ i £ M;

– индекс j обозначает состояние объекта или класс:        1£ j £ W;

– Pij – условная вероятность наблюдения i-го значения фактора у объектов в j-го класса;

– Pi – безусловная вероятность наблюдения i-го значения фактора по всей выборке.

Из (12) видно, что формула Харкевича для семантической меры информации по сути является логарифмом от формулы Байеса для апостериорной вероятности (отношение условной вероятности к безусловной). Вопрос об эквивалентности выражений (11) и (12) рассмотрим позднее.

Известно, что классическая формула Шеннона для количества информации для неравновероятных событий преобразуется в формулу Хартли при условии, что события равновероятны, т.е. удовлетворяет фундаментальному принципу соответствия. Поэтому теория информации Шеннона справедливо считается обобщением теории Хартли для неравновероятных событий. Однако, выражения  (11) и (12) при подстановке в них реальных численных значений вероятностей Pij, Pj и Pi не дает количества информации в битах, т.е. для этого выражения не выполняется принцип соответствия, обязательный для более общих теорий. Возможно, в этом состоит причина довольно сдержанного, а иногда и скептического отношения специалистов по теории информации Шеннона к семантической теории информации Харкевича.

Причину этого мы видим в том, что в выражениях (11) и (12) отсутствуют глобальные параметры конкретной модели W и M, т.е. в том, что А.Харкевич в своем выражении для количества информации не ввел зависимости от мощности пространства будущих состояний объекта W и количества значений факторов M, обуславливающих переход объекта в эти состояния.

Поставим задачу получить такое обобщение формулы Харкевича, которое бы удовлетворяло тому же самому принципу соответствия, что и формула Шеннона, т.е. преобразовывалось в формулу Хартли в предельном детерминистском равновероятном случае, когда каждому классу (состоянию объекта) соответствует один признак (значение фактора), и каждому признаку – один класс, и эти классы (а, значит и признаки), равновероятны, и при этом каждый фактор однозначно, т.е. детерминистским образом определяет переход объекта в определенное состояние, соответствующее классу.

Будем искать это обобщение (12) в виде:

( 13 )

Найдем такое выражение для коэффициента Y, названого нами в честь А.Харкевича "коэффициентом эмерджентности Харкевича", которое обеспечивает выполнение для выражения (13) принципа соответствия с классической формулой Хартли (1) и ее системным обобщением (2 и 3) в равновероятном детерминистском случае.

Для этого нам потребуется выразить вероятности Pij, Pj и Pi через частоты наблюдения признаков по классам (см. таблица 3). В таблице 3 рамкой обведена область значений, переменные определены ранее.

Таблица 3 – МАТРИЦА ЧАСТОТ

 

Классы

Сумма

1

...

j

...

W

Значения факторов

1

 

 

 

...

 

 

 

 

 

 

i

 

 

...

 

 

 

 

 

 

M

 

 

 

Суммарное

количество

признаков

 

 

 

 

Суммарное

количество

объектов

обучающей

выборки

 

 

 

 

2.2.3. Алгоритм формирования матрицы
абсолютных частот

Объекты обучающей выборки описываются векторами (массивами)   имеющихся у них признаков:

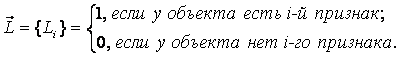
Первоначально в матрице абсолютных частот все значения равны нулю. Затем организуется цикл по объектам обучающей выборки. Если предъявленного объекта относящегося к j-му классу есть i-й признак, то:

Здесь можно провести очень интересную и важную аналогию между способом формирования матрицы абсолютных частот и работой многоканальной системы выделения полезного сигнала из шума. Представим себе, что все объекты, предъявляемые для формирования обобщенного образа некоторого класса в действительности являются различными реализациями одного объекта – "Эйдоса" (в смысле Платона), по-разному зашумленного различными случайными обстоятельствами. И наша задача состоит в том, чтобы подавить этот шум и выделить из него то общее и существенное, что отличает объекты данного класса от объектов других классов. Учитывая, что шум чаще всего является "белым" и имеет свойство при суммировании с самим собой стремиться к нулю, а сигнал при этом наоборот возрастает пропорционально количеству слагаемых, то увеличение объема обучающей выборки приводит ко все лучшему отношению сигнал/шум в матрице абсолютных частот, т.е. к выделению полезной информации из шума. Примерно так мы начинаем постепенно понимать смысл фразы, которую мы сразу не расслышали по телефону и несколько раз переспрашивали. При этом в повторах шум не позволяет понять то одну, то другую часть фразы, но в конце-концов за счет использования памяти и интеллектуальной обработки информации мы понимаем ее всю. Так и объекты, описанные признаками, можно рассматривать как зашумленные фразы, несущие нам информацию об обобщенных образах классов: "Эйдосах" [203-208], к которым они относятся. И эту информацию мы выделяем из шума при синтезе модели.

 

Для выражения (11):

( 14 )

Для выражений (12) и  (13):

( 15 )

Для выражений (11), (12) и  (13):

( 16 )

В (16) использованы обозначения:

Nij – суммарное количество наблюдений в исследуемой выборке факта: "действовало i-е значение фактора и объект перешел в j-е состояние";

Nj  – суммарное количество встреч различных факторов у объектов, перешедших в j-е состояние;

Ni  – суммарное количество встреч i-го фактора у всех объектов исследуемой выборки;

N   – суммарное количество встреч различных факторов у всех объектов исследуемой выборки.

 

2.2.4. Формирование матрицы условных
и безусловных вероятностей
(относительных частот)

На основе анализа матрицы частот (таблица 3) классы можно сравнивать по наблюдаемым частотам признаков только в том случае, если количество объектов по всем классам одинаково, как и суммарное количество признаков по классам. Если же они отличаются, то корректно сравнивать классы можно только по условным и безусловным вероятностям наблюдения признаков, посчитанных на основе матрицы частот (таблица 3) в соответствии с выражениями (14) и (15), в результате чего получается матрица условных и безусловных вероятностей (процентных распределений) (таблица 4).

 

Таблица 4 – МАТРИЦА УСЛОВНЫХ И БЕЗУСЛОВНЫХ ВЕРОЯТНОСТЕЙ

 

Классы

Безусловная

вероятность

признака

1

...

j

...

W

Значения факторов

1

 

 

 

...

 

 

 

 

 

 

i

 

 

...

 

 

 

 

 

 

M

 

 

 

Безусловная

вероятность

класса

 

 

 

 

 

 

При расчете матрицы условных и безусловных вероятностей Nj из таблицы 3 могут браться либо из предпоследней, либо из последней строки. В 1-м случае Nj  представляет собой "Суммарное количество признаков у всех объектов, использованных для формирования обобщенного образа j-го класса", а во 2-м случае, это "Суммарное количество объектов обучающей выборки, использованных для формирования обобщенного образа j-го класса", соответственно получаем различные, хотя и очень сходные семантические информационные модели, которые мы называем СИМ-1 и СИМ-2. Оба этих вида моделей поддерживаются системой "Эйдос".

 

Эквивалентность выражений (11) и (12) устанавливается, если подставить в них выражения вероятности Pij, Pj и Pi  через частоты наблюдения признаков по классам из (14), (15) и (16). В обоих случаях из выражений (11) и (12) получается одно и тоже выражение (17):

( 17 )

А из (13) выражение (18), с которым мы и будем далее работать.

( 18 )

При взаимно-однозначном соответствии классов и признаков в равновероятном детерминистском случае имеем (таблица 5):

 

Таблица 5 – МАТРИЦА ЧАСТОТ В РАВНОВЕРОЯТНОМ ДЕТЕРМИНИСТСКОМ СЛУЧАЕ

 

Классы

Сумма

1

...

j

...

W

Значения факторов

1

1

 

 

 

 

1

...

 

1

 

 

 

1

i

 

 

1

 

 

1

...

 

 

 

1

 

1

M

 

 

 

 

1

1

Сумма

1

1

1

1

1

N

 

В этом случае к каждому классу относится один объект, имеющий единственный признак. Откуда получаем для всех i и j (19):

( 19 )

Таким образом, обобщенная формула А.Харкевича (18) с учетом (19) в этом случае приобретает вид:

( 20 )

откуда:

( 21 )

или, учитывая выражение для коэффициента эмерджентности Хартли (8):

( 22 )

Подставив коэффициент эмерджентности А.Харкевича (21) в выражение (18), получим:

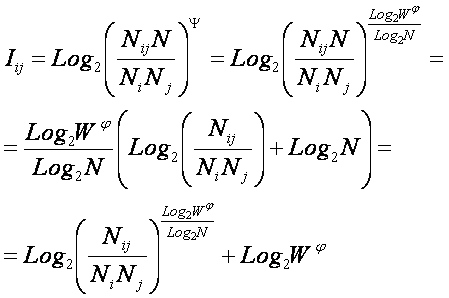
или окончательно:

( 23 )

Отметим, что 1-я задача получения системного обобщения формул Хартли и Харкевича и 2-я задача получения такого обобщения формулы Харкевича, которая удовлетворяет принципу соответствия с формулой Хартли – это две разные задачи. 1-я задача является более общей и при ее решении, которое приведено выше, автоматически решается и 2-я задача, которая является, таким образом, частным случаем 1-й.

Однако, представляет самостоятельный интерес и частный случай, в результате которого получается формула Харкевича удовлетворяющая в равновероятном детерминистском случае принципу соответствия с классической формулой Хартли (1), а не с ее системным обобщением (2) и (3). Ясно, что эта формула получается из (23) при j=1.

( 24 )

Из выражений (21) и (22) видно, что в этом частном случае, т.е. когда система эквивалентна множеству (M=1), коэффициент эмерджентности А.Харкевича приобретает вид:

( 25 )

На практике для численных расчетов на удобнее пользоваться не выражениями (23) или (24), а формулой (26), которая получается непосредственно из (18) после подстановки в него выражения (25):

( 26 )

 

В классическом анализе Шеннона идет речь лишь о передаче символов по одному информационному каналу от одного источника к одному приемнику. Его интересует прежде всего передача самого сообщения.

В данной работе ставится другая задача: идентифицировать или распознать информационный источник по сообщению от него. Поэтому метод Шеннона был обобщен путем учета в математической модели возможности существования многих источников информации, о которых к приемнику по зашумленному каналу связи приходят не отдельные символы-признаки, а сообщения, состоящие из последовательностей символов (признаков) любой длины.

Следовательно, ставится задача идентификации информационного источника по сообщению от него, полученному приемником по зашумленному каналу. Метод, являющийся обобщением метода К.Шеннона, позволяет применить классическую теорию информации для построения моделей систем распознавания образов и принятия решений, ориентированных на применение для синтеза адаптивных АСУ сложными объектами.

Для решения поставленной задачи необходимо вычислять не средние информационные характеристики, как в теории Шеннона, а количество информации, содержащееся в конкретном i-м признаке (символе) о том, что он пришел от данного j-го источника информации. Это позволит определить и суммарное количество информации в сообщении о каждом информационном источнике, что дает интегральный критерий для идентификации или прогнозирования состояния объекта.

Логично предположить, что среднее количество информации, содержащейся в системе признаков о системе классов

( 27 )

является ничем иным, как усреднением (с учетом условной вероятности наблюдения) "индивидуальных количеств информации", которые содержатся в конкретных признаках о конкретных классах (источниках), т.е.:

( 28 )

Это выражение определяет так называемую "плотность информации", т.е. количество информации, которое содержится в одном отдельно взятом факте наблюдения i-го символа (признака) на приемнике о том, что этот символ (признак) послан j-м источником.

Если в сообщении содержится M символов, то суммарное количество информации о принадлежности данного сообщения j-му информационному источнику (классу) составляет:

( 29 )

Необходимо отметить, что применение сложения в выражении (29) является вполне корректным и оправданным, так как информация с самого начала вводилась как аддитивная величина, для которой операция сложения является корректной.

Преобразуем выражение (29) к виду, более удобному для применения на практике для численных расчетов. Для этого традиционным для теории информации Шеннона способом выразим вероятности встреч признаков через частоты их наблюдения:

( 30 )

Подставив (30) в (29), получим:

( 31 )

Если ранжировать классы в порядке убывания суммарного количества информации о принадлежности к ним, содержащейся в данном сообщении (т.е. описании объекта), и выбирать первый из них, т.е. тот, о котором в сообщении содержится наибольшее количество информации, то мы получим обоснованную статистическую процедуру, основанную на классической теории информации, оптимальность которой доказывается в фундаментальной лемме Неймана-Пирсона [5, 45].

Подставим значения вероятностей из (30) в (28) и получим выражением для плотности информации Шеннона, выраженное не через вероятности, а через частоты наблюдения символов, которые рассматриваются как признаки объектов, т.е. количество информации, содержащееся в отдельном i-м признаке о том, что другом конце канала связи находится j-й объект (32):

( 32 )

Сравнивая выражения (23) и (32) видим, что в системном обобщении формулы Харкевича 1-е слагаемое практически тождественно выражению Шеннона для плотности информации, а 2-е слагаемое представляющем собой плотность информации по Хартли.

 Различия состоят в том, что в выражении (23) это слагаемое возведено в степень, имеющую смысл коэффициента эмерджентности Харкевича. Поэтому вполне оправданным называть это слагаемое не коэффициентом эмерджентности Харкевича, а коэффициентом эмерджентности Шеннона-Харкевича. Необходимо отметить также, что значения частот в этих формулах связаны с вероятностями несколько различным образом (выражения 14-16 и 30).

Из этого следует также, что полученное выражение (23) представляет собой нелинейную суперпозицию выражений для плотности информации Шеннона и Хартли, и, таким образом, является  обобщающим выражением для плотности информации, которое при различных условиях асимптотически переходит в классические выражения Хартли и Харкевича, а от выражения Шеннона отличается лишь константой, т.е. 2-м слагаемым, характеризующим мощность множества состояний объекта в модели.

Это позволяет нам обоснованно высказать гипотезу о том, что системная теория информации (СТИ), базирующаяся на выражении (23) для плотности информации, является более общей, чем теории Хартли, Шеннона и Харкевича и асимптотически связана с ними через принцип соответствия (рисунок 7).

 

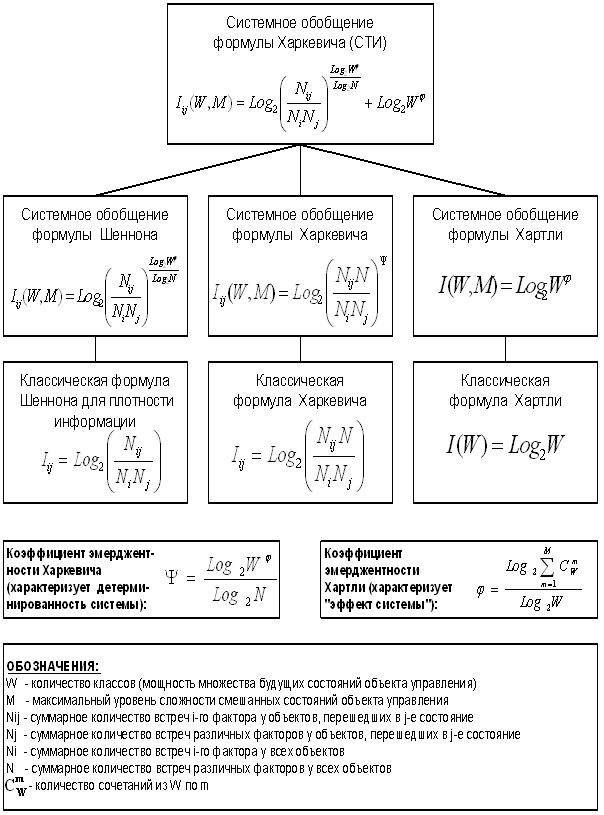
Рисунок 7. Генезис системной (эмерджентной)
теории информации

 

 

 

2.2.5. Взаимосвязь системной меры
целесообразности информации
со статистикой c2 и новая мера
уровня системности предметной области

Статистика c2 представляет собой сумму вероятностей совместного наблюдения признаков и объектов по всей корреляционной матрице или определенным ее подматрицам (т.е. сумму относительных отклонений частот совместного наблюдения признаков и объектов от среднего):

,

( 33 )

где

 Nij – фактическое количество встреч i-го признака у объектов j-го класса;

 t    –  ожидаемое количество встреч i-го признака у объектов j-го класса (34).

.

( 34 )

Отметим, что статистика c2 математически связана с количеством информации в системе признаков о классе распознавания в соответствии с системным обобщением формулы Харкевича для плотности информации (18):

,

( 35 )

а именно, из (34) и (35) получаем:

.

( 36 )

Из (36) очевидно:

.

( 37 )

Сравнивая выражения (33) и (37), видим, что числитель в выражении (33) под знаком суммы отличается от выражения (37) только тем, что в выражении (37) вместо значений Nij и t взяты их логарифмы. Так как логарифм является монотонно возрастающей функцией аргумента, то введение логарифма не меняет общего характера поведения функции.

Фактически это означает, что:

.

( 38 )

Из изложенного следует интерпретация системной меры информации (35) с учетом статистики c2 (33): если фактическая вероятность наблюдения i-го при­знака при предъявлении объекта j-го класса равна ожидаемой (средней), то наблюдение этого признака не несет никакой информации о принадлежности объекта к данному классу. Если она выше средней, то это свидетельствует в пользу того, что предъявлен объект данного класса, если  ниже – то другого.

Поэтому наличие статистической связи (информации) между признаками и классами распознавания, т.е. отличие вероятностей их совместных наблюдений от предсказываемого в соответствии со случайным нормальным распределением, приводит к увеличению фактической статистики c2 по сравнению с теоретической величиной.

Из этого следует возможность использования в качестве количественной меры степени выраженности закономерностей в предметной области не матрицы абсолютных частот и меры c2, а новой меры H, основанной на матрице информативностей и системном обобщении формулы Харкевича для количества информации:

,

( 39 )

где

– средняя информативность признаков по матрице информативностей.

Меру H в выражении (39) предлагается назвать обобщенным критерием степени сформированности модели Харкевича.

Значение данной меры показывает среднее отличие количества информации в факторах о будущих состояниях активного объекта управления от среднего количества информации в факторе (которое при больших выборках близко к 0). По своей математической форме эта мера сходна с мерами для значимости (интегральной информативности) факторов и степени сформированности образов классов и коррелирует с объемом неортонормированного семантического информационного пространства классов и семантического информационного пространства атрибутов.

Вышеописанная математическая модель обеспечивает инвариантность результатов ее синтеза относительно следующих параметров обучающей выборки: суммарное количество и порядок ввода анкет обучающей выборки; количество анкет обучающей выборки по каждому классу распознавания; суммарное количество признаков во всех анкетах обучающей выборки; суммарное количество признаков по классам распознавания; количество признаков и их порядок в отдельных анкетах обучающей выборки. Это обеспечивает высокую степень качества решения задач распознавания на неполных и разнородных (в вышеперечисленных аспектах) данных как обучающей, так и распознаваемой выборки, т.е. при таких статистических характеристиках потоков этих данных, которые чаще всего и встречается на практике и которыми невозможно или очень сложно управлять.

 

2.2.6. Получение матрицы знаний
(информативностей)

На основе анализа матрицы условных и безусловных вероятностей (таблица 4) наблюдений признаков по классам и всей выборке можно сравнивать признаки друг с другом по их роли для сравнения классов друг с другом и конкретных объектов с обобщенными классами. При этом существует 3 основных группы признаков:

Группа 1-я. Которые в одном классе встречаются, а в других нет. Это детерминистские признаки, обнаружение такого признака у объекта однозначно определяет его принадлежность к соответствующему классу.

Группа 2-я. Которые в одном классе встречаются чаще, чем в других. Это статистические признаки, обнаружение такого признака у объекта несет некоторую информацию о его принадлежности к соответствующему классу.

Группа 3-я. Которые в разных классах встречаются одной и той же вероятностью. Это признаки, обнаружение которых у объекта не несет никакой информации о его принадлежности к тем или иным классам.

Таким образом мы видим, что если используя таблицу 4 анализировать условные вероятности (или процентные распределения) признаков по классам, то можно вынести правдоподобные суждения о принадлежности объектов, обладающих этими признакам к тем или иным классам.

Однако в таком методе сравнения есть по крайней мере два существенных недостатка:

1. Для того, чтобы отнести признак к одной из вышеперечисленных групп необходимо сравнивать вероятности его наблюдения по классам, т.е. каждый раз при таком сравнении выполнять соответствующую необходимую для этого работу.

2. При отнесении признака ко 2-й группе этого самого по себе еще недостаточно для его использования с целью идентификации объекта, а необходимо еще оценить количество информации, которое содержится в факте обнаружения у объекта этого признака о принадлежности этого объекта к каждому из классов, а для этого необходим соответствующий математический и численный метод.

Что касается 1-го недостатка, то о нем можно сказать, что для реальных задач большой размерности выполнение этого сравнения вручную практически невозможно, а значит тем более невозможно и использование результатов этого сравнения для решения задач идентификации, прогнозирования и поддержки принятия решений, а тем более для исследования предметной области путем исследования ее модели. Все это обусловлено тем, что результат сравнения вероятностей встречи признака по классам не представляется при ручной обработке в количественной форме некоторого одного числа: частного критерия, величина и знак которого отражали бы результат такого сравнения.

2-й недостаток преодолевается методом, который предложен А.Харкевичем в выражениях (11) и (12) и уточнен нами в системном обобщении этих выражений (18). В этом методе предложено сравнивать не условные вероятности наблюдения признаков по различным классам друг с другом, а условную вероятность наблюдения признака по классу с безусловной вероятностью его наблюдения по всей выборке.

Это предложение по своей сути полностью соответствует известному статистическому методу отклонений от средних и нормативному подходу, когда в качестве базы сравнения выбирается норма, т.е. среднее по всей группе. На основе этого подхода формируются и критерии сравнения, т.е. можно сказать, что критериальный подход изначально основан на нормативном.

Если такое сравнение провести по всем признакам и классам, то получится матрица, снимающая оба указанных недостатка: используя выражение (18) и данные таблицы 3 непосредственно прямым счетом получаем матрицу знаний (таблица 6):

 

Таблица 6 – МАТРИЦА ЗНАНИЙ (ИНФОРМАТИВНОСТЕЙ)

 

Классы

Значимость

фактора

1

...

j

...

W

Значения факторов

1

 

 

...

 

 

 

 

 

 

i

 

 

...

 

 

 

 

 

 

M

 

 

Степень

редукции

класса

s1

 

sj

 

sW

Здесь – это среднее количество знаний в i-м значении фактора:

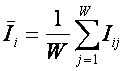
При расчете матрицы знаний Nj из таблицы 3 могут браться либо из предпоследней, либо из последней строки. В 1-м случае Nj представляет собой "Суммарное количество признаков у всех объектов, использованных для формирования обобщенного образа j-го класса", а во 2-м случае, это "Суммарное количество объектов обучающей выборки, использованных для формирования обобщенного образа j-го класса", соответственно получаем различные, хотя и очень сходные семантические информационные модели, которые мы называем СИМ-1 и СИМ-2. Оба этих вида моделей поддерживаются системой "Эйдос".

 

Количественные значения коэффициентов Iij таблицы 6 являются знаниями о том, что "объект перейдет в j-е состояние" если "на объект действует i-е значение фактора".

Принципиально важно, что эти весовые коэффициенты не определяются экспертами на основе опыта интуитивным неформализуемым способом, а рассчитываются непосредственно на основе эмпирических данных на основе теоретически обоснованной модели, хорошо зарекомендовавшей себя на практике при решении широкого круга задач в различных предметных областях.

Когда количество информации Iij>0 – i–й фактор способствует переходу объекта управления в j-е состояние, когда Iij<0 – препятствует этому переходу, когда же Iij=0 – никак не влияет на это. В векторе i-го фактора (строка матрицы информативностей) отображается, какое количество информации о переходе объекта управления в каждое из будущих состояний содержится в том факте, что данный фактор действует. В векторе j-го состояния класса (столбец матрицы информативностей) отображается, какое количество информации о переходе объекта управления в соответствующее состояние содержится в каждом из факторов.

Таким образом, матрица знаний (информативностей) (таблица 6) является обобщенной таблицей решений, в которой входы (факторы) и выходы (будущие состояния объекта управления) связаны друг с другом не с помощью классических (Аристотелевских) импликаций, принимающих только значения: "Истина" и "Ложь", а различными значениями истинности, выраженными в битах и принимающими значения от положительного теоретически-максимально-возможного ("Максимальная степень истинности"), до теоретически неограниченного отрицательного ("Степень ложности").

Фактически предложенная модель позволяет осуществить синтез обобщенных таблиц решений для различных предметных областей непосредственно на основе эмпирических исходных данных и продуцировать на их основе прямые и обратные правдоподобные (нечеткие) логические рассуждения по неклассическим схемам с различными расчетными значениями истинности, являющимся обобщением классических импликаций.

Таким образом данная модель позволяет рассчитать какое количество информации содержится в любом факте о наступлении любого события в любой предметной области, причем для этого не требуется повторности этих фактов и событий. Если же эти повторности осуществляются и при этом наблюдается некоторая вариабельность значений факторов, обуславливающих наступление тех или иных событий, то модель обеспечивает многопараметрическую типизацию, т.е. синтез обобщенных образов классов или категорий наступающих событий с количественной оценкой степени и знака влияния на их наступление различных значений факторов. Причем эти значения факторов могут быть как количественными, так и качественными и измеряться в любых единицах измерения, в любом случае в модели оценивается количество информации которое в них содержится о наступлении событий, переходе объекта управления в определенные состояния или просто о его принадлежности к тем или иным классам.

 

2.2.7. Решение задач идентификации
(распознавания образов), прогнозирования
и поддержки принятия решений

Данная модель позволяет прогнозировать поведение объекта управления при воздействии на него не только одного, но и целой системы факторов:

( 40 )

В теории принятия решений скалярная функция Ij векторного аргумента называется интегральным критерием. Основная проблема состоит в выборе такого аналитического вида функции интегрального критерия, который обеспечил бы эффективное решение сформулированной выше задачи АСУ.

Учитывая, что частные критерии (18) имеют смысл количества информации, а информация по определению является аддитивной функцией, предлагается ввести интегральный критерий, как аддитивную функцию от частных критериев в виде:

( 41 )

В выражении (41) круглыми скобками обозначено скалярное произведение, т.е. свертка. В координатной форме это выражение имеет вид:

,

( 42 )

где:

– вектор j-го класса-состояния объекта управления;

 – вектор состояния предметной области, включающий все виды факторов, характеризующих объект управления, возможные управляющие воздействия и окружающую среду (массив-локатор), т.е.:

В реализованной модели значения координат вектора состояния предметной области принимались равными либо 1 (фактор действует), либо 0 (фактор не действует).

Таким образом, интегральный критерий представляет собой суммарное количество информации, содержащееся в системе значений факторов различной природы (т.е. факторах, характеризующих объект управления, управляющее воздействие и окружающую среду) о переходе объекта управления в то или иное будущее состояние.

В многокритериальной постановке задача прогнозирования состояния объекта управления, при оказании на него заданного многофакторного управляющего воздействия Ij, сводится к максимизации интегрального критерия:

( 43 )

т.е. к выбору такого состояния объекта управления, для которого интегральный критерий максимален.

Задача принятия решения о выборе наиболее эффективного управляющего воздействия является обратной задачей по отношению к задаче максимизации интегрального критерия (идентификации и прогнозирования), т.е. вместо того, чтобы по набору факторов прогнозировать будущее состояние объекта, наоборот, по заданному (целевому) состоянию объекта определяется такой набор факторов, который с наибольшей эффективностью перевел бы объект управления в это состояние.

Предлагается еще одно обобщение фундаментальной леммы Неймана-Пирсона, основанное на косвенном учете корреляций между информативностями в векторе состояний при использовании средних по векторам. Соответственно, вместо простой суммы количеств информации предлагается использовать корреляцию между векторами состояния и объекта управления, которая количественно измеряет степень сходства этих векторов:

( 44 )

где:

  – средняя информативность по вектору класса;

  – среднее по вектору идентифицируемой ситуации (объекта).

– среднеквадратичное отклонение информативностей вектора класса;

         – среднеквадратичное отклонение по вектору распознаваемого объекта.

Выражение (44) получается непосредственно из (42) после замены координат перемножаемых векторов их стандартизированными значениями:

Необходимо отметить, что выражение для интегрального критерия сходства (42) по своей математической форме является корреляцией двух векторов. Это означает, что если эти вектора являются суммой двух сигналов: полезного и белого шума, то при расчете интегрального критерия белый шум практически не будет играть никакой роли, т.е. его корреляция с самими собой равна нулю по определению. Поэтому интегральный критерий сходства объекта со случным набором признаков с любыми образами классов, или реального объекта с образами классов, сформированными случайным образом, будет равен нулю. Это означает, что выбранный интегральный критерий сходства является высокоэффективным средством подавления белого шума и выделения полезной информации из шума, который неизбежно присутствует в эмпирических данных.

Важно также отметить неметрическую природу предложенного интегрального критерия сходства, благодаря чему его применение является корректным и при неортонормированном семантическом информационном пространстве, каким оно в подавляющем количестве случае и является, т.е. в общем случае.

Результат прогнозирования поведения объекта управления, описанного данной системой факторов, представляет собой список его возможных будущих состояний, в котором они расположены в порядке убывания суммарного количества информации о переходе объекта управления в каждое из них.

 

2.2.8. Сравнение, идентификация
и прогнозирование как разложение векторов
объектов в ряд по векторам классов
(объектный анализ)

Выше были введены неметрические интегральные критерии сходства объекта, описанного массивом-локатором Li с обобщенными образами классов Iij (выражения 40-42).

Для непрерывного случая выражение (42) принимает вид:

.

( 45 )

Таким образом, выражение (45) представляет собой обобщение интегрального критерия сходства конкретного объекта и обобщенного класса (42) для непрерывного случая в координатной форме.

Отметим, что коэффициенты ряда Фурье (24) по своей математической форме и смыслу сходны с ненормированными коэффициентами корреляции, т.е. по сути скалярными произведениями для непрерывных функций в координатной форме: выражением (45) между разлагаемой в ряд кривой f(x) и функциями Sin и Сos различных частот и амплитуд [5].

,

( 46 )

где  n={1, 2, 3,…} – натуральное число.

Из сравнения выражений (45) и (46) следует вывод о том, что процесс идентификации и прогнозирования (распознавания), реализованный в предложенной математической модели, может рассматриваться как разложение вектора-локатора распознаваемого объекта в ряд по векторам информативностей классов распознавания (которые представляют собой произвольные функции, сформированные при синтезе модели путем многопараметрической типизации на основе эмпирических данных).

Например, результаты идентификации представим на рисунке 8:

 

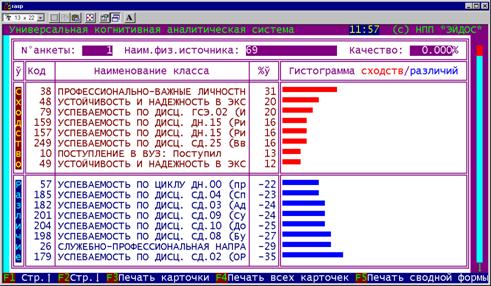
Рисунок 8. Пример разложения профиля курсанта усл.№69
в ряд по обобщенным образам классов

 

Продолжая развивать аналогию с разложением в ряд, данный результат идентификации можно представить в векторной аналитической форме:

или в координатной форме, более удобной для численных расчетов:

,

( 47 )

Предполагается, что . Таким образом массив-локатор, характеризующий распознаваемый объект, рассматривается как сумма произведений профилей классов на интегральный критерий сходства массива-локатора с этими профилями (т.е. взвешенная суперпозиция или разложение в ряд по профилям классов).

В выражении (47):

I(j) – интегральный критерий сходства массива-локатора, описывающего состояние объекта и j-го класса, рассчитываемый, согласно выражений (42) или (44):

( 48 )

I(i,j) – вектор обобщенного образа j-го класса, координаты которого рассчитываются в соответствии с системным обобщением формулы Харкевича (18):

.

( 49 )

Примечание: обозначения I(i,j) и Iij, и т.п. эквивалентны. Смысл всех переменных, входящих в выражения (48) и (49) раскрыт выше.

При дальнейшем развитии данной аналогии естественно возникают вопросы: о полноте, избыточности и ортонормированности системы векторов классов как функций, по которым проводится разложение вектора объекта; о сходимости, т.е. вообще возможности и корректности такого разложения.

В общем случае вектор объекта совершенно не обязательно должен разлагаться в ряд по векторам классов таким образом, что сумма ряда во всех точках точно совпадала со значениями исходной функции. Это означает, что система векторов классов может быть неполна по отношению к профилю распознаваемого объекта, и, тем более, всех возможных объектов.

Предлагается считать не разлагаемые в ряд, т.е. плохо распознаваемые объекты, суперпозицией хорошо распознаваемых объектов ("похожих" на те, которые использовались для формирования обобщенных образов классов), и объектов, которые и не должны распознаваться, так как объекты этого типа не встречались в обучающей выборке и не использовались для формирования обобщенных образов классов, а также не относятся к представляемой обучающей выборкой генеральной совокупности.

Нераспознаваемую компоненту можно рассматривать либо как шум, либо считать ее полезным сигналом, несущим ценную информацию о неисследованных объектах интересующей нас предметной области (в зависимости от целей и тезауруса исследователей). Первый вариант не приводит к осложнениям, так как примененный в математической модели алгоритм сравнения векторов объектов и классов, основанный на вычислении нормированной корреляции Пирсона (сумма произведений), является весьма устойчивым к наличию белого шума в идентифицируемом сигнале. Во втором варианте необходимо дообучить систему распознаванию объектов, несущих такую компоненту (в этой возможности и заключается адаптивность модели). Технически этот вопрос решается просто копированием описаний плохо распознавшихся объектов из распознаваемой выборки в обучающую, их идентификацией экспертами и дообучением системы. Кроме того, может быть целесообразным расширить справочник классов распознавания новыми классами, соответствующими этим объектам, и осуществить пересинтез модели.

Однако на практике гораздо чаще наблюдается противоположная ситуация (можно даже сказать, что она типична), когда система векторов избыточна, т.е. в системе классов распознавания есть очень похожие классы (между которыми имеет место высокая корреляция, наблюдаемая в режиме: "кластерно-конструктивный анализ"). Практически это означает, что в системе сформировано несколько практически одинаковых образов с разными наименованиями. Для исследователя это само по себе является очень ценной информацией. Однако если исходить только из потребности разложения распознаваемого объекта в ряд по векторам классов (чтобы определить суперпозицией каких образов он является, т.е. "разложить его на компоненты"), то наличие сильно коррелирующих друг с другом векторов представляется неоправданным, так как просто увеличивает размерности данных, внося в них мало нового по существу. Поэтому возникает задача исключения избыточности системы классов распознавания, т.е. выбора из всей системы классов распознавания такого минимального их набора, в котором профили классов минимально коррелируют друг с другом, т.е. ортогональны в фазовом пространстве признаков. Это условие в теории рядов называется "ортонормируемостью" системы базовых функций, а в факторном анализе связано с идеей выделения "главных компонент".

В предлагаемой математической модели реализованы два варианта выхода из данной ситуации:

1) исключение неформирующихся, расплывчатых классов;

2) объединение почти идентичных по содержанию (дублирующих друг друга) классов.

Однако выбрать нужный вариант и реализовать его, используя соответствующие режимы, пользователь технологии АСК-анализа должен сам. Вся необходимая и достаточная информация для принятия соответствующих решений предоставляется пользователю инструментария АСК-анализа.

Если считать, что функции образов составляют формально-логическую систему, к которой применима теорема Геделя, то можно сформулировать эту теорему для данного случая следующим образом: "Для любой системы базисных функций в принципе всегда может существовать по крайней мере одна такая функция, что она не может быть разложена в ряд по данной системе базисных функций, т.е. функция, которая является ортонормированной ко всей системе базисных функций в целом". Поэтому для адекватного отражения подобных функций в модели необходимо повышение размерности семантического информационного пространства.

Очевидно, не взаимосвязанными друг с другом могут быть только четко оформленные, детерминистские образы, т.е. образы с высокой степенью редукции ("степень сформированности конструкта"). Поэтому в процессе выявления взаимно-ортогональных базисных образов, в первую очередь, будут выброшены аморфные "расплывчатые" образы, которые связаны практически со всеми остальными образами.

В некоторых случаях результат такого процесса представляет интерес, и это делает оправданным его реализацию. Однако можно предположить, что наличие расплывчатых образов в системе является оправданным, так как в этом случае система образов не будет формальной и подчиняющейся теореме Геделя. Следовательно, система распознавания будет более полна в том смысле, что увеличится вероятность идентификации любого объекта, предъявленного ей на распознавание. Конечно, уровень сходства с аморфным образом не может быть столь высоким, как с четко оформленным. Поэтому в этом случае более уместно применить термин "ассоциация" или нечеткая, расплывчатая идентификация, чем "однозначная идентификация".

Итак, можно сделать следующий вывод: допустимость в математической модели СК-анализа не только четко оформленных (детерминистских) образов, но и образов аморфных, нечетких, расплывчатых является важным достоинством данной модели. Это обусловлено тем, что данная модель обеспечивает корректные результаты анализа, идентификации и прогнозирования даже в тех случаях, когда модели идентификации и информационно-поисковые системы детерминистского типа традиционных АСУ практически неработоспособны. В этих условиях данная модель СК-анализа работает как система ассоциативной (нечеткой) идентификации.

Таким образом, в предложенной семантической информационной модели при идентификации и прогнозировании, по сути, осуществляется разложение векторов идентифицируемых объектов по векторам классов распознавания, т.е. осуществляется "объектный анализ" (по аналогии с спектральным, гармоническим или Фурье-анализом), что позволяет рассматривать идентифицируемые объекты как суперпозицию обобщенных образов классов различного типа с различными амплитудами (25). При этом вектора обобщенных образов классов, с математической точки зрения, представляют собой произвольные функции и не обязательно образуют полную и не избыточную (ортонормированную) систему функций.

Для любого объекта всегда существует такая система базисных функций, что вектор объекта может быть представлен в форме линейной суперпозиции (суммы) этих базисных функций с различными амплитудами. Это утверждение, по-видимому, является одним из следствий фундаментальной теоремы А.Н. Колмогорова, доказанной им в 1957 году (О представлении непрерывных функций нескольких переменных в виде суперпозиций непрерывных функций одного переменного и сложения // Докл. АН СССР, Т. 114, С. 953–956, 1957).

Теорема Колмогорова: Любая непрерывная функция от n переменных F(x1, x2,..., xn) может быть представлена в виде:

,

где gj и hij – непрерывные функции, причем hij не зависят от функции F.

Эта теорема означает, что для реализации функций многих переменных достаточно операций суммирования и композиции функций одной переменной. Удивительно, что в этом представлении лишь функции gj зависят от представляемой функции F, а функции hij универсальны. Необходимо отметить, что теорема Колмогорова является обобщением теоремы В.И. Арнольда (1957), которая дает решение 13-й проблемы Гильберта.

К сожалению,  определение вида функций hij и gj для данной функции F представляет собой математическую проблему, для которой пока не найдено общего строгого решения.

В данной работе предлагается рассматривать предлагаемую семантическую информационную модель как один из вариантов решения этой проблемы. В этом контексте функция F интерпретируется как образ идентифицируемого объекта, функция hij – образ j-го класса, а функция gj –  мера сходства образа объекта с образом класса.

 

Таким образом В работе кратко описана математическая сущность предложенной автором системной теории информации СТИ), являющейся математической моделью системно-когнитивного анализа (СК-анализ) и реализуемой в его программном инструментарии – универсальной аналитической системе "Эйдос" [223, 224, 228].

 

2.3. Методика численных расчетов АСК-анализа

 

2.3.1. Детальный список БКОСА и их алгоритмов

В таблице 7 приведен детальный список базовых когнитивных операций системного анализа, которым соответствует 24 алгоритма, которые здесь привести нет возможности из-за их объемности. Но они все приведены в полном виде в работе [5].

 

Таблица 7 – ДЕТАЛЬНЫЙ СПИСОК БАЗОВЫХ КОГНИТИВНЫХ ОПЕРАЦИЙ СИСТЕМНОГО АНАЛИЗА (БКОСА)

№

 алгоритма

Код БКОСА

по схеме

СК-анализа

№

БКОСА

Наименование БКОСА

Полное наименование базовых когнитивных операций системного анализа (БКОСА)

 

1.1

1

Присвоение
имен

Присвоение имен классам
(интенсиональная, интегральная репрезентация)

 

1.2

Присвоение имен атрибутам
(экстенсиональная, дискретная репрезентация)

1

2.1.

2

Восприятие

Восприятие и запоминание исходной обучающей
информации

2

2.2.

Репрезентация. Сопоставление индивидуального
опыта с коллективным (общественным)

3

3.1.1.

3

Обобщение

(синтез,
индукция).

Накопление первичных данных

4

3.1.2.

Исключение артефактов

5

3.1.3.

Расчет истинности смысловых связей между
предпосылками и результатами
(обобщенных таблиц решений)

6

3.2.

Определение значимости шкал и градаций факторов, уровней Мерлина

7

3.3.

Определение значимости шкал и градаций классов, уровней Мерлина

8

4.1.

4

Абстраги-

рование

Абстрагирование факторов (снижение размерности семантического пространства факторов)

9

4.2.

Абстрагирование классов (снижение размерности семантического пространства классов)

10

5.

5

Оценка
адекватности

Оценка адекватности информационной модели
предметной области

11

7.

6

Сравнение, идентификация и прогнозирование

Сравнение, идентификация и прогнозирование. Распознавание состояний конкретных объектов (объектный анализ)

12

9.1.

7

Анализ,

дедукция
и абдукция

Анализ, дедукция и абдукция классов (семантический анализ обобщенных образов классов, решение
обратной задачи прогнозирования)

13

9.2.

Анализ, дедукция и абдукция факторов
(семантический анализ факторов)

14

10.1.1.

8

Классификация
и генерация

конструктов

Классификация обобщенных образов классов

15

10.1.2.

Формирование бинарных конструктов классов

16

10.1.3.

Визуализация семантических сетей классов

17

10.2.1.

Классификация факторов

18

10.2.2.

Формирование бинарных конструктов факторов

19

10.2.3.

Визуализация семантических сетей факторов

20

10.3.1.

9

Содержательное
сравнение

Содержательное сравнение классов

21

10.3.2.

Расчет и отображение многомногозначных когнитивных диаграмм, в т.ч. диаграмм Мерлина

22

10.4.1.

Содержательное сравнение факторов

23

10.4.2.

Расчет и отображение многомногозначных когнитивных диаграмм, в т.ч. инвертированных диаграмм Мерлина

24

11.

10

Планирование

и управление

Многовариантное планирование и принятие решения о применении системы управляющих факторов

 

 

2.3.2. Иерархическая структура данных семантической информационной модели
СК-анализа

На рисунке 9 приведена в обобщенном виде иерархическая структура баз данных семантической информационной модели системно-когнитивного анализа. На этой схеме базы данных обозначены прямоугольниками, а базовые когнитивные операции системного анализа, преобразующие одну базу в другую – стрелками с надписями. Имеются также базовые когнитивные операции, формирующие выходные графические формы. Из этой схемы видно, что одни базовые когнитивные операции готовят данные для других операций, относящихся к более высоким уровням иерархии системы процессов познания. Этим определяется возможная последовательность выполнения базовых когнитивных операций.

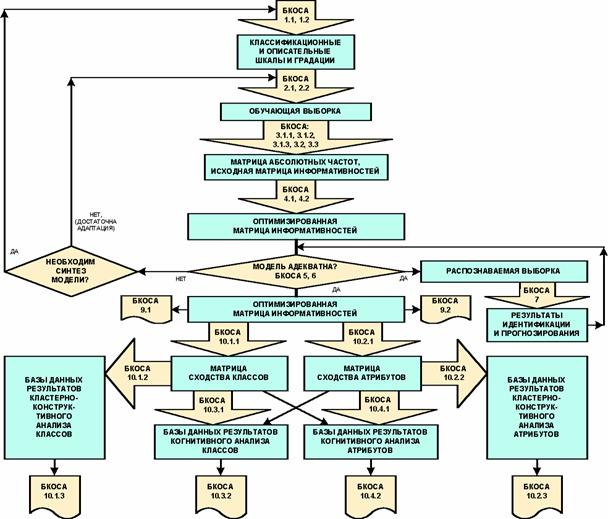
Рисунок 9. Иерархическая структура данных СК-анализа

 

2.4. Специальный программный инструментарий АСК-анализа – система "Эйдос"

 

2.4.1. Цели и основные функции системы "Эйдос"

Универсальная когнитивная аналитическая система "Эйдос" является отечественным лицензионным программным продуктом [222-236], созданным исключительно с использованием официально приобретенного лицензионного программного обеспечения. По системе "Эйдос" и различным аспектам ее применения имеется 12 научных монографий и учебных пособий с грифами УМО и министерства [1-12], а также около 200 научных публикаций ряда авторов [66-264]. Титульная видеограмма системы приведена на рисунке 10:

 

Рисунок 10. Титульная видеограмма системы "Эйдос"

 

Система "Эйдос" является одним из элементов предлагаемого решения проблемы и достижения цели данной работы, т.к. она обеспечивает решение следующих задач:

1. Синтез и адаптация семантической информационной модели предметной области, включая объект активный управления и окружающую среду.

2. Идентификация и прогнозирование состояния активного объекта управления, а также разработка управляющих воздействий для его перевода в заданные целевые состояния.

3. Углубленный анализ семантической информационной модели предметной области.

Таким образом, система "Эйдос" является инструментарием, решающим проблему данной работы.

 

2.4.1.1. Синтез содержательной информационной модели предметной области

Для разработки информационной модели предметной области необходимо владеть основными принципами ее когнитивной структуризации и формализованного описания. Синтез содержательной информационной модели включает следующие этапы:

1. Формализация (когнитивная структуризация предметной области).

2. Формирование исследуемой выборки и управление ею.

3. Синтез или адаптация модели.

4. Оптимизация модели.

5. Измерение адекватности модели (внутренней и внешней, интегральной и дифференциальной валидности), ее скорости сходимости и семантической устойчивости.

 

2.4.1.2. Идентификация и прогнозирование
состояния объекта управления,
выработка управляющих воздействий

Данный вид работ включает:

1. Ввод распознаваемой выборки.

2. Пакетное распознавание.

3. Вывод результатов распознавания и их оценку.

2.4.1.3. Углубленный анализ содержательной
информационной модели предметной
области

Углубленный анализ выполняется в подсистеме "Типология" и включает:

1. Информационный и семантический анализ классов и признаков.

2. Кластерно-конструктивный анализ классов распознавания и признаков, включая визуализацию результатов анализа в оригинальной графической форме когнитивной графики (семантические сети классов и признаков).

3. Когнитивный анализ классов и признаков (когнитивные диаграммы и диаграммы Вольфа Мерлина).

2.4.2. Обобщенная структура системы "Эйдос"

Данной обобщенной структуре соответствуют и структура управления и дерево диалога системы (таблица 8):

 

Таблица 8 – ОБОБЩЕННАЯ СТРУКТУРА СИСТЕМЫ "ЭЙДОС"
(текущей версии 12.5 от 12.10.2008)

Подсистема

Режим

Функция

Операция

1.

Формализация ПО

1. Классификационные шкалы и градации

2. Описательные шкалы (и градации)

3. Градации описательных шкал (признаки)

4. Иерархические уровни систем

1. Уровни классов

2. Уровни признаков

5. Программные интерфейсы для импорта данных

1. Импорт данных из TXT-фалов стандарта DOS-текст

2. Импорт данных из DBF-файлов стандарта проф. А.Н.Лебедева

3. Импорт из транспонированных DBF-файлов проф. А.Н.Лебедева

4. Генерация шкал и обучающей выборки RND-модели

5. Генерация шкал и обучающей выборки для исследования чисел

6. Транспонирование DBF-матриц исходных данных

7. Импорт данных из DBF-файлов стандарта Евгения Лебедева

6. Почтовая служба по НСИ

1. Обмен по классам

2. Обмен по обобщенным признакам

3. Обмен по первичным признакам

7. Печать анкеты

2.

Синтез СИМ

1. Ввод–корректировка обучающей выборки

2. Управление обучающей выборкой

1. Параметрическое задание объектов для обработки

2. Статистическая характеристика, ручной ремонт

3. Автоматический ремонт обучающей выборки

3. Синтез семантической информационной модели СИМ

1. Расчет матрицы абсолютных частот

2. Исключение артефактов (робастная процедура)

3. Расчет матрицы информативностей СИМ-1 и сделать ее текущей

4. Расчет условных процентных распределений СИМ-1 и СИМ-2

5. Автоматическое выполнение режимов 1–2–3–4

6. Сходимость и устойчивость СИМ

1. Сходимость и устойчивость СИМ

2. Зависимость валидности СИМ от объема обучающей выборки

7. Расчет матрицы информативностей СИМ-2 и сделать ее текущей

4. Почтовая служба по обучающей информации

5. Синтез СИМ и измерение ее адекватности

3.

Оптимизация СИМ

1. Формирование ортонормированного базиса классов

2. Исключение признаков с низкой селективной силой

3. Удаление классов и признаков, по которым недостаточно данных

4. Разделение классов на типичную и нетипичную части

5. Генерация сочетанных признаков и перекодирование обучающей выборки

4.

Распознавание

1. Ввод–корректировка распознаваемой выборки

2. Пакетное распознавание

3. Вывод результатов распознавания

1. Разрез: один объект – много классов

2. Разрез: один класс – много объектов

4. Почтовая служба по распознаваемой выборке

5. Построение функций влияния

6. Докодирование сочетаний признаков в распознаваемой выборке

5.

Типология

1. Типологический анализ классов распознавания

1. Информационные (ранговые) портреты (классов)

2. Кластерный и конструктивный анализ классов

1 Расчет матрицы сходства образов классов

2. Генерация кластеров и конструктов классов

3. Просмотр и печать кластеров и конструктов

4. Автоматическое выполнение режимов: 1,2,3

5. Вывод 2d семантических сетей классов

3. Когнитивные диаграммы классов

2. Типологический анализ первичных признаков

1. Информационные (ранговые) портреты признаков

2. Кластерный и конструктивный анализ признаков

1. Расчет матрицы сходства образов признаков

2. Генерация кластеров и конструктов признаков

3. Просмотр и печать кластеров и конструктов

4. Автоматическое выполнение режимов: 1,2,3

5. Вывод 2d семантических сетей признаков

3. Когнитивные диаграммы признаков

6. СК-анализ СИМ

1. Оценка достоверности заполнения объектов

2. Измерение адекватности семантической информационной модели

3. Измерение независимости классов и признаков

4. Просмотр профилей классов и признаков

5. Графическое отображение нелокальных нейронов

6. Отображение Паретто-подмножеств нейронной сети

7. Классические и интегральные когнитивные карты

7. Сервис

1. Генерация (сброс) БД

1. Все базы данных

2. НСИ

1. Всех баз данных НСИ

2. БД классов

3. БД первичных признаков

4. БД обобщенных признаков

3. Обучающая выборка

4. Распознаваемая выборка

5. Базы данных статистики

2. Переиндексация всех баз данных

3. Печать БД абсолютных частот

4. Печать БД условных процентных распределений СИМ-1 и СИМ-2

5. Печать БД информативностей СИМ-1 и СИМ-2

6. Интеллектуальная дескрипторная информационно–поисковая система

7. Копирование основных баз данных СИМ

8. Сделать текущей матрицу информативностей СИМ-1

9. Сделать текущей матрицу информативностей СИМ-1

 

Подробнее подсистемы, режимы, функции и операции, реализуемые системой "Эйдос", описаны в работах [1-12].

 

1.5. Выводы

Из вышеизложенного можно сделать обоснованный вывод о том, что математическая модель, методика численных расчетов (структуры данных и алгоритмы), специальный программный инструментарий СК-анализа (система "Эйдос"), а также методика и технология их применения являются адекватным инструментом для прогнозирования и поддержки принятия решений в растениеводстве.
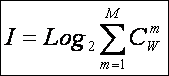
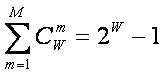
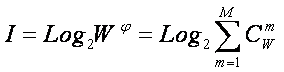
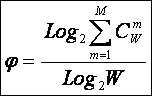
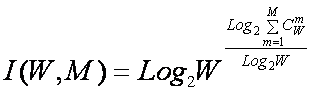
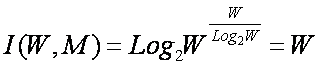
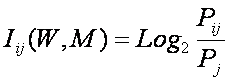
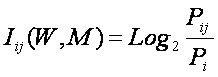
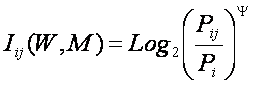
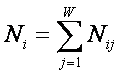
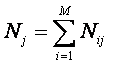
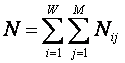
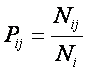
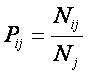
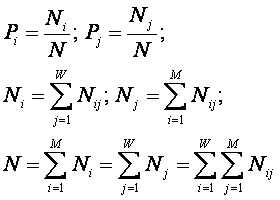
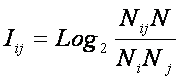
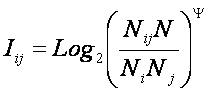
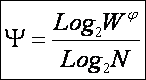
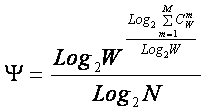
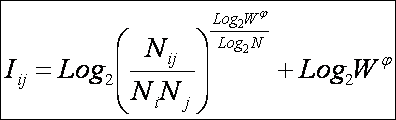
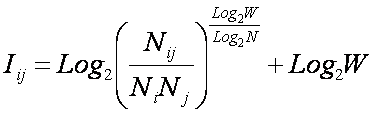
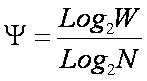
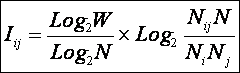
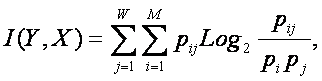
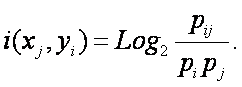
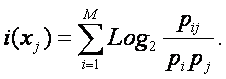
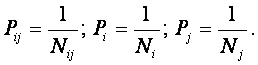
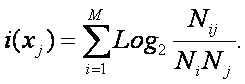
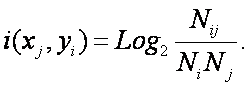
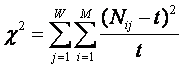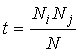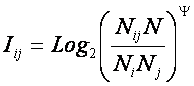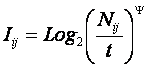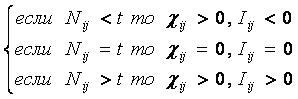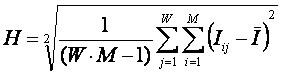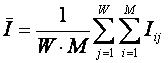
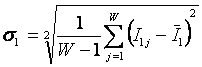
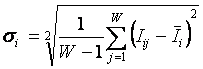
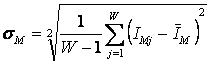
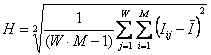
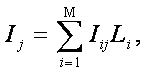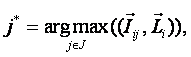
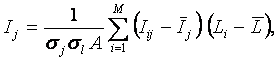
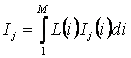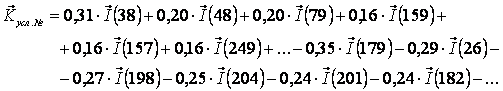
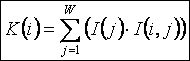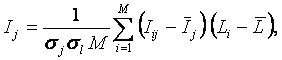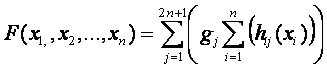