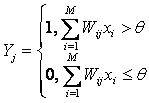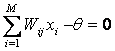1

1.3.5. ЛЕКЦИЯ-11.
Нейронные сети

Учебные вопросы

1. Биологический нейрон и формальная модель нейрона Маккалоки и Питтса.

2. Возможность решения простых задач классификации непосредственно одним нейроном.

3. Однослойная нейронная сеть и персептрон Розенблата.

4. Линейная разделимость и персептронная представляемость.

5. Многослойные нейронные сети.

6. Проблемы и перспективы нейронных сетей.

7. Модель нелокального нейрона и нелокальные интерпретируемые нейронные сети прямого счета.

В разделах 1.3.5.1 и 1.3.5.3 широко использованы материалы лекций по теории и приложениям искусственных нейронных сетей, размещенные в Internet Сергеем А. Тереховым, Лаборатория Искусственных Нейронных Сетей НТО-2, ВНИИТФ, Снежинск (http://alife.narod.ru/lectures/neural/Neu_index.htm) [237].

1.3.5.1. Биологический нейрон и формальная модель нейрона Маккалоки и Питтса

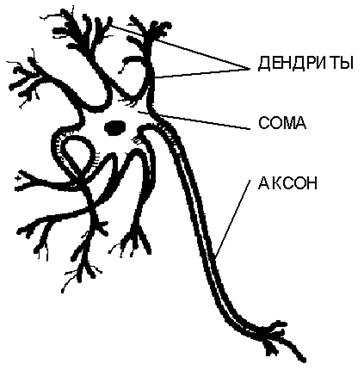
Биологический нейрон имеет вид, представленный на рисунке 73:

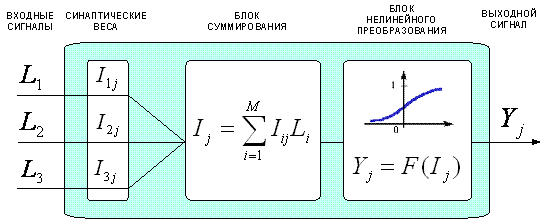
В 1943 году Дж. Маккалоки и У. Питт предложили формальную модель биологического нейрона как устройства, имеющего несколько входов (входные синапсы – дендриты), и один выход (выходной синапс – аксон) (рисунок 74).

Дендриты получают информацию от источников информации (рецепторов) L_i, в качестве которых могут выступать и нейроны. Набор входных сигналов {L_i} характеризует объект, его состояние или ситуацию, обрабатываемую нейроном.

Рисунок 73. Структура биологического нейрона

Рисунок 74. Классическая модель нейрона Дж. Маккалоки
и У. Питта (1943) в обозначениях системной теории информации

Каждому i-му входу j-го нейрона ставится в соответствие некоторый весовой коэффициент I_ij, характеризующий степень влияния сигнала с этого входа на аргумент передаточной (активационной) функции, определяющей сигнал Y_j на выходе нейрона. В нейроне происходит взвешенное суммирование входных сигналов, и далее это значение используется как аргумент активационной (передаточной) функции нейрона. На рисунке 74 данная модель приведена в обозначениях, принятых в настоящей работе.

1.3.5.2. Возможность решения простых задач классификации непосредственно одним нейроном

Представим себе, что необходимо решать задачу определения пола студентов по их внешне наблюдаемым признакам.

Есть, конечно, и более надежные способы, но мы их рассматривать не будем, т.к. они требуют дополнительных затрат для получения исходной информации и превращают задачу в тривиальную.

Поэтому будем рассматривать такие описательные шкалы и градации:

1. Длина волос: длинные, средние, короткие.

2. Наличие брюк: да, нет.

3. Использование духов или одеколона: да, нет.

Составим таблицу для определения весовых коэффициентов (таблица 33).

Таблица 33 – ОПРЕДЕЛЕНИЕ ВЕСОВЫХ
КОЭФФИЦИЕНТОВ НЕЙРОНОВ НЕПОСРЕДСТВЕННО
НА ОСНОВЕ ЭМПИРИЧЕСКИХ ДАННЫХ

Описательные шкалы и градации	Классификационные шкалы и градации
Описательные шкалы и градации	Юноши	Девушки
*Длина волос:*
– длинные	5	15
– средние	10	10
– короткие	15	5
*Наличие брюк:*
– да;	30	10
– нет	0	20
*Использование духов или одеколона:*
– да;	5	20
– нет	25	10

Пусть столбцы этой таблицы соответствуют состояниям нейрона, а строки – дендритам, соединенным с соответствующими органами восприятия, которые способны устанавливать наличие или отсутствие соответствующего признака.

Тогда один из простейших способов определить значения весовых коэффициентов на дендритах будет заключаться в том, чтобы на пересечениях строк и столбцов просто проставить суммарное количество студентов в обучающей выборке, обладающих данным признаком.

Если нейрон должен выдавать высокий выходной сигнал, когда на входе ему предъявляется юноша и низкий – когда девушка, то весовые коэффициенты на дендритах берутся из столбца: "Юноши". И наоборот, если нейрон должен выдавать высокий выходной сигнал, когда на входе ему предъявляется девушка и низкий – когда юноша, то весовые коэффициенты на дендритах берутся из столбца: "Девушки".

Можно представить себе сеть из двух нейронов, в которой весовые коэффициенты на дендритах взяты из столбцов: "Юноши" и "Девушки".

Большее количество нейронов для решения данной задачи будет избыточным. Его имеет смысл использовать в том случае, когда мы хотим повысить надежность идентификации объектов нейронной сетью и различные сходные по смыслу нейроны будут использовать независимые друг от друга рецепторы.

Например, если мы не только видим идентифицируемый объект, но можем его и обонять, и ощупывать, то это повышает надежность его идентификации. В этом состоит общепринятый в физике критерий реальности – принцип наблюдаемости, согласно которому объективное существование установлено для тех объектов и явлений, существование которых установлено несколькими, по крайней мере, двумя, независимыми способами.

В общем случае в нейронной сети каждому классу (градации классификационной шкалы) будет соответствовать один нейрон и объект, признаки которого будут измерены рецепторами на входе нейронной сети, будет идентифицирован сетью как класс, соответствующий нейрону с максимальным уровнем сигнала на выходе.

Психологические тесты обычно позволяют тестировать респондента сразу по нескольким шкалам. Очевидно, нейронные сети, реализующие эти тесты, будут иметь как минимум столько нейронов, сколько шкал в психологическом тесте.

1.3.5.3. Однослойная нейронная сеть и персептрон Розенблата

Исторически первой искусственной нейронной сетью, способной к перцепции (восприятию) и формированию реакции на воспринятый стимул, явился Perceptron Розенблатта (F.Rosenblatt, 1957). Термин " Perceptron" происходит от латинского perceptio, что означает восприятие, познавание. Русским аналогом этого термина является "Персептрон". Его автором персептрон рассматривался не как конкретное техническое вычислительное устройство, а как модель работы мозга. Современные работы по искусственным нейронным сетям редко преследуют такую цель.

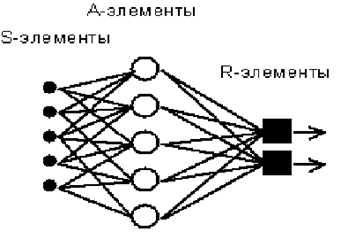
Простейший классический персептрон содержит элементы трех типов (рисунок 75), назначение которых в целом соответствует нейрону рефлекторной нейронной сети, рассмотренному выше.

Рисунок 75. Элементарный персептрон Розенблатта

S-элементы – это сенсоры или рецепторы, принимающие двоичные сигналы от внешнего мира. Каждому S-элементу соответствует определенная градация некоторой описательной шкалы.

Далее сигналы поступают в слой ассоциативных или A-элементов (показана часть связей от S к A-элементам). Только ассоциативные элементы, представляющие собой формальные нейроны, выполняют совместную аддитивную обработку информации, поступающей от ряда S-элементов с учетом изменяемых весов связей (рисунок 75). Каждому A-элементу соответствует определенная градация некоторой классификационной шкалы.

R-элементы с фиксированными весами формируют сигнал реакции персептрона на входной стимул. R-элементы обобщают информацию о реакциях нейронов на входной объект, например могут выдавать сигнал об идентификации данного объекта, как относящегося к некоторому классу только в том случае, если все нейроны, соответствующие этому классу выдадут результат именно о такой идентификации объекта. Это означает, что в R-элементах может использоваться мультипликативная функция от выходных сигналов нейронов. R-элементы также, как и A-элементы, соответствует определенным градациям классификационных шкал.

Розенблатт считал такую нейронную сеть трехслойной, однако по современной терминологии, представленная сеть является однослойной, так как имеет только один слой нейропроцессорных элементов.

Если бы R-элементы были тождественными по функциям A-элементам, то нейронная сеть классического персептрона была бы двухслойной. Тогда бы A-элементы выступали для R-элементов в роли S-элементов.

Однослойный персептрон характеризуется матрицей синаптических связей ||W|| от S- к A-элементам. Элемент матрицы отвечает связи, ведущей от i-го S-элемента (строки) к j-му A-элементу (столбцы). Эта матрица очень напоминает матрицы абсолютных частот и информативностей, формируемые в семантической информационной модели, основанной на системной теории информации.

С точки зрения современной нейроинформатики однослойный персептрон представляет в основном чисто исторический интерес, вместе с тем на его примере могут быть изучены основные понятия и простые алгоритмы обучения нейронных сетей.

Обучение классической нейронной сети состоит в подстройке весовых коэффициентов каждого нейрона.

Пусть имеется набор пар векторов {x^a, y^a}, a = 1..p, называемый обучающей выборкой, состоящей из p объектов.

Вектор {x^a} характеризует систему признаков конкретного объекта a обучающей выборки, зафиксированную S-элементами.

Вектор {y^a} характеризует картину возбуждения нейронов при предъявлении нейронной сети конкретного объекта a обучающей выборки:

Будем называть нейронную сеть обученной на данной обучающей выборке, если при подаче на вход сети вектора {x^a} на выходе всегда получается соответствующий вектор {y^a}, т.е. каждому набору признаков соответствуют определенные классы.

Ф.Розенблаттом предложен итерационный алгоритм обучения из 4-х шагов, который состоит в подстройке матрицы весов, последовательно уменьшающей ошибку в выходных векторах:

*Шаг 0:*	Начальные значения весов всех нейронов полагаются *случайными*.
*Шаг 1:*	Сети предъявляется входной образ x^a, в результате формируется выходной образ.
*Шаг 2:*	Вычисляется вектор ошибки, делаемой сетью на выходе.
*Шаг 3:*	Вектора весовых коэффициентов корректируются таким образом, что величина корректировки пропорциональна ошибке на выходе и равна нулю если ошибка равна нулю: – модифицируются только компоненты матрицы весов, отвечающие ненулевым значениям входов; – знак приращения веса соответствует знаку ошибки, т.е. положительная ошибка (значение выхода меньше требуемого) проводит к усилению связи; – обучение каждого нейрона происходит *независимо* от обучения остальных нейронов, что соответствует важному с биологической точки зрения, принципу *локальности* обучения.
*Шаг 4*:	Шаги 1-3 повторяются для всех обучающих векторов. Один цикл последовательного предъявления всей выборки называется эпохой. Обучение завершается по истечении нескольких эпох, если выполняется по крайней мере одно из условий: – когда итерации сойдутся, т.е. вектор весов перестает изменяться; – когда полная просуммированная по всем векторам абсолютная ошибка станет меньше некоторого малого значения.

Данный метод обучения был назван Ф.Розенблаттом "методом коррекции с обратной передачей сигнала ошибки". Имеется в виду передача сигнала ошибка от выхода сети на ее вход, где и определяются, и используются весовые коэффициенты. Позднее этот алгоритм назвали "d-правилом".

Данный алгоритм относится к широкому классу алгоритмов обучения с учителем, т.к. в нем считаются известными не только входные вектора, но и значения выходных векторов, т.е. имеется учитель, способный оценить правильность ответа ученика, причем в качестве последнего выступает нейронная сеть.

Розенблаттом доказана "Теорема о сходимости обучения" по d-правилу. Эта теорема говорит о том, что персептрон способен обучится любому обучающему набору, который он способен представить. Но она ничего не говорит о том, какие именно обучающие наборы он способен представить. Ответ на этот вопрос мы получим в следующем разделе.

1.3.5.4. Линейная разделимость и персептронная представляемость

При прямоугольной передаточной функции (1) каждый нейрон представляет собой пороговый элемент, который может находиться только в одном из двух состояний:

– возбужденном (активном), если взвешенная сумма входных сигналов больше некоторого порогового значения;

– заторможенном (пассивном), если взвешенная сумма входных сигналов меньше некоторого порогового значения.

( 1 )

Следовательно, при заданных значениях весов и порогов, каждый нейрон имеет единственное определенное значение выходной активности для каждого возможного вектора входов. При этих условиях множество входных векторов, при которых нейрон активен (Y=1), отделено от множества векторов, на которых нейрон пассивен (Y=0) гиперплоскостью (2).

( 2 )

Следовательно, нейрон способен отделить только такие два множества векторов входов, для которых существует гиперплоскость, отделяющая одно множество от другого. Такие множества называют линейно разделимыми.

Необходимо отметить, что линейно-разделимые множества являются составляют лишь очень незначительную часть всех множеств. Поэтому данное ограничение персептрона является принципиальным. Оно было преодолено лишь в 80-х годах путем введения нескольких слоев нейронов в сетях Хопфилда и неокогнитроне Фукушимы.

В завершении остановимся на некоторых проблемах, которые остались нерешенными после работ Ф.Розенблатта:

1. Возможно ли обнаружить линейную разделимость классов до обучения сети?

2. Как определить скорость обучения, т.е. количество итераций, необходимых для достижения заданного качества обучения?

3. Как влияют на результаты обучения последовательность предъявления образов и их количество?

4. Имеет ли алгоритм обратного распространения ошибки преимущества перед простым перебором весов?

5. Каким будет качество обучения, если обучающая выборка содержит не все возможные на практике пары векторов и какими будут ответы персептрона на новые вектора, отсутствующие в обучающей выборке?

Особенно важным представляется последний вопрос, т.к. индивидуальный опыт принципиально всегда не является полным.

1.3.5.5. Многослойные нейронные сети

1.3.5.5.1. Многослойный персептрон

Каким же образом в многослойных (иерархических) нейронных сетях преодолевается принципиальное ограничение однослойных нейронных сетей, связанное с требованием линейной разделимости классов?

Часто то, что не удается сделать сразу, вполне возможно сделать по частям. Для этого изменяются задачи, решаемые слоями нейронной сети. Оказывается в 1-м слое не следует пытаться на основе первичных признаков, фиксируемых рецепторами, сразу идентифицировать классы, а нужно лишь сформировать линейно-разделимую систему вторичных признаков, которую уже во 2-м слое связать с классами (рисунок 76).

Рисунок 76. Двух-слойный персептрон [233]

В многослойной сети выходные сигналы нейронов предыдущего слоя играют роль входных сигналов для нейронов последующего слоя, т.е. нейроны предыдущего слоя выступают в качестве рецепторов для нейронов последующего слоя.

Связи между смежными слоями нейронов будем называть непосредственными, а связи между слоями, разделенными N промежуточных слоев, будем называть связями N-го уровня опосредованности. Непосредственные связи – это связи 0-го уровня опосредованности. Промежуточные слои нейронов в многослойных сетях называют скрытыми.

Персептрон переводит входной образ, определяющий степени возбуждения рецепторов, в выходной образ, определяемый нейронами самого верхнего уровня, которых обычно, не очень много. Состояния возбуждения нейронов на верхнем уровне иерархии сети характеризуют принадлежность входного образа к тем или иным классам.

Таким образом, многослойный персептрон – это обучаемая распознающая система, реализующая корректируемое в процессе обучения линейное решающее правило в пространстве вторичных признаков, которые обычно являются фиксированными случайно выбранными линейными пороговыми функциями от первичных признаков.

При обучении на вход персептрона поочередно подаются сигналы из обучающей выборки, а также указания о классе, к которому следует отнести данный сигнал. Обучение перцептрона заключается в коррекции весов при каждой ошибке распознавания, т. е. при каждом случае несовпадения решения, выдаваемого персептроном, и истинного класса. Если персептрон ошибочно отнес сигнал, к некоторому классу, то веса функции, истинного класса увеличиваются, а ошибочного уменьшаются. В случае правильного решения все веса остаются неизменными.

Этот чрезвычайно простой алгоритм обучения обладает замечательным свойством: если существуют значения весов, при которых выборка может быть разделена безошибочно, то при определенных, легко выполнимых условиях эти значения будут найдены за конечное количество итераций.

При идентификации, распознавании, прогнозировании на вход многослойного персептрона поступает сигнал, представляющий собой набор первичных признаков, которые и фиксируются рецепторами. Сначала вычисляются вторичные признаки. Каждому такому вторичному признаку соответствует линейная от первичных признаков. Вторичный признак принимает значение 1, если соответствующая линейная функция превышает порог. В противном случае она принимает значение 0. Затем для каждого из классов вычисляется функция, линейная относительно вторичных признаков. Перцептрон вырабатывает решение о принадлежности входного сигнала к тому классу, которому соответствует функция от вторичных параметров, имеющая наибольшее значение.

Показано, что для представления произвольного нелинейного функционального отображения, задаваемого обучающей выборкой, достаточно всего двух слоев нейронов. Однако на практике, в случае сложных функций, использование более чем одного скрытого слоя может давать экономию полного числа нейронов.

1.3.5.5.2. Модель Хопфилда

В модели Хопфилда (J.J.Hopfield, 1982) впервые удалось установить связь между нелинейными динамическими системами и нейронными сетями.

Модель Хопфилда является обобщением модели многослойного персептрона путем добавления в нее следующих двух новых свойств:

1. В нейронной сети все нейроны непосредственно связаны друг с другом: силу связи i-го нейрона с j-м обозначим как W_ij.

2. Связи между нейронами симметричны: W_ij=W_ji, сам с собой нейрон не связан W_ii=0.

Каждый нейрон может принимать лишь два состояния, которые определяются по классической формуле (1). Изменение состояний возбуждения всех нейронов может происходить либо последовательно, либо одновременно (параллельно), но свойства сети Хопфилда не зависят от типа динамики.

Сеть Хопфилда способна распознавать объекты при неполных и зашумленных исходных данных, однако не может этого сделать, если изображение смещено или повернуто относительно его исходного состояния, представленного в обучающей выборке.

1.3.5.5.3. Когнитрон и неокогнитрон Фукушимы

В целом когнитрон (K.Fukushima, 1975) представляет собой иерархию слоев, последовательно связанных друг с другом, как в персептроне. Однако, при этом есть два существенных отличия:

1. Нейроны образуют не одномерную цепочку, а покрывают плоскость, аналогично слоистому строению зрительной коры человека.

2. Когнитрон состоит из иерархически связанных слоев нейронов двух типов – тормозящих и возбуждающих.

В когнитроне каждый слой реализует свой уровень обобщения информации:

– входные слои чувствительны к отдельным элементарным структурам, например, линиям определенной ориентации или цвета;

– последующие слои реагируют уже на более сложные обобщенные образы;

– в слое наивысшего уровня иерархии активные нейроны определяют результат работы сети – узнавание определенного образа, при этом результатам распознавания соответствуют те нейроны, активность которых оказалась максимальной.

Однако добиться независимости (инвариантности) результатов распознавания от размеров и ориентации изображений удалось лишь в неокогнитроне, который был разработан Фукушимой в 1980 году и представляет собой как бы суперпозицию когнитронов, обученных распознаванию объектов различных типов, размеров и ориентации.

1.3.5.6. Проблемы и перспективы нейронных сетей

На наш взгляд к основным проблемам нейронных сетей можно отнести:

1. Сложность содержательной интерпретации смысла интенсивности входных сигналов и весовых коэффициентов ("проблема интерпретируемости весовых коэффициентов").

2. Сложность содержательной интерпретации и обоснования аддитивности аргумента и вида активационной (передаточной) функции нейрона ("проблема интерпретируемости передаточной функции").

3. "Комбинаторный взрыв", возникающий при определении структуры связей нейронов, подборе весовых коэффициентов и передаточных функций ("проблема размерности").

4. "Проблема линейной разделимости", возникающая потому, что возбуждение нейронов принимают лишь булевы значения 0 или 1.

Проблемы интерпретируемости приводят к снижению ценности полученных результатов работы сети, а проблема размерности – к очень жестким ограничениям на количество выходных нейронов в сети, на количество рецепторов и на сложность структуры взаимосвязей нейронов с сети. Достаточно сказать, что количество выходных нейронов в реальных нейронных сетях, реализуемых на базе известных программных пакетов, обычно не превышает несколько сотен, а чаще всего составляет единицы и десятки.

Проблема линейной разделимости приводит к необходимости применения многослойных нейронных сетей для реализации тех приложений, которые вполне могли бы поддерживаться сетями с значительно меньшим количеством слоев (вплоть до однослойных), если бы значения возбуждения нейронов были не дискретными булевыми значениями, а континуальными значениями, нормированными в определенном диапазоне.

Перечисленные проблемы предлагается решить путем использования модели нелокального нейрона, обеспечивающего построение нейронных сетей прямого счета.

1.3.5.7. Модель нелокального нейрона и нелокальные интерпретируемые нейронные сети прямого счета

1.3.5.7.1. Метафора нейросетевого представления семантической информационной модели

В данной работе предлагается представление, согласно которому каждый нейрон отражает определенное будущее состояние активного объекта управления, а нейронная сеть в целом – систему будущих состояний, как желательных (целевых), так и нежелательных. Весовые коэффициенты на дендритах нейронов имеют смысл силы и направления влияния факторов на переход активного объекта управления в то или иное будущее состояние. Таким образом, предложенная в данной работе семантическая информационная модель в принципе допускает представление в терминах и понятиях нейронных сетей. Однако при более детальном рассмотрении выясняется, что семантическая информационная модель является более общей, чем нейросетевая и для полного их соответствия необходимо внести в нейросетевую модель ряд дополнений.

1.3.5.7.2. Соответствие основных терминов и понятий

Предлагается следующая система соответствий, позволяющая рассматривать термины и понятия из теории нейронных сетей и предложенной семантической информационной модели практически как синонимы. Нейрон – вектор обобщенного образа класса в матрице информативностей. Входные сигналы – факторы (признаки). Весовой коэффициент – системная мера целесообразности информации. Обучение сети – адаптация модели, т.е. перерасчет значений весовых коэффициентов дендритов для каждого нейрона (матрицы информативностей) и изменение вида активационной функции. Самоорганизация сети – синтез модели, т.е. изменение количества нейронов и дендритов, изменение количества нейронных слоев и структуры связей между факторами и классами, а затем адаптация (перерасчет матрицы информативностей). Таким образом, адаптация – это обучение сети на уровне изменения информационных весовых коэффициентов и активационной функции, а синтез – на уровне изменения размерности и структуры связей нейронов сети. 1-й (входной) слой нейронной сети – формирование обобщенных образов классов. Сети Хопфилда и Хэмминга – обучение с учителем, сопоставление описательной и классификационной информации, идентификация и прогнозирование. 2-й слой, сети Хебба и Кохонена – самообучение, анализ структуры данных без априорной классификационной информации, формирование кластеров классов и факторов. 3-й слой – формирование конструктов (в традиционных нейронных сетях не реализовано). Необходимо отметить, что любой слой нейронной сети является в предлагаемой модели не только обрабатывающим, но и выходным, т.е. с одной стороны дает результаты обработки информации, имеющие самостоятельное значение, а с другой – поставляет информацию для последующих слоев нейронной сети, т.е. более высоких уровней иерархии информационной системы (в полном соответствии с формализуемой когнитивной концепцией).

1.3.5.7.3. Гипотеза о нелокальности нейрона и информационная нейросетевая парадигма

Модель нелокального нейрона: так как сигналы на дендритах различных нейронов вообще говоря коррелируют (или антикоррелируют) друг с другом, то, значения весовых коэффициентов, а значит и выходное значение на аксоне каждого конкретного нейрона вообще говоря не могут быть определены с использованием значений весовых коэффициентов на дендритах только данного конкретного нейрона, а должны учитывать интенсивности сигналов на всей системе дендритов нейронной сети в целом (рисунок 77).

Рисунок 77. Модель нелокального нейрона

в обозначениях системной теории информации

За счет учета корреляций входных сигналов (если они фактически присутствуют в структуре данных), т.е. наличия общего самосогласованного информационного поля исходных данных всей нейронной сети (информационное пространство), нелокальные нейроны ведут себя так, как будто связаны с другими нейронами, хотя могут быть и не связаны с ними синаптически по входу и выходу ни прямо, ни опосредованно. Самосогласованность семантического информационного пространства [81, 109, 120] означает, что учет любого одного нового факта в информационной модели вообще говоря приводит к изменению всех весовых коэффициентов всех нейронов, а не только тех, на рецепторе которых обнаружен этот факт и тех, которые непосредственно или опосредованно синаптически с ним связаны.

В традиционной (т.е. локальной) модели нейрона весовые коэффициенты на его дендритах однозначно определяются заданным выходом на его аксоне и никак не зависят от параметров других нейронов, с которыми с нет прямой или опосредованной синаптической связи. Это связано с тем, что в общепринятой энергетической парадигме Хопфилда весовые коэффициенты дендритов имеют смысл интенсивностей входных воздействий. В методе "обратного распространения ошибки" процесс переобучения, т.е. интерактивного перерасчета весовых коэффициентов, начинается с нейрона, состояние которого оказалось ошибочным и захватывает только нейроны, ведущие от рецепторов к данному нейрону. Корреляции между локальными нейронами обусловлены сочетанием трех основных причин:

– наличием в исходных данных определенной структуры: корреляцией входных сигналов;

– синаптической связью локальных нейронов;

– избыточностью (дублированием) нейронной сети.

1.3.5.7.4. Решение проблемы интерпретируемости весовых коэффициентов (семантическая мера целесообразности информации и закон Фехнера)

В данной работе предлагается использовать такие весовые коэффициенты дендритов, чтобы активационная функция была линейной, т.е. по сути была равна своему аргументу: сумме. Этому условию удовлетворяют весовые коэффициенты, рассчитываемые с применением системного обобщения формулы Харкевича [81].

Очень важно, что данная мера, удовлетворяет известному эмпирическому закону Г.Фехнера (1860), согласно которому существует логарифмическая зависимость между интенсивностью фактора и величиной отклика на него биологической системы (в частности, величина ощущения прямо пропорциональна логарифму интенсивности раздражителя).

Предлагается информационный подход к нейронным сетям, по аналогии с энергетическим подходом Хопфилда (1980).

Суть этого подхода состоит в том, что интенсивности входных сигналов рассматриваются не сами по себе и не с точки зрения только их интенсивности, а как сообщения, несущие определенное количество информации или дезинформации о переходе нейрона и моделируемого им активного объекта управления в некоторое будущее состояние.

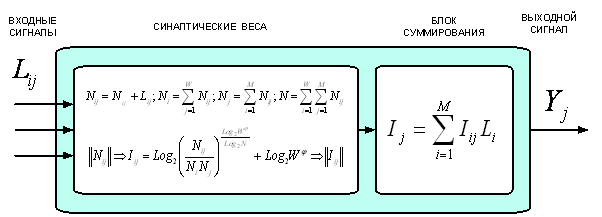
Под интенсивностью входного сигнала на определенном дендрите мы будем понимать абсолютную частоту (количество) встреч фактора (признака), соответствующего данному дендриту, при предъявлении нейронной сети объекта, соответствующего определенному нейрону. Таким образом матрица абсолютных частот рассматривается как способ накопления и первичного обобщения эмпирической информации об интенсивностях входных сигналов на дендритах в разрезе по нейронам.

Весовые коэффициенты, отражающие влияние каждого входного сигнала на отклик каждого нейрона, т.е. величину его возбуждения или торможения, представляют собой элементы матрицы информативностей, получающиеся из матрицы абсолютных частот методом прямого счета с использованием выражения для семантической меры целесообразности информации [81].

При этом предложенная мера семантической целесообразности информации, как перекликается с нейронными сетями Кохонена, в которых также принято стандартизировать (нормализовать) входные сигналы, что позволяет в определенной мере уйти от многообразия передаточных функций.

Наличие ясной и обоснованной интерпретации весовых коэффициентов, как количества информации, позволяет предложить в качестве математической модели для их расчета системную теорию информации (СТИ).

1.3.5.7.5. Семантическая информационная модель, как нелокальная нейронная сеть

Учитывая большое количество содержательных параллелей между семантической информационной моделью и нейронными сетями предлагается рассматривать данную модель как нейросетевую модель, основанную на системной теории информации. В данной модели предлагается вариант решения важных нейросетевых проблем интерпретируемости и ограничения размерности за счет введения меры целесообразности информации (системное обобщение формулы Харкевича), обеспечивающей прямой расчет интерпретируемых весовых коэффициентов на основе непосредственно эмпирических данных. Итак, в данной работе предлагается новый класс нейронных сетей, основанных на семантической информационной модели и информационном подходе. Для этих сетей предлагается полное наименование: "Нелокальные интерпретируемые нейронные сети прямого счета" и сокращенное наименование: "Нелокальные нейронные сети".

Нелокальная нейронная сеть является системой нелокальных нейронов, обладающей качественно новыми (системными, эмерджентными) свойствами, не сводящимися к сумме свойств нейронов. В такой сети поведение нейронов определяется как их собственными свойствами и поступающими на них входными сигналами, так и свойствами нейронной сети в целом, т.е. поведение нейронов в нелокальной нейронной сети согласовано друг с другом не только за счет их прямого и опосредованного синаптического взаимодействия (как в традиционных нейронных сетях), но за счет общего информационного поля весовых коэффициентов всех нейронов данной сети.

1.3.5.7.6. Гипотеза о физической природе нелокального взаимодействия нейронов в нелокальной нейронной сети

В данной работе предлагается математическая модель, численный метод и программный инструментарий нелокальных нейронных сетей (универсальная когнитивная аналитическая система "Эйдос"), успешно апробированные в ряде предметных областей. Данная система обеспечивает неограниченное количество слоев ННС при максимальном количестве весовых коэффициентов в слое до 16 миллионов в версии 9.0 и до 4000 выходных нейронов, а в текущей версии 12.5 эти количества ограничены практически только емкостью диска. Но если рассматривать нелокальную нейронную сеть как модель реальных "биологических" нейронных сетей, то ясно, что формальной модели недостаточно и необходимо дополнить ее физической моделью о природе каналов нелокального взаимодействия нейронов в данной сети.

По мнению автора данный механизм основан на парадоксе Эйнштейна-Подольского Розена (ЭПР) [10, 109, 264]. По мнению автора, физическая реализация нелокальных нейронов может быть осуществлена за счет соединения как минимум одного дендрита каждого нейрона с датчиком микротелекинетического воздействия, на который человек может оказывать влияние дистанционно. Некоторые из подобных датчиков описаны в работе [27] и на сайте автора по адресу: http://lc.kubagro.ru/History/vega-72/page_01.htm. По мнению автора, мозг может рассматриваться как оптимальная среда для редукции мыслей, в этом смысле квантовые компьютеры, основанные не на математических и программных моделях, а на физических нелокальных нейронах, могут оказаться во многих отношениях функционально эквивалентными физическому организму.

1.3.5.7.7. Решение проблемы интерпретируемости передаточной функции

Вопрос об интерпретируемости передаточной функции нейрона включает два основных аспекта:

1) об интерпретируемости аргумента передаточной функции;

2) об интерпретируемости вида передаточной функции.

1. Возникает естественный вопрос о том, чем обосновано включение в состав модели нейрона Дж. Маккалоки и У. Питтом именно аддитивного элемента, суммирующего входные сигналы, а не скажем мультипликативного или в виде какой-либо другой функции общего вида. По мнению автора такой выбор обоснован и имеет явную и убедительную интерпретацию именно в том случае, когда весовые коэффициенты имеют смысл количества информации, т.к. в этом случае данная мера представляет собой неметрический критерий сходства, основанный на лемме Неймана-Пирсона [194]. Сумма весовых коэффициентов, соответствующих набору действующих факторов (входных сигналов) дает величину выходного сигнала на аксоне каждого нейрона.

2. Вид передаточной функции содержательно в теории нейронных сетей явно не обосновывается. Предлагается гипотеза, что на практике вид передаточной функции подбирается таким образом, чтобы соответствовать смыслу подобранных в данном конкретном случае весовых коэффициентов. Так как при применении в различных предметных областях смысл весовых коэффициентов в явном виде не контролируется и может отличаться, то выбор вида передаточной функции позволяет частично компенсировать эти различия.

Предлагаемый интерпретируемый вид весовых коэффициентов обеспечивает единую и стандартную интерпретацию аргумента и значения передаточной функции независимо от предметной области. Поэтому в нелокальной нейронной модели передаточная функция нейрона всегда линейна (аргумент равен функции). Следовательно в модели нелокального нейрона блок суммирования по сути дела объединен с блоком нелинейного преобразования (точнее, второй отсутствует, а его роль выполняет блок суммирования), в отличие от стандартных передаточных функций локальных нейронов: логистической, гиперболического тангенса, пороговой линейной, экспоненциально распределенной, полиномиальной и импульсно-кодовой.

Нелокальные нейроны как бы "резонируют" на ансамбли входных сигналов, причем этот резонанс может быть обоснованно назван семантическим (смысловым), т.к. весовые коэффициенты рассчитаны на основе предложенной семантической меры целесообразности информации. Таким образом, разложение вектора идентифицируемого объекта в ряд по векторам обобщенных образов классов осуществляется на основе семантического резонанса нейронов выходного слоя на ансамбль входных сигналов (признаков, факторов).

1.3.5.7.8. Решение проблемы размерности

Вместо итерационного подбора весовых коэффициентов путем полного перебора вариантов их значений при малых вариациях (методы обратного распространения ошибки и градиентного спуска к локальному экстремуму) предлагается прямой расчет этих коэффициентов на основе процедуры и выражений, обоснованных в предложенных системной теории информации и семантической информационной модели. Выигрыш во времени и используемых вычислительных ресурсах, получаемый за счет этого, быстро возрастает при увеличении размерности нейронной сети.

1.3.5.7.9. Решение проблемы линейной разделимости

Вводятся промежуточные линейно-разделимые классы распознавания, которые рассматриваются как вторичные признаки при идентификации объектов с ранее не разделимыми классами. Это решение соответствует введению дополнительных слоев нейронной сети.

В системе "Эйдос" функция представления нейронов предыдущего слоя в качестве рецепторов последующего слоя автоматизирована, что в случае необходимости позволяет в полуавтоматическом режиме преобразовать однослойную сеть с линейно-неразделимыми классами в иерархическую нейронную сеть в которой эти классы линейно-разделены относительно вторичных признаков в слоях более высоких уровней иерархии.

1.3.5.7.10. Моделирование причинно-следственных цепочек в нейронных сетях и семантической информационной модели

Факторы описывают причины, а классы – следствия. Но и следствия в свою очередь являются причинами более отдаленных последствий. Предлагаемая семантическая информационная модель позволяет рассматривать события, обнаружение которых осуществляется в режиме идентификации, как причины последующих событий, т.е. как факторы, их вызывающие. При этом факт наступления этих событий моделируется путем включения в модель факторов, соответствующих классам (событиям). В нейронных сетях этот процесс моделируется путем включения в сеть дополнительных нейронных слоев и создания обратных связей между слоями, обеспечивающих передачу в предыдущие слои результатов работы последующих слоев.

1.3.5.7.11. Моделирование иерархических структур обработки информации

Рассмотрим иерархическую структуру информации на примере использования психологического теста для оценки психологических качеств сотрудников и влияния этих качеств на эффективность работы фирмы. В нейронной сети иерархическим уровням обработки информации соответствуют слои, поэтому далее будем использовать термины "слой нейронной сети" и "иерархический уровень обработки информации" как синонимы. Рецепторы дают информацию по ответам сотрудника на опросник, нейроны 1-го слоя дают оценку психологических качеств и сигнал с их аксонов является входным для нейронов 2-го слоя, дающих оценку качества работы фирмы. В семантической информационной модели существует три варианта моделирования подобных иерархических структур обработки информации:

1. Заменить все слои одним слоем и выявлять зависимости непосредственно между исходными данными с первичных рецепторов и интересующими итоговыми оценками, например, ответами сотрудников на вопросы и результатами работы фирмы. Этот подход эффективен с прагматической точки зрения, но дает мало информации для теоретических обобщений.

2. Каждый слой моделируется отдельной семантической информационной моделью, включающей свои классификационные и описательные шкалы и градации, обучающую выборку, матрицы абсолютных частот и информативностей. Вся система иерархической обработки информации моделируется системой этих моделей, взаимосвязанных друг с другом по входу-выходу: результаты классификации объектов обучающей выборки 1-й моделью рассматриваются как свойства этих объектов во 2-й модели, в которой они используются для классификации 2-го уровня. Например, психологические качества сотрудников, установленные в результате психологического тестирования, рассматриваются как свойства сотрудников, влияющие на эффективность работы фирмы. Данный подход эффективен и с прагматической, и с теоретической точек зрения, но является громоздким в программной реализации.

3. Моделирование каждого слоя соответствующими подматрицами матриц абсолютных частот и информативностей (таблица 34).

Примечание: в таблице 34 представлена именно логическая структура данных, т.е. в реальных базах данных нет записей, содержащих информацию о влиянии рецепторов n-го слоя на нейроны слоев, номера которых не равны n.

Этот вариант обладает преимуществами первых двух и преодолевает их недостатки. В нем применяется следующий итерационный алгоритм послойного расчета, где n={1, 2, …, N}, N – количество слоев нейронной сети:

Шаг n: расчет весовых коэффициентов n-го слоя, идентификация объектов обучающей выборки в нейронах n-го слоя, если слой (n+1) существует, то занесение в обучающую выборку в качестве свойств объектов (n+1)-го слоя результатов их идентификации в нейронах n-го слоя.

Таблица 34 – ЛОГИЧЕСКАЯ СТРУКТУРА ДАННЫХ, СООТВЕТСТВУЮЩАЯ ТРЕХСЛОЙНОЙ НЕЛОКАЛЬНОЙ НЕЙРОННОЙ СЕТИ

Рецепторы – факторы, влияющие на поведение объекта управления	Нейроны - будущие состояния объекта управления			Дифференцирующая способность входного сигнала
	Нейроны 1-го слоя: психологические качества сотрудников	Нейроны 2-го слоя: успешность деятельности сотрудника	Нейроны 3-го слоя: успешность деятельности фирмы	Дифференцирующая способность входного сигнала
Рецепторы 1-го слоя: ответы сотрудников на вопросы анкеты	Весовые коэффициенты 1-го слоя	– – –	– – –
Рецепторы 2-го слоя: психологические качества сотрудников	– – –	Весовые коэффициенты 2-го слоя	– – –
Рецепторы 3-го слоя: успешность деятельности сотрудника	– – –	– – –	Весовые коэффициенты 3-го слоя
Степень обученности нейрона				Степень обученности нейронной сети

1.3.5.7.12. Нейронные сети и СК-анализ

Известные в литературе нейронные сети, в отличие от предлагаемой семантической информационной модели и нелокальных нейронных сетей, не обеспечивают реализацию всех базовых когнитивных операций, входящих в когнитивный конфигуратор. В частности, традиционные нейронные сети решают лишь задачу идентификации (прогнозирования) и не обеспечивают решение обратной задачи (дедукции), необходимой для принятия решения о выборе многофакторного управляющего воздействия. Кроме того не решается вопрос об уменьшении размерности нейронной сети без ущерба для ее адекватности (абстрагирование).

Результаты численного моделирования и исследования свойств нейронных сетей этого класса при управлении в АПК и других предметных областях позволяют предположить, в качестве модели реальных когнитивных процессов они обладает более высокой адекватностью, чем нейронные сети других типов.

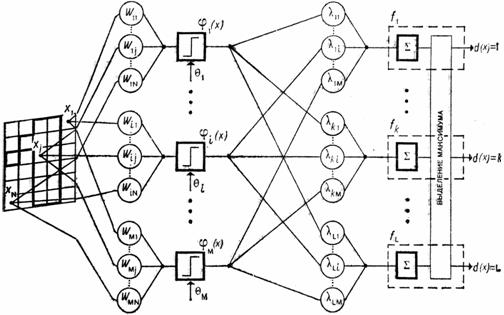
1.3.5.7.13. Графическое отображение нейронов, Паррето-подмножеств нелокальной нейронной сети, семантических сетей, когнитивных карт и диаграмм в системе "Эйдос"

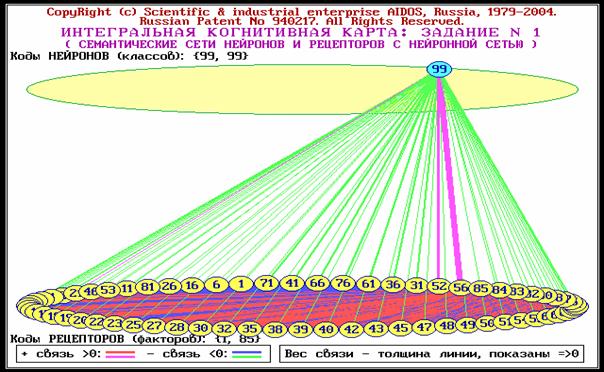
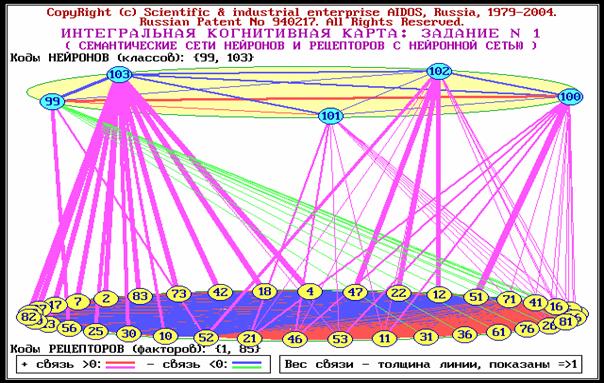
Для каждого технологического фактора в соответствии с предложенной моделью определяется величина и направление его влиянии на осуществление всех желаемых и не желаемых хозяйственных ситуаций. Для каждой ситуации эта информация отображается в различных текстовых и графических формах, в частности в форме нелокального нейрона (рисунок 78).

На данной и последующих графических диаграммах цвет линии означает знак связи (красный – положительная, синий – отрицательная), а толщина – ее модуль.

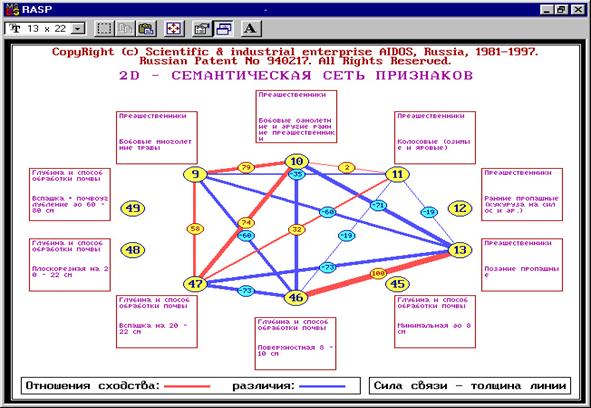
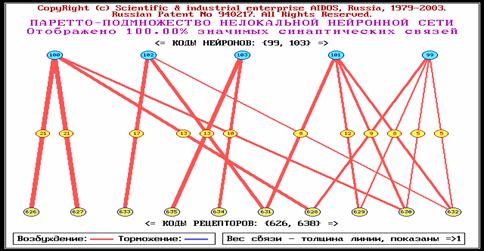
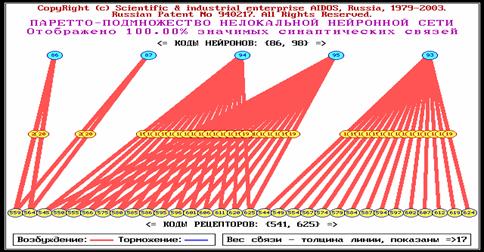
Паретто-подмножеством нелокальной нейронной сети будем называть ее подмножество, включающее наиболее значимые связи. Пример графического отображения такого подмножества приведен в таблицах 35 – 37.

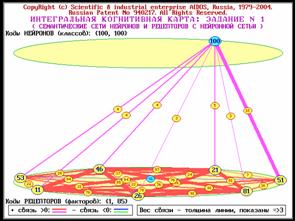
Факторы (сигналы с рецепторов) в модели нелокального нейрона взаимосвязаны друг с другом. Эти связи графически отображаются в форме семантической сети (рисунок 78).

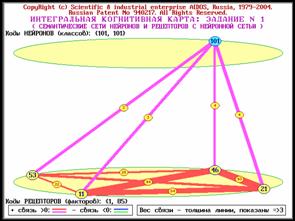
Структуру любой линии связи семантической сети можно детально изучить в когнитивной диаграмме (рисунок 79).

Дополнение модели нейрона связями факторов позволяет построить классическую когнитивную карту ситуации (будущего состояния АОУ). Необходимо отметить, что все указанные графические формы генерируются системой "Эйдос" автоматически в соответствии с созданной моделью.

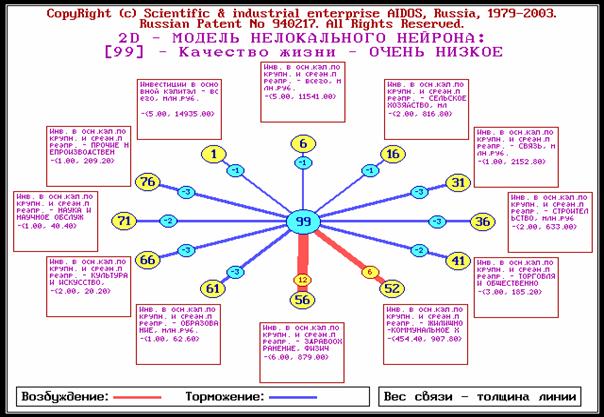
Нелокальный нейрон представляет собой будущее состояние объекта управления с изображением наиболее сильно влияющих на него факторов с указанием силы и направления (способствует-препятствует) их влияния (рисунок 80).


	Рисунок 78. Отображение результатов кластерно-конструктивного анализа факторов в форме семантической сети (когнитивной карты) в системе "Эйдос"

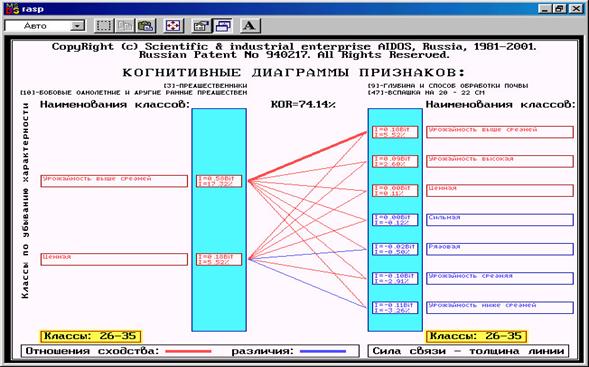
	Рисунок 79. Когнитивная диаграмма кластера факторов: "Глубина и способ обработки почвы: вспашка на 20-22 см – Предшественники: Бобовые однолетние и другие ранние предшественники", генерируемая системой "Эйдос"

Рисунок 80. Примеры нелокальных нейронов, отражающих влияние инвестиций на уровень качества жизни в регионе (система "Эйдос")

Нейронная сеть представляет собой совокупность взаимосвязанных нейронов. В классических нейронных сетях связь между нейронами осуществляется по входным и выходным сигналам, а в нелокальных нейронных сетях [109] – на основе общего информационного поля.

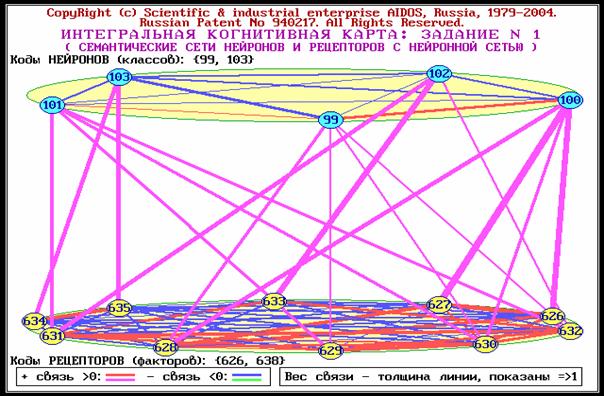
В таблице 35 приводится классификация причинно-следственных связей по рангам. Эта классификация использована для отображения параметров заданий на генерацию и соответствующих фрагментов нейронных сетей (таблица 36). Фрагменты нейронной сети со связями 0-го уровня опосредованности, т.е. соответствующие смежным слоям многослойной сети, показаны на голубом фоне. В пустых клетках таблицы 35 могут быть отображены фрагменты нейронной сети, аналогичные показанным. Однако новой информации, по сравнению с уже показанными, они не содержат, т.к. практически они образуются из них путем перемены местами нейронов и рецепторов (инвертирования – отражения относительно горизонтальной оси). Сгенерированные по этим заданиям фрагменты нейронной сети приведены в форме, позволяющей составить из них многослойную нейронную сеть (таблицы 36 и 37). эти таблицы взяты из работы [248].

Система "Эйдос" обеспечивает построение любого подмножества многослойной нейронной сети с заданными или выбираемыми по заданным критериям рецепторами и нейронами, связанными друг с другом связями любого уровня опосредованности.

Таблица 35 – ВИДЫ КАУЗАЛЬНЫХ СВЯЗЕЙ МЕЖДУ ОБЪЕКТАМИ РАЗЛИЧНЫХ УРОВНЕЙ ИЕРАРХИЧЕСКОЙ МОДЕЛИ И СООТВЕТСТВУЮЩИЕ ФРАГМЕНТЫ НЕЙРОННОЙ СЕТИ

Факторы (наименования, коды)		Классы (наименования, коды)
Факторы (наименования, коды)		Уровень качества жизни	Годы	Частные критерии уровня качества жизни
Наименования	Коды	99-103	86-98	1-85
Годы	626-638
Частные критерии уровня качества жизни	541-625
Первичные факторы (инвестиции)	1-85

Таблица 36 – ФРАГМЕНТЫ МНОГОУРОВНЕВОЙ СЕМАНТИЧЕСКОЙ ИНФОРМАЦИОННОЙ МОДЕЛИ И НЕЙРОННОЙ СЕТИ С НЕПОСРЕДСТВЕННЫМИ СВЯЗЯМИ

Уровень

Нейронная сеть

№

Наимено-

вание

Уровни качества Жизни (значения Интегрального критерия уровня качества жизни)

Годы

Вторичные факторы (частные критерии уровня качества жизни)

Первичные факторы

Таблица 37 – ФРАГМЕНТЫ МНОГОУРОВНЕВОЙ СЕМАНТИЧЕСКОЙ ИНФОРМАЦИОННОЙ МОДЕЛИ И МНОГОСЛОЙНОЙ НЕЙРОННОЙ СЕТИ СО СВЯЗЯМИ РАЗЛИЧНОЙ СТЕПЕНИ ОПОСРЕДОВАННОСТИ

Уровень		Нейронная сеть
№	Наимено- вание	Слои со связями 0-го уровня опосредованности	Слои со связями 1-го уровня опосредованности	Слои со связями 1-го уровня опосредованности	Слои со связями 2-го уровня опосредованности
4 3	Уровни качества Жизни (значения Интегрального критерия уровня качества жизни) Годы
3 2	Годы Вторичные факторы (частные критерии уровня качества жизни)
2 1	Вторичные факторы (частные критерии уровня качества жизни) Первичные факторы

Обучение нелокальной нейронной сети

В классических нейронных сетях обучение состоит в таком подборе весовых коэффициентов на дендритах, что минимизируется ошибка выходного сигнала сети по сравнению с эталонным. Этот вид обучения аналогичен обучению человека с уже сформированным мозгом, т.е. в достаточно зрелом возрасте, когда структура нейронной сети уже сформирована и фиксирована.

Однако в раннем возрасте и до наступления зрелости может быть основную роль играет другой вид обучения, который состоит в том, что формируется и перестраивается сама структура нейронной сети. Этот процесс включает:

– формирование новых связей между уже существующими нейронами;

– формирование новых нейронов;

– формирование связей между уже существующими и новыми нейронами;

– формирование связей между новыми нейронами;

– формирование новых нейронных систем (ансамблей) и слоев.

В классической нейронной сети обучение в каждом конкретном случае затрагивает лишь те нейроны, которые физически связаны с входными рецепторами и конкретными выходными аксонами.

В нелокальной нейронной сети могут возникать и новые связи между рецепторами и аксонами (адаптивность СИМ и ННС), а также добавляться новые рецепторы и нейроны (пересинтез СИМ и ННС).

Классические когнитивные карты

Классическая когнитивная карта представляет собой нейрон, соответствующий некоторому состоянию объекта управления с рецепторами, каждый из которых соответствует фактору в определенной степени способствующему или препятствующему переходу объекта в это состояние. Рецепторы соединены связями как с нейроном, так и друг с другом. Связи рецепторов с нейроном отражают силу и направление влияния факторов, а связи рецепторов друг с другом, отображаемые в форме семантической сети факторов, – сходство и различие между рецепторами по характеру их влияния на объект управления. Таким образом, классическая когнитивная карта представляет собой нейрон с семантической сетью факторов, изображенные на одной диаграмме (рисунок 81).



Рисунок 81. Примеры классических когнитивных карт, отражающих влияние структуры инвестиций на уровень качества жизни

Обобщенные когнитивные карты

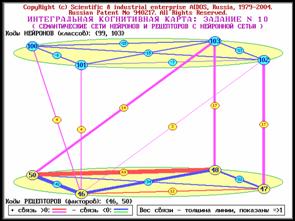
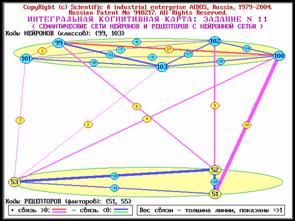
Если объединить несколько классических когнитивных карт на одной диаграмме и изобразить на ней также связи между нейронами в форме семантической сети классов, то получим обобщенную (интегральную) когнитивную карту. На рисунке 82 приведена обобщенная когнитивная карта, отражающая результаты идентификации лет с помощью интегрального критерия уровня качества жизни, на рисунке 83 – влияние инвестиций на уровень качества жизни.

Рисунок 82. Результаты оценки лет с 1991 по 2003
с помощью интегрального критерия уровня качества жизни

Рисунок 83. Обобщенная (интегральная) когнитивная карта,
визуализирующая связи 2-й степени опосредованности МСИМ между структурой инвестиций и уровнем качества жизни

Система "Эйдос" обеспечивает построение любого подмножества многоуровневой семантической информационной модели с заданными или выбираемыми по заданным критериям рецепторами и нейронами, связанными друг с другом связями любого уровня опосредованности в форме классических и обобщенных когнитивных карт. В частности, в системе полуавтоматически формируется задание на генерацию подмножеств обобщенной когнитивной карты, показанных на рисунках 84.


Рисунок 84. Примеры подмножеств интегральной когнитивной карты, отражающие влияние объемов инвестиций по конкретным отраслям на уровень качества жизни населения региона (система "Эйдос")

Резюме

Предлагается модель нелокального нейрона, являющаяся обобщением классической модели Дж. Маккалоки и У. Питтса. Суть нелокальности данной модели состоит в том, что весовые коэффициенты каждого нейрона зависят не только от нейронов, прямо или косвенно соединенных с ним синаптически, но и от всех остальных нейронов сети, не затрагиваемых при обратном распространении ошибки от данного нейрона. Предлагается новый класс нейронных сетей: "Нелокальные интерпретируемые нейронные сети прямого счета" (нелокальные нейронные сети – ННС). Организация ННС обеспечивает один из вариантов решения традиционных для нейронных сетей проблем:

– содержательной интерпретации смысла интенсивности входных сигналов и весовых коэффициентов ("проблема интерпретируемости весовых коэффициентов");

– содержательной интерпретации и обоснования аддитивности аргумента и вида активационной (передаточной) функции нейрона ("проблема интерпретируемости передаточной функции");

– "Комбинаторного взрыва" при определении структуры связей нейронов, подборе весовых коэффициентов и передаточных функций ("проблема размерности");

– "проблема линейной разделимости классов" в случае отсутствия вариабельности весовых коэффициентов нейронов, соответствующих тем или иным классам.

Математическая модель ННС основана на предложенной автором системной теории информации и семантической информационной модели автоматизированного системно-когнитивного анализа (АСК-анализ), и в отличие от известных нейронных сетей, обеспечивают автоматизацию всех 10 базовых когнитивных операций, образующих "когнитивный конфигуратор". Предложены не только математическая модель, но также и соответствующий численный метод (включая алгоритмы и структуры данных), а также программный инструментарий нелокальных нейронных сетей (универсальная когнитивная аналитическая система "Эйдос" версии 12.5), успешно апробированные в ряде предметных областей. Данная система обеспечивает неограниченное количество слоев ННС при максимальном количестве весовых коэффициентов в слое до 16 миллионов (в текущей версии), до 4000 выходных нейронов, а также автоматическую визуализацию и запись в виде графических файлов сформированных моделей нелокальных нейронов и Паретто-подмножеств нелокальной нейронной сети.

Контрольные вопросы

1. Биологический нейрон и формальная модель нейрона Маккалоки и Питтса.

2. Возможность решения простых задач классификации непосредственно одним нейроном.

3. Однослойная нейронная сеть и персептрон Розенблата.

4. Линейная разделимость и персептронная представляемость.

5. Многослойные нейронные сети.

6. Многослойный персептрон.

7. Модель Хопфилда.

8. Когнитрон и неокогнитрон Фукушимы.

9. Проблемы и перспективы нейронных сетей.

10. Модель нелокального нейрона и нелокальные интерпретируемые нейронные сети прямого счета.

11. Метафора нейросетевого представления семантической информационной модели.

12. Соответствие основных терминов и понятий.

13. Гипотеза о нелокальности нейрона и информационная нейросетевая парадигма.

14. Решение проблемы интерпретируемости весовых коэффициентов (семантическая мера целесообразности информации и закон Фехнера).

15. Семантическая информационная модель, как нелокальная нейронная сеть.

16. Гипотеза о физической природе нелокального взаимодействия нейронов в нелокальной нейронной сети.

17. Решение проблемы интерпретируемости передаточной функции.

18. Решение проблемы размерности.

19. Решение проблемы линейной разделимости.

20. Моделирование причинно-следственных цепочек в нейронных сетях и семантической информационной модели.

21. Моделирование иерархических структур обработки информации.

22. Нейронные сети и СК-анализ.

23. Графическое отображение нейронов, Паррето-подмножеств нелокальной нейронной сети, семантических сетей, когнитивных карт и диаграмм в системе "Эйдос".