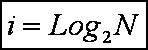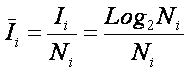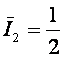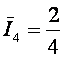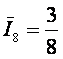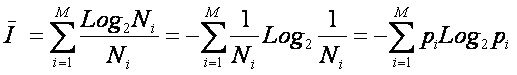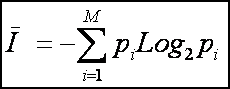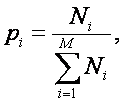1

1.3.3. ЛЕКЦИЯ-9.
Математические методы
и автоматизированные системы
поддержки принятия решений

Учебные вопросы

1. Многообразие задач принятия решений.

2. Языки описания методов принятия решений.

3. Выбор в условиях неопределенности.

4. Решение как компромисс и баланс различных интересов. О некоторых ограничениях оптимизационного подхода.

5. Экспертные методы выбора.

6. Юридическая ответственность за решения, принятые с применением систем поддержки принятия решений.

7. Условия корректности использования систем поддержки принятия решений.

8. Хранилища данных для принятия решений.

1.3.3.1. Многообразие задач принятия решений

1.3.3.1.1. Принятие решений, как реализация цели

Определение: принятие решения есть действие над множеством альтернатив, в результате которого исходное множество альтернатив сужается. Это действие называется "выбор".

Выбор является действием, придающим всей деятельности целенаправленность. Именно через акты выбора реализуется подчиненность всей деятельности определенной цели или совокупности взаимосвязанных целей.

Таким образом, для того, чтобы стал возможен акт выбора, необходимо следующее:

Порождение или обнаружение множества альтернатив, на котором предстоит совершить выбор.

Определение целей, ради достижения которых осуществляется выбор.

Разработка и применение способа сравнения альтернатив между собой, т.е. определение рейтинга предпочтения для каждой альтернативы, согласно определенным критериям, позволяющим косвенно оценивать, насколько каждая альтернатива соответствует цели.

Современные работы в области поддержки принятия решений выявили характерную ситуацию, которая состоит в том, что полная формализация нахождения наилучшего (в определенном смысле) решения возможна только для хорошо изученных, относительно простых задач, тогда как на практике чаще встречаются слабо структурированные задачи для которых полностью формализованных алгоритмов не разработано (если не считать полного перебора и метода проб и ошибок). Вместе с тем, опытные, компетентные и способные специалисты, часто делают выбор, который оказывается достаточно хорошим. Поэтому современная тенденция практики принятия решений в естественных ситуациях состоит в сочетании способности человека решать неформализованные задачи с возможностями формальных методов и компьютерного моделирования: диалоговые системы поддержки принятия решений, экспертные системы, адаптивные человеко-машинные автоматизированные системы управления, нейронные сети и когнитивные системы.

1.3.3.1.2. Принятие решений, как снятие неопределенности (информационный подход)

Процесс получения информации можно рассматривать как уменьшение неопределенности в результате приема сигнала, а количество информации, как количественную меру степени снятия неопределенности.

Но в результате выбора некоторого подмножества альтернатив из множества, т.е. в результате принятия решения, происходит тоже самое (уменьшение неопределенности).

Это значит, что каждый выбор, каждое решение порождает определенное количество информации, а значит может быть описано в терминах теории информации.

Простейшее понятие об информации (подход Хартли).

Будем считать, что если существует множество элементов и осуществляется выбор одного из них, то этим самым сообщается или генерируется определенное количество информации. Эта информация состоит в том, что если до выбора не было известно, какой элемент будет выбран, то после выбора это становится известным.

Найдем вид функции, связывающей количество информации, получаемой при выборе некоторого элемента из множества, с количеством элементов в этом множестве, т.е. с его мощностью. История науки не сохранила для нас вывода формулы для количества информации, предложенной Хартли. Поэтому в данной работе мы, стараясь следовать сложившейся традиции, попытаемся реконструировать его возможный ход мысли.

На качественном уровне его рассуждения могли выглядеть следующим образом.

Если множество элементов, из которых осуществляется выбор, состоит из одного-единственного элемента, то ясно, что его выбор предопределен, т.е. никакой неопределенности выбора нет. Таким образом, если мы узнаем, что выбран этот единственный элемент, то, очевидно, при этом мы не получаем никакой новой информации, т.е. получаем нулевое количество информации.

Если множество состоит из двух элементов, то неопределенность выбора минимальна. В этом случае минимально и количество информации, которое мы получаем, узнав, что совершен выбор одного из элементов. Минимальное количество информации получается при выборе одного из двух равновероятных вариантов. Это количество информации принято за единицу измерения и называется "бит".

Чем больше элементов в множестве, тем больше неопределенность выбора, тем больше информации мы получаем, узнав о том, какой выбран элемент.

На количественном уровне эти рассуждения могли бы иметь следующий вид.

Рассмотрим множество, состоящее из чисел в двоичной системе счисления длиной i двоичных разрядов. При этом каждый из разрядов может принимать значения только 0 и 1 (таблица 32).

Таблица 32 – К ЭВРИСТИЧЕСКОМУ ВЫВОДУ ФОРМУЛЫ КОЛИЧЕСТВА ИНФОРМАЦИИ ПО ХАРТЛИ

Кол-во двоичных разрядов (i) и кол-во состояний N, которое можно пронумеровать i-разрядными двоичными числами				Основание системы счисления и номера разрядов
				10		16	2
4	3	2	1	2	1	1	4	3	2	1
16	8	4	2	0	0	0	0	0	0	0
			2	0	1	1	0	0	0	1
				0	2	2	0	0	1	0
				0	3	3	0	0	1	1
				0	4	4	0	1	0	0
				0	5	5	0	1	0	1
				0	6	6	0	1	1	0
				0	7	7	0	1	1	1
				0	8	8	1	0	0	0
				0	9	9	1	0	0	1
				1	0	A	1	0	1	0
				1	1	B	1	0	1	1
				1	2	C	1	1	0	0
				1	3	D	1	1	0	1
				1	4	E	1	1	1	0
				1	5	F	1	1	1	1
***	***	***	***	*	*	*	*	*	*	*

Анализируя таблицу 32 можно заметить, что при увеличении количества разрядов в двоичных числах на один количество состояний, которые можно пронумеровать с помощью этих чисел возрастает в два раза:

Кол-во двоичных разрядов (i)	Кол-во состояний N, которое можно пронумеровать i-разрядными двоичными числами
Кол-во двоичных разрядов (i)
1	2
2	4
3	8
4	16
***	***
i

Аналогичное утверждение верно для чисел в любой системе счисления: при увеличении количества разрядов в числах в системе счисления с основанием E на один количество состояний, которые можно пронумеровать с помощью тих чисел возрастает в E раз. Например, при дописывании нуля к десятичному числу справа оно увеличивается в 10 раз, к двоичному – в два раза, к шестнадцатеричному – в 16 раз.

Итак, из таблицы 32 видно, что количество этих чисел (элементов) в множестве равно:

Рассмотрим процесс выбора чисел из рассмотренного множества. До выбора вероятность выбрать любое число одинакова. Существует объективная неопределенность в вопросе о том, какое число будет выбрано. Эта неопределенность тем больше, чем больше N – количество чисел в множестве, а чисел тем больше – чем больше разрядность i этих чисел.

Примем, что выбор одного числа дает нам следующее количество информации:

Таким образом, количество информации, содержащейся в двоичном числе, равно количеству двоичных разрядов в этом числе. Это количество информации i мы получаем, когда случайным равновероятным образом выпадает одно из двоичных чисел, записанных i разрядами, или из некоторого множества выбирается объект произвольной природы, пронумерованный этим числом (предполагается, что остальные объекты этого множества пронумерованы остальными числами и этим они и отличаются).

Это выражение и представляет собой формулу Хартли для количества информации. Отметим, что оно полностью совпадает с выражением для энтропии (по Больцману и Эшби), которая рассматривалась ими как количественная мера степени неопределенности состояния системы.

Сам Хартли, возможно, пришел к своей мере на основе эвристических соображений, подобных только что изложенным, но в настоящее время строго доказано, что логарифмическая мера для количества информации однозначно следует из этих двух постулированных им условий.

Таким образом, информация по своей сущности теснейшим и органичным образом связана с выбором и принятием решений.

Отсюда следует простейшее на первый взгляд заключение: "Для принятия решений нужна информация, без информации принятие решений невозможно, значение информации для принятия решений является определяющим, процесс принятия решений генерирует информацию".

Мера Шеннона, как обобщение меры Хартли для неравновероятных событий.

Представим себе, что имеются объекты различных видов, причем:

– всего имеется M видов объектов;

– объектов каждого i-го вида имеется N_i:

Пусть, например, в мешке имеются бильярдные шары, на которых написаны числа 2, 4, 8 и имеется:

– 4 шара с надписью "2", т.е. N₂=2;

– 4 шара с надписью "4", т.е. N₄=4:

– 8 шаров с надписью "8", т.е. N₈=8:

			2	2
		4	4	4	4
8	8	8	8	8	8	8	8

всего, 14 шаров.

Тогда по Хартли, если мы извлекаем один из объектов i-го вида, то получаем I_i бит информации

В частности:

– при извлечении шара с надписью "2" мы получаем бит информации;

– при извлечении шара с надписью "4" мы получаем бит информации;

– при извлечении шара с надписью "8" мы получаем бит информации;

В среднем по , т.е. на один объект i-го вида:

Или количественно в нашем примере:

Сумма этих средних будет равна:

Последнее выражение – это и есть формула Шеннона, которая, таким образом, позволяет рассчитать средневзвешенное количество информации, приходящееся на один объект, получаемое при предъявлении объектов различных видов, причем внутри объектов каждого вида выбор равновероятен, а количество объектов разного вида вообще говоря различно.

При переходе от частот к вероятностям в формуле Шеннона использованы элементарные свойства логарифмов и введено обозначение: 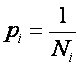, которое традиционно интерпретируется как вероятность встречи объектов i-го вида.

По мнению автора это не совсем точно, т.к. из элементарной теории вероятностей известно, что в общем случае вероятность определяется иначе, а именно как отношение количества событий определенного вида к общему количеству всех возможных событий всех видов.

Если использовать приведенные выше обозначения, то эта вероятность должна выражаться следующей формулой:

Из сравнения этих выражений видно, что общее выражение переходит в 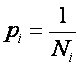в случае, когда все N_i=1 и сумма всех N_i=N.

Количественно:

Если количество объектов каждого вида одинаково, то формула Шеннона преобразуется в формулу Хартли.

Отметим, что идентификация объектов, как относящихся к тому или иному виду (i-му виду) осуществляется на основе признаков этих объектов. В простейшем варианте это может быть и один признак, например номер вида на бильярдном шаре, но в реальных случаях признаков может быть очень много и их различные наборы сложным и неоднозначным образом могут быть связаны с принадлежностью объектов к тем или иным классам.

Но главный вывод от этого не изменяется: формула Шеннона дает средневзвешенное количество информации, приходящееся на один объект, получаемое при предъявлении объектов различных видов (классов), отличающихся своими наборами признаков. Мера Шеннона является обобщением меры Хартли для неравновероятных событий.

1.3.3.1.3. Связь принятия решений и распознавания образов

Распознавание образов есть решение задачи идентификации состояния объекта или системы, отнесение его к той или иной классификационной категории.

Распознавание образов и принятие решений тесно взаимосвязаны:

– само распознавание безусловно представляет собой принятие решения об отнесении состояния системы к той или иной категории;

– от того, к какой категории отнесено состояние системы самым непосредственным образом зависят и решения по управлению этой системой;

– математический аппарат распознавания образов и принятия решений имеет очень много аналогий, а иногда и просто является тождественным (например, сведение многокритериальной задачи к однокритериальной).

1.3.3.1.4. Классификация задач принятия решений

Множественность задач принятия решений связана с тем, что каждая компонента ситуации, в которой осуществляется принятие решений может реализовываться в качественно различных вариантах.

Вот только некоторые из этих вариантов:

Множество альтернатив с одной стороны может быть конечным, счетным или континуальным, а с другой – закрытым (т.е. известным полностью), или открытым (включающим неизвестные элементы).

Оценка альтернатив может осуществляться по одному или нескольким критериям, которые, в свою очередь, могут иметь количественный или качественный характер.

Режим выбора может быть однократным (разовым), или многократным, повторяющимся, включающим обратную связь по результатам выбора, т.е. допускающим обучение алгоритмов принятия решений с учетом последствий предыдущих выборов.

Последствия выбора каждой альтернативы могут быть точно известны заранее (выбор в условиях определенности), иметь вероятностный характер, когда известны вероятности возможных исходов после сделанного выбора (выбор в условиях риска), или иметь неоднозначный исход с неизвестными вероятностями (выбор в условиях неопределенности).

Ответственность за выбор может отсутствовать, быть индивидуальной или групповой.

Степень согласованности целей при групповом выборе может варьироваться от полного совпадения интересов сторон (кооперативный выбор), до их противоположности (выбор в конфликтной ситуации). Возможны также промежуточные варианты: компромисс, коалиция, нарастающий или затухающий конфликт.

Различные сочетания перечисленных вариантов и приводят к многочисленным задачам принятия решений, которые изучены в различной степени.

1.3.3.2. Языки описания методов принятия решений

Об одном и том же явлении можно говорить на различных языках различной степени общности адекватности. К настоящему времени сложилось три основных языка описания выбора.

Самым простым и наиболее развитым и наиболее популярным является критериальный язык.

1.3.3.2.1. Критериальный язык

Название этого языка связано с основным предположением, состоящим в том, что каждую отдельно взятую альтернативу можно оценить некоторым конкретным (одним) числом, после чего сравнение альтернатив сводится к сравнению соответствующих им чисел.

Пусть, например, {X} - множество альтернатив, а x – некоторая определенная альтернатива, принадлежащая этому множеству: xÌX. Тогда считается, что для всех x может быть задана функция: q(x), которая называется критерием (критерием качества, целевой функцией, функцией предпочтения, функцией полезности и т.п.), обладающая тем свойством, что если альтернатива x1 предпочтительнее x2: (обозначается: x1 > x2),

то:

q(x1) > q(x2).

При этом выбор сводится к отысканию альтернативы с наибольшим значением критериальной функции.

Однако, на практике использование лишь одного критерия для сравнения степени предпочтительности альтернатив оказывается неоправданным упрощением, т.к. более подробное рассмотрение альтернатив приводит к необходимости оценивать их не по одному, а по многим критериям, которые могут иметь различную природу и качественно отличаться друг от друга.

Например, при выборе наиболее приемлемого для пассажиров и эксплуатирующей организации типа самолета на определенных видах трасс сравнение идет одновременно по многим группам критериев: техническим, технологическим, экономическим, социальным, эргономическим и др.

Многокритериальные задачи не имеют однозначного общего решения. Поэтому предлагается много способов придать многокритериальной задаче частный вид, допускающий единственное общее решение. Естественно, что для разных способов эти решения являются в общем случае различными. Поэтому едва ли не главное в решении многокритериальной задачи - обоснование данного вида ее постановки.

Используются различные варианты упрощения многокритериальной задачи выбора. Перечислим некоторые из них.

1. Условная максимизация (находится не глобальный экстремум суперкритерия, или, как его еще называют, интегрального критерия, а локальный экстремум основного критерия).

2. Поиск альтернативы с заданными свойствами.

3. Нахождение множества Парето.

4. Сведение многокритериальной задачи к однокритериальной, путем ввода суперкритерия.

Рассмотрим подробнее формальную постановку метода сведения многокритериальной задачи к однокритериальной.

Введем суперкритерий q₀(x), как скалярную функцию векторного аргумента:

q₀(x)= q₀((q₁(x), q₂(x),..., q_n(x)).

Суперкритерий позволяет упорядочить альтернативы по величине q₀, выделив тем самым наилучшую (в смысле этого критерия). Вид функции q₀ определяется тем, как конкретно мы представляем себе вклад каждого критерия в суперкритерий. Обычно используют аддитивные и мультипликативные функции:

Коэффициенты s_i обеспечивают:

1. Безразмерность или единую размерность числа a_iq_i/s_i (различные частные критерии могут иметь разную размерность, и тогда над ними нельзя производить арифметических операций и свести их в суперкритерий).

2. Нормировку, т.е. обеспечение условия: b_iq_i/s_i<1.

Коэффициенты a_i и b_i отражают относительный вклад частных критериев q_i в суперкритерий.

Итак, в многокритериальной постановке задача принятия решения о выборе одной из альтернатив сводится к максимизации суперкритерия.

Основная проблема в многокритериальной постановке задачи принятия решений состоит в том, что необходимо найти такой аналитический вид коэффициентов a_i и b_i, который бы обеспечил следующие свойства модели:

1. Высокую степень адекватности предметной области и точке зрения экспертов.

2. Минимальные вычислительные трудности максимизации суперкритерия, т.е. Его расчета для разных альтернатив.

3. Устойчивость результатов максимизации суперкритерия от малых возмущений исходных данных.

Устойчивость решения означает, что малое изменение исходных данных должно приводить к малому изменению величины суперкритерия, и, соответственно, к малому изменению принимаемого решения. То есть практически на тех же исходных данных должно приниматься или тоже самое, или очень близкое решение.

1.3.3.2.2. Язык последовательного бинарного выбора

Язык бинарных отношений является обобщением многокритериального языка и основан на учете того факта, что когда мы даем оценку некоторой альтернативе, то эта оценка всегда является относительной, т.е. явно или чаще неявно в качестве базы или системы отсчета для сравнения используются другие альтернативы из исследуемого множества или из генеральной совокупности. Мышление человека основано на поиске и анализе противоположностей (конструктов), поэтому, нам всегда проще выбрать один из двух противоположных вариантов, чем один вариант из большого и никак неупорядоченного их множества.

Таким образом, основные предположения этого языка сводятся к следующему:

1. Отдельная альтернатива не оценивается, т.е. критериальная функция не вводится.

2. Для каждой пары альтернатив некоторым образом можно установить, что одна из них предпочтительнее другой, либо они равноценны или несравнимы.

3. Отношение предпочтения в любой паре альтернатив не зависит от остальных альтернатив, предъявленных к выбору.

Существуют различные способы задания бинарных отношений: непосредственный, матричный, с использованием графов предпочтений, метод сечений и др.

Отношения между альтернативами одной пары выражают через понятия эквивалентности, порядка и доминирования.

1.3.3.2.3. Обобщенный язык функций выбора

Язык функций выбора основан на теории множеств и позволяет оперировать с отображениями множеств на свои подмножества, соответствующие различным вариантам выбора, без необходимости перечисления элементов. Этот язык является весьма общим и потенциально позволяет описывать любой выбор. Однако, математический аппарат обобщенных функций выбора в настоящее время еще только разрабатывается и проверяется в основном на задачах, которые уже решены с помощью критериального или бинарного подходов.

1.3.3.2.4. Групповой выбор

Пусть имеется группа лиц, имеющих право принимать участие в коллективном принятии решений. Предположим, что эта группа рассматривает некоторый набор альтернатив, и каждый член группы осуществляет свой выбор. Ставится задача о выработке решения, которое определенным образом согласует индивидуальные выборы и в каком-то смысле выражает "общее мнение" группы, т.е. принимается за групповой выбор.

Естественно, различным принципам согласования индивидуальных решений будут соответствовать различные групповые решения.

Правила согласования индивидуальных решений при групповом выборе называются правилами голосования. Наиболее распространенным является "правило большинства", при котором за групповое решение принимается альтернатива, получившая наибольшее число голосов.

Необходимо понимать, что такое решение отражает лишь распространенность различных точек зрения в группе, а не действительно оптимальный вариант, за который вообще никто может и не проголосовать. "Истина не определяется путем голосования", самой распространенной точкой зрения может быть и заблуждение.

Кроме того, существуют так называемые "парадоксы голосования", наиболее известный из которых парадокс Эрроу.

Эти парадоксы могут привести, и иногда действительно приводят, к очень неприятным особенностям процедуры голосования: например бывают случаи, когда группа вообще не может принять единственного решения (нет кворума или каждый голосует за свой уникальный вариант, и т.д.), а иногда (при многоступенчатом голосовании) меньшинство может навязать свою волю большинству, как это было на президентских выборах в США "Буш – Гор".

1.3.3.3. Выбор в условиях неопределенности

Выбор в условиях определенности – это частный случай выбора в условиях неопределенности (когда неопределенность близка к нулю).

Но неопределенность чего конкретно имеется в виду?

В современной теории выбора считается, что в задачах принятия решений существует три основных вида неопределенности:

1. Информационная (статистическая) неопределенность исходных данных для принятия решений.

2. Неопределенность последствий принятия решений (выбора).

3. Расплывчатость в описании компонент процесса принятия решений.

Рассмотрим их по порядку.

1.3.3.3.1. Информационная (статистическая) неопределенность в исходных данных

Данные, полученные о предметной области, не могут рассматриваться как абсолютно точные. Кроме того, очевидно, эти данные нас интересуют не сами по себе, а лишь в качестве сигналов, которые, возможно, несут определенную информацию о том, что нас в действительности интересует.

То есть, реалистичнее считать, что мы имеем дело с данными, не только зашумленными и неточными, но еще и косвенными, а возможно и не полными.

Кроме того эти данные касаются не всей исследуемой (генеральной) совокупности, а лишь определенного ее подмножества, о котором мы смогли фактически собрать данные, однако при этом мы хотим сделать выводы о всей совокупности, причем хотим еще и знать достоверность этих выводов.

В этих условиях используется теория статистических решений.

В этой теории существует два основных источника неопределенности. Во-первых, неизвестно, какому распределению подчиняются исходные данные. Во-вторых, неизвестно, какое распределение имеет то множество (генеральная совокупность), о котором мы хотим сделать выводы по его подмножеству, образующему исходные данные.

Статистические процедуры это и есть процедуры принятия решений, снимающих оба эти виды неопределенности.

Необходимо отметить, что существует ряд причин, которые приводят к некорректному применению статистических методов:

1. Статистические выводы, как и любые другие, всегда имеют некоторую определенную надежность или достоверность. Но, в отличие от многих других случаев, достоверность статистических выводов известна и определяется в ходе статистического исследования.

2. Качество решения, полученного в результате применения статистической процедуры зависит, от качества исходных данных.

3. Не следует подвергать статистической обработке данные, не имеющие статистической природы.

4. Необходимо использовать статистические процедуры, соответствующие уровню априорной информации об исследуемой совокупности (например, не следует применять методы дисперсионного анализа к негауссовым данным). Если распределение исходных данных неизвестно, то надо либо его установить, либо использовать несколько различных методов и сравнить результаты. Если они сильно отличаются - это говорит о неприменимости некоторых из использованных процедур.

1.3.3.3.2. Неопределенность последствий

Когда последствия выбора той или иной альтернативы однозначно определяются самой альтернативой, тогда можно не различать альтернативу и ее последствия, считая само собой разумеющимся, что выбирая альтернативу мы в действительности выбираем ее последствия.

Однако, в реальной практике нередко приходится иметь дело с более сложной ситуацией, когда выбор той или иной альтернативы неоднозначно определяет последствия сделанного выбора.

В случае дискретного набора альтернатив и исходов их выбора, при условии, что сам набор возможных исходов общий для всех альтернатив, можно считать, что различные альтернативы отличаются друг от друга распределением вероятностей исходов. Эти распределения вероятностей вообще говоря могут зависеть от результатов выбора альтернатив и реально наступивших в результате этого исходов. В простейшем случае исходы равновероятны. Сами исходы обычно имеют смысл выигрышей или потерь и выражаются количественно.

Если исходы равны для всех альтернатив, то выбирать нечего. Если же они различны, то можно сравнивать альтернативы, вводя для них те или иные количественные оценки. Разнообразие задач теории игр связано с различным выбором числовых характеристик потерь и выигрышей в результате выбора альтернатив, различными степенями конфликтности между сторонами, выбирающими альтернативы и т.д.

1.3.3.3.3. Расплывчатая неопределенность

Любая задача выбора является задачей целевого сужения множества альтернатив. Как формальное описание альтернатив (сам их перечень, перечень их признаков или параметров), так и описание правил их сравнения (критериев, отношений) всегда даются в терминах той или иной измерительной шкалы (даже тогда, когда тот, кто это делает, не знает об этом).

Известно, все шкалы размыты, но в разной степени. Под термином "размытие" понимается свойство шкал, состоящее в том, что всегда можно предъявить такие две альтернативы, которые различимы, т.е. различны в одной шкале и неразличимы, т.е. тождественны в другой - более размытой. Чем меньше градаций в некоторой шкале, тем более она размыта.

Таким образом, мы можем четко видеть альтернативы, и одновременно нечетко их классифицировать, т.е. иметь неопределенность в вопросе о том, к каким классам они относятся.

Уже в первой работе по принятию решений в расплывчатой ситуации Беллман и Заде выдвинули идею, состоящую в том, что и цели, и ограничения должны представляться как размытые (нечеткие) множества на множестве альтернатив.

1.3.3.4. Решение как компромисс и баланс различных интересов. О некоторых ограничениях оптимизационного подхода

Во всех рассмотренных выше задачах выбора и методах принятия решений проблема состояла в том, чтобы в исходном множестве найти наилучшие в заданных условиях, т.е. оптимальные в определенном смысле альтернативы.

Идея оптимальности является центральной идеей кибернетики и прочно вошла в практику проектирования и эксплуатации технических систем. Вместе с тем эта идея требует осторожного к себе отношения, когда мы пытаемся перенести ее в область управления сложными, большими и слабо детерминированными системами, такими, например, как социально-экономические системы.

Для этого заключения имеются достаточно веские основания. Рассмотрим некоторые из них.

1. Оптимальное решение нередко оказывается неустойчивым: т.е. незначительные изменения в условиях задачи, исходных данных или ограничениях могут привести к выбору существенно отличающихся альтернатив.

2. Оптимизационные модели разработаны лишь для узких классов достаточно простых задач, которые не всегда адекватно и системно отражают реальные объекты управления. Чаще всего оптимизационные методы позволяют оптимизировать лишь достаточно простые и хорошо формально описанные подсистемы некоторых больших и сложных систем, т.е. позволяют осуществить лишь локальную оптимизацию. Однако, если каждая подсистема некоторой большой системы будет работать оптимально, то это еще совершенно не означает, что оптимально будет работать и система в целом. То есть оптимизация подсистемы совсем не обязательно приводит к такому ее поведению, которое от нее требуется при оптимизации системы в целом. Более того, иногда локальная оптимизация может привести к негативным последствиям для системы в целом.

3. Часто максимизация критерия оптимизации согласно некоторой математической модели считается целью оптимизации, однако в действительностью целью является оптимизация объекта управления. Критерии оптимизации и математические модели всегда связаны с целью лишь косвенно, т.е. более или менее адекватно, но всегда приближенно.

Итак, идею оптимальности, чрезвычайно плодотворную для систем, поддающихся адекватной математической формализации, нельзя перенести на сложные системы. Конечно, математические модели, которые удается иногда предложить для таких систем, можно оптимизировать. Однако всегда следует учитывать сильную упрощенность этих моделей, а также то, что степень их адекватности фактически неизвестна. Поэтому не известно, какое чисто практическое значение имеет эта оптимизация. Высокая практичность оптимизации в технических системах не должна порождать иллюзий, что она будет настолько же эффективна при оптимизации сложных систем. Содержательное математическое моделирование сложных систем является весьма затруднительным, приблизительным и неточным. Чем сложнее система, тем осторожнее следует относится к идее ее оптимизации.

Поэтому, при разработке методов управления сложными, большими слабо детерминированными системами, основным является не оптимальность выбранного подхода с формальной математической точки зрения, а его адекватность поставленной цели и самому характеру объекта управления.

1.3.3.5. Экспертные методы выбора

При исследовании сложных систем часто возникают проблемы, которые по различным причинам не могут быть строго поставлены и решены с применением разработанного в настоящее время математического аппарата. В этих случаях прибегают к услугам экспертов (системных аналитиков), чей опыт и интуиция помогают уменьшить сложность проблемы.

Однако, необходимо учитывать, что эксперты сами представляют собой сверхсложные системы, и их деятельность сама зависит от многих внешних и внутренних условий. Поэтому в методиках организации экспертных оценок большое внимание уделяется созданию благоприятных внешних и психологических условий для работы экспертов.

На работу эксперта оказывают влияние следующие факторы:

– ответственность за использование результатов экспертизы;

– знание того, что привлекаются и другие эксперты;

– наличие информационного контакта между экспертами;

– межличностные отношения экспертов (если между ними есть информационный контакт);

– личная заинтересованность эксперта в результатах оценки;

– личностные качества экспертов (самолюбие, конформизм, воля и др.)

Взаимодействие между экспертами может как стимулировать, так и подавлять их деятельность. Поэтому в разных случаях используют различные методы экспертизы, отличающиеся характером взаимодействия экспертов друг с другом: анонимные и открытые опросы и анкетирования, совещания, дискуссии, деловые игры, мозговой штурм и т.д.

Существуют различные методы математической обработки мнений экспертов. Экспертам предлагают оценить различные альтернативы либо одним, либо системой показателей. Кроме того им предлагают оценить степень важности каждого показателя (его "вес" или "вклад"). Самим экспертам также приписывается уровень компетентности, соответствующий его вкладу в результирующее мнение группы.

Развитой методикой работы с экспертами является метод "Дельфи". Основная идея этого метода состоит в том, что критика и аргументация благотворно влияет на эксперта, если при этом не задевается его самолюбие и обеспечиваются условия, исключающие персональную конфронтацию.

Необходимо особо подчеркнуть, что существует принципиальное различие в характере использования экспертных методов в экспертных системах и в поддержке принятия решений. Если в первом случае от экспертов требуется формализация способов принятия решений, то во втором, лишь само решение, как таковое.

Поскольку эксперты привлекаются для реализации именно тех функций, которые в настоящее время или вообще не обеспечиваются автоматизированными системами, или выполняются ими хуже, чем человеком, то перспективным направлением развития автоматизированных систем является максимальная автоматизация этих функций.

1.3.3.6. Юридическая ответственность за решения, принятые с применением систем поддержки принятия решений

Необходимо отметить, что система поддержки принятия решений (СППР) не является физическим или юридическим лицом и не может нести ответственность за те или иные решения, которые принимаются с ее использованием.

Согласно действующему сейчас и в обозримой перспективе законодательству автоматизированную систему невозможно привлечь к административной или уголовной ответственности. Но это не означает, что в будущем подобные вопросы не возникнут по поводу созданных методами генной инженерии искусственных разумных биологических систем, которые автором совместно с Л.А.Бакурадзе в 1980 году были названы "квазибиологические роботы", или по поводу клонов, не ассоциированных в общечеловеческую социальную среду.

Ответственность за принятое решение всегда несет специалист, или, как говорят, "лицо, принимающее решения" (ЛПР).

Вместе с тем при выработке решения это лицо может обращаться к различной справочной информации, а также консультироваться со специалистами в различных предметных областях. При этом справочная информация может извлекаться по запросам из баз данных, а консультации могут происходить не с самими специалистами лично, а с автоматизированными системами поддержки принятия решений, в которых в формализованном и обобщенном виде содержаться знания многих специалистов.

Но в какой форме содержаться консультирующая информация и знания – это сути дела не меняет, т.е. ответственность за принятое решение все равно всегда лежит на лице, его приявшем, а не на консультирующих или поддерживающих решения системах. Поэтому эти системы и называются не "системы принятия решений", а лишь "системы поддержки принятия решений".

Особым случаем являются автоматизированные системы управления оружием, например, создаваемые в США в рамках программы "Стратегической оборонной инициативы" (СОИ). В этих системах человек может участвовать в процессе принятия решений лишь на этапах их создания, т.к. в на боевом дежурстве систем для участия человека просто не будет времени. И тем ни менее и эти системы принимают решения не самостоятельно, а на основе анализа фактической информации по тем критериям и алгоритмам, которые заложил в них человек. Таким образом, в подобных системах человек становится заложником своих же решений, принятых им ранее.

1.3.3.7. Условия корректности использования систем поддержки принятия решений

Этих условий три:

1. Само решение о выборе той или иной конкретной системы поддержки принятия решений должно приниматься лицом, принимающим решения, который и будет пользоваться ее рекомендациями, либо подчиненными ему компетентными специалистами по его личному поручению.

2. Сам выбор системы поддержки принятия решений должен осуществляться, как правило, не по их специальным, или, тем более, рекламным описаниям и литературным данным, а по результатам сравнительных испытаний на реальных примерах из практики работы организации.

3. Выбранная система должна быть официально принятой для решения тех задач, для решения которых она будет использоваться, т.е. должна быть сертифицирована.

Под сертификацией понимается:

– апробация системы поддержки принятия решений и оценка адекватности рекомендуемых ей решений на ряде реальных задач, которые возникали в прошлом или возникают в течение определенного периода экспериментальной эксплуатации;

– придание системе поддержки принятия решений юридического статуса, который предписывает и лицам принимающим решения "принимать к сведению" рекомендации системы.

Для сертификации системы создается соответствующая компетентная и полномочная комиссия, которая в течение определенного времени изучает систему и выдаваемые ею рекомендации на предмет адекватности складывающимся ситуациям. Результаты работы комиссии оформляются в форме юридического документа, имеющего силу в ведомстве или организации, в которых будет применяться система.

В этом документе описывается круг задач, для решения которых применяется система, инфраструктура и технология ее применения, а также определяются обязанности и персональная ответственность специалистов по эксплуатации системы.

Если система не сертифицирована, то ее применение некорректно с юридической точки зрения. На практике это происходит гораздо чаще, чем многие представляют, например, с системами бухгалтерского учета или психологическими тестами, которые распространяются на пиратских компакт-дисках, не локализованы для регионов и организаций применения, не адаптированы для решения задач, для решения которых они фактически применяются.

1.3.3.8. Хранилища данных для принятия решений

В разделе 4.2.5. данной работы мы рассматривали иерархическую систему обработки информации в которой на различных уровнях производятся различные операции по обработке данных, информации и знаний:

– на 1-м уровне накапливаются данные мониторинга;

– на 2-м уровне осуществляется анализ данных мониторинга с целью выявления в них зависимостей, что позволяет содержательно интерпретировать данные, т.е. генерировать информацию путем анализа данных;

– на 3-м уровне знание зависимостей в данных мониторинга используется для прогнозирования;

– на 4-м уровне возможности многовариантного прогнозирования и решения обратной задачи прогнозирования позволяют вырабатывать рекомендации и решения по достижению поставленных целей, т.е. генерировать и использовать знания путем системной обработки информации.

Выполнение операций каждого последующего уровня возможно только построения предыдущего уровня. Здесь уместно провести аналогию со строительством здания: пока не выполнен фундамент – не возводят стены, пока не возведены стены – не делают крышу, пока нет крыши – не проводят отделку и т.д. Аналогично, чтобы вытащить внутреннюю матрешку сначала надо раскрыть внешнюю. Могут существовать и более сложные алгоритмы, определяющие последовательность, например, типа используемых в игре "Ханойская башня".

Таким образом, фундаментом для генерации информации и знаний являются данные мониторинга.

Хранилище Данных (ХД или Data warehouses) – это база данных, хранящая данные, агрегированные по многим измерениям. Данные из ХД никогда не удаляются. Пополнение ХД происходит на периодической основе. При этом автоматически формируются новые агрегаты данных, зависящие от старых. Доступ к ХД организован особым образом на основе модели многомерного куба.

Итак, Хранилище Данных – это не автоматизированная система принятия решений, не экспертная система, не система логического вывода, а "всего лишь" оптимально организованная база данных, обеспечивающая максимально быстрый и комфортный доступ к информации, необходимой при принятии решений.

Принять любое управленческое решение, невозможно не обладая необходимой для этого информацией, обычно количественной. Для этого необходимо создание хранилищ данных (Data warehouses), то есть процесс сбора, отсеивания и предварительной обработки данных с целью предоставления результирующей информации пользователям для статистического анализа (а нередко и создания аналитических отчетов). Ральф Кимбалл (Ralph Kimball), один из авторов концепции хранилищ данных сформулировал основные требования к ним:

– поддержка высокой скорости получения данных из хранилища;

– поддержка внутренней непротиворечивости данных;

– возможность получения и сравнения так называемых срезов данных (slice and dice);

– наличие удобных утилит просмотра данных в хранилище;

– полнота и достоверность хранимых данных;

– поддержка качественного процесса пополнения данных.

Типичное хранилище данных, как правило, отличается от обычной реляционной базы данных.

Во-первых, обычные базы предназначены для того, чтобы помочь пользователям выполнять повседневную работу, тогда как хранилища данных предназначены для принятия решений. Например, продажа товара и выписка счета производятся с использованием базы данных, предназначенной для обработки транзакций, а анализ динамики продаж за несколько лет, позволяющий спланировать работу с поставщиками, - с помощью хранилища данных.

Во-вторых, обычные базы данных подвержены постоянным изменениям в процессе работы пользователей, а хранилище данных относительно стабильно: сведения в нем обычно обновляются согласно расписанию (например, еженедельно, ежедневно или ежечасно – в зависимости от потребностей). В идеале процесс пополнения представляет собой просто добавление новых данных за определенный период времени без изменения прежней информации, уже находящейся в хранилище.

В-третьих, обычные базы данных чаще всего являются источником данных, попадающих в хранилище. Кроме того, хранилище может пополняться за счет внешних источников, например статистических отчетов.

Для более полного ознакомления с концепцией хранилищ данных рекомендуется обратиться к Internet-источникам.

Контрольные вопросы

1. Многообразие задач принятия решений.

2. Принятие решений, как реализация цели.

3. Принятие решений, как снятие неопределенности (информационный подход).

4. Связь принятия решений и распознавания образов.

5. Классификация задач принятия решений.

6. Языки описания методов принятия решений.

7. Критериальный язык.

8. Язык последовательного бинарного выбора.

9. Обобщенный язык функций выбора.

10. Групповой выбор.

11. Выбор в условиях неопределенности.

12. Информационная (статистическая) неопределенность в исходных данных.

13. Неопределенность последствий.

14. Расплывчатая неопределенность.

15. Решение как компромисс и баланс различных интересов. О некоторых ограничениях оптимизационного подхода.

16. Экспертные методы выбора.

17. Юридическая ответственность за решения, принятые с применением систем поддержки принятия решений.

18. Условия корректности использования систем поддержки принятия решений.

19. Хранилища данных для принятия решений.