4.2. Постановка агрометеорологических задач выбора микрозон и культур для
выращивания
4.2.1. Актуальность исследования
Накоплен многолетний фактографический
материал по выращиванию плодовых культур в разных условиях среды. Однако, этот
материал находится в форме бумажных документов различных стандартов, что не
позволяет обработать его с применением современных математических методов и
компьютерных технологий и выявить причинно-следственные зависимости в системе генотип-среда.
Интересы сельскохозяйственной науки и практики требуют активного использования
этой информации для мониторинга, анализа, прогнозирования и поддержки
управленческих решений по выращиванию плодовых культур и сортов.
4.2.2. Общие положения
В данном разделе формулируются частные и обеспечивающие задачи,
необходимые для решения задачи прогнозирования количественных и качественных
результатов выращивания заданной культуры в заданной точке. Это задачи
выявления причинно-следственных закономерностей между метофакторами и
результатами выращивания, прогнозирования периодов фенофаз по динамике
метеопараметров, а также задачи триангуляции и пространственной интерполяции.
Показана взаимосвязь между этими задачами в контексте раскрытия логики решения
основной задачи.
4.2.3. Основная
задача исследования и этапы ее решения
Прогнозирование количественных и качественных результатов выращивания
различных культур в заданных точках (микрозонах). На основе решения данной основной
задачи для различных культур и точек выращивания могут быть решены
следующие две подзадачи:
1. Определен потенциал выращивания заданной культуры в различных
микрозонах.
2. Определен потенциал выращивания различных культур в заданной
микрозоне.
Результаты решения 1-й подзадачи подаются в наглядной и удобной
для принятия решений форме геоинформационной визуализации в виде зональных
географических карт, на которых зоны с одинаковым потенциалом для выращивания
некоторой культуры закрашены одним условным цветом.
Решение основной задачи состоит из двух этапов.
На 1-м этапе выявляются причинно-следственные зависимости между метеоусловиями и
результатами выращивания сельскохозяйственных культур.
На 2-м этапе используются знания выявленных причинно-следственных зависимостей для
прогнозирования количественных и качественных результатов выращивания заданной
культуры в конкретном пункте выращивания.
Будем считать, что биологический потенциал географической точки
определяется многолетней динамикой метеопараметров в этой точке.
Отметим, что влияние почв и агротехнологий в данном исследовании не
учитывается, но предлагаемые математические модели и реализующий их программный
инструментарий пригодны и для этого (имеется положительный опыт в этом направлении).
Решение основной задачи базируется на гипотезе о том, что
закономерности влияния динамики метеопараметров на переход культуры от одной
фенофазы к другой и на количественные и качественные результаты ее выращивания
определяются только генотипом данной культуры и не меняются от
точки к точке и в течение времени для данной культуры. Если данная гипотеза
верна, то закономерности влияния факторов среды на результаты выращивания
данной культуры, выявленные на основе обработки эмпирических данных, полученных
за определенный период времени в одних точках, применимы для прогнозирования
результатов выращивания этой культуры и в других точках.
Известно (Драгавцев А.П.), что влияние одних и тех же метеопараметров
на количественные и качественные результаты выращивания культуры зависит не
только от самих значений этих метеопараметров, но в огромной степени – от
фенофазы, в течение которой эти параметры действовали. Поэтому вся метеоинформация
должна обрабатываться с привязкой к периодам фенофаз, характеризующим темп биологического
времени для различных культур, а не просто – к физическому (календарному)
времени.
В принципе многие закономерности влияния метеоусловий на результаты
выращивания известны и описаны в специальной литературе, в том числе и авторами
данного исследования [11, 12, 13, 15, 38, 45, 47]. Однако для достижения цели
исследования все эти задачи должны быть решены на новом качественном уровне,
соответствующем современному уровню развития математических методов и
информационных технологий, в частности в рамках одной инструментальной
системы. Дело в том, что решение этих задач, реализованное в различных
инструментальных системах, не обеспечивает возможности обмена информацией между
ними, а значит, проведения реальных исследований и прогнозирования в промышленном
режиме.
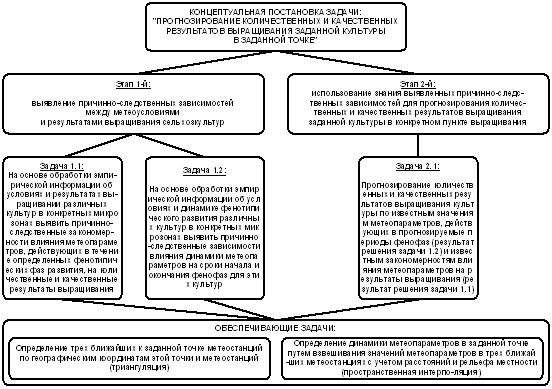
Рассмотрим подробнее, каким образом осуществляется декомпозиция
основной задачи в определенную последовательность этапов, частных и обеспечивающих задач (рисунок 90).
Этап 1-й:
выявление причинно-следственных зависимостей между метеоусловиями и результатами
выращивания сельскохозяйственных культур
Задача 1.1: На основе обработки эмпирической информации об
условиях и результатах выращивании различных культур в конкретных микрозонах выявить
причинно-следственные закономерности влияния метеопараметров, действующих
в течение определенных фенотипических фаз развития, на количественные и
качественные результаты выращивания.
Исходные данные:
– фактические периоды начала и окончания фенофаз;
– фактические посуточные значения метеопараметров.
Результат решения:
Для каждого значения каждого метеопараметра, действующего в период
определенной фенофазы, установлены сила и направление его влияния на
количественные и качественные результаты выращивания каждой конкретной
культуры.
Однако в данном пункте выращивания может и не быть метеостанции для
регистрации метеопараметров.
Поэтому задача 1.1 не может быть решена без решения задачи
пространственной интерполяции: определение значений метеопараметров
в заданной точке по их значениям в точках нахождения трех ближайших метеостанций
путем взвешивания значений с учетом поправок на рельеф и расстояния. Данная
задача, в свою очередь, предполагает предварительное решение задачи
триангуляции: определение трех ближайших к заданной точке
метеостанций по географическим координатам этой точки и метеостанций.
Последняя задача связана с необходимостью преобразования значений метеопараметров,
известных для нерегулярной сетки (решетки), в узлах которой расположены метеостанции,
в регулярную сетку потенциальных точек выращивания, которая более удобна для
геоинформационной визуализации.
Для потенциальных точек выращивания, по которым необходимо
прогнозировать количественные и качественные результаты, периоды начала и
окончания различных фенофаз для различных культур, неизвестны.
Поэтому возникает задача 1.2: на основе обработки
эмпирической информации об условиях и динамике фенотипического развития
различных культур в конкретных микрозонах выявить причинно-следственные
зависимости влияния динамики метеопараметров на сроки начала и окончания
фенофаз для этих культур.
Исходные данные:
– фактические периоды начала и окончания фенофаз;
– динамика метеопараметров.
Результат решения:
Математическая модель и методика численных расчетов, позволяющие с
минимальной погрешностью определить сроки наступления и окончания фенофаз для
различных культур как в фактических, так и предполагаемых точках их выращивания
по известной динамике метеопараметров в этих точках.
Задача 1.2 так же, как и 1.1 включает в качестве вспомогательных задачи
триангуляции и пространственной интерполяции.
Этап 2-й: использование знания выявленных причинно-следственных
зависимостей для прогнозирования количественных и качественных результатов выращивания
заданной культуры в конкретном пункте выращивания
Когда задачи 1-го этапа реализованы, то решение основной задачи
сводится к выполнению следующих шагов:
1. Определение трех ближайших к заданной точке метеостанций по
географическим координатам этой точки и метеостанций (триангуляция).
2. Определение динамики метеопараметров в заданной точке путем
взвешивания значений метеопараметров в трех ближайших метеостанциях с учетом
расстояний и рельефа местности (пространственная интерполяция).
3. Прогнозирование наиболее вероятных сроков начала и окончания фенофаз
для заданной культуры в заданной точке по известной динамике метеопараметров (задача
1.2).
4. Задача 2.1: Прогнозирование
количественных и качественных результатов выращивания культуры по известным значениям
метеопараметров, действующих в прогнозируемые периоды фенофаз (результат
решения задачи 1.2), и известным закономерностям влияния метеопараметров
на результаты выращивания (результат решения задачи 1.1).
Каждая из этих задач имеет свою формальную постановку, которую мы далее
коротко рассмотрим.
4.2.4. Формальная постановка частных и обеспечивающих
задач
Задача
1.1
На основе обработки эмпирической информации об условиях
и результатах выращивании различных культур в конкретных микрозонах выявить
причинно-следственные закономерности влияния метеопараметров,
действующих в течение определенных фенотипических фаз развития, на
количественные и качественные результаты выращивания.
Исходные данные
– фактические периоды начала и окончания фенофаз;
– фактические посуточные значения метеопараметров.
Алгоритм решения
Применяются два основных метода решения данной задачи:
1. Метод оценки индексов среды и экологической пластичности сортов по
продуктивности.
2. Метод автоматизированного системно-когнитивного анализа
(АСК-анализ).
1-й метод подробно рассмотрен в фундаментальной монографии [11],
поэтому освещать его нецелесообразно.
2-й метод основан на системной теории информации и автоматизации
системного анализа путем его декомпозиции по базовым когнитивным операциям [31].
Суть это метода состоит в том, что:
– для формализации результатов выращивания используются две
классификационные шкалы: шкала качества и шкала количества;
– для формализации действия метеофакторов применяются описательные
шкалы, соответствующие сочетаниям: фенофаза ´ метеопараметр;
– для формализации опыта выращивания используется обучающая выборка,
включающая в формальном виде описания всех случаев выращивания всех культур во
всех микрозонах, по которым есть информация по первым двум группам шкал;
– на основе предыдущего осуществляется синтез семантической
информационной модели (СИМ), отражающей силу и направление влияния всех
значений метеофакторов, действующих во всех фенофазах, на количественные и
качественные результаты выращивания сельскохозяйственных культур;
– СИМ проверяется на адекватность (верифицируется) и оптимизируется, из
нее исключаются артефакты и незначимая исходная информация, а также градации
классификационных и описательных шкал, по которым оказалось недостаточно
данных;
– проводится системно-когнитивный анализ СИМ, включающий изучение
системы детерминации будущих состояний объекта управления, сходства и различия
будущих состояний по системе детерминации, сходства и различия факторов по их
влиянию на объект управления, построение семантических сетей классов и
факторов, когнитивных диаграмм, классических и интегральных когнитивных карт.
Результат решения
Для каждого значения каждого метеопараметра, действующего в период
определенной фенофазы, установлены сила и направление его влияния на
количественные и качественные результаты выращивания каждой конкретной культуры
и строятся уравнения регрессии.
Задача 1.2
На основе обработки эмпирической информации об условиях
и динамике фенотипического развития различных культур в конкретных микрозонах выявить
причинно-следственные зависимости влияния динамики метеопараметров на сроки
начала и окончания фенофаз для этих культур.
Исходные данные
– фактические периоды начала и окончания фенофаз;
– динамика метеопараметров.
Алгоритм решения
Считается, что на сроки наступления и окончания фенофаз в основном
оказывают влияние накопительные значения средней температуры. Однако в
специальной литературе нигде не конкретизируется математическая модель и
методика численных расчетов, позволяющие действительно прогнозировать эти
сроки, не сравниваются различные модели по погрешности прогнозирования (степени
адекватности).
Поэтому возникает ряд вопросов, например:
– средние каких температур использовать: воздуха или почвы,
минимальной, средней или максимальной;
– с какой календарной даты или фенофазы начинать накопление;
– какие конкретные значения сумматора соответствуют началу или
окончанию тех или иных фаз у тех или иных культур.
По сути, эту математическую модель необходимо разработать и
верифицировать самим, что входит в задачи данного исследования.
Результат решения
Математическая модель и методика численных расчетов, позволяющие с
минимальной погрешностью определить сроки наступления и окончания фенофаз для
различных культур как в фактических, так и предполагаемых точках их выращивания
по известной динамике метеопараметров в этих точках.
Задача 2.1
Прогнозирование количественных и качественных результатов выращивания
культуры по известным значениям метеопараметров, действующих в прогнозируемые
периоды фенофаз (результат решения задачи 1.2) и известным
закономерностям влияния метеопараметров на результаты выращивания (результат
решения задачи 1.1).
Исходные данные
– фактические значения метеопараметров за ряд лет в данной точке.
Алгоритм решения
Для всех лет, по которым в базе метеоданных имеется информация о
значениях метеопараметров, прогнозируются количественные и качественные
результаты выращивания конкретной культуры, а затем за исследуемый период
подсчитывается средняя вероятность получения различных результатов выращивания.
Предполагается, что погода изменяется медленно, генотип еще медленней, и
поэтому определенная таким образом вероятность имеет силу и на данный момент
времени.
Результат решения
Вероятности различных количественных и качественных результатов
выращивания различных культур в заданных точках. Например, вероятность получения
высокого урожая абрикоса 1-го сорта в данной точке составляет 72 %.
Задача
триангуляции
Определение трех ближайших к заданной точке метеостанций
по географическим координатам этой точки и метеостанций (триангуляция).
Исходные данные
Географические координаты метеостанций и точек выращивания. Для
метеостанций сетка нерегулярная, а для точек выращивания, как правило,
регулярная (квадратная с равным шагом ячейки).
Алгоритм решения
Существуют различные оптимальные по различным критериям и просто
рациональные алгоритмы решения этой задачи, например алгоритм Делоне. Однако в
данном случае их применение вряд ли оправданно, т. к. вычислительные ресурсы
стандартного персонального компьютера вполне позволяют решить эту задачу
простейшим в реализации "методом прямого перебора в течение вполне приемлемого
реального времени", тем более эта задача может решаться редко, т. к.
исходные данные меняются очень редко и незначительно.
Шаг 0:
Вход.
Шаг 1:
Организуется цикл по потенциальным точкам выращивания.
Шаг 2:
Организуется цикл по метеостанциям.
Шаг 3:
Географические координаты преобразуются в декартовы (что вполне корректно из-за
очень небольших угловых расстояний между точкой выращивания и метеостанцией).
Шаг 4:
Вычисляется расстояние по поверхности Земли между текущей точкой и метеостанцией.
Шаг 5:
Результат вычисления расстояний заносится в первую базу данных.
Шаг 6:
Все метеостанции рассмотрены?
Если нет – переход на шаг 3, иначе – на 7.
Шаг 7:
Сортировка 1-й базы данных (расстояний от заданной точки до метеостанций) в
порядке увеличения расстояния.
Шаг 8:
Выбрать из базы данных три метеостанции с минимальными расстояниями до заданной
точки выращивания и поместить эту информацию во 2-ю базу данных.
Шаг 9:
Все точки выращивания просмотрены?
Если нет – переход на шаг 2, иначе – на 10.
Шаг 10.
Выход.
Результат решения
База данных, в которой содержится информация о всех точках выращивания
и трех ближайших к каждой точке метеостанциях.
Задача
пространственной интерполяции
Определение динамики метеопараметров в заданной точке
путем взвешивания значений метеопараметров в трех ближайших метеостанциях с
учетом расстояний и рельефа местности (пространственная интерполяция). Эта задача называется также задачей
"восстановления полей элементов в узлах регулярной сетки".
Исходные данные:
– известны суточные значения ряда метеопараметров в точках расположения
метеостанций;
– известны три ближайшие к любой заданной точке метеостанции.
Алгоритм решения
Восстановление полей элементов численными методами, получившее название
объективного анализа, в настоящее время широко применяется в гидрометеорологии
не только в научных исследованиях, но и в оперативной практике. Независимо от
применяемых методов расчета, все известные схемы объективного анализа
предусматривают предвычисление значений элемента в узлах регулярной сетки по
данным окружающих пунктов наблюдений.
Из численных методов восстановления полей элементов наиболее широко
известны метод оптимальной интерполяции, метод полиномиальной аппроксимации,
метод последовательных приближений. Имеется ряд других методов, многие из
которых представляют собой модификации перечисленных методов.
В отечественной гидрометеорологии наибольшее распространение получил
метод оптимальной интерполяции. В кратком изложении суть метода сводится к
следующему.
1. Описываем пункты наблюдений, используя для этого крупномасштабные
карты: гипсометрическую, почвенную, ландшафтную. Снимаются географические
координаты пункта, его декартовы координаты по условной сетке с шагом
2. Описываем узлы регулярной сетки. С этой целью определяем для каждого
узла все указанные выше характеристики, а также ближайшие оказывающие влияние
метеостанции.
3. Вводим необходимую гидрометеорологическую информацию по станциям
региона.
4. Используем комплекс программ, реализующих метод оптимальной
интерполяции.
Метод реализован на IBM PC. Проведенные контрольные расчеты показали
работоспособность созданных программ, а также адекватность полученных данных
реальным условиям.
Результат решения
Значения всех метеопараметров на любые сутки прошедшего периода можно
считать достоверно известными для любой географической точки, находящейся между
метеостанциями.
4.2.5. Выводы
Сформулированные задачи, будучи реализованные в одной программной
системе, обеспечивают решение основной задачи, поставленной в настоящем
исследовании: прогнозирование количественных и качественных результатов
выращивания различных культур в заданных точках (микрозонах). Необходимо
отметить, что данная система позволяет реализовать не все перечисленные задачи
и находится в постоянном совершенствовании и развитии.