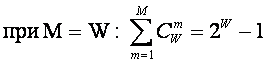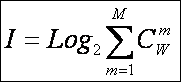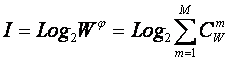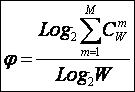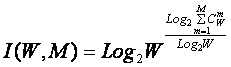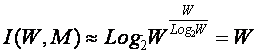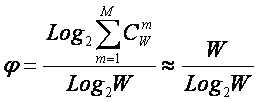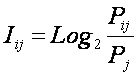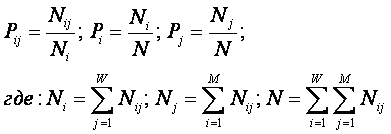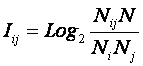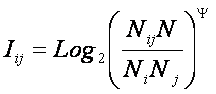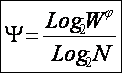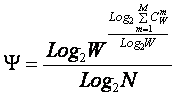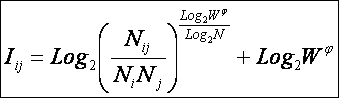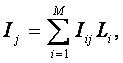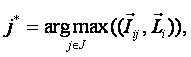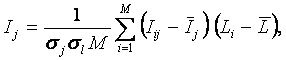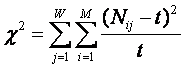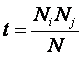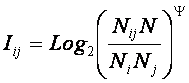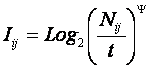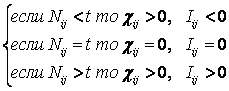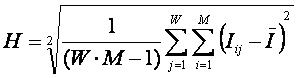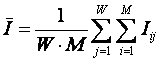1

1.2. Системная теория информации и семантическая информационная модель

В данной монографии системную теорию информации и семантическую информационную модель подробно рассматривать нецелесообразно, т.к. их детальному изложению посвящены работы [31, 35]. Поэтому здесь дан лишь краткий экскурс в эту тему. При этом некоторые разделы будут кратко раскрыты, а некоторые лишь названы.

1.2.1. Программа системного обобщения математики и предпосылки системной теории информации

Дадим определение понятия «система» классическим способом, т.е. путем его подведения под более общее понятие, каковым является понятие «множество» и выделение специфических признаков. Система представляет собой множество элементов, объединенных в целое за счет взаимодействия элементов друг с другом, т.е. за счет отношений между ними, и обеспечивающая преимущества в достижении целей. Преимущества в достижении целей обеспечиваются за счет системного эффекта. Системный эффект состоит в том, что свойства системы не сводятся к сумме свойств ее элементов, т.е. система как целое обладает рядом новых, т.е. эмерджентных свойств, которых не было у ее элементов. Уровень системности тем выше, чем выше интенсивность взаимодействия элементов системы друг с другом, чем сильнее отличаются свойства системы от свойств входящих в нее элементов, т.е. чем выше системный эффект, чем значительнее отличается система от множества. Элементы взаимодействуют (вступают в отношения) друг с другом с помощью имеющихся у них общих свойств, а также свойств, которые коррелируют между собой. Таким образом, система обеспечивает тем большие преимущества в достижении целей, чем выше ее уровень системности. В частности, система с нулевым уровнем системности вообще ничем не отличается от множества образующих ее элементов, т.е. тождественна этому множеству и никаких преимуществ в достижении целей не обеспечивает. Этим самым обеспечивается выполнение принципа соответствия между понятиями системы и множества. Из соблюдения это принципа для понятий множества и системы следует и его соблюдение для понятий, основанных на теории множеств и их системных обобщений.

На этой основе можно ввести и новое научное понятие: понятие «антисистемы», применение которого оправдано в случаях, когда централизация (монополизация, интеграция) не только не дает положительного эффекта, но даже сказывается отрицательно. Антисистемой называется система с отрицательным уровнем системности, т.е. это такое объедение некоторого множества элементов за счет их взаимодействия в целое, которое препятствует достижению целей.

Фундаментом, находящимся в самом основании современной математики, является теория множеств. Эта теория лежит и в основе самого глубокого на сегодняшний день обоснования таких базовых математических понятий, как «число» и «функция». Определенный период этот фундамент казался незыблемым. Однако вскоре работы целой плеяды выдающихся ученых XX века, прежде всего Давида Гильберта, Бертрана Рассела и Курта Гёделя, со всей очевидностью обнажили фундаментальные логические и лингвистические проблемы, в частности проявляющиеся в форме парадоксов теории множеств, что в свою очередь привело к появлению ряда развернутых предложений по пересмотру самых глубоких оснований математики [34].

В задачи данной монографии не входит рассмотрение этой интереснейшей проблематики, а также истории возникновения и развития понятий числа и функции. Отметим лишь, что кроме рассмотренных в литературе вариантов существует возможность обобщения всех понятий математики, базирующихся на теории множеств, в частности теории информации, путем тотальной замены понятия множества на понятие системы и тщательного отслеживания всех последствий этой замены. Это утверждение будем называть «программной идеей системного обобщения понятий математики».

Строго говоря, реализация данной программной идеи потребует прежде всего системного обобщения самой теории множеств и преобразование ее в математическую теорию систем, которая будет плавно переходить в современную теорию множеств при уровне системности стремящемся к нулю. При этом необходимо заметить, что существующая в настоящее время наука под названием «Теория систем» ни в коей мере не является обобщением математической теории множеств и ее не следует путать с математической теорией систем. Вместе с тем, на наш взгляд, существуют некоторые возможности обобщения ряда понятий математики и без разработки математической теории систем. К таким понятиям относятся прежде всего понятия «информация» и «функция».

Системному обобщению понятия информации посвящены работы [31, 34, 35, 74] и другие, поэтому в данной монографии этом вопросе мы останавливаться не будем. Отметим лишь, что на основе предложенной системной теории информации (СТИ) были разработаны математическая модель и методика численных расчетов (структуры данных и алгоритмы), а также специальный программный инструментарий (система «Эйдос») автоматизированного системно-когнитивного анализа (АСК-анализ), который представляет собой системный анализ, автоматизированный путем его рассмотрения как метода познания и структурирования по базовым когнитивным операциям.

В СК-анализе теоретически обоснована и реализована на практике в форме конкретной информационной технологии процедура установления новой универсальной, сопоставимой в пространстве и времени, ранее не используемой количественной, т.е. выражаемой числами, меры соответствия между событиями или явлениями любого рода, получившей название «системная мера целесообразности информации», которая по существу является количественной мерой знаний [35]. Это является достаточным основанием для того, чтобы назвать эти числа «когнитивными» от английского слова "cognition" – "познание".

В настоящее время функция понимается как соответствие друг другу нескольких множеств чисел. Поэтому виды функций можно классифицировать по крайней мере в зависимости от:

– природы этих чисел (натуральные, целые, дробные, действительные, комплексные и т.п.);

– количества и вида множеств чисел, связанных друг с другом в функции (функции одного, нескольких, многих, счетного или континуального количества аргументов, однозначные и многозначные функции, дискретные или континуальные функции) [34];

– степени жесткости и меры силы связи между множествами чисел (детерминистские функции, функции, в которых в качестве меры связи используется вероятность, корреляция и другие меры);

– степени расплывчатости чисел в множествах и самой формы функции (четкие и нечеткие функции, использование различных видов шкал, в частности интервальных оценок).

Так как функции, выявляемые модели предметной области методом АСК-анализа, связывают друг с другом множества когнитивных чисел, то предлагается называть их «когнитивными функциями». Учитывая перечисленные возможности классификации когнитивные функции, можно считать недетерминистскими многозначными функциями многих аргументов, в которых в качестве меры силы связи между множествами используется количественная мера знаний, т.е. системная мера целесообразности информации, основанными на интервальных оценках, номинальных и порядковых шкалах и шкалах отношений. Отметим, что детерминистские однозначные функции нескольких аргументов могут рассматриваться как частный случай когнитивных функций, к которому они сводятся при анализе жестко детерминированной предметной области, скажем явлений, описываемых классической физикой.

Итак, предлагается программная идея системного обобщения понятий математики, в частности теории информации, основанных на теории множеств, путем замены понятия множества на более общее и содержательное понятие системы, а затем последовательного сквозного и тщательного прослеживания всех последствий этой замены.

Частично эта идея была реализована при разработке автоматизированного системно-когнитивного анализа (АСК-анализа), математическая модель которого основана на системном обобщении формул для количества информации Хартли и Харкевича. Реализация следующего шага: системного обобщения понятия функциональной зависимости рассматривается в работе [34], в ней же вводятся новые научные понятия и соответствующие термины: «когнитивные функции» и «когнитивные числа». На численных примерах показано, что АСК-анализ обеспечивает выявление когнитивных функциональных зависимостей в многомерных зашумленных фрагментированных данных.

Далее в работах [31, 34] рассмотрены следующие аспекты семантической информационной модели СК-анализа.

1.2.2. Теоретические основы системной теории информации

1.2.2.1. Требования к математической модели и численной мере

1.2.2.2. Выбор базовой численной меры:

– абсолютная, относительная и аналитическая информация;

– выбор в качестве базовой численной меры количества информации.

1.2.2.3. Конструирование системной численной меры на основе базовой:

– системное обобщение формулы Хартли для количества информации;

– гипотеза о законе возрастания эмерджентности и следствия из него;

– системное обобщение классической формулы Харкевича, как количественная мера знаний;

– генезис системной (эмерджентной) теории информации.

1.2.3. Семантическая информационная модель СК-анализа

1.2.3.1. Формализм динамики взаимодействующих семантических информационных пространств. Двухвекторное представление данных:

– семантические пространства классов и атрибутов;

– требования к системам координат, свойства векторов классов и атрибутов, решение проблемы снижения размерности описания и ортонормирования.

1.2.3.2. Применение классической теории информации К.Шеннона для расчета весовых коэффициентов и мер сходства:

– формальная постановка задачи;

– информация как мера снятия неопределенности;

– количество информации в индивидуальных событиях и лемма Неймана-Пирсона.

1.2.3.3. Математическая модель метода распознавания образов и принятия решений, основанного на системной теории информации.

Системное обобщение формулы Хартли

В выражении (3) приведено системное обобщение формулы Хартли для равновероятных состояний объекта управления.

(1)		(4)
(2)		(5)
(3)	с очень малой и быстро уменьшающейся погрешностью	(6)

W – количество чистых (классических) состояний системы.

j – коэффициент эмерджентности Хартли (уровень системной организации объекта, имеющего W чистых состояний).

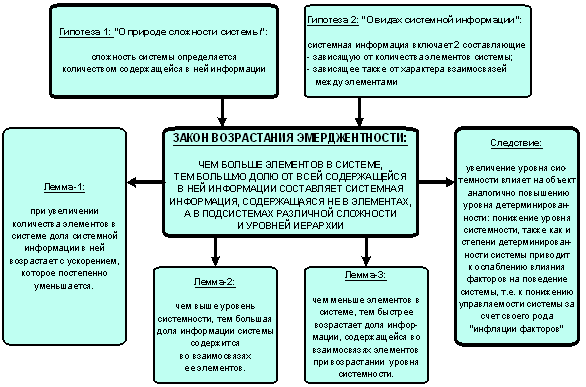
Гипотеза о Законе возрастания эмерджентности

Исследование математических выражений системной теории информации (7 – 12) позволило сформулировать гипотезу о существовании "Закона возрастания эмерджентности". Суть этой гипотезы в том, что в самих элементах системы содержится сравнительно небольшая доля всей содержащейся в ней информации, а основной ее объем составляет системная информация, содержащаяся в подсистемах различного уровня иерархии.

Различие между классическим и предложенным системным понятиями информации соответствует различию между понятиями МНОЖЕСТВА И СИСТЕМЫ, на основе которых они сформированы.

	(7)		(8)
	(9)		(10)
	(11)		(12)

Математическая формулировка:

Интерпретация (рисунок 16)

Рисунок 16. Гипотеза о законе возрастания эмерджентности

Системное обобщение формулы Харкевича

Ниже приведен вывод системного обобщения формулы Харкевича, а именно:

– классическая формула Харкевича через вероятности перехода системы в целевое состояние при условии сообщения ей определенной информации и самопроизвольно (13);

– выражение классической формулы Харкевича через частоты (14, 15);

– вывод коэффициента эмерджентности Харкевича на основе принципа соответствия с выражением Хартли в детерминистском случае (16 –19);

– вывод системного обобщения формулы Харкевича;

– окончательное выражение для системного обобщения формулы Харкевича (21).

Классическая формула Харкевича

(13)

P_ij – вероятность перехода объекта управления в j-е состояние в условиях действия i-го фактора;

P_j – вероятность самопроизвольного перехода объекта управления в j-е состояние, т.е. в условиях отсутствия действия i-го фактора или в среднем.

Известно, что корреляция не является мерой причинно-следственных связей. Если корреляция между действием некоторого фактора и переходом объекта управления в определенное состояние высока, то это еще не значит, что данный фактор является причиной этого перехода. Для того чтобы по корреляции можно было судить о наличии причинно-следственной связи необходимо сравнить исследуемую группу с контрольной группой, т.е. с группой, в которой данный фактор не действовал.

Также и высокая вероятность перехода объекта управления в определенное состояние в условиях действия некоторого фактора сама по себе не говорит о наличии причинно-следственной связи между ними, т.е. о том, что данный фактор обусловил переход объекта в это состояние. Это связано с тем, что вероятность перехода объекта в это состояние может быть вообще очень высокой независимо от действия фактора. Поэтому в качестве меры силы причинной обусловленности определенного состояния объекта действием некоторого фактора Харкевич предложил логарифм отношения вероятностей перехода в объекта в это состояние в условиях действия фактора и при его отсутствии или в среднем (13).

Таким образом семантическая мера информации Харкевича является мерой наличия причинно-следственных связей между факторами и будущими состояниями объекта управления, что делает ее целесообразным ее применение для синтеза математических моделей систем управления.

Выражение классической формулы Харкевича через частоты фактов

(14)

(15)

Вывод коэффициента эмерджентности Харкевича на основе принципа соответствия с выражением Хартли в детерминистском случае

Однако мера Харкевича (13) не удовлетворяет принципу соответствия мерой Хартли как мера Шеннона, т.е. не переходит в меру Хартли в детерминистском случае, т.е. когда каждому будущему состоянию объекта управления соответствует единственный уникальный фактор и между факторами и состояниями имеется взаимно однозначное соответствие (17).

(16)

(17)

Откуда:

(18)

(19)

Вывод системного обобщения формулы Харкевича

(20)

Окончательное выражение для системного обобщения формулы Харкевича

(21)

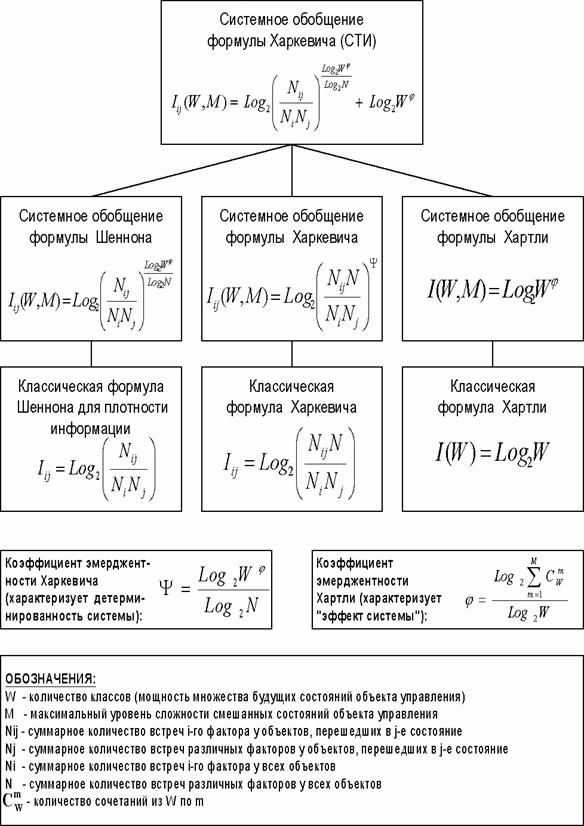
Связь системной теории информации (СТИ) с теорией Хартли-Найквиста-Больцмана и теорией Шеннона

Связь между выражениями для плотности информации в теориях Хартли, Шеннона и СТИ приведена на рисунке 17.

Рисунок 17. Связь между выражениями для плотности информации в теориях Хартли, Шеннона и СТИ

Интерпретация коэффициентов эмерджентности СТИ

Интерпретация коэффициентов эмерджентности, предложенных в рамках системной теории информации, приведена на рисунке 18.

Рисунок 18. Интерпретация смысла коэффициентов эмерджентности СТИ

Коэффициент эмерджентности Хартли j (4) представляет собой относительное превышение количества информации о системе при учете системных эффектов (смешанных состояний, иерархической структуры ее подсистем и т.п.) над количеством информации без учета системности, т.е. этот коэффициент является аналитическим выражением для уровня системности объекта.

Коэффициент эмерджентности Харкевича Y, изменяется от 0 до 1 и определяет степень детерминированности системы.

Таким образом, в предложенном системном обобщении формулы Харкевича (21) впервые непосредственно в аналитическом выражении для самого понятия "Информация" отражены такие фундаментальные свойства систем, как "Уровень системности" и "Степень детерминированности" системы.

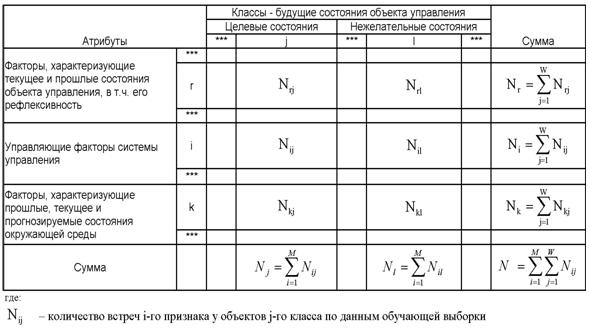
Матрица абсолютных частот

Основной формой первичного обобщения эмпирической информации в модели является матрица абсолютных частот (таблица 6).

Таблица 6 – МАТРИЦА АБСОЛЮТНЫХ ЧАСТОТ

В этой матрице строки соответствуют градациям факторов, столбцы – будущим целевым и нежелательным состояниям объекта управления, а на их пересечении приведено количество наблюдения фактов (по данным обучающей выборки), когда действовал некоторый i-й фактор и объект управления перешел в некоторое j-е состояние.

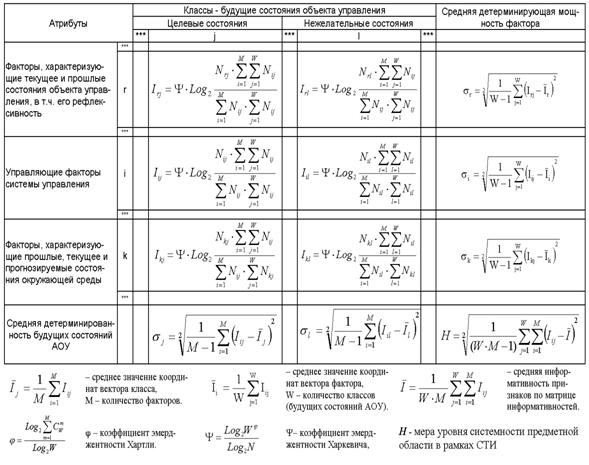
Матрица информативностей

Непосредственно на основе матрицы абсолютных частот с использованием системного обобщения формулы Харкевича (21) рассчитывается матрица информативностей (таблица 7).

Таблица 7 – МАТРИЦА ИНФОРМАТИВНОСТЕЙ

Матрица информативностей является универсальной формой представления смысла эмпирических данных в единстве их дискретного и интегрального представления (причины – последствия, факторы – результирующие состояния, признаки – обобщенные образы классов, образное – логическое, дискретное – интегральное).

Весовые коэффициенты матрицы информативностей непосредственно определяют, какое количество информации Iij система управления получает о наступлении события: "объект управления перейдет в j–е состояние", из сообщения: "на объект управления действует i–й фактор".

Когда количество информации Iij>0 – i–й фактор способствует переходу объекта управления в j–е состояние, когда Iij<0 – препятствует этому переходу, когда же Iij=0 – никак не влияет на это.

Таким образом, предлагаемая семантическая информационная модель позволяет непосредственно на основе эмпирических данных и независимо от предметной области рассчитать, какие количество информации содержится в любом событии о любом другом событии.

Этот вывод является ключевым для данной работы, т.к. конкретно показывает возможность числовой обработки в СК-анализе как числовой, так и нечисловой информации.

Матрица информативностей является также обобщенной (неклассической) таблицей решений, в которой входы (факторы) и выходы (будущие состояния объекта управления) связаны друг с другом не с помощью классических (Аристотелевских) импликаций, принимающих только значения: "Истина" и "Ложь", а различными значениями истинности, выраженными в битах и принимающими значения от положительного теоретически-максимально-возможного, до теоретически неограниченного отрицательного. Некоторые неклассические высказывания, генерируемые на основе матрицы информативности, приведены на плакате.

Неметрический интегральный критерий сходства, основанный на лемме Неймана-Пирсона

В выражениях (22 – 24) приведен неметрический интегральный критерий сходства, основанный на фундаментальной лемме Неймана-Пирсона, обеспечивающий идентификацию и прогнозирование в предложенных неортонормированных семантических пространствах с финитной метрикой, в которых в качестве координат векторов будущих состояний объекта управления и факторов выступает количество информации, рассчитанное в соответствии с системной теорией информации (21), а не Булевы координаты или частоты, как обычно.

(22)

(23)

Или в координатной форме:

(24)

(25)

– вектор j–го состояния объекта управления;

– вектор состояния предметной области, включающий все виды факторов, характеризующих объект управления, возможные управляющие воздействия и окружающую среду (массив–локатор), т.е.:

(26)

(27)

– средняя информативность по вектору класса;

– среднее по вектору идентифицируемой ситуации (объекта).

– среднеквадратичное отклонение информативностей вектора класса;

– среднеквадратичное отклонение по вектору распознаваемого объекта.

Оценка адекватности семантической информационной модели в СК-анализе

Под адекватностью модели СК-анализа понимается ее внутренняя и внешняя дифференциальная и интегральная валидность. Понятие валидности является уточнением понятия адекватности, для которого определены процедуры количественного измерения, т.е. валидность – это количественная адекватность. Это понятие количественно отражает способность модели давать правильные результаты идентификации, прогнозирования и способность вырабатывать правильные рекомендации по управлению.

Под внутренней валидностью понимается валидность модели, измеренная после синтеза модели путем идентификации объектов обучающей выборки.

Под внешней валидностью понимается валидность модели, измеренная после синтеза модели путем идентификации объектов, не входящих в обучающую выборку.

Под дифференциальной валидностью модели понимается достоверность идентификации объектов в разрезе по классам.

Под интегральной валидностью средневзвешенная дифференциальная валидность.

Возможны все сочетания: внутренняя дифференциальная валидность, внешняя интегральная валидность и т.д.

1.2.4. Некоторые свойства математической модели (сходимость, адекватность, устойчивость и др.)

1.2.4.1. Непараметричность модели. Робастные процедуры и фильтры для исключения артефактов

Предложенная семантическая информационная модель является непараметрической, т.к. базируется на системной теории информации [31], которая никоим образом не основана на предположениях о нормальности распределений исследуемой выборки.

Под робастными понимаются процедуры, обеспечивающие устойчивую работу модели на исходных данных, зашумленных артефактами, т.е. данными, выпадающими из общих статистических закономерностей, которым подчиняется исследуемая выборка.

Критерий выявления артефактов, реализованный в СК-анализе, основан на том, что при увеличении объема статистики частоты значимых атрибутов растут, как правило, пропорционально объему выборки, а частоты артефактов так и остаются чрезвычайно малыми, близкими к единице. Таким образом, выявление артефактов возможно только при достаточно большой статистике, т.к. в противном случае недостаточно информации о поведении частот атрибутов с увеличением объема выборки.

В модели реализована такая процедура удаления наиболее вероятных артефактов, и она, как показывает опыт, существенно повышает качество (адекватность) модели.

Кроме того, в работах [31, 34] подробнее рассмотрены следующие вопросы:

– формальная постановка основной задачи рефлексивной АСУ активными объектами и ее декомпозиция:

– декомпозиция основной задачи в ряд частных подзадач:

Решение задачи 1: "Синтез семантической информационной модели активного объекта управления";

Решение задачи 2: "Адаптация модели объекта управления";

Решение задачи 3: "Разработка алгоритмов решения основных задач АСУ";

Решение подзадачи 3.1: "Расчет влияния факторов на переход объекта управления в различные состояния (обучение, адаптация)";

Решение подзадачи 3.2: "Прогнозирование поведения объекта управления при конкретном управляющем воздействии и выработка многофакторного управляющего воздействия (обратная задача прогнозирования)";

Решение подзадачи 3.3: "Выявление факторов, вносящих основной вклад в детерминацию состояния АОУ; снижение размерности модели при заданных ограничениях";

Решение подзадачи 3.4: "Сравнение влияния факторов. Сравнение состояний объекта управления";

– семантический информационный анализ;

– кластерно-конструктивный анализ и семантические сети;

– когнитивные диаграммы классов и признаков;

– содержательное (смысловое) сравнение классов;

– содержательное (смысловое) сравнение признаков;

– обоснование сопоставимости частных критериев Iij;

Теорема-1: Индивидуальные количества информации, содержащейся в признаках объекта о принадлежности к классам, сопоставимы между собой;

Теорема-2: Величины суммарной информации, рассчитанные для одного объекта и разных классов, сопоставимы друг с другом;

Теорема-3: Величины суммарной информации, рассчитанные для разных объектов и разных классов, а также классов и классов, признаков и признаков, взаимно-сопоставимы;

Теорема-4: Неметрический интегральный критерий сходства, основанный на модифицированной формуле А.Харкевича и обобщенной лемме Неймана-Пирсона, аддитивен;

Обобщение интегральной модели путем учета значений выходных параметров объекта управления.

1.2.4.2. Зависимость информативностей факторов от объема обучающей выборки

1.2.4.3. Зависимость адекватности семантической информационной модели от объема обучающей выборки (адекватность при малых и больших выборках)

1.2.4.4. Семантическая устойчивость модели

1.2.4.5. Зависимость некоторых параметров модели от ее ортонормированности:

– зависимость адекватности модели от ее ортонормированности;

– зависимость уровня системности модели от ее ортонормированности;

– зависимость степени детерминированности модели от ее ортонормированности.

1.2.5. Взаимосвязь математической модели СК-анализа с другими моделями.

1.2.5.1. Взаимосвязь системной меры целесообразности информации со статистикой Х² и новая мера уровня системности предметной области.

В (28 – 33) показана связь системной меры целесообразности информации с известным критерием c², а также предложен новый критерий уровня системности предметной области, являющийся нормированным объемом семантического пространства (34, 35).

(28)

(29)

– N_ij – фактическое количество встреч i-го признака у объектов j-го класса;

– t – ожидаемое количество встреч i-го признака у объектов j-го класса.

(30)		(31)
(32)		(33)
	(34)	(35)

Предлагается более точный критерий уровня системности модели является объем неортонормированного семантического пространства, рассчитанный как объем многомерного параллелепипеда, ребрами которого являются оси семантического пространства. Однако для этой меры сложнее в общем виде записать аналитическое выражение и для ее вычисления могут быть использованы численные методы с использованием многомерного обобщения смешанного произведения векторов.

Абстрагирование (ортонормирование) существенно уменьшает размерность семантического пространства без существенного уменьшения его объема.

1.2.5.2. Сравнение, идентификация и прогнозирование как разложение векторов объектов в ряд по векторам классов (объектный анализ).

1.2.5.3. Системно-когнитивный и факторный анализ. СК-анализ, как метод вариабельных контрольных групп.

1.2.5.4. Семантическая мера целесообразности информации и эластичность:

– эластичность в непрерывном случае;

– эластичность в дискретном случае;

– свойства эластичности.

1.2.5.5. Связь семантической информационной модели с нейронными сетями:

– метафора нейросетевого представления семантической информационной модели;

– соответствие основных терминов и понятий;

– недостатки нейронных сетей и пути их преодоления в семантической информационной модели;

– гипотеза о нелокальности нейрона и информационная нейросетевая парадигма;

– решение проблемы интерпретируемости весовых коэффициентов (семантическая мера целесообразности информации и закон Фехнера);

– семантическая информационная модель, как нелокальная нейронная сеть;

– гипотеза о физической природе нелокального взаимодействия нейронов в нелокальной нейронной сети;

– решение проблемы интерпретируемости передаточной функции;

– решение проблемы размерности;

– моделирование причинно-следственных цепочек в нейронных сетях и семантической информационной модели;

– моделирование иерархических структур обработки информации;

– нейронные сети и СК-анализ.

1.2.5.6. Математический метод СК-анализа в свете идей интервальной бутстрепной робастной статистики объектов нечисловой природы

Постановка проблемы

Современный этап развития информационных технологий характеризуется быстрым ростом производительности компьютеров облегчением доступа к ним. С этим связан возрастающий интерес к использованию компьютерных технологий для организации мониторинга различных объектов, анализа данных, прогнозирования и управления в различных предметных областях. И у исследователей, и у руководителей, имеются определенные ожидания и надежды на повышение эффективности применения компьютерных технологий.

Однако на пути реализации этих ожиданий имеются определенные сложности, связанные с относительным отставанием в развитии математических методов и реализующего их программного инструментария.

И анализ, и прогнозирование, и управление самым непосредственным образом основываются на математическом моделировании объектов. Математическое моделирование в свою очередь предполагают возможность выполнения всех арифметических операций (сложение, вычитание, умножение и деление) над отображениями объектов в моделях и над их элементами.

В практике интеллектуального анализа данных в экономике, социологии, психологии, педагогике и других предметных областях все чаще встречаются ситуации, когда необходимо в рамках единой математической модели совместно обрабатывать числовые и нечисловые данные.

В свою очередь числовые данные могут быть различной природы и, соответственно, измеряться в самых различных единицах измерения. Ясно, что арифметические операции можно выполнять только над числовыми данными, измеряемыми в одних единицах измерения.

Данные нечисловой природы, т.е. различные факты и события, характеризуются тем, что с ними вообще нельзя выполнять арифметические операции.

Соответственно, возникает потребность в математических методах и программном инструментарии, обеспечивающих совместную сопоставимую обработку разнородных числовых данных и данных нечисловой природы.

Традиционные пути решения проблемы

Традиционно при необходимости проведения подобных исследований реализуется один из двух вариантов, т.е. либо изучается подмножество однородных по своей природе данных, измеряемых в одних единицах измерения; либо перед исследованием данные приводятся к сопоставимому виду, например, широко используются процентные или другие относительные величины, реже – стандартизированные значения.

Ясно, что первый вариант является не решением проблемы, а лишь ее вынужденным обходом, обусловленным ограничениями реально имеющегося в распоряжении исследователей инструментария.

Второй вариант лишь частично решает проблему, т.к. хотя и снимает различие в единицах измерения, но не преодолевает принципиального различия между количественными и качественными (нечисловыми) величинами и не позволяет обрабатывать их совместно в рамках единой модели.

В последние годы развивается ряд новых методов статистики, полный обзор которых дан в работах А. И. Орлова [http://antorlov.chat.ru]. Прежде всего, это интервальная статистика, статистика объектов нечисловой природы, робастные, бутстрепные и непараметрические методы.

В частности методы интервальной статистики, позволяют сводить числовые величины к фактам попадания их значений в определенные интервалы, т.е. к событиям. При этом преодолевается проблема различия в размерности числовых величин. Это обеспечивает также обработку числовых величин, как событий совместно с информацией о других событиях, связанных с объектами нечисловой природы. Таким образом, интервальные методы сводят обработку числовых величин к методам обработки нечисловой информации и позволяет обрабатывать их единообразно по одной методике. И это является очень важным достижением.

Идея решения проблемы

Это, в общем-то, вполне очевидный и естественный ход. Однако достигается этот результат дорогой ценой, т.е. путем сведения числовых величин к нечисловым, т.е. путем сведения их к "низменному типу", что приводит к утрате ряда возможностей обработки. Это происходит потому, что для числовых величин существует гораздо больше методов и возможностей обработки, чем для нечисловых.

По нашему мнению более предпочтительным является противоположный подход, основанный на введении некоторой количественной меры, позволяющей единым и сопоставимым образом описывать как числовые данные различной природы, так и нечисловые величины с использованием всего арсенала возможностей, имеющегося при обработке числовых данных.

Аналогично, если у нас есть документы стандартов "Документ Word" и "Текст-DOS" и мы хотели бы обрабатывать их все в одном редакторе, то это можно сделать либо преобразовав все документы Word в "низменный стандарт" "Текст-DOS", либо наоборот, преобразовав "досовские" документы в формат Word.

В 1979 году разработана, а в 1981 году впервые применена математическая модель, обеспечивающая реализацию этой идеи. В последующем этот математический аппарат был развит в ряде работ, основной из которых является [31], был разработана соответствующая ему методика численных расчетов, включающая структуры данных и алгоритмы базовых когнитивных операций, а также создана программная система "Эйдос", реализующая математическую модель и методику численных расчетов [31, 34].

Предложенный метод получил название "Системно-когнитивный анализ" (СК-анализ) [31]. В СК-анализе нечисловым величинам тем же методом, что и числовым, приписываются сопоставимые в пространстве и времени, а также между собой, количественные значения, позволяющие обрабатывать их как числовые.

СК-анализ включает следующие этапы:

1. Когнитивная структуризация, а затем и формализация предметной области.

2. Ввод данных мониторинга в базу прецедентов за период, в течение которого имеется необходимая информация в электронной форме.

3. Синтез семантической информационной модели (СИМ).

4. Оптимизация СИМ.

5. Проверка адекватности СИМ (измерение внутренней и внешней, дифференциальной и интегральной валидности).

6. Анализ СИМ.

7. Решение задач идентификации состояний объекта управления, прогнозирование и поддержка принятия управленческих решений по управлению с применением СИМ.

На первых двух этапах СК-анализа, детально рассмотренных в работе [31], числовые величины сводятся к интервальным оценкам, как и информация об объектах нечисловой природы (фактах, событиях). Этот этап реализуется и в методах интервальной статистики.

На третьем этапе СК-анализа всем этим величинам по единой методике, основанной на системном обобщении семантической теории информации А.Харкевича, сопоставляются количественные величины, с которыми в дальнейшем и производятся все операции моделирования.

Под внутренней валидностью понимается валидность модели, измеренная после синтеза модели путем идентификации объектов обучающей выборки. Под внешней валидностью понимается валидность модели, измеренная после синтеза модели путем идентификации объектов, не входящих в обучающую выборку. Под дифференциальной валидностью модели понимается достоверность идентификации объектов в разрезе по классам. Под интегральной валидностью средневзвешенная дифференциальная валидность. Возможны все сочетания: внутренняя дифференциальная валидность, внешняя интегральная валидность и т.д.

Основная идея бутстрепа по Б.Эфрону [31] состоит в том, что методом Монте-Карло (статистических испытаний) многократно извлекаются выборки из эмпирического распределения. Эти выборки, естественно, являются вариантами исходной, напоминают ее.

Эта идея позволяет сконструировать алгоритм измерения адекватности модели, состоящий из двух этапов:

1. Синтез модели на одном случайном подмножестве обучающей выборки.

2. Измерение валидности модели на оставшемся подмножестве обучающей выборки, не использованном для синтеза модели.

Поскольку оба случайных подмножества имеют переменный состав по объектам обучающей выборки, то подобная процедура должна повторяться много раз, после чего могут быть рассчитаны статистические характеристики адекватности модели, например, такие как:

– средняя внешняя валидность;

– среднеквадратичное отклонение текущей внешней валидности от средней и другие.

Достоинство бутстрепного подхода к оценке адекватности модели состоит в том, что он позволяет измерить внешнюю валидность на уже имеющейся выборке и изучить статистические характеристики, характеризующие адекватность модели при изменении объема и состава выборки.

Непараметричность модели. Робастные процедуры и фильтры для исключения артефактов

Выводы

Интервальные оценки сводят анализ чисел к анализу фактов и позволяют обрабатывать количественные величины как нечисловые данные. Это ограничивает возможности обработки количественных величин методами обработки нечисловых данных. В математической модели СК-анализа, основанной на системной теории информации, наоборот, качественным, нечисловым данным, сопоставляются количественные величины. Это позволяет использовать все возможности количественных методов для исследования нечисловых данных.

Таким образом, в СК-анализе числовые и нечисловые данные обрабатываются единообразно на основе единой математической модели как числовые данные.

Реализованный в математической модели СК-анализа метод измерения ее адекватности относится к бутстрепным методам.

В модели реализована робастная процедура выявления и устранения артефактов в СК-анализе.