ЛР-8:
"Идентификация трехмерных тел
по их ортогональным проекциям"

Краткая теория

Когда мы зрительно воспринимаем окружающую действительность, то постоянно решается задача идентификации трехмерных тел по их проекциям. При этом мы можем наблюдать одну, две или даже три проекции тела.

Одну проекцию мы наблюдаем при наблюдении тела на достаточно большом расстоянии, при котором бинокулярность зрения несущественна, или при монокулярном наблюдении за очень короткое время, за которое точка зрения на тело не меняется или оно не успевает повернутся.

Ясно, что наиболее сложными условиями для идентификации формы тела являются те, когда мы видим лишь одну его проекцию (большое расстояние и малое время наблюдения).

Задание

1. Формализовать задачу.

1.1. Сконструировать классификационные шкалы и градации.

1.2. Сконструировать описательные шкалы и градации.

1.3. Сгенерировать обучающую выборку.

2. Осуществить синтез и верификацию (измерение адекватности) семантической информационной модели.

3. Провести системно-когнитивный анализ модели:

3.1. Решить задачи идентификации и прогнозирования.

3.2. Сгенерировать информационные портреты классов и факторов, т.е. решить обратную задачу прогнозирования (результаты отобразить в графической форме двухмерных и трехмерных профилей классов и факторов).

3.3. Провести кластерно-конструктивный анализ классов и факторов (результаты отобразить в форме семантических сетей классов и факторов).

3.4. Осуществить содержательное сравнение классов и факторов (результаты отобразить в форме когнитивных диаграмм классов и факторов).

3.5. Построить нелокальные нейроны и интерпретируемые нейронные сети.

3.6. Построить классические когнитивные модели (отобразить в форме когнитивных карт).

3.7. Построить интегральные когнитивные модели (отобразить в форме интегральных когнитивных карт).

Пример решения

1. Формализовать задачу.

1.1. Сконструировать классификационные шкалы и градации.

Так как задачей является идентификация формы тела, то в качестве классов выберем для исследования простые и широко известные формы: шар, тетраэдр, куб, конус, пирамиду, призму и цилиндр, а также их наблюдения по две ортогональные проекции, которые будем обозначать числами 11, 12, 23, и одно наблюдение сразу трех проекций: 123 (таблица 84). Одновременно или последовательно наблюдаются проекции, в данном случае неважно.

Таблица 84 – КЛАССИФИКАЦИОННЫЕ
ШКАЛЫ И ГРАДАЦИИ

Код	Наимено- вание	Код	Наимено-вание	Код	Наимено- вание	Код	Наимено-вание
1	Шар	11	Куб	21	Пирамида	31	Призма
2	Шар-11	12	Куб-11	22	Пирамида-11	32	Призма-11
3	Шар-12	13	Куб-12	23	Пирамида-12	33	Призма-12
4	Шар-22	14	Куб-23	24	Пирамида-23	34	Призма-23
5	Шар-123	15	Куб-123	25	Пирамида-123	35	Призма-123
6	Тетраэдр	16	Конус	26	Цилиндр
7	Тетраэдр-11	17	Конус-11	27	Цилиндр-11
8	Тетраэдр-12	18	Конус-12	28	Цилиндр-12
9	Тетраэдр-23	19	Конус-23	29	Цилиндр-23
10	Тетраэдр-123	20	Конус-123	30	Цилиндр-123

1.2. Сконструировать описательные шкалы и градации.

Проекциями перечисленных трехмерных тел на взаимно-ортогональные плоскости являются двухмерные фигуры: круг, квадрат и треугольник. Соответственно, сконструируем и описательные шкалы и градации, чтобы они позволяли отразить все варианты проекций трехмерных тел (таблица 85).

Таблица 85 – ОПИСАТЕЛЬНЫЕ ШКАЛЫ И ГРАДАЦИИ

Код	Наименование
[1]	ВИД СПЕРЕДИ:
1	Круг
2	Квадрат
3	Треугольник
[2]	ВИД СБОКУ:
4	Круг
5	Квадрат
6	Треугольник
[3]	ВИД СВЕРХУ:
7	Круг
8	Квадрат
9	Треугольник

1.3. Сгенерировать обучающую выборку.

Чтобы сгенерировать обучающую выборку составим таблицу 86, в которой в наглядной форме изобразим проекции выбранных нами тел на ортогональные плоскости.

Таблица 86 – КОДИРОВАНИЕ ПРОЕКЦИЙ ТЕЛ
ДЛЯ ОБУЧАЮЩЕЙ ВЫБОРКИ

Код	Тело	Проекции	1-я проекция X«Y вращение вокруг Z 1			2-я проекция X«Z вращение вокруг Y 2			3-я проекция Y«Z вращение вокруг X 3
			X	Y	Z	X	Y	Z	X	Y	Z
1	Шар	Вид	O	O	O	O	O	O	O	O	O
		Код	1	4	7	1	4	7	1	4	7
2	Тетраэдр	Вид
		Код	3	6	9	3	6	9	3	6	9
3	Куб	Вид									
		Код	2	5	8	2	5	8	2	5	8
4	Конус	Вид			O	O				O
		Код	3	6	7	1	6	9	3	4	9
5	Пирамида	Вид								
		Код	3	6	8	2	6	9	3	5	9
6	Цилиндр	Вид			O	O				O	
		Код	2	5	7	1	5	8	2	4	8
7	Призма	Вид									
		Код	2	5	9	3	5	8	2	6	8

С использованием таблицы 86 составим таблицу 87 с обучающей выборкой.

Таблица 87 – ФОРМА ДЛЯ ВВОДА ОБУЧАЮЩЕЙ ВЫБОРКИ

Код	Наименование	Классы			Признаки
		1	2	3	Проекция-1			Проекция-2			Проекция-3
					1	2	3	4	5	6	7	8	9
1	Шар	1			1	4	7
2	Шар-11	2			1	4	7	1	4	7
3	Шар-12	3			1	4	7				1	4	7
4	Шар-22	4						1	4	7	1	4	7
5	Шар-123	5			1	4	7	1	4	7	1	4	7
6	Тетраэдр	6			3	6	9
7	Тетраэдр-11	7			3	6	9	3	6	9
8	Тетраэдр-12	8			3	6	9				3	6	9
9	Тетраэдр-23	9						3	6	9	3	6	9
10	Тетраэдр-123	10			3	6	9	3	6	9	3	6	9

Продолжение таблицы 87

Код	Наименование	Классы			Признаки
		1	2	3	Проекция-1			Проекция-2			Проекция-3
					1	2	3	4	5	6	7	8	9
11	Куб	11			2	5	8
12	Куб-11	12			2	5	8	2	5	8
13	Куб-12	13			2	5	8				2	5	8
14	Куб-23	14						2	5	8	2	5	8
15	Куб-123	15			2	5	8	2	5	8	2	5	8
16	Конус	16			3	6	7
17	Конус-11	17			3	6	7	1	6	9
18	Конус-12	18			3	6	7				3	4	9
19	Конус-23	19						1	6	9	3	4	9
20	Конус-123	20			3	6	7	1	6	9	3	4	9
21	Пирамида	21			3	6	8
22	Пирамида-11	22			3	6	8	2	6	9
23	Пирамида-12	23			3	6	8				3	5	9
24	Пирамида-23	24						2	6	9	3	5	9
25	Пирамида-123	25			3	6	8	2	6	9	3	5	9
26	Цилиндр	26			2	5	7
27	Цилиндр-11	27			2	5	7	1	5	8
28	Цилиндр-12	28			2	5	7				2	4	8
29	Цилиндр-23	29						1	5	8	2	4	8
30	Цилиндр-123	30			2	5	7	1	5	8	2	4	8
31	Призма	31			2	5	9
32	Призма-11	32			2	5	9	3	5	8
33	Призма-12	33			2	5	9				2	6	8
34	Призма-23	34						3	5	8	2	6	8
35	Призма-123	35			2	5	9	3	5	8	2	6	8

2. Осуществить синтез и верификацию (измерение адекватности) семантической информационной модели.

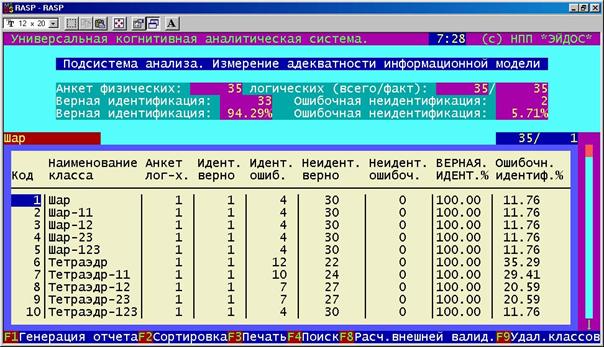
Вводим классификационные и описательные шкалы и градации (в 1-м и 2-м режимах 1-й подсистемы), а также обучающую выборку (в 1-м режиме 2-й подсистемы) в систему "Эйдос" и осуществляем синтез модели (в 5-й функции 3-го режима 2-й подсистемы), а затем ее верификацию (во 2-м режиме 6-й подсистемы). В результате получаем семантическую информационную модель, обладающую достаточно высокой степенью адекватности: 94,29%, чтобы результаты ее исследования можно было считать исследованием самой моделируемой предметной области (рисунок 181).

Рисунок 181. Экранная форма по измерению адекватности СИМ

3. Провести системно-когнитивный анализ модели:

3.1. Решить задачи идентификации и прогнозирования.

После выполнения 2-го режима 4-й подсистемы "Распознавание" в 1-й функции 3-го режима 4-й подсистемы получаем итоговую форму по результатам идентификации (таблица 88).

Таблица 88 – ИТОГОВЫЕ РЕЗУЛЬТАТЫ ИДЕНТИФИКАЦИИ

Объект		Класс		Сходство
Код	Наименован.	Код	Наименован.
1	Шар	1	Шар	94,083
2	Шар-11	1	Шар	76,819
3	Шар-12	1	Шар	76,819
4	Шар-23	1	Шар	76,819
5	Шар-123	1	Шар	54,319
6	Тетраэдр	6	Тетраэдр	94,257
7	Тетраэдр-11	6	Тетраэдр	76,960
8	Тетраэдр-12	6	Тетраэдр	76,960
9	Тетраэдр-23	6	Тетраэдр	76,960
10	Тетраэдр-123	6	Тетраэдр	54,419
11	Куб	11	Куб	94,189
12	Куб-11	11	Куб	76,905
13	Куб-12	11	Куб	76,905
14	Куб-23	11	Куб	76,905
15	Куб-123	11	Куб	54,380
16	Конус	16	Конус	92,171
17	Конус-11	17	Конус-11	75,941
18	Конус-12	20	Конус-123	77,354
19	Конус-23	20	Конус-123	82,367
20	Конус-123	20	Конус-123	69,532

Продолжение таблицы 88

Объект		Класс		Сходство
Код	Наименован.	Код	Наименован.
21	Пирамида	21	Пирамида	94,257
22	Пирамида-11	22	Пирамида-11	66,725
23	Пирамида-12	23	Пирамида-12	64,571
24	Пирамида-23	24	Пирамида-23	62,412
25	Пирамида-123	32	Призма-11	44,934
26	Цилиндр	26	Цилиндр	92,128
27	Цилиндр-11	27	Цилиндр-11	77,694
28	Цилиндр-12	27	Цилиндр-11	77,694
29	Цилиндр-23	30	Цилиндр-123	82,136
30	Цилиндр-123	30	Цилиндр-123	69,328
31	Призма	31	Призма	94,189
32	Призма-11	32	Призма-11	67,933
33	Призма-12	33	Призма-12	63,420
34	Призма-23	34	Призма-23	62,412
35	Призма-123	32	Призма-11	44,934

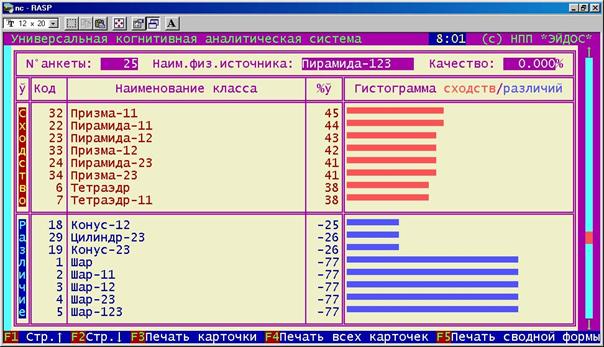
Из таблицы 88 видно, что объект "Пирамида-123" неверно идентифицирован как класс "Призма-11". В остальных случаях тип объекта идентифицирован верно, что не исключает в ряде случаев неверной идентификации вида проекции (что, конечно, не имеет отношения к телам Платона – первым трем классам). Карточка, дающая расшифровку результатов идентификации 25-го объекта "Пирамида-123", представлена на рисунке 182.

Рисунок 182. Карточка результатов идентификации объекта 25.

Если проанализировать коды признаков призмы и пирамиды, то можно увидеть, что они одни и те же, и отличие состоит лишь в количестве повторностей признаков. Это и является причиной сложностей при дифференцировании этих объектов.

3.2. Сгенерировать информационные портреты классов и факторов, т.е. решить обратную задачу прогнозирования (результаты отобразить в графической форме двухмерных и трехмерных профилей классов и факторов).

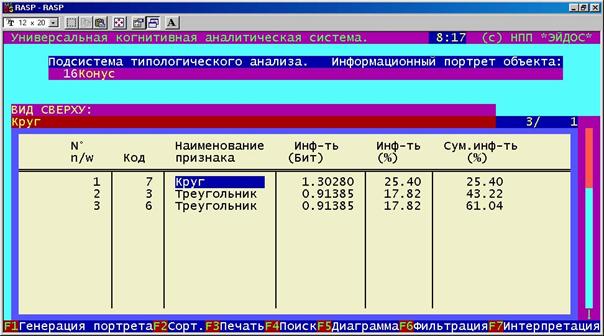
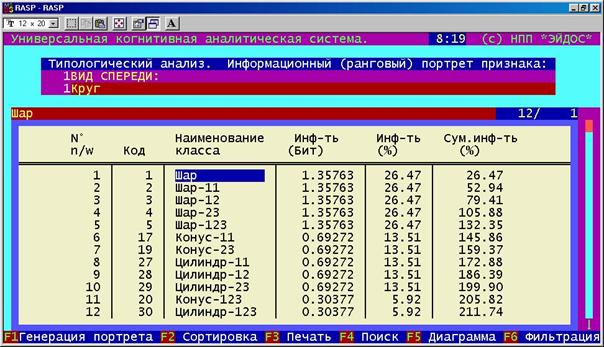
В 1-й функции 1-го режима 5-й подсистемы системы "Эйдос" получим информационный портрет класса, а в 1-й функции 2-го режима той же подсистемы – информационный портрет признака (рисунок 183).

Рисунок 183. Примеры информационных портретов
классов и признаков

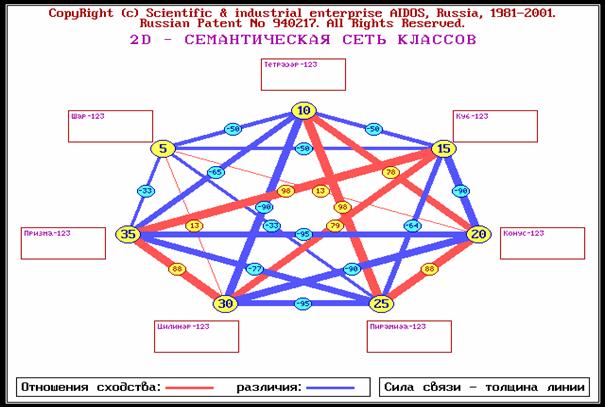
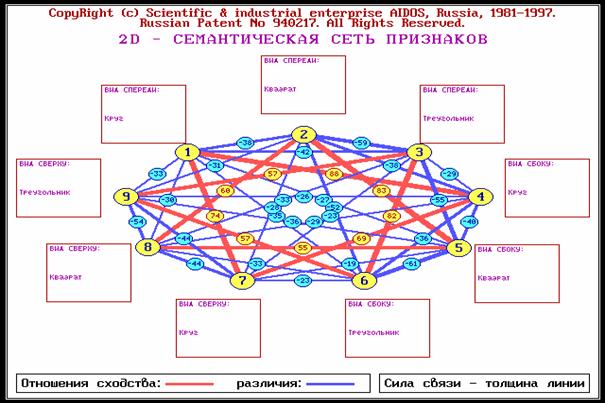
3.3. Провести кластерно-конструктивный анализ классов и факторов (результаты отобразить в форме семантических сетей классов и факторов).

В 5-й операции 2-й функции 1-го и 2-го режимов 5-й подсистемы получим семантические сети классов и факторов (рисунок 184).

Рисунок 184. Примеры семантических сетей классов и факторов

Интерпретацию семантических сетей дать самостоятельно.

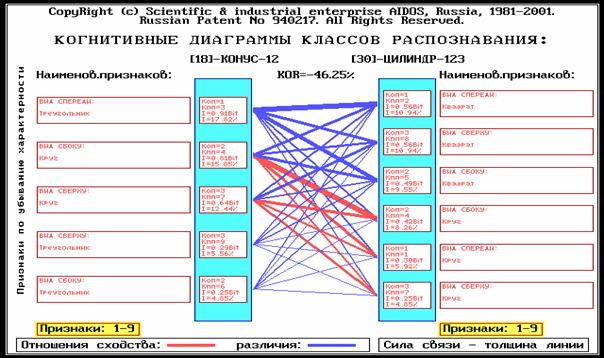
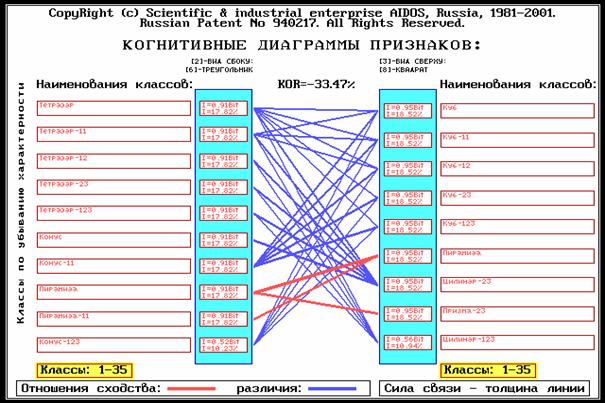
3.4. Осуществить содержательное сравнение классов и факторов (результаты отобразить в форме когнитивных диаграмм классов и факторов).

В 3-й функции 1-го и 2-го режимов 5-й подсистемы получим когнитивные диаграммы классов и признаков (рисунок 185).

Рисунок 185. Пример когнитивных диаграмм, содержащих результаты содержательного сравнения классов и факторов

Из диаграммы классов мы видим, что основной вклад в сходство конуса и цилиндра вносит то, что одна из проекций у них одинаковая, т.е. круг, а основной вклад в различие – что остальные проекции у конуса – треугольник, а у цилиндра – квадрат.

Из диаграммы сравнения признаков мы видим, что такие проекции есть и у пирамиды, и у призмы, а в различие – то, что эти проекции характерны для различных тел.

Задания 3.5 – 3.7 выполнить самостоятельно.

Контрольные опросы

1. Что называется ортогональными проекциями тел?

2. В чем заключается сложность идентификации тел по их ортогональным проекциям?

3. За счет чего облегчается задача идентификации тел по их проекциям при наблюдении с нескольких точек или в движении?

Литература по лабораторной работе

1. Луценко Е.В. Теоретические основы и технология адаптивного семантического анализа в поддержке принятия решений (на примере универсальной автоматизированной системы распознавания образов "ЭЙДОС-5.1"). - Краснодар: КЮИ МВД РФ, 1996. - 280с.

2. Луценко Е. В. Автоматизированный системно-когнитивный анализ в управлении активными объектами (системная теория информации и ее применение в исследовании экономических, социально-психологических, технологических и организационно-технических систем): Монография (научное издание). – Краснодар: КубГАУ. 2002. – 605 с.