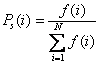1

1.3.6. ЛЕКЦИЯ-12.
Генетические алгоритмы
и моделирование биологической эволюции

Учебные вопросы

1. Основные понятия, принципы и предпосылки генетических алгоритмов.

2. Пример работы простого генетического алгоритма.

3. Достоинства и недостатки генетических алгоритмов.

4. Примеры применения генетических алгоритмов.

1.1.6.1. Основные понятия, принципы и предпосылки генетических алгоритмов

Генетические Алгоритмы (ГА) – это адаптивные методы функциональной оптимизации, основанные на компьютерном имитационном моделировании биологической эволюции. Основные принципы ГА были сформулированы Голландом (Holland, 1975), и хорошо описаны во многих работах и на ряде сайтов в Internet.

В настоящее время существует ряд теорий биологической эволюции (Ж.-Б.Ламарка, П.Тейяра де Шардена, К.Э.Бэра, Л.С.Берга, А.А.Любищева, С.В.Мейена и др.), однако, ни одна из них не считается общепризнанной. Наиболее известной и популярной, конечно, является теория Чарльза Дарвина, которую он представил в работе "Происхождение Видов" в 1859 году.

Эта теория, как и другие, содержит довольно много нерешенных проблем, глубокое рассмотрение которых далеко выходит за рамки данной работы. Здесь мы можем отметить лишь некоторые наиболее известные из них. Как это ни парадоксально, но несмотря на то, что сам Чарльз Дарвин назвал свою работу "Происхождение Видов" но как раз именно происхождения видов она и не объясняет. Дело в том, что возникновение нового вида "по алгоритму Дарвина" является крайне маловероятным событием, т.к. для этого требуется случайное возникновение в одной точке пространства и времени сразу не менее 100 особей нового вида, т.е. особей, которые могли бы иметь плодовитое потомство. При меньшем количестве особей вид обречен на вымирание. Поэтому процесс видообразования на основе случайных мутаций должен был бы занять несуразно много времени (по некоторым оценкам даже в намного раз больше, чем время существования Вселенной). Кроме того, "алгоритм Дарвина" не объясняет явной системности в многообразии возникающих форм, типа закона гомологичных рядов Н.И. Вавилова. Поэтому Л.С. Берг предложил очень интересную концепцию номогенеза – закономерной или направленной эволюции живого. В этой концепции предполагается, что филогенез имеет определенное направление и смена форма является не случайной, а задается некоторым вектором, природа которого не ясна. Идеи номогенеза глубоко разработал и развил А.А. Любищев, высказавший гипотезу о математических закономерностях, которые определяют многообразие живых форм. Кроме того, Дарвин не смог показать механизм наследования, при котором поддерживается и закрепляется изменчивость. Это было на пятьдесят лет до того, как генетическая теория наследственности начала распространяться по миру, и за тридцать лет до того, как "эволюционный синтез" укрепил связь между теорией эволюции и молодой генетикой.

Тем ни менее и не смотря на свои недостатки, именно теория Дарвина традиционно и моделируется в ГА, хотя, конечно, это не исключает возможности моделирования и других теорий эволюции в ГА. Более того, возможно именно такое компьютерное моделирование и сравнение его результатов с картиной реальной эволюции жизни на Земле может быть и сыграет положительную роль в дальнейшей разработке наиболее адекватной теории биологической эволюции.

Теория Дарвина применима не к отдельным особям, а к популяциям – большому количеству особей одного вида, т.е. способных давать плодовитое потомство, находящейся в определенной статичной или динамичной внешней среде.

В основе модели эволюции Дарвина лежат случайные изменения отдельных материальных элементов живого организма при переходе от поколения к поколению. Целесообразные изменения, которые облегчают выживание и производство потомков в данной конкретной внешней среде, сохраняются и передаются потомству, т.е. наследуются. Особи, не имеющие соответствующих приспособлений, погибают, не оставив потомства или оставив его меньше, чем приспособленные (считается, что количество потомства пропорционально степени приспособленности). Поэтому в результате естественного отбора возникает популяция из наиболее приспособленных особей, которая может стать основой нового вида.

Естественный отбор происходит в условиях конкуренции особей популяции, а иногда и различных видов, друг с другом за различные ресурсы, такие, например, как пища или вода. Кроме того, члены популяции одного вида часто конкурируют за привлечение брачного партнера. Те особи, которые наиболее приспособлены к окружающим условиям, будут иметь относительно больше шансов воспроизвести потомков. Слабо приспособленные особи либо совсем не произведут потомства, либо их потомство будет очень немногочисленным. Это означает, что гены от высоко адаптированных или приспособленных особей будут распространятся в увеличивающемся количестве потомков на каждом последующем поколении.

Таким образом, по сути дела каждый конкретный генетический алгоритм представляют имитационную модель некоторой определенной теории биологической эволюции или ее варианта. Вместе с тем необходимо отметить, что сами исследователи биологической эволюции пока еще не до конца определились с критериями и методами определения степени существенности для поддерживаемой ими теории эволюции тех или иных биологических процессов, которые собственно и моделируются в генетических алгоритмах.

1.1.6.2. Пример работы простого генетического алгоритма

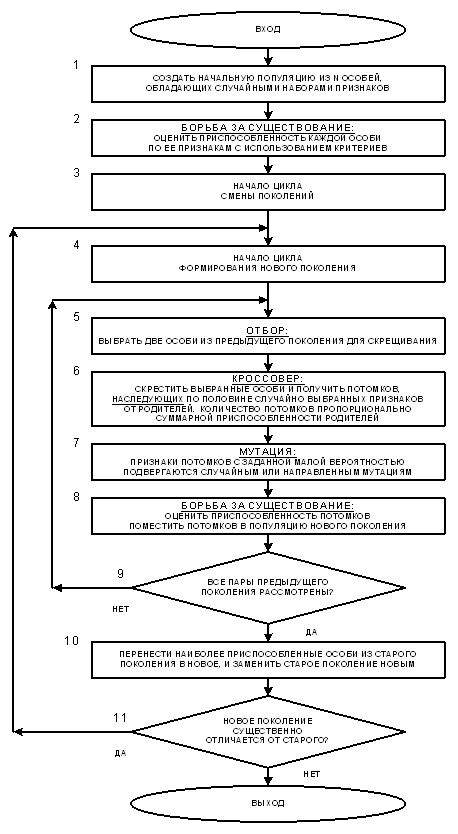
На рисунке 85 приведен пример простого генетического алгоритма.

Рисунок 85. Простой генетический алгоритм

Работа ГА представляет собой итерационный процесс, который продолжается до тех пор, пока поколения не перестанут существенно отличаться друг от друга, или не пройдет заданное количество поколений или заданное время. Для каждого поколения реализуются отбор, кроссовер (скрещивание) и мутация. Рассмотрим этот алгоритм.

Шаг 1: генерируется начальная популяция, состоящая из N особей со случайными наборами признаков.

Шаг 2 (борьба за существование): вычисляется абсолютная приспособленность каждой особи популяции к условиям среды f(i) и суммарная приспособленность особей популяции, характеризующая приспособленность всей популяции. Затем при пропорциональном отборе для каждой особи вычисляется ее относительный вклад в суммарную приспособленность популяции P_s(i), т.е. отношение ее абсолютной приспособленности f(i) к суммарной приспособленности всех особей популяции (3):

( 3 )

В выражении (3) сразу обращает на себя внимание возможность сравнения абсолютной приспособленности i-й особи f(i) не с суммарной приспособленностью всех особей популяции, а со средней абсолютной приспособленностью особи популяции (4):

( 4 )

Тогда получим (5):

( 5 )

Если взять логарифм по основанию 2 от выражения (5), то получим количество информации, содержащееся в признаках особи о том, что она выживет и даст потомство (6).

( 6 )

Необходимо отметить, что эта формула совпадает с формулой для семантического количества информации Харкевича, если целью считать индивидуальное выживание и продолжение рода. Это значит, что даже чисто формально приспособленность особи представляет собой количество информации, содержащееся в ее фенотипе о продолжении ее генотипа в последующих поколениях.

Поскольку количество потомства особи пропорционально ее приспособленности, то естественно считать, что если это количество информации:

– положительно, то данная особь выживает и дает потомство, численность которого пропорциональна этому количеству информации;

– равно нулю, то особь доживает до половозрелого возраста, но потомства не дает (его численность равна нулю);

– меньше нуля, то особь погибает до достижения половозрелого возраста.

Таким образом, можно сделать фундаментальный вывод, имеющий даже мировоззренческое звучание, о том, что естественный отбор представляет собой процесс генерации и накопления информации о выживании и продолжении рода в ряде поколений популяции, как системы.

Это накопление информации происходит на различных уровнях иерархии популяции, как системы, включающей:

– элементы системы: отдельные особи;

– взаимосвязи между элементами: отношения между особями в популяции, обеспечивающие передачу последующим поколениям максимального количества информации об их выживании и продолжении рода (путем скрещивания наиболее приспособленных особей и наследования рациональных приобретений);

– цель системы: сохранение и развитие популяции, реализуется через цели особей: индивидуальное выживание и продолжение рода.

Фенотип соответствует генотипу и представляет собой его внешнее проявление в признаках особи. Особь взаимодействует с окружающей средой и другими особями в соответствии со своим фенотипом. В случае, если это взаимодействие удачно, то особь передает генетическую информацию, определяющую фенотип, последующим поколениям.

Шаг 3: начало цикла смены поколений.

Шаг 4: начало цикла формирования нового поколения.

Шаг 5 (отбор): осуществляется пропорциональный отбор особей, которые могут участвовать в продолжении рода. Отбираются только те особи популяции, у которых количество информации в фенотипе и генотипе о выживании и продолжении рода положительно, причем вероятность выбора пропорциональна этому количеству информации.

Шаг 6 (кроссовер): отобранные для продолжения рода на предыдущем шаге особи с заданной вероятностью P_c подвергаются скрещиванию или кроссоверу (рекомбинации).

Если кроссовер происходит, то потомки получают по половине случайным образом определенных признаков от каждого из родителей. Численность потомства пропорциональна суммарной приспособленности родителей. В некоторых вариантах ГА потомки после своего появления заменяют собой родителей и переходят к мутации.

Если кроссовер не происходит, то исходные особи – несостоявшиеся родители, переходят на стадию мутации.

Шаг 7 (мутация): выполняются операторы мутации. При этом признаки потомков с вероятностью P_m случайным образом изменяются на другие. Отметим, что использование механизма случайных мутаций роднит генетические алгоритмы с таким широко известным методом имитационного моделирования, как метод Монте-Карло.

Шаг 8 (борьба за существование): оценивается приспособленность потомков (по тому же алгоритму, что и на шаге 2).

Шаг 9: проверяется, все ли отобранные особи дали потомство.

Если нет, то происходит переход на шаг 5 и продолжается формирование нового поколения, иначе – переход на следующий шаг 10.

Шаг 10: происходит смена поколений:

– потомки помещаются в новое поколение;

– наиболее приспособленные особи из старого поколения переносятся в новое, причем для каждой из них это возможно не более заданного количества раз;

– полученная новая популяция замещает собой старую.

Шаг 11: проверяется выполнение условия останова генетического алгоритма. Выход из генетического алгоритма происходит либо тогда, когда новые поколения перестают существенно отличаться от предыдущих, т.е., как говорят, "алгоритм сходится", либо когда пройдено заданное количество поколений или заданное время работы алгоритма (чтобы не было "зацикливания" и динамического зависания в случае, когда решение не может быть найдено в заданное время ).

Если ГА сошелся, то это означает, что решение найдено, т.е. получено поколение, идеально приспособленное к условиям данной фиксированной среды обитания.

Иначе – переход на шаг 4 – начало формирования нового поколения.

В реальной биологической эволюции этим дело не ограничивается, т.к. любая популяция кроме освоения некоторой экологической ниши пытается также выйти за ее пределы освоить и другие ниши, как правило "смежные". Именно за счет этих процессов жизнь вышла из моря на сушу, проникла в воздушное пространство и поверхностный слой почвы, а сейчас осваивает космическое пространство.

Конечно, реальные генетические алгоритмы, на которых проводятся научные исследования, чаще всего мало похожи на приведенный пример. Исследователи экспериментируют с различными параметрами генетических алгоритмов, например: способами отбора особей для скрещивания; критериями приспособленности и жесткостью влияния факторов среды; способами выбора признаков, передающихся от родителей потомкам (рецессивные и не рецессивные гены и т.д.); интенсивностью, видом случайного распределения и направленностью мутаций; различными подходами к воспроизводству и отбору.

Поэтому под термином "генетические алгоритмы" по сути дела надо понимать не одну модель, а довольно широкий класс алгоритмов, подчас мало похожих друг на друга.

В настоящее время рассматривается много различных операторов отбора, кроссовера и мутации: турнирный отбор (Brindle, 1981; Goldberg и Deb, 1991), реализует n турниров, чтобы выбрать n особей, при этом каждый турнир построен на выборке k элементов из популяции, и выбора лучшей особи среди них (наиболее распространен турнирный отбор с k=2); элитный отбор (De Jong, 1975) гарантируют, что при отборе обязательно будут выживать лучший или лучшие члены популяции совокупности (наиболее распространена процедура обязательного сохранения только одной лучшей особи, если она не прошла как другие через процесс отбора, кроссовера и мутации); двухточечный кроссовер (Cavicchio, 1970; Goldberg, 1989c) и равномерный кроссовер (Syswerda, 1989) отличаются способами наследования потомками признаков родителей.

Не смотря на то, что модели биологической эволюции, реализуемые в ГА, обычно сильно упрощены по сравнению с природным оригиналом, тем ни менее ГА являются мощным средством, которое может с успехом применяться для решения широкого класса прикладных задач, включая те, которые трудно, а иногда и вовсе невозможно, решить другими методами.

1.1.6.3. Достоинства и недостатки генетических алгоритмов

Однако, ГА не гарантирует обнаружения глобального решения за приемлемое время. ГА не гарантируют и того, что найденное решение будет оптимальным решением. Тем ни менее они применимы для поиска "достаточно хорошего" решения задачи за "достаточно короткое время". ГА представляют собой разновидность алгоритмов поиска и имеют преимущества перед другими алгоритмами при очень больших размерностях задач и отсутствия упорядоченности в исходных данных, когда альтернативой им является метод полного перебора вариантов.

В случаях, когда задача может быть решена специально разработанным для нее методом, практически всегда такие методы будут эффективнее ГА как по быстродействию, так и по точности найденных решений.

Главным же достоинством ГА является то, что они могут применяться для решения сложных неформализованных задач, для которых не разработано специальных методов, т.е. ГА обеспечивают решение проблем. Но даже в тех случаях, для которых хорошо работают существующие методики, можно достигнуть интересных результатов сочетая их с ГА.

1.1.6.4. Примеры применения генетических алгоритмов

Данный раздел основан на статье Алексея Андреева "Электродарвин" (http://www.fuga.ru/articles/2004/03/genetic-pro.htm), к которой мы и отсылаем за очень интересными подробностями.

В 1994 году Эндрю Кин из университета Саутгемптона использовал генетический алгоритм в дизайне космических кораблей. За основу была взята модель опоры космической станции, спроектированной в NASA из которой после смены 15 поколений, включавших 4.500 вариантов дизайна, получилась модель, превосходящая по тестам тот вариант, что разработали люди.

Аналогичный генетический алгоритм был использован NASA при разработке антенны для спутника.

Джон Коза из Стэнфорда разработал технологию генетического программирования, в которой результатом эволюции становятся не отдельные числовые параметры "особей", а целые имитационные программы, которые являются виртуальными аналогами реальных устройств. Эта технология позволила компании Genetic Programming повторить 15 человеческих изобретений, 6 из которых были запатентованы после 2000 года, то есть представляют собой самые передовые достижения, а один из контроллеров, "выведенных" в GP, даже превосходит аналогичную человеческую разработку.

Сейчас плоды электронной эволюции можно найти в самых разных сферах: от двигателя самолета Boeing 777 до новых антибиотиков.

Генетические алгоритмы представляют собой компьютерное моделирование эволюции. Материальное воплощение сконструированных таким образом систем до сих пор была невозможна без участия человека. Однако интенсивно ведутся работы, результатом которых является уменьшение зависимости машинной эволюции от человека. Эти работы ведутся по двум основным направлениям:

1. Естественный отбор, моделируемый ГА, переносится из виртуального мира в реальный, например, проводятся эксперименты по реальным битвам роботов на выживание.

2. Интеллектуальные системы, основанные на ГА, конструируют роботов, которые в принципе могут быть изготовлены на автоматизированных заводах без участия человека.

Пример воплощения ГА в реальной битве роботов на выживание: в 2002 году в британском центре Magna открылся павильон Live Robots, где боролись за выживание 12 роботов двух видов: "гелиофаги", способные добывать электроэнергию с использованием солнечных батарей; "хищники", которые могли получать электроэнергию только от гелиофагов. Выжившие роботы загружали свои "гены" в погибших и, таким образом, образовывали новые поколения. Те хищники, которые забирали всю энергию у гелиофагов, теряли источник питания и погибали, не передавая свою тактику потомкам, поступавшие же "более разумно" продолжили свой род. В результате возникла равновесная сбалансированная искусственная экосистема с двумя популяциями.

Пример конструирования роботов роботами: в Brandeis University была создана программа Golem, которая сама конструировала роботов. В программу была база деталей, а также механизм мутаций и функция пригодности для "отсеивания" неудачников – тех, кто не научился двигаться. После 600 поколений за несколько дней программа получила модели трех ползающих роботов. Показательно, что роботы оказались симметричными, хотя симметрия никак не была явно прописана в правилах эволюции и исходных данных. Это означает, что она появилась в ходе моделирования машинной эволюции как полезная черта, позволяющая двигаться прямолинейно.

Контрольные вопросы