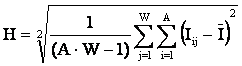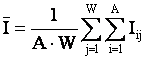3.6. ВЫВОДЫ

 

1. В третьей главе сформулированы требования к математической модели и к численной мере, а затем обоснован выбор базовой численной меры.

Для этого рассмотрены три вида информации: абсолютная, относительная и аналитическая информация и отдано предпочтение аналитической форме информации, к которой принадлежат относительные вероятности, относительные проценты и количество информации. Вместо традиционных мер, основанных на понятии "стоимости" и "полезности" предложено использовать информационную меру. Рассмотрены различные аспекты применения теории информации для анализа процесса труда и средств труда как информационных систем. Показано, что принятие решения об управляющем воздействии и управление есть обратный процесс по отношению к идентификации и прогнозированию, т.е. познанию. Показана связь количества (синтаксиса) и качества (содержания, семантики) информации, записываемой в структуре предмета труда, с меновой и потребительной стоимостью. Сформулирована информационная теория стоимости, в которой информация рассматривается как сущность стоимости и как "первичный" и по сути единственный товар. Рассмотрены вопросы определения стоимости и амортизация интеллектуальных систем и баз знаний. Показано, что их стоимость генераторов информации  возрастает в процессе эксплуатации. С позиций теории информации раскрыт фундаментальный источник экономической эффективности АСУ и систем интеллектуальной обработки данных: понижение энтропии объекта управления как приемника сообщений в результате получения управляющей информации. Сделан вывод о целесообразности выбора в качестве базовой численной меры количества информации. Поставлена задача выбора или конструирования конкретной численной меры, основанной на понятии информации.

2. В классической теории информации Шеннона, созданной на основе обобщения результатов Больцмана, Найквиста и Хартли, само понятие информации определяется на основе теоретико-множественных и комбинаторных представлений на основе анализа поведения классического макрообъекта, который может переходить только в четко фиксированные альтернативные редуцированные состояния. Однако, квантовые объекты и сложные активные рефлексивные системы могут оказываться одновременно в двух и более альтернативных для классических объектов состояниях. Такие состояния будем называть смешанными. Таким образом наблюдается картина последствий, не сводящаяся к простой сумме последствий альтернативных вариантов, т.е. очень напоминающая квантовое физическое явление, которое называется интерференцией плотности вероятности. Это явление, безусловно имеющее системный характер, предлагается называть "интерференция последствий выбора".

3. Предлагается обобщение классической теория информации Хартли-Шеннона путем рассмотрения квантовых и активных объектов в качестве объектов, на основе анализа которых формируется само основополагающее понятие информации. Обобщенную таким образом теорию информации предлагается называть системной или эмерджентной теорией информации (было бы удачным назвать ее и квантовой, но этот термин уже используется в другом смысле). Основным отличием эмерджентной теории информации от классической является учет свойства системности, как фундаментального и универсального свойства всех объектов, на уровне самого понятия информации, а не только в последующем изложении, как в классической теории.

4. Предложена системная модификация формулы Хартли для количества информации:

где:

W – количество чистых (классических) состояний системы;

– сочетания "по m" классических состояний.

Так как , то при M=1 выполняется принцип соответствия, являющийся обязательным для более общей теории. Данная формула дает верхнюю оценку возможного количества информации  состоянии системы, т.к. возможны различные правила запрета и реальное количество возможных состояний системы будет меньшим, чем .

Предложено приближенное выражение для системной модификации формулы Хартли (при M=W):

При W>4 погрешность данного выражения не превышает 1%.

Дополнительная информация, которую мы получаем из поведения объекта в СТИ, по сути дела является информацией о множестве всех его возможных состояний, как системы, элементом которой является объект в некотором данном состоянии.

5. Численные расчеты и аналитические выкладки показывают, что при возрастании количества элементов в системе доля системной информации в поведении ее элементов возрастает, причем возрастает ускоренно. Это обнаруженное нами свойство систем предлагается назвать "Законом возрастания эмерджентности".

6. Предложена системная модификация классической формулы А.Харкевича, являющееся нелинейной суперпозицией классических выражением для плотности информации Шеннона и количества информации Хартли.

где: j – коэффициент эмерджентности Хартли (уровень системной организации объекта, имеющего W чистых состояний):

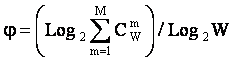
Полученное выражение учитывает как взаимосвязь между признаками (факторами) и будущими, в т.ч. целевыми состояниями объекта управления, так и мощность множества будущих состояний. Кроме того она объединяет возможности интегрального и дискретного описания объектов, что является основой формализации смысла, а также удовлетворяет принципу соответствия, т.е. преобразуется в формулу Хартли в предельном случае, когда каждому классу (состоянию объекта) соответствует один признак (фактор), и каждому признаку – один класс, и эти классы (а, значит и признаки), равновероятны.

7. Все это делает выражение оптимальным по сформулированным критериям для целей построения семантической информационной модели активных объектов управления и для применения для синтеза рефлексивных АСУ активными системами.

8. В предложенной семантической информационной модели генерируется обобщенная таблица решений, в которой входы (факторы) и выходы будущие состояния активного объекта управления (АОУ) связаны друг с другом не с помощью классических (Аристотелевских) импликаций, принимающих только значения: "Истина" и "Ложь", а различными значениями истинности, выраженными в битах и принимающими значения от положительного теоретически-максимально-возможного ("Максимальная степень истинности"), до теоретически неограниченного отрицательного ("Степень ложности"). Синтез обобщенных таблиц решений для различных предметных областей осуществляется непосредственно на основе эмпирических исходных данных, на основе этих таблиц продуцируются прямые и обратные правдоподобные (нечеткие) логические рассуждения по неклассическим схемам с различными расчетными значениями истинности, являющимся обобщением классических импликаций. При этом в прямых рассуждениях как предпосылки рассматриваются факторы, а как заключение – будущие состояния АОУ, а в обратных – наоборот. Степень истинности i-й предпосылки – это количество информации Iij, содержащейся в предпосылке о наступлении j-го будущего состояния активного объекта управления.

9. Евклидово расстояние в качестве меры сходства объекта с классом, класса с классом и атрибута с атрибутом не применимо, т.к. информационное семантическое пространство вообще говоря неортонормированно, расстояние Махалонобиса также неприменимо, т.к. измеряет расстояние от центроида, а не между векторами, поэтому на основе леммы Неймана-Пирсона в качестве неметрической меры сходства предложено использовать суммарное количество информации. Если предпосылок несколько, то степень истинности наступления j-го состояния АОУ равна суммарному количеству информации, содержащемуся в них об этом:

Или в координатной форме:

,

где:  – вектор j–го состояния объекта управления, координаты которого в информационном семантическом пространстве рассчитываются согласно системного обобщения формулы Харкевича, приведенной в п.6;   – булев вектор состояния предметной области, включающий все виды факторов, характеризующих объект управления, возможные управляющие воздействия и окружающую среду (массив–локатор).

10. Предложенная семантическая информационная модель позволяет решать задачи идентификации и прогнозирования развития активных систем (разложение вектора объекта по векторам классов – "Объектный анализ"), а также вырабатывать эффективные управляющие воздействия путем решения обратной задачи прогнозирования и применения элементов нетрадиционной логики и правдоподобных (нечетких) рассуждений. В ней объединены преимущества содержательных и статистических моделей, созданы предпосылки для реализации АСК-анализа.

11. Исследована взаимосвязь примененной в модели семантической меры Харкевича со статистикой Х2, и, на этой основе, предложена новая статистическая мера наличия причинно-следственных связей H, основанная на модифицированной формуле Харкевича:

где:

– средняя информативность признаков по матрице информативностей.

Обоснована устойчивость модели при малых выборках, дано обоснование сопоставимости частных критериев, разработана интерпретация распознавания как объектного анализа (разложение вектора объекта в ряд по векторам классов), предложены робастные процедуры, а также процедуры обеспечения структурной репрезентативности выборки.

12. Предложен коэффициент эмерджентности Хартли j, который представляет собой относительное превышение количества информации о системе при учете системных эффектов (смешанных состояний, иерархической структуры ее подсистем и т.п.) над количеством информации без учета системности, т.е. этот коэффициент отражает уровень системности объекта. Уровень системности объекта изменяется от 1 (системность минимальна, т.е. отсутствует) до W/Log2W (системность максимальна). Для каждого количества элементов системы существует свой максимальный уровень системности, который никогда реально не достигается из-за действия правил запрета на реализацию в системе ряда подсистем различных уровней иерархии.

Предложен коэффициент эмерджентности Харкевича Y, который изменяется от 0 до 1 и определяет степень детерминированности системы:

Y=1 соответствует полностью детерминированной системе, поведение которой однозначно определяется действием минимальным количеством факторов, которых столько же, сколько состояний системы;

Y=0 соответствует полностью случайной системе, поведение которой никак не зависит действия факторов независимо от их количества;

0<Y<1 соответствуют большинству реальных систем поведение которых зависит от многих факторов, число которых превосходит количество состояний системы, причем ни одно из состояний не определяется однозначно никакими сочетаниями действующих факторов.

Увеличение уровня системности влияет на семантическую информационную модель аналогично повышению уровня детерминированности. Понижение уровня системности, также как и степени детерминированности системы приводит к ослаблению влияния факторов на поведение системы, т.е. к своего рода "инфляции факторов".

Основной вывод по результатам третьей главы:

В предложенном системном обобщении формулы Харкевича впервые непосредственно в аналитическом выражении для самого понятия "Информация" отражены такие фундаментальные свойства систем, как "Уровень системности" и "Степень детерминированности" системы, кроме того это выражение (как и формула Шеннона) удовлетворяет принципу соответствия с выражением Хартли в детерминистском случае, учитывает понятие цели, мощность множества будущих состояний объекта управления, объединяет возможности интегрального и дискретного описания объектов. По этим причинам полученное выражение является оптимальным в качестве основы для построения математической модели рефлексивных АСУ активными объектами.
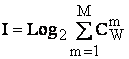
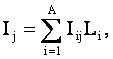