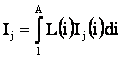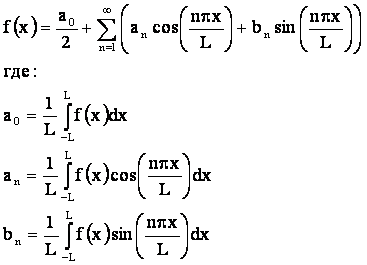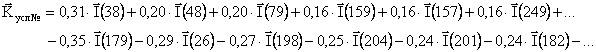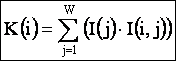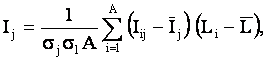3.5. СРАВНЕНИЕ, ИДЕНТИФИКАЦИЯ И ПРОГНОЗИРОВАНИЕ КАК ОБЪЕКТНЫЙ АНАЛИЗ
(РАЗЛОЖЕНИЕ ВЕКТОРОВ ОБЪЕКТОВ В РЯД ПО ВЕКТОРАМ КЛАССОВ)
В разделе 3.4 были введены неметрические интегральные критерии сходства объекта, описанного массивом-локатором Li с векторами обобщенных образов классов Iij (выражения 3.57 и 3.55)
|
|
В выражении (3.82) круглыми скобками обозначено скалярное произведение. В координатной форме это выражение имеет вид:
|
|
,где:
– вектор j–го состояния
объекта управления;
– вектор
состояния предметной области, включающий все виды факторов, характеризующих
объект управления, возможные управляющие воздействия и окружающую среду
(массив–локатор), т.е.:
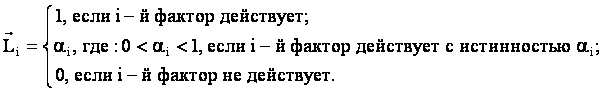
Для непрерывного случая выражение (3.81) принимает вид:
|
|
Таким образом, выражение (3.82) представляет собой вариант выражения (3.80) интегрального критерия сходства объекта и класса для непрерывного случая в координатной форме.
Интересно и очень важно отметить, что коэффициенты ряда Фурье по своей
математической форме и смыслу сходны с ненормированными коэффициентами
корреляции, т.е. по сути скалярными произведениями для непрерывных функций в
координатной форме: выражение (3.82), между разлагаемой в ряд кривой f(x) и функциями Sin и Сos различных частот и амплитуд на отрезке [–L, L] [3]:
|
|
где: n={1, 2, 3,…} – натуральное число.
Из сравнения выражений
(3.82) и (3.83) следует вывод, что процесс идентификации и прогнозирования
(распознавания), реализованный в предложенной математической модели, может
рассматриваться как разложение вектора распознаваемого объекта в ряд по
векторам классов распознавания.
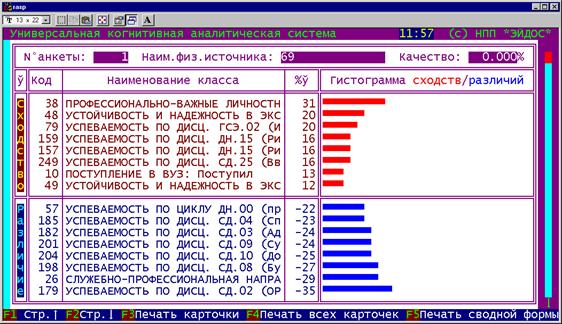
Например, при результатах идентификации, представленных
на рисунке (3.16):
|
|
|
Рисунок 3. 16.
Пример разложения профиля курсанта усл.№69 |
Продолжая развивать аналогию с разложением в ряд, данный
результат идентификации можно представить в векторной аналитической форме:
|
|
Или в координатной форме, более удобной для
численных расчетов:
|
|
где:
I(j)
– интегральный критерий сходства массива-локатора, описывающего состояние
объекта, и j-го класса, рассчитываемый согласно выражения
(3.57):
|
|
(3.57) |
I(i,j)
– вектор обобщенного образа j-го класса, координаты которого рассчитываются в
соответствии с системным обобщением формулы Харкевича
(3.28):
|
|
(3.28) |
Примечание: обозначения I(i,j) и Iij, и т.п.
эквивалентны. Смысл всех переменных, входящих в выражения (3.28) и (3.57) раскрыт
в разделе 3.1.3 данной работы.
При дальнейшем развитии данной аналогии естественно
возникают вопросы:
– о полноте, избыточности и ортонормированности системы векторов классов как функций,
по которым будет вестись разложение вектора объекта;
– о сходимости, т.е. вообще возможности и корректности такого разложения.
В общем случае вектор объекта совершенно не
обязательно должен разлагаться в ряд по векторам классов таким образом, что
сумма ряда во всех точках точно совпадала со значениям исходной функции. Это означает, что система
векторов классов не обязательно будет полна по отношению к профилю распознаваемого
объекта, и, тем более, всех возможных объектов. Предлагается считать не разлагаемые в ряд, т.е. плохо распознаваемые объекты суперпозицией хорошо распознаваемых объектов ("похожих" на те, которые
использовались для формирования образов), и объектов, которые и не должны распознаваться, так как объекты этого типа не встречались в обучающей выборке и не
использовались для формирования обобщенных образов классов.
Нераспознаваемую компоненту можно рассматривать либо как шум, либо считать ее полезным
сигналом, несущим ценную информацию о еще не исследованных
объектах интересующей нас предметной области (в зависимости от целей и
тезауруса исследователей). Первый вариант не приводит к осложнениям, так как
примененный в математической модели алгоритм сравнения векторов объектов и классов, основанный на
вычислении нормированной корреляции Пирсона (сумма произведений), является весьма
устойчивым к наличию белого шума в идентифицируемом сигнале. Во втором
варианте необходимо дообучить систему распознаванию объектов, несущих такую компоненту (в этой возможности и заключается
адаптивность модели). Технически этот вопрос решается просто копированием описаний плохо распознавшихся объектов из распознаваемой выборки в обучающую, их идентификацией экспертами и дообучением системы. Кроме того, может быть целесообразным расширить справочник
классов распознавания новыми классами, соответствующими этим объектам.
Но на практике гораздо чаще наблюдается противоположная
ситуация (можно даже сказать, что она типична), когда система векторов
избыточна, т.е. в системе классов распознавания есть очень похожие классы (между которыми имеет место высокая
корреляция, наблюдаемая в режиме: "кластерно–конструктивный анализ"). Практически это
означает, что в системе сформировано несколько практически одинаковых образов с
разными наименованиями. Для исследователя это само по себе является очень
ценной информацией. Однако, если исходить только из
потребности разложения распознаваемого объекта в ряд по векторам классов (чтобы
определить суперпозицией каких образов он является, т.е. "разложить его на
компоненты"), то наличие сильно коррелирующих друг с другом векторов представляется неоправданным, так как просто
увеличивает размерности данных, внося в них мало нового по существу. Поэтому возникает задача исключения избыточности системы классов
распознавания, т.е. выбора из всей системы классов распознавания такого
минимального их набора, в котором профили классов минимально коррелируют друг с другом, т.е. ортогональны
в фазовом пространстве признаков. Это условие в теории рядов называется
"ортонормируемостью" системы базовых функций, а в факторном анализе связано с идеей выделения "главных компонент".
В предлагаемой математической модели есть два варианта выхода из данной ситуации: исключение неформирующихся, расплывчатых или дублирующих классов; объединение почти идентичных по
содержанию классов.
Но выбрать вариант и реализовать его, используя
соответствующие режимы, пользователь технологии АСК-анализа
должен сам. Вся необходимая и достаточная информация для принятия
соответствующих решений предоставляется пользователю системы.
Если считать, что функции образов образуют
формально–логическую систему, к которой применима теорема Геделя, то можно сформулировать эту теорему для данного случая следующим
образом: "Для любой системы базисных функций всегда существует
по крайней мере одна такая функция, что она не может быть разложена в ряд по
данной системе базисных функций, т.е. всегда
существует функция, которая является ортонормированной ко всей системе базисных функций в целом".
Очевидно, не взаимосвязанными друг с другом могут быть только четко оформленные, детерминистские
образы, т.е. образы с высокой степенью редукции ("степень сформированности конструкта"). Поэтому в процессе выявления взаимно–ортогональных базисных
образов в первую очередь будут выброшены аморфные "расплывчатые"
образы, которые связаны практически со всеми остальными образами.
В некоторых случаях результат такого процесса
представляет интерес и это делает оправданным его реализацию. Однако можно предположить, что и наличие расплывчатых
образов в системе является оправданным, так как в этом случае система образов
не будет формальной и подчиняющейся теореме Геделя, следовательно, система распознавания будет более полна в том смысле, что повысится
вероятность идентификации любого объекта,
предъявленного ей на распознавание. Конечно, уровень сходства с аморфным образом не
может быть столь же высоким, как с четко оформленным, поэтому в этом
случае может быть более уместно применить термин
"ассоциация" или нечеткая, расплывчатая идентификация, чем
"однозначная идентификация".
Итак, можно сделать следующий вывод: возможность наличия
в системе не только четко оформленных (детерминистских) образов, но и образов
аморфных, нечетких, расплывчатых является важным достоинством перспективной
системы распознавания, так как обеспечивает ей возможность устойчивой работы даже в тех
случаях, в которых системы распознавания (идентификации) и
информационно–поисковые системы детерминистского типа практически неработоспособны.
В этих условиях перспективная система
работает как система ассоциативной идентификации.
Таким
образом, в предложенной семантической информационной модели при идентификации и
прогнозировании по сути дела осуществляется разложение векторов
идентифицируемых объектов по векторам классов распознавания, т.е. осуществляется "объектный анализ" (по аналогии с спектральным, гармоническим или Фурье–анализом), что позволяет
рассматривать идентифицируемые объекты как суперпозицию обобщенных
образов классов различного типа с различными амплитудами (3.84). При этом
вектора обобщенных образов классов с математической точки зрения представляют собой
произвольные функции, и не обязательно образуют полную и не избыточную
(ортонормированную) систему функций.
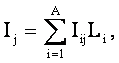