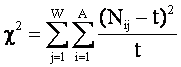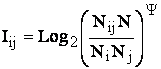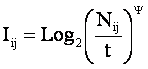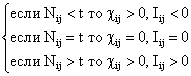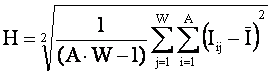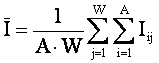3.4. СВЯЗЬ СИСТЕМНОГО
ОБОБЩЕНИЯ ИНФОРМАЦИОННОЙ МЕРЫ ХАРКЕВИЧА СО СТАТИСТИКОЙ c2 И НОВАЯ МЕРА УРОВНЯ СИСТЕМНОСТИ ПРЕДМЕТНОЙ ОБЛАСТИ
Статистика c2 представляет собой сумму вероятностей совместного наблюдения признаков и объектов по всей корреляционной матрице или определенным ее подматрицам (т.е. сумму относительных отклонений частот совместного наблюдения признаков и объектов от среднего):
|
|
где:
– Nij
– фактическое количество встреч i-го признака у объектов j-го класса;
– t –
ожидаемое количество встреч i-го признака у объектов j-го класса.
|
|
Нельзя не обратить внимание
на то, что статистика c2 математически простым
образом связана с количеством информации в системе признаков о классе
распознавания, в соответствии с системным обобщением формулы Харкевича для плотности информации (3.28)
|
|
а именно из (3.76) и (3.77) получаем:
|
|
Из (3.78) очевидно:
|
|
Сравнивая выражения (3.75) и (3.79), видим, что числитель в выражении (3.75) под знаком суммы отличается от выражения (3.79) только тем, что в выражении (3.79) вместо значений Nij и t взяты их логарифмы. Так как логарифм является монотонно возрастающей функцией аргумента, то введение логарифма не меняет общего характера поведения функции.
Фактически это означает, что:
|
|
Если фактическая
вероятность наблюдения i–го признака при
предъявлении объекта j–го класса равна ожидаемой (средней),
то наблюдение этого признака не несет
никакой информации о принадлежности объекта к данному классу. Если же она
выше средней – то это говорит в пользу того, что предъявлен
объект данного класса, если же ниже – то другого.
Поэтому наличие
статистической связи (информации) между признаками и классами распознавания, т.е. отличие вероятностей их совместных наблюдений от
предсказываемого в соответствии со случайным нормальным распределением,
приводит к увеличению фактической статистики c2 по сравнению
с теоретической величиной.
Из этого следует возможность использования в качестве количественной меры степени
выраженности закономерностей в предметной области использовать не матрицу
абсолютных частот и меру c2, а новую меру
основанную на матрице информативностей
и системном обобщении формулы Харкевича для
количества информации:
|
|
где:
|
|
– средняя информативность признаков по матрице информативностей. |
Значение данной меры показывает среднее отличие
количества информации в факторах о будущих состояниях активного объекта
управления от среднего количества информации в факторе (которое при больших
выборках близко к 0). По своей математической форме эта мера сходна с мерами
для значимости факторов и степени сформированности
образов классов и коррелирует с объемом пространства
классов и пространства атрибутов.
Описанная выше математическая модель обеспечивает инвариантность
результатов обучения Системы относительно следующих параметров обучающей выборки:
1. Суммарное количество и порядок ввода анкет обучающей выборки.
2. Количество анкет обучающей выборки по каждому классу распознавания.
3. Суммарное количество признаков во всех анкетах обучающей выборки.
4. Суммарное количество признаков по эталонным описаниям различных
классов распознавания.
5. Количество признаков и их порядок в отдельных анкетах
обучающей выборки.
Это обеспечивает высокое
качество решения задач системой распознавания на неполных и разнородных (в вышеперечисленных
аспектах) данных как обучающей, так и распознаваемой выборки, т.е. при таких
статистических характеристиках потоков этих данных, которые чаще всего и
встречается на практике и которыми невозможно или очень сложно управлять.