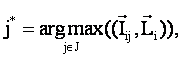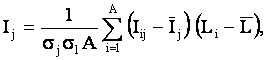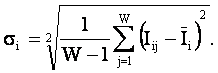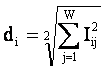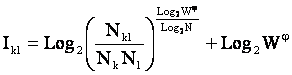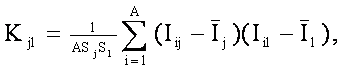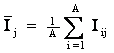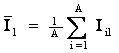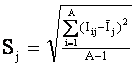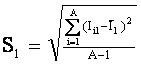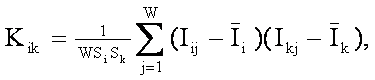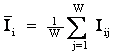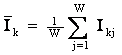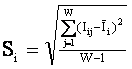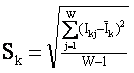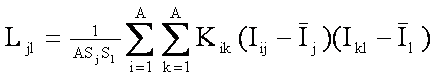3.2. СЕМАНТИЧЕСКАЯ ИНФОРМАЦИОННАЯ МОДЕЛЬ АСК-АНАЛИЗА

Основная проблема, решаемая в аналитической модели: выбор способа вычисления весовых коэффициентов, отражающих степень и характер влияния факторов на переход активного объекта управления в различные состояния.

Основное отличие предлагаемого подхода от методов обобщения экспертных оценок состоит в том, что в предлагаемом подходе от экспертов требуется лишь само решение, а весовые коэффициенты автоматически подбираются в соответствии с моделью таким образом, что в сходных случаях будут приниматься решения, аналогичные предлагаемым экспертами. В традиционных подходах от экспертов требуют либо самих весовых коэффициентов, либо правил принятия решения (продукций).

3.2.1. Формализм динамики взаимодействующих семантических информационных пространств. Двухвекторное представление данных.

Не всегда и не все классы являются атрибутами, также не всегда и не все атрибуты являются классами по смыслу. Поэтому традиционное представление данных в форме одной матрицы с одинаковыми строками и столбцами представляется нецелесообразным и предлагается более общее – двухвекторное представление.

В предлагаемой математической модели формальное описание объекта представляет собой совокупность его интенсионального и экстенсионального описаний. Интенсиональное (дискретное) описание – это последовательность информативностей (но не кодов) тех и только тех признаков, которые реально фактически встретились у данного конкретного объекта. Экстенсиональное (континуальное) описание состоит из информативностей (но не кодов) тех классов распознавания, для формирования образов которых по мнению экспертов целесообразно использовать интенсиональное описание данного конкретного объекта. Именно взаимодействие и взаимная дополнительность этих двух взаимоисключающих видов описания объектов формирует то, что психологи, логики и философы называют "смысл".

Таким образом формальное описание объекта в предлагаемой модели состоит из двух векторов. Первый вектор описывает к каким обобщенным категориям (классам распознавания) относится объект с точки зрения экспертов (вектор субъективной, смысловой, человеческой оценки). Второй же вектор содержит информацию о том, какими признаками обладает данный объект (вектор объективных характеристик). Необходимо особо подчеркнуть, что связь этих двух векторов друг с другом имеет вообще говоря не детерминистский, а вероятностный, статистический характер.

Если объект описан обоими векторами, то это описание можно использовать для формирования обобщенных образов классов распознавания, а также для проверки степени успешности выполнения этой задачи.

Если объект описан только вторым вектором – вектором признаков, то его можно использовать только для решения задачи распознавания (идентификации), которую можно рассматривать как задачу восстановления вектора классов данного объекта по его известному вектору признаков.

Предлагаемая модель удовлетворяет принципу соответствия, т.е. в ней одновекторный вариант описания предметной области получается как некоторое подмножество из возможных в ней вариантов, определяемое двумя ограничениями:

– справочник классов распознавания тождественно совпадает со справочником признаков;

– наличие какого-либо признака у объекта обучающей выборки однозначно (детерминистским образом) определяет принадлежность этого объекта к соответствующему классу распознавания (взаимно-однозначное соответствие классов и признаков).

Очевидно, эти ограничения приводят и к соответствующим ограничениям, накладываемым в свою очередь на варианты обработки информации и анализа данных в подобных системах.

Если говорить конкретнее, такая модель данных стирает различие между атрибутами и классами и не позволяет решать ряд задач, в которых эта абстракция является недопустимым упрощением. Эти задачи будут подробнее рассмотрены ниже.

Семантические пространства классов и атрибутов

Наглядно модель данных целесообразно представить себе в виде двух взаимосвязанных фазовых (т.е. абстрактных) пространств, в первом из которых осями координат служат шкалы атрибутов (пространство атрибутов), а во втором – шкалы классов (пространство классов).

В пространстве атрибутов векторами являются объекты обучающей выборки и обобщенные образы классов. Вектор класса представляет собой массив координат в фазовом пространстве, каждый элемент массива, т.е. координата, соответствует определенному атрибуту, а значение этой координаты – весовому коэффициенту, отражающему количество информации, содержащееся в факте наблюдения данного атрибута у объекта о принадлежности этого объекта к данному классу. В пространстве классов векторами являются атрибуты. Вектор атрибута представляет собой массив координат в фазовом пространстве, каждый элемент массива, т.е. координата, соответствует определенному классу, а значение этой координаты – весовому коэффициенту, отражающему количество информации, содержащееся в факте наблюдения объекта данного класса о том, что у этого объекта будет определенный атрибут.

Таким образом, выбор смысла и математической формы значений весовых коэффициентов вводит метрику в этих фазовых пространствах. Это самым существенным образом отличает предложенные семантические информационные пространства классов и атрибутов от семантического пространства, используемого в основном в психологии, в котором осями являются признаки (шкалы), а значениями координат по осям являются – градации признаков.

Однако этого недостаточно. Чтобы над векторами в фазовых пространствах можно было корректно выполнять стандартные операции сложения, вычитания, скалярного и векторного умножения, выполнять преобразования системы координат, переход от одной системы координат к другой, и вообще применять аппарат линейной алгебры и аналитической геометрии, что представляет большой научный и практический интерес и является очень актуальным, необходимо корректно ввести в этих пространствах системы координат т.е. системы отсчета, удовлетворяющие определенным требованиям.

Требования к системам координат, свойства векторов классов и атрибутов, решение проблемы снижения размерности описания и ортонормирования

В качестве осей координат пространства атрибутов целесообразно выбрать вектора атрибутов, обладающие следующими свойствами:

1. Их должно быть минимальное количество, достаточное для полного описания предметной области.

2. Эти вектора должны пересекаться в одной точке.

3. Значения координат вектора должны измеряться в одной единице измерения, т.е. должны быть сопоставимы.

Для выполнения первого требования необходимо, чтобы математическая форма и смысл весовых коэффициентов были выбраны таким образом, чтобы модули векторов атрибутов в пространстве классов были пропорциональны их значимости для решения задач идентификации, прогнозирования и управления. Причем наиболее значимые вектора атрибутов не должны коррелировать друг с другом, т.е. должны быть ортонормированны. В этом случае при удалении векторов с минимальными модулями автоматически останутся наиболее значимые практически ортонормированные вектора, которые можно принять за базисные, т.е. в качестве осей системы координат.

Второе требование означает, что минимальное расстояние между этими векторами в пространстве классов должно быть равно нулю.

Третье требование предполагает соответствующий выбор математической формы для значений координат.

Эти идеальные требования практически никогда не будут соблюдаться на практике с абсолютной точностью. Однако этого и не требуется. Достаточно, чтобы реально выбранные в качестве базисных атрибуты отображались в пространстве классов векторами, для которых эти требования выполняются с точностью, достаточной для применения соответствующих математических моделей и математического аппарата на практике.

Аналогично обстоит дело и с минимизацией размерности пространства классов. В качестве базисных могут выбраны вектора классов, имеющие максимальную длину и взаимно (попарно) ортонормированные.

Очевидно, задача выбора базисных векторов имеет не единственное решение, т.е. может существовать несколько систем таких векторов, которые можно рассматривать как результат действия преобразований системы координат, состоящих из смещений и поворотов.

3.2.2. Конструирование максимального конфигуратора предметной области (когнитивная структуризация, формализация предметной области, шкалы и градации)

Полное описание типов измерительных шкал дается в [4]

В данной работе предлагается следующие определения.

Шкала – это способ классификации объектов по наименованиям или степени выраженности некоторого свойства.

Градация – это положение на шкале (или интервал, диапазон), соответствующее наименованию или определенной степени выраженности свойства.

Формализация предметной области это процесс состоящий из двух основных этапов:

1. Конструирование шкал и градаций для описания и кодирования состояний объекта управления и факторов, влияющих на его поведение.

2. Отнесение состояний объекта управления и факторов к определенным градациям соответствующих шкал.

Понятие шкалы тесно связано с ключевым понятием когнитивной психологии: понятием конструкта, более того, практически является синонимом или формальным аналогом этого понятия. Конструктом называется понятие, имеющее полюса, противоположные по смыслу, и ряд промежуточных градаций. Познание состоит в создании (генерировании) новых конструировании конструктов и их использовании для ориентации в предметной области. Таким образом формализация предметной области по сути дела представляет собой ее познание, т.е. когнитивную структуризацию. В приведенной таблице 3.10 дана характеристика измерительных шкал согласно [4].

Таблица 3. 10 – ХАРАКТЕРИСТИКА И ПРИМЕРЫ ИЗМЕРИТЕЛЬНЫХ ШКАЛ

Конечно, наименования могут быть присвоены градациям всех видов измерительных шкал.

Шкалы классов

Очень плодотворным является представление классов распознавания, как некоторых областей в фазовом пространстве, в котором в качестве осей координат выступают некоторые шкалы. Классы распознавания могут рассматриваться, также, как градации (конкретные значения, заданные с некоторой точностью, или диапазоны - зоны), заданные на этих шкалах. Количество шкал, тип шкал и количество градаций на них в предлагаемой модели задает сам пользователь.

Если представить эти шкалы как оси координат, то, очевидно, наиболее обобщенным классам распознавания соответствуют зоны на самих осях. Кроме того возможны варианты сочетаний по 2 оси, соответствующие областям на координатных плоскостях. Существуют также области в фазовом пространстве, образованные сочетаниями градаций сразу n-го количества шкал, где n <= N, где N - размерность фазового пространства. Естественно, пользователь может исследовать только те классы, которые его интересуют, сознательно принимая решение не рассматривать остальных. Но он должен знать, что и остальные классы также могут быть сформированы и исследованы, а для этого нужно иметь их классификацию, принцип разработки которой мы только что рассмотрели.

Конкретными реализациями обобщенных категорий могут быть объекты, их состояния или ситуации (но применять мы, как правило, будем термин "объекты", всегда имея в виду и остальные возможные варианты). Синонимами понятия "класс распознавания" являются применяющиеся в специальной литературе термины "объекты", "категории", "образы", "эталоны", "типы", "профили".

Когда классы распознавания сформированы с ними могут осуществляться три основные операции:

– сравнение конкретных объектов, их состояний или ситуаций с классами;

– сравнение классов друг с другом;

– вывод информации о содержании обобщенного образа класса в форме таблиц или графических диаграмм.

Шкалы атрибутов

Конкретные объекты, предъявляемые Системе в качестве примеров или реализаций некоторых обобщенных классов (прецедентов), описываются на языке атрибутов, т.е. признаков.

Признаки могут иметь любую природу, в частности:

– объективную - физическую, химическую и др. (вес, температура, рост);

– социально-экономическую (меновую и потребительную стоимость, степень амортизации, процент дивидендов);

– эмоционально-психологическую (привлекательный, предупредительный, исполнительный, конфликтный и т.п.).

Система признаков двухуровневая, что позволяет формализовать (шкалировать) не только качественные (да/нет), но и количественные (числовые) признаки, а также позволяет обрабатывать вопросы со многими, в том числе и неальтернативными вариантами ответов. Вопрос с вариантами ответов можно рассматривать как шкалу с градациями. Такое понимание позволяет "ввести в оборот" хорошо разработанную теорию шкалирования, что является весьма ценным. В предлагаемой модели нет ограничений на тип и количество шкал, а также на количество градаций в них (за исключением суммарного общего количества градаций. Нет в предлагаемой модели и таких искусственных ограничений, как, например, необходимость одинакового количества градаций во всех шкалах, или необходимость использовать только шкалы только одного какого-либо типа, и т.п., которые, как правило, встречаются в других системах.

В принципе могут быть сконструированы системы признаков, представляемые деревьями трех и более уровней, однако программно реализовывать их нецелесообразно, т.к. они все сводятся к двухуровневым деревьям (вопросы с вариантами ответов).

Данная структура системы признаков относится к закрытому типу с множественным выбором. Это также не является ограничением, т.к. к данной системе могут быть сведены результаты тестирования с помощью тестов других видов: как открытых, так и закрытых, как с вербальным стимульным материалом, так и с невербальным (рисуночные тесты, тесты на конструирование, на ассоциации и т.п.).

Кинематическая и динамическая интерпретация модели

Шкалы классов (атрибутов) можно представить себе в качестве осей координат в некотором абстрактном семантическом пространстве. Тогда каждый атрибут (класс) в этом пространстве будет отображаться вектором, координатами которого являются значения информативностей. Динамика атрибута (класса) будут отображаться в этом пространстве в виде траектории. Для анализа кинематики и динамики факторов, объектов и классов могут быть адаптированы и применены понятия и законы теоретической механики, а также математический аппарат линейной алгебры и аналитической геометрии, обобщенные для неортонормированных пространств.

Например, в качестве системы отсчета в пространстве атрибутов могут быть выбраны вектора нескольких классов, наиболее сильно отличающихся друг от друга (наиболее близкие к ортонормированным).

Уровни системной организации классов

Классы распознавания могут относится к различным уровням иерархии какой-либо системы. Например, это могут быть конкретные студенты, группы, курсы, факультеты, учебные заведения, районы, регионы и т.д. В предлагаемой модели предусмотрена возможность работы с классами распознавания, относящимися не только к некоторому диапазону градаций шкал (кодов), но и к заданному диапазону уровней организации. Сами эти уровни могут иметь любой смысл, какой именно - определяет сам пользователь. Классификатор уровней классов входит в состав нормативно-справочной информации. Работа с уровнями предоставляет ряд преимуществ, по сравнению с использованием диапазонов кодов:

– классы распознавания, относящиеся к одному уровню, могут идти в справочнике в любом порядке;

– изменять коды уровней значительно легче, чем переделывать справочники, к тому же это не требует перекодирования обучающей выборки;

– уровни классов имеют самостоятельный смысл, тогда как выделение диапазонов кодов выглядит более искусственным приемом.

Уровни системной организации атрибутов

В предлагаемой модели предусмотрена возможность работы с уровнями признаков, относящимися не только к некоторому диапазону градаций (кодов), но и к заданному диапазону уровней организации. Сами эти уровни могут иметь любой смысл, какой именно – определяет сам пользователь. Например, для интегрального описания индивидуальности могут быть введены уровни качеств личности: генетически обусловленные (конституционные), социально-обусловленные (связанные с воспитанием, образованием, влиянием среды), отражающие текущее состояние. При этом в последующем анализе могут быть выявлены взаимосвязи между признаками различных уровней, т.е. может быть определено, какие конституционные качества необходимы для того, чтобы возникли определенные социально-обусловленные качества, и какие какими не должны быть первые и вторые, чтобы человек не мог оказаться в определенных нежелательных текущих состояниях. Классификатор уровней классов входит в состав нормативно-справочной информации. Работа с уровнями предоставляет ряд преимуществ, по сравнению с использованием диапазонов кодов:

– признаки, относящиеся к одному уровню, могут идти в справочнике в любом порядке;

– изменять коды уровней значительно легче, чем переделывать справочники, к тому же это не требует перекодирования обучающей выборки;

– уровни признаков имеют самостоятельный смысл, тогда как выделение диапазонов кодов выглядит более искусственным приемом.

3.2.3. Применение классической теории информации К.Шеннона для расчета весовых коэффициентов и мер сходства

Формально, распознавание есть не что иное, как принятие решения о принадлежности распознаваемого объекта или его состояния к определенному классу (классам) [251, 277]. Из этого следует внутренняя и органичная связь методов распознавания образов и принятия решений. Аналитический обзор позволяет сделать вывод, что наиболее глубокая основа этой связи состоит в том, что и распознавание образов, и принятие решений есть прежде всего снятие неопределенности. Распознавание снимает неопределенность в вопросе о том, к какому классу относится распознаваемый объект. Если до распознавания существовала неопределенность в вопросе о том, к какому классу относится распознаваемый объект или его состояние, то в результате распознавания эта неопределенность уменьшается, причем возможно и до нуля (когда объект идентифицируется однозначно). Принятие решения (выбор) также снимает неопределенность в вопросе о том, какое из возможных решений будет принято, если существовало несколько альтернативных вариантов решений и принимается одно из них.

Для строгого исследования процессов снятия неопределенности оптимальным является применение аппарата теории информации, которая как бы специально создана для этой цели. Из этого непосредственно следует возможность применения методов теории информации для решения задач распознавания и принятия решений в АСУ. Таким образом, теория информации может рассматриваться как единая основа методов распознавания образов и принятия решений.

Формальная постановка задачи

В рефлексивных АСУ активными объектами модели распознавания образов и принятия решений применимы в подсистемах идентификации состояния АОУ и выработки управляющего воздействия: идентификация состояния АОУ представляет собой принятие решения о принадлежности этого состояния к определенной классификационной категории (задача распознавания); выбор многофакторного управляющего воздействия из множества возможных вариантов представляет собой принятие решения (обратная задача распознавания).

Распознавание образов есть принятие решения о принадлежности объекта или его состояния к определенному классу. Если до распознавания существовала неопределенность в вопросе о том, к какому классу относится распознаваемый объект или его состояние, то в результате распознавания эта неопределенность уменьшается, в том числе может быть и до нуля (когда объект идентифицируется однозначно). Из данной постановки непосредственно следует возможность применения методов теории информации для решения задач распознавания образов и принятия решений в АСУ.

Информация как мера снятия неопределенности

Как было показано выше, теория информация применима в АСУ для решения задач идентификации состояния сложного объекта управления (задача распознавания) и принятия решения о выборе многофакторного управляющего воздействия (обратная задача распознавания).

Так в результате процесса познания уменьшается неопределенность в наших знаниях о состоянии объекта познания, а в результате процесса труда (по сути управления) – уменьшается неопределенность поведения продукта труда (или объекта управления). В любом случае количество переданной информации представляет собой количественную меру степени снятия неопределенности.

В данном разделе, основываясь на работе [347], приведем математический аппарат из теории информации К.Шеннона, позволяющий решить эти задачи на основе построения и применения информационной модели АОУ.

Процесс получения информации можно интерпретировать как изменение неопределенности в вопросе о том, от какого источника отправлено сообщение в результате приема сигнала по каналу связи.

Формально эту модель можно представить следующим образом. Пусть есть два взаимосвязанных множества:

1. Множество из N информационных источников {x_i}, априорные вероятности предъявления которых равны p(x_i).

2. Множество из M признаков {y_j}, которые встречаются с априорными вероятностями p(y_j) и условными вероятностями: p(x_i|y_j).

Априорная вероятность наблюдения признака – это средняя вероятность его наблюдения при предъявлении информационных источников (объектов) из исходного множества, а условная вероятность – вероятность его наблюдения при предъявлении определенного из них.

До получения информации ситуация характеризуется неопределенностью того, от какого источника она будет направлена, т.е. априорной энтропией:

(3. 30)

Допустим, что множества информационных источников и сообщений о них никак не связаны (представляют собой независимые события), т.е. связаны совершенно случайным образом. Это означает, что события из этих двух множеств независимы друг от друга.

Пусть, например, p_ij – есть вероятность наступления события (x_i,y_j), т.е. вероятность того, что если в сообщении был признак y_j, то это сообщение от источника x_i:

pij=pipj.

(3. 31)

Тогда в соответствии с фундаментальным определением Шеннона, энтропия множества XY, являющегося объединением множеств источников и сообщений, будет иметь вид:

(3. 32)

Подставив в эту формулу выражение для вероятности (3.31), получим:

Здесь использовано классическое определение энтропии (3.30):

(3.30)

и учтено условие нормировки вероятностей: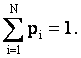

Таким образом, для независимых источников и сообщений получаем:

H(XY)=H(X)+H(Y).

(3. 33)

Обобщим это выражение на тот случай , когда содержание сообщений связано с тем, от какого они информационного источника. Этот случай представляет для нас особый интерес, т.к. именно в этом случае по сообщению можно определить источник.

Будем считать, что энтропия объединения множеств информационных источников и сообщений XY по прежнему определяется выражением Шеннона:

(3. 34)

Однако вероятность совместного наступления зависимых событий:

– "активен i–й информационный источник";

– "в сообщении наблюдается j–й признак"

будет равна

(3. 35)

где: – условная вероятность наблюдения признака y_j в информационном сообщении от источника x_i. Тогда, аналогично для энтропии объединенного множества получим выражение:

(3. 36)

H(XY)=H(X)+H(Y|X).

(3. 37)

В этом выражении учтено условие нормировки: 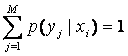, а также приведенное выше выражение для энтропии H(X). Второе слагаемое обозначим: H(Y|X) и назовем условной энтропией множества признаков из сообщений от информационных источников:

(3. 38)

Учитывая (3.35), окончательно получаем:

(3. 39)

Условной энтропией H(Y|X) измеряется степень неопределенности множества Y после снятия неопределенности множества X. Так как, очевидно, (x_i,y_j)=(y_j,x_i), то аналогично, условной энтропией H(X/Y) измеряется степень неопределенности множества X после снятия неопределенности множества Y:

H(XY)=H(X)+H(Y|X)=H(Y)+H(X|Y)=H(YX).

(3. 40)

Фактически, условная энтропия H(X/Y) показывает нам, насколько много информации для идентификации информационных источников мы в среднем получаем из сообщений от них.

Информация, как мера соответствия объектов обобщенным образам классов

Количество информации является мерой соответствия распознаваемого объекта (его состояния) обобщенному образу класса, определенное на основе информации о признаках этого объекта.

Количество информации есть количественная мера степени снятия неопределенности: информация, содержащаяся в множестве Y относительно множества X есть уменьшение степени неопределенности множества X, возникающее в результате снятия неопределенности множества Y.

В нашем случае первое множество – это множество признаков наблюдаемого объекта, а второе – множество классов. До наблюдения объекта с системой признаков Y неопределенность наших знаний о принадлежности этого объекта к классу была H(X) (априорная энтропия), после наблюдения системы признаков Y эта неопределенность уменьшилась и стала равна H(X|Y) (апостериорная энтропия). Количество информации о том, что наблюдаемый объект с системой признаков Y относится к классу X, равно уменьшению неопределенности наших знаний об этом, которое произошло в результате обнаружения у объекта признаков, т.е. равно разности априорной и апостериорной энтропии этого класса:

(3. 41)

Если после обнаружения системы признаков неопределенность знаний о принадлежности объекта к классу стала равна нулю H(X|Y)=0, т.е. это стало известно точно, то количество информации просто равно априорной энтропии. Если же это стало известно лучше, но еще не до конца, то количество информации будет меньше, чем априорная энтропия как раз на величину оставшейся, т.е. еще не снятой неопределенности. Поэтому энтропия – это недостающая информация.

Перепишем выражение (3.41) в явной форме, подставив в него выражения для априорной и апостериорной энтропии из (3.30) и (3.39):

(3. 42)

Учитывая, что

(3. 43)

получаем выражение для среднего количества информации, которое содержится в сообщениях об источниках информации

или окончательно:

(3. 44)

Находим выражение, связывающее информацию и взаимную энтропию, основываясь на (3.44):

(3. 45)

Учитывая в выражении (3.44), что p_ij=p_ji (условие симметричности) получаем:

I(X,Y)=I(Y,X),

(3. 46)

т.е. количество информации в признаках об объектах (сообщениях об источниках информации) то же самое, что и в объектах о признаках или в источниках информации о сообщениях, так как это одна и та же информация. По этой причине эту информацию иногда называют взаимной, так как она отражает определенное отношение двух множеств и не существует сама по себе независимо от них или только когда есть лишь одно из них.

Подставляя H(X|Y) из (3.40) в выражение (3.45) получаем:

(3. 47)

Таким образом, энтропия системы, состоящей из объединения двух подсистем, меньше суммы индивидуальных энтропий этих подсистем на величину взаимной информации, содержащейся в каждой из подсистем относительно другой подсистемы.

АСУ как раз и выступает информационным системообразующим фактором, объединяющим подсистемы в единую систему, имеющую меньшую суммарную энтропию, чем ее части.

Это очень похоже на своеобразный информационный аналог известного в физике "дефекта масс". Так называется физический эффект, состоящий в том, что масса системы меньше сумм масс ее частей на величину массы, соответствующей энергии их взаимодействия [25, 30]. Подобные аналогии могут быть продолжены значительно дальше [152]. Из этого следует, что по крайней мере для информационных систем информация это и есть то интегрирующее начало, которое делает систему системой, объединяя ее части в целое, т.е. по сути дела информация есть то, без чего система разрушается на части.

Количество информации в индивидуальных событиях и лемма Неймана–Пирсона

Следуя традиции, заложенной Шенноном, до сих пор анализировалось среднее количество информации, приходящееся на любую пару состояний (x_i,y_j) объекта X и сообщения Y. Эта характеристика естественна при рассмотрении особенностей стационарно функционирующих информационных систем, когда играют роль лишь их среднестатистические характеристики.

В классическом анализе Шеннона идет речь лишь о передаче символов по одному информационному каналу от одного источника к одному приемнику. Его интересует прежде всего передача самого сообщения.

В данном исследовании ставится другая задача: идентифицировать информационный источник по сообщению от него. Поэтому метод Шеннона был обобщен путем учета в математической модели возможности существования многих источников информации, о которых к приемнику по зашумленному каналу связи приходят не отдельные символы–признаки, а сообщения, состоящие из последовательностей символов (признаков) любой длины.

Следовательно, ставится задача идентификации информационного источника по сообщению от него, полученному приемником по зашумленному каналу. Метод, являющийся обобщением метода К.Шеннона, позволяет применить классическую теорию информации для построения моделей систем распознавания образов и принятия решений, ориентированных на применение для синтеза адаптивных АСУ сложными объектами.

Для решения поставленной задачи необходимо вычислять не средние информационные характеристики, а количество информации, содержащееся в конкретном j–м признаке (символе) о том, что он пришел от данного i–го источника информации. Это позволит определить и суммарное количество информации в сообщении о каждом информационном источнике, что дает интегральный критерий для идентификации или прогнозирования состояния АОУ.

Логично предположить, что среднее количество информации, содержащейся в системе признаков о системе классов

(3. 48)

является ничем иным, как усреднением (с учетом условной вероятности наблюдения) "индивидуальных количеств информации", которые содержатся в конкретных признаках о конкретных классах (источниках), т.е.:

(3. 49)

Это выражение определяет так называемую "плотность информации", т.е. количество информации, которое содержится в одном отдельно взятом факте наблюдения j–го символа (признака) на приемнике о том, что этот символ (признак) послан i–м источником.

Если в сообщении содержится M символов, то суммарное количество информации о принадлежности данного сообщения i–му информационному источнику (классу) составляет:

(3. 50)

Необходимо отметить, что применение сложения в выражении (3.43) является вполне корректным и оправданным, так как информация с самого начала вводилась как аддитивная величина, для которой операция сложения является корректной.

Преобразуем выражение (3.50) к виду, более удобному для практического применения (численных расчетов). Для этого, следуя [347], выразим вероятности встреч признаков через частоты их наблюдения:

(3. 51)

Подставив (3.44) в (3.25), получим:

(3. 52)

Если ранжировать классы в порядке убывания суммарного количества информации о принадлежности к ним, содержащейся в данном сообщении (т.е. описании объекта), и выбирать первый из них, т.е. тот, о котором в сообщении содержится наибольшее количество информации, то мы получим обоснованную статистическую процедуру, основанную на классической теории информации, оптимальность которой доказывается в фундаментальной лемме Неймана–Пирсона [234].

Сравнивая выражения (3.52) и (3.28) видим, что в системное обобщенное формулы Харкевича входит слагаемое, сходное с выражением Шеннона для плотности информации. Различия состоят в том, что в выражении (3.28) это слагаемое возведено в степень, имеющую смысл коэффициента эмерджентности Харкевича. Необходимо отметить, что значения частот в этих формулах связаны с вероятностями несколько различным образом (выражения 3.20 и 3.51).

Если ранжировать классы в порядке убывания суммарного количества информации о принадлежности к ним, содержащейся в данном сообщении (т.е. описании объекта), и выбирать первый из них, т.е. тот, о котором в сообщении содержится наибольшее количество информации, то мы получим обоснованную статистическую процедуру, основанную на классической теории информации, оптимальность которой доказывается в фундаментальной лемме Неймана–Пирсона [234].

Таким образом, распознавание образов есть принятие решения о принадлежности объекта или его состояния к определенному классу. Если до распознавания существовала неопределенность в вопросе о том, к какому классу относится распознаваемый объект или его состояние, то в результате распознавания эта неопределенность уменьшается, в том числе может быть и до нуля. Понятие информации может быть определено следующим образом: "Информация есть количественная мера степени снятия неопределенности". Количество информации является мерой соответствия распознаваемого объекта (его состояния) обобщенному образу класса.

Количество информации имеет ряд вполне определенных свойств. Эти свойства позволяют ввести понятие "количество информации в индивидуальных событиях", которое является весьма перспективным для применения в системах распознавания образов и поддержки принятия решений.

3.2.4. Математическая модель метода распознавания образов и принятия решений, основанного на системной теории информации

Формальная постановка основной задачи рефлексивной АСУ активными объектами и ее декомпозиция

Рассмотрим некоторые основные понятия, необходимые для дальнейшего изложения. При этом будут использованы как литературные данные, так и результаты, полученные в предыдущих главах данной работы.

Принятие решения в АСУ – это выбор некоторого наиболее предпочтительного управляющего воздействия из исходного множества всех возможных управляющих воздействий, обеспечивающего наиболее эффективное достижение целей управления. В результате выбора неопределенность исходного множества уменьшается на величину информации, которая порождается самим актом выбора [277]. Следовательно, теория информации может быть применена как для идентификации состояний объекта управления, так и для принятия решений об управляющих воздействиях в АСУ.

Модель АСУ включает в себя: модель объекта управления, модель управляющей подсистемы, а также модель внешней среды. Управляющая подсистема реализует следующие функции: идентификация состояния объекта управления, выработка управляющего воздействия, реализация управляющего воздействия.

С позиций теории информации сложный объект управления (АОУ) может рассматриваться как шумящий (определенным образом) информационный канал, на вход которого подаются входные параметры , представляющие собой управляющие воздействия, а также факторы предыстории и среды, а на выходе фиксируются выходные параметры , связанные как с входными параметрами, так и с целевыми и иными состояниями объекта управления.

Одной из основных задач АСУ является задача принятия решения о наиболее эффективном управляющем воздействии. В терминах теории информации эта задача формулируется следующим образом: зная целевое состояние объекта управления, на основе его информационной модели определить такие входные параметры , которые с учетом предыстории и актуального состояния объекта управления, а также влияния среды с наибольшей эффективностью переведут его в целевое состояние, характеризующееся выходными параметрами .

С решением этой задачи тесно связана задача декодирования теории информации: "По полученному в условиях помех сообщению определить, какое сообщение было передано" [309]. Для решения данной задачи используются коды, корректирующие ошибки, а в более общем случае, - различные методы распознавания образов.

Учитывая вышесказанное, предлагается рассматривать принятие решения об управляющем воздействии в АСУ как решение обратной задачи декодирования, которая формулируется следующим образом: "Какое сообщение необходимо подать на вход зашумленного канала связи, чтобы на его выходе получить заранее заданное сообщение". Данная задача решается на основе математической модели канала связи.

Декомпозиция основной задачи в ряд частных подзадач

Построение аналитической модели АОУ затруднено из-за отсутствия или недостатка априорной информации об объекте управления, а также из-за ограниченности и сложности используемого математического аппарата. В связи с этим предлагается путь решения данной проблемы, состоящий в поэтапном решении следующих задач:

1–я задача: разработать абстрактную модель более общего класса (содержательную информационную);

2–я задача: обучить абстрактную информационную модель путем учета информации о реальном поведении АОУ, поступающей в процессе экспериментальной эксплуатации АСУ; на этом этапе адаптируется и конкретизируется абстрактная модель АОУ, т.е. в ней все более точно отражаются взаимосвязи между входными параметрами и состояниями АОУ;

3–я задача: на основе конкретной содержательной информационной модели разработать алгоритмы решения следующих задач АСУ:

3.1. Расчет влияния факторов на переход АОУ в различные возможные состояния (обучение, адаптация).

3.2. Прогнозирование поведения АОУ при конкретном управляющем воздействии и выработка многофакторного управляющего воздействия (основная задача АСУ).

3.3. Выявление факторов, вносящих основной вклад в детерминацию состояния АОУ; контролируемое удаление второстепенных факторов с низкой дифференцирующей способностью, т.е. снижение размерности модели при заданных ограничениях.

3.4. Сравнение влияния факторов. Сравнение состояний АОУ.

Сформулируем предлагаемую абстрактную модель АОУ, опишем способ ее конкретизации и приведем алгоритмы решения задач адаптивных АСУ АОУ на основе данной модели.

Решение задачи 1: "Синтез семантической информационной модели активного объекта управления"

Исходные данные для выявления взаимосвязей между факторами и состояниями объекта управления предлагается представить в виде корреляционной матрицы – матрицы абсолютных частот (таблица 3.11):

Таблица 3. 11 – МАТРИЦА АБСОЛЮТНЫХ ЧАСТОТ

В этой матрице в качестве классов (столбцов) приняты будущие состояния объекта управления, как целевые, так и нежелательные, а в качестве атрибутов (строк) – факторы, которые разделены на три основных группы, математически обрабатываемые единообразно: факторы, характеризующие текущее и прошлые состояния объекта управления; управляющие факторы системы управления; факторы, характеризующие прошлые, текущее и прогнозируемые состояния окружающей среды. Отметим, что форма таблицы 3.11 является универсальной формой представления непосредственно эмпирических данных в единстве их дискретного и интегрального представления (причины – следствия, факторы – результирующие состояния, признаки – обобщенные образы классов, образное – логическое и т.п.).

Управляющие факторы объединяются в группы, внутри каждой из которых они альтернативны (несовместны), а между которыми - нет (совместны). В этом случае внутри каждой группы выбирают одно из доступных управляющих воздействий с максимальным влиянием. Варианты содержательной информационной модели без учета прошлых состояний объекта управления и с их учетом, аналогичны, соответственно, простым и составным цепям Маркова, автоматам без памяти и с памятью.

В качестве количественной меры влияния факторов, предложено использовать обобщенную формулу А.Харкевича (3.28), полученную на основе предложенной эмерджентной теории информации. При этом по формуле (3.28) непосредственно из матрицы абсолютных частот (таблица 3.11) рассчитывается матрица информативностей (таблица 3.12), которая и представляет собой основу содержательной информационной модели предметной области:

Таблица 3. 12 – МАТРИЦА ИНФОРМАТИВНОСТЕЙ

Весовые коэффициенты таблицы 3.12 непосредственно определяют, какое количество информации I_ij система управления получает о наступлении события: "активный объект управления перейдет в j–е состояние", из сообщения: "на активный объект управления действует i–й фактор".

Принципиально важно, что эти весовые коэффициенты не определяются экспертами неформализуемым способом, а рассчитываются непосредственно на основе эмпирических данных и удовлетворяют всем ранее сформулированным требованиям, т.е. являются сопоставимыми, содержательно интерпретируемыми, отражают понятия "достижение цели управления" и "мощность множества будущих состояний объекта управления" и т.д.

В данном исследовании обосновано, что предложенная информационная мера обеспечивает сопоставимость индивидуальных количеств информации, содержащейся в факторах о классах, а также сопоставимость интегральных критериев, рассчитанных для одного объекта и разных классов, для разных объектов и разных классов.

Когда количество информации I_ij>0 – i–й фактор способствует переходу объекта управления в j–е состояние, когда I_ij<0 – препятствует этому переходу, когда же I_ij=0 – никак не влияет на это. В векторе i–го фактора (строка матрицы информативностей) отображается, какое количество информации о переходе объекта управления в каждое из будущих состояний содержится в том факте, что данный фактор действует. В векторе j–го состояния класса (столбец матрицы информативностей) отображается, какое количество информации о переходе объекта управления в соответствующее состояние содержится в каждом из факторов.

Таким образом, матрица информативностей (таблица 3.12) является обобщенной таблицей решений, в которой входы (факторы) и выходы (будущие состояния АОУ) связаны друг с другом не с помощью классических (Аристотелевских) импликаций, принимающих только значения: "Итина" и "Ложь", а различными значениями истинности, выраженными в битах и принимающими значения от положительного теоретически-максимально-возможного ("Максимальная степень истинности"), до теоретически неограниченного отрицательного ("Степень ложности").

Фактически предложенная модель позволяет осуществить синтез обобщенных таблиц решений для различных предметных областей непосредственно на основе эмпирических исходных данных и продуцировать на их основе прямые и обратные правдоподобные (нечеткие) логические рассуждения по неклассическим схемам с различными расчетными значениями истинности, являющимся обобщением классических импликаций (таблица 3.13):

Таблица 3. 13 – ПРЯМЫЕ И ОБРАТНЫЕ ПРАВДОПОДОБНЫЕ ЛОГИЧЕСКИЕ
ВЫСКАЗЫВАНИЯ С РАСЧЕТНОЙ (В СООТВЕТСТВИИ С СТИ)
СТЕПЕНЬЮ ИСТИННОСТИ ИМПЛИКАЦИЙ

Приведем пример более сложного высказывания, которое может быть рассчитано непосредственно на основе матрицы информативностей – обобщенной таблицы решений (таблица 3.13):

Если A, со степенью истинности a(A,B) детерминирует B, и если С, со степенью истинности a(C,D) детерминирует D, и A совпадает по смыслу с C со степенью истинности a(A,C), то это вносит вклад в совпадение B с D, равный степени истинности a(B,D).

При этом в прямых рассуждениях как предпосылки рассматриваются факторы, а как заключение – будущие состояния АОУ, а в обратных – наоборот: как предпосылки – будущие состояния АОУ, а как заключение – факторы. Степень истинности i-й предпосылки – это просто количество информации I_ij, содержащейся в ней о наступлении j-го будущего состояния АОУ. Если предпосылок несколько, то степень истинности наступления j-го состояния АОУ равна суммарному количеству информации, содержащемуся в них об этом. Количество информации в i-м факторе о наступлении j-го состояния АОУ, рассчитывается в соответствии с выражением (3.28) СТИ.

Прямые правдоподобные логические рассуждения позволяют прогнозировать степень достоверности наступления события по действующим факторам, а обратные – по заданному состоянию восстановить степень необходимости и степень нежелательности каждого фактора для наступления этого состояния, т.е. принимать решение по выбору управляющих воздействий на АОУ, оптимальных для перевода его в заданное целевое состояние.

Необходимо отметить, что предложенная модель, основывающаяся на теории информации, обеспечивает автоматизированное формирования системы нечетких правил по содержимому входных данных, как и комбинация нечеткой логики Заде-Коско с нейронными сетями Кохонена [184]. Принципиально важно, что качественное изменение модели путем добавления в нее новых классов не уменьшает достоверности распознавания уже сформированных классов. Кроме того, при сравнении распознаваемого объекта с каждым классом учитываются не только признаки, имеющиеся у объекта, но и отсутствующие у него, поэтому предложенной моделью правильно идентифицируются объекты, признаки которых образуют множества, одно из которых является подмножеством другого (как и в Неокогнитроне К.Фукушимы) [184].

Данная модель позволяет прогнозировать поведение АОУ при воздействии на него не только одного, но и целой системы факторов:

(3. 53)

В теории принятия решений скалярная функция I_j векторного аргумента называется интегральным критерием. Основная проблема состоит в выборе такого аналитического вида функции интегрального критерия, который обеспечил бы эффективное решение сформулированной выше задачи АСУ.

Учитывая, что частные критерии (3.28) имеют смысл количества информации, а информация по определению является аддитивной функцией, предлагается ввести интегральный критерий, как аддитивную функцию от частных критериев в виде:

(3. 54)

В выражении (3.54) круглыми скобками обозначено скалярное произведение. В координатной форме это выражение имеет вид:

,

(3. 55)

где:

– вектор j–го состояния объекта управления;

– вектор состояния предметной области, включающий все виды факторов, характеризующих объект управления, возможные управляющие воздействия и окружающую среду (массив–локатор), т.е.:

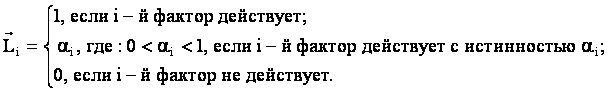В реализованной модели значения координат вектора состояния ПО принимались равными либо 1 (фактор действует), либо 0 (фактор не действует).

Таким образом, интегральный критерий представляет собой суммарное количество информации, содержащееся в факторах различной природы (т.е. факторах, характеризующих объект управления, управляющее воздействие и окружающую среду) о переходе активного объекта управления в целевое состояние.

В многокритериальной постановке задача прогнозирования состояния объекта управления, при оказании на него заданного многофакторного управляющего воздействия I_j, сводится к максимизации интегрального критерия:

(3. 56)

т.е. к выбору такого состояния объекта управления, для которого интегральный критерий максимален.

Задача принятия решения о выборе наиболее эффективного управляющего воздействия является обратной задачей по отношению к задаче максимизации интегрального критерия (идентификации и прогнозирования), т.е. вместо того, чтобы по набору факторов прогнозировать будущее состояние АОУ, наоборот, по заданному (целевому) состоянию АОУ определяется такой набор факторов, который с наибольшей эффективностью перевел бы объект управления в это состояние.

Предлагается еще одно обобщение этой фундаментальной леммы, основанное на косвенном учете корреляций между информативностями в векторе состояний при использовании средних по векторам. Соответственно, вместо простой суммы количеств информации предлагается использовать корреляцию между векторами состояния и объекта управления, которая количественно измеряет степень сходства этих векторов:

(3. 57)

где:

– средняя информативность по вектору класса;

– среднее по вектору идентифицируемой ситуации (объекта).

– среднеквадратичное отклонение информативностей вектора класса;

– среднеквадратичное отклонение по вектору распознаваемого объекта.

Выражение (3.57) получается непосредственно из (3.55) после замены координат перемножаемых векторов их стандартизированными значениями:

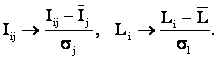
Результат прогнозирования поведения объекта управления, описанного данной системой факторов, представляет собой список его возможных будущих состояний, в котором они расположены в порядке убывания суммарного количества информации о переходе объекта управления в каждое из них.

Сравнения результатов идентификации и прогнозирования с опытными данными, с использованием выражений (3.57) и (3.55), показали, что при малых выборках они практически не отличаются, но при увеличении объема выборки до 400 и более (независимо от предметной области) выражение (3.57) дает погрешность идентификации (прогнозирования) на 5% – 7% меньше, чем (3.55). Поэтому в предлагаемой модели используется мера сходства (3.58).

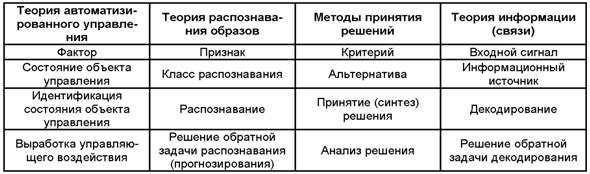
В связи с тем, что в дальнейшем изложении широко применяются понятия теории АСУ, теории информации (связи), теории распознавания образов и методов принятия решений, приведем таблицу соответствия наиболее часто используемых нами терминов из этих научных направлений, имеющих сходный смысл (таблица 3.14):

Таблица 3. 14 – СООТВЕТСТВИЕ ТЕРМИНОВ
РАЗЛИЧНЫХ НАУЧНЫХ НАПРАВЛЕНИЙ

Вывод системного обобщения формулы Харкевича (3.28) приведен в разделе 3.1 данной работы. Чрезвычайно важное для данного исследования выражение (3.28) заслуживает специального комментария. Прежде всего нельзя не обратить внимания на то, что оно по своей математической форме, т.е. формально, ничем не отличается от выражения для превышения сигнала над помехой для информационного канала [309]. Из этого, на первый взгляд, внешнего совпадения следует интересная интерпретация выражения (3.28). А именно: можно считать, что обнаружив некоторый i–й признак у объекта, предъявленного на распознавание, мы тем самым получаем сигнал, содержащий некоторое количество информации

о том, что этот объект принадлежит к j–му классу. По–видимому, это так и есть, однако чтобы оценить насколько много или мало этой информации нами получено, ее необходимо с чем–то сравнить, т.е. необходимо иметь точку отсчета или базу для сравнения. В качестве такой базы естественно принять среднее по всем признакам количество информации, которое мы получаем, обнаружив этот j–й класс:

Иначе говоря, если при предъявлении какого–либо объекта на распознавание у него обнаружен i–й признак, то для того, чтобы сделать из этого факта обоснованный вывод о принадлежности этого объекта к тому или иному классу, необходимо знать и учесть, насколько часто вообще (т.е. в среднем) обнаруживается этот признак при предъявлении объектов данного класса.

Фактически это среднее количество информации можно рассматривать как некоторый "информационный шум", который имеется в данном признаке и не несет никакой полезной информации о принадлежности объектов к тем или иным классам. Полезной же информацией является степень отличия от этого шума. Таким образом классическому выражению Харкевича (3.12) для семантической целесообразности информации может быть придан более привычный для теории связи вид:

который интерпретируется как вычитание шума из полезного сигнала. Эта операция является совершенно стандартной в системах шумоподавления.

Если полезный сигнал выше уровня шума, то его обнаружение несет информацию в пользу принадлежности объекта к данному классу, если нет – то, наоборот, в пользу не принадлежности.

Возвращаясь к выражению (3.12), необходимо отметить, что сам А.А.Харкевич рассматривал как вероятность достижения цели, при условии, что система получила информацию , а – как вероятность ее достижения при условии, что система этой информации не получала. Очевидно, что фактически соответствует вероятности случайного угадывания объектом управления правильного пути к цели, или, что тоже самое, вероятности самопроизвольного, т.е. без оказания управляющих воздействий, достижения АОУ целевого заданного состояния.

Необходимо отметить также, что каждый признак объекта управления как канала связи может быть охарактеризован динамическим диапазоном, равным разности максимально возможного (допустимого) уровня сигнала в канале и уровня помех в логарифмическом масштабе:

Максимальное количество информации, которое может содержаться в признаке, полностью определяется количеством классов распознавания W и равно количеству информации по Хартли: I=Log₂W.

Динамический диапазон признака является количественной мерой его полезности (ценности) для распознавания, но все же предпочтительней для этой цели является среднее количество полезной для классификации информации в признаке, т.е. исправленное выборочное среднеквадратичное отклонение информативностей:

(3. 58)

Очевидна близость этой меры к длине вектора признака в семантическом пространстве атрибутов:

(3. 59)

В сущности выражение (3.58) просто представляет собой нормированный вариант (3.59).

Решение задачи 2: "Адаптация модели объекта управления"

На основе обучающей выборки, содержащей информацию о том, какие факторы действовали, когда АОУ переходил в те или иные состояния, методом прямого счета формируется матрица абсолютных частот, имеющая вид, представленный в таблице 3.11. Необходимо отметить, что в случае АОУ в большинстве случаев нет возможности провести полный факторный эксперимент для заполнения матрицы абсолютных частот. В данной работе предполагается, что это и не обязательно, т.е. на практике достаточно воспользоваться естественной вариабельностью факторов и состояний АОУ, представленных в обучающей выборке. С увеличением объема обучающей выборки в ней со временем будут представлены все практически встречающиеся варианты сочетаний факторов и состояний АОУ.

В соответствии с выражением (3.28), непосредственно на основе матрицы абсолютных частот |||| (таблица 3.11) рассчитывается матрица информативностей факторов |||| (таблица 3.12).

Количество информации в i–м факторе о наступлении j–го состояния АОУ является статистической мерой их связи и количественной мерой влияния данного фактора на переход АОУ в данное состояние.

Решение задачи 3: "Разработка алгоритмов решения основных задач АСУ"

Как было показано в разделе 3.2, решение задачи 3 предполагает решение следующих подзадач.

Решение подзадачи 3.1: "Расчет влияния факторов на переход объекта управления в различные состояния (обучение, адаптация)"

При изменении объема обучающей выборки или изменении экспертных оценок прежде всего пересчитывается матрица абсолютных частот, а затем, на ее основании и в соответствии с выражением (28), - матрица информативностей. Таким образом, предложенная модель обеспечивает отображение динамических взаимосвязей, с одной стороны, между входными и выходными параметрами, а с другой, - между параметрами и состояниями объекта управления. Конкретно, это отображение осуществляется в форме так называемых векторов факторов и состояний.

В профиле (векторе) i–го фактора (строка матрицы информативностей) отображается, какое количество информации о переходе АОУ в каждое из возможных состояний содержится в том факте, что данный фактор действует.

В профиле (векторе) j–го состояния АОУ (столбец матрицы информативностей) отображается, какое количество информации о переходе АОУ в данное состояние содержится в каждом из факторов.

Решение подзадачи 3.2: "Прогнозирование поведения объекта управления при конкретном управляющем воздействии и выработка многофакторного управляющего воздействия (обратная задача прогнозирования)"

Прогнозирование состояния АОУ осуществляется следующим образом:

1. Собирается информация о действующих факторах, характеризующих состояние предметной области (активный объект управления описывается факторами, характеризующими его текущее и прошлые состояния; управляющая система характеризуется технологическими факторами, с помощью которых она оказывает управляющее воздействие на активный объект управления; окружающая среда характеризуется прошлыми, текущими и прогнозируемыми факторами, которые также оказывают воздействие на активный объект управления).

2. Для каждого возможного будущего состояния АОУ подсчитывается суммарное количество информации, содержащееся во всей системе факторов (согласно п.1), о наступлении этого состояния.

3. Все будущие состояния АОУ ранжируются в порядке убывания количества информации об их осуществлении.

Этот ранжированный список будущих состояний АОУ и представляет собой первичный результат прогнозирования.

Если задано некоторое определенное целевое состояние, то выбор управляющих воздействий для фактического применения производится из списка, в котором все возможные управляющие воздействия расположены в порядке убывания их влияния на перевод АОУ в данное целевое состояние. Такой список называется информационным портретом состояния АОУ [152].

Управляющие воздействия могут быть объединены в группы, внутри каждой из которых они альтернативны (несовместны), а между которыми - нет (совместны). В этом случае внутри каждой группы выбирают одно из фактически доступных управляющих воздействий с максимальным влиянием на достижение заданного целевого состояния АОУ.

Однако выбор многофакторного управляющего воздействия нельзя считать завершенным без прогнозирования результатов его применения. Описание АОУ в актуальном состоянии состоит из списка факторов окружающей среды, предыстории АОУ, описания его актуального (исходного) состояния, а также выбранных управляющих воздействий. Имея эту информацию по каждому из факторов в соответствии с выражением (7), нетрудно подсчитать, какое количество информации о переходе в каждое из состояний содержится суммарно во всей системе факторов. Данный метод соответствует фундаментальной лемме Неймана–Пирсона, содержащей доказательство оптимальности метода выбора той из двух статистических гипотез, о которой в системе факторов содержится больше информации. В то же время он является обобщением леммы Неймана–Пирсона, так как вместо информационной меры Шеннона используется системное обобщение семантической меры целесообразности информации Харкевича.

Предлагается еще одно обобщение этой фундаментальной леммы, основанное на косвенном учете корреляций между информативностями в профиле состояния при использовании среднего по профилю. Соответственно, вместо простой суммы количеств информации предлагается использовать ковариацию между векторами состояния и АОУ, которая количественно измеряет степень сходства формы этих векторов.

Результат прогнозирования поведения АОУ, описанного данной системой факторов, представляет собой список состояний, в котором они расположены в порядке убывания суммарного количества информации о переходе АОУ в каждое из них.

Решение подзадачи 3.3: "Выявление факторов, вносящих основной вклад в детерминацию состояния АОУ; снижение размерности модели при заданных ограничениях"

Естественно считать, что некоторый фактор является тем более ценным, чем больше среднее количество информации, содержащееся в этом факторе о поведении АОУ [152]. Но так как в предложенной модели количество информации может быть и отрицательным (если фактор уменьшает вероятность перехода АОУ в некоторое состояние), то простое среднее арифметическое информативностей может быть близко к нулю. При этом среднее будет равно нулю и в случае, когда все информативности равны нулю, и тогда, когда они будут велики по модулю, но с разными знаками. Следовательно, более адекватной оценкой полезности фактора является среднее модулей или, что наиболее точно, исправленное (несмещенное) среднеквадратичное отклонение информативностей по профилю признака.

Ценность фактора по сути дела определяется его полезностью для различения состояний АОУ, т.е. является его дифференцирующей способностью или селективностью.

Необходимо также отметить, что различные состояния АОУ обладают различной степенью обусловленности, т.е. в различной степени детерминированы факторами: некоторые слабо зависят от учтенных факторов, тогда как другие определяются ими практически однозначно. Количественно детерминируемость состояния АОУ предлагается оценивать стандартным отклонением информативностей вектора обобщенного образа данного состояния.

Предложено и реализовано несколько итерационных алгоритмов корректного удаления малозначимых факторов и слабодетерминированных состояний АОУ при заданных граничных условиях [152]. Решение задачи снижения размерности модели АОУ при заданных граничных условиях позволяет снизить эксплуатационные затраты и повысить эффективность РАСУ АО.

Решение подзадачи 3.4: "Сравнение влияния факторов. Сравнение состояний объекта управления"

Факторы могут сравниваться друг с другом по тому влиянию, которое они оказывают на поведение АОУ. Сами состояния могут сравниваться друг с другом по тем факторам, которые способствуют или препятствуют переходу АОУ в эти состояния. Это сравнение может содержать лишь результат, т.е. различные степени сходства/различия (в кластерном анализе), или содержать также причины этого сходства/различия (в когнитивных диаграммах).

Эти задачи играют важную роль в теории и практике РАСУ АО при необходимости замены одних управляющих воздействий другими, но аналогичными по эффекту, а также при изучении вопросов семантической устойчивости управления (различимости состояний АОУ по детерминирующим их факторам).

Этот анализ проводится над классами распознавания и над признаками. Он включает: информационный (ранговый) анализ; кластерный и конструктивный анализ, семантические сети; содержательное сравнение информационных портретов, когнитивные диаграммы.

Семантический информационный анализ

Предложенная математическая модель позволяет сформировать информационные портреты обобщенных эталонных образов классов распознавания и признаков.

Портреты классов распознавания представляют собой списки признаков в порядке убывания содержащегося в них количества информации о принадлежности к этим классам.

Информационный портрет класса распознавания показывает нам, каков информационный вклад каждого признака в общий объем информации, содержащейся в обобщенном образе этого класса.

В подходе к решению задач рефлексивных АСУ АО, основанном на применении методов распознавания образов, классам распознавания соответствуют, во–первых, исходные, а во–вторых, результирующие, в том числе целевые состояния объекта управления. Это значит, что в первом случае портреты классов используются для идентификации исходного состояния АОУ, потому что именно с ними сравнивается состояние объекта управления, а во втором – для выработки управляющего воздействия, так как его выбирают в форме суперпозиции неальтернативных факторов из информационного портрета целевого состояния, оказывающих наибольшее влияние на перевод АОУ в это состояние.

Портреты признаков представляют собой списки классов распознавания в порядке убывания количества информации о них, которое содержит данный признак. По своей сути информационный портрет признака раскрывает нам смысл данного признака, т.е. его семантическую нагрузку. В теории и практике рефлексивных АСУ АО информационный портрет фактора является развернутой количественной характеристикой, содержащей информацию о силе и характере его влияния на перевод АОУ в каждое из возможных результирующих состояний, в том числе в целевые. Информационные портреты классов и признаков допускают наглядную графическую интерпретацию в виде двухмерных (2d) и трехмерных (3d) диаграмм.

Кластерно–конструктивный анализ и семантические сети

Кластеры представляют собой такие группы классов распознавания (или признаков), внутри которых эти классы наиболее схожи друг с другом, а между которыми наиболее различны [76, 81, 85, 107, 179, 219, 294]. В данной работе, в качестве классов распознавания рассматриваются как исходные, так и результирующие, в том числе целевые состояния объекта управления, а в качестве признаков – факторы, влияющие на переход АОУ в результирующие состояния.

Исходные состояния АОУ, объединенные в кластер, характеризуются общими или сходными методами перевода в целевые состояния. Результирующие состояния АОУ, объединенные в кластер, являются слаборазличимыми по факторам, детерминирующим перевод АОУ в эти состояния. Это означает, что одно и то же управляющее воздействие при одних и тех же предпосылках (исходном состоянии и предыстории объекта управления и среды) могут привести к переводу АОУ в одно из результирующих состояний, относящихся к одному кластеру. Поэтому кластерный анализ результирующих состояний АОУ является инструментом, позволяющим изучать вопросы устойчивости управления сложными объектами.

При выборе управляющего воздействия как суперпозиции неальтернативных факторов часто возникает вопрос о замене одних управляющих факторов другими, имеющими сходное влияние на перевод АОУ из данного текущего состояния в заданное целевое состояние. Кластерный анализ факторов как раз и позволяет решить эту задачу: при невозможности применить некоторый управляющий фактор его можно заменить другим фактором из того же кластера.

При формировании кластеров используются матрицы сходства объектов и признаков, формируемые на основе матрицы информативностей.

В соответствии с предлагаемой математической моделью могут быть сформированы кластеры для заданного диапазона кодов классов распознавания (признаков) или заданных диапазонов уровней системной организации с различными критериями включения объекта (признака) в кластер.

Эти критерии могут быть сформированы автоматически либо заданы непосредственно. В последнем уровне кластеризации, в частности при задании одного уровня, в кластеры включаются не только похожие, но и все непохожие объекты (признаки), и, таким образом, формируются конструкты классов распознавания и признаков.

В данной работе под конструктом понимается система противоположных (наиболее сильно отличающихся) кластеров, которые называются "полюсами" конструкта, а также спектр промежуточных кластеров, к которым применима количественная шкала измерения степени их сходства или различия [152, 325].

Понятия "кластер" и "конструкт" тесно взаимосвязаны:

– так как положительный и отрицательный полюса конструкта представляют собой кластеры, в наибольшей степени отличающиеся друг от друга, то конструкты могут быть получены как результат кластерного анализа кластеров;

– конструкт может рассматриваться как кластер с нечеткими границами, включающий в различной степени, причем не только в положительной, но и отрицательной, все классы (признаки).

В теории рефлексивных АСУ АО, конструктивный анализ позволяет решить такие задачи, как:

1. Определение в принципе совместимых и в принципе несовместимых целевых состояний АОУ. Совместимыми называются целевые состояния, для достижения которых необходимы сходные предпосылки и управляющие воздействия, а несовместимыми – для которых они должны быть диаметрально противоположными. Например, обычно сложно совмещаются такие целевые состояния, как очень высокое качество продукции и очень большое ее количество.

2. Определение факторов, имеющих не только сходное (это возможно и на уровне кластерного анализа), но и совершенно противоположное влияние на поведение сложного объекта управления.

Современный интеллект имеет дуальную структуру и, по сути дела, мыслит в системе кластеров и конструктов. Поэтому инструмент автоматизированного кластерно–конструктивного анализа может быть успешно применен для рефлексивного управления активными объектами.

Необходимо отметить, что формирование кластеров затруднено из-за проблемы комбинаторного взрыва, так как требует полного перебора и проверки "из n по m" сочетаний элементов (классов или признаков) в кластеры. Конструкты же формируются непосредственно из матрицы сходства прямой выборкой и сортировкой, что значительно проще в вычислительном отношении, так как конструктов значительно меньше, чем кластеров (всего n²). Поэтому учитывая, что при формировании конструктов автоматически формируются и их полюса, т.е. кластеры, в предложенной математической модели реализован не кластерный анализ, а сразу конструктивный (как более простой в вычислительном отношении и более ценный по получаемым результатам).

Диаграммы смыслового сходства–различия классов (признаков) соответствуют определению семантических сетей [244], т.е. представляют собой ориентированные графы, в которых признаки соединены линиями, соответствующими их смысловому сходству–различию.

Когнитивные диаграммы классов и признаков

В предложенной в настоящем исследовании математической модели в обобщенной постановке реализована возможность содержательного сравнения обобщенных образов классов распознавания и признаков, т.е. построения когнитивных диаграмм [152].

В информационных портретах классов распознавания мы видим, какое количество информации о принадлежности (или не принадлежности) к данному классу мы получаем, обнаружив у некоторого объекта признаки, содержащиеся в информационном портрете. В кластерно–конструктивном анализе мы получаем результаты сравнения классов распознавания друг с другом, т.е. мы видим, насколько они сходны и насколько отличаются. Но мы не видим, какими признаками они похожи и какими отличаются, и какой вклад каждый признак вносит в сходство или различие некоторых двух классов.

Эту информацию мы могли бы получить, если бы проанализировали и сравнили два информационных портрета. Эту работу и осуществляет режим содержательного сравнения классов распознавания.

Аналогично, в информационных портретах признаков мы видим, какое количество информации о принадлежности (или не принадлежности) к различным классам распознавания мы получаем, обнаружив у некоторого объекта данный признак. В кластерно–конструктивном анализе мы получаем результаты сравнения признаков друг с другом, т.е. мы видим, насколько они сходны и насколько отличаются. Но мы не видим, какими классами они похожи и какими отличаются, и какой вклад каждый класс вносит в смысловое сходство или различие некоторых двух признаков.

Эту информацию мы могли бы получить, если бы проанализировали и сравнили информационные портреты двух признаков. Эту работу и осуществляет режим содержательного (смыслового) сравнения признаков.

Содержательное (смысловое) сравнение классов

Обобщим математическую модель, предложенную и развиваемую в данной главе, на случай содержательного сравнения двух классов распознавания: J–го и L–го.

Признаки, которые есть по крайней мере в одном из классов, будем называть связями, так как благодаря тому, что они либо тождественны друг другу, либо между ними имеется определенное сходство или различие по смыслу, они вносят определенный вклад в отношения сходства/различия между классами.

Список выявленных связей сортируется в порядке убывания модуля силы связи, причем учитывается не более заданного количества связей.

Пусть, например:

у J–го класса обнаружен i–й признак,

у L–го класса обнаружен k–й признак.

Используем те же обозначения, что и в разделе 3.1.

На основе обучающей выборки системой рассчитывается матрица абсолютных частот встреч признаков по классам (таблица 3.11).

В разделе 3.1. получено выражение (3.28) для расчета количества информации в i–м признаке о принадлежности некоторого конкретного объекта к j–му классу (плотность информации), которое имеет вид:

(3.28)

Аналогично, формула для количества информации в k–м признаке о принадлежности к L–му классу имеет вид:

(3. 60)

Вклад некоторого признака i в сходство/различие двух классов j и l равен соответствующему слагаемому корреляции образов этих классов, т.е. просто произведению информативностей

(3. 61)

Классический коэффициент корреляции Пирсона, количественно определяющий степень сходства векторов двух классов: j и l, на основе учета вклада каждой связи, образованной i–м признаком, рассчитывается по формуле

(3. 62)

где:

	– средняя информативность признаков j–го класса;
	– средняя информативность признаков L–го класса;
	– среднеквадратичное отклонение информативностей признаков j–го класса;
	– среднеквадратичное отклонение информативностей признаков L–го класса.

Проанализируем, насколько классический коэффициент корреляции Пирсона (3.62) пригоден для решения важных задач:

– содержательного сравнения классов;

– изучения внутренней многоуровневой структуры класса.

Упростим анализ, считая, что средние информативности признаков по обоим классам близки к нулю, что при достаточно больших выборках (более 400 примеров в обучающей выборке) практически близко к истине.

Каждое слагаемое (3.61) суммы (3.62) отражает связь между классами, образованную одним i–м признаком. I–я связь существует в том и только в том случае, если i–й признак есть у обоих классов. Поэтому эти связи уместно называть одно–однозначными.

Этот подход можно назвать классическим для когнитивного анализа. Рассмотрим когнитивную диаграмму, приведенную на стр. 222 работы классика когнитивной психологии Р.Солсо [296] (рисунок 3.12)

Рисунок 3. 12
. Когнитивная диаграмма
из классической работы Роберта Солсо [296].

В данной когнитивной диаграмме наглядно в графической форме показано сравнение классов (обобщенных образов) "Малиновка" и "Птица" разных уровней общности по их атрибутам (признакам).

Как видно из данной диаграммы, в ней:

1. Все атрибуты имеют одинаковый вес, т.е. не учитывается, что некоторые атрибуты более важны для идентификации класса, чем другие. Это соответствует предположению, что этот вес равен по модулю 1 для всех атрибутов.

2. Все признаки имеют одинаковый знак, т.е. они все характерны для классов и нет атрибутов нехарактерных. Это соответствует предположению, что вес всех признаков положительный, т.е. все призхнаки вносят вклад в сходство и нет признаков, вносящих вклад в различие.

3. Классы сравниваются только по тем атрибутам, которые есть одновременно у них обоих, т.е. признаки, имеющиеся у обоих классов вносят вклад в сходство классов, а признаки, которые есть только у одного из классов не вносят никакого вклада ни в сходство классов, ни в различие. Это соответствует предположению, что атрибуты ортонормированы, т.е. корреляция их друг с другом равна 0 (атрибуты семантически не связаны).

Каждое из этих трех допущений является довольно сильным и желательно их снять и, тем самым, обобщить принцип построения когнитивных диаграмм, приведенный в данном примере.

Но это означает, что данный подход не позволяет сравнивать классы, описанные различными, т.е. непересекающимися наборами признаков. Но даже если общие признаки и есть, то невозможность учета вклада остальных признаков является недостатком классического подхода, так как из содержательного анализа связей неконтролируемо исключается потенциально существенная информация. Таким образом, классический подход имеет ограниченную применимость при решении задачи №1. Для решения задачи №2 подход, основанный на формуле (3.62), вообще не применим, так как различные уровни системной организации классов образованы различными признаками и, следовательно, между уровнями не будет ни одной одно–однозначной связи.

Основываясь на этих соображениях, предлагается в общем случае учитывать вклад в сходство/различие двух классов, который вносят не только общие, но и остальные признаки. Логично предположить, что этот вклад (при прочих равных условиях) будет тем меньше, чем меньше корреляция между этими признаками.

Следовательно, для обобщения выражения для силы связи (3.61) необходимо умножить произведение информативностей признаков на коэффициент корреляции между ними, отражающий степень сходства или различия признаков по смыслу.

Таким образом, будем считать, что любые два признака (i,k) вносят определенный вклад в сходство/различие двух классов (j,l), определяемый сходством/различием признаков и количеством информации о принадлежности к этим классам, которое содержится в данных признаках:

(3. 63)

где – классический коэффициент корреляции Пирсона, количественно определяющий степень сходства по смыслу двух признаков: i и k, на основе учета вклада каждой связи, образованной содержащейся в них информацией о принадлежности к j–му классу

(3. 64)

где

	– средняя информативность координат вектора i–го признака;
	– средняя информативность координат вектора k–го признака;
	– среднеквадратичное отклонение координат вектора i–го признака;
	– среднеквадратичное отклонение координат вектора k–го признака.

Коэффициент корреляции между признаками (3.64) рассчитывается на основе всей обучающей выборки, а не только объектов двух сравниваемых классов. Так как коэффициент корреляции между признаками (3.64) практически всегда не равен нулю, то каждый признак i образует связи со всеми признаками k, где k={1,...,A}, а каждый признак k в свою очередь связан со всеми остальными признаками. Это означает, что выражение (3.63) является обобщением (3.61) с учетом много–многозначных связей.

На основе этих представлений сформулируем выражение для обобщенного коэффициента корреляции Пирсона между двумя классами: j и l, учитывающего вклад в их сходство/различие не только одно–однозначных, но и много–многозначных связей, образуемых коррелирующими признаками. Когнитивные диаграммы с много–многозначными связями предлагается называть обобщенными когнитивными диаграммами.

(3. 65)

где K_ik определяется выражением (3.64).

Сравним классический (3.62) и обобщенный (3.65) коэффициенты корреляции Пирсона друг с другом. Очевидно, при i=k (3.65) преобразуется в (3.62), т.е. соблюдается принцип соответствия. Отметим, что модель позволяет задавать минимальный коэффициент корреляции (порог) между признаками, образующими учитываемые связи. При пороге 100% отображаются только одно–однозначные связи, учитываемые в классическом коэффициенте корреляции (3.62). Из выражений (3.62) и (3.65) видно, что

(3. 66)

так как в обобщенном коэффициенте корреляции учитываются связи между классами, образованные за счет учета корреляций между различными признаками. Ясно, что отношение

(3. 67)

отражает степень избыточности описания классов. В модели имеется возможность исключения из системы признаков наименее ценных из них для идентификации классов. При этом в первую очередь удаляются сильно коррелирующие друг с другом признаки. В результате степень избыточности системы признаков уменьшается, и она становится ближе к ортонормированной.

Рассмотрим вопрос о единицах измерения, в которых количественно выражаются связи между классами.

Сходство двух признаков выражается величиной от – 1 до +1.

Максимальная теоретически возможная информативность признака в Bit выражается формулой

(3. 68)

где N_obj – количество классов.

Таким образом, максимальная теоретически возможная сила связи R_max равна

(3. 69)

Сила связи в диаграммах выражается в процентах от максимальной теоретически возможной силы связи.

На графической диаграмме отображается 8 наиболее сильных по модулю связей, рассчитанных согласно формуле (3.60), причем знак связи изображается цветом (красный +, синий – ), а величина – толщиной линии. Имеется возможность выводить диаграммы только с положительными или только с отрицательными связями (для не цветных принтеров).

Диаграммы Мерлина [143, 189] представляют собой частный случай обобщенных когнитивных диаграмм (т.е. с много–многозначными связями), т.е. диаграммы Мерлина – это когнитивные диаграммы, формируемые в соответствии с предложенной моделью при следующих граничных условиях:

1. Класс сравнивается сам с собой.

2. Фильтрация левого и правого информационных портретов выбрана по уровням системной организации признаков (в данном случае – уровням Мерлина).

3. Левый класс отображается с фильтрацией по одному уровню системной организации, а правый – по другому.

4. Диалог задания вида диаграмм предоставляет пользователю возможность задать следующие параметры:

– способ нормирования толщины линий, отображающих связи: нормирование по текущей диаграмме или по всем диаграммам;

– способ фильтрации признаков в информационных портретах диаграммы: по диапазону признаков или по диапазону уровней системной организации (уровням Мерлина);

– сами диапазоны признаков или уровней для левого и правого информационных портретов;

– максимальное количество связей, отображаемых на диаграмме;

– уровень сходства признаков, образующих одну связь, отображаемую на диаграмме: от 0 до 100%. При уровне сходства 100% в диаграммах отображаются только связи, образованные теми признаками, которые есть в обоих портретах одновременно, т.е. взаимно–однозначные связи. При уровне сходства менее 100% вообще говоря связи становятся много–многозначными, так как каждый признак корреляционно связан со всеми остальными;

– уровень сходства классов, отображаемых на диаграмме.

Таким образом, в предлагаемой математической модели в общем виде реализована возможность содержательного сравнения обобщенных образов состояний АОУ и факторов, т.е. построения когнитивных диаграмм [152, 277], веса атрибутов определяются автоматически на основе исходных данных в соответствии с математической моделью и могут принимать различные по величине положительные и отрицательные значения. Кроме того на основе кластерного анализа атрибутов определяются корреляции между ними, которые учитываются при определении вклада атрибутов в сходство или различие классов. Поэтому отношения между атрибутами разных классов в когнитивной диаграмме не "один к одному", как в диаграмме на рисунке 3.12, а "многие ко многим".

В информационном портрете состояния АОУ показано, какое количество информации о принадлежности (не принадлежности) АОУ к данному состоянию, а также о переходе (не переходе) АОУ в данное состояние содержится в том факте, что на АОУ действуют факторы, содержащиеся в данном информационном портрете.

Кластерно–конструктивный анализ дает результат сравнения состояний АОУ друг с другом, т.е. показывает, насколько эти состояния сходны друг с другом и насколько отличаются друг от друга. Но он не показывает, какими факторами эти состояния АОУ похожи и какими отличаются, и какой вклад каждый фактор вносит в сходство или различие каждых двух состояний. Чтобы получить эту информацию, необходимо проанализировать два информационных портрета, что и делается при содержательном сравнении состояний АОУ .

Смысл и значение диаграмм Мерлина применительно к проблематике АСУ состоит в том, что они наглядно представляют внутреннюю структуру детерминации состояний АОУ, т.е. показывают, каким образом связаны друг с другом факторы и будущие состояния АОУ.

Таким образом:

– для моделирования процессов принятия решений в адаптивных АСУ сложными системами целесообразно применение многокритериального подхода с аддитивным интегральным критерием, в котором в качестве частных критериев используется семантическая мера целесообразности информации (Харкевич, 1960);

– предложенная математическая модель обеспечивает эффективное решение следующих задач, возникающих при синтезе адаптивных АСУ АОУ: разработка абстрактной информационной модели АОУ; адаптация и конкретизация абстрактной модели на основе апостериорной информации о реальном поведении АОУ; расчет влияния факторов на переход АОУ в различные возможные состояния; прогнозирование поведения АОУ при конкретном управляющем воздействии и выработка многофакторного управляющего воздействия (основная задача АСУ); выявление факторов, вносящих основной вклад в детерминацию состояния АОУ; контролируемое удаление второстепенных факторов с низкой дифференцирующей способностью, т.е. снижение размерности модели при заданных ограничениях; сравнение влияния факторов, сравнение целевых и других состояний АОУ.

Предложенная методология, основанная на теории информации, обеспечивает эффективное моделирование задач принятия решений в адаптивных АСУ сложными системами.

Содержательное (смысловое) сравнение признаков

Предложенная математическая модель позволяет осуществить содержательное сравнение информационных портретов двух признаков.

Выявляются классы, которые есть по крайней мере в одном из векторов. Такие классы называются связями, так как благодаря тому, что они либо тождественны друг другу, либо между ними имеется определенное сходство или различие, они вносят определенный вклад в отношения сходства/различия между признаками по смыслу.

Все связи между признаками сортируются в порядке убывания модуля, в соответствии с определенными ограничениями, связанными с тем, что нет необходимости учитывать очень слабые связи.

Для каждого класса известно, какое количество информации о принадлежности к нему содержит данный признак – это информативность. Здесь необходимо уточнить, что информативность признака – это не только количество информации в признаке о принадлежности к данному классу, но и количество информации в классе о том, что при нем наблюдается данный признак, т.е. это взаимная информация класса и признака.

Если бы классы были тождественны друг другу, т.е. это был бы один класс, то его вклад в сходство/различие двух признаков был бы просто равен соответствующему данному классу слагаемому корреляции этих признаков, т.е. просто произведению информативностей.

Но поскольку это в общем случае это могут быть различные классы, то, очевидно, необходимо умножить произведение информативностей на коэффициент корреляции между классами.

Таким образом, будем считать, что любые два класса (j,l) вносят определенный вклад в сходство/различие двух признаков (i,k), определяемый сходством/различием этих классов и количеством информации о принадлежности к ним, которое содержится в данных признаках

(3. 70)

Вывод формулы (3.70) обобщенного коэффициента корреляции Пирсона для двух признаков совершенно аналогичен выводу формулы (3.65), поэтому он здесь не приводится. Формулы для всех входящих в (3.70) величин приведены выше в предыдущем разделе.

Так же, как и в режиме содержательного сравнения классов, в данном режиме сила связи выражается в процентах от максимальной теоретически–возможной силы связи. На диаграммах отображается 16 наиболее значимых связей, рассчитанных согласно этой формуле, причем знак связи изображается цветом (красный +, синий –), а величина – толщиной линии. Имеется возможность вывода диаграмм только с положительными или только с отрицательными связями.

Математическая модель позволяет получить обобщенные инвертированные когнитивные диаграммы для любых двух заданных признаков, для пар наиболее похожих и непохожих признаков, для всех их возможных сочетаний, а также инвертированные диаграммы Мерлина.

Необходимо отметить, что понятия, соответствующие по смыслу терминам "обобщенная инвертированная когнитивная диаграмма" и "инвертированная диаграмма Мерлина" не упоминаются даже в фундаментальных руководствах по когнитивной психологии [296] и впервые предложены в [143, 152]. Эти диаграммы представляют собой частный случай обобщенных когнитивных диаграмм признаков, формируемых в соответствии с предложенной математической моделью при следующих ограничениях:

1. Признак сравнивается сам с собой.

2. Выбрана фильтрация левого и правого вектора по уровням системной организации классов (аналог уровней Мерлина для свойств).

3. Левый вектор отображается с фильтрацией по одному уровню системной организации классов, а правый – по другому.

Обоснование сопоставимости частных критериев I_ij

Применение этого метода корректно, если можно сравнивать суммарное количество информации о переходе АОУ в различные состояния, рассчитанное в соответствии с выражением (3.62), т.е. если они сопоставимы друг с другом.

Будем считать, что величины сопоставимы тогда и только тогда, когда одновременно выполняются следующие три условия:

1. Сопоставимы индивидуальные количества информации, содержащейся в признаках о принадлежности к классам.

2. Сопоставимы величины, рассчитанные для одного объекта и разных классов.

3. Сопоставимы величины, рассчитанные для разных объектов и разных классов.

Очевидно, для решения всех этих вопросов необходимо дать точное и полное определение самого термина "сопоставимость".

Считается, что величины сопоставимы, если существует некоторая количественная шкала для измерения этих величин.

Таким образом, в нашем случае сопоставимость обеспечивается, если на шкале определены направление и единица измерения, а также есть абсолютный минимум (ноль) или максимум.

Докажем теоремы о выполнении условий сопоставимости для упрощенной и полной информационных моделей объектов и классов распознавания. Для этого рассмотрим вышеперечисленные необходимые и достаточные условия сопоставимости для упрощенной и полной информационных моделей.

Теорема-1: "О сопоставимости индивидуальных количеств информации, содержащейся в признаках объекта о принадлежности к классам"

В упрощенной информационной модели класса и информационной модели объекта принято, что все признаки имеют одинаковый вес, который равен 1, если признак есть у класса, и 0, если его нет. Уже одним этим обеспечивается сопоставимость индивидуальных количеств информации в упрощенной модели.

В полной модели количество информации рассчитывается в соответствии с модифицированной формулой Харкевича (3.28). Таким образом, в полной информационной модели класса для каждого признака известно, какое количество информации о принадлежности к данному классу он содержит. Это количество информации может быть положительным, нулевым и отрицательным, но не может превосходить некоторой максимальной величины, определяемой количеством классов распознавания: I=Log₂W (мера Хартли), где W – количество классов распознавания. Следовательно, для полной информационной модели сопоставимость индивидуальных количеств информации также обеспечивается, так как для них применима шкала отношений.

Это означает, что индивидуальные количества информации можно суммировать и ввести интегральный критерий как аддитивную меру от индивидуальных количеств информации, что и т.д.

Теорема-2: "О сопоставимости величин суммарной информации, рассчитанных для одного объекта и разных классов"

В упрощенной информационной модели вариант расстояния Хэмминга, в котором учитываются только совпадения 1 (т.е. существующих признаков), для кодовых слов объекта и класса равно:

(3. 71)

где – кодовое слово (профиль, массив–локатор) j–го класса;

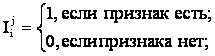
L_i – кодовое слово (профиль, массив–локатор) объекта.

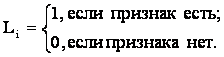
Пусть длина кодового слова (количество признаков) равна А. Длины кодовых слов объекта и классов одинаковы. Признаки могут принимать значения {0,1}. Тогда из этих условий и выражения (3.71) следует:

(3. 72)

Но выражение (3.72) является математическим определением шкалы отношений, что означает полную сопоставимость предложенной меры сходства для упрощенной информационной модели одного объекта и многих классов, что и т.д.

В полной информационной модели мера сходства объекта с классом имеет вид, определяемый выражением (3.70).

Очевидно, величина нормирована:

(3. 73)

что и доказывает применимость шкалы отношений и полную сопоставимость меры сходства для полной информационной модели одного объекта и многих классов.

Это значит, что можно сравнивать меры сходства данного объекта с каждым из классов и ранжировать классы в порядке убывания сходства с данным объектом, что и т.д.

Теорема-3: "О сопоставимости величин суммарной информации, рассчитанных для разных объектов и разных классов, а также классов и классов, признаков и признаков"

Очевидно, величина , рассчитанная по формуле (3.70) для различных объектов и классов нормирована:

(3. 74)

что и доказывает применимость шкалы отношений и полную сопоставимость мер сходства для полной информационной модели многих объектов и многих классов.

Это значит, что можно сравнивать меры сходства различных объектов с классами распознавания и делать выводы о том, что одни объекты распознаются лучше, а другие хуже на данном наборе классов и признаков, что и т.д.

Аналогичные рассуждения верны и для сравнения векторов классов друг с другом, а также векторов признаков друг с другом, что позволяет применить модели кластерно–конструктивного анализа и алгоритмы построения семантических сетей, что и т.д.

Теорема-4: "Об аддитивности неметрического интегрального критерия сходства, основанного на модифицированной формуле А.Харкевича и обобщенной лемме Неймана-Пирсона"

Рассмотрим информационные модели распознаваемого объекта и классов распознавания, т.е. модели, основанные на теории кодирования – декодирования. Эта модель является упрощенной, но достаточно адекватной для решения вопроса об аддитивности меры сходства объектов и классов.

Информационная модель распознаваемого объекта представляет собой двоичное слово, каждый разряд которого соответствует определенному признаку. Если признак есть у распознаваемого объекта, то соответствующий разряд имеет значение 1, если нет – то 0. Двоичное слово с установленными в 1 разрядами, соответствующими признакам распознаваемого объекта, называется его кодовым словом.

Упрощенная информационная модель класса распознавания есть двоичное слово, каждый разряд которого соответствует определенному признаку. Соответствие между двоичными разрядами и признаками для классов то же самое, что и для распознаваемых объектов. Если признак есть у класса, то соответствующий разряд имеет значение 1, если нет – то 0. Двоичное слово с установленными в 1 разрядами, соответствующими признакам класса, называется его кодовым словом.

Такая модель класса является упрощенной, так как в ней принято, что все признаки имеют одинаковый вес равный 1, если он есть у класса, и 0, если его нет, тогда как в полной информационной модели класса для каждого признака известно, какое количество информации о принадлежности к данному классу он содержит. Это количество информации может быть положительным, нулевым и отрицательным, но не может превосходить некоторой максимальной величины, определяемой количеством классов распознавания: I=Log₂N (мера Хартли), где N – количество классов.

Таким образом, в упрощенной информационной модели различные классы распознавания отличаются друг от друга только наборами признаков, которые им соответствуют.

При использовании этих упрощенных моделей задача распознавания объекта сводится к задаче декодирования, т.е. кодовые слова объектов рассматриваются как искаженные зашумленным каналом связи кодовые слова классов. Распознавание состоит в том, что по кодовому слову объекта определяется наиболее близкое ему в определенном смысле кодовое слово класса. При этом естественной и наиболее простой мерой сходства между распознаваемым объектом и классом является расстояние Хэмминга между их кодовыми словами, т.е. количество разрядов, которыми они отличаются друг от друга.

Рассмотрим теперь вопрос об аддитивности количества информации как частного критерия в интегральном критерии.

Известно [234], что существует всего два варианта формирования интегрального критерия из частных критериев: аддитивный и мультипликативный, поэтому задача сводится к выбору одного из этих вариантов.

Рассмотрим эти варианты. Пусть кодовое слово объекта состоит из N разрядов. Тогда добавление еще одного разряда, отображающего имеющийся (1) или отсутствующий (0) признак, приведет к различным результатам в случаях, когда интегральный критерий есть аддитивная и мультипликативная функция индивидуальных количеств информации в признаках (таблица 3.15):

Таблица 3. 15 – СРАВНЕНИЕ АДДИТИВНОГО И МУЛЬТИПЛИКАТИВНОГО
ВАРИАНТОВ ИНТЕГРАЛЬНОГО КРИТЕРИЯ

Дополнительный признак	Аддитивная функция:	Мультипликативная функция:
Есть (1)
Нет (0)

Здесь предполагается, что: I=f(n), f(1)=1, f(0)=0.

Итак, если функция аддитивна – добавление еще одного разряда увеличит количество информации в кодовом слове на 1 бит, если соответствующий признак есть, и не изменит этого количества, если его нет; если же функция мультипликативна, – то это не изменит количества информации в кодовом слове, если соответствующий признак есть, и сделает его равным нулю, если его нет.

Очевидно, мультипликативный вариант интегрального критерия не соответствует классическим представлениям о природе информации, тогда как аддитивный вариант полностью им соответствует: требование аддитивности самой меры информации было впервые обосновано Хартли в 1928 году, подтверждено Шенноном в 1948 году, и в последующем развитии теории информации никогда не подвергалось сомнению. На аддитивности частных критериев, имеющих смысл количества информации, основана известная лемма Неймана-Пирсона [234, стр.152].

Таким образом, аддитивность интегрального критерия, основанного на частных критериях, имеющих смысл количества информации, можно считать обоснованной, что и т.д.

Обобщение интегральной модели путем учета значений выходных параметров объекта управления

Выходные параметры– это свойства объекта управления, зависят от входных параметров (в том числе параметров, характеризующих среду) и связанны с его целевым состоянием сложным и неоднозначным способом:

Задача идентификации состояния АОУ по его выходным параметрам решается подсистемой идентификации управляющей подсистемы, работающей на принципах системы распознавания образов. При этом классами распознавания являются выходные состояния АОУ, а признаками – его выходные параметры.

Подсистема выработки управляющих воздействий, также основанная на алгоритмах распознавания образов, обеспечивает выбор управления , переводящего объект управления в целевое состояние .

При этом последовательно решаются следующие две обратные задачи распознавания:

во–первых, по заданному целевому состоянию определяются наиболее характерные для данного состояния выходные параметры объекта управления:

во–вторых, по определенному на предыдущем шаге набору выходных параметров определяются входные параметры , с наибольшей эффективностью переводящие объект управления в данное целевое состояние с этими выходными параметрами:

1. Показано, что определенная ограниченность подхода Шеннона, рассмотренная в четвертой главе данной работы, преодолевается в апостериорном подходе. Обосновано, что одной из наиболее перспективных конкретизаций апостериорного подхода, является подход, предложенный в 1960 году А.А.Харкевичем [234, 309, 330, 347]. Для моделирования процессов принятия решений в адаптивных АСУ сложными системами предложено применить многокритериальный подхода с аддитивным интегральным критерием, в котором в качестве частных критериев используется семантическая мера целесообразности информации. При апостериорном подходе количество информации оценивается косвенно: по изменению степени целесообразности поведения системы, получившей эту информацию. В результате получения информации поведение системы улучшается (растет выигрыш), а в результате получения дезинформации – ухудшается (растет проигрыш). Известны и более развитые обобщения [234], основанные на интересных и правдоподобных идеях, однако они наталкиваются на значительные математические трудности и намного более сложны в программной реализации, поэтому их рассмотрение в данном исследовании признано нецелесообразным.

2. Предложенная математическая модель обеспечивает эффективное решение следующих задач, возникающих в адаптивных АСУ СС:

– разработка абстрактной информационной модели АОУ;

– адаптация и конкретизация абстрактной модели на основе информации о реальном поведении АОУ;

– расчет влияния факторов на переход АОУ в различные возможные состояния;

– прогнозирование поведения АОУ при конкретном управляющем воздействии и выработка многофакторного управляющего воздействия (основная задача АСУ);

– выявление факторов, вносящих основной вклад в детерминацию состояния АОУ; контролируемое удаление второстепенных факторов с низкой дифференцирующей способностью, т.е. снижение размерности модели при заданных граничных условиях;

– сравнение влияния факторов, сравнение целевых и других состояний АОУ.

3. Таким образом, предложенная методология, основанная на теории информации, обеспечивает эффективное моделирование задач принятия решений в адаптивных АСУ сложными системами.

4. На примере метода сведения многокритериальной задачи принятия решений к однокритериальной показана глубокая внутренняя взаимосвязь данной модели с математической моделью распознавания образов. На этой основе введено понятие "интегрального метода" распознавания и принятия решений и, после изложения основных понятий теории информации, предложена базовая математическая модель "интегрального метода", основанная на теории информации. Показано, что теория информации может рассматриваться как единая основа методов РО и ПР, распознавание образов как принятие решения о принадлежности объекта к классу распознавания, прогнозирование как распознавание будущих состояний, принятие решения об управляющем воздействии на объект управления в АСУ как решение обратной задачи распознавания.

5. Проведено исследование базовой математической модели на примере решения основной задачи АСУ: задача принятия решения о наиболее эффективном управляющем воздействии. Осуществлена декомпозиция основной задачи в последовательность частных задач для каждой из которых найдено решение, показана взаимосвязь основной задачи АСУ с задачей декодирования теории информации.
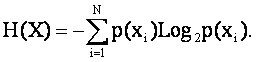
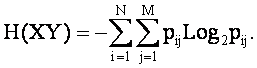
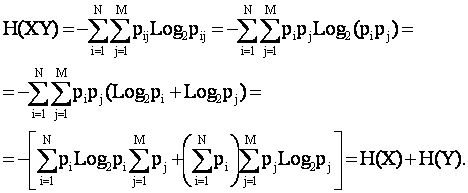
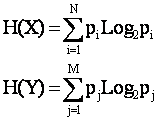
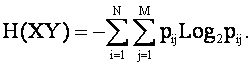
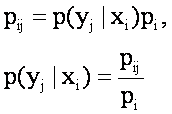
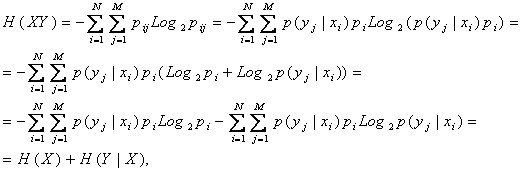
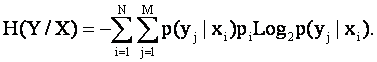
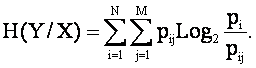
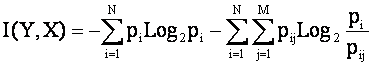
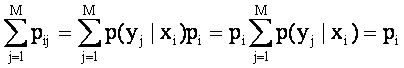
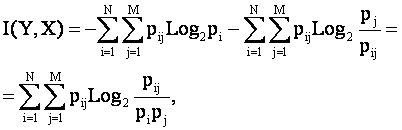
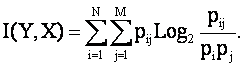
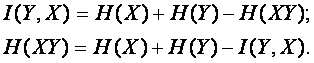
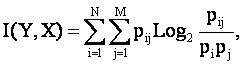
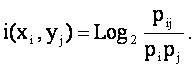
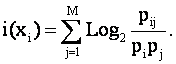
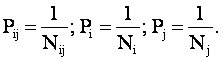
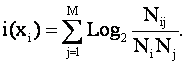
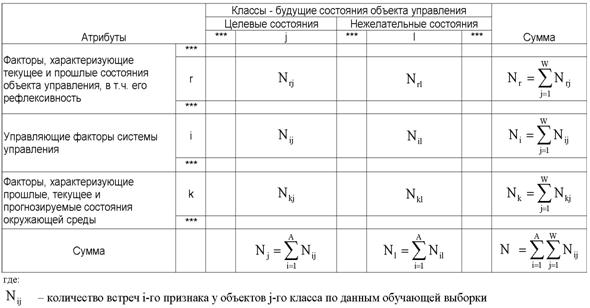
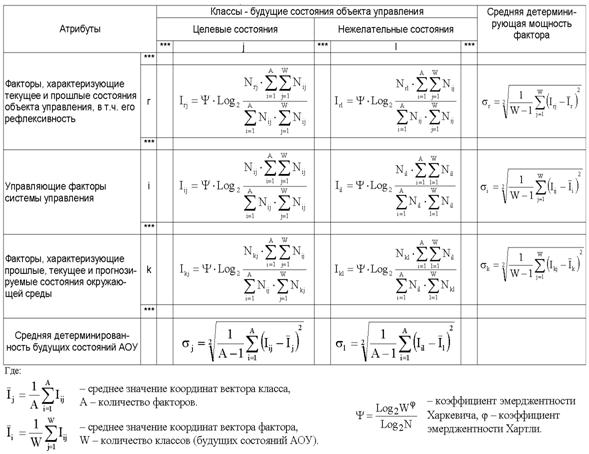
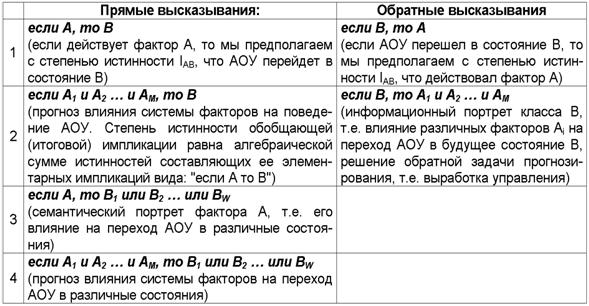
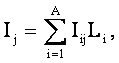