МОДЕЛИРОВАНИЕ ПРИНЯТИЯ РЕШЕНИЙ
В АДАПТИВНЫХ АСУ СЛОЖНЫМИ СИСТЕМАМИ
НА ОСНОВЕ ТЕОРИИ ИНФОРМАЦИИ

 

В.С.Симанков, Е.В.Луценко

 

Принятие решения в АСУ – это выбор некоторого наиболее предпочтительного управляющего воздействия из исходного множества всех возможных управляющих воздействий, обеспечивающего наиболее эффективное достижение целей управления. В результате выбора неопределенность исходного множества уменьшается на величину информации, которая порождается самим актом выбора [1]. Это значит, что теория информации применима как для описания процессов принятия решений, так и для построения модели АСУ.

Модель АСУ включает в себя: модель объекта управления, модель управляющей подсистемы, а также модель внешней среды. Управляющая подсистема реализует следующие функции: идентификация состояния объекта управления, выработка управляющего воздействия, реализация управляющего воздействия.

С позиций теории информации сложный объект управления (СОУ) может рассматриваться как шумящий (определенным образом) информационный канал, на вход которого подаются входные параметры , представляющие собой управляющие воздействия, а также факторы предыстории и среды, а на выходе фиксируются выходные параметры , связанные как с входными параметрами, так и с целевыми и иными состояниями объекта управления.

Одной из основных задач АСУ является задача принятия решения о наиболее эффективном управляющем воздействии. В терминах теории информации эта задача формулируется следующим образом: зная целевое состояние объекта управления, на основе его информационной модели, определить такие входные параметры , которые с учетом предыстории и актуального состояния объекта управления, а также влияния среды, с наибольшей эффективностью переведут его в целевое состояние, характеризующееся выходными параметрами .

С решением этой задачи тесно связана задача декодирования теории информации: по полученному в условиях помех сообщению определить, какое сообщение было передано [2]. Для решения данной задачи используются коды, корректирующие ошибки, а в более общем случае, - различные методы распознавания образов.

Учитывая вышесказанное, авторы предлагают рассматривать принятие решения об управляющем воздействии в АСУ как решение обратной задачи декодирования: что надо передать, чтобы получить заранее заданное сообщение. Данная задача решается на основе математической модели канала связи. В случае, когда каналом связи является объект управления, его модель - передаточная функция.

Построение аналитической модели СОУ затруднено отсутствием или недостатком априорной информации об объекте управления [2], а также ограниченностью и сложностью используемого математического аппарата. В связи с этим предлагается путь решения данной проблемы, состоящий в поэтапном решении следующих задач.

1-я задача: отказавшись от попыток построения конкретной содержательной аналитической модели СОУ, разработать абстрактную модель более общего класса (матричную информационную);

2-я задача: "обучить" абстрактную информационную модель, "наполнив" ее информацией о реальном поведении СОУ, поступающей в процессе экспериментальной эксплуатации АСУ; на этом этапе адаптируется и конкретизируется абстрактная модель СОУ, т.е. в ней все более точно отражаются взаимосвязи между входными параметрами и состояниями СОУ;

3-я задача: на основе конкретной содержательной информационной модели разработать алгоритмы решения следующих задач АСУ:

3.1. Расчет влияния факторов на переход СОУ в различные возможные состояния (обучение, адаптация).

3.2. Прогнозирование поведения СОУ при конкретном управляющем воздействии и выработка многофакторного управляющего воздействия (основная задача АСУ).

3.3. Выявление факторов, вносящих основной вклад в детерминацию состояния СОУ; контролируемое удаление второстепенных факторов с низкой дифференцирующей способностью, т.е. снижение размерности модели при заданных граничных условиях.

3.4. Сравнение влияния факторов. Сравнение состояний СОУ.

Сформулируем абстрактную модель, опишем способ ее конкретизации и приведем алгоритмы решения задач адаптивных АСУ СОУ на основе данной модели.

Решение задачи №1. Модель должна обеспечивать отражение взаимосвязей между входными и выходными параметрами СОУ и окружающей среды (факторами), с одной стороны, и состояниями СОУ, с другой стороны. Как было показано выше, построить содержательную аналитическую модель СОУ не представляется возможным из–за дефицита априорной информации. Остается вариант использования феноменологической аналитической модели, например регрессионного типа, однако и для ее построения необходима исходная информация, которая, как это следует непосредственно из определения СОУ, может быть только апостериорной. Общепринятой стандартной формой представления исходной информации для статистического анализа является матричная.

Поэтому предлагается представить информационную модель СОУ адаптивной АСУ в форме двумерной матрицы, столбцы которой соответствуют целевым и другим состояниям СОУ, а строки – входным параметрам, т.е. факторам (табл. 1):

 

Таблица 1 - МАТРИЧНАЯ ИНФОРМАЦИОННАЯ МОДЕЛЬ
СЛОЖНОГО ОБЪЕКТА УПРАВЛЕНИЯ АДАПТИВНОЙ АСУ

Факторы

Состояния СОУ

Дифференцирующая
мощность фактора

...

j

...

...

        

i

  

 

...

        

Детерминируемость
состояния СОУ

  

 

 

Элементами матрицы являются частные критерии , отражающие влияние i-го фактора на перевод СОУ в j-е состояние.

Выбор конкретного вида частных критериев является одним из ключевых моментов в построении информационной модели СОУ. В качестве предлагается применить семантическую меру целесообразности информации, введенную в 1960 году А.А.Харкевичем [1] на основе апостериорного подхода. Сущность этого подхода состоит в том, что количество информации оценивается по изменению степени целесообразности поведения системы в результате сообщения ей данной информации [11]. Но именно это и делается в АСУ: управляющая подсистема оказывает на СОУ управляющее воздействие с целью перевести его в целевое состояние. Управляющее воздействие в АСУ является прежде всего информационным воздействием, т.е. некоторым сообщением. В наших обозначениях мера Харкевича имеет вид:

.

(1)

Целесообразность выбора именно данной меры обусловлена самим смыслом величин и , обозначающих соответственно вероятность перехода СОУ в j-е состояние под воздействием i-го фактора и вероятность случайного перехода СОУ в то же состояние.

Выражение (1) непосредственно определяет, какое количество информации АСУ получает о наступлении события: {СОУ перейдет в j-е состояние}, из сообщения: {на СОУ действует i-й фактор}. Когда количество информации >0 – i-й фактор способствует переходу СОУ в j-е состояние, когда <0 – препятствует этому переходу, когда же =0 – никак не влияет на это.

Решение задачи №2. На основе обучающей выборки, содержащей информацию о том, какие факторы действовали, когда СОУ переходил в те или иные состояния, методом прямого счета формируется матрица абсолютных частот, имеющая следующий вид (таблица 2):

 

Таблица 2 - МАТРИЦА АБСОЛЮТНЫХ ЧАСТОТ

Факторы

Состояния СОУ

Сумма

...

j

...

...

        

i

  

 

...

        

Сумма

  

 

где – количество переходов СОУ в j-е состояние при действующем i-м факторе по данным обучающей выборки.

Необходимо отметить, что в случае СОУ в большинстве случаев нет возможности провести полный факторный эксперимент для заполнения матрицы абсолютных частот. Авторы выдвигают гипотезу, что в этом и нет необходимости, т.е. достаточно воспользоваться естественной вариабельностью факторов и состояний СОУ, представленных в обучающей выборке. С увеличением объема обучающей выборки в ней будут представлены все практически встречающиеся варианты.

Подставив в (1) и , рассчитанные из данной корреляционной матрицы по очевидным формулам: , , получим

(2)

Окончательное выражение для расчета количества информации в i-м факторе о переходе СОУ в j-е состояние имеет вид:

(3)

где - нормировочный коэффициент, переводящий количество информации в двоичные единицы измерения информации – биты с учетом количества возможных состояний СОУ: W, а также общего количества зарегистрированных факторов N [5].

В соответствии с выражением (3), непосредственно на основе матрицы абсолютных частот |||| (таблица 2) рассчитывается матрица информативностей факторов |||| (таблица 1). Количество информации в i-м факторе о наступлении j-го состояния СОУ является статистической мерой их связи и количественной мерой влияния данного фактора на осуществление перехода СОУ в данное состояние.

Решение задачи 3 предполагает решение следующих подзадач.

Решение задачи 3.1. При изменении объема обучающей выборки или изменении экспертных оценок, прежде всего пересчитывается матрица абсолютных частот, а затем, на ее основании и в соответствии с выражением (3) - матрица информативностей. Таким образом, предложенная модель обеспечивает отображение динамических взаимосвязей, с одной стороны, между входными и выходными параметрами, а с другой, - между параметрами и состояниями объекта управления. Конкретно, это отображение осуществляется в форме так называемых профилей факторов и состояний.

Профилем i-го фактора называется строка матрицы информативностей. В профиле фактора отображается, какое количество информации о переходе СОУ в каждое из возможных состояний содержится в том факте, что данный фактор действует.

Профилем j-го состояния СОУ называется столбец матрицы информативностей. В профиле состояния СОУ отображается, какое количество информации о переходе СОУ в данное состояние содержится в каждом из факторов.

Решение задачи 3.2 (основная задача АСУ). Данная модель позволяет прогнозировать поведение СОУ при воздействия на него не только одного, но и целой системы факторов:

(4)

В теории принятия решений [2] скалярная функция векторного аргумента называется интегральным критерием. Основная проблема состоит в выборе такого аналитического вида интегрального критерия, который обеспечил бы эффективное решение задачи АСУ.

Учитывая, что частные критерии (1) имеют смысл количества информации, а информация по определению является аддитивной функцией [2, 11], авторы предлагают ввести интегральный критерий, как аддитивную функцию от частных критериев:

(5)

где:

– профиль j-го состояния СОУ;

– профиль текущего состояния СОУ (массив-локатор), т.е.:

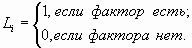
В выражении (5) скобками () обозначено скалярное произведение. Перепишем это выражение в координатной форме:

,

(6)

В многокритериальной постановке задача прогнозирования состояния СОУ, при оказании на него заданного многофакторного управляющего воздействия , сводится к максимизации интегрального критерия:

(7)

т.е. к выбору такого состояния СОУ, для которого интегральный критерий максимален.

Задача принятия решения о выборе наиболее эффективного управляющего воздействия является обратной задачей по отношению к задаче максимизации интегрального критерия, т.е. вместо того, чтобы по набору факторов прогнозировать состояние СОУ, необходимо, наоборот, по заданному (целевому) состоянию СОУ определить такой набор факторов, который с наибольшей эффективностью перевел бы объект управления в это состояние.

Как было показано при решении задачи 3.1, профиль состояния показывает, какое количество информации о переходе СОУ в данное состояние содержится в каждом из факторов.

Факторы могут быть разделены на зависящие и не зависящие от воли человека в данной АСУ, т.е. соответственно:

1) на управляющие воздействия (технологии);

2) факторы окружающей среды, а также факторы, характеризующие предысторию и актуальное состояние СОУ.

Возникает вопрос: достаточно ли знания актуального состояния объекта управления и среды для прогнозирования их развития при различных вариантах управляющего воздействия, или необходимо знать предысторию, т.е. “путь” по которому объект управления и среда попали в свое актуальное состояние? По мнению авторов, в общем случае предыстория развития СОУ безусловно влияет на его переходы в будущие состояния. В предлагаемой методологии нет необходимости решать этот вопрос на основании каких-либо априорных предположений, так как сама система распознавания на этапе обучения определяет ценность тех или иных факторов (признаков), в том числе и предшествующих состояний СОУ, для решения задачи идентификации и прогнозирования.

В предлагаемой методологии влияние предшествующих состояний СОУ можно учесть двумя способами:

введя более подробную классификацию актуальных состояний, некоторые из которых, по-видимому тождественные, как раз и будут отличаться только своей предысторией;

расширив список факторов, потенциально влияющих на поведение СОУ, факторами, связанными с его предшествующими состояниями.

Это различие соответствует различию между простыми и составными цепями Маркова, автоматами без памяти и с памятью.

Если задано некоторое определенное целевое состояние, то выбор управляющих воздействий для фактического применения производится из списка, в котором все возможные управляющие воздействия расположены в порядке убывания влияния на перевод СОУ в данное целевое состояние. Такой список называется информационным портретом состояния СОУ [5].

Управляющие воздействия могут быть объединены в группы, внутри каждой из которых они альтернативны, а между группами - нет. В этом случае внутри каждой группы выбирают одно из доступных управляющих воздействий с максимальным влиянием.

Однако выбор многофакторного управляющего воздействия нельзя считать завершенным без прогнозирования результатов его применения. Описание СОУ в актуальном состоянии состоит из списка факторов окружающей среды, предыстории СОУ, описания его актуального состояния, а также выбранных управляющих воздействий. Имея эту информацию по каждому из факторов в соответствии с выражением (6), нетрудно подсчитать, какое количество информации о переходе в каждое из состояний содержится суммарно во всей системе факторов.

Этот метод соответствует фундаментальной лемме Неймана-Пирсона, содержащей доказательство оптимальности метода выбора той из двух статистических гипотез, о которой в системе факторов содержится больше информации. В то же время он является обобщением леммы Неймана-Пирсона, так как, по предложению авторов вместо информационной меры Шеннона используется обобщенная мера семантической информации Харкевича [2, 4, 5, 11].

Предлагается еще одно обобщение этой фундаментальной леммы, основанное на косвенном учете корреляций между информативностями в профиле состояния при использовании среднего по профилю. Соответственно, вместо простой суммы количеств информации предлагается использовать ковариацию между профилями состояния и СОУ, которая количественно измеряет степень сходства формы этих профилей:

(8)

где:

A – количество факторов в профиле СОУ;

– средняя информативность по профилю j-го состояния СОУ;

– среднее по профилю текущего состояния СОУ;

– среднеквадратичное отклонение информативностей в профиле j-го состояния СОУ;

– среднеквадратичное отклонение профиля текущего состояния СОУ;

Выражение (8) получается непосредственно из (6) после замены координат перемножаемых векторов их стандартизированными значениями:

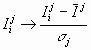
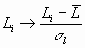
Результат прогнозирования поведения СОУ, описанного данной системой факторов, представляет собой список состояний, в котором они расположены в порядке убывания суммарного количества информации о переходе СОУ в них.

Применение этого метода корректно, если можно сравнивать суммарное количество информации о переходе СОУ в различные состояния, рассчитанное в соответствии с выражением (8), т.е. если они сопоставимы друг с другом. Сопоставимость обеспечивается тем, что информация измеряется в относительных шкалах [2]. Это следует из того, что, во-первых, вклад каждого частного критерия в интегральный критерий измеряется в одних и тех же единицах измерения, а именно: единицах измерения информации (битах), и, во-вторых, существует абсолютный максимум количества информации в факторе, определяемый только количеством возможных состояний СОУ и не зависящий от количества факторов.

Было осуществлено [5] сравнительное экспериментальное исследование результатов прогнозирования на основе критерия Неймана-Пирсона и на основе его обобщения, предложенного авторами. Это исследование показало, что на малых выборках ошибка прогнозирования на основе этих двух критериев практически одинакова, но с увеличением объема выборки качество прогнозирования на основе обобщенного критерия все более значительно превосходит результаты, полученные на основе традиционного метода.

На практике этапы выработки варианта многофакторного управляющего воздействия на СОУ и прогнозирование результатов его применения могут многократно повторяться до тех пор, пока не будет определен вариант управления, удовлетворяющий критериям эффективности.

Решение задачи 3.3. Естественно считать, что некоторый фактор является тем более ценным, чем больше среднее количество информации, содержащееся в этом факторе о поведении СОУ [5]. Однако, так как в предложенной модели количество информации может быть и отрицательным (если фактор уменьшает вероятность перехода СОУ в некоторое состояние), то простое среднее арифметическое информативностей может быть близко к нулю. При этом среднее будет равно нулю и в случае, когда все информативности равны нулю, и тогда, когда они будут велики по модулю, но с разными знаками. Следовательно, более адекватной оценкой полезности фактора, по мнению авторов, является среднее модулей или лучше исправленное (несмещенное) среднеквадратичное отклонение информативностей по профилю признака.

Ценность фактора по сути дела определяется его полезностью для различения состояний СОУ, т.е. есть дифференцирующей способностью.

Необходимо также отметить, что различные состояния СОУ обладают различной степенью обусловленности, т.е. в различной степени детерминированы факторами: некоторые слабо зависят от учтенных факторов, тогда как другие определяются ими практически однозначно. Количественно детерминируемость состояния СОУ предлагается оценивать стандартным отклонением информативностей профиля данного состояния.

Предложено и реализовано несколько итерационных алгоритмов корректного удаления малозначимых факторов и слабодетерминированных состояний СОУ при заданных граничных условиях [5]. Решение задачи снижения размерности модели СОУ при заданных граничных условиях позволяет снизить эксплуатационные затраты и повысить эффективность АСУ СОУ.

Решение задачи 3.4. Факторы могут сравниваться друг с другом по тому влиянию, которое они оказывают на поведение СОУ. Сами состояния могут сравниваться друг с другом по тем факторам, которые способствуют или препятствуют переходу СОУ в эти состояния. Это сравнение может содержать лишь результат, т.е. различные степени сходства/различия (в кластерном анализе), или содержать также причины этого сходства/различия (в когнитивных диаграммах).

Данные задачи АСУ играют важную роль при необходимости замены одних управляющих воздействий другими, но аналогичными по эффекту, а также при изучении вопросов устойчивости управления (различимости состояний СОУ по детерминирующим их факторам).

В результате кластерного анализа в кластеры объединяются наиболее схожие друг с другом состояния СОУ (или факторы), а состояния (или факторы), наиболее сильно отличающиеся друг от друга, автоматически оказываются в разных кластерах [3 - 5].

При формировании кластеров используются матрицы сходства состояний СОУ и факторов, формируемые на основе матрицы информативностей.

В соответствии с математической моделью могут быть сформированы кластеры для заданного диапазона кодов состояний СОУ (факторов) или заданных диапазонов уровней системной организации, с различными критериями включения состояния (фактора) в кластер.

Эти критерии могут быть сформированы автоматически или заданы пользователем. Имеется режим кластеризации, при котором в кластеры включаются не только похожие, но и все непохожие состояния (факторы), и, таким образом, формируются конструкты классов распознавания и признаков.

Конструктом является понятие, имеющее противоположные по смыслу полюса и целый спектр промежуточных смысловых значений, а также количественную шкалу для измерения этих значений [8, 9].

Понятия “кластер” и “конструкт” тесно взаимосвязаны.

Положительный и отрицательный полюса конструкта представляют собой кластеры, в наибольшей степени отличающиеся друг от друга. Конструкт может рассматриваться как кластер с нечеткими границами, включающий в различной степени (причем не только в положительной, но и в отрицательной) все состояния (факторы).

Необходимо отметить, что формирование кластеров сталкивается с проблемой комбинаторного взрыва, так как требует полного перебора и проверки "из n по m" сочетаний элементов (состояний или факторов) в кластеры [3]. Конструкты же формируются непосредственно из матрицы сходства прямой выборкой и сортировкой, что значительно проще в вычислительном отношении, так как конструктов значительно меньше, чем кластеров (всего n2). Естественно, при формировании конструктов автоматически формируются и их полюса, т.е. кластеры, что и реализовано в математической модели, предложенной одним из авторов [5].

Диаграммы смыслового сходства-различия состояний СОУ (факторов) соответствуют определению семантических сетей [8], т.е. представляют собой ориентированные графы, в которых признаки соединены линиями, соответствующими их смысловому сходству (различию) (рисунок 1):

 

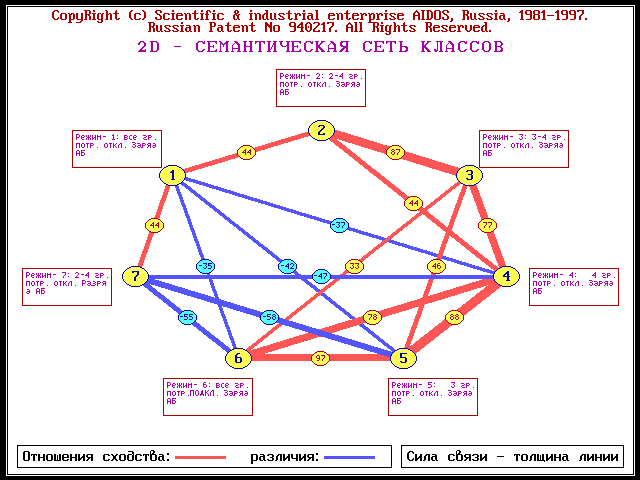
Рис. 1. Пример семантической сети режимов энергораспределения автономной комбинированной фотоветроэлектроэнергетической системы (ФВЭС)

 

В предлагаемой математической модели в общем виде реализована возможность содержательного сравнения обобщенных образов состояний СОУ и факторов, т.е. построения когнитивных диаграмм [4, 5].

В информационном портрете состояния СОУ показано, какое количество информации о принадлежности (не принадлежности) СОУ к данному состоянию, а также о переходе (не переходе) СОУ в данное состояние содержится в том факте, что на СОУ действуют факторы, содержащиеся в данном информационном портрете.

Кластерно-конструктивный анализ дает результат сравнения состояний СОУ друг с другом, т.е. показывает, насколько эти состояния сходны друг с другом и насколько отличаются друг от друга. Но он не показывает, какими факторами эти состояния СОУ похожи и какими отличаются, и какой вклад каждый фактор вносит в сходство или различие каждых двух состояний. Чтобы получить эту информацию, необходимо проанализировать два информационных портрета, что и делается при содержательном сравнении состояний СОУ .

Кластерно-конструктивный анализ факторов осуществляется так же, как и анализ состояний.

Авторы предлагают учитывать вклад в сходство/различие двух состояний СОУ, который вносят не только общие для них факторы, но и такие, которые есть только у одного из них, а у другого отсутствуют. Логично предположить, что этот вклад (при прочих равных условиях) будет тем меньше, чем меньше корреляция между профилями этих факторов, т.е. их сходство по смыслу.

Диаграммы Мерлина [6] представляют собой частный случай обобщенных когнитивных диаграмм [8] (т.е. с много-многозначными связями), т.е. диаграммы Мерлина - это когнитивные диаграммы, формируемые в соответствии с предложенной моделью при следующих граничных условиях [4, 5]:

1) состояние СОУ сравнивается само с собой, но с различной фильтрацией;

2) фильтрация левого и правого портрета выбрана по уровням системной организации факторов (в данном случае - уровням Мерлина);

3) левое состояние отображается с фильтрацией по одному уровню системной организации, а правое - по другому.

Выводы. Для моделирования процессов принятия решений в адаптивных АСУ сложными системами представляется перспективным применение многокритериального подхода с аддитивным интегральным критерием, в котором в качестве частных критериев используется семантическая мера информации, полученная А.А.Харкевичем в 1960 году [1] на основе апостериорной теории информации, являющейся обобщением классической теории Шеннона.

Предложенная математическая модель обеспечивает эффективное решение следующих задач, возникающих в адаптивных АСУ СОУ:

разработка абстрактной информационной модели СОУ;

адаптация и конкретизация абстрактной модели на основе информации о реальном поведении СОУ;

расчет влияния факторов на переход СОУ в различные возможные состояния;

прогнозирование поведения СОУ при конкретном управляющем воздействии и выработка многофакторного управляющего воздействия (основная задача АСУ);

выявление факторов, вносящих основной вклад в детерминацию состояния СОУ; контролируемое удаление второстепенных факторов с низкой дифференцирующей способностью, т.е. снижение размерности модели при заданных граничных условиях;

сравнение влияния факторов, сравнение целевых и других состояний СОУ.

Таким образом, предложенная методология, основанная на теории информации, обеспечивает эффективное моделирование задач принятия решений в адаптивных АСУ сложными системами.

 

Литература

1. Харкевич А.А. О ценности информации.- В сб.: Проблемы кибернетики.-М., Физматгиз, 1960, Вып. 4. С.53-57.

2. Перегудов Ф.И.,Тарасенко Ф.П., Введение в системный анализ.-М.: Высшая школа, 1989.-367с.

3. Дюран Б.,Оделл П. Кластерный анализ /Пер с англ. -М.: Статистика, 1977.
-125С.

4. Луценко Е.В. Когнитивная аналитическая система "ЭЙДОС-6.0", как инструмент исследования интегральной индивидуальности по Вольфу Мерлину., -В сб.: Актуальные проблемы социально-правовой подготовки специалистов и перспективы совершенствования системы комплектования ОВД. –Краснодар: КЮИ МВД РФ, 1997. - С.146-152.

5. Луценко Е.В. Теоретические основы и технология адаптивного семантического анализа в поддержке принятия решений (На примере универсальной автоматизированной системы распознавания образов "ЭЙДОС-5.1"). –Краснодар: КЮИ МВД РФ, 1996. 280с.

6. Мерлин В.С. Очерк интегрального исследования индивидуальности.-М., 1986.

7. Симанков В.С. Планирование определительных испытаний и оптимизация интервальных оценок при исследовании надежности электрических цепей. –Краснодар, 1981.-11с.-Рукопись предоставл. Красн. политехн. иститутом Деп. в ВИНИТИ, 1982. №D/987.

8. Солсо Р.Роберт, Когнитивная психология/Пер.с англ. - М.: Тривола, 1996. - 600с.: ил.

9. Франселла Ф., Банистер Д. Новый метод исследования личности (руководство по репертуарным личностным методикам) /Пер.с англ.-М.: Прогресс, 1987. –230с.

10. Хартли Р.В.Л. Передача информации. - В кн.: Теория информации и ее приложения/Под ред. А.А.Харкевича.-М.: Физматгиз, 1959.

11. Шилейко А.В., Кочнев В.Ф., Химушин Ф.Ф. Введение в информационную теорию систем. -М.: Радио и связь. 1985. –278с.