Е.В.Луценко

Кубанский государственный технологический университет

Рассмотрим пример, поясняющий понятие "интерференция последствий выбора". Пусть студент одновременно поступает в два высших учебных заведения и получает два высших образования (сейчас это возможно). По окончании обучения выбор "куда пойти работать" является не простой суммой вариантов выбора по каждой из специальностей, а качественно иным, включающим также новые области, не входящие ни в один из вариантов. Эти новые области его работы образуются за счет того, что свойства, полученные студентом при получении 1-го и 2-го высшего образования, взаимодействуют друг с другом и образуют систему свойств, предоставляющую ему новые возможности, не входящие ни в один из вариантов, взятый сам по себе.

Таким образом наблюдается картина последствий, не сводящаяся к простой сумме последствий альтернативных вариантов, т.е. очень напоминающая квантовое физическое явление, которое называется интерференцией плотности вероятности. Это явление безусловно имеет системный характер, т.е. свойства системы в целом не сводится к алгебраической сумме свойств ее частей.

Обобщим классическое дерево вероятностей таким образом, чтобы оно позволяло теоретически отображать явление интерференции альтернатив:

Классическое дерево вероятностей. С середины 80–х годов школа И.Пригожина развивает подход, согласно которому в развитии любой системы (в том числе и человека) чередуются периоды, в течение которых система ведет себя то как "в основном детерминированная", то как "в основном случайная".

Удобным формальным средством визуализации этой идеи является "классическое дерево вероятностей" (терм.авт.), в котором точки бифуркации изображаются узлами, а участки детерминистского развития системы – дугами.

С позиций развиваемых в настоящей статье, перспективным является представление о том, что узлы в диаграмме "дерева вероятностей", – это этапы принятия решений, а дуги – этапы их реализации. Существенным является то, что после реализации некоторого конкретного решения система с необходимостью оказывается в очередной точке бифуркации.

Рассмотрим упрощенный пример.

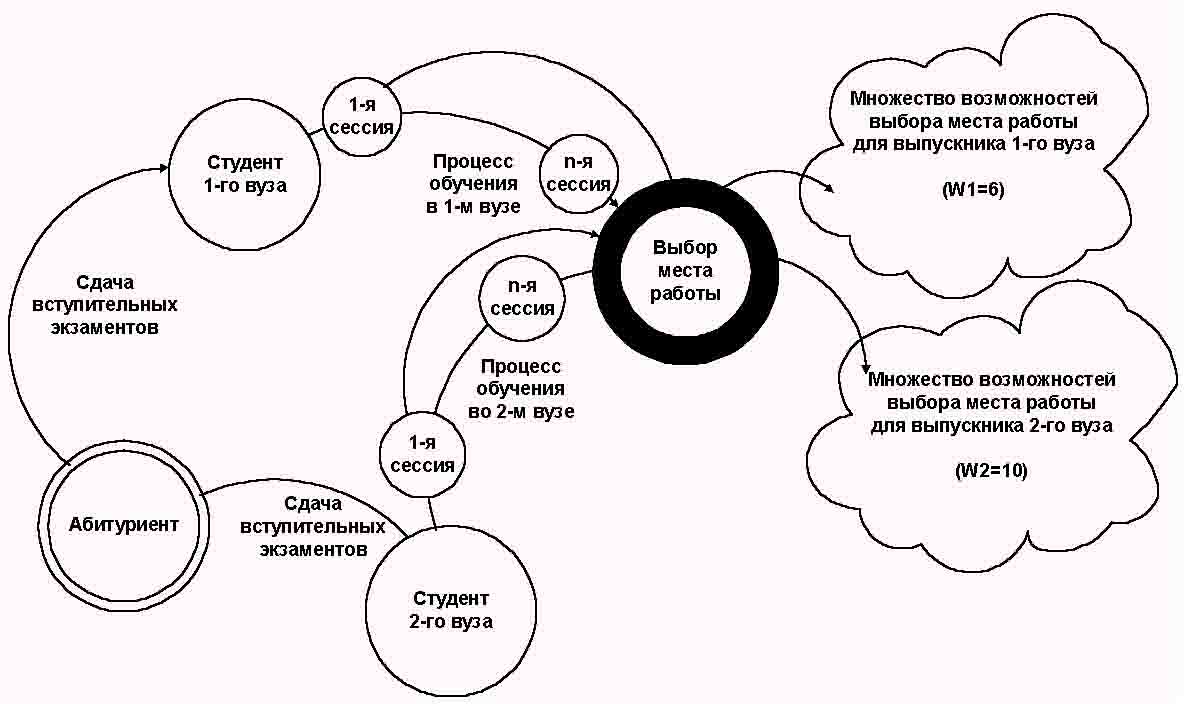
Молодой человек в начальном состоянии, изображенном на диаграмме (рисунок4), находится в точке бифуркации "абитуриент".

В этой точке в процессе сдачи вступительных экзаменов определяется, станет ли он студентом. существует две альтернативы, изображенные дугами:

1. Он поступает на очное отделение и учится в течение 5 лет (дуга: "обучение в вузе").

2. Он не поступает и сразу оказывается в точке бифуркации: "выбор места работы".

После окончания учебы выпускник, т.е. молодой специалист, также оказывается в точке бифуркации: "выбор места работы". Однако, не смотря на то, что у людей с высшим образованием и без него точки бифуркации "выбор места работы" совпадают по названию, по содержанию они существенно отличаются, из-за чего, собственно, на диаграмме и изображено два различных состояния с таким названием. Дело в том, что возможности выбора места работы самым существенным образом зависят от пути по которому человек перешел в данную точку бифуркации, т.е. зависят от его предыстории: множество альтернатив, доступных для человека без высшего образования в данной точке бифуркации, является подмножеством альтернатив, доступных для человека с высшим образованием.

Глубокую аналогию можно провести между рассмотренным примером поведения активной системы "человек" и квантовым движением микрообъекта, движение которого осуществляется путем чередования редуцированных и квантовых состояний. В соответствии с соотношением неопределенностей Гейзенберга в редуцированном состоянии определенными являются координаты квантового объекта, но неопределенным направление и скорость движения, а в виртуальном, наоборот, определенными являются направление и скорость движения, но неопределенными координаты. Это означает, что редуцированные состояния можно изобразить точками бифуркаций на "дереве вероятностей", а виртуальные, соответственно, дугами. В редуцированном состоянии как бы определяется направление будущего перемещения, а в виртуальном – реализуется это решение. Для человека в редуцированных состояниях точно известно, кем он является в настоящее время, но неизвестно кем он может стать в будущем, а в виртуальных, наоборот, его текущее состояние не фиксировано, т.е. он находится "в стадии трансформации", зато известно кем он станет в результате этой трансформации. Эта глубокая аналогия позволяет выдвинуть гипотезу, что развитие человека можно представить как его движение в некотором абстрактном фазовом суперпространстве развития.

Естественно, реальная система управления должна устойчиво управлять объектом управления не только на "детерминистских" участках его истории, но и в точках, в которых его дальнейшее поведение становится в высокой степени неопределенным и непредсказуемым. Отметим, что классический подход к управлению ориентирован именно на управление системами на детерминистских участках их эволюции, когда объект управления в течение длительного времени можно с достаточной точностью рассматривать как лишенный внутренней активности и обоснованно абстрагироваться от того, что это в общем случае не так.

Однако в ряде случаев, такое упрощенное представление об объекте управления является неадекватным и необходимо разрабатывать подходы к управлению системами, в поведении которых существенную роль играет их внутренняя активность, в частном случае - свобода воли.

Плодотворная аналогия движением активных и квантовых систем будет продолжена и развита ниже, т.к. это позволяет открыть много новых для теории автоматизированного управления аспектов исследования активных систем, а также дает надежду на возможность применения в будущем хорошо развитого математического аппарата квантовой теории поля (КТП) для решения задач управления активными объектами

Уровни бифуркаций. Как показано выше, в точке бифуркации принимается решение о дальнейшем пути эволюции системы, а на детерминистском этапе принятое решение реализуется. После окончания реализации принятого решения система опять попадает в состояние бифуркации.

На этом уровне абстрагирования и детализации этап реализации решения представляется однородным и лишенным какой-либо внутренней структуры. Однако при более детальном рассмотрении выясняется, что этап реализации некоторого важного решения (решения 1-го уровня) сам состоит из определенной последовательности этапов, на которых принимаются определенные решения (решения 2-го уровня), вытекающие из решения 1-го уровня и этапов их реализации.

Если продолжить пример, приведенный в предыдущем разделе, то дугу "Процесс обучения в вузе" можно представить в форме последовательности точек бифуркации, соответствующих сдаче сессий. В этих точках бифуркации определяется (принимается решение), будет ли студент обучаться в вузе на следующем семестре или на следующем курсе. Однако само решение о сдаче сессий фактически предопределено поступлением в вуз, т.е. с этой точки зрения является реализацией решения, т.е. детерминистским этапом. Таким образом, классификация того или иного этапа как бифуркационного или детерминистского является в определенной мере относительной.

Снятие неопределенности, как результат передачи информации. Рассмотрим систему: "человек – объект" в точке бифуркации, т.е. в точке, в которой снимается (уменьшается) неопределенность в поведении одного из элементов этой системы. Информация есть количественная мера снятия неопределенности, поэтому рассмотрим два основных направления информационных потоков, которые возможны в этой системе:

1. От человека к объекту: "Труд".

2. От объекта к человеку: "Познание".

В результате труда, который с позиций, развиваемых в данной работе, представляет собой управляющее, по существу информационное, воздействие на предмет труда, снимается неопределенность состояния предмета труда, в результате чего он трансформируется в продукт труда. В результате познания снимается неопределенность наших представлений об объекте познания, т.е. снимается неопределенность в состоянии человека, в результате чего он трансформируется из "незнающего" в "знающего".

Таким образом наблюдается картина последствий, не сводящаяся к простой сумме последствий альтернативных вариантов, т.е. очень напоминающая квантовое физическое явление, которое называется интерференцией плотности вероятности. Это явление безусловно имеет системный характер, т.е. свойства системы в целом не сводится к алгебраической сумме свойств ее частей.

Обобщим классическое дерево вероятностей таким образом, чтобы оно позволяло теоретически отображать явление интерференции альтернатив (рисунок5):

Однако квантовые объекты могут оказываться одновременно в двух и более альтернативных для классических объектов состояниях. Такие состояния будем называть смешанными.

Например электрон может интерферировать сам на себе, проходя одновременно через две щели. При этом наблюдаются эффекты, не сводящиеся к суперпозиции классических состояний, т.е. имеющие существенно квантовый, системный, эмерджентный характер.

Основным отличием эмерджентной теории информации от классической является учет свойства системности, как фундаментального и универсального свойства всех объектов, на уровне самого понятия информации, а не только в последующем изложении, как в классической теории.

Достаточно рассмотреть квантовое обобщение теории Хартли, т.к. путь вывода теории Шеннона из теории Хартли широко известен. Ричард Фейнман в основополагающей работе "Характер физических законов" рассматривает пример интерференции электрона на двух щелях, причем наблюдается это процесс с помощью Комптон-эффекта, т.е. путем рассеяния фотонов на электроне. При этом электрон всегда наблюдается в форме объекта с размером порядка длины волны света, и как выяснилось, его свойства самым существенным образом зависят от его наблюдаемого, а значит и фактического размера. Мы не будем детально приводить известную аргументацию Р.Фейнмана и коснемся лишь моментов, играющих ключевую роль в квантовом (системном) обобщении понятия "информация".

Когда длина волны фотонов порядка расстояния между щелями или больше, то видно, как он проходит через экран "накрывая" обе щели одновременно. В этом случае за ними наблюдается сложная интерференционная картина, нисколько не напоминающая сумму или суперпозицию классических распределений за 1-й и 2-й щелями, т.е. не являющуюся их суммой (рисунок 7):

Введем следующие обозначения:

Тогда:

откуда:

Если вероятность прохождения электрона через каждую из W щелей одинакова, то по классической теории Хартли в самом факте пролета электрона через одну из щелей содержится количество информации:

где W – количество щелей, или, в общем случае, классических состояний объекта.

В соответствии с концепцией эмерджентной теорией информации предлагается ввести в это выражение параметр j , учитывающий квантовые системные эффекты, т.е. учитывающих возможность нахождения объекта в смешанных состояниях. В результате количество состояний объекта возрастает и, следовательно, так же возрастает и количество информации, которое мы получаем, когда узнаем, что он перешел в одно из этих состояний:

где j – степень эмерджентности системы (синоним: уровень системности объекта), в частности:

Для деструктивных систем свойства целого меньше свойств частей, для классических систем они совпадают, для синтетических систем свойства целого больше свойств частей и не сводятся к ним.

На первый взгляд можно было бы просто увеличить количество состояний системы W за счет учета смешанных состояний. Однако этот путь не удовлетворяет известному принципу соответствия, который в данном контексте требует, чтобы в предельном случае более общая теория переходила в уже известную классическую.

Теорема Эшби описывает систему в точке бифуркации, причем по сути он при этом использует понятие "степень эмерджентности объекта", хотя в явном виде и не вводит его. Более того, он указывает на источник эмерджентности: – взаимодействие частей и связывает уровень системности или уровень системной организации с степенью взаимодействия этих частей.

Таким образом, и теоретико-информационное рассмотрение сложных активных самоорганизующихся систем, каким является человек и системы с участием человека, и рассмотрение квантовых систем, приводит к необходимости разработки эмерджентной теории информации, в которой используется обобщенное понятие информации, учитывающее эффект системности с помощью коэффициента эмерджентности.

Сравнивая выражения (6) и (3) видим, что новые дополнительные состояния, образующиеся за счет квантовых и системных эффектов, математически учитываются совершенно аналогично.

Тогда в 1-м случае, если мы узнаем, что выпускник устроился на определенное место работы, то мы получаем

информации, во 2-м случае, соответственно:

Но в 3-м случае мы получаем не

как можно было бы ожидать, если бы не было интерференции последствий, т.е. системного эффекта, а:

16 дополнительных состояний (мест работы) выпускника в 3-м случае образовались за счет системного эффекта (эмерджентности) и являются "смешанными", образующимися за счет одновременного наличия у выпускника свойств, полученных при окончании и 1-й, и 2-й специальности, поэтому, учитывая выражения (5) и (6), получаем:

Откуда:

Следовательно, одновременное окончание двух специальностей в рассмотренном случае дает системный эффект 1,25.

Литература: